Preprint
Article
Machine Learning Prediction of Phase and Tensile Properties of High Entropy Alloys Manufactured by Selective Laser Melting
Altmetrics
Downloads
159
Views
100
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
14 February 2024
Posted:
14 February 2024
You are already at the latest version
Alerts
Abstract
The utilization of selective laser melting (SLM) for high entropy alloys (HEAs) holds significant promise in commercial applications, and substantial experimental research efforts have been directed toward this domain. To take advantage of the reported experimental data of SLM manufactured (SLM-ed) HEAs and reduce unnecessary experimentation, this study incorporates machine learning (ML) techniques for the phase and tensile properties prediction of SLM-ed HEAs, thus presenting a novel avenue for accelerating the discovery of new SLM-ed HEAs. Through the adjustment of material descriptors and machine learning models, a model has been developed with an impressive accuracy of 93.8% in distinguishing between face-centered cubic (FCC), body-centered cubic (BCC), and dual-phase (FCC+BCC). Additionally, optimized models have been devised for the prediction of tensile properties, namely ultimate tensile strength (UTS), yield strength (YS), and elongation (δ), achieving noteworthy MAPEs (mean absolute percentage errors) of 10.33%, 8.55%, and 28.48%, respectively. Furthermore, several HEAs were fabricated using SLM, and the experimental outcomes exhibited a favorable alignment with the predicted results. These efforts carry significant implications in advancing the utilization of SLM for HEAs.
Keywords:
Subject: Chemistry and Materials Science - Materials Science and Technology
1. Introduction
High entropy alloys (HEAs) have gained attention because they offer high strength, good thermal stability, and impressive corrosion resistance, making them suitable for many applications [1,2]. Additive manufacturing (AM), often referred to as three-dimensional (3D) printing, creates parts directly from a digital 3D model, layer by layer. This enables the production of large parts with intricate designs and internal features [3,4]. AM methods in HEAs, such as directed energy deposition (DED), selective laser melting (SLM), electron beam melting (EBM), and direct ink writing (DIW), are being explored to meet the demands of modern industry. Among these, SLM technology is notable for its fast cooling and precision [5,6].
Numerous experiments have been conducted with selective laser melting manufactured (SLM-ed) HEAs. However, experimental research is costly and not very efficient when it comes to developing new SLM-ed HEAs. It is crucial to have highly accurate predictions for the development of unexplored SLM-ed HEAs to minimize unnecessary experiments.
Materials genome engineering (MGE) introduces a novel approach to expedite and cost-effectively develop new materials based on the reported research [7]. Machine learning (ML) has gained popularity as an efficient tool in the MGE area, with numerous studies highlighting its application in HEAs [8]. In the ML methodology, a surrogate model (referred to as "f") is established to discern the relationship between the specific property of interest (termed "Y") and a set of material descriptors (referred to as "X"). This relationship is expressed as Y = f(X). The effectiveness of ML predictions depends on the combined influence of material descriptors (X) and the model (f), which significantly guides the subsequent design of innovative materials. Therefore, when faced with a specific problem, it becomes crucial to identify the optimal combination of the model (f) and material descriptors (X). When optimizing material descriptors, screening is always chosen as a method to reduce material descriptor numbers and shorten the model training time, also reducing the complexity of model training, thereby reducing the phenomenon of model overfitting.
The phase composition of SLM-ed HEAs significantly impacts their properties and formability. HEAs with a single-phase face-centered cubic (FCC) structure tend to be ductile and exhibit good SLM formability but have relatively low strength. In contrast, single-phase body-centered cubic (BCC) HEAs typically offer high strength but are often brittle and possess poor SLM formability. Dual-phase HEAs can strike a balance between ductility and strength [9]. Consequently, the ability to design HEAs with the desired crystal structure is crucial for the development of new HEAs with improved properties and favorable SLM formability. Given the intricate composition of HEAs and the vast number of potential combinations, accurately predicting the stable structure or phase formation of unexplored HEAs is highly desirable. Some efforts have been directed toward phase prediction of HEAs using machine learning. For example, Zhang et al. [10] did highly accurate phase prediction of as-cast HEAs with a rational selection of material descriptors, the phase prediction accuracy was up to 91.3%. Kevin et al. [11] proposed a novel high-throughput approach, called “ML-HEA”, for coupling thermodynamic and chemical features with a random forest machine learning model for predicting the solid solution forming ability. Of the 1,110 quaternary and 130 quinary systems, the ML-HEA model predicts 436 quaternaries and 91 quinaries will form an FCC or BCC solid solution. Wu et al. [12] uncovered the eutectics design by machine learning in the Al–Co–Cr–Fe–Ni high entropy system, set up three steps for the design of EHEAs and experimental test the designed EHEAs, results showed that the designed EHEAs exhibited excellent mechanical properties indicating that purpose-oriented design of EHEA can be realized with ML. Ankit et al. [13] implement ML tools, to predict the crystallographic phase of low-, medium- and high-entropy alloys composed of a family of 5 refractory elements. The ML results in conjunction with experimental validation, reveal that the mean melting point and electronegativity difference exert the strongest contributions to the phase formation in these alloys.
However, the HEAs in these works were mostly manufactured by traditional methods like arc melting. The phase composition of HEAs manufactured by SLM may be different from that of traditional methods due to the higher cooling rate of SLM. For example, Zhou et al. [14] manufactured Al0.5FeCoCrNi by SLM. The gas-atomized powder originally had two phases, including the FCC and BCC phases. However, only the FCC phases in the SLM-ed Al0.5FeCoCrNi were detected which indicates that the BCC phases transform into the FCC phases during the SLM process.
In the area of properties prediction of HEAs by ML, Rao et al. [15] proposed an active learning strategy to accelerate the design of novel high entropy Invar alloys with extremely low thermal expansion. Li et al. [16] and Yao et al. [17] did some research on the prediction of the hardness of HEAs by ML. However, until now, tensile properties prediction of HEAs has not been reported yet. Tensile properties are incredibly significant among material properties, especially in engineering and material sciences. They describe the response of a material to forces applied in tension (pulling) and are fundamental in understanding how a material behaves under stress [18]. Thus, a high-accuracy ML model used for predicting the tensile properties of SLM-ed HEAs is very necessary. The tensile tests are always used to test the strength of a material and the UTS, YS, and are achieved after a successful tensile test. Thus, the prediction of the UTS, YS, and was studied in this research.
2. Methodology
The flowchart of our strategy to search for the best combination of material descriptors and machine learning model for a given materials problem is shown in Figure 1. The purple area is the preparation work for ML, it consists of two main parts, dataset preparation, and ML model preparation. Dataset preparation includes data collection, material descriptors construction, and material descriptors selection. ML model preparation is constructing an ML model pool according to the target requirements. Then the models work with the prepared dataset, as shown in the yellow area of Figure 1. The prepared dataset will be divided into K parts, select one of them as the test set each time, and use the remaining K-1 as the training set, and perform a total of K times. This ensures that each sample becomes a test set. This process is called crossover. During crossover, whether an accuracy or error is set to compare the predicted and actual labels of the testing set. This is the evaluation process. After that, we compared model accuracies or errors of these models with their corresponding material descriptor subset. The classifier model with the highest accuracy or the regressor model with the lowest error was chosen as the best model for phase formation and tensile properties prediction, respectively, and the corresponding material descriptor subset was chosen as the key material descriptors.
After creating the best ML model with a descriptor subset, it is generally necessary to perform prediction and experimental verification to assess its real-world performance and validate its effectiveness. This will help to test the performance of the ML model in the new data and avoid overfitting the historical data. This process is called experimental verification.
2.1. Data Collection
A dataset consisting of 49 SLM-ed HEAs with no Non-metallic elements added for which phase formation was available, and 35 of them have tensile properties information with no post-processing like annealing, was compiled from ScienceDirect literature sources (seen in supplementary material Table S1). In the work of ML prediction for phase formation, two primary phases were considered in this research: the body-centered cubic (BCC) phase and the face-centered cubic (FCC) phase. As a result, each alloy within our dataset may exhibit a phase configuration of either a single BCC phase, a single FCC phase, or FCC + BCC phases. In the work of ML prediction for tensile properties, the values of UTS, YS, and corresponding to each SLM-ed HEA were collected.
Thus, the initial dataset includes the phase information (FCC, BCC, or FCC + BCC) of 49 SLM-ed HEAs and corresponding chemical compositions. Among them, 35 of them have information on tensile properties (UTS, YS, and ). Phase information and tensile properties are our targeted responses and the chemical compositions will be used to calculate the material descriptors in the following procedure.
2.2. Material Descriptors Construction
One of the key factors in governing the performance of an ML model lies in the selection of material descriptors. Therefore, it is imperative to establish a comprehensive set of material descriptors with general applicability [19].
A set of material descriptors that have the potential to influence the phase formation or tensile properties of HEAs was assembled in this procedure. It contains 13 empirical material descriptors and 40 self-defined material descriptors. Among the 13 empirical material descriptors, 12 of them have been previously proposed in the literature by Zhang et al. [10] or Ankit et al. [13] and VED is the newly added empirical material descriptor in this work, as shown in Table 1. The basic thermodynamic descriptors consist of the mixing enthalpy (), the mixing entropy (), and a descriptor () designed to quantify the dominance of entropy to enthalpy [20]. The elemental descriptor includes the valence electron concentration (VEC), the difference in the Pauling electronegativities (), the Allen electronegativities (), the atomic size difference (), and a geometrical descriptor (γ) [21].
Volume energy density (VED) has an important influence on SLM with different manufacturing parameters, and it was always been used to explain the different results of SLM by different SLM parameters [4]. Thus, it was used as one of the empirical descriptors of SLM-ed HEAs and VED was defined by the following equation:
where, is the laser power (W); is the scanning velocity (mm/s); is the hatching space (μm); and is the layer thickness (μm).
Furthermore, the dataset incorporates 20 elemental parameters that approximately reflect bond strength and electrochemical properties. These parameters include characteristics like melting temperature (TM), ionization energy (IE), work function (WF), and so on, as shown in Table 2.
Each elemental parameter of a HEA in our composition space can be represented by the molar average value ( ) of an elemental parameter ( ) through
where is the mole fraction of the th element. Another way to describe each HEA is to calculate the mismatch value ( ) between elemental parameters ( ) of its components. The is given by
where is the mole fraction of the th element and is the molar average value obtained by Equation (2). Thus, 40 self-defined material descriptors are introduced and may contribute to the phase formation or tensile properties of HEAs as well. In total, the material descriptor space contains 53 material descriptors.
The compositions of SLM-ed HEAs are used to calculate the 53 descriptors according to the formulas listed in Table 1, Equations (2), and (3) with the input of the properties of elements in Table 1 and Table 2. The properties of elements were found on the websites of webelements (https://www.webelements.com/) and periodictable (www.periodictable.com). As we can readily get access to these elemental properties, all the descriptors are available for our training data.
Our material descriptors vary in magnitudes, units, and ranges. As most of the machine learning algorithms use Euclidean distance between two data points, material descriptors with high magnitudes will weigh more compared with those of low magnitudes. To bring all material descriptors to the same level of magnitudes, each material descriptor is normalized through the Min-Max Normalization to make it in the range of [0, 1]. The Min-Max Normalization function is as follows:
where and are the maximum and minimum values of descriptor X of our training data, respectively.
2.3. Material Descriptor Selection and Evaluation
To select the key material descriptors, we computed a total of 53 material descriptors and then applied a three-step material descriptor selection method. The first step is correlation screening to quickly remove redundant material descriptors. We calculated the Pearson correlation coefficient [22] between any two material descriptors X and Y based on the following equation:
where and are the values of two material descriptors in the -th alloy (i = 1, 2, …, 49), and are the average values of these two material descriptors in all 49 alloys. The values of Pearson correlation coefficient r between different material descriptors were shown in Figure 2. VED was not used in the correlation screening because some VEDs were not given in the references. Values of | r | > 0.75 imply a strong linear correlation between the two material descriptors X and Y, indicating that they carry the same or similar information and hence have the same or similar influences on material properties [23]. In this case, we choose one of these two material descriptors as input to establish models. 22 input features were selected after correlation screening. They are VED, VEC, , , , , , , , , , , , , , , , , , , , .
The second step is recursive elimination. Linear and Random Forest regressors were used in recursive elimination for they are two popular algorithms in ML, each with its advantages [24]. The dataset was divided into a training set and a test set randomly, and then the model with 22 input features and corresponding output features, "feature importance ranking" was achieved after that, the feature with the worst correlation was removed, and then the procedure was repeated until the remaining number of material descriptors reached the set number. For phase prediction, we perform the elimination recursively from 1 material descriptor to 12 material descriptors 8 times. And 8×12 groups of material descriptor subsets were achieved after recursive elimination. For tensile properties prediction, we perform the elimination recursively from 1 material descriptor to 12 material descriptors once. 12 groups of material descriptor subsets were achieved after recursive elimination.
The third step is exhaustive screening. We establish a series of models by using all exhaustive combinations of the remaining material descriptors from the recursive elimination step as inputs. For phase prediction, we built ML classifiers. For tensile properties prediction, we built ML regressors. For each material descriptor subset from the recursive elimination step, we evaluate its classification accuracy or mean absolute percentage error (MAPE).
In the process of building classifiers, two classifiers are trained according to whether the HEA contains FCC, or BCC or not. During predicting, when the output of a classifier is 1, it represents that the sample contains that phase. If both of the two classifiers predict correctly, the final classifier is correct, and it is included in the final accuracy.
In the process of building regressors, the regressors are trained for each tensile property, the UTS, YS, and , respectively. During predicting, is used to calculate the error between the predicted properties and tested properties, and MAPE is used to evaluate the model with its corresponding material descriptor subset.
where, is the error corresponding to property P, such as UTS, YS, and ; is the value of the actual property; is the value of the predicted property. N is the total number of samples.
Five-fold cross-validation was utilized in this work. The dataset is divided randomly into 5 roughly equal-sized subsets. 4 of them belong to the training set and 1 of them belongs to the testing set. The ML classifiers or regressors are built on the training set, and classification accuracy or MAPE is obtained by comparing the predicted and actual labels of the testing set. This process is repeated five times, with each of the 5 subsets used once as the testing set. The final classification accuracy or MAPE is obtained by averaging the classification accuracies or MAPEs from the five subsets.
Finally, for each phase classifier model, 8×12 groups of classification accuracies with the corresponding material descriptor subsets were achieved. For each tensile properties regressor model, 12 groups of MAPEs with the corresponding material descriptor subsets were achieved. The model with the highest accuracy among these classifier models with its corresponding material descriptor subset was chosen as the best model for phase prediction. The models with the lowest MAPE among these regressor models with their corresponding material descriptor subsets were chosen as the best models for properties prediction.
2.4. ML Prediction and Experimental Verification
The machine learning calculations were performed using Python language in the Anaconda platform with jupyter notebook. These classifiers and regressors were implemented in the scikit-learn library, along with pandas, matlotlib, seaborn, numpy, and scipy libraries.
9 HEAs with common metal elements were selected and experimentally synthesized by SLM with an SLM machine (HANS-100, Han’s Laser, Shenzhen, China) [25]. The initial powder may be commercial pre-alloyed powder or elemental powders, as shown in Table 3. Some of them were mixed in an agate jar by the ball milling machine (PM4L, DROIDE, Shanghai, China) at a speed of 150 rpm for half an hour. Specimens measuring 10×10×10 mm were produced (detailed manufacturing information is in supplementary materials Figure S1 and Table S2). The relative density (RD) of samples with good formability was measured using the Archimedes method using a density meter (ZMD-2, FANGRUI, Shanghai, China).
Samples with the highest density among these samples manufactured by different parameters were selected to do the X-ray diffraction (XRD) analyses. XRD analyses were determined on the X-Y plane using an X-ray diffractometer (D8 Advance, Bruker, Karlsruhe, Germany) with Cu Kα radiation at a scanning rate of 10° min−1, and a 2θ angle ranging from 20° to 120°.
Among these XRD tested samples, the processing parameters of HEAs manufactured with no cracks and having an RD higher than 98% were selected to prepare tensile test samples and the tensile testing was conducted on a universal testing machine (EM6.304-L 30 kN, TSMT, Shenzhen, China) at a speed of 0.5 mm/min at room temperature on dog-bone-shaped samples (a gauge length of 25 mm, width of 5 mm, and thickness of 2 mm).
3. Case study 1: Phase Formation of SLM-ed HEAs
3.1. Construction of a Model Pool
In this study, the ML models pool consists of 8 widely used classification models. These include a linear discriminant analysis (LDA), a decision tree model (D-tree), a Bayes classifier (Bayes), a random forest model (RF), and support vector machine with a linear kernel (SVM.lin), a polynomial kernel (SVM.poly), a radial basis function kernel (SVM.rbf) or a sigmoid kernel (SVM.sigm).
3.2. Classification Accuracy
The 8×12 groups of classification accuracies with the corresponding material descriptor subsets for each model achieved in Section 2.3 were shown in Figure 3, the cyan lines are the average accuracies of these ML models. In the LDA model, recursive elimination can improve the performance of the model, and in other models, recursive elimination can reduce the cost of model training (with appropriate quantities of material descriptors) without affecting the accuracy (performance) of the model.
The highest classification accuracy value for each model and its corresponding material descriptor subset are shown in Table 4. If two material descriptor subsets have the same highest accuracy of a model, the subset with fewer material descriptors was chosen. This indicates that these fewer material descriptors are the key material descriptors. That will help to reduce the workload of preparing material descriptors for ML of unexplored SLM-ed HEAs.
The highest accuracy of 0.9381 happens in the Bayes model with a material descriptor subset consisting of only 2 descriptors (VED and ). LDA and RF models also have a high accuracy of 0.9143 and 0.9095 (exceeding 0.900), respectively. But they need more material descriptors, 7 and 4, respectively. The D-tree model also has a high accuracy of 0.9095 with 2 material descriptors subsets with 5 material descriptors. By contrast, the SVM models have lower accuracies than those of the above models. The highest accuracy of the SVM models is 0.8418, it happens when using the VM.rbf or SVM.poly model with a material descriptor of . The highest accuracy of SVM.lin with material descriptors of VED and VEC is 0.7000, the highest accuracy of SVM.sigm with a material descriptor of VED is 0.6952, both are very low.
3.3. Prediction and Experimental Verification
Given the good classification performance of the Bayes model with a material descriptor subset consisting of VED and , the trained classification model then can be used to predict phases of un-explored SLM-ed HEAs.
4. Case Study 2: Tensile Properties of SLM-ed HEAs
4.1. Construction of Model Pool
In this study, the ML models pool consists of 2 widely used regressor models. These include a random forest model (RF) and a support vector machine (SVM).
4.2. The Results of MAPEs
12 groups of MAPEs with the corresponding material descriptor subsets for each model achieved in Section 2 are obtained after running the program. The lowest MAPE for each model and its corresponding material descriptor subset are shown in Table 6.
The lowest MAPEs for predicting UTS, YS, and all happen in the RF model with a material descriptor subset recursive eliminated by the RF regressor. The lowest MAPE of 10.33% for predicting UTS when working with a material descriptor subset consisting of only 2 descriptors ( and ). The lowest MAPE of 8.55% for predicting YS when working with a material descriptor subset consisting of only 1 descriptor (). The lowest MAPE for predicting occurs when working with a material descriptor subset consisting of 7 descriptors (, , , , , , ), though the value of MAPE is a little high, which is 28.48%.
The lowest MAPEs when predicting UTS, YS, and in in the SVM model are all higher than those in the RF model.
4.3. Prediction and Experimental Verification
The results are shown in Table 7. , , are the ultimate tensile strength, yield strength, and elongation, respectively, which are predicted by RF model with the lowest MAPEs when working with the corresponding material subset achieved in Section 4.2. , , are the experimental tested results of tensile strength, yield strength, and elongation on the SLM-ed samples. in Equation (6) is used to calculate the error between the predicted properties and tested properties
In the prediction of the UTS and YS, the errors are less than 20%. However, the errors are a little large when predicting , exceeding 20%. Figure 5 shows the room-temperature tensile stress-strain curve of these HEA samples. HEA A2 with FCC+BCC phases has higher strength and lower elongation than other HEAs with a single FCC phase, which fits well with the results of other research [9].
4. Discussion
4.1. Relationship between Key Material Descriptors and Phase Formation
The descriptors of VED and are the key material descriptors when predicting the phase formation of SLM-ed HEAs. In SLM, VED represents the amount of energy delivered to a unit volume of material. It significantly affects the heating and cooling rates during the rapid solidification of the melted material. Guo et al. [26] found that the duplex microstructure of AlCoCrFeNi2.1 underwent a morphological evolution from lamellar structure to cellular structure as laser energy input reduced. Ren et al. [27] also found that samples manufactured with a higher laser power and a lower laser scan speed are characteristic of a larger interlamellar due to a lower cooling rate (dT/dt = G × u), which originated from a smaller thermal gradient (G) and a slower solidification rate (u). The above findings show that VED has an important influence on the microstructures of dual-phase HEAs. Zhou et al. [14] and Sun et al. [28] both manufactured a HEA with a composition of Al0.5FeCoCrNi by SLM, but the SLM-ed samples showed different phases. One was FCC only and the other showed dual-phase with FCC phase and BCC phase. Low VED can lead to rapid heating and subsequent rapid cooling, impacting the phase transformation behavior of the material. Different phases in a material often have distinct formation kinetics. Low VED can lead to quicker solidification, potentially favoring the formation of metastable phases or amorphous structures due to insufficient time for atoms to arrange into the equilibrium phase [29].
Zhang et al [30] compared the atomic size mismatch () of various HEAs at different compositions. Interestingly, FCC solid solutions tend to have smaller values, and BCC solid solutions exhibit larger values. For intermediate , HEA may have a mixture of BCC and FCC solid solutions. Wang et al. [31] suggested that the structure changing from an FCC to a BCC structure with compositions can be attributed to the atomic-level strain energy [32]. Specifically, the FCC structure has the highest packing efficiency for identical hard spheres, and for a metallic solid solution FCC phase, the constitute elements often have similar atomic sizes. Since Al has a relatively larger atomic size compared to many 3d-transition metal elements (e.g., Cr, Fe, Co, Ni, and Cu), its addition may result in significant atomic-level strains in the FCC lattice. With increasing Al contents, the accumulated atomic-level strains may eventually destabilize the FCC structure, triggering the FCC-to-BCC transition [33,34]. With a lower packing efficiency in the BCC phase, the strain energy is largely released. Atomic size mismatch () can create strain within the crystal lattice, influencing the likelihood of forming specific phases or altering phase stability. These strains can favor the formation of certain phases over others, especially if the lattice strain promotes the formation of metastable phases [35].
4.2. Relationship between key material descriptors and tensile properties
The descriptors of the second ionization energy variance (), the third ionization energy variance () are the key material descriptors when predicting the UTS of SLM-ed HEAs. The mechanical strength of a metal is largely determined by the bond energy among atoms [36]. It is well known that metallic bonds result from the interaction between atomic cores and their free electrons, and thus the magnitude of free electron density of a metallic alloy is one of the important factors that control the strength of a metal [37]. The contribution of each atom to the free electron density is mainly determined by the ability of an atom to donate electrons. The greater the ability of an atom to donate electrons, the larger the contribution of the atom to the free electron density, and thus the stronger the metallic bonding. Zhang et al. [38] proposed a machine-learning approach to dramatically enhance the combined UTS and electric conductivity of alloys. Application of this approach to SSCA (solid solution strengthened conductive copper alloys) demonstrates that the key elemental feature for UTS of an alloy is the absolute electronegativity variance. The absolute electronegativity can be estimated from the first ionization energy and electron affinity. The first ionization energy is the amount of energy required to remove an electron from an atom to vacuum. The electron affinity energy indicates the amount of energy released when an atom acquires an electron. Here, most of the SLM-ed HEAs in the database are 3d transition metal CCAs that contain at least 4 of the 9 following elements: Al, Co, Cr, Cu, Fe, Mn, Ni, Ti, and V as described by Miracle [1]. The outermost electrons of these elemental atoms are 2-3. The second and third ionization energy is the amount of energy required to remove the second and third electron from an atom to vacuum. The greater the ability of an atom to donate electrons. A larger second ionization energy variance () or third ionization energy variance () indicates the ability of each element in the alloy to donate electrons has a large variation. It is reasonable to speculate that an element with a larger second or third ionization energy contributes to the weakening of the alloy or lowering of the alloy strength. Therefore, it is not difficult to understand that the second ionization energy variance (), the third ionization energy variance () of the alloy are also two of the most important factors affecting the UTS.
The descriptor of the electronegativity (Allen) variance () is the key material descriptor when predicting the YS of SLM-ed HEAs. For the SLM-ed HEAs, possible strengthening mechanisms include solid-solution hardening (), grain size hardening (), and precipitation hardening (). And the YS of SLM-ed HEAs is a simple summation of the individual contributions, expressed as [39]:
Poletti et al. [40] found that HEA formation can be correlated to the HRRs (Hume-Rothery rules) using the electronegativity (Allen) variance (). Leong et al. [41] did some research on electronegativity and enthalpy of mixing biplots for High Entropy Alloy solid solution prediction, they found that electronegativity (Allen) is better suited to predict solid-solution stability when utilizing only one parameter among electronegativity (Allen), electronegativity (Pauling) and electronegativity (Mulliken). The greater the electronegativity (Allen) variance () between the elements of SLM-ed HEAs, the stronger the chemical affinity between the solute and the solvent element, which is likely to have smaller solubility [42]. Thus, the electronegativity (Allen) variance () has a great influence on the solid-solution hardening () and then affects the YS of SLM-ed HEAs.
The MAPE when predicting the of SLM-ed HEAs is a little large. This may be attributed to the big difference in residual stress of SLM-ed HEAs after SLM with different SLM machines. However, the can be optimized by post-annealing or other post-heat treatment means after SLM [43]. The descriptors of the average Pauling electronegativity value (), the electronegativity (Allen) variance (), the second ionization energy variance (), the third ionization energy variance (), the quantum number variance (), the work function variance () and the Column variance () are the key material descriptors when predicting the of SLM-ed HEAs. Among them, is the key material descriptor when predicting the YS, , are the key material descriptors when predicting the UTS. The average Pauling electronegativity value (), the quantum number variance () and the Column variance () may also affect the plastic deformation just like the electronegativity (Allen) variance () because they all relate with the difficulty with which an atom loses electrons. The work function variance () has something to do with the Elastic Modulus, found in the research of Li et al. [44].
5. Conclusions
In summary, we propose a framework to select the best combination of material descriptors subset and ML models. We apply it in the prediction of phase formation and tensile properties of SLM-ed HEAs.
By adjusting material descriptors and machine learning models, an optimized Bayes model for classification has been established, achieving a remarkable 93.8% accuracy in distinguishing between body-centered cubic (BCC), face-centered cubic (FCC), and dual-phase (FCC+BCC) HEAs. Moreover, optimized Random Forest models for predicting the tensile properties (the ultimate tensile strength, yield strength, and elongation) achieved remarkable MAPEs (mean absolute percentage errors) of 10.33%, 8.55%, and 28.48%, respectively. Furthermore, several HEAs were manufactured by SLM and the experimental results showed good agreement with the predicted results. These efforts carry significant implications in advancing the utilization of SLM for HEAs.
Supplementary Materials
The following supporting information can be downloaded at: www.mdpi.com/xxx/s1.
Acknowledgments
This work was financially supported by, Natural Science Foundation of Guangdong Province (Grant No. 2023A1515011641), Key field research projects in Foshan City (Grant No. 2120001009232), Shenzhen Science and Technology Program (Grant No. GJHZ20220913143012022), the School-level scientific research project of Shenzhen Institute of Technology (Grant No. 2211017), Guangdong HUST Industrial Technology Research Institute, Guangdong Provincial Key Laboratory of Manufacturing Equipment Digitization (Grant No. 2020B1212060014), the Postdoctoral Science Foundation of China (Grant No. 2022M710503), the Natural Science Foundation Commission of Chongqing (Grant No. CSTB2022NSCQ-BHX0029).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Miracle, D.B.; Senkov, O.N.; Wilks, J. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Fang, Q.; Shi, Y.; Tor, S.B.; Chua, C.K.; Zhou, K. Recent Advances on High-Entropy Alloys for 3D Printing. Adv. Mater. 2020, 32, e1903855. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Niu, P.; Yuan, T.; Cao, P.; Chen, C.; Zhou, K. Selective laser melting of an equiatomic CoCrFeMnNi high-entropy alloy: Processability, non-equilibrium microstructure and mechanical property. J. Alloy. Compd. 2018, 746, 125–134. [Google Scholar] [CrossRef]
- Brif, Y.; Thomas, M.; Todd, I. The use of high-entropy alloys in additive manufacturing. Scr. Mater. 2015, 99, 93–96. [Google Scholar] [CrossRef]
- Moghaddam, A.O.; Shaburova, N.A.; Samodurova, M.N.; Abdollahzadeh, A.; Trofimov, E.A. Additive manufacturing of high entropy alloys: A practical review. J. Mater. Sci. Technol. 2020, 77, 131–162. [Google Scholar] [CrossRef]
- Rickman, J.; Lookman, T.; Kalinin, S. Materials informatics: From the atomic-level to the continuum. Acta Mater. 2019, 168, 473–510. [Google Scholar] [CrossRef]
- Meredig, B.; Agrawal, A.; Kirklin, S.; Saal, J.E.; Doak, J.W.; Thompson, A.; Zhang, K.; Choudhary, A.; Wolverton, C. Combinatorial screening for new materials in un-constrained composition space with machine learning. Phys. Rev. B 2014, 89, 094104. [Google Scholar] [CrossRef]
- Su, Y.; Luo, S.; Wang, Z. Microstructure evolution and cracking behaviors of additively manufactured AlxCrCuFeNi2 high entropy alloys via selective laser melting. J. Alloy. Compd. 2020, 842, 155823. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, C.; Wang, C.; Antonov, S.; Xue, D.; Bai, Y.; Su, Y. Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models. Acta Mater. 2020, 185, 528–539. [Google Scholar] [CrossRef]
- Kaufmann, K.; Vecchio, K.S. Searching for high entropy alloys: A machine learning approach. Acta Mater. 2020, 198, 178–222. [Google Scholar] [CrossRef]
- Wu, Q.F.; Wang, Z.J.; Hu, X.B.; Zheng, T.; Yang, Z.S.; He, F.; Li, J.J.; Wang, J.C. Uncovering the eutectics design by machine learning in the Al-Co-Cr-Fe-Ni high entropy system. Acta Mater. 2019, 182, 278–286. [Google Scholar] [CrossRef]
- Roy, A.; Babuska, T.; Krick, B. Balasubramanian G, Machine learned feature identification for predicting phase and Young’s modulus of low-, medium- and high-entropy alloys. Scr. Mater. 2020, 185, 152–158. [Google Scholar] [CrossRef]
- Zhou, P.; Xiao, D.; Wu, Z.; Ou, X. Al0.5FeCoCrNi high entropy alloy prepared by selective laser melting with gas-atomized pre-alloy powders. Mater. Sci. Eng. A 2018, 739, 86–89. [Google Scholar] [CrossRef]
- Rao, Z.; Tung, P.-Y.; Xie, R.; Wei, Y.; Zhang, H.; Ferrari, A.; Klaver, T.; Körmann, F.; Sukumar, P.T.; da Silva, A.K.; et al. Machine learning–enabled high-entropy alloy discovery. Science 2023, 378, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, S.; Liu, D.; Zou, R.; Yang, Z. Hardness prediction of high entropy alloys with machine learning and material descriptors selection by improved genetic algorithm. Comput. Mater. Sci. 2022, 205, 111185. [Google Scholar] [CrossRef]
- Chang, Y.-J.; Jui, C.-Y.; Lee, W.-J.; Yeh, A.-C. Prediction of the Composition and Hardness of High-Entropy Alloys by Machine Learning. JOM 2019, 71, 3433–3442. [Google Scholar] [CrossRef]
- Zbigniew, H. Stachurski, Mechanical behavior of materials, second edition, ANU, Australia, 2009.
- Ghiringhelli, L.M.; Vybiral, J.; Levchenko, S.V.; Draxl, C.; Scheffler, M. Big data of materials science: Critical role of the descriptor. Phys. Rev. Lett. 2015, 114, 105503. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.; Lin, J.; Chen, G.; Liaw, P. Solid-solution phaseformation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Roy, A.; Balasubramanian, G. Predictive descriptors in machine learning and data-enabled explorations of high-entropy alloys. Comput. Mater. Sci. 2021, 193, 110381. [Google Scholar] [CrossRef]
- Pearson, K. Note on regression and inheritance in the case of two parents. Proc. R. Soc. 1895, 58, 240–242. [Google Scholar]
- Yuan, R.; Liu, Z.; Balachandran, P.V.; Xue, D.; Zhou, Y.; Ding, X.; Sun, J.; Xue, D.; Lookman, T. Accelerated discovery of large electrostrains in BaTiO3-based piezoelectrics using active learning. Adv. Mater. 2018, 30, 1702884. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Lozano, C.; Seoane, J.A.; Gestal, M.; Gaunt, T.R.; Dorado, J.; Campbell, C. Texture classification using feature selection and kernel-based techniques. Soft Comput. 2015, 19, 2469–2480. [Google Scholar] [CrossRef]
- Tan, X.; Chen, D.; Xu, J.; Chen, H.; Peng, X.; Guo, L.; Xiao, H.; Zhang, Q. High-strength Fe32Cr33Ni29Al3Ti3 fabricated by selective laser melting. J. Mater. Res. Technol. 2023, 27, 3701–3711. [Google Scholar] [CrossRef]
- Guo, Y.; Su, H.; Zhou, H.; Shen, Z.; Liu, Y.; Zhang, J.; Liu, L.; Fu, H. Unique strength-ductility balance of AlCoCrFeNi2.1 eutectic high entropy alloy with ultra-fine duplex microstructure prepared by selective laser melting. J. Mater. Sci. Technol. 2022, 111, 298–306. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, Y.; Zhao, D.; Chen, Y.; Guan, S.; Liu, Y.; Liu, L.; Peng, S.; Kong, F.; Poplawsky, J.D.; et al. Strong yet ductile nanolamellar high-entropy alloys by additive manufacturing. Nature 2022, 608, 62–68. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Peng, W.X.; Yang, L.L.; Fang, L. Effect of SLM Processing Parameters on Microstructures and Mechanical Properties of Al0.5CoCrFeNi High Entropy Alloys. Metals 2020, 10, 292. [Google Scholar] [CrossRef]
- Jiang, K.; Yin, G.; Gao, H.; Tian, W. Influence of rapid heating and cooling combined with deformation at ultrahigh strain rates on the microstructure evolution of pure titanium shaped charge liner. Mater. Charact. 2018, 142, 211–218. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Z.P.; Ma, S.G.; Liaw, P.K.; Tang, Z.; Cheng, Y.Q.; Gao, M.C. Guidelines in predicting phase formation of high-entropy alloys. MRS Commun. 2014, 4, 57–62. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Chen, G. Atomic packing efficiency and phase transition in a high entropy alloy. J. Alloy. Compd. 2009, 478, 321–324. [Google Scholar] [CrossRef]
- Egami, T.; Waseda, Y. Atomic size effect on the formability of metallic glasses. J. Non-Crystalline Solids 1984, 64, 113–134. [Google Scholar] [CrossRef]
- Ma, S.G.; Zhang, S.F.; Gao, M.C.; Liaw, P.K.; Zhang, Y. A successful synthesis of the CoCrFeNiAl0.3 single-crystal, high-entropy alloy by Bridgman solidification. JOM 2013, 65, 1751–1758. [Google Scholar] [CrossRef]
- Tang, Z.; Gao, M.C.; Diao, H.; Yang, T.; Liu, J.; Zuo, T.; Zhang, Y.; Lu, Z.; Cheng, Y.; Zhang, Y.; et al. Aluminum alloying effects on lattice types, microstructures, and mechanical behavior of high-entropy alloys systems. JOM 2013, 65, 1848–1858. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Pearson, R.G. Absolute electronegativity and absolute hardness of Lewis acids and bases. J. Am. Chem. Soc. 1985, 107, 6801–6806. [Google Scholar] [CrossRef]
- Daw, M.S.; Foiles, S.M.; Baskes, M.I. The embedded-atom method: a review of theory and applications. Mater. Sci. Rep. 1993, 9, 251–310. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, H.; He, X.; Wang, C.; Jiang, L.; Chen, L.-Q.; Xie, J. Dramatically Enhanced Combination of Ultimate Tensile Strength and Electric Conductivity of Alloys via Machine Learning Screening. Acta Mater. 2020, 200, 803–810. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Yang, T.; Tong, Y.; Wang, J.; Luan, J.H.; Jiao, Z.B.; Chen, D.; Yang, Y.; Hu, A.; Liu, C.T.; Kai, J.J. Heterogeneous precipitation behavior and stacking-fault-mediated deformation in a CoCrNi-based medium-entropy alloy. Acta Mater. 2017, 138, 72–82. [Google Scholar] [CrossRef]
- Poletti, M.; Battezzati, L. Electronic and thermodynamic criteria for the occurrence of high entropy alloys in metallic systems. Acta Mater. 2014, 75, 297–306. [Google Scholar] [CrossRef]
- Leong, Z.; Huang, Y.; Goodall, R.; Todd, I. Electronegativity and enthalpy of mixing biplots for High Entropy Alloy solid solution prediction. Mater. Chem. Phys. 2018, 210, 259–268. [Google Scholar] [CrossRef]
- Gottstein, G. Physical Foundations of Material Science, Physical Foundations of Materials Science. 2004.
- Yang, F.; Wang, L.; Wang, Z.; Wu, Q.; Zhou, K.; Lin, X.; Huang, W. Ultra strong and ductile eutectic high entropy alloy fabricated by selective laser melting. J. Mater. Sci. Technol. 2022, 106, 128–132. [Google Scholar] [CrossRef]
- Li, Q.; Hua, G.; Lu, H.; Yu, B.; Li, D.Y. Understanding the Effect of Plastic Deformation on Elastic Modulus of Metals Based on a Percolation Model with Electron Work Function. JOM 2018, 70, 1130–1135. [Google Scholar] [CrossRef]
Figure 1.
Flowchart of our strategy to search for the best combination of material descriptors and machine learning model for a given materials problem.
Figure 1.
Flowchart of our strategy to search for the best combination of material descriptors and machine learning model for a given materials problem.
Figure 2.
The Pearson correlation coefficients between material descriptors.
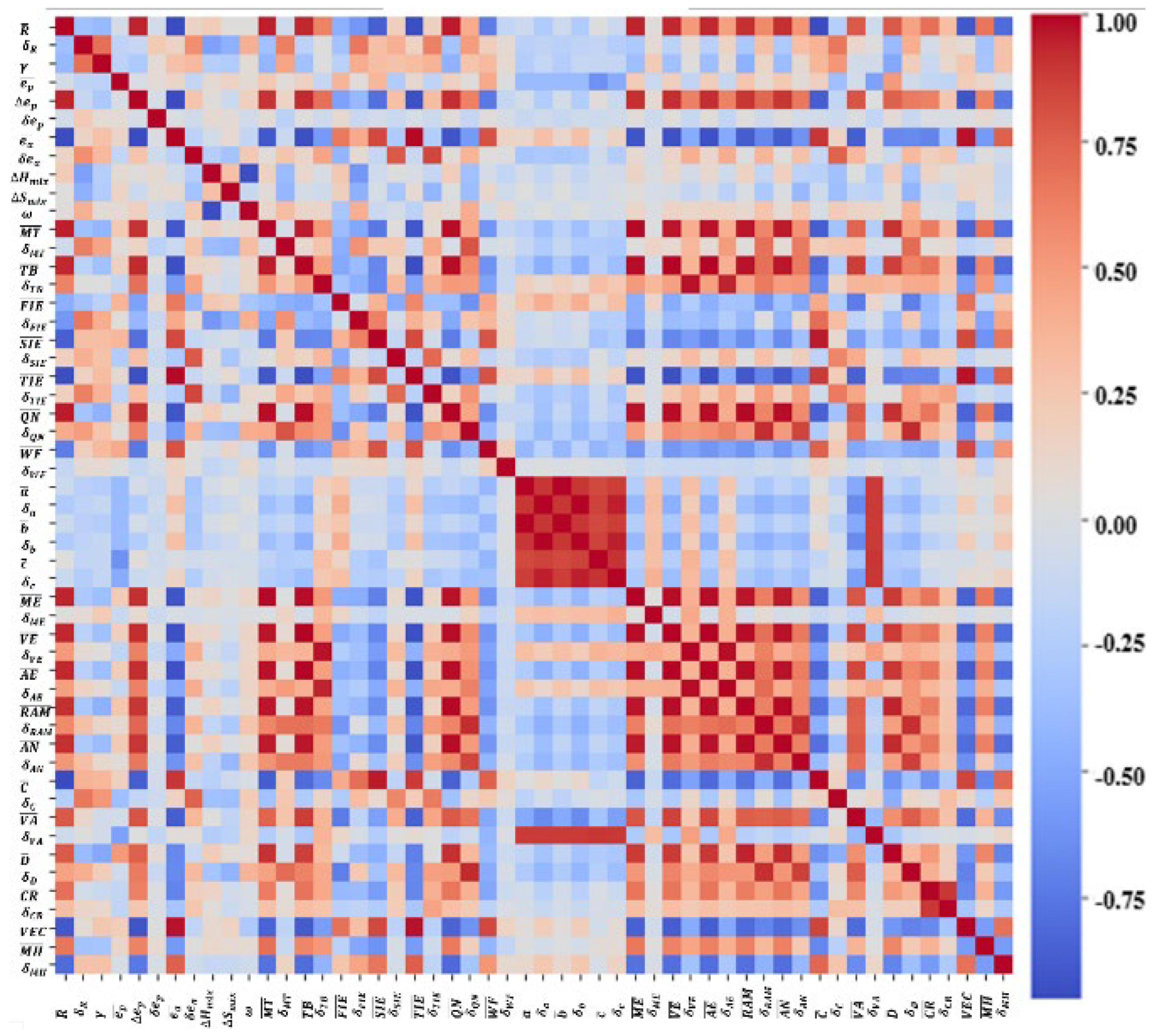
Figure 3.
The classification accuracies of different models in phase prediction.
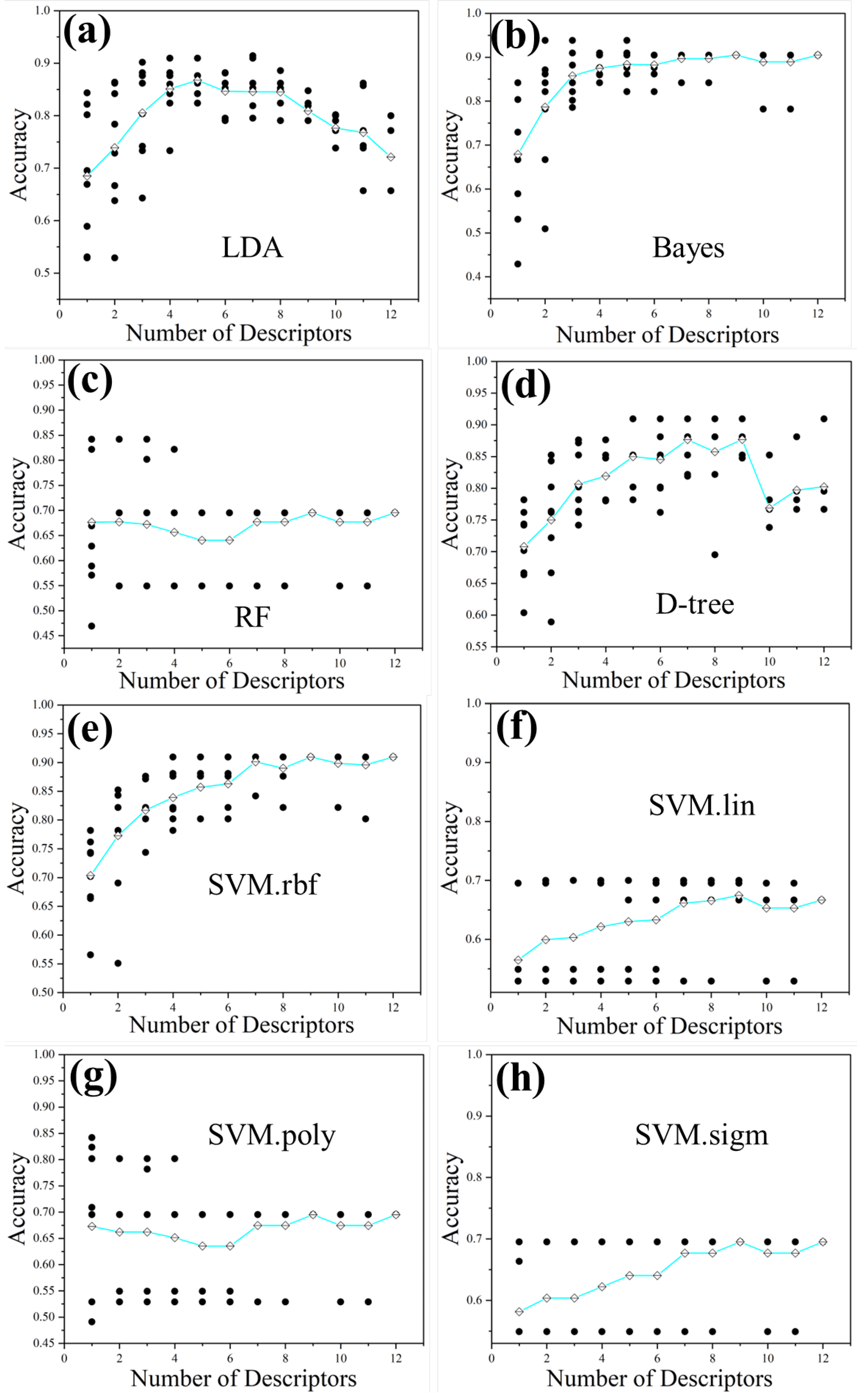
Figure 4.
XRD results of these experimental synthesized HEAs.
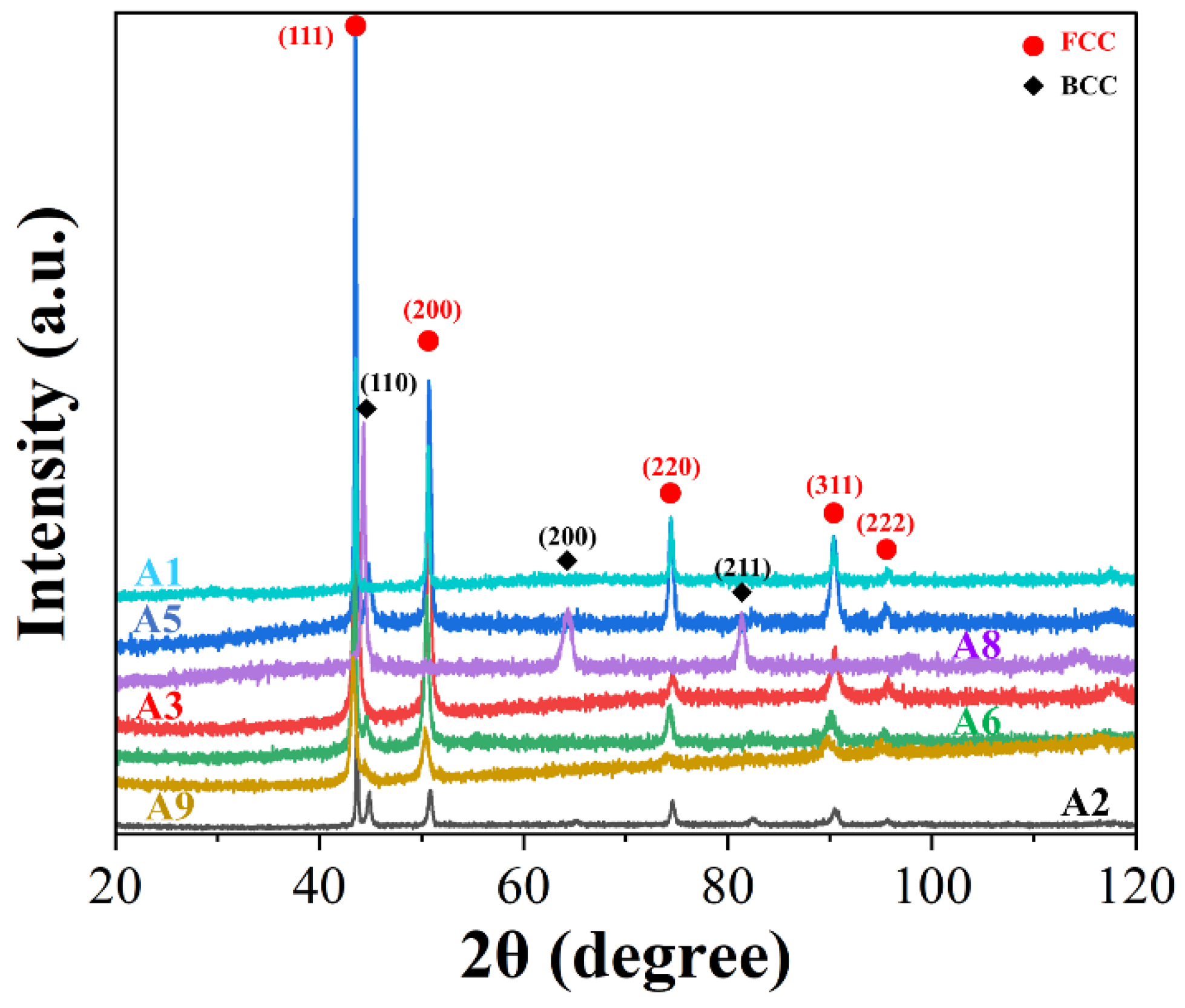
Figure 5.
Tensile test results of these experimental synthesized HEAs.
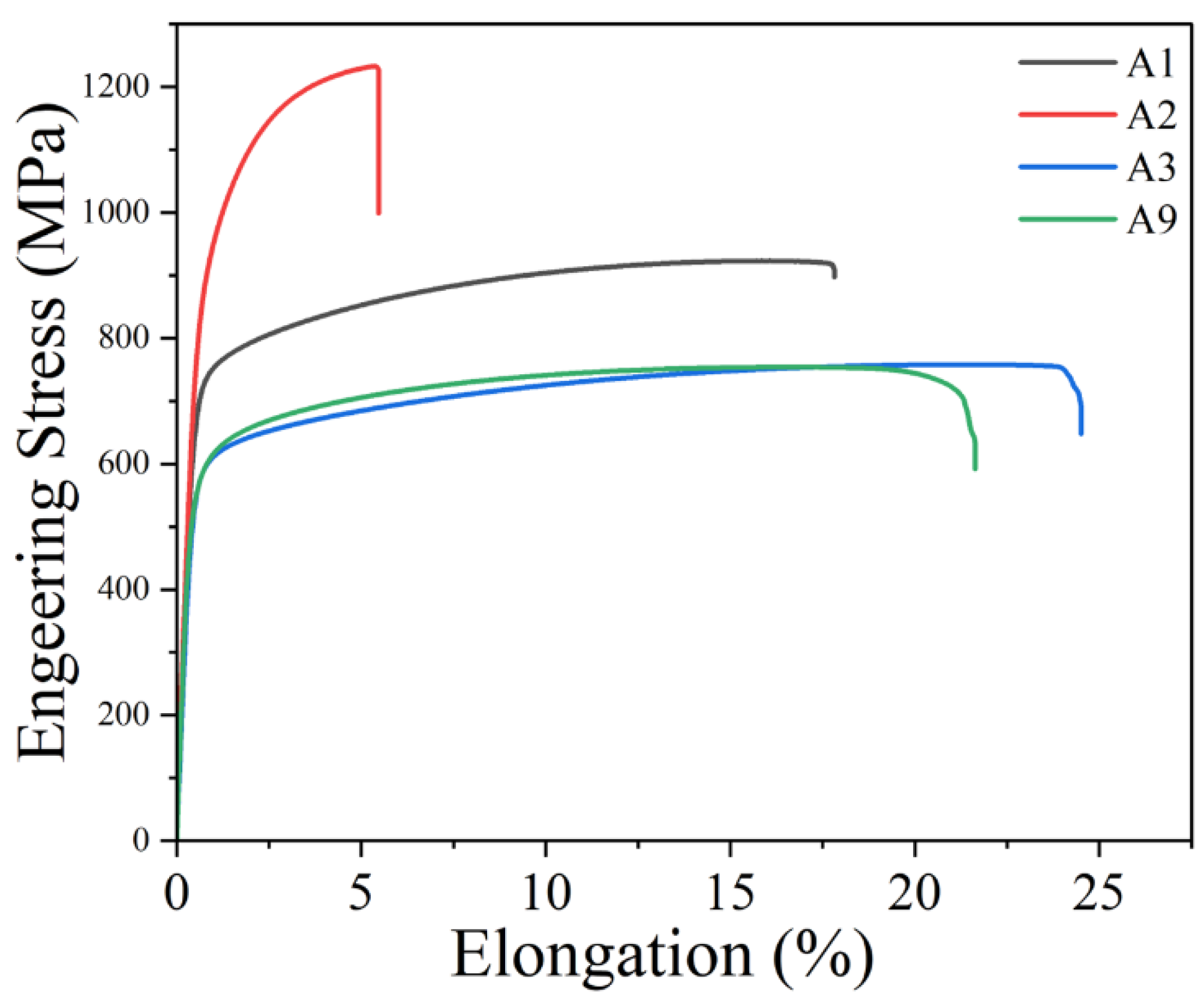
Table 1.
The empirical descriptors.
| Description | Abbreviation | Formula |
|---|---|---|
| Atomic Size | R | |
| Electronegativity (Pauling) |
; ; |
|
| Electronegativity (Allen) | ||
| Valence Electron Concentration | ||
| Mixing Entropy | ||
| Mixing Enthapy | ||
| Combining effects of Mixing Entropy and Mixing Enthapy | ||
| Combining effects of Mixing Entropy and Atomic Size Mismatch | ||
| Volume Energy Density | VED |
Table 2.
The elemental parameters for self-defined descriptors.
| Description | Abbreviation | Description | Abbreviation |
|---|---|---|---|
| Melting Point | TM | Atom Volume | VA |
| First Ionization Energy | FIE | Boiling Temperature | TB |
| Second Ionization Energy | SIE | Vaporization Enthalpy | VE |
| Third Ionization Energy | TIE | Melting Enthalpy | ME |
| Work Function | WF | Atomization Enthalpy | AE |
| Atomic Number | AN | Covalent Radii | CR |
| Quantum Number | QN | Density | D |
| Column in the Periodic Table | C | Lattice Constant | a/b/c |
| Relative Atom Mass | RAM | Morse Hardness | MH |
Table 3.
The powder, formability, and highest RD of 9 newly SLM-ed HEAs.
| HEA | Composition | Powder | Formability | Highest RD |
|---|---|---|---|---|
| A1 | (FeNi)67Cr15Mn10Al3Ti5 | Mixed (Fe+ Ni+ Cr+ Mn+ Al+ Ti) | ✓ | 98.2% |
| A2 | Fe30Cr33Ni29Al3Ti3 | pre-alloyed | ✓ | 99.4% |
| A3 | Fe30Cr33Ni44.2Al3Ti3 | Mixed (A2 + Ni) | ✓ | 99.4% |
| A4 | AlCrCuFeNi | pre-alloyed | × | × |
| A5 | AlCrCuFeNi2.67 | Mixed (A4 + Ni) | ✓ | 97.0% |
| A6 | AlCrCuFe2Ni2.34 | Mixed (A4+ Fe+ Ni) | ✓ | 98.2% |
| A7 | AlMoCrFeNi2 | pre-alloyed | × | × |
| A8 | AlMoCrFe8.76Ni2 | Mixed (A7 + Fe) | ✓ | 97.2% |
| A9 | AlMoCrFe8.76Ni3.26 | Mixed (A7 + Fe + Ni) | ✓ | 98.4% |
Table 4.
The highest classification accuracy of each model and its corresponding material descriptor subset.
Table 4.
The highest classification accuracy of each model and its corresponding material descriptor subset.
| ML model | Material descriptor subset | Accuracy |
|---|---|---|
| LDA | VED, , , , , , | 0.9143 |
| Bayes | VED, | 0.9381 |
| RF | VED, , , | 0.9095 |
| D-tree |
VED, VEC, , , VED, VEC, , , |
0.9095 0.9095 |
| SVM.rbf | 0.8418 | |
| SVM.lin | VED, VEC | 0.7000 |
| SVM.poly | 0.8418 | |
| SVM.sigm | VED | 0.6952 |
Table 5.
The phase formation predicted by ML and identified by XRD.
| HEA | Composition | XRD identified | ML predicted |
Match |
|---|---|---|---|---|
| A1 | (FeNi)67Cr15Mn10Al3Ti5 | FCC | FCC | ✓ |
| A2 | Fe30Cr33Ni29Al3Ti3 | FCC + BCC | FCC + BCC | ✓ |
| A3 | Fe30Cr33Ni44.2Al3Ti3 | FCC | FCC | ✓ |
| A5 | AlCrCuFeNi2.67 | FCC + BCC | FCC + BCC | ✓ |
| A6 | AlCrCuFe2Ni2.34 | FCC + BCC | FCC + BCC | ✓ |
| A8 | AlMoCrFe8.76Ni2 | BCC | BCC | ✓ |
| A9 | AlMoCrFe8.76Ni3.26 | FCC | FCC | ✓ |
Table 6.
The lowest MAPE of each model and its corresponding material descriptor subset.
| Tensile property | ML Model | Material descriptor subset | MAPE |
|---|---|---|---|
| UTS | RF | , | 10.33% |
| UTS | SVM | VED, , , , , , , , , , , | 23.41% |
| YS | RF | 8.55% | |
| YS | SVM | , , | 24.83% |
| RF | , , , , , , | 28.48% | |
| SVM | 50.47% |
Table 7.
The tensile properties predicted by ML and tested results.
| HEA |
(MPa) |
UTS (MPa) |
(%) |
(MPa) |
YS (MPa) |
(%) |
(%) |
(%) |
(%) |
|---|---|---|---|---|---|---|---|---|---|
| A1 | 871 | 923 | 6 | 697 | 692 | 1 | 22 | 18 | 22 |
| A2 | 1175 | 1267 | 8 | 866 | 915 | 5 | 7 | 5 | 40 |
| A3 | 850 | 724 | 17 | 630 | 553 | 14 | 31 | 22 | 41 |
| A9 | 862 | 754 | 14 | 621 | 547 | 14 | 32 | 22 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






