1. Introduction
Regression is the most used statistical method, applied for various purposes, and in different scientific disciplines, including metrology. The basic purpose of regression is the prediction of a value that has not been measured, but which can be estimated based on the regression line or regression plane. So, for example, a regression can be used to predict the cutting temperature and surface roughness during the face milling process [
1], or for predicting and monitoring vibrations on a lathe machine [
2]. Regression can also be used to characterize various devices and sensors: for atomic force microscope characterization [
3] or magnetic field sensors characterization [
4]. It is most often used in calibration: from calibrating pressure against ruby fluorescence shift [
5] to calibration that describes the pressure sensitivities of the optical fibre sensors [
6]. Furthermore, regression is often used in interlaboratory comparison studies of calibration standards in different fields [
7,
8], or for the analysis of different physical constants [
9,
10].
The application of regression involves measuring the value of the response variable that corresponds to the given values of the explanatory variable [
11]. There are existing numerous regression techniques that can be used to determine the relationship between these variables [
12]. Among all, a straight-line relationship is the simplest one. This, the most common way of connecting only one independent (explanatory) variable and the dependent (response) variable, is called univariate linear regression. The subject of this paper concerns the risk assessment for linear univariate regression models in metrology.
All recommendations and standards related to metrology are issued by the international metrology organization International Bureau of Weights and Measures (Bureau International des Poids et Mesures, BIPM). The basic procedure for risk assessment for an item of interest is given by the guide Evaluation of measurement data – The role of measurement uncertainty in conformity assessment 106:2012 [
13]. However, this method of risk assessment, well-known in metrology, has not been applied for regression so far. According to [
14] (p. 15), and [
15,
16] guidelines called JCGM 107, for the application of the least squares method, the most famous method for determining the coefficients of the regression line, are still in preparation. It is not yet known whether these guidelines will include a risk assessment.
Risk assessment is carried out in the process of assessing the conformity of a product with specified requirements. Two types of risks may arise during conformity assessment. The producer’s risk refers to situations where measurements or products meet the re-quired specifications but are rejected as non-conforming. Consumer risk refers to situations when products or measurements are accepted as conformed but do not meet specifications. Whether a product conforms to the given specifications or not is determined based on measurements. The measured value of the item of interest must be within the given tolerance interval. The measurement uncertainty that occurs during measurement may lead to incorrect decisions regarding the acceptance of a non-compliant product or the rejection of a product that meets the specifications. This happens when the measurement is close to either the lower limit of the tolerance interval
or upper limit of the tolerance interval
, and the measurement uncertainty associated with that measured value goes over the tolerance interval
[
17,
18,
19,
20,
21].
It is important to emphasize that the tolerance interval in the metrology domain is different from the regression tolerance interval in the statistical domain. The statistical tolerance regions also known as simultaneous tolerance intervals, are constructed so that, with a certain level of confidence, contain a specified proportion of the population in future sampling [
22,
23]. For reasons that will be elaborated upon further in the text, it is not feasible to apply these simultaneous tolerance intervals for the model of risk assessment in regression presented in this paper. The tolerance interval in the metrology domain is established by the manufacturer in its specifications for a particular measuring device, or this interval is determined by the applicable standards.
The risk assessment method outlined in this paper can be applied not only in metrology but also in general in all regression models, regardless of the area in which the data originates. Therefore, this manuscript gives alternative values for the tolerance interval that can be used when the values for the tolerance interval provided by the manufacturer are unavailable.
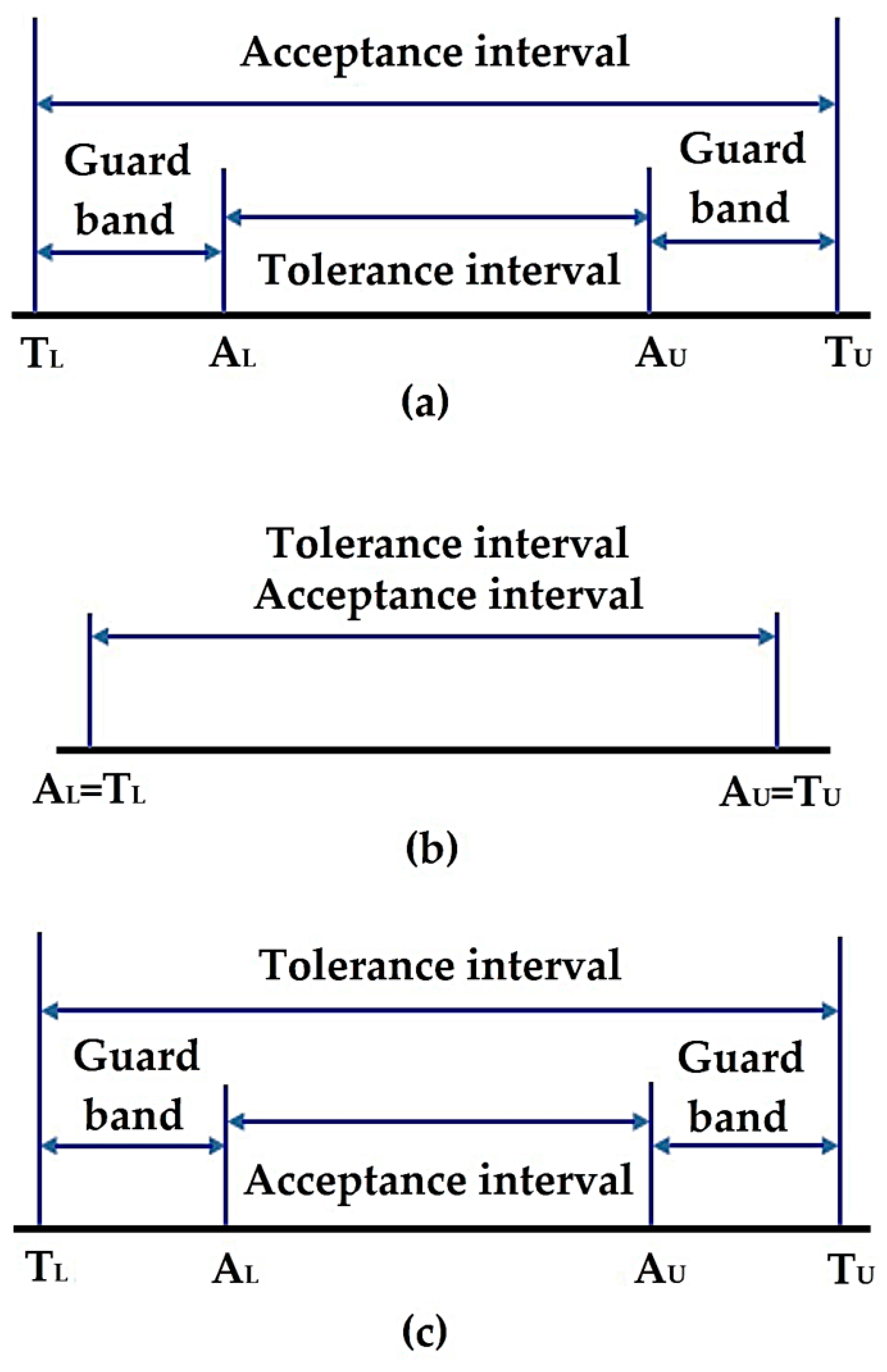
To reduce the impact of measurement uncertainty on risk assessment, an acceptance interval
is introduced into the procedure for evaluating the conformity of products with the prescribed specifications, in addition to the tolerance interval. The marks
and
represents lower and upper limits of the acceptance interval, respectively. Acceptance and tolerance intervals can be in different mutual relations [
24]. The limits of the tolerance interval and the acceptance interval depend on the properties of the measurand. These can be semi-open or semi-closed intervals [
25]. Furthermore, that can be closed intervals, as in this case. If the tolerance interval is within the acceptance interval, it is a model of minimization of the producer’s risk, as illustrated in
Figure 1a. If the tolerance interval is outside the acceptance interval, it is a consumer risk minimization model (
Figure 1c) [
26]. A special situation when tolerance and acceptance interval overlap, is when it is valid that
, and
. This is called shared risk (
Figure 1b).
The guard band of length , between the tolerance interval and the acceptance interval, ensures a reduction in the probability of making wrong decisions. In practice, it is commonly recommended to minimize the consumer’s risk to enhance the quality of the delivered products. However, it is feasible to set the length of the guard band so that both the customer and the producer are satisfied.
When measuring, it is assumed that the object of interest has a measurable property
with possible values
It is natural to assume that there exists historical data about the item of interest, such as those found in manuals, scientific papers, data from previous measurements, and the like. Also, one can talk about prior beliefs of the measurer based on experience about possible values that will be obtained during the measurement, or about the possible distribution of parameters that describe the measured data. Such data are treated as random variables. Knowledge about these data is given by prior distribution, that is, by probability density function (PDF), designated with
[
13]. Depending on the available data, the prior can be a non-parametric, one-parameter or two-parameter distribution [
27,
28]. According to the principle of maximum entropy (PME), if data for two moments are available, a two-parameter distribution is used for the prior [
29,
30,
31]. In this manuscript, the prior is a normal distribution whose parameters are the best estimate of a measurand
, with an associated standard measurement uncertainty
.
The data associated with the measurements
are also treated as a random variable. The values that this random variable can take are denoted by
Random variable
, is modeled via the likelihood function for normal distribution and denoted by
[
13]. The formula for the likelihood function involves standard measurement uncertainty
of some future measurement.
Global consumer’s risk
and global producer’s risk
are calculated probabilistically, using Bayes’ theorem. This is done by combining information on the prior distribution and the likelihood function, that is, by combining information on the random variables Y and
[
13,
19], [
32,
33]. If the values for
Y are outside the tolerance interval, and the values for
within the acceptance interval, it is about the global consumer’s risk
If the values for Y are within the tolerance interval, and the values for
are outside the acceptance interval, it is about the global producer’s risk
.
The risk assessment method can be applied when product quality is evaluated based on only one measured quantity [
13]. For example: when determining the roundness deviation of the inner ring of the bearing [
34], or when estimating the thickness of the epoxy coating applied to water pipes [
25]. This approach can also be used to evaluate conformity with the specifications for each, distinct property of the item of interest [
35]. It is also possible to assess the risk of multi-component models where several factors can affect the quality of the product [
36,
37]. Examples include risk assessment in food quality control and food supplements [
38,
39], risk assessment in drug quality control [
40], air quality control [
41], the chromatography process [
42], pharmaceutical equivalence studies when comparing generic and reference drugs [
43], and other related areas.
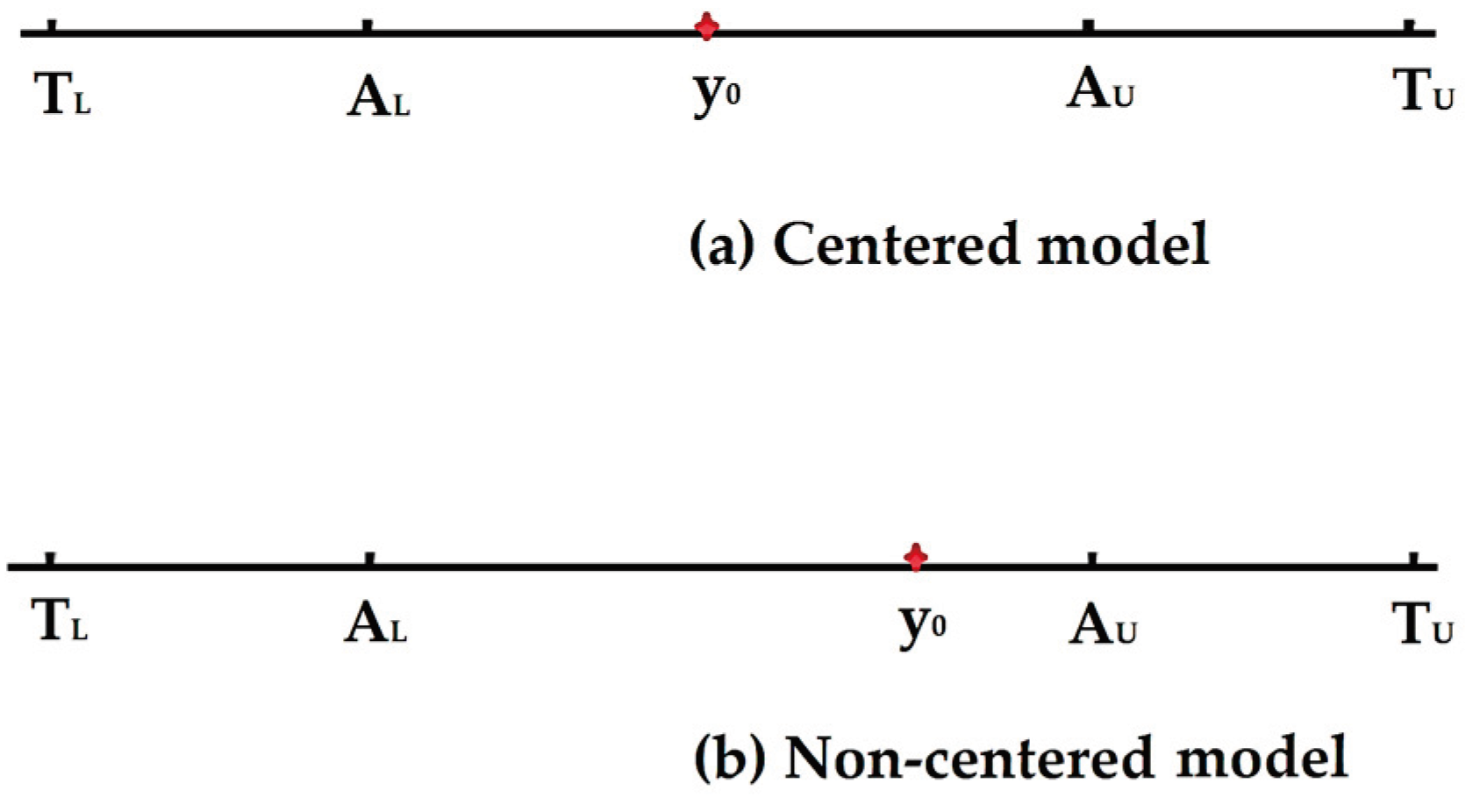
When the tolerance interval and acceptance interval are closed intervals, and in the case of risk evaluation for a single property of an item of interest, there exist two distinct models for the risk assessment: centered, and non-centered models (
Figure 2).
For the centered model, the best estimate of a measurand is exactly in the middle of the acceptance and tolerance interval, which is not the case with the non-centered model. This approach to risk assessment for a single measurable property, based on intervals of tolerance and acceptance, yields only one numerical value for the global risk of the producer, i.e. the consumer. It is evident that this method naturally can be extended to the two-dimensional case, where the outcomes are iso-risk curves, or to the three-dimensional case, where the results are risk surfaces, as demonstrated in this paper.
3. Results and Discussions
3.1. Graphical Risk Analysis
Graphical risk analysis was carried out by monitoring the behavior of the global risk of the producer and the global risk of the consumer along the moderate scale, along the guard band axis, and monitoring the behavior of the risk concerning the assumed value of measurement uncertainty of a future inspection process.
3.1.1. Behaviors of a Global Consumer and Producer Risk Along the Moderate Scale
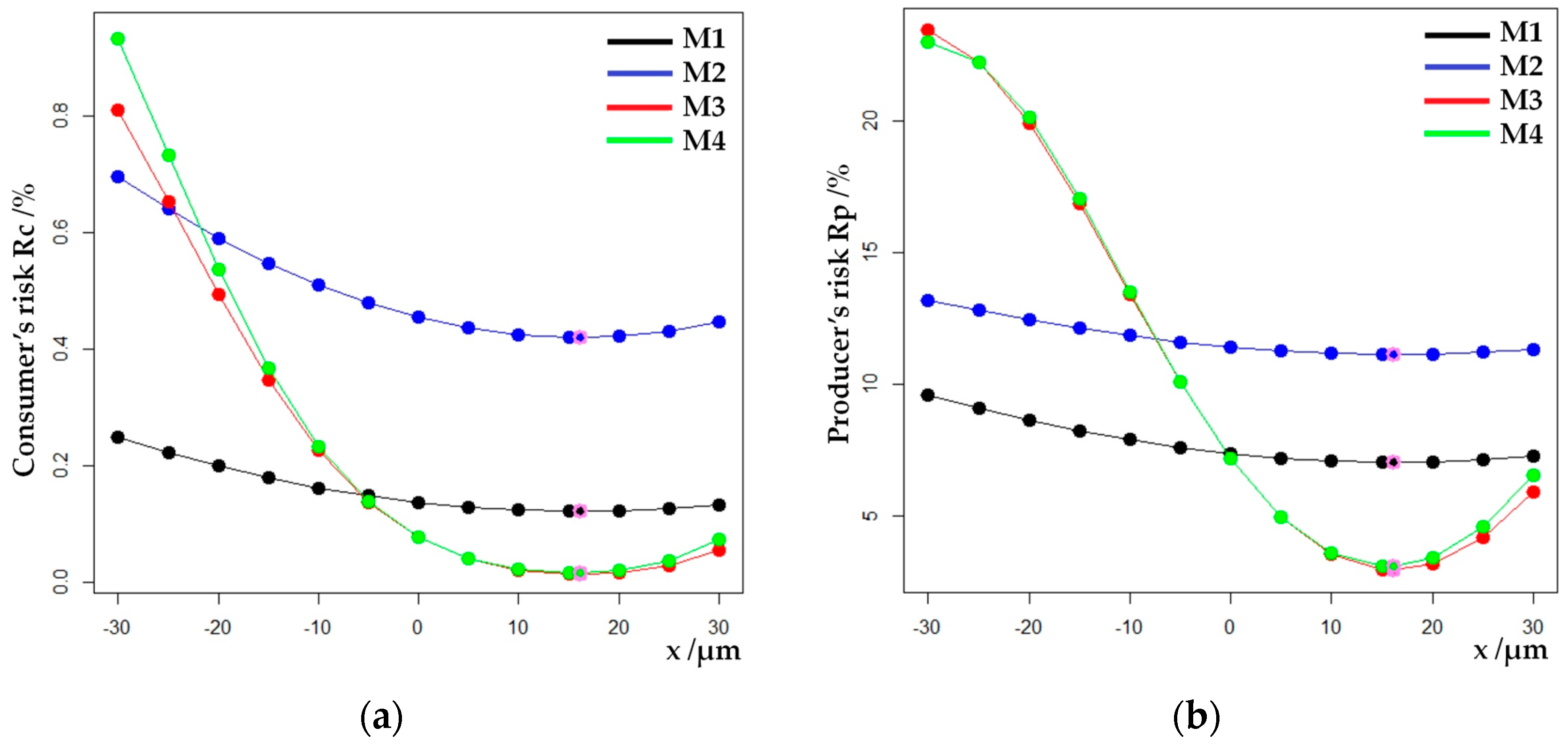
The behavior of the global producer’s risk
and global consumer’s risk
along the moderate scale depends on the values of the slope
and intercept
of the regression line. The risk curves for
and
along the moderate scale are parabolas with an upward opening. The minimum of these parabolas is located at the intersection of the regression line
and the line
. The position of the minimum at the moderate scale is indicated by
and is represented by the following expression:
It is easy to show how the minimal values of the global risk of producers and consumers along the moderate scale in all analyzed models are achieved for
µm (
Figure 5).
Parabolas are translated to the right when
i.e., if
and
, or if, as is the case here,
and
. That is the reason why the risk parabolas, i.e., the iso-risk curves along the moderate scale depicted in
Figure 5, are asymmetric. In all models, due to translation, the values of global risk for producers and consumers on the left side of the moderate scale are higher compared to the risk values on the right side of the moderate scale. This disparity is readily apparent in
Figure 4, as evidenced by the proportion of the regression line’s length located on the right side of the intersection of the regression line and the
line, in contrast to the proportion located on the left side of the intersection of the regression line and the
line. Therefore, the calculated global risks of producers and consumers can be seen as risks of deviation of the regression line from the
line.
In the case of a regression line where and , or and the parabolas would be translated to the left. The minimal values for the parabolas of the global risk of producers and consumers then would be located at the point of the moderate scale and would be calculated from equation (34).
The line marked with
and given by the equation:
is axisymmetric to the regression line. These lines are axisymmetric concerning
For the
worth
and conversely, for the
worth
The global risks of producers and consumers calculated for the line
are equal to the risks calculated for the regression line from equation (10) up to the order of magnitude ranging from
do
depending on the observed model and assuming that the line
is obtained under identical conditions as the regression line, with identical values for
and
and identical values for tolerance intervals and acceptance intervals. The same applies to conformance probability.
Due to the narrower range of the tolerance interval ∆T, the M2 model exhibits higher values of the global risk of producers and consumers across the entire moderate scale than the M1 model. The width of the tolerance interval of the M3 model is greater than the width of the tolerance interval of the M4 model, except in the middle of the scale, in the point
. At this point on the moderate scale, the width of the tolerance interval for both models is equal and amounts to
(
Table 3). Consequently, the global risks of producers and consumers in the M3 model are lower than those in the M4 model (
Figure 5a,b). In these two models, the risk values coincide at the point of minimum,
The iso-risk curves of models M1 and M2, along the moderate scale, exhibit stable behavior with a narrower range of value changes. These models behave differently compared to the M3 and M4 models. In models M3 and M4, the range of variations in producer and consumer risk values is significantly greater. In the case of consumer risk, the iso-risk curves for models M3 and M4 intersect those for models M1 and M2 (
Figure 5a). The same applies to iso-risk curves of producers (
Figure 5b). All models are shown on the same scale for comparison. That is why the iso-risk curves for models M1 and M2 do not have such a prominent parabola shape compared to models M3 and M4.
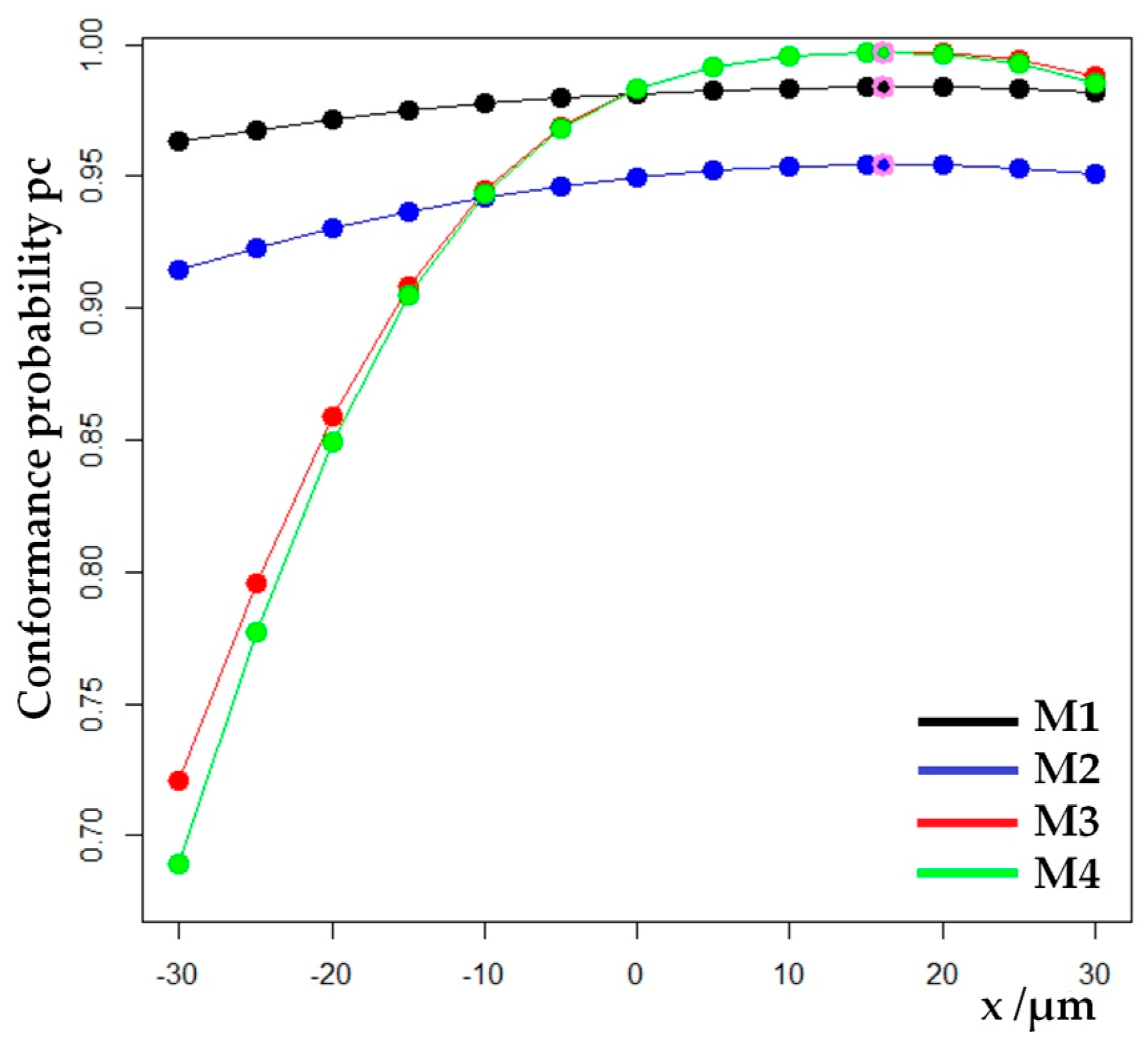
The maximal value for conformance probability is reached precisely at the point
where the global risk of the producer
and the global risk of the consumer
have a minimal value (
Figure 6).
Higher risk values result in lower values for the conformance probability and vice versa. This can be observed when comparing models M1 and M2, i.e., M3 and M4, as well as all models (
Figure 6). Models M3 and M4 have the same value for conformance probability at the point of moderate scale,
Other points of the moderate scale show higher values for conformance probabilities for model M3 than for model M4. The lowest values for conformance probability are found on the left side of the moderate scale for all models. The values for
drop to 72% for the M3 model, or even 69% for the M4 model. Hence, it is possible to conclude that models M3 and M4 attach greater importance to risks at the edges of the scale.
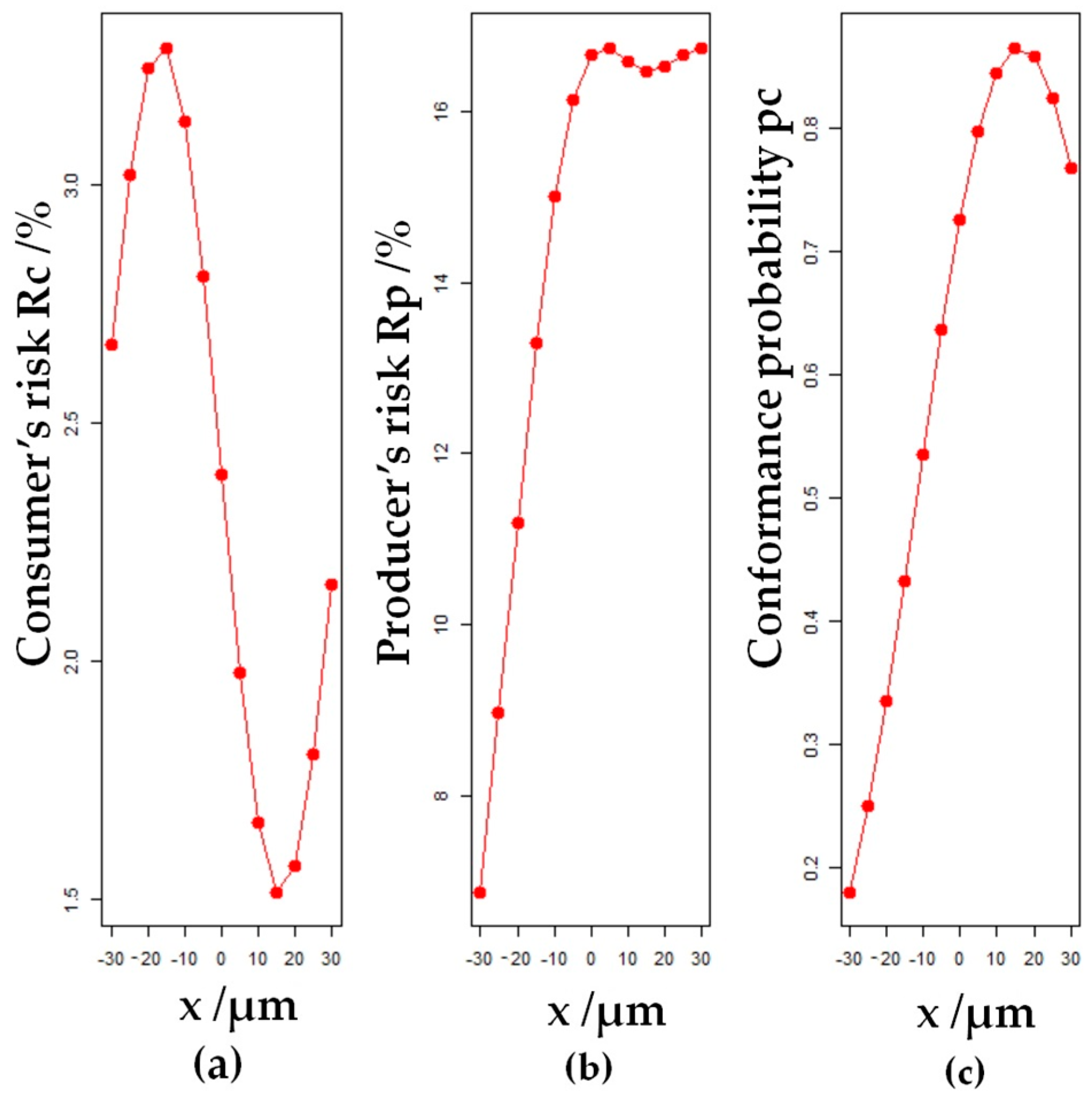
On the graphs of models M3 and M4, which show the behavior of the global risk of the producers, anomalies on the left edge of the scale can be observed (
Figure 5b). Anomalies mean that the iso-risk curves deviate from the parabola graph. At the point of the moderate scale
µm, the global risk of the producer for the M3 model is greater than the global risk of the producer for the M4 model. These anomalies occur when the tolerance interval is too narrow. If the range of the tolerance interval is too narrow, the regression line crosses the acceptance line, or both lines, the acceptance and tolerance line (or acceptance and tolerance curves). In that case, the risk graphs are no longer parabolas (
Figure 7).
Figure 7 illustrates the presence of anomalies, i.e., the deviations of the iso-risk curve from the parabola graph. Such deviations are obtained when, for example, with the M3 model, a too-narrow tolerance interval range of
is set. In that scenario, the regression line intersects the lower acceptance curve
and the lower tolerance curve
. Anomalies may manifest themselves for both the global consumer’s risk and global producer’s risk (
Figure 7a,b). The graph for conformance probability clearly shows that the model behaves badly on the left side of the moderate scale, where the conformance probability falls below 20% (
Figure 7c). The primary drawback of the described method for risk assessment in regression is excessively narrow tolerance interval. It is necessary to expand its span to resolve the issue. To stay within the 6-sigma range used in statistics, a tolerance interval width was set to
in the M3 model. The anomaly is not completely resolved by this. The regression line for
intersects the lower acceptance curve
. The iso-risk curves for the global producer’s risk
diverge from the parabola graph on the left edge of the moderate scale (
Figure 5b). For this reason, the range of tolerance intervals should be further expanded. The deviation from the parabola graph is even more noticeable with the M4 model. With this model, the regression line intersects the lower line of the acceptance interval
already by
In both models, M3 and M4, anomalies occur for the values of the multiplicative factor
which is related to the model of minimization of global consumer’s risk (
Figure 1c). The specified values of the multiplicative factor
were calculated numerically. Also, although the regression line in models M3 and M4 intersects the lower acceptance curve (line)
, it fails to intersect the lower tolerance curve (line)
. For the M2 model, it is sufficient to set
to prevent the regression line from intersecting either the tolerance interval or acceptance interval.
3.1.2. Behaviors of a Global Consumer’s and Producer’s Risk Along the Guard Band Axis
Depending on the multiplicative factor
where
according to equation (24), the guard band
can have a positive or negative value or be equal to zero. If
it is about the model of the minimization of global producer’s risk (
Figure 1a). If
it is a shared risk model (
Figure 1b). For
it is a model for minimizing the global consumer risk (
Figure 1c). It is natural to observe the behavior of the global risk of producers and consumers along the guard band axis. In general, if it is
then for
and
holds that
and
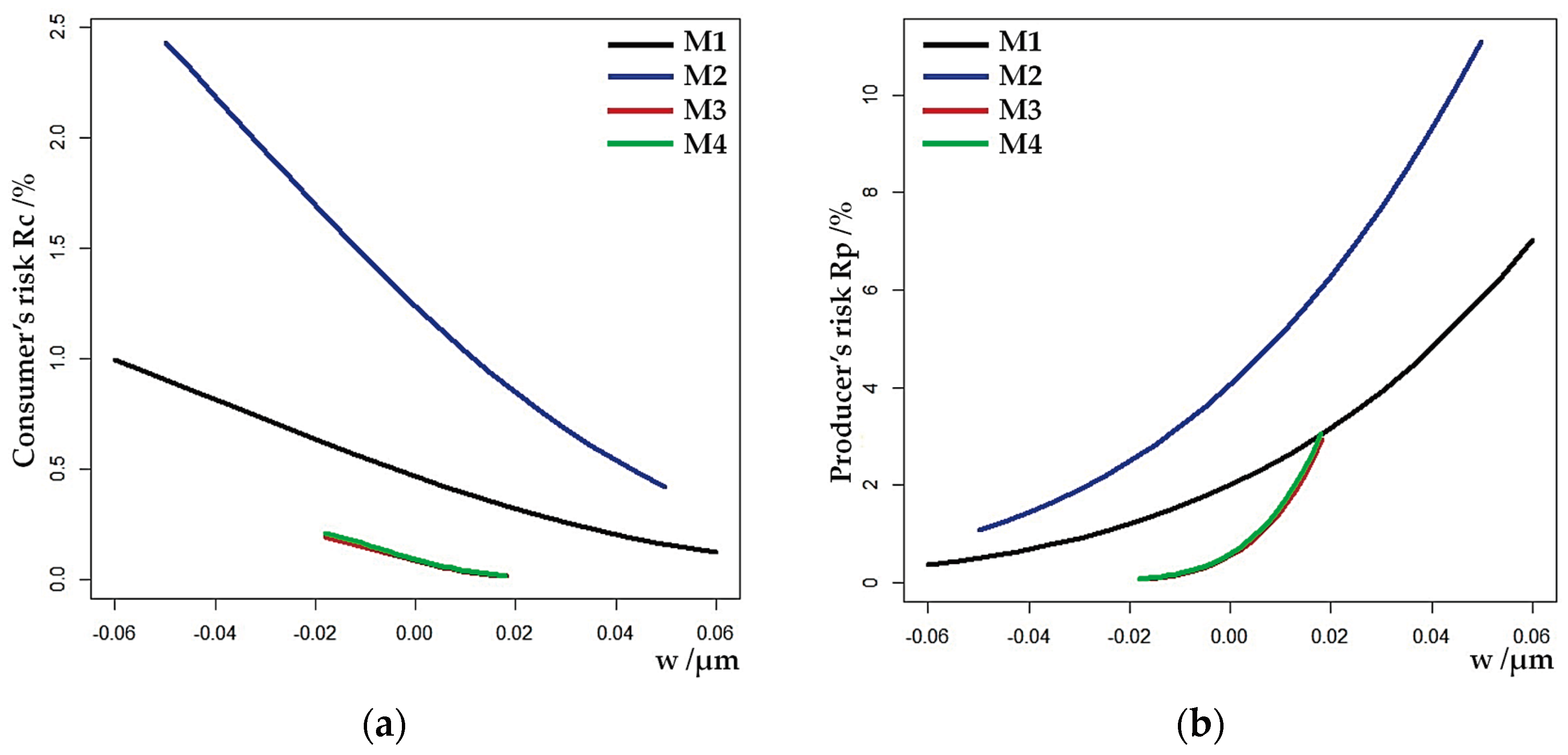
Simplified, the consumer’s risk decreases along the guard band axis as depicted in
Figure 8a, whereas the producer’s risk increases along the guard band axis as depicted in
Figure 8b.
Figure 8 shows the curves of the minimum of the global producer’s and consumer’s risk calculated numerically along the guard band axis at points
. These are the curves where the risks, for each model are the least. Due to the described construction of acceptance and tolerance intervals, risks are assessed for intervals of varying lengths along the guard band axis. The values of measurement uncertainties calculated using LRA,
are considerably smaller in comparison with
It is therefore pointless to compare all models for the same tolerance interval
µm given by the manufacturer. For the measurement uncertainty
the tolerance interval selected in this manner will be too wide, resulting in negligible risk values
and
for models M3 and M4, while the conformance probability will be equal to one. The M4 model’s curve of minimum for global producer’s risk intersects the curve of minimum of the M1 model (
Figure 8b).
The conformance probability for the curve of minimum in each model is determined by the straight line along the guard band axis. These values remain the same for all points For models M1, M2, M3 and M4 respectively worth: , and .
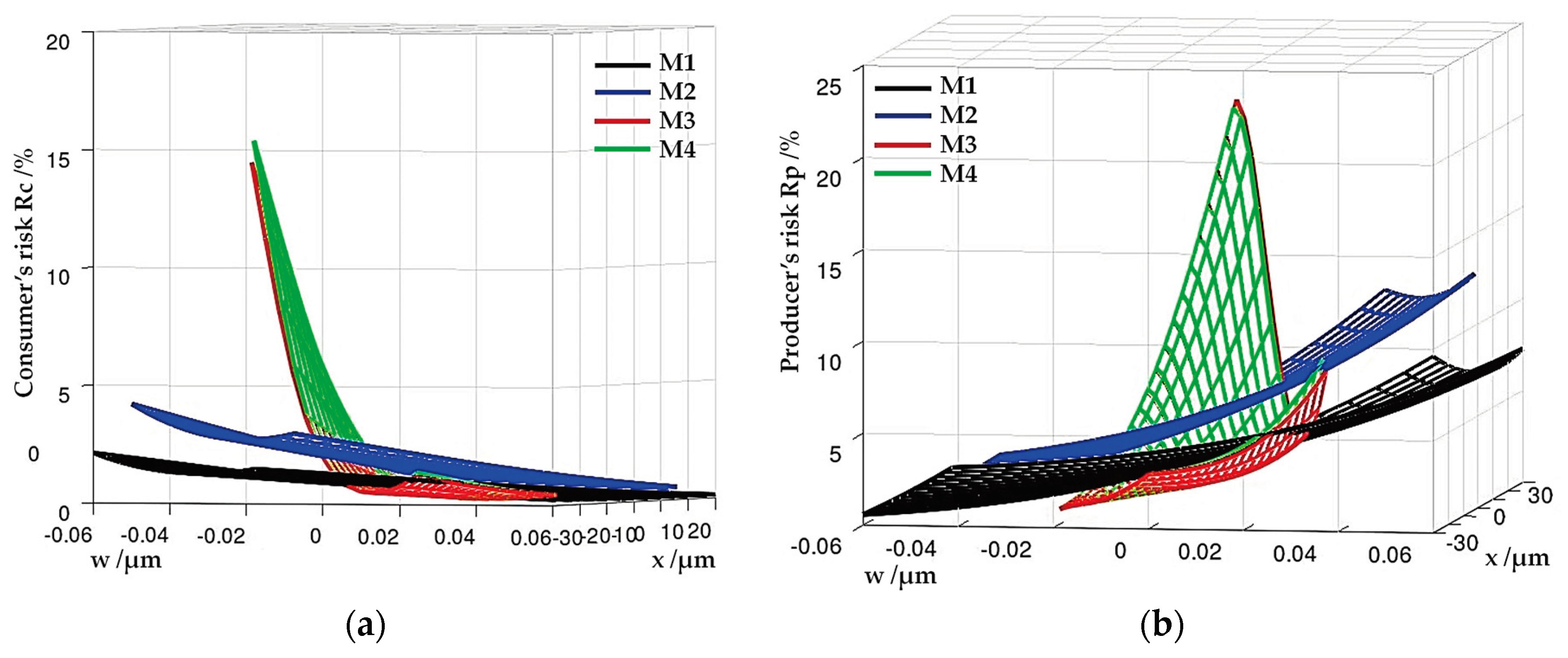
The described behavior of the global producer’s risk
and the global consumer’s risk
along the moderate scale and the guard band axis can be easily noticed by observing the risk surfaces shown in
Figure 9. From the picture, it is evident that there are areas where the global risk of the producer and the global risk of the consumer of models M3 and M4 are lower than the risk of the models M1 and M2.
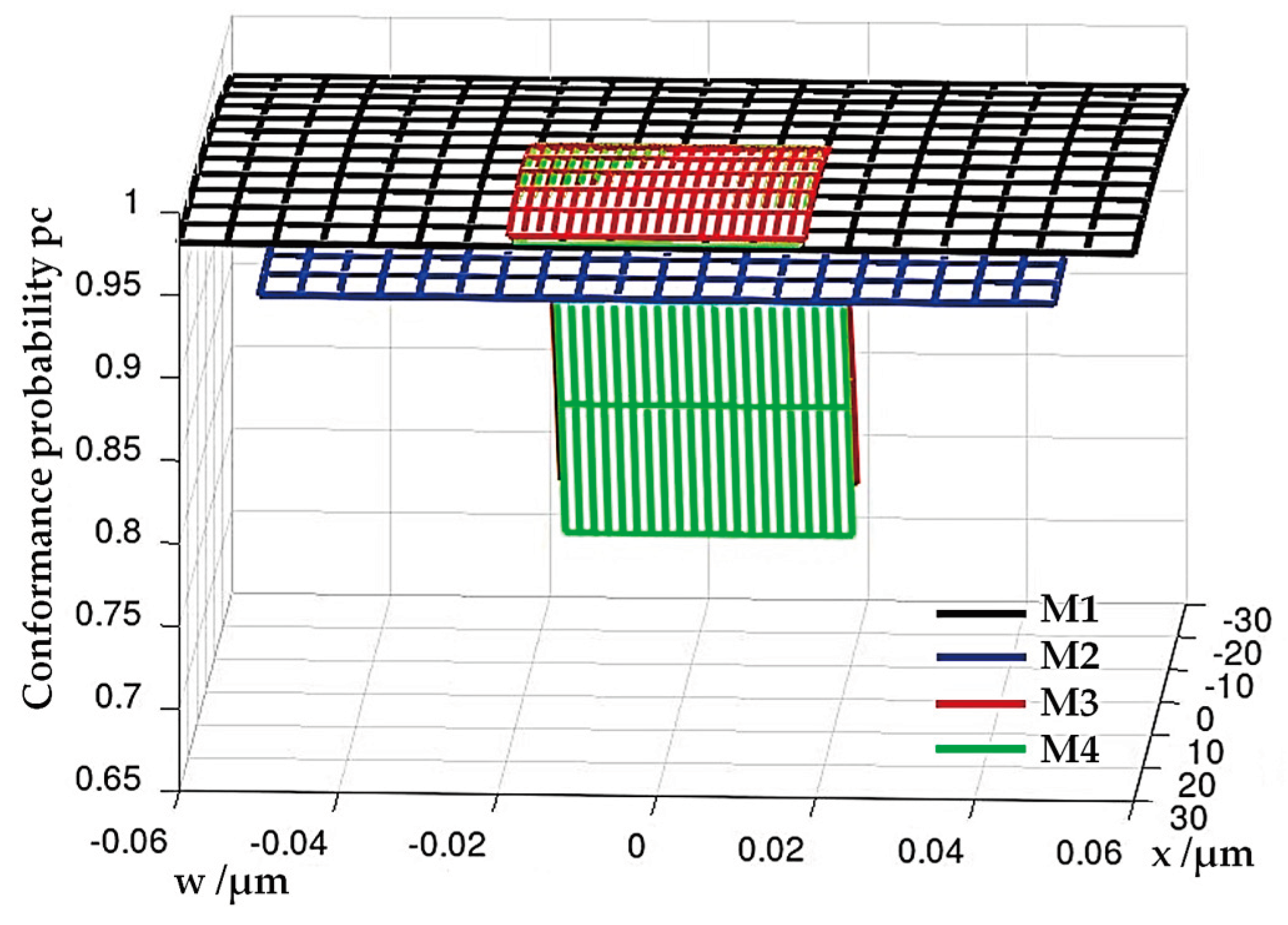
The conformance probability curves along the moderate scale are as in
Figure 6, but the conformance probability surfaces were evaluated for intervals of different ranges along the guard band scale (
Figure 10).
3.1.3. Behaviour of a Global Consumer’s and Producer’s Risk with the Changes of Measurement Uncertainty of a Future Inspection Process
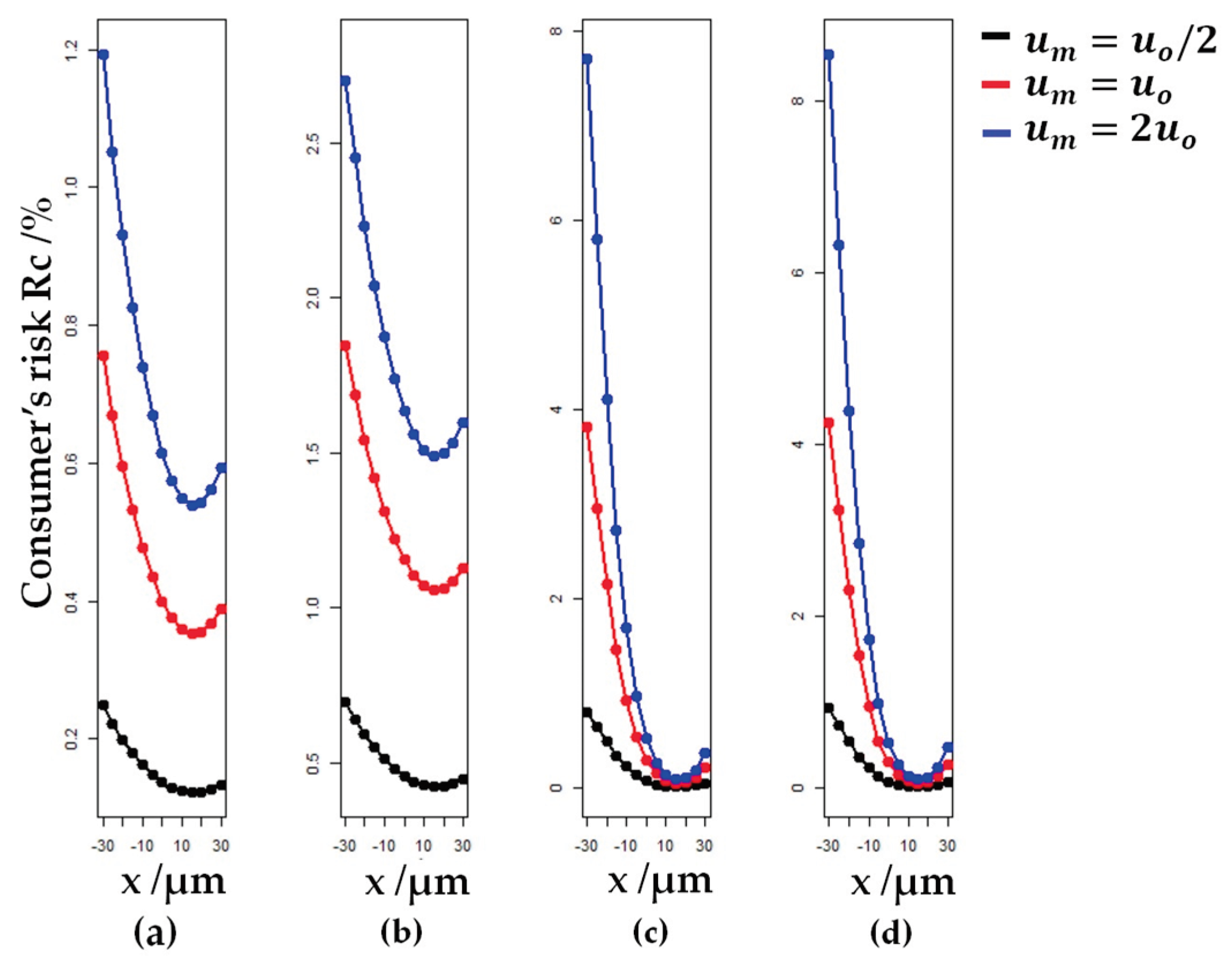
The behavior of the global producer’s risk and the global consumer’s risk across all models were tested for three different assumed values of measurement uncertainty of a futured inspection process: for and for
With the increase in measurement uncertainty
, the global consumer’s risk
also increase (
Figure 11).
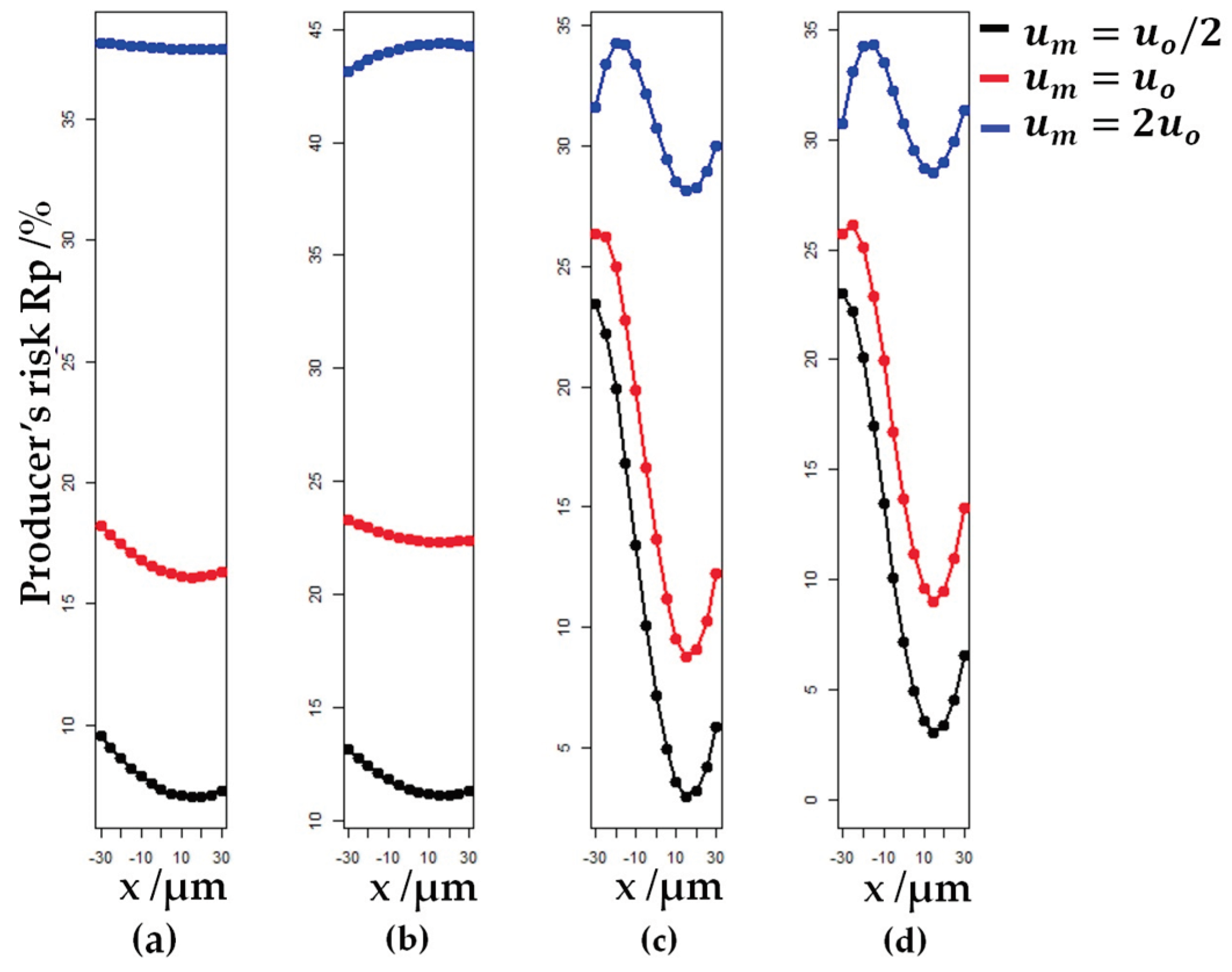
Additionally, with the increase in measurement uncertainty value
, the producer’s risk also rises
(
Figure 12).
It is evident that, in addition to the range of the tolerance interval to the occurrence of anomalies in the behavior of the global producer’s risk
, measurement uncertainty
also has an impact. Deviation from the parabolic curve becomes more pronounced, (
Figure 12c,d). Graphs can completely alter their behavior, as is the case in model M2. When it is worth that
, the graph of the global producer’s risk
is a parabola with a downward opening (
Figure 12b). For
the regression line is not outside the tolerance interval or the acceptance interval, in none of the mentioned case. To avoid anomalies in the behavior of the risk curves for
, it is necessary to expand the ranges of tolerance intervals. For model M2, this range should be set to at least
, for model M3 to
and for model M4 to
. This prevents anomalies in the graphs for all values of
.
According to equation (33), the expression for conformance probability
is independent of the measurement uncertainty
of a future inspection process. Therefore, the graphs for conformance probability for all tested values of measurement uncertainty
are as shown in
Figure 6, and for the 3D case, as shown in
Figure 10.
3.2. Comparison of Models by Root Mean Squared Error
There are lots of evaluation metrics for regression [
61,
62]. The most common are the mean squared error (MSE) and the root of the mean squared error (RMSE). RMSE is a more suitable statistical indicator compared to MSE because it is measured in the same units as the targeted variable, which allows for easier interpretation and comparison of models [
63]. RMSE values range from zero to infinity. The lower RMSE values, closer to zero, indicate better model performance [
64]. This metric is sensitive to large deviations of the measured values from the reference values [
65].
The comparison of risk models using the RMSE metric was conducted both graphically and quantitatively. The targeted variables in the model comparison are global producer’s and consumer’s risk and conformance probability. Comparisons were conducted for each point on the moderate scale
and for all measurements
. If
denotes the global consumer’s risk, calculated for each realization of the sample
, then the RMSE for the global consumer’s risk, for a chosen fixed value
can be calculated according to the following equation:
Analogously, by introducing the notations
and
, can be obtained the expressions for the RMSE of the individual measurements
for the global producer’s risk and conformance probability, respectively. These metrics quantify the deviation of the calculated risk for each measurement point from the fitted risk surfaces shown in
Figure 9, or from the fitted surfaces for conformance probability shown in
Figure 10.
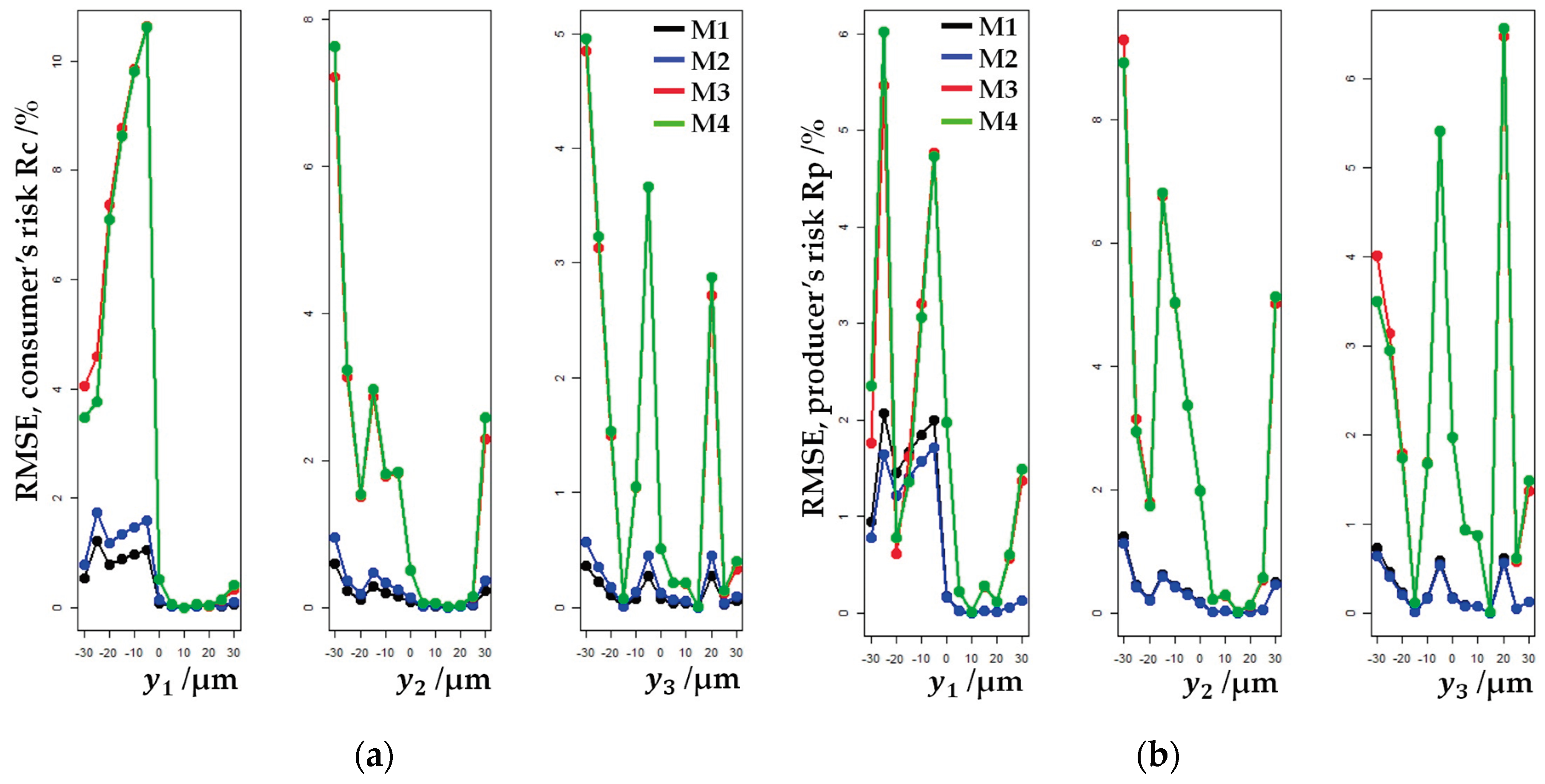
The RMSE metric exhibits higher values for those points on the moderate scale for which the deviation of measured values is greater relative to the scale values (
Figure 13).
The calculated RMSE values indicate that the models M3 and M4 better detect deviations of the risks, calculated for the points of the moderate scale, from the risk surfaces. This is particularly true for the sample realization
on the negative part of the scale (
Table 1). All the points on the moderate scale, for models M1 and M2, for each measurement
and each value of
falls within the tolerance interval and acceptance interval. The same holds for all models, for measurements
, and for each value of
. For model M3, the value
µm is already outside the tolerance interval and acceptance interval for
. As consequences, there is a higher producer’s and consumer’s risk for the mentioned measurement, and ultimately, higher RMSE values for that measurement. For
, all other values of the negative portion of the moderate scale
, are outside the tolerance interval, that is, between the tolerance interval and the acceptance interval. From
to
, all 6 measurements on the negative part of the moderate scale from sample
are outside the tolerance interval and outside the acceptance interval. In the model M4, all points in the negative portion of the moderate scale are located outside the tolerance and the acceptance intervals, for
to
.
Analogously, the RMSE values for conformance probability are higher in points where the measured values significantly diverge from the values of the moderate scale, in contrast to measurements with minor deviations from the moderate scale (
Figure S2).
The total value of the RMSE for each model
for the consumer’s risk, calculated for each measurement
is denoted as
and obtained from the equation:
Expressions for the total value of RMSE for the global producer’s risk and conformance probability are denoted as
and
, respectively. The values of these quantities are calculated analogously to the equation (37).
Each measurement
contributes to the determination of the parameters of the regression line and the determination of the risk surfaces and surfaces for conformance probability [
46], [
47] (pp. 76-78). Therefore, the total RMSE value for global consumer’s risk was additionally calculated for each model. This value is labeled as
, and was calculated according to the following equation:
The total value of RMSE for the global producer’s risk,
, and the total value of RMSE for conformance probability,
are obtained in the same manner as in equation (38). The results of the quantitative analysis for all models, considering all defined values for RMSE given in equations (36-38), are presented in
Table 4.
Quantitative analysis reveals that models M3 and M4 are better detecting deviations from measured values from values on a moderate scale. Consequently, all RMSE values for these models are higher compared to models M1 and M2. For all individual measurements , it holds that , which is understandable given that model M1 has a broader tolerance interval compared to model M2. Furthermore, for RMSE values associated with the producer’s risk, it holds that for all measurements . When comparing models M3 and M4, it is evident that for the first sample realization , wherein significant deviations of measured values from reference values were observed in the negative part of the moderate scale, the RMSE values indicate that and For measurements and , the reverse inequalities hold true. Additionally, it can be observed that for sample realization , the RMSE values and are significantly higher compared to the values for measurements and . Despite having a broader tolerance interval across almost all points on the moderate scale, model M3 exhibits higher RMSE values for , , and . For all measurements , it holds that , and likewise
3.3. Comparison of Models Using Metrics Related to the Confusion Matrix
Recent studies have shown that risk assessment models can be compared using metrics relates to the confusion matrix [
18,
34]. Expressions for evaluating the global risk of producers and consumers from equations (29) and (32) are a kind of classifier that sorts measurements as falsely rejected (FR) and falsely accepted (FA), so that
and
. Considering that the measurements that are within the tolerance interval and the acceptance interval were defined as true positive (TP) and that the measurements that are outside the acceptance interval and tolerance interval were defined as true negative (TN), it is feasible to construct a confusion matrix [
18]. For the confusion matrix constructed in this way, it is especially true that
=1. In addition, it holds that
and that
[
18]. For a well-performed measurement, it is always the case that
i.e., it is about imbalanced data [
66]. Since in the measurements there is always exist a measurement uncertainty, in practice it is assumed that the risks
and
are always present and that their values differ from zero. Theoretically, in metrology, these values can be equal to zero, but not simultaneously.
The models outlined in the article can be evaluated by utilizing any of the commonly recognized metrics: accuracy, precision, recall, F1 score, Matthew’s correlation coefficient (MCC), Cohen’s Kappa, etc. [
67,
68]. A comparison of models by using metrics associated with confusion matrices was conducted for the area enclosed by the moderate scale and guard band axes.
In this article, the F1 score and diagnostic odds ratio (DOR) were chosen for model comparison. The F1 score is the harmonic mean of precision and recall. According to [
18] in the metrological sense, it can be written in the form:
This metric is conveniently used in binary classification when it is necessary to recognize and classify a specific class of confusion matrix [
69]. Here it is the TP class. Standard values of the F1 score range from
. In the metrological sense, the values 0 and 1 should be excluded. If the value of the F1 score were to be zero, it would be true that
thereby indicating there is no TP measurement. Also, if the value of the F1 score were to be one, it would mean that
, which is impossible because of measurement uncertainty. This is the rationale behind why the values of the F1 score, in the realm of metrology, ought to be within the interval
. The model’s performances are better for the values of the F1 score that are closer to the one. Furthermore, the curves of the F1 score along the guard band axis pass through the intersection of the precision and recall curves. That characteristic intersection point is obtained for that value of the guard band for which
[
18]. The lengths of the acceptance intervals are chosen precisely so that the intersection of the risk surfaces will be visible on the graphs (
Figures S3–S6). Like the risk surfaces, the F1 score surfaces for models M1 and M2 behave differently compared to models M3 and M4 (
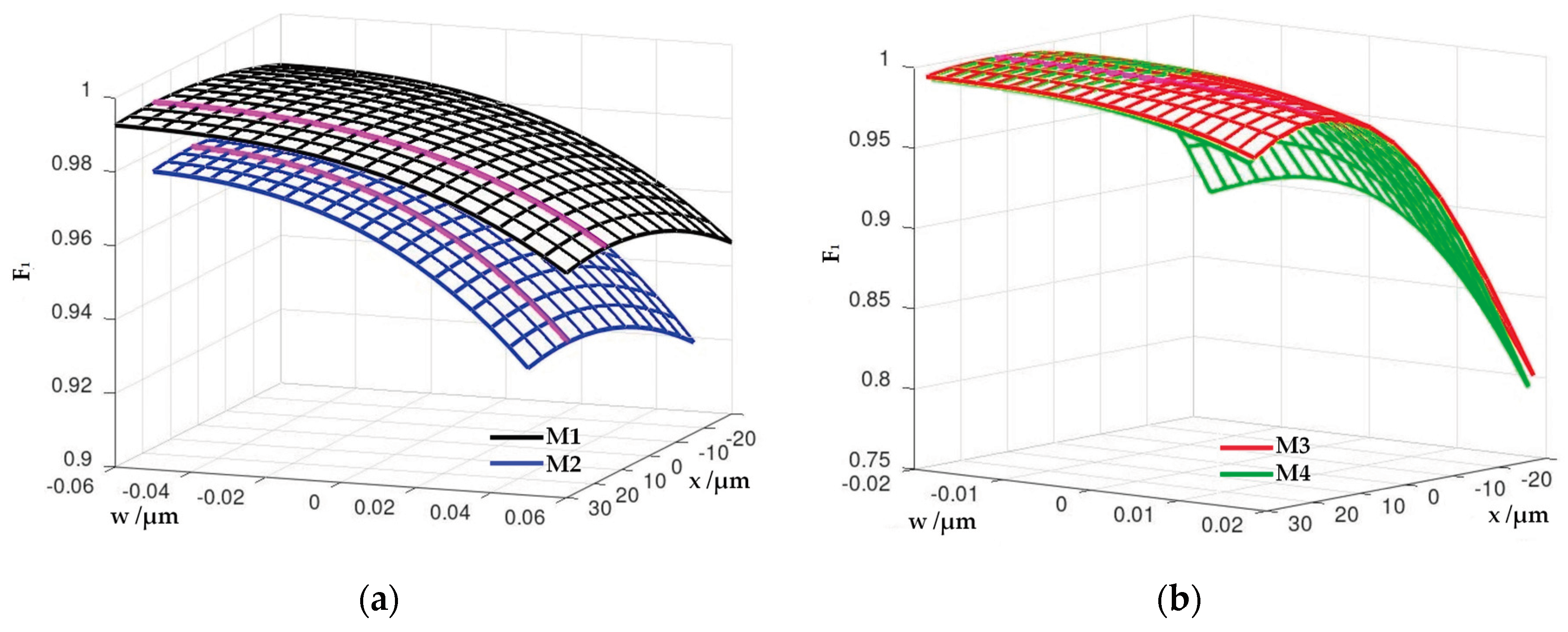
Figure 14).
For models M1 and M2, the F1 score decreases along the guard band axis. In contrast, the F1 score curves of models M3 and M4, along the moderate scale, have the maximum values at the points By using F1 score, it can be seen that models M3 and M4 better detect deviations of the measured values from the reference values of the moderate scale on the edge portions of the guard band axis. For all models, the maximal values of the F1 score along the guard band axis are found at points .
The comparison of risk assessment models was additionally performed using the DOR metric. DOR is the ratio of the probability of true positive measurements among falsely rejected measurements and the probability of falsely accepted measurements among true negative measurements [
70]. It can be calculated from the following equation written in metrology terms:
Standard values for the DOR are in the range
If the value for DOR were equal to zero, it would mean that
, that is, that
. This would mean that the measurement disastrously was carried out. Therefore, in the metrological sense, the values of DOR must be in the interval
Models that possess DOR values exceeding one are more effective in detecting probabilities of TP measurements among FR measurements [
71]. The minimal value of DOR along the guard band axis is achieved for the shared risk model when the length of the guard band is
. The highest values for DOR are achieved for the low rate of the global consumer’s and producer’s risk [
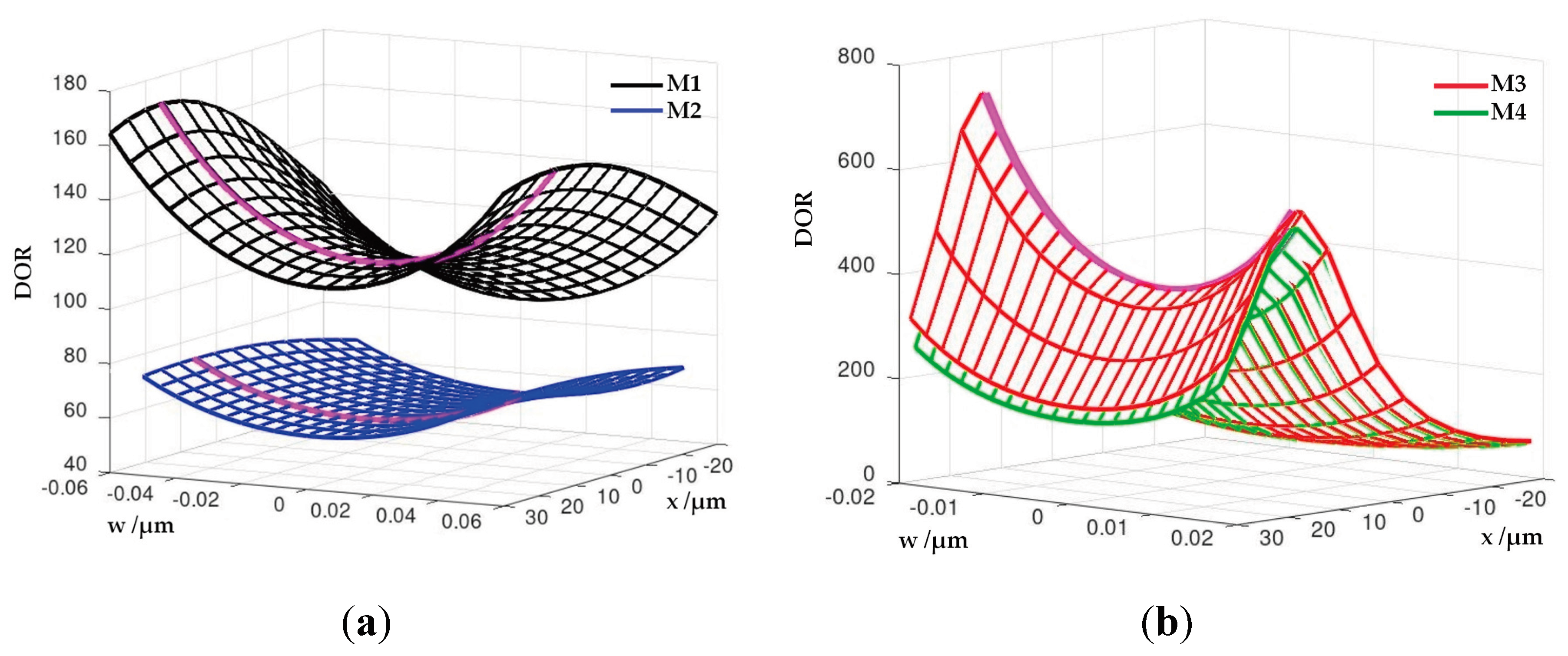
72]. Therefore, this metric is deemed suitable for identifying the line located in the plane that is enclosed by the moderate scale and by guard band axis, along which the risks are the smallest. As can be seen from
Figure 15a,b, the curve that indicates the maximum values for the DOR is situated just above the line that traverses the points
. DOR for M3 and M4 models detects this curve extremely well (
Figure 15b).
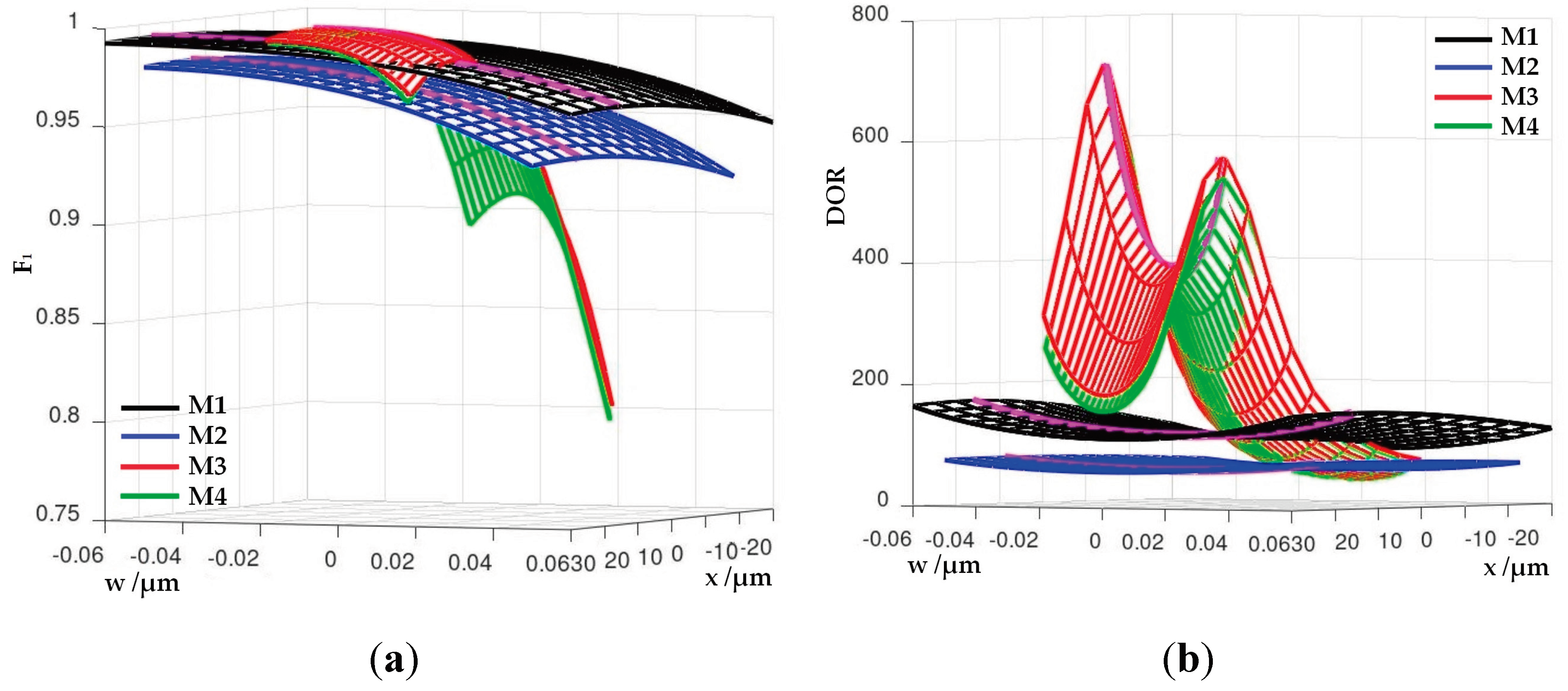
Similarly to the surfaces of the risks (
Figure 9), there is an area where the F1 score of the models M3 and M4 has a higher value than the F1 score of the models M1 and M2 (
Figure 16a). Analogously, there is an area where the DOR of models M3 and M4 has lower values compared to models M1 and M2 (
Figure 16b).
Figure 1.
Interrelationships of tolerance interval and acceptance interval: (
a) Minimizing producer risk; (
b) Shared risk; (
c) Minimizing consumer risk [
26].
Figure 1.
Interrelationships of tolerance interval and acceptance interval: (
a) Minimizing producer risk; (
b) Shared risk; (
c) Minimizing consumer risk [
26].
Figure 2.
Minimization of consumer risk: (a) Centered model; (b) Non-centered model.
Figure 2.
Minimization of consumer risk: (a) Centered model; (b) Non-centered model.
Figure 3.
The measurement uncertainty of the fitted regression line, according to the law of propagation of uncertainties.
Figure 3.
The measurement uncertainty of the fitted regression line, according to the law of propagation of uncertainties.
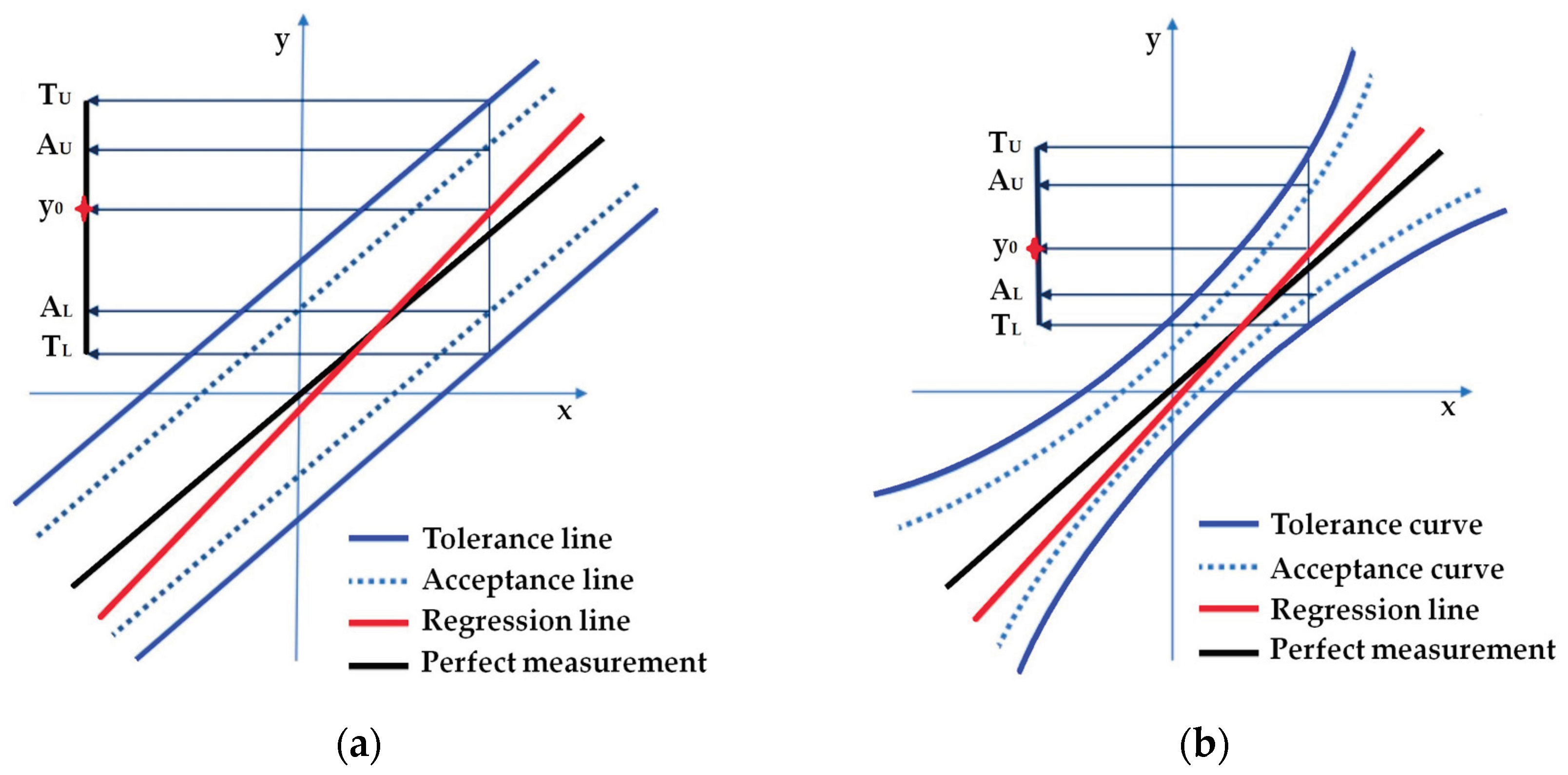
Figure 4.
Spatial extension of the risk assessment model in the case of consumer risk minimization: (a) Linearized model; (b) Non-linearized model.
Figure 4.
Spatial extension of the risk assessment model in the case of consumer risk minimization: (a) Linearized model; (b) Non-linearized model.
Figure 5.
Comparison of behavior of consumer’s risk and producer’s risk, along the moderate scale for all four models, : (a) Consumer’s risk; (b) Producer’s risk. A violet circle indicates the point of minimum for the risks and .
Figure 5.
Comparison of behavior of consumer’s risk and producer’s risk, along the moderate scale for all four models, : (a) Consumer’s risk; (b) Producer’s risk. A violet circle indicates the point of minimum for the risks and .
Figure 6.
Comparison of behavior of conformance probability along the moderate scale for all four models, . A violet circle indicates the point of maximum for conformance probability .
Figure 6.
Comparison of behavior of conformance probability along the moderate scale for all four models, . A violet circle indicates the point of maximum for conformance probability .
Figure 7.
An example of anomalies in the behavior of global consumer’s and producer’s risks along the moderate scale for the case of , , : (a) Consumer’s risk; (b) Producer’s risk; (c) Conformance probability.
Figure 7.
An example of anomalies in the behavior of global consumer’s and producer’s risks along the moderate scale for the case of , , : (a) Consumer’s risk; (b) Producer’s risk; (c) Conformance probability.
Figure 8.
Curves of a minimum of the global risk of consumers and producers evaluated along the guard band axis at points , , ; (a) Consumer’s risk; (b) Producer’s risk.
Figure 8.
Curves of a minimum of the global risk of consumers and producers evaluated along the guard band axis at points , , ; (a) Consumer’s risk; (b) Producer’s risk.
Figure 9.
Risk surfaces; (a) Consumer’s risk; (b) Producer’s risk.
Figure 9.
Risk surfaces; (a) Consumer’s risk; (b) Producer’s risk.
Figure 10.
Conformance probability surfaces.
Figure 10.
Conformance probability surfaces.
Figure 11.
Behaviors of a global consumer’s risk along the moderate scale with the changes of measurement uncertainty , : (a) Model M1; (b) Model M2; (c) Model M3; (d) Model M4.
Figure 11.
Behaviors of a global consumer’s risk along the moderate scale with the changes of measurement uncertainty , : (a) Model M1; (b) Model M2; (c) Model M3; (d) Model M4.
Figure 12.
Behaviors of a global producer’s risk along the moderate scale with the changes of measurement uncertainty , : (a) Model M1; (b) Model M2; (c) Model M3; (d) Model M4.
Figure 12.
Behaviors of a global producer’s risk along the moderate scale with the changes of measurement uncertainty , : (a) Model M1; (b) Model M2; (c) Model M3; (d) Model M4.
Figure 13.
The comparison of the RMSE values of each individual model, calculated in the values of the moderate scale , for each sample realization : (a) Consumer’s risk; (b) Producer’s risk.
Figure 13.
The comparison of the RMSE values of each individual model, calculated in the values of the moderate scale , for each sample realization : (a) Consumer’s risk; (b) Producer’s risk.
Figure 14.
Comparison of risk models using F1 score: (a) F1 score for models M1 and M2; (b) F1 score for models M3 and M4. The curve of maximums along the guard band axis for all models is marked in pink.
Figure 14.
Comparison of risk models using F1 score: (a) F1 score for models M1 and M2; (b) F1 score for models M3 and M4. The curve of maximums along the guard band axis for all models is marked in pink.
Figure 15.
Comparison of the risk models using DOR: (a) DOR surfaces for models M1 and M2; (b) DOR surfaces for models M3 and M4. The curve of maximums for all models is marked in pink.
Figure 15.
Comparison of the risk models using DOR: (a) DOR surfaces for models M1 and M2; (b) DOR surfaces for models M3 and M4. The curve of maximums for all models is marked in pink.
Figure 16.
Comparison of models using F1 score and DOR surfaces. (a) F1 score; (b) DOR. The curve of maximums for all models is marked in pink.
Figure 16.
Comparison of models using F1 score and DOR surfaces. (a) F1 score; (b) DOR. The curve of maximums for all models is marked in pink.
Table 1.
Calibration of probes in the measuring range of
µm [
44].
Table 1.
Calibration of probes in the measuring range of
µm [
44].
| Reference value x / µm |
1st measurement y1 / µm |
2nd measurement y2 / µm |
3rd measurement y3 /µm |
| −30 |
−30.10 |
−30.02 |
−30.05 |
| −25 |
−25.12 |
−25.05 |
−25.05 |
| −20 |
−20.10 |
−20.05 |
−20.05 |
| −15 |
−15.10 |
−15.00 |
−15.05 |
| −10 |
−10.10 |
−10.00 |
−10.05 |
| −5 |
−5.10 |
−5.05 |
−5.06 |
| 0 |
0.00 |
0.00 |
0.00 |
| 5 |
4.98 |
4.98 |
5.00 |
| 10 |
9.99 |
10.00 |
10.02 |
| 15 |
14.99 |
15.00 |
15.00 |
| 20 |
20.00 |
20.00 |
20.05 |
| 25 |
25.00 |
25.02 |
25.00 |
| 30 |
30.00 |
30.05 |
30.00 |
Table 2.
Uncertainty budget for probe in the measuring range
µm [
44].
Table 2.
Uncertainty budget for probe in the measuring range
µm [
44].
|
Probability distribution |
Standard uncertainty / µm |
| ULM device |
Normal |
0.1 |
| Linear error of the probe I |
Rectangular |
0.000184462 |
| Linear error of the dial probe II |
Rectangular |
0.065909762 |
| Resolution |
Rectangular |
0.034641016 |
| Combined measurement uncertainty of the probe |
0.1247 |
Table 3.
Overview of model properties.
Table 3.
Overview of model properties.
| Model |
Uncertainty |
Tolerance interval |
M1
Linearized model |
|
µm |
M2
Linearized model |
|
|
M3
Non-linearized model |
|
|
M4
Linearized model |
|
|
Table 4.
RMSE values for global consumer’s and producer’s risk and conformance probability, by models and sample realization and in total.
Table 4.
RMSE values for global consumer’s and producer’s risk and conformance probability, by models and sample realization and in total.
| RMSE, global consumer’s risk |
|
/ µm
|
/%
|
/%
|
/%
|
/%
|
|
0.63 |
0.94 |
5.40 |
5.27 |
|
0.22 |
0.35 |
2.55 |
2.68 |
|
0.17 |
0.27 |
2.11 |
2.16 |
|
0.40 |
0.60 |
3.66 |
3.63 |
| RMSE, global producer’s risk |
|
/ µm
|
/%
|
/%
|
/%
|
/%
|
|
1.16 |
0.97 |
2.40 |
2.52 |
|
0.46 |
0.42 |
4.03 |
3.97 |
|
0.35 |
0.32 |
2.92 |
2.87 |
|
0.75 |
0.64 |
3.19 |
3.18 |
| RMSE, conformance probability |
|
/ µm
|
|
|
|
|
|
0.022 |
0.039 |
0.356 |
0.358 |
|
0.007 |
0.014 |
0.092 |
0.100 |
|
0.005 |
0.010 |
0.078 |
0.083 |
|
0.013 |
0.025 |
0.217 |
0.220 |