Prerpints.org logo
Preprint
Review

Navigating the Depths: A Comprehensive Review of Numerical Groundwater Models – Objectives, Advantages & Challenges

Altmetrics

Downloads

240

Views

151

Comments

0

Submitted:

16 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts
Abstract
The Earth's fresh water resources predominantly is groundwater that is pumped out due to rapid urbanization and aggravated by climate change. Groundwater modeling is a crucial tool for understanding aquifer systems, employing 1D, 2D, and 3D numerical models with distinct applications. One-dimensional models focus on vertical dynamics, examining aquifer properties and simulating vertical contaminant transport. Two-dimensional models extend to regional scales, considering horizontal variations and assessing groundwater-surface water interactions, making them valuable for watershed-scale studies. Three-dimensional models provide a comprehensive representation of hydrogeological systems, capturing intricate flow patterns and aiding site-specific assessments. Comparative analysis reveals model strengths and limitations, emphasizing the importance of calibration for reliable results. Case studies showcase practical applications, such as 1D models in flooding analysis and 2D models for simulating debris flows. Three-dimensional modeling proves essential for understanding complex river-aquifer exchange fluxes. Future directions call for a global groundwater platform to address data variability and technical challenges. Despite substantial investments required, the anticipated returns in scientific advancements, societal benefits, and economic gains are expected to outweigh the initial costs. This review aims in highlighting the significance of advancing all three-dimension groundwater modeling for sustainable water resource management and environmental protection.
Keywords: 
Subject: Environmental and Earth Sciences  -   Environmental Science

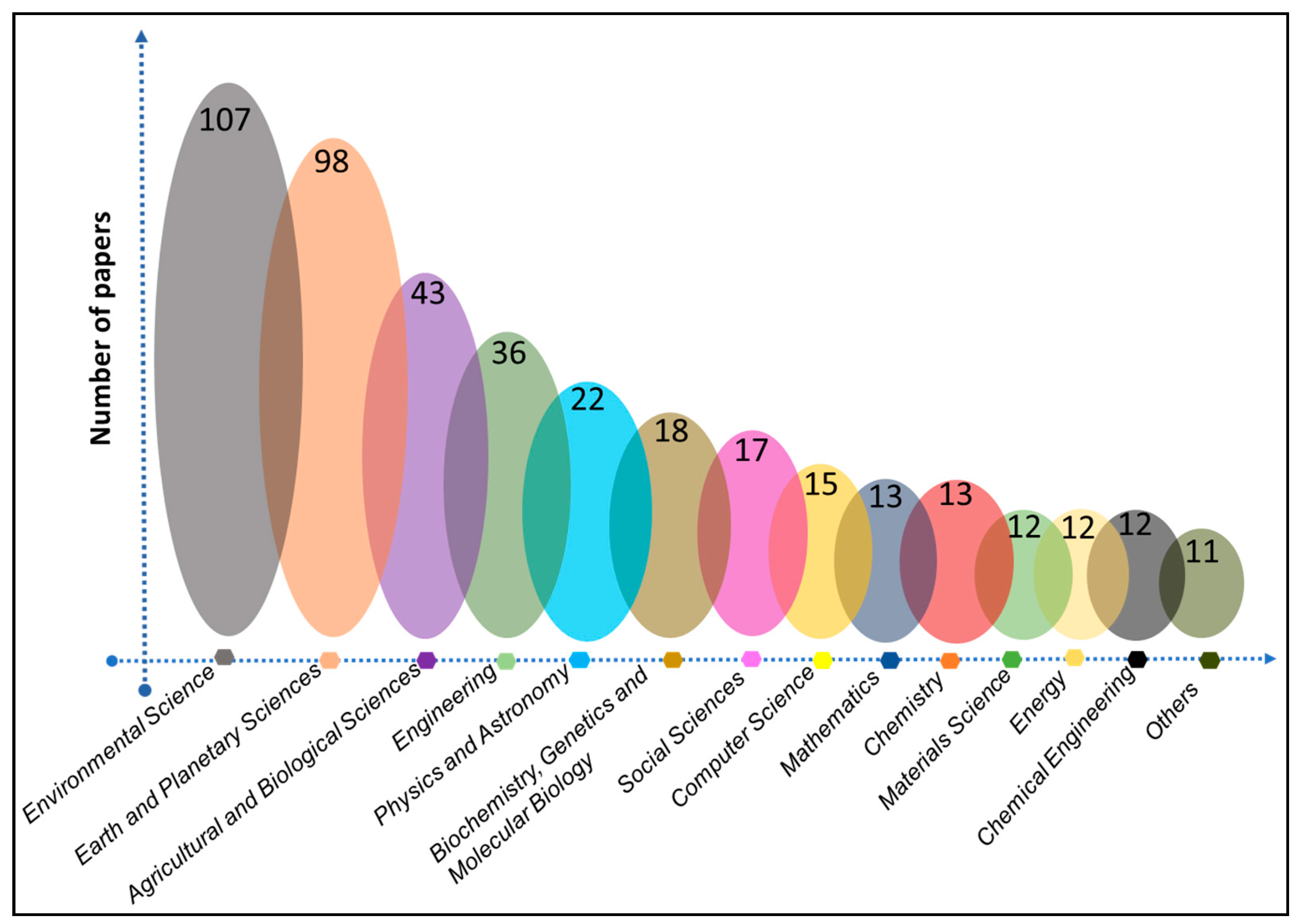
1. Background

A model serves as a representation of a physical system, aiming to forecast its behavior over time. Models can take the form of conceptual, physical, or mathematical representations. Conceptual models depict a system using general rules and concepts, while physical models are scaled-down replicas of the actual system. Mathematical models represent a system using mathematical concepts and language, categorized as analytical or numerical[1]. Analytical models offer closed-form solutions expressed as mathematical analytic functions, requiring minimal data but suitable for simple problems. In contrast, numerical models utilize a numerical time-stepping procedure to comprehend a model's behavior over time, making them more applicable for complex issues. Groundwater modeling involves replicating the behavior of an aquifer system through controlled physical or mathematical means[2,3]. This tool is designed to assist hydrogeologists as well as civil engineers in gaining a comprehensive understanding of groundwater systems, as well as in their development, management, and protection. The groundwater algorithms present a simplified representation of complicated aquifer systems, offering valuable information with a reasonable degree of confidence [4,5,6]. Groundwater modelers seek a systematic understanding of the groundwater system, incorporating field investigations and data collection on water levels, aquifer thickness, recharge and discharge rates, and aquifer parameters. These variables, along with factors such as limits, initial circumstances, and time-space differentiation, are incorporated into the model to generate both quantitative evidence and qualitative information within a predictive framework. Recent years have seen a discernible increase in research activity in this sector, as Figure 1 illustrates. To evaluate the effectiveness of the suggested models, more research in a variety of geographic areas is still required.
Various methods exist for groundwater modeling, with the "finite difference" and "finite element" methods being the most commonly used numerical approaches, each with its own advantages and disadvantages [7,8]. Groundwater modeling is crucial for sustainable groundwater resource management, aiding decisions on development programs concerning both quality and quantity. Groundwater models serve multiple purposes, acting as interpretive tools for analyzing flow patterns and contaminant transport, predictive tools for forecasting future changes, generic tools for evaluating groundwater dynamics and development scenarios, visualizing tools for communication, investigating the impact of well abstraction, understanding contaminant pathways, modeling sea water intrusion, and analyzing management programs' effects on groundwater systems, both quantitatively and qualitatively[9,10,11,12,13].
The primary objective of groundwater modeling is to replicate the flow of groundwater and the transport of pollutants within it. Flow models focus on quantities, aiming to determine the solution for h = f(x, y, z, t), where h represents groundwater head and x, y, z, and t denote spatial and temporal coordinates. On contrary, transport models address the quality of groundwater, seeking the solution for c = f(x, y, z, t), where c represents the concentration of pollutants[2,14]. Flow models are essential for interpreting observed heads, comprehending the response of a groundwater system to various recharge and discharge factors, anticipating decline, estimating water-based balances, and determining the catchment regions of wells. These models play an essential part in offering a useful understanding of the shifting patterns of groundwater circulation. In contrast, transport models are specifically designed for interpreting concentration data, conducting mass balances of contaminants, predicting the spread of pollutant plumes, designing pump and treat management strategies, planning monitoring approaches, and assessing risks associated with waste disposal [15,16]. These models are essential tools for evaluating the movement and impact of pollutants within groundwater systems, contributing to effective environmental management and decision-making [17,18]. Hence, a comprehensive understanding of general aspects related to groundwater flow and transport models is indispensable for their accurate application, reliable interpretation of results, and effective contribution to decision-making processes in various fields, including hydrogeology, environmental science, and water resource management.

2. Scope of groundwater numerical models (1D, 2D & 3D)

2.1. D Groundwater Numerical Models: Understanding Vertical Dynamics

Numerical groundwater models have become an indispensable tool for understanding and managing underground water resources. The scope of these models, ranging from 1D to 3D representations, provides a comprehensive approach to simulating complex hydrogeologic processes. In the area of 1D models, which focus primarily on vertical flow dynamics, researchers have explored their utility in analyzing aquifer properties such as hydraulic conductivity and porosity, as well as in simulating vertical contaminant transport phenomena [19]. These models provide valuable insight into groundwater flow behavior in vertical columns and aid in decision making for well placement and groundwater remediation strategies.

2.2. D Groundwater Numerical Models: Assessing Horizontal Variations

Numerical 2D groundwater models go beyond vertical dynamics and also include horizontal variations in hydraulic properties and boundary conditions. These models, which are widely used in groundwater studies at the regional scale, provide a more realistic representation of subsurface heterogeneity and flow paths [20,21]. By simulating interactions between aquifers, rivers and surface waters, 2D models facilitate the assessment of groundwater-surface water connections and the effect of land-use change on groundwater resources [22,23]. In addition, advances in computing technology have improved the efficiency and accuracy of 2D simulations, making them indispensable for sustainable groundwater management and this model pertain to a vertical plane, with an assumption that groundwater conditions repeat across parallel vertical planes. Examples of such models include spacing equations for subsurface drains and the application of groundwater energy balance to drainage equations [4]

2.3. D Groundwater Numerical Models: Comprehensive Representation

As the pinnacle of numerical groundwater modelling, 3D models provide a comprehensive representation of subsurface hydrogeologic systems by accounting for spatial variability in all three dimensions. These models, characterized by their ability to capture complicated flow patterns and heterogeneity, are invaluable for site-specific assessments and detailed groundwater management [24]. By integrating geological, hydrological and geophysical data, 3D models provide unparalleled insight into groundwater flow dynamics, contaminant transport ways and the influence of human activities on aquifer sustainability. The scope of 3D numerical groundwater models continues to expand with advances in computational capabilities and data integration techniques, promising greater accuracy and reliability in addressing today's water resource challenges. Harbaugh, 1989 revealed the 3D groundwater flow equation is addressed within the core of every grid cell using a linear function. This approach enables the integration of certain nonlinear processes into the linear equations, thereby facilitating the derivation of an approximate solution.

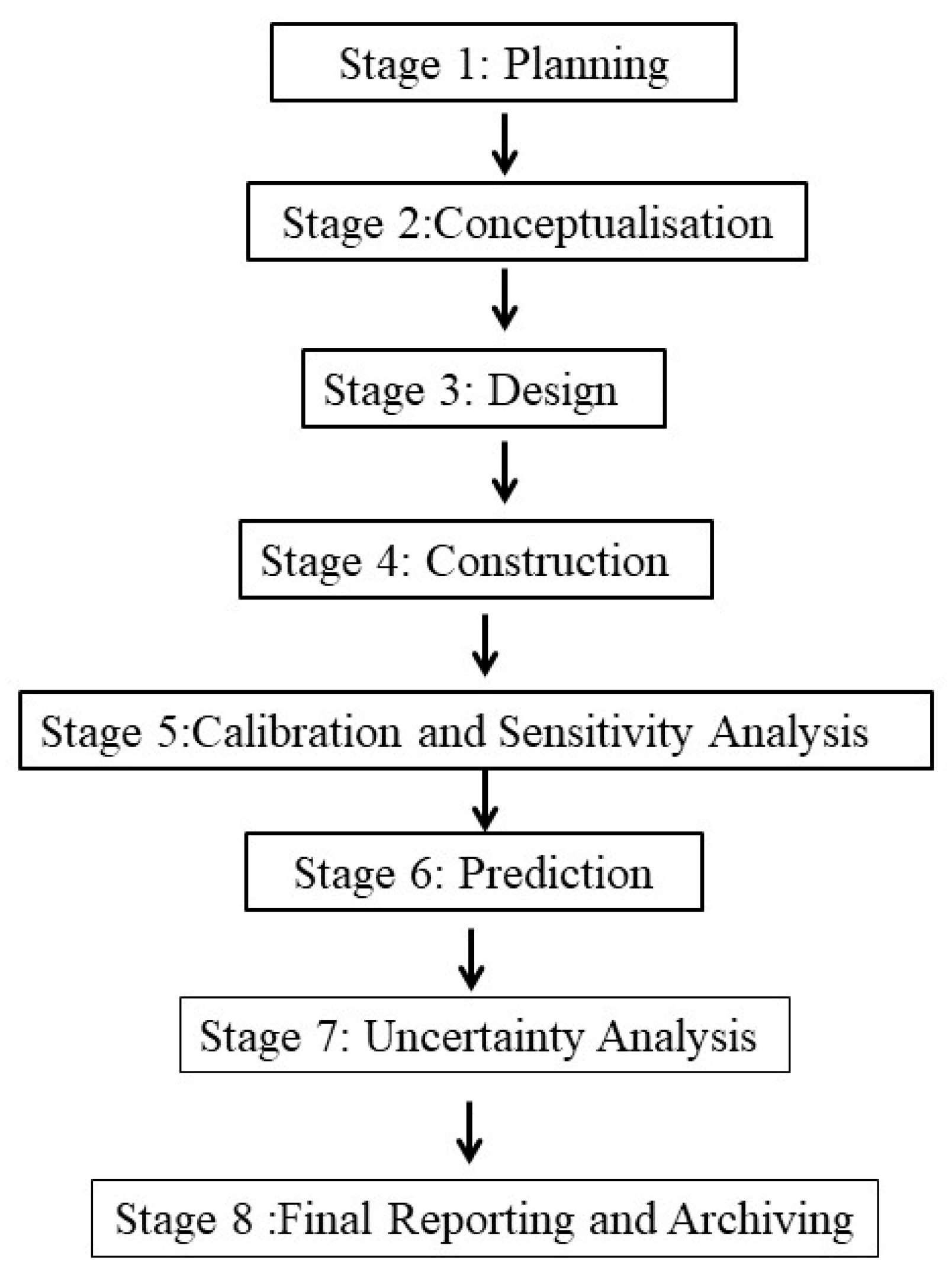
3. Basics of groundwater numerical models (1D, 2D & 3D)

Groundwater numerical modelling is an important tool for understanding the complex behavior of water flow and transport processes in the subsurface. In the basic field of 1D numerical groundwater models, the focus is on the vertical dynamics within the aquifer system. These models represent aquifers as one-dimensional columns and allow the simulation of groundwater flow along vertical profiles and the transport of contaminants through the subsurface [25,26]. By using mathematical equations such as Darcy's law and the advection-dispersion equations, 1D models provide insight into the movement of water and solutes in a simplified yet informative way.
Beyond the vertical representation, 2D numerical groundwater models introduce horizontal variability into the simulation domain. This extension enables the consideration of lateral flow components and spatial heterogeneity within the aquifer system. By incorporating additional dimensions, these models improve the accuracy of predictions of groundwater flow patterns and contaminant migration in heterogeneous subsurface environments [15]. In addition, 2D models facilitate the assessment of groundwater-surface water interactions, contributing to comprehensive water resource management strategies at the regional scale.
Numerical 3D models are at the forefront of groundwater modelling, providing a three-dimensional representation of subsurface hydrogeologic systems. By accounting for variations in hydraulic properties and boundary conditions in all spatial dimensions, 3D models provide a detailed understanding of groundwater flow behaviour in complex geologic environments [27,28,29]. These models enable the simulation of complicated flow patterns and capture the effects of geologic structures such as faults and strata on groundwater movement and contaminant transport. As computational capabilities continue to increase, 3D numerical groundwater models hold great promise for addressing increasingly complex challenges in groundwater resource management and environmental remediation.

4. Applications of groundwater numerical models (1D, 2D & 3D)

Groundwater numerical models, spanning 1D, 2D, and 3D representations, are indispensable tools in hydrogeology, environmental science, and water resources management. These models find diverse applications across various fields, offering in-sights into complex groundwater flow patterns, contaminant transport processes, and aquifer behavior. In the context of 1D models, applications often focus on simulating vertical flow processes, such as groundwater recharge, discharge, and solute transport. They are frequently used to analyze pumping impacts on groundwater levels, evaluate well-field management strategies, and assess contaminant migration in vertical aquifer profiles. For instance, Hydrus-1D program utilizes numerical methods to solve the Richards equation, employing the finite element method to analyze the flow of water in soil with varying saturation levels. [30]
Expanding to 2D groundwater numerical models broadens the scope of applications, allowing for the simulation of lateral groundwater flow, groundwater-surface water interactions, and contaminant transport across a two-dimensional plane. These models are instrumental in studying regional groundwater flow dynamics, assessing the impacts of land-use changes on groundwater resources, and predicting the migration of pollutants from various sources [31]. Furthermore, 2D models play a crucial role in watershed-scale hydrological studies, aiding in understanding groundwater flow within river basins and predicting aquifer responses to hydrological changes and climate variability. FEFLOW, a numerical groundwater model, is capable of simulating various aspects of groundwater behaviour. It is capable of accurately modelling flow, groundwater sources age, and mass, along with heat transport, as well as groundwater and transport of pollutants in both 2D and 3D scenarios, whether transient or steady state. The study was conducted by Li and colleagues. Li et al. [32,33] developed a thorough model to comprehend how regional hydrological processes are affected by water-saving measures. This model mimics the groundwater flow in the area as well as the water balance in China's Vadose Zone. It incorporates groundwater model flow (FEFLOW) under GIS and conceptual models in the Vadose zone with different landscape units. Similarly, a numerical simulation of thermohydraulic-mechanical-chemical (THMC) processes in porous and fractured media that uses the finite element technique (FEM) to provide flow equation solutions is called OpenGeoSys. Furthermore, it finds application across the disciplines of hydro-geology, waste deposition, geothermal energy, hydrology, and water resource management.
Preprints 99099 g003
Figure 2. Schematic procedure of the integrated model with landscape unit-based conceptual models and FEFLOW [31]
Figure 2. Schematic procedure of the integrated model with landscape unit-based conceptual models and FEFLOW [31]
Preprints 99099 g003
A software tool called HYDRUS was used to simulate the transport of solutes, heat, and water in 2D and 3D variably drenched media. It consists of computational finite element models. To model the movement of the water, Hydrus 2D combined implicit splitting time methods with the Galerkin finite element approach. Although it was intended to mimic soil infiltration, its adaptability indicated that it would yield positive outcomes for other kinds of porous media. Xu et al. [34] suggested using the Hydrus 2D model to study the flow of water in a heterogeneous soil. Mekala et al. [35] predicted the water flow and nitrogen species transport in an unsaturated subsurface system with variable irrigation and moisture conditions using Hydrus 2D. In this work, they developed an experimental model to comprehend and forecast the transportation of nitrogen compounds while avoiding the uncertainty that arises from changing environmental and climatic conditions in field data.
Incorporating three-dimensional (3D) groundwater models further enhances the capability to represent aquifer heterogeneity and simulate complex flow patterns. These models are employed in a wide range of applications, including aquifer characterization, groundwater resource management, contaminant remediation design, and environ-mental impact assessment. By integrating geological, hydrological, and chemical data, 3D groundwater models provide valuable insights into subsurface flow processes, facilitate the identification of contamination sources, and support decision-making for sustainable groundwater use and protection. The three-dimensional solute reactive transport model, or RT3D, for instance, is a module in MODFLOW that was utilized to solve coupled partial differential equations that illustrate the transport of many stationary pollutants or species in saturated groundwater systems. Furthermore, Wu et al. [36] proposed the optimization of groundwater management by combining a genetic algorithm with MODFLOW and RT3D to enhance the searching efficiency and obtain the best solution for groundwater management problems. Similarly, the propagation of a point source TCE contamination was simulated using the transient transport model MT3DMS. This work's primary objective is to assess if EPM is appropriate for use in significant contaminated sites in the Karst region [37]. In certain investigations, the Modular 3-D Transport Model (MT3D) and MODFLOW are combined with the Water Quality Analysis Simulation (WSAP) to assess how a trans-basin water diversion project will affect groundwater [38].
A number of water movement processes are simulated by the MIKE SHE modelling system, including evapotranspiration, saturated groundwater flow, channel and canopy interception following precipitation, and key quality components. Investigating the relationship between surface and groundwater is made easier by the 3D finite difference groundwater flow found in MIKE SHE [39]. For managing and balancing the water across the basin, a linear reservoir groundwater approach is available. Additionally, a completely distributed rainfall-runoff modelling is included. In order to replicate contaminant passage for source water protection and groundwater age studies, it also incorporates completely dynamic random walk particle tracking. A MIKE-SHE model was created by Fouad et al. [40] to aid in management choices and the evaluation of hydrological mitigation strategies. When it was not possible to represent every component of the water cycle, the MIKE-SHE proved to be an effective and popular tool in numerous research on watersheds. The integration of several hydrological processes at various timescales resulted in programme flexibility. Every hydrological system on a catchment scale was covered. The hydrologic simulation is composed of a number of processes, including evapotranspiration, channel/surface aquifer exchanges, unsaturated and saturated flow, and overland and channel flow.

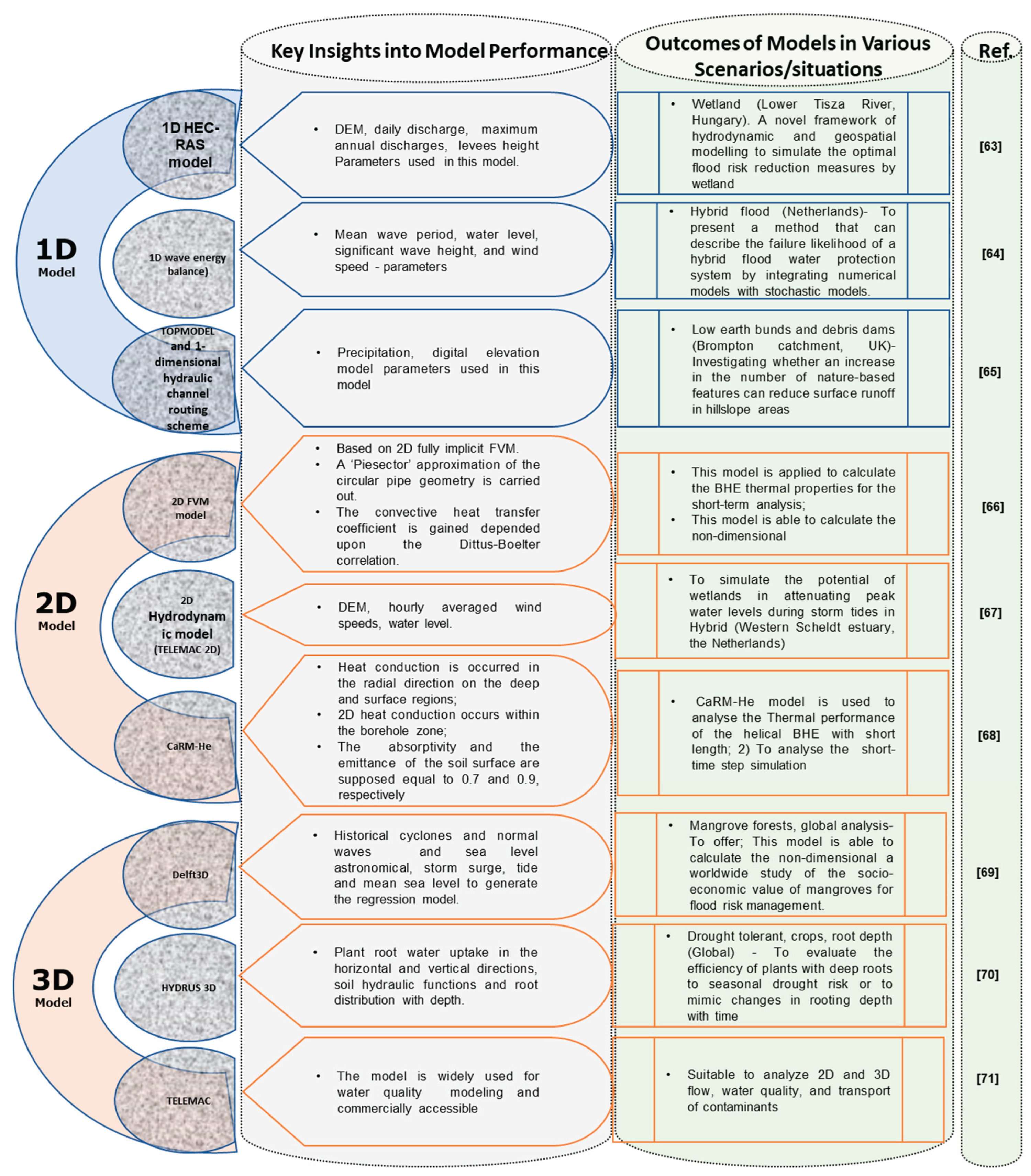
5. Comparative analysis: Advantages, Drawbacks and Solutions

Water quality models are broadly classified into two types one is physical and another is mathematical models [41]. In addition, these models can be classified into 1D, 2D, and 3D based on the level of the complexity of the computer replica, the data requirements (including comprehensive records and limited data specification predictions), the type of approach used (such as physically based, conceptual, and empirical), the type of pollutant being modelled (such as nutrients, sediment, and salts), the regions of application, the nature of the model (whether it is deterministic or stochastic), the state being analyzed (whether it is a steady state or flexible simulation), and the spatial analysis method used (whether it is lumped or distributed) [42]. Table 1 summarizes the benefits, drawbacks, suitability, and underlying assumptions of 1D, 2D, and 3D models. Alternatively, models can be classified as tactical, operational, strategic, or directed models, depending on their extent and spatial scales [43]. The SKM (2011) classification scheme categorizes the water's quality models into catchment, in-stream, and ecological response models. Utilizing the rainfall-runoff mechanism as a basis, catchment models simulate the corresponding loads of pollutants. Simulated in-stream models represent in-stream aquatic quality processes and the hydrodynamic behaviour of flows. Ecological response models represent how an ecosystem reacts to stresses, such as changes in flow and water quality. Three categories exist for models of water quality: dynamic/stochastic, constant state, and dynamic models. Steady-state models are employed to analyze prolonged patterns and perform regular surveillance. Dynamic/stochastic models are designed for capturing short-term fluctuations, ongoing monitoring, and long-term patterns. Dynamic models are designed primarily for short-term mobility and continuous tracking to facilitate operational management [44]. Water modelling models can be categorized as simulation or optimization models [45]. The simulation model delineates and portrays alterations in water quality through a mathematical framework. Optimization models are frequently used to determine the minimum amount of alternative data required before conducting the model simulation. Models are commonly categorized based on their complexity, the water they are used for, and the water quality metrics they can predict. Applying a complicated model to a specific scenario becomes exceedingly challenging and costly due to the data needed [46]. The primary controlling principle for model development is the law of preservation of energy, momentum, and mass preservation [47]. Various formulas can be utilized to construct a water quality model, with a specific choice depending on the parameters to be modelled [48]. A variety of water quality models, such as Agricultural Non-Point Source, AGWA, ANSWERS-2000, APEX, AQUA-TOX, BASINS, EFDC, EPD-RIV1, GLEAMS/CREAMS, HSPF, KINEROS2, LSPC, MIKE SHE, NLEAP, PRMS, QUAL2E, QUAL2K, SWAT, SWMM, WAM, WARMF, WASP7, WCS, and AquaChem, have been employed for the analysis of water quality.
Table 2. An overview of Groundwater Numerical Models.
Table 2. An overview of Groundwater Numerical Models.
Scope Advantages Challenges Assumptions
1D models
  • Analysis of aquifer characteristics like hydraulic conductivity and porosity
  • Simulation of vertical contaminant transport phenomena
  • Insight into groundwater flow behavior in vertical columns
  • Decision support for well placement and groundwater remediation strategies
  • Applied rapidly to analyze lake and reservoir water with no prior calibration and with a limited database of measurements
  • The most straightforward and often employed techniques for analyzing the quality of river water
  • They cannot estimate the temporal fluctuation of concentration.
  • They do not encompass the intricate chemical, physical, and biological processes occurring in water.
  • Usually applicable to rivers, as well as estuaries as well as lakes with significant length-width ratios.
  • Applicable in extensive watercourses, rivers, brooks, and constricted passages
2D models
  • Incorporation of horizontal variations in hydraulic properties and boundary conditions
  • Realistic representation of subsurface heterogeneity and flow pathways
  • Assessment of groundwater-surface water interactions
  • Analysis of the influences of land-use changes on groundwater resources
  • Specific characteristics can be analyzed at various time intervals, such as hourly, daily, weekly, monthly, and yearly.
  • It is important to assess water quality at different depths.
  • This process necessitates meticulous calibration and is very responsive to variations in numerous factors of water quality.
  • The models necessitate a greater amount of data and more proficient analytical users compared to one-dimensional models.
  • Applicable for simulating water quality primarily in reservoirs, deep rivers, and lakes.
  • Assumes substantial variations in water quality throughout both the lateral and longitudinal profiles of the watercourse.
3D models
  • Comprehensive representation of subsurface hydrogeological systems
  • Capture of intricate flow patterns and heterogeneity
  • Site-specific assessments for detailed groundwater resource management
  • Addressing contemporary water resource challenges with improved accuracy and reliability
  • Must determine the geographic arrangement of predicted water quality variable levels.
  • The models are infrequently utilized due to the intricate nature of the evaluated issues.
  • They require substantial quantities of data and a greater number of proficient analytical professionals.
  • Relevant for investigating alterations in the water quality of dams, lakes, deep rivers, water bodies, estuaries, and seabays

7. Case Studies and Practical Implementations

7.1. Real-world Examples of 1D Model Applications

The objective of hydrological modelling is to concentrate on the individual movements within a hydrological system, which are influenced by several factors such as the concentration of the flows, the properties of the soil, land, climate, and river. The precision of modelling mostly be determined by on the accurate estimation of important factors that are precipitation, evapotranspiration, interception, infiltration, and runoff estimation. They plan an important role in hydrological modelling. It is important to note that the accuracy of any model's results heavily relies on the accuracy of the information being supplied and the underlying assumptions of the conceptual model. We discuss various 1D model applications in the real-world scenario.

7.1.1. Flooding Model

The variability and arrangement of rainfall resulting from climate changes are significant causes for worry. Precipitation is the primary determinant of flash flood events, although several additional factors contribute to their occurrence. These factors include natural elements such as watershed features, soil type, and land use cover, as well as human activities along the river and floodplain. All of these factors collectively contribute to an increased frequency of floods. Various academics have utilized hydrological modelling to analyze floods in the river as well as floodplain systems [7,49,50].
Choosing appropriate cross sections for representing a river's natural geometry is crucial for the effectiveness of 1D hydraulic models. However, there are limited guidelines for determining the optimal space between cross sections based on the specific hydraulic problem. To address this issue, we compare high-resolution digital terrain models of the river Po in Italy and the River Severn in the United Kingdom. These models allow us to create hypothetical topographical ground surveys with varying cross section spacing, which can be used as input for a standard 1D model. By simulating historical and synthetic flood events for both river reaches, we analyze the impact of survey resolution on the accuracy and performance of standard 1D models.
Selecting an appropriate selection of cross sections is vital for accurately reflecting the natural shape of a river, which significantly impacts the effectiveness of 1D hydraulic computations. Nevertheless, there are scarce criteria for determining the most appropriate spacing among cross-sections, taking into account the particular hydraulic issue at hand. Castellarin et al. [51] examine this matter through the comparison of the high-resolution digital topography simulations of the river sections: the river Po in Italy and the river Severn in the United Kingdom. The models facilitated the creation of a sequence of hypothetical topographic ground examinations with varying intervals across cross-sections that could be utilized as input for a conventional 1D model. The results were examined by recreating both the past and artificial flood occurrences for the two sections of the rivers to measure the precision in evaluating how the resolution of surveys affects the effectiveness of conventional 1D models.

7.1.2. One-dimensional modelling of aquifer contamination

Given the current conditions [16,52], the problem of groundwater contamination is now more crucial than ever for the utilization of finite freshwater resources. Modelling this process is crucial for comprehending the current state and forecasting the future condition of aquifers. The primary benefit of this approach is the absence of the requirement for meshing the solution range, resulting in a reduction in the computational time needed to execute the computations. This study investigates the modelling of contaminant transmission in groundwater employing the Meshless Local Petrov Galerkin Method (MLPG) in a homogeneous mode. To address this issue, the equations that governed the problem were discretized utilizing the Petrov-Galerkin local method. Additionally, the shape function was approximated using the moving least squares approach. The findings obtained from this approach were compared to the exact results, demonstrating the satisfactory precision of the Petrov-Galerkin local method [26,53] in a one-dimensional model. Two more mesh-less models, RPCM-GCT and MWS-GCT, have been designed specifically for highly advective flows. Their effectiveness has been confirmed with the major transport process of advection [6].
The commonly utilized one-dimensional software includes Hydrologic Engineering Centre's River Analysis System (HEC-RAS), a publicly available program for 1D models with GIS integration developed by Brunner, and MIKE [54], a 1D river modelling software capable of conducting flood analysis, dam break analysis, as well as water purity evaluation.

7.2. Case Studies Highlighting 2D Model Successes

Numerical model techniques particularly 2D models play a significant role to find the particular reasons and effects for topographic and climate deviations which are the chief reasons of sudden flooding in tropical zones, for debris flow simulation, and saltwater intrusion in coastal aquifers.
FLO 2D is a hydrological model that ensures the preservation of volume, facilitates the analysis of flood routing, and operates on a grid system to accurately define flood risks and establish regulations for floodplain zoning. FLO 2D is a versatile tool for simulating many flood scenarios, including over-bank floods, unconfined flows over complicated terrains, split channels, mud or debris flows, and urban flooding. Recent works have focused on utilizing the FLO 2D model for simulating debris flows, dam breaks, hydrodynamic modelling, and mudflows [20,50].
The practical applicability of two-dimensional flow of groundwater simulations is significantly restricted when dealing with actual geometries. Groundwater flow opposite to the shoreline is often disrupted in real-world scenarios, making it impossible to accurately represent and model the issue using a cross-section. These circumstances commonly arise, for example, around individual wells where groundwater is drawn or infiltrated, in polder regions wherein regulated phreatic groundwater levels result in radial flow patterns, or in areas with intricate hydrogeologic geometries.

7.3. Three-Dimensional Modelling in Complex Hydrogeological Environments

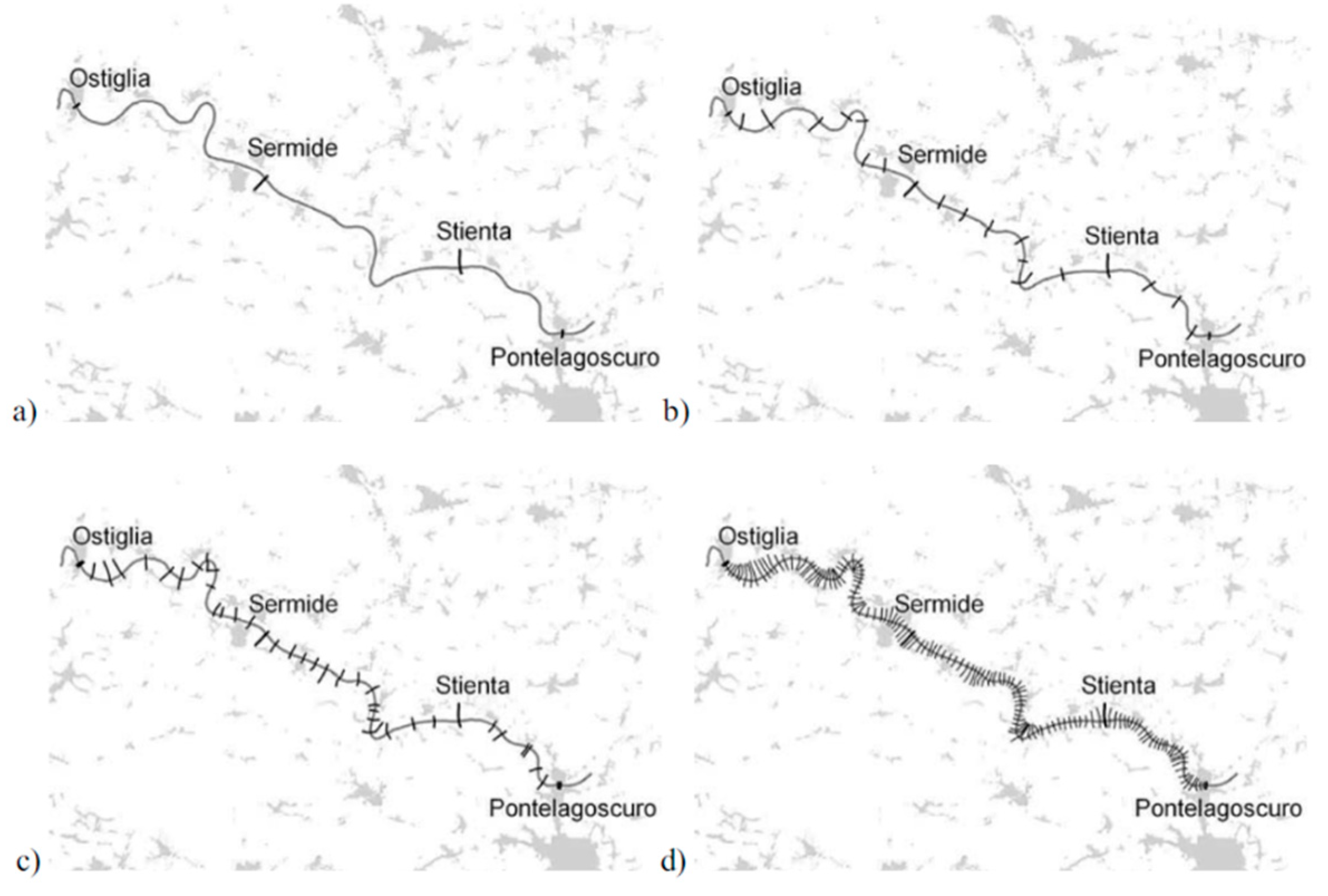
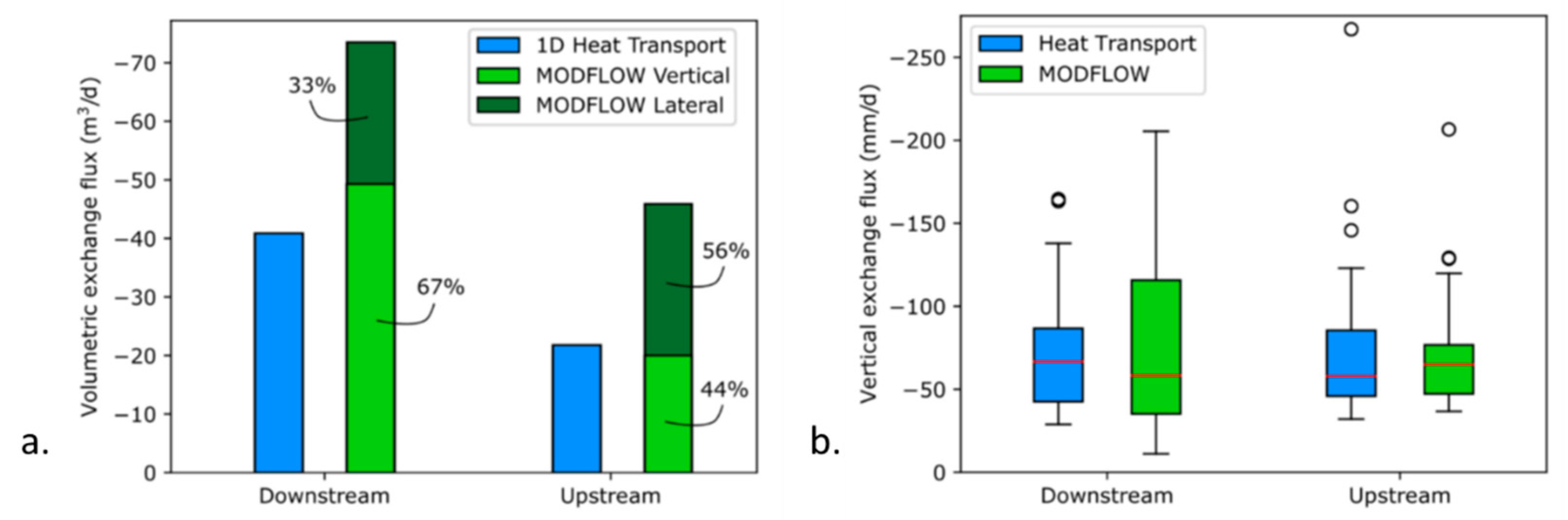
7.3.1. Study of river-aquifer exchange fluxes 1D Versus 3D ground water

The relationship connecting groundwater as well as rivers is crucial in resolving a diverse array of modern concerns. Hence, it is imperative to get a thorough comprehension of the exchange mechanisms between these entities to safeguard our water resources. The exchange flux, often referred to as the Darcy flux, is a crucial measure for characterizing the connections amongst groundwater and surface water. It represents the flow that takes place within rivers, riverbeds, and interconnected aquifers [54,55].
In study by Ghysels et al. [56], the researchers examined the spatial distribution of exchange fluxes between rivers and aquifers at the meter scale using two different approaches. The first approach involved the use of the 1D heat tracer method, while the second approach utilized numerical groundwater flow modelling. These methods were applied to two sections of a River in Belgium. In order to create maps that show the distribution of the exchange between the river and the aquifer, the researchers calculated the fluxes of vertical exchange at specific points in time using 115 temperature profiles of the riverbed. The estimation was derived from a straightforward one-dimensional quantitative approach to the heat transfer equation. A comparative analysis was performed using these regionally dispersed flux estimates to assess the agreement between the 1D analytical outcome and the flux estimates derived from a mathematical 3D groundwater model utilizing MODFLOW, which measures fluxes determined by Darcy's law. This model utilizes extremely detailed information on watercourse hydraulic conductivity to accurately replicate the variability of the riverbed.
Even though both methods utilized possess their own advantages and limitations, it remains possible to conduct a robust comparison of flux estimates from the 3D modelling of groundwater flow to those acquired through the application of the 1D heat transport equation. This comparison leads to the conclusion that significant non-vertical flow components exist in both sections of the river. The non-vertical flow experiences a notable increase towards the riverbanks, while quasi-vertical flow is only observed near the centre of the river[57]. The study emphasizes the need to be careful when inferring the overall interchange fluxes of the riverbed using just 1D solutions. These solutions do not take into account horizontal or lateral fluxes and are prone to underestimate the entire exchange flow. Numerical groundwater circulation models offer the benefit of being physically based and mechanistic simulations. They allow for the straightforward simulation of river-aquifer exchange fluxes in three dimensions. Furthermore, they enable the examination of lateral exchange patterns across the banks.
There are different types of 3D software to study the groundwater flow viz., MODFLOW, MT3DMS, SEAWAT, PHT3D, PHT3D and FEMWATER which are used for simulating groundwater flow, transport of contaminated substances, organic pollutants, and salt water. MODFLOW is the widely used 3D groundwater flow model software and SEAWAT is particularly used to model scenarios where saltwater intrusion and organic pollutant migration occur simultaneously.
Groundwater modeling plays a pivotal role in comprehending and overseeing hydrogeological systems. A comparative analysis (Figure 3) underscores the distinctive contributions and applications of 1D, 2D, and 3D groundwater models, offering valuable insights for researchers, practitioners, and decision-makers in hydrogeology and water resources management.
Table 2. Groundwater Numerical Models case studies.
Table 2. Groundwater Numerical Models case studies.
Model used Country Specific site Modelling Characteristics Major findings Reference
MODFLOW
 Central Mexico Morelia–Queréndaro aquifer (AMQ) springs, piezometric levels, natural terrain elevations, and groundwater extractions Weighted recharge was obtained using the map of potential recharge zones [58]
SEAWAT India Nagapattinam ,Tamil Nadu Permeability (K) assignation, importing of observation well data for head, concentration, and discharge; and.
parameters Cl and TDS at each observation well		 Fluctuation in TDS concentrations which was indicated by often a rise in TDS followed by a sharp drop [59]
FEFLOW Xinjiang, China
 The Sangong River watershed Permeation coefficient, rate of groundwater recharge, bottom elevation of the water-barrier of
phreatic aquifer and top elevation of the aquifer		 Models can be used to simulate the effects of regional vegetation change on the groundwater depth. [60]
FEMWATER Northern central Europe Nysa Łużycka River, the north-western part of the waste soil bank and its surroundings
 Hydraulic conductivity ks, differential water capacity F(h), volume moisture content θ(h) and relative hydraulic conductivity kr(h) Designing of dewatering system extending and monitoring system of potential threat of slope stability of the waste soil bank [61]
SUTRA Iran East Azerbaijan province The population size and the number of generations of the CACO optimization algorithm are adjusted based on the given stopping criteria Used to assess the current and projected future status of groundwater resources [62]
Preprints 99099 g004
Figure 3. River Po: control sections Sermide and Stienta and cross-sectional locations for different resolution models: a) PO-4; b) PO- 21; c) PO-41; and d) PO-140 gray areas represent municipalities [51].
Figure 3. River Po: control sections Sermide and Stienta and cross-sectional locations for different resolution models: a) PO-4; b) PO- 21; c) PO-41; and d) PO-140 gray areas represent municipalities [51].
Preprints 99099 g004
Preprints 99099 g005
Figure 4. a) Comparison of volumetric exchange flux estimated based on the 1D analytical solution (blue) and the groundwater flow model (green) for the downstream and upstream sections; b) Boxplots of vertical fluxes simulated with heat transport modelling (blue) and groundwater modelling (green) for both the downstream and upstream sections [56].
Figure 4. a) Comparison of volumetric exchange flux estimated based on the 1D analytical solution (blue) and the groundwater flow model (green) for the downstream and upstream sections; b) Boxplots of vertical fluxes simulated with heat transport modelling (blue) and groundwater modelling (green) for both the downstream and upstream sections [56].
Preprints 99099 g005
Preprints 99099 g006
Figure 5. Comparative Analysis of 1D, 2D, and 3D Models: Key Insights and Outcomes [63,64,65,66,67,68,69,70,71].
Figure 5. Comparative Analysis of 1D, 2D, and 3D Models: Key Insights and Outcomes [63,64,65,66,67,68,69,70,71].
Preprints 99099 g006

9. Future Directions and Innovations

The modelling of hydrology has significantly enhanced our ability to analyze and understand complex systems of water. Groundwater models will play a key role in developing adaptive management strategies involving real-time monitoring, continuous model updates, and dynamic decision-making. However, the need for a groundwater modelling dataset, platforms and understanding on circulation phenomena is required. The conceptual challenges involved in developing a global groundwater platform involves developing a framework that can accommodate the complexity and variability of different hydrogeologic systems across continents while acknowledging its interconnectivity [46]. Moreover, the technical limitation to reliably represent mass fluctuations at resolutions on the order of 10–100s of meters hinders the accuracy. A nuanced understanding of different hydrogeologic settings is required for developing models capable of capturing the variability in groundwater behavior and to bridge the gaps in datasets [72]. To determine the depth of productive aquifers, depth-to-bedrock and sediment thickness maps are instrumental. However, it's important to note that existing depth-to-bedrock maps can vary and even present contradictions due to differences in data sources and methodologies. Since, sediment thickness maps complement these assessments further validation considering regional variations and the specific characteristics of each map is critical. Further, existing datasets related to lithology, hydrogeology, and hydrofacies are predominantly two-dimensional, lacking a consistent global-scale 3D representation. While sedimentary basins may possess data suitable for extending these datasets vertically, such information is often not compiled or easily accessible[73]. This underscores the need for international collaboration in assembling and sharing vertical data could help to integrate groundwater modelling seamlessly in global circulation models. Conversely, in upland and mountainous regions dominated by fractured rocks, there is a notable scarcity of 3D spatial data on aquifer conditions and properties [74]. This highlights a gap in understanding for such areas and suggests a need for increased data collection and modeling efforts. The use of evapotranspiration, heat flow, temperature and sensible heat flux as tracer to estimate groundwater movements has increased the reliability, while large scale simulations are yet to incorporate [75]. The incorporation of developing tools, such as artificial intelligence and machine learning is expected to enhance the predictive capabilities of groundwater models[76]. These technologies can analyze vast datasets, identify patterns, and improve model calibration, providing more accurate and reliable predictions.

10. Conclusion

There is considerable optimism regarding the future of hydrological modelling, as continuous efforts are being made to enhance current models and establish novel methodologies. would pave the way to more accurate measurements. Increased emphasis on involving local communities and stakeholders in the modeling process will enhance the social acceptance and relevance of groundwater models. This in turn could be useful while implementing the policies devised from the simulations. As the importance of groundwater transcends regional boundaries, there is a growing emphasis on international collaboration and data sharing. Establishing a Global Groundwater Platform necessitates significant investments on both national and international scales. However, the anticipated returns, spanning scientific advancements, societal benefits, and economic gains, are expected to outweigh the initial costs.

Acknowledgement

The authors greatly acknowledge the Global Centre for Environmental Remediation (GCER), College of Engineering, Science & Environment, ATC Building, The University of Newcastle, Callaghan, NSW-2308, Australia for providing research facilities and also thankful to Tamil Nadu Agricultural University, Coimbatore, Tamil Nadu, India for extending support under GoI-ICAR-NAHEP-IDP for International Training Program.

References

  1. Sharan, A.; Datta, B.; Lal, A.; Kotra, K.K. Management of Saltwater Intrusion Using 3D Numerical Modelling: A First for Pacific Island Country of Vanuatu. Environ Monit Assess 2024, 196, 120. [CrossRef]
  2. Lal, A.; Datta, B. Performance Evaluation of Homogeneous and Heterogeneous Ensemble Models for Groundwater Salinity Predictions: A Regional-Scale Comparison Study. Water Air Soil Pollut 2020, 231, 1–21. [CrossRef]
  3. El-Rawy, M.; Batelaan, O.; Buis, K.; Anibas, C.; Mohammed, G.; Zijl, W.; Salem, A. Analytical and Numerical Groundwater Flow Solutions for the FEMME-Modeling Environment. Hydrology 2020, 7, 27. [CrossRef]
  4. Oosterbaan, R.J.; Boonstra, J.; Rao, K. The Energy Balance of Groundwater Flow. In Proceedings of the Subsurface-Water Hydrology: Proceedings of the International Conference on Hydrology and Water Resources, New Delhi, India, December 1993; Springer, 1996; pp. 153–160.
  5. Di Salvo, C. Groundwater Hydrological Model Simulation. Water (Switzerland) 2023, 15.
  6. Swain, S.; Taloor, A.K.; Dhal, L.; Sahoo, S.; Al-Ansari, N. Impact of Climate Change on Groundwater Hydrology: A Comprehensive Review and Current Status of the Indian Hydrogeology. Appl Water Sci 2022, 12. [CrossRef]
  7. Kumar, V.; Sharma, K.V.; Caloiero, T.; Mehta, D.J.; Singh, K. Comprehensive Overview of Flood Modeling Approaches: A Review of Recent Advances. Hydrology 2023, 10, 141. [CrossRef]
  8. Shah, T.; Molden, D.; Sakthivadivel, R.; Seckler, D. The Global Groundwater Situation: Overview of Opportunities and Challenges; 2000;
  9. Bhunia, G.S.; Chatterjee, U. Chapter 15 - Ground Water Depletion and Climate Change: Role of Geospatial Technology for a Mitigation Strategy. In Climate Change, Community Response and Resilience; Chatterjee, U., Shaw, R., Bhunia, G.S., Setiawati, M.D., Banerjee, S., Eds.; Elsevier, 2023; Vol. 6, pp. 291–304 ISBN 978-0-443-18707-0.
  10. Patle, G.T.; Singh, D.K.; Sarangi, A.; Sahoo, R.N. Modelling of Groundwater Recharge Potential from Irrigated Paddy Field under Changing Climate. Paddy and Water Environment 2017, 15, 413–423. [CrossRef]
  11. Nema, P.; Nema, S.; Roy, P. An Overview of Global Climate Changing in Current Scenario and Mitigation Action. Renewable and Sustainable Energy Reviews 2012, 16, 2329–2336.
  12. Li, R.; Merchant, J.W. Modeling Vulnerability of Groundwater to Pollution under Future Scenarios of Climate Change and Biofuels-Related Land Use Change: A Case Study in North Dakota, USA. Science of The Total Environment 2013, 447, 32–45. [CrossRef]
  13. Amanambu, A.C.; Obarein, O.A.; Mossa, J.; Li, L.; Ayeni, S.S.; Balogun, O.; Oyebamiji, A.; Ochege, F.U. Groundwater System and Climate Change: Present Status and Future Considerations. J Hydrol (Amst) 2020, 589. [CrossRef]
  14. Norouzi Khatiri, K.; Nematollahi, B.; Hafeziyeh, S.; Niksokhan, M.H.; Nikoo, M.R.; Al-Rawas, G. Groundwater Management and Allocation Models: A Review. Water (Basel) 2023, 15, 253. [CrossRef]
  15. Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic press, 2015; ISBN 0080916384.
  16. Das, S.; Eldho, T.I. Effectiveness of Meshless Methods for Advection Dominant Groundwater Contaminant Transport Problems. Eng Anal Bound Elem 2023, 157, 565–577. [CrossRef]
  17. Tootoonchi, F.; Todorović, A.; Grabs, T.; Teutschbein, C. Uni- and Multivariate Bias Adjustment of Climate Model Simulations in Nordic Catchments: Effects on Hydrological Signatures Relevant for Water Resources Management in a Changing Climate. J Hydrol (Amst) 2023, 623, 129807. [CrossRef]
  18. Valencia Cotera, R.; Guillaumot, L.; Sahu, R.-K.; Nam, C.; Lierhammer, L.; Máñez Costa, M. An Assessment of Water Management Measures for Climate Change Adaptation of Agriculture in Seewinkel. Science of The Total Environment 2023, 885, 163906. [CrossRef]
  19. Bear, J.; Beljin, M.S.; Ross, R.R. Ground Water Issue Fundamentals of Ground-Water Modeling; 1992;
  20. Lanni, C.; Mazzorana, B.; Macconi, P.; Bertagnolli, R. Suitability of Mono-and Two-Phase Modeling of Debris Flows for the Assessment of Granular Debris Flow Hazards: Insights from a Case Study. In Proceedings of the Engineering Geology for Society and Territory-Volume 2: Landslide Processes; Springer, 2015; pp. 537–543.
  21. Kalugin, A.S. The Impact of Climate Change on Surface, Subsurface, and Groundwater Flow: A Case Study of the Oka River (European Russia). Water Resources 2019, 46, S31–S39. [CrossRef]
  22. Mizyed, N. Climate Change Challenges to Groundwater Resources: Palestine as a Case Study. J Water Resour Prot 2018, 10, 215–229. [CrossRef]
  23. Rouhullah Ali, S.; Khan, J.N.; Pandey, Y.; Din Dar, M.U.; Shafi, M.; Hassan, I. Modeling the Impacts of Climate Change on Groundwater Resources: A Review.
  24. Zhang, B.; Zeng, F.; Wei, X.; Khan, U.; Zou, Y. Three-Dimensional Hierarchical Hydrogeological Static Modeling for Groundwater Resource Assessment: A Case Study in the Eastern Henan Plain, China. Water (Basel) 2022, 14, 1651. [CrossRef]
  25. Bear, J. Fundamentals of Ground-Water Modeling; Superfund Technology Support Center for Ground Water, Robert S. Kerr …, 1992;
  26. Bazari, S.; Akbarpour, A.; Zooghi, M.J. One-Dimensional Modeling of Aquifer Contamination Using a Meshless Method. Journal of Health sciences and Technology 2018, 2, 23–28. [CrossRef]
  27. Wood, W.W.; Imes, J.L. Dating of Holocene Ground-Water Recharge in Western Part of Abu Dhabi (United Arab Emirates): Constraints on Global Climate-Change Models. In Developments in Water Science; Alsharhan, A.S., Wood, W.W., Eds.; Elsevier, 2003; Vol. 50, pp. 379–385 ISBN 0167-5648.
  28. Zhu, K.; Cheng, Y.; Zhou, Q.; Kápolnai, Z.; Dávid, L.D. The Contributions of Climate and Land Use/Cover Changes to Water Yield Services Considering Geographic Scale. Heliyon 2023, 9, e20115. [CrossRef]
  29. Ejaz, F.; Guthke, A.; Wöhling, T.; Nowak, W. Comprehensive Uncertainty Analysis for Surface Water and Groundwater Projections under Climate Change Based on a Lumped Geo-Hydrological Model. J Hydrol (Amst) 2023, 626, 130323. [CrossRef]
  30. Wu, Q.; Wang, G.; Zhang, W.; Cui, H.; Zhang, W. Estimation of Groundwater Recharge Using Tracers and Numerical Modeling in the North China Plain. Water (Basel) 2016, 8, 353. [CrossRef]
  31. Sarma, R.; Singh, S.K. Simulating Contaminant Transport in Unsaturated and Saturated Groundwater Zones. Water Environment Research 2021, 93, 1496–1509. [CrossRef]
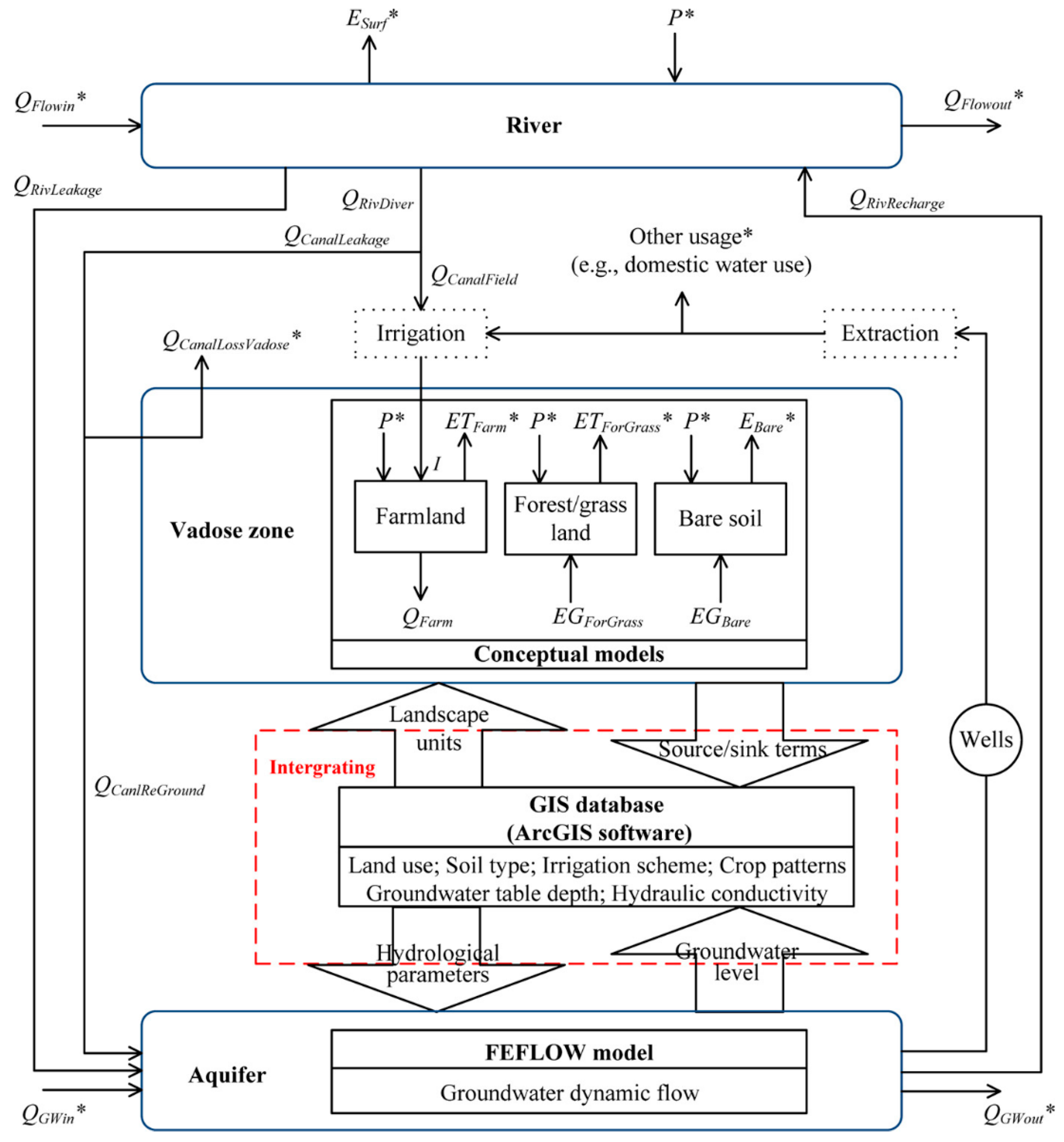
  32. Li, J.; Mao, X.; Li, M. Modeling Hydrological Processes in Oasis of Heihe River Basin by Landscape Unit-Based Conceptual Models Integrated with FEFLOW and GIS. Agric Water Manag 2017, 179, 338–351. [CrossRef]
  33. Sharan, A.; Lal, A.; Datta, B. Evaluating the Impacts of Climate Change and Water Over-Abstraction on Groundwater Resources in Pacific Island Country of Tonga. Groundw Sustain Dev 2023, 20, 100890. [CrossRef]
  34. Xu, X.; Kalhoro, S.A.; Chen, W.; Raza, S. The Evaluation/Application of Hydrus-2D Model for Simulating Macro-Pores Flow in Loess Soil. International Soil and Water Conservation Research 2017, 5, 196–201. [CrossRef]
  35. Mekala, C.; Nambi, I.M. Understanding the Hydrologic Control of N Cycle: Effect of Water Filled Pore Space on Heterotrophic Nitrification, Denitrification and Dissimilatory Nitrate Reduction to Ammonium Mechanisms in Unsaturated Soils. J Contam Hydrol 2017, 202, 11–22. [CrossRef]
  36. Wu, M.; Wu, J.; Liu, J.; Wu, J.; Zheng, C. Effect of Groundwater Quality on Sustainability of Groundwater Resource: A Case Study in the North China Plain. J Contam Hydrol 2015, 179, 132–147. [CrossRef]
  37. Ghasemizadeh, R.; Yu, X.; Butscher, C.; Hellweger, F.; Padilla, I.; Alshawabkeh, A. Equivalent Porous Media (EPM) Simulation of Groundwater Hydraulics and Contaminant Transport in Karst Aquifers. PLoS One 2015, 10, e0138954. [CrossRef]
  38. Jia, H.; Liang, S.; Zhang, Y. Assessing the Impact on Groundwater Safety of Inter-Basin Water Transfer Using a Coupled Modeling Approach. Front Environ Sci Eng 2015, 9, 84–95. [CrossRef]
  39. Zhang, J.; Zhang, M.; Song, Y.; Lai, Y. Hydrological Simulation of the Jialing River Basin Using the MIKE SHE Model in Changing Climate. Journal of Water and Climate Change 2021, 12, 2495–2514. [CrossRef]
  40. Fouad, M.; Hussein, E.E.; Jirka, B. Assessment of Numerical Groundwater Models. Int J Sci Eng Res 2018, 9, 951–974.
  41. Bedi, S.; Samal, A.; Ray, C.; Snow, D. Comparative Evaluation of Machine Learning Models for Groundwater Quality Assessment. Environ Monit Assess 2020, 192, 1–23. [CrossRef]
  42. Tsakiris, G.; Alexakis, D. Karstic Spring Water Quality: The Effect of Groundwater Abstraction from the Recharge Area. Desalination Water Treat 2014, 52, 2494–2501. [CrossRef]
  43. Ejigu, M.T. Overview of Water Quality Modeling. Cogent Eng 2021, 8, 1891711. [CrossRef]
  44. Whitehead, P.G.; Leckie, H.; Rankinen, K.; Butterfield, D.; Futter, M.N.; Bussi, G. An INCA Model for Pathogens in Rivers and Catchments: Model Structure, Sensitivity Analysis and Application to the River Thames Catchment, UK. Science of the Total Environment 2016, 572, 1601–1610. [CrossRef]
  45. Burigato Costa, C.M. da S.; da Silva Marques, L.; Almeida, A.K.; Leite, I.R.; de Almeida, I.K. Applicability of Water Quality Models around the World—a Review. Environmental Science and Pollution Research 2019, 26, 36141–36162. [CrossRef]
  46. Condon, L.E.; Kollet, S.; Bierkens, M.F.P.; Fogg, G.E.; Maxwell, R.M.; Hill, M.C.; Fransen, H.H.; Verhoef, A.; Van Loon, A.F.; Sulis, M. Global Groundwater Modeling and Monitoring: Opportunities and Challenges. Water Resour Res 2021, 57, e2020WR029500. [CrossRef]
  47. Chapra, S.C.; Dolan, D.M.; Dove, A. Mass-Balance Modeling Framework for Simulating and Managing Long-Term Water Quality for the Lower Great Lakes. J Great Lakes Res 2016, 42, 1166–1173. [CrossRef]
  48. Olowe, K.O. Assessment of Some Existing Water Quality Models. Nature Environment & Pollution Technology 2018, 17.
  49. Anees, M.T.; Abdullah, K.; Nordin, M.N.M.; Ab Rahman, N.N.N.; Syakir, M.I.; Kadir, M.O.A. One-and Two-Dimensional Hydrological Modelling and Their Uncertainties. Flood Risk Manag 2017, 11, 221–244.
  50. Anees, M.T.; Abdullah, K.; Nawawi, M.N.M.; Ab Rahman, N.N.N.; Piah, A.R.M.; Zakaria, N.A.; Syakir, M.I.; Omar, A.K.M. Numerical Modeling Techniques for Flood Analysis. Journal of African Earth Sciences 2016, 124, 478–486. [CrossRef]
  51. Castellarin, A.; Di Baldassarre, G.; Bates, P.D.; Brath, A. Optimal Cross-Sectional Spacing in Preissmann Scheme 1D Hydrodynamic Models. Journal of Hydraulic Engineering 2009, 135, 96–105.
  52. Das, S.; Eldho, T.I. Simulation of Reactive Transport in Porous Media Using Meshless Local Petrov Galerkin (MLPG) and Combination of Meshless Weak and Strong (MWS) Form Methods. J Contam Hydrol 2022, 251, 104104. [CrossRef]
  53. Syarifudin, A.; Satyanaga, A.; Destania, H.R. Application of the HEC-RAS Program in the Simulation of the Streamflow Hydrograph for Air Lakitan Watershed. Water (Basel) 2022, 14, 4094. [CrossRef]
  54. Conant Jr, B.; Robinson, C.E.; Hinton, M.J.; Russell, H.A.J. A Framework for Conceptualizing Groundwater-Surface Water Interactions and Identifying Potential Impacts on Water Quality, Water Quantity, and Ecosystems. J Hydrol (Amst) 2019, 574, 609–627.
  55. Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring Methods for Groundwater, Surface Water and Their Interactions: A Review. Hydrology and Earth System Sciences Discussions 2006, 3, 1809–1850.
  56. Ghysels, G.; Anibas, C.; Awol, H.; Tolche, A.D.; Schneidewind, U.; Huysmans, M. The Significance of Vertical and Lateral Groundwater–Surface Water Exchange Fluxes in Riverbeds and Riverbanks: Comparing 1D Analytical Flux Estimates with 3D Groundwater Modelling. Water (Basel) 2021, 13, 306. [CrossRef]
  57. Refsgaard, J.C.; Højberg, A.L.; Møller, I.; Hansen, M.; Søndergaard, V. Groundwater Modeling in Integrated Water Resources Management—Visions for 2020. Groundwater 2010, 48, 633–648. [CrossRef]
  58. Navarro-Farfán, M. del M.; García-Romero, L.; Martínez-Cinco, M.A.; Hernández-Hernández, M.A.; Sánchez-Quispe, S.T. Comparison between MODFLOW Groundwater Modeling with Traditional and Distributed Recharge. Hydrology 2024, 11, 9. [CrossRef]
  59. Gopinath, S.; Srinivasamoorthy, K.; Saravanan, K.; Suma, C.S.; Prakash, R.; Senthilnathan, D.; Chandrasekaran, N.; Srinivas, Y.; Sarma, V.S. Modeling Saline Water Intrusion in Nagapattinam Coastal Aquifers, Tamilnadu, India. Model Earth Syst Environ 2016, 2, 1–10. [CrossRef]
  60. Zhao, C.; Wang, Y.; Chen, X.I.; Li, B. Simulation of the Effects of Groundwater Level on Vegetation Change by Combining FEFLOW Software. Ecol Modell 2005, 187, 341–351. [CrossRef]
  61. Wienclaw, E.; Koda, E.; Marek, Z.; Kaczarewski, T. FEMWATER Flow Model of Waste Soil Bank from Lignite Open Pit Mine. Annals of Warsaw University of Life Sciences-SGGW. Land Reclamation 2007, 151–158. [CrossRef]
  62. Mostafaei-Avandari, M.; Ketabchi, H.; Shaker-Soureh, F. Managerial Sustainability Indices for Improving the Coastal Groundwater Decisions by a Parallel Simulation–Optimization Model. Environ Monit Assess 2023, 195, 100. [CrossRef]
  63. Yavuzturk, C.; Spitler, J.D. A Short Time Step Response Factor Model for Vertical Ground Loop Heat Exchangers. ASHRAE Trans 1999, 105, 475–485.
  64. Stark, J.; Plancke, Y.; Ides, S.; Meire, P.; Temmerman, S. Coastal Flood Protection by a Combined Nature-Based and Engineering Approach: Modeling the Effects of Marsh Geometry and Surrounding Dikes. Estuar Coast Shelf Sci 2016, 175, 34–45. [CrossRef]
  65. Zarrella, A.; De Carli, M. Heat Transfer Analysis of Short Helical Borehole Heat Exchangers. Appl Energy 2013, 102, 1477–1491.
  66. Guida, R.J.; Swanson, T.L.; Remo, J.W.F.; Kiss, T. Strategic Floodplain Reconnection for the Lower Tisza River, Hungary: Opportunities for Flood-Height Reduction and Floodplain-Wetland Reconnection. J Hydrol (Amst) 2015, 521, 274–285. [CrossRef]
  67. Vuik, V.; Van Vuren, S.; Borsje, B.W.; van Wesenbeeck, B.K.; Jonkman, S.N. Assessing Safety of Nature-Based Flood Defenses: Dealing with Extremes and Uncertainties. Coastal engineering 2018, 139, 47–64. [CrossRef]
  68. Metcalfe, P.; Beven, K.; Hankin, B.; Lamb, R. A Modelling Framework for Evaluation of the Hydrological Impacts of Nature-based Approaches to Flood Risk Management, with Application to In-channel Interventions across a 29-km2 Scale Catchment in the United Kingdom. Hydrol Process 2017, 31, 1734–1748.
  69. Menéndez, P.; Losada, I.J.; Torres-Ortega, S.; Narayan, S.; Beck, M.W. The Global Flood Protection Benefits of Mangroves. Sci Rep 2020, 10, 1–11. [CrossRef]
  70. Ghazouani, H.; Rallo, G.; Mguidiche, A.; Latrech, B.; Douh, B.; Boujelben, A.; Provenzano, G. Assessing Hydrus-2D Model to Investigate the Effects of Different on-Farm Irrigation Strategies on Potato Crop under Subsurface Drip Irrigation. Water (Basel) 2019, 11, 540. [CrossRef]
  71. Ziemińska-Stolarska, A.; Skrzypski, J. Review of Mathematical Models of Water Quality. Ecological Chemistry and Engineering S 2012, 19, 197–211. [CrossRef]
  72. of Groundwater in the World Water Quality Alliance, F. ASSESSING GROUNDWATER QUALITY: A GLOBAL PERSPECTIVE Importance, Methods and Potential Data Sources Friends of Groundwater in the World Water Quality Alliance (WWQA);
  73. Wu, W.Y.; Lo, M.H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.F.; Ducharne, A.; Yang, Z.L. Divergent Effects of Climate Change on Future Groundwater Availability in Key Mid-Latitude Aquifers. Nat Commun 2020, 11. [CrossRef]
  74. Arboleda Obando, P.F.; Ducharne, A.; Cheruy, F.; Jost, A.; Ghattas, J.; Colin, J.; Nous, C. Influence of Hillslope Flow on Hydroclimatic Evolution under Climate Change. Earths Future 2022, 10, e2021EF002613. [CrossRef]
  75. Dembélé, M.; Salvadore, E.; Zwart, S.; Ceperley, N.; Mariéthoz, G.; Schaefli, B. Water Accounting under Climate Change in the Transboundary Volta River Basin with a Spatially Calibrated Hydrological Model. J Hydrol (Amst) 2023, 626, 130092. [CrossRef]
  76. Lal, A.; Naidu, R.; Datta, B. Applications of Machine Learning Models for Solving Complex Groundwater Modelling, Monitoring and Management Problems. In Groundwater in Arid and Semi-Arid Areas: Monitoring, Assessment, Modelling, and Management; Springer, 2023; pp. 177–196.
Preprints 99099 g001
Figure 1. Distribution of subject areas researched extensively on numerical groundwater models domain.
Figure 1. Distribution of subject areas researched extensively on numerical groundwater models domain.
Preprints 99099 g001
Preprints 99099 g002
Figure 2. Ground water modelling process.
Figure 2. Ground water modelling process.
Preprints 99099 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
The Process of Groundwater Salinization on the Ca Mau Peninsula (Mekong Delta, Vietnam): Evaluation of Saltwater Intrusion Pathways via Scenario Calculations Applying a 3D Groundwater Model

Tran Viet Hoan

et al.

,

2023

Groundwater Modelling Quality in the Cold Region of the Athabasca River Basin

Tesfa Worku Meshesha

et al.

,

2020

A Step-Wise Modelling Approach to Identifying Structural Features That Control Groundwater Flow in a Folded Carbonate Aquifer System

Elisabetta Preziosi

et al.

,

2022

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated