Preprint

Article

On the Nature of Time, Space and Matter: Energy Elements, Hierarchical World, and a Classical Interpretation on Quantum Mechanics

Altmetrics

Downloads

128

Views

Comments

Guohua Tao^*

This version is not peer-reviewed

Submitted:

18 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts

Abstract

Time and space are fundamental concepts for characterizing and understanding our world. Despite of continuous curiosity and extensive studies, the nature of time and space remains elusive, and the underlying quantum structure is unclear. Here we propose a molecular model based on energy space decomposition to incorporate time and space synthetically in a unified framework. In the proposed model, the multipole expansion of action mapped to energy modules in scalar, vector, and matrix forms, results in the generators of time, space, and a material framework, cloud. And the invariance of time, space and cloud transformation corresponds to the conservation of energy, momentum, and mass, respectively. The classification of energy modules reveals a periodicity of energy elements, which constructs a hierarchical world in a molecular framework with dynamics represented by energy transformations. Here the role of time and space could switch from each other, and motion is attributed to the coupling of particle with intermediate bosons, corresponding to energy transformations among different energy modules. The application on Bohr model demonstrates that this picture provides a consistent classical interpretation to the foundation of quantum mechanics, and suggests an atomic model for gravitation.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

The current space-time paradigm on our universe established by Newton and reformed by Einstein, forms a well-organized framework to allow complex reality to be placed into order. Based on this space-time framework, modern science has been developed with the ambition to describe everything quantitatively in terms of fundamental particles and interactions [1,2,3]. Nevertheless, over the science tower built on the theoretical foundation of celebrated relativity and quantum mechanics, there are still some fundamental open problems wandering around, including the interpretation on foundations of quantum mechanics [4,5,6,7], the unification of theory of general relativity (GR) and quantum mechanics [8,9,10] and therefore the unification of all fundamental interactions. In our opinion, the key to solve these hardcore problems is indeed the fully understanding of the framework on which these theories were built, i.e., the space-time structure [10,11,12].

According to GR, space-time is a unified assembly and the geometry of which delivers gravitational interactions [13]. One well-known prediction [14,15] made by GR claims that stars may collapse into compact objects such as black hole [16], and space-time becomes singular within the trapped surface. Although the existence of the singularity renders a promising picture for the evolution of the early universe, the validity of GR in the strong gravity regime is questionable and mathematical incompleteness implies that alternative paradigms are worthwhile investigated.

Notably GR itself is a classical theory, and extensive and intensive efforts [17,18,19,20,21,22,23,24] have been devoted to the understanding of fundamental laws of physics in the extremely small and large scales, and at extremely low and high energy density, with hope to finalize a unified theory which incorporates both GR and quantum mechanics. In particular, recent successful detections of gravitational wave offer great opportunities to collect useful information on strong gravitational interactions [25]. Theoretical developments such as loop quantum gravity [19,20], and causal dynamical triangulations (CDT) [21], extend gravity into quantum regime in which the space-time singularity is avoided. On the other hand, all other three fundamental interactions, i.e., strong, weak, and electromagnetic interactions have been systematically incorporated into the field theory of quantum mechanics [1,26]. Nevertheless, constructing a final theory for everything is notably challenging. Especially, the understanding of the nature of space-time and gravitation is incomplete. Prevailing strategies in the field of quantum gravity for quantization of gravitational fields/interactions mainly take two pathways: through either quantization of spacetime structure directly from the GR perspective or quantization of dynamical spacetime on a static background from the quantum field theory (QFT) perspective. Spacetime and its geometrical properties (gravitation) thus emerge from collective quantum dynamics of many-body systems comprising fundamental entities of no direct spatiotemporal interpretation [27,28,29]. The nature of fundamental entities and the collective dynamics remain to be explored.

On the other hand, ambiguities and inconsistencies still exist in quantum mechanics regarding in particularly the role of time and its characterization [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50], which are normally entangled with conceptual difficulties in interpretations. In most practical applications, space and time are introduced ad hoc as mathematical variables in current theories with no detailed interpretations [47,48,49,50]. Although attempts have been made [36,37,38,43,44,45,46] to formulate a unified framework for both time and space at an equal footing, in accordance with theory of relativity, the fundamental difference between time and space calls for viable models with detailed underlying mechanisms rather than just the purely mathematical representation. In addition, conventional wisdoms suggest that in general but see [51,52], quantum effects of gravitation would come in approaching the Planck scale, which is beyond the reach of current technologies [11], and therefore information is extremely lacking for the model construction.

In this paper, we extend our recent work [53] on the energy space decomposition to propose a straightforward molecular interpretation to the structure of the space-time and matter energy transformation in a quantum mechanical framework. The model constructs a representation space based on elementary basis associated with different forms of energy modules, e.g., primitive matter state and radiation state. Our analysis indicates that energy modules are fundamental elements following a periodic rule in pretty much the same way as that for chemical elements. The energy elements and their transformations generate the world and everything. For instance, the classification of energy modules identifies the generators of time, space and a framework on which matter and energy can generate, transport and transform. In addition, dynamics may be attributed to energy transformation among different forms of energy modules with time and space treated synthetically in a unified framework. In particular, the analysis reveals that time and space could exchange their roles through a quantum phase transition. Different from the conventional space-time representation, the relativistic energy momentum relation is naturally built in as chemical transformation of energy modules (or elements) in the energy tensor representation of quantum mechanics [53], which results in a consistent classical interpretation on the underlying mechanism of quantum mechanics. In this molecular framework, electromagnetic interactions and gravity are incorporated in a natural way without the ad hoc expansion of dimensionality of space-time or internal gauge groups. The large and small scales and the external and internal regimes are unified in one paradigm of a hierarchical energy space while simplicity retains. In contrast to the conventional GR or QFT based models, spacetime may be generated from a single (fundamental) entity at different levels of energy hierarchy, while gravitational interaction is attributed to radiation state (graviton) at certain energy hierarchy with no empirical potential introduced. Consistently, the spacetime singularity is avoided since we argue that there is no spacetime for a single point (state).

The paper is organized as the follows. In section II, we first construct a tensor representation of energy space based on primitive energy modules, resulting in a modular energy space (MES). Then a molecular origin of time, space and matter is proposed, and a special energy pathway of time space transformation is discussed. Afterwards a mechanism for the motion of a particle based on energy transformations is suggested. Section III demonstrates that the application of our model on hydrogen atom reproduces the results of Bohr model in a consistent classical picture and suggests a new atomic model for gravitation. Section IV discusses the hierarchical structure of energy modules, the mapping of energy transformation with quantum dynamics, and our interpretation to the foundation of quantum mechanics. Section V concludes. The appendix further illustrates the construction of energy modules, the periodic generation of energy elements, and some details on quantum dynamics and relativistic effects.

2. Theory and Models

2.1. Energy Space Decomposition

One of the most fundamental questions is what time and space come from? To provide a possible answer to it, let us start from a heuristic quantum representation of energy space. Energy is commonly taken as a universal scalar to quantify a system of interest and different forms of energy may transform among one another. Given the fact that in general, a system of interest can be described in terms of energy states as done in conventional quantum mechanics [54,55], the identification and classification of the energy basis (modules) and energy transformations in a framework of energy space would be of fundamental importance. Instead of classifying energy as a scalar according to the resources, or physical effects, we identify and construct the energy basis in a tensor form based on mathematical structures. Therefore, the resulting energy space is a tensor space rather than a Hilbert space comprising (scalar) energy eigenstates. In addition, there is neither predefined space-time nor ad hoc parameters (so there is no Hilbert space in prior) while we construct everything from the proposed most fundamental objects, or the corresponding mathematical identities, i.e., primitive energy basis.

Consider an isolated fundamental object with no internal structure; its property may be quantified in terms of the total energy E that remains constant. We could associate this fundamental object with the primitive unit based on which general objects may be constructed, just like the atom in the primitive atomic theory. Mathematically this object can be represented algebraically as an element (of a set), or geometrically a point (in a space). To quantify such a system, we can map it to a zero-order tensor, i.e., a scalar. A set of scalars may form a scalar space (i.e., a zero-order tensor space) which can be used to quantify a composite system consisting of multiple non-interacting primitive objects. In the simplest example of a system including identical non-interacting primitive objects, we can assign the unity 1 (in terms of energy E) for each primitive object (versus 0 for nothing). Therefore, we indeed have a scalar energy space with the basis mapped to an energy quantum or energy atom (see Appendix A for further discussions). Of course, for a system containing more than one objects, the relation between different objects, i.e., interactions or transformations, would be interesting. In the mathematical model, if we take the objects as elements, their relations thus can be represented in terms of tensors formed by a set of elements. For instance, the interactions (or transformations) of two scalars may be represented by vectors; and similarly, the relations of vectors may be described by matrices, and so on. Therefore, we can construct vector space (or tensor space) to quantify complicated systems involving nontrivial interactions. Geometrically if we represent the elements as points, and their relations as lines connecting different points, we end up with a net representation.

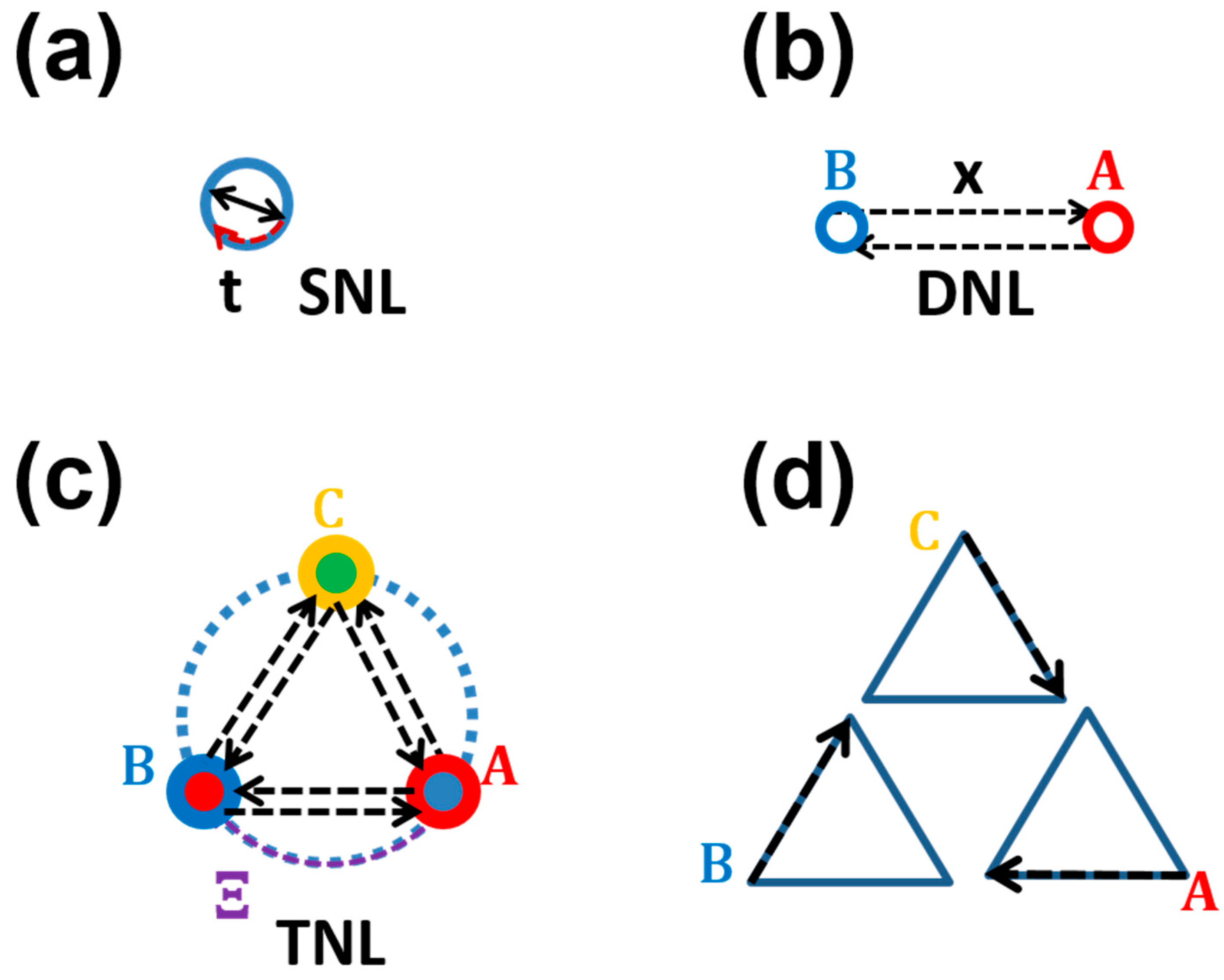
Consider the relation between two types of elements A and B, one class of relationship could be they transform into each other directly. Assuming that A and B have identical characteristic values in metric energy, i.e. E(A)=E(B), the transformations

A \overset{G}{\to} B

and

A \overset{F}{\leftarrow} B

are energy conserved. Here we define the metric of the energy space to be

E (X) = |e_{X}| = \sqrt{⟨e_{X}| e_{X}⟩}, f o r X = A, o r B

(1)

with

e_{X}

the energy (tensor) of the element X in a general sense, and

⟨. .| . .⟩

denotes the inner product [56]. For instance, the metric energy of the zero-order tensor is its absolute value; that of the first order tensor is the magnitude of the energy vector, and that of the second order tensor can be defined as the square root of the trace of the inner product of the energy matrix.

For simplicity, we start from considering the scalar case such that

e_{A} = E, a n d e_{B} = - E

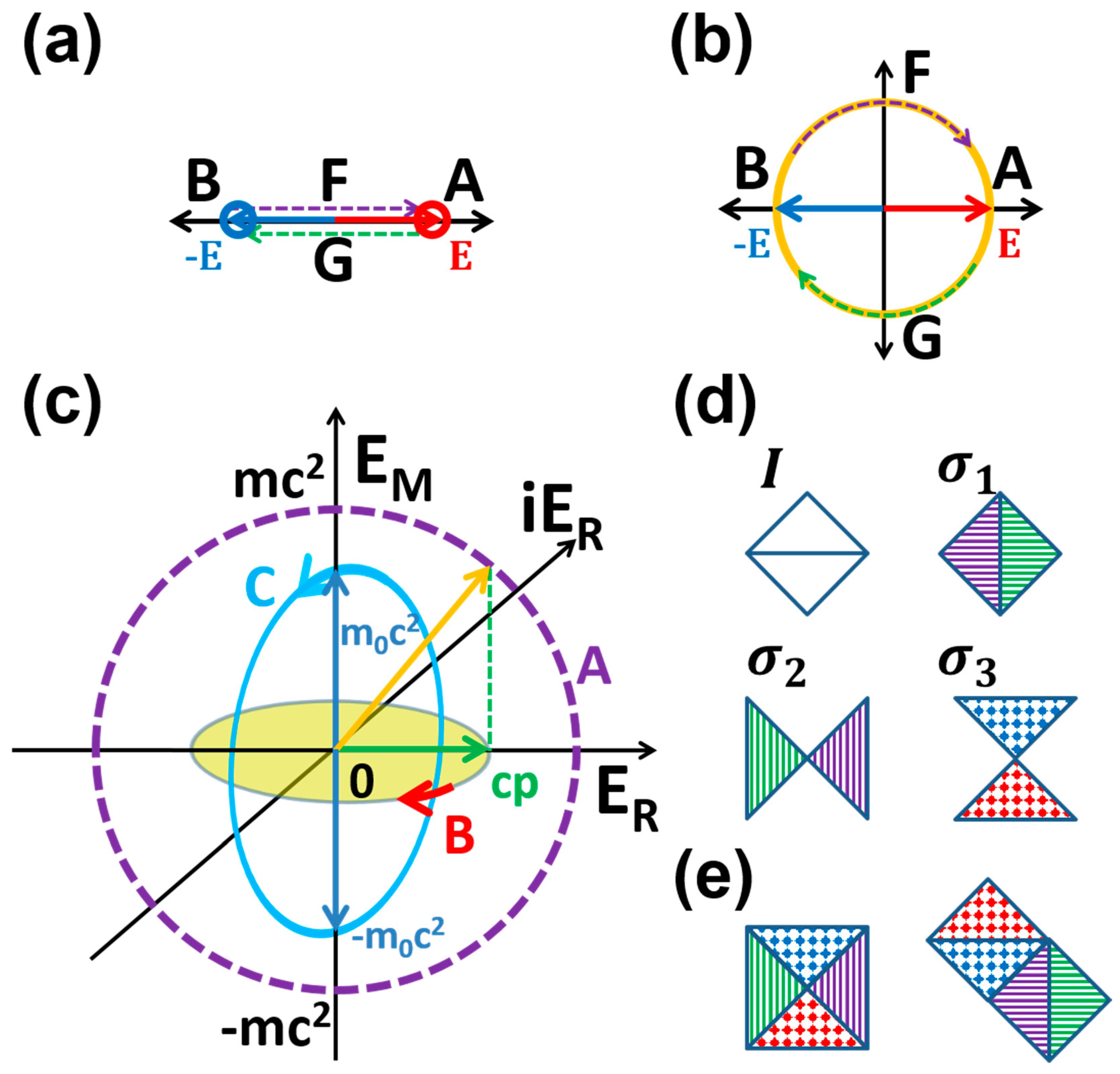
, representing for a symmetric pair of elements A and B with opposite scalar energy values. To quantify this system beyond the scalar representation, the interactions between A and B are represented by vectors F and G connecting two scalars. Thus, the one-dimensional (1D) energy space is generated upon the introduction of the interactions. Specifically, the system can be mapped to 1D Euclidean space, and the two elements correspond to the ending points of the segment of [–1, 1], while their relations correspond to the connecting lines in-between, as shown in Figure 1a as the net representation of the system. Here we may map the discrete transformation in Figure 1a to a Z₂ group, say an inversion group I = {e, i}, while the transformations F and G are not unique. Alternatively, we may follow a unitary transformation via intermediate states (continuous transformation may result as the number of intermediate states approaches infinity) satisfying energy conservation, as shown in Figure 1b. In the latter case, the original space is expanded if we consider the intermediate states along the transformation path as new elements. Indeed, the energy space may be mapped to a two dimensional (2D) Euclidean space or complex plane, and the two extremes on the imaginary axis may be taken as new basis (element) identified with intermediate bosons. It is worth noting that this type of transformation allows the conversion of different types of energy basis.

One way to understand the interaction induced difference between A and B is that they are the effective (or renormalized) elements for two original objects A0 and B0 with different values of energy, say

E_{a}

and

E_{b}

. In fact, it is easy to see that

E = E_{a} - \bar{E} = - (E_{b} - \bar{E})

, with

\bar{E} = (E_{a} + E_{b}) / 2

. When

E_{a} = E_{b}

, it is reduced to the scalar case. While when

E_{a} = - E_{b}

, we arrive at the case just considered with the maximal energy fluctuation for a given energy. On the other hand, we may regard the difference between A and B coming from the sign (phase rather than magnitude) of the energy. Thus, the interaction between A and B can be represented by the internal energy transformation associated with the orientation of the energy vector connecting A and B as a whole. Again, if intermediate states are allowed, they can be mapped to the surface of sphere in the high dimensional space. Nevertheless, it seems that only for the 2D energy space (Figure 1b), well defined order for all the states can be identified, i.e., clockwise and counterclockwise. In another word, a 2D energy space with magnitude E and phase

θ

as the polar coordinates allows for uniquely defined global order among all involved states while maintains unitary energy transformation.

To obtain a quantitative description, we may construct a 2D vector space with the basis

ϕ_{1} = (\binom{1}{0})

and

ϕ_{2} = (\binom{0}{1})

representing for A and B respectively. Therefore, the transformations F and G may be represented in terms of matrices, e.g.,

F = (\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix})

and

G = (\begin{matrix} 0 & 0 \\ 1 & 0 \end{matrix})

. It is easy to see that

F G = (\begin{matrix} 1 & 0 \\ 0 & 0 \end{matrix})

and

G F = (\begin{matrix} 0 & 0 \\ 0 & 1 \end{matrix})

. If we associate A, B with FG and GF, respectively, these transformations form a four-dimensional (4D) state space

H_{2 \times 2}

. This scheme just expands the dimensionality of the state space from 2 to 4, and therefore treats both the primitive elements and transformations in the 2D space at an equal footing as new basis in the 4D state space. Note that here the expanded state space is a generalized state space. One may ask if such a generalization could be related with the symmetry of the state space structure. However, the set of (

M_{2 \times 2} = \{A, B, F, G\}

) does not form a group.

Of course, this basis is not unique, and other types of basis may be constructed. Our strategy in the present work is to start from primitive energy elements and systematically construct energy modules (or molecules) of higher levels to form a hierarchical structure of energy space. This is just like to synthesize materials bottom-up from atoms to molecules and other higher-level structures. On the other hand, this construction allows representing the system of interest in the decomposed MES top-down to deeper hierarchies.

To elaborate our idea, consider again the above two-state system. Here we suggest an alternative simple mapping scheme. For instance, A and B could be identified with elements in the energy space specified in terms of a particular degree of freedom (DOF), say spin (not necessary to be the charge spin) so that S(A)=1 and S(B)=-1. For example, S could be the projection operator, which quantifies A and B with the coordinates of 1 and -1, respectively. While the coordinates of F and G may be taken as i and –i, respectively upon the projection of S. Now we see that the set of S(A), S(B), S(F), and S(G) forms a group isomorphic to the group of Z4, which can be mapped to the four basis in the complex plane as we just mentioned.

Specifically, a second order basis may be constructed by the direct sum of the primitive basis

ϕ_{1}

and

ϕ_{2}

, i.e.

A = I \equiv (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}), F = i A, B = - A, a n d G = - i A

(2a)

Here the operator S can be taken as the identity

2 \times 2

matrix. The continuous transformation of the A and B states may be captured by forming a basis using exponential functions, i.e.

A \leftrightarrow e^{i θ} I; B \leftrightarrow - A; F \leftrightarrow i A; G \leftrightarrow - i A

(2b)

As the angle variable

θ

varies from 0 to

2 π

, the system transforms from state A to states F, B, and G, respectively. The generalization of coordinates (of the elements) from real to complex plane introduces F and G as energy elements and allows the energy transformation to be continuous (or performed in a closed connected space, Figure 1b).

Alternative basis equivalent to Eq. 2 can be straightforwardly constructed. For instance, we can take

A = σ_{1} \equiv (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix})

(3a)

A = σ_{2} \equiv (\begin{matrix} 0 & - i \\ i & 0 \end{matrix})

(3b)

A = σ_{3} \equiv (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix})

(3c)

Here the

σ_{i = 1,2, 3}

are the three Pauli matrices, and other elements F, B, G are given by the same relation as in Eq. 2. It is easy to see that the basis in Eq. 2 and Eq. 3 can form a larger group of

C 4 = Z 4 ⨂ P

(

P = \{I, σ_{1}, σ_{2}, σ_{3}\}

), and the basis in Eq. 3 may be generated from that in Eq. 2 by a unitary transformation. This scheme can be generalized to higher dimensional systems. For instance, the higher order basis may be constructed by the direct sum of the basis A and B, and the dimension of the base space is thus expanded from 2 to 4 (see Appendix A for details).

The primitive energy basis could be chosen as energy eigenstates of the system Hamiltonian, which can be mapped to the basis functions, e.g.

ϕ_{1,2} \to ϕ_{\pm} = e^{\mp i ω t}

. The corresponding primitive pair basis can be written by, i.e.

ϕ = (\begin{matrix} ϕ_{+} \\ ϕ_{-} \end{matrix})

(4)

If the primitive basis is mapped to the two elements A and B in Figure 1b, then the single primitive pair basis can be mapped to the vector

\vec{S}

, just like a rod with two ends, or a chemical bond with two atoms. The same four-state space mentioned above may be represented in terms of this primitive pair basis, e.g.,

E 4 = \{1, - 1, i, - i\}

. Note that the resulting space is not the energy space directly formed by primitive energy atoms, but a function (energy) space formed by function basis, which can represent the symmetry of the relation (or transformation) of the system (structure).

Other construction schemes based on primitive pair states exist for high order energy basis. One possibility is to use the linear combination of the primitive basis of the four-state system [53], i.e.

φ_{1} = \frac{1}{\sqrt{2}} (ϕ_{1} + ϕ_{2}); φ_{2} = \frac{1}{\sqrt{2}} (ϕ_{1} - ϕ_{2});

(5a)

φ_{3} = \frac{1}{\sqrt{2}} i (ϕ_{1} + ϕ_{2}); φ_{4} = \frac{1}{\sqrt{2}} i (ϕ_{1} - ϕ_{2});

(5b)

This scalar representation can be mapped to the vector form in terms of the primitive pair basis, i.e.

φ_{1} = (\begin{matrix} ϕ_{+} \\ ϕ_{-} \end{matrix}); φ_{2} = (\begin{matrix} ϕ_{+} \\ - ϕ_{-} \end{matrix}); φ_{3} = i (\begin{matrix} ϕ_{+} \\ ϕ_{-} \end{matrix}); φ_{4} = i (\begin{matrix} ϕ_{+} \\ - ϕ_{-} \end{matrix});

(5c)

Physically, the two bases in Eq. 5a may be mapped to the bonding and anti-bonding states of the energy modules of two primitive energy elements, while the two bases in Eq.5b correspond to the radiation states associated with the bond formation/breakage. These four bases span the same 4D state space

H_{2 \times 2}

. In the same spirit, another equivalent basis may be given by

φ_{1} = \frac{1}{\sqrt{2}} (ϕ_{1} + i ϕ_{2}); φ_{2} = \frac{1}{\sqrt{2}} (i ϕ_{1} + ϕ_{2});

(6a)

φ_{3} = \frac{1}{\sqrt{2}} i (ϕ_{1} + i ϕ_{2}) = \frac{1}{\sqrt{2}} (i ϕ_{1} - ϕ_{2}); φ_{4} = \frac{1}{\sqrt{2}} (- ϕ_{1} + {i ϕ}_{2});

(6b)

Since this composite basis is the unitary transformation of the primitive energy elements, and it is well-known that continuous transformation may be generated by three Pauli matrices as generators, we associate the three generators of Pauli matrices with different types of energy transformation and energy modules. The three types of unitary transformation generated by the Pauli matrices are [57]:

U_{i} (θ) = c o s θ / 2 + i σ_{i} s i n θ / 2

(7)

It is easy to see that the set of basis in Eq. 1 and 2 correspond to the transformations

U_{2} (\frac{π}{2}), U_{1} (\frac{π}{2})

, respectively. And the transformation

U_{3} (\frac{π}{2})

generates the third type of basis, i.e.

φ_{1} = \frac{1 + i}{2} ϕ_{1}; φ_{2} = \frac{1 - i}{2} ϕ_{2};

(8a)

φ_{3} = \frac{- 1 + i}{2} ϕ_{1}; φ_{4} = \frac{1 + i}{2} ϕ_{2};

(8b)

These are the energy modules used in our previous work [53] to represent the solution of Schrödinger Equation for a four-state system.

Energy transformation among the energy modules may be quantified, for example, by the unitary transformations in Eq. 7, which correspond to the rotation in energy space along a specific axis determined by the three Pauli matrices (Figure 1c). As a result, the energy space can be decomposed in three-dimensional (3D) space with each isosurface of total energy as a Bloch sphere. The three Pauli matrices, together with the identity transformation I, constitute generators of unitary group U(2), which are widely applied in quantum mechanics to quantify the symmetry of the system [58,59]. Nevertheless, the same symmetry or the same math may be interpreted in dramatically different ways. Then the question is how we choose what these abstract mathematical elements and corresponding transformations are responsible for? Or what is the mapping between this mathematical structure and the realistic system of interest?

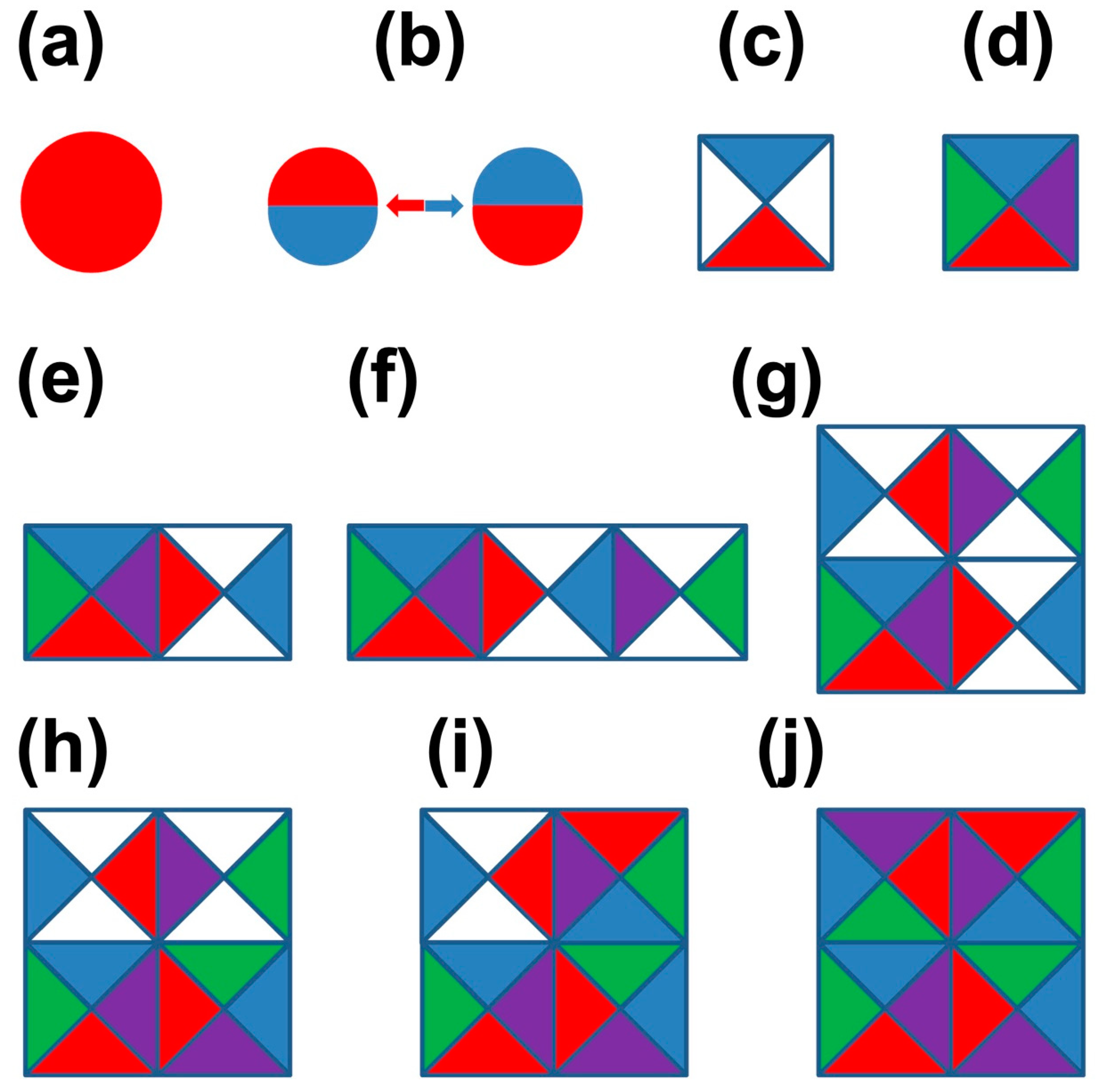
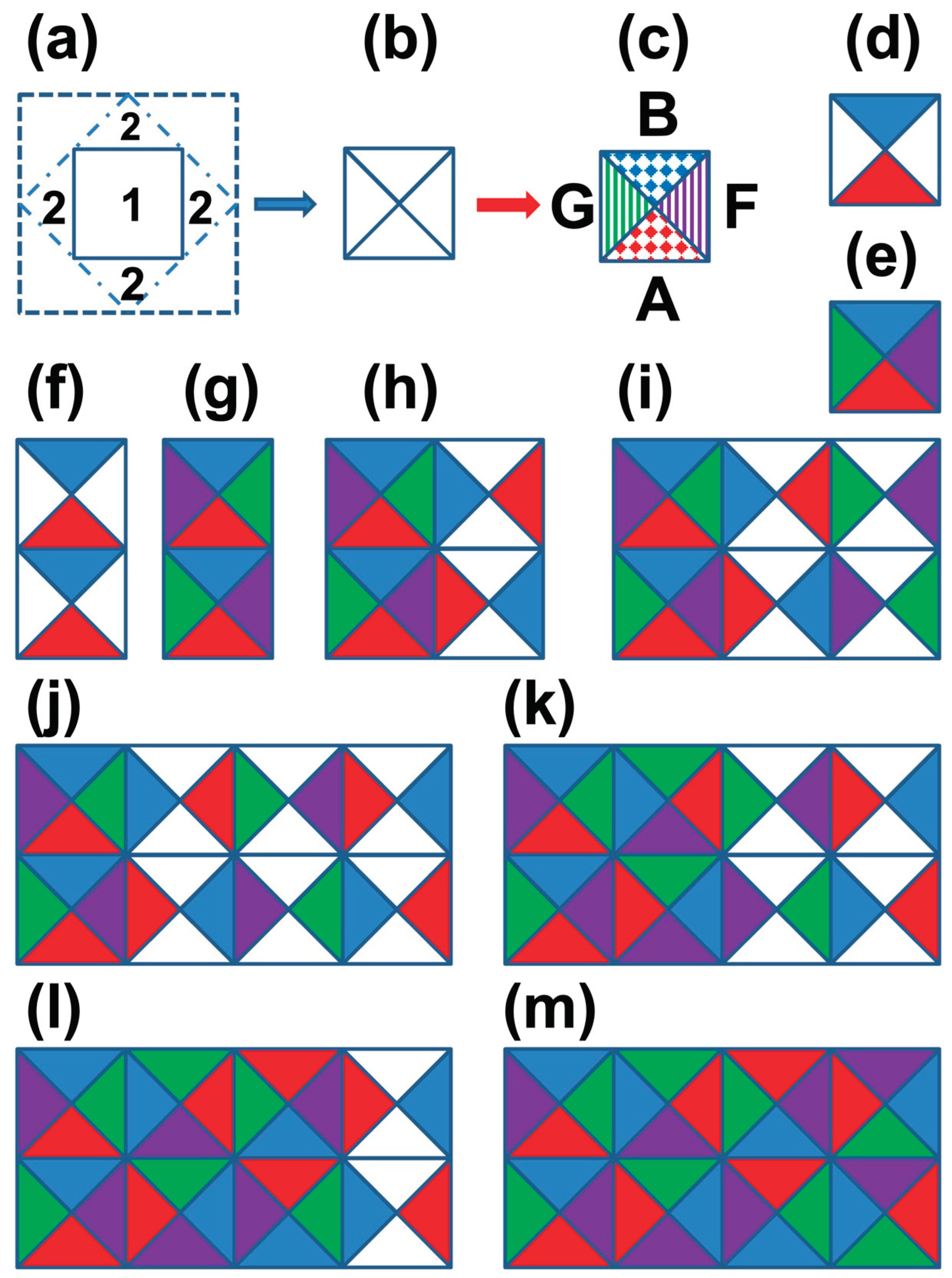
The mapping we focus on in this work is between the energy elements (and their transformations) and the elementary structure (and dynamics) of our world. We may start from identifying the three energy pair states dictated by the three Pauli matrices with different forms of fundamental energy modules, and we name them as shion, kongon and yunon [60], respectively. Together with the pair state associated with the identity matrix in Eq. 2 (we name it as benon), we obtain a group of generators of energy elements. These energy modules (Eq. 3, see Figure 1d for a 2D representation) constructed from the direct sum of the first order primitive energy basis (or energy elements), are associated with four types of elementary energy transformation (EET).

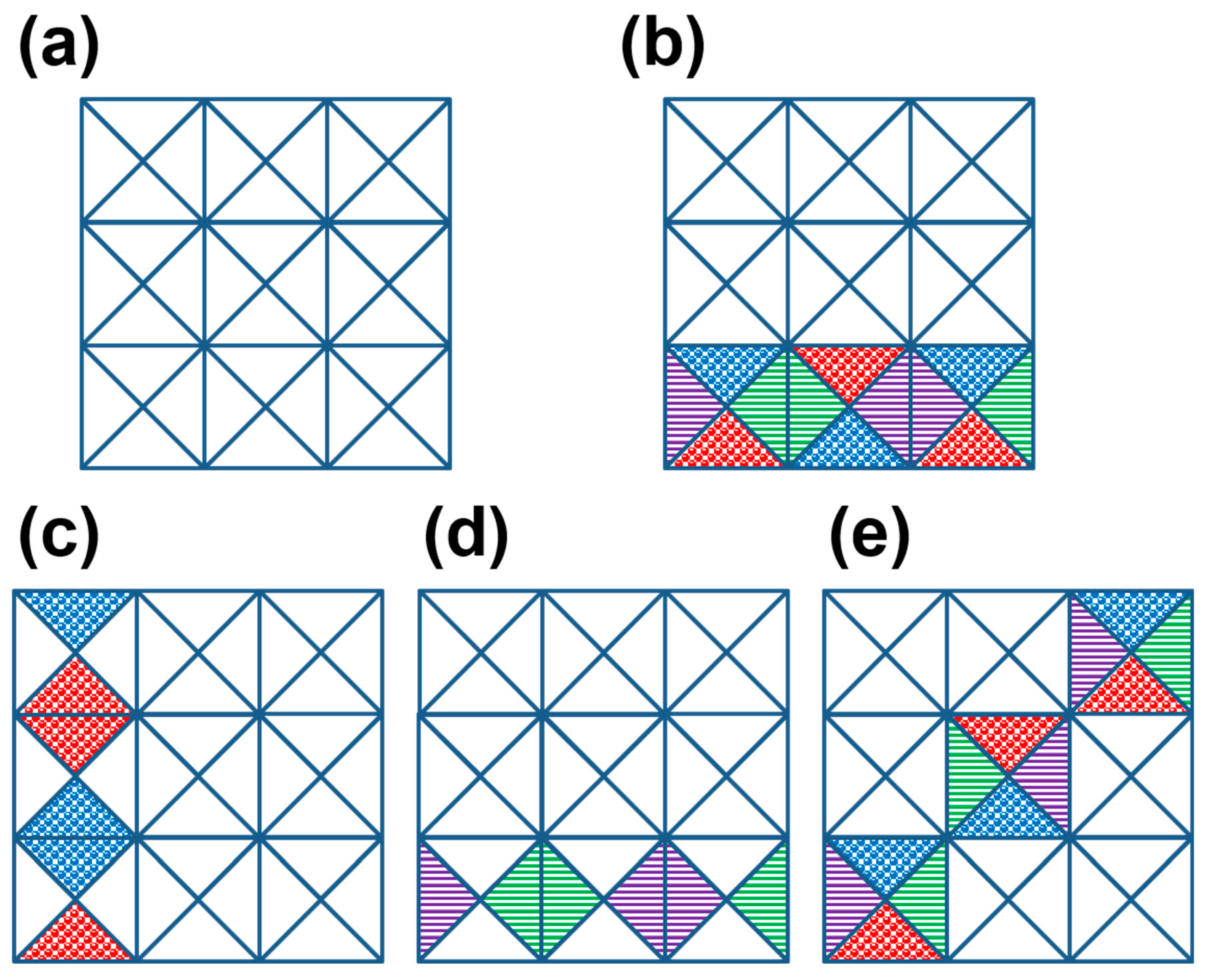
Our main postulation in this work is that energy fluctuation and transformation may be represented in terms of primitive energy basis (may be further identified with matter and radiation state), which can be associated with EET that generates time, space, cloud (see below), or other types of (higher level) structures. The model also maps quantum dynamics (motion in space-time) in energy space in terms of EET, with the space-time evolution of the system of interest represented by energy transformation among different energy modules. Combining the fundamental energy modules and elementary energy transformations, we construct a modular energy space (MES) as a framework to quantify or represent our world. In another word, the world can be generated from energy modules and energy transformations, in the same way as generating crystals from unit cells (see Figure 1e for representative energy cells) and symmetry transformation. Note that in our modular framework of energy transformation, time and space are quantized as the corresponding energy basis is quantized. In addition, there is no predefined spacetime or coordinates. One may create mathematical framework such as vector space to quantify the system, and even define nontrivial operation rules such as derivatives to describe spacetime transformations. Interactions (in particular the gravity) can be associated with coordinates based geometric objects such as curvature and connection [3,13,19,61]. However, geometrization based on nontrivial operation of simple basis is not the only way to quantify complex interactions. In fact, MES introduces hierarchical basis (energy modules) which may simplify the operation rules for high level interactions. This strategy also goes beyond the measurement description on the interactions in relative state or relational quantum mechanics [62,63].

The classification of energy modules in our mapping scheme not only results in a well-organized MES but also maps abstract energy basis to physical objects, thus provides quantitative descriptions of the structure, properties and transformations of the system of interest as what a conventional wave function can do. In another word, the wave function of the system may be represented in terms of its projection on energy modules in MES, which however has a well-defined deterministic interpretation in contrast to the conventional statistical interpretation. In addition, the evolution of the wave function can be characterized by the phase of the energy or the effective angle of the vector (and object) in MES. This is reminiscent of the de Broglie-Madelung-Bohm representation of the wave function of action angle variables, i.e.

ψ ~ A e^{i S / ℏ},

(9a)

for which the action S = \int p d q - E d t .

(9b)

And the amplitude A is associated with the probability density, which is responsible for quantum potential [6,7] causing quantum deviations from the classical dynamics. Note that the action may be represented by the integral of a generalized Lagrangian, i.e.

S = \int L (q, \dot{q}, σ) d σ .

(10)

Here q is generalized coordinate, (e.g., x or t),

\dot{q} = \frac{d q}{d σ}

is the generalized velocity, and

σ

is the affine parameter which characterizes the integration path. If we take

σ = t

, then Eq. 10 reduces to the action of the conventional Lagrangian

L (q, \dot{q}, t)

In contrast, the wave function in MES takes a new form in terms of action represented in the decomposed energy space, i.e.

ψ = e^{i S (E) / ℏ},

(11a)

which can be further expanded into a series:

ψ = e^{i / ℏ \sum_{n} S_{n}} .

(11b)

To interpret the physical meaning of the proposed wave function, considering the case there is only the first term, which represents for the scalar contribution to the action, i.e.

S_{1} = \int L_{1} d t = \int (H_{1} - E_{1}) d t,

(11c)

the corresponding wave function given by Eq. 11a reads:

ψ = e^{i \int L_{1} d t / ℏ} = e^{i \int (H_{1} - E_{1}) d t / ℏ} .

(11d)

Here

L_{1}

is the scalar Lagrangian,

H_{1} \equiv L_{1} + E_{1}

is the generalized energy and

E_{1}

is reference energy, i.e., the constant energy of a fundamental unit (e.g., energy atom). Assuming that a quantum mechanical system can be described by a wave function in the form of Eq. 11a-d, the time evolution of the system satisfies the first order ordinary differential equation (ODE) for a scalar energy state, i.e.

i ℏ \frac{d}{d t} ψ = (E_{1} - H_{1}) ψ .

(11e)

Here it is clear that explicit time dependence comes from the scalar energy fluctuation with respect to the reference (stationary) state, while the reference state may have internal time if it is multicomponent (see Appendix). In terms of internal time

τ

, time dependent Schrödinger equation for the reference state reads.

i ℏ \frac{\partial}{\partial τ} ψ = E_{1} ψ .

(11f)

In particular, when

H_{1} = 0

, which means there is no additional DOF other than the internal DOFs, the explicit time coincides with the internal time

τ

. On the other hand, the stationary state (eigenstate) is obtained when there is no energy fluctuation (

H_{1} = E_{1}

), i.e.,

H_{1} ψ = E_{1} ψ,

(11g)

with the eigenvalue of

E_{1}

. This corresponds to the case that internal DOFs are responsible for all the contributions to the generalized energy. These two cases represent for the two perspectives (interpretations) to the energy of the system, which may help illustrate the foundation of timeless quantum mechanics [62,64].

The single state case in Eq. 11c can be straightforwardly generalized to a multistate system, and the corresponding multistate quantum dynamics equation for an n-state system reads:

i ℏ \frac{d}{d t} ψ_{n} = (E_{n} I - H_{n}) ψ_{n} .

(11h)

with

ψ_{n}

the n-component wave function,

H_{n}

the corresponding generalized Hamiltonian represented by a

n \times n

matrix, and I the identity matrix. Eq. 11h can be solved routinely by diagonalizing the Hamiltonian matrix resulting in a representation (vector) space spanned by energy eigenstates [54]. It implies that unless all states are degenerated, explicit time dependence exists for multistate (n>1) systems. In addition, the hierarchical decomposition of the action (Eq. 11b) suggests that external and global time may be registered in a different hierarchy from the one where the system of interest is. Our model does not rely on the concept of position and the probability, and therefore seems to have no “problem of time” [10]. Note that the integral in the definition of action may be reduced to a discretized sum if only a quantum clock is available.

What is new here in Eq. 11a is that we represent the action and the corresponding Lagrangian (e.g., Eq. 11c-d) in the energy space in terms of a generalized Hamiltonian in the tensor form, rather than in the conventional space-time or momentum space. Specifically, we associate the n-th order action

S_{n}

with a generalized Hamiltonian tensor

H_{n}

corresponding to the contribution from the n-body (energy module) interactions, which can be further decomposed into the sum of irreducible tensors of rank l:

S_{n} = \int (H_{n} - E_{n} I) d t = \int (\sum_{0}^{n - 1} H_{n l} - E_{n} I) d t .

(12a)

As an example, let us explain our mapping scheme by considering a two-state system. The action is now decomposed into two terms corresponding to the contributions from the time integral of the scalar and vector energy (tensors), respectively, i.e.

\begin{array}{l} S_{2} = \int (H_{2} - E_{2} I) d t = \int (H_{20} + H_{21} - E_{2} I) d t \\ = \int (E_{20} - E_{2}) I d t + \int E_{21} \cdot σ d t . \end{array}

(12b)

To illustrate explicitly the mathematical structure of the energy space, a matrix representation is used in the last step of Eq. 12b (see Appendix A for details). The first term represents for the scalar transformation of the energy space discussed in Eq. 11. Here let us focus on the second term. As shown in the construction of energy modules, the vector transformation of energy modules can be represented by the generators of SU(2) group, i.e. the three Pauli matrices, which may be mapped to the three components of the irreducible spherical tensor of rank 1, different from the zeroth rank scalar tensor. Physically, these three types of vector transformation correspond to the rotations in the energy space shown in Figure 1a-c, in the 1, 2 and 3 dimensional space, respectively. And if we denote the two body inter-module energy transform rate as c, which is a constant in the free space, i.e., without higher order interactions, then the action can be rewritten into

\int E_{21} \cdot σ d t = \int \frac{E_{21}}{λ} T \cdot σ d λ t / T = \int \frac{E_{21}}{c} \cdot d x .

(12c)

Here we define the vector

x \equiv σ c t

, and

c = λ / T

given by the ratio of the characteristic length and time of energy modules.

Similarly, the tensor expansion of action for a three-state system results in the form of integrals of various types:

S_{3} = \int (H_{3} - E_{3} I) d t = \int {E'}_{3} d t + \int p_{3} \cdot d x + \int m_{3} : d Ξ .

(12d)

where

{E'}_{3} = E_{30} - E_{3} I, p_{3} = \frac{E_{31}}{c}, m_{3} = \frac{E_{32}}{c^{2}}

, and

Ξ = ω r r

. Thus, they represent for the contribution of multipole terms of scalar, vector, and second order tensor (matrix), respectively, which again may be mapped to different types of energy transformation in MES. Higher order terms could be included explicitly; otherwise, we might be able to regard Eq.12d as a period of three loop, and represent higher order terms by using the same energy modules renormalized at different levels.

The tensor expansion of the generalized action in Eq. 12 suggests that the scalar fluctuation of action generates (scalar) energy (shion, or scalar mass state), and the corresponding scalar energy transformation creates time. Similarly, the vector fluctuation of action generates momentum (kongon, or radiation state), and vector energy (radiation) transformation creates space; the matrix fluctuation of action generates mass, and matrix energy transformation creates cloud (see Figure 2). This mapping scheme may be extended to higher-level expansions, which corresponds to the generation of higher dimensional space. Here our model implies that there may exist different levels of expansion: for the first level, there exist only scalar module; for the second level, there are both scalar and vector modules; and for the third level, there exist scalar, vector and matrix (second order tensor) modules, and so on. This seems exactly the same rule followed by chemical elements to fill in the periodic table. And it is the set of quantum numbers to determine the energy levels. Therefore, we propose that energy elements follow the same filling rule. For instance, the principal quantum number determines the level, and the angular momentum quantum number determines the sublevel, i.e., l=0 (scalar), l=1(vector), and l=2(matrix). (See Appendix A for further details). Correspondingly it suggests that there exist different levels (hierarchies) of worlds or universes, i.e., scalar energy (time) world, vector energy (time space) world, and matrix energy (e.g., time-space-cloud) world, etc.

To make the connection with conventional quantum dynamics, we consider a simple particle moving in 1D space with a constant momentum, and rewrite the three matrix expansion terms of action in Eq. 12d in an equivalent form in terms of the generators of energy transformation using Pauli matrices, i.e.

S = - E \int (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) d t + p \int (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) d x + m \int (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) d Ξ,

(13)

which are mapped to the contributions to the action from the energy modules of shion, kongon and yunon in MES, respectively. Note that the last term may be combined with the first two terms resulting in a renormalized space-time. Then Eq. 11 can be reduced to the conventional wave function

ψ ~ e^{- i (k x - w t)}

. In addition, Eq. 13 may be mapped to a two-state system resulting in the Klein Gordon Equation. On the other hand, Eq. 11-13 can be straightforwardly generalized to the more complicated cases, through a variety of ways including dimensional expansion and time discretization. For instance, the wave function for a system of two two-state particles (four-state) may be obtained from Eq. 11 using a Hamiltonian expanded in

4 \times 4

matrices and a time discretized form may be given by:

S_{1} = - E \sum (\begin{matrix} I \\ - I \end{matrix}) ∆ t,

(14a)

S_{2} = p \sum (\begin{matrix} I \\ - I \end{matrix}) ∆ x;

(14b)

S_{3} = m \sum (\begin{matrix} I \\ - I \end{matrix}) ∆ Ξ;

(14c)

The corresponding wave function apparently satisfies the Schrödinger equation.

Note that the wave function in Eq. 11 represents for the single trajectory in the energy space, and the ensemble of trajectories may be used for a collection of particles exactly like applying statistical mechanics based on classical trajectories for complex systems. And the initial condition of the ensemble is thus given by

ψ (\{c_{E}\}, 0)

, which is the wave function at time 0, with the coordinates

\{c_{E}\}

(projections on energy modules). This is in contrast to the de Broglie-Madelung-Bohm representation in Eq. 9, which itself is a nonlocal wave function with a time dependent magnitude associated with the probability density (therefore the statistical interpretation has already built-in for the single trajectory). In addition, all the time dependent parts are incorporated into the exponential term in Eq. 11, which is in fact the time evolution operator with respect to a non-interacting hierarchical reference state if we write the action into the time integral of the corresponding Hamiltonian, i.e.

e^{i / ℏ \int \sum_{n} (H_{n} - E_{n} I) d t} .

(15a)

Therefore, it is not surprising that Eq. 11a indeed describes the time evolution of the system in the energy representation and satisfies Schrödinger Equation, which also bears the feature of the matrix representation as suggested in Heisenberg’s matrix mechanics [54,55].

To compare with the conventional definition of the action in Eq. 9, we write the action in Eq. 11 as

S = \int p d x - H d t \leftrightarrow S = \int (H - E) d t .

(15b)

Here we generalize the first term in the conventional action into the energy tensor in energy space (c.f. Eq. 11 and 12) and identify the conventional (scalar) Hamiltonian as the total energy of the system. The system Hamiltonian matrix may be constructed from the energy tensor (see Appendix A), and when applying the stationary phase condition (or equivalently the principle of least action), we obtain the Newton equation, i.e.

\frac{\partial p}{\partial t} = - \frac{\partial E}{\partial x} = F;

(16a)

and similarly, \frac{\partial p}{\partial Ξ} = \frac{\partial m}{\partial x} .

(16b)

In addition, from the constructed wave function, the relativistic Klein-Gordon (or multistate Schrödinger) equation follows, i.e.

\frac{\partial^{2}}{\partial t^{2}} ψ = c^{2} \frac{\partial^{2}}{\partial x^{2}} ψ + c^{4} \frac{\partial^{2}}{\partial Ξ^{2}} ψ .

(16c)

Note that our formalism implies that the unitary transformation with invariant time and space guarantees energy and momentum conservations, respectively, whereas that with invariant cloud guarantees mass conservation. In addition, this hierarchical world picture built on MES suggests a molecular interpretation to the renormalization in conventional quantum theory for fundamental particles and interactions (to be further investigated in future works).

2.2. Time Space Transformation

The equivalency of energy momentum relation in MES and space-time dynamics (both are related to each other through integral transformations) facilitates detailed analysis on the structure of energy space and stimulate new physical insights into energy transformation. For instance, energy transformation is apparently not necessary to be unimodular, described by the three Pauli matrices. In fact, any trajectory in the energy space may correspond to a particular energy transformation pathway, just as a trajectory in the phase space representing for a particular space-time transformation of the system of interest.

To illustrate the MES perspective on energy transformation, let us consider a free particle in 1D space. According to the wave function in terms of energy tensor expansion of action, the equation of motion (EOM) is a generalized Klein Gordon equation (Eq. 16):

- ℏ^{2} \frac{\partial^{2}}{\partial t^{2}} ψ^{'} = (- ℏ^{2} c^{2} \nabla^{2} {- ℏ^{2} c}^{4} \frac{\partial^{2}}{\partial Ξ^{2}}) ψ^{'},

(17)

and the solution may take the form of

ψ (x, t, Ξ) ~ e^{i (k x - ω t + μ Ξ)}

(18a)

with

k, ω

are the wave vector and frequency, respectively. Following the pattern in the conventional form, the additional third term in the phase comprises

Ξ = 2 π ν σ

, the cloud area rate in the cloud (space), and the associated variable

μ = m_{0} / ℏ

, called the wave matrix. Here the energy relation (or energy representation of EOM in MES) reads:

E^{2} = E_{R}^{2} + E_{M}^{2} .

(18b)

As radiation energy (or k) decreases, a pure mass state may be obtained when all attached intermediate bosons leave away.

If the square of radiation energy further decreases (k becomes into imaginary, i.e.,

k = i κ

), we may have

ψ (x, t) ~ e^{- κ x - i ω t + i μ Ξ},

(19a)

and E^{2} = - E_{R}^{2} + E_{M}^{2} .

(19b)

Now radiation becomes internal and may be written into

\frac{ℏ c}{ξ} = \frac{ℏ}{ξ / c} = \frac{ℏ v}{ξ_{0}},

(20)

with

ξ

being the coherence length of internal radiation, and the Compton wavelength

ξ_{0} = \frac{ℏ}{m_{0} c}

. Therefore Eq. 19 indicates that as the coherence length decreases to the Compton wavelength or the internal time

ξ / c

decreases to the characteristic time (or the effective velocity of the confined particle increases from zero to the speed of light), the mass state may turn into (or is balanced by) a coherence state in full. The resulting state can be associated with the MLNP, generated from mass state by approaching full quantum coherence (QC) in the internal limit.

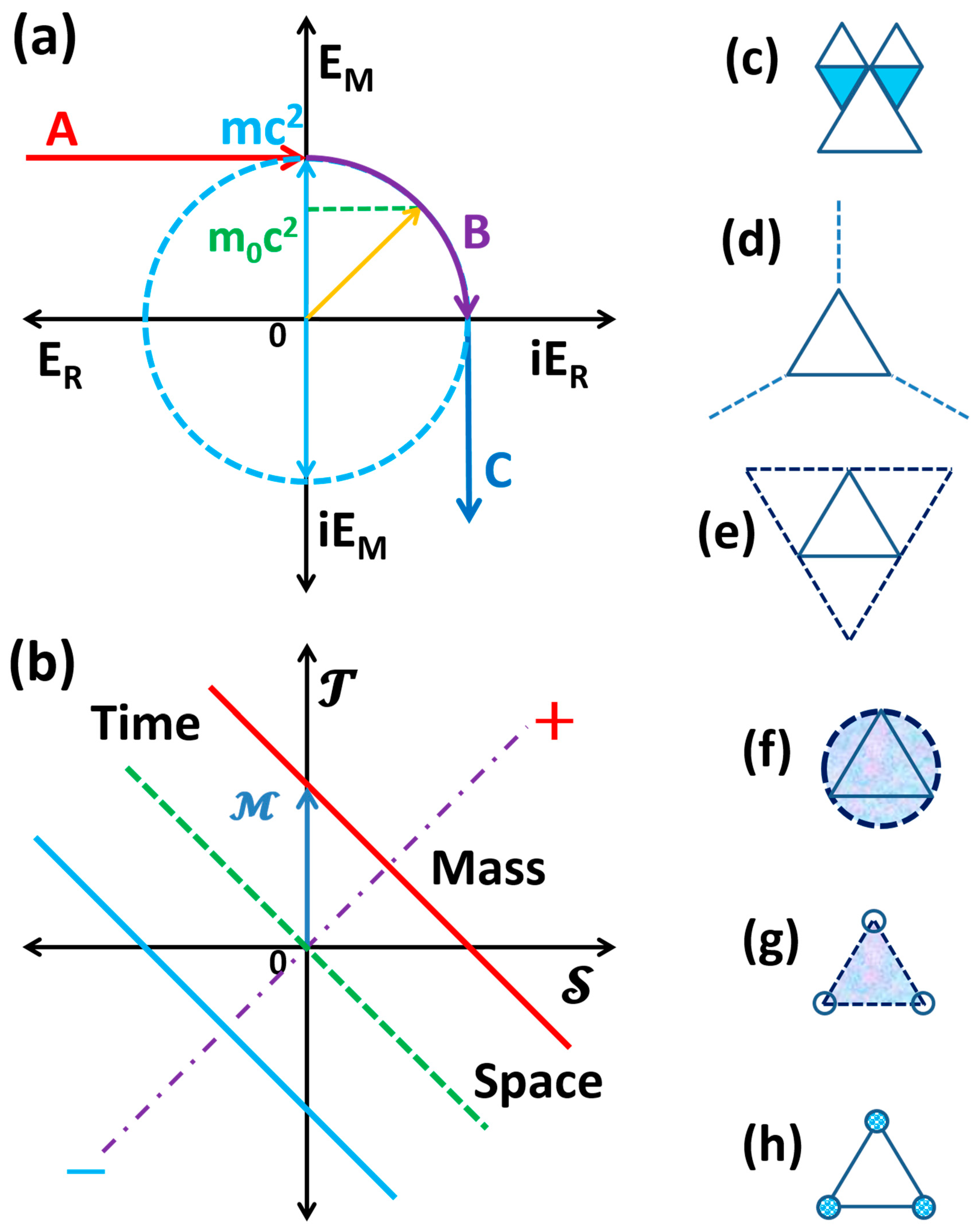
Clearly, Eq. 18 and 19 represent for two classes of states: one is free wave and the other is confined wave corresponding to external and internal QC, respectively. They are involved in two typical routes (A and B) shown in Figure 3a. At the point where the MLNP is generated, the original total energy of the particle decreases to zero. As the coherence length further decreases or the radiation energy further increases, the square of the total energy would become negative (route C in Figure 3a,

ω = i Ω

). Then we have

ψ (x, t) ~ e^{- κ x + Ω t + i μ Ξ},

(21a)

and - E^{2} = - E_{R}^{2} + E_{M}^{2} .

(21b)

Here to retain the positivity of energy square, we explicitly extract the negative sign out in Eq. 19b and 21b. After rearranging the order of terms, well-behaved energy relation recovers as shown in Table I. And this operation implies certain transformation may occur as the nature of pathways changes. Indeed, Figure 3b illustrates transitions among different regimes in a generalized energy space via characteristic lines:

T = S + M

(22)

with

T {\equiv E}^{2}, S \equiv E_{R}^{2}, M \equiv E_{M}^{2}

. Accordingly, the energy space is decomposed into the time-like, mass-like and space-like sectors. The time-like domain corresponds to the external world, and the space-like domain is associated with the internal world, in which the role of time and space shifts, i.e., the internal radiation behaves like shion whereas the internal mass state behaves like radiation. Interestingly external radiation pair state may generate vast space in the time-like domain whereas internal radiation pair state could generate various time loops in the spatial confined space-like domain. In comparison with energy transformation in the previous section, the pathways A and C here describe open systems while pathway B is for closed systems, the same as those captured by three Pauli matrices. Alternatively, we may regard the pathways A and C as physical transformations (magnitude changed) while those defined by Pauli matrices as chemical transformations (module changed).

Table 3. a, in line with the corresponding wavefunction, D’Alembertian operator, and transformation angle

θ

Table 3. a, in line with the corresponding wavefunction, D’Alembertian operator, and transformation angle

θ

Route	A (Time-like)	B (Mass-like)	C (Space-like)
Energy relation	$E^{2} = E_{R}^{2} + E_{M}^{2}$	$E^{2} = - E_{R}^{2} + E_{M}^{2}$	$- E^{2} = - E_{R}^{2} + E_{M}^{2}$
Rearranged	$E^{2} = E_{R}^{2} + E_{M}^{2}$	$E_{M}^{2} = E^{2} + E_{R}^{2}$	$E_{R}^{2} = E^{2} + E_{M}^{2}$
states	$e^{i (k x - ω t + μ Ξ)}$	$e^{- κ x - i ω t + i μ Ξ}$	$e^{- κ x + Ω t + i μ Ξ}$
Operator upon basis change	$\nabla_{c t}^{2} - \nabla_{x}^{2}$	$\nabla_{c t}^{2} + \nabla_{x}^{2}$	$\nabla_{x}^{2} - \nabla_{c t}^{2}$
$θ$	0	$(0, π / 2)$	$π / 2$

From the time-like domain to the space-like domain (route A vs. route C), the mass energy term in the energy relation keeps invariant while the total energy changes from scalar (mass) energy to radiation energy, which implies that the role of two components switches, and correspondingly the role of time and space switches. From route A to B, the external time is substituted by the characteristic time associated with the rest mass, and the external world turns into an internal world. The role of time and space switches along route B in the mass-like domain as the connection between routes A and C. From route B to C internal radiation (with the feature of internal time) increases (Figure 3c-h). If we define the spatial basis in the space-like domain to be ct, and the time to be x/c, then the energy relation (and physical laws) would be invariant.

To be specific, instead of transforming state variables, the basis transformation in route B may be obtained by the following mapping:

(\begin{matrix} c t \\ x \end{matrix}) = (\begin{matrix} σ c o s θ \\ σ s i n θ \end{matrix}),

(23a)

which gives the transformation of the line elements, i.e.

(\begin{matrix} d σ \\ σ d θ \end{matrix}) = (\begin{matrix} c o s θ & s i n θ \\ - s i n θ & c o s θ \end{matrix}) (\begin{matrix} d c t \\ d x \end{matrix}) .

(23b)

In the time-like domain (

θ = 0

), we have

σ = c t

; while in the space-like domain (

θ = π / 2

σ = x

; and in the mass-like domain in between transformation between time and space occurs. Such basis transformation provides a new perspective different from analytical continuation of corresponding variables into complex plane [65,66,67].

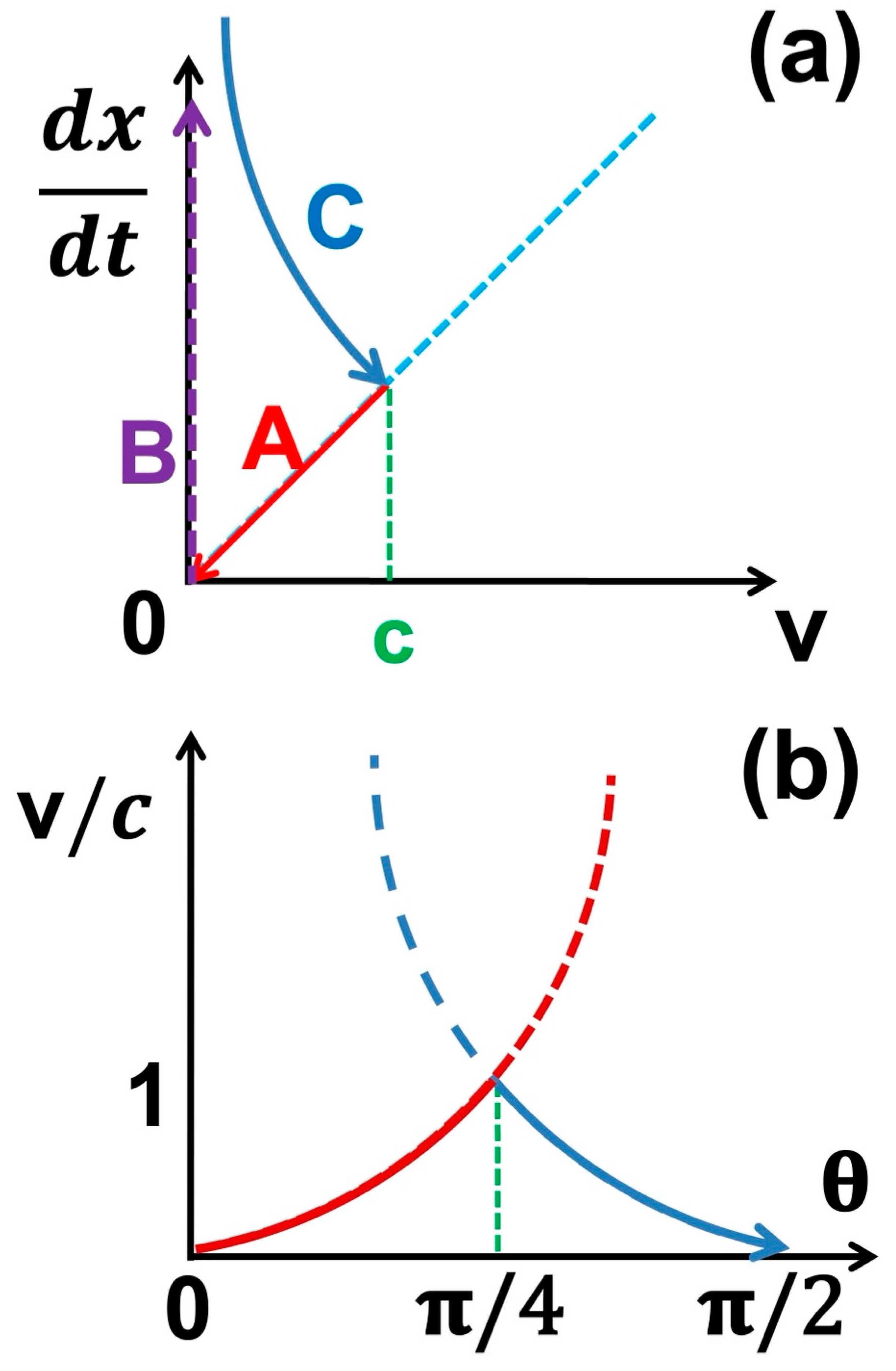
This timespace transformation (TT) may correspond to a quantum phase transition. The crossover behavior is illustrated in Figure 4a. In the time-like domain (external world), the velocity decreases from c to zero, as external intermediate bosons being detached. The mass-like domain in the expanded energy space connecting both time-like and space-like domains in which the role of time and space is exchanged so that the rate dx/dt switches from zero to infinity. Note that for fixed

θ

\frac{d x}{d t} = c t a n θ

in Eq. 23b, and therefore

θ

serves as the order parameter of phase transition (Figure 4b). At

θ = π / 4

, time and space become degenerated, marking the transition point in the mass-like domain. In the space-like domain, if the confined internal intermediate bosons can be excited, the velocity could also increase from zero to c, approaching a limit to form a closed loop in the diagram.

The TT transformation can be associated with the yunon transformation generated by the Pauli matrix

σ_{3}

, which may involve both particle and antiparticle in the same way as the annihilation of particle and antiparticle into radiation corresponding to the kongon transformation generated by the Pauli matrix

σ_{2}

. The kongon and yunon may be mapped to the external flux and internal coherence, respectively, both of which are key components of the constructed energy space at different levels of the hierarchical structure. The kongon transforms energy among different modules in the same framework while by contrast the yunon transforms energy within the same module. The free kongon propagates at the light speed marked the interface separating the internal and external worlds. In the internal world, kongon becomes time-like whereas the shion becomes space-like which however does not have to be bounded by a confined length.

2.3. Energy Dynamics

A quantum theory of motion is one of the key components of the foundation of quantum mechanics. The standard quantum theory suggests that motion is captured by the time evolution of the probabilistic wave (function) in space and the concept of classical trajectory is discarded. In the de Broglie-Madelung-Bohm representation, the trajectory concept is restored and motion is attributed to the propagation of the wave front [6,7,68] of a nonlocal wave. While in relativistic quantum mechanics, the energy momentum relation indicates that the moving particle may be regarded as the compound of pure (rest) mass state and radiation state carrying a specific momentum [53]. Since the dynamics of a system of interest is represented by energy transformation in the proposed MES framework, such a mapping or quantization results in a classical like deterministic trajectory in energy space and provides a molecular interpretation on the underlying mechanism. The question is how exactly this coherent compound works? Here we elaborate the idea and illustrate how energy transports in the generated space-time.

As shown in our previous work [53], the basis associated with the identity matrix (benon) could form the underlying framework for energy transformation by setting the energy module as the ground state. Therefore, it may provide the base as both the support and interface for energy quanta represented by primitive energy modules, as shown in Figure 5a for a possible configuration of the generated space. Note that this generated space is the real space, which is one particular representation of the general energy space. The background space may comprise (infinitely) many energy modules in the ground state, while the dynamics of the considered energy quantum could proceed as exciton transport (Figure 5b) and the energy transformation among different modules play a decisive role in energy transport. Note that the constituent modules of the background space have their own spacetime structures, which make it possible to illustrate the underlying molecular mechanism of quantum dynamics in spacetime, in contrast to the various quantum gravity models [27,28,29].

The time evolution of a system can thus be represented by the unitary transformation of the state determined by the action angle variable, provided the total energy be conserved. And the action involves the contributions from the elementary operations corresponding to different energy modules (Eq. 12). As an example, Figure 5c-e display the space-time diagram for three types of motions of a single energy quantum, i.e., time evolution, space evolution, and space-time evolution. This modular energy diagram (MED) can also be used to illustrate the energy transformation in a generalized energy space (not shown). The equation of motion in the time dominated domain (Figure 3) is given by

E^{2} = E_{R}^{2} + E_{M}^{2}

, in which energy (shion) comprises the contributions from kongon and yunon, which may transform between each other. Alternatively, if the energy transformation proceeds along the space dominated path, then EOM would be

E_{R}^{2} = E^{2} + E_{M}^{2}

. Similarly, energy transport may also occur in a mass dominated domain in which energy transforms between shion and kongon, with the corresponding EOM

E_{M}^{2} = E^{2} + E_{R}^{2}

Then what exactly takes place on the microscopic scale and what is the underlying molecular mechanism? Now consider an energy quantum with a specific momentum, the dynamical process may be described by the elementary operations involving three Pauli matrices, e.g.,

σ_{2} σ_{3}

(see Figure 6a). Each of such elementary operation makes a forward move of 1/4 unit cell along the direction of the momentum. After each of such move, the role of time and space, and therefore the role of matter and radiation are switched. Once the four steps complete, the original state of the energy quantum recovers, and a whole period is achieved. For each step the mass state operates, the clock starts to run; whereas when the radiation state operates, the position varies. And the alternative activation of shion and kongon results in a limiting (light) speed of the radiation particle.

To further illustrate energy transformation in the Hamiltonian form, let us first consider a molecular model based on primitive energy modules for a single intermediate boson or radiation particle (e.g., photon). We start from a four-state model [53], for which the multistate quantum dynamics equation reads:

i ℏ \frac{d}{d t} (\begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix}) = (\begin{matrix} I m_{0} c^{2} & i σ \cdot c p \\ - i σ \cdot c p & - I m_{0} c^{2} \end{matrix}) (\begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix}),

(24a)

with the up and down components for each ψ_{i} = (\begin{matrix} ψ_{i}^{u} \\ ψ_{i}^{d} \end{matrix}), i = 1,2

(24b)

Note that Eq. 24a is ODE since the generalized Hamiltonian in energy space (no position or momentum space) is used. For simplicity, we assume that the radiation particle propagates freely along the z axis with a momentum of p, that is

p_{x} = p_{y} = 0

, then the Eq. 24 becomes into

i ℏ \frac{d}{d t} (\begin{matrix} \begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix} \\ \begin{matrix} ψ_{3} \\ ψ_{4} \end{matrix} \end{matrix}) = (\begin{matrix} \begin{matrix} m_{0} c^{2} & i c p \\ - m_{0} c^{2} \end{matrix} & 0 \\ 0 & \begin{matrix} m_{0} c^{2} \\ - i c p & - m_{0} c^{2} \end{matrix} \end{matrix}) (\begin{matrix} \begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix} \\ \begin{matrix} ψ_{3} \\ ψ_{4} \end{matrix} \end{matrix}) .

(25)

Here we model a single radiation particle in MES as a compound of different energy modules, e.g., two shions plus one directional kongon [69]. And it propagates like an energy train as energy transforms between different forms and transports among different modules along the z axis. Starting from the configuration given by Eq. 25, a straightforward calculation using the unitary transformation suggested in previous work [53], results in the multicomponent wave function as the follows:

\begin{array}{l} Ψ_{1} = e^{- i ω t} - \frac{i c p}{2 E} (e^{- i ω t} + e^{i ω t}); ψ_{2} = e^{i ω t}; \\ ψ_{3} = e^{- i ω t}; ψ_{4} = e^{i ω t} + \frac{i c p}{2 E} (e^{- i ω t} + e^{i ω t}) . \end{array}

(26)

The results indicate that the energy flow of kongon pull the energy train running along the z axis, during the first 1/4 period. Once the energy train moves one step forward, the modules in the middle (H₂₂ and H₃₃ in bold) can combine together to transform into a yunon,

i ℏ \frac{d}{d t} ψ = (\begin{matrix} \begin{matrix} i c p \\ m_{0} c^{2} \end{matrix} & 0 \\ 0 & \begin{matrix} - m_{0} c^{2} \\ - i c p & m_{0} c^{2} \\ - m_{0} c^{2} \end{matrix} \end{matrix}) ψ

(27)

and the Hamiltonian becomes into

H (t + ∆ τ) = (\begin{matrix} \begin{matrix} i c p \\ m_{0} c^{2} \end{matrix} & 0 \\ \begin{matrix} m_{0} c^{2} \\ - i c p \end{matrix} & \begin{matrix} m_{0} c^{2} \\ m_{0} c^{2} \end{matrix} \end{matrix}) .

(28)

Now, it is time for kongon to move forward as yunon serves as both the interface and the driving force between adjacent kongons, and the particle propagating line shifts to the kongon and at this step kongon and yunon play the same role of shion and kongon in the previous step, respectively. The solution can be found following the same strategy as in previous work [53], which indicates that the kongon propagates one step forward through the mediation of yunon (see the Appendix A for details). In the next step, yunon transforms back to shion again, and energy transformation occurs through the time line again under the help of kongon. Altogether the energy train moves forward a distance of one module of kongon during the half period of shion. This corresponds to half wavelength noting the sign change of shion. The next half period follows the same pattern and this three-module “photon” propagates at a constant velocity of

v = \frac{δ L}{δ τ} = \frac{λ}{T} = c,

(29)

Here the T and

λ

are the charachteristic time and length of the corresponding energy quanta, i.e., shion and kongon, respectively.

Inspired by the relativistic energy momentum relation, we propose that [53] the motion of a massive particle is attributed to the carriage of a moving energy quantum or a radiation particle (e.g., the three-module “photon” considered above), just like a passenger on an energy train. Here we explain this molecular model in more details. Consider a particle of mass m coupled with a single intermediate boson of momentum p along the z axis, the corresponding multistate quantum dynamics equation may be written by

I ℏ \frac{d}{d t} (\begin{matrix} \begin{matrix} \begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix} \\ ψ_{3} \end{matrix} \\ \begin{matrix} ψ_{4} \\ ψ_{5} \end{matrix} \end{matrix}) = (\begin{matrix} \begin{matrix} m_{0} c^{2} & i c p \end{matrix} & \begin{matrix} m c^{2} \\ - m c^{2} \end{matrix} \\ \begin{matrix} - m_{0} c^{2} \end{matrix} & \begin{matrix} m_{0} c^{2} \\ - i c p & - m_{0} c^{2} \end{matrix} \end{matrix}) .

(30)

In comparison with Eq. 25, the attached particle is sitting on the energy train (Figure 6b). When the train starts to move, it transports along the z axis the same way as that in the single “photon” case in the first 1/4 period. However, when energy module transforms from shion into kongon, the existing massive particle would block the way of energy transformation and extra time is required for the completeness of transformation. The transition time for the compound is

\frac{τ^{'}}{τ_{0}} = \frac{\sqrt{{(m_{0} c^{2})}^{2} + {(p c)}^{2}}}{p c} = \frac{E}{p c} .

(31)

Once the transition completes, the energy transport follows the same flowchart as that in Eqs. 25-28 and therefore the velocity of the moving particle is given by

v = \frac{L}{τ^{'}} = c \frac{p c}{E} = v .

(32a)

Alternatively, to carry the massive particle, part of the energy of the radiation particle has to be used to power the cloud transformation (Figure 6c-e), which costs extra time on motions orthogonal to the momentum of the radiation particle. And the energy partition on these two types of motions is proportional to the energy ratio of the radiation and the massive particles, i.e.

\frac{p c}{m_{0} c^{2}} = \frac{v}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} .

(32b)

Here the same velocity of the massive particle is obtained. Our analysis indicates that it is the energy transport among energy modules responsible for the motion of a particle. And elementary building blocks such as shion, kongon, and yunon (plus benon) constitute matter, transformation and our world (see further discussions below).

If we represent energy modules in the form of second order tensor, i.e., matrix, the energy transport may be described by Liouville equation in terms of density matrix according to the mapping between energy modules and density matrices. Let us take a two-state model to explain the molecular framework for energy transport. The dynamics of the system can be generated by Liouville equation as the follows:

\frac{d ρ}{d t} = \frac{i}{ℏ} [ρ, H],

(33)

with

ρ

the density matrix,

H

Hamiltonian, and

ℏ

the circular Planck constant. Eq. 33 may be rewritten in the form of optical Bloch equation [70],

\frac{d}{d t} D = (\begin{matrix} 0 & - w & v \\ w & 0 & - u \\ - v & u & 0 \end{matrix}) D

(34a)

with the definition of

D \equiv (\begin{matrix} P \\ C \\ F \end{matrix}) = (\begin{matrix} ρ_{11} - ρ_{22} \\ ρ_{12} + ρ_{21} \\ (ρ_{12} - ρ_{21}) \end{matrix}),

(34b)

which may be mapped to three Pauli matrices. Eq. 34 can be solved routinely and the solution has been widely applied as a key component for dynamics of a system involving a large number of degrees of freedom [57,70]. The space-time evolution of the system thus can be well-captured by the rotation of the unimodular vector on the surface of Bloch sphere.

To apply this density matrix representation to describe energy transformation in the energy space, Eq. 34 has to be recast into a quantized energy space and generalized to incorporate multiple modules. Let us again take the example of a massless boson (e.g., photon) comprising six primitive energy modules. Suppose that at the initial time, a radiation particle represented by a compound of two shions and one kongon carrying an energy quantum of cp (c.f. Eq. 25) moves at a constant speed of c. The EOM of the particle can be obtained by discretizing Eq. 34 into the following steps, i.e.

First step:

P \to C

P (t + ∆ τ) = P (t) - w C (t) ∆ τ

(35a)

C (t + ∆ τ) = w C (t) ∆ τ

(35b)

Second step:

F \to F'

F (t + ∆ τ) = F (t) - u C (t) ∆ τ

(36a)

F' (t + ∆ τ) = F' (t) + u C (t) ∆ τ

(36b)

Third step:

P \to C

P (t + 2 ∆ τ) = P (t + ∆ τ) + v F' (t + ∆ τ) ∆ τ

(37a)

C (t + 2 ∆ τ) = - v F' (t + ∆ τ) ∆ τ

(37b)

These three primitive steps constitute one elementary step for the energy transport, after which the particle moves forward half period of characteristic time (and length). Here the propagation of the particle is fully quantum in each step, resulting in EOM in the kinetic form, which corresponds to the first three steps considered in the multistate quantum dynamics equation (c.f. Eq. 25-28). If the energy modules can be further divided, for instance, if the time can be discretized into N small segments, resulting a smaller time step, i.e.,

∆ τ = ∆ t / N

, then the discrete kinetic Eqs. 35-37 would become to a conventional continuous EOM as the number of steps N tends to infinite at the classical limit. Therefore, for each smaller time step

∆ τ

, the particle moves only a small fraction of the characteristic length, say l/N (see Figure 6f for an example case). Note that the speed of the particle is unchanged (the radiation particle with different wavelength travels at the same speed of light). Also, the radiation particle carried by a classical particle has a typical energy much lower than mass energy of the massive particle itself, so that the massive particle could be quite localized in comparison with the characteristic length

λ

3. Applications

3.1. Atomic Model

The energy tensor representation of the space-time structure and dynamics offers new physical insights into the atomic structure, and a consistent classical quantum mechanical interpretation can be obtained for Bohr’s atomic model of hydrogen atom without the aid of the ad hoc correspondence principle. First, we start for the stationary states. According to Dirac, the state corresponds to a particular type of motion [71]. On the other hand, our classical quantum theory suggests that motion is attributed to the attached radiation particle. It is therefore natural to propose that the state quantization is attributed to the quantization of radiation. Next, we will show that this is in fact the truth.

The energy of the electron in hydrogen atom may be obtained by the Dirac equation including both the mass energy and radiation energy:

E = \sqrt{m^{2} c^{4} + p^{2} c^{2}} \approx m c^{2} + \frac{p^{2} c^{2}}{2 m c^{2}} .

(38)

Thus, if the second term in Eq. 38 is identified with the interaction potential caused by the internal radiation, we arrive at

r_{0} = \frac{4 π ε_{0} ℏ^{2}}{m e^{2}},

(39a)

and E = m c^{2} + \frac{e^{2}}{8 π ε_{0} r_{0}} .

(39b)

These are in fact the Bohr radius and the ground state energy of the electron, respectively. Note that in Eq. 38 and 39b, we do not include explicitly the potential term, the effective interaction responsible for the specific motion. In another word, in our model it is the radiation generates motion and dynamics and we do not need to introduce extra ad hoc potentials. The proposed potential free model suggests that the (generalized) Lagrangian

L = T = H

, and Eqs. 11e and 11h are essentially the Schrödinger equations except that the sign of the time flips, which can be understood as the time used becomes effectively internal. Surely, the inter-state interactions mediated by radiation states may be modeled by potentials or external fields used in conventional treatments [72,73,74]. However, we believe that the introduction of sometimes empirical potentials is one of the main sources causing misleading inconsistencies and technical difficulties in conventional theories.

Interestingly, if the radiation is further split into n parts, then the energy of the corresponding stationary states follows the result of Bohr model for the energy level of hydrogen atom.

r_{n} = \frac{4 π ε_{0} n^{2} ℏ^{2}}{m e^{2}} = n^{2} r_{0},

(40a)

and E_{n} = E - m c^{2} = \frac{e^{2}}{8 π ε_{0} n^{2} r_{0}} = \frac{E_{1}}{n^{2}} .

(40b)

Thus, we see again that the inter-state interactions mediated by radiation can be represented in terms of an effective electromagnetic potential and the state quantization is due to the radiation quantization. Here in our model radiation creates “space” and constructs the quantized orbits on which electron can travel via energy train. The transition between the stationary states requires energy transformation for the electron transfer between energy trains running on the corresponding orbitals. In addition, the angular momentum quantization can be obtained from the radiation quantization:

|l| = m v r = \oint p d q = \frac{ℏ}{n r_{0}} 2 π r_{n} = n h .

(41)

Note that here we do not introduce the correspondence principle. While on the other hand, Eq. 40 indicates that the energy of the radiation (or momentum) reduces to 1/n while the radius of the classical orbit increases by

n^{2}

, therefore the frequency of the electron motion for the n-th stationary state decreases to

1 / n^{3}

. This indicates that when the state transition occurs, the classical transition frequency approaches to the frequency difference between the adjacent energy levels as the quantum number of the state increases. In fact, the classical limit is a natural consequence in our model. The above analysis be can straightforwardly applied to other hydrogen-like systems, in the same way as Bohr model.

3.2. Gravitation

In addition, our model can be extended to gravitational interactions. Simply replacing the electronic interaction by gravitational interaction in Eq. 39 gives:

r_{0} = \frac{ℏ^{2} (M + m)}{G M^{2} m^{2}},

(42a)

and E = m c^{2} + \frac{G M}{2 r_{0}} \frac{M m}{M + m} .

(42b)

Here M and m are the mass of the two interacting objects, and G is the gravitational constant. Again, the interaction energy in Eq. 42b is represented in terms of the effective gravitational potential. Since for gravitation there is no “gravitational charge” discovered so far, here we use the hydrogen atom as an effective mass unit and express the mass in Eq 42 in terms of relative mass with respect to the effective mass unit, i.e.,

m_{H}

. This gives the gravitational Bohr radius as:

r_{0} = \frac{ℏ^{2} (N_{M} + N_{m})}{G m_{H}^{3} N_{M}^{2} N_{m}^{2}} \geq \frac{2 ℏ^{2}}{G m_{H}^{3} N_{M}^{3}},

(43)

where

N_{M}

and

N_{m}

are the number of effective particles of the two interacting objects, and the equality holds when they are equal in mass (assuming the total number of effective particles being constant). As an estimate on the order of magnitude, if

N_{M} = 0.4 \times 10^{8}

, then

r_{0} ~ 1

. On the other hand, putting in the masses of Sun and Earth in Eq. 43 gives

r_{0} ~ 10^{- 135}

. This extremely small number is because that for the Sun-Earth system, both two objects comprise a huge number of particles, therefore, the effective radiation particle is not primitive.

Careful examination on the many-body interactions reals that for the composite objects, the inter-state interaction can be represented by an effective radiation also comprising a number of primitive particles. If we assume that the gravitational interaction is an effective potential mediated by a coherent radiation particle of an ensemble of N intermediate bosons, then an effective gravitational Bohr radius reads:

r_{0} = \frac{ℏ^{2} (N_{M} + N_{m})}{G m_{H}^{3} N^{2}} \geq \frac{2 ℏ^{2}}{G m_{H}^{3} N},

(44a)

with N = \sqrt{N_{M} N_{m}} .

(44b)

Now if

N = 10^{23}

, then

r_{0} ~ 1

. In fact, we can define a new constant, a gravitational Mole radius as:

r_{G} \equiv \frac{2 ℏ^{2}}{G m_{H}^{3} N_{A}} = 0.12 m,

(44c)

with

N_{A}

the Avogadro constant, which is appropriate for gravitational interactions in the composite systems. For example, Eq. 44c indicates that the ground state of two one-mole Hydrogen like drops features a gravitational wavelength of about 1m, which might be suitable for a promising experimental setup for verifying quantum gravity [75].

Similar to the electromagnetic case, if the ground state gravitational radiation is split into n parts, the energy of the corresponding higher-level stationary states can be obtained by:

r_{n} = \frac{n^{2} ℏ^{2} (N_{M} + N_{m})}{G m_{H}^{3} N^{2}} = n^{2} r_{0},

(45a)

and E_{n} = E - m c^{2} = \frac{G M}{2 r_{n}} \frac{M m}{M + m} = \frac{E_{1}}{n^{2}} .

(45b)

Obviously, the Earth orbit is a highly “Rydberg” state with an extremely large quantum number of the energy level. If the orbit radius of

1.5 \times 10^{11}

m is used, then the quantum number

n ~ 10^{19}

. This indicates that a huge number of radiation particles are generated upon the fission of the original single coherent radiation, and the generated space is classical and full of radiation. Thus, the application of our model on both electromagnetic and gravitational systems suggests that there seems no borderline between the quantum and classical worlds, rather there are big and small energy particles and deterministic dynamics may become statistical as the number of small particles increases astronomically.

4. Discussions

4.1. Energy Transformation

The hierarchical structure of energy space deserves further clarifications. The mapping of a complex system in modular energy space (MES) resolves the representation into two parts: the basis and its mathematical structure, or equivalently the energy elements and their transformations. The same system of interest can be represented by either simple (primitive) basis (normally) resulting in a complicated but high-resolution representation, or equivalently complex basis with a relatively simple but coarse-grained representation. The appropriate choice of the basis sets the focus on specific levels of the structure, manifesting the power of mathematical mappings. For instance, the solution of Schrodinger equation for the four-state model in our previous work [53] may be represented by either primitive energy basis, i.e.,

ϕ_{\pm}

, or the constructed higher order complex energy modules. Ideally, these higher order energy modules can be classified systematically based on some specific generating rules. The one we proposed in this work is just an example of infinitely many possibilities (but perhaps the first one to manifest the molecular structure of the energy space). According to the generating rule (see Appendix A for details), the mathematical transformation of primitive basis results in a higher level (2^nd) of energy modules (Eq. 2). And the particle pair states MLNP in [53] are the third order of energy modules made of these 2^nd order energy modules. These hierarchical energy modules constitute fundamental elements to represent or construct the system of interest. In another word, all components and fundamental structures of the world, including time, space, and matter, can be represented by energy elements. On the other hand, in the same way as constructing our world by using atoms and molecules of chemical elements, we are allowed to synthesize the molecules and compounds of energy elements, and the world. Note that the hierarchical nature of the energy modules in the tensor form makes our molecular model distinct from existing literature such as those based on modular variables [76] and energy momentum tensor [77].

As said, the multidimensionality and the hierarchical feature of MES may result in different pictures from different perspectives on the same structure. For instance, the representation of the system would be different using different equivalent basis (e.g., Eq. 3), and therefore the interpretation of the same mathematical structure would be different, which however may be associated with different realistic processes. For another example, the TT transformation in Figure 3 may correspond to the transition from a rotational yunon to a kongon, and then a shion. Both examples demonstrate that the same mathematical framework could be mapped to different physical models or processes. And we believe that MES, if effectively constructed, could facilitate the systematic analysis of energy space structure and therefore the rational design of new pathways of energy transformations.

In the case of TT, it is worth noting that in the space-like domain, the Lagrangian is formally invariant under TT, so that the equation of motion is also invariant. In contrast to the external world, the frame (length) keeps immortal, and time is confined, as the role of time and space exchanges after TT. Similarly, the role of the identity matrix and the first Pauli matrix switches, both of which are associated with the exchange of the role between the (confined) mass energy and internal radiation energy. The confined radiation may be represented in terms of closed time loop (CTL), and fast CTL carries more internal energy. Here CTL is the component of the system, which is different from the closed timelike curves [78]. This picture just offers one scheme to map the mathematical framework to physical models that could occur in reality. As said, the same framework may represent different scenarios when different mapping schemes are adopted. For instance, if the imaginary time formalism [79] is applied, the space-like domain in Figure 4 may be mapped to thermal states of the system. And it is interesting to see the connection between these two scenarios, considering internal motions can be associated with temperature. Note that the above analysis can be generalized to the 3D space. As shown in Figure 4c-h, TT results in exchange in the dimensionality of the time and space variables through the mass-like domain, indicating topological transformation occurs in both directions on the domain borders, and there might have only two dimensions exist in some intermediate regimes. This argument is somehow consistent with the prediction of CDT on dimensionality reduction [21], while it deserves further investigations.

4.2. Energy Quantization and Quantum Mechanics

Energy quantization and the quantization of other physical quantities associated with the Planck constant h set up the foundation of quantum mechanics [54]. However, the conventional representations of quantum mechanics overemphasize on either mathematical representation and manipulations or measurable physical realities, while the chemical transformation of fundamental elements or basis that can manifest the underlying mechanism of quantum mechanics is rarely investigated. For example, in conventional quantum mechanics, the wave function can be represented by energy basis, position basis, momentum basis and function basis in Hilbert space. Then what are these bases and what are the relation or interactions among them? Without answering these fundamental questions, the full story cannot be understood just like the fact that the crystal structure cannot be fully obtained based only on space lattice and symmetry transformation unless one knows what the lattice point really is or what the motif mapped to the lattice point is.

In this work, we try to uncover the molecular mechanisms of quantum mechanics by introducing the modular energy space (MES), which results in an energy tensor representation (not the conventional scalar energy representation) of quantum mechanics in terms of classified energy basis (modules). Here any physical quantity including time, space, and matter can be represented by fundamental energy modules and elementary energy transformations in a unified molecular framework. For example, the fundamental energy modules kongon and yunon are coherently incorporated within the same framework of energy space, and the transformation of different types of energy modules is given by the EOM (Eq. 16) while there is no inhomogeneous component as suggested in the conventional spacetime representation [6,7].

In MES, we have pure states associated with particle-like or wave-like elements, which implies that in principle, deterministic identification of particle and/or wave is possible. Nevertheless, these are fundamental elements while in our model realistic objects comprise multiple primitive energy elements. In fact, the undetermined phase factor in conventional wave function may be associated with the transformation among different energy modules. Thus, conventional experimental measurements would result in wave particle duality, consistent with current observations. Therefore, our formalism not only provides a molecular model for energy transformation, but also suggests a consistent classical interpretation on quantum mechanics. Although it is illuminating to make interpreting mappings of quantum mechanics by using well-studied classical systems including mechanical or hydrodynamic analogs [80,81,82], and some models seem well represent the characteristics of quantum mechanics, we note that our model by contrast features a unique hierarchical nature on representing the state space starting from the fundamental entities, which is supposed to get rid of any ambiguity in the model construction on the phenomenological level.

According to Eq. 12, the wave function in MES has a well-defined physical interpretation in terms of energy modules, and its phase could have three contributions from the corresponding action, namely, the dynamic phase associated with time, the geometric phase associated with space, and the mass phase associated with cloud. Since coherence among different states (or energy modules) is also incorporated in our model of wave function, therefore the Aharonov Anandan (AA) phase is also included [56]. In comparison with the de Broglie-Madelung-Bohm representation, the mass phase in our model plays a role of the amplitude there. In general, the amplitude may be represented by the projection of the system on energy modules (i.e., coordinates) in MES in multidimensions with all basis treated at an equal footing. And the appropriate choice of energy modules could result in a deterministic representation of the system of interest. We believe that our model has some advantages since it incorporates the transformation between the external and the internal worlds and there seems no need to introduce an abstract quantum potential.

Going beyond the kinetic perspective of motion, our molecular model of quantum dynamics offers new insights into the trajectory representation of a moving object. In the proposed model, the space and time are evolved through energy transformation proceeding on a quantum net of primitive energy modules. The dynamics of both the massive and massless particles are therefore determined by the trajectory of energy transformation. For free particles, the trajectory is a straight line followed the least action principle. Whereas in case of that the interactions of particle and surrounding environment are not negligible, the trajectory may become random and motion becomes statistically undetermined. Here is the reason why the statistical representation of quantum dynamics comes in, and the corresponding wave function becomes probabilistic. Thus, we advocate the picture of that the origin of probability of wave in wave quantum mechanics lies in the system environment interactions [5], just like Brownian motion in classical mechanics [68].

In agreement with de Broglie-Madelung-Bohm representation, the deterministic EOM of quantum dynamics in MES results from the Hamilton Jacobi equation. By expanding the action in the tensor form, the system is represented in the expansion in terms of energy modules exactly in the same way as normal modes (of harmonic oscillators) in classical mechanics. Therefore, the state function of a system in MES obeys the superposition principle the same as classical wavelike normal mode models. On the other hand, energy transformation among different energy modules occurs via particle like energy quanta. The molecular picture of MES thus seems to explain all the major paradoxes and puzzles of quantum mechanics. Here we state that quantum mechanics is essentially the same as classical mechanics in the energy space, and energy transformation in energy modules and quantum dynamics are naturally relativistic. All these evidences indicate that we have obtained a unified framework incorporating existing fundamental theories including classical mechanics, quantum mechanics, and theory of relativity.

It is worth mentioning that deterministic quantum mechanics has been recently formulated in the cellular automaton (CA) model [83,84], which manifests a viable classical interpretation to quantum dynamics [for a variety of different forms of classical interpretations, see for example, [85,86]. Note that the CA model was built in a predefined space-time, therefore efforts have to be made to interpret the conventional puzzles of quantum mechanics such as locality, and wave function collapse, which are avoided in our molecular model in the energy space.

One of the uncertainties of the proposed model is the nature of the proposed fundamental object. For simplicity, we assume that this fundamental object has no internal structure and can be characterized by a single scalar, i.e., its energy E. If such energy atom does exist, then what is the exact value of its energy E? This quantity may be related with the fundamental properties of the universe. So far we do not have a determined answer for it but take it as a reference unit or an energy measure, like the atomic unit. It is also possible that the object with no internal structure is only the idealistic basis for the model construction while the realistic fundamental object may have internal structures. In fact, in the Appendix A, the possibility of a quantum clock with internal states is discussed. And the energy elements may also start from the second hierarchy of the primitive basis. Note that the internal and external worlds are dual concepts in our hierarchical framework. Thus, it will be of great importance how we interpret the constituent energy elements if the proposed hierarchical world model is the truth. Further investigations are under the way.

5. Concluding Remarks

Modular energy space (MES) is constructed based on a set of energy modules generated from primitive energy basis. Within this framework, we generalize the action integral to a tensor decomposition form. Such a systematical expansion of action results in an energy tensor (ET) representation of quantum mechanics, which provides new insights into the structure of energy space and a consistent classical interpretation on quantum mechanics. For example, the wave function is represented fully as a function of action in a deterministic form. Facilitated by MES analysis, we propose that scalar energy transformation generates time, vector energy transformation generates space, and tensor energy transformation may generate cloud. The corresponding energy transformations may be represented by a group of composite energy modules including the generators of U(2) group comprising identity matrix and three Pauli matrices. The classification of energy modules reveals a periodicity of energy elements, and a hierarchical picture on the structure and transformation of the world may be constructed. This leads to a molecular interpretation on the nature of time, space, matter, and our world.

The ET representation of quantum mechanics suggests a molecular mechanism for motion, through the coupling of particle and intermediate bosons. The proposed formalism manifests energy transformation between matter and radiation, and equivalently dynamics transformation between time and space. We show that energy space can be decomposed into time-like, mass-like and space-like domains. And timespace transformation occurred in the mass-like domain exchanges the roles of time and space, indicating a quantum phase transition between external and internal worlds.

In addition, the ET interpretation on quantum mechanics incorporates relativistic energy momentum relation as a chemical transformation of energy elements following a simple geometric relation, and new molecular insights into some fundamental issues including wave particle duality, the existence of a limited speed of light, and the quantization of electromagnetic and gravitational interactions are thus obtained. For example, the application on hydrogen atom reproduces the results of Bohr model together with a consistent classical interpretation on quantum mechanics. The generalization of the idea on gravitational interactions suggests a new atomic model manifesting the natural transition from the quantum to classical world. Here electromagnetic and gravitational interactions and the small and large scales are incorporated in a unified molecular framework.

In summary, this work developed a promising strategy to construct a unified theory.

Data Availability Statement

No Data associated in the manuscript.

Acknowledgments

We acknowledge the support from National Science Foundation of China (21673012) and Peking University Shenzhen Graduate School.

Conflicts of Interest

The author declares no competing financial interests.

Appendix A

1. Generation of time and space

Here we suggest a generation scheme for the energy space in multidimensions. Consider a system comprising N energy modules, Schrodinger equation reads:

i ℏ \frac{\partial}{\partial t} ψ_{n} = H ψ_{n} = E_{n} ψ_{n}

(A.1.1)

with

ψ_{n}

and

E_{n}

the eigenfunction and eigenvalue of energy for the n-th state. And we have the wave function in a generic form of

ψ_{n} = e^{- i 2 π (\frac{E_{n} t}{h})} = e^{- i ω_{n} t},

(A.1.2a)

Here E_{n} = ℏ ω_{n} .

(A.1.2b)

Eq. A1.2a is a periodic function with represented values given in Table A1.1.

Table A1. 1.

$E_{n} > 0$ , $T_{n} = h / E_{n}$
$θ$	0	$π / 2$	$π$	$3 π / 2$	$2 π$
t/ $T_{n}$	0	1/4	1/2	3/4	1
$e^{- i ω_{n} t}$	1	-i	-1	i	1

Let us start from considering a scalar space, then the rank of the state space is zero, i.e.

K = 0,

(A1.3a)

and there is only one state (represented by a single point in the state space), i.e.

N_{K} (d) = d^{K} = {(n s)}^{K} = 1 .

(A1.3b)

Here d is the dimension of the base space, s is the number of components for each basis or the dimension of the internal space of basis, and n is the number of basis. In this case, without loss of generality, we may set the energy of the state is zero, i.e.,

E_{0} = 0

. And if we associate the phase of the wave function in Eq. A1.2 with the state in the energy space, then it can take only a single value of 1 (here we refer the single state to a determined state with no other possibilities), which means that the time t is immortal or there is no time. Nontrivial structures can only be generated at higher levels. For example, the original single energy atom may split into two parts, the wave functions of the two components are

ψ_{1} = ψ_{2} = e^{- i ω t},

(A1.4a)

with E_{1} = E_{2} = ℏ ω .

(A1.4b)

Now if we allow the energy of the whole system to fluctuate between the two components, then the wave function may take two values, i.e., 1 and -1, and we may associate the two modules with the phase values of 1, and -1, respectively. Note that here time can take only the discrete values, i.e., integer number times of half period. Thus, we have a quantum clock comprising two states, with the time to be determined by the number of cycles the system switched between the two states. As we mentioned in the text, these two states may be mapped to the two ends of a line segment, which can be generated from the bisection of the original whole segment. This generation scheme can be applied to generate higher dimensional state space, resulting in a hierarchical state space self-similarly mapped to a one-dimensional segment [87] corresponding to a scalar energy space with all states are energy degenerated. And we can create a clock walking ergodic in the state space (say along the path AGBF in Figure 1a), which tends to run continuously as the number of states goes to infinity in the classical limit. Note that the dimension of the scalar space, which can be associated with time, is always one even if there are multiple particles (n>1) or multiple components (s>1) in this scalar space, (

e . g . N_{K} = 1

For the state space of rank one, i.e., K=1, let us consider a simple case of two-state system, i.e.

d = 2, and N_{K} = d^{K} = 2

(A1.5)

The corresponding wave functions are

ψ_{n} = e^{- i ω_{n} t}, (n = 1, 2)

(A1.6a)

with E_{n} = ℏ ω_{n}

(A1.6b)

Without loss of generality, we may associate the two states with the energy values of E, and -E, respectively, which correspond to two points in the energy space (Figure 1a). And they are separated from each other by the intermediate radiation states, or in another word, radiation generates space. The vector energy transformation between these two states is associated with real energy transfer from one state to another through intermediate bosons, different from the scalar case in Eq. A1.4 where only the phase of the energy varies. Here the state space is 2D with the dimensionality of the basis state being 2, either two single component basis or equivalently one single two-component state of

ψ = (\begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix})

This example indicates that alternative interpretations or mapping schemes exist. For instance, we may increase the dimensionality of the state space, by expanding the dimensionality of the base space from either external or internal perspectives. In the case of that K is zero, the state space is one dimensional regardless of the basis dimensionality (all components are degenerated internal states), and the energy space is scalar (the eigenvalue takes only one number). When the energy space is a vector space and K=1, there are more than one non-degenerated states with more than one eigenvalues. These external states are separable because of the existence of the intermediate radiation states (and the space they create). For the two-state system we considered as an example, the eigenvalues are extended from one positive number in the scalar case to two real numbers in the vector case, so that the degeneracy is broken. To further expand the dimensionality of the basis space from 2 to 4, one may think of expanding the eigenvalue space form real to complex plane. However, for complex eigenvalues, the generic form of wave function in Eq. A1.2a would become exponential. One strategy to circumvent this problem is to make the corresponding dual variables complex too. For instance, for additional two (radiation) states with energy eigenvalues of

\pm i

, the corresponding dual variable also takes complex values, i.e.

t \to \pm i t

. In another word, when we introduce new energy basis, new dimensions are generated. These can be associated with additional space dimensions since they are fundamentally different from the time dimension. This illustrates the strategy of energy space decomposition and how the conventional scalar energy space is resolved in terms of classified energy modules. This same space generating strategy applied to the state space of dimensionality of four would generate the conventional 4D space-time.

2. The energy basis in expanded space

We can construct the higher order energy basis in an expanded base space by using generating schemes. For instance, to generate a four-state energy basis, a direct sum of the energy basis in Eq. 3 results in

A = I_{4} \equiv (\begin{matrix} \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} & 0 \\ 0 & \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \end{matrix}), F = i A, B = - A, a n d G = - i A

(A2.1a)

A = (\begin{matrix} \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} & 0 \\ 0 & \begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix} \end{matrix}), F = (\begin{matrix} \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} & i I \\ - i I & \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \end{matrix}),

B = I_{4}, a n d G = (\begin{matrix} \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} & I \\ I & \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \end{matrix})

(A2.1b)

Eq. A2.1b is a vector basis by contrast. And other forms of basis may be obtained by using different combinations. According to the generating schemes for energy basis, the representation of the system in the energy space can be straightforwardly obtained. For instance, the representation space for the self-similar scheme is a degenerated scalar space, and different states can be identified by the phase. For the space-generating scheme, the representation space could be one dimensional real axis, or two-dimensional complex plane, etc.

3. The energy representation of the system

Here we consider two examples to show the energy representation of the system. The first is the two-state system, and we write the system Hamiltonian in terms of energy modules.

H = (\begin{matrix} H_{11} & H_{12} \\ H_{21} & H_{22} \end{matrix}) = E_{20} I + E_{21}^{i} \cdot σ_{i} (i = 1,2, 3),

(A3.1)

E_{20} = \frac{1}{2} T r H, E_{21}^{i} = \frac{1}{2} T r (H σ_{i})

Here

σ_{i}

are Pauli Matrices. And for a three-state system, the Hamiltonian reads:

H = (\begin{matrix} H_{11} & H_{12} & H_{13} \\ H_{21} & H_{22} & H_{23} \\ H_{31} & H_{32} & H_{33} \end{matrix}) = E_{30} I + E_{31}^{i} \cdot λ_{i} + E_{32}^{j} \cdot λ_{j}, (i = 1 - 3, j = 4 - 8)

E_{30} = \frac{1}{3} T r H, E_{31}^{i} = \frac{1}{2} T r (H λ_{i}),

E_{32}^{j} = \frac{1}{2} T r (H λ_{j}) f o r j \neq 8; E_{32}^{8} = \frac{1}{3} T r (H λ_{8})

(A3.2)

Note that

λ

is the unnormalized Gell-Mann matrix.

To determine the energy representation of the system from Eq. 14, we transform the other types of energy basis (modules) into the same time basis. Therefore, the space contribution becomes into

(\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) \to \frac{1}{2} (\begin{matrix} 1 & i \\ i & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) (\begin{matrix} 1 & - i \\ - i & 1 \end{matrix}) \to (\begin{matrix} 0 & i \\ - i & 0 \end{matrix})

(A3.3a)

And the system Hamiltonian reads:

H = (\begin{matrix} m c^{2} & i p c \\ - i p c & - m c^{2} \end{matrix})

(A3.3b)

in the rest frame, which becomes diagonalized in the renormalized new time basis as shown in Eq. 14. Note that Eq. A3.3 takes the form for the two-state system in our previous work [53].

4. Periodicity of energy elements

The classification of the energy modules results in a periodic table of energy elements. In analogy with that for chemical elements, here we identify energy elements according to a set of quantum numbers, which may be mapped to the hierarchical multipole expansion of action. The first is the hierarchy (principle) quantum number n, which corresponds to the level of the expansion hierarchy and may be associated with a composite energy module comprising of n primitive modules. The second is the space (angular momentum) quantum number l, which is mapped to the spherical harmonic terms (space) of multipole expansion of action for a specific shell. The third is the dimension (magnetic) quantum number m, which is associated with the basis of a specific space with a particular n and l. The fourth is the module (spin) quantum number s, which specifies the polarization of the energy fluctuation and may be associated with the primitive energy modules (say

ϕ_{+} a n d ϕ_{-}

) for

s = \pm \frac{1}{2}

, respectively. Here we prefer to use new names for these quantum numbers since energy modules generate everything and no physical variables including time and space are predefined. The allowed values of n, l, and m followed the same rule as that for chemical elements in the conventional quantum mechanical definition. For instance, n=3 for the third shell elements, and l can be 0, 1, and 2, associated with the scalar, vector, and matrix space, respectively. The corresponding m value takes 0 for l=0; 0,

\pm 1

for l=1; and

0, \pm 1, \pm 2

for l=2, and the dimensionality of the space is 1, 3, and 5, respectively.

Let us explain how the energy elements can be constructed. Note that the hierarchy quantum number is connected with the rank of the state space (A1.3). The K=0 case corresponds to the scalar energy space, and the zeroth order primitive module can be used to construct higher level structures. Here the first energy element H(1) is a single state representing for a constant base with no internal structure (Figure A1a), which may be associated with a primitive atom or element, or mathematically a point. However, this does not mean that there is any singular point in modular energy space since there is no space-time for a single state. The scalar energy fluctuation of a primitive energy atom results in the second element H(2) (Figure A1b), which can be represented by a module with two internal states (see discussions on the case considered in Eq. A1.4). And there are only two configurations, which can be identified with the particle and its antiparticle of H(2). The oscillation between the two configurations may be used to construct a two-state clock. The two configurations are indistinguishable to each other since there is only one connecting path between two components. In another word, there is no direction of the path (time). We can assign H(1) with n=1, l=0, and configuration

{1 s}^{1}

, following the same labelling scheme of chemical elements. Similarly the configuration of H(2) is

{1 s}^{2}

. These first two elements are in the first period, which represents for the first hierarchy scalar world, i.e., time world.

Figure A1. Energy elements in a two-dimensional representation. (a) The primitive energy module is the first energy element represented by a single state as base (ground state). Note that we can always reset the energy of the ground state as zero, so this corresponds to a plain background. Energy fluctuations of the plain background correspond to excited states mapped to the higher order energy basis, or subsequent energy elements. (b) the second element represented in terms of the primitive pair state of the module. (c-j) the energy elements in the second hierarchy, i.e., the element of number 3-10. Only the outmost valence shell is shown.

The second period of energy elements is built on the second hierarchy based on the first scalar world. For simplicity, in the following, we only mention the outmost energy hierarch, i.e., the valence hierarchy (or valence shell, also borrowed from chemistry). The valence shell of the first element of the second period H(3) is associated with a composite module with two distinguished components (in contrast to the indistinguishable two states of H(2)), which may be represented by a single square module in a two dimensional representation with the primitive pair state

(\begin{matrix} ϕ_{+} \\ ϕ_{-} \end{matrix})

being occupied [its antiparticle is

(\begin{matrix} ϕ_{-} \\ ϕ_{+} \end{matrix})

, not shown] , so we have n=2, l=0, and the valence configuration is

{2 s}^{1}

. The second unoccupied pair state in the square module serves as the spacer to distinguish the two configurations of H(3). When it is occupied, the full square module is obtained with four components in total corresponding to a four-state quantum clock in a 1D representation, or an internal world with internal time and internal space in a 2D representation. This square module can be mapped to the next element H(4) and its valence configuration is

{2 s}^{2}

The space quantum number l is 1 for the second period of energy elements, and therefore there are both time and space (worlds) in this hierarchy. Following the rules underlying the periodicity of chemical elements, the subsequent energy elements in the second period H(5)-H(10) can be generated by filling the primitive energy module of the second period, i.e. the pair state, into the energy diagram ordinally, as shown in Figure A1e-j. Note that the configuration of H(7) (

{2 s}^{2} 2 p^{3}

) follows Hund’s rule, forming a closed space “path” in a bigger square module (Figure A1g). While the fully filled energy hierarchy is a closed time space world (Figure A1j). Interestingly, the energy diagram is equivalent to that of a system comprising a particle/antiparticle pair (each represented by a square module) fully correlated with two intermediate bosons.

The energy elements may have different representations (or interpretations). Here is presented an alternative scheme to construct the energy elements at a different hierarchy. We start from a primitive module with two internal states, the case we considered in Eq. A1.4. There are only two configurations, which can be identified with the particle and its antiparticle of the first energy element H(1). This construction results in the first order energy modules. The first order energy modules for K=1 may be mapped to the second Brillouin zone in the previous 2D representation if we regard the zero-order primitive module as the first Brillouin zone. Thus, we end up with a compact square module as the first order module if the reduced zone scheme is taken (Figure A2a-c), which can be used as the basic building block for energy elements. Now the first element H(1) may be represented by a single square module in a 2D representation using the primitive pair state

(\begin{matrix} ϕ_{+} \\ ϕ_{-} \end{matrix})

as the primitive basis [the corresponding antiparticle is

(\begin{matrix} ϕ_{-} \\ ϕ_{+} \end{matrix})

] , and the configuration is

{1 s}^{1}

. The second element H(2) can be mapped to the full square module with both two pair states occupied, thus its configuration is

{1 s}^{2}

. The first period of two elements can be associated with the first hierarchy time world. And higher hierarchy worlds correspond to other periods of energy elements consistent with the tensor expansion of the action in the text. As an example, Figure A2d-m displays the energy diagrams of energy elements in the first two periods.

In this representation, all energy elements are generated by the energy fluctuations on a plain background, in an analogy with excitons generated in crystals. In comparison with the generating scheme starting from the zeroth order primitive module, which produces static structures (elements), the second scheme starting from the first order primitive modules results in dynamical structures (elements). Specifically, time world generated in the first scheme is a two-state system corresponding to a static clock, while the time world generated in the second scheme and represented by a single square module with the two internal pair states including both matter and radiation states, may be regarded as a running clock. This is consistent with our molecular theory of dynamics in which radiation states are responsible for the motion of the clock (see the comparison between elements H(2) [Figure A1b, and Figure A2e] and H(10) [Figure A1j, and Figure A2m]). Clearly much work has to be done to identify the proposed energy elements and investigate their properties. We leave further discussions on energy elements in future work.

Figure A2. Energy elements represented in an alternative scheme. (a) The primitive energy module (the square labeled by 1) may be represented by a square state for ground state (1) and excited state (2) by mapping the higher order energy basis into the same square (b), an example is given in (c). (d) The first energy element represented in terms of the primitive pair state of the square module. (e) the second element; (f-m) the energy elements in the second hierarchy, i.e. the element of number 3-10. Only the outmost valence shell is shown.

5. Quantum dynamic of a single radiation state

The dynamics of the kongon under the mediation of yunon is give as the follows. The Schrodinger equation for the evolved states reads:

ℏ \frac{\partial}{\partial x} (\begin{matrix} \begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix} \\ \begin{matrix} ψ_{3} \\ ψ_{4} \end{matrix} \end{matrix}) = (\begin{matrix} \begin{matrix} i c p & 0 \\ V & α \end{matrix} & 0 \\ 0 & \begin{matrix} i c p & V \\ 0 & β \end{matrix} \end{matrix}) (\begin{matrix} \begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix} \\ \begin{matrix} ψ_{3} \\ ψ_{4} \end{matrix} \end{matrix})

(A5.1)

Here

α a n d β

represent the dynamical occupation of the corresponding modules. Following the same strategy in our previous work [53], the solution of Eq. A5.1 can be found as the follows:

(I): $α = 0 a n d β = 0;$

$(\begin{matrix} \begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix} \\ \begin{matrix} ψ_{3} \\ ψ_{4} \end{matrix} \end{matrix}) = (\begin{matrix} \begin{matrix} \frac{i c p}{E} e^{i p x / ℏ} \\ \frac{V}{E} e^{i p x / ℏ} \end{matrix} \\ \begin{matrix} e^{i p x / ℏ} \\ 0 \end{matrix} \end{matrix})$

(A5.2a)
(II): $α = i c p a n d β = i c p$

$(\begin{matrix} \begin{matrix} ψ_{1} \\ ψ_{2} \end{matrix} \\ \begin{matrix} ψ_{3} \\ ψ_{4} \end{matrix} \end{matrix}) = (\begin{matrix} \begin{matrix} 0 \\ e^{i p x / ℏ} \end{matrix} \\ \begin{matrix} \frac{i c p}{E} e^{i p x / ℏ} \\ \frac{V}{E} e^{i p x / ℏ} \end{matrix} \end{matrix})$

(A5.2b)

From Eq. A5.2, it is clear that kongon moves one step forward.

6. The relativistic effect in MES

The relativistic effects may be explained within the framework of MES. Consider a moving frame with a velocity of v, which may be associated with a system of total energy E comprising a rest mass m carrying radiation with momentum p. Different from the conventional mathematical perspective, a moving frame is intrinsically physical in our formalism. Therefore, it is not surprised that the spacetime transformation would deviate from the linear Galilean transformation. Indeed, we can show Lorentz transformation is obeyed and the well-known relativistic effects may be interpreted in a synthetic way. Assuming that the mass and radiation comprising a and b primitive energy modules, respectively, then we have

\frac{h / p}{\sqrt[2]{{(\frac{h}{m c^{2}})}^{2} + {(\frac{h}{p c})}^{2}}} = \frac{b c τ}{\sqrt[2]{{(a τ)}^{2} + {(b τ)}^{2}}} = v

. That means that

\frac{t'}{τ} = \frac{1}{γ}, a n d \frac{l'}{l} = \frac{1}{γ}

. Or in another word, the moving clock rans slowly and ruler becomes shorten.

Also relativistic invariance is naturally built in in MES. In the action angle representation, the wave function can be written by

ψ ~ e^{i S / ℏ}

(A6.1a)

for which the action is given by the integral of a generalized Lagrangian, i.e.

S = \int L (q, \dot{q}, σ) d σ .

(A6.1b)

Here we can take the proper time to be the affine parameter, i.e.

σ = τ

The differential action in a classical picture is

d S = p d q - E d t = γ p d λ - γ E d τ

(A6.1c)

The second equivalence follows due to the transformation with

d λ = \frac{d q}{γ}; d τ = \frac{d t}{γ}; γ = \frac{1}{\sqrt{1 - β^{2}}} and β = \frac{v}{c}

(A6.1d)

The equation of motion results from the principle of least action, i.e.

F = \frac{d (γ p)}{d τ} = - \frac{\partial (γ E)}{\partial λ}

(A6.2)

The result is consistent with the principle of relativity, i.e. physical laws should be invariant in different inertial frames.

For a particle in a gravitational field in 3D, Eq. A6.2 gives a modified force

F_{r} = - \frac{γ \partial (E (γ))}{\partial r} = - \frac{L^{2}}{m r^{3}} + γ^{2} \frac{G M m}{r^{2}}

(A6.3)

with an additional factor of

γ^{2}

with respect to the force in the rest frame. L is the angular momentum,

G

is the gravitational constant, and M is the mass of source. This produces exactly the same result as that provided by GR in the weak field limit [13,88]. For instance, it would make the relativistic correction for the procession of Mercury’s perihelion to be 43”/century. To reach the result from Eq. A6.3, we effectively pick up the whole system as the reference frame. And the moving object in this frame carries a number of intermediate bosons, resulting in a scaling factor in physical quantities including mass, time, and force, etc. But all these quantities are measured in the reference frame and the space is unscaled, because the moving object changes while radiation does not. Note that when the velocity approaches to the speed of light, the scaling factor

γ

diverges. This artifact is attributed to the single body approximation, and if the full two body motion is considered, the radius should be rescaled or the reduced mass should be used. Then when the velocity increases, there is a limit as the two interacting objects have equal mass and the divergence is thus avoided. Also Eq. A6.3 may be obtained from Eq. 42 from an energy perspective, so that we have successfully extend the MES framework to incorporate gravitational interactions.

References

Weinberg, S. Essay: Half a Century of the Standard Model. Phys. Rev. Lett. 2018, 121, 220001. [Google Scholar] [CrossRef]
Leor Barack et al. Black holes, gravitational waves and fundamental physics: a roadmap. Class. Quantum Grav. 2019, 36, 143001. [CrossRef]
L. Heisenberg, A systematic approach to generalisations of General Relativity and their cosmological implications. Physics Reports 2019, 796, 1–113. [CrossRef]
H. Nikoli´c, Quantum Mechanics: Myths and Facts. Found. Phys. 2007, 37, 1563–1611. [CrossRef]
A. Bassi, K. Lochan, S. Satin, T. P. Singh, and H. Ulbricht, Models of wave-function collapse, underlying theories, and experimental tests. Rev. Mod. Phys. 2013, 85, 471–527. [CrossRef]
Bohm, D. A suggested interpretation of the quantum theory in terms of hidden variables, I. Phys. Rev. 85:166–179 (1952); II. 180-193 (1952).
Holland, P. R., 1993, The Quantum Theory of Motion: An Account of the de Broglie-Bohm Causal Interpretation of Quantum Mechanics (Cambridge University Press, Cambridge, England).
Roger Penrose, On the Gravitization of Quantum Mechanics 1: Quantum State Reduction. Found Phys 2014, 44, 557–575. [CrossRef]
K Krasnov and R Percacci Gravity and unification: a review. Class. Quantum Grav. 2018, 35, 143001. [CrossRef]
Kiefer, C. (2020). Space, Time, Matter in Quantum Gravity. In: De Bianchi, S., Kiefer, C. (eds) One Hundred Years of Gauge Theory. Fundamental Theories of Physics, vol 199. Springer, Cham. [CrossRef]
Giovanni Amelino-Camelia, Quantum-Spacetime Phenomenology. Living Rev. Relativity 2013, 16, 5. [CrossRef]
't Hooft G Time, the Arrow of Time, and Quantum Mechanics. Front. Phys. 2018, 6, 81. [CrossRef]
J. B. Hartle, Gravity: An Introduction to Einstein’s General Relativity. Addison-Wesley, San Francisco, 2003 (Reprinted in China).
Penrose, A. Gravitational Collapse and Spacetime Singularities. Phys. Rev. Lett. 1965, 14, 57. [Google Scholar] [CrossRef]
Senovilla, J.M.; Garfinkle, D. The 1965 Penrose singularity theorem. Class. Quantum Grav. 2015, 32, 124008. [Google Scholar] [CrossRef]
V. Cardoso, P. Pani, Testing the nature of dark compact objects: a status report. Living Reviews in Relativity 2019, 22, 4. [CrossRef]
Porto R, A. The effective field theorist’s approach to gravitational dynamics. Phys. Rep. 2016, 633, 1–104. [Google Scholar] [CrossRef]
M. Levi, Effective field theories of post-Newtonian gravity: a comprehensive review. Rep. Prog. Phys. 2020, 83, 075901. [CrossRef]
Rovelli, Loop Quantum Gravity. Living Rev. Relativity 2008, 11, 5. [CrossRef] [PubMed]
Ashtekar and P. Singh, Loop quantum cosmology: a status report. Class. Quantum Grav. 2011, 28, 213001. [CrossRef]
Loll, R. Quantum gravity from causal dynamical triangulations: A review. Class. Quantum Grav. 2019, 37, 013002. [Google Scholar] [CrossRef]
J. B. Jiménez, L. Heisenberg, G. J. Olmo, D. Rubiera-Garcia. Born–Infeld inspired modifications of gravity. Physics Reports 2018, 727, 1–129. [CrossRef]
P. K Schwartz and D. Giulini. Post-Newtonian corrections to Schrodinger equations in gravitational fields. Class. Quantum Grav. 2019, 36, 095016. [CrossRef]
Singh, A. Quantum space, quantum time, and relativistic quantum mechanics. Quantum Stud.: Math. Found. 2022, 9, 35–53. [Google Scholar] [CrossRef]
M. Miller, N. Yunes, The new frontier of gravitational waves. Nature 2017, 568, 469.
S. Weinberg. The quantum theory of fields. Vol. I. Cambridge University Press, Cambridge. 1995 (Reprinted in China).
Oriti, D. (2018). Spacetime as a Quantum Many-Body System. In: Angilella, G., Amovilli, C. (eds) Many-body Approaches at Different Scales. Springer, Cham. [CrossRef]
Oriti, Group field theory as the second quantization of loop quantum gravity. Class. Quantum Gravity 2016, 33(8), 085005. [CrossRef]
Gaberdiel, M.R. (2018). String Theory and Spacetime Geometry. In: Rowe, D., Sauer, T., Walter, S. (eds) Beyond Einstein. Einstein Studies, vol 14. Birkhäuser, New York, NY. [CrossRef]
V. Giovannetti, S. Lloyd, and L. Maccone, Quantum time. Phys. Rev. D 2015, 92, 045033.
N. Page and W. K. Wootters, Evolution without evolution. Phys. Rev. D 1983, 27, 2885.
B. S. DeWitt, Quantum theory of gravity. I. The canonical theory. Phys. Rev. 1967, 160, 1113. [CrossRef]
N. Grot, C. Rovelli, and R.S. Tate, Time of arrival in quantum mechanics. Phys. Rev. A 1996, 54, 4676. [CrossRef] [PubMed]
J. Kijowski, On the time operator in quantum mechanics and the Heisenberg uncertainty relation for energy and time. Rep. Math. Phys. 1974, 6, 361. [CrossRef]
J. Kijowski, Comment on “Arrival time in quantum mechanics” and “Time of arrival in quantum mechanics”. Phys. Rev. A 1999, 59, 897. [CrossRef]
Hans-Thomas Elze, Emergent discrete time and quantization: relativistic particle with extra-dimensions. Physics Letters A 2003, 310, 110–118. [CrossRef]
Eduardo, O. Dias, Quantum formalism for events and how time can emerge from its foundations. PHYSICAL REVIEW A 2021, 103, 012219. [Google Scholar]
Horwitz, L.P. On the definition and evolution of states in relativistic classical and quantum mechanics. Found Phys 1992, 22, 421–450. [Google Scholar] [CrossRef]
Horwitz, L.P. Spin and entanglement in general relativity. Eur. Phys. J. Plus 2021, 136, 32. [Google Scholar] [CrossRef]
J. Leon and L. Maccone, The Pauli objection. Found. Phys. 2017, 47, 1597. [CrossRef]
S. Khorasani, Time Operator in Relativistic Quantum Mechanics. Commun. Theor. Phys. 2017, 68, 35. [CrossRef]
Wendel, L. Martínez, and M. Bojowald, Physical Implications of a Fundamental Period of Time. Phys. Rev. Lett. 2020, 124, 241301. [Google Scholar] [CrossRef]
Altaie MB, Hodgson D and Beige A Time and Quantum Clocks: A Review of Recent Developments. Front. Phys. 2022, 10, 897305. [CrossRef]
N. L. Diaz, J. M. Matera, and R. Rossignoli, Spacetime quantum actions. Phys. Rev. D 2021, 103, 065011. [CrossRef]
Giacomini, F. Spacetime Quantum Reference Frames and Superpositions of Proper Times. Quantum 2021, 5, 508. [Google Scholar] [CrossRef]
Capellmann, H. Space-Time in Quantum Theory. Found Phys 2021, 51, 44. [Google Scholar] [CrossRef]
Vaccaro J., A. The quantum theory of time, the block universe, and human experience. Phil. Trans. R. Soc. A 2018, 376, 20170316. [Google Scholar] [CrossRef]
Schild, Time in quantum mechanics: A fresh look at the continuity equation. PHYSICAL REVIEW A 2018, 98, 052113. [CrossRef]
Lizzia, P. Vitaleb, Time discretization from noncommutativity. Physics Letters B 2021, 818, 136372. [Google Scholar] [CrossRef]
Das, S. Das, E. C. Vagenas. Discreteness of space from GUP in strong gravitational fields. Phys. Lett. B 2020, 809, 135772. [Google Scholar] [CrossRef]
S. Bose, A. Mazumdar, G. W. Morley, H. Ulbricht, M. Toroš, M. Paternostro, A. A. Geraci, P. F. Barker, M. S. Kim, and G. Milburn, Spin Entanglement Witness for Quantum Gravity. PRL 2017, 119, 240401.
C. Marletto and V. Vedral, Gravitationally Induced Entanglement between Two Massive Particles is Sufficient Evidence of Quantum Effects in Gravity. PRL 2017, 119, 240402. [CrossRef] [PubMed]
Tao, G. Dynamical Coupling between Particle and Antiparticle in Relativistic Quantum Mechanics: A Multistate Perspective on the Energy–Momentum Relation. Symmetry 2023, 15, 1649. [Google Scholar] [CrossRef]
Messiah, Quantum Mechanics (Dover, Mineola, 1999).
Landau, L. D., and E. M. Lifshitz, 1976, Quantum Mechanics (Pergamon Press, New York), 3rd ed.
Zeng, J. Y. 2014, Quantum Mechanics I, II (Fifth Ed. Science Press, Beijing, China).
Cohen-Tannoudji, C.; Diu, B.; Laloe, F. Quantum Mechanics; Wiley: New York, 1977.
W. H. Klink and W. Schweiger, 2018, Relativity, Symmetry, and the Structure of Quantum Theory, Volume 2: Point form relativistic quantum mechanics (Bristol: IOP Publishing).
Simulik, V.M.; Krivsky, I.Y. Quantum-Mechanical Description of the Fermionic Doublet and its Link with the Dirac Equation. Ukr. J. Phys. 2018, 58, 1192. [Google Scholar] [CrossRef]
Here shion, kongon, yunon, and benon origin from Chinese of time, space, cloud, and base.
Kapustin and M. Touraev 2021 Non-relativistic geometry and the equivalence principle. Class. Quantum Grav. 38 135003.
Rovelli, C. Relational quantum mechanics. Int. J. Theor. Phys. 1996, 35, 1637–1678. [Google Scholar] [CrossRef]
Everett, H. Relative state formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
Dah-Wei Chiou Timeless path integral for relativistic quantum mechanics Class. Quantum Grav. 2013, 30, 125004. [CrossRef]
W. H. Miller and T. F. George. Analytic Continuation of Classical Mechanics for Classically Forbidden Collision Processes. J. Chem. Phys. 1972, 56, 5668. [CrossRef]
E. Pollak and W. H. Miller, New Physical Interpretation for Time in Scattering Theory. Phys. Rev. Lett. 1984, 53, 115. [CrossRef]
W. Koch and D. J. Tannor, Multivalued Classical Mechanics Arising from Singularity Loops in Complex Time. J. Chem. Phys. 2018, 148, 084108. [CrossRef] [PubMed]
de Broglie, L. The reinterpretation of wave mechanics. Found Phys. 1970, 1, 5–15. [Google Scholar] [CrossRef]
This directional kongon comprises two primitive energy modules with the same momentum, in contrast to the directionless kongon, including a pair of kongon with opposite momentum. Also note that this model of radiation particle is not photon, but only an analogy of photon. According to our formalism, photon is the radiation particle at only a particular hierarchy.
Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: Oxford, U.K., 1995.
P. A. M. Dirac, The Principles of Quantum Mechanics, 4th Ed. Oxford University Press: Oxford, U.K., 1958 (Reprinted in China).
F.J. Dyson, The radiation theories of Tomonaga, Schwinger, and Feynman. Phys. Rev. 1949, 75, 486. [CrossRef]
Carbonell, J., de Soto, F. & Karmanov, V.A. Three Different Approaches to the Same Interaction: The Yukawa Model in Nuclear Physics. Few-Body Syst 2013, 54, 2255–2269.
Yuri, N. Obukhov, Alexander J. Silenko, and Oleg V. Teryaev, General treatment of quantum and classical spinning particles in external fields. Phys. Rev. D 2017, 96, 105005. [Google Scholar]
C. Rovelli, Considerations on Quantum Gravity Phenomenology. Universe 2021, 7, 439. [CrossRef]
Laurent Freidel, Robert G. Leigh, and Djordje Minic, Quantum spaces are modular. Phys. Rev. D 2016, 94, 104052.
Sbitnev, V. Quaternion Algebra on 4D Superfluid Quantum Space-Time: Can Dark Matter Be a Manifestation of the Superfluid Ether? Universe 2021, 7, 32. [Google Scholar] [CrossRef]
Luminet, J.-P. Closed Timelike Curves, Singularities and Causality: A Survey from Gödel to Chronological Protection. Universe 2021, 7, 12. [Google Scholar] [CrossRef]
V. S. Popov. Imaginary-Time Method in Quantum Mechanics and Field Theory. Physics of Atomic Nuclei 2005, 68, 686–708. [CrossRef]
Drezet, P. Jamet, D. Bertschy, A. Ralko, and C. Poulain, Mechanical analog of quantum bradyons and tachyons. PHYSICAL REVIEW E 2020, 102, 052206. [CrossRef] [PubMed]
F. Marino, Massive phonons and gravitational dynamics in a photon-fluid model. PHYSICAL REVIEW A 2019, 100, 063825. [CrossRef]
J. W.M. Bush, Pilot-Wave Hydrodynamics. Annu. Rev. Fluid Mech. 2015, 47, 269–92. [CrossRef]
't Hooft G Deterministic Quantum Mechanics: The Mathematical Equations. Front. Phys. 2020, 8, 253. [CrossRef]
't Hooft, G. The cellular automaton interpretation of quantum mechanics. In: Fundamental Theories of Physics, 1st Edn., Vol. 185. Cham: Springer International Publishing (2016).
Tao, “Coherence-controlled nonadiabatic dynamics via state-space decomposition: A consistent way to incorporate ehrenfest and born–oppenheimer-like treatments of nuclear motion”. J. Phys. Chem. Lett. 2016, 7, 4335–4339. [CrossRef]
G. Tao, “Multi-state trajectory approach to non-adiabatic dynamics: General formalism and the active state trajectory approximation”. J. Chem. Phys. 2017, 147, 044107. [CrossRef]
G. Tao, Y. Tan, Modular Tensor Diagram Approach for the Construction of Spin Eigenfunctions: The Case Study of Exciton Pair States. J. Phys. Chem. A 2020, 124, 5435–5443. [CrossRef]
B. Schutz, 2009, A First Course in General Relativity, 2nd Ed. (Cambridge University Press, Reprinted in China).

Figure 1. Energy modules and transformations in modular energy diagram. (a) Transformation between two states through two vector intermediate bosons. (b) unitary transformation between two states in expanded space; (c) three types of transformation associated with Pauli matrices; and (d) corresponding primitive pair basis; (e) composite basis comprising primitive basis states can form different unit cells.

Figure 3. Timespace transformation in modular energy diagram. (a) Three representative routes of transformation represented by pathways in different domains in energy space. A: mass with external radiation; B: mass transforms into MLNP; C: mass becomes imaginary. (b) Timespace transformation (TT) in generalize energy space. Characteristic lines show energy momentum relation in a linear form in the positive (+, M>0) and negative (-, M<0) worlds, which is separated by the zero-mass line (green dashed). Red line passes through the time-like, mass-like, and space-like domains corresponding to the routes A, B, and C, respectively. TT results in a flip of the time-like and space-like domains and the role exchange in time and space. Purple line marks the degenerated state of time and space. Note that the three domains here refer to the energy space, which are different from the ones in the space-time diagram in GR. Also timespace used in TT reminds its different nature from the conventional space-time paradigm. (c-h) modular basis evolves in the quantum phase transition induced by TT: (c) Moving mass carrying intermediate bosons. (d) and (e) Space turns from external into internal world at the border of A and B regimes. (f) Degenerated states of time and space. (g) and (h) Role exchanges in time and space at the border of B and C regimes.

Figure 4. Quantum phase transition induced by timespace transformation. (a) The rate dx/dt vs. the apparent velocity v for routes A, B, and C in Figure 3a. Timespace transformation (TT) in route B switches time and space, results in divergence in dx/dt. But v does not diverge. (b) Quantum phase transition due to TT in the mass-like domain. The critical point is marked by the order parameter

θ = \frac{π}{4}

, where the transition takes place with the role of time and space exchanged.

θ = \frac{π}{4}

, where the transition takes place with the role of time and space exchanged.

Figure 5. Energy transport in modular energy diagram. (a) Quantum net framework built on primitive energy modules. (b) 1D transport for a single energy quantum. Shown from the left the dynamics of a square module in three consecutive time slices. Panels c-e show the space-time diagram for a single energy module. (c) Time evolution of a shion. (d) Space evolution of a kongon. (e) Space-time evolution of a yunon.

Figure 6. Energy transport in modular energy diagram. (a) Molecular model for a single radiation particle. Shown from the bottom the dynamics in the first half period. Panels b-e show the 1D free motion of a five-module massive particle carried by a three-module radiation particle. Note that the central four-module yunon requires extra time for transformation. (f) The same single radiation particle but spanning over four square energy modules.

Figure 2. Energy modules and transformations in the multipole expansion of action. (a) Scalar transformation through single node loop (SNL); (b) vector transformation through double node loop (DNL); (c) matrix transformation through triple node loop (TNL); and (d) three types of transformation represented by primitive triplet basis.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Nature of Time, Space and Matter: Energy Elements, Hierarchical World, and a Classical Interpretation on Quantum Mechanics

Abstract

1. Introduction

2. Theory and Models

2.1. Energy Space Decomposition

2.2. Time Space Transformation

2.3. Energy Dynamics

3. Applications

3.1. Atomic Model

3.2. Gravitation

4. Discussions

4.1. Energy Transformation

4.2. Energy Quantization and Quantum Mechanics

5. Concluding Remarks

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

1. Generation of time and space

2. The energy basis in expanded space

3. The energy representation of the system

4. Periodicity of energy elements

5. Quantum dynamic of a single radiation state

6. The relativistic effect in MES

References

MDPI Initiatives

Important Links

Subscribe