1. Introduction
Aerodynamic stall phenomena are important in many engineering applications that influence critical operating limits and system performance. Aerodynamic hysteresis, which is observed both in experiments and in computational simulations under static and dynamic conditions is an important feature of the stall region [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11]. Stall prediction using wind tunnel tests or computer simulations is challenging due to the high sensitivity of flow separation respectively to experimental testing conditions or computational models and solvers.
Strong turbulence in the wind tunnel flow and vibrations of the test model mounting system can cause premature transitions between the branches of static hysteresis [
6]. In computational simulations, there is also an observed sensitivity to the numerical solver, grid resolution, turbulence model, etc. [
11]. Albeit the complications, it is important to improve the understanding of the flow physics of this phenomenon to develop more reliable modeling of stall aerodynamics. Applications where static hysteresis exists range from wind turbines and micro air vehicles operating at low Reynolds numbers to the problem of loss of control in-flight (LOC-I) of transport aircraft for which modeling of stall/post-stall aerodynamics at high Reynolds numbers is required [
12].
There are many wind tunnel results that show static hysteresis in the separated flow region. For instance, occurrence of static aerodynamic hysteresis in flow past the NACA 0018 airfoil in the range of Reynolds numbers from
to
was shown in [
4,
5,
13]. It was also shown that aerodynamic static hysteresis can exists even at high Reynolds number
and may be even enlarged with a circular bump on the leading edge of the pressure side of the airfoil [
7]. CFD predictions of such static hysteresis phenomena on 2D airfoils using the URANS equations in OpenFOAM [
14,
15] with the SA (1-eqn) and SST (2-eqns) turbulence models have also been successful [
13,
16]. The use of an algebraic turbulence model such as the Baldwin-Lomax also deemed sufficient for capturing static hysteresis on the NACA 0012 airfoil at
, but was associated with a very strong buffeting even after introducing a special stabilizing numerical procedure [
10].
In this paper, we consider three-dimensional separated flow with the existence of aerodynamic static hysteresis on NACA 0018 finite aspect wing with
at moderate Reynolds numbers
and
. For the conducted URANS simulations with the use of SST turbulence model an open source CFD code OpenFOAM was used. The obtained simulation results were compared with wind tunnel data from [
8]. To the best knowledge of the authors, this is the first simulation results of aerodynamic static hysteresis loops for a three-dimensional wing configuration matching the experimental data and showing the development of flow asymmetry at high angles of attack. This shows the applicability of URANS simulations for evaluation of separated flows forming with bi-stable flow structures and static hysteresis in aerodynamic loads. The simulations were carried out using a pseudo-transient continuation algorithm based dual time solver developed in OpenFOAM as proposed in [
17]. The methodology involved driving the residuals of segregated equations to zero (or at least to a truncation error) in every time step to ensure full convergence of the flow variables [
14,
15].
This paper also introduces a novel phenomenological method for modelling static hysteresis manifesting bi-stable separated flow structures. A concept of such bifurcation modelling of static hysteresis was proposed in [
18] and some of its implementations were discussed early in [
13,
19,
20,
21].
The application of the proposed phenomenological model in this paper and its validation against experimental results is shown in
Section 4. The CFD simulation results are presented in the paper as follows. The computational framework including the geometry, grid and other numerical setup are discussed in
Section 2. Computational results for static hysteresis obtained for Reynolds numbers of
and
using OpenFOAM are shown in
Section 3. This section also includes the skin friction visualization patterns and three dimensional streamlines for bi-stable flow structures. The concluding remarks and future work is presented in
Section 5.
2. Computational Framework
Within this section, the discussion revolves around the computational framework employed for simulating static and dynamic hysteresis. This includes the geometrical attributes of the NACA 0018 wing, the governing equations, and the numerical settings applied in OpenFOAM.
The finite aspect NACA 0018 wing with
was made up from the two-dimensional NACA 0018 section profile with rounded tips at its ends. The wing span of the NACA 0018 was measured at
and the chord length is
. A blunt trailing edge was implemented similar to as that in the wind tunnel wing geometry. The incorporation of rounded tips aimed to facilitate a smooth flow attachment to the wing edges and support the proper development of wing tip vortices. The adopted geometry of the considered wing is illustrated in
Figure 1. The boundaries of the virtual wind tunnel are positioned at a distance of 50 chord lengths in the upstream, downstream, and sideways directions. Consequently, there is no need for blockage corrections in the Computational Fluid Dynamics (CFD) results obtained in this setup.
The inlet is subjected to a Dirichlet velocity-inlet boundary condition, complemented by a Neumann-type zero-gradient pressure boundary condition. Meanwhile, at the outlet, a zero-gradient velocity outlet boundary condition is applied, and the pressure is prescribed with a fixed value of . Slip boundary conditions are adopted for the wind tunnel walls. To replicate wind tunnel conditions, the turbulent kinetic energy at the inlet is set to a fixed value based on a turbulence intensity of . For the solid rotating surfaces, specifically the NACA 0018 wing, a "movingWallVelocity" boundary condition is implemented to ensure a zero-flux condition during dynamic or quasi-steady oscillations.
The computational grids are generated using ICEM CFD software, incorporating an O-grid topology for seamless wrapping of the O-type blocking around the wing with a blunt trailing edge. This approach facilitates the creation of a high-quality structured grid with favorable cell determinant values for the hexahedral cells. Utilizing O-type blocking ensures a well-defined boundary layer, maintaining optimal values for cell skewness and orthogonality. The ratios of cell area and volume transitions fall within the range of
, allowing a maximum change of 20 percent. This ensures that large gradients in flow scalar and vector variables are avoided during the simulation. The boundary layer comprises 30 adjacent layers with a growth rate of
. The height of the first cell layer is determined by a non-dimensional wall distance of
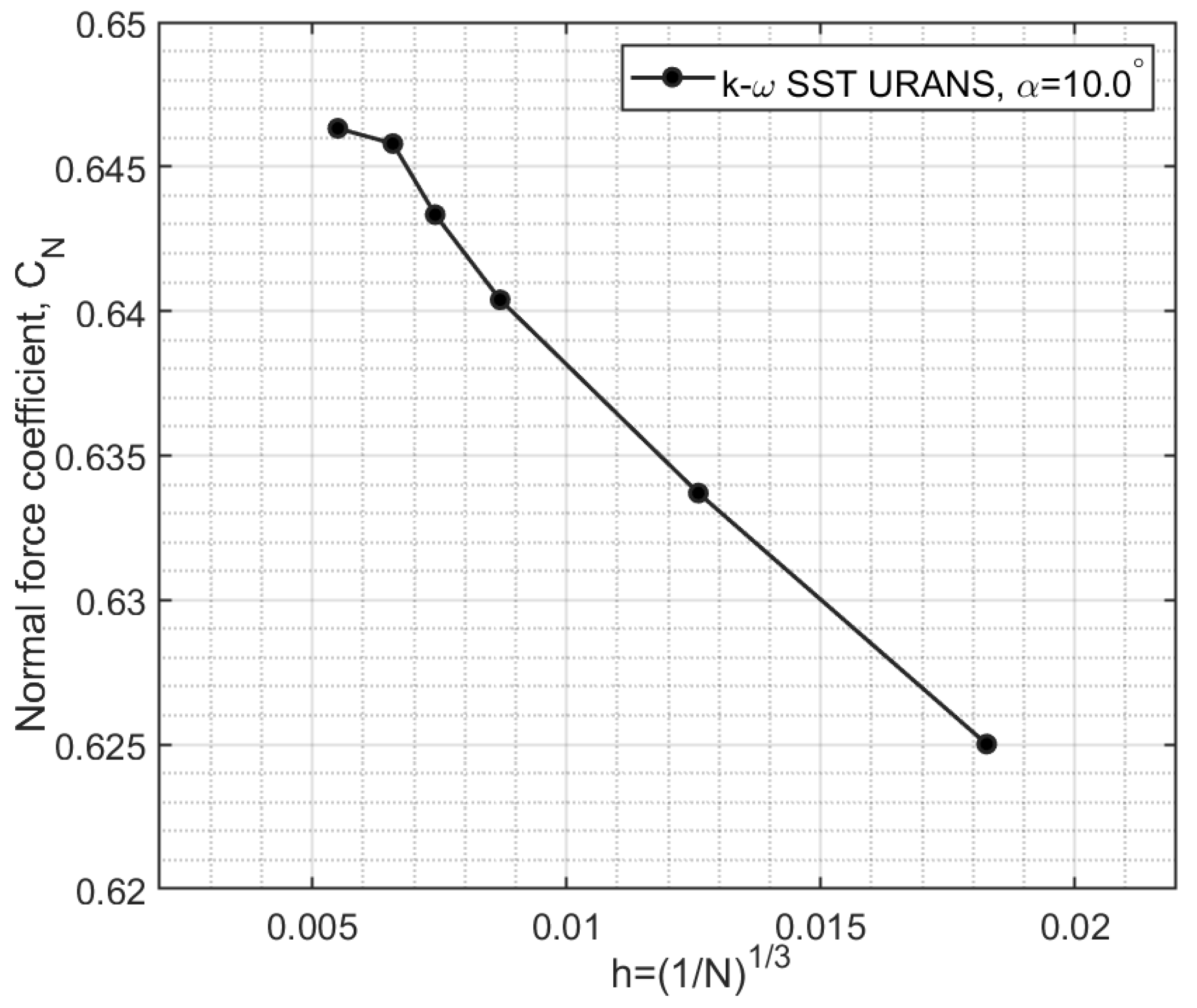
, enabling the use of a no-wall-function low Reynolds number approach. Following a thorough grid independence study, a mesh size of 3.5 million elements was found to be sufficient for this study as shown in
Figure 2.
The flow conditions, characterized by a relatively low Mach number of
, allows the consideration of incompressible fluid flow. The Navier-Stokes (NS) equations governing incompressible fluid flow are the continuity (
1) and the momentum equation (
2):
For flow conditions characterized by high Reynolds numbers, the computational demands associated with the Direct Numerical Simulation (DNS) of Eqns. (
1) and (
2) typically surpass the current computational capabilities. To address the effects of turbulence in a more computationally feasible manner, the Unsteady Reynolds-Averaged Navier-Stokes (URANS) equations are often employed. These represent a time-averaged approximation of the Navier-Stokes equations, with the averaging process introducing additional terms known as Reynolds stresses. Describing these stresses necessitates the inclusion of empirical equations, either algebraic or differential, to close the computational model. The majority of URANS turbulence models rely on an eddy viscosity concept, analogous to the kinematic viscosity of the fluid, to characterize the turbulent mixing or diffusion of flow momentum. In linear turbulence models, the Reynolds stresses resulting from averaging are modelled using the Boussinesq assumption (
3):
In this study, the SST (Shear-Stress Transport) two-equation turbulence model, as proposed by Menter [
22], is utilized. This model is widely applied in aeronautical applications, particularly for external aerodynamics involving adverse pressure gradients and strongly separated flow conditions [
11,
22]. The authors also have previously employed the SST model for capturing static hysteresis phenomena for the NACA 0018 2D airfoil [
13]. The SST model solves two equations, one for the turbulent kinetic energy (
k) and the second for evaluating
, which represents the specific dissipation rate of turbulence.
Following a meticulous evaluation and testing of various finite volume schemes and solvers available in OpenFOAM, as outlined in
Table 1, the Pre-conditioned Conjugate (PCG) solver coupled with the Geometric Algebraic Multi-Grid method (GAMG) as a pre-conditioner seemed as the most efficient algorithm for driving unsteady residuals to zero at each time level. By employing the GAMG pre-conditioner with 10-30 iterations and applying pre and post-smoothing of residuals for 2-3 levels, it was observed that only 10-30 iterations of the PCG Solver were required to reduce the residual (in the outer iterations) to nearly zero. The gradients of the flow quantities are computed using the second-order accurate Gauss linear scheme with limiters based on cell center values. The divergence of the vector velocity field and the scalar turbulent quantities is estimated with second-order accuracy using the "cellLimited Gauss linear" scheme in OpenFOAM. A linear interpolation scheme is utilized for estimating the contribution of cell center variables to the faces.
The estimation of the time derivatives in OpenFOAM for the case studies involved in this research is accomplished using the dual time stepping method, which has been well established for steady state problems [
23,
24]. More particularly, the time integration technique proposed in [
17] was adopted, which was verified and tested for several dynamic hysteresis and quasi-steady hysteresis cases.
4. Phenomenological Bifurcation Model
This section presents a phenomenological model of aerodynamic hysteresis, reflecting the empirical properties of aerodynamic loads in the stall zone. The proposed formulation for the phenomenological model is adapted to the available experimental data [
8] and the CFD simulation results presented above.
The formulation of the phenomenological model should reflect the effects observed in experiments and computer simulations of the delay in the onset of flow separation, as well as its reattachment, compared to static conditions. It was shown that the flow separation delay is proportional to the rate of change of the angle of attack
due to the improvement of the pressure gradient in the region of the leading edge [
1]. Flow reattachment when returning to lower angles of attack also exhibits similar behavior. A key feature of the phenomenological model is the need to reflect the existence of bi-stable separated structures that create static hysteresis loops and also dynamic transitions between branches of static hysteresis under unsteady conditions.
The phenomenological model, originally proposed in [
18], was based on the use of a first-order nonlinear dynamic system, including a folded equilibrium surface with bifurcation points bounding the static hysteresis zone, representing flows with a non-unique structure. A simplified model [
18] for aerodynamic loads taking into account a single separated flow structure in the stall zone, presented in [
26], demonstrated good agreement with experimental data obtained in a wind tunnel for a number of delta wings, as well as for aircraft performing Cobra maneuver. The used representation is based on introduction of an internal variable x characterising position of vortex breakdown or flow separation point governed by a first order linear differential equation characterising variation of the internal state variable in transitional motion conditions. The delay of stall was described by using the delay argument
. Recently, this delay-relaxation model attracted attention of researchers and showed its efficiency in many applications ranging from separation flow control and gust alleviation [
5,
27] to transport aircraft dynamic maneuvers [
28].
With introduction of the normalised internal state variable
the aerodynamic loads depend not only on angle of attack
and its rate of change
, but also on state variable
x, for example, the normal force coefficient in the stall region can be represented with nonlinear function
, reflecting the influence of internal variable
x on the aerodynamic loads. This general function should have the following properties:
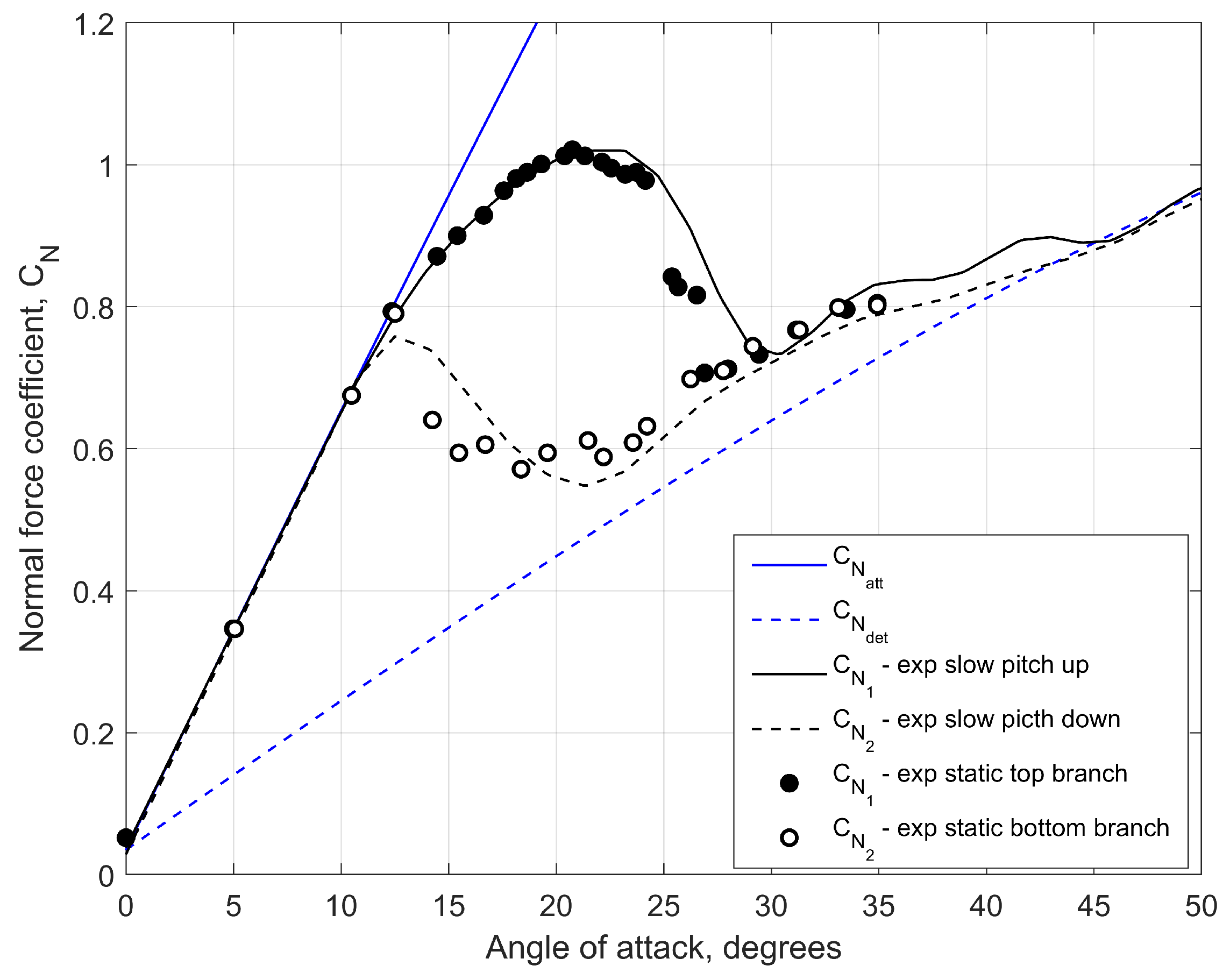
and
, where
is the dependence of the normal force coefficient under attached flow conditions which is extended above the stall region, and
represents the dependence of the normal force coefficient under fully separated flow conditions which is extended below the stall region (see
Figure 12).
In case of a single flow structure the dynamic behaviour of the internal state variable
is described by the following first order linear relaxation differential equation:
where
is a normalised internal state variable characterising the location of flow separation,
corresponds to the conditions of an attached flow and
corresponds to the conditions of a completely detached flow,
characterises the location of flow separation under static conditions,
is the delayed angle of attack, where the delay is proportional to the rate of change of the angle of attack
and
and
are the time constants, which characterise the relaxation process and the delay effect, respectively.
The transition of flow from attached conditions to completely detached conditions in the dependence
considering that most of the normal force is generated in the area close to the leading edge of the wing, the following approximation is accepted:
where
. According to the Kirchhoff formula for a fully separated flow with a constant pressure zone behind an airfoil [
5,
26,
28] this function with account of Eqn.
5 is represented as
. This formula clearly shows that the normal force coefficient
is mainly generated in the immediate vicinity of the leading edge
, where about
of normal force can be lost upon transition to a completely separated flow regime. This is confirmed by the classical distribution of
along the airfoil.
There is a wealth of experimental data showing the existence of static hysteresis in aerodynamic loads within the stall region, such as the experimental data and CFD simulation results for the NACA 0018
presented above in this paper. However, the linear relaxation Eqn.
4 does not allow bi-stable solutions at the same angle of attack, so it must be modified to accommodate the phenomenon of static hysteresis.
To achieve this transformation, we modify Eqn.
4 to the following nonlinear form:
where
is the hysteresis morphing function,
is the saddle disturbance function. The choice of these two functions, which we present below, is based on the creation of three different equilibrium solutions in the stall region by shaping the function
as a closed curve in the form of an ellipse and the function
, which is non-zero only in the vicinity of two saddle points of a nullcline set of points defined by equation
and function
is required for tuning the relaxation time in the phenomenological model.
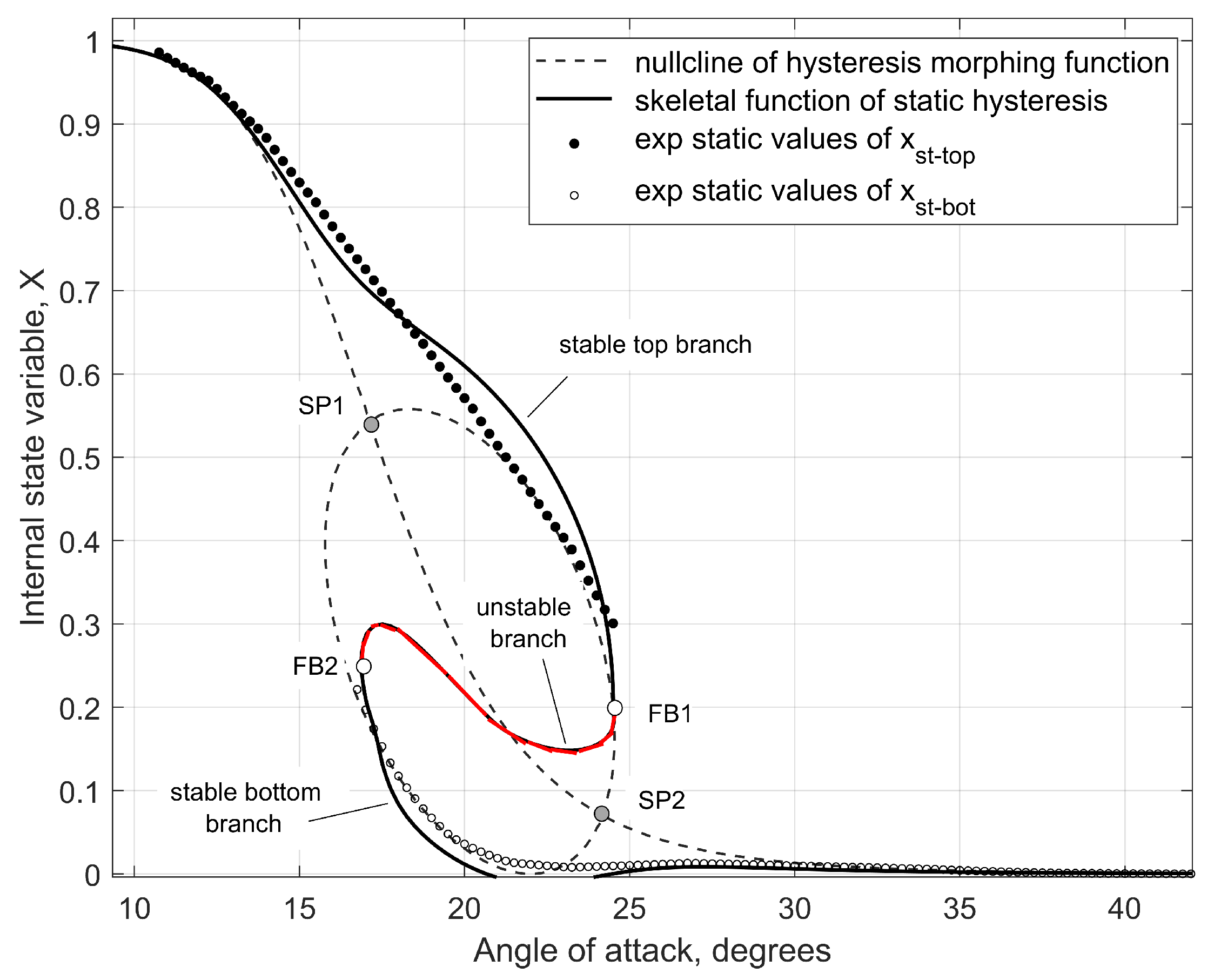
Figure 13 graphically presents major constructions in designing the nonlinear functions in Eqn.
6. The dashed lines represent the nullcline set of points defined by equation
. The function
is crossing the ellipse defined by the morphing function
in two saddle points
and
. These two saddle points are structurally unstable and functions
applied in the vicinity of saddle points will transform the nullcline set of points into continuous folded curve which shapes a skeletal function for static hysteresis. This curve includes two stable branches of static hysteresis, one on the top with
and one on the bottom with
. The intermediate branch (red segment) represents unstable solution of Eqn.
6 which separates regions of attraction of stable branches (two black segments). Two fold bifurcation points
and
on the skeletal curve indicate jump-like transition from one stable branch of static hysteresis to another stable branch depending on the direction of angle of attack variation. The presented skeletal hysteresis function has been adapted to the experimental positions of
for the top and bottom branches of static hysteresis
and
. More details about the constructed functions are given in the
Appendix A.
The characteristic time scale
in the case of Eqn.
6 is now expressed as:
where
. This means that when approaching the bifurcation points of static hysteresis
and
the relaxation time is approaching infinity
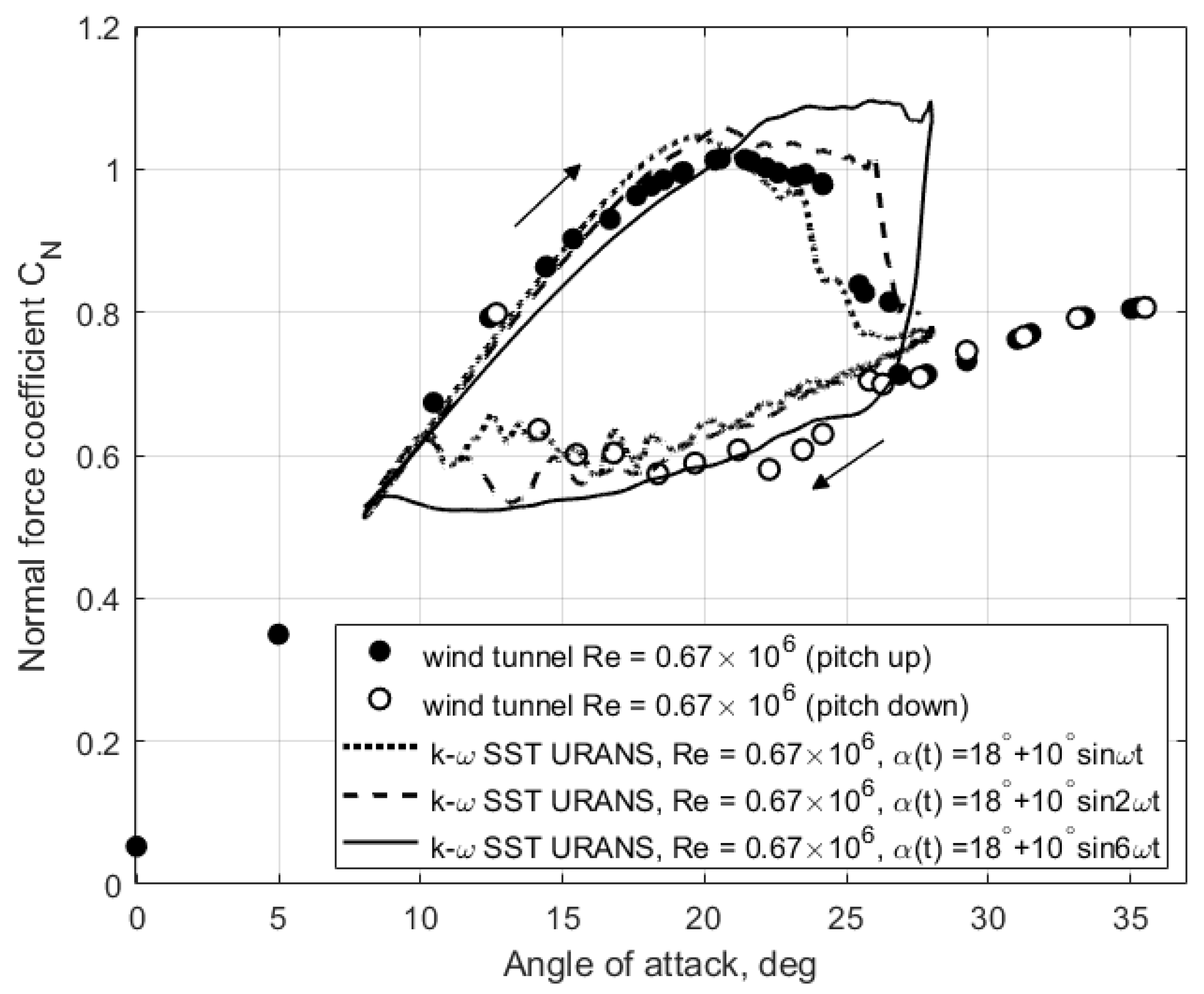
. This explains a significant expansion of the hysteresis loops in unsteady conditions with very slow variation of the angle of attack
deg/s (see
Figure 11).
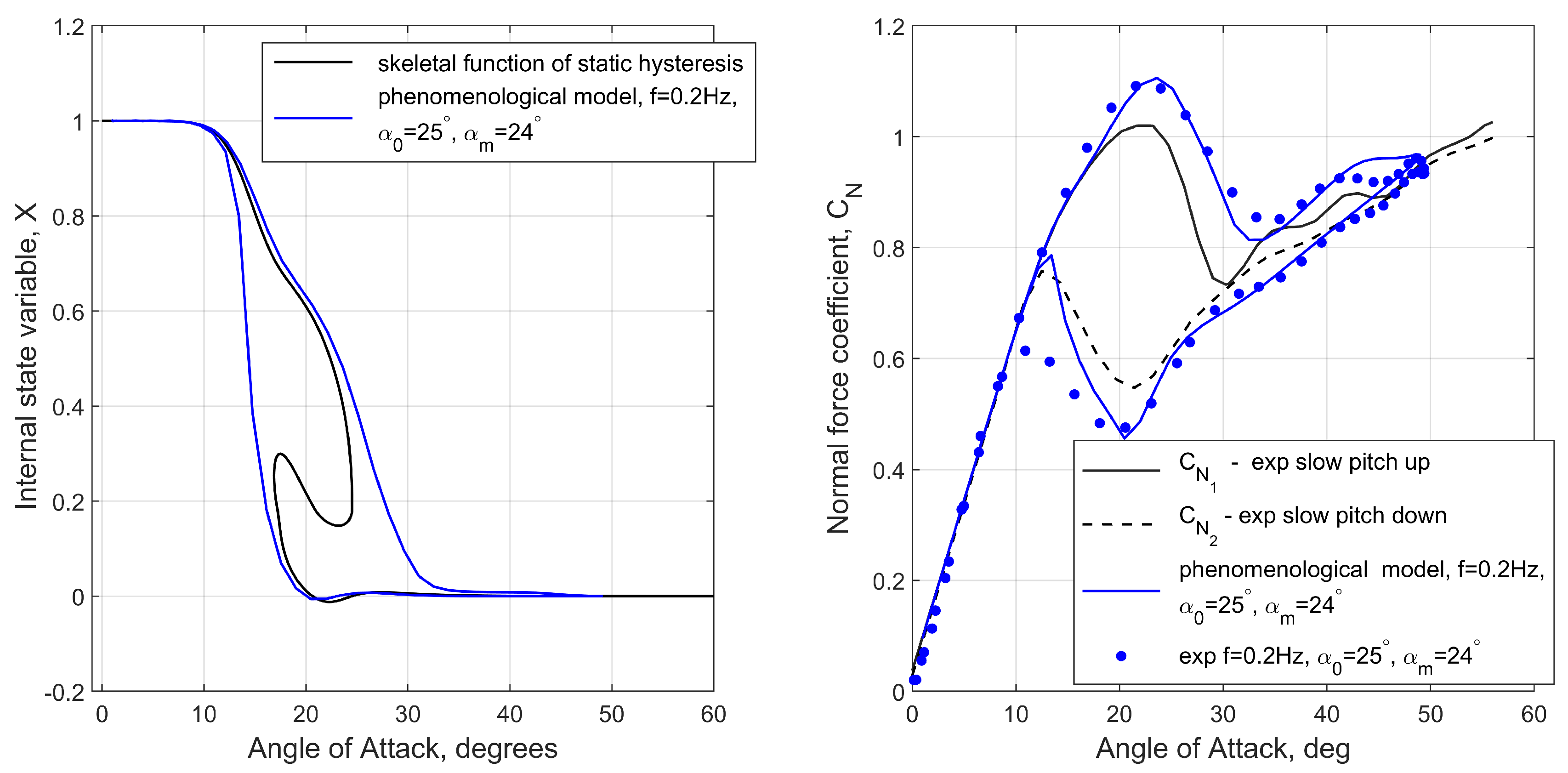
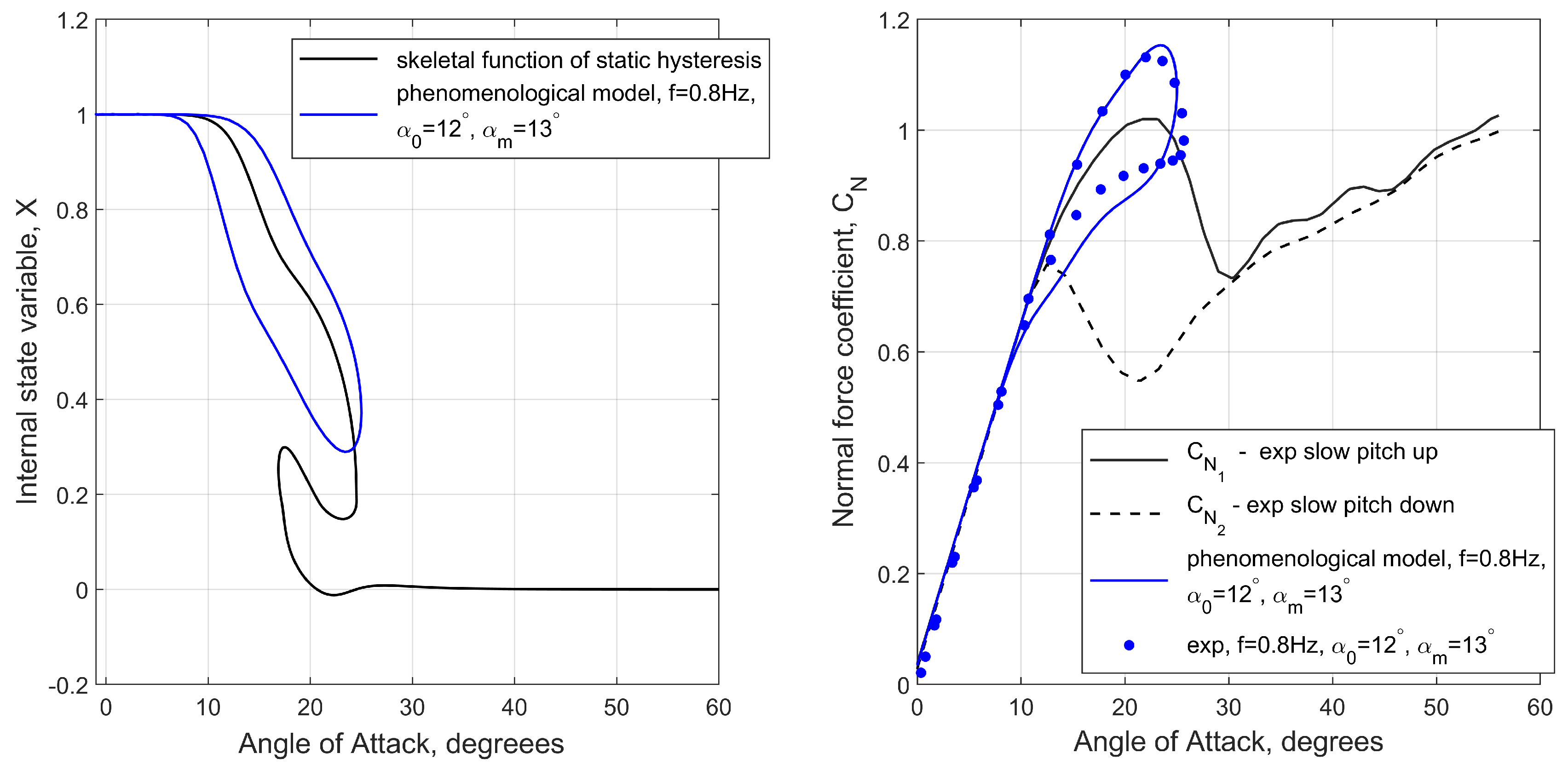
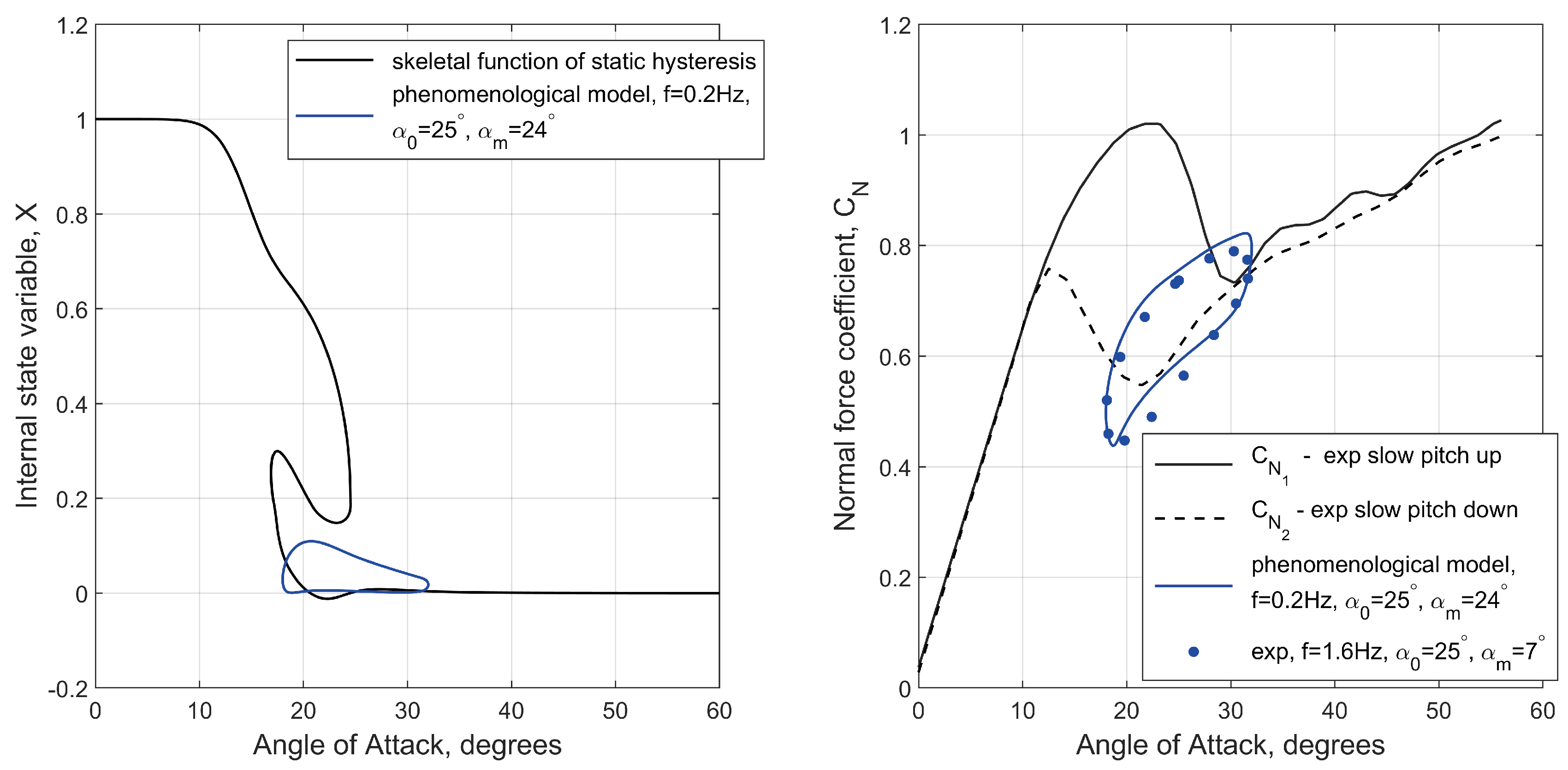
Figure 14 shows that the constructed nonlinear functions shown in
Figure 13 accurately model the quasi-static hysteresis giving good match with the experimental data. Three different cases of dynamic hysteresis were modelled, (a) the loop around the static hysteresis zone shown in
Figure 15, (b) the loop on the top branch of
reaching the bifurcation point
shown in
Figure 16 and (c) the loop on the bottom branch of
reaching‘ the bifurcation point
shown in
Figure 17. The images on the left in Figs.
Figure 15,
Figure 16 and
Figure 17 show dynamic variations of the internal state variable
with respect to the skeletal function of static hysteresis. The phenomenological modelling results in all three cases (a),(b) and (c) are very close to the experimental wind tunnel data different amplitudes and frequencies of oscillation. The tuning of the nonlinear function
in the model Eqn.
6 was carried out manually by a trial and error method for an ensemble of the considered processes. A formal mathematical approach for the parameter identification of phenomenological bifurcation models needs further research.
Figure 1.
NACA 0018 wing geometry.
Figure 1.
NACA 0018 wing geometry.
Figure 2.
Normal force coefficient variation against grid resolution parameter h from the conducted mesh independence study.
Figure 2.
Normal force coefficient variation against grid resolution parameter h from the conducted mesh independence study.
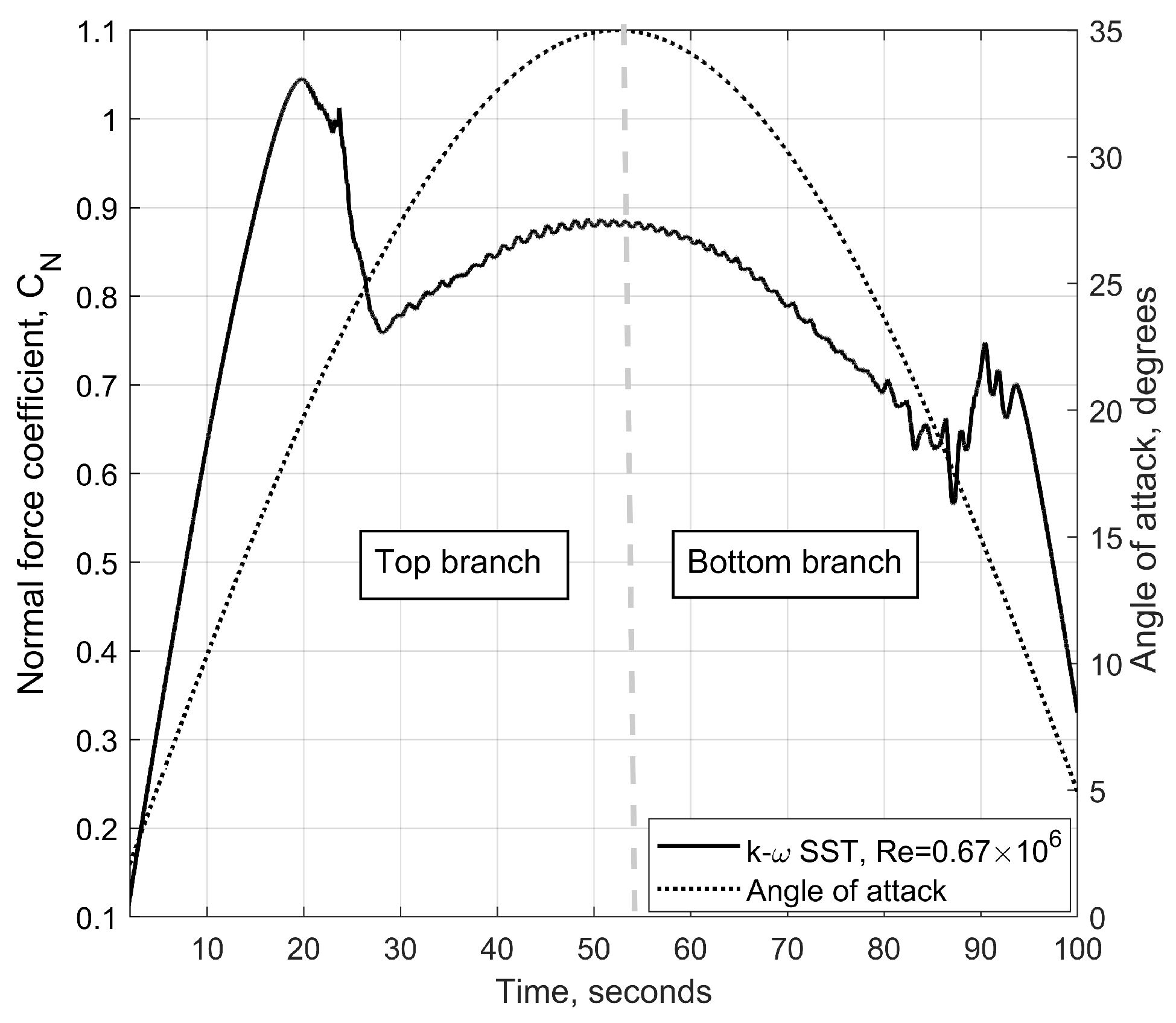
Figure 3.
Normal force coefficient (primary y axis) and angle of attack (secondary y axis) variation with physical time for the static hysteresis loop obtained at .
Figure 3.
Normal force coefficient (primary y axis) and angle of attack (secondary y axis) variation with physical time for the static hysteresis loop obtained at .
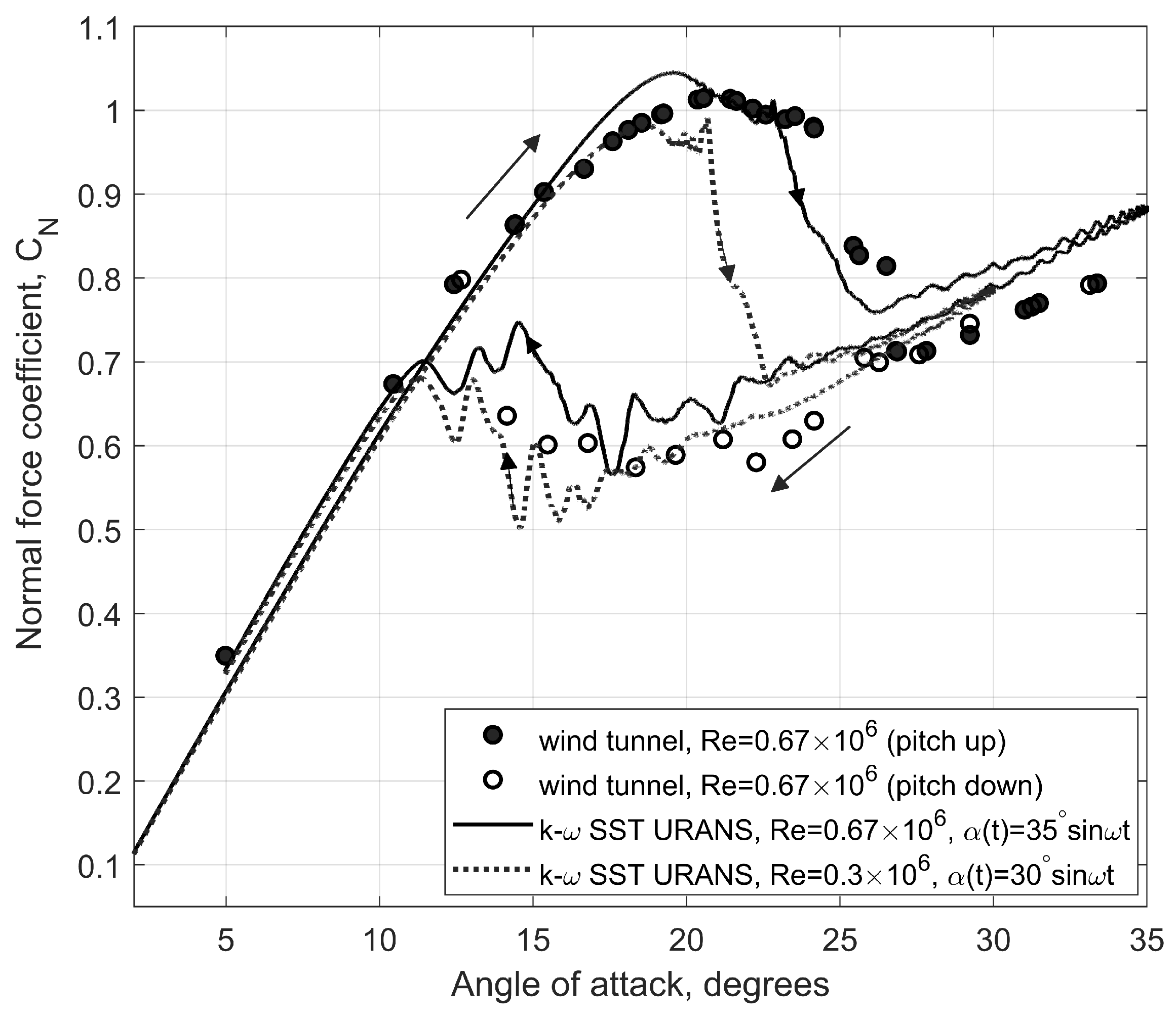
Figure 4.
Normal force coefficient
vs
during the pitch up and pitch down phases: CFD simulations and wind tunnel data from [
8].
Figure 4.
Normal force coefficient
vs
during the pitch up and pitch down phases: CFD simulations and wind tunnel data from [
8].
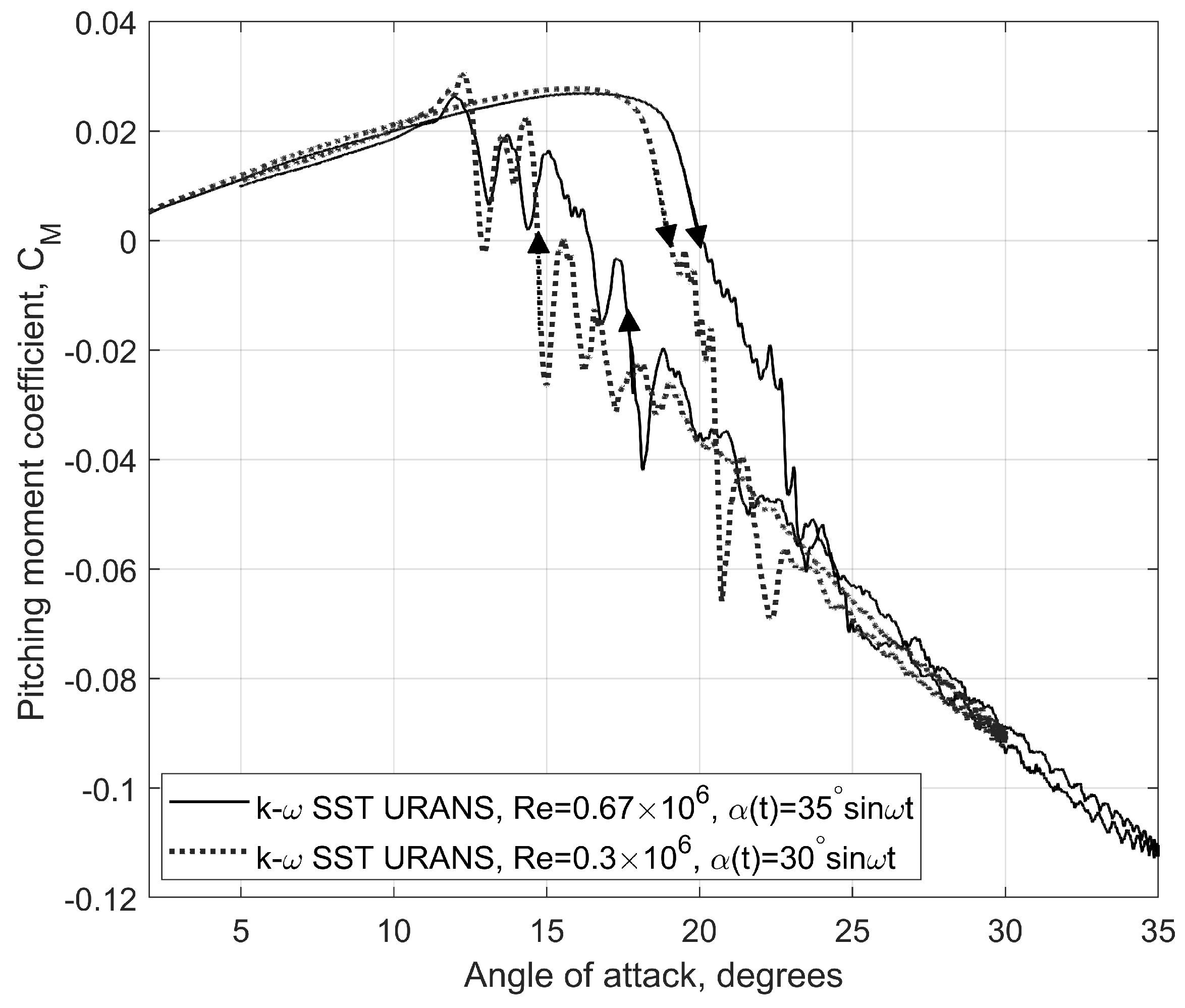
Figure 5.
Pitching moment coefficient vs during the pitch up and pitch down phases.
Figure 5.
Pitching moment coefficient vs during the pitch up and pitch down phases.
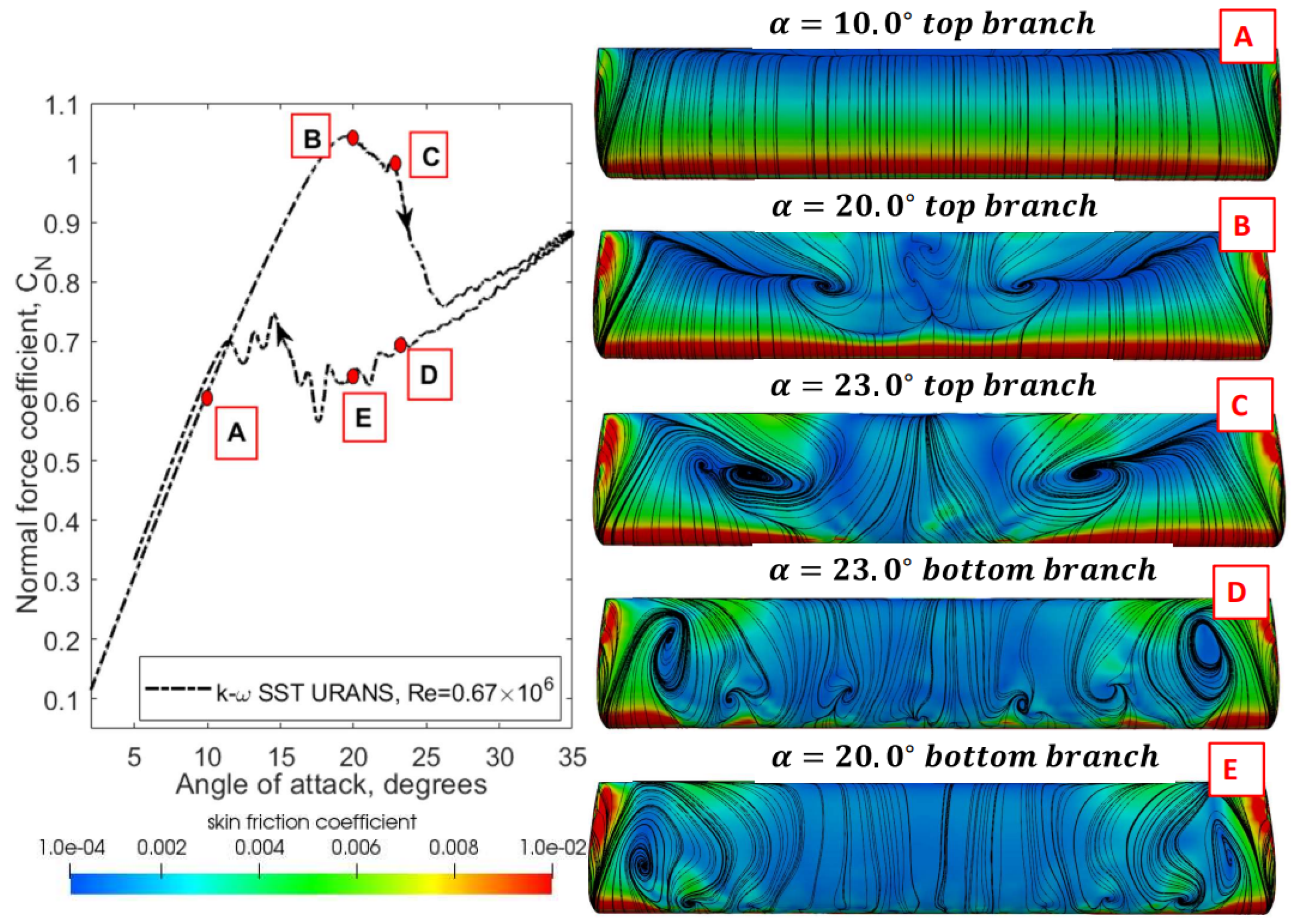
Figure 6.
Contours of skin friction superimposed on surface streamline patterns on the NACA 0018 wing during the pitch up and pitch down phases of aerodynamic static hysteresis.
Figure 6.
Contours of skin friction superimposed on surface streamline patterns on the NACA 0018 wing during the pitch up and pitch down phases of aerodynamic static hysteresis.
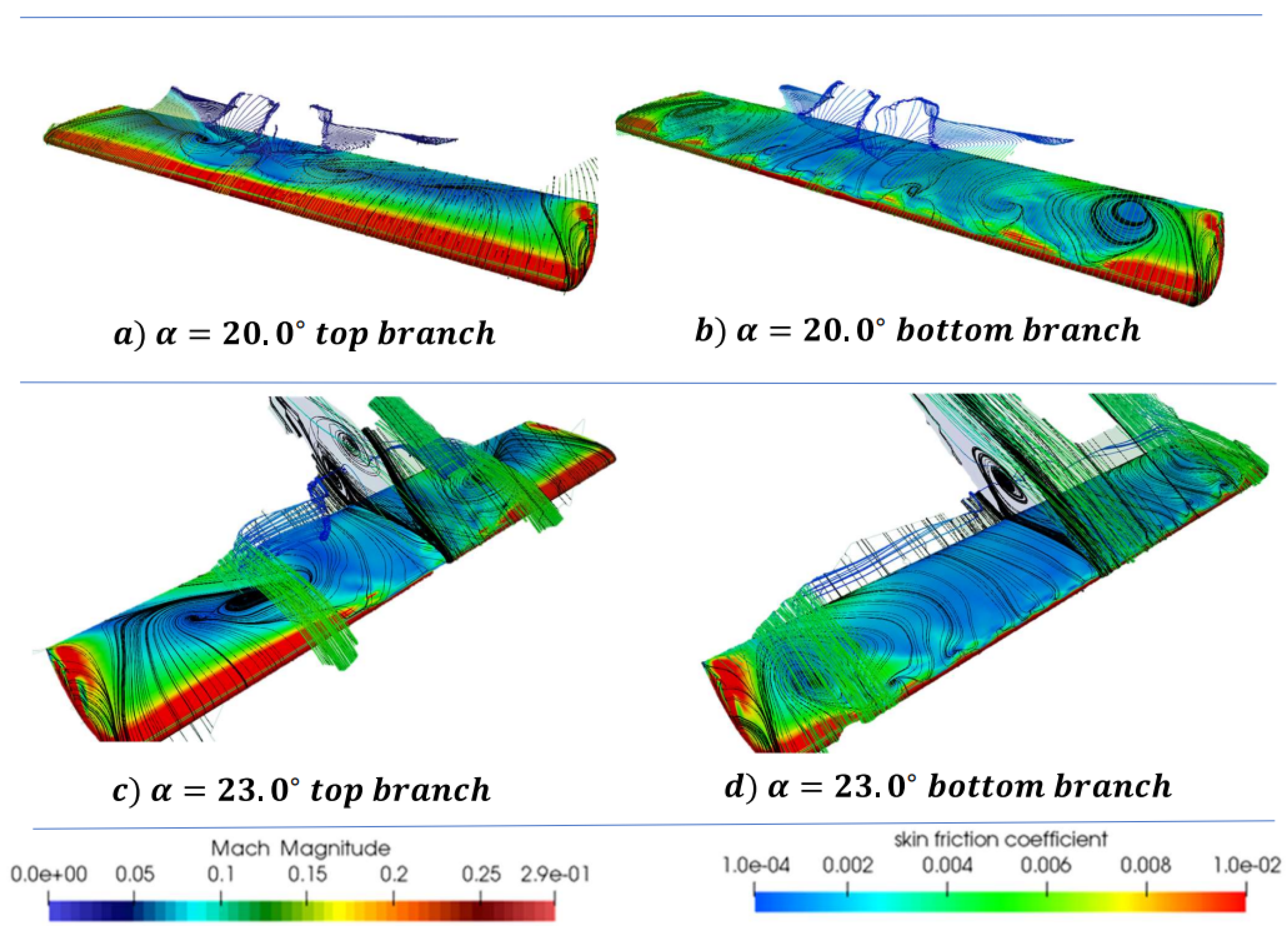
Figure 7.
3D streamlines of velocity field and contours of skin friction superimposed on surface streamline patterns on the NACA 0018 wing during the pitch up and pitch down phases at and .
Figure 7.
3D streamlines of velocity field and contours of skin friction superimposed on surface streamline patterns on the NACA 0018 wing during the pitch up and pitch down phases at and .
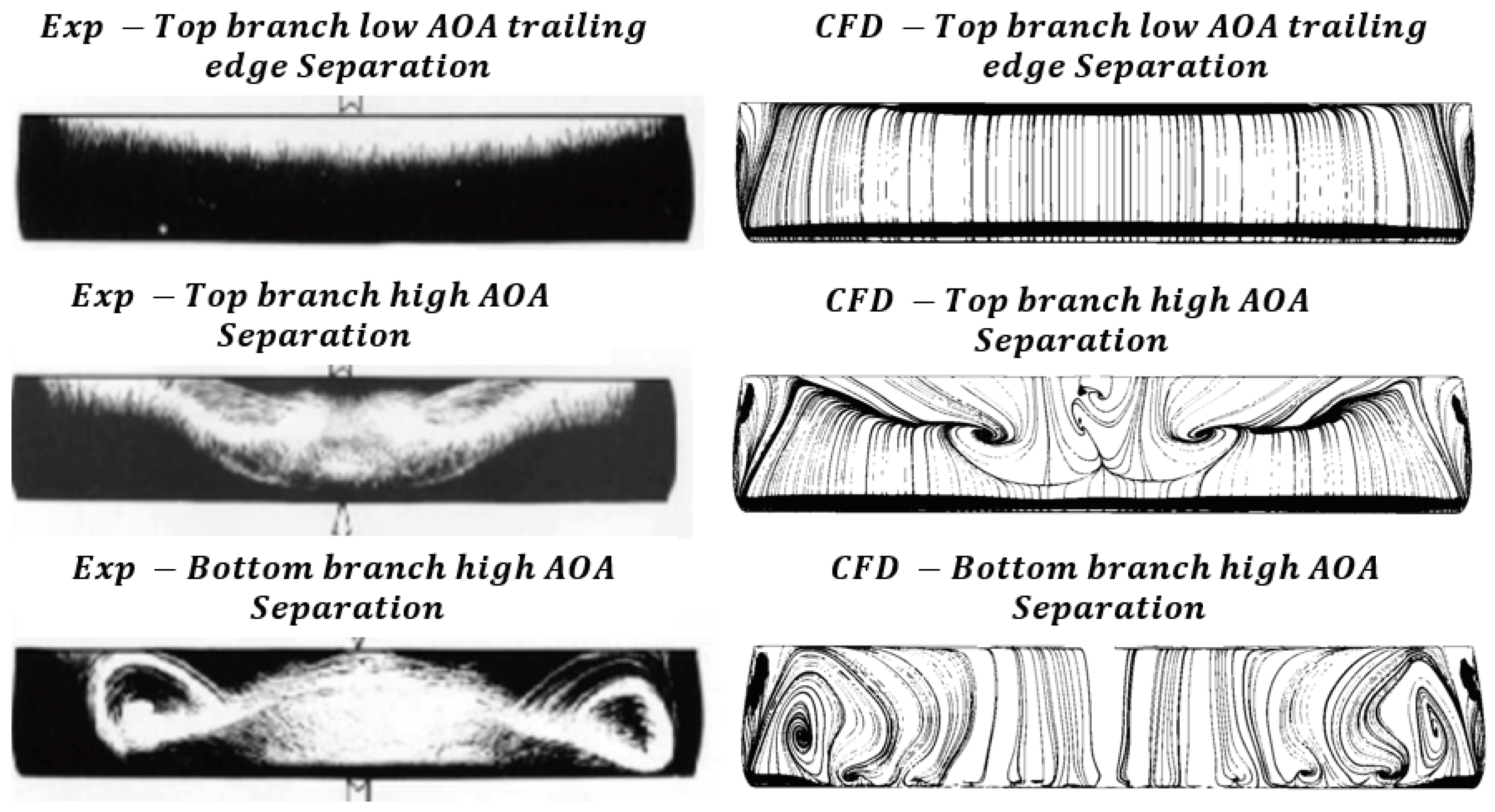
Figure 8.
Qualitative comparison of wind tunnel oil flow visualization [
25] and CFD surface streamline patterns on the top and bottom branches of aerodynamic hysteresis.
Figure 8.
Qualitative comparison of wind tunnel oil flow visualization [
25] and CFD surface streamline patterns on the top and bottom branches of aerodynamic hysteresis.
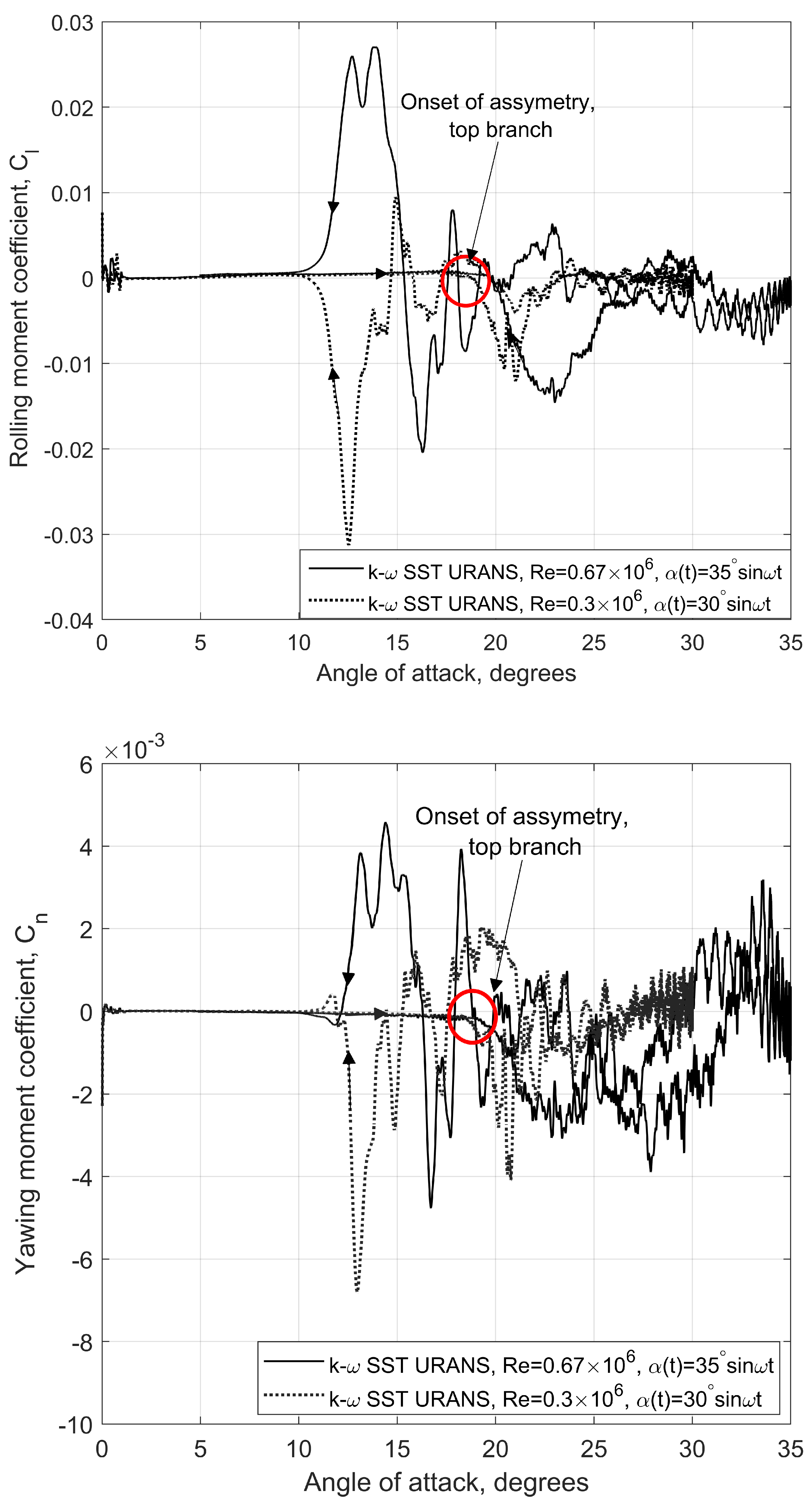
Figure 9.
Rolling and yawing moment coefficients (, ) from CFD simulations vs during the pitch up and pitch down phases.
Figure 9.
Rolling and yawing moment coefficients (, ) from CFD simulations vs during the pitch up and pitch down phases.
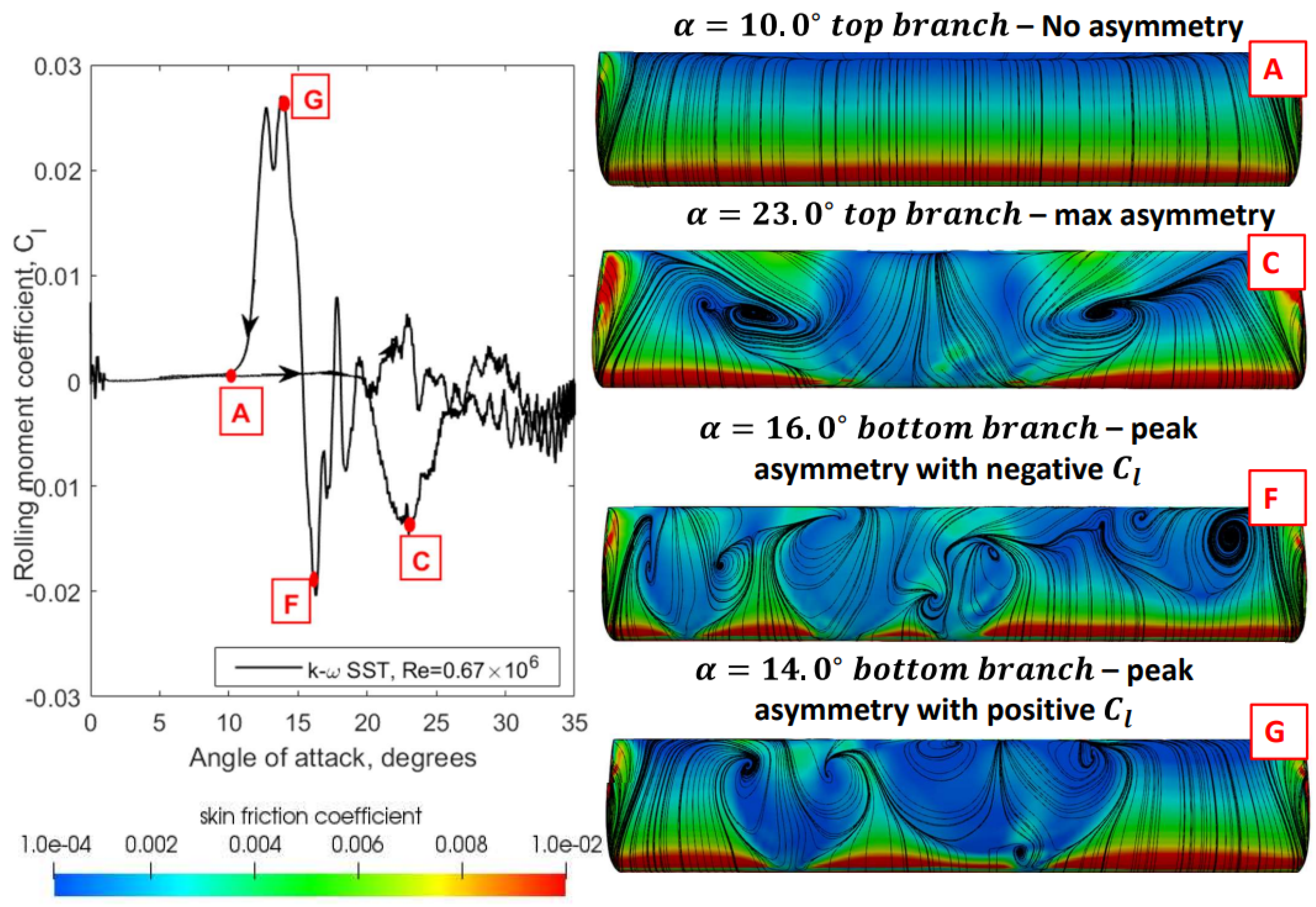
Figure 10.
Contours of skin friction superimposed on surface streamline patterns on the NACA 0018 wing during the pitch up and pitch down phases of aerodynamic static hysteresis showing development of flow asymmetry.
Figure 10.
Contours of skin friction superimposed on surface streamline patterns on the NACA 0018 wing during the pitch up and pitch down phases of aerodynamic static hysteresis showing development of flow asymmetry.
Figure 11.
Normal force coefficient from computational simulations at different rotational frequencies with and amplitude .
Figure 11.
Normal force coefficient from computational simulations at different rotational frequencies with and amplitude .
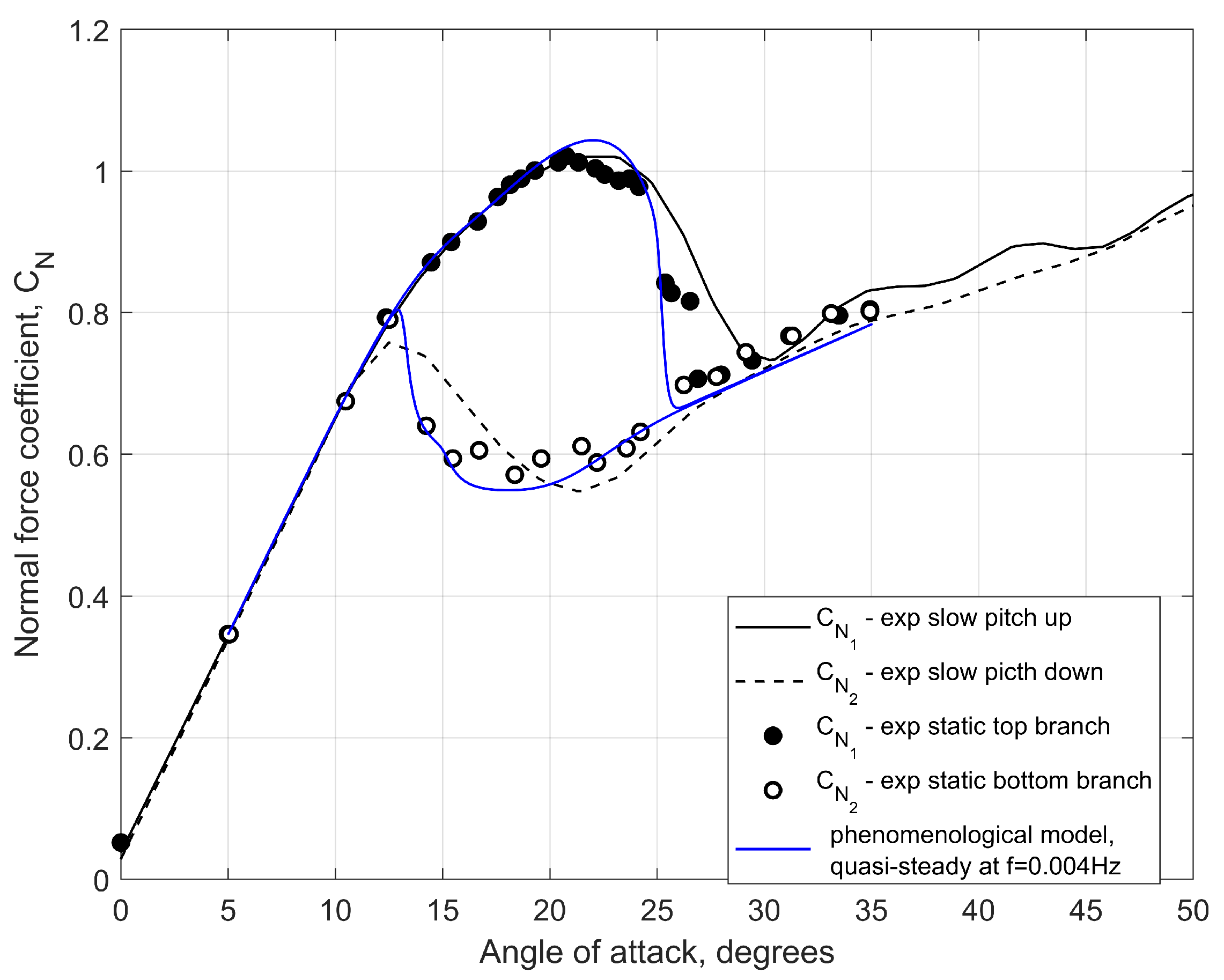
Figure 12.
Normal force coefficient of NACA 0018 wing at : 1) static test points, 2) slow pitch up and pitch down measurements and 3) approximation lines for fully attached and fully detached flow conditions, and .
Figure 12.
Normal force coefficient of NACA 0018 wing at : 1) static test points, 2) slow pitch up and pitch down measurements and 3) approximation lines for fully attached and fully detached flow conditions, and .
Figure 13.
Phenomenological model skeletal function of static hysteresis based on experimental data.
Figure 13.
Phenomenological model skeletal function of static hysteresis based on experimental data.
Figure 14.
Normal force coefficient for a very slow change in angle of attack based on phenomenological modeling and experimental results at .
Figure 14.
Normal force coefficient for a very slow change in angle of attack based on phenomenological modeling and experimental results at .
Figure 15.
Internal state variable and normal force coefficient : comparison of phenomenological results with experimental data at where Hz.
Figure 15.
Internal state variable and normal force coefficient : comparison of phenomenological results with experimental data at where Hz.
Figure 16.
Internal state variable and normal force coefficient : comparison of phenomenological results with experimental data at where Hz.
Figure 16.
Internal state variable and normal force coefficient : comparison of phenomenological results with experimental data at where Hz.
Figure 17.
Internal state variable and normal force coefficient : comparison of phenomenological results with experimental data at where Hz.
Figure 17.
Internal state variable and normal force coefficient : comparison of phenomenological results with experimental data at where Hz.
Table 1.
Finite volume solvers of OpenFOAM used in the study
Table 1.
Finite volume solvers of OpenFOAM used in the study
| Method |
equations |
preconditioner |
tolerance |
iterations |
| Pre-conditioned Conjugate Gradient (PCG) |
pressure-correction |
Multi-Grid GAMG |
1e-06 |
50 |
| smoothSolver |
Momentum/ turbulence |
none |
1e-10 |
10 |
Table 2.
Summary of the considered case studies.
Table 2.
Summary of the considered case studies.
| case |
k |
M |
Re |
|
Amplitude,
|
| 1 |
|
|
|
|
|
| 2 |
varying |
|
|
|
|