Retarded Gravity in Disk Galaxies

1. Introduction

From an empirical perspective general relativity (GR) is known to be verified by many different types of observations [5,6,15,16,29]. However, currently Einstein’s general relativity is at a rather difficult position. It has much support from observational evidence while also having serious challenges. The observational verifications it has gained in both cosmology and astrophysics are in doubt due to the fact that it needs to include unconfirmed ingredients, dark matter and energy, in order to achieve successes on the larger scales of galaxies, clusters of galaxies and universe as a whole. In most cases the unconfirmed ingredient is used while at the same time practitioners neglect a major ingredient of general relativity, the phenomenon of retardation, that negates Newtonian action at a distance.

Indeed, the dark matter enigma has not only been with the astronomical community since the 1930s (or perhaps even since the 1920s when it was known as the question of missing mass), but it has become prevalent as more dark matter (and a more serious neglect of retardation) has had to be postulated on larger scales as those scales were scrutinized. A very detailed and costly forty-years underground and accelerator search failed to prove its existence. The dark matter enigma has become even more problematic in recent years as the Large Hadron Collider failed to find any super symmetric particles, not only the astro-particle community’s preferred form of dark matter, but an essential ingredient that string theory needs, and it is that same string theory that is expected to quantize gravity.

As early as 1933, Zwicky noted that a group of galaxies within the Comma Cluster have velocities that are significantly higher than that predicted by the virial calculations based on Newtonian theory [4,45]. He calculated that the amount of matter required to account for the velocities could be 400 times greater than that of visible matter (this was later mitigated somewhat). Of course, if Zwicky would have use the retarded gravity version of the virial theory [43] no significant problem would arise. In 1959, on a smaller galactic scale, Volders observed that stars in the outer rims of a nearby spiral galaxy (M33) do not move as they should [26]. That is to say that the velocities do not decrease as $1/\sqrt{r}$. This discrepancy was further established in later years. During the seventies Rubin and Ford [19,20] have shown that for a rather large sample of spiral galaxies the velocities at the outer rim of galaxies do not decrease. Rather, in the general case, they attain a plateau (or continue increasing) at some velocity different for each galaxy. In previous works it was shown that such velocity curves can be deduced directly from GR if retardation is not neglected. The derivation of the retardation effect is described in previous publications [27,28,32,33,34,35,36,37]. The mechanism is strongly connected to the dynamics of the density of matter inside the galaxy, or more specifically to the densities’ second derivative. The density can change due to the depletion of gas in the galaxies surrounding (in which case the second derivative of the galaxies’ total mass is negative [35]) but can also be affected by dynamical processes involving star formation and supernovae explosions [27,28]. It was determined that all possible processes can be captured by three different length scales: the typical length of the density gradient, the typical length of the velocity field gradient and the dynamical length scale. It is the shortest among those length scales that determine the significance of retardation [38].

The famous relation of Tully and Fisher [24] connecting the baryonic mass of a galaxy to the fourth power of its rim velocity can also be deduced from retarded gravity [39].

Retarded gravity does not affect only slowly moving particles but also photons. Although the mathematical analysis is slightly different in both cases [38,41], it is concluded that the apparent "dark mass" must be the same as in the galactic rotation curves.

While the standard dark matter paradigm may still prevail, the current situation is alarming enough to contemplate the possibility that this prevailing paradigm might at least be reconsidered. We mention a few difficulties that add doubt to this common idea:

First, in order to comply with said observations and structure formation simulations a list of properties has been attributed to DM [4], which will not be listed here. However, to date, 50 years since its inception, DM has not been observed nor could any known particles be identified with its properties.

Second, dark matter simulations are notorious for having a core-cusp problem. Navarro-Frenk-White (NFW) [17] is the most common dark matter profile used today to fit rotation curves and is the outcome of Cold Dark Matter (CDM) simulations. However, NFW doesn’t do so well, especially in Low Surface Brightness galaxies (LSBs). Its predictions for rotational velocities and actual observations often appear to be in tension. More specifically, an NFW profile predicts a "cuspy" inner region for a dark halo (i.e. the inner density is changing fast) while observations prefer a "core-like" (approximately constant density) behavior. Of course, many attempts have been made over the years to resolve this problem, but those were very limited. They included more ad hoc assumptions and more free parameters, and one could not avoid the feeling that those were mainly introduced to keep the current paradigm alive.

Third, Sancisi’s Law [21] is a significant and quite general observation. The problems it creates apply to all kinds of dark halos. It states that "for any feature in the luminosity profile there is a corresponding feature in the rotation curve and vice versa". In other words, small changes in the baryonic mass distribution ("features") can be seen in the total velocity distribution, i.e. in the rotation curve. It is quite unexpected from a dark-matter perspective: the dark halo is much more massive according to standard modelling than the baryons. Therefore, in most regions, fluctuations in the baryonic distribution should not affect the velocity distribution contrary to observations. The problem in LSBs is even worse. In LSBs the dark halo is believed to be dominant in every radius. Still, the velocity distribution presents each and every "baryonic bump". It seems that somehow, the total velocity "cares" about small baryonic fluctuations.

Thus there is indeed room for the present suggestion. Unlike other theories that suggest modifying general relativity such as Milgrom’s MOND [13], Mannheim’s Conformal Gravity [10,11] or Moffat’s MOG [14], the current approach does not do so. We adhere strictly to Occam’s razor, as suggested by Newton and Einstein. It seeks to replace dark matter with effects within the standard General Relativity itself. Notice, however, that the connection between retardation and MOND was recently elucidated [44], showing in what sense low acceleration MOND criteria can be derived from retardation theory and how MOND interpolation function can be a good approximation to retarded gravity.

We emphasize that appreciable retardation effects do not require that velocities of matter in the galaxy are high (although this may help), in fact the vast majority of galactic bodies (stars, gas) are slow with respect to the speed of light. In other words, the ratio of $\frac{v}{c}\ll 1$. Typical velocities in galaxies are 100 km/s, which makes this ratio $0.001$ or smaller. To obtain appreciable retardation effects what is needed is a small typical gradient scale with respect to the size of the system [38]. It was shown that retardation effects may become significant even at low speeds, provided that the distance over a typical length scale is large enough.

Within the solar system retardation effects are not appreciable [40,42]. However, galaxies’ velocity curves indicate that the retardation effects cannot be neglected beyond a certain distance [27,28,35]. The purpose of this study is to establish the empirical basis for the retarded gravity theory. It expands previous work analysing eleven galaxies [28] to the current application of a larger sample of 143 galaxies. Those 143 galaxies originated from the SPARC Galaxy collection are of different types, sizes and luminosities. We show that in most cases we obtain an excellent fit without postulating dark matter or modifying general relativity.

2. Retardation Effects Beyond the Newtonian Approximation

The mathematical similarities between GR and Electromagnetic (EM) theory have not gone unnoticed. While exact solutions of GR have proven challenging due to the non-linear nature of the Einstein equations, within the weak field approximation the equations are linear, therefore superposable, yielding a Retarded Potential [9,29] similar to that of EM theory [8,23]. The form of the equations in both case is related to the structure of the constant Lorentzian metric [30,31].

Thus the retarded gravitational potential $\varphi$ is given in Equation (21) of [35]:

$$\varphi =-G\int \frac{\rho ({\overrightarrow{x}}^{\prime },t-\frac{R}{c})}{R}{d}^3{x}^{\prime }$$

(1)

The notations used are the same as in [35] and will not be redefined here.

When focusing on the far field solutions of the Retarded Potential given in equation (1), in a similar manner to EM theory, the exciting possibility of gravitational waves has risen [9,29]. For many years, the community has focused on this possibility of Gravitational Waves, which have only recently been observed [2] with much excitement, creating new possibilities. Since the far field approach is not suitable within galaxies, or even at their edges, as the galaxy is the source system, retardation theory [33,34,35,36,37,38,39,41] focuses on the near field solutions, yielding a near field regime.

Using equation (1) we may derive the force per unit mass:

$$\begin{array}{ccc}\hfill \overrightarrow{F}& =& -\overrightarrow{\nabla }\varphi ={\overrightarrow{F}}_{Nr}+{\overrightarrow{F}}_r\hfill \\ \hfill {\overrightarrow{F}}_{Nr}& =& -G\int \frac{\rho ({\overrightarrow{x}}^{\prime },t-\frac{R}{c})}{R^2}\widehat{R}{d}^3{x}^{\prime },\widehat{R}\equiv \frac{\overrightarrow{R}}{R}\hfill \\ \hfill {\overrightarrow{F}}_r& \equiv & -\frac{G}{c}\int \frac{{\rho }^{\left(1\right)}({\overrightarrow{x}}^{\prime },t-\frac{R}{c})}{R}\widehat{R}{d}^3{x}^{\prime },{\rho }^{\left(n\right)}\equiv \frac{{\partial }^n\rho }{\partial t^n}.\hfill \end{array}$$

(2)

Thus a retarded potential does not simply imply a retarded Newtonian force ${\overrightarrow{F}}_{Nr}$, but in addition a pure "retardation" force ${\overrightarrow{F}}_r$ which decreases more slowly than the Newtonian force with distance, explaining the peculiar form of the galactic rotation curves. We emphasize that this result is independent of any perturbation expansion in the delay time $\frac{R}{c}$ as was done in [35]. However, the perturbation expansion does shed some light on the nature of those force terms as is explained below.

The duration $\frac{R}{c}$ may be tens of thousands of years, but may be short with respect to the duration in which the galactic density changes considerably. Thus, we write a Taylor series for the density:

$$\rho ({\overrightarrow{x}}^{\prime },t-\frac{R}{c})=\sum _{n=0}^{\infty }\frac{1}{n!}{\rho }^{\left(n\right)}({\overrightarrow{x}}^{\prime },t){(-\frac{R}{c})}^n.$$

(3)

By inserting Equations (3) into Equation (1), we will obtain:

$$\begin{array}{ccc}\hfill \varphi & =& {\varphi }_2+{\varphi }_{(n>2)}\hfill \\ \hfill {\varphi }_2& =& -G\int \frac{\rho ({\overrightarrow{x}}^{\prime },t)}{R}{d}^3{x}^{\prime }+\frac{G}{c}\int {\rho }^{\left(1\right)}({\overrightarrow{x}}^{\prime },t)d^3{x}^{\prime }-\frac{G}{2c^2}\int R{\rho }^{\left(2\right)}({\overrightarrow{x}}^{\prime },t)d^3{x}^{\prime }\hfill \\ \hfill {\varphi }_{(n>2)}& =& -G\sum _{n=3}^{\infty }\frac{{(-1)}^n}{n!c^n}\int R^{n-1}{\rho }^{\left(n\right)}({\overrightarrow{x}}^{\prime },t)d^3{x}^{\prime }\hfill \end{array}$$

(4)

The Newtonian potential is the first term, the second term has null contribution, and the third term is the lower order correction to the Newtonian theory:

$${\varphi }_r=-\frac{G}{2c^2}\int R{\rho }^{\left(2\right)}({\overrightarrow{x}}^{\prime },t)d^3{x}^{\prime }$$

(5)

The expansion given in Equation (4), being a Taylor series expansion, is only valid for limited radii determined by the convergence of the infinite sum:

$$R<c{T}_{max}\equiv R_{max}$$

(6)

hence the current approximation can only be used in the near field regime, this is to be contrasted with the far field approximation used for gravitational radiation [3,6,18]. The restriction is even more severe when one uses a second order expansion as was done in [35].

If $n>2$ terms can be neglected, the total force per unit mass can be approximated by:

$$\begin{array}{ccc}\hfill \overrightarrow{F}& \simeq & {\overrightarrow{F}}_N+{\overrightarrow{F}}_{ar}\hfill \\ \hfill {\overrightarrow{F}}_N& =& -\overrightarrow{\nabla }{\varphi }_N=-G\int \frac{\rho ({\overrightarrow{x}}^{\prime },t)}{R^2}\widehat{R}{d}^3{x}^{\prime },\widehat{R}\equiv \frac{\overrightarrow{R}}{R}\hfill \\ \hfill {\overrightarrow{F}}_{ar}& \equiv & -\overrightarrow{\nabla }{\varphi }_r=\frac{G}{2c^2}\int {\rho }^{\left(2\right)}({\overrightarrow{x}}^{\prime },t)\widehat{R}{d}^3{x}^{\prime }.\hfill \end{array}$$

(7)

In the above ${\overrightarrow{F}}_N$ is a non retarded Newtonian force. To see how this comes about from the existence of a Newtonian retarded force and retardation force as defined in equation (2) please consult [37]. The cancellation of the first order term in $\frac{1}{c}$ is indeed remarkable as was pointed out by Feynman [7] with respect to the electromagnetic case. For large distances, $r=|\overrightarrow{x}|\to \infty$, such that $\widehat{R}\simeq \frac{\overrightarrow{x}}{|\overrightarrow{x}|}\equiv \widehat{r}$; thus, we obtain:

$${\overrightarrow{F}}_{ar}=\frac{G}{2c^2}\widehat{r}\int {\rho }^{\left(2\right)}({\overrightarrow{x}}^{\prime },t)d^3{x}^{\prime }=\frac{G}{2c^2}\widehat{r}\ddot{M},\ddot{M}\equiv \frac{d^{2}M}{d{t}^2}.$$

(8)

The above approximation is rather useful as dominant retardation effect occur usually outside the main mass of the galaxy. As the galaxy attracts intergalactic gas, its mass becomes larger and therefore $\dot{M}>0$; however, as the intergalactic gas is depleted, the rate at which the mass is accumulated must decrease and therefore $\ddot{M}<0$. This is of course a much oversimplified description of the overall situation in which star formation and supernovae explosions affect the mass accretion rate of the galaxy.

Thus, in the galactic case:

$${\overrightarrow{F}}_{ar}=-\frac{G}{2c^2}\left|\ddot{M}\right|\widehat{r}$$

(9)

and the retardation force is attractive.

${\overrightarrow{F}}_N$ first introduced by Newton is attractive, however, the retardation force ${\overrightarrow{F}}_r$ may be either attractive or repulsive. Newtonian force decreases as $\frac{1}{R^2}$, however, the retardation force does not depend on distance as long as the Taylor approximation given in Equation (3) holds. Below a certain distance, the Newtonian force dominates, but for larger distances the retardation force has the upper hand. Newtonian force can be neglected for distances significantly larger compared to the retardation distance:

$$R\gg R_r\equiv c\Delta t$$

(10)

$\Delta t$ is a duration associated with the second order derivative of the density $\rho$. For $R\ll R_r$, retardation can be neglected and only Newtonian forces need to be considered; this is the situation in the solar system.

One may claim that since for the galaxy $\ddot{M}<0$ and the total mass is conserved it must be that $\ddot{M}>0$ for the matter outside the galaxy and thus retardation forces ${\overrightarrow{F}}_{ar}$ inside and outside the galaxy should cancel out. This argument, however, is incorrect because equation (7) is only valid when $\frac{R}{c}$ is small, it is certainly not small if the rest of the universe outside the galaxy is taken into account. We have shown in [37] by a detailed model that a retardation force exist regardless if one assumes the expansion of equation (3) or not.

3. Methodological Remarks

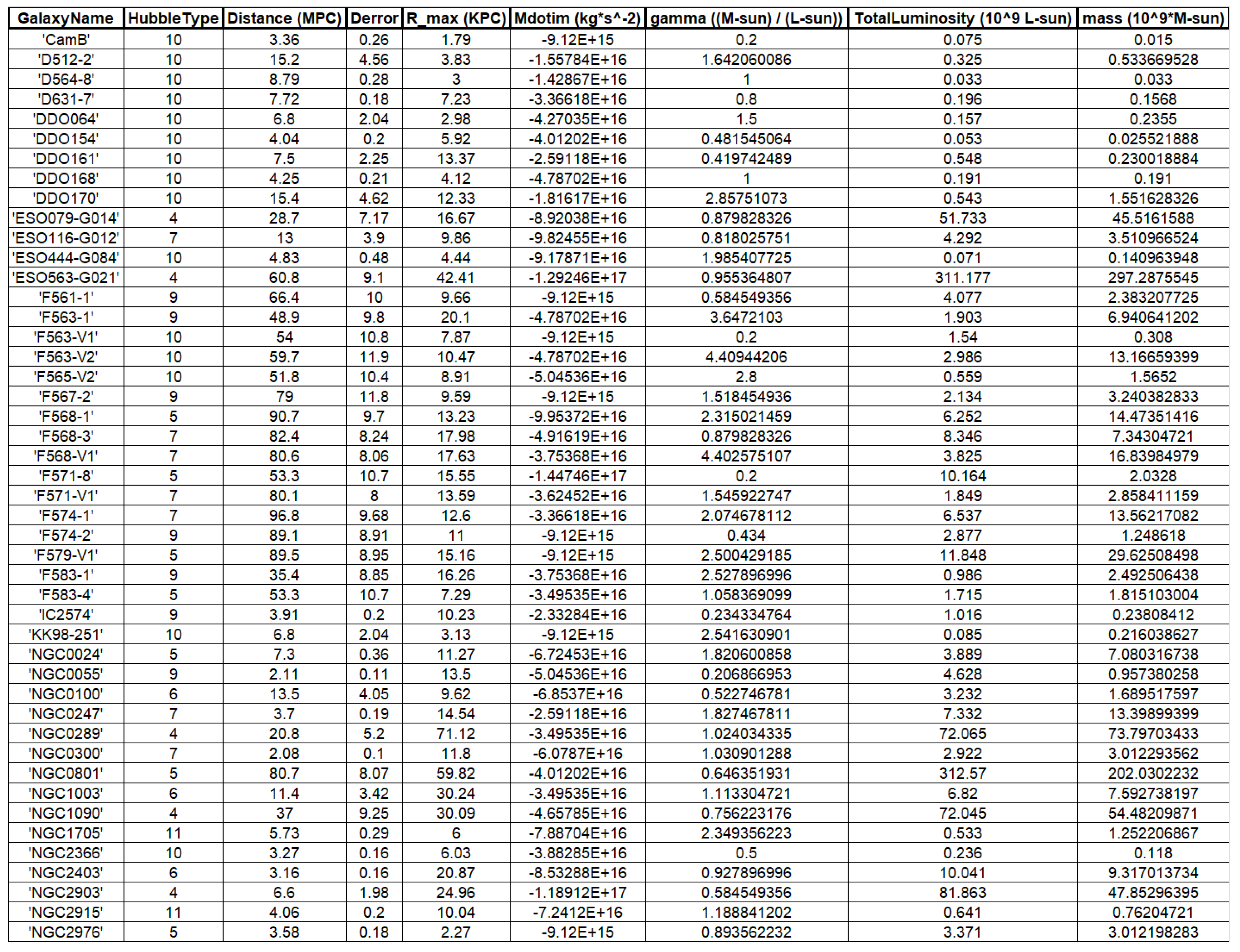
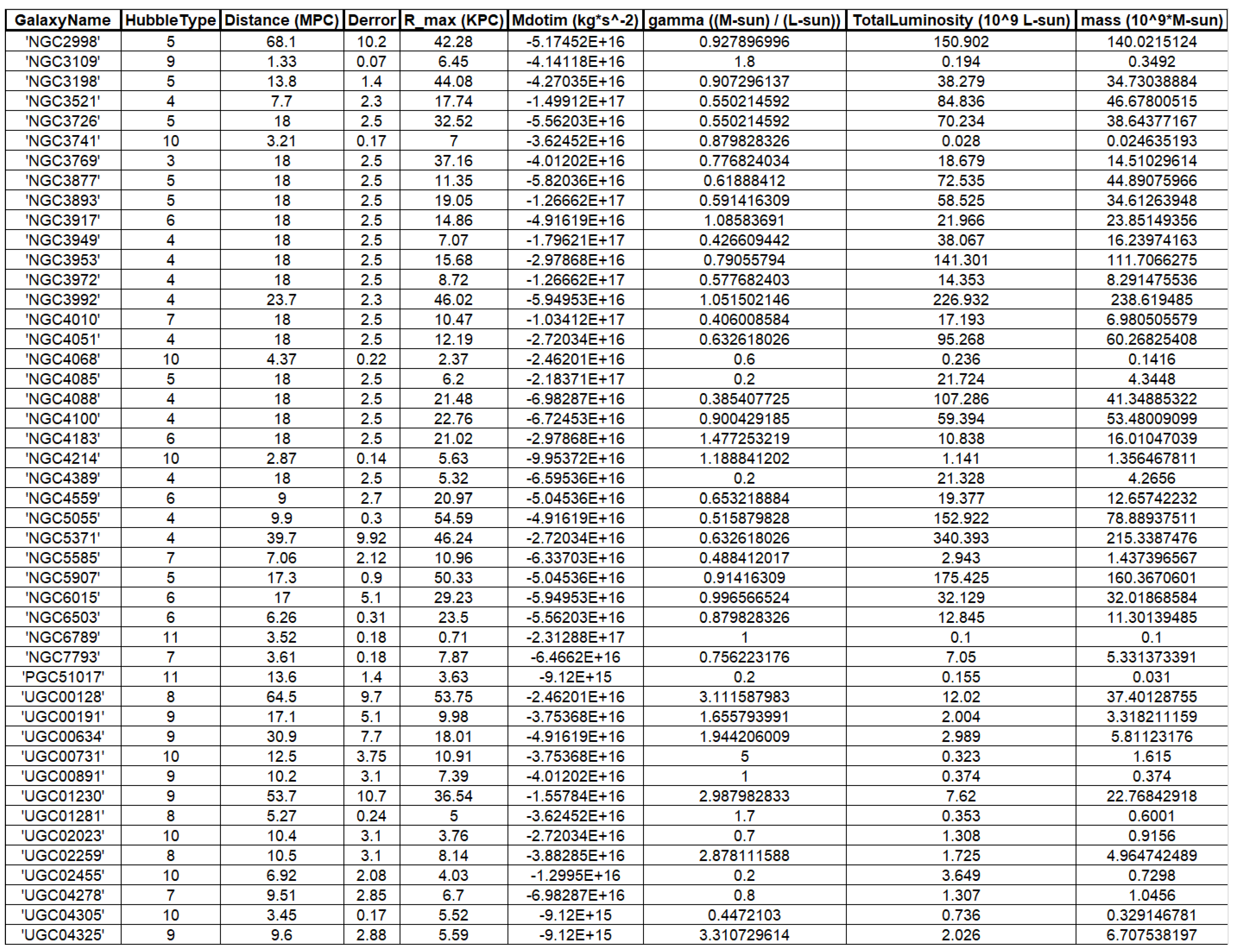
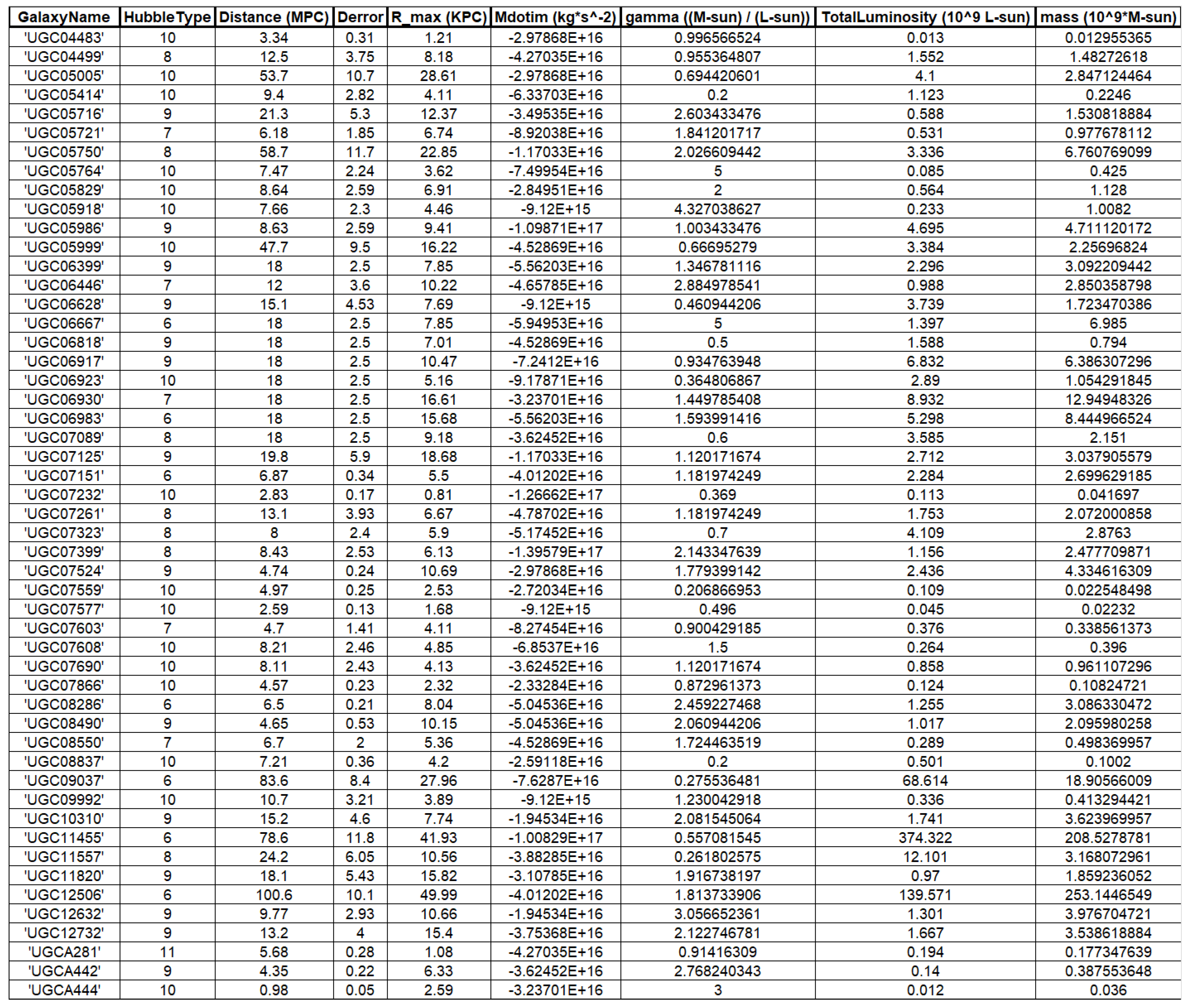
Our goal is to fit a large number of rotation curves using the retardation model. In order to accomplish this goal, we rely on the publicly available SPARC database of [12]. The database includes galaxies with extended 21-cm rotation curves spanning a large range of luminosities and radii. Galactic rotation curves are calculated in this work by the well known formula:

$$\frac{v_{\theta }^2}{r}=F$$

(11)

in which we use the notation of [35]. However, unlike other authors we do not neglect the retardation effect and thus:

$$\frac{v_{\theta }^2}{r}=F=F_N+F_{ar}=F_N+\frac{G}{2c^2}\left|\ddot{M}\right|,$$

(12)

In the above we use the approximation given in equation (9) which will suffice in most cases, and allows automatization of the curve fitting process. However, to obtain high quality results more detailed modelling of the density is required as described in [35]. Each observed rotation curve in the database is accompanied by the Newtonian velocity components of its stellar disk $v_{disk}\left(r\right)=\sqrt{r{F}_{Ndisk}}$, galactic bulge $v_{bulge}\left(r\right)=\sqrt{r{F}_{Nbulge}}$, and gaseous disk $v_{gas}\left(r\right)=\sqrt{r{F}_{Ngas}}$. Those correspond to the expected circular Newtonian velocities (i.e. the models) produced by each galactic component. For simplicity, in this study we selected only galaxies with no bulge components.

Let us now take a closer look at our model and discuss its different terms. Equation (12) can be rewritten in the following form:

$$v_{predicted}\left(r\right)=\sqrt{(M/L)·v_{disk}^2\left(r\right)+v_{gas}^2\left(r\right)+\frac{Gr}{2c^2}\left|\ddot{M}\right|},$$

(13)

where $M/L$ is the stellar-disk mass-to-light ratio which signifies the fact that mass is not observed directly but is derived from the (absolute) luminosity of the galaxy. The model the contains, therefore, two free parameters: $M/L$ and $|\ddot{M}|$ ($v_{disk}$ corresponds to a disk velocity contribution for a mass-to-light of unity, that is the mass to light ration of the sun).

Let us briefly discuss the different velocity components. The publicly-available velocity distribution $v_{disk}\left(r\right)$ of each galaxy (i.e., prediction for the disk) was numerically obtained from the corresponding light distribution of that galaxy. The light distribution of a galaxy traces the stellar mass distribution. Therefore, given the light distribution (combined with the chosen $M/L$), the gravitational and velocity fields of the disk component could be derived. The publicly-available velocity distribution $v_{gas}\left(r\right)$ of each galaxy was numerically derived from observed neutral hydrogen. The gaseous disk component may also contribute to the overall velocity, especially in low-luminosity galaxies. The disk and gas components of each galaxy, $v_{disk}\left(r\right)$ and $v_{gas}\left(r\right)$ are available online in [12] as numerical data files. Sanders & McGaugh [22] provides more details on the extraction of these components.

In order to fit the model (i.e., equation (13)) to a given observed rotation curve, we use the least-squares method. We search for the values of $M/L$ and $|\ddot{M}|$ that minimize ${\chi }^2$ in each galaxy; that is to say, the best-fit values of those two parameters. This is done through a dedicated MATLAB script that searches the values iteratively. It starts with a 2-dimensional grid of initial guesses. From each point on the grid it tries to find a close local minimum. It then combine the results to get a global minimum. The $M/L$ value is found from the inner Newtonian part of the rotation curve simplifying the parameter search.

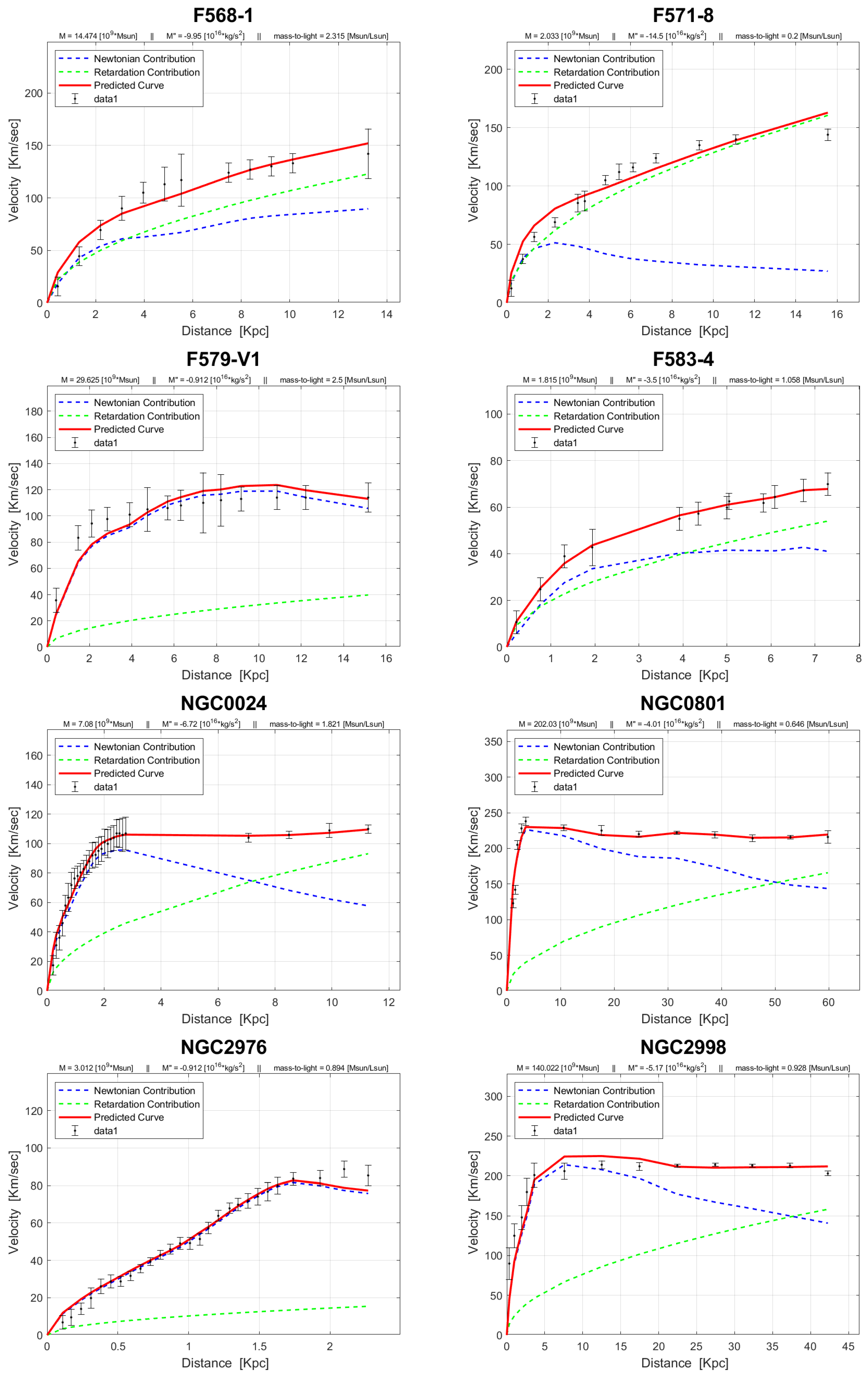
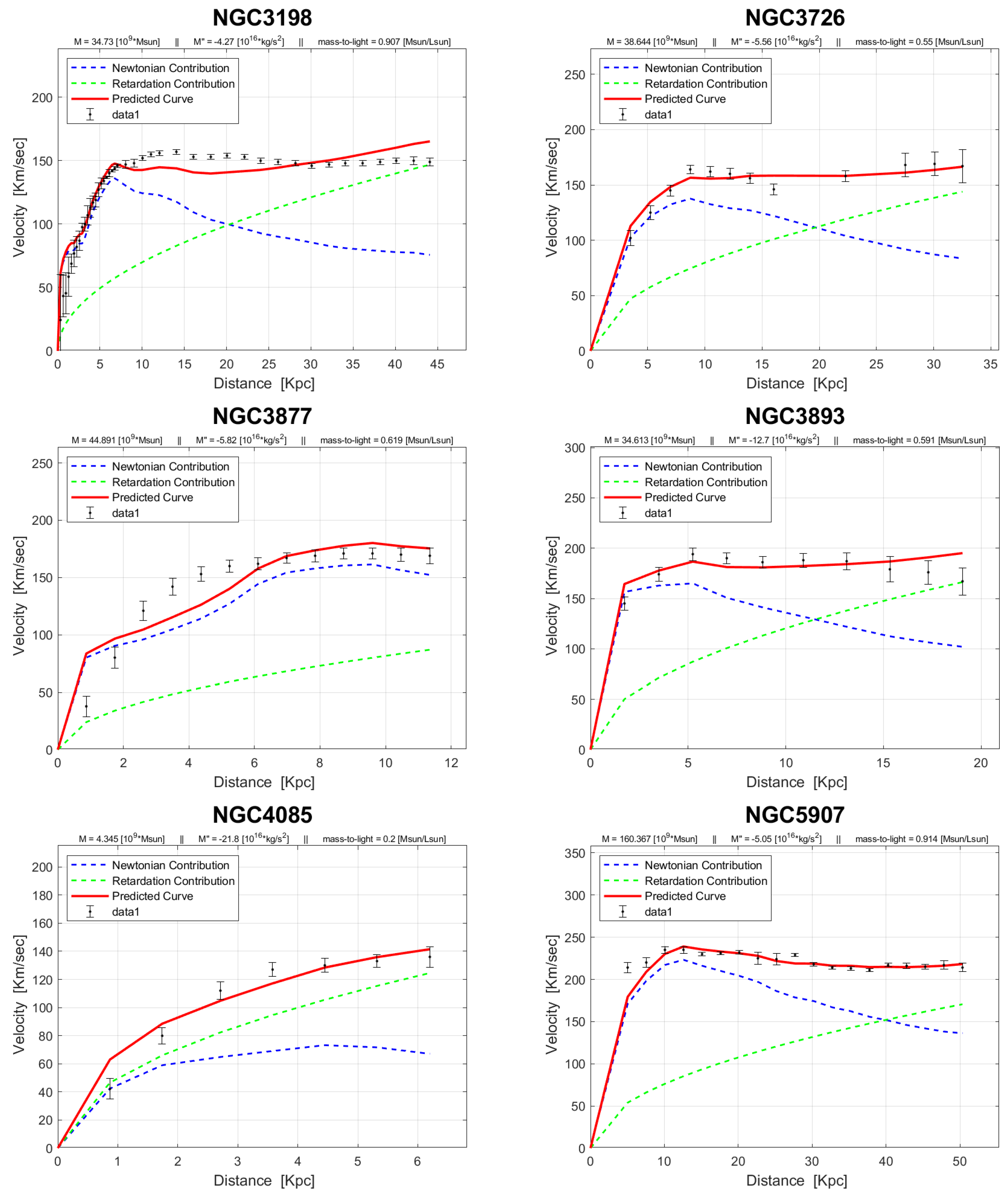
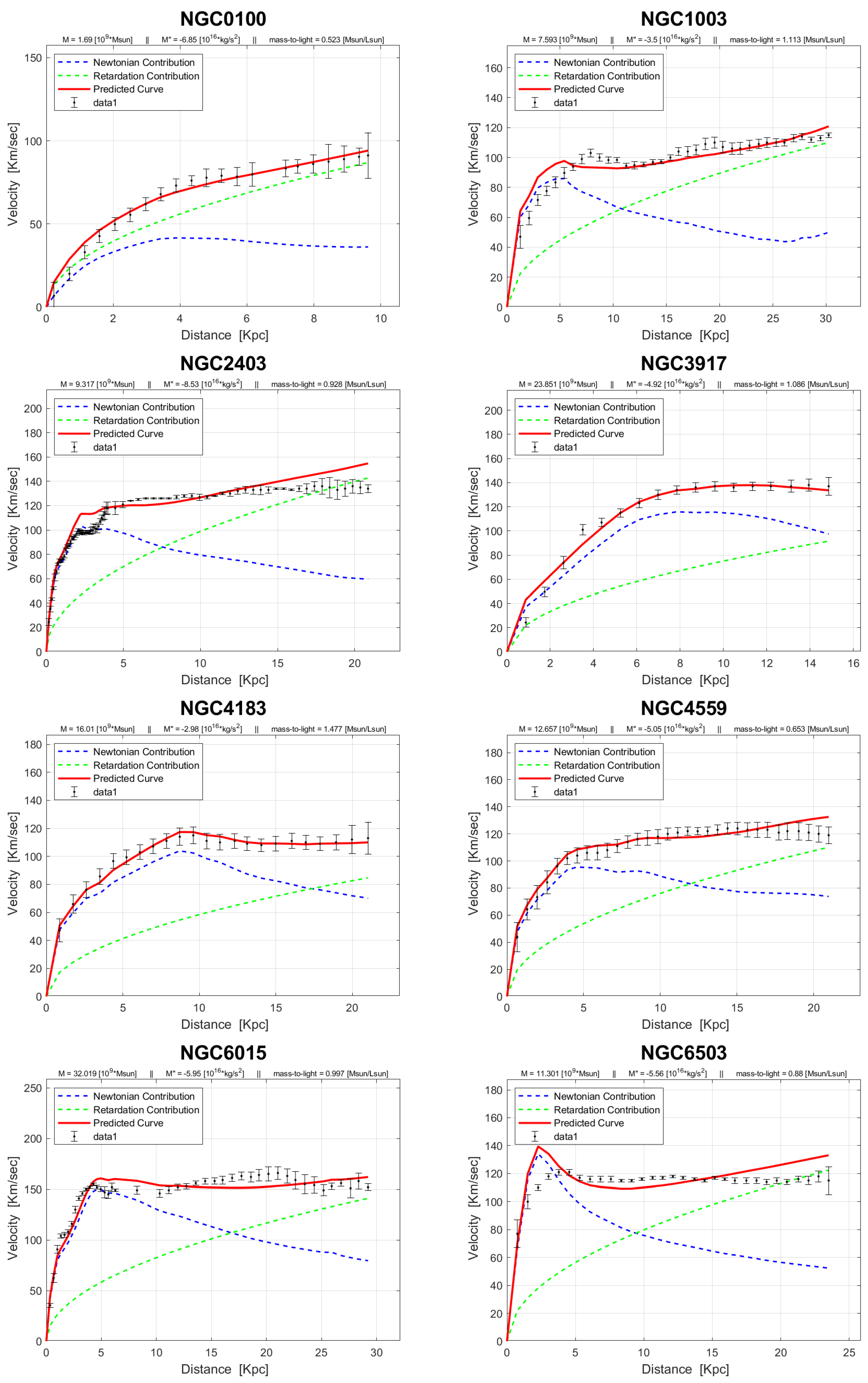
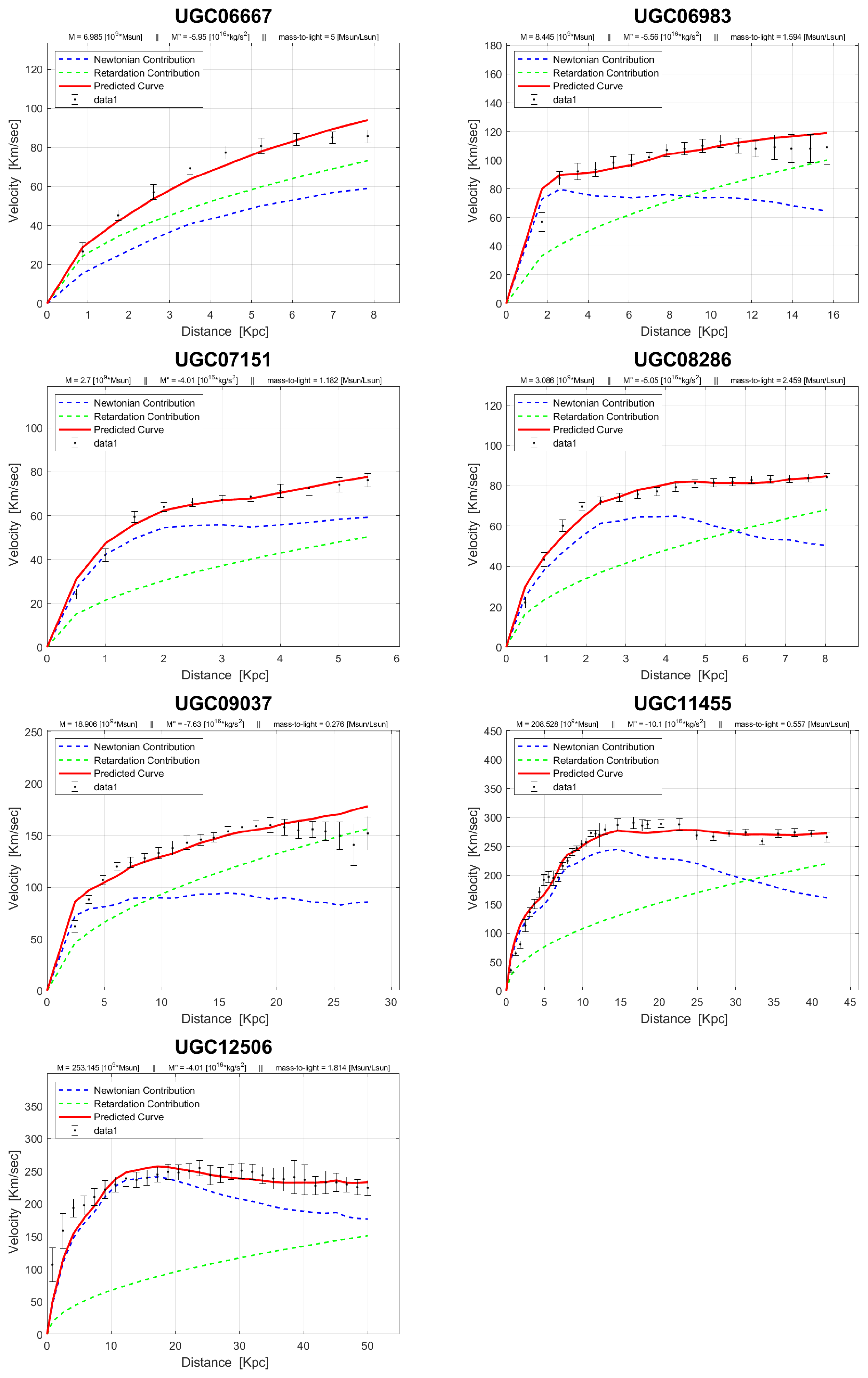
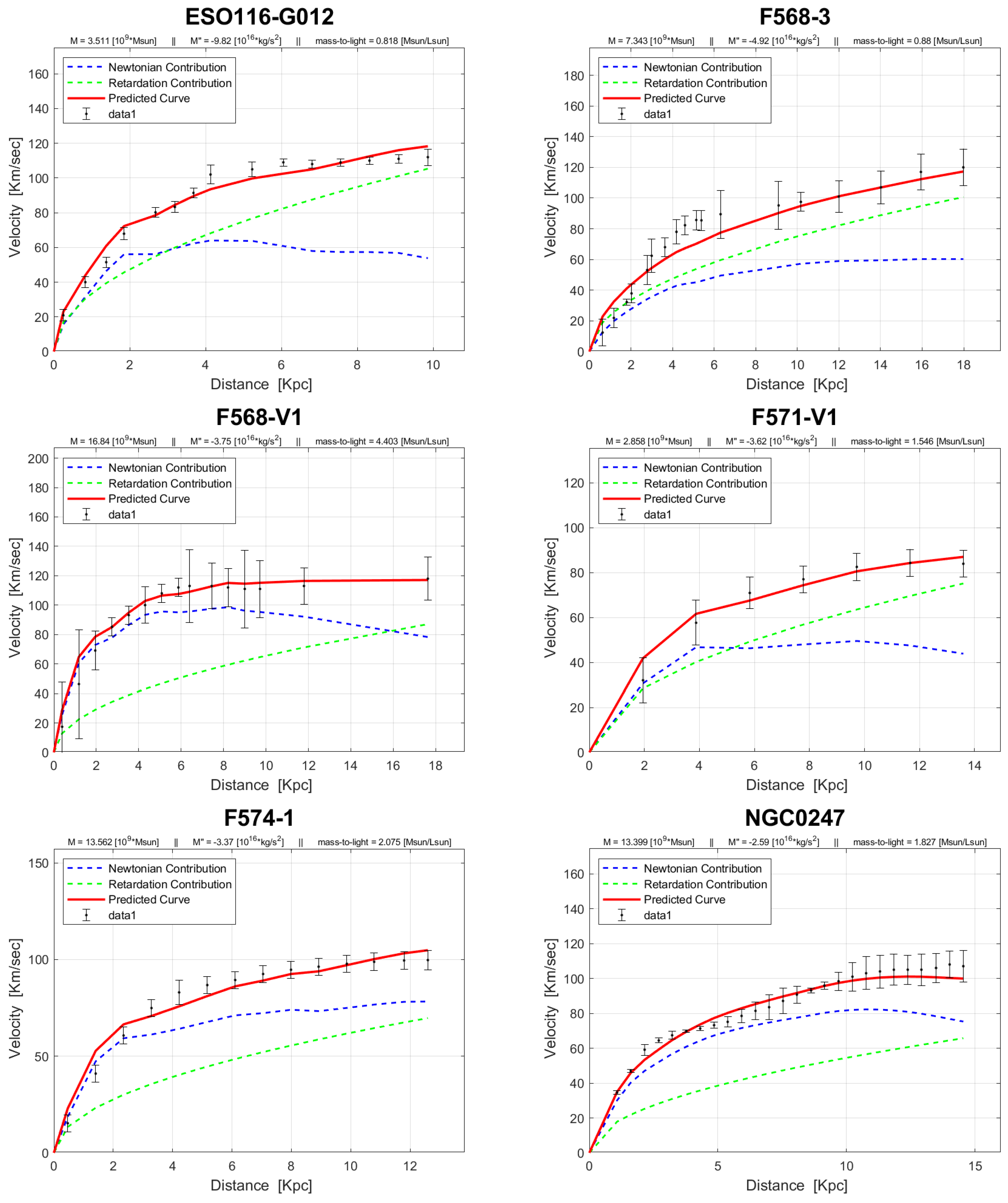
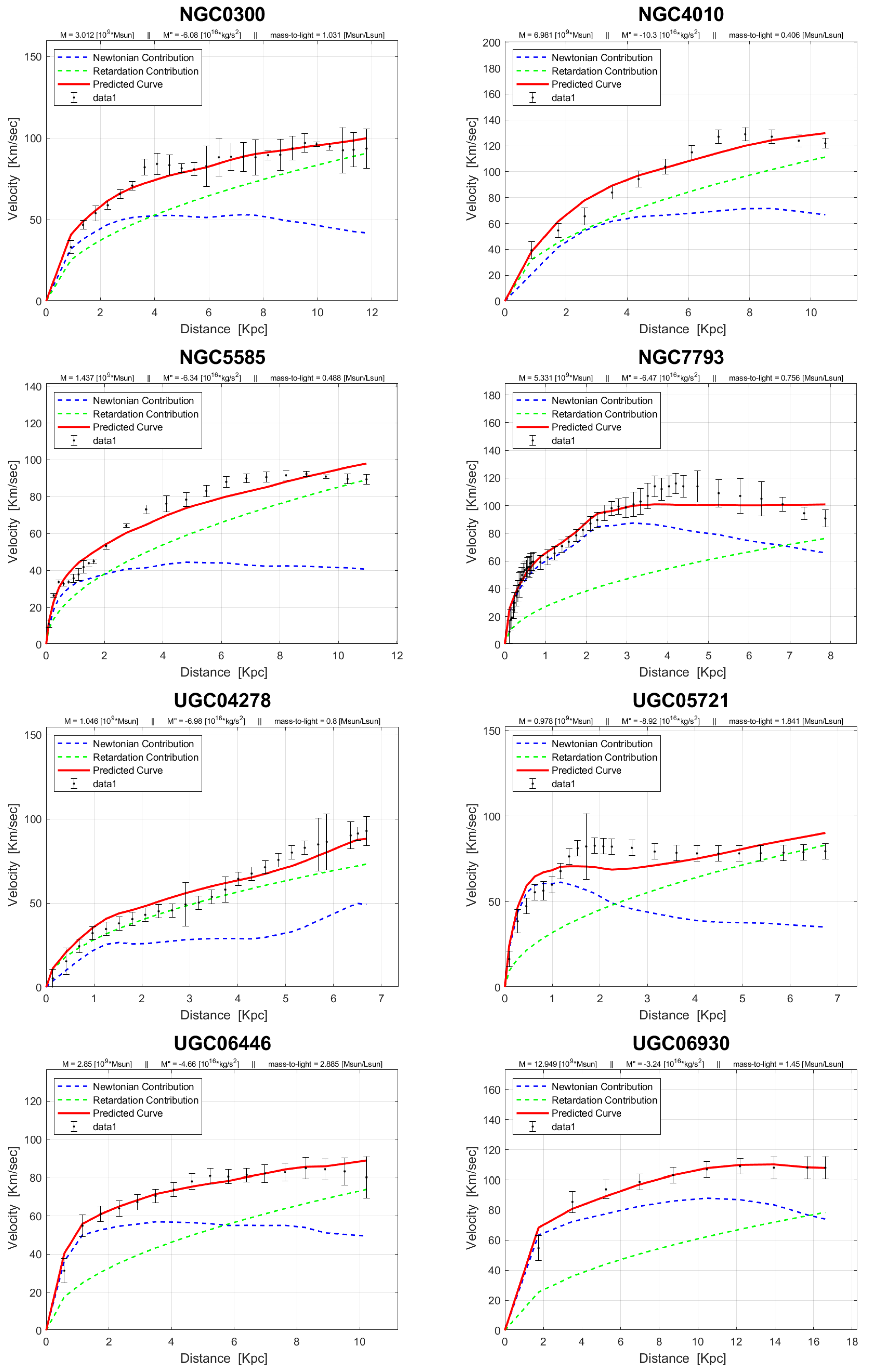
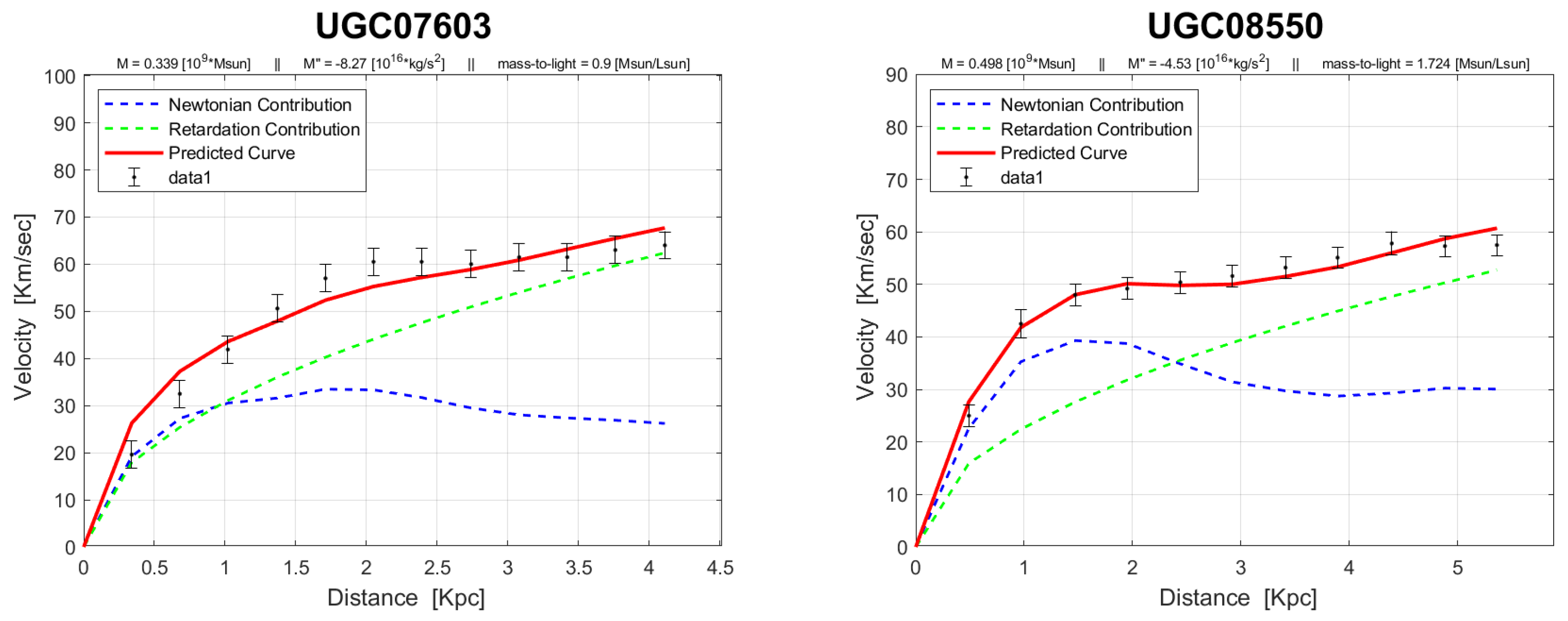
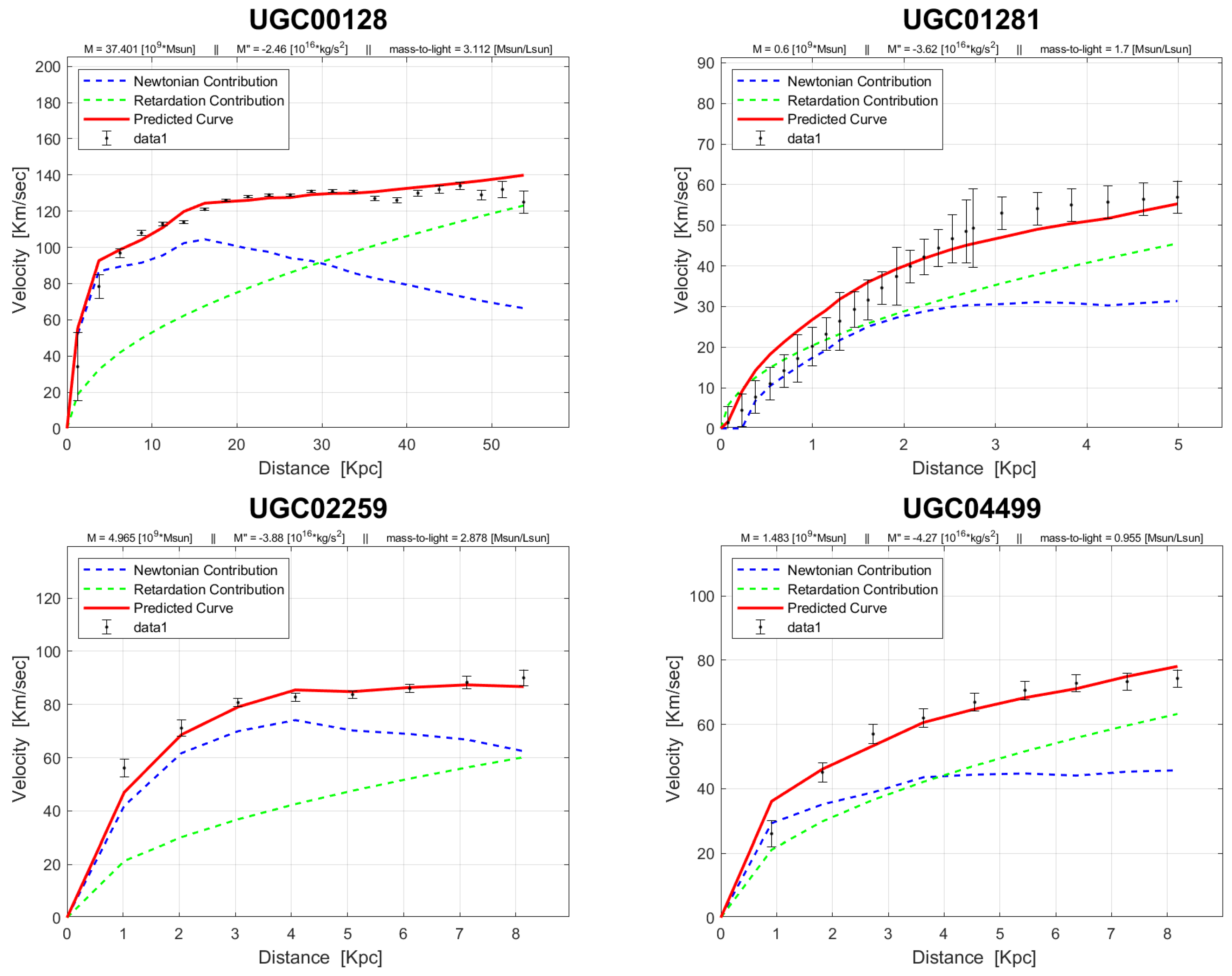
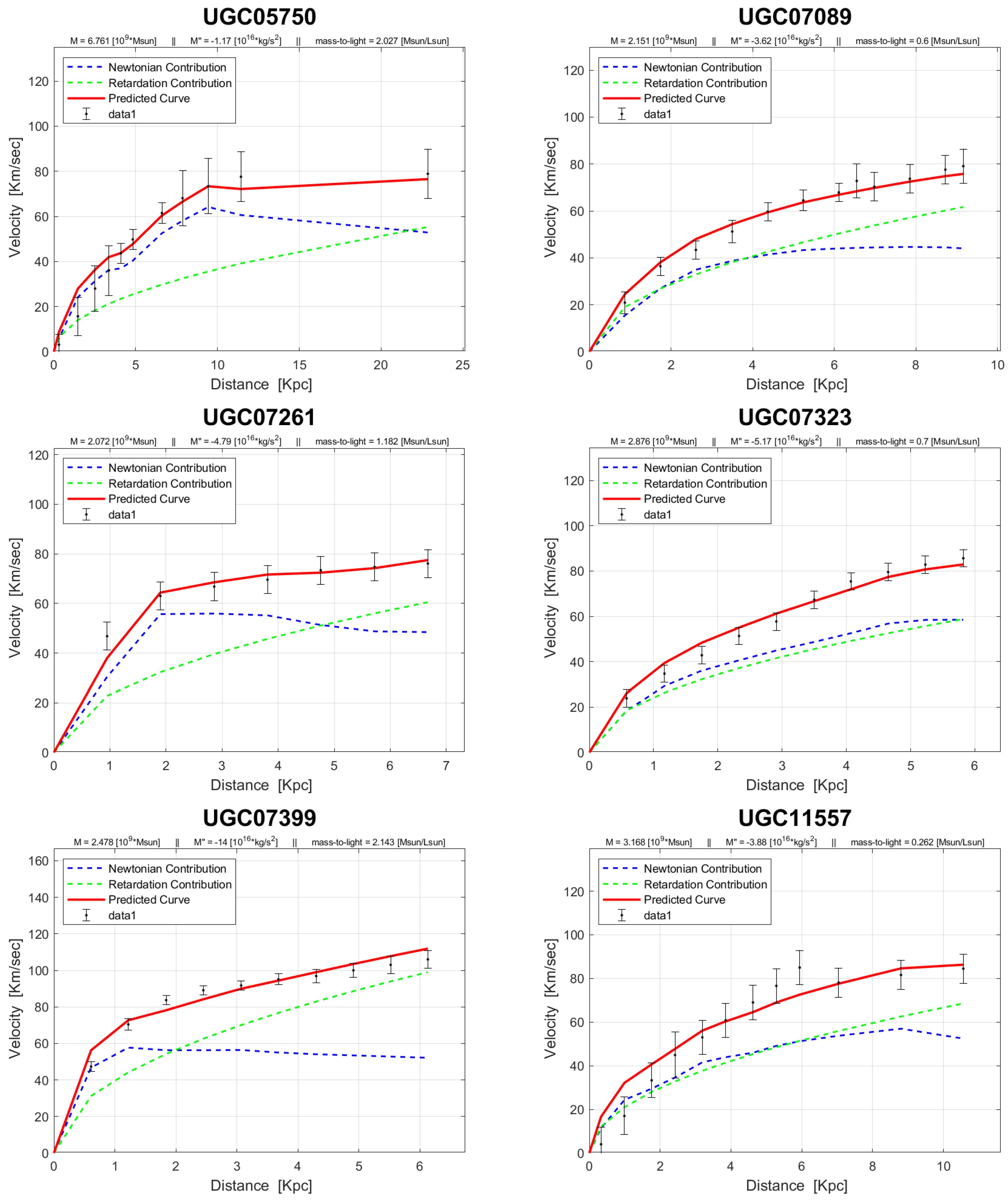
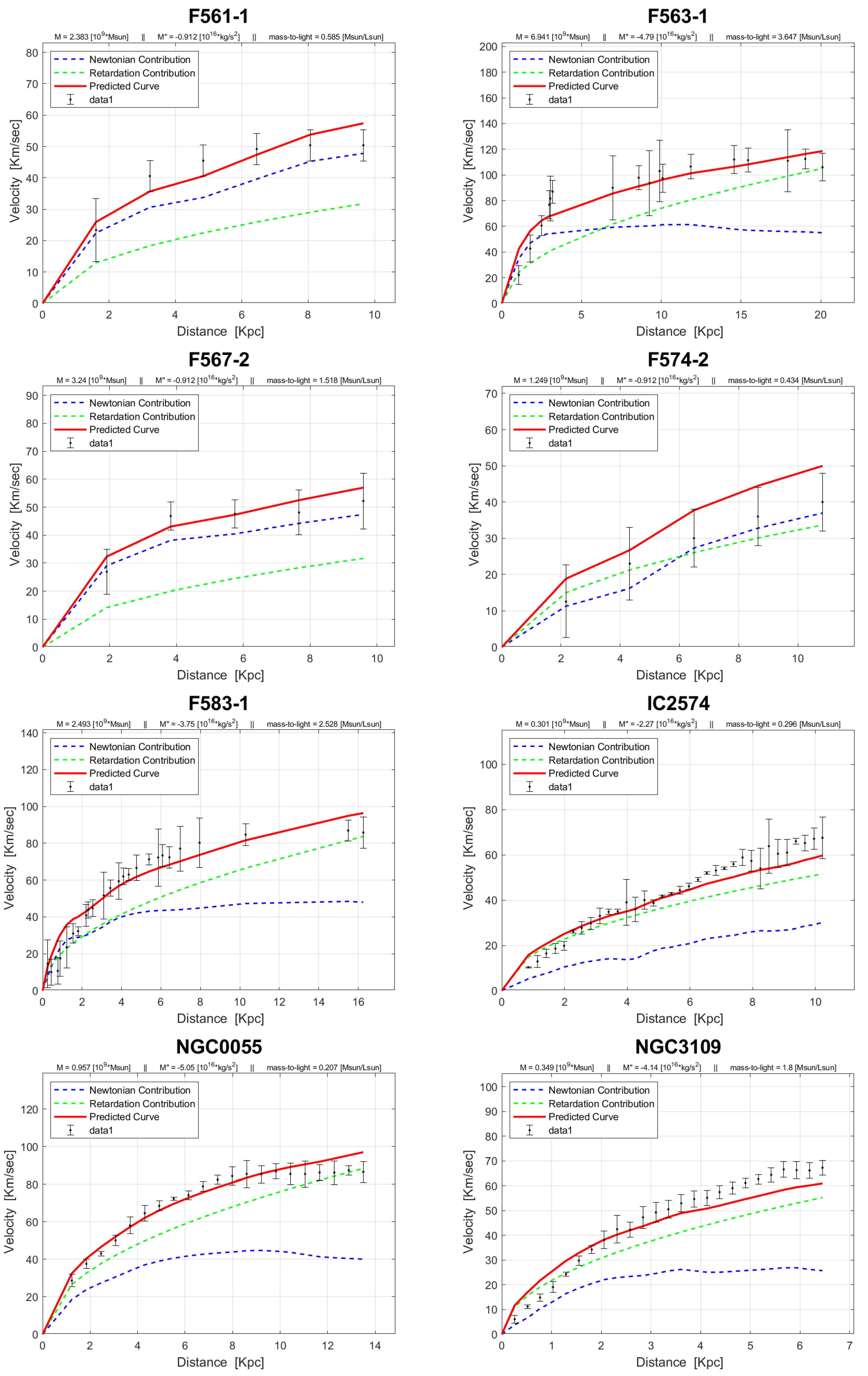
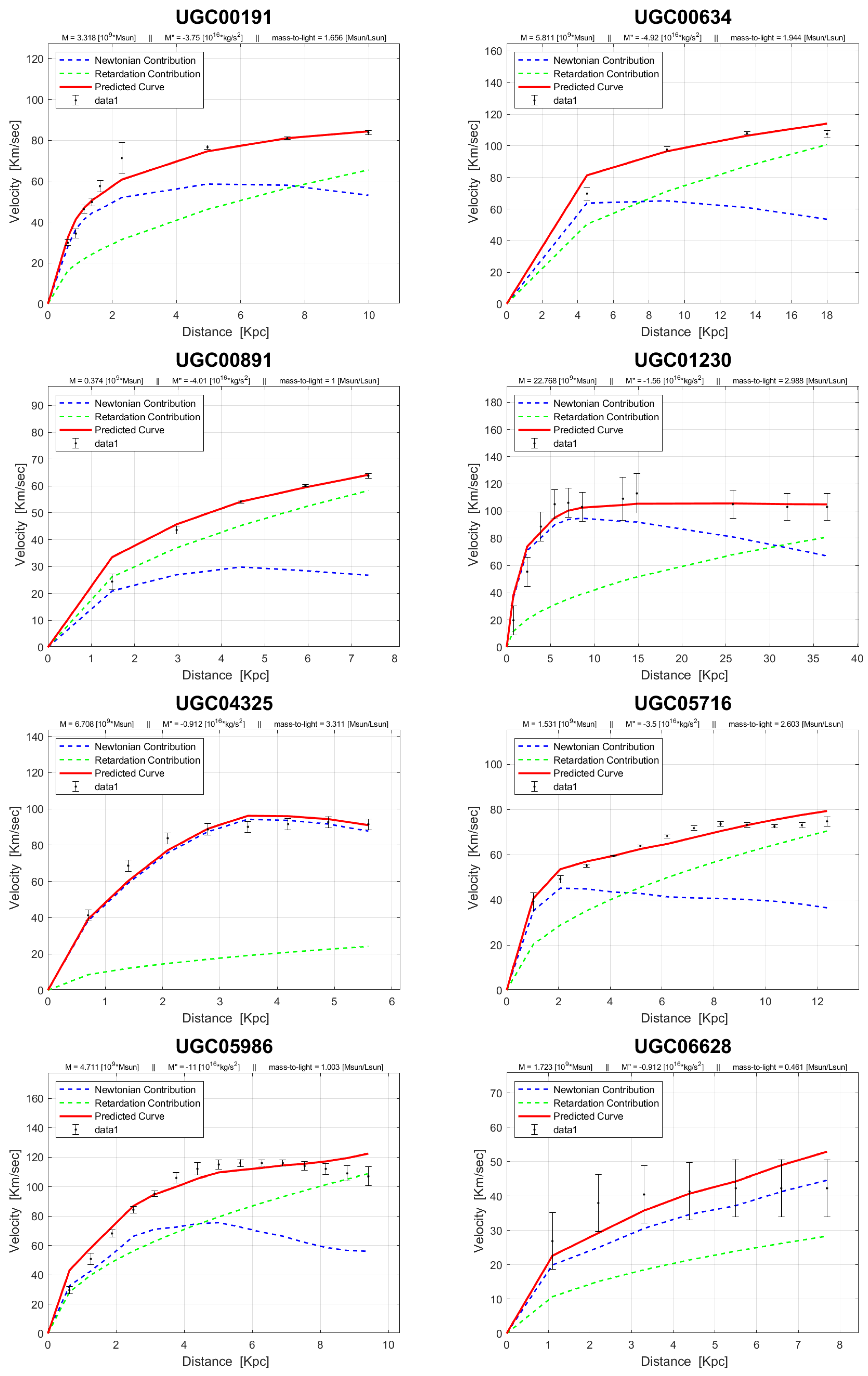
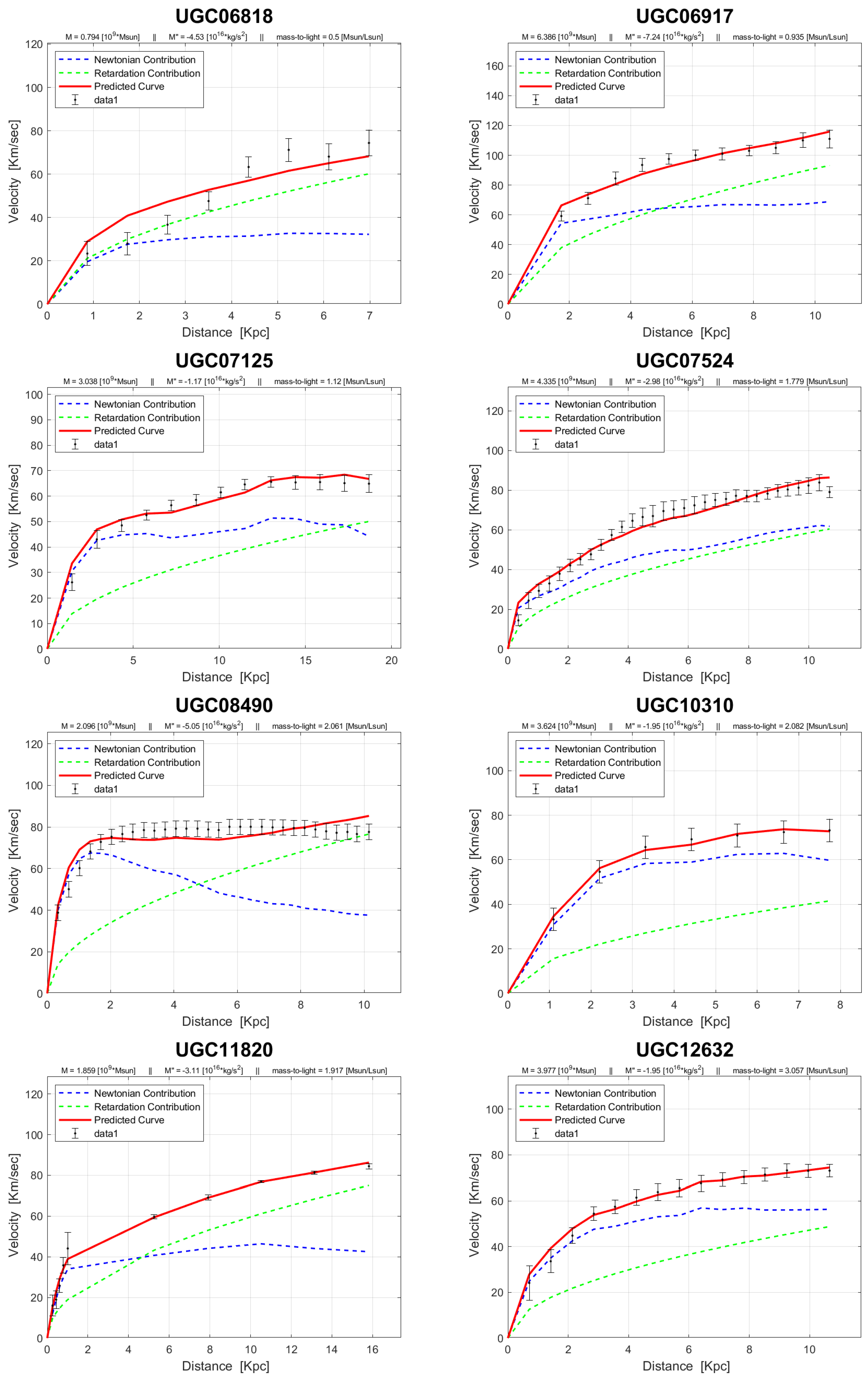
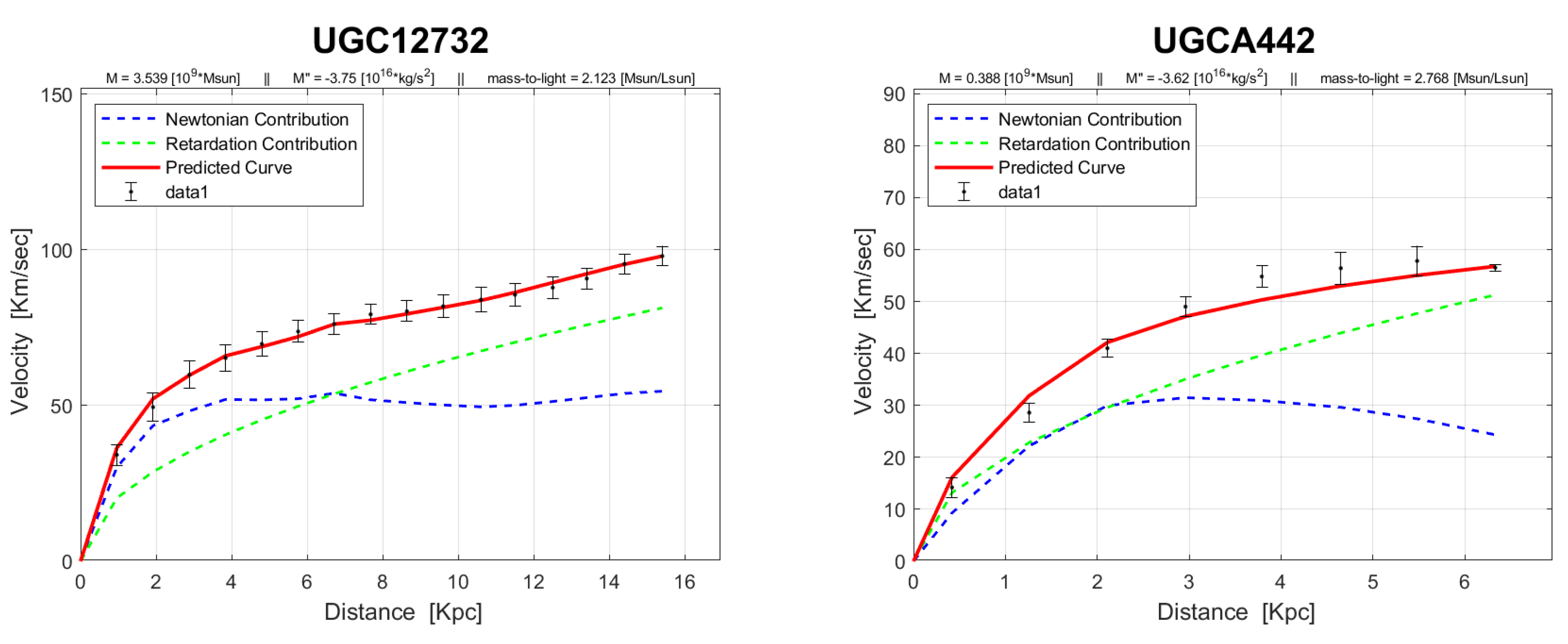
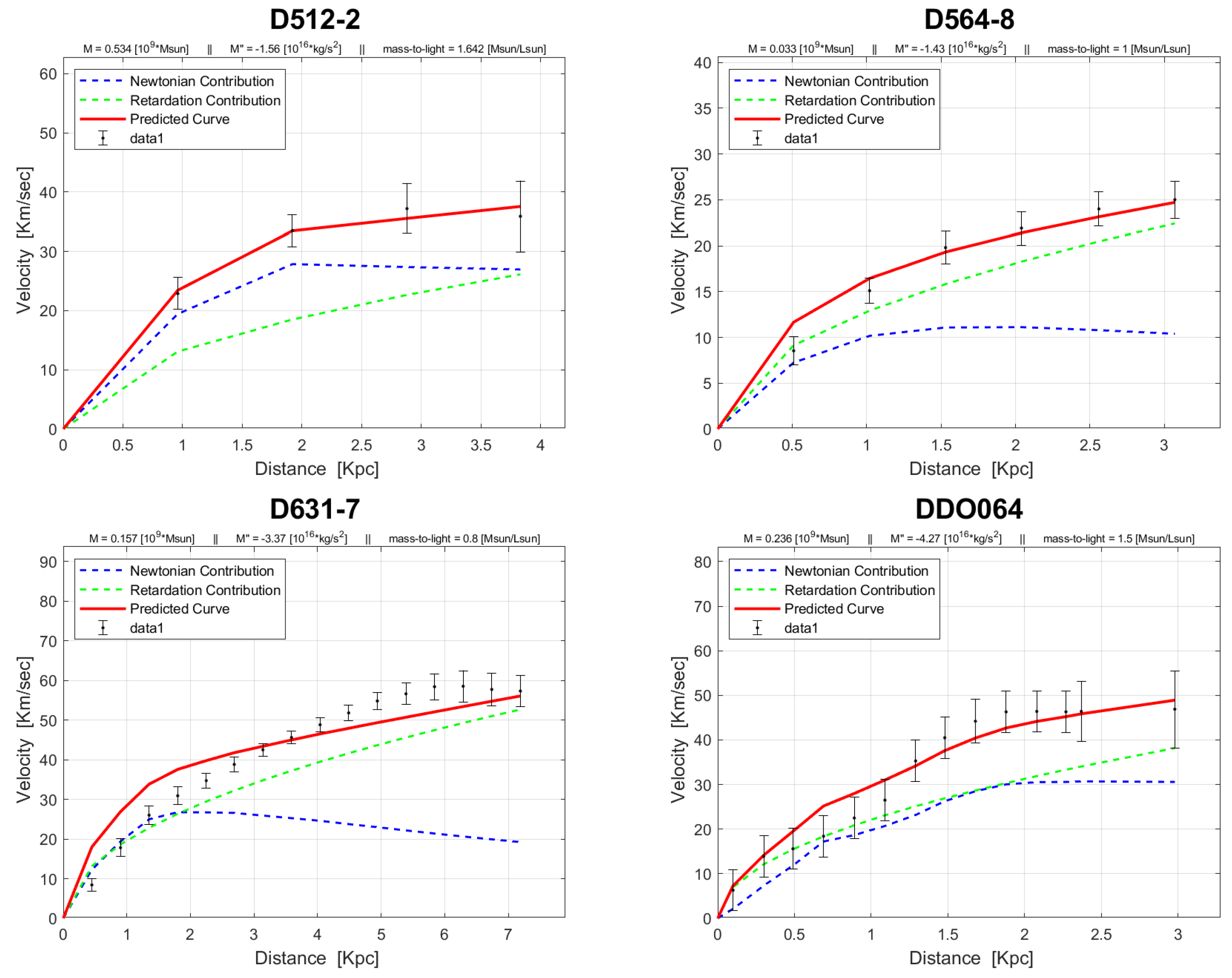
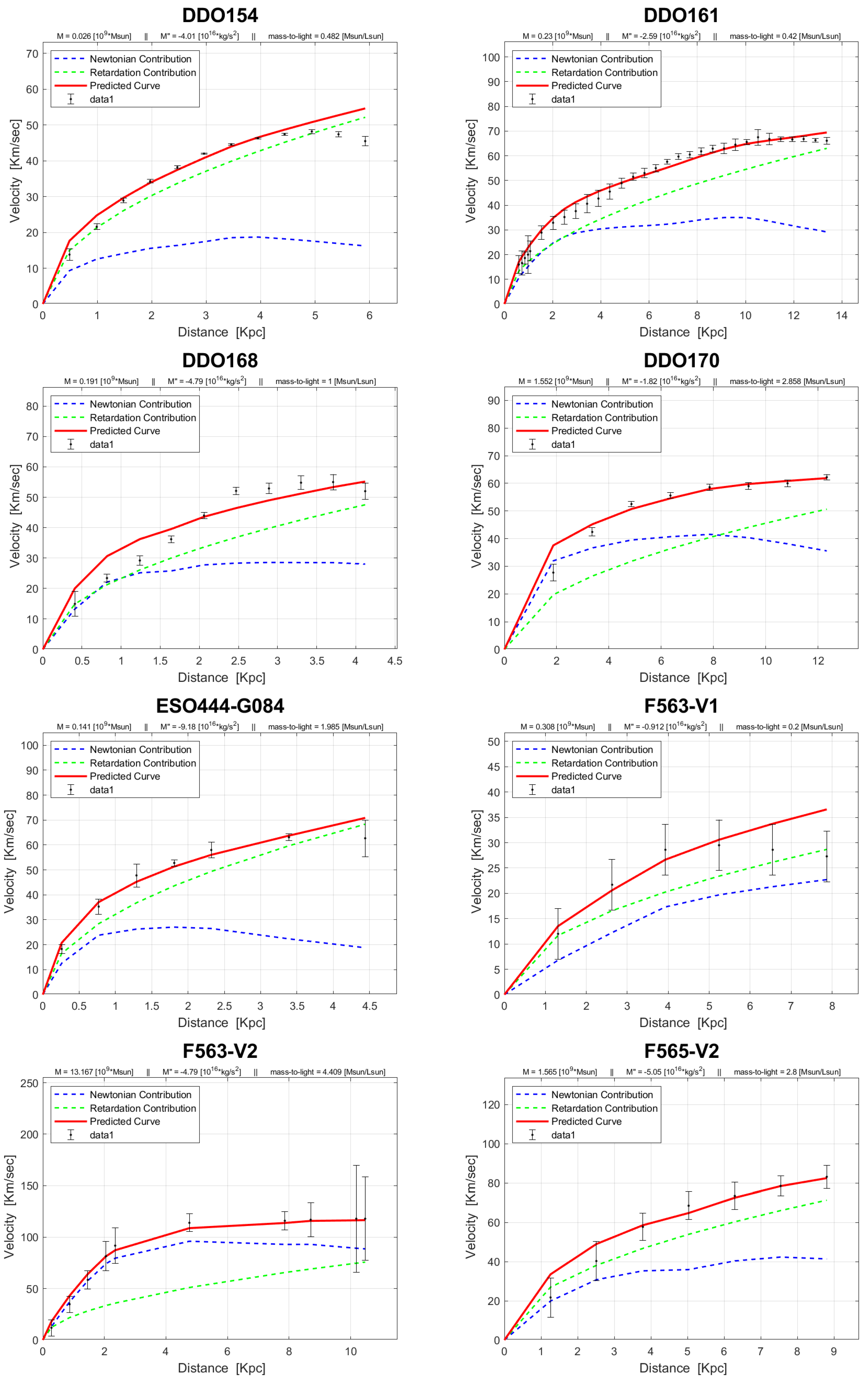
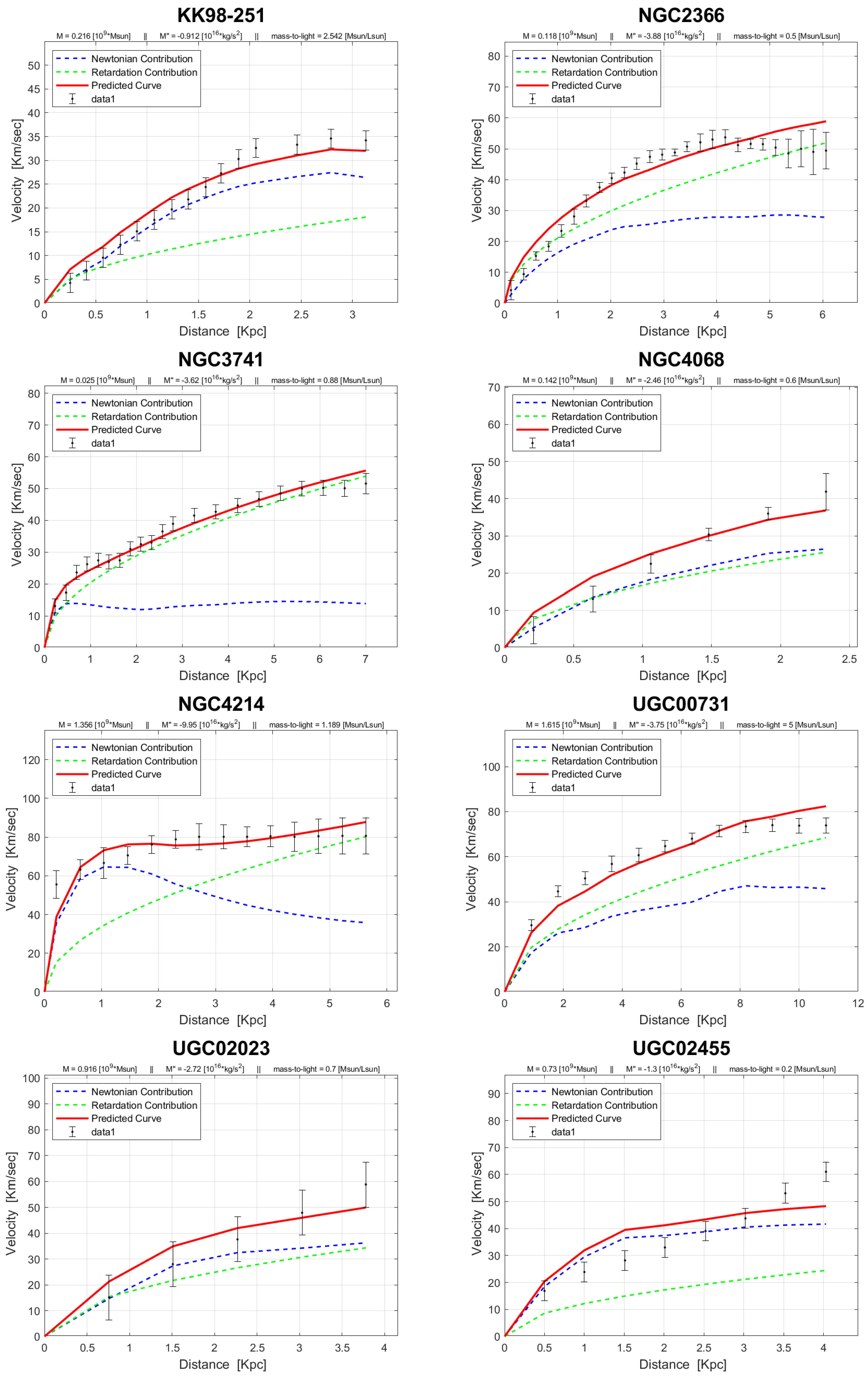
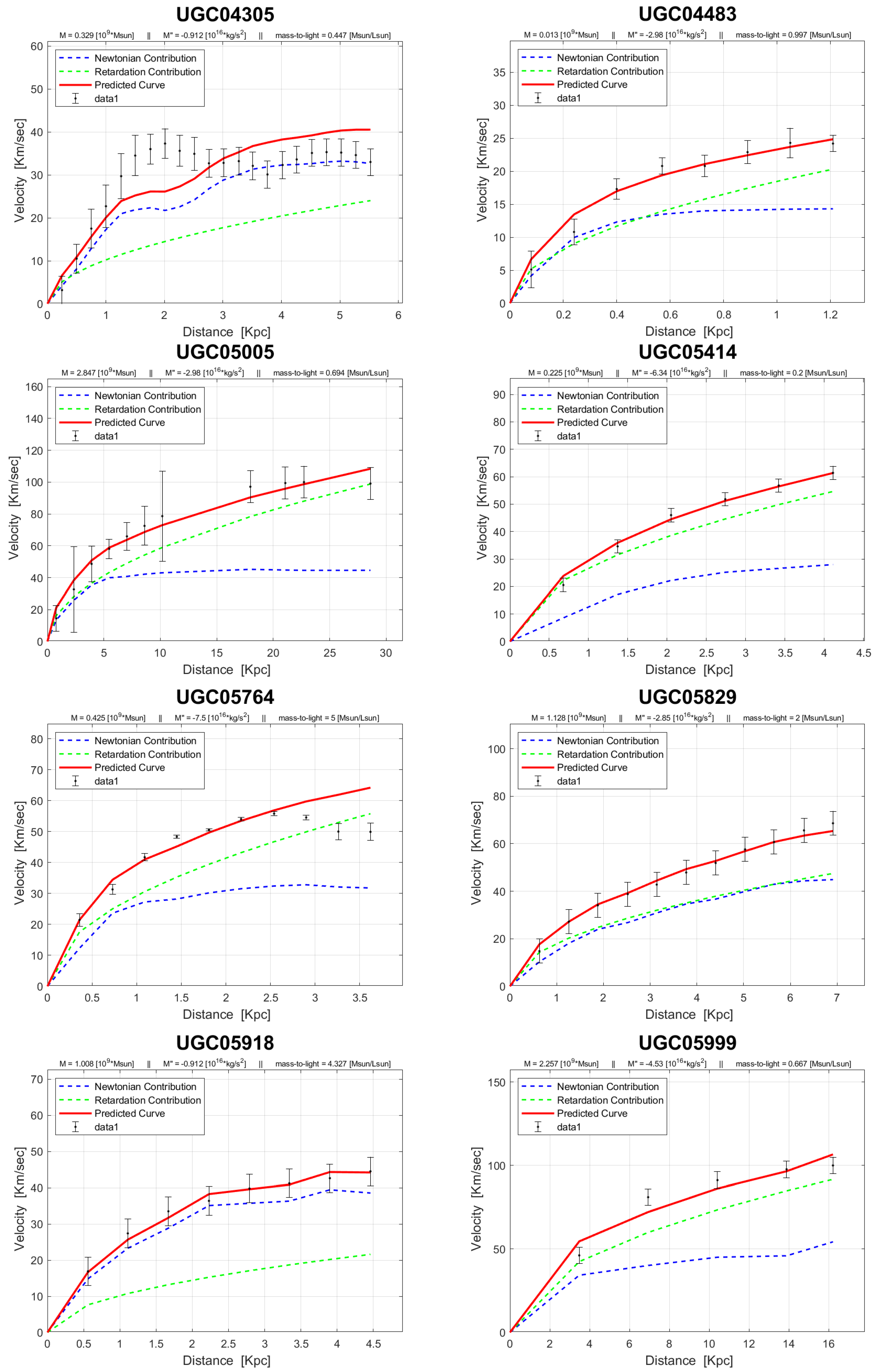
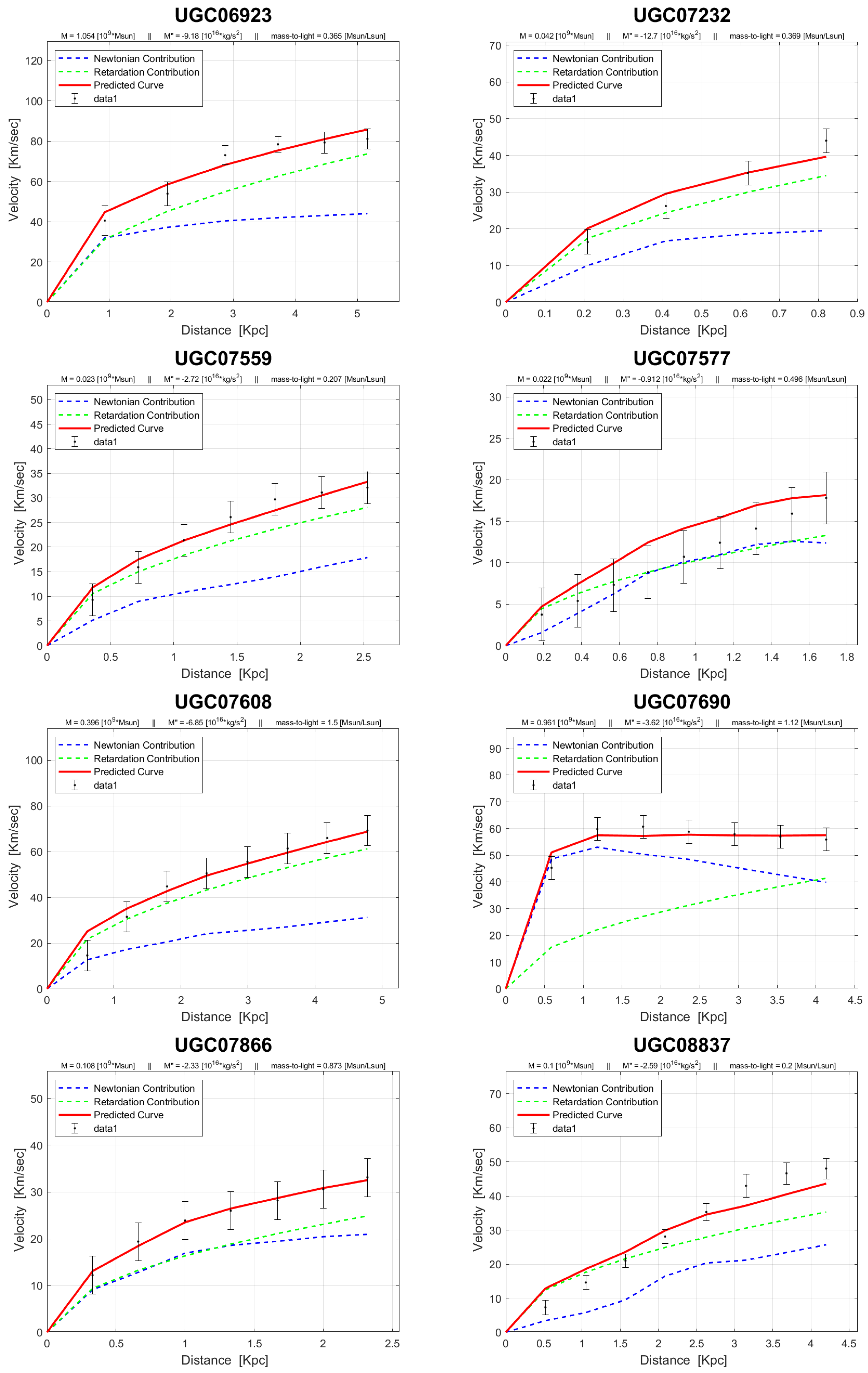
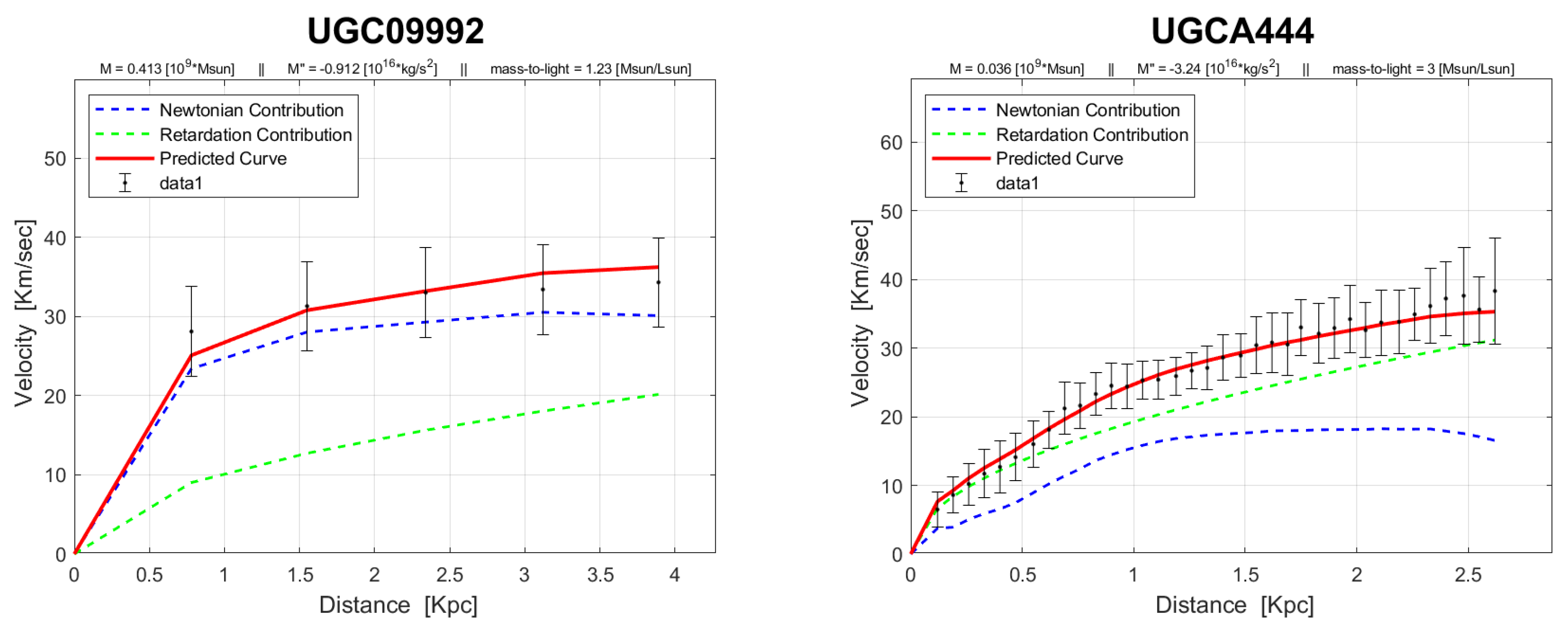
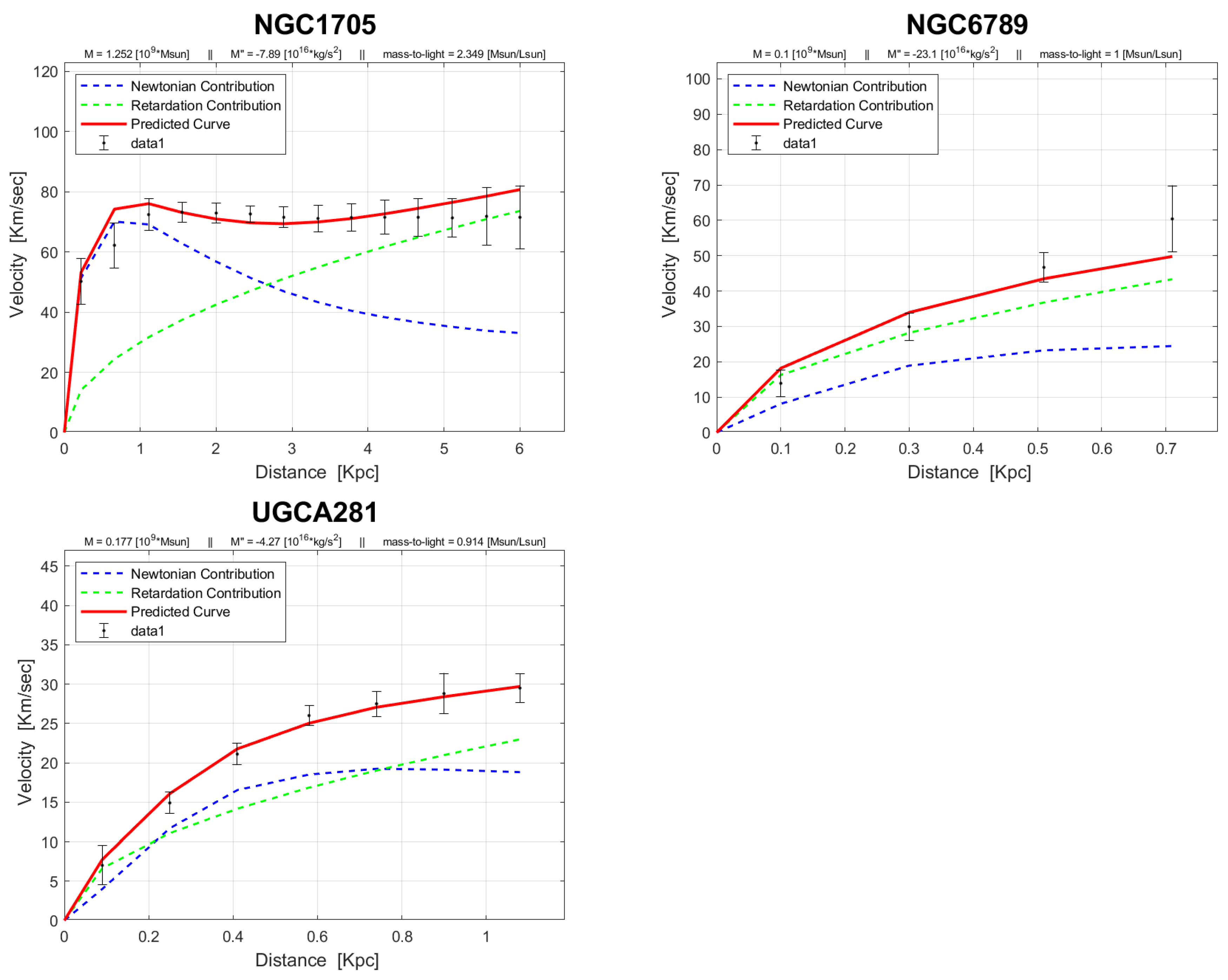
4. Rotation Curves

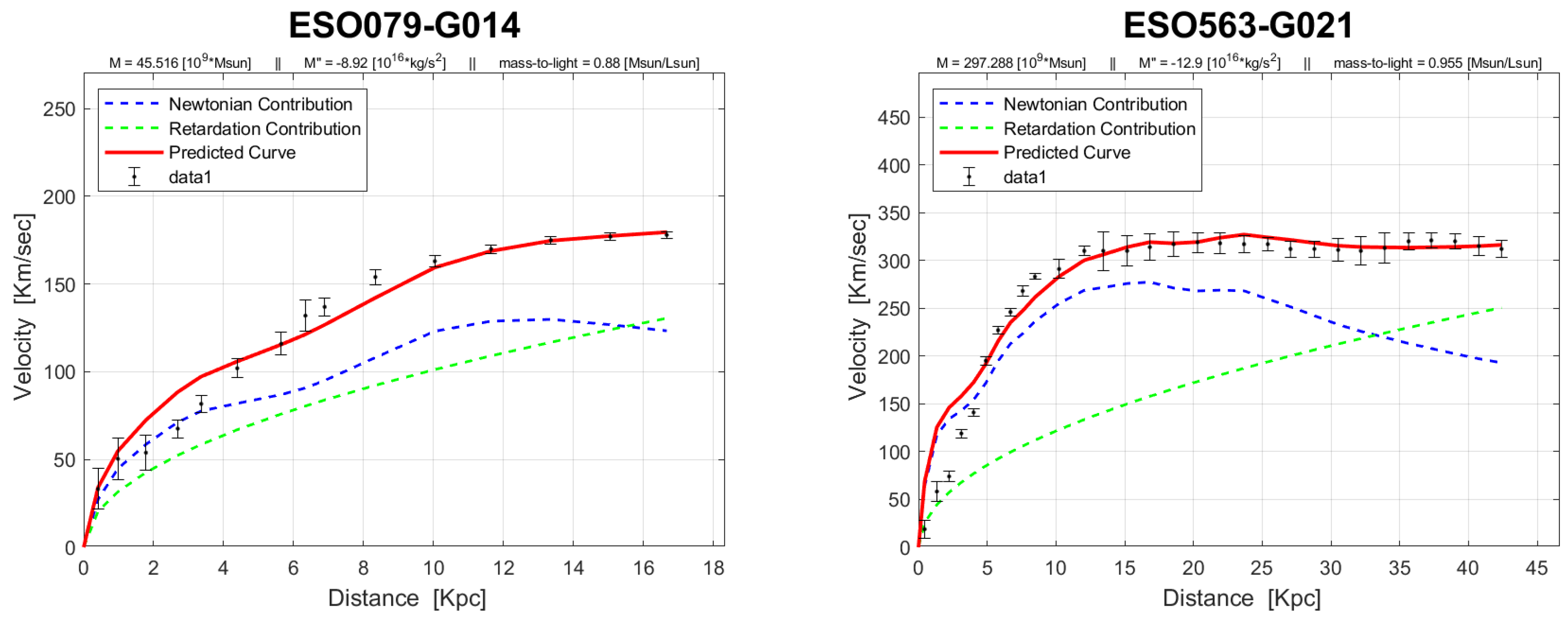
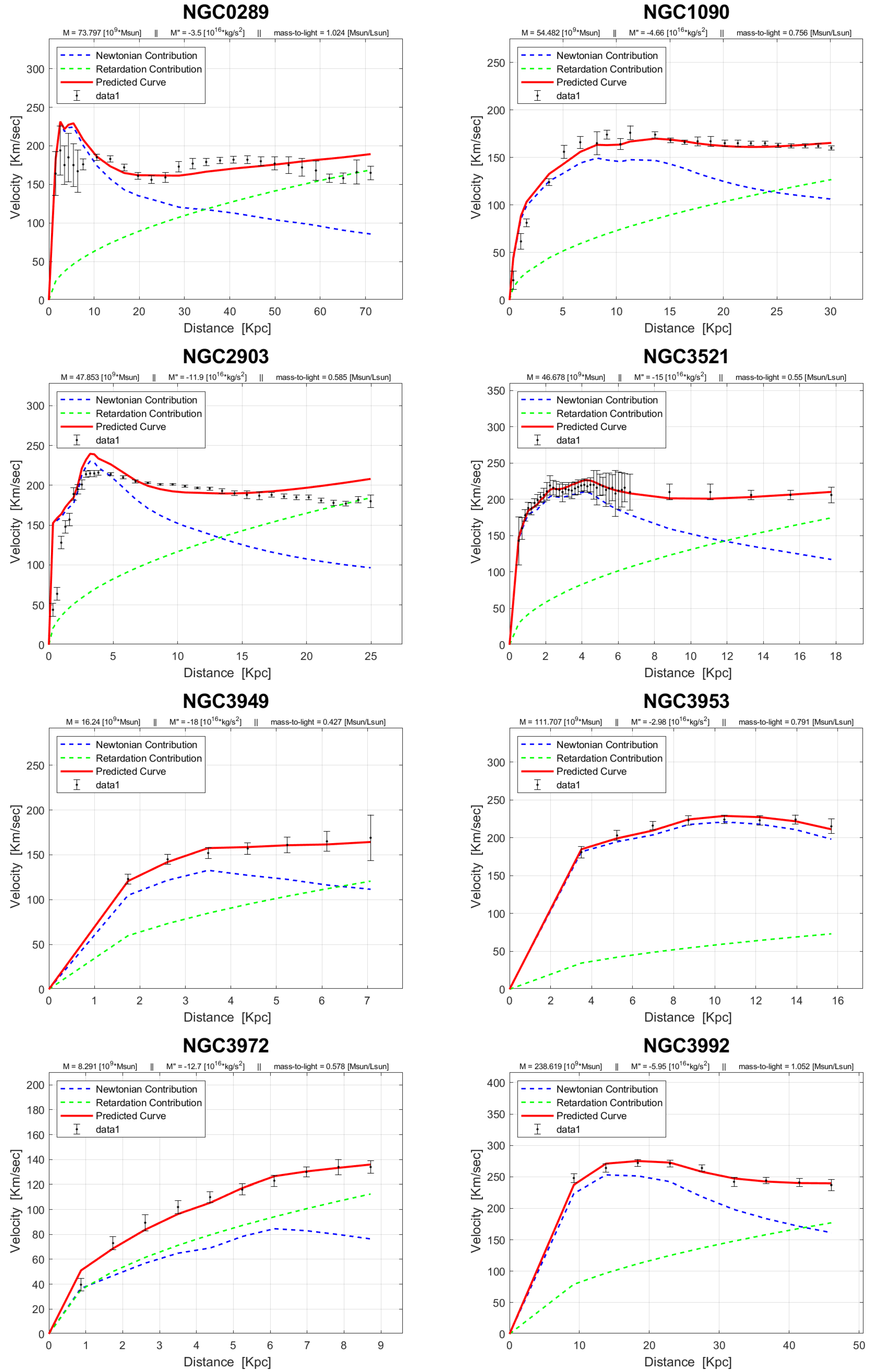
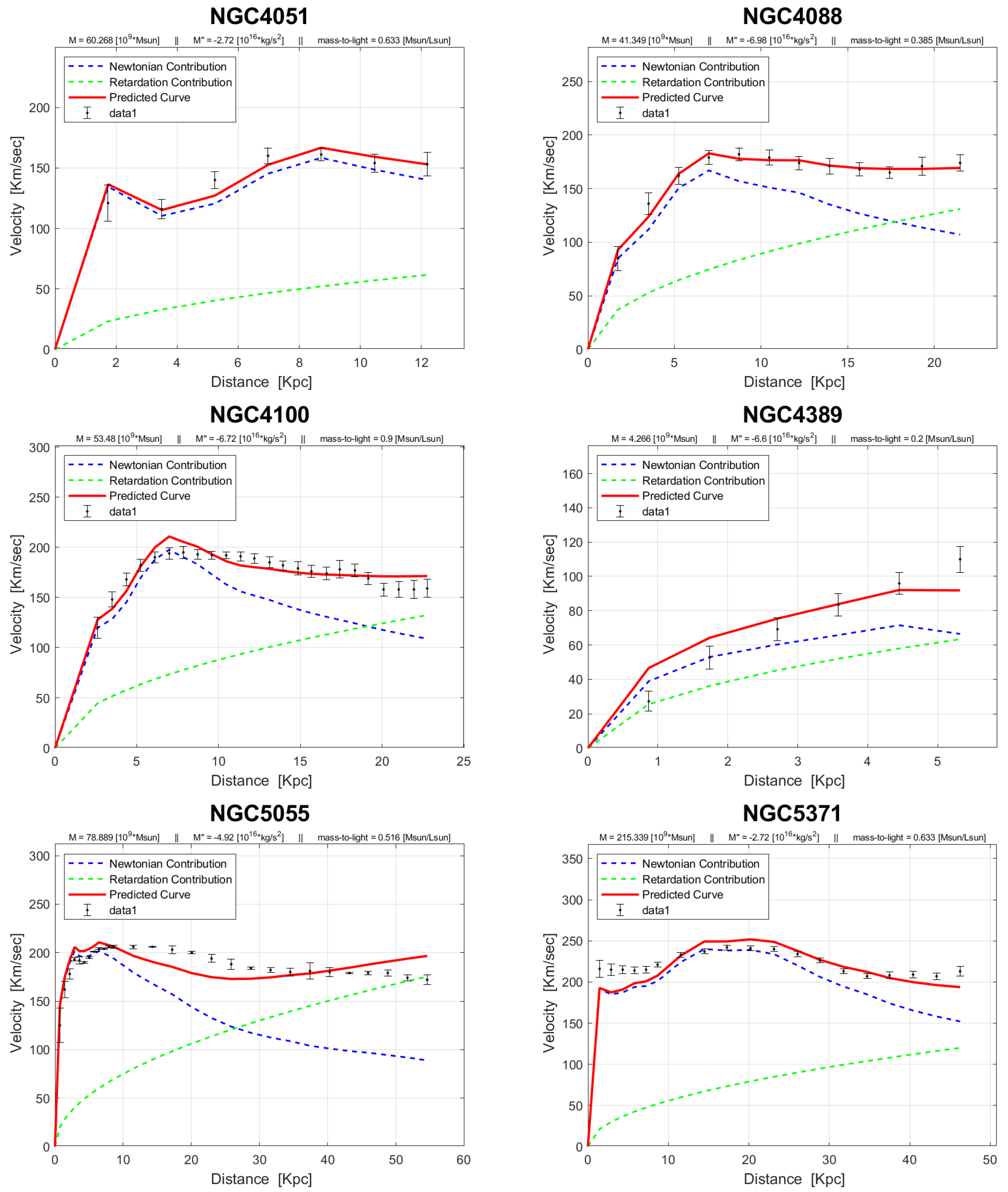
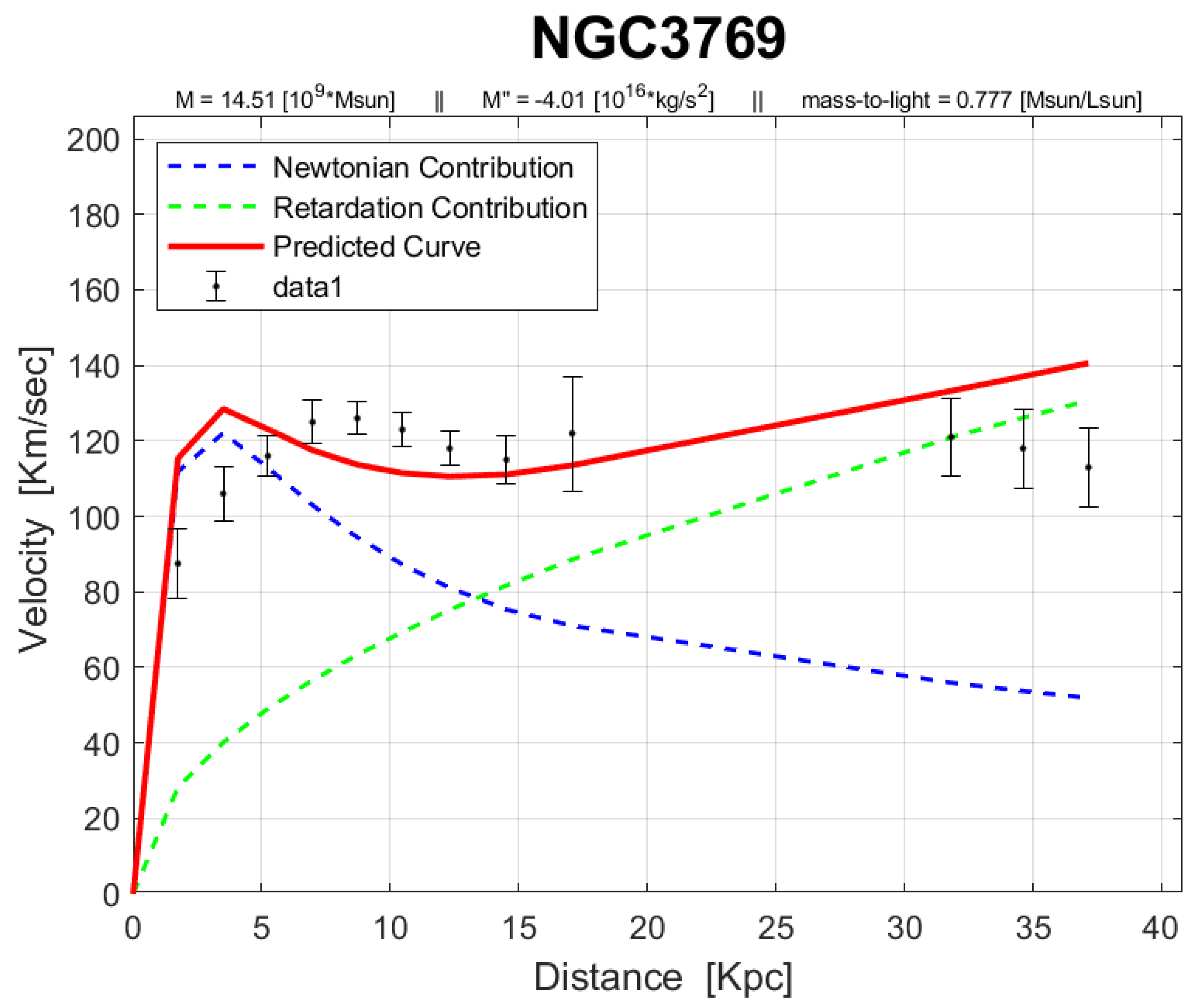
The rotation curves of the 143 galaxies from the SPARC Galaxy collection are given below. It is worth noting that the SPARC Galaxy collection contains 175 galaxies, but for the sake of simplicity we took galaxies in which the size of the bulge is very small so that we can neglect the height of the galaxy in the z axis in relation to the size of the galaxy in the x, y plane. We performed a fitting for each galaxy by finding two parameters: mass to light ratio and the absolute value of the second derivative of the mass. We arranged the sample results according to Hubble morphological sequence - the classification scheme for galaxies introduced by Edwin Hubble in 1926. It is often colloquially known as the Hubble tuning-fork diagram because the shape in which it is traditionally represented resembles a tuning fork. Hubble’s scheme divided regular galaxies into three broad classes – ellipticals, lenticulars and spirals – based on their visual appearance (originally on photographic plates). A fourth class contains galaxies with an irregular appearance.

Figure 1. Edwin Hubble’s classification scheme.

Figure 1. Edwin Hubble’s classification scheme.

In the following plots: the blue line describes the Newtonian contribution, the green line describes the contribution resulting from the retardation, the red line describes the joint contribution of the Newtonian force and the retardation force, and black dots describe the SPARC data. In addition, above each plot we indicate the values of the mass to light ratio, the second mass derivative, and the total mass of the galaxy. The total mass is calculated from the $M/L$ that was found, and is not a free parameter. The results of this procedure are shown in Appendix A, from which it is clear that most rotation curves are fitted quite well.

5. Correlations

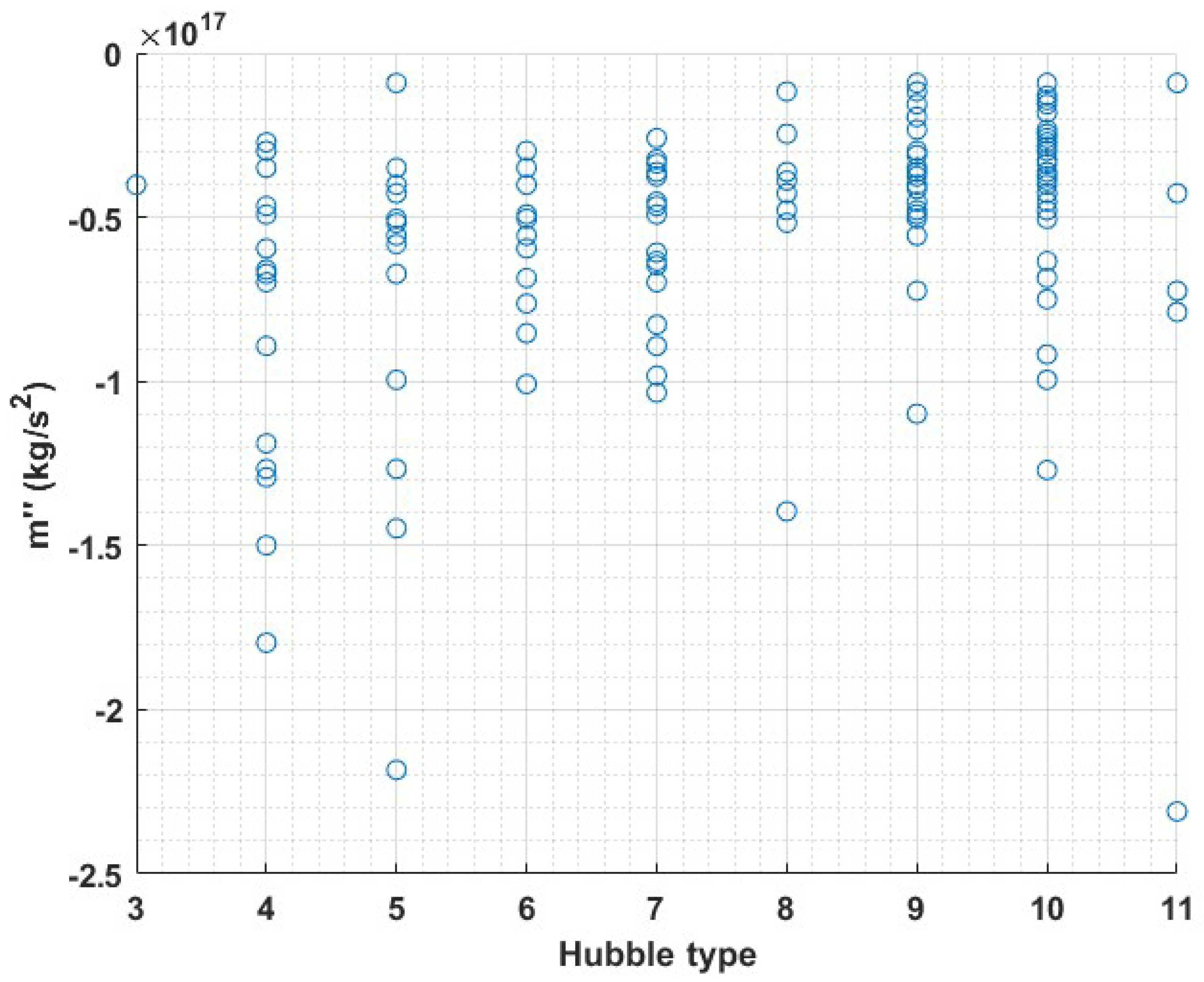
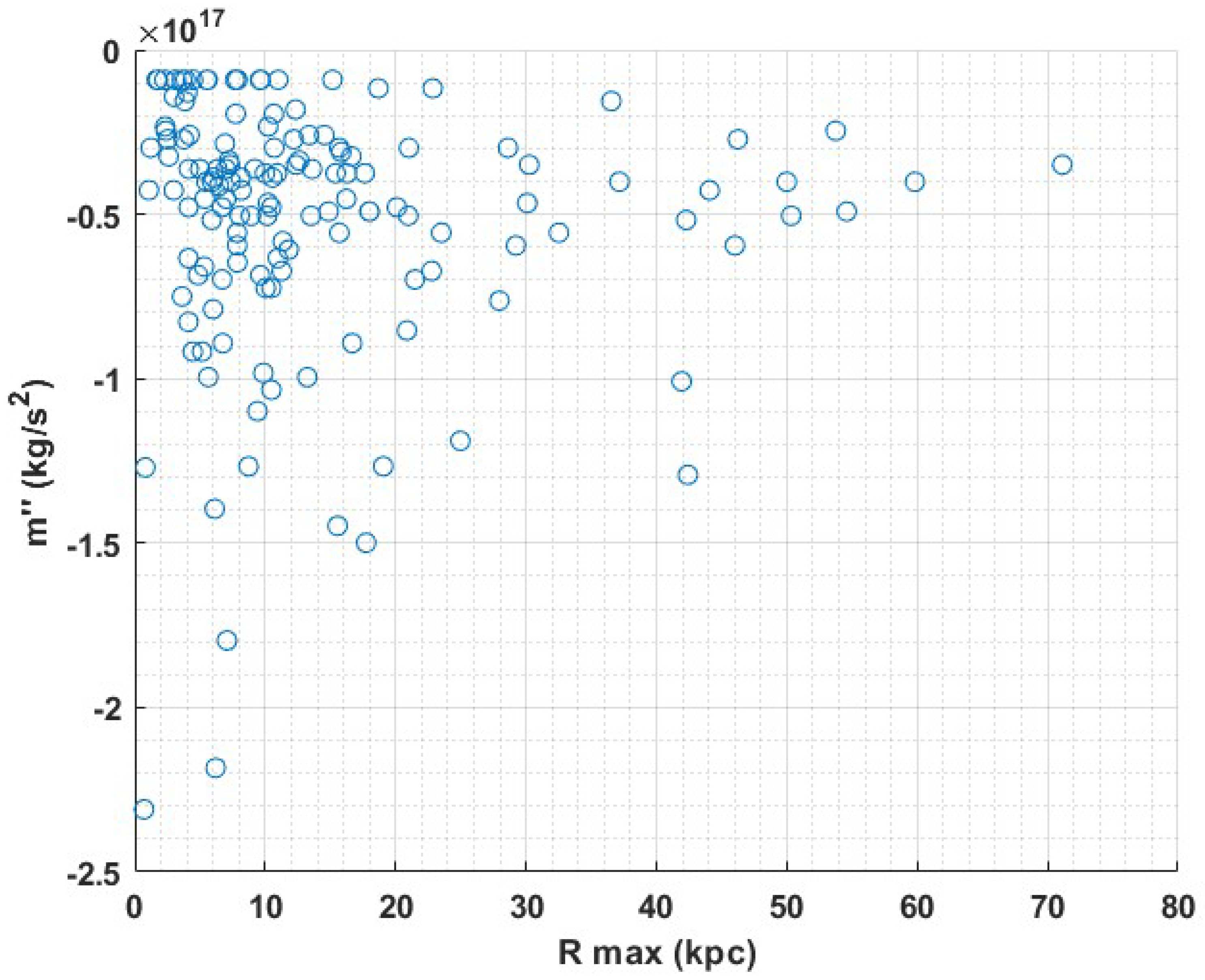
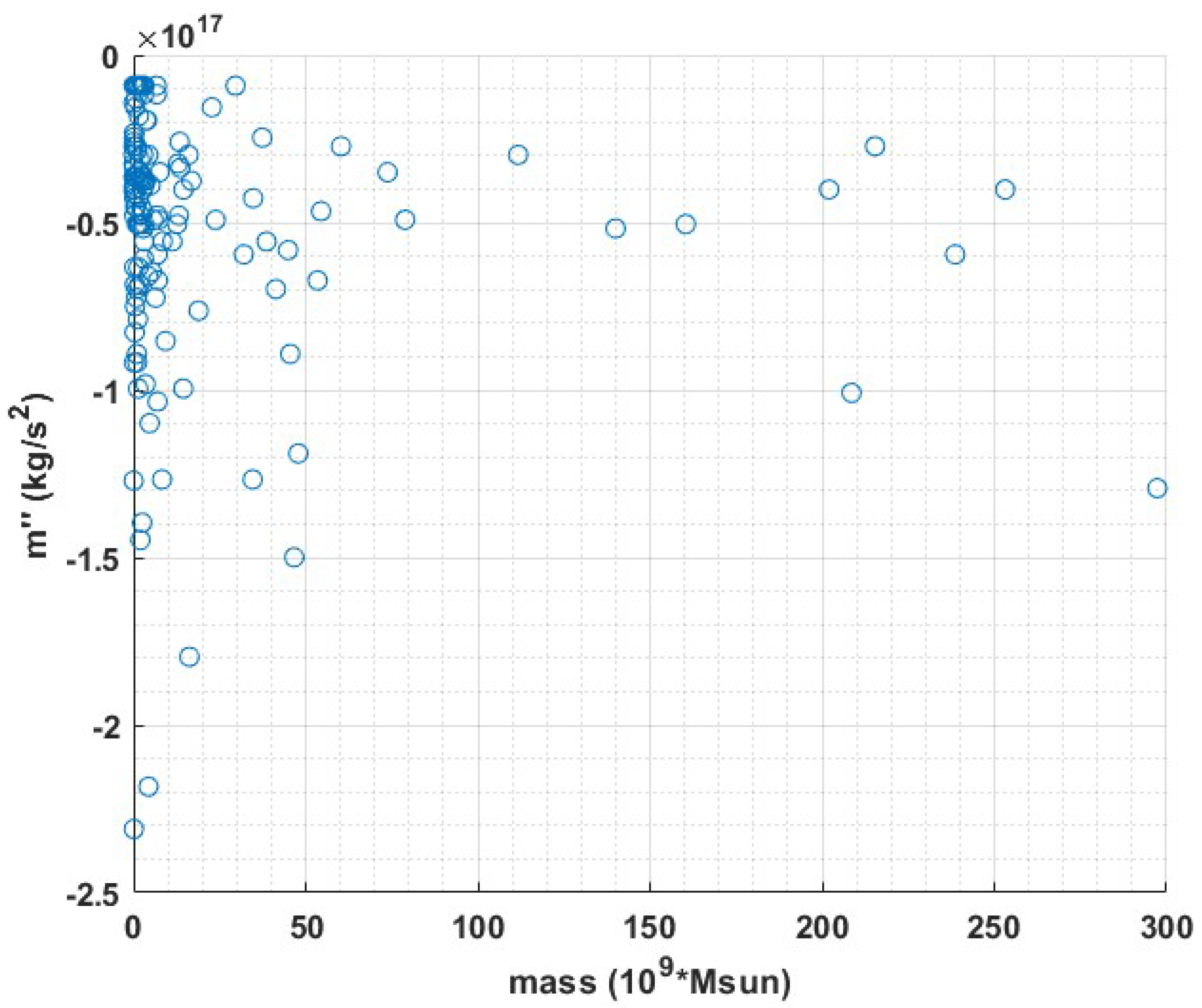
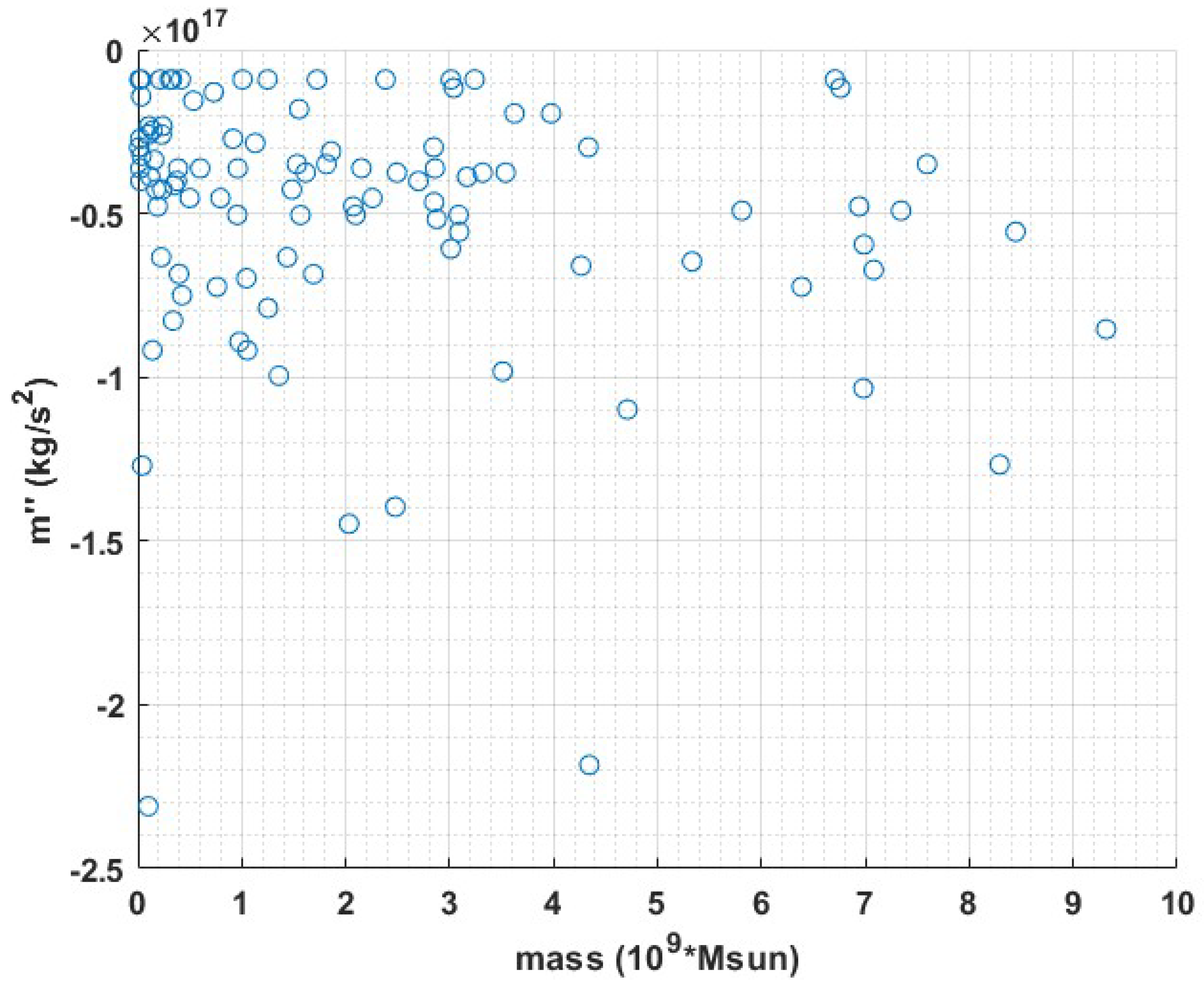
In this study, we attempted to address the missing mass problem by fitting the rotation curves of 143 galaxies using the retardation model. Summarizing tables of the relevant galactic parameters are given in the appendix. We used a rough retardation model of a single parameter which is the magnitude of the second derivative of the mass. We were able to explain the observed discrepancies with Newtonian action at a distance gravity, within General Relativity and without the need to postulate the existence of dark matter. Importantly, we found no correlations between the size of the second derivative of the mass and the radius or mass of the galaxies, nor was there any correlation between the size of the second derivative and the type of the galaxy according to the Hubble classification. This could indicate that our proposed solution does not depend on the size, mass, or type but rather on its history. Nevertheless almost all second derivatives are of the same order of magnitude. Below are graphs describing the size of the second derivatives as a function of radius, mass, and type.

Figure 2. The size of the second derivative of the mass vs. the Hubble type: .0 = S0, 1 = Sa, 2 = Sab, 3 = Sb, 4 = Sbc, 5 = Sc, 6 = Scd, 7 = Sd, 8 = Sdm, 9 = Sm, 10 = Im, 11 = BCD.

Figure 2. The size of the second derivative of the mass vs. the Hubble type: .0 = S0, 1 = Sa, 2 = Sab, 3 = Sb, 4 = Sbc, 5 = Sc, 6 = Scd, 7 = Sd, 8 = Sdm, 9 = Sm, 10 = Im, 11 = BCD.

Figure 3. The size of the second derivative of the mass vs. the size of the galaxy.

Figure 3. The size of the second derivative of the mass vs. the size of the galaxy.

Figure 4. The size of the second derivative of the mass vs. the galactic mass.

Figure 4. The size of the second derivative of the mass vs. the galactic mass.

Figure 5. The size of the second derivative of the mass vs. the galactic mass for galaxies with a mass smaller than ${10}^{9}Msun$. No obvious correlation can be found also in this limited set.

Figure 5. The size of the second derivative of the mass vs. the galactic mass for galaxies with a mass smaller than ${10}^{9}Msun$. No obvious correlation can be found also in this limited set.

6. Conclusions

Lorentz symmetry group excludes action at a distance potentials in the weak field approximation of GR, and thus only retarded solutions are allowed. Retardation is intuitively more significant when bigger distances and bigger second derivatives are present. We have demonstrated in [35] that the current approach does not require that the velocities in the system, v, to be high, as most galactic entities (stars, gas) are subluminal with $\frac{v}{c}\ll 1$. Typical velocities in galaxies are at the order of $100\frac{km}{s}$ (see figures above), which makes this ratio $0.001$ or smaller. However, every gravitational system has a retardation distance, beyond which the retardation effect cannot be ignored. This follows because mass is exchanged between each natural system and its surroundings. For example, the solar wind in the solar system and on a much larger scale, galaxies that accrete intergalactic gas. This means that all systems have a finite retardation distance. The question is thus quantitative. The change of mass of the sun is minute and thus the retardation distance of the solar system is much larger than the size of the system allowing us to neglect retardation effects. However, for the M33 galaxy [35] the velocity curve indicates that the retardation effects cannot be neglected beyond a certain distance which was calculated to be roughly $R_r=4.54$ kpc. Similar analysis for other galaxies of different types has shown similar results [27,28] as was shown in the current paper. In [35] we demonstrated using a detailed model that this does not require high velocity of gas or stars and is perfectly consistent with the current observational knowledge of galactic and extra galactic material content and dynamics. Of course $|\ddot{M}|$ cannot be constant over the entire life time of the galaxy, for a simple model based on intergalactic mass depletion see [35].

We point out that if the mass outside a galaxy is still abundant (or totally consumed) $\ddot{M}\simeq 0$ and the retardation force should vanish. In this case, no "missing mass" phenomenon is expected. This was indeed reported [25] for the galaxy NGC1052-DF2 and for a few more ultra diffuse galaxies.

We note that the same physics that causes the gravitational radiation recently discovered is also responsible for the peculiar galactic rotation curves. The second order expansion in equation (4) is only valid for limited radii:

$$R<c{T}_{max}\equiv R_{max}$$

(14)

That is to the near field, this is acceptable since the extension of the rotation curve in galaxies is the same order of magnitude as the size of the galaxy itself. An opposite case in which the size of the object is much smaller than the distance to the observer will result in a different approximation leading to the famous quadruple equation of gravitational radiation as predicted by Einstein [6] and verified indirectly in 1993 by Russell A. Hulse and Joseph H. Taylor, Jr. for which they justly received the Nobel Prize. The Hulse-Taylor binary pulsar offered indirect evidence of the existence of gravitational waves [18]. On 11 February 2016, the LIGO and Virgo Scientific Collaboration announced they had made a direct observation of gravitational waves. The observation was made five months earlier, on 14 September 2015, using the Advanced LIGO detectors. The gravitational waves was caused by the merging of a binary black hole system [3]. Thus we study a near field case of gravitational radiation while previous art contains far field demonstrations.

To conclude this section we would like to mention the remarkable theory of conformal gravity put forward by Mannheim [10,11]. The approach practiced in this paper leads to a Newtonian potential plus a linear potential. Such potential types can also be derived from different theoretical considerations of conformal gravity. Indeed, on purely phenomenological grounds such fits have essentially already been published in the literature. While those fits looked reasonable they treat the coefficient of the linear potential as a variable that changes from galaxy to galaxy, this element which also arise in the current work is not in line with conformal gravity in which the coefficient of the linear potential is supposed to be a new universal constant of nature. This can be easily explained with retardation theory in which a variable $\ddot{M}$ seems reasonable depending on the dynamical conditions of various galaxies and the history of their creation.

Retardation Theory’s approach satisfies Occam’s razor rule and does not affect observations which are beyond the near-field regime [37], and therefore, does not clash with GR theory and its observations. Most of the 143 galaxies that were modelled in this work fit quite well with only a simple approximation to retarded gravity, other may benefit from a more detailed modelling as was done in [35]. Of course, in some cases the cylindrical symmetry approximation that we assume will not suffice.

Finally, the paper does not discuss dark matter in cosmological context. This is left for future works.