Preprint

Article

Simple Modeling and Analysis of Total-Ionizing-Dose Effects on Radio-Frequency Low-Noise Amplifier

Altmetrics

Downloads

135

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

20 February 2024

Posted:

21 February 2024

You are already at the latest version

Alerts

Abstract

In this study, the degradation characteristics of radio-frequency (RF) low-noise amplifier (LNA) based on silicon-germanium (SiGe) heterojunction bipolar transistors (HBTs) due to total ionizing dose (TID) are investigated. The small-signal equivalent model of a SiGe HBT is utilized to analyze circuit-level performance including the input and the output matching and noise figure (NF). As a target circuit, an LNA with a cascode common-emitter stage with emitter degeneration is studied and the equation of each performance parameter is derived. The RF LNA fabricated using commercial 350 nm SiGe technology was exposed to X-ray irradiation with the total dose up to 3 Mrad (SiO2). The experimental results exhibit that modeled device parameters estimate the degraded circuit performance. In addition, the relative impact of each parameter on the circuit metrics is revealed, which is expected from the derived design equations. The key device parameters for modeling TID-induced circuit degradations include the base resistance, the transconductance, and the base-to-emitter capacitance.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Silicon-germanium heterojunction bipolar transistors (SiGe HBTs) have demonstrated promising suitability for a variety of wireless and communication applications, exhibiting good radio-frequency (RF) performance parameters such as high unity-gain frequency (f_T) and maximum oscillation frequency (f_MAX) [1-3]. Moreover, in order to investigate their potential usage in extreme environment (e.g. space), radiation effects of SiGe HBTs on the electrical characteristics have been studied in the literature [2,4] and the research findings show that SiGe HBTs can maintain performance up to tens of krad of ionizing dose [4-6]. This property is fundamentally attributed to device physics that the operation of SiGe HBTs is not highly dependent on the quality of the oxide layer as typical metal-oxide-semiconductor (MOS)-based devices [2,7]. Still, SiGe HBTs undergo performance degradation in device characteristics due to total ionizing dose (TID) and the important mechanism is the trap generation in the emitter-base spacer and the shallow trench insulation (STI) oxide, leading to an increase in the base current [8-10].

One of the essential circuit blocks in a radio-frequency (RF) applications is the low-noise amplifier (LNA). It is designed to present matched impedance to the input for good signal reception, providing sufficient gain for the subsequent stages and minimizing noise contribution for better noise performance of the receiver system [11,12]. Regarding radiation effects, SiGe LNAs suffer from variations in input and output impedances, reduced signal gain, and an increase in noise figure (NF) [13], most of which are attributed to the degradations of active devices such as SiGe HBTs [14,15]. Whereas there have been some papers of TID effects on SiGe LNAs in the literature, however, few studies have been conducted with a primary focus on the modeling side of the changes in the device parameters. The analysis of the effect of TID on the parameters of SiGe HBTs will be helpful to understand and evaluate performance changes and it will be beneficial for developing radiation-hardening design techniques.

This paper is organized as follows. Section 2 explains the schematic and the analysis of the LNA, using the small-signal models SiGe HBTs which will be used for modeling TID-induced performance degradations. In Section 3, details of the experimental set-up and performance variations of the SiGe LNA due to X-ray irradiation will be presented. In Section 4, based on the small-signal model and the equivalent circuit, we discuss modeling results and analyze the impact of each parameter of a SiGe HBT on LNA performance. Lastly, Section 5 summarizes and concludes the findings of this work.

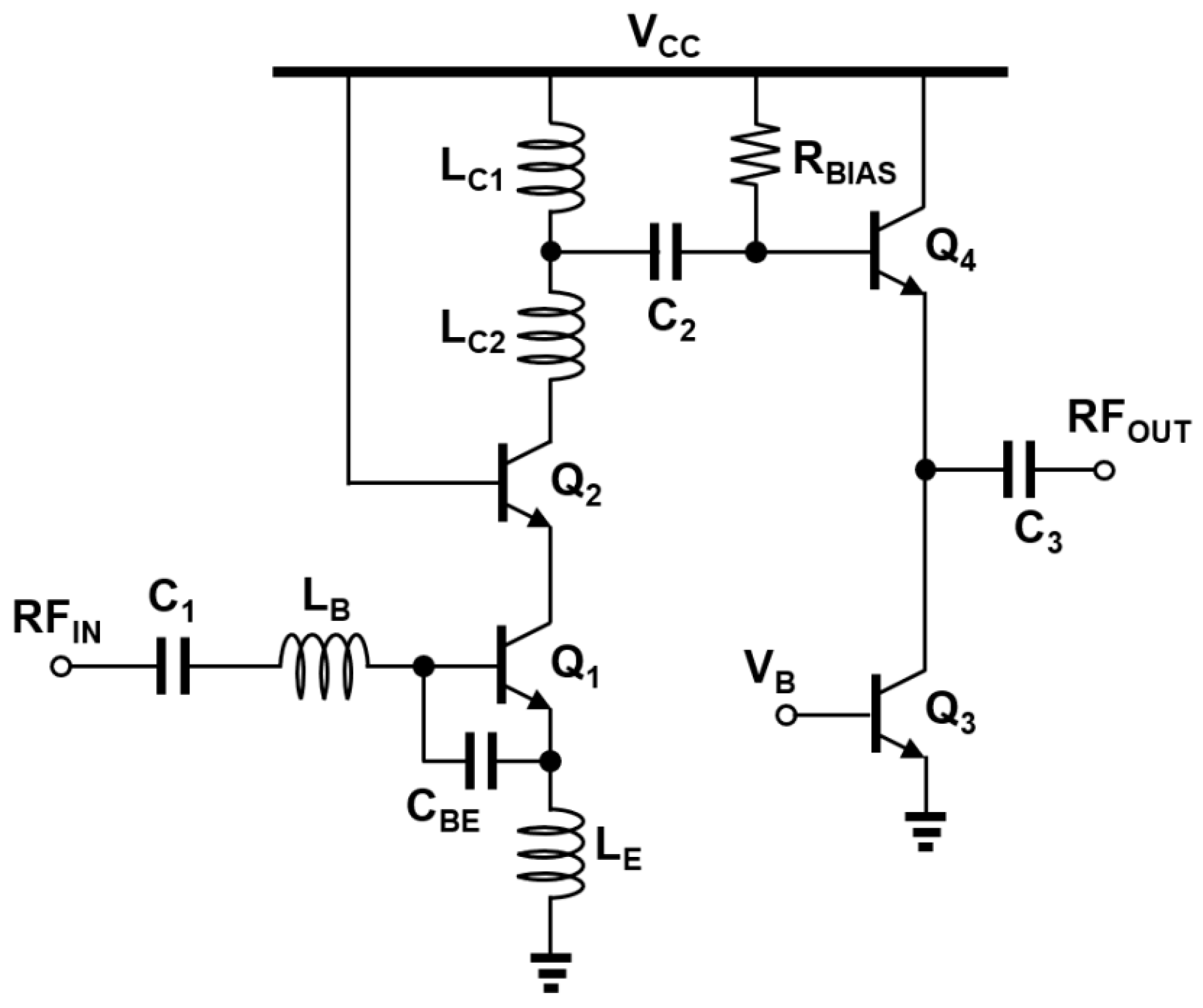
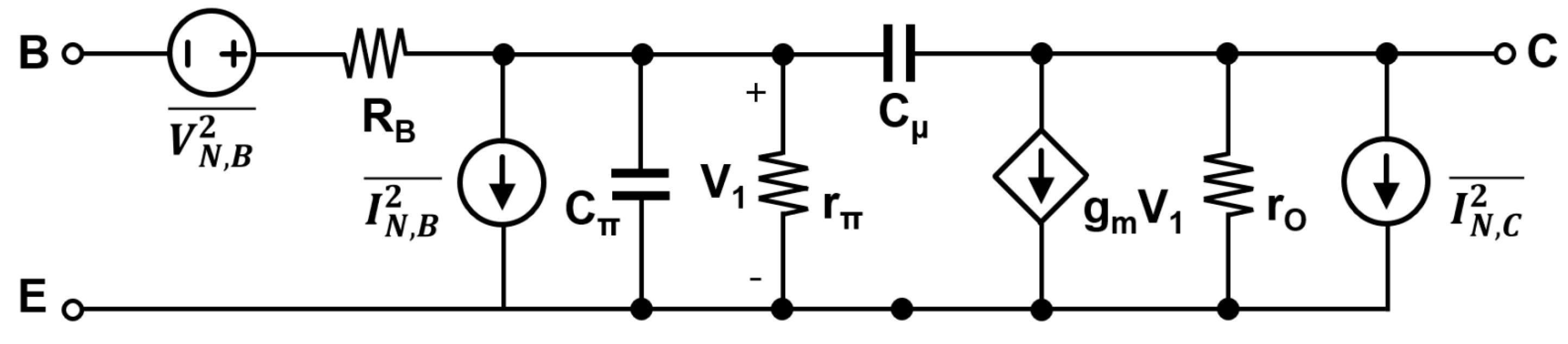
2. LNA Schematic and Device Modeling

An RF LNA is the first gain stage in a receiver and it plays a key role in 1) impedance matching between the antenna and the chip and 2) the system's noise performance. At the same time, it should provide sufficient gain to maintain the quality and strength of the incoming signal. In the aspect of small-signal operation, circuit performance is measured with S-parameters: S₂₁, S₁₁, and S₂₂ represent power gain, input matching, and output matching, respectively [16]. In addition, noise performance is read, using noise figure (NF) in the unit of dB [17]. Linearity properties of an LNA are important as well, but they are out of scope in this study.

With SiGe technology, the target LNA employed SiGe HBTs for good achieving gain, matching, and noise optimization. The schematic of the SiGe LNA for narrowband applications is shown in Figure 1. Overall, the LNA is based on a cascode common-emitter (Q₁ and Q₂) stage as a main stage [5] and the second stage (Q₃ and Q₄) act as a buffer for output impedance matching. In the former, Q₁ is the input transistor that receives the signal. Q₁, C_BE, L_E, and L_B collectively form the input matching network and the optimum noise impedance simultaneously. Q₂ is a cascode stage to improve gain performance and to suppress the Miller effects associated with the parasitic base-collector capacitance C_μ1 (see in Figure 2) [18]. The emitter inductor L_E generates real impedance at the base terminal of Q₁ and provides negative feedback for stability and the base-to-emitter capacitance C_BE along with C_π1 (see in Figure 2) is be tuned for input and noise matching. The second branch is configured as an emitter-follower stage, providing decoupling between the first stage and the load. Lc₁ and Lc₂ are optimized for peak gain and resonance of the first stage at the operation frequency, respectively. Lastly, C₁ and C₃ are for dc blocking and R_BIAS is for biasing Q₄.

For a theoretical analysis, the small-signal model of a SiGe HBT was constructed as shown in Figure 2 [19,20]. Whereas the complete small-signal equivalent model is much more complex, critical device parameters for modeling were selected for simple, yet insightful equations at the cost of accuracy. In this model, g_m, r_π, R_B, r_O, C_π, and C_μ are the small-signal transconductance, the emitter-to-base resistance, the base parasitic resistance, the collector-to-emitter resistance, the base-to-emitter capacitance, and the base-to-collector capacitance, respectively. Regarding noise sources

\bar{V_{N . B}^{2}}

is the thermal noise of the R_B,

\bar{I_{N . B}^{2}}

is shot noise associated with I_B, and

\bar{I_{N . C}^{2}}

is shot noise associated with I_C.

In order to conduct a theoretical analysis, equations to derive device parameters are presented below [21]. The transconductance (g_m) is obtained by taking the derivative of I_C with respect to V_BE and R_B is determined by using Z-parameters. And C_π and C_μ can be determined from Y-parameters. To extract device parameters, the following equations were derived and applied to design kit models of SiGe HBTs. In the following equations, β and ω refers to the current gain and the angular frequency, respectively.

g_{m} = \frac{\partial I_{C}}{\partial V_{BE}}

(1)

R_{B} = Re (Z_{11} - Z_{12})

(2)

r_{π} = Re (Z_{12}) = \frac{β}{g_{m}}

(3)

r_{O} = \frac{\partial V_{CE}}{I_{C}}

(4)

C_{π} = \frac{Im (Y_{11} + Y_{12})}{ω}

(5)

C_{μ} = - \frac{Im (- Y_{12})}{ω}

(6)

The parameters of the SiGe HBT used in the LNA were extracted and small-signal modeling was conducted, using the equivalent circuit and Equations (1)-(6) [19,21]. Then, the next step is to match the circuit performance such as matching, gain, and noise figure, using design equations. Analyze input and output impedance, gain and noise with small signal model parameters. First, the input impedance is an essential factor that ensures signal transfer with minimum reflections, and it is derived with L_B, L_E, C_BE, C_π1, and g_m1 under the assumption of very large r_o and C₁ and negligible C_μ. The input impedance of the LNA is shown in Equation (7), where the real and the imaginary terms should be matched to 50 Ω and 0 Ω eventually.

Z_{IN} = [\frac{1}{{sC}_{BE}} | | (R_{B} + \frac{1}{{sC}_{π 1}})] + s (L_{E} + L_{B}) + \frac{g_{m 1} L_{E}}{C_{π 1} + C_{BE} + {sC}_{π 1} C_{BE} R_{B}}

(7)

To analyze the output impedance of the LNA, the circuit is simplified as illustrated in Figure 3a. The cascode part of the first branch is treated as Z_CAS and it is assumed to be a very large impedance or an open. Then, the remaining circuitry can be modeled as a parallel RLC as shown in Figure 3b. The output impedance (Z_OUT) equation is given by

Z_{OUT} = (R_{B 4} + \frac{1}{{sC}_{2}} + {sL}_{C 1}) | | \frac{1}{g_{m 4}}

(8)

From Figure 3b, the equivalent model contains three components and their expressions are given as follows:

R_{P} = \frac{1}{1 + g_{m 4} R_{B 4}}

(9)

L_{P} = \frac{C_{2}}{g_{m 4}}

(10)

C_{P} = g_{m 4} L_{C 1}

(11)

Z_{OUT} = R_{P} ||L_{P}|| C_{P}

(12)

From Equations (8) and (12), R_B4 > 1/g_m4, and as shown in Figure 2, (R_B4 + 1/sC₂ + sL_C1) and 1/g_m4 are connected in parallel. Therefore, the magnitude of Z_OUT varies between R_B4||1/g_m4 and 1/g_m4 in the range of operation frequency. That is, the output impedance is affected by R_B4 and g_m4 of Q₄. This is confirmed in detail by the degradation modeling in Section 4.

The gain of the LNA is derived in Equation (13), which is a simplified gain expression without the contribution of the second branch. From this, it is shown that the gain of the LNA is affected by g_m1, g_m2, C_π1, and C_π2.

A_{V, LNA} = \frac{g_{m 1} Z_{L}}{1 + {sL}_{E} g_{m 1} + s^{2} (L_{E} + L_{B}) (C_{BE} + C_{π 1})}

(13)

Z_{L} = \frac{L_{C 1}}{L_{C 1} + L_{C 2}}

(14)

Achieving low noise contribution from an LNA is important requirement. In Figure 2, the thermal noise of the base resistor (R_B) and the shot noise of the base and collector currents are included, which are the main sources of noise in SiGe HBTs. While there are other factors that affect noise performance under radiation effects, such as changes in LNA gain, noise matching, biasing conditions and etc., however, the noise sources in the small-signal model of the SiGe HBTs are considered for modeling noise figure of the LNA. The device noise equations and output noise voltage equation are shown as follows.

\bar{I_{N . B}^{2}} = 2 {qI}_{B}

(15)

\bar{I_{N . C}^{2}} = 2 {qI}_{C}

(16)

\bar{V_{N . B}^{2}} = 4 {kTR}_{B}

(17)

\bar{V_{N . HBT}^{2}} = 2 {qI}_{C} r_{O}^{2} + 4 {kTR}_{B} A_{V, HBT}^{2} + 2 q {(R_{B} | | \frac{1}{{sC}_{π}})}^{2} r_{O}^{2} g_{m} I_{B}

(18)

Using the above analysis and equations, the performance degradation of the SiGe LNA due to TID was modeled and the results are presented in the next section.

3. Experimental Results

3.1. Test Setup for Performance Measurement

The RF SiGe LNAs were fabricated using the GlobalFoundries 350nm SiGe BiCMOS technology, which featured a peak f_T and f_MAX of 23 GHz and 110 GHz, respectively [22-24]. Figure 4 shows the chip micrograph of an LNA sample. For S-parameter measurement, a network analyzer (Agilent PNA E8364B), custom-designed PCBs, and a probe station were used. Noise performance was characterized with a noise source (N4002A) and a PXA signal analyzer (N9030A). The supply voltage of the LNA was 2.5 V and the bias current of I_BIAS1 and I_BIAS2 were 830 μA and 600 μA, respectively. In addition, for the radiation experiment, an Aracor X-ray source was used with total dose up to 3 Mrad (SiO₂) [25-27]. The LNA samples were irradiated under unbiased conditions and the time between irradiation and measurement was about 24 hours. The pre-rad condition showed that the peak gain of the LNA was 12.8 dB at 6 GHz, and the corresponding noise figure (NF) was 3.4 dB. The input- and the output-matched frequencies were observed at 5 GHz and 5.8 GHz, respectively.

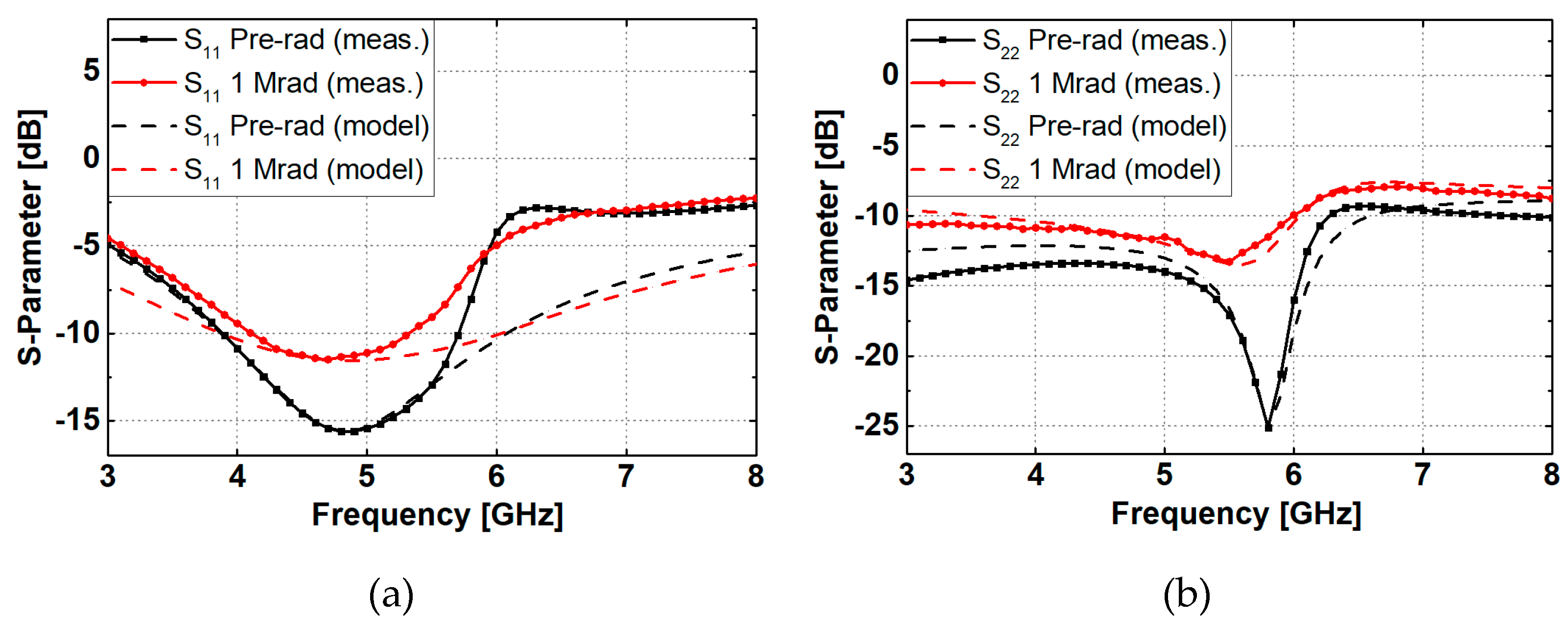
3.2. Performance Degradations and Modeling

After the radiation experiment, branch currents did not show significant changes, implying the collector currents of the SiGe HBTs were about the same. But the base current gradually increased as the total dose accumulated, resulting in a decrease in current gain [28]. In general, the performance of SiGe HBT LNAs was influenced by several factors including the changes in the internal resistances and capacitances, transconductance, and/or current gain [4,29]. In this work, passive devices such as capacitors and inductors as external components were assumed to have little effects on performance degradation [30]. In addition, small-signal modeling was conducted for the pre-rad and the 1 Mrad cases.

Figure 5 shows the input matching (S₁₁) and the output matching (S₂₂) of the SiGe LNA for pre-rad and 1 Mrad cases. Comparing S₁₁ and S₂₂ response, the S-parameter values increased at the matched frequencies, showing degradations in signal transfer characteristics. Regarding the locations of resonant frequencies, there was no noticeable frequency shift between the pre-rad and 1 Mrad irradiation. Figure 6 shows the performance changes in the power gain (S₂₁) and NF. Similar to the S₁₁ and the S₂₂ cases, unfavorable shifts (e.g., a reduction of gain and an increase in NF) in a vertical direction were observed, but there were no horizontal shifts.

From Equation (7), (12), (13), and (18), the key LNA characteristics are determined by the device parameters including C_π g_m, and R_B. Thus, it is important to investigate the impact of TID to device parameters and relate them to circuit operation. Due to the irradiation, traps are generated in the EB spacer region of a SiGe HBT, leading to an increase in the dielectric constant from incomplete coupling and eventually to greater EB junction capacitance [4,31]. With regard to transconductance, X-ray irradiation induces degradations in diffusion length and carrier mobility, thereby reducing g_m. As the accumulate dose increases, g_m will decrease, lowering overall gain of the circuit [4,29,30]. Next, after irradiation R_B will increase due to the reduction of charge carriers, as traps generated capture a more portion of electrons. Moreover, dopants tend to be deactivated under the increased fluence, further raising the base resistance [32-35]. Therefore, it is reasonable to assume that combined changes of C_π, g_m and R_B will modify circuit response in terms of S-parameters and NF after X-ray irradiation.

To capture and represent the degradation characteristics, simulations using the small-signal model were conducted. For example, as shown in Equation (13), the gain of the LNA is highly affected by the transconductance (g_m) of the input SiGe HBT, whereas the NF is degraded by the R_B and g_m [see Equation (18)]. It can be estimated that S₂₁ degrades after X-ray irradiation due to a reduction of g_m. A similar degradation trend is expected in NF of the LNA as well. As shown in Figure 5 and Figure 6, the modeled results were matched well around the resonant frequencies in terms of S-parameters and NF. As frequencies move away from the center, however, some discrepancies such as magnitude and slope differences were observed, exhibiting the limitations of using simplified device models and ignored other circuit parameters.

Figure 7a,b shows the degradations in the input and the output impedance matching with reference to the pre-rad results, respectively. This indicates that the dose can cause poorer matching at the target frequency, resulting in unwanted ripples or instability. In Figure 8a, the gain decreases as the total dose increases, and in Figure 8b, the NF characteristics degrade monotonically. When the TID reached 3 Mrad, however, unlike the previous case, a slight performance recovery was observed. This is due to the annealing effect in the device as the X-ray irradiation time increases, which recovers some performance loss and the degree of recovery over a period may vary depending on the temperature and the irradiation time [8,36]. Table 1 summaries the overall changes in performance parameters under different TID.

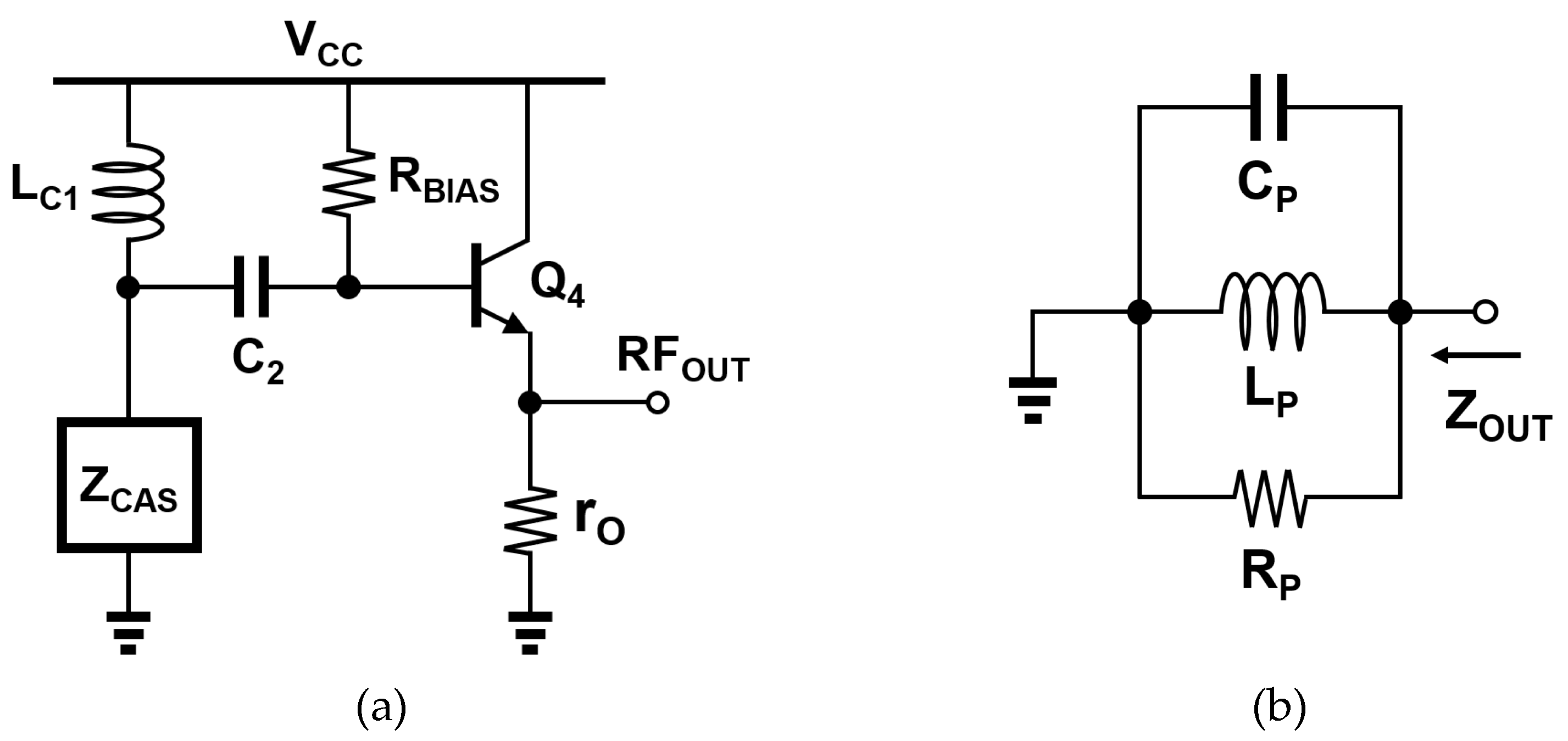
4. Analysis and Discussion

The degradation characteristics of SiGe HBTs due to ionizing radiation tend to decrease in g_m and increase resistances and capacitances. Based on this trends, simulations were conducted using the small-signal model of SiGe HBTs. The input and the output matching are affected by R_B, C_π, and g_m as shown in Equation (7) and (8). Changes of S₁₁ (ΔS₁₁) are influenced by ΔR_B with 73% and ΔC_π1 with 23% as illustrated in Figure 9a. For output matching, ΔS₂₂ has the largest dependency on g_m4 by 60%, followed by R_B (30%) and g_m5 (5%) (see Figure 9b). In Figure 9, other parameters contributed to ΔS₁₁ and ΔS₂₂, but their portion is only 4% and 5%, respectively.

Gain changes (ΔS₂₁) was mostly affected by the decrease in g_m (see Figure 10a). ΔS₂₁ is almost dominated by Δg_m1 (about 60%), whereas the contributions of other transconductance and C_π1 much less. Regarding noise modeling, since NF is proportional to resistance and inversely proportional to g_m, it can be predicted that noise figure performance degrades as g_m decreases and R_B increases (see Figure 10b). As expected, the small-signal model simulation shows that Δg_m1 and ΔR_B1 have the most influence on NF. Like the input and output return loss, NF and S₂₁ in Figure 10 shows remaining contributions of 10% and 4%, respectively. In the case of NF, the derivation assumes perfect impedance matching conditions. Due to TID irradiation, however, this condition may be valid as inferred from the degradations in S₁₁. Therefore, to improve the modeling accuracy of NF will require more parameters to be included in the analysis stage.

Table 2 compares how much a parameter in the small-signal model contributes to circuit degradation. In the table, C_π refers to the combined effect of the ΔC_π1 and ΔC_π4, whereas g_m is for Δg_m1, Δg_m2, and Δg_m4. It shows the relative portion of each parameter to the changes in circuit performance caused by TID, assuming that all SiGe HBTs exhibit degradations with the same ratio. For input matching and NF, R_B had the most significant impact on performance degradation by 73% and 56%, respectively. For output matching and power gain, g_m contributed the most significant portion by 65% and 88%, respectively.

Table 3 shows the variation in parameter values for SiGe HBTs before and after the X-ray irradiation. In this analysis, all devices are assumed to have the same rate of degradation regardless of bias conditions or size. The above discussion, in turn, implies that proper modeling of key device parameters can predict the overall degradation characteristics of a SiGe LNA with a reasonable accuracy. With prior knowledge of device parameter values over TID irradiation, the model will better estimate the performance degradation of the circuit.

5. Summary

Degradation characteristics of RF SiGe LNA due to TID was investigated using a small-signal equivalent model of a SiGe HBT. Among device parameters of a SiGe HBT, g_m, C_π, and R_B were mostly responsible for performance degradations of the LNA. Based on the analytic equations, the case of 1 Mrad (SiO₂) dose was modeled and the degradations in S-parameters and NF were replicated. The proposed approach will be helpful to understand the relationship between device parameters and circuit operation. In addition, it can predict the degree of degradation in RF SiGe LNA due to TID effectively, which will be useful in the estimation of radiation hardness.

Author Contributions

Conceptualization, T.K. and I.S.; methodology, T.K., I.S.; software, J.L.; validation, T.K., M.-K.C., and I.S.; formal analysis, T.K., J.L., and I.S.; investigation, T.K., M.-K.C.; resources, D.M.F., J.D.C., and I.S.; data curation, J.L.; writing—original draft preparation, T.K., G.R., and I.S.; writing—review and editing, M.-K.C. and I.S.; visualization, T.K.; supervision, J.D.C. and I.S.; project administration, J.D.C. and I.S.; funding acquisition, J.D.C. and I.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT). (No. NRF-2022M1A3B8076511, NRF-2022M3I7A1085472, and RS-2023-00212268). In addition, this work was supported in part by Institute of Information & communications Technology Planning & Evaluation (IITP) under the artificial intelligence semiconductor support program to nurture the best talents (IITP-2024-RS-2023-00253914) grant funded by the Korea government (MSIT). The EDA tool was supported by the IC Design Education Center (IDEC), Korea.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Cressler, J.D. SiGe HBT Technology: A New Contender for Si-Based RF and Microwave Circuit Applications. IEEE Transactions on Microwave Theory and Techniques, 1998, vol. 46, pp. 572-589.
Song, I.; Cardoso, A. S.; Ying, H.; Cho, M. -K.; Cressler, J. D. Cryogenic Characterization of RF Low-Noise Amplifiers Utilizing Inverse-Mode SiGe HBTs for Extreme Environment Applications. IEEE Transactions on Device and Materials Reliability, 2018, vol. 18, pp. 613-619.
Cressler, J. D. On the Potential of SiGe HBTs for Extreme Environment Electronics. In Proceedings of the IEEE, 2005, vol. 93, pp. 1559-1582.
4. Zhuoqi Li.; Shuhuan Liu.; Xiaotang Ren.; Mathew Adefusika Adekoya.; Jun Zhang.; Shuangying Liu. Experimental Investigation on the Degradation of SiGe LNAs under Different Bias Conditions Induced by 3 MeV Proton Irradiation. Nuclear Engineering and Technology, 2022, vol. 54, pp. 661-665.
5. Song, I.; Jung, S.; Lourenco, N. E.; Raghunathan, U. S.; Fleetwood, Z. E.; Zeinolabedinzadeh, S.; Gebremariam, T. B.; Inanlou, F.; Roche, N. J.-H.; Khachatrian, A.; McMorrow, D.; Buchner, S. P.; Melinger, J. S.; Warner, J. H.; Paki-Amouzou, P.; Cressler, J. D. Design of Radiation-Hardened RF Low-Noise Amplifiers Using Inverse-Mode SiGe HBTs. IEEE Transactions on Nuclear Science, 2014, vol. 61, pp. 3218-3225.
6. Teng, J. W.; Ildefonso, A.; Tzintzarov, G. N.; Ying, H.; Moradinia, A.; Wang, P. F.; Li, Xun.; Zhang, E. X.; Fleetwood, D. M.; Cressler, J. D. Variability in Total-Ionizing-Dose Response of Fourth-Generation SiGe HBTs. IEEE Transactions on Nuclear Science, 2021, vol. 68, pp. 949-957.
7. Cressler, J. D. Radiation Effects in SiGe Technology. IEEE Transactions on Nuclear Science, 2013, vol. 60, pp. 1992-2014. [CrossRef]
Nergui, D.; Teng, J. W.; Hosseinzadeh, M.; Mensah, Y.; Li, K.; Gorchichko, M.; Ildefonso, A.; Ringel, B. L.; Zhang, E. X.; Fleetwood, D. M.; Cressler, J. D. Total-Ionizing-Dose Response of SiGe HBTs at Elevated Temperatures. IEEE Transactions on Nuclear Science, 2022, vol. 69, pp. 1079-1084.
Wachter, M. T.; Ildefonso, A.; Fleetwood, Z. E.; Lourenco, N. E.; Tzintzarov, G.; McMorrow, D.; Roche, N. J.-H.; Khachatrian, A.; McMarr, P.; Hughes, H.; Warner, J. H.; Paki, P.; Cressler, J. D. The effects of total ionizing dose on the transient response of SiGe BiCMOS technologies. In 2016 16th European Conference on Radiation and Its Effects on Components and Systems (RADECS), Bremen, Germany, 2016, pp. 1-5. [CrossRef]
Wang, X.; Li, X.; Zhang, J.; Heini, M.; Liu, M.; Liu, H. Effects of Total Ionizing Dose on Low Frequency Noise Characteristics in SiGe HBT. In 2023 5th International Conference on Radiation Effects of Electronic Devices (ICREED). Kunming, China, 2023, pp. 1-5. [CrossRef]
11. Davulcu, M.; Çalışkan, C.; Kalyoncu, İ.; Gurbuz, Y. An X-Band SiGe BiCMOS Triple-Cascode LNA With Boosted Gain and P1dB. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, vol. 65, pp. 994-998. [CrossRef]
Song, I.; Cho, M. K.; Oakley, M. A.; Ildefonso, A.; Ju, I.; Buchner, S. P.; McMorrow, D.; Paki, P.; Cressler, J. D. On the Application of Inverse-Mode SiGe HBTs in RF Receivers for the Mitigation of Single-Event Transients. IEEE Transactions on Nuclear Science, 2017, vol. 64, pp. 1142-1150. [CrossRef]
Zhuoqi Li.; Shuhuan Liu.; Mathew Adefusika Adekoya.; Xiaotang Ren.; Jun Zhang.; Shuangying Liu.; Long Li. Radiation response of SiGe low noise amplifier irradiated with different energy protons. Microelectronics Reliability, 2021, vol. 127, ISSN 0026-2714.
Sarker, M.A.R.; Jung, S.; Ildefonso, A.; Khachatrian, A.; Buchner, S.P.; McMorrow, D.; Paki, P.; Cressler, J.D.; Song, I. Mitigation of Single-Event Effects in SiGe-HBT Current-Mode Logic Circuits. Sensors 2020, 20, 2581. [CrossRef] [PubMed]
Zhang, J.; Guo, Q.; Guo, H.; Lu, W.; He, C.; Wang, X.; Li, P.; Liu, M. Impact of Bias Conditions on Total Ionizing Dose Effects of 60Coγ in SiGe HBT. IEEE Transactions on Nuclear Science, 2016, vol. 63, pp. 1251-1258. [CrossRef]
Kobal, E. Siriburanon, T.; Staszewski. R. B.; Zhu, A. A Compact, Low-Power, Low-NF, Millimeter-Wave Cascode LNA With Magnetic Coupling Feedback in 22-nm FD-SOI CMOS for 5G Applications. IEEE Transactions on Circuits and Systems II: Express Briefs, 2023, vol. 70, pp. 1331-1335. [CrossRef]
Jia, X.; Niu, G. Impact of Correlated RF Noise on SiGe HBT Noise Parameters and LNA Design Implications. IEEE Transactions on Electron Devices, 2014, vol. 61, pp. 2324-2331. [CrossRef]
Song, I.; Ryu, G.; Jung, S.H.; Cressler, J.D.; Cho, M.-K. Wideband SiGe-HBT Low-Noise Amplifier with Resistive Feedback and Shunt Peaking. Sensors 2023, 23, 6745. [Google Scholar] [CrossRef] [PubMed]
Lee, Seonghearn.; Ryum, B. R.; Kang, S. W. A New Parameter Extraction Technique for Small-Signal Equivalent Circuit of Polysilicon Emitter Bipolar Transistors. IEEE Transactions on Electron Devices. 1994, vol. 41, pp. 233-238. [CrossRef]
Sarker, M.A.R.; Song, I. Design and Analysis of fT-Doubler-Based RF Amplifiers in SiGe HBT Technology. Electronics 2020, 9, 772. [Google Scholar] [CrossRef]
Lee, K.; Choi, K.; Kook, S. H.; Cho, D. H.; Park, K. W.; Kim, B. Direct Parameter Extraction of SiGe HBTs for the VBIC Bipolar Compact Model. IEEE Transactions on Electron Devices, 2005, vol. 52, pp. 375-384. [CrossRef]
22. SiGe Power Amplifier Platforms. gf.com/wp-content/uploads/2021/12/GF21-SiGe-PA-0705.pdf (16, 2, 2024).
Sirohi, S.; Sirohi, S.; Jain, V.; Raman, A.; Nukala, B.; Veeramani, E.; Adkisson, J. W.; Joseph, A. Impact of Emitter Width Scaling on Performance and Ruggedness of SiGe HBTs for PA Applications. In 2018 IEEE BiCMOS and Compound Semiconductor Integrated Circuits and Technology Symposium (BCICTS), San Diego, CA, USA, 2018, pp. 182-185. [CrossRef]
Song, I.; Cho, M; K.; Lourenco, N. E.; Fleetwood, Z. E.; Jung, S.; Roche, N. J.-H.; Khachatrian, A.; Buchner, S. P.; McMorrow, D.; Paki, P.; Cressler, J. D. The Use of Inverse-Mode SiGe HBTs as Active Gain Stages in Low-Noise Amplifiers for the Mitigation of Single-Event Transients. IEEE Transactions on Nuclear Science, 2017, vol. 64, pp. 359-366. [CrossRef]
Gorchichko, M.; Cao, Y.; Zhang, E. X.; Yan, D.; Gong, H.; Zhao, S. E.; Wang, P.; Jiang, R.; Liang, C.; Fleetwood, D. M.; Schrimpf, R. D.; Reed, R. A.; Linten, D. Total-Ionizing-Dose Effects and Low-Frequency Noise in 30-nm Gate-Length Bulk and SOI FinFETs With SiO2/HfO2 Gate Dielectrics. IEEE Transactions on Nuclear Science, 2020, vol. 67, pp. 245-252. [CrossRef]
Lambert, D.; Gaillardin, M.; Raine, M.; Paillet, P.; Duhamel, O.; Marcandella, C.; Martinez, M.; Rostand, N.; Lagutère, T.; Aubert, D.; Assaillit, G.; Delbos, C. TID Effects Induced by ARACOR, 60Co, and ORIATRON Photon Sources in MOS Devices: Impact of Geometry and Materials. IEEE Transactions on Nuclear Science, 2021, vol. 68, pp. 991-1001. [CrossRef]
Gaillardin, M.; Lambert, D.; Aubert, D.; Raine, M.; Marcandella, C.; Assaillit, G.; Auriel, G.; Martinez, M.; Duhamel, O.; Ribière, M.; Rostand, N.; Lagutère, T.; Paillet, P.; Delbos, C.; Poujols, D.; Ritter, S. Investigations on Spectral Photon Radiation Sources to Perform TID Experiments in Micro- and Nano-Electronic Devices. IEEE Transactions on Nuclear Science, 2021, vol. 68, pp. 928-936. [CrossRef]
Shiming Zhang.; Cressler, J. D.; Guofu Niu.; J, C.; Marshall.; W, P.; Marshall.; Kim, H.S.; Reed, Robert A.; Palmer, M. J.; Joseph, Alvin J.; Harame, D. L. The effects of operating bias conditions on the proton tolerance of SiGe HBTs. Solid-State Electronics, 2003, vol. 47, pp. 1729-1734.
Yabin Sun.; Ziyu Liu.; Jun Fu.; Xiaojin Li.; Yanling Shi. Investigation of total dose effects in SiGe HBTs under different exposure conditions. Radiation Physics and Chemistry, 2018, vol. 151, pp. 84-89.
Habeenzu, B. Effect of electron radiation on small-signal parameters of NMOS devices at mm-wave frequencies. Microelectronics Reliability, 2020, vol. 107, ISSN 0026-2714. (www.sciencedirect.com/science/article/pii/S0026271419306699).
Prakash, A.P.G.; Pradeep. T.M.; Hegde, V.N.; Pushpa, N.; Bajpai, P.K.; Patel, S.P.; Trivedi, T.; Bhushan. K.G. Comparison of effect of 5 MeV proton and Co-60 gamma irradiation on silicon NPN rf power transistors and N–channel depletion MOSFETs. Radiat. Eff. Defect Solid, 2017, vol. 172, pp. 952-963. [CrossRef]
32. Wei-Min Lance Kuo.; Yuan Lu.; Floyd, B.A.; Haugerud, B.M.; Sutton, A.K.; Krithivasan, R.; Cressler, J.D.; Gaucher, B.P.; Marshall, P.W.; Reed, R.A.; Freeman, G. Proton radiation response of monolithic Millimeter-wave transceiver building blocks implemented in 200 GHz SiGe technology. IEEE Transactions on Nuclear Science, 2004, vol. 51, pp. 3781-3787. [CrossRef]
Yuan Lu.; Cressler, J.D.; Krithivasan, R.; Ying Li.; Reed, R.A.; Marshall, P.W.; Polar, C.; Freeman, G.; Ahlgren, D. Proton tolerance of third-generation. 0.12 /spl mu/m 185 GHz SiGe HBTs. IEEE Transactions on Nuclear Science, 2003, vol. 50, pp. 1811-1815. [CrossRef]
Shiming Zhang.; Guofu Niu.; J. D. Cressler.; S. D. Clark and D. C. Ahlgren. The effects of proton irradiation on the RF performance of SiGe HBTs. IEEE Transactions on Nuclear Science, 1999, vol. 46, pp. 1716-1721. [CrossRef]
Jia, X.; Niu, G. Impact of Correlated RF Noise on SiGe HBT Noise Parameters and LNA Design Implications. IEEE Transactions on Electron Devices, 2014, vol. 61, pp. 2324-2331. [CrossRef]
Nergui, D.; Teng, J. W.; Hosseinzadeh, M.; Mensah, Y.; Li, K.; Gorchichko, M.; Ildefonso, A.; Ringel, B. L.; Zhang, E. X.; Fleetwood, D. M.; Cressler, J. D. "Total-Ionizing-Dose Response of SiGe HBTs at Elevated Temperatures. IEEE Transactions on Nuclear Science, 2022, vol. 69, pp. 1079-1084. [CrossRef]

Figure 1. Circuit schematic of RF SiGe LNA.

Figure 2. Small-signal equivalent a model of a SiGe HBT.

Figure 3. (a) Schematic to calculate the output impedance of the LNA (b) Simplified RLC-equivalent model of the output impedance.

Figure 4. Microphotograph of the fabricated SiGe LNA.

Figure 5. Measured and the modeled S-parameters: (a) S₁₁ (input matching) (b) S₂₂ (output matching) of the SiGe LNA.

Figure 6. Measured and the modeled (a) S₂₁ (power gain) and (b) noise figure (NF) of the SiGe LNA.

Figure 7. Performance degradation with reference to the pre-rad condition for different total-dose cases (a) S₁₁ (b) S₂₂ of the SiGe LNA.

Figure 8. Performance degradation with reference to the pre-rad condition for different total-dose cases (a) S₂₁ (b) NF of the SiGe LNA.

Figure 9. Contribution of each parameter to performance degradation in the LNA (a) Relative contributions to ΔS₁₁ (b) Relative contributions to ΔS₂₂.

Figure 10. Contribution of each parameter to performance degradation in the LNA (a) Relative contributions to ΔS₂₁ (b) Relative contributions to ΔNF.

Table 1. Degradation of LNA Performance due to TID. (Maximum or Minimum Values).

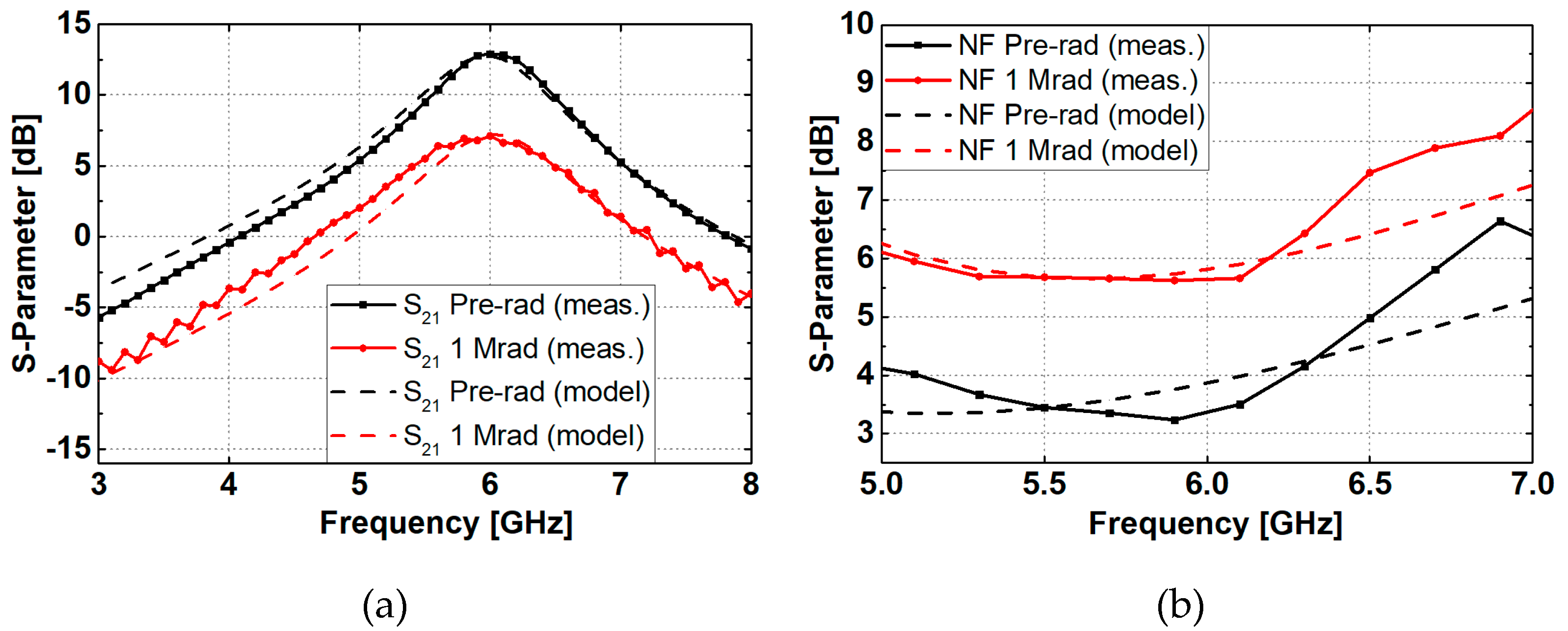
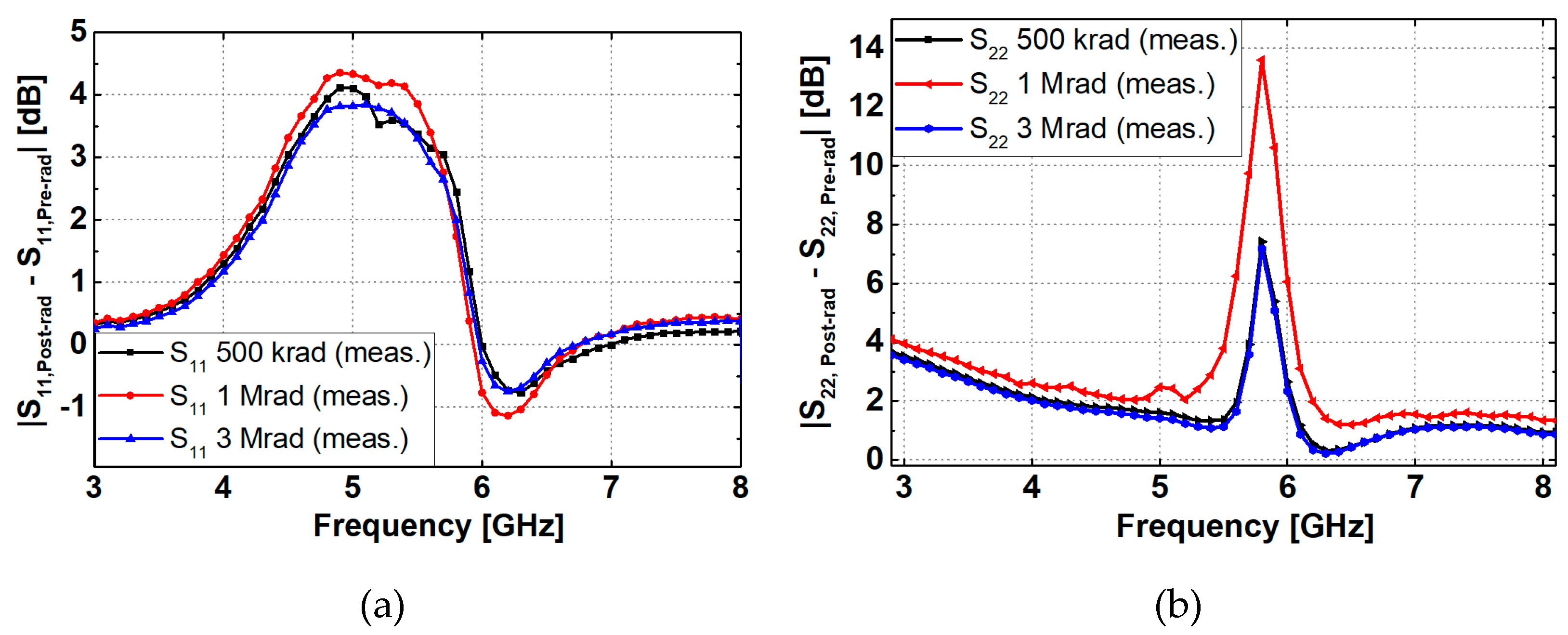
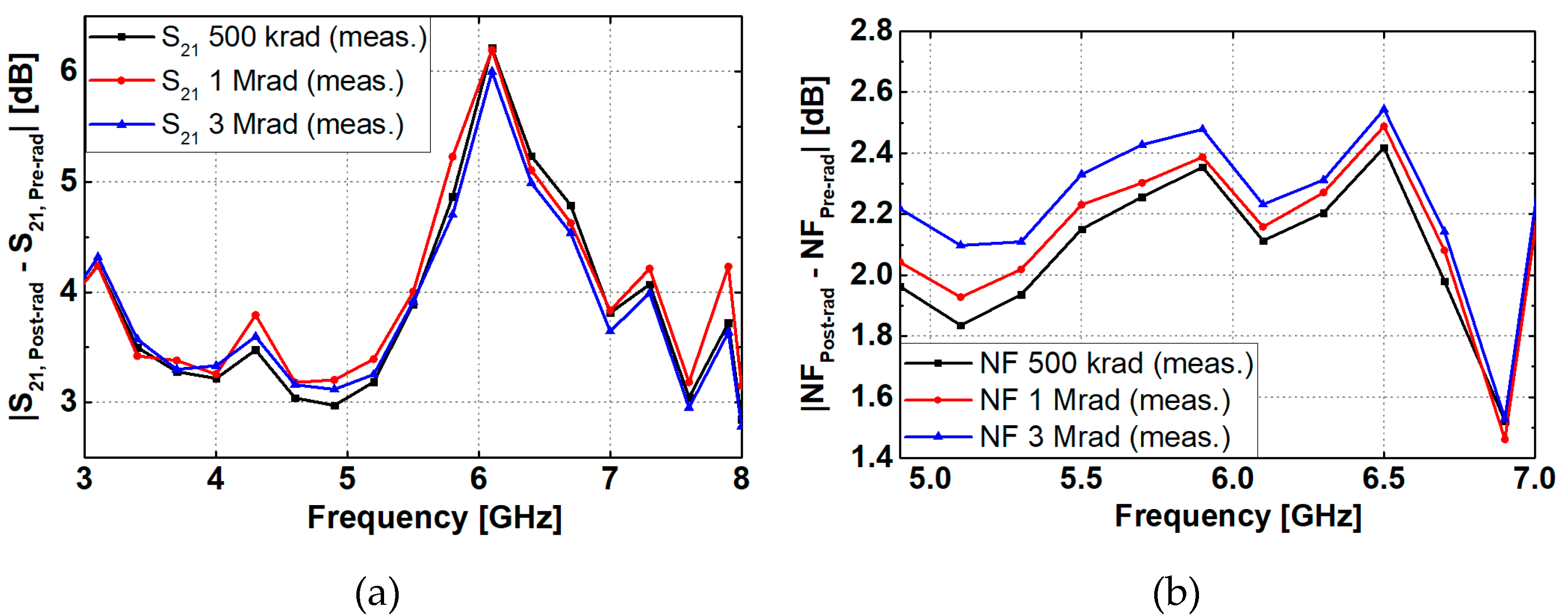
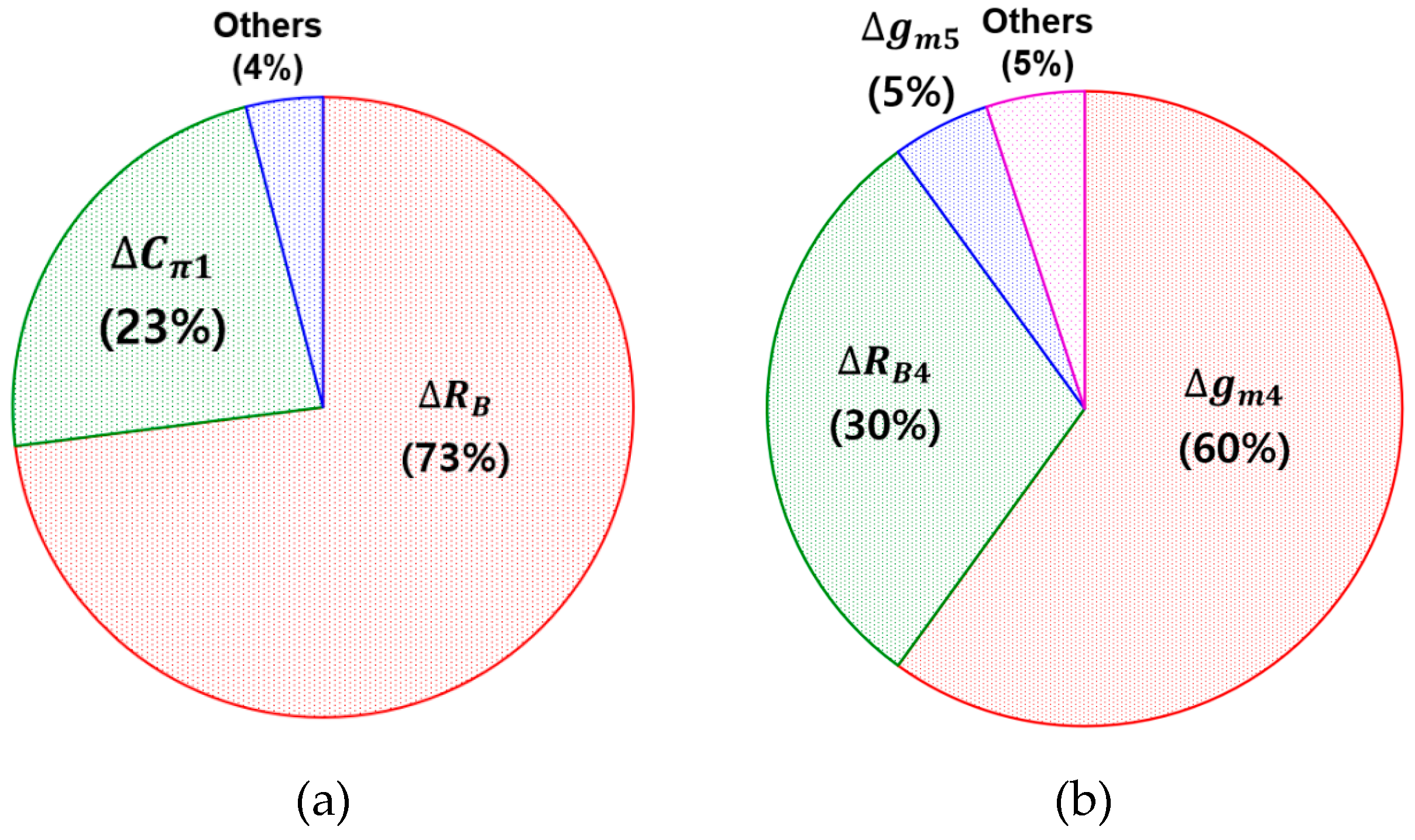
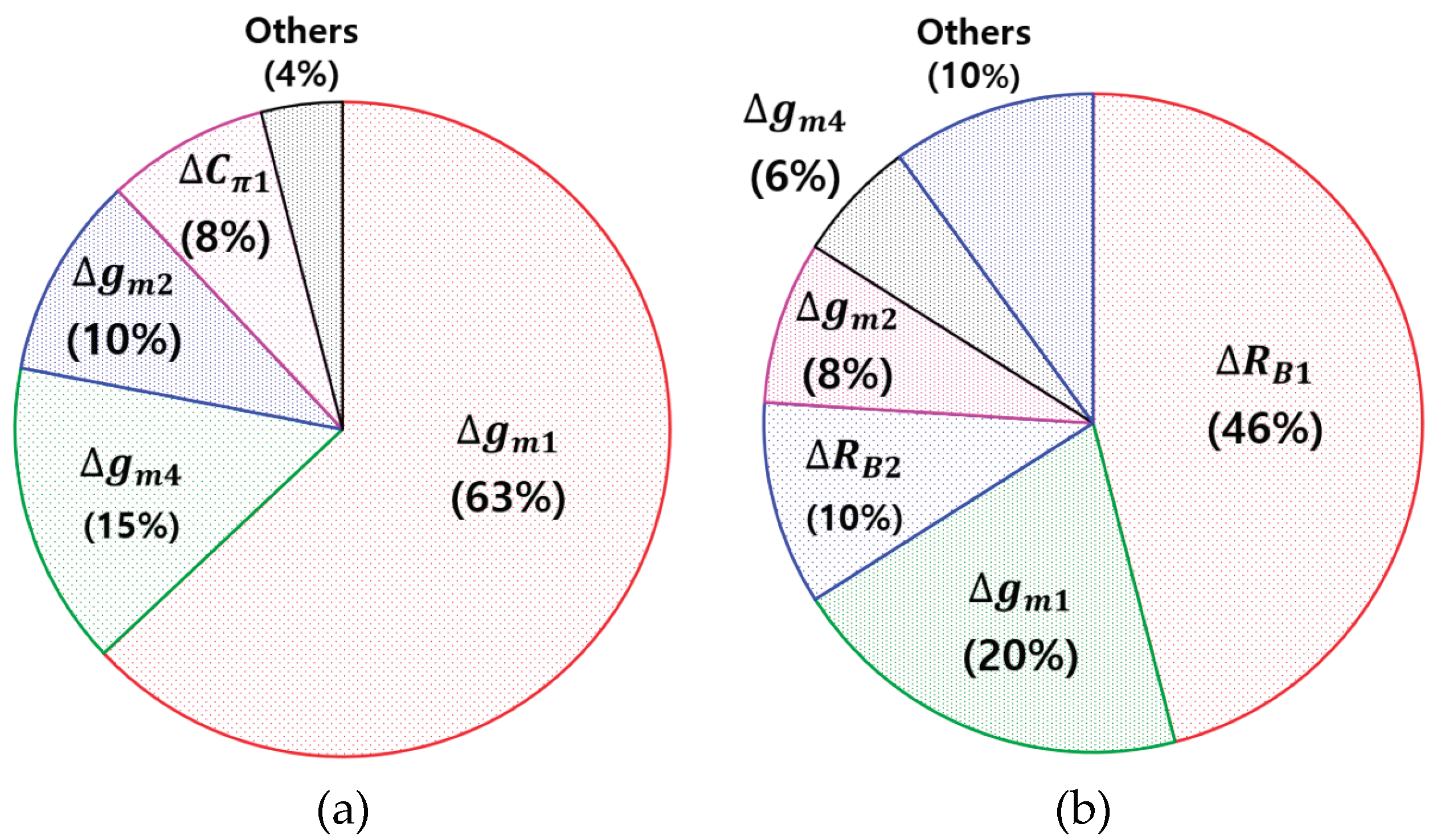
Total dose	S₁₁	S₂₂	S₂₁	NF
Pre-rad	-15.62 dB	-23.66 dB	12.89 dB	3.45 dB
500 krad	-11.52 dB	-17.11 dB	7.34 dB	5.6 dB
1 Mrad	-11.27 dB	-11.19 dB	7.14 dB	5.66 dB
3 Mrad	-11.79 dB	-17.36 dB	7.55 dB	5.78 dB

Table 2. The Impact of Device Parameters on the LNA Performance Degradation by TID.

Parameter	ΔS₁₁	ΔS₂₂	ΔS₂₁	ΔNF
C_π	23%	-	8%	-
g_m	-	65%	88%	34%
R_B	73%	30%	-	56%

Table 3. Device Parameter Values for Pre-rad and Post-rad Conditions.

Parameter	Unit	Pre-rad	Post-rad (1 Mrad)
C_π1, C_π2	fF	250	330
C_π4	fF	240	320
g_m1, g_m2	mS	45	30
g_m4	mS	17	11
R_B1, R_B2	Ω	97	170
R_B4	Ω	80	140

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.