Submitted:
22 February 2024
Posted:
22 February 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Expansion Mechanisms in Battery Cells
2.1. Reversible Expansion
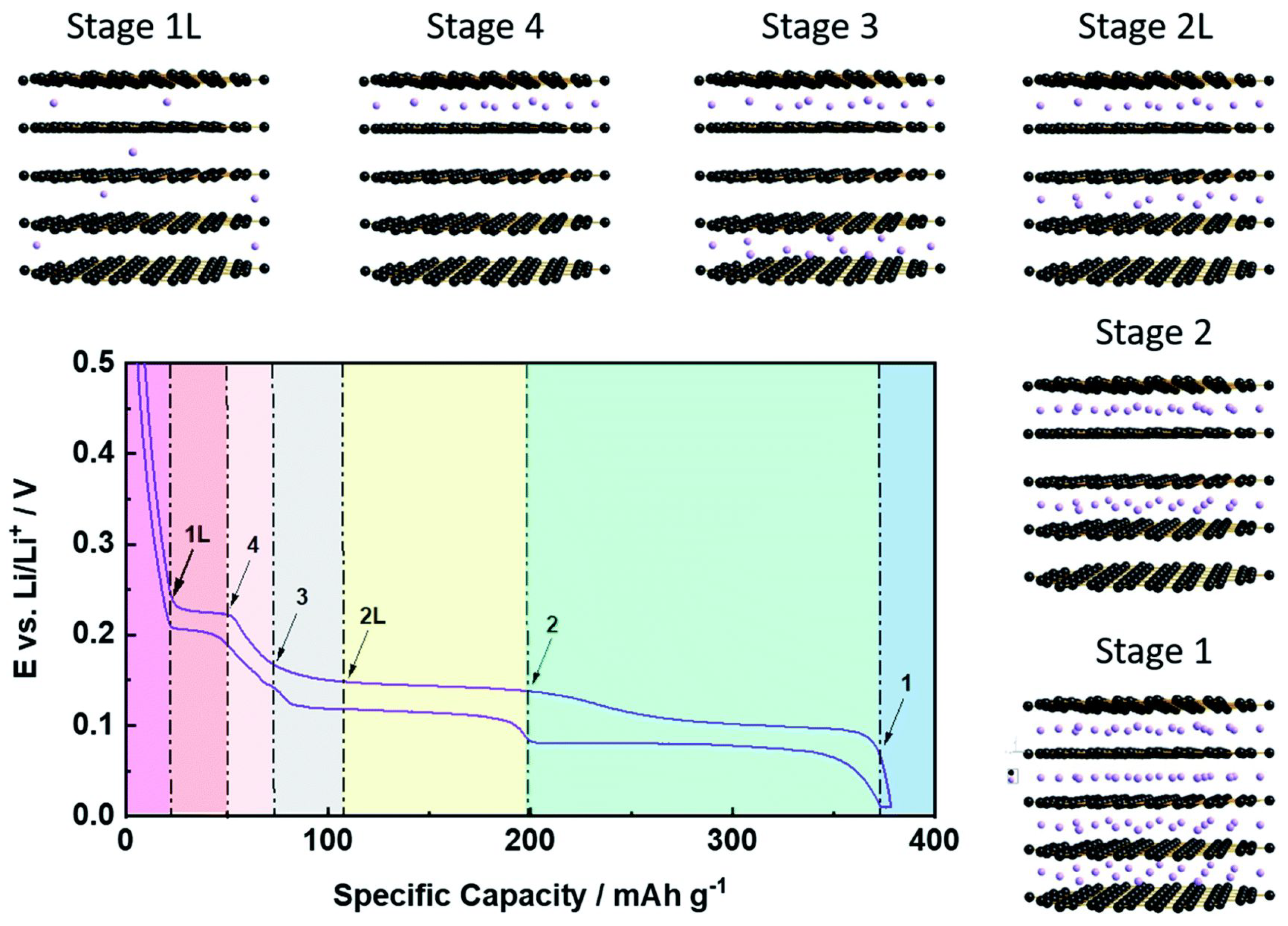
2.1.1. Anodes
2.1.2. Cathode
2.1.3. Thermal Expansion
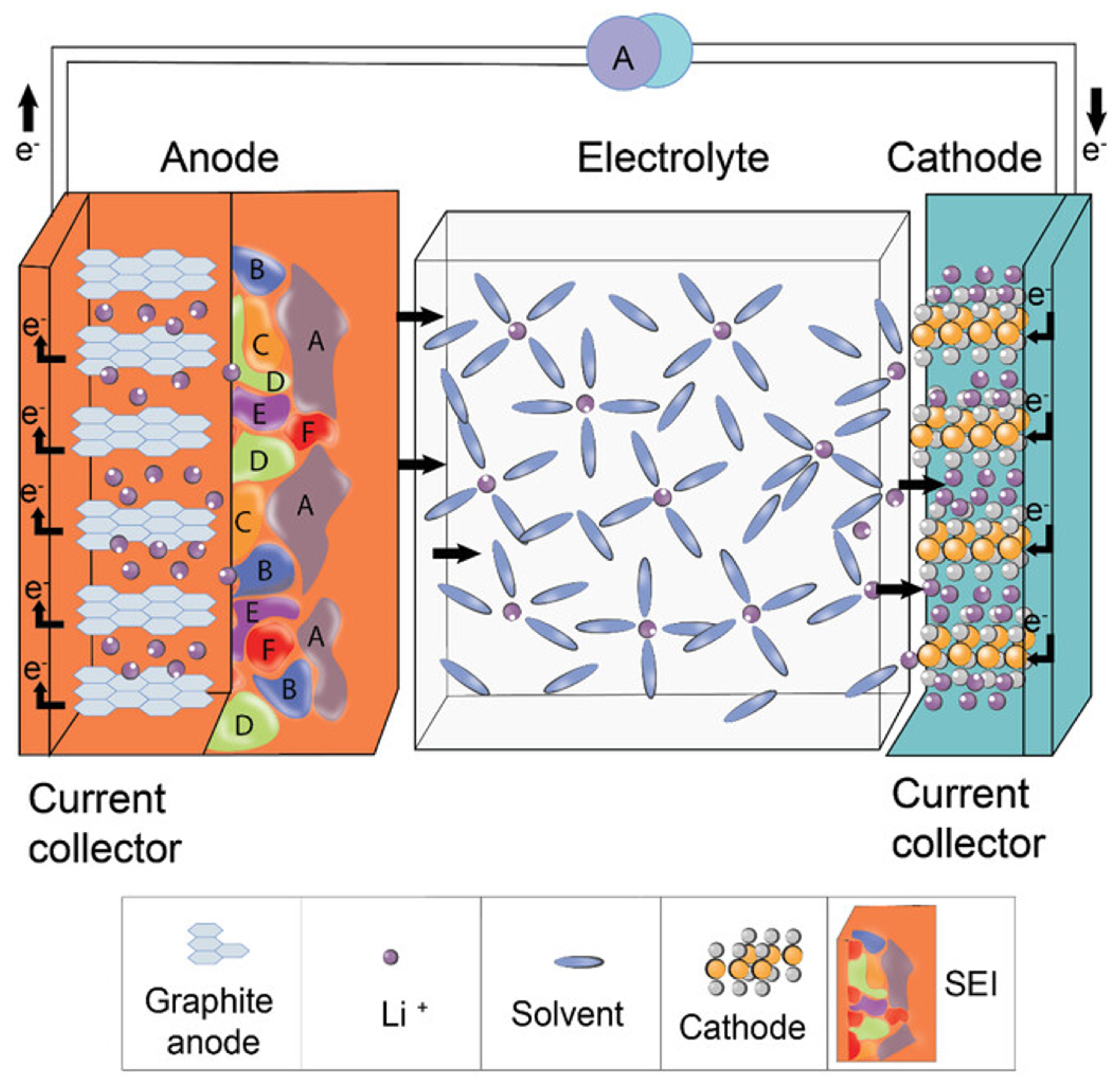
2.2. Irreversible Expansion
2.2.1. Solid-Electrolyte-Interface Layer
2.2.2. Lithium Plating
2.2.3. Gas Generation
3. Measurement of Expansion in Lithium-Ion Battery Cells
3.1. Contact Approaches
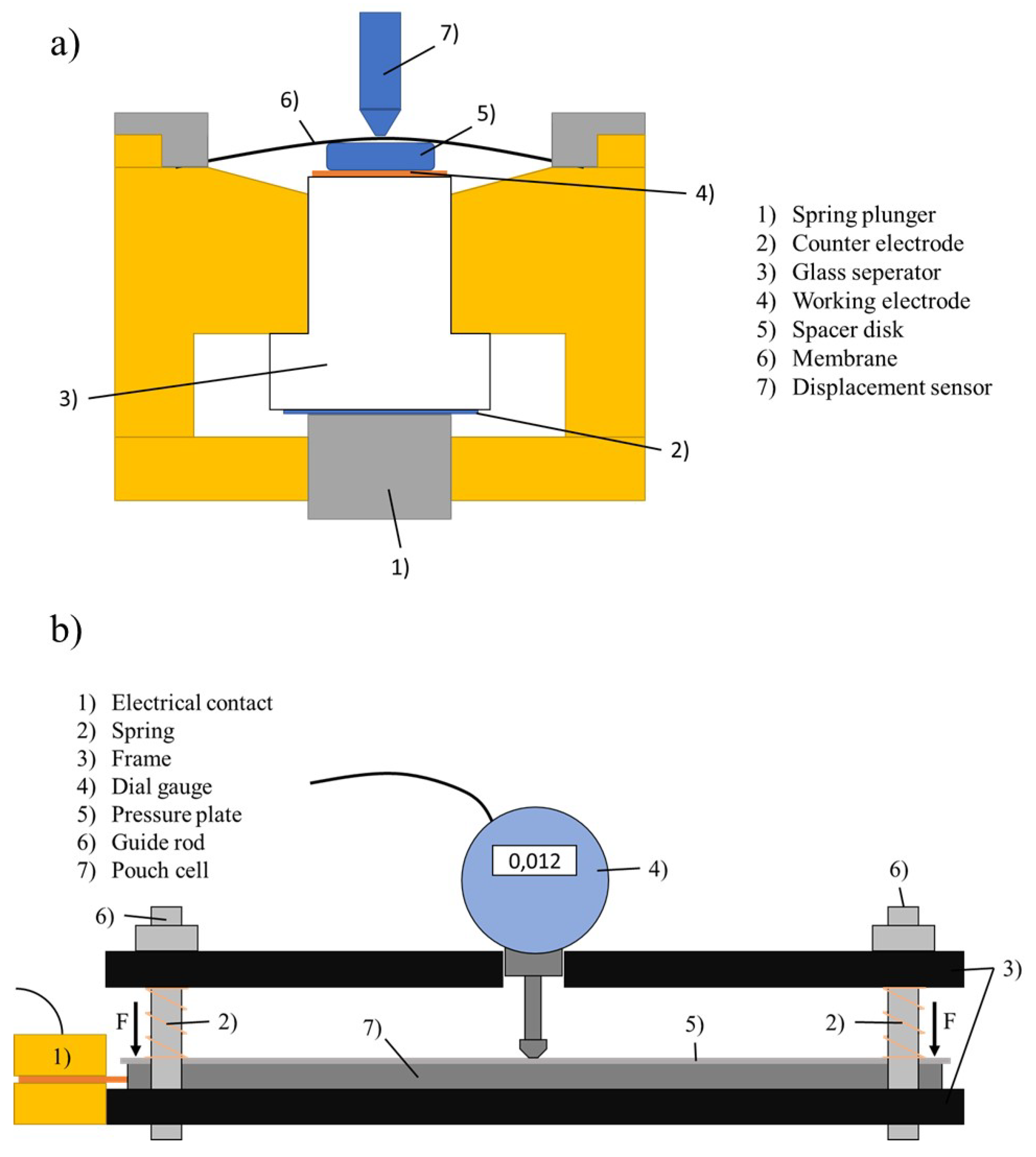
3.1.1. Dilatometer
3.1.2. Buoyancy Measurements
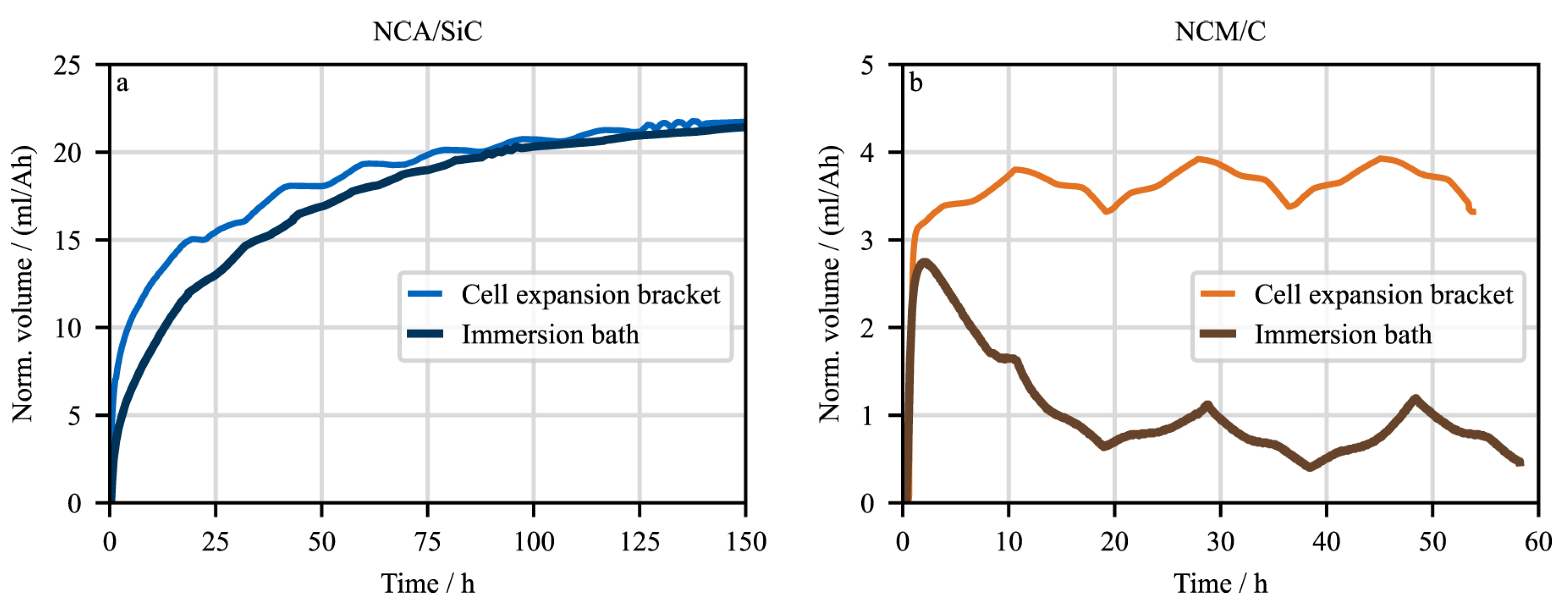
3.1.3. Strain Measurement
Strain Gauges
Optical Fiber Sensors
3.2. Non-Contact Approaches
3.2.1. Radiological Imaging
X-ray Imaging
Neutron Imaging
3.2.2. Optical Imaging
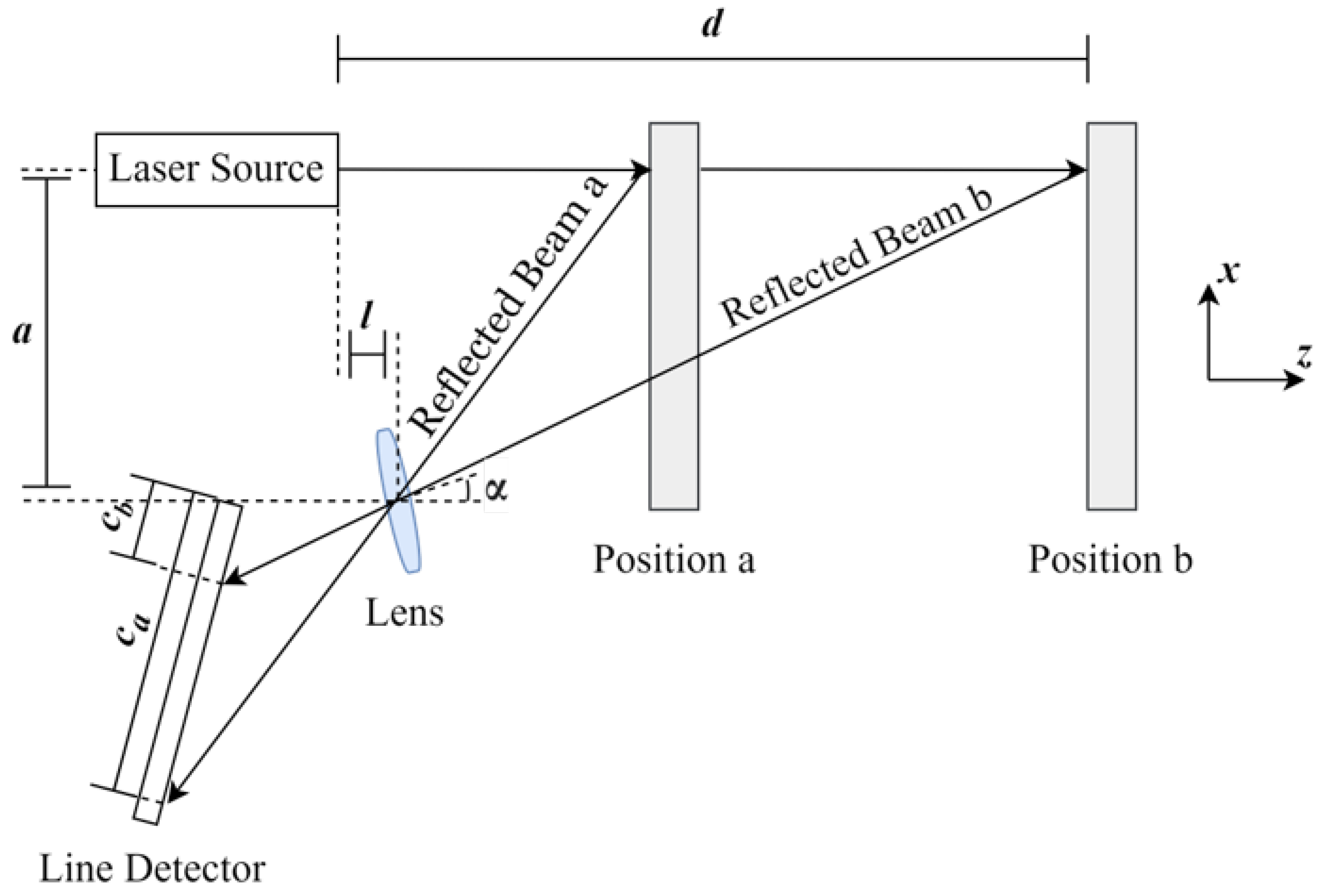
Laser Triangulation
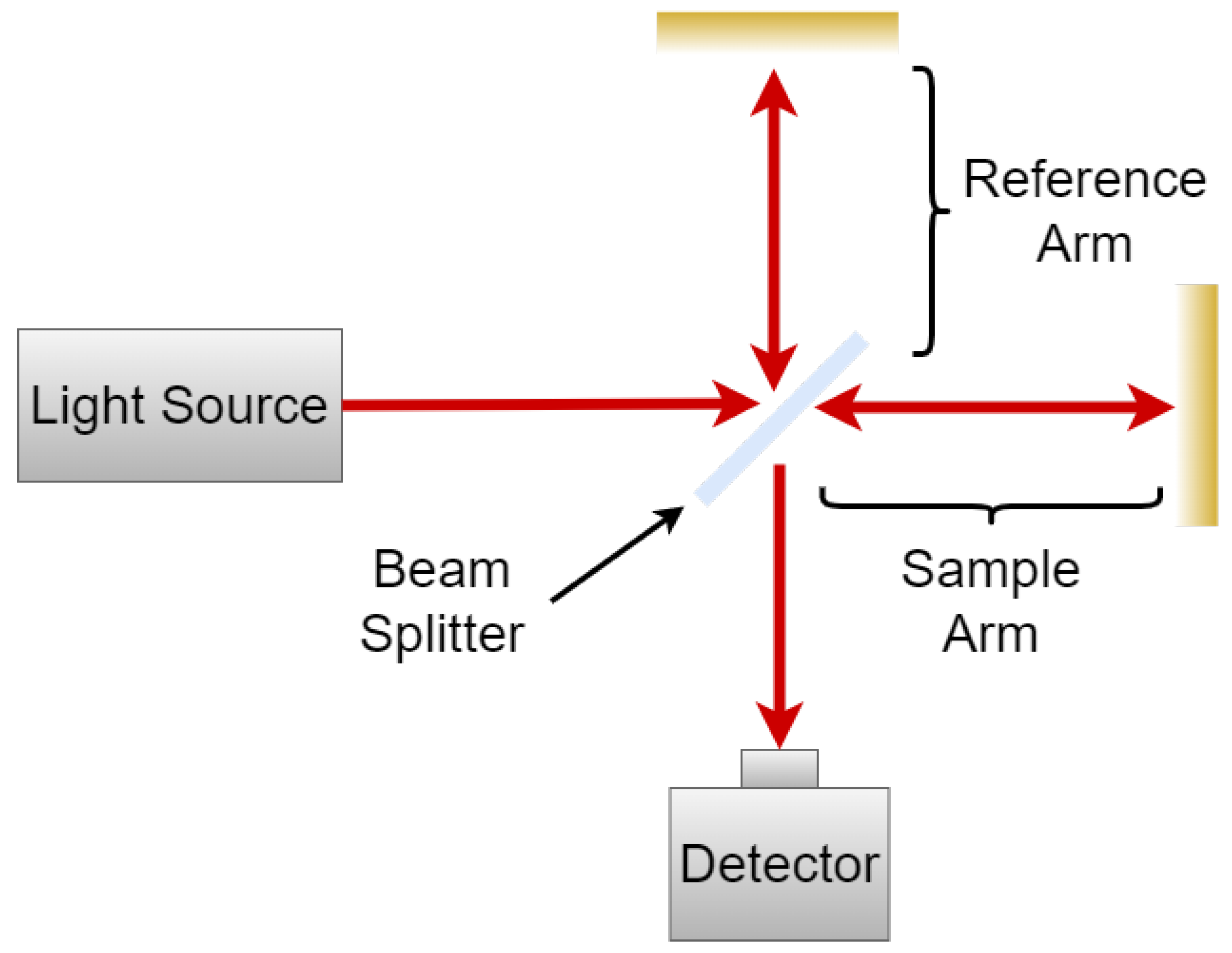
Interferometric Measurements
Structured Light
Digital Image Correlation
4. Comparison of Techniques
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Geels, F.W. Disruption and low-carbon system transformation: Progress and new challenges in socio-technical transitions research and the Multi-Level Perspective. Energy Research & Social Science 2018, 37, 224–231. [Google Scholar] [CrossRef]
- Budde-Meiwes, H.; Drillkens, J.; Lunz, B.; Muennix, J.; Rothgang, S.; Kowal, J.; Sauer, D.U. A review of current automotive battery technology and future prospects. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering 2013, 227, 761–776. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, R.; Wang, J.; Wang, Y. Current and future lithium-ion battery manufacturing. iScience 2021, 24, 102332. [Google Scholar] [CrossRef]
- Ren, D.; Xie, L.; Wang, L.; He, X. A practical approach to predict volume deformation of lithium–ion batteries from crystal structure changes of electrode materials. Int J Energy Res 2021, 45, 7732–7740. [Google Scholar] [CrossRef]
- Siegel, J.B.; Stefanopoulou, A.G.; Hagans, P.; Ding, Y.; Gorsich, D. Expansion of Lithium Ion Pouch Cell Batteries: Observations from Neutron Imaging. J. Electrochem. Soc. 2013, 160, A1031–A1038. [Google Scholar] [CrossRef]
- Heubner, C.; Schneider, M.; Michaelis, A. Detailed study of heat generation in porous LiCoO2 electrodes. J. Power Sources 2016, 307, 199–207. [Google Scholar] [CrossRef]
- Liu, X.M.; Arnold, C.B. Effects of Cycling Ranges on Stress and Capacity Fade in Lithium-Ion Pouch Cells. J. Electrochem. Soc. 2016, 163, A2501–A2507. [Google Scholar] [CrossRef]
- Sturm, J.; Spingler, F.B.; Rieger, B.; Rheinfeld, A.; Jossen, A. Non-Destructive Detection of Local Aging in Lithium-Ion Pouch Cells by Multi-Directional Laser Scanning. J. Electrochem. Soc. 2017, 164, A1342–A1351. [Google Scholar] [CrossRef]
- Bernhard, R.; Metzger, M.; Gasteiger, H.A. Gas Evolution at Graphite Anodes Depending on Electrolyte Water Content and SEI Quality Studied by On-Line Electrochemical Mass Spectrometry. J. Electrochem. Soc. 2015, 162, A1984–A1989. [Google Scholar] [CrossRef]
- Deich, T.; Storch, M.; Steiner, K.; Bund, A. Effects of module stiffness and initial compression on lithium-ion cell aging Deich 2021 // Effects of module stiffness and initial compression on lithium-ion cell aging. J. Power Sources 2021, 506, 230163. [Google Scholar] [CrossRef]
- Deich, T.; Hahn, S.L.; Both, S.; Birke, K.P.; Bund, A. Validation of an actively-controlled pneumatic press to simulate automotive module stiffness for mechanically representative lithium-ion cell aging. J Energy Storage 2020, 28, 101192. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Sheldon, B.W. Deformation and stress in electrode materials for Li-ion batteries. Prog. Mater. Sci. 2014, 63, 58–116. [Google Scholar] [CrossRef]
- Nazari, P.; Bäuerle, R.; Zimmermann, J.; Melzer, C.; Schwab, C.; Smith, A.; Kowalsky, W.; Aghassi-Hagmann, J.; Hernandez-Sosa, G.; Lemmer, U. Piezoresistive Free-standing Microfiber Strain Sensor for High-resolution Battery Thickness Monitoring. Adv. Mater. 2023, 35, e2212189. [Google Scholar] [CrossRef]
- Pfrang, A.; Kersys, A.; Kriston, A.; Scurtu, R.G.; Marinaro, M.; Wohlfahrt-Mehrens, M. Deformation from Formation Until End of Life: Micro X-ray Computed Tomography of Silicon Alloy Containing 18650 Li-Ion Cells. J. Electrochem. Soc. 2023, 170, 030548. [Google Scholar] [CrossRef]
- Piątek, J.; Afyon, S.; Budnyak, T.M.; Budnyk, S.; Sipponen, M.H.; Slabon, A. Sustainable Li–Ion Batteries: Chemistry and Recycling. Adv. Energy Mater. 2021, 11. [Google Scholar] [CrossRef]
- Adenusi, H.; Chass, G.A.; Passerini, S.; Tian, K.V.; Chen, G. Lithium Batteries and the Solid Electrolyte Interphase (SEI)—Progress and Outlook. Adv. Energy Mater. 2023, 13, 2203307. [Google Scholar] [CrossRef]
- Placke, T.; Kloepsch, R.; Dühnen, S.; Winter, M. Lithium ion, lithium metal, and alternative rechargeable battery technologies: the odyssey for high energy density. J Solid State Electrochem 2017, 21, 1939–1964. [Google Scholar] [CrossRef]
- Das, D.; Manna, S.; Puravankara, S. Electrolytes, Additives and Binders for NMC Cathodes in Li-Ion Batteries—A Review. Batteries 2023, 9, 193. [Google Scholar] [CrossRef]
- Graae, K.V.; Li, X.; Sørensen, D.R.; Ayerbe, E.; Boyano, I.; Sheptyakov, D.; Jørgensen, M.R.V.; Norby, P. Time and space resolved operando synchrotron X-ray and Neutron diffraction study of NMC811/Si–Gr 5 Ah pouch cells. J. Power Sources 2023, 570, 232993. [Google Scholar] [CrossRef]
- Bauer, M.; Wachtler, M.; Stöwe, H.; Persson, J.V.; Danzer, M.A. Understanding the dilation and dilation relaxation behavior of graphite-based lithium-ion cells. J. Power Sources 2016, 317, 93–102. [Google Scholar] [CrossRef]
- Gantenbein, S.; Schönleber, M.; Weiss, M.; Ivers-Tiffée, E. Capacity Fade in Lithium-Ion Batteries and Cyclic Aging over Various State-of-Charge Ranges. Sustainability 2019, 11, 6697. [Google Scholar] [CrossRef]
- Sethuraman, V.A.; Hardwick, L.J.; Srinivasan, V.; Kostecki, R. Surface structural disordering in graphite upon lithium intercalation/deintercalation. J. Power Sources 2010, 195, 3655–3660. [Google Scholar] [CrossRef]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Birkenmaier, C.; Bitzer, B.; Harzheim, M.; Hintennach, A.; Schleid, T. Lithium Plating on Graphite Negative Electrodes: Innovative Qualitative and Quantitative Investigation Methods. J. Electrochem. Soc. 2015, 162, A2646–A2650. [Google Scholar] [CrossRef]
- Mercer, M.P.; Peng, C.; Soares, C.; Hoster, H.E.; Kramer, D. Voltage hysteresis during lithiation/delithiation of graphite associated with meta-stable carbon stackings. J. Mater. Chem. A 2021, 9, 492–504. [Google Scholar] [CrossRef]
- Clerici, D.; Mocera, F.; Somà, A. Experimental Characterization of Lithium-Ion Cell Strain Using Laser Sensors. Energies 2021, 14, 6281. [Google Scholar] [CrossRef]
- Asenbauer, J.; Eisenmann, T.; Kuenzel, M.; Kazzazi, A.; Chen, Z.; Bresser, D. The success story of graphite as a lithium-ion anode material – fundamentals, remaining challenges, and recent developments including silicon (oxide) composites. Sustainable Energy & Fuels 2020, 4, 5387–5416. [Google Scholar] [CrossRef]
- Ghosh, A.; Ghamouss, F. Role of Electrolytes in the Stability and Safety of Lithium Titanate-Based Batteries. Front. Mater. 2020, 7. [Google Scholar] [CrossRef]
- Lv, W.; Gu, J.; Niu, Y.; Wen, K.; He, W. Review—Gassing Mechanism and Suppressing Solutions in Li 4 Ti 5 O 12 -Based Lithium-Ion Batteries. J. Electrochem. Soc. 2017, 164, A2213–A2224. [Google Scholar] [CrossRef]
- Han, C.; He, Y.B.; Liu, M.; Li, B.; Yang, Q.H.; Wong, C.P.; Kang, F. A review of gassing behavior in Li 4 Ti 5 O 12 -based lithium ion batteries. J. Mater. Chem. A 2017, 5, 6368–6381. [Google Scholar] [CrossRef]
- He, Y.B.; Li, B.; Liu, M.; Zhang, C.; Lv, W.; Yang, C.; Li, J.; Du, H.; Zhang, B.; Yang, Q.H.; Kim, J.K.; Kang, F. Gassing in Li(4)Ti(5)O(12)-based batteries and its remedy. Sci Rep 2012, 2, 913. [Google Scholar] [CrossRef] [PubMed]
- Sauerteig, D.; Ivanov, S.; Reinshagen, H.; Bund, A. Reversible and irreversible dilation of lithium-ion battery electrodes investigated by in-situ dilatometry. J. Power Sources 2017, 342, 939–946. [Google Scholar] [CrossRef]
- Nemeth, T.; Schröer, P.; Kuipers, M.; Sauer, D.U. Lithium titanate oxide battery cells for high-power automotive applications – Electro-thermal properties, aging behavior and cost considerations. J Energy Storage 2020, 31, 101656. [Google Scholar] [CrossRef]
- Song, T.; Jeon, Y.; Paik, U. Si nanotubes array sheathed with SiN/SiOxNy layer as an anode material for lithium ion batteries. Journal of Electroceramics 2014, 32, 66–71. [Google Scholar] [CrossRef]
- Zhang, X.; Weng, J.; Ye, C.; Liu, M.; Wang, C.; Wu, S.; Tong, Q.; Zhu, M.; Gao, F. Strategies for Controlling or Releasing the Influence Due to the Volume Expansion of Silicon inside Si-C Composite Anode for High-Performance Lithium-Ion Batteries. Materials 2022, 15. [Google Scholar] [CrossRef] [PubMed]
- Shen, T.; Yao, Z.; Xia, X.; Wang, X.; Gu, C.; Tu, J. Rationally Designed Silicon Nanostructures as Anode Material for Lithium–Ion Batteries. Adv Eng Mater 2018, 20. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Pan, D. Solutions for the problems of silicon-carbon anode materials for lithium-ion batteries. R. Soc. open sci. 2018, 5, 172370. [Google Scholar] [CrossRef] [PubMed]
- Zuo, X.; Zhu, J.; Müller-Buschbaum, P.; Cheng, Y.J. Silicon based lithium-ion battery anodes: A chronicle perspective review. Nano Energy 2017, 31, 113–143. [Google Scholar] [CrossRef]
- Zhao, X.; Lehto, V.P. Challenges and prospects of nanosized silicon anodes in lithium-ion batteries. Nanotechnology 2021, 32, 042002. [Google Scholar] [CrossRef]
- Dou, F.; Weng, Y.; Wang, Q.; Chen, G.; Liu, H.; Shi, L.; Zhang, D. In situ imaging analysis of the inhibition effect of functional coating on the volume expansion of silicon anodes. Chemical Engineering Journal 2021, 417, 128122. [Google Scholar] [CrossRef]
- Luo, W.; Chen, X.; Xia, Y.; Chen, M.; Wang, L.; Wang, Q.; Li, W.; Yang, J. Surface and Interface Engineering of Silicon–Based Anode Materials for Lithium–Ion Batteries. Advanced Energy Materials 2017, 7. [Google Scholar] [CrossRef]
- Popp, H.; Koller, M.; Jahn, M.; Bergmann, A. Mechanical methods for state determination of Lithium-Ion secondary batteries: A review. J Energy Storage 2020, 32, 101859. [Google Scholar] [CrossRef]
- Noerochim, L.; Suwarno, S.; Idris, N.H.; Dipojono, H.K. Recent Development of Nickel-Rich and Cobalt-Free Cathode Materials for Lithium-Ion Batteries. Batteries 2021, 7, 84. [Google Scholar] [CrossRef]
- Rieger, B.; Schlueter, S.; Erhard, S.V.; Jossen, A. Strain Propagation in Lithium-Ion Batteries from the Crystal Structure to the Electrode Level. J. Electrochem. Soc. 2016, 163, A1595–A1606. [Google Scholar] [CrossRef]
- Li, L.; Luo, C.; Zou, J.; Ran, Q.; Chen, P.; Wang, X.; Zhao, Y.; Wang, L.; Zheng, J.; Niu, X. Prelithiated FeS2 cathode with alleviated volume expansion toward improved cycling performance. Solid State Ionics 2021, 368, 115696. [Google Scholar] [CrossRef]
- Mao, C.; An, S.J.; Meyer, H.M.; Li, J.; Wood, M.; Ruther, R.E.; Wood, D.L. Balancing formation time and electrochemical performance of high energy lithium-ion batteries. J. Power Sources 2018, 402, 107–115. [Google Scholar] [CrossRef]
- Hemmerling, J.; Guhathakurta, J.; Dettinger, F.; Fill, A.; Birke, K.P. Non-Uniform Circumferential Expansion of Cylindrical Li-Ion Cells—The Potato Effect. Batteries 2021, 7, 61. [Google Scholar] [CrossRef]
- Zhang, X.; He, J.; Zhou, J.; Chen, H.; Song, W.; Fang, D. Thickness evolution of commercial Li-ion pouch cells with silicon-based composite anodes and NCA cathodes. Sci. China Technol. Sci. 2021, 64, 83–90. [Google Scholar] [CrossRef]
- Li, T.; Yuan, X.Z.; Zhang, L.; Song, D.; Shi, K.; Bock, C. Degradation Mechanisms and Mitigation Strategies of Nickel-Rich NMC-Based Lithium-Ion Batteries. Electrochem. Energ. Rev. 2020, 3, 43–80. [Google Scholar] [CrossRef]
- Zhang, G.; Li, M.; Ye, Z.; Chen, T.; Cao, J.; Yang, H.; Ma, C.; Jia, Z.; Xie, J.; Cui, N.; Xiong, Y. Lithium Iron Phosphate and Layered Transition Metal Oxide Cathode for Power Batteries: Attenuation Mechanisms and Modification Strategies. Materials 2023, 16. [Google Scholar] [CrossRef] [PubMed]
- Mei, W.; Duan, Q.; Lu, W.; Sun, J.; Wang, Q. An investigation on expansion behavior of lithium ion battery based on the thermal-mechanical coupling model. J Clean Prod 2020, 274, 122643. [Google Scholar] [CrossRef]
- Vorwerk, P.; Hahn, S.K.; Daniel, C.; Krause, U.; Keutel, K. Detection of Critical Conditions in Pouch Cells Based on Their Expansion Behavior. Batteries 2022, 8, 42. [Google Scholar] [CrossRef]
- Oh, K.Y.; Epureanu, B.I. A novel thermal swelling model for a rechargeable lithium-ion battery cell. J. Power Sources 2016, 303, 86–96. [Google Scholar] [CrossRef]
- Liu, G.; Ouyang, M.; Lu, L.; Li, J.; Han, X. Analysis of the heat generation of lithium-ion battery during charging and discharging considering different influencing factors. J Therm Anal Calorim 2014, 116, 1001–1010. [Google Scholar] [CrossRef]
- Piłatowicz, G.; Marongiu, A.; Drillkens, J.; Sinhuber, P.; Sauer, D.U. A critical overview of definitions and determination techniques of the internal resistance using lithium-ion, lead-acid, nickel metal-hydride batteries and electrochemical double-layer capacitors as examples. J. Power Sources 2015, 296, 365–376. [Google Scholar] [CrossRef]
- Yoo, K.; Kim, J. Thermal behavior of full-scale battery pack based on comprehensive heat-generation model. J. Power Sources 2019, 433, 226715. [Google Scholar] [CrossRef]
- Zhai, Q.; Xu, X.; Kong, J.; Liu, M.; Xu, P.; Heidarshenas, B.; Wang, Q.; Zhou, F.; Wei, H. 3D Simulation Study on Thermal Behavior and Thermal Stress of Lithium–Ion Battery. Energy Tech 2023, 11. [Google Scholar] [CrossRef]
- Mei, W.; Chen, H.; Sun, J.; Wang, Q. Numerical study on tab dimension optimization of lithium-ion battery from the thermal safety perspective. Appl. Therm. Eng. 2018, 142, 148–165. [Google Scholar] [CrossRef]
- Wang, S. Entropy and heat generation of lithium cells/batteries. Chinese Physics B 2016, 25, 010509. [Google Scholar] [CrossRef]
- Bree, G.; Hao, H.; Stoeva, Z.; John Low, C.T. Monitoring state of charge and volume expansion in lithium-ion batteries: an approach using surface mounted thin-film graphene sensors. RSC advances 2023, 13, 7045–7054. [Google Scholar] [CrossRef] [PubMed]
- McBrayer, J.D.; Apblett, C.A.; Harrison, K.L.; Fenton, K.R.; Minteer, S.D. Mechanical studies of the solid electrolyte interphase on anodes in lithium and lithium ion batteries. Nanotechnology 2021, 32, 502005. [Google Scholar] [CrossRef] [PubMed]
- Jankowski, P.; Wieczorek, W.; Johansson, P. SEI-forming electrolyte additives for lithium-ion batteries: development and benchmarking of computational approaches. J Mol Model 2017, 23, 6. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, Y.; Sun, H.; Yuan, T.; Gong, Y.; Liu, X.; Chen, T. Impact of Surface Structure on SEI for Carbon Materials in Alkali Ion Batteries: A Review. Batteries 2023, 9, 226. [Google Scholar] [CrossRef]
- Zhu, T.; Hu, Q.; Yan, G.; Wang, J.; Wang, Z.; Guo, H.; Li, X.; Peng, W. Manipulating the Composition and Structure of Solid Electrolyte Interphase at Graphite Anode by Adjusting the Formation Condition. Energy Tech 2019, 7, 1900273. [Google Scholar] [CrossRef]
- Schomburg, F.; Drees, R.; Kurrat, M.; Danzer, M.A.; Röder, F. Characterization of the Solid–Electrolyte Interphase Growth During Cell Formation Based on Differential Voltage Analysis. Energy Tech 2023, 11. [Google Scholar] [CrossRef]
- Peled, E.; Menkin, S. Review—SEI: Past, Present and Future. J. Electrochem. Soc. 2017, 164, A1703–A1719. [Google Scholar] [CrossRef]
- Louli, A.J.; Ellis, L.D.; Dahn, J.R. Operando Pressure Measurements Reveal Solid Electrolyte Interphase Growth to Rank Li-Ion Cell Performance. Joule 2019, 3, 745–761. [Google Scholar] [CrossRef]
- Pinson, M.B.; Bazant, M.Z. Theory of SEI Formation in Rechargeable Batteries: Capacity Fade, Accelerated Aging and Lifetime Prediction. J. Electrochem. Soc. 2013, 160, A243–A250. [Google Scholar] [CrossRef]
- Bitzer, B.; Gruhle, A. A new method for detecting lithium plating by measuring the cell thickness. J. Power Sources 2014, 262, 297–302. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. The Effects of Defects on Localized Plating in Lithium-Ion Batteries. J. Electrochem. Soc. 2015, 162, A1365–A1373. [Google Scholar] [CrossRef]
- Janakiraman, U.; Garrick, T.R.; Fortier, M.E. Review—Lithium Plating Detection Methods in Li-Ion Batteries. J. Electrochem. Soc. 2020, 167, 160552. [Google Scholar] [CrossRef]
- Lin, X.; Khosravinia, K.; Hu, X.; Li, J.; Lu, W. Lithium Plating Mechanism, Detection, and Mitigation in Lithium-Ion Batteries. Prog Energy Combust Sci. 2021, 87, 100953. [Google Scholar] [CrossRef]
- Waldmann, T.; Hogg, B.I.; Wohlfahrt-Mehrens, M. Li plating as unwanted side reaction in commercial Li-ion cells – A review. J. Power Sources 2018, 384, 107–124. [Google Scholar] [CrossRef]
- Münster, P.; Diehl, M.; Frerichs, J.E.; Börner, M.; Hansen, M.R.; Winter, M.; Niehoff, P. Effect of Li plating during formation of lithium ion batteries on their cycling performance and thermal safety. J. Power Sources 2021, 484, 229306. [Google Scholar] [CrossRef]
- Rowden, B.; Garcia-Araez, N. A review of gas evolution in lithium ion batteries. Energy Reports 2020, 6, 10–18. [Google Scholar] [CrossRef]
- James, J.D.; Spittle, J.A.; Brown, S.G.R.; Evans, R.W. A review of measurement techniques for the thermal expansion coefficient of metals and alloys at elevated temperatures. Meas. Sci. Technol. 2001, 12, R1–R15. [Google Scholar] [CrossRef]
- Michael, H.; Jervis, R.; Brett, D.J.L.; Shearing, P.R. Developments in Dilatometry for Characterisation of Electrochemical Devices. Batteries & Supercaps 2021, 4, 1378–1396. [Google Scholar] [CrossRef]
- Moyassari, E.; Roth, T.; Kücher, S.; Chang, C.C.; Hou, S.C.; Spingler, F.B.; Jossen, A. The Role of Silicon in Silicon-Graphite Composite Electrodes Regarding Specific Capacity, Cycle Stability, and Expansion. J. Electrochem. Soc. 2022, 169, 010504. [Google Scholar] [CrossRef]
- Biberacher, W.; Lerf, A.; Besenhard, J.O.; Möhwald, H.; Butz, T. A high resolution dilatometer for in situ studies of the electrointercalation of layered materials. Materials Research Bulletin 1982, 17, 1385–1392. [Google Scholar] [CrossRef]
- Huesker, J.; Froböse, L.; Kwade, A.; Winter, M.; Placke, T. In Situ Dilatometric Study of the Binder Influence on the Electrochemical Intercalation of Bis(trifluoromethanesulfonyl) imide Anions into Graphite. Electrochimica Acta 2017, 257, 423–435. [Google Scholar] [CrossRef]
- Bazlen, S.; Heugel, P.; von Kessel, O.; Commerell, W.; Tübke, J. Influence of charging protocols on the charging capability and aging of lithium-ion cells with silicon-containing anodes. Journal of Energy Storage 2022, 49, 104044. [Google Scholar] [CrossRef]
- Rieger, B.; Schlueter, S.; Erhard, S.V.; Schmalz, J.; Reinhart, G.; Jossen, A. Multi-scale investigation of thickness changes in a commercial pouch type lithium-ion battery. J. Energy Storage 2016, 6, 213–221. [Google Scholar] [CrossRef]
- Göttlinger, M.; Daubinger, P.; Stracke, W.; Hartmann, S.; Giffin, G.A. Influence of external pressure on silicon electrodes in lithium-ion cells. Electrochimica Acta 2022, 419, 140354. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Stress evolution and capacity fade in constrained lithium-ion pouch cells. J. Power Sources 2014, 245, 745–751. [Google Scholar] [CrossRef]
- Oh, K.Y.; Epureanu, B.I.; Siegel, J.B.; Stefanopoulou, A.G. Phenomenological force and swelling models for rechargeable lithium-ion battery cells. J. Power Sources 2016, 310, 118–129. [Google Scholar] [CrossRef]
- Chae, S.; Ko, M.; Kim, K.; Ahn, K.; Cho, J. Confronting Issues of the Practical Implementation of Si Anode in High-Energy Lithium-Ion Batteries. Joule 2017, 1, 47–60. [Google Scholar] [CrossRef]
- Grimsmann, F.; Brauchle, F.; Gerbert, T.; Gruhle, A.; Knipper, M.; Parisi, J. Hysteresis and current dependence of the thickness change of lithium-ion cells with graphite anode. J Energy Storage 2017, 12, 132–137. [Google Scholar] [CrossRef]
- Jahn, L.; Katzer, F.; Danzer, M.A. Combined dilatometry and voltage analysis for a reliable detection of lithium deposition on graphitic anodes. J. Power Sources 2022, 520, 230870. [Google Scholar] [CrossRef]
- Michelini, E.; Höschele, P.; Heindl, S.F.; Erker, S.; Ellersdorfer, C. Experimental Investigation on Reversible Swelling Mechanisms of Lithium-Ion Batteries under a Varying Preload Force. Batteries 2023, 9, 218. [Google Scholar] [CrossRef]
- Mohtat, P.; Lee, S.; Siegel, J.B.; Stefanopoulou, A.G. Towards better estimability of electrode-specific state of health: Decoding the cell expansion. J. Power Sources 2019, 427, 101–111. [Google Scholar] [CrossRef]
- Müller, V.; Scurtu, R.G.; Richter, K.; Waldmann, T.; Memm, M.; Danzer, M.A.; Wohlfahrt-Mehrens, M. Effects of Mechanical Compression on the Aging and the Expansion Behavior of Si/C-Composite|NMC811 in Different Lithium-Ion Battery Cell Formats. J. Electrochem. Soc. 2019, 166, A3796–A3805. [Google Scholar] [CrossRef]
- Nagayama, M.; Ariyoshi, K.; Yamamoto, Y.; Ohzuku, T. Characterization of Lithium Insertion Electrodes by Precision Dilatometer: Area-Specific Deformation of Single Electrode. J. Electrochem. Soc. 2014, 161, A1388–A1393. [Google Scholar] [CrossRef]
- Sauerteig, D.; Hanselmann, N.; Arzberger, A.; Reinshagen, H.; Ivanov, S.; Bund, A. Electrochemical-mechanical coupled modeling and parameterization of swelling and ionic transport in lithium-ion batteries. J. Power Sources 2018, 378, 235–247. [Google Scholar] [CrossRef]
- Schmider, D.; Bessler, W.G. Thermo-Electro-Mechanical Modeling and Experimental Validation of Thickness Change of a Lithium-Ion Pouch Cell with Blend Positive Electrode. Batteries 2023, 9, 354. [Google Scholar] [CrossRef]
- Stock, S.; Diller, F.; Böhm, J.; Hille, L.; Hagemeister, J.; Sommer, A.; Daub, R. Operando Analysis of the Gassing and Swelling Behavior of Lithium-ion Pouch Cells during Formation. J. Electrochem. Soc. 2023, 170, 060539. [Google Scholar] [CrossRef]
- Grimsmann, F.; Gerbert, T.; Brauchle, F.; Gruhle, A.; Parisi, J.; Knipper, M. Determining the maximum charging currents of lithium-ion cells for small charge quantities. J. Power Sources 2017, 365, 12–16. [Google Scholar] [CrossRef]
- Waluś, S.; Offer, G.; Hunt, I.; Patel, Y.; Stockley, T.; Williams, J.; Purkayastha, R. Volumetric expansion of Lithium-Sulfur cell during operation – Fundamental insight into applicable characteristics. Energy Stor. Mater. 2018, 10, 233–245. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, H.M.; Ahn, S. Battery dimensional changes occurring during charge/discharge cycles—thin rectangular lithium ion and polymer cells. J. Power Sources 2003, 119-121, 833–837. [Google Scholar] [CrossRef]
- Louli, A.J.; Li, J.; Trussler, S.; Fell, C.R.; Dahn, J.R. Volume, Pressure and Thickness Evolution of Li-Ion Pouch Cells with Silicon-Composite Negative Electrodes. J. Electrochem. Soc. 2017, 164, A2689–A2696. [Google Scholar] [CrossRef]
- Berckmans, G.; de Sutter, L.; Marinaro, M.; Smekens, J.; Jaguemont, J.; Wohlfahrt-Mehrens, M.; van Mierlo, J.; Omar, N. Analysis of the effect of applying external mechanical pressure on next generation silicon alloy lithium-ion cells. Electrochimica Acta 2019, 306, 387–395. [Google Scholar] [CrossRef]
- Yoon, D.h.; Marinaro, M.; Axmann, P.; Wohlfahrt-Mehrens, M. Communication—Quantitative Analysis of Consumption of Fluoroethylene Carbonate Additives on Silicon Alloy Anodes. J. Electrochem. Soc. 2018, 165, A2467–A2469. [Google Scholar] [CrossRef]
- Marinaro, M.; Yoon, D.h.; Gabrielli, G.; Stegmaier, P.; Figgemeier, E.; Spurk, P.C.; Nelis, D.; Schmidt, G.; Chauveau, J.; Axmann, P.; Wohlfahrt-Mehrens, M. High performance 1.2 Ah Si-alloy/Graphite|LiNi 0.5 Mn 0.3 Co 0.2 O 2 prototype Li-ion battery. J. Power Sources 2017, 357, 188–197. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Li, D.; Hu, J.; Xu, J.; Dang, D.; Xiao, X.; Cheng, Y.T. Mechanical Property Evolution of Silicon Composite Electrodes Studied by Environmental Nanoindentation. Advanced Energy Materials 2018, 8. [Google Scholar] [CrossRef]
- Li, J.Y.; Xu, Q.; Li, G.; Yin, Y.X.; Wan, L.J.; Guo, Y.G. Research progress regarding Si-based anode materials towards practical application in high energy density Li-ion batteries. Materials Chemistry Frontiers 2017, 1, 1691–1708. [Google Scholar] [CrossRef]
- Jin, C.; Wang, Y.; Borujerdi, A.S.; Li, J. Stress evolution and thickness change of a lithium-ion pouch cell under various cycling conditions. Journal of Power Sources Advances 2022, 16, 100103. [Google Scholar] [CrossRef]
- Grimsmann, F.; Brauchle, F.; Gerbert, T.; Gruhle, A.; Parisi, J.; Knipper, M. Impact of different aging mechanisms on the thickness change and the quick-charge capability of lithium-ion cells. J Energy Storage 2017, 14, 158–162. [Google Scholar] [CrossRef]
- Oh, K.Y.; Siegel, J.B.; Secondo, L.; Kim, S.U.; Samad, N.A.; Qin, J.; Anderson, D.; Garikipati, K.; Knobloch, A.; Epureanu, B.I.; Monroe, C.W.; Stefanopoulou, A. Rate dependence of swelling in lithium-ion cells. J. Power Sources 2014, 267, 197–202. [Google Scholar] [CrossRef]
- Aiken, C.P.; Xia, J.; Wang, D.Y.; Stevens, D.A.; Trussler, S.; Dahn, J.R. An Apparatus for the Study of In Situ Gas Evolution in Li-Ion Pouch Cells. J. Electrochem. Soc. 2014, 161, A1548–A1554. [Google Scholar] [CrossRef]
- Leißing, M.; Horsthemke, F.; Wiemers-Meyer, S.; Winter, M.; Niehoff, P.; Nowak, S. The Impact of the C–Rate on Gassing During Formation of NMC622 II Graphite Lithium–Ion Battery Cells. Batteries & Supercaps 2021, 4, 1344–1350. [Google Scholar] [CrossRef]
- Self, J.; Aiken, C.P.; Petibon, R.; Dahn, J.R. Survey of Gas Expansion in Li-Ion NMC Pouch Cells. J. Electrochem. Soc. 2015, 162, A796–A802. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Xiong, D.J.; Petibon, R.; Du, C.Y.; Dahn, J.R. Gas Evolution during Unwanted Lithium Plating in Li-Ion Cells with EC-Based or EC-Free Electrolytes. J. Electrochem. Soc. 2016, 163, A3010–A3015. [Google Scholar] [CrossRef]
- Xiong, D.J.; Petibon, R.; Madec, L.; Hall, D.S.; Dahn, J.R. Some Effects of Intentionally Added Water on LiCoO 2 /Graphite Pouch Cells. J. Electrochem. Soc. 2016, 163, A1678–A1685. [Google Scholar] [CrossRef]
- Ellis, L.D.; Allen, J.P.; Thompson, L.M.; Harlow, J.E.; Stone, W.J.; Hill, I.G.; Dahn, J.R. Quantifying, Understanding and Evaluating the Effects of Gas Consumption in Lithium-Ion Cells. J. Electrochem. Soc. 2017, 164, A3518–A3528. [Google Scholar] [CrossRef]
- Krause, L.J.; Chevrier, V.L.; Jensen, L.D.; Brandt, T. The Effect of Carbon Dioxide on the Cycle Life and Electrolyte Stability of Li-Ion Full Cells Containing Silicon Alloy. J. Electrochem. Soc. 2017, 164, A2527–A2533. [Google Scholar] [CrossRef]
- Milien, M.S.; Hoffmann, J.; Payne, M.; Lucht, B.L. Effect of Electrolyte Additives on Li 4 Ti 5 O 12 Cycling Performance and Gas Evolution. J. Electrochem. Soc. 2018, 165, A3925–A3931. [Google Scholar] [CrossRef]
- Guillot, S.L.; Usrey, M.L.; Peña-Hueso, A.; Kerber, B.M.; Zhou, L.; Du, P.; Johnson, T. Reduced Gassing In Lithium-Ion Batteries With Organosilicon Additives. J. Electrochem. Soc. 2021, 168, 030533. [Google Scholar] [CrossRef]
- Rodrigues, M.T.F.; Trask, S.E.; Shkrob, I.A.; Abraham, D.P. Quantifying gas generation from slurries used in fabrication of Si-containing electrodes for lithium-ion cells. J. Power Sources 2018, 395, 289–294. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, X.; Jia, S.; Jin, Y.; Xu, S.; Chen, J. High precision strain monitoring for lithium ion batteries based on fiber Bragg grating sensors. J. Power Sources 2019, 433, 226692. [Google Scholar] [CrossRef]
- Hickey, R.; Jahns, T.M. Measuring Individual Battery Dimensional Changes for State-of-Charge Estimation using Strain Gauge Sensors. ECCE 2019; IEEE: Piscataway, NJ, 2019; pp. 2460–2465. [Google Scholar] [CrossRef]
- Choi, W.; Seo, Y.; Yoo, K.; Ko, T.J.; Choi, J. Carbon Nanotube-Based Strain Sensor for Excessive Swelling Detection of Lithium-Ion Battery. 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII). IEEE, 2019, pp. 2356–2359. [CrossRef]
- Willenberg, L.K.; Dechent, P.; Fuchs, G.; Sauer, D.U.; Figgemeier, E. High-Precision Monitoring of Volume Change of Commercial Lithium-Ion Batteries by Using Strain Gauges. Sustainability 2020, 12, 557. [Google Scholar] [CrossRef]
- Wahl, M.S.; Spitthoff, L.; Muri, H.I.; Jinasena, A.; Burheim, O.S.; Lamb, J.J. The Importance of Optical Fibres for Internal Temperature Sensing in Lithium-ion Batteries during Operation. Energies 2021, 14, 3617. [Google Scholar] [CrossRef]
- Du, W.; Tao, X.M.; Tam, H.Y.; Choy, C.L. Fundamentals and applications of optical fiber Bragg grating sensors to textile structural composites. Composite Structures 1998, 42, 217–229. [Google Scholar] [CrossRef]
- Helsztynski, J.; Lewandowski, L.; Jasiewicz, W.; Jedrzejewski, K.P. Interferometric fiber Bragg gratings. In Proc. SPIE; Vol. 5576, pp. 37–41. [CrossRef]
- Cheng, X.; Pecht, M. In Situ Stress Measurement Techniques on Li-ion Battery Electrodes: A Review. Energies 2017, 10, 591. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, X.; Jia, S.; Xu, S.; Chen, J. Design of a sensitivity-enhanced FBG strain sensor and its application in state estimation for lithium-ion battery. AOPC 2019: Optical Fiber Sensors and Communication; Zhang, J., Fu, S., Yang, J., Eds.; SPIE: Bellingham, Washington, USA, 2019; Proceedings of SPIE, p. 10. [Google Scholar] [CrossRef]
- Komma, J.; Schwarz, C.; Hofmann, G.; Heinert, D.; Nawrodt, R. Thermo-optic coefficient of silicon at 1550 nm and cryogenic temperatures. Appl. Phys. Lett. 2012, 101, 041905. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. Journal of Lightwave Technology 1997, 15, 1442–1463. [Google Scholar] [CrossRef]
- Novais, S.; Nascimento, M.; Grande, L.; Domingues, M.F.; Antunes, P.; Alberto, N.; Leitão, C.; Oliveira, R.; Koch, S.; Kim, G.T.; Passerini, S.; Pinto, J. Internal and External Temperature Monitoring of a Li-Ion Battery with Fiber Bragg Grating Sensors. Sensors 2016, 16. [Google Scholar] [CrossRef]
- Alcock, K.M.; Grammel, M.; González-Vila, Á.; Binetti, L.; Goh, K.; Alwis, L.S. An accessible method of embedding fibre optic sensors on lithium-ion battery surface for in-situ thermal monitoring. Sensors and Actuators A: Physical 2021, 332, 113061. [Google Scholar] [CrossRef]
- Unterkofler, J.; Glanz, G.; Koller, M.; Klambauer, R.; Bergmann, A. Strain Compensation Methods for Fiber Bragg Grating Temperature Sensors Suitable for Integration into Lithium-Ion Battery Electrolyte. Batteries 2023, 9, 34. [Google Scholar] [CrossRef]
- Nascimento, M.; Ferreira, M.; Pinto, J. Simultaneous Sensing of Temperature and Bi-Directional Strain in a Prismatic Li-Ion Battery. Batteries 2018, 4, 23. [Google Scholar] [CrossRef]
- Yang, G.; Leitão, C.; Li, Y.; Pinto, J.; Jiang, X. Real-time temperature measurement with fiber Bragg sensors in lithium batteries for safety usage. Measurement 2013, 46, 3166–3172. [Google Scholar] [CrossRef]
- Sommer, L.W.; Raghavan, A.; Kiesel, P.; Saha, B.; Schwartz, J.; Lochbaum, A.; Ganguli, A.; Bae, C.J.; Alamgir, M. Monitoring of Intercalation Stages in Lithium-Ion Cells over Charge-Discharge Cycles with Fiber Optic Sensors. J. Electrochem. Soc. 2015, 162, A2664–A2669. [Google Scholar] [CrossRef]
- Rao, Y.J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355–375. [Google Scholar] [CrossRef]
- Sommer, L.W.; Kiesel, P.; Ganguli, A.; Lochbaum, A.; Saha, B.; Schwartz, J.; Bae, C.J.; Alamgir, M.; Raghavan, A. Fast and slow ion diffusion processes in lithium ion pouch cells during cycling observed with fiber optic strain sensors. J. Power Sources 2015, 296, 46–52. [Google Scholar] [CrossRef]
- Meyer, J.; Nedjalkov, A.; Doering, A.; Angelmahr, M.; Schade, W. Fiber optical sensors for enhanced battery safety. Fiber Optic Sensors and Applications XII; Pickrell, G.; Udd, E.; Du, H.H., Eds. SPIE, 2015, SPIE Proceedings, p. 94800Z. [CrossRef]
- Raghavan, A.; Kiesel, P.; Sommer, L.W.; Schwartz, J.; Lochbaum, A.; Hegyi, A.; Schuh, A.; Arakaki, K.; Saha, B.; Ganguli, A.; Kim, K.H.; Kim, C.; Hah, H.J.; Kim, S.; Hwang, G.O.; Chung, G.C.; Choi, B.; Alamgir, M. Embedded fiber-optic sensing for accurate internal monitoring of cell state in advanced battery management systems part 1: Cell embedding method and performance. J. Power Sources 2017, 341, 466–473. [Google Scholar] [CrossRef]
- Bae, C.J.; Manandhar, A.; Kiesel, P.; Raghavan, A. Monitoring the Strain Evolution of Lithium–Ion Battery Electrodes using an Optical Fiber Bragg Grating Sensor. Energy Technol. 2016, 4, 851–855. [Google Scholar] [CrossRef]
- Nascimento, M.; Novais, S.; Ding, M.S.; Ferreira, M.S.; Koch, S.; Passerini, S.; Pinto, J.L. Internal strain and temperature discrimination with optical fiber hybrid sensors in Li-ion batteries. J. Power Sources 2019, 410-411, 1–9. [Google Scholar] [CrossRef]
- Yu, Y.; Vincent, T.; Sansom, J.; Greenwood, D.; Marco, J. Distributed internal thermal monitoring of lithium ion batteries with fibre sensors. J Energy Storage 2022, 50, 104291. [Google Scholar] [CrossRef]
- Ghannoum, A.; Nieva, P. Graphite lithiation and capacity fade monitoring of lithium ion batteries using optical fibers. J Energy Storage 2020, 28, 101233. [Google Scholar] [CrossRef]
- Gardner, C.; Langhammer, E.; Du, W.; Brett, D.J.L.; Shearing, P.R.; Roberts, A.J.; Amietszajew, T. In-Situ Li-Ion Pouch Cell Diagnostics Utilising Plasmonic Based Optical Fibre Sensors. Sensors 2022, 22. [Google Scholar] [CrossRef]
- Bonefacino, J.; Ghashghaie, S.; Zheng, T.; Lin, C.P.; Zheng, W.; Blanquer, L.A.; Huang, J.; Gervillié, C.; Tam, H.Y.; Tarascon, J.M.; Boles, S.T. High-Fidelity Strain and Temperature Measurements of Li-Ion Batteries Using Polymer Optical Fiber Sensors. J. Electrochem. Soc. 2022, 169, 100508. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, Q.; Zheng, Y.; Xu, Y.; Chen, Y.; Ni, J.; Zhao, Y. Recent Progress in Lithium-Ion Battery Safety Monitoring Based on Fiber Bragg Grating Sensors. Sensors 2023, 23. [Google Scholar] [CrossRef]
- Pietsch, P.; Hess, M.; Ludwig, W.; Eller, J.; Wood, V. Combining operando synchrotron X-ray tomographic microscopy and scanning X-ray diffraction to study lithium ion batteries. Scientific reports 2016, 6, 27994. [Google Scholar] [CrossRef]
- Withers, P.J.; Bouman, C.; Carmignato, S.; Cnudde, V.; Grimaldi, D.; Hagen, C.K.; Maire, E.; Manley, M.; Du Plessis, A.; Stock, S.R. X-ray computed tomography. Nature Reviews Methods Primers 2021, 1. [Google Scholar] [CrossRef]
- Maire, E.; Withers, P.J. Quantitative X-ray tomography. International Materials Reviews 2014, 59, 1–43. [Google Scholar] [CrossRef]
- Brunke, O.; Brockdorf, K.; Drews, S.; Müller, B.; Donath, T.; Herzen, J.; Beckmann, F. Comparison between x-ray tube-based and synchrotron radiation-based mCT. Developments in X-Ray Tomography VI; Stock, S.R., Ed. SPIE, 2008, SPIE Proceedings, p. 70780U. [CrossRef]
- Brant, W.R.; Schmid, S.; Du, G.; Gu, Q.; Sharma, N. A simple electrochemical cell for in-situ fundamental structural analysis using synchrotron X-ray powder diffraction. Journal of Power Sources 2013, 244, 109–114. [Google Scholar] [CrossRef]
- Su, L.; Choi, P.; Parimalam, B.S.; Litster, S.; Reeja-Jayan, B. Designing reliable electrochemical cells for operando lithium-ion battery study. MethodsX 2021, 8, 101562. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.; Li, Y.; Alsem, D.H.; So, H.; Lee, S.C.; Bai, P.; Cogswell, D.A.; Liu, X.; Jin, N.; Yu, Y.s.; Salmon, N.J.; Shapiro, D.A.; Bazant, M.Z.; Tyliszczak, T.; Chueh, W.C. Origin and hysteresis of lithium compositional spatiodynamics within battery primary particles. Science 2016, 353, 566–571. [Google Scholar] [CrossRef]
- Borkiewicz, O.J.; Shyam, B.; Wiaderek, K.M.; Kurtz, C.; Chupas, P.J.; Chapman, K.W. The AMPIX electrochemical cell: a versatile apparatus for in situ X-ray scattering and spectroscopic measurements. J Appl Crystallogr 2012, 45, 1261–1269. [Google Scholar] [CrossRef]
- Bond, T.; Zhou, J.; Cutler, J. Electrode Stack Geometry Changes during Gas Evolution in Pouch-Cell-Type Lithium Ion Batteries. J. Electrochem. Soc. 2017, 164, A6158–A6162. [Google Scholar] [CrossRef]
- Beattie, S.D.; Larcher, D.; Morcrette, M.; Simon, B.; Tarascon, J.M. Si Electrodes for Li-Ion Batteries—A New Way to Look at an Old Problem. J. Electrochem. Soc. 2008, 155, A158. [Google Scholar] [CrossRef]
- Obrovac, M.N.; Krause, L.J. Reversible Cycling of Crystalline Silicon Powder. J. Electrochem. Soc. 2007, 154, A103. [Google Scholar] [CrossRef]
- Fister, T.T.; Goldman, J.L.; Long, B.R.; Nuzzo, R.G.; Gewirth, A.A.; Fenter, P.A. X-ray diffraction microscopy of lithiated silicon microstructures. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef]
- Wang, X.; Sone, Y.; Kuwajima, S. In Situ Investigation of the Volume Change in Li-ion Cell with Charging and Discharging. J. Electrochem. Soc. 2004, 151, A273. [Google Scholar] [CrossRef]
- Finegan, D.P.; Scheel, M.; Robinson, J.B.; Tjaden, B.; Di Michiel, M.; Hinds, G.; Brett, D.J.L.; Shearing, P.R. Investigating lithium-ion battery materials during overcharge-induced thermal runaway: an operando and multi-scale X-ray CT study. Physical chemistry chemical physics 2016, 18, 30912–30919. [Google Scholar] [CrossRef]
- Trease, N.M.; Ko ster, T.K.J.; Grey, C.P. In Situ NMR Studies of Lithium Ion Batteries. Interface magazine 2011, 20, 69–73. [Google Scholar] [CrossRef]
- Le Houx, J.; Kramer, D. X-ray tomography for lithium ion battery electrode characterisation — A review. Energy Reports 2021, 7, 9–14. [Google Scholar] [CrossRef]
- Zhou, H.; An, K.; Allu, S.; Pannala, S.; Li, J.; Bilheux, H.Z.; Martha, S.K.; Nanda, J. Probing Multiscale Transport and Inhomogeneity in a Lithium-Ion Pouch Cell Using In Situ Neutron Methods. ACS Energy Letters 2016, 1, 981–986. [Google Scholar] [CrossRef]
- Calzada, E.; Schillinger, B.; Grünauer, F. Construction and assembly of the neutron radiography and tomography facility ANTARES at FRM II. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2005, 542, 38–44. [Google Scholar] [CrossRef]
- Clerici, D.; Mocera, F.; Somà, A. Electrochemical–mechanical multi-scale model and validation with thickness change measurements in prismatic lithium-ion batteries. J. Power Sources 2022, 542, 231735. [Google Scholar] [CrossRef]
- Rieger, B.; Schuster, S.F.; Erhard, S.V.; Osswald, P.J.; Rheinfeld, A.; Willmann, C.; Jossen, A. Multi-directional laser scanning as innovative method to detect local cell damage during fast charging of lithium-ion cells. J. Energy Storage 2016, 8, 1–5. [Google Scholar] [CrossRef]
- Yang, H.; Tao, W.; Zhang, Z.; Zhao, S.; Yin, X.; Zhao, H. Reduction of the Influence of Laser Beam Directional Dithering in a Laser Triangulation Displacement Probe. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.; Ding, W.; Huang, R.; Fu, Y.; Xu, F. Research progress of laser triangulation on-machine measurement technology for complex surface: A review. Measurement 2023, 216, 113001. [Google Scholar] [CrossRef]
- Kienle, P.; Batarilo, L.; Akgül, M.; Köhler, M.H.; Wang, K.; Jakobi, M.; Koch, A.W. Optical Setup for Error Compensation in a Laser Triangulation System. Sensors 2020, 20. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Wang, Z.; Jia, G.; Li, X.; Zhang, Y. Field imaging system for hyperspectral data, 3D structural data and panchromatic image data measurement based on acousto-optic tunable filter. Optics express 2018, 26, 17717–17730. [Google Scholar] [CrossRef] [PubMed]
- Bohn, G.; Taub, J.; Linke, A.; Bayer, S.; Oeser, D.; Ziegler, A.; Ettl, P.; Ackva, A. High-resolution Interferometric Measurement of Thickness Change on a Lithium-Ion Pouch Battery. IOP Conf. Ser.: Earth Environ. Sci. 2019, 281, 012030. [Google Scholar] [CrossRef]
- Bohn, G.; Taub, J.; Oeser, D.; Ziegler, A.; Gielinger, S. Fast and High Resolution Expansion Measurement at an Audi e-tron Battery Cell. 2022 IEEE Vehicle Power and Propulsion Conference (VPPC). IEEE, 2022, pp. 1–6. [CrossRef]
- Xu, Z.; Shilpiekandula, V.; Youcef-toumi, K.; Yoon, S.F. White-light scanning interferometer for absolute nano-scale gap thickness measurement. Optics express 2009, 17, 15104–15117. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, P.; Tereschenko, S.; Xie, W. Fundamental aspects of resolution and precision in vertical scanning white-light interferometry. Surf. Topogr.: Metrol. Prop. 2016, 4, 024004. [Google Scholar] [CrossRef]
- Krause, T.J.H. Self-witnessing coherent imaging for automatic noise filtering and artifact removal in laser process monitoring. Thesis, Queen’s University, Kingston, Ontario, Canada, 2022.
- Yang, K.; Sheng, Z.; Chen, B.; Li, X.; Fu, Y. Dual-surface li-ion battery deformation measurement by temporal electronic speckle pattern interferometry. International Conference on Optical and Photonic Engineering (icOPEN 2022); Zuo, C.; Wang, H.; Feng, S.; Kemao, Q., Eds. SPIE, 24.11.2022 - 27.11.2022, p. 94. [CrossRef]
- Yang, L.; Xie, X.; Zhu, L.; Wu, S.; Wang, Y. Review of electronic speckle pattern interferometry (ESPI) for three dimensional displacement measurement. Chin. J. Mech. Eng. 2014, 27, 1–13. [Google Scholar] [CrossRef]
- Zhang, Z.; Towers, C.E.; Towers, D.P. Time efficient color fringe projection system for 3D shape and color using optimum 3-frequency Selection. Optics express 2006, 14, 6444–6455. [Google Scholar] [CrossRef]
- Griffin, P.M.; Narasimhan, L.S.; Yee, S.R. Generation of uniquely encoded light patterns for range data acquisition. Pattern Recognition 1992, 25, 609–616. [Google Scholar] [CrossRef]
- van der Jeught, S.; Dirckx, J.J.J. Deep neural networks for single shot structured light profilometry. Optics express 2019, 27, 17091–17101. [Google Scholar] [CrossRef] [PubMed]
- Geng, J. Structured-light 3D surface imaging: a tutorial. Adv. Opt. Photon. 2011, 3, 128. [Google Scholar] [CrossRef]
- Ishii, I.; Yamamoto, K.; Doi, K.; Tsuji, T. High-speed 3D image acquisition using coded structured light projection. 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2007, pp. 925–930. [CrossRef]
- Wang, Z. Review of real-time three-dimensional shape measurement techniques. Measurement 2020, 156, 107624. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A state of the art in structured light patterns for surface profilometry. Pattern Recognition 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Schreier, H.; Orteu, J.J.; Sutton, M.A. Image Correlation for Shape, Motion and Deformation Measurements; Springer US: Boston, MA, 2009. [Google Scholar] [CrossRef]
- Gao, Y.; Cheng, T.; Su, Y.; Xu, X.; Zhang, Y.; Zhang, Q. High-efficiency and high-accuracy digital image correlation for three-dimensional measurement. Optics and Lasers in Engineering 2015, 65, 73–80. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Boukhtache, S.; Abdelouahab, K.; Berry, F.; Blaysat, B.; Grédiac, M.; Sur, F. When Deep Learning Meets Digital Image Correlation. Optics and Lasers in Engineering 2021, 136, 106308. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, L.; Yao, X. StrainNet-3D: Real-time and robust 3-dimensional speckle image correlation using deep learning. Optics and Lasers in Engineering 2022, 158, 107184. [Google Scholar] [CrossRef]
- Luo, J.; Dai, C.Y.; Wang, Z.; Liu, K.; Mao, W.G.; Fang, D.N.; Chen, X. In-situ measurements of mechanical and volume change of LiCoO2 lithium-ion batteries during repeated charge–discharge cycling by using digital image correlation. Measurement 2016, 94, 759–770. [Google Scholar] [CrossRef]
- Leung, P.K.; Moreno, C.; Masters, I.; Hazra, S.; Conde, B.; Mohamed, M.R.; Dashwood, R.J.; Bhagat, R. Real-time displacement and strain mappings of lithium-ion batteries using three-dimensional digital image correlation. J. Power Sources 2014, 271, 82–86. [Google Scholar] [CrossRef]
- Mutscheller, A. Safety Standards of Protection against X-ray Dangers. Radiology 1928, 10, 468–476. [Google Scholar] [CrossRef]
- Keshavamurthy, R.S.; Kumar, D.S. Radiation safety and radiation shielding design. In Physics of Nuclear Reactors; Elsevier, 2021; pp. 635–694. [CrossRef]
- Bilderback, D.H.; Elleaume, P.; Weckert, E. Review of third and next generation synchrotron light sources. Journal of Physics B: Atomic, Molecular and Optical Physics 2005, 38, S773–S797. [Google Scholar] [CrossRef]
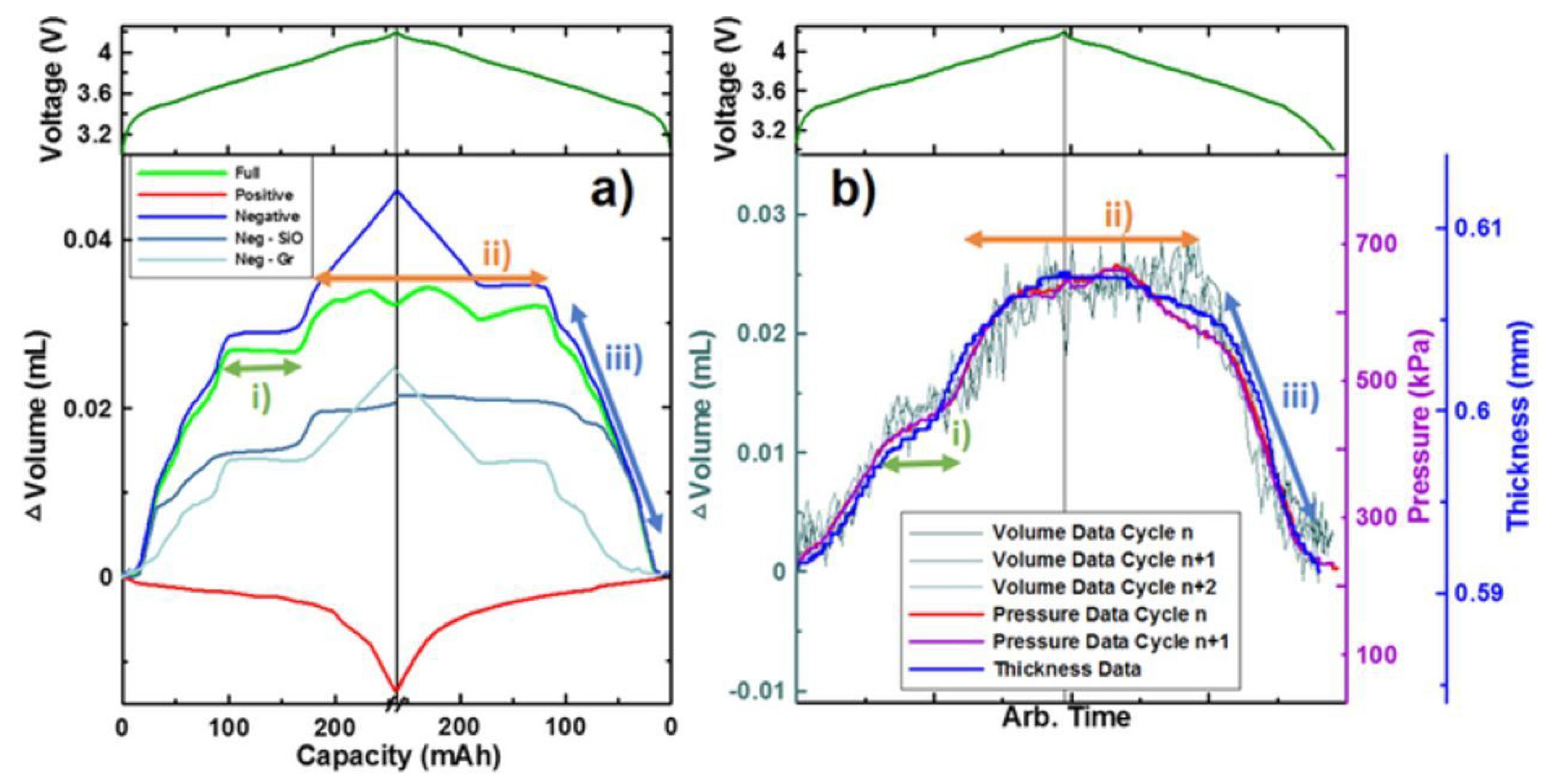


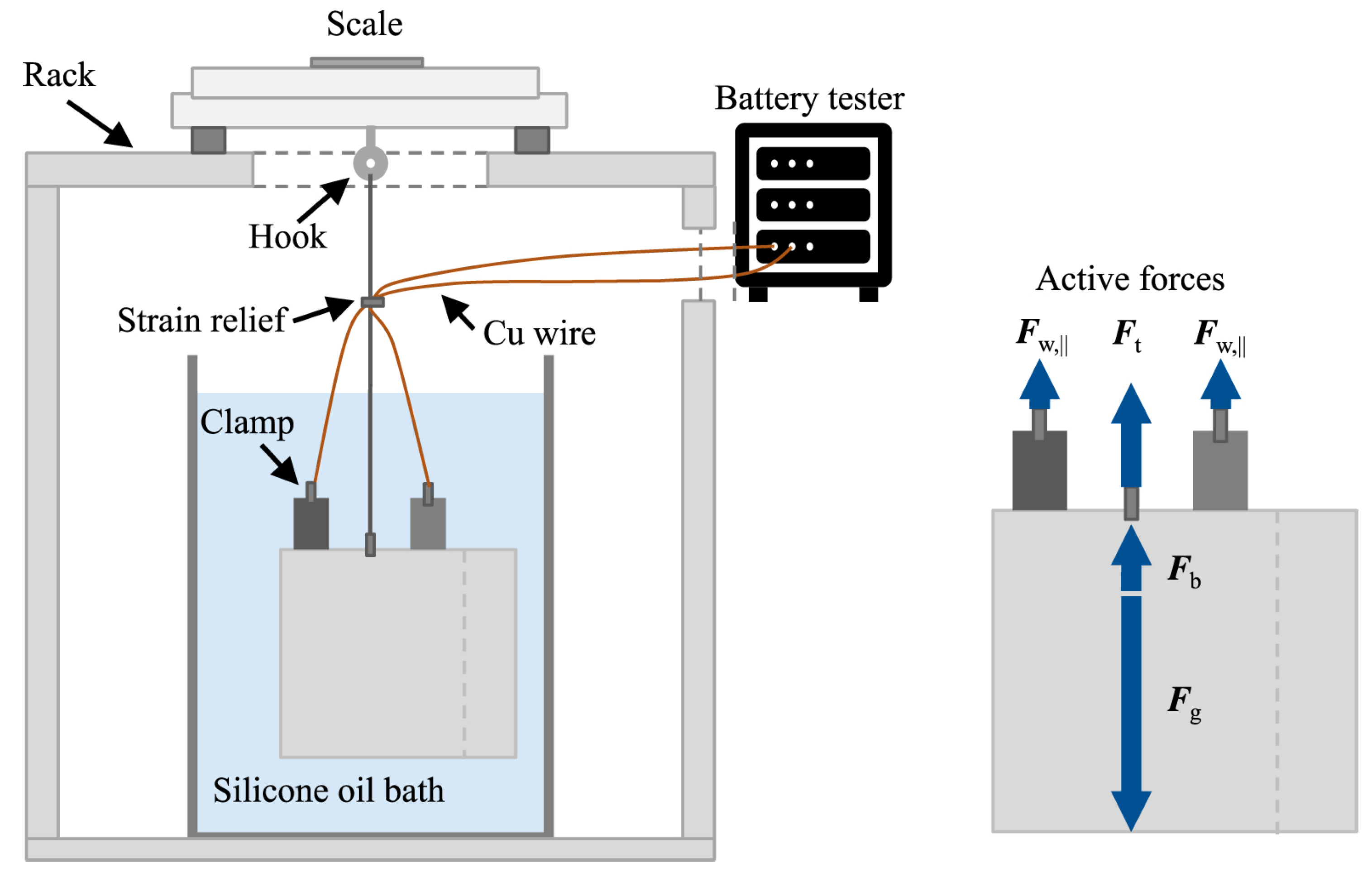

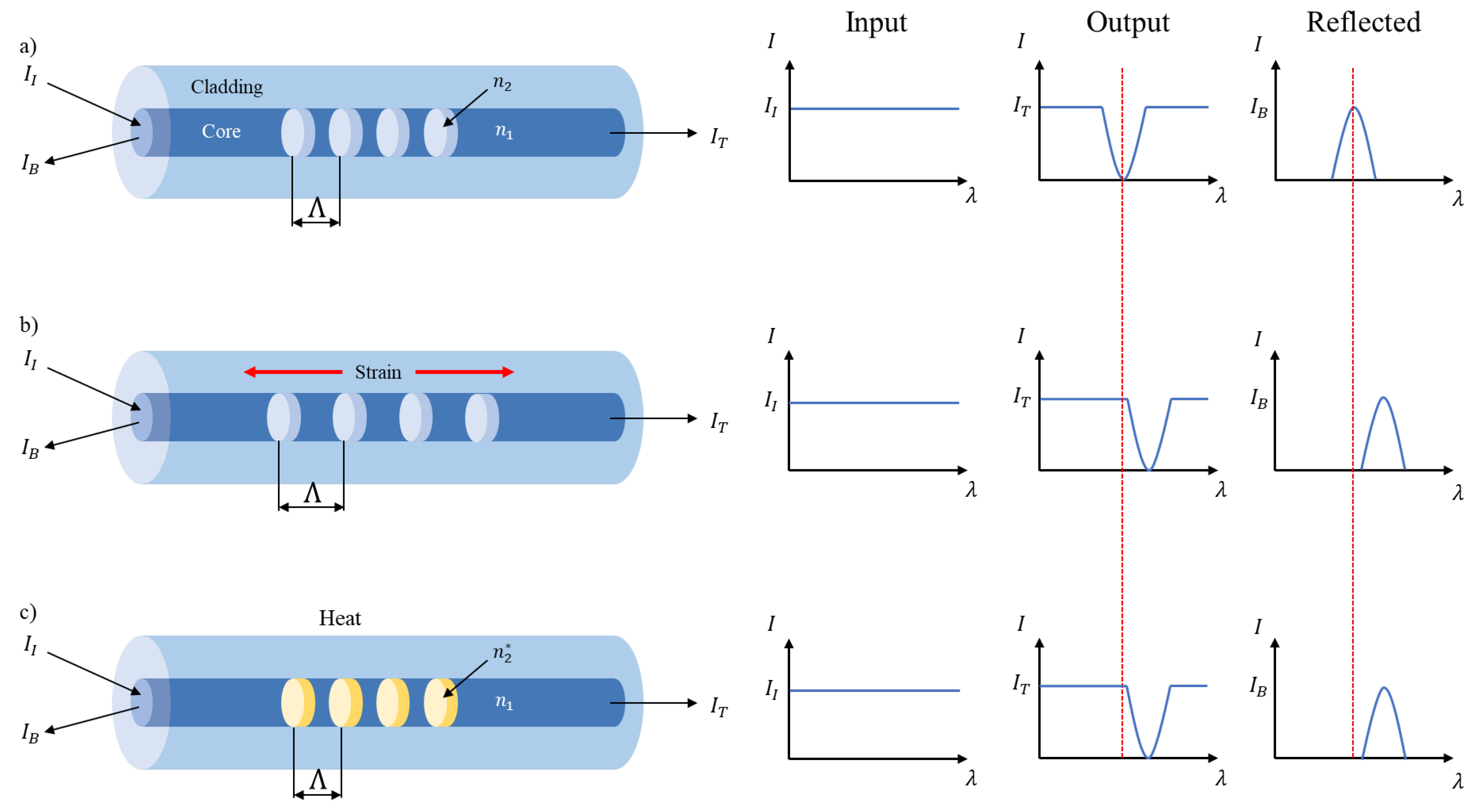
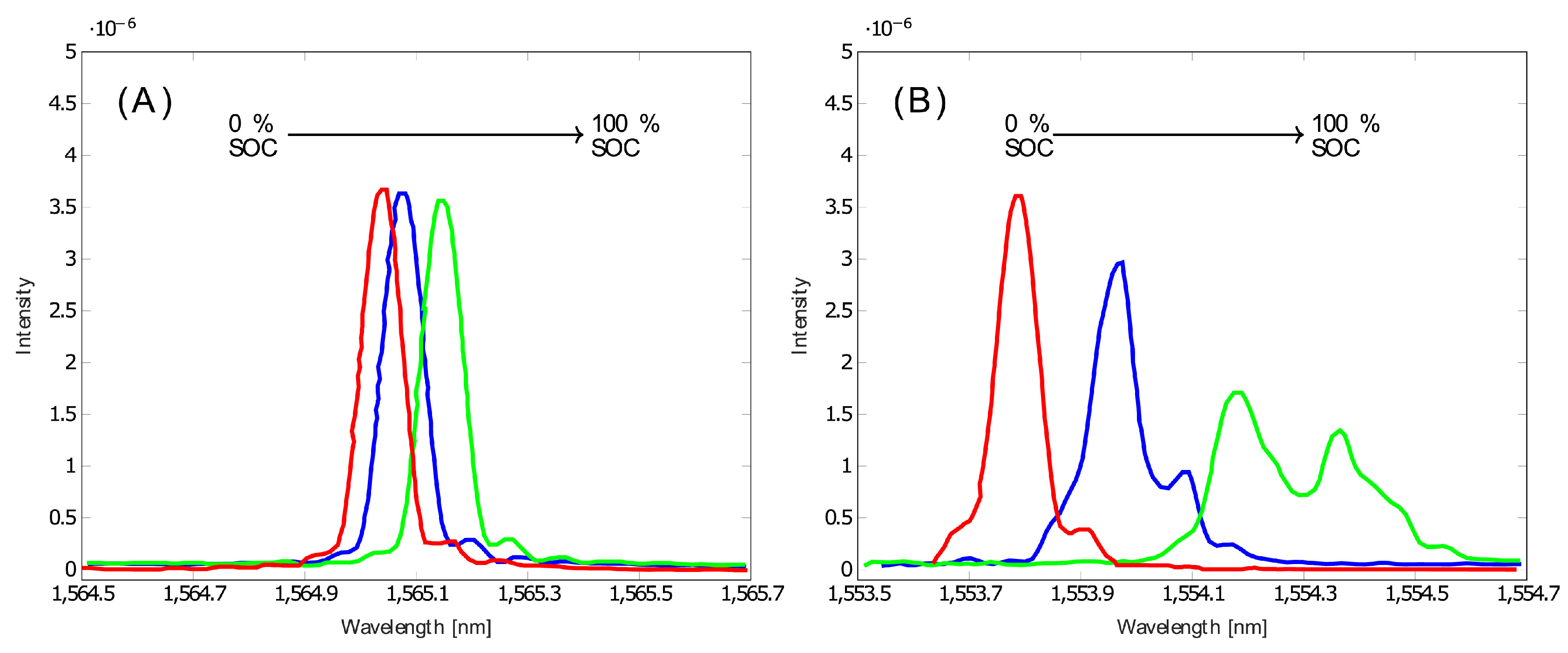

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




