Removable Singularities of Harmonic Functions on Stratified Sets

1. Introduction

Description of removable singularities for solutions of partial differential equations in a given functional space traditionally attracts a great attention of researchers. The classical result in this direction is the theorem claiming removability of a relatively closed set of zero (harmonic) capacity for a bounded harmonic function on a domain of Euclidean space ${\mathbb{R}}^n$.

In this paper we prove an analog of this theorem for bounded harmonic functions in the sense of the “soft Laplacian” on stratified sets with flat interior strata.

The main result asserts that, for a bounded harmonic function on an n-dimensional stratified set satisfying the “strong sturdiness condition”, a relatively closed set is removable whenever its intersection with the closure of any n-dimensional stratum has capacity zero in that stratum.

This result can become one of the main technical components for extending the well-known Poincaré–Perron’s method of proving the solvability of the Dirichlet problem for a soft Laplacian. Previously (see [1]) this could only be done in the two-dimensional case.

2. Preliminaries

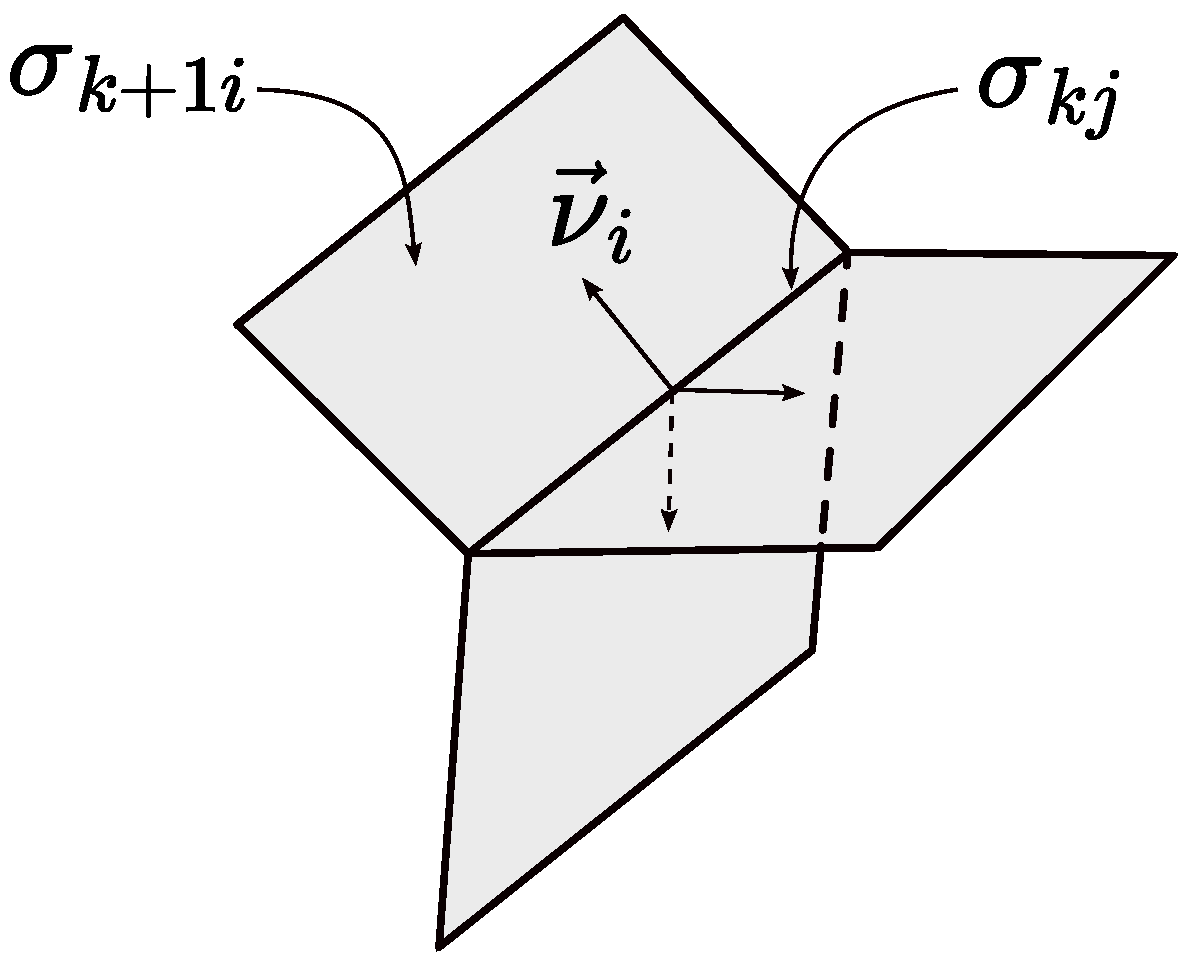
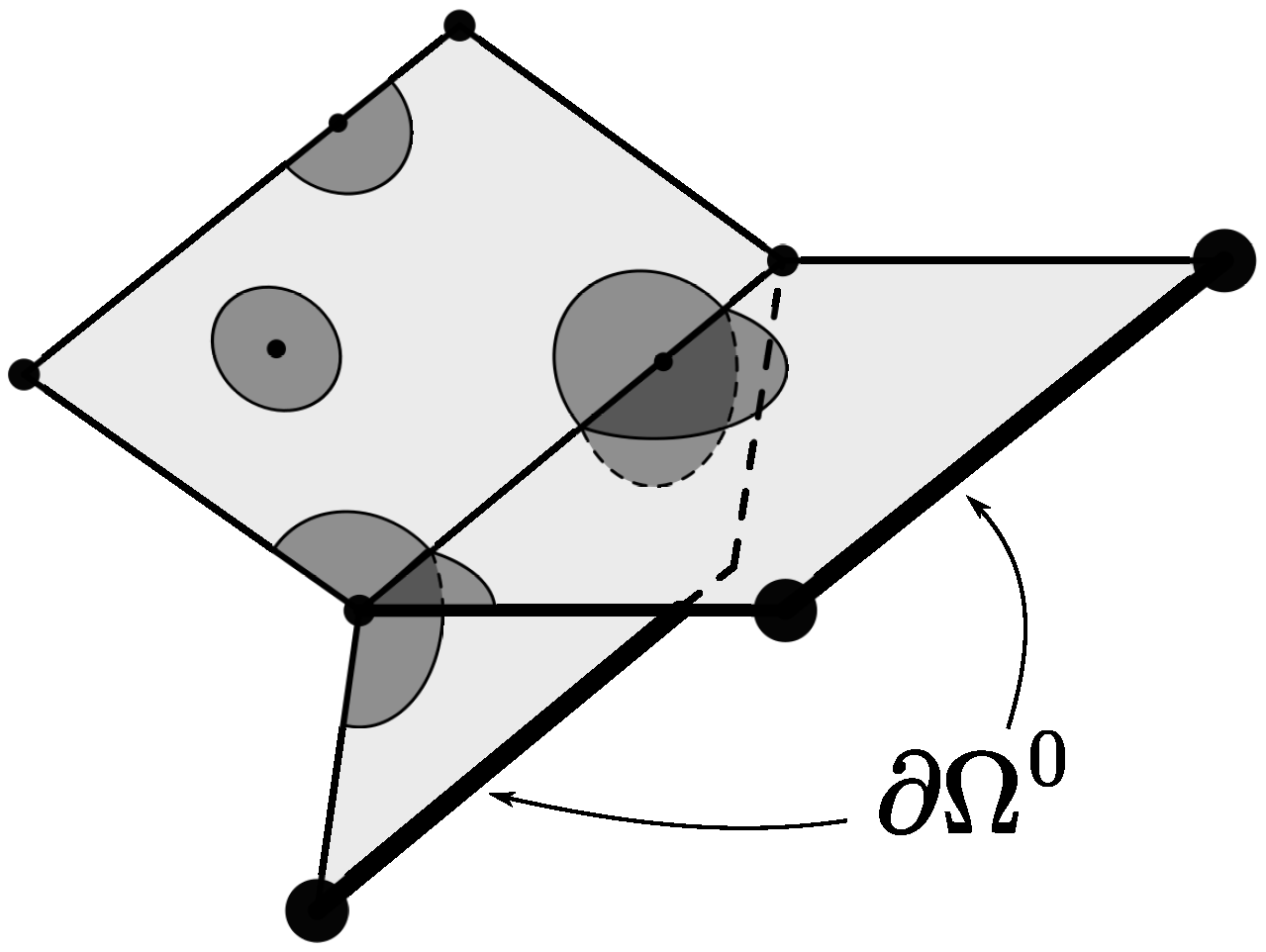
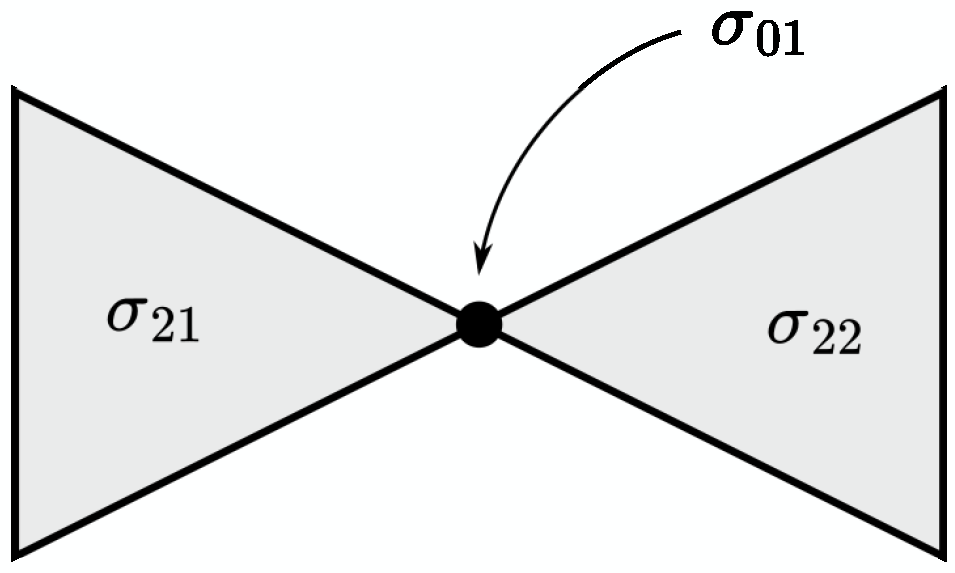
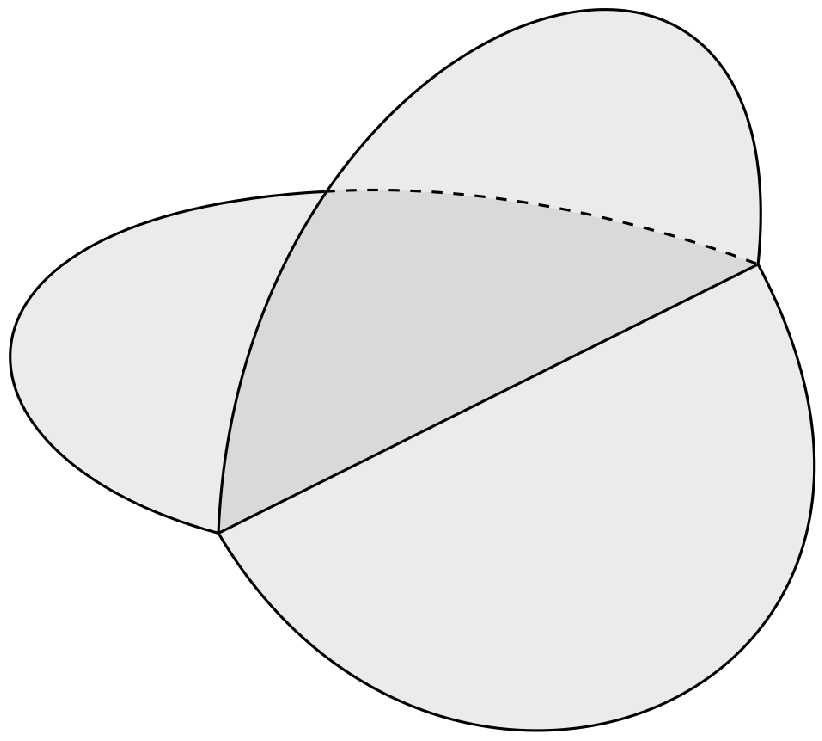
2.1. Stratified Sets

In this paper by a stratified set $\mathsf{\Omega }$ we mean a connected subset of the Euclidean space ${\mathbb{R}}^N$ which consists of finitely many pairwise disjoint connected (boundaryless) submanifolds, called strata. The set of all strata is denoted by $\mathsf{\Sigma }$, while the strata themselves by ${\sigma }_{kj}$:

$$\mathsf{\Omega }=\bigcup _{{\sigma }_{kj}\in \mathsf{\Sigma }}{\sigma }_{kj}.$$

The first subscript indicates the dimension of a stratum, while the second enumerates the strata of the given dimension. We impose the following requirements on the mutual disposition of strata:

• the closure ${\overline{\sigma }}_{kj}$ of every stratum is compact and the boundary $𝜕{\sigma }_{kj}={\overline{\sigma }}_{kj}\setminus {\sigma }_{kj}$ is the union of some strata in $\mathsf{\Sigma }$;
• for any two strata ${\sigma }_{kj},{\sigma }_{mi}\in \mathsf{\Sigma }$ the intersection of their closures ${\overline{\sigma }}_{kj}\cap {\overline{\sigma }}_{mi}$ either is empty or consists of some strata in $\mathsf{\Sigma }$.

Henceforth the relation ${\sigma }_{kj}\prec {\sigma }_{mi}$ designates that ${\sigma }_{kj}\subset 𝜕{\sigma }_{mi}$. In this case we say that the strata are contiguous (to one another).

We will use the interior metric d on $\mathsf{\Omega }$, defining $d(X,Y)$ as usual to be the infimum of the lengths of curves through $X,Y\in \mathsf{\Omega }$ in $\mathsf{\Omega }$. It is easy to see that the metric topology agrees with the topology induced in $\mathsf{\Omega }$ by the inclusion $\mathsf{\Omega }\subset {\mathbb{R}}^N$. All topological notions below will refer to this topology.

Also we represent $\mathsf{\Omega }$ as the union ${\mathsf{\Omega }}^{\circ }\cup 𝜕{\mathsf{\Omega }}^{\circ }$ (“interior” and “boundary”) in which ${\mathsf{\Omega }}^{\circ }$ is an open connected subset of $\mathsf{\Omega }$ composed of some strata in $\mathsf{\Sigma }$ and satisfying the equality $\overline{{\mathsf{\Omega }}^{\circ }}=\mathsf{\Omega }$; the remaining part $𝜕{\mathsf{\Omega }}^{\circ }=\mathsf{\Omega }\setminus {\mathsf{\Omega }}^{\circ }$ is then the topological boundary of ${\mathsf{\Omega }}^{\circ }$.

Definitions for stratified set and related notions in a more general setting can be found in [2,3]. To a great extent these definitions are inspired by [4].

In this paper all interior strata are assumed flat in the following sense: every stratum ${\sigma }_{kj}\subset {\mathsf{\Omega }}^{\circ }$ is a subdomain of a k-dimensional affine subspace of ${\mathbb{R}}^N$.

2.2. Stratified Measure

We call a set $\omega \subset \mathsf{\Omega }$ μ-measurable if every intersection ${\sigma }_{kj}\cap \omega$ is measurable with respect to the k-dimensional Lebesgue measure on ${\sigma }_{kj}$. It is easy to see that the set ${\mathcal{M}}_{\mathsf{\Omega }}$ of all $\mu$-measurable sets is a $\sigma$-algebra on $\mathsf{\Omega }$. The stratified measure ${\mu }_{\mathsf{\Omega }}$ on $\mathsf{\Omega }$ (more precisely on ${\mathcal{M}}_{\mathsf{\Omega }}$) is defined as

$${\mu }_{\mathsf{\Omega }}\left(\omega \right)=\sum _{{\sigma }_{kj}\in \mathsf{\Sigma }}{\mu }^k\left({\omega }_{kj}\right),$$

where ${\mu }^k\left({\omega }_{kj}\right)$ is the k-dimensional Lebesgue measure of the set ${\omega }_{kj}=\omega \cap {\sigma }_{kj}$. Measurability of a function $f:\mathsf{\Omega }\to \mathbb{R}$ is defined routinely: f is $\mu$-measurable if all Lebesgue sets $L_f\left(c\right)=\{X\in \mathsf{\Omega }:f\left(X\right)\le c\}$ belong to ${\mathcal{M}}_{\mathsf{\Omega }}$ for $c\in \mathbb{R}$. It is easy to see that the Lebesgue integral of a $\mu$-measurable function over a $\mu$-measurable set $\omega$ reduces to the sum

$$\underset{\omega }{\int }fd{\mu }_{\mathsf{\Omega }}=\sum _{{\sigma }_{kj}\in \mathsf{\Sigma }}\underset{{\omega }_{kj}}{\int }fd{\mu }^k.$$

We will frequently omit $\mathsf{\Omega }$ in the notation ${\mu }_{\mathsf{\Omega }}$, hoping that the stratified set under consideration is uniquely identified by the context.

2.3. Divergence and Laplacian

Henceforth by ${\overrightarrow{C}}^1\left({\mathsf{\Omega }}^{\circ }\right)$ we mean the space of tangent vector fields F on ${\mathsf{\Omega }}^{\circ }$ whose restrictions $\overrightarrow{F}{|}_{{\sigma }_{ki}}$ to the strata ${\sigma }_{ki}\subset {\mathsf{\Omega }}^{\circ }$ belong to the spaces $C^1\left({\sigma }_{kj}\right)$.

The divergence of a vector field $\overrightarrow{F}\in {\overrightarrow{C}}^1\left(\mathsf{\Omega }\right)$ at a point $X\in {\sigma }_{kj}\subset {\mathsf{\Omega }}^{\circ }$ is defined to be

$$\nabla ·\overrightarrow{F}\left(X\right)={\nabla }_k·\overrightarrow{F}\left(X\right)+\sum _{{\sigma }_{k+1i}\succ {\sigma }_{kj}}\overrightarrow{F}(X+0·{\overrightarrow{\nu }}_i)·{\overrightarrow{\nu }}_i,$$

where the summation is carried out over all $(k+1)$-dimensional strata ${\sigma }_{k+1i}$ contiguous to ${\sigma }_{kj}$. Here ${\nabla }_k$ on the right-hand side denotes the operator of the conventional k-dimensional divergence applied to the restriction $\overrightarrow{F}{|}_{kj}$ of $\overrightarrow{F}$ to ${\sigma }_{kj}$, ${\overrightarrow{\nu }}_i$ is the unit inward normal to ${\sigma }_{kj}$ in ${\sigma }_{k+1j}$ at X, and $\overrightarrow{F}(X+0·{\overrightarrow{\nu }}_i)$ is the limit of $\overrightarrow{F}\left(Y\right)$ as $Y\in {\sigma }_{k+1i}$ tends to X inside ${\sigma }_{k+1i}\succ {\sigma }_{kj}$ in the direction of ${\nu }_i$. See Figure 1 for illustration.

The so-defined divergence is a genuine analog of the classical one. It can be shown (see [5,6]) that, as in the ordinary setup, the divergence $\nabla ·\overrightarrow{F}\left(X\right)$ is the density of the flux of the vector field $\overrightarrow{F}$ at X with respect to the stratified measure $\mu$ defined in the previous section. Furthermore, for $F\in {\overrightarrow{C}}^1\left({\mathsf{\Omega }}^{\circ }\right)$ we have the following stratified analog of the divergence theorem (the sign “−” is caused by the choice of the inward normal):

$${\int }_{{\mathsf{\Omega }}^{\circ }}\nabla ·\overrightarrow{F}d\mu =-{\int }_{𝜕{\mathsf{\Omega }}^{\circ }}{\overrightarrow{F}}_{\nu }d\mu ,$$

(1)

where for $X\in {\sigma }_{kj}\subset 𝜕{\mathsf{\Omega }}^{\circ }$

$${\overrightarrow{F}}_{\nu }\left(X\right)=\sum \overrightarrow{F}(X+0·{\nu }_i)·{\nu }_i$$

with the summation taken over all ${\sigma }_{k+1i}\succ {\sigma }_{kj}$ not lying in $𝜕{\mathsf{\Omega }}^{\circ }$.

For a sufficiently smooth scalar function u its gradient $\nabla u$ is a tangent vector field (in this case $\nabla u$ is simply the collection of the gradients of the restrictions of u to the strata). It would be rather natural to define the Laplacian on a stratified set as $\Delta u=\nabla ·(\nabla u)$. The so-defined Laplacian is often called “hard”. At present the qualitative theory of harmonic functions in the sense of this Laplacian is developed weakly. Therefore, here we restrict ourselves to considering the so-called “soft” Laplacian.

We call a stratum ${\sigma }_{kj}$ free if it is not contiguous to any stratum of greater dimension. The soft Laplacian of a function u on ${\mathsf{\Omega }}^{\circ }$ is defined to be

$$\tilde{\Delta }u=\nabla ·(p\nabla u),$$

(2)

where $p=1$ on the free strata and $p=0$ on the remaining strata.

The explicit expression of the soft Laplacian at the points of free strata coincides with the ordinary Laplacian (in the case of nonflat strata, with the Laplace–Beltrami operator).

If the stratum ${\sigma }_{kj}$ is not free but there exist free strata ${\sigma }_{k+1i}\succ {\sigma }_{kj}$ then at a point $X\in {\sigma }_{kj}$ the expression of the soft Laplacian looks like

$$\tilde{\Delta }u\left(X\right)=\sum _{{\sigma }_{k+1i}\succ {\sigma }_{kj}}\nabla u(X+0·{\overrightarrow{\nu }}_i)·{\overrightarrow{\nu }}_i,$$

where the summation is taken over all free strata ${\sigma }_{k+1i}\succ {\sigma }_{kj}$.

Finally, if a stratum is neither free nor contiguous to any free stratum of dimension greater than one then, in accord with (2), on this stratum we have $\tilde{\Delta }u=0$.

For an open set $U\subset {\mathsf{\Omega }}^{\circ }$ we denote by ${\tilde{C}}_{\mathrm{loc}}^2\left(U\right)$ the set of functions $u:U\to \mathbb{R}$ that satisfy the following conditions:

• u is continuous on U;
• for every free stratum ${\sigma }_{ni}$ the restriction ${u|}_{U\cap {\sigma }_{ni}}$ is twice continuously differentiable and the gradient $\nabla u$ of the restriction has a continuous extension to each point $X\in U\cap {\sigma }_{n-1j}$ of any interior stratum ${\sigma }_{n-1j}$ contiguous to ${\sigma }_{ni}$.

A function $u:U\to \mathbb{R}$ is said to be harmonic on U if $u\in {\tilde{C}}_{\mathrm{loc}}^2\left(U\right)$ and u satisfies the equation

$$\tilde{\Delta }u\left(X\right)=0$$

(3)

for all $X\in U$.

2.4. Mean Value Theorem and Harnack’s Inequality

The functions on a stratified set which are harmonic in the sense of the soft Laplacian inherit a number of important properties of the ordinary harmonic functions. In particular, valid are analogs of the Mean Value Theorem and Harnack’s inequality.

We call a ball $B_r\left(X_0\right)=\{X\in \mathsf{\Omega }:d(X,X_0)<r\}$ admissible or, in more detail, an open ball of admissible radius $r>0$ with center $X_0$, if r is less than the distance from $X_0$ to any stratum whose closure does not contain $X_0$. In that event, the set $S_r\left(X_0\right)=\{X\in \mathsf{\Omega }:d(X,X_0)=r\}$ is called an admissible sphere. Figure 2 shows several examples of admissible balls.

Admissible balls and spheres get a natural stratification from $\mathsf{\Omega }$. For example, for an admissible sphere S all nonempty intersections ${\sigma }_{kj}\cap S$, ${\sigma }_{kj}\in \mathsf{\Sigma }$, are its $(k-1)$-dimensional strata. The stratified measure ${\mu }_S$ on a stratified sphere S is defined as for any other stratified set (see Section 1.2).

Let $\mathsf{\Omega }$ be a stratified set in which all free strata have the same dimension n. Then $p=1$ on all n-dimensional strata and p vanishes on all other strata in $\mathsf{\Sigma }$.

For $X_0\in {\mathsf{\Omega }}^{\circ }$ and an admissible sphere $S_r\left(X_0\right)$, consider the spherical mean:

$$M\left[S_r\left(X_0\right)\right]u=\frac{1}{|S_r\left(X_0\right){|}_p}{\int }_{S_r\left(X_0\right)}pud{\mu }_S,$$

where $|S_r\left(X_0\right){|}_p={\int }_{S_r\left(X_0\right)}pd{\mu }_S$.

Theorem 1 

(Mean Value Theorem). [7] Let Ω be a stratified set whose free strata have the same dimension, let u be a harmonic function on ${\mathsf{\Omega }}^{\circ }$, and let $S_r\left(X_0\right)$, $X_0\in {\mathsf{\Omega }}^{\circ }$, be an admissible sphere. Then

$$M\left[S_r\left(X_0\right)\right]u=u\left(X_0\right).$$

Remark 1. 

A similar assertion is true with the means calculated over admissible balls in place of admissible spheres.

Theorem 2 

(Harnack’s Inequality). [8] Let Ω be a stratified set and let K be an arbitrary compact set in ${\mathsf{\Omega }}^{\circ }$. Then the inequality

$$\underset{X\in K}{sup}u\left(X\right)\le C\underset{X\in K}{inf}u\left(X\right)$$

holds for every nonnegative harmonic function u on ${\mathsf{\Omega }}^{\circ }$ with a constant $C=C(K,{\mathsf{\Omega }}^{\circ })$ independent of u.

3. Removable Singularity Theorem

3.1. Statement

Given a stratified set $\mathsf{\Omega }$, denote by ${\mathsf{\Sigma }}^k$ the union of all interior strata of dimension k and denote by ${\mathsf{\Sigma }}_k$ the union of all interior strata of dimension at most k:

$${\mathsf{\Sigma }}^k=\bigcup _{j:{\sigma }_{kj}\subset {\mathsf{\Omega }}^{\circ }}{\sigma }_{kj},{\mathsf{\Sigma }}_k=\bigcup _{l=0}^k{\mathsf{\Sigma }}^l.$$

A stratified set $\mathsf{\Omega }$ is called sturdy ( see [8]) if all free strata have the same dimension n and the set ${\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}$ is connected. Let us call $\mathsf{\Omega }$ strongly sturdy if all free strata have the same dimension n and, for every $X\in {\mathsf{\Sigma }}_{n-2}$, there exists an admissible ball $B_r\left(X\right)$ such that the set $B_r\left(X\right)\setminus {\mathsf{\Sigma }}_{n-2}$ is connected.

The following theorem is the main result of the present article.

Theorem 3 

(Removable Singularity Theorem). Let Ω be a strongly sturdy stratified set, $S\subset {\mathsf{\Omega }}^{\circ }$ a relatively closed set whose intersection with the closure of any free stratum has harmonic capacity zero in the affine space including the stratum, and $u:{\mathsf{\Omega }}^{\circ }\setminus S\to \mathbb{R}$ a bounded harmonic function. Then u has a harmonic extension to all of ${\mathsf{\Omega }}^{\circ }$.

The theorem is a straightforward consequence of the next two lemmas.

Lemma 1. 

Under the conditions of Theorem 3 the function u extends to a bounded harmonic function on ${\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}$.

Lemma 2. 

Let Ω be a strongly sturdy stratified set of dimension n and $u:{\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}\to \mathbb{R}$ a bounded harmonic function. Then u has a harmonic extension to all of ${\mathsf{\Omega }}^{\circ }$.

Remark 2. 

The strong sturdiness condition is essential.

As an example, consider a two-dimensional set $\mathsf{\Omega }$ composed of two planar triangles with one common vertex ${\sigma }_{01}$ and no other points in common (see Figure 3). Put $𝜕{\mathsf{\Omega }}^{\circ }=⌀$, i.e., ${\mathsf{\Omega }}^{\circ }=\mathsf{\Omega }$. The function u, equal to 0 on one triangle and to 1 on the other, is harmonic on $\mathsf{\Omega }\setminus {\sigma }_{01}$, but fails to have a harmonic extension to all of $\mathsf{\Omega }$.

Proof of Lemma 1. 

It suffices to prove that, for every point $X_0\in {\mathsf{\Sigma }}^n\cup {\mathsf{\Sigma }}^{n-1}$ and any admissible ball $B_r\left(X_0\right)$, the restriction ${u|}_{B_r\left(X_0\right)\setminus S}$ admits an extension to a bounded harmonic function on $B_r\left(X_0\right)$.

If $X_0\in {\mathsf{\Sigma }}^n$ then the existence of a sought extension follows from the removability of a relatively closed set of capacity zero for bounded harmonic functions on subdomains of ${\mathbb{R}}^n$. Therefore, suppose that $X_0$ belongs to an $(n-1)$-dimensional stratum ${\sigma }_{n-1}$ and let $B_r\left(X_0\right)$ be an admissible ball. Without loss of generality, we assume $\mathsf{\Omega }$ to be the closed stratified ball $B_r\left(X_0\right)\cup S_r\left(X_0\right)$ in which $B_r\left(X_0\right)$ serves as the interior and $S_r\left(X_0\right)$ as the boundary (see Figure 4).

Let ${\sigma }_{n1},\cdots ,{\sigma }_{nm}$ be all strata contiguous to ${\sigma }_{n-1}$.

If we have exactly two strata, ${\sigma }_{n1}$ and ${\sigma }_{n2}$, then $B_r\left(X_0\right)$ (with its interior metric) is isometric to the usual Euclidean ball B of radius r in ${\mathbb{R}}^n$; moreover, ${\sigma }_{n1}$ and ${\sigma }_{n2}$ go under isometry into half-balls separated by the $(n-1)$-dimensional disk that is the image of ${\sigma }_{n-1}$. The function $\tilde{u}$ corresponding to u under the isometry is an ordinary harmonic function on $B\setminus \tilde{S}$, where $\tilde{S}$ is the image of $S\cap B_r\left(X_0\right)$ under the isometry. Applying the standard removable singularity theorem to $\tilde{u}$, we obtain a harmonic extension of $\tilde{u}$ to B. Executing the inverse isometry, we get a harmonic extension of u to $B_r\left(X_0\right)$.

If we have an odd number of strata then we double their number by slightly rotating the ball $B_r\left(X_0\right)$ around ${\sigma }_{n-1}$ and extend u to the new strata by using this rotation.

Thus, we may assume that there are $2l$ strata in total, ${\sigma }_{nj}$, $j=1,\cdots ,2l$, contiguous to ${\sigma }_{n-1}$. Again we take a Euclidean ball B of radius r in ${\mathbb{R}}^n$ divided into two half-balls $B^1$ and $B^2$ resting on an equatorial $(n-1)$-dimensional disk D. Let $J\subset \{1,2,\cdots ,2l\}$ be an arbitrary collection of l distinct numbers and let $\overline{J}$ be the complementary collection. Now, map ${\sigma }_{nj}\cup {\sigma }_{n-1}$, $j\in J$, onto $B^1\cup D$ and map ${\sigma }_{n\overline{j}}\cup {\sigma }_{n-1}$, $\overline{j}\in \overline{J}$, onto $B^2\cup D$ isometrically so that the stratum ${\sigma }_{n-1}$ go onto D. Let $\tilde{S}$ be the union of the images of $({\sigma }_{nj}\cup {\sigma }_{n-1})\cap S$ over all j under the isometry. Translating u by isometry from ${\sigma }_{nj}\cup {\sigma }_{n-1}$ to $B^1\cup D$, we receive functions $u_j$, $j\in J$. Proceeding similarly, we also receive functions $u_{\overline{j}}$, $\overline{j}\in \overline{J}$. It is easily seen that the function $u_J$, equal to ${\sum }_{j\in J}{u}_j$ on $(B^1\cup D)\setminus \tilde{S}$ and equal to ${\sum }_{\overline{j}\in \overline{J}}{u}_{\overline{j}}$ on $(B^2\cup D)\setminus \tilde{S}$ (notice that both the functions agree on the intersection of their domains), is an ordinary harmonic function on $B\setminus \tilde{S}$. Applying to it the standard removable singularity theorem, we get a harmonic extension of $u_J$ to the whole ball B. Since this is true for every collection J, an easy combinatorics shows that each individual function $u_j$ gets an extension rather than their combination. Returning to u, we obtain an extension of u to the whole set ${\sigma }_{nj}\cup {\sigma }_{n-1}$ for every j; furthermore, the resultant function is harmonic on the whole ball $B_r\left(X_0\right)$. □

Proof of Lemma 2. 

Equation (3) imposes no conditions on the strata of dimension $\le n-2$. Thus, the lemma asserts in fact that u extends continuously to ${\mathsf{\Omega }}^{\circ }$.

We extend u from ${\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}$ to ${\mathsf{\Omega }}^{\circ }$ by using spherical means. To this end, we state the following lemma whose proof is postponed to the next section.

Lemma 3 

(Equality of Means). Under the conditions of Theorem 3, for every $X_0\in {\mathsf{\Omega }}^{\circ }$ and any admissible radii $r_1$ and $r_2$ the equality of means holds:

$$M\left[S_{r_1}\left(X_0\right)\right]u=M\left[S_{r_2}\left(X_0\right)\right]u.$$

Leaning on this lemma, we put

$$M\left(X\right)=M\left[S_r\left(X\right)\right]u,X\in {\mathsf{\Omega }}^{\circ },$$

where r is any admissible radius.

Note that

$$u\left(x\right)=M\left(X\right)\mathrm{for}X\in {\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}.$$

Let us prove by induction on k decreasing from $k=n-1$ to 0 that $M\left(X\right)$ is continuous on ${\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{k-1}$. Then $M\left(X\right)$ will give us the sought extension of u.

The induction base is trivial. Suppose that $M\left(X\right)$ is continuous on ${\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_k$, $k<n-1$, and hence harmonic on ${\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_k$. Take $X_0\in {\sigma }_k$ for a k-dimensional stratum ${\sigma }_k\subset {\mathsf{\Omega }}^{\circ }$. We are to prove that

$$\underset{X\to X_0}{lim}M\left(X\right)=M\left(X_0\right).$$

(4)

This will justify the induction step and, therefore, complete the proof of Lemma 2.

Lemma 4. 

$\underset{X\to X_0,X\in {\sigma }_k}{lim}M\left(X\right)=M\left(X_0\right).$

Proof. Let $X_i\in {\sigma }_k$, $i=1,2,\cdots$, and $X_i\to X_0$ as $i\to \infty$. Let $S_r\left(X_0\right)$ be an admissible sphere and let $B_R\left(X_0\right)$ be an admissible ball of a greater radius, $R>r$. Since the points $X_i$ lie on the same stratum as $X_0$, the translated spheres $S_r\left(X_i\right)$ are admissible, too, and lie within $B_R\left(X_0\right)$ for i large enough. For $Z\in B_R\left(X_0\right)\setminus {\mathsf{\Sigma }}_{n-2}$, define

$$u_i\left(Z\right)=u(Z+(X_i-X_0)).$$

The sequence $u_i$ converges pointwise to u and is uniformly bounded. Therefore,

$${\int }_{S_r\left(X_0\right)}p{u}_{i}d{\mu }_S\to {\int }_{S_r\left(X_0\right)}pud{\mu }_S.$$

Hence,

$$M\left(X_i\right)=M\left[S_r\left(X_i\right)\right]u=M\left[S_r\left(X_0\right)\right]u_i\to M\left[S_r\left(X_0\right)\right]u=M\left(X\right),$$

which finishes the proof of the lemma. □

Lemma 5. 

$m:=\underset{X\to X_0,X\in \mathsf{\Omega }\setminus {\sigma }_k}{lim\; inf}M\left(X\right)=M\left(X_0\right)$.

Proof. Choose $X_i\in \mathsf{\Omega }\setminus {\sigma }_k$ so that $X_i\to X_0$ and $M\left(X_i\right)\to m$. Let $L_k$ be the k-dimensional affine plane including ${\sigma }_k$. Let $Y_i$ be the projection of $X_i$ to $L_k$. Since $X_i\to X_0$ and $Y_i\to X_0$, the balls $B_{r_i}\left(Y_i\right)$, $r_i=2|X_i-Y_i|$, are admissible for i large enough (see Figure 5).

Since $r_i\to 0$, while m is the lower limit of $M\left(X\right)$ at $X_0$, it follows that

$$m_i:=\underset{X\in B_{r_i}\left(Y_i\right)\setminus {\sigma }_k}{inf}M\left(X\right)\to m\mathrm{as}i\to \infty .$$

(5)

Indeed, for any $\epsilon >0$ there exists $Z_i\in B_{r_i}\left(Y_i\right)\setminus {\sigma }_k$ such that

$$M\left(Z_i\right)-\epsilon <m_i\le M\left(X_i\right).$$

Then

$$\underset{i\to \infty }{lim\; inf}M\left(Z_i\right)-\epsilon \le \underset{i\to \infty }{lim\; inf}{m}_i,$$

(6)

$$\underset{i\to \infty }{lim\; sup}{m}_i\le \underset{i\to \infty }{lim}M\left(X_i\right)=m.$$

(7)

Notice that $Z_i\to X_0$ as $i\to \infty$. Therefore,

$$\underset{i\to \infty }{lim\; inf}M\left(Z_i\right)\ge m.$$

(8)

Inequalities (6) and (8) imply the inequality

$$m-\epsilon \le \underset{i\to \infty }{lim\; inf}{m}_i$$

which, by the arbitrariness of $\epsilon$, yields

$$m\le \underset{i\to \infty }{lim\; inf}{m}_i.$$

(9)

In turn, (9) and (7) mean the validity of (5).

Put

$$u_i\left(X\right):=M\left(X\right)-m_i,X\in B_{r_i}\left(Y_i\right)\setminus {\sigma }_k.$$

Then $u_i$ are nonnegative bounded functions harmonic on $B_{r_i}\left(Y_i\right)\setminus {\sigma }_k$ according to the induction assumption; moreover, $u_i\left(X_i\right)\to 0$ as $i\to \infty$.

Since all $Y_i$ and $X_0$ lie on the same stratum, all (admissible) balls $B_{r_i}\left(Y_i\right)$ are similar to one admissible ball $B_r\left(X_0\right)$. Let $T_i:B_{r_i}\left(Y_i\right)\to B_r\left(X_0\right)$ denote the corresponding similarity transformation. Then

$$T_i\left(Y_i\right)=X_0,\mathrm{dist}(T_i\left(X_i\right),{\sigma }_k)=r/2,|T_i\left(X_i\right)-X_0|=r/2.$$

For $Z\in B_r\left(X_0\right)$, define

$${\overline{u}}_i\left(Z\right):=u_i\left(T_i^{-1}\left(Z\right)\right).$$

Then ${\overline{u}}_i$ are nonnegative bounded harmonic functions on $B_r\left(X_0\right)\setminus {\sigma }_k$.

Let $H\subset B_r\left(X_0\right)\setminus {\sigma }_k$ be an arbitrary compact set. Since all points $T_i\left(X_i\right)$ are at a positive distance from the boundary of $B_r\left(X_0\right)\setminus {\sigma }_k$, there exists a compact set $K\subset B_r\left(X_0\right)\setminus {\sigma }_k$ including H as well as all the points $T_i\left(X_i\right)$. Taking it into account that ${\overline{u}}_i\left(T_i\left(X_i\right)\right)=u_i\left(X_i\right)\to 0$ as $i\to \infty$ and applying Harnack’s inequality to the functions ${\overline{u}}_i$ on $B_r\left(X_0\right)\setminus {\sigma }_k$ and the compact set K (it is here that we use the strong sturdiness condition of $\mathsf{\Omega }$), we conclude that the functions ${\overline{u}}_i$ converge uniformly to zero on K and, in consequence, on H.

Since the compact set H can be taken arbitrarily close to ${\sigma }_k$ and the ${\overline{u}}_i$ are uniformly bounded, the means of ${\overline{u}}_i$ over the spheres with center $X_0$ tend to zero. Indeed, let C be an upper bound for the functions ${\overline{u}}_i$ and let $\epsilon >0$ be arbitrary. For $\rho >0$, put

$${\sigma }_k\left(\rho \right)=\{Z\in B_r\left(X_0\right):\mathrm{dist}(Z,{\sigma }_k)<\rho \}.$$

Choose $\rho$ so small that

$$|S_{r/2}\left(X_0\right)\cap {\sigma }_k\left(\rho \right){|}_p<\epsilon {\left|S_{r/2}\left(X_0\right)\right|}_p/\left(2C\right).$$

Now, take the compact set

$$H=S_{r/2}\setminus {\sigma }_k\left(\rho \right).$$

Choose N so as to have ${\overline{u}}_i\left(Z\right)<\epsilon /2$, $Z\in H$, for $i>N$. Then for $i>N$

$$\begin{array}{c}M\left[S_{r/2}\left(X_0\right){\overline{u}}_i\right]=\frac{1}{|S_{r/2}\left(X_0\right){|}_p}\left\{{\int }_H\overline{p}{u}_{i}d{\mu }_S+{\int }_{S_{r/2}\setminus H}p{\overline{u}}_{i}d{\mu }_S\right\}\hfill \\ \hfill \hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\frac{1}{|S_{r/2}\left(X_0\right){|}_p}\left({\epsilon \left|H\right|}_p/2+C{|S_{r/2}\left(X_0\right)\setminus H|}_p\right)\le \epsilon .\end{array}$$

For $S_{r_i/2}\left(Y_i\right)=T_i^{-1}{S}_{r/2}\left(X_0\right)$ we obtain

$$M\left[S_{r_i/2}\left(Y_i\right)\right]u_i=M\left[S_{r/2}\left(X_0\right)\right]{\overline{u}}_i\to 0(i\to \infty ).$$

Therefore, $M\left(Y_i\right)\to m$ as $i\to \infty$, because the spherical means of the functions $M\left(X\right)$ and $u\left(X\right)$ coincide in view of the equality $M\left(X\right)=u\left(X\right)$ for $X\in {\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}$.

From Lemma 4 we also have $M\left(Y_i\right)\to M\left(X_0\right)$. Hence, $m=M\left(X_0\right)$. □

Lemma 6. 

$M\left(X_0\right)=\underset{X\to X_0,X\in \mathsf{\Omega }\setminus {\sigma }_k}{lim\; sup}M\left(X\right)$.

For a proof, it suffices to apply Lemma 5 to the function $-u$, leaning upon the equality $lim\; inf(-u)=-lim\; supu$.

Lemmas 5 and 6 yield ${lim}_{X\to X_0}M\left(X\right)=M\left(X_0\right)$. This and Lemma 4 imply (4), thus finishing the proof of Lemma 2.

4. Proof of Lemma 3

4.1. Gradient Estimate

We need an estimate for the gradient of a harmonic function on a stratified set. In the classical case when u is a bounded harmonic function on a domain $G\subset {\mathbb{R}}^n$ we have the following gradient estimate:

$$|\nabla u\left(X\right)|\le \frac{n}{\rho \left(X\right)}\underset{G}{sup}\left|u\right|,$$

where $\rho \left(X\right)=\mathrm{dist}(X,𝜕G)$ (see, for instance, [9]). We prove a similar estimate in the stratified setup.

Theorem 4 

(Gradient Estimate). Let Ω be a stratified set whose free strata have the same dimension n and let $u:{\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}\to \mathbb{R}$ be a bounded harmonic function. Then for every $X\in {\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}$ the estimate holds:

$$|\nabla u\left(X\right)|\le \frac{C}{\rho \left(X\right)}\underset{{\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}}{sup}\left|u\right|,$$

where $C=C\left(\mathsf{\Omega }\right)$ is a constant depending only on the structure of the stratified set Ω, and $\rho \left(X\right)=\mathrm{dist}(X,{\mathsf{\Sigma }}_{n-2}\cup 𝜕{\mathsf{\Omega }}^{\circ })$.

We first give an estimate over admissible balls.

Lemma 7. 

For every $X_0\in {\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}$ and any admissible ball $B_r\left(X_0\right)$ the estimate holds:

$$|\nabla u\left(X\right)|\le \frac{C}{r}\underset{B_r\left(X_0\right)}{sup}\left|u\right|,X\in B_{r/2}\left(X_0\right),$$

where $C=C\left(\mathsf{\Omega }\right)$ is a constant depending only on the structure of Ω.

Proof. 

We use the same trick as in the proof of Lemma 1.

If $X_0$ belongs to an n-dimensional stratum, then the required estimate follows from the above-mentioned classical result. We therefore assume that $X_0$ belongs to some $(n-1)$-dimensional stratum ${\sigma }_{n-1}$ and let $B_r\left(X_0\right)$ be an admissible ball. Without loss of generality, we consider $\mathsf{\Omega }$ to be the closed stratified ball $B_r\left(X_0\right)\cup S_r\left(X_0\right)$ in which $B_r\left(X_0\right)$ serves as interior and $S_r\left(X_0\right)$ as boundary (Figure ??).

Let ${\sigma }_{n1},\cdots ,{\sigma }_{nm}$ be all strata contiguous to ${\sigma }_{n-1}$.

If we have only two strata, ${\sigma }_{n1}$ and ${\sigma }_{n2}$, then $B_r\left(X_0\right)$ (with its interior metric) is isometric to the ordinary Euclidean ball of radius r in ${\mathbb{R}}^n$; moreover, under the isometry the strata ${\sigma }_{n1}$ and ${\sigma }_{n2}$ go onto two half-balls separated by an $(n-1)$-dimensional disk which is the image of ${\sigma }_{n-1}$. The function $\tilde{u}$ corresponding to u under the isometry is an ordinary harmonic function on the Euclidean ball and the required estimate is valid for it. By isometry, the required estimate holds for u, too.

Proceeding as in the proof of Lemma 1, we may assume that we have $2l$ strata ${\sigma }_{nj}$, $j=1,\cdots ,2l$, contiguous to ${\sigma }_{n-1}$. Repeating the construction from the proof of Lemma 1, we take a Euclidean ball B of radius r in ${\mathbb{R}}^n$ divided into two half-balls $B^1$ and $B^2$ resting on an $(n-1)$-dimensional disk D. Next, for an arbitrary collection $J\subset \{1,2,\cdots ,2l\}$ of l distinct numbers and the complementary collection $\overline{J}$, we obtain the functions $u_j$ on $B^1\cup D$, $j\in J$, and the functions $u_{\overline{j}}$ on $B^2\cup D$, $\overline{j}\in \overline{J}$, that correspond to the functions ${u|}_{{\sigma }_{nj}\cup {\sigma }_{n-1}}$, $j\in J$, and the functions ${u|}_{{\sigma }_{n\overline{j}}\cup {\sigma }_{n-1}}$, $\overline{j}\in \overline{J}$, by isometry. Then the function $u_J$, equal to ${\sum }_{j\in J}{u}_j$ on $B^1\cup D$ and equal to ${\sum }_{\overline{j}\in \overline{J}}{u}_{\overline{j}}$ on $B^2\cup D$, is an ordinary harmonic function on B and for it we have the required estimate. Since this is true for any J, an easy combinatorics shows that the sought estimate is valid for each function $u_j$, $j=1,\cdots ,2l$, and by isometry for the function u. □

Another proof can be accessed by utilizing the Poisson integral representation in admissible stratified balls centered at points of an $(n-1)$-dimensional stratum.

The following lemma is quite evident geometrically.

Lemma 8. 

If $X\in {\mathsf{\Sigma }}^n$ then $\mathrm{dist}(X,{\mathsf{\Sigma }}_{n-1}\cup 𝜕{\mathsf{\Omega }}^{\circ })$ is an admissible radius for X. There exists $\alpha \in (0,1]$ (depending on Ω) such that if $X\in {\mathsf{\Sigma }}^{n-1}$ then $\alpha \mathrm{dist}(X,{\mathsf{\Sigma }}_{n-2}\cup 𝜕{\mathsf{\Omega }}^{\circ })$ is an admissible radius for X.

Proof of Theorem 4. 

Take $X\in {\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}$ and

$$\rho =\mathrm{dist}(X,{\mathsf{\Sigma }}_{n-2}\cup 𝜕{\mathsf{\Omega }}^{\circ }).$$

If $\mathrm{dist}(X,{\mathsf{\Sigma }}^{n-1})<\alpha \rho /4$ then there is an $(n-1)$-dimensional stratum ${\sigma }_{n-1}$ and a point $X_0\in {\sigma }_{n-1}$ such that $X\in B_{\alpha \rho /4}\left(X_0\right)$. Observe that $\mathrm{dist}(X_0,{\mathsf{\Sigma }}_{n-2}\cup 𝜕{\mathsf{\Omega }}^{\circ })>\rho /2$. By Lemma 8, $\alpha \rho /2$ is an admissible radius for $X_0$ and by Lemma 7

$$|\nabla u\left(X\right)|\le \frac{2C}{\alpha \rho }\underset{B_{\alpha \rho /2}\left(X_0\right)}{sup}\left|u\right|.$$

If $\mathrm{dist}(X,{\mathsf{\Sigma }}^{n-1})\ge \alpha \rho /4$ then, by Lemma 8, $\alpha \rho /4$ is an admissible radius for X and by Lemma 7

$$|\nabla u\left(X\right)|\le \frac{4C}{\alpha \rho }\underset{B_{\alpha \rho /4}\left(X\right)}{sup}\left|u\right|.$$

Anyway we get the required estimate. □

4.2. Gradient Flux

Theorem 5. 

Let Ω be a stratified set whose free strata have the same dimension n and let $u:{\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}\to \mathbb{R}$ be a bounded harmonic function. Then $\nabla u$ has zero flux through any admissible sphere $S_r\left(X\right)$:

$${\int }_{S_r\left(X\right)}{(p\nabla u)}_{\nu }d{\mu }_S=0.$$

(10)

Proof. 

If $B_r\left(X\right)\cap {\mathsf{\Sigma }}_{n-2}=⌀$ then the conclusion of the lemma follows from the application of the divergence theorem, which is expressed by (1), to the vector field $p\nabla u\in {\overrightarrow{C}}^1\left(B_r\left(X\right)\right)$, with the equality $\nabla ·(p\nabla u)=0$ taken into account.

Therefore, assume $B_r\left(X\right)\cap {\mathsf{\Sigma }}_{n-2}\ne ⌀$. Let

$${\sigma }_{d_{1}1},{\sigma }_{d_{2}1},\cdots ,{\sigma }_{d_2{j}_2},\cdots ,{\sigma }_{d_{k}1},\cdots ,{\sigma }_{d_k{j}_k}$$

be all strata whose closures contain X and dimensions do not exceed $n-2$. Consider the dimensions to increase:

$$d_1<d_2<\cdots <d_k\le n-2.$$

Note that there is exactly one stratum, ${\sigma }_{d_{1}1}$, of dimension $d_1$, and $X\in {\sigma }_{d_{1}1}$.

Let $0<{\rho }_1<r$ and

$${\sigma }_{d_{1}1}\left({\rho }_1\right)=\{Z\in B_r\left(X\right):\mathrm{dist}(Z,{\sigma }_{d_{1}1})<{\rho }_1\}.$$

Choose ${\rho }_2$, $0<{\rho }_2<{\rho }_1$, so that the sets

$${\sigma }_{d_{2}j}\left({\rho }_2\right)=\{Z\in B_r\left(X\right):\mathrm{dist}(Z,{\sigma }_{d_{2}j})<{\rho }_2\}\setminus {\sigma }_{d_{1}1}\left({\rho }_1\right)$$

be pairwise disjoint for $j=1,\cdots ,j_2$ and do not intersect the strata ${\sigma }_{d_{i}j}$, $i>2$, that are not contiguous to ${\sigma }_{d_{2}j}$.

Proceeding by induction, finally choose ${\rho }_k$, $0<{\rho }_k<{\rho }_{k-1}$, so that the sets

$${\sigma }_{d_{k}j}\left({\rho }_k\right)=\{Z\in B_r\left(X\right):\mathrm{dist}(Z,{\sigma }_{d_{k}j})<{\rho }_k\}\setminus \bigcup _{i\le k-1,s}{\sigma }_{d_{i}s\left({\rho }_i\right)}$$

be pairwise disjoint for $j=1,\cdots ,j_k$.

Put for $l=1,\cdots ,k$

$$\mathsf{\Sigma }({\rho }_1,\cdots ,{\rho }_l)=\bigcup _{i\le l,s}{\sigma }_{d_{i}s\left({\rho }_i\right)}$$

and consider the stratified set

$${\mathcal{P}}_l=\left(B_r\left(X\right)\cup S_r\left(X\right)\right)\setminus \mathsf{\Sigma }({\rho }_1,\cdots ,{\rho }_l)$$

with boundary

$$𝜕{\mathcal{P}}_l^{\circ }=\left(S_r\left(X\right)\setminus \mathsf{\Sigma }({\rho }_1,\cdots ,{\rho }_l)\right)\cup \bigcup _{i\le l,s}{\mathsf{\Gamma }}_{d_{i}s}^l,$$

where

$${\mathsf{\Gamma }}_{d_{i}s}^l={\mathsf{\Gamma }}_{d_{i}s}^l({\rho }_1,\cdots ,{\rho }_l)=\{Z\in B_r\left(X\right):\mathrm{dist}(Z,{\sigma }_{d_{i}s})={\rho }_i\}\setminus \mathsf{\Sigma }({\rho }_1,\cdots ,{\rho }_l).$$

Figure 6 shows what remains after erasing the “cylinders” ${\sigma }_{d_{k}j}\left({\rho }_k\right)$ from the ball; in three-dimensional space the process of constructing ${\mathcal{P}}_l$ is not very diverse and might involve only one or two steps in dependence of the dimension of the stratum containing the center of the ball. In this figure the invisible part of the sphere is also included into the boundary $𝜕{\mathcal{P}}_l^{\circ }$.

Inducting on l decreasing from $l=k$ to 0, let us prove that

$${\int }_{𝜕{\mathcal{P}}_l^{\circ }}{(p\nabla u)}_{\nu }d\mu =0,$$

(11)

where $d\mu$ is the stratified measure on $𝜕{\mathcal{P}}_l^{\circ }$.

Take $l=k$. The set $\mathsf{\Sigma }({\rho }_1,\cdots ,{\rho }_k)$ represents a neighborhood of the set ${\mathsf{\Sigma }}_{n-2}\cap B_r\left(X\right)$. Then $p\nabla u\in {\overrightarrow{C}}^1\left({\mathcal{P}}_k^{\circ }\right)$, and the divergence theorem (see (1)) gives

$${\int }_{𝜕{\mathcal{P}}_k^{\circ }}{(p\nabla u)}_{\nu }d\mu =0,$$

which justifies the induction base.

Assuming (11) true, let us validate the equality for $l-1$. We have

$$𝜕{\mathcal{P}}_l^{\circ }=\left(𝜕{\mathcal{P}}_{l-1}^{\circ }\setminus \bigcup _s{\sigma }_{d_{l}s}\left({\rho }_l\right)\right)\cup \bigcup _s{\mathsf{\Gamma }}_{d_{l}s}^l.$$

Hence,

$${\int }_{𝜕{\mathcal{P}}_{l-1}^{\circ }\setminus {\bigcup }_{s=1}^{j_l}{\sigma }_{d_{l}s}\left({\rho }_l\right)}{(p\nabla u)}_{\nu }d\mu =\sum _{s=1}^{j_l}{\int }_{{\mathsf{\Gamma }}_{d_{l}s}^l}{(p\nabla u)}_{\nu }d\mu ,$$

(12)

where the signs of the integrals on the right-hand side are chosen in accord with the fact that ${\mathsf{\Gamma }}_{d_{l}s}^l$ as part of the boundary of ${\sigma }_{d_{l}s}\left({\rho }_l\right)$.

The next relations will be justified below:

$$\underset{{\rho }_l\to 0}{lim}{\int }_{𝜕{\mathcal{P}}_{l-1}^{\circ }\setminus {\bigcup }_{s=1}^{j_l}{\sigma }_{d_{l}s}\left({\rho }_l\right)}{(p\nabla u)}_{\nu }d\mu ={\int }_{𝜕{\mathcal{P}}_{l-1}^{\circ }}{(p\nabla u)}_{\nu }d\mu ,$$

(13)

$$\underset{{\rho }_l\to 0}{lim}{\int }_{{\mathsf{\Gamma }}_{d_{l}s}^l({\rho }_1,\cdots ,{\rho }_l)}{(p\nabla u)}_{\nu }d\mu =0.$$

(14)

Applying them, we get from (12):

$${\int }_{𝜕{\mathcal{P}}_{l-1}^{\circ }}{(p\nabla u)}_{\nu }d\mu =0,$$

completing validation of the induction step.

Since $𝜕{\mathcal{P}}_0^{\circ }=S_r\left(X\right)$, the equality (11) for $l=0$ coincides with (10).

To finish the proof of the theorem, it remains to justify (13) and (14).

Since $p=1$ on the strata of dimension n and $p=0$ on the other strata, we have

$${\int }_{𝜕{\mathcal{P}}_{l-1}^{\circ }}{(p\nabla u)}_{\nu }d\mu =\sum _j{\int }_{{\sigma }_{nj}\cap 𝜕{\mathcal{P}}_{l-1}^{\circ }}{(\nabla u)}_{\nu }d{\mu }^{n-1},$$

(15)

where the summation is over all n-dimensional strata whose closures contain X, and $d{\mu }^{n-1}$ is the surface $(n-1)$-measure.

By Theorem 4, the estimate holds:

$$|\nabla u\left(Z\right)|\le \frac{C}{\mathrm{dist}(Z,{\mathsf{\Sigma }}_{n-2})}.$$

(16)

The following lemma is rather obvious and we leave it without proof.

Lemma 9. 

Let $L_d$ be a d-dimensional affine subspace of ${\mathbb{R}}^n$, $d\le n-2$, and G an $(n-1)$-dimensional compact peacewise smooth surface in ${\mathbb{R}}^n$ which is smooth in a neighborhood of the intersection $G\cap L_d$ and is transversal to $L_d$. Then the function

$$f\left(x\right)=\frac{1}{\mathrm{dist}(x,L_d)}$$

is integrable with respect to the surface $(n-1)$-measure on G.

Note that for $Z\in {\sigma }_{nj}$

$$\frac{1}{\mathrm{dist}(Z,{\mathsf{\Sigma }}_{n-2})}\le \sum _{i,s}\frac{1}{\mathrm{dist}(Z,L_{d_{i}s})},$$

where $L_{d_{i}s}$ is the affine subspace including ${\sigma }_{d_{i}s}$, and $\mathrm{dist}(Z,L_{d_{i}s})$ is the distance from Z to $L_{d_{i}s}$ inside $L_{nj}$. From (15)–(16) and Lemma 9 we then conclude that ${(p\nabla u)}_{\nu }$ is $\mu$-integrable on $𝜕{\mathcal{P}}_{l-1}^{\circ }$. This proves (13).

By analogy to (15), we have

$${\int }_{{\mathsf{\Gamma }}_{d_{l}s}^l({\rho }_1,\cdots ,{\rho }_l)}{(p\nabla u)}_{\nu }d\mu =\sum _j{\int }_{{\sigma }_{nj}\cap {\mathsf{\Gamma }}_{d_{l}s}^l}{(\nabla u)}_{\nu }d{\mu }^{n-1},$$

(17)

with the summation taken over the n-dimensional strata contiguous to ${\sigma }_{d_{l}s}$.

Fix a stratum ${\sigma }_{nj}$ contiguous to ${\sigma }_{d_{l}s}$ and consider

$$\phi \left({\rho }_l\right)={\int }_{{\sigma }_{nj}\cap {\mathsf{\Gamma }}_{d_{l}s}^l({\rho }_1,\cdots ,{\rho }_l)}{(\nabla u)}_{\nu }d{\mu }^{n-1}={\int }_{{\sigma }_{nj}\cap {\mathsf{\Gamma }}_{d_{l}s}^l({\rho }_1,\cdots ,{\rho }_l)}\frac{𝜕u}{𝜕\nu }d{\mu }^{n-1}.$$

(18)

First, suppose that $d_l\le n-3$. In view of (16),

$$|\phi \left({\rho }_l\right)| \le {\int }_{{\sigma }_{nj}\cap {\mathsf{\Gamma }}_{d_{l}s}^l({\rho }_1,\cdots ,{\rho }_l)}\frac{C}{\mathrm{dist}(Z,{\mathsf{\Sigma }}_{n-2})}d{\mu }^{n-1}.$$

(19)

The following assertion is proven by straightforward calculations.

Lemma 10. 

Let $L_d\subset L_m$ be a d-dimensional and an m-dimensional affine subspaces of ${\mathbb{R}}^n$, $d\le m\le n-2$, let ${\sigma }_d\subset L_d$ be a bounded open subset, and

$$\mathsf{\Gamma }\left(\rho \right)=\{x\in {\mathbb{R}}^n:\mathrm{dist}(x,{\sigma }_d)=\rho \}.$$

Then

$${\int }_{\mathsf{\Gamma }\left(\rho \right)}\frac{1}{\mathrm{dist}(x,L_m)}d{\mu }^{n-1}=C(d,m,n){\rho }^{n-d-2}{\mu }^d\left({\sigma }_d\right).$$

From (19) and Lemma 10 we obtain ${lim}_{{\rho }_l\to 0}\phi \left({\rho }_l\right)=0$ when $d_l\le n-3$.

Now, we examine the case $d_l=n-2$. In this case $l=k$ and $d_k=n-2$. To simplify notations, we henceforth denote ${\rho }_k$ by $\rho$, the stratum ${\sigma }_{nj}$ by ${\sigma }_n$, the stratum ${\sigma }_{d_{k}s}$ by ${\sigma }_{n-2}$, and denote ${\mathsf{\Gamma }}_{d_{k}s}^k({\rho }_1,\cdots ,{\rho }_k)$ by $\mathsf{\Gamma }\left(\rho \right)$. Then

$$\mathsf{\Gamma }\left(\rho \right)=\{Z\in {\sigma }_n\cap B_r\left(X\right):\mathrm{dist}(Z,{\sigma }_{n-2})=\rho \}\setminus \mathsf{\Sigma }({\rho }_1,\cdots ,{\rho }_{k-1})$$

and $\mathsf{\Sigma }({\rho }_1,\cdots ,{\rho }_{k-1})$ is a neighborhood of $𝜕{\sigma }_{n-2}\cap B_r\left(X\right)$.

Let us show that the limit ${lim}_{\rho \to 0}\phi \left(\rho \right)$ exists. Fix an arbitrary admissible value $\overline{\rho }>0$ for ${\rho }_k$ and, considering $\rho \in (0,\overline{\rho })$, define the stratified set

$$\mathcal{Q}=\{Z\in {\sigma }_n\cap B_r\left(X\right):\rho \le \mathrm{dist}(Z,{\sigma }_{n-2})\le \overline{\rho }\}\setminus \mathsf{\Sigma }({\rho }_1,\cdots ,{\rho }_{k-1}),$$

whose interior ${\mathcal{Q}}^{\circ }$ and boundary $𝜕\mathcal{Q}$ are determined relative to the topology of $\mathsf{\Omega }$. Note that $p\nabla u\in {\overrightarrow{C}}^1\left(\mathcal{Q}\right)$ and by the divergence theorem

$${\int }_{𝜕\mathcal{Q}}{(p\nabla u)}_{\nu }d\mu =0.$$

Hence,

$$\phi \left(\rho \right)={\int }_{\mathsf{\Gamma }\left(\rho \right)}\frac{𝜕u}{𝜕\nu }d{\mu }^{n-1}={\int }_{𝜕\mathcal{Q}\setminus \mathsf{\Gamma }\left(\rho \right)}{(p\nabla u)}_{\nu }d\mu .$$

The last integral can be treated in the same way as in the deduction of (13). This proves the existence of the limit ${lim}_{\rho \to 0}\phi \left(\rho \right)$.

Suppose this limit is nonzero, say ${lim}_{\rho \to 0}\phi \left(\rho \right)>0$.

Denote by G the projection of $\mathsf{\Gamma }\left(\overline{\rho }\right)$ to ${\sigma }_{n-2}$,

$$\tilde{\mathsf{\Gamma }}\left(\rho \right)=\{Z\in {\sigma }_n\cap B_r\left(X\right):\mathrm{dist}(Z,G)=\rho \}$$

and

$$\tilde{\phi }\left(\rho \right)={\int }_{\tilde{\mathsf{\Gamma }}\left(\rho \right)}\frac{𝜕u}{𝜕\nu }d{\mu }^{n-1}.$$

If $\overline{\rho }$ is small enough, the $(n-2)$-measure of the difference between G and the projection of $\mathsf{\Gamma }\left(\rho \right)$ to ${\sigma }_{n-2}$ is arbitrarily small for $\rho \in (0,\overline{\rho })$. In view of Theorem 4 and Lemma 10 applied with $d=m=n-2$, we conclude that for $\overline{\rho }>0$ sufficiently small, the values of the functions $\phi \left(\rho \right)$ and $\tilde{\phi }\left(\rho \right)$ differ by a quantity which is arbitrarily small for $\rho \in (0,\overline{\rho })$ and, in consequence, the following inequality holds (with some $\delta$):

$$\tilde{\phi }\left(\rho \right)\ge \delta >0,\rho \in (0,\overline{\rho }).$$

(20)

Look at the integral

$${\int }_0^{\overline{\rho }}\frac{\tilde{\phi }\left(\rho \right)}{\rho }d\rho ={\int }_0^{\overline{\rho }}\frac{1}{\rho }\left({\int }_{\tilde{\mathsf{\Gamma }}\left(\rho \right)}\frac{𝜕u}{𝜕\nu }d{\mu }^{n-1}\right)d\rho .$$

In the n-dimensional affine subspace $L_n$ including ${\sigma }_n$, consider the coordinates $(z^{\prime },\rho ,\theta )$, where $z^{\prime }$ are the Cartesian coordinates of the projection $Z^{\prime }$ of $Z\in L_n$ to the affine $(n-2)$-dimensional subspace $L_{n-2}$ including ${\sigma }_{n-2}$, and $(\rho ,\theta )$ are the polar coordinates with center $Z^{\prime }$ in the plane orthogonal to $L_{n-2}$ in $L_n$.

Since

$$d{\mu }^{n-1}=\rho d{z}^{\prime }d\theta ,$$

we have

$$\begin{array}{c}{\int }_0^{\overline{\rho }}\frac{1}{\rho }\left({\int }_{\tilde{\mathsf{\Gamma }}\left(\rho \right)}\frac{𝜕u}{𝜕\nu }d{\mu }^{n-1}\right)d\rho ={\int }_0^{\overline{\rho }}{\int }_G{\int }_{\mathsf{\Phi }}\frac{𝜕u}{𝜕\rho }(z^{\prime },\rho ,\theta )d\theta d{z}^{\prime }d\rho \hfill \\ \hfill \hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\int }_G{\int }_{\mathsf{\Phi }}\left(u(z^{\prime },\overline{\rho },\theta )-u(z^{\prime },0,\theta )\right)d\theta d{z}^{\prime }\le C\underset{B_r\left(X\right)\setminus {\mathsf{\Sigma }}_{n-2}}{sup}\left|u\right|,\end{array}$$

(21)

i.e., the integral is finite. On the other hand, by (20) the integral must diverge. This contraction completes the proof of relation (14), as well as the proof of Theorem 5. □

4.3. Proof of Lemma 3

Without loss of generality, we assume $\mathsf{\Omega }$ to have the structure of a stratified ball of admissible radius with center at a point $X_0$. Consider spherical coordinates $(r,\varphi )$ with center $X_0$. Then

$$\frac{1}{r^{n-1}}d{\mu }^{n-1}=d\varphi .$$

For $\delta >0$ small enough, we have

$$\frac{M\left[S_{r+\delta }\left(X_0\right)\right]u-M\left[S_r\left(X_0\right)\right]u}{\delta }=\frac{1}{\omega }{\int }_{\mathsf{\Phi }}\frac{u(r+\delta ,\varphi )-u(r,\varphi )}{\delta }d\varphi ,$$

where $\mathsf{\Phi }$ is the set of directions corresponding to the $(n-1)$-dimensional regions of the stratified sphere $S_r\left(X_0\right)$. Since u is smooth on the n-dimensional strata, it follows that as $\delta \to 0$

$$\frac{u(r+\delta ,\varphi )-u(r,\varphi )}{\delta }\to \frac{𝜕u(r,\varphi )}{𝜕r}.$$

By the finite increment formula, we have for some $r^{*}\in (r,r+\delta )$

$$\left|\frac{u(r+\delta ,\varphi )-u(r,\varphi )}{\delta }\right|=\left|\frac{𝜕u(r^{*},\varphi )}{𝜕r}\right|\le |\nabla u(r^{*},\varphi )|.$$

By Theorem 4

$$\begin{array}{cc}\hfill |\nabla u(r^{*},\varphi \left)\right|& \le \frac{C}{\mathrm{dist}(X(r^{*},\varphi ),{\mathsf{\Sigma }}_{n-2}\cup 𝜕{\mathsf{\Omega }}^{\circ })}\underset{{\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}}{sup}\left|u\right|\hfill \\ \hfill & \le \frac{C}{\mathrm{dist}(X(r,\varphi ),{\mathsf{\Sigma }}_{n-2}\cup 𝜕{\mathsf{\Omega }}^{\circ })}\underset{{\mathsf{\Omega }}^{\circ }\setminus {\mathsf{\Sigma }}_{n-2}}{sup}\left|u\right|.\hfill \end{array}$$

The last inequality holds because the distance from X to ${\mathsf{\Sigma }}_{n-2}$ increases when X moves from $X_0$ along a radius. Thus,

$$\frac{u(r+\delta ,\varphi )-u(r,\varphi )}{\delta }$$

is dominated by an integrable function. By Lebesgue’s dominated convergence theorem

$$\frac{M\left[S_{r+\delta }\left(X\right)\right]u-M\left[S_r\left(X\right)\right]u}{\delta }\to \frac{1}{\omega }{\int }_{\mathsf{\Phi }}\frac{𝜕u(r,\varphi )}{𝜕r}d\varphi =\frac{1}{\omega r^{n-1}}{\int }_{S_r\left(X\right)}\frac{𝜕u(r,\varphi )}{𝜕\nu }d{\mu }^{n-1}.$$

The last integral vanishes in virtue of Theorem 5.

Thus,

$$\frac{d}{dr}M\left[S_r\left(X\right)\right]=0$$

and the value of $M\left[S_r\left(X\right)\right]$ does not depend on r, which completes the proof of Lemma 3.