Prerpints.org logo
Preprint
Article

Distributed Temperature Sensing through Network Analysis Frequency-Domain Reflectometry

Altmetrics

Downloads

95

Views

55

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 February 2024

Posted:

26 February 2024

You are already at the latest version

Alerts
Abstract
In this paper, we propose and demonstrate a network analysis optical frequency domain reflectometer (NA-OFDR) for distributed temperature measurements at high spatial (down to 3 cm) and temperature resolution. The system makes use of a frequency-stepped, continuous-wave (cw) laser, whose output light is modulated using a vector network analyzer. The latter is also used to demodulate the amplitude of the beat signal obtained by coherently mixing the Rayleigh backscattered light with a local oscillator. The system is capable of high measurand resolution (50 mK at 3-cm spatial resolution), thanks to the high sensitivity of coherent Rayleigh scattering to temperature. Furthermore, compared to the conventional optical-frequency domain reflectometry (OFDR), the proposed system does not rely on the use of a tunable laser, therefore it is less prone to limitations related to the laser coherence or sweep nonlinearity. Two configurations are analyzed, both numerically and experimentally, based on either a double sideband or single sideband modulated probe light. The results confirm the validity of the proposed approach.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Distributed optical fiber sensors can monitor the continuous spatial profile of temperature and strain, usually exploiting some scattering mechanism occurring in optical fibers [1]. Distributed sensors based on Brillouin scattering are capable of long range [2], and in some cases high spatial resolution [3,4,5] measurements. However, the measurand resolution is somewhat limited by the relatively low sensitivity of the Brillouin frequency shift to temperature (≈1 MHz/°C) and strain (≈50 kHz/µε). Instead, distributed sensors based on Rayleigh scattering benefit from a much larger sensitivity of the Rayleigh spectrum to these measurands (≈1.3 GHz/°C and 150 MHz/με, respectively) [6]. In order to measure the Rayleigh spectral shift, two approaches are commonly adopted: the Optical Frequency-Domain Reflectometry (OFDR), operating in the frequency domain, and the phase-sensitive Optical Time-Domain Reflectometry (Φ−OTDR), operating in the time-domain. In the former approach, the backscatter Rayleigh complex field is typically acquired by scanning the frequency of a tunable laser over a wide range, while recovering the positional information through Fourier transform [6]; in the Φ−OTDR approach, instead, the Rayleigh backscatter is acquired using a pulsed source, while scanning the laser frequency over a relatively narrow range [7]. In both cases, the temperature (or strain) variations are recovered by cross correlating the Rayleigh spectra acquired in two consecutive measurements. Comparing the two approaches, the time-domain configuration is less prone to laser coherence limitations; in fact, a km-scale sensing range can be easily reached. Furthermore, the scan of the laser frequency can be avoided by using linearly chirped probe pulses, enabling faster, single-shot measurements [8]. Nonetheless, the use of a pulsed source usually involves a trade-off between the signal-to-noise ratio (SNR) and the spatial resolution: using a shorter pulse improves the spatial resolution at the cost of a lower backscattered energy [9]. On the other hand, the OFDR approach ensures a finer spatial resolution, owing to the much larger amount of energy injected into the fiber. As a matter of fact, commercial OFDR equipment can reportedly perform distributed temperature measurements with a temperature resolution of ± 0.1°C and a spatial resolution of 1 cm [10].
Recently, we have demonstrated a novel OFDR method based on a single-frequency laser and a vector network analyzer (VNA) [11]. In this technique, named NA-OFDR, the VNA output is employed to impress a small sinusoidal modulation to the laser light, while the backscatter signal is mixed with a local oscillator and demodulated by the VNA. Finally, the acquired data are inverse Fourier transformed to recover the spatial information, at a spatial resolution determined by the modulation frequencies scanned by the VNA [12]. In Ref. [11] the NA-OFDR method was applied to detect vibrations (strain) at a rate much larger than what is commonly allowed by OFDR. In this paper, the same NA-OFDR configuration is employed for static temperature measurements. Compared to the conventional OFDR method, the NA-OFDR keeps high spatial resolution capabilities, with the added advantage of not requiring a tunable laser nor a trigger interferometer.
Compared to the NA-OFDR configuration recently applied to vibration sensing, the method proposed here has two fundamental differences: first, we use the amplitude rather than the phase of the Rayleigh backscattered light. Second, the coherent Rayleigh trace is acquired for a discrete set of laser frequencies, which permits to reconstruct the Rayleigh spectrum at each fiber position. The temperature information is then recovered by cross correlating the Rayleigh spectra acquired in two consecutive measurements, as in conventional OFDR sensors.
In analogy to Ref. [11], two modulation formats of the probe light are analyzed here: single sideband (SSB), and double sideband (DSB) modulation. In the following, the two configurations are first numerically analyzed and then experimentally assessed, demonstrating their capability to realize distributed measurements with high spatial and temperature resolution.

2. Numerical analysis

The model developed in Ref. [11] describes the baseband transfer function of the fiber, as obtained by coherently mixing the Rayleigh backscatter excited by a DSB or an SSB-modulated probe with a local oscillator and demodulated by the VNA. The model calculates the Rayleigh backscatter assuming a random distribution of the scatterers along the fiber. For an optical fiber with N scatterers, the VNA output using a DSB- or SSB-modulated probe is given by [11]:
S 21 D S B ( ω m ) ∝ ∑ i = 1 N 4 a i c o s ( 2 k 0 z i ) e j ( − 2 ω m v z i )
S 21 S S B ( ω m ) ∝ ∑ i = 1 N 2 a i e x p ( 2 j k 0 z i ) e j ( − 2 ω m v z i )
In Eqs. (1-2), z i and a i are the positions and reflection coefficients of the N scatterers; k 0 = ω 0 v is the wavenumber corresponding to the laser angular frequency ω 0 , v = c n is the phase velocity, and ω m is the angular frequency modulation impressed by the VNA. Given the scatterers distribution, Eqs. (1-2) can be used to calculate S 21 ( ω m ) for a discrete set of modulation frequencies ω m . Then, the spatial distribution of the Rayleigh scatter amplitude (and phase) is obtained by applying an inverse Fourier transform to S 21 ( ω m ) and converting the time coordinate into a spatial one using z = v g 2 t , v g being the group velocity of the optical guided mode. The choice of the modulation frequencies ω m is related to the fiber length and target spatial resolution, according to the following relationships [12]:
S R = π v g ω m , m a x − ω m , m i n
L m a x = π v g Δ ω m
where S R is the spatial resolution, L m a x is the maximum length of the fiber, ω m , m a x and ω m , m i n are the maximum and minimum modulation angular frequencies, respectively, and Δ ω m is the angular modulation frequency step.
Since the temperature (or strain) change is recovered from the shift of the Rayleigh backscatter power in the laser-frequency domain, the coherent Rayleigh trace must be computed over a range of laser frequencies [7]. When some temperature or strain perturbation acts on the fiber, the positions z i of the scatterers falling within the perturbed area are progressively shifted by an amount depending on the applied perturbation, while all scatterers after the perturbed area are shifted by the same quantity. Furthermore, the refractive index in the perturbed area changes due to thermo-optic or elasto-optic effect [13]. The new distribution of the scatterers can then be used to recalculate the fiber response over the same set of laser frequencies. Finally, as the Rayleigh spectrum has a speckle-like appearance, the temperature (or strain) induced shift is determined, at each fiber position, by cross correlating the Rayleigh spectrum with the one measured under known environmental conditions, as in conventional OFDR sensors.
At first, we analyze the fiber response in absence of perturbations, by calculating the autocorrelation of the Rayleigh spectrum. In the following, we assume a fiber length of 60 m and an average distance between the scatterers equal to 1 mm. The spatial resolution was set to 1 m or 10 cm, by calculating S 21 ( ω m ) up to ω m , m a x = 2 π × 100   M H z or 2 π × 1   G H z , respectively. Note that, the average distance between the scatterers was, in both cases, much shorter than the spatial resolution, thus meeting the requirements discussed in Ref. [13]. The laser frequency was varied over an interval of 10 GHz, with a frequency step of 25 MHz. The results relative to a DSB-, or SSB-modulated probe are visualized in Figure 1. The simulation data indicate that, for an SSB modulated-probe, the 3-dB bandwidth of the autocorrelation increases from ≈ 61 MHz at SR = 1 m, to ≈ 339 MHz at SR = 10 cm. For a DSB-modulated probe, the autocorrelation follows a similar behavior, with the 3-dB bandwidth increasing from ≈ 75 MHz at SR = 1 m, to ≈ 297 MHz at SR = 10 cm. The broadening of the correlation peak, similar to the one observed in time-domain schemes [14], is explained by considering that, a sharper spatial resolution implies a smaller distance between the most distant scatterers inside each resolution cell. Consequently, the interference fringes in the Rayleigh spectrum spread out, with a consequent broadening of the correlation curve. Therefore, setting a sharper spatial resolution will inevitably restrict the smallest detectable temperature (or strain) change.
More simulations were performed by varying the temperature along a 2-m central region of the fiber, from 0 °C to 0.2 °C. For these simulations, the spatial resolution was set to 1 m. We show in Figure 2 the cross-correlation of the Rayleigh spectra at the center of the hotspot, computed after scaling the spectra such that their autocorrelations at zero lag equal unity. As expected, the correlation peak shifts to the left, by an amount proportional to the temperature variation. In addition, the figure reveals that, in case of a DSB-modulated probe the amplitude of the correlation peak oscillates with the applied perturbation, while remaining more uniform in case of an SSB-modulated probe. Still, we attribute this behavior to the interference of the Rayleigh traces produced by the two probe sidebands [15]. Obviously, a too weak correlation peak could prevent a correct estimate of the Rayleigh frequency shift, whenever its amplitude falls below the background noise or the sidelobes level. Therefore, according to our analysis, the SSB modulation scheme should be preferred to the DSB modulation scheme to ensure reliable measurements.

3. Experimental results

Figure 3 shows the experimental setup used for measuring the coherent Rayleigh traces based on the here proposed NA-OFDR approach. The setup is essentially identical to the one employed in Ref. [11] for distributed vibration measurements, with the only addition of a tunable frequency shifter (composed by an SSB electro-optic modulator driven by an RF source) placed immediately after the laser. In brief, the light from a 1550-nm narrowband laser is first sent to the frequency shifter. The frequency-shifted light is then split by a 90/10 optical coupler to separate the probe light (upper branch) from the local oscillator (lower branch). The former is intensity-modulated by an electro-optic modulator (EOM1) biased at its null point and driven by the output port of the VNA, and then amplified by an erbium-doped fiber amplifier (EDFA). In the DSB-modulated probe configuration, the amplified probe is directly launched into the sensing fiber. Instead, in case of SSB-modulation, a narrowband (≈ 8 GHz FWHM) fiber Bragg grating (FBG) is inserted before the sensing fiber, selecting only one of the two sidebands generated by EOM1. Note that, for SSB modulation tests an offset of 8 GHz is applied to the modulation frequencies scanned by the VNA, ensuring that the two sidebands produced by EOM1 are separated by at least 2×8 = 16 GHz. In the receiver path, the backscattered light is mixed with the local oscillator, while the beat signal is detected through a photodetector connected to the input port of the VNA. Note that, in SSB-modulated probe experiments the local oscillator is frequency upshifted through another electro-optic modulator (EOM2) driven by an RF synthesizer at a frequency of 8 GHz. This permits to balance the offset applied to the VNA modulation frequency sweep. The same offset is also applied to the photodetector output through an RF mixer, upshifting the frequency of the beat signal by 8 GHz and thus ensuring that the VNA input sweeps the same range of its output [11]. In both cases, the mixed light is sent to a 4-GHz photodetector. For SSB experiments, the presence of EOM2 and the RF mixer in the receiver path resulted in an additional insertion loss of 8 dB, compared to DSB experiments. Finally, we observe that, while in the conventional OFDR both the probe light and local oscillator are frequency-swept, in the NA-OFDR scheme only the frequency of the probe light is swept, while the local oscillator has a fixed frequency, in analogy to the time-gated digital OFDR method [16].
For our experiments, a ≈ 55-m single-mode fiber (the AcoustiSens® by OFS) was employed as the fiber under test (FUT). This fiber provides a 13-dB enhanced Rayleigh scattering power compared to conventional single-mode fibers, while ensuring a relatively low attenuation loss (≈ 0.7 dB/km). Note that, even if the fiber has a weak grating inscribed along its length, its behavior in terms of Rayleigh backscatter is still well described by the conventional 1-D model used for simulations [11]. For each test, the state-of-polarization of the local oscillator was adjusted to maximize the average power of the detected signal. In DSB-modulated probe experiments, the laser frequency was varied by 10 GHz with a step of 25 MHz by means of the frequency shifter. Instead, in SSB-modulated probe experiments the laser frequency was swept by 4 GHz only. The reason of such reduced sweep stems from the necessity, in case of SSB-modulated probe experiments, to keep the selected probe sideband within the reflection bandwidth of the FBG, while varying both the laser frequency and the VNA modulation frequency. In case of DSB experiments, instead, no FBG was employed, therefore the laser frequency range was only limited by the bandwidth of our frequency shifter. All tests were carried out setting an IF bandwidth of the VNA equal to 100 kHz.
The first experiments were conducted sweeping the VNA modulation frequency from 1 MHz to 100 MHz, with a step of 1 MHz. These settings resulted in a spatial resolution of 1 m. A hotspot was realized by immersing a 3-m central piece of the FUT in a water bath, whose temperature was monitored through a thermocouple. As an example, we show in Figure 4 the cross-correlation of the Rayleigh spectra acquired for a water temperature variation of 0.1 °C (corresponding to a Rayleigh frequency shift of ≈-130 MHz). The same graphs also show the retrieved Rayleigh frequency shift profile. From the measurements, we derive an average temperature variation in the hotspot region equal to ≈ 0.14 °C for DSB measurements, and ≈ 0.13 °C for SSB measurements (a precalibrated factor of -1.33 GHz/K was used for frequency shift/temperature conversion). The discrepancy between the nominal and measured temperature is mostly attributed to the limited accuracy with which the temperature in the water bath could be set. Note that, in both DSB and SSB experiments, the absolute Rayliegh frequency shift (≈130 MHz) was much less than the laser frequency sweep, thus ensuring a correct result of the cross-correlation [17].
In order to have a more comprehensive assessment of the sensor performance, we have repeated the measurement for several water bath temperatures at a step of 0.1 °C. The results are summarized in Figure 5. We note that the DSB-modulated probe experiments were taken varying the temperature of the water bath up to ≈ 2.9°C, against the ≈ 1.1°C of SSB-modulated probe experiments. Such a difference derives from the different range swept by the laser frequency in the two configurations (10 GHz for the DSB probe, 4 GHz for the SSB probe). We also observe that, the hotspot size in the reconstructed profiles is progressively reduced when increasing the temperature variation. This is attributed to errors in the frequency shift estimation near the transition regions, due to the finite spatial resolution [14]. The average standard deviation of the temperature profiles outside the hotspot was ≈ 7 mK in DSB measurements, and ≈11 mK in SSB measurements. The difference between the temperature uncertainties of the two schemes is to be attributed to the lower SNR of SSB measurements, as already discussed. In both figures, the inset shows the amplitude of the correlation peak at the hotspot position. It is seen that, in both cases the correlation peak decays when increasing the temperature variation, as an obvious consequence of the limited range of the scanned laser frequencies. We also notice that the correlation peak amplitude for the DSB probe experiments does not exhibit the strong oscillations predicted by our numerical analysis. This can be attributed to the very short period of these oscillations, which are hard to be observed experimentally. For example, the simulation data in Figure 2 indicate a period of these oscillations of only 25 MHz, which corresponds to a temperature period of less than 20 mK. In practical conditions, it is difficult to control the temperature with such accuracy. In other words, the temperature fluctuations of the water bath during the acquisition of the Rayleigh traces may induce a “smearing out” of the measurement data, compared to simulation.
Further experiments were carried by scanning the VNA modulation frequency up to 3 GHz, while keeping the frequency step equal to 1 MHz. This resulted in a spatial resolution of ≈ 3 cm. For these tests, two 5-cm pieces of the same FUT, distant ≈1.7 m each other, were fixed through silicone thermal grease to a Peltier cell connected to a PID controller. A 1.2-mm thermistor-bead was also fixed to the border of the Peltier cell, using the same thermal grease. The thermoelectric system formed by the Peltier cell, the thermistor and the PID controller, allowed us to control the temperature of the fiber pieces fixed to the Peltier cell with a precision better than 0.1 °C. As in the previous tests, the laser frequency was scanned by 10 GHz for DSB experiments, or 4 GHz for SSB experiments, while the frequency step was set to 50 MHz. As an example, we show in Figure 6 the cross-correlation of the Rayleigh spectra, acquired for a nominal temperature variation of the Peltier cells equal to 1°C, with superimposed the retrieved Rayleigh frequency shift profiles.
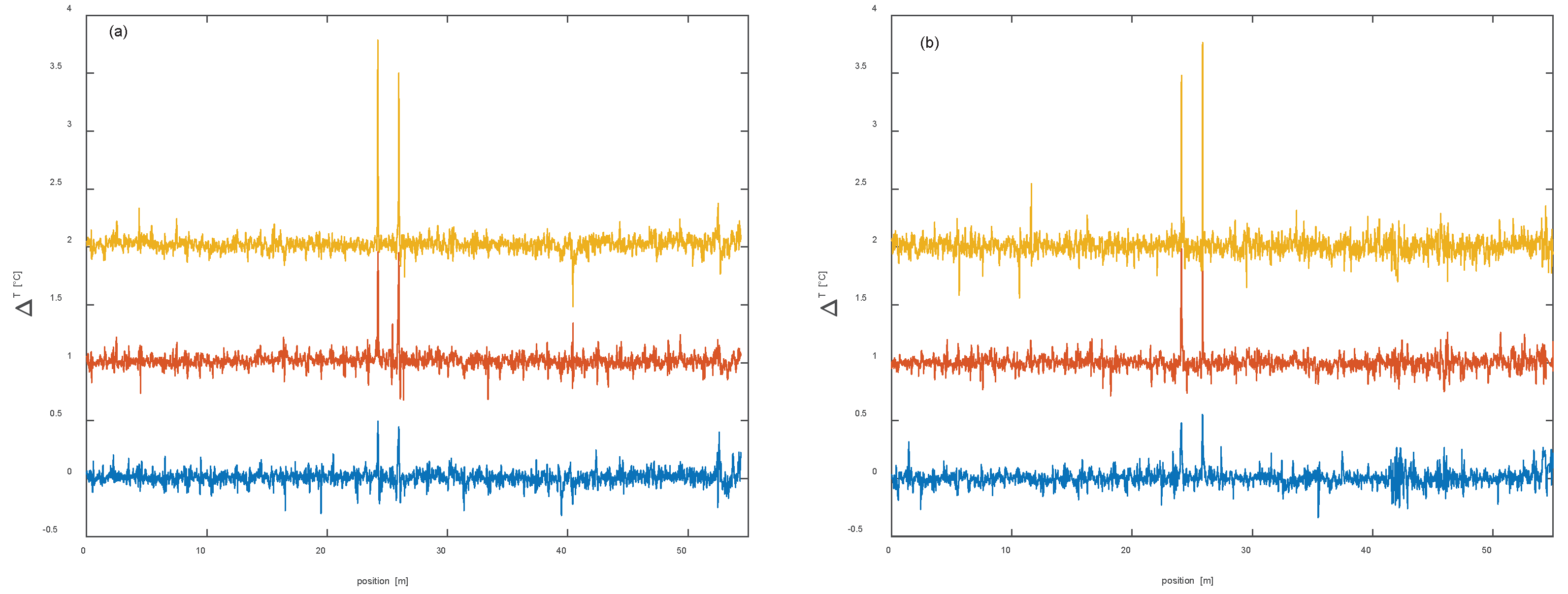
Finally, we show in Figure 7 the temperature profiles acquired for a nominal change of the temperature at the two hotspot positions equal to 0.5°C, 1°C and 1.5 °C, respectively.
We notice that, while both configurations detect the two hotspots, the SSB measurements are slightly noisier than the DSB measurements: specifically, the standard deviation of the temperature values measured outside the perturbed zones (averaged over the three tests) was ≈ 51 mK for the DSB measurements, and ≈ 55 mK for the SSB measurements. Still, we attribute this difference to the lower SNR of SSB measurements. As regards the temperature at the hotspots, the maximum deviation between the measured and nominal temperature was 0.28°C for the DSB measurements, and 0.26°C for the SSB measurements. We mostly attribute these errors to the difficulty of controlling the temperature of the fiber at the hotspots. In fact, even though the Peltier cell could control the temperature with a precision better than 0.1°C, only a portion of the fiber was in contact with the cell, while the rest was exposed to air. While the results in Figure 7 show that DSB and SSB modulation formats provide similar performance, we must recall that these results have been obtained adopting two different laser frequency sweeps. Interestingly, truncating the DSB measurements to the same laser frequency sweep adopted for SSB measurements (4 GHz), the standard deviation of the temperature values outside the hotspots increased to 81 mK, which was worse than SSB measurements, despite the 8-dB SNR advantage. Thus, it may be argued that, if a fair comparison between the two configurations could be made (i.e., ensuring the same SNR and the same laser frequency sweep range), the SSB configuration is expected to provide more accurate results than the DSB configuration, in analogy to what presented in Ref. [11].

4. Conclusions

In this paper, the NA-OFDR scheme was demonstrated for distributed temperature (and strain) measurements. The scheme is capable of high spatial and temperature resolution; therefore, it can find application whenever small, localized temperature changes must be detected. While the experiments have been performed applying small temperature variations, larger variations could be accommodated by setting the reference to the measurement immediately preceding each new measurement and summing incremental spectral shifts across all times [8,18].
Compared to the conventional OFDR method, the NA-OFDR method does not rely on a tunable laser, therefore it is less prone to the limitations imposed by the phase noise and nonlinearity of the frequency sweep [19]. Furthermore, the use of a VNA for signal demodulation is compatible with high-resolution Brillouin sensing [5], which makes this technique ready to be extended to hybrid multiparameter sensing [20,21]. Finally, the technique can be easily combined with the method demonstrated in Ref. [11] for vibration measurements, therefore it is well suited for simultaneous static and dynamic measurements.
One major issue is the frequency drift of the laser source, which causes a progressive degradation of the cross-correlation quality. In our measurements, we observed a significant drop in the correlation peak amplitude when correlating a reference trace with a measurement taken after several minutes. As a future development, we plan to improve the long-term stability of our system by locking the laser frequency to the absorption line of a gas molecule as in Ref. [7].

Author Contributions

Conceptualization, A.M. and R.V.; methodology, A.M and R. Z.; software, R.Z.; validation, R.Z. and R. V.; writing—original draft preparation, A.M.; writing—review and editing, L.Z.; funding acquisition, L.Z and A.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Italian Ministry of Education, PRIN 2022 PNRR “TU-LEARN.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are available upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hartog, A.A. An Introduction to Distributed Optical Fibre Sensors, 1st ed.; CRC Press, 2008. [Google Scholar]
  2. Soto, M.A.; et al. Extending the Real Remoteness of Long-Range Brillouin Optical Time-Domain Fiber Analyzers. J. Light. Technol. 2014, 32, 152–162. [Google Scholar] [CrossRef]
  3. Hotate, K.; Tanaka, M. Distributed fiber Brillouin strain sensing with 1-cm spatial resolution by correlation-based continuous-wave technique. IEEE Photonics Technol. Lett. 2002, 14, 179–181. [Google Scholar] [CrossRef]
  4. Li, W.; Bao, X.; Li, Y.; Chen, L. Differential pulse-width pair BOTDA for high spatial resolution sensing. Opt. Express 2008, 16, 21616–21625. [Google Scholar] [CrossRef] [PubMed]
  5. Bernini, R.; Minardo, A.; Zeni, L. Distributed Sensing at Centimeter-Scale Spatial Resolution by BOFDA: Measurements and Signal Processing. IEEE Photon. J. 2012, 4, 48–56. [Google Scholar] [CrossRef]
  6. Froggatt, M.; Moore, J. High-spatial-resolution distributed strain measurement in optical fiber with Rayleigh scatter. Appl. Opt. 1998, 37, 1735–1740. [Google Scholar] [CrossRef] [PubMed]
  7. Koyamada, Y.; Imahama, M.; Kubota, K.; Hogari, K. Fiber-Optic Distributed Strain and Temperature Sensing With Very High Measurand Resolution Over Long Range Using Coherent OTDR. J. Light. Technol. 2009, 27, 1142–1146. [Google Scholar] [CrossRef]
  8. Pastor-Graells, J.; Martins, H.F; Garcia-Ruiz, A.; Martin-Lopez, S.; Gonzalez-Herraez, M. Single-shot distributed temperature and strain tracking using direct detection phase-sensitive OTDR with chirped pulses. Opt. Express 2016, 24, 13121–13133. [Google Scholar] [CrossRef] [PubMed]
  9. Palmieri, L.; Schenato, L.; Santagiustina, M.; Galtarossa, A. Rayleigh-Based Distributed Optical Fiber Sensing. Sensors 2022, 22, 6811. [Google Scholar] [CrossRef]
  10. Available online: https://lunainc.com/sites/default/files/assets/files/resource-library/LUNA-Data-Sheet-OBR-4600-V2.pdf (accessed on 22 February 2024).
  11. Zahoor, R.; Vallifuoco, R.; Catalano, E.; Bernini, R.; Zeni, L.; Minardo, A. Distributed Vibration Sensing through a Network Analysis Optical Frequency-Domain Reflectometer. J. Light. Technol. [CrossRef]
  12. MacDonald, R.I. Frequency domain optical reflectometer. Appl. Opt. 1981, 20, 1840–1844. [Google Scholar] [CrossRef]
  13. Liokumovich, L.B.; Ushakov, N.A.; Kotov, O.I.; Bisyarin, M.A; Hartog, A.H. Fundamentals of Optical Fiber Sensing Schemes Based on Coherent Optical Time Domain Reflectometry: Signal Model Under Static Fiber Conditions. J. Light. Technol. 2015, 33, 3660–3671. [Google Scholar] [CrossRef]
  14. Lu, X.; Soto, M.A; Thévenaz, L. Temperature-strain discrimination in distributed optical fiber sensing using phase-sensitive optical time-domain reflectometry. Opt. Express 2017, 25, 16059–16071. [Google Scholar] [CrossRef] [PubMed]
  15. Koshikiya, Y.; Fan, X.; Ito, F. Long Range and cm-Level Spatial Resolution Measurement Using Coherent Optical Frequency Domain Reflectometry With SSB-SC Modulator and Narrow Linewidth Fiber Laser. J. Light. Technol. 2008, 26, 3287–3294. [Google Scholar] [CrossRef]
  16. Wang, S.; Fan, X.; Liu, Q.; He, Z. Distributed fiber-optic vibration sensing based on phase extraction from time-gated digital OFDR. Opt. Express 2015, 23, 33301–33309. [Google Scholar] [CrossRef] [PubMed]
  17. Feng, K.; Cui, J.; Jiang, D.; Dang, H.; Jin, Y.; Sun, X.; Niu, Y.; Tan, J. Improvement of the strain measurable range of an OFDR based on local similar characteristics of a Rayleigh scattering spectrum. Opt. Lett. 2018, 43, 3293–3296. [Google Scholar] [CrossRef] [PubMed]
  18. Chen, C.; Gao, S.; Chen, L.; Bao, X. Distributed High Temperature Monitoring of SMF under Electrical Arc Discharges Based on OFDR. Sensors 2020, 20, 6407. [Google Scholar] [CrossRef] [PubMed]
  19. Zhong, H.; Fu, C.; Li, P.; Du, B.; Du, C.; Meng, Y.; Yin, X.; Liao, C.; Wang, Y. Ultra-linear broadband optical frequency sweep for a long-range and centimeter-spatial-resolution OFDR. Opt. Lett. 2023, 48, 4540–4543. [Google Scholar] [CrossRef] [PubMed]
  20. Coscetta, A.; Catalano, E.; Cerri, E.; Cennamo, N.; Zeni, L.; Minardo, A. Hybrid Brillouin/Rayleigh sensor for multiparameter measurements in optical fibers. Opt. Express 2021, 29, 24025–24031. [Google Scholar] [CrossRef] [PubMed]
  21. Huang, L.; Fan, X.; He, Z. Scanning-free hybrid Rayleigh–Brillouin distributed fiber-optic sensing system. Opt. Lett. 2023, 48, 4629–4632. [Google Scholar] [CrossRef] [PubMed]
Preprints 99783 g001
Figure 1. Autocorrelation of the Rayleigh spectrum as computed for (a) a DSB-, or (b) an SSB-modulated probe.
Figure 1. Autocorrelation of the Rayleigh spectrum as computed for (a) a DSB-, or (b) an SSB-modulated probe.
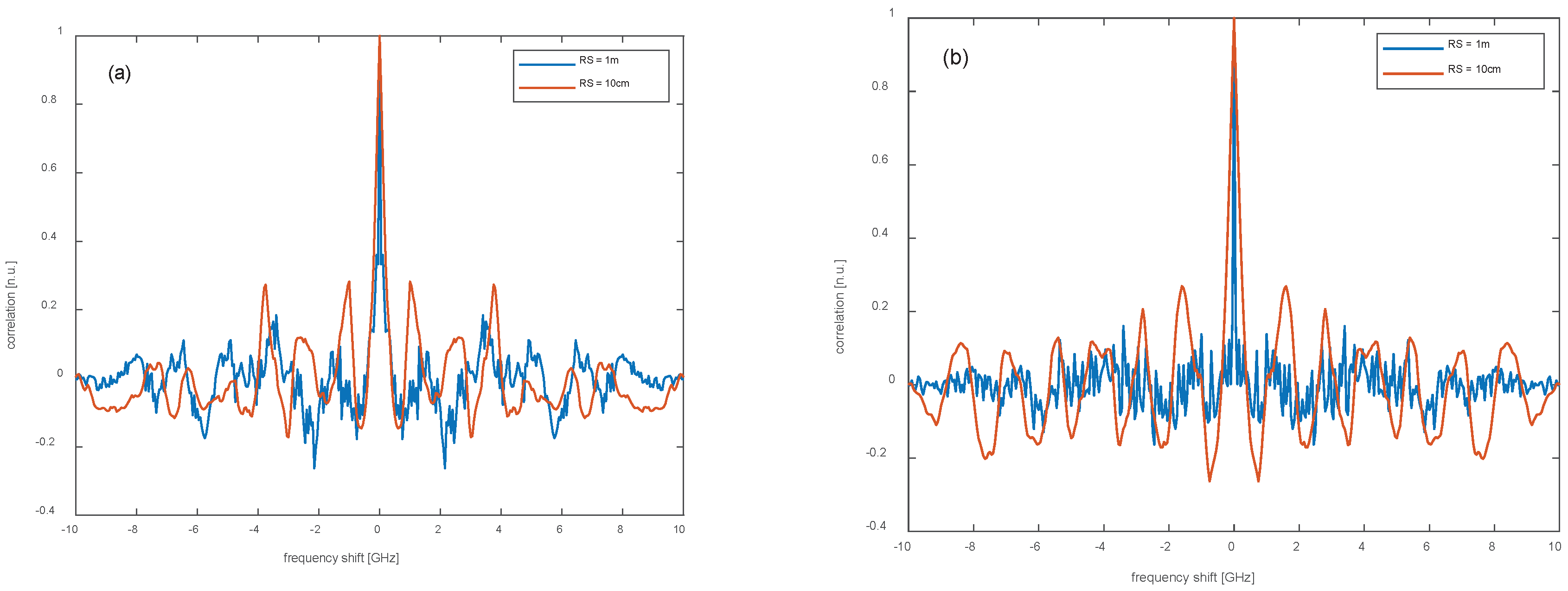
Preprints 99783 g001
Preprints 99783 g002
Figure 2. Cross-correlation of the Rayleigh spectrum as computed for (a) a DSB-, or (b) an SSB-modulated probe. The insets show the amplitude of the correlation peak versus the perturbation-induced spectral shift.
Figure 2. Cross-correlation of the Rayleigh spectrum as computed for (a) a DSB-, or (b) an SSB-modulated probe. The insets show the amplitude of the correlation peak versus the perturbation-induced spectral shift.
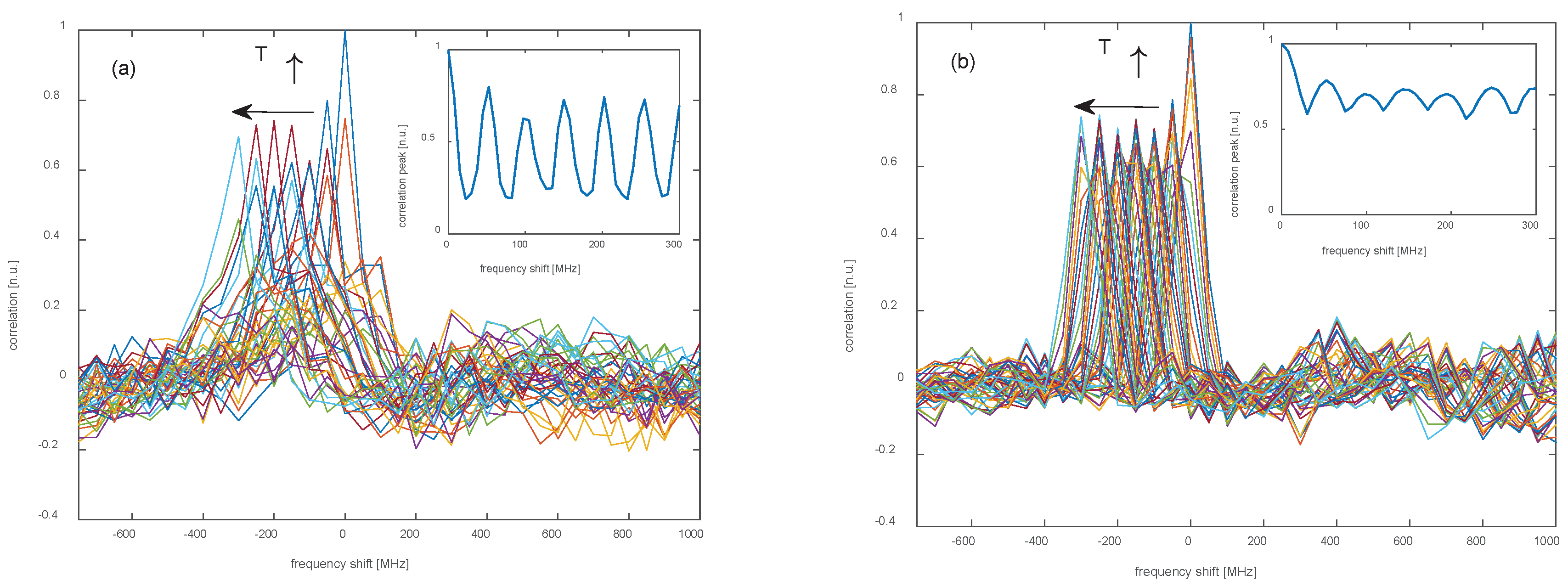
Preprints 99783 g002
Preprints 99783 g003
Figure 3. Experimental setup for NA-OFDR temperature measurements. The components inside the red dashed box are used only for SSB-modulated probe measurements. EDFA: Erbium-doped fiber amplifier; FBG: fiber Bragg grating; EOM: electro-optic modulator; VNA: vector network analyzer.
Figure 3. Experimental setup for NA-OFDR temperature measurements. The components inside the red dashed box are used only for SSB-modulated probe measurements. EDFA: Erbium-doped fiber amplifier; FBG: fiber Bragg grating; EOM: electro-optic modulator; VNA: vector network analyzer.
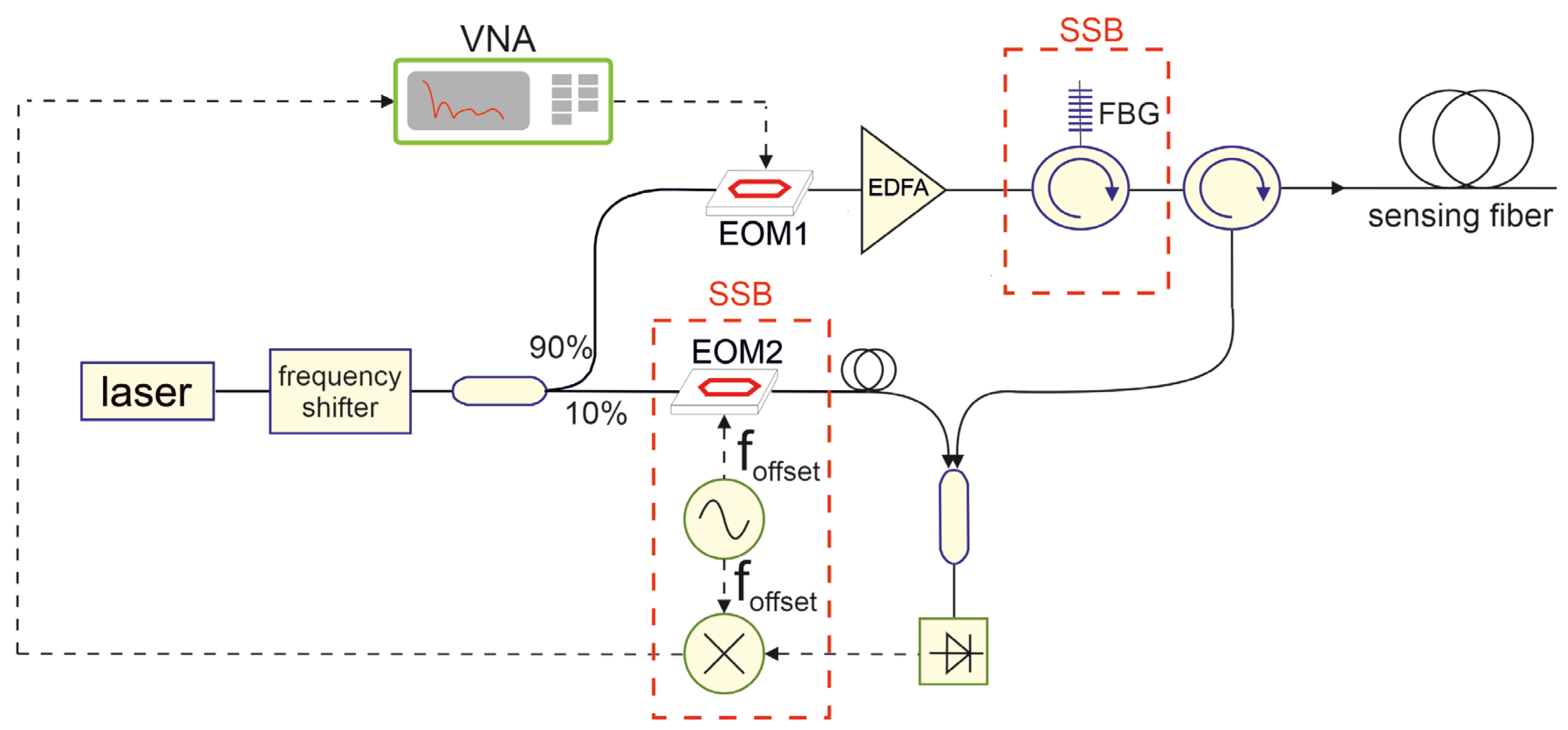
Preprints 99783 g003
Preprints 99783 g004
Figure 4. Cross-correlation of the Rayleigh spectra acquired using a (a) DSB- or (b) SSB-modulated probe, with a nominal temperature variation of 0.1 °C in the middle. The spatial resolution was set to 1 m. The superimposed black lines represent the Rayleigh frequency shift profile.
Figure 4. Cross-correlation of the Rayleigh spectra acquired using a (a) DSB- or (b) SSB-modulated probe, with a nominal temperature variation of 0.1 °C in the middle. The spatial resolution was set to 1 m. The superimposed black lines represent the Rayleigh frequency shift profile.
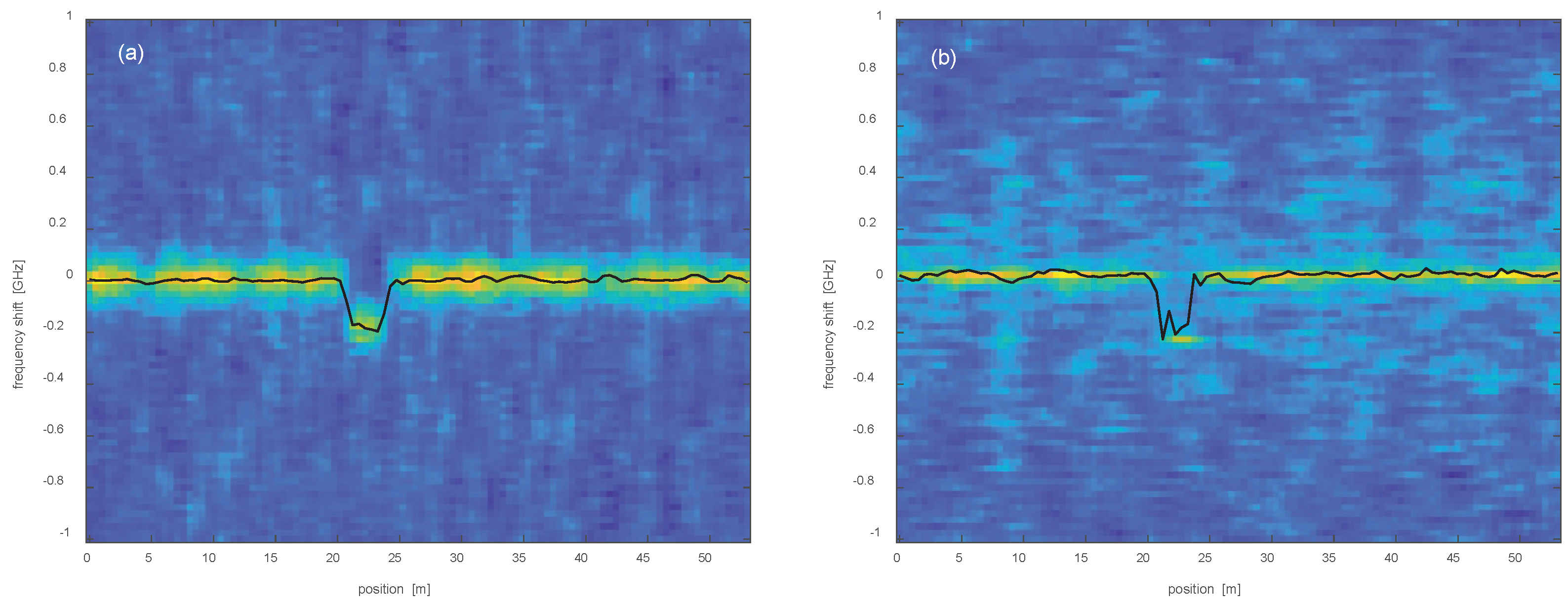
Preprints 99783 g004
Preprints 99783 g005
Figure 5. Temperature profiles acquired using (a) a DSB- or (b) an SSB-modulated probe, at a spatial resolution of 1 m. .
Figure 5. Temperature profiles acquired using (a) a DSB- or (b) an SSB-modulated probe, at a spatial resolution of 1 m. .
Preprints 99783 g005
Preprints 99783 g006
Figure 6. Cross-correlation of the Rayleigh spectra acquired using a a (a) DSB- or (b) SSB-modulated probe, with a nominal temperature variation of 1 °C in the middle. The spatial resolution was set to ≈3 cm. The superimposed black lines represent the Rayleigh frequency shift profile.
Figure 6. Cross-correlation of the Rayleigh spectra acquired using a a (a) DSB- or (b) SSB-modulated probe, with a nominal temperature variation of 1 °C in the middle. The spatial resolution was set to ≈3 cm. The superimposed black lines represent the Rayleigh frequency shift profile.
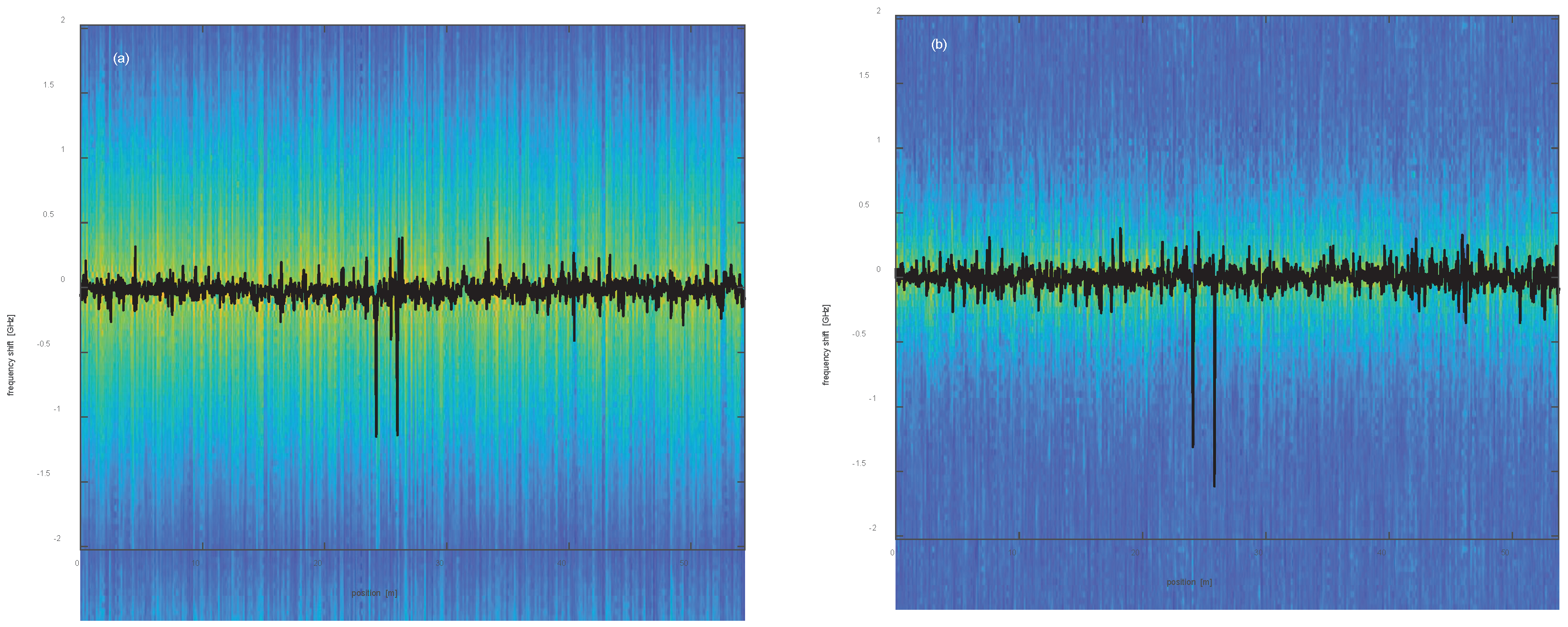
Preprints 99783 g006
Preprints 99783 g007
Figure 7. Temperature profiles acquired using (a) a DSB- or (b) an SSB-modulated probe, at a spatial resolution of ≈3 m. The profiles are vertically shifted by 1°C each other for clarity purposes.
Figure 7. Temperature profiles acquired using (a) a DSB- or (b) an SSB-modulated probe, at a spatial resolution of ≈3 m. The profiles are vertically shifted by 1°C each other for clarity purposes.
Preprints 99783 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated