Prerpints.org logo
Preprint
Article

Numerical Simulation of Polyacrylamide Hydrogel Prepared by Thermal Initiated Frontal Polymerization

Altmetrics

Downloads

121

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

24 February 2024

Posted:

26 February 2024

You are already at the latest version

Alerts
Abstract
Frontal Polymerization (FP) is recognized as a polymer synthesis method capable of generating a highly localized and self-propagating exothermic front, considered a more rapid and energy-efficient manufacturing scheme for polymer-based fiber-reinforced composite materials. This study conducts a numerical investigation based on the Finite Element Method into the initiation and propagation of frontal polymerization of acrylamide. Utilizing Differential Scanning Calorimetry (DSC) experiments, the study phenomenologically tests the curing kinetics reactions of acrylamide (AM) in deep eutectic solvent (DES)-based polymerizable systems, thereby establishing a curing kinetics model for the autocatalytic reaction of polyacrylamide. By coupling the heat conduction diffusion equation of the frontal polymerization reaction, the Finite Element Method is employed to solve the reaction-diffusion model, aiming to explore the evolution of temperature and degree of curing during the manufacturing process. The results demonstrate the reliability and accuracy of the nth-order autocatalytic model in the study of curing kinetics for DES-based synthesis, indicating that the front propagation speed of the AM-based FP reaction is influenced by the activation temperature, duration of activation temperature, and initial temperature of the solution. Experimental validation of the polyacrylamide manufacturing through frontal polymerization corroborates the accuracy and reliability of the model predictions, providing a reference for the numerical model study and temperature control in the synthesis of acrylamide composite hydrogels via FP.
Keywords: 
Subject: Chemistry and Materials Science  -   Applied Chemistry

1. Introduction

Thermoset polymer-based composite materials are widely used in various engineering applications due to their superior mechanical properties and environmental resistance. However, the composite material manufacturing processes based on autoclaves and heated molds require significant capital investment, and the large-scale curing processes involving high temperature and pressure necessitate complex, time-consuming curing cycles and substantial energy expenditure[1]. Frontal Polymerization (FP) represents a valuable alternative synthesis approach for polymer-based composites. This reaction features a highly localized and self-propagating exothermic reaction zone, offering a cheaper, faster, and more energy-efficient option for composite material manufacturing[2]. It enables the rapid fabrication of certain composite material components, providing a more efficient method to overcome the limitations of traditional high-temperature, high-pressure curing processes[3].
Numerous types of polymers can undergo Frontal Polymerization (FP), with the primary characteristic being that the polymerization reaction is highly exothermic, and the reaction rate must be sufficiently high so that the energy released far exceeds the thermal energy lost to the environment. To date, explored FP reactions mainly include the anionic and cationic polymerization of epoxy resins[4,5,6], free radical polymerization of olefins[7,8,9], addition polymerization of polyurethanes[10,11,12], and ring-opening metathesis polymerization of dicyclopentadiene (DCPD)[13,14,15]. High-performance composite hydrogel materials have also been synthesized through FP[16]. Jiang Yang et al.[17,18] have used acrylamide (AAc), acrylamide (AM), and choline chloride (ChCl) in specific molar ratios to synthesize deep eutectic solvents (DESs) for preparing macroporous polyacrylamide hydrogels. This method surpasses conventional techniques, emphasizing simplicity, environmental sustainability, rapidity, and energy conservation. At ambient temperature, introducing an initiator and cross-linker into DESs rapidly solidifies monomer solutions into hydrogels, demonstrating significant potential for expeditious biomedical fabrication[16].
During the development of numerical analysis for Frontal Polymerization (FP), Goldfeder et al.[9] predicted the degree of monomer conversion and front velocity in an adiabatic acrylate FP system based on initial reactant concentration and initial solution temperature, further studying the FP process in non-adiabatic environments. Viner et al.[19] modified this model to accommodate non-polymeric fillers undergoing phase transitions. Frulloni et al.[5] employed an axisymmetric finite difference model with the Alternating Direction Implicit method to model FP in epoxy resins, investigating the effects of resin physicochemical properties and boundary conditions on FP evolution. Goli et al.[20] solved transient coupled diffusion-reaction equations based on the Prout-Tompkins model using the Finite Element Method (FEM) to describe FP in dicyclopentadiene (DCPD). The preparation of high-performance composite hydrogels through frontal polymerization has also been extensively studied; however, these studies have focused on chemical modification, with less numerical analysis on the propagation aspect. There is a lack of effective predictive models for the front conversion speed and temperature propagation speed during the FP synthesis process of hydrogel monomers[21]. This investigation delves into the curing kinetics of acrylamide-based hydrogels within deep eutectic solvents (DES), concentrating on the rates of initiation and progression of Frontal Polymerization (FP) in the matrix. By integrating an intricate curing kinetics model with the heat conduction equation, the Finite Element Method (FEM) is deployed to predict propagation velocities and temperature distributions within a two-dimensional adiabatic framework accurately. This methodology enables precise alignment with experimental observations, affirming the model’s accuracy in simulating FP dynamics.

2. Methods

2.1. Basic mechanism of FP communication

Acrylamide-based hydrogels, favored for their reactivity with electrophiles and free radicals, are predominantly synthesized through free radical polymerization[22]. The kinetics of free radical polymerization follow three basic steps (initiation, propagation, termination) [9]:
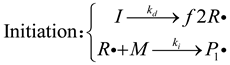
Preprints 99771 i001
Preprints 99771 i002
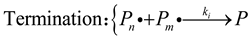
Preprints 99771 i003
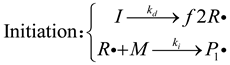
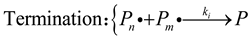
I represents the initiator,   R · is the initial free radical, M is the monomer, P j · is a polymer free radical of length j, P is a chemically inactive polymer, all substances with chemical activity are denoted with a dot beside them, f is the efficiency of the initiator, which is generally 0.5. Due to their high reactivity, a minimal fraction of free radicals generated by decomposition react with monomers. The reaction rate constant, k i , varies with temperature, following Arrhenius law. Initially, these reactions occur simultaneously.
The front-end polymerization of DEMs, a complex multiphysics phenomenon, involves both physical and chemical material transformations. Initiated by Potassium Persulfate (KPS), the process converts a DEMs solution, containing Acrylamide (AM) and Choline Chloride (ChCl), from liquid to solid-state gel polymer, with the conversion degree (α) indicating rapid change. This study bifurcates into analyzing the polymerization's solidification kinetics and its thermal conduction diffusion dynamics.

2.2. Curing Kinetics Model

In solidification reaction kinetics, key parameters include apparent activation energy, frequency factor, and reaction order, with the apparent activation energy indicating the reaction's difficulty level. The system must exceed this energy threshold for a successful reaction, while a higher frequency factor accelerates the reaction. The presence of simultaneous mechanistic reactions complicates maintaining a stable apparent activation energy, making its accurate determination essential. Kinetic models of solidification are categorized into phenomenological and mechanistic types. Phenomenological models rely on semi-empirical equations to analyze kinetics without focusing on chemical details, facilitating their broad application. The solidification kinetics rate equation is then derived based on these principles:
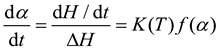Preprints 99771 i004
where dα/dt is the solidification rate, t is the reaction time, α is the degree of conversion, ΔH is the total heat of solidification reaction, f(α) is the solidification kinetics model, dependent on the reactants, K(T) is a function of temperature and follows the Arrhenius law[23]：
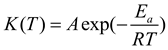
Preprints 99771 i005
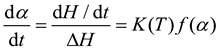
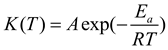
In equation (2), A represents the pre-exponential factor, Ea is the apparent activation energy, and R is the Avogadro gas constant. By combining equations (1) and (2), we can obtain
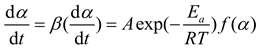
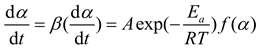
Preprints 99771 i006
Logarithmizing both sides of equation (3) yields
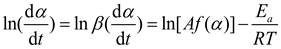
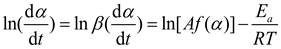
Preprints 99771 i007
Selecting an appropriate f(α) function is pivotal for analyzing FP solidification kinetics. Despite the concurrent multiple reactions, simplification to a single representative reaction is standard. With various chemical reactions modeled differently, identifying a model that aligns with the specific system or reaction type is critical. The nth order model, for its simplicity, is the preferred approach in current applications to describe solidification kinetics：
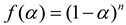
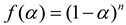
Preprints 99771 i008
The characteristic of an nth order reaction is that the reaction rate is maximum at t=0, where n is the reaction order. At this time, equation (4) becomes:
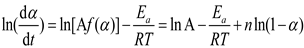
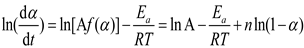
Preprints 99771 i009
A non-linear relationship between ln[Af(α)] and ln(1−α) suggests an autocatalytic solidification reaction[24]. Per the Sesták-Berggren autocatalytic model[25], a maximum exothermic peak occurring within 30% to 40% of the reaction process signifies that the reaction adheres to autocatalytic kinetics：
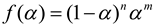Preprints 99771 i010
where m and n are the independent reaction orders of the autocatalytic reaction model. At this time, the kinetic equation can be transformed into equation (8)
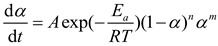
Preprints 99771 i011
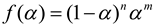
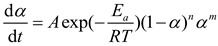
Logarithmizing both sides of the equation yields Equation (9).
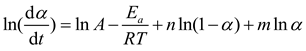
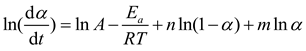
Preprints 99771 i012
By setting s=m/n, it follows that:
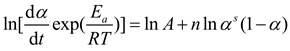
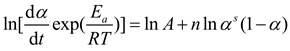
Preprints 99771 i013
To further investigate the coefficients of solidification kinetics, the Malek method is employed to determine the appropriate kinetic model function for the solidification reaction[26]. The Malek method calculates kinetic parameters to identify the specific kinetic model by constructing two critical parameters, y(α) and z(α).
Preprints 99771 i014
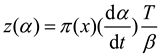
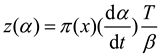
Preprints 99771 i015
In Equations (11) and (12),   x = E a / R T ，where the mean value of Ea is determined through the Flynn-Wall-Ozawa (FWO) method among others for conversion rate analysis[27]. The calculation of Ea at different heating rates β and the same conversion rate allows for the determination of its mean value. The function π(x) an be represented by Equation (12) as proposed by Senum-Yang[23].
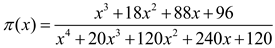
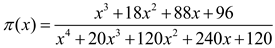
Preprints 99771 i016
By analyzing the relationship curve of ln ⁡ [ ( d α / d t ) e x ]   a n d   with α in the interval (0.2, 0.8), the kinetic parameters (n, m, and ln A) can be determined, where α m = m / ( m + n ) . Through substitution, it is possible to derive s = α m / ( 1 − α m ) . By determining n from the fitting curve, m can subsequently be calculated using m = sn.

2.3. Heat diffusion transfer model

The initiation and unidirectional propagation of DEMs polymerization assume isotropic thermal conductivity within the solution. Heat transfer in FP reactions is governed by the classical heat conduction equation, necessitating the resolution of a set of nonlinear partial differential equations regarding α and temperature[28]：
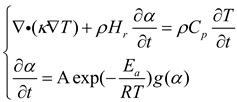
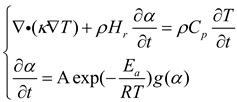
Preprints 99771 i017
In the equation, κ (W/(m·K)) denotes thermal conductivity, ρ ( kg/m³) density, C p ( J/kg·K) specific heat capacity, and Hr ( J/kg) the total enthalpy of exothermic reaction. The relationship in equation (14) outlines the cure kinetics associated with exothermic reactions. Cure kinetics parameters are derived by conducting nonlinear fitting on the cure rate evolution curves extracted from DSC experiments
In this experiment, the corresponding boundary conditions and initial conditions are:：
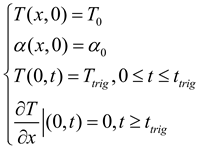Preprints 99771 i018
where Ttrig denotes the time taken to apply a triggering temperature at the boundary end to initiate frontal polymerization, T0 represents the initial temperature of the solution, and α0 indicates the initial degree of cure of the solution[28].

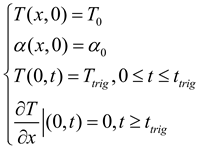
3. Experiment and Discussion

3.1. Material preparation

Materials: Acrylamide (AM), Choline Chloride (ChCl), and Potassium Persulfate (KPS) were all purchased from Shanghai Aladdin Biochemical Technology Co., Ltd. All reagents were of analytical grade and were used directly after purchase.
The preparation of DEMs is illustrated in Figure 1[18]. Specifically, ChCl is selected as the hydrogen bond acceptor (HBA) and AM as the hydrogen bond donor (HBD). The two materials were vigorously stirred in an 80°C oil bath until a uniform, transparent, and clear liquid was obtained. After cooling to approximately 33°C, the initiator KPS was added, and the mixture was left to await the application of an initiating heat source. The molar ratio of AM to ChCl was 2:1, with KPS constituting 0.5% of the mass. The melting point of the DEM was 31°C. This study aims to explore the free radical polymerization reaction in a binary mixture system without crosslinking and to measure the heat released during the formation of linear polymer chains through frontal polymerization.

3.2 Non-isothermal isothermal DSC experiment

To examine the curing kinetics of AM-based DEMs, multiple preliminary DSC trials were conducted using a Mettler-Toledo DSC3 calorimeter, revealing the temperature response of DEMs around 30°C. Early in the curing process, endothermic activity results in negative DSC curve values, indicating the absence of FP reaction initiation, as depicted in Figure 2. This figure shows the exothermic curing curves of DEMs under various heating rates β (1, 3, 5, 7, 9 K/min), alongside their characteristic temperature plots, where the activation energy for the curing reaction is measured. With only a single exothermic peak present in all curves in Figure 2, it suggests that the DEMs system maintains a relatively uniform curing environment[29,30]. It is observed that with an increase in heating rate, the initial reaction temperature ( T i ), peak exothermic temperature ( T p ), and reaction termination temperature ( T f ) all escalate. Increased heating rates shorten the residence time at specific temperatures, leading to inadequate curing. The system thus requires further curing at elevated temperatures. This thermal lag effect accentuates the temperature differential and increases the thermal inertia per unit time, shifting the exothermic peak towards higher temperatures[31].
Figure 3 reveals a linear correlation between the curing reaction's characteristic temperatures and the heating rate across various stages. By extrapolating to a zero heating rate, the onset of the reaction is identified at 307.7K, with the peak exothermic temperature at 325.5K and the reaction completion at 342.5K. The curing involves numerous simultaneous polymerization reactions, complicating the maintenance of a stable apparent activation energy. Figure 4, derived using the Flynn-Wall-Ozawa method, showcases the ln(dα/dt)-1/T curve for conversion rates spanning 0.2 to 0.8, yielding an average activation energy (Ea) of 89.567 kJ/mol.
As depicted in Figure 5, further analysis of the ln[Af(α)] versus ln(1-α) relationship indicates that ln[Af(α)] and ln(1-α) do not follow a simple linear relationship, suggesting that the reaction system does not conform to an nth-order reaction model[24].
Table 1 presents the maximum values of dα/dt、y(α), and z(α) as αp、αm、αp∞, respectively. By correlating these with the conversion rate, the parameters, including the statistical averages of αm and αp∞, are calculated. Figure 6 displays normalized plots of y(α) and z(α), where their peak characteristic values satisfy 0<αm<αp and αp∞≠0.632,. According to the Malek method criteria, the curing process of this system is aptly described by the Sesták-Berggren dual-parameter autocatalytic kinetics model[25]. The relationship curves of ln[(dα/dt)ex] and ln[αs(1-α)] within the conversion rate interval of (0.2, 0.8), as shown in Figure 7, facilitate the calculation of the autocatalytic model's kinetic parameters m, n, and ln A.
To validate the precision of the kinetic equation (15) for the curing process, we juxtaposed the DSC experimental outcomes across diverse heating rates against the forecasts derived from the equation's fitting curves, as shown in Figure 8. The curves generated by the autocatalytic model closely match the experimental curves over a range of heating rates, although deviations emerge in the advanced stages of the curing reaction. These variances between experimental and theoretical figures at higher temperatures signal a shift in the reaction dynamics from being chemically controlled to diffusion controlled, underscoring the complex nature of the curing process.
Overall, the non-isothermal curing reaction of the AM-based DEMs system can be described using an autocatalytic reaction model, which corresponds to the autocatalytic kinetics model as follows:
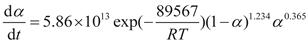
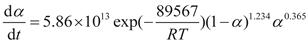
Preprints 99771 i019

3.3. Numerical simulation

The nonlinear partial differential equation delineated in Equation (13) was solved numerically utilizing the Finite Element Analysis (FEA) software ABAQUS, which is adept for general heat transfer problems not involving intricate internal heat generation. Figure 9(b) showcases typical temperature and cure degree profiles within a liquid DEMs domain (initial temperature T0 = 305 K) over a length of r = 5 mm, adequate for capturing the stable propagation of the polymerization front. A minimal initial cure degree α0 = 0.0001 ensured that the cure degree field calculations were non-zero. The experimental setup, conducted in cylindrical tubes, was represented computationally through an axisymmetric two-dimensional model. The thermodynamic properties of the AM-based DEMs solution are summarized in Table 2. To initiate polymerization, a triggering temperature of trig = 474K was applied at the domain's left boundary for 0.2 seconds, effectively initiating the FP reaction. The simulation employed an initial mesh of 15600 elements and a time step of 0.001 seconds, with a refined mesh size of 0.1mm×0.1mm to accurately capture the narrow advancing front, yielding a simulated average front velocity of 2.7 mm/s, as depicted in figures (c) and (d).
Figure 10 illustrates the impact of the duration of the applied triggering temperature on the propagation velocity of the frontal interface. As the duration of the trigger increases from 0.1 seconds to 1 second, the average frontal velocity escalates from 2 mm/s to 3.2 mm/s. Beyond a 1-second duration, this acceleration reaches a plateau due to the heat generated by the material being sufficient to activate the frontal polymerization process. At shorter triggering durations, heating is confined to the material's surface, leaving deeper regions at relatively lower temperatures. This expression has been refined for enhanced precision, conciseness, and academic rigor.
Figure 11 demonstrates the initiator temperature's impact on frontal velocity, revealing a modest increase with temperature under a fixed 0.2s trigger duration. This velocity includes an initial phase of rapid heating and a subsequent self-sustaining FP polymerization phase. Results indicate a convergence of these phases at elevated temperatures, with the self-propagation speed reaching a peak rather than continuously increasing. The influence of the initial applied temperature diminishes as propagation is primarily driven by the polymerization's exothermic heat, leading to velocity stabilization.
Figure 12 underscores the significant role of the system's initial temperature, T0, on FP velocity. Higher initial temperatures markedly accelerate the propagation speed; for instance, at T0 = 321K, the speed is approximately 1.5 times greater than at 289K, suggesting that beyond DEMs' FP initiation temperature, bulk polymerization dominates. This implies that a higher T0, without surpassing the initiation threshold, effectively enhances FP polymerization speed, aligning with SCI journal requirements for conciseness and academic rigor.

3.4. Model validation

In order to assess the accuracy of the curing kinetics simulations by fitting analysis, we employed a thermal initiation technique using acrylamide-based deep eutectic compounds (DEMs) to initiate the frontal polymerization process. The experimental arrangement, as illustrated in Figure 13, involved using molds crafted from alumina silicate ceramic fiber boards for insulation, which encapsulated the test tube to diminish thermal losses within the FP reaction's diffusive environment. After introducing the initiator KPS into the DEMs, the mixture was rapidly transferred to the test tube. Once settled, the FP reaction was initiated by applying heat to the upper end of the tube with a soldering iron. The process's temperature distribution and diffusion velocity were documented using thermal infrared imaging.
Figure 14 presents the experimental measurements of Tmax and its temperature distribution, noting a thermal peak at 141.1°C and a propagation velocity of 1.5mm/s. The observed distribution of thermal hotspots from the infrared imaging aligns closely with the patterns predicted by numerical simulations, validating the model's capacity to precisely represent the temperature profiles and propagation speeds characteristic of FP reactions. Nevertheless, the simulations are observed to predict higher Tmax values, a discrepancy attributed to the model's limitations in capturing microscale phenomena and accounting for the thermal diffusion through the experimental insulation. This discrepancy underscores the necessity for enhancing the granularity and accuracy of the simulations to better reflect the nuanced behaviors observed in FP reactions.

4. Conclusion

In this study, a comprehensive examination of the cure kinetics of acrylamide DEMs was conducted, employing the DSC non-isothermal test method to fit and validate a cure kinetics model against empirical data. The employment of the nth-order autocatalytic model was substantiated through this process, affirming its robustness and precision in the analysis of DEM-type syntheses' cure kinetics.
Subsequent finite element numerical simulations shed light on the dynamics influencing the characteristic temperatures and velocities within the FP reaction mechanism. It was elucidated that both the duration and increment of trigger temperatures transiently augment front speeds until equilibrium is attained, underscoring the critical role of initial liquid temperature in modulating FP front velocities.
Comparative evaluation of simulation predictions against experimental outcomes highlighted a propensity for simulations to overestimate, attributed to experimental measurement variances and temperature control sensitivities. Nonetheless, the congruence in overall temperature profiles and peak temperature features between simulations and experiments underscores the simulations' value in reliably forecasting the rapid curing behaviors of hydrogel composite materials synthesized via the FP method. This concordance suggests that numerical simulation can serve as a pivotal tool for guiding experimental design and optimization strategies.The findings of this study not only validate the applied cure kinetics model and simulation approach but also augment the understanding of temperature's effect on polymerization reactions, offering a methodological and theoretical basis for enhancing material synthesis and application.

Author Contributions

Methodology, validation, data curation, and writing—original draft preparation, Y.X.; Investigation, writing—review and editing, S.L.; resources and funding acquisition, P.W.; conceptualization, supervision, and project administration, S.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (NSFC11902232).

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Abliz, D.; Duan, Y.; Steuernagel, L.; Xie, L.; Li, D.; Ziegmann, G. Curing methods for advanced polymer composites - a review. Polymers and Polymer Composites, 2013, 21(6), 341-348. [CrossRef]
  2. Davtyan, S. P.; Berlin, A. A.; Tonoyan, A. O. Advances and problems of frontal polymerization processes. Review Journal of Chemistry, 2011, 1(1), 56-92. [CrossRef]
  3. Robertson, I. D.; Yourdkhani, M.; Centellas, P. J.; Aw, J. E.; Ivanoff, D. G.; Goli, E.; Lloyd, E. M.; Dean, L. M.; Sottos, N. R.; Geubelle, P. H.; Moore, J. S.; White, S. R. Rapid energy-efficient manufacturing of polymers and composites via frontal polymerization. Nature, 2018, 557(7704), 223-227. [CrossRef]
  4. Mariani, A.; Bidali, S.; Fiori, S.; Sangermano, M.; Malucelli, G.; Bongiovanni, R.; Priola, A. Uv-ignited frontal polymerization of an epoxy resin. Journal of Polymer Science Part A: Polymer Chemistry, 2004, 42(9), 2066-2072.
  5. Frulloni, E.; Salinas, M. M.; Torre, L.; Mariani, A.; Kenny, J. M. Numerical modeling and experimental study of the frontal polymerization of the diglycidyl ether of bisphenol a/diethylenetriamine epoxy system. Journal of Applied Polymer Science, 2005, 96(5), 1756-1766. [CrossRef]
  6. Scognamillo, S.; Bounds, C.; Thakuri, S.; Mariani, A.; Wu, Q.; Pojman, J. A. Frontal cationic curing of epoxy resins in the presence of defoaming or expanding compounds. Journal of Applied Polymer Science, 2014, 131(11).
  7. McFarland, B.; Popwell, S.; Pojman, J. A. Free-radical frontal polymerization with a microencapsulated initiator:  Characterization of microcapsules and their effect on pot life, front velocity, and mechanical properties. Macromolecules, 2006, 39(1), 55-63.
  8. Nason, C.; Roper, T.; Hoyle, C.; Pojman, J. A. Uv-induced frontal polymerization of multifunctional (meth)acrylates. Macromolecules, 2005, 38(13), 5506-5512. [CrossRef]
  9. Goldfeder, P. M.; Volpert, V. A.; Ilyashenko, V. M.; Khan, A. M.; Pojman, J. A.; Solovyov, S. E. Mathematical modeling of free-radical polymerization fronts. The Journal of Physical Chemistry B, 1997, 101(18), 3474-3482. [CrossRef]
  10. Mariani, A.; Bidali, S.; Fiori, S.; Malucelli, G.; Sanna, E. Synthesis and characterization of a polyurethane prepared by frontal polymerization. e-Polymers, 2003, 3(1). [CrossRef]
  11. Chen, S.; Sui, J.; Chen, L.; Pojman, J. A. Polyurethane–nanosilica hybrid nanocomposites synthesized by frontal polymerization. Journal of Polymer Science Part A: Polymer Chemistry, 2005, 43(8), 1670-1680. [CrossRef]
  12. Fiori, S.; Mariani, A.; Ricco, L.; Russo, S. First synthesis of a polyurethane by frontal polymerization. Macromolecules, 2003, 36(8), 2674-2679. [CrossRef]
  13. Robertson, I. D.; Pruitt, E. L.; Moore, J. S. Frontal ring-opening metathesis polymerization of exo-dicyclopentadiene for low catalyst loadings. ACS Macro Letters, 2016, 5(5), 593-596. [CrossRef]
  14. Alzari, V.; Nuvoli, D.; Sanna, D.; Ruiu, A.; Mariani, A. Effect of limonene on the frontal ring opening metathesis polymerization of dicyclopentadiene. Journal of Polymer Science Part A: Polymer Chemistry, 2016, 54(1), 63-68. [CrossRef]
  15. Ruiu, A.; Sanna, D.; Alzari, V.; Nuvoli, D.; Mariani, A. Advances in the frontal ring opening metathesis polymerization of dicyclopentadiene. Journal of Polymer Science Part A: Polymer Chemistry, 2014, 52(19), 2776-2780. [CrossRef]
  16. Sennakesavan, G.; Mostakhdemin, M.; Dkhar, L. K.; Seyfoddin, A.; Fatihhi, S. J. Acrylic acid/acrylamide based hydrogels and its properties - a review. Polymer Degradation and Stability, 2020, 180, 109308. [CrossRef]
  17. Yapeng,C.; Shilin,Y.; Shengfang,L.;Tao,Z. Preparation of Macroporous Hydrogel by Frontal Polymerization of Deep Eutectic Solvent and Its Swelling and Adsorption Performance [J]. Polymeric Materials Science and Engineering, 2021, 37(9): 141-148.
  18. Jiang, Y.; Li, S.; Chen, Y.; Yan, S.; Tao, M.; Wen, P. Facile and green preparation of superfast responsive macroporous polyacrylamide hydrogels by frontal polymerization of polymerizable deep eutectic monomers. Industrial & Engineering Chemistry Research, 2020, 59(4), 1526-1533. [CrossRef]
  19. Viner, V. G.; Pojman, J. A.; Golovaty, D. The effect of phase change materials on the frontal polymerization of a triacrylate. Physica D: Nonlinear Phenomena, 2010, 239(11), 838-847. [CrossRef]
  20. Goli, E.; Robertson, I. D.; Geubelle, P. H.; Moore, J. S. Frontal polymerization of dicyclopentadiene: A numerical study. The Journal of Physical Chemistry B, 2018, 122(16), 4583-4591. [CrossRef]
  21. Chang,L.; Xinhui,H.; Yuxin,H. Preparation of mesoporous - molecular -sieve/polydicyclopentadiene composites[J]．Acta Materiae Compositae Sinica, 2012, 29(2): 65-72.
  22. Kobayashi, Shiro. Encyclopedia of polymeric nanomaterials. Berlin, Heidelberg: Springer Berlin Heidelberg, 2015. 1654-1658.
  23. Senum, G.; Yang, R. Rational approximations of the integral of the arrhenius function. Journal of thermal analysis, 1977, 11, 445-447. [CrossRef]
  24. Jouyandeh, M.; Paran, S. M. R.; Jannesari, A.; Puglia, D.; Saeb, M. R. Protocol for nonisothermal cure analysis of thermoset composites. Progress in Organic Coatings, 2019, 131,333-339. [CrossRef]
  25. Choe, Y.; Kim, W. Cure reactions of epoxy/anhydride/(polyamide copolymer) blends. Macromolecular Research, 2002, 10(5), 259-265. [CrossRef]
  26. Málek, J. Kinetic analysis of crystallization processes in amorphous materials. Thermochimica Acta, 2000, 355(1-2), 239-253. [CrossRef]
  27. Popescu, C. Integral method to analyze the kinetics of heterogeneous reactions under non-isothermal conditions a variant on the ozawa-flynn-wall method. Thermochimica Acta, 1996, 285(2), 309-323. [CrossRef]
  28. Goli, E.; Parikh, N. A.; Yourdkhani, M.; Hibbard, N. G.; Moore, J. S.; Sottos, N. R.; Geubelle, P. H. Frontal polymerization of unidirectional carbon-fiber-reinforced composites. Composites Part A: Applied Science and Manufacturing, 2020, 130, 105689. [CrossRef]
  29. Hayaty, M.; Honarkar, H.; Beheshty, M. H. Curing behavior of dicyandiamide/epoxy resin system using different accelerators. Iranian Polymer Journal, 2013, 22, 591-598. [CrossRef]
  30. Saad, G. R.; Abdallah, H. M.; Aziz, M. S. A.; Mohamed, N. A.; Sabaa, M. W. Cure kinetics and thermal stability of maleimide modified epoxy tgic/cpe powder coating system. Thermochimica Acta, 2015, 617, 191-199. [CrossRef]
  31. Mafi, R.; Mirabedini, S.; Naderi, R.; Attar, M. Effect of curing characterization on the corrosion performance of polyester and polyester/epoxy powder coatings. Corrosion Science, 2008, 50(12), 3280-3286. [CrossRef]
Preprints 99771 g001
Figure 1. Schematic diagram of the synthesis and preparation of DEM[18].
Figure 1. Schematic diagram of the synthesis and preparation of DEM[18].
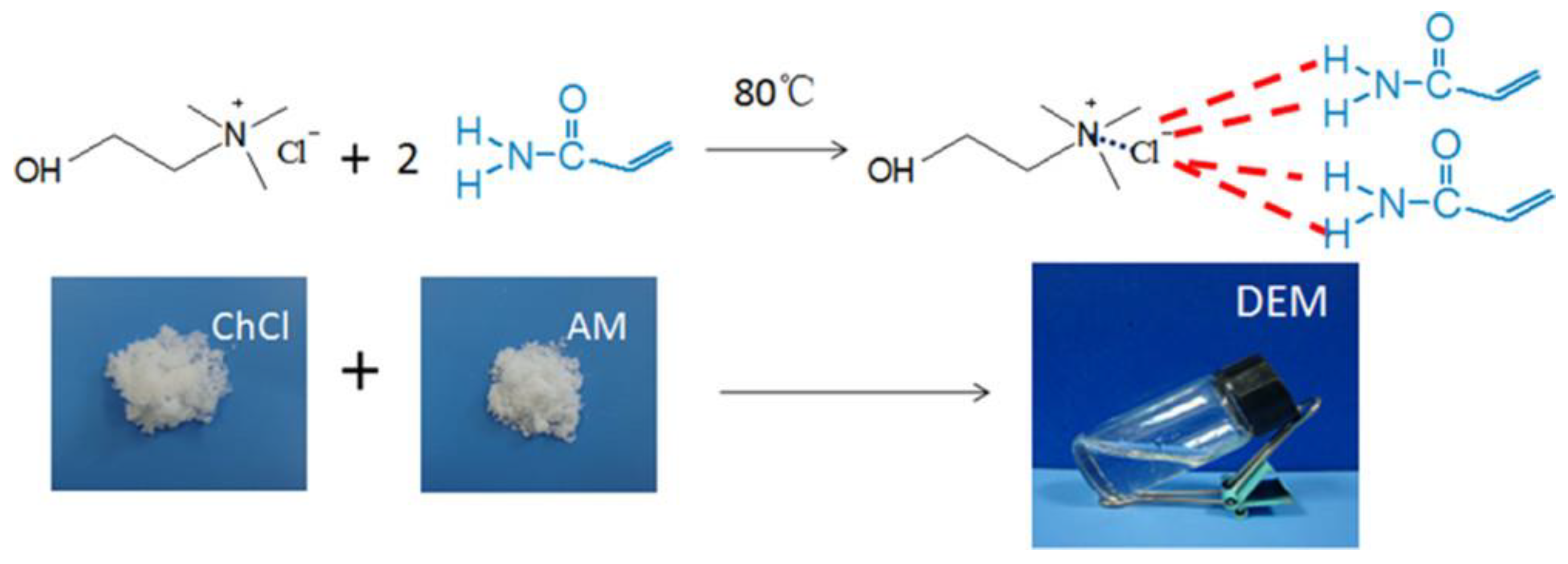
Preprints 99771 g001
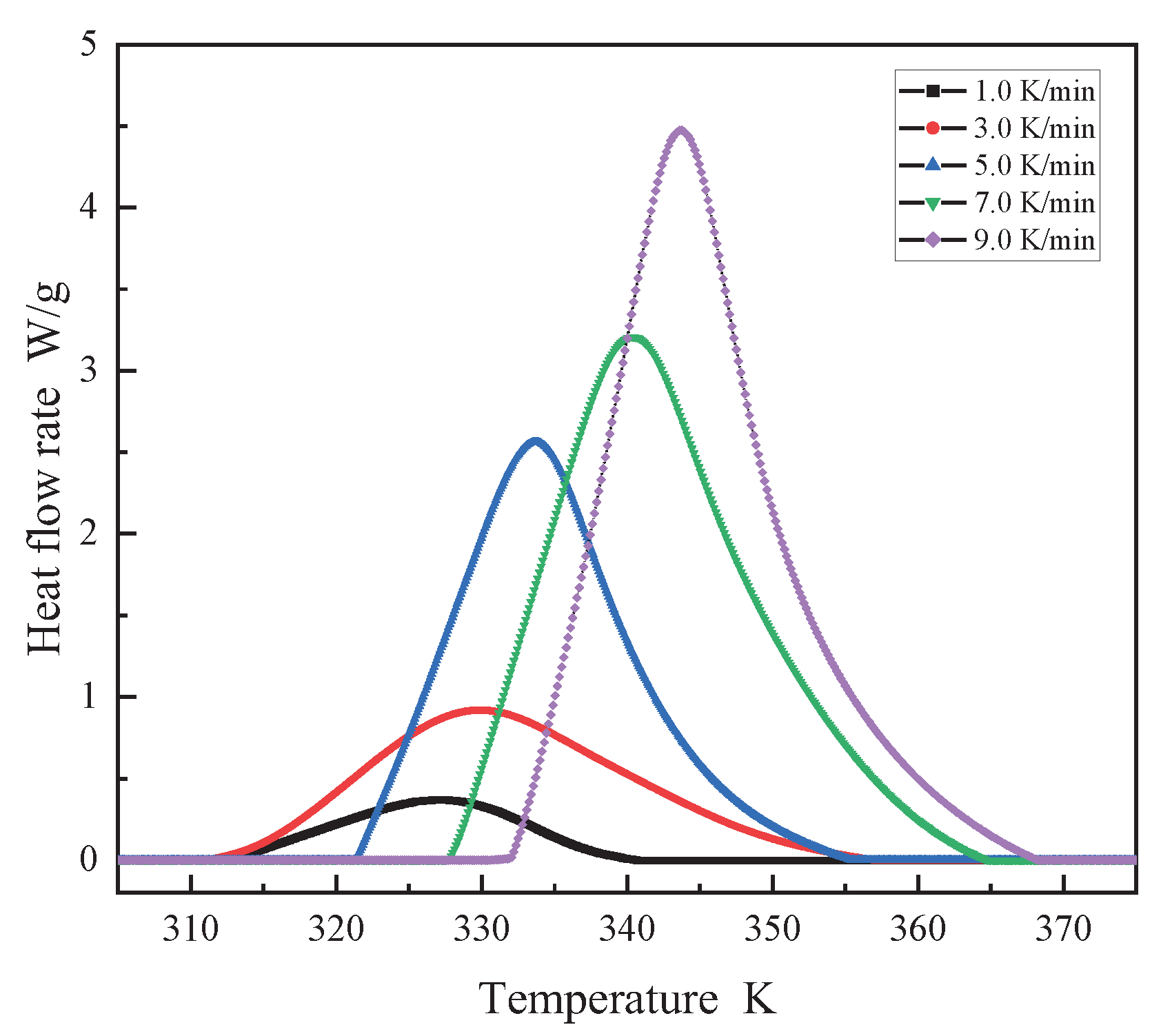
Preprints 99771 g002
Figure 2. DSC curves of DEM under different heating rates.
Figure 2. DSC curves of DEM under different heating rates.
Preprints 99771 g002
Preprints 99771 g003
Figure 3. The relationship between Characteristic temperature T and heating rate β.
Figure 3. The relationship between Characteristic temperature T and heating rate β.
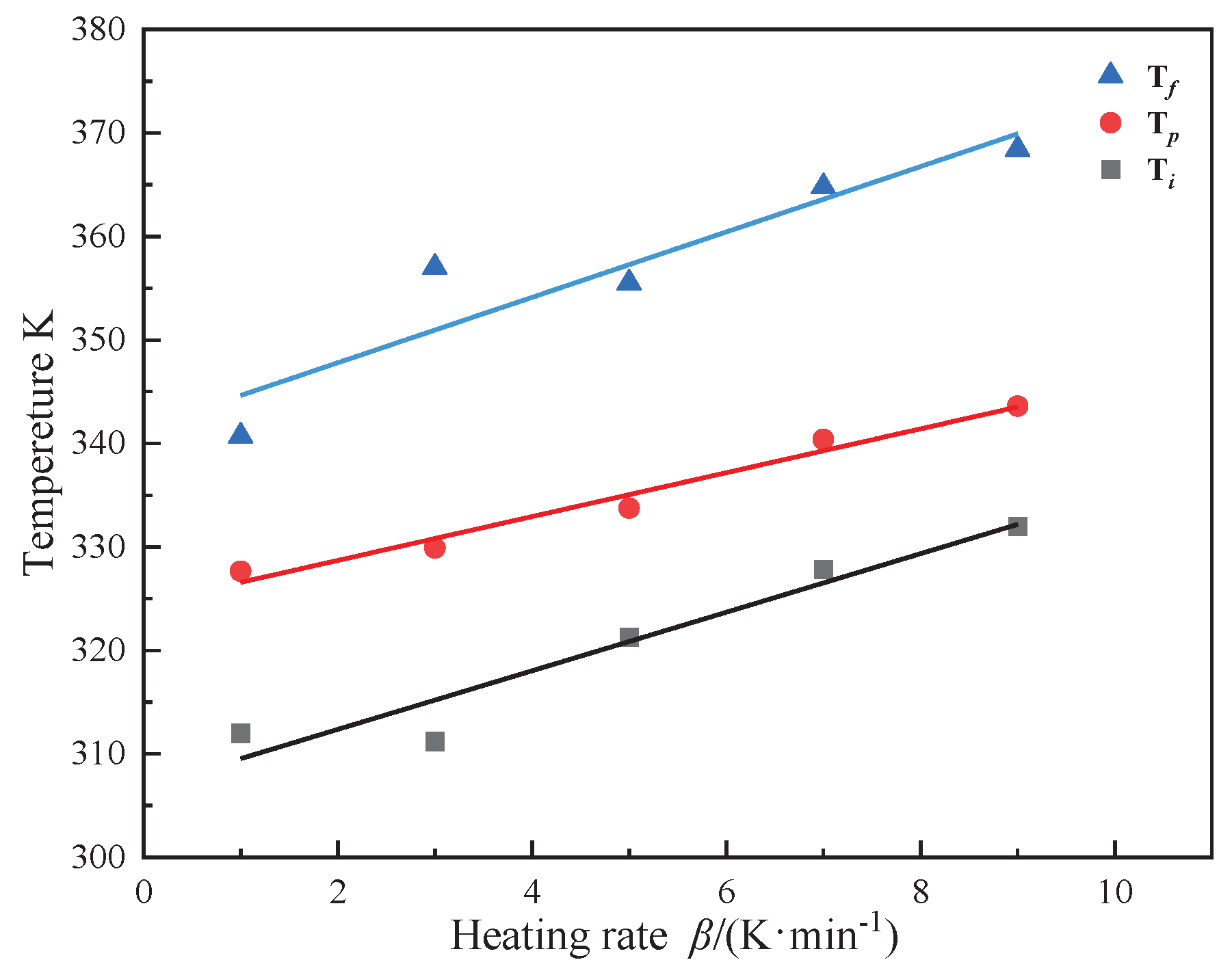
Preprints 99771 g003
Preprints 99771 g004
Figure 4. Analysis of activation energy curve using FWO methond.
Figure 4. Analysis of activation energy curve using FWO methond.
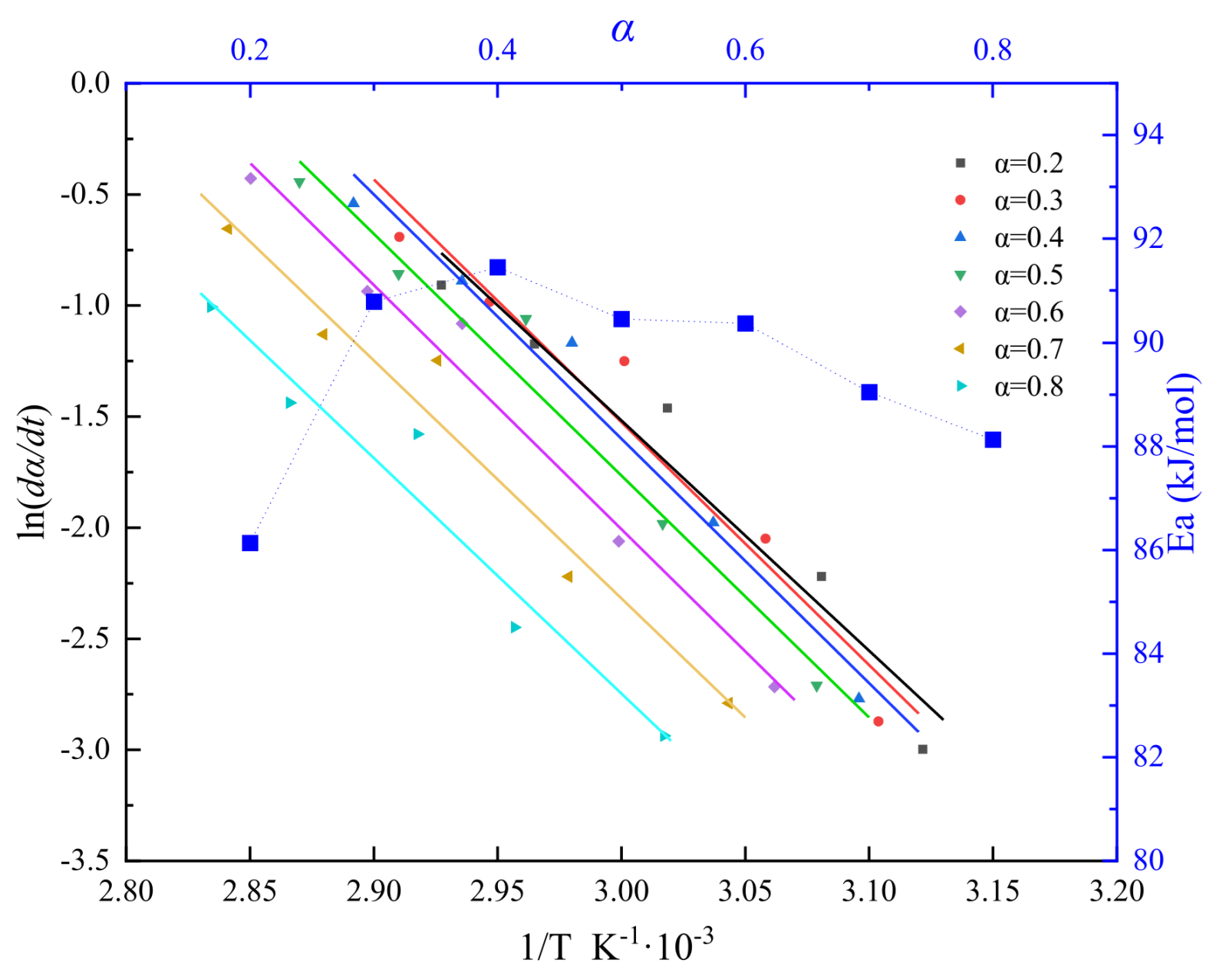
Preprints 99771 g004
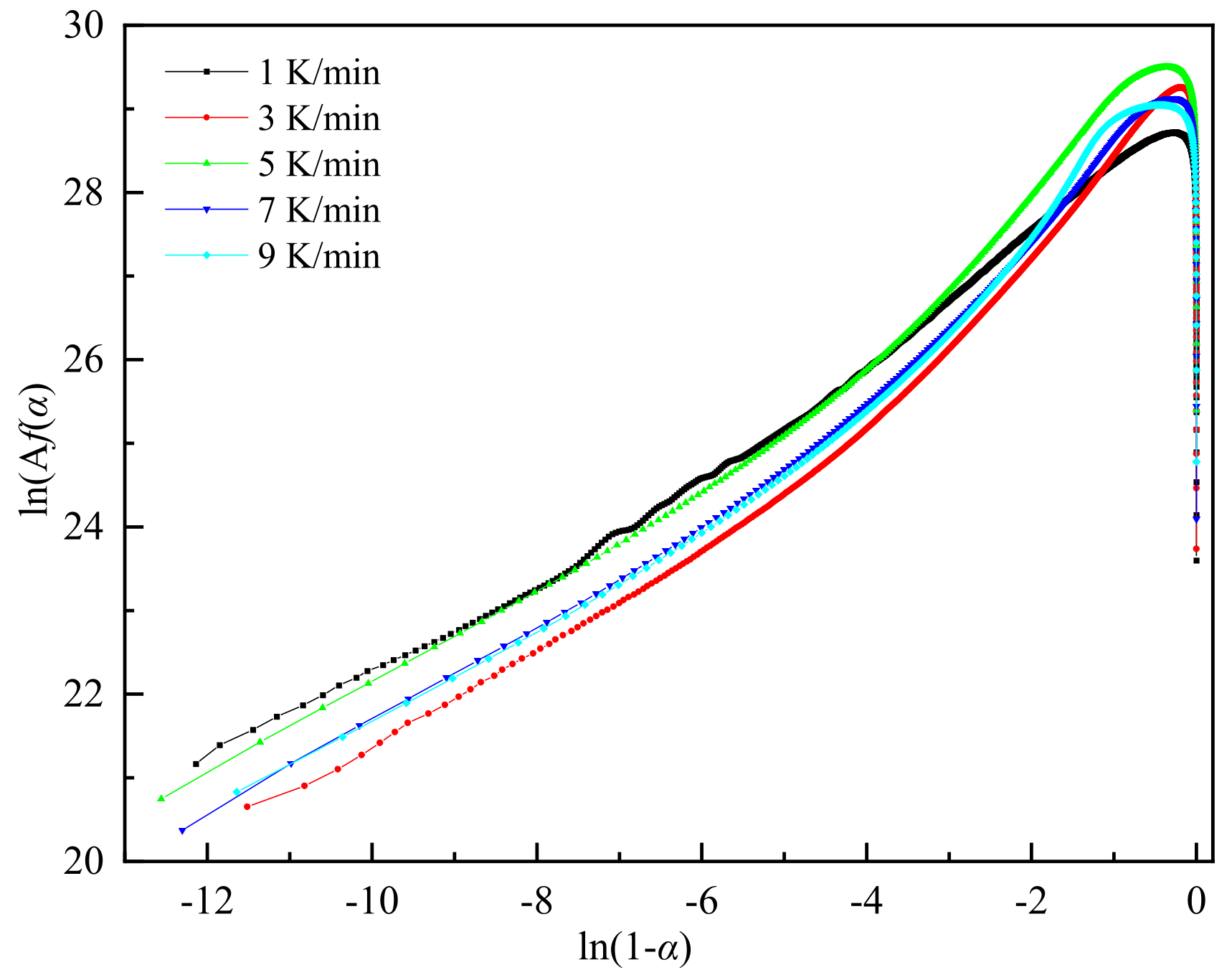
Preprints 99771 g005
Figure 5. Plots of ln[Af(α)] versus ln(1-α) of the DEM at different heating rates.
Figure 5. Plots of ln[Af(α)] versus ln(1-α) of the DEM at different heating rates.
Preprints 99771 g005
Preprints 99771 g006
Figure 6. Plots of normalized y(α) and z(α) against α.
Figure 6. Plots of normalized y(α) and z(α) against α.
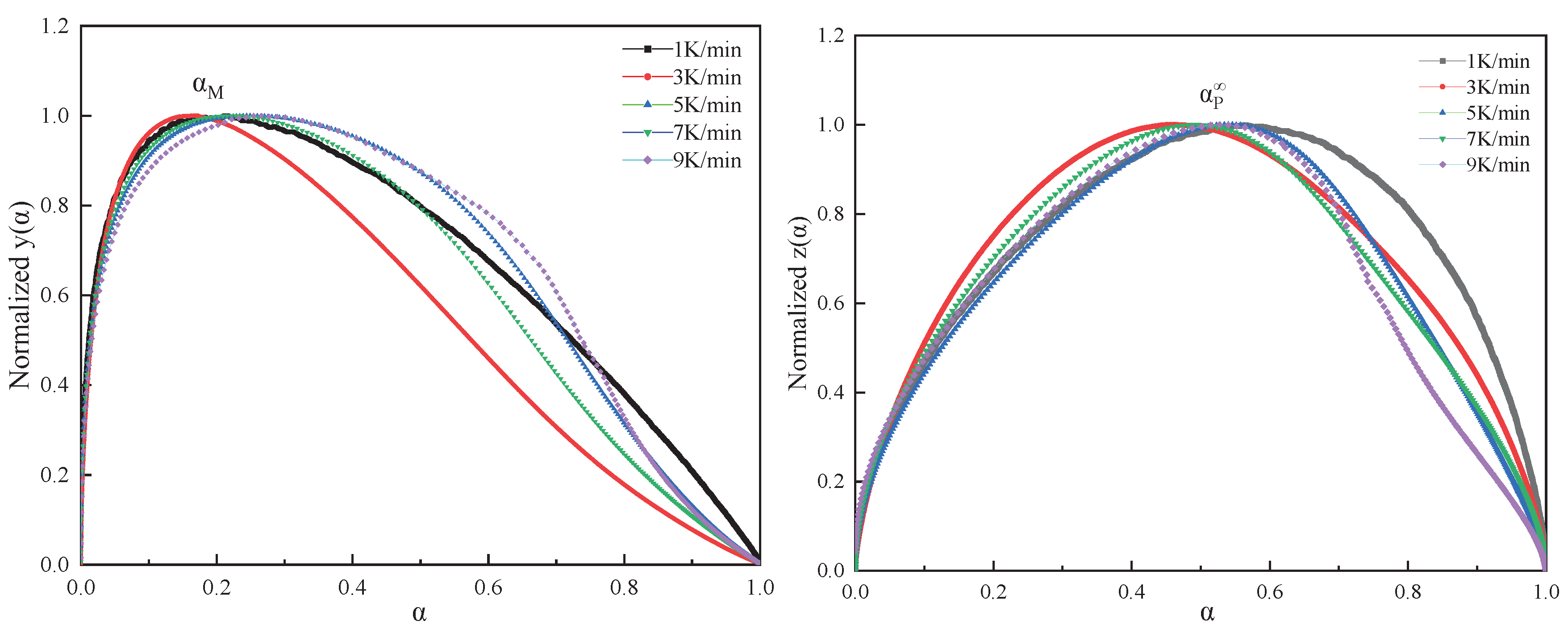
Preprints 99771 g006
Preprints 99771 g007
Figure 7. Plots of ln[(dα/dt)ex] against [αs(1-α)].
Figure 7. Plots of ln[(dα/dt)ex] against [αs(1-α)].
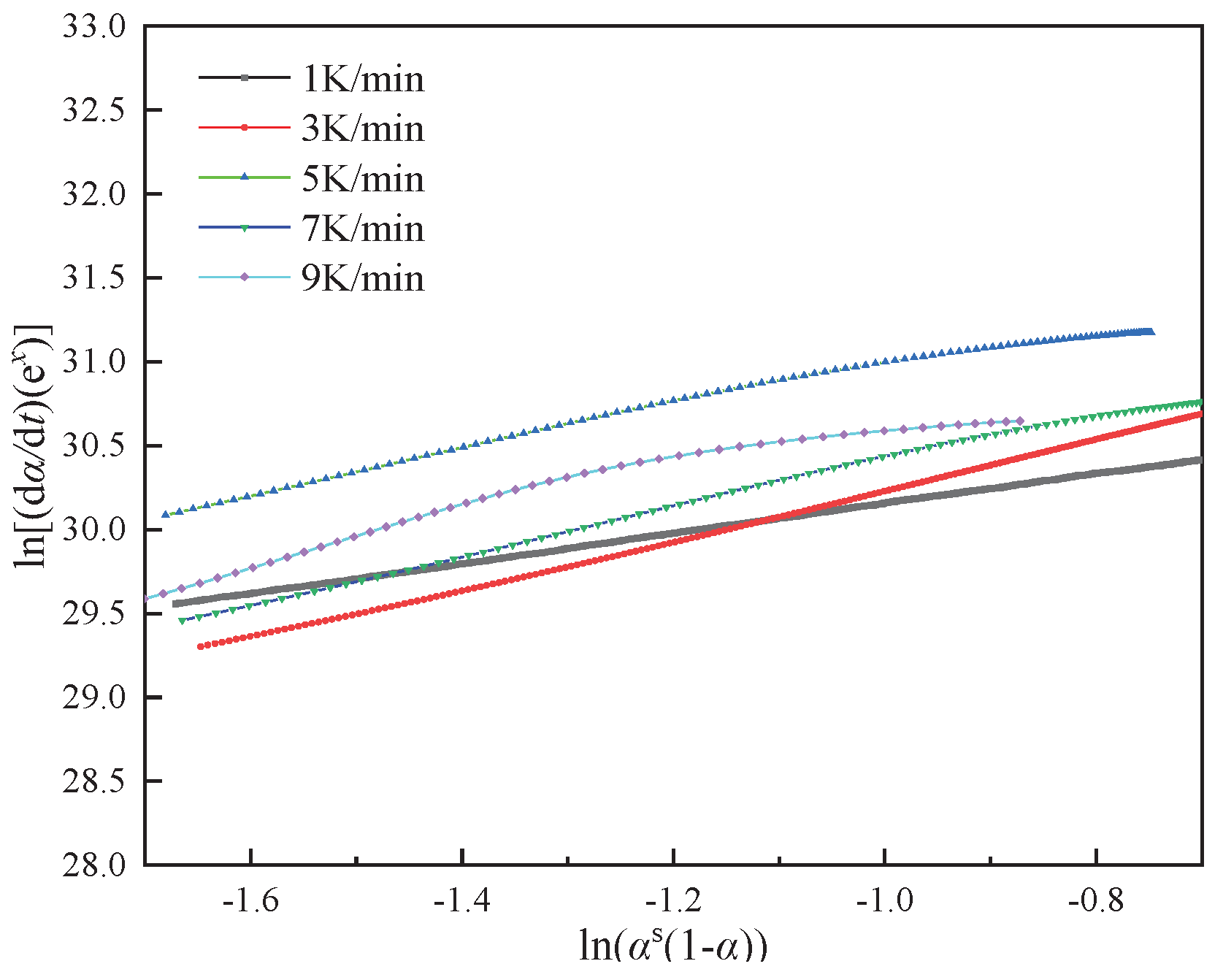
Preprints 99771 g007
Preprints 99771 g008
Figure 8. Comparing the autocatalytic reaction rate model with DSC data: black lines denote experimental values, colored lines indicate fits.
Figure 8. Comparing the autocatalytic reaction rate model with DSC data: black lines denote experimental values, colored lines indicate fits.
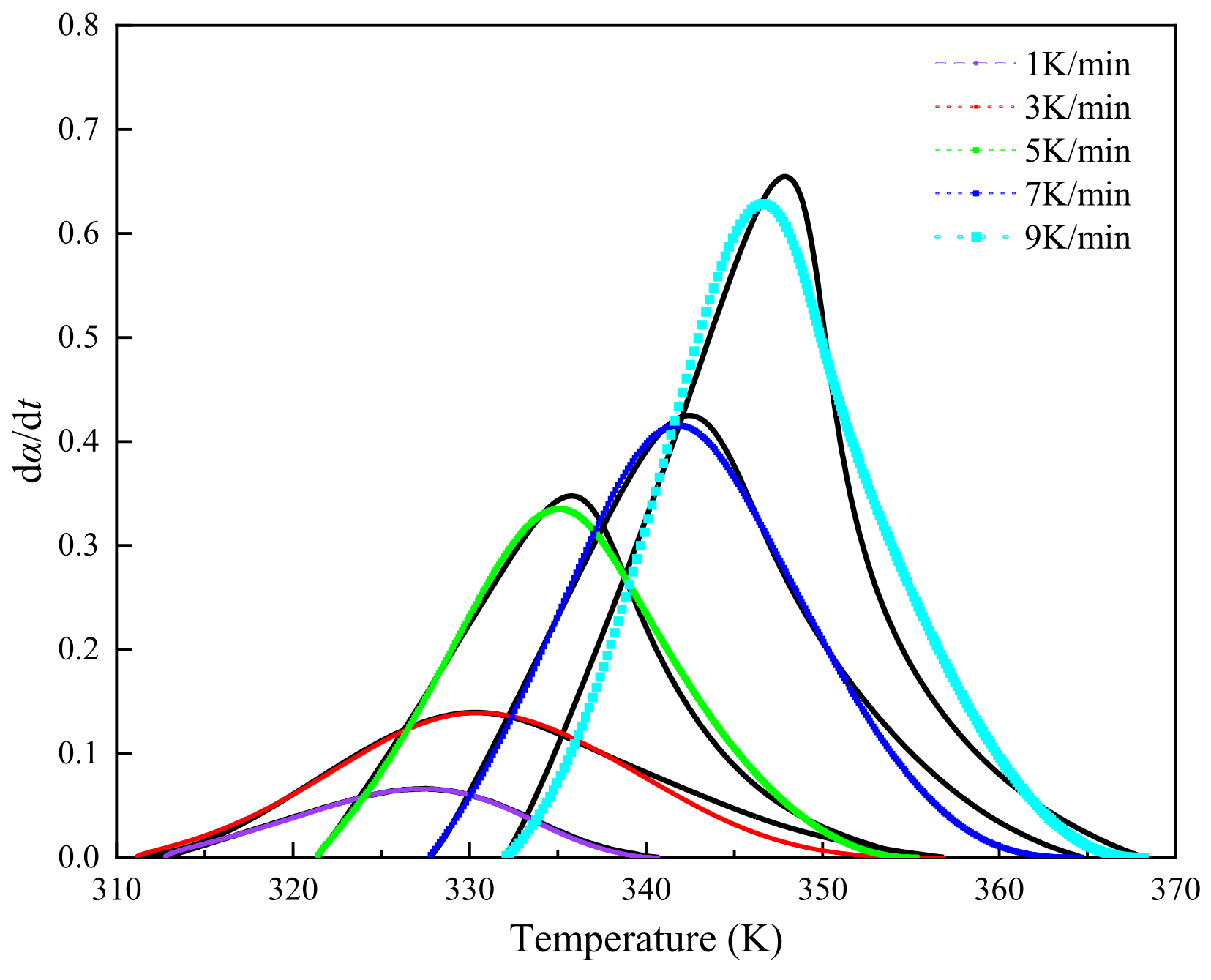
Preprints 99771 g008
Preprints 99771 g009aPreprints 99771 g009b
Figure 9. Numerical simulation calculation chart of FP based on AM. (a) Simulation calculation model diagram; (b) Curing degree and temperature curve of the propagation front-end;(c) Simulation distribution of propagation temperature；(d) Simulation distribution of propagation curing degree.
Figure 9. Numerical simulation calculation chart of FP based on AM. (a) Simulation calculation model diagram; (b) Curing degree and temperature curve of the propagation front-end;(c) Simulation distribution of propagation temperature；(d) Simulation distribution of propagation curing degree.
Preprints 99771 g009aPreprints 99771 g009b
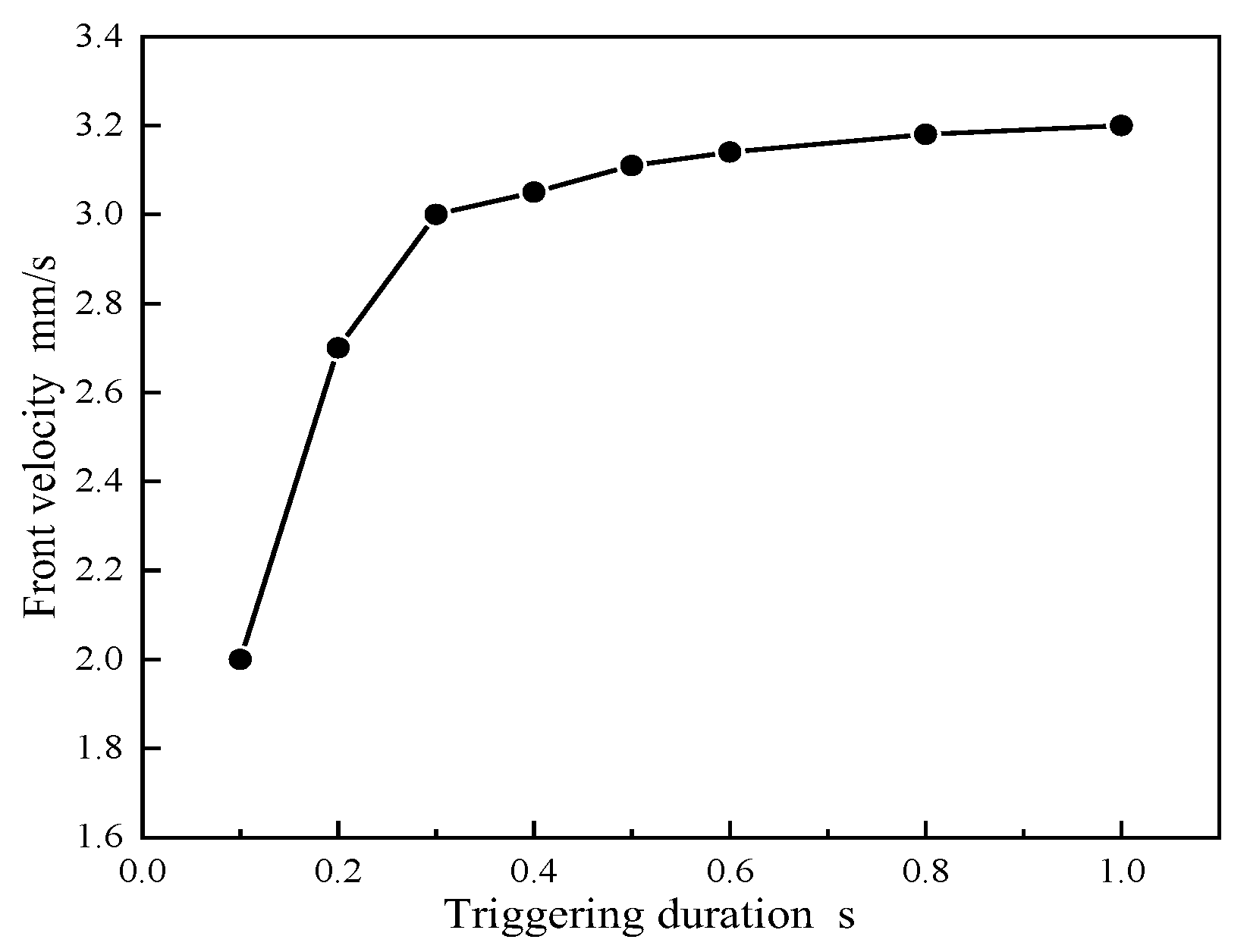
Preprints 99771 g010
Figure 10. Impact of trigger time on front-end speed.
Figure 10. Impact of trigger time on front-end speed.
Preprints 99771 g010
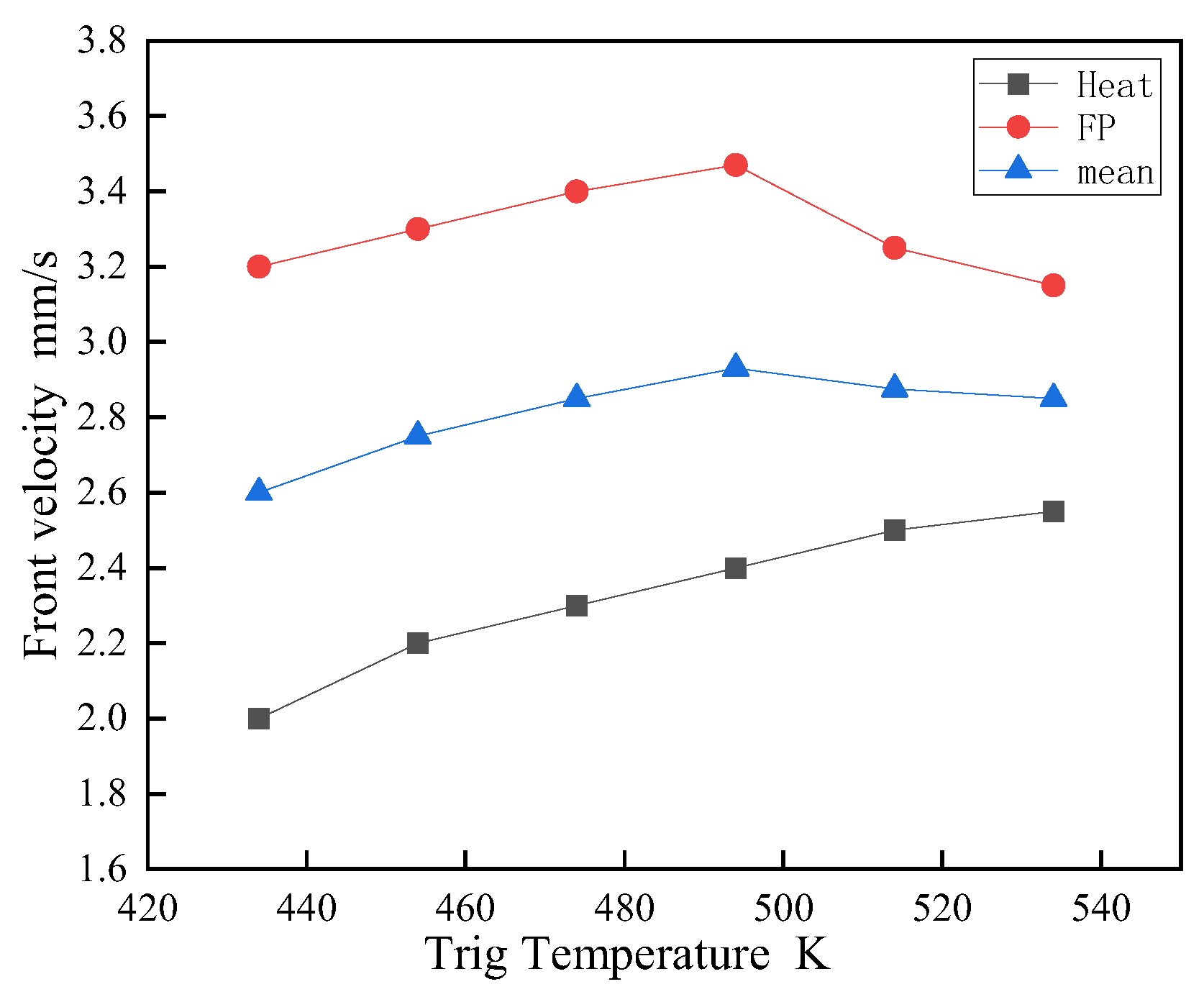
Preprints 99771 g011
Figure 11. Diagram of the influence of different triggering temperatures on front-end speed.
Figure 11. Diagram of the influence of different triggering temperatures on front-end speed.
Preprints 99771 g011
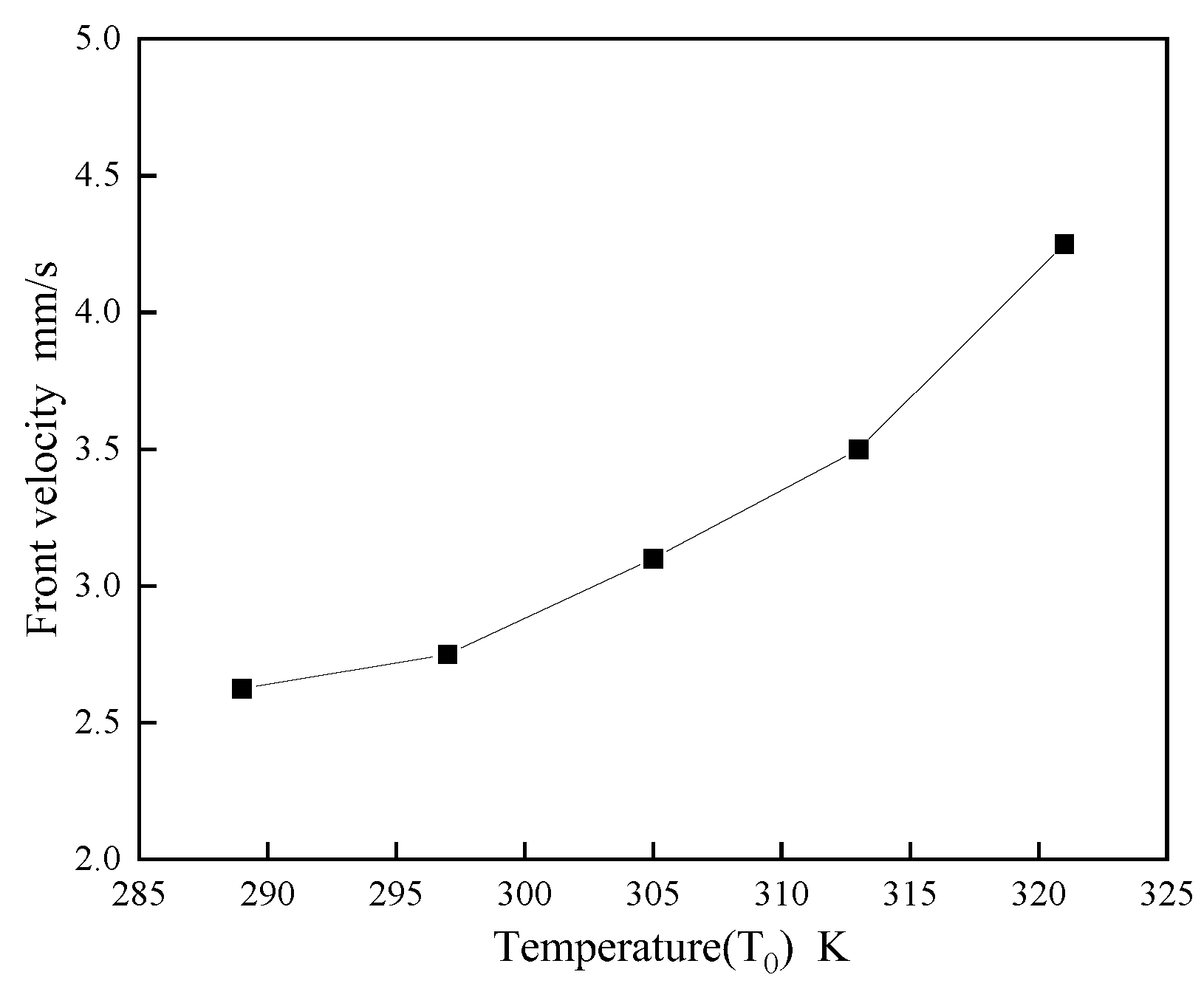
Preprints 99771 g012
Figure 12. Diagram of the influence of system temperature T0 on front-end speed.
Figure 12. Diagram of the influence of system temperature T0 on front-end speed.
Preprints 99771 g012
Preprints 99771 g013
Figure 13. Schematic diagram of FP experimental model.
Figure 13. Schematic diagram of FP experimental model.
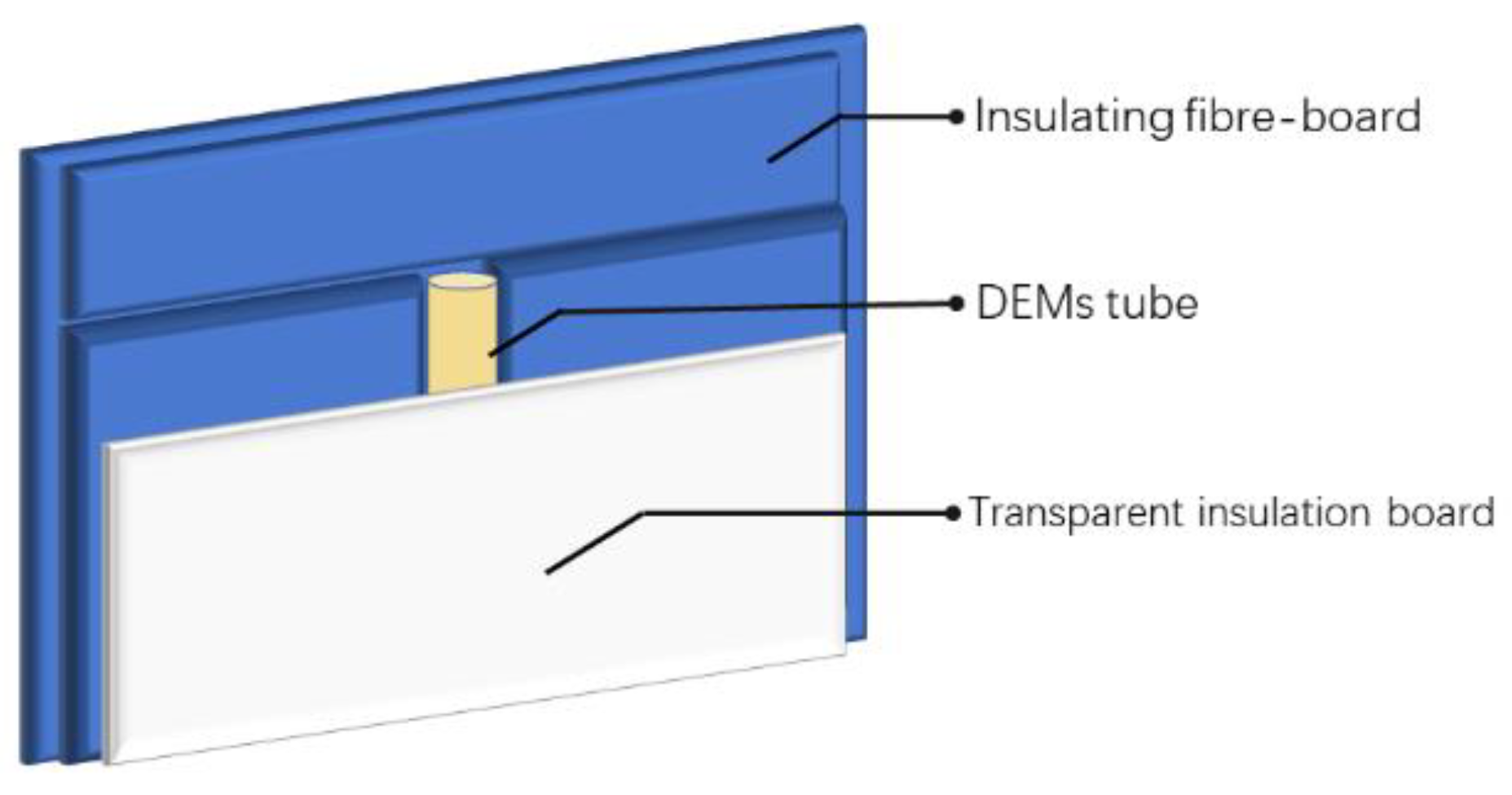
Preprints 99771 g013
Preprints 99771 g014
Figure 14. FP propagation infrared image of DEM.
Figure 14. FP propagation infrared image of DEM.
Preprints 99771 g014
Table 1. Characteristic conversion peaks and kinetic parameters from autocatalytic models across varied heating rates.
Table 1. Characteristic conversion peaks and kinetic parameters from autocatalytic models across varied heating rates.
β αp αm αp∞ n m lnA
1 0.561 0.214 0.561 0.883 0.240 31.035
3 0.478 0.189 0.468 1.490 0.347 31.725
5 0.534 0.249 0.540 1.133 0.376 32.073
7 0.485 0.222 0.489 1.357 0.386 31.750
9 0.556 0.267 0.527 1.309 0.476 31.927
mean 0.523 0.223 0.517 1.234 0.365 31.702
Table 2. Thermophysical parameters of DEMs based on AM.
Table 2. Thermophysical parameters of DEMs based on AM.
Monomer κ （W/m*k） ρ(kg/m3) C p (J/kg*K) Hr（J/g） T0(K)
AM 0.25 900 1990 406.05 305
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated