Prerpints.org logo
Preprint
Article

Novel Method for Determining Fibrin/Fibrinogen Degradation Product and Fibrinogen Threshold Criteria by Artificial Intelligence in Cases of Massive Hemorrhage during Delivery with Hematuria

Altmetrics

Downloads

85

Views

59

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 February 2024

Posted:

27 February 2024

You are already at the latest version

Alerts
Abstract
(1) Background: Although diagnostic criteria for massive hemorrhage with organ dysfunction such as disseminated intravascular coagulation associated with delivery have been empirically established based on clinical findings, strict logic has yet to be used to establish numerical criteria. (2) Methods: A dataset of 107 deliveries with ≥2,000 g of blood loss, among 13,368 deliveries from nine national perinatal centers in Japan between 2020 and 2023 was obtained. Twenty-three patients had fibrinogen levels <170 mg/dl, which is the initiation of coagulation system failure per our previous reports. Three of these patients had hematuria. We used six machine learning methods to identify the borderline criteria dividing the fibrinogen/fibrin/fibrinogen degradation product (FDP) planes, using 15 coagulation fibrinolytic factors. (3) Results: The boundaries of hematuria development on a two-dimensional plane of fibrinogen and FDP were obtained. If the FDP–fibrinogen/3–60 (mg/dl) value is positive, this indicates hematuria; otherwise, the case is non-hematuria, as demonstrated by the support vector machine method that seemed the most appropriate. (4) Conclusions: The borderline criterion dividing the fibrinogen/FDP plane for patients with hematuria that could be considered organ dysfunction in massive hemorrhage during delivery was obtained using artificial intelligence, and this method seemed to be useful.
Keywords: 
Subject: Medicine and Pharmacology  -   Obstetrics and Gynaecology

1. Introduction

Massive hemorrhage continues to be one of the most severe complications in pregnant women. Massive hemorrhage during delivery can be classified into consumption coagulopathy with coagulation abnormalities, such as disseminated intravascular coagulation (DIC) resulting from abruptio placentae, and dilutional coagulopathy without coagulation abnormalities, such as atonic bleeding [1]. DIC is a systemic disease affecting the coagulation system, simultaneously causing procoagulant factor activation, fibrinolytic activation, and consumptive coagulopathy that can ultimately lead to organ dysfunction and death [2]. As DIC can be significant causes of maternal mortality, the pathogenesis of the disease needs to be understood. DIC should be appropriately diagnosed because massive hemorrhage during delivery due to consumption coagulopathy may require treatment for correction of coagulation abnormalities. DIC during pregnancy is one of the chief causes of maternal mortality worldwide [3], with a frequency of 0.03% [4] to 0.35% [5]. DIC can originate from and cause damage to the microvasculature; this, if sufficiently severe, can lead to organ dysfunction [6]. However, although numerical diagnostic criteria for DIC associated with delivery have been empirically established based on clinical findings such as the presence or absence of organ dysfunction and laboratory findings of coagulation and fibrinolysis factors, strict logic has yet to be used to establish numerical criteria.
Fibrin/fibrinogen degradation products (FDPs) represent a key factor concerning DIC. Excessive FDP with diminished or normal systemic fibrinolytic activity suggests that local intravascular fibrin deposition and fibrinolysis occurred in normal parturition and in bleeding complications in pregnancy [7]. We reported the criterion values of coagulation and fibrinolytic system collapse based on FDP, focusing on the fibrinogen behavior, using mathematical methods such as data distribution function evaluation and differential equations in massive hemorrhage during delivery without organ dysfunction [8]. When the fibrinogen level fell below 237 mg/dl, the FDP distribution became abnormal, which began the abnormal coagulation/fibrinolysis system. When it fell below 170 mg/dl, the coagulation/fibrinolysis system failed (P<0.05). The borderline value of FDP in organ dysfunction cases was expected to be even higher. This classification showed good agreement with the clinical status [9].
Artificial intelligence (AI) has recently become a more common and easily applied tool in medical science. Some AI applications involve medical imaging [10,11,12,13,14,15,16,17,18,19,20], though some do not [21,22,23,24,25]. Machine learning is part of the concept of AI and can acquire rules for judging unknown data by learning patterns latent in the data. Machine learning enables the learning and classification of observed data. An optimal method can be chosen from among various machine learning algorithms. Machine learning can computationally classify the data, resultantly determining the data boundaries.
The present study was a prospective study in which we collected cases of massive hemorrhage during delivery with hematuria that could be assumed as organ dysfunction, and we developed a method to mathematically determine the FDP boundaries for hematuria.
We used the method to analyze 15 coagulation/fibrinolysis-related factors, selecting factors that correlate with fibrinogen and FDP and that would facilitate rapid clinical results and avoid multicollinearity with each other. Then, after performing supervised learning using machine learning, we determined the criterion line dividing the plane of fibrinogen and FDP. We used the same factors selected to create a discriminant analysis function [26] to obtain the boundaries, which we compared with the boundaries created by machine learning.

2. Materials and Methods

This multicenter prospective case series study including human subjects was approved by the National Hospital Organization (NHO) Central Research Ethics Committee (R1-1009002). The participants were women who gave birth at any of nine NHO perinatal centers (NHO Okayama Medical Center, NHO Saga Hospital, NHO Nagasaki Medical Center, NHO Mie Chuo Medical Center, NHO Higashihiroshima Medical Center, NHO Kure Medical Center, NHO Kyoto Medical Center, NHO Shikoku Medical Center for Children and Adults, and NHO Kokura Medical Center) in Japan between August 2020 and September 2023. We used fully deidentified data for deliveries with ≥2,000 g of blood due to hemorrhage within 24 hours after delivery. Blood sampling was performed when needed, and blood test data analyzed in the study were collected. Obstetric management, blood product transfusion, and determining the cause of bleeding were performed at the attending physicians’ discretion at each center. Data from the first measurement for each patient were used for analysis.
All procedures were performed in accordance with the ethical standards of the responsible committees on human experimentation (institutional and national) and the Helsinki Declaration of 1964 and its later amendments. Written informed consent was obtained from all patients for which identifying information is included in this article.
Based on the results of our previous study [8], we used only data for fibrinogen <170 mg/dl, which was a criterion for coagulation system failure. In the present study, we defined the appearance of hematuria as organ dysfunction.
Let the set of factors of the complete data obtained be {α,β,γ, ...}. Let {α,β,γ, ...} be the set of factors of the complete data obtained. Let A and B be the sets of factors significantly related to element α and another element β, respectively. Here, a contribution rate >0.49 is used as the criterion. The elements of the A∪B set are classified into the following sets P, Q, R.
P = x x ∈ A ,   x ∉ B ,   x ∉ Φ }   … .
Q = y y ∉ A ,   y ∈ B ,   y ∉ Φ }   … .
R = z z ∈ A ,   z ∈ B ,   z ∉ Φ }   … .
, where cr(v,w) is the contribution rate between v and w, then,
c r x s , x t < C R ;   s ≠ t ,   ∀ x s ∈ P ,   ∀ x t ∈ P   … .
c r y s , y t < C R ;   s ≠ t ,   ∀ y s ∈ Q ,   ∀ y t ∈ Q   … .
c r z s , z t < C R ;   s ≠ t ,   ∀ z s ∈ R ,   ∀ z t ∈ R   … .
Here, CR = 0.64. When N(P), N(Q), and N(R) are the number of elements in P, Q, and R, respectively, we have the following vectors,
{ α ,   β ,   x 1 ,   x 2 , … , x N P ,     y 1 ,   y 2 , … , y N Q ,   z 1 ,   z 2 , … , z N ( R ) }   … .
The classifiers were created by labeling cases with and without organ dysfunction and by performing supervised machine learning. We used logistic regression [27], random forest [28], nearest neighbors [29], naïve Bayes [30], neural network [31], and support vector machine [32] as machine learning methods.
Then, when the regression functions are f, g, and h,
x ~ i = f i α ;   i = { 1 ,   2 ,   … ,   N P }   … .
y ~ j = g j β ;   j = { 1 ,   2 ,   … ,   N Q }   … .
z ~ k = h k α , β ;   k = { 1 ,   2 ,   … ,   N R }   … .
{ α ,   β ,   x ~ 1 ,   x ~ 2 , … , x ~ N P ,   y ~ 1 ,   y ~ 2 , … , y ~ N Q ,   z ~ 1 ,   z ~ 2 , … , z ~ N ( R ) }   … .
This vector was substituted into the classifier to obtain the classification in {α,β}. In this study, α and β were calculated as fibrinogen and FDP, respectively.
Next, a discriminant analysis was performed using this vector.
Then, a single regression function α ~ = f β was obtained using the same method with fibrinogen as the dependent variable and FDP as the independent variable. The organ dysfunction criterion values for FDP alone were then determined.
We examined the performance of each machine learning method, and comprehensively determined the optimal boundary criterion.
Development environment for analysis and statistics
The computing environment comprised a Mac Pro running OS X 13.1 (Apple Inc.; Cupertino, CA, USA) and Mathematica 13.0 (Wolfram Research; Champaign, IL, USA). The data distribution analysis, discriminant analysis, linear regression analysis, machine learning, Mann–Whitney test, and t-test were carried out with this setup.

3. Results

During the study period, 322 women fulfilled the inclusion criteria from among 13,368 deliveries at all participating centers. Of these women, 132 were enrolled, while 25 were excluded because required data were missing. In this study’s final sample of 107 women, there were 23 with fibrinogen <170 mg/dl. Three were classified as organ dysfunction cases because they had hematuria corresponding to marked activation of the coagulation-fibrinolytic system, while the remaining 20 were non-organ dysfunction cases. Antiplasmin (AP), activated partial thromboplastin time (APTT), antithrombin (AT), D-dimer, FDP, fibrin monomer complex (FMC), fibrinogen, hemoglobin (Hgb), Hgb/fibrinogen, hematocrit (Hct), α2 plasmin inhibitor plasmin complex (PIC) [33], platelet (Plt), prothrombin time (PT-sec) [5], prothrombin time-international normalized ratio (PT-INR), and thrombin antithrombin complex (TAT) [33] were obtained as factors for the complete data. Among these 15 factors, those with a significant difference between patients with organ dysfunction and without organ dysfunction were FDP, D-dimer, TAT, Hgb/fibrinogen, fibrinogen, PT-sec, and PT-INR in the t-test, and FDP, D-dimer, TAT, Hgb/fibrinogen, fibrinogen, PT-INR, PT-sec, and PIC in the Mann–Whitney test in descending order of P-value from the t-test (Table 1). In both tests, FDP had the most statistically significant difference.
Among the 13 factors other than fibrinogen and FDP, Hgb/fibrinogen, PT-sec, and PT-INR were strongly correlated with fibrinogen, while D-dimer and PIC were strongly correlated with FDP. To avoid multicollinearity, regression functions were created to obtain Hgb/fibrinogen and PT-sec from fibrinogen and D-dimer from FDP (Table 2).
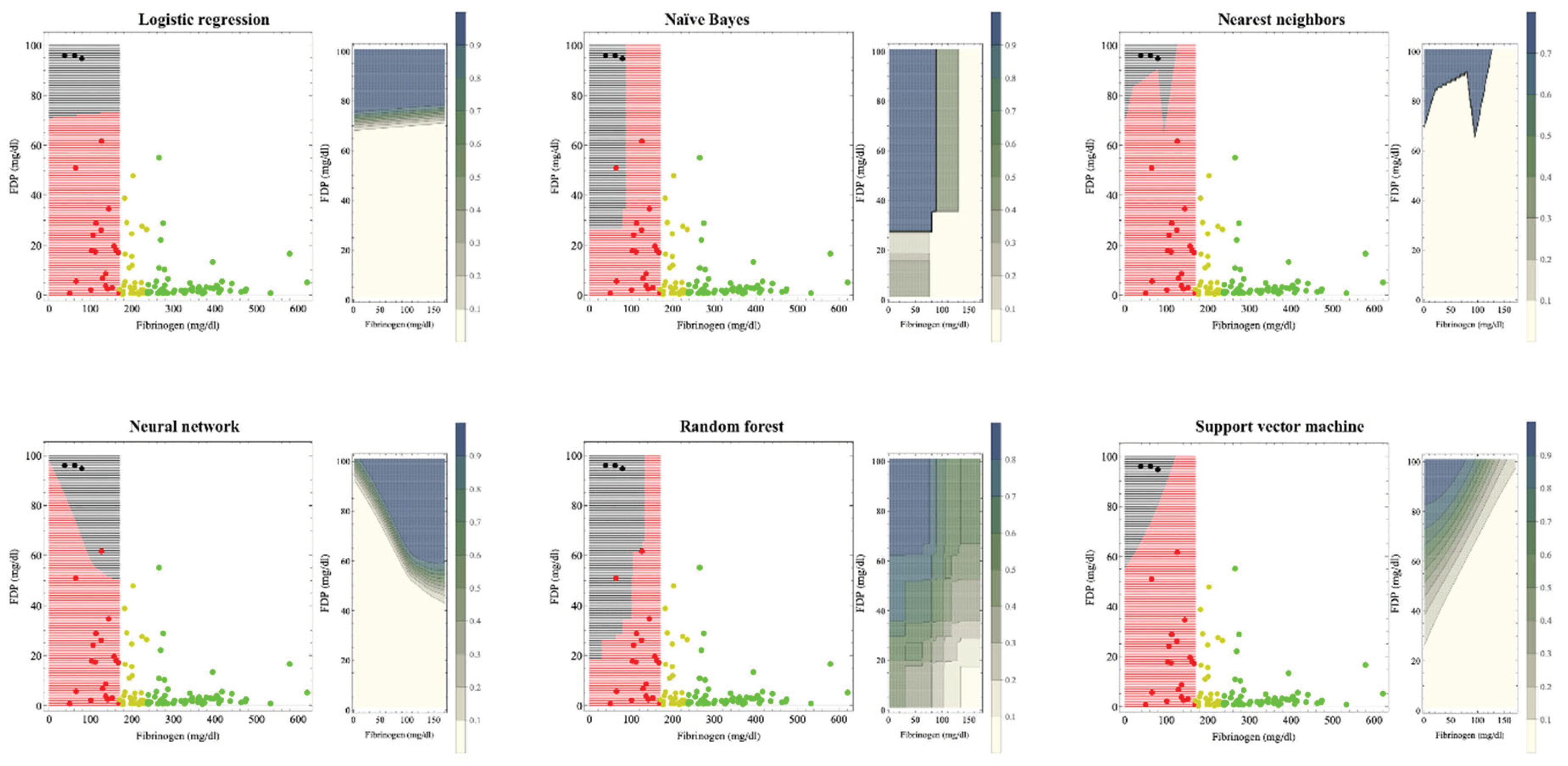
Figure 1 shows the hematuria boundaries that, based on machine learning, could be recognized as organ dysfunction in massive hemorrhage during delivery. In previous studies [8], the reference values for fibrinogen were 237 mg/dl and 170 mg/dl for the onset and breakdown of coagulopathy, respectively. Machine learning was used to perform supervised learning on cases with fibrinogen levels <170 mg/dl. The patient was considered to have hematuria if the estimated probability of developing hematuria by each machine learning method was >0.5. The crude areas where organ dysfunction occurs are: logistic regression: FDP >75 mg/dl; naïve Bayes: fibrinogen <100 mg/dl and FDP >30 mg/dl; nearest neighbors: fibrinogen <120 mg/dl and FDP> 80 mg/dl; neural network: FDP >50 mg/dl; random forest: fibrinogen <150 mg/dl and FDP> 40 mg/dl; and support vector machine shows that if the FDP–fibrinogen/3–60 (mg/dl) value is positive, this indicates hematuria; otherwise the case is non-hematuria because FDP decreases from 100 to 60 mg/dl as the fibrinogen level decreases from 120 mg/dl to zero.
For the left figure of each method, black areas indicate areas of organ dysfunction. The green, yellow, red, and black dots indicate cases without coagulopathy, with coagulopathy, with disrupted coagulopathy, and with organ dysfunction, respectively. Our previous study used fibrinogen criteria values of 237 and 170 mg/dl for the development and disruption of coagulopathy, respectively.8 Machine learning was trained on red and black cases with fibrinogen levels <170 mg/dl. The crude areas where organ dysfunction occurs are: logistic regression; FDP >75 mg/dl, naïve Bayes; fibrinogen <100 mg/dl and FDP >30 mg/dl, nearest neighbors; fibrinogen <120 mg/dl and FDP >80 mg/dl, neural network; FDP >50 mg/dl, random forest, fibrinogen <150 mg/dl and FDP >40 mg/dl; support vector machine shows that the boundary by whether FDP–fibrinogen/3–60 (mg/dl) is positive because FDP decreases from 100 to 60 mg/dl as the fibrinogen level decreases from 120 mg/dl to zero.
In the contour graph on the right figure of each method, as shown in the legend bar, the darker the color, the higher the probability of hematuria. If the estimated probability of developing hematuria was >0.5, the patient was considered to have hematuria in the left figure. As coagulopathy is generally accompanied by a fibrinogen decrease and FDP increase, support vector machine, neural network, and naïve Bayes, whose contour lines change stepwise, seemed to be a good fit.
The boundary by support vector machine method that does not include the fibrinogen 170 mg boundary seemed most appropriate for clinical use.
Table 3 shows the performance of classifiers on the boundaries in the fibrinogen and FDP planes of hematuria occurrence by the different machine learning methods. All methods demonstrated high accuracy values >0.91. All methods demonstrated high values of the area under the characteristic curve (AUC) >0.95. Class mean class entropy [34,35] was smaller in the logistic regression, naïve Bayes, and neural network methods.
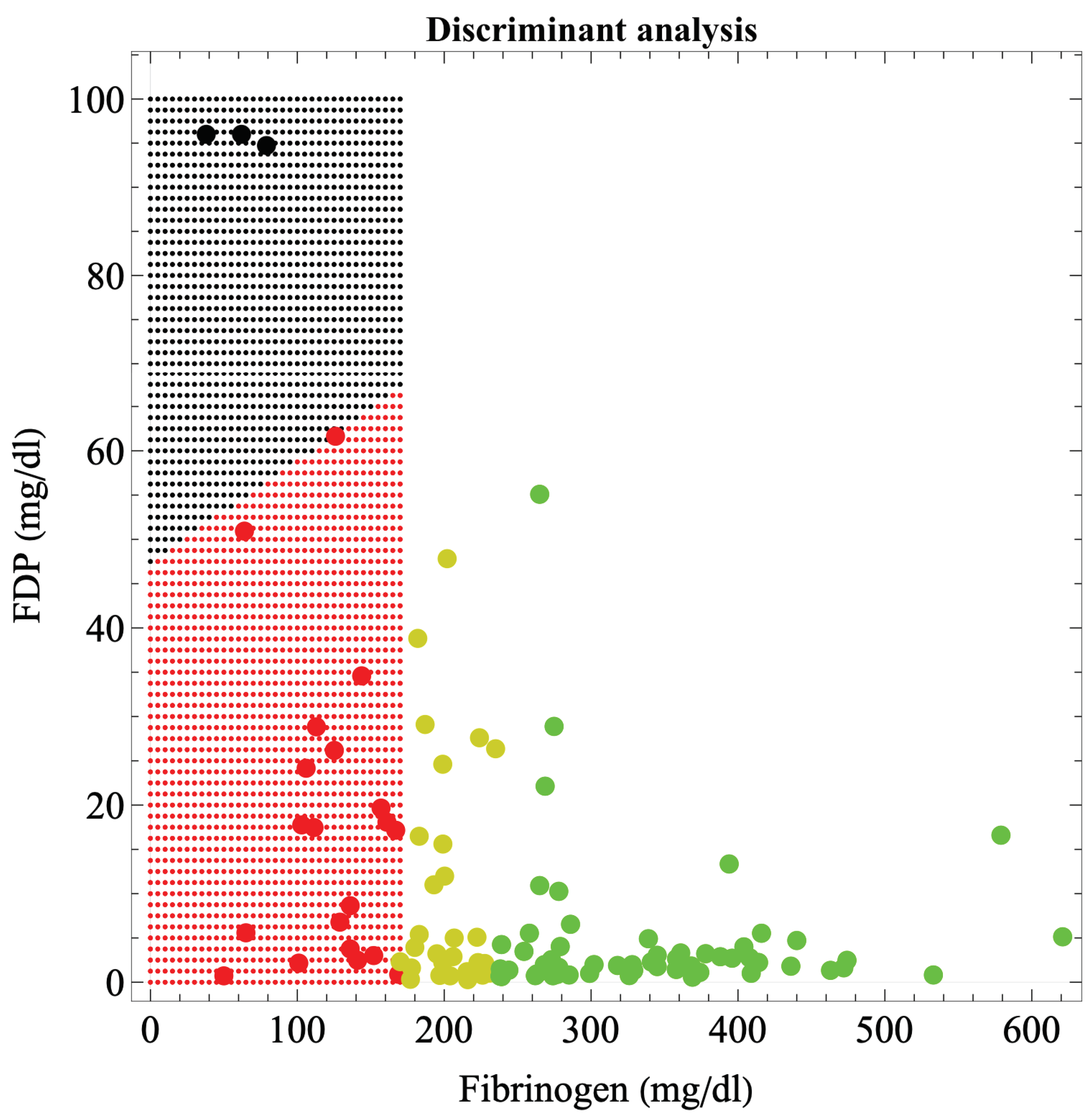
Figure 2 shows the boundaries of hematuria occurrence in massive hemorrhage during delivery, based on discriminant analysis. The boundary was a straight line connecting (0, 50) and (170, 68) in the fibrinogen-FDP coordinates. The discriminant function was: 50.693 – 0.00106 × fibrinogen – 0.52723 × FDP – 0.04314 × Hgb/fibrinogen-0.6978 × PT-sec – 0.02844 × D-dimer; η2=0.775 meaning moderate fit (P = 3.37×10−9), error probability = 0.4186%.
The FDP criterion value for hematuria development was determined from the FDP value alone, independent of fibrinogen. The relationship between fibrinogen and FDP was y ~ = β 0 + β 1 x ;   x ; F D P ,   y ; f i b r i n o g e n ,   β 0 = 132.905 ± 9.571   P = 4.719 × 10 − 12 ,   β 1 ; − 0.6613 ± 0.2327   P = 9.760 × 10 − 3 ,   R 2 = 0.278 . Table 4 shows the comparison of the performance of the classifiers by machine learning method. The FDP criteria were 84.96, 101.16, 73.38, 86.94, 92.23, and 79.67 for logistic regression, random forest, nearest neighbors, naïve Bayes, neural network, and support vector machine, respectively. All AUC values were >0.958, and the positive diagnostic rate was excellent, at ≥0.956, except for random forest.

4. Discussion

We presented a method for obtaining the boundaries of hematuria development associated with massive hemorrhage during delivery, on a two-dimensional plane consisting of fibrinogen and FDP. Each machine learning method and discriminant analysis presented a variety of candidate boundaries. As shown in Table 3, the performance of the machine learning classifier and the fit of the discriminant analysis function were both generally excellent. The different methods gave various boundaries and criteria; however, as they are all mathematically correct, it was not desirable to simply determine a single boundary or a criterion statistically, or to adopt an average of the values. Boundaries should ultimately be determined comprehensively based on clinical judgment, though data analysis should eliminate subjective judgments to the greatest possible extent. As coagulopathy is generally accompanied by decreased fibrinogen and increased FDP, the support vector machine, neural network, and naïve Bayes methods are well suited for this purpose because the contour lines change in a stepwise manner. Additionally, neither contains a fibrinogen 170 mg/dl boundary. Based on these findings, the support vector machine and naïve Bayes methods appeared suitable for predicting hematuria in patients with massive hemorrhage during delivery. The boundary by whether FDP–fibrinogen/3–60 (mg/dl) is positive by the support vector machine method seemed the most appropriate for clinical use, though naïve Bayes, which has a very low value of class mean class entropy, may be optimal (Figure 1, Table 3). Erez et al. [36] reported that the definition of DIC by the Scientific and Standardization Committee on DIC of the International Society on Thrombosis and Haemostasis indicated that (1) DIC is always secondary to other causes, one being obstetric-related, such as abruption placentae [37], (2) DIC represents systemic pathological activation of coagulation, and (3) DIC is a process that originates in the microvasculature, or the vascular endothelium, resulting in organ damage from microthrombi [38]. As hematuria alone does not necessarily indicate organ dysfunction, yet is almost always considered to be nearly a state of organ dysfunction, and as it is impractical to biopsy microthrombi in the kidneys of pregnant women in delivery who are hemorrhaging, there is value in defining the onset of hematuria associated with massive hemorrhage during delivery as a type of clinical DIC and analyzing and applying the findings to clinical practice.
Although there are many coagulation and fibrinolytic factors in addition to, for example, complete blood counts and platelets, in a massive hemorrhage under the urgent circumstances of delivery, factors should be selected so that only those for which test results are available as quickly as possible are used to predict organ dysfunction and initiate preventive treatment. We, therefore, sought a criterion for determining organ dysfunction based solely on fibrinogen and FDP, factors for which results are known relatively quickly. As information on related factors such as Hgb/fibrinogen ratio, PT-sec, and D-dimer also exist behind these factors, the five-dimensional factors are projected onto a two-dimensional plane using a regression function, and not simply boundaries determined from fibrinogen and FDP information alone. We also obtained only the boundaries of the FDP in one dimension (Table 4). Clinicians would find the boundaries created from fibrinogen and FDP in a two-dimensional plane (Figure 1 and Figure 2) more clinically convincing than the one-dimensional FDP boundaries, because the fibrinogen estimates from the FDP are less precise. This is because, even at fibrinogen <170 mg/dl, consumption coagulopathy with FDP elevation and dilutional coagulopathy without FDP elevation were mixed; thus, the correlation between fibrinogen and FDP is no longer accurate (R2=0.278). Therefore, boundaries in a two-dimensional plane are more realistic and suitable for clinical applications than one-dimensional criterion. Although a boundary surface in a higher-dimensional space would be more accurate, recognizing and handling a boundary surface that divides a space of more than three dimensions is challenging; therefore, a boundary in a two-dimensional plane appears to be the most appropriate. The recognition of boundary surfaces in three-dimensional space and beyond will become easier to understand if the space is subdivided; that is, if the dimension is lowered by dividing the space into cases under certain conditions.
In this case, the boundary values are obtained in a two-dimensional plane from multidimensional factors, but by extending the above-described method, boundary surfaces can be obtained in three-dimensional or greater space. This can be applied not only to the analysis of the coagulation-fibrinolytic system in massive hemorrhage but also can be further generalized to other research areas. Care must be taken, however, combining factors to be selected to avoid multicollinearity. There are no set rules for combining these factors, and these must be handled on a case-by-case basis, which complicates the creation of the regression function. The discriminant analysis showed results comparable with those of machine learning, though it is only a linear combination of factors. However, since each factor is supposedly related to the others, AI classifiers are generally more suitable, especially in the future. Naturally, if more cases (e.g., more than 1,000) can be accumulated, including many organ dysfunction cases, AI using deep learning [39] should provide more reliable boundaries than machine learning or discriminant analysis.
In the present study, we sought the boundary between the two classifications of the presence or absence of organ dysfunction, but more than three classifications are still obtainable by extending the above-described method. The present analysis was limited to fibrinogen <170 mg/dl, where the coagulation system is disrupted, in accordance with our previous report [8], but it is also possible to create boundaries between three or more regions, including normal conditions.
The most statistically significant difference in FDP was between organ-dysfunctional and non-organ-dysfunctional cases with fibrinogen <170 mg/dl. This suggests FDP is the most important factor in determining organ dysfunction. Regarding hemorrhage, we suggest the validity of using FDP to predict severe organ dysfunction, focusing on the dynamics of fibrinogen, which is involved in both coagulation and fibrinolysis.
There were some limitations in this study. First, the number of organ dysfunction cases (three) was low. The results were acceptable despite there being only three cases of organ dysfunction because the cases’ laboratory values were widely apart and extremely abnormal. However, the frequency of detection of hematuria was 2.27% (3/132) of the number of cases in which the amount of bleeding was ≥2,000 g at delivery, and only 0.0244% (3/13, 368) of all deliveries; thus, accumulating cases of organ dysfunction such as hematuria is not easy, but, ideally, more data from more organ dysfunction cases would be added to the analysis. Additionally, although fibrinogen and FDP were selected as the two items for which rapid test results were clinically obtainable, the ability to obtain rapid results for both at the same time depends on medical institutions’ facilities and testing methods’ advances. In facilities where only fibrinogen results are available, fibrinogen <100 mg/dl, and in facilities where only FDP is available, FDP >60 mg/dl should be considered as an indication of organ dysfunction occurrence. Furthermore, although it is not our contention, some factor other than fibrinogen and FDP may be better suited for predicting organ dysfunction. Finally, although there were no deaths in this study and hematuria was used as organ dysfunction, there is no fixed definition of organ dysfunction. Data ideally should be analyzed with other indicators, such as death, renal dysfunction, postpartum sequelae, and histopathological abnormalities. The use of these severe cases would lead to different results.
Although each machine learning method proposed various boundaries, the results of naïve Bayes, support vector machine, and discriminant analysis seem clinically acceptable, and the boundary by whether FDP–fibrinogen/3–60 (mg/dl) is positive by support vector machine seemed the most appropriate for clinical use thus far. In the future, if more types of organ dysfunction, or data on cases of organ dysfunction, can be added, a more reliable region will be available. Even if the definition of organ dysfunction is changed, or many factors, including unknown ones, are added to the definition of organ dysfunction, the method presented in this study, which is based on AI using multiple factors correlated with fibrinogen and FDP and avoiding multicollinearity to obtain the boundary line dividing the plane of fibrinogen and FDP, can be expected to be a useful criterion for organ dysfunction occurrence.

Author Contributions

Conceptualization, Y.M., K.T. and I.Y.; methodology, Y.M.; software, Y.M.; validation, Y.M., K.T., I.Y., K.T., Y.M., N.T., T.M., I.E., K.M. and K.K.; formal analysis, Y.M.; investigation, Y.M..; resources, Y.M., K.T.; data curation, K.T., I.Y., K.T., Y.M., N.T., T.M., I.E., K.M. and K.K.; writing—original draft preparation, Y.M.; writing—review and editing, Y.M.; visualization, Y.M.; supervision, K.T. and I.Y.; project administration, K.T..; funding acquisition, K.T. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the grants from the National Hospital Organization. The funding source had no role in the design, practice, or analysis of this study. This research was funded by the grants from the National Hospital Organization, grant number. R1-1009002. The APC was funded by the National Hospital Organization, grant number. R1-1009002.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the National Hospital Organization (NHO) Central Research Ethics Committee (R1-1009002).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The datasets generated during the current study are available from the corresponding author upon reasonable request.

Acknowledgments

We thank the following clinicians who helped in the recruitment of participants: Sachie Suga and Megumi Koga at NHO Nagasaki Medical Center, Makoto Nomiyama and Yuko Oshima at NHO Saga Hospital, Kyohei Yamaguchi and Ryoun Cho at NHO Mie Chuo Medical Center, Takashi Kodama and Takako Sadakane at NHO Higashihiroshima Medical Center, and Aki Nagao at NHO Shikoku Medical Center for Children and Adults.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Tada, K.; Miyagi, Y.; Yasuhi, I.; Yoshida, M.; Yorozu, M,; Maegawa, Y,; Okura, N.; Kawakami, K.; Yamaguchi, K.; Ogawa, M.; Kodama, T.; Nomiyama, M.; Mizunoe, T. Clinical features of dilutional coagulopathy in massive obstetrical hemorrhage: A multicenter retrospective case series study. Journal of Japan Society of Perinatal and Neonatal Medicine 2020, 56, 417-423.
  2. Venugopal, A. Disseminated intravascular coagulation. Indian J Anaesth. 2014, 58, 603-608. [CrossRef]
  3. Gulumser, C., Engin-Ustun, Y., Keskin, L., Celen, S., Sanisoglu, S., Karaahmetoglu, S., Ozcan, A., Sencan, I. Maternal mortality due to hemorrhage: population-based study in Turkey. J Matern Fetal Neonatal Med 2019, 32, 3998–4004. [CrossRef]
  4. Rattray, D.D.; O’Connell, C.M.; Baskett, T.F. Acute disseminated intravascular coagulation in obstetrics: a tertiary centre population review (1980 to 2009). J Obstet Gynaecol Can 2012, 34, 341–347. [CrossRef]
  5. Erez, O.; Novack, L.; Beer-Weisel. R.; Dukler, D.; Press, F.; Zlotnik, A.; Than, N.G.; Tomer, A.; Mazor M. DIC score in pregnant women–a population based modification of the International Society on Thrombosis and Hemostasis score. PLoS One 2014, 9:e93240. [CrossRef]
  6. Taylor, F.B. Jr.; Toh, C.H.; Hoots, W.K.; Wada, H.; Levi, M. Towards definition, clinical and laboratory criteria, and a scoring system for disseminated intravascular coagulation. Thromb Haemost 2001, 86, 1327–1330. [CrossRef]
  7. Bonnar, J.; Davidson, J.F.; Pidgeon, C.F.; McNicol, G.P.; Douglas, A.S. Fibrin Degradation Products in Normal and Abnormal Pregnancy and Parturition. Br Med J 1969, 19, 137–140. [CrossRef]
  8. Miyagi, Y.; Tada, K.; Yasuhi, I.; Maekawa, Y.; Okura, N.; Kawakami. K.; Yamaguchi. K.; Ogawa. M.; Kodama. T.; Nomiyama. M.; Mizunoe. T.; Miyake. T. New method for determining fibrinogen and FDP threshold criteria by artificial intelligence in cases of massive hemorrhage during delivery. J Obstet Gynaecol Res 2020, 46, 256–265. [CrossRef]
  9. Tada, K.; Miyagi, Y.; Kumazawa, K.; Tsukahara, S.; Okimoto, N.; Yoshida, M.; Ooka, N. Feasibility of Applying Novel FDP Threshold Criteria to DIC Diagnostic Scoring Systems in Japanese Women with Placental Abruption. Eur J Clin Biomed Sci 2022, 8, 27-32. [CrossRef]
  10. Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi. N. Deep Learning to predicting live births and aneuploid miscarriages from images of blastocysts combined with maternal age. Int J Bioinfor Intell Comput 2022, 1, 10-21. [CrossRef]
  11. Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi. N. Predicting a live birth by artificial intelligence incorporating both the blastocyst image and conventional embryo evaluation parameters. Artif Intell Med Imaging 1(3):94-107, 2020. [CrossRef]
  12. Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi. N. Feasibility of artificial intelligence for predicting live birth without aneuploidy from a blastocyst image. Reprod Med Biol 2019, 18, 204-211. [CrossRef]
  13. Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi. N. Feasibility of deep learning for predicting live birth from a blastocyst image in patients classified by age. Reprod Med Biol 18: 190-203, 2019. [CrossRef]
  14. Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi. N. Feasibility of predicting live birth by combining conventional embryo evaluation with artificial intelligence applied to a blastocyst image in patients classified by age. Reprod Med Biol 2019, 18, 344–356. [CrossRef]
  15. Miyagi Y, Hata T, Miyake T. Fetal brain activity and the free energy principle. J Perinat Med 2023, 51, 925-931. [CrossRef]
  16. Miyagi, Y, Hata, T, Bouno, S, Koyanagi, A, Miyake, T. Artificial intelligence to understand fluctuation of fetal brain activity by recognizing facial expressions. Int J Gynecol Obstet 2023, 161, 877-885. [CrossRef]
  17. Miyagi, Y.; Hata, T.; Bouno, S.; Koyanagi, A.; Miyake, T. Recognition of Facial Expression of Fetuses by Artificial intelligence (AI). J Perinat Med 2021, 49, 596-603. [CrossRef]
  18. Miyagi, Y.; Hata, T.; Bouno, S.; Koyanagi, A.; Miyake, T. Recognition of Fetal Facial Expressions using Artificial Intelligence Deep Learning. Donald School J Ultrasound Obstet Gynecol 2021, 15, 223-228. [CrossRef]
  19. Miyagi, Y.; Takehara, K.; Miyake, T. Application of deep learning to the classification of uterine cervical squamous epithelial lesion from colposcopy images. Mol Clin Oncol 2019, 11, 583-589. [CrossRef]
  20. Miyagi, Y.; Takehara, K.; Nagayasu, Y.; Miyake, T. Application of deep learning to the classification of uterine cervical squamous epithelial lesion from colposcopy images combined with HPV types. Oncology Letters 2020, 19, 1602-1610. [CrossRef]
  21. Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi. N. New methods for comparing embryo selection methods by applying artificial intelligence: Comparing embryo selection AI for live births. BJHMR 2022, 9, 36–44. [CrossRef]
  22. Miyagi, Y.; Fujiwara, K.; Nomura, H.; Yamamoto, K.; Coleman, R.L. Feasibility of New Method for the Prediction of Clinical Trial Results Using Compressive Sensing of Artificial Intelligence. BJHMR 2023, 10, 237-267. [CrossRef]
  23. Miyagi, Y.; Miyake, T. Potential of artificial intelligence for estimating Japanese fetal weights. Acta Medica Okayama 2020, 74, 483-493. [CrossRef]
  24. Miyagi, Y.; Fujiwara, K.; Oda, T.; Miyake, T.; Coleman, R.L. Studies on Development of New Method for the Prediction of Clinical Trial Results Using Compressive Sensing of Artificial Intelligence. In Theory and Practice of Mathematics and Computer Science; Editor Ferreira, M.A.M., Ed.; Book Publisher International, Hooghly, West Bengal, India, 2020; pp. 101-108. Print ISBN: 978-93-90206-63-6, eBook ISBN: 978-93-90206-64-3.
  25. Miyagi, Y.; Fujiwara, K.; Oda, T.; Miyake. T.; Coleman, R.L. Development of New Method for the Prediction of Clinical Trial Results Using Compressive Sensing of Artificial Intelligence. J Biostat Biometric App 2018, 3, 202, 2018.
  26. Huberty, C.J. Discriminant Analysis. Rev Educ Res 1975, 45, 543–598. [CrossRef]
  27. Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: a methodology review. J Biomed Inform 2002, 35, 352-359. [CrossRef]
  28. Breiman, L. Random forests. Mach Learn 2001, 45, 5-32. [CrossRef]
  29. Friedman, J.; Baskett, F.; Shustek, L. An algorithm for finding nearest neighbors. IEEE Trans Comput 1975, 100, 1000-1006. [CrossRef]
  30. Ben-Bassat, M.; Klove, K.L.; Weil, M.H. Sensitivity analysis in Bayesian classification models: multiplicative deviations. IEEE Trans Pattern Anal Mach Intell 1980, 3, 261-266. [CrossRef]
  31. Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature. 1986, 323, 533-536. [CrossRef]
  32. Tsochantaridis, I.; Joachims, T.; Hofmann, T.; Altun, Y. Large margin methods for structured and interdependent output variables. J Mach Learn Res 2005, 6, 1453-1484.
  33. Asakura, H.; Takahashi, H.; Uchiyama, T.; Eguchi, Y.; Okamoto, K.; Kawasugi, K.; Madoiwa, S.; Wada, H. DIC subcommittee of the Japanese Society on Thrombosis and Hemostasis. Proposal for new diagnostic criteria for DIC from the Japanese Society on Thrombosis and Hemostasis. Thromb J 2016, 14, 42. [CrossRef]
  34. Pincus, S.; Singer, B.H. Randomness and degrees of irregularity. Proc Natl Acad Sci USA 1996, 93, 2083–2088. [CrossRef]
  35. Jamin, A.; Humeau-Heurtier, A. (Multiscale) Cross-Entropy Methods: A Review. Entrop. 2020, 22, 45. [CrossRef]
  36. Ere0,z O.; Othman, M.; Rabinovich, A.; Leron, E.; Gotsch, F.; Thachil, J. DIC in Pregnancy - Pathophysiology, Clinical Characteristics, Diagnostic Scores, and Treatments. J Blood Med 2022, 13, 21-44. [CrossRef]
  37. Levi, M.; Toh, C.H.; Thachi,l J.; Watson, H,G. Guidelines for the diagnosis and management of disseminated intravascular coagulation. Br J Haematol 2009, 145, 24–33. [CrossRef]
  38. Thachil, J. Disseminated Intravascular Coagulation: A Practical Approach. Anesthesiology 2016, 125, 230–236. [CrossRef]
  39. Deng, L.; Yu, D. “Deep Learning: Methods and Applications”, Foundations and Trends® in Signal Processing: 2014, 7, 197-387. [CrossRef]
Preprints 99815 g001
Figure 1. Boundary of hematuria occurrence in heavy bleeding during delivery by machine learning, i.e., the boundary of organ dysfunction occurrence. The results of each machine learning method are shown in two sets of figures. The left figure of the set shows the scatterplot of the data and the boundaries of the hematuria occurrence, and the right shows the contours of the estimated probability of hematuria occurrence, divided into 10 segments from 0% to 100%.
Figure 1. Boundary of hematuria occurrence in heavy bleeding during delivery by machine learning, i.e., the boundary of organ dysfunction occurrence. The results of each machine learning method are shown in two sets of figures. The left figure of the set shows the scatterplot of the data and the boundaries of the hematuria occurrence, and the right shows the contours of the estimated probability of hematuria occurrence, divided into 10 segments from 0% to 100%.
Preprints 99815 g001
Preprints 99815 g002
Figure 2. Boundary of hematuria occurrence in major hemorrhage at parturition by discriminant analysis; i.e., the boundary of organ dysfunction occurrence. Black areas indicate areas of organ dysfunction. The green, yellow, red, and black dots indicate cases without coagulopathy, with coagulopathy, with disrupted coagulopathy, and with organ dysfunction, respectively. Our previous study used fibrinogen criteria values of 237 and 170 mg/dl for the development and disruption of coagulopathy, respectively.8 The boundary was a straight line connecting (0, 50) and (170, 68) in the fibrinogen-FDP coordinates. The discriminant function was: 50.693 – 0.00106 × fibrinogen – 0.52723 × FDP – 0.04314 × Hgb/fibrinogen – 0.6978 × PT-sec – 0.02844 × D-dimer; η 2 = 0.775 that means moderate fit (P = 3.37×10-9), error probability = 0.4186%.
Figure 2. Boundary of hematuria occurrence in major hemorrhage at parturition by discriminant analysis; i.e., the boundary of organ dysfunction occurrence. Black areas indicate areas of organ dysfunction. The green, yellow, red, and black dots indicate cases without coagulopathy, with coagulopathy, with disrupted coagulopathy, and with organ dysfunction, respectively. Our previous study used fibrinogen criteria values of 237 and 170 mg/dl for the development and disruption of coagulopathy, respectively.8 The boundary was a straight line connecting (0, 50) and (170, 68) in the fibrinogen-FDP coordinates. The discriminant function was: 50.693 – 0.00106 × fibrinogen – 0.52723 × FDP – 0.04314 × Hgb/fibrinogen – 0.6978 × PT-sec – 0.02844 × D-dimer; η 2 = 0.775 that means moderate fit (P = 3.37×10-9), error probability = 0.4186%.
Preprints 99815 g002
Table 1. Comparison of factors for organ dysfunction and non-organ dysfunction cases in data with fibrinogen <170 mg/dl. Factors are listed in order of decreasing P-value of t-test.
Table 1. Comparison of factors for organ dysfunction and non-organ dysfunction cases in data with fibrinogen <170 mg/dl. Factors are listed in order of decreasing P-value of t-test.
Organ Dysfunction (Hematuria) Non-Organ Dysfunction t-Test Mann–Whitney Test
Factors Mean ± SD Min Max Median 0.25 quantile 0.75 quantile Mean ± SD Min Max Median 0.25 quantile 0.75 quantile P-value P-value
FDP 95.58 ± 0.73 94.73 96 96 94.73 96 17.52 ± 16.8 0.72 61.64 17.31 3.01 24.16 1.03×10−7 0.0053
DD 350.63 ± 189.25 135.4 491 425.5 135.4 491 47.77 ± 54.65 3 219 34.05 10.61 47.9 3.32×10−6 0.0092
TAT 120. ± 0.0 120 120 120 120 120 67.53 ± 42.88 15.4 120 63.25 19.9 113 2.80×10−5 0.0319
Hgb/fbg 139.08 ± 73.17 56.96 197.37 162.9 56.96 197.37 61.42 ± 24.9 30.18 112 53.96 42.64 66.67 0.0009 0.0399
fbg 59.67 ± 20.6 38 79 62 38 79 122.82 ± 34.2 50 169 127.5 103 143.8 0.0057 0.0198
PT-sec 17.3 ± 2.14 15.6 19.7 16.6 15.6 19.7 13.62 ± 2.24 10.1 18.2 13.2 12 14.4 0.0145 0.0318
PT-INR 1.61 ± 0.2 1.46 1.84 1.53 1.46 1.84 1.22 ± 0.25 0.96 2 1.11 1.06 1.22 0.0174 0.0317
PIC 38.13 ± 26.67 17.7 68.3 28.4 17.7 68.3 8.87 ± 8.02 0.3 27.3 6.45 2 14.6 0.1962 0.0121
AP 45.33 ± 11.93 32 55 49 32 55 53.7 ± 14.28 34 93 52.5 42 56 0.3479 0.4107
AT 52.67 ± 19.01 34 72 52 34 72 45.2 ± 13.15 27 82 43 39 49 0.3925 0.4364
APTT 54.3 ± 19.54 39.3 76.4 47.2 39.3 76.4 46.28 ± 17.05 29.7 93.6 40.65 32.5 51.8 0.4624 0.3858
FMC 166.33 ± 121.48 27 250 222 27 250 184.12 ± 83.87 19.2 250 250 124 250 0.7477 0.6223
Hgb 7.37 ± 2.8 4.5 10.1 7.5 4.5 10.1 6.82 ± 1.26 5 10.2 6.85 5.6 7.3 0.7692 0.6809
Plt 105.33 ± 34.95 76 144 96 76 144 99.65 ± 33.7 39 183 88 78 119 0.7887 0.8190
Hct 21.8 ± 8.02 13.5 29.5 22.4 13.5 29.5 20.78 ± 3.74 15 30.6 20.7 17.3 22.5 0.8473 0.7492
AP, antiplasmin; APTT, activated partial thromboplastin time. AT, antithrombin; DD, D-dimer; fbg, fibrinogen; FDP, fibrin/fibrinogen degradation products; FMC, fibrin monomer complex; Hgb, hemoglobin; Hct, hematocrit; PIC, α2 plasmin inhibitor/plasmin complex; Plt, platelet; PT, prothrombin time; PT-INR, prothrombin time-international normalized ratio; SD, standard deviation; TAT, thrombin antithrombin III complex.
Table 2. Regression functions from fibrinogen to Hgb/fbg and PT-sec and from fibrin/fibrinogen degradation products to D-dimer while avoiding multicollinearity.
Table 2. Regression functions from fibrinogen to Hgb/fbg and PT-sec and from fibrin/fibrinogen degradation products to D-dimer while avoiding multicollinearity.
Formula Estimate ± SE P-Value AIC R-Squared
Hgb/fbg = β0+β1 Fbg β0, 174.41 ± 15.277;
β1, −0.898 ± 0.126		 β0, 1.81×10−10; β1, 5.31×10−7 213.79 0.7057
PT-sec = β0+β1 fbg β0, 19.681 ± 1.118;
β1, −0.048 ± 0.009		 β0, 4.80×10−14; β1, 3.30×10−5 93.54 0.5679
D-dimer = β0+β1 FDP β0, −9.535 ± 20.235;
β1, 3.4946 ± 0.492		 β0, 0.642; β1; 5.24×10−7 265.83 0.7061
AIC, Akaike’s information criterion; fbg, fibrinogen; FDP; fibrin/fibrinogen degradation products, Hgb, hemoglobin; PT, prothrombin time; SE, standard error.
Table 3. Comparison of the performance of classifiers on the boundaries in the fibrinogen and fibrin/fibrinogen degradation product planes of hematuria occurrence in parturient hemorrhage by different machine learning methods. All methods demonstrated high accuracy values >0.91. All methods demonstrated high AUC values >0.95. Class mean class entropy was smaller in the logistic regression, naïve Bayes, and neural network methods.
Table 3. Comparison of the performance of classifiers on the boundaries in the fibrinogen and fibrin/fibrinogen degradation product planes of hematuria occurrence in parturient hemorrhage by different machine learning methods. All methods demonstrated high accuracy values >0.91. All methods demonstrated high AUC values >0.95. Class mean class entropy was smaller in the logistic regression, naïve Bayes, and neural network methods.
Accuracy ± SD AUC Class Mean Class Entropy Cohen’s Kappa F1 Score PPV, Precision Sensitivity, Recall Specificity
Logistic regression 1.000 ± 0.22 1.000 1.417×10−4 1.000 1.000 1.000 1.000 1.000
Naïve Bayes 0.9565 ± 0.04 0.9583 5.097×10−5 0.8321 0.8571 0.7500 1.000 0.950
Nearest neighbors 1.000 ± 0.22 1.000 0.3285 1.000 1.000 1.000 1.000 1.000
Neural network 1.000 ± 0.22 1.000 2.253×10−5 1.000 1.000 1.000 1.000 1.000
Random forest 0.9130 ± 0.06 1.000 0.2407 0.7013 0.7500 0.6000 1.000 0.9000
Support vector machine 0.9565 ± 0.04 1.000 0.4967 0.7767 0.8000 1.000 0.6667 1.000
AUC, area under the characteristic curve; SD, standard deviation.
Table 4. Comparison of the performance of classifiers on the boundaries of fibrin/fibrinogen degradation products (FDPs) for hematuria occurrence in parturient hemorrhage by different machine learning methods. Class mean entropy was smaller for the logistic regression, naïve Bayes, and neural network methods. The classifiers by the logistic regression, naïve Bayes, and neural network methods were equally superior.
Table 4. Comparison of the performance of classifiers on the boundaries of fibrin/fibrinogen degradation products (FDPs) for hematuria occurrence in parturient hemorrhage by different machine learning methods. Class mean entropy was smaller for the logistic regression, naïve Bayes, and neural network methods. The classifiers by the logistic regression, naïve Bayes, and neural network methods were equally superior.
FDP Criteria (mg/dl) Accuracy ± SD AUC Class Mean Entropy Cohen’s Kappa F1 Score PPV, Precision Sensitivity, Recall Specificity
Logistic regression 84.96 1.000 ± 0.22 1.000 1.417×10−5 1.000 1.000 1.000 1.000 1.000
Naïve Bayes 86.94 0.9565 ± 0.04 0.958 5.097×10−5 0.832 0.857 0.750 1.000 0.950
Nearest neighbors 73.38 1.000 ± 0.22 1.000 0.3285 1.000 1.000 1.000 1.000 1.000
Neural network 92.23 1.000 ± 0.22 1.000 3.569×10−4 1.000 1.000 1.000 1.000 1.000
Random forest 101.16 0.9130 ± 0.06 1.000 0.2407 0.701 0.750 0.600 1.000 0.900
Support vector machine 79.67 0.9565 ± 0.04 1.000 0.4967 0.7767 0.800 1.000 0.6667 1.000
AUC, area under the characteristic curve; SD, standard deviation.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated