Queuing-Inventory System with Catastrophes in the Warehouse: Case Rare Catastrophes

Preprint

Article

Queuing-Inventory System with Catastrophes in the Warehouse: Case Rare Catastrophes

Altmetrics

Downloads

111

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 February 2024

Posted:

27 February 2024

You are already at the latest version

Alerts

Abstract

A model of a single-server queuing-inventory system (QIS) with catastrophes and a finite waiting room for consumer customers (c-customers) has been developed. When a catastrophe occurs, all inventory in the system's warehouse is destroyed, but c-customers in the system are still waiting for restocking. In addition to c-customers, negative customers (n-customers) are also taken into account, which displaces one c-customers (if any). The policy (?, ?) is used to replenish stocks. If upon arrival of the c-customer the inventory level is zero, then according to Bernoulli’s scheme this c-customer is either lost or joining the queue. The mathematical model of the studied QIS is constructed in the form of a two-dimensional continuous-time Markov chain (2D CTMC). Exact and approximate methods for calculating the steady-state probabilities of constructed 2D CTMCs are developed and closed-form expressions are derived for calculating the performance measures. The results of numerical experiments are presented, demonstrating the high accuracy of the developed approximate formulas, as well as the behavior of performance indicators depending on the reorder point. In addition, an optimization problem is solved to obtain the optimal reorder point to minimize the expected total cost.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

MSC: 60J28; 60K25; 90B05; 90B22

1. Introduction

To increase the adequacy of the developed mathematical models of a real queuing-inventory systems (QISs), it is necessary to take into account the possibility of various risks. Among these risks, catastrophes (disasters) that lead to the destruction of all (or part) of inventories are more important. Generally speaking, in real systems, catastrophes are rare events. However, the rate of catastrophes is not so rare that it should not be taken into account when developing mathematical models of the real QISs. In other words, catastrophes are rare events, but they must be taken into account, since they significantly affect the performance of the system. Unfortunately, this real risk is not taken into account in the vast majority of works devoted to QISs models.

Note that in the available literature, the issues of the impact of catastrophes on the operation of classical queuing systems have been studied in detail, see, for instance, [1,2,3,4,5,6,7]. These issues have been studied in connection with assessing the reliability of servers in queuing systems, since in them catastrophes are interpreted as failure of the system servers, see [8,9] and their references lists.

The catastrophes in a QISs warehouse gives rise to new problems, and these problems have been poorly studied in the available literature. Models of QMS with randomly catastrophes that destroy only one item in a warehouse were developed in works [10,11], in which catastrophes are interpreted as destructive customers. Recently, QISs models with the possibility of a catastrophe destroying all items in the warehouse have been considered in [12]. The vast majority of works, including the mentioned papers devoted to models with catastrophes, study QISs models with an infinite queue. To analyze such models, the well-established in classical book [13] matrix-geometric method (MGM) is often used, for more detailed describing and applications of MGM see recent two volume books [14,15] as well as book [16]. However, models with an infinite queue are not adequate to the real situation, since in real QISs, as a rule, there are finite waiting room. However, models of QISs with finite waiting room for c-customers have been poorly studied, see works [17,18,19,20,21,22,23].

This work is a continuation of the research begun in the indicated above work [12]. Namely, here we study a Markov QIS model with catastrophes that destroy the entire warehouse and with a finite buffer for waiting consumer customers (c-customers). Note that imposing a restriction on the length of the queue of c-customers leads to a fundamental change (compared to the infinite model) in the methodology for studying the system. In addition, new performance measures of the system appear here. We understand that the Poisson/exponential assumption is a rough approximation to the real situation, but, firstly, this paper is one of the first works in this direction, and secondly, here a methodology for studying these systems is proposed.

The main contributions of this work can be summarized as follows:

Exact and approximate methods to study QIS model with finite waiting room are developed.
High-accurate closed-form approximate formulas for calculating the steady-state probabilities, as well as performance measures of the investigated QIS in the case of rare catastrophes are developed.
The developed approximate formulas make it possible to calculate the performance measures of large-scale QISs using closed-form formulas and minimize the expected total cost (ETC) by choosing the optimal value of reorder point.

This paper is organized as follows. In Section 2, we describe the model of investigated finite QIS. Exact and approximate methods to calculate the steady-state probabilities as well as performance measures are developed in Section 3. The results of numerical examples are shown in Section 4. Concluding remarks are given in Section 5.

2. The Model

Consider single server finite QIS in which warehouse has maximum capacity

S

. Input flow of homogeneous c-customers forms Poisson process with rate

λ^{+}

. Customer homogeneity means that each customer requires the same amount of inventory. The service times of the c-customers are independent identically distributed (i.i.d.) random variables with a common average value

μ^{- 1}

and at the end of service the inventory level decreases by one unit. The waiting room for queuing c-customers has a finite size

R, R < \infty

. This means that if, when a c-customer arrives, there are already

R

c-customers in the queue, then the arriving new c-customer is lost with probability (w.p.) 1; otherwise, the arriving c-customer will join the queue if the server is busy. A combined sales scheme is used, i.e., if upon arrival of c-customer inventory level is zero, then, in accordance to the Bernoulli trials, it either, w.p.

φ_{1}

joins the queue (backorder sale scheme), or w.p.

φ_{2} = 1 - φ_{1}

leaves the system without inventory (lost sale scheme).

Along with c-customers, the system also receives a Poisson flow of negative customers (n-customers) with rate

λ^{-}

. Negative customers require no service or inventory, but upon the arrival of n-customers, one c-customer is pushed out from the system, if any. Procedure of pushing out the c-customer is managed as follows: (1) if there is a queue of c-customers, then only the c-customer is pushed out of the queue; (2) if there is no queue of c-customers but only c-customer is on server, then a n-customer force out of the system a c-customer which is on server (in these cases the inventory level does not change, since it is assumed that stocks are released after the completion of servicing a c-customer); (3) if there are no c-customers in the system (in queue or on server), then arrived n-customer does not affect the operation of the system.

Catastrophes form a Poisson flow with parameter κ, and when a catastrophe occurs, all inventory items are instantly destroyed. A catastrophe destroys even items that are in the status of release to the c-customer. In this case, the interrupted c-customer returns to the queue, i.e., the catastrophe only destroys the inventory and does not force c-customers out of the system. Catastrophes does not affect the operation of the system warehouse, if the inventory level is zero.

In order to be specific, here

(s, S)

inventory replenishment policy is considered (sometimes this policy is called “Up to

S

” as well). This means that when the inventory level drops to the order replenishment point

s

0 \leq s < S,

a replenishment order is placed and upon replenishment, the inventory level is restored to level

S

, regardless of how many items were in inventory.

The lead times of the replenishments i.i.d. random variables with a common average value

ν^{- 1}

The problem is to find the joint distribution of the number of c-customers in the system and the inventory level of the system, as well as to calculate the key performance measures: the average number of items in warehouse, the average order size, the average reorder rate, includes the average length of the queue and loss rate of c-customers.

3. Steady-State Analysis

In this section, the Markov model is developed and both exact and approximate methods to calculate the steady-state probabilities are proposed.

3.1. An Exact Approach

In this subsection, an exact method to calculate the steady-state probabilities as well as performance measures is proposed. As in Melikov et al (2023) [12], let

X_{t}

be the number of с-customers at time

t

and

Y_{t}

be the inventory level at time

t

. So, the process

Z_{t} = \{(X_{t}, Y_{t}), t \geq 0\}

forms a two-dimensional continuous time Markov chain (2D CTMC) with state spac

E = ⋃_{m = 0}^{S} E_{m},

(1)

where

E_{m} = \{(0, m), (1, m), \dots, (R, m)\}

is the subset of states in which inventory level is equal to

m, m = 0,1, \dots, S .

The transition rate from state

(n_{1}, m_{1})

to state

(n_{2}, m_{2})

is denoted by

q ((n_{1}, m_{1}), (n_{2}, m_{2}))

. By taking into account the assumptions related to operating of the investigated QIS, we conclude that these transitions rates are calculated as follows

q ((n_{1}, m_{1}), (n_{2}, m_{2})) = \{\begin{matrix} λ^{+} φ_{1}, & m_{2} = m_{1} = 0, n_{2} = n_{1} + 1, \\ λ^{+}, & m_{2} = m_{1} > 0, n_{2} = n_{1} + 1, \\ λ^{-}, & m_{2} = m_{1}, n_{2} = n_{1} - 1, \\ μ, & m_{2} = m_{1} - 1, n_{2} = n_{1} - 1, \\ κ, & m_{1} > 0, m_{2} = 0, n_{2} = n_{1}, \\ ν, & m_{1} \leq s, m_{2} = S, n_{2} = n_{1} . \end{matrix}

(2)

From relations (2) we conclude that each state of the constructed 2D CTMC can be reached from any other state through a finite number of transitions, i.e. considered chain is an irreducible one. In other words, for any positive values of the initial parameters, a stationary mode is existing. Let us denote by 𝑝(𝑛, 𝑚) the probability of the state (𝑛, 𝑚) ∈ 𝐸. These probabilities can be obtained by solving the system of balance equations (SBE) which is constructed by using relations (2).

\begin{matrix} Case 1 : When (n, 0) \in E_{0} : \\ (λ^{+} φ_{1} χ (n < R) + λ^{-} χ (n > 0) + ν) p (n, 0) = λ^{+} φ_{1} p (n - 1,0) (n > 0) \\ + λ^{-} p (n + 1,0) χ (n < R) + μ p (n + 1,1) χ (n < R) + κ \sum_{m = 1}^{S} p (n, m) . \end{matrix}

(3)

\begin{matrix} Case 2 : When (n, m) \in E_{m}, 0 < m \leq s : \\ (λ^{+} χ (n < R) + λ^{-} χ (n > 0) + ν + μ + κ) p (n, m) = λ^{+} p (n - 1, m) χ (n > 0) \\ + λ^{-} p (n + 1, m) χ (n < R) + μ p (n + 1, m + 1) χ (n < R) . \end{matrix}

(4)

\begin{matrix} Case 3 : When (n, m) \in E_{m}, s < m < S : \\ (λ^{+} χ (n < R) + λ^{-} χ (n > 0) + μ + κ) p (n, m) = λ^{+} p (n - 1, m) χ (n > 0) \\ + λ^{-} p (n + 1, m) χ (n < R) + μ p (n + 1, m + 1) χ (n < R) . \end{matrix}

(5)

\begin{matrix} Case 4 : When (n, S) \in E_{S} : \\ (λ^{+} χ (n < R) + λ^{-} χ (n > 0) + μ + κ) p (n, S) = λ^{+} p (n - 1, S) χ (n > 0) \\ + λ^{-} p (n + 1, S) χ (n < R) + μ p (n + 1, m + 1) χ (n < R) + ν \sum_{m = 0}^{s} p (n, m) . \end{matrix}

(6)

Here and below, χ

(A)

denotes the indicator function of the event

A

. To SBE (3)-(6), a normalization condition should be added, i.e.

\sum_{(n, m) \in E} p (n, m) = 1 .

(7)

The constructed SBE (3)-(7) is a system of linear algebraic equations of dimension

(R + 1) \cdot (S + 1)

and it can be solved numerically by using well-known software in case the moderate values of the parameters

R

and

S

After calculating the steady-state probabilities, key performance measures of the QIS under study can be determined using a standard technique. The performance measures are divided into two groups: (1) inventory-related performance measures and (2) queuing-related performance measures. The first group of performance measures includes the average number of items in warehouse

(S_{a v})

, the average order size

(V_{a v})

and the average reorder rate

(R R)

The average number of items in warehouse (i.e. the average inventory level) is calculated as mathematical expectation of the appropriate random variable and is given by

$S_{a v} = \sum_{m = 1}^{S} m \sum_{n = 0}^{R} p (n, m) .$

(8)
Similar to (8), the average order size (i.e. the average size of replenished items from external source) is calculated as mathematical expectation of the appropriate random variable and is calculates as follows

$V_{a v} = \sum_{m = S - s}^{S} m \sum_{n = 0}^{R} p (n, S - m) .$

(9)
An inventory order is placed in two cases: (1) when the inventory level drops to the reorder point $s$ after completing customer service in states $(n, s + 1) \in E_{s + 1}$ , and (2) when catastrophes occur the in states $(n, m) \in E_{m}, m > 0 .$ Therefore, the average reorder rate is calculated as follows

$R R = μ \sum_{n = 1}^{R} p (n, s + 1) + κ (1 - \sum_{n = 0}^{R} p (n, 0)) .$

(10)

The second group of performance measures includes the average length of the queue

(L_{a v})

and loss rate of c-customers

(L R)

The average length of the queue is calculated as mathematical expectation of the appropriate random variable and is given by

$L_{a v} = \sum_{n = 1}^{R} n \sum_{m = 0}^{S} p (n, m) .$

(11)
Losing c-customers occurs in three cases: (1) if at the time the c-customer arrives the waiting room is full (with probability 1), i.e. when the system are in one of the states $(R, m) \in E_{m}$ , $m = 0,1, \dots, S,$ (2) if at the time the c-customer arrives, the inventory level is zero and waiting room is not full (with probability $φ_{2}$ ), i.e, when system are in one of the states $(n, 0) \in E_{0}$ , $n < R,$ (3) when n-customer arrived, it displaced one c-customer. Therefore, the loss rate of c-customers is calculated as follows

$L R = λ^{+} \sum_{m = 0}^{S} p (R, m) + λ^{+} φ_{2} \sum_{n = 0}^{R - 1} p (n, 0) + λ^{-} (1 - \sum_{m = 0}^{S} p (0, m)) .$

(12)

As it was mentioned above, the proposed exact approach can be used for investigation the QIS model with moderate state space. Computational difficulties arise for large-scale models, and an approximate method for calculating steady-state probabilities is then required. Below we develop an approximate method for solving this problem, which can be used in cases of rare catastrophes.

3.2. An Approximate Approach

In this subsection, we derive the closed-form approximate solution for steady-state probabilities of the investigated 2D CTMC, by using space merging approach, see [24]. This approach is highly accurate for systems with rare catastrophes, i.e. we will assume that

κ ≪ m i n (λ^{+}, λ^{-}, μ) .

Note that the last assumption is not extraordinary, since in the opposite case (i.e. when the level of catastrophes is close to the rate of c-customers, the speed of their service, the rate of n-customers) the QIS under consideration is generally not effective.

In the case where the above assumption is fulfilled, the basic requirement for an adequate application of space merging method is satisfied. In this case, transition rates between states in each subset

E_{m}

(see (1)) are much great than the transition rates between states from different subsets. So, in accordance to the space merging algorithm, each subset of states

E_{m}

in (1) is combined into one merged state

< m >

, and the following merging function is determined in the initial state space (1)

: U (n, m) = < m >, (n, m) \in E

. The merged states form the set

\hat{E} = \{< m > : m = 0,1, \dots, S\} .

The approximate values of steady-state probabilities,

\hat{p} (m, n),

are calculate as follows

\hat{p} (n, m) \approx ρ_{m} (n) π (< m >)

(13)

where

ρ_{m} (n)

denotes probability of state

(n, m)

within subset

E_{m}

and

π (< m >)

denotes probability of merged state

< m > \in \hat{E}

From relations (2) we conclude that the steady-state probabilities

ρ_{0} (n), n = 0,1, \dots, R,

within a split model with the state space

E_{0}

coincide with the stationary distribution of a finite one-dimensional birth-death process in which birth rate is

λ^{+} φ_{1}

while death rate is

λ^{-}

. By the same way, from relations (2) we conclude that the steady-state probabilities

ρ_{m} (n), m > 0, n = 0,1, \dots, R,

within a split model with the state space

E_{m}

are independent on

m,

and coincide with the stationary distribution of a finite one-dimensional birth-death process in which birth rate is

λ^{+}

while death rate is

λ^{-}

. In other words, steady-state probabilities within split models are calculated as

ρ_{m} (n) = \{\begin{matrix} θ^{n} \frac{1 - θ}{1 - θ^{R + 1}}, & m > 0, n = 0,1, \dots, N, \\ θ_{0}^{n} \frac{1 - θ_{0}}{1 - θ_{0}^{R + 1}}, & m = 0, n = 0,1, \dots, N, \end{matrix}

(14)

where

θ_{0} = λ^{+} φ_{1} / λ^{-}, θ = θ_{0} / φ_{1} .

Note 1. To simplify the notation, below the subscript

m

for cases

m > 0

is omitted in state probabilities

ρ_{m} (n) .

In cases

θ = 1

and/or

θ_{0} = 1

, all state probabilities

ρ_{m} (n) = 1 / (R + 1)

for any

n, n = 0,1, \dots, R,

and

m, m = 0,1, \dots, S

Let us denote the rate of transition from the merged state

< m_{1} >

to the merged state

< m_{2} >

q (< m_{1} >, < m_{2} >)

. Then, taking into account relations (2) and (14), we obtain the following formulas for calculating the indicated rates (all other transition rates are zero):

\begin{matrix} Case 0 \leq m \leq s : \\ q (< m >, < S >) = ν \sum_{n = 0}^{R} ρ_{m} (n) = ν \end{matrix}

(15)

\begin{matrix} Case m > 0 : \\ q (< m >, < 0 >) = κ \sum_{n = 0}^{R} ρ_{m} (n) = κ; \end{matrix}

(16)

q (< m >, < m - 1 >) = μ \sum_{n = 1}^{R} ρ_{m} (n) = μ (1 - ρ (0)) .

(17)

In other words, merged model represents one-dimensional Markov chain with state space

\hat{E}

where transition rates between states are calculated via formulas (15)-(17). Using the approach proposed in [12], we obtain the following closed-form formulas for calculating the probabilities of merged states:

π (0) = \frac{1 + b c}{1 + d c},

(18)

π (1) = d π (0) - b,

(19)

π (m) = a_{m} π (1), 2 \leq m \leq S,

(20)

where

d = \frac{ν + κ}{μ (1 - ρ (0))}, b = \frac{κ}{μ (1 - ρ (0))},

c = \sum_{m = 1}^{S} a_{m}, a_{m} = \{\begin{matrix} {(1 + d)}^{m - 1}, & if 1 \leq m \leq s + 1, \\ {(1 + d)}^{s} {(1 + b)}^{m - s - 1}, & if s + 1 < m \leq S . \end{matrix}

Eventually, taking into account formulas (13), (14), (18)-(20), we conclude that an approximate values of performance measures (8)-(12) can be calculated using the following explicit formulas

S_{a v} = \sum_{m = 1}^{S} m π (m);

(21)

V_{a v} = \sum_{m = S - s}^{S} m π (S - m);

(22)

R R = μ (1 - ρ (0)) π (s + 1) + κ (1 - π (0));

(23)

L_{a v} = \sum_{n = 1}^{R} n (ρ_{0} (n) π (0) + ρ (n) (1 - π (0)));

(24)

\begin{matrix} L R = λ^{+} φ_{2} π (0) (1 - ρ_{0} (0)) + λ^{+} ρ_{0} (R) π (0) + λ^{+} (1 - π (0)) ρ (R) + \\ + λ^{-} (π (0) (1 - ρ_{0} (0)) + (1 - π (0)) (1 - ρ (0))) \end{matrix}

(25)

4. Numerical Experiments

Based on the purpose of the paper, we conducted numerical experiments that have three goals: (1) estimation of the accuracy of the proposed approximate formulas; (2) study the behavior of the performance measures versus initial parameters and (3) solve the optimization problem.

4.1. Accuracy of the Developed Approximate Formulas

The accuracy of the developed approximate formulas is investigated via numerical experiments. For this purpose, exact values of the steady-state probabilities (SSP) are determined from SBE (3)-(7) for the QIS with maximum capacity of warehouse

S = 50

and buffer size

R = 30,

dimension of SBE is equal to 1581. The accuracy of the developed approximate formulas can be estimated using several norms, e.g. cosine similarity, Euclidean distance, Jaccard norm etc. To be specific, here we use a simple norm, that is, the maximum errors when calculating SSPs. Results of numerical experiments are shown in Table 1. In this table, along with an indication of the accuracy of calculating the SSPs, results are given that indicate the accuracy of calculating the performance measures (8)-(12). From this table, we conclude that the accuracy of the developed formulas to calculation of the SSPs as well as performance measures are sufficiently. From this table it is also clear that the accuracy of calculating the SSPs is greater than the accuracy of calculating performance indicators. This was to be expected, since the performance indicators are calculated through SSPs using operations of multiplication by large numbers, see formulas (8)-(12) and (21)-(25). We conducted a large number of experiments and demonstrated only a small part of them here. An interesting result of these experiments is that increasing the size of the system (i.e. increasing

S

and

R

) leads to an increase in the accuracy of the approximate results.

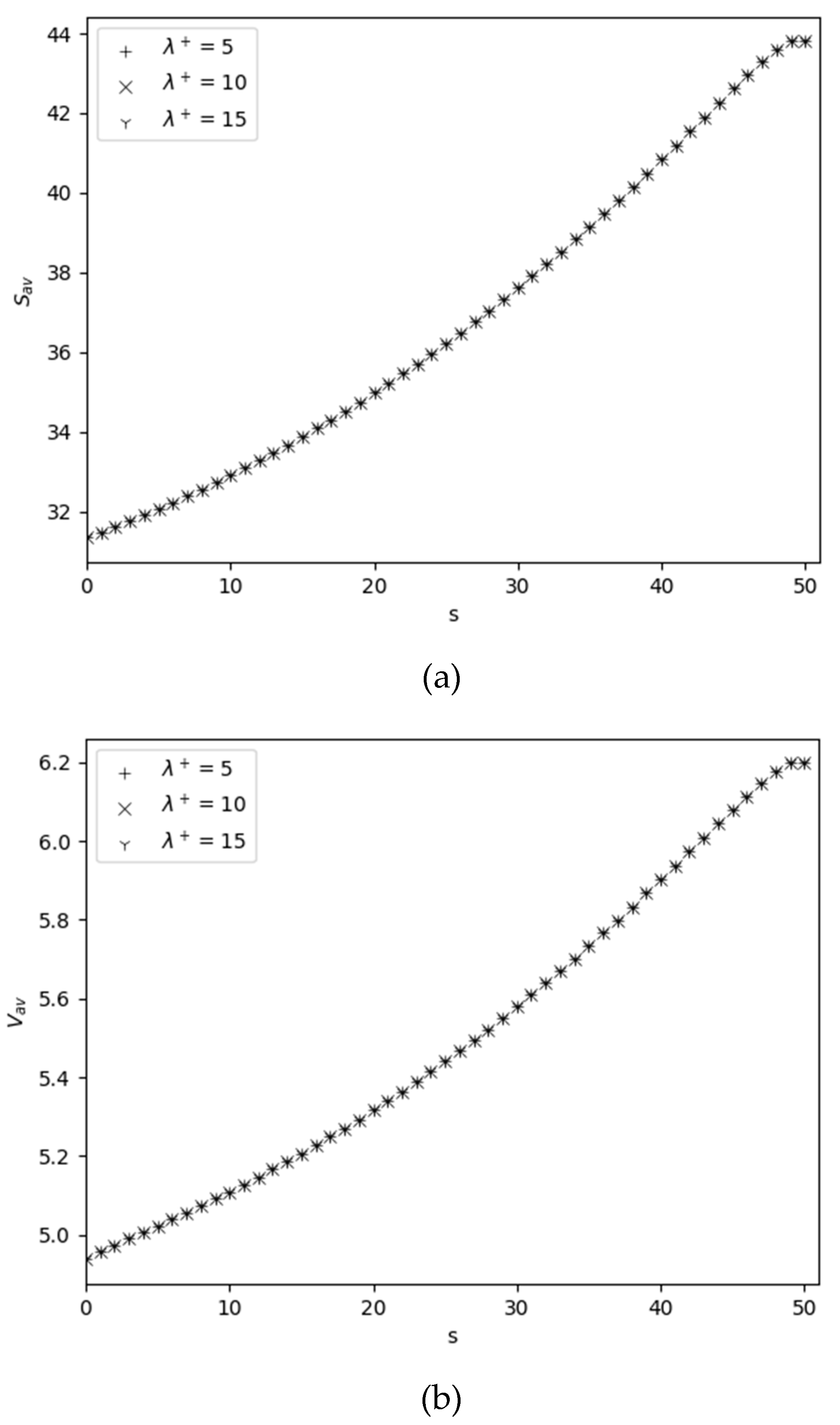
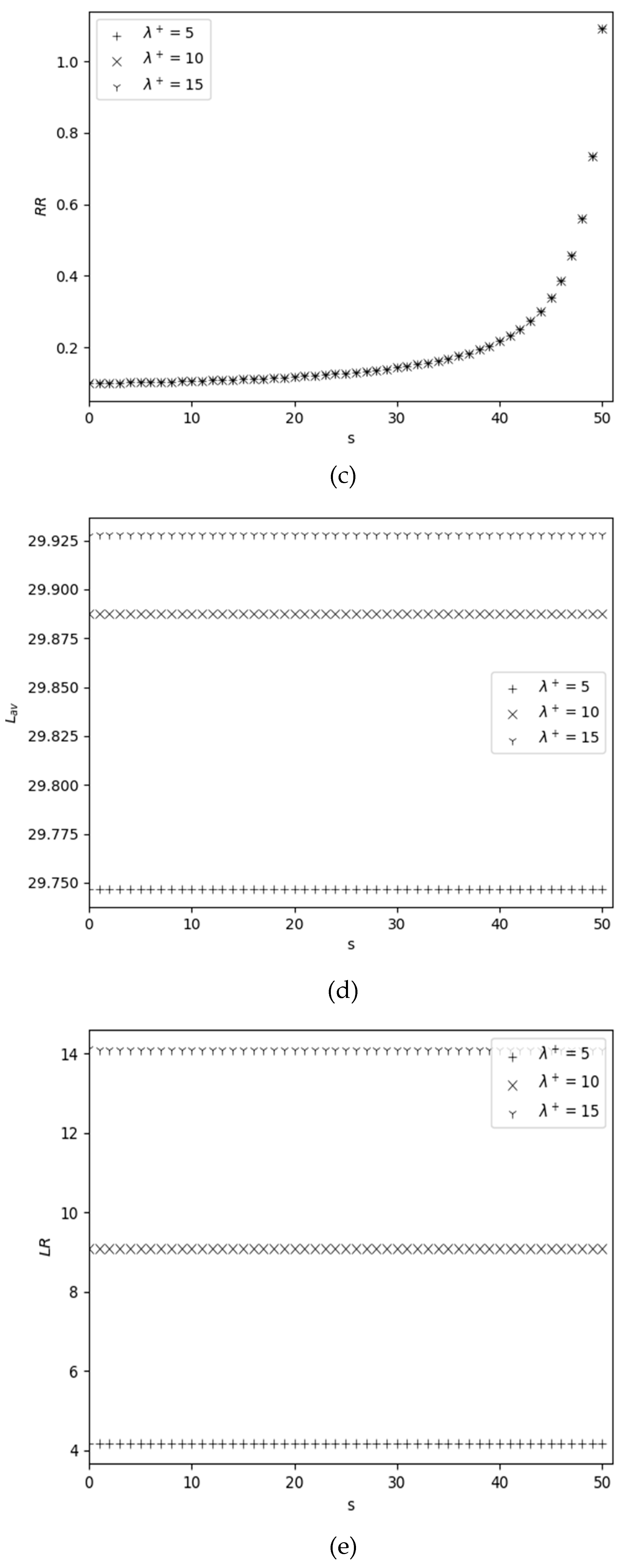
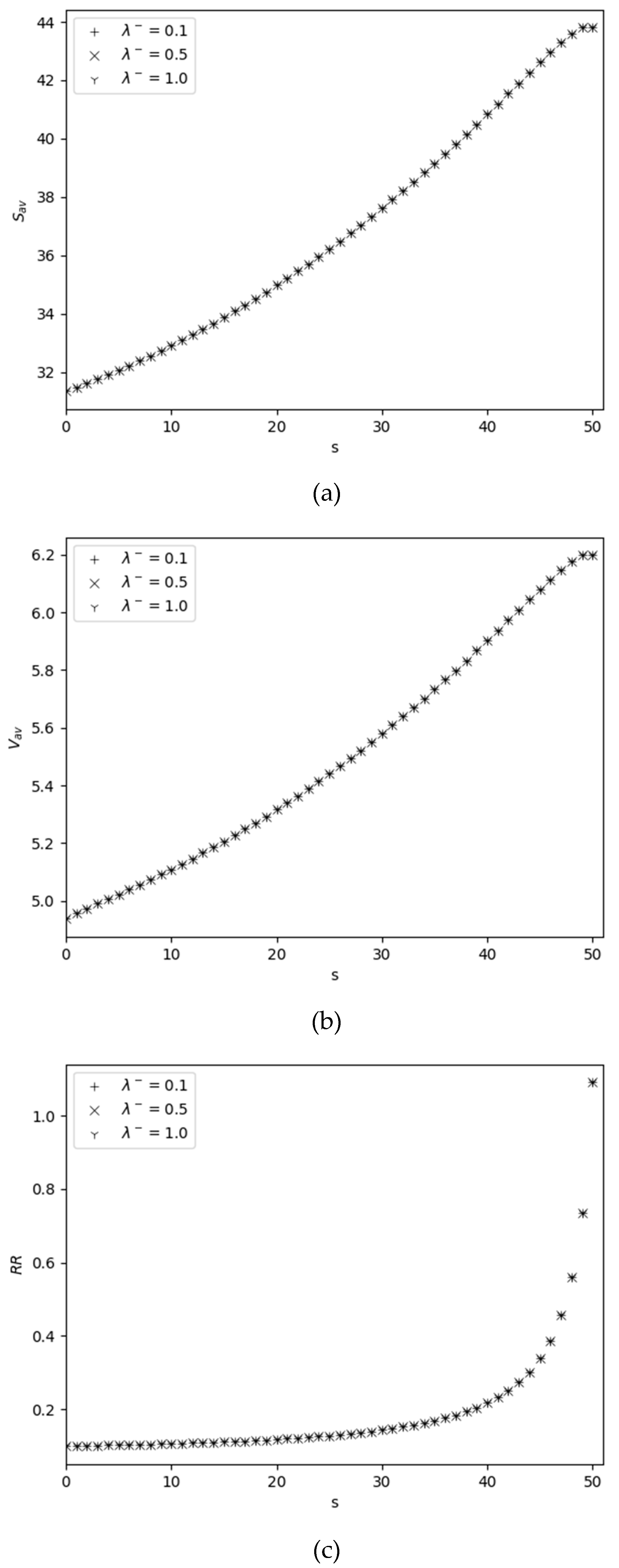
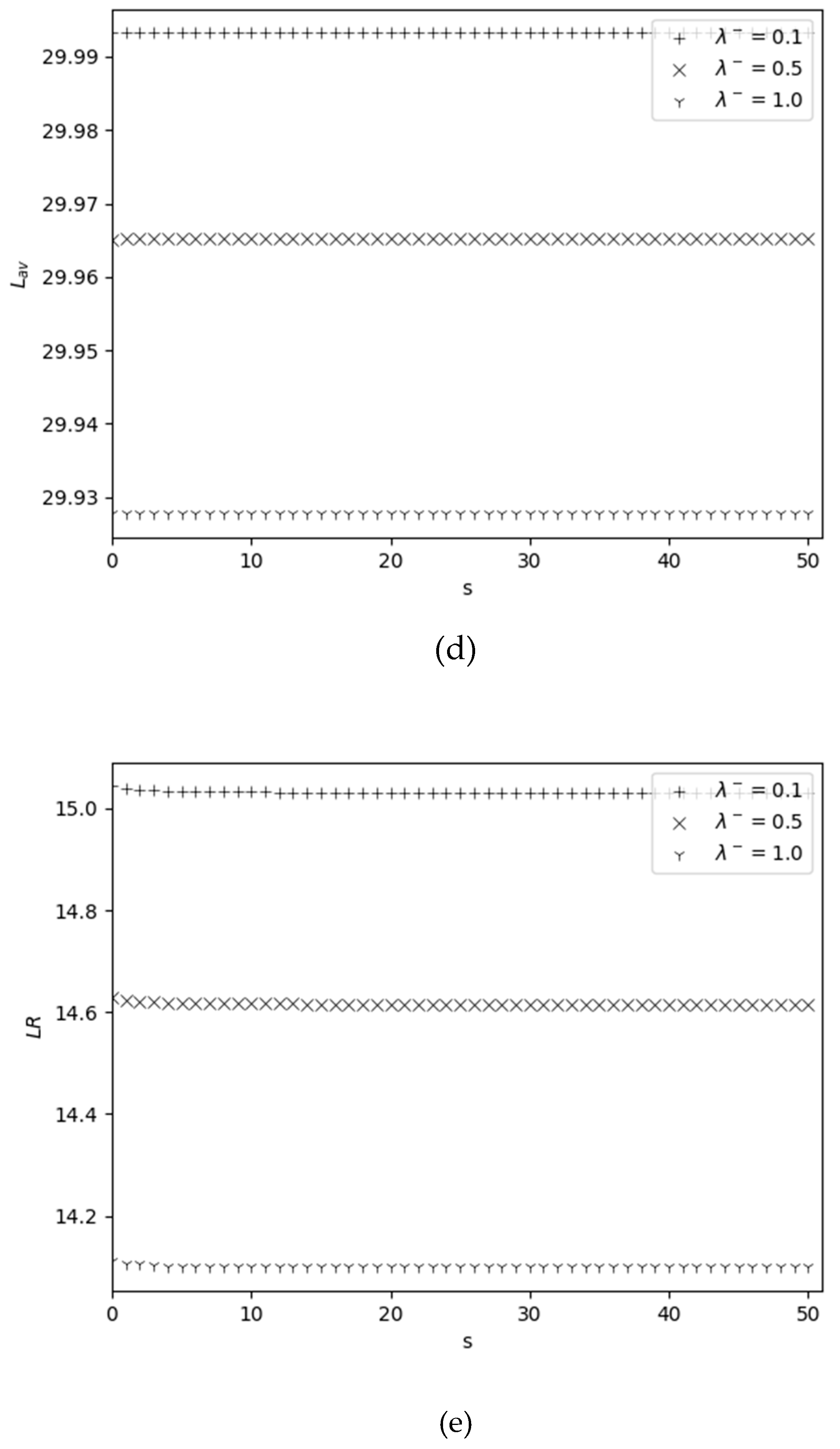
4.2. Behavior of Performance Measures Versus Reorder Point

Performance measures are computed and numerically illustrated for different sets of values for the input parameters. In all experiments the values of following parameters are fixed:

S = 50, N = 30, φ_{1} = 0.4, κ = 0.1 .

So, Figure 1 shows the behavior of performance measures as a functions of reorder point

s

for the three different values of

λ^{+}

. From these plots, we conclude that inventory-related performance measures are almost independent of the rate of c-customers, but significantly dependent on the reorder point, see Figure 1, (a), (b) and (c). Note that all inventory-related performance measures are increasing functions versus reorder point. Measure

S_{a v}

is an increasing function versus

s

, and this fact was expected, see Figure 1 (a). At first glance, the increasing of

V_{a v}

versus

s

seems unexpected, see Figure 1 (b). However, this fact has the following explanation: as

s

increases, the reorder rate increases (see Figure 1 (c)), and as a result, the average order size increases. The

R R

is an increasing function with respect to

s

because as

s

increases, the probability that the inventory level is positive, also increases and hence

R R

becomes an increasing function, see formula (10) as well. For the selected data the rate of its increase becomes very high at large (possible) values of the reorder point, see Figure 1 (c). Opposite, the queuing-related performance measures are almost independent of the reorder point, see Figure 1, (d) and (e). For selected initial data the average number of customers in queue

(L_{a v})

for all values of

λ^{+}

are very close to buffer size (

R = 30

), see Figure 1 (d). Therefore, loss rate

(L R)

is very close to

λ^{+}

, see Figure 1 (e).

The dependence of performance measures on

s

and

λ^{-}

is shown in Figure 2. It is interesting to note that here behavior, even absolute values of the inventory-related performance measures (see Figure 2, (a)-(c)), are same as in Figure 1 (a)-(c). From Figure 2 (d) we conclude that

L_{a v}

is almost independent of

s

and the rate of its decreasing versus

λ^{-}

is very small, i.e., increasing

λ^{-}

even by ten times leads to a change in the value of

L_{a v}

in the second digit after the decimal point. Similarly, from Figure 2 (e) we conclude that

L R

is also almost independent of

s

, but here the rate of its decrease compared to

λ^{-}

is noticeable.

The dependence of performance measures on

s

and

μ

is shown in Figure 3. An increase in

S_{a v}

with respect to

s

is obvious, since an increase in

s

leads to an increase in the rate of filling the warehouse to its maximum size, see Figure 3 (a); on the other hand,

S_{a v}

is a decreasing function versus

μ

because an increase in

μ

results in an increase in the rate at which inventory is sold. Since

S_{a v}

is a decreasing function with respect to

μ

, therefore

V_{a v}

is increasing with respect to

μ

, see Figure 3 (b); an increase in

s

leads to increasing the probability that the inventory level drops to zero due to catastrophes, i.e., average order size is also increasing function versus

s

. Measure

R R

is an increasing function with respect to

s

, since increasing of

s

leads to increasing the probability that the stock level is greater than zero, i.e., the rate of replenishment of stocks due to catastrophes also increases, see Figure 3(c); this measure is also an increasing function with respect to

μ

, since an increase in

μ

leads to increasing the probability that the inventory level drops to the re-order point

s

, i.e., the rate of replenishment increases (see formula (9) also). From Figure 3(d) we conclude that

L_{a v}

is an increasing function versus

s

and a decreasing function versus

μ

. And for large values of

s

, i.e.,

s > 25,

the value of

L_{a v}

is practically independent of

μ

. These facts are expected. Measure

L R

is decreasing function versus on both

s

and

μ

, see Figure 3 (e). The decrease of this function with respect to

s

is obvious, but its decrease relative to

μ

is not evident at first glance. The last fact has the following explanation: an increase in

μ

leads to increasing the probability that the inventory level is zero, i.e., the loss probability of arriving customers also increases and hence the measure

L R

becomes increasing. However, the rate of increasing of

L R

versus

μ

is very small, i.e., increasing

μ

even by three times leads to a change in the value of

L R

in the second digit after the decimal point.

The dependence of performance measures on

s

and ν is shown in Figure 4. Measure

S_{a v}

is an increasing one with respect to both

s

and ν, see Figure 4 (a). Indeed, an increase in

s

and ν leads to an increase in the rate of filling the warehouse to its maximum size. Measure

V_{a v}

is increasing versus

s

, while it is decreasing function versus ν. Here

V_{a v}

is decreasing versus ν, since

S_{a v}

is a increasing function with respect to ν, see Figure 4 (b); the increase in

V_{a v}

with respect to

s

is explained as above, i.e., as s increases, the probability of inventory levels falling to zero due to catastrophes also increases, so the average order size is also an increasing function with respect to

s

. Measure

R R

is an increasing one with respect to both

s

and ν, since an increase in both

s

and ν leads to increasing the probability that the stock level is greater than zero, hence the rate of replenishment of inventory due to catastrophes also increases, see Figure 4(c). From Figure 4 (d) we conclude that the

L_{a v}

is almost constant (does not decrease) depending on

s

and ν; only for small values of

s

, i.e. s<10, we observe insignificant differences between the values of

L_{a v}

for different values of ν. Measure

L R

is a decreasing function with respect to both

s

and ν, see Figure 4 (e). Such behavior of this measure is expected, since an increase in both

s

and ν leads to an increase in the average inventory level and, as a consequence, to a decrease in

L R

4.5. Optimization Problem

Third goal of performing numerical experiments is solving the optimization problem. To be specific, here minimization of Expected Total Cost (ETC) is considered. In this problem it is assumed that all load parameters as well as structural parameters of the QIS are fixed and only controllable parameter is reorder point. Similar to Melikov et al (2023) [12], ETC is defined as follows:

E T C (s) = (K + c_{r} \cdot V_{a v}) \cdot R R + c_{h} \cdot S_{a v} + c_{p s} \cdot κ \cdot S_{a v} + c_{l} \cdot L R + c_{w} {\cdot L}_{a v},

(26)

where

K

is the fixed price of one order,

c_{r}

is the unit price of the order size,

c_{h}

is the unit inventory storage price per unit of time,

c_{p s}

is the price of unit inventory destruction,

c_{l}

is the cost for a single c-customer loss,

c_{w}

is the price per unit time of queuing delay for a single c-customer.

The problem is to find a value (optimal) of

s

that minimizes (26). For any values of initial parameters this problem has solution since admissible set for values of

s

is finite and discrete, i.e.,

0 \leq s \leq S - 1 .

Coefficients in (26) for hypothetical model are selected as

K = 10, c_{r} = 15, c_{h} = 10, c_{l} = 450, c_{w} = 400, c_{p s} = 15

. Some results of the minimization of (26) are demonstrated in Table 2. Here we assume that

N = 30, φ_{1} = 0.4, λ^{+} = 15, λ^{-} = 1, κ = 0.1, μ = 2, ν = 1 .

Optimal solution for indicated values of

S

s * = 0

. For completeness, Table 2 shows the values of the performance measures in the optimal solution, as well as the minimum value of the expected total cost that denoted by

E T C * .

5. Conclusions

The model of single-server QIS with catastrophes in the warehouse and finite waiting room for consumer customers was proposed. When a catastrophe occurs, the entire inventory, as well as items that were in the status of release to the consumer, are instantly destroyed. However, catastrophes do not force consumers out of the system. It is assumed that if the inventory level upon arrival of consumer customer is zero, then, in accordance to the Bernoulli trials, it either joined the queue of infinite length, or left the system unserved. In the system “Up to S” replenishment policy is applied. In addition to c-customers, negative customers also enter the system. When a negative customer arrives, one of the consumers, if any, is pushed out. The mathematical model of the investigated QIS is constructed as two-dimensional Markov chain. Both exact and approximate methods for calculating steady-state probabilities and performance measures of the QIS under study are proposed. The exact method is based on balance equations while the approximate method is based on the space merging approach. It is noted that the proposed approximate method has high accuracy in the case of rare catastrophes. Closed-form formulas for calculating the performance measures were proposed. The results of numerical experiments are demonstrated.

A direction for further research should be the study of similar models with MAP flows of c- customers and/or n-customers, as well as with the PH distribution of service times for c-customers and/or lead times.

Author Contributions

Conceptualization, A.M.; methodology, A.M. and J.S.; software, L.P.; investigation, A.M., J.S. and L.P.; writing-review and editing, A.M., J.S. and L.P.; supervision and project administration, A.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Chakravarthy, S.R. A catastrophic queueing model with delayed action. Appl. Math. Model. 2017, 46, 631–649. [Google Scholar] [CrossRef]
Kumar, D.; Singh, B.G. Transient Solution of a Two Homogeneous Servers Markovian Queueing System with Environmental, Catastrophic and Restoration Effects, Int. J. Math. & Statistics Studies, 2024, 12, 45–53. [Google Scholar]
Demircioglu, M.; Bruneel, H.; Wittevrongel, S. Analysis of a Discrete-Time Queueing Model with Disasters. Mathematics 2021, 9, 3283. [Google Scholar] [CrossRef]
Kumar, B.K.; Arivudainambi, D. Transient solution of an M/M/1 queue with catastrophes. Comp. and Math. with Appl. 2000, 40, 1233–1240. [Google Scholar] [CrossRef]
Jain, N.K.; Rakesh, K. Transient solution of a catastrophic-cum-restorative queuing problem with correlated arrivals and variable service capacity. Int. J. of Inform. & Manag. Sci. 2007, 18, 461–465. [Google Scholar]
Jain, N.K.; Singh, B.G. A queue with varying catastrophic intensity. Int. J. Comput. & Appl. Math 2010, 5, 41–46. [Google Scholar]
Singh, B.G.; Niwas, B.R. Time dependent analysis of a queueing system incorporating the effect of environment, catastrophe and restoration. J. Reliability and Statistical Studies 2015, 8, 29–40. [Google Scholar]
Krishnamoorthy, A.; Joshua, A.N.; Mathew, A.P. The k-out-of-n: G System Viewed as a Multi-Server Queue. Mathematics 2024, 12, 210. [Google Scholar] [CrossRef]
Rykov, V.; Kochueva, O.; Farkhadov, M. Preventive Maintenance of a k-out-of-n System with Applications in Subsea Pipeline Monitoring. J. Mar. Sci. Eng. 2021, 9, 85. [Google Scholar] [CrossRef]
Melikov, A.; Mirzayev, R.R.; Nair, S.S. Numerical investigation of double source queuing-inventory systems with destructive customers. J. Comput. Syst. Sci. Int. 2022a, 61, 581–598. [Google Scholar] [CrossRef]
Melikov, A.; Mirzayev, R.R.; Nair, S.S. Double Sources Queuing-Inventory System with Hybrid Replenishment Policy. Mathematics 2022b, 10, 2423. [Google Scholar] [CrossRef]
Melikov, A.; Poladova, L.; Edayapurath, S.; Sztrik, J. Single-Server Queuing-Inventory Systems with Negative Customers and Catastrophes in the Warehouse. Mathematics 2023, 11, 2380. [Google Scholar] [CrossRef]
Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; The Johns Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]
Chakravarthy, S.R. Introduction to Matrix-Analytic Methods in Queues; John Wiley & Sons, Inc.: London, UK, 2022; Volume 1. [Google Scholar]
Chakravarthy, S.R. Introduction to Matrix-Analytic Methods in Queues; John Wiley & Sons, Inc.: London, UK, 2022; Volume 2. [Google Scholar]
Dudin, A.N.; Klimenok, V.I.; Vishnevsky, V.M. The Theory of Queueing Systems with Correlated Flows; Springer Nature Switzerland AG: Basel, Switzerland, 2020. [Google Scholar]
Amirthakodi, M.; & Sivakumar, B. (2019). An inventory system with service facility and feedback customers. Int. J. Ind. & Syst. Eng. 2019, 33, 374–411.
Amirthakodi, M.; Sivakumar, B. An inventory system with service facility and finite orbit size for feedback customers. OPSEARCH. 2015, 52, 225–255. [Google Scholar] [CrossRef]
Amirthakodi, M.; Radhamani, V.; Sivakumar, B. (2015) A perishable inventory system with service facility and feedback customers. Ann Oper Res. 2015, 233, 25–55. [Google Scholar] [CrossRef]
Sivakumar, B.; Elango, C.; & Arivarignan, G. A Perishable Inventory System with Service Facilities and Batch Markovian Demands. Int. J Pure & Appl. Math. 2006, 32, 33–49. [Google Scholar]
Devi, P.C.; Sivakumar, B.; Krishnamoorthy,A. Optimal Control Policy of an Inventory System with Postponed Demand. RAIRO-Oper. Res. 2016, 50, 145–155. [Google Scholar] [CrossRef]
Varghese, D.T.; Shajin, D. State Dependent Admission of Demands in a Finite Storage System. Int. J. Pure & Appl. Math. 2018, 118(20), 917–922. [Google Scholar]
Jenifer, J.S.A.; Sangeetha, N.; Sivakumar, B. Optimal Control of Service Parameter for a Perishable Inventory System with Service Facility, Postponed Demands and Finite Waiting Hall. Int. J. Inform. & Manag. Sci. 2014, 25, 349–370. [Google Scholar]
Melikov, A.; Mirzayev, R.R.; Sztrik, J. Double Sources QIS with Finite Waiting Room and Destructible Stocks. Mathematics 2023, 11, 226. [Google Scholar] [CrossRef]

Figure 1. Dependency of performance measures on

s

for different

λ^{+}

Figure 1. Dependency of performance measures on

s

for different

λ^{+}

Figure 2. Dependency of performance measures on

s

for different

λ^{-}

Figure 2. Dependency of performance measures on

s

for different

λ^{-}

Figure 3. Dependency of performance measures on

s

for different

μ

Figure 3. Dependency of performance measures on

s

for different

μ

Figure 4. Dependency of performance measures on

s

for different v.

Figure 4. Dependency of performance measures on

s

for different v.

Table 1. Dependence of the absolute error of the SSPs and performance measures vs

s

;

λ^{+} = 15, λ^{-} = 1, μ = 2, κ = 0.1, ν = 1, φ_{1} = 0.4 .

Table 1. Dependence of the absolute error of the SSPs and performance measures vs

s

;

λ^{+} = 15, λ^{-} = 1, μ = 2, κ = 0.1, ν = 1, φ_{1} = 0.4 .

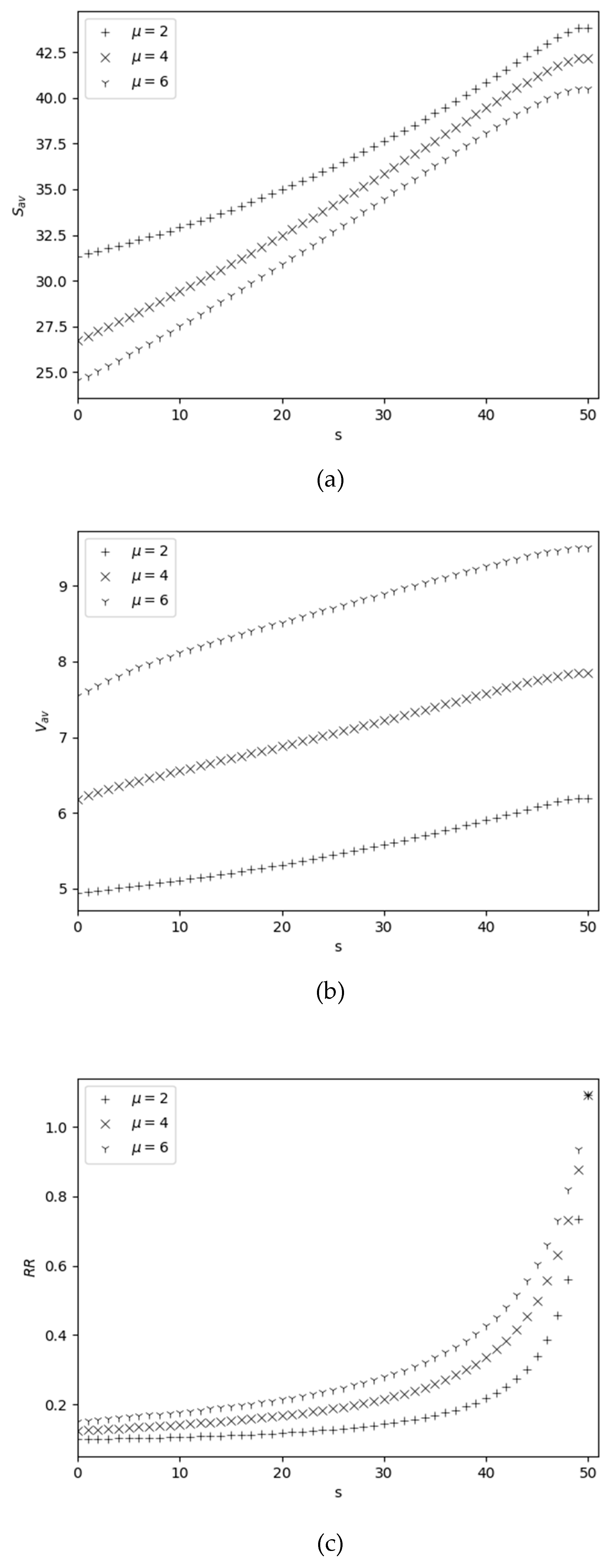
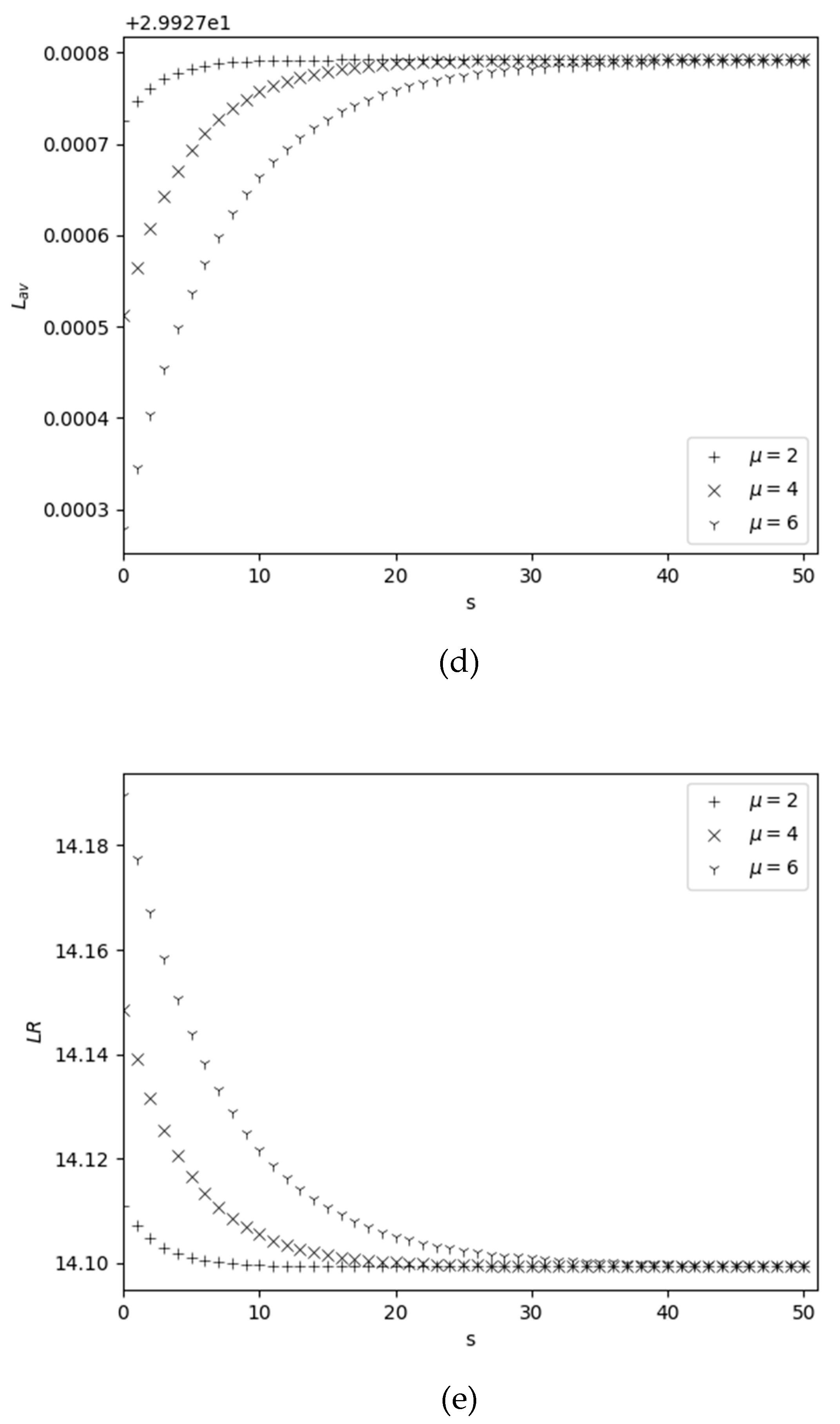
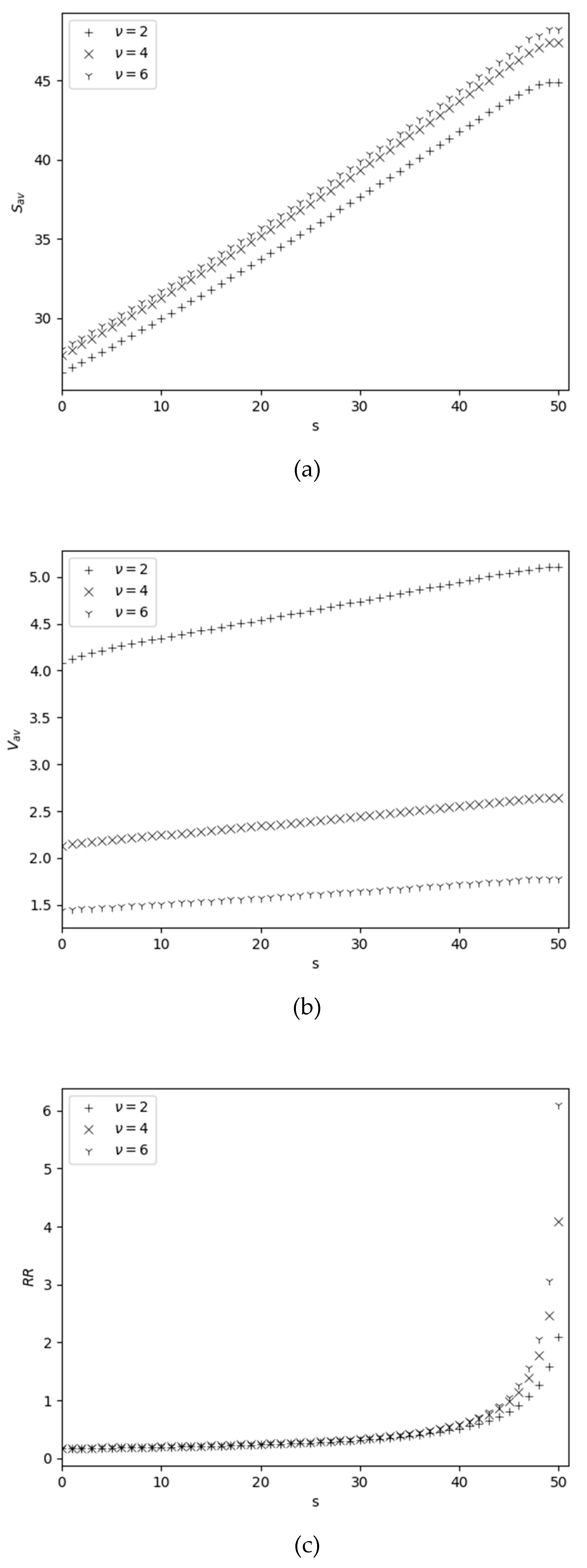
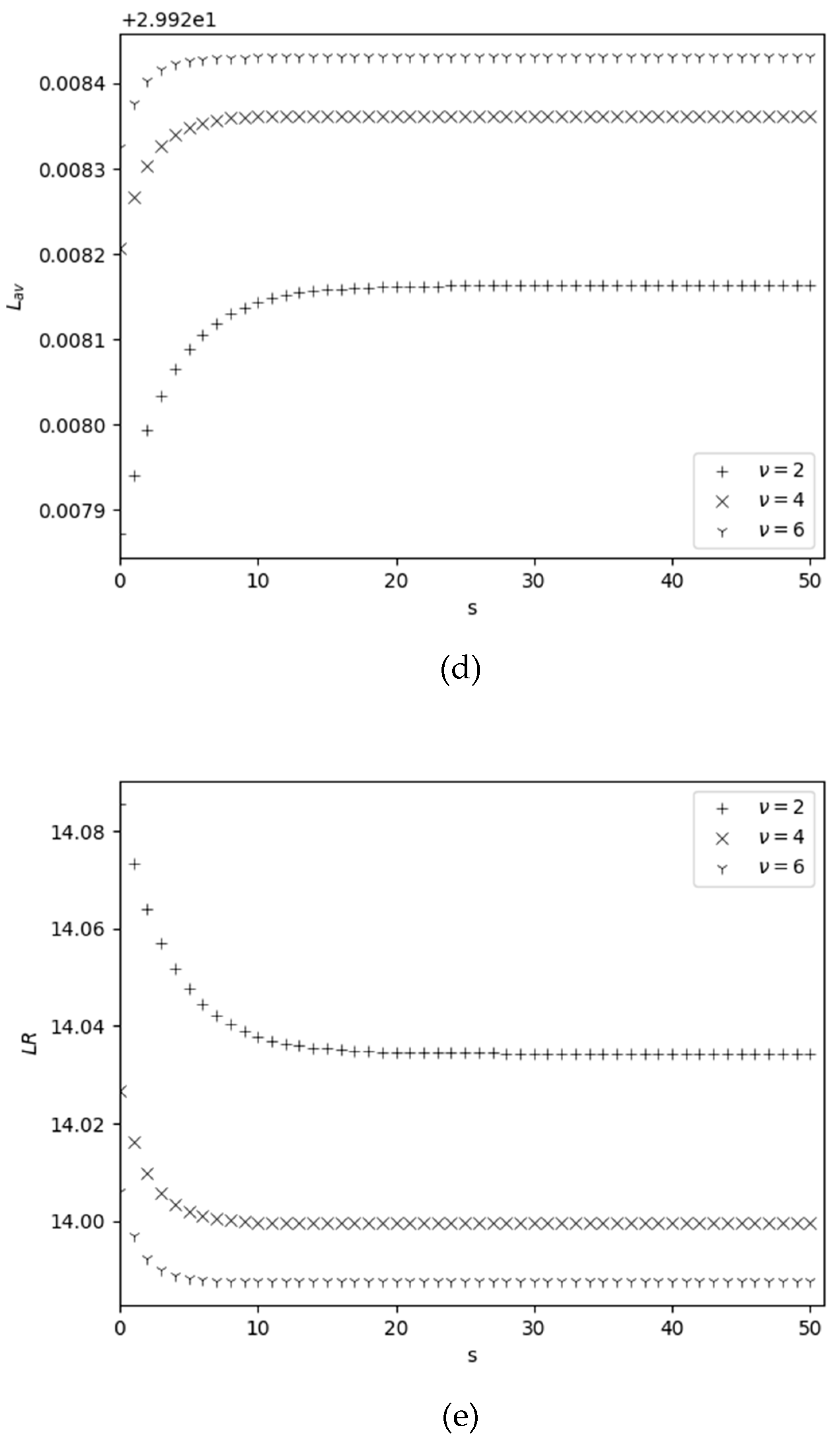
$s$	Max of error for SSPs	Error for
$s$	Max of error for SSPs	$S_{a v}$	$V_{a v}$	$R R$	$L_{a v}$	$L R$
0	$1.17 \times 10^{- 3}$	$7.01 \times 10^{- 2}$	$1.12 \times 10^{- 1}$	$1.23 \times 10^{- 2}$	$1.41 \times 10^{- 1}$	$1.54 \times 10^{- 2}$
5	$1.02 \times 10^{- 3}$	$6.05 \times 10^{- 1}$	$1.13 \times 10^{- 2}$	$1.05 \times 10^{- 2}$	$1.02 \times 10^{- 1}$	$1.27 \times 10^{- 2}$
10	$2.15 \times 10^{- 3}$	$3.11 \times 10^{- 2}$	$2.29 \times 10^{- 2}$	$1.91 \times 10^{- 2}$	$1.17 \times 10^{- 1}$	$1.36 \times 10^{- 2}$
15	$8.77 \times 10^{- 4}$	$4.02 \times 10^{- 2}$	$3.01 \times 10^{- 2}$	$5.14 \times 10^{- 2}$	$1.43 \times 10^{- 1}$	$1.78 \times 10^{- 2}$
20	$7.01 \times 10^{- 4}$	$3.18 \times 10^{- 1}$	$6.08 \times 10^{- 2}$	$4.02 \times 10^{- 2}$	$2.01 \times 10^{- 1}$	$2.15 \times 10^{- 2}$
25	$3.73 \times 10^{- 3}$	$5.02 \times 10^{- 2}$	$7.11 \times 10^{- 2}$	$2.72 \times 10^{- 2}$	$2.02 \times 10^{- 1}$	$3.01 \times 10^{- 2}$
30	$2.16 \times 10^{- 3}$	$1.08 \times 10^{- 2}$	$4.33 \times 10^{- 2}$	$5.05 \times 10^{- 2}$	$1.04 \times 10^{- 1}$	$2.02 \times 10^{- 2}$
35	$2.41 \times 10^{- 3}$	$3.13 \times 10^{- 1}$	$1.02 \times 10^{- 1}$	$1.92 \times 10^{- 2}$	$1.51 \times 10^{- 1}$	$1.32 \times 10^{- 2}$
40	$1.24 \times 10^{- 3}$	$1.02 \times 10^{- 1}$	$8.12 \times 10^{- 2}$	$1.82 \times 10^{- 2}$	$1.11 \times 10^{- 1}$	$1.03 \times 10^{- 2}$
45	$3.45 \times 10^{- 3}$	$1.03 \times 10^{- 1}$	$2.01 \times 10^{- 1}$	$1.09 \times 10^{- 2}$	$1.21 \times 10^{- 1}$	$1.17 \times 10^{- 2}$

Table 2. Optimization problem results.

$S$	$S_{a v}$	$V_{a v}$	$R R$	$L_{a v}$	$L R$	$E T C *$
50	28.07176	1.439081	0.172690	29.92832	13.98755	18981.34
55	31.23721	1.493466	0.162924	29.92834	13.98755	19059.21
60	34.46487	1.548604	0.154860	29.92835	13.98755	19138.86
65	37.75379	1.604545	0.148112	29.92836	13.98755	19220.23
70	41.10292	1.661316	0.142398	29.92837	13.98755	19303.25

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Queuing-Inventory System with Catastrophes in the Warehouse: Case Rare Catastrophes

Abstract

1. Introduction

2. The Model

3. Steady-State Analysis

3.1. An Exact Approach

3.2. An Approximate Approach

4. Numerical Experiments

4.1. Accuracy of the Developed Approximate Formulas

4.2. Behavior of Performance Measures Versus Reorder Point

4.5. Optimization Problem

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe