Kinematics Comparison of Volleyball Jump Serve Technique under Two Serving Line Conditions

In volleyball, the jump serve is a fundamental and crucial skill that is one of the most commonly used serving techniques. This study aimed to examine the kinematic differences between straight line (SL) and diagonal line (DL) in volleyball jump serves by focusing on torso and attack arm joint motions. Three-dimensional coordinate data were captured using a motion capture system (200 Hz) in 14 right-handed male professional volleyball players who performed SL and DL jump serves. This result suggests that the pelvis and torso backward rotation angles during the arm-clocking phase were smaller when performing DL serves. During ball contact, the servers exhibited greater forward rotation angles of the pelvis and torso to control the upper body facing the diagonal direction of the target zone. In addition, lowering the forward tilt angle of the trunk helped the servers maintain body balance in the air and increased their wrist flexion angle, preventing the ball from flying out of bounds when performing DL. These findings highlight the importance of controlling pelvic and torso rotations in the transverse plane when adjusting for different serving lines. These insights can guide volleyball athletes and coaches in refining their serving techniques.

Keywords:

Subject: Social Sciences - Tourism, Leisure, Sport and Hospitality

1. Introduction

Volleyball is a team sport that requires repeated high-intensity movements. Each player must quickly and accurately execute skill-specific actions such as spiking and blocking to win a game [1]. The serve is a critical volleyball skill in determining the match’s outcome. It is the only volleyball movement unaffected by the opposing team’s tactics and behaviour [2,3]. An accurate and powerful serve results in direct scoring opportunities and disrupts the tactical layout of the opposing team, considerably increasing the winning percentage of the game [2,4,5]. The jump serve, characterized by its explosive power, fast ball speed, and higher direct points, is a crucial serving technique [3,6]. Therefore, studying the techniques and mechanics of the jump serve is paramount in understanding and improving volleyball performance, as it significantly impacts the outcome of the game.

Previous biomechanical studies on jump serve examined various aspects of the technique. Lima et al. [2] analysed the relationship between ball and arm speeds in male players. Bari et al. [4] determined each kinematic parameter associated with the effect of a jump serve by building a multiple regression model. Jang et al. [7] investigated the effects of core muscle fatigue on the movements of the trunk and the attack-arm joints during the execution of a jump serve. Reeser et al. [8] compared the biomechanics differences in the upper limbs in various volleyball spike and serve techniques. However, despite its importance in the game, the jump serve has received relatively less attention in detailed biomechanical analysis than other techniques, such as spike. Most volleyball biomechanics research focuses on spike action on motion characteristics and muscle exertion of the lower limbs in the last step before take-off and motion of the arm swing [8,9,10,11,12,13,14,15,16,17,18]. Despite the significance of the jump serve in volleyball, it has received relatively little attention in detailed biomechanical analyses, particularly regarding different serving lines. This gap in research highlights the need for further exploration into this crucial aspect of volleyball.

In volleyball, the server needs to select different serving lines depending on the position of the opponent’s receiver. The straight line and diagonal line serve are two commonly used serving lines, each with distinct characteristics and tactical significance. Some analytical studies on volleyball serve reception tactics have indicated that avoiding libero and spiking the ball between other players makes the serve more aggressive [19]. The position of the receiver and the 10-foot line are essential factors in the receiver’s success [20,21]. Different serving lines cause the ball to fly with different trajectories and landing points. This can force the opposing receiver to move greater distances to catch the ball, thereby increasing the difficulty for the receiver and the likelihood of turnover. However, a detailed biomechanical analysis of different lines serving is yet to be performed. Therefore, a detailed analysis of how the jump-serve motion is adjusted when serving along different lines would provide a deeper understanding of the jump-serve technique.

This study aimed to better understand the motion control at different serving lines during the aerial spiking of a jump serve. We compared the kinematics and selected parameters between the straight line (SL) and diagonal line (DL) for professional volleyball players. We hypothesised that the motions of the upper torso and attack arm would contribute to adjusting different serving lines. Therefore, by clarifying the movement differences between the two lines, we aimed to reveal the biomechanical mechanisms and motor control strategies behind these adjustments, providing coaches and athletes with specific and practical guidance for teaching and training.

2. Materials and Methods

2.1. Participants

In total, 14 right-handed professional male volleyball players from local volleyball clubs voluntarily participated in this study. Their mean age, height, weight, and volleyball experiences were (21.14 ± 5.39) years, (1.95 ± 0.06) m, (85.93 ± 11.49) kg, and (8.50 ± 3.37) years, respectively. Players had experience using jump serves in their practices and national or regional competitions. Therefore, they could competently perform jump serves. No participant had suffered a severe neuromuscular or skeletal injury 3 months before data collection. All participants provided written informed consent before the experiment, and the local Ethics Committee approved all procedures.

2.2. Experiment

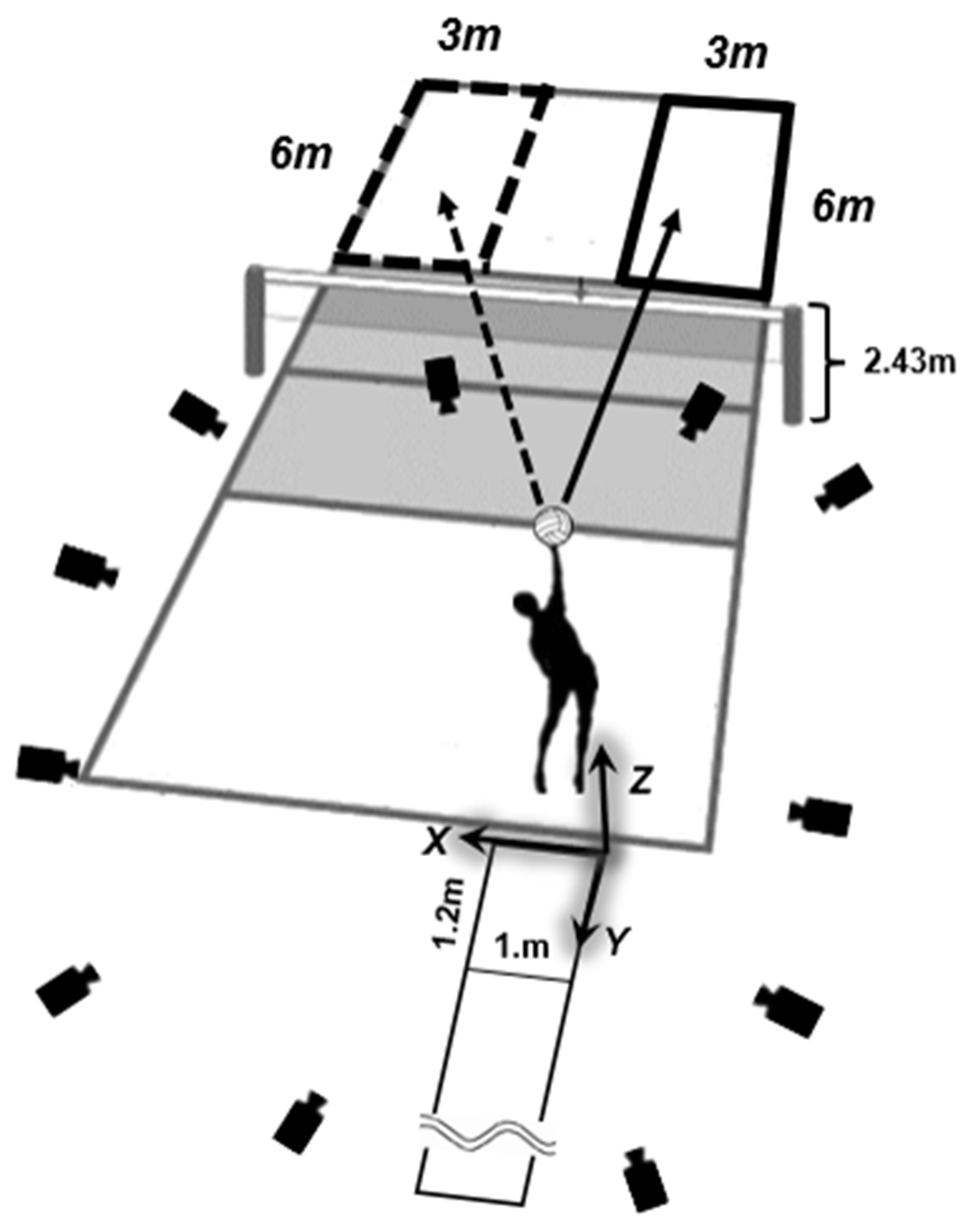
Figure 1 illustrates the experimental field setup. The experiment was conducted in a regulation-sized volleyball hall (length: 18 m; width: 9 m), and the net’s height was set at 2.43 m. A 12-camera motion capture system (Qualisys Track Manager, Qualisys, Sweden) was used to capture three-dimensional coordinate data of the reflective markers during the jump serve at 200 Hz. The ball speed was measured using a volleyball pocket radar gun (Smart Coach, Pocket Radar Inc., Santa Rosa, USA). The global coordinate system was set as a right-handed orthogonal reference frame. The positive Z-axis was vertically up, the Y-axis was opposite to the serve’s direction, and the X-axis ran from the right to the left view from a right-handed player.

2.3. Procedure

Each participant wore close-fitting clothing and their own sports shoes after a warm-up. A set of 47 markers (diameter:14 mm) were paced to the head vertex, left/right tragus, anterior/posterior shoulders, left/right acromions, suprasternal notch, xiphoid process, fifth cervical vertebrae, tenth thoracic vertebrae, left/right lateral costal borders (tenth rib), third metacarpal hands, medial/lateral wrist joints, medial/lateral elbow joints, left/right toes, first and fifth metatarsal, calcaneal tuberosities, medial/lateral malleolus, medial/lateral knee joints, left/right greater trochanters, left/right anterior iliac spines, and left/right superior iliac spines. Subsequently, the participants performed a jump serve with maximal effort, aiming to serve the ball in two target zones (each 6 m long and 3 m wide). The sequence began by serving along the SL (represented by the solid black line in Figure 1), followed by the DL (indicated by the dotted black line in Figure 1). For SL and DL jump serves, each participant was asked to execute a ball toss and run-up along an SL behind the end line of the court. In the last step before the jump take-off, participants were asked to execute a serve within a specified area (1.2 m long and 1 m wide), as shown in Figure 1. A jump serve was successful if the ball crossed the net and landed in the target zone. Two experimental assistants were present: the first stood behind the target area and observed if the ball landed in the target area, and the other observed whether the ball touched the net. The participants repeated the jump serve until they completed each serving line in three trials. The SL and DL trials with the highest ball speeds were selected for subsequent movement analysis.

2.4. Data Processing

All data processing was performed using MATLAB 2016a (MathWorks Inc., Natick, MA, USA). The raw coordinates of the marker trajectories were smoothed using a low-pass Butterworth filter, and the cutoff frequency was set at 15 Hz. The pelvic and torso motion angles were calculated according to the global coordinate system. The pelvic (or torso) rotation angle was defined as the angle formed by the line connecting the right anterior and left anterior iliac spine markers with the X-axis of the global coordinate system [22]. Similarly, the torso rotation angle was defined using right and left shoulder markers. The trunk tilt angle was defined as the angle formed by the line connecting the mid-hip and shoulder virtual markers along the Z-axis in the YZ plane. The positive and negative values correspond to the forward (serving direction) and backward directions (opposite serving direction).

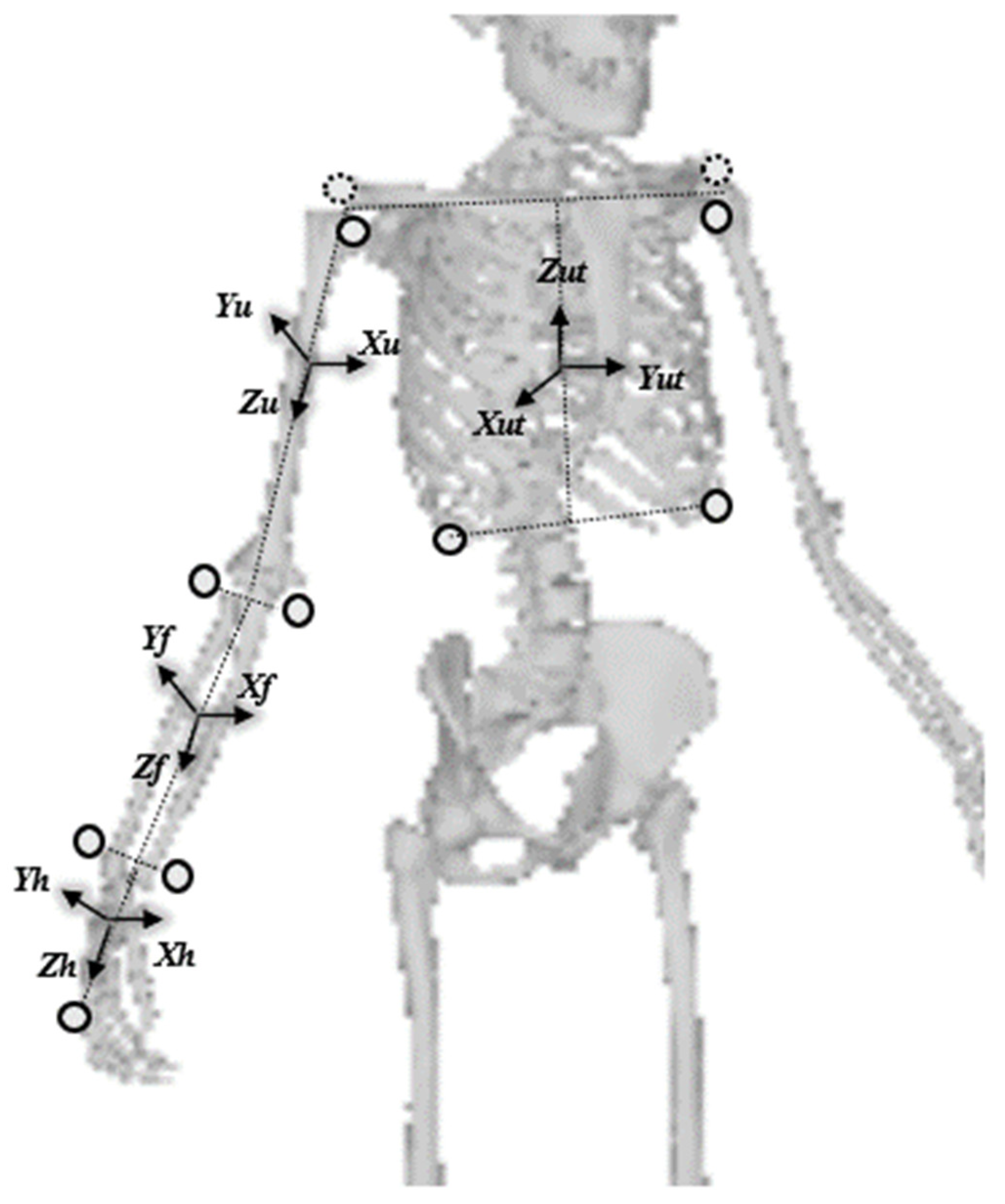
The three joint angles (shoulder, elbow, and wrist) of the attack’s arm were calculated as distal segments relative to the proximal segments. The shoulder flexion/extension and horizontal abduction/adduction were calculated based on the orientation of the upper arm segment relative to the upper torso segment. In addition, shoulder external/internal rotations, as adopted from previous studies [23,24], were calculated using the forearm segment orientation relative to the upper torso segment. Elbow flexion was calculated based on the forearm segment orientation relative to the upper arm segment. The wrist flexion/extension and supination/pronation were calculated based on the hand segment orientation relative to the forearm segment. Figure 2 shows the definitions of the coordinate systems for the upper torso, arm, and forearm segments. For the upper torso segment, referring to a previous study [25], Zut is the vector from the mid-rib to the mid-shoulder; Yut is the cross-product of Zut and the vector from the mid-right shoulder to the mid-left shoulder; and Xut is the cross-product of Yut and Zut. For the upper arm, Zu is the vector from the mid-right shoulder to the mid-right elbow; Yu is the cross-product of Zu and the vector from the medial elbow to the lateral elbow, and Xu is the cross-product of Yu and Zu. For the forearm, Zf is the vector from the mid-right elbow to the mid-right wrist, Yf is the cross-product of Zf, and the vector is from the medial to the lateral wrist, where Xf is the cross-product of Yf and Zf. For the hand, Zh is the vector from the mid-right wrist to the third metacarpal hand, Yh is the cross-product of Zh and the vector from the medial to the lateral wrist, and Xh is the cross-product of Yh and Zh. The angles were calculated using Euler (xyz sequence). The angular velocity variables were calculated for each angle using a three-point method for numerical differentiation.

2.5. Analysis of Phases

This study’s analytical phase encompassed the period from take-off (T-OFF) to landing. T-OFF denoted the precise moment both feet were lifted off the ground, verified by the vertical ground reaction force (GRF) < 5 N. Conversely, landing (L-ON) signified the instant of the maximum downward vertical velocity of the center of mass (CoM). The CoM’s position was approximated using anthropometric inertial parameters reported by Ae et al. [26]. The Maximum shoulder external (MSE) rotation refers to the moment of peak external rotation of the shoulder during motion. The timing of ball contact (BC) was based on previous research [15,24] and is defined as the instant when the horizontal velocity of the attack arm’s hand reaches its maximum. The jump serve was divided into the arm-cocking (T-OFF to MSE), arm-acceleration (MSE to BC), and follow-through (BC to L-on) phases. All angular variables were normalized to a standard deviation of 100% of the normalized time.

2.6. Statistical Analysis

Descriptive statistics are expressed as mean ± standard deviation. Normality was tested using the Shapiro–Wilk test. A paired t-test was used for a normal distribution to determine the differences in ball and hand speeds, angle variables, and angular velocity variables between SL and DL. The Wilcoxon signed-rank test was used to determine these differences without a normal distribution. Statistical significance was set at p < 0.05. All tests were performed using the free statistical software JASP (https://jasp-stats.org/).

3. Results

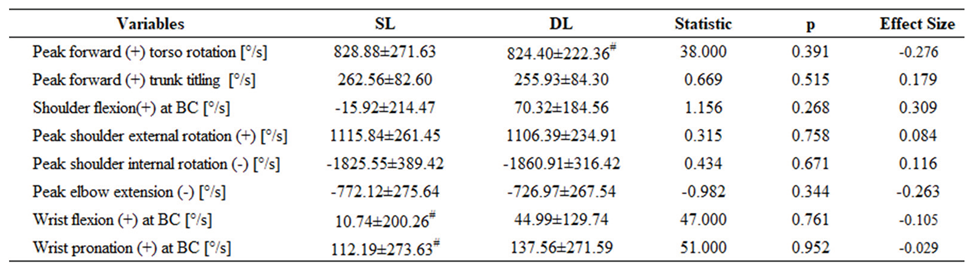
First, we compared both lines’ maximum ball and bat speeds at the BC. The ball speed in the SL was 100.29±7.45 km/h, which was significantly greater than that in the DL (96.21±6.74 km/h). However, the hand speed at BC in the SL was 16.46±1.50 m/s, significantly smaller than that in the DL (17.25±1.39) (Table 1).

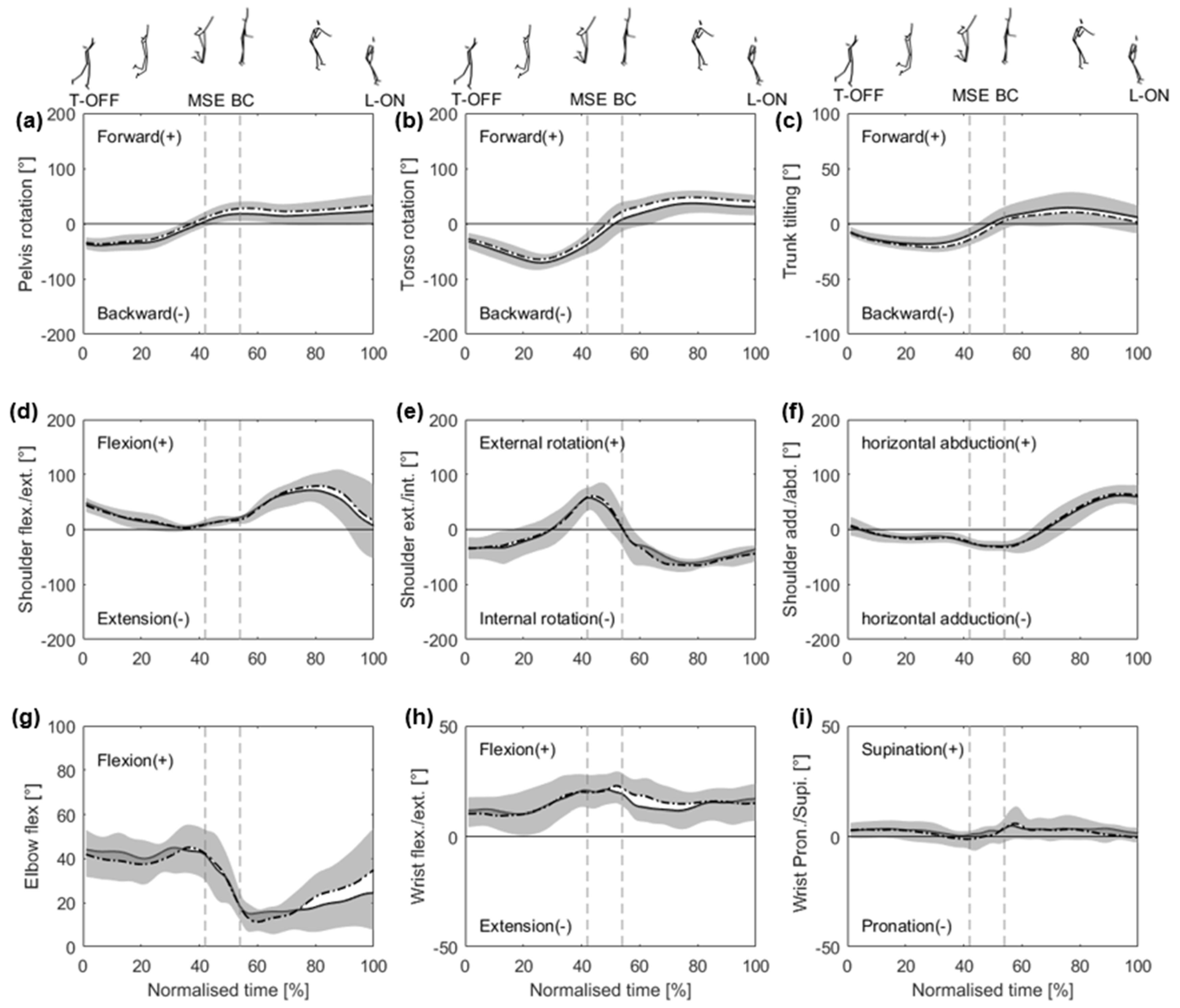
Figure 3 presents the between-line differences in angle. From T-OFF time, both lines pelvic rotation angle (a) decreased backward (-). Subsequently, they turned forward (+) from MSE and increased gradually, and the angles at BC in the SL were 19.12 ± 12.46°, which was significantly smaller than those in the DL (26.93 ± 10.76°) (Table 1). The torso rotation angles (b) and trunk tilting (c) exhibit similar patterns in both lines. They decreased backward (-) from approximately 30% of the normalized time and then increased in the forward direction (+) from the MSE and BC phases. Statistical results found that the peak torso backward rotation in the SL (-73.51±11.19°) was significantly greater than that in the DL (-66.52±10.84°), whereas the forward rotation at BC in the SL (8.78±13.70°) was significantly smaller than that in the DL (18.81±9.94°). In addition, the peak forward (+) titling at BC (6.97±6.80°) in the SL was significantly greater than those in the DL (-22.37±3.76; 2.91±6.85°) (Table 1). The angle of the wrist joint was kept in flexion for the whole phase, and the wrist flexion angle at BC in the SL was 20.84 ± 5.55°, which was significantly smaller than that in the DL (23.44 ± 5.44°) (Table 1).

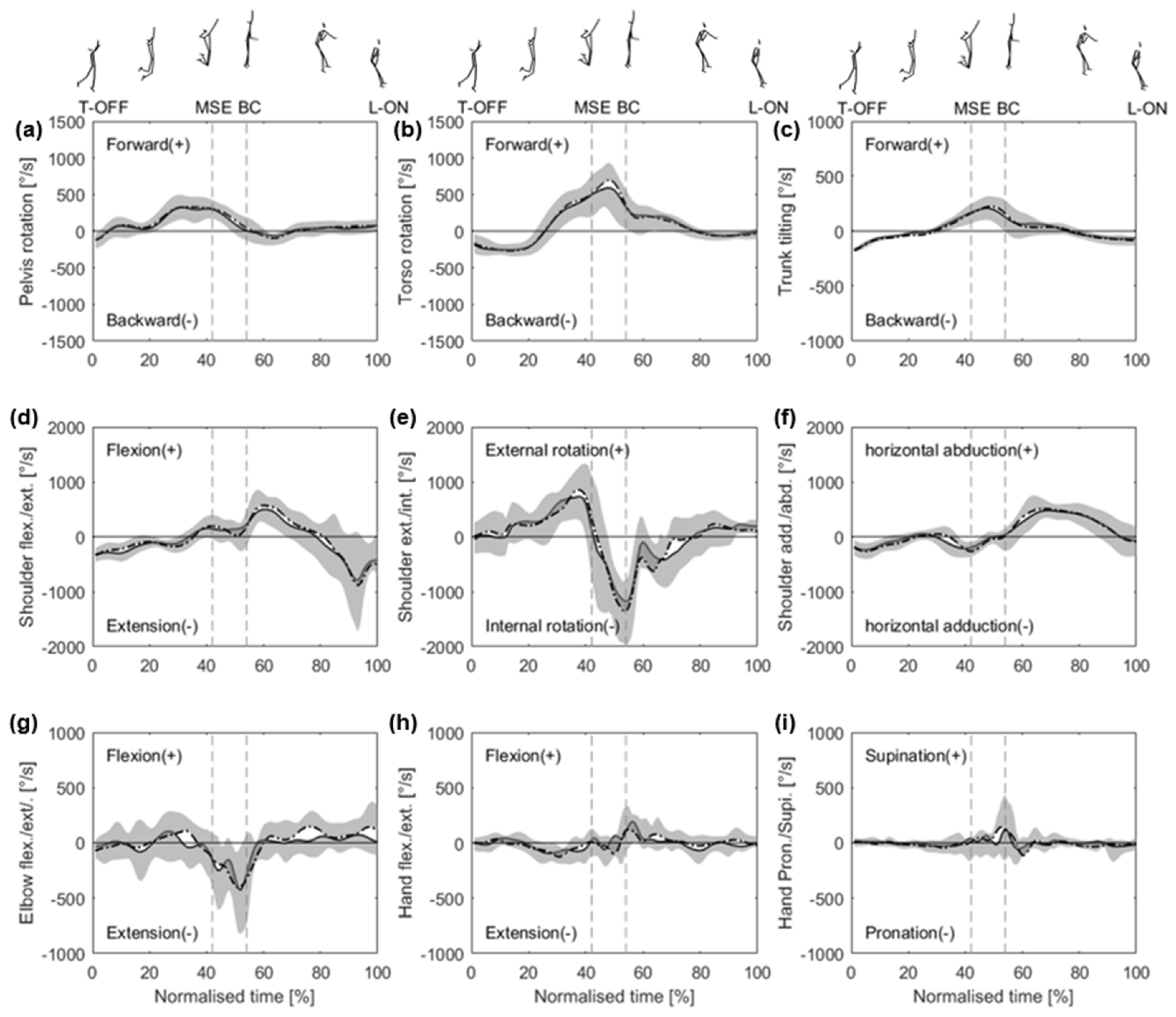
Figure 4 presents the between-line differences in angular velocity. The pelvis (a), trunk (b), and trunk tilting (c) rotation and joint motions of the shoulder and elbow, which are indicated by (d), (e), (f), and (g), exhibited similar patterns in both lines. The peak forward torso, shoulder external, and shoulder internal rotation in DL were greater than those in SL; these parameters showed no significant differences between SL and DL (Table 2).

4. Discussion

This study aimed to clarify the kinematic differences in the upper torso motion and joint angles of the attacking arm under two serving lines (SL and DL) during a jump serve. The main findings revealed that DL exhibited a smaller peak backward torso rotation than SL. DL demonstrated greater forward pelvic rotation, forward torso rotation, smaller trunk forward tilt, and greater wrist flexion angle than SL in BC. These results partially supported the study’s hypothesis, suggesting that serving lines can be altered by adjusting the pelvis and upper torso rotation.

Notably, DL demonstrated a greater hand speed at BC than SL; however, the maximum ball speed was less than that at SL (Table 1). Previous research on jump serves by Lima et al. [2] reported a stronger correlation between hand swing and ball speeds. However, our findings do not support this conclusion because the speed and trajectory of the ball are influenced by various external factors such as air resistance and gravity [1]. A diagonal ball travels a longer distance in the air than a straight ball (Figure 1), meaning that it is subjected to more air resistance, which indirectly causes a reduction in ball speed.

In the arm-cocking phase (0% to MSH), the participants showed smaller backward rotation angles of the pelvis and torso in the DL than in the SL (Figure 3 a and b). The peak backward rotation of the torso in the DL was smaller than that in the SL (Table 1). This phase prepares the motion for the subsequent arm-acceleration phase (MSE to BC). The pelvis and torso were smaller in the DL, perhaps because the servers needed to control the body rotation more finely to rotate the pelvis and torso to a greater range in the spiking direction during the arm-acceleration phase. Subsequently, the angles of the pelvis and torso in both lines rapidly rotated in the forward direction in the arm-acceleration phase (Figure 2 and b). The statistical analysis revealed that the pelvis and torso angles in the DL were significantly larger than those in the SL at BC (Table 1). A closer observation of the pelvis and torso value at BC indicated that the pelvis (19.12±12.46) and torso of the DL (26.94±10.76) rotated approximately 7° and 10° more than SL (8.78±13.70; 18.81±9.94), respectively (Table 1). These findings suggest that when serving a DL ball, athletes require a greater rotation angle than that for an SL ball so that the upper torso faces the diagonal direction as much as possible to increase the ability to accurately serve the ball in the target area.

Regarding the trunk tilting angle, the DL position showed a smaller forward tilting angle than the SL position during BC (Figure 3 (c)). Wagner et al. [24] showed that the forward trunk tilt angle during a volleyball spike is approximately 10°. We inferred that during a diagonal rather than during a straight serve, the athletes’ upper-body rotation toward the DL could put the body in an unstable position. This necessitates a reduction in the forward trunk tilt to enhance body balance in the air.

Regarding the wrist joint angle (Figure 3 (i)) of the attacking arm, we observed that at BC, the flexion angle of DL was more significant greater than that of SL (Table 1). DL has a longer ball flight distance; players must increase their hand speed to achieve this flight distance when serving a DL. However, this can easily result in the ball falling out of bounds. Notably, some studies have indicated that the speed and attack angle of the hand can change the ball trajectory [1,27]. Therefore, we considered that they flexed the wrist to lower the attacking angle of the spike position, lowering the ball’s flight trajectory and ensuring that the ball landed accurately in the DL target zone.

As described anticipation but sacrifice ball speed to some extent. Finally, it is essential to maintain the almost inv above, our knowledge of the trunk’s (pelvis and upper torso) rotation angle will guide players and coaches regarding adjustments to different serving lines. For example, when adjusting to serve a diagonal ball, the server can attempt to increase the pelvis and upper torso rotation angle, ensuring that the front of the trunk faces the target zone as much as possible. Therefore, it is necessary to know that a diagonal ball can interfere with the opponent’s ariant motion pattern of the attack arm while serving different lines. Wrist flexion can control a ball’s flight trajectory and landing position but does not adjust its direction.

Limitations

This study has some limitations. First, the experimental design employed a fixed service position. However, in an actual game, servers would serve the ball from other positions depending on their preferences. Second, the findings on the DL serve were exclusively applicable to right-handed players. Finally, in BC, hand speed in the DL was greater than that in the SL; however, the reasons for this were not explained in depth. In most explosive-hitting sports, the trunk and extremities joint and segmental rotation velocity mainly produce the end-segment speed. During the arm-acceleration phase, the tendencies for peak torso forward rotation (Figure 4 (b)) and shoulder internal rotation (Figure 4 (e)) were greater in the DL than in the SL; however, no significant differences were found. Future studies should analyse the inverse dynamics of the joint moments and power characteristics to provide more comprehensive information. To our knowledge, this is the first biomechanical analysis of kinematic differences at different serving lines during a volleyball jump serve. These results will be practical for volleyball practitioners and coaches.

5. Conclusions

We compared the kinematic differences between SL and DL volleyball jump serve techniques. This study suggests that servers can generate faster balls when serving in the SL direction than in the DL direction. During the arm-acceleration phase, when the servers serve the ball in the DL direction, they rotate their pelvis and torso at smaller backward angles and then exhibit greater forward pelvic and torso rotation angles to control the trunk facing the diagonal direction of the target zone. In addition, during BC, lowering the forward trunk tilt and increasing the wrist flexion angle help to maintain body balance and control the ball’s flight trajectory. The findings of this study indicate that controlling pelvis and upper torso rotations is crucial for different service lines.

Author Contributions

Conceptualization, L.L. and Z.C.; methodology, Z.C.; software, L.L.; validation, L.L. and Z.C.; formal analysis, L.L.; investigation, L.L. and Z.C.; resources, L.L., D.Z. and Z.C.; data curation, Z.C.; writing—original draft preparation, L.L.; writing—review and editing, L.L., D.Z., Z.T. and Z.C.; visualization, L.L.; supervision, Z.T. and Z.C.; project administration, Z.T. and Z.C.; funding acquisition, L.L., D.Z., and Z.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Shanghai Municipal Science and Technology Commission (grant number: 22dz1204900), Shanghai Sports Science and Technology Program (grant number: 22J013), and Shanghai Research Institute of Sports Science (Shanghai Anti-Doping Agency) Research Initiation Foundation Program (grant number: 2023TKS-TYQD001).

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Shanghai Research Institute of Sports Science Ethics Committee (protocol code LLSC20230015 and September 21, 2023).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data are not publicly available due to privacy or ethical restrictions.

Acknowledgments

The authors thank all the participants for their cooperation.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Reeser, J.C.; Bahr, R. Handbook of sports medicine and science: Volleyball, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
Lima, R.; Afonso, J.; Silva, A.F.; Silva, R.; Clemente, F.M. Relationships between ball speed and arm speed during the volleyball serve in youth elite male players, and why statistical significance might be misleading. Proceedings of the Institution of Mechanical Engineers 2021, 235, 122–130. [Google Scholar] [CrossRef]
Moras, G.; Buscà, B.; Peña, J.; Rodríguez, S.; Vallejo, L.; Tous-Fajardo, J.; Mujika, I. A comparative study between serve mode and speed and its effectiveness in a high-level volleyball tournament. Journal of Sports Medicine and Physical Fitness 2008, 48, 31–36. [Google Scholar] [PubMed]
Bari, M.A.; Al Mijbilee, A.A.A.; Nuhmani, S.; Iqbal, A.; Alghadir, A.H. Analysis of the kinematic variables that predict jump serve efficacy among volleyball players. Medicine (Baltimore) 2023, 102, e34471. [Google Scholar] [CrossRef] [PubMed]
Melnyk, A.; Liakhova, T. Jump serve performed by volleyball players of different qualifications. Pedagogy of Health 2022, 1, 29–33. [Google Scholar] [CrossRef]
Mackenzie, S.; Kortegaard, K.; Levangie, M.; Barro, B. Evaluation of two methods of the jump float serve in volleyball. J Appl Biomech 2012, 28, 579–586. [Google Scholar] [CrossRef]
Jang, B.; Rusdiana, A.; Sudin, S. Three-Dimensional Kinematical Analysis of Jump Serve In Volleyball: Muscle Fatigue Effects. Annals of Applied Sport Science 2022, 10. [Google Scholar] [CrossRef]
Reeser, J.C.; Fleisig, G.S.; Bolt, B.; Ruan, M. Upper limb biomechanics during the volleyball serve and spike. Sports Health 2010, 2, 368–374. [Google Scholar] [CrossRef] [PubMed]
Coleman, S.G.; Benham, A.S.; Northcott, S.R. A three-dimensional cinematographical analysis of the volleyball spike. J Sports Sci 1993, 11, 295–302. [Google Scholar] [CrossRef] [PubMed]
Fuchs, P.X.; Fusco, A.; Bell, J.W.; von Duvillard, S.P.; Cortis, C.; Wagner, H. Movement characteristics of volleyball spike jump performance in females. J Sci Med Sport 2019, 22, 833–837. [Google Scholar] [CrossRef]
Fuchs, P.X.; Menzel, H.K.; Guidotti, F.; Bell, J.; von Duvillard, S.P.; Wagner, H. Spike jump biomechanics in male versus female elite volleyball players. J Sports Sci 2019, 37, 2411–2419. [Google Scholar] [CrossRef]
Fuchs, P.X.; Mitteregger, J.; Hoelbling, D.; Menzel, H.K.; Bell, J.W.; von Duvillard, S.P.; Wagner, H. Relationship between general jump types and spike jump performance in elite female and male volleyball players. Applied Sciences, 2021, 11, 1–8. [Google Scholar] [CrossRef]
Giatsis, G.; Tilp, M. Spike Arm Swing Techniques of Olympics Male and Female Elite Volleyball Players (1984-2021). J Sports Sci Med 2022, 21, 465–472. [Google Scholar] [CrossRef] [PubMed]
Irawan, F.A.; Permana, D.F.W.; Nurrahmad, L.; Anam, K.; Hadi, H.; Romadhoni, S.; Ghassani, D.S. A Motion Analysis of volleyball open spike: Kinematics and performance. International Journal of Human Movement and Sports Sciences 2023, 11, 134–142. [Google Scholar] [CrossRef]
Serrien, B.; Ooijen, J.; Goossens, M.; Baeyens, J.-P. A Motion Analysis in the volleyball spike - Part 1: Three-dimensional kinematics and performance. International Journal of Human Movement and Sports Sciences 2016, 4, 70–82. [Google Scholar] [CrossRef]
Tai, W.H.; Te Peng, H.; Song, C.Y.; Lin, J.Z.; Yu, H.B.; Wang, L.I. Dynamic characteristics of approach spike jump tasks in male volleyball players. Applied Sciences 2021, 11. [Google Scholar] [CrossRef]
Tilp, M.; Wagner, H.; Müller, E. Differences in 3D kinematics between volleyball and beach volleyball spike movements. Sports Biomech 2008, 7, 386–397. [Google Scholar] [CrossRef]
Wagner, H.; Tilp, M.; von Duvillard, S.P.; Mueller, E. Kinematic analysis of volleyball spike jump. Int J Sports Med 2009, 30, 760–765. [Google Scholar] [CrossRef] [PubMed]
Fernandez-Echeverria, C.; Gil, A.; Moreno, A.; Claver, F.; Moreno, M.P. Analysis of the variables that predict serve efficacy in young volleyball players. International Journal of Performance Analysis in Sport 2015, 15, 172–186. [Google Scholar] [CrossRef]
Paulo, A.; Zaal, F.T.; Fonseca, S.; Araújo, D. Predicting Volleyball Serve-Reception. Front Psychol 2016, 7, 1694. [Google Scholar] [CrossRef]
Paulo, A.; Zaal, F.T.J.M.; Seifert, L.; Fonseca, S.; Araújo, D. Predicting volleyball serve-reception at group level. J Sports Sci 2018, 36, 2621–2630. [Google Scholar] [CrossRef]
Liu, L.; Deguchi, T.; Shiokawa, M.; Ishii, T.; Oda, Y.; Shinya, M. A biomechanics analysis of the judo osoto-gari technique: Comparison of black belt and white belt judokas. Sports Biomechanics 2021, 1–13. [Google Scholar] [CrossRef] [PubMed]
Ishida, K.; Murata, M.; Hirano, Y. Shoulder and elbow kinematics in throwing of young baseball players. Sports Biomech 2006, 5, 183–196. [Google Scholar] [CrossRef] [PubMed]
Wagner, H.; Pfusterschmied, J.; Tilp, M.; Landlinger, J.; von Duvillard, S.P.; Müller, E. Upper-body kinematics in team-handball throw, tennis serve, and volleyball spike. Scand J Med Sci Sports 2014, 24, 345–354. [Google Scholar] [CrossRef]
Ae, K.; Koike, S.; Fujii, N.; Ae, M.; Kawamura, T. Kinetic analysis of the lower limbs in baseball tee batting. Sports Biomech 2017, 16, 283–296. [Google Scholar] [CrossRef]
Ae, M.; Tang, H.; Yokoi, T. Estimation of inertia properties of the body segments in Japanese athletes (in Japanese). Biomechanisms 1992, 11, 23–33. [Google Scholar] [CrossRef]
Kao, S.S.; Sellens, R.W.; Stevenson, J.M. A mathematical model for the trajectory of a spiked volleyball and its coaching application. Journal of Applied Biomechanics 2016, 10, 95–109. [Google Scholar] [CrossRef]

Figure 1. Experimental environment.

Figure 2. Definitions of segments coordinate systems for the upper torso, upper torso, forearm, and hand.

Figure 3. Mean (standard deviation) time-series data of trunk and attack arm angle. Solid line: straight line (SL); dotted line: diagonal line (DL); MSE: maximum shoulder external rotation; BC: ball contact.

Figure 4. Mean (standard deviation) time-series data of trunk and attack arm angular velocity. Solid line: straight line (SL); dotted line: diagonal line (DL); MSE: maximum shoulder external rotation; BC: ball contact.

Table 1. Comparison of ball and hand speeds and angle variables between SL and DL.

Table 2. Comparison of angular velocity variables between SL and DL.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer