1. Introduction and the Model
Optical solitons are a broad class of self-trapped states maintained by the interplay of nonlinearity and dispersion or diffraction in diverse photonic media [
1,
2]. In addition to that, dissipative optical solitons are supported by the equilibrium of loss and gain or pump, concomitant to the nonlinearity-dispersion/diffraction balance [
3,
4]. Dissipative solitons have been studied in detail, theoretically and experimentally, in active setups, with the loss compensated by local gain (essentially, provided by lasing), being modelled by one- and two-dimensional (1D and 2D) equations of the complex Ginzburg-Landau (CGL) type [
5,
6].
In passive nonlinear optical cavities, the losses are balanced by the pump field supplied by external laser beams, with the appropriate models provided by the Lugiato-Lefever (LL) equations [
7]. This setting was also studied in the 1D and 2D forms [
8,
9,
10,
11]. Widely applied in nonlinear optics, the LL equations play a crucial role in understanding fundamental phenomena such as the modulation instability (MI) and pattern formation in dissipative environments [
8,
10,
13,
15,
18,
19,
20,
23,
25,
27]. Its relevance extends to the exploration of complex dynamics of various nonlinear photonic modes, tremendously important applications being the generation of Kerr solitons and frequency combs in passive cavities [
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
21,
22,
23,
24], as well the generation of terahertz radiation [
25]. In addition to rectilinear cavity resonators, circular ones can be used too [
26]. In many cases, they operate in the whispering-gallery regime [
27,
28,
29,
30,
31,
32].
In most cases, solutions of the one- and two-dimensional LL equations are looked for under the action of the spatially uniform pump, which approximately corresponds to the usual experimental setup. However, the use of localized (focused) pump beams is possible too, which makes it relevant to consider LL equations with the respective shape of the pump terms. In fact, truly localized optical modes in the cavities can be created only in this case, otherwise the uniform pump supports nonzero background of the optical field. In particular, exact analytical solutions of the LL equations with the 1D pump represented by the delta-function, and approximate solutions maintained by the 2D pump in the form of a Gaussian were reported in Ref. [
33]. In Ref. [
26], the LL equation for the ring resonator with localized pump and loss terms produced nonlinear resonances leading to multistability of nonlinear modes and coexisting solitons, that are associated with spectrally distinct frequency combs.
Further, solutions for fully localized robust pixels with zero background were produced by the 2D LL equation, incorporating the spatially uniform pump, self-focusing or defocusing cubic nonlinearity, and a tight confining harmonic-oscillator potential, were reported in Ref. [
34]. Additionally, this model with a vorticity-carrying pump gives rise to stable vortex pixels. In particular, in the case of the self-defocusing sign of the nonlinear term, the pixels with zero vorticity, and with vorticity
, were predicted analytically by means of the Thomas-Fermi (TF) approximation.
In this work, we introduce the 2D LL equation for complex amplitude field
, with the cubic or cubic-quintic nonlinearity:
and a confined pump beam. Here
is the loss parameter,
and
corresponds, respectively, to the self-focusing and defocusing Kerr (cubic) nonlinearity,
or
represents the self-defocusing or focusing quintic nonlinearity (which often occurs in optical media [
35,
36,
37], in addition to the cubic term), parameter
defines the cavity mismatch,
, in terms of the linearized LL equation, and
represents the confined pump beam with real amplitude
, radial width
W, and integer vorticity
, written in terms of polar coordinates
. Vortex beams, shaped by the passage of the usual laser beam through an appropriate phase mask, are available in the experiment [
37].
Stationary solutions of Eq. (
1) are characterized by values of the total power (alias norm),
and angular momentum,
(with * standing for the complex conjugate), even if the power and angular momentum are not dynamical invariants of the dissipative equation (
1). In the case of the axisymmetric solutions with vorticity
S, i.e.,
, the expressions for the power and angular momentum are simplified:
Our objective is to construct
stable ring-shaped vortex solitons (representing vortex pixels, in terms of plausible applications), as localized solutions of Eq. (
1) with the same
S as in the pump term (
2). It is a challenging problem, as it is well known from the work with models based on the nonlinear Schrodinger and CGL equations that, in the absence of the tight confining potential, vortex-ring solitons are vulnerable to the splitting instability, which may be considered as MI of the ring against azimuthal perturbations which break its axial symmetry [
2,
38]. The azimuthal MI is driven by the self-focusing nonlinearity, and inhibited by the self-defocusing.
To produce stationary solutions for the vortex solitons in an approximate analytical form (parallel to the numerical solution), we employ a variational approximation (VA). Our results identify regions of the existence and stability of the vortex solitons with
in the space of parameters of Eqs. (
1) and (
2) (in particular, in the plane of
) for both signs of the cubic nonlinearity,
, while the mismatch parameter is fixed to be
by dint of scaling. The stability areas are vast, provided that the loss coefficient
is, roughly speaking, not too small. A majority of the results are produced for the pure cubic model, with
, but the effect of the quintic term, with
, is considered too. Quite surprisingly, a stability area for the vortices with
is found even in the case of
, when both the cubic and quintic terms are self-focusing, which usually implies strong propensity to the azimuthal instability of the vortex rings [
38].
The rest of the paper is structured as follows. The analytical approach, based on the appropriate VA, is presented in
Section 2. An asymptotic expression for the tail of the vortex solitons, decaying at
, is found too in that section. Systematically produced numerical results for the shape and stability of the vortex solitons are collected (and compared to the VA predictions) in
Section 3. The paper is concluded by
Section 4.
3. Numerical Results
Simulations of Eq. (
1) were conducted by means of the split-step pseudo-spectral algorithm. The solution started from the zero input, and was running until convergence to an apparently stable stationary profile. This profile was then compared to its VA counterpart, produced by a numerical solution of Eqs. (
18) and (
19) with the same values of parameters
,
,
g, and
,
W,
S (see Eq. (
2)). The results are presented below by varying, severally, loss
, vorticity
S, the pump’s width
W and strength
, and, eventually, the quintic coefficient
g. The findings are eventually summarized in the form of stability charts plotted in
Figure 11.
3.1. Variation of the Loss Parameter
In
Figure 2(a) we display the cross-section (drawn through
) of the variational and numerical solutions for the stable vortex solitons obtained with
,
, and
, while the other parameter are fixed as
(the self-focusing cubic nonlinearity),
,
,
, and
. The accuracy of the VA-predicted solutions presented in
Figure 2(a) is characterized by the relative power difference from their numerically found counterparts, which is
,
, and
for
respectively. Thus, the VA accuracy improves with the increase of
.
Similar results for the self-repulsive nonlinearity,
, are presented in
Figure 2(b), which shows an essentially larger discrepancy between the VA and numerical solutions,
viz.,
,
, and
for the same set (
28) of values of the loss parameter, other coefficients being the same as in
Figure 2(a).
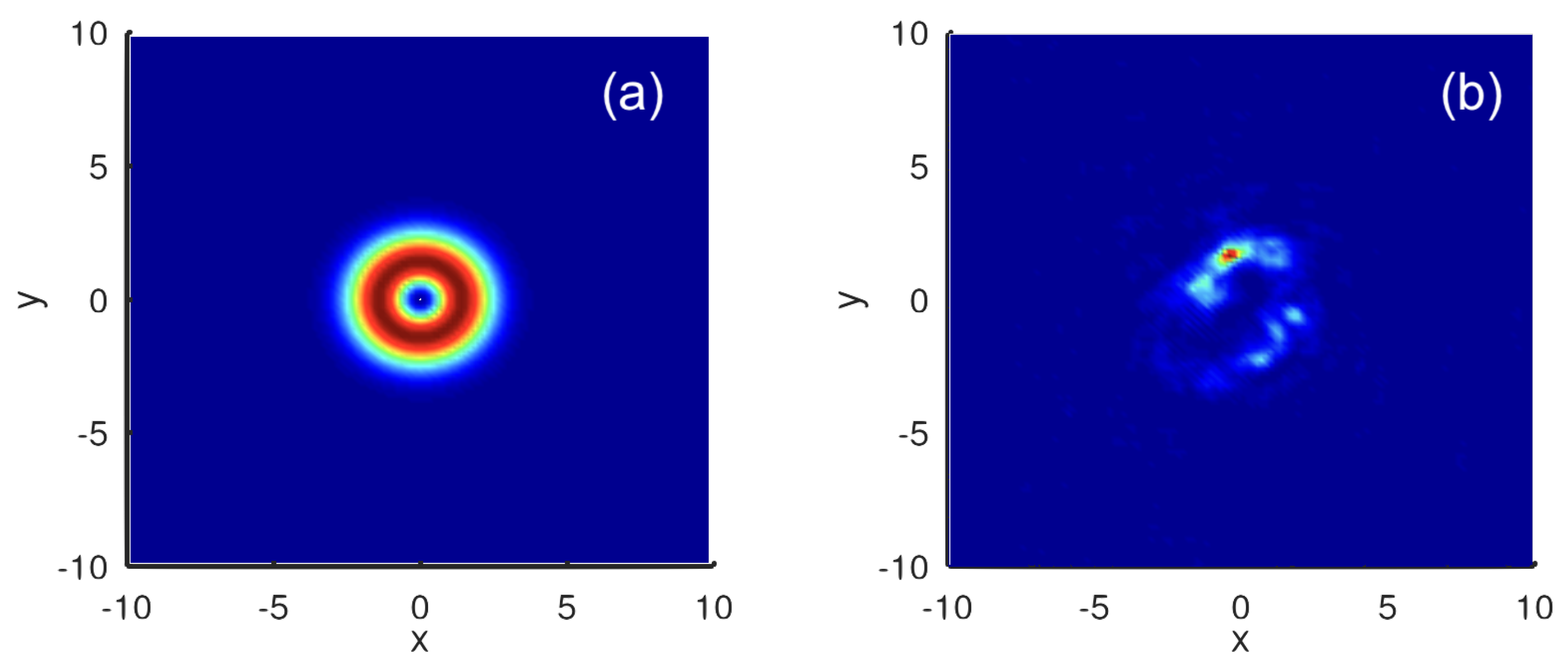
There is a critical value of
below which the vortex solitons are unstable. As an example,
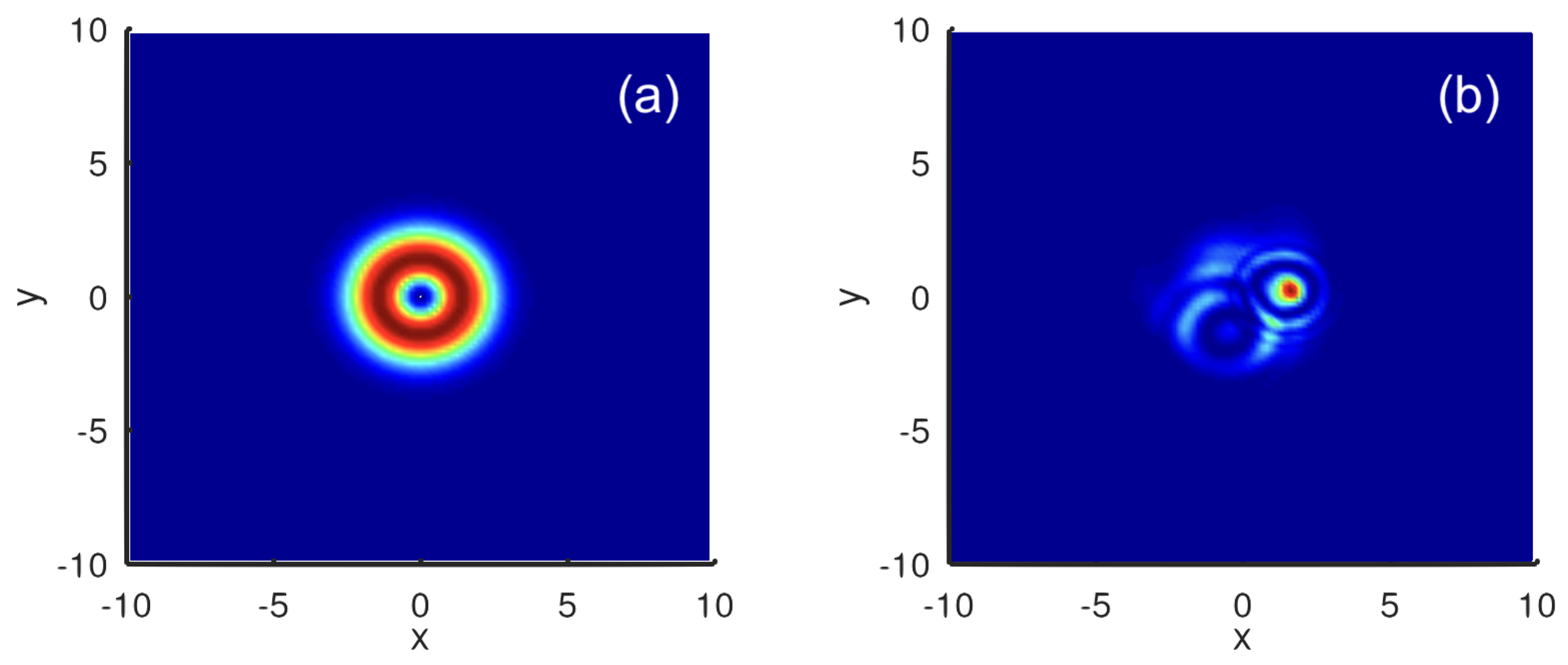
Figure 3 shows the VA-predicted and numerically produced solutions for
and
(the self-focusing nonlinearity). The observed picture may be understood as a result of the above-mentioned azimuthal MI which breaks the axial symmetry of the vortex soliton. More examples of the instability of this type are displayed below. For the values of other parameters fixed as in
Figure 3, the instability boundary is
. The stabilizing effect of the loss at
is a natural feature. On the other hand, the increase of
leads to decrease of the soliton’s amplitude, as seen in
Figure 2.
In the case of the self-defocusing (), all the numerically found vortex modes are stable, at least, at , although the discrepancy in the values of the power between these solutions and their VA counterparts is very large at small , exceeding at . At still smaller values of , the relaxation of the evolving numerical solution toward the stationary state is very slow, which makes it difficult to identify the stability.
3.2. Variation of the pump’s vorticity S
To analyze effects of the winding number (vorticity)
S, we here fix
(the pure cubic nonlinearity) and set
,
,
in Eqs. (
1) and (
2). In the self-focusing case (
), the numerically produced solutions are stable for
and 2, and unstable for
. In the former case, the power difference between the VA and numerical solutions is
and
for
and 2, respectively, i.e., the VA remains an relatively accurate approximation in this case.
In the self-defocusing case (), considering the same values of the other parameters as used above, the numerical solution produces stable vortex solitons at least until . As above, the accuracy of VA is much lower for than for the self-focusing case (), with the respective discrepancies in the power values being , , , , and for , 2, 3, 4, and 5, respectively.
3.3. Variation of the Pump’s Width W
To address the effects of the variation of parameter
W in Eq. (
2), we here fix
,
,
, and
. In
Figure 4(a), the power of the VA-predicted and numerically found stable vortex-soliton solutions is plotted as a function of
W for both the self-focusing and defocusing cases, i.e.,
and
, respectively. In the former case, the azimuthal MI sets in at
, see an example in
Figure 4(b) for
.
In the self-focusing case, , the azimuthal MI for the solitons with higher vorticities, , 3, 4, or 5, sets in at , , , and , respectively. In the self-defocusing case, no existence/stability boundary was found for the vortex modes with , , and (at least, up to ). At higher values of the vorticity, the localized vortices do not exist, in the defocusing case, at and , for , and , respectively.
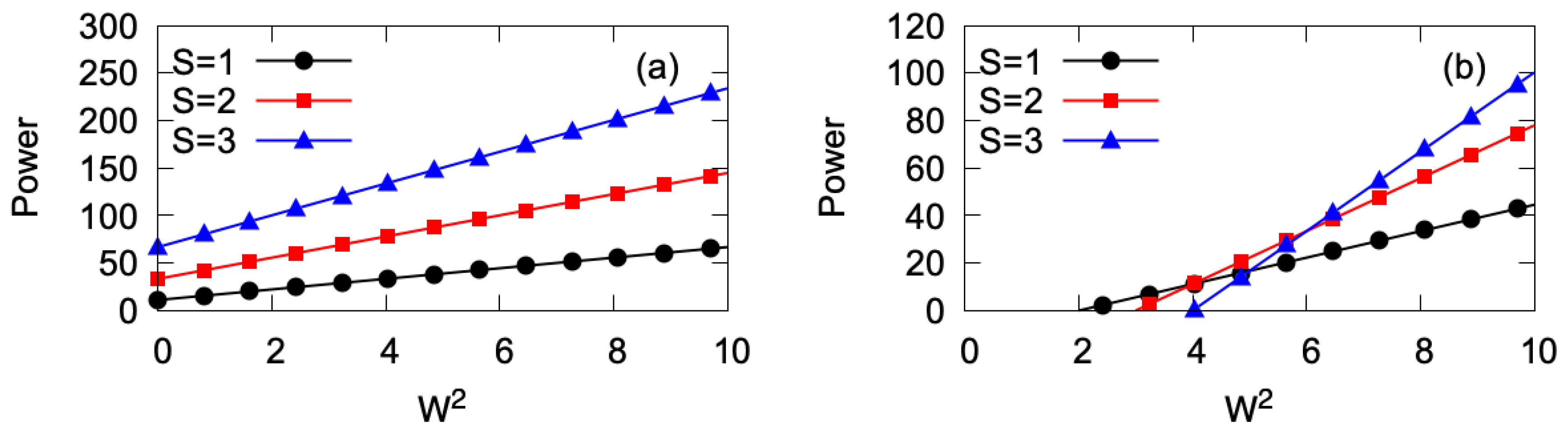
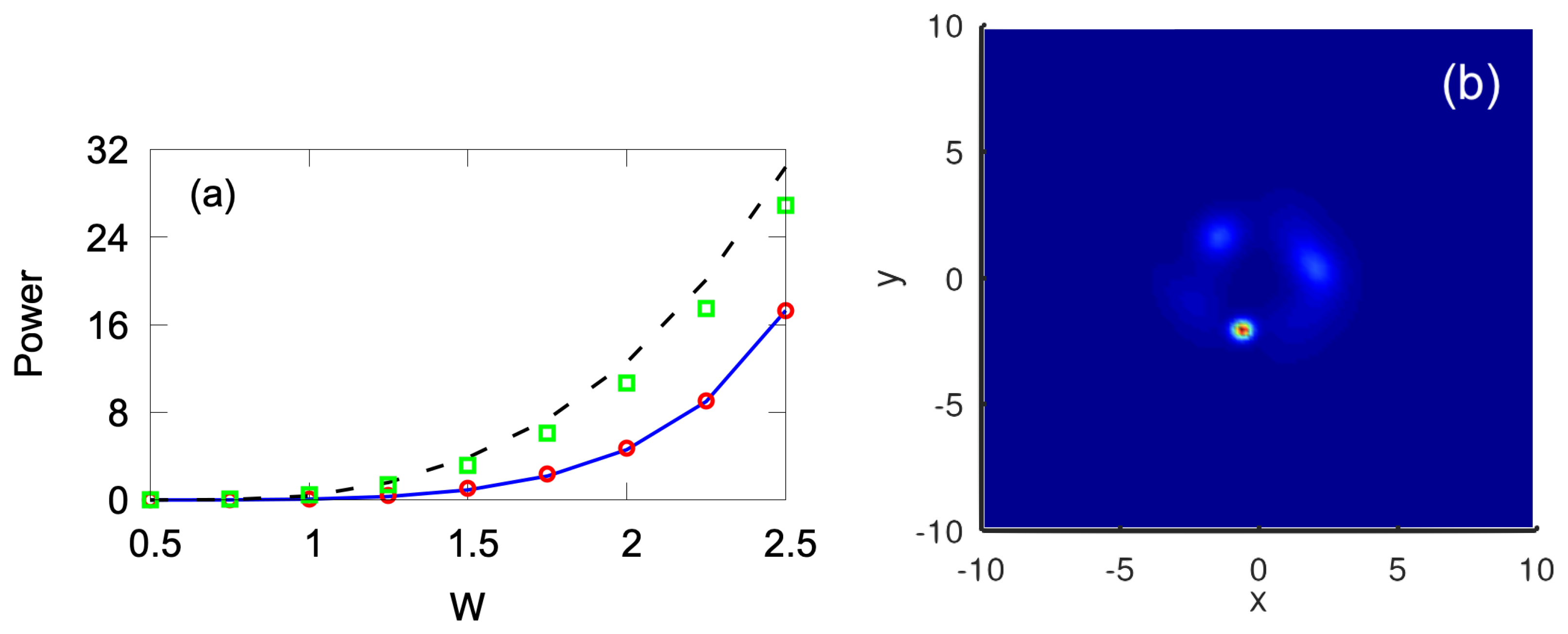
3.4. Variation of the Pump’s Strength
Effects of the variation of
are reported here, fixing other parameters as
,
, and
. In the case of the cubic self-focusing,
, the vortex soliton with
are subject to MI at
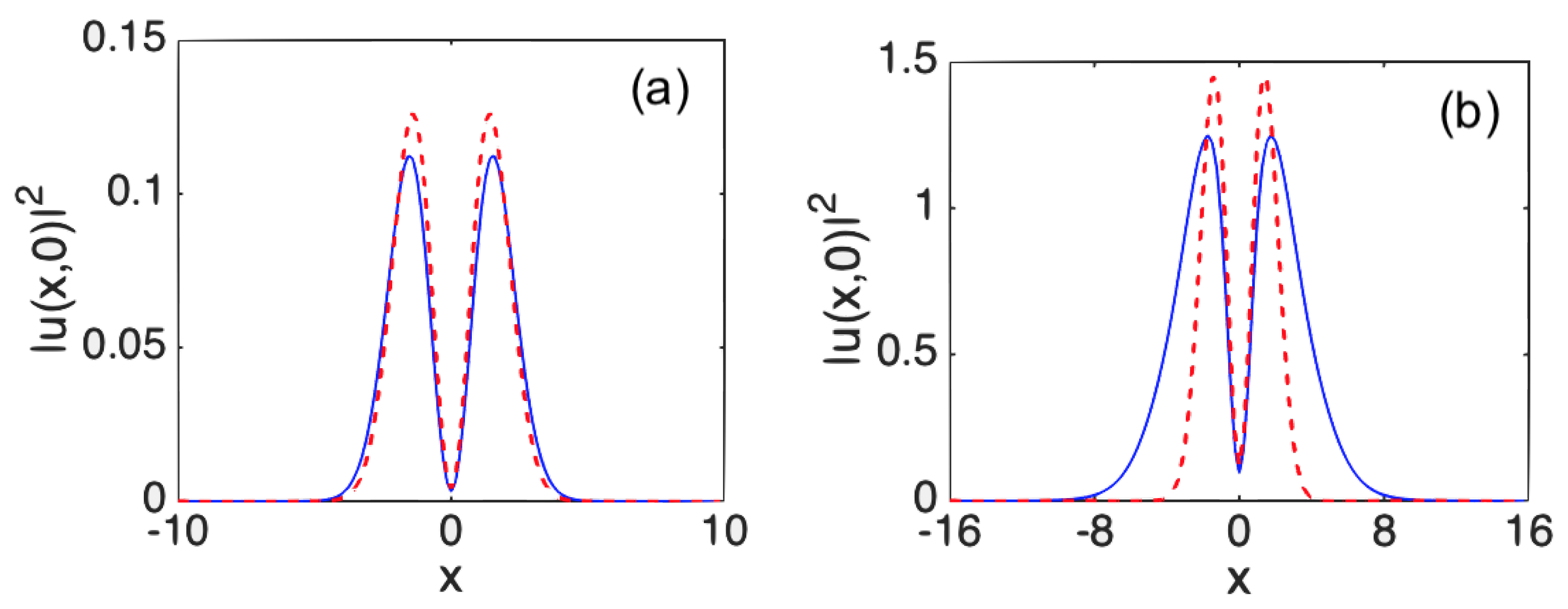
. As a typical example, in
Figure 5 we display the VA-predicted solution alongside the result of the numerical simulations for
. For higher vorticities,
, 3, 4, and 5, the azimuthal instability sets in at
,
,
, and
, respectively. Naturally, the narrow vortex rings with large values of
S are much more vulnerable to the azimuthal MI.
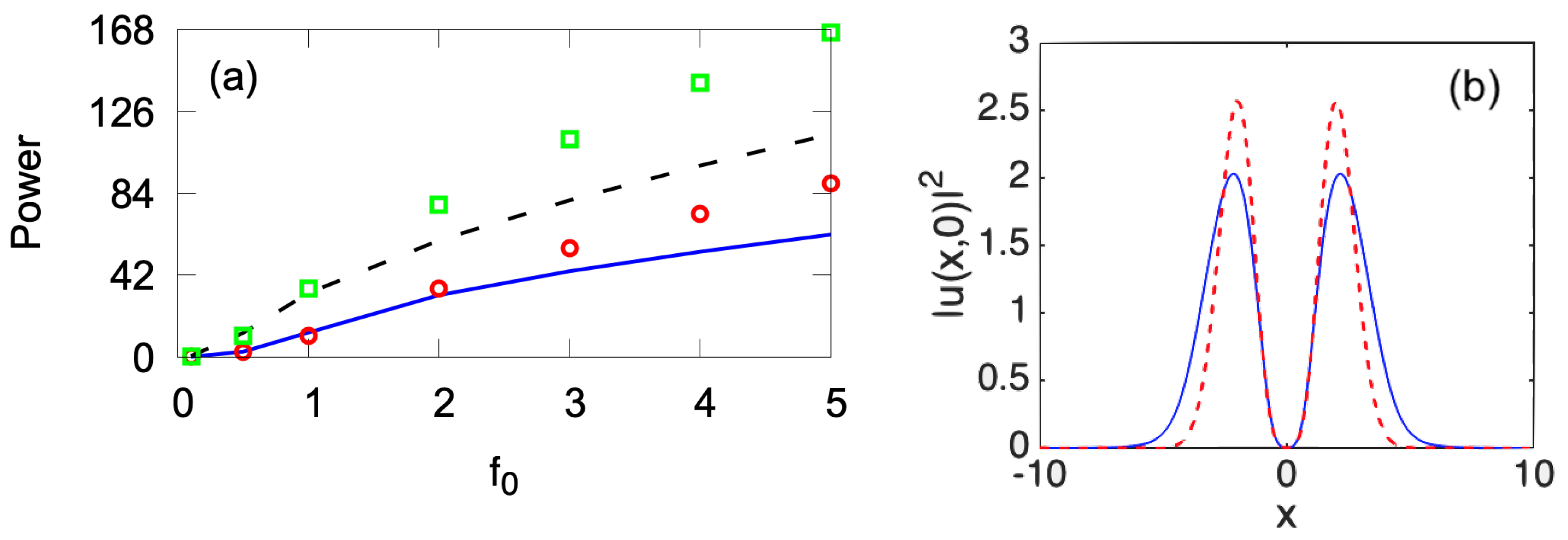
The power of the vortex solitons with
and 2, as produced by the VA and numerical solution, is plotted vs. the pump amplitude
in
Figure 6(a). As an example,
Figure 6(b) showcases an example of the cross-section profile of the vortex soliton with
, demonstrating the reliability of the VA prediction. In the range of
, the highest relative difference in the power between the numerical and variational solutions cases is
and
for
and
, respectively.
Figure 5.
(a) The VA-predicted profile of
in the self-focusing case, with parameters
,
,
,
,
, and
. (b) The unstable solution, produced, at
, by the simulations of Eq. (
1) for the same parameters.
Figure 5.
(a) The VA-predicted profile of
in the self-focusing case, with parameters
,
,
,
,
, and
. (b) The unstable solution, produced, at
, by the simulations of Eq. (
1) for the same parameters.
Figure 6.
(a) The power versus for the confined vortex modes in the self-focusing case (). The VA solutions for and 2 are shown by solid blue and dashed black lines, respectively. The corresponding numerical solutions are represented by red circles and green squares, respectively. Recall that the numerical solutions are stable, in this case, at and , for and 2, respectively. (b) The VA-predicted and numerically obtained (the dashed red and solid blue lines, respectively) profiles of the stable solution with and , drawn as cross sections through . The other parameters are , , , .
Figure 6.
(a) The power versus for the confined vortex modes in the self-focusing case (). The VA solutions for and 2 are shown by solid blue and dashed black lines, respectively. The corresponding numerical solutions are represented by red circles and green squares, respectively. Recall that the numerical solutions are stable, in this case, at and , for and 2, respectively. (b) The VA-predicted and numerically obtained (the dashed red and solid blue lines, respectively) profiles of the stable solution with and , drawn as cross sections through . The other parameters are , , , .
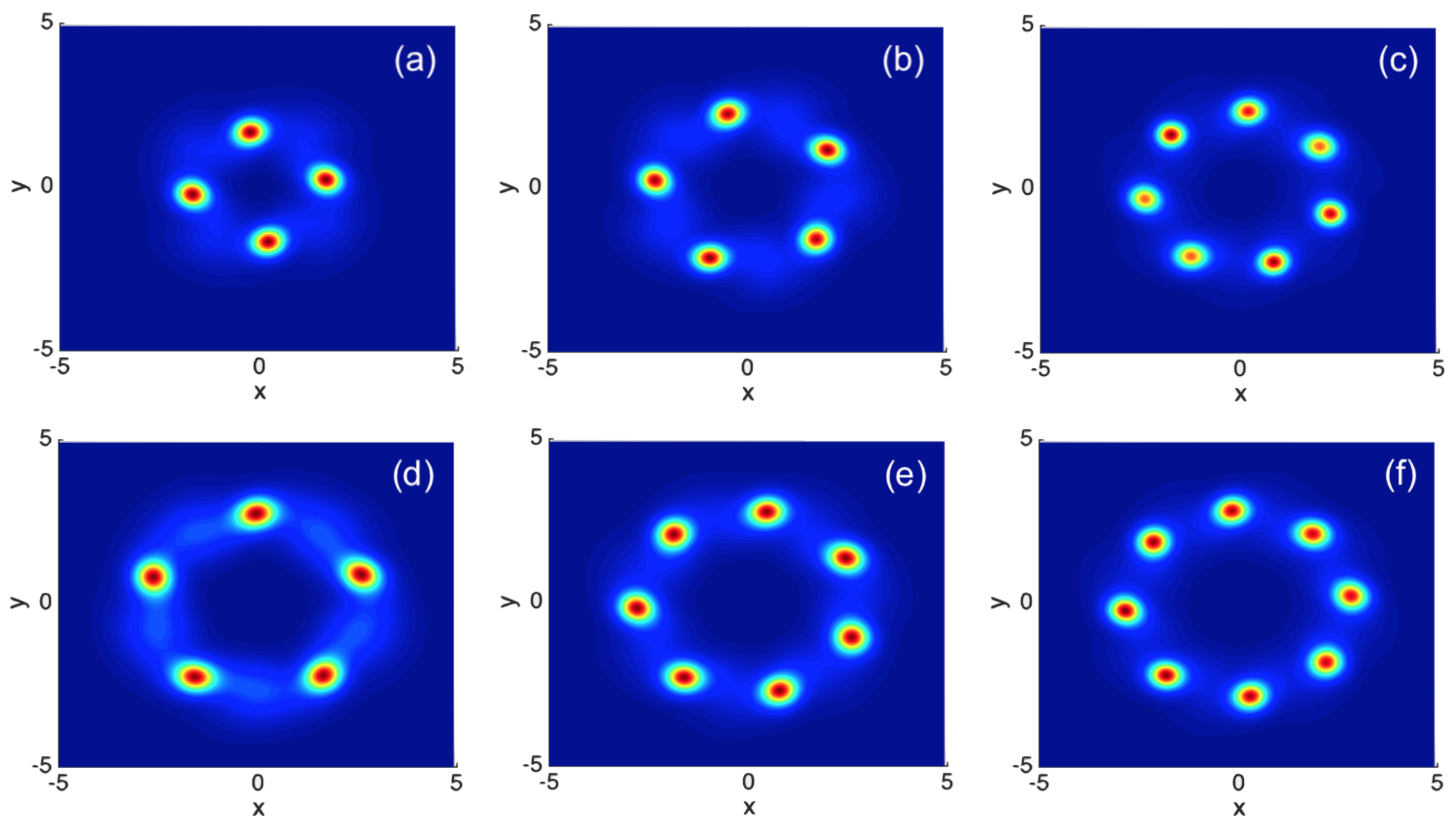
It is relevant to mention that the “traditional” azimuthal instability of vortex-ring solitons with winding number
S demonstrates fission of the original axially symmetric shape into a set consisting of a large number
of symmetrically placed localized fragments [
2,
38], while the above examples, displayed in
Figure 3(b),
Figure 4(b), and
Figure 5(b), demonstrate the appearance of a single bright fragment and a “garbage cloud” distributed along the original ring. At larger values of
, our simulations produce examples of the “clean” fragmentation,
viz., with
produced by the unstable vortex rings with
in
Figure 7(a),
produced by
and 3 in (b) and (d),
by
and 3 in (c) and (e), and
by
in (f). These outcomes of the instability development are observed at the same evolution time
as in
Figure 3(b),
Figure 4(b), and
Figure 5(b).
In self-defocusing case,
, a summary of the results produced by the VA and numerical solution for the stable vortex solitons with
and 2, in the form of the dependence of their power on
, is produced in
Figure 8(a) (cf.
Figure 6(a) for
). Naturally, the VA-numerical discrepancy increases with the growth of the pump’s strength,
, see an example in
Figure 8(b). Unlike the case of
, in the case of the self-defocusing the vortex modes with
remain stable, at least, up to
(here, we do not dot consider the case of
).
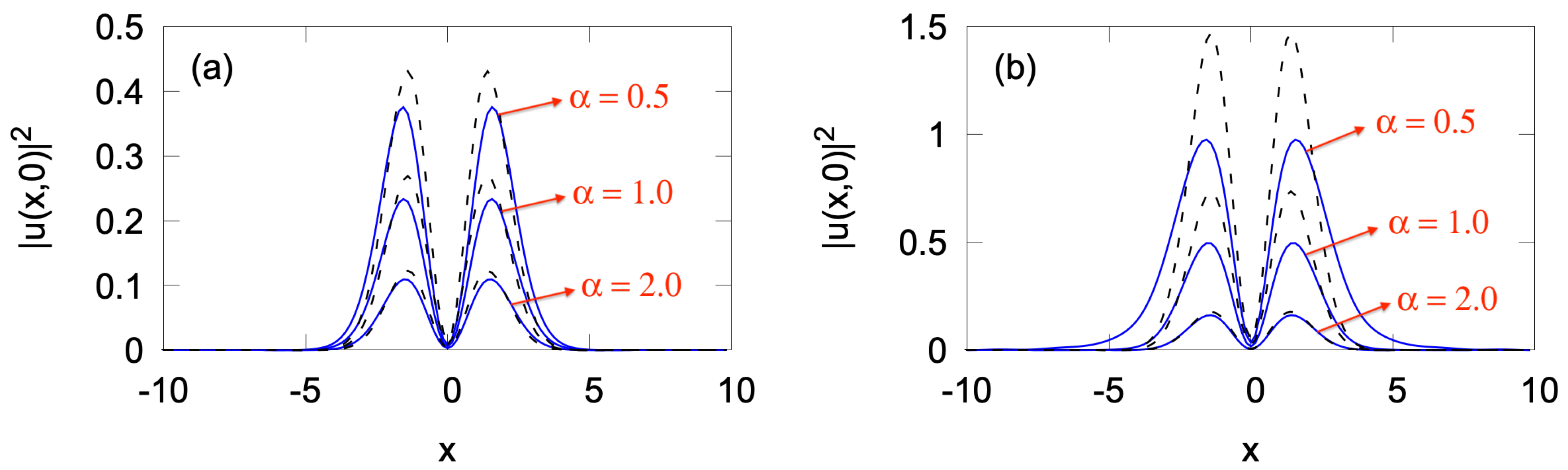
3.5. Influence of the Quintic Coefficient g
In the above analysis, the quintic term was dropped in the LL equation (
1), setting
. To examine the impact of this term, we first address the case shown above in
Figure 3, which demonstrated that the vortex soliton with
, as a solution to Eqs. (
1) and (
2) with
,
and
,
, was unstable if the loss parameter fell below the critical value,
. We have found that, adding to Eq. (
1) the quintic term with either
or
(the self-focusing or defocusing quintic nonlinearity, respectively) leads to the
stabilization of the vortex mode displayed in
Figure 3, which was unstable in the absence of the quintic term. This conclusion seems surprising because, in most cases, the inclusion of the self-focusing quintic nonlinearity gives rise to the supercritical collapse in 2D, making all solitons strongly unstable [
2,
38]. However, as it can be concluded from the stability charts displayed below in
Figure 11, the stabilizing effect of the quintic self-focusing occurs only at moderately small powers. In the general case, solitons stability regions shrinks under the action of the quintic self-focusing quintic term, with
.
In the presence of the quintic term, the comparison of the numerically found stabilized vortex-soliton profiles with their VA counterparts, with parameters produced by a numerical solution of Eqs. (
18) and (
19), is presented in
Figure 9. Similar to the results for the LL equation with the cubic-only nonlinearity, the VA is essentially more accurate in the case of the self-focusing sign of the quintic term (
) than in the opposite case,
. In particular, in the case shown in
Figure 9, the power-measured discrepancy for
and
is, respectively,
and
.
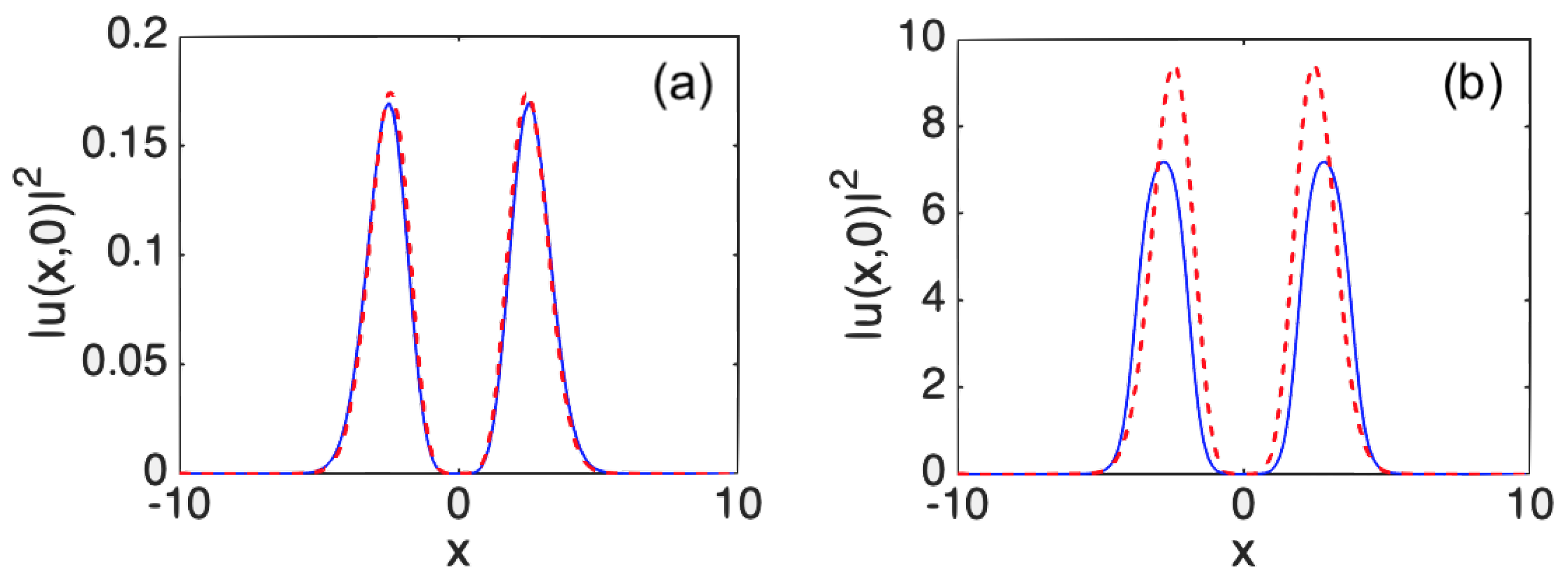
Figure 9.
Cross-section profiles (drawn through
) for stable vortex solitns with
, produced by Eq. (
1) with the quintic self-focusing,
(a) or defocusing,
(b) term. In both cases, the cubic self-focusing cubic term, with
, is present. The numerically found profiles and their VA-produced counterparts are displayed, respectively, by the solid blue and dashed lines. Other parameter are
,
, and
,
.
Figure 9.
Cross-section profiles (drawn through
) for stable vortex solitns with
, produced by Eq. (
1) with the quintic self-focusing,
(a) or defocusing,
(b) term. In both cases, the cubic self-focusing cubic term, with
, is present. The numerically found profiles and their VA-produced counterparts are displayed, respectively, by the solid blue and dashed lines. Other parameter are
,
, and
,
.
Another noteworthy finding is the stabilization of higher-vorticity solitons by the quintic term. For instance, it was shown above that, for parameters
,
,
,
, and
(the cubic self-focusing) all vortex solitons with
, produced by Eq. (
1), were unstable. Now, we can demonstrate that the soliton with
can be stabilized by adding a self-defocusing quintic with a small coefficient, just
, see
Figure 10(b). As a counter-intuitive effect, the stabilization of the same soliton by the self-focusing quintic term is possible too, but the necessary coefficient is large,
, see
Figure 10(a) (recall that
is sufficient for the stabilization of the vortex soliton with
and
in
Figure 9(a)). For the stabilized vortex modes shown in
Figure 10(a), in the case when both the cubic and quintic terms are self-focusing, the relative power-measured discrepancy between the numerical and VA-predicted solutions is very small,
, while in the presence of the weak quintic self-defocusing in
Figure 10(b) the discrepancy is
.
Figure 10.
Cross-section profiles (drawn through
) of vortex solitons with
, stabilized by the self-focusing (a) or defocusing (b) quintic tterm in Eq. (
1), with the respective coefficient
or
, other parameters being
(cubic self-focusing),
,
, and
,
in Eq. (
2). The numerically found solutions and their VA-predicted counterparts are presented by the solid blue and dashed red lines, respectively.
Figure 10.
Cross-section profiles (drawn through
) of vortex solitons with
, stabilized by the self-focusing (a) or defocusing (b) quintic tterm in Eq. (
1), with the respective coefficient
or
, other parameters being
(cubic self-focusing),
,
, and
,
in Eq. (
2). The numerically found solutions and their VA-predicted counterparts are presented by the solid blue and dashed red lines, respectively.
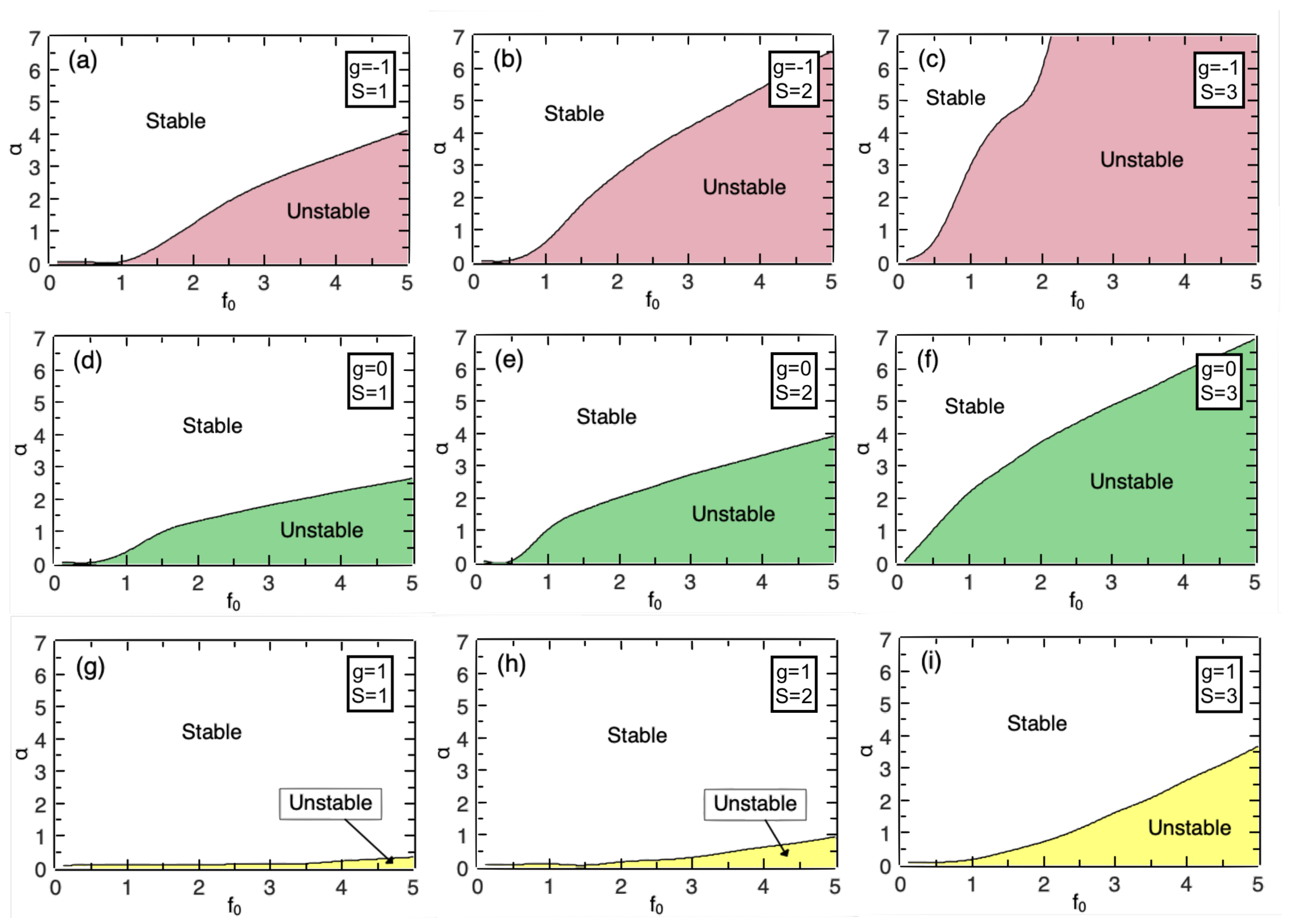
3.6. Stability Charts in the Parameter Space
The numerical results produced in this work are summarized in the form of stability areas plotted in
Figure 11 in the parameter plane
, for the vortex-soliton families with winding numbers
, 2, 3, and three values of the quintic coefficient,
, 0,
, while the cubic term is self-focusing,
, and the width of the pump beam is fixed,
. In addition to that, stability charts corresponding to the combination of the cubic self-defocusing (
) and quintic focusing (
), also for
, are plotted in
Figure 12.
The choice of the parameter plane
is relevant, as the strength of the pump beam,
, and loss the coefficient,
, and are amenable to accurate adjustment in the experiment (in particular,
may be tuned by partially compensating the background loss of the optical cavity by a spatially uniform pump, taken separately from the confined pump beam). As seen in all panels of
Figure 11 and
Figure 12, the increase of
naturally provides effective stabilization of the vortex modes, while none of them may be stable at
, in agreement with the known properties of vortex-soliton solutions to the 2D nonlinear Schrödinger equation with the cubic and/or cubic-quintic nonlinearity [
2,
38]. The apparent destabilization of the vortices with the increase of the pump’s amplitude
is explained by the ensuing enhancement of the destabilizing nonlinearity. Other natural features exhibited by
Figure 11 are the general stabilizing/destabilizing effect of the quintic self-defocusing/focusing, and expansion of the splitting-instability area with the increase of
S (the latter feature is also exhibited by
Figure 12).
Figure 11.
Stability areas for families of the vortex solitons with winding numbers
,
and 3, in the plain of the loss coefficient (
) and amplitude of the pump beam (
), for three different values of the quintic coefficient,
(recall that
and
correspond, respectively, to the self-focusing and defocusing). Other parameters of Eqs. (
1) and (
2) are
(the self-focusing cubic term),
, and
.
Figure 11.
Stability areas for families of the vortex solitons with winding numbers
,
and 3, in the plain of the loss coefficient (
) and amplitude of the pump beam (
), for three different values of the quintic coefficient,
(recall that
and
correspond, respectively, to the self-focusing and defocusing). Other parameters of Eqs. (
1) and (
2) are
(the self-focusing cubic term),
, and
.
Figure 12.
The same as in
Figure 11, but for
and
(the cubic self-defocusing and quintic focusing terms).
Figure 12.
The same as in
Figure 11, but for
and
(the cubic self-defocusing and quintic focusing terms).
The instability mode which determines the boundary of the stability areas in
Figure 11 and
Figure 12 is the breaking of the axial symmetry of the vortex rings by azimuthal perturbations, as shown above in
Figure 3(b),
Figure 4(b), and
Figure 5(b). The destabilization through the spontaneous splitting of the rings into symmetric sets of fragments (see
Figure 7) occurs deeply inside the instability area, at larger values of
.
4. Conclusions
We have introduced the two-dimensional LL (Lugiato-Lefever) equation including the self-focusing or defocusing cubic or cubic-quintic nonlinearity and the confined pump with embedded vorticity (winding number), . Stable states in the form of vortex solitons (rings) with the same S are obtained, in parallel, in the semi-analytical form by means of the VA (variational approximation) and numerically, by means of systematic simulations of the LL equation starting from the zero input. The VA provides much more accurate results in the case of the self-focusing nonlinearity than for the defocusing system. Stability areas of the vortex solitons with are identified in the plane of experimentally relevant parameters, viz., the pump amplitude and loss coefficient, for the self-focusing and defocusing signs of the cubic and quintic terms. Stability boundaries for the vortex rings are determined by the onset of the azimuthal instability breaking their axial symmetry. These findings suggest new possibilities for the design of tightly confined optical modes, such as vortex pixels.
As an extension of this work, it may be interesting to construct solutions pinned to a symmetric pair of pump beams with or without intrinsic vorticity. In this context, it is possible to consider the beam pair with identical or opposite vorticities. In the case of the self-focusing sign of the nonlinearity, one may expect onset of spontaneous breaking of the symmetry in the dual-pump configuration.