Tsallis Distribution as a Λ-Deformation of the Maxwell-Jüttner Distribution

Preprint

Article

Tsallis Distribution as a Λ-Deformation of the Maxwell-Jüttner Distribution

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Jean-Pierre Gazeau^*

This version is not peer-reviewed

Submitted:

28 February 2024

Posted:

29 February 2024

You are already at the latest version

Alerts

Abstract

Currently, there is no widely accepted consensus regarding a consistent thermodynamic framework within the special relativity paradigm. However, by postulating that the inverse temperature 4-vector, denoted as β, is future-directed and timelike, intriguing insights emerge. Specifically, it is demonstrated that the q-dependent Tsallis distribution can be conceptualized as a de-Sitterian deformation of the relativistic Maxwell-Jüttner distribution. In this context, the curvature of the de Sitter space-time is characterized by Λ/3, where Λ represents the cosmological constant within the ΛCDM standard model for Cosmology. For a simple gas composed of particles with proper mass m, and within the framework of quantum statistical de Sitterian considerations, the Tsallis parameter q exhibits a dependence on the cosmological constant given by q=1+ℓcΛ/n where ℓc=ℏ/mc is the Compton length of the particle and n is a positive numerical factor. This formulation establishes a novel connection between the Tsallis distribution, quantum statistics, and the cosmological constant, shedding light on the intricate interplay between relativistic thermodynamics and fundamental cosmological parameters.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Preamble: Temperature, Heat, Entropy, that Obscure Objects of Desire

It is opportune to start out this contribution by quoting what de Broglie was writing in [1] about the relation between entropy invariance and relativistic variance of temperature (translated from french):

It is well known that entropy, alongside the spacetime interval, electric charge, and mechanical action, is one of the fundamental “invariants” of the theory of relativity. To convince oneself of this, it is enough to recall that, according to Boltzmann, the entropy of a macroscopic state is proportional to the logarithm of the number of microstates that realize that state. To strengthen this reasoning, one can argue that, on the one hand, the definition of entropy involves a integer number of microstates, and, on the other hand, the transformation of entropy during a Galilean reference frame change must be expressed as a continuous function of the relative velocity of the reference frames. Consequently, this continuous function is necessarily constant and equal to unity, which means that entropy is constant.

Let us now give more insights about what “relativistic thermodynamics” could be. In relativistic thermodynamics (i.e., in accordance with special relativity) there exist three points of view [2], distinguished from the way heat

Δ Q

and temperature T transform under a Lorentz boost from frame

R_{0}

(e.g., laboratory) to comoving frame

R

with velocity

v = v \hat{n}

relative to

R_{0}

and Lorentz factor

γ (v) = \frac{1}{\sqrt{1 - v^{2} / c^{2}}} .

(1)

(a): the covariant viewpoint (Einstein [3], Planck [4], de Broglie [1] ...),

$Δ Q = Δ Q_{0} γ^{- 1}, T = T_{0} γ^{- 1} .$

(2)
(b): the anti-covariant one (Ott [5], Arzelies [6], ...),

$Δ Q = Δ Q_{0} γ, T = T_{0} γ .$

(3)
(c): the invariant one, “nothing changes” (Landsberg [7,8], ...),

$Δ Q = Δ Q_{0}, T = T_{0} .$

(4)

Also note that for some authors (Landsberg [9], Sewell [10], ...) “there is no meaningful law of temperature under boosts”.

In this paper we adopt the viewpoint Section a and review de Broglie’s arguments in Section 2. In Section 3 we remind the construction of the so-called Maxwell-Jütner distribution presented by Synge in . We then present in Section 4 the de Sitter space-time, its geometric description as a hyperboloid embedded in the

1 + 4

Minkowski space-time, and give some insights of the fully covariant quantum field theory of free scalar massive elementary systems propagating on this manifold. We then develop in Section 5 our arguments in favor a a novel connection between the Tsallis distribution, quantum statistics, and the cosmological constant, shedding light on the intricate interplay between relativistic thermodynamics and fundamental cosmological parameters. A few comments end our paper in Section 6.

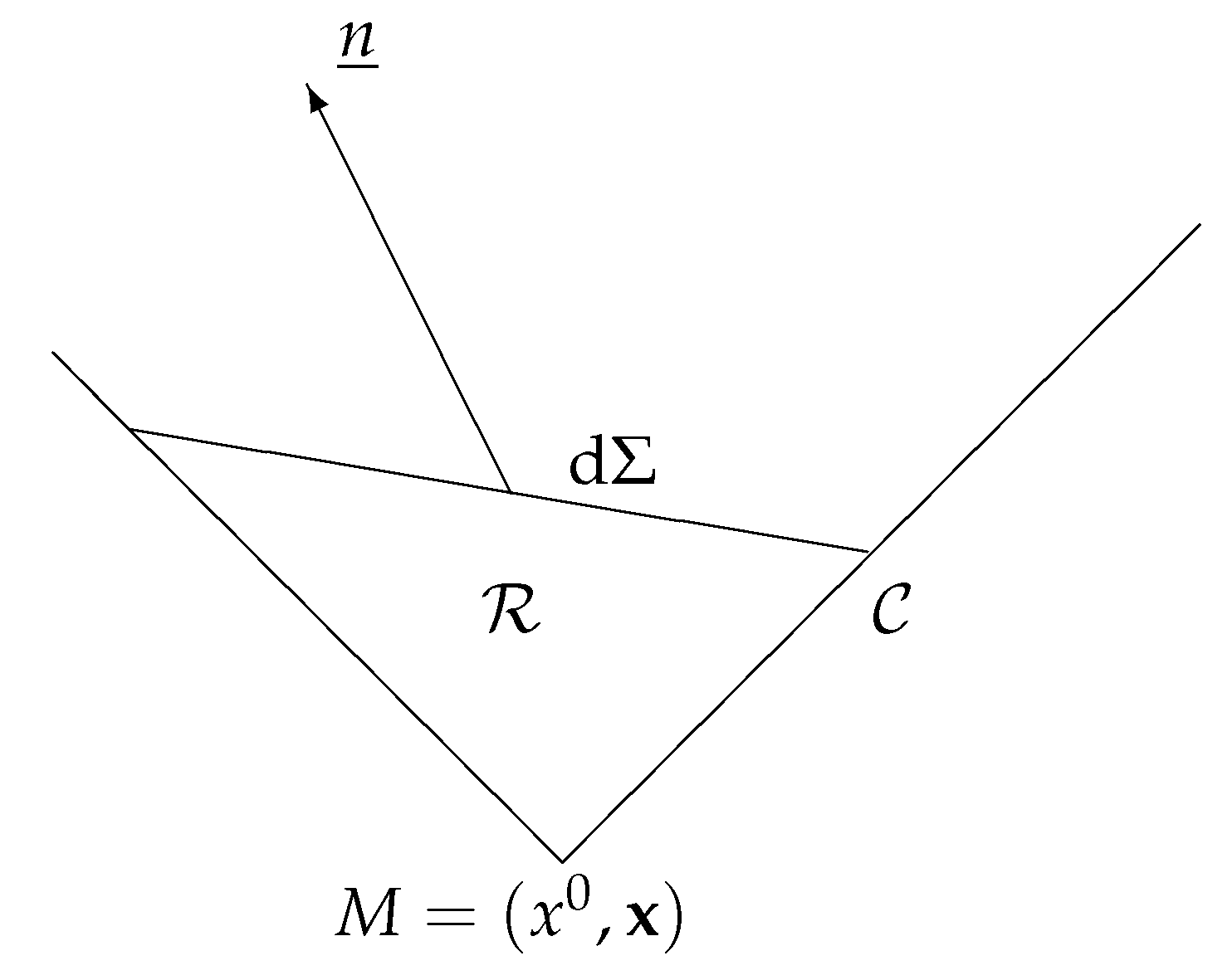
2. Relativistic Covariance of Temperature According to de Broglie (1948)

We here give an account of the de Broglie arguments given in [1] in favour of the covariant viewpoint (a).

Let us consider a body

B

with proper frame

R_{0}

, and total proper mass

M_{0}

. It is assumed to be in thermodynamical equilibrium with temperature

T_{0}

and fixed volume

V_{0}

(e.g., a gas enclosed with surrounding rigid wall). Let us then observe

B

from an inertial frame

R

in which

B

has constant velocity

v = v \hat{n}

relative to

R_{0}

. We suppose that a source in

R

provides

B

with heat

Δ Q

. In order to keep the velocity

v

B

constant a work W has to be done on

B

. Its proper mass is consequently modified

M_{0} \to M_{0}^{'}

. Then, from energy conservation,

(M_{0}^{'} - M_{0}) γ c^{2} = Δ Q + W, γ = γ (v) = \frac{1}{\sqrt{1 - v^{2} / c^{2}}},

(5)

and the relativistic 2nd Newton law,

Δ P = M_{0}^{'} γ v - M_{0} γ v = \int F d t = \frac{1}{v} \int F v d t = \frac{W}{v},

(6)

we derive

Δ Q = \frac{c^{2}}{v^{2}} γ^{- 2} W = (M_{0}^{'} - M_{0}) c^{2} γ^{- 2} .

(7)

In the frame

R_{0}

there is no work done (the volume is constant), there is just transmitted heat

Δ Q_{0} = (M_{0}^{'} - M_{0}) c^{2}

. By comparison with (7) one infers that heat transforms as

Δ Q = Δ Q_{0} γ^{- 1} .

(8)

Since the entropy

S = \int \frac{d Q}{T}

is relativistic invariant,

S = S_{0}

, temperature finally transforms as

T = T_{0} γ^{- 1}

(9)

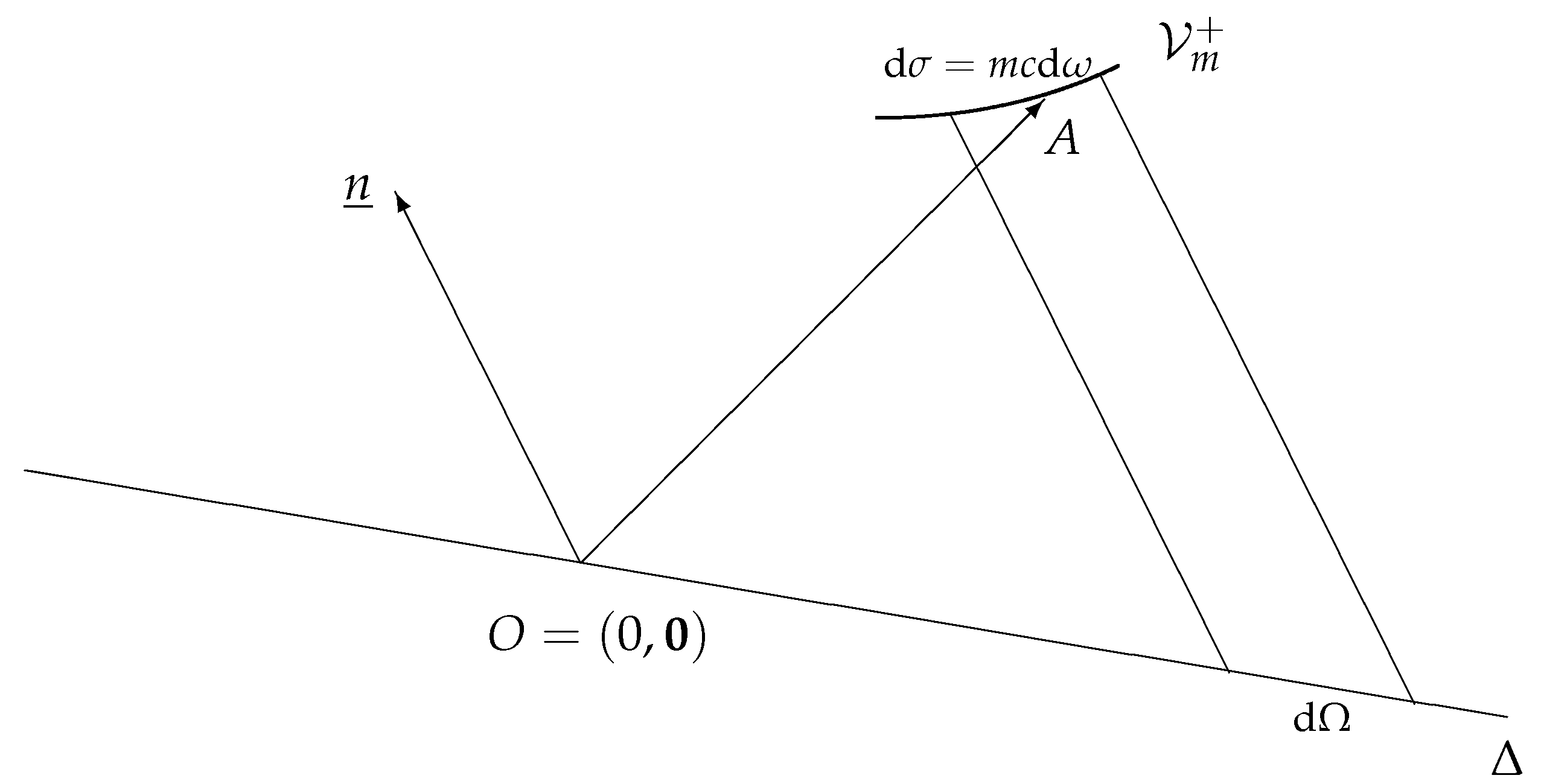
3. Maxwell-Jüttner Distribution

We now present a relativistic version of the Maxwell-Bolztman distribution for simple gases, namely Maxwell-Jüttner distribution. We follow the derivation given by Synge in [14], see also [15], and the recent [16] for a comprehensive list of references. Note that this distribution is defined on the mass hyperboloid and not expressed in terms of velocities (see the recent [17] and references therein).

Our notations [18] for event 4-vector

\underset{̲}{x}

in the Minkowskian space-time

M_{1, 3}

and for 4-momentum

\underset{̲}{k}

are the following:

M_{1, 3} ∋ \underset{̲}{x} = (x^{μ}) = (x^{0} = x_{0}, x^{i} = - x_{i}, i = 1, 2, 3) \equiv (x^{0}, x),

(10)

equipped with the metric

d s^{2} = {(d x^{0})}^{2} - d x \cdot x \equiv g_{μ ν} d x^{μ} d x^{ν}

g_{μ ν} = diag (1, - 1, - 1, - 1)

\underset{̲}{k} = (k^{μ}) = (k^{0}, k) .

(11)

The Minkowskian inner product is noted by:

\underset{̲}{x} \cdot \underset{̲}{x^{'}} = g_{μ ν} x^{μ} {x^{'}}^{ν} = x^{μ} x_{μ}^{'} = x^{0} {x^{'}}^{0} - x \cdot x^{'}

(12)

Let

\underset{̲}{k}

be a 4-momentum pointing toward point A of the mass shell hyperboloid

V_{m}^{+} = {\underset{̲}{k}, \underset{̲}{k} \cdot \underset{̲}{k} = m^{2} c^{2}}

, and an infinitesimal hyperbolic interval at A, with length

d σ = m c d ω,

(13)

where

d ω = \frac{d^{3} k}{k_{0}}

is the Lorentz-invariant element on

V_{m}^{+}

. Given a time-like unit vector

\underset{̲}{n}

, and a straight line

Δ

passing through the origin and orthogonal (in the

M_{1, 3}

metric sense) to

\underset{̲}{n}

, denote by

d Ω

the length of the projection of

d σ

Δ

along

\underset{̲}{n}

. As is illustrated in Figure 1, one easily proves that

d Ω = | \underset{̲}{k} \cdot \underset{̲}{n} | d ω (= d^{3} k i f \underset{̲}{n} = (1, 0)) .

(14)

The sample population consists of those particles with world lines cutting the infinitesimal space-like segment

d Σ

orthogonal to the time-like unit vector

\underset{̲}{n}

, as is shown in Figure 2.

Every particle that traverses the segment

C

of the null cone between M and

d Σ

must also traverse

d Σ

(causal cone). Consequently, regardless of the collisions that take place within the infinitesimal region

R

bounded by M, the segment of the light cone

C

, and

d Σ

, the number of particles crossing

Σ

is predetermined as the number crossing

C

ν = \underset{̲}{N} \cdot \underset{̲}{n} d Σ = d Σ \int_{V_{m}^{+}} N (\underset{̲}{x}, \underset{̲}{k}) d Ω,

(15)

where

\underset{̲}{N}

is the numerical-flux 4-vector and

N (\underset{̲}{x}, \underset{̲}{k})

is the distribution function. By the conservation of 4-momentum at each collision in a simple gas, the flux of 4-momentum across

d Σ

is predetermined as the flux across

C

T_{μ} \cdot \underset{̲}{n} d Σ = d Σ \int_{V_{m}^{+}} N (\underset{̲}{x}, \underset{̲}{k}) c k_{μ} d Ω,

(16)

where

\underset{̲}{\underset{̲}{T}} = (T_{μ ν})

is the energy-momentum tensor.

The most probable distribution function

N

at M is that which maximizes the following entropy integral

F = - d Σ \int_{V_{m}^{+}} N (\underset{̲}{x}, \underset{̲}{k}) log N (\underset{̲}{x}, \underset{̲}{k}) d Ω .

(17)

Variational calculus with 5 Lagrange

\underset{̲}{x}

-dependent multipliers

α

and

η_{μ}

associated with constraints on

ν

and

T_{μ} \cdot \underset{̲}{n}

respectively leads to the solution

N (\underset{̲}{x}, \underset{̲}{k}) = C (\underset{̲}{x}) exp (- \underset{̲}{η} (\underset{̲}{x}) \cdot \underset{̲}{k}), C = e^{α - 1} .

(18)

Scalar C and time-like 4-vector

\underset{̲}{η}

are determined by the constraints on

ν = \underset{̲}{N} \cdot \underset{̲}{n} d Σ

and

T_{μ} \cdot \underset{̲}{n} d Σ

C \int_{V_{m}^{+}} k_{μ} e^{- \underset{̲}{η} \cdot \underset{̲}{k}} d ω = N_{μ}, C \int_{V_{m}^{+}} c k_{μ} k_{ν} e^{- \underset{̲}{η} \cdot \underset{̲}{k}} d ω = T_{μ ν} .

(19)

established by taking into account that

\underset{̲}{n}

is arbitrary.

With the equations of conservation

\underset{̲}{\partial} \cdot \underset{̲}{N} = 0, \underset{̲}{\partial} \cdot T_{μ} = 0,

(20)

we finally get as many equations as the 19 functions of

\underset{̲}{x}

C, \underset{̲}{η}, \underset{̲}{N}, T

. The following partition function is essential for all relevant calculations.

Z (η) : = \int_{V_{m}^{+}} e^{- \underset{̲}{η} \cdot \underset{̲}{k}} \frac{d^{3} k}{k_{0}} = \frac{4 π m c}{\sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}} K_{1} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}})

(21)

where

K_{ν}

is the modified Bessel function [19]. Hence, the components of the numerical flux 4-vector

\underset{̲}{N}

and of the energy tensor

\underset{̲}{\underset{̲}{T}}

in (19) are given in terms of derivatives of Z and finally in terms of Bessel functions by

\begin{matrix} N_{μ} & = - C \frac{\partial Z}{\partial η^{μ}} = C \frac{4 π m^{2} c^{2} η_{μ}}{\underset{̲}{η} \cdot \underset{̲}{η}} K_{2} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}), \end{matrix}

(22)

\begin{matrix} T_{μ ν} & = C c \frac{\partial^{2} Z}{\partial η^{μ} \partial η^{ν}} = C 4 π m^{2} c^{3} [m c \frac{K_{3} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}})}{{(\underset{̲}{η} \cdot \underset{̲}{η})}^{3 / 2}} η_{μ} η_{ν} - \frac{K_{2} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}})}{\underset{̲}{η} \cdot \underset{̲}{η}} g_{μ ν}] . \end{matrix}

(23)

For a simple gas consisting of material particles of proper mass m the components of the energy-momentum tensor

\underset{̲}{\underset{̲}{T}}

are given by

T_{μ ν} = (ρ + p) u_{μ} u_{ν} - p g_{μ ν},

(24)

where

ρ

is the mean density, p is the pressure, and

\underset{̲}{u} = (u_{μ} = \frac{d x_{μ}}{d s})

\underset{̲}{u} \cdot \underset{̲}{u} = 1

, is the mean 4-velocity of the fluid. Hence, by identification with (), Synge [14] proved that a relativistic gas consisting of material particles of proper mass m is a perfect fluid through the relations:

\begin{matrix} u_{μ} & = \frac{η_{μ}}{\sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}}, \end{matrix}

(25)

\begin{matrix} ρ + p & = C 4 π m^{3} c^{4} \frac{K_{3} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}})}{\sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}}, \end{matrix}

(26)

\begin{matrix} p & = C 4 π m^{2} c^{3} \frac{K_{2} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}})}{\underset{̲}{η} \cdot \underset{̲}{η}} . \end{matrix}

(27)

From () and () we derive the expression of the density:

ρ = C \frac{4 π m^{3} c^{4}}{\sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}} \frac{K_{1} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}) + K_{3} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}})}{2} = - C \frac{4 π m^{3} c^{4}}{\sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}} K_{2}^{'} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}) .

(28)

Let us define the invariant quantity, i.e., the projection of the numerical flux () along the 4-velocity of the fluid,

N_{0} = \underset{̲}{N} \cdot \underset{̲}{u} = C \frac{4 π m^{2} c^{2}}{\sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}} K_{2} (m c \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}}) .

(29)

This expression, which represents the number of particles per unit length (“numerical density”) in the rest frame of the fluid (

u_{0} = 1

), allows us to determine the function

C = C (\underset{̲}{x})

and to eventually write the distribution (18) as:

N (\underset{̲}{x}, \underset{̲}{k}) = \frac{N_{0}}{m^{2} c k_{B} T_{a} K_{2} (m c^{2} / k_{B} T_{a})} exp (- \frac{c \underset{̲}{u} \cdot \underset{̲}{k}}{k_{B} T_{a}}) .

(30)

The term

T_{a} : = c / (k_{B} \sqrt{\underset{̲}{η} \cdot \underset{̲}{η}})

, where

k_{B}

is the Boltzmann constant, is a “relativistic” absolute temperature. It is precisely the relativistic invariant, which might fit pointview (c).

Note that with this expression, () reads as the usual gas law:

p = N_{0} k_{B} T_{a} .

(31)

The Maxwell-Boltzmann non relativistic distribution (in the space of momenta) is recovered by considering the limit at

k_{B} T_{a} ≪ m c^{2}

in the rest frame of the fluid:

\begin{matrix} K_{2} (\frac{m c^{2}}{k_{B} T_{a}}) \approx \sqrt{\frac{π k_{B} T_{a}}{2 m c^{2}}} e^{- \frac{m c^{2}}{k_{B} T_{a}}} \\ \Rightarrow N (\underset{̲}{x}, \underset{̲}{k}) \\ \approx N_{0} {(2 π m k_{B} T_{a})}^{- 3 / 2} exp (- \frac{k_{0} c - m c^{2}}{k_{B} T_{a}}) \approx N_{0} {(2 π m k_{B} T_{a})}^{- 3 / 2} exp (- \frac{k^{2}}{2 m k_{B} T_{a}}) . \end{matrix}

(32)

3.1. Inverse Temperature 4-Vector

The found distribution (30) on the Minkowskian mass shell for a simple gas consisting of particles of proper mass m leads us to introduce the relativistic thermodynamic, future directed, time-like 4-coldness vector

\underset{̲}{β}

, as the 4-version of the reciprocal of the thermodynamic temperature (see also [2]):

\frac{c \underset{̲}{u}}{k_{B} T_{a}} \equiv \underset{̲}{β} = (β^{0} = β_{0} > 0, β^{i} = - β_{i}) = (β_{0}, β),

(33)

with absolute coldness as relativistic invariant,

\sqrt{\underset{̲}{β} \cdot \underset{̲}{β}} = \frac{c}{k_{B} T_{a}} \equiv β_{a} .

(34)

It is precisely the way as the component

β_{0}

transforms under a Lorentz boost,

β_{0}^{'} = γ (v) (β_{0} - v \cdot β / c)

, which explains the way the temperature transforms à la de Broglie,

T \mapsto T^{'} = T γ^{- 1}

. So, in the sequel, we call Maxwell-Jüttner distribution the following relativistic invariant:

N (\underset{̲}{β}, \underset{̲}{k}) = \frac{N_{0}}{m c K_{1} (m c β_{a})} exp (- \underset{̲}{β} \cdot \underset{̲}{k}),

(35)

where the space-time dependence holds through the coldness 4-vector coldness field

\underset{̲}{β} = \underset{̲}{β} (\underset{̲}{x})

4. deSitter Material

We now turn our attention to the de Sitter (dS) space-time and some important features of a dS covariant quantum field theory.

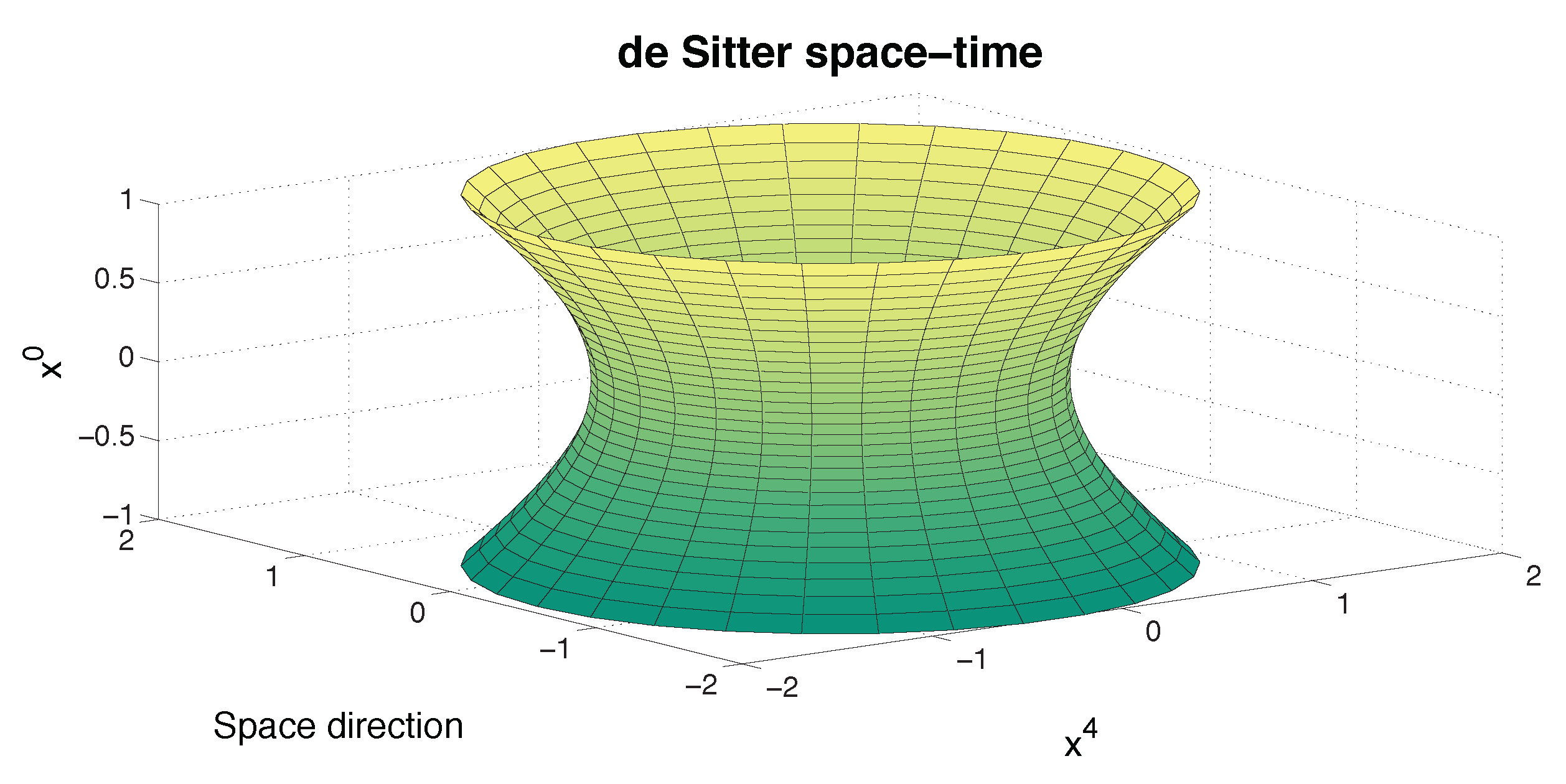
4.1. de Sitter Geometry

The de Sitter space-tiem can be viewed as a hyperboloid embedded in a five-dimensional Minkowski space

M_{1, 4}

with metric

g_{α β} =

diag

(1, - 1, - 1, - 1, - 1)

(see Figure 3). Of course, one should keep in mind that all choices of one point in the manifold as an origin are physically equivalent, like are the points of the Minkowski space-time

M_{1, 3}

M_{R} \equiv {x \in R^{5}; x^{2} = g_{α β} x^{α} x^{β} = - R^{2}},, α, β = 0, 1, 2, 3, 4,

(36)

where the pseudo-radius R (or inverse of curvature) is given by

R = \sqrt{\frac{3}{Λ}}

within the cosmological

Λ

CDM standard model. The de Sitter symmetry group is the group SO₀

(1, 4)

of proper (i.e.,

det . = 1

) and orthochronous (to be precised later) transformations of the manifold (36). This group has ten (Killing) generators

K_{α β} = x_{α} \partial_{β} - x_{β} \partial_{α}

4.2. Flat Minkowskian Limit of de Sitter Geometry

Let us choose the global coordinates

c t \in R, n \in S^{2}, r / R \in [0, π]

for the dS manifold

M_{R}

. They are defined by:

\begin{matrix} M_{R} ∋ x & = (x^{0}, x^{1}, x^{2}, x^{3}, x^{4}) \equiv (x^{0}, x, x^{4}) \\ = (R sinh (c t / R), R cosh (c t / R) sin (r / R) n, R cosh (c t / R) cos (r / R)) \equiv x (t, x) . \end{matrix}

(37)

At the limit

R \to \infty

the manifold

M_{R} \to M_{1, 3}

, the Minkowski spacetime tangent to

M_{R}

at, say, the de Sitter point

O_{d S} = (0, 0, R)

, chosen as origin, since then

M_{R} ∋ x \underset{R \to \infty}{\approx} (c t, r = r n, R) \equiv (\underset{̲}{ℓ}, R), \underset{̲}{ℓ} \in M_{1, 3} .

(38)

At this limit, the de Sitter group becomes the Poincaré group:

lim_{R \to \infty} {SO}_{0} (1, 4) = P_{+}^{↑} (1, 3) = M_{1, 3} ⋊ {SO}_{0} (1, 3) .

(39)

Consistently, the ten de Sitter Killing generators contract (in the Wigner-Inonü sense) to their Poincaré counterparts

K_{μ ν}

Π_{μ}

μ = 0, 1, 2, 3

, after rescaling the four

K_{4 μ} ⟶ Π_{μ} = K_{4 μ} / R

4.3. de Sitter plane waves as binomial deformations of Minkowskian plane waves

The de Sitter (scalar) plane waves are defined [20] as

ϕ_{τ, ξ} (x) = {(\frac{x \cdot ξ}{R})}^{τ}, x \in M_{R}, ξ \in C_{1, 4},

(40)

where

C_{1, 4} = {ξ \in R^{5}, ξ \cdot ξ = 0}

is the null cone in

M_{1, 4}

. They are solutions of the Klein-Gordon-like equation

\frac{1}{2} M_{α β} M^{α β} ϕ_{τ, ξ} (x) \equiv R^{2} □_{R} ϕ_{τ, ξ} (x) = τ (τ + 3) ϕ_{τ, ξ} (x),

where

M_{α β} = - i (x_{α} \partial_{β} - x_{β} \partial_{α})

is the quantum representation of the Killing vector

K_{α β}

, and

□_{R}

stands for the d’Alembertian operator on

M_{R}

. For the values

τ = - \frac{3}{2} + i ν, ν \in R,

(41)

they describe free quantum motions of “massive” scalar particles on

M_{R}

. The term “massive” is justified by the flat Minkowskian limit

R \to \infty

, i.e.

Λ \to 0

. This limit is understood as follows.

(i): First one has the Garidi [21] relation between proper mass m (curvature independent) of the spinless particle and the parameter $ν \geq 0$ :

$m = \frac{ℏ}{R c} {[ν^{2} + \frac{1}{4}]}^{1 / 2} \Leftrightarrow ν = \sqrt{\frac{R^{2} m^{2} c^{2}}{ℏ^{2}} - \frac{1}{4}} \underset{R large}{\approx} \frac{R m c}{ℏ} = \frac{m c}{ℏ} \sqrt{\frac{3}{Λ}} .$

(42)

The quantity $\frac{ℏ c ν}{R}$ is a kind of at rest desitterian energy, which is distinct of the proper mass energy $m c^{2}$ if $Λ \neq 0$ .
(ii): Then, with the mass shell parametrisation $ξ = (ξ^{0} = \frac{k_{0}}{m c}, ξ = \frac{k}{m c}, ξ^{4} = 1) \in C_{1, 4}^{+}$ , one obtains at the limit $R \to \infty$ :

$ϕ_{τ, ξ} (x) = {(x \cdot ξ / R)}^{- 3 / 2 + i ν} \underset{R \to \infty}{\to} e^{i \underset{̲}{k} \cdot \underset{̲}{ℓ} / ℏ}, \underset{̲}{ℓ} = (c t, r) .$

(43)

This relation allows to consider the functions (40) as deformation of the plane waves propagating in the Minkowskian space-time

M_{1, 4}

. This pivotal property justifies the name “dS plane waves” granted to the functions (40).

4.4. Analytic Extension of dS Plane Waves for dS QFT

The dS plane waves

ϕ_{τ, ξ} (x) = {(\frac{x \cdot ξ}{R})}^{τ}

τ = - 3 / 2 + i ν

, are not defined on all

M_{R}

due to the possible change of sign of

x \cdot ξ

. A solution to this drawback is found through the extension to the tubular domains in the complexified hyperboloid

M_{R}^{C} = \{z = x + i y \in C^{5}, z^{2} = g_{α β} z^{α} z^{β} = - R^{2}

or equivalently

x^{2} - y^{2} = - R^{2}, x \cdot y = 0\}

T^{\pm} : = T^{\pm} \cap M_{R}^{C}, T^{\pm} : = M_{1, 4} + i V^{\pm},

(44)

where the forward and backward light cones

V^{\pm} : = \{x \in M_{1, 4}, x^{0} ≷ \sqrt{x^{2} + {(x^{4})}^{2}}\}

allow for a causal ordering in

M_{1, 4}

Then the extended plane waves

ϕ_{τ, ξ} (z) = {(\frac{z \cdot ξ}{R})}^{τ}

are globally defined for

z \in T^{\pm}

and

ξ \in C_{1, 4}^{+}

These analytic extensions allow for a consistent QFT for free scalar fields on

M_{R}

: the two-point Wightman function

W_{ν} (x, x^{'}) = 〈 Ω, ϕ (x) ϕ (x^{'}) Ω 〉

can be extended to the complex covariant, maximally analytic, two-point function having the spectral representation in terms of these extended plane waves:

W_{ν} (z, z^{'}) = c_{ν} \int_{V_{m}^{+} \cup V_{m}^{-}} {(z \cdot ξ)}^{- 3 / 2 + i ν} {(ξ \cdot z^{'})}^{- 3 / 2 - i ν} \frac{d k}{k_{0}}, z \in T^{-}, z^{'} \in T^{+} .

(45)

Details are found in [20] and in the recent volume [22].

4.5. KMS Interpretation of $W_{ν} (z, z^{'})$ Analyticity

From the analyticity of

W_{ν} (z, z^{'})

we deduce that

W_{ν} (x, x^{'})

defines a

2 i π R / c

periodic analytic function of t, whose domain is the periodic cut plane

C_{x, x^{'}}^{cut} = {t \in C, Im (t) \neq 2 n π R / c, n \in Z} \cup {t, t - 2 i n π R / c \in I_{x, x^{'}}, n \in Z},

(46)

where

I_{x, x^{'}}

is the real interval on which

{(x - x^{'})}^{2} < 0

. Hence

W_{ν} (z, z^{'})

is analytic in the strip

{t \in C, 0 < Im (t) < 2 i π R / c},

(47)

and satisfies:

W_{ν} (x^{'} (t + t^{'}, x), x) = lim_{ϵ \to 0^{+}} W_{ν} ((x, x^{'} (t + t^{'} + 2 i π R / c - i ϵ, x)), t^{'} \in R .

(48)

This is a KMS relation at (∼ Hawking) temperature

T_{Λ} = \frac{ℏ c}{2 π k_{B} R} : = \frac{ℏ c}{2 π k_{B}} \sqrt{\frac{Λ}{3}} .

(49)

5. de Sitterian Tsallis Distribution

5.1. Tsallis Entropy and Distribution, a Short Reminder

Given a discrete (resp. continuous) set of probabilities

{p_{i}}

(resp. continuous

x \mapsto p (x)

) with

\sum_{i} p_{i} = 1

(resp.

\int p (x) d x = 1

) , and a real q, the Tsallis entropy [23] is defined as

S_{q} (p_{i}) = k \frac{1}{q - 1} (1 - \sum_{i} p_{i}^{q}) r e s p . S_{q} [p] = \frac{1}{q - 1} (1 - \int {(p (x))}^{q} d x) .

(50)

q \to 1

S_{q} (p_{i}) \to S_{BG} (p) = - k \sum_{i} p_{i} ln p_{i}

(Boltzmann-Gibbs). The Tsallis entropy is non additive : for two independent systems A and B, for which

p (A \cup B) = p (A) p (B)

S_{q} (A \cup B) = S_{q} (A) + S_{q} (B) + (1 - q) S_{q} (A) S_{q} (B)

. A Tsallis distribution is a probability distribution derived from the maximization of the Tsallis entropy under appropriate constraints. The so-called q-exponential Tsallis distribution has the probability density function

(2 - q) λ {[1 - (1 - q) λ x]}^{1 / (1 - q)} \equiv (2 - q) λ e_{q} (- λ x),

(51)

where

q < 2

and

λ > 0

(rate), arises from the maximization of the Tsallis entropy under appropriate constraints, including constraining the domain to be positive. More details are given for instance in [24].

Let us now show how the Tsallis distribution can be viewed as a

Λ

-deformation of the Maxwell-Jüttner distribution.

5.2. Coldness in de Sitter

In analogy with the de Sitter plane waves, we introduce the following distributions on the subset

\sim V_{m}^{+}

of the null cone

C_{1, 4}^{+} = {ξ \in M_{1, 4}, ξ \cdot ξ = 0, ξ^{0} > 0}

ϕ_{τ, ξ} (x) = {(\frac{b \cdot ξ}{B})}^{τ}, b \in M_{B}, ξ = (\frac{k^{0}}{m c} > 0, \frac{k}{m c}, - 1),

(52)

where one should note the negative value

- 1

for

ξ_{4}

, and

M_{B} \equiv {b \in M_{1, 4}, b^{2} = g_{α β} b^{α} b^{β} = - B^{2}}, α, β = 0, 1, 2, 3, 4,

(53)

is the manifold of the “deSitterian 5-vector coldness fields”

b = b (x)

Like for

M_{R}

we use global coordinates on

M_{B}

β^{0} \in R, β = ∥ β ∥ n \in R^{3}, ∥ β ∥ / B \in [0, π],

(54)

with

\begin{matrix} M_{B} ∋ b \equiv b (\underset{̲}{β}) = (b^{0}, b^{1}, b^{2}, b^{3}, b^{4}) \equiv (b^{0}, b, b^{4}) \\ = (B sinh (β^{0} / B), B cosh (β^{0} / B) sin (∥ β ∥ / B) n, - B cosh (β^{0} / B) cos (∥ β ∥ / B)), \end{matrix}

(55)

in such a way that at large B we recover the Minkowskian coldness

\underset{̲}{β}

M_{B} ∋ b \underset{B \to \infty}{\sim} (\underset{̲}{β}, B) .

We now need to connect the desitterian coldness scale B with

Λ

. Inspired by the relativistic invariant

β_{a} = \frac{c}{k_{B} T_{a}}

and the KMS temperature

T_{Λ} = \frac{ℏ c}{2 π k_{B}} \sqrt{\frac{Λ}{3}}

we write

B \propto \frac{2 π}{ℏ} \sqrt{\frac{3}{Λ}}, i . e . B = \frac{n}{ℏ \sqrt{Λ}},

(56)

where

n

is a numerical factor. Note that with the values

Λ_{current} = 1.1056 \times 10^{- 52} m^{- 2}, ℏ = 1.054571817 . . . \times 10^{- 34} J s,

one obtains

B \approx 0.9 \times 10^{60} n

SI (inverse of a momentum).

5.3. A de Sitterian Tsallis Distribution

We now consider the distribution on

M_{B} \times V_{m}^{+}

with

B = \frac{n}{ℏ \sqrt{Λ}}

N (b, \underset{̲}{k}) = C_{B} {(\frac{b \cdot ξ}{B})}^{- m c B} = C_{B} {(\frac{b^{0}}{B} \frac{k^{0}}{m c} - \frac{b}{B} \cdot \frac{k}{m c} + \frac{b^{4}}{B})}^{- m c B} .

(57)

b \in M_{B}, ξ = (\frac{k^{0}}{m c} > 0, \frac{k}{m c}, - 1),

where the constant

C_{B}

involves an associated Legendre function of the First Kind [25].

With the global coordinates (55) and with the constraint

β^{0} / B \in [0, π / 2)

, the distribution

N (b, \underset{̲}{k})

reads

\begin{matrix} N (b, \underset{̲}{k}) \\ = C_{B} {(cosh (β^{0} / B) cos (∥ β ∥ / B) + sinh (β^{0} / B) \frac{k^{0}}{m c} - cosh (β^{0} / B) sin (∥ β ∥ / B) \frac{n \cdot k}{m c})}^{- m c B} \\ = C_{B} exp [- m c B log (cosh (β^{0} / B) cos (∥ β ∥ / B))] \times \\ \times exp [- m c B log (1 + \frac{sinh (β^{0} / B) \frac{k^{0}}{m c} - cosh (β^{0} / B) sin (∥ β ∥ / B) \frac{n \cdot k}{m c}}{cosh (β^{0} / B) cos (∥ β ∥ / B)})] . \end{matrix}

(58)

At large B this expression becomes the Maxwell-Jüttner distribution:

N (b, \underset{̲}{k}) \underset{B \to \infty}{\sim} C_{B} e^{- \underset{̲}{β} \cdot \underset{̲}{k}} .

Hence, going back to the original expression

\begin{matrix} N (b, \underset{̲}{k}) & = C_{B} {(\frac{b \cdot ξ}{B})}^{- m c B} = C_{B} {(\frac{b^{0}}{B} \frac{k^{0}}{m c} - \frac{b}{B} \cdot \frac{k}{m c} + \frac{b^{4}}{B})}^{- m c B} \\ = C_{B} {(\frac{b^{4}}{B})}^{- m c B} {(1 + \frac{\underset{̲}{b} \cdot \underset{̲}{k}}{b^{4} m c})}^{- m c B}, \underset{̲}{b} : = (b^{0}, b), \end{matrix}

and introducing

q = 1 + \frac{1}{m c B} = 1 + \frac{ℏ \sqrt{Λ}}{m c n},

(59)

we finally get the Tsallis-type distribution

N (b, \underset{̲}{k}) = C_{B} {(\frac{b^{4}}{B})}^{- m c B} {(1 - (1 - q) \frac{B}{b^{4}} \underset{̲}{b} \cdot \underset{̲}{k})}^{\frac{1}{1 - q}} .

(60)

Analogously to (21) and all subsequent determinations of thermodynamical quantities, the following partition function is essential for their transcriptions to the de Sitter case:

\begin{matrix} Z_{dS} (b, \underset{̲}{k}) & = {(\frac{b^{4}}{B})}^{- m c B} \int_{V_{m}^{+}} {(1 + \frac{\underset{̲}{b} \cdot \underset{̲}{k}}{b^{4} m c})}^{- m c B} \frac{d^{3} k}{k_{0}} \end{matrix}

(61)

\begin{matrix} = 4 π m^{2} c^{2} {(\frac{b^{4}}{B})}^{- m c B} \int_{0}^{\infty} {(1 + (\frac{b_{0}}{b^{4}}) cosh t)}^{- m c B} {sinh}^{2} t d t . \end{matrix}

(62)

With the following integral representation of the associated Legendre function of the First Kind

P_{ν}^{μ} (z)

[25],

P_{ν}^{μ} (z) = \frac{2^{- ν} {(z^{2} - 1)}^{- μ / 2}}{Γ (- ν - μ) Γ (ν + 1)} \int_{0}^{\infty} {(z + cosh t)}^{- ν - μ - 1} {sinh}^{2 ν + 1} t d t,

(63)

valid for

z \notin (- \infty, - 1]

and

Re (- μ) > Re (ν) > - 1

, the function (61) reads as

Z_{dS} (b, \underset{̲}{k}) = {(8 π)}^{3 / 2} Γ (1 - m c B) {(\frac{B}{b_{0}})}^{m c B} {(\frac{B^{2} - b \cdot b}{b_{0}^{2}})}^{m c B / 2 - 3 / 4} P_{1 / 2}^{m c B - 3 / 2} (\frac{b^{4}}{b_{0}}) .

(64)

6. Conclusions

In this contribution, we have forged a groundbreaking link between the Tsallis distribution, quantum statistics, and the cosmological constant, illuminating the complex interplay between relativistic thermodynamics and a fundamental cosmological parameter.

Our key findings are encapsulated in the formulas (59) and (60). The intricate technical details of the associated thermodynamic features (flux number, energy-momentum tensor, etc.) in the de Sitter space-time, along with their physical (and astrophysical!) implications, are reserved for future exploration.

Funding

This research received no external funding.

Conflicts of Interest

The author declare no conflicts of interest.

References

de Broglie, L. Sur la variance relativiste de la température. Cahiers de la Physique 1948, 31-32, 1–11. [Google Scholar]
Wu, Z. C. Inverse Temperature 4-vector in Special Relativity. Eur. Phys. Lett. 2009, 88, 20005. [Google Scholar] [CrossRef]
Einstein, A. , Ueber das Relativitaetsprinzip und die aus demselben gezogenen Folgerungen. Jahrb. Rad. u. Elektr. 1907, 4. [Google Scholar]
Planck, M. Ann Physik. Lpz. Ser. 1908, 26, 1–35. [Google Scholar]
Ott, H. Lorentz-Transformation der Wärme und der Temperatur. Zeitschr. Phys. 1963, 175, 70–104. [Google Scholar] [CrossRef]
Arzeliès, H. , Transformation relativiste de la température et de quelques autres grandeurs thermodynamiques. Nuov. Cim. 1965, 35, 792–804. [Google Scholar] [CrossRef]
Landsberg, P. T. Does a Moving Body Appear Cool? Nature 1966, 212, 571–572. [Google Scholar] [CrossRef]
Landsberg, P. T. Does a Moving Body Appear Cool? Nature 1967, 214, 903–904. [Google Scholar] [CrossRef]
Landsberg, P. T.; Matsas, G. E. A. Laying the ghost of the relativistic temperature transformation. Phys. Lett. A 1996, 223, 401–403. [Google Scholar] [CrossRef]
Sewell, G. L. On the question of temperature transformations under Lorentz and Galilei boosts. J. Phys. A: Math. Theor. 2008, 41, 382003. [Google Scholar] [CrossRef]
Jüttner, F. Das maxwellsche gesetz der geschwindigkeitsverteilung in der relativtheorie. Ann. Phys. 1911, 339, 856–882. [Google Scholar] [CrossRef]
van Dantzig, D. On the phenomenological thermodynamics of moving matter. Physica VI 1939, 673–704. [Google Scholar] [CrossRef]
Taub, A. H. Relativistic Ranirine-Hugoniot Equations. Phys. Rev. 1948, 74, 328–334. [Google Scholar] [CrossRef]
Synge, J. L. The Relativistic Gas; North-Holland Publishing Company, 1957. [Google Scholar]
Gazeau, J.-P.; Graffi, S. Quantum Harmonic Oscillator: a Relativistic and Statistical Point of View. Boll.U.M.I. 1997, Ser.VII , XI-A, 815–839. [Google Scholar]
Chacón-Acosta, G.; Dagdug Hugo, L.; Morales-Técotl, A. Manifestly covariant Jüttner distribution and equipartition theorem. Phys. Rev. E 2010, 81, 021126. [Google Scholar] [CrossRef] [PubMed]
Curado, E. M. F.; Cedeño, C. E.; Soares, I. D.; Tsallis, C. Relativistic gas: Lorentz-invariant distribution for the velocities. Chaos 2022, 32, 103110. [Google Scholar] [CrossRef] [PubMed]
Landau, L. D.; Lifshitz, E. M. The Classical Theory of Fields. Vol. 2 (4th ed.). Butterworth-Heinemann, 1980.
Magnus, W. Formulas and Theorems for the Special Functions of Mathematical Physics. 3rd edition, Springer-Verlag, Berlin and Heidelberg, 1966.
Bros, J.; Gazeau, J.-P.; Moschella, U. ; Quantum Field Theory in the de Sitter Universe. Phys. Rev. Lett. 1994, 73, 1746–1749. [Google Scholar] [CrossRef] [PubMed]
Garidi, T. What is mass in desitterian physics?. arXiv:hep-th/0309104 (hep-th).
Enayati, M.; Gazeau, J.-P.; Pejhan, H.; Wang, A. The de Sitter (dS) Group and its Representations, An Introduction to Elementary Systems and Modeling the Dark Energy Universe. Synthesis Lectures on Mathematics & Statistics (SLMS), Springer 2022.
Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics-an overview after 20 years. Braz. J. Phys 2009, 39, 337–356. [Google Scholar] [CrossRef]
Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions With Formulas, Graphs, and Mathematical Tables. Handbook of mathematical functions National Bureau of Standards (1964).

Figure 1.

\underset{̲}{n}

is a time-like unit vector,

Δ

is a straight line passing through the origin and orthogonal (in the Minkowskian metric sense) to

\underset{̲}{n}

. The 4-momentum

\underset{̲}{k} = (k^{μ}) = (k^{0}, k)

points toward a point A of the mass shell hyperboloid

V_{m}^{+} = {\underset{̲}{k}, \underset{̲}{k} \cdot \underset{̲}{k} = m^{2} c^{2}}

d Ω

is the length of the projection, along

\underset{̲}{n}

, of an infinitesimal hyperbolic interval at A of length

d σ = m c d ω

Figure 1.

\underset{̲}{n}

is a time-like unit vector,

Δ

is a straight line passing through the origin and orthogonal (in the Minkowskian metric sense) to

\underset{̲}{n}

. The 4-momentum

\underset{̲}{k} = (k^{μ}) = (k^{0}, k)

points toward a point A of the mass shell hyperboloid

V_{m}^{+} = {\underset{̲}{k}, \underset{̲}{k} \cdot \underset{̲}{k} = m^{2} c^{2}}

d Ω

is the length of the projection, along

\underset{̲}{n}

, of an infinitesimal hyperbolic interval at A of length

d σ = m c d ω

Figure 2.

C

is the portion of the null cone starting at the event

M = (x^{0}, x)

and limited by the infinitesimal space-like segment

d Σ

orthogonal to the time-like unit vector

\underset{̲}{n}

R

is the region delimited by M, the portion of the light cone

C

, and

d Σ

Figure 2.

C

is the portion of the null cone starting at the event

M = (x^{0}, x)

and limited by the infinitesimal space-like segment

d Σ

orthogonal to the time-like unit vector

\underset{̲}{n}

R

is the region delimited by M, the portion of the light cone

C

, and

d Σ

Figure 3. The de Sitter space-time as viewed as a one-sheet hyperboloid embedded in Minkowski space

M_{1, 4}

Figure 3. The de Sitter space-time as viewed as a one-sheet hyperboloid embedded in Minkowski space

M_{1, 4}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Tsallis Distribution as a Λ-Deformation of the Maxwell-Jüttner Distribution

Abstract

1. Preamble: Temperature, Heat, Entropy, that Obscure Objects of Desire

2. Relativistic Covariance of Temperature According to de Broglie (1948)

3. Maxwell-Jüttner Distribution

3.1. Inverse Temperature 4-Vector

4. deSitter Material

4.1. de Sitter Geometry

4.2. Flat Minkowskian Limit of de Sitter Geometry

4.3. de Sitter plane waves as binomial deformations of Minkowskian plane waves

4.4. Analytic Extension of dS Plane Waves for dS QFT

4.5. KMS Interpretation of W ν ( z , z ′ ) Analyticity

5. de Sitterian Tsallis Distribution

5.1. Tsallis Entropy and Distribution, a Short Reminder

5.2. Coldness in de Sitter

5.3. A de Sitterian Tsallis Distribution

6. Conclusions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.5. KMS Interpretation of $W_{ν} (z, z^{'})$ Analyticity