Preprint

Article

The Basic k-ϵ Model and a New Fundamentally Based Model of Anisotropic Inhomogeneous Turbulence Compared with DNS of Channel Flow at High Reynolds Number

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

J.J.H. Brouwers^*

This version is not peer-reviewed

Submitted:

02 March 2024

Posted:

04 March 2024

You are already at the latest version

Alerts

Abstract

Predictions of mean values of statistical variables of large scale turbulent flow by the widely used basic k-ϵ model and a new fundamentally based model are verified against published results of Direct Numerical Simulations DNS of the Navier-Stokes equations. The verification concerns turbulent channel flow at shear Reynolds numbers of 950, 2000 and 104. The basic k-ϵ model is largely based on empirical formulations accompanied by calibration constants. This contrasts with the new model where descriptions of leading statistical quantities are based on the general principles of statistical turbulence at large Reynolds number. Predicted values of major output variables such as turbulent viscosity, diffusivity of passive admixture, temperature, and fluid velocities compare well with DNS in case of the new model. Significant differences are seen in case of the basic k-ϵ model.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

The description of turbulence has been an issue right from the beginning. A solid starting point for analysis are the Navier-Stokes equations which describe the flow. These can be time averaged resulting in equations for mean values of velocity, pressure and temperature. Problem are the average values of the products of the fluctuating quantities in the non-linear convection terms in the equations. They describe the effect of fluctuations on mean flow quantities. Proposed representations of average nonlinear convective fluctuations have been of a hypothetical nature by drawing analogies with molecular chaos. Boussinesq [1] was the first to follow this line of thinking by introducing the gradient hypothesis: the averaged nonlinear fluxes are proportional to the derivative of the mean flow quantity proceeded by a constant termed turbulent viscosity or turbulent diffusion coefficient. Several versions and extensions based on the same idea have since then been put forward by the pioneers of turbulence theory: Taylor [2], Prandtl [3], and Von Karman [4] among others. They form also the basis of many of today’s computer models used in engineering and environmental analysis: Hanjalic and Launder [5], Bernard and Wallace [6].

An offspring of the afore mentioned concept is the basic k-

ϵ

model widely used in engineering and environmental analysis [5,6]. The average value of momentum fluxes is described by the gradient of the mean velocity. Fluctuations are isotropic and the coefficient proceeding the gradient equals

c_{μ} \frac{k^{2}}{ϵ}

where k is mean kinetic energy of fluctuations,

ϵ

is mean energy dissipation rate and

c_{μ}

is a calibration constant. The model is completed by equations for k and

ϵ

. The gradient hypothesis is also applied to several other flux terms in the equations with different values of the calibration constants.

Problem with the gradient based models is their hypothetical origin and lack of uniqueness. Starting from a sketchy analogy with laminar diffusion almost limitless forms of gradient representations and proceeding functional dependencies can be devised. A new development which surpasses these limitations is the statistical description of anisotropic inhomogeneous turbulence: Brouwers [7,8,9]. Turbulence at high Reynolds number is featured by unstable eddies of whirling irregular fluid velocities whose behaviour is governed by domination of the inertial forces in the momentum balance: Monin and Yaglom, Vol. II, Ch.8 [10]. The eddies start at sizes of the configuration and break down to ever smaller ones until the point where viscous forces become into play at sizes of a few millimeter. Here the theory of small viscous scales of Kolmogorov comes into play [10]. Building on this framework of high Reynolds turbulence and using the methods of stochastic theory of Van Kampen [11] and Stratonovich [12] explicit statistical descriptions of governing variables are obtained. They are the leading terms of asymptotic expansions based on small value of the inverse of the universal Lagrangian Kolmogorov constant. Results represent unique descriptions of turbulent flow statistics up to deviations due to truncated higher order terms.

An opportunity for testing the outcome of the turbulence models is provided by the results of Direct Numerical Simulation DNS of the Navier-Stokes equations. With the evolution of modern computer power it has become possible to generate a wealth of accurate data on turbulent flow at high Reynolds number. Most interestingly are the recent DNS data of turbulent channel flow of Hoyas et all [13,14] and Kuerten et all [15]. Fluctuating channel velocities are strongly fundamentally based and averages of flow quantities vary strongly with distance from the wall. Inhomogeneity and anisotropy are the characteristics of turbulence in practice. The DNS data thus provide a meaningful test case for models. In this paper a detailed comparison is presented of the DNS data with the predictions of the basic k-

ϵ

model and the new fundamentally based model, also referred to as fundamental model.

2. The Basic k- $ϵ$ Model and the New Fundamental Model

Considered is turbulent flow of an incompressible fluid or an almost incompressible fluid, e.g. a liquid or a gas flowing at speeds where the square of the Mach number is small. The density

ρ

is taken constant. Turbulent fluctuations measured at a fixed point in space are treated as a statistical process which is stationary or almost stationary in time compared to the time of velocity fluctuations. Statistical averages follow from time averaging over sufficiently long time intervals. The time averaged representation of the Navier-Stokes equations is given by

Conservation of mass:

\frac{\partial u_{i}}{\partial x_{i}} = 0

(1)

Conservation of momentum:

\frac{\partial u_{i}}{\partial t} + u_{j} \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial < u_{i}^{'} u_{j}^{'} >}{\partial x_{j}} = - \frac{\partial p}{\partial x_{i}}

(2)

Conservation of energy:

\frac{\partial θ}{\partial t} + u_{j} \frac{\partial θ}{\partial x_{j}} + \frac{\partial < u_{j}^{'} θ^{'} >}{\partial x_{j}} = 0

(3)

where angled brackets represent statistical averaging, t and x are time and space coordinate, u, p, and

θ

are mean or time-averaged values of fluid velocity, pressure, and temperature and

u'

and

θ'

represent fluctuations of velocity and temperature, that is velocity and temperature minus their mean value. As we are concerned with flow at high Reynolds number the contributions of the viscous forces and heat conductivity present in the Navier-Stokes equations have been dropped. Their effect can be disregarded when considering the main flow governed by instability of inviscid flow outside small boundary layers The average temperature in energy equation (3) can also be used to describe the average distribution of passive or almost passive admixture in the fluid. Restricting the formulation of the conservation equations to an incompressible or almost incompressible fluid implies that the solution of (1) and (2) is not affected by the value of the conservative scalar temperature. The representation holds as long as the changes in temperature or admixture imposed at external boundary conditions are of limited magnitude.

2.1. Turbulent Diffusion in the Basic k- $ϵ$ Model

The appearance of turbulent fluxes in the convection terms of the averaged conservation equations results in an unclosed set of equations for mean flow variables. It is known as the closure problem. To resolve this issue a diffusion hypothesis has been introduced in the basic k-

ϵ

model. In this hypothesis turbulent fluxes are treated as isotropic and are described by [5,6].

< u_{j}^{'} u_{i}^{'} > = \frac{2}{3} k δ_{i j} - ν_{t} (\frac{\partial u_{j}}{\partial x_{i}} + \frac{\partial u_{i}}{\partial x_{j}})

(4)

< u_{j}^{'} θ^{'} > = - ν_{t} \frac{\partial θ}{\partial x_{j}}

(5)

where

ν_{t}

is a scalar which represents diffusivity or turbulent viscosity and which is defined by

ν_{t} = c_{μ} \frac{k^{2}}{ϵ}

(6)

and where k is average kinetic energy of fluctuations,

k = \frac{1}{2} < {u_{i}^{'}}^{2} >

and

ϵ = \frac{1}{2} ν < {(\frac{\partial u_{i}^{'}}{\partial x_{j}} + \frac{\partial u_{j}^{'}}{\partial x_{i}})}^{2} >

is average energy dissipation rate with

ν

being kinematic viscosity;

c_{μ}

in (4) and (5) is a calibration constant whose value is usually taken as

0.09

[5,6]. In Equation (5) correction factors are sometimes added to the diffusion constant, i.e. a turbulent Prandtl number and a turbulent Schmidt number in case of temperature and admixture respectively. But these numbers are generally close to unity and are omitted here.

2.2. Turbulent Diffusion in the Fundamentally Based Model

The derivation of the fundamental model starts from a Langevin equation for fluid particle velocity [8,9,10]. In this equation the limiting form of Kolmogorov’s theory of small scales is implemented, i.e. the limiting form of this theory when times characteristic for the velocity fluctuations are much larger than the time of the viscous scales. This is the case when the Reynolds number is large: Kolmogorov [16]. A further step is an expansion in terms of the inverse of the Kolmogorov constant

C_{0}

. Matching predictions with data of measurements and DNS reveals values of

C_{0}

around

6 - 7

; in the present analysis a value of 7 is adopted. Furthermore the area where the Lagrangian description applies can be reduced to a point in the Eulerian flow description in the limit of small

{C_{0}}^{- 1}

. In this way Lagrangian based descriptions are connected to Eulerian ones. The following descriptions for the flux terms are obtained [8,9]

< u_{j}^{'} u_{i}^{'} > = \frac{2}{3} (k + D_{n k} \frac{\partial u_{n}}{\partial x_{k}}) δ_{i j} - D_{i k} \frac{\partial u_{j}}{\partial x_{k}} - D_{j k} \frac{\partial u_{i}}{\partial x_{k}}

(7)

< u_{j}^{'} θ^{'} > = - D_{i k} \frac{\partial θ}{\partial x_{k}}

(8)

where the fundamentally based diffusion tensor

D_{i j}

is described by

D_{i J} = 2 C_{0}^{- 1} ϵ^{- 1} σ_{i n} σ_{n j} + 2 C_{0}^{- 2} ϵ^{- 2} σ_{l i} σ_{j k} u_{n} \frac{\partial σ_{l k}}{\partial x_{n}} - 4 C_{0}^{- 2} ϵ^{- 1} σ_{k j} u_{n} \frac{\partial}{\partial x_{n}} (ϵ^{- 1} σ_{i m} σ_{m k})

(9)

and

σ_{i n} = < u_{i}^{'} u_{n}^{'} >

(10)

is co-variance or Reynolds stress. Relations (8) - (10) are part of the description which holds in the entire flow configuration (except from the thin viscous layers at walls) once they are coupled to conservation equations (1) - (3). In this way change of turbulent flux at each point x as described by (7) and (8) is connected to change in kinetic energy and energy dissipation. Although the presence of

ν

in the expression for energy dissipation

ϵ = \frac{1}{2} ν < {(\frac{\partial u_{i}'}{\partial x_{j}} + \frac{\partial u_{j}'}{\partial x_{i}})}^{2} >

may suggest otherwise,

ϵ

is a characteristic of the main inviscid flow outside the boundary layers [10]. The magnitude of gradients of velocity is governed by the small viscous scales of turbulence. It scales as

1 / \sqrt{ν}

and makes the magnitude of

ϵ

independent of

ν

. This independency is reflected in the equations for k and

ϵ

presented in the next section.

The above expressions for diffusion of the fundamental model reveal dependency on mean gradients which are of a more complex structure than those of the basic k-

ϵ

model. It reflects the anisotropy of the fluctuating velocity field and reveals a more complex dependency of flow statistics.

Application of the fundamentally based diffusion approximation to a scalar as done in Equation (8) is only justified if the scalar is a conservative scalar [8,9]. The value of the conservative scalar is constant when following a fluid particle and fluctuates in value in a fixed coordinate system only due to fluctuations of the fluid particle. This is the case for temperature in an incompressible fluid such as liquids. It is approximately correct if the fluid is almost incompressible as is the case in gases flowing at speeds where the square of the Mach number is small. The scalar representation can also be applied to passive or almost passive admixture in fluids such as aerosols in air [7,8,9]. It leads to errors when applied to non-conservative scalars such as kinetic energy and pressure: see section 5.

3. Equations for k and $ϵ$

Implementing the expressions for turbulent diffusion of the basic k-

ϵ

model and the fundamental model in the averaged conservation equations introduces two unknowns: the mean kinetic energy k and the mean energy dissipation rate

ϵ

. Equations for k and

ϵ

can be obtained from the Navier-Stokes equations [8,9]. Our aim is to describe the flow away from thin viscous controlled layers near walls being in size a few millimeters only. In line with this approach the contributions in the equations for k and

ϵ

from laminar viscosity will be disregarded ( just as we did in conservation equations (1), (2) and (3)). To provide boundary conditions at the wall the viscous layer is surpassed by applying the solutions of the log layer at

x = 0

: [5,6].

The equation for k reads as [5,6]

\frac{\partial k}{\partial t} + u_{i} \frac{\partial k}{\partial x_{i}} + \frac{\partial < u_{i}^{'} k^{'} >}{\partial x_{i}} + ρ^{- 1} \frac{\partial < u_{i}^{'} p^{'} >}{\partial x_{i}} = P - ϵ

(11)

where P is mean production of turbulent fluctuations defined by

P = σ_{i j} \frac{\partial u_{i}}{\partial x_{j}}

(12)

and where

k^{'}

and

p^{'}

are the fluctuating parts of kinetic energy and pressure, respectively, that is the kinetic energy and dissipation rates minus their time-averaged values. There are two turbulent flux terms in Equation (11), i. e. the third and fourth term on the LHS of (11), which need to be modelled. In the basic k-

ϵ

model both terms are lumped together [5,6] and are described by:

Basic k-ϵ model

< u_{i}^{'} k^{'} > + ρ^{- 1} < u_{i}^{'} p^{'} > = - \frac{ν_{t}}{σ_{k}} \frac{\partial k}{\partial x_{i}}

(13)

where

σ_{k}

is a calibration constant which is usually taken unity:

σ_{k} = 1

[5,6].

Fundamental model

The theory underlying the fundamental model provides general expressions for turbulent scalar fluxes which are free from calibration factors. However, these expressions are only valid for conservative scalars and lead to disagreement with DNS results when applied to turbulent fluxes of kinetic energy and pressure [8]. A fall back to empirical construction is needed. It reads as

< u_{i}^{'} k^{'} > + ρ^{- 1} < u_{i}^{'} p^{'} > = - c_{k} D_{i j} \frac{\partial k}{\partial x_{j}}

(14)

where it is noted that if k were a conserved scalar its diffusion should be described by

D_{i j} \frac{\partial k}{\partial x_{j}}

. The factor

c_{k}

represents correction for non-conservative behaviour and includes the relative small contribution [8] of pressure diffusion. The above relations for diffusion of kinetic energy and pressure will be compared and calibrated with DNS results in Section 5.

The equation for

ϵ

conventionally applied in CFD models [5,6] is largely an empirical construction. Its basic k-

ϵ

form follows from the Navier-Stokes equations. It contains a number of terms which are governed by the small viscous scales. These terms are generally replaced by expressions which meet the criteria of matching to the results of decaying grid turbulence and the log layer of turbulent channel flow. The equation reads as

Basic k-ϵ model

\frac{\partial ϵ}{\partial t} + \frac{\partial u_{i} ϵ}{\partial x_{i}} = \frac{\partial}{\partial x_{i}} (\frac{ν_{t}}{σ_{ϵ}} \frac{\partial ϵ}{\partial x_{i}}) + (c_{ϵ 1} P - c_{ϵ 2} ϵ) \frac{ϵ}{k}

(15)

Fundamental model

\frac{\partial ϵ}{\partial t} + \frac{\partial u_{i} ϵ}{\partial x_{i}} = \frac{\partial}{\partial x_{i}} (\frac{D_{i j}}{σ_{ϵ}^{*}} \frac{\partial ϵ}{\partial x_{j}}) + (c_{ϵ 1} P - c_{ϵ 2} ϵ) \frac{ϵ}{k}

(16)

The constant

c_{ϵ}

ensures matching with the case of grid turbulence. Its value is usually taken to be

1.9

which is somewhat less than the theoretical limit value of 2 for infinite Reynolds number: George [17]. The von Karman constant

κ

is equal to

0.4

. In case of the basic k-

ϵ

model the calibration constant

σ_{ϵ}

is usually taken to be around

1.3

and

c_{ϵ 1}

is specified by the equation (eq. (8.41) of [16])

\frac{\sqrt{c_{μ}} σ_{ϵ}}{κ^{2}} (c_{ϵ 2} - c_{ϵ 1}) = 1

(17)

The values appropriate for

c_{ϵ 1}

and

σ_{ϵ}^{*}

in case of the fundamental model are determined in section 6.

4. Channel Flow

Objective is to compare the results of the basic k-

ϵ

model and the fundamental model with those of DNS of channel flow. The channel consists of parallel planes in between which the mean velocity

u_{1}

is unidirectional in the direction

x_{1}

parallel to the planes. Its magnitude and the value of statistical averages related to velocity fluctuations only change in the direction

x_{2}

normal to the planes. For channel flow there is an exact solution for the mean pressure [9] which reads as

\frac{p}{ρ} = - u_{τ}^{2} \frac{x_{1}}{H} - σ_{22}

(18)

where

u_{τ}

is shear velocity and

2 H

is channel height. The shear velocity is determined by the pressure drop in direction

x_{1}

at given

u_{1}

. There are theoretical and experimentally confirmed relations for the relationship determining

u_{τ}

. Another exact result for channel flow is the description of the co-variance

σ_{12}

< u_{1}^{'} u_{2}^{'} >

σ_{12} = - u_{τ}^{2} (1 - \frac{x_{2}}{H})

(19)

which is valid outside the thin viscous layer at the wall [9].

In the subsequent analysis of channel flow we shall make use of dimensionless formulations:

u_{i}

is made dimensionless by

u_{τ}

σ_{i j}

and

\frac{p}{ρ}

u_{τ}^{2}

x_{1}

and

x_{2}

by H, P and

ϵ

\frac{u_{τ}^{3}}{H}

; the subscript₂ of

x_{2}

will be dropped. In this new notation Equations (18) and (19) become

\frac{p}{ρ} = - x_{1} - σ_{22}

(20)

which is valid outside the thin viscous layer at the wall.

σ_{12} = - (1 - x)

(21)

Furthermore Equation (12) becomes

P = (1 - x) \frac{d u_{1}}{d x}

(22)

The above solutions follow from the averaged momentum equations adopted to the case of channel flow [9]. A complete specification of all variables follows from the expressions for turbulent fluxes and the equations for k and

ϵ

. In case of channel flow these reduce to:

Basic k-ϵ model

\begin{matrix} σ_{11} = σ_{22} = σ_{33} & = \frac{2}{3} k \end{matrix}

(23a)

\begin{matrix} σ_{12} & = - ν_{t} \frac{d u_{1}}{d x} \end{matrix}

(23b)

\begin{matrix} < θ^{'} u_{2}^{'} > & = - ν_{t} \frac{d θ}{d x} \end{matrix}

(23c)

\begin{matrix} ν_{t} & = c_{μ} \frac{k^{2}}{ϵ} \end{matrix}

(23d)

\begin{matrix} \frac{d}{d x} (\frac{ν_{t}}{σ_{k}} \frac{d k}{d x}) + P - ϵ & = 0 \end{matrix}

(23e)

\begin{matrix} \frac{d}{d x} (\frac{ν_{t}}{σ_{ϵ}} \frac{d ϵ}{d x}) + (c_{ϵ 1} P - c_{ϵ 2} ϵ) \frac{ϵ}{k} & = 0 \end{matrix}

(23f)

Fundamental model:

\begin{matrix} σ_{22} & = \frac{2}{3} (k + D_{12} \frac{d u_{1}}{d x}) \end{matrix}

(24a)

\begin{matrix} σ_{33} & = σ_{22} \end{matrix}

(24b)

\begin{matrix} σ_{11} & = \frac{2}{3} (k - 2 D_{12} \frac{d u_{1}}{d x}) \end{matrix}

(24c)

\begin{matrix} σ_{12} & = - D_{22} \frac{d u_{1}}{d x} \end{matrix}

(24d)

\begin{matrix} < θ^{'} u_{2}^{'} > & = - D_{22} \frac{d θ}{d x} \end{matrix}

(24e)

\begin{matrix} D_{12} & = \frac{2}{ϵ C_{0}} σ_{12} (σ_{11} + σ_{22}) \end{matrix}

(24f)

\begin{matrix} D_{22} & = \frac{2}{ϵ C_{0}} (σ_{12}^{2} + σ_{22}^{2}) \end{matrix}

(24g)

\begin{matrix} c_{k} \frac{d}{d x} (D_{22} \frac{d k}{d x}) + P - ϵ & = 0 \end{matrix}

(24h)

\begin{matrix} \frac{1}{σ_{ϵ}^{*}} \frac{d}{d x} (D_{22} \frac{d ϵ}{d x}) + (c_{ϵ 1} P - c_{ϵ 2} ϵ) \frac{ϵ}{k} & = 0 \end{matrix}

(24i)

In the subsequent sections we shall compare the above descriptions with results of DNS.

5. Testing the Diffusion Representations by DNS

In the derivation of equations for the mean values of flow quantities use has been made of the diffusion representation of mean fluxes, i.e. the mean value of products of fluctuating quantities. Their correctness and accuracy will be assessed by comparison with DNS results published for friction Reynolds numbers

R e_{τ} = u_{τ} \frac{H}{ν}

of 950 [15], 2000 [13] and

10^{4}

[14]. The comparison is focussed on the flow in the main region, the region outside the thin boundary layer at the wall. In the main region flow statistics are governed by unstable large eddies governed by inertia forces while the effect of viscosity in this region is negligibly small. The presented basic k-

ϵ

and fundamental model intend to describe these statistics. The boundary layer is governed by viscous forces and is situated in the region

x < \frac{100}{R e_{τ}}

, that is,

x < 0.1, 0.05

and

0.01

for

R e_{τ} = 950, 2000,

and

10^{4}

respectively. The DNS results of the boundary layer near

x = 0

are omitted in this analysis.

5.1. Diffusion of Momentum

In case of channel flow turbulent momentum transport is apparent in the equation

< u_{1}^{'} u_{2}^{'} > = - v_{D N S} \frac{d u_{1}}{d x}

(25)

where

ν_{D N S}

is turbulent viscosity according to the DNS results, that is the value calculated from eq. (25) when substituting the values of

< u_{2}^{'} u_{1}^{'} >

and

\frac{d}{d x} u_{1}

obtained from DNS data. The value according to the basic k-

ϵ

model

ν_{t}

is given by Equation (6) and that according to the fundamental model

D_{22}

by Equation (24g) whereby the RHS’s of these equations are evaluated from the DNS data. The DNS data which were used are those of

R e_{τ} = 10^{4}

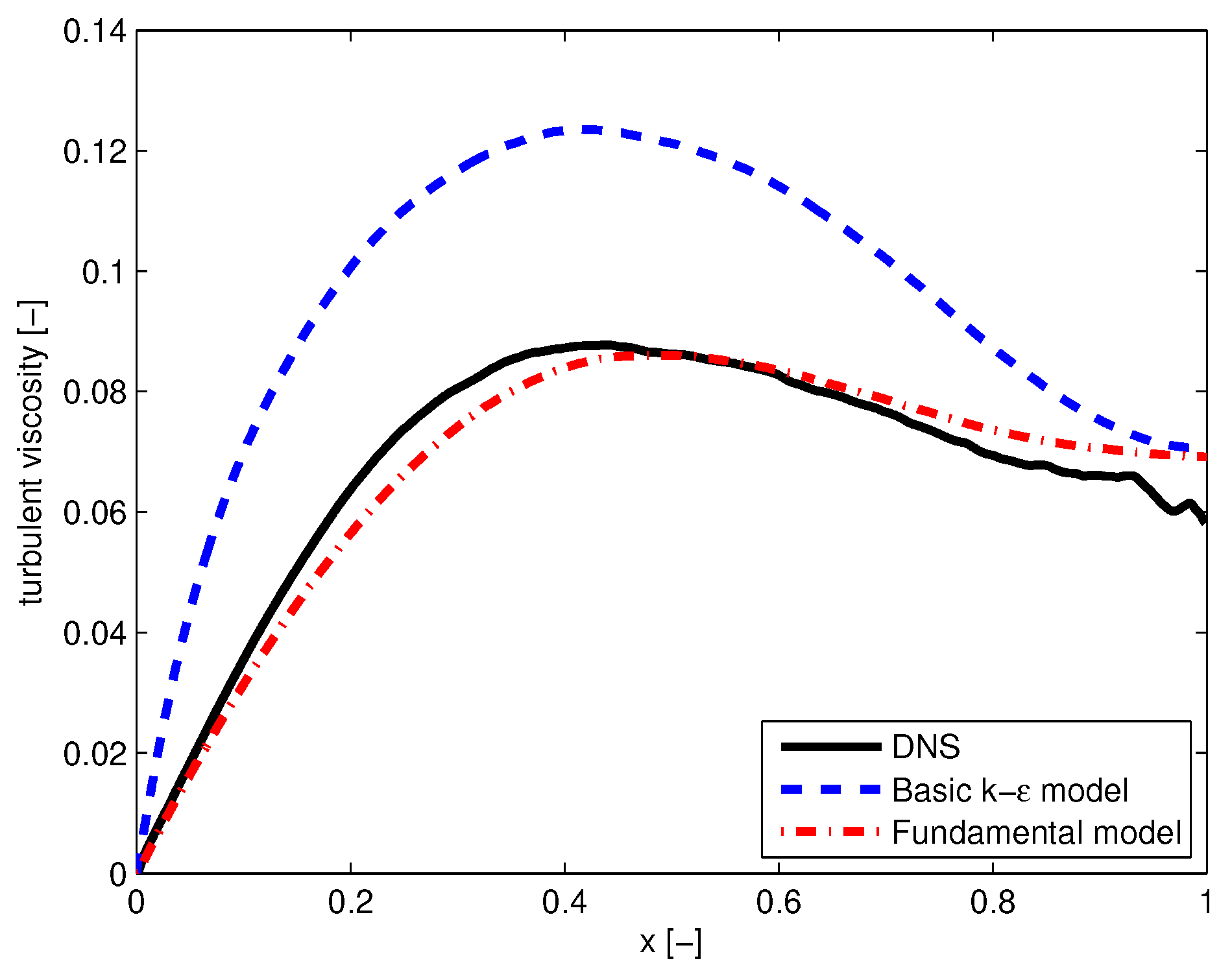
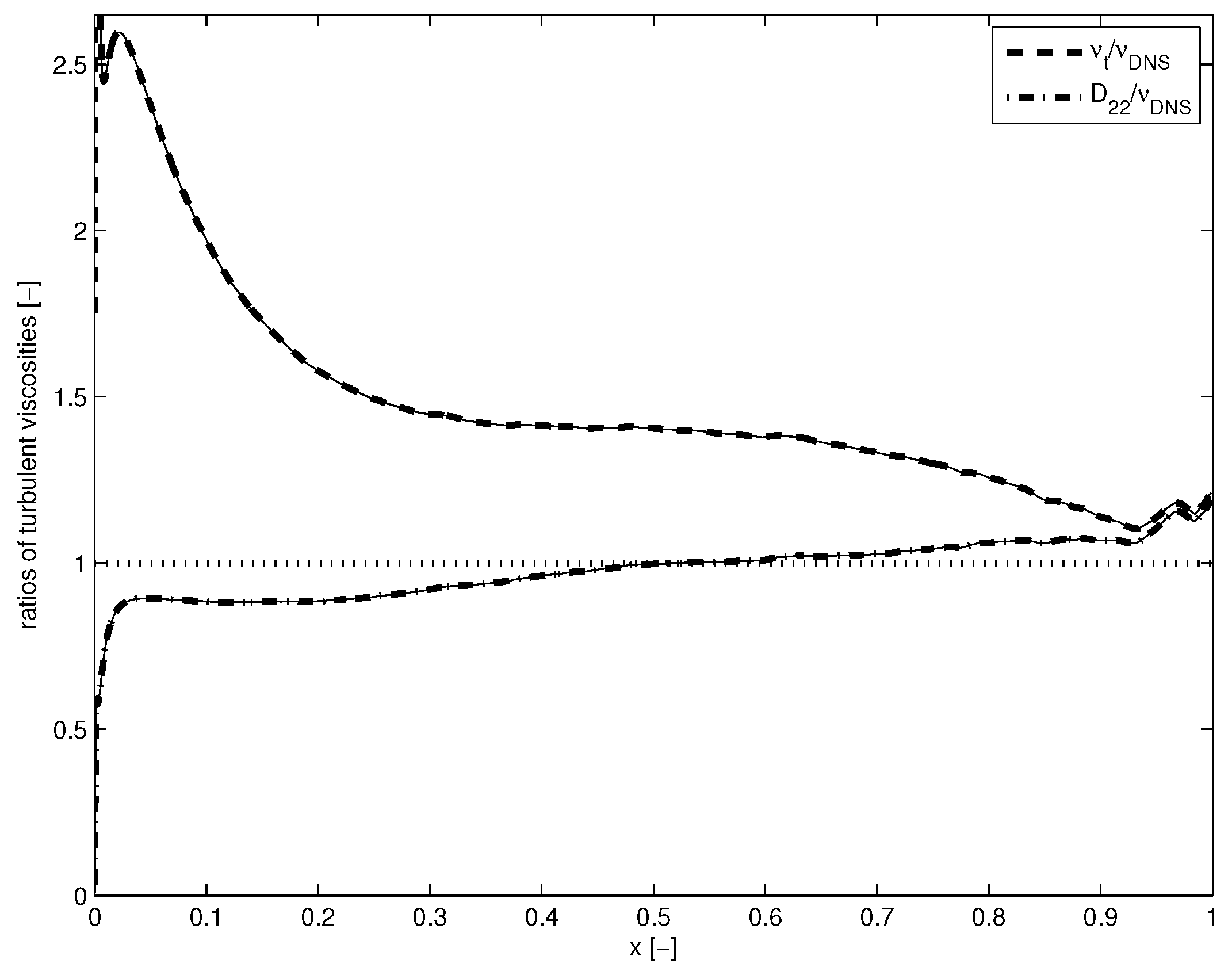
[14]. The three turbulent viscosities thus calculated have been shown as a function of x in Figure 1. The ratios

\frac{ν_{t}}{ν_{D N S}}

and

\frac{D_{22}}{ν_{D N S}}

versus x have been shown in Figure 2. Disregarding the thin viscous layer at the wall, the fundamental model gives satisfactory agreement over the entire x range without the use of calibration factors. Deviations are less than

10 %

from the DNS results. They can be ascribed to truncation of the higher order terms in the expansions in powers of

C_{0}^{- 1}

which were used in the theory leading to the presented expressions [8,9]. The same conclusion was arrived at when using the DNS data of

R e_{τ} = 2000

[9,13]. The basic k-

ϵ

model on the other hand disagrees quite a lot from DNS. The disagreement is largest at small x and gradually becomes smaller when approaching the central axis of the channel:

x = 1

. The dependency on x is apparently not well captured by representation (23d), in contrast with (24g) which shows satisfactory agreement over the entire range.

5.2. Diffusion of Temperature

Temperature is a conservative quantity in incompressible flow at high Reynolds number where heat conductivity by molecular vibration is negligibly small outside thin layers at the walls. From the theory underlying the fundamental model it follows that the thermal diffusion constant equals

D_{i k}

: cf. eq.(8). In case of channel flow it becomes

D_{22}

and becomes equal to that of turbulent viscosity: cf. Equations (24d)–(24e). This result is confirmed by Lagrangian based DNS of channel flow at

R e_{τ} = 950

[15] where the thermal diffusion coefficient according to DNS,

\frac{< u_{2}^{'} θ^{'} >}{\frac{d θ}{d x}}

is compared to that of the fundamentally based model

D_{22}

.The agreement closely resembles that shown in Figure 1 and Figure 2, c.q.,

\frac{< u_{2}^{'} u_{1}^{'} >}{\frac{d u_{1}}{d x}}

and

D_{22}

. Deviations of the predictions of the basic k-

ϵ

model are likely equally large as those shown in Figure 1 and Figure 2.

5.3. Diffusion of Kinetic Energy and Pressure

In the case of the basic k-

ϵ

model fluxes of kinetic energy and pressure are lumped together: Equation (13) For channel flow these become

< k^{'} u_{2}^{'} > + < p^{'} u_{2}^{'} > = - \frac{ν_{t}}{σ_{k}} \frac{d k}{d x}

(26)

From eq.(14) we have for the fundamental model

< k^{'} u_{2}^{'} > + < p^{'} u_{2}^{'} > = - c_{k} D_{22} \frac{d k}{d x}

(27)

The description is used in the numerical solution of the equation for k in Section 6.

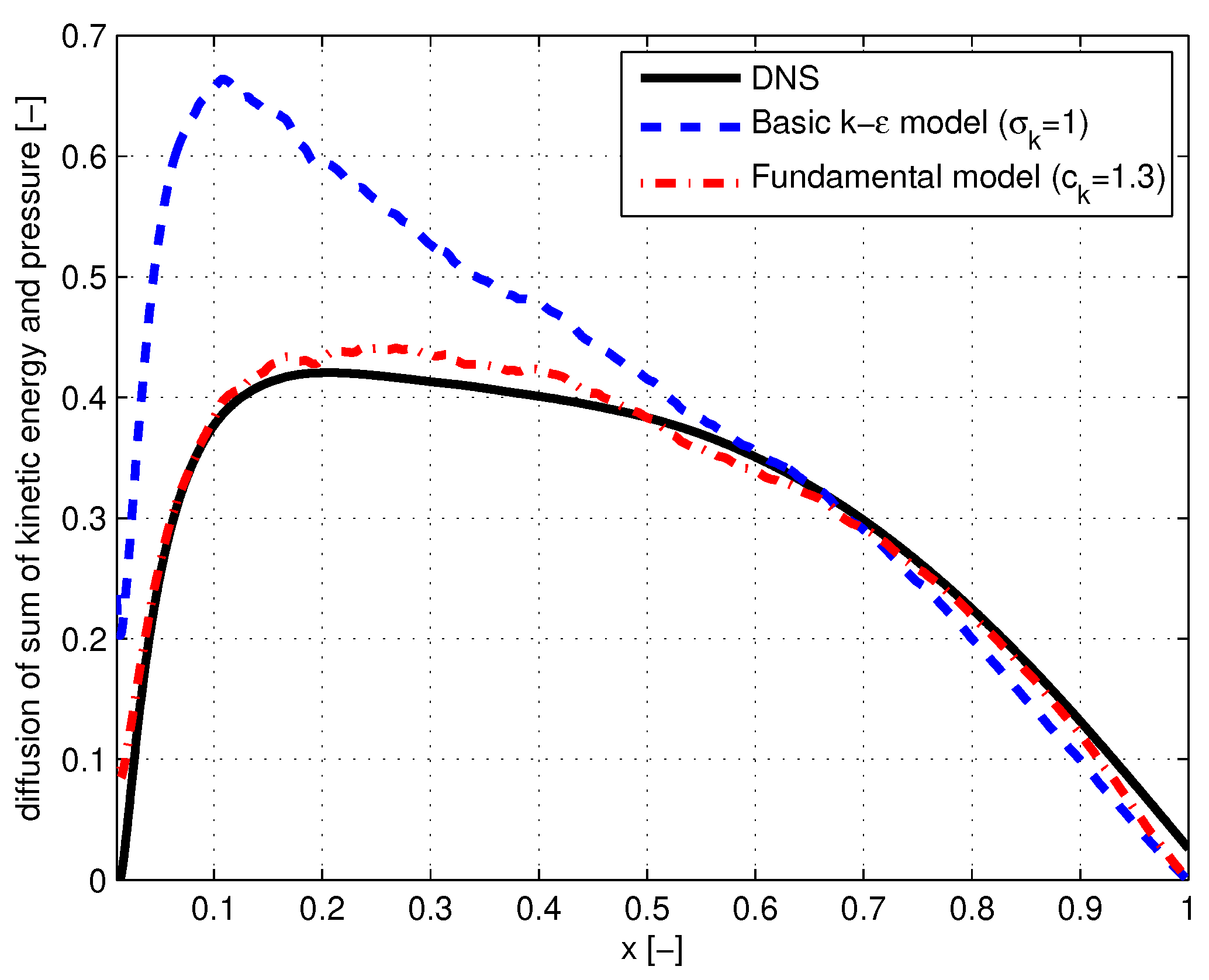
In Figure 3 we have shown the sum of both fluxes versus x when the RHS’s of (26) and (27) are evaluated by the DNS data. Values for the calibration constants

σ_{k}

and

c_{k}

of 1 and

1.3

were taken. Also is shown the value of the sums obtained by direct calculation of their values using DNS of

R e_{τ} = 10^{4}

. The empirical construction of Equation (27) based on the fundamental model gives surprisingly good agreement. The agreement extends over the entire x-range and is obtained with the calibration constant

c_{k} = 1.3

5.4. Diffusion of Energy Dissipation

DNS data do not provide information of average values of products of velocity fluctuations and dissipation fluctuations. Direct verification of the diffusion representation is thus not possible. Further, the differential equation for mean energy dissipation in both models is largely an empirical construction. What is still possible is to verify the values of quantities obtained from the solutions of the coupled differential equations for mean kinetic energy and mean energy dissipation with the DNS data. This is the subject of the next section.

6. Solutions of k and $ϵ$ Compared with DNS

In the previous section predictions of individual components of the models were verified by DNS. Further testing is executed by comparing numerically obtained solutions of the model equations as a whole with DNS.

6.1. Equations and Boundary Conditions

Model equations are given by coupled differential equations for mean kinetic energy and mean energy dissipation. For mean energy dissipation the variable G is introduced which is defined by

G = κ ϵ x

(28)

Near the wall outside the viscous layer solutions should comply with the solutions of the log layer. Inertial subrange asymptotics [18] reveal that production P and dissipation

ϵ

are equal in this region:

P = ϵ

. Furthermore,

κ \frac{d u_{1}}{d x} = 1

so that

G = 1

. DNS results show values of G in the log layer which are between

0.9

and 1 [13,14]. In the present analysis the theoretical value of 1 is taken. Making use of relations (21), (23b), (23d) and (28) differential equations (23e) and (23f) can be transformed into the following coupled equations for k and G appropriate for the basic k-

ϵ

model.

Basic k-ϵ model equations:

\frac{κ^{2}}{σ_{k}} \frac{x}{G} \frac{d}{d x} (\frac{A x}{G} \frac{d k}{d x}) + \frac{{(1 - x)}^{2}}{A} - 1 = 0

(29)

\frac{κ^{2}}{σ_{ϵ}} \frac{x^{2}}{G^{2}} \frac{d}{d x} (\frac{A x}{G} \frac{d}{d x} (\frac{G}{x})) + \frac{1}{k} (\frac{c_{ϵ 1} {(1 - x)}^{2}}{A} - c_{ϵ 2}) = 0

(30)

where

A = c_{μ} k^{2}

(31)

where values of the empirical constants will be taken in agreement with [5,6]:

κ = 0.4

c_{μ} = 0.09

σ_{k} = 1

σ_{ϵ} = 1.3

c_{ϵ 1} = 1.49

c_{ϵ 2} = 1.9

. The boundary conditions are

x = 0; k = \frac{1}{\sqrt{c_{μ}}}; G = 1

(32)

x = 1; \frac{d k}{d x} = 0; \frac{d G}{d x} = G

(33)

The boundary condition for k at

x = 0

follows from relations (21) (23b) and (23d) noting that

ϵ = \frac{d u_{1}}{d x}

in the log layer. The boundary condition for G at

x = 1

corresponds to zero slope of

ϵ

x = 1

The equations appropriate for the fundamental model follow from (24h) and (24i) upon using (28), (21), (24a)–(24g).

Fundamental model equations:

\frac{c_{k} κ^{2} x}{G} \frac{d}{d x} (B \frac{x}{G} \frac{d k}{d x}) + \frac{{(1 - x)}^{2}}{B} - 1 = 0

(34)

\frac{κ^{2} x^{2} k}{G^{2} σ_{ϵ}^{*}} \frac{d}{d x} (B \frac{x}{G} \frac{d \frac{G}{x}}{d x}) + \frac{c_{ϵ 1} {(1 - x)}^{2}}{B} - c_{ϵ 2} = 0

(35)

and

B = \frac{2}{C_{0}} (σ_{12}^{2} + σ_{22}^{2}) = \frac{2}{C_{0}} ({(1 - x)}^{2} + σ_{22}^{2})

(36)

In these equations k and

σ_{22}

are related to each other by an algebraic relation which is obtained by systematic elimination of

ϵ^{- 1} \frac{d u_{1}}{d x}

σ_{12}

σ_{11}

σ_{33}

D_{12}

D_{22}

from Equations (21), (24a) and (24g)

k = σ_{22} \frac{3 σ_{22}^{2} + {(1 - x)}^{2}}{2 (σ_{22}^{2} - {(1 - x)}^{2})}

(37)

The relation can be used to eliminate

σ_{22}

from (34)–(35) resulting in two differential equations for k and G. However, analysis of the above relation for k shows that in an area close to

x = 0

according to (37)

σ_{22}

can have two values for one value of k. Verification of (37) using the results of DNS confirms the correctness of the equation and the double dependency in this area. The other way around is not the case: for each value of

σ_{22}

there is only one value of k possible. The easiest approach is then to substitute for k relation (37) into the two differential equations (34) and (35) and solve for

σ_{22}

and G. The value of k is subsequently obtained from (37). The boundary conditions are

x = 0; G = 1; σ_{22} = \sqrt{\frac{C_{0}}{2} - 1}

(38)

x = 1; \frac{d σ_{22}}{d x} = 0; \frac{d G}{d x} = G

(39)

where the boundary condition for

σ_{22}

x = 0

follows from Equations (21), (24d) and (24g) noting that

ϵ = \frac{d u_{1}}{d x}

in the log layer. As in the basic k-

ϵ

model

c_{ϵ 2} = 1.9

. A value of

c_{k}

1.3

was established in Section 5.3 (Figure 3). A value of

σ_{ϵ}^{*}

0.2

is found to lead to the best agreement with DNS.

The value of

c_{ϵ 1}

follows from Equation (35) by letting x approach

x = 0

. It yields the relation

c_{ϵ 1} = c_{ϵ 2} - \frac{k_{0} κ^{2}}{σ_{ϵ}^{*}}

(40)

which is analogous to eq.(17) in case of the basic k-

ϵ

model;

k_{0}

is the value of k at

x = 0

obtained from eq.(37). For

c_{ϵ 2} = 1.9

C_{0} = 7

σ_{ϵ}^{*} = 0.2

and

k_{0} = 4.48

c_{ϵ 1} = - 1.68

. This suggests negative production. However, for the first term on the LHS of eq.(35) one can write

x^{2} \frac{d}{d x} (B \frac{x}{G} \frac{d \frac{G}{x}}{d x}) = x^{2} \frac{d}{d x} (\frac{B}{G} \frac{d G}{d x}) - x \frac{d B}{d x} + B

(41)

where the last two terms have the same character as that of production and make the total of production-like-terms positive.

6.2. Numerical Solution

Numerical instability is encountered when solving Equations (29)-(30) and (34)-(35), a feature not uncommon for k-

ϵ

equations: Lew et all [19]. Way out is to convert the equations into a diffusion problem by adding the terms

\frac{d k}{d t}

and

\frac{d G}{d t}

on the RHS of (29)-(30),

\frac{d σ_{22}}{d t}

and

\frac{d G}{d t}

on the RHS of (34)-(35) and solving starting from a suitably chosen initial solution at

t = 0

: Borse [20]. After sufficient time the solution has converged to the desired stationary result.

Another difficulty encountered in the execution of the numerical calculations concerned the boundary condition for G at

x = 1

: cf. Equations (33) and (39). These were replaced by

(d / d x) G = 0

x = 1

. The effect of this simplification is limited to a small region near

x = 1

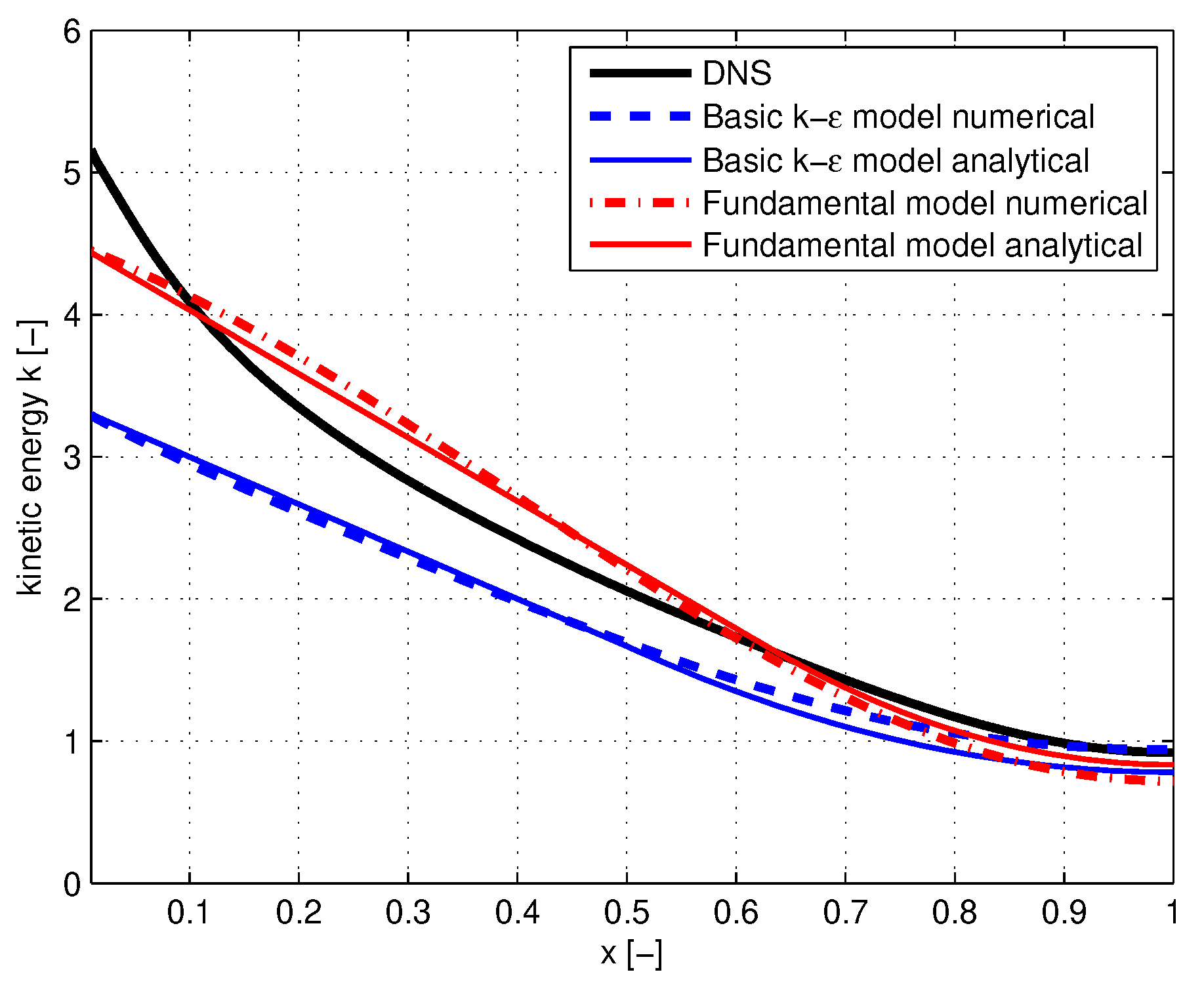
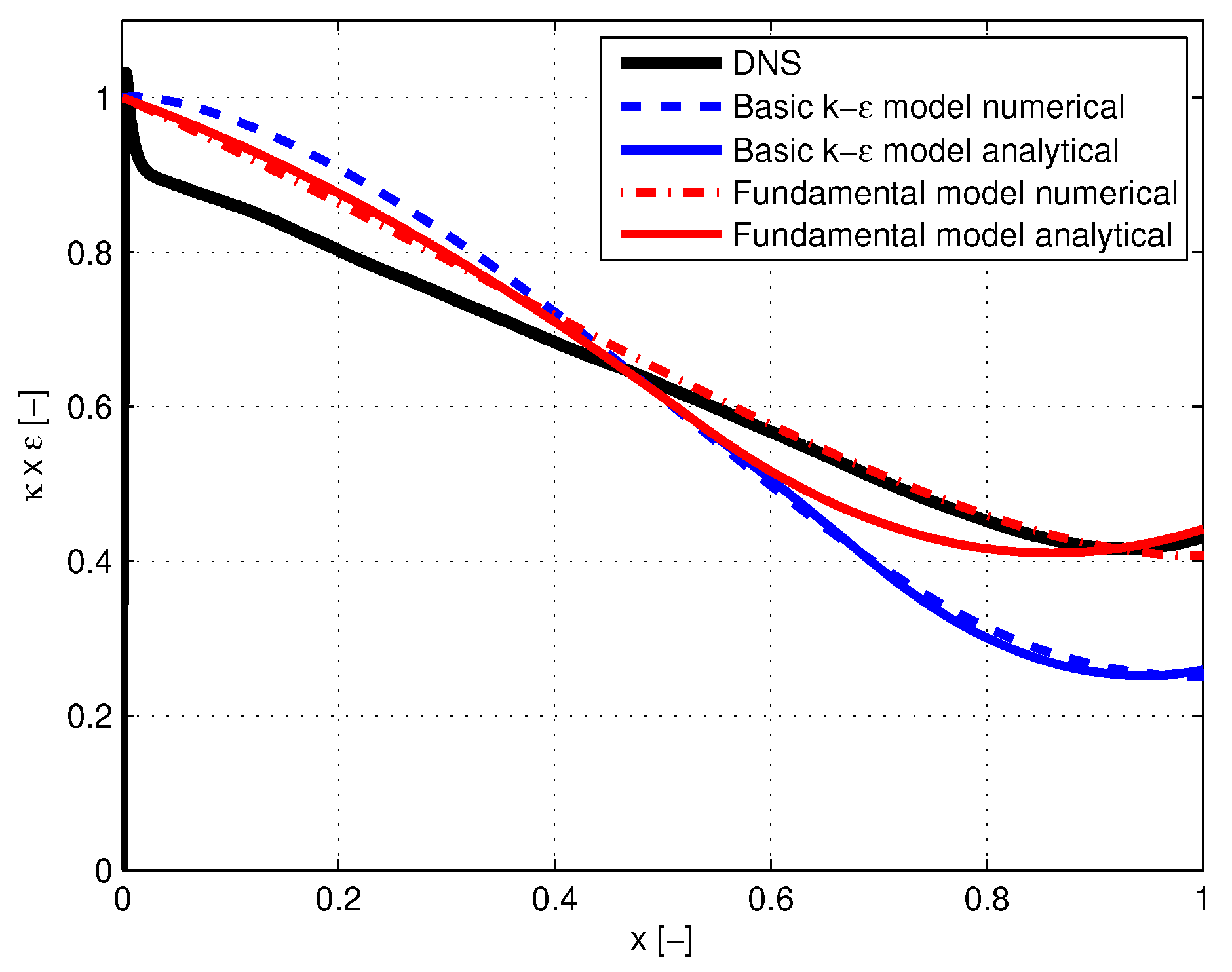
In Figure 4 and Figure 5 are respectively shown the distributions versus x of kinetic energy k and energy dissipation rate G according DNS, according the basic k-

ϵ

model calculated from Equations (29) - (30) and according to the fundamentally based model calculated from Equations (34) - (35).

6.3. Analytical Solution

Distinction is made between the area near the wall referred to as outer region and the area near the centre of the channel referred to as inner region. The outer region is the area where production and dissipation of energy are dominant. Turbulent diffusion of kinetic energy and pressure and turbulent diffusion of dissipation are negligibly small. It is the area where the log layer description for mean flow applies and where production equals dissipation [21]. In the inner region turbulent diffusion of kinetic energy and pressure and turbulent diffusion of dissipation are important and in balance with energy dissipation while production is negligibly small. For each of these regions analytical solutions can be derived which are subsequently matched to arrive at a complete solution.

6.3.1. Solutions for k and G in the Outer Region

Solutions valid in the outer region are obtained by retaining the second and third term in eqs.(28) and eqs.(33) yielding

A = {(1 - x)}^{2}

and

B = {(1 - x)}^{2}

or in terms of k and

σ_{22}

Basic k-ϵ model:

k = \frac{1}{\sqrt{c_{μ}}} (1 - x)

(42)

Fundamental model:

σ_{22} = \sqrt{(\frac{C_{0}}{2} - 1)} (1 - x)

(43)

Using the relation between k and

σ_{22}

x = 0

according to the fundamental model, cf. Equation (37), we have

Fundamental model:

k = k_{0} (1 - x)

(44)

where

k_{0}

is the value of k at

x = 0

k_{0} = \frac{1}{2} \sqrt{(\frac{C_{0}}{2} - 1)} (\frac{3 C_{0} - 4}{C_{0} - 4})

(45)

which amounts to

k_{0} = 4.48

for

C_{0} = 7

. To derive the equations for G applicable in the outer region the second and third term of Equation (41) need to be taken into account (and replacing B by A in Equation (41) in case of the basic k-

ϵ

model). Noting that in the outer region

A = {(1 - x)}^{2}

and

B = {(1 - x)}^{2}

one obtains for G from Equation (30) using relation (17) and from Equation (35) using relation (40) the result

Basic k-ϵ model and Fundamental model:

G = (1 - x) \sqrt{(1 + x)}

(46)

The above descriptions for k and G are rather simple, They compare well with the numerical results for values of x up to about

0.5

. At greater distances from the wall they start to deviate and fail to meet the conditions of zero slope at

x = 1

. To overcome this deficiency solutions valid for the inner region are developed.

6.3.2. Solutions for k in the Inner Region

Solutions for k are developed by describing k by a series of successive powers of

η = 1 - x

. The linear term in

η

is omitted in order to satisfy the zero-slope condition at

η = 0

. Disregarding terms of

O (η^{3})

and higher we write for k

k = k_{1} + a η^{2}

(47)

where

k_{1}

is the value of k at

x = 1

;

k_{1}

and a are to be determined. Substituting expression (47) in Equation (29) and (34) and equating the leading terms of

O (η^{0})

we obtain for a in case of the basic k-

ϵ

and fundamental models respectively the relations

2 a \frac{c_{μ} κ^{2} k_{1}^{2}}{σ_{k}} = G_{1}^{2}

(48)

and

\frac{16 a c_{k} κ^{2} k_{1}^{2}}{9 C_{0}} = G_{1}^{2}

(49)

where

G_{1}

is the value of G at

η = 0

. In deriving result (49) we took for

σ_{22}

η = 0

the value

\frac{2}{3} k_{1}

in accordance with Equation (37). The boundary between inner and outer region is defined by

η_{0} = 1 - x_{0}

. At this boundary the value of k and its slope should match the values according to those of the outer region. This yields the relations:

k_{1} + a η_{0}^{2} = \frac{η_{0}}{\sqrt{c_{μ}}}; k_{1} + a η_{0}^{2} = η_{0} k_{0}

(50)

2 a η_{0} = \frac{1}{\sqrt{c_{μ}}}; 2 a η_{0} = k_{0}

(51)

for basic k-

ϵ

and fundamental model respectively. From Equations (47)-(51) the following solutions are obtained:

For the basic k- $ϵ$ model:

η_{0} = 4 σ_{k} G_{1}^{2} \frac{\sqrt{c_{μ}}}{κ^{2}}; k_{1} = \frac{η_{0}}{2 \sqrt{c_{μ}}}; a = \frac{1}{2 \sqrt{c_{μ}} η_{0}}

(52)

and for the fundamental model

η_{0} = \frac{9 G_{1}^{2} C_{0}}{2 κ^{2} k_{0}^{3} c_{k}}; k_{1} = \frac{k_{0} η_{0}}{2}; a = \frac{k_{0}}{2 η_{0}}

(53)

The above solution parameters can be determined by implementing the values of the system parameters

σ_{k}, c_{μ}, κ, C_{0}, k_{0}

and

c_{k}

. The value of

G_{1}

is taken from the numerical results:

G_{1} = 0.25

in case of the basic k-

ϵ

model and

G_{1} = 0.44

in case of the fundamental model. An alternative approach to determine

G_{1}

is to couple the above analytical solution of k to that of G presented in Section 6.3.3 below. It yields values for

G_{1}

without recourse to the numerical results. The values are practically equal to those of the numerical results.

A complete analytical description of k for outer and inner region is obtained from Equations (41) and (44) when

x \leq x_{0}

and Equations (47) and (52) when

x \geq x_{0}

where

x_{0} = 0.47

in case of the basic k-

ϵ

model and

x_{0} = 0.33

in case of the fundamental model. The result has been shown in Figure 4 by solid blue and red lines.

6.3.3. Solutions for G in the Inner Region

For G in the inner region the following expansion is used

G = G_{1} (1 - η) + a η^{2} .

(54)

where the linear term

G_{1} η

is introduced to satisfy the boundary condition at

x = 1

: cf. Equations (33) and (39). The values of

G_{1}

and a are to be determined. Substituting description (54) into Equations (30) and (35) and equating the leading terms of

O (η^{0})

yields

a = α G_{1}^{3}

(55)

where

α = \frac{σ_{ϵ} c_{ϵ 2}}{2 κ^{2} c_{μ} k_{1}^{3}}

(56)

and

α = \frac{9 C_{0} σ_{ϵ}^{*} c_{ϵ 2}}{16 κ^{2} k_{1}^{3}}

(57)

for basic k-

ϵ

model and fundamental model respectively. At the boundary of inner and outer region

η = η_{1}

the values of G and its slope according to outer and inner regions should become equal. It yields the relations

η_{1} \sqrt{(2 - η_{1})} = (1 - η_{1}) G_{1} + α G_{1}^{2} η_{1}^{2}

(58)

\frac{(2 - \frac{3}{2} η_{1})}{\sqrt{2 - η_{1}}} = - G_{1} + 2 α G_{1}^{2} η_{1}

(59)

Eliminating

G_{1}

from the above equations yields the following irreducible equation for

η_{1}

α = \frac{2}{η_{1}^{4}} \frac{{(1 - \frac{η_{1}}{2})}^{3}}{{(1 - \frac{η_{1}}{4})}^{3}} (1 - \frac{3 η_{1}}{4} + \frac{η_{1}^{2}}{4})

(60)

The value of

α

follows from Equation (56) using the system values for the various parameters and taking for

k_{1}

the value of the numerical calculations, i.e.

k_{1} = 0.8

, with the result that

α = 134

and

α = 18

in case of the basic k-

ϵ

model and the fundamental model respectively. By iteration one finds from eqs (60) for the basic k-

ϵ

model

η_{1} = 0.31 (x_{1} = 0.69)

and for the fundamental model

η_{1} = 0.47 (x_{1} = 0.53)

. A complete analytical description of G for outer and inner region is obtained from Equation (46) when

x \leq x_{1}

and Equations (54)-(56) when

x \geq x_{1}

. The result has been shown in Figure 5 by solid blue and red lines.

6.4. Discussion of Results

Numerical and analytical solutions for kinetic energy k and energy dissipation

ϵ

, the latter in terms of

G = κ x ϵ

, have been developed for the basic k-

ϵ

model and a new fundamentally based model. The solutions were compared with DNS results and have been shown in Figure 4 and Figure 5. Conclusions are:

Analytical solutions agree in a satisfactory manner with numerical solutions. The analytical solutions reveal the relative contributions of turbulent diffusion, energy production and energy dissipation in outer and inner region of the channel. They show to what extent the descriptions are empirically or fundamentally based and depend on calibration factors.
Solutions for k in the in the outer region $(x \leq 0.33)$ according to the fundamental model do not depend on calibration constants. They have a fundamental basis. The differences with DNS can be ascribed to errors as a result of truncation in the expansion with respect to $C_{0}^{- 1}$ which underlies the fundamental model.
Solutions for k in the inner region $(x \geq 0.33)$ according to the fundamental model depend on the calibration factor $c_{k}$ .
Solutions for k in both the outer and inner region according to the basic k- $ϵ$ model depend on the calibration factors $c_{μ}$ and $σ_{k}$ .
Solutions for G in the outer region according to the fundamental model and the basic k- $ϵ$ model, $(x \leq 0.53)$ and $(x \leq 0.69)$ do not depend on calibration factors. Differences with DNS are due to some deviation between the value of production and dissipation in this area.
Solutions for G in the inner region according to the fundamental model and the basic k- $ϵ$ model, $(x \geq 0.69)$ and $(x \geq 0.53)$ respectively, depend on the calibration factors $σ_{ϵ}^{*}$ and $σ_{ϵ}$ .
Using standard calibration constants in the solutions of the basic k- $ϵ$ model results in notable deviations compared to DNS. The deviations can be reduced by recalibrating $σ_{ϵ}$ , $c_{μ}$ and $σ_{k}$ . Deviations between diffusion constants remain significant because of different functional dependencies: Figure 1, Figure 2 and Figure 3.

7. Velocity Distributions

The basic k-

ϵ

model is based on the assumption of an isotropic turbulence field. It cannot predict anisotropic behaviour of co-variances or turbulent stresses. In case of the fundamental model the distribution of

σ_{22}

follows from the solution of eqs.(34) According to Equation (24b)

σ_{33} = σ_{22}

while

σ_{11} = \frac{1}{2} k - σ_{22}

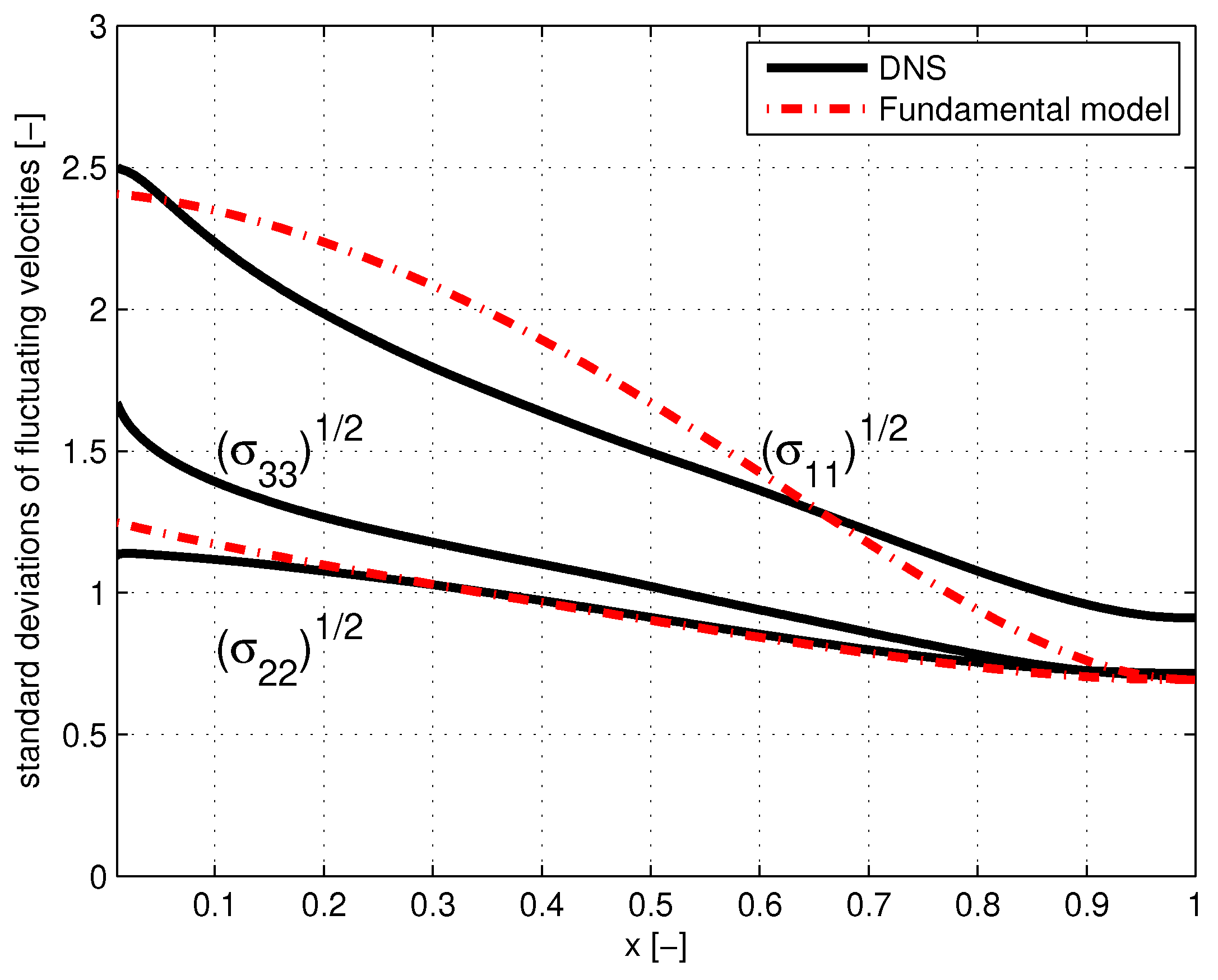
where k is given by Equation (37). In Figure 6 the distribution versus x is shown of the calculated values of the standard deviations of the fluctuations

\sqrt{σ_{11}}

\sqrt{σ_{22}}

and

\sqrt{σ_{33}}

according to the fundamental model and the results of DNS. Deviations are similar to those shown in [9] and are ascribed to truncation of the expansions of

C_{0}^{- 1}

which underlies the theory of the fundamental model. Deviations of the three variances

σ_{11}, σ_{22}, σ_{33}

from k which describe anisotropy are next to leading order in the

C_{0}^{- 1}

expansion (cf. Equation (24a) - (24c)) and therefore more sensitive to truncation error.

For the gradient of the mean flow the following relations can be derived. For the basic k-

ϵ

model from eqs (21) and (23b)

\frac{d u_{1}}{d x} = \frac{1 - x}{ν_{t}}

(61)

For the fundamental model from eqs (21) and (24d)

\frac{d u_{1}}{d x} = \frac{1 - x}{D_{22}}

(62)

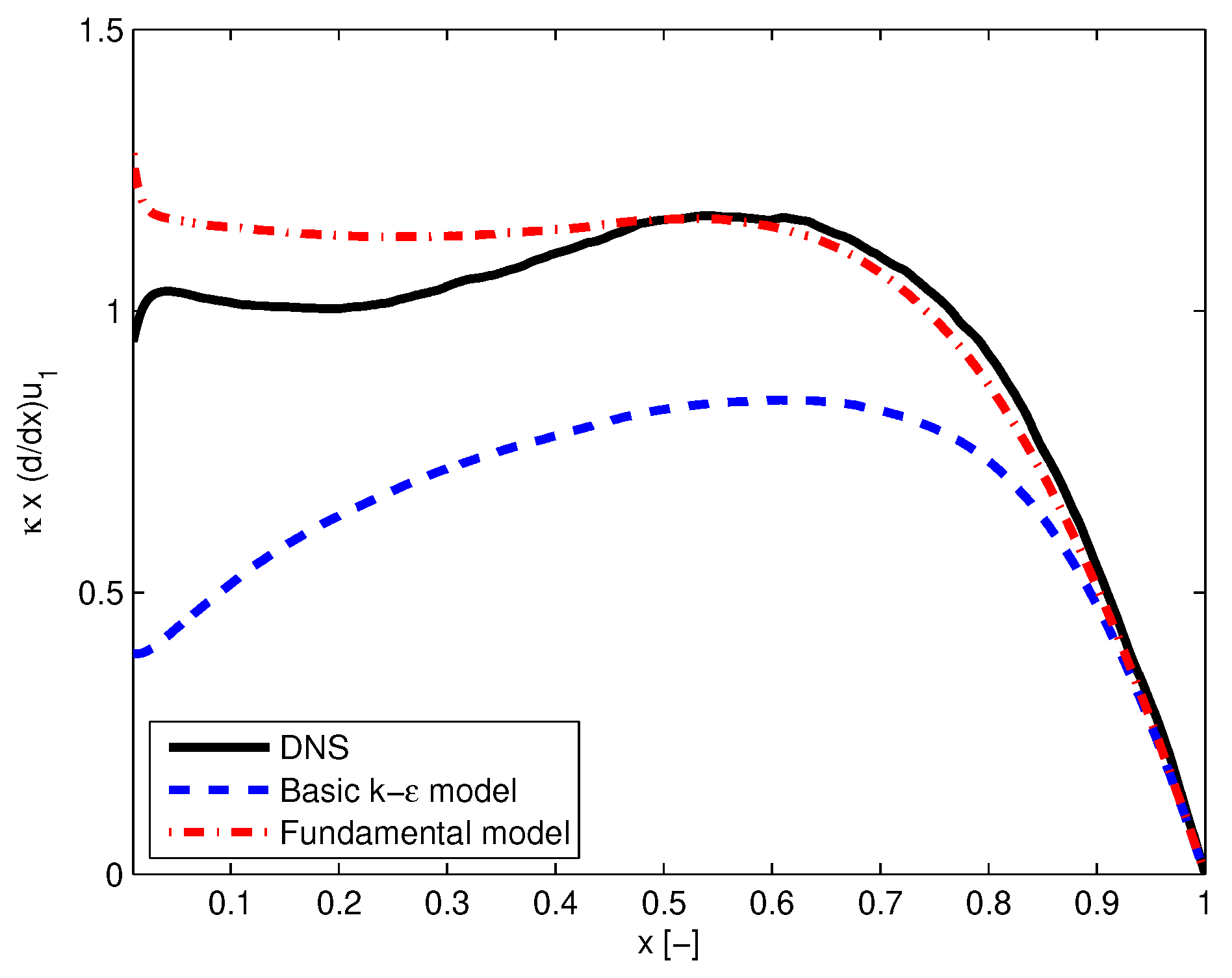
In Figure 7 the distributions versus x are shown of

κ x \frac{d u_{1}}{d x}

according to DNS, the basic k-

ϵ

model and the fundamental model. The deviations between DNS and basic k-

ϵ

model are similar to those shown for

ν_{D N S}

and

ν_{t}

shown in Figure 1 and Figure 2. Similarly the agreement between

ν_{D N S}

and

D_{22}

shown in Figure 1 and Figure 2. According to (21):

P = (1 - x) \frac{d u_{1}}{d x}

which indicates that disagreement of production with DNS in case of the basic k-

ϵ

model is similar to that shown in Figure 7 and that agreement of production with DNS in case of the fundamental model is similar to that shown in Figure 7.

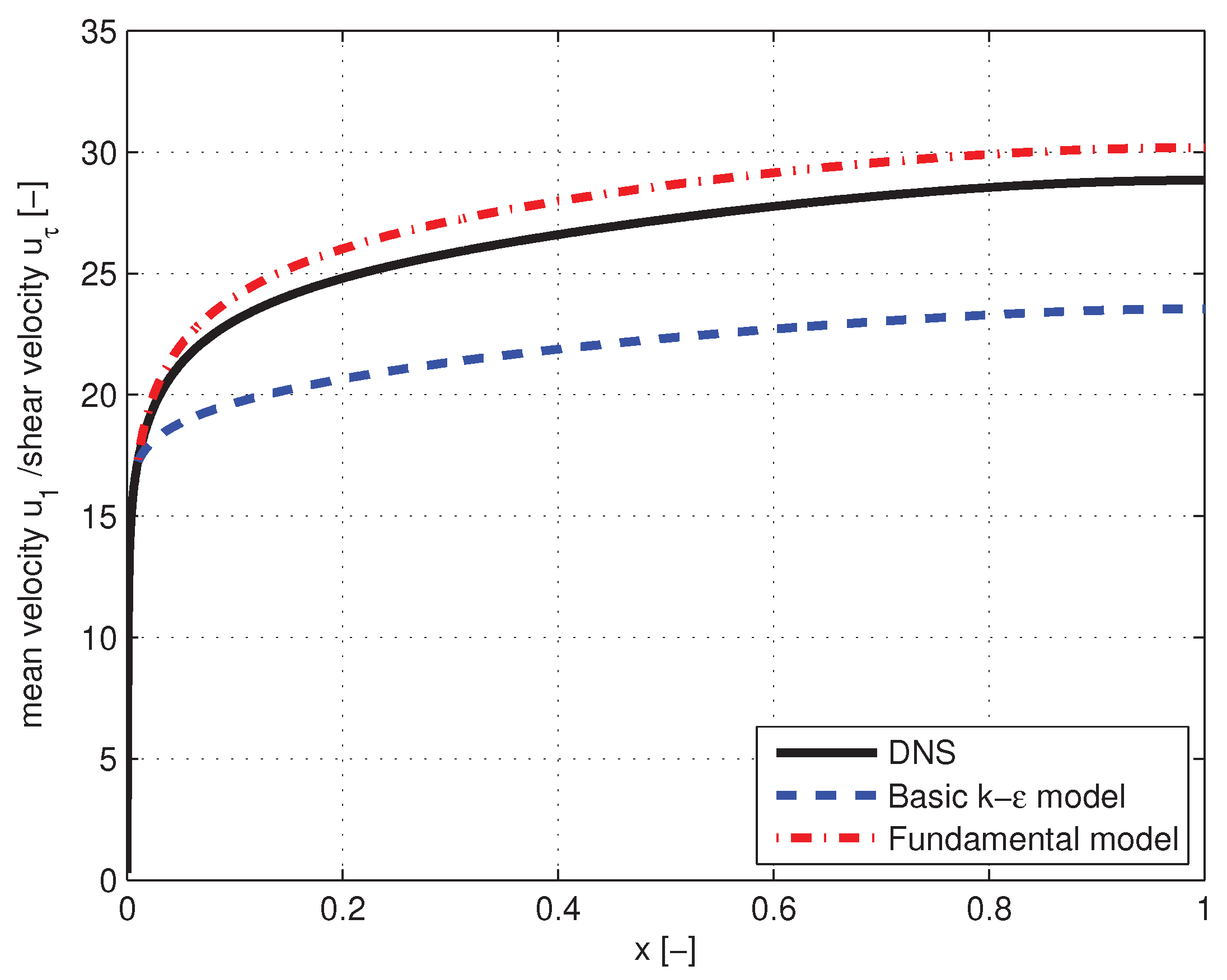
The distribution of mean velocity

u_{1}

predicted by the basic k-

ϵ

model and the fundamental model are obtained by integration of the RHS’s of Equations (61) and (62). Because the models do not describe the velocity in the viscous layer at the wall the integration starts at some distance from the wall for which the position

x = \frac{100}{R e_{τ}}

is taken. The value of

u_{1}

at this point according to the DNS results of

R e_{τ} = 10^{4}

is 17.2 which agrees with the values obtained from measurements: Monin and Yaglom, Vol. I, fig. 25 [21]. The results of the integration are shown in Figure 8, where the distributions of mean velocity of the two models and of DNS are presented. It is seen that for equal shear velocity, that is for equal longitudinal pressure gradient in the channel, the fundamental model somewhat overestimates mean velocity, by

5 %

while the basic k-

ϵ

model underestimates by

18 %

8. Conclusions

An analysis has been presented of two models for determining mean values of turbulent flow variables: velocities

u_{i}

, pressure p, turbulent diffusion

D_{i j}

, kinetic energy k and energy dissipation

ϵ

. The two models are the basic k-

ϵ

model widely used in engineering applications and environmental analysis [5,6], and a new fundamentally based model which is derived from recently published statistical descriptions of inhomogeneous anisotropic turbulence [7,8,9]. The analysis was focused on turbulent channel flow which is highly anisotropic and inhomogeneous. It is of direct relevance to applications of duct flows, turbulent boundary layers around bodies and the atmospheric surface layer around the earth. Model predictions were verified against published results of direct numerical simulations DNS for shear Reynolds numbers of 950 [15], 2000 [13] and

10^{4}

[14]. The comparison was focussed on the regions outside the thin viscous boundary layers of a few millimeters at the wall. The development status of DNS is mature; its results can serve as a reliable source for verifying model predictions.

The basic k-

ϵ

model is built on an empirical isentropic representation of the turbulence field. It contains a gradient hypothesis for turbulent diffusion which is supplemented by calibration constants. Using conventionally proposed values for the calibration constants [5,6] model predictions of several variables are found to deviate remarkably from the results of DNS. A summary has been given in Table 1.

The fundamental model is derived from a theory which has a fundamental basis [7,8,9]. Expressions for turbulent diffusion of momentum and of conservative scalars such as temperature and passive admixture (smoke, aerosols) are of a general nature. They are free from calibration constants. They are found to agree in a satisfactory manner with DNS results at all distances x from the wall (outside the thin boundary layer at the wall). The theory underlying the fundamental model does not provide generally valid expressions for turbulent diffusion of the non-conservative scalars kinetic energy, pressure, energy dissipation. The non-conservative diffusion terms are only important for the determination of k and

ϵ

in the inner half of the channel. Here non-conservative behaviour has been modeled by using the diffusion expressions of conservative scalars provided with calibration factors. A summary is given in Table 1.

A general limitation of empirical models is that they lack a fundamental basis. It is uncertain whether the modelled terms are correctly described by their dependencies on variables. The addition of calibration factors tempers inaccuracies of prediction to some extent. At the same time they need to be specified for each new case. Models which are derived from generally valid principles do not suffer from these limitations. The presented fundamental model contains descriptions of several variables which satisfy this criterion. Calibration factors are absent and applicability can be expected to exceed that of channel flow. What is still missing in the fundamental model are fundamental expressions for non-conservative scalars. Their development eliminates the remaining empirical factors.

Funding

This research received no external funding.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

B.G.J. Ruis and H.S. Janssen are acknowledged for performing numerical calculations; G.M. Janssen for preparing the manuscript.

Conflicts of Interest

The author declares no conflict of interest.

References

Boussinesq, J. Mem.pres.par.div. savantis a l’acad. sci. de Paris, 1877, 23, 1, 1-680, 1877, 24, 2, 726-736.
Taylor, G.I. Phil.Trans. 1915, A215, 1-26, and Proc.Roy.Soc.(London), 1932, A135, 685-701.
Prandtl, L. Zeits. f. Math.u. Mech., 1925, 5, 136-139.
Karman, Th. von. Nachr. Ges. Wiss. Goettingen, Math. Phys., 1930, Klasse 58-76.
Hanjali´c, K.; Launder, B. Modelling Turbulence in Engineering and the Environment: Second-Moment Routes to Closure; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
Bernard, P.S.; Wallace, J.K. Turbulent Flow: Analysis, Measurement and Prediction; Wiley: New Jersey, NJ, USA, 2002. [Google Scholar]
Brouwers, J.J.H. Statistical description of turbulent dispersion. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 066309. [Google Scholar] [CrossRef] [PubMed]
Brouwers, J.J.H. Statistical Models of Large Scale Turbulent Flow. Flow Turbul. Combust. 2016, 97, 369–399. [Google Scholar] [CrossRef]
Brouwers, J.J.H. Statistical Descriptions of Inhomogeneous fundamentally based Turbulence Mathematics 2022, 10, 4619.
Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics, Vol II, Ch 8; Dover: New York, NY, USA, 2007. [Google Scholar]
van Kampen, N.G. Stochastic Processes in Physics and Chemistry, 3rd ed.; Elsevier: New York, NY, USA, 2007. [Google Scholar]
Stratonovich, R.L. Topics in the Theory of Random Noise; Gordon and Breach: New York, NY, USA, 1967; Volume 1. [Google Scholar]
Hoyas, S.; Jiménez, J. Scaling of the velocity fluctuations in turbulent channels up to Re_τ=2003. Phys. Fluids 2006, 18, 011702. [Google Scholar] [CrossRef]
Hoyas, S.; Oberlack, M.; Alcántara-Ávila, F.; Kraheberger, S.V.; Laux, J. Wall turbulence at high friction Reynolds numbers. Phys.Rev. Fluids 2022, 7, 014602. [Google Scholar] [CrossRef]
Kuerten, J.; Brouwers, J.J.H. Lagrangian statistics of turbulent channel flow at Re_τ=950 calculated with direct numerical simulation and Langevin models. Phys. Fluids 2013, 25, 105108. [Google Scholar] [CrossRef]
Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akad.Nauk. Sssr Dokl. 1941, 30, 301–305. [Google Scholar]
George, W.K. The Decay of Homogeneous Isotropic Turbulence. Phys.Fluids A 1992, 4, 1492–1509. [Google Scholar] [CrossRef]
Brouwers, J.J.H. Dissipation equals Production in the Log Layer of Wall Induced Turbulence. Phys.Fluids 2007, 19(10), 101702. [Google Scholar] [CrossRef]
Lew,A.J.; Gustavo, C.; Carrica,B.; Carrida, P.M. Int. J. Computational Fluid Dynamics. 2001,14:3, 201-209. [CrossRef]
Borse,G.J. Numerical Methods with Matlab, Ch.22, PWS Publishing, Boston, USA, 1997. ISBN 0534938221.
Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics, Vol I. Dover: New York, NY, USA, 2007.

Figure 1. Turbulent viscosities according to

ν_{D N S}

R e_{τ} = 10^{4}

, fundamental model

D_{22}

and basic k-

ϵ

model

ν_{t}

versus dimensionless distance from the wall x. Results from DNS are represented by the solid line, from the fundamental model by dashdot line and from the basic k-

ϵ

model by dashed line.

Figure 1. Turbulent viscosities according to

ν_{D N S}

R e_{τ} = 10^{4}

, fundamental model

D_{22}

and basic k-

ϵ

model

ν_{t}

versus dimensionless distance from the wall x. Results from DNS are represented by the solid line, from the fundamental model by dashdot line and from the basic k-

ϵ

model by dashed line.

Figure 2. Ratio of turbulent viscosity of the fundamental model to that of DNS at

R e_{τ} = 10^{4}

\frac{D_{22}}{ν_{D N S}}

(lower line) and ration of turbulent viscosity of the basic k-

ϵ

model to that of DNS at

R e_{τ} = 10^{4}

\frac{ν_{t}}{ν_{D N S}}

(upper line) versus dimensionless distance from the wall x.

Figure 2. Ratio of turbulent viscosity of the fundamental model to that of DNS at

R e_{τ} = 10^{4}

\frac{D_{22}}{ν_{D N S}}

(lower line) and ration of turbulent viscosity of the basic k-

ϵ

model to that of DNS at

R e_{τ} = 10^{4}

\frac{ν_{t}}{ν_{D N S}}

(upper line) versus dimensionless distance from the wall x.

Figure 3. Sum of turbulent fluxes of kinetic energy and pressure versus dimensionless distance from the wall x. The solid line is the sum according to DNS at

R e_{τ} = 10^{4}

, the dashdot line according to an empirical construction using the fundamental model and the dashed line the empirical construction of the basic k-

ϵ

model.

Figure 3. Sum of turbulent fluxes of kinetic energy and pressure versus dimensionless distance from the wall x. The solid line is the sum according to DNS at

R e_{τ} = 10^{4}

, the dashdot line according to an empirical construction using the fundamental model and the dashed line the empirical construction of the basic k-

ϵ

model.

Figure 4. Distribution versus x of kinetic energy k according to DNS (solid line), according to the numerically and analytically assessed basic k-

ϵ

model ( dashed and full line respectively), and according to the numerically and analytically assessed fundamental model (dashdot and full line respectively).

Figure 4. Distribution versus x of kinetic energy k according to DNS (solid line), according to the numerically and analytically assessed basic k-

ϵ

model ( dashed and full line respectively), and according to the numerically and analytically assessed fundamental model (dashdot and full line respectively).

Figure 5. Distribution versus x of kinetic energy G according to DNS (solid line), according to the numerically and analytically assessed basic k-

ϵ

model ( dashed and full line respectively), and according to the numerically and analytically assessed fundamental model (dashdot and full line respectively).

Figure 5. Distribution versus x of kinetic energy G according to DNS (solid line), according to the numerically and analytically assessed basic k-

ϵ

model ( dashed and full line respectively), and according to the numerically and analytically assessed fundamental model (dashdot and full line respectively).

Figure 6. Distribution versus x of the standard deviations of fluctuating velocities

\sqrt{σ_{11}}

\sqrt{σ_{22}}

and

\sqrt{σ_{33}}

according to DNS (solid line) and the fundamental model (dashdot line).

Figure 6. Distribution versus x of the standard deviations of fluctuating velocities

\sqrt{σ_{11}}

\sqrt{σ_{22}}

and

\sqrt{σ_{33}}

according to DNS (solid line) and the fundamental model (dashdot line).

Figure 7. Distribution versus x of

κ x \frac{d u_{1}}{d x}

according to DNS (solid line), the basic k-

ϵ

model (dashdot line)and the fundamental model ( dashed line).

Figure 7. Distribution versus x of

κ x \frac{d u_{1}}{d x}

according to DNS (solid line), the basic k-

ϵ

model (dashdot line)and the fundamental model ( dashed line).

Figure 8. Distribution of mean velocity divided by shear velocity versus x according to DNS (solid line), the basic k-

ϵ

model (dashdot line)and the fundamental model ( dashed line).

Figure 8. Distribution of mean velocity divided by shear velocity versus x according to DNS (solid line), the basic k-

ϵ

model (dashdot line)and the fundamental model ( dashed line).

Table 1. Predictions of the basic k-

ϵ

model and the fundamentally based model compared with DNS of turbulent channel flow

Table 1. Predictions of the basic k-

ϵ

model and the fundamentally based model compared with DNS of turbulent channel flow

variable	basic k- $ϵ$ model	fundamentally based model
Turbulent viscosity	Empirical Equation (23d) Significant deviations Figure 1 and Figure 2	Fundamentally based Equation (24d) Satisfactory agreement: Figure 1 and Figure 2
Turbulent diffusion of temperatures, smokes, aerosols	Empirical Equation (23c) Significant deviations similar to Figure 1 and Figure 2	Fundamentally based Equation (24e) Satisfactory agreement similar to Figure 1 and Figure 2
Tubulent diffusion of kinetic energy and pressure	Empirical Equation (26) Deviations Figure 3	Empirical Equation (27) Satisfactory agreement Figure 3
Mean value of kinetic energy	Empirical Equation (29) Deviations Figure 4	In the outer half of the channel: fundamentally based Equation (55). In the inner half: empirical Equation (55). Satisfactory agreement Figure 4
Mean value of energy dissipation rate	In the outer half of the channel: fundamentally based Equation (46) In the inner half: empirical Equation (55). Deviations: Figure 5	In the outer half of the channel: fundamentally based Equation (46). In the inner half: empirical Equation (55). Satisfactory agreement: Figure 5
RMS values of fluctuations	No prediction	Qualitative agreement Figure 6
Mean value of velocity	Empirical Equation (61) Deviations Figure 7 and Figure 8	Fundamentally based Equation (62) Satisfactory agreement Figure 7 and Figure 8

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Basic k-ϵ Model and a New Fundamentally Based Model of Anisotropic Inhomogeneous Turbulence Compared with DNS of Channel Flow at High Reynolds Number

Abstract

1. Introduction

2. The Basic k- ϵ Model and the New Fundamental Model

2.1. Turbulent Diffusion in the Basic k- ϵ Model

2.2. Turbulent Diffusion in the Fundamentally Based Model

3. Equations for k and ϵ

4. Channel Flow

5. Testing the Diffusion Representations by DNS

5.1. Diffusion of Momentum

5.2. Diffusion of Temperature

5.3. Diffusion of Kinetic Energy and Pressure

5.4. Diffusion of Energy Dissipation

6. Solutions of k and ϵ Compared with DNS

6.1. Equations and Boundary Conditions

6.2. Numerical Solution

6.3. Analytical Solution

6.3.1. Solutions for k and G in the Outer Region

6.3.2. Solutions for k in the Inner Region

6.3.3. Solutions for G in the Inner Region

6.4. Discussion of Results

7. Velocity Distributions

8. Conclusions

Funding

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2. The Basic k- $ϵ$ Model and the New Fundamental Model

2.1. Turbulent Diffusion in the Basic k- $ϵ$ Model

3. Equations for k and $ϵ$

6. Solutions of k and $ϵ$ Compared with DNS