Prerpints.org logo
Preprint
Communication

Generalized Electron Emission Theory for One-Dimensional Conducting Materials

Altmetrics

Downloads

96

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 February 2024

Posted:

06 March 2024

You are already at the latest version

Alerts
Abstract
This research focuses on exploring generalized electron emissions in one-dimensional conducting materials, specifically examining field emission and thermionic emission. Additionally, the study investigates one-dimensional thermal radiation. The current density is derived for both one-dimensional thermionic emission and one-dimensional field emission. A generalized current density in one dimension is devised, taking into account arbitrary accelerating fields and temperature conditions. The formula for the one-dimensional current density is depicted with accelerating field and temperature across various work function materials. The current is also represented as a function of both temperature and electric field for various temperatures.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

Photons are emitted by a heated object. Max Planck’s exploration of blackbody radiation led to the discovery of angular momentum quantization and the Planck constant (h) [1]. The Planck constant, along with its reduced form (h/2π), representing the minimum action, serves as the foundation for quantization, encompassing phenomena such as photons, Josephson constant, von Klitzing constant, conductance quantum, inverse conductance quantum, and magnetic flux quantum [2]. The study of n-dimensional blackbody radiation revealed generalized Planck energy and the Stefan-Boltzmann law [3]. The characteristics of thermal radiation were deduced across arbitrary fractional dimensions, ascertainable through the measurement of spectral radiance [4]. The extent of thermal radiation is influenced by the dimensions of the object. As the size of the object decreases significantly, quantum effects become apparent due to the minimum wavelength of photons being comparable to the size of the object. Researchers examined the size-dependent impact on the energy density of thermal radiation [5,6,7]. Investigations also delved into the concept of effective temperature, particularly in cases of non-uniform temperature distributions within the object [8,9,10]. Additionally, thermionic emission, wherein electrons with energy levels surpassing their work function are emitted from a heated conducting metal, has been studied. Initially, thermionic emission was investigated in metallic materials [11], while subsequent studies extended to semiconductor materials to explore scaling laws [12]. The derivation of thermionic emission current density was conducted for a two-dimensional crystal material and generalized for arbitrary dimensions [13,14]. In conducting metals, electrons near the Fermi energy level undergo quantum tunneling when subjected to a strong electric field, a phenomenon referred to as field emission. The exploration of field emission began in metallic materials utilizing quantum mechanical tunneling principles [15]. Comprehensive investigations were carried out on both field emission and field ionization phenomena [16]. Superconducting niobium cavities are extensively utilized for accelerating electrons or heavy ions. However, in high-accelerating electric fields, field emissions originating from micron-sized particles or surface irregularities in these niobium superconducting cavities can lead to performance degradation. Thorough research efforts have been undertaken to comprehend the impacts of field emission on these niobium superconducting cavities [17,18,19,20]. Furthermore, research has explored field emission phenomena in carbon nanotubes and carbon nanotube field emitter arrays [21,22,23], with efforts to calculate the generalized current density for field emission across arbitrary dimensions [24]. Additionally, a comprehensive electron emission theory has been developed by integrating field emission as well as thermionic emission principles within two-dimensional conducting materials [25].
In this study, we compute the universal current density encompassing both thermally emitted electrons and field emitted electrons within one-dimensional materials. We delve into the spectral radiance of one-dimensional entities. The current density is specifically determined for generalized thermionic emission and generalized field emission within the one-dimensional framework. A comprehensive, one-dimensional current density is then calculated to accommodate diverse electric fields and temperatures. Furthermore, the expression of this current density varies with temperature and electric field for various work functions.

2. Thermal Radiation in One Dimension

One-dimensional blackbody radiation arises from an infinite array of modes within a one-dimensional cavity, where photon energy is quantized. This quantized photon energy can be represented as
E i = n i h ν ,
where h denotes the Planck constant, n i denotes a positive integer, and ν denotes the frequency. According to Planck’s distribution, the mean photon count is calculated as
n ¯ p h = 1 e x p ( h   ν k B T ) − 1 ,
where k B stands for the Boltzmann constant and T stands for the absolute temperature.
The mean energy within the mode is given by
E ¯ = h ν e x p ( h   ν k B T ) − 1 .
The spectral density for one-dimensional blackbody radiation, derived from Planck’s radiation law, is expressed as
u ( ν , T ) = ( 4 c ) ν e x p ( h   ν k B T ) − 1 ,
where c represents the speed of light.
The energy density for photon energy E at temperature T is formulated as
u ( E , T ) = ( 4 h c ) E e x p ( E k B T ) − 1 .
The energy density of the photon gas, assuming an infinite body length, and integrating Eq. (5) from zero to infinity, yields
u ( T ) = ( 4 h c ) ∫ 0 ∞ E d E e x p ( E k B T ) − 1 .
By introducing x = E / k B T , Eq. (6) is simplified to
u ( T ) = ( 4 ( k B T ) 2 h c ) ∫ 0 ∞ ( x d x e x p ( x ) − 1 ) .
Eq. (7) can be evaluated to obtain
u B T = 4 k B T 2 h c π 2 6 ,
which represents one-dimensional blackbody radiation. This derivation follows the conventional approach for one-dimensional blackbody radiation, where the radiation’s maximum wavelength is large enough to approximate the minimum energy to zero. In a one-dimensional blackbody, the energy density is proportional to T 2 , contrasting with a three-dimensional blackbody, where the energy density is proportional to T 4 .
The spectral radiance in one dimension is given by [4]
Φ v = 4 π h v e x p ( h v / k B T ) − 1 .
This spectral radiance can be represented in terms of dimensionless photon energy as ( h   ν k B T ) .

3. One-dimensional Thermionic Emission

At zero temperature, electrons within a conductor occupy energy levels up to Fermi energy. As the temperature increases, some electrons are excited to energy levels exceeding the work function. Electrons thermally emitted in this process, possessing energy surpassing the vacuum energy, participate in thermionic emissions.
The one-dimensional kinetic energy of an electron is given by
E 1 D = 1 2 m v x 2 ,
where m denotes the electron mass and v x denotes the electron velocity in the x-direction. This Eq. (10) can also be represented as E 1 D ( k x ) = ℏ 2 k x 2 2 m when incorporating the wave number, given the electron’s velocity is significantly lower than the light speed. The electron velocity can be expressed as v x = ℏ k m by considering v x = 1 ℏ ∇ k x E ( k x ) .
The one-dimensional current density associated with thermionic emission becomes
J 1 D = e ∫ 0 ∞ d v x v x n ( v x ) D ( E x ) ,
where n signifies the density of electrons, D represents the tunneling probability, and e denotes the electric charge. The electron density, represented as n ( E ) = g ( E ) f ( E ) , incorporates the density of states g(E) and the Fermi factor f(E), indicating the probability of a specific state having energy E. When the electron energy exceeds the vacuum energy, the tunneling probability is 1. Utilizing Eq. (11), the thermionic current density in one dimension is derived as
  J 1 D = e ∫ 0 ∞ ( d E x m ) ( 2 m h ) D ( E x ) e x p E x − E F k B T + 1 ,
where E F represents the Fermi energy and k B denotes the Boltzmann constant. Taking into account the vacuum energy, Eq. (12) is rewritten as:
  J 1 D = 2 e k B T h ∫ Φ w + E F ∞ d E x / k B T e x p E x − E F k B T + 1 ,
where Φ W denotes the work function of the one-dimensional material. By introducing x = E x − E F k B T , Eq. (13) can be expressed
J 1 D = 2 e k B T h ∫ Φ w k B T ∞ d x e x p x + 1 .
Integration of Eq. (14) yields
J 1 D = 2 e k B T h [ l o g ( 1 + e Φ w k B T ) − Φ w k B T ] .
Eq. (15) can alternatively be written as
J 1 D = 2 e k B T h [ l o g ( 1 + e − Φ w k B T ) ] .
Eq. (16) stands for the thermionic current density in one-dimensional materials. This current density formula (16) is applicable across varying work functions and temperatures.
When the work function of Φ W is much bigger than thermal energy of k B T , Eq. (14) simplifies to:
J 1 D = 2 e h k B T ∫ Φ w k B T ∞ e x p − x d x .
From Eq. (17), the thermionic current density for one-dimensional materials is obtained as
J 1 D = 2 e k B T h e − Φ w k B T .
This Eq. (18) represents the one-dimensional current density for thermionic emission.
When thermally excited electrons have energy exceeding the vacuum energy, they might undergo reflection at the boundary between the metal and vacuum. The generalized one-dimensional current density for thermally emitted electrons is then described as
J 1 D = ( 1 − r ) 2 e k B T h e − Φ w k B T ,
where r denotes the probability of reflection for the electrons.

4. One-Dimensional Field Emission

In a metal, free electrons adhere to a Fermi-Dirac distribution. Concerning field emission, the current density in a one-dimensional conductor is as follows
J 1 D = e ∫ 0 E F d v x v x n 1 D ( E x ) D ( E x ) ,
where v x represents the x-directional velocity of electrons, E F signifies the Fermi energy, n 1 D denotes the one-dimensional density of electrons, and D represents the tunneling probability. D ( E x ) signifies the probability of tunneling, indicating the likelihood that an electron with energy E x traverses into a vacuum through the potential barrier
Figure 1 depicts a schematic representation of one-dimensional field emission, showcasing the application of the x-directional electric field to the conducting material. The electron tunneling probability D for the conductor exposed to a steady electric field is provided by [15]
D = ( 4 E x E F + Φ w − E x E F + Φ w ) e − 4 k ( E F + Φ w − E x ) 3 / 2 / 3 F ,
where k = 8 π 2 m h 2 signifies the electron wave number, E x denotes the electron energy along the x-direction, Φ w represents the work function of the metal, and F signifies the accelerating field to the metal. The electron tunneling probability described by Eq. (21) is contingent on the Fermi energy, work function, and accelerating electric field.
The expression for the field emission current density in a one-dimensional conductor, derived from Eq. (20), is presented as follows
J 1 D = 2 e h ∫ 0 E F d E x D ( E x ) e x p E x − E F k B T + 1 ,
where D ( E x ) denotes the probability of electron tunneling.
When considering the electron tunneling probability from Eq. (21) and the limit at zero temperature, the expression for the one-dimensional current density in the field emission, represented by Eq. (22), simplifies to:
J 1 D = 8 e h ∫ 0 E F d E x ( E F − E x E F ) ( E x E F + Φ w − E x E F + Φ w ) e − 4 k ( E F + Φ w − E x ) 3 / 2 / 3 F .
By substituting E x with E F − x and assuming prevalent electron tunneling in the vicinity of the Fermi energy, the approximated current density for the field emission, denoted as Eq. (23), is obtained as
J 1 D = 8 e h Φ w ( E F + Φ w ) 1 E F e − 4 k Φ w 3 / 2 / 3 F ∫ 0 ∞ d x x e − 2 x k Φ w / F .
Using Eq. (24), the expression for the current density in the case of one-dimensional field emission is derived as
J 1 D = e h F 2 4 π 2 m ( E F + Φ w ) E F Φ w e − 4 k Φ w 3 / 2 / 3 F ,
where m denotes the electron mass. Eq. (25) illustrates the one-dimensional current density for field emission, indicating the number of quantum tunneled electrons per unit time. This current increases with higher electric field strength and decreases with a reduction in the work function.

5. Comprehensive Electron Emission Theory in One Dimension

The generalized electron emission in one-dimensional materials can be computed for arbitrary electric fields and temperatures. Based on Eq. (22), the current of one-dimensional field emission is approximately determined for diverse temperature conditions.
J 1 D = 8 e h [ ∫ 0 E F + Φ W d E x ( E x E F + Φ w − E x E F + Φ w ) l n ( 1 + e x p ( − E x − E F k B T ) e − 4 k ( E F + Φ w − E x ) 3 / 2 / 3 F ] .
Combining Eq. (18) and Eq. (26), the generalized one-dimensional current density for arbitrary accelerating fields and temperatures is represented as
J 1 D U F = 2 e h [ k B T e − Φ w k B T + 4 ∫ 0 E F + Φ W d E x ( E x − E F E F ) ( E x E F + Φ w − E x E F + Φ w ) l n ( 1 + e x p ( − E x − E F k B T ) e − 4 k ( E F + Φ w − E x ) 3 / 2 / 3 F ] .
The one-dimensional current density derived from the unified theory encompassing both field emission and thermionic emission can be computed using Eq. (27). This comprehensive theory of electron emission serves to elucidate the emission behavior of electrons from one-dimensional conducting materials such as carbon nanotubes. It is noteworthy that the dimension of the one-dimensional current density is electrical current (A), whereas for the three-dimensional current density, it is electrical current divided by area (A/m2).

6. Results and Discussions

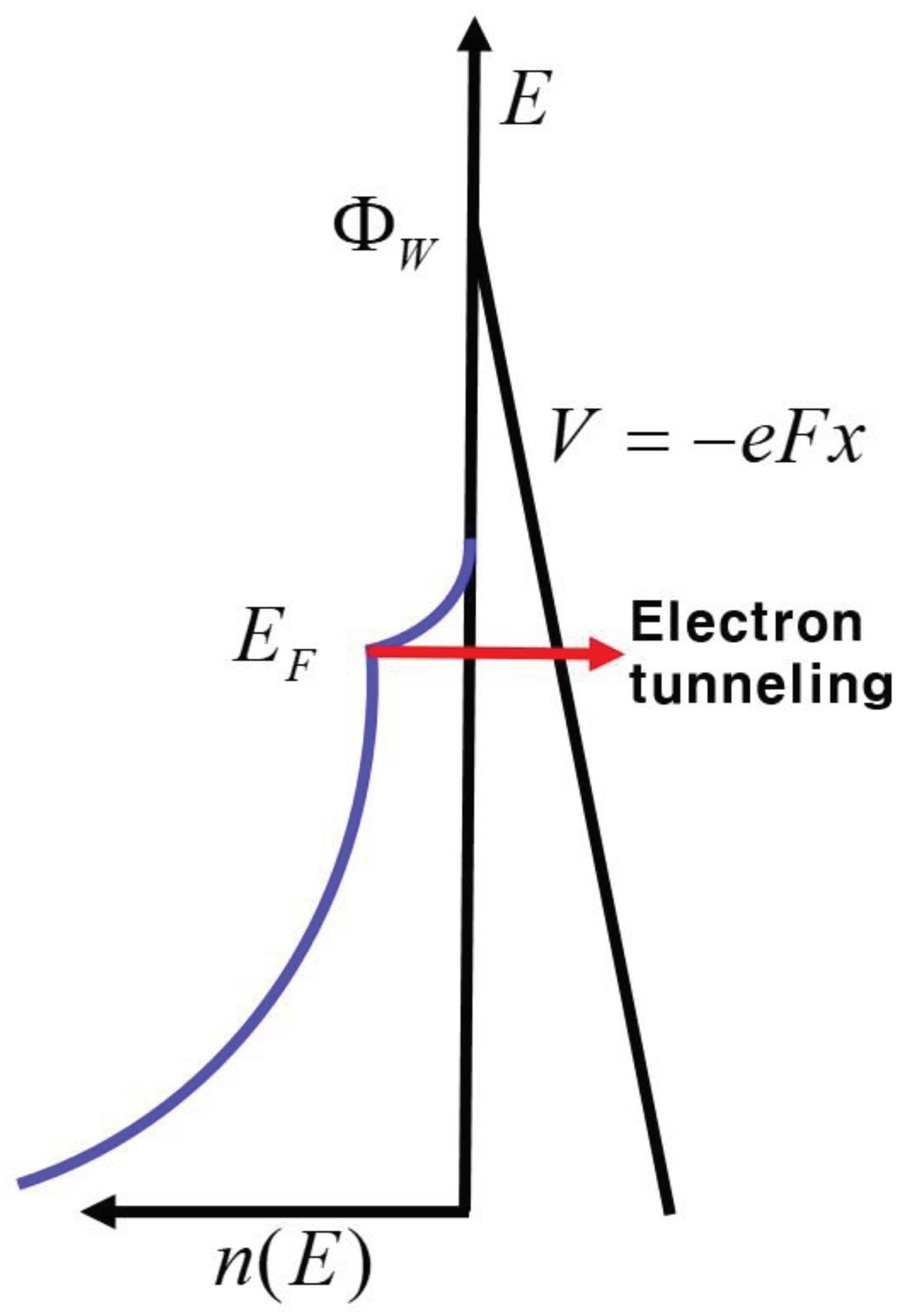
Figure 1 depicts a schematic representation of one-dimensional electron emission. A robust local electric field is directed along the x-axis within the metal. At zero temperature, electrons occupy energy levels up to Fermi energy. As temperature rises, these electrons become excited, reaching energy levels exceeding Fermi energy and, subsequently, surpassing the work function. Thermally excited electrons, whose energy levels exceed that of the vacuum, participate in thermionic emissions. On the other hand, under a strong electric field, electrons with energy levels below the vacuum energy engage in quantum tunneling, constituting the generalized field emission.
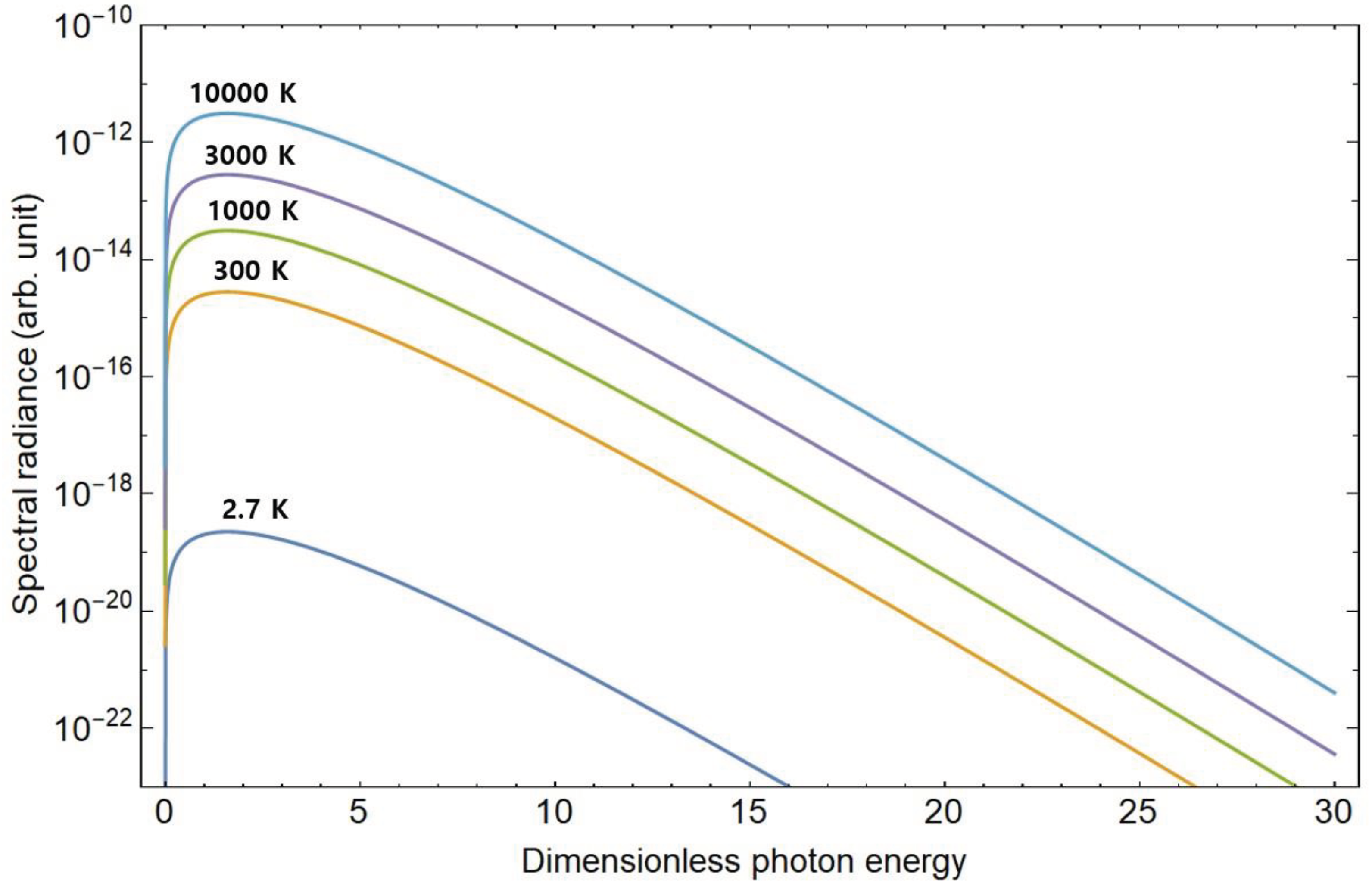
Figure 2 depicts the spectral radiance for various temperatures in one-dimensional materials, presented in terms of dimensionless photon energy. The spectral radiance, as defined in Eq. (9), is expressed as dimensionless photon energy ( h ν k B T ) for various temperatures in one-dimensional materials. The temperature sequence in Figure 2, progressing from bottom to top, corresponds to 2.7 K, 300 K, 1000 K, 3000 K, and 10000 K, respectively. It is noteworthy that the unit of one-dimensional energy density is joules per meter (J/m), while the unit for the three-dimensional energy density is joules per cubic meter (J/m³).
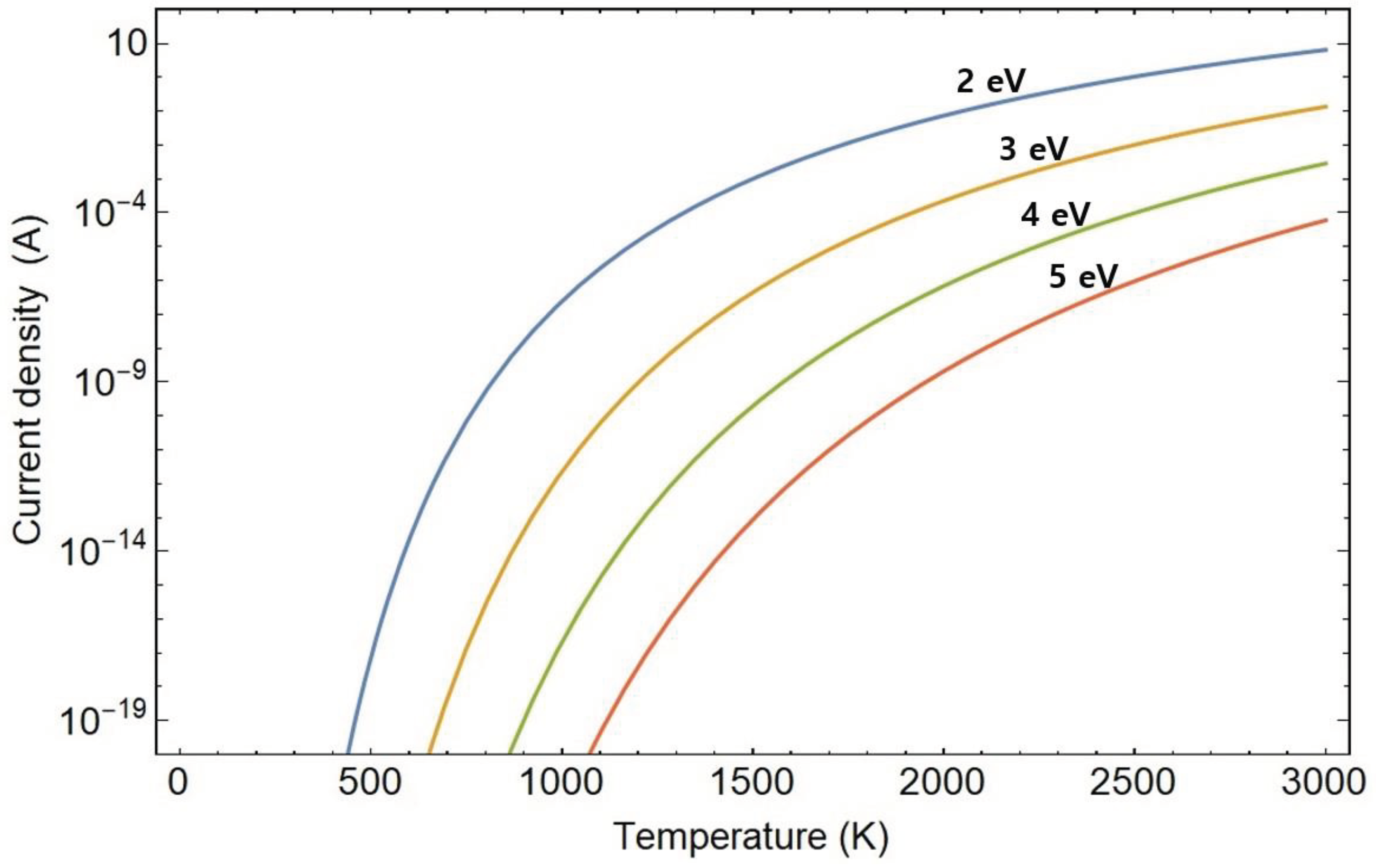
In Figure 3, the variation of one-dimensional current density with temperature is presented for different materials characterized by distinct work functions. The calculation of one-dimensional current density is performed for materials with a Fermi energy of 4.57 eV and varying work functions from 2 to 5 eV. The observed trend indicates that the one-dimensional current density rises with increasing temperature and decreasing work function.
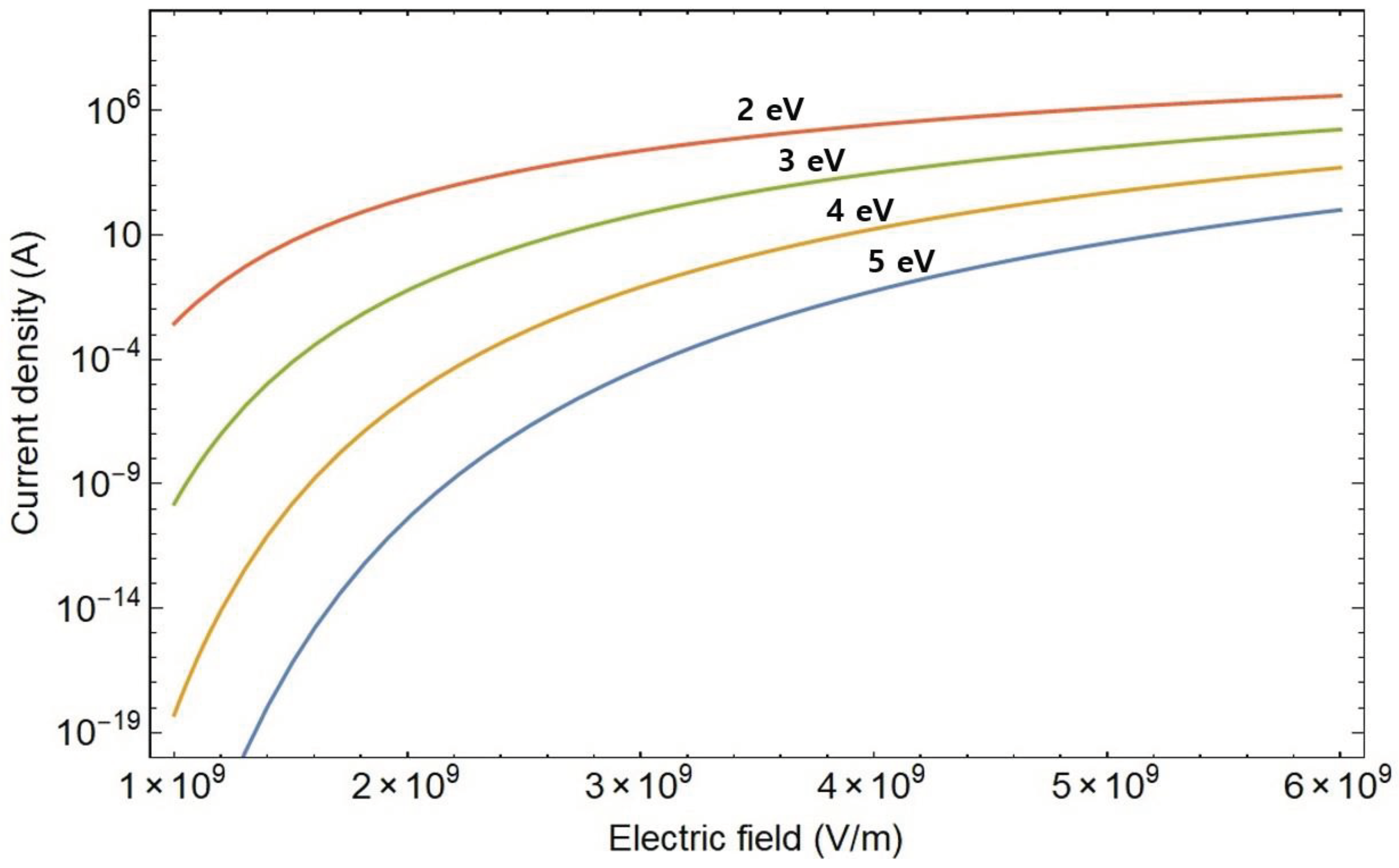
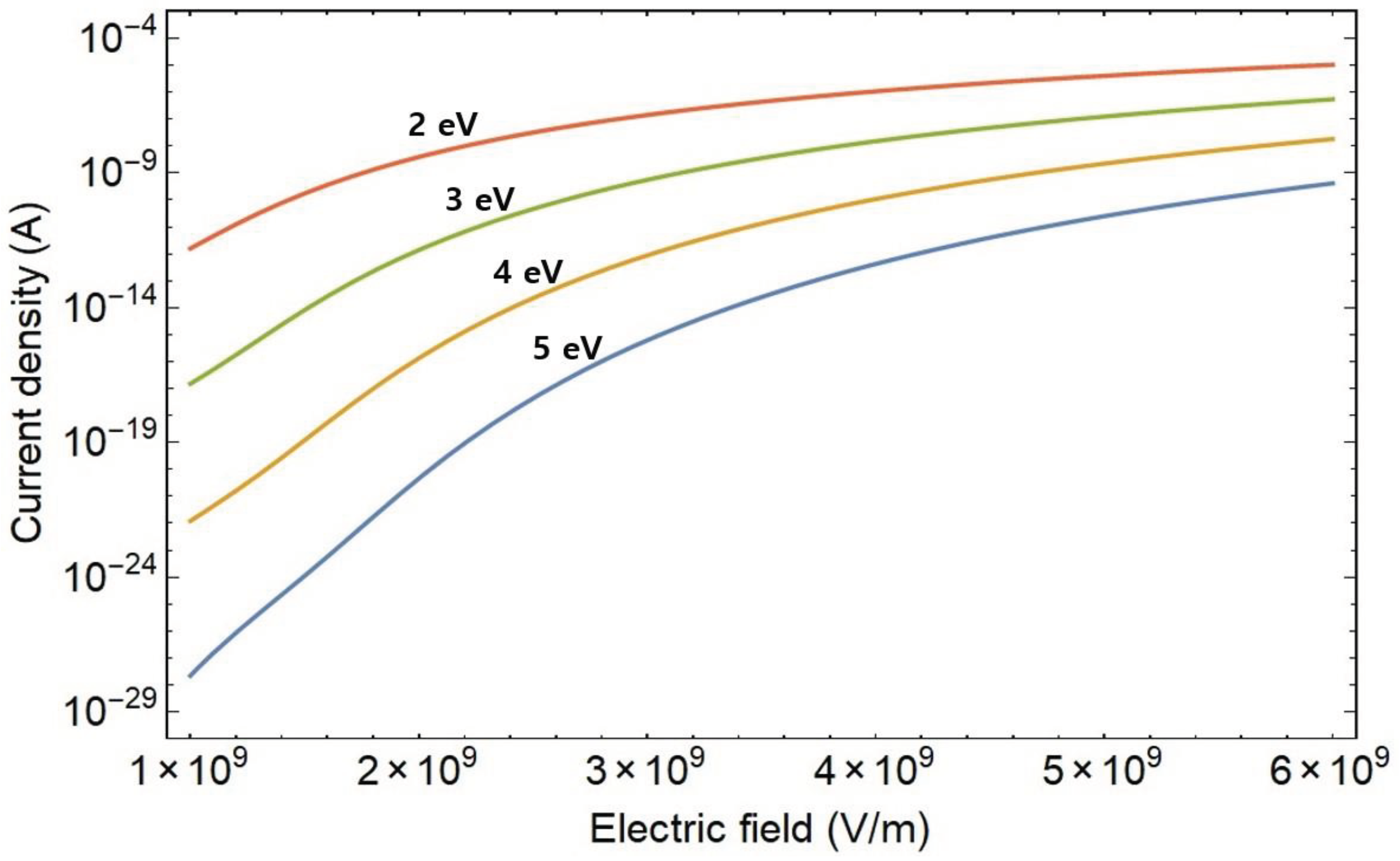
Figure 4 illustrates the one-dimensional current density plotted against the electric field for various materials characterized by various work functions. The calculation of one-dimensional current is conducted for materials with a fixed Fermi energy of 4.57 eV and varying work functions ranging from 2 to 5 eV. It is observed that the one-dimensional current density of the conducting material increases with an increase in the electric field and a decrease in the work function.
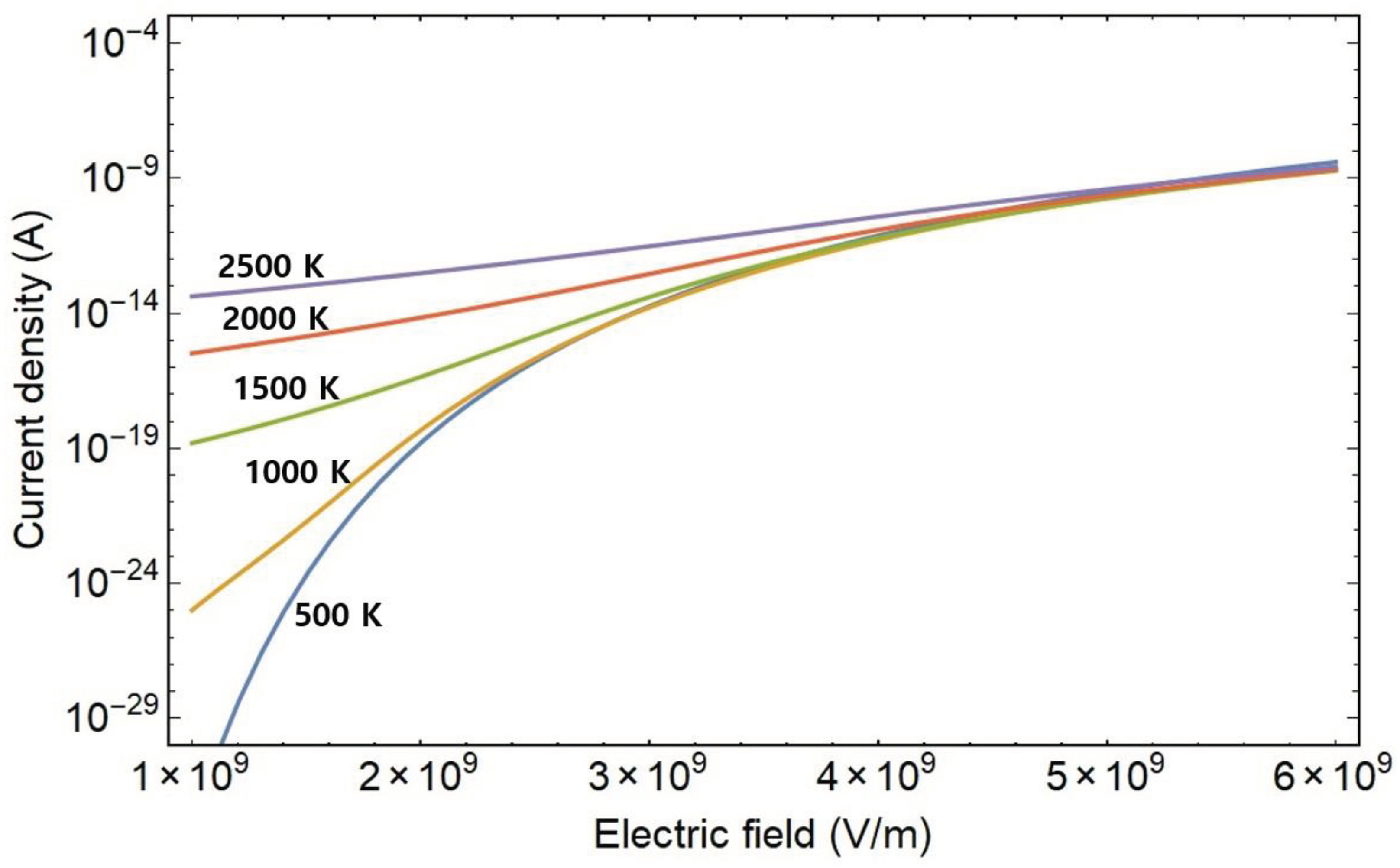
In Figure 5, the one-dimensional current density of carbon nanotubes is presented as a function of the electric field. The work function and Fermi level function for carbon nanotubes are specified as 4.56 eV and 4.57 eV, respectively. The temperatures range from 500 K to 2500 K, progressing from bottom to top. The depicted trend reveals that the current density emitted from carbon nanotubes rises with increases in both the temperature and the applied accelerating field.
Figure 6 illustrates the variation of one-dimensional current density with the applied electric field for various work functions, maintaining a constant temperature of 1000 K. The depicted graph presents a sequence of work functions ranging from 2 to 5 eV, from top to bottom. The observed trend indicates that the current density increases with a rise in the applied accelerating field.
This research is valuable for understanding electron emissions originating from both electric potential energy and thermal energy within diverse one-dimensional materials.

7. Conclusion

We have formulated a comprehensive electron emission theory that covers arbitrary thermal energy and electric potential energy across various one-dimensional materials. The analysis includes the spectral radiance for one-dimensional thermal radiation, illustrated with dimensionless photon energy across various temperatures in such materials. Additionally, calculations for the thermionic and field emission current densities are conducted for one-dimensional conductors. The generalized current densities, applicable at any temperature and under an applied electric field, are derived and computed for one-dimensional materials. The resulting one-dimensional current density is depicted as a function of temperature and accelerating field, considering different materials with varying work functions. Furthermore, the electron emission current for carbon nanotubes is shown for temperature and accelerating field, providing insights into their emission behavior.

Author Contributions

H.K.: Conceptualization, data curation, investigation, writing—original draft, writing—review and editing. C.P.; data curation, investigation, validation, writing—review and editing. S.Y.; investigation, validation, funding acquisition, writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This study was carried out as part of an inter-ministerial collaboration project supported by the Korea Institute for Advancement of Technology (KIAT) under the Ministry of Trade, Industry and Energy (MOTIE) (Project No. P0022203).

Data Availability Statement

Data is available on request.

Acknowledgments

The authors would like to thank all the researchers who discuss about electron emissions in RAON.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Planck, M. On the law of distribution of energy in the normal spectrum. Ann. Phys. 1901, 309, 553. [Google Scholar] [CrossRef]
  2. Kim, H.; Jeon, S.; Jung, Y.; Kim, J. Magnetic heating effect for quarter-wave resonator (QWR) superconducting cavities. Quantum Beam Sci. 2023, 7, 21. [Google Scholar] [CrossRef]
  3. Landsberg, P.T.; De Vos, A. The Stefan-Boltzmann constant in n-dimensional space. J. Phys A Math. Gen. 1989, 22, 1073. [Google Scholar] [CrossRef]
  4. Kim, H.; Kim, W.; Park, G.T.; Shin, I.; Choi, S.; Jeon, D.O. Generalized thermal radiation from arbitrary fractional dimension. Infrared Phys. Technol. 2014, 67, 600. [Google Scholar] [CrossRef]
  5. Yu, S.J.; Youn, S.J.; Kim, H. Size effect of thermal radiation. Physica B 2010, 405, 638. [Google Scholar] [CrossRef]
  6. Kim, H.; Youn, S.J.; Yu, S. J. Finite size effect of one-dimensional thermal radiation. J. Korean Phys. Soc. 2010, 56, 554. [Google Scholar] [CrossRef]
  7. Kim, H.; Chu, S.; Lee, Y.H. Size effect of two-dimensional thermal radiation. Phys. Lett. A 2011, 375, 2661. [Google Scholar] [CrossRef]
  8. Kim, H.; Han, M.S.; Perello, D.; Yun, M. Effective temperature of thermal radiation from non-uniform temperature distributions and nanoparticles. Infrared Phys. Technol. 2013, 60, 7. [Google Scholar] [CrossRef]
  9. Kim, H.; Park, C.S.; Han, M.S. Effective temperature of two- dimensional material for non-uniform temperature distribution. Opt. Commun. 2014, 325, 68. [Google Scholar] [CrossRef]
  10. Kim, H.; Kim, W.; Park, G.T.; Park, C.S.; Cho, H.D. Size effect of the effective temperature in one-dimensional material. Infrared Phys. Technol. 2014, 67, 49. [Google Scholar] [CrossRef]
  11. Richardson, O.W. On the negative radiation from hot platinum. Math. Proc. Camb. Philos. Soc. 1901, 11, 286. [Google Scholar]
  12. Ang, Y.S.; Yang, H.Y.; Ang, L.K. Universal scaling laws in Schottky heterostructures based on two-dimensional materials. Phys. Rev. Lett. 2018, 121, 056802. [Google Scholar] [CrossRef] [PubMed]
  13. Wei, X.; Chen, Q.; Peng, L. Electron emission from a two-dimensional crystal with atomic thickness. AIP Advances 2013, 3, 042130. [Google Scholar] [CrossRef]
  14. Kim, H.; Lee, J. K. Generalized thermionic emission for arbitrary dimension. J. Korean Phys. Soc. 2019, 74, 701. [Google Scholar] [CrossRef]
  15. Fowler, R.H.; Nordheim, L.W. Electron emission in intense electric fields. Proc. Roy. Soc. A. 1928, 119, 173. [Google Scholar]
  16. Gomer, R. Field Emission and Field Ionization; Harvard University Press: Boston, MA, USA, 1961. [Google Scholar]
  17. Schwettmant, H. A.; Turneaure, J.P.; Waites, R.F. Evidence for surface-state-enhanced field emission in rf superconducting cavities. J. Appl. Phys. 1974, 45, 914. [Google Scholar] [CrossRef]
  18. Klein, U.; Turneaure, J. Field emission in superconducting RF cavities. IEEE Trans. Magn. 1983, 19, 1330. [Google Scholar] [CrossRef]
  19. D. Moffat, D.; et al. Studies on the nature of field emission sites. In Proc. 5th Int. Conf. RF Superconductivity (SRF’91), Hamburg, Germany, 1991. SRF91D02; p. 245.
  20. Sakai, H.; Cenni, E.; Enami, K.; Furuya, T.; Sawamura, M.; Shinoe, K.; Umemori, K. Field emission studies in vertical test and during cryomodule operation using precise x-ray mapping system. Phys. Rev. Accel. Beams. 2019, 22, 022002. [Google Scholar] [CrossRef]
  21. de Heer, W.A.; Chatelain, A.; Ugarte, D. A carbon nanotube field-emission electron source. Science 1995, 290, 1179. [Google Scholar] [CrossRef]
  22. Bonard, J.; Kind, H.; Stockli, T.; Nilsson, L. Field emission form carbon nanotubes: the first five years. Solid-State Electron 2001, 45, 893. [Google Scholar] [CrossRef]
  23. Chouhan, V.; Noguchi, T.; Kato, S. Field emission from optimized structure of carbon nanotube field emitter array. J. Appl. Phys. 2016, 119, 134303. [Google Scholar] [CrossRef]
  24. Kim, H.; Lee, J.K.; Park, C.-S. Generalized n-dimensional field emission. J. Korean Phys. Soc. 2021, 79, 363. [Google Scholar] [CrossRef]
  25. Kim, H.; Lee, S. Unified theory of thermionic and field emission for two-dimensional conducting materials. J. Korean Phys. Soc. 2022, 80, 167. [Google Scholar] [CrossRef]
Preprints 100213 g001
Figure 1. Diagram illustrating generalized electron emission in one-dimensional materials. An accelerating field is directed along the x-axis and applied to the metal. Thermally excited electrons with energy levels surpassing the vacuum threshold engage in thermionic emissions. Electrons experiencing a strong electric field, with energy levels below the vacuum threshold, partake in quantum tunneling, constituting the generalized field emission.
Figure 1. Diagram illustrating generalized electron emission in one-dimensional materials. An accelerating field is directed along the x-axis and applied to the metal. Thermally excited electrons with energy levels surpassing the vacuum threshold engage in thermionic emissions. Electrons experiencing a strong electric field, with energy levels below the vacuum threshold, partake in quantum tunneling, constituting the generalized field emission.
Preprints 100213 g001
Preprints 100213 g002
Figure 2. Spectral radiance presented as dimensionless photon energy for various temperatures in one-dimensional materials. The spectral radiance, as defined in Eq. (9), is represented with dimensionless photon energy ( x = h ν k B T ) across different temperatures in one-dimensional materials. The sequence of temperatures, ranging from bottom to top, corresponds to 2.7, 300, 1000, 3000, and 10000 K, respectively.
Figure 2. Spectral radiance presented as dimensionless photon energy for various temperatures in one-dimensional materials. The spectral radiance, as defined in Eq. (9), is represented with dimensionless photon energy ( x = h ν k B T ) across different temperatures in one-dimensional materials. The sequence of temperatures, ranging from bottom to top, corresponds to 2.7, 300, 1000, 3000, and 10000 K, respectively.
Preprints 100213 g002
Preprints 100213 g003
Figure 3. One-dimensional current density with temperature for various materials characterized by distinct work functions. The calculation of one-dimensional current density is conducted for materials with a Fermi energy of 4.57 eV and various work function materials, specifically 2, 3, 4, and 5 eV, respectively.
Figure 3. One-dimensional current density with temperature for various materials characterized by distinct work functions. The calculation of one-dimensional current density is conducted for materials with a Fermi energy of 4.57 eV and various work function materials, specifically 2, 3, 4, and 5 eV, respectively.
Preprints 100213 g003
Preprints 100213 g004
Figure 4. One-dimensional current density plotted against the accelerating field for materials with varying work functions. The calculation involves determining the one-dimensional current density for materials with a common Fermi energy of 4.57 eV and different function materials, specifically 2, 3, 4, and 5 eV, respectively.
Figure 4. One-dimensional current density plotted against the accelerating field for materials with varying work functions. The calculation involves determining the one-dimensional current density for materials with a common Fermi energy of 4.57 eV and different function materials, specifically 2, 3, 4, and 5 eV, respectively.
Preprints 100213 g004
Preprints 100213 g005
Figure 5. One-dimensional current density of carbon nanotubes plotted against the accelerating field. In the case of carbon nanotubes, the work function and Fermi level are specified as 4.56 eV and 4.57 eV, respectively. The represented temperatures ascend from bottom to top, representing 500, 1000, 1500, 2000, and 2500 K, respectively.
Figure 5. One-dimensional current density of carbon nanotubes plotted against the accelerating field. In the case of carbon nanotubes, the work function and Fermi level are specified as 4.56 eV and 4.57 eV, respectively. The represented temperatures ascend from bottom to top, representing 500, 1000, 1500, 2000, and 2500 K, respectively.
Preprints 100213 g005
Preprints 100213 g006
Figure 6. One-dimensional current density plotted against the applied electric field for materials featuring various work functions, all at a constant temperature of 1000 K. In the sequence from top to bottom, the depicted work functions correspond to 2, 3, 4, and 5 eV, respectively.
Figure 6. One-dimensional current density plotted against the applied electric field for materials featuring various work functions, all at a constant temperature of 1000 K. In the sequence from top to bottom, the depicted work functions correspond to 2, 3, 4, and 5 eV, respectively.
Preprints 100213 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated