Prerpints.org logo
Preprint
Review

Hox Gene Collinearity with Pulling Physical Forces Create a Hox Gene Clustering in Embryos of Vertebrates, Invertebrates, Complete or Split Clutters

Altmetrics

Downloads

105

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 March 2024

Posted:

05 March 2024

You are already at the latest version

Alerts
Abstract
Hox gene clusters are crucial in Embryogenesis. It was observed that some Hox genes are located in order along the telomeric to centromeric direction of the DNA sequence: Hox1, Hox2, Hox3…. These genes are expressed in the same order in the ontogenetic units of the Drosophila embryo along the Anterior-Posterior axis. The two entities (genome and embryo) differ significantly in linear size and in-between distance. This strange phenomenon was named Spatial Collinearity (SP). Later, it was observed that, particularly in the Vertebrates, a Temporal Collinearity (TC) coexists: first is Hox1 expressed, later Hox2 and even later Hox3,…,. According to a Biophysical Model (BM), pulling forces act at the anterior end of the cluster while a cluster fastening applies at the posterior end. Hox clusters are irreversibly elongated along the force direction. During Evolution, the elongated Hox clusters are broken at variable lengths thus split clusters may be created. An Empirical Rule was formulated distinguishing development due to a complete Hox cluster from development due to split Hox clusters. BM can ‘explain’ this Empirical Rule. In a spontaneous mutation where the cluster fastening is dismantled, a weak pulling force automatically shifts the cluster inside the Hox activation domain. This cluster translocation can probably explain the absence of Temporal Collinearity in Drosophila.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

In 1978 E.B. Lewis discovered a fundamental property of  Developmental Biological: Hox Gene Collinearity (HGC). HGC is the  long- range interaction of entities where the archetypical example is the Coulomb force relating material objects at different geometric ranges. In particular, HGC correlates genes (entities inside the cell nucleus) with embryonic units. These entities are quite apart from each other.
Hox genes play an important role in the development of most animals and plants. Some Hox genes form clusters which are crucial for the Embryogenesis of Metazoa. The importance of this clustering was noticed by Lewis who studied the genetics of Drosophila [1]. He observed that some genes of the genome (later coined Hox genes) were located in order along the telomeric to centromeric direction and were denoted (Hox1, Hox2, Hox3…). Lewis noticed that the genes of these clusters were expressed in the same order along the anterior-posterior axis of the Drosophila embryo (Figure 1) [1]. This is an astonishing event since this correlation occurs between extremely distant domains - in one hand the gene sequence in the cell nucleus and in the other the Drosophila embryo. Biomolecular interactions alone  cannot create such correlations [2]. This surprising phenomenon was named Spatial Collinearity (SC). Some years later, another collinearity was observed particularly in the Vertebrates: Temporal Collinearity (TC). According to TC, the first Hox gene (Hox1) of the Hox cluster starts being expressed. Later, Hox2 is expressed and even later Hox3 followed until all Hox genes are expressed following the sequence Hox1, Hox2, Hox3… [3].
In order to explain these phenomena, I proposed in 2001 a Biophysical Model (BM) according to which, pulling physical forces could explain the experimental findings [2,4] (Figure 1a, b). Several predictions of BM were compared to many collected data and the comparison confirmed BM [5,6].  
A simple heuristic expression for these pulling forces F was proposed [7,8].
F = N * P
In Eq.(1), F is a simplification of the pulling Coulomb force since the distance between the electric charges (N and P) is missing. This ‘quasi Coulomb force’ F is applied at the telomeric end of the Hox cluster. It turns out that this arbitrary omission of the Coulomb range reflects a deep connection of these ‘quasi- Coulomb’ forces to the fundamental phenomenon of Symmetry (see Section 2.1 and Section 2.2). Ν and P stand for the negative and positive electric charges acting on a Hox cluster. In the above heuristic formulation, the Hox cluster consists of a deployed finite sequence of Hox genes along the telomeric to centromeric ends of the cluster (Hox1, Hox2, Hox3…). The numbers assign the gene order in the cluster. These numbers determine the order membership to the Paralogy Group (PG). (Here is followed Duboule’s definition of PG [9]).
As mentioned above, (N) represents the microscopic contribution to F and it is a real entity – the negative electric charge of the DNA sequence in the cell nucleus. (P) represents a positively charged molecular structure located opposite the telomeric end of the Hox cluster (Figure 1). Contrary to N, P is a fictitious entity as yet, standing for the embryonic-macroscopic contribution to F. Note that the known morphogens of the present time like Sonic Hedgehog, Fibroblast Growth Factors, Retinoic Acid and the plethora of other morphogenetic factors were fictitious fifty years ago. The existence of P does not contradict any First Principle so it is legitimate to anticipate its existence as advocated in [4]. F pulls the Hox genes sequentially out of the cluster (Figure 1). As mentioned already, Eq.(1) is a heuristic expression that was successfully tested in several experiments [5,6,7,8].
Hox genes control the normal development of animals (wild type). Spontaneous mutation of these genes cause severe malformations (Homeosis), consisting of parts of the animal growing in the wrong location of the body. In Homeosis PG ordering is violated.
About twenty years ago, an important advancement was achieved concerning the transfer of specific molecules from outside the cell into the inner domain of the cell nucleus [10,11,12,13]. For example, it was noticed that significant amounts of Activin are gathered outside the cell nucleus. Controlled amounts of this activin were transduced inside the nucleus causing specific modifications on the genome. It is assumed that BM combined with the action of transduction technology can affect Hox gene expression. This possibility is incorporated in the present Review.
BM is based on the hypothesis that pulling forces are applied at the telomeric end of the Hox cluster. This hypothesis was elaborated in detail and it was concluded that the cluster is elongated along the direction of the force [14]. This BM prediction wash later confirmed [15,16,17]. In some cases the measured elongation of the activated Hox cluster was five times longer than the length of the inactive Hox cluster [16]. When Hox cluster activation is initiated, a weak force (F1) pulls the first gene of the cluster (Hox1) out of its niche toward the interchromosome domain (ICD) (Figure 1(a), (b)).
Particularly Hox1 is directed towards the transcription factory domain (TFD) where Hox gene activation (expression) is possible [18,19]. The pulling forces increase irreversibly: i) increasing along the gene location from Hox1 towards Hox13 (Hox1 → Hox13), and ii) following the time course t1 → t3. Under force F2 (F2 > F1) Hox1 and Hox2 are extruded from their niche. This process continues until all Hox genes of a complete Hox cluster are transferred in the TFD. In the mechanical analogue, for the efficient function of an elongated elastic spring, besides the pulling force at one of its ends, a proper fastening should be applied at its other end. Accordingly, the Hox cluster should be fastened at the centromeric end of the cluster (Figure 1(b)).
The Vertebrate Hox clusters comprise four homologue clusters (HoxA, HoxB, HoxC, and HoxD) as shown in Figure 1(c) [11]. Each homologue cluster is included in a separate chromosome. In these homologue clusters the PG identity is conserved. However, in the course of Evolution, modifications of the mouse genes are possible up to the point of gene deletion. This ordered mouse Hox clusters remind of a ‘ratchet’ allowing motion in one irreversible direction only [8]. Note that some ‘teeth’ of the ratchet may be missing (corresponding to Hox genes deleted in the course of Evolution).
Besides Vertebrates, the contemporary cephalochordate Amphioxus is a descendant of the ancestor Amphioxus. This ancestor Amphioxus was the ancestor of both Drosophila and vertebrates [9]. Amphioxus lived after the Cambrian period of evolutionary explosion 500 million years ago (Mya). Vertebrates and Drosophila appeared a few Mya later. Amphioxus has 14 Hox genes whereas vertebrates and Drosophila have 13 (Hox14 is missing).

2. Symmetries

2.1. Symmetry

Symmetry is the cornerstone of Science and several other human intellectual activities. Many distinguished scientists have proposed their definition of the term. When an action is applied on any material object (or physical system) it causes its change. If this change leaves the system invariant, the system is symmetric. This means that any point of the system moves to another point contained in the system. I consider the compact definition of Frank Wilczek (in the form of an aphorism) is appropriate: Symmetry is a change without change [20]. The human intellect incorporates a wider realm than pure scientific thinking. Therefore, Wilczek’s definition of Symmetry could be complemented with unusual thoughts e.g. ‘Symmetry is complicated, ‘Symmetry is beautiful’ or even ‘lack of symmetry is ugly’.

2.2. Noether’s Theory in Developmental Biology

In 1918 Emmy Noether formulated and proved in Classical Mechanics a fundamental theorem on Symmetry. In simple terms, Noether proved that any physical system obeying a symmetry law is escorted by a conserved physical quantity [20,21]. For example, if the physical system is invariant under time translations (that means it is independent of when is put the origin of measuring the time) the energy of the system is conserved [20,21]. The significance of Noether’s theory is evident. Its applications extend from the symmetries in Classical Mechanics to the complicated symmetries of the elementary particles – the numerous constituents of the universe [20,21,22].
Besides the obvious external symmetries in Space and Time, there appeared in the last century the need to introduce several internal symmetries and particularly in the field of elementary particles where these material constituents are given exotic names like bosons, quarks, charmed particles, mesons etc [22,23]. Historically, in 1932, W. Heisenberg was the first who introduced such esoteric terms (e.g. the isotopic spin or isospin to described the symmetry of interchanging protons and neutrons under the strong nuclear interactions [23]
Another important application of Noether’s theory is the following: assume that the equations of a dynamic system are invariant under space translations. According to Noether’s theory such a symmetric system is necessarily followed by a conserved quantity - in this case it is the momentum. [22,23].
The heuristic equation introduced in the Introduction has the form
F = N * P
which is a ’quasi’ Coulomb force. The proper Coulomb force (CF) is
CF = (Q1 * Q2)/ R2
CF is a long-range force since its range R is unlimited. In contrast, the quasi-Coulomb force F has no geometric range since it depends only on the electric charges N and P. The electric charges Q1 and Q2 may be attractive (if one charge is positive and the other negative) or repulsive (if both charges are either positive or negative).
In the quasi-Coulomb force F, the dependence on R is missing. This arbitrary absence of Geometry is motivated by sheer simplicity as mentioned in the Introduction. However, it turns out that this simplicity is unexpectedly related to the internal Symmetries [23].
Among its numerous applications, Noether’s theory was used in the study of important biological issues. Self-similarity is the particular symmetry of objects which, although different, they look the same if depicted under suitable scale units. Such objects are the fractals where the part looks like the whole [24]. A typical example is the Barnsley fern that can be easily drawn using a computer program. B. Mandelbrot invented this branch of Applied Mathematics and introduced the term of fractals [24].
Self-similarity is a continuous symmetry applying to all spatial lengths. The finite sequence of ordered Hox genes associated with the ordered embryonic units constitute a very limited ‘primitive’ self similarity since it applies to only two discrete spatial dimensions. Consequently, it is expected that only a remnant symmetry to emerge as shown in Figure 1(c).
In this Figure, in the mouse homologue Hox gene clusters only PG is preserved. The set of Hox genes is reminiscent of an irreversibly advancing ‘ratchet’ where some Hox genes are missing [8]. In this remnant self-similarity, only PG ordering is conserved and it is here assumed that it constitutes the conserved quantity of Noether’s theory. Some Hox genes of the cluster may fade out up to extinction during the Whole Genome Duplication of the evolutionary process, as mentioned above [8,11].
In another biological application, Noether’s theory was recently used in a comparison of DNA sequences of different animal phyla [25].
In any measurement, Symmetry in a variable quantity requires that this variable is absent in its constituent equations. In order to clarify this point, it is followed the reasoning of Iliopoulos [23]. Consider a completely symmetric body (e.g. the sphere in 3D space) as described in a Cartesian system of axes (x, y, z) or a Polar coordinates system ( z, φ, θ). Any measurement in the sphere contains the variable angles θ and φ. It turns out that the constituent equation of the sphere is:
x2+ y2 + z2 = R2
where R is the radius of the sphere. In this equation, the variables (θ, φ) are indeed missing in agreement with the above symmetry requirement: no angular dependence is involved [23].
In Eq.(1) for the quasi-Coulomb force F, the term R-2 is missing, so F is an even simpler equation than the proper Coulomb force. The meaning of this omission is that the heuristic pulling force of the BM is a quantity independent of the 3D geometric space:
Note that in this space, the symmetry of F becomes internal, reminiscent of Heisenberg’s internal variable- the isotopic spin [23].

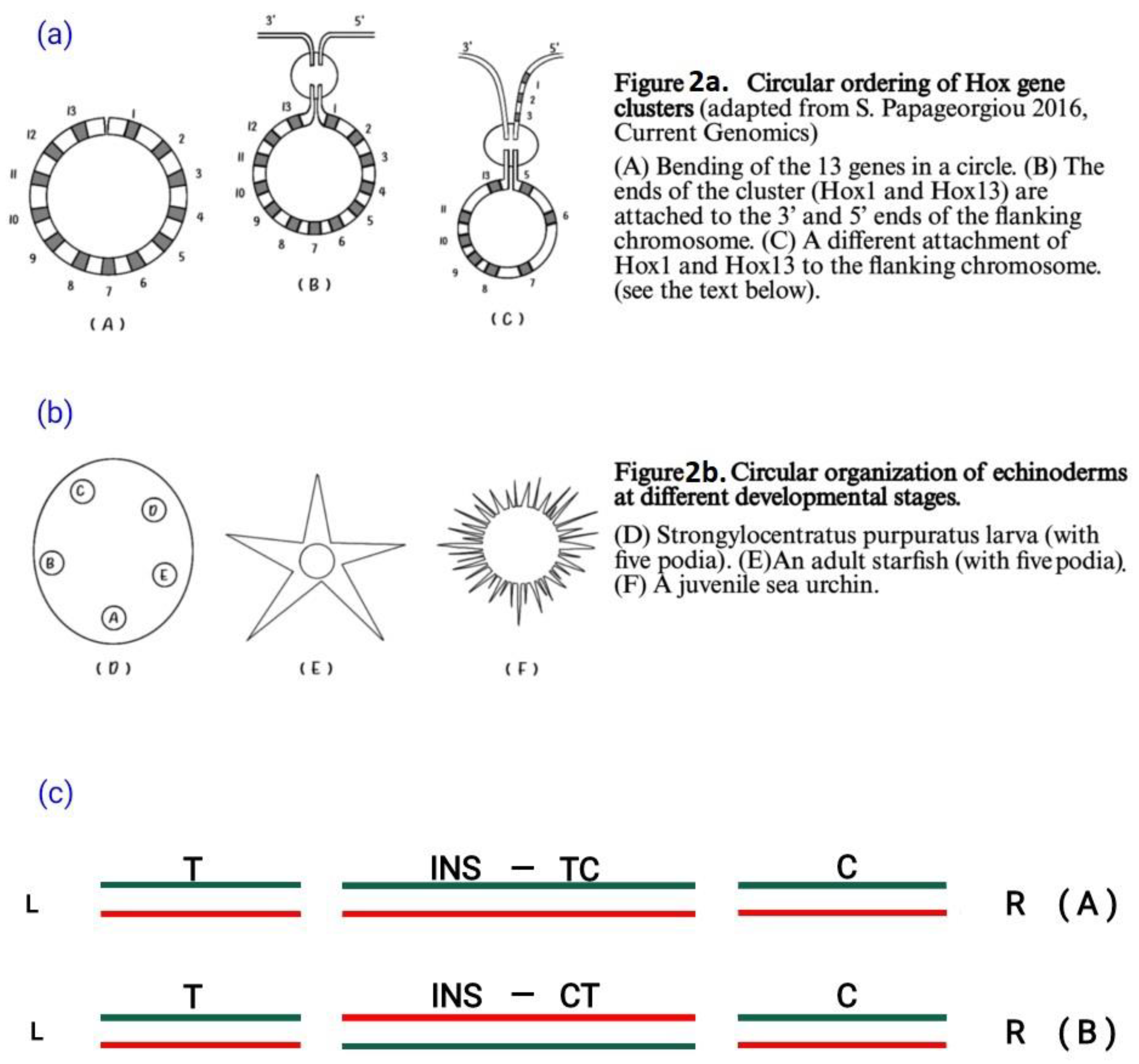
3. Insertion of a DNA Fragment in a Hosting DNA Sequence

Besides the ordering of Hox genes on a finite straight line, in many early larva embryos (e.g. the echinoderms) a circular ordering is superimposed on this finite line as shown in Figure 2a(A).
In Figure 2a(B) the two ends of the circular cluster are attached to the 3’ and 5’ ends of the flanking chromosome. If the 3’ end of the flanking chromosome is attached to Hox1 (and 5’ to Hox13) no novelty is created and A.planci normal Hox gene order gene is reproduced (Figure 2aB). In contrast, if the 5’ end of the flanking chromosome is attached to Hox1, Hox2. Hox3 (shown in Figure 2aC) a novelty is created. A second breaking follows leading to a new Hox gene order which corresponds to the Hox gene order of the sea urchin [8].
The circular Hox gene clusters can be incorporated in the flanking DNA sequence of the genome. A recent review by T. Hanscom refers to the well known technique of double strand break (DSB) [26,27]. In the above review, besides the usual medical applications of the DSB methodology, it is extensively emphasized the novel trends of research to explore how DSB can leverage genome evolution. In Figure 2(c) the incorporation of a Hox cluster (INS---) in the flanking genome is schematically depicted.

3. Complete vs Split Hox Clusters

Hox Gene Collinearity (both Spatial and Temporal) has been unequivocally confirmed in the Vertebrates. However, in recent years it was found that this is not true in many other animal species, particularly in invertebrates. For instance, it was observed that Hox collinearity is violated in the lophotrochozoa and this violation was associated with the brachiopods whose Hox cluster is broken [26,27]. In brachiopods both spatial and temporal collinearities are violated, while lophotrochozoan morphological novelties result from Hox Collinearity violation [26]. It was argued above that for the insertion of a circularly organized Hox cluster in the flanking genome, a break (split) of the cluster is necessary. It is clear that Hox cluster splitting is a necessary step for evolutionary novelties.
It has been emphasized that tight Hox clustering is lost during Evolution [28,29,30,31]. More specifically D. Ferrier and P. Holland observed that Hox clusters are constrained by TC in their gene order [28,29]. Moreover, complete Hox clusters are associated with the spectrum of Hox gene expressions along the whole Anterior – Posterior embryonic axis. Otherwise, if the gene expression does not extend along the whole A-P axis, the Hox gene cluster is split. In this cluster splitting tendency, the Hox clusters ‘may fall apart when TC is no more needed for [28,29]. Similar arguments were put forward by several other authors before and after the above observation [29,30].
Drosophila has a typically split Hox cluster. The Drosophila Hox cluster has 13 genes consisting of two subclusters ANT-C and BX-C depicted in Figure 3 [29].
Drosophila, together with the vertebrate Hox cluster, originates from a large ancestral Hox cluster. Cloning had later identified Amphioxus as the common ancestor of insects and vertebrates [28], and a one-to-one correspondence between the Amphioxus Hox genes and the Drosophila Hox genes was confirmed [28,29]. However in this correspondence some Drosophila Hox genes of the ANT-C subcluster developed novel evolutionary non-Hox functions. For instance, the Drosophila complex of Hox genes (zen1, zen2, bcd) corresponds to the ancestral Amphioxus Hox3 gene. Some Central genes have evolved from tandem evolutionary duplications [29]. (See in [29] Figure 1). The BX-C subcluster consists of the 3 last genes (Ubx, Abd-A, Abd-B) of the Drosophila Hox cluster. The summarizing conclusion from the above analysis is that TC is responsible for a complete Hox cluster. If this is not possible (or not needed) the Hox cluster is split [28]. In any case SC is a necessity for a Hox cluster.
As stressed above, if TC extends to a fraction only of the Hox cluster range, the cluster is expected to split. In a way, Hox expression in a range between Anterior and Posterior ends (‘space’) is translated into ‘time)’- where TC coordinates a ‘Hox clock’- more exactly a ‘Hox timer’ since the time course is irreversible [30].

4. Discussion

4.1. Empirical Rule on Complete and Split Hox Clusters

With the above established knowledge, D. Duboule formulated recently a useful Empirical Rule (ER) for the Hox Gene clusters [30]: ‘A complete Hox cluster controlling development in time along the Anterior-Posterior axis is non-split, whereas animals developing according to a time-independent mechanism to produce their main body axis are licensed to split their clusters…
In a significant experiment of extended posterior upstream excisions, T. Kondo and D. Duboule had noticed that several Hox gene expressions (and particularly Hoxd4 and Hoxd10) were unexpectedly absent as if Temporal Collinearity (TC) had disappeared [30]. In this case, TC disappearance is not real - it is only fictitious [31]. However, in a different interpretation of the above Kondo and Duboule experiment a ‘prediction in retrospect’ of BM was formulated according to which TC disappears really (and not fictitiously) [32,33,34]. (Notice analogies in the following section 4.2 and section 4.3).

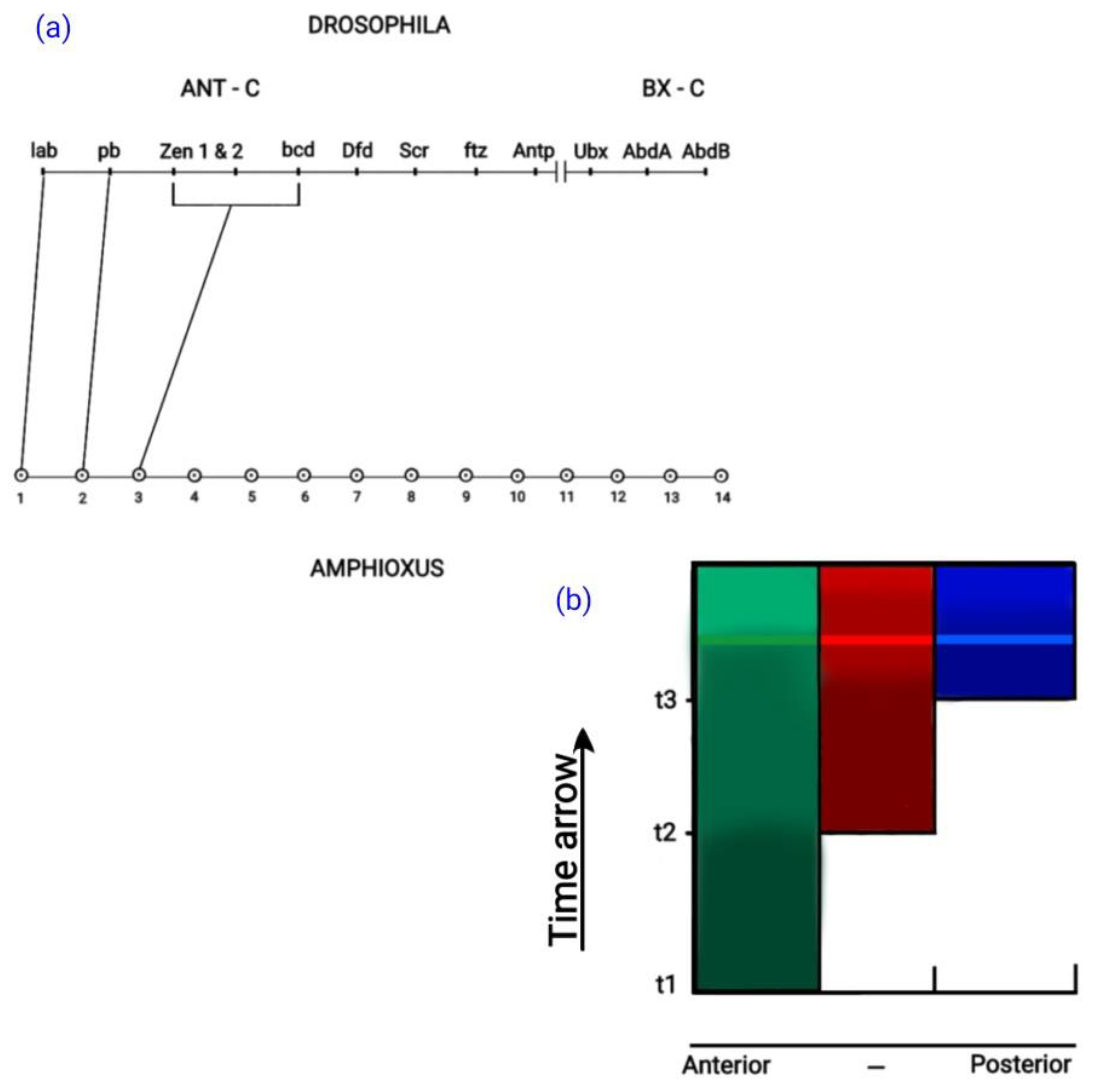
4.2. Development in the Secondary Developmental Axis

In chick limbs, it was observed that the apical ectodermal ridge (AER) controls development responding to morphogen Fibroblast Growth Factor (FGF) [32]. The last Hox13 gene of the cluster switches off when the AER is cut-off. [32]. the consequences from this experiment are illuminating [32]: Hox13 expression can be initiated again if beads soaked in FGF are implanted distally. This can occur after a fixed time interval. If the FGF dose is increased the Hox13 rescue occurs earlier. Furthermore, the rate of Hox13 spreading is faster initially and slower at later stages - a sign that passive diffusion is the main mechanism of signal propagation [32]. In the above chick limb bud experiment in the secondary developmental axis, Hox13 expression is most sensitive to AER excision [32]. However, Hox10 and Hox11 are less sensitive to this excision indicating that TC is not uniform along the developmental axis.

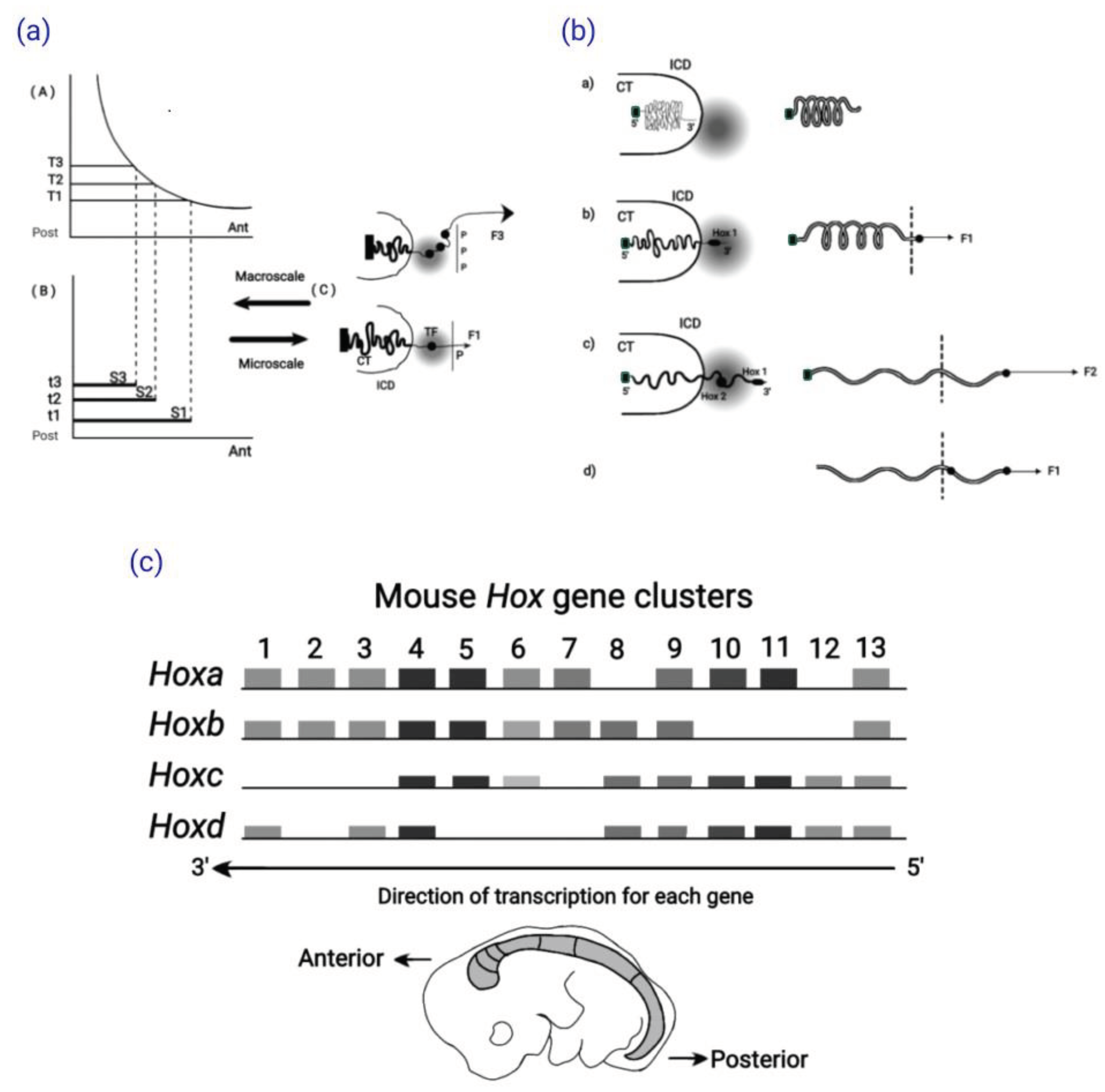
4.3. Development in the Mouse Primary Anterior-Posterior Axis

It is interesting to compare the above limb findings in to a similar experiment of upstream DNA excision in mouse embryos as described in [33,34]. In this excision experiments, TC disappearance was in agreement with the BM pulling forces model [33]. According to BM it is eventually expected TC to reappear. This expectation remains to be tested [33]. To this end it was proposed the reverse experimental path - the insertion of TGF-beta signals. (A detailed description is included in [34]). The proposed disappearance experiment and the eventual reappearance of TC is not completed. The direct course of disappearance is confirmed but the palindromic course of TC reappearance remains to be tested and its eventual experimental confirmation will be decisive [34].

4.4. Quantitative Collinearity

Relying on Lewis observation [1], A. Durston proposed a Hox cluster property (Posterior Prevalence) (PP) to guarantee the dominance of posterior Hox gene expressions over simultaneously expressed anterior Hox expressions [35,36].
Besides Spatial and Temporal collinearities, a third collinearity has also been traced: Quantitative Collinearity (QC). This was a puzzling issue and for a long time it was examined following a parallel path with the PP hypothesis. QC is determined following two directions in the two-dimensional plane. First is the direction along the down-up time irreversible direction (Figure 3b) and second is the expression intensity along the Anterior- Posterior axis. For the HoxD expression in a sequence of cells along the horizontal dashed line, the intensity is stronger at the posterior side (Figure 3b) [14]. The intensity at any point depends on its distance from the morphogen source. It turns out that in the limb, passive Diffusion is the main signal propagating mechanism whose size of spreading depends on the vicinity to the morphogen source [4,14]. It was measured that this size is higher near the morphogen source compared to the size of spreading at a distant location [32]. A similar mechanism applies for the expression of split clusters as mentioned in Section 3.

4.5. A Spontaneous Mutation in the Drosophila Case

In the Introduction it was stressed that spontaneous genetic mutations can lead to evolutionary novelties as in the case of Homeosis. If, in a spontaneous Drosophila mutation, the Hox cluster fastening is dismantled as shown in Figure 1(b), the slightest pulling force will automatically shift the cluster in the transcription factory domain. The repercussion on both genetic structure and function of the cluster will be dramatic: TC will automatically (and not gradually) disappear (Figure 1(b)).
According to the generally accepted argument mentioned before, TC is constrained to inexistence if TC is no more needed [28,29,30,31]. This occurs when the complete Hox cluster slides inside the transcription factory domain Therefore, the loss of TC in Drosophila could be ascribed to a spontaneous genetic mutation that suppresses Hox cluster fastening.

5. Complex Expression Patterns

According to BM, it is expected that complex patterns can be created by splitting the early (simply connected) Hox gene expression into expression domains separated by a ‘ditch’ zone (cf. Figure 4a) [37,38]. This splitting was already confirmed in 2013 [37]. Following this line of thought [37,38], BM predicts that a small DNA strip containing (Hox10 and Hox11) has a strange expression behavior in time (Figure 4). These genes can be pushed in and out of the Hox cluster activation domain which is depicted in the dark blue `circle ( Figure 4b). In the left graph, Hox10, Hox11, Hox12 are activated. In the middle graph, (Hox10, Hox11) are pushed out of the activation domain. In the right graph, (Hox10, Hox11) reenter later in the activation domain following the increased force of BM in the time course [37,38].
Recently it was unexpectedly observed in limb digit condensations a local expression disappearance in the interdigital area as shown in Figures { 2 (m, o) and 2 (n, p)} of [39]. These figures are reminiscent of the (Hox10,Hox11) disappearance in Figure 4b of the present Reviewed. The above reminiscence is a further confirmation of the BM pulling forces.
It is interesting that the theoretical prediction ‘Biophysics precedes Biochemistry’ [38] was experimentally confirmed soon after ‘…structural organization of HoxD cluster may predate transcriptional activation’ [16].

6. Recent Findings Caused by BM Physical Forces

6.1.a Physical Forces May Cause a Tension in the Hox Clusters

New technological advances (e.g. STORM- the Stochastic Optical Reconstruction Microscopy) made possible the measurement of quantities and properties that were inaccessible before. Physical tension in Hox clusters is such a case and more specifically the tension of DNA topological domains which are important for Hox gene activation. Amândio et al. have recently measured mouse HoxD clusters under physical tension [40]. The origin of this tension is elusive. This team has even considered the possibility of the BM physical forces to be responsible for this phenomenon. In this case they argue that ‘the forces would be generated by the local chromatin interactions themselves, rather than through an asymmetrically localized point of attachment to the nuclear environment’ [40]. Indeed this is possible and it is worth further examining.

6.1.b Proposal for a Test of 6.1a

The origin of the tension due to BM pulling forces could be tested by manipulating the HoxD cluster by gradual fastening deletions (Figure 1b). Suppose that the manipulations start with a cluster under full tension. If the origin of tension is due to BM pulling forces, it is expected that this tension will gradually end up to a cluster with completely deleted tension. This is a worth performing experiment.

6.2. Confirmation That FGF Causes the Necessary (but Not Sufficient) Condition for Limb Growth

As early as 2001 it was observed in C. Tickle’s Laboratory that FGF signaling in the chick limb is only necessary but not sufficient for the expression of the last gene of the HoxA cluster [32]. Recently this important finding was further confirmed by Sedas- Perez et al. using novel genetic techniques [39]. It was found out that Fgf signaling creates a permissive environment necessary for the HoxA13 gene expression for both the mouse and the chick. Furthermore, Fgf signaling is unexpectedly dispensable once it is activated. (Note that the author of the present Review contributed a theoretical elaboration which, instead of Hox gene expression above one threshold, HoxA13 is expressed between two thresholds - a lower and an upper [32]).

7. Conclusions and Predictions

7.1

According to the conventional representation, the DNA sequence is deployed along a meandering one-dimensional line. However, it is more realistic if this deployment expands as a long two dimensional strip with the DNA sequence gaining another degree of topological freedom. Besides DNA bending and stretching, another topological operation is possible: tape twisting that leads to a ‘Moebius strip’ [8]. Furthermore, the two-dimensional bendings and twistings may be extended to 3-dimensional surfaces the so called ‘Moebius torus’ that can accommodate more realistic DNA sequential structures [8].

7.2

. Besides Hox gene quantitative collinearity, Figure 3 can also describe the split Hox cluster activation. It is strange that so divergent phenomena can be described by the same mechanism. This may hint at a scarcity or universal parsimony of the developmental mechanisms. Is this an evolutionary advantage or disadvantage? I believe this is an evolutionary advantage since it can accommodate several divergent developmental pathways, as for instance in the case of primary and secondary developmental axes. Note that the morphogen source in the limb is located at a quite different position - namely the AER in the distal tip of the bud [32].

7.3

According to chick limb bud experiments, morphogen signaling for Hox gene expression is necessary but not sufficient [32]. Therefore complementary cues must come into play for a proper gene expression. For instance such cues could distinguish gene expression in liver cells from heart cells or even when this should occur.
The BM forces vary along the developmental axes following the distances from their origin. Passive diffusion is the main signaling mechanism and the closer to the source origin the stronger the force as noticed in [32]. For a more accurate source localization, more accurate recent techniques have been exploited (CRISP technology).
In the chick limb experiments mentioned above, the excision of the morphogen source causes the disappearance of HoxA13 at the distant tip [33,34]. However, this expression reappears by exposure of the bud to an FGF soaked bead. It would be interesting to perform the analogous experiment in the primary mouse axis and compare the results as proposed in [34].

Epilogue

All Natural Sciences are interconnected with the other branches of human intellectual activity. A short epistemological overview is included in [41].

List of Abbreviations

AER Apical Ectodermal Ridge
BM Biophysical Model
CF Coulomb Force
CT Chromatin territory
DSB Double Strand Break
ER Empirical Rule
FGF Fibroblast Growth Factor
HGC Hox Gene Collinearity
ICD Interchromosome domain
Mya Million years ago
PG Paralogy Group
PP Posterior Prevalence
QC Quantitative Collinearity
Quasi Coulomb force
SC SpatialCollinearity
TC TemporalCollinearity
TFD Transcription Factory Domain
wt wild type

References

  1. Lewis E.B A gene complex controlling segmentation in Drosophila. Nature 1978 Hox genes 276, 565.
  2. Papageorgiou S. A physical force may expose express in a morphogenetic density gradient. Bull. Math.Biol. 2001, 63,185-200. [CrossRef] [PubMed]
  3. Dollé P et al., HOX-4 and the morphogenesis of mammalian genitalia. Genes and Development 1991,. [CrossRef]
  4. Papageorgiou S. Pulling forces acting on Hox gene clusters cause expression collinearity. Int.J. Dev.Biol.2006, 50, 301-308. [CrossRef] [PubMed]
  5. Tarchini B, Duboule D Control Hoxd genes collinearity during animal development. Dev Cell 2006, 10, 93-103. [CrossRef] [PubMed]
  6. Tschopp P et al. Uncoupling time and space in the collinear regulation of hox genes.PLOS Genetics 2009, 5(3). [CrossRef]
  7. Papageorgiou S. A biophysical mechanism may control the collinearity of hoxd genes duting the early phase of limb development. Dev Growth & Differ 2011, 3, 275-280. [CrossRef]
  8. Papageorgiou S Physical laws shape up Hox gene collinearity. J. Dev. Biol. 2021, 9, 17. [CrossRef]
  9. Duboule D The rise and fall of Hox gene clusters. Development 2007, 134, 2549-2560 I. [CrossRef]
  10. Shimizu K, Gurdon J.B. A quantitative analysis of signal transduction from activin receptor to nucleus. Proc. Nat. Academy of Sci.1999, 8;96(12): 6791-96. [CrossRef]
  11. Afzal Z, Krumlauf R. Transacriptional regulation and implications for controlling Hox gene expression J. Dev. Biol.2022, 10; 10(1):4. [CrossRef]
  12. Simeoni I , Gurdon J.B. Interpretation of BMP signaling in early Xenopus development Dev.Biol. 2007, 308 (1): 82-92. [CrossRef]
  13. Bourillot Y-P et al. A changing morphogen gradient is interpreted by continuous transduction flow. Development 2002, 129(9): 2167-80. [CrossRef]
  14. Papageorgiou S Comparison of models for the collinearity of Hox genes in the developmental axes of vertebrates. Curr. Genomics 2012, 13(3): 245-51. [CrossRef]
  15. NoordermeerD et al. Temporal dynamics and development memory of 3D chromatin architecture at hox gene loci., eLIFE2014, 3, e0255. [CrossRef]
  16. Fabre P et al, .Nanoscale spatial organization of the HoxD gene cluster organization in distinct transcriptional states Proc. Nat. Acad. Sci.2015, 112, 13964- 13969. [CrossRef]
  17. Fabre P et al,. Visualizing HoxD gene cluster at the nanoscale level. Cold Spring Harb.Symp. Quant. Biol. 2015, 80, 9-16. [CrossRef] [PubMed]
  18. Papantonis A, Cook P.R. Fixing the model for transcription: the DNA moves, not the polymerase. Transcription 2011, 2(1) :41-44. [CrossRef]
  19. Brackley C.A. et al, Complex small-world regulatory networks emerge from the 3D organization of the human genome. Nat. Commun. 2021, 12(1): 5756. [CrossRef]
  20. Wilczek F, A Beautiful Question, 2015, Allen Lane Editions .
  21. Marinho R.M., Noether’s theorem in Classical Mechanics revisited. Eur. J. Phys. 2006, 28, 37-43. [CrossRef]
  22. Papageorgiou S, Hox gene collinearity may be related to Noether Theory on Symmetry and its linked conserved quantity. J. Multidiscipl. Sci. J 2020, 3, 13. [CrossRef]
  23. Iliopoulos J, Aux origins de la masse: particules élémentaires et symmetries fondamentales, 2014, Editions EDPSciences, Paris, France.
  24. Mandelbrot B.B. ‘The Fractal Geometry of Nature’, 1982, Editions Freeman, New York.
  25. 25. Almirantis Y, Provata A, Li W, Noether’s Theory as a metaphor for Chargaff’s 2nd parity rule in Genomics. J. Mol. Evol.,2022,. [CrossRef]
  26. Hanscom T et al., Regulation of Error-Prone DNA Double-Strand Break Repair and its impact on genome evolution, 2020, Cells 9, 165. [CrossRef]
  27. Schiemann S.M., Heznol A. et al. Clustered brachiopod Hox genes are not expressed collinearly and are associated with lophotrochozoan. PNAS USA 2017, 114(10) E1913-E1922. [CrossRef]
  28. Ferrier D, Holland P. Cionaintestinalis ParaHox genes: Evolution of Hox/ParaHox cluster integrity, developmental mode, and temporal collinearity. Mol. Phyl. Evol.2002, 24:412-417. [CrossRef]
  29. Ferrier D in ‘HOX GENE EXPRESSION’ Editor S. Papageorgiou, Landes Bioscience and Springer Science, 2007, USA.
  30. Duboule D The (unusual) heuristic value of Hox gene clusters: a mater of time? Dev. Biol.2022, 484:75-87. [CrossRef]
  31. Kondo T, Duboule D Breaking collinearity in the mouse HoxD complex. Cell 1999, 97, 407-417. [CrossRef]
  32. Vargesson N et al. Characterisation of HoxA gene expression in the chick limb bud in response to FGF. Dev. Dynamics 2001,. [CrossRef]
  33. 33. Papageorgiou S. The multiple roles of Temporal Collinearity in Hox gene clustering Preprints. [CrossRef]
  34. Papageorgiou S Disappearance of Temporal collinearity in Vertebrates and its eventual Reappearance Biology 2021, 10(10): 1018. [CrossRef]
  35. Durston A.J. Global Posterior Prev9alence is unique to Vertebrates: a dance to the music of Time? Dev. Dynamics 2012, 241: 179-1807. [CrossRef]
  36. Durston A, Some questions and answers about the role of Hox Temporal Collinearity. [CrossRef]
  37. Andrey G. et al. A switch between topological domains underlies HoxD genes colline arity in mouse limbs. Science 2013, 340/1234167. [CrossRef]
  38. Papageorgiou S. Biophysics precedes Biochemistry in Hox Gene Collinearity. http://webmedcentralplus.com/ article_ view/405.
  39. Sedas Perez S, et al. Fgf signalling triggers an intrinsic mesodermal timer that determines the duration of limb patterning. Nature Com. 2023, 14(1), 5841. [CrossRef]
  40. Amândio A.R. et al. Sequential in cis mutagenesis in vivo reveals various functions for CTCF sites at the mouse HoxD cluster. Genes & Development 2021, 35(21-22):1490-1509. [CrossRef]
  41. Papageorgiou S. In ‘Chaos, Information processing and Paradoxical Games’ Editors Nicolis G - Basios V, World Scientific, 2015.
Preprints 100448 g001
Figure 1. 1(a). Macro-scale and Micro-scale Hox gene clustering (adapted from S. Papageorgiou, Biology 2017: 6, 32). (A) Morphogen Gradient Concentration (T1, T2. T3). The gradient peak is located at the posterior end. ( B) Time sequence (t1, t2, t3) combine with (T1, T2,T3) for expression domains S1, S2, S3 of Hox1, Hox2, Hox3. (C) (bottom) a small force F1 pulls Hox1 out of the chromatin territory (CT) toward the Interchromosome Domain (ICD) and the Transcription Factory (TF) regime (grey domain). Polar Molecule P is located opposite the telomeric end of the cluster. At a later stage (top), a stronger force F3 (3P) pulls Hox1, Hox2, Hox3 out of CT toward TF. 1(b). Mechanical analogue of Hox cluster decondensation(adapted from S. Papageorgiou, Current Genomics 2012, 13:3). a) (left) Before gene activation, Hox cluster is compacted inside (CT). (right) Mechanical analogue: uncharged elastic spring fixed at its left end. b) (left) BM pulling force decondenses the cluster and Hox1 is extruded in (ICD) in the transcription factory (TF) domain (shadow disc) The cluster is fastened posteriorily. (right) A small force F1slightly expands the spring and black spot moves beyond the dashed line. Spring fixed posteriorily. c) (left) Hox cluster is further decondensed and Hox1, Hox2, Hox3 move in (ICD). (right) F2> F1 and the spring is further expanded. d) (left) The fastening of the cluster is removed and, with a slight force F1, the cluster can slide beyond the dashed line. (right) the loose spring slides freely beyond the dashed line. 1(c) Mouse Hox Gene Clusters (adapted from Z. Afzal and R. Krumlauf, J DevBiol 2022) HoxA, HoxB, HoxC and HoxD are depicted in the direction of transcription for each gene. The mouse embryo is shown in the Anterior – Posterior direction of Figure 1a where the gradient peak is at the posterior end ( Figure 1a).
Figure 1. 1(a). Macro-scale and Micro-scale Hox gene clustering (adapted from S. Papageorgiou, Biology 2017: 6, 32). (A) Morphogen Gradient Concentration (T1, T2. T3). The gradient peak is located at the posterior end. ( B) Time sequence (t1, t2, t3) combine with (T1, T2,T3) for expression domains S1, S2, S3 of Hox1, Hox2, Hox3. (C) (bottom) a small force F1 pulls Hox1 out of the chromatin territory (CT) toward the Interchromosome Domain (ICD) and the Transcription Factory (TF) regime (grey domain). Polar Molecule P is located opposite the telomeric end of the cluster. At a later stage (top), a stronger force F3 (3P) pulls Hox1, Hox2, Hox3 out of CT toward TF. 1(b). Mechanical analogue of Hox cluster decondensation(adapted from S. Papageorgiou, Current Genomics 2012, 13:3). a) (left) Before gene activation, Hox cluster is compacted inside (CT). (right) Mechanical analogue: uncharged elastic spring fixed at its left end. b) (left) BM pulling force decondenses the cluster and Hox1 is extruded in (ICD) in the transcription factory (TF) domain (shadow disc) The cluster is fastened posteriorily. (right) A small force F1slightly expands the spring and black spot moves beyond the dashed line. Spring fixed posteriorily. c) (left) Hox cluster is further decondensed and Hox1, Hox2, Hox3 move in (ICD). (right) F2> F1 and the spring is further expanded. d) (left) The fastening of the cluster is removed and, with a slight force F1, the cluster can slide beyond the dashed line. (right) the loose spring slides freely beyond the dashed line. 1(c) Mouse Hox Gene Clusters (adapted from Z. Afzal and R. Krumlauf, J DevBiol 2022) HoxA, HoxB, HoxC and HoxD are depicted in the direction of transcription for each gene. The mouse embryo is shown in the Anterior – Posterior direction of Figure 1a where the gradient peak is at the posterior end ( Figure 1a).
Preprints 100448 g001
Preprints 100448 g002
Figure 2. c (A) L: Double Strand Break Left (T) and Right (C). In the middle (INS) follows orientation (T→C) R. (B) L: Double Strand Break Left (T) and Right (C). In the middle (INS) follows orientation (T←C) R In (A) the inserted graft in the middle (INS) follows the orientation T→ C. In (B) the inserted graft in the middle (INS) follows the reverse orientation (T ← C).
Figure 2. c (A) L: Double Strand Break Left (T) and Right (C). In the middle (INS) follows orientation (T→C) R. (B) L: Double Strand Break Left (T) and Right (C). In the middle (INS) follows orientation (T←C) R In (A) the inserted graft in the middle (INS) follows the orientation T→ C. In (B) the inserted graft in the middle (INS) follows the reverse orientation (T ← C).
Preprints 100448 g002
Preprints 100448 g003
Figure 3. 3a. The ANT-C and BX-C subclusters of Drosophila and the complete Amphioxus cluster (adapted from D.E.K. Ferrier in Hox Gene Expression editor S. Papageorgiou. Editions Springer and Landes Bioscience 2007). A part only of the cluster correspondence between Drosophila and Amphioxus. The Drosophila [Zen1&2, bcd ] genes have evolved from the ancestral Amphioxus 3 gene. 3b. Quantitative Collinearity The split clusters of section 3 and Quatitative collinearity of section 4.3 are represented by the same Figure. The horizontal narrow strip (above t3) is in agreement with PP- the intensity of the posterior part of the strip is stronger than the anterior part. (See Section 4.4).
Figure 3. 3a. The ANT-C and BX-C subclusters of Drosophila and the complete Amphioxus cluster (adapted from D.E.K. Ferrier in Hox Gene Expression editor S. Papageorgiou. Editions Springer and Landes Bioscience 2007). A part only of the cluster correspondence between Drosophila and Amphioxus. The Drosophila [Zen1&2, bcd ] genes have evolved from the ancestral Amphioxus 3 gene. 3b. Quantitative Collinearity The split clusters of section 3 and Quatitative collinearity of section 4.3 are represented by the same Figure. The horizontal narrow strip (above t3) is in agreement with PP- the intensity of the posterior part of the strip is stronger than the anterior part. (See Section 4.4).
Preprints 100448 g003
Preprints 100448 g004
Figure 4. 4a. Hox10 expression at stage E11.5 with a ‘ditch’ zone separating distal domain 2 from proximal domain 1. A and P are the anterior and posterior ends of the limb. 4b. Big blue discs indicate the expression domain of the Hox genes. In the left domain, [Hox10, Hox11, Hox12 ] are activated. Hox13 is not yet activated. In the middle domain, [Hox12, Hox13] are activated but [Hox11, Hox10] are pushed out of the activation domain. In the right domain all Hox genes are activated and [Hox11, Hox10] reenter in the activation domain.
Figure 4. 4a. Hox10 expression at stage E11.5 with a ‘ditch’ zone separating distal domain 2 from proximal domain 1. A and P are the anterior and posterior ends of the limb. 4b. Big blue discs indicate the expression domain of the Hox genes. In the left domain, [Hox10, Hox11, Hox12 ] are activated. Hox13 is not yet activated. In the middle domain, [Hox12, Hox13] are activated but [Hox11, Hox10] are pushed out of the activation domain. In the right domain all Hox genes are activated and [Hox11, Hox10] reenter in the activation domain.
Preprints 100448 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated