Preprint

Article

DECLAREd: A Polytime LTL_f Fragment

Altmetrics

Downloads

186

Views

111

Comments

A peer-reviewed article of this preprint also exists.

Giacomo Bergami^*

This version is not peer-reviewed

Submitted:

10 March 2024

Posted:

11 March 2024

You are already at the latest version

Alerts

Abstract

This paper considers a specific fragment of Linear Temporal Logic for Finite traces, DECLAREd, which, to the best of our knowledge, we prove for the first time to be a {polytime} fragment of LTLf. We derive this in terms of the following ancillary results: we propose a set of novel LTLf equivalence rules that, when applied to \LTLf specifications, lead to an equivalent specification which can be computed faster by any existing verified temporal artificial intelligence task. We also introduce the concept of temporal non-simultaneity, prescribing that two activities shall never satisfy the same atom, and temporal short-circuit, that occurs when a specification interpreted in LTL would accept an infinitely long trace while, on LTLf, it can be rewritten so to postulate the absence of certain activity labels. We test these considerations over formal synthesis (Lydia), SAT-Solvers (AALTAF) and formal verification (KnoBAB) tools, where formal verification can be also run on top of a relational database and can be therefore expressed in terms of relational query answering. We show that all these benefit from the aforementioned assumptions, as running their tasks over a rewritten equivalent specification will improve their running times.

Keywords:

Subject: Computer Science and Mathematics - Logic

Verified Artificial Intelligence [1] calls for exact procedures ascertaining whether a model of the system

S

abides by the specifications in

Φ

through yes or no answers (

S ⊧ Φ

) when written in a formalism for efficient computations, either for verifying the compliance of a system to a specification (formal verification [2]) or for producing a system abiding by a given specification (formal synthesis [3]). This can be determined after a specification mining phase used to extract

Φ

from a system

S

[4]; these considerations bridge temporal reasoning with artificial intelligence, as in both we can extract a specification from the data that can be used to determine decision problems. Under these assumptions, we are then interested in a temporal description of such systems, when different runs are collected as logs

S

and referred to as traces

σ \in S

. These are temporally ordered records of observed and completed (or aborted) labelled activities. We are then interested in temporal specifications expressible over a fragment of Linear Temporal Logic for Finite traces (LTL_f), where LTL_f assumes that there is only one possible immediately following event to another and that the traces of interest contain a finite number of events. The major difference between LTL [5] and LTL_f is that, while the former might also prescribe the need for traces of infinite length, the latter will discard any temporal behaviour requiring such infinite traces to occur. This is evident from their procedural characterization through automata: while LTL models can be expressed as Büchi automata, LTL_f can be conveniently represented as NFAs only accepting finite traces [6]. To the best of our knowledge, this paper studies these situations for the first time and refers to them as temporal short-circuits:

Example 1.

Let us assume to have a temporal specification

Φ = □ (a \Rightarrow ⊚ c) \land □ (c \Rightarrow ⊚ a)

: while the interpretation of the former in LTL accepts any trace either containing neithera-s norc-s or accepting either

{(ac)}^{ω}

{(ca)}^{ω}

where ω is the first infinite ordinal, the latter can never occur inLTL_f, thus prescribing the absence of anya-s orc-s from the patterns. By interpreting Φ inLTL_f, we can then express it equivalently to

□ \neg a \land □ \neg c

(§2.2) while preferring the latter representation as it completely removes the need to check whether the constraint leads to infinite behaviour never expressible in finite traces.

Declarative languages in the context of Business Process Management (BPM) such as Declare [7] ease the practitioners’ task to understand complex log patterns of interest in a straightforward way: by restricting the set of all the possible temporal behaviours of interest to the one in Table 1, we can conveniently extract compact specifications in which conformance checking tasks determine the abidance by the hospitalization procedures [8]. These specifications do not necessarily have to be hard-coded, but can be mined from such logs [4]. For BPM, each event is associated with exactly one single label [9] and, under the occasion that each event is also dataful and therefore associated with some data payload, we can always generate a finite set of mutually exclusive atoms partitioning the data space into non-overlapping intervals [10]. This ensures the theoretical possibility of defining atoms so an event will satisfy at most one of them. This evidence is also corroborated by data as represented in the real world: recent work on time series segmentation showed the possibility of representing a time series as a sequence of dichotomous increase and non-increase events [11] as well as the transitioning of a system into distinct non-overlapping states [12]. Furthermore, different types of malware can be distinguished just from the distinct name of the system calls being invoked at the operative system level [13,14]. As it is a common assumption in specification mining algorithms using Declare to return a finite conjunction of specifications, it is quite common to return inconsistent specifications under the temporal non-simultaneity axiom (§2.3) when support metrics below

100 %

are considered for increasing the algorithmic recall (see Example 2). Declare works under such an axiom, as BPM’s practitioners implicitly assume that each trace event corresponds to explicitly one activity event, where all the distinct activity labels are assumed to be mutually exclusive predicates. Detecting this in advance will prevent running any verified temporal artificial intelligence technique on such specifications for the aforementioned practical scenarios, as no trace will ever satisfy an inconsistent specification.

Example 2.

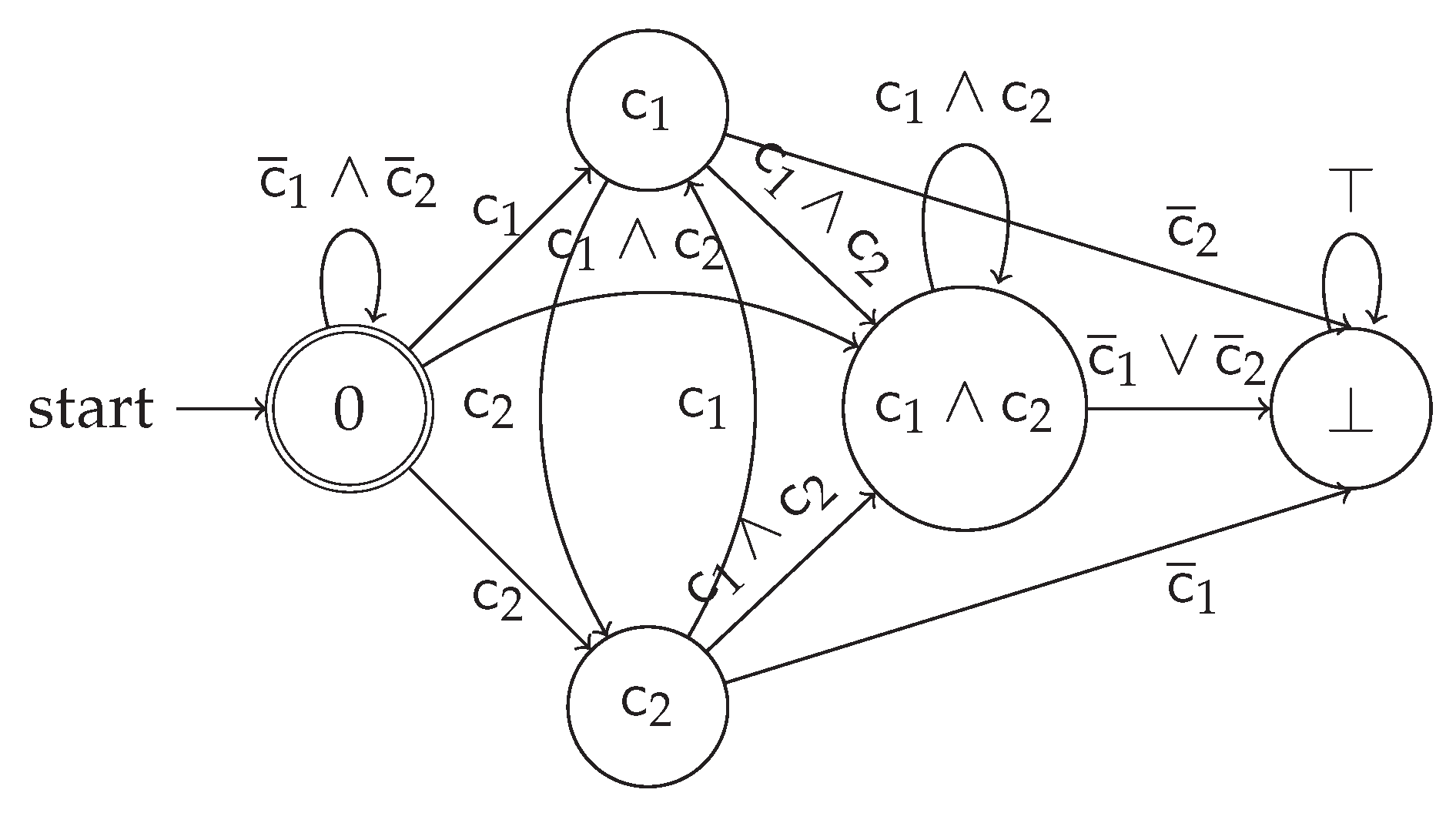
Let us assume to have the following log

S = {acdefac, adcfeadad, acugac, addadduadd}

As “a” appears in all traces, we return

◊ a

(

Exists (a)

in Declare) as well as postulating that, when anaactivity occurs in the log, this is immediately followed byc

50 %

of the times (

□ (a \Rightarrow ⊚ c)

ChainResponse (a, c)

in DECLAREd with

50 %

support) and by the remaining

50 %

percent by d (

□ (a \Rightarrow ⊚ d)

ChainResponse (a, d)

). Under the assumption of Axiom ax:tns, the occurrence of any “

a

” cannot possibly occur, thus rewriting the two latter statements as

□ \neg a

. Still, this conflicts with the first occurrence clause, thus generating a globally un-satisfiable specification ⊥.

This paper focuses on a DECLARE fragment, DECLAREd ( Table 1), which is still affected by the aforementioned problem. These two preliminary definitions, where the second is optional, alongside the determination of a set of equivalence rules for DECLAREd (fig:rewriting) and the definition of an algorithm for DECLAREd rewriting

Φ_{d}

(§3) lead to our major result, that our proposed algorithm runs in

P o l y (n)

(§4). In fact, such algorithm1 will return ⊥ if the module has inconsistencies, ⊤ if this is detected trivially true, and a rewritten set of DECLAREd clauses

Φ_{d}^{'}

when possible. As a byproduct of the previous result, we show that such running times were not achieved by other tools not running on the same fragment:

Our rewritten equivalent specification $Φ_{d}^{'}$ speeds up the time of existing verified temporal artificial intelligence algorithms (§1) if compared with their runtime over the original specification $Φ_{d}$ , thus proving that such algorithms do not support the notion of temporal short-circuit (§5.1).
Under temporal non-simultaneity, the time required for both running a verified temporal artificial intelligence task and computing $Φ_{d}^{'}$ is also smaller than the running time of running such tasks over $Φ$ (§5.2).

Graph Notation. (See §A) We denote a (finite) graph G as a pair

(V, E)

, where V is a set of vertices and

E \subseteq V^{2}

is a set of directed edges; to denote a vertex (or edge) set of a graph G, we use the notation

V_{G}

(or

E_{G}

O u t_{G} (u)

(or

I n_{G} (u)

) is the set of the vertices reachable through the outgoing (or incoming) edges for

v \in V_{G}

. Removing a vertex

u \in V_{G}

from a graph G (

V_{G}^{-} (v)

) requires also removing all the incoming and outgoing edges from a graph while removing an edge

(u, v) \in E_{G}

from such a graph (

E_{G}^{-} (u, v)

) also requires removing the nodes u or v if such removal nullifies the degree of such nodes.

℘ (S)

is the powerset of S. We represent a (hash)multimapf associating a single activity in

Σ

to a finite subset of

Σ

as a finite function

f : Σ \to ℘ (Σ)

where, for each

x \in Σ

not being a key for the multimap, we guarantee

f (x) = ⌀

and

f (x) \neq ⌀

otherwise; an empty multimap f returns ⌀ for each

x \in Σ

D e l_{f} (x)

removes x as a key of the multimap while

P u t_{f} (x, u)

adds u to the set of values associated to x in f. Given V a set of vertices and

ι : | V | \leftrightarrow {0, \dots, | V | - 1}

a bijection enumerating each vertex in V to, a directed circulant graph

C_{L}^{n, \pm}

on n vertices has each vertex

v \in V

adjacent to the immediately preceding and following vertices in V in the order expressed within a set of natural numbers

L \in ℘ (N)

, i.e.

E_{C_{L}^{n, \pm}} : = \{(u, v) \in V^{2} | \exists k \in L . ι (v) = (ι (u) \pm k) mod n\}

. Given this, we define

C_{{1}}^{n, +}

as a cyclic graph representing exactly one chain and

C_{{0, \dots, n - 1}}^{n, \pm}

is a complete graph.

1. Brief Related Work

Formal Synthesis.

Lydia2 [3] generates a DFA for a LTL_f specification

Φ

such that it will accept a trace

σ

iff.

σ ⊧ Φ

. This works over a finite alphabet

Σ

inferred from such formula. The authors efficiently do so by exploiting a compositional bottom-up approach after rewriting a LTL_f formula into an equivalent LDL_f one. Automata operations are implemented using MONA for compact representation. Benchmarks show the effectiveness of such an approach if compared to competing ones. By considering the effects of specification rewriting in automata generation, we want to verify whether temporal short-circuit rewriting tasks are already occurring over Lydia while building the automaton instead of pursuing the approach in §2.2 (see lemr-1 vs. coroll1).

Formal Verification.

KnoBAB3 [2] is a tool implementing the semantics for LTL_f operators into custom relational operators (xtLTL_f) providing a 1-to-1 mapping with the former. This was achieved by adequately representing all the traces in a log

S

under a main memory columnar representation. Its architecture stores all the activities associated to traces’ events in an ActivityTable, which is then sorted by increasing activity id in

Σ

, trace id, and event id. At loading time, the system also builds up a CountingTable, which determines the number of occurrences of each activity label per trace. This architecture supports MAX-Sat queries, declarative confidence and support, and returning the traces satisfying a given clause alongside its associated activated and target conditions (

σ ⊧ Φ

for

σ \in S

). As KnoBAB outperforms existing tools for formal verification, we take this as a computational model of reference for determining the computational complexity of formal verification tasks over given specifications

Φ_{d}

in xtLTL_f (see lem-1).

SAT-Solvers.

AALTAF4 [15] is a SAT-checker determining whether an LTL_f formula is satisfiable by generating a corresponding transition system where each state represents subformulæ of the original LTL_f specification while leveraging traditional SAT-solvers. Differently from KnoBAB, which determines whether traces in a log satisfy an LTL_f specification expressed in algebraic terms (xtLTL_f) or not, AALTAF is more general than this and determines whether no traces will ever satisfy a given specification, thus determining its unsatisfiability, or whether there might exist a finite trace allowing this. This paper will show that DECLAREd provides a polytime fragment of LTL_f for which our equational rewriting algorithm (§3) also provides a decidable polyspace decision function for satisfiability (see thm).

LTL_f Modulo Theories

While LTL_f is generally known as a decidable language, most recent research [16] also consider decidable fragments of LTL_f also involving first-order logic arithmetic properties. Differently from our proposed characterization, events are not labelled as required when actions need to be ascertained. Furthermore, none of the proposed decidable fragments with arithmetic properties involves considerations on polytime complexity, while still referring to polyspace complexity.

2. Preliminaries

We consider temporal specifications

Φ_{d}

expressed in DECLAREd as a finite set of clauses from tab:dt being instantiated over a finite set of possible activity labels

Σ

. By interpreting this as conjunctive models [10], we can equivalently represent

Φ_{d}

as the finite conjunction of the LTL_f semantics associated to such clauses, i.e.

Φ \equiv ⋀_{c_{l} \in Φ_{d}} [[c_{l}]]

. We use both notations interchangeably. Proofs are postponed to the Appendix.

2.1. Rewriting Rules

fig:rewriting identifies any possible rewriting of the DECLAREd clauses into Absence or Exists, while determining the effects of the latter when interfering with the templates’ activation (A) or target (B) conditions. If available, we are also interested in rewriting rules to identify an inconsistency leading to an unsatisfiable specification ⊥. We now consider rewriting rules not assuming the temporal non-simultaneity axiom, thus remarking on the possibility of encoding these in already-existing tools as an LTL_f pre-processing step without any further assumption. As

AltPrecedence (a, b)

can be rewritten as the LTL_f expression associated to

Precedence (a, b)

as well as

□ (b \to ⊚ (\neg b U a))

, we named AltPrecedence rewriting rules only the ones related to this LTL_f expression. We omit the proofs, but the reader can easily verify their correctness by checking that both sides of the equivalences generate the same automata5.

In all the rules, we assume that

a \neq b

where

a, b \in Σ

. Other rewriting rules (Lemma A6) are implicitly assumed in forthcoming algorithmic subroutines (sec:subrout) and while loading and indexing specifications (algo:load).

2.2. Temporal Short-Circuit Rewriting

A finite conjunction ofLTL_f statements

φ : = ⋀_{i} φ_{i}

leads to atemporal short-circuitif this can be rewritten as a finitary conjunction, either

φ^{'} : = ⋀_{j} □ \neg a_{j}

φ^{'} : = ⋀_{j} ◊ a_{j}

, for each distinct atom

a_{j}

freely occurring in φ when

φ^{'}

is not syntactically equivalent to φ. We apply a(temporal) short-circuit rewritingto aLTL_f specification Φ if we replace any sub-formula φ in Φ leading to a temporal short-circuit with

φ^{'}

Short-circuits based on ChainResponse boil down to the absence of each of its atoms:

Lemma 1.

Given

A = {c_{1}, c_{2}, \dots, c_{n}} \subseteq Σ

Φ^{'} : = ⋀_{c_{i} \in A} □ \neg c_{i}

is equivalent to

Φ : = □ (c_{n} \Rightarrow ⊚ c_{1}) \land ⋀_{\overset{i \in N}{1 \leq i < n}} □ (c_{i} \Rightarrow ⊚ c_{i + 1})

inLTL_f.

Such a rewriting will streamline formal verification tasks:

Lemma 2.

Given

A = {c_{1}, c_{2}, \dots, c_{n}} \subseteq Σ

, computing

Φ^{'} : = ⋀_{c_{i} \in A} □ \neg c_{i}

in lieu of

Φ : = □ (c_{n} \Rightarrow ⊚ c_{1}) \land ⋀_{\overset{i \in N}{1 \leq i < n}} □ (c_{i} \Rightarrow ⊚ c_{i + 1})

always leads to a positive average speed-up.

After representing all the

ChainResponse (a, c)

in a input specification as a graph

G^{cr}

with edge

a \to c \in E_{G^{cr}}

and nodes

a, c \in V_{G^{cr}}

, we can show as a corollary of the first lemma that this boils down to removing all circuits appearing over some nodes

β^{cr} \subseteq V_{G^{cr}}

and rewriting such clauses as

(⋀_{v \in β^{cr}} Absence (v)) \land (⋀_{\overset{u \to v \in E_{G^{cr}}}{u, v \notin β^{cr}}} ChainResponse (u, v))

in polytime on the size of

Φ

(Corollary A1). We can infer similar lemmas for AltResponse in terms of rewriting such resulting temporal short-circuits to absences (arlemma) thus resulting in time speed-up (coroll3).

2.3. Temporal Non-Simultaneity

Axiom 1

(Temporal Non-Simultaneity). Given the set of all the possible activity labels Σ, we prescribe that no distinct activity could occur simultaneously in the same instant of time. This can be expressed as

\forall a, b \in Σ . a \neq b \Rightarrow □ (a \land b \Rightarrow ⊥)

As we assume a finite set of activity labels

Σ

to be fully known from our specification or data, we can represent this axiom as an extension of the properties

Φ

to be checked as a new property

Φ_{↓ Σ} : = Φ \land ⋀_{\overset{a, b \in Σ}{a \neq b}} □ (a \land b \Rightarrow ⊥)

. As prior approaches using LTL_f did not consider this assumption,

Φ

should be directly stated as

Φ_{↓ Σ}

for both Lydia and AALTAF. On the other hand, our solver Reducer only takes

Φ_{d}

as it works under such an axiom. KnoBAB automatically assumes that each distinct activity label is different from the rest, thus entailing an implicit semantic difference between different types of events.

Rewriting Rules

We can identify that the following rewriting rule holds for

c \neq b

Σ

, as we can never have an event being labelled with both

c

and

b

after the same occurring event:

{[ChainResponse (a, b) \land ChainResponse (a, c)]}_{↓ Σ} \equiv Absence (a)

Temporal Short-Circuit Rewriting

We now consider temporal short-circuit rewriting rules that only hold under temporal non-simultaneity. For

a \neq b

Σ

, as any b shall always occur after the first occurring a for Response, we can express it as:

□ {(a \to ◊ b)}_{↓ Σ} \equiv □ (a \to ⊚ ◊ b)

Due to this, we need to discard the eventuality that

| A | = 1

, as

□ (a \to ◊ a)

is, on the other hand, trivially true and leads to no temporal short-circuit.

Lemma 3.

Given

A = {c_{1}, c_{2}, \dots, c_{n}} \subseteq Σ

with

| A | = n > 2

Φ^{'} : = ⋀_{c_{i} \in A} □ \neg c_{i}

is equivalent to

Φ : = {[□ (c_{n} \Rightarrow ◊ c_{1}) \land ⋀_{\overset{i \in N}{1 \leq i < n}} □ (c_{i} \Rightarrow ◊ c_{i + 1})]}_{↓ Σ}

inLTL_f.

Lemma 4.

Given

A = {c_{1}, c_{2}, \dots, c_{n}} \subseteq Σ

with

| A | = n > 2

, computing

Φ^{'} : = ⋀_{c_{i} \in A} □ \neg c_{i}

in lieu of

Φ : = {[□ (c_{n} \Rightarrow ◊ c_{1}) \land ⋀_{\overset{i \in N}{1 \leq i < n}} □ (c_{i} \Rightarrow ◊ c_{i + 1})]}_{↓ Σ}

always leads to a positive average speed-up.

3. Reducer: Equational Rewriting

The Reducer algorithm for rewriting

Φ_{d}

into

Φ_{d}^{'}

proceeds as follows: after showing the subroutines for removing redundant clauses from the specification while propagating the detection of an inconsistency towards the function call chain (§3.1), we outline how a specification

Φ_{d}

can be efficiently loaded as a collection of graphs

G^{★}

for each DECLAREd template ★ for clause indexing (§3.2). After applying the aforementioned equivalence rules (§3.3), we apply the temporal short-circuit rewriting (§3.4) before returning the rewritten specification

Φ_{d}^{'}

from the edges remaining from

G^{★}

and values in an F map storing Absence and Exists clauses. Upon detecting the joint satisfaction of an Absence(x) and Exists(x) for an activity label x, we immediately detect an inconsistency for which we return ⊥. If the resulting specification appears to be empty in spite of no inconsistency being detected, we then obtain a trivially true specification ⊤. Otherwise, we return a rewritten specification

Φ_{d}^{'}

3.1. Algorithmic Subroutines

Algorithm 1 shows crucial algorithmic subroutines ensuring to propagate the detection of an absence/presence of an activity label while dealing with clauses

c_{l}

derivable from the input specification

Φ_{d}

clauses of the specification.

Let F be a finite multimap associating each activity label

a \in Σ

to a set of booleans, where true (and false) denotes that

Exists (a)

(and

Absence (a)

) can be inferred from the specification. If both

Exists (a)

and

Absence (a)

are entailed, we deem the overall specification as inconsistent, for which we will return ⊥. Ex in L. 1 (and Abs in L. 2) returns false whether the addition of Exists (or an Absence) to a specification makes it explicitly inconsistent.

Clear at L. 4 removes all the clauses in which activation condition x would never occur per Absence(x). For

Choice (x, b)

, this triggers the generation of Exists(b) which, in turn, might lead to an inconsistent specification (L. 6 and 7). For Precedence(x,b), the absence of the activation requires Absence(b), which is then in turn added while testing for the specification’s inconsistency (L. 10). The function returns true if the specification is not currently detected as inconsistent (L. 12).

Reduce at L. 15 can be applied to templates ★ such as ChainResponse, Response, and AltResponse for implementing a cascade effect upon the specification supporting

Absence (x)

by also requiring that the associated activations should be absent from the specification (L. 22). We return true if no inconsistency was detected, and false otherwise. This idea was revised so as to be applied to Precedence (L. 32): for this, the absence of the activation triggers the necessity of the second argument to be absent as well, thus enforcing to visit the graph towards the outgoing edges (L. 39). We also ensure to remove all the vertices and edges associated with x (L. 40).

Dually, Expand^re works by recursively applying the head from the tail of the RespExistence clauses upon the request that an event x shall exist in the data (L. 56). As this trivially exists, we remove all the clauses having this condition in the head of such rules (L. 53) while, if x appears as a second argument of a

NegSuccession (u, x)

, we still postulate for the absence of u from the specification (L. 54).

3.2. Specification Loading as Graphs

algo:load shows the process of loading and indexing the clauses from

Φ_{d}

in primary memory.

We add Absence and Exists in map F; at this stage, the specification is deemed inconsistent (returning ⊥) if a given activity label a is required to both appear and be absent from each trace.

Binary clauses

★ (a, b)

are loaded as edges

(a, b)

of a graph

G^{★}

where

V_{G^{★}} \subseteq Σ

. Clauses being the conjunction of other clauses are then rewritten into their constituents;

AltPrecedence (a, b)

is rewritten into

Precedence (a, b)

, to be stored in an edge

(a, b)

for

G^{p}

, and

□ (b \to ⊚ (\neg b W a))

, to be stored in an edge

(b, a)

for

G^{ap -}

. For binary clauses entailing the universal truth ⊤ when both arguments are associated with the same activity label (e.g., Response), we avoid inserting this clause as an edge. For other clauses (e.g., AltResponse, L. 42), this same situation might be rewritten as the absence of a specific activity label which, if leading to an inconsistency, also immediately ensures to return an empty specification. Conversely, a Choice having both arguments being the same boils down to an Exists, which is also added in place of Choice (L. 57), while we might never have an ExclChoice where both arguments are the same (L. 62). For clauses being symmetric (e.g., Choice), we avoid duplicated entries by preferring only one of the two equivalent writings (e.g., Choice(a,b) over Choice(b,a) for

a ⪯ b

, L. 58).

3.3. Applying Equational Rewriting

Equational rewriting for rules in fig:rewriting is run as follows: we consider each graph in order of appearance in §2.1 and we iterate over its edges. For each of these, we detect their match with one of the cases appearing in the first binary clause

★ (a, b)

on the left-hand side of the formula, and we look up for the occurrence of any clause appearing in the same hand-side.

If the condition described by the left-hand side is then reflected by the specification represented by edges for graphs

G^{★}

and F, we determine the rewriting strategy depending on the definition of the right-hand side. If the latter is ⊥, we immediately return it and detect an unsatisfiable model. Also, we remove any edge

(a, b)

from

G^{★}

★ (a, b)

does not appear on the right-hand side of the formula, and we add any edge

† (a, b)

G^{†}

not appearing on the left-hand side. If an

Exists (a)

(or

Absence (a)

) appears only on the right-hand side, we add it by invoking Ex(a) (or Abs(a)), while immediately returning an empty specification if an inconsistency is detected while doing so. These methods are also changed according to the interdependencies across templates: e.g., the generation of new Exists(x) for RespExistence rules triggers Expand

^{re}

(x) instead, and the Absence(x) for NotCoExistence invokes Reduce

^{ch}

(x) which, in turn, will also call for Expand

^{re}

(x) as per alg:asur; Absence(x) for RespExistence will call for Reduce

^{re}

(x). Similar considerations can be provided for other templates and rules. This process does not clear out clauses, as we at least fill in F, from which we are also returning Exists or Absence for

Φ_{d}^{'}

After applying the rules on a single graph

G^{†}

, we then iterate over all the activities x required to be absent by the specification (

false \in F (x)

), for which we run all the

R e d u c e^{★} (x)

methods and

C l e a r (x)

, through which we propagate the effect of requiring the absence of a specific activity label to all the clauses in the specification. If, while doing so, any inconsistency is detected by returning a false, we immediately return ⊥ (see absurdity).

3.4. Applying Short-Circuit Rewriting

This further algorithmic step is run after running the AltPrecedence Rules and before running the RespExistence ones, thus potentially reducing the number of clauses to be considered due to the absence of a specific activity label.

We prefer to detect the existence of a circuit

v_{α_{1}} \to \dots \to v_{α_{n}} \to v_{α_{1}}

of length

n + 1

through a DFS visit of the graph with back-edge detection [17]. Once we detect a circuit, we generate Absence(

v_{α_{i}}

) clauses for each node

v_{α_{i}}

in it, while removing such nodes from the graph. The latter operation is efficiently computed by creating a view over such a graph through an absence set R which will contain all of the nodes in the circuit being removed. Then, for each graph traversal, we avoid starting the visit from nodes in R and we avoid traversing edges leading to nodes in R. This avoids extremely costly graph restructuring operations. As by construction we cannot have a single non-connected node as each clause is represented by one single edge, if at the end of this reduction process we obtain nodes with zero degrees, such nodes were previously connected to nodes belonging to cycles and that were therefore also part of cycles: those also constitute Absence clauses.

For all the novel

Absence (a)

clauses being inserted in the specification in lieu of the detected temporal short-circuits, we also run all the available Reduce^★(x) methods as well as Clear(x), thus ensuring a cascading effect removing the remaining clauses that will never be activated while keeping searching for inconsistencies via sub-routine calls.

4. A PolyTime $(| Φ_{d} |)$ SAT-Solver for DECLAREd

This section is mainly to prove that satisfiability in DECLAREd can be carried out in polytime over the size of the original specification

| Φ_{d} |

; this strengthens the previous informal results over conformance checking provided over KnoBAB over such a fragment. We twin this result with the overall algorithmic correctness.

Theorem 1.

The Reducer specification rewriting process is a decidable SAT-Solver for DECLAREd running in

P o l y (| Φ_{d} |)

-time.

Proof.

The main lemmas supporting this proof are reported in the appendix. First, we need to prove that the previous section describes an always-terminating computation: given subrouteDec,exploadDec,rewritingDec and shortDec, we have that each previous subsection in §3 describes a polytime procedure. The composition of each single non-mutually-recursive sub-routine terminates and leads to a polytime decision function.

Last, we discuss the correctness of the resulting procedure. If

Φ_{d}

in input were a tautology, all the clauses in the original specification would have been cancelled out as they would have trivially held, thus providing no further declarative clause to be returned (tautology). If, on the other hand, any inconsistency was detected, the computation would have stopped before returning the reduced specification, thus ignoring all the remaining rewriting steps (absurdity). If neither of the previous cases holds, we have then by exclusion a satisfiable specification

Φ_{d}

which is also rewritten into an equivalent specification

Φ_{d}^{'}

under the temporal non-simultaneity axiom (Axiom 1). □

5. Empirical Evaluation

We determine a set of activity labels

Σ

from the Cybersecurity dataset [14] and by creating 8 distinct subsets

A_{1}, \dots, A_{8} \subseteq Σ

of size

| A_{i} | = 2^{i}

such that

A_{i} \subset A_{j}

for each

1 \leq i < j \leq 8

. We then consider each

A_{i}

as a set of vertices for which we instantiate a complete graph, a cyclic graph representing a chain, and a circulant graph

C_{{0, 1, 2, 3}}^{| A_{i} |, \pm}

. Given each of these graphs g, we then generate a specification

Φ_{i}^{c, g}

for each of these

A_{i}

by interpreting each edge

(a, b) \in A_{i}^{2}

in the generated graph as a declarative clause:

c=ChainResponse: $ChainResponse (a, b)$
c=Precedence: $Precedence (a, b)$
c=Response: $Response (a, b)$
c=RespExistence+Exists: $RespExistence (a, b)$
c=RespExistence+ExclChoice+Exists: $RespExistence (a, b)$ ,

$ExclChoice (a, b)$

For the last two cases, we also add a clause

Exists (u)

for

u = min A_{i}

. Given the same

A_{i}

and u, we also generate two other specifications

Φ_{i}^{c, g}

where clauses are instead generated for each activity label

a \in A_{i}

c=(Chain+Alt)Response: $ChainResponse (a, a)$ ,

$AltResponse (a, a)$
c=ChainResponseAX: $ChainResponse (u, a)$ .

We then expect that, if any of the aforementioned verified temporal artificial intelligence tasks provide no LTL_f or Declarative rule rewriting as per this paper, running any verified temporal artificial intelligence task over a

Φ_{i}^{g, c}

being generated from

g = C_{{0, \dots, | Σ_{i} | - 1}}^{| A_{i} |, \pm}

will take more time than running it over a

Φ_{i}^{g^{'}, c}

where

g^{'} = C_{{0, 1, 2, 3}}^{| A_{i} |, \pm}

, which in turn will take more time than running a specification

Φ_{i}^{g^{''}, c}

generated over

g^{''} = C_{{1}}^{| A_{i} |, +}

. This last consideration also includes the aforementioned rewriting task in its worst-case scenario. As we are expecting that, for each c, each of these

Φ_{i}^{c, g}

for any of such graphs g will be then always rewritten into the same specification

Φ_{i}^{' c}

, we are expecting to have similar running times for each rewritten specification, as we expect the running time in the latter to be dependant on the number of atoms/vertices and not on the number of clauses as the former.

Each of these generated specifications is then fed to our rewriting algorithm, which returns the specification in both the LTL_f representation required by Lydia and AALTAF and the declarative specification for KnoBAB. We discard parsing and query plan generation times for each solution: running times for Lydia only considered the time required for generating the DFA from the LTL_f formula as per their internal main-memory representation. For the formal verification task run in KnoBAB as a relational database query, we consider a sample of 9 traces from the original log over which we run the generated specifications. To alleviate potential out-of-memory issues, we test the specifications in batches of 10 at a time, thus sacrificing greater query plan minimization with the certainty of completing the computation without out-of-memory errors. On the other hand, the two aforementioned tools do not require a log to work, for which it is sufficient to have a specification. The dataset for specifications and logs is available online6.

We present a condensed version of the benchmarks, while §Appendix E gives more extensive plots.

5.1. Rule Rewriting without Temporal Non-Simultaneity

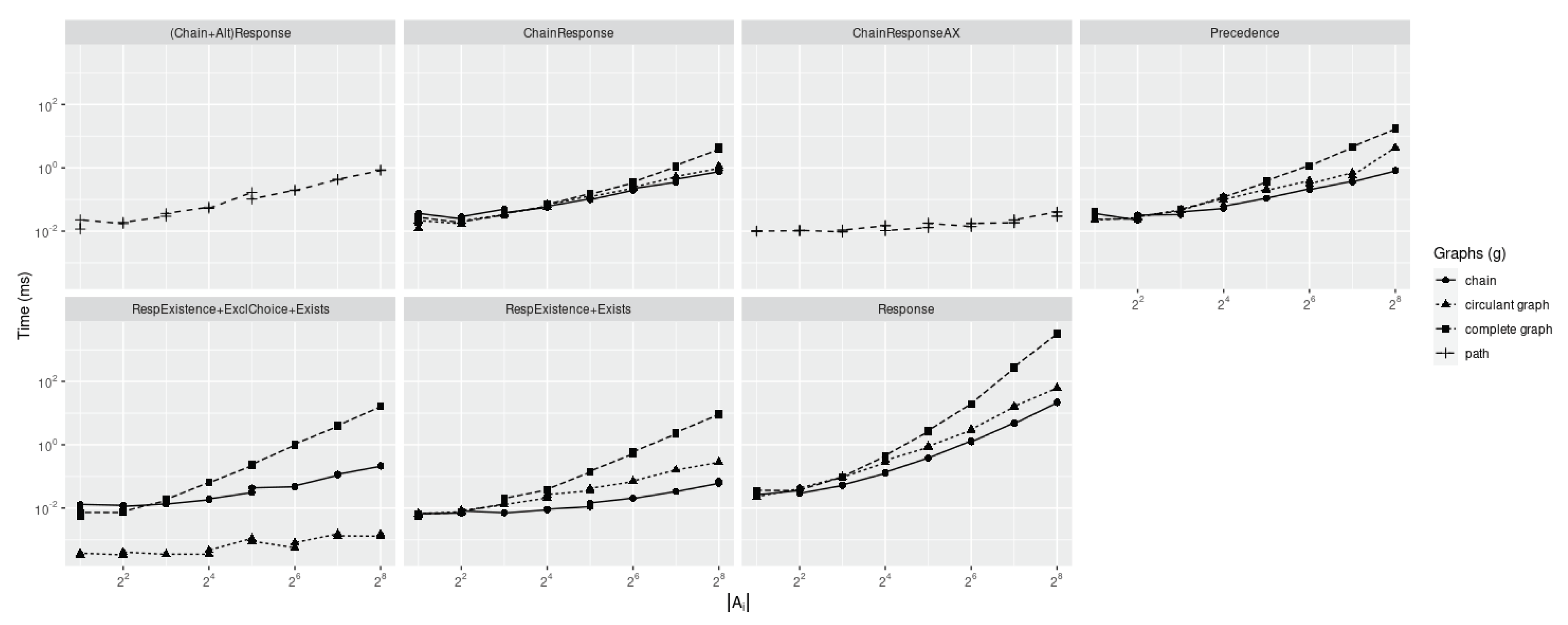
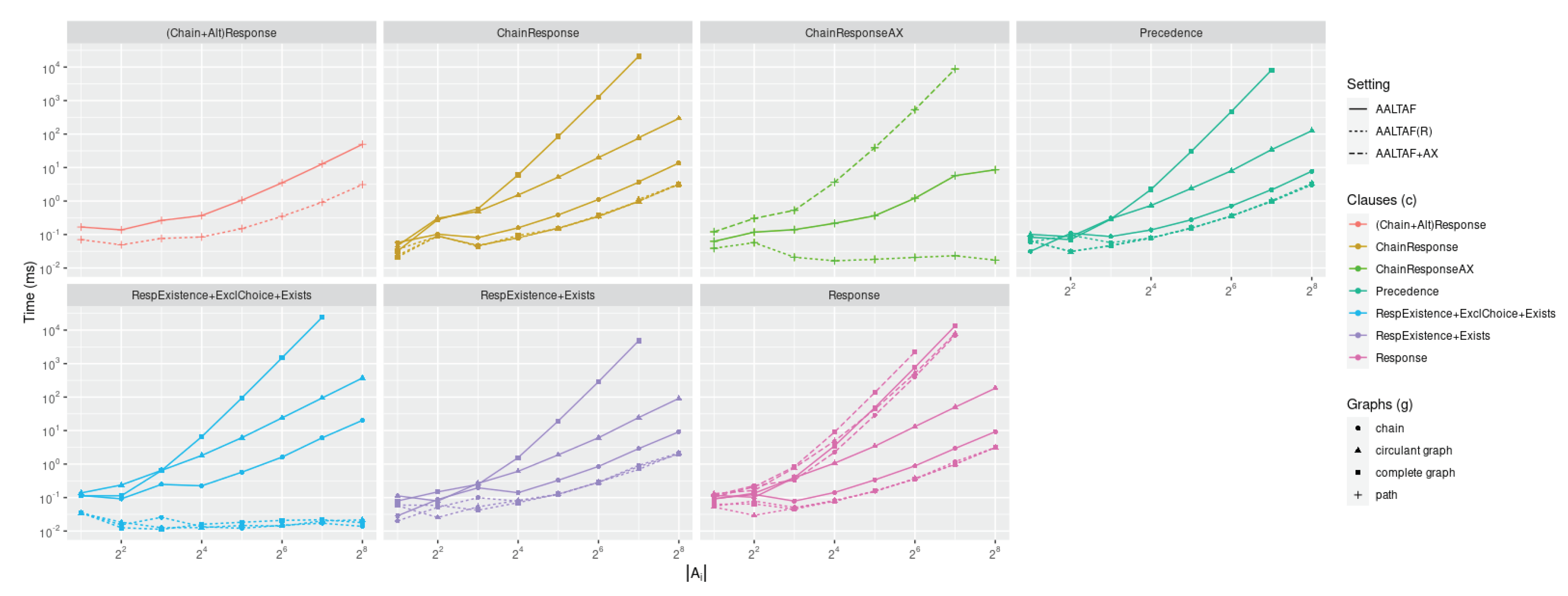
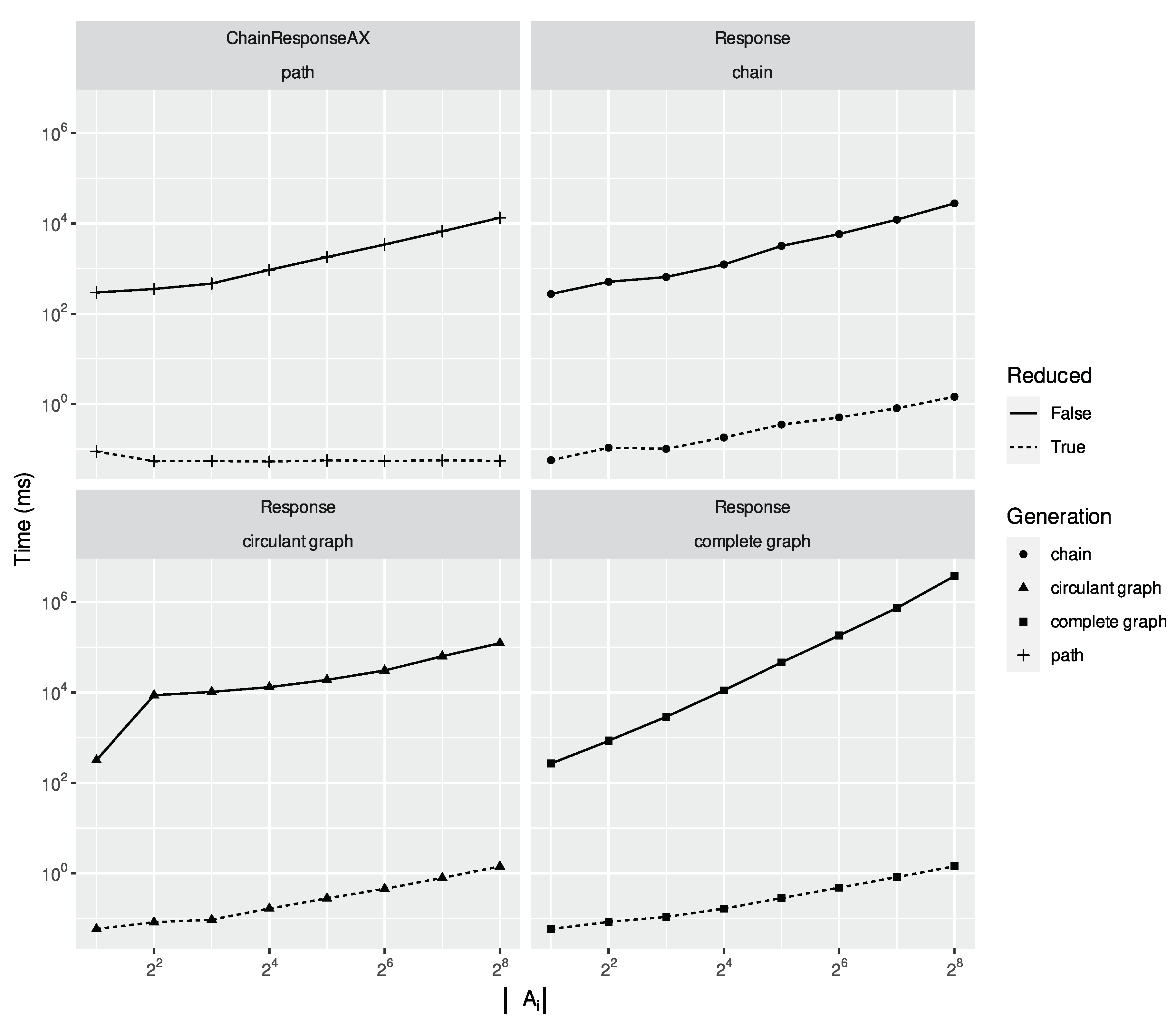
We now consider all the resulting specifications being generated except Response and ChainResponseAX, which are discussed in the next subsection as they assume the temporal non-simultaneity axiom. The ones here discussed are a mere application of temporal short-circuit rewriting. Therefore, this section aims at remarking on the generality of our result, which can be shown even without assuming ax:tns.

Each plot in fig:bennoax is grouped by c and the black solid line refers to the time required for the solver to generate

{Φ_{d}}_{i}^{' c}

from

{Φ_{d}}_{i}^{c, g}

in milliseconds. Missing data points refer to data points not being collected as the solutions went out of primary memory. For both Lydia and AALTAF, we consider running those over both the non-rewritten specification

Φ_{i}^{c, g}

as well as over the rewritten one

Φ_{i}^{' c}

(LYDIA(R) and AALTAF(R) in fig:bennoax). In its worst-case scenario, Reducer has a running time comparable to AALTAF over the non-reduced specification while, in the best-case scenario, it has a running time inferior or comparable to AALTAF over the rewritten specification. This ensures that running our solver as a pre-processing mechanism can benefit existing verified temporal artificial intelligence algorithms.

Given these experiments, such tools did not support our suggested rewriting rules. Otherwise, the tasks’ running time on the original specification

Φ_{i}^{c, g}

would have been comparable to the one for

Φ_{i}^{' c}

plus the running time for Reducer. Since experimental evidence suggests that the running time for

Φ_{i}^{c, g}

is always greater than the one for

Φ_{i}^{' c}

, we have thus empirically demonstrated both the novelty and necessity of these rewriting rules in the aforementioned tools. fig:knonoax shows the benchmarks for the formal verification task running on KnoBAB. This plot was separated from the rest to improve the plot’s readability. Even in this scenario, the formal verification task over the reduced specification comes, in the worst case scenario, with a running time comparable to the one over the original specification while, in the best case scenario, we have a speed-up of seven orders of magnitude, as all the tasks requiring the access to the ActivityTable are rewritten into clauses that can leverage the sole CountingTable. This also remarks that the query plan minimisation strategy cannot satisfactorily outperform any declarative specification pre-processing strategy, leading to a resulting reduced specification, as its associated running time would have had a comparable running time otherwise.

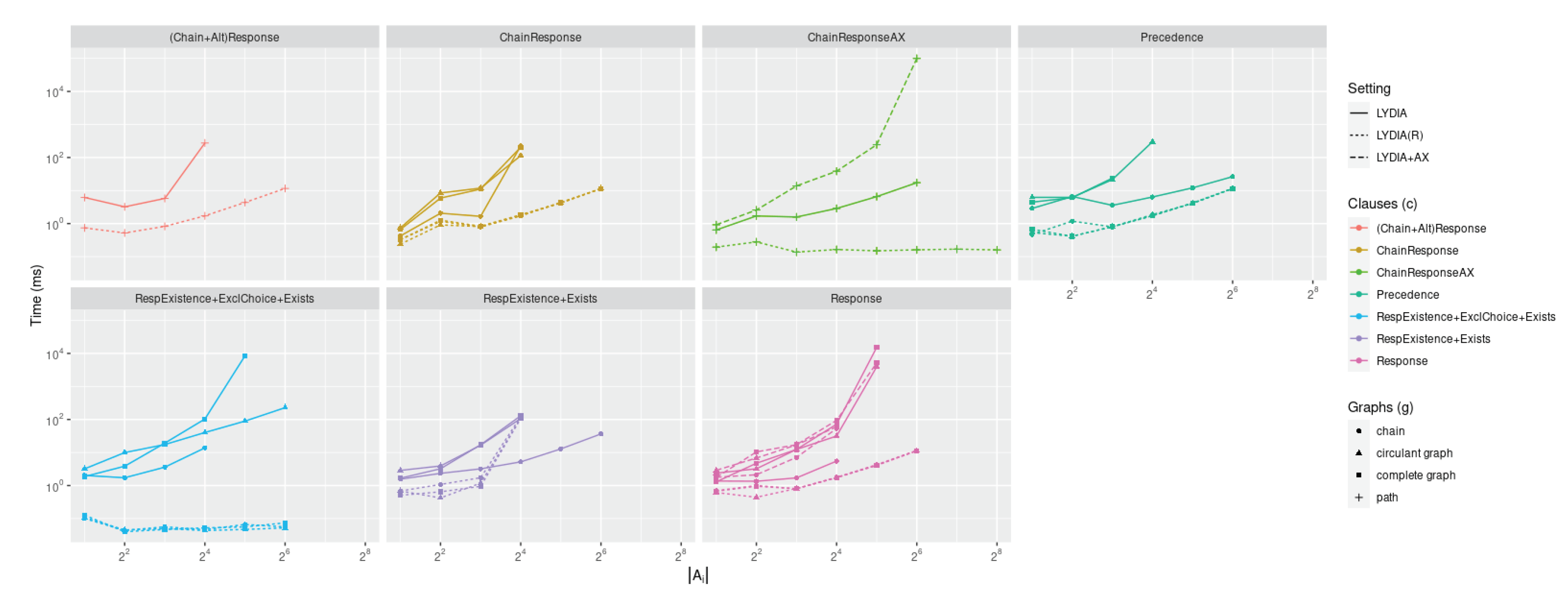
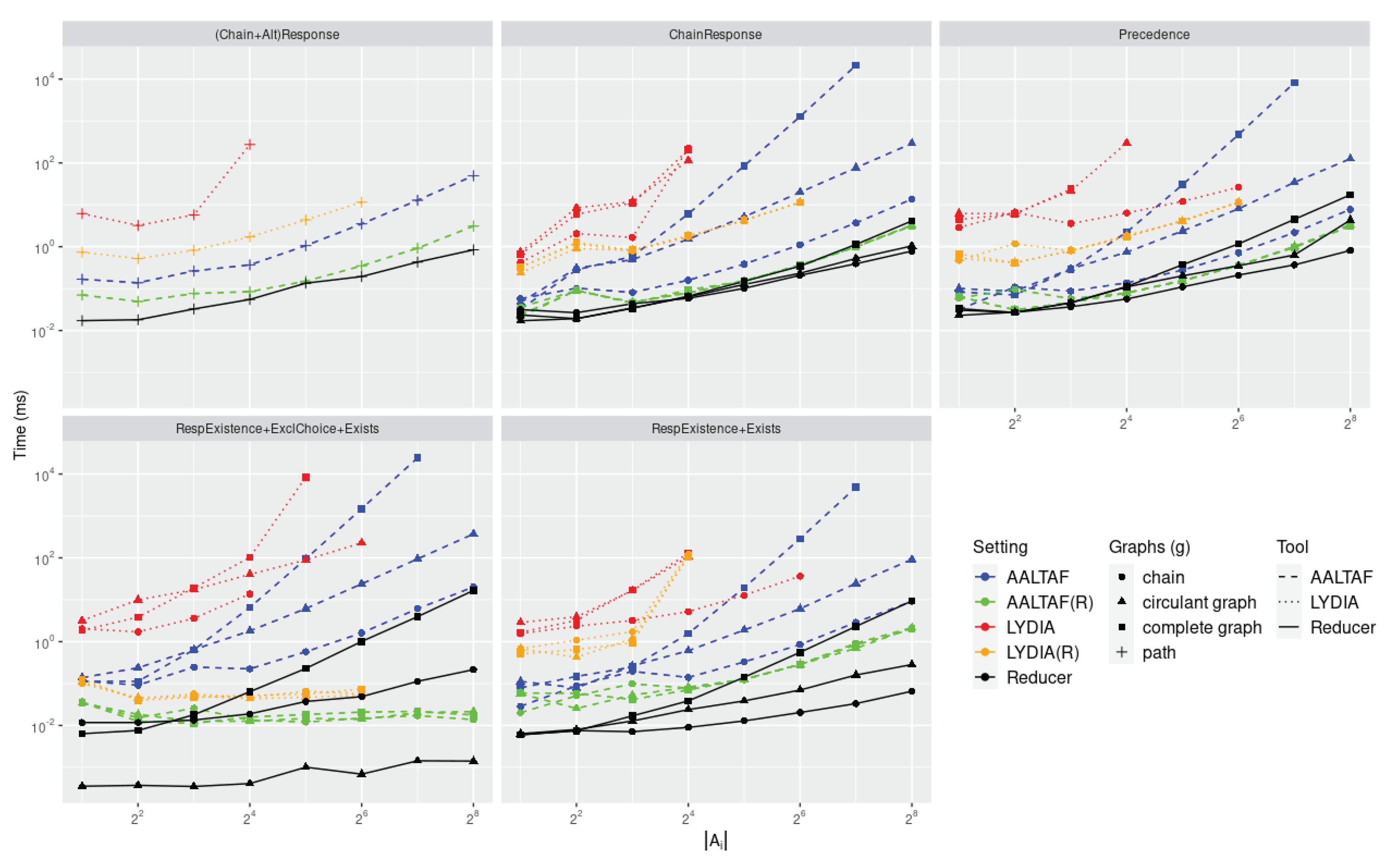
5.2. Rule Rewriting Requiring Temporal Non-Simultaneity

We now consider rewriting rules assuming the temporal non-simultaneity axiom. For this, we then need to compare the running time for

{(Φ_{i}^{c, g})}_{↓ A_{i}}

where the axiom is grounded over the finite set of activity labels

A_{i}

to the one resulting from the rewriting process by

{Φ_{i}^{c}}^{'}

. In fig:benax, we give running times for

Φ_{i}^{c, g}

for detecting any additional overheads being implied by the instantiation of the axiom over the atoms in

A_{i}

. If both Lydia and AALTAF supported LTL_f rewriting rules as per this paper, carrying a task over

{(Φ_{i}^{c, g})}_{↓ A_{i}}

would have a comparable running time to

{Φ_{i}^{c}}^{'}

, while a considerable overhead for computing

{(Φ_{i}^{c, g})}_{↓ A_{i}}

if compared to

Φ_{i}^{c, g}

denotes that the additional rules coming from the instantiation to the axiom provide a significant computational burden rather than helping in simplifying the specification.

This set of experiments confirms all our previous observations from the previous set-up regarding comparisons between our specification rewriting strategy and the existing verified temporal artificial intelligence tasks. We observe that, in the best-case scenario, such tasks exhibit a running time for

{(Φ_{i}^{c, g})}_{↓ A_{i}}

comparable to the one for

Φ_{i}^{c, g}

while, in the worst-case scenario, they increase their computational gap proportionally to the increase of the number of clauses. Still, the tasks running over

{Φ_{i}^{c}}^{'}

are consistently outperforming the same tasks running in

{(Φ_{i}^{c, g})}_{↓ A_{i}}

while also guaranteeing to minimise the out-of-memory exceptions. In the case of AALTAF, these are then completely nullified. Similar considerations can be drawn for running formal specification tasks over the 9 traces sampled from our Cybersecurity scenario, fig:knoax shows that running

{Φ_{d}}_{i}^{'}

gives speed-ups between 3 and 7 orders of magnitude by consistently exploiting the CountingTable instead of the ActivityTable if compared to the running times for the original specification

{Φ_{d}}_{i}^{c, g}

6. Conclusion and Future Works

This paper showed for the first time the existence of a polytime fragment of LTL_f, DECLAREd by simply circumscribing the temporal expressiveness of the language. This was possible by observing differences between LTL_f and LTL and, to some extent, assuming mutually exclusive conditions across events. We, therefore, design a scalable SAT-Solver working under equational rewriting, thus rewriting a temporal specification into an equivalent and more tractable rewritten temporal specification

Φ_{d}^{'}

. Future works will analyse DECLAREd’s time complexity by also considering first-order arithmetic conditions [16]. Experiments on Lydia remarked that the latter does not support adequate rewriting for internal formula minimisation as computing

{(Φ_{i}^{c, g})}_{↓ A_{i}}

is always slower than

Φ_{i}^{' c}

: no algebraic rewriting is considered, as the minimisation steps are only performed while composing the DFA and never at the LTL_f level. Running Lydia on

Φ_{i}^{' c}

significantly improves the running time for temporal formal synthesis. Future works will assess whether the construction of the DFA over the alphabet

{{c} | c \in Σ} \cup {⌀}

instead of

℘ (Σ)

per Axiom 1, where ⌀ denotes any other atom not in

Σ

, will boost the algorithm. We will also consider using graph equi-joins in lieu of product construction for conjunction of states, as the former technique already proved to be more efficient than traditional automata composition for DFA generation over

Φ

s [18].

Experiments on AALTAF showed it does not exploit rewriting rules as introduced in this paper: computing

{(Φ_{i}^{c, g})}_{↓ A_{i}}

is also more costly than

Φ_{i}^{c, g}

, and the computation over

Φ_{i}^{' c}

as generated by our solver is always faster than computing either

{(Φ_{i}^{c, g})}_{↓ A_{i}}

Φ_{i}^{c, g}

, thus remarking the benefit of our approach in rewriting the formula. Future works will consider generalising the rewiring rules here defined for DECLAREd, a fragment of LTL_f, so as to be implemented in any LTL_f tool considering such a rewriting step.

Last, our tool also proved to be beneficial as a specification preprocessing step for optimising formal verification tasks over relational databases, as computing

Φ_{d}^{'}

is always faster than computing

Φ_{d}

. Future work will consider defining a query plan optimisation strategy not only by computing each shared sub-expression within a given specification once, but also implementing suitable algebraic rewriting rules while supporting Axiom 1.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The author declares no conflicts of interest.

Appendix A. Formal Definition

We now provide the formal definition of some operators that were given informally at the end of the Introduction.

Appendix A.1. Graph Operations

O u t_{G} (u) : = \{v \in V_{G} | (u, v) \in E_{G}\}

I n_{G} (v) : = \{u \in V_{G} | (u, v) \in E_{G}\}

D e g_{G} (v) : = | O u t_{G} (v) | + | I n_{G} (v) |

E_{G}^{+} (α, β) : = (V_{G} \cup {α, β}, E_{G} \cup {(α, β)})

V_{G}^{-} (α) : = (V_{G} ∖ {α}, {(u, v) \in E | u \neq α \land v \neq α})

\begin{matrix} E_{G}^{-} (α, β) : = \\ (V_{G} ∖ {u | (α, β) \in E_{G} \land (u = α \lor u = β) \land D e g_{G} (u) = 1}, \\ {(u, v) \in E_{G} | u \neq α \land v \neq β}) \end{matrix}

Appendix A.2. Multimap Operations

D e l_{f} (x) : = y \mapsto \{\begin{matrix} ⌀ & y = x \\ f (y) & y \neq x \end{matrix}

P u t_{f} (x, v) : = y \mapsto \{\begin{matrix} f (x) \cup {v} & y = x \\ f (y) & y \neq x \end{matrix}

Appendix B. Short-Circuit Rewriting: Time Complexity

The following rewriting lemmas will heavily rely upon the algorithm outlined in [6] for generating an NFA out of a temporal specification

Φ

. We will use this algorithm to prove that, upon applying this algorithm and minimising the resulting non-deterministic automaton, we will obtain automata equivalently expressing the total absence of the activity labels being represented within the specification. As the size of the resulting graph is exponential over the number of the clauses of the graph, we show that any algorithm using this approach for detecting short-circuit rewriting will take at least ExpTime over the size of the specification

Φ_{d}

to detect this. On the other hand, the next section shows a convenient algorithm for detecting those in polytime over the size of the specification. Please also observe that we provide generic proofs for each of the following lemmas, not necessarily requiring that all the activity labels in

A \subseteq Σ

shall be considered mutually exclusive.

Appendix B.1. Automata-Based Strategy

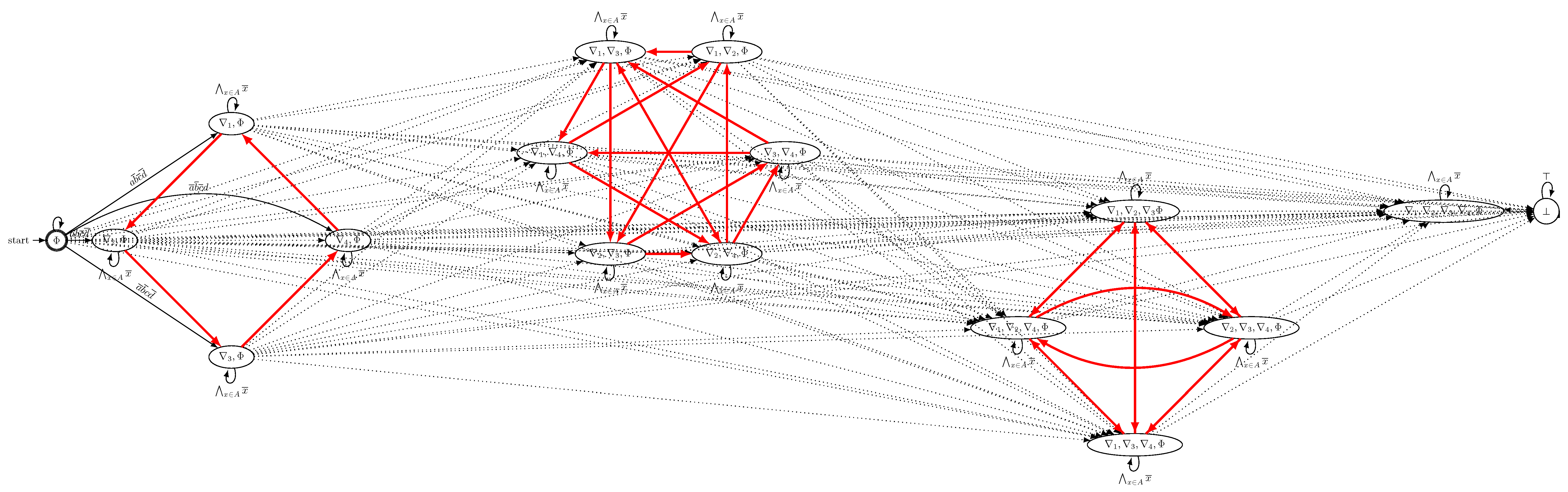
Figure A1. Representation of the NFA associated to

Φ_{d} = {ChainResponse (c_{i}, c_{i + 1 mod 2})}_{i \in {1, 2}}

before minimisation for lemr-1.

Figure A1. Representation of the NFA associated to

Φ_{d} = {ChainResponse (c_{i}, c_{i + 1 mod 2})}_{i \in {1, 2}}

before minimisation for lemr-1.

Proof

(Proof for lemr-1). Please observe that the following proof works independently from the non-simultaneity axiom: as we will show, the activation of at least one condition in A will require to verify all the requirements in the specification indefinitely, thus never leading to an acceptance state. So, we now prove this for A not necessarily containing mutually exclusive activity labels.

For this, let us define an atom substitution function

ρ

{[c_{i} \mapsto c_{(i + 1 mod | Σ |)}]}_{1 \leq i \leq n}

indicating the next required atom to follow according to the formula requirements. The generic formula for a ChainResponse temporal short-circuit leads to the NFA that can be constructed as follows: an initial state

q_{0}

being also the sole acceptance state, having a self-loop for

⋀_{a \in A} \neg a

, a sink falsehood state ⊥ having a self-loop as the only outgoing edge with the universal truth formula ⊤; for each

S \in ℘ (A) ∖ {\emptyset}

, we generate a new state S associated to the formula

S_{ϕ} = S_{ϕ}^{+} \land S_{ϕ}^{-}

with

S_{ϕ}^{+} = ⋀_{a \in S} a

and

S_{ϕ}^{-} : = ⋀_{a \in A ∖ S} \neg a

, describing the actions that were performed to each this system state. For each of these, where we outline the following edges:

an edge $q_{0} \overset{S_{ϕ}}{\to} S$ : this requires that, as soon as at least one of the activities in A is run, then we need to follow the requirements associated to the specification;
an edge $S \overset{\neg (ρ S_{ϕ}^{+})}{\to} ⊥$ : this requires that, as soon as we miss one of the transition conditions requiring that each of the activities being true in S should then immediately move to the immediately following activities $ρ S$ , we then violate the specification;
for each $T \in ℘ (A) ∖ {\emptyset}$ , we define a new edge $S \overset{T_{ϕ}}{\to} T$ if $ρ S \subseteq T$ : we connect each of such states not only to the immediately following actions as per $ρ$ , but we also assume that further activation conditions must hold.

Please observe that, as soon as all the activities in A are activated, all are then required to be always true, thus having that the state A will have as outgoing edges its self-loop, prescribing that all the conditions in A must hold, and a transition towards ⊥ as soon as at least one of these conditions are no more satisfied. After minimising this DFA, we can observe that we obtain

q_{0}

, still an initial acceptance state retaining its self-loop, and ⊥, also retaining its self-loop while having an edge labelled as

⋁_{a \in A} a

coming from

q_{0}

, thus entailing a DFA accepting only the traces where none of the atoms in A. Thus, we proved the correctness of our reduction into a conjunction of DECLAREd absences for each activity label in A.

As the number of states is in

O (| ℘ (A) |)

, the generation of the automaton will take at least exponential time over the size of the ChainResponse short-circuit, also corresponding to the size of

A \subseteq Σ

. □

Figure A2. Representation of the NFA associated to

Φ = ⋀_{1 \leq i \leq 3} □ (c_{i} \Rightarrow ⊚ ◊ c_{i + 1 mod 3})

before minimisation for b1lemma.

Figure A2. Representation of the NFA associated to

Φ = ⋀_{1 \leq i \leq 3} □ (c_{i} \Rightarrow ⊚ ◊ c_{i + 1 mod 3})

before minimisation for b1lemma.

Figure A3. Representation of the NFA associated to

Φ = {AltResponse (c_{i}, c_{i + 1 mod 4})}_{1 \leq i \leq 4}

before minimisation for arlemma.

Figure A3. Representation of the NFA associated to

Φ = {AltResponse (c_{i}, c_{i + 1 mod 4})}_{1 \leq i \leq 4}

before minimisation for arlemma.

Lemma A1.

Given

A = {c_{1}, c_{2}, \dots, c_{n}} \subseteq Σ

with

| A | > 2

Φ^{'} : = ⋀_{c_{i} \in A} □ \neg c_{i}

is equivalent to

Φ : = [□ (c_{n} \Rightarrow ⊚ ◊ c_{1}) \land ⋀_{\overset{i \in N}{1 \leq i < n}} □ (c_{i} \Rightarrow ⊚ ◊ c_{i + 1})]

inLTL_f.

Proof.

Differently from the previous proof, where the NFA automaton could have been greatly simplified due to the involvement of ⊚ within the construction, the proof for this lemma needs to be handled with greater care. Before starting, we remind the reader of the special temporal properties holding in LTL_f:

□ ϕ = ϕ \land ⊚ □ ϕ

□ (ϕ \land ϕ^{'}) = □ ϕ \land □ ϕ^{'}

, and

◊ ϕ = ϕ \lor ⊚ ◊ ϕ

The activation of a i-th clause at any state S while constructing the NFA by

c_{i} \in A

“generates” the corresponding target condition to be met

\nabla_{i} : = ◊ (c_{(i + 1 mod | A |)})

expressed as

\nabla_{i} \equiv (c_{(i + 1 mod | A |)} \lor ⊚ \nabla_{i})

by the special temporal property of the eventuality operator. By running [6], we also generate

2^{| A |}

states, where the sole initial and acceptance state associated to

Φ

, and the other states S are associated to the formulæ in

S = {S^{'} \cup {Φ} | S^{'} \in ℘ ({\nabla_{i} | c_{i} \in A}) ∖ {\emptyset}}

, none of which is an accepting state. No explicit falsehood sink state is present, as the invalidation of one of the

\nabla_{i}

will actually require never having an event

c_{i + 1 mod | A |}

, for which we would still transit across non-accepting states in

S

indefinitely. We then identify the following transitions among such states:

(1): $Φ \overset{⋀_{c_{i} \in A} \neg c_{i}}{\to} Φ$ : if none of the clauses is activated, we trigger no activation condition $c_{i}$ leading into a $\nabla_{i}$ target requirement to be met; we, therefore, persist on the same initial accepting state.
(2): $Φ \overset{⋀_{\nabla_{i} \in S} c_{i} \land ⋀_{\nabla_{j} \notin S} \neg c_{j}}{\to} S$ for each $S \in S$ : when at least one activity label in $Φ$ activates one clause, we transit to a state representing the activation of the specific clause.
(3): $S \overset{F}{\to} S$ for each $S \in S$ : for remaining in the same state, we require that no other condition $c_{i}$ not appearing as $\nabla_{i} \in S$ shall be activated, otherwise, we will be transiting towards another state. Furthermore, we require that the activation of any $c_{i + 1 mod | A |}$ for which both $\nabla_{i + 1 mod | A |}$ and $\nabla_{i}$ appear in S should also require the activation of the activity $c_{i}$ as, otherwise, we will reduce the number of $\nabla_{i}$ , thus ending into a state containing a subset of activated conditions: this is enforced by the construction of $Φ$ . Given this, we obtain the following formulation for F:

$\underset{\nabla_{i + 1 mod | A |}, \nabla_{i} \in S}{⋀} (c_{i + 1} \Rightarrow c_{i}) \land \underset{\nabla_{j} \notin S}{⋀} \neg c_{j}$

Please observe that we do not require that $⋀_{\nabla_{i + 1 mod | A |} \notin S, \nabla_{i} \in S} (c_{i})$ should also hold, as the eventuality of the condition for the target condition does not strictly require that such condition must immediately hold in a subsequent step, so either the possibility of $c_{i}$ being still activated or its opposite are both considered.
(4): ${\nabla_{j}}_{j \in S^{'}} \cup {Φ} \overset{F}{\to} {\nabla_{j}}_{j \in S^{''}} \cup {Φ}$ with $S^{'} \subset S^{''}$ : we need to ensure that the conditions appearing only in $S^{''}$ are newly activated, while the ones being active in $S^{'}$ shall be kept active in $S^{''}$ ; given this, we obtain the following F:

$\underset{\begin{matrix} i \in S^{''} ∖ S^{'} \cup \\ {j | (j = 1 \land | A | \in S^{'}) \lor (j \neq 1 \land j - 1 \in S^{'})} \end{matrix}}{⋀} c_{i} \land (\underset{i \in {1, \dots, | A |} ∖ (S \cup S^{'})}{⋀} \neg c_{i})$
(5): ${\nabla_{j}}_{j \in S^{'}} \cup {Φ} \overset{F}{\to} {\nabla_{j}}_{j \in S^{''}} \cup {Φ}$ with $S^{'} \supset S^{''}$ : this transition can only occur if, by attempting to consume $\nabla_{i}$ with $i \in S^{'}$ by executing an action $c_{i + 1 mod | A |}$ , this leads to generating $\nabla_{i + 1 mod | A |}$ appearing in $S^{''} \cap S^{'}$ or, otherwise, we would have transited towards another state. This then provides a restriction of the states towards which we can transit and the states that can move backwards. F can be then defined as:

$\underset{\begin{matrix} i \in S^{'}, \\ i + 1 mod | A | \in S^{'} \cap S^{''} \end{matrix}}{⋀} c_{i + 1 mod | A |} \land \underset{i \in {1, \dots, | A |} ∖ (S^{''} \cup S^{'})}{⋀} \neg c_{i}$
(6): ${\nabla_{j}}_{j \in S^{'}} \cup {Φ} \overset{F}{\to} {\nabla_{j}}_{j \in S^{''}} \cup {Φ}$ with $S^{'} \neq S^{''}$ : otherwise, we can transit ${\nabla_{j}}_{j \in S^{'}} \cup {Φ} \overset{F}{\to} {\nabla_{j}}_{j \in S^{''}} \cup {Φ}$ with $S^{'} \neq S^{''}$ at the following conditions: for each $j \in S^{'}$ , either $(j + 1 mod | A |) \in S^{''}$ or $j \in S^{''}$ . If those conditions had not been met, given the previous considerations, it would not have been possible to transit exactly between these two states.

As we can observe from the former transitions, once one trace event satisfies a condition in A, we will always navigate towards states in

S

without ever having the possibility of going back to the initial and sole accepting state

Φ

, as we must perennially guarantee that the conditions in A shall be eventually satisfied in turns, thus entailing that no finite trace will ever satisfy such conditions. As the number of states required for generating these formulae is therefore exponential in the size of both

Φ

and A as

| Φ | = | A |

by construction, by assuming that the most efficient algorithm for generating such automaton from the LTL_f specification will take at least a time comparable to the size of the graph without any additional computation overhead, we therefore have that such algorithm will take at least an exponential time on the size of the specification, thus in

o (2^{| A |})

Similarly to the previous lemma, even in this scenario, the minimisation of such automaton will lead to one being equivalent to the one predicate the absence of all the activities in A.

□

Proof

(Proof for lemwdue). It derives as a corollary from b1lemma, which holds independently from the non-simultaneity axiom. □

Lemma A2.

Given

A = {c_{1}, c_{2}, \dots, c_{n}} \subseteq Σ

Φ^{'} : = ⋀_{c_{i} \in A} □ \neg c_{i}

is equivalent to

Φ : = □ (c_{n} \Rightarrow ⊚ (\neg c_{n} U c_{1})) \land ⋀_{\overset{i \in N}{1 \leq i < n}} □ (c_{i} \Rightarrow ⊚ (\neg c_{i} U c_{i + 1}))

inLTL_f.

Proof.

We proceed similarly to the previous lemma where now, due to the adoption of the Until operator, we change the definition of

\nabla_{i}

per its special property as follows:

\nabla_{i} : = c_{i + 1 mod | A |} \lor (\neg c_{i} \land \neg c_{i + 1 mod | A |} \land ⊚ \nabla_{i})

prescribing that in any subsequent step

c_{i}

can never occur until the first occurrence of

c_{i + 1 mod | A |}

. Furthermore, similarly to the ChainResponse case, we add a falsehood sink state, towards each state will transit upon violation of the conditions prohibited by

\nabla_{i}

. In fact, this lemma restricts the expected behaviour in the former lemma, as we now prescribe that

c_{i}

, once activating a clause thus adding

\nabla_{i}

to a state, cannot occur before the occurrence of

c_{i + 1 mod | A |}

or, otherwise, we have to transit towards a never-accepting sink falsehood state. Consequently, except for the sink falsehood state, I could loop over any other state only if none of the activities in A are considered. We now stress the main differences from the definition of the transition functions if compared with the previous lemma:

(1): $Φ \overset{⋀_{c_{i} \in A} \neg c_{i}}{\to} Φ$ : Same as per the previous lemma.
(2): $Φ \overset{⋀_{\nabla_{i} \in S} c_{i} \land ⋀_{\nabla_{j} \notin S} \neg c_{j}}{\to} S$ for each $S \in S$ : Same as per the previous lemma.
(3): $S \overset{F}{\to} S$ for each $S \in S$ : As per previous observation, this is now changed to $F = ⋀_{c_{i} \in A} \neg c_{i}$ , as performing none of the states that are recorded in A is the only possible way not to transit into any other state.
(4): ${\nabla_{j}}_{j \in S^{'}} \cup {Φ} \overset{F}{\to} {\nabla_{j}}_{j \in S^{''}} \cup {Φ}$ with $S^{'} \subset S^{''}$ : Same as per previous lemma.
(5): ${\nabla_{j}}_{j \in S^{'}} \cup {Φ} \overset{F}{\to} {\nabla_{j}}_{j \in S^{''}} \cup {Φ}$ with $S^{'} \supset S^{''}$ . This type of transition never occurs similarly to lemr-1. Without any loss of generality, let us assume that $S^{'} = {i, j, k}$ and $S^{''} = {i, j}$ as in the previous lemma: allowing such transition would require to have an event abiding by $c_{k + 1 mod | A |}$ for which either $i = k + 1 mod | A |$ or $j = k + 1 mod | A |$ . The only possible way to make this admissible is to make also $\nabla_{i}$ (or $\nabla_{j}$ ) move with a corresponding $c_{i + 1 mod | A |}$ (or $c_{j + 1 mod | A |}$ ) action; still, this would have contradicted the assumption that i and j are not moving, and therefore this action would either violate $\nabla_{i}$ or $\nabla_{j}$ , which is then impossible. Therefore, executing any of the activation conditions $c_{i}$ for $i \in S^{'}$ being explicitly prohibited by the corresponding $\nabla_{i}$ will just move the current source state of interest towards the sink falsehood state.
(6): ${\nabla_{j}}_{j \in S^{'}} \cup {Φ} \overset{F}{\to} {\nabla_{j}}_{j \in S^{''}} \cup {Φ}$ with $S^{'} \neq S^{''}$ : otherwise, as observed in the previous point, we can move towards a new state by either consuming a $c_{i + 1 mod | A |}$ with $i \in S^{'}$ leading to an $i + 1 mod | A | \in S^{''}$ , or by ensuring a $c_{j + 1 mod | A |}$ with $j + 1 mod | A | \in S^{''} ∖ S^{'}$ and $j \notin S^{'}$ for not violating an already-activated condition. Overall, we can observe that this leads to never transiting from a state containing more activation conditions towards one containing less than those, at any rate.

Under all the remaining circumstances, we transit from S towards the falsehood sink state. Similarly, as in the previous construction, we can observe that any algorithm generating such a graph before minimisation will take an exponential time on the size of both the specification

Φ

and A. □

Appendix B.2. Proposed Methodology

In this section, we show an efficient algorithm for detecting short-circuit rewritings within the DECLAREd fragment in polytime over the size of the specification.

Corollary A1.

We can rewrite

Φ_{d}

containing aChainResponseshort-circuit in polytime on the size of

Φ_{d}

Proof.

Given the construction sketched in §2.2, the best case scenario for

Φ

constitutes in

Φ

containing exactly one single ChainResponse circuit, for which we obtain a graph

G^{cr}

representing itself a cycle of size

| Φ |

. By adopting a DFS visit for detecting a cycle, we take

O (V + E)

to recognize the whole graph

G^{cr}

as a cycle.

In the worst-case scenario,

Φ

contains a conjunction of clauses

⋀_{\overset{a, c \in Σ}{a \neq c}} ChainResponse (a, c)

leading to a fully connected graph

G^{cr}

. Within this scenario, the worst-case scenario for detecting a cycle is detecting a cycle of size 2 after fully visiting

G^{cr}

. After doing so, we remove the two nodes from

G^{cr}

and repeat the visit over such a reduced graph. If we always assume to detect cycles of size 2 for each visit, we will end up running

\frac{| V^{cr} |}{2}

visits of the graph, and the overall time complexity becomes

\sum_{i = 0}^{| V^{cr} | / 2} (| V^{cr} | - 2 i + (| V^{cr} {| - 2 i)}^{2}) \in O (| V^{cr} |^{3})

□

As a further corollary from this, we immediately deduce that our strategy from §3.4 is far way more efficient than generating a DFA associated with a formula for then minimising it as in lemr-1, as in the best case scenario we still have to generate an exponential number of states in the size of A, while in our proposed approach we do not. This is possible as our current envisioned approach assumes lemr-1 to hold without needing to go through the aforementioned exponential construction algorithm.

Corollary A2.

We can rewrite

Φ_{d}

containing aResponseshort-circuit in polytime on the size of

Φ_{d}

Proof.

This can be considered a further corollary of coroll1, as both the graph visit and construction phase are completely independent of the nature of the clause, which is completely neglected and sketched in terms of mutual dependencies across activity labels through a dependency graph. Similar conclusions then hold, also in terms of time complexity for the graph visit. □

Corollary A3.

We can rewrite

Φ_{d}

containing anAltResponseshort-circuit in polytime on the size of

Φ_{d}

Proof.

As per coroll2, the goal is closed similarly to b1lemma due to the same way the graph is constructed independently from its associated LTL_f semantics. □

Appendix C. Formal Verification Speedup

While the previous section clarified that, by assuming a templated temporal language, we can rewrite temporal short-circuits in polynomial time, this section remarks the benefits of the aforementioned rewriting within formal verification tasks, as all aforementioned state-of-the-art algorithms in these regard do not contemplate clause rewriting. This will then provide a theoretical validation over the empirical results provided in the main paper.

While considering the computational complexity associated with formal verification tasks, we assume the KnoBAB computational model, where the entire set of traces within a log is considered, and each trace is not necessarily computed one at a time. Therefore, we interpret the LTL_f computation for each trace in the log regarding the associated xtLTL_f operators in KnoBAB [2].

Proof

(Proof for lemuno). Given

| | S | |

the number of all the events in the log obtained by summing up all the trace lengths in

S

| | S | |

denotes the number of all the events in the entire log in all traces. We also denote

# a

as the number of all the events in

S

having “

a

” as an activity label.

Using KnoBAB as a computational model for computing LTL_f via xtLTL_f, we can determine

σ, t ⊧ ⊚ c_{i}

# c_{i}

time. As the number of all the events not being

c_{i}

S

| | S | | - # c_{i}

, computing

σ, t ⊧ \neg c_{i}

requires

| | S | | - # c_{i}

time. Under the KnoBAB intermediate result representation assumption, all the intermediate results from xtLTL_f expressions are pre-sorted by trace id and temporal position, we can compute either

σ, t ⊧ φ \land φ^{'}

σ, t ⊧ φ \land φ^{'}

in at most

| φ | + | φ^{'} |

time. Per each clause occurring in the specification, we are interested in computing

ϕ = c_{i} \Rightarrow ⊚ c_{i + 1 mod | A |}

. We can then

ϕ

(\neg c_{i}) \lor (c_{i} \land ⊚ c_{i + 1 mod | A |})

: as we observe that the next

⊚ φ

operator provides a linear scan of the input operator, this computation can be carried out in an overall

| | S | | - # c_{i} + # c_{i} + 2 # c_{i + 1 mod | A |}

generating, in the worst case scenario, data in the size of

| | S | |

. Furthermore, we observe that computing this for each clause in

Φ

leads to a total time of

| A | | | S | | + 2 | | S | |

. Therefore, computing

σ, t ⊧ □ ϕ

as an xtLTL_f operator over all events satisfying

σ, t ⊧ ϕ

will take at most

| | S | | log | | S | |

per clause, thus adding up to

| A | | | S | | log | | S | |

. Furthermore, the cost of computing the conjunction among the result of all such clauses adds up to

| A | | | S | |

in its worst-case scenario.

On the other hand, computing each

□ \neg c_{i}

in the resulting specification

Φ^{'}

requires KnoBAB to check in the counting table for each trace that

c_{i}

occurs zero times with a linear scan; thus,

Φ^{'}

can be computed in

2 | A | | S | = 2 l e

time, as we also need to encompass the time required for computing the disjunction between all the data being computed per traces.

For

l : = | | S | | > 0

and

e : = | A | > 0

, we therefore compute the positive speed-up by expressing it as the ratio between the time complexity for computing a formal verification task composed by ChainRespons-es leading to a temporal short-circuit and the one for computing an equivalent set of absence clauses after short-circuit rewriting. From this ratio, we observe that the computation of the rewritten specification leads to a positive speed-up over the former, as the the resulting value is always greater or equal than zero:

\frac{l e (1 + \frac{2}{e}) + l e log l + l e}{2 l e} \geq 1 \Leftrightarrow \frac{2}{e} + log l \geq 0

□

Proof

(Proof for lemdue ). We use the proof for lem-1 as a calque for this other speed-up analysis, where we only have to change

ϕ

c_{i} \Rightarrow ◊ c_{i + 1 mod | A |}

thus focussing our analysis on

σ, t ⊧ ϕ

: this can be then equivalently expressed as

σ, t ⊧ \neg c_{i} \lor (c_{i} \land ◊ c_{i + 1 mod | A |})

, where

φ \land ◊ φ^{'}

is computed using a specific derived operator taking

| φ | | φ^{'} | log | φ^{'} |

time. For each clause, this leads to

| | S | | - # c_{i} + # c_{i} \cdot # c_{i + 1 mod | A |} log # c_{i + 1 mod | A |}

time per clause computing

ϕ

returning, in the worst case scenario,

| | S | |

events; all the clauses take at most

| | S | (| A | - 1) + | | S | | k log k

time to compute this expression by assuming

k ≃ # c_{1} ≃ \dots ≃ # c_{| A |} ≃ \frac{| | S | |}{| A |}

. As in the previous Lemma, the computation of the associated □ operator for each

□ ϕ

per each of the

| A |

clauses will take at most

| A | | | S | | log | | S | |

time. The time for computing

Φ^{'}

is also

2 l e

as per the previous Lemma.

Similarly to the previous lemma, we then compute the ratio between the time complexity for formal verification over AltResponse-es leading to a temporal short-circuit and the one over the equivaletly rewritten specification. As the ratio between the former and the latter is strictly greater than zero, the rewriting leads to a speed-up at least proportional to the size of the log and traces for

l : = | | S | | > 0

and

e : = | A | > 0

\frac{l (e - 1) + l k log k + l e log l + l e}{2 l e} = \frac{1 - \frac{1}{e} + \frac{k log k}{e} + log l + 1}{2} \geq 1

Thus entailing an always positive speed-up for formal verification tasks for sufficiently large

k, l, e \to \infty

. □

Lemma A3.

Given

A = {c_{1}, c_{2}, \dots, c_{n}} \subseteq Σ

, computing

Φ^{'} : = ⋀_{c_{i} \in A} □ \neg c_{i}

in lieu of

Φ : = □ (c_{n} \Rightarrow ⊚ (\neg c_{n} U c_{1})) \land ⋀_{\overset{i \in N}{1 \leq i < n}} □ (c_{i} \Rightarrow ⊚ (\neg c_{i} U c_{i + 1}))

always leads to a positive average speed-up.

Proof.

We can exploit a similar formulation as per lem-1 and lemre-2, where we now only need to consider that

\neg c_{i} U c_{i + 1 mod | A |}

will come at the cost of

(| | S | | - # c_{i})^{2} # c_{i + 1 mod | A |}

. This computation will generate at most data in the size of

| | S | | - # c_{i}

, as the latter data within the first operand of the Until will also contain the events satisfying the condition in the second argument, thus leading to an additional

| | S | | - # c_{i}

cost for computing the associated ⊚ operator. As the previous clauses, in the worst case scenario each clause will take

(| | S | | - # c_{i})^{2} # c_{i + 1 mod | A |} + | | S | | - # c_{i}

to compute and, when considering all the clauses so far, this adds up to

{| | S | |}^{3} {(1 - \frac{| | S | |}{| A |})}^{2} + | | S | | (| A | - 1)

for each clause by considering

# c_{i} ≃ # c_{i + 1 mod | A |} ≃ \frac{| | S | |}{| A |}

So, as this increases the overall time complexity for each clause, we also obtain as per lemre-2 an always positive speed-up. □

Appendix D. DECLAREd SAT

This section remarks that the rule rewriting strategy outlined in this paper can be used as a SAT-solver for DECLAREd. After showing the correctness of this procedure (§Appendix D.1), we finally show that the underlying time complexity of the overall procedure is in polynomial time (§D.2).

Appendix D.1. Correctness

Lemma A4.

If the specification is a tautology, then the formula is completely rewritten into ⊤.

Proof.

algo:load is the only part detecting trivially-holding conditions: this occurs all the time that an edge is not added in

G^{★}

for a clause with the template ★ while invoking neither Abs nor Ex, as these would otherwise trigger the generation of Absence and Exists clauses at the end of the computation. In fact, any further clause rewriting resulting from applying the rewriting rules as described in §3.3 always invokes one of the two former functions, thus not necessarily guaranteeing that an empty specification will be returned. Therefore, the aforementioned algorithm is the only point in the code where the non-insertion of clauses jointly with the lack of the invocation of Abs/Ex might lead to the generation of an empty specification. As the clauses that were not inserted in the specification were actually trivially true, if we obtain a specification with empty graphs and an empty F, we infer that the overall specification is also trivially true. Therefore, in this situation, we return ⊤ as a resulting

Φ^{'}

for

Φ_{d}^{'}

. □

Lemma A5.

If the specification is unsatisfiable, then the computation abruptedly terminates while returning ⊥

Proof.

We observe that we detect the specification as unsatisfiable only under three circumstances, whether (i)

\exists x \in d o m (F) . | F (x) | = 2

, thus implying by algorithmic construction that the absurd condition

Absence (x) \land Exists (x)

should hold, (ii) whether we trigger a rewriting rule leading to ⊥, and (iii) at loading time. This proof follows from the assumption that no further inconsistency can be detected from the described rules and algorithms.

The first scenario requires checking, each time a new

Absence (x)

Exists (x)

clause is generated, to always check for (i) while ensuring that the detection of (i) is propagated through the function call chain. The second condition requires iterating over all the edges and correctly detecting the conditions leading to ⊥ from fig:rewriting while applying the rewriting rules as per §3.3: the return of ⊥ in this occasion is described in this section. The third scenario is as described in algo:load. We close the two last sub-goals as we covered all the possible cases leading to a direct inconsistency.

This leads to then proving the remaining first sub-goal. First, we can prove that detecting an inconsistent specification is propagated backwards given the function call stack. Let us now focus on the sub-routines in alg:asur: we observe that Abs/Ex returns false when a specification is being detected as inconsistent, while all the other sub-routines in the same Algorithm immediately return false upon calling any of the other functions when at least one call detects such an inconsistency. As the generation of

Absence (x)

Exists (x)

is also achieved by calling the previous functions, we always ensure that any potential inconsistency is detected. Furthermore, the code guarantees that any call to Reduce and Clear returning false immediately returns ⊥: this in fact holds as the respective functions guarantee that explicit application of the rewriting rules involving each clause that we know per Absence(x) that will be never activated, thus guaranteeing an a posteriori rewriting of the specification even after scanning all of the clauses associated to the same template as per §3.3. For NotCoExistence, we also guarnatee that this detection occurs by directly calling Reduce

^{ch}

instead, thus also leading to the generation of Exists clauses. Dually, this also holds for the generation of new Exists(x) rules, which are then leading to the invocation of the Expand

^{re} (x)

sub-routine which, in turn, is also checking for Ex(x). Thus we can observe that our algorithm guarantees that all of the rules are properly expanded as well as always updating on the current state for the existence/absence of inconsistencies, thus leading to correctly detecting an inconsistency if any. As the rewriting rules provide all the possible combinations for which the absence or the presence of specific activity labels might generate further activation or target conditions, we immediately ensure to return an inconsistent specification upon detection given the rewriting rules completely describing the language. □

Last, we also provided some unit tests for ensuring, to the best of our knowledge, the correctness of the implemented solution: https://anonymous.4open.science/r/DECLAREd-B1BF/tests.cpp.

Appendix D.2. Convergence in PolyTime(Φ d )

We now prove the lemmas dealing with DECLAREd’s decidability and polynomial time complexity for each sub-routine within our equational rewriting algorithm.

Lemma A6.

The sub-routines in alg:asur always terminate in polynomial time.

Proof.

We now analyse each declared sub-routine. Before doing so, we observe that no rule generates activity labels that are not originally considered within the original specification

Φ_{d}

, thus ensuring that the computation will always terminate. Given

Σ

the set of all the activity labels occurring in the original specification

Φ_{d}

, we can only have

| Σ |

distinct calls to these functions and, given that no rule in both fig:rewriting and temporal short-circuit rewriting generates novel activity labels not occurring in the formula, we are never expecting having

| d o m (F) | > | Σ |

, thus ensuring the non-divergence of our computation. This assumption (A1) is then transferred to each call of the following functions:

Ex(x):: This function takes note that the specification requires, at some point of the rewriting, that x shall exist anytime in a trace; this mainly updates a hashmap F and immediately returns a boolean value determining whether this is also associated to an absence, for which then F will be associated to two distinct values instead of one. Therefore, this trivially terminates in $O (1)$ .
Abs(x):: This function is the exact dual of the previous one, as it predicates the absence of an event associated with an activity label x. Even in this case, this function always terminates in $O (1)$ .
Clear(x):: This function calls only other functions for removing vertices and edges from a graph associated with a clause template, which functions are non-recursive and trivially terminating. Furthermore, this function only reduces the previously loaded and indexed information, except for the clauses associated with calls to Ex(x) and Abs(x), used to detect inconsistencies within the temporal specification. This is carried out in linear time over the size of the currently-loaded specification.
Reduce $^{★}$ (x) for $★ \neq ch$ :: This function mainly describes an iterative backward DFS visit over a $G^{★}$ graph with $★ \neq p$ using toremove as a stack by traversing all the edges in the graph backwards from x; we avoid in-definitively traversing loops in the graph by remembering which nodes were already visited and popped from the aforementioned stack (visited). This call jointly with Clear(x) ensures that no clause containing $x \in Σ$ as an activity label will be returned in the resulting specification, as this function will remove all the vertices representing the activity label x. Henceforth, even this function does not generate new data jointly with A1. Overall, the algorithm is then guaranteed always to terminate in polynomial time over the size of the specification.
Reduce $^{p}$ (x):: we can draw similar considerations as the previous algorithm, as the main difference is merely in the direction of the graph visit: we are now traversing the edges forward instead than in reverse ( $\forall a, b \in Σ . Precedence (a, b) \land Absence (a) \equiv Absence (a) \land Absence (b)$ , Line 56 also in fig:rewriting). Vertices from the $G^{p}$ are also explicitly covered in this function (L. 40), as this is not considered as part of Clear(x); this ensures that this function cannot be called with the same argument x.
Expand $^{re}$ (x):: Notwithstanding that this function is the dual of the previous, this works similarly: when a new Exists(x) DECLAREd clause is attempted to be generated, we ensure that this will not trigger another rewriting annihilating some RespExistence clauses ( $\forall a, b \in Σ . RespExistence (a, b) \land Exists (a) \equiv Exists (a) \land Exists (b)$ , Line 56). Similarly to the previous steps, we are not adding information in the graph $G^{re}$ that we are traversing, rather than removing those, thus ensuring to avoid unnecessary re-computations over the same activity label $x \in Σ$ . Furthermore, we remove any occurrence of a Choice clause that might be trivialised by the existence of x ( $\forall a, b \in Σ . Choice (a, b) \land (Exists (a) \lor Exists (b)) \equiv (Exists (a) \lor Exists (b))$ , Line 52) as well as checking whether the existence of x might lead to inconsistencies related to the required absence of the label expressed in the target condition at Line 54:

$\forall a, b \in Σ . NegSuccession (a, b) \land Exists (a) \equiv Absence (b)$

Similarly to the other sub-routines, this function is gradually reducing the number of the clauses which are potentially rewritten in Exists/Absence: due to (A1), this procedure is also guaranteed to terminate.
Reduce $^{★}$ (x) for $★ = ch$ :: This provides a restriction to the case $★ \neq ch$ inasmuch as the activity labels in toremove are not visited from the stack, rather than being used for calling Expand $^{re}$ which, in turn, is also a terminating function. Overall, Reduce is always terminating independently from ★.

Overall, we conclude that each of the sub-routines is guaranteed to terminate in at most polynomial time while also guaranteeing to reduce the information being stored in the graphs associated with each declarative template. □

Lemma A7.

The computation allowing the expansion of some DECLAREd clauses while loading those in the appropriate graphs

G^{★}

for each template ★ terminates in linear time over the size of the specification (algo:load).

Proof.

First, as the

Φ_{d}

set is always finite under the assumption that this algorithm works by loading specification as written in a computer, then this algorithm will always take a finite time to linearly iterate over all the finite set of DECLAREd clauses being represented in the specification. Next, each invocation to Ex and Abs is guaranteed to terminate in

O (1)

due to Lemma A6. Furthermore, while graphs are instantiated by adding edges (and therefore the corresponding nodes if missing), we are never traversing those. As per previous considerations, at this stage we also consider expansion rules rewriting some of the given clauses in

Φ

as other clauses. As this expansion does not trigger any further rewriting rule in fig:rewriting, we are simply adding new clauses without being stuck in never-ending cycles. This also goes hand in hand with (A1) from the previous lemma, as we generate clauses without inferring new activity labels not in the original specification. Therefore, even this algorithmic step is guaranteed to terminate in most linear time concerning the specification size. □

Corollary A4.

The computation of short-circuit rewriting is guaranteed to terminate in a polytime over the size of the original specification.

Proof.

This can be seen as a further corollary of Corollary A1, Corollary A2, and Corollary A3: as the composition of distinct terminating function calls leads to an overall terminating computation, we guarantee that all the short-circuit rewritings lead to a terminating computation in polytime over the size of the original specification,

Φ_{d}

. □

Lemma A8.

The computation of the rewriting rules leads to a terminating procedure.

Proof.

Last, we consider the termination for the procedure sketched in §3.3. In the worst case scenario, we are never generating an inconsistency, thus never abruptedly terminating the procedure by returning an inconsistent ⊥ specification. If no rewriting rule is ever triggered, we then simply linearly iterate over all the edges of the graphs

G^{★}

for each template ★ without triggering any of the past functions. Furthermore, the iteration over the domain of F will be always be the same. Therefore, no additional overhead is introduced and the procedure terminates. On the other hand, we trigger at least one rewriting rule that, per the (A1) assumption, never generates a clause containing an activity label that was not present in

Σ

: under this, all the previous functions are also guaranteed not to generate more information than the one being available in

Σ

. Furthermore, this computation never generates new edges to be visited, as the only expansion phase occurs as described in exploadDec. At most. we trigger the deletion of edges from the graph in

O (1)

that we are currently generating or the generation of novel Exists/Absence clauses, but we never generate other clauses. Furthermore, the graphs are mainly depleted after iterating over the edges, by invoking Reduce or Clear functions for each x s.t.

F (x) = false

after the aforementioned edge iteration. Even in this scenario, the computation is guaranteed to converge in polynomial time: as we mainly boil down the clauses to absences and existentials while ensuring to remove entailing clauses, and given that the number of such templates is finite, we therefore guarantee to converge in at most polynomial time over the size of the declarative specification. □

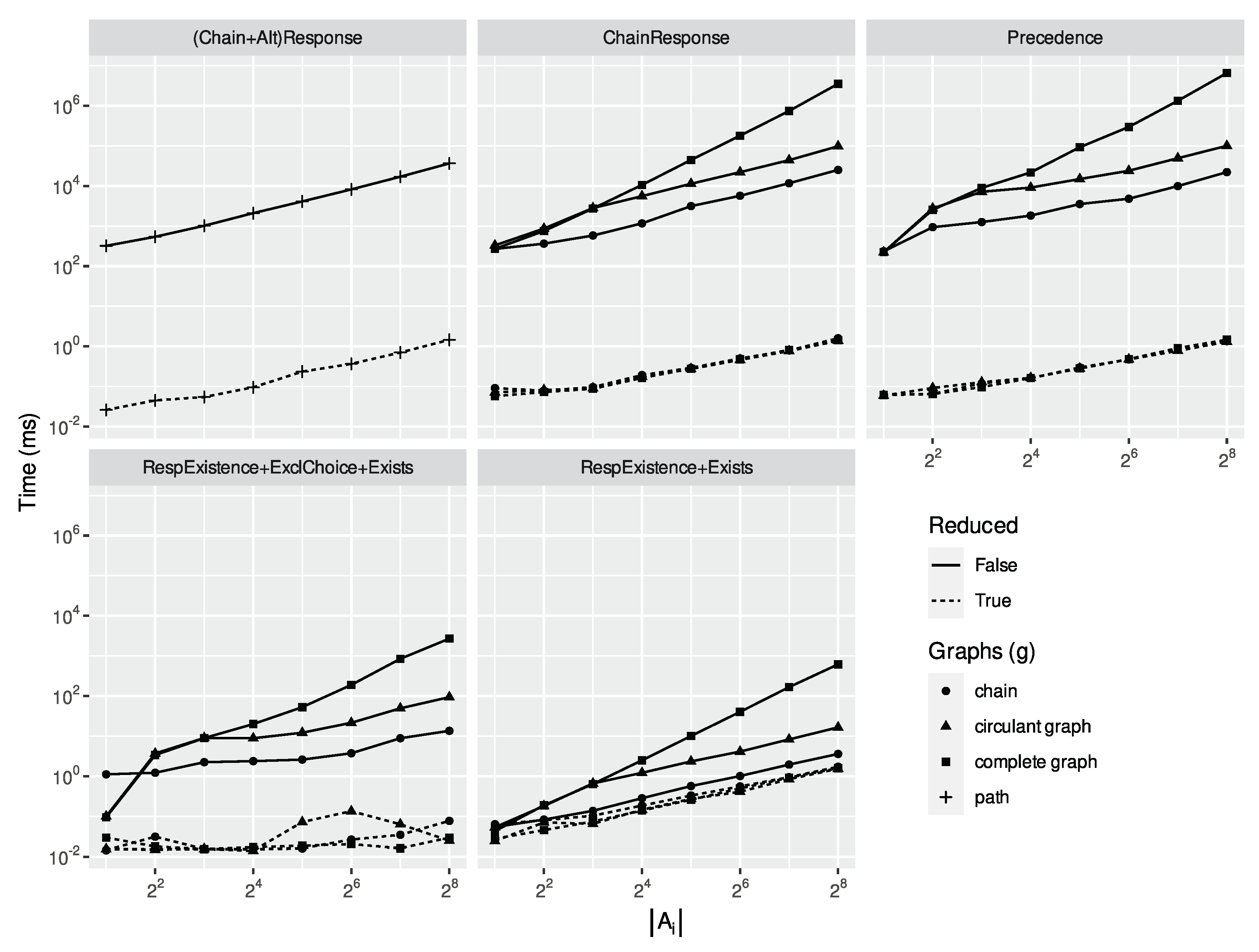
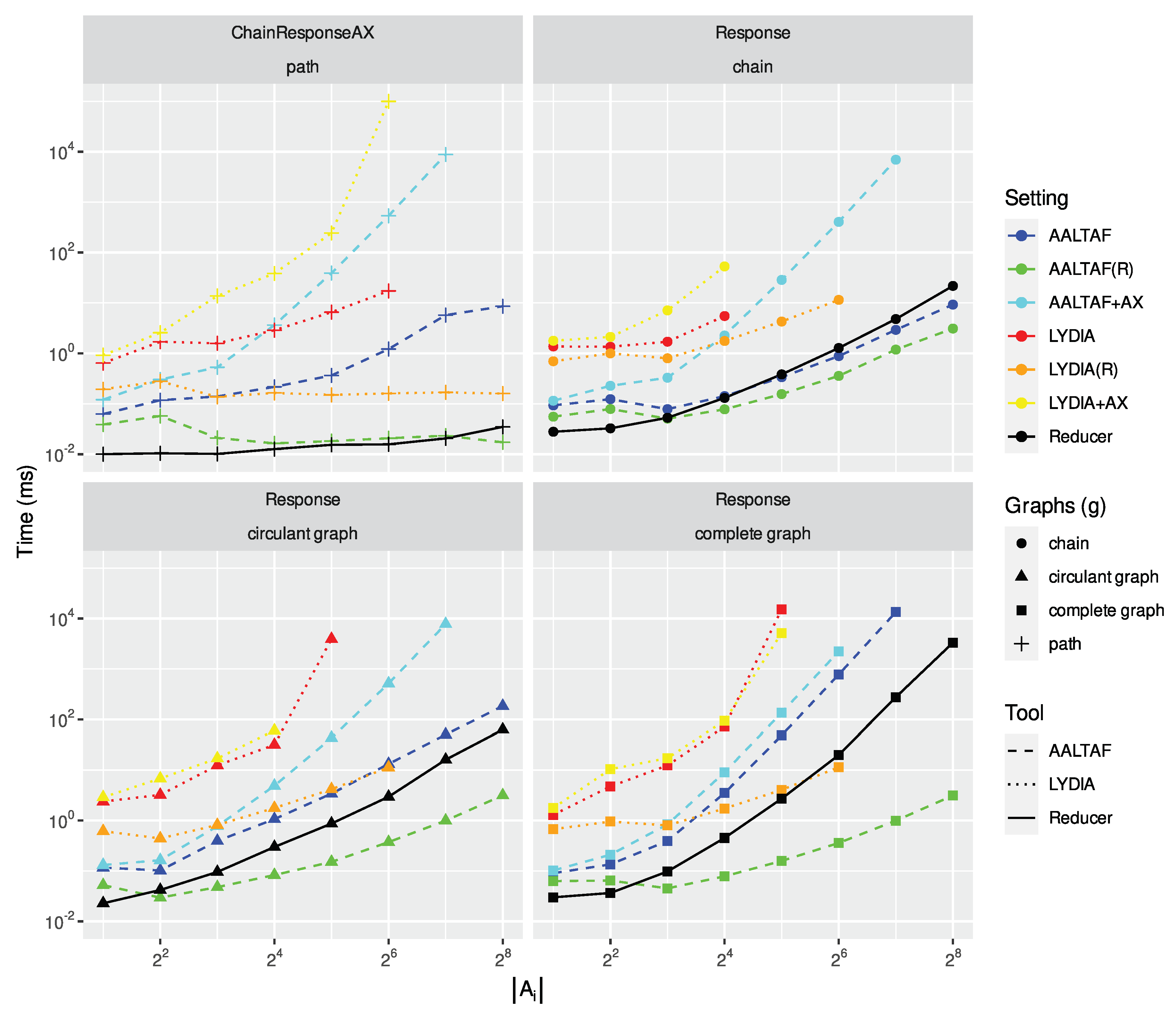
Appendix E. Detailed Benchmarks

This section provides the aforementioned benchmarks in a greater size, so as to better remark the running times associated with each single algorithm. As in the main paper, missing data points for specific

2^{i}

values of

| Σ |

refer to missing data points due to out-of-memory issues while dealing with the automaton representation of the LTL_f formula. fig:allReducer provides all the running times for the reducer, while fig:allLydia andfig:allAaltaf refers to the running time of the formal synthesis (Lydia) and SAT-Checker (AALTAF) tasks over different specifications representations.

Figure A4. Running times for rewriting

Φ_{d}

Φ_{d}^{'}

Figure A4. Running times for rewriting

Φ_{d}

Φ_{d}^{'}

Figure A5. Running times for Lydia for both

Φ_{i}^{c, g}

(LYDIA),

Φ_{i}^{' c}

(LYDIA(R)) and

{(Φ_{i}^{c, g})}_{↓ Σ}

(LYDIA+AX)

Figure A5. Running times for Lydia for both

Φ_{i}^{c, g}

(LYDIA),

Φ_{i}^{' c}

(LYDIA(R)) and

{(Φ_{i}^{c, g})}_{↓ Σ}

(LYDIA+AX)

Figure A6. Running times for AALTAF for both

Φ_{i}^{c, g}

(AALTAF),

Φ_{i}^{' c}

(AALTAF(R)) and

{(Φ_{i}^{c, g})}_{↓ Σ}

(AALTAF+AX)

Figure A6. Running times for AALTAF for both

Φ_{i}^{c, g}

(AALTAF),

Φ_{i}^{' c}

(AALTAF(R)) and

{(Φ_{i}^{c, g})}_{↓ Σ}

(AALTAF+AX)

References

Bergami, G. Streamlining Temporal Formal Verification over Columnar Databases. Information 2024, 15. [Google Scholar] [CrossRef]
Bergami, G.; Appleby, S.; Morgan, G. Quickening Data-Aware Conformance Checking through Temporal Algebras. Inf. 2023, 14, 173. [Google Scholar] [CrossRef]
De Giacomo, G.; Favorito, M. Compositional Approach to Translate LTLf/LDLf into Deterministic Finite Automata. Proceedings of the International Conference on Automated Planning and Scheduling 2021, 31, 122–130. [Google Scholar] [CrossRef]
Bergami, G.; Appleby, S.; Morgan, G. Specification Mining over Temporal Data. Computers 2023, 12. [Google Scholar] [CrossRef]
Pnueli, A. The temporal logic of programs. In Proceedings of the 18th Annual Symposium on Foundations of Computer Science (sfcs 1977); 1977; pp. 46–57. [Google Scholar] [CrossRef]
Giacomo, G.D.; Masellis, R.D.; Montali, M. Reasoning on LTL on Finite Traces: Insensitivity to Infiniteness. In Proceedings of the Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, July 27 -31, 2014, Québec City, Québec, Canada; pp. 20141027–1033. [CrossRef]
Pesić, M.; Schonenberg, H.; van der Aalst, W.M. DECLARE: Full Support for Loosely-Structured Processes. In Proceedings of the 11th IEEE International Enterprise Distributed Object Computing Conference (EDOC 2007); 2007; pp. 287–287. [Google Scholar]
Xu, H.; Pang, J.; Yang, X.; Yu, J.; Li, X.; Zhao, D. Modeling clinical activities based on multi-perspective declarative process mining with openEHR’s characteristic. BMC Medical Informatics and Decision Making 2020, 20, 303. [Google Scholar] [CrossRef] [PubMed]
Giacomo, G.D.; Maggi, F.M.; Marrella, A.; Patrizi, F. On the Disruptive Effectiveness of Automated Planning for LTLf-Based Trace Alignment. In Proceedings of the Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, February 4-9, 2017, San Francisco, California, USA; pp. 20173555–3561. [CrossRef]
Bergami, G.; Maggi, F.M.; Marrella, A.; Montali, M. Aligning Data-Aware Declarative Process Models and Event Logs. In Proceedings of the Business Process Management; Polyvyanyy, A.; Wynn, M.T.; Van Looy, A.; Reichert, M., Eds., Cham; 2021; pp. 235–251. [Google Scholar]
Huo, X.; Hao, K.; Chen, L.; song Tang, X.; Wang, T.; Cai, X. A dynamic soft sensor of industrial fuzzy time series with propositional linear temporal logic. Expert Systems with Applications 2022, 201, 117176. [Google Scholar] [CrossRef]
Wang, C.; Wu, K.; Zhou, T.; Cai, Z. Time2State: An Unsupervised Framework for Inferring the Latent States in Time Series Data. Proc. ACM Manag. Data 2023, 1. [Google Scholar] [CrossRef]
Yazi, A.F.; Çatak, F.Ö.; Gül, E. Classification of Methamorphic Malware with Deep Learning(LSTM). In Proceedings of the 27th Signal Processing and Communications Applications Conference, SIU 2019, Sivas, Turkey, April 24-26, 2019. IEEE, Sivas, Turkey, 24-26 April 2019; 2019; pp. 1–4. [Google Scholar]
Catak, F.O.; Ahmed, J.; Sahinbas, K.; Khand, Z.H. Data augmentation based malware detection using convolutional neural networks. PeerJ Computer Science 2021, 7, e346. [Google Scholar] [CrossRef] [PubMed]
Li, J.; Pu, G.; Zhang, Y.; Vardi, M.Y.; Rozier, K.Y. SAT-based explicit LTLf satisfiability checking. Artificial Intelligence 2020, 289, 103369. [Google Scholar] [CrossRef]
Geatti, L.; Gianola, A.; Gigante, N.; Winkler, S. Decidable Fragments of LTL_f Modulo Theories. In Proceedings of the ECAI; Gal, K.; et al.. 2023. [Google Scholar]
Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd Edition. MIT Press, 2009. [Google Scholar]
Bergami, G. Fast Synthetic Data-Aware Log Generation for Temporal Declarative Models. In Proceedings of the Proceedings of the 6th Joint Workshop on Graph Data Management Experiences & Systems (GRADES) and Network Data Analytics (NDA), New York, NY, USA, 2023; GRADES & NDA ’23.

1	https://anonymous.4open.science/r/DECLAREd-B1BF
2	https://github.com/whitemech/lydia
3	https://github.com/datagram-db/knobab
4	https://github.com/lijwen2748/aaltaf
5	An on-line tool is available here: http://ltlf2dfa.diag.uniroma1.it/
6	https://drive.google.com/drive/folders/1EK44vwSBVdz_A17XZintDP1eeEoBh53Q?usp=sharing

Figure 1. Some rewriting Rules for DECLAREd (§3.3)

Figure 2. Comparing the specification reducer’s running time with the ones of Lydia and AALTAF running over

Φ_{i}^{c, g}

vs. running over

Φ_{i}^{' c}

(LYDIA(R) and AALTAF(R) respectively).

Figure 2. Comparing the specification reducer’s running time with the ones of Lydia and AALTAF running over

Φ_{i}^{c, g}

vs. running over

Φ_{i}^{' c}

(LYDIA(R) and AALTAF(R) respectively).

Figure 3. Comparing different running times of KnoBAB over

Φ_{d}

(False) vs.

Φ_{d}^{'}

(True).

Figure 3. Comparing different running times of KnoBAB over

Φ_{d}

(False) vs.

Φ_{d}^{'}

(True).

Figure 4. Comparing the specification reducer’s running time with the ones of Lydia and AALTAF running over

Φ_{i}^{c, g}

vs. running over

Φ_{i}^{' c}

(LYDIA(R) and AALTAF(R) respectively) and the grounded representation

{(Φ_{i}^{c, g})}_{↓ A_{i}}

(LYDIA+AX and AALTAF+AX respectively).

Figure 4. Comparing the specification reducer’s running time with the ones of Lydia and AALTAF running over

Φ_{i}^{c, g}

vs. running over

Φ_{i}^{' c}

(LYDIA(R) and AALTAF(R) respectively) and the grounded representation

{(Φ_{i}^{c, g})}_{↓ A_{i}}

(LYDIA+AX and AALTAF+AX respectively).

Figure 5. Comparing different running times of KnoBAB over

Φ_{d}

(False) vs.

Φ_{d}^{'}

(True).

Figure 5. Comparing different running times of KnoBAB over

Φ_{d}

(False) vs.

Φ_{d}^{'}

(True).

Table 1. DECLAREd: our Declare’s subset of interest, where A (respectively, B) denote activation (resp., target) conditions.

Exemplifying clause ( $c_{l}$ )	LTL_f Semantics ( $〚 c_{l} 〛$ )
Exists(A)	$◊ A$
Absence(A)	$□ \neg A$
Choice( $A, A^{'}$ )	$◊ A \lor ◊ A^{'}$
NotCoExistence( $A, A^{'}$ )	$\neg (◊ A \land ◊ A^{'})$
ExlChoice( $A, A^{'}$ )	$〚 Choice (A, A^{'}) 〛 \land 〚 NotCoExistence (A, A^{'}) 〛$
RespExistence( $A, B$ )	$◊ A \Rightarrow ◊ B$
CoExistence( $A, B$ )	$〚 RespExistence (A, B) 〛 \land 〚 RespExistence (B, A) 〛$
Precedence( $A, B$ )	$\neg B W A$
Response( $A, B$ )	$□ (A \Rightarrow ◊ B)$
Succession( $A, B$ )	$〚 Precedence (A, B) 〛 \land 〚 Response (A, B) 〛$
NegSuccession( $A, B$ )	$□ (A \Rightarrow \neg ◊ B)$
ChainPrecedence( $A, B$ )	$□ (⊚ A \Rightarrow B)$
ChainResponse( $A, B$ )	$□ (A \Rightarrow ⊚ B)$
ChainSuccession( $A, B$ )	$〚 ChainPrecedence (B, A) 〛 \land 〚 ChainResponse (A, B) 〛$
AltResponse( $A, B$ )	$□ (A \Rightarrow ⊚ (\neg A U B))$
NegChainSuccession( $A, B$ )	$□ (A \Leftrightarrow ⊚ \neg B)$
AltPrecedence( $A, B$ )	$〚 Precedence (A, B) 〛 \land □ (B \Rightarrow ⊚ (\neg B W A))$
AltSuccession( $A, B$ )	$〚 AltPrecedence (A, B) 〛 \land 〚 AltResponse (A, B) 〛$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

DECLAREd: A Polytime LTLf Fragment

Abstract

1. Brief Related Work

Formal Synthesis.

Formal Verification.

SAT-Solvers.

LTLf Modulo Theories

2. Preliminaries

2.1. Rewriting Rules

2.2. Temporal Short-Circuit Rewriting

2.3. Temporal Non-Simultaneity

Rewriting Rules

Temporal Short-Circuit Rewriting

3. Reducer: Equational Rewriting

3.1. Algorithmic Subroutines

3.2. Specification Loading as Graphs

3.3. Applying Equational Rewriting

3.4. Applying Short-Circuit Rewriting

4. A PolyTime ( | Φ d | ) SAT-Solver for DECLAREd

5. Empirical Evaluation

5.1. Rule Rewriting without Temporal Non-Simultaneity

5.2. Rule Rewriting Requiring Temporal Non-Simultaneity

6. Conclusion and Future Works

Funding

Institutional Review Board Statement

Informed Consent Statement

Conflicts of Interest

Appendix A. Formal Definition

Appendix A.1. Graph Operations

Appendix A.2. Multimap Operations

Appendix B. Short-Circuit Rewriting: Time Complexity

Appendix B.1. Automata-Based Strategy

Appendix B.2. Proposed Methodology

Appendix C. Formal Verification Speedup

Appendix D. DECLAREd SAT

Appendix D.1. Correctness

Appendix D.2. Convergence in PolyTime(Φ d )

Appendix E. Detailed Benchmarks

References

MDPI Initiatives

Important Links

Subscribe

DECLAREd: A Polytime LTL_f Fragment

LTL_f Modulo Theories

4. A PolyTime $(| Φ_{d} |)$ SAT-Solver for DECLAREd