Influence of Knowledge Uncertainties on the Safety Assessment of Existing Post-tensioned Concrete Bridges

Preprint

Article

Influence of Knowledge Uncertainties on the Safety Assessment of Existing Post-tensioned Concrete Bridges

Altmetrics

Downloads

Views

Comments

Alberto Poeta,

Fabio Micozzi^*

,Laura Gioiella,Andrea Dall'Asta

Alberto Poeta,

Fabio Micozzi^*

,Laura Gioiella,Andrea Dall'Asta

This version is not peer-reviewed

Submitted:

05 March 2024

Posted:

06 March 2024

You are already at the latest version

Alerts

Abstract

The assessment of existing bridges constitutes a serious challenge for the researchers since their safety evaluation is a complex task due to several sources of uncertainty affecting the parameters identified in the knowledge process. In particular, a high level of uncertainties may arise in the case of prestressing systems requiring special investigation strategies and experimental technologies. The paper aims to investigate how the knowledge uncertainties influence the safety assessment of existing post-tensioned bridges. The semi-probabilistic approach is used, and uncertainties related to the knowledge process are described considering the number of tests, the confidence level assumed for the estimation of the problem parameters, and the measurement errors of in-situ tests. Results concerning a typical post-tensioned bridge are reported and the variability of the outcomes is discussed and compared with a reference case of “perfect knowledge”. The main results of the study confirm the general robustness of the semi-probabilistic Eurocodes safety format and provide an overview of dispersion due to different choices about the number of tests and confidence level. The measurement errors may lead to significant under-estimation of the computed structural capacity with respect to the reference one.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Existing bridges constitute a significant portion of the transport infrastructure. A large part of them, although designed according to old Codes, is still in service. Such infrastructures can suffer the effects of both natural hazard (e.g. earthquakes [1,2] and floods [3]) and anthropic loads. It is quite common to find bridges subjected to actions larger than the actions considered in the design, due to the increasing of the total traffic and travelling loads. Furthermore, many bridges have exceeded their design lifetime and some of them show a significant degradation due to environmental effects and, in some cases, to insufficient maintenance interventions. These aspects have been highlighted by the unexpected collapses of bridges occurred worldwide in the recent past, causing economic and social losses. Among them, the collapse of the Fossano overpass in Cuneo in 2016 (IT), the Polcevera viaduct in Genova in 2019 (IT), the Troja footbridge in Prague in 2017 (RC), the Nanfangao bridge in Taiwan in 2019, and the most recent Fern Hollow Bridge in 2022 in Pittsburgh (US).

From the economical point of view, some recent studies have estimated the budget to renovate bridges in different countries. The COST ACTION 345 report [4] estimated a budget of about 400 billion Euros for the replacement costs of one million of existing bridges in the 27 European countries. In 2013 the Federal Highway Administration [5] estimated that approximately the 25 percent of US bridges were either structurally deficient or functionally obsolete; while in the same year the ASCE Infrastructure Report Card [5] estimated that the annual investment necessary for the improvement of US existing bridges was nearly 20 billion dollars. All these aspects stress the urgency of having an efficient and effective evaluation of the structural reliability of existing bridges to give support to stakeholders in optimizing the maintenance/restoration interventions, and in properly allocating the limited maintenance budgets [6].

In many countries the majority of bridge stock consists of simply supported Prestressed Concrete beams. Among them the Post Tensioned (PT) concrete bridges are a large part of the population, as in the case of Italy [7]. They are a critical set since the assessment of their vulnerability is affected by a notable level of uncertainties. Such uncertainties concern the knowledge of the state of conservation of the precompression system, which cannot be investigated through visual inspection or conventional tests. In the US, this aspect is treated by a specific guideline: the Federal Highway Administration-HRT-13-028 [8]. Such document provides protocols for sampling grout from tendons, and methods for the detection of grout deficiencies with reference to test techniques used in the American context. The guideline provides a rational approach to extract statistically significant number of grout samples to define the corrosion susceptibility and recommendation for repair/rehabilitation procedures. In England, this topic is treated by the Highway England CS 465 [9] and CS 464 [10]. The first document provides a management procedure for risk review, risk assessment and risk management for post-tensioned concrete bridge. The second, contains requirements related to Non-Destructive Testing (NDT) of highways structures. In Italy, a recent guideline [11] introduced a multi-level analysis for the risk assessment of existing bridges. This document suggests the executions of special inspections for PT bridges through a detailed study of the conditions of the post-tensioned cable system, based on the detection and quantification of defects. Data collected from visual inspections and in situ tests, specific for PT cables, are combined for an overall assessment of the pre-stressing system.

In most practical cases, the evaluation of the structural reliability is carried out through the semi-probabilistic approach [12]. In this case, the uncertainties concerning the problem are considered through (deterministic) characteristic parameters combined with partial factors, calibrated according to target values of the probability of failure. The partial factors suggested in most of national and international Standards have been developed for the assessment of new structures [12]. However, this approach is suitable for existing structures too, and proposals for partial factors have been developed. For example, the Fib 80 code [13], proposes two different partial factor formats, enabling the incorporation of specific reliability-related aspects for not deteriorated existing structures by considering the actual material properties. This way, all prior data collected from existing design specification and/or original design documents can be combined with information provided by material investigation (both non-destructive and destructive tests) and by visual inspections (e.g. [14,15]). An increase in the number of tests and in the confidence level leads to a reduction in the level of uncertainties of the design parameters estimated. However, a large number of tests is not always feasible and a balance between costs and approximation of the safety estimation should be found. In the field of reliability assessment of existing structures, it can be of interest to include time varying phenomena, as ageing, damage, and deterioration; some studies are currently on-going concerning these topics ([16,17,18,19]).

The outcome of the semi-probabilistic reliability assessment of new structure is a deterministic safety ratio, i.e. the capacity/demand ratio, and it derives from the knowledge of deterministic design parameters, based on statistical properties of the basic variables. On the contrary, in the case of existing structures, the safety ratio becomes an uncertain quantity since the statistical properties of the basic variables are not known in advance and they can only be estimated from a limited amount of information. The study reported in [20] has underscored the significant impact of knowledge uncertainties on the reliability assessment of existing structures. However, no previous studies have examined this effect on PT members, which are characterized by a greater complexity, a higher number of basic variables, and potentially large uncertainties about measurement errors.

In this paper the reliability assessment of existing PT beams is performed by the semi-probabilistic approach, and the influence of the uncertainties affecting the knowledge process on the following statistical distribution of the safety ratio is evaluated and discussed. More precisely, the design parameters required by the semi-probabilistic approach are estimated, based on the outcomes of in-situ inspections and tests. The influence on the statistical distribution of the safety ratio of three parameters, (i) the number of tests, (ii) the confidence level chosen for the estimation of the design parameters, and (iii) the measure errors related to test techniques, is investigated.

Three different scenarios have been considered. In the first one an ideal condition of “perfect knowledge” is assumed. Safety checks performed in this condition lead to the reference solution of safety ratios, that is assumed as the real one. In the second scenario the knowledge process is considered: the influence of the number of tests on the safety checks is studied, considering also different choices for the confidence level assumed for the estimation of the parameters. In the third scenario, the error affecting the experimental measures is introduced. The probabilistic distribution of the capacity/demand ratio following different choices regarding number of tests, confidence levels and measure uncertainties is obtained using a Monte Carlo simulation, evaluating and discussing the overall probability to observe values larger than the reference one, i.e. values on the un-safe side. Finally, it is worth to recall that this study focuses only on the propagation of uncertainties from the knowledge process towards the estimation of the safety ratio and the results do not depend on the choice of the set of partial factors.

2. Reliability Evaluation and Notation

Reliability assessment is generally based on the definition of a response function (or limit state function)

g (x) : R^{n} \to R

, where

x

is a vector collecting the so-called basic variables, or state variables (e.g. geometry, material properties, load magnitude and others), strictly necessary to evaluate the performance indicator

g

. Failure occurs if the response function is below a threshold

\bar{g}

, i.e.

g (x) < \bar{g}

Due to different sources of uncertainties [21], the basic variables

x

are described by a vector of random variables (r.v.)

X

, whose statistical properties are provided by the joint probability distribution function

f_{X} (x)

, so that the failure probability

P_{f}

, which is a probabilistic measure of the structural performance [22], can be evaluated by:

P_{f} = \int I (x) f_{X} (x) d x

(1)

where the index function

I (x)

in Equation (1) is defined as follows:

I (x) = 1

g (x) < \bar{g}

, otherwise

I (x) = 0

. The system response is satisfactory if

P_{f} < \bar{P_{f}}

in which the target value

\bar{P_{f}}

, is usually based on the evaluation of economic and social consequences due to failure.

Response function

g (x)

is often expressed by introducing two separate quantities related to the strength of the system

r (x)

, and to the effects of the external actions

e (x)

, whose most diffused expressions are the safety margin

z (x)

, defined by Equation (2), and the safety ratio

y (x)

, defined by Equation (3).

z (x) = r (x) - e (x)

(2)

y (x) = r (x) / e (x)

(3)

The failure condition is attained when

z < 0

y < 1

Given that

X

is a r.v., previous functions provide r.v. denoted as

G = g (X)

Z = z (X)

Y = y (X)

. Consequently, using for example the safety margin, the probability of failure

P_{f}

can be computed by integrating the probability distribution of

Z

over the unsafe domain, as shown in Equation (4).

P_{f} = P [Z = R - E < 0] = \int_{- \infty}^{0} f_{Z} (z) d z

(4)

The reliability assessment is often carried out by an approximated approach (the semi-probabilistic formulation [12]) deriving from

X

a set of deterministic “design” parameters

ϑ_{d}

and estimating, through these parameters, the safety ratio as shown in Equation (5). The parameters

ϑ_{d}

are usually obtained from strength and action descriptors reduced or amplified by calibrated partial factors, in order to obtain probability of failures close to the threshold when

y_{d} (ϑ_{d}) = r (ϑ_{d}) / e (ϑ_{d})

(5)

is equal to 1. In the case of existing structures, as those considered in this study, the properties

f_{X} (x)

X

can be only estimated by a reduced number of imprecise tests. Consequently, using the semi-probabilistic approach, the components of

ϑ_{d}

are no more deterministic values, but they are r.v.

{\bar{Θ}}_{d}

, that collect possible estimations

{\bar{ϑ}}_{d}

ϑ_{d}

. For example, the expected variability of

{\bar{ϑ}}_{d}

reduces by increasing the number of tests. Consequently, the expected safety ratio

{\bar{Y}}_{d} = y_{d} ({\bar{Θ}}_{d})

is a r.v. too.

3. Safety Assessment of Existing PT Bridges

As previously stated, the semi-probabilistic approach is used in the following for the safety assessment. First, the basic random variables

X

, chosen in this study to characterize the PT bridge properties are defined, and the related deterministic parameters

ϑ_{d}

required for the safety checks are introduced. Successively, the safety checks with respect to two failure conditions that are mainly influenced by the prestressing system: bending failure and shear failure, are described. Finally, the methods used for the estimation of

{\bar{ϑ}}_{d}

from experimental tests are discussed.

3.1. Basic Random Variables and Parameters for the Semi-Probabilistic Method

The basic variable vector

x

generally collects geometrical, mechanical, and material properties. In the problem analysed in this study vector

x

is defined as follows

x = [A_{p}, P_{p t}, f_{u p}, f_{y s}, f_{c}]

(6)

where the collected quantities describe the uncertain basic properties of the beam. More in detail

A_{p}

denotes the wires area;

P_{p t}

the current prestressing force;

f_{u p}

the ultimate strength of prestressing steel;

f_{y s}

the yielding strength of the rebar; and

f_{c}

the concrete strength. All the other basic variables (e.g. the beam width, the cable path, and so on), not contained in vector

x

, are assumed as known quantities described by deterministic values.

It is assumed that the components of

x

are statistically independent. They describe physical quantities that cannot be lower than 0, therefore their probability distribution describing the statistical properties of each random variable is assumed to be log-normal.

The parameters

ϑ_{d}

required in the semi-probabilistic approach based on the partial factors for the safety checks are

ϑ_{d} = [A_{p m}, P_{p t_m}, f_{y s d}, f_{u p d}, f_{c d}]

(7)

The vector

ϑ_{d}

encompasses the mean values of the wires area

A_{p m}

; the mean value of the current prestressing force

P_{p t_m}

; and the design values of the strength of materials

f_{y s d}

f_{u p d}

f_{c d}

derived by the ratio between their characteristic value and the relevant partial factor.

3.2. Failure Condition Modalities and Safety Checks

The safety checks are carried out by evaluating the safety ratio

y_{d}

of Equation (5), using the partial factor method. The considered checks are related to shear and to bending moment; both the failure conditions are considered since they are significantly influenced by the precompression system. The design values of resistances and actions have been computed using the same partial factors

γ

used for new structures as suggested in [12].

More in detail, the shear is checked at the first cracked section of the beam. The literature provides several studies with refined and complex formulas to predict the shear capacity of prestressed concrete members [23,24]s. In the following, the shear capacity is calculated according to the recommendations proposed by Italian Standard [25] and Eurocode [26] through the formulas for elements with and without shear-reinforcement. The relative variation is expected to be similar using more refined shear resistance models. In case of shear reinforcement, the shear capacity is derived using the following expressions

V_{R d, 1} = m i n (V_{R s d}, V_{R c d})

(8)

V_{R s d} = 0.9 d \frac{A_{s w}}{s} f_{y s d} (\cot δ + \cot ϑ) \sin δ

(9)

V_{R c d} = 0.9 d b_{w} α_{c} υ f_{c d} (\cot δ + \cot ϑ) / (1 + {c o t}^{2} ϑ)

(10)

where

d

is the effective height of the cross-section;

b_{w}

is the minimum width between tension and compression chord;

ϑ

is the angle between the concrete compression strut and the beam axis perpendicular to the shear action;

δ

is the angle between shear reinforcement and the beam axis perpendicular to the shear force;

A_{s w}

is the cross-sectional area of the shear reinforcement;

s

is the spacing of the stirrups;

f_{y s d}

is the design value of the rebar yielding strength obtained as

f_{y s k} / γ_{s}

, where

γ_{s}

is a partial factor equal to 1.15;

α_{c}

is the coefficient taking into account the state of stress in the compression chord;

f_{c d}

is the design value of the concrete strength obtained as

f_{c k} / γ_{c}

, where

γ_{c}

is a partial factor equal to 1.5; and

υ

is the strength reduction factor for concrete cracked in shear. Further information can be found in chapters 4.1.2.3.5.2 of [25] and 6.2.3 of [26].

The shear capacity for unreinforced cracked concrete is calculated trough the following equation.

V_{R d, 2} = m a x \{[C_{R d, c} k {(100 ρ_{1} f_{c k})}^{1 / 3} + k_{1} σ_{c p}] b_{w} d; (v_{m i n} + 0.15 σ_{c p}) b_{w} d\}

(11)

where

d

is the effective height of the cross-section;

b_{w}

is the smallest width of the cross-section in tensile area;

k

is a parameter depending on

d

;

f_{c k}

is the characteristic value of the concrete compressive strength;

C_{R d, c}

and

k_{1}

are parameters whose values are defined in national annexes, however their recommended values are

0.18 / γ_{c}

and

0.15

, respectively;

v_{m i n}

is a parameter that depends on

f_{c k}

, and

k

;

ρ_{1}

is a ratio depending on the area of tensile reinforcement,

b_{w}

, and

d

;

σ_{c p}

is the axial stress in the cross section defined as the ratio between the actual prestressing force

P_{p t_m}

, and the area of concrete

A_{c}

of the cross section. Further information can be found in chapter 4.1.2.3.5.1 of [25] and 6.2.2 of [26].

In the case of post-tensioned prestressed elements, the shear contribution given by the vertical component of the prestressing force,

V_{c p}

, shall be added to obtain the total shear capacity,

V_{R d}

. This component can be computed as

V_{c p} = P_{p t_m} \sin α_{c p}

(12)

where

P_{p t_m}

is the prestressing force of the cross-section; and

α_{c p}

is the angle between the prestressing force and the longitudinal axes of the beam. In the shear check the resultant cable is adopted for the prestressing force and its location.

For both the cases, the safety shear ratio

y_{d, s}

is calculated as follows and its greater value is chosen

y_{d, s} = m a x (\frac{V_{c p} + V_{R d, 1}}{V_{e d}}, \frac{V_{c p} + V_{R d, 2}}{V_{e d}})

(13)

where

V_{e d}

is the shear action acting on the section under investigation.

In the case of bending check over a generic cross section, the resistant bending moment,

M_{R d}

, can be computed as

M_{R d} = T d^{*}

(14)

T = f_{y p d} A_{p m} + f_{y s d} A_{s}

(15)

where

T

is the resultant tensile force containing the contributions given by the resultant cable, and by the reinforcement steel located under the neutral axis at the ultimate condition;

f_{y p d}

is the design value of the yielding strength of prestressing steel obtained as

f_{y p k} / γ_{s}

;

A_{s}

is the area of the reinforcing steel;

d^{*}

is the arm between the two resultant compressive and tensile forces. The bending check is usually carried out at the midpoint of the simply supported beam since that section is the most stressed one.

The safety bending ratio is obtained as

y_{d, b} = \frac{M_{R d}}{M_{e d}}

(16)

where

M_{e d}

is the design bending moment due to external actions.

A safety check is satisfied if this ratio is equal or greater than 1. Moreover, in this paper the envelope

y_{d}

is used, considering both the checks and calculated as

y_{d} = m i n (y_{d, b}, y_{d, s})

(17)

Previous Equations (10)–(12) and (14) are sensitive to the characteristics of the post-tensioning system that in turn involves the area of the cables

A_{p m}

, the actual prestressing force

P_{p t_m}

, and the characteristic yield stress of the harmonic steel

f_{y p k}

. The resistant bending moment is clearly sensitive to

A_{p m}

and

f_{y p k}

, while the shear resistance is, instead, sensitive to the prestressing force. The

P_{p t_m}

influences Equation (10) through the term

α_{c}

representing the compressive state of the section given by the prestressing system, while

P_{p t_m}

explicitly appears in Equations (11) and (12). Moreover, all the previous parameters indirectly influence the shear capacity because they sway the position of the first cracked section in which

V_{c p}

is different. By reducing the prestressing action, the first cracked section moves towards the beam support, resulting in a higher

V_{e d}

3.3. Estimation of the Design Parameters Based on Experimental Measurements

The semi-probabilistic method requires that some design parameters

ϑ_{d}

X

are estimated from a limited number

n

of tests providing samples

\bar{x}

. Estimated parameters are r.v.

{\bar{ϑ}}_{d}

and the confidence

α = P [{\bar{ϑ}}_{d} < ϑ_{d}]

is the probability that the estimated parameter is lower than the actual value. If the Cumulative Density Function (CDF) of

{\bar{ϑ}}_{d}

is available, it is possible to define the limit value

{\bar{ϑ}}_{d}^{\propto}

of the estimated quantity, such that

F_{{\bar{ϑ}}_{d}} ({\bar{ϑ}}_{d}^{\propto}) = α

For example, being

X

a single valued normally distributed r.v. whose standard deviation

σ_{X}

is known, it is possible to estimate the mean

X_{m}

by the sample mean

{\bar{x}}_{m} = \frac{1}{n} \sum_{i = 1}^{n} x_{i}

(18)

The estimation of the mean is a normally distributed r.v., whose expected value is equal to the real mean,

µ_{\bar{X}} = µ

, and the standard deviation depends on

σ_{X}

and on the number of tests,

σ_{{\bar{X}}_{n}} = σ_{X} / \sqrt{n}

. Once both mean and standard deviation of

{\bar{X}}_{m}

are known, the probability density function (pdf) of

{\bar{X}}_{m}

is known and it is possible to evaluate

{\bar{x}}_{m}^{\propto}

corresponding to the desired confidence level. Many times, instead, the standard deviation

σ_{X}

is not known, and in this case

{\bar{X}}_{m}

is distributed according to a Student’s t-Distribution depending on both the sample mean and the sample standard deviation [22].

Furthermore, existing bridges differ from new structures as the data used in their assessment can be related to experimental measurements. Every time a measurement is done, its value is affected by error due to the accuracy of the instrument, the environmental conditions, and the operator execution. Consequently, the measurement error introduces an additional variability of the samples, leading to a higher dispersion in the parameter

{\bar{ϑ}}_{d}

and to a further dispersion of possible values caught from the probability distribution of the basic variables. The outcomes of the tests carried out to evaluate the sample

x_{i}

is a r.v.

X_{e r r}

that can be expressed as

X_{e r r} = x_{i} \cdot ε (c_{v_{ε}})

(19)

where

ε (c_{v_{ε}})

is a log-normally distributed random variable, having zero as log-mean and coefficient of variation equal to

c_{v_{ε}}

In conclusion, the distribution of the safety ratio deduced from estimated parameters, is influenced by the effective knowledge of each parameter that, in turn, depends on the number of tests

n

, the confidence level

α

assumed in its estimation, and the

c_{v_{ε}}

describing the measurement error.

4. Case Study Evaluated through Three Different Knowledge Scenarios

In this chapter, either the adopted methods for the estimation of the set of the parameters

{\bar{ϑ}}_{d}

from the information received by experimental campaigns, and the way to consider the knowledge uncertainties are showed in an application concerning a real existing PT bridge, by considering different combinations of

n

α

and

c_{v_{ε}}

. First, the case study is introduced, then the three considered knowledge scenarios are described.

4.1. Case Study Features

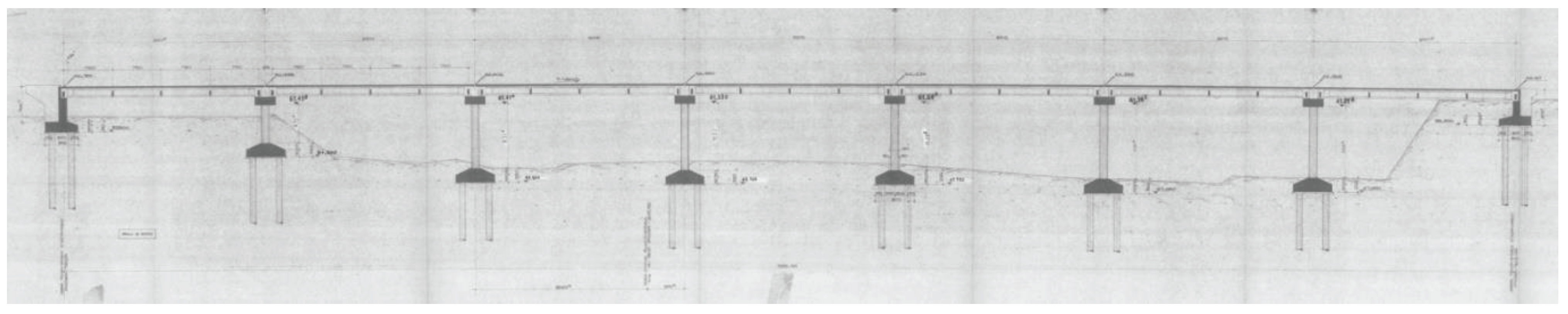
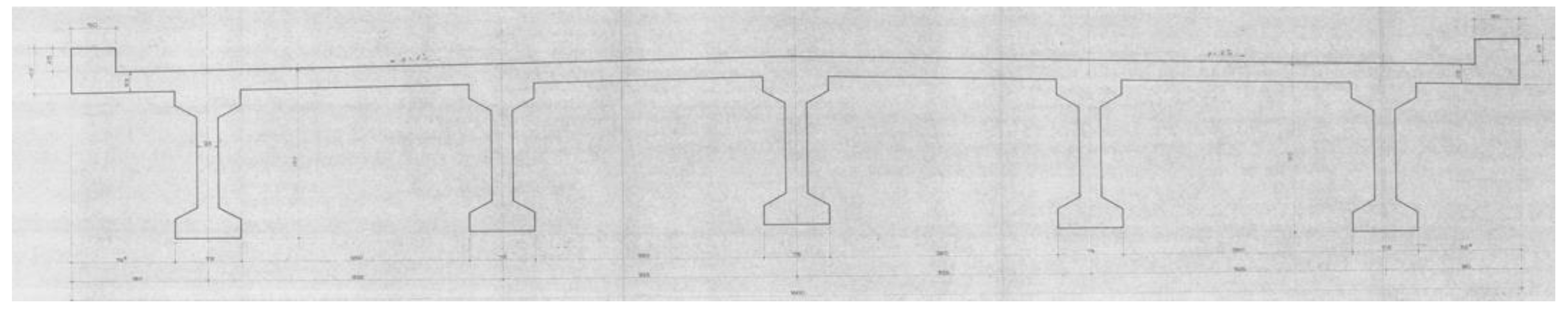
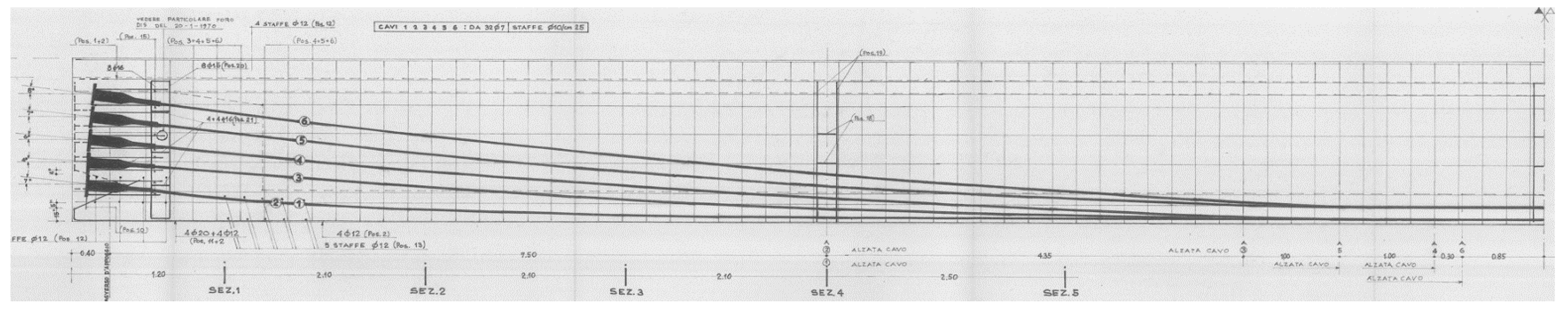
The case study is a typical post-tensioned bridge (Figure 1), with a simple support static scheme and span length equal to 30 m. The deck is made of 5 cast-in-place prestressed I-beams, a slab of 0.23 m thick, and 5 prestressed crossbeams. The original drawing of the cross section of the bridge is reported in Figure 2. Every beam (Figure 3) is prestressed by 6 cables and each cable is composed of 34 strands with diameters of 7 mm. The prestressing procedure has been carried out in two different construction stages. In the first stage, the 4 lower cables have been tensioned after the curing of beam concrete. Later, after the slab and crossbeam casting, the 2 remaining cables, the upper ones, have been tensioned. The original drawing of the position of the cables along the beam (Figure 4) is reported below. It is important to underline that information about bridge geometry, material characteristics, construction stages, and prestressing force have been derived from both original drawings and design reports. The compressive cubic strength of the concrete used for the beam is

R_{c k}

= 45 MPa, while the one used for the slab is equal to 40 MPa. FeB44k steel has been used for the rebars. Prestressing strands present a characteristic ultimate strength equal to

f_{p t k}

= 1800 MPa. Each cable has a cross section area equal to

A_{p}

= 12.32 cm². The mean value of the prestressing stress applied to the cables is equal to

σ_{p t}

= 1189.6 MPa.

The actions

E_{d}

are evaluated according to [28] (Load Model 1). The SAP2000 [29] software has been used to determine the most relevant external effects on the deck. For the safety checks only the most loaded beam is examined.

4.2. Perfect Knowledge Scenario

The perfect knowledge scenario is a theoretical condition that could be hypothetically achieved if an infinite number of tests are carried out, and if test procedures are not affected by errors. In such an ideal scenario, the probability distributions of the basic variables are known and consequently the components of the vector

ϑ_{d}

are deterministic and they can be directly computed from the characteristic values and the partial factors. The characteristic values of the material strengths are calculated as the 5% percentile of their probability distributions, according to the current safety format [12]. For what concerns the cables area, the nominal value has been used as suggested by the Standard [12]. For what concerns the prestressing action, the Standard [12] recommends using either the mean value

P_{m}

or, if relevant, the upper

P_{k, u p}

and lower

P_{k, l o w}

characteristic values. In this case, the mean value is adopted. Starting from the initial prestressing force and subtracting the immediate and long-term prestress losses, the nominal value of the prestressing force, is obtained for each cable. The resultant cable force has been computed at all the sections for the safety check calculations.

In this case, the safety ratios (

y_{d, s}

y_{d, b}

y_{d}

) are deterministic results and they are used for the comparison with the following scenarios simulating the experimental campaigns.

Table 1 shows the probability distributions of

X

and their related parameters

ϑ_{d}

in the perfect knowledge scenario. The mean values of the geometric basic variable

{(A}_{p})

and of the strengths of materials

{(f}_{c}

f_{u p}

f_{y s})

are obtained from the information specified in the original technical drawings (terms with the subscript ‘op’ in Table 1), while their coefficients of variation are acquired from the literature. The mean value of the current prestressing force,

P_{p t}

, is obtained by subtracting from the initial prestressing force,

P_{p t_i}

, declared in the original design, the prestress losses

{Δ P}_{p t}

(either long-term and immediate ones), calculated following the approach proposed in [26]. For

P_{p t}

a unique coefficient of variation

c_{v_{p}}

, is adopted, it includes the uncertainties related to the initial force applied to the cables, as well as uncertainties related to immediate and long-term losses. The global coefficient of variation

c_{v_{p}}

can be obtained according to [30], as follows:

c_{v_{p}} = \frac{\sqrt{{(c_{v_{F}} \cdot µ_{F})}^{2} + {(c_{v_{l o s s e s_l t}} \cdot µ_{l o s s e s_l t})}^{2} + {(c_{v_{l o s s e s_s t}} \cdot µ_{l o s s e s_s t})}^{2}}}{µ_{F} + µ_{l o s s e s_l t} + µ_{l o s s e s_s t}}

(20)

where

c_{v_{F}}

and

µ_{F}

are the coefficient of variation and the mean value of initial prestressing force, respectively;

c_{v_{l o s s e s_l t}}

and

µ_{l o s s e s_l t}

are , the coefficient of variation and the mean value of long-term prestress losses, respectively;

c_{v_{l o s s e s_s t}}

and

µ_{l o s s e s_s t}

are the immediate ones. All the coefficients of variation of Equation (20) have been obtained with reference to [31] and they have been assumed constants and equal to their mean values. For the application of the safety format, the equivalent cable of the post-tensioned system is adopted.

Once the parameters

ϑ_{d}

are obtained, the safety ratios

y_{d}

for the perfect knowledge scenario can be determined and they are equal to:

$y_{d, s}$ = $V_{r d}$ / $V_{e d}$ = 0.97
$y_{d, b}$ = $M_{r d}$ / $M_{e d}$ = 1.09
$y_{d}$ = ${m i n (y}_{d, s}$ , $y_{d, b})$ = 0.97

4.3. Partial Knowledge Assessment

The partial knowledge scenario refers to a condition in which only a reduced number of tests is carried out, and a variability of

{\bar{ϑ}}_{d}

arises due to the uncertain estimation of basic variables. Such a scenario is simulated starting from the probability distribution

f_{X} (x)

of the random variables

X

, and from the fixed number of tests

n

chosen. Many test campaigns involving the same number of tests are simulated; each simulation, composed by a different set of samples, leads to a different estimation of the probability distribution of the parameters, given the confidence factor

α

, and consequently to different values

{\bar{ϑ}}_{d}

of the estimated r.v.

{\bar{Θ}}_{d}

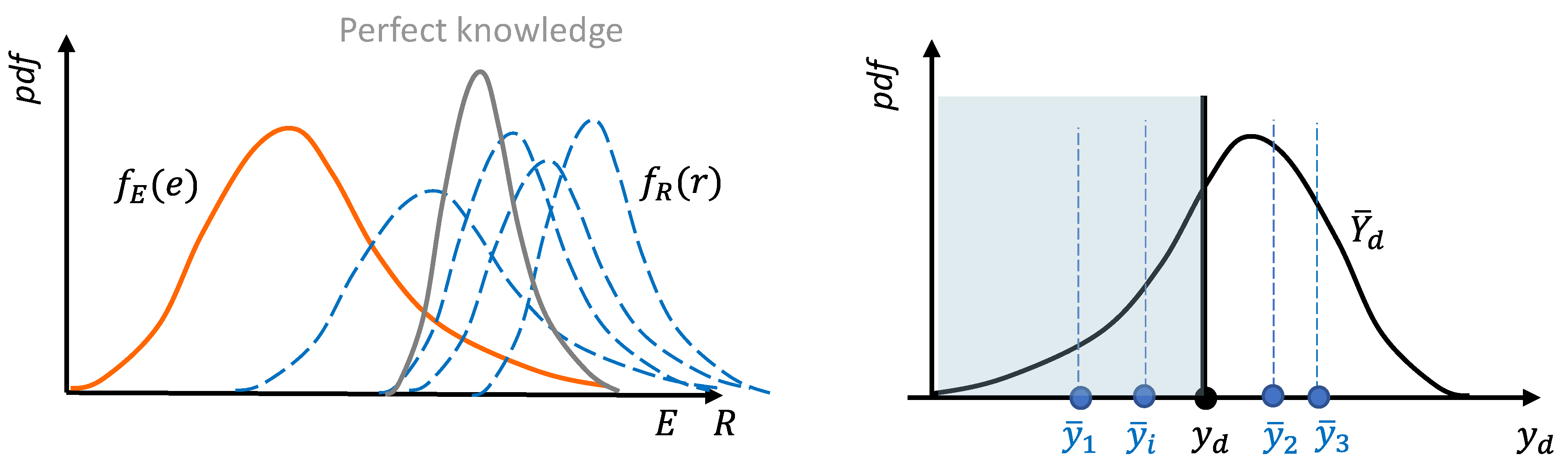
. From the latter, a probability distribution of the estimated safety ratio

{\bar{Y}}_{d}

follows (Figure 5) and the properties of this distribution can be studied in order to evaluate the reliability of the method. It is interesting, indeed, to evaluate the probability that the estimated value

{\bar{y}}_{d}

is lower than the reference value

y_{d}

. This probability is equal to the value assumed by the Cumulative Density Function (CDF) at the reference value,

F_{{\bar{Y}}_{d}} (y_{d})

or, equivalently, the area under the function

f_{{\bar{Y}}_{d}} (y_{d})

evaluated on the domain

{{\bar{y}}_{d} < y}_{d}

(Figure 5).

The parameters are estimated through the recommendations contained in [12] following the condition of unknown variance

σ

of the basic variable distributions.

The characteristic values of the materials (

f_{c k}

f_{y s k}

f_{u p k}

) are calculated through the Coverage Method [34,35]. The characteristic value is obtained from the following formula:

{\bar{f}}_{k} = m - k_{p} \cdot s

(21)

where

{\bar{f}}_{k}

is the estimated characteristic value,

m

is the sample mean,

s

is the sample standard deviation, and

k_{p}

is the estimation coefficient, calculated in Equation (22) and depending on the probability

p

corresponding to the desired

k

-percentile

f_{k}

, on the confidence level

α

, and on the sample size

n

k_{p} (p, α, n) = - t (p, α, n) / \sqrt{n}

(22)

where

t (p, α, n)

is the

α

-percentile of the generalised noncentral t-Distribution [36], corresponding to the probability

p

and with

n - 1

degrees of freedom.

The mean values of the wires area (

A_{p m}

) and of the prestressing force

P_{p t_m}

, derived from samples, are estimated using the t-Student method [22] adopting the case of no prior information about the variable. The estimation of the mean value is obtained from the following formula:

{\bar{X}}_{m} = m + t_{α} \frac{s}{\sqrt{n}}

(23)

where

{\bar{X}}_{m}

is the estimation of the mean value,

m

and

s

are the mean and the standard deviation of the sample,

n

is the number of samples, and

t_{α}

is the percentile of the t-Distribution with degree of freedom

n - 1

corresponding to a confidence level

α

By increasing the number of tests, the parameter estimation improves, and the sample distribution approximates better and better the probability density function of the population.

Once the parameters

{\bar{ϑ}}_{d}

have been calculated, it is possible to carry out the safety checks and to obtain the safety measure

{\bar{y}}_{d}

. A Monte Carlo simulation [22] is applied to obtain the probability distribution of the safety ratio

{\bar{Y}}_{d}

. With the aim at evaluating how much uncertainties on the design parameters affect the estimated

{\bar{y}}_{d}

, the probability to stay into the safe domain

{{\bar{y}}_{d} < y}_{d}

is calculated.

4.4. Assessment through Tests with Measurement Error Scenario

In this scenario, the

{\bar{ϑ}}_{d}

are obtained in a similar way, but in this case the measurement error is also considered. According to the paragraph 3.3, the error is added to each sample value, by considering a probability distribution of the erroneous measurement having a coefficient of variation

c_{v, ε}

and a mean value equal to the one of the samples itself.

5. Parametric Analysis and Related Results

This section presents the evaluation of the safety ratio

y_{d}

and its variability in the two scenarios simulating the performance of experimental campaigns.

In both scenarios, different analyses have been carried out by choosing different number

n

of tests and by exploring the

α

range [0.50-0.95] with the aim of observing how

F_{{\bar{Y}}_{d}} (y_{d})

changes. The following hypotheses have been assumed in the parametric analysis: in the first scenario, the same values of

n

and

α

are assumed for all the parameters

{\bar{ϑ}}_{d}

and no measurement error is considered. In the second scenario, the measurement error is added, by considering different values of the coefficient of variation

c_{v_{ε}}

5.1. Outcomes of the Assessment through Tests without Measurement Error

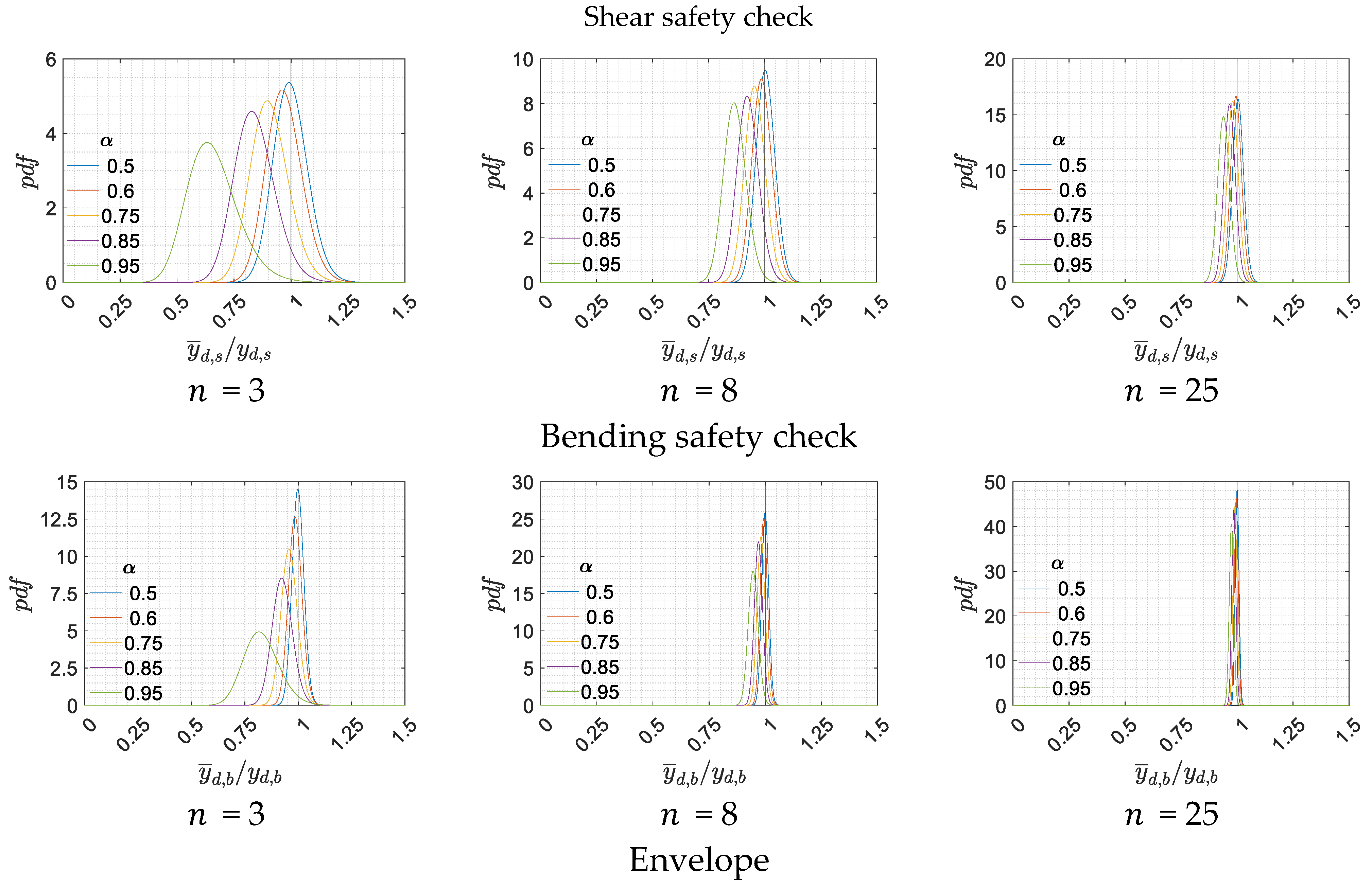
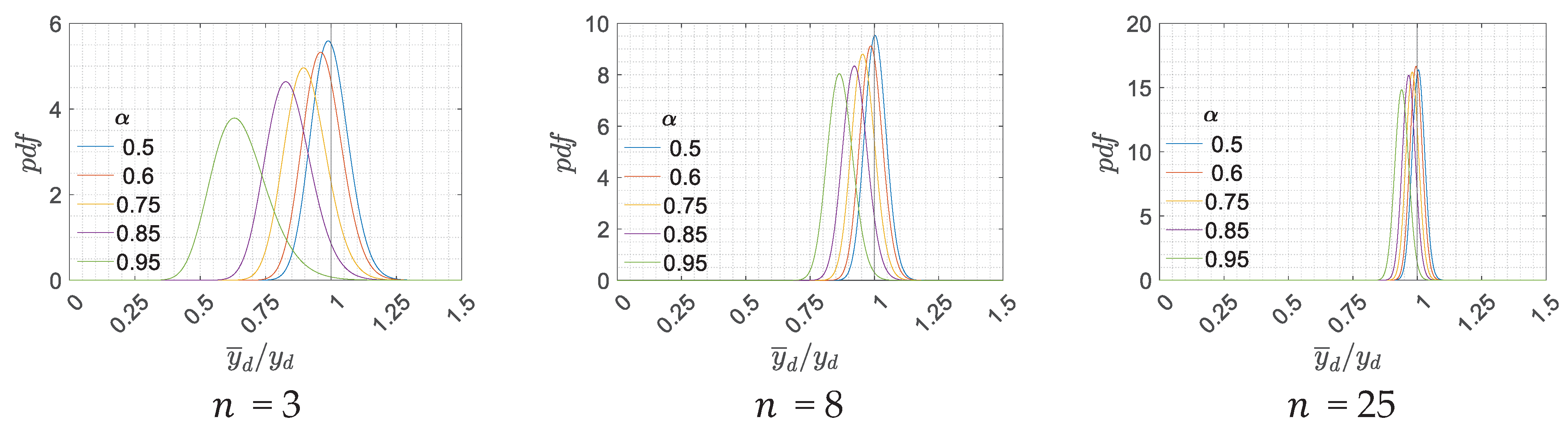
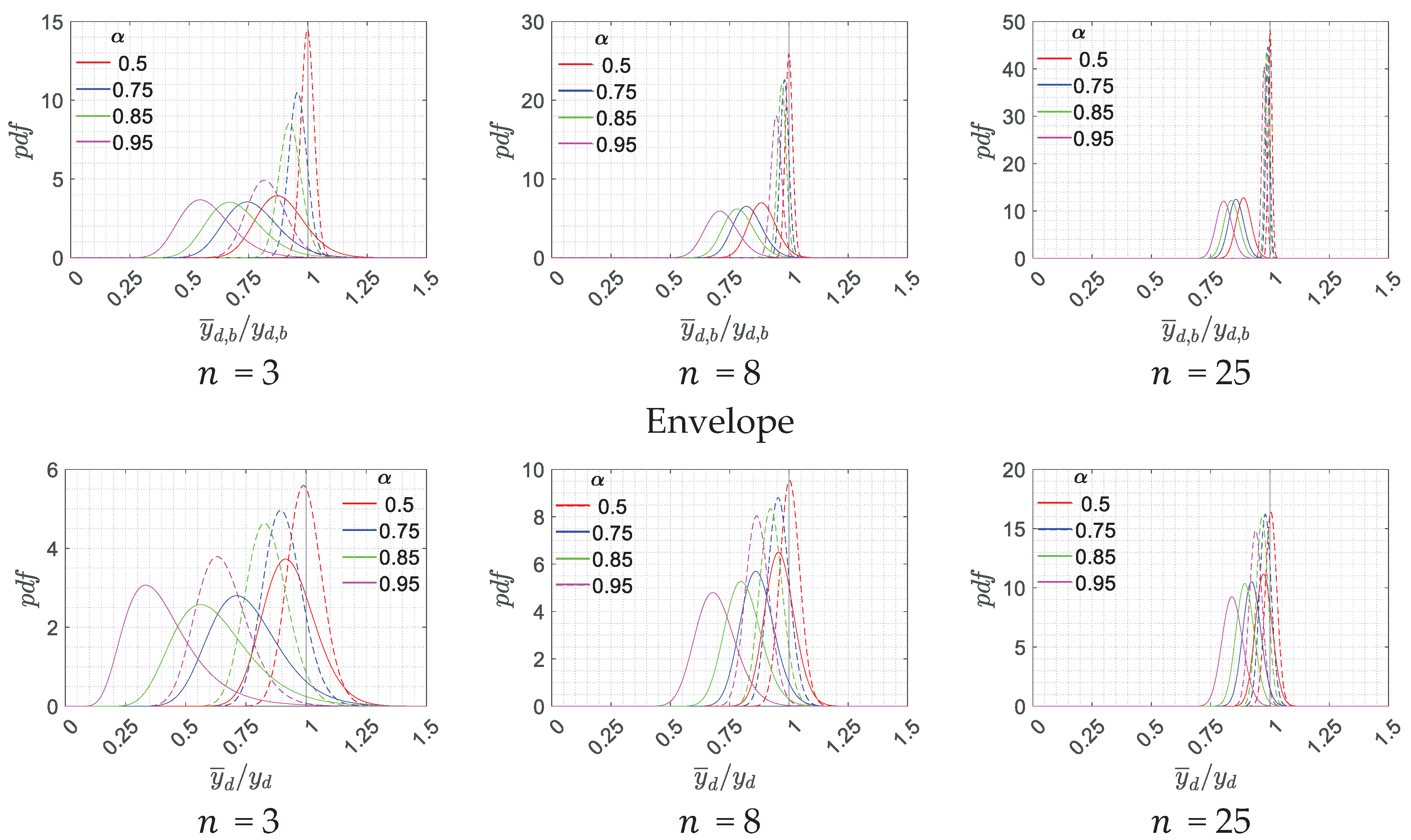
Such a scenario simulates a possible experimental campaign conducted on the case study without considering any measurement error. The results obtained are reported in Figure 6 and in Figure 7. Figure 6 shows the pdfs of the shear safety ratio

{\bar{y}}_{d, s}

, of the bending one

{\bar{y}}_{d, b}

, and the pdfs of their envelopes

{\bar{y}}_{d}

, obtained for different values of

n

and

α

. To make the comparison easier, for all the three safety ratios the nondimensional ratio

{\bar{y}}_{d} / y_{d}

is reported. In this way, the value 1 is the boundary between estimations of the capacity/demand ratio higher or lower than the reference case of perfect knowledge.

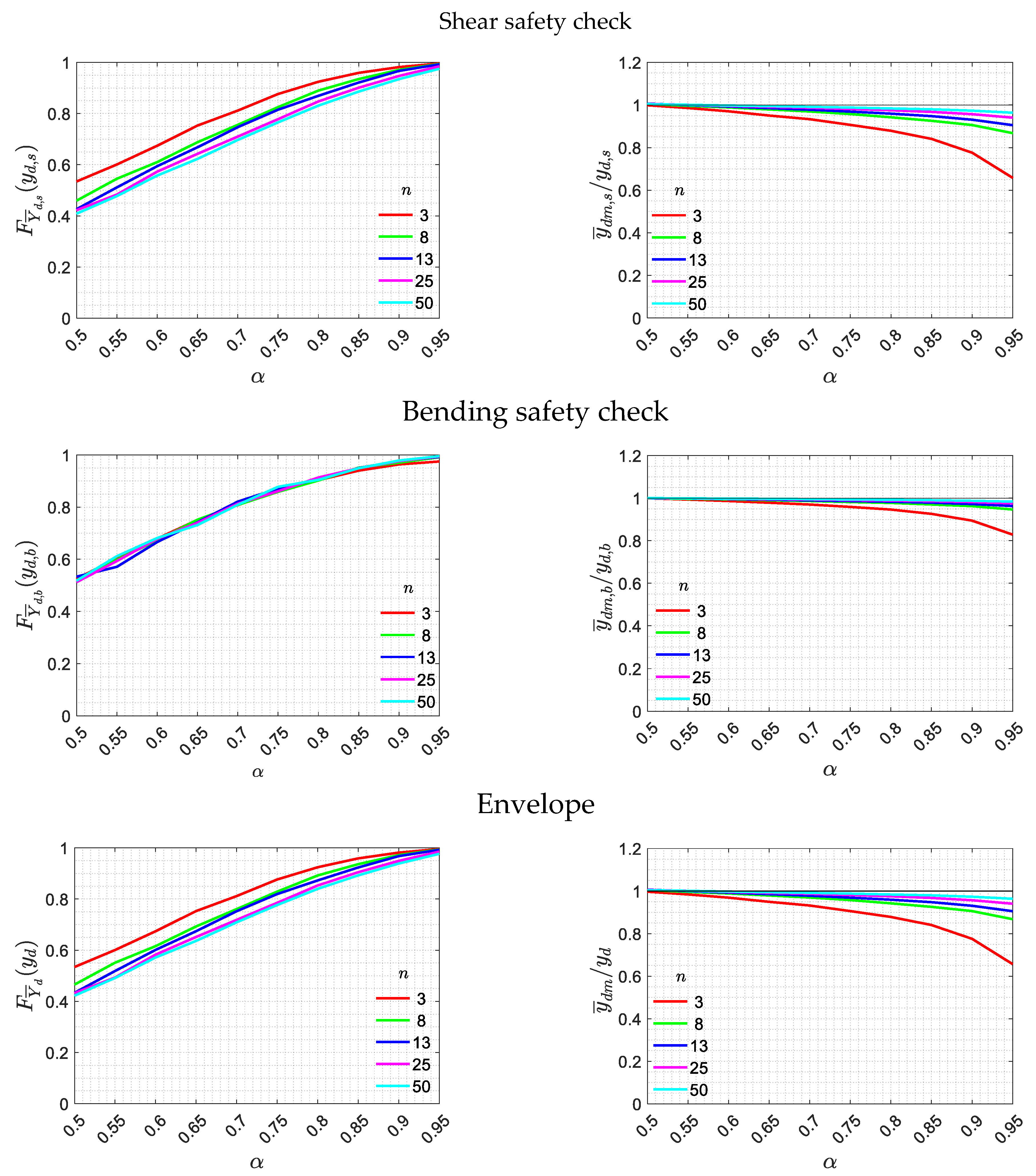
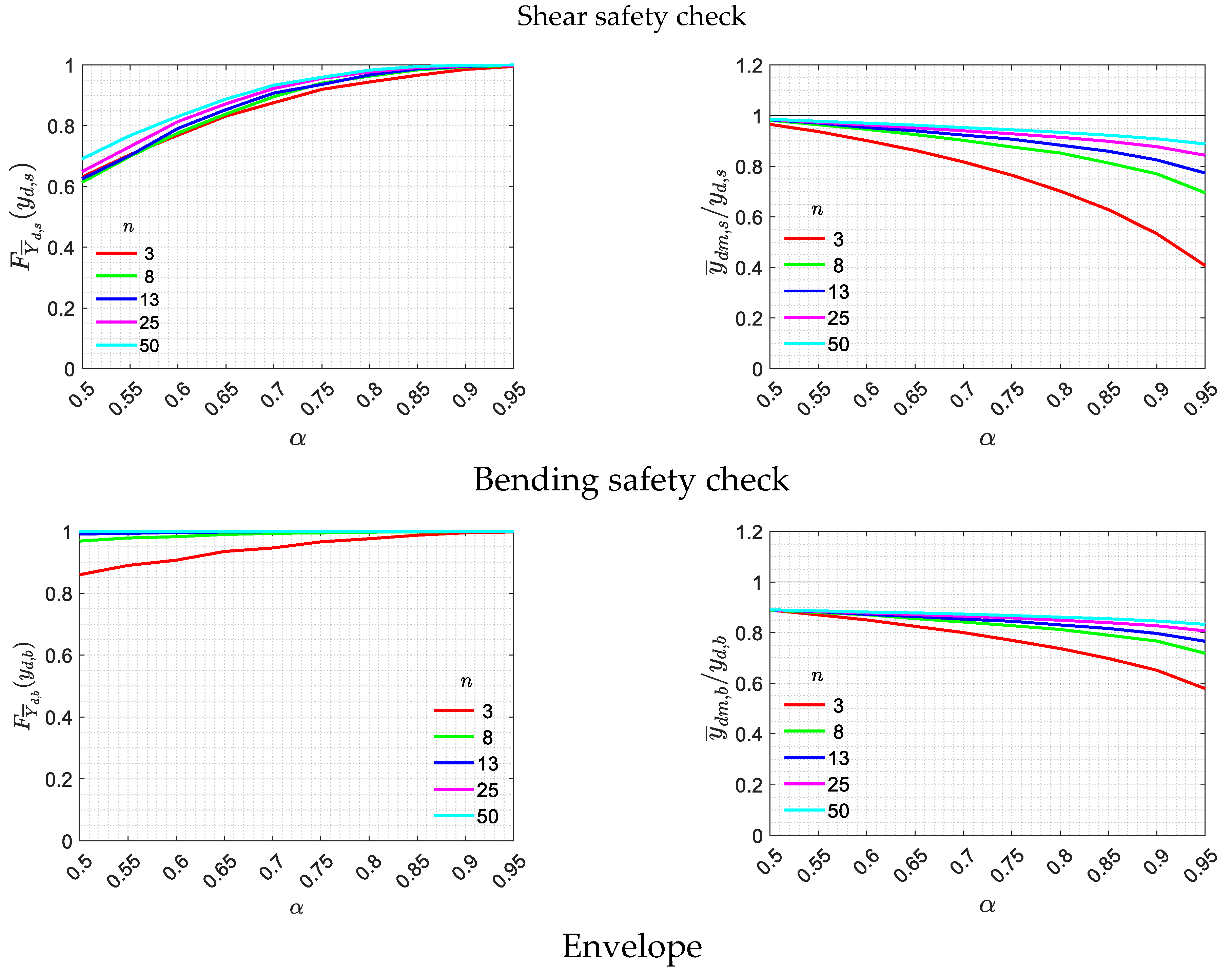
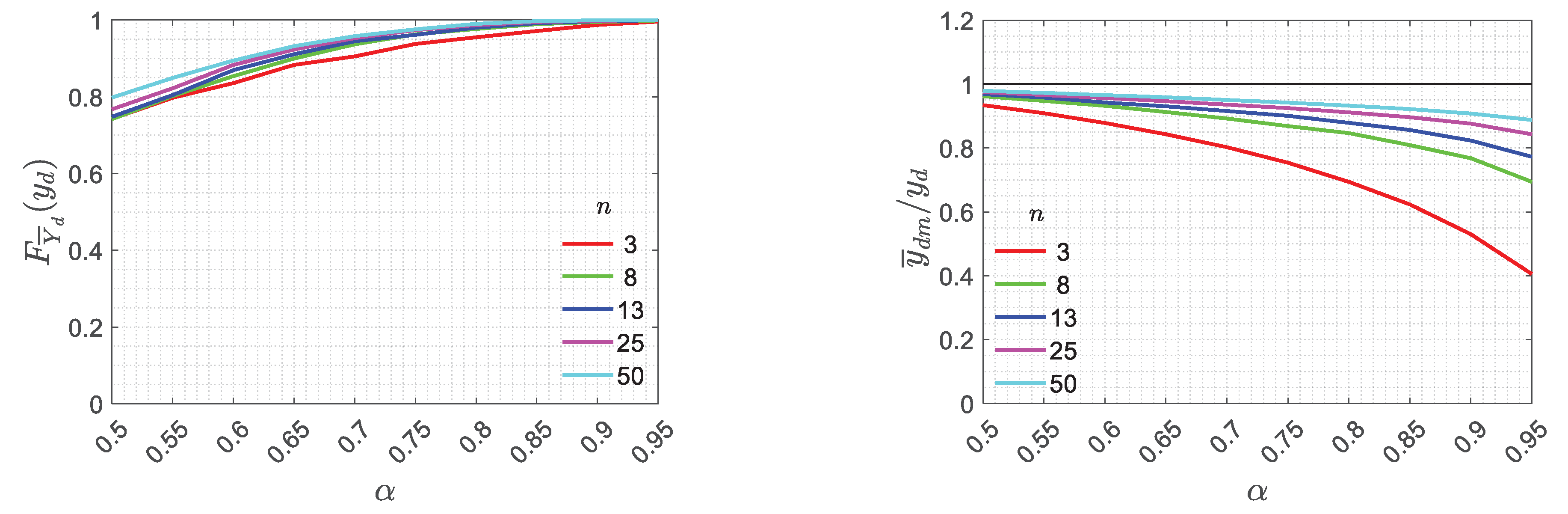
Figure 7 reports, instead, the trends of the CDF of

{\bar{Y}}_{d}

evaluated at the reference value,

F_{{\bar{Y}}_{d}} (y_{d}),

and of the mean value

{\bar{y}}_{d m} = E [{\bar{Y}}_{d}]

in the nondimensional form, by varying the confidence level

α

and the number of tests

n

. It is important to underline that the choice of the partial factors do not affect the nondimensional reported results, since they appear both on

{\bar{y}}_{d}

and

y_{d}

With the aim of understanding the results of this scenario in a clearer way, Table 2, Table 4 and Table 6 display the numerical values obtained for the probability of estimating values of the safety ratio lower than the reference one

F_{{\bar{Y}}_{d}} (y_{d})

, for the case of shear, bending, and envelope checks, while Table 3, Table 5 and Table 7 contain the numerical results relevant to the ratio

{\bar{y}}_{d} / y_{d}

The results reported in the previous figures (Figure 6 and Figure 7) and tables (Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7) are discussed first with reference to the different number of tests

n

, and successively by analysing the effect of variations of confidence

α

within the range considered.

Different choices on the number of tests

n

have a significant impact on the results obtained. By comparing the results of Figure 6 it is observed that by increasing the number of tests, the dispersion of the probability distributions reduces, and the mean value get closer to the reference scenario. This behaviour is expected as a higher number of tests leads to a better evaluation of the model uncertainties. On the other hand, by reducing

n

, the probability distributions move away from the reference scenario toward the safety zone (i.e. a capacity/demand ratio estimation lower than the reference scenario), but, at the same time, they are characterized by a greater standard deviation. Moreover, the shear dispersion is generally greater than the bending one. This aspect can be explained by the fact that the number of r.v. involved in

y_{d, b}

is lower than the number of the r.v. involved in

y_{d, s}

. The different choices of

n

result in changes in the probability distributions, which in turn, affect the probability

F_{{\bar{Y}}_{d}} (y_{d})

of staying within the safety zone

{{\bar{y}}_{d} < y}_{d}

For what concerns the results for the shear check depicted in Figure 7 (first row), taking a low value of

n

leads to a larger, i.e. safer, value of

F_{{\bar{Y}}_{d, s}} (y_{d, s})

and to a conservative value of

{\bar{y}}_{d m, s} / y_{d, s}

because the methods used to calculate

{\bar{ϑ}}_{d}

(see Equations (21) and (23)) produce conservative values of the estimated parameters thanks to the coefficient

k_{p}

, (see Equation (22)), and to the percentile

t_{α}

of the t-Distribution. This behaviour is also observed for the bending check (Figure 7) where the variation of

n

results in different values of

{\bar{y}}_{d m, b} / y_{d, b}

. As already observed in Figure 6, the different number of random variables involved in the estimation of

y_{d, b}

has an effect also in the trends of the ratio

{\bar{y}}_{d m, b} / y_{d, b}

of Figure 7, which are closer to each other with respect to those of the ratio

{\bar{y}}_{d m, s} / y_{d, s}

As expected, the choice of the confidence level

α

also produces different results. By increasing

α

, the mean value of the probability distributions (Figure 6) shifts to the left, providing an average value that is always smaller than the reference one. The safety check is statistically more precautionary, but at the same time, less accurate, since the dispersion increases, and a significant underestimation of the safety coefficient is likely to be obtained. The mean values reported in Figure 6 start from 1 for

α

equal to 0.5 and decrease in precautionary manner as

α

increases. This reduction is more pronounced with a small number of tests. At the same time, as already observed from the perspective of different

n

, the dispersion of the distribution

{\bar{y}}_{d} / y_{d}

increases. This aspect negatively influences the probability

F_{{\bar{Y}}_{d}} (y_{d})

to obtain values of

{\bar{y}}_{d}

lower than the reference value

y_{d}

. Once fixed

α

, the trend of

F_{{\bar{Y}}_{d}} (y_{d})

does not excessively change by varying the number

n

of tests. By assuming as a reference value the confidence level

α

equal to 0.75, as recommended by [12] and [34], the probability

F_{{\bar{Y}}_{d}} (y_{d})

is around 0.8 for different

n

and

α

(Figure 7).

5.2. Outcomes of the Assessment through Tests with Measurement Error

In addition to previous uncertainties related to test numbers and confidence factors, the current scenario also considers the impact of the measurement error on the safety assessment. Since in the literature there are no information about the measurement errors regarding tests for the survey of the prestressing system, in this work a credible coefficient of variation

c_{v_{ε}}

equal to 0.10 is assumed for the basic random variables selected in the previous sections. However, with the aim of providing a more general overview of the potential influence of this parameter for measurement systems more or less accurate than the previous ones, the main results have been also evaluated for different values of

c_{v_{ε}}

. In detail, results concerning

c_{v_{ε}} = 0.05

and

c_{v_{ε}} = 0.20

are reported and discussed at the end of this section.

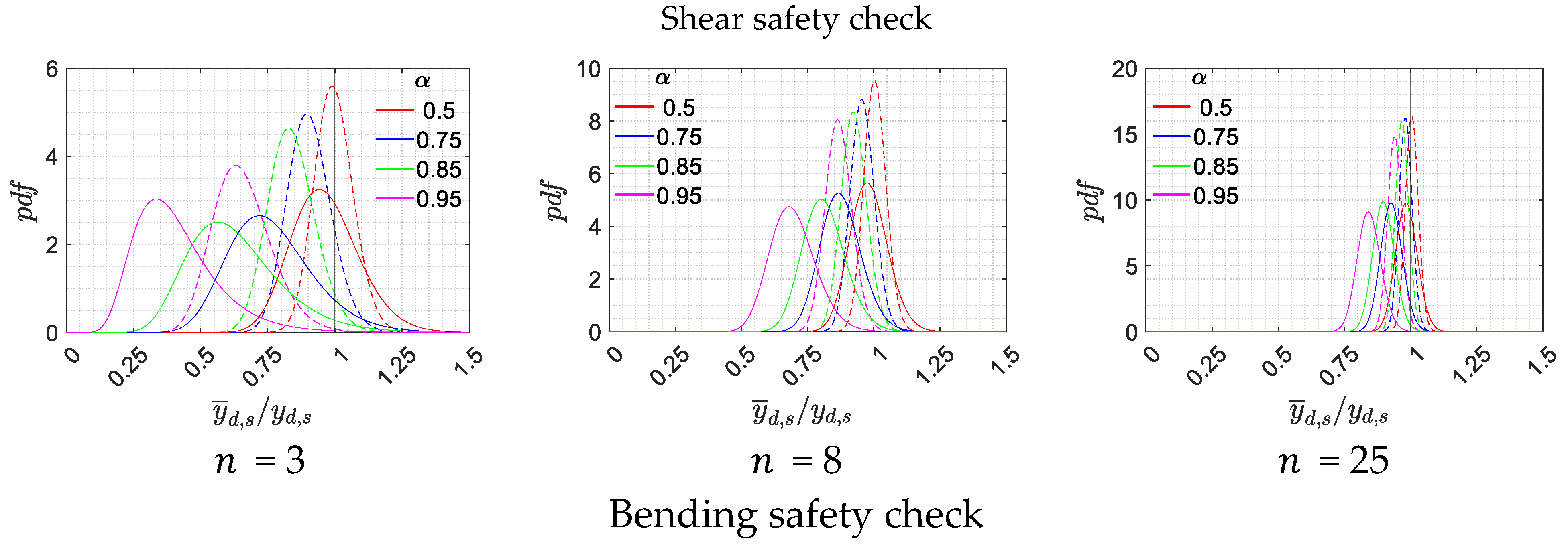
The obtained results for

c_{v_{ε}}

equal to 0.10 are reported in Figure 8 and Figure 9. Figure 8 shows the differences between the probability distribution with and without measurement error, depicted by solid and dashed lines, respectively, for the same values of

n

adopted in the previous section (Figure 6). The results are reported in term of shear, bending and envelope checks.

Figure 9 reports the trends of

F_{{\bar{Y}}_{d}} (y_{d})

and the mean values

{\bar{y}}_{d m}

, obtained by varying

n

and

α

. Even in this scenario, the probability of obtaining a bending check worse than the shear check is low.

With the aim of understanding the results of this scenario in a clearer way, Table 8, Table 10 and Table 12 display the numerical results for the shear, bending and envelope checks of

F_{{\bar{Y}}_{d}} (y_{d})

, while Table 9, Table 11 and Table 13 contain those related to

{\bar{y}}_{d} / y_{d}

The comparison depicted in Figure 8 shows that this additional uncertainty source shifts the probability distribution toward conservative

{\bar{y}}_{d}

values. Given the same values of

α

and

n

, this translation is more pronounced with respect to the previous case (no measurement error) and the dispersion is larger. From the combination of these two factors, it follows that the probability

F_{{\bar{Y}}_{d}} (y_{d})

of obtaining values of

{\bar{y}}_{d}

lower than the reference one is enhanced and the mean value

{\bar{y}}_{d m}

reduces, with respect to the previous scenario. Similar trends are observed for all the values of

α

and

n

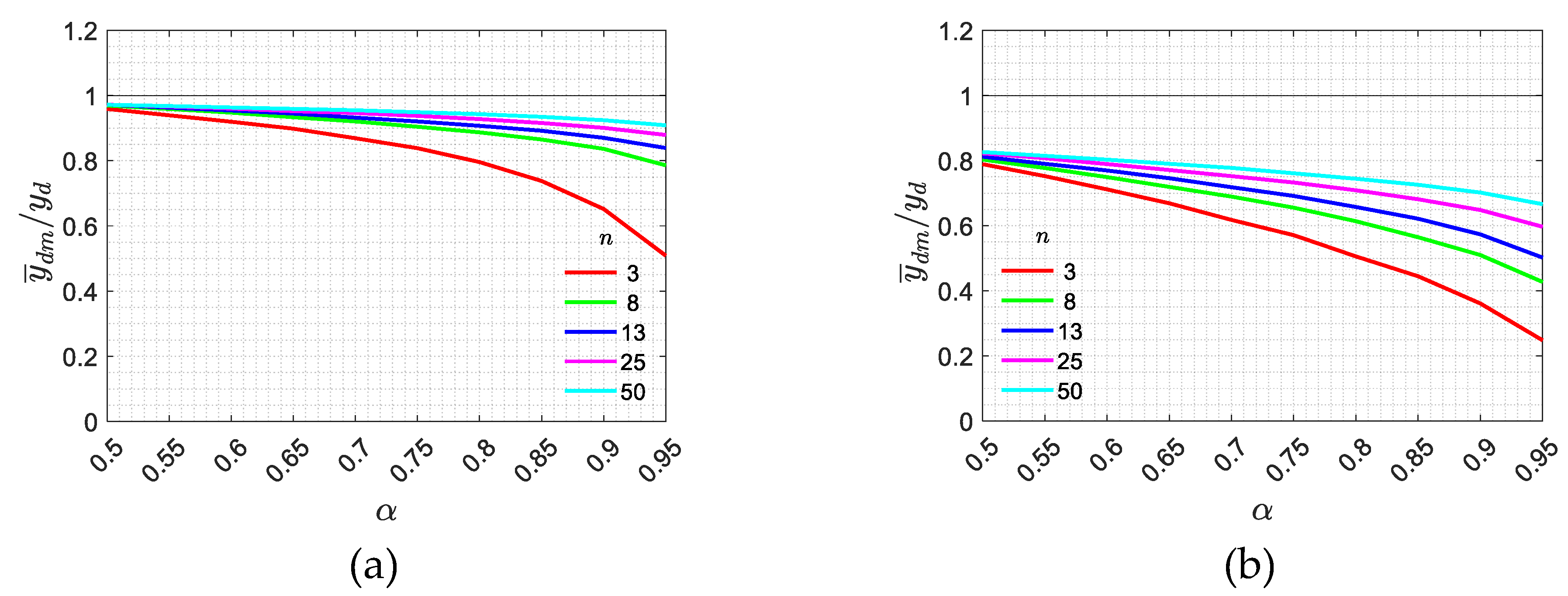
Aiming at observing how much the structural safety is affected by different measurement errors, the results for

c_{v_{ε}}

equal to 0.05 (Figure 10a) and 0.20 (Figure 10b) are reported only for

{\bar{y}}_{d m} / y_{d}

relevant to the envelope case. Figure 10 shows that the measurement error significantly influences the final value of the estimated capacity mean

{\bar{y}}_{d m}

It is also worth to observe that, by increasing the measurement error variability, the probability to have a safe estimation of

{\bar{y}}_{d}

increases. The uncertainty due to the measurement error introduces an extra variability of the measured quantity that implies a further safety on the final results. This is a remarkable difference between new structures and existing ones, and it should be considered within the safety format to avoid over-conservative safety assessments.

6. Conclusions

In this paper the uncertainties affecting the safety assessment based on the semi-probabilistic approach for existing post-tensioned prestressed bridges is studied. The knowledge process is simulated by the Monte Carlo method, and it is defined by (i) the number

n

of tests, (ii) the confidence level

α

used for the estimation of the design parameters, and (iii) the coefficient of variation

c_{v_{ε}}

of the measurement error. Some strengths and weakness of the safety format applied to this type of post-tensioned prestressed structures are highlighted in the following.

The safety format is robust since different levels of $n$ and $α$ lead almost always to a conservative estimation of the capacity/demand ratio. Namely the probability to obtain estimated safety ratios ${\bar{y}}_{d}$ lower than the reference value $y_{d}$ is high and often close to 1. As expected, this probability increases by increasing the number of tests and the confidence level. For the value of confidence $α$ equal to 0.75, recommended by the Eurocodes [12,34], the probability $F_{{\bar{Y}}_{d}} (y_{d})$ to have a safety estimation of ${\bar{y}}_{d}$ is high in both the scenarios, with and without the measurement error.
Results depend on the expressions used for the estimation of the design parameters ${\bar{ϑ}}_{d}$ , and relevant underlying assumption. The Eurocode formulas, based on Coverage Method and t-Student method, provide satisfactory results.
In the scenario that neglects the measurement error, high values of the confidence factor $α$ , approximately larger than 0.8, do not notably improve the result $F_{{\bar{Y}}_{d}} (y_{d})$ , but significantly reduce the expected value ${\bar{y}}_{d, m}$ of ${\bar{Y}}_{d}$ . Thus, it becomes very probable to obtain under-estimation of the safety ratio, and, in a misleading way, the structure could appear to be not adequate.
Measurement error significantly influences the results. The safety format still provides conservative results, but the probability of under-estimate the structural capacity is more and more increased.

Presented results refer to a quite diffused girder typology, but they cannot be considered definitive, and the problem requires further investigations. Furthermore, a credible variability of the outcomes provided by the measurement errors has been considered (coefficient of variation equal to 0.1), but few studies exist about this topic, especially for what concerns tests and technologies for the estimation of the tensile force and strength of prestressing cable [37], as well as of the detrimental effects of corrosion [18,19].

References

Scozzese, F.; Minnucci, L. Seismic Risk Analysis of Existing Link Slab Bridges Using Novel Fragility Functions. Applied Sciences 2023, 14, 112. [Google Scholar] [CrossRef]
Minnucci, L.; Scozzese, F.; Carbonari, S.; Gara, F.; Dall’Asta, A. Innovative Fragility-Based Method for Failure Mechanisms and Damage Extension Analysis of Bridges. Infrastructures 2022, 7, 122. [Google Scholar] [CrossRef]
Ragni, L.; Scozzese, F.; Gara, F.; Tubaldi, E. Dynamic Identification and Collapse Assessment of Rubbianello Bridge.; Guimarães, Portugal, 2019; pp. 619–626.
COST 345. Procedures for the assessment of Highway Structures. Final Report, Reports of Working Groups 1-6. 2004.
Zhang, W.; Wang, N. Bridge Network Maintenance Prioritization under Budget Constraint. Structural Safety 2017, 67, 96–104. [Google Scholar] [CrossRef]
Frangopol, D.M. Life-Cycle Performance, Management, and Optimisation of Structural Systems under Uncertainty: Accomplishments and Challenges ¹. Structure and Infrastructure Engineering 2011, 7, 389–413. [Google Scholar] [CrossRef]
Pinto, P.E.; Franchin, P. Issues in the Upgrade of Italian Highway Structures. Journal of Earthquake Engineering 2010, 14, 1221–1252. [Google Scholar] [CrossRef]
Federal Highway Administration-HRT-13-028: Guidelines for Sampling, Assessing, and Restoring Defective Grout in Prestressed Concrete Bridge Post-Tensioning Duts. 2013.
Highways England. CS 465 Management of Post-Tensioned Concrete Bridges. 2020.
Highways England. CS 464 Non-destructive testing on highways structures. 2020.
Italian Ministry of Infrastructures and Transport, Decree 01/07/2022, n. 204, Guidelines on Risk Classification and Management, Safety Assessment and Monitoring of Existing Bridges, Italian Minestry of Infrastrucures and Transport: Rome, Italy, 2020.
CEN EN 1990 Eurocode 0- Basis of Structural Design. CEN 2002, Brussels.
fib. Bullettin N°80. Partial Safety factor Methods for Existing Structures, Lausanne. 2016.
Gino, D.; Castaldo, P.; Bertagnoli, G.; Giordano, L.; Mancini, G. Partial Factor Methods for Existing Structures According to Fib Bulletin 80: Assessment of an Existing Prestressed Concrete Bridge. Structural Concrete 2020, 21, 15–31. [Google Scholar] [CrossRef]
Lara, C.; Tanner, P.; Zanuy, C.; Hingorani, R. Reliability Verification of Existing RC Structures Using Partial Factors Approaches and Site-Specific Data. Applied Sciences 2021, 11, 1653. [Google Scholar] [CrossRef]
Frangopol, D.M.; Kim, S. Service Life, Reliability and Maintenance of Civil Structures. In Service Life Estimation and Extension of Civil Engineering Structures; Elsevier, 2011; pp. 145–178 ISBN 978-1-84569-398-5.
Cesare, M.A.; Santamarina, C.; Turkstra, C.; Vanmarcke, E.H. Modeling Bridge Deterioration with Markov Chains. J. Transp. Eng. 1992, 118, 820–833. [Google Scholar] [CrossRef]
Ma, Y.; Zhang, J.; Wang, L.; Liu, Y. Probabilistic Prediction with Bayesian Updating for Strength Degradation of RC Bridge Beams. Structural Safety 2013, 44, 102–109. [Google Scholar] [CrossRef]
Vereecken, E.; Lombaert, G.; Caspeele, R. Bayesian Assessment of the Remaining Prestressing Reinforcement in Existing Concrete Bridges. In fib symposium proceedings 2021, 1386–1397. [Google Scholar]
Caspeele, R.; Taerwe, L. Influence of Concrete Strength Estimation on the Structural Safety Assessment of Existing Structures. Construction and Building Materials 2014, 62, 77–84. [Google Scholar] [CrossRef]
Paté-Cornell, ME. Uncertainties in risk analysis: Six levels of treatment. Reliability Engineering & System Safety. 1996, 54, 95–111. [Google Scholar] [CrossRef]
Ang AH-S, Tang WH, Ang AH-S. Probability Concepts in Engineering: Emphasis on Applications in Civil & environmental Engineering, 2nd ed; Wiley, New York, 2007.
Huber, P.; Huber, T.; Kollegger, J. Experimental and Theoretical Study on the Shear Behavior of Single- and Multi-span T- and I-shaped Post-tensioned Beams. Structural Concrete 2020, 21, 393–408. [Google Scholar] [CrossRef]
Herbrand M, Kueres D, Classen M, Hegger J. Experimental Investigations on the Shear Capacity of Prestressed Concrete Continuous Beams with Rectangular and I-Shaped Cross-Sections. In: Hordijk DA, Luković M, editors. High Tech Concrete: Where Technology and Engineering Meet, Cham: Springer International Publishing; 2018, p. 658–66. [CrossRef]
Italian Ministry of Infrastrucutures and Transport. Decree 17/01/2018, n.42. Adjournament of >; Italian Ministry of Infrastructures and Transports: Rome, Italu, 2018. [Google Scholar]
CEN EN 1992-1 Eurocode 2- Design of Concrete Structures, Part1: CEN 2005. Brussels.
Birgin, H.B.; Laflamme, S.; D’Alessandro, A.; Garcia-Macias, E.; Ubertini, F. A Weigh-in-Motion Characterization Algorithm for Smart Pavements Based on Conductive Cementitious Materials. Sensors 2020, 20, 659. [Google Scholar] [CrossRef] [PubMed]
CEN EN 1991. Eurocode 1 – Actions on Structures, CEN 2005. Brussels.
CSI. SAP200. Computers and Structures Inc. Berkley, CA. CSI. SAP200. Computers and Structures Inc. Berkley, CA.
Lemons, D.S.; Langevin, P. An Introduction to Stochastic Processes in Physics: Containing “On the Theory of Brownian Motion” by Paul Langevin, Translated by Anthony Gythiel; Johns Hopkins University Press: Baltimore, 2002; ISBN 978-0-8018-6866-5. [Google Scholar]
Joint Committee on Structural Safety. JCSS Probabilistic Model Code, Part 3: Resistance Models. 2002.
Wisniewski, D.F. Safety Formats for the Assessment of Concrete Bridges. 2007.
CEN. EN 10138-2. Prestressing Steels – Part 2: Wire. 2000 Brussels.
Leonardo da Vinci Pilot Project CZ/02/B/F/PP-134007. Handbook 2. Reliability Backgrounds, Guide to the basis of structural reliability and risk engineering related to Eurocodes, supplemented by practical example. 2005.
Holický M, Vorlíček M. Statistical Procedures for Design Assisted by Testing 1996. [CrossRef]
Owen, D.B. A Survey of Properties and Applications of the Noncentral T-Distribution. Technometrics 1968, 10, 445. [Google Scholar] [CrossRef]
Morelli, F.; Panzera, I.; Piscini, A.; Salvatore, W.; Chichi, F.; Marconi, G.; Maestrini, D.; Gammino, M.; Mori, M. X-Ray Measure of Tensile Force in Post-Tensioned Steel Cables. Construction and Building Materials 2021, 305, 124743. [Google Scholar] [CrossRef]

Figure 1. Original longitudinal profile of the bridge.

Figure 2. Original cross-section of the bridge deck.

Figure 3. Side, horizontal and cross section original view of the beam.

Figure 4. Original location of the strands along the beam.

Figure 5. Safety assessment based on a partial knowledge.

Figure 6. pdfs of the ratio

{\bar{y}}_{d} / y_{d}

, for different values of

α

and

n

Figure 6. pdfs of the ratio

{\bar{y}}_{d} / y_{d}

, for different values of

α

and

n

Figure 7. Diagrams of

F_{{\bar{Y}}_{d}} (y_{d})

and

{\bar{y}}_{d m} / y_{d}

with

α

and

n

for shear, bending and envelope checks.

Figure 7. Diagrams of

F_{{\bar{Y}}_{d}} (y_{d})

and

{\bar{y}}_{d m} / y_{d}

with

α

and

n

for shear, bending and envelope checks.

Figure 8. pdfs of the ratio

{\bar{y}}_{d} / y_{d}

, for different values of

α

and

n

by considering the measurement error.

Figure 8. pdfs of the ratio

{\bar{y}}_{d} / y_{d}

, for different values of

α

and

n

by considering the measurement error.

Figure 9. Diagram of

F_{{\bar{Y}}_{d}} (y_{d})

and

{\bar{y}}_{d m} / y_{d}

with

α

and

n

for shear, bending and envelope checks.

Figure 9. Diagram of

F_{{\bar{Y}}_{d}} (y_{d})

and

{\bar{y}}_{d m} / y_{d}

with

α

and

n

for shear, bending and envelope checks.

Figure 10. Diagram of

{\bar{y}}_{d m} / y_{d}

related to the envelope check by varying

α

and

n

with measurement error equal to 0.05 (a) and 0.20 (b).

Figure 10. Diagram of

{\bar{y}}_{d m} / y_{d}

related to the envelope check by varying

α

and

n

with measurement error equal to 0.05 (a) and 0.20 (b).

Table 1. Probability distributions of the basic variables and related design parameters.

Basic variables	Distribution type	Distribution parameters $µ, c_{v}$	Parameter references	Design parameters
$f_{c}$	Log-Normal	$f_{c m} = R_{c k, o p} \cdot 0.83 + 8$ [MPa] $c_{v} = 0.10$	[25] [32]	$f_{c d} = \frac{f_{c k}}{γ_{c}} = 21.7$ [MPa]
$f_{u p}$	Log-Normal	$f_{u p m} = f_{u k, o p} \cdot 1.04$ [MPa] $c_{v} = 0.025$	[31] [31]	$f_{u p d} = \frac{f_{u p k}}{γ_{s}} = 1475$ [MPa]
$f_{y s}$	Log-Normal	$f_{y m s} = f_{y k, o p} + 2 \cdot 30$ [MPa] $c_{v} = 0.025$	[31] [31]	$f_{y s d} = \frac{f_{y s k}}{γ_{s}} = 305.6$ [MPa]
$A_{p}$ (single strand)	Log-Normal	$A_{p m} = A_{p m, o p}$ $c_{v} = 0.02$	[12] [33]	$A_{p m} = 12.32$ [cm²]
$P_{p t}$	Log-Normal	$P_{p t m} = P_{p t i, o p} - {Δ P}_{p t}$ $c_{v_{p}} = 0.08$	Equation (20)	$P_{p t m} = 1221.81$ [kN] (mid-span)

Table 2. Numerical values of

F_{{\bar{Y}}_{d, s}} (y_{d, s})

for different values of

α

and

n

Table 2. Numerical values of

F_{{\bar{Y}}_{d, s}} (y_{d, s})

for different values of

α

and

n

$F_{{\bar{Y}}_{d, s}} (y_{d, s})$		$α$
$F_{{\bar{Y}}_{d, s}} (y_{d, s})$		0.50	0.60	0.75	0.85	0.95
$n$	3	0.53	0.67	0.87	0.95	0.99
	8	0.46	0.61	0.82	0.93	0.99
	25	0.42	0.57	0.78	0.99	0.99

Table 3. Numerical values of

{\bar{y}}_{d m, s} / y_{d, s}

for different values of

α

and

n

Table 3. Numerical values of

{\bar{y}}_{d m, s} / y_{d, s}

for different values of

α

and

n

${\bar{y}}_{d m, s} / y_{d, s}$		$α$
${\bar{y}}_{d m, s} / y_{d, s}$		0.50	0.60	0.75	0.85	0.95
$n$	3	1	0.97	0.90	0.84	0.66
	8	1	0.99	0.96	0.92	0.87
	25	1	0.99	0.98	0.97	0.94

Table 4. Numerical values of

F_{{\bar{Y}}_{d, b}} (y_{d, b})

for different values of

α

and

n

Table 4. Numerical values of

F_{{\bar{Y}}_{d, b}} (y_{d, b})

for different values of

α

and

n

$F_{{\bar{Y}}_{d, b}} (y_{d, b})$		$α$
$F_{{\bar{Y}}_{d, b}} (y_{d, b})$		0.50	0.60	0.75	0.85	0.95
$n$	3	0.52	0.68	0.86	0.94	0.98
	8	0.52	0.67	0.86	0.94	0.99
	25	0.51	0.68	0.86	0.95	0.99

Table 5. Numerical values of

{\bar{y}}_{d m, b} / y_{d, b}

for different values of

α

and

n

Table 5. Numerical values of

{\bar{y}}_{d m, b} / y_{d, b}

for different values of

α

and

n

${\bar{y}}_{d m, b} / y_{d, b}$		$α$
${\bar{y}}_{d m, b} / y_{d, b}$		0.50	0.60	0.75	0.85	0.95
$n$	3	1	0.98	0.96	0.93	0.83
	8	1	0.99	0.98	0.97	0.95
	25	1	0.99	0.99	0.99	0.97

Table 6. Numerical values of

F_{{\bar{Y}}_{d}} (y_{d})

for different values of

α

and

n

Table 6. Numerical values of

F_{{\bar{Y}}_{d}} (y_{d})

for different values of

α

and

n

$F_{{\bar{Y}}_{d}} (y_{d})$		$α$
$F_{{\bar{Y}}_{d}} (y_{d})$		0.50	0.60	0.75	0.85	0.95
$n$	3	0.53	0.67	0.88	0.96	0.99
	8	0.47	0.62	0.83	0.94	0.99
	25	0.43	0.58	0.78	0.90	0.97

Table 7. Numerical values of

{\bar{y}}_{d m} / y_{d}

for different values of

α

and

n

Table 7. Numerical values of

{\bar{y}}_{d m} / y_{d}

for different values of

α

and

n

${\bar{y}}_{d m} / y_{d}$		$α$
${\bar{y}}_{d m} / y_{d}$		0.50	0.60	0.75	0.85	0.95
$n$	3	1	0.97	0.91	0.84	0.66
	8	1	0.99	0.96	0.93	0.87
	25	1	0.99	0.98	0.97	0.94

Table 8. Numerical values of

F_{{\bar{Y}}_{d, s}} (y_{d, s})

for different values of

α

and

n

with the measurement error.

Table 8. Numerical values of

F_{{\bar{Y}}_{d, s}} (y_{d, s})

for different values of

α

and

n

with the measurement error.

$F_{{\bar{Y}}_{d, s}} (y_{d, s})$	$α$
$F_{{\bar{Y}}_{d, s}} (y_{d, s})$	0.50		0.60	0.75	0.85	0.95
$n$	3	0.63	0.77	0.92	0.97	0.99
	8	0.61	0.78	0.94	0.98	0.99
	25	0.65	0.81	0.95	0.99	0.99

Table 9. Numerical values of

{\bar{y}}_{d m, s} / y_{d, s}

for different values of

α

and

n

with the measurement error.

Table 9. Numerical values of

{\bar{y}}_{d m, s} / y_{d, s}

for different values of

α

and

n

with the measurement error.

${\bar{y}}_{d m, s} / y_{d, s}$		$α$
${\bar{y}}_{d m, s} / y_{d, s}$		0.50	0.60	0.75	0.85	0.95
$n$	3	0.96	0.90	0.76	0.63	0.40
	8	0.98	0.94	0.88	0.81	0.69
	25	0.98	0.96	0.93	0.89	0.84

Table 10. Numerical values of

F_{{\bar{Y}}_{d, b}} (y_{d, b})

for different values of

α

and

n

with the measurement error.

Table 10. Numerical values of

F_{{\bar{Y}}_{d, b}} (y_{d, b})

for different values of

α

and

n

with the measurement error.

$F_{{\bar{Y}}_{d, b}} (y_{d, b})$		$α$
$F_{{\bar{Y}}_{d, b}} (y_{d, b})$		0.50	0.60	0.75	0.85	0.95
$n$	3	0.89	0.93	0.97	0.99	1
	8	0.97	0.99	0.99	1	1
	25	1	1	1	15	1

Table 11. Numerical values of

{\bar{y}}_{d m, b} / y_{d, b}

for different values of

α

and

n

with the measurement error.

Table 11. Numerical values of

{\bar{y}}_{d m, b} / y_{d, b}

for different values of

α

and

n

with the measurement error.

${\bar{y}}_{d m, b} / y_{d, b}$		$α$
${\bar{y}}_{d m, b} / y_{d, b}$		0.50	0.60	0.75	0.85	0.95
$n$	3	0.89	0.85	0.77	0.70	0.58
	8	0.89	0.87	0.83	0.79	0.72
	25	0.89	0.87	0.86	0.84	0.81

Table 12. Numerical values of

F_{{\bar{Y}}_{d}} (y_{d})

for different values of

α

and

n

with the measurement error.

Table 12. Numerical values of

F_{{\bar{Y}}_{d}} (y_{d})

for different values of

α

and

n

with the measurement error.

$F_{{\bar{Y}}_{d}} (y_{d})$		$α$
$F_{{\bar{Y}}_{d}} (y_{d})$		0.50	0.60	0.75	0.85	0.95
$n$	3	0.75	0.83	0.93	0.97	0.99
	8	0.74	0.85	0.96	0.99	0.99
	25	0.77	0.88	0.97	0.99	0.99

Table 13. Numerical values of

{\bar{y}}_{d m} / y_{d}

for different values of

α

and

n

with the measurement error.

Table 13. Numerical values of

{\bar{y}}_{d m} / y_{d}

for different values of

α

and

n

with the measurement error.

${\bar{y}}_{d m} / y_{d}$		$α$
${\bar{y}}_{d m} / y_{d}$		0.50	0.60	0.75	0.85	0.95
$n$	3	0.93	0.88	0.75	0.62	0.41
	8	0.96	0.91	0.87	0.81	0.69
	25	0.98	0.96	0.92	0.89	0.84

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Influence of Knowledge Uncertainties on the Safety Assessment of Existing Post-tensioned Concrete Bridges

Abstract

1. Introduction

2. Reliability Evaluation and Notation

3. Safety Assessment of Existing PT Bridges

3.1. Basic Random Variables and Parameters for the Semi-Probabilistic Method

3.2. Failure Condition Modalities and Safety Checks

3.3. Estimation of the Design Parameters Based on Experimental Measurements

4. Case Study Evaluated through Three Different Knowledge Scenarios

4.1. Case Study Features

4.2. Perfect Knowledge Scenario

4.3. Partial Knowledge Assessment

4.4. Assessment through Tests with Measurement Error Scenario

5. Parametric Analysis and Related Results

5.1. Outcomes of the Assessment through Tests without Measurement Error

5.2. Outcomes of the Assessment through Tests with Measurement Error

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe