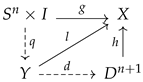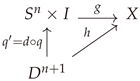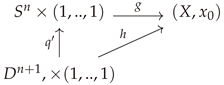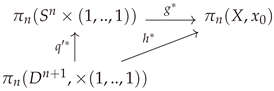1. Motivation
In physics, fiber bundles and homotopy theory are fundamental for understanding fields and forces, offering a geometric interpretation of various physical phenomena, including gauge theories and aspects of general relativity. [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15]. Employing the language of fiber bundles offers significant advantages in studying the phase transitioning systems. Fiber bundles are able to reveal the contrast between local simplicity and global complexity making these differences the key points in understanding topological properties of the symmetry breaking systems. Additionally, the homotopy lifting property on a fiber bundle enables conversion from
relative homotopy groups to
absolute homotopy group:
, naturally extending the results of [
2]. In the fiber bundle framework, every path in a topological space
X based at
will be lifted to a unique path on fiber bundle
G (with a fiber
H and a base
) starting at
and ending in fiber
H up to homotopy. In first section, we show how fibers and bases of fiber bundles together with homotopy can be used to define the notions of an
order parameter space,
topological defect,
symmetry breaking,
phases and
phase transitions. The Defect and Fiber structure theorems we present in the second section of this work allow us to expose explicitly the mathematical conditions at which long exact homotopy sequence of the absolute homotopy group can be used to track the stability of a topological defect in successive phase transitions. Finally, we provide the examples of how these theorems may be used on the most well-studied condensed matter phase transitioning system- superfluid Helium [
16,
17,
18,
19,
20].
2. Preliminary Knowledge
Suppose that B and H are Hausdorff topological spaces. A fiber bundle G with base B and fiber H is a Hausdorff topological space X together with a continuous map (called projection map) with the following properties:
For each , the preimage of of is homeomorphic to H
For each , ∃ neighborhood fibers are homeomorphic to , such that is the map and
Equivalence relation is a binary relation which is reflexive (), symmetric (), and transitive ().
Equivalence class is a subset , such that , and never a case for , but . The equivalence class to which n belongs is denoted as . All elements of X equivalent to each other are also elements of the same equivalence class. The equivalence class of a path f under the equivalence relation of homotopy called the homotopy class of f.
The n-th homotopy group . Let be n-cube consisting of points in Euclidean n-space, such that , . Setting or gives us the -face, and union of such -faces forms the boundary of . Consider maps of into X, such that maps into , then the elements of are homotopy classes of such maps. Alternatively, an element of can be defined as a homotopy class of maps of into X, with , where is the reference point on to which the boundary is squished.
Normal subgroup. The subgroup is called normal if and only if for . Equally, a subgroup is normal if and only if .
Quotient space. The left coset of is a subset of . Collection of all cosets of H is denoted by , so elements of are cosets, not elements of G. If H is a normal subgroup of G, then can be turned into a group and we call the quotient group.
Covering theorem. Let be the covering space for X, such that there exists a projection map , such that . Then exists induced homomorphism , such that is the isomorphism onto for .
Universal property: Let X be a space and ∼ equivalence relation on X with corresponding quotient space . The projection map has the universal property: for a given map , such that if , there ∃ a unique map , such that . Every map lifts to a map on X that is constant on equivalence classes.
Homotopy Lifting Property. A fiber bundle
G with the base
B and projection map
has the homotopy lifting property with respect to all CW pairs
[
21]
Although some of the order parameter spaces can be directly observed by physicists in condensed matter laboratories, the topological defects defined as the elements of the
the homotopy group are not easily related to the physical realms. The term "defect" is quite ambiguous and used in various disciplines implying different meanings [
22,
23,
24,
25]. In this work, a topological defect is referred to a mathematical structure uniquely associated to a phenomena observed by physicists in the laboratory. The observed phenomena by experimentalists will be referred as
physical defects. For example, if two physical defects, such as vortices or phonons, are observed in some condensed matter experiment, we associate each observed physical defect to a unique element of the fundamental group of the parameter space and call it a topological defect.
Order parameter space and topological defects. Let G be having a structure of fiber bundle of dimension m with fiber H of dimension k, and base of dimension . The projection map is given by , where and denotes the coset . The base is called the order parameter space of dimension . The elements of the n-th homotopy group are called topological defects (or simply defects).
Symmetry breaking. Let G be a group corresponding to the maximal symmetries of some physical system named K. We say that system K undergoes symmetry breaking if exists a normal subgroup H in G and continuous map . Then H represent the set of symmetries the system X is invariant after the symmetry breaking, and the quotient group represents the symmetries under which X is no longer invariant.
Symmetry breaking may also be discussed in the language of fiber bundles. For some arbitrary system K with its maximal symmetries described by the fiber bundle G, single spontaneous symmetry breaking is given by the short fiber bundle sequence , where N is the fiber of G, which represents the unbroken or remaining symmetries in the system G and the base represents the group of broken symmetries.
Phases and transitions. Let G be a group of the maximal symmetries of the considered system and have a structure of the fiber bundle. Let be a closed subgroup of G and be a closed subgroup of , so that . The number of such closed "nested" subgroups in G is called the number of phases which the system can transit to, and our case is given for the two phases. The system is said to experience two-phase transitions, if there exists a continuous map p from .
3. The Defect and Fiber Structure Theorems
Local cross section f. Let
N be a closed subgroup of
G, so that
N is a point
. A local cross section of
N in
G is a function
f that continuously mapping a neighborhood
of
into
G such that
for
. Such
f exists for every fiber bundle
G over
[
26].
Fiber structure theorem. Let be a closed subgroup of G such that it admits a local cross section f, and be a closed subgroup of : , and let be the the map induced by the inclusion of cosets. Two statements can be made:
Statement 1. has a fiber bundle structure relative to p with the fiber , and the group of the bundle is with being the largest subgroup of invariant in acting in as left translations. There exists a short homotopy sequence group, ( In other notation, .
Statement 2. For path-connected base , there exists a long homotopy sequence:
Proof:
Proof of statement 1. By the bundle structure theorem in [
26], one can assign a bundle structure to
relative to
p with the fiber
.
Proof of statement 2: By Proposition 4.48 in [
21], a fiber bundle
, (base is
and fiber
), has the homotopy lifting property with respect to all CW pairs
. By Theorem 4.41 and Proposition 4.1 in [
21], there exists a long exact homotopy sequence
Corollary. For two phase-transitions, the long homotopy sequence,
, where the fiber is , the fiber bundle is , and the base is and the short sequence is . However, if is trivial, then the original fiber bundle is reduced to , with the reduced fiber , and the base , so the short sequence for the reduced fiber bundle becomes , and the long homotopy sequence becomes
Stability lemma. For a topological space X, these conditions are equivalent:
Any map is homotopic without regard to basepoints to a constant map, with image a point
Any map extends to a map
for all
Proof:
Consider with the defined equivalence relation ∼ on it and I being dimensional version of the interval . The map collapsing the top of the mapping cylinder to a single point gives us a quotient cone . Consider a given map that is homotopic without regard to a basepoints to a constant map with image a point, so that for . Then by the universal property, there exists a unique map , such that , and every map lifts to a map from that is constant on equivalence classes. Define a map , such that for . Then, again, by the universal property, exists a unique map such that and every map lifts to a map from Y that is constant on equivalence classes. Denote map , so now . Then and , so any map extends to a map .
Adopt the second diagram from the part above and consider that any map
extends to a map
. Moreover, consider the map
to be restriction of the map
.
Consider the based homotopy class . Since is deformation contractible to a point, any image of the loop of can also be deformation-contracted to a point. So the images of loops of and are homotopy equivalent to a point, hence is trivial .
Adopting a hypothesis that is trivial , consider any map and let , with for some . Then is nullhomotopic.
Physical stability theorem. Let r be an arbitrary dimension of the physical defect bounded to dimensional space. An dimensionalphysical defect cannot be physically stable if its associated homotopy class is homotopic to a constant map (or, equivalently, the fundamental group is trivial).
Proof: If the is trivial, then by Stability lemma, any map from is homotopic without regard to basepoints to a constant map, having a point as its image. So, any topological defects formed in is homotopic to a point, and hence associated physical defects cannot be stable.
4. Examples in Condensed Matter Physics
4.1. Superfluid Helium 4
From physics experiments, superfluid Helium 4 is known to have only one superfuid phase and the complex order parameter described by
[
27].
To connect mathematical language with the physics language, let G be having a structure of a fiber bundle represent all the symmetries of Helium 4 before the transition to its superfluid phase, and be s closed subgroup of G representing the remaining symmetries after the system underwent the phase transition from conventional fluid to the superfluid. Then the base of the fiber bundle is representing the order parameter of the superfluid, so that .
Unlike the order parameter space, it is challenging to observe
G and
in the laboratory, however one can deduce
G topological structure from the long homotopy sequence and assuming that
is trivial. Given relatively simple nature of the order parameter, one may only consider lower order fundamental groups in the long homotopy sequence:
Setting , one arrives to a part in a long homotopy sequence . Because the long homotopy sequence is exact, each map is a homomorphism such that the image of each map is equal to the kernel of the following map. For example, the image of the map f is trivial, which means that the kernel of g is also trivial, and hence the image of g must be trivial as well. Given that is trivial, the kernel of j must be , so the image of g is . As result, g is isomorphism of with . From these results, we can deduce the Trivial fiber theorem for the transitioning systems with maximal symmetries described by fiber bundle G and single trivial fiber :
The Trivial Fiber Theorem: Suppose that G is a fiber bundle with the fiber and base . If and are both trivial, then is isomorphic .
Although the fiber bundle G for superfluid Helium 4 is experimentally not accessible, from the the fact that is isomorphic to and that is trivial, the second fundamental group is also trivial.
Similarly, consider another part of the long homotopy sequence Since is trivial and since is also trivial, given that there is only one element and hence the number of connected components, we deduce that isomorphic to Z, since . This result means that the fiber bundle G of superfluid Helium 4 contains non-contractible loops whose behavior is very much like the behavior of loops .
The Physical Stability Theorem can be applied to discuss the stability of physical defects which can be observed in superfluid Helium 4.
For given dimension of physical space, such as a bulk of superfluid Helium 4, and r being the physical dimension of a defect,
The 0-dimensional defects cannot be stable since is trivial,
There exist 1-dimensional stable defects since ,
The 2-dimensional defects cannot be stable since is trivial.
One does not need to consider scenario representing 3D topological defect in the system, because it is physically impossible. In fact, the dimensional physical space may be considered isomorphic to dimensional Euclidean space, ,and the defect space of dimension r is isomorphic to dimensional Euclidean space , . So, space-wise, . To illustrate this idea in an explicit example, consider the topological space , which can be envisioned as observing the cross section of a conventional three-dimensional space formed by Cartesian coordinates with removed axis, let it be z -axis for convenience. Removing the z axis leads to a cross-section is missing a point, resulting in the space behavior equivalent to with a missing point. Three dimensional topological defect would be equivalent to an object embedded in , and hence having it in 3D topological medium would lead to minus behavior, leading to breaking the continuous space apart, which might cost infinitely amount of energy.
Bundle structure theorem: Suppose
G is a matrix Lie group and
H is a closed subgroup of
G: Then
G has the structure of a fibre bundle with base
and fiber
H, where projection map
is given by
, with
denoting the coset
Prove is given for Proposition 13.8 in [
28].
4.2. Stability of the Defects in Superfluid Helium 3
The order parameter space for superfluid Helium 3 is given as
, which we refer as the
initial base space [
29]. Given that the base space is a matrix Lie group
, it is having a structure of a fiber bundle
G with its own fibers
representing remaining symmetries, and bases
, corresponding to the order parameters of various phases by the Bundle structure theorem [
19]. We convert the results of [
30] for continuous symmetries to a fiber-bundle language (
Table 1), and apply Stability lemma and Physical Stability theorem in
Table 2 for some of the phases of superfluid Helium 3, where each fundamental group’s multiplication rule dictates the behavior of the zero-dimensional and 1-dimensional physical defects.
Although the phase diagram of superfluid Helium 3 is very complex [
31], for simplicity of the argument, consider only two phases of superfluid Helium 3 called
phase-A and
phase-B to illustrate usage of Fiber structure theorem. Additionally, consider a part of a phase diagram where phase-B follows from phase-A. In a physical laboratory, such scenario may happen if pressure remains fixed during the experiment, but the temperature gradually lowered, leading to encountering phase-A and followed by phase B [
19]. The defects formed during phase-A may transit to the phase-B, and stability of those defects may be studied using the long homotopy sequence of the Fiber structure theorem. For example, in 3-dimensional case (
), by statements of Physics stability theorem, the 0-dimensional defects (often referred as
monopoles by physicists) represented by the second homotopy group of the order parameter space
, where
i corresponds to the number of phases. So, for phase-A, the order parameter space would be given by
, where
is the group of symmetries under which the system remains invariant even at phase-A after the transition. Similarly,
, where
is the remaining symmetries for
G during phase-B, and
is a closed subgroup of
while
is a closed subgroup of
G admitting a local cross section
f. Then, for the 0-dimensional objects, according to the second statement of the Fiber structure theorem, a part of the long homotopy sequence:
To illustrate an example, for the simplicity of the argument consider dipole-locked phase-A of superfluid Helium 3 transitioning to the phase-B. The order parameter for dipole-locked phase-A is given by
and the group of remaining symmetries
consists of the identity alone. Similarly, for the phase-B,
with
. So, the fiber
reduces to
given the triviality of
,
[
4,
11,
27].
The long homotopy sequence may be used to evaluate stability of physical defects formed from one phase to another. For example, by Physical stability theorem,
and hence dipole-locked phase-A supports stable 1d-defects. To evaluate the question whether these 1d-defects remain stable as superfluid Helium 3 enters the phase-B, consider the relevant part of the long homotopy sequence
Using Seifert-van Kampen Theorem,
, which infinite abelian group consisting of pairs
where first element
a belongs to the cyclic group of order two
and second element
b belongs to
Z, the group of integers under addition. So the partial sequence becomes
The stability of 1d-defects of dipole-locked phase-A in phase-B depends on whether elements of remain non-trivial when mapped to . If non-trivial element of maps to a trivial element of , then 1d-defects corresponding to these elements are considered unstable in the order parameter space of phase-B.
For the 1d defects to be stable, the element of (which is ) must map to an element of that is not in the kernel of the subsequent map to . If the map from to sends this element to a non-trivial element, then the 1d-defects are stable in the total space , because they are not "killed" when projecting down to .
Given the homotopy sequence , where the map is the inclusion of cosets from to , we analyze the stability of strings. The first map in the sequence, from to , likely maps into as or a similar structure. The second map, the inclusion of cosets, maps elements from to , where typically the Z component maps to the identity. If the inclusion map preserves the part, then non-trivial strings in remain non-trivial in , indicating stability.
Similarly, the long homotopy sequence may be used to determine 0-dimensional defects, such as monopoles as superfluid Helium 3 undergoes transition from dipole-locked phase-A to phase-B [
2]. Considering the homotopy sequence for monopoles, which are classified by the second homotopy group
:
A monopole represented by an element in
is stable if it maps to the trivial element in
, which suggests the absence of an attachment to higher-dimensional defects. Conversely, if the element maps to a non-trivial element in
, the monopole is considered unstable as it indicates an attachment to a higher-dimensional defect or transformation into a 1d-defect in the space
. For a monopole to be stable, its corresponding element must not be in the kernel of the map from
to
. So, in the given fibration with
and
, the relevant part of the long exact sequence is:
This sequence indicates that the second homotopy group is trivial for both the total space and the base space. Consequently, there are no non-trivial monopole defects to consider, and thus, by definition, any monopoles would be stable [
32,
33]. However, this stability is somewhat vacuous since the triviality of the groups suggests the absence of monopoles in the spaces under consideration due to Physical stability theorem.
4.3. Combined Effects in KLS Cosmic Walls
Various sequential symmetry breaking scenarios described in [
2] and corresponding references in detail. For example, given the context of polar distorted
B phase (PdB) phase in the KLS walls, the combined topological objects are described by the relative homotopy group
, where
and
corresponding the vacuum spaces. Using the homotopy lifting properties, such relative homotopy group can be converted to the absolute homotopy group
with the fiber bundle
G and corresponding fiber
N and base
B. So in such formalism, the fiber
is
, the fiber bundle
and base
, and using Statement 1 in the Fiber structure theorem, the short homotopy sequence group
By applying the Physical stability theorem and Statement 2 of the Fiber structure theorem, one may recover results of [
2,
16] on exact sequence of homomorphism.
Acknowledgments
I would like to express my gratitude and appreciation to Professor Grigory Volovik for his valuable recommendations which have significantly enhanced the scope of this paper, extending the relevance of the presented theorems from condensed matter to cosmic phase transitions. Many thank you to Professor Jon McCammond for all the guidance, patience and support for my transition from physics to pure mathematics. Additionally, I would like to thank the department of mathematics in Princeton University for hosting me once in a while and providing the best productive environment and inspiration. Special thank you to my PhD advisor Professor Dirk Bouwmeester for all the inspiration and supporting my passion for topology.
References
- T. W. B. Kibble, T. T. W. B. Kibble, T. Vachaspati, Monopoles on strings, J. Phys. G 42 (2015) 094002. [CrossRef]
- G. E. Volovik, K. G. E. Volovik, K. Zhang, String monopoles, string walls, vortex skyrmions, and nexus objects in the polar distorted b phase of he-3, Physical Review Research 2 (2020) 023263. [CrossRef]
- F. A. Bais, The topology of monopoles crossing a phase-boundary, Phys. Lett. B 98 (1981) 437–442. [CrossRef]
- N. D. Mermin, The topological theory of defects in ordered media, Reviews of Modern Physics 51 (3) (1979) 591–648. [CrossRef]
- P. Grinevich, G. P. Grinevich, G. Volovik, Topology of gap nodes in superfluid 3he: Homotopy group for 3he-b disclination, Journal of Low Temperature Physics 72 (1988) 371–380. [CrossRef]
- G. E. Volovik, The Universe in a Helium Droplet, Oxford University Press, 2010. [CrossRef]
- R. Kennedy, C. R. Kennedy, C. Guggenheim, Homotopy theory of strong and weak topological insulators, Phys. Rev. B 91 (2015) 245148. [CrossRef]
- A.-C. Davis, R. Brandenberger (Eds.), Formation and Interactions of Topological Defects: Proceedings of a NATO Advanced Study Institute on Formation and Interactions of Topological Defects, held August 22–September 2, 1994, in Cambridge, England, Vol. 349 of NATO Science Series B:, Publisher Name, Cambridge, England, 1994. 22 August.
- G. Toulouse, M. Kléman, Principles of a classification of defects in ordered media, Journal de Physique Lettres 37 (6) (1976) 149–151. [CrossRef]
- V. Poénaru, Superalgebras and Confinement in Condensed Matter Physics, Vol. 59, Springer, 2023.
- M. Nakahara, Geometry, Topology and Physics, 2nd Edition, Graduate Student Series in Physics, 2003.
- T. W. B. Kibble, Classification of topological defects and their relevance to cosmology and elsewhere, Vol. 549 of NATO Science Series (Series C: Mathematical and Physical Sciences), Springer, Dordrecht, 2000, pp. 7–31.
- G. E. Volovik, The superfluid universe, Volume! 156 (2010) 570–618. [CrossRef]
- R. P. Huebener, N. Schopohl, G. E. Volovik, Vortices in unconventional superconductors and superfluids, 2002. [CrossRef]
- V. M. H. Ruutu, V. Eltsov, A. J. Gill, A. J. Gill, T. W. B. Kibble, M. Krusius, Y. Makhlin, Y. Makhlin, B. Plaçais, G. E. Volovik, G. E. Volovik, W.-B. Xu, Vortex formation in neutron-irradiated superfluid 3he as an analogue of cosmological defect formation, Nature 382 (1996) 334–336. [CrossRef]
- J. Mäkinen, V. Dmitriev, J. Nissinen, J. Rysti, G. Volovik, A. Yudin, K. Zhang, V. Eltsov, Half-quantum vortices and walls bounded by strings in the polar-distorted phases of topological superfluid 3he, Nature Communications 10 (237) (2019) 1–10. [CrossRef]
- G. E. Volovik, The Universe in a Helium Droplet, Oxford University Press, Oxford, 2003.
- G. Volovik, Exotic Properties of Superfluid Helium 3, Modern Condensed Matter Physics, World Scientific, Singapore, 1992.
- D. Vollhardt, Superfluid Phases of Helium 3, Taylor and Francis Group, 1990.
- A. J. Leggett, Superfluidity, Rev. Mod. Phys. 71 (1999) S318–S323. [CrossRef]
- A. Hatcher, Algebraic Topology, Cambridge University Press, 2002.
- P. M. Chaikin, T. C. Lubensky, Principles of Condensed Matter Physics, Cambridge University Press, 1995. [CrossRef]
- R. Durrer, Topological defects in cosmology, New Astronomy Reviews 43 (2-4) (1999) 111–156. [CrossRef]
- A. Ardaşeva, A. Doostmohammadi, Topological defects in biological matter, Nature Reviews Physics 4 (2022) 354–356. [CrossRef]
- L. Giomi, Z. Kos, M. Ravnik, A. Sengupta, Cross-talk between topological defects in different fields revealed by nematic microfluidics, Proc. Natl. Acad. Sci. U. S. A. 114 (29) (2017) E5771–E5777. [CrossRef]
- N. E. Steenrod, The Topology of Fibre Bundles, Princeton University Press, 1951.
- A. J. Leggett, Quantum Liquids: Bose Condensation and Cooper Pairing in Condensed-Matter Systems, Oxford University Press, 2021.
- B. C. Hall, Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Vol. 222 of Graduate Texts in Mathematics, Springer, 2015. [CrossRef]
- G. Volovik, The Universe in a Helium Droplet, Internet Archive, 2013, accessed: 2013-10-05 15:45:38.
- C. Bruder, D. Vollhardt, Symmetry and stationary points of a free energy: The case of superfluid He3, Physical Review B 34 (1) (1986) 131–146. [CrossRef]
- N. D. Mermin, D. M. Lee, Superfluid helium 3, Scientific American 235 (6) (1976) 56–71. https://www.jstor.org/stable/24950505.
- M. M. Salomaa, Monopoles in the rotating superfluid helium-3 a–b interface, Nature 326 (1987) 367–370. [CrossRef]
- O. V. Lounasmaa, E. Thuneberg, Vortices in rotating superfluid 3he, Proceedings of the National Academy of Sciences 96 (14) (1999) 7760–7767. [CrossRef]
Table 1.
Fibers and Base spaces for phases of superfluid Helium 3.
Table 1.
Fibers and Base spaces for phases of superfluid Helium 3.
| i |
|
|
| (1) |
|
|
| (2) |
|
|
| (3) |
|
|
| (4) |
|
|
| (5) |
|
|
| (6) |
|
|
| (7) |
|
|
| (8) |
|
|
| (10) |
|
|
| (11) |
|
|
Table 2.
0-dimensional and 1-dimensional defects represented by and correspondingly for a base space for each of the phase of superfluid Helium 3.
Table 2.
0-dimensional and 1-dimensional defects represented by and correspondingly for a base space for each of the phase of superfluid Helium 3.
| i |
|
for 0d-defects |
for 1d-defects |
| (1) |
|
|
|
| (2) |
|
|
|
| (3) |
|
|
|
| (4) |
|
|
|
| (5) |
|
|
|
| (6) |
|
|
|
| (7) |
|
|
|
| (8) |
|
|
|
| (10) |
|
|
|
| (11) |
|
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).