1. Introduction
Photovoltaic (PV) systems require accurate modelling and monitoring to ensure their profitability. The amount of irradiance at the site, the GPI, is the foundation of designing, modelling and monitoring PV systems. The global plane-of-array irradiance (GPI) comprises the plane-of-array’s (POA) direct beam, ground and diffuse irradiance components. GPI is used to model and monitor PV systems, as this shows the amount of generated solar power and, therefore, one of the most important contributing factors to designing a PV system. The global horizontal irradiance (GHI), direct normal irradiance (DNI) and diffuse horizontal irradiance (DHI) components are required to calculate these irradiance components.
Irradiance components with a transposition model calculate GPI (
) as
is the direct beam irradiance,
is the ground-reflected irradiance, and
is the diffuse irradiance component in the POA. GHI, DNI and DHI components are required to calculate
,
and
. The sum of the DNI projected onto the horizontal surface using the cosine of the solar zenith angle
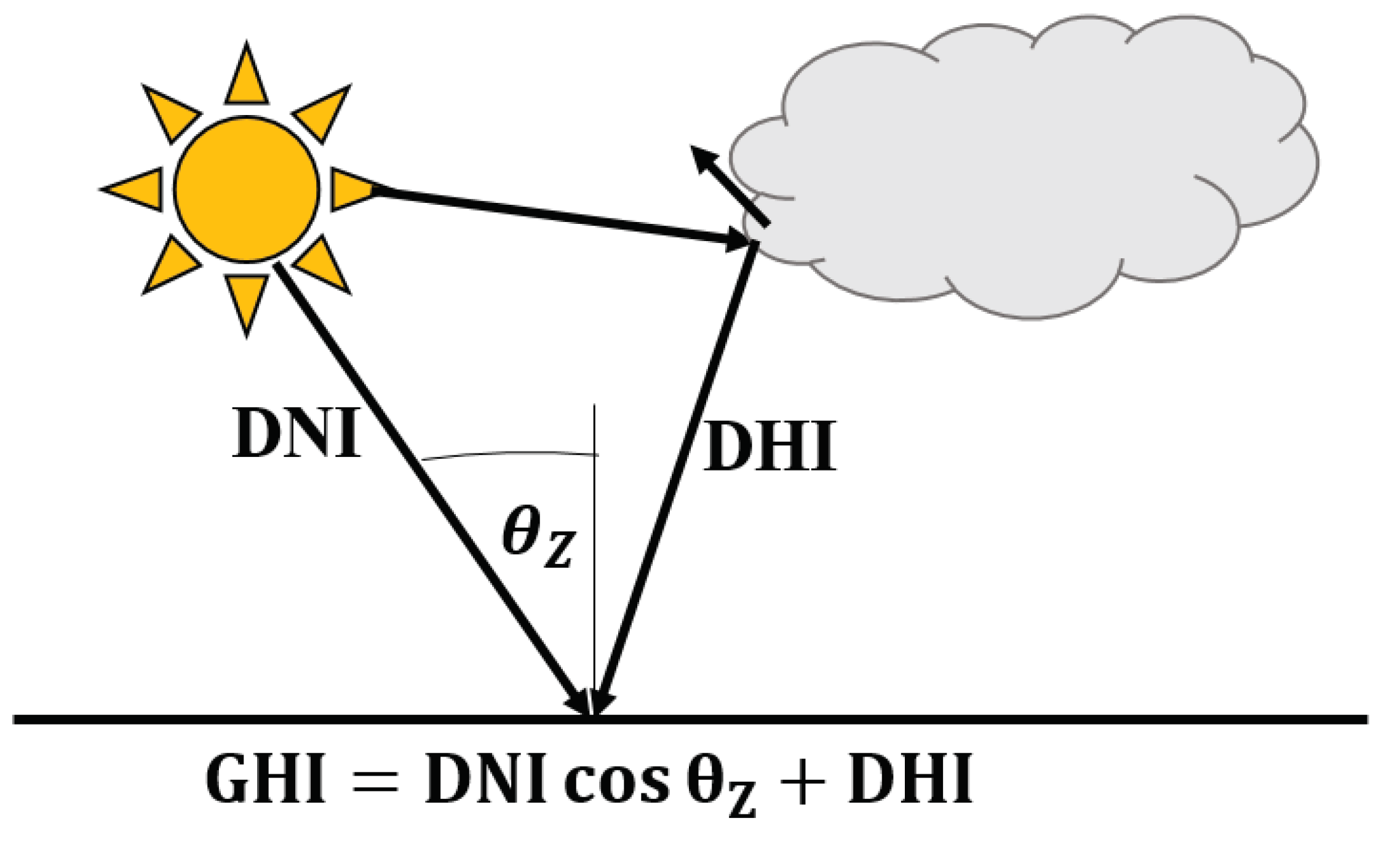
, and DHI gives the GHI, shown in
Figure 1, [
1]:
GHI, DHI, and DNI units are in .
Most ground-based stations have at least measurements of GHI. Other measurements include radiometric data such as DNI, DHI and ultra-violet, and meteorologic data such as the temperature, pressure, rainfall, relative humidity, wind direction and wind speed. Pyranometers measure DHI and GHI, and the pyrheliometer measures DNI.
GHI is measured with a hemispherical view and is mounted horizontally. Similar in setup to other pyranometers, the DHI pyranometer includes the additional feature of being shaded from direct sunlight. The pyrheliometer has a narrow view that only measures the beam directly from the Sun and is usually a Sun tracker for increased accuracy [
2]. The irradiance measurements are converted to
and logged accordingly.
Calibrating the equipment to the ISO 9060:1990 standard is necessary, and it is advisable to undergo recalibration every two years to ensure the reliability of measurements. The maintenance required is to clean the domes and regularly check and replace the desiccant, which keeps the instruments dry internally.
GHI, DNI and DHI are interdependent; therefore, having only two irradiance measurements is sufficient to estimate the third using the decomposition models (also sometimes called separation models) [
3]. If only the GHI is available, the DNI and DHI also are estimated using the decomposition models. The transposition models calculate GPI using the irradiance components. Therefore, GHI, DHI and DNI correlations are usually empirically expressed as a decomposition model [
4].
Indices are relationships between different irradiance components. Decomposition and transposition models utilise these relationships.
The definition of the direct beam transmittance
and diffuse transmittance
is
Liu and Jordan defined the
as
All K-values (, and ) are unitless.
The extraterrestrial irradiance on a normal surface
depends on the day of the year
The Solar Constant is usually 1,367 .
Determining the horizontal extraterrestrial irradiance
involves multiplying it by the cosine of
as expressed in Equation (
7):
Multipredictor decomposition models can improve accuracy compared to single predictor models [
6]. However, the disadvantage is that multiple measurements must be available, which is not always the case for developing countries or brand-new sites of PV installations.
Boland
et al. and Ridley
et al. developed a logistical model to estimate solar diffuse radiation [
7,
8]. Soares
et al., Talvitie
et al., and Kalyanam and Hoffmann have proposed machine-learning-based models to predict solar diffuse and direct components [
9,
10,
11]. Bessafi
et al. have proposed a satellite-based decomposition model as an alternative to ground-based measurements [
12], and Janjai
et al. have proposed statistical models for estimating diffuse radiation [
13].
Decomposition models have been developed by assessing previous models and improving the accuracy of these estimations. As more data and measurements become available, researchers have the opportunity to develop models for different climates and temporal resolutions. Most models predominantly use
. Some of the variables used in the decomposition models are the solar altitude angle
and dew point temperature
. Using
as the main predictor in decomposition models is popular because of its simplicity and applicability [
6].
Orgill and Hollands developed a relationship between the
and
[
14], and Erbs
et al. extended the
-
relationship to latitudes from 31 to 42
∘ North [
15]. Louche
et al. established a GHI and DNI relationship for a Mediterranean site to estimate
using
[
16].
The Direct Insolation Simulation Code (DISC) was developed by Maxwell [
17], and Perez
et al. developed the Dirint model with the hopes of increasing the performance of the DISC model [
18]. The Dirint model of Perez
et al. has shown superior performance when estimating the DNI [
19].
In Korea, Lee
et al. developed a model using 6 Korean locations [
20], and Lee
et al. developed a new model using Maxwell’s DISC model by refitting the coefficients [
3]. Skartveit and Olseth developed a DNI estimation model using the solar elevation angle for Norway based on hourly GHI and DHI records [
21].
Lam and Li derived
for Hong Kong [
22]. Reindl
et al. determined
using two models with
and
[
23].
The main limitations of decomposition models are that some have limited climate scope, and the dataset’s temporal resolution affects the irradiance estimation accuracy. A decomposition model in a tropical climate may be unsuitable for a desert climate and vice versa. Intra-hourly-based models perform differently from daily- or monthly-based models, which is why many available decomposition models exist.
Several regions, such as Belgium [
4], China [
24], the USA [
19], and North Africa [
25], evaluated the accuracy of decomposition models.
Gueymard and Ruiz-Arias provided an extensive study of 140 available decomposition models. The authors state that the predicted DNI’s accuracy highly depends on the decomposition model. Validation studies exist but are limited to a few models and test stations, i.e. biased to a specific location or climate [
26]. Research indicates that no decomposition model has been developed and validated for South Africa.
Laiti
et al. state that, in general, decomposition models tend to overestimate DHI and underestimate DNI and typically, models tend to underestimate DHI in overcast periods and overestimate during clear-sky periods [
19].
Higher resolution data include higher
values, resulting in extreme overestimations of DNI. These hourly DNI estimates have higher accuracy than 1-minute DNI estimates. Subhourly estimations would be highly beneficial for real-time monitoring and forecasting of solar power [
26].
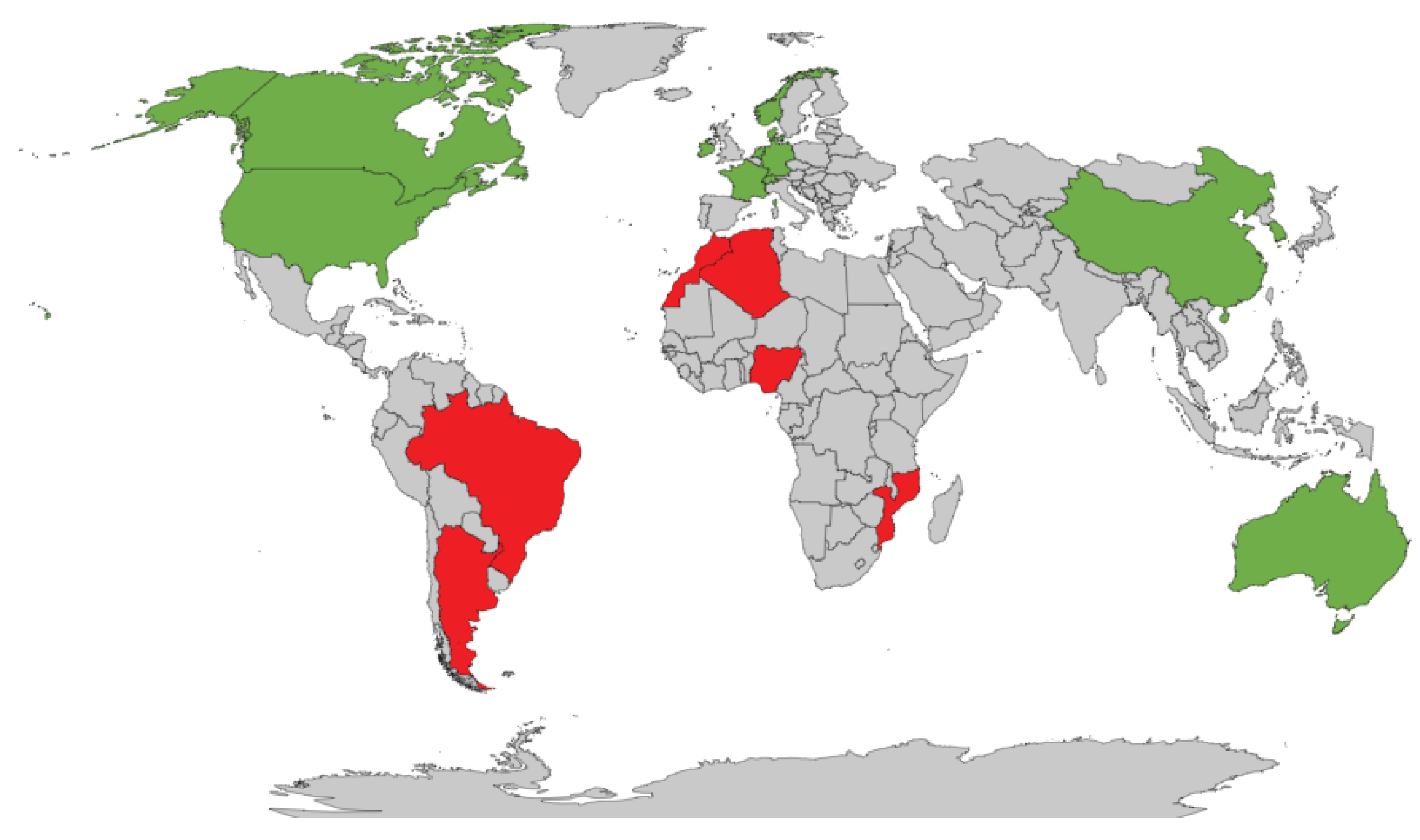
Figure 2 visualises the testing and validation countries of common decomposition models in green of models such as Orgill and Hollands, Erbs
et al., Louche
et al., Reindl
et al., DISC (Maxwell), Dirint (Perez
et al.), Lee
et al., Lee
et al., Skartveit and Olseth and Lam and Li) [
3,
14,
15,
16,
17,
18,
20,
21,
22,
23].
The development of the decomposition model in South America includes Brazil [
28], Argentina and Brazil [
29]. Northern African models include Nigeria [
30], Algeria [
31] and Morocco [
32].
Engerer developed a model for Australia and observed that the model only slightly outperformed the Dirint model [
33]. The BRL model by Ridley
et al. developed a method to construct multiple variable logistic models for the diffuse solar fraction, which includes Mozambique [
8].
Figure 2 represents these discussed models [
8,
28,
29,
30,
31,
32,
33] in red.
South African research on decomposition models includes the following: Tsubo and Walker published the only Southern African-based study on the relationship between radiation and
[
34]. However, this relationship is with photosynthetically active radiation related to agricultural practices, not PV systems. Clear-sky model assessments and validation studies have been performed by [
35] and [
36] for Southern African countries. Clear-sky models simplify atmospheric attenuation to estimate solar irradiance under clear-sky conditions and do not represent decomposition models and is not include these studies as comparison models, as they are irrelevant to the research.
Mahachi’s thesis assessed decomposition and transposition models in South Africa and showed that the models tend to overestimate the DHI but underestimate the DNI [
37]. Furthermore, the DISC and Dirint decomposition models showed the most accurate estimations of the DNI and DHI for the South African climatic conditions [
38].
As discussed, decomposition models are empirical relationships between GHI, DHI and DNI. All three irradiance components are required to estimate GPI. Decomposition models are useful as it reduces the measurement equipment by decomposing one irradiance component into two other; for example, use GHI to estimate DHI and DNI.
Most decomposition models are not universally applicable and localised to a specific climate, and the temporal resolution is not always transferable. There has not been extensive literature published representing the Southern African region in decomposition models, which this research article will attempt to address.
2. Model Development
The methodology to develop a novel decomposition model is based on selected data from the automated QC procedure and addresses three geographical models:
a localised decomposition model, which is site-specific;
a clustered decomposition model, which encapsulates several sites to group an area based on their geographical location;
and a regional (Southern African) model, which encapsulates the data from the SAURAN network for developing a model specific to Southern Africa.
2.1. SAURAN Database
Table 1 summarises the SAURAN stations’ corresponding geographical information, such as latitude, longitude, and elevation above sea level.
Table 3 shows the data points available for the model development, taken from
Table 2. Further, the data points assessed are
between 0.175 and 0.875.
The data points are hourly measurements of the GHI, DNI and DHI. The split of the train-validation-test datasets is 50:25:25, with the exceptions of two datasets, ILA and MIN. The ILA and MIN have a 0:0:100 data split and are two unknown datasets as part of the test study.
Table 3 also shows each station’s mean GHI, DNI, and DHI determined after applying the QC procedure.
Table 2.
SAURAN database and dataset sizes from [
39].
Table 2.
SAURAN database and dataset sizes from [
39].
| Station |
Dataset size |
Start Date |
End Date |
| Before QC |
After QC |
| CSIR |
46,434 |
26,539 |
11 March 2017 |
31 October 2022 |
| CUT |
28,077 |
14,619 |
24 October 2017 |
31 October 2022 |
| FRH |
40,895 |
22,233 |
7 February 2017 |
24 February 2022 |
| GRT |
18,541 |
9774 |
27 November 2013 |
24 January 2016 |
| HLO |
21,532 |
11,728 |
8 October 2015 |
27 October 2020 |
| ILA |
8832 |
4676 |
13 October 2021 |
31 October 2022 |
| KZH |
52,323 |
38,898 |
7 December 2015 |
07 August 2022 |
| KZW |
20,291 |
10,756 |
7 December 2015 |
12 December 2018 |
| MIN |
8185 |
4423 |
28 October 2021 |
31 October 2022 |
| MRB |
4201 |
2462 |
17 March 2017 |
22 October 2019 |
| NMU |
39,969 |
23,130 |
10 December 2015 |
30 September 2022 |
| NUST |
52,004 |
27,401 |
26 July 2016 |
31 October 2022 |
| PMB |
9773 |
5415 |
13 July 2021 |
31 October 2022 |
| RVD |
63,716 |
34,457 |
27 March 2014 |
28 July 2021 |
| SALT |
14,151 |
9908 |
21 July 2017 |
22 December 2020 |
| STA |
40,256 |
21,751 |
7 December 2015 |
19 April 2021 |
| SUN |
87,720 |
47,733 |
24 May 2010 |
31 October 2022 |
| SUT |
1715 |
902 |
8 February 2017 |
20 April 2017 |
| UBG |
38,917 |
20,646 |
26 November 2014 |
6 November 2020 |
| UFS |
31,665 |
17,152 |
16 January 2014 |
30 August 2017 |
| UNV |
59,100 |
33,144 |
23 April 2015 |
31 October 2022 |
| UNZ |
56,399 |
30,373 |
11 July 2014 |
31 October 2022 |
| UPR |
78,792 |
42,128 |
19 September 2013 |
31 October 2022 |
| VAN |
24,701 |
13,234 |
26 August 2016 |
10 July 2019 |
Table 3.
Model development stations indicating the mean GHI, DNI and GHI and sizes of training, validation and testing sets.
Table 3.
Model development stations indicating the mean GHI, DNI and GHI and sizes of training, validation and testing sets.
| Station |
Mean1
|
|
Dataset2
|
|
Cluster Allocation |
|
GHI []
|
DNI []
|
DHI []
|
Total |
Train |
Validation |
Test |
| CSIR |
575 |
599 |
167 |
|
14,991 |
7,495 |
3,748 |
3,748 |
|
2 |
| CUT |
609 |
639 |
159 |
|
9,161 |
4,580 |
2,290 |
2,291 |
|
2 |
| FRH |
544 |
583 |
151 |
|
12,224 |
6,112 |
3,056 |
3,056 |
|
4 |
| GRT |
573 |
624 |
151 |
|
5,788 |
2,894 |
1,447 |
1,447 |
|
4 |
| HLO |
550 |
608 |
138 |
|
7,061 |
3,530 |
1,765 |
1,766 |
|
1 |
| ILA |
589 |
680 |
131 |
|
2,709 |
0 |
0 |
2,709 |
|
1 |
| KZH |
533 |
517 |
179 |
|
8,782 |
4,391 |
2,195 |
2,196 |
|
3 |
| KZW |
531 |
511 |
184 |
|
5,945 |
2,972 |
1,486 |
1,487 |
|
3 |
| NMU |
556 |
545 |
165 |
|
10,562 |
5,281 |
2,640 |
2,641 |
|
4 |
| NUST |
614 |
670 |
149 |
|
15,901 |
7,950 |
3,975 |
3,976 |
|
1 |
| MIN |
564 |
573 |
161 |
|
2,761 |
0 |
0 |
2,761 |
|
2 |
| RVD |
630 |
729 |
125 |
|
19,624 |
9,812 |
4,906 |
4,906 |
|
1 |
| SUN |
556 |
645 |
133 |
|
28,508 |
14,254 |
7,127 |
7,127 |
|
1 |
| UBG |
591 |
602 |
158 |
|
12,137 |
6,068 |
3,034 |
3,035 |
|
2 |
| UFS |
567 |
654 |
137 |
|
10,257 |
5,128 |
2,564 |
2,565 |
|
2 |
| UNV |
579 |
524 |
197 |
|
15,874 |
7,937 |
3,968 |
3,969 |
|
2 |
| UNZ |
530 |
528 |
176 |
|
10,055 |
5,027 |
2,514 |
2,514 |
|
3 |
| UPR |
568 |
609 |
163 |
|
28,089 |
14,044 |
7,022 |
7,023 |
|
2 |
| VAN |
597 |
683 |
126 |
|
7,860 |
3,930 |
1,965 |
1,965 |
|
1 |
2.2. Comparison Metrics
The comparison metrics are the root mean square error (RMSE), mean absolute error (MAE) and mean bias error (MBE).
where
is the measured value, and
is the predicted value. A low RMSE and MAE indicate a good model, whereas an MBE should be closer to zero. RMSE indicates the concentration of data around the line of best fit. Therefore, a smaller RMSE is indicative of a more accurate model.
The Pearson correlation coefficient
r indicates the correlation between data:
In Equation (
9),
and
represent the individual points with index
i and
and
represent the mean of the
x and
y sample set. An
r closer to -1 has a negative correlation, meaning if one variable increases, the other decreases. In contrast, if
r is closer to 1, it has a positive correlation, meaning if one variable increases, the other would also [
41].
Statistical indicators used for the comparison metrics are the MBE, RMSE and MAE, all expressed as a percentage of the mean measured DNI [
26] and
. Further comparison metrics are two MAE
-intervals:
and
.
The MBE indicates whether a model over or underestimates the DNI, and the RMSE indicates the deviation of the errors. A significant difference between MAE and RMSE indicates a larger variance in the data. Lower RMSE and MAE are ideal, whereas an MBE closer to zero is optimal. The MAE is an unbiased estimator and also evaluates the two intervals. Lower and higher indicate overcast and clear-sky conditions, respectively. Therefore, the two intervals assess the models under varying weather conditions.
2.3. Regression and Fitting
The relationship between two variables is quantified using statistical methods like regression. Regression techniques can be linear, multi-linear and non-linear.
The definition of a linear relationship is
where
y is the response,
x is the regressor,
is the intercept, and
is the slope. A regression analysis quantifies the strength of a relationship between
y and
x [
41].
The least squares method estimates
and
so that the sum of the squares of the residuals is at a minimum. The residual sum of squares is denoted as
and is the sum of squares of the errors about the regression line. Thus, the minimisation of
where
denotes the predicted or fitted value.
The coefficient of determination,
, indicates how good the fit of a model is and is a number between zero and one.
A higher
-value indicates that the model explains the variation in the response variable around its mean, and the regression model fits the observation better [
41].
Polynomial regression is the modelling of a dependent,
y, as an
-degree polynomial of
x
Exponential regression is where the best fit of an equation is an exponential function, like
or
Multi-linear regression has multiple variables, which is the outcome of a response variable
2.4. Software Development Tools
The model development utilises a combination of data science applications and modelling. The primary tool is the open-source language Python with the anaconda interface [
42], and various available libraries [
43,
44,
45].
2.5. Baseline Models
Three comparative models are used as a baseline to compare the new models. Based on the literature, the DISC and Dirint models performed well for Southern African climates [
38,
46].
The Dirint [
18] and Lee [
3] models are also used for comparison because their foundation is similar to the DISC model [
17].
Maxwell’s DISC quasi-physical approach has three assumptions [
3]:
The relative air mass is the dominant parameter affecting the relationship between and ;
The physical model used to calculate
will provide a physically-based reference from which the changes in
can be calculated (see Equation (
20) below);
Seasonal, annual and climate variations in the relationship between and are fully accounted for by parametric functions in that relate to , cloud cover and PW vapour.
The absolute AM (
) is the pressurised normalisation of AM, expressed as
where
P refers to the atmospheric pressure at the test site, and
is the atmospheric pressure at sea level.
The modelled DNI is determined using Equation (
3):
where
and
The clear-sky limit
is a polynomial in
:
Two intervals determine the coefficients and : and .
Maxwell’s model possesses a different functional form because the quasi-physical approach is applied; therefore, it partially reflects the physics involved in the atmospheric transmission of solar radiation [
3]. The
,
and
parameters were fitted based on solar radiation data from Atlanta, Georgia, USA, 1981 [
17]. Maxwell adopted the Bird clear-sky model for
(see Equation (
22)). The parameters
,
and
, as described in Equations (
23) and (
24), were then fitted based on the dataset.
The DISC model, termed ‘quasi-physical’, combines a clear-sky model with experimental fits for other sky conditions. The model is a clear-sky irradiance attenuated by a function of
. Maxwell derived the empirical regressions from 12 years of recorded radiation data at 70 stations [
4,
17].
The Dirint model is based on the DISC model and was developed by Perez
et al. [
18]. The goal was to improve the accuracy of the DISC model by Maxwell [
17].
The Dirint model uses a clearness index variation parameter
:
Furthermore, a stability index parameter
:
considers the previous (
), current (
i) and next hourly (
) record. When the preceding or hourly record is missing,
is
A low
is a stable condition, whereas a high
characterises unstable conditions, which allows the distinction between hazy and partly cloudy conditions. The
is an adequate atmospheric PW estimator [
18]. The Dirint model’s atmospheric PW (
W) is estimated using:
The Dirint is a four-dimension conditional model, having the
,
,
and
W. Based on the four-dimensional model, the calculation of hourly DNI is
where
Coefficients and are from a complex lookup table.
Lee
et al. created a new model for Korea with the same format as Maxwell’s DISC model.
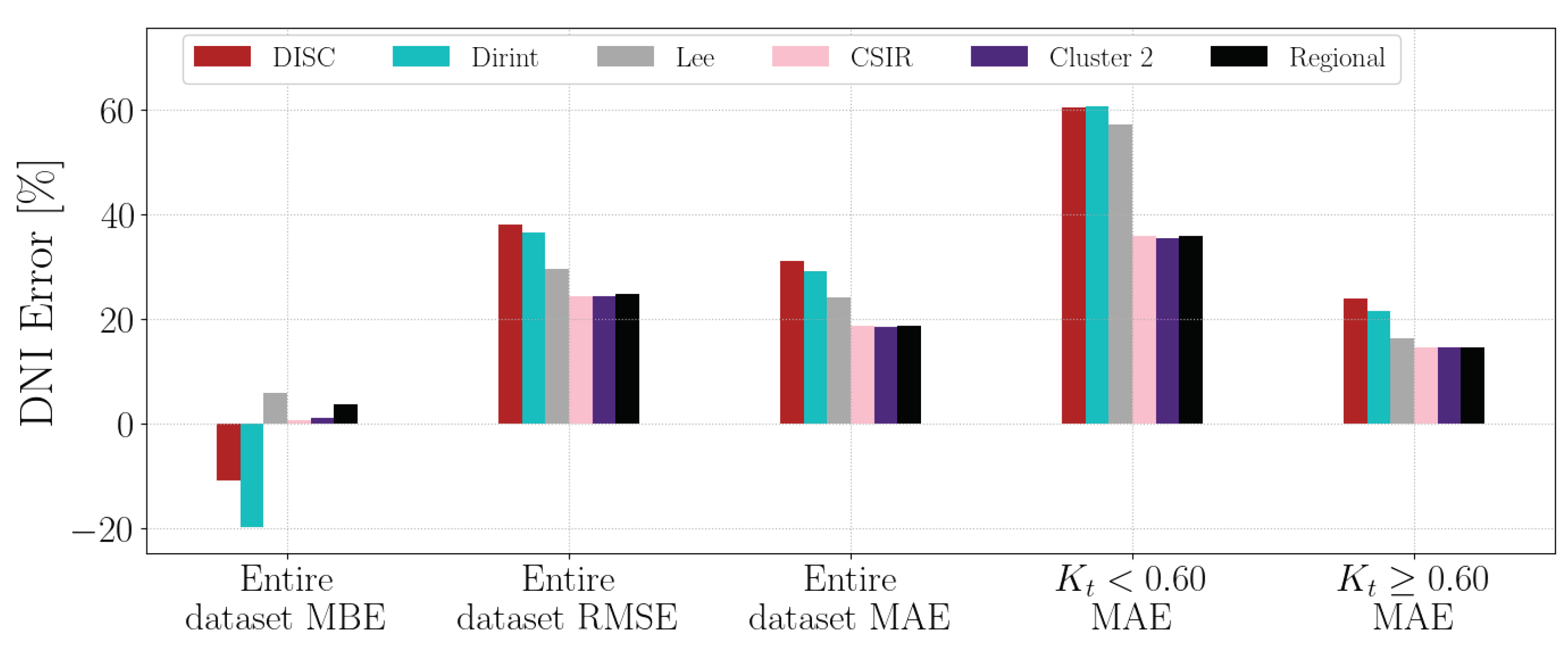
The evaluation consists of comparing the localised, clustered and regional models against the three baseline models: DISC, Dirint and Lee. The DISC and Dirint models were selected based on their performance in estimating DNI for Southern African climates. The Lee and Dirint models have foundational similarities to the DISC model. These models consider whether the newly developed decomposition model improves the accuracy of hourly DNI estimations for Southern Africa. The accuracy evaluation uses the comparison metrics discussed in the next section.
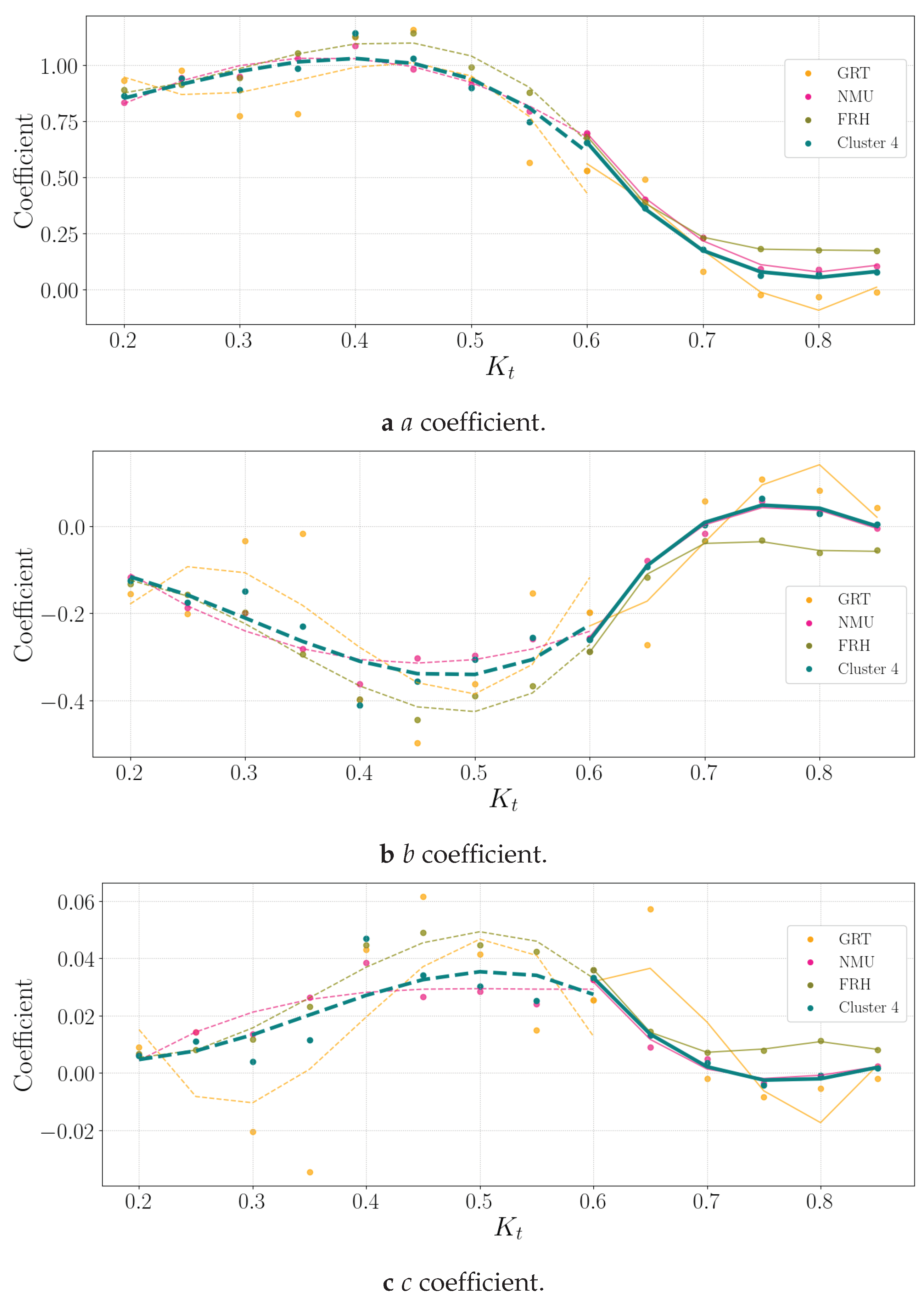
2.6. Decomposition Model Development Methodology
The methodology builds on the DISC model. The DISC model stands out as one of the better-performing models for estimating DNI for South Africa [
38]. Its simplicity is evident in its lack of need for a complex four-dimensional lookup table, unlike the Dirint model.
The original DISC model uses Equation (
21), an exponential function. However, the regression model for an exponential function, as discussed in
Section 2.3, showed difficulty in finding optimal
a,
b and
c coefficients in all cases. Instead, a second-order polynomial function of
is a suitable substitute with similar regression results.
The training set then fits
a,
b and
c for intervals
and
:
and the validation and testing sets evaluate the model’s accuracy.
Each model development undergoes the following initial processing steps:
Empirical formulae estimate , , pressure, , and . From this, the assessment of available models aids in developing a new model;
Data is split into intervals of 0.05 , starting from 0.175 to 0.875;
is then modelled as Equation (
34);
The interval or intervals are then fitted against the function to determine Equation (
34) to determine the
a,
b and
c coefficients using a least squares regression analysis;
From the
-interval function, the
-
,
-
and
-
coefficients are fitted to a polynomial of Equation (
35) with regards to
;
These equations can be used to determine
and
, which, in turn, calculates the DNI (see Equations (
19) and (
20)).
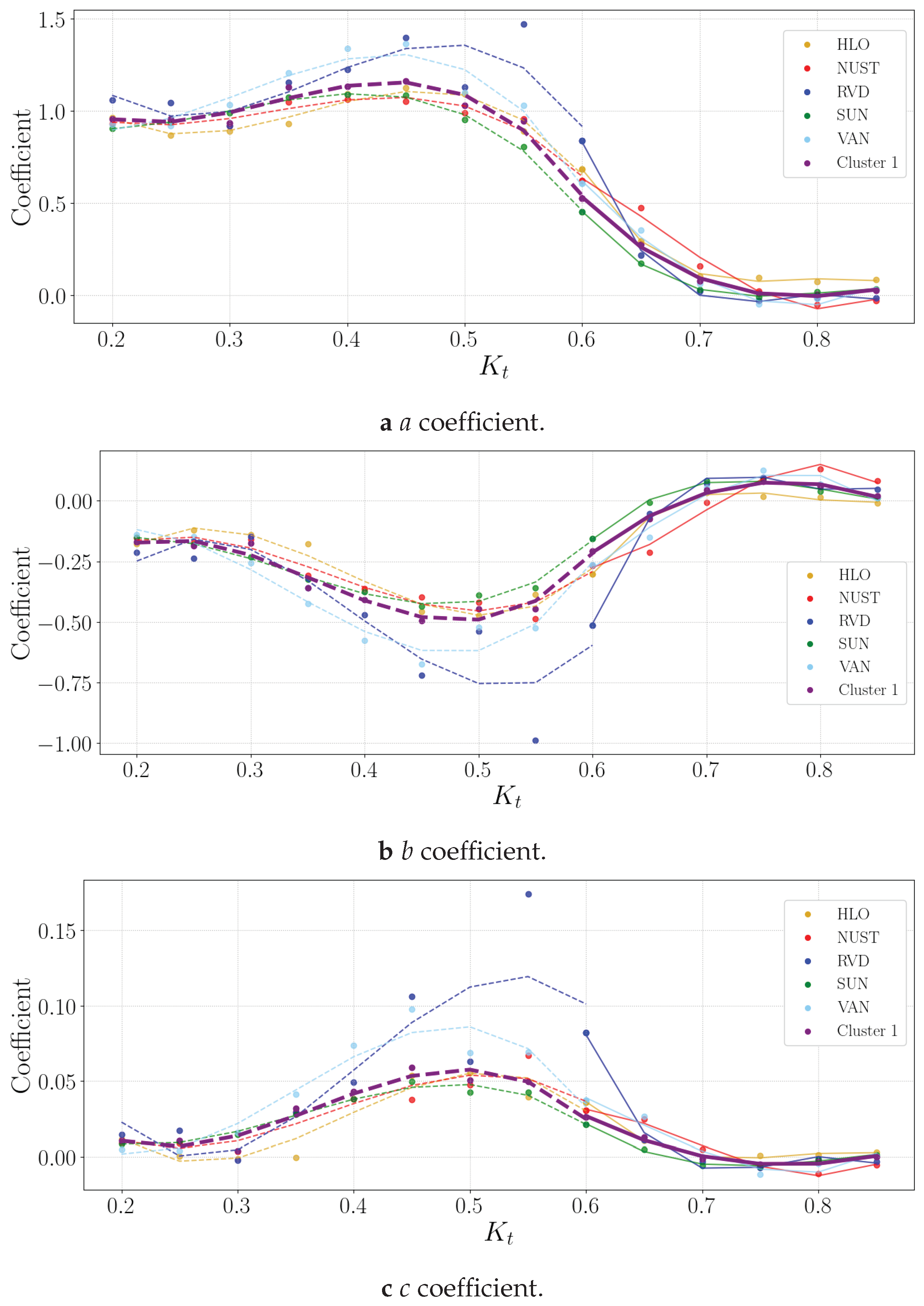
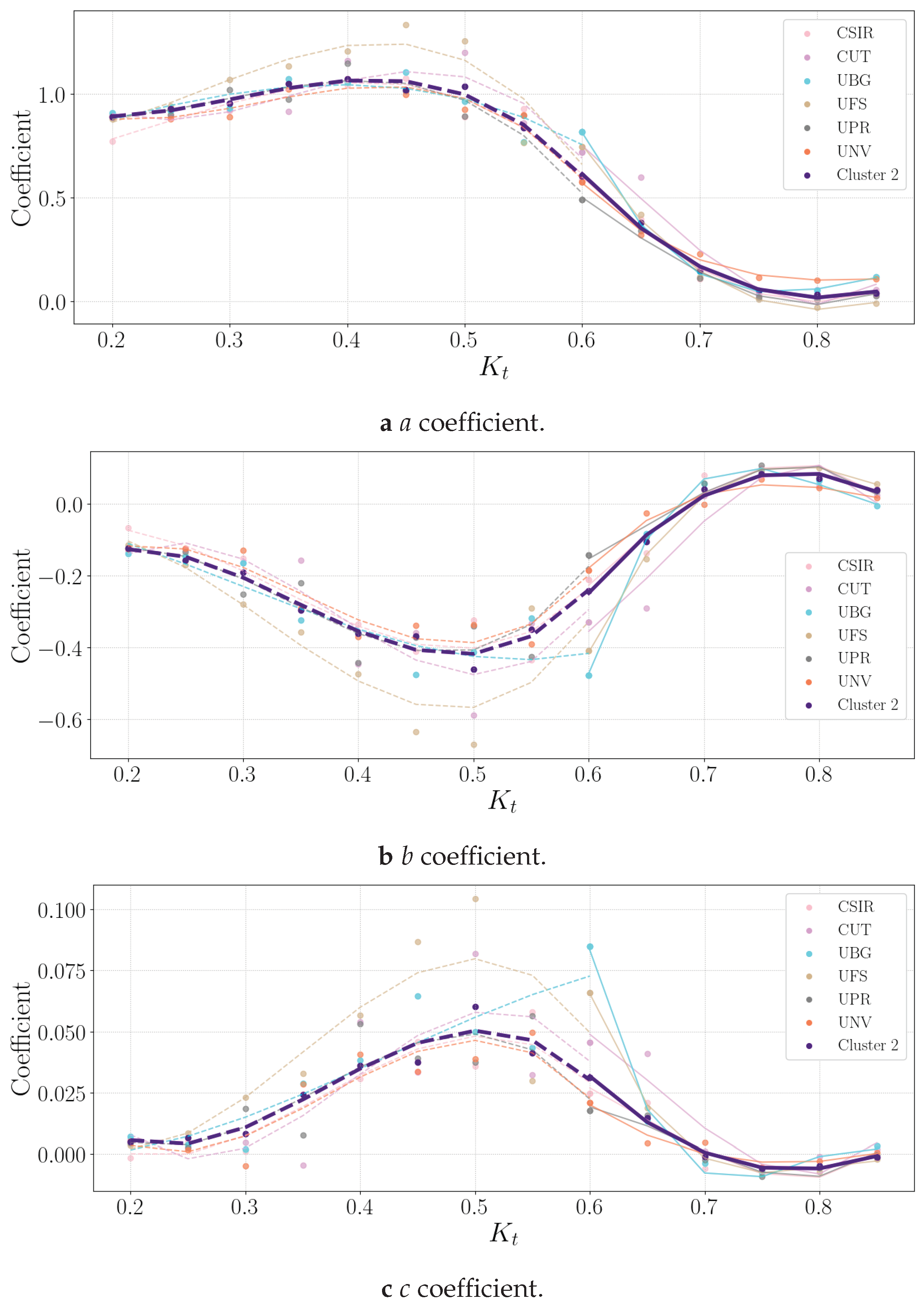
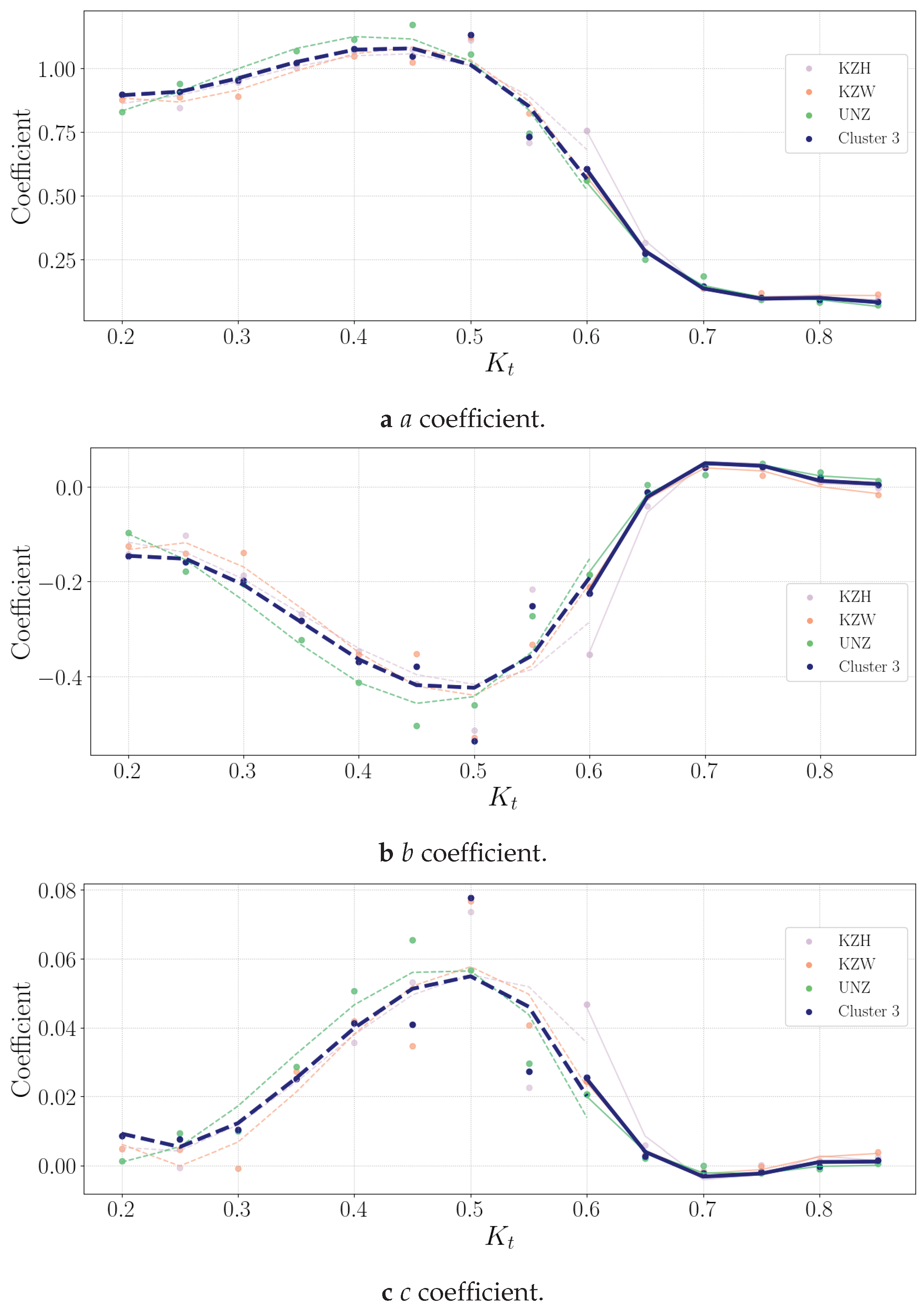
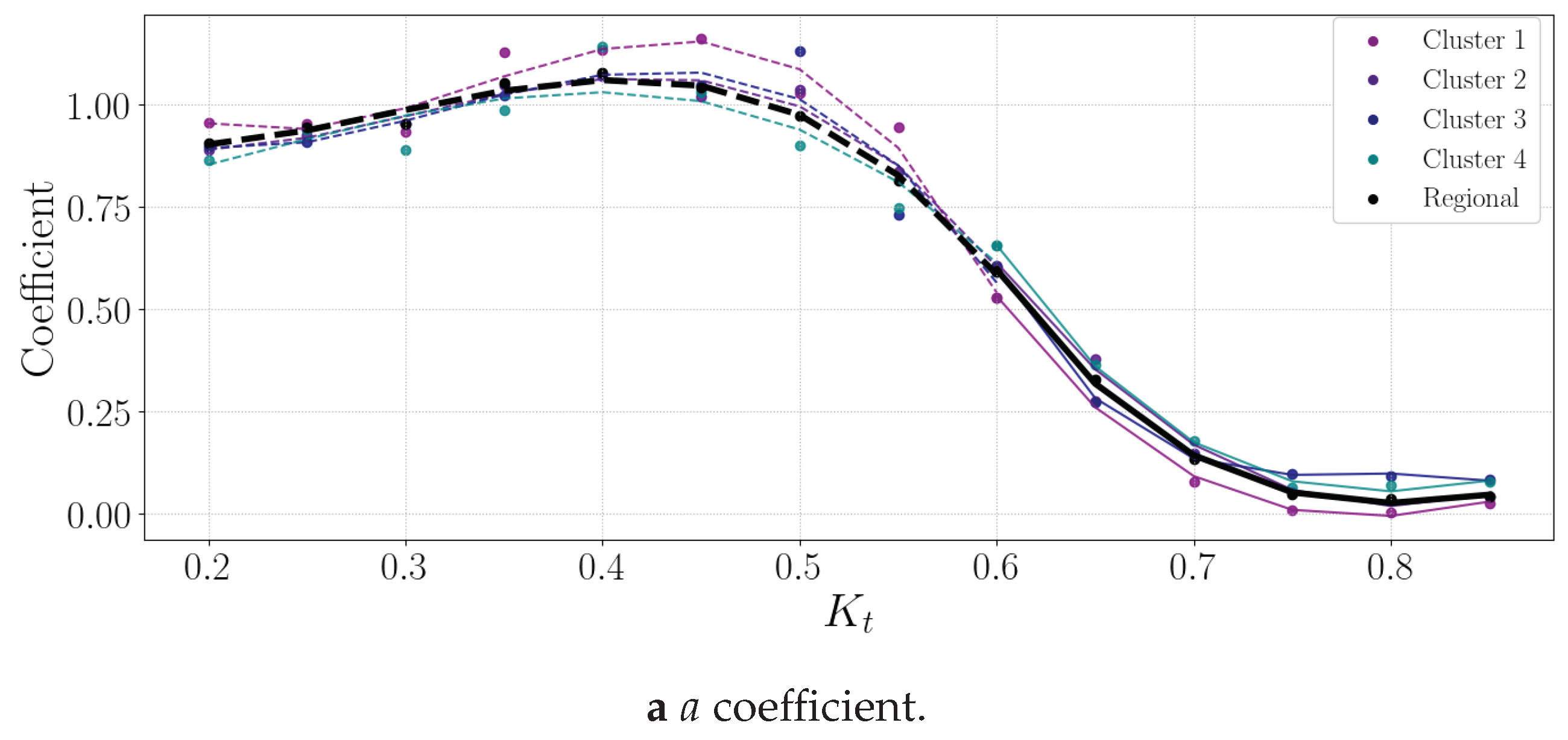
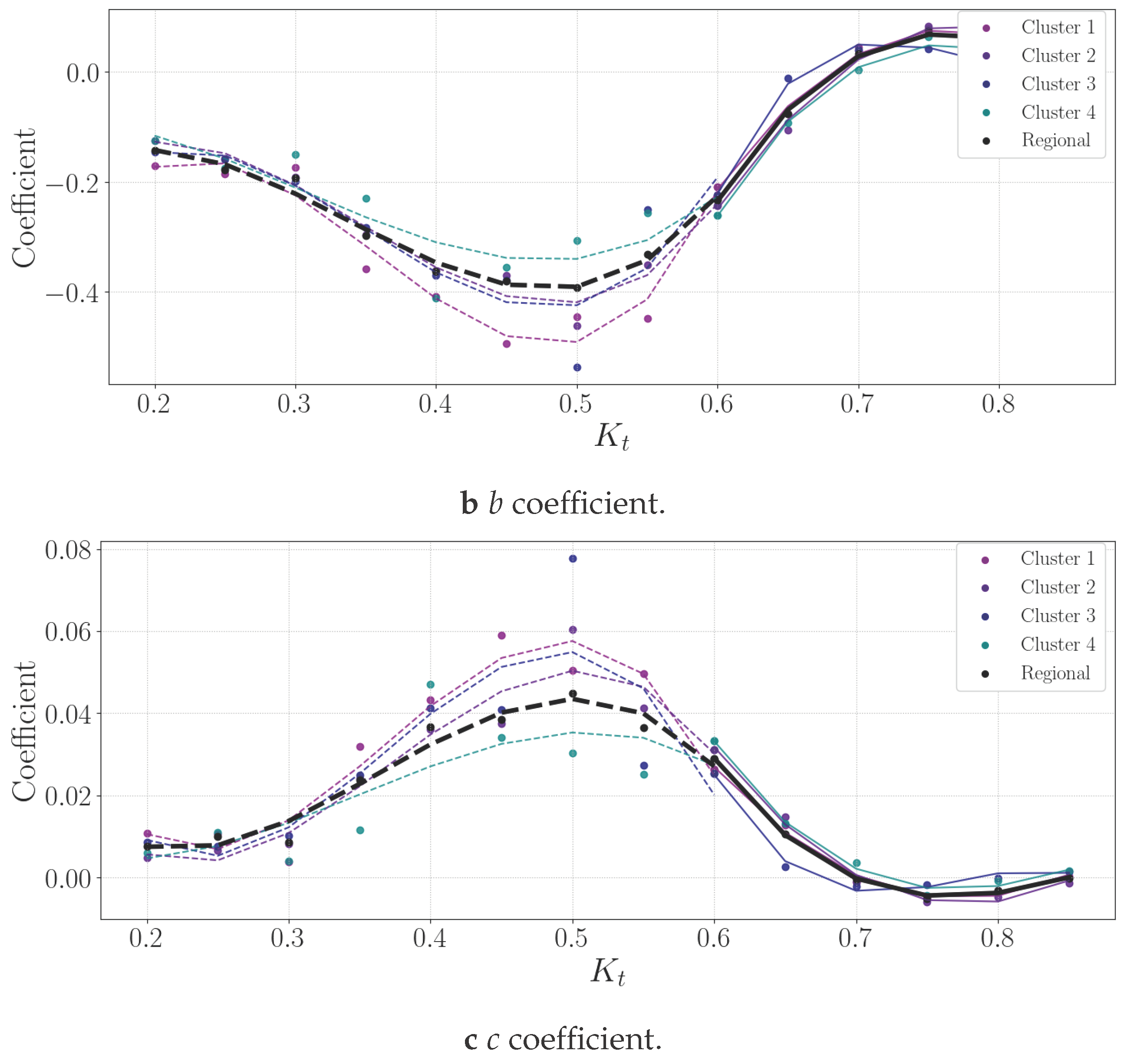
For each SAURAN station, a localised decomposition model is developed. A clustered decomposition model describes an area with similar irradiance patterns using the clustered areas discussed in [
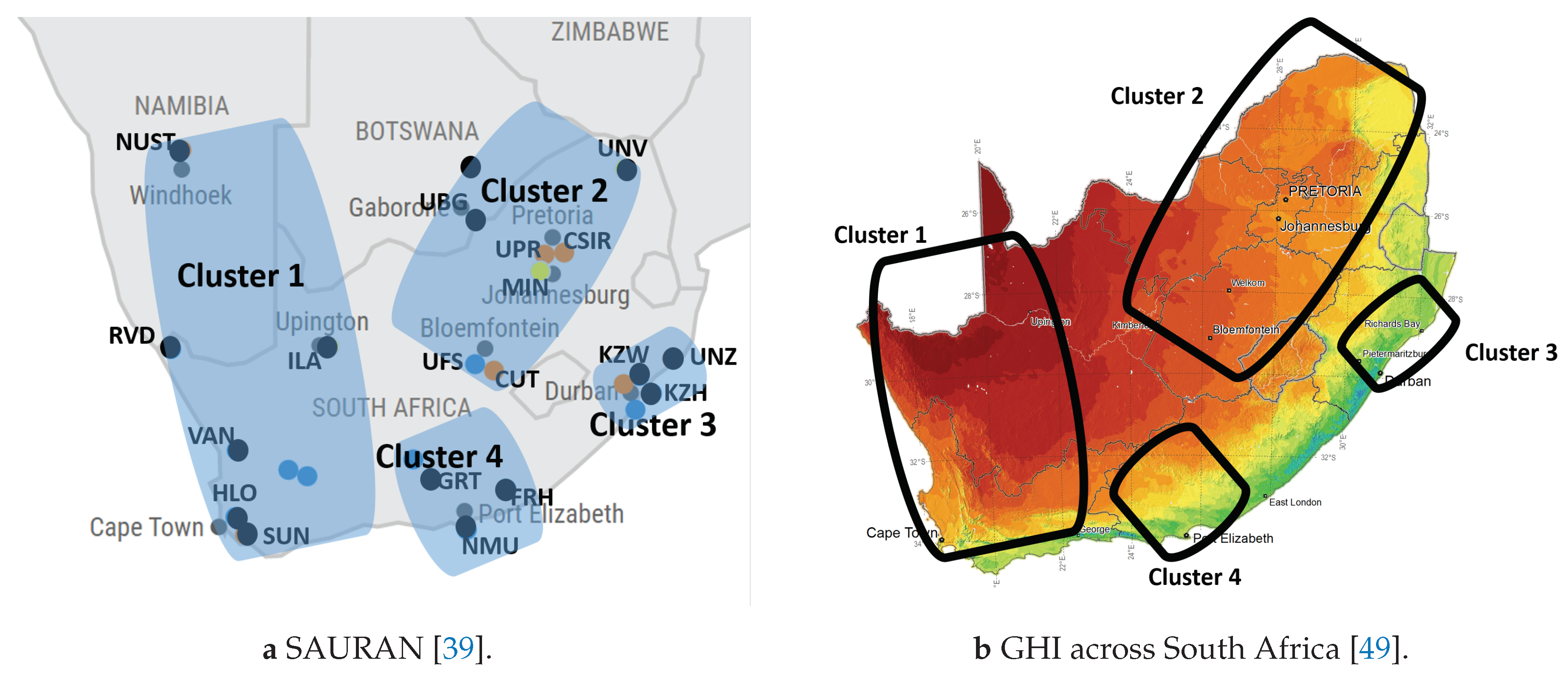
40]. Farmer and Rix first presented a two-cluster correlation map using the SAURAN database [
48] and, by using this approach, this study formulated four clusters instead of two in Southern Africa, as shown in
Figure 3a.
Figure 3a shows the clusters’ geographical location, and
Figure 3b shows the penetration levels of GHI.
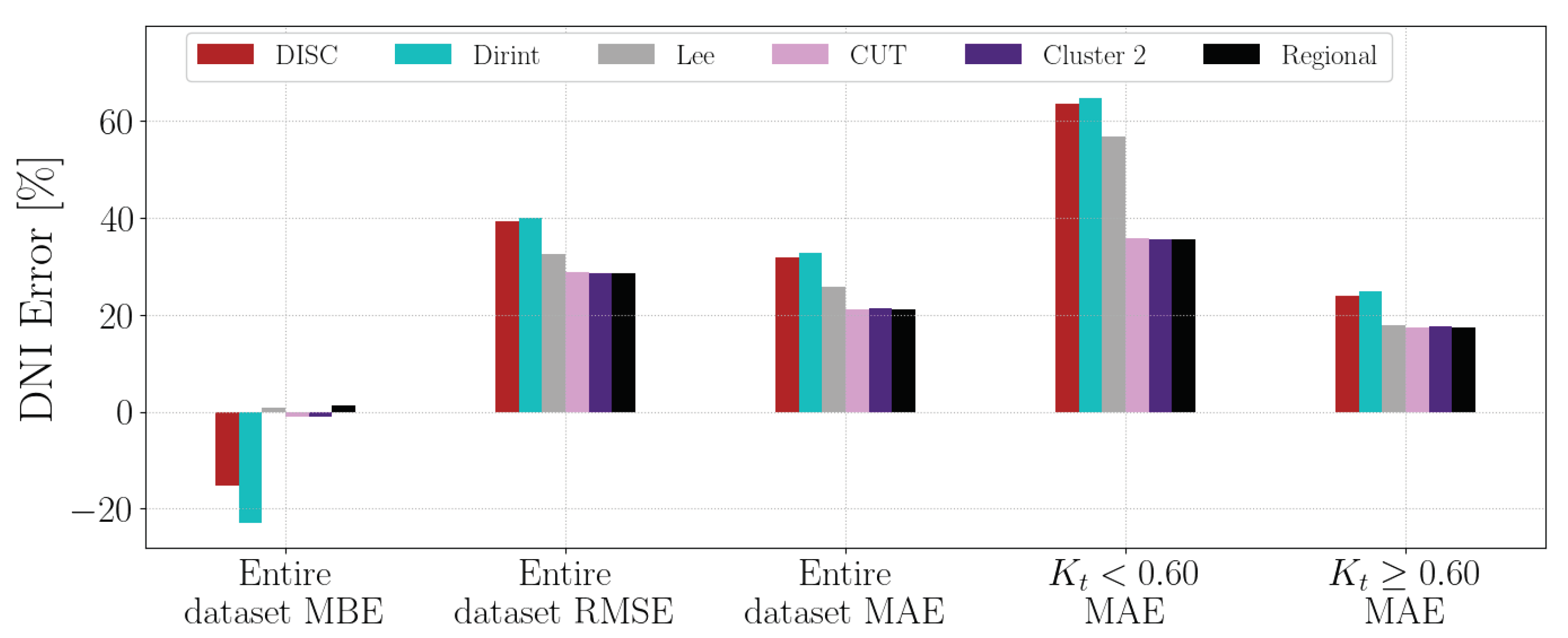
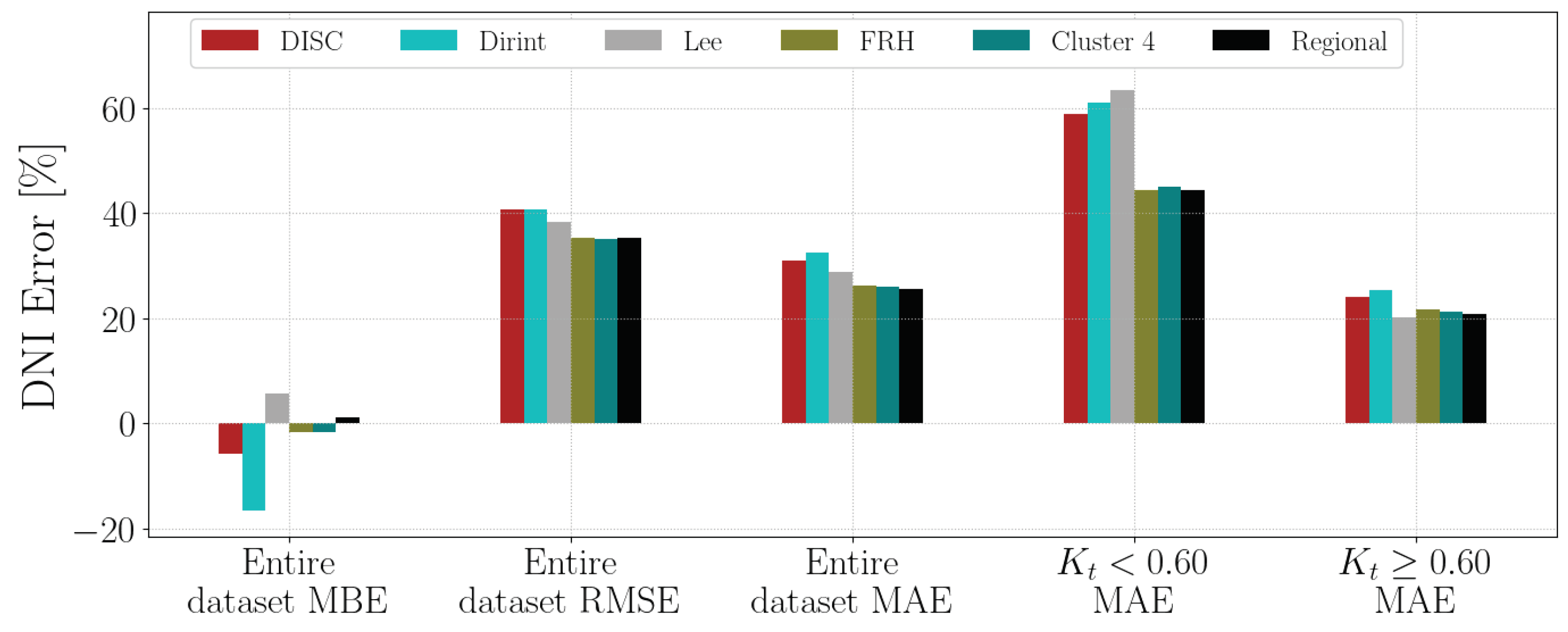
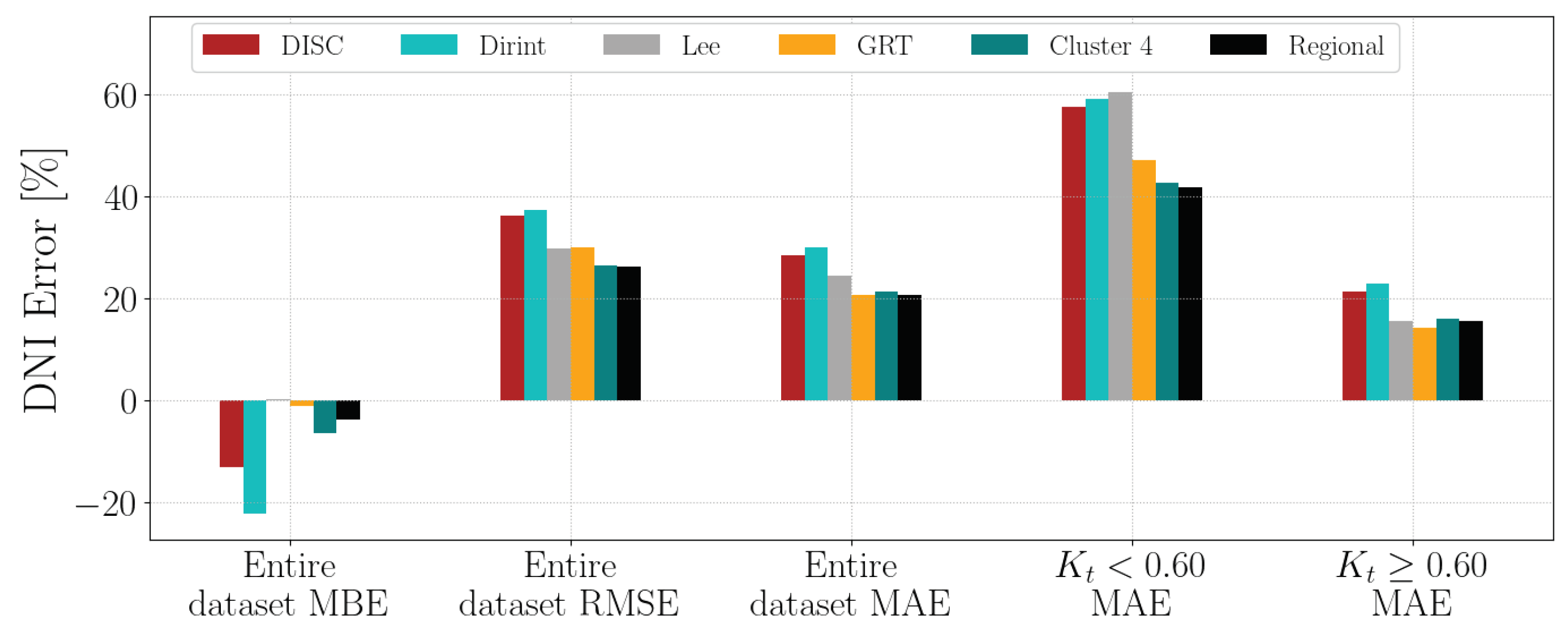
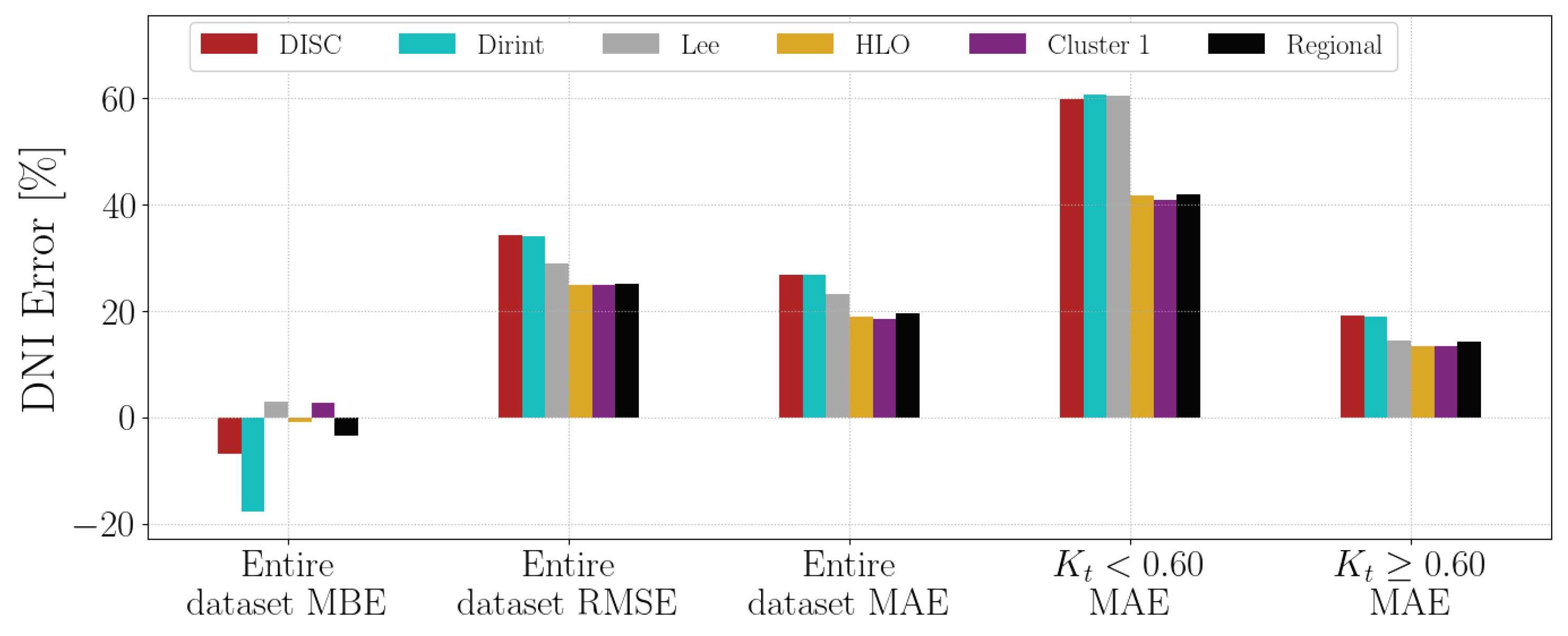
Table 4 shows the different clusters’ training sets’ mean GHI, DNI and DHI.
Figure 3.
Clusters within the Southern African context.
Figure 3.
Clusters within the Southern African context.
Cluster 1 receives the most GHI and DNI, and Cluster 3 receives the least, as evident from Figure fig:Clustersb. The different climates are also evident in these clusters: Cluster 3 is more humid and receives, on average, more DHI than Cluster 1.
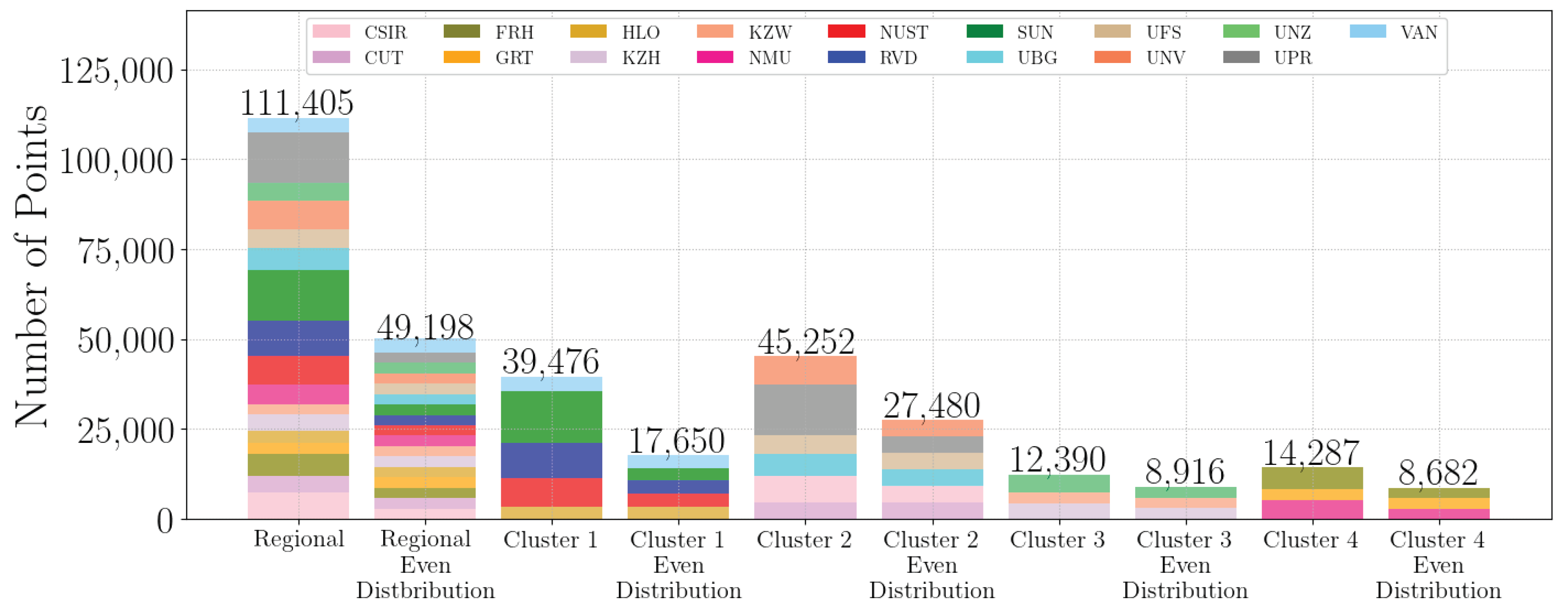
Figure 4 shows how the cluster data is combined. Each cluster and the regional (Southern African) model are combined with even distributions of datasets to avoid introducing a bias, as some stations are over-represented in the original data set. Some stations, such as the SUN, UPR and RVD stations, have considerably more data available as they are either older stations or have not been closed down.
The different stations have varying climates, and therefore, a larger representation of one station will result in a biased model towards that station. The advantage of the even distribution is that every station is sufficiently represented and will not cause a model bias, but this reduces the amount of available data.
Cluster 2’s stations have higher elevation and summer humidity due to its warm, rainy summers and dry, cold winters. The expected annual irradiance levels are lower, as seen in
Figure 3b. The stations have higher humidity because of their location and higher DHI levels.
The two stations in Cluster 2, UPR and CSIR, are expected to have more diffuse particles due to the higher air pollution levels and, therefore, higher DHI levels. Cluster 2 has a large bias of the data from Pretoria, South Africa, from the CSIR and UPR datasets.
Cluster 4 has lower annual irradiance levels, as seen in
Figure 3b, and FRH and NMU are closer to the coastline, whereas GRT is inland.
Figure 1.
The irradiance relationships between GHI, DNI, DHI and .
Figure 1.
The irradiance relationships between GHI, DNI, DHI and .
Figure 2.
Validation sites of discussed decomposition models.
Figure 2.
Validation sites of discussed decomposition models.
Figure 4.
Distribution of data within clusters.
Figure 4.
Distribution of data within clusters.
Table 1.
SAURAN station summary [
39,
40].
Table 1.
SAURAN station summary [
39,
40].
| |
Name (Location) |
Coordinates |
Elevation |
| |
|
(Lat (∘S), Long (∘E)) |
(m) |
| CSIR |
CSIR Energy Centre (Pretoria, South Africa) |
25.747, 28.279 |
1400 |
| CUT |
Central University of Technology (Bloemfontein, South Africa) |
29.121, 26.216 |
1397 |
| FRH |
University of Fort Hare (Alice, South Africa) |
32.785, 26.845 |
540 |
| GRT |
Graaff-Reinet (Graaff-Reinet, South Africa) |
32.485, 24.586 |
660 |
| HLO |
Mariendal (Mariendal, South Africa) |
33.854, 18.824 |
178 |
| ILA |
Ilanga CSP Plant (Upington, South Africa) |
28.490, 21.520 |
884 |
| KZH |
University of KwaZulu-Natal Howard College (Durban, South Africa) |
29.871, 30.977 |
150 |
| KZW |
University of KwaZulu-Natal Westville (Durban, South Africa) |
29.817, 30.945 |
200 |
| MIN |
CRSES Mintek (Johannesburg, South Africa) |
26.089, 27.978 |
1521 |
| NMU |
Nelson Mandela University (Gqeberha, South Africa) |
34.009, 25.665 |
35 |
| NUST |
Namibian University of Science and Technology (Windhoek, Namibia) |
22.565, 17.075 |
1683 |
| RVD |
Richtersveld (Alexander Bay, South Africa) |
28.561, 16.761 |
141 |
| SUN |
Stellenbosch University (Stellenbosch, South Africa) |
33.935, 18.867 |
119 |
| UBG |
Gaborone (Gaborone, Botswana) |
24.661, 25.934 |
1014 |
| UFS |
University of Free State (Bloemfontein, South Africa) |
29.111, 26.185 |
1491 |
| UNV |
Venda (Vuwani, South Africa) |
23.131, 30.424 |
628 |
| UNZ |
University of Zululand (KwaDlangezwa, South Africa) |
28.853, 31.852 |
90 |
| UPR |
University of Pretoria (Pretoria, South Africa) |
25.753, 28.229 |
1410 |
| VAN |
Vanrhynsdorp (Vanrhynsdorp, South Africa) |
31.617, 18.738 |
130 |
Table 4.
Clusters mean irradiances.
Table 4.
Clusters mean irradiances.
| |
Mean 4
|
| |
GHI |
DNI |
DHI |
| |
[] |
[] |
[] |
| Cluster 1 |
592 |
669 |
135 |
| Cluster 2 |
583 |
604 |
165 |
| Cluster 3 |
534 |
523 |
178 |
| Cluster 4 |
557 |
579 |
158 |
Table 5.
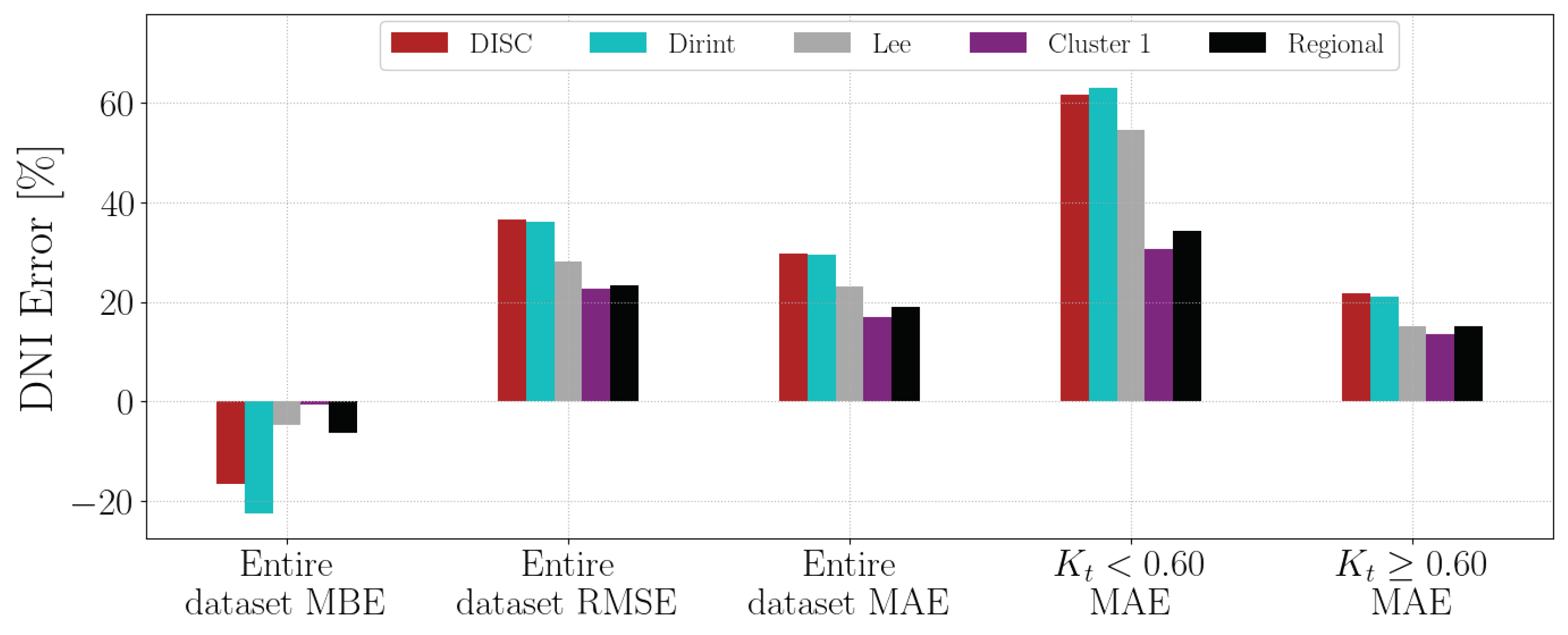
Hourly validation results of decomposition model development for CSIR.
Table 5.
Hourly validation results of decomposition model development for CSIR.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
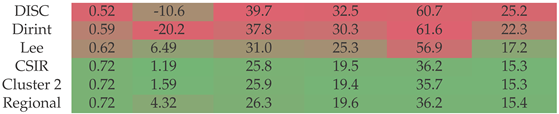 |
Table 6.
Hourly validation results of decomposition model development for CUT.
Table 6.
Hourly validation results of decomposition model development for CUT.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
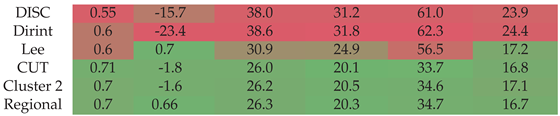 |
Table 7.
Hourly validation results of decomposition model development for FRH.
Table 7.
Hourly validation results of decomposition model development for FRH.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
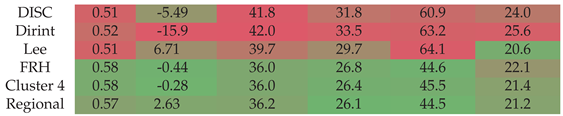 |
Table 8.
Hourly validation results of decomposition model development for GRT.
Table 8.
Hourly validation results of decomposition model development for GRT.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
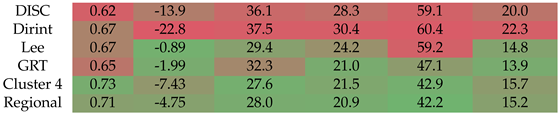 |
Table 9.
Hourly validation results of decomposition model development for HLO.
Table 9.
Hourly validation results of decomposition model development for HLO.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
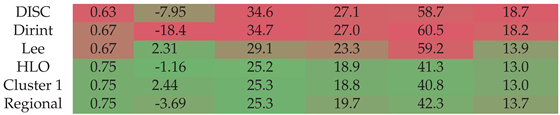 |
Table 10.
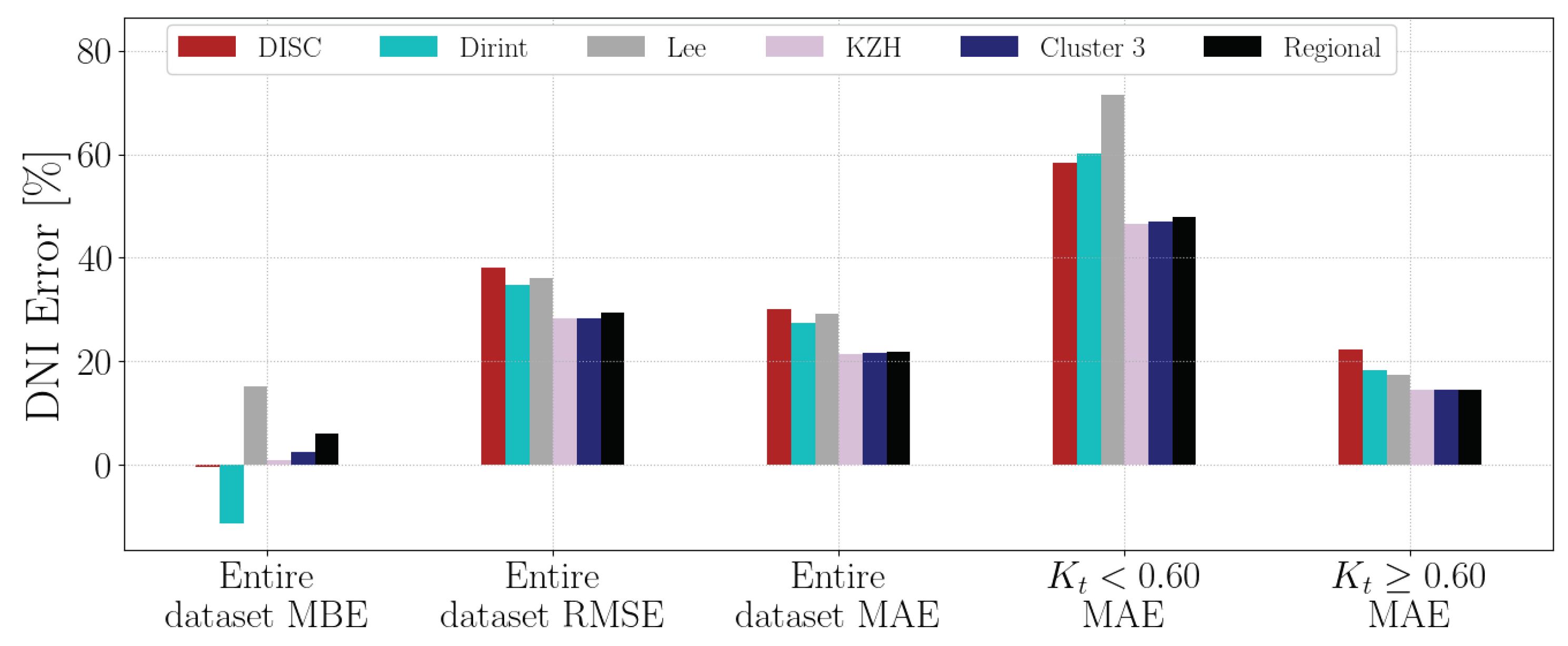
Hourly validation results of decomposition model development for KZH.
Table 10.
Hourly validation results of decomposition model development for KZH.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
 |
Table 11.
Hourly validation results of decomposition model development for KZW.
Table 11.
Hourly validation results of decomposition model development for KZW.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
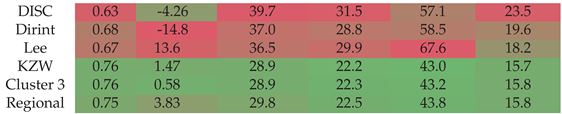 |
Table 12.
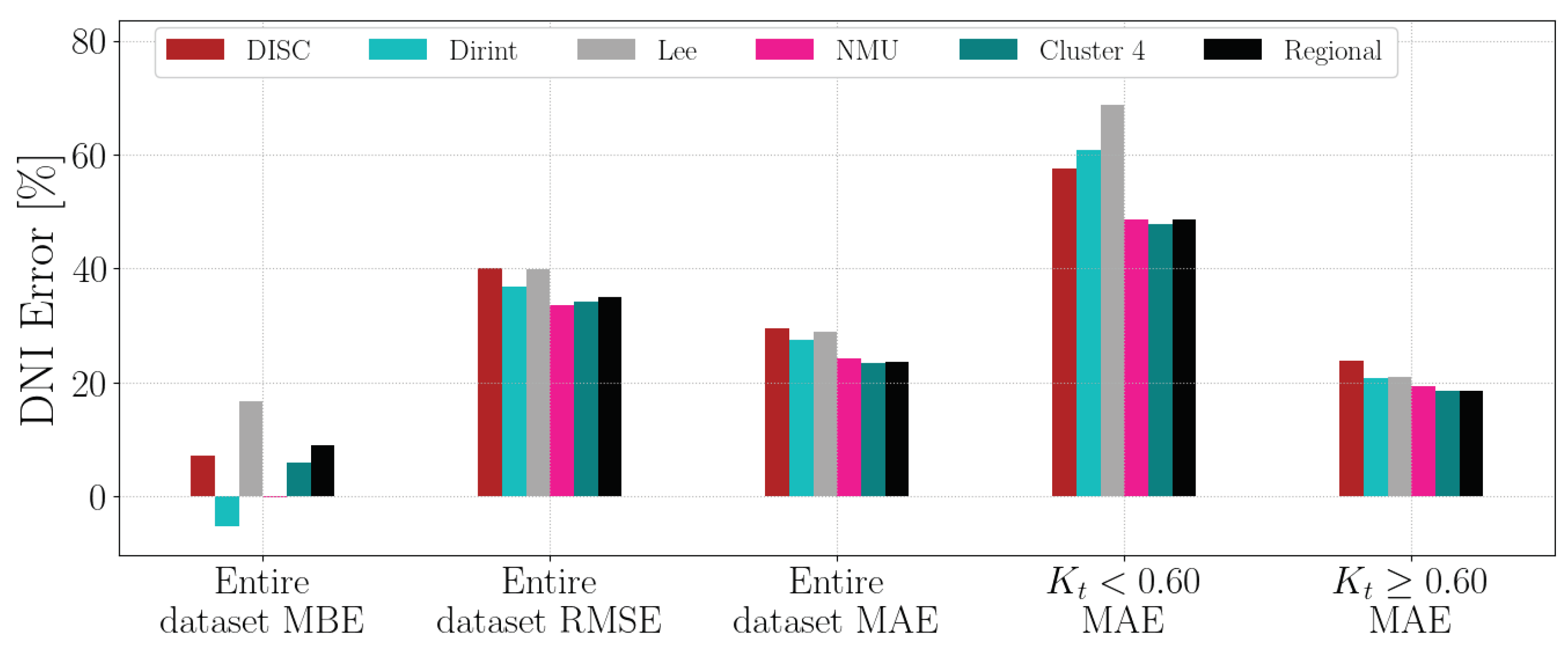
Hourly validation results of decomposition model development for NMU.
Table 12.
Hourly validation results of decomposition model development for NMU.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
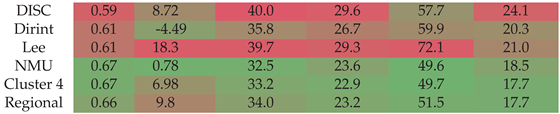 |
Table 13.
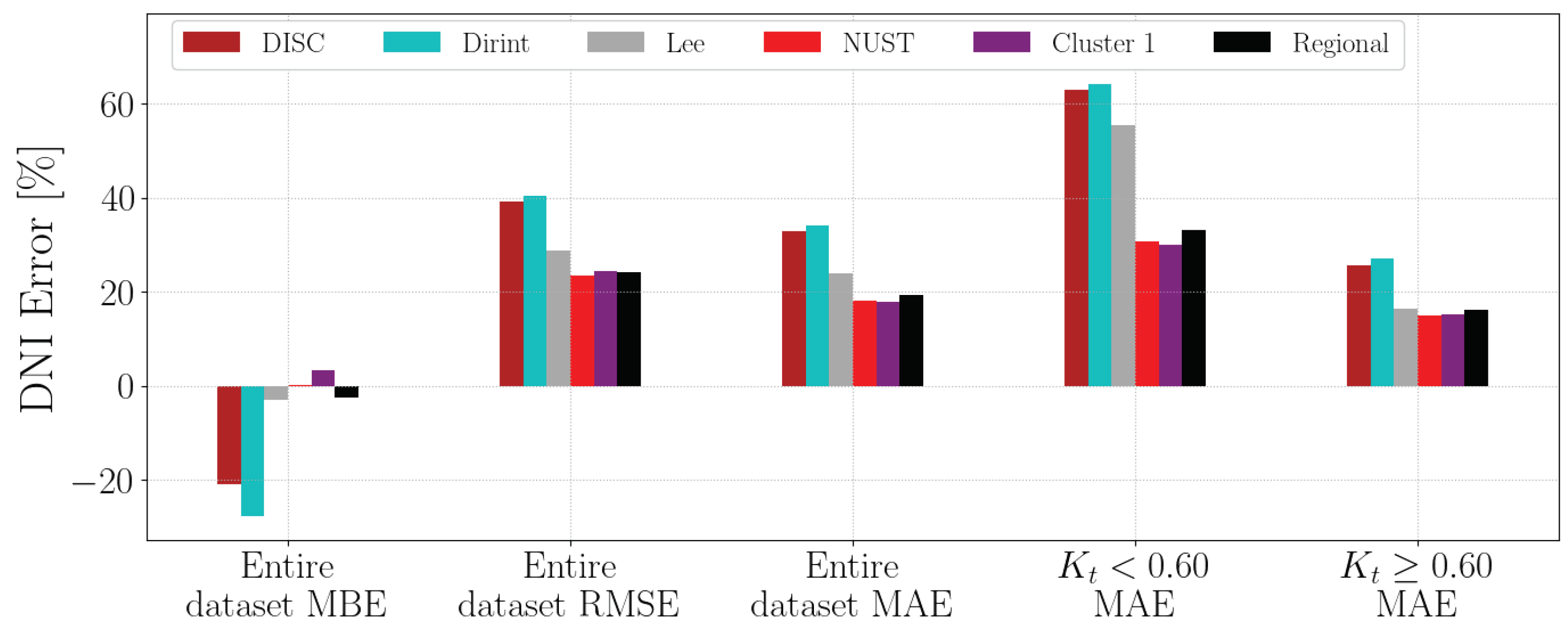
Hourly validation results of decomposition model development for NUST.
Table 13.
Hourly validation results of decomposition model development for NUST.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
 |
Table 14.
Hourly validation results of decomposition model development for RVD.
Table 14.
Hourly validation results of decomposition model development for RVD.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
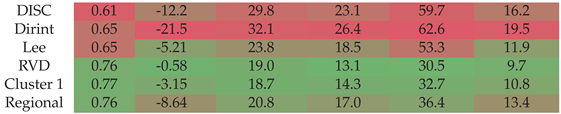 |
Table 15.
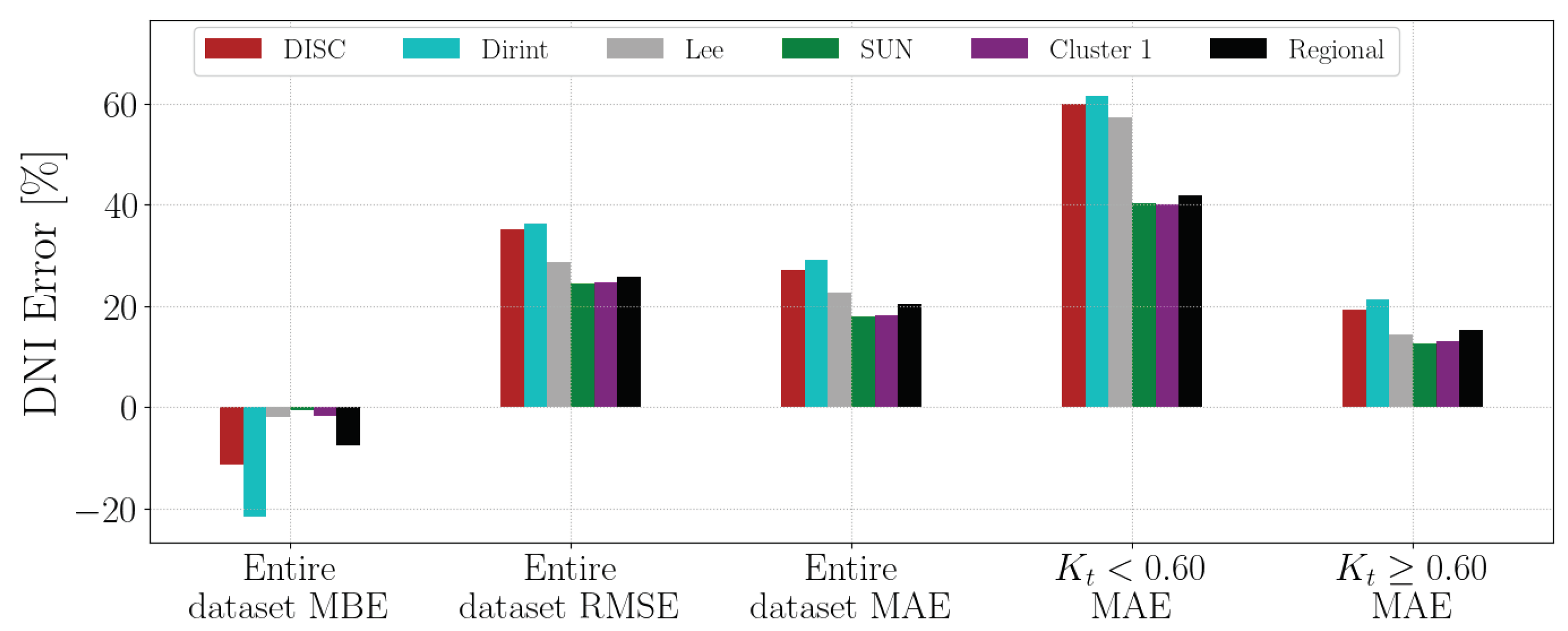
Hourly validation results of decomposition model development for SUN.
Table 15.
Hourly validation results of decomposition model development for SUN.
| Model |
Entire Dataset |
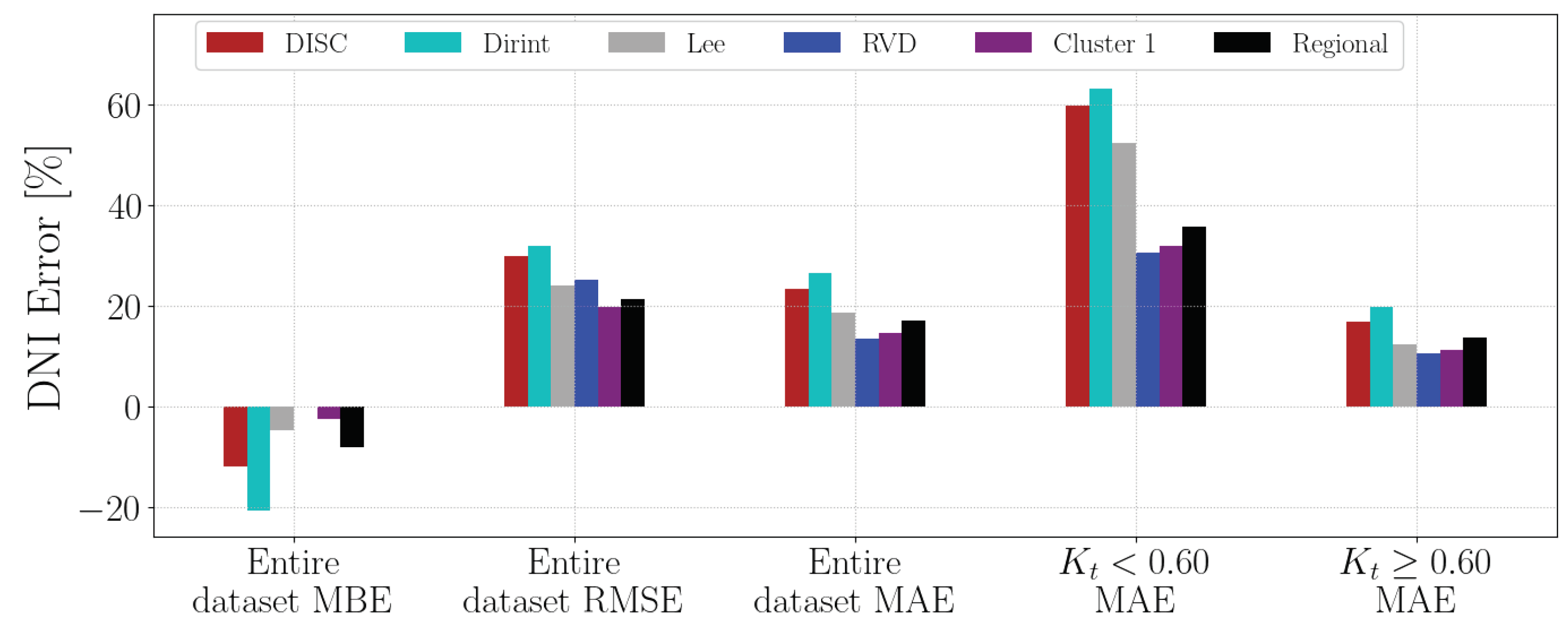
|
|
|
MBE [%] |
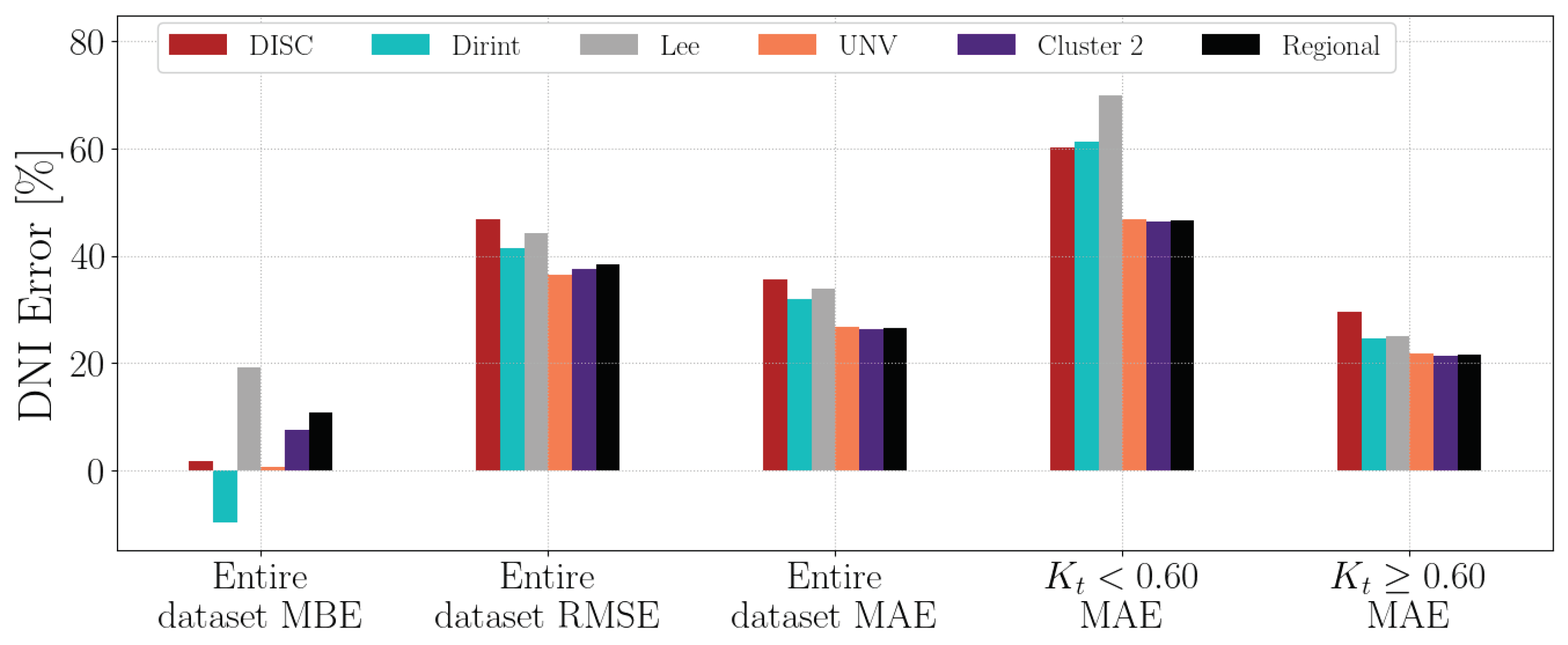
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
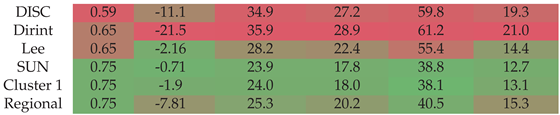 |
Table 16.
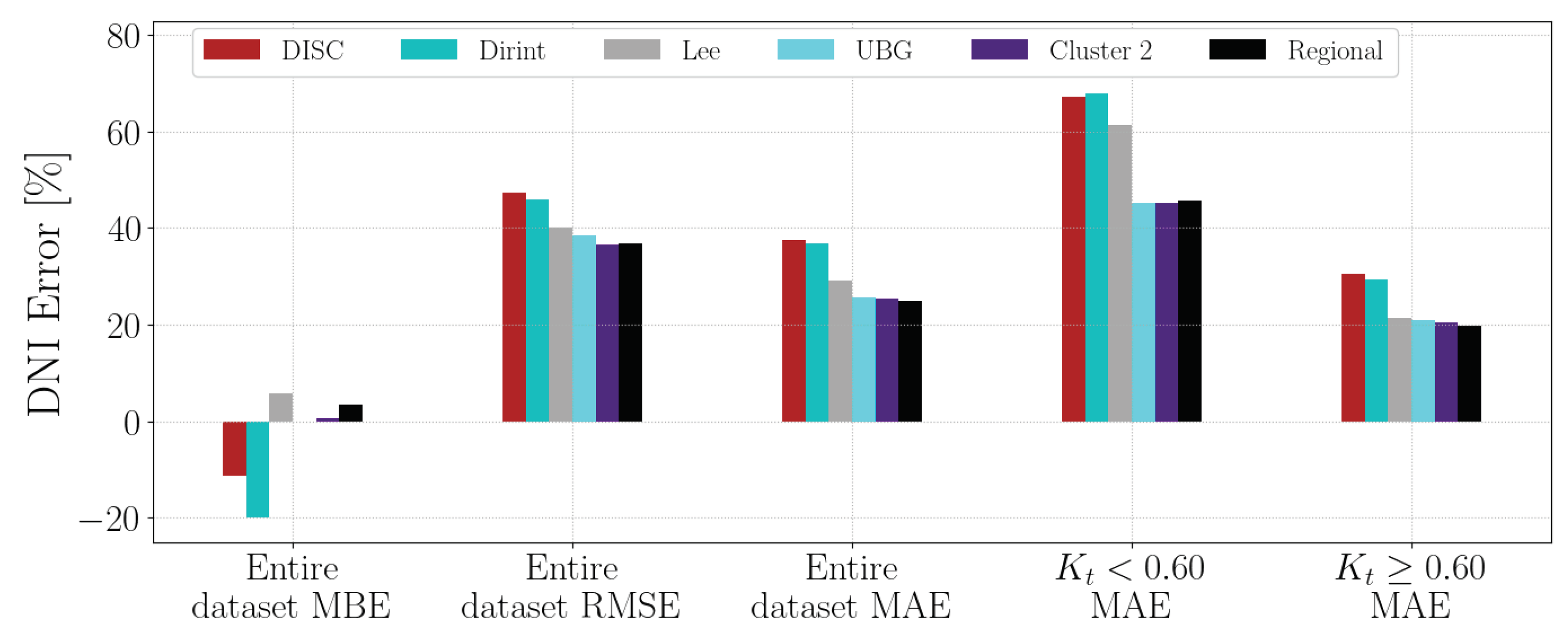
Hourly validation results of decomposition model development for UBG.
Table 16.
Hourly validation results of decomposition model development for UBG.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
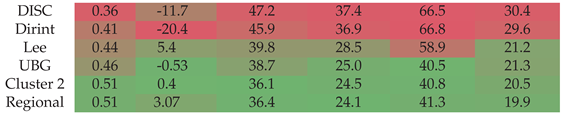 |
Table 17.
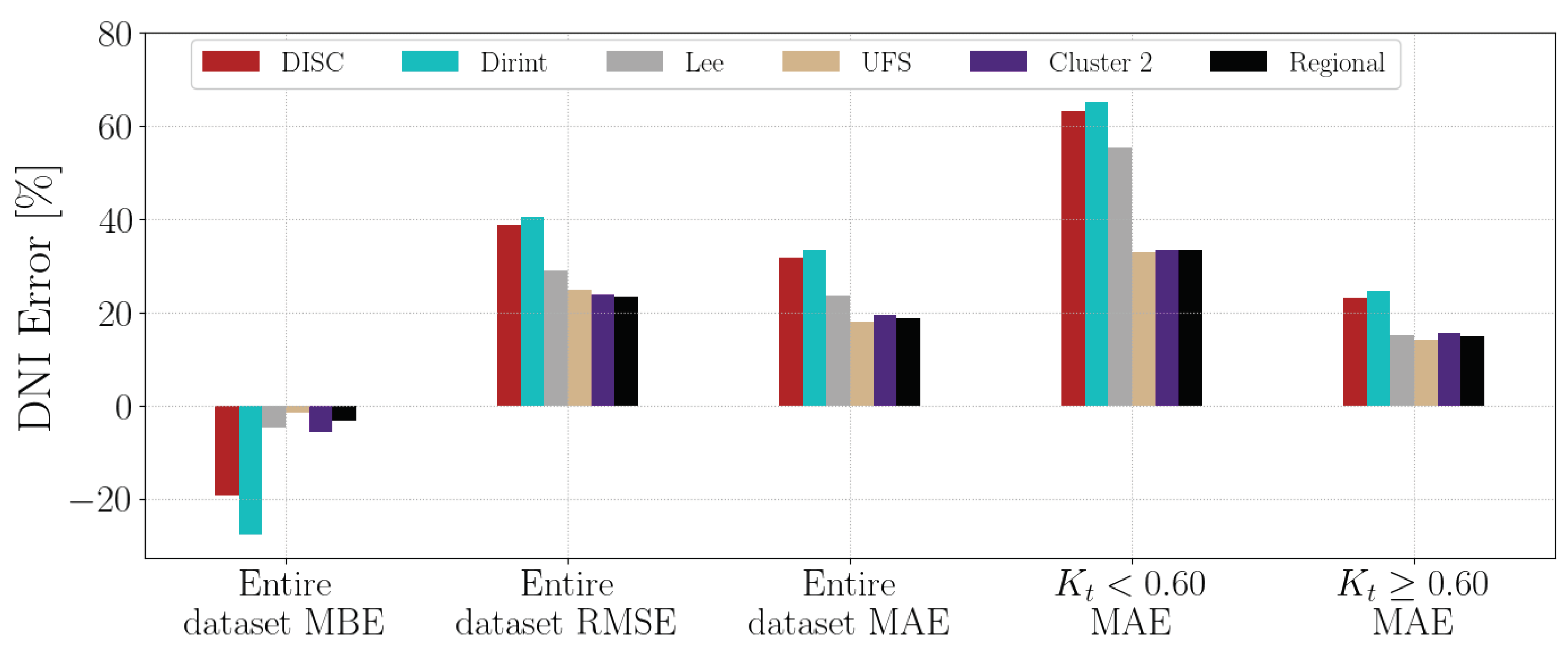
Hourly validation results of decomposition model development for UFS.
Table 17.
Hourly validation results of decomposition model development for UFS.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
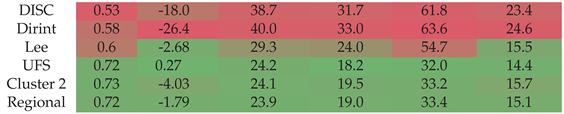 |
Table 18.
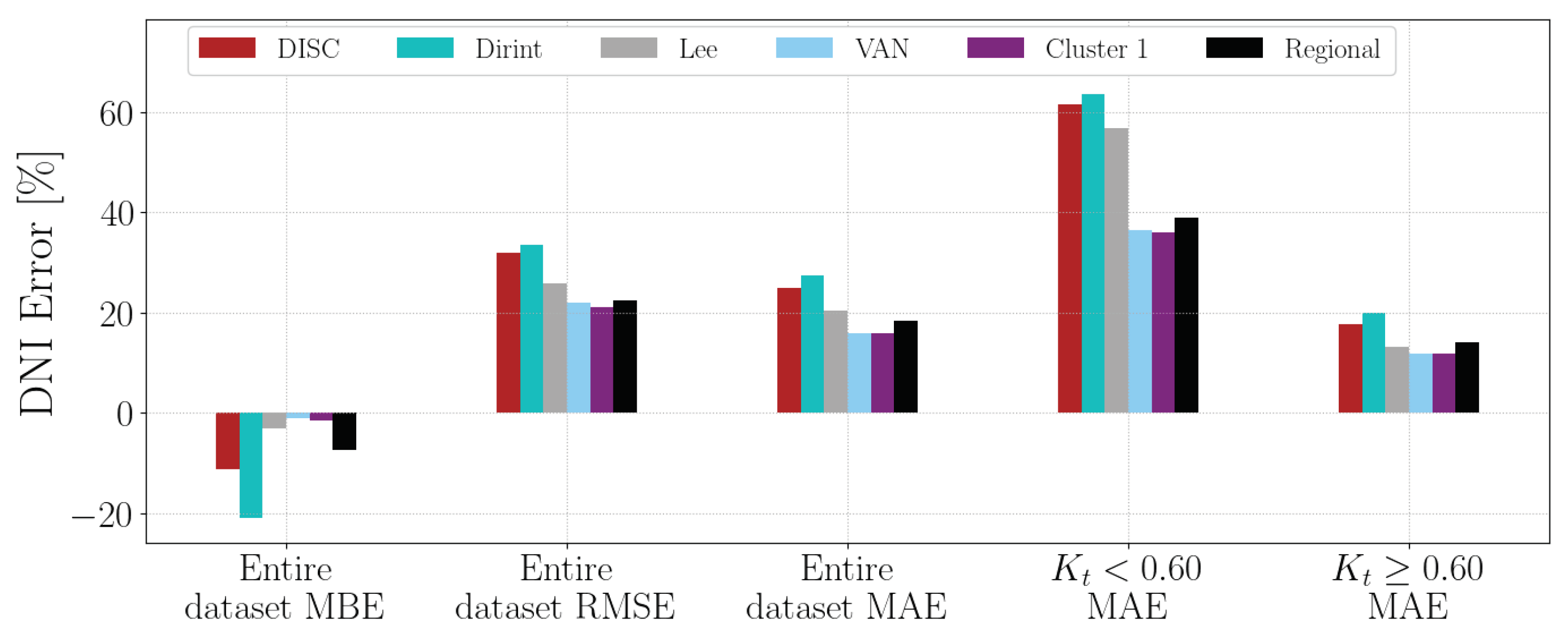
Hourly validation results of decomposition model development for UNV.
Table 18.
Hourly validation results of decomposition model development for UNV.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
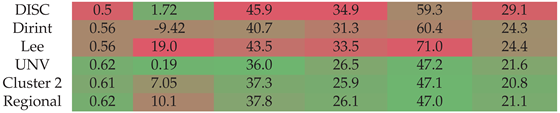 |
Table 19.
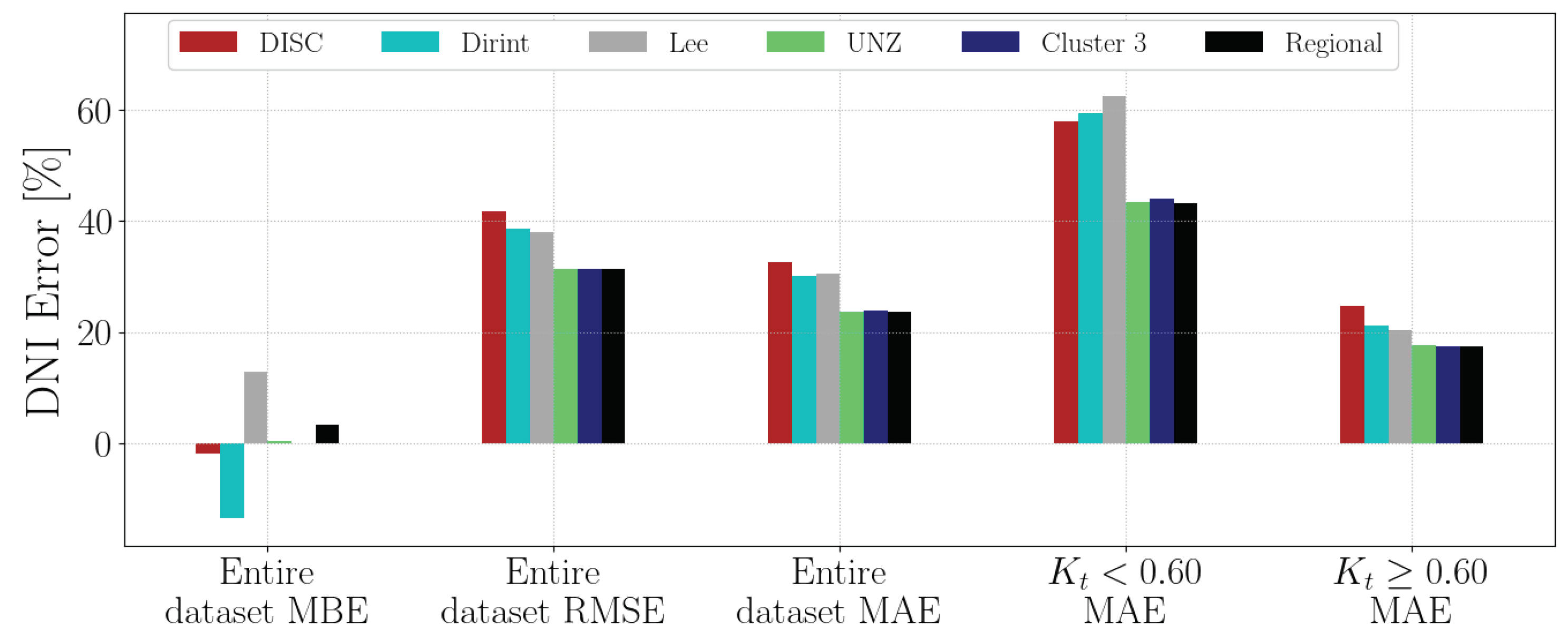
Hourly validation results of decomposition model development for UNZ.
Table 19.
Hourly validation results of decomposition model development for UNZ.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
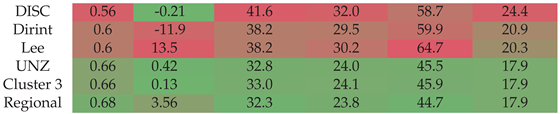 |
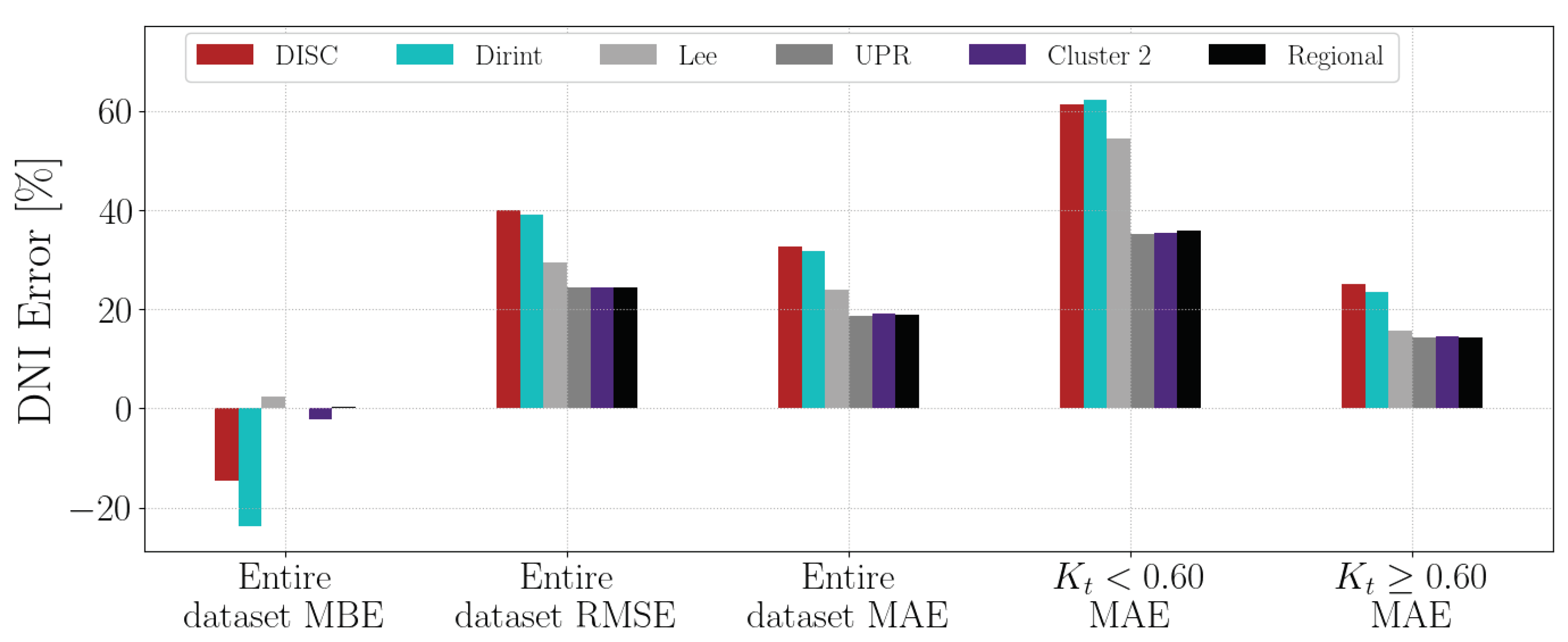
Table 20.
Hourly validation results of decomposition model development for UPR.
Table 20.
Hourly validation results of decomposition model development for UPR.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
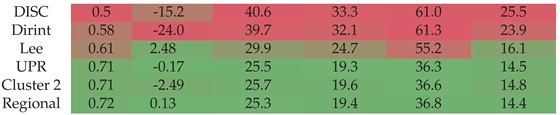 |
Table 21.
Hourly validation results of decomposition model development for VAN.
Table 21.
Hourly validation results of decomposition model development for VAN.
| Model |
Entire Dataset |
|
|
|
MBE [%] |
RMSE [%] |
MAE [%] |
MAE [%] |
MAE [%] |
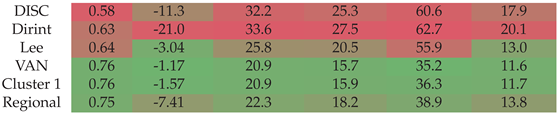 |
Table 22.
Summary of test and validation sets of stations outperforming baseline models.
Table 22.
Summary of test and validation sets of stations outperforming baseline models.
| Dataset |
Localised model |
|
Cluster model |
|
Regional model |
| outperforms |
|
outperforms |
|
outperforms |
| baseline models |
|
baseline models |
|
baseline models |
| Test |
Validation |
|
Test |
Validation |
|
Test |
Validation |
| CSIR |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| CUT |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| FRH |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| GRT |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| HLO |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| ILA |
- |
✓ |
|
- |
✓ |
|
- |
✓ |
| KZH |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| KZW |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| MIN |
- |
✓ |
|
- |
✓ |
|
- |
✓ |
| NMU |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| NUST |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| RVD |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| SUN |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| UBG |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| UFS |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| UNV |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| UNZ |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| UPR |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |
| VAN |
✓ |
✓ |
|
✓ |
✓ |
|
✓ |
✓ |