Prerpints.org logo
Preprint
Article

Why Does Cross-Sectional Analyst Coverage Incorporate Market-Wide Information?

Altmetrics

Downloads

119

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 March 2024

Posted:

12 March 2024

You are already at the latest version

Alerts
Abstract
This paper shows that the empirical distribution of cross-sectional analyst coverage in China's stock markets follows an exponential law in a given month from 2011 to 2020. The findings hold in both the emerging (Shanghai) and the developed market (Hong Kong). Moreover, the unique distribution parameter (i.e., mean) is directly related to the amount of market-wide information. Average analyst coverage exhibits a significant negative predictive power for stock-market uncertainty, highlighting the role of security analysts in diminishing the total uncertainty. The exponential law can be derived from the maximum entropy principle (MEP). When analysts, who are constrained by average ability in generating information (i.e., the first-order moment), strive to maximize the amount of market-wide information, this objective yields the exponential distribution. Contrary to the conventional wisdom that security analysts specialize in the generation of firm-specific information, empirical findings suggest that analysts primarily produce market-wide information for 25 countries. Nevertheless, it remains unclear why cross-sectional analyst coverage reflects market-wide information, this paper provides an entropy-based explanation.
Keywords: 
Subject: Social Sciences  -   Decision Sciences

1. Introduction

Sell-side analysts are among the most influential information producers in financial markets, playing a crucial role for both investors and managers. Numerous empirical studies have documented the impact of analyst attention (i.e., coverage) on investors’ decisions (e.g., [10,14]), as well as on corporate activities such as investment and financing, innovation (e.g., R&D), acquisition, and earnings management (e.g., [4,6,11,23]).
However, contrary to the conventional wisdom that security analysts specialize in collecting and disseminating firm-specific information, empirical findings indicate that analysts predominantly generate market-wide information for 25 countries [3,9]. It remains unclear why analyst reports reflect market-wide information rather than firm-specific information. To deeply understand the underling mechanism, we examine the empirical distribution of cross-sectional analyst coverage.
This paper illustrates that the empirical distribution of analyst coverage for China’s listed companies maintains an exponential structure in a given month from 2011 to 2020. Our findings are consistent in both the Shanghai and Hong Kong stock markets. Since the system information of exponential distribution can be fully characterized by the mean value, we expect that aggregate analyst coverage can help reduce total uncertainty for both investors and managers. This paper provides evidences that aggregate (or say average) analyst coverage, denoted by λ − 1 , exhibits a strong negative predictive power for stock-market uncertainty.
Given that cross-sectional analyst coverage is exponentially distributed, a natural question is how the exponential structure occurs. Motivated by [19], who draw on the maximum entropy principle (MEP) to interpret the asymmetric Laplace-shaped distribution of Tobin’ Q. We utilize the MEP to derive the exponential distribution of analyst coverage. The central idea is that when analysts, who are constrained by limited average ability in producing information (i.e., the first-order moment), aim to maximize the amount of market-wide information, this objective can yield an exponential distribution. To the best of our knowledge, it has not been documented in the previous literature that cross-sectional analyst coverage follows an exponential law. Our study is the first to provide an explanation for why analyst coverage predominantly incorporates market-wide information.
Our findings have some important implications. Firstly, sell-side analysts primarily generate market-wide information. Secondly, almost all relevant studies claim that coverage proxies should be used in logarithmic form to mitigate the influence of outliers, however, our results suggest that the exponential structure would be distorted when logarithmic transformation is performed. Thirdly, because more than half of the firms have the similar coverage, future research should be extra cautious when using coverage proxies in cross-sectional and particularly in portfolio analyses.
The rest of this paper is organized as follows. Section 2 reports the empirical distribution of cross-sectional analyst coverage in Chinese stock markets. Section 3 provides a potential mechanism for the exponential law. In Section 4, we make concluding discussions.

2. Exponentially distributed cross-sectional analyst coverage

Assume a random variable X is exponentially distributed, it can be written as,
Exp [ λ ] : f [ x ] = λ e − λ x
where x > 0 , λ > 0 , f [ x ] is the probability density function (PDF) with E [ X ] = D [ X ] = λ − 1 . Empirically, it is better to work with the complementary cumulative distribution function i.e., CCDF: P [ X > x ] = e − λ x . The parameter λ can be obtained by the slope of straight line on a semi-log scale: log ( CCDF ) vs. x.
We examine the empirical distribution of cross-sectional analyst coverage in China’s stock markets. The sample consists of all common stocks listed on the Shanghai Stock Exchange (SSE) and the Hong Kong Stock Exchange (HK) from January 2011 to January 2020. The data are all from the Wind database.

2.1. Evidence from the Shanghai and Hong Kong stock markets

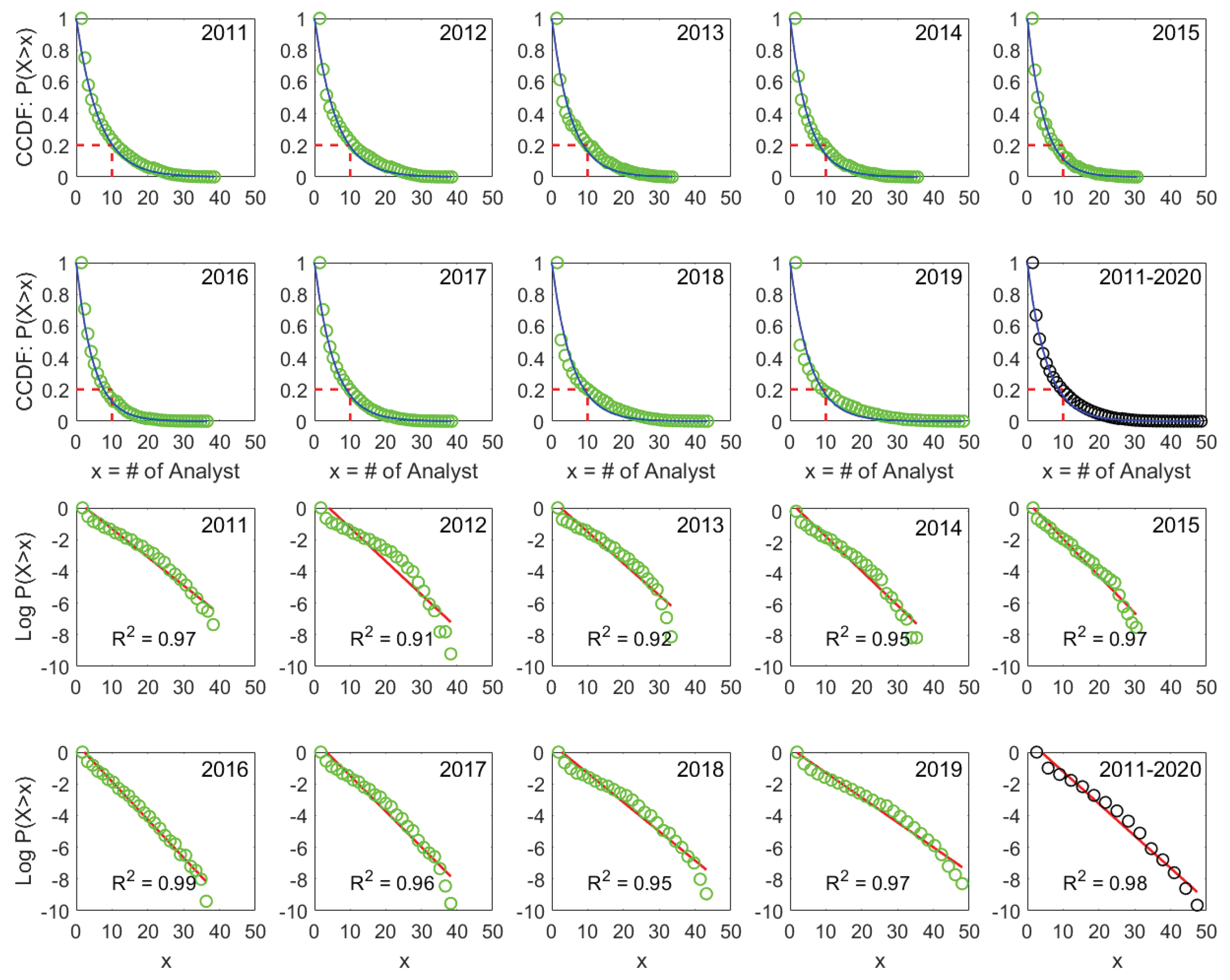
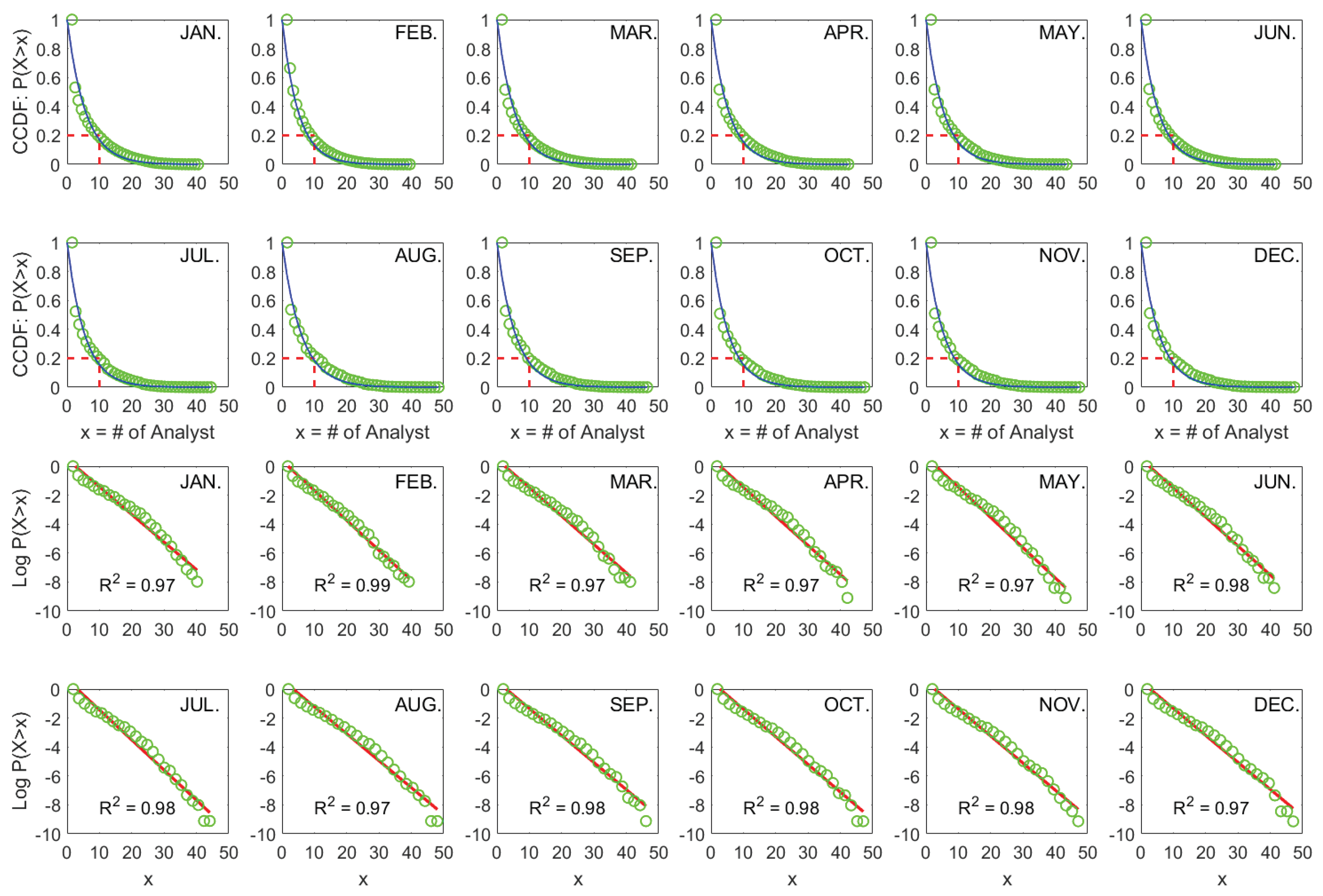
The monthly results are shown in Figure 1. Two things are evident. First, the CCDFs show the highly skewed structure of cross-sectional analyst coverage, and we can observe that the percent of firms with coverage below 10 is about 80%, i.e., a very high proportion of firms are covered by a small number of analysts, while certain firms have substantial coverage. Second, and most importantly, the empirical distributions are well fitted by Exp [ λ ] on both linear (CCDF vs. x) and semi-log (log CCDF vs. x) scales, where exponential fits are denoted as blue and red lines, respectively.
One might be intrigued by the goodness of fit, we thus present the regression R2 in each semi-log subplot. On average, the R2 is as high as 98% for the period 2011-2020. Notably, we do not exclude any coverage data based on any firm characteristics, which ensures that our findings provide a clean and complete picture of attention allocation structure of sell-side analysts.
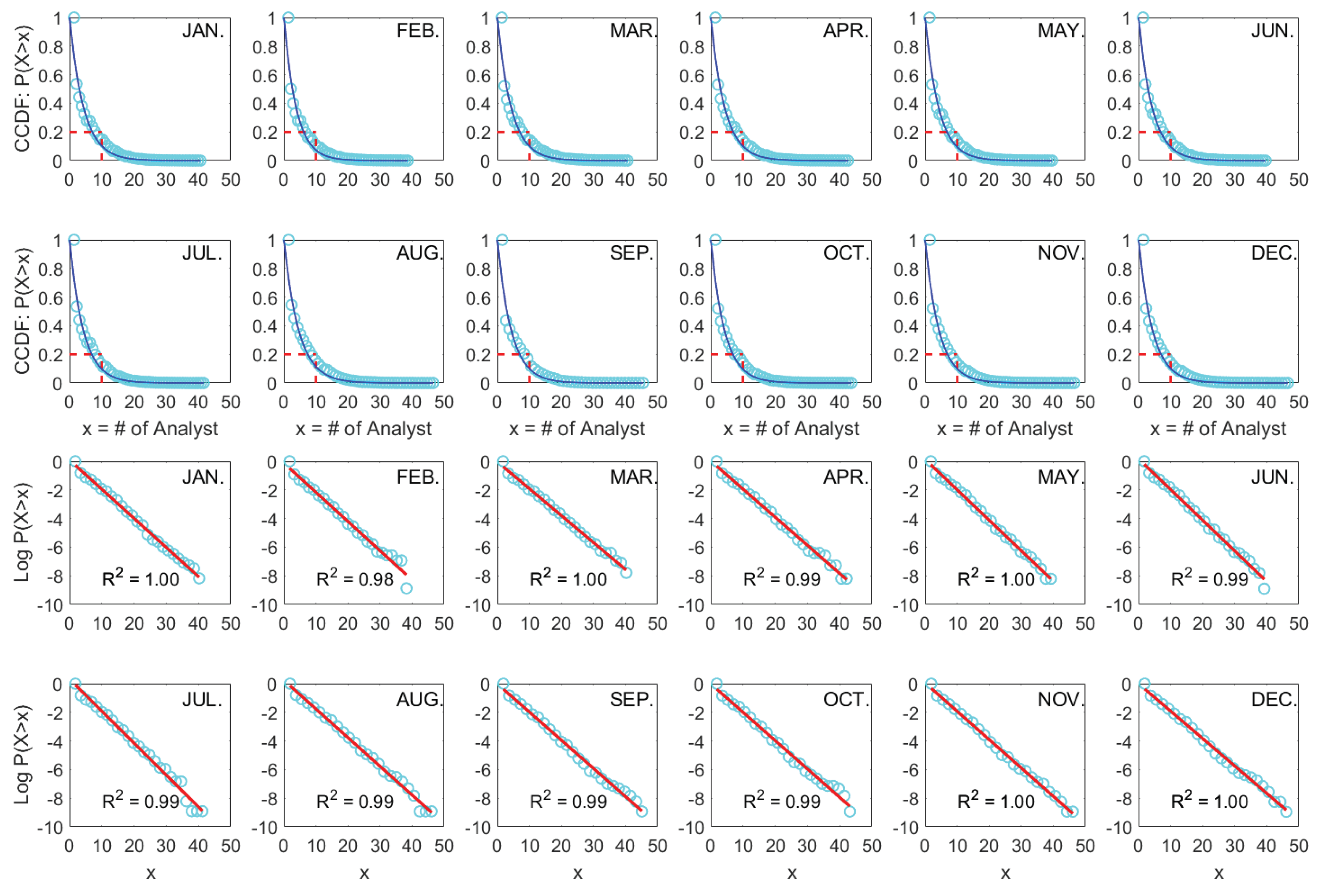
Furthermore, as shown in Figure 2, a consistent exponential pattern of cross-sectional analyst coverage is evident for the Hong Kong stock market (HK), indicating that our findings are consistent in both emerging and developed stock markets.
This paper argues that using coverage proxy to measure the amount of firm-specific information poses a serious inference problem. It is impossible that the amounts of information for firms with zero-coverage are exactly equal. After excluding firms with no coverage, 80 % of firms have almost the same small amount of analyst coverage. In any case, one cannot state that the majority of firms with approximate amount of coverage have similar firm-specific information environments.
Given the finding that sell-side analyst mainly generates market-wide information (see [3,9]), we go one step further and directly examine whether aggregate analyst coverage is related to stock-market uncertainty. In this paper, aggregate analyst coverage is denoted by the inverse of parameter λ , since λ − 1 fully characterizes the mean value of cross-sectional analyst coverage. The finding has many implications, and the most critical one is that aggregate analyst coverage exhibits a negative predictive power for stock-market uncertainty. If analysts have no advantage over insiders in generating firm-specific information, focusing on providing market-wide information becomes an inevitable choice. Next, we test the hypothesis that aggregate analyst coverage (denoted by λ − 1 ) can help reduce the expected total uncertainty.

2.2. Predicting stock-market uncertainty

We examine the forecasting power of aggregate analyst coverage denoted by λ − 1 for stock-market uncertainty based on the following time-series predictive regression,
U t , t + h j = α + δ λ t − 1 + Controls + ε t , t + h
where U t , t + h j is the stock-market uncertainty over the prediction horizon h, where h = 1 , 6 and 12 months, and j denotes two uncertainty proxies, which are market-level cash-flow volatility (i.e., CFV) and investor search volume (i.e., Search). λ t − 1 is the inverse of the parameter of exponentially distributed analyst coverage in month t, which captures continuous-varying marker information flows. We also control for a linear time trend and lagged stock-market uncertainty up to 5 lags.
Our analysis in Table 1 is motivated by [8], who theoretically show that the expected amount of information generated equals the expected reduction in uncertainty. The idea is consistent with the foundational work in information theory [20]. Concretely, we construct two proxies for stock-market uncertainty that are closely related to managers and investors, respectively. One is market-level cash flow volatility i.e., CFVt (e.g., [2,17]), which directly measures the uncertainty of operating management. The other is investor search volume denoted as Searcht. Because theories of rational information acquisition predict that investors’ information-search demand increases in the uncertainty about asset payoffs (e.g., [1,18]).
Table 1 suggests that an increase in aggregate analyst coverage is associated with an expected decrease in manager uncertainty (Panel A) and investor uncertainty (B), respectively. The results remain robust after controlling for a linear time trend and lagged stock-market uncertainty up to five lags in models (2), (4), and (6). In summary, we conclude that aggregate analyst coverage can alleviate total uncertainty for both investors and managers. Moreover, a higher aggregate analyst coverage also precedes lower market-wide cash holdings and the absolute magnitude of unexpected earnings, as well as greater capital expenditures and long-term debt. For more comprehensive and detailed evidence, see [12,16].

3. MEP generates the exponential distribution

Finally, this paper attempts to provide a potential generation mechanism for the exponentially distributed analyst coverage. Motivated by [19], who draw on the maximum entropy principle (MEP) to interpret the asymmetric Laplace distribution of Tobin’ Q. In what follows we utilize the MEP to derive the exponential law. The idea of MEP is that in making inferences on the basis of partial information we must use the probability distribution that achieves maximum entropy [13].
Suppose that our only knowledge of analysts coverage distribution is the mean value (i.e., limited average-ability in producing information). Mathematically, the maximum entropy problem subject to the first-order moment constraint is as follows,
max { f [ x ] ≥ 0 | x ∈ R + } h ( f [ x ] ) = − ∫ x f [ x ] log f [ x ] d x s . t . ∫ x f [ x ] d x = 1 , E [ X ] = ∫ x x f [ x ] d x = μ x
The Lagrangian associated with this programming problem is,
J ( f [ x ] ) = − ∫ x f [ x ] log f [ x ] d x + λ 1 ( ∫ x f [ x ] d x − 1 ) + λ 2 ( ∫ x x f [ x ] d x − μ x )
Taking the first-order condition and solving for f [ x ] yields,
f * [ x ; λ ] = λ e − λ x , E [ X ] = λ − 1
The solution is an exponential distribution fully characterized by unique parameter λ . Note that this entropy maximization property is perhaps the main reason why we encounter exponential distributions so frequently in mathematics and physics. Additionally, the concept of maximum-entropy optimization has been advocated in economic analysis (see [7,21]).
The first-order moment constrain condition is natural due to the fact that analysts have limited average capability in providing information. One might ask what entropy i.e., h ( f [ x ] ) means in our case. In the Shannon theory, this answer is clear. The average amount of information is given by the information entropy i.e., h ( f [ x ] ) , as Shannon pointed out [20]. Because analyst coverage can be viewed as a standard information source, maximizing the objective function is equivalent to maximizing the amount of market-wide information. Similarly, suppose we do not have any knowledge about distribution, the solution of maximum-entropy optimization is the Uniform distribution. In this case, when each firm has a same coverage (no firm-specific information), the amount of market-wide information attains the maximum value. In both cases, sell-side analysts generate market-wide information, not firm-specific information.

4. Conclusion and discussion

Contrary to the conventional wisdom that sell-side analysts specialize in collecting and disseminating firm-specific information, it is found that demonstrate that analysts predominantly generate market-wide information for 25 countries [3,9]. However, it is still unclear why analyst coverage reflects market-wide information rather than firm-specific information. To understand the underling reasons, we examine the empirical distribution of cross-sectional analyst coverage.
This paper shows the following key findings: (i) the empirical frequency distribution of cross-sectional analyst coverage follows an exponential law, observed in both the Shanghai and Hong Kong stock markets; (ii) an increase in aggregate analyst coverage is associated with and an expected decrease in total uncertainty; (iii) when analysts, who are constrained by limited average ability in producing information (i.e., the first-order moment), strive to maximize the amount of market-wide information, this objective yields the exponential distribution.
In summary, our findings offer two main insights. First, sell-side analysts in China’s stock markets predominantly contribute to market-wide information, illuminating their role in mitigating total uncertainty. Second, future research should be extra cautious when using coverage proxies in cross-sectional and portfolio analyses due to potential inference issues. Strictly speaking, it is advisable to carefully re-evaluate previous cross-sectional findings, if feasible.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant No. [71671134]. The authors are grateful to the editor and anonymous referees for helpful comments. They are solely responsible for the specific views and any errors in the preceding article. Finally, one of the authors, Hou Y.F., would like to thank Li M.Y. and Hu C.Y. for useful discussions to this work.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. The yearly results for Shanghai stock market (SSE)

Preprints 101136 g0a1
Figure A1. Exponential fits of complementary cumulative distribution functions (CCDFs) of cross-sectional analyst coverage (x) on the linear (blue) and semi-log (red) scales for each year from 2011 to 2020 in the Shanghai stock market (SSE).
Figure A1. Exponential fits of complementary cumulative distribution functions (CCDFs) of cross-sectional analyst coverage (x) on the linear (blue) and semi-log (red) scales for each year from 2011 to 2020 in the Shanghai stock market (SSE).
Preprints 101136 g0a1

References

  1. Benamar, H.; Foucault, T.; Vega, C. Demand for information, uncertainty, and the response of US Treasury securities to news. The Review of Financial Studies 2021, 34, 3403–3455. [Google Scholar] [CrossRef]
  2. Bloom, N. The impact of uncertainty shocks. Econometrica 2009, 77, 623–685. [Google Scholar]
  3. Chan, K.; Hameed, A. Stock price synchronicity and analyst coverage in emerging markets. Journal of Financial Economics 2006, 80, 115–147. [Google Scholar] [CrossRef]
  4. Chen, T.; Harford, J.; Lin, C. Do analysts matter for governance? Evidence from natural experiments. Journal of Financial Economics 2006, 115, 383–410. [Google Scholar] [CrossRef]
  5. Da, Z.; Engelberg, J.; Gao, P. In search of attention. The Journal of Finance 2011, 66, 1461–1499. [Google Scholar] [CrossRef]
  6. Derrien, F.; Kecskes, A. The real effects of financial shocks: Evidence from exogenous changes in analyst coverage. The Journal of Finance 2013, 68, 1407–1440. [Google Scholar] [CrossRef]
  7. Foley, D. A statistical equilibrium theory of markets. Journal of Economic Theory 1994, 62, 321–345. [Google Scholar] [CrossRef]
  8. Frankel, A.; Kamenica, E. Quantifying information and uncertainty. American Economic Review 2019, 109, 3650–3680. [Google Scholar] [CrossRef]
  9. Gao, K.; Lin, W.; Yang, L.; Chan, K. The impact of analyst coverage and stock price synchronicity: Evidence from brokerage mergers and closures. American Economic Review 2020, 33, 101190. [Google Scholar] [CrossRef]
  10. Guo, L.; Li, F.; Wei, K. Security analysts and capital market anomalies. Journal of Financial Economics 2020, 137, 204–230. [Google Scholar] [CrossRef]
  11. He, J.; Tian, X. The dark side of analyst coverage: The case of innovation. Journal of Financial Economics 2013, 109, 856–878. [Google Scholar] [CrossRef]
  12. Hou, Y.; Hu, C. Understanding the role of aggregate analyst attention in resolving stock market uncertainty. Finance Research Letters 2023, 57, 104183. [Google Scholar] [CrossRef]
  13. Jaynes, E. Information theory and statistical mechanics. Physical Review 1957, 106, 620. [Google Scholar] [CrossRef]
  14. Kelly, B.; Ljungqvist, A. Testing asymmetric-information asset pricing models. The Review of Financial Studies 2012, 25, 1366–1413. [Google Scholar] [CrossRef]
  15. Lee, C.; So, E. Uncovering expected returns: Information in analyst coverage proxies. The Review of Financial Studies 2017, 124, 331–348. [Google Scholar] [CrossRef]
  16. Loh, R.; Stulz, R. Is sell-side research more valuable in bad times? The Journal of Finance 2018, 73, 959–1013. [Google Scholar] [CrossRef]
  17. Minton, B.; Schrand, C. The impact of cash flow volatility on discretionary investment and the costs of debt and equity financing. Journal of Financial Economics 1999, 54, 423–460. [Google Scholar] [CrossRef]
  18. Neilson, J. Investor information gathering and the resolution of uncertainty. Journal of Accounting and Economics 2022, 74, 101513. [Google Scholar] [CrossRef]
  19. Scharfenaker, E.; dos Santos, P. The distribution and regulation of Tobin’s q. Economics Letters 2015, 137, 191–194. [Google Scholar] [CrossRef]
  20. Shannon, C. A mathematical theory of communication. The Bell System Technical Journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
  21. Sims, C. Implications of rational inattention. Journal of Monetary Economics 2003, 50, 665–690. [Google Scholar] [CrossRef]
  22. White, H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 1980, 48, 817–838. [Google Scholar] [CrossRef]
  23. Yu, F. Analyst coverage and earnings management. Journal of Financial Economics 2008, 88, 245–271. [Google Scholar] [CrossRef]
Preprints 101136 g001
Figure 1. Exponential fits of complementary cumulative distribution functions (CCDFs) of cross-sectional analyst coverage (x) on the linear (blue) and semi-log (red) scales for each month from 2011 to 2020 in the Shanghai stock market (SSE).
Figure 1. Exponential fits of complementary cumulative distribution functions (CCDFs) of cross-sectional analyst coverage (x) on the linear (blue) and semi-log (red) scales for each month from 2011 to 2020 in the Shanghai stock market (SSE).
Preprints 101136 g001
Preprints 101136 g002
Figure 2. Exponential fits of complementary cumulative distribution functions (CCDFs) of cross-sectional analyst coverage (x) on the linear (blue) and semi-log (red) scales for each month from 2011 to 2020 in the Hong Kong stock market (HK).
Figure 2. Exponential fits of complementary cumulative distribution functions (CCDFs) of cross-sectional analyst coverage (x) on the linear (blue) and semi-log (red) scales for each month from 2011 to 2020 in the Hong Kong stock market (HK).
Preprints 101136 g002
Table 1. Diminishing the expected stock-market uncertainty.
Table 1. Diminishing the expected stock-market uncertainty.
Panel A. Predicting future manager uncertainty proxied by cash-flow volatility CFVt,t+h
(1) (2) (3) (4) (5) (6)
CFVt,t+1 CFVt,t+1 CFVt,t+6 CFVt,t+6 CFVt,t+12 CFVt,t+12
λ t − 1 − 1 . 38 * * * − 0 . 16 * * − 1 . 42 * * * − 0 . 52 * * * − 1 . 42 * * * − 0 . 61 * * *
[ − 8.29 ] [ − 2.27 ] [ − 8.68 ] [ − 3.57 ] [ − 9.47 ] [ − 5.25 ]
Trend No Yes No Yes No Yes
Lagged CFV No Yes No Yes No Yes
N 108 108 102 102 96 96
adj.R2 0.31 0.86 0.42 0.82 0.50 0.86
ADF.prob 1× 10 − 3 1× 10 − 3 5× 10 − 3 1× 10 − 3 2× 10 − 3 5× 10 − 3
Panel B. Predicting future investor uncertainty proxied by information demand Searcht,t+h
Searcht,t+1 Searcht,t+1 Searcht,t+6 Searcht,t+6 Searcht,t+12 Searcht,t+12
λ t − 1 − 0 . 40 * * * − 0 . 34 * * * − 0 . 39 * * * − 0 . 20 * * * − 0 . 34 * * * − 0 . 26 * * *
[ − 4.65 ] [ − 4.04 ] [ − 9.22 ] [ − 7.16 ] [ − 8.87 ] [ − 6.22 ]
Trend No Yes No Yes No Yes
Lagged Search No Yes No Yes No Yes
N 108 108 102 102 96 96
adj.R2 0.22 0.58 0.40 0.65 0.42 0.71
ADF.prob 1× 10 − 3 1× 10 − 3 1× 10 − 2 5× 10 − 3 1× 10 − 2 1× 10 − 2
Note: This table reports time-series predictive regressions of expected stock-market uncertainty on aggregate analyst coverage denoted as λ t − 1 . The dependent variables are the future market-level cash-flow volatility i.e., CFVt,t+h (Panel A) and investor search volume i.e., Searcht,t+h (Panel B), which measure the manager and investor uncertainty, respectively. Controls in models (2), (4), and (6) include a linear time trend and lagged market-uncertainty up to 5 lags. To address concerns about spurious regression, we utilize the ADF tests. The sample period is 2011−2020. The t-statistics in brackets are adjusted for heteroskedasticity [22]. *, **, and *** indicate significance at the 10 % , 5 % , and 1 % levels, respectively.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated