Submitted:
05 March 2024
Posted:
11 March 2024
You are already at the latest version
Abstract
Keywords:
0. Introduction
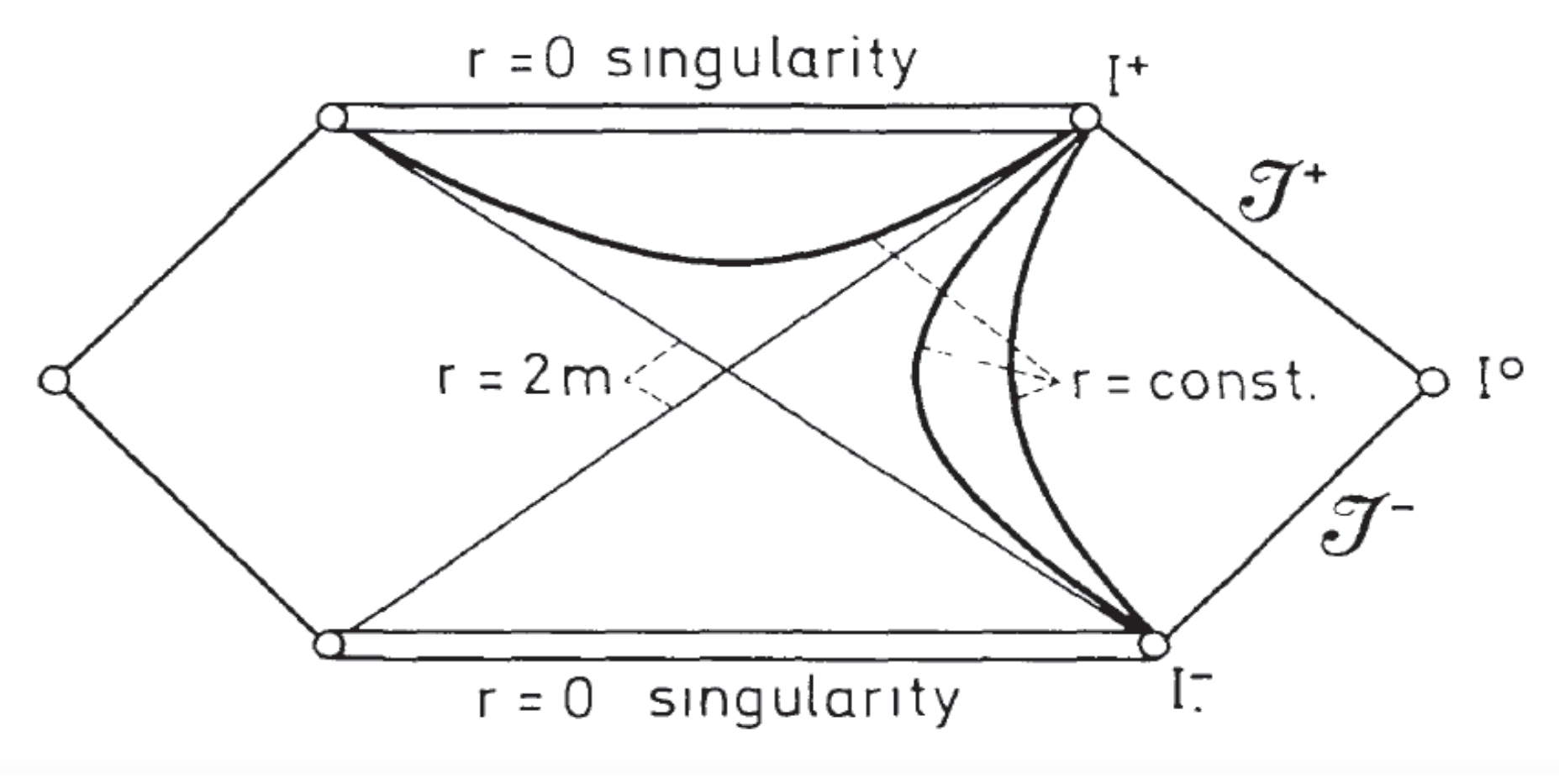
1. Standard Formulation of the Black Hole Evaporation
2. Black Hole Evaporation as a Consequence of Spontaneous Symmetry Breaking
2.1. Emission of Particles
2.2. The Connection of with the Particle Statistic
3. Curvature Effects Appearing from the Particle Lagrangian
4. Conclusions
References
- S, Carrol, Spacetime and Geometry: An Introduction to General Relativity, San Francisco: Addison-Wesley, ISBN 978-0-8053-8732-2; R. M. Walt, (1984), General Relativity, University of Chicago Press. ISBN 978-0-226-87033-5. [CrossRef]
- R. P. Kerr, Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics, Physical Review Letters. 11 (5): 237–238, (1963); H. Reissner, Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie, Annalen der Physik (in German). 50 (9): 106–120, (1916). [CrossRef]
- S. W. Hawking, Particle creation by black Holes, Commun. Math. Phys. 43 (1975) 199-220; Erratum: Commun.Math.Phys. 46 (1976) 206. [CrossRef]
- J. B. Hartle and S. W. Hawking, Phys. Rev. D 13, 2188. [CrossRef]
- S. W. Hawking, Breakdown of predictability in gravitational collapse, Physical Review D. 14 (10): 2460–2473, (1976). [CrossRef]
- N. Zettili, Quantum Mechanics: Concepts and Applications, John Wiley and sons Ltd., ISBN-13: 978-0470026793; S. S. Sakurai and J. Napolitano, Modern Quantum Mechanics, Cambridge U. Press, ISBN-13: 978-1108473224.
- L. Susskind, The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics, Little, Brown. p. 10. ISBN 9780316032698, (2008), L. Susskind and J. Lindesay, Black Holes, Information and the String Theory Revolution, World Scientific, 2005, pp. 69-84; ISBN 978-981-256-083-4.
- G. Dvali and C. Gomez, [arXiv:1005.3497[hep-th]]; G. Dvali, S. Folkerts and C. Germani, Phys.Rev.D84:024039, 2011.
- I. Arraut, Black-Hole evaporation and quantum-depletion in Bose–Einstein condensates, Mod.Phys.Lett.A 36 (2021) 02, 2150006; I. Arraut, Black-hole evaporation from the perspective of neural networks, EPL 124 (2018) 5, 50002. [CrossRef]
- I. Arraut, Black-hole evaporation from the perspective of neural networks, EPL 124 (2018) 5, 50002. [CrossRef]
- Peskin M. E and Schroeder D. V., An introduction to Quantum Field Theory, CRC press, Taylor and Francis group, 6000Broken Sound Parkway, NW Suite 300, Boca Raton Fl. 33487-2742, (2018).
- Claudia de Rham, Gregory Gabadadze, and Andrew J. Tolley, Resummation of Massive Gravity, Phys.Rev.Lett. 106 (2011) 231101. [CrossRef]
- Claudia de Rham and Gregory Gabadadze, Generalization of the Fierz-Pauli action, Phys.Rev.D 82 (2010) 044020. [CrossRef]
- H. Kodama and I. Arraut, Stability of the Schwarzschild–de Sitter black hole in the dRGT massive gravity theory, PTEP 2014 (2014) 023E02. [CrossRef]
- I. Arraut, Path-integral derivation of black-hole radiance inside the de-Rham–Gabadadze–Tolley formulation of massive gravity, Eur.Phys.J.C 77 (2017) 8, 501. [CrossRef]
- I. Arraut, On the apparent loss of predictability inside the de-Rham-Gabadadze-Tolley non-linear formulation of massive gravity: The Hawking radiation effect, EPL 109 (2015) 1, 10002. [CrossRef]
- Ernst C.G. Stückelberg, (1938). Die Wechselwirkungskräfte in der Elektrodynamik und in der Feldtheorie der Kräfte, Helvetica Physica Acta (in German). 11: 225.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



