Prerpints.org logo
Preprint
Article

Tunnel Effect in Acoustics

Altmetrics

Downloads

68

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 March 2024

Posted:

11 March 2024

You are already at the latest version

Alerts
Abstract
Traversal time in tunneling effect for ultrasonic waves in tapered waveguides is derived considering its analogy with quantum and electromagnetic waves tunneling. If, as traversal time, the so called phase time is considered, the ultrasonic wavepacket shows the equivalent in acoustics of superluminality i.e. the derived velocity , crosses the limit of bulk transverse ultrasonic waves in the medium of the waveguide that is the equivalent of c in the quantum and electromagnetic cases. Graphs clearly illustrating this so called Hartman effect are obtained confirming the experimental results in the three different fields.
Keywords: 
Subject: Physical Sciences  -   Acoustics

1. Introduction

The existence of a formal analogy among the equations that govern wave propagation, allows to extend, in some cases, the results to phenomena whose study originates in areas of different physical disciplines. This is the case, for example, of the phenomenon of the so-called superluminal propagation of evanescent waves, whose name directly recalls the field of electromagnetism but which also has close analogies in quantum physics and, as demonstrated in this paragraph, even in acoustics. The unifying concept is that of the propagation of an impulse or a wave packet in a medium with a strong or anomalous dispersion: a packet of acoustic, electromagnetic or quantum wave pobability density waves can therefore be considered equivalent.
Let us therefore imagine not a monochromatic wave but a wavepacket limited in time and space with a central carrier frequency and an envelope with modulated amplitude which, therefore, introduces components at different frequencies through Fourier analysis: the so-called phase velocity V f = ω / k can be identified as the velocity of the crests of the carrier frequency, but already Lord Rayleigh [1] identified the fact that the packet envelope moves with the group velocity V g = d ω / d k (at first order) which has, in the case of anomalous dispersion, peculiar characteristics e.g. can become negative when the frequency decreases rather than increases with increasing k.
Anomalous dispersion was first studied for mechanical oscillators [2] and later, by Sommerfeld and Brillouin, in materials that absorb light in which the group velocity can be greater than c (velocity of light in vacuum) or even negative within the absorption [3]. The phase velocity can be greater than c in many cases, for example inside waveguides but this does not create problems because, representing the velocity of a continuous series of crests, this does not carry the signal information.
On the other end, if the group velocity is identified as the velocity at which a signal (information) travels, the problem of the limit of the principle of causality set by the constancy of the velocity of light in the vacuum of special relativity immediately arises, but this identification is possible only in cases of "normal" dispersion where the deformation of the packet is slight and the group velocity remains below the velocity c.
Sommerfeld and Brillouin then continued to define signal velocity as that of the point of rise of the signal intensity equal to half its steady-state value, which can be demonstrated to proceed at the group velocity, but they introduced the concept of "velocity of the wave front" ideally defined as that of a discontinuity in the signal of the step function type with infinite derivative and it is this last velocity, certainly carrying information, which is subject to the limitation of the velocity c just as the velocity, to be defined, with which the energy is transported [3,4].
All these velocities, in a non-dispersive medium coincide and are equivalent, for elastic waves, to the bulk transverse waves velocity of that medium while, for electromagnetic waves, is the velocity of light in that medium or c if it is a vacuum. However, it must be noted that, the definition of a wave front with infinite derivative (vertical slope) is only ideal, requiring an infinite bandwidth in the frequency components which is unachievable in any real signal generator. In reality, physical signal generators only produce finite spectra due to their natural inertia in reaching the steady-state amplitude (impossibility of a vertical rise of the wave front) and the necessarily finite content of energy in the signal because an infinite frequency bandwidth would require, due to the Plank relation E = ℏ ω , an infinite energy.
The limitation of the frequency bandwidth for a physical detector highlights the limits of reasoning based on classical physics. In the latter case, a "classical" detector can detect a theoretically small quantity of energy as desired, whereas a physical detector needs at least a quantum of energy ℏ ω . Regardless of the interpretation, when we talk about propagation at superluminal velocity we are referring to a clear and measurable effect that involves the group velocity and therefore requires the use of a wave packet. This effect has been predicted theoretically and measured experimentally in different conditions: for example in anomalous dispersion zones near an absorption line [5,6,7], in nonlinear [8] and linear gain lines [9,10,11], in a active plasma [12], optically [13] and finally in a tunnel effect barrier [14,15,16].
This last physical situation in which superluminal wavepackets are found, is the one we want to take into consideration here because there is a close analogy between the quantum tunneling effect of a particle through a potential barrier and the crossing of a zone, limited in space, in which propagation is prohibited for both electromagnetic and acoustic guided wave packets.
The so-called Hartman effect [17] has been theoretically analyzed [18] and experimentally measured [16,19] for which the crossing time of a quantum potential barrier [20] initially increases with the dimensions of the barrier and then rapidly reaches a constant value, which is of the order of magnitude of the inverse of the carrier frequency of the wave packet, independent of the dimensions of the barrier. It is immediate that, by simply defining the velocity of crossing the barrier as the ratio between its dimensions and the time taken to cross it, the velocity grows with the dimensions of the barrier when the time reaches a constant value, until it reaches superluminal values.
It is necessary to point out, however, in this phenomenon that the time considered is that of detecting the half height of the rise of the wave front, therefore we are talking about observation of the packet envelope which should correspond to the group velocity, on the other hand the superluminal velocity defined in this way is not a real velocity that can be defined at every point, since, inside the barrier where the waves are evanescent, there is no defined propagation and corresponding velocity. Other possible definitions of the tunneling crossing time and the corresponding velocity are possible although the interpretations are not univocal [21,22].

2. Analogy between the Quantum Tunneling Effect and Evanescent, Electromagnetic or Acoustic Guided Waves

Recall that the Schrödinger equation leads to a negative kinetic energy in the case of tunneling since the potential energy V is greater than the total energy of the particle E: if we write the equation for a one-dimensional barrier
d 2 ψ d x 2 + 2 m ℏ 2 ( E − V ) ψ = 0 .
Its monochromatic solution leads to evanescent modes within the barrier (where V>E) of the type
ψ ( V > E ) = A e − q x + B e + q x
where q is such that, having defined the free de Broglie wavenumber as k = 2 m E / ℏ 2 , that becomes k ′ = 2 m ( E − V ) / ℏ 2 if a potential V < E is present, is defined as q = − ı k ′ = 2 m ( V − E ) / ℏ 2 inside the barrier wher V > E .
So, defining for the barrier a characteristic k 0 = k 2 + q 2 = 2 m V / ℏ 2 , then it is possible to write down the Schrödinger equation as
d 2 ψ d x 2 + ( k 2 − k 0 2 ) ψ = 0 .
The Schrödinger equation is then completely analogous to the Helmholtz equation for guided waves. This equation is applicable to both guided electromagnetic waves and guided acoustic waves, where ψ represents the electric field inside the waveguide in the former case and the polarized displacement in the horizontal transverse direction, relative to the typical waveguide axis, of the so-called SH (Shear Horizontal) in the latter case of acoustic guided waves.
For guided waves, k is then the wavenumber of the bulk waves of the fields in the material medium considered while k 0 is the cut-off wavenumber of the guide such that k 0 = n π / b where n = 1 , 2 , 3 . . . is the order of the possible propagation modes inside a guide of thickness b.
In a wave guide it is therefore possible to simulate a potential barrier by narrowing the guide along a section d in such a way that, there, k 0 > k and therefore the propagation wave number in the direction of the guide axis β = k 2 − k 0 2 , becomes imaginary giving rise to evanescent waves inside the narrowed part of the guide. For the electromagnetic waves k = ω / v where v is the bulk velocity of the wave in the material while for the ultrasonic SH waves k = ω / V s with V s the velocity of the transverse bulk waves in the medium considered.
The quantum tunneling effect happens when the particle, represented by a wave packet of the probability density wave function with central frequency corresponding to the De Broglie wavelength, passes through an area in which a forbidden potential barrier is present, therefore it has a precise analogy with the propagation of a packet of electromagnetic or acoustic waves within a tapered guide in such a way that the waves are evanescents in the narrowed, limited area representing the barrier.
The equations describing the quantum tunneling effect can be transformed in the ones describing the propagation, in a waveguide, trough a forbidden barrier with the substitution
ℏ m ⟶ v 2 ω
where v is the bulk electromagnetic wave velocity or the bulk ultrasonic wave transverse velocity in the material that constitutes the waveguide.

3. A Possible Definition of Traversal Time: The Phase Time

Let’s consider the solution of a one-dimensional Schrödinger equation for a given value of energy E, in presence of a potential barrier V. The solution can be expressed in three parts, ψ 1 ( x ) , ψ 1 ( x ) and ψ 1 ( x ) respectively the wave function, on the left, inside and on the rigth of the barrier:
ψ 1 ( x ) = A e + ı k x + B e − ı k x ψ 2 ( x ) = C e − q x + D e + q x ψ 3 ( x ) = F e + ı k x .
Considering a rectangular shaped potential barrier placed along the x axes between positions x = 0 and x = d , the boundary conditions of continuity of the wave function and of its derivative leads to a system for the wave amplitudes to solve:
A + B = C + D ı k ( A − B ) = − q ( C − D ) C e − q d + D e + q d = F e ı k d − q ( C e − q d − D e + q d ) = ı k F e ı k d .
Eliminating the amplitudes B, C e D, it is possible to find the complex transmission coefficient T e ı α such that
T e ı α ≡ F A = 4 ı k q − ( q − ı k ) 2 e q d + ( q + ı k ) 2 e − q d e − ı k d ,
and an analogous expression for the reflection coefficient R = B / A .
It is given a wavepacket strickly picked around a value k, inpinging on the barrier; its Fourier components will be of the form T ( k ) exp [ ı α ( k ) + ı k x − ı E ( k ) t / ℏ ] . The transmitted wavepacket will be thus described by the expression
ψ T = 1 2 π ∫ − ∞ + ∞ T ( k ) e ı α ( k ) e k x e − ı ω ( k ) t d k
where, for a particle, ω ( k ) = E ( k ) / ℏ .
The phase time is the time associated with a recognizable element of the packet such as, for example, the peak to which we assign a position x ( t ) . To follow the peak, we can use the stationary phase method: we rewrite the exponential in the integral as e ı F ( k ) where F ( k ) represents the total changing of phase of the individual components, with a phase shift due to propagation with the path inside the barrier, included. The method, therefore, consists in neglecting the contribution to the integral in the regions in which F ( k ) varies rapidly with k, since the rapid oscillations of the function tend to give a null contribution to the integral. The main contribution to the integral comes instead from the regions around the extremal points of F ( k ) , those where the first derivative with respect to k vanishes [14]. This leads to the equation
d α d k + x ( t ) − d ω d k t = 0 ;
thus the process of tunneling through a barrier of length d leads to a spatial delay δ x = d α / d k and the traversal phase time t T ϕ is defined as the ratio of the spatial delay due to the overall phase shift to the group velocity v g [23].
From equation (7)
F A e ı k d = T 1 / 2 e ı ( α ( k ) + k d ) = 2 k q 2 k q cosh ( q d ) − ı ( k 2 − q 2 ) sinh ( q d )
so the phase displacement
α ( k ) + k d = tan − 1 k 2 − q 2 2 k q tanh ( q d ) .
The phase time for the barrier crossing is then
t T ϕ = 1 v g d d k ( α ( k ) + k d ) = m ℏ k q 2 q d k 2 ( q 2 − k 2 ) + k 0 4 sinh ( 2 q d ) 4 k 2 q 2 + k 0 4 sinh ( q d )
The time defined in this way is certainly an important reference concept, but it is necessary to mention why this definition does not conclude the theoretical discussion, indeed other definitions of traversal time have been hypothesized and the problem is still open.

3.1. Problems with Phase Time

Let’s consider the reflection phase time t R ϕ (defined in the same way as t T ϕ but now for the reflected particle) and the dwell time t D ϕ (Dwell time) [24] defined as the average time spent by the particle in a certain spatial interval ( x 1 , x 2 ) , which may possibly include the expression barrier having the expression
t D ϕ = 1 j ( k ) ∫ x 1 x 2 | ψ ( x , k ) | 2 d x
that is the ratio between the number of the particles in the interval that includes the barrier and the flux of the incident probability density J ( k ) = ℏ k / m .
Then, necessarily, the condition t D ϕ = R t R ϕ + T t T ϕ where R and T are respectively the reflexion and transmission coefficients, should be satisfied. In our case, instead, there is an additional sinusoidal term [14,21,25]:
t D ϕ = R t R ϕ + T t T ϕ + R k v g sin ( Φ − 2 k x 1 )
where Φ is the phase displacement of the reflected wave. This term represents the interference between the reflected wave function and the one incident on the barrier. Since, to define the velocity of crossing the barrier we need the actual traversal time taken by the particle (or by the wave packet) to cross it, the phase transmission time t T ϕ as defined above, cannot represent the actual traversal time because it contains an additional interference term in which the contributions of transmission and reflection are not separable.

4. S H Modes in Ultrasonic Waveguides

It’s given an ultrasonic rectangular waveguide, characterized by an ideally infinite length (direction z) along which the waves propagate, an ideally infinite width (direction y) and a finite thickness b (direction x) comparable with the wavelength. The normal stress free condition at the surface of the waveguide rules the propagation of the possible modes. With respect to the waveguide it is possible to distinguish three polarization of the ultrasonic waves. The longitudinal one L and, of the two shear, the one polarized in the vertical direction ( S V ) along the thickness and the other polarized in the horizontal direction ( S H ) along the width of the waveguide.
When a shear horizontal wave is reflected at the interface constitute by the waveguide surfaces, the boundary conditions are fully satisfied by a reflection in another S H wave, while the shear vertical S V is partially reflected and partially transformed in a longitudinal L and so the longitudinal generates at reflection both the S V and L kind. So two kind of modes can propagate along the waveguide, the pure shear modes, horizontally polarized, S H and modes that are a combination of longitudinal ad shear vertical polarization called Lamb modes.
Let’s focus on the S H modes that have a dispersion relation that is the analogous of the electromagnetic and quantum cases and has an analytic expression for the function ω ( k ) while the dispersion relation for Lamb waves must be solved numerically to obtain the function ω ( k ) . From a mathematical point of view it is possible to define a displacement vector u → , a scalar potential ϕ and a vector potential ψ → such that
u → = ∇ ϕ + ∇ × ψ → .
Through Christoffel equation for isotropic medium [26] it is possible to demonstrate that the shear waves depend only on ψ → with a wave equation
Δ ψ → − 1 V s 2 ∂ 2 ψ → ∂ t 2 = 0
where v s is the shear bulk velocity v s = μ / ρ and μ is the shear modulus [27].
In the rectangular waveguide the S H waves reflect on itself back and forth between the sufaces. Their shear wavenumber vector of modulus k s = ω / v s , has transversal component k t s along y direction and component β along the direction of propagation z. S H waves have the only displacement component along the horizontal direction x so the vector potential ψ → has the only component along the vertical y direction such that
ψ y = A e − ı β z cos ( k t s y + α )
and
u x = − ∂ ψ ∂ z = ı β ψ y = ı β A e − ı β z cos ( k t s y + α ) .
The boundary conditions impose the component of the stress, normal to the surfaces
T x y = μ ∂ u x ∂ y = ı β k t s μ A e − ı β z sin ( k t s y + α ) ,
to be null at y = ± b / 2 . This leads to α = 0 and to the ondition of transverse resonance given by
k t s = n π b ( n ∈ N ) .
So a number n of S H modes exist that satisfy the boundary conditions and that have a wavenumber of propagation β such that
β 2 = k t s 2 − n π b 2 = ω v s 2 − n π b 2 .
This dispersion relation is the analogous of that of the electromagnetic waveguide. Excluding the n = 0 mode, that is simply a shear bulk wave propagating parallel to the z direction, all the other modes have a cut-off frequency below which, the mode is evanescent.

5. Phase Time for S H Ultrasonic Waves

The transmission phase time t T ϕ , as defined in section (Section 3), is an important reference concept that can be defined also in the acoustic field. Let’s consider its expression for a potential barrier simulated by a zone in which the waves become evanescent (e.g. an area with less thickness than a waveguide such that the frequency is under the cut-off limit) for S H waves. A waveguide of thickness b is considered in which the propagation of a particular S H mode is possible with dispersion dispersion equation (21)
β = ω 2 v s 2 − n π b 2
where the wave vector β → , of the propagating wave along the waveguide, is real and the propagating mode has expression
ψ = ψ 0 e ı ( β x − ω t )
In the narrowed section of the waveguide of length d, if the thickness b ′ is such that b ′ < n π v s / ω , the correspondent β ′ becomes imaginary and it is substituted by
q = ı β ′ = n π b ′ 2 − ω 2 v s 2
and the wave becomes evanescent with expression
ψ = ψ 0 e − q x e ı ω t .
Defining, then,
k 0 = n π b ′ 2 − n π b 2 ,
the traversal phase time for S H waves has an expression analogous to (12)
t T ϕ = 1 v g q 2 q d β 2 ( q 2 − β 2 ) + k 0 4 sinh ( 2 q d ) 4 β 2 q 2 + k 0 4 sinh ( q d )
where the group velocity is v g = v s 2 β / ω .

6. Results

6.1. Theorical Results for SH Waves

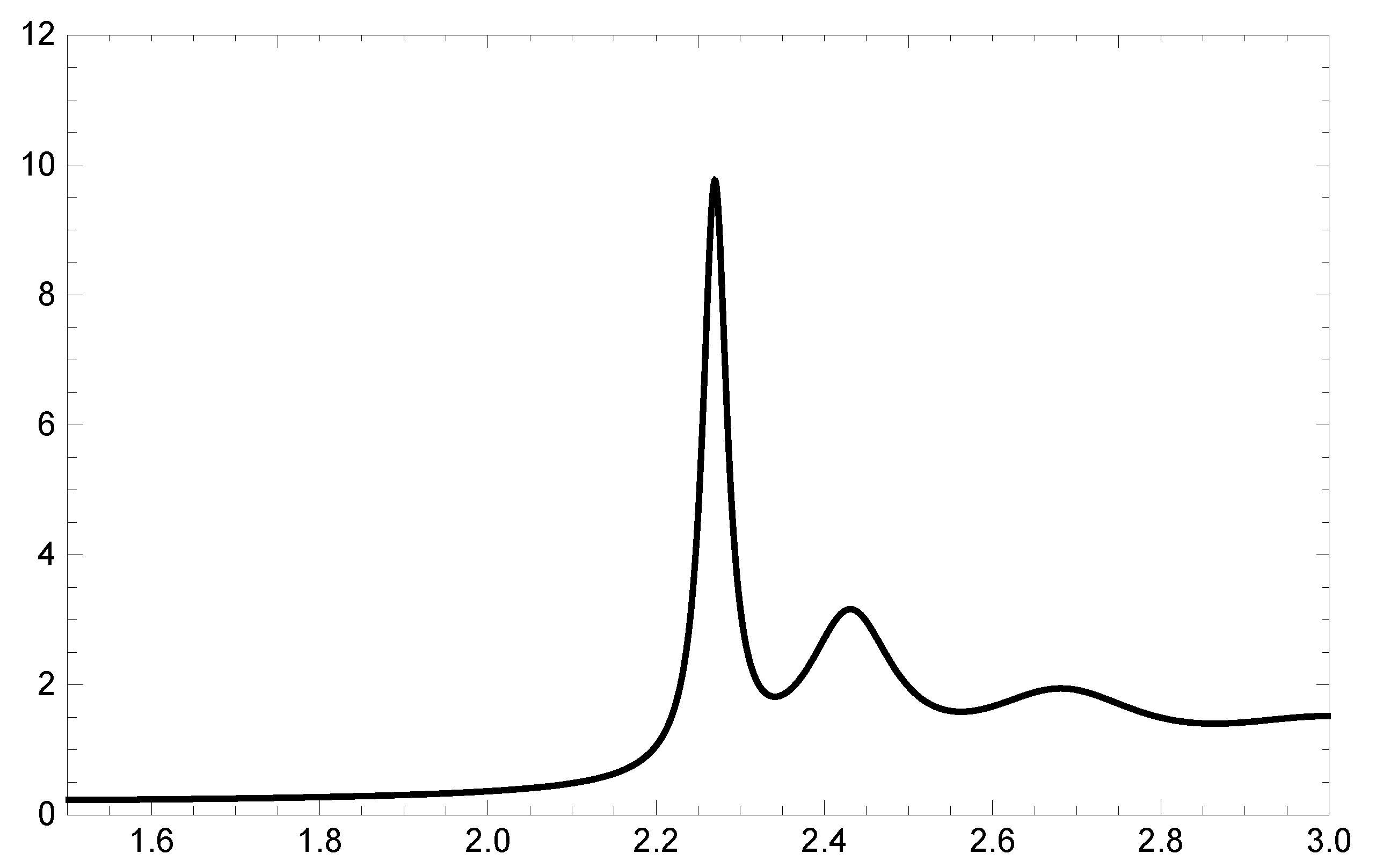
In a concrete example, we can consider a waveguide with thickness b = 2 mm tapered in an area with a smaller thickness b ′ = 0.7 mm, of length d; the velocity of the transverse waves is set to v s = 3100 m/s typical of aluminum. In this case it is found that the cut-off frequency of the evanescent wave zone is ν 0 = 2.214 MHz. In Figure 1 the phase time is graphed as a function of frequency for the first mode n = 1 and a barrier d = 3 mm long. To be noted the barrier resonances above the cutoff frequency and the monotonic decrease in traversal time below the cutoff frequency.
If we then consider, for example, a frequency ν = 2.200 MHz (wavelength λ = 1.41 mm) just below the cut-off frequency ν 0 = 2.214 MHz in Table 1 are indicated the values of the transversal phase time τ T ϕ and the corresponding traversal velocity V T defined as the ratio between the length of the barrier (evanescent zone) and the traversal phase time, corresponding to different lengths d of the barrier. It is possible to note the so called Hartman effect for which the traversal time tends to a constant limit value, independent by the barrier length, resulting in rapid increasing in traversal velocity; the effect happens when, increasing the barrier length d, it becomes opaque i.e. β d ≫ 1 . Remembering that the velocity of bulk transverse waves v s = 3100 m/s represents the analogue of the velocity of light in the medium that constitutes the electromagnetic wave guide, it is possible to note that, with these parameters, the acoustic analogous of the apparent superluminal behavior, is already reached with a barrier length corresponding to few wavelenghts of the signal.
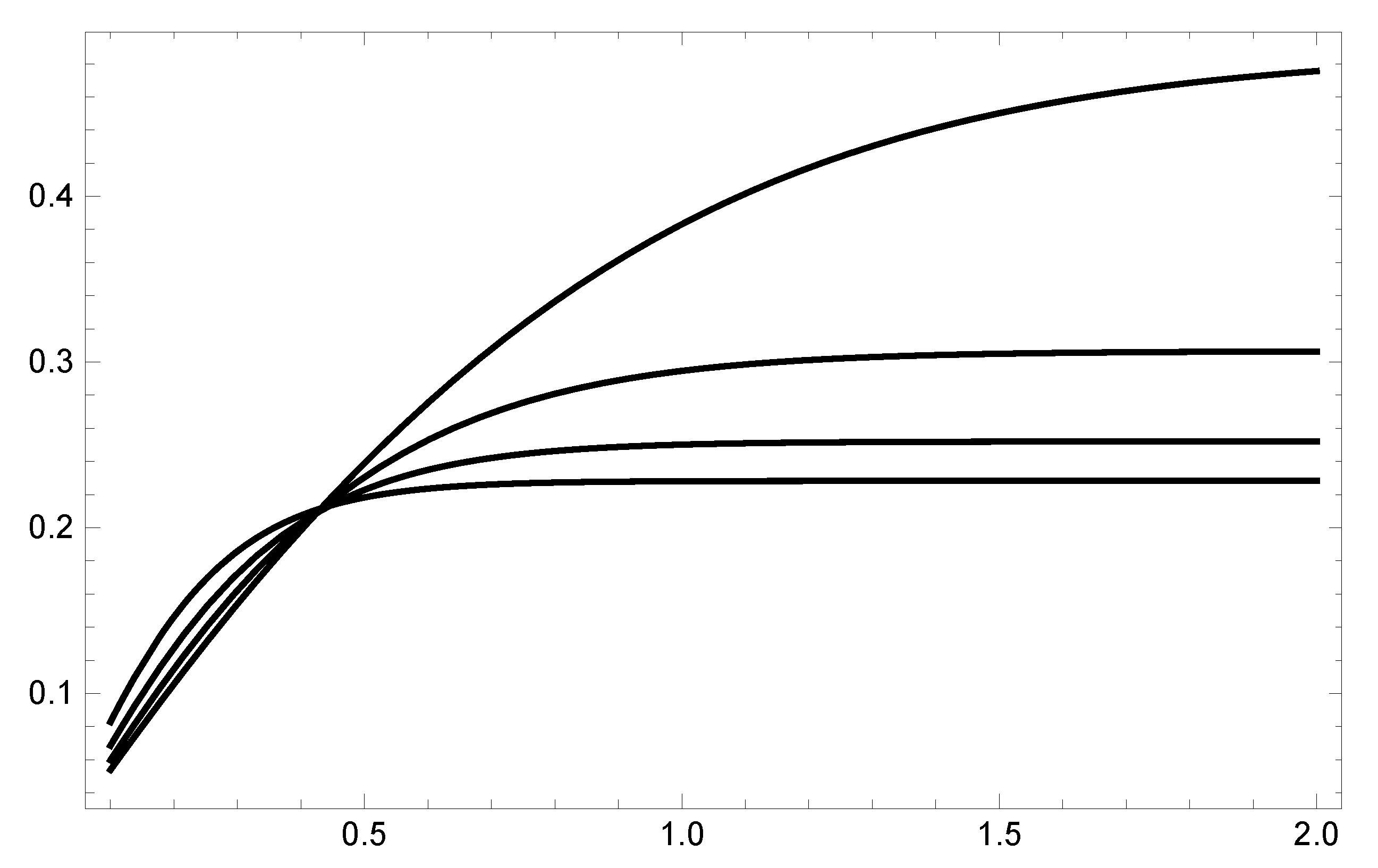
At lower frequencies then, i.e. further inside the potential well, the Hartman effect is reached even for shorter barrier lengths and the value of the traversal time limit decreases slightly and it is within the order of magnitude of a fraction of a microsecond.
This is graphed in Figure 2 where the phase time is in function of the barrier length for several frequencies under the cut-off. The plateau of constant phase time, showing the Hartman effect, is reached, for lower frequencies at shorter barrier lengths.
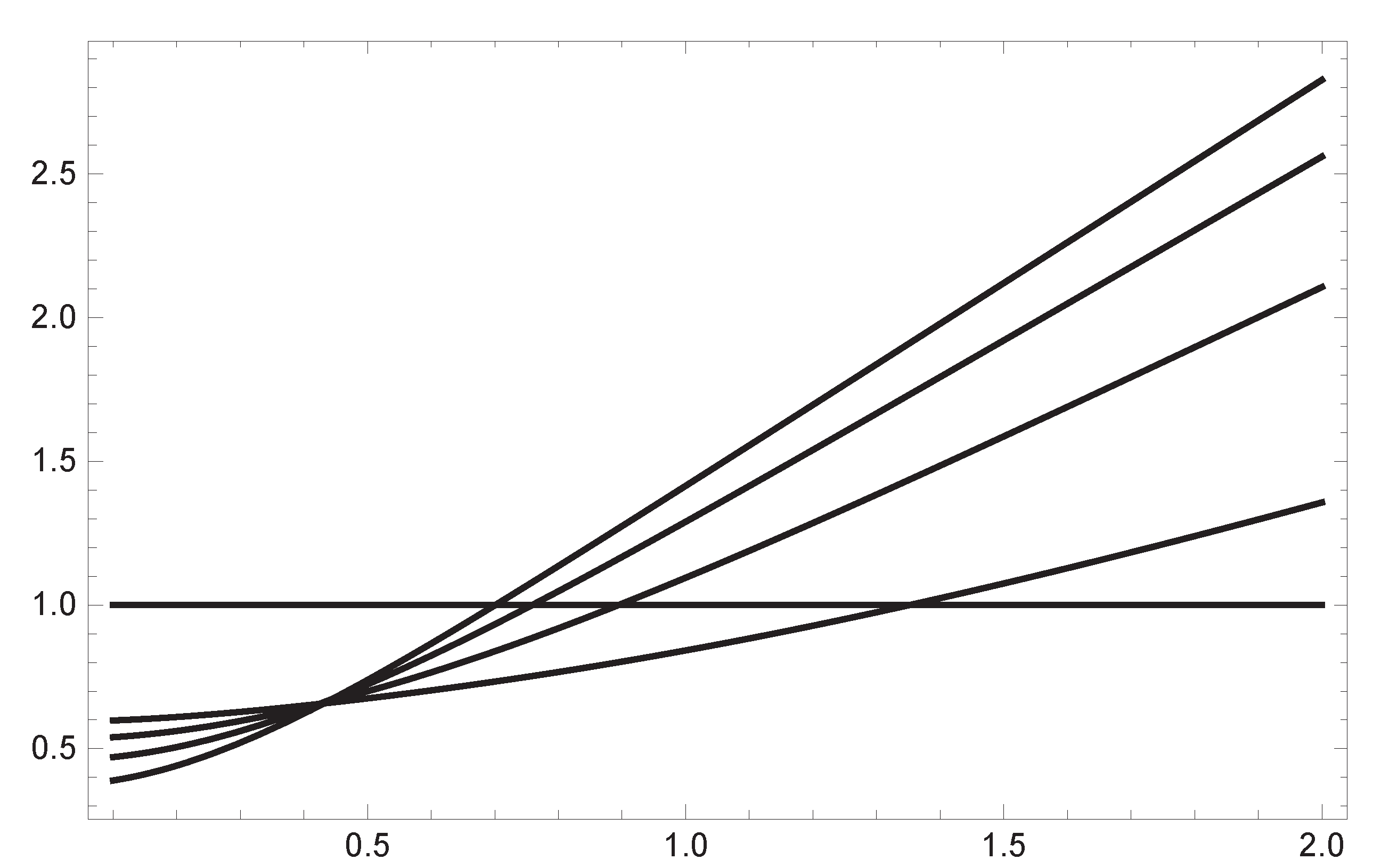
Defining the traversal velocity as the ratio between barrier length and phase time increment during the crossing, in Figure 3 it is possible to see at which barrier length, the value of this velocity goes above the limit velocity of shear bulk waves in the material, for different frequencies. The lower the frequency, the shorter barrier length is necessary to cross above this limit.

6.2. Some Experimental Results in Literature

Traversal time measurements in the tunneling effect in quantum mechanics pose several problems for issues related to non-invasive measurements of quantum objects [20]. In electromagnetism and acoustics, measurements of the delay of the packet envelope were instead carried out for different frequencies and in different situations in which evanescent waves were involved.
Table 2 lists some experimental results in photonics (tunneling between two FTIR total internal reflection prisms, photonic chain of dielectric layers, tapered waveguide), in guided microwaves and in guided Lamb waves.
Table 2 shows experimental results that support a hypothesis made by Nimtz and Stahlhofen [35] for which the traversal time is of the order of magnitude of the reciprocal of the frequency used. This is found for both electromagnetic waves and acoustic waves. This fact, combined with the Hartman effect of independence of the traversal time from the length of the barrier for "opaque" barriers (beyond a minimum length) leads to the possibility of an envelope of the wave packet traveling at very large velocities, even superluminal for electromagnetic waves and beyond the maximum elastic velocity of the considered medium for elastic waves.
We remember that in any case in particular conditions, the velocity of the envelope does not correspond to the velocity of information transfer, therefore the causality principle of special relativity remains intact.

7. Conclusions

Following the formal analogy among quantum, electromagnetic and acoustic waves, the problem of determination of the traversal time of a potential barrier by evanescent acoustic waves has been addressed. The analogy has been demonstrated for the S H (shear horizontal) modes in a rectangular waveguide that have the same analytical form of dispersion relation as quantum and electromagnetic waves; then with an appropriate tapering of the waveguide a potential barrier has been simulated. The article focused in particular on the determination of the so called phase time i.e. the temporal delay due to a phase displacement for a wavepacket crossing a region of forbidden propagation, putting in evidence the so called Hartman effect also for acoustic modes.
The Hartman effect happens for opaque barriers when the length d is such that β d ≫ 1 . The typical traversal time, in that case, is found for S H waves and compared with other results in literature obtained in different fields, confirming the conjecture that the traversal phase time is proportional to the inverse of the typical frequency of the phenomenon independently from the length of the opaque barrier.
This leads to an increasing of traversal velocity defined as barrier length divided by the phase time, well above the velocity limit relative to the phenomenon in object, which, for acoustic shear guided waves, is the shear velocity of bulk waves in the material of which the waveguide is made and that is the analogous of the ligth c velocity in electromagnetic and quantum fields.

Conflicts of Interest

The author declare no conflict of interest.

References

  1. Lord Rayleigh, Nature (London) XXIV, 1881, 382.
  2. Lord Rayleigh, Philos. Mag. XLVIII, 1889, 151.
  3. Brillouin, L. Wave propagation and group velocity, Academic Press, New York, 1960.
  4. Winful, H.G. Group delay, stored energy, and the tunnelling of evanescent electromagnetic waves. Phys. Rev. E 2003, 68. [Google Scholar]
  5. Garrett, C.G.B.; McCumber, D.E. Phys. Rev. A 1970, 1, 305. [CrossRef]
  6. Chu, S.; Wong, S. Linear pulse propagation in an absorbing medium. Pys. Rev. Lett. 1982, 48, 738. [Google Scholar] [CrossRef]
  7. Akulshin, A.M.; Barreiro, S.; Lezama, A. Pys Rev. Lett. 1999, 83, 4277. [CrossRef]
  8. Basov, N. G et al. Sov. Phys. JETP 1966, 23, 16. [Google Scholar]
  9. Chiao, R.Y. Phys Rev. A 1993, 48, R34. [CrossRef]
  10. Steinberg, A.M.; Chiao, R.Y. Phys. Rev. A 1994, 49, 2071. [CrossRef]
  11. Li-Gang, W.; Nian-Hua, L.; Qiang, L.; Shi-Yao, Z. Effect of coherence on the superluminal propagation of light pulses through anomalously dispersive media with gain. Europhys. Lett. 2002, 60, 834. [Google Scholar]
  12. Fisher, D.L.; Tajima, T.; Downer, M.C.; Siders, C.W. Phys. Rev. E 1995, 51, 4860.
  13. Steinberg, A. M.; Kwiat, P.G.; Chiao, R.Y. Measurement of the single-photon tunnelling time. Phys. Rev. Lett. 1993, 71, 708–711. [Google Scholar] [CrossRef]
  14. Hauge, E.H.; Støvneng, J.A. Tunneling times: a critical review. Rev. Mod. Phys. 1989, 61, 917–936. [Google Scholar] [CrossRef]
  15. Ranfagni, A.; Mugnai, D.; Fabeni, P.; Pazzi, G.P. Delay-time measurements in narrowed waveguides as a test of tunnelling. Appl. Phys. Lett. 1991, 58, 774. [Google Scholar] [CrossRef]
  16. Enders, A.; Nimtz, G. Evanescent-mode propagation and quantum tunneling. Phys. Rev. E 1993, 48, 632–634. [Google Scholar] [CrossRef] [PubMed]
  17. Hartman, T.H. Tunneling of a wave packet. J. Appl. Phys. 1962, 33, 3427. [Google Scholar] [CrossRef]
  18. Ghatak, A.; Banerjee, S. Appl. Opt. 1989, 28, 1960.
  19. Spielmann, Ch.; Szipöcs, R.; Stingl, A.; Krausz, F. Tunneling of optical pulses through photonic band gaps. Phys. Rev. Lett. 1994, 73, 2308. [Google Scholar] [CrossRef]
  20. Muga, J.G.; Leavens, C.R. Arrival time in quantum mechanics. Phys. Reports 2000, 338, 353–438. [Google Scholar] [CrossRef]
  21. Büttiker, M. Larmor precession and the traversal time for tunnelling. Phys. Rev. B 1983, 27, 6178–6188. [Google Scholar] [CrossRef]
  22. Winful, H.G. Tunneling time, the Hartman effect and superluminality: a proposed resolution of an old paradox. Physics Reports 2006, 436, 1–69. [Google Scholar] [CrossRef]
  23. Landauer, R.; Martin, Th. Barrier interaction time in tunnelling. Rev. of Mod. Phys. 1994, 66, 217–227. [Google Scholar] [CrossRef]
  24. Leavens, C.R.; Aers, G.C. Dwell time and phase times for transmission and reflection. Phys. Rev. B 1989, 39, 1202–1206. [Google Scholar] [CrossRef] [PubMed]
  25. Landauer, R.; Martin, Th. Time delay in wave packet tunnelling. Solid State Commun. 1992, 84, 115–117. [Google Scholar] [CrossRef]
  26. Slawinski, M, A. Waves and rays in elastic continua, World Scientific, 2010.
  27. Salencon J. Handbook of continuum mechanics: general concepts, thermoelasticity, springer science & business media, 2001.
  28. Balcou, Ph.; Dutriaux, L. Phys. Appl. Rev. Lett. 1997, 78, 851. [CrossRef]
  29. Mugnai, D.; Ranfagni, A.; Ronchi, L. The queston of tunneling time duration: a new experimental test at microwave scale. Phys, Lett. A 1998, 247, 281. [Google Scholar] [CrossRef]
  30. Carey, J.J.; Zawadzka, J.; Jaroszynski, D.; Wynne, K. Phys. Rev. Lett. 2000, 84, 1431. [CrossRef] [PubMed]
  31. Haibel, A.; Nimtz, G. Universal tunnelling time in photonic barrier. Ann. Phys. 2001, 10 Ed. 8, 707–712. [Google Scholar] [CrossRef]
  32. Nimtz, G.; Enders, A.; Spieker, H. J. Phys. I. 1994, 4, 565.
  33. Enders, A.; Nimtz, G. J. Phys. I. 1992, 2, 1693.
  34. Alippi, A.; Germano, M.; Bettucci, A.; Farrelly, F.A.; Muzio, G. Traversal time of acoustic plate waves through a tunneling section. Phys. Rev. E 1998, 57, 4907–4910. [Google Scholar] [CrossRef]
  35. Nimtz, G.; Stahlhofen, A. A. Universal tunneling time for all fields. Ann. Phys. 2008, no.6, 17, 374–379. [Google Scholar] [CrossRef]
Preprints 101082 g001
Figure 1. Phase time (in μ s) vs. frequency (in MHz). To be noted the resonances due to the narrowed section of the waveguide, above the cut-off frequency of 2.214MHz and the almost constant value below the cut-off.
Figure 1. Phase time (in μ s) vs. frequency (in MHz). To be noted the resonances due to the narrowed section of the waveguide, above the cut-off frequency of 2.214MHz and the almost constant value below the cut-off.
Preprints 101082 g001
Preprints 101082 g002
Figure 2. Phase time (in μ s) vs. barrier length (in mm) for some frequencies under the cut-off: looking at the plateau on the right of the figure (Hartman effect) the curves from the bottom to the top are respectively at frequency of 1.5, 1.7, 1.9 and 2.1 MHz. To be noted that the deeper the frequency is under cut-off, the sooner (at a shorter barrier length) the plateau of constant phase time (Hartman effect) is reached.
Figure 2. Phase time (in μ s) vs. barrier length (in mm) for some frequencies under the cut-off: looking at the plateau on the right of the figure (Hartman effect) the curves from the bottom to the top are respectively at frequency of 1.5, 1.7, 1.9 and 2.1 MHz. To be noted that the deeper the frequency is under cut-off, the sooner (at a shorter barrier length) the plateau of constant phase time (Hartman effect) is reached.
Preprints 101082 g002
Preprints 101082 g003
Figure 3. Defining the velocity through the barrier as barrier length/phase time, in figure is represented on the vertical axis the ratio between this velocity and the velocity v s of the bulk transverse waves in the medium (3100 m/s in this case) that is the velocity in the acoustic case correspondent to "c of the electromagnetic case. On the horizontal axes is the barrier length in mm. The horizontal line represents the limit of acoustic analogous of superluminality. The curves are at different frequencies of 1.5, 1.7, 1.9 and 2.1 MHz. To be noted that the curves cross the limit sooner (shorter barrier) for lower frequencies (deep under the cut-off) and later for higher frequencies (closer to the cut-off).
Figure 3. Defining the velocity through the barrier as barrier length/phase time, in figure is represented on the vertical axis the ratio between this velocity and the velocity v s of the bulk transverse waves in the medium (3100 m/s in this case) that is the velocity in the acoustic case correspondent to "c of the electromagnetic case. On the horizontal axes is the barrier length in mm. The horizontal line represents the limit of acoustic analogous of superluminality. The curves are at different frequencies of 1.5, 1.7, 1.9 and 2.1 MHz. To be noted that the curves cross the limit sooner (shorter barrier) for lower frequencies (deep under the cut-off) and later for higher frequencies (closer to the cut-off).
Preprints 101082 g003
Table 1. Traversal phase time and velocity for different lengths of the barrier for S H waves at frequency ν = 2.200 MHaz and cut-off frequency ν 0 = 2.214 MHz.
Table 1. Traversal phase time and velocity for different lengths of the barrier for S H waves at frequency ν = 2.200 MHaz and cut-off frequency ν 0 = 2.214 MHz.
Barrier length d(mm) Traversal phase time t T ϕ ( μ s) Traversal velocity V T (m/s)
]1*3 1.0646 2818.0
]1*8 1.3489 5930.6
]1*13 1.3543 9598.9
]1*18 1.3544 13290.2
]1*23 1.3544 16981.9
]1*28 1.3544 20673.7
Table 2. Experimental results in literature.
Table 2. Experimental results in literature.
Barrier type Reference Traversal time 1/frequency
FTIR Balcou and Dutriax [28] 40 fs 11.3 fs
FTIR Mugnai et al. [29] 134 ps 100 ps
FTIR Carey et al. [30] ≈ 1 ps 3 ps
FTIR Haibel and Nimtz [31] 117 ps 120 ps
Photonic chain Steinberg et al. [13] 1.47 fs 2.3 fs
Photonic chain Spielmann et al. [19] 2.7 fs 2.7 fs
Photonic chain Nimtz et al. [32] 81 ps 115 ps
Photonic waveguide Enders and Nimtz [33] 81 ps 115 ps
Microwave waveguide Ranfagni et al. [15] ≈ 1 ns ≈ 1 ns
Ultrasonic waveguide Alippi et al. [34] 0.5 μ s 0.65 μ s
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated