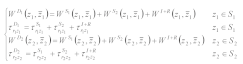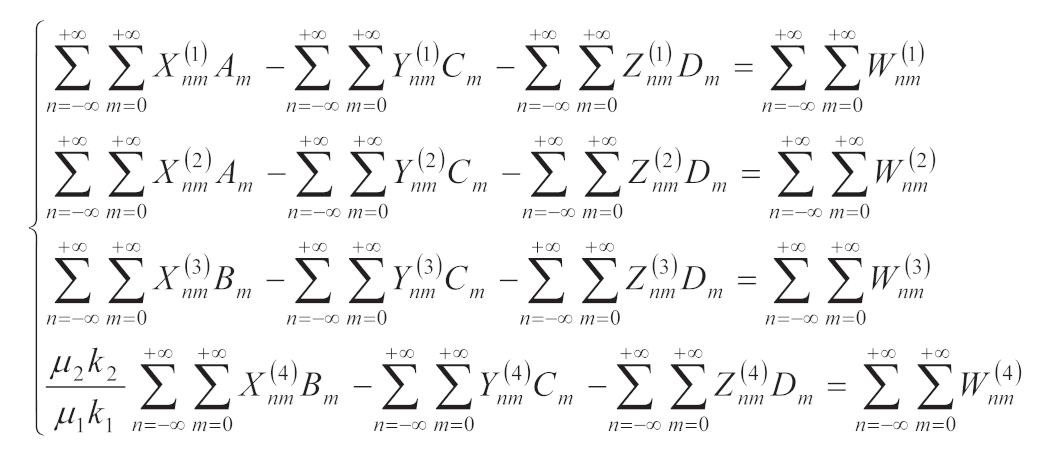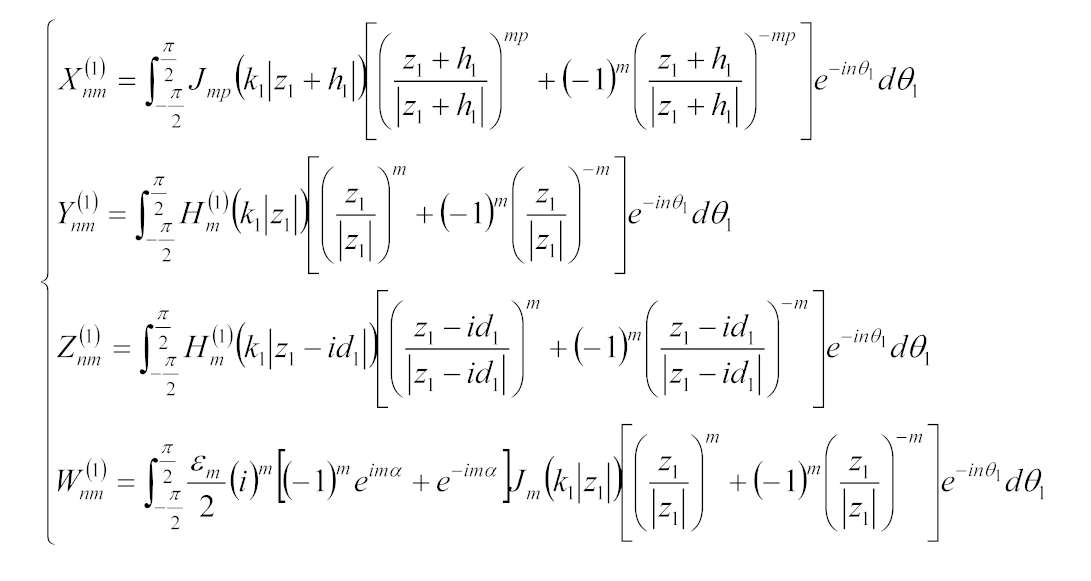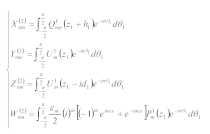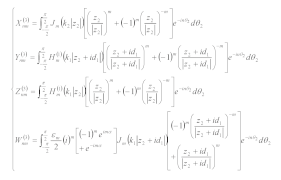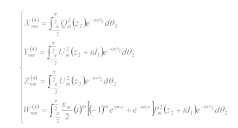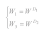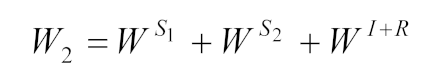1. Introduction
Earthquake is a very serious natural disaster. It is a worldwide problem to accurately predict earthquakes. To reduce the damage caused by earthquakes, improving the seismic capacity of structures and evaluating the seismic damage is a key point in the field of earthquake engineering. Through previous studies, it is found that under the same seismic load, different local topography will have different effects.
Shear horizontal wave (SH wave) can make the surface shake in the horizontal direction, which is the main cause of earthquake disasters. Many scholars have done a lot of research on the response of different terrains to SH waves. Xu and Han [
1] studied the scattering of plane SH waves by multiple semi-cylindrical canyons. Numerical results and discussions of displacements and phases on the surface of the canyons are given. By using the accurate region-matching technique to derive a rigorous series solution, Chang et al. [
2] studied the scattering of SH waves by a circular sectorial canyon. Combining the region-matching technique and a periodic indirect boundary element method (PIBEM), Ba and Liang [
3] discussed the scattering and diffraction of plane SH waves by periodic alluvial valleys embedded in a layered half-space. Yang et al. [
4] investigated the scattering of SH waves around a circular canyon in radial inhomogeneous wedge space. By transforming the governing equation with variable coefficients into a standard Helmholtz equation, the corresponding analytical solution is derived. Qi et al. [
5] discussed the scattering of steady-state shear horizontal guided waves from the elastic strip media with multiple semi-cylindrical depressions on the surface and obtained the analytical solution.
The real situation is usually very complex, which is the coupling of many different structures. In this paper, the scattering of SH waves on a hill joined with an alluvial valley is studied. The final solution of the surface response is obtained by using the analytical method.
2. Model Simplification and Partition
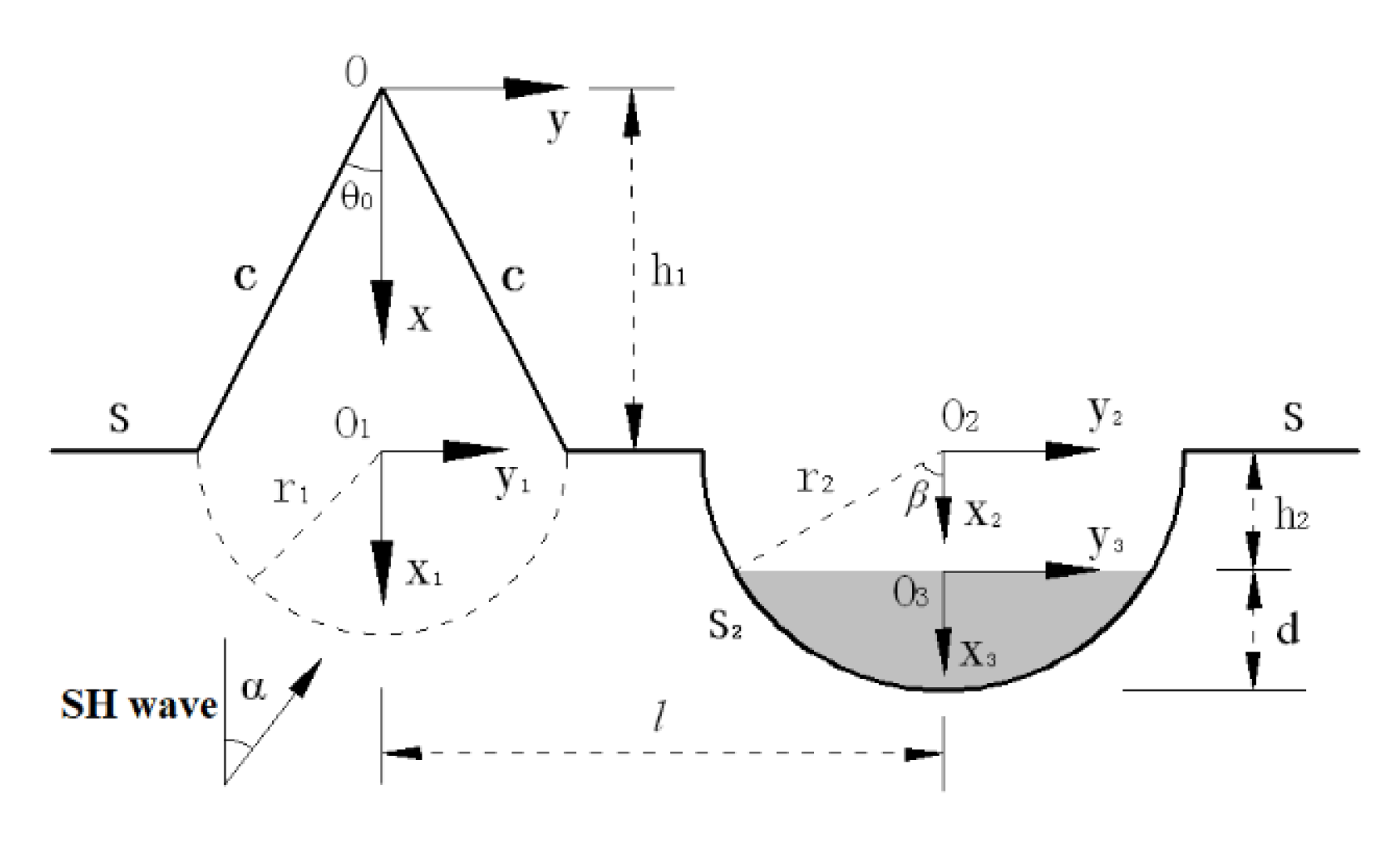
The hill is simplified as an isosceles triangle, and the alluvial valley is simplified as a semicircle. The simplified model and related parameters are shown in
Figure 1. The horizontal surface, the hypotenuse of the triangle, and the boundary of the semicircle are marked as
S,
C, and
S2, respectively. The mass density of the foundation and sediment is
ρ1 and
ρ2, and the shear modulus is
µ1 and
µ2. SH waves incident in the plane along the
X1-O1-Y1 coordinate system at the angle of
α.
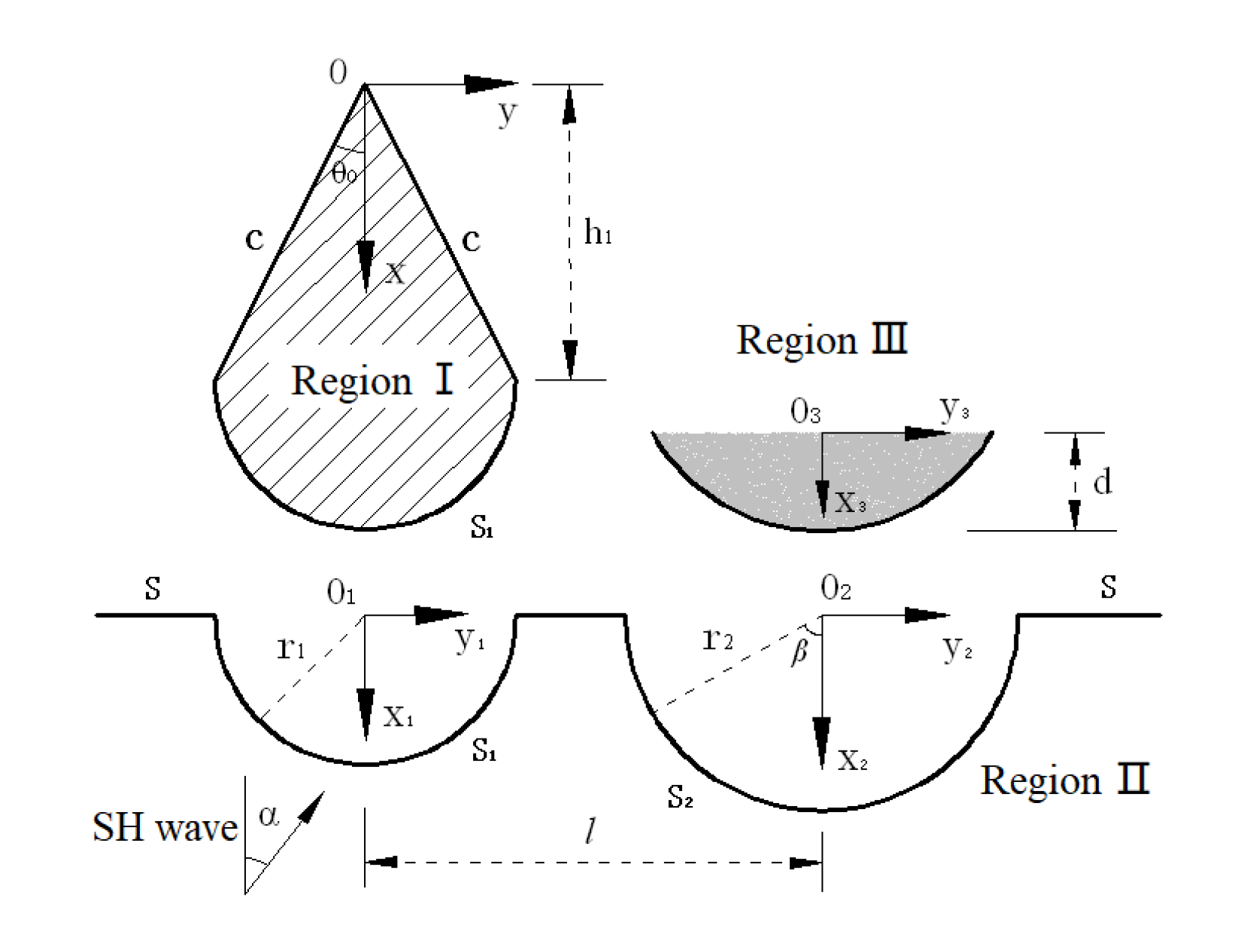
The method of “partition and combination” is used to study this complex terrain. As shown in
Figure 2, a semicircular virtual boundary
S1 is created with
O1 as the center and
r1 as the radius. Taking
S1 and
S2 as the interface, the model is divided into 3 regions.
Wave functions satisfying the boundary conditions are constructed by using the wave function expansion method and coordinate moving method [
6,
7,
8]. According to the continuous conditions of displacement and stress on the common boundary, the equations are established to solve the unknown coefficients in the wave function of each term. Finally, the dynamic response of each position on the surface can be obtained.
3. Construction of Wave Functions
For steady state, the governing equation of SH waves in isotropic homogeneous and continuous media can be expressed as [
9,
10]
where
W is the displacement function,
k=
ω/
Cs,
ω is frequency,
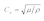
is the shear wave velocity.
In polar coordinates, the corresponding stress component is
3.1. Wave Function in Region Ι
The zero-stress condition on the boundary C is
The standing wave function satisfying the governing Equation (1) and boundary condition (3) can be expressed as [
11]
where Am is the constant to be solved, W0 is the displacement amplitude. p=π/(2θ0). Jmp(·) is a Bessel function with mp ranks.
The wave function needs to satisfy the continuity condition on
S1 boundary [
12,
13]. According to the moving coordinate method, Equation (4) in
the coordinate system can be expressed as
The corresponding stress can be expressed as
where
3.2. Wave Function in Region Ш
The boundary condition of the upper surface of sediment can be expressed as
The standing wave function satisfying condition (8) and Equation (1) can be expressed as
where Bm is the constant to be solved.
According to the moving coordinate method, Equation (9) in
the coordinate system can be expressed as
The corresponding stress can be expressed as
3.3. Scattering Waves in RegionⅡ
In region Ⅱ, there are two scattering waves on each boundary because the scattering waves generated by the two depressions interfere with each other. The functions that satisfy the governing equation and the boundary condition can be expressed in the form of multipolar coordinates as [
14,
15,
16]
The corresponding stress can be expressed as
where
Cm,
Dm are the constant to be solved.
is Hankel function of the first kind, and
3.4. Incident and Reflected Waves
In the complex plane
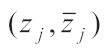
, the incident and reflected waves can be expressed as
The corresponding stress can be expressed as
where

, and
4. Establishment of Equations
Wave functions in each region satisfy the continuous conditions of displacement and stress on the common boundary, thus the equations of unknown coefficients can be established as (22). Because there are many parameter variables, the solution is very complex. Due to the space limitation, this article only considers the special case of d=r2.
Expanding (22) by Fourier series in the complex domain, the following equations are obtained
The expression of each function is
(23) are four infinite series equations with unknown coefficients. Finally, the unknown coefficients are obtained by programming.
5. Results Analysis
There is only a standing wave in region Ⅰ and region Ⅲ, so the total wave field is
The total wave field in region Ⅱ consists of three parts:
The incident wave amplitude W0 is assumed to be 1.0. y1=0 represents the vertex of the hill, y1=±r1 represents the intersection of the hill and the horizontal plane, |y1|<r1 represents the points on the surface of the hill, y1/r1=d1 represents the center of the alluvial valley. Through numerical examples, the influence of different SH wave numbers (η=2r1/λ), incident angle, and other parameters on the amplitude of surface displacement is analyzed.
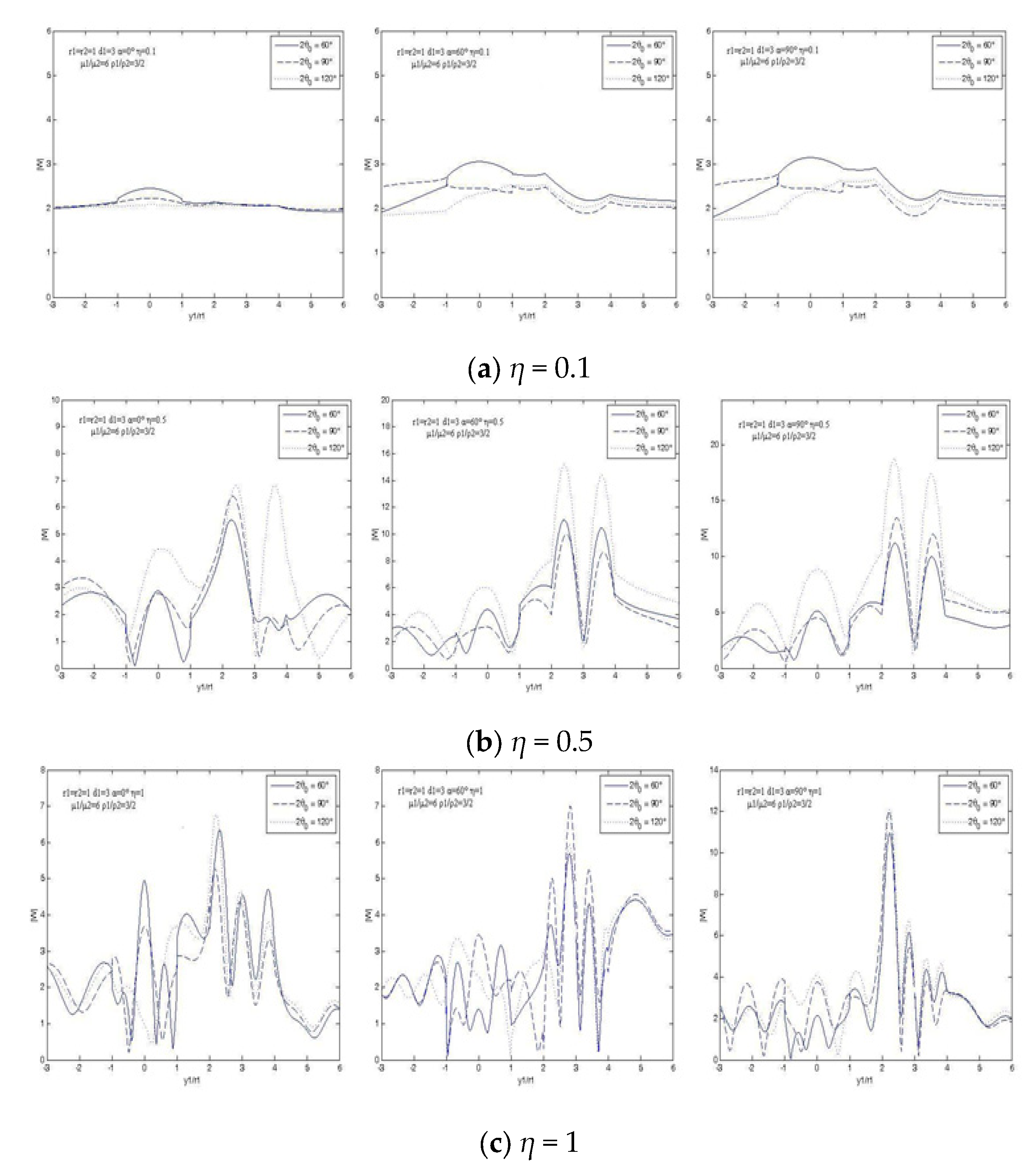
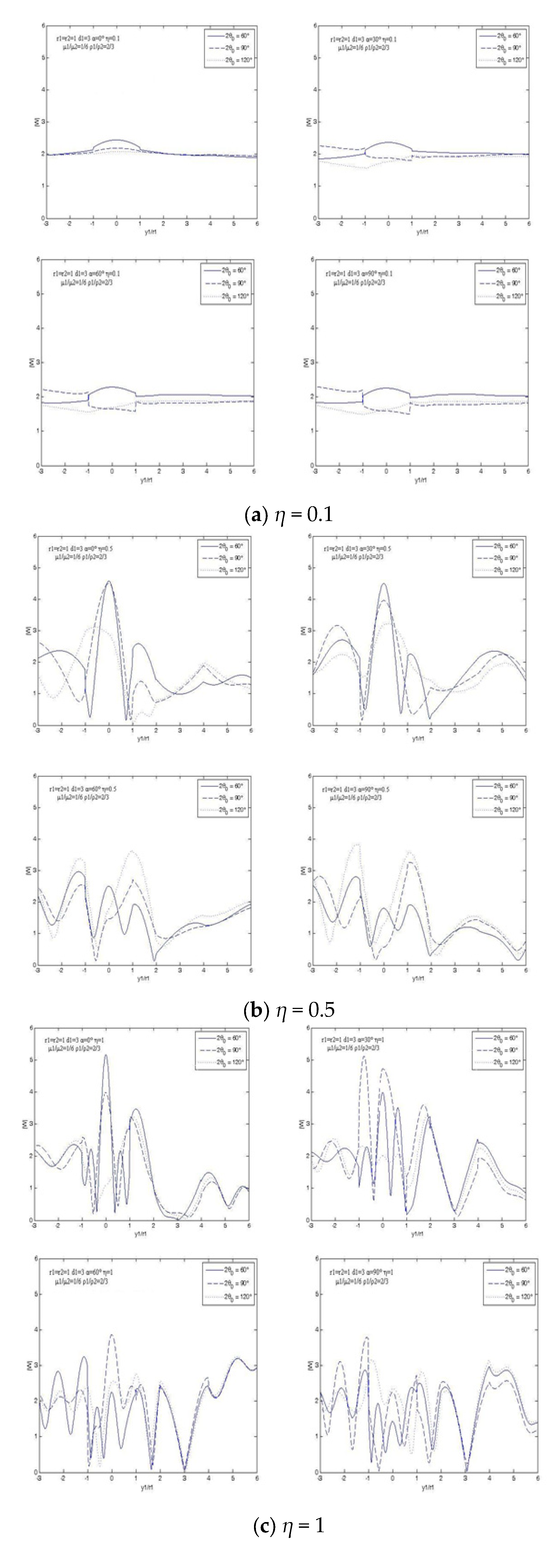
When the sediment is softer than the foundation, the variation of surface displacement amplitude with different wave numbers and incident angles is shown in
Figure 3. When the wave number is small, the surface displacement changes little, which is similar to the quasi-static problem. With the increase of wave number, the change of surface displacement becomes more and more intense, and the maximum value of displacement amplitude gradually approaches the alluvial valley. When
η≥0.5, the surface displacement amplitude in the valley is more than 10, which is 5 times that when the SH wave incident on the horizontal surface.
When the sediment is harder than the foundation, the surface displacement amplitude with different wave numbers and incident angles is shown in
Figure 4, which is much smaller than in
Figure 3. The surface displacement in the valley is generally smaller than that of the hill. The maximum value appears at the top of the hill (
η=1,
α=0°), which is 5.2. When
α=0°, the ground motion of the hill increases with the decrease of the vertex angle, and the opposite is true for
α>0°.
The average value of surface displacement on the hill is set as
e1. When the SH waves only incident on the hill, the average value of surface displacement is set as
e2. Let
e=
e1/
e2. Taking the distance between hill and valley as abscissa and
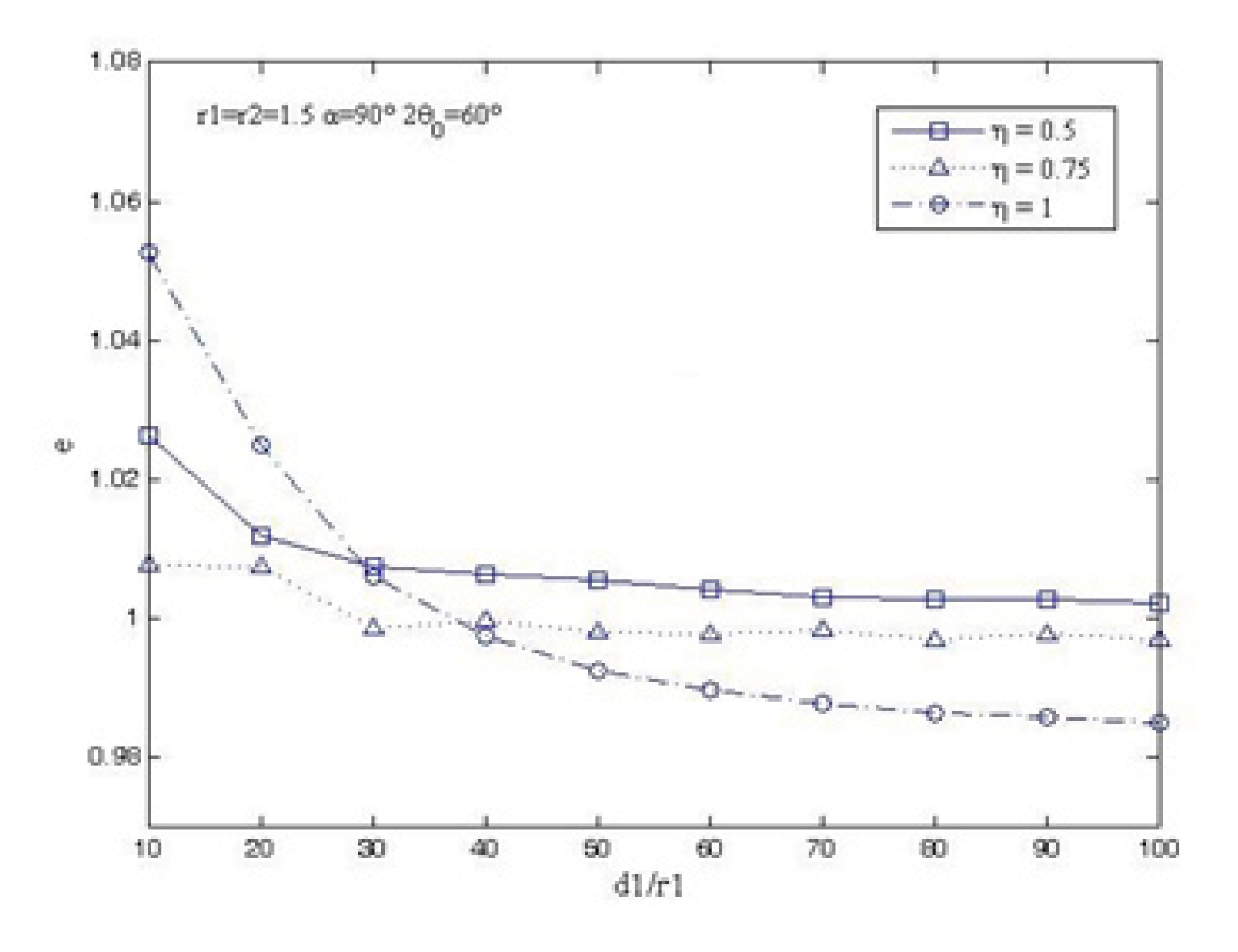
e as ordinate, the results are shown in
Figure 5. With the increase of distance,
e is closer to 1. When
d1>30
r1, the difference between
e and 1 is less than 0.02. At this time, the interaction between the hill and the valley can be ignored.
6. Conclusions
Based on elastic wave dynamics and the knowledge of complex functions, the scattering of SH waves on a triangular hill joined with a semicircular alluvial valley is studied. The conclusions are as follows:
1) When the sediment is softer than the foundation, the surface displacement is relatively large as a whole. The maximum value appears near the center of the valley, which is more than 5 times when SH waves incident into the infinite half-space.
2) When the sediment is harder than the foundation, the influence of the valley on the hill is small. The maximum surface displacement appears at the top of the hill, which is more than 2 times when SH waves incident into the infinite half-space.
3) When the distance between the hill and the valley is more than 30 times the half-width of the bottom of the hill, the interaction can be ignored.
Author Contributions
Conceptualization, Jianze Liu and Guangzheng Wang; Funding acquisition, Fazhan Yang and Xuefeng Zhang; Methodology, Jianze Liu, Yang Li and Zhuang Wang; Project administration, Jianze Liu; Software, Jianze Liu and Guangzheng Wang; Visualization, Jianze Liu and Fazhan Yang; Writing – original draft, Jianze Liu and Zhuang Wang; Writing – review & editing, Jianze Liu, Yang Li and Zhuang Wang.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declared no potential conflicts of interest concerning the research, authorship, and/or publication of this article.
References
- Xu, Y.Y.; Han, F. Scattering of SH-waves by multiple semi-cylindrical canyons. Earthquake Engineering and Engineering Vibration 1992, 12, 12–18. [Google Scholar]
- Chang, K.H.; Tsaur, D.H.; Wang, J.H. Scattering of SH waves by a circular sectorial canyon. Geophysical Journal International 2013, 195, 532–543. [Google Scholar] [CrossRef]
- Ba, Z.N.; Liang, J.W. Dynamic response analysis of periodic alluvial valleys under incident plane SH-waves. Journal of Earthquake Engineering 2016, 21, 531–550. [Google Scholar] [CrossRef]
- Yang, Z.L.; Li, X.Z.; Song, Y.Q. Scattering of SH waves around circular canyon in inhomogeneous wedge space. Geophysical Journal International 2020, 223, 45–56. [Google Scholar] [CrossRef]
- Qi, H.; Yang, R.J.; Guo, J. Scattering of SH wave by multiple semi-cylindrical depressions in an elastic strip. Explosion and Shock Waves 2020, 40, 29–41. [Google Scholar]
- Shyu, W.S.; Teng, T.J.; Yeh, C.S. Surface motion of two canyons for incident SH waves by hybrid method. Procedia Engineering 2014, 79, 533–539. [Google Scholar] [CrossRef]
- Han, F.; Liu, D.K. Research of scattering of plane SH-wave by a semi-cylindrical canyon. Journal of Harbin University of Civil Engineering and Architecture 1990, 23, 24–31. [Google Scholar]
- Shashi, K.; Swapan, K.C. Influence of scattering of SH-waves in dynamic interaction of shear wall with soil layers. Earthquake Engineering and Engineering Vibration 2020, 19, 583–595. [Google Scholar]
- Lv, X.T.; An, J.B. Ground motion of a semi-cylindrical hill joined with a semi-cylindrical alluvial valley under incident SH-waves. Journal of Vibration and Shock 2014, 33, 127–131. [Google Scholar]
- Liu, Z.X.; Yu, Q.; He, Y. Effect of randomness of geotechnical medium on the seismic ground motion amplification effect of a sedimentary valley. Acta Seismologica Sinica 2017, 39, 764–777. [Google Scholar]
- Chen, S.H.; Zhang, Y.S. Dynamic responses of canyon with multiple arc-shaped layers under incidence of plane SV waves. Chinese Journal of Geotechnical Engineering 2017, 39, 1074–1081. [Google Scholar]
- Gai, Z.X.; Chen, C.X. Localized boundary element method for seismic wave surface scattering problems: 2D SH case. Chinese Journal of Geophysics 2020, 63, 2274–2280. [Google Scholar]
- Xu, H.N.; Zhang, Y.; Huang, Q.Y. Ground motion of underground complicated circular lining structure by out-plane wave. Earthquake Engineering and Engineering Dynamics 2019, 39, 154–159. [Google Scholar]
- Ma, R.; Li, Y.Q.; Jing, L.P. Influence of a semi-circular canyon site on ground surface displacement due to incidence of elastic waves. Earthquake Engineering Journal 2019, 41, 392–398. [Google Scholar]
- Liu, Q.J.; Wu, Z.Y.; Vincent, W.L. Scattering and reflection of SH waves around a slope on an elastic wedged space. Earthquake Engineering and Engineering Vibration 2019, 18, 255–266. [Google Scholar] [CrossRef]
- Zhou, F.X.; Pang, B.B.; Zhai, R.Z. Effect of circular tunnels on earthquake subground motions: Incidence of SH wave. Earthquake Engineering Journal 2018, 40, 873–878. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
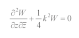
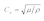 is the shear wave velocity.
is the shear wave velocity.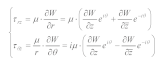
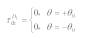
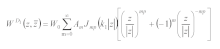
 the coordinate system can be expressed as
the coordinate system can be expressed as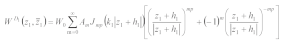

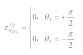
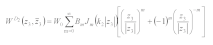
 the coordinate system can be expressed as
the coordinate system can be expressed as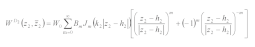
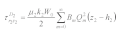
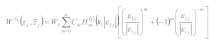
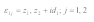
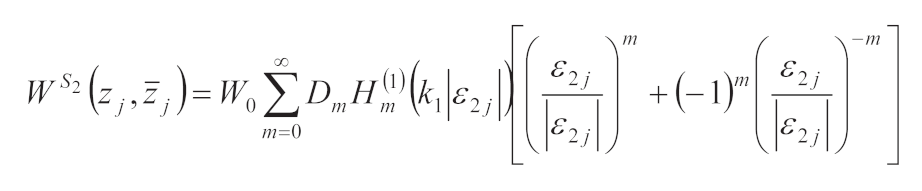
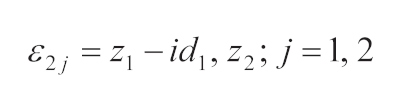
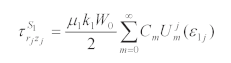
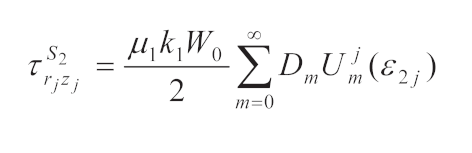
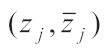 , the incident and reflected waves can be expressed as
, the incident and reflected waves can be expressed as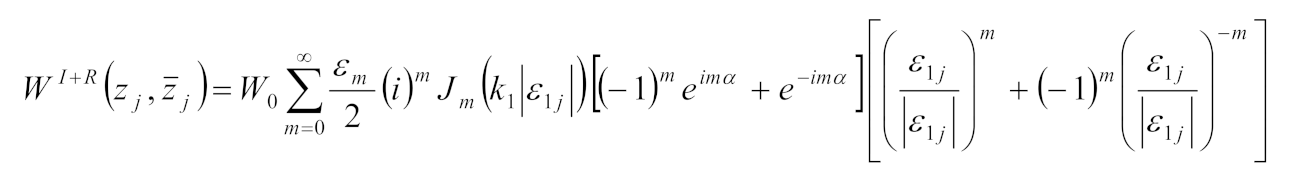
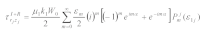
 , and
, and