Prerpints.org logo
Preprint
Article

Lower Extremity Joint Kinetics during Walk–to–Run and Run–to–Walk Transitions

Altmetrics

Downloads

87

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 March 2024

Posted:

12 March 2024

You are already at the latest version

Alerts
Abstract
Lower extremity joint kinetic factors are thought to modulate walk–to–run transition (WRT) and run–to–walk transition (RWT). This study aimed to investigate joint stiffness and energetic patterns during the WRT and RWT processes and identify whether gait transitions occurred within a single step or not. Ten healthy subjects participated in treadmill WRT (1.8 m/s – 2.4 m/s) and RWT (2.4 m/s – 1.8 m/s) tests. We investigated two steps before transition (S–2, S–1), two steps after transition (S1, S2) and the transition step (S0). We found significant differences between S2 and S–2 for ankle joint stiffness during WRT and RWT (p < 0.001); and for hip joint stiffness, we found significant differences between S1 and S–1 during WRT and RWT (p ≤ 0.001). Additionally, stance phase mechanical energy generation was observed to transfer from proximal to distal joints at S0 during WRT, and from distal to proximal at S0 during RWT. Transition step ankle kinematic and kinetic patterns were similar to the target locomotion task gait format in both WRT and RWT. Moreover, RWT required longer adaptation time compared with WRT. These findings indicate that WRT and RWT were modulated before and after the actual transitions, not within a single step. Redistribution of joint mechanical work generation was related to gait transition triggers, which modulate the WRT and RWT process.
Keywords: 
Subject: Public Health and Healthcare  -   Other

1. Introduction

Walking and running have different gait characteristics [1] and whole body center of mass (COM) dynamic patterns [2,3,4]. The transition between the walking inverted pendulum and running spring mass paradigm is primarily determined by stance phase lower extremity kinetic factors [5,6]. When walking at a constantly increasing speed or running at a constantly decreasing speed, walk–to–run transition (WRT) or run–to–walk transition (RWT) dependably occurs at a preferred transition speed (PTS) [7]. The magnitude of acceleration and deceleration affects the speed at which gait transition occurs [8].
Previous studies have investigated different factors to explain gait transition mechanisms. Generally, there have been four proposed gait transition triggers: metabolic energy cost, mechanical cost, mechanical load, cognitive and perceptual modulation [9]. From a biomechanical perspective, mechanical cost and mechanical load may be the more important factors contributing to gait transition [6,9]. With regard to mechanical cost, muscle properties [10,11] and power generation efficiency [10] are related to mechanical energy expenditure [12]. Specifically, when walking compared with running at speeds above the PTS, or running compared with walking at speeds below PTS, more muscle fiber work is required, respectively [12]. There seems to be a feedback system associated with the neuromusculoskeletal system [10] to help minimize mechanical cost of locomotion [3,9,13,14], which triggers gait transition. Mechanical load trigger [6] is known as a protective muscle stress reduction and injury prevention mechanism [9,15,16]. Specifically, when walking above PTS or running below PTS, the protective mechanism minimizes peak loads to reduce injury risk [6,17,18], which leads to gait transition. Other studies have suggested that gait transition is an active, non–spontaneous reorganization process, based on the non–linear behavior of the vertical ground reaction force, joint kinetics and muscle activity patterns before the gait transition [19,20,21].
Lower extremity joint level kinetic patterns are closely related to musculoskeletal system mechanical efficiency and mechanical load mechanisms, which help to modulate gait transition. Previous studies have investigated lower extremity joint mechanics in walking and running across different speeds [22,23], the joint kinetic characteristics around the PTS [6,10], and gait kinematics and kinetics during the transition [2,17,18,24,25,26]. It was reported that different locomotion speeds or tasks would result in the changes of joint level stiffness, mechanical work and power parameters [22], and that ankle and hip joint mechanics contribute to the WRT [6]. Specifically, lower extremity joint power generation tended to shift from hip to ankle joint, when running above PTS compared with walking, as it is beneficial for positive mechanical work and power generation, as well as improving gait mechanical efficiency by switching gait patterns [6,10]. Additionally, a switch from walking to running near PTS has been reported to reduce the effort of ankle and hip muscles [6]. These findings indicate the joint power transfer phenomenon between the ankle and hip is related to the gait transition trigger mechanisms [6]. Whether lower extremity joint kinetics are different within each step, and the mechanical work and power transfer between each joint still exists during both WRT and RWT processes remains unknown and needs further investigation.
Previous studies which focused on incremental locomotion protocols around PTS reported that gait transition happened instantaneously at the transition step, and the change of joint kinetic parameters were regarded as mechanical trigger components to modulate gait transition [6,18]. Another study focused on continuous protocols suggested that gait transition was an active reorganization process rather than an instantaneous event, due to the non–linear patterns in some joint kinematic and kinetic parameters among steps before WRT [20]. Most previous studies were either focused on joint mechanics among the steps before WRT, or the comparisons between different locomotion tasks around PTS. With these contradictions and gaps, if we regard before, during and after transition as a whole process, no studies have investigated joint kinetics during both WRT and RWT processes. From the joint kinetics aspect, it remains unknown whether WRT and RWT occurs instantaneously at the transition step only, or are modulated before and after transition.
The change of locomotion tasks or speeds is known to affect changes in joint mechanics: faster locomotion speeds required higher mechanical work and power generation [6,10,22,27], depending on modulation of lower extremity joint stiffness and moment angular impulse. Joint stiffness reflects joint elastic spring–like behavior under loading [22,28], and moment angular impulse represents the joint moment executed over time [29]. Both parameters reflect dynamic loading and response, and they are regarded as the end–effect of muscle functions during locomotion [6,22]. However, it remains unknown how continuously accelerated or decelerated locomotion speed influences the joint stiffness and moment angular impulse during transitions between walking and running. Further investigation can be helpful to identify whether the modulation of joint kinetics is an active reorganization process before and after transition, or if it occurs solely within the transition step. Moreover, lower extremity joints play different functional roles between stance and swing phase in both walking and running across different speeds [22]. Whether WRT and RWT require different functional roles for lower extremity joints, and the differences between joint kinetic patterns remains unknown, both need further investigation.
In this study, we aimed to investigate lower extremity joints stance phase dynamic loading and response, as well as stance and swing phase joint energetics during WRT and RWT processes. Further investigation of these patterns during WRT and RWT will benefit future lower extremity assistive device development, which might be designed to meet multiple locomotion tasks and be better suited to gait transition. Since lower extremity joint kinetic parameters increase with locomotion speeds [22], and the distal end joint generates more mechanical work when running above PTS [6,30], we hypothesized that: (1) lower extremity joint stiffness would increase during the WRT, and decrease during the RWT; (2) joint work and extensor moment angular impulse would increase during the WRT, and decrease during the RWT process; (3) distal end joint will generate more mechanical energy in stance phase during WRT, and decrease during the RWT process.

2. Materials and Methods

2.1. Participants

Ten middle age healthy subjects (5 males, 5 females, 50.7 ± 6.0 years, 173.4 ± 11.4 cm, 69.7 ± 14.9 kg) participated in the study. All subjects signed informed written consent approved by the university’s institutional review board (RCS #07302015.030) before participation. All subjects self–reported to be free of lower extremity musculoskeletal injuries which would affect walking and running for the past 6 months.

2.2. Experimental Protocol and Data Collection

Fifty–five retro–reflective markers were placed on the skin surface of the subjects, based on a previously published whole body marker set [31]. Before the formal test, subjects were provided with 10–minutes treadmill acceleration and deceleration practice. Then subjects were asked to complete the WRT protocol: walking on a force–instrumented treadmill (Bertec, Inc., Columbus, OH) at 1.8 m/s for 30 seconds, then the treadmill was constantly accelerated at 0.1 m/s2 up to 2.4 m/s. Subjects were asked to transition to a running gait whenever they felt ready during the acceleration process. After transitioning to a running gait, they ran at 2.4 m/s for another 30 seconds, before the treadmill was slowed down and stopped to allow a short break. Next, subjects completed the RWT protocol: running at 2.4 m/s for 30 seconds, then the treadmill was constantly decelerated at −0.1 m/s2 down to 1.8 m/s. Subjects were asked to transition to a walking gait whenever they felt ready during the deceleration process. Once they transitioned to a walking gait, they walked at 1.8 m/s for another 30 seconds. Treadmill acceleration and deceleration magnitude for the WRT and RWT protocols were chosen based on previous work [26]. Subjects were required to complete at least two WRT and RWT trials. Segmental kinematic data were collected at 120 Hz using an 8–camera motion capture system (Motion Analysis Corp., Santa Rosa, CA). Ground reaction force data were collected at 1200 Hz using the force–instrumented treadmill. Kinematic and kinetic data were filtered with a low–pass fourth–order Butterworth filter at 6 Hz and 50 Hz, respectively, based on previous studies [22,23,32,33,34].

2.3. Data Analysis

The transition step (S0) was determined based on the number of swing phases in vertical ground reaction force (GRF) data [19,20,21]. Specifically, the first step with double swing phases was regarded as S0 during WRT, and the first step with a single swing phase was regarded as S0 during RWT [19,20,21]. Vertical GRF threshold was set at 20 N to identify the stance phase between heel strike and toe off. All outcome variable calculations and analyses were focused on two steps before gait transition (S–2, S–1), the transition step (S0) and two steps after transition (S1, S2) for both WRT and RWT. Lower extremity joint angles, moments and net joint powers were calculated using an inverse dynamics model in Visual 3D (C–Motion, Inc., Germantown, MD). Joint stiffness ( K j o i n t ) was calculated as the change in sagittal plane joint moment ( ∆ M j o i n t ) divided by sagittal plane joint angular displacement ( ∆ θ j o i n t ) in the braking phase of ground contact [28,35], expressed as:
K j o i n t = ∆ M j o i n t ∆ θ j o i n t ,
Stance and swing phase joint positive work ( W j o i n t + ) and negative work ( W j o i n t − ) were calculated as the sum of all positive or negative net joint power integrated over time, respectively [27]. Stance phase joint extensor moment angular impulse ( I j o i n t ) was calculated as the sum of all stance phase extensor joint moment integrated over time [36,37]. Total lower extremity joint support moment impulse ( I t o t a l ) was calculated as the sum of ankle, knee and hip joint stance phase extensor moment angular impulse [36,37], expressed as
I t o t a l = I a n k l e + I k n e e + I h i p ,
Group average net joint power curves were plotted for each of the five steps analyzed for the WRT and RWT trials. Stance phase sagittal plane ankle joint angle–moment curves were averaged for further analysis.
Joint stiffness ( K j o i n t ), joint work ( W j o i n t ) and moment impulse ( I j o i n t ) were examined for differences between joints, and steps before, during and after the transition using 2–way ANOVAs (joint × step) for WRT and RWT in SPSS (V22.0, IBM, Armonk, NY). Total joint support moment impulse ( I t o t a l ) was examined using a 1–way ANOVA to compare between the five steps tested during WRT and RWT, respectively. Initial alpha level was set to 0.05. When main effect or interaction effects were detected, Bonferroni adjustments were used for pairwise comparison. The post–hoc alpha level was adjusted based on the comparison numbers. Joint level main effect pairwise comparison adjusted α was set at 0.0167, step main effect pairwise comparison adjusted α was set at 0.005. Joint × step interaction effect pairwise comparison α was set at 0.0011. Additionally, to identify whether each transition step is the walking or running pattern, paired t–test was conducted between peak ankle angle and moment during each transition step and the actual walking and running conditions between 1.8 m/s – 2.2 m/s from the previous studies with the same subjects [23].

3. Results

3.1. Joint Stiffness

Joint stiffness ( K j o i n t ) mean values are presented in Table 1. During WRT, K h i p was higher than K k n e e at S1 (p < 0.001), and K a n k l e was higher than K k n e e at S1 and S2 (p  ≤ 0.001). Within K a n k l e , S2 was higher than S–2, S–1 and S0 (p < 0.001); within K h i p , S1 was higher than S–2 and S–1 (p < 0.001). During RWT, K k n e e was lower than K a n k l e (p < 0.001) and K h i p (p < 0.001) at both S–2 and S–1. Within K a n k l e , S2 was lower than S–2 and S–1 (p < 0.001); S–1 was higher than S1 and S2 (p  ≤ 0.001) within K h i p .

3.2. Joint Mechanical Work

WRT W j o i n t mean values are presented in Table 2. During the WRT trials, stance phase W a n k l e + was higher than W k n e e + at S–2, S–1 and S2 (p < 0.001), W a n k l e + was also higher than W h i p + at S1 and S2 (p < 0.001), W k n e e + was higher than W h i p + at S1 and S2 (p  ≤ 0.001). Within W h i p + in stance, S–2 was higher than S1 and S2 (p < 0.001), S–1 was higher than S0, S1 and S2 (p < 0.001). Stance phase W k n e e − was higher than W a n k l e − at S–1 (p < 0.001), W k n e e − was also higher than W h i p − at S1 and S2 (p  ≤ 0.001). Within W a n k l e − in stance, S–2 was lower than S1 and S2 (p < 0.001), S–1 was lower than S1 and S2 (p < 0.001). During WRT in swing phase, W h i p + was higher than W a n k l e + and W k n e e + at all steps between S–2 and S2 (p < 0.001); within W h i p + , S–2 was lower than S1 (p < 0.001). Swing phase W k n e e − was higher than W a n k l e − and W h i p − at all steps (p < 0.001); among steps between S–1 and S1, W h i p − was higher than W a n k l e − (p < 0.001); within W k n e e − , S–2 and S–1 were lower than all steps between S0 and S2, respectively (p < 0.001).
For the RWT trials, W j o i n t mean values are presented in Table 3. Stance phase W a n k l e + was higher than W k n e e + and W h i p + at all steps between S–2 and S0, respectively (p  ≤ 0.001); W k n e e + was higher than W h i p + at S–2 and S–1 (p  ≤ 0.001). Within W a n k l e + in stance, S–2 was higher than S2 (p < 0.001); within W k n e e + , S–1 was higher than S1 (p = 0.001); within W h i p + , S–2 and S–1 were lower than steps between S1 and S2 (p  ≤ 0.001). Stance phase W a n k l e − was lower than W k n e e − at S1 and S2 (p < 0.001); within W a n k l e − , S–2 and S–1 were higher than all steps between S0 and S2 (p  ≤ 0.001). During RWT in swing phase, for positive work many significant differences were detected. Except for W k n e e + at S1, W h i p + was higher than W a n k l e + and W k n e e + among all other steps between S–2 and S2 (p < 0.001); W a n k l e + was higher than W k n e e + at S–1 (p < 0.001). Swing phase W k n e e − was higher than W a n k l e − and W h i p − at all steps, respectively (p < 0.001); W h i p − was also higher than W a n k l e − at all steps between S–1 and S2 (p  ≤ 0.001); within W k n e e − , S2 was lower than S–2 and S–1 (p < 0.001), and S0 was lower than S–1 (p < 0.001).

3.3. Joint Moment Angular Impulse

During WRT in stance phase (Table 4), I a n k l e was higher than I h i p at all steps, respectively (p  ≤ 0.001), I a n k l e was higher than I k n e e at S–2 and S–1 (p < 0.001), and I k n e e was higher than I h i p at S1 (p < 0.001); within I k n e e , S–2 was lower than S1 and S2 (p < 0.001), and S–1 was lower than S1 (p < 0.001); S–2 and S–1 was higher than all steps between S1 and S2 (p < 0.001), and S0 was higher than S1 (p < 0.001) within I h i p . During RWT in stance phase (Table 4), I a n k l e was higher than I h i p at all steps (p < 0.001), and I k n e e was higher than I h i p at S–2 and S–1 (p < 0.001); within I k n e e , S1 was lower than S–2 and S–1 (p < 0.001); within I h i p , S–2 was lower than S1 and S2 (p < 0.001), S–1 was lower than S2 (p < 0.001).

3.4. Joint Mechanical Power

During WRT trials, net joint power characteristics in all three joints at S0 were observed to be similar to running gait patterns (Figure 1). Stance phase peak power increased and time to peak power reduced at S0 compared with the previous walking stride. Specifically, peak negative ankle and knee joint power were 123% and 84% higher, respectively at S0 than S–1. The time to peak positive ankle and peak negative hip power were 52% and 59% lower, respectively at S0 than S–1. At S0 for the RWT process, joint power patterns tended to be a combination of both walking and running (Figure 2). Specifically, stance phase peak negative ankle and knee joint power were 94% and 41% lower, respectively at S0 than S–1. The peak negative ankle and knee joint power were 79% and 51% higher, respectively at S0 than S1.

4. Discussion

This study aimed to investigate lower extremity joint stance phase loading and response patterns, and functional roles of lower extremity joints in stance and swing phase during WRT and RWT processes. The hypothesis that K j o i n t would increase during WRT and decrease during RWT was partially supported. Specifically, K k n e e tended to remain unchanged across transition steps, K a n k l e and K h i p tended to increase from S0 to S2 during WRT, and decrease from S0 to S2 during RWT (Table 1). This indicates that the transition between walking and running has greater influence on ankle and hip joint dynamic loading and response rather than the knee. A previous study reported higher K a n k l e and K h i p in running compared with walking at the same speed [22], which supports the current gait transition findings. Additionally, K a n k l e and K h i p were both significantly different between steps before and after transition. This indicates both WRT and RWT were modulated over more than a single transition step. It also supports and expands the previous finding that ankle and hip mechanics would not only contribute to the WRT, but also the RWT at transition step [6].
The hypothesis that W j o i n t + , W j o i n t − and I j o i n t would increase during WRT and decrease during RWT was also partially supported. Specifically, only W a n k l e + and W k n e e + increased during WRT and decreased during RWT, which supported the hypothesis. During WRT stance phase, W a n k l e + and W k n e e + were 34% and 60% higher, respectively at S0 compared with S–1; while for W h i p + there was a significant decrease at S0 compared with S–1 (Table 2). This indicates W j o i n t + did not gradually change among the five steps during WRT, but rather changed instantaneously at the transition step and continue to modulate in the following steps. Furthermore, W a n k l e + and W k n e e + were higher compared to W h i p + within steps between S1 and S2, indicating that when switching from walking to running gait, the ankle and knee joint played more dominant roles in stance phase energy generation at S0 and the following steps (S1, S2). This observation agrees with previous reports [25]. Decreasing W h i p + while increasing W a n k l e + within the steps from S0 to S2 compared with previous steps before the transition indicated that during the WRT process, stance phase energy generation tended to transfer from proximal to distal. The redistribution of W j o i n t + among lower extremity joints at S0 was related to the mechanical load and efficiency trigger mechanisms which help modulate WRT: it would be favorable for hip muscles by reducing hip peak power and work at S0 during WRT [6,12,38]; and it would be more efficient for ankle plantar flexor power generation between S0 and S2 during WRT [6]. All these factors have been related to switching gait patterns from walking to running and should contribute to improving gait mechanical efficiency during the WRT [6,10].
During RWT stance phase, the ankle and knee played more dominant roles in energy generation within the pre–transition steps (S–2, S–1) (Table 3). The W a n k l e + and W k n e e + at S0 were 28% and 42% lower than at S–1, respectively; while W h i p + at S0 was 78% higher than at S–1 (Table 3). This indicates during RWT stance phase, energy generation tended to transfer from distal to proximal, and that W a n k l e + and W k n e e + decreased while W h i p + increased during and after transition. This may be due to a reduced requirement of ankle plantar flexor power and force generation efficiency in walking compared with running at S0 during RWT [6,10]. A previous study investigated walking and running across different speeds, reporting that the percentage and amount of W j o i n t + contributed to the total lower extremity positive work at fast walking speeds (1.8 and 2.0 m/s) were around 45% for W a n k l e + and 24% for W h i p + [22]; at slow running speeds (1.8 and 2.2 m/s), and that W a n k l e + contributed to 65% while W h i p + accounted for only 6% of total work also support the current finding that W j o i n t + would transfer between lower extremity joints when locomotion tasks changed between walking and running, even within the similar locomotion speed range [22]. The non–linear change of W j o i n t + generation at S0 to S2 compared with the pre–transition steps (S–2, S–1) also implied RWT occurred at the transition step and then continues to modulate during the following steps.
The energy generation transfer phenomenon among lower extremity joints at S0 during both WRT and RWT may be attributed to lower extremity distal joints having higher energy generation efficiency, or less required effort when running at speeds above PTS [6,10], and vice versa for the proximal joints when walking at speeds below PTS. Stance phase energy generation transfer was sensitive at transition step (S0) for both WRT and RWT. The redistribution of W j o i n t + and transfer mechanism can be attributed to the combined choice of gait transition trigger mechanisms: optimization of mechanical work efficiency, and minimization of musculoskeletal system effort at the transition step [6,10], both factors which help to modulate gait transitions. In the present study, the knee joint played an important function during both WRT and RWT stance phase energy absorption. In swing phase for both transition types, the hip and knee joints played dominant roles in energy generation and absorption.
During both WRT and RWT, I a n k l e accounted for more than 57% of I t o t a l at S–2 and S–1 during WRT, as well as at S1 and S2 during RWT (Table 4). This observation suggests that walking stance phase relies more on ankle plantar flexor moment for providing total body support and forward propulsion during both transitions. Additionally, I a n k l e was determined by ankle plantar flexor muscle moment and stance time. Stance time was changeable due to the continuous changing speed protocol in this study, while I a n k l e consistently contributed to nearly 50% of I t o t a l among all steps. This indicates ankle plantar flexor muscle force and moment compensate for the changeable stance time length, and they would help to maintain a relatively consistent I a n k l e output to support and move the body forward efficiently during the transitions between different locomotion tasks. During WRT, I k n e e at S0 was 70% higher than at S–1, indicating that additional knee joint extensor muscle work is needed in terminal stance phase at S0 to drive the body transitioning from walking to running gait, especially in preparation for the first flight phase immediately after the stance phase of S0.
Since ankle joint kinetics contribute to and help modulate both WRT and RWT, we further examined the stance phase sagittal plane ankle angle–moment relationship during both transitions (Figure 3). The ankle angle–moment relationship displayed a clockwise hysteresis curve [23,28,39,40]. The ascending phase can be regarded as a dynamic loading period, and the descending phase considered as an energy generation period [39].
During WRT trials, S–2 was similar to a standard walking gait pattern, however S1 and S2 exhibited a typical running gait pattern (Figure 3) [22,23]. No statistically significant difference (p > 0.05) between WRT peak ankle angle and moment at S–2, S–1 with actual walking at 1.8 m/s and 2.0 m/s, as well as the comparisons between S1, S2 during WRT with actual running at 2.2 m/s from previous study [23] confirm the above assumption. At S–1, the ankle started to plantar flex in mid–stance phase and the early plantar flexion movement resulted in peak ankle moment decreasing from 1.9 Nm/kg at S–2 to 1.6 Nm/kg at S–1 in terminal stance phase. This indicates that the ankle joint started to prepare for gait transition at S–1 due to the constantly accelerated speed. At S0, the curve was similar to a typical running gait pattern. Specifically, after initial contact, the ankle dorsiflexed to around –13°. Compared with S1 and S2, a relatively wide–open area between the ascending and descending phase at S0 indicated additional energy generation was needed at S0 to modulate and prepare for the following running strides during WRT. A significant difference (p = 0.002) between WRT peak ankle angle at S0 and actual walking at 2.0 m/s, as well as no significant difference between S0 at WRT and actual running at 1.8 m/s and 2.2m/s (p > 0.05) from previous study [23] also validates S0 at WRT is close to a running pattern.
During the RWT process, S–2, S–1 exhibited a typical running kinematic and kinetic pattern, while S1, S2 was similar to a walking pattern (Figure 3). No statistically significant difference (p > 0.05) between S–2, S–1 and actual running at 2.2 m/s, as well as between S1, S2 and actual walking at 1.8 m/s from previous [23] study further confirms this observation. A four–phase pattern was observed at S0. After initial contact, the ankle dorsiflexed to a smaller angle, around –5° in the ascending phase, then plantar flexed with a slight increase in ankle moment. This may be attributed to the constantly decelerating speed, along with an increase in stance time. Compared with a typical walking condition, the energy generation period during S0 was observed to be earlier. The ankle kinematic and kinetic pattern at S0 were both closer to the walking gait pattern. No statistically significant difference (p > 0.05) of peak ankle angle and moment between S0 at RWT and actual walking at 2.0 m/s, as well as significant difference (p < 0.05) between S0 and actual running at 1.8 m/s or 2.2 m/s from previous study [23] also validates it.
A unique ankle angle–moment curve pattern at S0 was observed in both WRT and RWT. During WRT, it was similar to a running gait pattern; however, it appeared to be a combination of both walking and running conditions during RWT, with the kinematic and kinetic values closer to the walking gait pattern. This observation reveals that during RWT a longer time was needed to adjust and modulate the motor response compared with the WRT. For both WRT and RWT, we recorded the treadmill instantaneous speed at S0 as the PTS. During WRT, the calculated PTS was 2.06 ± 0.09 m/s, and transition time was about 2.6 seconds (from 1.80 – 2.06 m/s). For the RWT, the calculated PTS was 1.97 ± 0.10 m/s, and transition time was about 4.3 seconds (from 2.40 – 1.97 m/s). These results confirm that subjects needed more time to modulate the RWT process compared with the WRT.
One limitation of this study is that only one magnitude of acceleration and deceleration was used for transitions. Different acceleration and deceleration magnitudes would likely affect the PTS and possibly the gait patterns of the transition step [8]. This limits the generalizability of our findings.

5. Conclusions

In conclusion, the reorganization processes of the WRT and RWT were modulated before and after transitions and gait transition is not a single step event. Both WRT and RWT exhibited unique ankle and hip joint stiffness characteristics at the transition step and then continued to modulate those patterns in subsequent steps. Stance phase energy generation tended to transfer from proximal to distal joints during WRT, and vice versa during the RWT process. Redistribution of joint mechanical work generation suggests that mechanical efficiency and load triggers were the key factors modulating the gait transition. Ankle kinematic and kinetic patterns at transition step were similar to the target locomotion task format in both WRT and RWT. With the same continuously accelerated or decelerated speed, it takes longer to modulate and finish the RWT than WRT. Overall, gait transitions appeared to distinctively affect lower extremity joint kinetic patterns.

Author Contributions

Conceptualization, L.J. and M.E.H.; methodology, L.J. and M.E.H.; software, L.J.; validation, L.J.; formal analysis, L.J.; investigation, L.J.; resources, M.E.H.; data curation, L.J.; writing—original draft preparation, L.J.; writing—review and editing, M.E.H.; visualization, L.J.; supervision, M.E.H.; project administration, L.J. and M.E.H.; funding acquisition, L.J. and M.E.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Betty Foster McCue Scholarship at the University of Oregon.

Institutional Review Board Statement

This study was conducted in accordance with the Declaration of Helsinki, and was approved by the Institutional Review Board of the University of Oregon (protocol #07302015.030).

Informed Consent Statement

Informed consent was obtained from all of the subjects involved in the study.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

We would like to thank Alex Denton and Zoey Kearns for their assistance in the data processing.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Lipfert, S.W.; Günther, M.; Renjewski, D.; Grimmer, S.; Seyfarth, A. A Model-Experiment Comparison of System Dynamics for Human Walking and Running. J Theor Biol 2011, 292C, 11–17. [Google Scholar] [CrossRef] [PubMed]
  2. Segers, V.; Aerts, P.; Lenoir, M.; De Clercq, D. Dynamics of the Body Centre of Mass during Actual Acceleration across Transition Speed. J Exp Biol 2007, 210, 578–585. [Google Scholar] [CrossRef] [PubMed]
  3. Farley, C.T.; Ferris, D.P. Biomechanics of Walking and Running: Center of Mass Movements to Muscle Action. Exerc Sport Sci Rev 1998, 26, 253–285. [Google Scholar] [CrossRef]
  4. Lipfert, S.W.; Günther, M.; Renjewski, D.; Grimmer, S.; Seyfarth, A. A Model-Experiment Comparison of System Dynamics for Human Walking and Running. J Theor Biol 2012, 292, 11–17. [Google Scholar] [CrossRef] [PubMed]
  5. Saibene, F.; Minetti, A.E. Biomechanical and Physiological Aspects of Legged Locomotion in Humans. Eur J Appl Physiol 2003, 88, 297–316. [Google Scholar] [CrossRef] [PubMed]
  6. Pires, N.J.; Lay, B.S.; Rubenson, J. Joint-Level Mechanics of the Walk-to-Run Transition in Humans. Journal of Experimental Biology 2014, 217, 3519–3527. [Google Scholar] [CrossRef] [PubMed]
  7. Raynor, A.J.; Yi, C.J.; Abernethy, B.; Jong, Q.J. Are Transitions in Human Gait Determined by Mechanical, Kinetic or Energetic Factors? Hum Mov Sci 2002, 21, 785–805. [Google Scholar] [CrossRef]
  8. Li, L. Stability Landscapes of Walking and Running near Gait Transition Speed. J Appl Biomech 2000, 16, 428–435. [Google Scholar] [CrossRef]
  9. Kung, S.M.; Fink, P.W.; Legg, S.J.; Ali, A.; Shultz, S.P. What Factors Determine the Preferred Gait Transition Speed in Humans? A Review of the Triggering Mechanisms. Hum Mov Sci 2018, 57, 1–12. [Google Scholar] [CrossRef]
  10. Farris, D.J.; Sawicki, G.S. The Mechanics and Energetics of Human Walking and Running: A Joint Level Perspective. J R Soc Interface 2012, 9, 110–118. [Google Scholar] [CrossRef]
  11. Neptune, R.R.; Clark, D.J.; Kautz, S. a. Modular Control of Human Walking: A Simulation Study. J Biomech 2009, 42, 1282–1287. [Google Scholar] [CrossRef] [PubMed]
  12. Sasaki, K.; Neptune, R.R. Muscle Mechanical Work and Elastic Energy Utilization during Walking and Running near the Preferred Gait Transition Speed. Gait Posture 2006, 23, 383–390. [Google Scholar] [CrossRef] [PubMed]
  13. Diedrich, F.J.; Warren, W.H. Why Change Gaits? Dynamics of the Walk-Run Transition. J Exp Psychol Hum Percept Perform 1995, 21, 183–202. [Google Scholar] [CrossRef]
  14. Minetti, A.E.; Ardigo, L.P.; Saibene, F. The Transition between Walking and Running in Humans: Metabolic and Mechanical Aspects at Different Gradients. Acta Physiol Scand 1994, 150, 315–323. [Google Scholar] [CrossRef] [PubMed]
  15. Farley, C.T.; Taylor, C.R. A Mechanical Trigger for the Trot-Gallop Transition in Horses. Science (1979) 1991, 253, 306–308. [Google Scholar] [CrossRef] [PubMed]
  16. Hreljac, A. Preferred and Energetically Optimal Gait Transition Speeds in Human Locomotion. Med Sci Sports Exerc 1993, 25, 1158–1162. [Google Scholar] [CrossRef] [PubMed]
  17. Hreljac, A. Determinants of the Gait Transition Speed during Human Locomotion: Kinematic Factors. J Biomech 1995, 28, 669–677. [Google Scholar] [CrossRef]
  18. Hreljac, A.; Imamura, R.T.; Escamilla, R.F.; Edwards, W.B.; MacLeod, T. The Relationship between Joint Kinetic Factors and the Walk-Run Gait Transition Speed during Human Locomotion. J Appl Biomech 2008, 24, 149–157. [Google Scholar] [CrossRef]
  19. Li, L.; Hamill, J. Characteristics of the Vertical Ground Reaction Force Component Prior to Gait Transition. Res Q Exerc Sport 2002, 73, 229–237. [Google Scholar] [CrossRef]
  20. Zhang, S.; Pan, J.; Li, L. Non-Linear Changes of Lower Extremity Kinetics Prior to Gait Transition. J Biomech 2018, 77, 48–54. [Google Scholar] [CrossRef]
  21. Li, L.; Ogden, L.L. Muscular Activity Characteristics Associated with Preparation for Gait Transition. J Sport Health Sci 2012, 1, 27–35. [Google Scholar] [CrossRef]
  22. Jin, L.; Hahn, M.E. Modulation of Lower Extremity Joint Stiffness, Work and Power at Different Walking and Running Speeds. Hum Mov Sci 2018, 58, 1–9. [Google Scholar] [CrossRef]
  23. Jin, L.; Hahn, M.E. Comparison of Lower Extremity Joint Mechanics between Healthy Active Young and Middle Age People in Walking and Running Gait. Sci Rep 2019, 9, 5568. [Google Scholar] [CrossRef]
  24. Segers, V.; Aerts, P.; Lenoir, M.; De Clercq, D. External Forces during Actual Acceleration across Transition Speed. J Appl Biomech 2008, 24, 340–350. [Google Scholar] [CrossRef]
  25. Segers, V.; De Smet, K.; Van Caekenberghe, I.; Aerts, P.; De Clercq, D. Biomechanics of Spontaneous Overground Walk-to-Run Transition. Journal of Experimental Biology 2013, 216, 3047–3054. [Google Scholar] [CrossRef] [PubMed]
  26. Segers, V.; Aerts, P.; Lenoir, M.; De Clercq, D. Spatiotemporal Characteristics of the Walk-to-Run and Run-to-Walk Transition When Gradually Changing Speed. Gait Posture 2006, 24, 247–254. [Google Scholar] [CrossRef] [PubMed]
  27. Schache, A.G.; Brown, N.A.T.; Pandy, M.G. Modulation of Work and Power by the Human Lower-Limb Joints with Increasing Steady-State Locomotion Speed. Journal of Experimental Biology 2015, 218, 2472–2481. [Google Scholar] [CrossRef] [PubMed]
  28. Kuitunen, S.; Komi, P. v; Kyröläinen, H.; Kyrolainen, H. Knee and Ankle Joint Stiffness in Sprint Running. Med. Sci. Sports Exerc. 2002, 34, 166–173. [Google Scholar] [CrossRef]
  29. Stefanyshyn, D.J.; Stergiou, P.; Lun, V.M.Y.; Meeuwisse, W.H.; Worobets, J.T. Knee Angular Impulse as a Predictor of Patellofemoral Pain in Runners. American Journal of Sports Medicine 2006, 34, 1844–1851. [Google Scholar] [CrossRef]
  30. Farris, D.J.; Sawicki, G.S. The Mechanics and Energetics of Human Walking and Running: A Joint Level Perspective. J R Soc Interface 2012. [Google Scholar] [CrossRef]
  31. Sawers, A.; Hahn, M.E. Regulation of Whole-Body Frontal Plane Balance Varies within a Step during Unperturbed Walking. Gait Posture 2012, 36, 322–324. [Google Scholar] [CrossRef] [PubMed]
  32. Russell Esposito, E.; Blanck, R.V.; Harper, N.G.; Hsu, J.R.; Wilken, J.M. How Does Ankle-Foot Orthosis Stiffness Affect Gait in Patients with Lower Limb Salvage? Clin Orthop Relat Res 2014, 472, 3026–3035. [Google Scholar] [CrossRef] [PubMed]
  33. Russell Esposito, E.; Choi, H.S.; Owens, J.G.; Blanck, R.V.; Wilken, J.M. Biomechanical Response to Ankle-Foot Orthosis Stiffness during Running. Clinical Biomechanics 2015, 30, 1125–1132. [Google Scholar] [CrossRef] [PubMed]
  34. Russell Esposito, E.; Ranz, E.C.; Schmidtbauer, K.A.; Neptune, R.R.; Wilken, J.M. Ankle-Foot Orthosis Bending Axis Influences Running Mechanics. Gait Posture 2017, 56, 147–152. [Google Scholar] [CrossRef] [PubMed]
  35. Hobara, H.; Baum, B.S.; Kwon, H.J.; Miller, R.H.; Ogata, T.; Kim, Y.H.; Shim, J.K. Amputee Locomotion: Spring-like Leg Behavior and Stiffness Regulation Using Running-Specific Prostheses. J Biomech 2013, 46, 2483–2489. [Google Scholar] [CrossRef] [PubMed]
  36. DeVita, P.; Hortobagyi, T. Age Causes a Redistribution of Joint Torques and Powers during Gait. J Appl Physiol 2000, 88, 1804–1811. [Google Scholar] [CrossRef] [PubMed]
  37. Winter, D.A.; Patla, A.E.; Frank, J.S.; Walt, S.E. Biomechanical Walking Pattern Changes in the Fit and Healthy Elderly. Phys Ther 1990, 70, 340–347. [Google Scholar] [CrossRef] [PubMed]
  38. Sasaki, K.; Neptune, R.R. Differences in Muscle Function during Walking and Running at the Same Speed. J Biomech 2006, 39, 2005–2013. [Google Scholar] [CrossRef]
  39. Crenna, P.; Frigo, C. Dynamics of the Ankle Joint Analyzed through Moment-Angle Loops during Human Walking: Gender and Age Effects. Hum Mov Sci 2011, 30, 1185–1198. [Google Scholar] [CrossRef]
  40. Gabriel, R.C.; Abrantes, J.; Granata, K.; Bulas-Cruz, J.; Melo-Pinto, P.; Filipe, V. Dynamic Joint Stiffness of the Ankle during Walking: Gender-Related Differences. Physical Therapy in Sport 2008, 9, 16–24. [Google Scholar] [CrossRef]
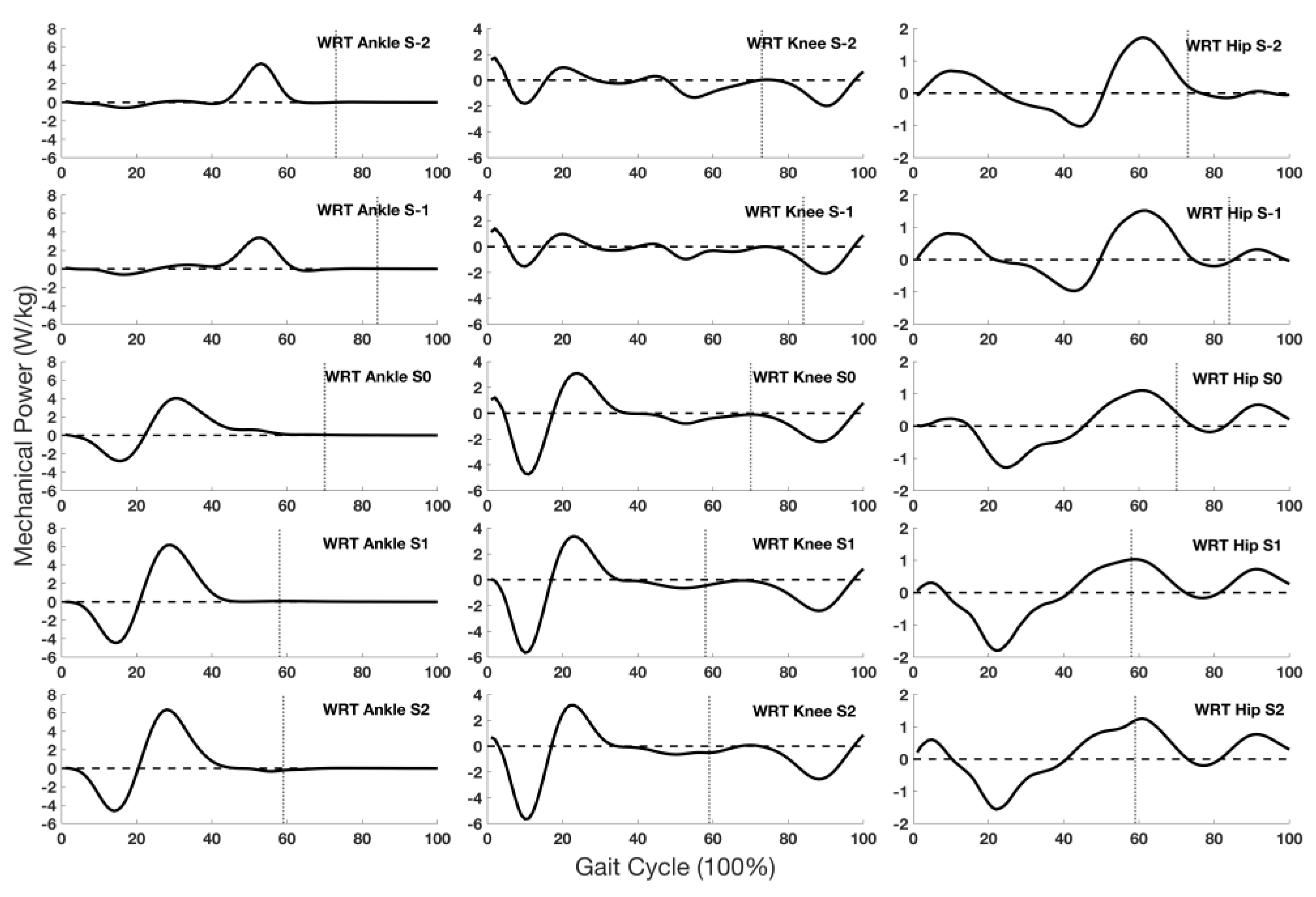
Preprints 101152 g001
Figure 1. Group average (n = 10) ankle, knee and hip (left to right) joint power curves across the WRT steps (S–2 top to S2 bottom). Vertical dash line is the boundary between stance and swing phase. Time normalized to whole gait cycle.
Figure 1. Group average (n = 10) ankle, knee and hip (left to right) joint power curves across the WRT steps (S–2 top to S2 bottom). Vertical dash line is the boundary between stance and swing phase. Time normalized to whole gait cycle.
Preprints 101152 g001
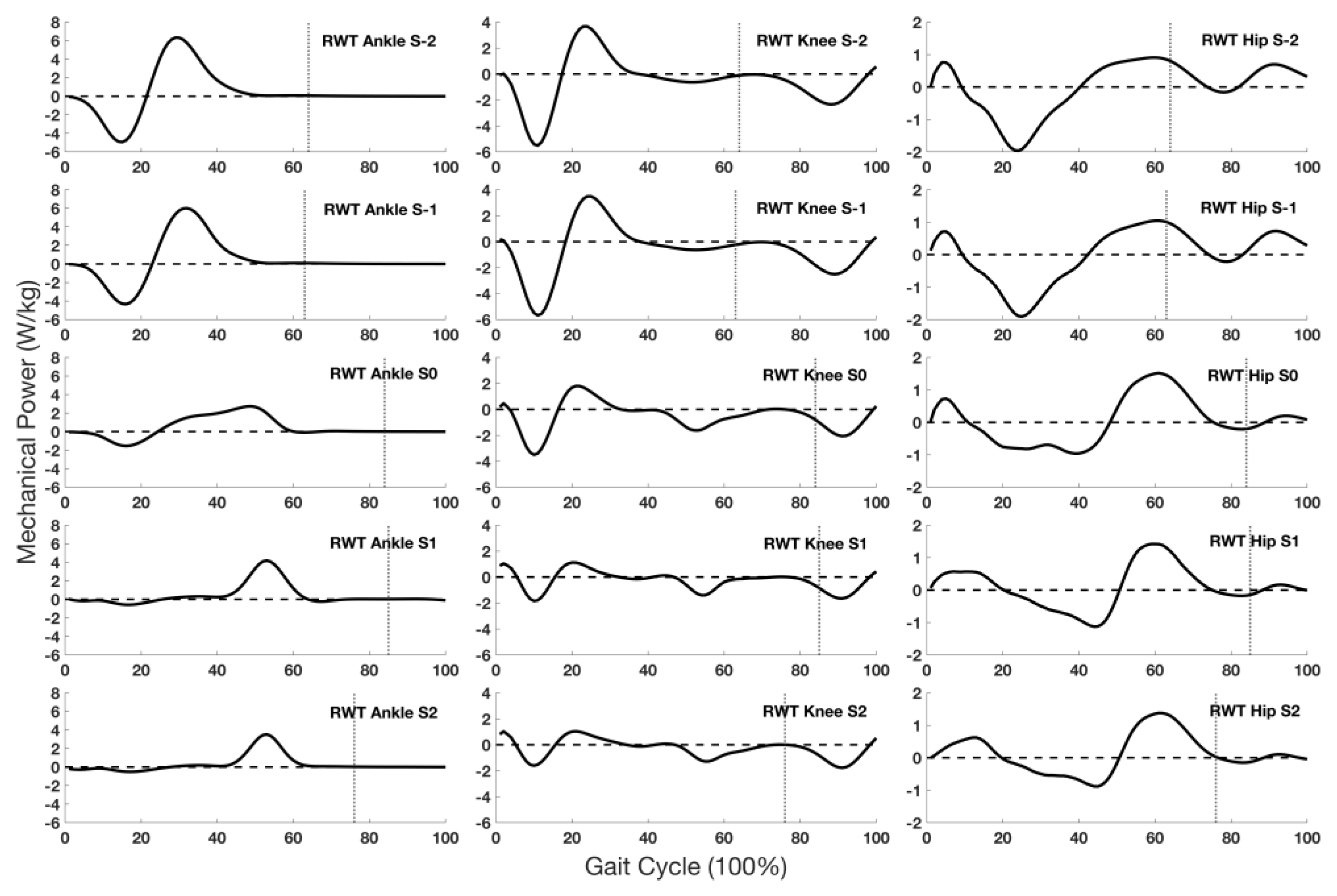
Preprints 101152 g002
Figure 2. Group average (n = 10) ankle, knee and hip (left to right) joint power curves across the RWT steps (S–2 top to S2 bottom). Vertical dash line is the boundary between stance and swing phase. Time normalized to whole gait cycle.
Figure 2. Group average (n = 10) ankle, knee and hip (left to right) joint power curves across the RWT steps (S–2 top to S2 bottom). Vertical dash line is the boundary between stance and swing phase. Time normalized to whole gait cycle.
Preprints 101152 g002
Preprints 101152 g003
Figure 3. Group average (n = 10) ankle joint angle–moment curves (stance phase only) across the WRT steps (left) and RWT steps (right).
Figure 3. Group average (n = 10) ankle joint angle–moment curves (stance phase only) across the WRT steps (left) and RWT steps (right).
Preprints 101152 g003
Table 1. Joint stiffness (Nm/kg/deg) across WRT and RWT steps. Sample Mean (SD); n = 10.
Table 1. Joint stiffness (Nm/kg/deg) across WRT and RWT steps. Sample Mean (SD); n = 10.
Joint Stiffness (Nm/kg/deg) Steps
S−2 S−1 S0 S1 S2
WRT
Ankle 0.13 (0.05) c 0.12 (0.04) c 0.16 (0.09) c 0.23 (0.11) b 0.24 (0.10) b,c
Knee 0.11 (0.05) 0.10 (0.03) 0.11 (0.06) 0.11 (0.05) a,b 0.11 (0.06) b
Hip 0.08 (0.03) d 0.08 (0.02) d 0.17 (0.09) 0.20 (0.06) a,d 0.24 (0.12)
RWT
Ankle 0.21 (0.09) e,g 0.18 (0.07) e,g 0.19 (0.10) 0.15 (0.06) 0.13 (0.06) g
Knee 0.12 (0.08) e,f 0.11 (0.07) e,f 0.12 (0.07) 0.12 (0.07) 0.09 (0.04)
Hip 0.21 (0.12) f 0.18 (0.07) f,h 0.12 (0.05) 0.11 (0.05) h 0.08 (0.05) h
a: Statistically significant differences between K h i p and K k n e e at S1 during WRT, (p < 0.001); b: differences between K a n k l e and K k n e e at S1 and S2 (p  ≤ 0.001) during WRT; c: differences between S2 and S−2, S2 and S−1, S2 and S0 (p < 0.001) during WRT, within K a n k l e ; d: differences between S1 and S−2, S1 and S−1 (p < 0.001) during WRT, within K h i p ; e: differences between K a n k l e and K k n e e at S−2 and S−1 (p < 0.001) during RWT; f: differences between K h i p and K k n e e at S−2 and S−1 (p < 0.001) during RWT; g: differences between S2 and S−2, S2 and S−1 (p < 0.001) during RWT, within K a n k l e ; h: differences between S−1 and S1, S−1 and S2 (p  ≤ 0.001) during RWT, within K h i p .
Table 2. Joint work (J/kg) across WRT steps. Sample Mean (SD); n = 10.
Table 2. Joint work (J/kg) across WRT steps. Sample Mean (SD); n = 10.
Joint Work (J/kg) Steps
S−2 S−1 S0 S1 S2
Stance Phase Positive Work
Ankle 0.40 (0.16) a 0.39 (0.13) a 0.55 (0.25) 0.63 (0.29) b 0.61 (0.23) a,b
Knee 0.21 (0.08) a 0.20 (0.08) a 0.37 (0.19) 0.31 (0.15) c 0.28 (0.14) a,c
Hip 0.20 (0.07) d 0.24 (0.08) e 0.09 (0.09) e 0.05 (0.05) b,c,d,e 0.06 (0.03) b,c,d,e
Stance Phase Negative Work
Ankle −0.10 (0.04) h −0.11 (0.06) f,i −0.28 (0.13) −0.36 (0.12) h,i −0.36 (0.08) h,i
Knee −0.30 (0.21) −0.24 (0.06) f −0.41 (0.32) −0.43 (0.18) g −0.41 (0.21) g
Hip −0.17 (0.12) −0.15 (0.08) −0.22 (0.18) −0.24 (0.19) g −0.19 (0.19) g
Swing Phase Positive Work
Ankle j 0.01 (0.00) 0.01 (0.00) 0.01 (0.00) 0.01 (0.00) 0.01 (0.00)
Knee k 0.02 (0.02) 0.02 (0.01) 0.01 (0.01) 0.01 (0.01) 0.03 (0.04)
Hip j,k 0.14 (0.03) l 0.13 (0.06) 0.21 (0.07) 0.23 (0.07) l 0.26 (0.11)
Swing Phase Negative Work
Ankle m −0.01 (0.03) <−0.01 (0.00) o <−0.01 (0.00) o <−0.01 (0.00) o −0.03 (0.10)
Knee m,n −0.23 (0.03) p −0.24 (0.04) q −0.31 (0.05) p,q –0.34 (0.06) p,q −0.35 (0.06) p,q
Hip n −0.03 (0.02) −0.02 (0.01) o −0.02 (0.01) o –0.02 (0.01) o −0.02 (0.01)
Note: W j o i n t < 0.01 indicates a negligible value. a: Statistically significant differences between W a n k l e + and W k n e e + at S−2, S−1 and S2 (p < 0.001) during stance; b: differences between W a n k l e + and W h i p + at S1 and S2 (p < 0.001) during stance; c: differences between W k n e e + and W h i p + at S1 and S2 (p  ≤ 0.001) during stance; d: differences between S−2 and S1, S−2 and S2 (p < 0.001) during stance, within W h i p + ; e: differences between S−1 and S0, S−1 and S1, S−1 and S2 (p < 0.001) during stance, within W h i p + ; f: Differences between W a n k l e − and W k n e e − at S−1 during stance, (p < 0.001); g: differences between W k n e e − and W h i p − at S1 and S2 (p  ≤ 0.001) during stance; h: differences between S−2 and S1, S−2 and S2 (p < 0.001) during stance, within W a n k l e − ; i: differences between S−1 and S1, S−1 and S2 (p < 0.001) during stance, within W a n k l e − ; j: differences between W h i p + and W a n k l e + during swing for all steps, (p < 0.001); k: differences between W h i p + and W k n e e + during swing for all steps, (p < 0.001); l: differences between S−2 and S1 during swing within W h i p + , (p < 0.001); m: differences between W k n e e − and W a n k l e − during swing for all steps, (p < 0.001); n: differences between W k n e e − and W h i p − during swing for all steps, (p < 0.001); o: differences between W a n k l e − and W h i p − during swing, for all steps between S−1 and S1, (p < 0.001); p: Differences between S−2 and all steps between S0 and S2 during swing, within W k n e e − , (p < 0.001); q: differences between S−1 and all steps between S0 and S2 during swing, within W k n e e − , (p < 0.001).
Table 3. Joint work (J/kg) across RWT steps. Sample Mean (SD); n = 10.
Table 3. Joint work (J/kg) across RWT steps. Sample Mean (SD); n = 10.
Joint Work (J/kg) Steps
S−2 S−1 S0 S1 S2
Stance Phase Positive Work
Ankle 0.67 (0.31) a,b,d 0.66 (0.33) a,b 0.50 (0.21) a,b 0.48 (0.34) 0.37 (0.20) d
Knee 0.33 (0.16) a,c 0.32 (0.15) a,c,e 0.21 (0.14) a 0.23 (0.17) e 0.19 (0.11)
Hip 0.06 (0.04) b,c,f 0.07 (0.05) b,c,g 0.16 (0.08) b 0.20 (0.06) f,g 0.18 (0.04) f,g
Stance Phase Negative Work
Ankle −0.41 (0.19) i −0.38 (0.18) j −0.17 (0.12) i,j −0.12 (0.08) h,i,j −0.10 (0.05) h,i,j
Knee −0.41 (0.21) −0.45 (0.24) −0.42 (0.22) −0.28 (0.10) h −0.26 (0.06) h
Hip −0.25 (0.22) −0.26 (0.18) −0.23 (0.18) −0.22 (0.15) −0.18 (0.11)
Swing Phase Positive Work
Ankle l 0.01 (0.00) 0.01 (0.00) m 0.01 (0.00) 0.01 (0.01) 0.01 (0.00)
Knee k 0.01 (0.01) <0.01 (0.00) m 0.01 (0.01) 0.02 (0.04) 0.01 (0.01)
Hip k,l 0.22 (0.09) 0.22 (0.09) 0.13 (0.04) 0.12 (0.06) 0.12 (0.03)
Swing Phase Negative Work
Ankle n <−0.01 (0.00) <−0.01 (0.00) p <−0.01 (0.00) p <−0.01 (0.00) p <−0.01 (0.00) p
Knee n,o −0.33 (0.09) q −0.34 (0.08) q,r −0.23 (0.05) r −0.21 (0.08) −0.21 (0.04) q
Hip o −0.01 (0.01) −0.02 (0.01) p −0.02 (0.01) p −0.02 (0.01) p −0.02 (0.01) p
Note: W j o i n t < 0.01 indicates a negligible value. a: Statistically significant differences between W a n k l e + and W k n e e + during stance for all steps between S−2 and S0, (p  ≤ 0.001); b: differences between W a n k l e + and W h i p + during stance for all steps between S−2 and S0, (p  ≤ 0.001); c: differences between W k n e e + and W h i p + at S−2 and S−1 during stance (p  ≤ 0.001); d: differences between S−2 and S2 during stance within W a n k l e + (p < 0.001); e: differences between S−1 and S1 during stance within W k n e e + (p = 0.001); f: differences between S−2 and steps between S1 and S2 during stance, within W h i p + (p  ≤ 0.001); g: differences between S−1 and steps between S1 and S2 during stance, within W h i p + (p  ≤ 0.001); h: differences between W a n k l e − and W k n e e − at S1 and S2 (p < 0.001) during stance; i: Differences between S−2 and steps between S0 and S2 during stance, within W a n k l e − (p  ≤ 0.001); j: differences between S−1 and steps between S0 and S2 during stance, within W a n k l e − (p  ≤ 0.001); k: differences between W h i p + and W k n e e + during swing for all steps, except for W k n e e + at S1, (p < 0.001); l: differences between W h i p + and W a n k l e + during swing for all steps, (p < 0.001); m: differences between W a n k l e + and W k n e e + at S−1 during swing (p < 0.001); n: differences between W k n e e − and W a n k l e − for all steps during swing (p < 0.001); o: differences between W k n e e − and W h i p − for all steps during swing (p < 0.001); p: differences between W a n k l e − and W h i p − for steps between S−1 and S2 during swing (p  ≤ 0.001); q: Differences between S2 and S−2, S2 and S−1 (p < 0.001) during swing, within W k n e e − ; r: differences between S−1 and S0 during swing, within W k n e e − , (p < 0.001).
Table 4. Joint stance phase extensor moment angular impulse (Nm · s/kg) and total joint support moment impulse (Nm · s/kg) across WRT and RWT steps. Sample Mean (SD); n = 10.
Table 4. Joint stance phase extensor moment angular impulse (Nm · s/kg) and total joint support moment impulse (Nm · s/kg) across WRT and RWT steps. Sample Mean (SD); n = 10.
Impulse   ( Nm · s/kg) Steps
S−2 S−1 S0 S1 S2
WRT
Ankle a 0.40 (0.12) b 0.36 (0.07) b 0.38 (0.12) 0.41 (0.15) 0.40 (0.11)
Knee 0.16 (0.12) b,d 0.14 (0.08) b,e 0.29 (0.19) 0.30 (0.14) c,d,e 0.26 (0.15) d
Hip a 0.12 (0.03) f 0.12 (0.02) g 0.10 (0.04) h 0.05 (0.03) c,f,g,h 0.07 (0.02) f,g
Total 0.68 (0.23) 0.62 (0.12) 0.77 (0.28) 0.76 (0.28) 0.73 (0.24)
RWT
Ankle i 0.46 (0.22) 0.44 (0.21) 0.41 (0.19) 0.44 (0.24) 0.37 (0.15)
Knee 0.30 (0.15) j,k 0.32 (0.15) j,k 0.25 (0.13) 0.18 (0.10) k 0.16 (0.08)
Hip i 0.06 (0.03) j,l 0.06 (0.04) j,m 0.08 (0.05) 0.12 (0.04) l 0.11 (0.04) l,m
Total 0.82 (0.36) 0.82 (0.36) 0.73 (0.33) 0.75 (0.37) 0.65 (0.24)
a: Statistically significant differences between I a n k l e and I h i p for all steps during WRT (p  ≤ 0.001); b: differences between I a n k l e and I k n e e at S−2 and S−1 (p < 0.001) during WRT; c: differences between I k n e e and I h i p at S1 during WRT (p < .001); d: differences between S−2 and S1, S−2 and S2 (p < 0.001) during WRT, within I k n e e ; e: differences between S−1 and S1 during WRT, within I k n e e (p < 0.001); f: differences between S−2 and S1, S−2 and S2 during WRT, within I h i p (p < 0.001); g: differences between S−1 and S1, S−1 and S2 during WRT, within I h i p (p < 0.001); h: differences between S0 and S1 during WRT, within I h i p (p < 0.001); i: differences between I a n k l e and I h i p for all steps during RWT (p < 0.001); j: differences between I k n e e and I h i p at S−2 and S−1 (p < 0.001) during RWT; k: differences between S1 and S−2, S1 and S−1 (p < 0.001) during RWT, within I k n e e ; l: differences between S−2 and S1, S−2 and S2 (p < 0.001) during RWT, within I h i p ; m: differences between S−1 and S2 during RWT, within I h i p (p < 0.001).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated