Direct and Indirect Effects of Mountain Heights on Heavy Rainfall in the Hokitika Region of New Zealand

Very heavy stratiform precipitation (> 200 mm/per day) occurred in the Hokitika region on the west coast of the South Island of New Zealand on 18 June 2015, under north-westerlies with small CAPE (< 25 J/kg). Analyses of model simulations and observations showed that this heavy rainfall was due to cold front lifting enhanced by orographic lifting over the Southern Alps. At 1.5 km grid-length, the model terrain underestimated the average height of the 103 tallest mountains over the South Island by ~ 800 m. This leads to weaker orographic lifting and mountain blocking, and a faster-moving and stronger cold front in the Hokitika region. As a result, large errors in the heavy rainfall prediction occur. By increasing either the resolved or the sub-grid mountain heights, the simulated rainfall errors were largely reduced through stronger orographic lifting and mountain blocking, and a better simulation of the cold front movement and strength. All the experiments have the same “flow-over” regime with mountain waves and/or wave breaking (Fm ranges 0.61 – 1.21). However, the rainfall amount and distribution on the windward side of mountains altered significantly. Our new findings were that the Southern Alps can have significant indirect effects on heavy rainfall by altering the speed and strength of the cold front, in addition to the well-known direct dynamical effects (i.e., orographic lifting and mountain blocking). A combination of these direct and indirect effects makes the heavy rainfall simulation sensitive to mountain heights even under the same “flow-over” regime.

Keywords:

Subject: Environmental and Earth Sciences - Atmospheric Science and Meteorology

1. Introduction

Mountains significantly affect the amount and distribution of rainfall through the nonlinear interactions of mountain blocking, orographic lifting, and land surface processes (Colle, 2004; Smith and Barstad, 2004; Yang and Chen, 2008; Houze, 2012; Colle et al., 2013; Chow et al., 2013; Stockham et al., 2018; Smith, 2019). In general, orographic lifting of airflow produces much more rainfall on the windward side of mountains than in the lee where descent of airflow occurs. For conditionally unstable airflow passing over a bell-shaped mountain ridge, idealized numerical experiments showed that the moist flow regimes (or precipitation distribution) can be controlled by the moist Froude number (defined as

F_{m} = \frac{U}{N_{m} h}

, where

U

is the basic-state wind speed,

N_{m}

the moist Brunt–Väisälä frequency, and

h

the maximum ridge height, Colle, 2004) and CAPE (convective available potential energy, Chen and Lin, 2005a, 2005b). Idealised numerical simulations of conditionally unstable flows past a mountain ridge performed by Miglietta and Rotunno (2009, 2010 and 2012) found that rainfall amount/rate and distribution can be controlled by a combination of the parameters

U

, CAPE,

N_{m}

h

, ridge half-width, tropopause height, LFC (level of free convection), and downdraft CAPE.

A cold front is one of the major weather systems causing heavy rainfall. Mountains can distort cold fronts by dynamically enhancing or slowing down their movement, and strengthen or weaken them (Egger and Hoinka, 1992; Colle et al., 1999; Steenburgh and Blazek, 2001; Schultz, 2004; Steenburgh et al., 2009; West and Steenburgh, 2010; etc.). The dynamical effects of mountains are determined by not only their height but also their aspect ratio or shape, and the mountain size (Smith, 1989; Yang and Chen, 2008). Therefore, in numerical weather prediction (NWP) of heavy rainfall, the height, size, and shape of mountains should be well described in the model’s terrain to accurately simulate a mountain’s dynamical effects.

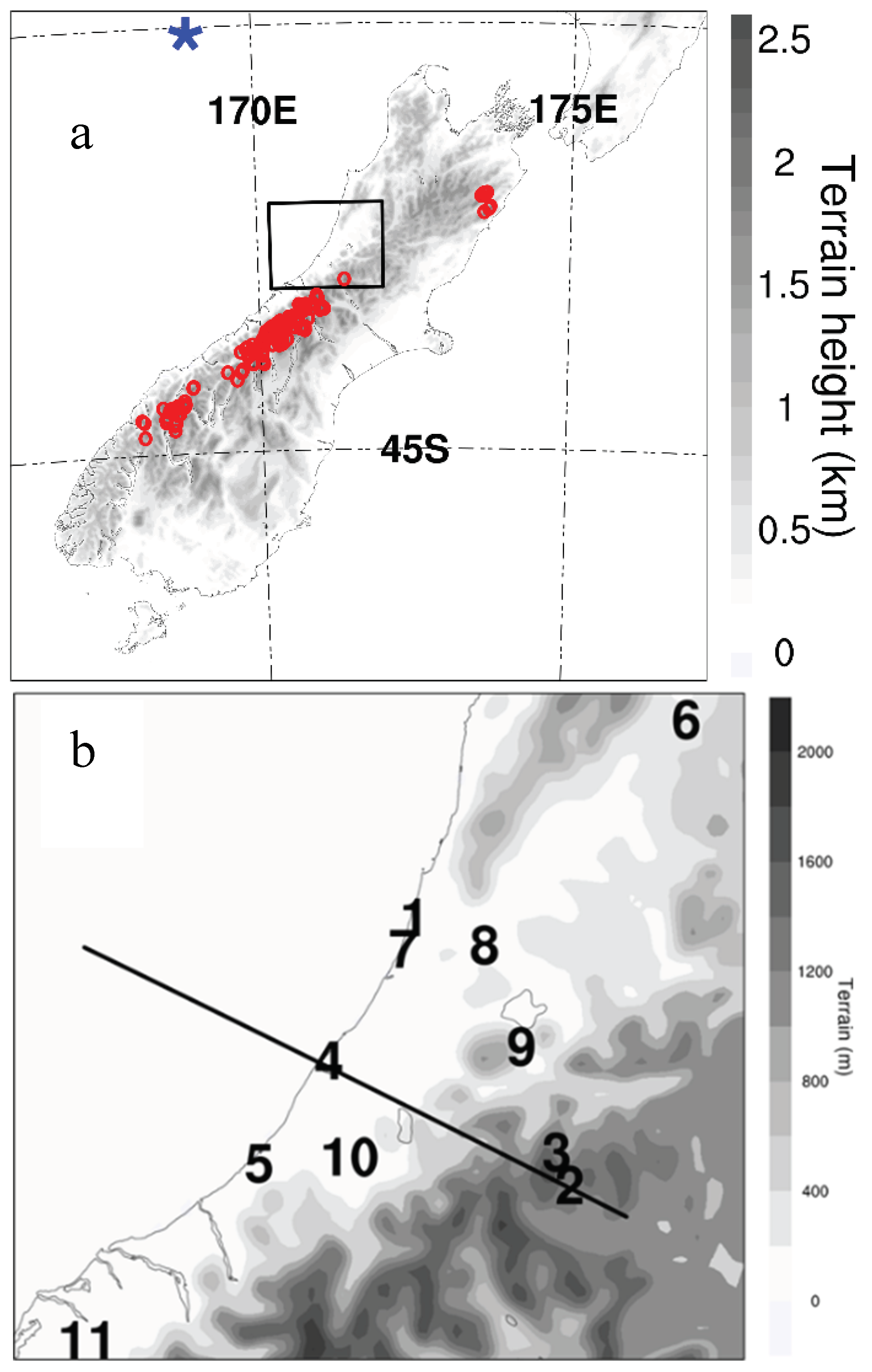
New Zealand’s South Island lies in the mid-latitude southwest Pacific, surrounded by ocean. The main mountain range, with a southwest to northeast orientation, is known as the Southern Alps (Figure 1a). Under the prevailing mid-latitude westerly winds, the western region of the South Island is generally the windward side and the eastern region is the lee side, with cold fronts being one of the major weather systems to produce rainfall in this region.

Overall, rainfall amounts are much higher over land areas than over the nearby sea and much more rainfall occurs over the western side of the South Island than over other parts of the country (Salinger, 1980; Tait and Fitzharris, 1998; Yang et.al., 2015; Shu et al., 2021) due to the orographic lifting of more consistent westerly airflows by the Southern Alps (Sturman and Wanner, 2001). Heavy rainfall frequently occurs in the Southern Alps. It is not uncommon that the total annual rainfall exceeds 10,000 mm or that daily maxima exceed 500 mm at some locations on the upper slopes (Griffiths and McSaveney, 1983a; Whitehouse, 1985; Henderson and Thompson, 1999; Griffiths, 2011). One example of a heavy rainfall event is one that occurred in the Hokitika region on the western side of the Southern Alps on 18 June 2015, with daily rainfall maxima greater than 200 mm.

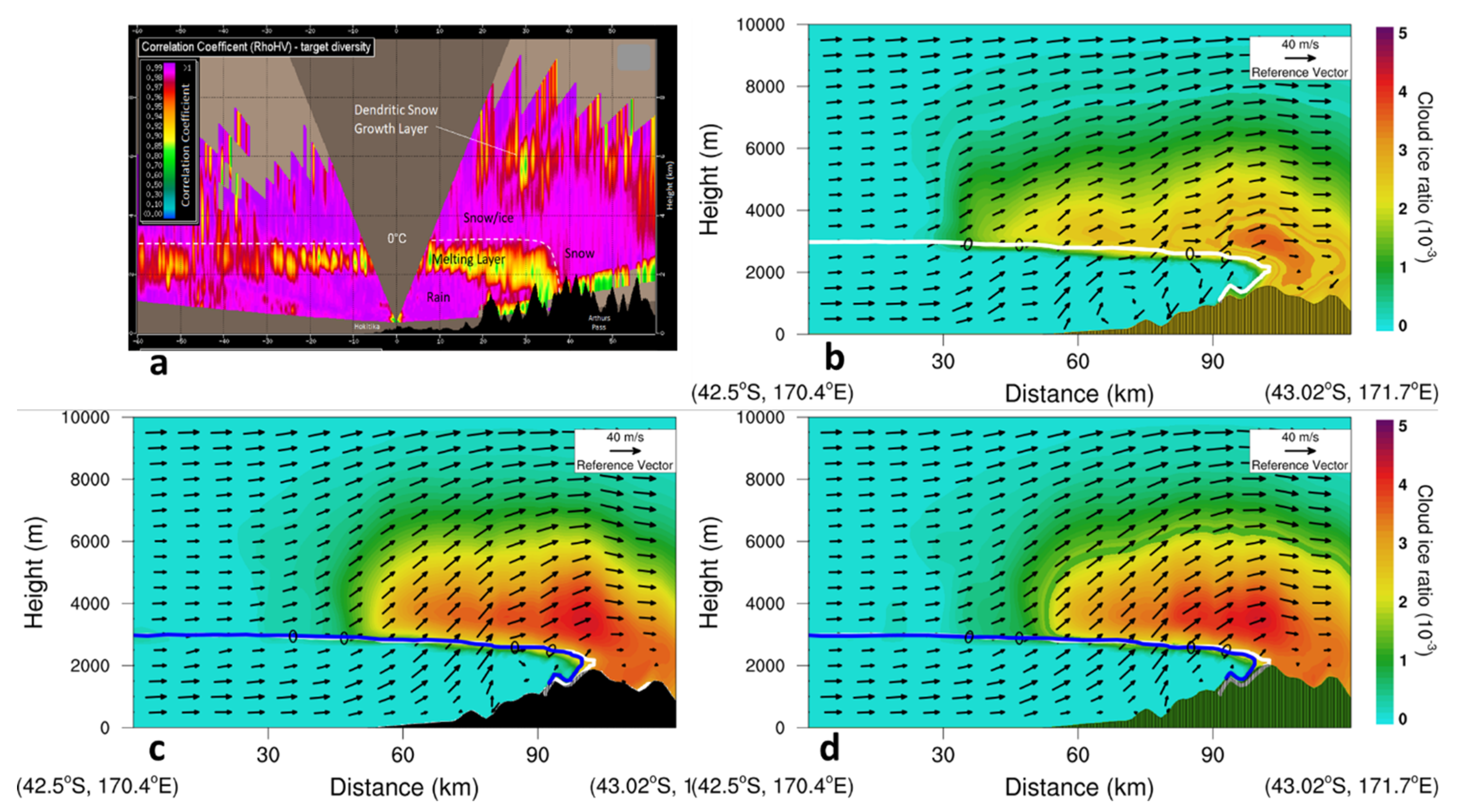
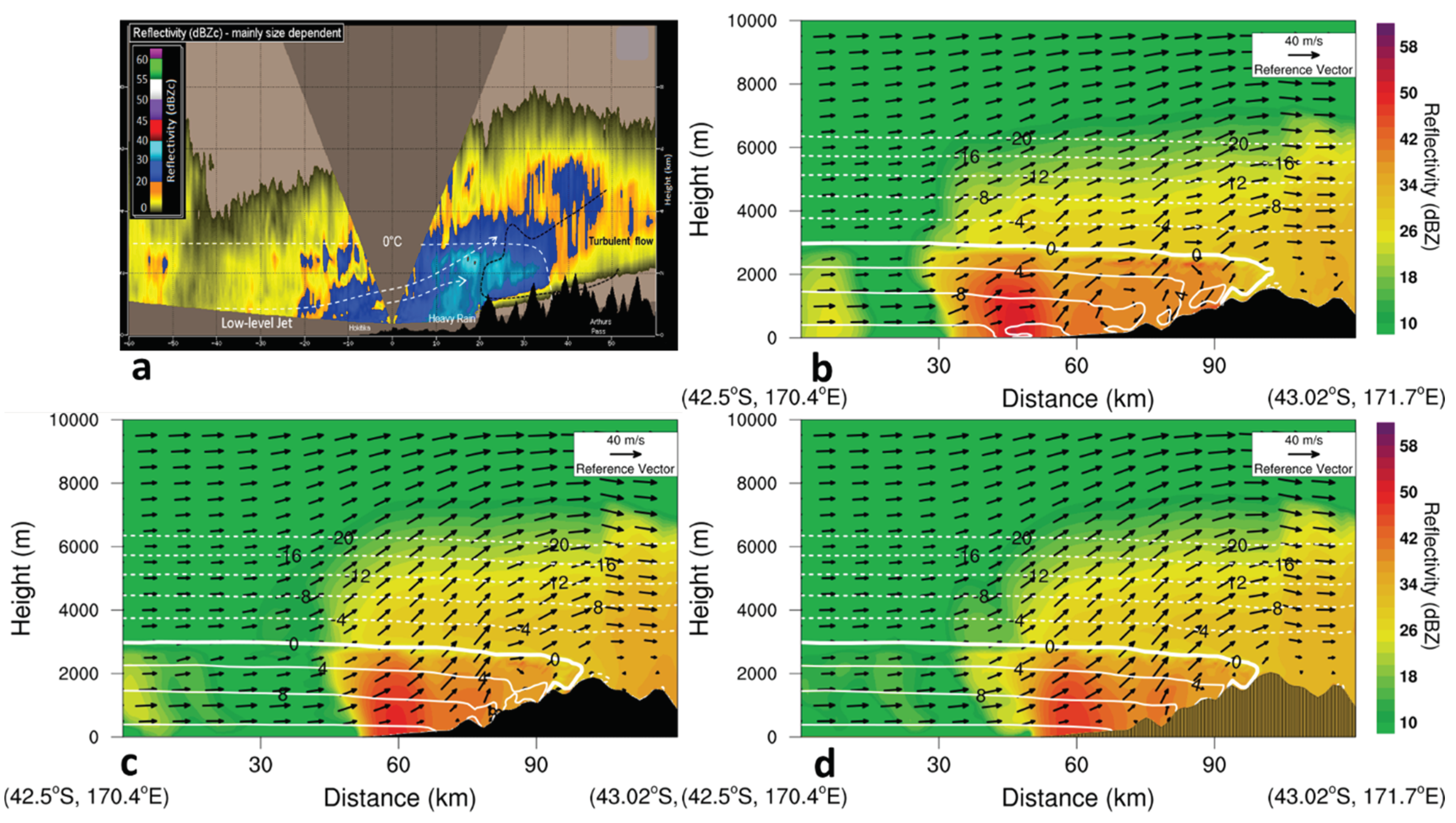
This study was initially motivated by a comparison of the New Zealand Convective-Scale Model (NZCSM, Yang et al., 2017) forecasts with the dual-polarisation radar observations of the New Zealand MetService at Hokitika for the same heavy rainfall event. See Crouch and Russell (2021) for more information about the radar observation analysis. An advantage of the dual-polarisation radar is the freezing level (0 °C air temperature height) can be reliably identified from the radar cross-section echo. A pronounced difference in the 0 °C air temperature curve between the simulation and the radar observations was the prominent eastern extension (~ 10 km) of the simulated 0 °C air temperature curve over the high mountains in the middle of the South Island around 1830 NZST on 18 June 2015 (Figure 2, see more information in Section 3). It is hypothesised that the eastern extension/penetration of the simulated 0 °C curve over the high mountains was due to the model terrain being lower than the actual terrain and weaker mountain blocking. Testing this hypothesis is one objective of this study. Furthermore, we will investigate the key processes leading to this heavy rainfall event, how well these processes are described in the model, and how these processes are affected by the mountain heights and the sub-grid mountain heights. Following the introduction, descriptions of the model and the weather situation are given in Section 2. Results showing the effects of resolved mountain heights are described in Section 3. The effects of sub-grid orographic information are described in Section 4 with a discussion is presented in Section 5 followed by concluding remarks.

2. Description of the model and the weather situation

The model used in this study is the regional configuration of the Met Office Unified Model (UM). The UM uses the ENDGame dynamical core which employs a semi-implicit semi-Lagrangian formulation to solve the non-hydrostatic, fully compressible deep-atmosphere equations of motion (Wood et al., 2014; Walters et al., 2017). Two domains with grid-lengths of 12 km and 1.5 km have been used in this study. The 12 km grid-length domain has almost the same domain size as the New Zealand Limited Area Model (NZLAM, 324x324 horizontal grid points, Yang et al., 2012), uses the GA6 physics settings (Walters et al., 2017), and was driven by Met Office global UM forecasts (N768, ~ 17 km grid-length). The 12-km grid-length domain provides lateral boundary conditions for the 1.5-km grid-length domain (1350x1200 horizontal grid points), which uses the first Regional Atmosphere and Land (RAL1) science configuration for mid-latitude regions (Bush et al., 2020), and had 70 vertical levels with the model top at 40 km. The model was initialized at 0000 NZST 18 June 2015 (CTRL, Table 1) and run for 36 hours.

On 18 June 2015, heavy rainfall occurred in the Hokitika region. The observed daily rainfall at 0900 NZST 19 June 2015 was ~ 211 mm at Hokitika Airport (Site 4 in Figure 1b), a new record, and ~ 330 mm at Inchbonnie, located on the windward foothills of the Southern Alps to the east of Hokitika (Site 9 in Figure 1b).

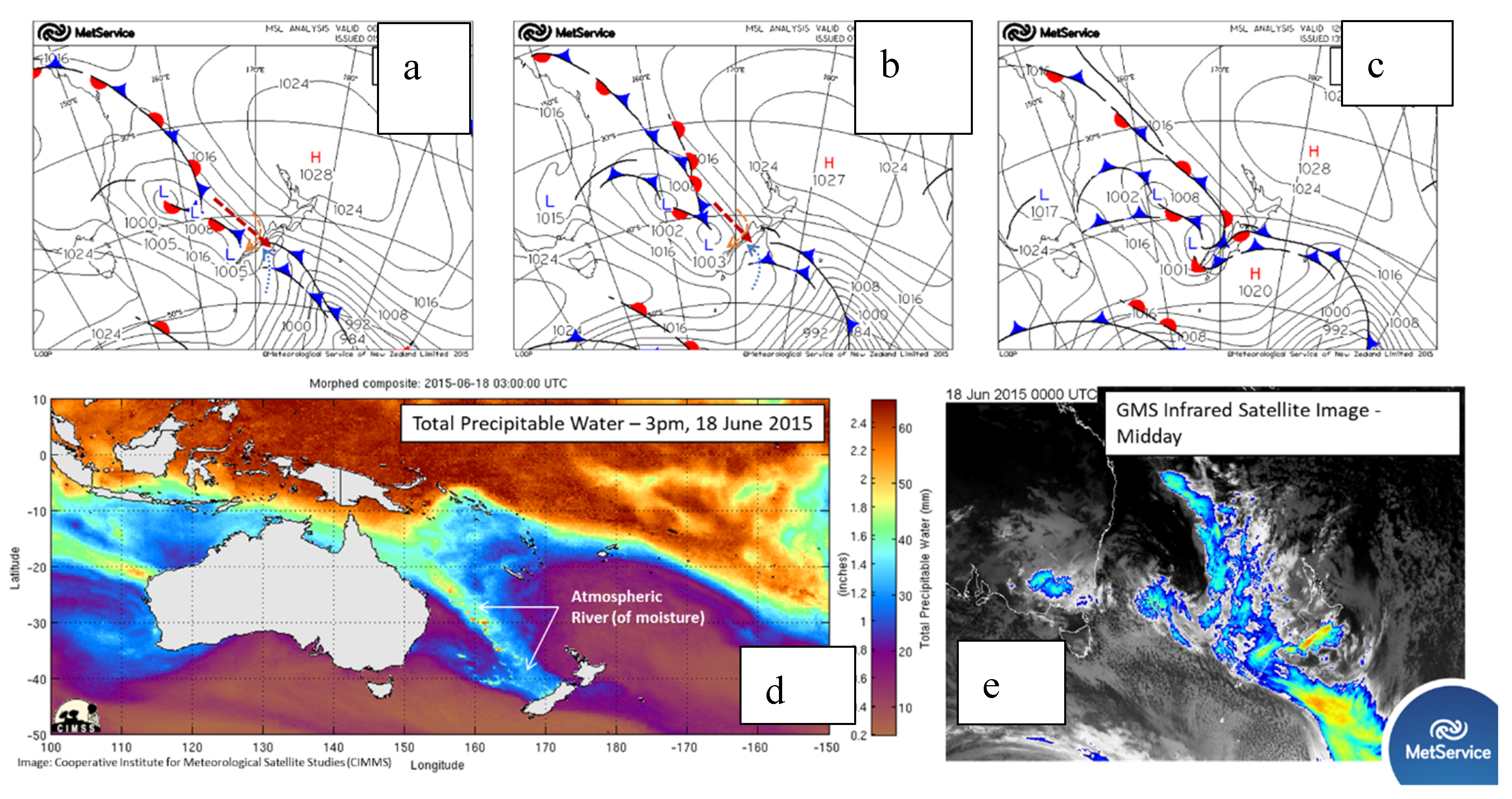
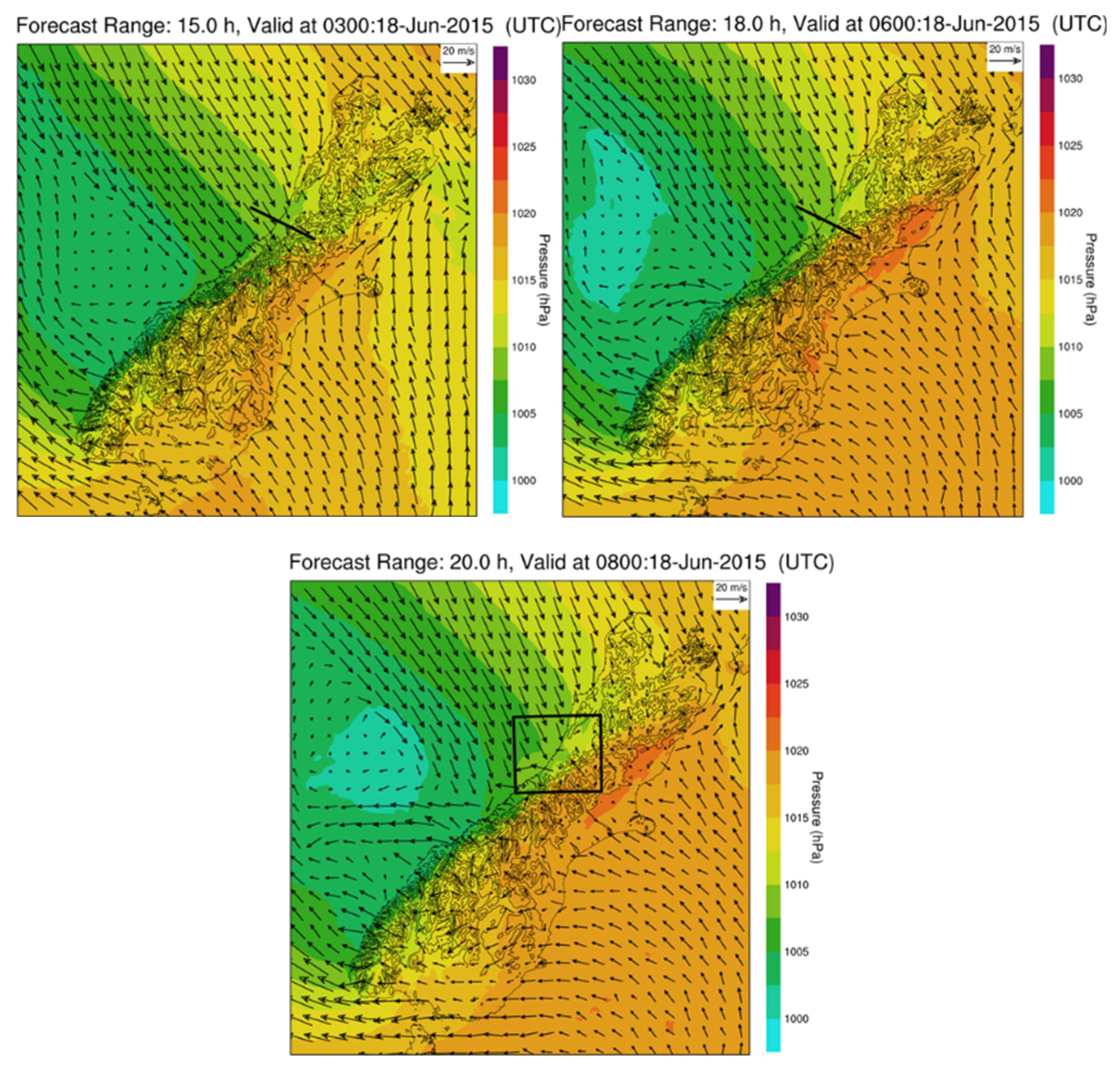
At the surface on 18 June 2015 (Figure 3), a high-pressure centre was observed to the southwest of New Zealand and another to the northeast. Between the two highs was a narrow trough of low pressure with northwest-southeast orientation crossing the South Island. The strong and warm northwest airflow associated with the low supplied abundant moisture (Figure 3), via an “atmospheric river”, a common moisture supply condition for heavy rainfall occurrence in New Zealand (Shu et al., 2021). A cold front with overall northwest-southeast orientation was found over the sea between the north-westerly moist warm air and the south-easterly and southerly cold air. This cold front gradually moved toward the northeast.

To the east side of the South Island at the surface, cold southerlies and south-easterlies were found behind the cold front (Figure 4). The cold front over land on the east of the South Island moved faster toward the north than that on the west, and had a southwest to northeast orientation, which is a typical orientation for cold fronts over the South Island (Smith et al., 1991; Sturman et al., 1992; Yang et al., 2012).

The southerly and south-easterly cold airflows near the surface gradually moved over the high mountains from the east of the Southern Alps and descended on the west side (Figure 4, Figure 5). To the west of the Southern Alps, the cold front at the surface was found between the cold air and the warm moist north-westerly airflow, and also had a southwest-northeast orientation (Figure 6), in significant contrast to the cold front over the sea that had a northwest-southeast orientation (Figure 3). The cold front over land gradually moved from the high mountains to the lowlands and coastal area (Figure 6). Around 1800 NZST, the cold front reached Hokitika Airport from the eastern lowlands. As described in detail later, the upward motion of the cold front, enhanced by orographic lifting, was the dominant dynamical process for the heavy rainfall occurrence in the Hokitika region, which was liquid precipitation. However, over the high mountains and the east side of the Southern Alps, heavy snow occurred on that day. In this study, we focused on the heavy liquid rainfall in the Hokitika region.

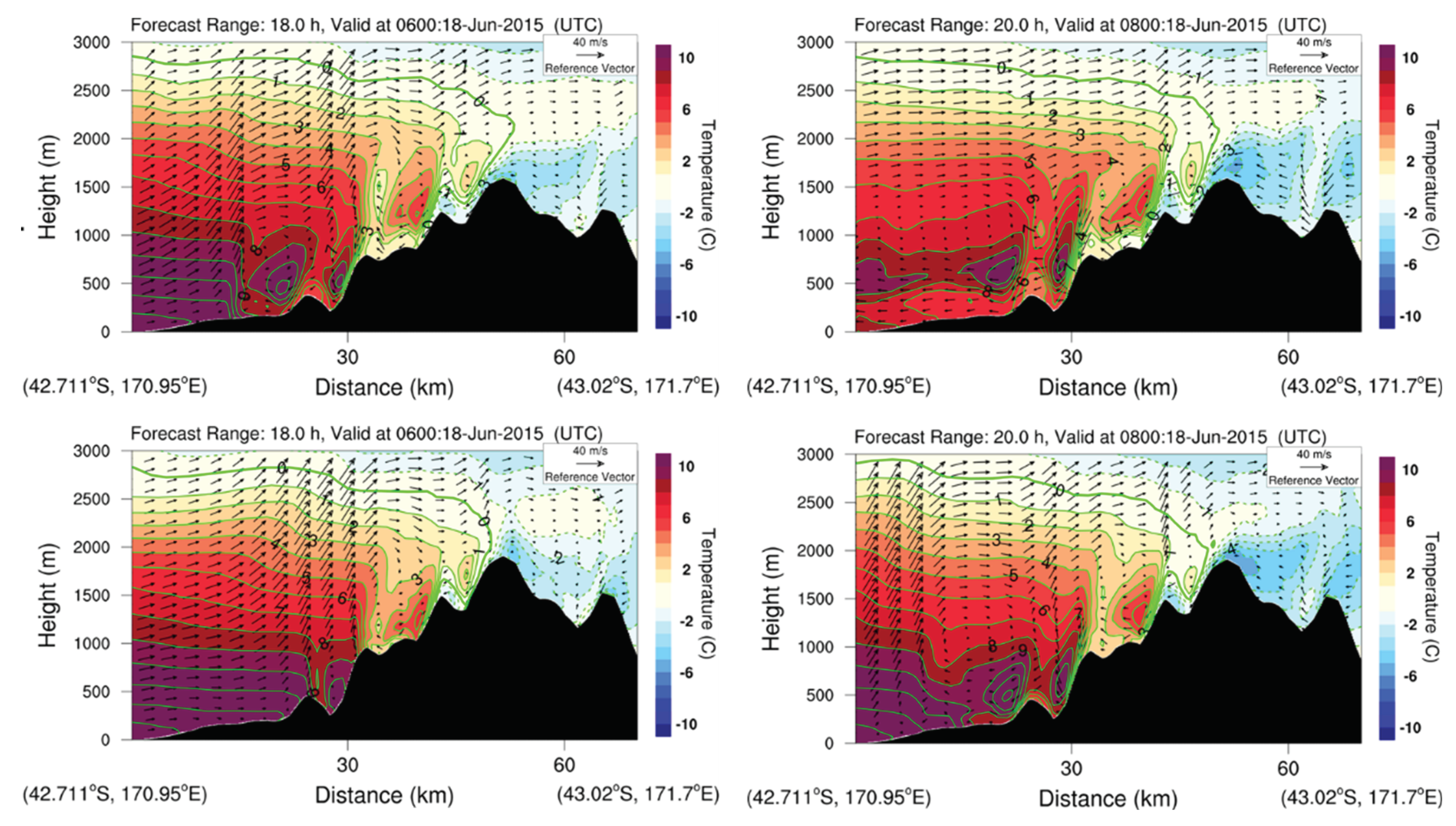
Figure 5. Cross-sections along the solid line in Figure 1b for the simulated winds and air temperature by CTRL at 1800 NZST (a) and 2000 NZST (b), and by 1.2X at 1800 NZST (c) and 2000 NZST (d) on 18 June 2015.

Figure 6. Simulated surface winds and air temperature by CTRL at 1500 NZST (a), 1800 NZST (b), and 2000 NZST (c), and by 1.2X at 1500 NZST (d), 1800 NZST (e), and 2000 NZST (f) on 18 June 2015. Blue dashed lines denote positions of the cold fronts. See Figure 4c for the location of the area.

3. Effects of model resolved mountain heights

The Southern Alps consist of many mountains with heights over 2000 m above sea-level. It is the combined effect of the many high mountains that contributes to the strong dynamic effects, such as mountain blocking and orographic lifting, rather than a single peak. To quantify how NZCSM’s model terrain underestimated the mountain heights, we calculated the average height of the 103 tallest mountains with the heights larger than 2400 m on the South Island (Figure 1a). The average height is ~ 2600 m. However, the average height of the corresponding mountains peaks in the model terrain of NZCSM is only ~ 1800 m. Overall, the model terrain underestimated the mountain heights by ~ 800 m. One of the major error sources comes from the smoothing which is applied to the terrain as standard in all NWP models to achieve dynamical stability. This led us to conduct numerical experiments where the terrain heights were uniformly increased, as a method of understanding the effects of the missing orography without compromising model stability.

In this study, the simulation using the original NZCSM terrain file is labelled CTRL. Numerical experiments where the model terrain is increased by 1.1 (1.1X), 1.2 (1.2X), 1.3 (1.3X), and 1.4 (1.4X) times the CTRL model terrain were conducted and labelled accordingly (Table 1). All the experiments used exactly the same lateral boundary conditions that were provided by the 12 km resolution simulations, and the same initial lower boundary conditions except for terrain heights. We will investigate how these different mountain heights affect the simulated air temperature, surface winds, cold front, and rainfall in the Hokitika region on 18 June 2015. For brevity and clarity, analyses are mainly presented for CTRL, 1.2X, and 1.3X.

The effect of mountains on the surrounding atmosphere can be determined by the mountain Rossby radius of deformation,

L_{R} = \frac{N h}{f},

where

f

is the Coriolis parameter,

h

is the mountain height, and

N

is the Brunt–Väisälä frequency. For the Southern Alps in the mid-latitudes with average mountain height ranges from 1800 m for CTRL to 2520 m for 1.4X, considering a typical value 0.01

s^{- 1}

for

N

L_{R}

ranges from ~ 180 km for CTRL to 250 km for 1.4X. This indicates that the influence of the Southern Alps on the environmental airflow extends 180 - 250 km away for all the experiments. To calculate the moist Froude Number

F_{m}

for the moist northwesterly airflows affecting the Southern Alps, a location (169°E and 40.1°S, Figure 1a) about 300 km to the northwest from Hokitika was chosen.

F_{m}

was calculated using model outputs at this location for the 0 – 3 km height layer around 1800 NZST 18 June 2015 when heavy rainfall started to occur at Hokitika (Table 1). The calculation of

F_{m}

used model outputs instead of observations because of a lack of radiosonde observation data over the sea to the west of the Southern Alps. In fact, using model forecasts is more appropriate than using observations because we investigated the effects of model terrain under the model atmosphere.

F_{m}

ranged 0.61 – 1.21 for the numerical experiments described earlier and was almost the same during the time periods of the intensive precipitation, indicating a “flow-over” regime with mountain waves (the gravity waves excited as airflow past mountains) and/or mountain wave breaking for the Southern Alps with the aspect ratio of ~ 1/4 (Smith, 1989; Epifanio, 2003).

3.1. CTRL simulation

As described earlier, cold air near the surface behind the cold front moved from the east side of the Southern Alps, passed over the high mountains and descended on the west side. The adiabatic descent gradually warmed the cold air near the surface. For CTRL (Figures 5a, b), when the cold front and the south-easterly cold air reached the low-lands in the Hokitika region at 1800 NZST 18 June, the air temperature was ~ 6°C near the surface, while it was ~ −4°C near the surface of the high mountains, a ~ 10°C increase due to the adiabatic descent warming. At 2000 NZST, the cold front and the cold south-easterlies moved further westward offshore on the west side (Figure 5b, Figure 6c). Immediately above the surface south-easterly cold airflows over the coastal area and lowlands, warmer airflows with an easterly wind direction were found for the 400 – 1000 m height layer (Figure 5b), and were the north-easterly barrier jets indicated by Crouch and Russell (2021) based on analysis of radar observations. Over the coastal area offshore, the barrier jets mixed with surface cold air, leading to the change of surface wind direction from south-easterly to easterly (Figure 6c). Barrier jets frequently occur in the coastal areas of the South Island (Revell et al., 2002; Yang et al., 2017). The warm north-westerly airflow (including the barrier jets) was lifted by the cold front (Figures 5a, b). This cold front lifting was further enhanced by the orographic lifting above (Figure 5) for the heavy rainfall production.

3.2. Effect of higher mountains on freezing heights

Figure 2 shows the dual-polarisation radar observations and the simulated ice ratio, air temperature, and winds. The freezing height, indicated by the 0° C curve over the western side of the Southern Alps, was simulated at ~ 3 km height for CTRL (white contour, Figure 2b), 1.2X and 1.3X (blue contours, Figures 2c, d), close to the dual-polarisation radar observations (white dotted line, Figure 2a). Compared with the radar observations, the eastern extension of the 0° C curve over high mountains in CTRL was largely corrected by the 1.2X and 1.3X experiments that exhibit a much smaller eastern extension of the 0° C curve over high mountains than CTRL. As analysed in Section 3.3 later, this was mainly due to weaker simulated north-westerly winds and weaker warm advection over the high mountains below 3 km height when compared against CTRL.

For the radar observations, the maximum cloud ice ratio (Figure 2a, shading) over high mountains extended over 5 km in height. This feature was better simulated by 1.2X and 1.3X than CTRL, which showed lower cloud ice ratio over high mountains than 1.2X and 1.3X (Figures 2b, c, d, shading).

3.3. Effects of higher mountains on air temperature, winds, and the cold front

With higher mountains in 1.2X and 1.3X than for CTRL (Figure 5, Figure 6 and Figure 7), three pronounced features can be found in the Hokitika region: i) the adiabatic descent warming of the south-easterly cold air near the surface was more significant with larger temperature increases (3 – 5 K) for 1.2X and 1.3X than for CTRL on the west lowlands after the cold air past over the high mountains; ii) the wind speed of the cold south-easterly winds near the surface behind the cold front was 2 – 5 m/s weaker and the westward movement of the cold front was slower for 1.2X and 1.3X, and iii) the orographic lifting of the north-westerly airflow above the easterly cold winds was stronger for 1.2X and 1.3X.

The westward movement of the cold front over land on the west side of the South Island was improved in the 1.2X and 1.3X simulations. In the Hokitika region, there are only four stations that have routine hourly observations for precipitation, surface winds and air temperature. Figure 7 shows the observations and simulations at the four stations (See Table 2 and Figure 1b for location details). Over the South Island, the passage of a cold front is also called a “southerly change” due to a pronounced wind change to southerly and a large drop in air temperature. At these sites, these features associated with the passage of the cold front were well captured and simulated. The simulation of these two features was better in the 1.2X and 1.3X experiments than in the CTRL. For example, at Mt. Philistine the passage of the cold front was observed during 1900 – 2000 NZST, while it was simulated at ~ 1800 NZST for 1.2X and 1600 – 1700 NZST for CTRL. At Greymouth, the passage of the cold front was simulated at 2100 – 2200 NZST, consistent with the observations, while it was simulated in 1900 – 2000 NZST for CTRL.

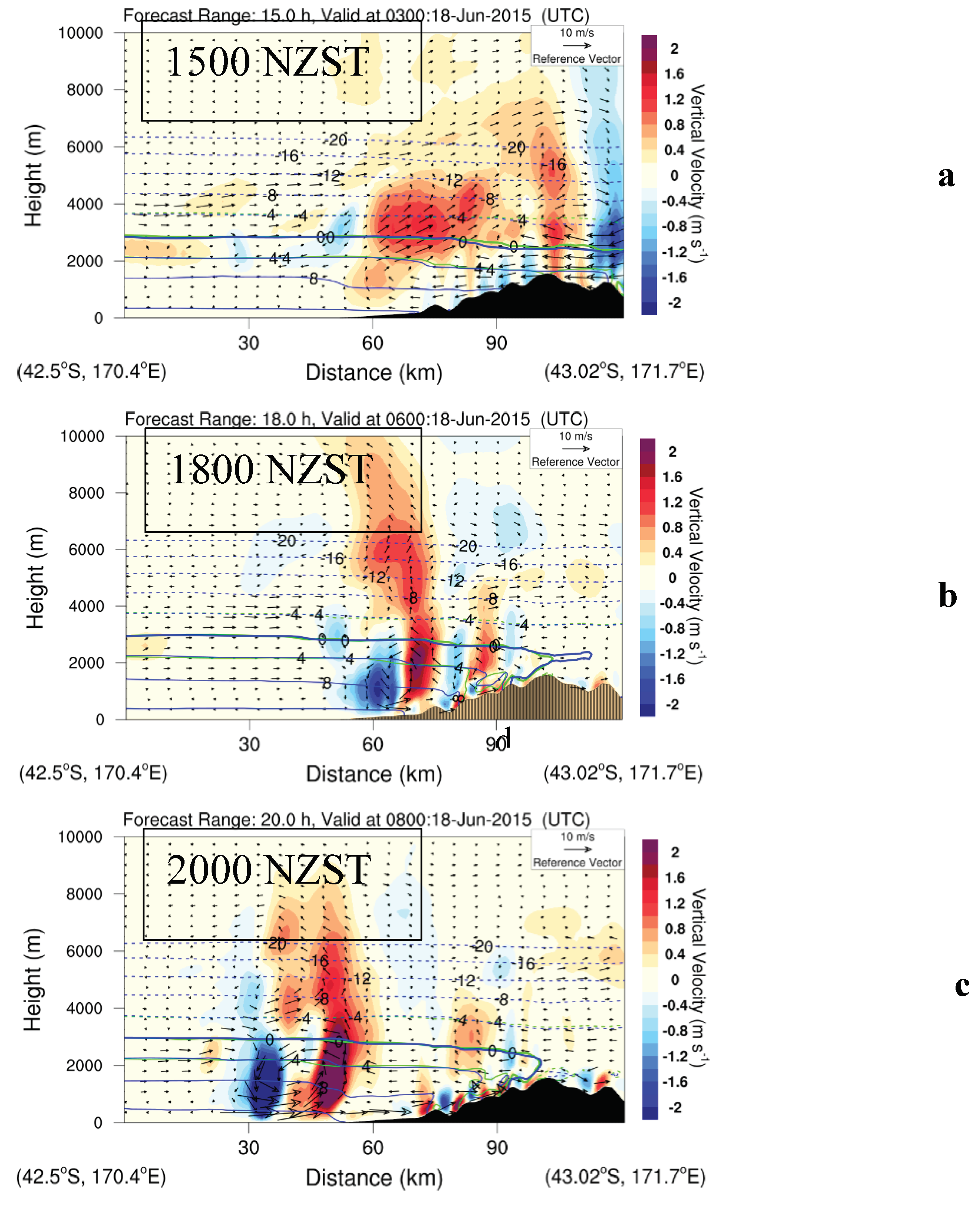
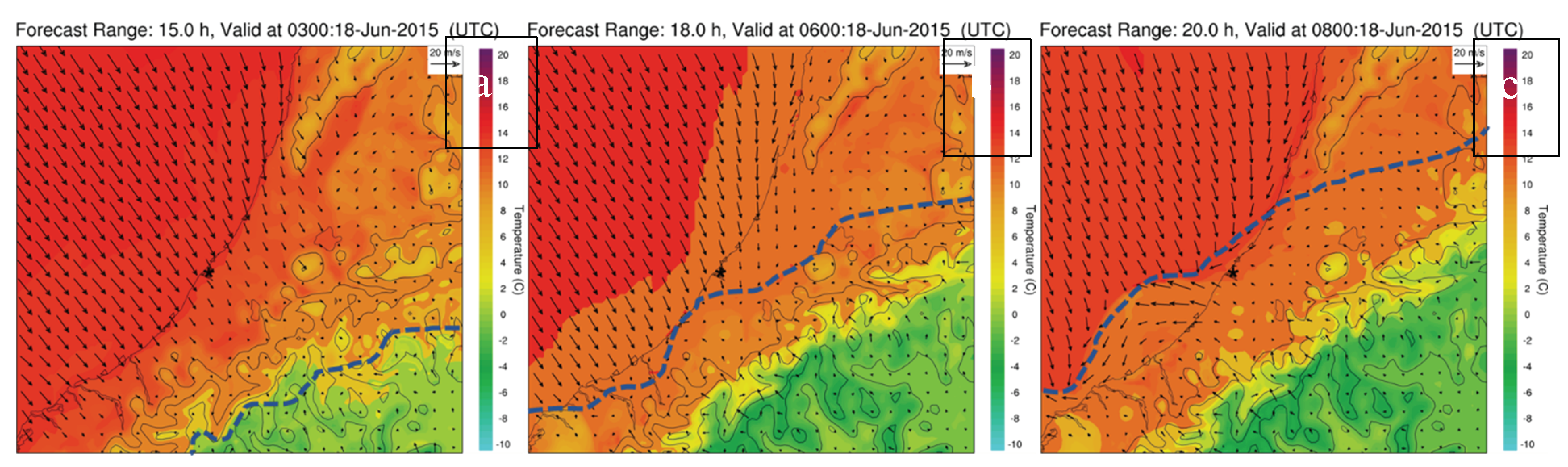
For the 1.2X and 1.3X simulations, the mountain blocking of the warm north-westerly airflow was enhanced. This can be clearly seen from the differences in simulated winds between CTRL and 1.2X and 1.3X (Figure 8). At 1500 NZST 18 June 2014, almost uniform north-westerly airflow moved toward the middle and upper South Island (Figure 4a). In the cross-section diagram (Figures 8a, b), stronger mountain blocking and orographic lifting led to an anomalous clockwise circulation cell over the western lowlands and high mountains for the 1.2X and 1.3X simulations. The lower branch of the cell was found below ~ 2 km height over the western lowlands and below ~ 3 km height over the high mountains, and consisted of easterly wind anomalies (weaker westerly winds, Figures 8a, b) due to stronger mountain blocking for higher mountains in 1.2X and 1.3X than in CTRL. Stronger orographic lifting (red shading) occurred above these easterly wind anomalies on the western side of the cell. The upper branch of the wind anomaly cell consisted of westerly wind anomalies (i.e. the stronger westerly winds) and leading to stronger descent of airflow over the high mountains in 1.2X and 1.3X relative to the CTRL (Figure 8a, b).

At 1800 NZST, the cold front reached the lowlands on the west coast. The uprising motion due to cold front lifting was found over the lowlands and was enhanced by the orographic lifting of the north-westerly airflow (Figure 5). This enhancement was stronger with the higher mountains in the 1.2X and 1.3X simulations due to stronger orographic lifting (Figures 8c, d).

The mountain blocking of the cold south-easterly airflow near the surface on the east side of the South Island was more significant for 1.2X and 1.3X than for CTRL, leading to the development of weaker easterly winds (i.e., westerly wind anomalies) near the surface over high mountains and over the slopes and lowlands on the west side for 1.2X and 1.3 X (Figures 8c – f). As the cold airflow passed over high mountains and descended on the west side, the adiabatic descent warming became more significant for 1.2X and 1.3X with higher mountains than CTRL. This led to higher air temperature ( 3 – 5 K) for the cold easterly winds near surface for 1.2X and 1.3X than CTRL (Figure 5). The weaker easterly cold winds with higher temperatures seen in 1.2X and 1.3X compared with CTRL slowed down the westward movement of the cold front over land to the west of the Southern Alps (Figures 8c-f). The mountain heights of the Southern Alps clearly affected the movement, speed and strength of the cold front.

At 1800 and 2000 NZST (Figures 8c-f), an anomalous anti-clockwise wind cell was found to the west of the strong anomalous uprising motion, which was caused by the difference in the position and strength of the cold front circulation between CTRL and 1.2X and 1.3X.

Above the cold air over the high mountains, the wind anomaly cell found at 1500 NZST was also found at 1800 NZST (Figures 8c, d). At 2000 NZST, the westerly winds below 3 km height over the high mountains were weaker due to higher mountains for 1.2X and 1.3X than for CTRL. This weakened the warm advection, so as to reduce the eastern extension of the 0°C curves over the high mountains below 3 km height (Figures 8c, d) for 1.2 X and 1.3X. Thus, the eastern extension of the simulated 0°C curve over the high mountains in CTRL was mainly due to stronger simulated north-westerly winds and warm advection over the high mountains below 3 km height as a result of weaker mountain blocking.

3.4. Rainfall

Figure 9 shows the observed and simulated radar reflectivity. Hokitika Airport is located approximately at the middle of the bottom x-axis. The observed maximum radar reflectivity (intense rainfall) was found over and to the east of Hokitika Airport at ~ 1830 NZST. For all the simulations at 1830 NZST, the simulated radar reflectivity maxima corresponded well to the uprising motion maximum, which was the cold front lifting enhanced by orographic lifting. For CTRL (Figure 9b), the simulated radar reflectivity maximum was found to the west of Hokitika airport due to the simulated fast movement of the cold front. For 1.2X and 1.3X, because of the slower movement of the cold front, the simulated radar reflectivity maximum was found over and to the east of Hokitika Airport, closer to observations than CTRL.

Table 2 shows the 24-h rainfall amount valid at 0900 NZST 19 June 2015 at 11 stations in the Hokitika region. With each increment in terrain height in the model by 0.1, 0.2, and 0.3 times (i.e., 1.1X, 1.2X, and 1.3X, respectively) the model terrain height of CTRL, the mean absolute errors (MAE) of daily rainfall at the 11 stations gradually decreased. The simulation of the daily rainfall amount in Hokitika region is improved by using higher terrain in 1.1X, 1.2X, and 1.3X than CTRL. For example., at Hokitika Airport the 24-h rainfall simulated by 1.3X (~ 198 mm) was closer to the observations (~ 211mm) than in the other simulations.

However, the MAE of the simulated rainfall in the Hokitika region becomes worse when the mountain height is increased from 1.3X to 1.4X (Table 2), even though the average mountain height of the Southern Alps for 1.4X is closer to the real height (~2600 m) than that of the 1.3X (Table 1). The performance of 1.4X in simulating rainfall ranks between 1.2X and 1.3X. This indicates that the envelope of the mountain range is now too high, and the blocking effect is now too strong. This effect is not unexpected when the model area-average elevation height is comparable to the observed point measurements of maximum height.

Table 2. 24-h rainfall accumulation (mm, valid at 0900 NZST 19 June 2015) for observations and simulations at 11 stations, and the mean absolute errors (MAE, the bottom row).

Station No.	Sta. Name	OBS	1.4X	1.3X	1.2X	1.1X	CTRL	OD
1	Greymouth	144.4	136.0	144.0	151.9	206.6	186.2	170.0
2	Arthurs Pass	81.0	130.2	113.7	123.0	114.1	82.3	129.4
3	Mt Philistine	163.0	107.6	113.4	107.7	93.4	87.5	117.5
4	Hokitika	211.3	167.6	197.7	178.4	144.7	140.2	163.9
5	Ross	188.5	240.2	184.0	133.0	121.6	106.5	129.7
6	Reefton	82.8	94.0	105.9	102.3	102.7	97.2	135.3
7	Paroa	144.9	139.6	156.9	216.2	171.7	118.6	228.3
8	Kokiri	180.6	177.2	178.8	171.2	156.3	147.9	170.4
9	Inchbonnie	327.9	210.8	248.9	247.0	247.0	231.8	258.9
10	Kowhitirangi	265.3	250.1	226.2	200.7	164.9	149.3	176.1
11	Lower Whataroa	274.7	180.7	169.9	192.8	139.4	113.8	179.6
MAE			42.2	33.6	48.2	63.2	66.1	57.9

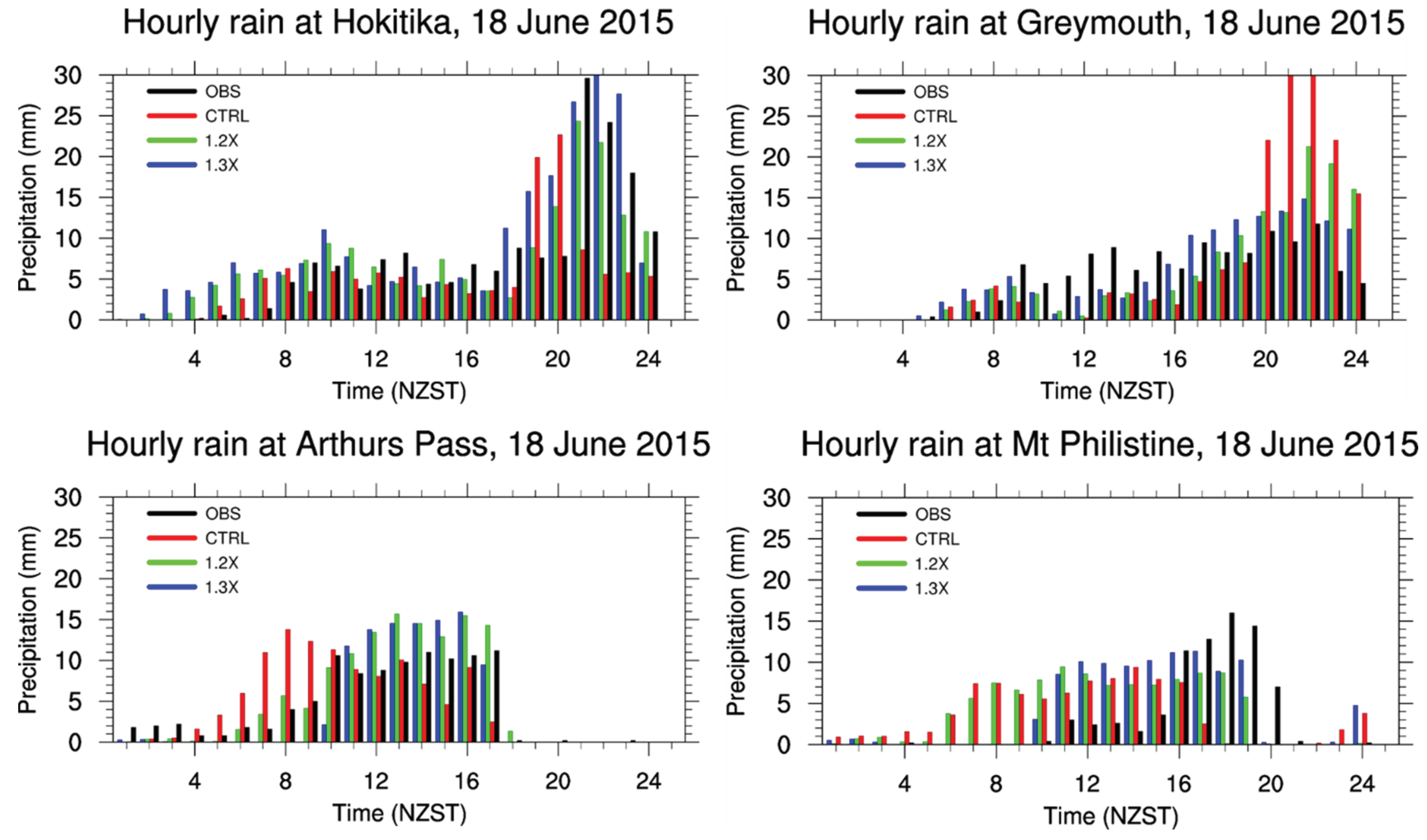
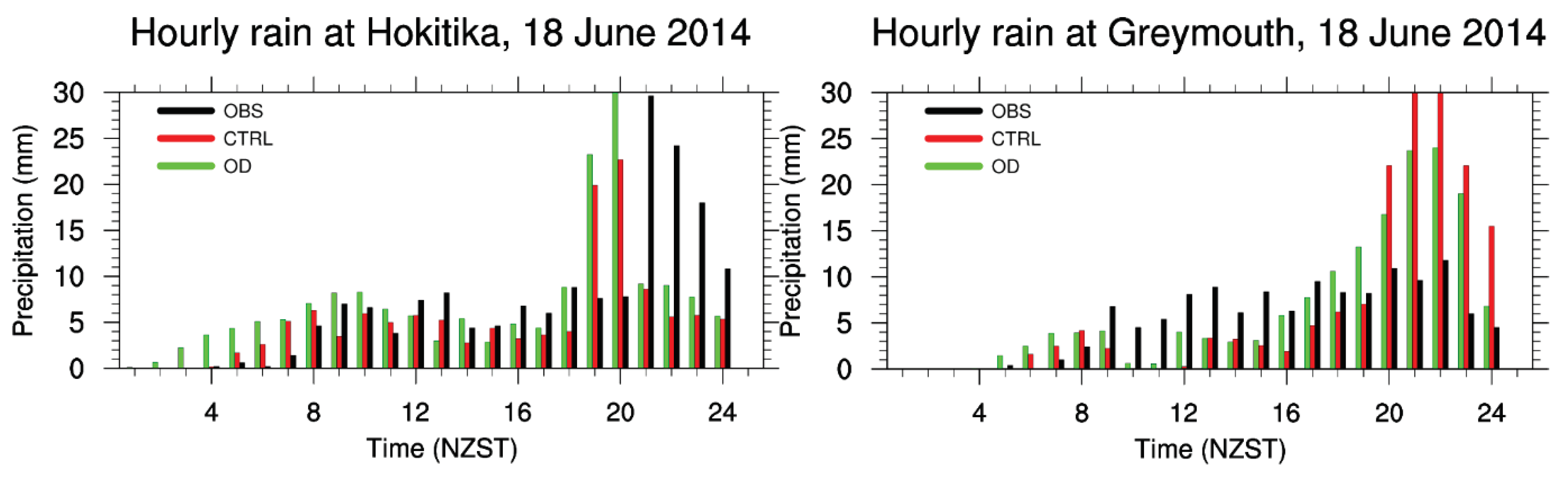
Among the 11 stations only 4 have hourly precipitation observations. Figure 10 shows the observed and simulated hourly rainfall by 1.2X and 1.3X at the four sites in the Hokitika region. Intensive rainfall occurred around the time of the passage of the cold front (comparing Figure 7 and Figure 10). Both the 1.2X and 1.3X simulations captured the hourly rainfall associated with the passage of the cold front in the evening more accurately than the CTRL in terms of both the amount and timing. Overall, CTRL simulated the occurrence of the intensive rainfall earlier than observations at Mt. Philistine, Hokitika and Arthurs Pass, and produced higher intensity rainfall than observed at Greymouth. These errors in CTRL were largely corrected in the 1.2X and 1.3X simulations. In addition, except at Arthurs Pass, the 24-h rainfall amount was also simulated more accurately by 1.2X and 1.3X than by the CTRL (Table 2).

As described earlier, the cold front lifting was enhanced by orographic lifting in the Hokitika region. This led to the intensive rainfall around the time of the cold front passage. For higher mountains in 1.2X and 1.3X than CTRL, the westward movement of the cold front and the orographic lifting over the west lands were better simulated by 1.2X and 1.3X. As a result, 1.2X and 1.3X performed better than CTRL in the Hokitika region in terms of daily rainfall amount and occurrence time of intensive rainfall.

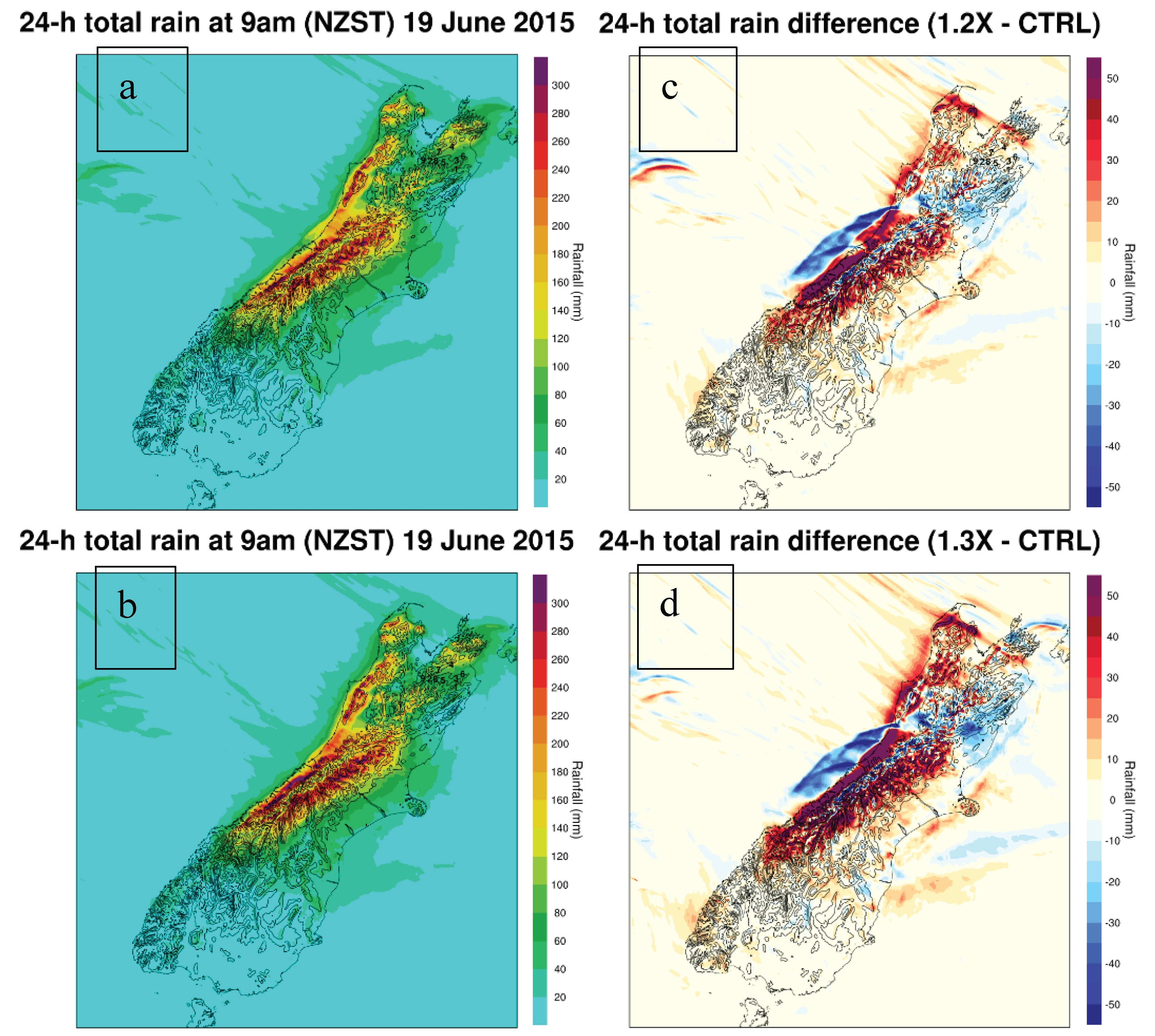
Figure 11 shows the daily rainfall and the differences in daily rainfall between 1.2X, 1.3X and CTRL. The difference in the vertical motions between CTRL and 1.2X or 1.3X due to differences in orographic lifting and the westward movement speed of the cold front led to pronounced differences in 24-h rainfall (Figure 11). More rainfall for 1.2X and 1.3X than CTRL was found over land, especially over windward slope, and less rainfall over the sea off the middle west coast. The same features were also found for 1.4X (Figure 12a).

The results drawn from rainfall analyses for different mountain heights indicated a significant indirect dynamical effect of the Southern Alps on heavy rainfall by affecting the movement speed and strength of the cold front. This is a new finding to our knowledge.

4. Effect of sub-grid terrain

In numerical weather and climate models, it is unavoidable that the actual mountain dynamical effects are underestimated by the model resolved mountains. To compensate for this underestimation, the effects of sub-grid mountains are considered and parameterisation schemes of sub-grid mountain dynamical effects have been developed (e.g., McFarlane, 1987; Lott and Miller, 1997; Webster et al., 2003, 2020).

In the RAL (Bush et.al., 2020) configuration used, the UM’s orographic drag scheme, and its parameterised sub-grid mountain blocking, are not included at the 1.5 km grid-length. To establish whether the sub-grid parametrisation can produce a realistic response in the cold-front structure, and resultant precipitation, we include the orographic drag scheme (Lott and Miller, 1997; Webster et al., 2020) in the 1.5 km simulation, using the same parameters (including sub-grid ancillary fields) as our 12 km simulation. This is likely to over-estimate the true sub-grid blocking, but as with the experiments in Section 3, our goal is not to produce the best simulation, but rather to explore the mechanisms affecting the dynamics. In particular, does the sub-grid parametrisation of mountain blocking produce the same response as increasing the resolved mountain heights. However, given the fractal nature of mountains, and uncertainties inherent in the parametrisation design, it does not represent an unrealistic experiment. This experiment is hereafter labelled as “OD” (Table 1).

For OD, the simulated mountain blocking and orographic lifting were stronger than for CTRL. This can be shown from the differences in winds between OD and CTRL (Figure 13a). Similar to 1.2X and 1.3X (Figures 7a, b), a clockwise wind anomaly cell along the vertical was also found over the western slopes and high mountains for OD. However, there is a pronounced difference between Figure 13 and Figure 7. Over the high mountains a deep uprising motion was found inside the cell for OD but not for 1.2X and 1.3X (Figure 7a, b, Figure 14a). At 1800 NZST, the wind anomaly cell found at 1500 NZST was not pronounced. The main difference was that the easterly wind anomalies corresponding to the lower branch of the cell were much weaker for OD than 1.2X and 1.3X (Figures 7c, d, Figure 13b). In other words, the simulated north-westerly airflows over the high mountains below 3 km height by OD were almost the same as those by CTRL (i.e., almost the same warm advection) around 1830 NZST. This led to almost the same easterly extension of the 0°C curve over the high mountains (not shown).

The near surface easterly cold winds over the high mountains and the western lowlands were weaker when simulated by OD than by CTRL (Figures 13b,c). As a result, the westward movement of the cold front in the west was slower for OD than for CTRL (Figures 6a,b,c, and Figures 14a, b, c). Compared with the 1.2X and 1.3X experiments, the simulated surface winds over land by OD in the Hokitika region were weaker (Figure 6, Figure 15).

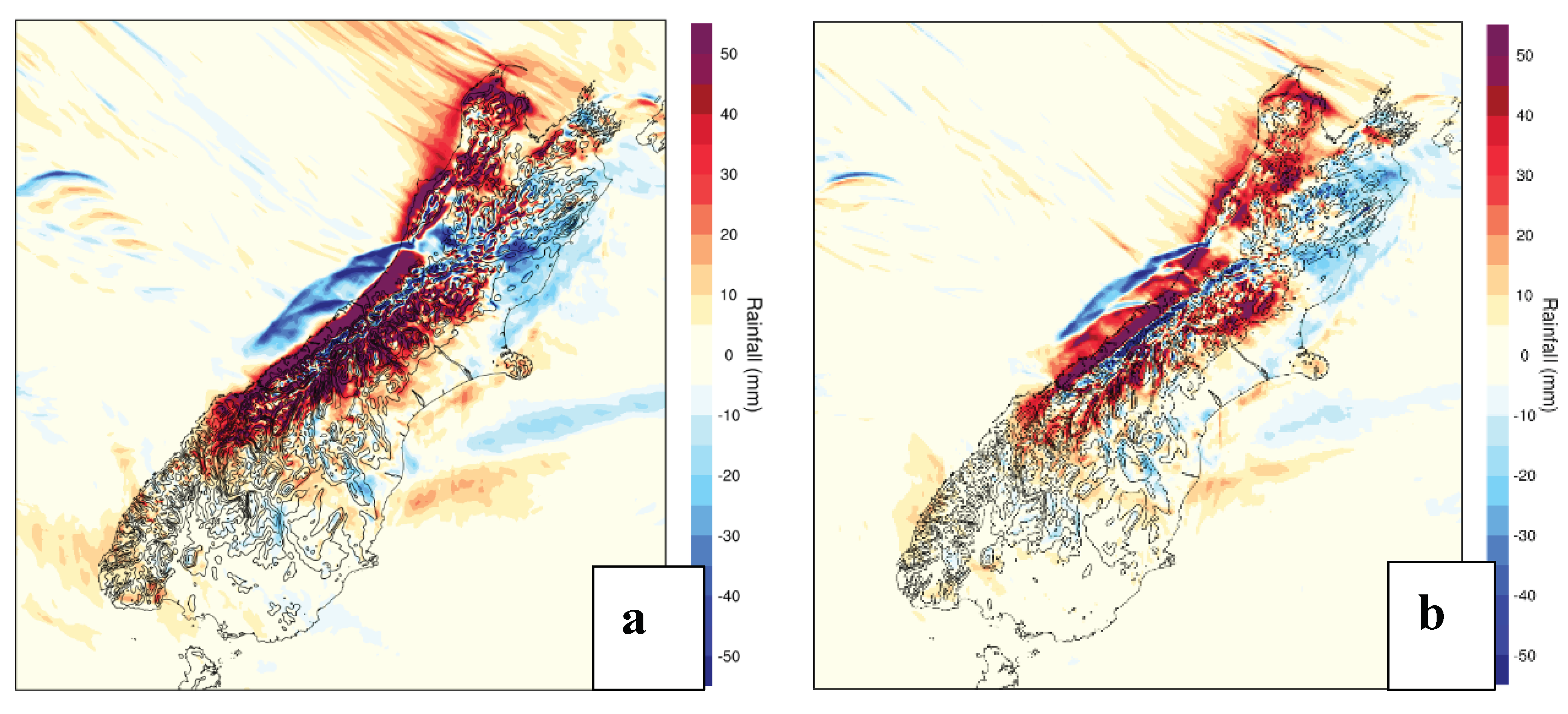
Similar to 1.2X and 1.3X, OD with stronger orographic lifting and slower westward movement of the cold front than CTRL led to better simulation of rainfall. Figure 12b shows the differences in 24-h rainfall between CTRL and OD. The patterns of these rainfall differences are very close to those of 1.2X (Figure 11c), 1.3X (Figure 11d), and 1.4X (Figure 12a). With respect to MAE of the simulated rainfall at the 11 sites in the Hokitika region (Table 2), OD is better than CTRL and 1.1X, but still not as good as 1.2X, 1.3X, and 1.4X. For the hourly rainfall at the four sites (Figure 15), regarding the rainfall amount and intensive rainfall time period, OD is also better than CTRL.

5. Discussion

For numerical weather and climate models, prediction errors are the result of a combination of errors and uncertainties in the initial conditions, lower boundary conditions, lateral boundary conditions (for regional models), model physics schemes, and the interactions of these errors. This makes it hard to isolate the greatest source of error.

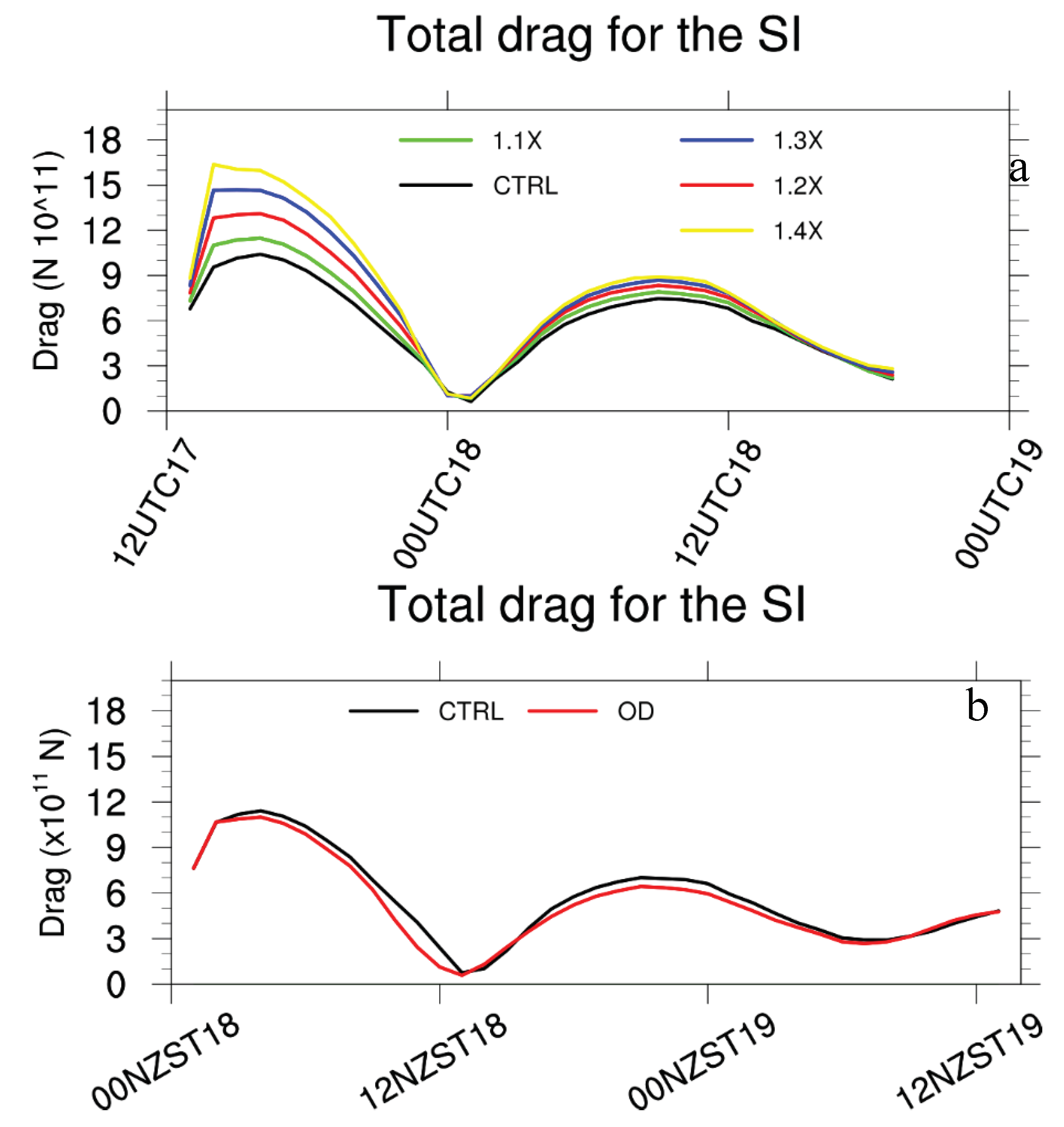
In this study, for the Southern Alps, the lower than reality model mountain heights imply weaker mountain dynamical forcing. This was supported by verifying model simulations with increasing model terrain heights against radar and meteorological station observations. Furthermore, underestimation of the dynamical effects of the Southern Alps can also be shown in the total mountain drag of the southern alps, which was calculated using the schemes described in Smith et al. (2006, Eqs. 1 - 3). The total mountain drag over the South Island increased due to the higher mountains in experiments 1.1X to 1.4X (Figure 16a). A minimum of the total mountain drag was found around midday of 18 June when the cold front reached the middle of the South Island. These opposing easterly and westerly mountain drags resulted in the minimum of the total mountain drag around the midday of 18 June. All these facts indicate that the model’s underestimation of peak heights over the Southern Alps was a large source of error for the Hokitika heavy rainfall simulation in this study.

When including sub-grid mountain dynamical forcing and sub-grid mountain blocking (OD experiment), the dynamical forcing of the Southern Alps was increased with better results as compared with CTRL. However, it remains unclear why the eastern extension of the 0°C isotherm over high mountains shown in CTRL at 1830 NZST was not corrected. Giving stronger orographic lifting and mountain blocking for OD than CTRL, it is unexpected that the total mountain drag over the Southern Alps simulated by OD was slightly smaller than CTRL (Figure 16b). These problems need to be investigated further.

Regarding effects of mountain heights on precipitation, what are the similarities and differences between this study and previous idealized numerical experiments? Answering this question is complicated because, in addition to the complex Southern Alps and the spatial variations of airflows, the presence of the cold front also played a key role for the occurrence of intensive rainfall in the Hokitika area on 18 June 2015.

This heavy rainfall event occurred under conditionally unstable northwesterly airflows, however, the CAPE was less than 25 J/kg (not shown). As a result, this heavy precipitation was of stratiform type (Crouch and Russell, 2021). For CTRL, 1.1X, 1.2X, 1.3X, and 1.4X,

F_{m}

ranges 0.61 – 1.21. For OD, the mean mountain height

h

is very hard to calculate.

F_{m}

for OD can only be estimated here. Giving stronger orographic lifting and mountain blocking for OD than CTRL, it is expected that

F_{m}

of OD is lower than that of CTRL (1.21). Because the performance of OD in rainfall simulation is worse than 1.2X, the

F_{m}

of OD is very likely larger than that of 1.2X (1.01), i.e., 1.01 <

F_{m}

< 1.21 (Table 1).

For the idealized numerical experiments conducted by Colle (2004),

F_{m}

(or the non-dimensional mountain height,

M_{m} = \frac{1}{F_{m}}

) was the main control parameter but CAPE was not calculated and shown. Very large CAPE (as a control parameter around 1000 J/kg or larger) was used in Chen and Lin (2005a, b) and Miglietta and Rotunno (2009, 2010), and the precipitation was convective type. In this study. the CAPE was very small (< 25 J/kg) and the precipitation was stratiform type. In addition, the activity of the cold front associated with the mid-latitude low played a key role in affecting the precipitation amount and distribution. Cold fronts were also found associated with the cold-air outflow caused by evaporative cooling of rain from precipitating convective cells in Miglietta and Rotunno (2009). However, they were not the kind of meso-scale to large-scale cold front found in this study. These differences make it very hard to compare our results with these idealised numerical experiments, or apply the theoretical results from these idealized numerical experiments to this heavy rainfall event.

Smith and Barstad (2004) applied their linear theory of orographic precipitation to the Olympic Range (2428 m at peak) in Washington State using idealised airflow with mean wind speed of 15 ms^-1 and a moist stability of 0.005

s^{- 1}

. This gives

F_{m} = 1.2

, which is close to that of CTRL. Maximum precipitation was found just upwind of the mountain peaks with some spillover, which shared some similarities to that of CTRL (Figure 11). However, there is significant difference between this study and the application case of Smith and Barstad (2004), i.e., the presence of the cold front in this study significantly affecting rainfall amount and distribution on the windward side.

Yang and Chen (2008) investigated the effects of the height and size of the island of Hawaii on the rainfall distribution under easterly trade wind flow, which has a moist conditionally unstable layer (2 km) with a low CAPE (100 J/kg). They indicated that in addition to island blocking and orographic lifting, terrain heights also affect rainfall distribution by affecting the land surface thermal forcing. In contrast, in this study the heavy rainfall event occurred at mid-latitude during wintertime when the land surface thermal forcing was very weak. This can be shown by the temporal variations of surface air temperature that the major variations were caused by the passage of cold fronts (Figure 7). Furthermore, in this study mountain heights affected rainfall amount and distribution by affecting the movement speed and strength of the cold front, in addition to mountain dynamical effects.

6. Conclusion

For the heavy rainfall that occurred in the Hokitika region in the late afternoon and evening of 18 June 2015, numerical experiments were conducted in this study to understand the causes leading to large errors in the 0°C isotherm height over high mountains compared with radar observations, the key processes that affected the heavy rainfall, and how well these key processes were described in the model.

Analyses of model outputs and observations showed that this heavy rainfall (daily maxima > 200 mm) was due to the lifting of the warm airflows by the cold front enhanced by orographic lifting.

In the experiments where the height of the Southern Alps was increased, the eastern extension error of the 0°C isotherm over high mountains was largely corrected. This error was due to stronger simulated north-westerly airflows (or stronger warm advection) below 3 km height over high mountains as a result of weaker mountain blocking (or lower mountains).

Weaker mountain blocking caused more significant descent of cold airflows on the west side of the Southern Alps, leading to stronger and faster movement of the cold front from highlands to the west coast. As a result, large errors occurred in the heavy rainfall simulation in the Hokitika region for lower mountain heights than the actual in CTRL.

By increasing the model-resolved terrain heights to be closer to the actual heights, the westward movement speed of the cold front and the cold front lifting enhanced by orographic lifting were better simulated. This led to better simulation of the magnitude and timing of the heavy rainfall associated with the passage of the cold front.

Turning on the sub-grid orographic drag scheme and enhancing sub-grid mountain blocking improved the simulation of mountain blocking, the cold front movement and orographic lifting, yielding a better simulation of this heavy rainfall case. These results indicate that even at 1.5 km grid lengths, mountain dynamical effects could be largely underestimated and thus result in large errors in heavy rainfall prediction in mountainous areas. Therefore, a consideration of the effects of (unresolved) sub-grid mountains may be a promising approach. These unresolved effects include both the impact of terrain which remains sub-grid to the resolved scale of the model, and terrain that is modified by the filtering applied to achieve dynamical stability. To do this requires further development of orographic drag parametrizations suitable for this scale.

All the experiments had the moist Froude Number

F_{m}

ranging 0.61 – 1.21, and, as a result, the same “flow-over” regimes with mountain waves and/or wave breaking (Smith, 1989; Epifanio, 2003) for an aspect ratio of ~ 1/4 for the Southern Alps. However, the rainfall amount and distribution, especially on the windward side (i.e., the Hokitika region) significantly differed due to different movement speed and strength of the cold front caused by different mountain heights. These facts revealed that in addition to the well-known direct dynamical effect (e.g., orographic lifting and mountain blocking), the Southern Alps also has significant indirect effect on the heavy rainfall by changing the strength and movement speed of the cold front. The combined direct and indirect dynamical effects of the Southern Alps on heavy rainfall make the precipitation simulation sensitive to mountain heights even under the same “flow-over” regime, a new finding to our knowledge.

Acknowledgments

This research was carried out under research collaboration SC0128 with the UK Met Office and supported by the NZ Government's Strategic Science Investment Fund (SSIF) through the NIWA programme Forecasting Weather Systems. The authors wish to thank MetService New Zealand for providing the dual-polarisation radar images and acknowledge the contribution of the New Zealand eScience Infrastructure (NeSI) to the results of this research. New Zealand's national compute and analytics services and team are supported by the NeSI and funded jointly by NeSI's collaborator institutions and through the Ministry of Business, Innovation and Employment. URL http://www.nesi.org.nz.

References

Bush, M.; Allen, T.; Bain, C.; Boutle, I.; et al. The first Met Office Unified Model–JULES Regional Atmosphere and Land configuration, RAL1. Geosci. Model Dev. 2020, 13, 1999–2029. [Google Scholar] [CrossRef]
Chow, F. K., De Wekker, S. F. J., and Snyder, B. J., Eds., (2013) Mountain Weather Research and Forecasting: Recent Progress and Current Challenges. Springer, 750 pp.
Colle, B.A.; Mass, C.F.; Smull, B.F. An observational and numerical study of a cold front interacting with the Olympic Mountains during COAST IOP5. Mon. Wea. Rev. 1999, 127, 1310–1334. [Google Scholar] [CrossRef]
Colle, B. Sensitivity of orographic precipitation to changing ambient conditions and terrain geometries: An idealized modeling perspective. J. Atmos. Sci. 2004, 61, 588–606. [Google Scholar] [CrossRef]
Colle, B.; Smith, R.B.; Wesley, D.A. (2013) Theory, observations, and predictions of orographic precipitation. Mountain Weather Research and Forecasting: Recent Progress and Current Challenges, F. K. Chow, S. F. J. De Wekker, and B. J. Snyder, Eds., Springer, 291–344.
Crouch, J.; Russell, F.M. South Island West Coast orographic rainfall – a polarimetric radar view. Weather & Climate. 2021, 41, 30–51. [Google Scholar]
Egger, J.; Hoinka, K.P. Fronts and orography. Meteor. Atmos. Phys. 1992, 48, 3–36. [Google Scholar] [CrossRef]
Epifanio, C.C. (2003) Lee vortices. In Encyclopedia of the Atmospheric Sciences, Cambridge University Press, 1150-60.
Griffiths, G.A.; McSaveney, M.J. Distribution of mean annual precipitation across some steep land regions of New Zealand. Journal of Science. 1983, 26, 197–209. [Google Scholar]
Griffiths, G. Drivers of extreme daily rainfalls in New Zealand. Weather and Climate 2011, 31, 24–49. [Google Scholar] [CrossRef]
Henderson, R.; Thompson, S. Extreme Rainfalls in the Southern Alps of New Zealand. Journal of Hydrology (New Zealand) 1999, 38, 309–330. [Google Scholar]
Houze, R.A., Jr. Orographic effects on precipitating clouds. Rev. Geophys. 2012, 50, RG1001. [Google Scholar] [CrossRef]
Lott, F.; Miller, M.J. A new subgrid-scale orographic drag parametrization: Its formulation and testing. Q. J. R. Meteorol. Soc. 1997, 123, 101–127. [Google Scholar]
McFarlane, N.A. The Effect of Orographically Excited Gravity Wave Drag on the General Circulation of the Lower Stratosphere and Troposphere. J. Atmos. Sci. 1987, 44, 1775–1800. [Google Scholar] [CrossRef]
Miglietta, M.M.; Rotunno, R. Numerical Simulations of Conditionally Unstable Flows over a Mountain Ridge. J. Atmos. Sci. 2009, 66, 1865–1885. [Google Scholar] [CrossRef]
Miglietta, M.M.; Rotunno, R. Numerical Simulations of Low-CAPE Flows over a Mountain Ridge. J. Atmos. Sci. 2010, 67, 2391–2401. [Google Scholar] [CrossRef]
Miglietta, M.M.; Rotunno, R. Application of Theory to Simulations of Observed Cases of Orographically Forced Convective Rainfall. Monthly Weather Review 2012, 140, 3039–3053. [Google Scholar] [CrossRef]
Revell, M.J.; Copeland, J.H.; Larsen, H.R.; Wratt, D.S. Barrier jets around the Southern Alps of New Zealand and their potential to enhance alpine rainfall. Atmospheric Research 2002, 61, 277–298. [Google Scholar] [CrossRef]
Salinger, M. J. New Zealand climate: I. Precipitation pattern. Mon. Weather Rev. 1980, 108, 1892–1904. [Google Scholar] [CrossRef]
Schultz, D. M. Cold fronts with and without prefrontal wind shifts in the central United States. Mon. Wea. Rev. 2004, 132, 2040–2053. [Google Scholar] [CrossRef]
Shu, J.; Shamseldin, A.Y.; Weller, E. The impact of atmospheric rivers on rainfall in New Zealand. Sci Rep 2021, 11, 5869. [Google Scholar] [CrossRef]
Smith, S. A.; Doyle, J. D.; Brown1, A. R.; Webster, S. Sensitivity of resolved mountain drag to model resolution for MAP case-studies. Q.J.R. Meteorol. Soc. 2006, 132, 1467–1487. [Google Scholar] [CrossRef]
Smith, R. B. , (1989) Hydrostatic flow over mountains. Advances in Geophysics, Vol. 31, Academic Press, 1–41.
Smith, R.B.; Barstad, I. A linear theory of orographic precipitation. J. Atmos. Sci. 2004, 61, 1377–1391. [Google Scholar] [CrossRef]
Smith, R. B. 100 Years of Progress on Mountain Meteorology Research. Meteorological Monographs 2019, 59, 20.1–2073. [Google Scholar] [CrossRef]
Smith, R.K.; Ridley, R.N.; Page, M.A.; Steiner, J.T.; Sturman, A.P. Southerly Changes on the East Coast of New Zealand. Monthly Weather Review 1991, 119, 1259–1282. [Google Scholar] [CrossRef]
Steenburgh, W.J.; Blazek, T.R. , Topographic distortion of a cold front over the Snake River Plain and central Idaho Mountains. Wea. Forecasting 2001, 16, 301–314. [Google Scholar] [CrossRef]
Steenburgh, W. J.; Neuman, C.R.; West, G.L.; Bosart, L.F. Discrete frontal propagation over the Sierra-Cascade Mountains and Intermountain West. Mon. Wea. Rev. 2009, 137, 2000–2020. [Google Scholar] [CrossRef]
Stockham, A.J.; Schultz, D.M.; Fairman, J.G., Jr.; Draude, A.P. Quantifying the Rain-Shadow Effect: Results from the Peak District, British Isles. Bulletin of the American Meteorological Society 2018, 99, 777–790. [Google Scholar] [CrossRef]
Sturman, A.P.; Smith, R.K.; Page, M.A.; et al. Meso-scale surface wind changes associated with the passage of cold fronts along the eastern side of the Southern Alps, New Zealand. Meteorl. Atmos. Phys. 1990, 42, 133–143. [Google Scholar] [CrossRef]
Sturman, A.P.; Wanner, H. A comparative review of the weather and climate of the New Zealand Southern Alps and the European Alps. Mountain Research and Development 2001, 21, 359–369. [Google Scholar] [CrossRef]
Tait, A.B.; Fitzharris, B.B. Relationships between New Zealand rainfall and south-west Pacific pressure patterns. Int. J. Climatol. 1998, 18, 407–424. [Google Scholar] [CrossRef]
Whitehouse, I.E. The frequency of high-intensity rainfalls in the central Southern Alps, New Zealand. Journal of the Royal Society of New Zealand 1985, 15, 213–226. [Google Scholar] [CrossRef]
Walters, D.; Boutle, I.; Brooks, M.; et al. The Met Office Unified Model Global Atmosphere 6. 0/6.1 and JULES Global Land 6.0/6.1 configurations, Geosci. Model Dev. 2017, 10, 1487–1520. [Google Scholar]
Webster, S.; Brown, A.R.; Cameron, D.R.; Jones, C.P. , Improvements to the representation of orography in the Met Office Unified Model. Q. J. R. Meteorol. Soc. 2003, 129, 1989–2010. [Google Scholar] [CrossRef]
Webster, S.; Wells, H.; Vosper, S.; Smith, S.A. (2020) Gravity Wave Drag, Unified Model Documentation Paper 022. UM Version: 11.7. Last Updated : 2020-02-17 (for vn11.6).
Wood, N.; Staniforth, A.; White, A.; et al. An inherently mass-conserving semi-implicit semi-Lagrangian discretization of the deep-atmosphere global non-hydrostatic equations. Q.J.R. Meteorol. Soc. 2014, 140, 1505–1520. [Google Scholar] [CrossRef]
Yang, Y.; Chen, Y. Effects of Terrain Heights and Sizes on Island-Scale Circulations and Rainfall for the Island of Hawaii during HaRP. Monthly Weather Review 2008, 136, 120–146. [Google Scholar] [CrossRef]
Yang, Y.; Uddstrom, M.; Revell, M.; Andrews, P.; Turner, R. Amplification of the impact of assimilating ATOVS radiances on simulated surface air temperatures over Canterbury by the Southern Alps, New Zealand. Mon. Wea. Rev. 2012, 140, 1367–1384. [Google Scholar] [CrossRef]
Yang, Y.; Andrews, P.; Carey-Smith, T.; Uddstrom, M.; Revell, M. Prediction of Moderate and Heavy Rainfall in New Zealand Using Data Assimilation and Ensemble. Advances in Meteorology 2015, 2015, 460243. [Google Scholar] [CrossRef]
Yang, Y.; Uddstrom, M.; Revell, M.; Moore, S.; Turner, R. Damaging Southerly Winds Caused by Barrier Jets in the Cook Strait and Wellington Region of New Zealand. Mon. Wea. Rev. 2017, 145, 1203–1220. [Google Scholar] [CrossRef]

Figure 1. (a) The Southern Alps showing terrain height from CTRL. (b) Locations of the 11 stations with daily rainfall observations chosen for verification in this study. See Table 2 for the name of each station. The mountain heights are shown in grey shading. The blue star and red dots in (a) denote the location where

F_{m}

was calculated and the locations of the 103 tallest mountains of the South Island with heights larger than 2400 m, respectively. The solid line in (b) is the transect for the cross-sections. The area of (b) is shown by the square in Figure 1a.

F_{m}

Figure 2. Dual-polarisation radar observations (Correlation Coefficient) (a), and simulated winds, ice ratio, and 0° C (white for CTRL) air temperature by CTRL (b), 1.2X (c), and 1.3X(d) at 1830 NZST 18 June 2015 along the solid line in Figure 1b.

Figure 3. The surface analysis weather chart (a) at 1200 NZST, (b) at 1800 NZST 18 June 2015, and (c) at 0000 NZST 19 June 2015; (d) Total Precipitable Water image for 1500 NZST 18 June 2015 from Cooperative Institute for Meteorological Satellite Studies (CIMMS); (e) GMS infrared satellite image at 1200 NZST 18 June 2015.

Figure 4. The simulated surface winds and pressure (1.5 km resolution, CTRL) initialized at 0000NZST 18 June 2015 at (a) 1500 NZST, (b) 1800 NZST, and (c) 2000 NZST on 18 June 2015. The solid line in (a) and (b) is the same as in Figure 1b and shows the position for cross-sections. The small square in (c) shows the area for Figure 6.

Figure 7. Observed and simulated (CTRL and 1.2X) hourly surface winds and air temperature at four stations in the Hokitika region. See Table 1 and Figure 1 for site locations.

Figure 8. Cross-sections along the solid line in Figure 1b for the difference in the simulated winds and vertical velocity between CTRL and 1.2X (the left panel) and 1.3X (the right panel). Green contours are air temperature simulated by CTRL. Blue contours are air temperature simulate by 1.2X (left panel) and by 1.3X (right panel).

Figure 9. Observations of radar reflectivity (a), and simulated winds, air temperature, and radar reflectivity by CTRL (b), 1.2X (c), and 1.3X (d) at 1830 NZST on 18 June 2015.

Figure 10. Observed (OBS) and simulated (CTRL, 1.2X, and 1.3X) hourly rainfall at four stations in the Hokitika region. See Table 2 and Figure 1 for site locations.

Figure 11. Simulated 24-h rainfall (mm, valid at 0900 NZST 19 June 2015) by 1.2X (a) and 1.3X (b), and the difference in 24-h rainfall between CTRL and 1.2X (c) and 1.3X (d).

Figure 12. Differences in 24-h rainfall (mm) valid at 0900 NZST 19 June 2015 between CTRL (a) 1.4X and (b) OD.

Figure 13. Cross-sections along the solid line in Figure 1b for the difference in the simulated winds and vertical velocity between CTRL and OD (OD – CTRL,). Green contours are air temperature simulated by CTRL. Blue contours are air temperature simulate by OD.

Figure 14. Simulated surface winds and pressure by OD at 1500 NZST (a), 1800 NZST (b), and 2000 NZST (c) on 18 June 2015. Blue dashed lines denote positions of the cold fronts. See Figure 4c for the location of the area.

Figure 15. Observed and simulated (CTRL, OD) hourly rainfall.

Figure 16. The total mountain drag of the South Island calculated from model simulations.

Table 1. Description of numerical experiments, the average height (h) of the Southern Alps mountains resolved by the model, and the moist Froude Number (

F_{m}

) calculated from the mean wind speed (~23 m/s) and mean moist Brunt–Väisälä frequency (0.0105

s^{- 1}

) for the 0 – 3 km layer at a location about 300 km to the northwest of Hokitika.

Table 1. Description of numerical experiments, the average height (h) of the Southern Alps mountains resolved by the model, and the moist Froude Number (

F_{m}

) calculated from the mean wind speed (~23 m/s) and mean moist Brunt–Väisälä frequency (0.0105

s^{- 1}

) for the 0 – 3 km layer at a location about 300 km to the northwest of Hokitika.

EXP	Description	h (m)	$F_{m}$
CTRL 1.1X 1.2X 1.3X 1.4X OD	Using the original terrain data generated by the nesting suite of UM Increasing the terrain height by 1.1 times of the terrain of CTRL Increasing the terrain height by 1.2 times of the terrain of CTRL Increasing the terrain height by 1.3 times of the terrain of CTRL Increasing the terrain height by 1.3 times of the terrain of CTRL the same as CTRL but turning on the sub-grid mountain blocking, the 5A scheme (Lott and Miller, 1997; Webster et al., 2020)	1800 1980 2160 2340 2520 1800	1.21 1.11 1.01 0.94 0.61 $1.01 < F_{m}$ <1.21

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer