Physical Experimental Study on the Wave Reflection and Run-Up of a New Ecological Hollow Cube

A new type of artificial block is proposed by modifying the traditional block. Based on the physical model experiment, the wave reflection and run-up characteristics of the new ecological blocks under regular waves were examined, and the influence of the height of the "planting trough" border on the hydrodynamic properties was analyzed. The results indicate that the wave reflection and run-up would decrease with a decrease in the breakwater slope. As wave height increases, wave run-up increases, and the reflection coefficient falls. Wave reflection and run-up increase with an increasing wave period. The relative depth of the water has a smaller impact on the wave reflection than the wave run-up. The reflection coefficient of the new ecological blocks is consistently lower than that of the conventional and continues to decrease as the border of the "planting trough" is raised. The raised borders prevent water loss in the trough, resulting in no significant improvement in the wave run-up performance of the new blocks. The reflection coefficient and the relative run-up R/H gradually increase with the average wave breaking parameter ξ increase. The crude permeability coefficients for the new blocks, New Heights 1 and New Heights 2, are 0.53, 0.53, and 0.54, respectively.

Keywords:

Subject: Engineering - Other

1. Introduction

Armour blocks are the main structures responsible for wave breaking and energy dissipation in coastal protection engineering, usually made of natural rock blocks or artificial concrete blocks [1]. The implementation of armour blocks on breakwaters [2] is a typical method of wave mitigation and marine disaster prevention. Unlike natural rock blocks, artificial armour blocks, such as accropides and hollow cubes, are easier to obtain and more stable. These artificial armour blocks are widely used in practical engineering for coastal protection [3]. The use of sheathing blocks, including Accropode^®, Xbloc^®, and Core-Loc^TM, has become a classic solution for the construction of coastal structures [2]. The development of new face protection blocks [4,5,6] has had a sustained impact on achieving better wave energy dissipation and low concrete consumption. It can be argued that there is a great deal of uncertainty about how to effectively protect littoral structures against longer and larger waves in coastal waters and that such structures will be more vulnerable to oceanic hazards associated with global warming [7]. Using artificial armour blocks in seawall and coastal protection projects effectively achieves the safety functions of disaster prevention and erosion control. However, these structures often have monotonous facades, rigid appearances, and poor landscape effects. Additionally, they tend to have less consideration for environmental impacts, leading to various ecological issues [7,8,9]. With the continuous improvement of environmental awareness, it is significant to enhance the ecological and landscape value of coastal protection projects while ensuring their safety functions [10].

Currently, the construction of ecological coastal protection projects can be divided into two main forms. The first form relies entirely on natural structures and materials for coastal protection, such as mangroves [11] or artificially cultivated reefs [12,13]. Natural breakwaters have great environmental properties but require larger construction spaces and longer construction periods. The second form involves the addition of ecological structures on the intertidal zone or the water-facing surface in front of traditional protection projects to alleviate negative impacts on the ecological environment [14]. Examples of this include adding rock cavities (pits or crevices) to the armour structure to provide additional habitat [15], thereby increasing biodiversity and richness, or combining vegetation with engineering structures to not only reduce wave action [16] but also provide habitat for organisms [17]. This mixed-design method reduces construction costs and applies to the ecological transformation of existing structures, making it widely used in practice [18].

Compared to areas such as the crest and hinterland, the wave-facing slope is directly exposed to wave action, experiencing more complex wave-dynamic conditions. This necessitates the use of armour blocks to dissipate wave energy, ensuring the safety and stability of the structure. Therefore, ecological design and implementation of wave-facing slopes are approached with relative caution, often prioritizing the fulfillment of the armour layer's wave-breaking and energy-dissipating functions before moderately pursuing enhancements in ecological greening effects. Mohammad [19] proposed a new type of environmentally friendly armour block that can support vegetation growth and evaluated its environmental and hydraulic performance through laboratory and field testing. Scheres and Schüttrumpf [20] outlined the structure, function, and current design practices of vegetation cover layers on embankment surfaces. Le Xuan [21] summarized the experiences and lessons learned from typical coastal protection projects in the Mekong Delta, Vietnam, and proposed a multi-line defense solution incorporating “seawall/coastal protection + mangroves + offshore breakwater.” And vegetation greening on the wave-facing slope to enhance the landscape effect. Chen [22] discussed the marine ecological protection and restoration plan; taking the Taiping Bay reclamation project in Dalian Port as an example, they proposed a sloping structure for the ecological seawall. Use blocks or fence panels as slope protection materials, and plant salt-alkali-tolerant plants such as shrubs and grass to improve the environmental and landscape qualities of the slope. Martínez [23] analyzed the stability of the newly developed environmental armour block, COASTALOCK, through physical model testing. This ecological block simulates natural rock pools and creates local ecosystems, promoting biodiversity.

This study shows that the ecological greening enhancement of an artificial block armour layer requires the block to have a certain cavity or groove to green plants on the soil cover or provide a habitat for marine organisms. Armor blocks are usually placed on slopes to reduce wave run-up while also producing ecological effects. There are few studies related to wave run-up on sloping armour blocks, but previous research related to wave run-up on sloping beaches or slopes is more adequate. Dutykh et al. [24] considered the problem of the long-wave run-up of rough bottoms and proposed a stochastic model to simulate natural bottom roughness. The effect of bottom roughness on the maximum run-up height is also investigated. A stochastic model describing the bottom irregularity is proposed, which has practical significance. Torsvik et al. [25] used numerical models based on the finite volume method applied to the modified NLSW and modified Peregrine equations (Durán et al., [26]; Dutykh et al., [27]) and emphasized the theoretical framework and the development of equations of motion for shallow water long waves. This provided an important basis for the subsequent discussion of tsunami wave propagation and run-up on sloping beaches. In addition, Didenkulova and Pelinovsky [28] investigated the effect of incident wave form on the extreme (maximum) characteristics (run-up and draw-down heights, run-up and draw-down velocities, and breaking parameters) of waves on the beach. Bouard et al. [29] studied the motion of the free surface of a fluid over a variable bottom in a long-wave asymptotic regime. And proved that the final impact of random topography is represented by a canonical process.

Based on the traditional four-legged hollow block, this paper proposes a new type of ecological armour block. Through physical model tests, it analyzes the block’s reflection coefficient and wave overtopping on the slope embankment. Meanwhile, the influence of the height of the upper frame of the block on the wave dissipation performance is also discussed. It is worth noting that the results of this paper are aimed at the breakwater in the construction stage; the planting groove has not been planted in the planting groove during the construction phase stage. The study analyzes the reflection of the block and run-up to ensure that the breakwater does not occur over the waves. Or storm surge and other extreme climatic conditions, such as planting grooves in the plant soil body, caused damage only to the block itself to resist the storm surge situation, so this paper studies the block in the absence of plants or the soil body of the situation. It may take a fairly long time before the vegetation fully grows up. It is necessary to study the stability of the armour blocks without vegetation.” The paper is organized as follows: Section 2 describes the model and the research methodology. Section 3 presents the results and discussion. Finally, Section 4 summarizes the main conclusions and recommendations of our study.

2. Materials and Methods

2.1. New Ecological Block

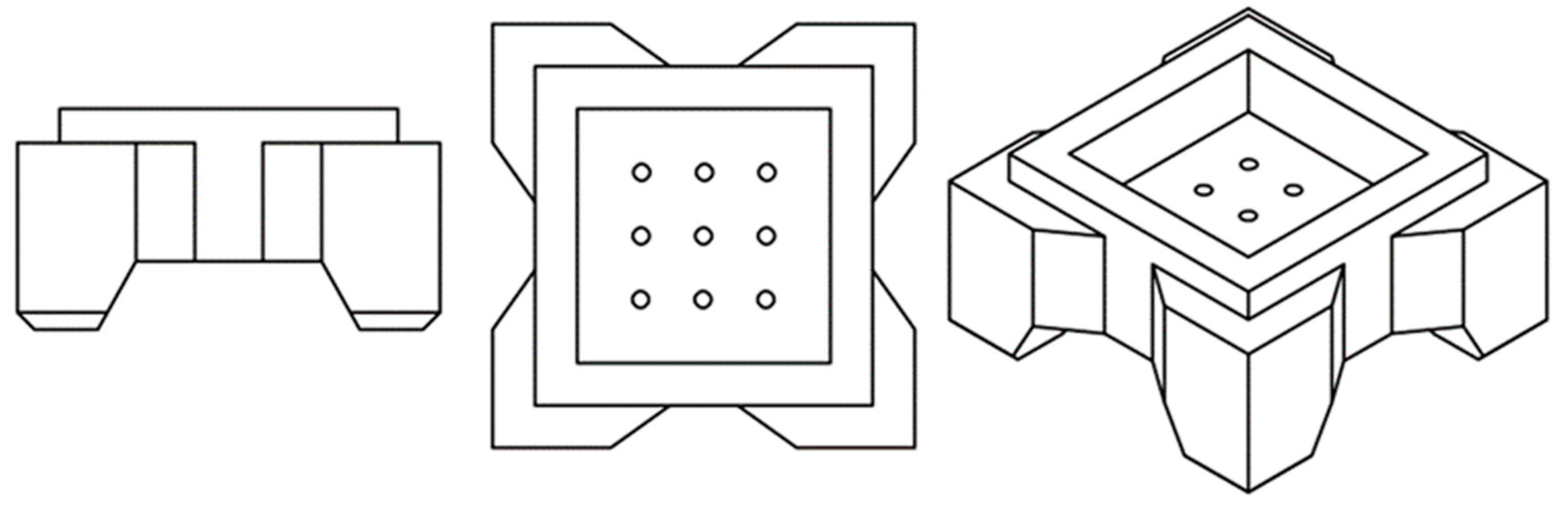
The new type of ecological armour block is transformed from the traditional four-legged hollow block. The four legs on the upper part of the conventional traditional block are removed, and the border is raised with appropriate surface excavation to form a “planting groove.” The block has the form in Figure 1. The wave dissipation mechanism of the block is as follows: During the wave run-up process, strong turbulence is generated when the wave enters the chamber formed in the block. During the interaction between the wave and the block, the energy is dissipated, thus achieving the purpose of wave dissipation. In this paper, we only consider the case where only the blocks are placed during the construction period of the breakwater or under extreme climatic conditions, and subsequently, the ecological performance of the breakwater can be improved by increasing the biomass of the tidal surface of the breakwater by planting coastal aquatic plants in the planting groove. However, it may take a considerable amount of time for the vegetation to fully grow. It is necessary to study the stability of armored blocks without vegetation.

Considering a new ecological conventional block with a side length of 2m (weighing approximately 5.5t), physical model tests were conducted following the principle of gravity similarity. The geometric scaling factor λ_l=25 and the time scaling factor λ_t=(λ_l)^0.5=5. New ecological blocks are placed on a smooth slope to study the reflection coefficient of the blocks and the wave run-up. Four different slope ratios were considered: 1:1.5, 1:2, 1:2.5, and 1:3. Additionally, three different water depths at the toe of the dike were considered: 7.5m, 8.75m, and 10m.

2.2. Model Experiment

2.2.1. Experimental Equipment and Instruments

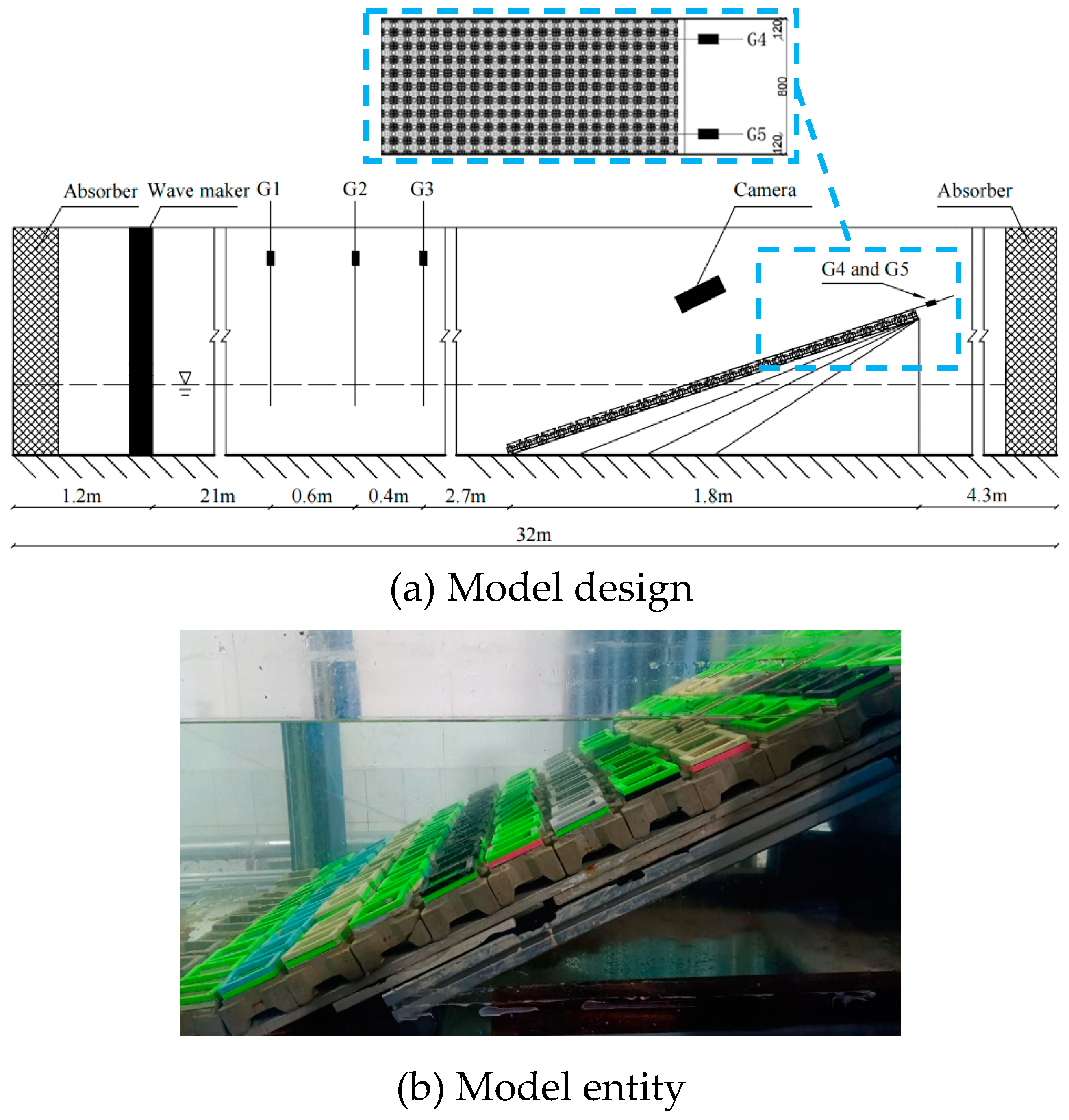
The physical modelling tests were undertaken in a two-dimensional wave flume at Zhejiang University of Water Resources and Electric Power in China. The flume has dimensions of 32.0 (L) × 0.8 (W) × 1.0 (H) m. Figure 2 illustrates a two-dimensional wave flume. The flume is equipped with a piston-type wave maker and an active wave absorption system (AWAS). Figure 3 illustrates the wavemaker. It can actively absorb secondary reflected waves, and the absorption rate of regular waves reaches more than 90%. Energy dissipation nets were installed on both ends of the flume to mitigate the effects of wave reflection. Wave height was measured using a DS30 multi-channel wave height acquisition system.

2.2.2. Model Work and Experimental Conditions

In general, the higher the frame of the “planting groove” of the new block, the larger the space and the better the wave dissipation effect. To investigate the effect of frame height on the wave dissipation performance, two modified blocks with different frame heights were made while maintaining the overall structure of the new block unchanged. The model section was a sloping structure consisting of two layers of impermeable tiles and aluminum profiles. The armour blocks were placed regularly on the slope using four different schemes. Figure 4 displays the armour blocks used in the model, from left to right; they correspond to the Conventional four-legged hollow block (referred to as the “conventional block”), the new ecological four-legged hollow block (referred to as the “new block”), and the modified blocks with one additional layer (referred to as “New High 1”) and two different layers (referred to as “New High 2”) of frame height for the new block. The prototype dimensions of each type of block are shown in Table 1.

Physical model test conditions were determined based on slope gradient, water depth, wave height, and period under different armour block schemes, as shown in Table 2. The experimental data and graphics are presented on a prototype scale. Regular waves were used in each set of test conditions and repeated twice to ensure the repeatability of the experimental data.

2.2.3. Experimental Layout

The model section is 24.7m from the wavemaker. For data collection, a wave gauge was set up at 2.7m, 3.1m, and 3.7m at the toe of the slope, respectively. Wave surface data is collected using three wave gauges, and then the data is imported into the two-point method twice [30] to obtain the average wave reflection coefficient. High-definition cameras were arranged vertically above and on the side of the slope to record the propagation and deformation of waves on the slope. In addition, one wave gauge was placed on each side of the second row of blocks on the slope to enable future wave run-up calculations. The specific experimental layout is shown in Figure 5.

3. Results and Discussion

3.1. Analysis of the Reflection Coefficient for the New Block

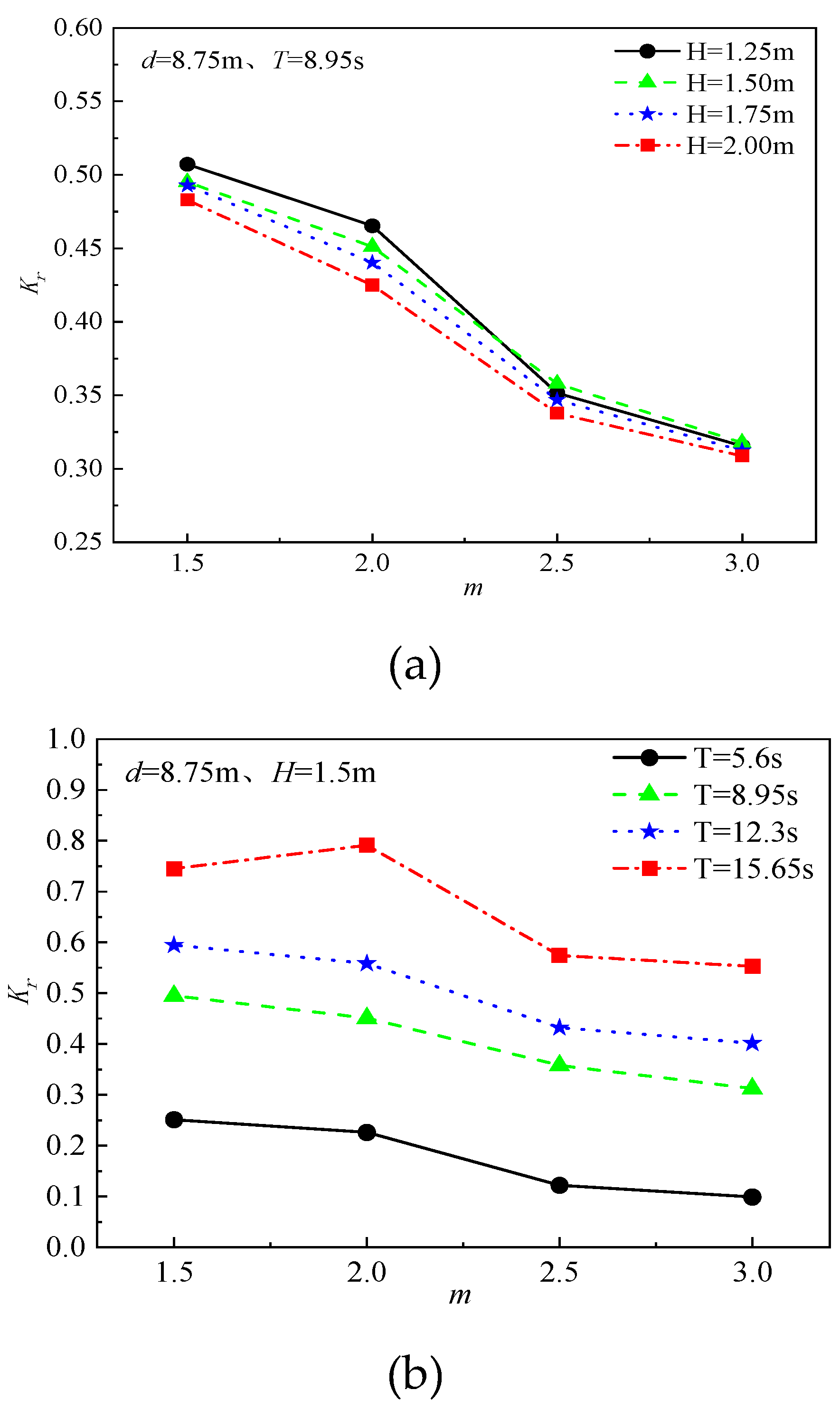
Typically, the factors affecting the wave attenuation effectiveness of armor block structures are slope gradient, incident wave characteristics, and water depth at the toe of the structure. Figure 6 shows the influence of slope gradient on the reflection coefficient of the new block type under different incident wave heights and periods when the test water depth is 8.75 m. The reflection coefficient decreases with a decrease in the slope gradient. At the same water depth, a gentle slope leads to a longer wave run-up distance on the slope. The increased friction on the slope and the turbulent flow inside the “planting groove” increase wave energy dissipation, reducing the reflected waves’ energy. For the same slope, the higher the wave height and the smaller the period, the lower the reflection coefficient. It may be that the increased steepness of the waves due to higher wave heights and smaller periods makes the waves more prone to breaking on the slope, and wave breaking consumes more energy. Moreover, as the slope gradient changes from 1:2.5 to 1:3, the rate of decrease in the reflection coefficient reduces. At a slope of 1:2.5, the new block almost achieves optimal wave dissipation.

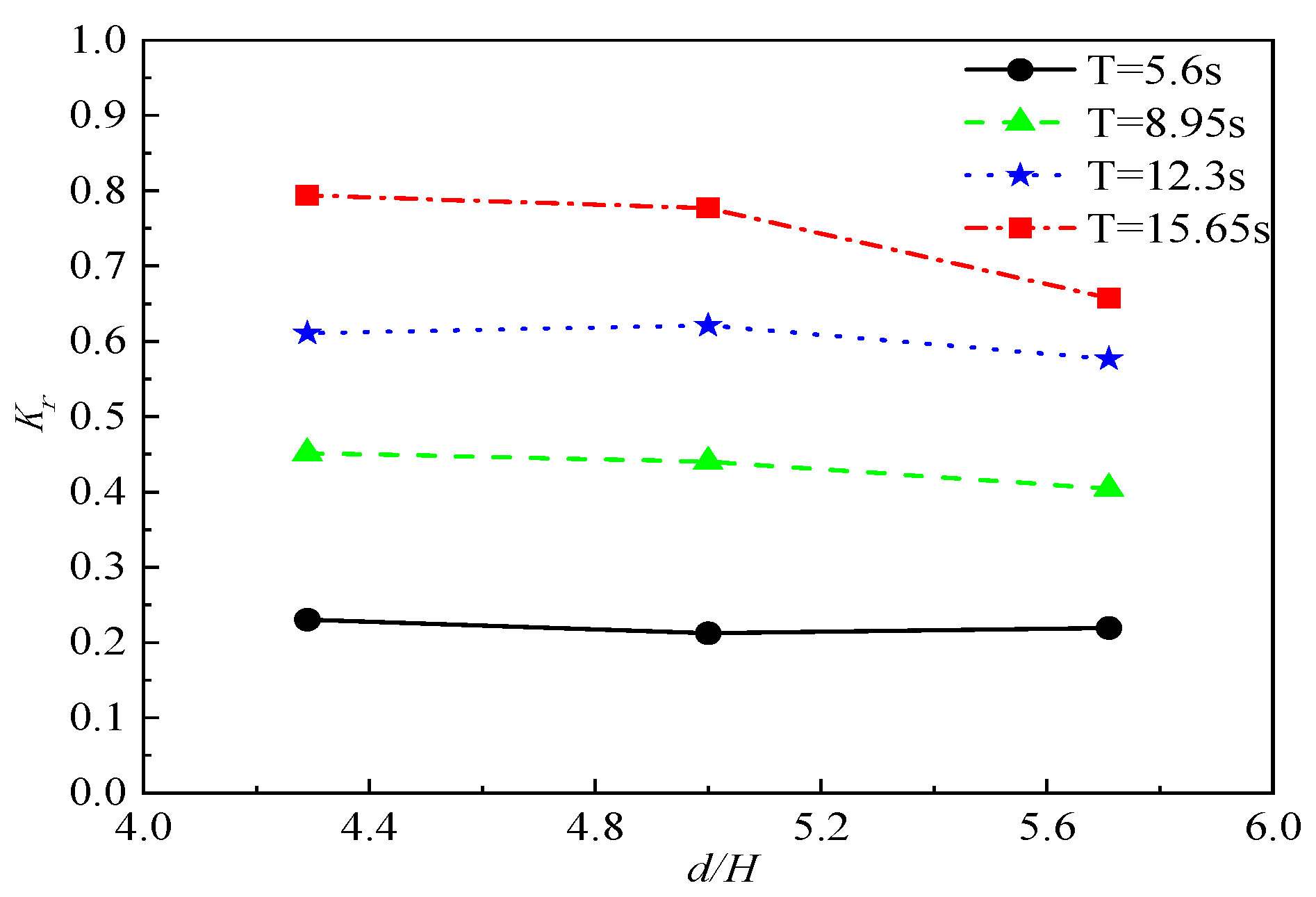
Figure 7 presents the relationship between the reflection coefficient and the relative water depth under different wave periods for a slope gradient of 1:2 and an incident wave height of 1.75m. Under the same incident wave conditions, the reflection coefficient slightly decreases with an increase in the relative water depth, but the reduction is small. It shows that the influence of the relative water depth on the reflection coefficient is insignificant.

3.2. Analysis of the Wave Run-up of the New Block

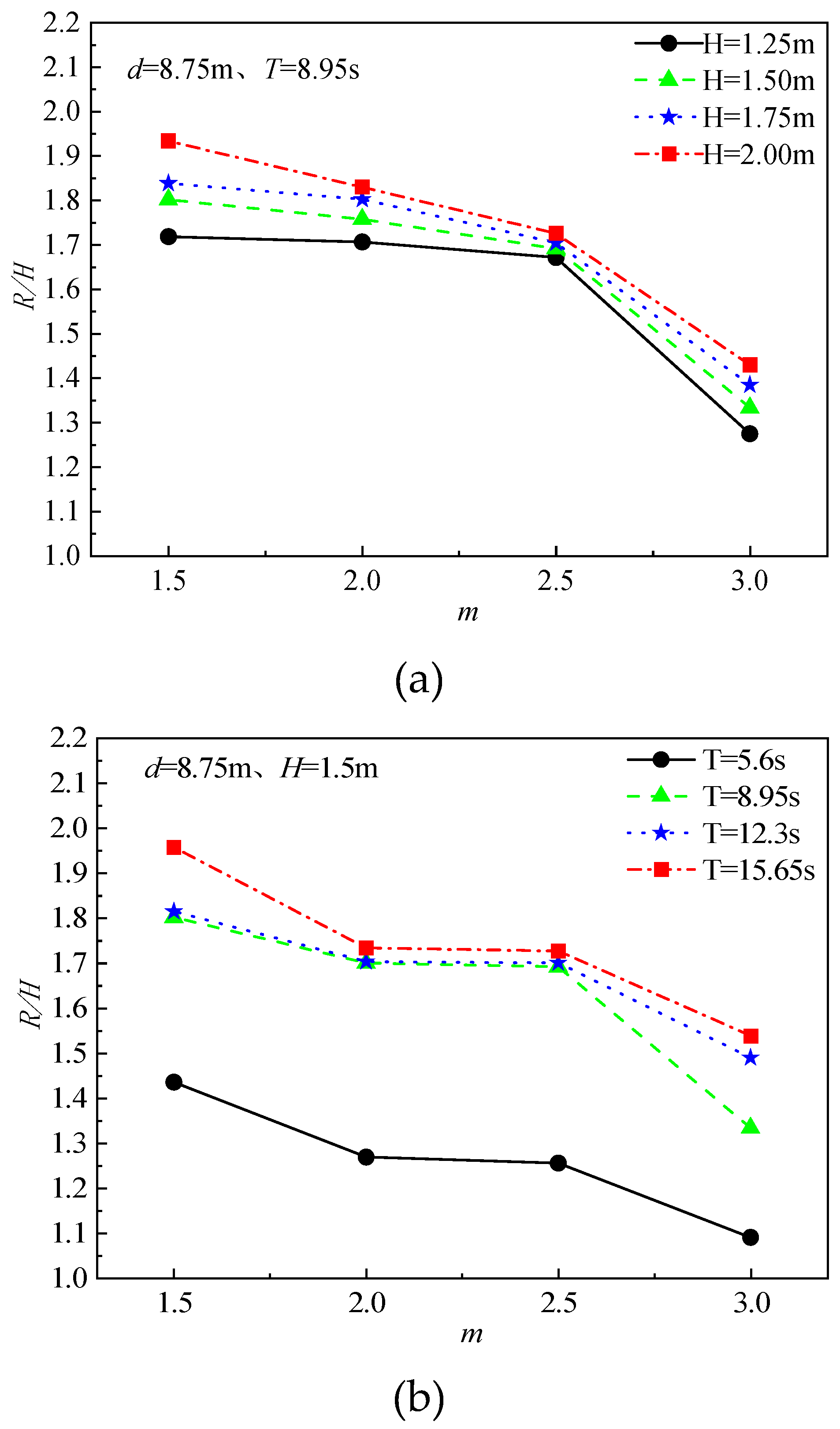
Figure 8 presents the influence of slope gradient on wave run-up under different incident wave conditions, with a water depth of 8.75 m. As the slope slows down, the relative wave run-up continues to decrease. In Figure 8a, the relative wave run-up falls slowly as the slope gradient changes from 1:1.5 to 1:2.5. The decrease becomes more significant when the slope gradient further decreases to 1:3. This might be because the wave reflection gradually weakens as the slope gradient changes from 1:1.5 to 1:2.5 (Figure 6). Meanwhile, the breaking waves continue to expand, increasing the energy dissipation from breaking. This increase outweighs the decrease in energy from reflected waves, resulting in a slight decline in wave run-up. Further reduction in slope gradient leads to a significant increase in energy dissipation due to slope friction and turbulence, causing a reduction in wave run-up. For slopes with the same gradient, larger incident wave heights result in a higher wave run-up. Furthermore, the wave run-up from waves with shorter periods is noticeably lower than from waves with longer periods.

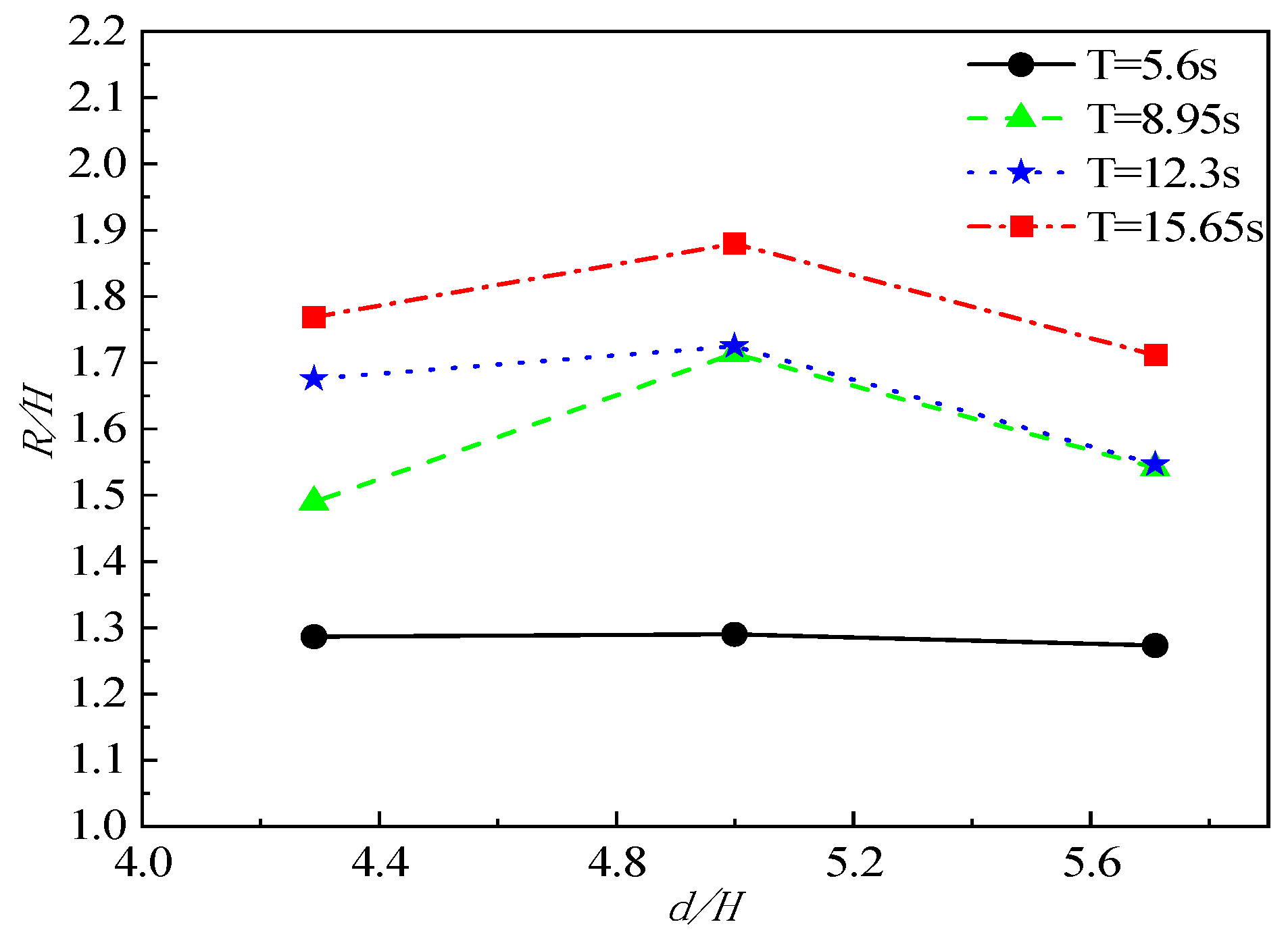
Figure 9 shows the relationship between wave run-up and relative water depth for a slope gradient of 1:2 and a wave height of 1.75m. Wave rise increases slowly and then decreases as the relative water depth increases. Taking T = 15.65 s as an example, with the relative water depth rising from 4.3 to 5.0, the relative wave run-up increases from 1.76 to 1.87. As the water depth increases, the relative run-up of the wave decreases to 1.7. For short waves with a period of 5.6 s, the relative water depth does not affect the wave’s relative run-up.

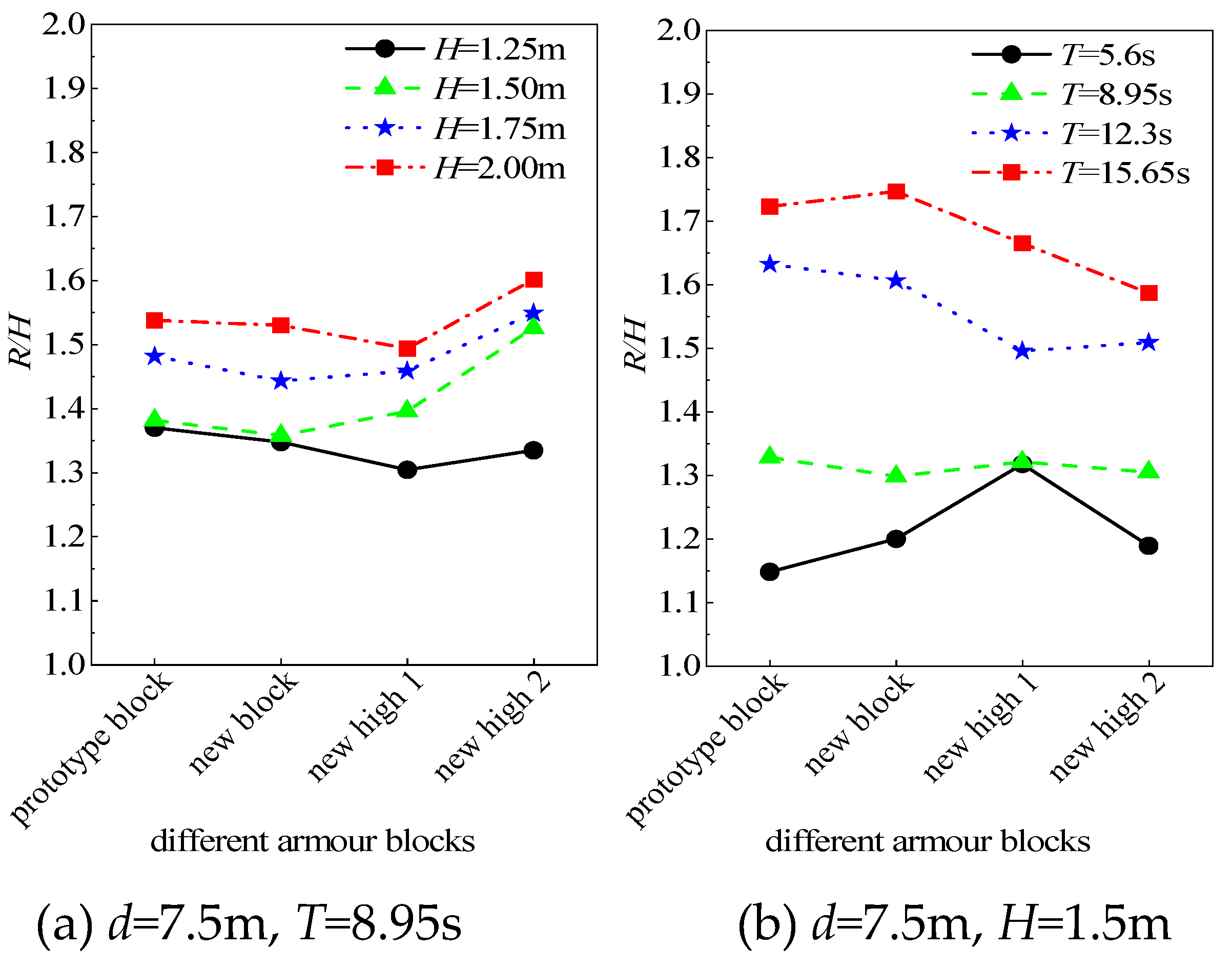
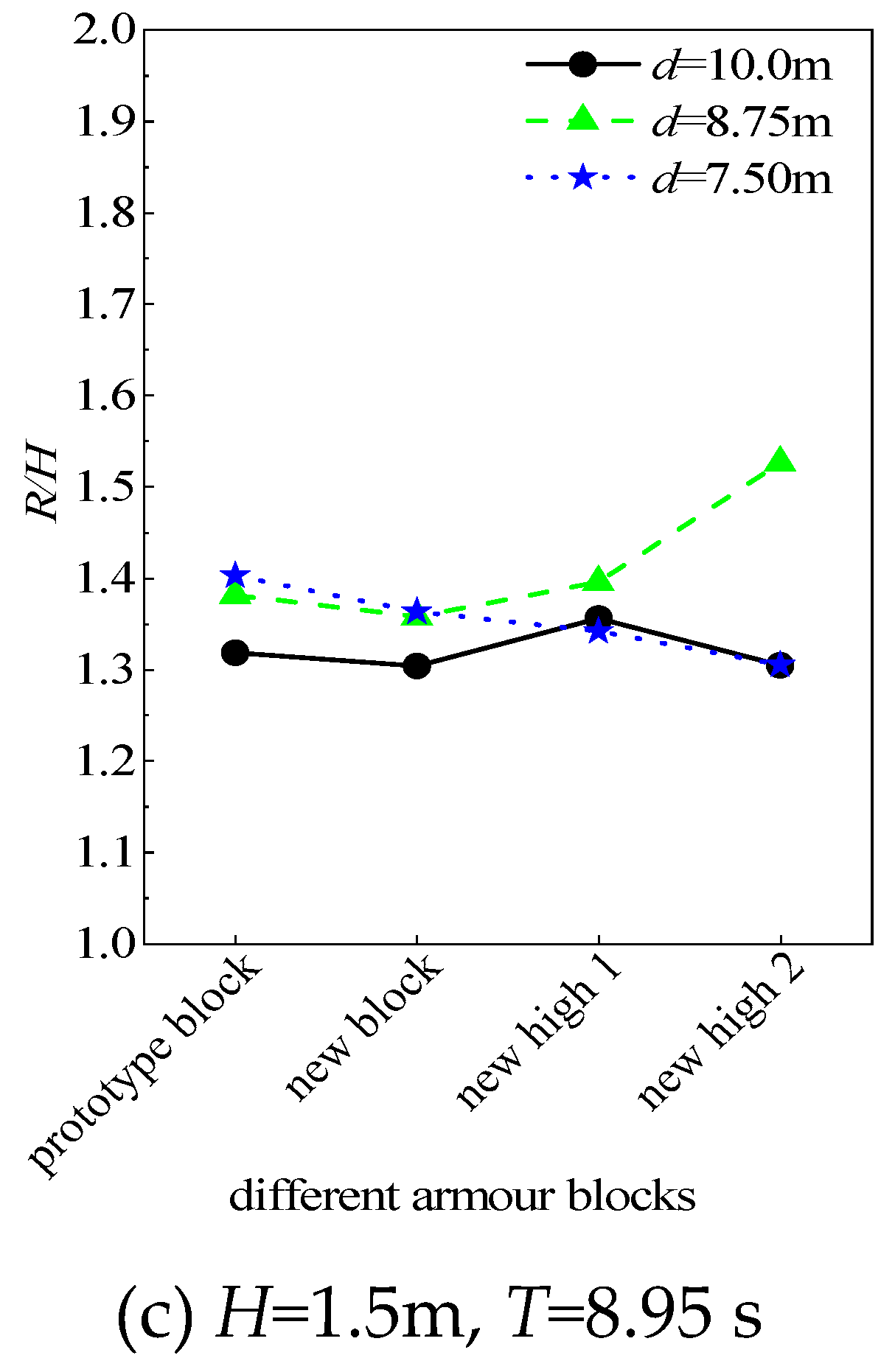
3.3. Comparison of Reflection Coefficient and Wave Run-Up for Different Blocks

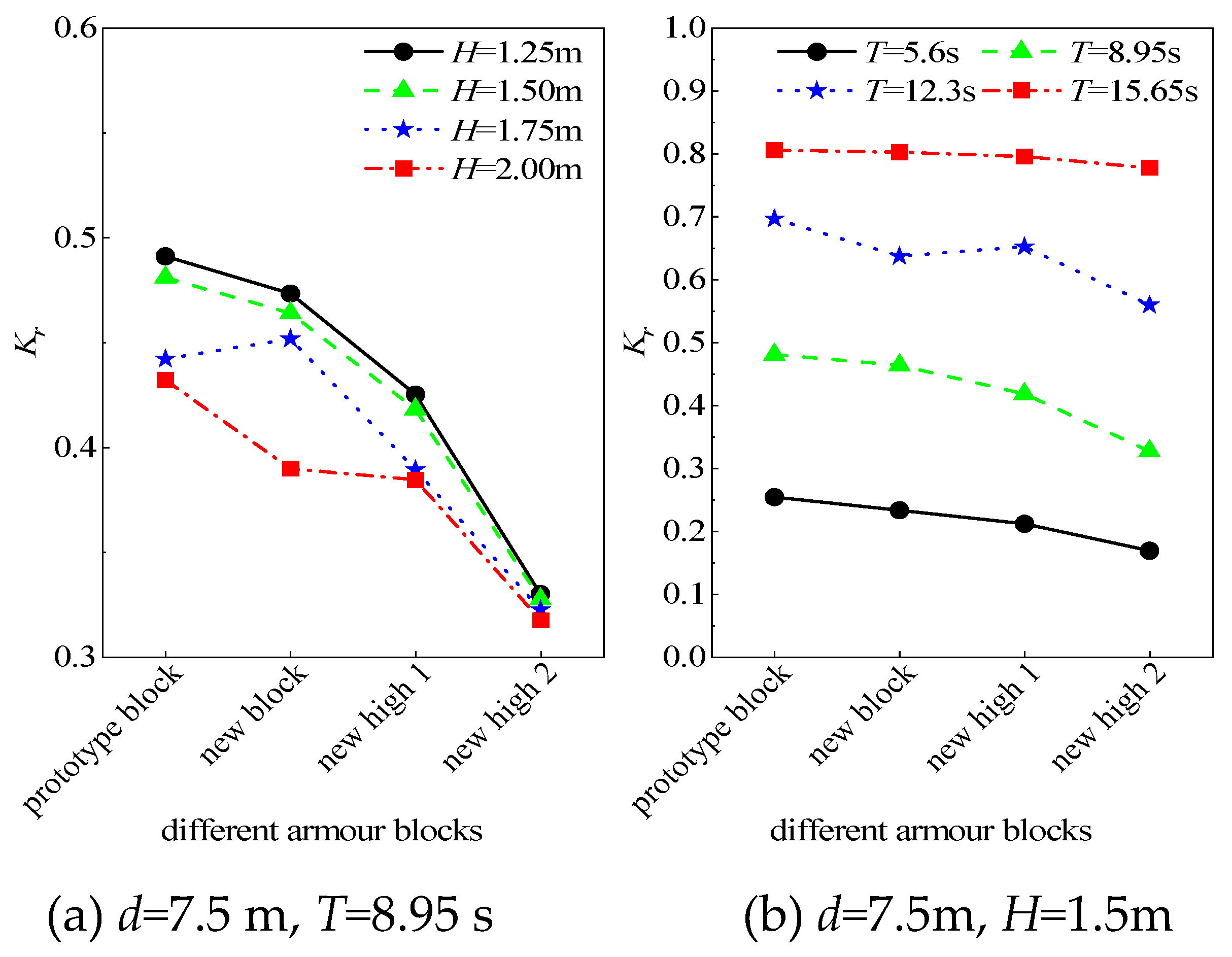
To investigate the differences in wave dissipation between a new block and the Conventional block, as well as the influence of different border heights on the reflection coefficient and wave run-up of the new block, Figure 10 and Figure 11 provide a comparison of the reflection coefficients and wave run-up for a different armour block. Figure 10a shows that the reflection coefficient of the new block is generally lower than that of the Conventional block. The latest block demonstrates better wave dissipation for larger wave heights than smaller ones. As the border height increases, the reflection coefficient of the waves significantly decreases, and the differences in reflection coefficients between different wave heights gradually reduce.

According to Figures 10b and 10c, for different wave periods and experiment water depths, the reflection coefficients of the new block are lower than those of the Conventional block. The wave dissipation effectiveness of the block improves with the increase in border height. The possible reason for this is that as the border height of the “planted groove” in the armour block increases, the surface of the block becomes more pronounced. There is increased frictional resistance on the breakwater slope, and the “planted groove” volume in the block also increases. As a result, more water flows into the groove during the run-up process, increasing turbulent energy consumption. Ultimately, this leads to a reduction in the energy of the reflected waves.

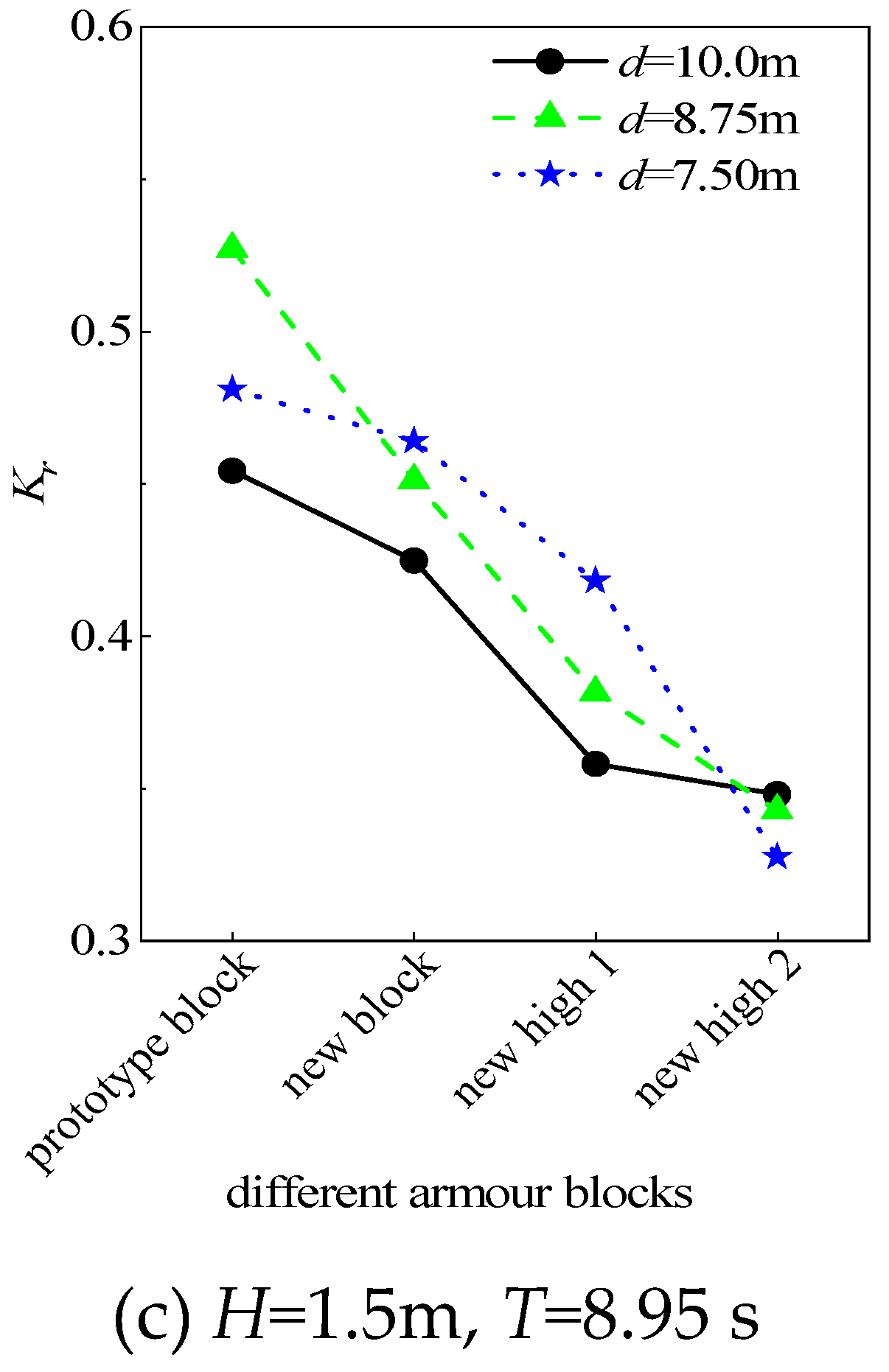
Figure 11 shows a comparison of the relative run-up between the different blocks. The wave run-up characteristics of the new block are not significantly better than those of the Conventional block. In fact, for larger wave heights, the wave run-up of the new block is even greater (Figure 11a). Furthermore, there is no apparent trend of decreased wave run-up with increasing border height. Based on the analysis of the experimental phenomena, the increase in the border’s height hinders the backflow of water on the slope. It prevents the timely discharge of water from the groove. It may reduce the resistance to wave climbing and lead to wave run-up.

As Figure 11 demonstrates, the armour block used in this study only varies in the height of the border; the pattern that may be found if the armour block is studied as a sloping surface with roughness is not clear. In this regard, Dutykh et al. [27] proposed a stochastic model describing the bottom roughness and quantified its effect using Monte-Carlo simulations, which showed that the bottom roughness magnitude σ decreases with the maximum wave run-up and increases with the regularity parameter r, and that the law holds for different variations of the bottom roughness and the regularity parameter. This study provides a supplement and basis for the effect of bottom roughness on the maximum wave run-up, and it also provides a new way of thinking about the approximation of the armourξblock into roughness for the study in this paper.

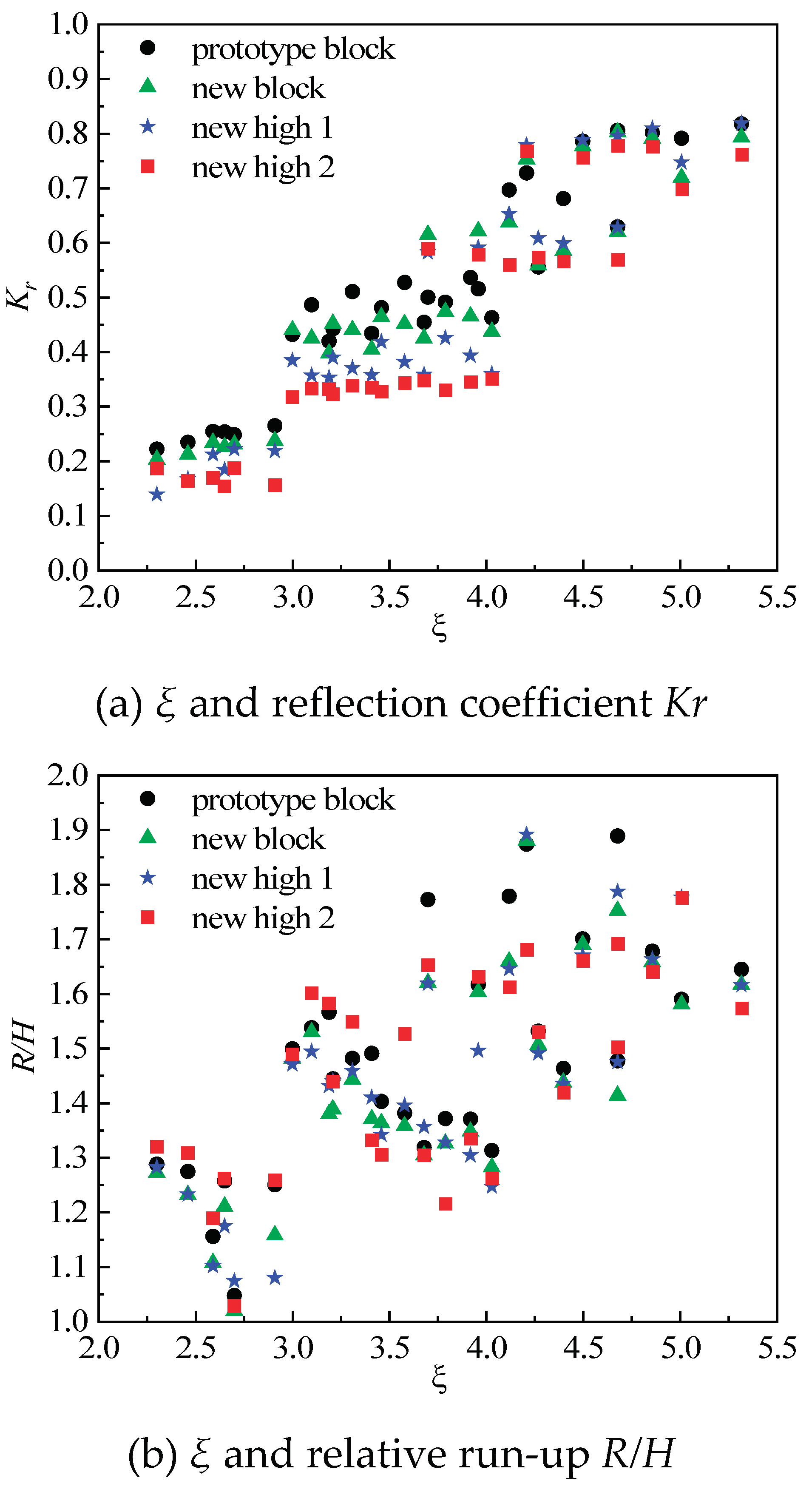
3.4. Influence of the Average Breaking Parameter ξ on the Reflection Coefficient and Wave Run-Up of New Blocks

Considering the significant impact of wave breaking on waves, the average breaking parameter ξ is introduced, with a value of tanα/(H/L)^0.5, where α represents the slope gradient and H and L represent the wave height and wavelength in front of the seawall. Figure 12a shows that the reflection coefficient increases with the average breaking parameter ξ. The reflection coefficients of the blocks are relatively concentrated when the average breaking parameter ξ ranges from 2.3 to 2.9; during this range, the reflection coefficients are relatively small. Within this range, the increment of reflection coefficients with the increase in the average breaking parameter ξ is relatively small. When ξ ranges from 3 to 4.1, the wave-breaking type changes from plunging to surging, and the overall reflection coefficient is noticeably greater than the reflection coefficient when ξ ranges from 2.3 to 2.9. Additionally, during this range, the reflection coefficient is concentrated and increases slowly with the increase in ξ. When ξ exceeds 4.2, the reflection coefficient is significantly larger and more dispersed, possibly due to longer wave periods resulting in poorer wave dissipation effectiveness of the blocks. The figure also indicates that the reflection coefficient of the new block is somewhat lower than that of the Conventional block, and this trend becomes more pronounced with the increase in border height. On average, the reflection coefficient of the new block is reduced by 4.25% compared to the Conventional block, with a reduction of 11.66% for New High 1 and 18.86% for New High 2.

For wave run-up, when ξ is between 2.3 and 2.9, the formation of plunging increases as ξ increases when waves backwash on the slope. The interaction between the plunging and the next incoming wave results in a gradual decrease in the next wave run-up, leading to a relatively smaller relative run-up R/H with the increase of ξ. When ξ is between 3 and 4.1, the overall relative run-up R/H is greater than when ξ is between 2.3 and 2.9. The predominant wave type formed at this time is surging. When surging breaks, the wave border peak becomes asymmetric, and the toe of the wave peak front begins to break, followed by a miscellaneous breaking situation in the front of the wave peak, climbing up the slope like a water surge. When ξ is greater than 4.2, the relative run-up R/H shows an increasing trend, possibly due to the excessively large wave period.

According to the “Code of Hydrology for Sea Harbour” [31] and the “Code for Design of Sea Dike Project” [32], for a single-slope seawall with a slope of 1:(1-5) and a foreshore slope of i≤1/50, the wave run-up of regular waves on the seawall can be calculated using the following formula:

R=K_△R₁H

(1)

R represents the wave run-up (m), with the still water level as the reference plane, positive in the upward direction; K_△ is the rough permeability coefficient related to the structure type of the sloping armour; H represents the wave height in front of the breakwater (m); R₁ is the wave run-up (m) when K = 1 and H = 1m.

Under the same working conditions, with all parameters in equation (1) being the same except for the turbulent permeability coefficient, the rough permeability coefficient for the four-legged hollow block specified in the code is 0.55. Based on the run-up of the Conventional four-legged hollow block and the new blocks, New High 1 and New High 2, the rough permeability coefficients for the new blocks, New High 1 and New High 2, calculated by the ratio method, are 0.53, 0.53, and 0.54, respectively.

Furthermore, The type of waves discussed in this study are regular waves, and nothing is yet known about how different incident wave shapes affect wave run-up, reflections, and breaking patterns. Torsvik et al. [25] discuss the propagation and run-up of tsunami waves on an inclined beach with wave dispersion. Wave flume experiments show that wave dispersion plays an important role in wave signal propagation and wave translation. However, the low sensitivity of the maximum wave run-up to dispersion effects suggests that the wave run-up can be adequately calculated by using non-dispersive model equations. This study is informative for future experimental design of armored blocks, and it is recommended that future studies related to armored blocks start with incident wave shapes to improve the practical applicability of the results.

4. Conclusions

A two-dimensional wave flume physical modeling test was done on the new ecological hollow blocks to find out how well they reflect waves and how much water they hold up while the breakwater was being built. The main conclusions of this study are as follows:

(1) The effects on the reflection coefficients of the new blocks are investigated by varying the incident wave height, period, water depth, and breakwater slope. The results show that: When the slope gradient increases from 1:1.5 to 1:3, the reflection coefficient of the new block decreases continuously. The reflection coefficient decreases with increasing wave run-up and decreasing period. In addition, it was found that the relative water depth had little effect on the reflection coefficient.

(2) The effect on the wave run-up in the new block was investigated by varying the incident wave height, period, water depth, and breakwater slope. The results showed that as the slope angle decreases, the relative run-up decreases sharply. The wave run-up increases as the wave height and period increase. Furthermore, an increase in relative water depth causes the relative run-up to first increase and then decrease, but the magnitude of the change is small.

(3) By comparing the reflection coefficient and wave run-up between the new block and the conventional block, it is concluded that the reflection coefficient of the new block is lower than that of the conventional block and further decreases with the elevation of the boundary of the "planting groove," but the wave run-up of the new block does not significantly decrease with the elevation of the boundary of the "planting groove.".

(4) Changing the average breaking parameter ξ had an impact on the reflection coefficient and wave run-up of the new blocks. The reflection coefficient gradually went up from 2.3 to 5.32, especially when ξ reached 2.9 and 4.1. The relative run-up R/H also went up, but there was a noticeable drop between ξ = 2.3 and 2.9 and 3.0 and 4.1. Compared with the conventional four-legged hollow blocks, the average reflection coefficients of the new blocks decreased by 4.25%, 11.66% for New Height 1, and 18.86% for New Height 2. In addition, the roughness coefficients were calculated to be 0.53, 0.53, and 0.54 for the new blocks, New Height 1, and New Height 2, respectively, based on comparisons with the conventional four-legged hollow block.

The results of this paper are only for the case of blocks without plants when they are in the construction period of the breakwater or when extreme weather intrusion occurs, and the case of placing plants in the blocks will be carried out in the next step.

Author Contributions

Conceptualization, H.Z., F.D., J.Y.; Methodology, H.Z., H.J.; Software, H.Z., W.G.; Validation, Q.L.; Investigation, H.Z., G.Y.; Formal Analysis, H.Z.; Resources, G.Y.; Data Curation, H.J.; Writing - Original Draft, H.Z., F.D.; Writing - Review & Editing, J.W., W.C.; Visualization, W.C.; Supervision, F.D., J.W.; Project Administration, W.G.; Funding Acquisition, F.D., Q.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Open Fund of Key Laboratory of Marine Spatial Resource Management Technology, Ministry of Natural Resources, Zhejiang Province, China, grant numbers KF-2022-110 and 2021GXNSFAA075003, and the Natural Science Foundation of ZheJiang province, grant numbers ZJWZ23E090009.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Acknowledgments

The authors acknowledge the editors and reviewers for their valuable comments and suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

References

Scaravaglione G, Latham J P, Xiang J, et al. Historical overview of the structural integrity of Concrete Armour Units[J]. Coast. Offshore Sci. Eng, 2022, 1: 68-98.
Bruce, T.; van der Meer, J.W.; Franco, L.; Pearson, J.M. Overtopping performance of different armour units for rubble mound breakwaters. Coast. Eng. 2009, 56, 166–179. [CrossRef]
Kudale, M., Prakash, K. and Kudale, A., 2021. Performance of concrete armour units of breakwaters in india - a review. International Journal of Civil Engineering and Technology, 12: 54-66. [CrossRef]
Safari, I.; Mouazé, D.; Ropert, F.; Haquin, S.; Ezersky, A. Hydraulic stability and wave overtopping of starbloc® armored mound breakwaters. Ocean Eng. 2018, 151, 268–275. [CrossRef]
Park, Y.H.; Oh, Y.M.; Ahn, S.M.; Han, T.H.; Kim, Y.T.; Suh, K.D.; Won, D. Development of a new concrete armor unit for high waves. J. Coast. Res. 2019, 35, 719–728. [CrossRef]
Tianjin Research Institute for Water Transport Engineering. A Comprehensive Type of Wave Damping Artificial Block and Embankment. CN 108385609 B, 27 October 2020. (In Chinese).
Isobe, M. Impact of global warming on coastal structures in shallow water. Ocean Eng. 2013, 71, 51–57. [CrossRef]
Hosseinzadeh N, Ghiasian M, Andiroglu E, et al. Concrete seawalls: A review of load considerations, ecological performance, durability, and recent innovations[J]. Ecological engineering, 2022, 178: 106573. [CrossRef]
Rella A, Perkol-Finkel S, Neuman A, et al. Challenges in applying ecological enhancement factors into coastal and marine concrete construction[M]//Coasts, Marine Structures and Breakwaters 2017: Realising the Potential. ICE Publishing, 2018: 823-832. [CrossRef]
Firth L B, Thompson R C, Bohn K, et al. Between a rock and a hard place: environmental and engineering considerations when designing coastal defence structures[J]. Coastal Engineering, 2014, 87: 122-135. [CrossRef]
Gedan K B, Kirwan M L, Wolanski E, et al. The present and future role of coastal wetland vegetation in protecting shorelines: answering recent challenges to the paradigm[J]. Climatic change, 2011, 106: 7-29. [CrossRef]
Meyer D L, Townsend E C, Thayer G W. Stabilization and erosion control value of oyster cultch for intertidal marsh[J]. Resto-ration Ecology, 1997, 5(1): 93-99. [CrossRef]
Piazza B P, Banks P D, La Peyre M K. The potential for created oyster shell reefs as a sustainable shoreline protection strategy in Louisiana[J]. Restoration Ecology, 2005, 13(3): 499-506. [CrossRef]
Dafforn K A, Glasby T M, Airoldi L, et al. Marine urbanization: an ecological framework for designing multifunctional artificial structures[J]. Frontiers in Ecology and the Environment, 2015, 13(2): 82-90. [CrossRef]
Ido S, Shimrit P F. Blue is the new green–ecological enhancement of concrete based coastal and marine infrastructure[J]. Eco-logical Engineering, 2015, 84: 260-272. [CrossRef]
Rosenberger D, Marsooli R. Benefits of vegetation for mitigating wave impacts on vertical seawalls[J]. Ocean Engineering, 2022, 250: 110974. [CrossRef]
Chapman M G, Underwood A J. Evaluation of ecological engineering of “armoured” shorelines to improve their value as habitat[J]. Journal of experimental marine biology and ecology, 2011, 400(1-2): 302-313. [CrossRef]
Sutton-Grier A E, Wowk K, Bamford H. Future of our coasts: The potential for natural and hybrid infrastructure to enhance the resilience of our coastal communities, economies and ecosystems[J]. Environmental Science & Policy, 2015, 51: 137-148. [CrossRef]
Mohamed T A, Alias N A, Ghazali A H, et al. Evaluation of environmental and hydraulic performance of bio-composite re-vetment blocks[J]. American Journal of Environmental Sciences, 2006, 2(4): 129-134.
Scheres B, Schüttrumpf H. Enhancing the ecological value of sea dikes[J]. Water, 2019, 11(8): 1617. [CrossRef]
Le Xuan T, Ba H T, Thanh V Q, et al. Evaluation of coastal protection strategies and proposing multiple lines of defense under climate change in the Mekong Delta for sustainable shoreline protection[J]. Ocean & Coastal Management, 2022, 228: 106301. [CrossRef]
Chen Y, Li Y, Shou Y, et al. Exploring the Ecological Impacts and Implementation Strategies of Reclamation in Taiping Bay of Dalian Port as an Example[J]. Journal of the Taiwan Institute of Chemical Engineers, 2023: 105023. [CrossRef]
Gutiérrez Martínez J, Bezner M, Molenkamp A, et al. Physical Evaluation Of The Hydrodynamic Stability Of An Eco-engineered Armouring Unit[J]. Coastal Engineering 2022, 2023, 37.
Dutykh D, Labart C, Mitsotakis D. Long wave run-up on random beaches[J]. Physical Review Letters, 2011, 107(18): 184504. [CrossRef]
Torsvik T, Abdalazeez A, Dutykh D, et al. Dispersive and nondispersive nonlinear long wave transformations: Numerical and experimental results[J]. Applied Wave Mathematics II: Selected Topics in Solids, Fluids, and Mathematical Methods and Complexity, 2019: 41-60. [CrossRef]
Durán, D. Dutykh, and D. Mitsotakis. Peregrie’s system revisited. In N. Abcha, E. Pelinovsky, and I. Mutabazi, editors, Nonlinear Waves and Pattern Dynamics, pages 3{43. Springer, 2018.
Dutykh D, Katsaounis T, Mitsotakis D. Finite volume schemes for dispersive wave propagation and runup[J]. Journal of Computational Physics, 2011, 230(8): 3035-3061. [CrossRef]
Didenkulova I I, Pelinovsky E N. Run-up of long waves on a beach: the influence of the incident wave form[J]. Oceanology, 2008, 48: 1-6. [CrossRef]
De Bouard A, Craig W, Díaz-Espinosa O, et al. Long wave expansions for water waves over random topography[J]. Nonline-arity, 2008, 21(9): 2143. [CrossRef]
Goda Y, Suzuki Y. Estimation of incident and reflected waves in random wave experiments[M]//Coastal Engineering 1976. 1976: 828-845. [CrossRef]
JTJ 213-1998, Code of Hydrology for Sea Harbour [S]]. (In Chinese).
GB/T 51015-2014, Code for Design of Sea Dike Project [S]]. (In Chinese).

Figure 1. Schematic diagram of the new type of ecological four-legged hollow block.

Figure 2. Wave flume.

Figure 3. Wavemaker.

Figure 4. Prototype block and the new block with different frame heights.

Figure 5. Model layout (units:m).

Figure 6. The variation of the reflection coefficient with the slope gradient.

Figure 7. The variation of the reflection coefficient with the relative water depth.

Figure 8. The variation of the wave run-up coefficient with slope gradient.

Figure 9. The variation of wave run-up with relative water depth at different wave periods.

Figure 10. Comparison of reflection coefficients for different armour blocks.

Figure 11. Comparison of wave relative run-up for different armour blocks.

Figure 12. The impact of ξ on reflection coefficient and run-up.

Table 1. Different prototype model sizes of armour blocks.

Block type	Length/m	Wide/m	Border height/m	Height /m
Conventional block	2	2	/	1.2
New block	2	2	0.16	1.04
New High 1	2	2	0.32	1.2
New High 2	2	2	0.48	1.36

Table 2. Experimental conditions of the physical model test. (prototype scale).

Block type	slope gradient m	Water depth d/m	Period T/s	Wave height H/m
Conventional block	1:2	8.75	5.6, 8.95, 12.3, 15.65	1.25, 1.5, 1.75, 2.0
		7.5, 10	8.95	1.25, 1.5, 1.75, 2.0
		7.5, 10	5.6, 12.3, 15.65	1.5
New block	1:1.5, 1:2, 1:2.5, 1:3	7.5, 8.75, 10	5.6, 8.95, 12.3, 15.65	1.25, 1.5, 1.75, 2.0
New High 1	1:2	8.75	5.6, 8.95, 12.3, 15.65	1.25, 1.5, 1.75, 2.0
		7.5, 10	8.95	1.25, 1.5, 1.75, 2.0
		7.5, 10	5.6, 12.3, 15.65	1.5
New High 2	1:2	8.75	5.6, 8.95, 12.3, 15.65	1.25, 1.5, 1.75, 2.0
		7.5, 10	8.95	1.25, 1.5, 1.75, 2.0
		7.5, 10	5.6, 12.3, 15.65	1.5

Table 3. Experimental conditions of the physical model test. (model scale).

Block type	slope gradient m	Water depth d/m	Period T/s	Wave height H/cm
Prototype block	1:2	0.35	1.12, 1.79, 2.46, 3.13	5, 6, 7, 8
		0.3, 0.4	1.79	5, 6, 7, 8
		0.3, 0.4	1.12, 2.46, 3.13	6
New block	1:1.5, 1:2, 1:2.5, 1:3	0.3, 0.35, 0.4	1.12, 1.79, 2.46, 3.13	5, 6, 7, 8
New High 1	1:2	0.35	1.12, 1.79, 2.46, 3.13	5, 6, 7, 8
		0.3, 0.4	1.79	5, 6, 7, 8
		0.3, 0.4	1.12, 2.46, 3.13	6
New High 2	1:2	0.35	1.12, 1.79, 2.46, 3.13	5, 6, 7, 8
		0.3, 0.4	1.79	5, 6, 7, 8
		0.3, 0.4	1.12, 2.46, 3.13	6

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer