1. Introduction
In optimization, the aim is to determine a best solution from a set of options for a specific problem [
1]. Mathematically, optimization problems consist of decision variables, constraints, and an objective function. The objective is to assign appropriate values to the decision variables in order to maximize or minimize the objective function while adhering to the problem's constraints [
2]. Regarding such optimization problems, problem solving techniques can be partitioned into two main groups: deterministic and stochastic approaches [
3]. Deterministic methods are particularly useful for solving linear, convex, low-dimensional, continuous, and differentiable problems [
4]. However, as problems become more intricate and dimensions increase, deterministic approaches may struggle with being trapped in local optima and providing suboptimal solutions [
5]. Conversely, within science, engineering, industry, technology, and practical applications, numerous intricate optimization problems exist that are characterized as non-convex, non-linear, discontinuous, non-differentiable, complex, and high-dimensional. Due to the inefficiencies and challenges associated with deterministic methods in addressing these optimization issues, scientists have turned to developing stochastic approaches [
6].
Metaheuristic algorithms stand out as highly effective stochastic methods capable of offering viable solutions for optimization challenges, all without requiring derivative information. They rely on random exploration within the solution space, utilizing random operators and trial-and-error strategies. Their advantages include straightforward concepts, straightforward implementation, proficiency in tackling varied optimization problems, no matter how complex or high-dimensional they may be, as well as adaptability to nonlinear and unfamiliar search spaces. As a result, the popularity and extensive use of metaheuristic algorithms continue to grow [
7]. In metaheuristic algorithms, the optimization process begins by randomly generating a set of candidate solutions at the start of the algorithm. These candidate solutions are then enhanced and modified by the algorithm during a certain number of iterations following its implementation steps. Upon completion of the algorithm, the best candidate solution found during its execution is put forward as the proposed solution to the problem [
8]. This random search element in metaheuristic algorithms means that achieving a global optimum cannot be guaranteed using these methods. Nonetheless, the solutions derived from these algorithms, being near the global optimum, are deemed acceptable as quasi-optimal solutions [
9].
For a metaheuristic algorithm to effectively carry out the optimization process, it needs to thoroughly explore the solution space on both a global and local scale. Global searching, through exploration, allows the algorithm to pinpoint the optimal area by extensively surveying all parts of the search space and avoiding narrow solutions. Local searching, through exploitation, helps the algorithm converge to solutions near a global optimum by carefully examining surrounding areas and promising solutions. Success in the optimization process hinges on striking a balance between exploration and exploitation during the search [
10]. Researchers' desire to improve optimization outcomes has resulted in the development of many metaheuristic algorithms.
The key question at hand is whether, based on the available metaheuristic algorithms, there remains a need in scientific research to develop new metaheuristic algorithms. The concept of No Free Lunch (NFL) [
11] addresses this by highlighting that while a metaheuristic algorithm may perform well in solving a particular set of optimization problems, it might not guarantee the same solution quality for different optimization problems. The NFL theorem suggests that there is no one-size-fits-all optimal metaheuristic algorithm for all types of optimization problems. It is conceivable that an algorithm may efficiently reach a global optimum for one problem but struggle to do so for another, possibly getting stuck at a local optimum. As a result, the success or failure of employing a metaheuristic algorithm for an optimization problem cannot be definitively assumed.
The novelty of this paper is the introduction of a new innovative bio-metaheuristic algorithm called Frilled Lizard Optimization (FLO) to solve optimization problems in different research fields and real-world applications. The main contributions of this investigation can be summarized as follows:
FLO is based on the imitation of the natural behavior of the frilled lizard in the wild.
The basic inspiration of FLO is derived from (i) the hunting strategy of the frilled lizard and (ii) the retreat of this animal to the top of the tree after feeding.
The theory of FLO is described and its implementation steps are mathematically modeled in two phases (i) exploration based on the simulation of the frilled lizard's attack towards the prey and (ii) exploitation based on the simulation of the retreat of the frilled lizard to the top of the tree after feeding.
The performance of FLO has been tested on fifty-two standard benchmark functions of various types of unimodal, high-dimensional multimodal, fixed-dimensional multimodal, and the CEC 2017 test suite.
FLO has been applied to real-world problems, and its performance is evaluated on twenty-two constrained optimization problems from the CEC 2011 test suite and four engineering design problems.
The results obtained from FLO are compared with the performance of other available metaheuristic algorithms.
This paper is organized as follows:
Section 2 contains a review of the relevant literature.
Section 3 describes the proposed Frilled Lizard Optimization (FLO) and gives a mathematical model. Then
Section 4 presents the results of our simulation studies.
Section 5 investigates the effectiveness of FLO in solving real-world applications, and
Section 6 provides some conclusions and suggestions for future research.
2. Literature Review
Metaheuristic algorithms are created by drawing upon a range of influences from natural phenomena, behaviors of living organisms in nature, biological sciences, genetics, physical laws, human behavior, and other evolutionary processes. These algorithms are categorized into four groups, namely swarm-based, evolutionary-based, physics-based, and human-based approaches – depending on the inspiration behind their design.
Swarm-based metaheuristic algorithms leverage inspiration from the collective behavior and strategies observed in various natural systems, particularly those of animals, aquatic organisms, and insects in the wild. The most frequent swarm-based metaheuristics are Particle Swarm Optimization (PSO) [
12], Ant Colony Optimization (ACO) [
13], Artificial Bee Colony (ABC) [
14], and Firefly Algorithm (FA) [
15]. PSO has replicated the collective movements of birds and fish as they search for food. ACO has imitated the behavior of ants in identifying the best path of communication between their colony and a food source. ABC has mirrored the actions of honey bees within a colony when seeking out food sources. FA draws inspiration from how fireflies communicate through optical signals. The most prominent natural behaviors among animals are foraging, hunting, migration, digging, and chasing, which have been sources of inspiration in the design of several metaheuristic algorithms such as: Greylag Goose Optimization (GGO) [
1], African Vultures Optimization Algorithm (AVOA) [
16], Marine Predator Algorithm (MPA) [
17], Gooseneck Barnacle Optimization Algorithm (GBOA) [
18], Grey Wolf Optimizer (GWO) [
19], electric eel foraging optimization (EEFO) [
20], White Shark Optimizer (WSO) [
21], Crested Porcupine Optimizer (CPO) [
22], Tunicate Swarm Algorithm (TSA) [
23], Orca Predation Algorithm (OPA) [
24], Honey Badger Algorithm (HBA) [
25], Reptile Search Algorithm (RSA) [
26], Golden Jackal Optimization (GJO) [
27], and Whale Optimization Algorithm (WOA) [
28].
Evolutionary-based metaheuristics are introduced, drawing inspiration from the fundamental concepts of genetics, biology, natural selection, survival of the fittest, and Darwin's evolutionary theory. Notable examples within this category include Genetic Algorithm (GA) [
29] and Differential Evolution (DE) [
30] are among the most popular evolutionary-based metaheuristic algorithms that are developed by imitating the generation process, biological which stand out as widely adopted algorithms. These evolutionary-based metaheuristics emulate various biological processes such as the generation mechanism, principles of genetics, natural selection, and the incorporation of random operators like selection, mutation, and crossover. Additionally, the Artificial Immune Systems (AISs) algorithm is conceived, taking cues from the human body's immune system and its adept defense mechanisms against germs and diseases [
31]. Other prominent members of evolutionary-based metaheuristics include Genetic programming (GP) [
32], Cultural Algorithm (CA) [
33], and Evolution Strategy (ES) [
34].
Physics-based metaheuristic algorithms are introduced, drawing inspiration from the modeling of forces, laws, phenomena, and other fundamental concepts in physics. Simulated Annealing (SA) [
35] , a widely employed physics-based metaheuristic algorithm, takes its design cues from the physical phenomenon of metal annealing. This process involves the melting of metals under heat, followed by a gradual cooling and freezing process to attain an ideal crystal structure. Gravitational Search Algorithm (GSA) [
36] is crafted by modeling physical gravitational forces and applying Newton's laws of motion. Concepts derived from cosmology and astronomy serve as the foundation for algorithms like Multi-Verse Optimizer (MVO) [
37] and Black Hole Algorithm (BHA) [
38]. Some other physics-based metaheuristic algorithms are: Thermal Exchange Optimization (TEO) [
39], Prism Refraction Search (PRS) [
40], Equilibrium Optimizer (EO) [
41], Archimedes Optimization Algorithm (AOA) [
42], Lichtenberg Algorithm (LA) [
43], Water Cycle Algorithm (WCA) [
44], and Henry Gas Optimization (HGO) [
45].
Human-based metaheuristic algorithms are introduced, seeking inspiration from the behaviors, decisions, thoughts, and various strategies exhibited by humans in both individual and social contexts. Teaching-Learning Based Optimization (TLBO) [
46] is one of the most widely used human-based metaheuristics, which imitates the relationships and educational interactions in the classroom between the teacher and students and among the students. A Mother Optimization Algorithm (MOA) is designed based on modeling Eshrat's care of her children [
9]. The strategy of the soldiers and their movements during a battle in ancient wars was the basic idea in the development of War Strategy Optimization (WSO) [
47]. The efforts of both the rich and the poor in the society to improve their financial and economic status has been the main idea in the design of Poor and Rich Optimization (PRO) [
48]. Some other human-based metaheuristic algorithms are: Coronavirus Herd Immunity Optimizer (CHIO) [
49], Gaining Sharing Knowledge based Algorithm (GSK) [
50], and Ali Baba and the Forty Thieves (AFT) [
51].
Based on the above literature review, no metaheuristic algorithm does exist based on the simulation of the natural behavior of frilled lizard in the wild. Meanwhile, the strategy of the frilled lizard during hunting and retreating to the top of the tree after feeding are intelligent processes that can be the basis for the design of a new optimizer. In order to address this gap, based on the mathematical modeling of two natural behaviors of the frilled lizard: (i) attacking the prey and (ii) retreating to the top of the tree, a new metaheuristic algorithm has been developed, which is discussed in the subsequent section.
3. Frilled Lizard Optimization
In this section, the source of inspiration used in the development and theory of Frilled Lizard Optimization (FLO) is stated. Then the corresponding implementation steps are mathematically modeled in order to be used for the solution of optimization problems.
3.1. Inspiration of FLO
The frilled lizard (Chlamydosaurus kingii), is a species of lizard from the family Agamidae, which is native to southern New Guinea and northern Australia [
52]. The frilled lizard is an arboreal species and diurnal that spends more than 90% of each day up in the trees [
53]. During the short time that this animal is on the ground, it is busy with feeding, socializing or traveling to a new tree [
52]. A frilled lizard can move bipedally and do this when hunting or escaping from predators. To keep balanced, it leans its head far back enough, so it lines up behind the tail base [
52,
54]. The total length of the frilled lizard is about 90 centimeters, a head-body length of 27 centimeters, and weighs up to 600 grams [
55]. The frilled lizard has a special wide and big head with a long neck to accommodate the frill. It has long legs for running and a tail that makes most of the total length of this animal [
56]. The male species is larger than the female species and has proportionally bigger jaw, head, and frill [
57]. A picture of a frilled lizard is shown in
Figure 1.
The main diet of the frilled lizard are insects and other invertebrates, although it also rarely feeds on vertebrates. Prominent prey includes centipedes, ants, termites, and moth larvae [
58]. The frilled lizard is a sit-and-wait predator that looks for potential prey. After seeing the prey, the frilled lizard runs fast on two legs and attacks the prey to catch it and feed on it. After feeding, the frilled lizard retreats back up a tree [
52].
Among the frilled lizard's natural behaviors, its sit-and-wait hunting strategy to catch prey and retreat to the top of the tree after feeding is much more prominent. These natural behaviors of frilled lizard are intelligent processes that are the fundamental inspiration in designing the proposed FLO approach.
3.2. Initialization of the Algorithm
The proposed FLO method is a metaheuristic algorithm that considers frilled lizards as its members. FLO efficiently discovers optimal solutions for optimization challenges by leveraging the search capabilities of its members within the problem-solving space. Each frilled lizard establishes value assignments for the decision variables according to its particular location in the problem-solving space. Consequently, every frilled lizard represents a potential solution that can be interpreted mathematically through a vector. Collectively, the frilled lizards constitute the FLO population, which can be mathematically characterized as a matrix using Equation (1). The initial placements of the frilled lizards within the problem-solving space are established through random initialization using Equation (2):
Here denotes the FLO population matrix, represents the th frilled lizard (candidate solution), denotes its th dimension in the search space (decision variable), gives the number of frilled lizards, is the number of decision variables, represents a random number from the interval , , and are a lower bound and an upper bound on the th. decision variable, respectively.
Considering that each frilled lizard represents a candidate solution for the problem, corresponding to each candidate solution, the corresponding objective function value can be calculated for the problem. The set of determined objective function values can be represented mathematically using the vector given in Equation (3):
Here denotes the vector of calculated objective function values and gives the evaluated objective function value corresponding to the th frilled lizard.
The determined objective function values are appropriate criteria for measuring the quality of the population individuals (i.e., candidate solutions). In particular, the best evaluated value for the objective function corresponds to the best individual of the population (i.e., the best candidate solution) and similarly, the worst evaluated value for the objective function corresponds to the worst individual of the population (i.e., the worst candidate solution). Since in each iteration of FLO, the position of the frilled lizards is updated in the solution space, new values are also evaluated for the objective function of the problem. Consequently, in each iteration the position of the best individual (i.e., the best candidate solution) must also be updated. At the end of the FLO implementation, the best candidate solution obtained during the iterations of the algorithm is presented as the solution to the problem.
3.3. Mathematical Modelling of FLO
In the FLO design, in each iteration, the position of the frilled lizard in the problem solving space is updated in two phases (i) exploration based on the simulation of the frilled lizard’s movement towards the prey during hunting and (ii) exploitation based on the simulation of the frilled lizard’s movement towards the top of the tree after feeding.
3.3.1. Phase 1: Hunting Strategy (Exploration)
One of the most characteristic natural behaviors of the frilled lizard is the hunting strategy of this animal. The frilled lizard is a sit-and-wait predator that attacks its prey after seeing it. The simulation of frilled lizard's movement towards the prey leads to extensive changes in the position of the population members in the problem-solving space and as a result increases the exploration power of the algorithm for global search. In the first phase of FLO, the position of the population individuals in the solution space of the problem is updated based on the frilled lizard's hunting strategy. In the design of FLO, for each frilled lizard, the position of other population members who have a better objective function value is considered as the prey position. According to this, the set of candidate preys' positions for each frilled lizard is determined using Equation (4):
Here, is the candidate preys set for the th frilled lizard, is the population member with a better objective function value than the th frilled lizard, and is its objective function value.
In the FLO design, it is assumed that the frilled lizard randomly chooses one of these candidate preys and attacks it. Based on the modeling of the frilled lizard's movement towards the chosen prey, a new position for each individual of the population has been calculated using Equation (5). Then, if the objective function value is better, this new position replaces the previous position of the corresponding individual using Equation (6):
Here, denotes the new suggested position of ith frilled lizard based on the first phase of FLO, represents its th dimension, denotes its objective function value, is a random number with a normal distribution from the interval , denotes the th dimension of the selected prey for the th frilled lizard, is a random number from the set , is the number of frilled lizards, and gives the number of decision variables.
3.3.2. Phase 2: Moving up the Tree (Exploitation)
After feeding, the frilled lizard retreats to the top of a tree near its position. Simulating the movement of the frilled lizard to the top of the tree leads to small changes in the position of the population individuals in the solution space of the problem and as a result, increasing the exploitation power of the algorithm for local search. In the second phase of FLO, the position of the population individuals in the solution space is updated based on the frilled lizard's strategy when retreating to the top of the tree after feeding.
Based on modeling the movement of the frilled lizard to the top of the nearby tree, a new position for each population individual is calculated using Equation (7). Then this new position, if it improves the objective function value, replaces the previous position of the corresponding individual using Equation (8):
Here denotes the new suggested position of the th frilled lizard based on the second phase of FLO, represents its th dimension, gives its objective function value, represents the iteration counter of the algorithm, and describes the maximum number of iterations of the algorithm.
3.4. Repetition Process, Pseudocode, and Flowchart of FLO
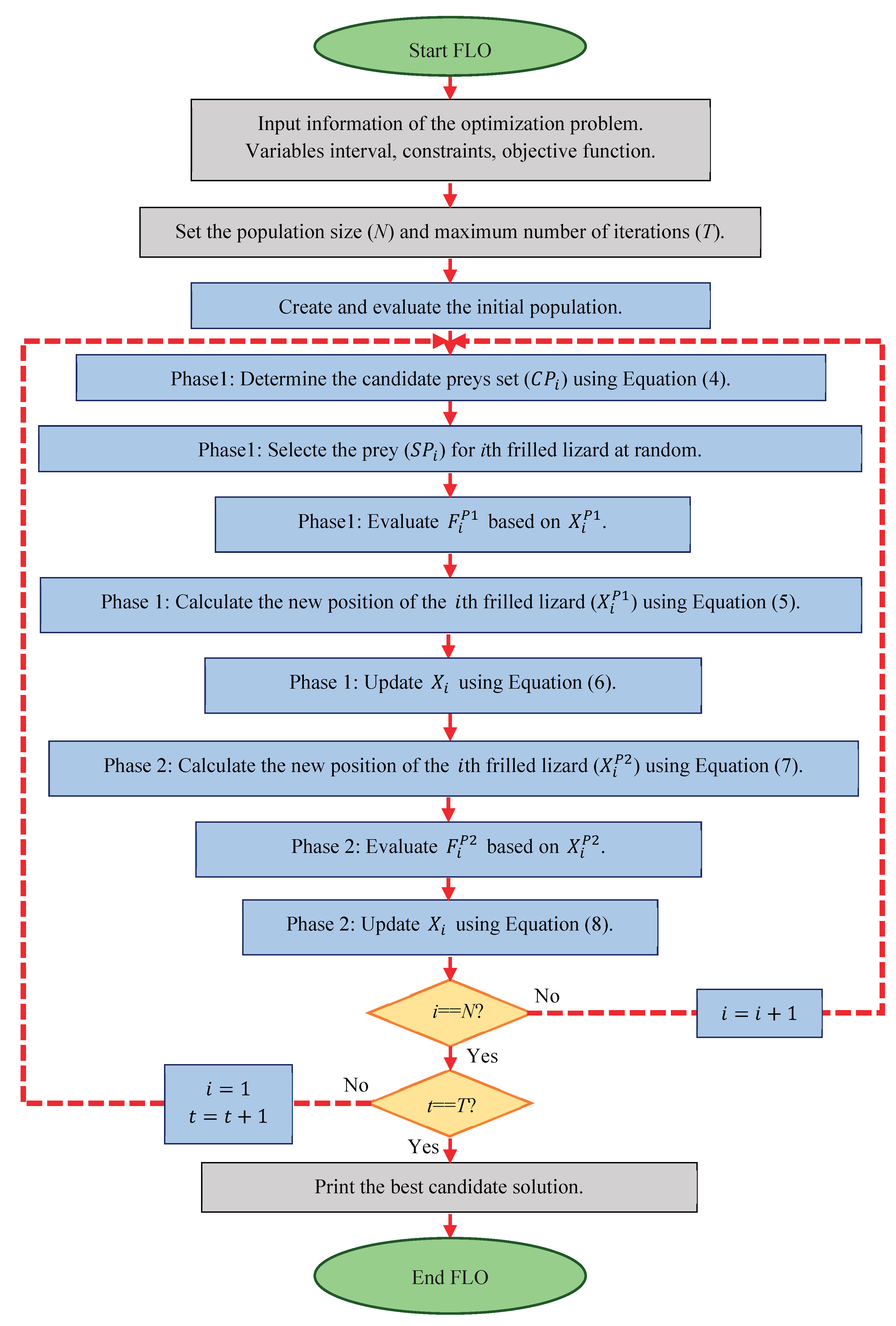
The first iteration of FLO is completed after updating the position of all frilled lizards in the problem solving space based on the first and second phases. After that, with the new updated values, the algorithm starts with the next iteration and the process of updating the position of the frilled lizards continues until the algorithm finishes using Equations (4) to (8). In each iteration, the best candidate solution is also updated and stored based on the comparison of the obtained objective function values. After the complete implementation of the algorithm, the best candidate solution obtained during the iterations of the algorithm is presented as the FLO solution for the given problem. The implementation steps of FLO are shown as a flowchart in
Figure 2, and its pseudocode is presented in Algorithm 1.
|
Algorithm 1. Pseudocode of FLO. |
| Start FLO. |
| 1. |
|
|
Input the problem information: variables, constraints, and the objective function. |
| 2. |
|
|
Set the FLO population size (N) and number of iterations (T). |
| 3. |
|
|
Generate the initial population matrix using Equation (2).
|
| 4. |
|
|
Evaluate the objective function. |
| 5. |
|
|
|
For to T
|
| 6. |
|
|
|
|
For to
|
| 7. |
|
|
|
|
Phase 1: Hunting strategy (exploration) |
| 8. |
|
|
|
|
|
Determine the candidate preys set using Equation (4).
|
| 9. |
|
|
|
|
|
Choose the prey for the ith frilled lizard at random. |
| 10. |
|
|
|
|
|
Calculate the new position of ith frilled lizard using Equation (5).
|
| 11. |
|
|
|
|
|
Update ith FLO member using Equation (6).
|
| 12. |
|
|
|
|
Phase 2: Moving up the tree (exploitation) |
| 13. |
|
|
|
|
|
Calculate the new position of ith frilled lizard using Equation (7).
|
| 14. |
|
|
|
|
|
Update ith frilled lizard using Equation (8).
|
| 15. |
|
|
|
|
end |
| 16. |
|
|
|
|
Save the best candidate solution so far. |
| 17. |
|
|
|
end |
| 18. |
|
|
Output the best quasi-optimal solution obtained with the FLO. |
| End FLO. |
3.5. Computational Complexity of FLO
In this subsection, the computational complexity of FLO is evaluated. The preparation and initialization steps of FLO have a computational complexity of O(Nm), where N denotes the number of frilled lizards and m gives the number of decision variables of the problem. In the FLO design, the position of each frilled lizard is updated in each iteration in two phases of exploration and exploitation. Therefore, the update process in FLO has a computational complexity of O(2TNm), where T is the maximum number of iterations of the algorithm. According to this, the overall computational complexity of the proposed FLO approach is
4. Simulation Studies and Results
In this section, the performance of the developed FLO algorithm in dealing with optimization tasks is evaluated. For this purpose, a set of fifty-two standard benchmark functions of unimodal, high-dimensional multimodal, fixed-dimensional multimodal types [
59], and the CEC 2017 test suite [
60] have been employed. The results obtained by using FLO have been compared with the performance of twelve well-known metaheuristic algorithms: GA [
29], PSO [
12], GSA [
36], TLBO [
46], MVO [
37], GWO [
19], WOA [
28], MPA [
17], TSA [
23], RSA [
26], AVOA [
16], and WSO [
21]. The values of the control parameters of the metaheuristic algorithms are determined in
Table 1. In order to optimize the objective functions F1 to F23, FLO and each of the competitive algorithms have been employed in 30 independent runs, where each run includes 30,000 function evaluations (FEs) and a population size of 30 is chosen. In handling the CEC 2017 test suite, the FLO approach and each of the competitive algorithms have been implemented in 51 independent runs, where each independent run includes
(
is the number of variables) of Fs and a population size of 30. The simulation outcomes are presented through six statistical indicators, namely mean, best, worst, standard deviation (std), median, and rank. To establish the ranking of the metaheuristic algorithms for optimizing each benchmark function, a comparison of the mean index values has been employed.
4.1. Evaluation of Unimodal Functions
The unimodal variables F1 to F7, due to not having a local optimum, are suitable criteria for measuring the ability of the metaheuristic algorithms in local exploitation and search. The implementation results of FLO and the competitive algorithms for the functions F1 to F7 are reported in
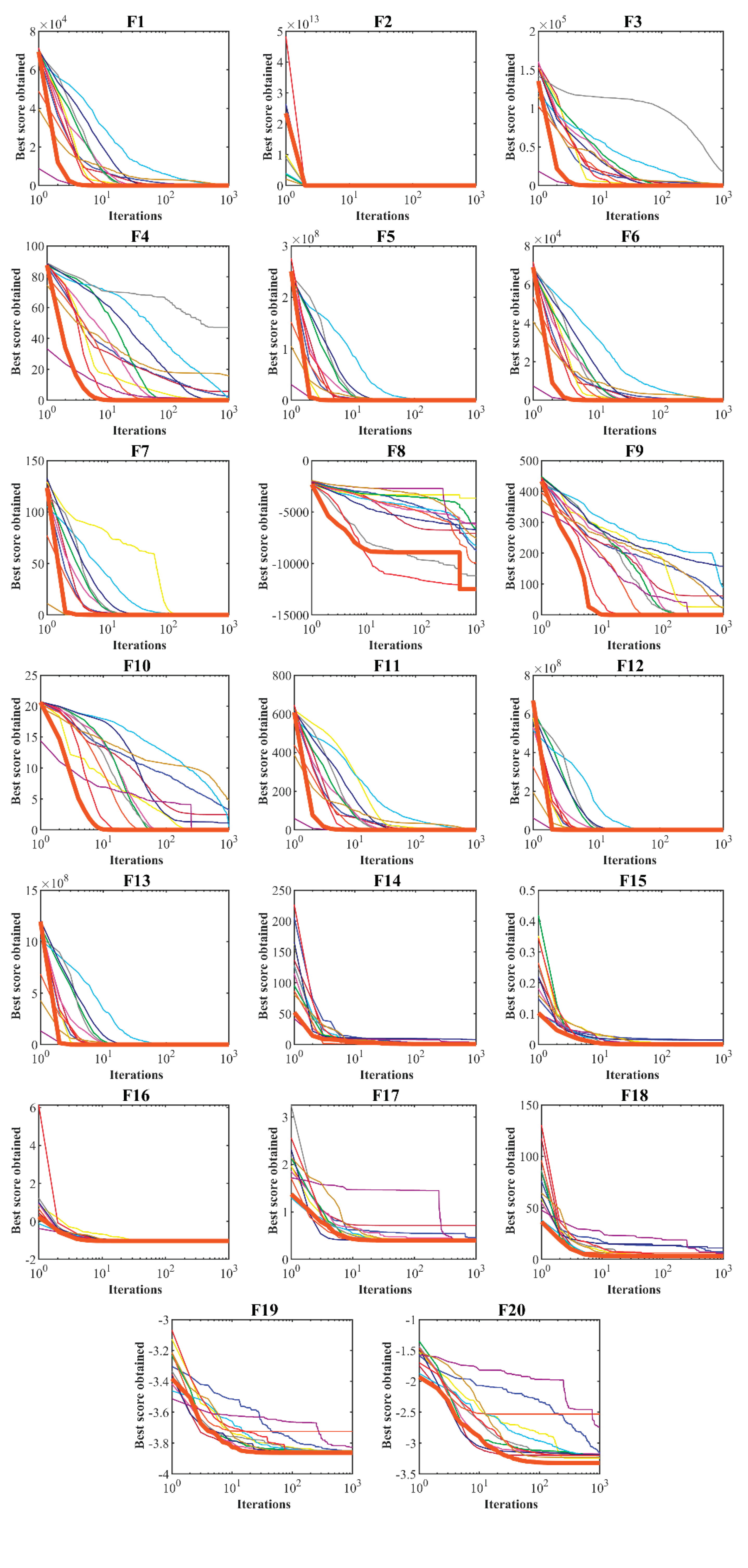
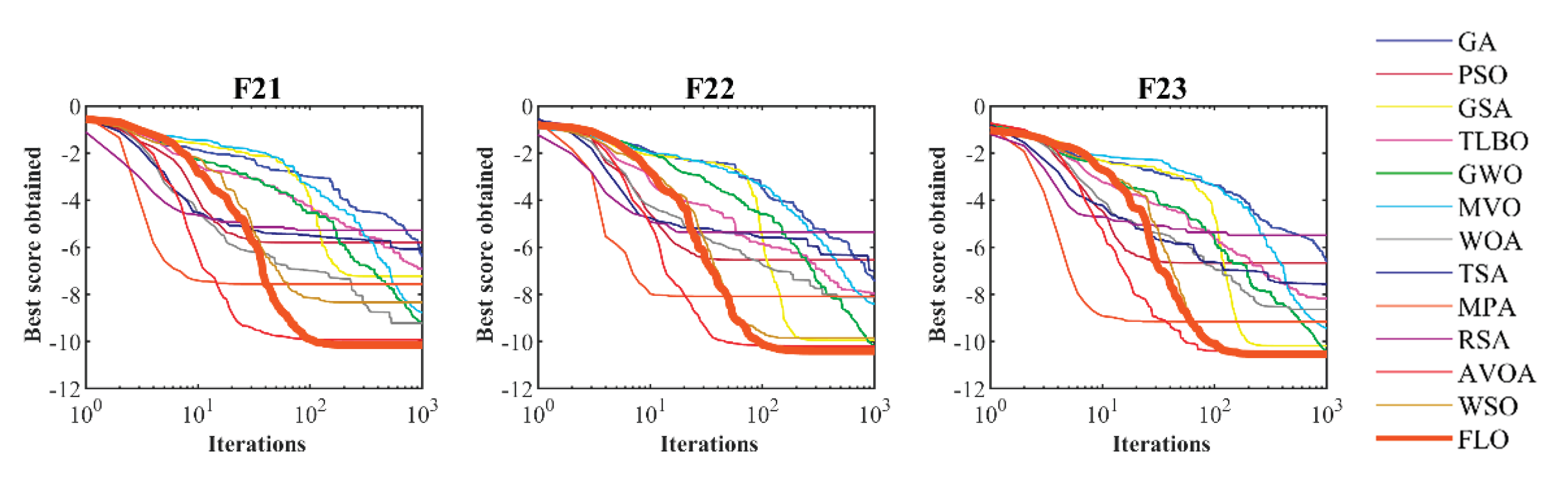
Table 2. Based on the results, FLO with high capability in exploitation and local search has been able to converge to the global optimum for the functions F1 to F6. Also, in solving the F7 function, FLO is the first best optimizer for this function. The comparison of the simulation results indicates that FLO, with its high exploitation ability, has delivered a superior performance in handling unimodal functions F1 to F7 against the competitive algorithms.
4.2. Evaluation of High-Dimensional Multimodal Functions
The high-dimensional multimodal functions F8 to F13, due to having multiple local optima, are suitable criteria for challenging the ability of the metaheuristic algorithms in global exploration and search. The optimization results for the functions F8 to F13 using FLO and the competitive algorithms are reported in
Table 3. Based on the obtained results, FLO with its high ability in exploration has been able to provide a global optimum for these functions by discovering the main optimal region in dealing with the F9 and F11 functions. Also, in order to optimize the functions F8, F10, F12, and F13, FLO is the first best optimizer for these functions. The analysis of the simulation results shows that FLO with high capability in exploration and global search in order to cross local optima and discover the main optimal area turned out to be superior in competition with the compared algorithms.
4.3. Evaluation of Fixed-Dimensional Multimodal Functions
The fixed-dimension multimodal functions F14 to F23, having a smaller number of local optima compared to functions F8 to F13, are suitable criteria for measuring the ability of the metaheuristic algorithms in balancing exploration and exploitation. The results of employing FLO and the competitive algorithms for the functions F14 to F23 are reported in
Table 4. It turned out that FLO is the best optimizer for functions F14 to F23. In cases where FLO has the same value for the mean index with some competitive algorithms, it has provided a more effective performance by providing a better value for the std index. The simulation results show that FLO, with an appropriate ability to balance exploration and exploitation, has a superior performance by providing better results for the benchmark functions in comparison with the competitive algorithms.
The convergence curves resulting from the execution of FLO and the competitive algorithms for the functions F1 to F23 are drawn in
Figure 3.
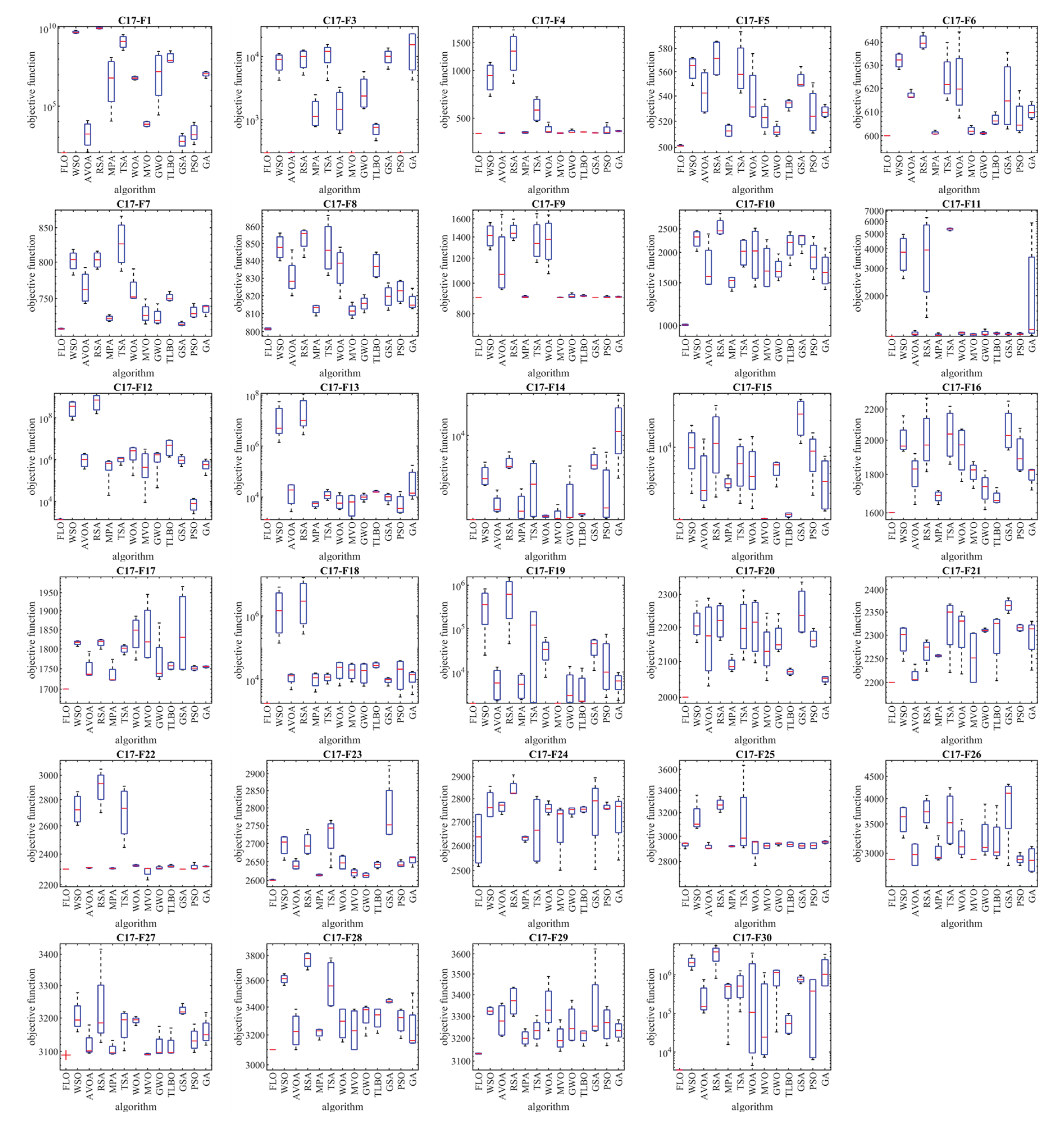
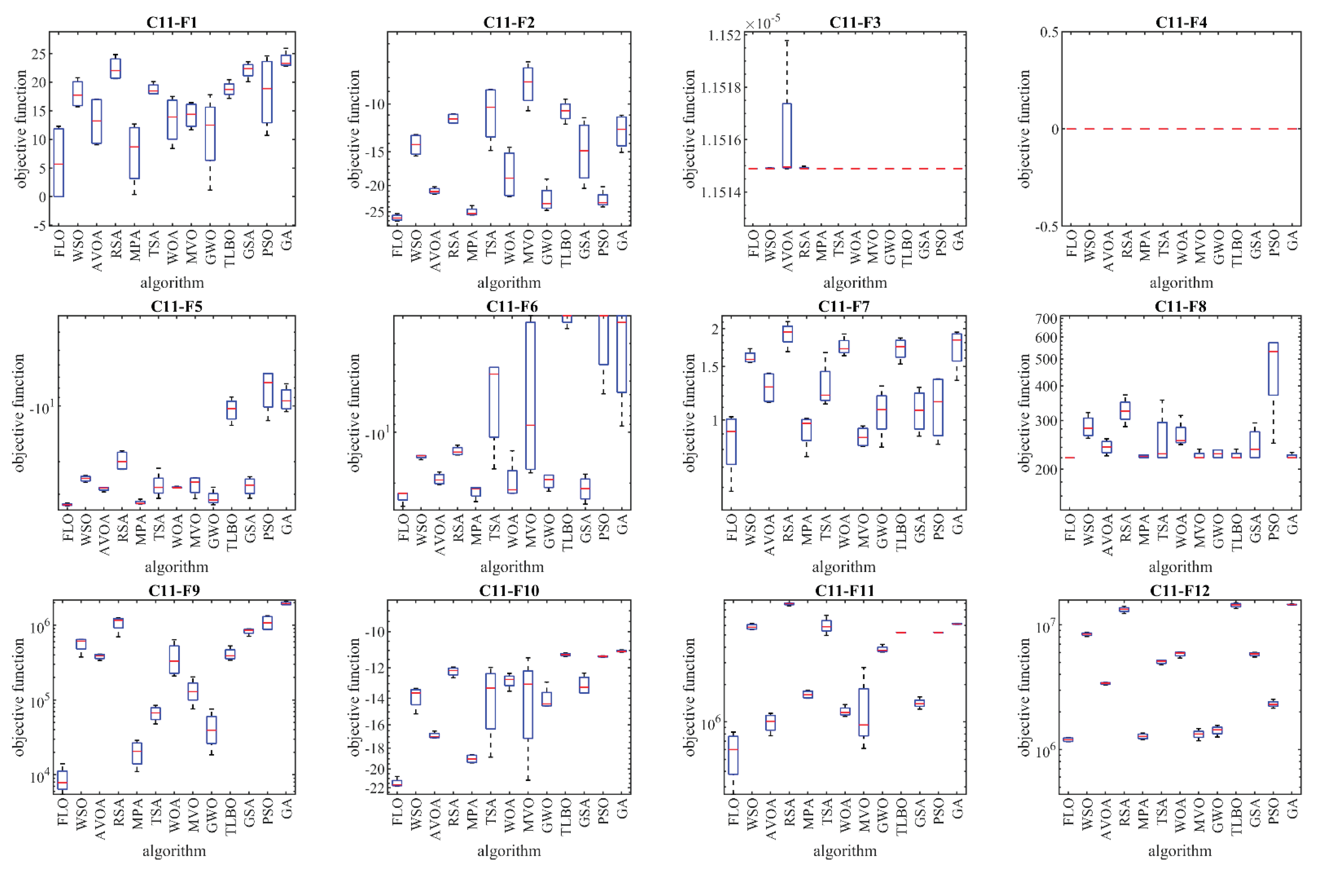
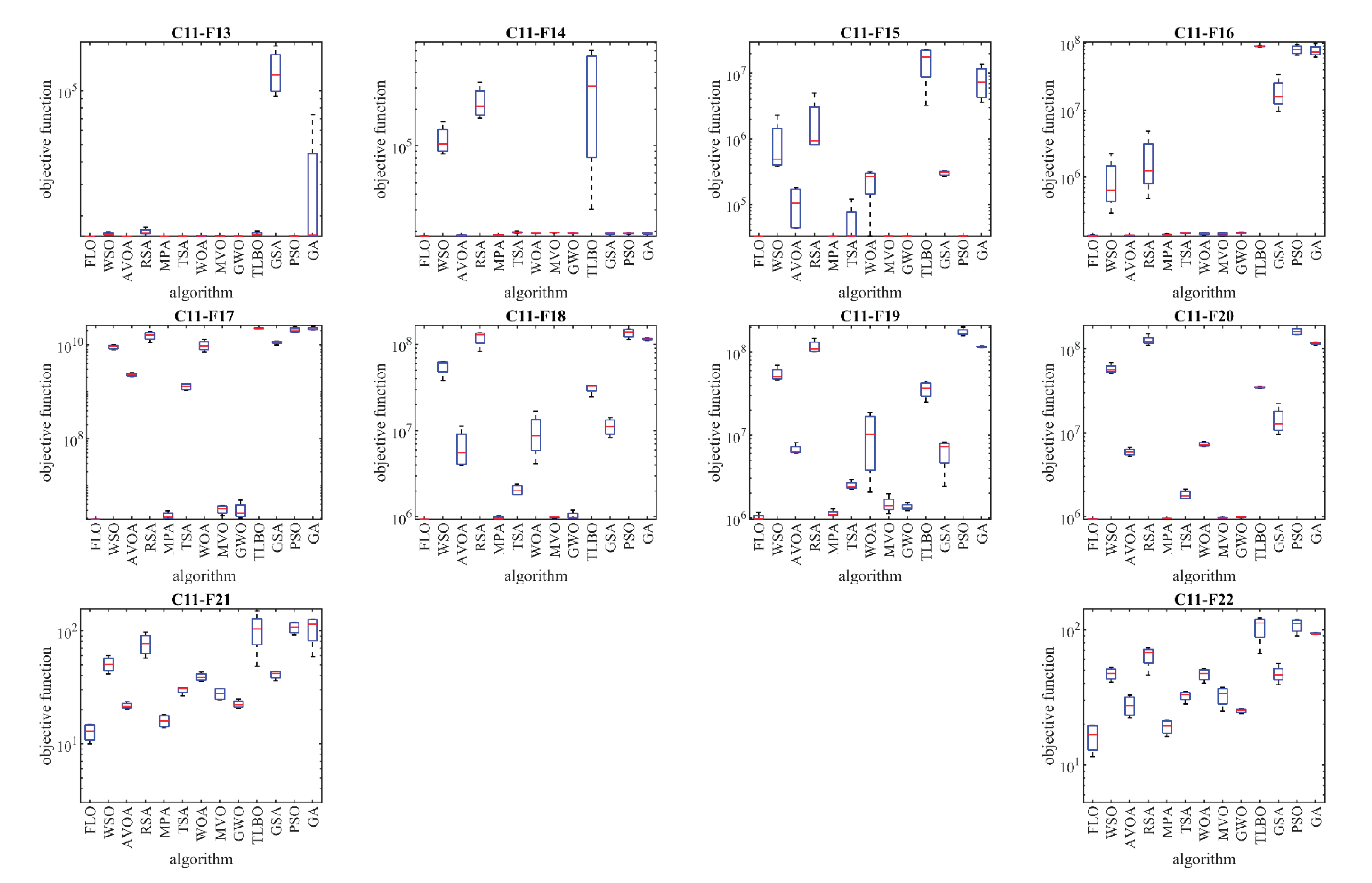
4.4. Evaluation of the CEC 2017 Test Suite
In this subsection, the efficiency of FLO in handling the CEC 2017 test suite is evaluated. The CEC 2017 test suite includes thirty standard benchmark functions consisting of three unimodal functions of C17-F1 to C17-F3, seven multimodal functions of C17-F4 to C17-F10, ten hybrid functions of C17-F11 to C17-F20, and ten composite functions of C17-F21 to C17-F30. From this test suite, the C17-F2 function was not included in the simulation studies due to the instability of the behavior. A complete description and the details of the CEC 2017 test suite can be found in [
60]. The optimization results of the CEC 2017 test suite using FLO and the competitive algorithms for the mentioned dimensions are reported in
Table 5. Also, the boxplot diagrams resulting from the performance of the metaheuristic algorithms on this test suite are shown in
Figure 4. Based on the obtained optimization results, FLO is the best approach for the functions: C17-F1, C17-F3 to C17-F21, C17-F23, C17-F24, and C17-F27 to C17-F30.
The optimization outcomes indicate that FLO has achieved favorable results for the benchmark functions due to its strong capabilities in both exploration and exploitation, as well as effectively balancing them throughout the search process. Through the comparison of the simulation results, it is clear that FLO surpasses the competitive algorithms for most benchmark functions, establishing itself as the top optimizer overall and demonstrating a superiority in handling the CEC 2017 test suite.
4.5. Statistical Analysis
A statistical analysis has been made to check whether the superiority of FLO against the competitive algorithms is significant from a statistical point of view. For this purpose, the non-parametric Wilcoxon rank sum test [
61] has been used, which is useful in determining a significant difference between the averages of two data samples. In the Wilcoxon rank sum test, it is investigated whether there is a significant difference between the performance of two algorithms by using an index called p-value. The results of implementing the Wilcoxon rank sum test on the results of FLO compared to each of the competitive algorithms are given in
Table 6. Based on the results, in cases where the p-value is less than 0.05, FLO has a statistically significant advantage in competition with the alternative metaheuristic algorithms. Basically, based on the statistical analysis, it is obvious that FLO has a significant statistical superiority compared to the competitive algorithms in handling all the studied benchmark functions.
Author Contributions
Conceptualization, M.D. and I.A.F.; methodology, M.D., O.A.B. and S.A.; software, I.A.F., O.A.B. and S.A.; validation, F.W., G.B. and O.P.M..; formal analysis, S.A., F.W. and G.B.; investigation, F.W. and O.P.M.; resources, O.A.B. and S.A.; data curation, I.A.F.; writing—original draft preparation, M.D., S.A., O.A.B. and I.A.F.; writing—review and editing, S.G., G.B. and I.L.; visualization, O.P.M. , I.L. and S.G.; supervision, M.D.; project administration, I.A.F.; funding acquisition, F.W. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Frilled lizard taken from: free media Wikimedia Commons.
Figure 1.
Frilled lizard taken from: free media Wikimedia Commons.
Figure 2.
Flowchart of FLO.
Figure 2.
Flowchart of FLO.
Figure 3.
Convergence curves of FLO and competitive algorithms performances for F1 to F23.
Figure 3.
Convergence curves of FLO and competitive algorithms performances for F1 to F23.
Figure 4.
Boxplot diagrams of FLO and the performance of the competitive algorithms for the CEC 2017 test suite.
Figure 4.
Boxplot diagrams of FLO and the performance of the competitive algorithms for the CEC 2017 test suite.
Figure 5.
Boxplot diagrams of FLO and the performances of the competitor algorithms on the CEC 2011 test suite.
Figure 5.
Boxplot diagrams of FLO and the performances of the competitor algorithms on the CEC 2011 test suite.
Figure 6.
Schematic of the pressure vessel design.
Figure 6.
Schematic of the pressure vessel design.
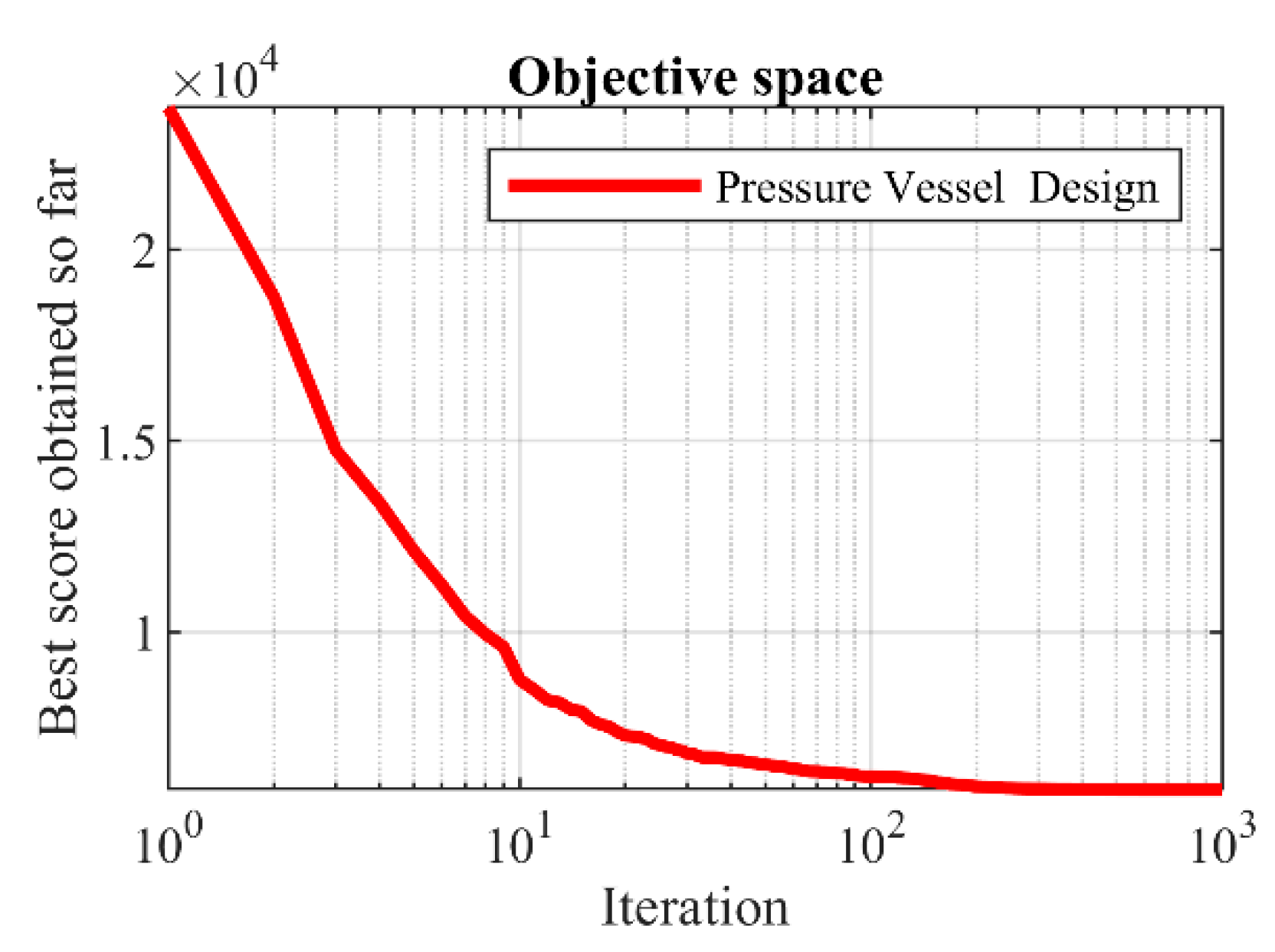
Figure 7.
FLO’s performance convergence curve for the pressure vessel design.
Figure 7.
FLO’s performance convergence curve for the pressure vessel design.
Figure 8.
Schematic of the speed reducer design.
Figure 8.
Schematic of the speed reducer design.
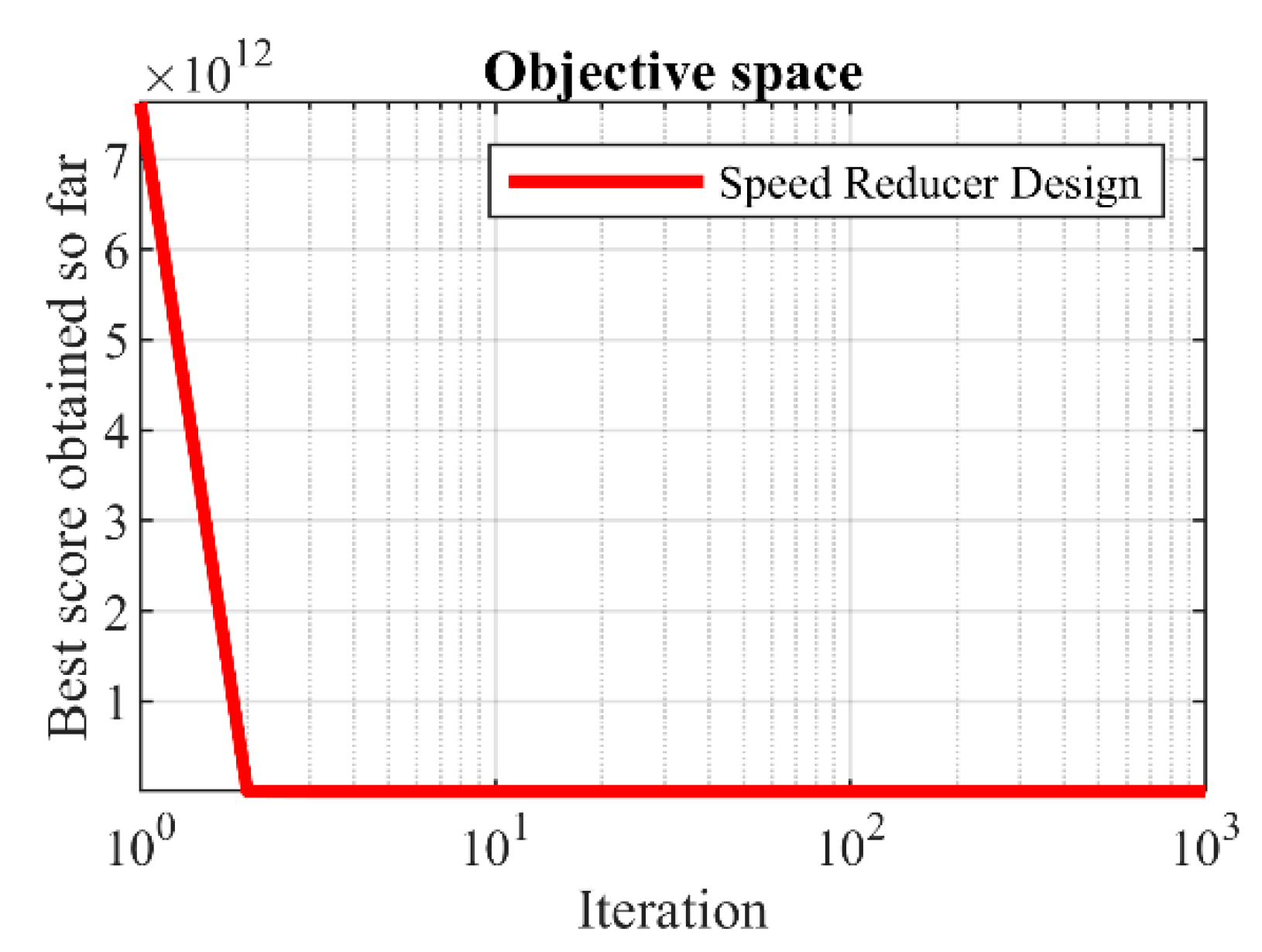
Figure 9.
FLO’s performance convergence curve for the speed reducer design.
Figure 9.
FLO’s performance convergence curve for the speed reducer design.
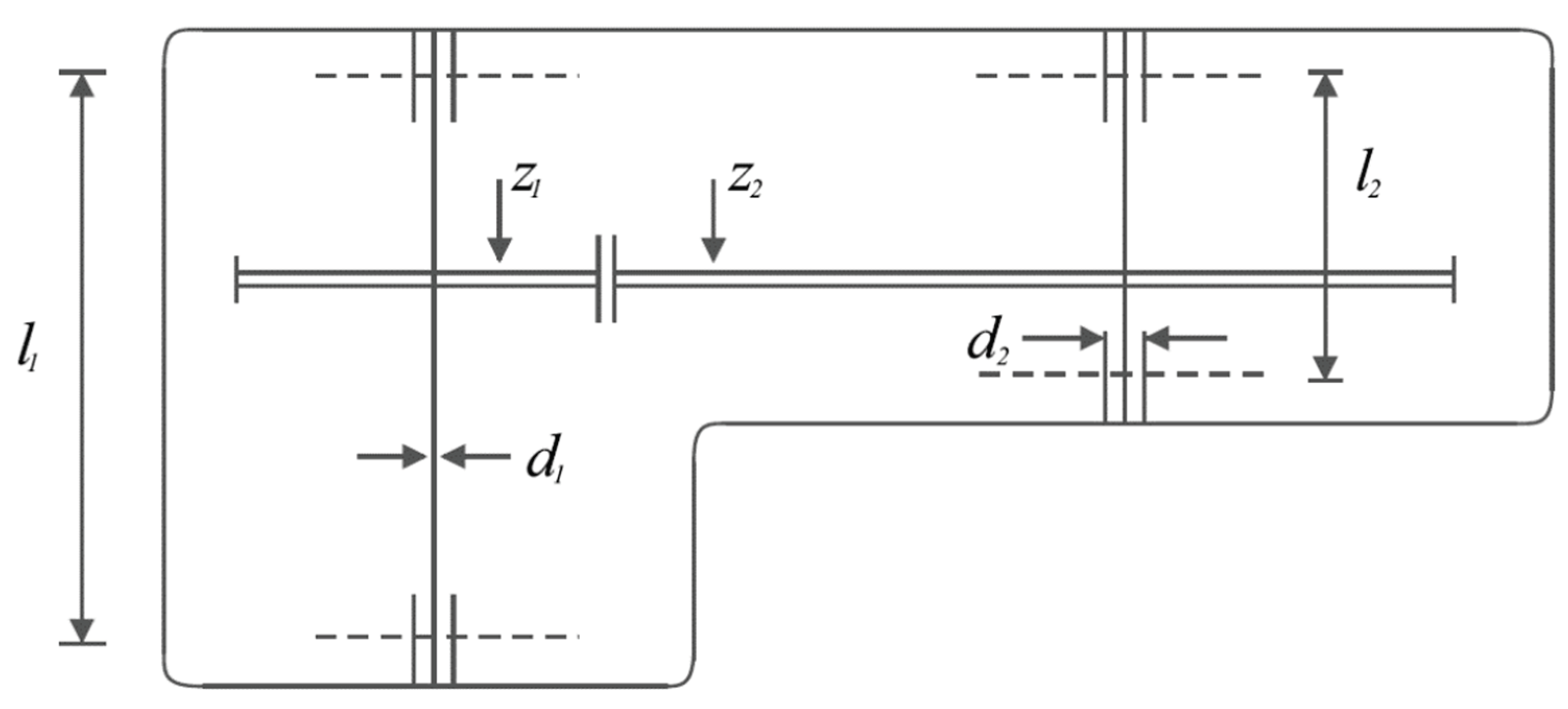
Figure 10.
Schematic of the welded beam design.
Figure 10.
Schematic of the welded beam design.
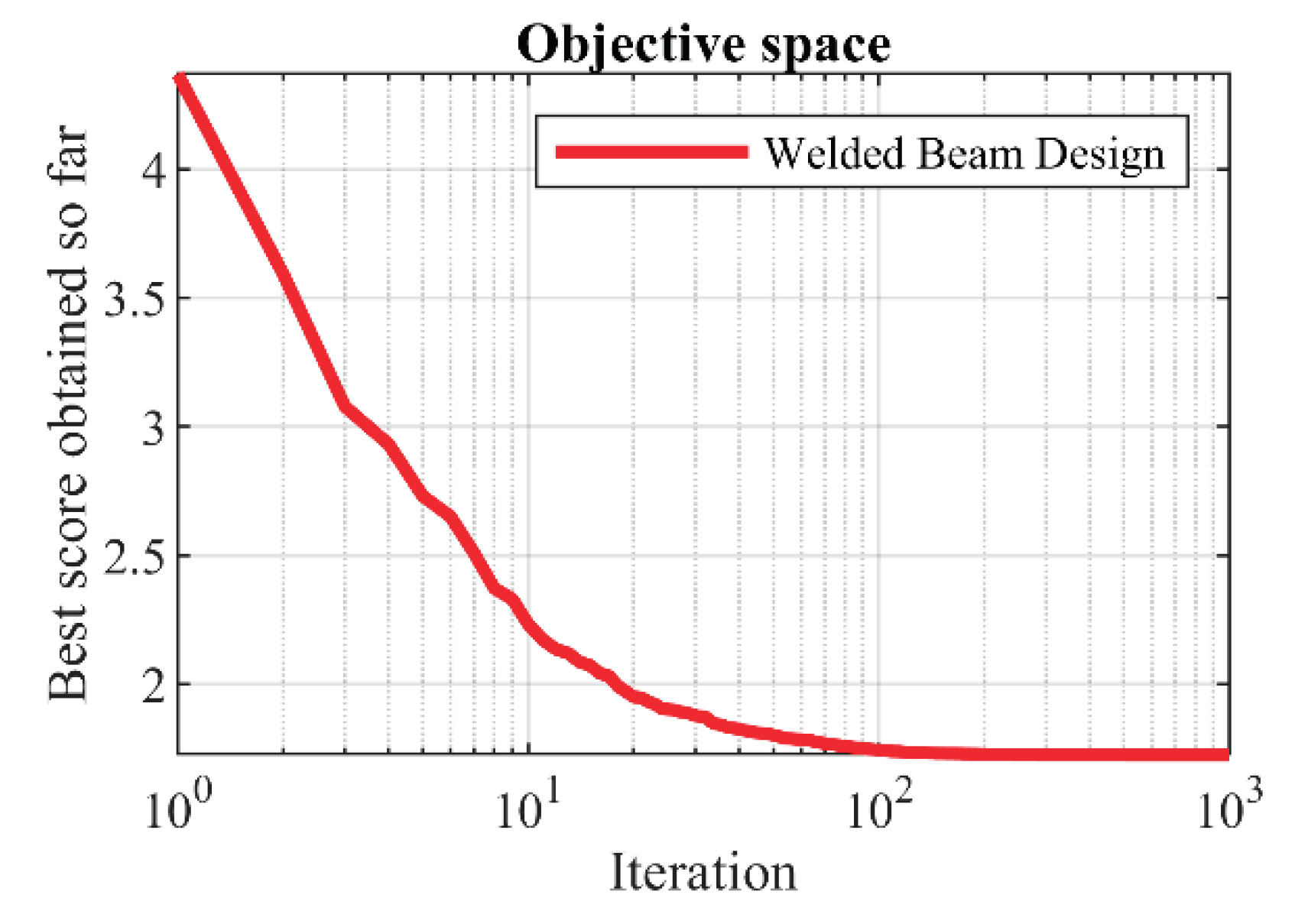
Figure 11.
FLO’s performance convergence curve for the welded beam design.
Figure 11.
FLO’s performance convergence curve for the welded beam design.
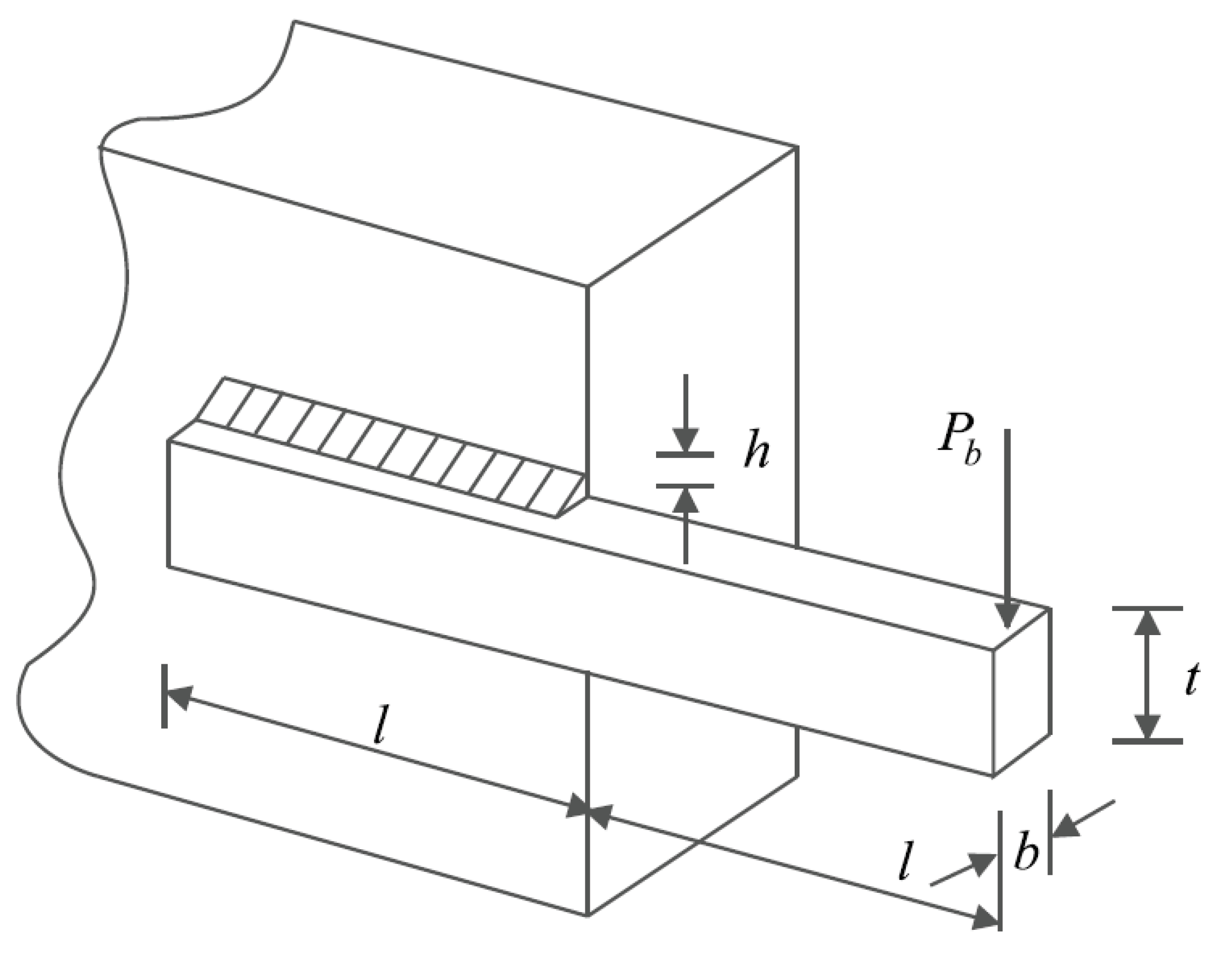
Figure 12.
Schematic of the tension/compression spring design.
Figure 12.
Schematic of the tension/compression spring design.
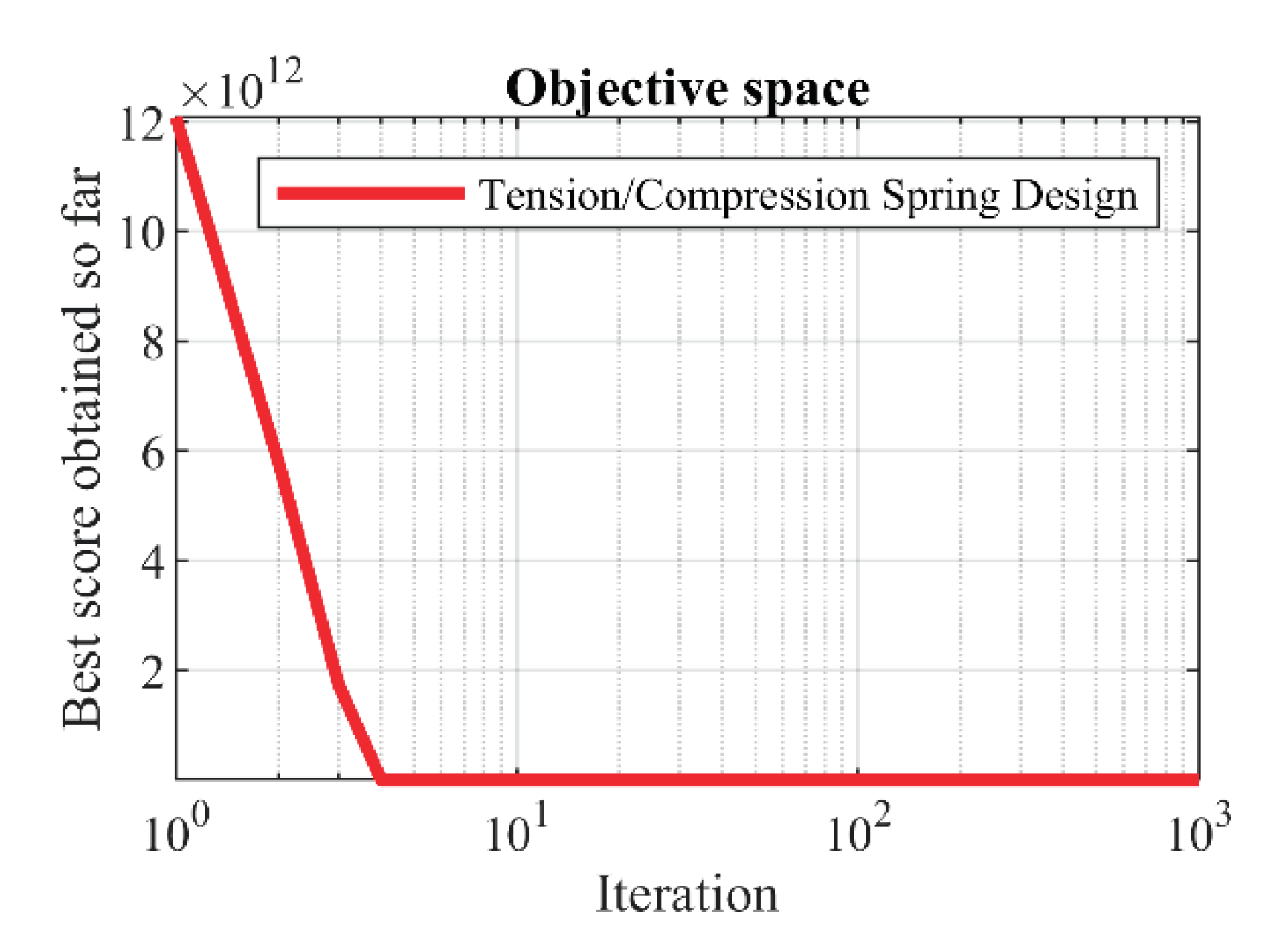
Figure 13.
FLO’s performance convergence curve for the tension/compression spring.
Figure 13.
FLO’s performance convergence curve for the tension/compression spring.
Table 1.
Control parameter values.
Table 1.
Control parameter values.
| Algorithm |
|
Parameter |
|
Value |
| GA |
|
|
|
|
| |
|
Selection |
|
Roulette wheel (Proportionate) |
| |
|
Crossover |
|
Whole arithmetic (Probability = 0.8, ) |
| |
|
Mutation |
|
Gaussian (Probability = 0.05) |
| PSO |
|
|
|
|
| |
|
Cognitive and social constant |
|
(C1, C2)
|
| |
|
Velocity limit |
|
10% of dimension range |
| |
|
Inertia weight |
|
Linear reduction from 0.9 to 0.1 |
| GSA |
|
|
|
|
| |
|
Alpha, G0, Rnorm, Rpower
|
|
20, 100, 2, 1 |
| TLBO |
|
|
|
|
| |
|
Teaching Factor (TF) |
|
TF = round
|
| MVO |
|
|
|
|
| |
|
wormhole existence probability (WEP) |
|
Min(WEP) = 0.2 and Max(WEP)=1. |
| |
|
Exploitation accuracy over the iterations (p) |
|
. |
| GWO |
|
|
|
|
| |
|
Convergence parameter (a) |
|
a: Linear reduction from 2 to 0. |
| WOA |
|
|
|
|
| |
|
Convergence parameter (a) |
|
a: Linear reduction from 2 to 0. |
| |
|
l |
|
is a random number in the range of |
| TSA |
|
|
|
|
|
|
Pmin and Pmax
|
|
1, 4 |
| |
|
c1, c2, c3 |
|
random numbers lie in the range of
|
| MPA |
|
|
|
|
| |
|
Constant number |
|
P=0.5 |
| |
|
Random vector |
|
R is a vector of uniform random numbers in
|
| |
|
Fish Aggregating Devices (FADs) |
|
𝐹𝐴𝐷𝑠=0.2 |
| |
|
Binary vector |
|
U= 0 or 1 |
| RSA |
|
|
|
|
| |
|
Sensitive parameter |
|
|
| |
|
Sensitive parameter |
|
|
| |
|
Evolutionary Sense (ES) |
|
ES: randomly decreasing values between 2 and −2 |
| WSO |
|
|
|
|
|
|
Fmin and Fmax
|
|
0.07, 0.75 |
| |
|
τ, ao, a1, a2 |
|
4.125, 6.25, 100, 0.0005 |
| AVOA |
|
|
|
|
| |
|
w |
|
2.5 |
| |
|
P1, P2, P3
|
|
0.6, 0.4, 0.6 |
| |
|
L1, L2
|
|
0.8, 0.2 |
Table 2.
Optimization results for the unimodal functions.
Table 2.
Optimization results for the unimodal functions.
| |
FLO |
AVOA |
WSO |
RSA |
MPA |
TSA |
WOA |
GWO |
MVO |
TLBO |
GSA |
PSO |
GA |
| F1 |
best |
0 |
4.822882 |
0 |
0 |
3.47E-52 |
1.32E-50 |
8.50E-171 |
0.096099 |
1.36E-61 |
5.35E-77 |
4.88E-17 |
0.000443 |
16.32806 |
| mean |
0 |
60.02965 |
0 |
0 |
1.75E-49 |
4.24E-47 |
1.30E-151 |
0.13629 |
1.61E-59 |
2.30E-74 |
1.21E-16 |
0.091953 |
27.78154 |
| median |
0 |
41.36897 |
0 |
0 |
3.79E-50 |
3.89E-48 |
2.00E-159 |
0.137102 |
9.80E-60 |
1.54E-75 |
1.03E-16 |
0.008853 |
25.68391 |
| worst |
0 |
217.602 |
0 |
0 |
1.51E-48 |
3.01E-46 |
2.40E-150 |
0.183344 |
7.03E-59 |
2.36E-73 |
3.40E-16 |
1.27308 |
51.8506 |
| std |
0 |
49.03061 |
0 |
0 |
3.65E-49 |
9.30E-47 |
5.60E-151 |
0.02579 |
1.99E-59 |
5.72E-74 |
6.65E-17 |
0.288752 |
9.721273 |
| rank |
1 |
11 |
1 |
1 |
5 |
6 |
2 |
9 |
4 |
3 |
7 |
8 |
10 |
| F2 |
best |
0 |
0.603391 |
1.20E-306 |
0 |
1.68E-29 |
1.84E-30 |
7.20E-118 |
0.145798 |
4.44E-36 |
8.04E-40 |
3.18E-08 |
0.041243 |
1.589689 |
| mean |
0 |
1.948988 |
9.90E-277 |
0 |
6.34E-28 |
1.92E-28 |
2.30E-105 |
0.236058 |
1.23E-34 |
6.16E-39 |
5.00E-08 |
0.815635 |
2.539698 |
| median |
0 |
1.39396 |
6.00E-290 |
0 |
3.20E-28 |
1.80E-29 |
3.10E-108 |
0.244414 |
5.92E-35 |
4.53E-39 |
4.67E-08 |
0.532063 |
2.497037 |
| worst |
0 |
6.781435 |
2E-275 |
0 |
4.29E-27 |
1.66E-27 |
2.50E-104 |
0.332 |
7.21E-34 |
2.22E-38 |
1.12E-07 |
2.270937 |
3.46705 |
| std |
0 |
1.648521 |
0.00E+00 |
0 |
1.02E-27 |
4.92E-28 |
6.40E-105 |
0.058527 |
1.82E-34 |
5.19E-39 |
1.74E-08 |
0.671498 |
0.506175 |
| rank |
1 |
11 |
2 |
1 |
7 |
6 |
3 |
9 |
5 |
4 |
8 |
10 |
12 |
| F3 |
best |
0 |
947.6498 |
0 |
0 |
5.64E-19 |
1.25E-21 |
1880.714 |
5.44143 |
2.15E-19 |
2.00E-29 |
224.0264 |
19.82675 |
1297.164 |
| mean |
0 |
1626.99 |
0 |
0 |
2.29E-12 |
1.08E-10 |
18179.06 |
14.54867 |
1.98E-14 |
3.50E-24 |
433.0901 |
353.5142 |
1975.532 |
| median |
0 |
1419.306 |
0 |
0 |
1.66E-13 |
9.79E-14 |
18511.54 |
10.81976 |
4.25E-16 |
3.68E-26 |
364.629 |
266.9079 |
1913.339 |
| worst |
0 |
3227.104 |
0 |
0 |
1.31E-11 |
1.78E-09 |
31594.58 |
44.57484 |
3.69E-13 |
3.28E-23 |
1080.509 |
933.9386 |
3150.434 |
| std |
0 |
583.2962 |
0 |
0 |
4.07E-12 |
4.05E-10 |
7950.636 |
10.00187 |
8.38E-14 |
1.01E-23 |
204.6704 |
267.9873 |
594.3514 |
| rank |
1 |
9 |
1 |
1 |
4 |
5 |
11 |
6 |
3 |
2 |
8 |
7 |
10 |
| F4 |
best |
0 |
10.85214 |
0.00E+00 |
0 |
2.75E-20 |
0.0000879 |
0.823893 |
0.242208 |
5.97E-16 |
5.29E-32 |
9.01E-09 |
2.085999 |
2.018782 |
| mean |
0 |
15.75337 |
3E-265 |
0 |
2.71E-19 |
4.03E-03 |
47.1994 |
0.49832 |
1.12E-14 |
1.67E-30 |
1.13E+00 |
5.719781 |
2.577042 |
| median |
0 |
16.18755 |
1.80E-282 |
0 |
2.36E-19 |
0.001339 |
50.48116 |
0.483681 |
5.78E-15 |
5.94E-31 |
0.826058 |
5.357815 |
2.53522 |
| worst |
0 |
21.70983 |
4.1E-264 |
0 |
8.75E-19 |
0.032632 |
83.53016 |
0.877153 |
5.23E-14 |
7.40E-30 |
4.488194 |
12.16864 |
3.636626 |
| std |
0 |
2.682766 |
0.00E+00 |
0 |
2.13E-19 |
0.007381 |
27.51566 |
0.178584 |
1.35E-14 |
2.23E-30 |
1.288828 |
2.325016 |
0.433841 |
| rank |
1 |
11 |
2 |
1 |
4 |
6 |
12 |
7 |
5 |
3 |
8 |
10 |
9 |
| F5 |
best |
0 |
1227.144 |
1.27E-06 |
7.93E-29 |
20.77433 |
23.38145 |
24.33873 |
25.16727 |
23.28628 |
23.30644 |
23.57596 |
23.93699 |
208.4007 |
| mean |
0 |
9836.204 |
1.30E-05 |
1.18E+01 |
21.24372 |
25.93746 |
24.87395 |
87.63958 |
24.21079 |
24.39873 |
40.1211 |
4200.597 |
542.2831 |
| median |
0 |
5109.367 |
8.55E-06 |
1.12E-28 |
21.21726 |
26.2519 |
24.67096 |
27.34075 |
23.89208 |
23.97967 |
23.99658 |
78.41897 |
433.1568 |
| worst |
0 |
84446.57 |
5.38E-05 |
26.40458 |
21.90432 |
26.31483 |
26.17246 |
344.199 |
24.734 |
26.18823 |
152.3277 |
82043.31 |
2055.752 |
| std |
0 |
18645.98 |
1.35E-05 |
1.37E+01 |
0.361087 |
0.732269 |
0.53677 |
94.27249 |
0.489025 |
0.869977 |
41.18185 |
18690.79 |
394.8645 |
| rank |
1 |
13 |
2 |
3 |
4 |
8 |
7 |
10 |
5 |
6 |
9 |
12 |
11 |
| F6 |
best |
0 |
15.44096 |
6.47E-09 |
3.336533 |
7.36E-10 |
2.325128 |
0.009582 |
0.072166 |
0.224723 |
0.212329 |
5.03E-17 |
0.00000173 |
14.21997 |
| mean |
0 |
91.90698 |
4.53E-08 |
5.881906 |
1.64E-09 |
3.353519 |
0.074298 |
0.137535 |
0.601908 |
1.1489 |
9.53E-17 |
5.78E-02 |
31.10185 |
| median |
0 |
63.37101 |
4.20E-08 |
6.270887 |
1.46E-09 |
3.457431 |
0.028788 |
0.145872 |
0.662447 |
1.108843 |
8.63E-17 |
0.001874 |
28.85646 |
| worst |
0 |
348.3797 |
1.24E-07 |
6.603377 |
4.37E-09 |
4.360664 |
0.297605 |
0.227803 |
1.140588 |
1.971716 |
1.65E-16 |
0.493414 |
57.16884 |
| std |
0 |
88.71011 |
3.05E-08 |
0.955084 |
8.69E-10 |
0.644215 |
0.094418 |
0.044022 |
0.284877 |
0.461983 |
3.45E-17 |
0.138033 |
12.58959 |
| rank |
1 |
13 |
4 |
11 |
3 |
10 |
6 |
7 |
8 |
9 |
2 |
5 |
12 |
| F7 |
best |
2.35E-06 |
1.22E-05 |
2.30E-06 |
5.58E-06 |
0.000102 |
0.001361 |
0.0000218 |
0.003619 |
0.000166 |
0.0000829 |
0.012869 |
0.062864 |
0.002764 |
| mean |
2.54E-05 |
8.43E-05 |
5.93E-05 |
2.97E-05 |
0.0005 |
0.003958 |
1.17E-03 |
0.010581 |
0.000759 |
1.40E-03 |
0.048101 |
0.16772 |
0.009646 |
| median |
1.83E-05 |
0.0000619 |
0.0000382 |
0.0000148 |
0.000488 |
0.003393 |
0.000748 |
0.010309 |
0.000772 |
0.001376 |
0.047213 |
0.161882 |
0.009274 |
| worst |
6.89E-05 |
3.10E-04 |
2.44E-04 |
1.23E-04 |
0.00082 |
0.009088 |
0.00492 |
0.020558 |
0.001783 |
0.002684 |
0.087051 |
0.374669 |
0.019985 |
| std |
2.02E-05 |
8.29E-05 |
6.81E-05 |
3.21E-05 |
0.0002 |
0.002175 |
0.001343 |
0.004677 |
0.000433 |
0.000817 |
0.023188 |
0.073415 |
0.004477 |
| rank |
1 |
4 |
3 |
2 |
5 |
9 |
7 |
11 |
6 |
8 |
12 |
13 |
10 |
| Sum rank |
7 |
15 |
72 |
20 |
32 |
50 |
48 |
36 |
59 |
35 |
54 |
65 |
74 |
| Mean rank |
1 |
2.142857 |
10.28571 |
2.857143 |
4.571429 |
7.142857 |
6.857143 |
5.142857 |
8.428571 |
5 |
7.714286 |
9.285714 |
10.57143 |
| Total rank |
1 |
2 |
12 |
3 |
4 |
8 |
7 |
6 |
10 |
5 |
9 |
11 |
13 |
Table 3.
Optimization results for the high-dimensional multimodal functions.
Table 3.
Optimization results for the high-dimensional multimodal functions.
| |
FLO |
AVOA |
WSO |
RSA |
MPA |
TSA |
WOA |
GWO |
MVO |
TLBO |
GSA |
PSO |
GA |
| F8 |
best |
-12622.8 |
-9319.44 |
-12574.2 |
-6277.23 |
-10663.1 |
-7789.11 |
-12572.1 |
-9494.05 |
-7348.84 |
-7525.59 |
-4717.57 |
-8584.04 |
-9939.5 |
| mean |
-12498.6 |
-7535.73 |
-12471.8 |
-6064.7 |
-9936.78 |
-6704.97 |
-11191.6 |
-8247.67 |
-6650.74 |
-6212.41 |
-3646.54 |
-7076.8 |
-8783.73 |
| median |
-12577.8 |
-7475.79 |
-12561.2 |
-6088.96 |
-9959.64 |
-6677.51 |
-12087.2 |
-8140.19 |
-6654.03 |
-6229.64 |
-3578.49 |
-7214.2 |
-8749.63 |
| worst |
-11936.3 |
-6637.72 |
-11957.2 |
-5569.4 |
-9389.03 |
-5089.32 |
-8167.12 |
-7387.54 |
-5723.04 |
-5269.79 |
-3021.3 |
-5668.31 |
-7523.94 |
| std |
194.2272 |
686.0549 |
179.0354 |
209.0513 |
341.0971 |
682.0853 |
1611.369 |
683.5917 |
439.8347 |
568.8056 |
464.0183 |
688.4831 |
597.0402 |
| rank |
1 |
7 |
2 |
12 |
4 |
9 |
3 |
6 |
10 |
11 |
13 |
8 |
5 |
| F9 |
best |
0 |
13.31572 |
0 |
0 |
0 |
81.74052 |
0 |
48.07879 |
0.00E+00 |
0 |
12.68706 |
36.24875 |
21.1603 |
| mean |
0 |
22.43339 |
0 |
0 |
0 |
157.6833 |
0 |
89.10431 |
1.55E-14 |
0 |
25.96315 |
61.67496 |
49.80422 |
| median |
0 |
20.66512 |
0 |
0 |
0 |
151.8098 |
0 |
88.42416 |
0.00E+00 |
0 |
24.01479 |
59.26511 |
47.92176 |
| worst |
0 |
41.85228 |
0 |
0 |
0 |
262.4813 |
0 |
135.9663 |
1.04E-13 |
0 |
44.40468 |
104.3443 |
70.04209 |
| std |
0 |
8.007302 |
0 |
0 |
0 |
47.39195 |
0 |
23.41107 |
3.02E-14 |
0 |
8.516422 |
17.5057 |
12.82893 |
| rank |
1 |
3 |
1 |
1 |
1 |
8 |
1 |
7 |
2 |
1 |
4 |
6 |
5 |
| F10 |
best |
8.88E-16 |
3.081216 |
8.88E-16 |
8.88E-16 |
8.88E-16 |
7.36E-15 |
8.88E-16 |
0.091628 |
7.36E-15 |
4.12E-15 |
4.24E-09 |
1.542411 |
2.62492 |
| mean |
8.88E-16 |
4.819446 |
8.88E-16 |
8.88E-16 |
3.96E-15 |
1.13E+00 |
3.80E-15 |
0.526357 |
1.53E-14 |
4.12E-15 |
7.48E-09 |
2.483992 |
3.256237 |
| median |
8.88E-16 |
4.717522 |
8.88E-16 |
8.88E-16 |
4.12E-15 |
2.03E-14 |
4.12E-15 |
0.176984 |
1.38E-14 |
4.12E-15 |
7.03E-09 |
2.490083 |
3.305859 |
| worst |
8.88E-16 |
7.467465 |
8.88E-16 |
8.88E-16 |
4.12E-15 |
3.072576 |
7.36E-15 |
2.290859 |
2.03E-14 |
4.12E-15 |
1.32E-08 |
4.606032 |
4.227951 |
| std |
0.00E+00 |
1.134893 |
0.00E+00 |
0.00E+00 |
7.38E-16 |
1.46E+00 |
2.11E-15 |
0.629188 |
3.30E-15 |
8.26E-31 |
2.17E-09 |
0.796999 |
0.36853 |
| rank |
1 |
11 |
1 |
1 |
3 |
8 |
2 |
7 |
5 |
4 |
6 |
9 |
10 |
| F11 |
best |
0 |
1.005423 |
0 |
0 |
0 |
0 |
0 |
0.231481 |
0 |
0 |
2.728462 |
0.002156 |
1.173211 |
| mean |
0 |
1.563093 |
0 |
0 |
0 |
0.008054 |
0 |
0.364028 |
0.00122 |
0 |
6.565133 |
0.168742 |
1.342053 |
| median |
0 |
1.458192 |
0 |
0 |
0 |
0.008191 |
0 |
0.379369 |
0 |
0 |
6.659052 |
0.111443 |
1.318588 |
| worst |
0 |
2.991765 |
0 |
0 |
0 |
0.018714 |
0 |
0.488181 |
0.017145 |
0 |
11.51061 |
0.797732 |
1.57193 |
| std |
0 |
0.504151 |
0 |
0 |
0 |
0.005847 |
0 |
0.076055 |
0.004166 |
0 |
2.528054 |
0.212292 |
0.115089 |
| rank |
1 |
7 |
1 |
1 |
1 |
3 |
1 |
5 |
2 |
1 |
8 |
4 |
6 |
| F12 |
best |
1.57E-32 |
0.868125 |
3.67E-10 |
0.700576 |
4.73E-11 |
0.944381 |
0.001117 |
0.00091 |
0.011442 |
0.021959 |
4.33E-19 |
0.0000973 |
0.055414 |
| mean |
1.57E-32 |
2.978079 |
2.35E-09 |
1.200098 |
1.85E-10 |
5.276134 |
0.018304 |
0.833065 |
0.036322 |
0.064967 |
1.91E-01 |
1.37E+00 |
0.250377 |
| median |
1.57E-32 |
2.63405 |
2.18E-09 |
1.265478 |
1.87E-10 |
3.920951 |
0.005268 |
0.382795 |
0.034529 |
0.062564 |
0.073046 |
1.170635 |
0.24084 |
| worst |
1.57E-32 |
6.729691 |
7.13E-09 |
1.499107 |
3.47E-10 |
12.87521 |
0.124691 |
3.504838 |
0.079043 |
0.123083 |
0.848666 |
4.753719 |
0.592794 |
| std |
2.86E-48 |
1.699748 |
1.54E-09 |
0.28233 |
8.93E-11 |
3.605398 |
0.037167 |
1.111915 |
0.01982 |
0.019465 |
0.285629 |
1.194504 |
0.128821 |
| rank |
1 |
12 |
3 |
10 |
2 |
13 |
4 |
9 |
5 |
6 |
7 |
11 |
8 |
| F13 |
best |
1.35E-32 |
12.567 |
1.04E-09 |
6.06E-32 |
9.07E-10 |
1.832961 |
0.033885 |
0.005868 |
0.0000427 |
0.536004 |
4.24E-18 |
0.008719 |
1.176729 |
| mean |
1.35E-32 |
3278.627 |
9.13E-09 |
2.86E-31 |
2.28E-03 |
2.474572 |
0.195464 |
0.029851 |
4.68E-01 |
1.00371 |
5.16E-02 |
3.285858 |
2.466324 |
| median |
1.35E-32 |
40.28554 |
5.94E-09 |
3.66E-31 |
2.57E-09 |
2.309059 |
0.15101 |
0.021526 |
0.471026 |
1.015205 |
1.62E-17 |
3.010954 |
2.611495 |
| worst |
1.35E-32 |
56617.17 |
3.47E-08 |
4.96E-31 |
0.023056 |
3.382691 |
0.637881 |
0.083455 |
0.865379 |
1.403745 |
0.872898 |
11.46312 |
3.588802 |
| std |
2.86E-48 |
12872.05 |
8.16E-09 |
2.09E-31 |
5.89E-03 |
0.518014 |
0.170514 |
0.02303 |
0.239555 |
0.214971 |
1.99E-01 |
2.816182 |
0.701 |
| rank |
1 |
13 |
3 |
2 |
4 |
11 |
7 |
5 |
8 |
9 |
6 |
12 |
10 |
| Sum rank |
6 |
11 |
53 |
27 |
15 |
52 |
18 |
32 |
39 |
32 |
44 |
50 |
44 |
| Mean rank |
1 |
1.83334 |
8.83334 |
4.5 |
2.5 |
8.66667 |
3 |
5.33334 |
6.5 |
5.33334 |
7.33334 |
8.33334 |
7.33334 |
| Total rank |
1 |
2 |
11 |
5 |
3 |
10 |
4 |
6 |
7 |
6 |
8 |
9 |
8 |
Table 4.
Optimization results for the fixed-dimensional multimodal functions.
Table 4.
Optimization results for the fixed-dimensional multimodal functions.
| |
FLO |
AVOA |
WSO |
RSA |
MPA |
TSA |
WOA |
GWO |
MVO |
TLBO |
GSA |
PSO |
GA |
| F14 |
best |
0.998004 |
0.998004 |
0.998004 |
0.998033 |
0.998004 |
1.903374 |
0.998004 |
0.998004 |
0.998004 |
0.998004 |
0.998004 |
0.998004 |
0.998004 |
| mean |
0.998004 |
1.089592 |
1.089412 |
2.920195 |
1.009791 |
7.965725 |
3.455667 |
2.430619 |
0.999055 |
0.999056 |
3.333745 |
3.365148 |
1.045199 |
| median |
0.998004 |
0.998004 |
0.998004 |
2.115668 |
0.998004 |
10.76083 |
2.805144 |
0.998014 |
0.998004 |
0.998004 |
2.722809 |
1.903377 |
0.998008 |
| worst |
9.98E-01 |
1.90E+00 |
2.81E+00 |
1.16E+01 |
1.23E+00 |
1.42E+01 |
9.89E+00 |
9.89E+00 |
1.02E+00 |
1.02E+00 |
1.09E+01 |
1.16E+01 |
1.90E+00 |
| std |
0 |
0.284 |
0.412 |
2.84 |
0.0537 |
4.69 |
3.47 |
2.74 |
0.00479 |
0.00479 |
2.56 |
3.52 |
0.206 |
| rank |
1 |
7 |
6 |
9 |
4 |
13 |
12 |
8 |
2 |
3 |
10 |
11 |
5 |
| F15 |
best |
0.000307 |
0.000308 |
0.000316 |
0.000772 |
0.000309 |
0.000317 |
0.000317 |
0.000324 |
0.000317 |
0.000327 |
0.000844 |
0.000308 |
0.000861 |
| mean |
0.000307 |
0.001349 |
0.000436 |
0.001135 |
0.001212 |
0.015074 |
0.003178 |
0.000849 |
0.002523 |
0.000654 |
0.002255 |
0.002388 |
0.014128 |
| median |
0.000307 |
0.000429 |
0.000429 |
0.001026 |
0.0016 |
0.000874 |
0.000429 |
0.000704 |
0.000736 |
0.000438 |
0.002087 |
0.000429 |
0.013087 |
| worst |
3.07E-04 |
1.87E-02 |
6.94E-04 |
2.77E-03 |
1.67E-03 |
1.01E-01 |
1.87E-02 |
2.20E-03 |
1.86E-02 |
1.29E-03 |
6.49E-03 |
1.87E-02 |
6.11E-02 |
| std |
2.59E-19 |
0.00417 |
0.0000907 |
0.000435 |
0.000552 |
0.0279 |
0.00679 |
0.000471 |
0.00562 |
0.000382 |
0.00128 |
0.0057 |
0.0151 |
| rank |
1 |
7 |
2 |
5 |
6 |
13 |
11 |
4 |
10 |
3 |
8 |
9 |
12 |
| F16 |
best |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03161 |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03163 |
| mean |
-1.03163 |
-1.0313 |
-1.0313 |
-1.02928 |
-1.02916 |
-1.02986 |
-1.0313 |
-1.0313 |
-1.0313 |
-1.03129 |
-1.0313 |
-1.0313 |
-1.03129 |
| median |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03119 |
-1.0316 |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03163 |
-1.03162 |
-1.03163 |
-1.03163 |
-1.03162 |
| worst |
-1.03E+00 |
-1.03E+00 |
-1.03E+00 |
-1.00E+00 |
-1.00E+00 |
-1.00E+00 |
-1.03E+00 |
-1.03E+00 |
-1.03E+00 |
-1.03E+00 |
-1.03E+00 |
-1.03E+00 |
-1.03E+00 |
| std |
1.87E-16 |
0.000853 |
0.000853 |
0.00652 |
0.00708 |
0.00657 |
0.000853 |
0.000853 |
0.000853 |
0.000853 |
0.000853 |
0.000853 |
0.000853 |
| rank |
1 |
6 |
2 |
10 |
11 |
9 |
4 |
3 |
5 |
8 |
2 |
2 |
7 |
| F17 |
best |
0.397887 |
0.397887 |
0.397887 |
0.398697 |
0.397887 |
0.397893 |
0.397888 |
0.397887 |
0.397887 |
0.397897 |
0.397887 |
0.397887 |
0.397887 |
| mean |
0.397887 |
0.397919 |
0.397919 |
0.409491 |
0.398387 |
0.397952 |
0.397919 |
0.397919 |
0.397919 |
0.397985 |
0.397919 |
0.713742 |
0.459977 |
| median |
0.397887 |
0.397894 |
0.397894 |
0.403269 |
0.397974 |
0.397917 |
0.397894 |
0.397894 |
0.397894 |
0.397969 |
0.397894 |
0.397913 |
0.397943 |
| worst |
3.98E-01 |
3.98E-01 |
3.98E-01 |
4.77E-01 |
4.01E-01 |
3.98E-01 |
3.98E-01 |
3.98E-01 |
3.98E-01 |
3.98E-01 |
3.98E-01 |
2.58E+00 |
1.63E+00 |
| std |
0 |
0.0000644 |
0.0000644 |
0.0181 |
0.000932 |
0.0000842 |
0.0000644 |
0.0000643 |
0.0000644 |
0.0000895 |
0.0000644 |
0.659 |
0.281 |
| rank |
1 |
4 |
2 |
10 |
9 |
7 |
6 |
5 |
3 |
8 |
2 |
12 |
11 |
| F18 |
best |
3 |
3.001243 |
3.001243 |
3.002335 |
3.013933 |
3.001249 |
3.001246 |
3.001243 |
3.001243 |
3.001244 |
3.001243 |
3.001243 |
3.00321 |
| mean |
3 |
3.265013 |
3.265014 |
5.79232 |
6.144686 |
11.00853 |
3.265025 |
3.265037 |
3.265013 |
3.265014 |
3.265013 |
3.265013 |
7.18414 |
| median |
3 |
3.035691 |
3.035691 |
3.08846 |
3.563655 |
3.099528 |
3.0357 |
3.035714 |
3.035692 |
3.035692 |
3.035691 |
3.035691 |
3.161867 |
| worst |
3.00E+00 |
5.41E+00 |
5.41E+00 |
2.88E+01 |
3.00E+01 |
8.41E+01 |
5.41E+00 |
5.41E+00 |
5.41E+00 |
5.41E+00 |
5.41E+00 |
5.41E+00 |
3.22E+01 |
| std |
1.19E-15 |
0.582 |
0.582 |
7.91 |
6.49 |
24.3 |
0.582 |
0.582 |
0.582 |
0.582 |
0.582 |
0.582 |
9.71 |
| rank |
1 |
2 |
6 |
10 |
11 |
13 |
8 |
9 |
5 |
7 |
4 |
3 |
12 |
| F19 |
best |
-3.86278 |
-3.86278 |
-3.86278 |
-3.85352 |
-3.86278 |
-3.86268 |
-3.86278 |
-3.86277 |
-3.86278 |
-3.86251 |
-3.86278 |
-3.86278 |
-3.86276 |
| mean |
-3.86278 |
-3.85019 |
-3.85019 |
-3.82664 |
-3.72454 |
-3.84982 |
-3.8488 |
-3.84804 |
-3.85019 |
-3.84918 |
-3.85019 |
-3.85019 |
-3.85004 |
| median |
-3.86278 |
-3.85056 |
-3.85056 |
-3.83066 |
-3.72574 |
-3.85052 |
-3.84988 |
-3.84899 |
-3.85056 |
-3.85015 |
-3.85056 |
-3.85056 |
-3.85049 |
| worst |
-3.86E+00 |
-3.81E+00 |
-3.81E+00 |
-3.77E+00 |
-3.29E+00 |
-3.81E+00 |
-3.81E+00 |
-3.81E+00 |
-3.81E+00 |
-3.81E+00 |
-3.81E+00 |
-3.81E+00 |
-3.81E+00 |
| std |
2.32E-15 |
0.0123 |
0.0123 |
0.0237 |
0.14 |
0.0121 |
0.0124 |
0.012 |
0.0123 |
0.0117 |
0.0123 |
0.0123 |
0.0124 |
| rank |
1 |
2 |
3 |
10 |
11 |
6 |
8 |
9 |
4 |
7 |
2 |
2 |
5 |
| F20 |
best |
-3.322 |
-3.31333 |
-3.2804 |
-3.0278 |
-3.22483 |
-3.31126 |
-3.31333 |
-3.30816 |
-3.31333 |
-3.29698 |
-3.31333 |
-3.31333 |
-3.23904 |
| mean |
-3.322 |
-3.23202 |
-3.19953 |
-2.74117 |
-2.52925 |
-3.18729 |
-3.19091 |
-3.18259 |
-3.20485 |
-3.17608 |
-3.24826 |
-3.196 |
-3.16292 |
| median |
-3.322 |
-3.24933 |
-3.19492 |
-2.82466 |
-2.58954 |
-3.17741 |
-3.19778 |
-3.18393 |
-3.22077 |
-3.17676 |
-3.25667 |
-3.2116 |
-3.17485 |
| worst |
-3.32E+00 |
-3.14E+00 |
-3.09E+00 |
-1.70E+00 |
-1.78E+00 |
-3.06E+00 |
-3.00E+00 |
-3.04E+00 |
-3.08E+00 |
-2.92E+00 |
-3.18E+00 |
-3.03E+00 |
-2.97E+00 |
| std |
4.53E-16 |
0.0502 |
0.0636 |
0.297 |
0.344 |
0.0699 |
0.0882 |
0.0802 |
0.0703 |
0.0927 |
0.0342 |
0.0841 |
0.0658 |
| rank |
1 |
3 |
5 |
12 |
13 |
8 |
7 |
9 |
4 |
10 |
2 |
6 |
11 |
| F21 |
best |
-10.1532 |
-10.1437 |
-10.1531 |
-5.50974 |
-10.1515 |
-10.1221 |
-10.1529 |
-10.1524 |
-10.153 |
-9.43287 |
-10.1531 |
-10.1362 |
-9.56481 |
| mean |
-10.1532 |
-8.33089 |
-9.92179 |
-5.27848 |
-7.55875 |
-6.07089 |
-9.22698 |
-9.2225 |
-8.76716 |
-6.91569 |
-7.22664 |
-5.79638 |
-6.37604 |
| median |
-10.1532 |
-9.88105 |
-9.95235 |
-5.30903 |
-7.90122 |
-5.07671 |
-9.88043 |
-9.8783 |
-9.77271 |
-7.16601 |
-9.69851 |
-5.15726 |
-7.0501 |
| worst |
-1.02E+01 |
-2.89E+00 |
-9.70E+00 |
-5.06E+00 |
-5.06E+00 |
-2.83E+00 |
-5.10E+00 |
-5.08E+00 |
-5.06E+00 |
-3.65E+00 |
-2.89E+00 |
-2.87E+00 |
-2.62E+00 |
| std |
2.12E-15 |
2.97 |
0.187 |
0.187 |
2.09 |
3.04 |
1.73 |
1.75 |
2.08 |
1.93 |
3.26 |
2.66 |
2.63 |
| rank |
1 |
6 |
2 |
13 |
7 |
11 |
3 |
4 |
5 |
9 |
8 |
12 |
10 |
| F22 |
best |
-10.4029 |
-10.4027 |
-10.4027 |
-5.56152 |
-10.4005 |
-10.3106 |
-10.4025 |
-10.3741 |
-10.376 |
-9.77163 |
-10.4027 |
-10.3804 |
-9.99024 |
| mean |
-10.4029 |
-9.84679 |
-10.1952 |
-5.35402 |
-8.0883 |
-6.9905 |
-10.1947 |
-8.10544 |
-8.40252 |
-7.96089 |
-9.94596 |
-6.53375 |
-7.43449 |
| median |
-10.4029 |
-10.1786 |
-10.2819 |
-5.44069 |
-9.04577 |
-7.67583 |
-10.2816 |
-9.92632 |
-9.98379 |
-8.27344 |
-10.211 |
-5.21856 |
-7.85052 |
| worst |
-1.04E+01 |
-3.41E+00 |
-9.93E+00 |
-5.09E+00 |
-5.09E+00 |
-2.12E+00 |
-9.93E+00 |
-2.17E+00 |
-3.29E+00 |
-4.32E+00 |
-5.26E+00 |
-2.97E+00 |
-2.89E+00 |
| std |
3.58E-15 |
1.56 |
0.189 |
0.189 |
2.13 |
3.38 |
0.189 |
2.82 |
2.54 |
1.58 |
1.14 |
3.28 |
1.86 |
| rank |
1 |
5 |
2 |
13 |
8 |
11 |
3 |
7 |
6 |
9 |
4 |
12 |
10 |
| F23 |
best |
-10.5364 |
-10.5286 |
-10.5286 |
-5.60303 |
-10.4492 |
-10.4288 |
-10.5284 |
-10.5277 |
-10.5286 |
-9.73892 |
-10.5286 |
-10.5196 |
-9.73355 |
| mean |
-10.5364 |
-10.4131 |
-10.4131 |
-5.48753 |
-9.15348 |
-7.57014 |
-10.4127 |
-8.63436 |
-9.43441 |
-8.1814 |
-10.1863 |
-6.66461 |
-6.60937 |
| median |
-10.5364 |
-10.4482 |
-10.4482 |
-5.52257 |
-9.54713 |
-9.95964 |
-10.4479 |
-10.3968 |
-10.4202 |
-8.70553 |
-10.4482 |
-4.32836 |
-7.12733 |
| worst |
-1.05E+01 |
-1.01E+01 |
-1.01E+01 |
-5.13E+00 |
-5.13E+00 |
-3.11E+00 |
-1.01E+01 |
-2.33E+00 |
-5.17E+00 |
-4.67E+00 |
-5.88E+00 |
-2.97E+00 |
-3.04E+00 |
| std |
2.82E-15 |
0.134 |
0.134 |
0.134 |
1.5 |
3.18 |
0.134 |
3.07 |
2.08 |
1.54 |
1.04 |
3.57 |
2.39 |
| rank |
1 |
2 |
3 |
13 |
7 |
10 |
4 |
8 |
6 |
9 |
5 |
11 |
12 |
| Sum rank |
10 |
33 |
44 |
105 |
87 |
101 |
66 |
66 |
50 |
73 |
47 |
80 |
95 |
| Mean rank |
1.00E+00 |
3.30E+00 |
4.40E+00 |
1.05E+01 |
8.70E+00 |
1.01E+01 |
6.60E+00 |
6.60E+00 |
5.00E+00 |
7.30E+00 |
4.70E+00 |
8.00E+00 |
9.50E+00 |
| Total rank |
1 |
2 |
3 |
12 |
9 |
11 |
6 |
6 |
5 |
7 |
4 |
8 |
10 |
Table 5.
Optimization results for the CEC 2017 test suite.
Table 5.
Optimization results for the CEC 2017 test suite.
| |
FLO |
WSO |
AVOA |
RSA |
MPA |
TSA |
WOA |
MVO |
GWO |
TLBO |
GSA |
PSO |
GA |
| C17-F1 |
mean |
100 |
5.47E+09 |
3736.741 |
9.92E+09 |
34277291 |
1.69E+09 |
6265768 |
7309.046 |
85692339 |
1.43E+08 |
728.1107 |
3057.613 |
11513604 |
| best |
100 |
4.53E+09 |
115.1723 |
8.57E+09 |
10886.23 |
3.62E+08 |
4562393 |
4650.116 |
27005.92 |
63693665 |
100.0187 |
338.6514 |
5962184 |
| worst |
100 |
7.01E+09 |
11575.72 |
1.18E+10 |
1.25E+08 |
3.68E+09 |
8249654 |
10768.56 |
3.11E+08 |
3.45E+08 |
1741.869 |
9048.114 |
16528771 |
| std |
0 |
1.13E+09 |
5637.763 |
1.54E+09 |
63646439 |
1.56E+09 |
1643381 |
3018.544 |
1.59E+08 |
1.43E+08 |
748.1019 |
4247.123 |
4651212 |
| median |
100 |
5.16E+09 |
1628.036 |
9.64E+09 |
6282818 |
1.36E+09 |
6125512 |
6908.755 |
15705576 |
81669353 |
535.2778 |
1421.844 |
11781730 |
| rank |
1 |
12 |
4 |
13 |
8 |
11 |
6 |
5 |
9 |
10 |
2 |
3 |
7 |
| C17-F3 |
mean |
300 |
8293.792 |
301.8391 |
9378.914 |
1375.654 |
10888.66 |
1688.689 |
300.053 |
2989.135 |
713.9977 |
9971.33 |
300 |
14356.74 |
| best |
300 |
4202.111 |
300 |
5061.044 |
777.166 |
4151.807 |
610.0958 |
300.0123 |
1492.915 |
466.305 |
6277.902 |
300 |
4233.022 |
| worst |
300 |
11094.74 |
303.9338 |
12545.46 |
2470.6 |
15390.93 |
3243.315 |
300.1207 |
5726.5 |
875.8003 |
13549.84 |
300 |
22687.57 |
| std |
0 |
3176.215 |
2.247148 |
3603.989 |
822.8102 |
5026.203 |
1306.484 |
0.050178 |
2057.025 |
189.0482 |
3158.628 |
4.89E-14 |
10152.4 |
| median |
300 |
8939.158 |
301.7113 |
9954.573 |
1127.425 |
12005.95 |
1450.672 |
300.0395 |
2368.563 |
756.9427 |
10028.79 |
300 |
15253.2 |
| rank |
1 |
9 |
4 |
10 |
6 |
12 |
7 |
3 |
8 |
5 |
11 |
2 |
13 |
| C17-F4 |
mean |
400 |
918.5001 |
404.6184 |
1324.333 |
406.5383 |
571.4825 |
424.4454 |
403.2412 |
411.4095 |
408.9142 |
404.4257 |
419.7445 |
414.3073 |
| best |
400 |
686.9377 |
401.2064 |
832.4566 |
402.378 |
475.6638 |
406.2617 |
401.5494 |
405.9193 |
408.1513 |
403.4619 |
400.1027 |
411.3519 |
| worst |
400 |
1127.349 |
406.3441 |
1806.129 |
411.0611 |
683.3579 |
471.5001 |
404.7584 |
427.5674 |
409.3958 |
405.9062 |
468.4064 |
417.9233 |
| std |
0 |
211.487 |
2.549157 |
437.6922 |
4.510676 |
107.2135 |
33.13703 |
1.757159 |
11.34448 |
0.561975 |
1.180512 |
34.5168 |
3.028779 |
| median |
400 |
929.8569 |
405.4616 |
1329.372 |
406.357 |
563.4541 |
410.0099 |
403.3286 |
406.0757 |
409.0548 |
404.1674 |
405.2343 |
413.977 |
| rank |
1 |
12 |
4 |
13 |
5 |
11 |
10 |
2 |
7 |
6 |
3 |
9 |
8 |
| C17-F5 |
mean |
501.2464 |
562.7628 |
543.267 |
571.5024 |
512.6851 |
563.2066 |
540.248 |
523.2985 |
512.8239 |
533.4614 |
552.8981 |
527.4234 |
527.5331 |
| best |
500.9951 |
548.6366 |
526.3694 |
557.1506 |
508.2448 |
542.4586 |
523.0456 |
510.0618 |
508.3883 |
528.0685 |
548.1185 |
510.9634 |
522.9067 |
| worst |
501.9917 |
572.071 |
561.7117 |
586.2257 |
517.6984 |
594.6685 |
575.476 |
537.3349 |
519.9718 |
536.9224 |
564.4298 |
550.8372 |
533.1848 |
| std |
0.523294 |
11.24763 |
19.528 |
17.00721 |
5.239914 |
24.39291 |
25.86418 |
11.99271 |
5.257986 |
4.097238 |
8.204426 |
19.37243 |
4.881442 |
| median |
500.9993 |
565.1717 |
542.4935 |
571.3166 |
512.3987 |
557.8496 |
531.2352 |
522.8986 |
511.4678 |
534.4273 |
549.5221 |
523.9465 |
527.0204 |
| rank |
1 |
11 |
9 |
13 |
2 |
12 |
8 |
4 |
3 |
7 |
10 |
5 |
6 |
| C17-F6 |
mean |
600 |
631.9679 |
617.0699 |
640.1193 |
601.1766 |
624.4721 |
622.8332 |
602.1188 |
601.1108 |
606.7637 |
616.9574 |
607.3227 |
610.1123 |
| best |
600 |
628.0964 |
616.08 |
636.953 |
600.7006 |
614.8572 |
607.4178 |
600.4653 |
600.5875 |
604.6901 |
602.8743 |
601.3351 |
606.8056 |
| worst |
600 |
635.2211 |
619.5846 |
644.3114 |
602.3635 |
639.8378 |
644.5482 |
604.2511 |
601.6942 |
609.997 |
635.6217 |
618.9817 |
614.2958 |
| std |
0 |
3.522076 |
1.770682 |
3.482394 |
0.835501 |
11.34888 |
16.46555 |
1.791659 |
0.482493 |
2.54797 |
15.95463 |
8.429568 |
3.496574 |
| median |
600 |
632.277 |
616.3074 |
639.6063 |
600.8212 |
621.5967 |
619.6833 |
601.8795 |
601.0807 |
606.1838 |
614.6668 |
604.4871 |
609.6739 |
| rank |
1 |
12 |
9 |
13 |
3 |
11 |
10 |
4 |
2 |
5 |
8 |
6 |
7 |
| C17-F7 |
mean |
711.1267 |
801.8243 |
764.7796 |
803.027 |
724.4458 |
826.7993 |
761.355 |
730.597 |
725.8017 |
751.4689 |
717.0341 |
732.4347 |
736.5061 |
| best |
710.6726 |
781.9245 |
743.4263 |
789.9792 |
720.2997 |
787.2738 |
750.5297 |
717.1182 |
717.3753 |
746.9989 |
714.7886 |
725.3833 |
726.3134 |
| worst |
711.7995 |
818.2036 |
792.1502 |
815.5044 |
728.797 |
867.6759 |
790.383 |
749.5856 |
743.0676 |
759.4706 |
720.7105 |
743.8261 |
741.0172 |
| std |
0.539366 |
16.11626 |
23.59666 |
12.6169 |
3.767224 |
36.78314 |
20.43924 |
14.38877 |
12.42733 |
5.871453 |
2.702113 |
8.863158 |
7.268468 |
| median |
711.0174 |
803.5845 |
761.771 |
803.3123 |
724.3433 |
826.1237 |
752.2536 |
727.8421 |
721.382 |
749.7031 |
716.3187 |
730.2647 |
739.3469 |
| rank |
1 |
11 |
10 |
12 |
3 |
13 |
9 |
5 |
4 |
8 |
2 |
6 |
7 |
| C17-F8 |
mean |
801.4928 |
847.9594 |
830.7179 |
852.9783 |
812.5179 |
847.6438 |
835.8856 |
811.6922 |
815.6551 |
837.214 |
819.6168 |
822.481 |
816.585 |
| best |
800.995 |
840.0504 |
820.0255 |
841.9218 |
808.7429 |
831.6806 |
818.3429 |
807.3408 |
810.3963 |
830.393 |
811.8696 |
815.4944 |
812.6473 |
| worst |
801.9912 |
856.225 |
846.3057 |
858.1424 |
814.642 |
866.671 |
847.9269 |
816.4079 |
820.5681 |
845.0906 |
827.2753 |
828.8525 |
824.2671 |
| std |
0.605411 |
7.772196 |
11.68425 |
7.882006 |
2.862269 |
16.39951 |
13.38181 |
3.92383 |
4.482335 |
7.915127 |
6.904175 |
6.97152 |
5.495759 |
| median |
801.4926 |
847.7811 |
828.2702 |
855.9245 |
813.3434 |
846.1118 |
838.6363 |
811.51 |
815.8281 |
836.6862 |
819.6612 |
822.7886 |
814.7128 |
| rank |
1 |
12 |
8 |
13 |
3 |
11 |
9 |
2 |
4 |
10 |
6 |
7 |
5 |
| C17-F9 |
mean |
900 |
1415.647 |
1184.109 |
1459.407 |
905.126 |
1374.025 |
1368.683 |
900.7903 |
911.7692 |
911.6633 |
900 |
904.1835 |
905.0408 |
| best |
900 |
1274.159 |
952.9809 |
1364.939 |
900.323 |
1164.299 |
1071.705 |
900.001 |
900.5653 |
907.1323 |
900 |
900.8869 |
902.7594 |
| worst |
900 |
1554.98 |
1650.596 |
1594.98 |
913.158 |
1658.273 |
1645.866 |
903.0715 |
932.6733 |
919.7283 |
900 |
912.149 |
908.9528 |
| std |
0 |
132.6979 |
340.4279 |
103.1532 |
6.084099 |
225.1024 |
254.5478 |
1.602111 |
15.86347 |
5.829805 |
0 |
5.66366 |
2.949944 |
| median |
900 |
1416.725 |
1066.429 |
1438.854 |
903.5116 |
1336.763 |
1378.581 |
900.0444 |
906.9191 |
909.8963 |
900 |
901.849 |
904.2254 |
| rank |
1 |
11 |
8 |
12 |
5 |
10 |
9 |
2 |
7 |
6 |
1 |
3 |
4 |
| C17-F10 |
mean |
1006.179 |
2273.607 |
1759.53 |
2541.66 |
1504.452 |
2008.524 |
2001.099 |
1762.429 |
1708.336 |
2144.709 |
2248.35 |
1923.739 |
1698.821 |
| best |
1000.284 |
2018.084 |
1472.325 |
2374.849 |
1382.178 |
1739.505 |
1438.96 |
1445.087 |
1526.348 |
1763.109 |
1975.334 |
1547.422 |
1405.051 |
| worst |
1012.668 |
2452.924 |
2381.05 |
2893.002 |
1577.649 |
2255.004 |
2513.204 |
2252.39 |
1968.77 |
2426.108 |
2351.688 |
2320.273 |
2084.862 |
| std |
7.010122 |
207.8178 |
449.5863 |
254.1133 |
96.96531 |
286.3359 |
547.0173 |
411.8901 |
198.0574 |
296.8361 |
192.0592 |
334.2969 |
307.0471 |
| median |
1005.882 |
2311.71 |
1592.372 |
2449.394 |
1528.991 |
2019.793 |
2026.115 |
1676.12 |
1669.112 |
2194.81 |
2333.189 |
1913.63 |
1652.685 |
| rank |
1 |
12 |
5 |
13 |
2 |
9 |
8 |
6 |
4 |
10 |
11 |
7 |
3 |
| C17-F11 |
mean |
1100 |
3792.805 |
1147.32 |
3913.816 |
1126.386 |
5353.182 |
1149.714 |
1126.836 |
1153.923 |
1149.669 |
1138.236 |
1142.466 |
2351.467 |
| best |
1100 |
2579.105 |
1116.633 |
1449.857 |
1112.878 |
5208.571 |
1112.643 |
1105.411 |
1121.094 |
1136.909 |
1119.165 |
1131.464 |
1114.678 |
| worst |
1100 |
4965.598 |
1199.302 |
6347.472 |
1157.346 |
5432.526 |
1171.319 |
1147.72 |
1225.241 |
1170.543 |
1166.94 |
1163.436 |
5860.164 |
| std |
0 |
1129.665 |
38.31996 |
2318.078 |
22.11378 |
104.8258 |
28.5344 |
22.26206 |
51.12907 |
15.28998 |
21.47371 |
15.1631 |
2463.985 |
| median |
1100 |
3813.26 |
1136.672 |
3928.967 |
1117.659 |
5385.816 |
1157.446 |
1127.106 |
1134.679 |
1145.613 |
1133.42 |
1137.481 |
1215.513 |
| rank |
1 |
11 |
6 |
12 |
2 |
13 |
8 |
3 |
9 |
7 |
4 |
5 |
10 |
| C17-F12 |
mean |
1352.959 |
3.46E+08 |
1076623 |
6.9E+08 |
555218.2 |
1017040 |
2302745 |
1006704 |
1384502 |
4942507 |
998167 |
7942.901 |
591852.2 |
| best |
1318.646 |
77501553 |
348274.8 |
1.53E+08 |
19458.1 |
527421.5 |
168030.9 |
8666.689 |
44473.99 |
1322697 |
464212.7 |
2491.975 |
171450.5 |
| worst |
1438.176 |
6.04E+08 |
1952421 |
1.21E+09 |
868884.4 |
1248617 |
3820158 |
3162122 |
2167137 |
8749709 |
1688039 |
13645.63 |
1044753 |
| std |
60.34215 |
2.8E+08 |
790170 |
5.61E+08 |
394089.6 |
358149.2 |
1787906 |
1534071 |
985273.1 |
4143007 |
545566.9 |
5351.454 |
377639 |
| median |
1327.506 |
3.51E+08 |
1002899 |
7E+08 |
666265.1 |
1146061 |
2611395 |
428012.7 |
1663199 |
4848812 |
920208 |
7817.002 |
575602.7 |
| rank |
1 |
12 |
8 |
13 |
3 |
7 |
10 |
6 |
9 |
11 |
5 |
2 |
4 |
| C17-F13 |
mean |
1305.324 |
16818760 |
17959.57 |
33627051 |
5343.993 |
12487.34 |
7441.547 |
6609.75 |
10102.15 |
16388.5 |
9879.403 |
6504.793 |
53288.07 |
| best |
1303.114 |
1403371 |
2692 |
2791832 |
3667.876 |
7450.198 |
3237.74 |
1384.282 |
6393.425 |
15476.72 |
4965.5 |
2355.43 |
8385.223 |
| worst |
1308.508 |
55824623 |
30752.64 |
1.12E+08 |
6529.18 |
19767.52 |
14850.39 |
12137.03 |
14101.13 |
18615.71 |
13903.43 |
16377.46 |
176137.9 |
| std |
2.393502 |
27444488 |
15277.22 |
54887056 |
1437.183 |
5598.534 |
5574.972 |
5865.593 |
3326.546 |
1578.577 |
3978.516 |
7008.283 |
86300.99 |
| median |
1304.837 |
5023524 |
19196.82 |
10040363 |
5589.459 |
11365.82 |
5839.029 |
6458.844 |
9957.02 |
15730.79 |
10324.34 |
3643.14 |
14314.57 |
| rank |
1 |
12 |
10 |
13 |
2 |
8 |
5 |
4 |
7 |
9 |
6 |
3 |
11 |
| C17-F14 |
mean |
1400.746 |
3939.312 |
2008.934 |
5264.816 |
1928.918 |
3345.285 |
1516.59 |
1568.362 |
2326.763 |
1586.904 |
5478.844 |
2962.532 |
12721.15 |
| best |
1400 |
3117.693 |
1673.286 |
4612.291 |
1434.307 |
1486.131 |
1480.161 |
1422.656 |
1461.054 |
1513.755 |
4535.374 |
1431.851 |
3678.382 |
| worst |
1400.995 |
5351.578 |
2798.455 |
6783.07 |
2872.227 |
5496.468 |
1555.51 |
1981.281 |
4889.386 |
1616.566 |
7425.724 |
6730.767 |
25320.97 |
| std |
0.523906 |
1086.154 |
558.4401 |
1073.877 |
710.2403 |
2246.597 |
40.54732 |
289.9705 |
1799.198 |
51.60308 |
1426.2 |
2666.975 |
9655.175 |
| median |
1400.995 |
3643.988 |
1781.998 |
4831.952 |
1704.569 |
3199.271 |
1515.345 |
1434.756 |
1478.307 |
1608.646 |
4977.139 |
1843.756 |
10942.63 |
| rank |
1 |
10 |
6 |
11 |
5 |
9 |
2 |
3 |
7 |
4 |
12 |
8 |
13 |
| C17-F15 |
mean |
1500.331 |
10098.58 |
5218.908 |
13616.4 |
3924.269 |
6887.913 |
6120.022 |
1540.983 |
5724.402 |
1704.856 |
23414.1 |
8840.912 |
4486.47 |
| best |
1500.001 |
2973.107 |
2060.565 |
2708.398 |
3187.379 |
2302.517 |
2003.782 |
1525.386 |
3527.032 |
1582.367 |
11023.57 |
2843.03 |
1882.431 |
| worst |
1500.5 |
17679.9 |
12395.04 |
29757.67 |
4821.345 |
12315.56 |
13198.16 |
1552.777 |
6787.366 |
1792.663 |
35125.15 |
14517.22 |
7878.356 |
| std |
0.247931 |
6463.467 |
5077.324 |
12437.92 |
713.8488 |
4531.581 |
5138.748 |
12.60171 |
1577.67 |
108.6858 |
12125.71 |
5138.289 |
3139.349 |
| median |
1500.413 |
9870.658 |
3210.011 |
10999.77 |
3844.176 |
6466.789 |
4639.074 |
1542.885 |
6291.604 |
1722.197 |
23753.83 |
9001.7 |
4092.546 |
| rank |
1 |
11 |
6 |
12 |
4 |
9 |
8 |
2 |
7 |
3 |
13 |
10 |
5 |
| C17-F16 |
mean |
1600.76 |
2003.841 |
1805.182 |
2007.682 |
1682.475 |
2037.911 |
1943.131 |
1811.714 |
1725.811 |
1675.298 |
2063.238 |
1916.854 |
1798.115 |
| best |
1600.356 |
1932.833 |
1641.383 |
1814.741 |
1640.895 |
1856.913 |
1761.641 |
1723.889 |
1615.517 |
1649.88 |
1939.83 |
1817.788 |
1716.236 |
| worst |
1601.12 |
2155.779 |
1919.398 |
2275.751 |
1712.433 |
2218.582 |
2068.663 |
1872.098 |
1820.735 |
1728.436 |
2253.981 |
2073.252 |
1828.527 |
| std |
0.332693 |
107.9397 |
123.3381 |
205.0407 |
32.40876 |
172.8169 |
153.6816 |
66.01326 |
89.17165 |
38.56257 |
150.4328 |
124.6204 |
57.53511 |
| median |
1600.781 |
1963.376 |
1829.974 |
1970.119 |
1688.287 |
2038.075 |
1971.11 |
1825.435 |
1733.496 |
1661.439 |
2029.57 |
1888.188 |
1823.848 |
| rank |
1 |
10 |
6 |
11 |
3 |
12 |
9 |
7 |
4 |
2 |
13 |
8 |
5 |
| C17-F17 |
mean |
1700.099 |
1815.785 |
1749.933 |
1815.932 |
1735.005 |
1800.085 |
1838.968 |
1839.831 |
1767.119 |
1757.185 |
1843.74 |
1751.289 |
1754.835 |
| best |
1700.02 |
1806.767 |
1733.703 |
1799.367 |
1721.462 |
1785.215 |
1772.092 |
1776.895 |
1723.964 |
1747.255 |
1746.952 |
1744.783 |
1751.768 |
| worst |
1700.332 |
1820.911 |
1793.046 |
1824.963 |
1773.372 |
1810.751 |
1885.438 |
1945.3 |
1868.057 |
1766.927 |
1967.462 |
1757.838 |
1757.219 |
| std |
0.163405 |
6.604172 |
30.34816 |
11.98474 |
26.95023 |
11.55193 |
51.8522 |
83.97523 |
71.2283 |
10.25543 |
118.4177 |
5.880496 |
2.593649 |
| median |
1700.022 |
1817.731 |
1736.491 |
1819.698 |
1722.593 |
1802.187 |
1849.171 |
1818.564 |
1738.228 |
1757.279 |
1830.274 |
1751.268 |
1755.175 |
| rank |
1 |
9 |
3 |
10 |
2 |
8 |
11 |
12 |
7 |
6 |
13 |
4 |
5 |
| C17-F18 |
mean |
1805.36 |
2790335 |
11621.85 |
5564458 |
10833.91 |
11819.61 |
22803.87 |
20498.52 |
19481.89 |
28855.77 |
9528.075 |
21406.05 |
12557.12 |
| best |
1800.003 |
143079.7 |
4773.511 |
275503.5 |
4103.869 |
7333.66 |
6341.191 |
8540.919 |
6218.404 |
23471.4 |
6286.716 |
2855.611 |
3398.068 |
| worst |
1820.451 |
8086661 |
15273.85 |
16153226 |
16174.54 |
15949.14 |
35793.67 |
32964.2 |
32845.25 |
36080.81 |
11621.21 |
39828.48 |
18092.38 |
| std |
10.59792 |
3874670 |
4958.103 |
7747506 |
5781.245 |
3773.409 |
14945.94 |
12109.03 |
14219.8 |
6108.088 |
2397.694 |
20100.54 |
6759.369 |
| median |
1800.492 |
1465801 |
13220.02 |
2914551 |
11528.62 |
11997.83 |
24540.31 |
20244.49 |
19431.95 |
27935.43 |
10102.19 |
21470.05 |
14369.02 |
| rank |
1 |
12 |
4 |
13 |
3 |
5 |
10 |
8 |
7 |
11 |
2 |
9 |
6 |
| C17-F19 |
mean |
1900.445 |
387325.3 |
6595.99 |
687462.2 |
5511.926 |
122623.9 |
34035.21 |
1914.421 |
5302.419 |
4631.324 |
39521.63 |
24406.65 |
6082.546 |
| best |
1900.039 |
24496.92 |
2170.349 |
44786.25 |
2308.105 |
1948.078 |
7524.944 |
1909.202 |
1943.66 |
2039.952 |
10888 |
2607.662 |
2205.951 |
| worst |
1901.559 |
818032 |
12978.45 |
1476750 |
9240.37 |
244893.5 |
62270.58 |
1923.745 |
13530.05 |
12241.53 |
57304.33 |
75127.73 |
9695.844 |
| std |
0.784167 |
360554.3 |
5534.839 |
680304 |
3721.021 |
146723.9 |
23668.24 |
7.235854 |
5837.141 |
5343.17 |
21892 |
36010.83 |
3254.361 |
| median |
1900.09 |
353386.2 |
5617.582 |
614156.2 |
5249.615 |
121827 |
33172.67 |
1912.368 |
2867.982 |
2121.906 |
44947.1 |
9945.598 |
6214.195 |
| rank |
1 |
12 |
7 |
13 |
5 |
11 |
9 |
2 |
4 |
3 |
10 |
8 |
6 |
| C17-F20 |
mean |
2000.312 |
2210.011 |
2166.568 |
2217.803 |
2090.167 |
2202.524 |
2201.759 |
2136.293 |
2165.937 |
2070.321 |
2247.759 |
2165.023 |
2049.043 |
| best |
2000.312 |
2154.567 |
2030.604 |
2160.675 |
2071.051 |
2104.208 |
2096.032 |
2045.847 |
2127.852 |
2059.553 |
2183.382 |
2141.464 |
2034.979 |
| worst |
2000.312 |
2278.59 |
2287.603 |
2271.927 |
2119.96 |
2313.389 |
2281.142 |
2241.642 |
2240.244 |
2080.497 |
2338.678 |
2196.123 |
2056.626 |
| std |
0 |
53.95395 |
121.7585 |
57.65849 |
22.07053 |
93.32007 |
93.18815 |
84.66573 |
53.35706 |
9.247632 |
79.56738 |
28.60972 |
10.51071 |
| median |
2000.312 |
2203.443 |
2174.032 |
2219.306 |
2084.828 |
2196.25 |
2214.931 |
2128.842 |
2147.827 |
2070.617 |
2234.488 |
2161.253 |
2052.284 |
| rank |
1 |
11 |
8 |
12 |
4 |
10 |
9 |
5 |
7 |
3 |
13 |
6 |
2 |
| C17-F21 |
mean |
2200 |
2290.968 |
2213.493 |
2265.597 |
2255.897 |
2322.324 |
2307.36 |
2251.936 |
2310.718 |
2297.422 |
2364.486 |
2316.097 |
2295.936 |
| best |
2200 |
2244.697 |
2204.034 |
2223.411 |
2253.464 |
2220.748 |
2217.975 |
2200.007 |
2306.605 |
2203.635 |
2347.406 |
2308.22 |
2225.954 |
| worst |
2200 |
2316.52 |
2238.126 |
2289.583 |
2258.376 |
2368.215 |
2350.548 |
2305.165 |
2315.574 |
2335.231 |
2381.419 |
2323.478 |
2329.794 |
| std |
0 |
35.24304 |
17.34766 |
30.82035 |
2.18896 |
72.54506 |
63.5482 |
63.15665 |
3.884515 |
66.31879 |
14.9697 |
7.903532 |
49.76087 |
| median |
2200 |
2301.327 |
2205.907 |
2274.697 |
2255.874 |
2350.166 |
2330.458 |
2251.285 |
2310.346 |
2325.411 |
2364.56 |
2316.346 |
2313.999 |
| rank |
1 |
6 |
2 |
5 |
4 |
12 |
9 |
3 |
10 |
8 |
13 |
11 |
7 |
| C17-F22 |
mean |
2300.073 |
2727.205 |
2308.786 |
2902.26 |
2304.896 |
2704.733 |
2323.277 |
2286.092 |
2308.412 |
2319.143 |
2300.006 |
2312.979 |
2317.535 |
| best |
2300 |
2604.512 |
2304.267 |
2697.974 |
2300.923 |
2445.851 |
2318.712 |
2230.996 |
2301.239 |
2313.024 |
2300 |
2300.624 |
2314.697 |
| worst |
2300.29 |
2863.201 |
2310.901 |
3052.187 |
2309.155 |
2908.01 |
2330.751 |
2305.182 |
2321.915 |
2330.62 |
2300.026 |
2344.466 |
2321.909 |
| std |
0.152789 |
125.676 |
3.213404 |
157.0784 |
3.653123 |
217.2198 |
5.66243 |
38.69394 |
10.01534 |
8.480752 |
0.013627 |
22.1532 |
3.245621 |
| median |
2300 |
2720.553 |
2309.989 |
2929.44 |
2304.752 |
2732.534 |
2321.822 |
2304.095 |
2305.248 |
2316.463 |
2300 |
2303.413 |
2316.766 |
| rank |
3 |
12 |
6 |
13 |
4 |
11 |
10 |
1 |
5 |
9 |
2 |
7 |
8 |
| C17-F23 |
mean |
2600.919 |
2695.142 |
2641.279 |
2698.593 |
2614.053 |
2720.959 |
2647.789 |
2619.87 |
2613.481 |
2641.744 |
2787.95 |
2643.451 |
2655.069 |
| best |
2600.003 |
2654.05 |
2630.016 |
2670.241 |
2611.708 |
2633.704 |
2630.257 |
2607.041 |
2607.705 |
2631.074 |
2724.222 |
2636.443 |
2635.506 |
| worst |
2602.87 |
2718.801 |
2658.663 |
2738.344 |
2616.681 |
2764.466 |
2667.61 |
2631.191 |
2620.042 |
2650.904 |
2923.517 |
2655.116 |
2663.229 |
| std |
1.39047 |
31.84495 |
14.22616 |
33.5504 |
2.494325 |
62.22928 |
21.21048 |
11.06898 |
6.713412 |
9.259933 |
98.62473 |
8.912385 |
13.94899 |
| median |
2600.403 |
2703.859 |
2638.218 |
2692.893 |
2613.911 |
2742.834 |
2646.645 |
2620.625 |
2613.089 |
2642.5 |
2752.031 |
2641.123 |
2660.77 |
| rank |
1 |
10 |
5 |
11 |
3 |
12 |
8 |
4 |
2 |
6 |
13 |
7 |
9 |
| C17-F24 |
mean |
2630.488 |
2774.562 |
2764.817 |
2845.426 |
2630.649 |
2667.52 |
2757.964 |
2682.241 |
2746.372 |
2753.283 |
2745.087 |
2762.814 |
2721.233 |
| best |
2516.677 |
2721.424 |
2731.165 |
2822.869 |
2614.606 |
2529.897 |
2729.886 |
2501.653 |
2720.269 |
2739.08 |
2503.872 |
2753.308 |
2541.917 |
| worst |
2732.32 |
2855.174 |
2784.603 |
2907.973 |
2639.658 |
2810.341 |
2790.428 |
2758.938 |
2759.651 |
2765.909 |
2894.23 |
2785.223 |
2809.443 |
| std |
122.6896 |
68.4245 |
26.78397 |
43.96585 |
11.87973 |
158.2364 |
26.36986 |
127.588 |
19.50185 |
13.53941 |
177.0559 |
15.83832 |
127.6645 |
| median |
2636.477 |
2760.824 |
2771.75 |
2825.431 |
2634.167 |
2664.92 |
2755.771 |
2734.188 |
2752.784 |
2754.072 |
2791.123 |
2756.364 |
2766.787 |
| rank |
1 |
12 |
11 |
13 |
2 |
3 |
9 |
4 |
7 |
8 |
6 |
10 |
5 |
| C17-F25 |
mean |
2932.639 |
3155.18 |
2913.894 |
3269.51 |
2918.209 |
3129.369 |
2908.071 |
2922.324 |
2938.568 |
2933.51 |
2922.491 |
2923.532 |
2951.829 |
| best |
2898.047 |
3064.544 |
2899.073 |
3202.552 |
2914.394 |
2906.642 |
2768.56 |
2901.85 |
2921.811 |
2915.723 |
2903.487 |
2898.655 |
2937.353 |
| worst |
2945.793 |
3355.646 |
2948.92 |
3343.189 |
2923.782 |
3641.612 |
2957.842 |
2943.71 |
2945.838 |
2952.119 |
2943.394 |
2946.537 |
2962.362 |
| std |
24.31643 |
142.1273 |
24.70364 |
61.2439 |
4.370192 |
363.6379 |
98.02209 |
24.7485 |
11.84326 |
21.01351 |
23.0419 |
27.38159 |
11.26241 |
| median |
2943.359 |
3100.264 |
2903.792 |
3266.149 |
2917.329 |
2984.611 |
2952.94 |
2921.869 |
2943.312 |
2933.1 |
2921.543 |
2924.469 |
2953.8 |
| rank |
7 |
12 |
2 |
13 |
3 |
11 |
1 |
4 |
9 |
8 |
5 |
6 |
10 |
| C17-F26 |
mean |
2900 |
3586.548 |
2978.206 |
3738.663 |
3009.357 |
3605.933 |
3177.182 |
2900.145 |
3257.787 |
3200.309 |
3841.837 |
2903.976 |
2897.274 |
| best |
2900 |
3249.585 |
2808.919 |
3421.475 |
2892.278 |
3139.18 |
2926.653 |
2900.111 |
2967.8 |
2911.806 |
2808.919 |
2808.919 |
2711.383 |
| worst |
2900 |
3826.851 |
3151.519 |
4068.773 |
3285.46 |
4241.393 |
3579.816 |
2900.189 |
3886.42 |
3855.646 |
4319.2 |
3006.985 |
3105.287 |
| std |
3.91E-13 |
292.2164 |
205.8885 |
293.9256 |
194.7487 |
567.5965 |
300.739 |
0.036902 |
445.4171 |
463.1248 |
736.9779 |
85.29239 |
210.1045 |
| median |
2900 |
3634.878 |
2976.193 |
3732.203 |
2929.845 |
3521.579 |
3101.13 |
2900.14 |
3088.464 |
3016.891 |
4119.614 |
2900 |
2886.213 |
| rank |
2 |
10 |
5 |
12 |
6 |
11 |
7 |
3 |
9 |
8 |
13 |
4 |
1 |
| C17-F27 |
mean |
3089.518 |
3205.957 |
3119.375 |
3228.207 |
3104.379 |
3177.675 |
3192.753 |
3091.585 |
3115.563 |
3114.565 |
3223.217 |
3135.116 |
3158.554 |
| best |
3089.518 |
3158.16 |
3095.187 |
3126.438 |
3092.187 |
3102.163 |
3177.187 |
3089.706 |
3094.336 |
3095.264 |
3211.305 |
3096.94 |
3118.73 |
| worst |
3089.518 |
3277.829 |
3179.042 |
3416.328 |
3132.899 |
3219.061 |
3204.273 |
3094.852 |
3174.984 |
3169.582 |
3244.326 |
3181.461 |
3216.271 |
| std |
2.76E-13 |
53.52379 |
42.0126 |
135.253 |
20.16865 |
55.77425 |
11.90539 |
2.548962 |
41.75977 |
38.63556 |
15.47514 |
37.43231 |
43.43005 |
| median |
3089.518 |
3193.919 |
3101.636 |
3185.032 |
3096.215 |
3194.737 |
3194.776 |
3090.89 |
3096.466 |
3096.708 |
3218.617 |
3131.032 |
3149.607 |
| rank |
1 |
11 |
6 |
13 |
3 |
9 |
10 |
2 |
5 |
4 |
12 |
7 |
8 |
| C17-F28 |
mean |
3100 |
3611.463 |
3233.144 |
3764.422 |
3215.961 |
3575.685 |
3282.736 |
3235.706 |
3339.606 |
3320.184 |
3443.108 |
3301.185 |
3243.164 |
| best |
3100 |
3563.288 |
3100 |
3683.905 |
3165.474 |
3405.693 |
3151.545 |
3100.121 |
3192.63 |
3211.49 |
3430.136 |
3175.433 |
3143.902 |
| worst |
3100 |
3652.954 |
3384.01 |
3822.542 |
3240.311 |
3780.33 |
3384.51 |
3384.011 |
3405.236 |
3384.247 |
3461.135 |
3384.221 |
3504.385 |
| std |
0 |
39.54602 |
132.2986 |
67.7661 |
36.47716 |
204.6273 |
126.0886 |
165.1629 |
103.9998 |
86.83885 |
15.12725 |
99.68882 |
184.0982 |
| median |
3100 |
3614.806 |
3224.283 |
3775.62 |
3229.03 |
3558.358 |
3297.444 |
3229.346 |
3380.28 |
3342.5 |
3440.581 |
3322.542 |
3162.184 |
| rank |
1 |
12 |
3 |
13 |
2 |
11 |
6 |
4 |
9 |
8 |
10 |
7 |
5 |
| C17-F29 |
mean |
3132.241 |
3324.262 |
3281.439 |
3370.25 |
3201.677 |
3234.136 |
3344.478 |
3201.267 |
3262.49 |
3211.02 |
3341.53 |
3263.344 |
3235.113 |
| best |
3130.076 |
3307.388 |
3208.777 |
3300.298 |
3165.245 |
3165.464 |
3233.56 |
3142.258 |
3188.769 |
3164.942 |
3231.698 |
3167.136 |
3187.368 |
| worst |
3134.841 |
3342.951 |
3360.613 |
3436.015 |
3242.35 |
3302.718 |
3488.455 |
3283.301 |
3374.431 |
3233.318 |
3624.637 |
3344.532 |
3283.168 |
| std |
2.61421 |
19.00098 |
82.36137 |
73.67541 |
35.72216 |
59.15374 |
112.573 |
62.88155 |
93.01789 |
33.76393 |
199.5837 |
84.79596 |
42.46644 |
| median |
3132.023 |
3323.354 |
3278.183 |
3372.344 |
3199.556 |
3234.181 |
3327.949 |
3189.755 |
3243.379 |
3222.909 |
3254.892 |
3270.854 |
3234.958 |
| rank |
1 |
10 |
9 |
13 |
3 |
5 |
12 |
2 |
7 |
4 |
11 |
8 |
6 |
| C17-F30 |
mean |
3418.734 |
2165720 |
287506.3 |
3584776 |
404550 |
599358.3 |
967621 |
295454.7 |
912690.3 |
59213.86 |
763371.5 |
377738.5 |
1489498 |
| best |
3394.682 |
1320162 |
102168.6 |
807160.4 |
15619.96 |
109607.9 |
4440.547 |
7339.401 |
32840.9 |
28649.75 |
586908.4 |
6321.34 |
512847.3 |
| worst |
3442.907 |
3250978 |
748843.2 |
5662047 |
597037.7 |
1267208 |
3652633 |
1126231 |
1320855 |
99321.06 |
974824 |
748878.9 |
3393200 |
| std |
29.24586 |
845640.7 |
324777.7 |
2140730 |
278078.7 |
518025.2 |
1887445 |
583462.4 |
637318.9 |
36349.97 |
169764.2 |
450721.6 |
1429827 |
| median |
3418.673 |
2045870 |
149506.7 |
3934949 |
502771.1 |
510308.6 |
106705.4 |
24124.27 |
1148533 |
54442.32 |
745876.8 |
377876.9 |
1025972 |
| rank |
1 |
12 |
3 |
13 |
6 |
7 |
10 |
4 |
9 |
2 |
8 |
5 |
11 |
| Sum rank |
38 |
319 |
177 |
351 |
106 |
284 |
239 |
116 |
188 |
191 |
238 |
183 |
197 |
| Mean rank |
1.310345 |
11 |
6.103448 |
12.10345 |
3.655172 |
9.793103 |
8.241379 |
4 |
6.482759 |
6.586207 |
8.206897 |
6.310345 |
6.793103 |
| Total rank |
1 |
12 |
4 |
13 |
2 |
11 |
10 |
3 |
6 |
7 |
9 |
5 |
8 |
Table 6.
Wilcoxon rank sum test results.
Table 6.
Wilcoxon rank sum test results.
| Compared Algorithm |
Test Functions |
| F1 to F7 |
F8 to F13 |
F14 to F23 |
CEC 2017 |
| FLO vs. AVOA |
2.93E-14 |
4.68E-08 |
1.39E-37 |
3.65E-22 |
| FLO vs. WSO |
1.79E-27 |
1.91E-24 |
2.02E-37 |
1.96E-24 |
| FLO vs. RSA |
4.12E-10 |
1.58E-14 |
1.39E-37 |
1.91E-24 |
| FLO vs. MPA |
9.78E-28 |
1.01E-17 |
2.02E-37 |
1.94E-21 |
| FLO vs. TSA |
9.78E-28 |
1.27E-23 |
1.39E-37 |
9.20E-24 |
| FLO vs. WOA |
2.36E-27 |
5.94E-14 |
1.39E-37 |
9.20E-24 |
| FLO vs. GWO |
9.78E-28 |
5.17E-19 |
1.39E-37 |
5.07E-24 |
| FLO vs. MVO |
9.78E-28 |
1.91E-24 |
1.39E-37 |
8.75E-22 |
| FLO vs. TLBO |
9.78E-28 |
6.76E-18 |
1.39E-37 |
3.57E-24 |
| FLO vs. GSA |
9.78E-28 |
1.91E-24 |
1.39E-37 |
1.55E-21 |
| FLO vs. PSO |
9.78E-28 |
1.91E-24 |
1.39E-37 |
1.49E-22 |
| FLO vs. GA |
9.78E-28 |
1.91E-24 |
1.39E-37 |
2.63E-22 |
Table 7.
Optimization results for the CEC 2011 test suite.
Table 7.
Optimization results for the CEC 2011 test suite.
| |
FLO |
AVOA |
WSO |
RSA |
MPA |
TSA |
WOA |
GWO |
MVO |
TLBO |
GSA |
PSO |
GA |
| C11-F1 |
best |
2E-10 |
15.71076 |
9.066921 |
20.62179 |
0.380394 |
17.94272 |
8.419541 |
1.141181 |
11.67985 |
17.18251 |
20.08481 |
10.70815 |
22.81227 |
| mean |
5.92E+00 |
17.99435 |
13.14302 |
22.38356 |
7.610637 |
18.74465 |
13.4423 |
10.99171 |
14.21507 |
18.77743 |
22.09735 |
18.27145 |
23.83473 |
| median |
5.687176 |
17.74842 |
13.22952 |
22.04179 |
8.683689 |
18.4701 |
13.92203 |
12.50987 |
14.38094 |
18.7476 |
22.36096 |
18.89069 |
23.29871 |
| worst |
12.30606 |
20.76982 |
17.04611 |
24.82885 |
12.69478 |
20.09569 |
17.50561 |
17.80591 |
16.41857 |
20.43201 |
23.58269 |
24.59626 |
25.92925 |
| std |
7.196379 |
2.60606 |
4.637594 |
2.136403 |
5.931504 |
1.059314 |
4.389729 |
7.430618 |
2.408351 |
1.40313 |
1.543546 |
6.81674 |
1.494991 |
| rank |
1 |
7 |
4 |
12 |
2 |
9 |
5 |
3 |
6 |
10 |
11 |
8 |
13 |
| C11-F2 |
best |
-27.0676 |
-15.5758 |
-21.5126 |
-11.7957 |
-25.7104 |
-14.8607 |
-21.9772 |
-24.7158 |
-10.5976 |
-11.8759 |
-20.5101 |
-23.9972 |
-15.0976 |
| mean |
-26.3179 |
-14.211 |
-20.9668 |
-11.3516 |
-25.073 |
-11.0667 |
-18.5091 |
-22.5833 |
-8.54387 |
-10.6677 |
-15.3823 |
-22.633 |
-12.7312 |
| median |
-26.3856 |
-14.1395 |
-21.0593 |
-11.3616 |
-25.4223 |
-10.2821 |
-18.8021 |
-23.3354 |
-8.29251 |
-10.5943 |
-14.8825 |
-23.1576 |
-12.4044 |
| worst |
-25.4328 |
-12.9891 |
-20.2358 |
-10.8875 |
-23.7372 |
-8.84169 |
-14.4552 |
-18.9464 |
-6.99281 |
-9.60622 |
-11.254 |
-20.2195 |
-11.0182 |
| std |
0.738935 |
1.387208 |
0.593111 |
0.509167 |
0.966972 |
2.990523 |
4.075175 |
2.675921 |
1.64456 |
0.990412 |
4.427235 |
1.741838 |
2.015308 |
| rank |
1 |
8 |
5 |
10 |
2 |
11 |
6 |
4 |
13 |
12 |
7 |
3 |
9 |
| C11-F4 |
best |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
| mean |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
| median |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
| worst |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
1.15E-05 |
| std |
2.00E-19 |
2.22E-11 |
2.55E-09 |
5.00E-11 |
1.25E-15 |
2.39E-14 |
6.15E-19 |
3.74E-15 |
9.98E-13 |
7.86E-14 |
2.00E-19 |
6.08E-20 |
2.77E-18 |
| rank |
1 |
11 |
13 |
12 |
6 |
8 |
4 |
7 |
10 |
9 |
3 |
2 |
5 |
| C11-F4 |
best |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| mean |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| median |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| worst |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| std |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| rank |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| C11-F5 |
best |
-34.7494 |
-25.9018 |
-29.1581 |
-22.0228 |
-33.8571 |
-31.5428 |
-27.7524 |
-34.1779 |
-31.7223 |
-12.7456 |
-31.5218 |
-11.9996 |
-10.7279 |
| mean |
-34.1274 |
-24.7516 |
-28.0779 |
-19.864 |
-33.2723 |
-27.0943 |
-27.5969 |
-31.5621 |
-26.9534 |
-10.5939 |
-27.3127 |
-8.41031 |
-9.27774 |
| median |
-34.1871 |
-24.6441 |
-27.771 |
-19.9721 |
-33.646 |
-27.5565 |
-27.7204 |
-32.2815 |
-25.8032 |
-10.3414 |
-26.7975 |
-7.48141 |
-9.39582 |
| worst |
-33.3862 |
-23.8166 |
-27.6116 |
-17.489 |
-31.9401 |
-21.7214 |
-27.1943 |
-27.5074 |
-24.4848 |
-8.94709 |
-24.1342 |
-6.67878 |
-7.59142 |
| std |
0.589989 |
0.95518 |
0.770371 |
2.52328 |
0.939346 |
4.252721 |
0.282677 |
2.997963 |
3.555513 |
1.70007 |
3.400906 |
2.637435 |
1.455951 |
| rank |
1 |
9 |
4 |
10 |
2 |
7 |
5 |
3 |
8 |
11 |
6 |
13 |
12 |
| C11-F6 |
best |
-27.4298 |
-14.5571 |
-20.4029 |
-13.6442 |
-25.7465 |
-16.4981 |
-22.9899 |
-22.38 |
-17.3952 |
-2.44646 |
-26.6323 |
-5.94001 |
-9.20345 |
| mean |
-24.1119 |
-13.9676 |
-19.0042 |
-12.965 |
-22.6108 |
-7.43437 |
-19.9336 |
-19.6085 |
-9.4219 |
-2.15053 |
-21.8798 |
-3.02392 |
-3.93842 |
| median |
-23.0059 |
-13.7835 |
-19.2017 |
-13.1341 |
-21.6869 |
-4.54604 |
-21.9278 |
-19.0489 |
-9.12028 |
-2.05189 |
-21.5738 |
-2.05189 |
-2.24917 |
| worst |
-23.0059 |
-13.7463 |
-17.2104 |
-11.9475 |
-21.3227 |
-4.1473 |
-12.8889 |
-17.9562 |
-2.05189 |
-2.05189 |
-17.7395 |
-2.05189 |
-2.05189 |
| std |
2.324951 |
0.414304 |
1.546268 |
0.826562 |
2.226773 |
6.363543 |
5.036499 |
2.223563 |
8.734288 |
0.207362 |
4.026194 |
2.0434 |
3.694555 |
| rank |
1 |
7 |
6 |
8 |
2 |
10 |
4 |
5 |
9 |
13 |
3 |
12 |
11 |
| C11-F7 |
best |
0.582266 |
1.546644 |
1.142773 |
1.679132 |
0.757596 |
1.129698 |
1.628575 |
0.814227 |
0.817307 |
1.528266 |
0.88491 |
0.831913 |
1.350761 |
| mean |
0.860699 |
1.607366 |
1.284792 |
1.921733 |
0.929758 |
1.302666 |
1.745163 |
1.067876 |
0.881104 |
1.720185 |
1.079947 |
1.123948 |
1.741991 |
| median |
0.91775 |
1.582628 |
1.284988 |
1.950134 |
0.974943 |
1.206637 |
1.716675 |
1.081482 |
0.875765 |
1.744987 |
1.076935 |
1.148661 |
1.835193 |
| worst |
1.025027 |
1.717562 |
1.426421 |
2.107532 |
1.011549 |
1.667694 |
1.918728 |
1.294312 |
0.955577 |
1.862501 |
1.28101 |
1.366556 |
1.946817 |
| std |
0.211503 |
0.081267 |
0.161509 |
0.187417 |
0.123219 |
0.258951 |
0.129822 |
0.207943 |
0.071645 |
0.153083 |
0.188418 |
0.290556 |
0.283994 |
| rank |
1 |
9 |
7 |
13 |
3 |
8 |
12 |
4 |
2 |
10 |
5 |
6 |
11 |
| C11-F8 |
best |
220 |
258.6912 |
223.6432 |
284.7586 |
220 |
220 |
245.4116 |
220 |
220 |
220 |
220 |
248.2351 |
220 |
| mean |
220 |
285.3233 |
240.5843 |
325.95 |
222.4592 |
257.5026 |
266.3147 |
227.3776 |
224.0986 |
224.0986 |
246.4917 |
470.865 |
222.5047 |
| median |
220 |
281.17 |
240.5843 |
324.1056 |
222.4592 |
227.3776 |
253.6089 |
227.3776 |
220 |
220 |
236.0957 |
531.6483 |
220 |
| worst |
220 |
320.262 |
257.5254 |
370.8302 |
224.9184 |
355.2553 |
312.6294 |
234.7551 |
236.3946 |
236.3946 |
293.7756 |
571.9284 |
230.0189 |
| std |
0 |
28.33492 |
15.32562 |
37.10878 |
2.984731 |
68.88765 |
32.70744 |
8.954192 |
8.616175 |
8.616175 |
36.77287 |
161.0301 |
5.26544 |
| rank |
1 |
10 |
6 |
11 |
2 |
8 |
9 |
5 |
4 |
4 |
7 |
12 |
3 |
| C11-F9 |
best |
5457.674 |
374781.4 |
336665.2 |
697814.5 |
11041.59 |
47806.58 |
208627.9 |
18499.88 |
75972.25 |
340166.3 |
708937.6 |
874293.6 |
1873402 |
| mean |
8789.286 |
560697.8 |
380695.1 |
1068617 |
20271.76 |
66589.3 |
377005.8 |
43236.71 |
134161.7 |
411177.8 |
828454.6 |
1089209 |
1954852 |
| median |
7828.591 |
611878.7 |
388154.1 |
1161468 |
20599.99 |
66996.02 |
330330.8 |
39412.95 |
128749.4 |
388492.1 |
856508.3 |
1074211 |
1938336 |
| worst |
14042.29 |
644252.5 |
409807.3 |
1253718 |
28845.46 |
84558.58 |
638733.6 |
75621.04 |
203175.8 |
527560.9 |
891864.2 |
1334122 |
2069334 |
| std |
3889.181 |
133563.1 |
33735.78 |
264941.7 |
8281.714 |
16458.05 |
206133.7 |
25372.04 |
55157.42 |
86679.05 |
85588.09 |
258343.4 |
101384.9 |
| rank |
1 |
9 |
7 |
11 |
2 |
4 |
6 |
3 |
5 |
8 |
10 |
12 |
13 |
| C11-F10 |
best |
-21.8299 |
-15.1474 |
-17.0907 |
-12.6209 |
-19.405 |
-18.8457 |
-13.5067 |
-14.5551 |
-21.1801 |
-11.3313 |
-13.6317 |
-11.3867 |
-11.0857 |
| mean |
-21.4889 |
-13.9334 |
-16.8991 |
-12.2327 |
-19.0152 |
-14.3551 |
-12.8304 |
-14.0677 |
-14.6685 |
-11.236 |
-13.1122 |
-11.3363 |
-11.0392 |
| median |
-21.669 |
-13.6326 |
-16.9924 |
-12.1747 |
-19.0175 |
-13.2966 |
-12.7347 |
-14.4077 |
-13.0427 |
-11.2352 |
-13.2437 |
-11.332 |
-11.0534 |
| worst |
-20.7878 |
-13.321 |
-16.521 |
-11.9607 |
-18.6207 |
-11.9813 |
-12.3453 |
-12.9002 |
-11.4084 |
-11.1423 |
-12.3297 |
-11.2945 |
-10.9644 |
| std |
0.498616 |
0.873428 |
0.27595 |
0.300903 |
0.421114 |
3.248101 |
0.512428 |
0.827904 |
4.63444 |
0.085067 |
0.667544 |
0.04007 |
0.055176 |
| rank |
1 |
7 |
3 |
10 |
2 |
5 |
9 |
6 |
4 |
12 |
8 |
11 |
13 |
| C11-F11 |
best |
260837.9 |
5557994 |
774810 |
8605193 |
1549827 |
4971008 |
1107924 |
3655950 |
612213.8 |
5205505 |
1268560 |
5226548 |
6108796 |
| mean |
571712.3 |
5828813 |
992977 |
8901363 |
1664311 |
5971920 |
1218465 |
3849509 |
1311819 |
5233232 |
1415206 |
5244366 |
6150774 |
| median |
598725.2 |
5779629 |
1011965 |
8954672 |
1654404 |
5848479 |
1192994 |
3765694 |
945640.2 |
5235642 |
1400232 |
5241956 |
6135506 |
| worst |
828560.9 |
6198000 |
1173167 |
9090917 |
1798611 |
7219712 |
1379948 |
4210699 |
2743783 |
5256141 |
1591802 |
5267002 |
6223290 |
| std |
260922.1 |
311888.7 |
182652.4 |
218241.7 |
126103.5 |
976503 |
121814.2 |
259907.3 |
1016990 |
23271.59 |
139894.1 |
21402.87 |
53468.09 |
| rank |
1 |
10 |
2 |
13 |
6 |
11 |
3 |
7 |
4 |
8 |
5 |
9 |
12 |
| C11-F12 |
best |
1155937 |
8077880 |
3283202 |
12348593 |
1198994 |
4777223 |
5416874 |
1260376 |
1175696 |
13547393 |
5521409 |
2148081 |
14426897 |
| mean |
1199805 |
8426155 |
3386135 |
13294942 |
1274918 |
5048294 |
5837448 |
1425143 |
1328064 |
14393299 |
5812159 |
2319287 |
14555006 |
| median |
1196965 |
8445689 |
3403596 |
13352032 |
1273202 |
5111608 |
5942811 |
1438043 |
1331765 |
14488324 |
5853035 |
2299989 |
14553136 |
| worst |
1249353 |
8735363 |
3454144 |
14127111 |
1354273 |
5192738 |
6047295 |
1564112 |
1473028 |
15049154 |
6021158 |
2529089 |
14686857 |
| std |
47157.58 |
286877.7 |
78506.39 |
766755.2 |
71443.68 |
202702 |
305338.9 |
132403.6 |
127721.8 |
662190.6 |
226324.5 |
165169.6 |
111676.6 |
| rank |
1 |
10 |
6 |
11 |
2 |
7 |
9 |
4 |
3 |
12 |
8 |
5 |
13 |
| C11-F13 |
best |
15444.19 |
15673.41 |
15447.01 |
15896.67 |
15460.95 |
15480.47 |
15492.04 |
15494.46 |
15487.9 |
15628.53 |
93207.96 |
15473.77 |
15460.54 |
| mean |
15444.2 |
15859.93 |
15448.01 |
16315.13 |
15463.27 |
15490.45 |
15535.98 |
15501.42 |
15508.25 |
15935.9 |
128965.6 |
15491.09 |
30083.63 |
| median |
15444.2 |
15727.24 |
15447.96 |
16004.54 |
15462.43 |
15489.09 |
15528.33 |
15498.88 |
15499.07 |
15806.47 |
122594.5 |
15481.38 |
15637.37 |
| worst |
15444.21 |
16311.82 |
15449.13 |
17354.77 |
15467.29 |
15503.13 |
15595.2 |
15513.47 |
15546.97 |
16502.13 |
177465.4 |
15527.81 |
73599.23 |
| std |
0.009091 |
319.7317 |
0.936378 |
734.5073 |
2.951184 |
11.77287 |
50.4487 |
8.855953 |
28.7804 |
415.6116 |
39873.02 |
26.01087 |
30492.98 |
| rank |
1 |
9 |
2 |
11 |
3 |
4 |
8 |
6 |
7 |
10 |
13 |
5 |
12 |
| C11-F14 |
best |
18241.58 |
85957.61 |
18404.38 |
169588 |
18524.65 |
19280.26 |
19076.34 |
19090.78 |
19324.11 |
30320.43 |
18806.64 |
18965.34 |
18831.17 |
| mean |
18295.35 |
113024.3 |
18520.66 |
230315.4 |
18609.59 |
19538.42 |
19231.08 |
19238.06 |
19425.84 |
312498.8 |
19097.29 |
19130.04 |
19117.21 |
| median |
18275.87 |
104003.8 |
18529.52 |
209852.9 |
18613.95 |
19391.67 |
19248.13 |
19218.59 |
19435.9 |
308198.1 |
19136.96 |
19138.94 |
19109.76 |
| worst |
18388.08 |
158132.1 |
18619.22 |
331967.8 |
18685.8 |
20090.09 |
19351.71 |
19424.28 |
19507.46 |
603278.4 |
19308.62 |
19276.94 |
19418.16 |
| std |
71.59938 |
33932.57 |
106.2459 |
76452.06 |
72.70982 |
390.523 |
133.2113 |
154.6878 |
81.27908 |
289123 |
228.3532 |
134.2236 |
252.1723 |
| rank |
1 |
11 |
2 |
12 |
3 |
10 |
7 |
8 |
9 |
13 |
4 |
6 |
5 |
| C11-F15 |
best |
32782.17 |
376496.4 |
43237.1 |
805730.9 |
32870.41 |
33048.29 |
33010.83 |
33043.73 |
33016.97 |
3251765 |
266808.2 |
33282.14 |
3635414 |
| mean |
32883.58 |
913742.5 |
108324.5 |
1926961 |
32948.76 |
54692.41 |
219807.3 |
33079.11 |
33101.38 |
15519775 |
301493.4 |
33290.62 |
7987262 |
| median |
32897.86 |
490250.6 |
104456.3 |
935843.3 |
32952.78 |
33191.73 |
265754.4 |
33064.22 |
33113.92 |
17841852 |
306962.8 |
33289.27 |
7312427 |
| worst |
32956.46 |
2297973 |
181148.2 |
5030428 |
33019.06 |
119337.9 |
314709.5 |
33144.26 |
33160.73 |
23143632 |
325240 |
33301.81 |
13688781 |
| std |
76.94696 |
973487 |
77908.34 |
2178087 |
64.00355 |
45299.42 |
133672.1 |
49.07491 |
66.50997 |
9507027 |
28571.3 |
8.604748 |
4845152 |
| rank |
1 |
10 |
7 |
11 |
2 |
6 |
8 |
3 |
4 |
13 |
9 |
5 |
12 |
| C11-F16 |
best |
131374.2 |
289911.4 |
133666.6 |
475920.9 |
135600.3 |
142488.4 |
136342.4 |
143409.4 |
133204.9 |
87188553 |
9569677 |
66243039 |
62144961 |
| mean |
133550 |
950389 |
135187.3 |
1960981 |
137683.4 |
145199.6 |
142217.9 |
145950.3 |
141860.1 |
89472496 |
18842170 |
80082023 |
76892038 |
| median |
133257.5 |
632638.2 |
135643.3 |
1246618 |
136879.5 |
145567.6 |
142484.3 |
144445.2 |
141757.3 |
89326420 |
15854250 |
79194589 |
73536101 |
| worst |
136310.8 |
2246368 |
135796 |
4874767 |
141374.4 |
147174.8 |
147560.5 |
151501.4 |
150721 |
92048591 |
34090502 |
95695874 |
98350989 |
| std |
2392.2 |
924912.3 |
1073.35 |
2079444 |
2709.018 |
2414.887 |
4923.103 |
3938 |
7730.783 |
2140935 |
11144663 |
13343828 |
16165669 |
| rank |
1 |
8 |
2 |
9 |
3 |
6 |
5 |
7 |
4 |
13 |
10 |
12 |
11 |
| C11-F17 |
best |
1916953 |
7.69E+09 |
2.12E+09 |
1.12E+10 |
1957612 |
1.06E+09 |
6.96E+09 |
2038930 |
2299063 |
2.16E+10 |
9.93E+09 |
1.85E+10 |
2.06E+10 |
| mean |
1926615 |
9.02E+09 |
2.33E+09 |
1.56E+10 |
2293290 |
1.29E+09 |
9.76E+09 |
3026639 |
3119727 |
2.25E+10 |
1.13E+10 |
2.10E+10 |
2.20E+10 |
| median |
1923412 |
9.20E+09 |
2.33E+09 |
1.61E+10 |
2151018 |
1.31E+09 |
9.55E+09 |
2583866 |
3212688 |
2.24E+10 |
1.16E+10 |
2.06E+10 |
2.13E+10 |
| worst |
1942685 |
1.00E+10 |
2.55E+09 |
1.91E+10 |
2913511 |
1.47E+09 |
1.30E+10 |
4899892 |
3754468 |
2.34E+10 |
1.20E+10 |
2.42E+10 |
2.49E+10 |
| std |
12003.53 |
1.08E+09 |
2.00E+08 |
3.55E+09 |
450632.8 |
2.22E+08 |
2.66E+09 |
1354721 |
706077.7 |
7.96E+08 |
9.67E+08 |
2.72E+09 |
2.04E+09 |
| rank |
1 |
7 |
6 |
10 |
2 |
5 |
8 |
3 |
4 |
13 |
9 |
11 |
12 |
| C11-F18 |
best |
938416.2 |
38056233 |
3961154 |
8.23E+07 |
949848.4 |
1798555 |
4141903 |
967157.9 |
964035.1 |
24725187 |
8352117 |
1.14E+08 |
1.11E+08 |
| mean |
942057.5 |
55335975 |
6591790 |
119000000 |
971938.3 |
2057336 |
9635664 |
1031700 |
988411.5 |
31196699 |
11194144 |
1.36E+08 |
1.15E+08 |
| median |
942553.5 |
60171362 |
5547873 |
1.29E+08 |
953682.2 |
2014229 |
8740133 |
978717.1 |
994949.5 |
33157306 |
11150777 |
1.39E+08 |
1.15E+08 |
| worst |
944706.9 |
62944940 |
11310259 |
136000000 |
1030540 |
2402332 |
16920486 |
1202207 |
999712.1 |
33746997 |
14122905 |
151000000 |
120000000 |
| std |
2774.139 |
12250909 |
3597267 |
2.65E+07 |
41194.04 |
305963.2 |
5671597 |
119728.3 |
17307.31 |
4553484 |
2710018 |
1.73E+07 |
3.64E+06 |
| rank |
1 |
10 |
6 |
12 |
2 |
5 |
7 |
4 |
3 |
9 |
8 |
13 |
11 |
| C11-F19 |
best |
967927.7 |
46475624 |
6108745 |
1.01E+08 |
1068411 |
2231819 |
2066743 |
1233805 |
1129215 |
25080259 |
2395060 |
1.58E+08 |
1.13E+08 |
| mean |
1025341 |
54468087 |
6693128 |
1.17E+08 |
1138554 |
2472748 |
10278052 |
1364982 |
1479593 |
35816486 |
6301409 |
1.74E+08 |
1.16E+08 |
| median |
983146.6 |
51071115 |
6276995 |
1.10E+08 |
1096048 |
2369288 |
10210584 |
1339636 |
1411616 |
36753610 |
7266724 |
1.68E+08 |
1.15E+08 |
| worst |
1167142 |
69254493 |
8109779 |
147000000 |
1293711 |
2920598 |
18624296 |
1546849 |
1965925 |
44678464 |
8277126 |
201000000 |
119000000 |
| std |
99675.04 |
10803670 |
999513.5 |
2.25E+07 |
109726.8 |
322083.5 |
8192328 |
137939.2 |
368407.8 |
8923056 |
2806570 |
1.97E+07 |
2.73E+06 |
| rank |
1 |
10 |
7 |
12 |
2 |
5 |
8 |
3 |
4 |
9 |
6 |
13 |
11 |
| C11-F20 |
best |
936143.2 |
50954706 |
5223024 |
1.10E+08 |
957152.3 |
1647208 |
6898584 |
977723.6 |
962978.5 |
34027686 |
9534816 |
1.46E+08 |
1.10E+08 |
| mean |
941250.4 |
57915854 |
5924708 |
1.26E+08 |
960470.6 |
1832300 |
7322355 |
998911.1 |
973018.6 |
34790803 |
14357706 |
1.60E+08 |
1.16E+08 |
| median |
940995.9 |
56061928 |
5900417 |
1.22E+08 |
961081.7 |
1770969 |
7251433 |
1001253 |
972340.5 |
34759730 |
12833683 |
1.60E+08 |
1.17E+08 |
| worst |
946866.6 |
68584856 |
6674976 |
150000000 |
962566.8 |
2140056 |
7887969 |
1015414 |
984414.7 |
35616065 |
22228640 |
174000000 |
120000000 |
| std |
5013.552 |
7896396 |
633442.1 |
1.77E+07 |
2451.631 |
245964.6 |
444598.3 |
17075.25 |
9907.006 |
694445.5 |
5830855 |
1.61E+07 |
4.38E+06 |
| rank |
1 |
10 |
6 |
12 |
2 |
5 |
7 |
4 |
3 |
9 |
8 |
13 |
11 |
| C11-F21 |
best |
9.974206 |
41.53049 |
20.3649 |
57.17792 |
13.78391 |
26.56174 |
35.6313 |
20.64111 |
24.52369 |
48.57262 |
35.96567 |
91.90592 |
59.07491 |
| mean |
12.71443 |
50.50227 |
21.70431 |
76.8985 |
15.95743 |
29.94194 |
38.96962 |
22.44344 |
27.63915 |
101.2915 |
40.89389 |
106.3608 |
103.21 |
| median |
12.95425 |
50.18166 |
21.46124 |
76.90776 |
15.89929 |
30.83809 |
38.56438 |
22.17047 |
27.67676 |
103.6709 |
41.89081 |
107.5927 |
113.8538 |
| worst |
14.97499 |
60.11528 |
23.52986 |
96.60055 |
18.24724 |
31.52984 |
43.11841 |
24.79172 |
30.67941 |
149.2516 |
43.82828 |
118.3517 |
126.0577 |
| std |
2.412667 |
8.418648 |
1.420534 |
18.29913 |
2.179408 |
2.41647 |
3.47749 |
1.927552 |
3.642786 |
43.35039 |
3.696548 |
13.67187 |
32.75307 |
| rank |
1 |
9 |
3 |
10 |
2 |
6 |
7 |
4 |
5 |
11 |
8 |
13 |
12 |
| C11-F22 |
best |
11.50133 |
40.80883 |
22.24877 |
46.17906 |
16.22029 |
28.20055 |
40.22051 |
23.95676 |
24.842 |
66.75931 |
39.13532 |
89.94588 |
92.17511 |
| mean |
16.12513 |
47.02927 |
27.52481 |
63.81642 |
19.10191 |
32.24992 |
46.54553 |
25.05548 |
32.40714 |
103.2154 |
46.90524 |
107.2767 |
93.11538 |
| median |
16.72317 |
47.34708 |
27.50942 |
67.79995 |
19.45731 |
33.00267 |
47.31893 |
25.18537 |
33.63111 |
111.9199 |
46.28905 |
110.3475 |
92.79237 |
| worst |
19.55286 |
52.6141 |
32.83162 |
73.4867 |
21.27275 |
34.79379 |
51.32375 |
25.89443 |
37.52432 |
122.2625 |
55.90755 |
118.4661 |
94.70167 |
| std |
4.197797 |
5.316853 |
5.254729 |
12.72251 |
2.533066 |
2.999636 |
5.265485 |
0.938547 |
5.947232 |
26.22423 |
7.253922 |
13.5143 |
1.170916 |
| rank |
1 |
9 |
4 |
10 |
2 |
5 |
7 |
3 |
6 |
12 |
8 |
13 |
11 |
| Sum rank |
22 |
109 |
191 |
231 |
55 |
146 |
145 |
97 |
118 |
222 |
157 |
198 |
224 |
| Mean rank |
1 |
4.954545 |
8.681818 |
10.5 |
2.5 |
6.636364 |
6.590909 |
4.409091 |
5.363636 |
10.09091 |
7.136364 |
9 |
10.18182 |
| Total rank |
1 |
12 |
2 |
4 |
13 |
3 |
11 |
6 |
9 |
7 |
10 |
5 |
8 |
| Wilcoxon: p-value |
9.77E-15 |
1.71E-15 |
1.71E-15 |
7.09E-15 |
3.66E-15 |
1.71E-15 |
7.10E-15 |
3.99E-12 |
5.36E-15 |
8.52E-15 |
2.54E-15 |
5.36E-15 |
Table 8.
Performance of the optimization algorithms for the pressure vessel design problem.
Table 8.
Performance of the optimization algorithms for the pressure vessel design problem.
| Algorithm |
Optimum variables |
Optimum cost |
| Ts |
Th |
R |
L |
| FLO |
0.7780271 |
0.3845792 |
40.312284 |
200 |
5882.8955 |
| WSO |
0.7780271 |
0.3845790 |
40.312281 |
200 |
5882.9011 |
| AVOA |
0.7780312 |
0.3845812 |
40.3125 |
199.99699 |
5882.9085 |
| RSA |
1.2457527 |
0.6715044 |
63.011657 |
29.541317 |
7988.1974 |
| MPA |
0.7780271 |
0.3845792 |
40.312284 |
200 |
5882.9013 |
| TSA |
0.7796786 |
0.3859699 |
40.39555 |
200 |
5912.596 |
| WOA |
0.9277593 |
0.4591628 |
46.950913 |
125.78933 |
6318.0671 |
| MVO |
0.8412891 |
0.4202776 |
43.571299 |
159.51516 |
6018.566 |
| GWO |
0.7785126 |
0.3859628 |
40.321643 |
199.96009 |
5891.0999 |
| TLBO |
1.6576806 |
0.4930712 |
48.594397 |
115.47982 |
11406.549 |
| GSA |
1.1728405 |
1.2516962 |
44.572154 |
189.66668 |
12726.817 |
| PSO |
1.6439969 |
0.6521499 |
65.916976 |
31.507574 |
10499.421 |
| GA |
1.4828762 |
0.8317876 |
60.436345 |
58.62914 |
11533.208 |
Table 9.
Statistical results of the optimization algorithms for the pressure vessel design problem.
Table 9.
Statistical results of the optimization algorithms for the pressure vessel design problem.
| Algorithm |
mean |
best |
worst |
std |
median |
rank |
| FLO |
5882.8955 |
5882.8955 |
5882.8955 |
1.92E-12 |
5882.8955 |
1 |
| WSO |
5892.2389 |
5882.9011 |
5975.0303 |
25.597613 |
5882.9017 |
3 |
| AVOA |
6260.4989 |
5882.9085 |
7187.8793 |
405.93922 |
6067.7468 |
5 |
| RSA |
13203.718 |
7988.1974 |
21708.462 |
3602.5764 |
12075.035 |
9 |
| MPA |
5882.9013 |
5882.9013 |
5882.9013 |
4.24E-06 |
5882.9013 |
2 |
| TSA |
6318.3698 |
5912.596 |
7078.0209 |
383.81952 |
6175.3376 |
6 |
| WOA |
8256.0687 |
6318.0671 |
13647.68 |
1937.652 |
7786.0827 |
8 |
| MVO |
6595.3898 |
6018.566 |
7192.4617 |
369.02769 |
6656.059 |
7 |
| GWO |
6028.1203 |
5891.0999 |
6766.8855 |
275.78721 |
5900.4533 |
4 |
| TLBO |
30997.684 |
11406.549 |
66934.242 |
15893.46 |
27298.577 |
12 |
| GSA |
22439.592 |
12726.817 |
35296.066 |
7732.2649 |
21527.451 |
10 |
| PSO |
32584.002 |
10499.421 |
56166.913 |
14879.262 |
35973.439 |
13 |
| GA |
27805.883 |
11533.208 |
50355.085 |
12475.479 |
24579.373 |
11 |
Table 10.
Performance of the optimization algorithms for the speed reducer design problem.
Table 10.
Performance of the optimization algorithms for the speed reducer design problem.
| Algorithm |
Optimum variables |
Optimum cost |
| b |
M |
p |
l1
|
l2
|
d1
|
d2
|
| FLO |
3.5 |
0.7 |
17 |
7.3 |
7.8 |
3.3502147 |
5.2866832 |
2996.3482 |
| WSO |
3.5000005 |
0.7 |
17 |
7.3000098 |
7.8000004 |
3.3502148 |
5.2866833 |
2996.3483 |
| AVOA |
3.5 |
0.7 |
17 |
7.3000007 |
7.8 |
3.3502147 |
5.2866832 |
2996.3482 |
| RSA |
3.591081 |
0.7 |
17 |
8.2108102 |
8.2554051 |
3.3555991 |
5.4809743 |
3180.6287 |
| MPA |
3.5 |
0.7 |
17 |
7.3 |
7.8 |
3.3502147 |
5.2866832 |
2996.3482 |
| TSA |
3.512746 |
0.7 |
17 |
7.3 |
8.2554051 |
3.3505367 |
5.2901744 |
3013.6687 |
| WOA |
3.5864383 |
0.7 |
17 |
7.3 |
8.0068571 |
3.3614768 |
5.2867549 |
3037.755 |
| MVO |
3.5022252 |
0.7 |
17 |
7.3 |
8.0658639 |
3.3693655 |
5.2868795 |
3008.0939 |
| GWO |
3.5006336 |
0.7 |
17 |
7.3050825 |
7.8 |
3.3637852 |
5.2887849 |
3001.4528 |
| TLBO |
3.5554343 |
0.7039501 |
26.213531 |
8.0919072 |
8.1411238 |
3.6597328 |
5.3387355 |
5243.4107 |
| GSA |
3.5226393 |
0.7027207 |
17.364783 |
7.8143829 |
7.8885518 |
3.4080837 |
5.3847634 |
3167.6764 |
| PSO |
3.5080871 |
0.7000711 |
18.082718 |
7.3978687 |
7.867227 |
3.5925551 |
5.3433467 |
3298.9223 |
| GA |
3.5770929 |
0.7054996 |
17.804212 |
7.7373556 |
7.8551847 |
3.6974126 |
5.3456293 |
3.34E+03 |
Table 11.
Statistical results of the optimization algorithms for the speed reducer design problem.
Table 11.
Statistical results of the optimization algorithms for the speed reducer design problem.
| Algorithm |
mean |
best |
worst |
std |
median |
rank |
| FLO |
2996.3482 |
2996.3482 |
2996.3482 |
9.58E-13 |
2996.3482 |
1 |
| WSO |
2996.6283 |
2996.3483 |
2998.7703 |
0.593604 |
2996.3642 |
3 |
| AVOA |
3000.8027 |
2996.3482 |
3010.9013 |
4.0273974 |
3000.7044 |
4 |
| RSA |
3273.4732 |
3180.6287 |
3331.0939 |
58.376714 |
3288.1754 |
9 |
| MPA |
2996.3482 |
2996.3482 |
2996.3482 |
3.23E-06 |
2996.3482 |
2 |
| TSA |
3031.7102 |
3013.6687 |
3045.2791 |
10.291508 |
3033.477 |
7 |
| WOA |
3148.2393 |
3037.755 |
3439.8167 |
107.88934 |
3115.2947 |
8 |
| MVO |
3029.4277 |
3008.0939 |
3069.3067 |
13.455894 |
3029.8624 |
6 |
| GWO |
3004.5239 |
3001.4528 |
3010.4183 |
2.5448163 |
3004.0121 |
5 |
| TLBO |
6.873E+13 |
5243.4107 |
4.975E+14 |
1.175E+14 |
2.692E+13 |
12 |
| GSA |
3449.2391 |
3167.6764 |
4062.9379 |
266.13006 |
3321.1203 |
10 |
| PSO |
1.014E+14 |
3298.9223 |
5.139E+14 |
1.258E+14 |
7.256E+13 |
13 |
| GA |
4.884E+13 |
3342.7177 |
3.152E+14 |
7.902E+13 |
1.957E+13 |
11 |
Table 12.
Performance of the optimization algorithms for the welded beam design problem.
Table 12.
Performance of the optimization algorithms for the welded beam design problem.
| Algorithm |
Optimum variables |
Optimum cost |
| h |
l |
t |
b |
| FLO |
0.2057296 |
3.4704887 |
9.0366239 |
0.2057296 |
1.7248523 |
| WSO |
0.2057296 |
3.4704887 |
9.0366239 |
0.2057296 |
1.7248523 |
| AVOA |
0.204974 |
3.4868751 |
9.0365185 |
0.2057344 |
1.7259067 |
| RSA |
0.1968043 |
3.5338976 |
9.9140767 |
0.2176511 |
1.972399 |
| MPA |
0.2057296 |
3.4704887 |
9.0366239 |
0.2057296 |
1.7248523 |
| TSA |
0.2042143 |
3.4950752 |
9.0638538 |
0.2061512 |
1.7337349 |
| WOA |
0.2136308 |
3.3314508 |
8.9745837 |
0.2208114 |
1.8201429 |
| MVO |
0.2059899 |
3.4648795 |
9.0445874 |
0.2060516 |
1.7283218 |
| GWO |
0.2055937 |
3.4736068 |
9.0362448 |
0.2057979 |
1.7255154 |
| TLBO |
0.313913 |
4.4099301 |
6.8250934 |
0.4224048 |
3.0076755 |
| GSA |
0.2927572 |
2.7308917 |
7.4410075 |
0.3066903 |
2.0800575 |
| PSO |
0.3704896 |
3.4252427 |
7.3653863 |
0.5694254 |
3.9945673 |
| GA |
0.2240807 |
6.8722146 |
7.7790615 |
0.3031552 |
2.7482044 |
Table 13.
Statistical results for the optimization algorithms for the welded beam design problem.
Table 13.
Statistical results for the optimization algorithms for the welded beam design problem.
| Algorithm |
mean |
best |
worst |
std |
median |
rank |
| FLO |
1.7246798 |
1.7246798 |
1.7246798 |
2.34E-16 |
1.7246798 |
1 |
| WSO |
1.7248526 |
1.7248523 |
1.7248578 |
1.269E-06 |
1.7248523 |
3 |
| AVOA |
1.7607647 |
1.7259067 |
1.8412254 |
0.0369935 |
1.7470447 |
7 |
| RSA |
2.1759749 |
1.972399 |
2.519308 |
0.1462171 |
2.1512469 |
8 |
| MPA |
1.7248523 |
1.7248523 |
1.7248523 |
3.40E-09 |
1.7248523 |
2 |
| TSA |
1.7429229 |
1.7337349 |
1.7520018 |
0.0056864 |
1.743018 |
6 |
| WOA |
2.3034718 |
1.8201429 |
4.0174423 |
0.6509517 |
2.08131 |
9 |
| MVO |
1.7410203 |
1.7283218 |
1.7744279 |
0.013955 |
1.7370004 |
5 |
| GWO |
1.7272229 |
1.7255154 |
1.7312168 |
0.0013824 |
1.7269807 |
4 |
| TLBO |
3.285E+13 |
3.0076755 |
3.17E+14 |
8.229E+13 |
5.6424231 |
12 |
| GSA |
2.4348133 |
2.0800575 |
2.7395728 |
0.1942722 |
2.4639914 |
10 |
| PSO |
4.53E+13 |
3.9945673 |
2.742E+14 |
8.886E+13 |
6.6680784 |
13 |
| GA |
1.112E+13 |
2.7482044 |
1.203E+14 |
3.506E+13 |
5.609433 |
11 |
Table 14.
Performance of the optimization algorithms for the tension/compression spring design problem.
Table 14.
Performance of the optimization algorithms for the tension/compression spring design problem.
| Algorithm |
Optimum variables |
Optimum cost |
| d |
D |
P |
| FLO |
0.0516891 |
0.3567177 |
11.288966 |
0.0126652 |
| WSO |
0.0516871 |
0.3566707 |
11.291725 |
0.0126652 |
| AVOA |
0.0511979 |
0.3450265 |
12.012341 |
0.0126701 |
| RSA |
0.0501506 |
0.3146926 |
14.669014 |
0.0131519 |
| MPA |
0.0516907 |
0.3567578 |
11.286619 |
0.0126652 |
| TSA |
0.0509975 |
0.3403048 |
12.334688 |
0.0126818 |
| WOA |
0.0511727 |
0.3444345 |
12.0511 |
0.0126706 |
| MVO |
0.0501506 |
0.3204164 |
13.852933 |
0.0127487 |
| GWO |
0.0519529 |
0.3630808 |
10.930013 |
0.0126706 |
| TLBO |
0.0675319 |
0.8850682 |
2.828481 |
0.0174182 |
| GSA |
0.055068 |
0.4400717 |
7.8639345 |
0.0130684 |
| PSO |
0.0674505 |
0.8819948 |
2.828481 |
0.0173176 |
| GA |
0.0679933 |
0.8927686 |
2.828481 |
0.0178071 |
Table 15.
Statistical results for the optimization algorithms for the tension/compression spring design problem.
Table 15.
Statistical results for the optimization algorithms for the tension/compression spring design problem.
| Algorithm |
mean |
best |
worst |
std |
median |
rank |
| FLO |
0.0126019 |
0.0126019 |
0.0126019 |
7.07E-18 |
0.0126019 |
1 |
| WSO |
0.0126761 |
0.0126652 |
0.012822 |
3.588E-05 |
0.0126656 |
3 |
| AVOA |
0.0133257 |
0.0126701 |
0.014115 |
0.000558 |
0.0132591 |
8 |
| RSA |
0.0132315 |
0.0131519 |
0.0133718 |
6.945E-05 |
0.013211 |
6 |
| MPA |
0.0126652 |
0.0126652 |
0.0126652 |
2.85E-09 |
0.0126652 |
2 |
| TSA |
0.0129549 |
0.0126818 |
0.0135043 |
0.0002418 |
0.0128831 |
5 |
| WOA |
0.013257 |
0.0126706 |
0.0144524 |
0.0006048 |
0.0130638 |
7 |
| MVO |
0.0163776 |
0.0127487 |
0.0177786 |
0.0016487 |
0.0172702 |
9 |
| GWO |
0.0127215 |
0.0126706 |
0.0129391 |
5.535E-05 |
0.0127191 |
4 |
| TLBO |
0.0179362 |
0.0174182 |
0.0185278 |
0.0003583 |
0.0178931 |
10 |
| GSA |
0.0192519 |
0.0130684 |
0.0315728 |
0.0042637 |
0.0188366 |
11 |
| PSO |
2.039E+13 |
0.0173176 |
3.618E+14 |
8.314E+13 |
0.0173176 |
13 |
| GA |
1.593E+12 |
0.0178071 |
1.647E+13 |
4.885E+12 |
0.0252274 |
12 |