Preprint
Article
Length of Stay Analysis of COVID-19 Intensive Care Unit Admissions Using Count Regression and Hurdle Regression Models: A Study in a Tertiary Hospital, Cape Town, South Africa
Altmetrics
Downloads
161
Views
64
Comments
0
This version is not peer-reviewed
Preprints on COVID-19 and SARS-CoV-2
Submitted:
14 March 2024
Posted:
18 March 2024
You are already at the latest version
Alerts
Abstract
Objective: To evaluate the variables influencing the length of stay (LoS) for COVID-19 ICU patients at Tygerberg Hospital (Cape Town) and to identify the covariates that significantly influenced it and any potential risk factors associated with LoS.
Methods and Results: Poisson, negative binomial (NB), Hurdle–Poisson, and
Hurdle–NB regression models were used to model the LoS in this prospective cohort study. The fitted models were compared using the Akaike information criterion (AIC), Vuong’s test criteria, and Rootograms. Based on the chosen performance criteria, the NB model provided the best fit outperforming other candidate models. The baseline LoS count was 8 days. On average, antibiotics reduced LoS by 0.74-fold (95% CI 0.62-0.89) compared to not taking antibiotics. The second wave had a significant effect on the average LoS, which decreased by 0.36-fold (95% CI 0.14-0.93) compared to the first wave. Average LoS increased by 1.01-fold (95% CI 1.01-1.02) for every one-year increase in the age of the patient and by 1.02-fold (95% CI 1.01-1.03) for every 1 unit increase in neutrophils. A 1 ng/L increase in log (TropT) levels decreased the average LoS by 0.87-fold (95% CI 0.81-0.93) similarly, a unit increase in the PF ratio decreased the average LoS by 0.998-fold (95% CI 0.997-0.999) respectively.
Conclusion: The study identified common clinical characteristics associated with length of stay in ICU for COVID-19 patients, including age at admission, PF ratio, neutrophils, TropT, Wave, and antibiotic use. These results can aid in identifying risk factors for increased length of stay, assist in healthcare systems planning, and aid in evaluating different models for analysing this type of data.
Keywords:
Subject: Medicine and Pharmacology - Epidemiology and Infectious Diseases
Introduction
Coronavirus is an infectious sickness known as coronavirus disease (COVID-19) caused by the SARS-Cov-2 virus, which the World Health Organization classified as a pandemic in March 2020 (World Health Organization, 2022) . Up until November 2022, COVID-19 had caused 637 million cases and more than 6.6 million fatalities globally since the first case was discovered in Wuhan in December 2019 (World Health Organization, 2022). The COVID-19 pandemic posed a serious threat to health systems that were forced to deal with an enormous spike in the number of patients who required hospitalization. The burden of the COVID-19 pandemic on health systems demonstrated the need for healthcare institutions to have agile and responsive management plans that anticipate hospital service demand and effectively make resources accessible when necessary.
Length of stay (LoS) measures the duration between a patient's admission to the hospital and their release (Thomas WJ, Guire KE & Horvat GG, 1997). LoS is a crucial measure of hospital efficiency and is used for functional evaluations to gauge management effectiveness and patient care quality. A shorter stay results in fewer patients needing hospital resources and more beds being available for patients, hence a surrogate measure of the cost of care. LoS reduction is associated with better clinical results, lower mortality for some conditions, and decreased risks of hospital-acquired opportunistic infections and drug adverse effects. LoS promotes bed turnover, lessens the burden of medical payments, and increases hospital profit margins while decreasing overall social expenditures. It is therefore imperative for researchers to identify the factors and characteristics that are linked to patients' longer or shorter hospital stays.
A meta-analysis and systematic review of 52 papers (Rees et al., 2020) compared the LoS of COVID-19 patients in China with patients in Europe, the U.S.A and the UK and research showed a significant difference in LoS between China (longer LoS) and other locations (shorter LoS). However, little information is available on the effects of age, disease severity, and the research period on LoS. In China research showed that the average age of patients with a longer LoS was higher than that of patients with an average LoS, while a retrospective study in Vietnam discovered that age was substantially connected with a lengthy hospital stay in COVID-19 patients. A territory-wide retrospective cohort study in Hong Kong, on 28-day in-hospital mortality and LoS, showed that there was a slight change in overall LoS before and after the years of the COVID-19 pandemic. Patients triaged as critical in the emergency department in 2020 had a 2.71-day shorter LoS than those in 2019i.
A retrospective study of COVID-19 hospitalized patients in China used multivariable and univariate logistic regression models to investigate the risk factors for a prolonged hospital LoS. Patients with a prolonged LoS were found to be older on average compared to those with a median LoS. The factors connected to the LoS were found using a time-to-event analysis using a Cox proportional hazard model (Guo et al., 2021). The predicted LoS of patients was necessary to model bed occupancy and create contingency plans, and factors associated with a longer hospital stay should be considered when setting up bed strength on a contingency basis. Researchers in artificial intelligence (AI) created algorithms to simulate bed occupancy and to create backup strategies.
Gamma regression and multivariable negative binomial models were employed in a different study in South Korea to identify the components that affect LoS. The study showed that COVID-19 patients’ average LoS in the hospital was 5.5 days (Jang et al., 2021). The average LoS also tended to be longer for older patients except for those 65 years of age or older who had a shortened hospital stay than the other groups. To effectively estimate the LoS and risk of mortality from a management perspective, a study in Dubai applied AI-based modelling by utilizing Decision Tree prediction models. These intelligent models could give clinicians the resources they need to enhance their management strategies and save lives.
Like many countries in Africa, South Africa’s health system faced unprecedented stressors and struggled to cope with the burden of COVID-19 ICU patients with high hospitalization rates. It was important to determine several variables of longer LoS.
This research study uses count regression and Hurdle regression models in conjunction with the already available predictors and influencing variables to analyze the LoS of COVID-19 ICU patients in Cape Town, South Africa. The objective is to evaluate the variables influencing the LoS for COVID-19 ICU patients and to identify the covariates that significantly influenced it and any potential risk factors associated with LoS.
Methods
Study Design
This prospective cohort study was conducted at Tygerberg Hospital (TBH) during the first two waves of the COVID-19 pandemic between 27 March 2020 and 10 February 2021. The TBH is a 1380-bed hospital that serves as the main teaching hospital for Stellenbosch University Faculty of Medicine and Health Sciences. TBH was designated as a centre for COVID-19 management with additional critical care services. It provides tertiary services to around 3.5 million people.
Study Population and Sample Size
The study included data from 488 adult patients admitted with severe COVID-19 pneumonia to the designated ICU during the above-mentioned dates waves. The diagnosis was confirmed with a positive SARS-CoV-2 polymerase chain reaction (PCR). Details regarding admission criteria to ICU are documented in the Western Cape Government’s provincial guidelines (Critical Care Society of Southern Africa, 2020).
Data Collection
Clinical data were extracted from ICU clinical notes and entered into a REDCap® (Research Electronic Data Capture, Stellenbosch, South Africa) database, a secure web application. Laboratory data were imported from the National Health Laboratory Service (NHLS) Laboratory Information System (TrakCare® Lab Enterprise) onto the REDCap database. Data quality assurance was undertaken by the research assistants and later verified by the supervisor of the research team to ensure data quality before analysis. Detailed information about the clinical parameters is defined in the previously published articles (Chapanduka et al., 2022; Zemlin et al., 2022).
Statistical Analysis
Descriptive statistics, such as frequency, percentage, and median with interquartile range (IQR), were used to summarize the patient characteristics. The generalized linear model (GLM) framework for regression models (Nelder & Wedderburn, 1972) was used to model the count outcome (LoS in ICU). For each predictor variable, bivariable count regressions were fitted and variables that had a p-value of less than 0.15 were a candidate for the multivariable model. Skewed variables were log-transformed to stabilize their variance. Statistical significance was declared at a p-value of less than 0.05. The most typical type of regression used to examine count data is Poisson regression, however, in practice, its assumptions are usually violated and models such as the negative binomial (NB) are preferred (Zeleke et al., 2022). Therefore, we assessed overdispersion using the overdisp package (Fávero et al., 2020) in STATA to directly propose consistent and adequate models (A. C. Cameron & Trivedi, 2010, 2013; A. Cameron & Trivedi, 2005). Both the Poisson and NB models were implemented using the glm function in the stats package (R Core Team, 2022) and the glm.nb function in the MASS package (Venables & Ripley, 2002) in R. To explore the impact of zero counts (observations), we used the Hurdle count model from the pscl package (Jackman, 2020) in R. This is a two-stage model: 1) Zero vs. non-zero (logistic regression); 2) Regression of counts > 0 (zero-truncated Poisson or NB). In other words, it combines a count data model and a zero Hurdle model by collapsing the count distribution into two categories (zero vs. larger counts), and then uses a truncated model, namely a Poisson or negative binomial distribution where zero has been excluded, for the positive counts (Andika et al., 2021; Rodriguez, 2013).
Model comparison was done using the likelihood ratio test for nested models and the information criterion for non-nested models (Akaike information criteria, AIC, and Bayesian information criteria, BIC). The model with the lowest AIC/BIC value among a group of potential models was considered the best. In addition, we used the Vuong test from the pscl package to compare two non-nested models fitted to the same data by maximum likelihood under the null hypothesis that the models are indistinguishable. Residual analysis was carried out using graphical techniques and rootograms (Kleiber & Zeileis, 2016) were used to assess the fit of the count regression models. Rootgrams are mainly useful for diagnosing and treating issues such as overdispersion and/or excess zeros in count data models and we created these plots using the countreg package (Zeileis et al., 2008; Zeileis & Kleiber, 2022) in R. All analyses were carried out using Stata (StataCorp, 2021) release 17 and R (R Core Team, 2022) release 4.2.1 with R Studio (RStudio Team, 2020).
Results
Descriptive Statistics
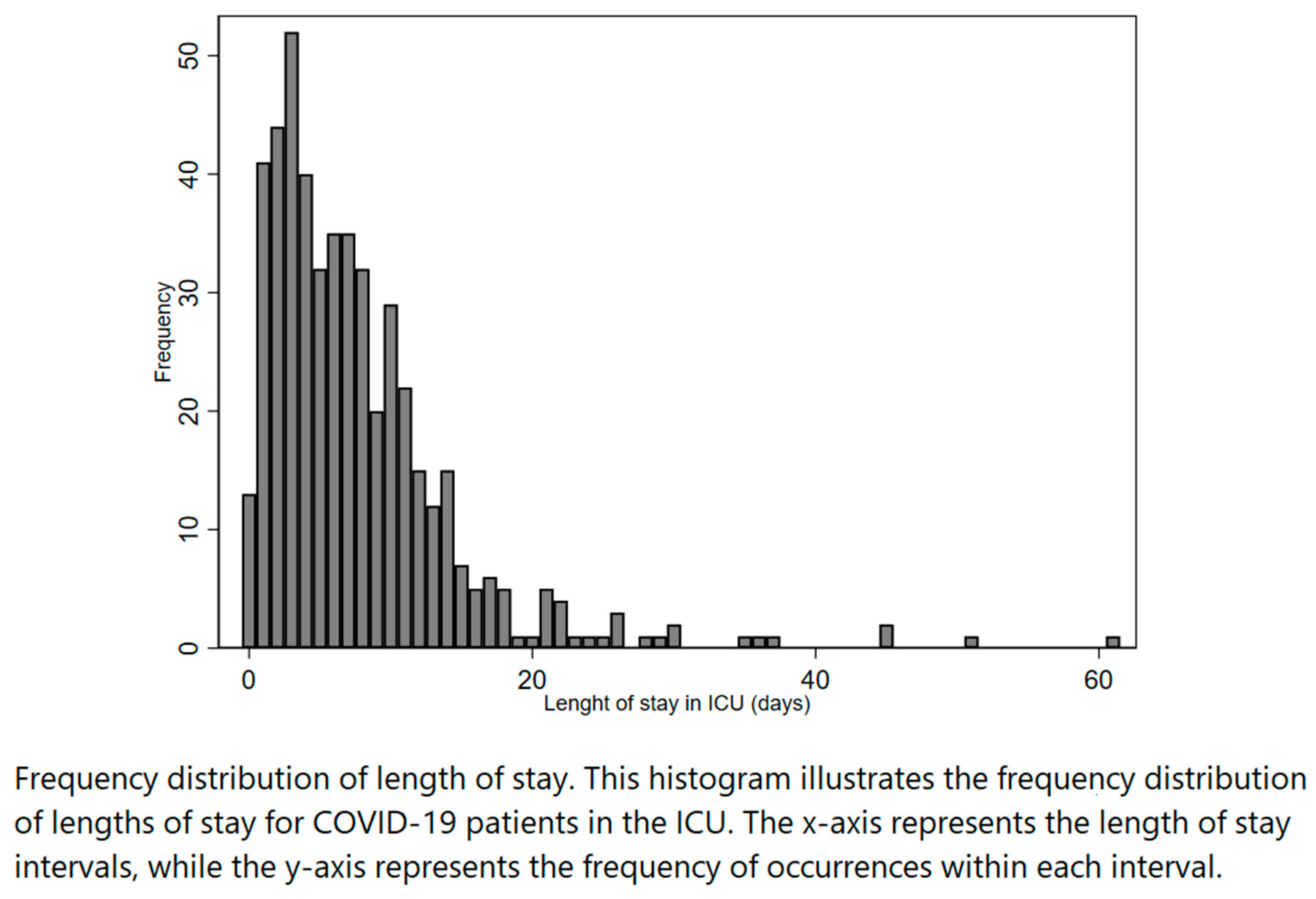
In this study, a total of 488 patients were admitted to ICU during the first (n=406) and the second (n=82) wave. The median length of stay in the ICU before death or discharge during the study period was 6 days (IQR 3-10). The distribution of length of stay was positively skewed, as shown in Figure 1.
Table 1 summarises the sociodemographic and clinical characteristics of the patients. Out of the study sample, 248 (51.5%) were males and the median age was 54 years (IQR 46-61). Underlying comorbidities were HIV (13.8%), hypertension (59.1%), diabetes mellitus (49.9%), hyperlipidaemia (10.1%), asthma (5.2%), chronic kidney disease (CKD) (3.9%), insulin resistance (4.3%), and chronic obstructive pulmonary disease (COPD) (2.8%). Non-invasive ventilation was necessary for 82.0% of the patients. The median time to ICU from admission was 1 day (IQR: 0 – 2). Clinical biomarkers included creatinine (median 77 μmol/L, IQR 63–106), D-dimer (median 1.06 ng/L, IQR 0.45–4.28), NT-proBNP (median 328 pg/ml, IQR 100–1166) and TropT (median 13 ng/L, IQR 8–32).
Univariate Analysis
The variance of the LoS was about 7 times greater than its mean (51.42 vs 7.70) suggesting the existence of overdispersion in the data. The formal test for overdispersion was carried out and we rejected the null hypothesis of equidispersion (uhat = 0.332, p-value < 0.001). Therefore, the univariate analysis was carried out using the negative binomial (NB) regression model to account for the overdispersion. Variables that were significantly associated with LoS in ICU were creatinine, lymphocytes, TropT, NT-proBNP, neutrophils, PF ratio, age at admission, gender, antibiotics, antivirals, hypertension, tuberculosis, wave, and the calendar season at admission (Table 2).
Multivariable Analysis
In the multivariable negative binomial regression analysis (Table 3), age at admission, PF ratio, neutrophils, TropT, wave and antibiotics were significantly associated with LoS in ICU. These variables were then used to fit the adjusted Poisson model and they were all significant (Table 3). However, as previously stated in the univariate analysis, there was overdispersion in the Poisson model. Table 4 reports the coefficients of the fitted Hurdle models. It summarises the count processes of the Hurdle–Poisson model and the Hurdle–NB model. In section (1), only the truncated process, i.e., positive counts, has been fitted. In section (2), zero counts were fitted through a binary logit model. The final interpretations were made based on the chosen model from these four count regression models.
Model Comparison
To prevent inaccurate results and misleading interpretations, a structured model comparison approach was essential.
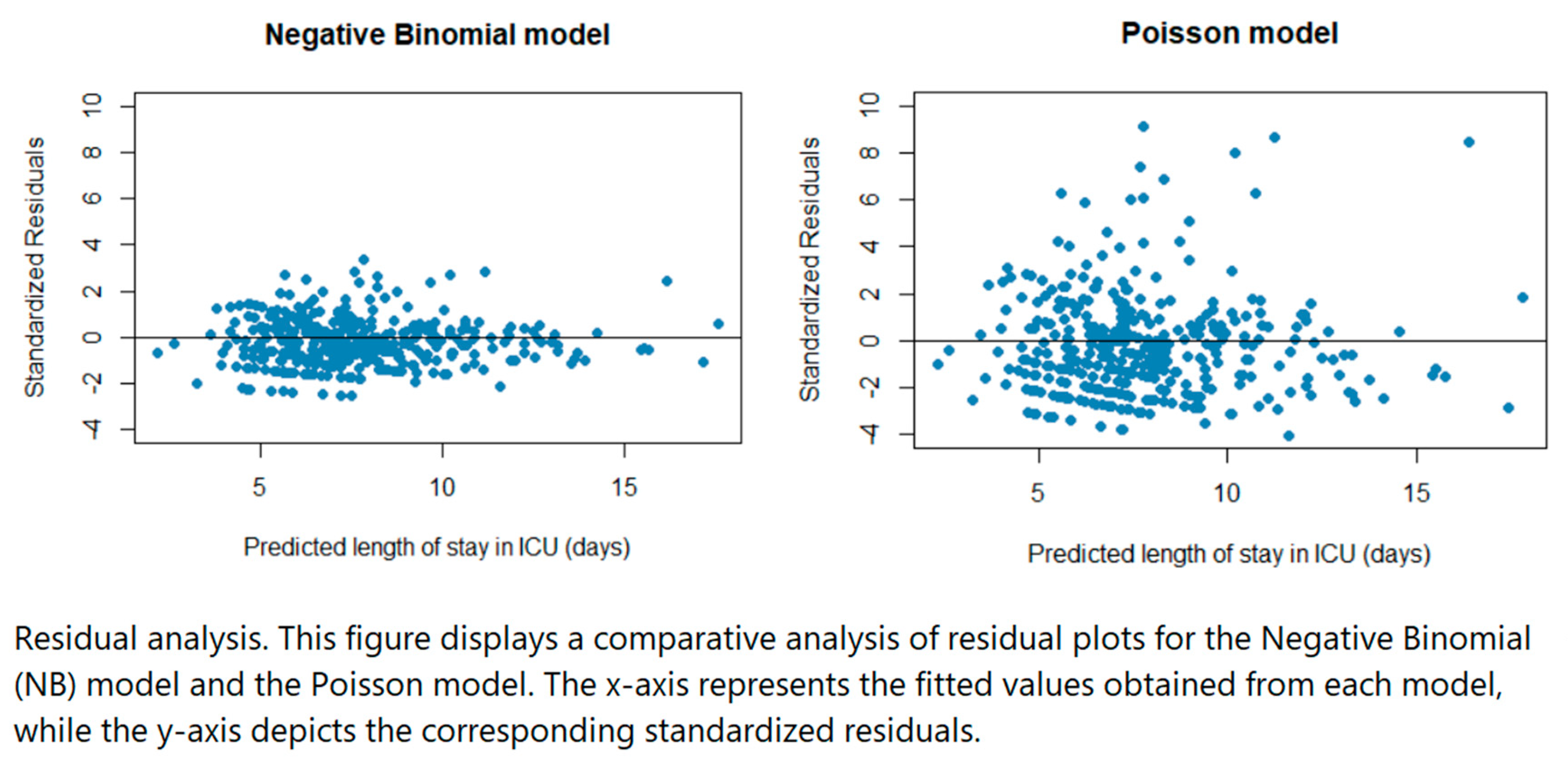
Residual plots were used to compare the Poisson model and the NB model. From the plots in Figure 2, the residuals were more spread out for the Poisson regression model (some residuals extending beyond 6) compared to the NB regression model indicating that the latter was likely more appropriate since the residuals of that model are smaller. A likelihood ratio test to determine if there was a difference in the fit of the two regression models gave significant results (p < 0.001) therefore we concluded that the NB regression model offered a significantly better fit to the data compared to the Poisson regression model.
The Poisson regression model had the largest AIC value followed by Hurdle–Poisson and the Hurdle–NB, whereas NB had the smallest AIC value confirming further that the latter was the best choice for this dataset (Table 5).
The comparison between the NB and Poisson models had a Vuong test statistic of 5.34 with a p-value < 0.001, indicating that the NB model provided a better fit. Similar results were obtained for other models (Table 6). We concluded that the preferred model was the NB model because it had the highest value of the Vuong test statistics and a significant p-value. There were no differences between the Poisson and Hurdle Poisson models, they were indistinguishable (p-value = 0.343).
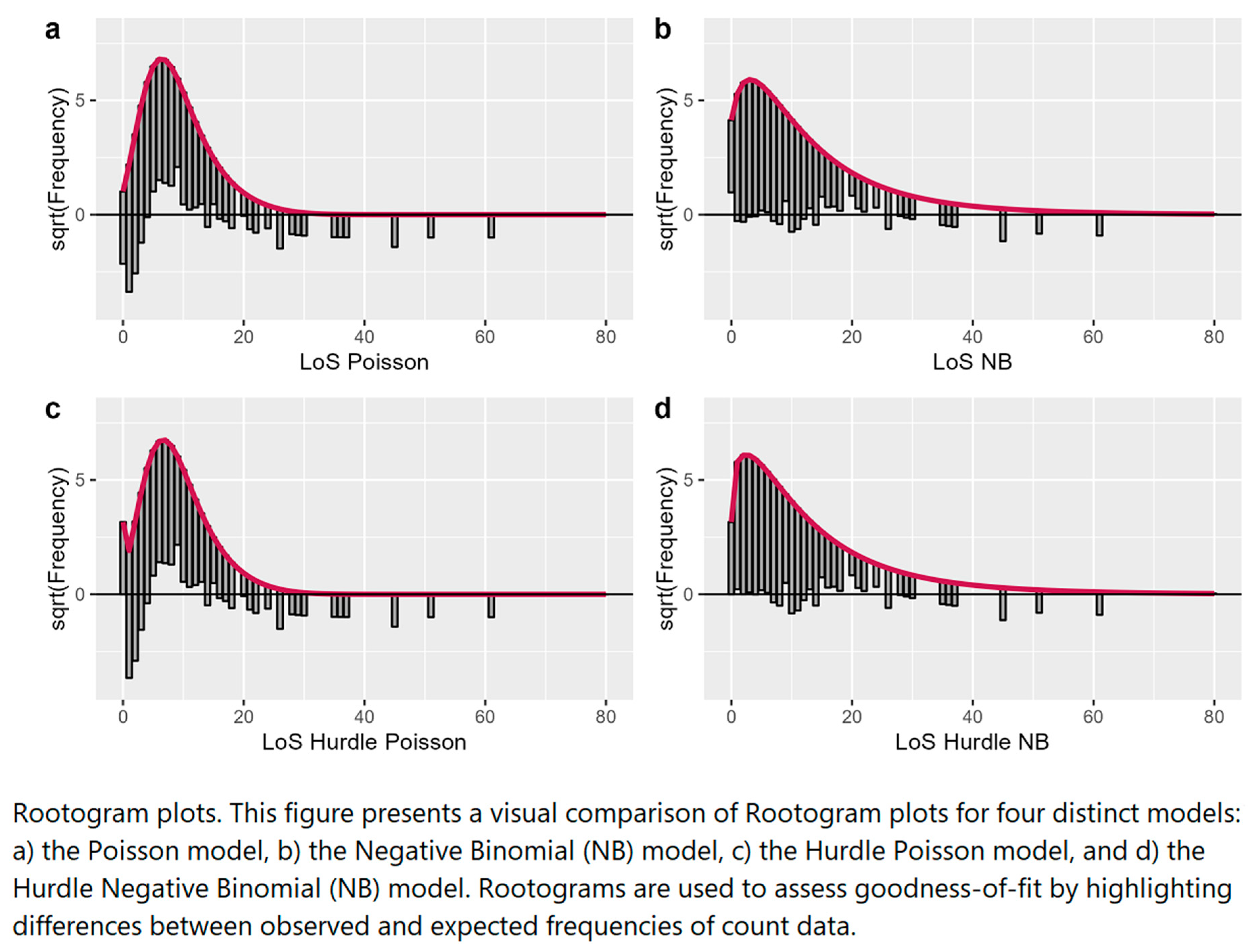
In the hanging Rootogram plots (Figure 3), the expected counts given the model, are shown by the thick red line. The grey bars represent observed counts, on the x-axis we have the count bin, and, on the y-axis, we have the square root of the observed or expected count. A reference line to estimate over- or underfitting is drawn at 0.
The plots for the NB and Hurdle–NB showed a much better fit with the data than the other models although some of the zero counts were slightly overfitted (over the line) for the NB model. The Poisson model showed a poorer fit; zero counts were under fitted (under the line) together with some low counts (between 1 and 5), and many count bins were overfitted (between 6 and 15). Similar conclusions were drawn for the Hurdle–Poisson model.
Factors Associated with Length of Stay in ICU
The incidence rate ratios (IRR) of the preferred model, negative binomial regression, are a measure of the association between the outcome (i.e., the LoS) and one of the predictor variables. Specifically, the IRR is the ratio of the expected LoS in one group to the expected LoS in another group, with all other predictor variables held constant (Table 3). Hence, an IRR greater (smaller) than one obtained for the predictors suggests longer (shorter) expected LoS in ICU. The baseline or average intercept LoS count was 8 days. On average, antibiotics reduced LoS by 0.74-fold (95% CI 0.62-0.89) compared to not taking antibiotics. The second wave had a significant effect on the average LoS, which decreased by 0.36-fold (95% CI 0.14-0.93) compared to the first wave. A 1 ng/L increase in log (TropT) levels decreased the average LoS by 0.87-fold (95% CI 0.81-0.93) similarly, a unit increase in the PF ratio decreased the average LoS by 0.998-fold (95% CI 0.997-0.999) respectively. Average LoS increased by 1.01-fold (95% CI 1.01-1.02) for every one-year increase in the age of the patient and by 1.02-fold (95% CI 1.01-1.03) for every 1 unit increase in neutrophils.
Discussion
To the best of our knowledge, this is the first study analysing the LoS of COVID-19 admissions in ICU using count regression and Hurdle regression models in Africa as most studies dichotomised the outcome (Birhanu et al., 2022; Pillai et al., 2022). This prospective cohort study investigated LoS based on 488 adult patients admitted with severe COVID-19 pneumonia between March 2020 and February 2021. LoS is an important quality indicator and efficiency measure in healthcare service provision. An accurate prediction of hospital LoS ensures that bed capacity is provided without restricting healthcare access for other patients. In general, most studies assessing hospital LoS among COVID-19 patients have been conducted in West Asia and Africa has the least number of studies (Alimohamadi et al., 2022).
In this study, after adjusting the known socio-demographic and clinical characteristics that may have affected LoS, the median LoS for COVID-19 ICU patients was 6 days before discharge or death. In general, this LoS is similar to the median LoS obtained in comparable studies. A retrospective study in Saudi Arabia established that LoS was 7 days (Alahmari et al.,2022) while a systematic review and meta-analysis study on LoS for COVID-19 patients, also established that LoS for hospitalized patients in Africa was 9 days compared to 21 days in South America (Alimohamadi et al, 2022). An analysis of COVID-19 hospitalizations in Italy also established that a median LoS was 6 days (Zekele et al.,2022)
The study identified hypertension (59.1%), diabetes mellitus (49.9%), HIV (13.8%), Hyperlipidaemia (10.1%), asthma (5.2%), insulin resistance (4.3%), chronic kidney disease (CKD) (3.9%), and chronic obstructive pulmonary disease (COPD) (2.8%) as common underlying comorbidities associated with COVID-19 ICU admission. Similar studies elsewhere also identified diabetes mellitus (23.6%), hypertension (22.5%), and cardiovascular disease (3.7%) as common comorbidities in COVID-19 patients (Alimohamadi et al., 2022). However, comparative retrospective studies in Saudi Arabia have shown that comorbidities had no statistically significant correlation with LoS (Alharbi et al, 2022). The study also showed that important clinical biomarkers in COVID-19 patients included creatinine, D-dimer, NT-proBNP and TropT.
Both univariate and multivariable analyses identified age at admission, PF ratio, neutrophils, TropT, Wave, and antibiotic use as common clinical characteristics associated with LoS in ICU. Our study results are aligned with the results of Alimohamadi et al., (2022), who also recognize age at admission as a common clinical characteristic associated with LoS in the ICU. They estimated LoS in COVID-19 patients above 60 years to be 17 days compared to LoS of 10 days for patients below 40 years of age. Although we found an association between LoS and antibiotics, their use in COVID-19 patients has been a topic of substantial debate and concern within the scientific community, as highlighted by several studies (Adebisi et al., 2021; Granata et al., 2022; Martin et al., 2023; Mustafa et al., 2021). These studies provide a broader context for understanding the challenges associated with antibiotic use during the COVID-19 pandemic. Our study's finding that antibiotics reduced LoS should be interpreted in light of these concerns.
Comparison of Regression Models
The NB regression model was found to be the best fit for observed count data, outperforming other candidate models such as the Poisson regression model. It captured the overdispersion in the data and had the highest value of the Voung test statistics and a significant p-value. The NB regression model was also preferred according to the Akaike Information Criterion (AIC), and Rootograms were used to understand the impacts of the predictors on the average LoS. The Hurdle models were not as good as the NB model in terms of fitting the data although they accounted for zero LoS in addition to the overdispersion.
Summarising Length of Stay
The study calculated incidence rate ratios to measure the association of LoS and various predictor variables and showed that predictor variables affected LoS differently. Using baseline or intercept LoS count of 8 days, antibiotic intake, second wave, increase in TropT, and increase in PF ratio were proven to reduce average LoS, while conversely, the age of the patient on admission and increase in neutrophils increased average LoS.
Limitations of the Study
We acknowledge the limitations of our study, particularly the lack of detailed information on the specific types and dosages of antibiotics prescribed. Our analysis, while indicating an association between antibiotics and reduced LoS, does not advocate for the routine use of antibiotics in COVID-19 patients. Instead, it underscores the complexity of factors influencing LoS, with antibiotics being just one aspect. The research recognises other factors outside the scope of this study that has the potential to impact LoS. These include delay in diagnosis, disease prognosis, delay in seeking medical care, differences in peak infection times and resource availability within healthcare facilities. Furthermore, LoS was also determined by the willingness to pay and country-specific factors like admission criteria which are also beyond the scope of this study. Additional confounders such as demographic and socio-economic variables, clinical characteristics, medical conditions, and laboratory tests for the patients, might be among the most important factors that could further explain the variability in LoS.
Conclusions
This prospective study estimated the LoS for COVID-19 ICU admission which is key in preparedness and planning for patients. We established common sociodemographic and clinical characteristics associated with COVID-19 patients' ICU admissions and disease severity. The study also showed that few COVID-19 patients in ICU required invasive ventilation, a key determinant of the cost of care during ICU admission. Both univariate and multivariable analyses identified age at admission PF ratio, neutrophils, TropT, Wave and Antibiotics as common clinical characteristics associated with LoS in ICU. Our results, when viewed in the context of existing literature (Adebisi et al., 2021; Granata et al., 2022; Martin et al., 2023; Mustafa et al., 2021), emphasize the need for cautious interpretation of observational data. We echo the recommendations from previous research, stating that antibiotics should only be prescribed in COVID-19 patients when there is a clear clinical indication of bacterial infection. Further research is warranted to better understand the nuanced relationship between antibiotic use and outcomes in COVID-19 patients, considering the multifaceted factors at play. The study also concluded that the NB regression model offered a significantly better fit to the data compared to the Poisson regression model after applying a likelihood ratio test to ascertain the difference in the fit of the two regression models. In addition, the NB regression model also had the highest value of the Voung test statistics and the smallest AIC making it the preferred model over the Hurdle models.
Author Contributions
Data curation: LNS and VND. Formal analysis: PS. Investigation: ZCC, AZ, and PSN. Methodology: PS, LNS and CN. Supervision: PSN, ZCC, and AZ. Writing – review & editing: PS, CN, LNS, JT, AEZ, ZCC, BWA, CFK, EMI, UL, VDN, TPJ, RTE, TEM, AZ, and PSN.
Funding
This work was carried out under the Stellenbosch University Special Vice-Rector (RIPS) Fund and the COVID-19 Africa Rapid Grant Fund supported under the auspices of the Science Granting Councils Initiative in Sub-Saharan Africa (SGCI) and administered by South Africa’s National Research Foundation (NRF) in collaboration with Canada’s International Development Research Centre (IDRC), the Swedish International Development Cooperation Agency (SIDA), South Africa’s Department of Science and Innovation (DSI), the Fonds de Recherche du Québec (FRQ), the United Kingdom’s Department of International Development (DFID), United Kingdom Research and Innovation (UKRI) through the Newton Fund, and the SGCI participating councils across 15 countries in sub-Saharan Africa.
Ethics
This study was approved by the Health Research Ethics Committee of Stellenbosch University, approval number: N20/04/002_COVID-19. Patient confidentiality was ensured by labelling data with a unique episode number. The research project followed the laid down guidelines for the ethical conduct of studies involving human participants.
Informed Consent Statement
The Investigators obtained ethical approval and waiver of consent from the Health Research Ethics Committee of the Faculty of Medicine and Health Sciences, Stellenbosch University, and the Research Committee of the Tygerberg Hospital.
Availability of data and materials
Data are available upon reasonable request from the corresponding author.
Acknowledgements
Sir Prof Alimuddin Zumla, is co-Principal Investigator of the (PANDORA-ID-NET), the Pan-African Network for Rapid Research, Response, Relief and Preparedness for Infectious Disease Epidemics, supported by the EDCTP. He receives a UK National Institutes of Health Research, Senior Investigator Award and is a Mahathir Foundation Science Award laureate.
Conflicts of Interest
All authors declare no conflicts of interest.
Abbreviations
LoS: Length of Stay, IRR: Incidence rate ratios, NB: Negative Binomial, COVID-19: Coronavirus Disease 2019; TropT: Troponin T, NtproBNP: N-terminal B-type natriuretic peptide; ICU: intensive unit care; NHLS: National Health Laboratory Service; PCR: Polymerase Chain Reaction; REDCap: Research Electronic Data Capture; SARS-COV-2: severe acute respiratory syndrome coronavirus 2; TBH: Tygerberg Hospital.
References
- Alahmari, A.K.; Almalki, Z.S.; Albassam, A.A.; Alsultan, M.M.; Alshehri, A.M.; Ahmed, N.J.; Alqahtani, A.M. Factors Associated with Length of Hospital Stay among COVID-19 Patients in Saudi Arabia: A Retrospective Study during the First Pandemic Wave. Healthcare 2022, 10, 1201. [Google Scholar] [CrossRef]
- Alharbi, A.A.; Alqumaizi, K.I.; Bin Hussain, I.; AlHarbi, N.S.; Alqahtani, A.; Alzawad, W.; Suhail, H.M.; Alamir, M.I.; Alharbi, M.A.; Alzamanan, H. Hospital length of stay and related factors for COVID-19 inpatients among the four southern regions under the proposed southern business unit of Saudi Arabia. Journal of Multidisciplinary Healthcare 2022, 825–836. [Google Scholar] [CrossRef]
- Alimohamadi, Y.; Yekta, E.M.; Sepandi, M.; Sharafoddin, M.; Arshadi, M.; Hesari, E. Hospital length of stay for COVID-19 patients: a systematic review and meta-analysis. Multidisciplinary Respiratory Medicine 2022, 17. [Google Scholar] [CrossRef]
- Guo, A.; Lu, J.; Tan, H.; Kuang, Z.; Luo, Y.; Yang, T.; Xu, J.; Yu, J.; Wen, C.; Shen, A. Risk factors on admission associated with hospital length of stay in patients with COVID-19: a retrospective cohort study. Scientific Reports 2021, 11, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.Y.; Seon, J.Y.; Yoon, S.J.; Park, S.Y.; Lee, S.H.; Oh, I.H. Comorbidities and factors determining medical expenses and length of stay for admitted COVID-19 patients in Korea. Risk Management and Healthcare Policy 2021, 14. [Google Scholar] [CrossRef]
- Thomas, W.J.; Guire, K.E.; Horvat, G.G. Is patient length of stay related to quality of care? Journal of Healthcare Management 1997, 42, 489–507. [Google Scholar]
- World Health Organization - Coronavirus Disease (COVID-19). Accessed December 2022. Available online: https://www.who.int/health-topics/coronavirus#tab=tab_1.
- World Health Organization - Weekly epidemiological update on COVID-19 - 30 November 2022. Accessed December 2022. Available online: https://www.who.int/publications/m/item/weeklyepidemiological- update-on-covid-19---30-november-2022.
- Adebisi, Y.A.; Jimoh, N.D.; Ogunkola, I.O.; Uwizeyimana, T.; Olayemi, A.H.; Ukor, N.A.; Lucero-Prisno, D.E. The use of antibiotics in COVID-19 management: a rapid review of national treatment guidelines in 10 African countries. Tropical Medicine and Health 2021, 49. [Google Scholar] [CrossRef] [PubMed]
- Andika, A.; Abdullah, S.; Nurrohmah, S. Hurdle Negative Binomial Regression Model. ICSA - International Conference on Statistics and Analytics 2019, 1, 57–68. [Google Scholar] [CrossRef]
- Birhanu, A.; Merga, B.T.; Ayana, G.M.; Alemu, A.; Negash, B.; Dessie, Y. Factors associated with prolonged length of hospital stay among COVID-19 cases admitted to the largest treatment center in Eastern Ethiopia. SAGE Open Medicine 2022, 10, 205031212110703. [Google Scholar] [CrossRef]
- Cameron, A.C.; Trivedi, P.K. Microeconometrics using stata. 2010. http://cameron.econ.ucdavis.edu/sfu2022/mus2_chapter28.pdf.
- Cameron, A.C.; & Trivedi, P.K. (2013). Regression analysis of count data. https://books.google.com/books?hl=en&lr=&id=qVEwBQAAQBAJ&oi=fnd&pg=PR15&dq=A.+C.+Cameron,+and+P.+K.+Trivedi,+Regression+Analysis+of+Count+Data,+Cambridge+University+Press,+Cambridge,+2013.&ots=RNjkie972b&sig=MYjmXNze0NzHKFNplX0xTlRoeDE.
- Cameron, A.; & Trivedi, P.; & Trivedi, P. (2005). Microeconometrics: methods and applications. [CrossRef]
- Chapanduka, Z.C.; Abdullah, I.; Allwood, B.; Koegelenberg, C.F.; Irusen, E.; Lalla, U.; Zemlin, A.E.; Masha, T.E.; Erasmus, R.T.; Jalavu, T.P.; et al. Haematological predictors of poor outcome among COVID-19 patients admitted to an intensive care unit of a tertiary hospital in South Africa. Plos ONE 2022, 17, e0275832. [Google Scholar] [CrossRef]
- Fávero, L.P.; Belfiore, P.; Santos, M.A.; Souza, R.F. Overdisp: A stata (and mata) package for direct detection of overdispersion in poisson and negative binomial regression models. Statistics, Optimization and Information Computing 2020, 8, 773–789. [Google Scholar] [CrossRef]
- Granata, G.; Schiavone, F.; Pipitone, G.; Taglietti, F.; Petrosillo, N. Antibiotics Use in COVID-19 Patients: A Systematic Literature Review. Journal of Clinical Medicine 2022, 11. [Google Scholar] [CrossRef]
- Jackman, S. (2020). {pscl}: Classes and Methods for {R} Developed in the Political Science Computational Laboratory. https://github.com/atahk/pscl/.
- Kleiber, C.; Zeileis, A. Visualizing Count Data Regressions Using Rootograms. The American Statistician 2016, 70, 296–303. [Google Scholar] [CrossRef]
- Martin, A.J.; Shulder, S.; Dobrzynski, D.; Quartuccio, K.; Pillinger, K.E. Antibiotic Use and Associated Risk Factors for Antibiotic Prescribing in COVID-19 Hospitalized Patients. Journal of Pharmacy Practice 2023, 36, 256–263. [Google Scholar] [CrossRef]
- Mustafa, L.; Tolaj, I.; Baftiu, N.; Fejza, H. Use of antibiotics in COVID-19 ICU patients. Journal of Infection in Developing Countries 2021, 15, 501–505. [Google Scholar] [CrossRef]
- Nelder, J.A.; Wedderburn, R.W.M. Generalized Linear Models. Journal of the Royal Statistical Society. Series A (General) 1972, 135, 370. [Google Scholar] [CrossRef]
- Pillai, J.; Mistry, P.P. K.; Le Roux, D.A.; Motaung, K.S. C.; Mokgatle, M.; Gaylard, P.; Cengiz, N.; Basu, D. Laboratory parameters associated with prolonged hospital length of stay in COVID-19 patients in Johannesburg, South Africa. South African Medical Journal 2022, 112, 201–208. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. (2022). R: A Language and Environment for Statistical Computing. https://www.r-project.org/.
- Rees, E.M.; Nightingale, E.S.; Jafari, Y.; Waterlow, N.R.; Clifford, S.; Carl, C.A.; Group, C.W.; Jombart, T.; Procter, S.R.; Knight, G.M. COVID-19 length of hospital stay: A systematic review and data synthesis. BMC Medicine 2020, 18. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, G. (2013). Models for Count Data With Overdispersion. Princeton Statistics, September 2007, 1–7. http://data.princeton.edu/wws509/notes/c4a.pdf. /: http, 20 September.
- RStudio Team. (2020). RStudio: Integrated Development Environment for R. http://www.rstudio.com/.
- StataCorp. (2021). Stata: Release 17. https://www.stata.com/.
- Venables, W.N.; Ripley, B.D. (2002). Modern Applied Statistics with S (Fourth). Springer. https://www.stats.ox.ac.uk/pub/MASS4/. /: Springer. https.
- Zeileis, A.; Kleiber, C. (2022). {countreg}: Count Data Regression. https://r-forge.r-project.org/projects/countreg/.
- Zeileis, A.; Kleiber, C.; Jackman, S. Regression Models for Count Data in {R}. Journal of Statistical Software 2008, 27. http://www.jstatsoft.org/v27/i08/. /: http.
- Zeleke, A.J.; Moscato, S.; Miglio, R.; Chiari, L. Length of Stay Analysis of COVID-19 Hospitalizations Using a Count Regression Model and Quantile Regression: A Study in Bologna, Italy. International Journal of Environmental Research and Public Health 2022, 19, 2224. [Google Scholar] [CrossRef] [PubMed]
- Zemlin, A.E.; Allwood, B.; Erasmus, R.T.; Matsha, T.E.; Chapanduka, Z.C.; Jalavu, T.P.; Ngah, V.; Sigwadhi, L.N.; Koegelenberg, C.F.; Irusen, E.; et al. Prognostic value of biochemical parameters among severe COVID-19 patients admitted to an intensive care unit of a tertiary hospital in South Africa. IJID Regions, 2022, 2, 191–197. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Frequency distribution of length of stay.
Figure 2.
Residual analysis.
Figure 3.
Rootogram plots.
Table 1.
Sociodemographic and clinical characteristics of the study sample (N=488).
| Variables | N | Category | Median (IQR) or n (%) |
| Gender | 482 | Male | 248 (51.5%) |
| HIV status | 392 | Yes | 54 (13.8%) |
| Smoking status | 273 | Current or past smoker | 59 (21.6%) |
| Hypertension | 464 | Yes | 274 (59.1%) |
| Asthma | 464 | Yes | 24 (5.2%) |
| Diabetes mellitus | 465 | Yes | 232 (49.9%) |
| Insulin resistance | 462 | Yes | 20 (4.3%) |
| Hyperlipidaemia | 464 | Yes | 47 (10.1%) |
| Tuberculosis | 464 | Yes | 460 (99.1%) |
| COPD | 462 | Yes | 13 (2.8%) |
| CKD | 463 | Yes | 18 (3.9%) |
| Ventilation | 488 | Invasive | 88 (18.0%) |
| Antibiotics | 466 | Yes | 293 (62.9%) |
| Antifungals | 466 | Yes | 5 (1.1%) |
| Antivirals | 466 | Yes | 85 (18.2%) |
| Anticoagulants | 466 | Yes | 426 (91.4%) |
| Corticosteroids | 466 | Yes | 397 (85.2%) |
| Wave | 488 | Second wave | 82 (16.8%) |
| Age (years) | 481 | median | 54 (46-61) |
| HbA1c | 374 | median | 7 (6-9) |
| Creatinine | 480 | median | 77 (63-106) |
| D-dimer | 462 | median | 1.06 (0.45-4.28) |
| Lymphocytes | 477 | median | 1 (1-2) |
| TropT | 417 | median | 13 (8-32) |
| NT-proBNP | 418 | median | 328 (100-1166) |
| Neutrophils | 478 | median | 10 (7-16) |
| CRP | 472 | median | 177 (109-271) |
| PF ratio | 468 | median | 76 (54-110) |
| Length of stay in ICU (days) | 488 | median | 6 (3-10) |
| Length of stay in hospital (days) | 486 | median | 9 (6-15) |
| Time to ICU from admission (days) | 488 | median | 1 (0-2) |
Abbreviations: (ICU) Intensive care unit; (HIV) human immunodeficiency virus; (Nt-proBNP) serum N-terminal pro b-type natriuretic peptide; (HbA1c) glycated haemoglobin; (Trop T) Troponin T.
Table 2.
Summary of IRR estimates from univariate analysis of NB model regression.
| Variables | IRR | 95% conf. interval | p-value |
| Gender (reference: Female) | 0.830 | (0.717; 0.962) | 0.013 |
| Antibiotics (reference: No) | 0.714 | (0.614; 0.830) | <0.001 |
| Antifungals (reference: No) | 0.661 | (0.310; 1.411) | 0.284 |
| Antivirals (reference: No) | 0.832 | (0.685; 1.012) | 0.065 |
| Anticoagulants (reference: No) | 1.205 | (0.920; 1.580) | 0.176 |
| Corticosteroids (reference: No) | 1.096 | (0.887; 1.354) | 0.396 |
| Smoking status (reference: Non-smoker) | 1.059 | (0.835; 1.344) | 0.637 |
| Hypertension (reference: No) | 1.144 | (0.983; 1.330) | 0.082 |
| Asthma (reference: No) | 0.826 | (0.587; 1.162) | 0.272 |
| Diabetes mellitus (reference: No) | 1.039 | (0.895; 1.206) | 0.617 |
| Insulin resistance (reference: No) | 0.872 | (0.602; 1.264) | 0.471 |
| Hyperlipidaemia (reference: No) | 1.032 | (0.807; 1.319) | 0.803 |
| HIV status (reference: Negative) | 0.855 | (0.674; 1.084) | 0.196 |
| Tuberculosis (reference: No) | 3.138 | (1.214; 8.112) | 0.018 |
| COPD (reference: No) | 0.756 | (0.475; 1.201) | 0.236 |
| CKD (reference: No) | 1.160 | (0.793; 1.697) | 0.444 |
| Ventilation (reference: Non-invasive) | 1.080 | (0.894; 1.306) | 0.425 |
| Wave (reference: First wave) | 1.517 | (1.257; 1.831) | <0.001 |
| Season (reference: Summer) | 1.000 | - | - |
| Autumn | 0.678 | (0.520; 0.884) | 0.004 |
| Winter | 0.677 | (0.535; 0.857) | 0.001 |
| Spring | 0.985 | (0.736; 1.319) | 0.919 |
| Age (years) | 1.010 | (1.003; 1.017) | 0.005 |
| HbA1c | 1.014 | (0.983; 1.047) | 0.383 |
| Creatinine | 0.999 | (0.998; 1.000) | 0.023 |
| D-dimer | 0.998 | (0.985; 1.011) | 0.744 |
| Lymphocytes | 1.019 | (1.002; 1.037) | 0.031 |
| Log (TropT) | 0.885 | (0.826; 0.948) | <0.001 |
| Log (NT-proBNP) | 0.947 | (0.903; 0.992) | 0.022 |
| Neutrophils | 1.006 | (1.003; 1.008) | <0.001 |
| CRP | 1.000 | (0.999; 1.001) | 0.984 |
| PF ratio | 0.999 | (0.997; 1.000) | 0.013 |
IRR: Incident Rate Ratio.
Table 3.
Summary of IRR estimates of the multivariable Poisson and NB model regression.
| Poisson model | Negative Binomial model | ||||||
| Variables | IRR | 95% conf. interval | p-value | IRR | 95% conf. interval | p-value | |
| Intercept | 8.013 | (6.344; 10.121) | <0.001 | 8.369 | (5.185; 13.507) | <0.001 | |
| Antibiotics (reference: No) | 1.000 | - | - | - | - | - | |
| Yes | 0.748 | (0.691; 0.810) | <0.001 | 0.743 | (0.624; 0.885) | 0.001 | |
| Wave (reference: First wave) | 1.000 | - | - | - | - | - | |
| Second wave | 0.275 | (0.167; 0.455) | <0.001 | 0.357 | (0.137; 0.929) | 0.035 | |
| Log (TropT) | 0.857 | (0.826; 0.888) | <0.001 | 0.869 | (0.809; 0.932) | <0.001 | |
| Neutrophils | 1.022 | (1.014; 1.029) | <0.001 | 1.018 | (1.005; 1.032) | 0.007 | |
| PF ratio | 0.998 | (0.998; 0.999) | <0.001 | 0.998 | (0.997; 0.999) | 0.003 | |
| Age (years) | 1.009 | (1.005; 1.012) | <0.001 | 1.008 | (1.001; 1.015) | 0.028 | |
| Log(alpha) | - | - | - | -0.796 | (-0.977; -0.615) | ||
IRR: Incident Rate Ratio.
Table 4.
Coefficients of the Hurdle–Poisson and Hurdle–NB models.
| Hurdle Poisson | Hurdle Negative Binomial | ||||||
|
|||||||
| Variables | Estimate | Std. Error | p-value | Estimate | Std. Error | p-value | |
| Intercept | 2.114 | 0.119 | <0.001 | 2.137 | 0.270 | <0.001 | |
| Antibiotics (reference: No) | - | - | - | - | - | - | |
| Yes | -0.275 | 0.041 | <0.001 | -0.304 | 0.098 | 0.002 | |
| Wave (reference: First wave) | - | - | - | - | - | - | |
| Second wave | -1.212 | 0.256 | <0.001 | -1.018 | 0.531 | 0.055 | |
| Log (TropT) | -0.145 | 0.019 | <0.001 | -0.145 | 0.040 | <0.001 | |
| Neutrophils | 0.020 | 0.003 | <0.001 | 0.018 | 0.007 | 0.014 | |
| PF ratio | -0.001 | 0.000 | <0.001 | -0.002 | 0.001 | 0.012 | |
| Age (years) | 0.007 | 0.002 | <0.001 | 0.007 | 0.004 | 0.072 | |
| Log(theta) | - | - | - | 0.626 | 0.118 | <0.001 | |
|
|||||||
| Variables | Estimate | Std. Error | p-value | Estimate | Std. Error | p-value | |
| Intercept | 2.426 | 2.101 | 0.248 | 2.426 | 2.101 | 0.248 | |
| Antibiotics (reference: No) | - | - | - | - | - | - | |
| Yes | -0.915 | 1.081 | 0.397 | -0.915 | 1.081 | 0.397 | |
| Wave (reference: First wave) | - | - | - | - | - | - | |
| Second wave | 8.935 | 3384.0 | 0.998 | 8.935 | 3384.0 | 0.998 | |
| Log (TropT) | -0.332 | 0.262 | 0.207 | -0.332 | 0.262 | 0.207 | |
| Neutrophils | 0.119 | 0.093 | 0.202 | 0.119 | 0.093 | 0.202 | |
| PF ratio | -0.006 | 0.004 | 0.122 | -0.006 | 0.004 | 0.122 | |
| Age (years) | 0.047 | 0.030 | 0.112 | 0.047 | 0.030 | 0.112 | |
Table 5.
Model comparison using AIC/BIC.
| Model | AIC | BIC |
| Poisson | 3185.4 | 3213.2 |
| Negative Binomial | 2348.2 | 2380.0 |
| Hurdle Poisson | 3164.6 | 3220.2 |
| Hurdle Negative Binomial | 2351.2 | 2410.8 |
Table 6.
Model comparison using the Vuong test.
| Model Comparison | Vuong Test Statistic | p-Value | Preferred Model |
| NB vs. Poisson | 5.34 | <0.001 | NB |
| NB vs. Hurdle Poisson | 5.43 | <0.001 | NB |
| NB vs. Hurdle NB | 4.96 | <0.001 | NB |
| Poisson vs. Hurdle Poisson | 0.40 | 0.343 | - |
| Hurdle NB vs. Poisson | 5.08 | <0.001 | Hurdle NB |
| Hurdle NB vs. Hurdle Poisson | 5.16 | <0.001 | Hurdle NB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Length of Stay Analysis of COVID-19 Intensive Care Unit Admissions Using Count Regression and Hurdle Regression Models: A Study in a Tertiary Hospital, Cape Town, South Africa
Perseverence Savieri
et al.
,
2024
Development and Validation of a Prediction Model for 28-Day in-Hospital Mortality in Critically Ill Patients with COVID-19
Paloma Ferrando-Vivas
et al.
,
2021
Trends in Intensive Care for Patients with COVID-19 in England, Wales and Northern Ireland
James C Doidge
et al.
,
2020
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated