1. Introduction
One of the most important partial differential equations in physics is the ordinary three-dimensional wave equation [
1,
2]. It was first derived by Leonhard Euler in the 18th century to describe the propagation of three-dimensional acoustic waves [
3,
4]. Although originally conceived to describe the propagation of acoustic waves without losses in homogeneous isotropic media, it was later found that under the same conditions,
1 the ordinary wave equation describes a variety of wave phenomena such as propagation of the waves in solids [
5], the propagation of mechanical stress waves [
6], the propagation of seismic waves [
7], and as shown by Maxwell in the 19th century [
8], the ordinary wave equation describes the propagation of electromagnetic waves.
Regardless of whether the wave equation describes a mechanical, acoustic, or electromagnetic wave, the ordinary three-dimensional wave equation reads:
where
u is the displacement,
c is the velocity of the wave propagation,
t is the time, and
is three dimensional Laplace operator. In general, the wave equation (
1) describes the propagation of a displacement, or a disturbance, propagating from the source to the receiver with finite velocity
c. In the case of an acoustic wave, the function
u represents the pressure or the velocity potential [
9,
10,
11]. For an electromagnetic wave, the function
u can be any Cartesian component of an electric or magnetic field [
12,
13].
A particularly important class of solutions to the ordinary wave equation are those that involve moving point sources. In the field of electrodynamics, the Liénard-Wiechert scalar and vector potentials are one example of such solutions [
14,
15]. These time retarded potentials are widely used for advanced electromagnetic calculations such as synchrotron, undulator, and radar radiation [
16,
17,
18]. For example, the scalar Liénard-Wiechert potential takes the following mathematical form:
where
,
is the position vector of a stationary receiver,
is the position vector of the moving source, and
is the retarded time that satisfies the following causal relationship:
Furthermore, the vectors
and
are given by:
Solutions to the ordinary wave equation for moving sources are also found in the field of acoustics. For example, Schmidt and Kuperman derived the solution to the ordinary wave equation for the harmonic point source moving with constant velocity along a straight line [
19]. Obrezanova and Rabinovich derived a two-dimensional solution for harmonic point source moving along arbitrary path [
20]. Lim and Ozard derived the solution caused by harmonic acoustic source moving along an arbitrary trajectory in 3D [
21] that has a mathematical form similar to Liénard-Wiechert scalar potential.
Modifying any of the point source solutions mentioned earlier to accommodate a moving receiver results in a violation of the ordinary wave equation. For example, if the receiver starts to move, then its position indicated by the vector
becomes the function of time, i.e.
. As it will be demonstrated later in this paper, if one substitutes
by
in the equation (
2), then
u is no longer the solution to the ordinary wave equation. The same applies to the acoustic point source solutions mentioned in the references [
19,
20,
21].
Thus, the ordinary wave equation has the ability to describe waves caused by moving sources, but it cannot describe the waves seen by the moving receiver. It is shown in this paper that the wave equation that admits the solutions where both the receiver and the source are permitted to move takes the following mathematical form:
where
is the velocity vector of the moving receiver, and where the operator
represents the operator
applied twice. If the receiver is stationary, then
, and the equation (
6) reduces to an ordinary wave equation.
The proof that for the moving receivers the wave equation (
6) is valid instead of the ordinary wave equation is organized as follows: in the
Section 2 we first mathematically define a wave function caused by stationary point source, and in the
Section 3 we use this wave function to derive the wave equation (
6) for the specific case of the moving receiver and the stationary source. Then in the
Section 4 Green’s function for the equation (
6) is derived. Finally, in the
Section 5, by using the derived Green’s function, the solutions to the wave equation (
6) are found where both the receiver and the source are permitted to move.
In conclusion, it is shown that instead of an ordinary wave equation, the equation (
6) is the governing wave equation when both the receiver and the source are permitted to move. If the receiver becomes stationary, then the wave equation (
6) reduces to an ordinary wave equation. This means that the ordinary wave equation can be considered a particular case of the wave equation for the moving receiver and the moving source. These findings are summarized in
Table 1, where the wave equation for the moving source and the moving receiver and its point-source solution is compared to the ordinary wave equation and respective point-source solution.
2. Free Space Wave Function for the Stationary Source and Moving Receiver
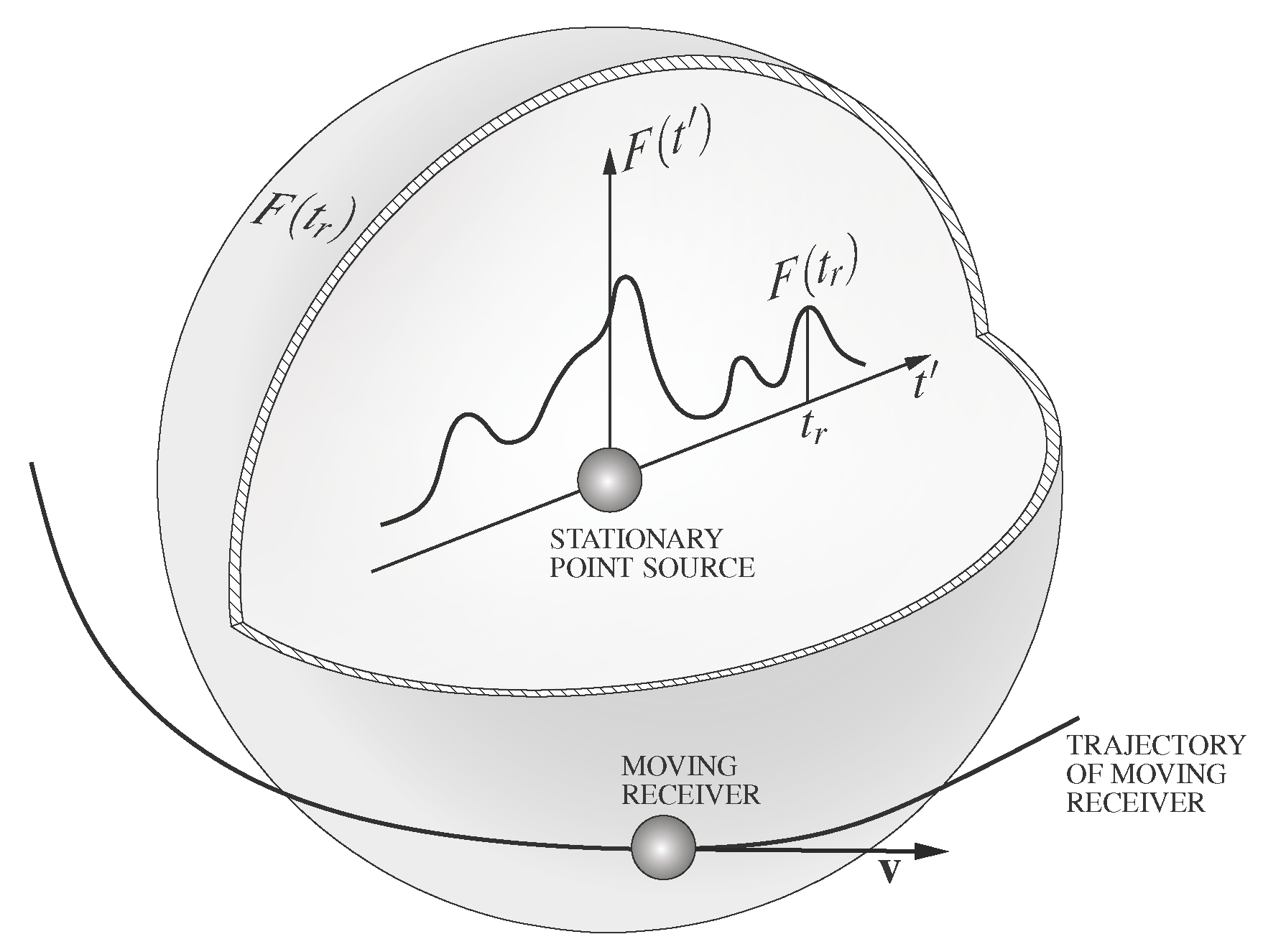
In this section, we mathematically describe the wave caused by a stationary point source. The wave is simply a disturbance emitted by the source at retarded time
that travels towards the receiver with finite velocity
c. Because the disturbance travels with finite velocity, this disturbance arrives at the moving receiver at the time
. This causal relationship can be represented by the following equation:
where we declare the time t as an independent variable.
In the expression (
7), the function
represents the distance between the location of the source at the time of emission
and the location of the moving receiver at the time
t when the wave emitted at the time
intercepts the receiver. This distance
can be written as:
where the vector is the position vector of the moving receiver at the time of wave reception, and the vector is the position vector of a stationary source.
A simple way to define the wave function
u that represents the disturbance traveling in time with velocity
c is by declaring:
where
F is any function twice differentiable. By substituting the equation (
7) into the equation (
9) we can equivalently write:
The equations (
9) and (
10) represent the disturbance that has the value
at the time of emission
. This disturbance travels towards the receiver with velocity
c, and it intercepts the moving receiver at the time
t. As indicated in
Figure 1, at the time of interception, the disturbance still has the value
.
From the equations (
9) and (
10), it is also clear that the wave function
u represents the spherical wave spreading equally in all directions away from the source. If something emits spherical waves from the position
, this also means that there is a point source located at the position
.
Furthermore, the equations (
9) and (
10) imply that the amplitude of the function
u does not change as the wave travels away from the source. In nature, the point sources usually generate diverging spherical waves whose amplitude is inversely proportional to the distance from the source. For example, the acoustic point source generates the diverging spherical waves [
22,
23], and the point source of electric potential waves and magnetic vector potential waves generates the diverging spherical waves [
24,
25]. Therefore, if the function
u is to represent the wave generated by a physical point source, the wave function
u must take the following mathematical form:
If the constant is added to the argument of the function
F, the function
u still satisfies the wave equation. Thus, for the sake of completeness, and for the reasons that will become apparent in the
Section 4 of this paper, we rewrite the wave function
u as follows:
where
a is any real constant. As shown in the
Section 4, this particular mathematical form of the wave function allows us to derive Green’s function for the wave equation for the moving receiver in a relatively straightforward manner.
3. The Wave Equation for the Moving Receiver and the Stationary Source
In this section, we derive the wave equation for the stationary point source and the moving receiver. Here, the position of the receiver is considered the function of time
t, i.e.
, and the position vector
of the stationary source is not considered a function of time:
The distance
between the source at the time of wave emission and the receiver at the time of wave interception is the function of time:
The derivative of the wave function
u given by the equation (
11) with respect to variable
can be calculated using the chain rule:
where
R is a shorthand notation for
, and where
and
. Note that because of the equation (
7), the derivative of the retarded time with respect to variable
is non-zero. This follows from the equation (
7) where we declared the variable
t as an independent variable, therefore, the retarded time
is the function of the variable
t, constant vector
, and the vector function
.
By differentiating the equation (
16) with respect to variable
, the second order derivative of the wave function
u is obtained as:
where
. The Laplacian of the function
u can now be written as the sum:
By differentiating the equation (
7) with respect to variable
it is obtained:
The derivative
can be obtained by differentiating the equation (
15) with respect to variable
as:
where
is
ith Cartesian component of the unit vector
given as:
Clearly, because the vector
is an unit vector, it can be written:
Using the equations (
19), (
20) and the equation (
22), one can calculate the sums found in the equation (
18) as:
where the symbol
represents the 3D Dirac’s delta function. The divergence of the unit vector
can be calculated as:
where
are Cartesian components of the vector
, i.e.
. Substituting the equations (
23) - (
28) into the equation (
18) yields:
After cancellation of the appropriate terms on the right-hand side of the equation (
29), the equation (
29) simplifies to:
We now introduce the operator
, where
is the velocity of the receiver:
By applying the operator
to the function
u it is obtained:
where
are Cartesian components of the vector
. Substituting the equations (
19) and (
20) into the equation (
32) it is obtained:
By differentiating the equation (
15) the time derivative
is obtained as:
Substituting the equation (
34) into the equation (
33) yields:
The second and the fourth right-hand side terms of the equation above cancel, thus, we may write:
By differentiating the equation (
7) with respect to time one obtains:
Substituting the equation (
37) into the equation (
36) yields:
Next we will apply the operator
to the equation (
38) to obtain:
where the operator
simply means the operator
applied twice. Substituting the equations (
19) and (
20) into the equation (
39) it is obtained:
Furthermore, substituting the equation (
34) into the equation (
40) yields:
The second and the fourth right-hand side terms cancel, therefore:
By substituting the equation (
37) into the equation (
42) it is obtained that:
Subtracting the equation (
43) divided by
from the equation (
30) yields the wave equation for the stationary source and the moving receiver:
where
F is any function such that
. This means that the function
F can even be a constant, which has applications in electrodynamics [
24]. It is also interesting to note that if the receiver becomes stationary, then
and the velocity of the receiver
. In that case, the wave equation for the stationary source and the moving receiver becomes the wave equation (
1).
4. The Green’s Function for the Wave Equation for the Moving Receiver and the Stationary Source
The free space Green’s function for the three-dimensional version of the wave equation is typically derived by the application of Fourier or Laplace transform [
26,
27], which is somewhat mathematically involving. For the wave equation given by the equation (
1), the Green’s function
G satisfies the following inhomogeneous wave equation:
Using Fourier’s or Laplace transform, one can solve the equation (
45) for the function
G to obtain Green’s function for the wave equation in an unbounded domain [
28,
29]:
which represents the effect of an impulse propagating away from the source located at the position
.
We are now interested in finding Green’s function for the wave equation for the moving receiver and the stationary source expressed by the equation (
44). Therefore, we need to find the function
G that satisfies the following inhomogeneous wave equation:
Instead of using Fourier or Laplace transform to find the function
G, we here take the simpler approach that takes advantage of the right-hand side of the equation (
44). If in the equation (
8) we replace the constant vector
by the constant vector
the function
u becomes:
Because
is a constant vector, the function
u still satisfies the wave equation for the moving observer and the stationary source given by the equation (
44). Now by letting
, where
is an independent real variable, the function
u becomes:
Note that because
is an independent variable, the function
u still satisfies the equation (
44). The function
F can be any differentiable function, thus, we choose
F to be the Dirac’s delta function divided by
:
With this choice, the function
u becomes:
Substituting the function
u into the equation (
44) yields:
The term
is non-zero only when
. In that case the Dirac delta function
becomes:
Substituting the equation (
53) into the equation (
52) yields:
Thus, it is evident that the function
u as defined by the equation (
51) is indeed Green’s function for the wave equation for the moving receiver and the stationary source:
Note the difference between the Green’s functions given by the equations (
46) and (
55): with the equation (
55), the receiver is allowed to move because its position is described by the position vector
. With the equation (
46), the receiver is not allowed to move because its position is described by the constant position vector
.
5. The Wave Equation for the Moving Source and the Moving Receiver
Thus far, it was assumed that the wave equation for the moving source and the stationary receiver given by the equation (
44) admits only the solutions in which the receiver is allowed to move, but the source is stationary. In this section, however, we are attempting to find the solution to the wave equation (
44) in which both the source and the receiver are allowed to move. If such solution exists, it satisfies the following inhomogeneous wave equation:
Furthermore, if the function
u is the solution to the equation (
56) then the distance
R between the location of the source at the time
when the wave was emitted and the location of the moving receiver at the time
t when this wave arrives at the receiver is the function of both the retarded time
and the time
t:
Substituting the equation (
57) into causal relationship given by the equation (
7) yields:
Note the difference between the equation (
44) and the equation (
56). In the equation (
44), the motion of the source is not allowed while the receiver can move along an arbitrary trajectory. In contrast, the equation (
56) allows both the source and the receiver to move along arbitrary trajectory.
Before we start the mathematical procedure of finding such solution, note that the right-hand side term of the equation (
56) is non-zero only when
. This can only happen if the source and the receiver occupy the same point in 3D space, that is, if the source and the receiver collide. In that case, the retarded time
is equal to present time
t, and we can write:
The Green’s function for the wave equation for the moving receiver and the stationary source allows us to write the solution to the equation (
59) as:
Substituting the equation (
55) into the equation (
60) yields:
The sifting property of Dirac’s delta function
picks out point
, thus, the equation (
61) becomes:
Using the following identity involving the Dirac’s delta function [
30,
31]:
where
is a differentiable function, and
is the solution to the equation
, one can write the Dirac’s delta function under the integral on the right-hand side of the equation (
62) as:
where
is the solution to the following equation:
By comparing the equations (
58) and (
65) it follows that the time
is:
Differentiating the expression in denominator of the equation (
64) while keeping in mind that
t is an independent variable yields:
Substituting the equation (
67) into the equation (
64) yields:
Using the equation (
66), i.e.
, yields:
If we assume that
the equation (
70) can be written as:
The equation (
70) can be written in more concise form as:
where the vectors
and
are given as:
Furthermore, substituting the equation (
71) into the equation (
62) yields:
Using the sifting property of the Dirac delta function, we can rid ourselves of the integral in the equation (
74) to obtain:
where
, where the retarded time
satisfies the equation (
58), and where the vector
is the function of both time
t and the retarded time
.
Put in other words, the function
u is the wave function when both the source and the receiver can move along arbitrary trajectories, and the function
u satisfies the wave equation (
56). This means that the equation (
44) derived in the
Section 3 of this paper is not only the wave equation for the moving receiver and the stationary source, but it is also the wave equation for the moving receiver and the moving source.
Note that the equation (
75) does not satisfy the ordinary wave equation given by the equation (
1). However, if the receiver becomes stationary, then
, and consequently, the velocity of the receiver
. In such a scenario, the wave equation for the moving source and the moving receiver (
56) simplifies to the ordinary wave equation, and the solution (
75) also simplifies to the solution to the ordinary wave equation. Thus, it is evident that the ordinary wave equation is a special case of the wave equation (
56).
From the point of view of electrodynamics, it is worth noting that if the function
F is a constant, such that
, and if the velocity of the receiver
, then the equation (
75) becomes the scalar Liénard-Wiechert potential caused by the moving point charge. This potential is also the solution to the ordinary wave equation because the receiver is stationary.
6. Summary and Discussion
In
Table 1, the results of the investigations conducted in this paper are concisely summarized. The table is divided into two parts: the first deals with the ordinary wave equation, and the second deals with the wave equation for the moving source and the moving receiver. The moving point-source solution to the ordinary wave equation and the corresponding parameters are obtained by setting
(and consequently
) in the equation (
59). As indicated in the
Table 1, the ordinary wave equation cannot have solutions where the receiver is in motion.
Although the point source solutions to ordinary wave equation are obtained from the equation (
59), these solutions can be verified in a different manner by using the differentiation techniques described in the
Appendix A. However, verifying the equations given in the
Table 1 using these differentiation techniques requires a significant amount of mathematical manipulation, which would significantly and unnecessarily lengthen this paper. Alternatively, advanced symbolic computation software such as
Mathematica, together with the techniques given in the
Appendix A, can be employed to verify the equations in
Table 1 in a different manner than the one presented in this paper.
The second part of the
Table 1 presents the wave equation for the moving source and the moving receiver and its general solution for the point sources. The equations given in the second part of this table represent the summary of the
Section 5 of this paper. As indicated in the second part of the
Table 1, the wave equation (
59) is more general than an ordinary wave equation because it admits the solutions for the moving receiver. In fact, it can be concluded that the ordinary wave equation is a particular case of the wave equation for the moving source and the moving receiver when
.
Table 1.
Comparison of ordinary wave equation and the wave equation for the moving source and the moving receiver. The ordinary wave equation does not allow the motion of the receiver, while the wave equation for the moving source and the moving receiver allows the motion of both the source and the receiver.
Table 1.
Comparison of ordinary wave equation and the wave equation for the moving source and the moving receiver. The ordinary wave equation does not allow the motion of the receiver, while the wave equation for the moving source and the moving receiver allows the motion of both the source and the receiver.
| Name of the equation |
Expression(s) |
Source motion allowed |
Receiver motion allowed |
| Ordinary wave equation |
|
| |
Point source solution: |
| |
|
|
X
|
| |
Parameters: |
| |
|
| |
|
| |
F - any function differentiable twice |
| |
a - any constant |
| the wave equation for the moving source and the moving receiver |
|
| |
Point source solution: |
| |
|
|
|
| |
Parameters: |
| |
|
| |
- the velocity of the receiver |
| |
|
| |
F - any function differentiable twice |
| |
a - any constant |
7. Conclusions
There are several principal results of this study, the foremost being a derivation of a three-dimensional wave equation that allows the motion of both the source and the receiver. Secondly, this study has demonstrated the inadequacy of the ordinary wave equation to admit the solutions where the receiver is allowed to move. Moreover, it was demonstrated that the ordinary wave equation represents a particular case of the wave equation derived in this paper. Therefore, it is concluded that the wave equation for the moving source and the moving receiver is a more general equation than the ordinary wave equation.
The third, but not less important result, is that the general point source solutions are derived for both the ordinary wave equation and for the wave equation for the moving source and the moving receiver. These solutions can be adapted for various physical problems involving wave propagation without losses in homogeneous isotropic media. Additionally, the free space Green’s function for the wave equation for the moving source and the moving receiver has also been derived.
Lastly, the wave equation for the moving source and the moving receiver has potential application in physics. In particular, the limitations of Liénard-Wiechert potentials in electrodynamics, namely their inability to represent moving receivers, can be resolved by altering these potentials. This modification could potentially aid with some modern challenges in the field of electrodynamics.