Prerpints.org logo
Preprint
Article

Instantaneous Relativistic Precession of Mercury

Altmetrics

Downloads

90

Views

24

Comments

0

This version is not peer-reviewed

Submitted:

16 March 2024

Posted:

18 March 2024

You are already at the latest version

Alerts
Abstract
The extra precession of Mercury - 42.9 seconds of arc per century - explained by General Relativity (GR), is the result of a secular addition of 5.02 × 10−7 rad. at the end of every orbit around the Sun. We will analyze, the instantaneous precession and its addition along one orbit, determine the magnitude and oscillations around the mean value, comparing key theoretical proposals. This angular precession, should be the result reaction of Mercury to the gravitoelectric action produced by the geometric curve space-time at each single point of the elliptic orbit. The better we should know about this instantaneous precession, the better we will determine the external action and its quantum core nature, if that is the case. The Doppler tracking of the MESSENGER spacecraft, produces only 1 m error, enough precision to deduce the complete geodesic orbit of Mercury as an open free-fall path, isolated from other planets gravitational interference. The aim of this article is also to encourage JPL, IMCCE. and other scientific teams to do so because, as far as I know, it has not been entirely measured yet, by accurately tracking that motion.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

As General Relativity has determined, Mercury without the gravitational actions of other planets, tracks a geodesic as an open free-fall path, embedded in a geometric curved space/time with no external forces and therefore, follows a rectilinear motion. As an isolated motion, precession could be deduced trough the Schwarzschild formulation. It is also deduced as result of the perturbing method that studies the effects over the orbit elements, solved with Gauss, Lagrange and Landau equations. This perturbation approach, can be adopted since the small additional accelerations involved related with the dominant inverse-square Newtonian law [1].
Relativistic precession, is the angle that turns and drags the axes of the regular elliptic orbit. Instantaneous precession should be an almost simultaneous reaction to an external perturbing gravitational action, in direct connection with the curvature’s intensity of the space–time at each single point of the trajectory.
Gravitation, produces gravitoelectric effects in any target, that should be also consistent with the quantization of the gravitational field. However, while many aspects of General Relativity have been tested, there is no direct evidence for that [2], and experimental support for the existence of gravitons remains weak [3].
Classic manuals and scientific research on GR, have usually focused on the cumulative secular precession -the “perihelion shift”-, measured in arc. sec./century and located in one unique point.
The main issue of that research, has been the mathematical calculation of the “perihelion shift” and also slight new contributions just to obtain an accurate measure of this specific point, that was the first crucial discovery of the GR, providing a solution to the anomaly observed by Le Verrier in 1859. It has to be encourage the efforts of qualified scientific teams searching for infinitesimal secular advance of the perihelion shift, due to the Lense-Thirring effect, (4,7 x 10−5 relative to GR), relativistic “cross-terms” in the post-Newtonian equations (3,7 x 10−6), 2PPN secular pericenter precession (6,6 x 10−8) [4]. This infinitesimal secular precession, means a tangential perihelion shift distance, between 10 mm and 2 m in each orbit as much, really difficult to become measurable in the near future, although its cumulative evolution. A significant research about the options to measure this effects are: [5,6]
The orbital precession –integral addition of the instantaneous angular one-, is a continuous turn of the orbit axes at every point of the trajectory, with periodic oscillations either in a forward or backward motion, just as an output effect of the external action exerted on the target at every instant. These oscillations would have amplitudes between 1 km or 22 km per orbit, however periodic and not cumulative, located in different true anomaly angles, with two or four peaks and significant dependence on eccentricity, according to the different theoretical proposals. Although relativistic precession is not a direct measure, it can be obtained removing the gravitational action of the other planets, modeling the orbit of Mercury as an open free-fall geodesic path.
Scientific works about instantaneous/orbital precession are very few, however highlight the formulations of M. Soffel [7,8]. R. Park, J. Williams and a JPL team, published a key article [9], that mentions the periodic effects of the perihelion motion using PPN parameters. The article asserts that the accuracy of typical spacecraft ranging is about 1 m and then, this periodic effect, can be easily measured by accurately tracking the motion of MESSENGER’s orbit about Mercury.
As far as I know, although accepting my limited knowledge about, it has not yet been full length accurate tracking measured. This future determination of the angular instantaneous and orbital precession, should answer next questions:
  • Is it right to accept a constant gradual angular precession?
  • How large are the magnitude of oscillations, if there are any?
  • Why those oscillations with that magnitude are located specifically in those true
  • anomaly angles?
  • What happens with the relation between eccentricity and oscillations?
  • Which of these theoretic proposals fits on the real angular/ orbital precession of
  • Mercury?
  • Does these oscillations give more information about the gravitational actions
  • that produces it?
  • What happens if none of these formulations works?

2. GR Precession; Classic Formulation

The equation of motion of the elliptic orbit is:
r = p 1 + e c o s ⁡ ( ∆ ( ) ) ϕ = t r u e a n o m a l y
where Δ(φ ), is a very small function that produces the orbit perturbation, from the newtonian-kepler ellipse. Misner et al. (1973) in his well known relativity textbook “Gravitation”[10], advanced a constant instantaneous precession.
δ(φ) = K= 3GM/c2p = constant precession. Δ(φ ) = K•φ
For one complete orbit, the relativistic precession is:
Δ ( 2 π ) = 2 π K = 6 π G M c 2 p r a d . / o r b i t
p = semi-latus; c = speed of light, and for Mercury :
Δ(2π) = 5.02 x 10−7 rad./orbit = 42.9 sec.arc./century
perihelion tangential shift ≈ 23.1 km./orbit.
The author mentioned that there are also periodic non cumulative effects ≈ 1 km amplitude, but in 1973 had not been determined experimentally.
This particular solution with a constant angular precession was, in my opinion [11], the first result obtained by Einstein in 1915 [12]

3. Schwarzschild Method

GR accepts also small periodic oscillations of the orbital precession based in Schwarzschild`s methodological approach: [13,14,15]
The trajectory of a massive particle is a geodesic, that satisfies the equation:
d 2 u d φ 2 + u = GM h 2 + 3 GM c 2   u 2 ; u = 1 / r   ; h   = angular   momentum / unit   of   mass
A particular integral of the equation is [15]:
r = p / ( 1 + e     cos φ +   α ( φ ) )   where α(φ) is the perturbing function.
α ( ϕ ) =   3 GM c 2 p [ 1 + e 2   1 2 1 6   c o s   2 ϕ + e ϕ sin ⁡ ϕ   ]   r a d .    
Professor Berry [16] obtains a very similar result although a different formulation.
α ( ) = GM c 2 p   [   ( 3 + 2 e 2   ) + ( 1 + 3 e 2 e )   cos   e 2 cos   2 + 3   e   sin   ]
The final precession at the end of a complete orbit Δ(2π) is the same as the expected one, but the intermediate values of the orbital precession Δ(φ ), are not now in a lineal progression as before. These periodic swing is the result of the angular precession that involves the terms cos2φ or cos2φ, and should produce, in my opinion, ≈0.25 km forward/backward shift, referred to the expected lineal precession, when φ = ± π/2.
The other terms of the equation, produces slight periodic variations of the radial distance, that should be confirmed, but not an angle perturbation.

4. The Laplace-Runge-Lenz and Perturbing Potential Methods

We can also study the effects of specific perturbing actions, method that should allow accurate results as those obtained solving the second order Schwarzschild differential equation. [11]
A solution to the orbital precession, is based on the Laplace-Runge-Lenz vector, located in the same plane as the orbit and pointing in the direction of the perihelion. Vector’s angular velocity, measures the precession if there is any external perturbation [17,18]. It is interesting to note that the L-R-L vector, is very similar to the Hamilton vector, unfortunately this last one has vanished from textbooks on classical mechanics in twentieth century.[19]
The instantaneous precession is δ(φ), (angular precession), so that the gradual addition along the orbit Δ(φ ) (orbital precession) as integral of δ(φ), has a continuous addition till its final value Δ(2π).
Angular precession under L-R-L method is then:
δ ( ϕ ) = K 1 e 1 + e   c o s ϕ 2 c o s ϕ r a d . / r a d . = a n g u l a r p r e c e s s i o n
The units/time of the mean angular precession should be: rad./sec. ≈ 8,3 x 10−7 rad./rad. The integral of this angular precession gives the orbital precession in each single point of the trajectory.
Δ ( ϕ ) = ∫ δ ( ϕ )   d ϕ = K 3 / 4 e 2 + 1 e s i n   ϕ + 1 2 s i n   2 ϕ + 1 12 e   s i n   3 ϕ + ϕ r a d .  
Another method is to analyze the effective GR potential where the last term, is the perturbation potential added to the classic newtonian one: [15,20]
V e f = − G M r + h 2 2 r 2 − G M h 2 c 2 r 3
Following reference [20], we can solve the equation of motion, to obtain the angular and orbital precession.
( ϕ ) = ∫ d u 2 E m h 2 + 2 G M h 2 u − u 2 − 2 V ( u ) m h 2
where u = (1+e z) ⁄ p ; then:
∆ ( ϕ ) = − 2 p G M e 2 ∫ z   dz 1 − z 2 d   V ( z ) dz
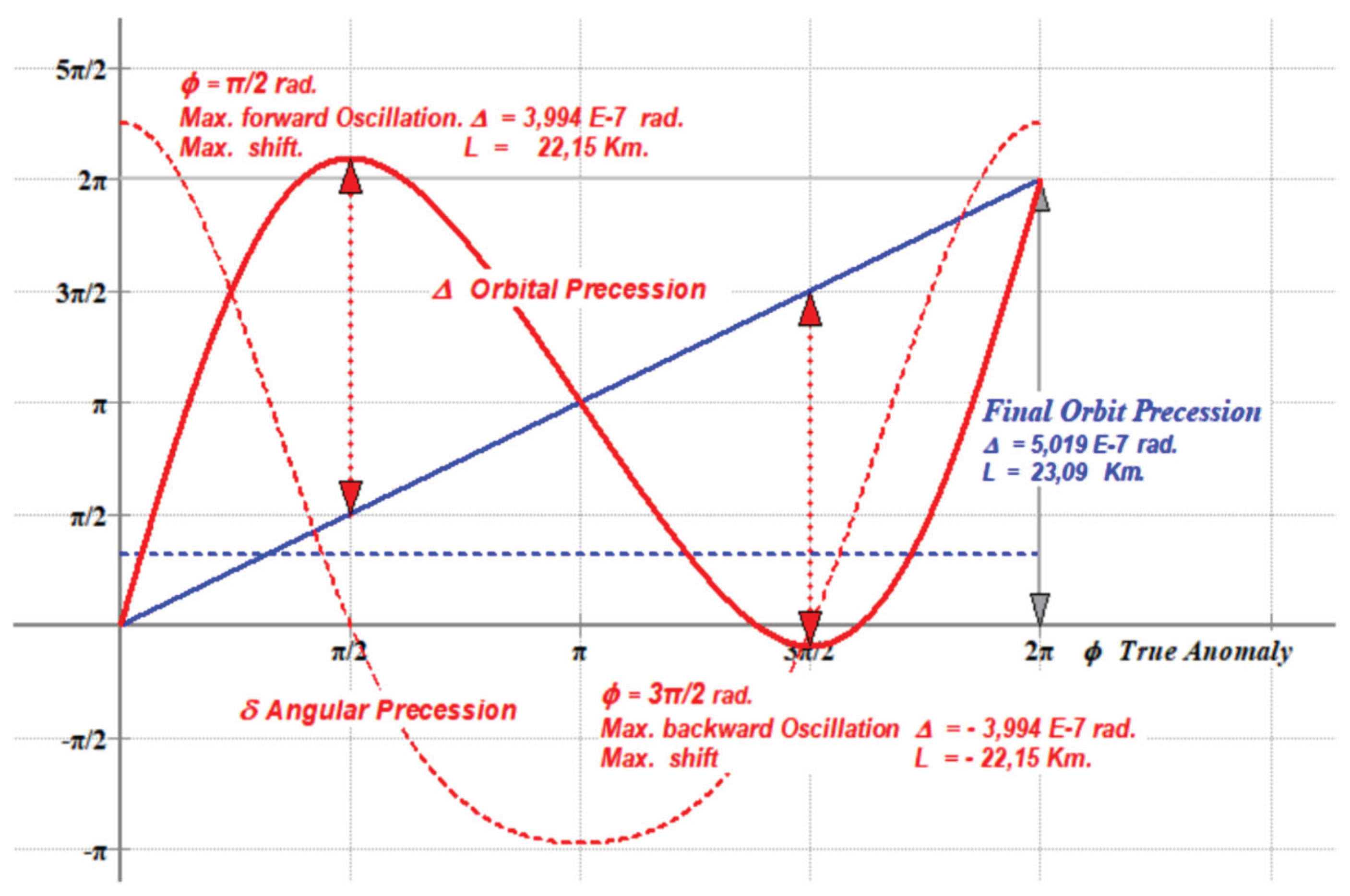
Preprints 101504 g001
Figure 1. Angular / Orbital precession. L-R-L and Perturbing Potential method (red). Constant angular precession; lineal orbital precession (blue).
Figure 1. Angular / Orbital precession. L-R-L and Perturbing Potential method (red). Constant angular precession; lineal orbital precession (blue).
Preprints 101504 g001
The result is just the same as before.
Underline that with this methods, the forward oscillation is located when φ < π. However, may this position, be consequence of a conventional criteria in the sign of precession. Using a negative sign or a π drag in true anomaly angle, results in a symmetric solution, very similar to the one obtained under the PPN formulation. The amplitude of oscillations, involves a shift about 22 km forward and backward.

5. Quantum Potential Transmission/Precession Reaction

Consider a gravitoelectric external action, either due to a relativistic gravitational disturbing potential, or a quantum field and gravitons transmission. We should accept that this precession has a virtually instantaneous transfer action inside the target.
This potential, should be continuously emitted and updated from its central focus whatever could be the space/time curvature and/or the background quantum transmission field. This continuous update, must also shape the general relativity curved space-time framework were, gravitational effects are not forces but the outcome of a “geometric”, but not frozen, structure of the universe.
Consider a target with a radial speed Vr related to the inertial frame, moving in the same forward direction as the potential emission. The transit time of the potential crossing through the target, will be larger related with the transit time when the object is in a rest position and will decrease, if they are moving in opposite directions. The larger or reduced transit time inside the target, is proportional to Vr/c, and potential with (Vr/c)2.
We assume potential’s transmission velocity, equal to that of light (c).[21,22]
Potential P(φ ) is then defined as a slight perturbation to the newtonian gravitational potential:
P ( ϕ ) = − GM r [ 1   ∓   V r c 2 ⁡ ] = − G M r + S ϕ   ;   S ϕ = ∓ G M r V r c 2
Potential S(φ) has a clear physical basis, consistent with the laws of impulse and momentum transfer, energy conservation and the action/reaction effect of the usual mechanics.
Point out also that, if we apply potential S(φ) to any sphere or any compact three-dimension target, the resultant ratio is three times (Vr/c)2. The transmission distance inside the target, has been enlarge with a new length, producing a light increase of the sphere´s active volume and mass, that involves a three times ratio compared with a single particle effect. [21].
Consider δ(φ) as the instantaneous angular precession at each single point of the newtonian-kepler ellipse, and as result of its gradual accumulation, the orbital precession will reach a final value Δ(2π) at the end of one orbit.
We will use Landau & Lifshitz formulation [20,23], and deduce the precession produced by a perturbing potential. This formula is valid as a theorem, suitable for any small perturbation whatever could be its physical origin and returning the exact value. Integration is performed over an unperturbed orbit [24].
Δ 2 π = ∂ ∂ h 2 h ∫ 0 π r 2   δ U   d ϕ
where δU is the perturbing potential/unit of mass.
The angular δ(φ) and orbital Δ(φ) precession are:
Δ ( ϕ ) = ∫ 0 ϕ δ ϕ   d ϕ = 3 G M c 2 p ∫ 0 ϕ s i n 2 ϕ 1 + e c o s ϕ 2 2 − e 2 + e c o s ϕ d ϕ
∆ = 3 G M c 2 p ϕ − sin ⁡ ϕ   ( e + c o s ϕ ) ( 1 + e cos )  
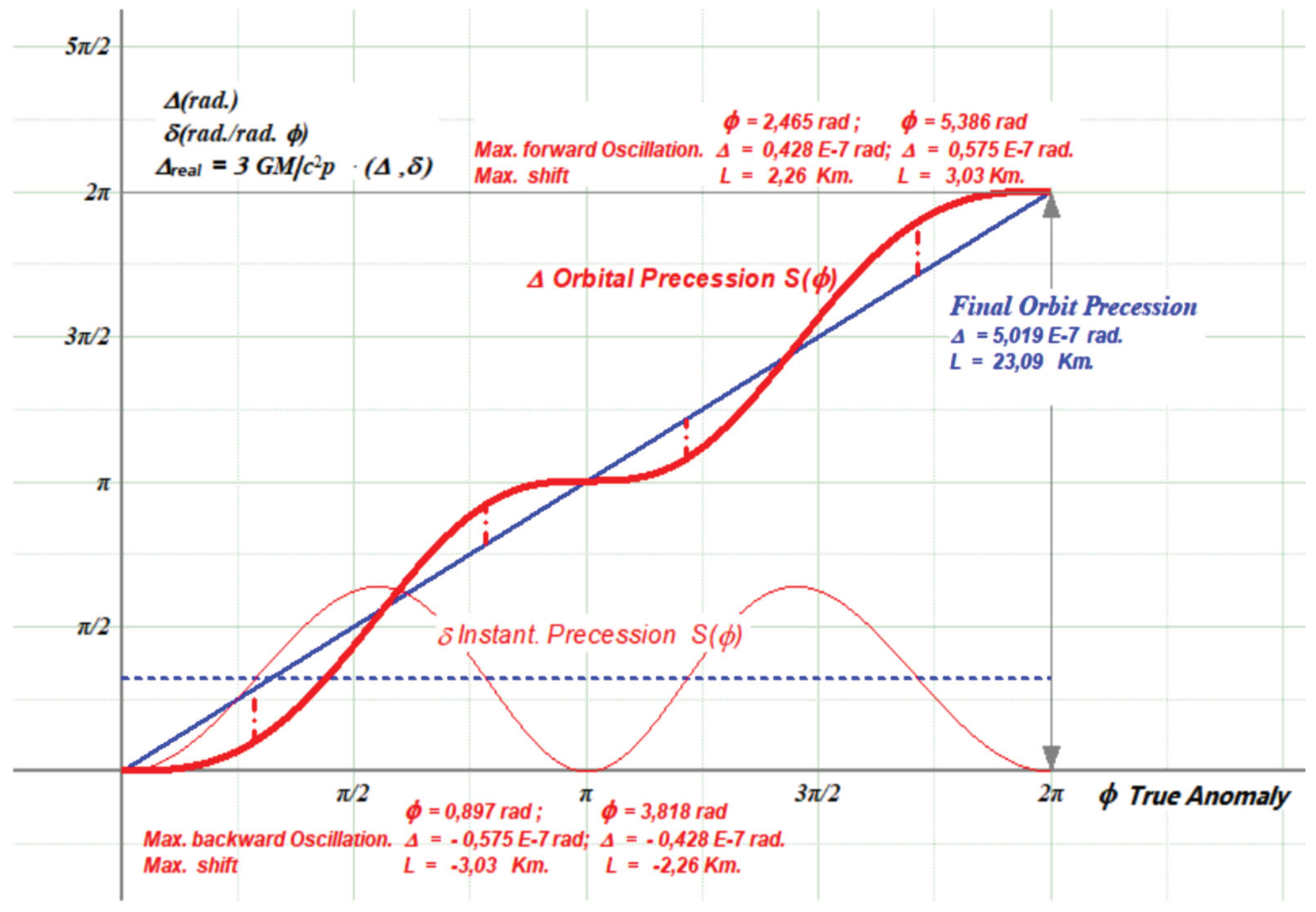
This method obtains an orbital precession with four peaks and a shift between 2-3 km, forward and backward motions. Angular precession has a maximum when φ = 1,73 and φ = 4,56 rad., where radial velocity is very near from its maximum; is null where radial velocity is also null.
Using Lagrange planetary perturbing equation, we reach a very similar result however the maximum angular precession is when φ = 1,42 and φ = 4,86 rad.
Preprints 101504 g002
Figure 2. Angular / Orbital precession. Perturbing potential action.
Figure 2. Angular / Orbital precession. Perturbing potential action.
Preprints 101504 g002

6. PPN Formulation

As we mentioned before, the most significant research about periodic relativistic precession, was performed by M.H.Soffel [7,8] using planetary perturbing equations, radial and transversal accelerations related with time, true anomaly and PPN parameters.
There are also other formulations of the perturbing gravitoelectric acceleration, where periodic effects could be deduced, however these specific proposals, are focused on the secular average shifts, at the perihelion over one complete orbit [25]:
A ( 1 p N ) = − μ c 2 r 2 v 2 − 4 μ r r ^ + 4 μ c 2 r 2 r ^   ∙ v v
and [26], the argument of perihelion:
d ω d t = 1 e p G M − R   c o s   ϕ + S 2 + e   c o s ϕ 1 + e   c o s ϕ   s i n ϕ
where R and S are the radial and tangential components of the perturbing acceleration.
Following Soffel proposal, R.S.Park, J.G.Williams and a JPL team in their significant article [9], displays the periodic orbital precession, the partial derivative with respect to the PPN parameters β, g and the solar oblatness effect.
The formulation of Soffel, is based on the Gauss planetary equation referred to the argument of the pericentre ω:
d ω dt = 1 − e 2 n a e [   S   cos ⁡ ϕ + T   ( 1 + r p )   sin ⁡ ϕ ]
where S and T are the radial and tangential components of the perturbing acceleration and φ is true anomaly angle.
This equation results in the angular precession:
δ ( ϕ ) r a d i a l = − 3 G M c 2 p cos ⁡ ϕ e 1 + e 2 + 2 3 e cos ⁡ ϕ − 4 3 e 2 c o s 2 ϕ
δ ( ϕ ) t a n g . = 3 G M c 2 p   4 3 2 + e cos ⁡ ϕ   s i n 2 ϕ
δ ( ϕ ) = − 3 GM c 2 p 3   e 2 3 e cos   ϕ + 5 3   cos   2 ϕ   1   rad . / rad .   ( <   >   d ω / d ϕ )
and then, orbital precession is:
Δ ( ϕ ) = ∫ 0 ϕ δ ϕ d ϕ = 3 GM c 2 p [ ϕ − 5 6 s i n 2 ϕ − 3 − e 2 3 e sin ⁡ ϕ ] r a d .    
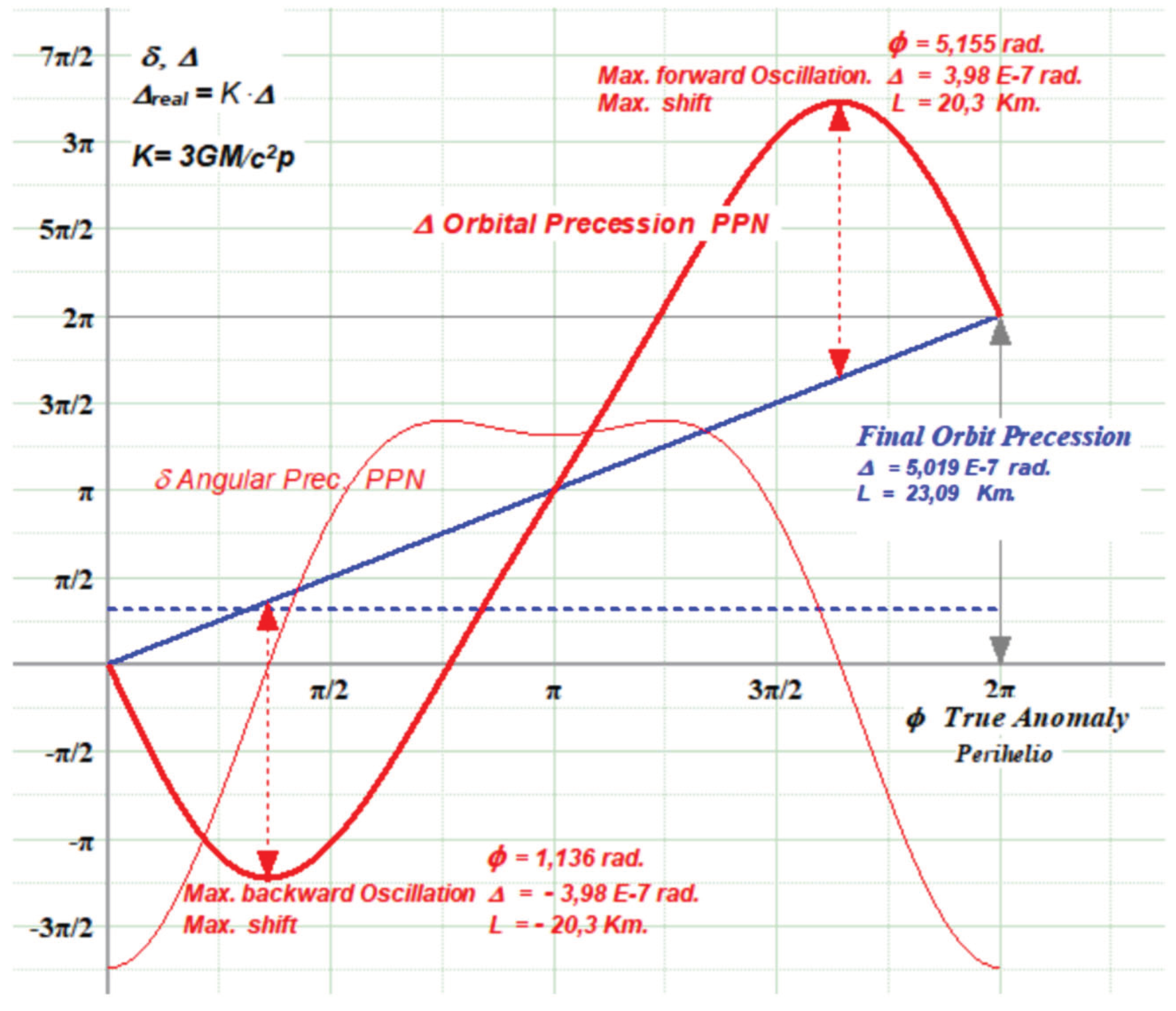
Preprints 101504 g003
Figure 3. Angular / Orbital precession. PPN formulation.
Figure 3. Angular / Orbital precession. PPN formulation.
Preprints 101504 g003
This method obtains an orbital precession with two peaks and a shift of 20.3 km, forward and backward motions. The equation has a term with an inverse proportion to eccentricity. Angular precession has positive maximums between φ = 2,37 and 3,91 and negative when φ = 0 and φ = 2π. This forward maximums are located when Mercury is in the farthest point from the Sun and the backward, in the nearest, results that should need a reasonable explanation.

7. Relativistic Gravitational Force

Theory of Special Relativity (SR) and gravity in flat space, was left aside since the GR success as a new science, a geometric space/time framework that gives an exact explanation of the anomalous perihelion shift of Mercury. However, there have been many authors trying to analyze and resolve this precession under SR method. In reference [27], there is a complete summary beginning with the early works in 1898, 1906, new research until 2022, and also mentions proposals about gravitational fields and rotational time dilation.
There is also a recent article with the title “Relativistic Gravitational Force”[28], that suggests to give up the principle of equivalence and focus again on SR. This proposal should reach the correct perihelion shift of Mercury, all of the classic experimental tests of GR, and also suggest the framework of quantum gravity. This method, developed within the same flat space/time as quantum field theory, could be helpful for a possible transition to the quantum regime.
Using Hamilton vector, this proposal assumes the next precession formula:
∆ ϕ = L μ α 2 e 2 ∫ 0 2 π k 1 r 3 + k 2 r 2 + k 3 r + k 4 d ϕ
Where L= h; μ = Mm/(M+m); α = GMm and k1 – k4 are constants with complex functions of G, M, m, h, c, and p.
Trying to convert that formula, although accepting any differ understanding of k- constants, we could obtain the next equations of the orbital precession along the orbit, and present two alternatives under a Taylor series potential equation.
Δ ( φ   )   ≈   3   GM c 2 p ( A ϕ 3 − B ϕ 2 + C ϕ )
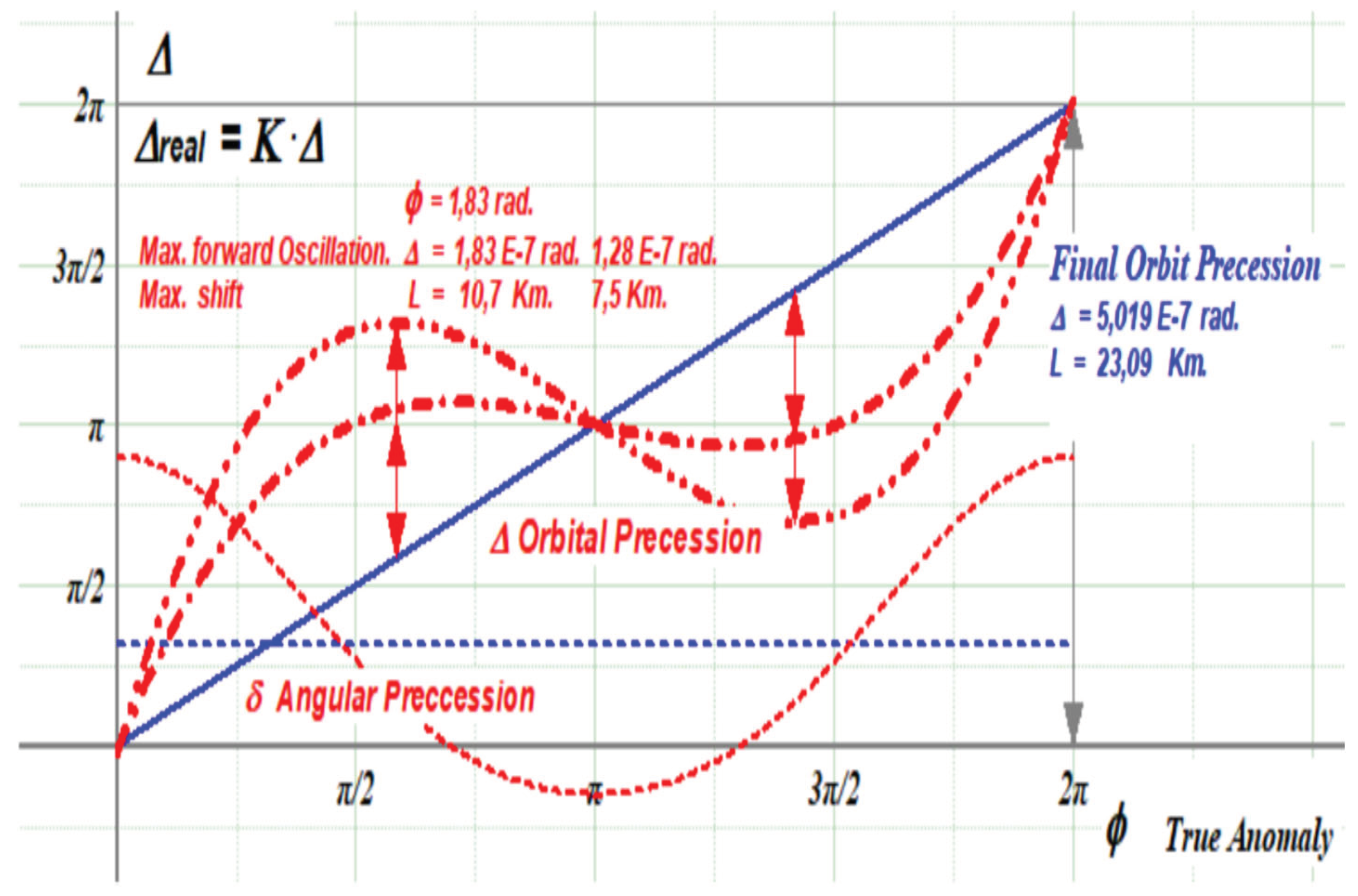
Preprints 101504 g004
Figure 4. Angular / Orbital precession. RGF formulation.
Figure 4. Angular / Orbital precession. RGF formulation.
Preprints 101504 g004
Orbital precession has a similar formulation as the Laplace-Runge-Lenz method, with forward motion peak when φ = 1.83 rad., backward when φ = 2.19 rad. and tangential shift between 7.5 and 10.7 km. However as before, a different criteria in the meaning of the ± sign, should produce a symmetric function similar as PPN equation.

8. Yukawa Gravitational Potential

The Yukawa potential is an alternative from the Newton law, characterized by a power-law formulation related with the dimensionless -α- (strength referred to gravity) and -λ- (range). The Yukawa potential should be the static limit of an interaction due to the exchange of virtual bosons or the possibility that a nonzero graviton mass could lead to this potential [29]. This potential can be also connected to mass terms which appears in addition to the theoretical field analog of the usual Hilbert-Einstein Lagrangian. [30]. The Yukawa potential is usually referred as one component of the fifth force.
Trying to unify gravity with the other three fundamental forces of Nature, new approaches could be deviations of the Newton law of gravitation [31]:
Y P o t . = − G M α r e x p . − r λ
The Yukawa-like fifth force, has only a radial perturbing acceleration:
A Y = − G M α r 2   1 + r λ   e x p . − r λ
Following Landau & Lifshitz formulation, we will obtain the angular/orbital precession [23,24]
Δ ( ϕ ) = ∫ δ ( ϕ )   d ϕ = α 2 e ∫ e x p . − r λ ( 1 + e c o s   ϕ ) 2 r λ 2 e + ( 1 + e 2 ) cos ⁡ ϕ − ( e + cos ⁡ ϕ ) d ϕ
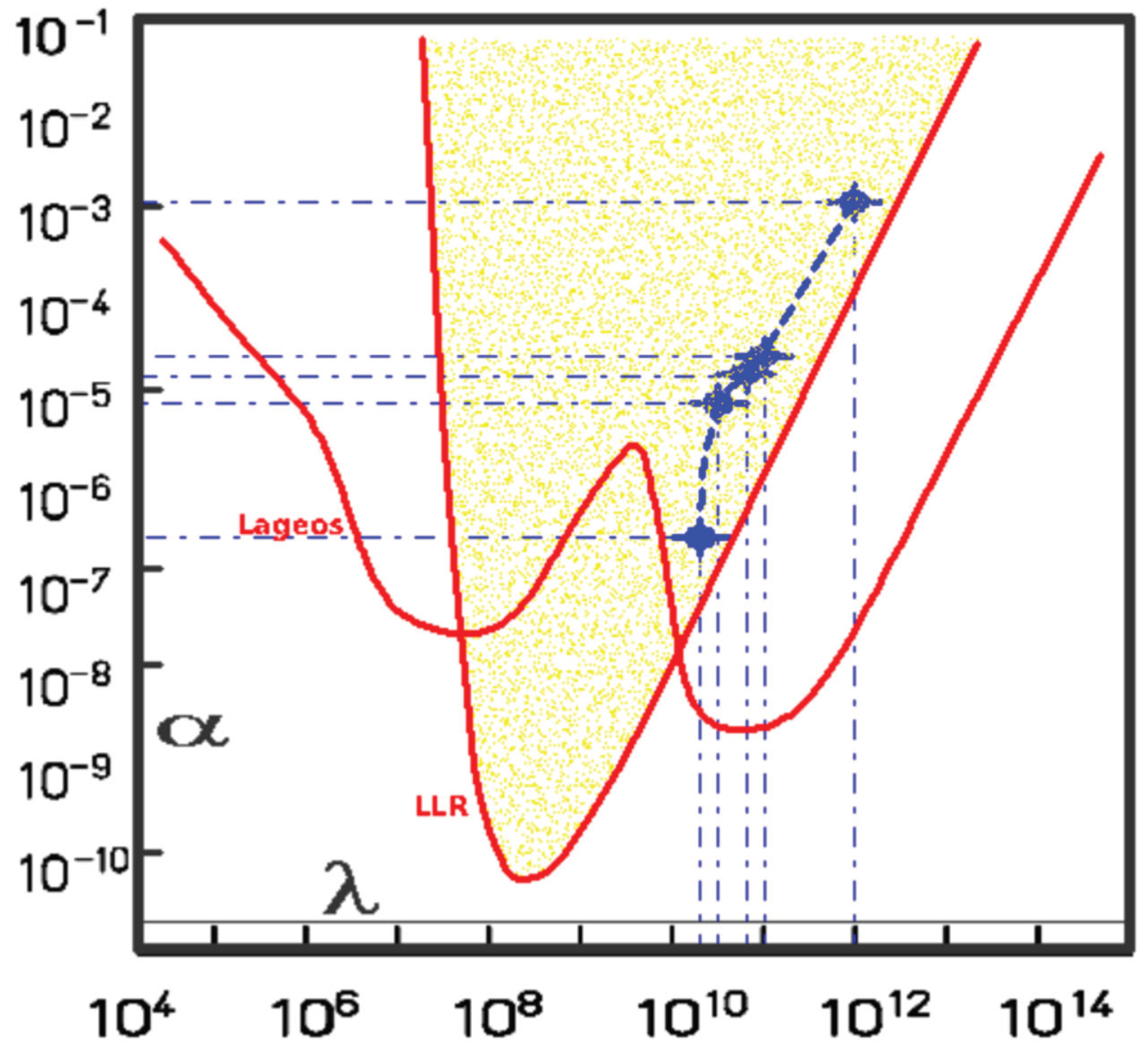
Δ(2π) is the relativistic precession at the perihelion and every pair of α and λ parameters, has a fixed constraint with it. As result of equations (25) and (26), each λ is linked with only one α that fits with the final precession:
Then, Δ(φ ) ≈ K x [Aφ 5 + Bφ 4 + Cφ 3 + Dφ 2 + Eφ ]
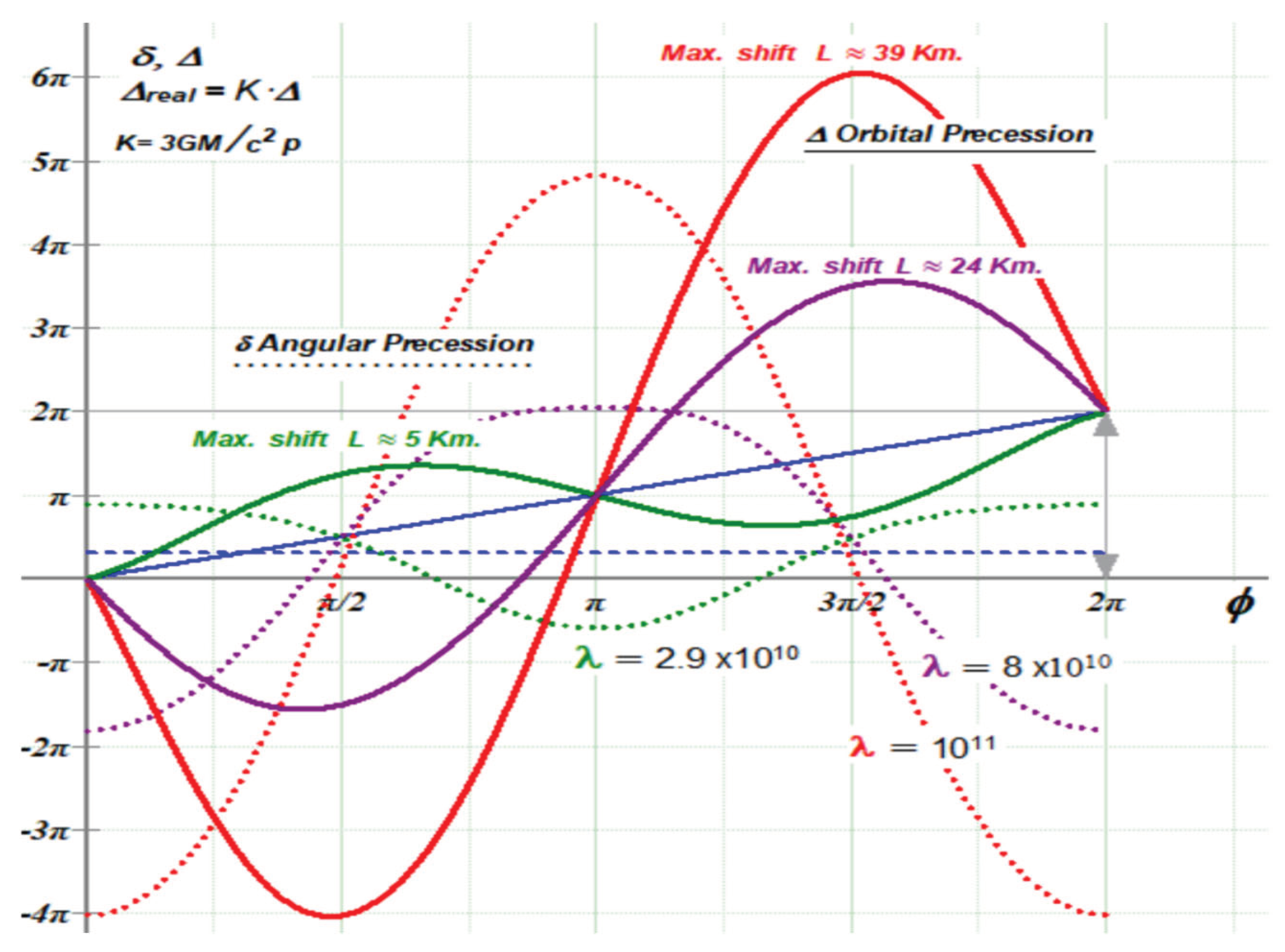
Orbital precession for λ = 8 x 1010, has similar evolution and maximum shifts as the PPN proposal. For other values, there are clear divergences between them.
Table 1. Examples of λ and α parameters.
Table 1. Examples of λ and α parameters.
 2,9 x 1010 5 x 1010 8 x 1010 1011 1012
2,5 x 10−7 9,3 x 10−6 1,6 x 10−5 2,1 x 10−5 1,1 x 10−3
Preprints 101504 g005
Figure 5. Represents some α and λ parameters over the LLR and Lageos aproach. [29].
Figure 5. Represents some α and λ parameters over the LLR and Lageos aproach. [29].
Preprints 101504 g005
Preprints 101504 g006
Figure 6. Angular / Orbital precession. Yukawa potential.
Figure 6. Angular / Orbital precession. Yukawa potential.
Preprints 101504 g006

9. The Effect of Eccentricity

The PPN, Yukawa and L-R-L methods, have an eccentricity inverse proportional term, associated with sinφ. When φ = 2π or φ = π, it has a null result, so final orbital precession in the perihelion, is not disturbed. However, the oscillations along the orbit are direct involved by that term, with increasing magnitudes as eccentricity decreases. Orbital precession under PPN proposal is:
Δ ( ϕ ) = 3 G M c 2 p [ ϕ − 5 6 s i n 2 ϕ − 3 − e 2 3 e sin ⁡ ϕ ]   r a d .  
Δ(φ) and maximum shifts in the peak point of each oscillation referred to the planets in the Solar system is:
Table 2. Peak orbital precession and shift in oscillations.
Table 2. Peak orbital precession and shift in oscillations.
Planets Excec. Semi latus (p) Δ(2) Perih.Shift Oscillation Max. Shift
m rad. km rad. ± Δ() rad. ~ ± km
Mercurio 0,20563 5,5461E+10 5,02E-07 23,1 1.13 & 5.15 3,98E-07 20,3
Venus 0,0068 1,0820E+11 2,57E-07 27,6 1.55 & 4.73 6,02E-06 652
Tierra 0,0167 1,4956E+11 1,86E-07 27,4 1.53 & 4.76 1,77E-06 265
Marte 0,0934 2,2594E+11 1,23E-07 25,5 1.34 & 4.95 2,12E-07 48
Júpiter 0,0484 7,7658E+11 3,58E-08 26,6 1.44 & 4.84 1,18E-07 92
Saturno 0,0538 1,4253E+12 1,95E-08 26,4 1.43 & 4.85 5,79E-08 82
Urano 0,0472 2,8686E+12 9,70E-09 26,6 1.45 & 4.84 3,28E-08 94
Neptuno 0,0086 4,5041E+12 6,18E-09 27,6 1.55 & 4.73 1,14E-07 515
Eccentricity has a clear influence in the peak orbital precession and tangential shift in the oscillations, as it happens with Venus, Neptune and the Earth. As the magnitudes are significant, it is necessary to confirm if those shifts have been really detected and observed by the tracking of the planets mentioned. These effect should be also confirmed with the Moon using the L.L.R. and also other moons with a very low eccentricity as there are some around Jupiter.
We should admit that any equation with an inverse proportional term, is also valid for very low eccentricities; otherwise, it is difficult to accept an “ad- hoc” formulation if the experimental tracking results, does not fit with the expected ones.

10. Conclusions

The geodesic orbit of Mercury is an open line, straight free fall path embedded in a curve space-time. This track is equivalent to the addition of an elliptic orbit, characterized with the usual osculating parameters, and a continuous turn of the orbit as a whole ensemble. This last motion is the precession, which can be displayed by an external perturbing action that, leaving aside the gravitational effect of the other planets of the Solar system, results in the GR precession. Usually, the research about this issue, has been focused on the angular distance within two consecutive perihelions, cumulative secular effect that represents the final precession at the end of each orbit, summarize as seconds of arc per century. Less interest has deserve the evolution of precession along the 87,9 days that takes Mercury to complete his orbit.
The angular instantaneous precession and its addition in the orbital precession, represents the reaction of the planet to an external perturbing action whatever could be the curve space-time producing an expected geodesic pattern, or/and a quantum field and graviton transmission. Underline that gravitational action is a single unique isue whatever could be cut off in its components, just to identify and study the perturbing actions and linked reactions.
Theoretic proposal mentioned in this work, have different results related with the angular/orbital precession in each point of the orbit. However there are similarities in their formulations and also clear divergences on the magnitude and peak location of them. It should be appropriate to explain gravitational action, linked with precession reaction, as a complete ensemble that involves theoretic and experimental tracking detection of this motion.
The theoretic research about this issue is unusual and as far as I know, the real tracking detection of the orbital precession, has not been totally performed. Tracking and model the complete orbit of Mercury as a free geodesic trajectory, should be incorporated in the Planetary Ephemeris Program, or other programs with comparable scope.[32]
The aim of this article is also to encourage JPL, IMCCE and other scientific teams to perform and publish it, and close an open issue concerning astrophysical research, related with the first and most crucial test of General Relativity.

Funding

This research received no external funding.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The author declare no conflict of interest.

References

  1. Iorio, L. Why Is the Mean Anomaly at Epoch Not Used in Tests of Non-Newtonian Gravity? Universe 2022, 8, 203. [Google Scholar] [CrossRef]
  2. 2. Wilczek, F; Krauss, L Using Cosmology to Establish the Quantization of Gravity. Phys. Rev. D. [CrossRef]
  3. 3. Parikh, M; Wilczek, F; Zahariade, G. The Noise of Gravitons. Int. J. Mod.Phy. Vol. /: (2020). https, 2020.
  4. Will, C. A new general relativistic contribution to Mercury’s perihelion advance. Phys. Rev. Lett. 120. 2018. [CrossRef] [PubMed]
  5. Iorio, L. Might the 2PN Perihelion Precession of Mercury Become Measurable in the Next Future? Universe 2023, 9, 37 https://www.mdpi.com/2218–1997/9/1/37. [Google Scholar] [CrossRef]
  6. Iorio, L. New general relativistic contributions to Mercury’s orbital elements and their measurability. Eur. Phys. J. C, 3: 80. [CrossRef]
  7. Soffel, M. Relativity in Astrometry, Celestial Mechanics and Geodesy; Springer-Verlag; Berlin, Germany, 1989; pp.
  8. Soffel, M.; Wen-Biao, H. Theory and Applications in Astronomy, Celestial Mechanics and Metrology; Springer Nature Switzerland. 2019.; pp. 329-331. [CrossRef]
  9. Park, R.; Williams, G. Precession of Mercury’s Perihelion from Ranging to the MESSENGER Spacecraft. The Astron. J. 1: (2017), 2017. [Google Scholar] [CrossRef]
  10. Misner, C. ; Thorne, Wheeler, J; Gravitation; Freeman and Co. S. Francisco. USA. 1973, pp. 1110, 1111. [Google Scholar]
  11. Bootello, J. Angular Precession of Elliptic Orbits. Mercury.; Int. J. Astron. & Astroph., 2012, 2, 249–255. [Google Scholar] [CrossRef]
  12. Einstein. The Collected Papers of A. Einstein, Vol. 6, Doc. 24. Princeton University Press, Princeton, USA. 1996,.
  13. Thornton, S; Marion, B. Classical Dynamics of Particles and Systems. Thomson Books/Cole.. 5ª ed. (2004). USA. pp.
  14. Carroll, S. Spacetime and Geometry. Addison Wesley. 2004. S. Francisco, USA,. pp.
  15. Hobson, M.; Efstathiou, G.; Lasenby, A. ; General Relativity. Cambridge University Press 2006. UK. pp. 230-233. [CrossRef]
  16. Berry, M. Principles of Cosmology and Gravitation. Cambridge University Press. Cambridge. 1976. UK. pp.
  17. Davies, D. Elementary Theory of Perihelion Precession. Am. J. Phys. [CrossRef]
  18. Stewart, M. Precession of the Perihelion of Mercury’s orbit. Am. J. Phys, 2005. [Google Scholar] [CrossRef]
  19. Muñoz, G. Vector constants of the motion and orbits in the Coulomb/Kepler problem. Am. J. Phys, 1292; 71. [Google Scholar]
  20. Adkins, G.; McDonnell, J. Orbital Precession Due to Central Force Perturbation. Phys. Rev. D, 75. [CrossRef]
  21. Bootello, J. Perturbing Potential and Orbit Dynamics. J. of Mod. Phys. 2013 Vol. 4; pp. /: 207-212 https. [CrossRef]
  22. 22. Bootello,J. Flyby orbits and perturbing potential. Adv. Spa. Res. [CrossRef]
  23. Landau, L; Lifshitz, M. Mekhanika. 3rd Ed. Butterwoth- Heinemann, 1976, Rep. 2000, Oxford, GB, pp. 30-40.
  24. Melnikov, V.; Kolosnitsyn, N. New Observational Tests of Non-Newtonian Interactions at Planetary and Binary Pulsar Orbital Distances. Gravit. & Cosmol. 2004. Vol.
  25. 25. Iorio,L. Is it possible to measure new general relativistic third-body effects on the orbit of Mercury with BepiColombo? Eur. Phys. J. C. [CrossRef]
  26. Will, C. On incorporating post-Newtonian effects in N-body dynamics. Phys. Rev. D. [CrossRef]
  27. McDonald, K. Special Relativity and the Precession of the Perihelion. J. H. Lab., Princeton University, /: NJ. 2023. http, 2023. [Google Scholar]
  28. Edvardsson, S. Relativistic gravitational force. Celest. Mech. Dyna. Astron. 2023. [Google Scholar] [CrossRef]
  29. Adelberger, E.; Heckel, B.; Nelson, A. Tests of the Gravitational Inverse-Square Law. Ann. Rev. Nuc. & Part. Sci. Vol. [CrossRef]
  30. Sereno, M.; Jetzer, Ph. Dark matter versus modifications of the gravitational inverse-square law: results from planetary motion in the Solar system, Month. Not. Royal Astron. Soc., Volume 371, Issue 2, 06, Pages 626-632. 20 September. [CrossRef]
  31. 31. Iorio,L. Constraints on the range λ of Yukawa-like modifications to the Newtonian inverse-square law of gravitation from Solar System planetary motions. J. H. En. Phys. [CrossRef]
  32. Chandler, J; Shapiro, I; et al. The Planetary Ephemeris Program: Capability, Comparison, and Open Source Availability, AJ 162 78 2021. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated