Optimal Position of Fixed crane and Dynamic Transport Truck Parking in Precast Building Construction Project

Preprint

Article

Optimal Position of Fixed crane and Dynamic Transport Truck Parking in Precast Building Construction Project

This version is not peer-reviewed.

Suphawut Malaikrisanachalee,

Narongrit Wongwai^*

Nujet Butsan

Suphawut Malaikrisanachalee,

Narongrit Wongwai^*

Nujet Butsan

This version is not peer-reviewed.

Altmetrics

Downloads

109

Views

Comments

Submitted:

19 March 2024

Posted:

19 March 2024

You are already at the latest version

Abstract

Efficient fixed crane position analysis is critical in precast buildings construction to maximize lifting efficiency for precast elements. The primary objective is to minimize the travel distances of fixed cranes, thereby enhancing operational efficiency and cost control. This involves strategically reducing the distances between the transport truck parking, where elements are stored, the fixed crane, and the construction installation point. Despite its significance, existing studies often overlook the dynamic movement efficiency of transport trucks, particularly when dealing with multiple transport trucks and various models of fixed cranes, rendering the opti-mization of this scenario a challenging NP-hard problem susceptible to combinatorial explosion. This study presents a novel mathematical model leveraging the Genetic Algorithm (GA). The model aims to solve optimal model and position of fixed cranes, along with identifying ideal positions for transport truck parking. The study's methodology is validated and demonstrated through a project case study. Comparative analyses between the proposed model and the original planning underscore a noteworthy 6% reduction in both duration and costs when lifting elements directly from transport trucks, as opposed to establishing an on-site stock yard. Furthermore, the developed GA exhibits a substantial improvement in final solutions, achieving a remarkable 30% reduction in both operational duration and costs. This research contributes valuable insights into fixed crane position analysis of precast building construction, providing foundation for enhanced operational efficiency and cost-effectiveness in the industry.

Keywords:

Subject:

Engineering - Civil Engineering

1. Introduction

At present, precast construction is widely employed in tall buildings within urban area [1,2]. The method statement encompasses the use of precast elements manufactured in facilities and their assembly at specific construction sites [3,4]. Fixed cranes, which function as extensive lifting equipment for assembling elements at construction sites [5], need precise positioning determined by calculations of crane height, operating radius, and permissible load [6], alongside considerations of the installation and removal procedures. The efficiency of fixed cranes significantly influences construction speed, impacting project duration and overall costs [7]. Hence, meticulous selection of the fixed crane model and its positioning is crucial [3]. In precast building construction sites, fixed cranes are selected to lift precast elements from transport trucks onto the evolving structure. The fixed load and dimensions of individual elements necessitate accurate alignment of the permissible load and allowable radius of fixed cranes with project specifications [8]. To minimize crane costs, efforts should focus on reducing their lifting load and the distances traveled during the installation of building structures [9]. In urban areas with limited construction space, stacking a substantial number of prefabricated elements is often unviable. Instead, the precast elements are transported to the sites via transport trucks and lifted directly from the trucks for installation onto the structure using the fixed crane. Therefore, it is essential to carefully consider the varying positions of the transport trucks when selecting the crane's position and model. Neglecting this aspect could lead to overestimating the fixed crane's allowable load, potentially resulting in serious accidents. Despite the incorporation of the direct lifting approach—lifting the elements directly from the transport truck to the structure—in fixed crane position analysis for precast building projects [10], this methodology falls short in accounting for dynamic transport truck parking positions, the crucial variable in fixed crane position analysis. In conventional construction practices, fixed cranes assume a vital function by facilitating the lifting of various construction materials, including formwork, steel bars, and concrete. The initial step involves determining the positioning of the crane based on the building's site, followed by strategically placing the stock yards nearby. Optimizing fixed crane positions traditionally focuses on minimizing processing duration and cost. In 1983, a scholar proposed an optimization model aimed at reducing the processing cost of the crane by determining the optimal crane position on the site [11]. Building upon continuous advancements in computer technology, Zhang et al. made significant progress by developing an optimization model for a single fixed crane, focusing on minimizing the crane's transport duration [12]. Then, the scholar team further improved this approach by incorporating stacking positions of materials as variables. They proposed a mixed integer programming model to determine both the fixed crane's position and the stocked positions of materials [13]. The scholar team introduced an optimization model for the simultaneous positioning of multiple fixed cranes and materials, considering the capacities of fixed cranes within conflicting ranges [9]. Another scholarly team proposed using mixed-integer linear programming to select the model and position of the fixed crane. This method determines which transport truck parks at an available position and matches each precast element type to its corresponding installation point [14]. However, their model still contains numerous variables and constraints that could lead to significant computational time and result in being trapped in local optimal solutions. A comprehensive optimization model concerning the selection of fixed crane models, quantities, and positions was introduced. This model incorporates a four-dimensional simulation to mitigate conflicts during fixed crane operations [15]. The working procedure in precast buildings is more intricate than in traditional ones, involving heavy and bulky elements, element rotation, positioning, and assembly assistance. Previous research, such as Lei et al.'s automated system for lifting path verification and Han et al.'s 3D simulation model for conflict mitigation, has considered the fixed crane’s jib length as a crucial factor [16,17]. Although there are similarities in fixed crane position analysis for both traditional and precast buildings, direct application is challenging due to the distinct complexities inherent in precast building projects. The permissible load of fixed cranes is a crucial factor due to the fixed load and size of precast elements. Moreover, while stock yards in traditional construction projects can vary, those in precast projects are typically fixed, posing unique challenges in crane position analysis. To enhance the efficiency of fixed cranes in precast projects, researchers have explored various methodologies. A genetic algorithms (GAs) model was proposed; however, it focused solely on one fixed crane and one transport truck position [8].

The primary objective of the study is to determine the optimal distance between the transport truck and the installation point, as well as the distance between the transport truck and the fixed crane. In this context, the positions of the transport trucks and the precast elements they carry are considered as variables. Various fixed crane positions are determined as variables for various transport truck parking points altogether.

Mathematical model devised for ascertaining the optimal positioning of fixed cranes and dynamic parking locations for transport trucks in precast building construction projects is formulated upon these conditions. Genetic algorithms (GAs) are utilized to tackle the optimization quandary, with the objective of minimizing fixed crane expenditures through the identification of the optimal crane setup, placement, and the most appropriate parking location for transport trucks. The optimization model's validation is demonstrated through illustrative case studies, serving as empirical evidence to corroborate the effectiveness and robustness of the model.

2. Model Formulation

Mathematical models have been developed to address the selection of crane models and their positioning for precast building projects during the construction phase. The objective equation is to minimize total cost of the fixed crane by determining the model, position of fixed crane and the parking position of the transport truck carried each precast element. To formulate mathematical model, we utilized information extracted from the case study project, including predetermined and limited crane positions and configurations. The height of the fixed cranes was a critical consideration to meet the building's height requirements, with adjustments made as the amount of fixed crane sections increased. Moreover, the transport truck capacity was considered to ensure the fulfillment of the construction site's requirements, recognizing the continuous transportation of elements from the factory to the construction site. Specific project-related data included comprehensive details about element demands (position, model, weight, and quantity) and the corresponding positions of installations. The operational cost of the fixed crane hinges on its model and operational duration.

In addition, this paper introduces certain assumptions. Firstly, for each lifting cycle, the fixed crane operates at a consistent rate under both full load and empty load conditions. Secondly, the maximum lifting height during each cycle corresponds to the building's height specifications. Thirdly, it is postulated that there are no conflicts among concurrently operating fixed cranes. Fourthly, the influence of element installation duration on the processing duration of the fixed crane is omitted. Lastly, it is assumed that multiple elements can be allocated for a specific transport truck parking spot. Lastly, it is assumed that multiple elements can be provided for a particular transport truck parking. A crucial operational sequence of the fixed crane involves initiating from the transport truck parking, elevating elements to the installation point, and subsequently returning from the installation point to the transport truck parking, thus facilitating the subsequent operation in this cyclical process. During a lifting cycle, the fixed crane traverses two identical distances, characterized by the first half involving the crane's movement while bearing a significant load, followed by the second half with an empty load. The exact processing rate is not exclusively dictated by the inherent speed of the fixed crane alone but also depends on the productivity of the fixed crane operator. The model calibrates the operator's productivity using a constant value, maintaining a consistent operational pace for the fixed crane regardless of load conditions. Consequently, the crane dedicates twice the duration for each hoisting task compared to a unidirectional journey. The model, structured around parameters such as the fixed crane's jib length, lifting capacity, operational efficiency, and associated selection costs, does not incorporate the crane's height as a criterion for assessment. Furthermore, once the fixed crane is selected and installed, reaching the maximum lifting height stipulations can be accomplished by augmenting the standard section of the tower. In such circumstances, as long as the lifting crane jib length and capacity prerequisites are satisfied, the fixed crane can adhere to the specifications. Nevertheless, it's worth noting that certain fixed cranes may not attain the necessary maximum lifting height stipulated by the building, which could potentially result in an incorrect model selection. In contrast to cast-in-place projects, fixed cranes involved in precast endeavors also play a vital role in the assembly of elements. Differences in assembly complexity and varying skill levels among personnel lead to distinct delay durations for the fixed crane to aid in assembly, affecting the project's advancement more than the duration needed for the fixed crane to hoist elements. Therefore, the model does not incorporate the influence of assembly duration on the fixed crane's operational duration. Because of the intermittent nature of transport truck deliveries, where elements are swiftly unloaded upon lifting and optimal position selection, the subsequent vehicle carrying the elements can pause at the spot where the previous vehicle halted. This mitigates the possibility of truck obstruction. Thus, the model posits that transport truck parking can be utilized repeatedly, enabling the delivery of multiple elements.

2.1. Fixed Crane Movements

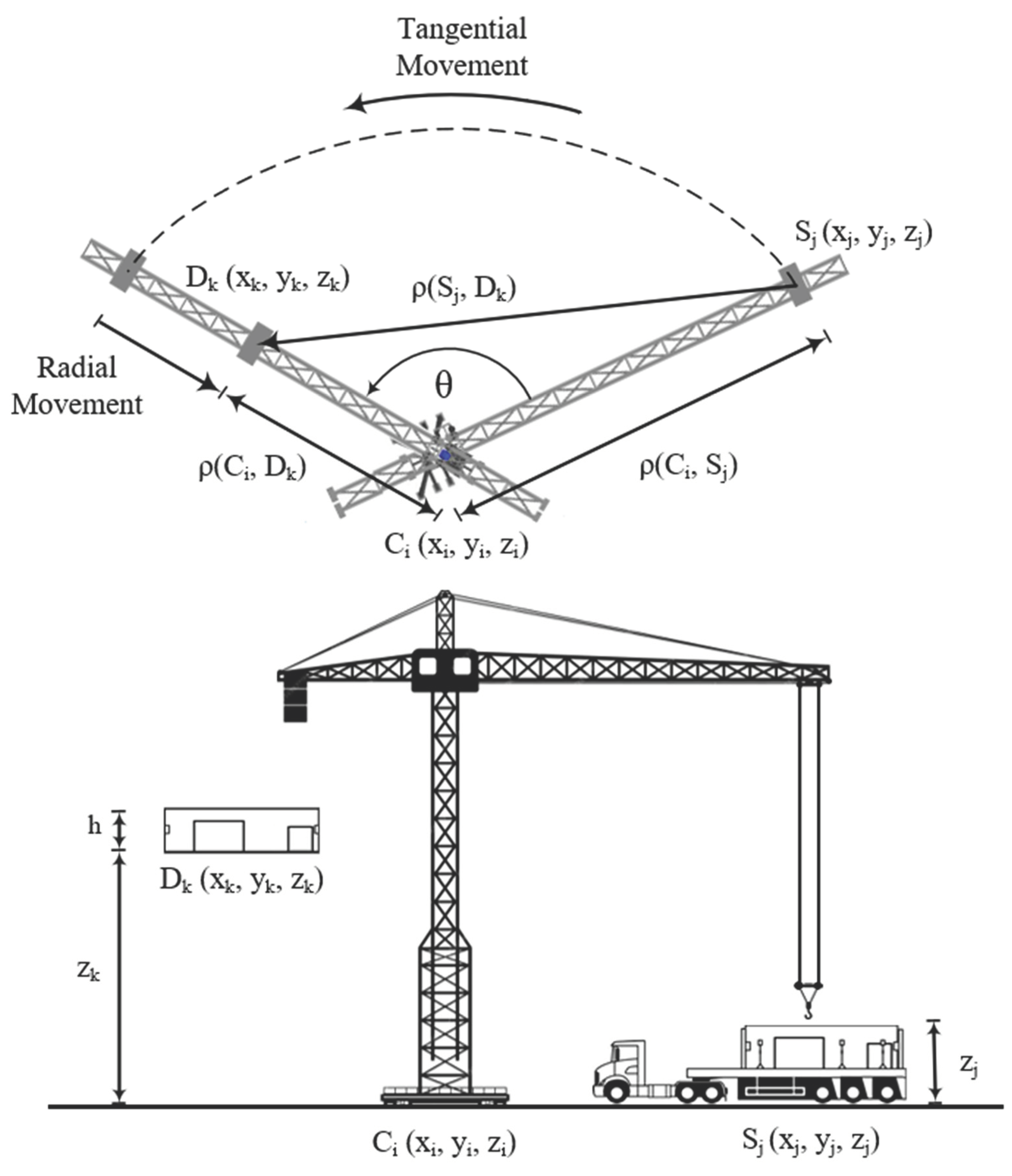
The motion of the fixed crane involves both plane and upright components. In the plane displacement, the trajectory of motion can be broken down into two components: the tangential motion of the boom and the radial motion of the hook along the boom, as illustrated in Figure 1. In Figure 1, (x_i, y_i, z_i) represents the position coordinates i of the fixed crane, (x_j, y_j, z_j) denotes the transport truck parking coordinates j of the transport truck, and (x_k, y_k, z_k) signifies the installation coordinates k.

Equations (1) to (3) denote the plane separation between the fixed crane's location, the parking spot of the transport truck, and the installation point.

ρ (C_{i,} S_{j}) = \sqrt{{(x_{i} - x_{j})}^{2} + {(y_{i} - y_{j})}^{2}}

(1)

ρ (C_{i,} D_{k}) = \sqrt{{(x_{i} - x_{k})}^{2} + {(y_{i} - y_{k})}^{2}}

(2)

ρ (S_{j,} D_{k}) = \sqrt{{(x_{j} - x_{k})}^{2} + {(y_{j} - y_{k})}^{2}}

(3)

Equation (4) illustrates the relationship between the distances

ρ (C_{i,} S_{j})

ρ (C_{i,} D_{k})

ρ (S_{j,} D_{k})

and the angle θ in accordance with the principles of trigonometry in three-dimensional space. Let

T_{(i, j, k)}^{r}

symbolize the duration required for the radial movement of the hook along the boom, while

V_{n}^{r}

denotes the speed associated with this radial motion.

{ρ (S_{j,} D_{k})}^{2} = {ρ (C_{i,} S_{j})}^{2} + {ρ (C_{i,} D_{k})}^{2} - 2 ρ (C_{i,} S_{j}) ρ (C_{i,} D_{k}) \cos θ (0 ≤ θ ≤ π)

(4)

Let

T_{(i, j, k)}^{r}

denote the duration required for the radial movement of the hook along the boom, and

V_{n}^{r}

represent the speed associated with this radial motion. The expression for

T_{(i, j, k)}^{r}

is provided by Equation (5).

T_{(i, j, k)}^{r} = \frac{|ρ (C_{i,} S_{j}) - ρ (C_{i,} D_{k})|}{V_{n}^{r}}

(5)

In 1999, an equation to depict the movements was formulated involved in calculating the processing duration of a fixed crane [12]. This study has selected this equation to represent the distance covered by the fixed crane in order to ascertain its processing duration. Additionally, we use Equation (4) to facilitate the calculation outlined in Equation (6).

T_{(i, j, k)}^{ω} = \frac{\cos^{- 1} \{({ρ (C_{i,} S_{j})}^{2} + {ρ (C_{i,} D_{k})}^{2} - {ρ (S_{j,} D_{k})}^{2}) / 2 ρ (C_{i,} S_{j}) ρ (C_{i,} D_{k})\}}{V_{n}^{ω}} (0 \leq \cos^{- 1} θ \leq π)

(6)

The synchronization of tangential and radial movements in the plane plane relies on the proficiency of the operator. To quantify this alignment, we introduce a constant value denoted as 'μ' measuring the coherence level between tangential and radial motions. The constant value 'μ' ranges from 0 to 1, wherein greater values signify superior alignment. For plane motion, if radial motion is more discrete, the plane processing duration

T_{(i, j, k)}^{h}

is longer. The expression for

T_{(i, j, k)}^{h}

is ultimately provided in Equation (7).

T_{(i, j, k)}^{h} = m a x (T_{(i, j, k)}^{r}, T_{(i, j, k)}^{ω}) + μ \cdot m i n (T_{(i, j, k)}^{r}, T_{(i, j, k)}^{ω})

(7)

Let

T_{(i, j, k)}^{v}

represent the upright movement duration of the fixed crane, and

V_{n}^{v}

represent the hook speed in the upright direction, as expressed by Equation (8).

T_{(i, j, k)}^{v} = \frac{(|z_{k} - z_{j}| + 2 h)}{V_{n}^{v}}

(8)

In addition, a discernible level of alignment arises between the plane and upright movements of the fixed crane. Introducing the constant value 'σ' to quantify this alignment, its values range from 0 to 1. A higher value of 'σ' indicates a lower level of operator proficiency, leading to more distinct plane and upright movements of the fixed crane. Therefore, the single processing duration

T_{(i, j, k)}

of the fixed crane is extended, as expressed by Equation (9).

T_{(i, j, k)} = m a x (T_{(i, j, k)}^{h}, T_{(i, j, k)}^{v}) + σ \cdot m i n (T_{(i, j, k)}^{h}, T_{(i, j, k)}^{v})

(9)

2.2. Decision Variables

The binary variable α_n indicates whether fixed crane model n is selected. The

α_{n}

value is set to one when fixed crane model n is selected; otherwise, it is set to zero, as shown in Equation (10). In the case of selecting only one model of fixed crane for installation in the construction project, the sum of binary variables from Equation (10) for all candidate models of fixed cranes is equal to one, as illustrated in Equation (11).

α_{n} = \{\begin{array}{l} 1, S e l e c t i n g t o w e r c r a n e t y p e n \\ 0, O t h e r w i s e \end{array}

(10)

\sum_{n = 1}^{N} α_{n} = 1

(11)

The binary variable

β_{(n, i)}

indicates whether the fixed crane model n is position at position i. The

β_{(i, n)}

value is one when fixed crane model n is located at position i; if not, it assumes a value of zero, as shown in Equation (12). In the case where the placement of fixed cranes is confined to a single position, the sum of binary variables from Equation (12) for all available positions where a fixed crane can be placed is equal to one, as illustrated in Equation (13).

β_{(n, i)} = \{\begin{array}{l} 1, P l a c i n g t o w e r c r a n e t y p e n a t l o c a t i o n i \\ 0, O t h e r w i s e \end{array}

(12)

The integer variable

γ_{(j, k)}

indicates whether the element at transport truck parking position j, identified by the integer index

S_{j}

is lifted and installed at installation point k, as shown in Equation (13).

γ_{(j, k)} = (S_{j}| S_{j} \in I n t e g e r)

(13)

2.3. Permissible Load of the Fixed Crane

The permissible load of a fixed crane is constrained, influenced by factors like distance and structure. Rigging and pulley weights are factored into the fixed crane lifting capacity calculation. To ensure the selected fixed crane meets permissible load, the parameter

W_{(i, j, k)}^{m a x}

is presented. It signifies the maximum permissible load of the model-n fixed crane at position i, considering the crane jib length'

L_{c}

' while transporting an element from transport truck parking j to installation point k.

W_{(i, j, k)}^{m a x}

depends on the distances between i and j (

ρ (C_{i,} S_{j})

) and i and k (

ρ (C_{i,} D_{k})

W_{(i, j, k)}

represents the weight of the element lifted by the fixed crane at position i from the transport truck parking at position j to be installed at installation point k. Additionally, constraints are imposed on the crane jib length'

L_{c}

' of the selected fixed crane, ensuring that the distances between i and j (

ρ (C_{i,} S_{j})

) and i and k (

ρ (C_{i,} D_{k})

) do not exceed the crane jib length'

L_{c}

'. To prevent exceeding the permissible load and ensure both the transport truck parking and installation point are within the crane jib length'

L_{c}

', we've introduced a penalty constant value '

p_{(i, j, k)}

'. This constant value is assigned a high or infinity value in case of conflicts, and it is multiplied with the objective equation to reduce the fitness value, as shown in Equation (14).

p_{(i, j, k)} = \{\begin{array}{l} \infty, W_{(i, j, k)} > W_{(i, j, k)}^{m a x} o r ρ (C_{i,} S_{j}) o r > L_{c} \\ 0, o t h e r w i s e \end{array}

(14)

2.4. Objective Equation

The objective equation, as presented in Equation (16), serves as a representation of the total processing cost (TC) involved in lifting elements from the transport truck parking to the installation point using a fixed crane within a feasible solution.

T_{(i, j, k)}

from Equation (9) encapsulates the comprehensive duration spent during a single fixed crane operation, encompassing the duration required for lifting the element from the transport truck parking position to the installation. Additionally, the duration for the fixed crane to return to the next transport truck parking position, facilitating subsequent lifting operations, is also denoted as

T_{(i, j, k)}

C_{n}

is a representation of the operating cost specific to fixed crane model 'n'. Equation (15) further integrates the penalty value from Equation (14) through multiplication. This integration serves to adjust the total processing cost (TC) in instances where conflicts arise with the capacity constraints on the selected fixed crane, encompassing both maximum permissible load and crane jib length. The resulting adjustment directly impacts the fitness value of the solution, leading to a reduction when conflicts occur.

T C = \sum_{n = 1}^{N} \sum_{i = 1}^{I} \sum_{j = 1}^{J} \sum_{k = 1}^{K} p_{(i, j, k)} (2 \cdot T_{(i, j, k)}) C_{n}

(15)

2.5. Genetic Algorithm

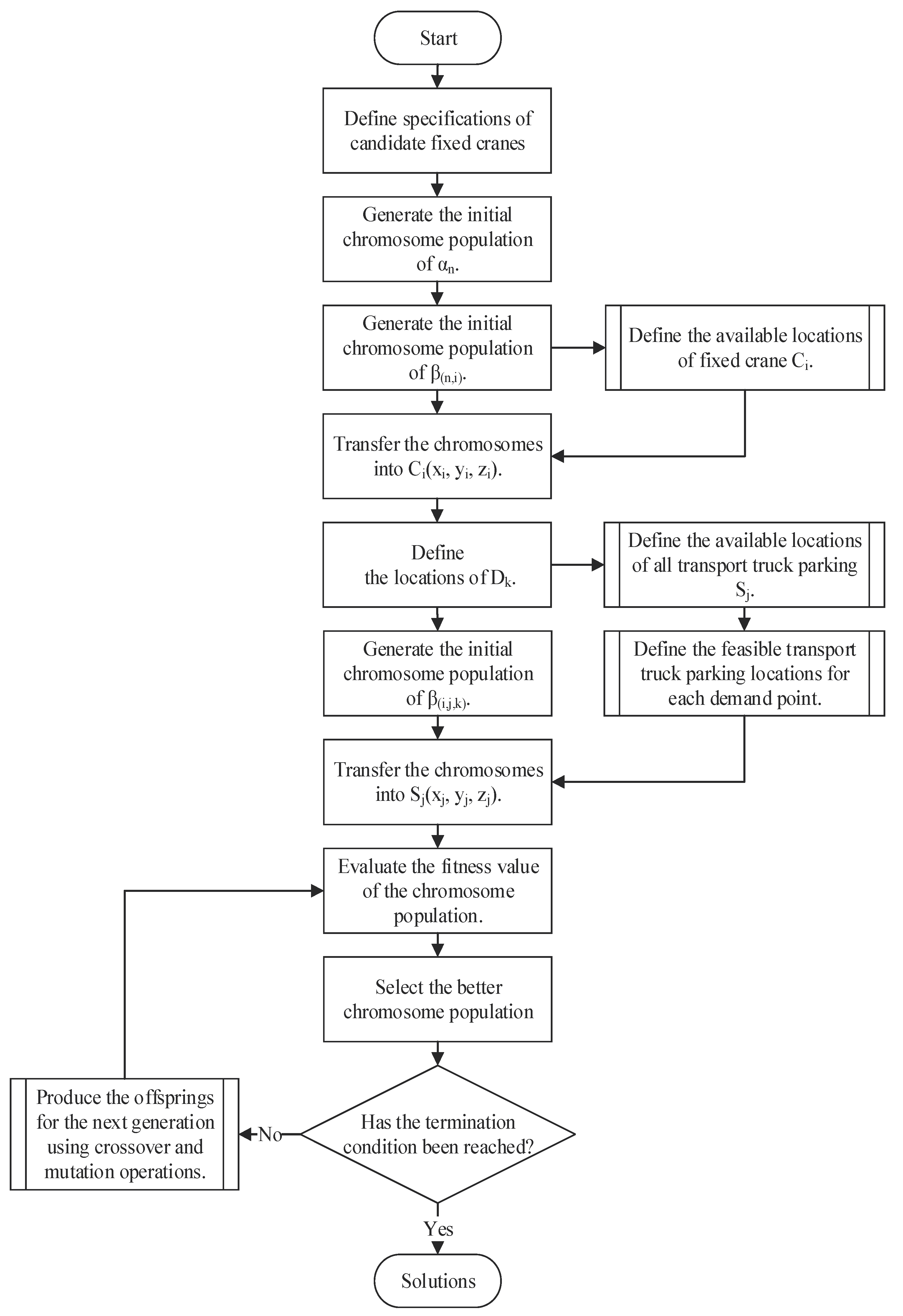
As shown in Figure 2, the genetic algorithm begins by defining the specifications of candidate fixed cranes. Subsequently, a set of fixed cranes is selected from the candidates by generating the initial chromosome population. Subsequently, the available positions for fixed cranes, demand points, and transport truck parking positions are determined by specifying their three-dimensional coordinates. The chromosome population is then generated, with each one mapped to various position points, including fixed crane positions, transport truck parking positions for each installation. The fitness value of the first generation is calculated using the defined fitness equation. The reproductions are applied to improve the chromosomes using crossover and mutation, resulting in the creation of new offspring. This iterative process continues until a termination condition is satisfied, typically defined as the absence of any further change or enhancement in the fitness value over a predetermined number of iterations, such as 5,000 attempts.

1. Generate chromosomes for the fixed crane selection, i.e., random numbers

α_{1}

α_{2}

α_{3}

,…,

α_{n}

\in

(0, 1), as shown in Figure 3.

2. Define coordinates of the available positions of fixed crane C₁(x₁, y₁, z₁), C₂(x₂, y₂, z₂) …, C_i(x_i, y_i, z_i).

3. Generate chromosomes for the fixed crane position, i.e., random numbers

β_{(n, 1)}

β_{(n, 2)}

β_{(n, 3)}

,…,

β_{(n, i)}

\in

(0, 1), as shown in Figure 4.

4. Transfer chromosomes for the feasible fixed crane positions into C_i(x_i, y_i, z_i).

5. Define coordinates of the installations D₁(x₁, y₁, z₁), D₂(x₂, y₂, z₂) …, D_k(x_k, y_k, z_k).

6. Define the coordinates of available transport truck parking position S₁(x₁, y₁, z₁), S₂(x₂, y₂, z₂), …, S_k(x_k, y_k, z_k)

7. Generate chromosomes for the feasible transport truck parking position for each installation, i.e., random numbers

γ_{(j, 1)}

γ_{(j, 2)}

γ_{(j, 3)}

,…,

γ_{(j, k)}

∈ Integers, as shown in Figure 5.

8. Transfer chromosomes for the feasible transport truck parking position for each installation pointinto S_j(x_j, y_j, z_j).

9. Evaluate the fitness value of the chromosome population, which will vary inversely with the objective value at position 'p,' as shown in Equation (16).

{F i t n e s s V a l u e}_{p} = \frac{1}{{T C}_{p}}

(16)

10. Crossover and mutation takes place.

11. Repeat the process until the termination condition has been reached.

12. Optimal solution is found.

3. Application with Case Study

The case study project is situated in Bangkok, Thailand. It features a high-rise precast residential building with usable area of 300,000 m² and construction space of approximately 15,000 m², as depicted in Figure 6.

The building rises to 30 stories, reaching a total height of 87 meters, and spans a width of 50 meters with a depth of 20 meters. The primary precast elements include facades, walls, and staircases, totaling 45 different models of elements. The required amount for each model of element and the weight of each element for the building are presented in Table 1.

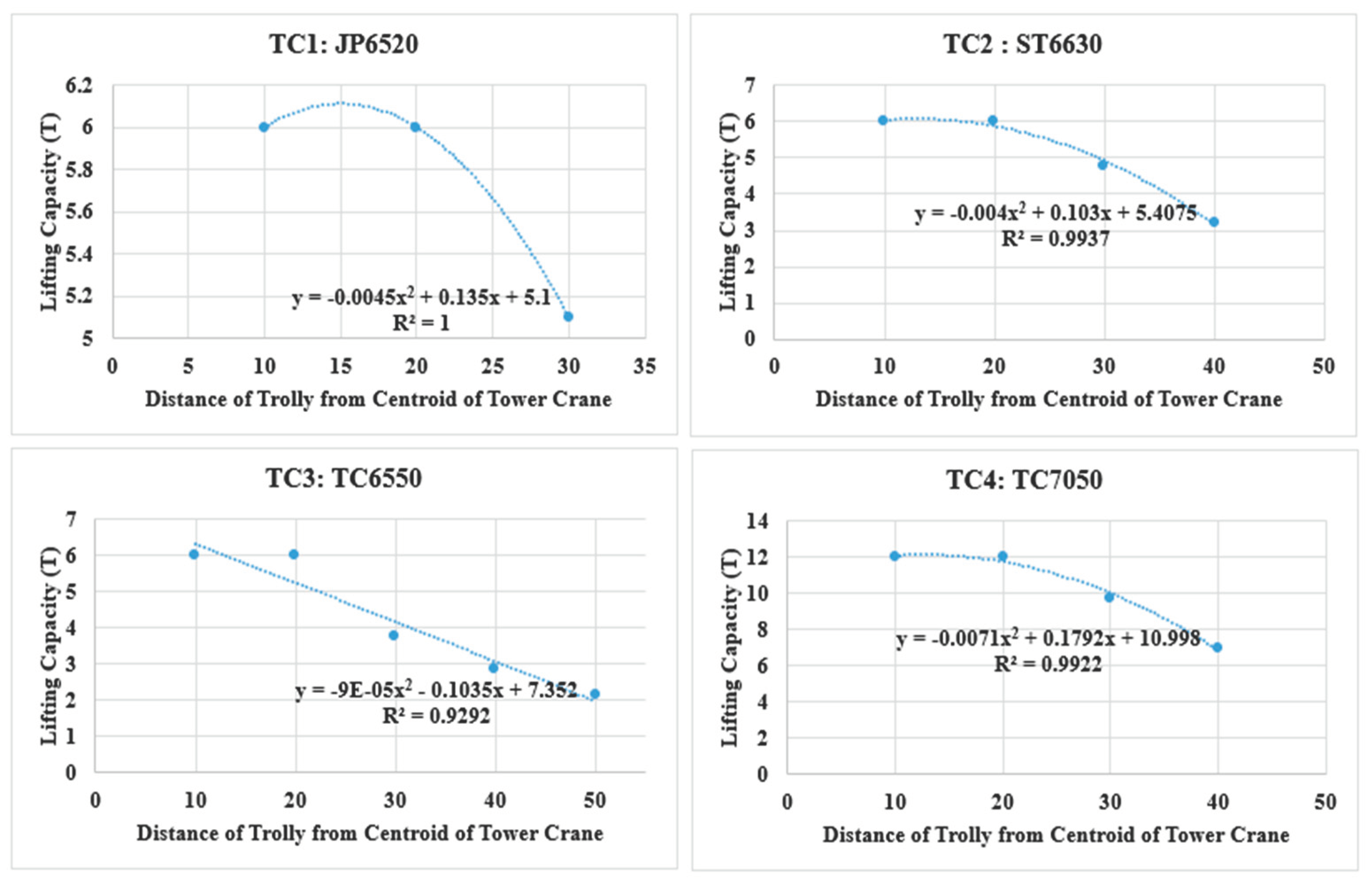
The fixed cranes in this construction site play a crucial role in both the upright and plane motion of various precast elements. Four candidate fixed cranes—JP6520, ST6630, TC6550, and TC7050—have been identified and are detailed in Table 2. The jib length for each fixed crane model remains fixed in this study, if the lifting height adequately meets the height of building. The fixed crane cost is directly associated with the model and processing duration. With predetermined jib lengths, information regarding the permissible load of each fixed crane at specified distances (refer to Table 2) and the fixed crane productivity rates (refer to Table 2) can be obtained from fixed crane specification received by the rental suppliers. Through correlation analysis, the permissible load equation for the candidate fixed crane can be derived, as illustrated in Figure 7.

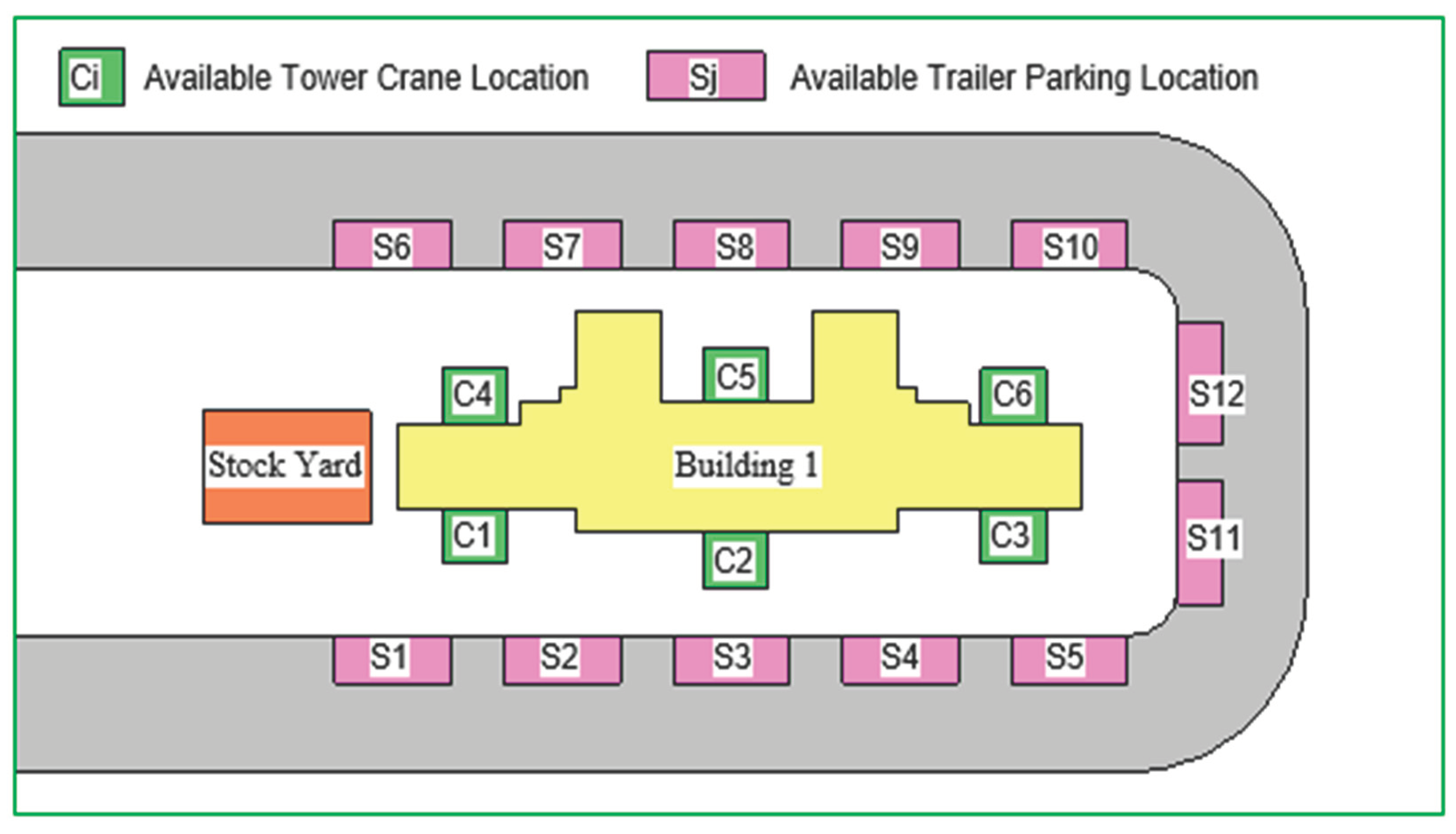
The project case study revealed of 6 available fixed crane positions. These fixed crane positions were represented by coordinate points. The specific coordinates of these available positions are detailed in Table 3. Temporary pavement has been designated for the precast buildings, serving as entrances and exits for transport trucks. All available transport truck parking positions are situated along the left side of the pavement to prevent obstruction of the pavement due to the transport truck parking. Each transport truck parking is strategically spaced to allow ample room for transport trucks to enter and exit. To ensure enough parking points for transport trucks, 12 available transport truck parking positions were established in the project, and the coordinates of these transport truck parking points are presented in Table 3.

4. Results and Discussion

Before deciding to directly lift precast elements from the transport truck for installation at various installations on the building, the project manager plans the arrangement of precast elements at a fixed stock yard. Subsequently, the fixed crane is then utilized to lift and install them. The position of a fixed stock yard for precast elements is illustrated in Figure 6, and its coordinate is shown in Table 3.

In the genetic algorithm (GA), each generation's population size is set at 100. The GA runs for 5,000 generations with a 0.1 mutation rate and a one-point crossover using a randomly determined crossover point. To automate data computation in the project case study, utilizing the mathematical model and GA, the solution is implemented through Visual Basic for Applications (VBA), yielding results presented in Table 4. 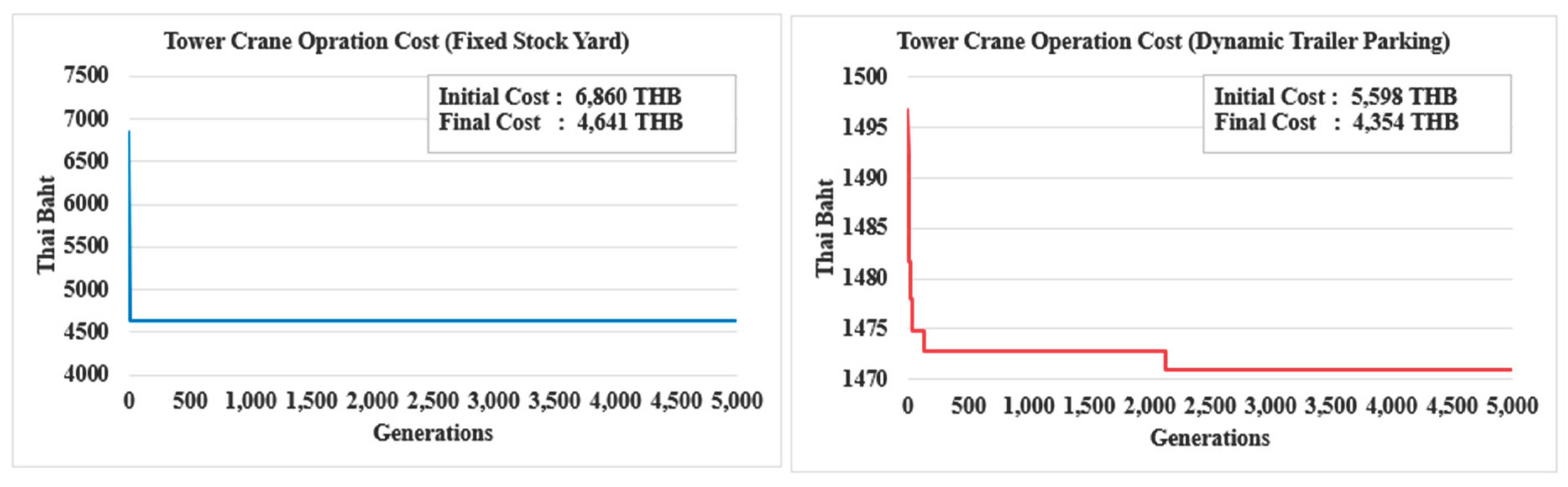Table 4 displays optimal fixed crane positions, selected models, and transport truck parking positions for each installation. It also reflects the project manager's choice between temporarily stocking precast elements at a fixed yard or lifting them directly from the transport truck. The GA demonstrates an approximate 1% reduction in both operational duration and cost per story from the initial to the final solution. With the building rising to 30 stories, this results in a 30% reduction in both operational duration and cost.

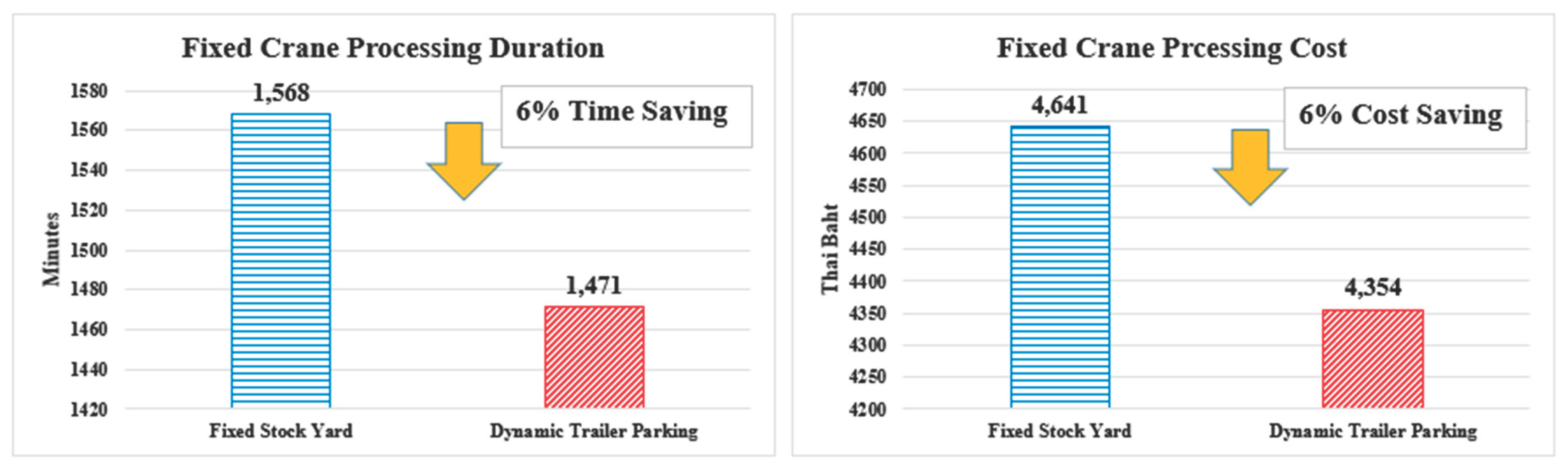
The substantial improvements in operational duration and cost by the GA are depicted in Figure 8 and Figure 9. Furthermore, the outcomes highlight that lifting precast elements directly from the transport truck, instead of the stock yard, can notably reduce operational duration and cost for the fixed crane by up to 6%, as shown in Figure 10.

5. Conclusions

Precast buildings, typically found in densely populated cities, pose challenges due to limited construction space. Construction sites often lack the capacity to store numerous prefabricated elements. While establishing a demountable stock yard on spare sites may seem like a solution, it results in resource wastage, increased on-site storage costs, and unnecessary double-handling of elements. Additionally, site constraints can compromise the optimal position of a stock yard, impacting fixed crane layout and further elevating crane workload and costs. Directly lifting elements from transport trucks to the site not only conserves space but also significantly reduces fixed crane workload, leading to cost savings.

In response to these challenges, this study proposed a Genetic Algorithm (GA) model for pre-construction fixed crane planning in high-rise building construction. The model considers the fixed crane model, crane position, and transport truck parking position with both duration and cost objectives. Key factors influencing fixed crane costs in the position analysis of precast building construction projects include the crane model and processing duration. Crane model must meet permissible load at the relevant jib length, while processing duration depends on the crane's distance from the transport truck parking and the installation.

With the installation point held constant, the study created a model to minimize the processing distance of the fixed crane, treating fixed crane and transport truck positions as variables. This model provides suggestions for crane position, model, and transport truck parking positions at the site. Comparisons between the study's model and the project manager's original planning reveal that lifting elements from transport trucks reduces the operational duration and cost of the fixed crane by 6% compared to setting up an on-site stock yard. Furthermore, the developed GA improves final solutions by reducing operational duration and cost by 30%. Experimental results affirm the model's effectiveness and validity.

This study investigates the impact of digital innovation through the utilization of the Genetic Algorithm (GA). The decision to employ the Genetic Algorithm is justified by its capacity to address specific requirements not met by alternative optimization methods, such as linear programming. Furthermore, the solution can be represented in a string format, encompassing the selection of the fixed crane's model, its position, and the parking position of the transport truck for each installation point, mirroring the chromosomes utilized in GA. Ultimately, achieving a near-optimal solution, which minimizes the processing duration of the fixed crane, is considered adequate for practical purposes.

Author Contributions

Conceptualization, S.M. and N.W.; Methodology, N.W.; Software, N.B.; Validation, N.W. and N.B.; Formal Analysis, S.M. and N.W.; Investigation, N.B.; Resources, N.W. and N.B.; Data curation, N.W. and N.B; Writing—original draft preparation, N.W. and N.B.; Writing—review and editing, S.M. and N.W.; Visualization, N.W.; Supervision, S.M.; Project administration, N.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Lawson, R.M.; Ogden, R.G.; Bergin, R. Application of Modular Construction in High-Rise Buildings. Journal of Architectural Engineering 2012, 18, 148–154. [Google Scholar] [CrossRef]
Shan, S.; Looi, D.T.-W.; Cai, Y.; Ma, P.; Chen, M.-T.; Su, R.; et al. Engineering modular integrated construction for high-rise building: A case study in Hong Kong. Proceedings of the Institution of Civil Engineers - Civil Engineering 2019, 172, 51–57. [Google Scholar] [CrossRef]
Zhang, Z.; Pan, W. Multi-criteria decision analysis for tower crane layout planning in high-rise. Automation in Construction 2021, 127, 103709. [Google Scholar] [CrossRef]
Masood, R.; Lim, J.B.; Gonzalez, V.A. Performance of the supply chains for New Zealand prefabricated. Sustainable Cities and Society 2021, 64, 102537. [Google Scholar] [CrossRef]
Kaveh, A.; Vazirinia, Y. Optimization of Tower Crane Location and Material Quantity Between Supply and Demand Points: A Comparative Study. Periodica Polytechnica Civil Engineering 2018, 62, 732–745. [Google Scholar] [CrossRef]
Nadoushani, Z.S.; Hammad, A.W.; Akbarnezhad, A. Location Optimization of Tower Crane and Allocation of Material Supply Points in a Construction Site Considering Operating and Rental Costs. Journal of Construction Engineering and Management 2018, 143, 04016089. [Google Scholar] [CrossRef]
Lu, Y.; Zhu, Y. Integrating Hoisting Efficiency into Construction Site Layout Plan Model for Prefabricated Construction. Journal of Construction Engineering and Management 2021, 147, 04021130. [Google Scholar] [CrossRef]
Hyun, H.; Park, M.; Lee, D.; Lee, J. Tower Crane Location Optimization for Heavy Unit Lifting in High-Rise Modular Construction. Buildings 2021, 11, 121. [Google Scholar] [CrossRef]
Ji, Y.; Leite, F. Optimized Planning Approach for Multiple Tower Cranes and Material Supply Points Using Mixed-Integer Programming. Journal of Construction Engineering and Management 2020, 146, 04020007. [Google Scholar] [CrossRef]
Thomas, H.R.; Ellis, R.D. Site Layout. In Construction Site Management and Labor Productivity Improvement: How to Improve the Bottom Line and Shorten the Project Schedule; Kindle, Ed.; American Society of Civil Engineers: Virginia, United States, 2017; pp. 79–87. [Google Scholar]
Rodriguez-Ramos, W.E.; Francis, R.L. Single Crane Location Optimization. Journal of Construction Engineering and Management 1983, 109, 355–482. [Google Scholar] [CrossRef]
Zhang, P.; Harris, F.C.; Olomolaiye, P.O.; Holt, G.D. Location Optimization for a Group of Tower Crane. Journal of Construction Engineering and Management 1999, 125, 69–131. [Google Scholar] [CrossRef]
Huang, C.; Wong, C.; Tam, C. Optimization of tower crane and material supply locations in a high-rise building site. Automation in Construction 2011, 20, 571–580. [Google Scholar] [CrossRef]
Zhou, C.; Dai, F.; Xiao, Z.; Liu, W. Location Optimization of Tower Cranes on High-Rise Modular Housing Projects. Buildings 2023, 13, 115. [Google Scholar] [CrossRef]
Younes, A.; Marzouk, M. Tower cranes layout planning using agent-based simulation considering. Automation in Construction 2018, 93, 348–360. [Google Scholar] [CrossRef]
Lei, Z.; Taghaddos, H.; Olearczyk, J.; Al-Hussein, M.; Hermann, U. Automated Method for Checking Crane Paths for Heavy Lifts in Industrial Projects. Journal of Construction Engineering and Management 2013, 139, 04013011. [Google Scholar] [CrossRef]
Han, S.H.; Hasan, S.; Bouferguène, A.; Al-Hussein, M.; Kosa, J. Utilization of 3D Visualization of Mobile Crane Operations for Modular Construction On-Site Assembly. Journal of Management in Engineering 2015, 31, 04014080. [Google Scholar] [CrossRef]

Figure 1. Fixed crane motions.

Figure 2. Genetic algorithm flowchart.

Figure 3. Chromosomes for selecting fixed crane model.

Figure 4. Chromosomes for the fixed crane position.

Figure 5. Chromosomes for the feasible transport truck parking position for each installation.

Figure 6. High-rise precast residential building project case study.

Figure 7. Permissible load equation of the candidate fixed crane from the correlation analysis.

Figure 8. Improvement fixed crane operational duration using genetic algorithm.

Figure 9. Improvement fixed crane operational cost using genetic algorithm.

Figure 10. Results between fixed stock yard and dynamic transport truck parking approach.

Table 1. Precast element installations for building 1 at 12^th floor.

Installation Point	Element Amount	Element Weight	Installation point Coordinates			Installation Point	Element Amount	Element Weight	Installation point Coordinates
	(pcs)	(Tones)	x	y	z		(pcs)	(Tones)	x	y	z
D1	1	3.348	27.9	53.5	34.8	D21	1	0.958	59.7	52.5	34.8
D2	1	3.348	68.7	53.5	34.8	D22	1	2.11	63.9	61.8	34.8
D3	1	2.403	30.9	53.5	34.8	D23	1	3.961	30	60.6	34.8
D4	1	2.461	48.9	52	34.8	D24	1	1.82	37.5	61	34.8
D5	1	2.461	51.6	52	34.8	D25	1	2.046	40.5	68.1	34.8
D6	1	2.304	45.3	66	34.8	D26	1	2.046	58.5	68.1	34.8
D7	1	2.304	54.3	66	34.8	D27	1	2.445	45.3	63	34.8
D8	1	2.248	27.6	55.2	34.8	D28	1	1.71	54	63	34.8
D9	1	2.304	43.5	68.1	34.8	D29	1	3.257	63	63	34.8
D10	1	2.304	55.5	68.1	34.8	D30	1	3.254	66.6	60.6	34.8
D11	1	2.736	39.9	66	34.8	D31	1	1.82	54.9	51.6	34.8
D12	1	2.736	59.7	66	34.8	D32	1	1.82	65.4	52.8	34.8
D13	1	2.736	27.6	60	34.8	D33	1	1.82	44.7	51.6	34.8
D14	1	2.736	69.9	60	34.8	D34	1	1.52	61.8	52.8	34.8
D15	1	2.67	27.6	55.8	34.8	D35	1	1.59	58.8	51.6	34.8
D16	1	2.67	69.9	57	34.8	D36	1	1.59	41.1	51.6	34.8
D17	1	2.67	69.9	54	34.8	D37	1	3.61	36	53.1	34.8
D18	1	1.347	38.1	61.2	34.8	D38	1	3.118	45	57.5	34.8
D19	1	0.98	39	63	34.8	D39	1	3.118	57	57.5	34.8
D20	1	0.958	39.9	51.6	34.8	D40	1	3.83	51	57.5	34.8

Table 2. Candidate fixed crane specification.

Model	Model	Crane jib length	Cost	Hook Lifting Speed	Boom Rotation Speed	Trolly Radial Speed	Constant value of Motion		Lifting Capacity
		(m)	(THB/min)	(m/min)	(θ/min)	(m/min)	α	β	10 m.	20 m.	30 m.	40 m.	50 m.
TC1	JP6520	30	1.48	36	0.7	30	0.2	0.7	6	6	5.1
TC2	ST6630	40	1.87	45	0.7	35	0.2	0.7	6	6	4.8	3.21
TC3	TC6550	50	2.16	40	0.7	50	0.2	0.7	6	6	3.77	2.86	2.14
TC4	TC7050	45	2.23	50	0.6	60	0.2	0.7	12	12	9.76	6.93

Table 3. Coordinates of available position of the fixed crane and the transport truck parking.

Available positions of the fixed crane				Available positions of the transport truck parking
Position	x	y	z	Position	x	y	z
C1	33	51	0	S1	27	43.5	2
C2	49.5	49.5	0	S2	37.5	43.5	2
C3	66	51	0	S3	48	43.5	2
C4	33	63.1	0	S4	57.6	43.5	2
C5	49.5	60	0	S5	67.2	43.5	2
C6	66	63.1	0	S6	27	70.5	2
				S7	37.5	70.5	2
				S8	48	70.5	2
				S9	57.6	70.5	2
				S10	67.2	70.5	2
				S11	72.4	51	2
				S12	72.4	63.1	2
				Stock Yard	25.5	55.8	0

Table 4. Genetic Algorithm Results.

Scenario	Stage	Selected Fixed crane	Selected Fixed crane Model	Selected Transport truck Parking for each Installation point Sj(DPk)	Fixed crane Operational Duration (min)	Fixed crane Operational Cost (THB)
Fixed Stock Yard	Initial Solution	TC3	TC6550	-	1,588	6,860
	Final Solution	TC1	JP6520	-	1,568	4,641
Dynamic Transport truck Parking	Initial Solution	TC2	ZTT6513	S1(DP4, DP5), S2(DP10, DP21, DP25), S3(DP16, DP22, DP23, DP34), S4(DP3, DP14, DP31), S5(DP15, DP36), S6(DP27, DP30, DP32), S7(DP1, DP6, DP18, DP26, DP29), S8(DP2, DP9, DP17, DP20), S9(DP12, DP38, DP40), S10(DP12, DP38, DP40), S11(DP7, DP8, DP11, DP13, DP19, DP24, DP28, DP35)	1,497	5,598
	Final Solution	TC1	JP6520	S1(DP5, DP20), S2(DP4, DP8, DP17, DP18, DP36, DP37, DP39), S3(DP30, DP38), S4(DP7, DP33), S5(DP35), S6(DP11, DP15, DP19), S7(DP24, DP25, DP27), S8(DP1, DP6, DP9, DP10, DP21, DP29), S9(DP12, DP23, DP28, DP31, DP32), S10(DP3, DP13, DP14, DP26), S11(DP2, DP16, DP22, DP34, DP40)	1,471	4,354

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimal Position of Fixed crane and Dynamic Transport Truck Parking in Precast Building Construction Project

Abstract

Keywords:

Subject:

1. Introduction

2. Model Formulation

2.1. Fixed Crane Movements

2.2. Decision Variables

2.3. Permissible Load of the Fixed Crane

2.4. Objective Equation

2.5. Genetic Algorithm

3. Application with Case Study

4. Results and Discussion

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe