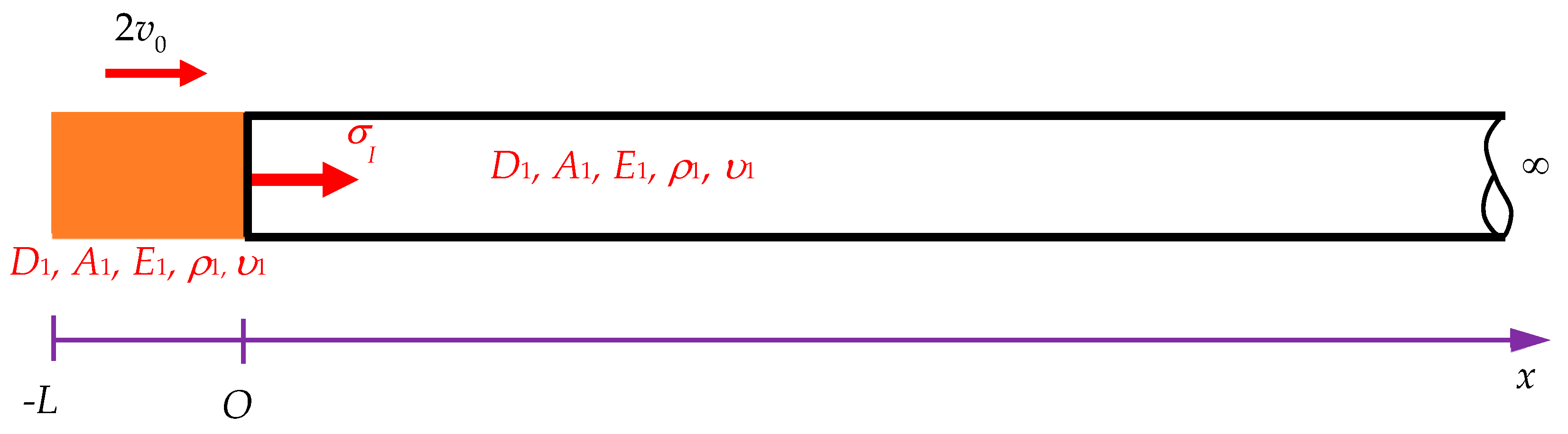1. Introduction
Stress wave propagation, particularly concerning the nondestructive testing (NDT) of structures, is an important field in engineering. The NDT method is crucial for assessing the safety, reliability, and efficiency of structures [
1,
2,
3,
4,
5] because it allows for the evaluation of structures and component integrity without causing damage. This approach is particularly vital for detecting defects or fractures in engineering structures [
6,
7,
8,
9,
10]. It is also used for structural analysis and optimization to enhance the bearing capacity of a structure [
11,
12]. The detection of the damage condition in rod-type structure elements embedded inside the medium is an important topic in the NDT field. Among the various theories introduced to understand the longitudinal wave propagation for the impact echo NDT method, Rayleigh–Love rod theory [
13] presents the closest modeling to the observed real behavior. This theory combines the effects of lateral inertia and Poisson’s ratio, often neglected in the traditional model of D’Alembert [
14]. Incorporating lateral inertia and Poisson’s ratio is crucial for analyzing longitudinal stress wave propagation in rods because it considerably affects wave behavior, as evidenced by the research provided by Yang et al. [
15,
16].
The primary goal of this research is to develop an NDT method aimed at identifying the positions of cross-sectional area changes based on forward analysis of stress wave propagation in rod. Since the exhibiting abrupt changes in cross-sectional area of a rod often indicates damage or defects in the rod type structure member. The theoretical foundation of this research is grounded in Rayleigh–Love rod theory [
13], which provides a comprehensive understanding of stress wave propagation in rod, particularly in the context of sudden cross-sectional changes. This complex theoretical approach enables a detailed analysis of the complex dynamics of wave propagation, including the critical effects of lateral inertia and Poisson’s ratio.
As depicted in
Figure 1, the model for this research is developed to determine the changing cross section
A2 and length
L1 based on stress wave propagation signals. The analysis delves into the reflection and transmission of waves in rods undergoing sudden changes in their cross-sectional area. These changes may be regarded as the main defects, such as cracks, necking, and corrosion in the rod. This aspect is crucial because the shape and intensity of stress waves are significantly affected at the discontinuity interface within a structure [
17,
18]. Previous studies [
17,
18] have documented the substantial influence of boundaries on wave behavior, particularly noting how sudden changes in cross-sectional area can modify wave propagation. However, these studies do not fully consider the specific effects of lateral inertia and Poisson’s ratio on stress wave propagation.
This research seeks to enrich the understanding of stress wave propagation in structures with abrupt cross-sectional changes by investigating the interaction between wave behavior and discontinuous cross-section areas. Moreover, the practical application of this research involves the numerical verification of an impact echo testing method. The striker rod is moved with an impact velocity of 2v0. Then, an incident wave and a contingent reflection wave are generated at the position of a cross-sectional area change. A signal is measured at a sensing site for back-calculation to determine the position and severity of a cross-sectional area change. This study aspires to advance the theoretical knowledge in the field and contribute practically to the NDT of defect assessment in rods.
2. Fundamental Theory of Stress Wave Propagation in a Rayleigh–Love Rod
This section provides the fundamental theory of stress wave propagation in a Rayleigh–Love rod, followed by the derived solution for the stress wave propagation equation in a Rayleigh–Love rod with a sudden variation in cross-sectional area.
2.1. Fundamental of Rayleigh- Love Theory
The Materials and Methods should be described with sufficient details to allow others to replicate and build on the published results.
The behavior of stress waves in a material is typically described by the wave equation. It also captures the relationship between the displacement of particles within the material and the rate at which these displacements change over time and space. This dynamic phenomenon is often attributed to the transmission of energy and momentum through the medium. The traditional wave equation for one-dimensional wave propagation in a rod is given by [
14]
where u (x, t) represents the axial (longitudinal) displacement of a point located at position x in the rod at time t, and c0 is the wave velocity without considering Poisson’s ratio effect. Herein, wave velocity is related to the mass density ρ and Young’s modulus E of the rod by using the equation .
Equation (1) provides a foundational understanding of wave propagation in rods. However, it does not fully reflect the wave behavior in rods as observed in the real world. Rayleigh and Love [
13] recognized this limitation. They conducted a study that resulted in the development of a revised wave equation that is in keeping with the dynamics of wave propagation in rods. An important feature of this modified equation is the incorporation of Poisson’s effect, an aspect that clears light on the transversal deformations during the wave’s movement. The detailed derivation of the modified wave equation presented by Rayleigh and Love [
13] is shown in
Appendix A. This derivation incorporates Poisson’s effect and provides a generalized representation of the deformation process. Applying Hooke’s law to correlate lateral strain with longitudinal stress and assuming uniaxial stress can simplify the complex relationships in the rod’s deformation. Then, the derivation utilizes the energy method, calculating the kinetic and potential energy densities to elucidate the rod’s dynamics. This step involves integrating these energy expressions over the rod’s cross section, with a focus on longitudinal and lateral displacements. A balance is established between the internal and external forces acting on the rod by employing Hamilton’s principle. Finally, an equation is derived using the variational method, accurately describing the stress wave propagation in the rod as follows
where
u is the axial displacement in the axial direction of stress wave propagation,
υ is Poisson’s ratio, and
κ is the radius of gyration of the cross section. Subject to the following boundary conditions, as shown in Eq. (A19) of
Appendix A, the stress equation can be expressed as
Various methods, such as separation of variables [
19,
20,
21], D’Alembert’s solution [
22,
23], finite difference method [
24], finite element method (FEM) [
25,
26], or Laplace transform [
27,
28,
29], can be employed to solve Eq. (2). The Laplace transform, a mathematical tool that transitions functions from the time domain to the
s-domain, offers an elegant method for simplifying and solving differential equations [
30]. When applied in wave propagation, this transform converts the original differential equation problem into an algebraic equation, making managing and solving easy. The solution is then converted back to the time domain using the inverse Laplace transform, which provides an accurate solution to the original wave propagation problem. Therefore, the Rayleigh–Love rod model, which considers the effects of lateral inertia, can be effectively solved with the Laplace transform. This analytical approach contributes to a detailed interpretation of the wave propagation dynamics and the consequential stress distribution, thereby providing substantial insights into the dynamic response of materials under stress wave propagation.
2.2. Solution of the Stress Wave Propagation Equation in a Rayleigh–Love Rod with a Sudden Cross-Sectional Area Variation
This research sets the approach based on the results of the Laplace transform method derived from Yang et al. [
16], and the exact solution for the transmitted and reflected stress waves in a Rayleigh–Love rod with a sudden cross-sectional variation is derived. Subsequently, a backward analysis method can be developed to determine the position of the changing cross section and the ratio of the reduced area to the original area, as illustrated in
Figure 1.
Yang et al. [
16] focused on building an impact model based on split Hopkinson tests. The process begins with a semi-infinite rod, known as the incident bar, being struck longitudinally by a striker bar. The traditional one-dimensional theory suggests that the resulting impact generates a rectangular pulse if both rods are composed of the same material and have identical cross-sectional areas. However, the distortions of the pulses are expected on theoretical grounds and observed during experiments. Yang et al. [
16] derived the analytical solutions for the longitudinal impact problems in dispersive rods. Their discussion focused on a situation where a semi-infinite Rayleigh–Love rod was impacted by a striker rod of length L with the same material and cross-sectional area as the Rayleigh–Love rod, as depicted in
Figure 2.
At the initial time
t = 0, a finite striker rod moving coaxially at an impact velocity of 2
v0 hits a stationary semi-infinite rod, with both rods assumed to be unstressed. Consequently, the initial conditions relating to the axial displacement
u can be expressed as follows:
The boundary conditions at the free end, where
, and at infinity are determined by
If the two rods are tightly bonded without separation following the collision, then the coupled continuity conditions at the contact surface
x = 0 can be established as
Yang et al. [
16] converted the values to dimensionless quantities for easy transformation by setting
,
,
,
,
,
, and
. The Laplace transform is employed to solve Eq. (2). The results in the
s domain are obtained as follows:
where is the displacement in the s domain.
Solving Eq. (8) with the boundary conditions can obtain the displacement function in the s domain as follows:
Utilizing an inverse Laplace transformation in Eq. (9) obtains the result in a semi-infinite rod as
The stress formula in Eq. (3) in a semi-infinite rod is determined as
From Eq. (10) and (11), Yang et al. [
16] provided the results of stress wave propagation in the semi-infinite Rayleigh–Love rod as follows:
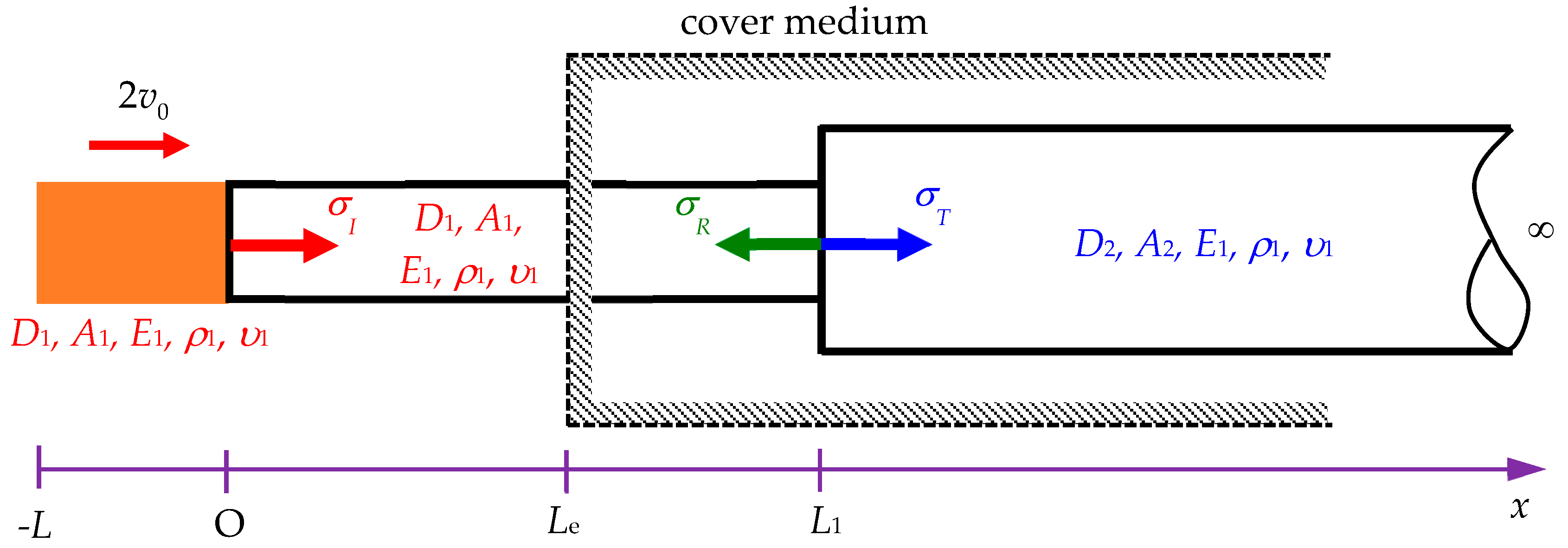
Equation (12) can efficiently present the stress wave propagation in the Rayleigh–Love rod model with a sudden cross-sectional variation, which is embedded inside a medium with x > Le. It cannot be identified from outside the structure, as depicted in
Figure 3. Interactions occur at the interface when a wave motion encounters a discontinuity in a rod. The incident wave approaches the disruption, leading to reflected and transmitted waves. The distinctiveness of the Rayleigh–Love model lies in its acute focus on the effects of lateral inertia, providing deep insights into the dynamics of wave behavior at rod discontinuities. This model, illustrated in
Figure 3, offers a comprehensive vision and theoretical representation of the problem to be investigated in this study. Converting the dimensionless quantities from Eq. (12) into dimensional quantities can simplify the analysis and obtain the following result:
where , is a variable in the contour integration of the Laplace inverse transform, ρ is the mass density, c is the longitudinal wave velocity of the elastic material, and v0 is the impact velocity.
In this study, the incident stress result is considered to determine the reflected stress
and transmitted stress
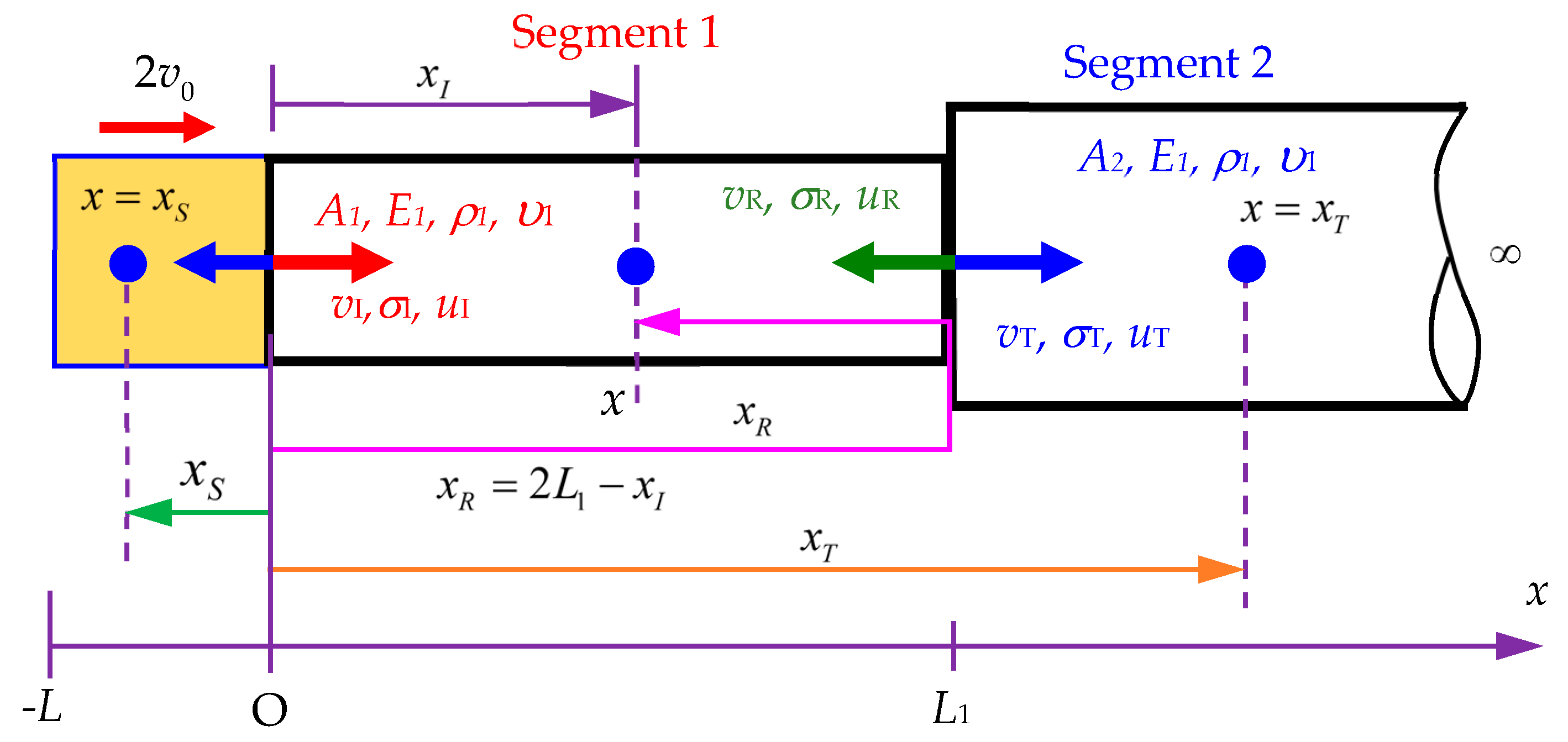
in a Rayleigh–Love rod with a sudden change in cross-sectional area under the effects of Poisson’s ratio and lateral inertia. Based on the balance of forces at the interface between two segments, the total force applied by segment 1 (from the incident and reflected waves) must be equal to the total force applied by segment 2 (from the transmitted wave), as shown in
Figure 4. Thus, the following equation is obtained:
where A1 and A2 are the cross-sectional areas of segment 1 and segment 2, respectively; σI, σR, and σT are the incident, reflected, and transmitted stresses, respectively.
Based on the continuity of velocity in
Figure 4, the velocity of the interface between the two segments must be the same, which is expressed as
The relationship between stress and velocity in the rod is shown as follows (
Appendix B):
where c is the longitudinal wave velocity of the elastic material, and v is the velocity of the material point under stress σ.
Based on Eq. (16), the velocity for incident, reflected, and transmitted waves can be, respectively, presented as
Substituting Eqs. (17) to (19) into Eq. (15) can obtain
Solving Eqs. (14) and (20) can obtain the reflected stress
and transmitted stress
as follows:
where the reflected ratio is
, and the transmitted ratio is
According to
Figure 3, the stress wave propagation
σ1 traveling along segment 1 is determined as
, where
x is the positions determined for the incident and reflected stresses (see
Figure 4).
The propagation of the transmitted stress propagation
σ2 traveling along segment 2 is determined as
, where x is the position determined for the transmitted stress.
The stress wave propagation in the striker rod is determined as follows:
, where x is the position for the determined stress wave in the striker rod.
When the Poisson’s ratio is set as zero, the incident stress, reflection stress, and transmitted stress are, respectively, expressed as follows:
The numerical integration provided by Yang et al. [
31] was utilized to obtain the stress wave propagation in a Rayleigh–Love rod to solve Eqs. (24) to (28). The process for solving Eqs. (29) to (31) can be seen in
Appendix C. The results obtained are subsequently compared with those from the FEM to verify the correctness of the proposed modeling and solving algorithm.
6. Conclusions
This paper presents a detailed study of the stress wave propagation in a Rayleigh–Love rod characterized by a sudden change in the cross-sectional area after a distance from the impacted end of the rod. Based on the analytical solution by Yang et al. [
16], the analytical solutions of the transmitted and reflected stresses in a Rayleigh–Love rod with sudden cross-section variation are obtained. This study highlights the influence of a sudden cross-sectional variation on wave behavior, triggering the reflections and transmissions at the interface of discontinuity. The role of Poisson’s effect is emphasized, shedding light on how it modulates wave behavior by generating additional waves and modulating the amplitudes of both reflected and transmitted waves.
Analyses for impact echo testing cases are also presented to identify the interface positions and cross-sectional area ratio in a Rayleigh–Love rod from the signal variations at specific positions. Examples solved by the FEM are provided to verify the correctness of the modeling and numerical algorithm to the analytical results of this study.
In addition to the forward analysis of Rayleigh–Love wave propagation in rods impacted by a striker rod, an NDT method is proposed to conduct the condition assessment of the rod type of the structure component with a sudden cross-sectional area change within a cover medium based on the measured signals at the measurable zone of the rod to be inspected.
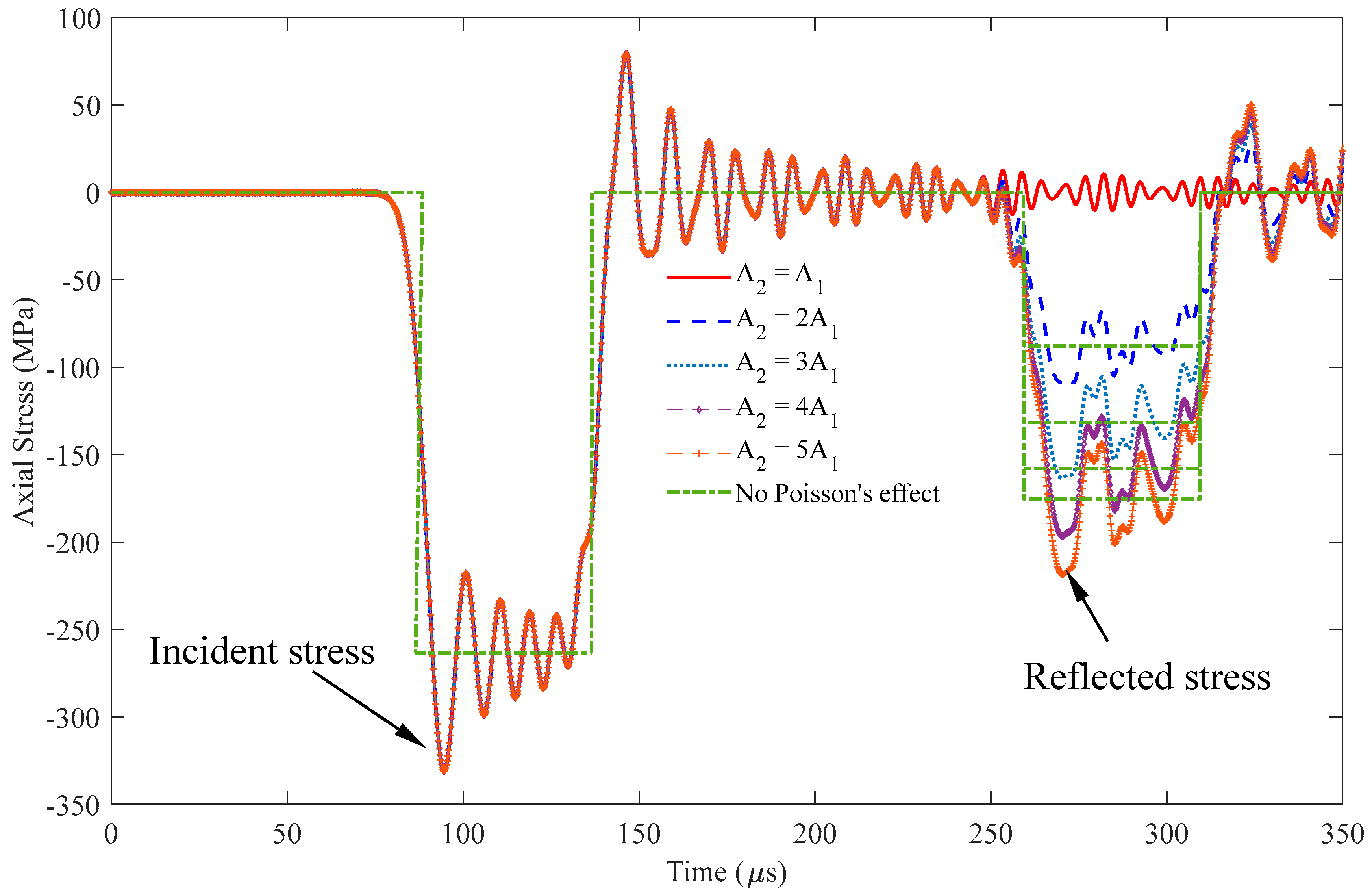
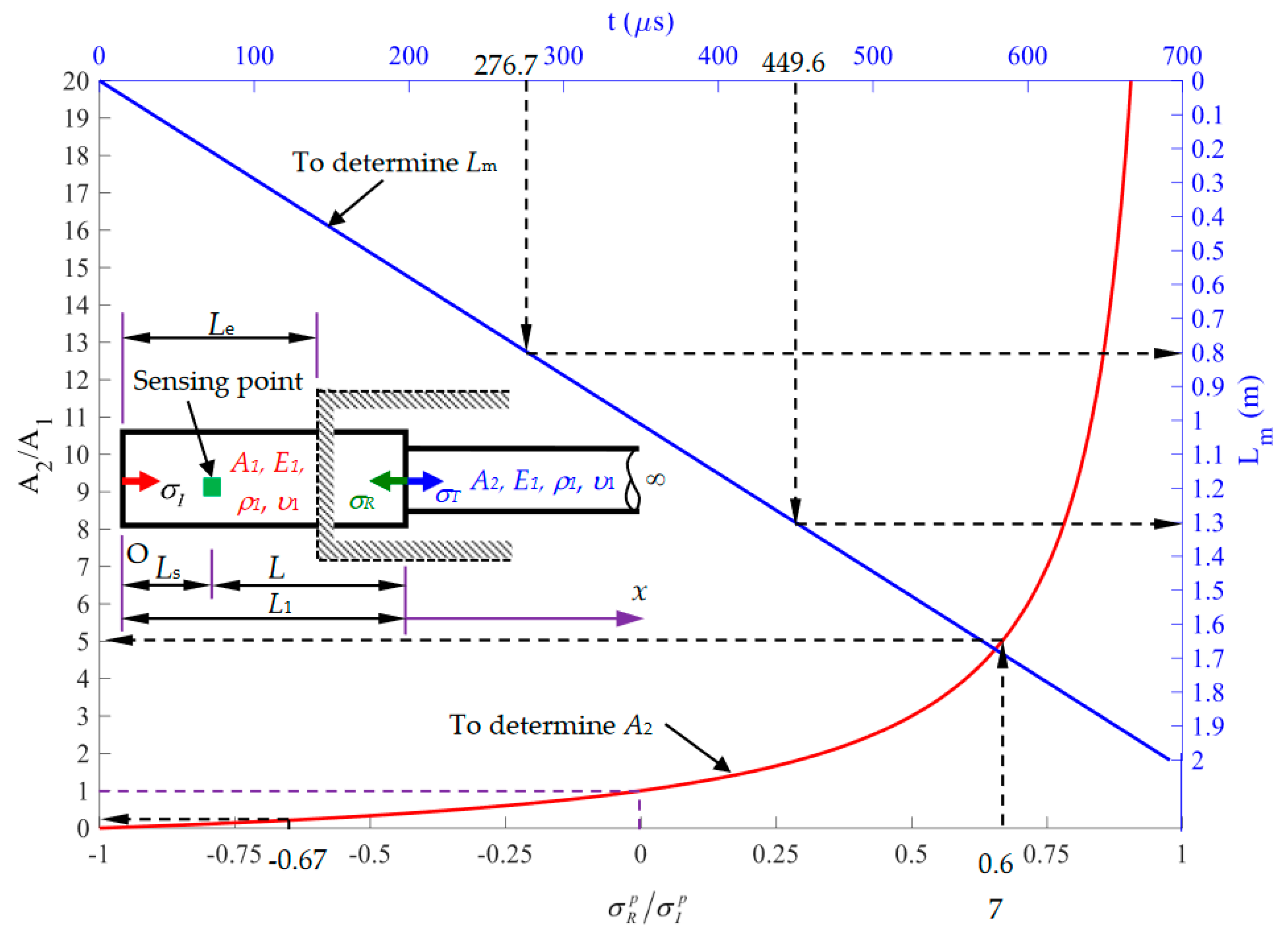
Investigation results show that when determining the cross-sectional area using the
σR/
σI ratio, the decision to consider or not consider Poisson’s ratio has little influence on the final ratio (
Figure 14). Including Poisson’s ratio leads to a similar rate of increase in amplitudes in the incident and reflected stress waves. As a result, the reflected ratio
remains nearly the same values, regardless of whether Poisson’s ratio is accounted for or not. However, in practical application, the first peak
and
values can be easily determined through measured signal, and the technique proposed in this study can be applied to conduct the nondestructive evaluation of the location and the ratio of the cross-sectional area change of a rod within a cover medium.
The condition in Example 1 is set as a rod with two segments of different cross-sectional areas, where cross-sectional area
A2 is greater than cross-sectional area
A1, as shown in
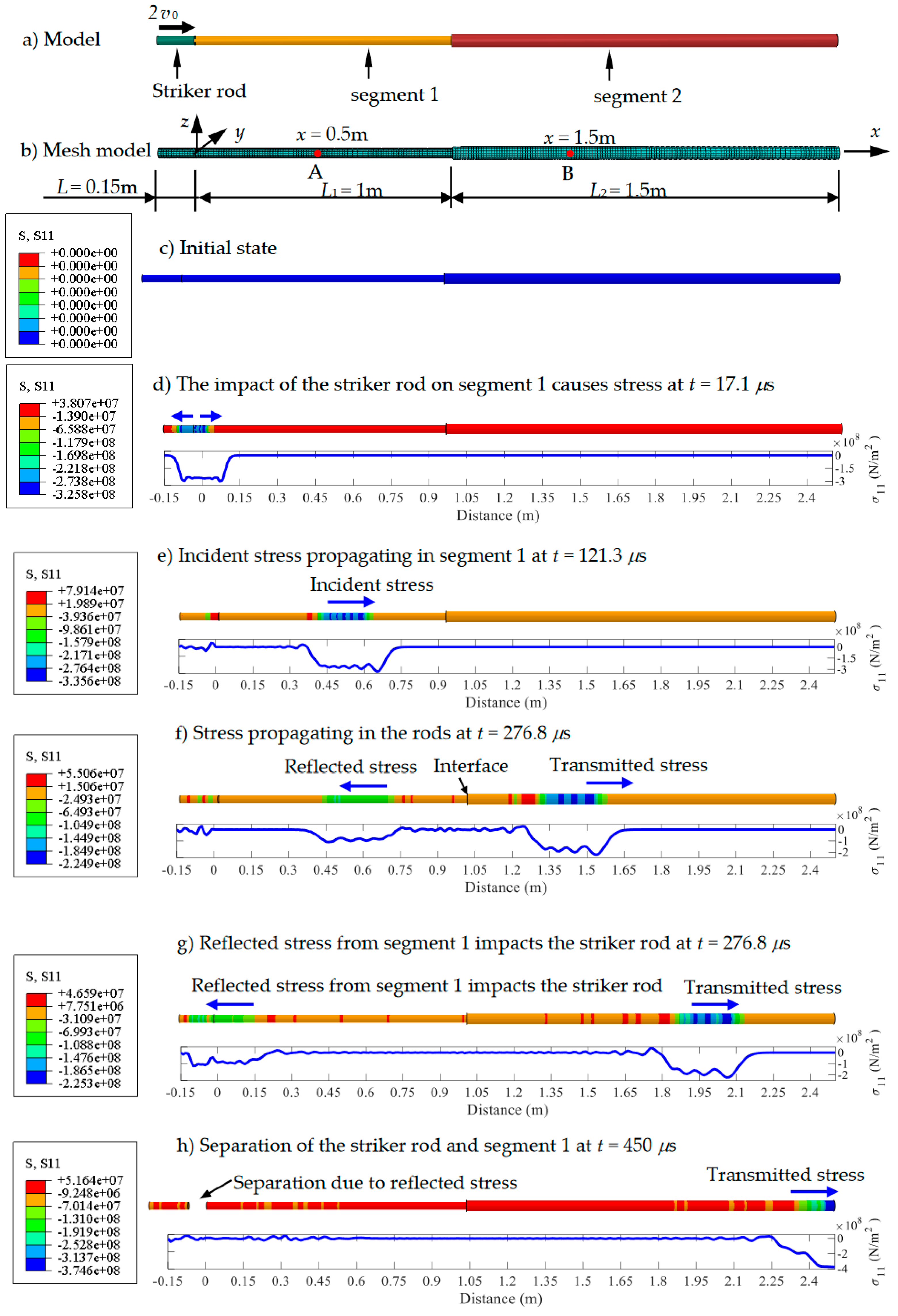
Figure 3. First, the accuracy of Eqs. (24) to (28) must be confirmed. Finding the difference between the results derived from these equations and those obtained from the FEM is necessary.
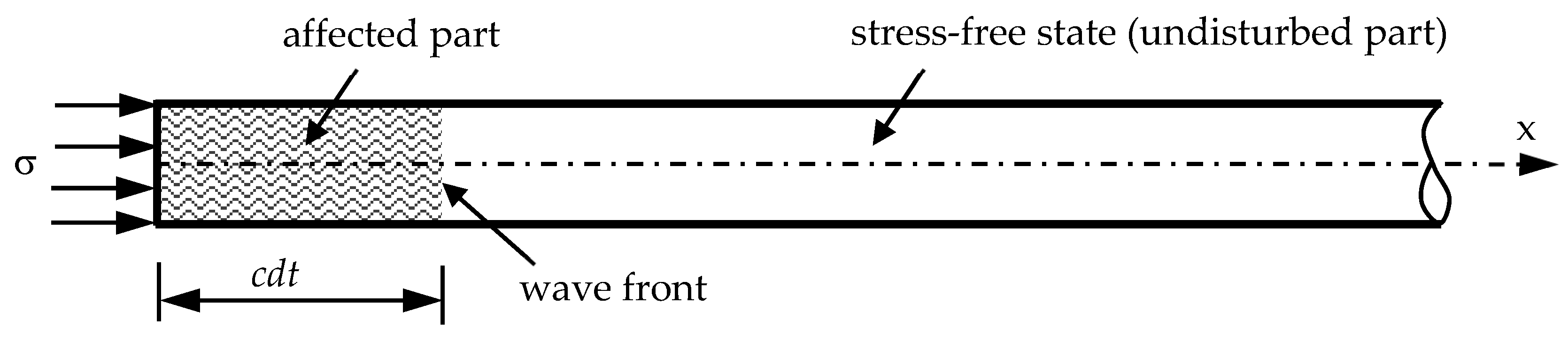
Figure 1.
Model for determining the changing cross section A2 and the length L1 embedded in a medium (x > Le) based on stress wave propagation theory. (Note: σI, σR, and σT represent the incident, reflected, and transmitted stresses, respectively; A1 and A2 are the cross-sectional areas of segments 1 and 2 of the semi-infinite rod, respectively; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the rod, respectively.)
Figure 1.
Model for determining the changing cross section A2 and the length L1 embedded in a medium (x > Le) based on stress wave propagation theory. (Note: σI, σR, and σT represent the incident, reflected, and transmitted stresses, respectively; A1 and A2 are the cross-sectional areas of segments 1 and 2 of the semi-infinite rod, respectively; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the rod, respectively.)
Figure 2.
Scheme of a semi-infinite rod under the impact of a striker rod. (Note: σI is the incident stress, D1 and A1 are the diameter and the cross-sectional area of the striker rod and the semi-infinite rod, respectively; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the two rods, respectively; 2v0 is the impact velocity, used to facilitate the application of the Laplace transform in later derivation.)
Figure 2.
Scheme of a semi-infinite rod under the impact of a striker rod. (Note: σI is the incident stress, D1 and A1 are the diameter and the cross-sectional area of the striker rod and the semi-infinite rod, respectively; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the two rods, respectively; 2v0 is the impact velocity, used to facilitate the application of the Laplace transform in later derivation.)
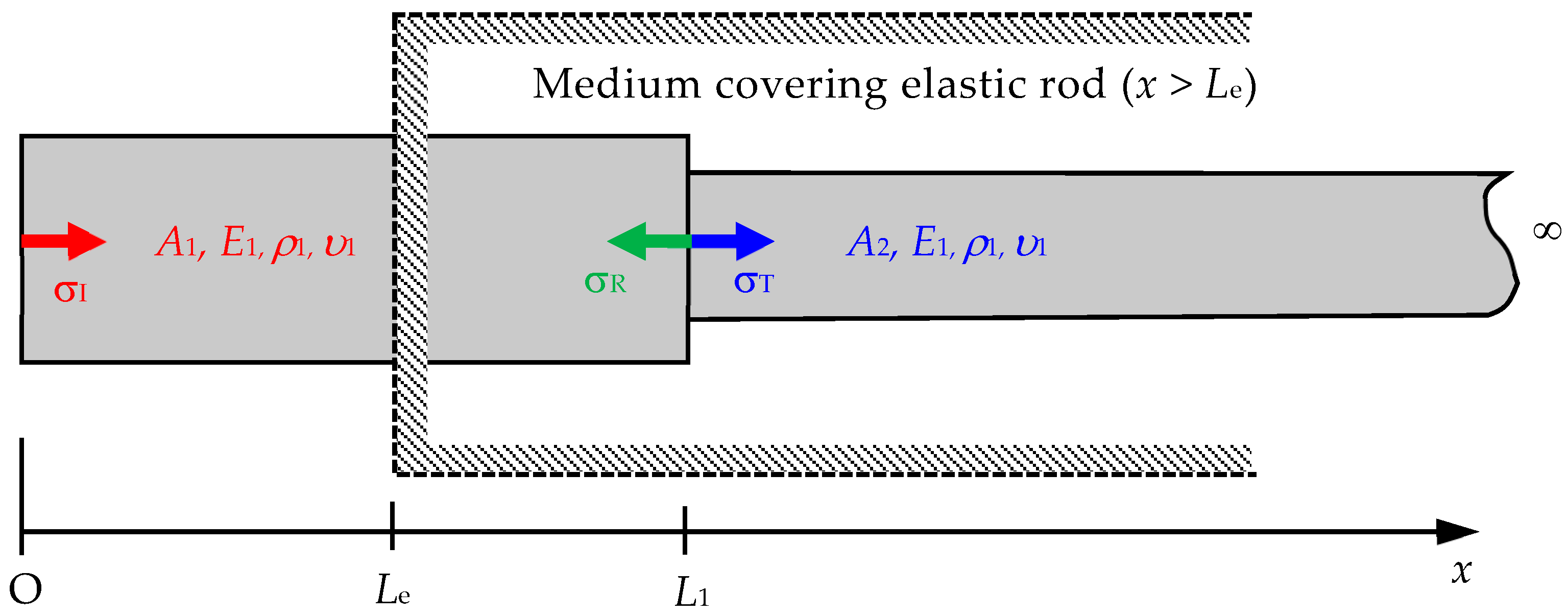
Figure 3.
Scheme of a Rayleigh–Love rod with a sudden cross-sectional area change within a cover medium of x > Le. (Note: σI, σR, and σT represent the incident, reflected, and transmitted stresses, respectively; D1 is the diameter of the striker rod and rod segment 1; D2 is the diameter of rod segment 2; A1 is the cross-sectional areas of the striker rod and rod segment 1; A2 is the cross-sectional area of rod segment 2; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the rod, respectively.)
Figure 3.
Scheme of a Rayleigh–Love rod with a sudden cross-sectional area change within a cover medium of x > Le. (Note: σI, σR, and σT represent the incident, reflected, and transmitted stresses, respectively; D1 is the diameter of the striker rod and rod segment 1; D2 is the diameter of rod segment 2; A1 is the cross-sectional areas of the striker rod and rod segment 1; A2 is the cross-sectional area of rod segment 2; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the rod, respectively.)
Figure 4.
The interface between the two segments of a Rayleigh–Love rod with the same material but different cross-sectional areas. (Note: vI, σI, and uI are the incident velocity, incident stress, and incident displacement of segment 1, respectively; vR, σR, and uR are the reflected velocity, reflected stress, and reflected displacement of segment 1, respectively; vR, σR, and uR are the transmitted velocity, transmitted stress, and transmitted displacement of segment 2, respectively; A1 and A2 are the cross-sectional areas of segment 1 and segment 2 of the semi-infinite rod, respectively; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the two rods, respectively; xI, xR and xT are the positions determined for the incident, reflected, and transmitted stresses in the semi-infinite rod, respectively; xS is the position determined stress in the striker rod).
Figure 4.
The interface between the two segments of a Rayleigh–Love rod with the same material but different cross-sectional areas. (Note: vI, σI, and uI are the incident velocity, incident stress, and incident displacement of segment 1, respectively; vR, σR, and uR are the reflected velocity, reflected stress, and reflected displacement of segment 1, respectively; vR, σR, and uR are the transmitted velocity, transmitted stress, and transmitted displacement of segment 2, respectively; A1 and A2 are the cross-sectional areas of segment 1 and segment 2 of the semi-infinite rod, respectively; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the two rods, respectively; xI, xR and xT are the positions determined for the incident, reflected, and transmitted stresses in the semi-infinite rod, respectively; xS is the position determined stress in the striker rod).
Figure 5.
Stress wave propagating in a Rayleigh–Love rod model using solid elements for cross-sectional area ratio A2/A1 = 2.
Figure 5.
Stress wave propagating in a Rayleigh–Love rod model using solid elements for cross-sectional area ratio A2/A1 = 2.
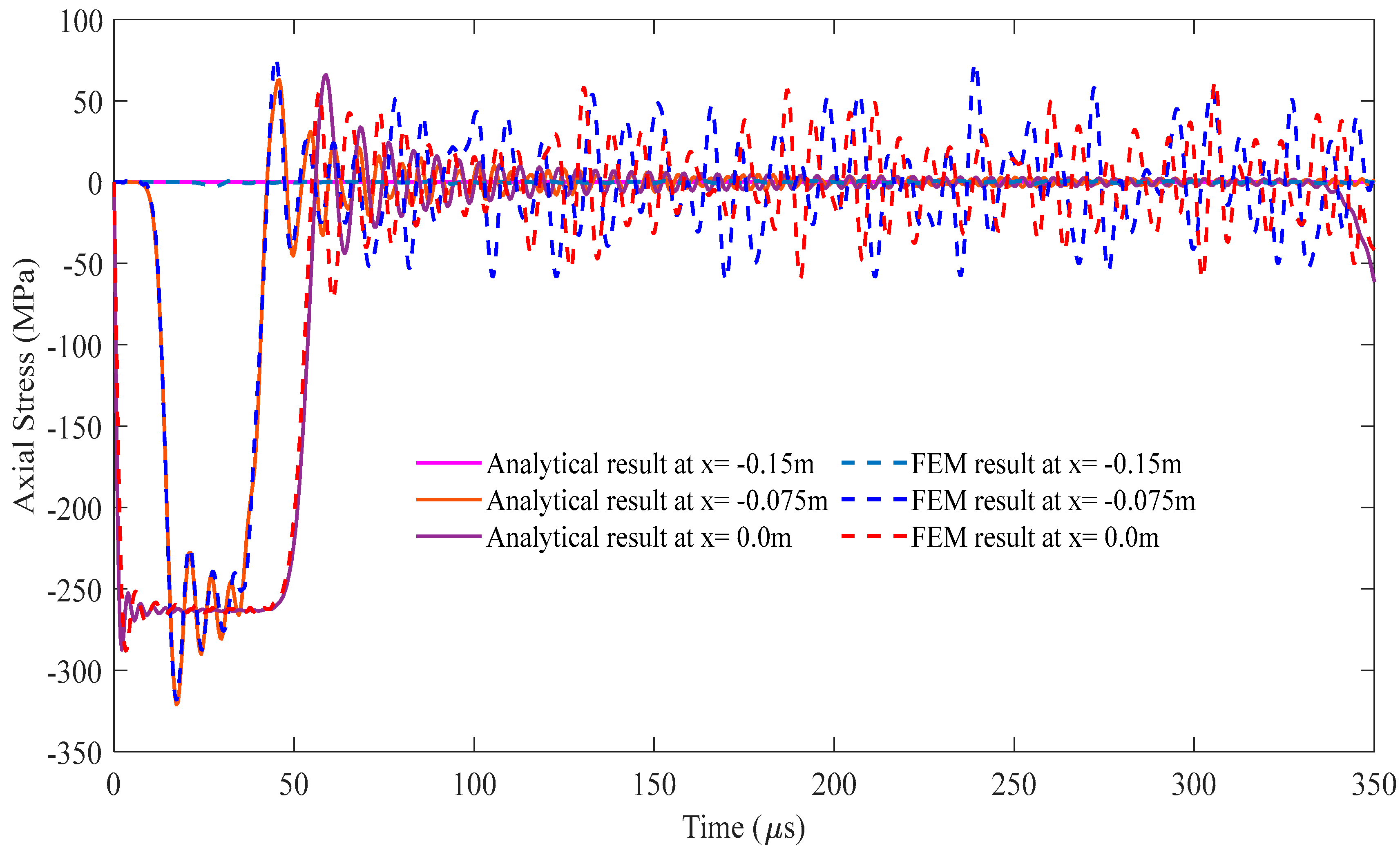
Figure 6.
Comparison of the stress wave propagation in the striker rod between the analytical solution and FEM results for the cross-sectional area ratio A2/A1 = 2.
Figure 6.
Comparison of the stress wave propagation in the striker rod between the analytical solution and FEM results for the cross-sectional area ratio A2/A1 = 2.
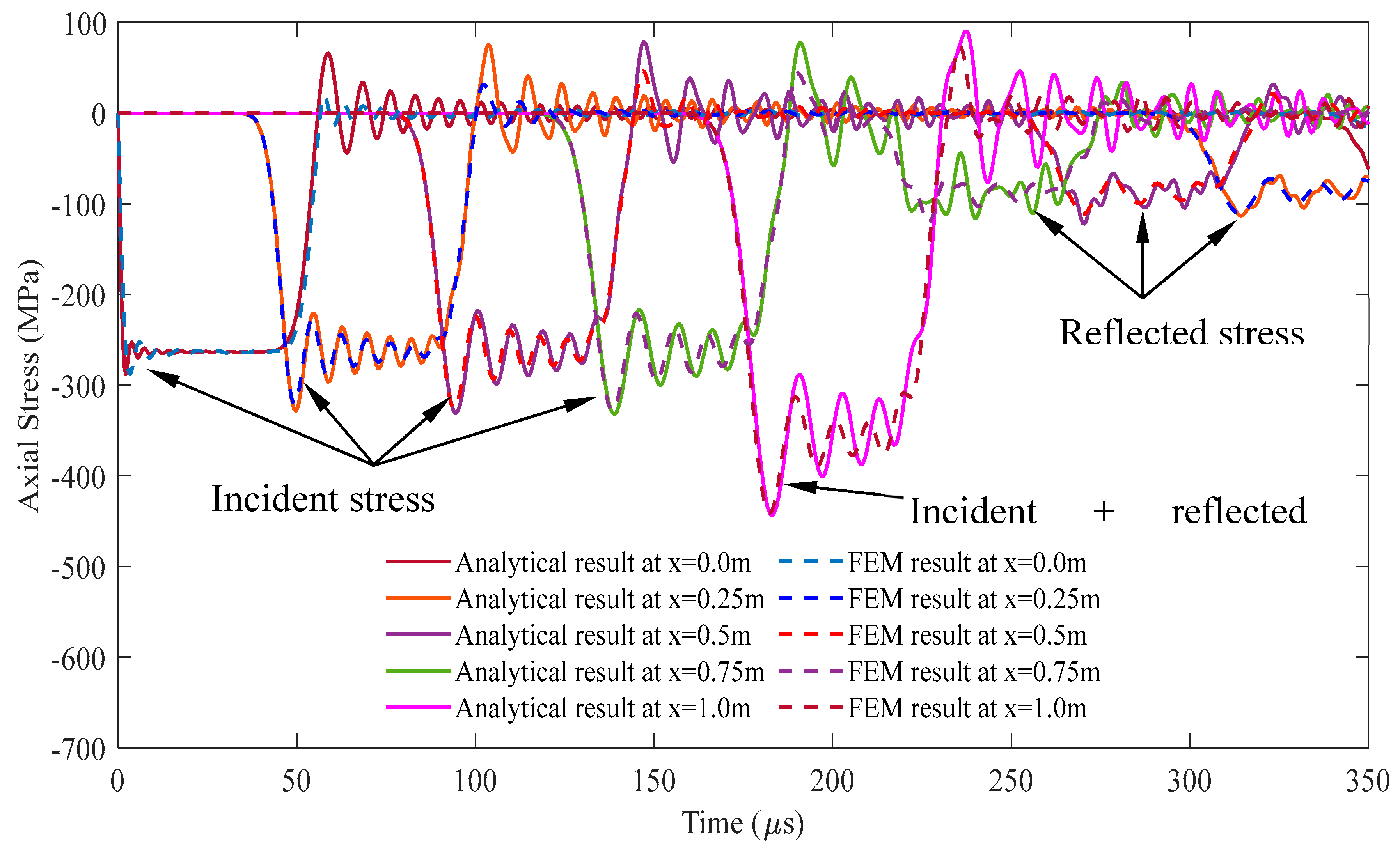
Figure 7.
Comparison of the stress wave propagation in segment 1 between the analytical solution and FEM results for the cross-sectional area ratio A2/A1 = 2.
Figure 7.
Comparison of the stress wave propagation in segment 1 between the analytical solution and FEM results for the cross-sectional area ratio A2/A1 = 2.
Figure 8.
Comparison of the stress wave propagation in segment 2 between the analytical solution and FEM results for the cross-sectional area ratio A2/A1 = 2.
Figure 8.
Comparison of the stress wave propagation in segment 2 between the analytical solution and FEM results for the cross-sectional area ratio A2/A1 = 2.
Figure 9.
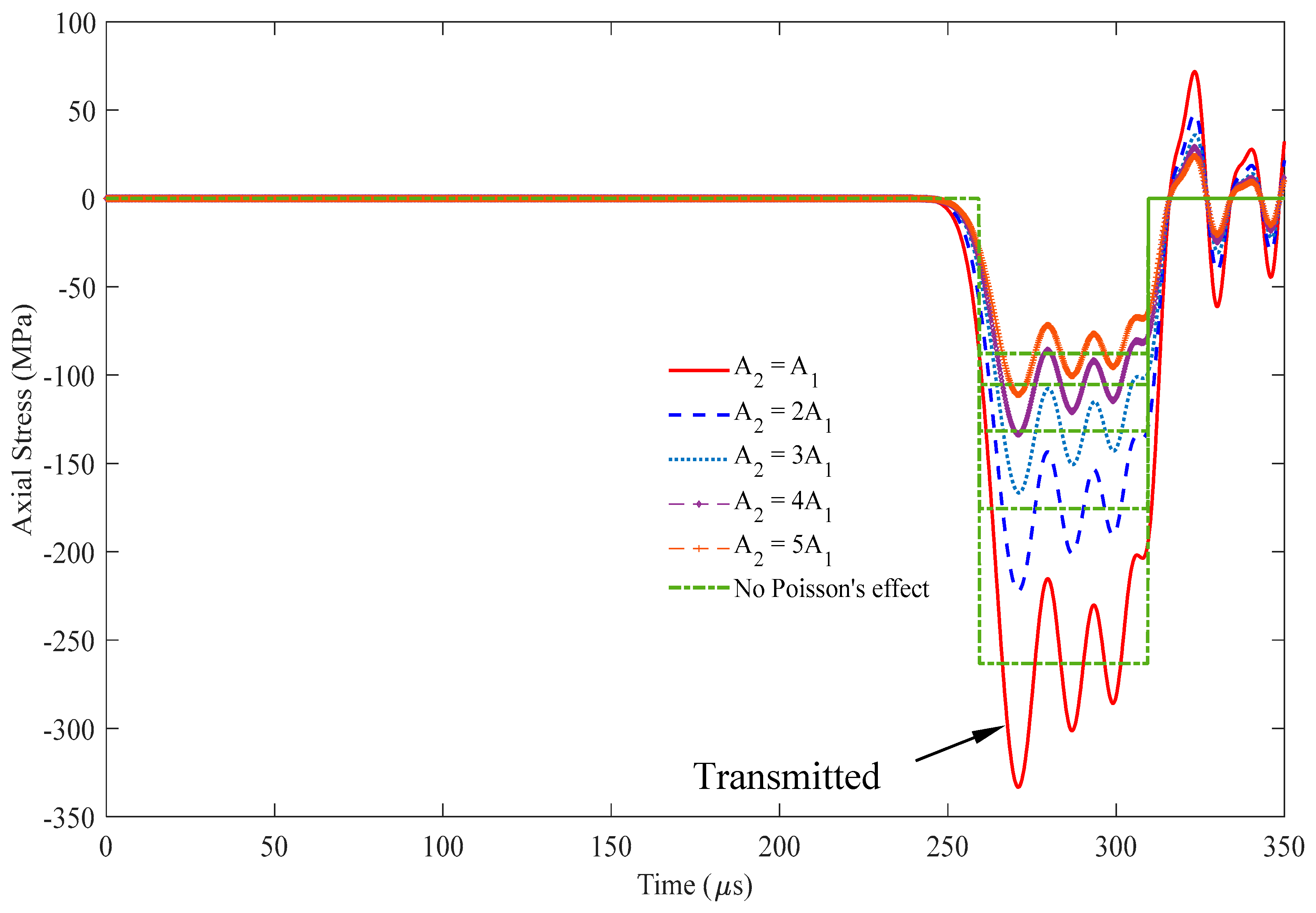
Stress wave propagation for the incident and reflected stresses in some cases of A2 ≥ A1 observed at x = 0.5 m (impact velocity 2v0 = 11.6 m/s).
Figure 9.
Stress wave propagation for the incident and reflected stresses in some cases of A2 ≥ A1 observed at x = 0.5 m (impact velocity 2v0 = 11.6 m/s).
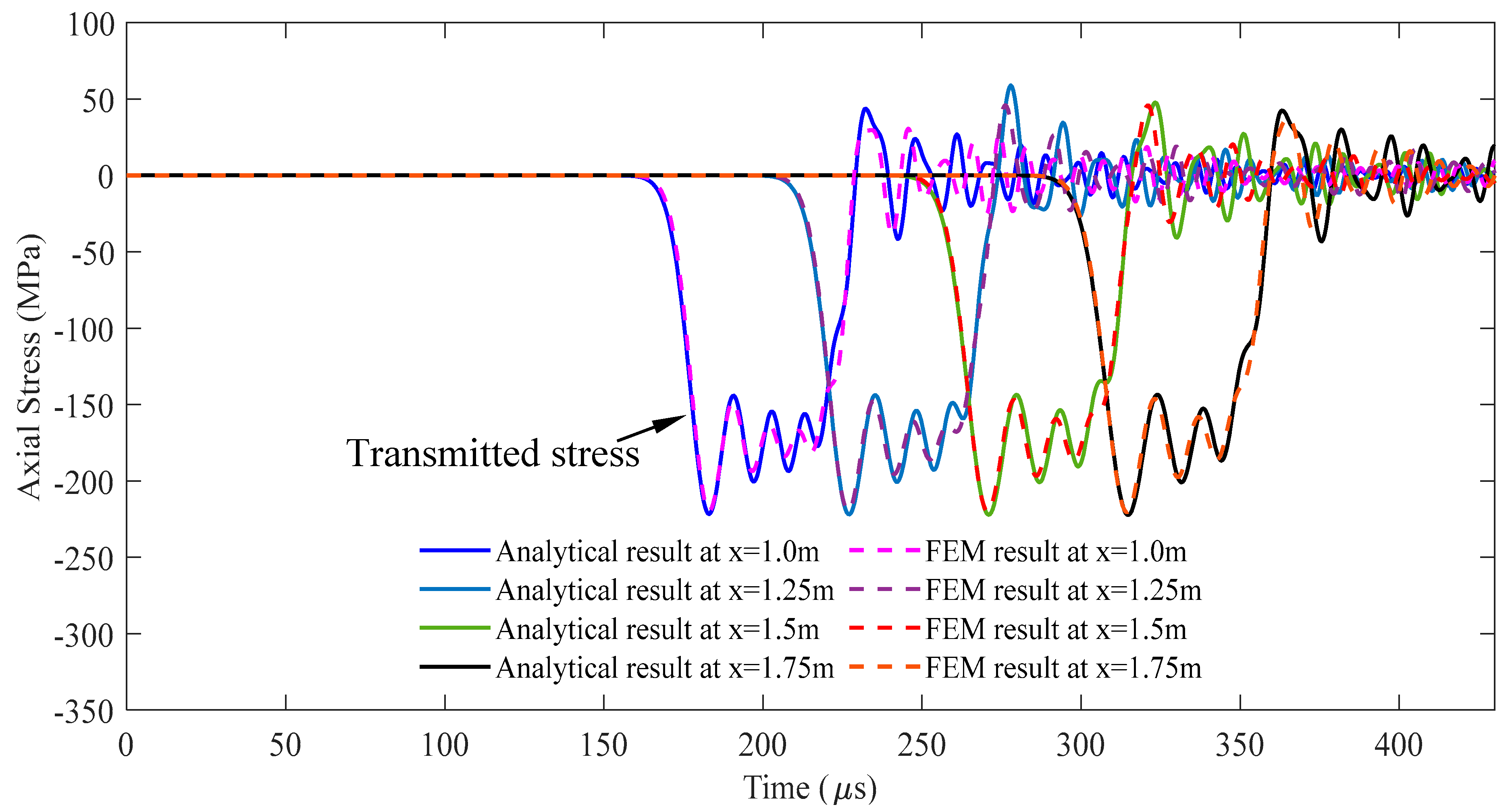
Figure 10.
Stress wave propagation for the transmitted waves in some cases of A2 ≥ A1 observed at x = 1.5 m (impact velocity 2v0 = 11.6 m/s).
Figure 10.
Stress wave propagation for the transmitted waves in some cases of A2 ≥ A1 observed at x = 1.5 m (impact velocity 2v0 = 11.6 m/s).
Figure 11.
Scheme of a Rayleigh–Love rod with a sudden cross-sectional area change from large to small embedded in a cover medium of x > Le. (Note: σI, σR, and σT represent the incident, reflected, and transmitted stresses, respectively; D1 is the diameter of the striker rod and rod segment 1; D2 is the diameter of rod segment 2; A1 is the cross-sectional areas of the striker rod and rod segment 1; A2 is the cross-sectional area of rod segment 2; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the rod, respectively.)
Figure 11.
Scheme of a Rayleigh–Love rod with a sudden cross-sectional area change from large to small embedded in a cover medium of x > Le. (Note: σI, σR, and σT represent the incident, reflected, and transmitted stresses, respectively; D1 is the diameter of the striker rod and rod segment 1; D2 is the diameter of rod segment 2; A1 is the cross-sectional areas of the striker rod and rod segment 1; A2 is the cross-sectional area of rod segment 2; E1, ρ1, and υ1 are Young’s modulus, mass density, and Poisson’s ratio of the rod, respectively.)
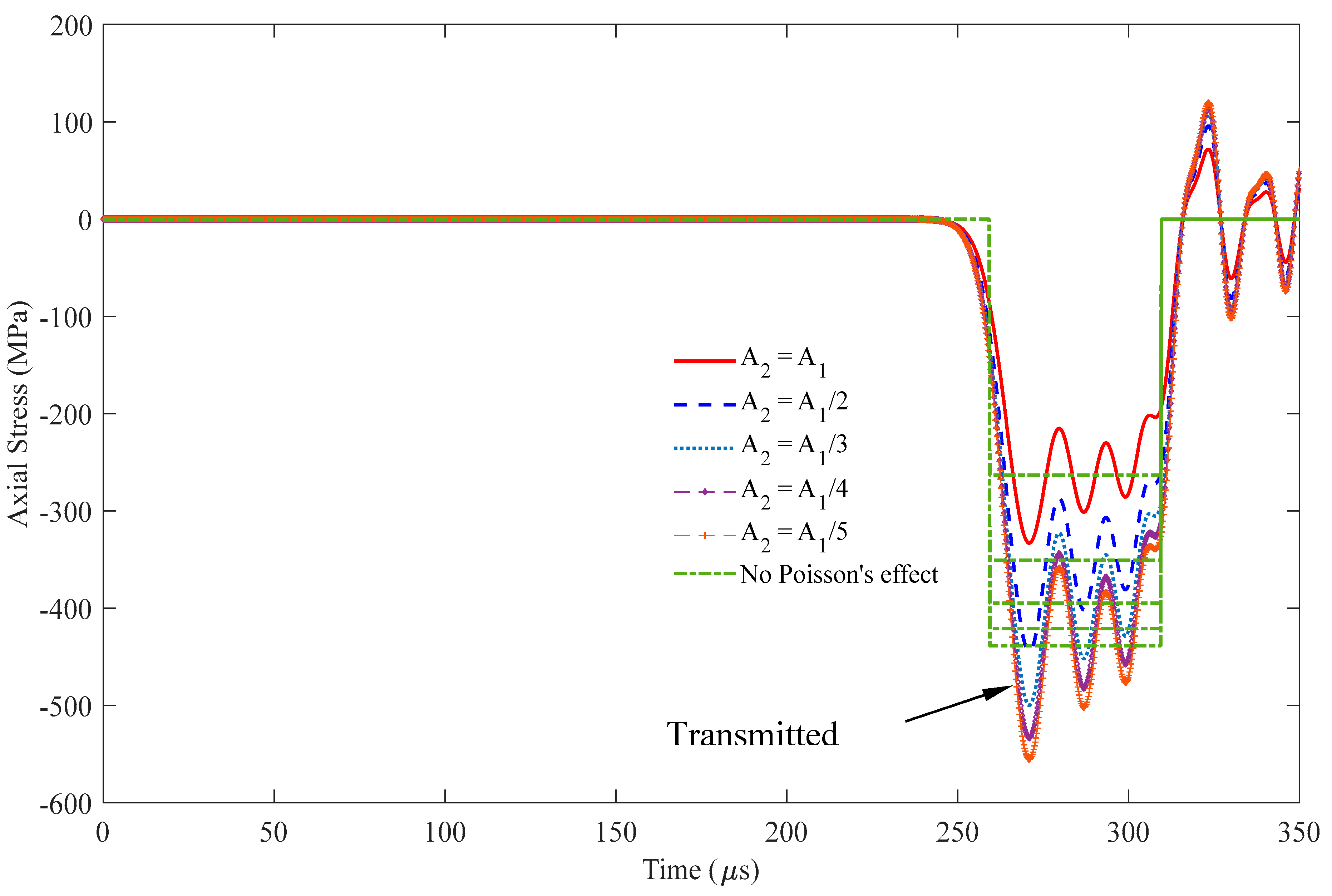
Figure 12.
Stress wave propagation for the incident and reflected waves in some cases of A2 ≤ A1 observed at x = 0.5 m (impact velocity of 2v0 = 11.6 m/s).
Figure 12.
Stress wave propagation for the incident and reflected waves in some cases of A2 ≤ A1 observed at x = 0.5 m (impact velocity of 2v0 = 11.6 m/s).
Figure 13.
Stress wave propagation for transmitted waves in some cases of A2 ≤ A1 observed at x = 1.5 m (impact velocity of 2v0 = 11.6 m/s).
Figure 13.
Stress wave propagation for transmitted waves in some cases of A2 ≤ A1 observed at x = 1.5 m (impact velocity of 2v0 = 11.6 m/s).
Figure 14.
Diagram for determining the length Lm and cross-sectional area A2.
Figure 14.
Diagram for determining the length Lm and cross-sectional area A2.
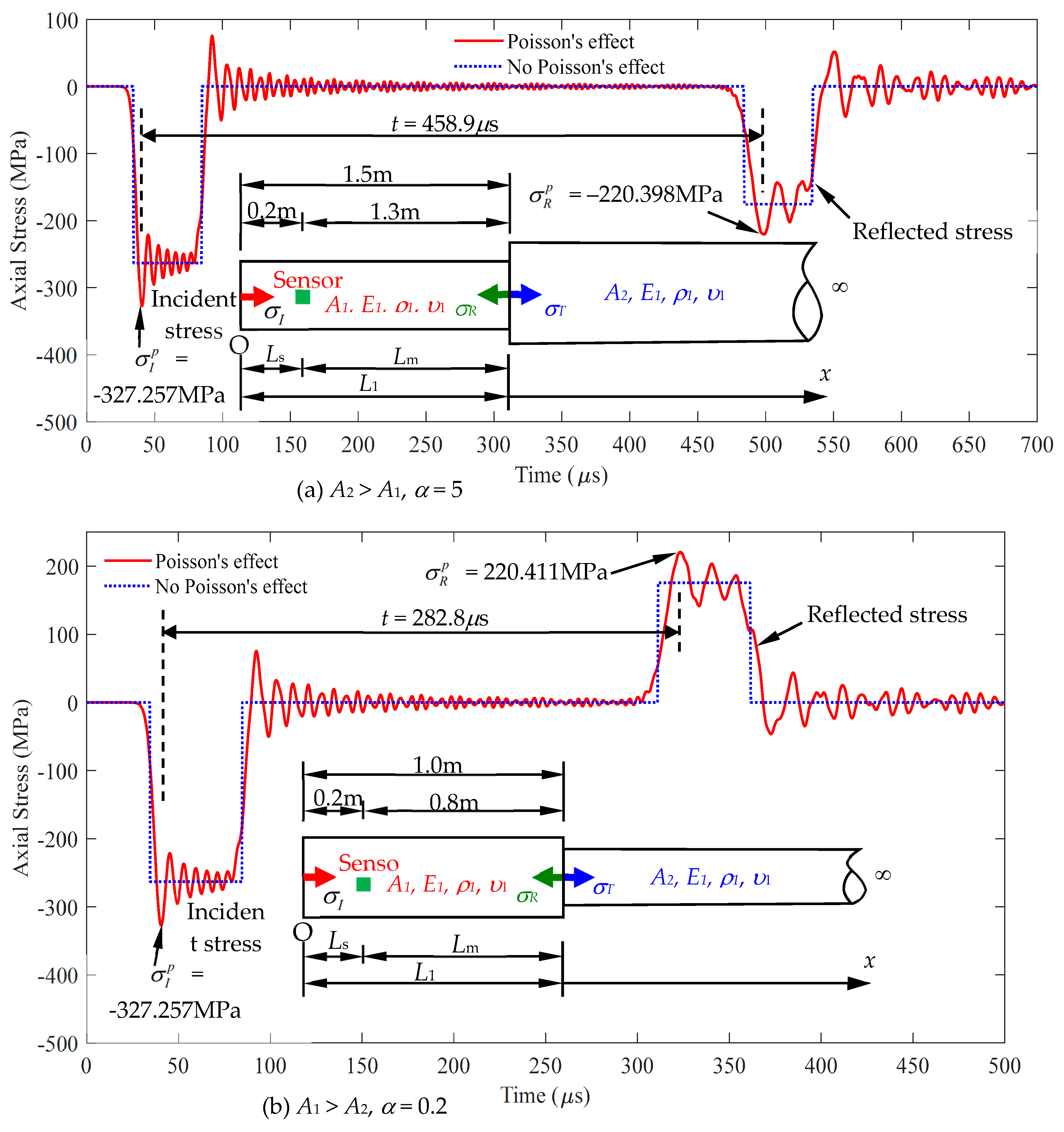
Figure 15.
The cross-sectional area A2 and length L1 determined based on the stress signal measured at x = Ls: (a) A2 > A1, (b) A1 > A2.
Figure 15.
The cross-sectional area A2 and length L1 determined based on the stress signal measured at x = Ls: (a) A2 > A1, (b) A1 > A2.
Figure 16.
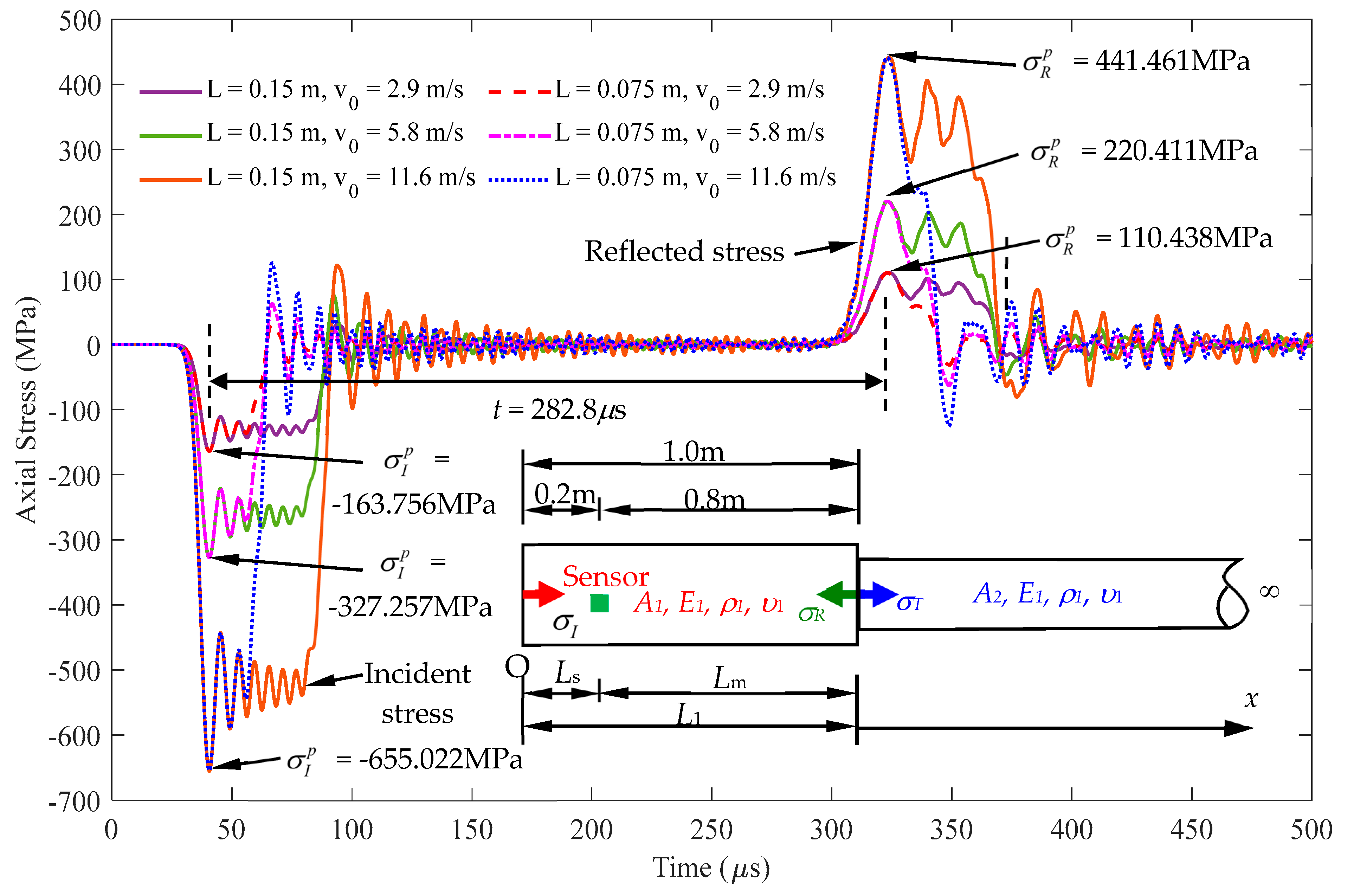
Determine the cross-sectional area A2 and length L1 based on the stress signal measured with different velocities and striker lengths at the position of x = Ls, A1 > A2, α = 0.2.
Figure 16.
Determine the cross-sectional area A2 and length L1 based on the stress signal measured with different velocities and striker lengths at the position of x = Ls, A1 > A2, α = 0.2.
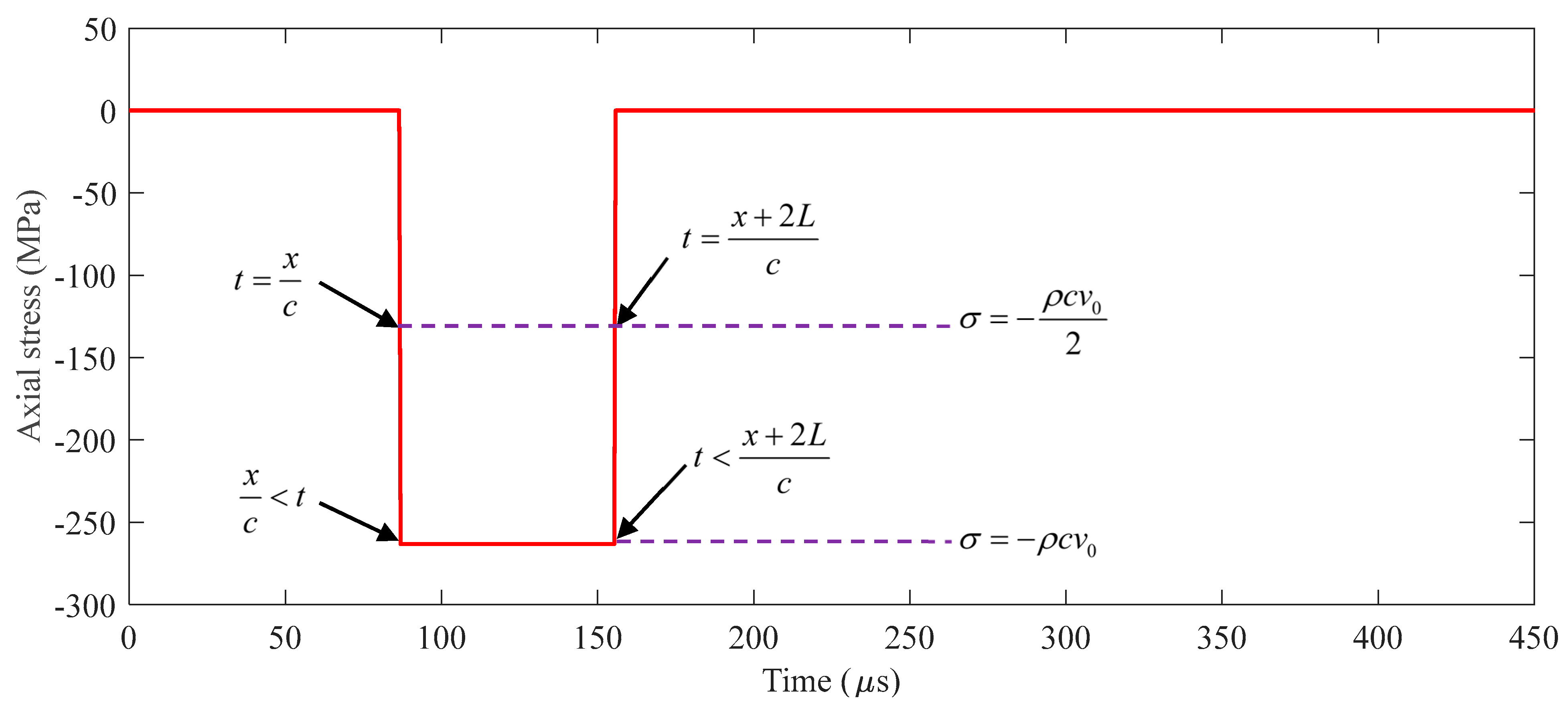
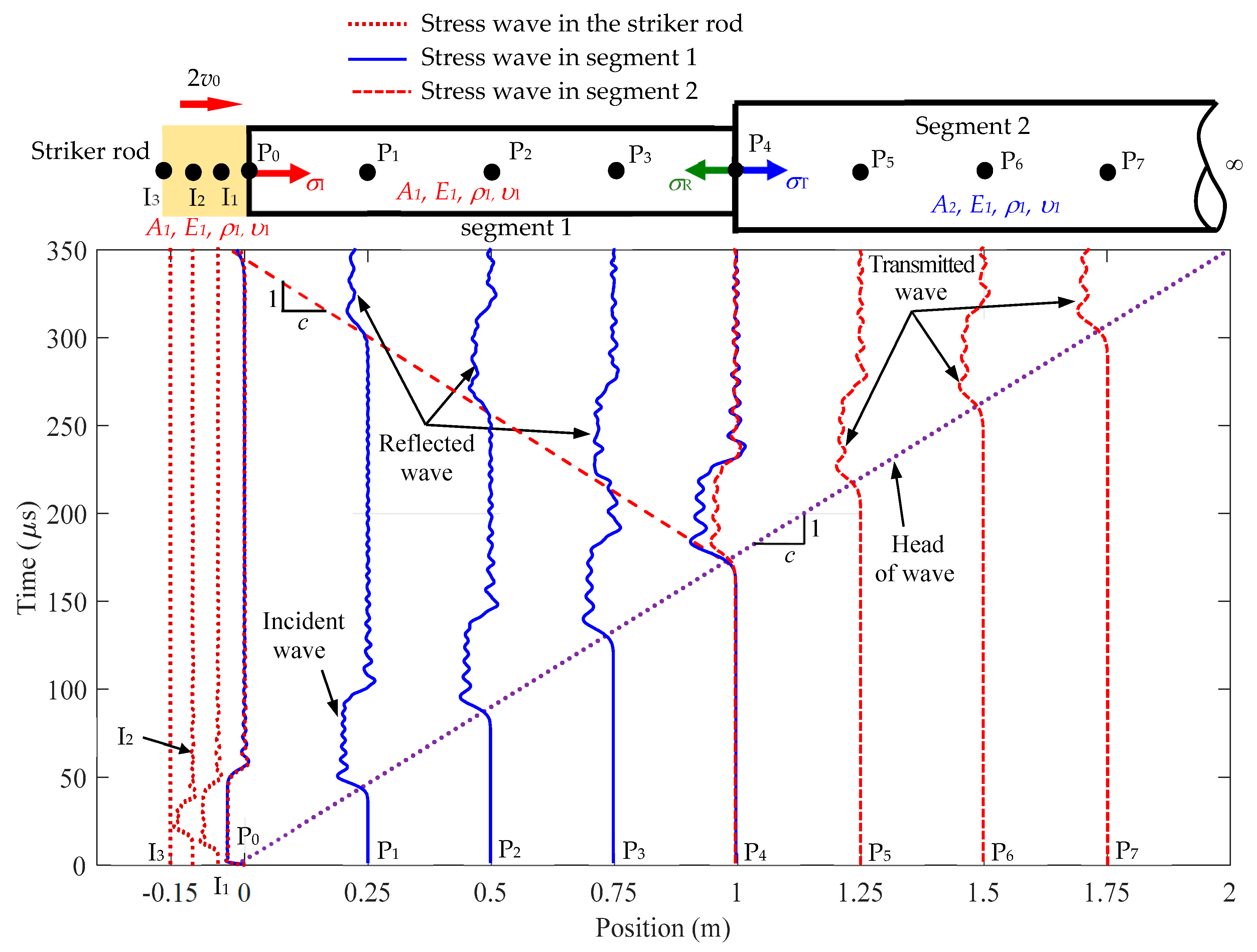
Figure 17.
Stress wave travel time history at various positions in the striker rod and Rayleigh–Love rod with a sudden cross-sectional area variation for the incident, reflected, and transmitted waves depending on position and time.
Figure 17.
Stress wave travel time history at various positions in the striker rod and Rayleigh–Love rod with a sudden cross-sectional area variation for the incident, reflected, and transmitted waves depending on position and time.
Table 1.
Parameters used in the Rayleigh–Love rod model
Table 1.
Parameters used in the Rayleigh–Love rod model
| Parameters |
Values |
|
| Diameter of the striker rod |
30 mm |
| Diameter of segment 1 |
30 mm |
| Diameters of segment 2 |
30, 42, 52, 60, 67 mm |
| Young modulus, E
|
195 GPa |
| Poisson’s ratio, υ
|
0.3 |
| Mass density, ρ
|
7,850 kg/m3
|
| Striker rod length, L
|
0.15m |
| Length of segment 1, L1
|
1 m |
| Length of segment 2, L2
|
1.5 m |
| Impact velocity, 2v0
|
11.6 m/s |
Table 2.
Reflected stresses in case of A2 ≥ A1
Table 2.
Reflected stresses in case of A2 ≥ A1
| A2/A1
|
|
|
Diff. (%) |
| 1 |
0 |
0 |
- |
| 2 |
−108.688 |
−87.762 |
23.84 |
| 3 |
−163.362 |
−131.643 |
24.09 |
| 4 |
−196.481 |
−157.972 |
24.38 |
| 5 |
−218.610 |
−175.524 |
24.55 |
Table 3.
Transmitted stresses in case of A2 ≥ A1
Table 3.
Transmitted stresses in case of A2 ≥ A1
| A2/A1
|
|
|
Diff. (%) |
| 1 |
−333.24 |
−263.286 |
26.57 |
| 2 |
−222.16 |
−175.524 |
26.57 |
| 3 |
−166.62 |
−131.643 |
26.57 |
| 4 |
−133.296 |
−105.314 |
26.57 |
| 5 |
−111.08 |
−87.762 |
26.57 |
Table 4.
Reflected stresses in case of A2 ≤ A1
Table 4.
Reflected stresses in case of A2 ≤ A1
| A2/A1
|
|
|
Diff. (%) |
| 1 |
0 |
0 |
- |
| 1/2 |
114.9129 |
87.762 |
30.94 |
| 1/3 |
170.8699 |
131.643 |
29.80 |
| 1/4 |
204.1672 |
157.9716 |
29.24 |
| 1/5 |
226.3654 |
175.524 |
28.97 |
Table 5.
Transmitted stresses in case of A2 ≤ A1
Table 5.
Transmitted stresses in case of A2 ≤ A1
| A2/A1
|
|
|
Diff. (%) |
| 1 |
−333.240 |
−263.286 |
26.57 |
| 1/2 |
−444.320 |
−351.048 |
26.57 |
| 1/3 |
−499.860 |
−394.929 |
26.57 |
| 1/4 |
−533.184 |
−421.2576 |
26.57 |
| 1/5 |
−555.400 |
−438.81 |
26.57 |
Table 6.
The initial impact kinetic energy
of the striker in each case in
Figure 16
Table 6.
The initial impact kinetic energy
of the striker in each case in
Figure 16
| No. |
Cross-section
(m2) |
Density
(kg/m3) |
Impact length
(m) |
Initial velocity
(m/s) |
Kinetic energy
(J) |
| 1 |
7.069*10-4
|
7850 |
0.15 |
2.9 |
3.500 |
| 2 |
5.8 |
14.000 |
| 3 |
11.6 |
55.999 |
| 4 |
0.075 |
2.9 |
1.750 |
| 5 |
5.8 |
7.000 |
| 6 |
11.6 |
27.999 |