Persistence and Stochastic Extinction in a Lotka-Volterra Predator-Prey Stochastically Perturbed Model

1. Introduction

Let us consider the classical predator-prey model [1,2,3,4,5]

$$\begin{gathered} \dot{x}=a_{1}x(1-b_{11}x-b_{12}y), \\ \dot{y}=-a_{2}y(1-b_{21}x), \end{gathered}$$

(1.1)

where all parameters are positive. This model was suggested independently by Volterra and Lotka, and its properties are well studied. Specifically, the model has three equilibria, namely (i) the zero equilibrium $E_0^{*}=(0,0)$, (ii) the predator-free equilibrium $E_x^{*}=(b_{11}^{-1},0)$ on the x-axis, and (iii) the positive equilibrium $E_{+}^{*}=(x^{*},y^{*})$, where both species coexist. Coordinates $x^{*}$ and $y^{*}$ are defined by the equalities

$$b_{11}{x}^{*}+b_{12}{y}^{*}=1,b_{21}{x}^{*}=1$$

(1.2)

with the solution

$$x^{*}=\frac{1}{b_{21}},y^{*}=\frac{b_{21}-b_{11}}{b_{12}{b}_{21}}=\frac{1-R_0^{-1}}{b_{12}},R_0=\frac{b_{21}}{b_{11}}.$$

(1.3)

Here, the parameter $R_0$ has a transparent biological meaning: it is the predator’s basic reproduction number, i.e., a number of the offspring that reach the reproductive age produced per capita of the predator under the most favourable conditions when $x=1/b_{11}$ and $y\to 0$. The concept of the basic reproduction number is originated in the infectious diseases dynamics, where it is proved to be exceptionally successful. We believe that this concept is very convenient in modelling population dynamics as well.

The principal global asymptotic properties of model (1.1) are summarized by the following theorem [1,3]:

Theorem 1.

For the system (1.1) the following statements are true:

(1) If $R_0>1$, then the coexisting equilibrium $E_{+}^{*}$ exists and is globally asymptotically stable, while the predator-free equilibrium $E_x^{*}$ is unstable (a saddle points).

(2) If $R_0\le 1$, then system (1.1) has no coexisting equilibrium state, and the equilibrium $E_x^{*}$ is globally asymptotically stable.

(3) The zero equilibrium $E_0^{*}$ is always unstable (a saddle point).

A principal property of the Lotka-Vo;terra model is its persistence. At the same time, it was observed that in real-life biosystems species can extinct due to stochastic fluctuations. Objectives of this paper is to analytically study how stochastic effects affect the model dynamics, and, in particular, its persistence and species extinction. We consider, therefore, the Lotka-Volterra model under stochastic perturbations of the white noise type that are postulated proportional to the system current state. Such type of perturbations appear to be the most natural for models motivated by biological applications.

To explore the persistence or stochastic extinction in the stochastic model, in this paper we employ a recently developed by the authors method [6,7] that is based on the direct Lyapunov method [8] and, in particular, on the development of ideas of R.Z. Khasminskii [9]. Specifically, in line with Khasminskii’s idea, we suggest that the sufficient conditions for the stochastic extinction are the conditions for the reversion of the stability of the trivial equilibrium state (so called “stabilisation by noise”). Application of this idea to the model ensures the precise sufficient conditions for species extinction (and, hence, the precise necessary conditions for persistence).

To apply the Khasmiskii’s idea to the models originated in mathematical biology, we extended it to multi-dimensional nonlinear systems and exploited the concept of the stability of invariant sets. That is, instead of the stability of the trivial equilibrium state of a linear 1-dim stochastic equation, as in [9], we study of the stability of the coordinate axes of a nonlinear stochastic system.

2. Predator-Prey Model under Stochastic Perturbations

Let $\{\Omega ,\mathfrak{F},\mathbf{P}\}$ be a complete probability space, $\{{\mathfrak{F}}_t,t\ge 0\}$ be a nondecreasing family of sub-$\sigma$-algebras of $\mathfrak{F}$, i.e., ${\mathfrak{F}}_{t_1}\subset {\mathfrak{F}}_{t_2}\subset \mathfrak{F}$ for $t_1<t_2$, $\mathbf{E}$ be the mathematical expectation with respect to the measure $\mathbf{P}$.

Let us assume that the model (1.1) is influenced by stochastic perturbations that are of the white noise type and are of magnitudes proportional to the current population size. Then the system of ordinary differential equations (1.1) transforms to the following system of Ito’s stochastic differential equations (SDE) [10]:

$$\begin{gathered} dx=a_{1}x(1-b_{11}x-b_{12}y)dt+{\sigma }_{1}xd{w}_1, \\ dy=-a_{2}y(1-b_{21}x)dt+{\sigma }_{2}yd{w}_2. \end{gathered}$$

(2.1)

Here ${\sigma }_1$ and ${\sigma }_2$ are constants, and $w_1\left(t\right)$ and $w_2\left(t\right)$ are the mutually independent ${\mathfrak{F}}_t$-adapted standard Wiener processes.

Before we proceed to the model analysis, let us recall the basic definition of persistence and extinction that are applicable to systems (1.1) and (2.1) [11,12,13]:

Definition 1.

Species x is weakly persistent if for all $x\left(0\right),y\left(0\right)>0$, ${lim}_{t\to +\infty }supx\left(t\right)>0$.

Species x is persistent if for all $x\left(0\right),y\left(0\right)>0$, ${lim}_{t\to +\infty }infx\left(t\right)>0$.

Species x is uniformly persistent if for all $x\left(0\right),y\left(0\right)>0$, ${lim}_{t\to +\infty }infx\left(t\right)>\epsilon >0$.

Species x extincts if for all $x\left(0\right),y\left(0\right)>0$, ${lim}_{t\to +\infty }supx\left(t\right)=0$.

The same definitions are applicable for species y.

By term "stochastic extinction" we imply the extinction due to stochastic processes only. That is, stochastic extinction occurs under the conditions when the corresponding deterministic system is persistent.

Lemma 1.

The positive quadrant ${\mathbf{R}}_{\ge 0}^2=\left\{(x,y)\right|x,y\ge 0\}$ is an invariant set of stochastic system (2.1).

For proof it is enough to note that the solution $\left(x\right(t),y(t\left)\right)$ of system (2.1) is presented in form [10]

$$\begin{array}{l}x\left(t\right)=x\left(0\right)exp\left\{{\int }_0^t\left(a_1(1-b_{11}x\left(s\right)-b_{12}y\left(s\right))-\frac{1}{2}{\sigma }_1^2\right)ds+{\sigma }_1{w}_1\left(t\right)\right\},\\ y\left(t\right)=y\left(0\right)exp\left\{{\int }_0^t\left(-a_2(1-b_{21}x\left(s\right))-\frac{1}{2}{\sigma }_2^2\right)ds+{\sigma }_2{w}_2\left(t\right)\right\}.\end{array}$$

Lemma 2.

If ${\sigma }_1^2\le 2a_1$, then set

$$M=\left\{(x,y)\left|x\in \left[0,\frac{1}{b_{11}}\left(1+\frac{{\sigma }_1^2}{2a_1}\right)\right],y\ge 0\right.\right\}\subset {\mathbf{R}}_{\ge 0}^2$$

is in mean a positive invariant and attractive set of system (2.1).

Proof. 

Let L be the generator [10] of system (2.1). The Lyapunov function $u(x,y)=x^2$ satisfies

$$Lu=2a_1{x}^2\left(1+\frac{{\sigma }_1^2}{2a_1}-b_{11}x-b_{12}y\right).$$

That is, ${\sigma }_1^2\le 2a_1$ ensures that $Lu<0$ for all $y\ge 0$, $x>{\displaystyle \frac{1}{b_{11}}}\left(1+{\displaystyle \frac{{\sigma }_1^2}{2a_1}}\right)$. By Dynkin’s formula [10]

$$\mathbf{E}u(x\left(t\right),y\left(t\right))-\mathbf{E}u(x\left(0\right),y\left(0\right))={\int }_0^t\mathbf{E}Lu(x\left(s\right),y\left(s\right))ds,$$

(5)

inequality $\mathbf{E}Lu\left(x\right(s),y(s\left)\right)<0$ for $s\in (0,t)$ implies that $\mathbf{E}u\left(x\right(t),y(t\left)\right)<\mathbf{E}u\left(x\right(0),y(0\left)\right)$. That is, for all $y\ge 0$ and $x>{\displaystyle \frac{1}{b_{11}}}\left(1+{\displaystyle \frac{{\sigma }_1^2}{2a_1}}\right)$ Lyapunov function $u\left(x\right)$ decreases as t grows. Therefore, the mathematical expectation of the solutions with positive initial conditions converge to the region M and remain there. □

We would like to remind that $K=1/b_{11}$ is the environment currying capacity for the prey. Lemma 2 implies that, due to stochastic fluctuations, in system (2.1) the mathematical expectation for the prey population exceeds the deterministic currying capacity K and varies within the range $\left[0,{\displaystyle \frac{1}{b_{11}}}\left(1+{\displaystyle \frac{{\sigma }_1^2}{2a_1}}\right)\right]$. This fact indicates a necessity to introduce, alongside to the deterministic currying capacity K, the stochastic currying capacity

$$\tilde{K}=K\left(1+\frac{{\sigma }_1^2}{2a_1}\right)\ge K.$$

Using this notation, set $M=\left\{(x,y)\right|x\in [0,\tilde{K}],y\ge 0\}$. Furthermore, the concept of stochastic crying capacity naturally leads to a concept of the stochastic predator’s basic reprobation number

$${\tilde{R}}_0=b_{21}\tilde{K}=\left(1+\frac{{\sigma }_1^2}{2a_1}\right)R_0=b_{21}\left(1+\frac{{\sigma }_1^2}{2a_1}\right)K.$$

Lemma 3.

If ${\sigma }_1^2>2a_1$, then the zero equilibrium $E_0^{*}$ is stable in probability.

Proof. 

Using the Lyapunov function $w\left(x\right)={\left|x\right|}^{1-{\displaystyle \frac{2a_1}{{\sigma }_1^2}}}$, for all $x,y\ge 0$ we have

$$\begin{array}{cc}\hfill Lw=& \left(1-\frac{2a_1}{{\sigma }_1^2}\right){\left|x\right|}^{-{\displaystyle \frac{2a_1}{{\sigma }_1^2}}}{a}_{1}x(1-b_{11}x-b_{12}y)-\frac{1}{2}\left(1-\frac{2a_1}{{\sigma }_1^2}\right){\displaystyle \frac{2a_1}{{\sigma }_1^2}}{\left|x\right|}^{-{\displaystyle \frac{2a_1}{{\sigma }_1^2}}-1}{\sigma }_1^2{x}^2\hfill \\ \hfill =& -a_1\left(1-\frac{2a_1}{{\sigma }_1^2}\right){\left|x\right|}^{1-{\displaystyle \frac{2a_1}{{\sigma }_1^2}}}\left(b_{11}x+b_{12}y\right)\le 0.\hfill \end{array}$$

Therefore, semi-axis $x=0,y\ge 0$ (as a solution of the first equation of system (2.1)) is stable in probability [9].

Next, consider Lyapunov function $v\left(y\right)=y^2$, if ${\sigma }_2^2<2a_2$, and $v\left(y\right)={\left|y\right|}^{1-{\displaystyle \frac{2a_2}{{\sigma }_2^2}}}$, if ${\sigma }_2^2\ge 2a_2$. If ${\sigma }_2^2<2a_2$, then

$$Lv=-2a_2{y}^2(1-b_{21}x)+{\sigma }_2^2{y}^2=-y^2[2a_2(1-b_{21}x)-{\sigma }_2^2].$$

From the above-said arguments, it follows that $x\to 0$, and, hence, the condition ${\sigma }_2^2<2a_2$ ensures that inequality $Lv\le 0$ holds for all $y\ge 0$.

If ${\sigma }_2^2\ge 2a_2$, then Lyapunov function $v\left(y\right)={\left|y\right|}^{1-{\displaystyle \frac{2a_2}{{\sigma }_2^2}}}$ satisfies

$$\begin{array}{ll}Lv& =-\left(1-\frac{2a_2}{{\sigma }_2^2}\right){\left|y\right|}^{-{\displaystyle \frac{2a_2}{{\sigma }_2^2}}}{a}_{2}y(1-b_{21}x)-\frac{1}{2}\left(1-\frac{2a_2}{{\sigma }_2^2}\right)\frac{2a_2}{{\sigma }_2^2}{\left|y\right|}^{-{\displaystyle \frac{2a_2}{{\sigma }_2^2}}-1}{\sigma }_2^2{y}^2\\ & =-a_2\left(1-{\displaystyle \frac{2a_2}{{\sigma }_2^2}}\right){\left|y\right|}^{1-{\displaystyle \frac{2a_2}{{\sigma }_2^2}}}(2-b_{21}x).\end{array}$$

(2.3)

As $x\to 0$ by the arguments above, we obtain that $Lv\le 0$ for all $x\le {\displaystyle \frac{2}{b_{21}}}$, $y\ge 0$. Therefore, in the both cases, namely for ${\sigma }_2^2<2a_2$ and ${\sigma }_2^2\ge 2a_2$, solution $y=0$ of the second equation of system (2.1) is stable in probability. That is, the zero equilibrium $E_0^{*}$ of system (2.1) is stable in probability [9]. This completes the proof. □

It was shown in [6], that the condition ${\sigma }_1^2\le 2a_1$ is the necessary condition for prey’s persistence. It is hardly surprising, that the extinction of prey immediately leads to the extinction of predators.

Authors also would like to mention that Lyapunov functions of the type that was used in the proof were invented by R.Z. Khasminskii [9]. The inversion of the stability for larger perturbations, such as Lemma 3 describes, is usually referred to as the stabilization by noise.

Lemma 4.

If ${\sigma }_2^2\ge 2a_2$ and $\widetilde{R_0}=R_0\left(1+{\displaystyle \frac{{\sigma }_1^2}{2a_1}}\right)\le 2$, then for the system of stochastic differential equations (2.1) the set $S=\left\{(x,0)\right|x\in [0,\tilde{K}]\}$ (an interval on the positive semi-axis $\{x\ge 0\}$) is stable in probability.

Proof. 

From (2.3), for Lyapunov function $v\left(y\right)={\left|y\right|}^{1-{\displaystyle \frac{2a_2}{{\sigma }_2^2}}}$, we have that $Lv\le 0$ holds for all $x\le 2b_{21}^{-1}$, $y\ge 0$. Therefore, the solution $y=0$ of the second equation of system (2.1) is stable in probability. Besides, $\widetilde{R_0}=b_{21}\tilde{K}=R_0\left(1+{\displaystyle \frac{{\sigma }_1^2}{2a_1}}\right)\le 2$ ensures that $x\le \tilde{K}\le 2b_{21}^{-1}$. Besides, by Lemma 2, for all positive initial conditions, there is a finite $t_1>0$ such that $\mathbf{E}x\left(t\right)\le \tilde{K}$ holds for all $t>t_1$.

That is, the lemma hypotheses ensue that $L\left(v\right(t\left)\right)\le 0$ holds for all positive initial condition and for $t>t_1$. This completes the proof. □

Summarizing statements of Lemmas 3 and 4, we come to the following theorem.

Theorem 2.

(1) Conditions ${\sigma }_2^2\ge 2a_2$ and $\widetilde{R_0}\le 2$ are sufficient conditions for the prey stochastic extinction (the extinction by probability).

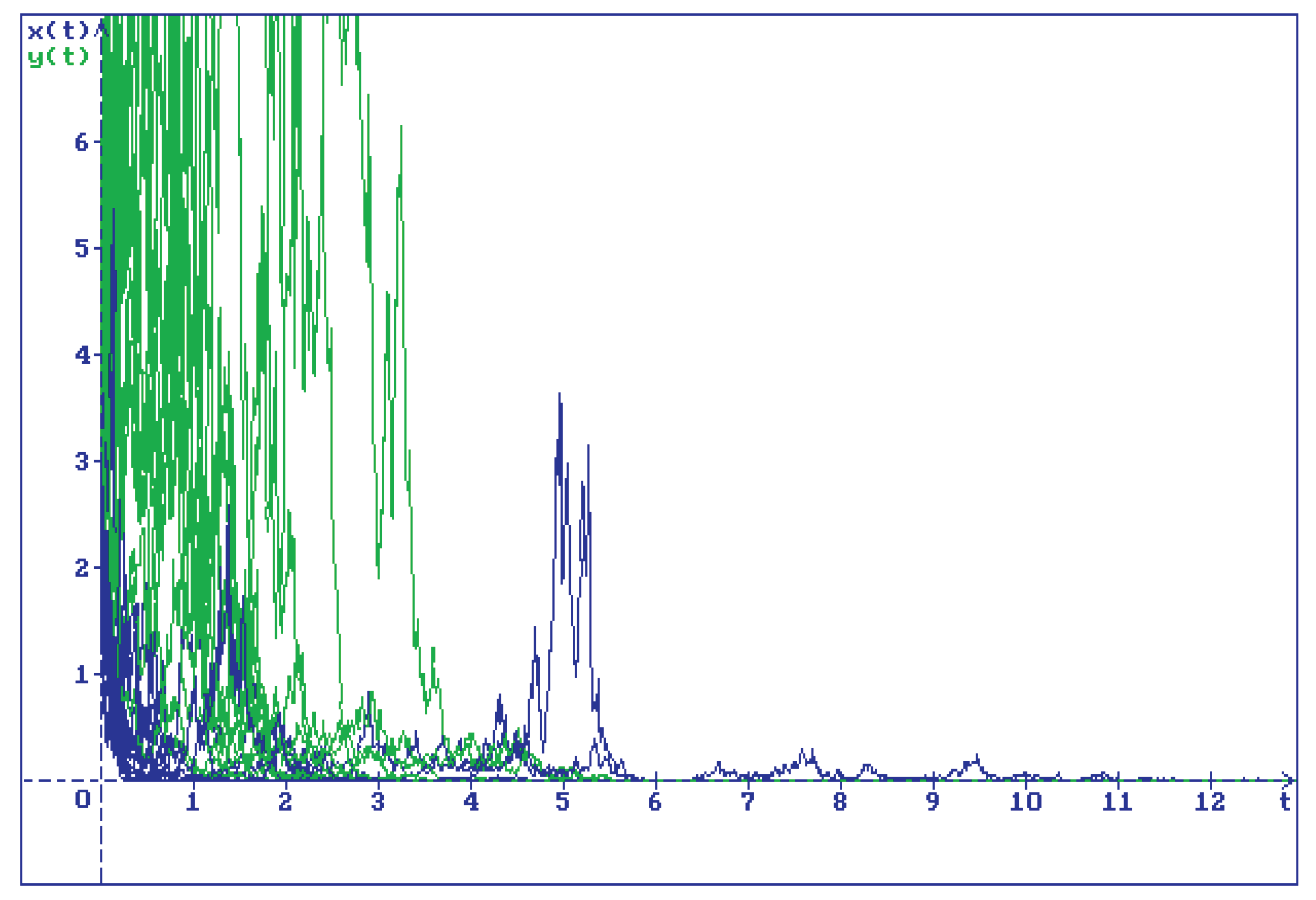
(2) If ${\sigma }_1^2>2a_1$, then both species, namely, the prey and the predator, extinct (by probability).

(3) ${\sigma }_1^2\le 2a_1$ is necessary for the stochastic system persistence.

(4) ${\sigma }_1^2\le 2a_1$ and either ${\sigma }_2^2<2a_2$, or $\widetilde{R_0}>2$ are necessary for predator’s persistence.

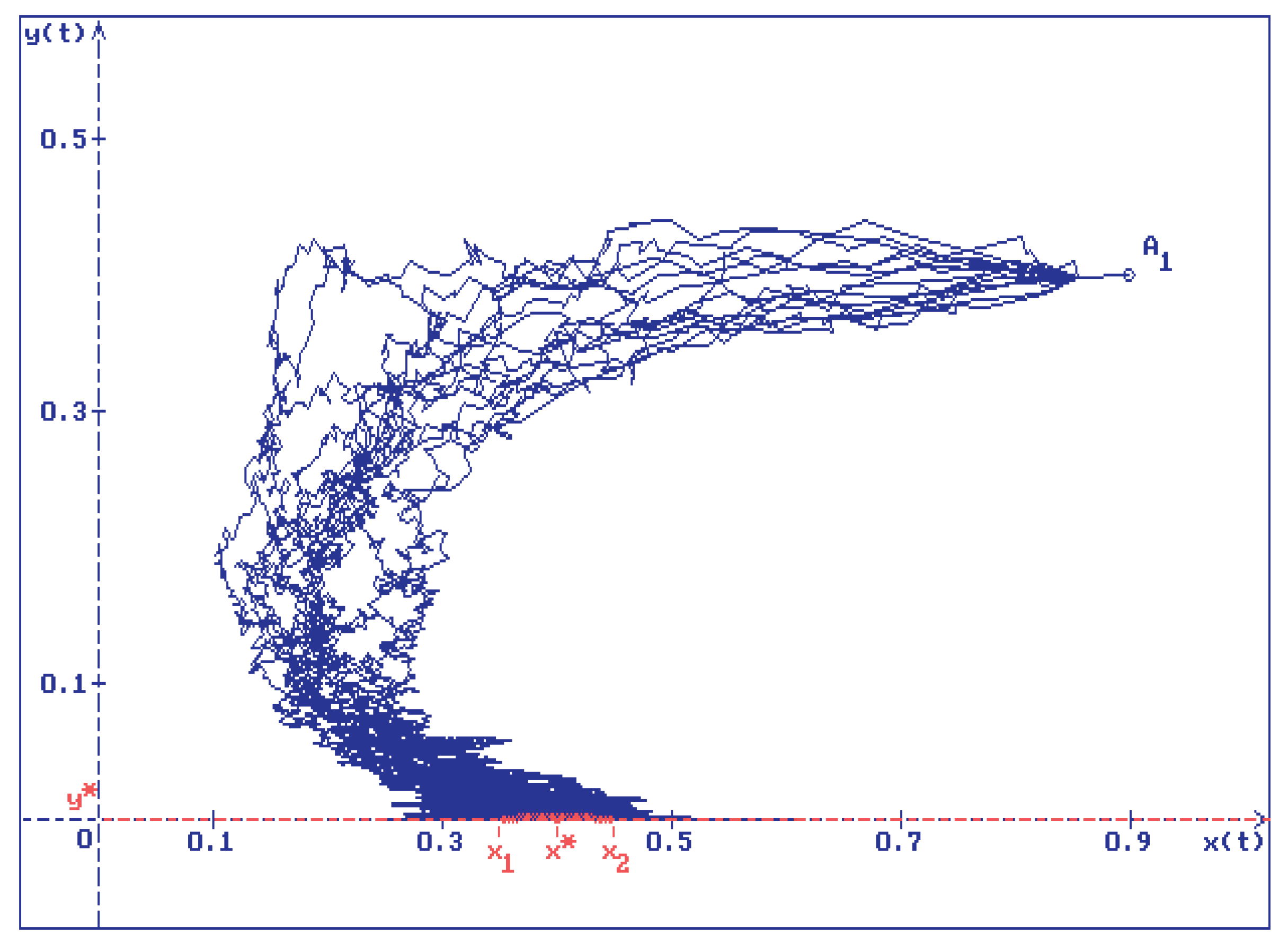
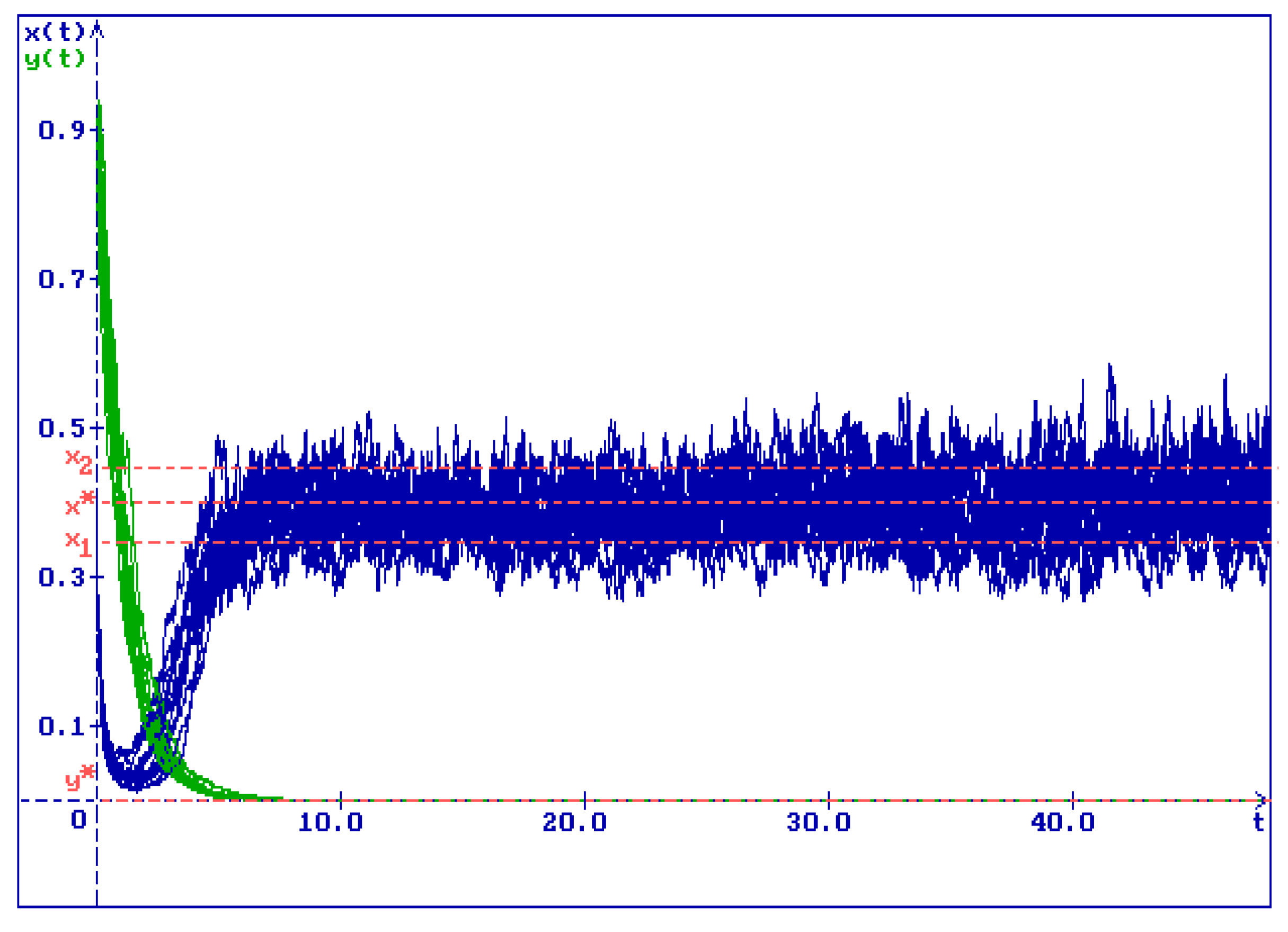
Figure 1 and Figure 2 illustrate the predator extinction due to stochastic perturbations for the case ${\sigma }_1^2<2a_1$ and ${\sigma }_2^2<2a_2$, respectively. Figure 3 illustrates the stochastic extinction of both species for case ${\sigma }_1^2>2a_1$ and ${\sigma }_2^2>2a_2$.

Note that for the numerical simulation of the Wiener process trajectories, a special algorithm described in detail in [8] has been used.

The authors would like to attract readers’ attention to the fact that in Figure 1 and Figure 2, as $y\to 0$, the prey population $x\left(t\right)$ oscillates around a certain interval $(x_1,x_2)$. (In Figure 1 and Figure 2, $(x_1,x_2)=(0.35,0.45)$.) In fact, in the absence of the predator (that is, for $y=0$), the first equation of the system of stochastic differential equations (2.1) is equivalent to the stochastically perturbed logistic equation of a single population growth that was studied by the authors in [6]. In [6], for this equation the authors established the existence of a stable in mean interval on the x-axis and show that the trajectories oscillate around this interval. (In notation of this paper, the interval is $(x_1,x_2)=\left({\displaystyle \frac{1}{b_{11}}}\left(1-{\displaystyle \frac{|{\sigma }_1|}{\sqrt{2a_1}}}\right),{\displaystyle \frac{1}{b_{11}}}\left(1+{\displaystyle \frac{|{\sigma }_1|}{\sqrt{2a_1}}}\right)\right)$.) Recalling that the x-axis is an invariant set of system (2.1) and that solutions are continuous, it is easy to see, that, as $y\to 0$, the solution of system (2.1) tends to that on the x-axis, and, hence, the interval $(x_1,x_2)$ in Figure 1 and Figure 2 corresponds to the stable interval found in [6].

3. Conclusions

In this paper, employing a recently developed by the authors technique based upon ideas of R.Z. Khasminskii, we found precise sufficient conditions for the stochastic species extinction and, hence, the precise necessary conditions for the species persistence for the classical Lotka-Volterra predator-prey model under stochastic perturbations proportional to the system current state. Please note that the found conditions of the extinction are sufficient, in probability. For this model, the stochastic extinction necessary occurs as a result of a phenomenon know as the stabilization by noise, and the conditions found in this paper are, in fact, the conditions for the reversion of the stability of the corresponding coordinate subspaces. This ensures that the conditions in this paper are the precise sufficient conditions for extinction, and, hence, the precise necessary conditions for the species persistence.

We would like to stress that the technique used in this paper can be applied for more complicated models (including nonlinear models), as well as for higher dimension models.