Preprint
Article
Developing Customized Lattice Structures Tailored to Mimic Closely Patients’ Bone Anisotropic Properties and Microarchitecture for Joint Reconstruction Applications
Altmetrics
Downloads
109
Views
50
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
21 March 2024
Posted:
23 March 2024
You are already at the latest version
Alerts
Abstract
Existing implants used with Total Knee Arthroplasty (TKA), Total Hip Arthroplasty (THA), and other joint reconstruction treatments, have displayed premature failures and frequent needs for revision surgery in recent years, particularly with young active patients who represent more than 55% of all joint reconstruction patients. Bone cement and stress shielding have been identified as the major reasons for premature joint failures. A breakdown of the cement may happen, and revision surgery may be needed because of the aseptic loosening. The significant mismatch of stiffness properties of patient trabecular bones and metallic implant materials in joint reconstruction surgery results in the stress shielding phenomenon. This could lead to significant bone resorption and increased risk of bone fracture and the aseptic loosening of implants. The present project introduces an approach for development of customized cellular structures to match the mechanical properties and architecture of human trabecular bone. It consists of four modules:1- characterization of geometry, microarchitecture, and stiffness properties of patient’s bones; 2- developing customized lattice structures tailored to mimic properties established in module 1; 3 - integration of developed lattice structure into full scale implant design and manufacturing; 4- implementation of the developed technology for use in implants that would overcome most of the issues related to aseptic loosening phenomenon. The present work aims at fulfilling the objectives of module 2 by exploring new designs of customized lattice structures and texture tailored to mimic closely patients’ bone anisotropic properties and that can incorporate an engineered biological press-fit fixation technique. The effects of various lattice design variables on mechanical performance of the structure are examined through systematic experimental plan using statistical design of experiments technique and analysis of variance method. All tested lattice designs were explored under realistic geometrical, biological, and manufacturing constraints. Of the four design factors examined in this study, strut thickness was found to have the highest percent contribution (41%) regarding the structure stiffness, followed by unit cell type, and cell size. Srut shape was found to have the lowest effect with only 11% contribution. The introduced solution offers lattice structure designs that can be adjusted to match bone stiffness distribution and promote bone ingrowth and hence eliminating the phenomenon of stress shielding while incorporating biological press-fit fixation technique.
Keywords:
Subject: Engineering - Bioengineering
1. Introduction
Existing implants used with Total Knee Arthroplasty (TKA), Total Hip Arthroplasty (THA), and other joint reconstruction treatments, have displayed premature failures and frequent needs for revision surgery in recent years, particularly with young active patients [1,2]. Ulrich et al. [1], found that the reviewed 237 THA revision procedures showed the overall mean time to revision was 83 months (close to 7 years), with failure reasons of aseptic loosening (51.9%), instability (16.9%), and infection (5.5%). Aseptic loosening is the most concern of revision rates for both TKA and THA. According to the historical growth trajectory, demand for joint replacements for young patients less than 65 years old was projected to be 52% for primary THAs and 55% to 62% for primary or revision TKAs by 2030 [2]. In recent years, researchers have discovered an effective solution for repairing bone defects caused by diseases or trauma, using the power of additive manufacturing (3D-printing) and the outstanding properties of titanium alloys, stainless steels and others. Specifically, Ti6Al4V is a titanium alloy with excellent biocompatibility, corrosion resistance, and combination of good load carrying capacity and toughness, make it the preferred choice for manufacturing of medical devices for orthopedic and dental applications [3,4,5].
Most joint replacements have severe stress shielding problems lead by metal implants that have much higher stiffness (elastic modulus) than that of bone. When metal implants are inserted into bone structures, bone suffers a lower strain energy density than the previous intact bone, resulting in stress shielding. This stress shielding phenomenon can cause significant bone resorption which lead to significantly increased risk of fracture and aseptic loosening [6,7,8]. Chmielewska and Dean [9], presented review highlights recent developments in devices for skeletal reconstruction that match the stiffness, while not interrupting the normal loading pattern of a healthy bone, and help to combat stress shielding and stress concentration. The presented review summarizes various approaches to achieve stiffness matching. Their review concluded that the introduced device must minimize, if not eliminate, interference with the normal stress-strain trajectories that the bone’s shape and mechanical properties, as well as the adjacent muscles, are adapted to. Arabnejad et al. [8], showed that a fully porous implant with an optimized material micro-structure can reduce the amount of bone loss secondary to stress shielding by 75% compared to a fully solid implant. Zimmer has introduced Trabecular Metal made of porous Tantalum that has an average modulus of elasticity from 2.5 to 3.9GPa compared with the reported modulus range of 0.1 to 1.5GPa for cancellous bone [10]. The introduced trabecular structure can only reduce the mismatch in average to 4:1, still high enough to cause stress shielding. Although bone cement had been the gold standard in the field of joint replacement surgery, its use has somewhat decreased because of the advent of press-fit implants which encourage bone ingrowth [11]. A press-fit implant is cementless and has porous features that allow biological fixation, which is important for young active patients. In a recent investigation [12], damage resistance of suggested four lattice structures (regular hexahedron, regular octahedron, rhombic dodecahedron, and body-centered cubic), was studied using gradient algorithm for stabilized and lightweight mandibular prostheses. The introduced algorithm was aided by finite element analysis to select an optimal lattice structure. The reported investigation has several limitations that would diminish the effectiveness of the proposed solution. The study assumed that fabricated orthopedic or dental implants would have homogeneous and isotropic properties, which is very difficult to achieve using additive manufacturing techniques. Secondly, the investigation considered only the effect of the type of lattice structure (four different types) and never looked at the effects of other lattice structure design parameters that could have significant effects in controlling stiffness properties and morphology of the porosity of the developed lattice structures.
Based on the above discussion, the present work aims at exploring new designs of customized lattice structures and texture tailored to mimic closely patients’ bone anisotropic properties and that can incorporate an engineered biological press-fit fixation technique. The introduced customized lattice structure will consider all design parameters that contribute to controlling stiffness properties and porosity of the developed customized structure. These designs could be created using additive manufacturing (AM) techniques for use with implants that would overcome most of the issues related to aseptic loosening and have greater success, especially in younger patients.
2. Investigation Approach
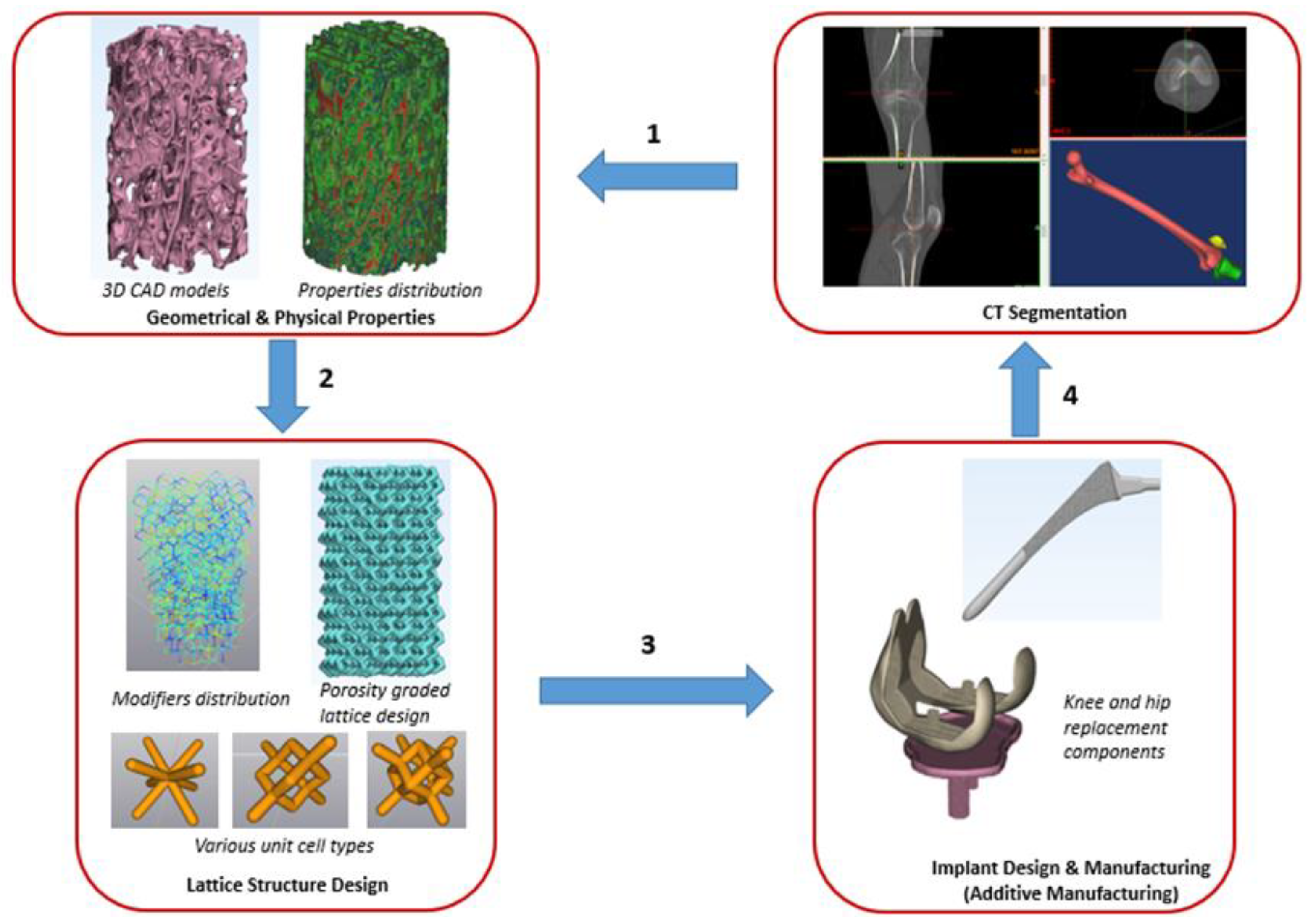
Ma and El-Gizawy [13] presented a conceptual approach for development of customized cellular structures to match the mechanical properties of human trabecular bone. Figure 1 shows key steps in our proposed approach needed for building an implant with properties mimicking those of patients’ bones. The workflow in the present approach is feasible for both patient-specific implant and population-based implant design.
Module 1 in the proposed approach, involves CT scan of the patients’ native bone, segmentation to get the 3D CAD models of the bone and characterization of geometry, microarchitecture, and stiffness properties of bones. These properties are crucial for designing and building optimized implants for joint and dental reconstruction applications. Module 2 covers the development of customized lattice structures tailored to mimic closely patients’ bone anisotropic properties and microarchitecture. Module 3 involves integration of porosity graded lattice to full scale implant design and manufacturing. Ultimately, all findings of the three modules will be utilized in module 4, implementation of the developed technology for use in implants that would overcome most of the issues related to aseptic loosening and have greater success, especially in younger patients.
2.1. Characterization of Geometry, Microarchitecture, and Stiffness Properties of Bones
Characterization of geometry, microarchitecture, and stiffness properties of bones required in module 1, has been accomplished and published in journal BioMed [14]. A summary of the findings is presented here to link them to the new work of module 2 presented in the current article.
Module 1 work presents evaluation and experimental verification using micro-CT scans for accurate characterization of geometry, microarchitecture, and stiffness properties of bones. The micro-CT scans of investigated bone reveal that the trabecular bone is highly anisotropic and heterogeneous. The results also showed considerable degree of parametric variability and uncertainty on microarchitecture and stiffness properties of patient’s trabecular bone. Probabilistic analyses of micro-CT data could consider these variabilities. They can aid in generating the required lattice structures of optimum implant designs that match closely patient bones and hence can overcome most of the issues related to aseptic loosening phenomenon and premature failure of the treated joints. 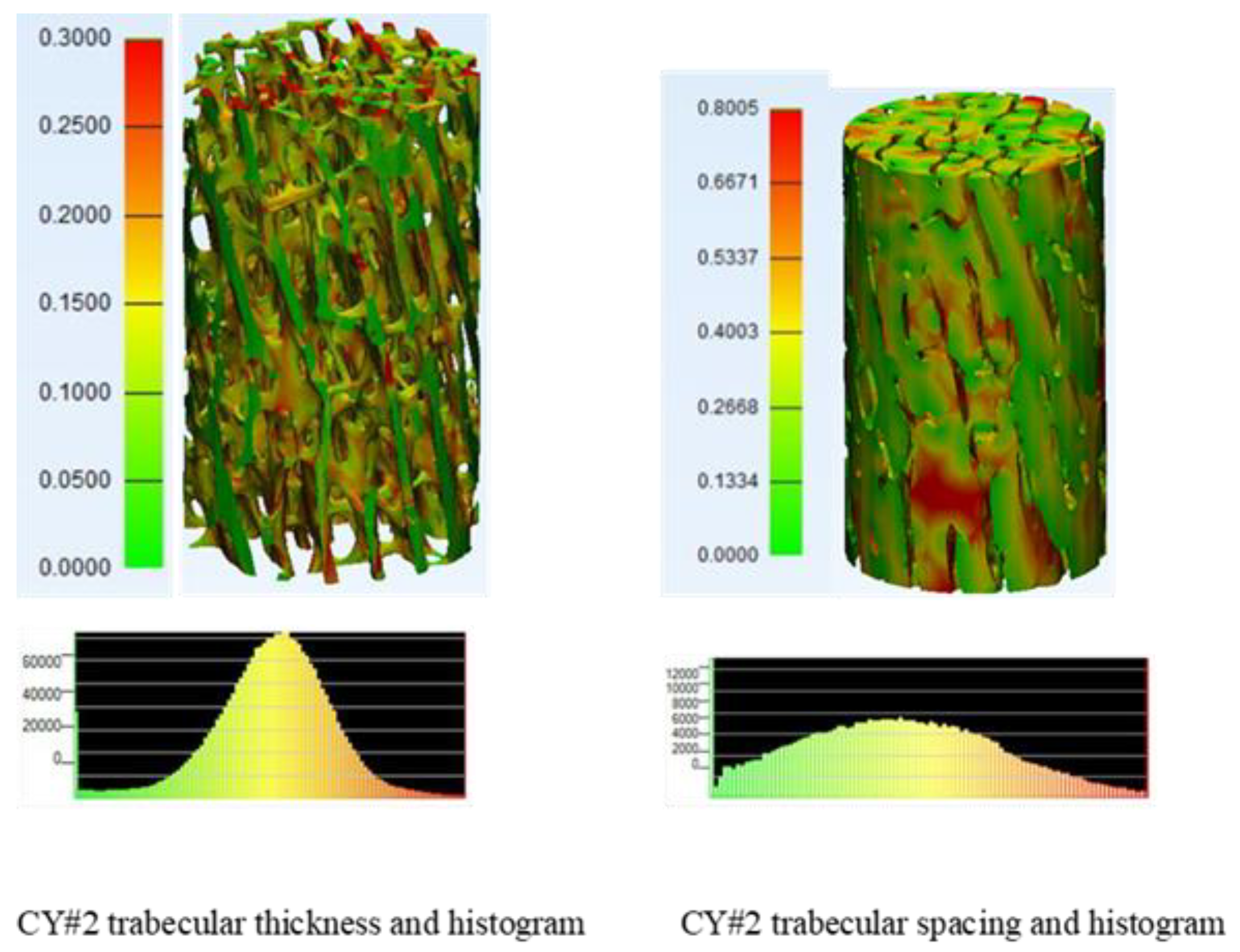Figure 2 shows trabecular thickness and trabecular spacing colored maps and histograms for typical cylindrical bone sample. Figure 3 displays bone properties assigned based on the gray scale values obtained from micro-CT data. The predicted modulus varied significantly from point to point within the tested sample with an average of 506.7 MPa and standard deviation of 238.06MPa. [14]. These observations mean that the mentioned microarchitecture parameters: trabecular thickness and spacing have significant degree of variability.
2.2. Design of Lattice Structures Adjusted to Match Bone Stiffness Distribution
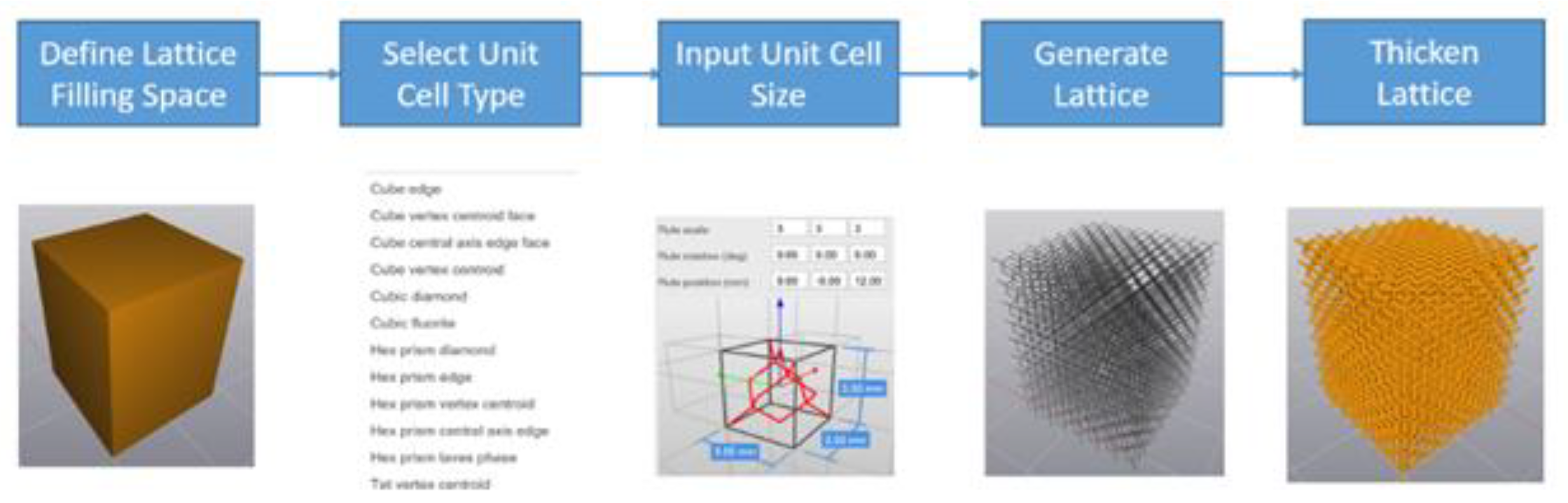
The following are the lattice structure important design factors that would affect the properties and performance of the developed lattice structure: unit cell type; unit cell size; strut shape; and strut thickness. Element software from Next-Gen Engineering Design Software (nTop) [15] is used to generate the 3D models of the lattices with the workflow shown in Figure 4. First, a solid part of which the boundary representing the design space (filling space) of the lattice is imported from a CAD system. Secondly, a unit cell type is selected from the existing library or from user-defined unit cell structures. Then unit cell size is selected for the assigned unit cell. After that a topological structure without assigned thickness is generated based on the unit cell type and size, to fill the design space imported in the first step. Finally, a 3D lattice structure is thickened out after defining the desired strut shape and thickness.
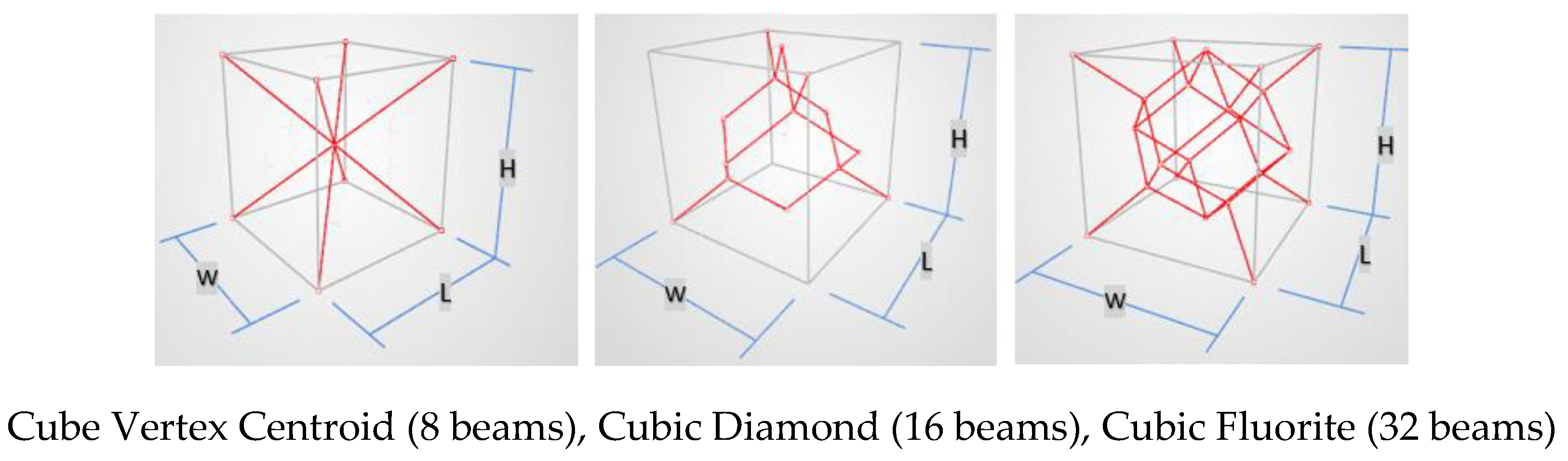
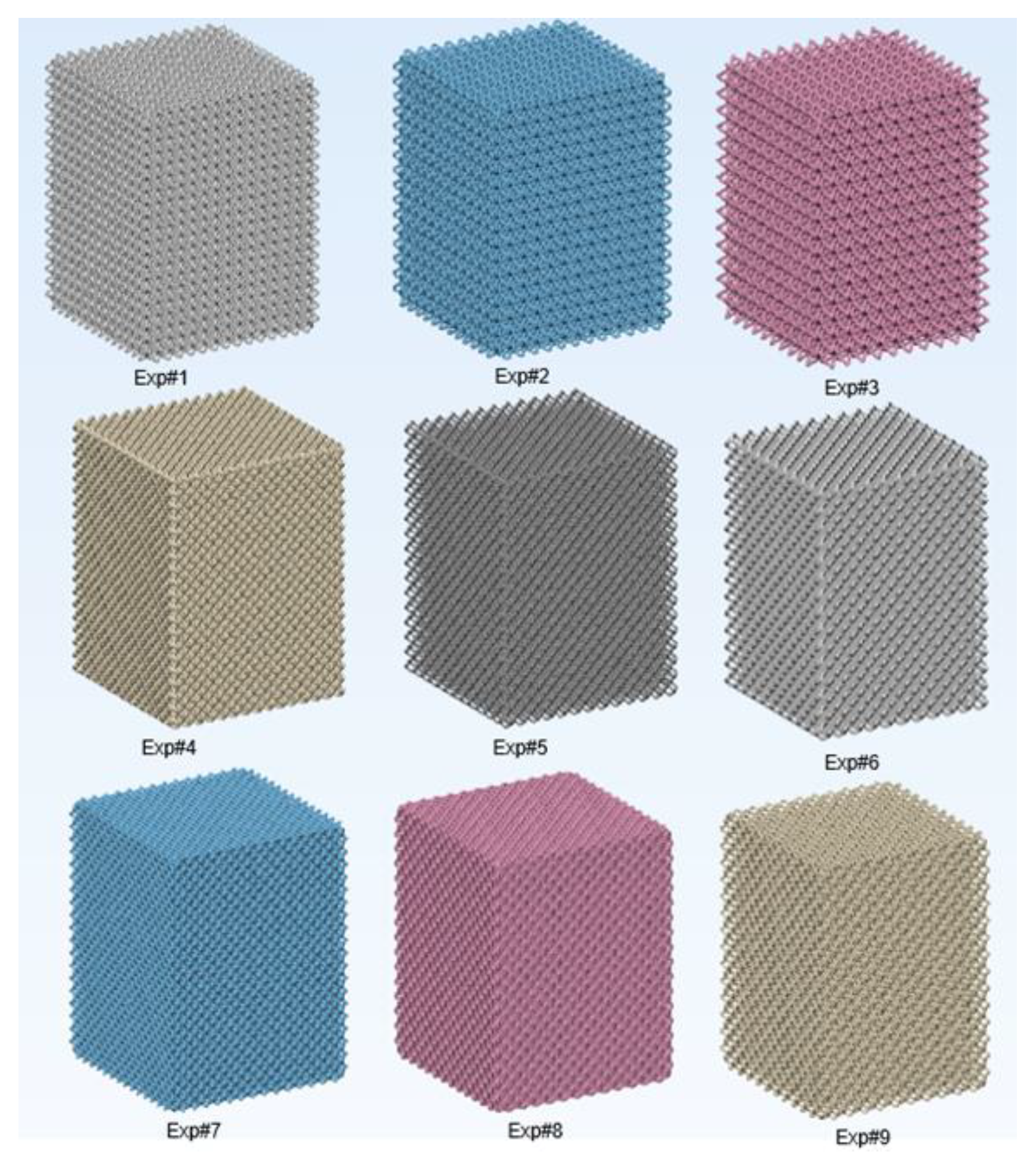
The selected unit cell types for the present investigation are cube vertex centroid, cubic diamond, and cubic fluorite, shown in Figure 5. They were selected because their overhang angles are 35.3 degrees for all beams used in the three configurations. This satisfies self-support requirement for building the lattice structure using additive manufacturing by Laser Powder Bed Fusion (L-PBF) method. The second design factor is strut thickness which is defined as the diameter of the equivalent circle that has the same area. Considering the minimum printable thickness for the L-PBF process of 200 μm, strut shapes of square, hexagon, and circle are considered. If the strut thickness is a, a circle’s diameter is a; a hexagon’s width and height are 0.95a and 1.10a respectively; and the side length of a square is 0.89a, to have the same cross-sectional area for the same strut thickness. A unit cell size of 1.2mm, 1.4mm, and 1.6mm, and a strut thickness of 0.23mm, 0.28mm, and 0.33mm were considered. Table 1 displays all factors and their alternative levels considered in present design.
2.3. Parametric Investigation of Lattice Structure Design
To investigate the effects of the lattice structure important design factors on the quality characteristics (properties and performance of the developed cellular structure), a standard orthogonal array for parametric investigation is used [16,17]. In this type of experimental design, partial factorial design of L9 (nine experiments to be conducted) is selected based on the number of factors and their levels to be tested. Three different samples were tested for each investigated lattice structure. The quality characteristics to be considered in this parametric study are the stiffness and yield strength properties of the lattice structure, subject to biological and manufacturing constraints dictated by the application of the device and the available manufacturing technology (L-PBF) for building these designs. 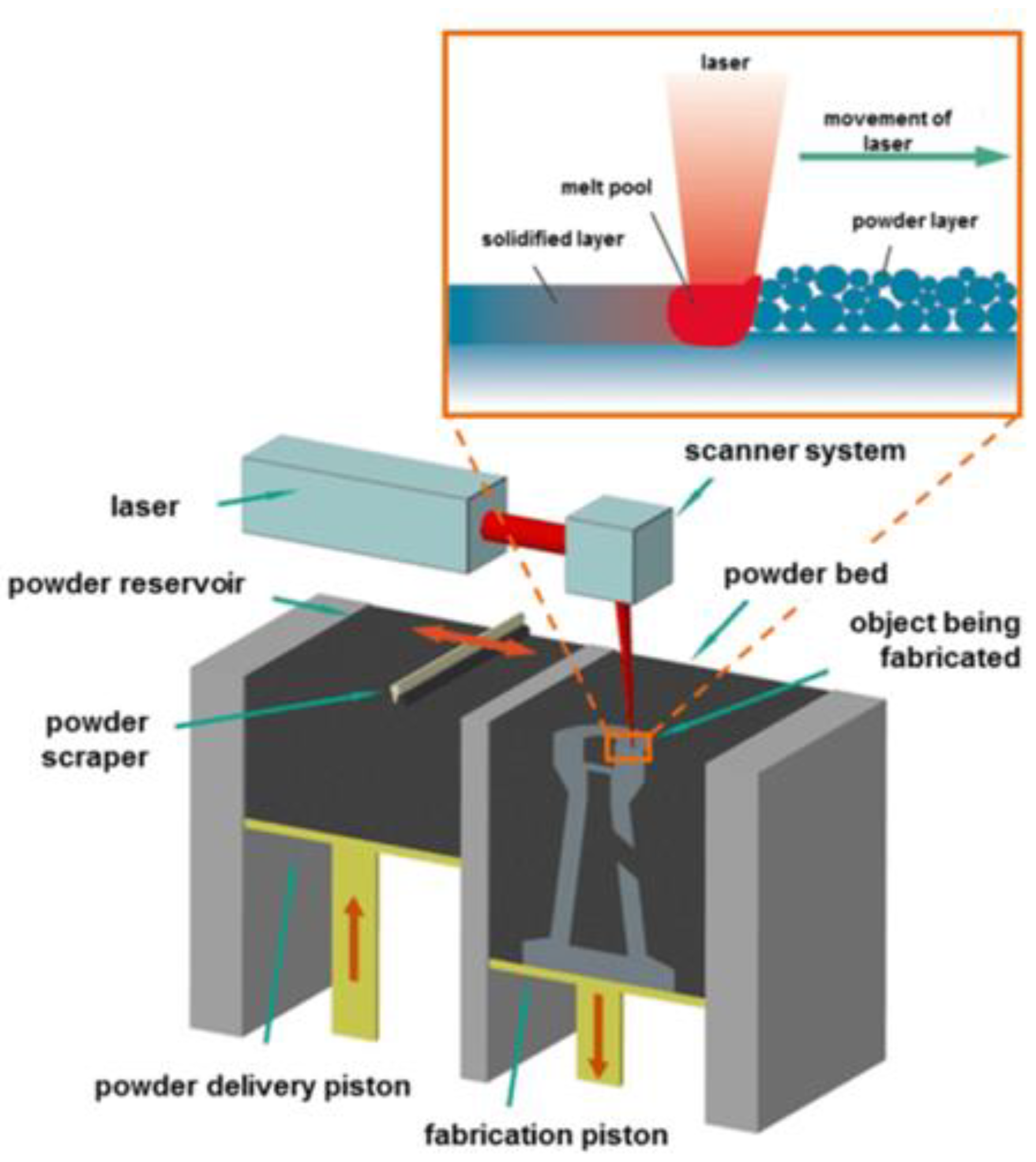Figure 6 shows the basic elements of the L-PBF process used in the present study. Table 2 displays the experimental Log of the used orthogonal array with all the four design parameters used and their levels. Figure 7 displays digital design models of the nine investigated lattice designs. Figure 8 shows all built samples ready for testing.
2.4. Materials and Fabrication of the Experimental Lattice Structures
The 3D printing Laser -Powder Bed Fusion (L-PBF) process system displayed in Fig. 6 is used for printing the examined designs. It is an EOS M290 machine available at Core Link Surgical, Inc., Saint Louis, MO. The used EOS M290 system has a building volume of 250mm x 250mm x 325mm, with a 400W Yb-fiber laser that allows a scanning speed up to 7m/s. All the designed parts are built with Ti64 material with optimized process parameters for lattice structures. The Ti64 powder has a particle size of 39 ± 3 µm according to analysis following the ISO 13320 Particle size analysis-laser diffraction methods. The chemical composition analysis of the used material is shown in Table 3. After the printing, the powders around the built parts are removed and the support structures are broken away. A high-speed rotary tool with conical carbide cutter was used to deburr the rough surfaces. A glass bead blasting process was conducted to remove the powders inside the lattice structures and improve the surface finish throughout the parts. Ultrasonic washing was done in various cycles with Steris CIP 100 cleaning solution and deionized water with elevated temperature. Finally, hot isostatic pressing (HIP) process was conducted to improve the mechanical performance of the parts according to the ASTM F3301. The HIP process was done in argon inert gas environment with a temperature of 954℃, and pressure of 103MPa for 3 hours.
2.5. Evaluation of Geometric Features of Printed Lattices
Geometrical features such as surface area, pore size, and porosity are recorded for each lattice design. Pore size is evaluated in the cross-sectional plane that has the largest void area, by measuring the largest diameter of the circle that can fit into the voids. Surface area, pore size, and porosity were evaluated on the as-designed models. Porosity is calculated by the volume fraction of the void space on the CAD models.
2.6. Characterization of Stiffness and Strength of Investigated Lattice Structures
DIC tracker that was used for measuring the axial deformation in the specimen.
The MTS Landmark system was used for the compression testing of all investigated lattice structures (see Figure 9). For accurate measurement of the specimen deformation, a Dantec Q-400 Digital Image Correlation (DIC) system was used for the measurement of the displacement of the bottom platen (see Figure 10), while the upper platen was fixed during testing. A light source was projected onto the testing area when two cameras took images from two different angles. The DIC sampling rate is 10Hz, i.e., the cameras took 10 images per second to capture the displacement change. A speckle pattern was sprayed in the front face of the DIC tracker with white color background and finely distributed black dots. The two cameras of the DIC system track the location of the black dots through taking pictures while the compression testing is running. During the tests, the bottom compression plate moves at a speed of 0.03mm/s upward to compress the lattices. The compression test setup is shown in Figure 9 and Figure 10. Compression forces during testing were collected from the data acquisition system of the MTS testing machine. Displacement (Deformation) data was calculated using image processing in ISTRA 4D software evaluation module. All collected data of forces and deformation for different tests were normalized to determine the stress-strain results associated with each test. Stress-Strain results for each test were plotted to illustrate the mechanical behavior of each investigated lattice structure. 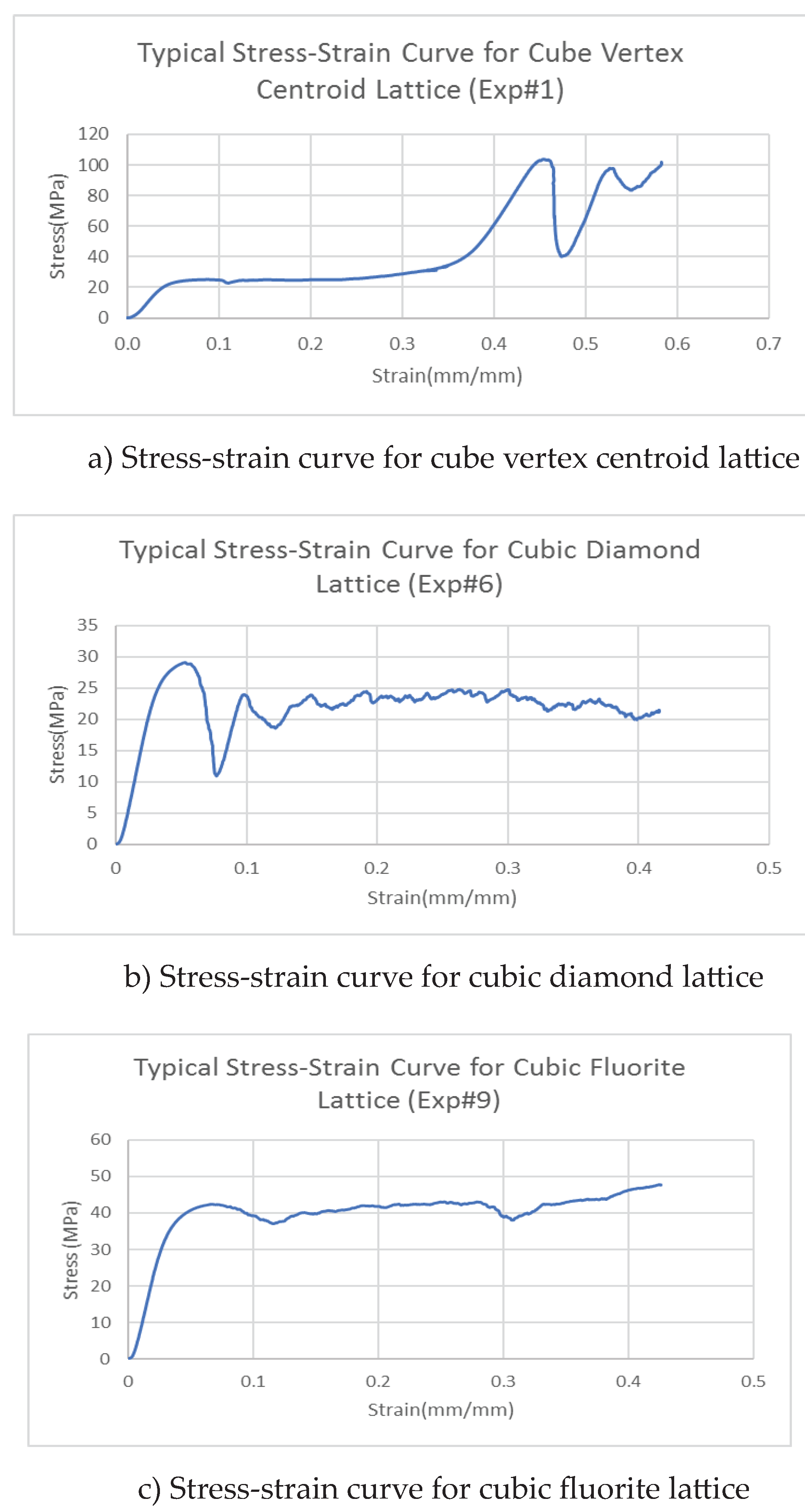Figure 11 displays stress-strain curves for three different lattice structures. Each of the displayed curves is unique and they are different from each other. The displayed curves show peaks and valleys very similar to the results obtained in compression testing of trabecular bone displayed in module 1, [14]. The slop of the linear portion of the stress-strain curve determines the elastic modulus of each lattice structure. At 0.2% offset strain the corresponding yield Strength of the specimens.
3. Results and Discussions
The developed approach is integrated with parametric investigation and involves both biological requirements and design for additive manufacturing by Laser -Powder Bed Fusion process (L-PBF). The presented solution offers lattice structure designs that can be adjusted to match bone stiffness distribution and promote bone ingrowth and hence eliminating the phenomenon of stress shielding while incorporating biological press-fit fixation technique. Table 4 summarizes the mean values of all measured properties of all nine lattices investigated with three samples tested for each design. All results are discussed in the light of how they affect the performance of patient’s specific lattice structures. Special attention is given to the significance of design parameters on stiffness property (modulus of elasticity) because of its direct effect on the phenomenon of stress shielding and implant potential failure.
3.1. Parametric Analysis of Design Parameters Effect on Lattice Microstructure
The output results (Table 4) show that different lattice designs have different quality characteristics that would enable the designer to choose the design that would satisfy most of the function requirements of the implant. The followings are explanation of various effects:
Surface Area.
Surface area affects the bone ingrowth as it provides an interface for the biological reaction. The surface area of 18x18x24mm block is 2376mm2, while lattices surface area varies from 14264.43 to 33566.66 mm2. This is 6 to 14 times of the block surface area. Unit cell type and unit cell size have the largest influence on the surface area, the maximum surface area occurs when the unit cell type is cubic fluorite that has the highest density of beams, and when unit cell size is 1.2mm, the smallest size. The specific levels are listed in the Experimental Log (Table 2).
Bore Size.
Bore size is the geometric property that would affect the growth of bone tissues into the implant to establish biological bond between the implant and the patient bone without need to introduce cement at the interface. Taniguchi et al. [18] have concluded that additive manufactured porous titanium implants with a pore size of 0.490–1.100mm exhibit a reasonable performance in vivo. The reported bore size (Table 4), ranges from 0.720 to 1.580 mm. Six out of the investigated nine lattices are within the recommended ranges. Based on the reported results, to reduce the pore size, a higher level of unit cell types (cubic diamond or cubic fluorite), and smaller unit cell size are recommended.
Porosity Distribution.
The optimum porosity is selected based on the resulting stiffness (modulus of elasticity), which should be close to the stiffness of the patient bone to avoid the stress shielding phenomenon. The experimental measurements (Table 4) of modulus of elasticity indicate that porosity in the range of 80-89% results in elastic modulus in the range of 1124.0 to 616.0 MPa. This range matches the ones for cancellous bone. Six out of nine investigated lattices are in this range.
3.2. Parametric Analysis of Structure Parameters’ Effects on Lattice Stiffness
Stiffness Properties (Modulus of Elasticity) of the implant has the most effects on its performance. Most of the existing joint metal implants could lead to stress shielding problems because of their much higher elastic modulus than that of bone. This could lead to reduction of the quality in the remaining bone, which would result to a significantly increased risk of fracture and aseptic loosening. Therefore, more detailed analysis of the experimentally determined stiffness of the investigated lattice structures are given below to examine the significance of the effects of each of the lattice design parameters on the structure stiffness. Table 5 displays modulus of elasticity mean value and standard deviation for each of the nine tested lattices. The reported stiffness varied in the range of 616.5 MPa to 5357.4 MPa depending on lattice design.
Analysis of Variance
The analysis of variance (ANOVA) technique [16] is used to predict the relative significance of the lattice design parameters on the stiffness (modulus of elasticity) of the structure. It gives the percentage of contribution of each factor, thus, providing a quantitative measure of the effects of various factors on design performance. The ANOVA results are shown below in Table 6. The error variance in the present analysis was obtained by pooling the sum of squares corresponding to the factor having the lowest mean square. Percentage contribution (ϱ, %) is calculated from the ratio, Sum of Squares due to the factor/Total Sum of Squares. Of the four design factors examined in this study, the Strut Thickness (D) was found to have the highest percent contribution (41%) regarding the structure stiffness, followed by Unit Cell Type (A), and Cell Size (B). Strut Shape (C) was found to have the lowest effect with only 11% contribution. The variance ratio, denoted by “F”, in Table 8, is the ratio of the mean square due to a factor and the error mean square. A large value of F means the effect of that factor is large compared to the error variance.
4. Conclusions
The present work aimed at exploring new designs of customized lattice structures and texture tailored to mimic closely patients’ bone anisotropic properties and that can incorporate an engineered biological press-fit fixation technique, to overcome most of the issues related to aseptic loosening phenomenon and risk of bone fracture.
An effective approach for development of customized cellular structures to match the mechanical properties and architecture of human trabecular bone, is introduced. It consists of four modules:1- characterization of geometry, microarchitecture, and stiffness properties of patient’s bones; 2- developing customized lattice structures tailored to mimic properties established in module 1; 3 - integration of developed lattice structure into full scale implant design and manufacturing; 4- implementation of the developed technology for use in implants design and fabrication.
Module 2 of the introduced approach is integrated with parametric investigation that involves both biological requirements and design for additive manufacturing by Laser -Powder Bed Fusion process (L-PBF). Of the four design factors examined in this study, strut thickness was found to have the highest percent contribution (41%) regarding the structure stiffness, followed by unit cell type, and cell size. Srut shape was found to have the lowest effect with only 11% contribution.
Results of the present investigation offer lattice structure designs that can be selected to match bone stiffness and promote bone ingrowth and hence eliminating the phenomenon of stress shielding while incorporating biological press-fit fixation technique.
Further investigation is needed to establish a predictive model based on the present experimental results to define optimum lattice design that will simultaneously meat target value for each of the required quality characteristics while minimizing variability of performance, that is, having a robust lattice design. This is necessary to complete all requirements of module 2 of the introduced approach.
Author Contributions
A.S.E.-G. made substantial contributions to research design, planning, coordination and management of all efforts, securing resources and drafting and submitting the final manuscript of this paper. X.M. made substantial contributions to research design, analysis and experimental work as part of his graduate research at the University of Missouri. J.C.A. made substantial contributions to research design including design, optimization, and supervising of the L-PBF process and finishing operations used for building all investigated designs with the required properties. A.A.M. made substantial contributions to the present research, updating and reviewing literature survey supporting the present results, securing additional resources from King Abdulaziz University paying for materials and supplies needed, reviewing and editing the final manuscript prior of submission for publication.
Funding
This research received no external funding.
Institutional Review Board Statement
This study did not require ethical approval.
Informed Consent Statement
No information was obtained from known patients or animals.
Data Availability Statement
All results regarding mechanical testing, geometrical measurements and statistical analysis of the results are available with Dr. A. S. El-Gizawy (corresponding author for the present article, and Dr. X Ma, (co-author of this article).
Acknowledgments
The authors wish to acknowledge the in-kind and financial support provided by Industrial Technology Development and Management (ITECH D&M), LLC, Columbia, Missouri, USA, for this research. Additionally, much gratitude is extended to Talissa Altes (MD) and Staff of the University Of Missouri Department of Radiology for sharing their CT scanner and expertise. Our appreciation is also extended to Robert Weinholtz, Frank Feng, and Matthew Maschmann of the University of Missouri Department of Mechanical and Aerospace Engineering for their valuable discussions and encouragement during the present project. We acknowledge also advice received from Benjamin Hansen (MD), and Ajay Aggarwal (MD) of Missouri Orthopedic Institute (MOI) regarding medical needs and importance of the proposed solutions.
References
- Ulrich SD, Seyler TM, Bennett D, Delanois RE, Saleh KJ, Thongtrangan I, Kuskowski M, Cheng EY, Sharkey PF, Parvizi J, Stiehl JB. Total hip arthroplasties: what are the reasons for revision? International Orthopedic. 32(5) (2008), 597-604. [CrossRef]
- Kurtz SM, Lau E, Ong K, Zhao K, Kelly M, Bozic KJ. Future young patient demand for primary and revision joint replacement: national projections from 2010 to 2030. Clinical Orthopaedics and Related Research®. 467(10) (2009), 2606-12. https://Doi.10.1007/s11999-009-0834-6.
- Hutmacher, D.W. Scaffolds in tissue engineering bone and cartilage. Biomaterials 2000, 21, 2427–2431. [Google Scholar] [CrossRef]
- Van Bael, S.; Kerckhofs, G.; Moesen, M.; Pyka, G.; Schrooten, J.; Kruth, J.P. Micro-CT-based improvement of geometrical and mechanical controllability of selective laser melted Ti6Al4V porous structures. Mater. Sci. Eng. A 2011, 528, 7423–7431. [Google Scholar] [CrossRef]
- Abdelrhman, Y.; Gepreel, M.A.; Kobayashi, S.; Okano, S.; Okamoto, T. Biocompatibility of new low-cost (alpha+beta)-type Ti-Mo-Fe alloys for long-term implantation. Mater. Sci. Eng. C Mater. Biol. Appl. 2019, 99, 552–562. [Google Scholar] [CrossRef]
- Huiskes R, Weinans H, Van Rietbergen B. The relationship between stress shielding and bone resorption around total hip stems and the effects of flexible materials. Clinical Orthopaedics and related research. ( 1992) Jan 1, 124–34.
- Ridzwan MI, Shuib S, Hassan AY, Shokri AA, Ibrahim MM. Problem of stress shielding and improvement to the hip implant designs: a review. J. Med. Sci. 7(3) (2007), 460-7. [CrossRef]
- Arabnejad S, Johnston B, Tanzer M, Pasini D. Fully porous 3D printed titanium femoral stem to reduce stress-shielding following total hip arthroplasty. Journal of Orthopedic Research. 35(8) (2017), 1774-83. [CrossRef]
- Agnieszka Chmielewska, David Dean. The role of stiffness-matching in avoiding stress shielding-induced bone loss and stress concentration-induced skeletal reconstruction device failure. Acta Biomaterialia 173 (2024) 51–65. [CrossRef]
- https://www.zimmerbiometdental.
- Vaishya R, Chauhan M, Vaish A. Bone cement. Journal of clinical orthopaedics and trauma. 4(4) (2013), 157-63.
- Liu, R.; Su, Y.; Yang, W.; Wu, K.; Du, R.; Zhong, Y. A Novel Design Method of Gradient Porous Structure for Stabilized and Lightweight Mandibular Prosthesis. Bioengineering. 2022, 9, 424. [Google Scholar] [CrossRef]
- Ma, X.; El-Gizawy, A.S. Development of customized cellular structures to match the mechanical properties of human trabecular bone. Solid Freeform Fabrication 2018: Annual International Solid Freeform Fabrication Symposium – An Additive Manufacturing Conference, August 13-15, 2018, 65, Austin, Texas, USA. [Google Scholar]
- El-Gizawy, A.S.; Ma, X.; Pfeiffer, F.; Schiffbauer, J.D.; Selly, T. Characterization of Microarchitectures, Stiffness and Strength of Human Trabecular Bone Using Micro-Computed Tomography (Micro-CT) Scans. BioMed 2023, 3, 89–100. [Google Scholar] [CrossRef]
- Next-Gen Engineering Design Software: nTop, www.ntop.com.
- Phadke, M.S. Quality Engineering Using Robust Design. Prentice Hall, Englewood, CA. 1989.
- Arnone, J.; El-Gizawy, A.S.; Ward, C.; Della Rocca, G.; Crist, B. An integrated computer-aided engineering approach for parametric investigation of locked plating systems design, ASME Transactions, J. Med. Devices 7:2, 1-8, 2013. [CrossRef]
- Taniguchi N, Fujibayashi S, Takemoto M, Sasaki K, Otsuki B, Nakamura T, et al. Effect of pore size on bone ingrowth into porous titanium implants fabricated by additive manufacturing: an in vivo experiment. Materials Science and Engineering: C. 2016;59: 690-701. [CrossRef]
Figure 1.
Proposed approach for development of customized orthopedic implants.
Figure 2.
Trabecular thickness and trabecular spacing colored maps and histograms for typical cylindrical bone samples. [14].
Figure 2.
Trabecular thickness and trabecular spacing colored maps and histograms for typical cylindrical bone samples. [14].
Figure 3.
Density and stiffness properties (MPa) Assigned Based on the Gray Scale Values [14].
Figure 3.
Density and stiffness properties (MPa) Assigned Based on the Gray Scale Values [14].
Figure 4.
The workflow of creating a periodic lattice structure with nTop Elements.
Figure 5.
Three-unit cell types investigated. The height (H), length (L) and width (W) of the external cubes are equal. Cell size=H=L=W.
Figure 5.
Three-unit cell types investigated. The height (H), length (L) and width (W) of the external cubes are equal. Cell size=H=L=W.
Figure 6.
Laser Powder Bed Fusion (L-PBF) system used for building all investigated samples.
Figure 7.
Digital design models of the investigated nine lattice structures.
Figure 8.
Experimental samples ready for testing.
Figure 9.
Compression Test Setup of Lattice Structures.
Figure 10.
Close view of compression test fixture displaying the specimen and the.
Figure 11.
Stress-Strain curves for three different lattice structures.
Table 1.
Factors and their Alternative levels considered in present lattice design.
| Factors (Design Paramters) |
Levels | |||
| 1 | 2 | 3 | ||
| Unit Cell Type (A) | Cube Vertex Centroid | Cubic Diamond | Cubic Fluorite | |
| Cell Size (B), mm | 1.2 | 1.4 | 1.6 | |
| Strut Shapes (C) | Square | Hexagon | Circle | |
| Strut Thickness (D), mm | 0.23 | 0.28 | 0.33 | |
Table 2.
Experimental log for parametric analysis.
| Experimental (Measurements)- Log | ||||
| Lattice Design (experiment) # |
Unit Cell Type A |
Cell Size, mm B |
Strut Shape C |
Strut Thickness, mm D |
| 1 | Cube Vertex Centroid | 1.2 | Square | 0.23 |
| 2 | Cube Vertex Centroid | 1.4 | Hexagon | 0.28 |
| 3 | Cube Vertex Centroid | 1.6 | Circle | 0.33 |
| 4 | Cubic Diamond | 1.2 | Hexagon | 0.33 |
| 5 | Cubic Diamond | 1.4 | Circle | 0.23 |
| 6 | Cubic Diamond | 1.6 | Square | 0.28 |
| 7 | Cubic Fluorite | 1.2 | Circle | 0.28 |
| 8 | Cubic Fluorite | 1.4 | Square | 0.33 |
| 9 | Cubic Fluorite | 1.6 | Hexagon | 0.23 |
Table 3.
Material chemical composition of Ti64 powder (wt.%).
| EOS Ti64 Material Composition | ||||||||
| Element | Ti | Al | V | O | N | C | H | Fe |
| wt-% | balance | 5.5-6.75 | 3.5-4.5 | <0.2 | <0.05 | <0.08 | <0.015 | <0.3 |
Table 4.
Summary of All Measured Properties (Mean Values) of Tested Lattices.
| Lattice Design # |
Surface Area, mm2 |
Pore Size, mm | Porosity, % | Compression Testing | |
|---|---|---|---|---|---|
| Elastic Modulus, MPa | Yield Strength, MPa | ||||
| Exp#1 | 21344.55 | 1.23 | 83.5 | 708.1 | 17.0 |
| Exp#2 | 18352.45 | 1.41 | 80.9 | 706.9 | 19.6 |
| Exp#3 | 14264.43 | 1.58 | 83.5 | 616.5 | 16.8 |
| Exp#4 | 25367.25 | 0.74 | 69.2 | 2513.3 | 58.2 |
| Exp#5 | 15098.33 | 1.08 | 89.0 | 688.1 | 16.8 |
| Exp#6 | 15296.34 | 1.12 | 85.0 | 1124.4 | 25.6 |
| Exp#7 | 33566.66 | 0.74 | 61.4 | 3345.9 | 99.6 |
| Exp#8 | 31190.34 | 0.72 | 52.3 | 5357.4 | 77.4 |
| Exp#9 | 21075.15 | 1.17 | 81.1 | 1248.5 | 30.3 |
Table 5.
Modulus of Elasticity Mean Value and Standard Deviation for Each of Tested Lattice Design.
| Experimental (Measurements)- Log |
Mean Modulus/Mpa |
Standard Deviation Modulus |
||||
| Lattice Design # |
Unit Cell Type |
Cell Size, mm |
Strut Shape |
Strut Thickness, mm |
µ | σ |
| 1 | Cube Vertex Centroid |
1.2 | Square | 0.23 | 708.1 | 76.5 |
| 2 | Cube Vertex Centroid |
1.4 | Hexagon | 0.28 | 706.9 | 56.2 |
| 3 | Cube Vertex Centroid |
1.6 | Circle | 0.33 | 616.5 | 50.9 |
| 4 | Cubic Diamond |
1.2 | Hexagon | 0.33 | 2513.3 | 398.3 |
| 5 | Cubic Diamond |
1.4 | Circle | 0.23 | 688.1 | 73.4 |
| 6 | Cubic Diamond |
1.6 | Square | 0.28 | 1124.4 | 164.3 |
| 7 | Cubic Fluorite |
1.2 | Circle | 0.28 | 3345.9 | 861.3 |
| 8 | Cubic Fluorite |
1.4 | Square | 0.33 | 5357.4 | 3055.8 |
| 9 | Cubic Fluorite |
1.6 | Hexagon | 0.23 | 1248.5 | 135.4 |
Table 6.
Analysis of Variance Regarding the Effects Design Parameters on Stiffness of the developed Design.
Table 6.
Analysis of Variance Regarding the Effects Design Parameters on Stiffness of the developed Design.
| ANOVA Table for Modulus of Elasticity | |||||
|---|---|---|---|---|---|
| Source | Degrees of Freedom D.F |
Sum of Squares, Sx |
Mean Square Vx=Sx/D.F |
Variance Ratio, F |
Percentage Contribution, ϱ (%) |
| Unit Cell Type A |
2 | 3,863,449 | 1,931,724 | 2.5 | 27 |
| Cell Size B |
2 | 2,999,370 | 1,499,685 | 1.94 | 21 |
| Strut Shape C |
2 | 1,542,907 | 771,454 | 1.0 | 11 |
| Strut Thickness D |
2 | 5,722,752 | 2,816,371 | 3.65 | 41 |
| Totals | 8 | 14,128,478 | 1,766,059 | 100 | |
| (Error) | (2) | (1,542,907) | (771,454) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated