Prerpints.org logo
Preprint
Article

Effect of Post-Processing Heat Treatment on the Micro-Contact Damage of Zirconia-Reinforced Lithium Silicate Dental Materials

Altmetrics

Downloads

83

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 March 2024

Posted:

25 March 2024

You are already at the latest version

Alerts
Abstract
Zirconia-reinforced lithium silicate (ZLS) is utilized as a material for prosthetic tooth crowns, offering enhanced strength compared to other dental glass-ceramics. In this study, we investigate a commercial ZLS material, provided in a fully crystallized form. We examine the effects of an optional post-processing heat treatment on micro-contact damage using controlled indentation tests simulating the primary modes of contact during chewing: axial and sliding. Our findings indicate that the heat treatment does not affect mechanical properties such as the elastic modulus, hardness and indentation fracture toughness. However, it does enhance the resistance to contact damage by fracture and chipping in both axial and sliding modes, as well as the resistance to crack initiation measured from sliding tests. This improvement is attributed to the refinement of the flaw population achieved through the heat treatment. The results are analysed within the framework of contact and fracture mechanics, and the implications for prosthetic dentistry are briefly discussed.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Modern dental prosthetic crowns predominantly utilize ceramic materials and their composites, chosen based on aesthetic and mechanical requirements, often involving tradeoffs. Among available options, dental zirconias are renowned for their superior strength and wear resistance, albeit potentially presenting challenges in machinability and aesthetics compared to less robust materials such as glass-ceramics or ceramic-polymer composites [1,2,3,4,5,6,7,8].
Zirconia-reinforced lithium silicate (ZLS) materials represent an advancement in dental glass-ceramics, offering enhanced strength and durability while maintaining excellent aesthetics. This is achieved by incorporating 10% zirconium oxide to the glass matrix to bolster strength and by limiting the size of lithium silicate crystallites [9]. Commercial ZLS dental materials are typically sourced in blocks (Figure 1(A)) ready for use in computer-aided design/computer-aided manufacturing (CAD/CAM) dentistry. According to the manufacturer specifications [9], one of such ZLS materials can be employed in as-received, already fully-crystallized condition which possess a natural tooth colour. An optional heat treatment (post-processing) is recommended to further enhance flexural and biaxial fracture strength by approximately ~150/160 MPa without changing the aesthetics.
A gap in the literature exists regarding the systematic examination of how post-processing treatments may impact the contact damage (e.g., fracture-induced chipping) of ZLS dental materials, beyond conventional mechanical property measurements. This is relevant because dental prosthetic crowns experience cyclic contacts against opposing dentition during chewing, involving a complex combination of axial and lateral forces, occasional bite overloads, and exposure to aggressive media where micron-sized abrasive particles may be present [6,10,11]. Mechanical degradation in the form of fracture and wear in turn has the potential to compromise the performance, strength and durability of the crown. Notably, the ability to resist mechanical degradation does not necessarily correlate with single-valued mechanical properties as measured from standardized tests [8].
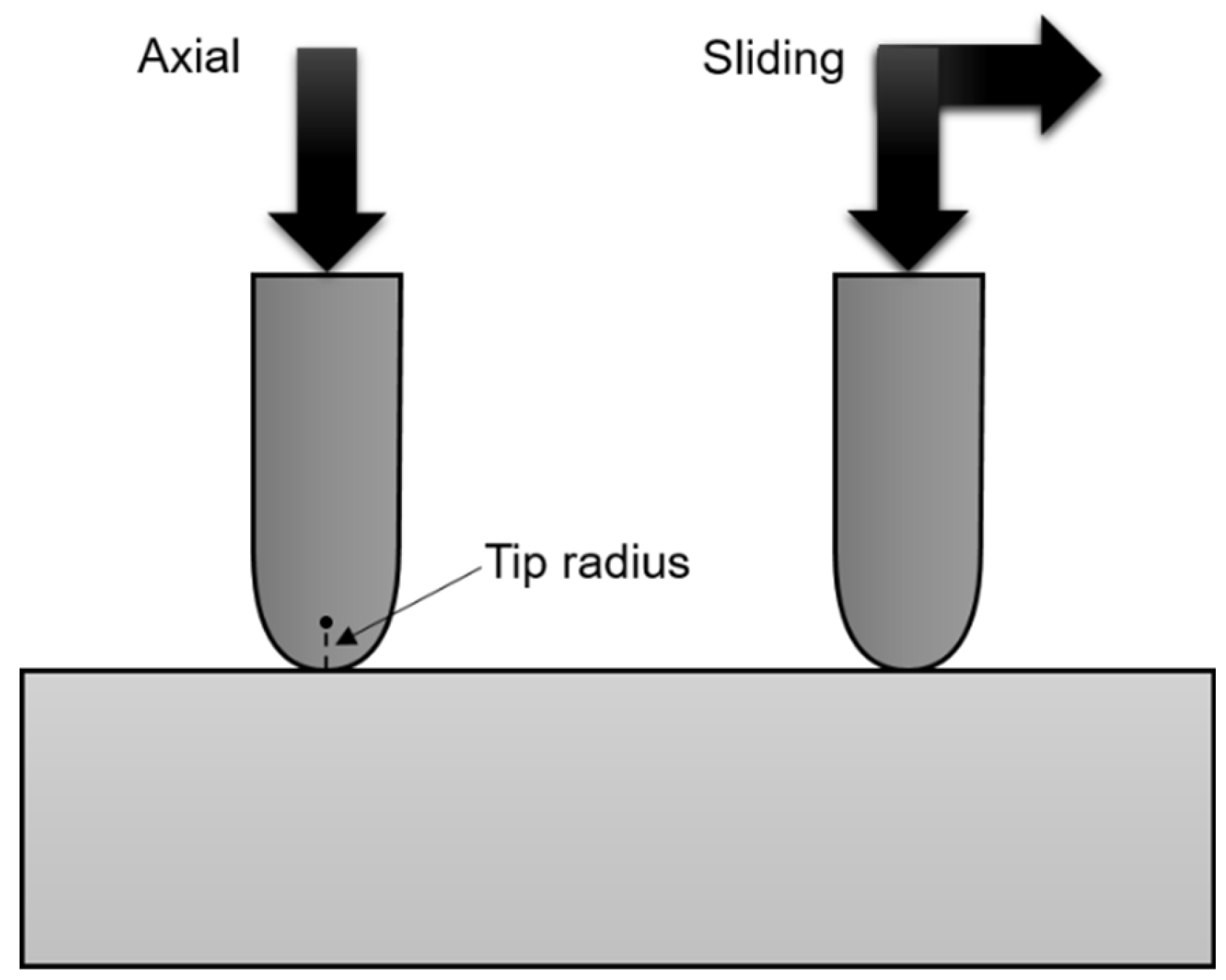
To address this gap, we investigate the fundamental contact damage of as-received (untreated) and heat-treated commercial ZLS glass-ceramics using controlled in-vitro indentation tests, in both axial and sliding configurations (Figure 2). The effects of contact/abrasive size are evaluated using tips of varying radii. Results are analysed with respect to the materials’ microstructure, within the framework of contact fracture mechanics. Furthermore, we briefly discuss the implications for prosthetic dentistry, with a view to providing insights for the selection of dental materials.

2. Experimental Procedure

The ZLS materials employed were obtained from commercially available CAD/CAM blocks (Celtra Duo HT, Dentsply Sirona, NC, USA). Plane parallel specimens for testing of thickness ≈1.2-1.5 mm were obtained by mechanical cutting from as-received (untreated) blocks. Half of the specimens were subsequently heat-treated in a dedicated furnace (Multimap Touch, Dentsply, PA, USA) in a dental/prosthetic facility (Clínica David Maestre, Valverde de Leganés, and LAB Dental, Badajoz, Spain), following the manufacturer’s specifications: initial heating to 500 ºC (soaking 3 min), followed by heating to 820ºC at 60ºC/min (soaking 1 min), and gradual cooling with the chamber closed until 500ºC, and then opening the furnace doors [7].
The test surfaces of all specimens were gently ground with fine sandpaper, lapped (30 μm), and polished with diamond suspensions using routine ceramographic methods. The polishing routine consisted of the following steps: 15 μm (10 min), 9 μm (10 min), 6 μm (10 min), 3 μm (15 min), and 1 μm (20 min).
The microstructure and fracture surface of the materials were observed by scanning electron microscopy (FE-SEM; Quanta 3D FEG, FEI, The Netherlands) using secondary and backscattered electrons at intermediate accelerating voltages (10-20 kV), without gold coating.
Relevant contact mechanical properties were measured by conventional indentation tests at room temperature in air. First, Hertzian tests were conducted (5535, Instron, Canton, MA, USA) on sputter-gold coated specimens, using loads in between 15 N and 1500 N, applied by WC spheres of radii 7.94 and 4.76 mm. The dimensions of the scars were subsequently measured by optical microscopy (Epiphot 300, Nikon, Tokyo, Japan) and, following procedures described elsewhere [12], stress-strain curves were constructed. For each material, the elastic modulus (E) was estimated from the linear part of the stress-strain curve [12,13]. Second, Vickers tests were performed with a diamond tip (MV-1, Matsuzawa, Japan), using a load of 9.8 N. A total of 10 indentations per material were conducted to determine the hardness (H) and fracture toughness (KIC) from the scar dimensions (measured by optical microscopy), using standard formulae [13,14].
Advanced indentation experiments were used to investigate micro-contact damage. Tests were performed at room temperature in air, using dedicated, computer-controlled equipment (Revetest RST3, Anton Paar, Graz, Austria). Rockwell-C (sphero-conical), diamond indenters of different radii (200 μm, and 20 μm) were employed. Tests were conducted in both axial and sliding loading configurations (see Figure 2). In the axial tests, for each material and tip size, separate pre-tests were performed at 50 N/min, progressively increasing maximum load at initial intervals of 20 N. The test surfaces were subsequently inspected by optical microscopy to determine the load range within which chipping takes place first. Such intervals were subsequently scanned in more detail, using loading steps between 1N and 5N. Every test was repeated ×3. Surfaces were again inspected after testing to accurately determine critical chipping loads. The criterion employed was that the critical chipping load was the smallest load for which all 3 of the 3 indentations at such load showed a well-formed chip particle. Tests were also conducted in sliding mode, ×3 for each material and tip size, using a sliding speed of 5 mm/min, at progressively increasing normal load from an initial value of 1 N (loading rate 100 N/min with the large tip; 25 N/min with the small tip). Test surfaces were subsequently examined by optical microscopy. For each test, critical chipping load was calculated from the corresponding microscopy image using the sliding speed and loading rate (more details in [6]).
Sliding tests using the larger tip (200 µm) were also employed to estimate the resistance to sliding fracture (σ*) of the materials. Tests were conducted in progressive loading under the following conditions: initial normal load 1 N, final normal load of 25 N, loading rate 25 N/min, and sliding rate 3 mm/min. A total of N=25 tests per material were performed. After each scratch test, the track was inspected in detail using the optical microscope to assess the critical fracture (normal) load (FC) and the contact radius (a) at the onset of cracking, as well as the coefficient of friction (f) logged by the equipment at that point. For each material, the σ* values were obtained from the experimental (FC, a, f) values using a contact mechanics model [15]. These were then sorted in ascending order, and a probability of failure value (Pf) was assigned to each one of them, using Pf =(i-0.5)/N, for the i-th value. A two-parameter Weibull probability function was employed to fit the data, from which the characteristic resistance to sliding fracture (σ0*) and Weibull modulus (m) were determined [16] (more details in [17]).
In selected cases, contact stresses were simulated using the software package FilmDoctor® (SIO®, Saxonian Institute of Surface Mechanics, Ruegen, Germany). The software calculates the elastic stress field in single-layer and multilayer systems, from the contact conditions and the materials’ elastic property values, using the extended Hertzian model [18].

3. Results and Discussion

Figures 1(B) and 1(C) show SEM micrographs representative of the microstructure of as-received and heat-treated ZLS dental glass-ceramics, respectively. At the microstructural scale, no significant differences can be detected between the two. Both microstructures exhibit a distribution of lithium-based crystals within a zirconia silicate glassy matrix. Crystal phase content is ≈50 vol%, and their compositions are known to be primarily Li2SiO3, followed by Li2Si2O5 and Li3PO4 [9,19,20]. Crystal sizes range from nanometric, beyond the current resolution, to micrometric. The majority of observed crystals appear rod-shaped, with an average size of 0.7 ± 0.1 μm and an aspect ratio of 3.5 ± 0.6 [7]. Hence, based on the SEM observations, the optional post-processing heat treatment does not significantly alter the relative phase content and crystallinity of the ZLS investigated materials. It is worth noting that this contrasts with other commercially available ZLS materials, which are supplied in pre-crystallized form and require a crystallization treatment to achieve both aesthetic and strength requirements [20].
The contact-mechanical properties of the ZLS materials investigated also appear to remain unaffected by the post-processing heat treatment. Elastic modulus, hardness and indentation fracture toughness values of 99 ± 6 GPa, 6.2 ± 0.2 GPa, and 0.70 ± 0.03 MPa·m1/2, respectively, were measured through Hertzian and Vickers tests in both as-received and heat-treated materials. In comparison to other dental glass-ceramics, ZLS materials generally exhibit improved mechanical properties, except for fracture toughness [4,6,7,17]. Lithium disilicate glass-ceramics, with their larger, interconnected crystals, demonstrate significantly higher toughness [7,17]. It is important to note that, while the Vickers indentation method may be considered less accurate than other techniques, it proves suitable for measuring the fracture toughness of the ZLS materials investigated and assessing any potential differences. This is because, under the load applied in our tests, the materials exhibit the required response, characterized by clean radial cracks observed on the surface [21,22].
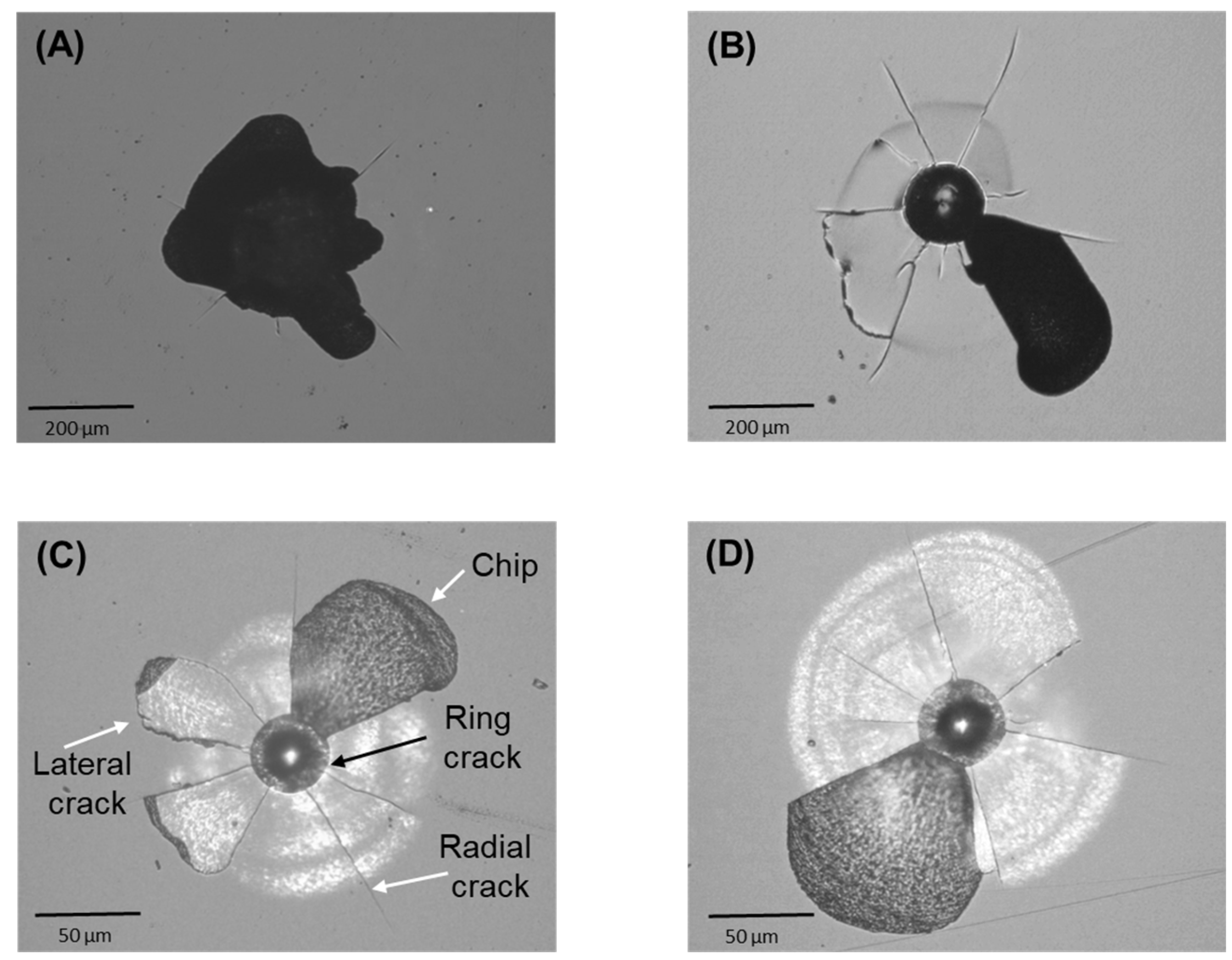
Controlled indentation tests with sphero-conical tips in both axial and sliding modes enable simulations of the fundamental modes of dental contact. Figure 3 presents micrographs illustrating the damage generated by axial contacts of different size (radius 200 μm and 20 μm) on both as-received and heat-treated ZLS glass-ceramics. When the applied load is sufficiently high, the concentrated stresses induce different fracture modes around the indentation site, including ring-like cracks around the circular contact, radial cracks perpendicular to the loading axis, and sub-surface lateral cracks (some reaching the surface). Of particular relevance in dentistry is the phenomenon of chipping, characterized by the wholesale dislodgement of material fragments (chips) due to the coalescence of cracks (typically radial and lateral) [23]. The loads required for the onset of fracture and chipping decrease with decreasing the tip radius from 200 μm to 20 μm. It is noteworthy that, in contrast with the previous single-value mechanical properties, the critical chipping load is influenced by the heat treatment. With the larger tip radius (200 μm), the critical chipping load for the as-received material was measured at 115 ± 5 N, while for the heat-treated material it was 130 ± 5 N—a 13 % increase. Similarly, with the smaller tip radius (20 μm), the critical chipping loads measured in as-received and heat-treated materials were 10 ±± 1 N and 12 ± 1 N, respectively, representing a 20 % increase.
Figure 4 presents panoramic micrographs of the damage resulting from sliding contacts of different size, at progressively increasing normal load, on the investigated ZLS glass-ceramics. With the larger tip (200 μm), low initial loads lead to surface smearing and deformation, evolving into fracture at intermediate loads. The first fracture mode is partial ring cracks, perpendicular to the sliding direction. Subsequent sliding leaves behind a series of parallel cracks in the wake of the contact, with progressively decreasing spacing. At higher loads, radial cracks extend outwards from the scratch track at an angle with the sliding direction. Ultimately, the coalescence of radial and partial ring/cone cracks results in material removal through chipping. As in the axial case, the loads required for the onset of fracture and chipping decrease with decreasing tip radius from 200 μm to 20 μm, with the heat treatment influencing the critical loads. With the larger tip (200 μm), the measured critical fracture and chipping loads were 5.4 ± 0.1 N and 54 ± 4 N (as-received), and 7.2 ± 0.1 N and 64 ± 4 N (heat-treated). With the smaller tip (20 μm), the critical fracture and chipping loads were 2.2 ± 0.1 N and 2.5 ± 0.3 N (as-received), and 2.5 ± 0.1 N and 2.7 ± 0.3 (heat-treated).
The fracture modes observed can be explained based on the analysis of the main components of the stress field generated by axial and sliding contacts. Figure 5 shows simulations of the cross-sectional distribution of normal and Von Mises stresses, induced by axial contacts of radii 200 μm and 20 μm, at a low reference load (1 N). The maximum tensile stress is located on the surface, right outside the contact circle. Because the maximum tensile stresses have radial direction, when their magnitude exceeds a critical value, they open ring-shaped cracks, as shown in the inset of Figure 5 (A) (high magnification detail) [12]. On the other hand, the maximum shear stress (Von Mises) is located below the surface, approximately at ~0.5a, with a the Hertzian contact radius, and is responsible for plastic and quasi-plastic deformation processes. Upon unloading, the residual elastic-plastic indentation stress field propagates some of the sub-surface microcracks previously generated, which eventually reach the contact surface with radial orientation (i.e., radial cracks, Figure 5(A) inset). Depending on the specific micro-crack orientation, propagation may be parallel to the contact surface, developing lateral cracks as observed for example in Figure 3(C) [12,13,14]. The simulations indicate that the greater pressures attained using smaller tips translate into an increase in both the maximum surface tensile stress and the sub-surface Von Mises stress with decreasing the contact size (Figures 5(C) and 5(D)). This explains, qualitatively, the lower loads required for chipping using the 20 μm tip compared to the 200 μm tip.
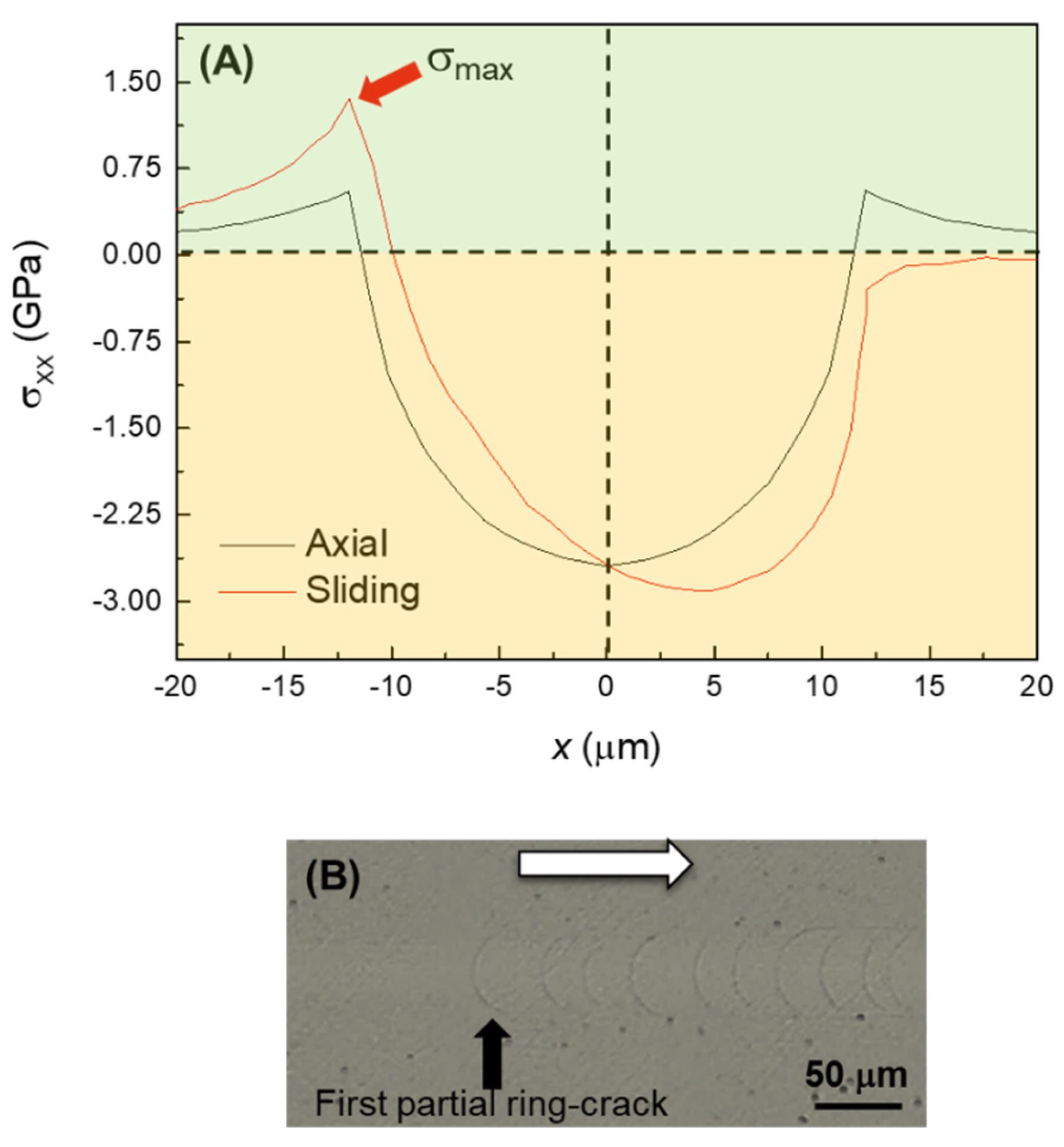
The addition of a lateral force upon sliding has a relatively minor effect on the Von Mises stress?it basically shifts the maximum slightly ahead of the normal axis [15]. However, it has a significant impact on the stress at the contact surface. In particular, friction increases the maximum tensile stress at the trailing half of the contact, while the stress at the leading half becomes compressive, as observed in the line graphs (Figure 6) of the normal stress distributions on the surface for the 200 μm tip (axial/frictionless vs. sliding/friction) [15]. This asymmetry of the maximum contact stress leads to the initial opening not of fully developed ring cracks, but of half rings (i.e., only in the rear edge of the contact, the so-called partial ring/cone cracks) [24]. A detail of such partial ring cracks upon sliding contact can be observed in Figure 6 (C). As in the axial case, subsequent increases in the applied load lead to the formation of radial cracks. In the sliding case, the moving tensile component of the stress field pulls the radial cracks forward, explaining the angle with respect to the sliding direction (e.g., white arrows in Figures 4(A) and 4(B)). Decreasing the contact size also translates into an increase of the magnitude of the stresses, again explaining the lower chipping loads measured with the 20 μm tip compared to the 200 μm tip. In fact, as a result of the greater contact pressure even at low loads, partial ring cracks are not observed with the smaller tip, and the initial fracture mode is radial cracking followed by chipping at low loads.
The fact that the initial fracture mode of the ZLS materials upon scratching with the larger 200 μm tip is that of partial ring cracks allows this test to be employed to assess the resistance to sliding fracture. The theoretical framework is provided by the expression from Hamilton and Goodman for the maximum tensile stress at the rear edge of a sliding Hertzian contact [15]:
σ m a x = P 0 1 − 2 υ 3 + 4 + υ 8 f
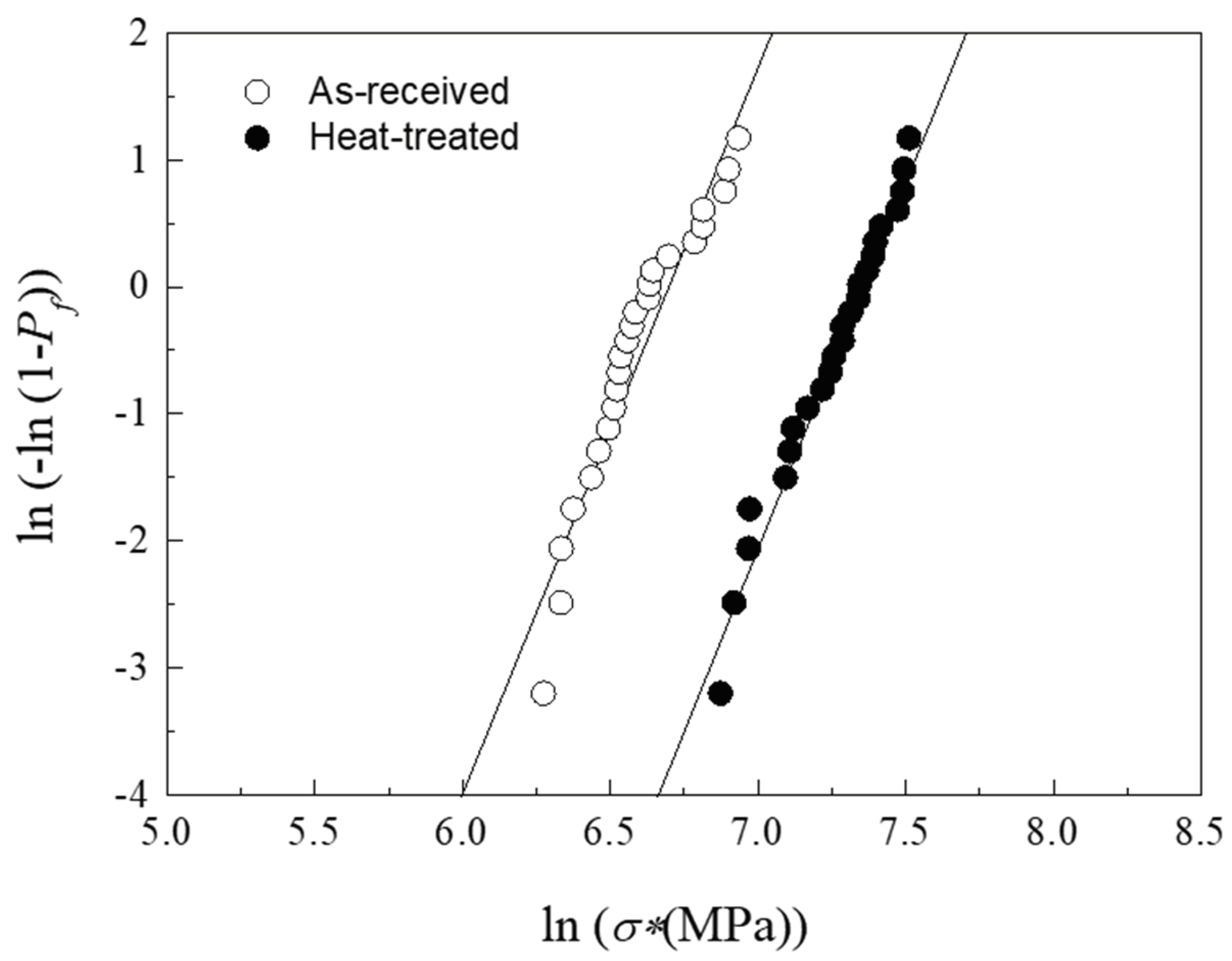
where P0 and f are the applied Hertzian pressure and coefficient of friction at that contact point, and υ the Poisson’s ratio of the material. Thus, measurement of the critical load FC and f at which the first partial ring crack appears (data collected by the equipment), allows an estimation of the material’s resistance to sliding fracture (σ*) using (1). To deal with the intrinsic variability of the fracture phenomenon in brittle materials, several tests were performed in as-received and heat-treated ZLS materials and analysed using Weibull statistics [17]. The results are shown in Figure 7, where Pf represents the probability of failure. As with the critical chipping loads, the post-processing heat treatment has a positive impact on the resistance to sliding fracture. However, in this case the extent of the improvement is significantly greater, with the heat-treated material showing a characteristic resistance σ0*=1587.6 MPa and Weibull modulus/reliability m=5.8 vs. σ0*=804.3 MPa and m=5.7 in the the as-received material.
The results obtained demonstrate that the optional post-processing heat treatment applied to ZLS materials does not significantly alter their single-value mechanical properties (E, H, KIC). However, it does increase the critical loads for chipping under any given contact configuration (axial, sliding) and size, as well as the sliding fracture strength. In essence, this treatment makes the materials more resistant to the initiation of cracks, and to material removal by crack coalescence processes. Given that the heat treatment does not significantly affect the observed crystallinity of the glass-ceramics (Figure 1), this effect is attributed to a refinement of the flaw population. Such defects are traditionally challenging to detect on polished surfaces such as the ones in Figure 1 [25,26], but they become apparent on fracture surfaces, as illustrated in Figure 8. The SEM images reveal the presence of defects, such as µm-sized voids [14], in both the as-received and the heat-treated materials. However, the frequency and size of these defects appear to be relatively smaller after the heat treatment. According to Griffith’s fracture mechanics relation (σF~c-1/2, with c representing the size of the critical defect precursor for fracture [13,14]), a reduction in the average defect size can in turn lead to an increase in the fracture strength of the heat-treated material without compromising aesthetics, aligning with the manufacturer’s specifications [9].
This study has significant implications in prosthetic dentistry and may aid in selecting materials with improved durability. Although the post-processing heat treatment for ZLS glass-ceramics involves greater processing cost and time, it results in improved mechanical stability of the prosthesis without sacrificing aesthetics. Similar treatments could be considered for other types of dental materials. Furthermore, the findings emphasize that single-value mechanical properties such as elastic modulus, hardness and fracture toughness may not adequately reflect prosthesis durability, adding to previous evidence obtained from wear tests on biphasic dental materials [8]. Material removal processes, such as chipping, involving complex interactions between different fracture modes, are best assessed by considering both mechanical properties and microstructural features (e.g., weak interfaces, defects).

4. Conclusions

We have investigated the effect of a post-processing heat treatment on the damage generated by micrometric axial and sliding contacts in ZLS dental glass-ceramics. Based on the results and analyses, the following conclusions can be drawn:
  • The heat treatment does not significantly alter the crystallinity of the ZLS glass-ceramics, but it does reduce the frequency and size of processing flaws compared to the untreated material.
  • Within experimental errors, the heat treatment does not impact the elastic modulus, hardness and indentation fracture toughness of the materials.
  • The heat treatment leads to an increase in critical loads for fracture and chipping in both axial and sliding contacts, with critical loads decreasing as the contact size decreases.
  • A significant improvement in fracture strength, as measured from scratch tests, is observed with statistical (Weibull) significance following the heat treatment.
  • The enhanced resistance to contact damage can be attributed to the refinement of the flaw population achieved through the heat treatment.

Author Contributions

Conceptualization, Estíbaliz Sánchez-González and Óscar Borrero-López; methodology, Estíbaliz Sánchez-González and Óscar Borrero-López; software, José A. Pérez and Fernando Rodríguez Rojas; validation, José A. Pérez and Estíbaliz Sánchez-González; formal analysis, Estíbaliz Sánchez-González; investigation, José A. Pérez and Estíbaliz Sánchez-González; resources, Estíbaliz Sánchez-González and Óscar Borrero-López; data curation, José A. Pérez, Fernando Rodríguez Rojas and Estíbaliz Sánchez-González; writing—original draft preparation, Estíbaliz Sánchez-González and Óscar Borrero-López; supervision, Estíbaliz Sánchez-González and Óscar Borrero-López; project administration, Estíbaliz Sánchez-González and Óscar Borrero-López; funding acquisition, José A. Pérez and Estíbaliz Sánchez-González. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data relating to the research is available to any researcher upon request to the authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. F. Zhang, H. Reveron, B.C. Spies, B. Van Meerbeek, J. Chevalier, Trade-off between fracture resistance and translucency of zirconia and lithium-disilicate glass ceramics for monolithic restorations, Acta Biomaterialia 91 (2019) 24-34. [CrossRef]
  2. Y. Zhang, I. Sailer, B.R. Lawn, Fatigue of dental ceramics, Journal of Dentistry 41(12) (2013) 1135-1147.
  3. J.J. Kruzic, J.A. Arsecularatne, C.B. Tanaka, M.J. Hoffman, P.F. Cesar, Recent advances in understanding the fatigue and wear behavior of dental composites and ceramics, Journal of the Mechanical Behavior of Biomedical Materials 88 (2018) 504-533. [CrossRef]
  4. M. Wendler, R. Belli, A. Petschelt, D. Mevec, W. Harrer, T. Lube, R. Danzer, U. Lohbauer, Chairside CAD/CAM materials. Part 2: Flexural strength testing, Dental Materials 33(1) (2017) 99-109.
  5. Borrero-Lopez, F. Guiberteau, Y. Zhang, B.R. Lawn, Wear of ceramic-based dental materials, Journal of the Mechanical Behavior of Biomedical Materials 92 (2019) 144-151.
  6. E. Sanchez-Gonzalez, O. Borrero-Lopez, F. Rodriguez-Rojas, M. Hoffman, F. Guiberteau, Chipping of ceramic-based dental materials by micrometric particles, Journal of the American Ceramic Society 106(2) (2023) 1309-1320. [CrossRef]
  7. F. Rodríguez-Rojas, O. Borrero-López, E. Sánchez-González, M. Hoffman, F. Guiberteau, On the durability of zirconia-reinforced lithium silicate and lithium disilicate dental ceramics under severe contact, Wear 508-509 (2022) 204460. [CrossRef]
  8. Borrero-Lopez, F. Guiberteau, Y. Zhang, B.R. Lawn, Inverse correlations between wear and mechanical properties in biphasic dental materials with ceramic constituents, Journal of the Mechanical Behavior of Biomedical Materials 105 (2020). [CrossRef]
  9. D. Sirona, Celtra® Duo. Zirconia – Reinforced Lithium Silicate (ZLS). Developed to make a difference. Brochure for the dental laboratory Dentsply, PA, USA.
  10. F. Rodriguez-Rojas, O. Borrero-Lopez, P.J. Constantino, A.G. Henry, B.R. Lawn, Phytoliths can cause tooth wear, Journal of the Royal Society Interface 17(172) (2020).
  11. W.H.O.O.a.E.H.T.. Hazard prevention and control in the work environment: airborne dust. https://apps.who.int/iris/handle/10665/66147, 1999).
  12. B.R. Lawn, Indentation of ceramics with spheres: A century after Hertz, Journal of the American Ceramic Society 81(8) (1998) 1977-1994.
  13. B.R. Lawn, Fracture of brittle solids, Cambridge University Press, Cambridge, UK, 1993. [CrossRef]
  14. D.J. Green, An introduction to the mechanical properties of ceramics, Cambridge University Press, Cambridge, UK, 1998.
  15. G.M. Hamilton, L.E. Goodman, Stress field created by a circular sliding contact, Journal of Applied Mechanics 33(2) (1966) 371-&. [CrossRef]
  16. A.s.f.t.a. materials, Standard Practice for Reporting Uniaxial Strength Data and Estimating Weibull Distribution Parameters for Advanced Ceramics, C1239, ASTM International, 2007.
  17. Estíbaliz Sánchez-González, Óscar Borrero-López, Fernando Rodríguez-Rojas, José Antonio Pérez, M. Hoffman, Fracture resistance of dental glass-ceramics under sliding contact, Ceramics International 49(19) (2023) 31727-31733. [CrossRef]
  18. N. Schwarzer, The extended Hertzian theory and its uses in analyzing indentation experiments, Philosophical Magazine 86(33-35) (2006) 5179-5197. [CrossRef]
  19. J. Lubauer, R. Belli, H. Peterlik, K. Hurle, U. Lohbauer, Grasping the Lithium hype: Insights into modern dental Lithium Silicate glass-ceramics, Dental Materials 38(2) (2022) 318-332. [CrossRef]
  20. R. Belli, M. Wendler, D. de Ligny, M.R. Cicconi, A. Petschelt, H. Peterlik, U. Lohbauer, Chairside CAD/CAM materials. Part 1: Measurement of elastic constants and microstructural characterization, Dental Materials 33(1) (2017) 84-98. [CrossRef]
  21. D.B. Marshall, R.F. Cook, N.P. Padture, M.L. Oyen, A. Pajares, J.E. Bradby, I.E. Reimanis, R. Tandon, T.F. Page, G.M. Pharr, B.R. Lawn, The Compelling Case for Indentation as a Functional Exploratory and Characterization Tool, Journal of the American Ceramic Society 98(9) (2015) 2671-2680. [CrossRef]
  22. G.R. Anstis, P. Chantikul, B.R. Lawn, D.B. Marshall, A critical-evaluation of indentation techniques for measuring fracture-toughness .1. direct crack measurements, Journal of the American Ceramic Society 64(9) (1981) 533-538.
  23. B.R. Lawn, Chipping: a pervasive presence in nature, science and technology, Journal of Materials Science 56(14) (2021) 8396-8405.
  24. B.R. Lawn, Partial cone crack formation in a brittle material loaded with a sliding spherical indenter, Proceedings of the Royal Society of London Series a-Mathematical and Physical Sciences 299(1458) (1967) 307-&.
  25. E. Sanchez-Gonzalez, P. Miranda, A. Diaz-Parralejo, A. Pajares, F. Guiberteau, Influence of zirconia sol-gel coatings on the fracture strength of brittle materials, Journal of Materials Research 20(6) (2005) 1544-1550. [CrossRef]
  26. N. Sheth, C. Greenley, R. Bermejo, J.C. Mauro, C.G. Pantano, S.H. Kim, Effects of acid leaching treatment of soda-lime silicate glass on crack initiation and fracture, Journal of the American Ceramic Society 104(9) (2021) 4550-4558. [CrossRef]
  27. F. Rodriguez-Rojas, O. Borrero-Lopez, E. Sanchez-Gonzalez, J.D. Rios, F. Guiberteau, Investigating correlations between translucency and wear resistance in lithium silicate-based dental glass-ceramics, Boletín de la Sociedad Española de Cerámica y Vidrio 63(1) (2024) 2-10. [CrossRef]
Preprints 102044 g001
Figure 1. (A) Photograph of an as-received ZLS CAD/CAM block. SEM micrographs representative of the microstructure of ZLS dental glass-ceramics (from [27]): (B) as-received, and (C) heat-treated.
Figure 1. (A) Photograph of an as-received ZLS CAD/CAM block. SEM micrographs representative of the microstructure of ZLS dental glass-ceramics (from [27]): (B) as-received, and (C) heat-treated.
Preprints 102044 g001
Preprints 102044 g002
Figure 2. Schematic (cross-sectional detail) of the axial and sliding contact configurations simulated by indentation tests. Not at scale.
Figure 2. Schematic (cross-sectional detail) of the axial and sliding contact configurations simulated by indentation tests. Not at scale.
Preprints 102044 g002
Preprints 102044 g003
Figure 3. Optical micrographs representative of the damage generated by axial contacts of different size in ZLS glass-ceramics: (A) as-received, tip radius 200 μm, load 115 N; (B) heat-treated, tip radius 200 μm, load 130 N; (C) as-received, tip radius 20 μm, load 10 N; (D) heat-treated, tip radius 20 μm, load 12 N.
Figure 3. Optical micrographs representative of the damage generated by axial contacts of different size in ZLS glass-ceramics: (A) as-received, tip radius 200 μm, load 115 N; (B) heat-treated, tip radius 200 μm, load 130 N; (C) as-received, tip radius 20 μm, load 10 N; (D) heat-treated, tip radius 20 μm, load 12 N.
Preprints 102044 g003
Preprints 102044 g004
Figure 4. Optical micrographs (panoramic) representative of the damage generated by sliding contacts of different size (progressive loading, from 1N to 100N with tip radius 200 μm and from 1N to 25N with tip radius 20 μm) in ZLS glass-ceramics: (A) as-received, tip radius 200 μm with white arrows pointing at radial cracks (from [6]); (B) heat-treated, tip radius 200 μm with white arrows pointing at radial cracks; (C) as-received, tip radius 20 μm (from [6]); (D) heat-treated, tip radius 20 μm. The black arrow indicates the direction of sliding.
Figure 4. Optical micrographs (panoramic) representative of the damage generated by sliding contacts of different size (progressive loading, from 1N to 100N with tip radius 200 μm and from 1N to 25N with tip radius 20 μm) in ZLS glass-ceramics: (A) as-received, tip radius 200 μm with white arrows pointing at radial cracks (from [6]); (B) heat-treated, tip radius 200 μm with white arrows pointing at radial cracks; (C) as-received, tip radius 20 μm (from [6]); (D) heat-treated, tip radius 20 μm. The black arrow indicates the direction of sliding.
Preprints 102044 g004
Preprints 102044 g005
Figure 5. FilmDoctor® simulations of the relevant components of the contact stress field induced on a model isotropic, elastic layer of elastic modulus 99 GPa (simulating ZLS) by a sliding contact (diamond indenter) at a reference applied load (axial) of 1 N: (A) tensile stress σxx, indenter radius 200 μm; (B) Von Mises stress, indenter radius 200 μm; (C) tensile stress σxx, indenter radius 20 μm; (D) Von Mises stress, indenter radius 20 μm. Cartesian coordinates are used, with z the normal loading direction. The contour plots show the stress at the xz cross-section. Positive stress values indicate tensile stress and negative values compressive stress. Note the different x- and z-axis scales used in each graph. The inset in (A) is an optical microscopy detail of the cracking modes generated by the stress field on the contact surface.
Figure 5. FilmDoctor® simulations of the relevant components of the contact stress field induced on a model isotropic, elastic layer of elastic modulus 99 GPa (simulating ZLS) by a sliding contact (diamond indenter) at a reference applied load (axial) of 1 N: (A) tensile stress σxx, indenter radius 200 μm; (B) Von Mises stress, indenter radius 200 μm; (C) tensile stress σxx, indenter radius 20 μm; (D) Von Mises stress, indenter radius 20 μm. Cartesian coordinates are used, with z the normal loading direction. The contour plots show the stress at the xz cross-section. Positive stress values indicate tensile stress and negative values compressive stress. Note the different x- and z-axis scales used in each graph. The inset in (A) is an optical microscopy detail of the cracking modes generated by the stress field on the contact surface.
Preprints 102044 g005
Preprints 102044 g006
Figure 6. (A) 2-D plot at the contact surface (z=0 μm) of the tensile stress σxx (for a reference load 1 N) on a model ZLS layer simulated by FilmDoctor® for purely axial (black line) and sliding (f=0.2, red line). Cartesian coordinates are used, with z the normal loading direction, and x the direction of sliding. The green and yellow regions correspond to tensile and compressive stresses, respectively. (B) Optical micrograph showing the onset of partial ring-cracking in a ZLS material upon sliding with a 200 μm tip. .
Figure 6. (A) 2-D plot at the contact surface (z=0 μm) of the tensile stress σxx (for a reference load 1 N) on a model ZLS layer simulated by FilmDoctor® for purely axial (black line) and sliding (f=0.2, red line). Cartesian coordinates are used, with z the normal loading direction, and x the direction of sliding. The green and yellow regions correspond to tensile and compressive stresses, respectively. (B) Optical micrograph showing the onset of partial ring-cracking in a ZLS material upon sliding with a 200 μm tip. .
Preprints 102044 g006
Preprints 102044 g007
Figure 7. Weibull plot of probability of failure (Pf) vs critical fracture stress (σ*) obtained from sliding tests with a 200 μm tip on as-received and heat-treated ZLS glass-ceramics. Symbols correspond to experimental data and solid lines are the best linear fit each data set.
Figure 7. Weibull plot of probability of failure (Pf) vs critical fracture stress (σ*) obtained from sliding tests with a 200 μm tip on as-received and heat-treated ZLS glass-ceramics. Symbols correspond to experimental data and solid lines are the best linear fit each data set.
Preprints 102044 g007
Preprints 102044 g008
Figure 8. SEM micrographs representative of the fracture surface of ZLS glass-ceramics: (A) as-received, with inset corresponding to a higher magnification detail: (B) heat-treated.
Figure 8. SEM micrographs representative of the fracture surface of ZLS glass-ceramics: (A) as-received, with inset corresponding to a higher magnification detail: (B) heat-treated.
Preprints 102044 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated