2. The 4th-BERRU-PM Posterior Distribution
The 4th-BERRU-PM Methodology [
1] uses the MaxEnt principle [
3] to combine the first four moments of the computed response distribution in parameters space (which were reviewed in Part 1 [
4]) with the first four moments of the distribution of measured model responses, which are assumed to be known and are defined below.
(i) The mean (or expected) values for the measured system responses, which will be denoted as , .
(ii) The covariances, denoted as , for two measured responses and , for . The covariances , , of the system responses are considered to be components of the -dimensional covariance matrix of system responses, which will be denoted as .
(iii) The triple correlations, denoted as , for three system responses denoted as , and , . The skewness of a response is denoted as .
(iv) The quadruple correlations, denoted as , for four system responses denoted as , , , , where . The kurtosis of a response will be denoted as .
The 4th-BERRU-PM posterior distribution derived by Cacuci [
1] using the MaxEnt principle [
3] has the following exponential form:
where the subscript “4” denotes “fourth-order,” the superscript “be” denotes “best-estimate,” and where:
The Lagrange multipliers in Eq. (2) have the following expressions:
4. Application of the 4th-BERRU-PM Methodology to the PERP Benchmark: Best-Estimate Predicted Moments of the Posterior Distribution of Responses and Parameters
This Section presents the results obtained by applying the 4th-BERRU-PM methodology to the PERP benchmark when several relatively imprecise experimental measurements of the benchmark’s leakage response have been performed, having a mean value neutrons/sec, and a relatively large standard deviation . These values were chosen in order to examine the effects of applying the 4th-BERRU-PM methodology to a case when the mean value of the measurements is “one experimental standard deviation” away from the computed values of the leakage response (since ).
Two cases will be considered regarding the precision of the model parameters, namely:
parameters having uniform standard deviations of 2%, which are expected to provide physically meaningful results, within the radius of convergence of the Taylor-series provided in Eq. (16); and
parameters having uniform standard deviations of 5%, which are expected to illustrate the results still obtainable not far outside the radius of convergence of the Taylor-series provided in Eq. (16).
The results to be presented in this Section will illustrate the effects of the parameters’ standard deviations on the following moments of the (MaxEnt) posterior distribution of model parameters, computed and measured response, as follows:
Subsection 4.1, below, will present results for the optimally predicted best-estimate leakage response value, denoted as and the predicted best-estimate standard deviation, denoted as , for ; it will be shown that is smaller than either the originally measured of computed response standard deviations.
Subsection 4.2, below, will present results for the best-estimate predicted correlations, denoted as , between the best-estimate posterior responses and model parameters.
Subsection 4.3, below, will present results for the calibrated best-estimate predicted values, denoted as , for the model parameters.
Subsection 4.4, below, will present results for the best-estimate values of the components of the predicted covariance matrix, denoted as , of the calibrated model parameters.
Subsection 4.5, below, will present results for the predicted values of the posterior triple-correlations among the predicted model parameters and leakage response, including the predicted skewness of the best-estimate predicted leakage response, denoted as , and the predicted skewness, denoted as , of the calibrated model parameters.
Subsection 4.6, below, will present results for the predicted values of the posterior quadruple-correlations among the predicted model parameters and leakage response, including the predicted kurtosis, denoted as , of the best-estimate predicted leakage response, and the predicted kurtosis, denoted as , of the calibrated model parameters.
The best-estimate moments mentioned above depend on the index , which will be used to indicate the order of the highest-order retained sensitivities in the respective expressions. The effects of the order of the sensitivities retained in these expressions will also investigated, as follows: (i) : only the 1st-order sensitivities are considered; (ii) : the first- and second-order sensitivities are included; (iii) : all sensitivities up to and including third-order are included; (iv) : all sensitivities up to and including fourth-order are included.
4.1. Effects of Sensitivities and Parameter Standard Deviations on the Predicted Value of the Best-Estimate Leakage Response and Its Corresponding Best-Estimate Standard Deviation
The results to be presented in this Subsection will illustrate the effects of the parameters’ standard deviations on the best-estimate leakage response value, denoted as , and the reduction of its accompanying predicted best-estimate standard deviation, denoted as , where the index indicates the order of the highest-order retained sensitivities. Three cases will be considered regarding the precision of the model parameters, as follows:
Subsection 4.1.1 presents results for parameters that are known with “high precision,” having uniform standard deviations of 2%, which are expected to provide physically meaningful results, within the radius of convergence of the Taylor-series provided in Eq. (16).
Subsection 4.1.2 presents results for parameters that are known with “medium precision,” having uniform standard deviations of 5%, which are expected to illustrate the results still obtainable not too far outside of the radius of convergence of the Taylor-series provided in Eq. (16).
Subsection 4.1.3 presents results for parameters that are known with “low precision,” having uniform standard deviations of 10%, which are expected to illustrate the results obtainable outside the radius of convergence of the Taylor-series provided in Eq. (16).
4.1.1. “High precision” parameters, having uniform relative standard deviations
The results of applying Eqs. (17)‒(33) to the PERP benchmark, in conjunction with the experimental information mentioned above (i.e.,
with
) are illustrated in
Figure 1,
Figure 2,
Figure 3 and
Figure 4, below, when considering that the parameters have been measured precisely, having uniform relative standard deviations of 2%. The results presented in
Figure 1 include only the first-order sensitivities of the leakage response with respect to the model parameters (total microscopic group cross sections). The results presented in
Figure 2 include the first- and second-order sensitivities. The results depicted in
Figure 3 include first- through third-order sensitivities, while the results depicted in
Figure 4 include all sensitivities up to (and including) fourth-order. The numerical values of the results depicted in
Figure 1,
Figure 2,
Figure 3 and
Figure 4 are tabulated in
Table 1. The results depicted in
Figure 1,
Figure 2,
Figure 3 and
Figure 4 are tabulated numerically in
Table 1, below.
The results presented in
Figure 1,
Figure 2,
Figure 3 and
Figure 4 and
Table 1 indicate that the application of the BERRU-PM methodology yields a best-estimate value for the predicted leakage response which is in-between the experimentally measured and computed values of this response (but closer to the more precisely known experimental value), with an accompanying predicted standard deviation which is smaller than either the measured or the computed standard deviations. Since the standard deviations (of 2%) for the model parameters are within the radius of convergence of the Taylor-series that represents the computed response in terms of parameter deviations, the contributions stemming from the higher-order sensitivities are expected to diminish with increasing order. This expectation is confirmed by the results shown in
Figure 1,
Figure 2,
Figure 3 and
Figure 4 and
Table 1, which indicate that the impact of the second- and higher-order sensitivities on the best-estimate predicted leakage response and accompanying predicted standard deviation are small.
4.1.2.“. Medium Precision” Parameters, Having Uniform Relative Standard Deviations
Figure 5,
Figure 6,
Figure 7 and
Figure 8, below, depict the results of applying Eqs. (17)‒(33) to the PERP benchmark, in conjunction with the same experimental information as mentioned above (i.e.,
with
), but considering that the parameters have been measured with a precision (qualified as being “medium”) which is typical of cross section measurements, having uniform relative standard deviations of 5%. The results presented in
Figure 5 include only the first-order sensitivities of the leakage response with respect to the model parameters (total microscopic group cross sections). The results presented in
Figure 6 include the first- and second-order sensitivities. The results depicted in
Figure 7 include first- through third-order sensitivities, while the results depicted in
Figure 8 include all sensitivities up to (and including) fourth-order. The numerical values of the results depicted in
Figure 5,
Figure 6,
Figure 7 and
Figure 8 are tabulated in
Table 2.
As indicated by the results shown in
Figure 5,
Figure 6,
Figure 7 and
Figure 8 and
Table 2, the contributions stemming from the higher-order sensitivities to the quantities
increase with increasing order of sensitivities retained, thus confirming the expectation that the parameter standard deviations are sufficiently large to cause divergence of the Taylor-series that is used to represent the expected value and the standard deviation of the computed response in terms of parameter standard deviations. Nevertheless, the application of the BERRU-PM methodology yields a best-estimate value for the predicted leakage response which falls in-between the experimentally measured and computed values of this response (but closer to the more precisely known experimental value), with an accompanying predicted standard deviation which is smaller than either the measured or the computed standard deviations. These results indicate that the application of the 4th-BERRU-PM methodology can produce physically useful/meaningful results even when the Taylor-series expansion of the response in terms of parameter standard deviations diverges slightly.
4.1.3.“. Low precision” parameters, having uniform relative standard deviations
Figure 9,
Figure 10,
Figure 11 and
Figure 12, below, depict the results of applying Eqs. (17)‒(33) to the PERP benchmark, in conjunction with the same experimental information as mentioned above (i.e.,
with
), but considering that the parameters have been measured with low precision, having uniform relative standard deviations of 10%. The results presented in
Figure 9 include only the first-order sensitivities of the leakage response with respect to the model parameters (total microscopic group cross sections). The results presented in
Figure 10 include the first- and second-order sensitivities. The results depicted in
Figure 11 include first- through third-order sensitivities, while the results depicted in
Figure 12 include all sensitivities up to (and including) fourth-order. The numerical values of the results depicted in
Figure 9,
Figure 10,
Figure 11 and
Figure 12 are tabulated in
Table 3.
The results presented in
Figure 9,
Figure 10,
Figure 11 and
Figure 12 and
Table 3 confirm the expectation that parameter standard deviations of 10% cause massive divergence of the Taylor-series used to represent the expected value and standard deviation of the computed response in terms of parameter standard deviations. Nevertheless, as indicated by the last column in
Table 3, the application of the BERRU-PM methodology yields a best-estimate value and reduced predicted standard deviation for the predicted leakage response which is close to the more precisely-known experimental values. These results indicate that the application of the 4th-BERRU-PM methodology predicts results that remain physically useful/meaningful even when the parameters uncertainties (measured by the respective standard deviations) are sufficiently large to cause indisputable divergence of the Taylor-series expansion of the response in terms of parameter deviations. However, since parameter standard deviations of 5% already cause the Taylor-series of the response, cf. Eq. (16), to diverge, and since microscopic cross sections are generally known with a precision of 5% or better, only parameter standard deviations of 2% and 5% will henceforth be considered for the subsequent illustrative applications of the 4th-BERRU-PM methodology to the PERP benchmark.
4.2. Effects of Sensitivities and Parameter Standard Deviations on the Predicted Values of the Best-Estimate Correlations between the Leakage Response and the Most Important Parameters
The components of the vectors , , of best-estimate correlations among the benchmark’s leakage response and parameters are computed using the expression provided in Eq. (35). The impact of the parameters’ precision and of the sensitivities of various orders will be illustrated below in Subsection 4.2.l (for “high precision parameters” having uniform relative standard deviations of 2%) and, respectively, Subsection 4.2.2 (for “medium precision parameters” having uniform relative standard deviations of 5%). All of the numerical results presented in this Section for the components of the vectors , , are in units of “[parameter units] x [response units]”, i.e., [barns x neutrons/sec], where 1 barn=10-24 cm2.
4.2.1. “High Precision” Parameters, Having Uniform Relative Standard Deviations
When only the first- and second-order sensitivities are considered, the numerical results for the components of the vectors
,
, are computed using the expression provided in Eq. (36). For the PERP benchmark, each of the vectors
and
has 180 components, as there are 180 parameters corresponding to the microscopic total cross sections for all 6 isotopes in the benchmark [
4]. When only the 1st-order sensitivities are considered, the numerical results for the components of the vector
for the top 10 parameters (ranked in the order of the magnitude of their 1st-order relative sensitivities) are presented in
Table 4. When both the 1st-order and 2nd-order sensitivities are considered, the numerical results for the components of the vector
for the top 10 parameters (also ranked in the order of the magnitude of their 1st-order relative sensitivities) are presented in
Table 5.
Comparing the results presented in
Table 4 and
Table 5 indicates the following conclusions:
- (i)
Even though the original correlations between the model parameters and the computed leakage response were negative, the best estimate correlations are positive, i.e., the components of and are all positive.
- (ii)
The absolute values of the components of and are all considerably smaller than the absolute values of the original correlations .
- (iii)
The values of the components of are larger than the corresponding components of , which indicates that the inclusion of the 2nd-order sensitivities reduces the best-estimate correlations between the best-estimate parameters and the predicted best-estimate leakage response.
When the third- and, respectively, fourth-order sensitivities are also included in addition to the first- and second-order sensitivities, the numerical results for the components of the vectors
,
, are computed using the expression provided in Eq. (37). The numerical results thus obtained for the components of the vector
and, respectively,
, for the top 10 parameters (ranked in the order of the magnitude of their 1st-order relative sensitivities), are presented in
Table 6 and
Table 7, respectively.
- (i)
All of the components of the original correlations and between the model parameters and the computed leakage response are negative. Furthermore, including the 3rd- and 4th-order sensitivities causes the absolute values of the components of to be larger than the corresponding components of the vector .
- (ii)
The components of the vectors , , representing the best-estimate correlations among the benchmark’s best-estimate leakage response and best-estimate parameters, are all positive.
- (iii)
The values of the components of are larger than the corresponding components of , which in turn are larger than the components of , which in turn are larger than the components of . This sequence of inequalities indicates that the inclusion of the successively higher-order sensitivities reduces successively the corresponding best-estimate correlations between the best-estimate parameters and the predicted best-estimate leakage response.
4.2.2. “Medium Precision” Parameters, Having Uniform Relative Standard Deviations
When the parameters are considered to be characterized by uniform relative standard deviations of 5%, the numerical results obtained for the components of the vectors
,
, of best-estimate correlations among the benchmark’s best-estimate leakage response and the top 10 parameters (ranked in the order of the magnitude of their 1st-order relative sensitivities), are presented in below in
Table 8,
Table 9,
Table 10 and
Table 11, respectively. As before, when only the first- and second-order sensitivities are considered, the numerical results for the components of the vectors
,
, are computed using the expression provided in Eq. (36). Similarly, when the third- and fourth-order sensitivities are also included, the numerical results for the components of the vectors
,
, are computed using the expression provided in Eq. (37).
Comparing the results presented in
Table 8,
Table 9,
Table 10 and
Table 11 with the corresponding results presented in
Table 4,
Table 5,
Table 6 and
Table 7 reveals that the larger parameters standard deviations (
) accentuate the characteristics displayed by the corresponding results for the smaller parameter standard deviations (
), as follows:
- (i)
Comparing the results in
Table 8 with the results presented in
Table 4 reveals that the components of the correlations
for
are considerably larger in absolute values than the components of the correlations
for
. Conversely (and consequently), the components of the best-estimate correlations
for
are considerably larger in absolute values than the components of the correlations
for
. Similar conclusion can be drawn by: (a) comparing the results in
Table 9 with the results presented in
Table 5; (b) comparing the results in
Table 10 with the results presented in
Table 6; and (c) comparing the results in
Table 11 with the results presented in
Table 7.
- (ii)
All of the conclusions previously drawn from the results obtained for the smaller parameter standard deviations (
) also hold for the larger parameters standard deviations (
), so they will not be repeated here, other than to note that these conclusions are even more evident/accentuated by the contrast between the original values for the correlations
(between the model parameters and computed leakage response) and the predicted best-estimate values for the posterior best-estimate correlations,
, between the calibrated best-estimate parameters and the best-estimate predicted response. In particular, the starkest contrasts among the original and predicted posterior values for the parameter-response correlations are evidenced by the results presented in
Table 11: the original components of the vector
all have large negative values of the order of
, while the posterior best-estimate correlations
have positive values of the order of
.
The overall conclusion that follows from the results presented in
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10 and
Table 11 is that the larger the parameter standard deviation and the higher the order of retained sensitivities, the larger the negative values of the original correlations among the model parameters and the leakage response, and the smaller the positive values of the best-estimate predicted posterior correlations among the best-estimate posterior calibrated model parameters and the predicted posterior leakage response.
4.3. Effects of Sensitivities and Parameter Standard Deviations on the Predicted Values of the Best-Estimate Calibrated Model Parameters
The best-estimate predicted values of the calibrated model parameters,
,
, are computed by using Eq. (40). All of the numerical results presented in this Section for the best-estimate predicted calibrated parameter values are in units of “barn”, where 1 barn=10-24 cm2.
Table 12 presents the results for the best-estimate predicted values for the top 10 calibrated model parameters (ranked in the order of the magnitude of their 1st-order relative sensitivities) for parameters that are measured with “high precision,” having uniform relative standard deviations
.
Table 13 presents the results for the best-estimate predicted values for the top 10 calibrated model parameters (ranked in the order of the magnitude of their 1st-order relative sensitivities) for parameters that are measured with “medium precision,” having uniform relative standard deviations
. For all of the results presented in these Tables, the nominal value of the measured response is
n/s, with a measured relative standard deviation
. The results presented in these Tables indicate that the calibration (i.e., adjustment) of each of the respective parameter’s nominal value is negligeable for the realistic values (2-5%) considered for the relative standard deviations for the parameters.
4.4. Effects of Sensitivities and Parameter Standard Deviations on the Predicted Values of the Components of the Covariance Matrix of Predicted Model Parameters
The components of the predicted posterior covariance matrix , , of the best-estimate calibrated parameters are computed by using Eq. (42). All of the numerical results presented in this Section for the components of the best-estimate parameter covariance matrices , , are in units of “,” i.e., . As before, all of the results presented in this Section were obtained by considering that the nominal value of the measured response is n/s, with a measured relative standard deviation .
The diagonal matrix of apriori variances for the top 10 model parameters (ranked in the order of the magnitude of their 1st-order relative sensitivities), which are considered to be uncorrelated, normally distributed, and having uniform relative standard deviations
, is presented in
Table 14, below.
Table 15,
Table 16,
Table 17 and
Table 18, below, present the results for the best-estimate predicted values for the components of the posterior matrices
,
.
The results presented in these Tables indicate that the variance of each of the calibrated predicted parameters has been significantly reduced by comparison to its original value. However, this reduction is not monotonic but oscillates with decreasing amplitudes as sensitivities of increasingly higher-order are considered. Furthermore, the originally uncorrelated parameters have become negatively correlated after the application of the 4th-BERRU-PM methodology. The impact of sensitivities higher than first-order is small.
The results for the top 10 model parameters (ranked in the order of the magnitude of their 1st-order relative sensitivities), which are considered to be uncorrelated, normally distributed, and having uniform relative standard deviations
, are presented in
Table 19,
Table 20,
Table 21,
Table 22 and
Table 23, below.
Table 19 presents the diagonal matrix of apriori parameter variances.
Table 20,
Table 21,
Table 22 and
Table 23 present the results for the predicted values for the components of the posterior matrices
,
.
The results presented above in
Table 20,
Table 21,
Table 22 and
Table 23 are similar to the results presented in
Table 15,
Table 16,
Table 17 and
Table 18, indicating that: (i) the variance of each of the calibrated predicted parameters is significantly reduced by comparison to its original value; this reduction is not monotonic but oscillates with decreasing amplitudes as sensitivities of increasingly higher-order are considered.; (ii) the originally uncorrelated parameters have become negatively correlated after the application of the 4th-BERRU-PM methodology; and (iii) the impact of sensitivities higher than first-order is small.
Recall that the Taylor-series expansion provided in Eq. (16) is divergent for parameter standard deviations of 5% and larger. Nevertheless, it is of interest to show that the application of the 4th-BERRU-PM methodology reduces the standard deviations of the predicted calibrated parameters even in such rather extreme situations, even if just the first- and second-order sensitivities are considered. In this vein,
Table 24,
Table 25 and
Table 26 present the results for the top 10 model parameters (ranked in the order of the magnitude of their 1st-order relative sensitivities), which are considered to be uncorrelated, normally distributed, and having uniform relative standard deviations
.
Table 24 presents the diagonal matrix of apriori parameter variances.
Table 25 and
Table 26 present the results for the predicted values for the components of the posterior matrices
,
. Remarkably, the results presented in these Tables are similar to the results presented in
Table 15,
Table 16,
Table 17 and
Table 18 (which were obtained for small parameter standard deviations, of 2%), thus indicating that: (i) the variance of each of the calibrated predicted parameters is significantly reduced by comparison to its original value; this reduction is not monotonic but oscillates with decreasing amplitudes as sensitivities of increasingly higher-order are considered; (ii) the originally uncorrelated parameters have become negatively correlated after the application of the 4th-BERRU-PM methodology.
4.5. Effects of Sensitivities and Parameter Standard Deviations on the Predicted Skewness of the Predicted Leakage Response and, respectively, Calibrated Model Parameters
The most important triple-correlation is the skewness of each individual best-estimate predicted response and calibrated parameters. The skewness of the predicted best-estimate leakage response, denoted as
, where the index “i" denotes the highest-order of sensitivities retained in the respective computation, is computed using the expression below:
where the expression of the triple-correlation
is provided in Eq. (45), while the expression of the standard deviation
is provided in one of Eqs. (30)‒(33), depending on the value of the index “i".
Similarly, the skewness of a predicted best-estimate calibrated parameter
,
will be denoted as
, where the index “i" denotes the highest-order of sensitivities retained in the respective computation, and is computed using the expression below:
In Eq. (74), the expression of the triple-correlation is provided in Eq. (57), while the standard deviation is the square-root of the respective diagonal element of , which is obtained using the expression provided in Eq. (42).
The numerical results obtained for the skewness
of the predicted best-estimate leakage response, and for the skewness
for each of the three most important predicted calibrated model parameters are presented below in
Table 27 and
Table 28, respectively.
The results presented in
Table 27 are for uniform relative standard deviations of 2% for the model parameters; recall that the Taylor-series expansion of the computed response in terms of parameter deviations provided in Eq. (16) is convergent for such small standard deviations. Recall that the measurements were considered to be normally distributed (thus having zero skewness); furthermore, the contribution of the initial skewness of the computed responses enters in the expression of the higher-order term
in Eq. (44), which was neglected by comparison to the other terms in this equation. Thus, the skewness of the measured response and the skewness of the computed responses do not influence the predicted skewness, within the second-order approximation inherent in the expression of the predicted skewness. When only the first-order sensitivities are considered, the small positive number for the predicted skewness in
Table 27 indicates that the MaxEnt distribution of the predicted best-estimate leakage response is slightly tilted to the right of the distribution’s mean value. However, when the second- and higher-order sensitivities are also considered, the MaxEnt distribution of the predicted best-estimate leakage response becomes tilted just slightly to the left of the distribution’s mean value, but the respective tilt is negligibly small. These results indicate that results based exclusively on first-order sensitivities are unreliable. It is therefore paramount to at least consider the second-order sensitivities, in addition to the first-order ones. The above conclusion holds both for the predicted leakage response and for the calibrated predicted parameters.
The results presented in
Table 28 for uniform parameter standard deviations of 5% indicate that the conclusions drawn from the results in
Table 27 also hold for these larger standard deviations, which are just outside the convergence radius of the Taylor-series in Eq. (16).
4.6. Effects of Sensitivities and Parameter Standard Deviations on the Predicted Kurtosis of the Predicted Leakage Response and, respectively, Calibrated Model Parameters
The most important quadruple-correlations are the individual kurtoses of the best-estimate predicted response and calibrated parameters. The kurtosis of the predicted best-estimate leakage response, denoted as
, where the index “i" denotes the highest-order of sensitivities retained in the respective computation, is computed using the expression below:
where the expression of the quadruple-correlation
is provided in Eq. (59), while the expressions of the standard deviation
are provided in the corresponding Eqs. (30)‒(33).
Similarly, the kurtosis of a predicted best-estimate calibrated parameter
,
will be denoted as
, where the index “i" denotes the highest-order of sensitivities retained in the respective computation, and is computed using the expression below:
In Eq. (76), the expression of the quadruple-correlation is provided in Eq. (68) while the standard deviation is the square-root of the respective diagonal element of , which is obtained using the expression provided in Eq. (42).
The numerical results obtained for the kurtosis
of the predicted best-estimate leakage response, and for the kurtosis
, for each of the three most important calibrated model parameters, are presented in
Table 29 and
Table 30, below.
The results presented in
Table 29 are for uniform relative standard deviations of 2% for the model parameters; recall that the Taylor-series expansion of the computed response in terms of parameter deviations provided in Eq. (16) is convergent for such small standard deviations. When only the first-order sensitivities are considered, the kurtosis of the MaxEnt distribution of the predicted best-estimate leakage response is somewhat “more peaked” than the initial normal distribution. However, when the second- and higher-order sensitivities are also considered, the MaxEnt distribution of the predicted best-estimate leakage response converges to the normal distribution (for which “kurtosis = 3.00”). The same trend is also observed for the most important parameters: recall that the parameters were considered to have initially been normally distributed and uncorrelated, which implies that the distribution of each parameter initially had the value “initial parameter kurtosis = 3.” The MaxEnt distribution of the best-estimate calibrated parameters also remains around the value (=3) of the corresponding normal distribution.
The results presented in
Table 30 for uniform parameter standard deviations of 5% indicate that the conclusions drawn from the results in
Table 29 also hold for these larger standard deviations, which are just outside the convergence radius of the Taylor-series in Eq. (16).
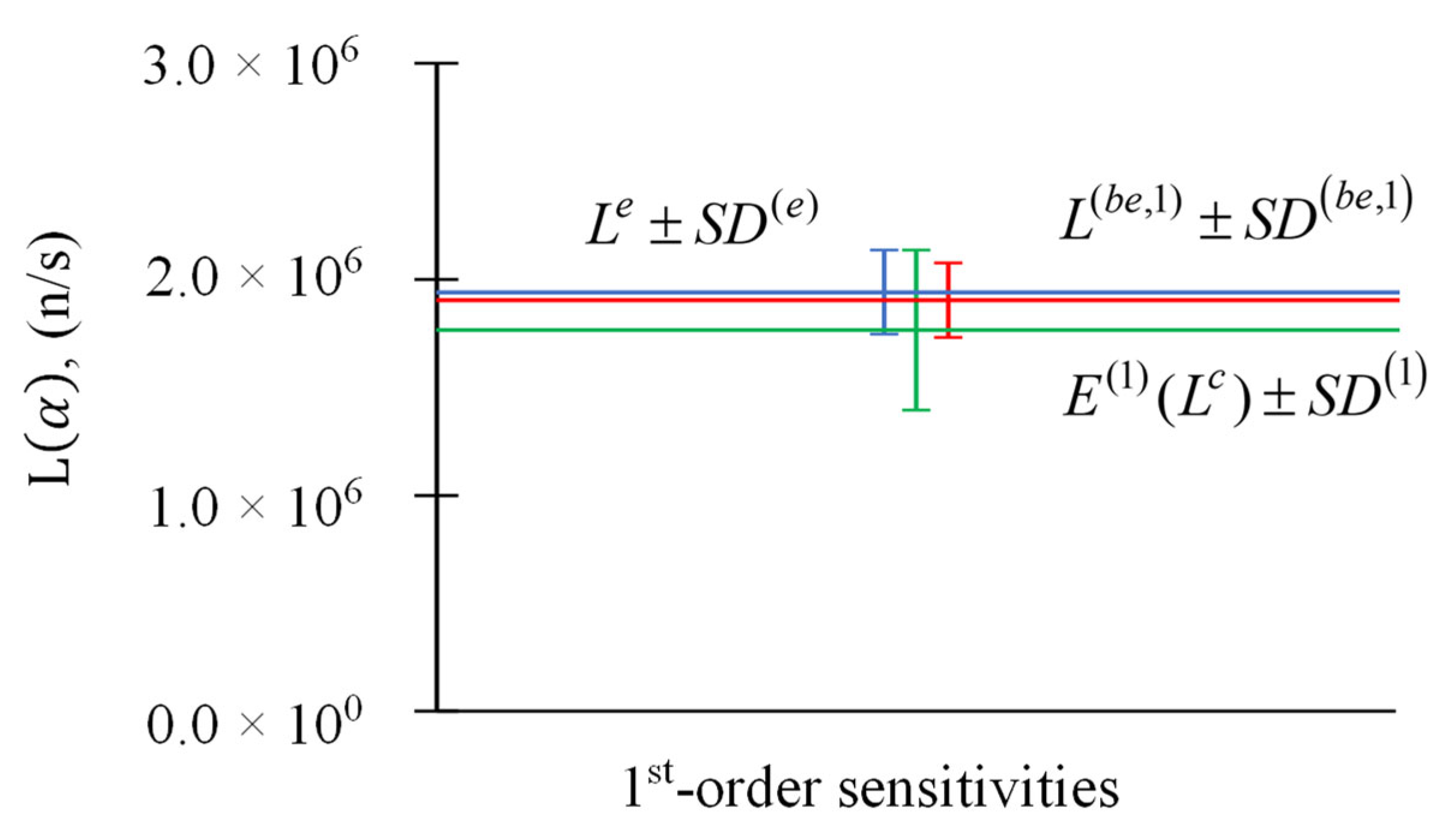
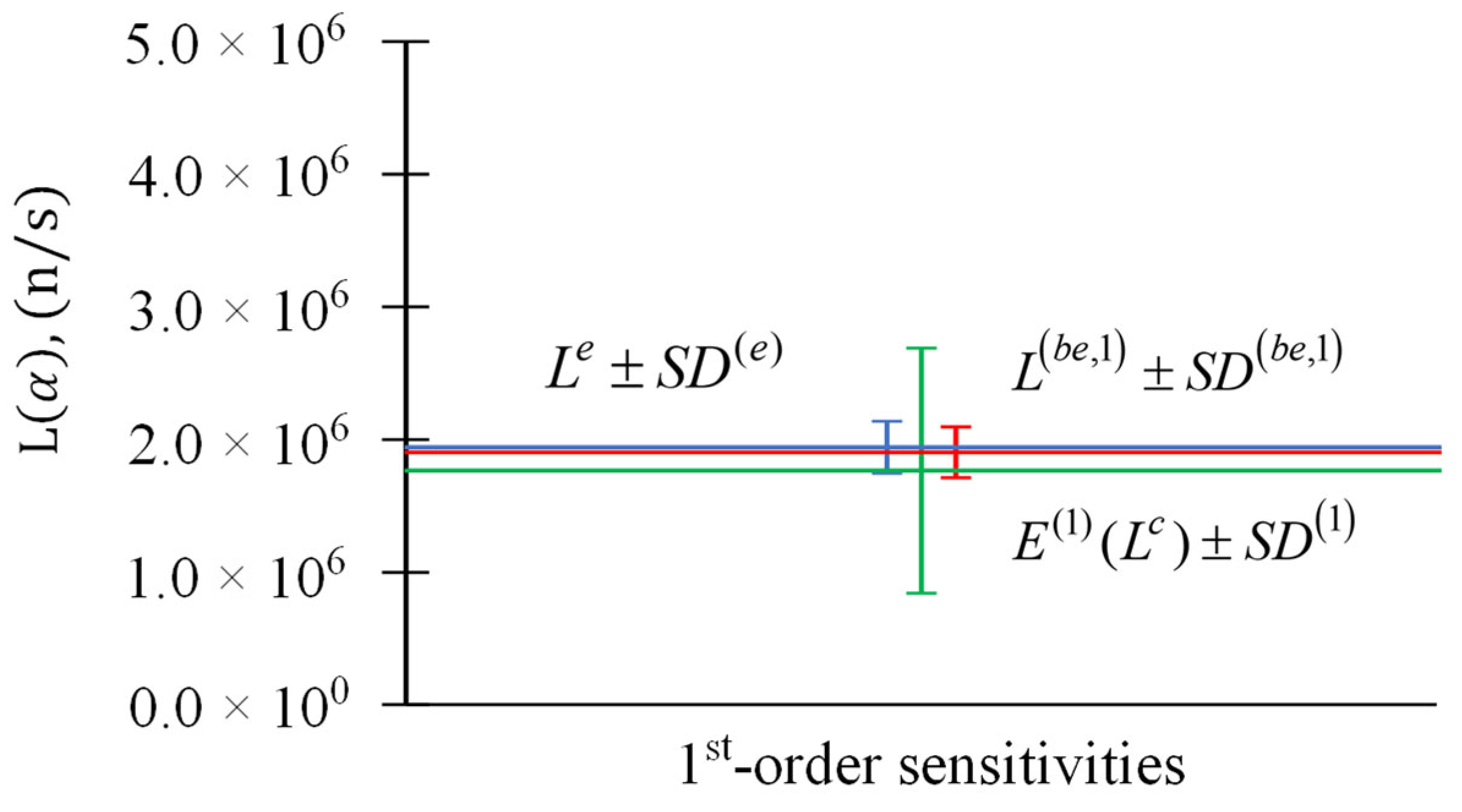
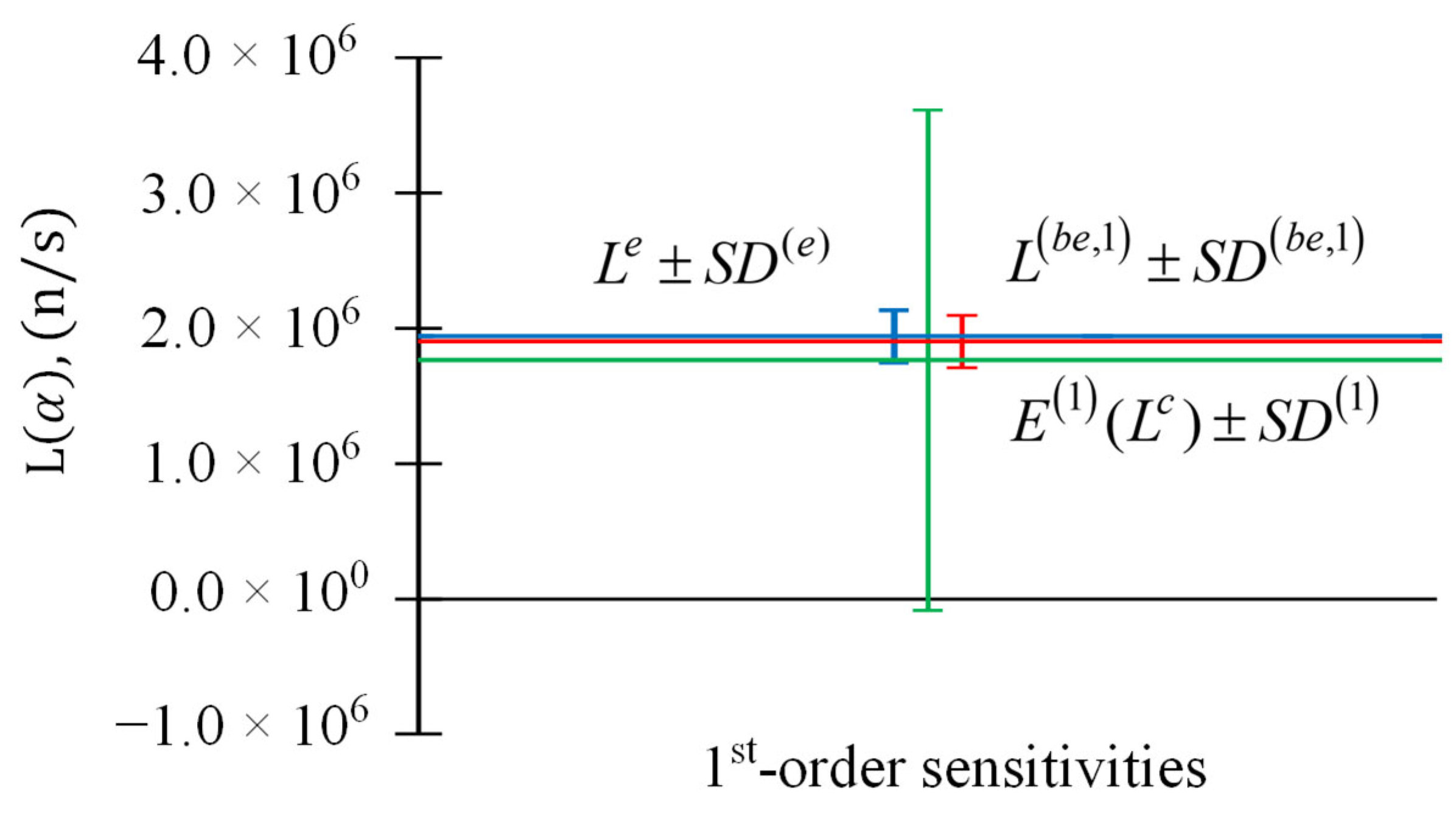
Figure 1.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including only first-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including only first-order sensitivities.
Figure 1.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including only first-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including only first-order sensitivities.
Figure 2.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first- and second-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first- and second-order sensitivities.
Figure 2.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first- and second-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first- and second-order sensitivities.
Figure 3.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first-, second, and third-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first-, second, and third-order sensitivities.
Figure 3.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first-, second, and third-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first-, second, and third-order sensitivities.
Figure 4.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first- through fourth-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first- through fourth-order sensitivities.
Figure 4.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first- through fourth-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first- through fourth-order sensitivities.
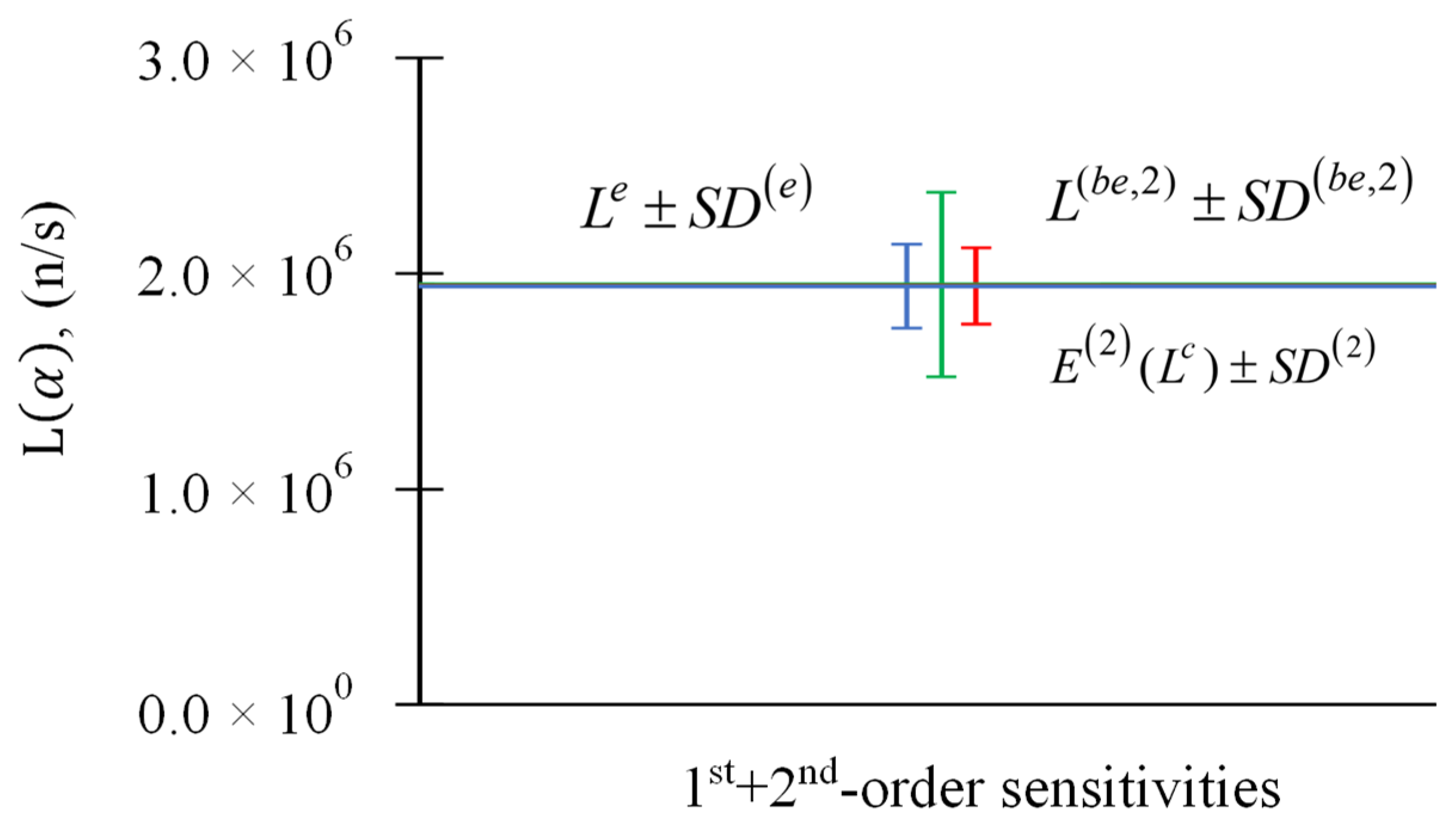
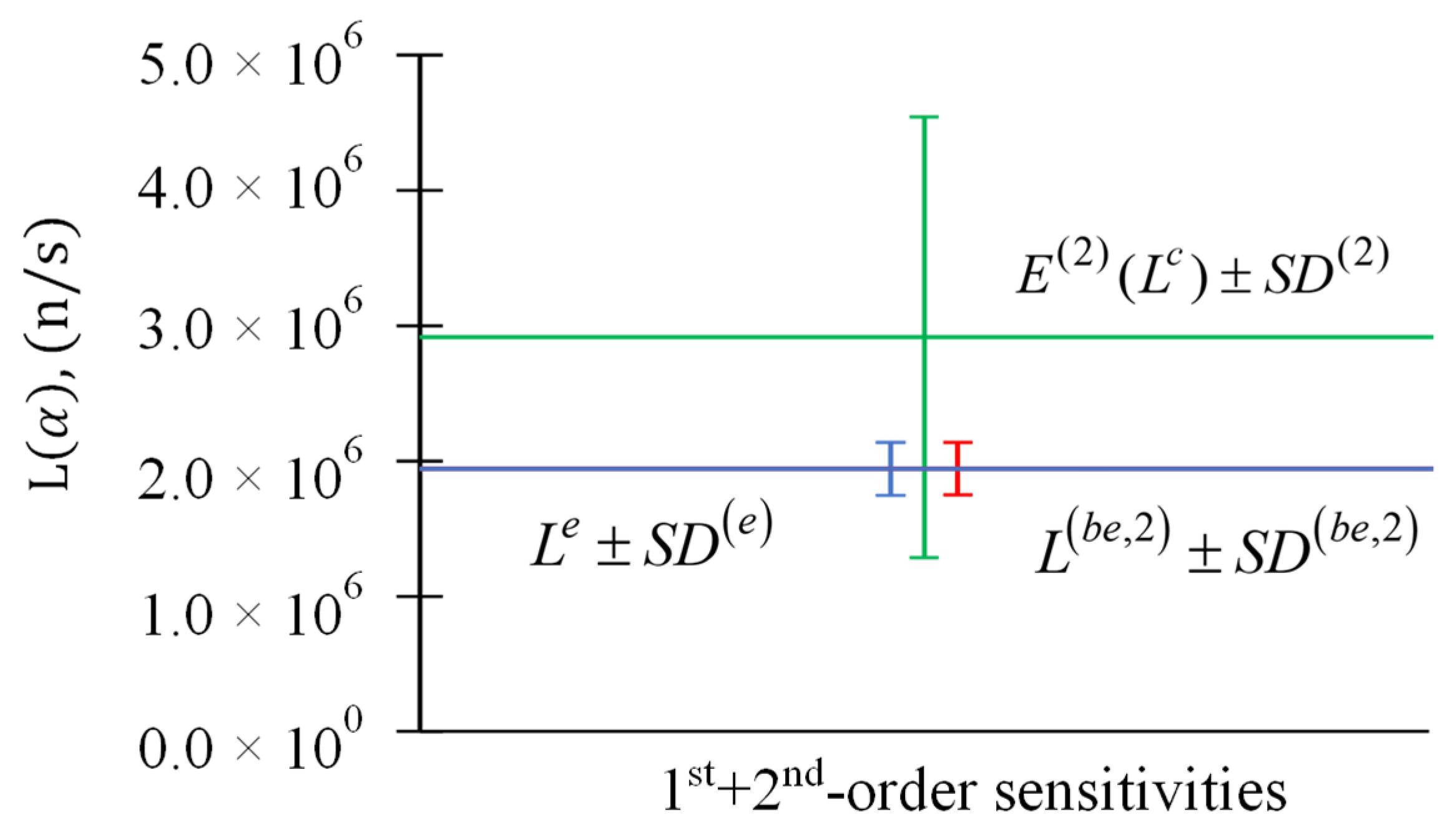
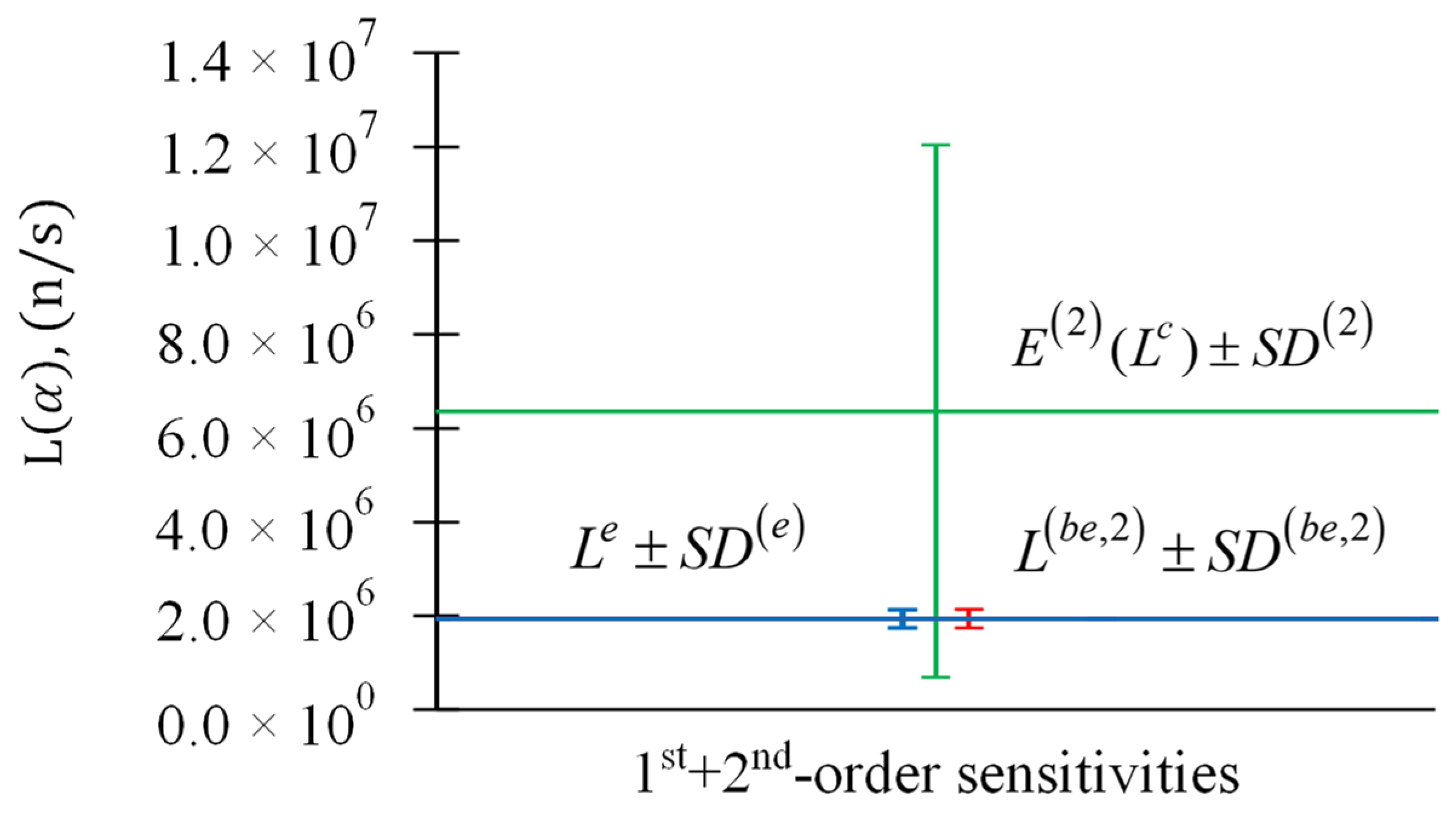
Figure 5.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including only first-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including only first-order sensitivities.
Figure 5.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including only first-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including only first-order sensitivities.
Figure 6.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first- and second-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first- and second-order sensitivities.
Figure 6.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first- and second-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first- and second-order sensitivities.
Figure 7.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first-, second, and third-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first-, second, and third-order sensitivities.
Figure 7.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first-, second, and third-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first-, second, and third-order sensitivities.
Figure 8.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first- through fourth-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first- through fourth-order sensitivities.
Figure 8.
Parameter relative standard deviations : (i) experimentally measured response and its standard deviation (blue); (ii) expected value of computed response and its standard deviation (green) including first- through fourth-order sensitivities; (iii) best-estimate predicted leakage response and its predicted best-estimate standard deviation (red) including first- through fourth-order sensitivities.
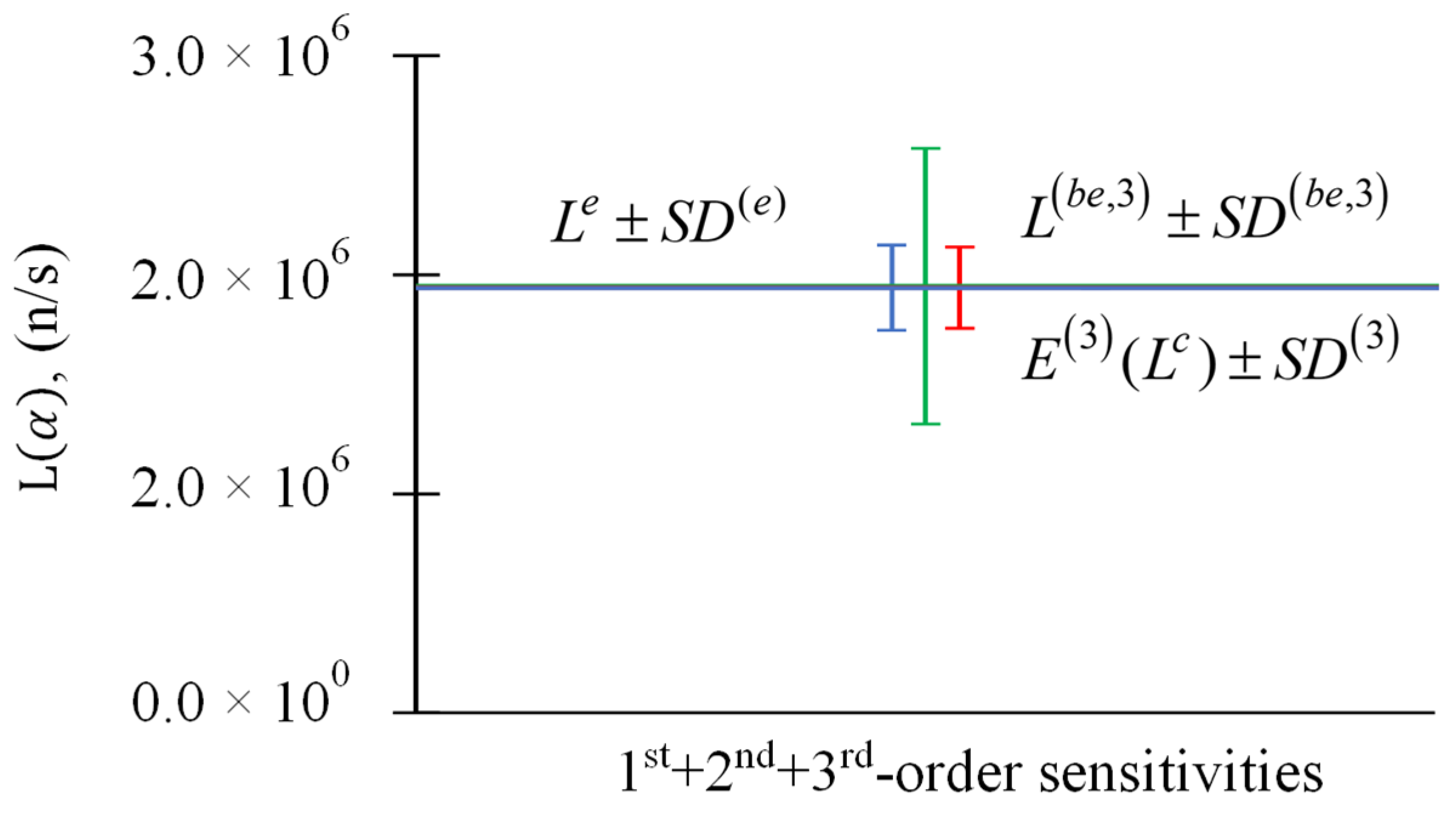
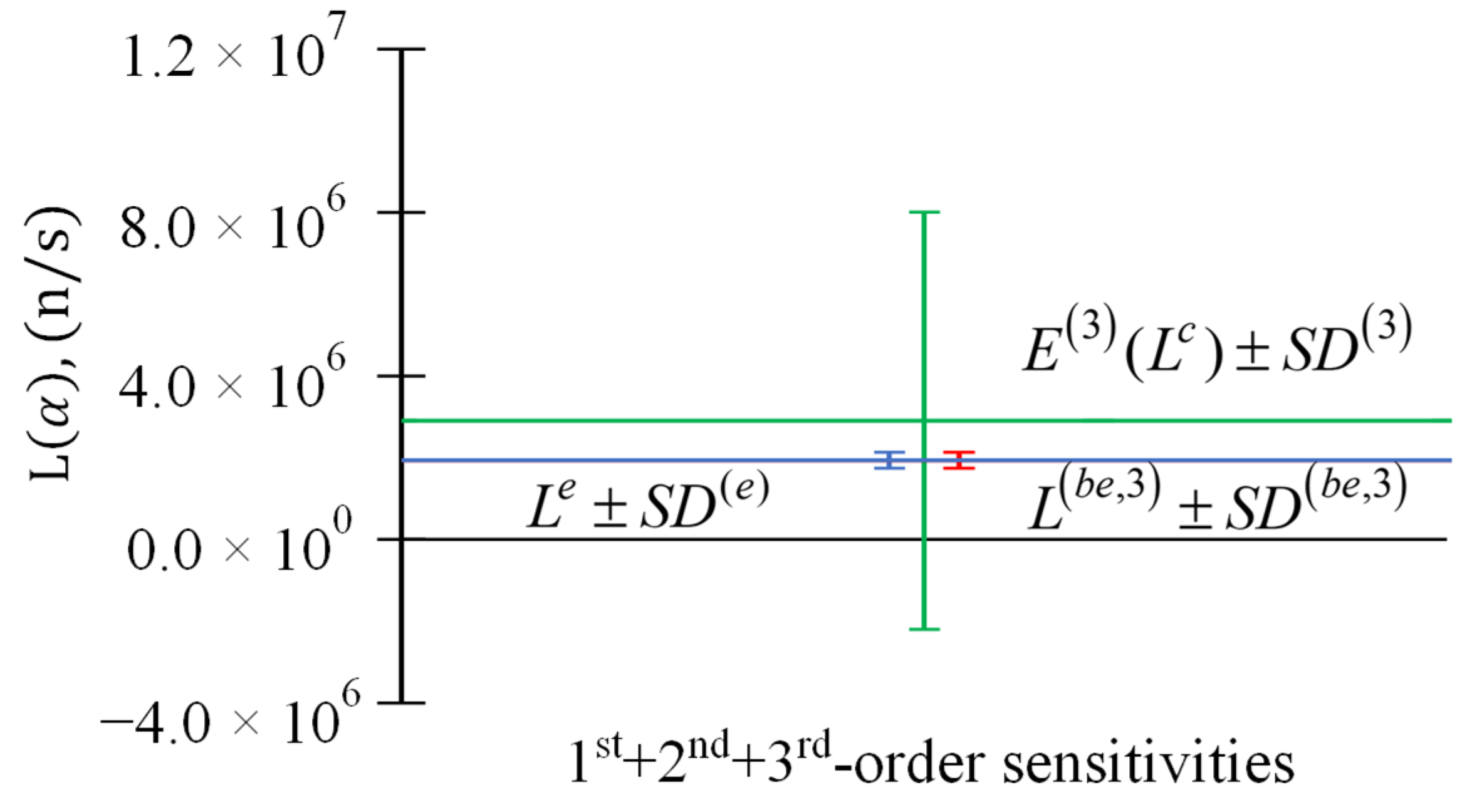
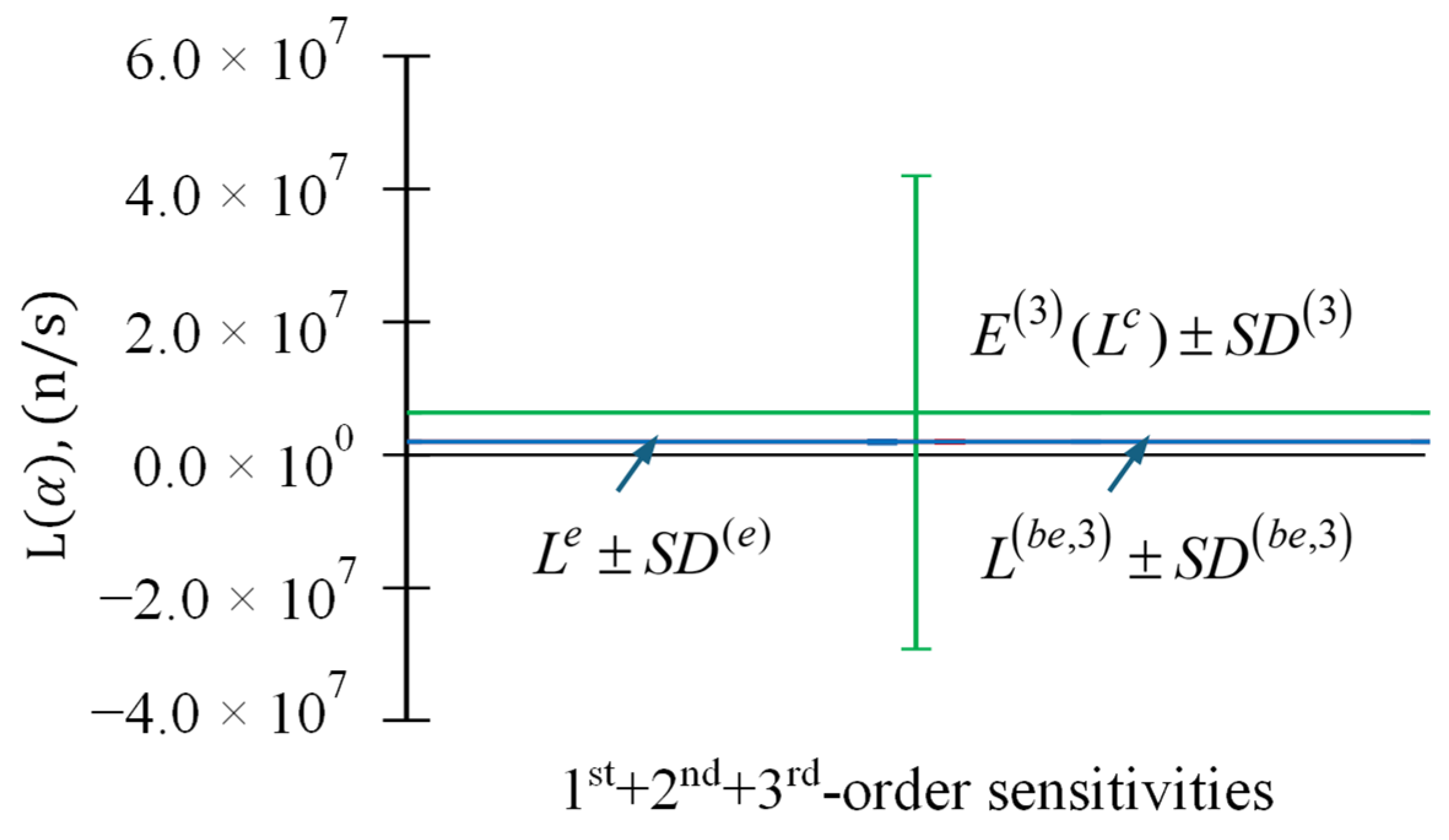
Figure 9.
Comparison of (in green), (in red), and (in blue), for response measurement for response measurement n/s, , and parameters . Only the 1st-order () sensitivities are considered.
Figure 9.
Comparison of (in green), (in red), and (in blue), for response measurement for response measurement n/s, , and parameters . Only the 1st-order () sensitivities are considered.
Figure 10.
Comparison of (in green), (in red), and (in blue), for response measurement for response measurement n/s, , and parameters . The 1st + 2nd-order () sensitivities are included.
Figure 10.
Comparison of (in green), (in red), and (in blue), for response measurement for response measurement n/s, , and parameters . The 1st + 2nd-order () sensitivities are included.
Figure 11.
Comparison of (in green), (in red), and (in blue), for response measurement for response measurement n/s, , and parameters . The 1st + 2nd + 3rd-order () sensitivities are included.
Figure 11.
Comparison of (in green), (in red), and (in blue), for response measurement for response measurement n/s, , and parameters . The 1st + 2nd + 3rd-order () sensitivities are included.
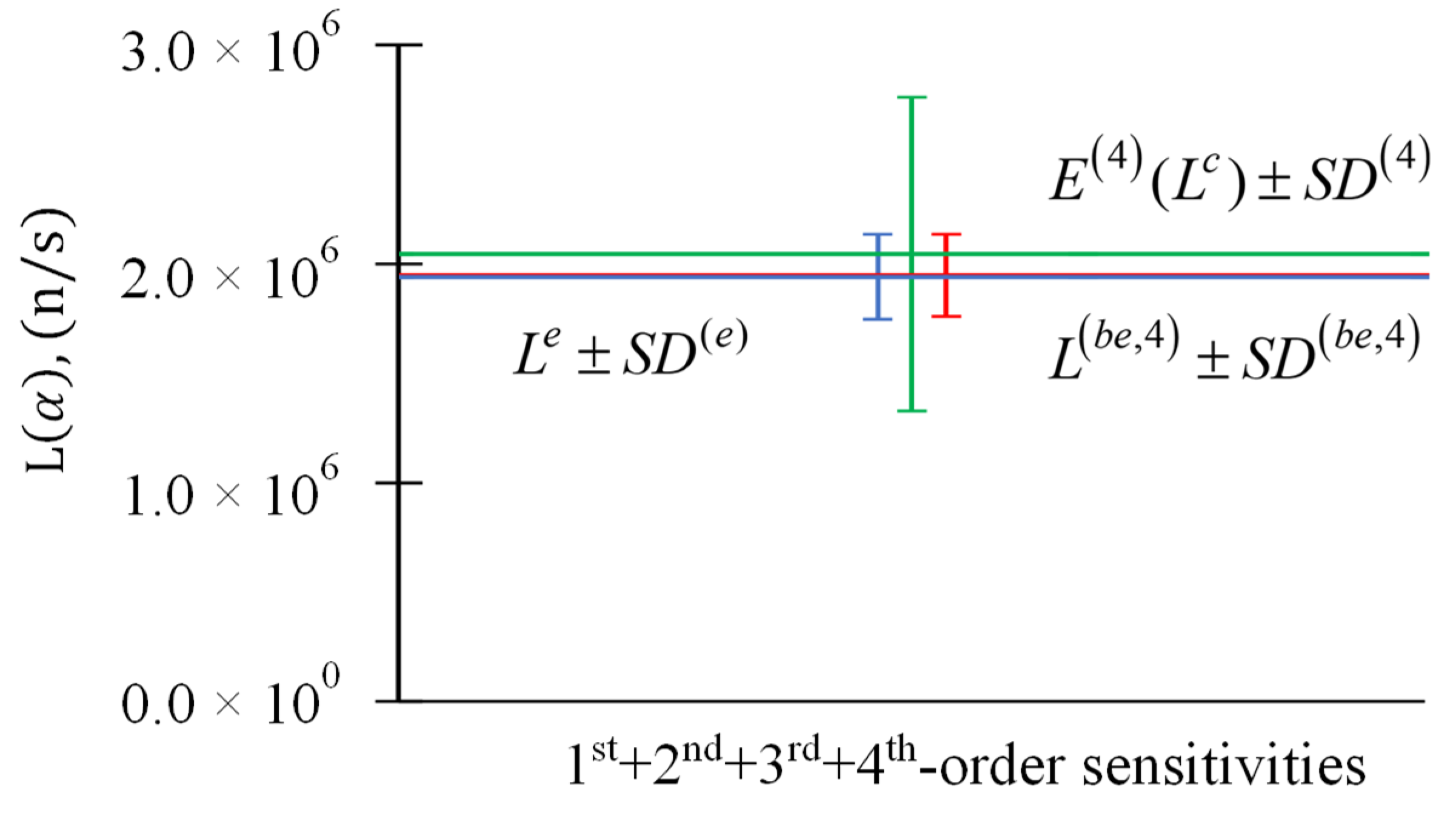
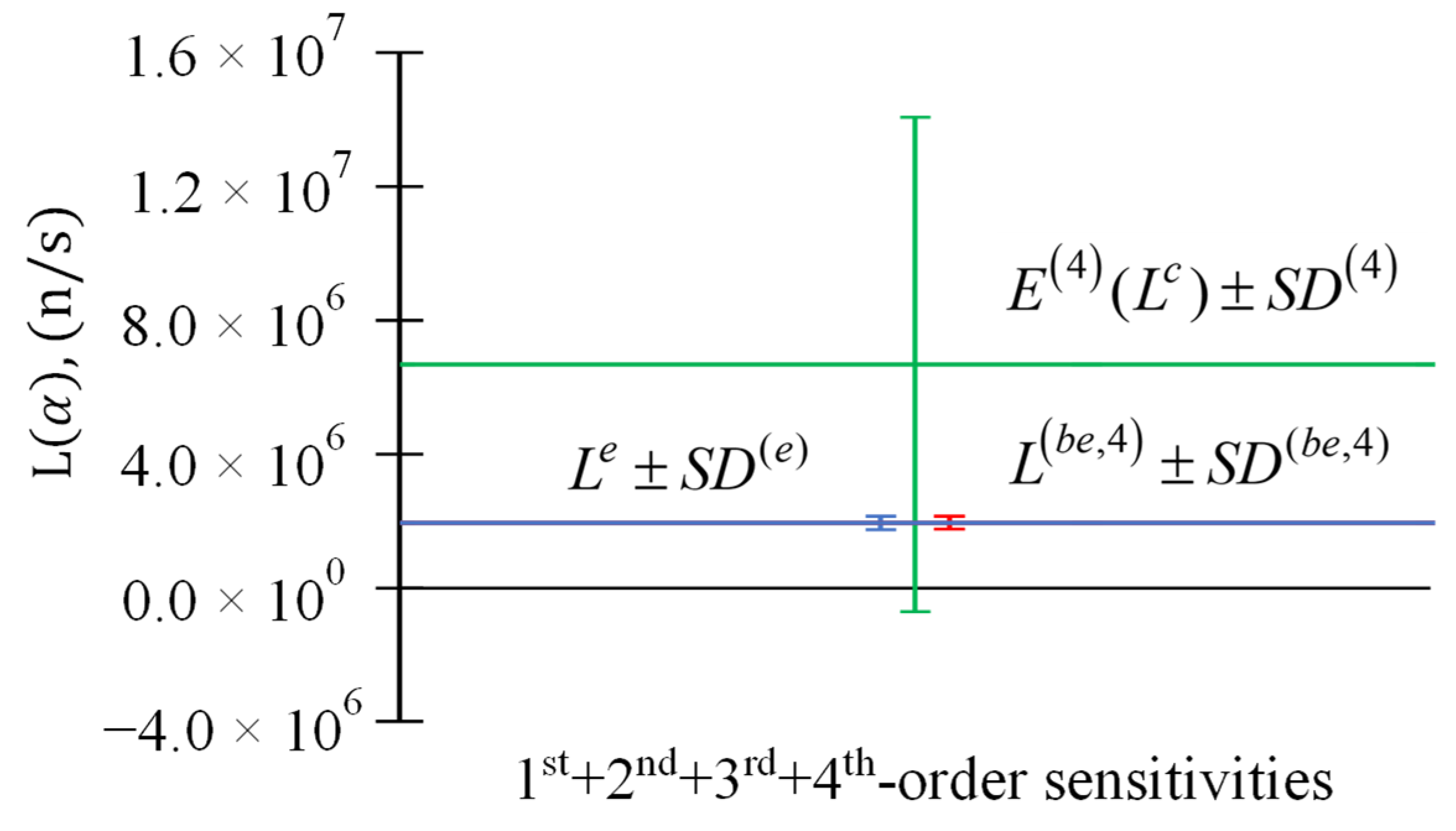
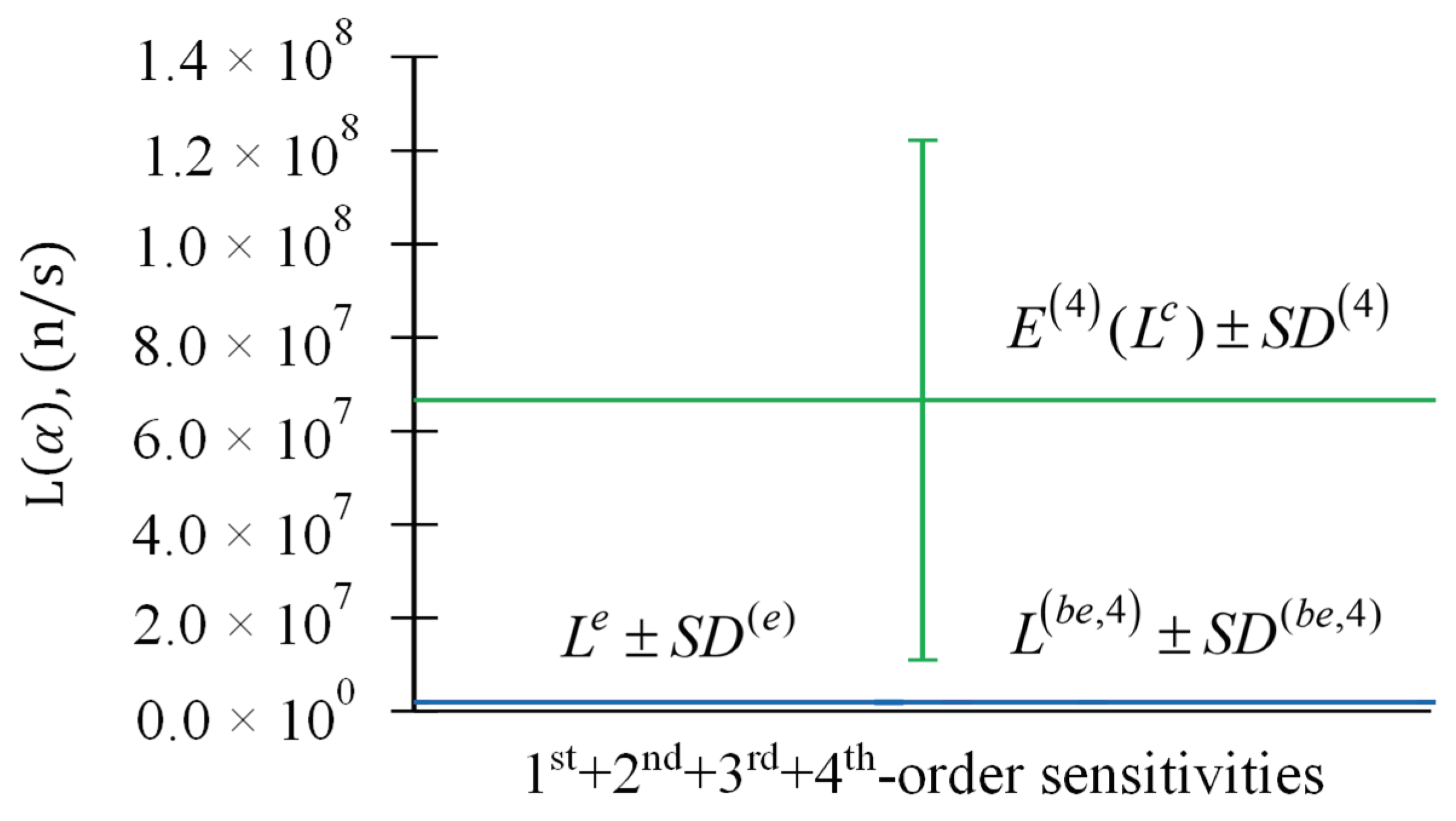
Figure 12.
Comparison of (in green), (in red), and (in blue), for response measurement for response measurement n/s, , and parameters . The 1st + 2nd + 3rd + 4th-order () sensitivities are included.
Figure 12.
Comparison of (in green), (in red), and (in blue), for response measurement for response measurement n/s, , and parameters . The 1st + 2nd + 3rd + 4th-order () sensitivities are included.
Table 1.
Results for and , , for response measurement n/s, , and parameters’ .
Table 1.
Results for and , , for response measurement n/s, , and parameters’ .
| Order of Sensitivities Considered |
(neutrons/sec) |
(neutrons/sec) |
(neutrons/sec) |
| 1st-order () |
1.941 × 106 ± 1.941 × 105 |
1.765 × 106 ± 3.698 × 105 |
1.903 × 106 ± 1.719 × 105 |
| 1st + 2nd-order () |
1.949 × 106 ± 4.276 × 105 |
1.943 × 106 ± 1.768 × 105 |
| 1st + 2nd + 3rd-order () |
1.949 × 106 ± 6.288 × 105 |
1.942 × 106 ± 1.855 × 105 |
| 1st + 2nd + 3rd + 4th-order () |
2.045 × 106 ± 7.157 × 105 |
1.948 × 106 ± 1.874 × 105 |
Table 2.
Results for and , , for response measurement n/s, , and parameters’ .
Table 2.
Results for and , , for response measurement n/s, , and parameters’ .
| Order of Sensitivities Considered |
(neutrons/sec) |
(neutrons/sec) |
(neutrons/sec) |
| 1st-order () |
1.941 × 106 ± 1.941 × 105 |
1.765 × 106 ± 9.246 × 105 |
1.934 × 106 ± 1.899 × 105 |
| 1st + 2nd-order () |
2.914 × 106 ± 1.629 × 106 |
1.955 × 106 ± 1.928 × 105 |
| 1st + 2nd + 3rd-order () |
2. 914 × 106 ± 5.103 × 106 |
1.943 × 106 ± 1.939 × 105 |
| 1st + 2nd + 3rd + 4th-order () |
6.681 × 106 ± 7.386 × 106 |
1.945 × 106 ± 1.940 × 105 |
Table 3.
Results for and , , for response measurement n/s, , and parameters’ .
Table 3.
Results for and , , for response measurement n/s, , and parameters’ .
| Order of Sensitivities Considered |
(neutrons/sec) |
(neutrons/sec) |
(neutrons/sec) |
| 1st-order () |
1.941 × 106 ± 1.941 × 105 |
1.765 × 106 ± 1.849 × 106 |
1.939 × 106 ± 1.931 × 105 |
| 1st + 2nd-order () |
6.363 × 106 ± 5.675 × 106 |
1.946 × 106 ± 1.940 × 105 |
| 1st + 2nd + 3rd-order () |
6.363 × 106 ± 3.561 × 107 |
1.941 × 106 ± 1.941 × 105 |
| 1st + 2nd + 3rd + 4th-order () |
6.662 × 106 ± 5.562 × 107 |
1.942 × 106 ± 1.941 × 105 |
Table 4.
Results for the components of when only the 1st-order sensitivities are considered for the top 10 parameters, with uniform parameters relative standard deviations .
Table 4.
Results for the components of when only the 1st-order sensitivities are considered for the top 10 parameters, with uniform parameters relative standard deviations .
| Ranking of parameter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Parameter |
|
|
|
|
|
|
|
|
|
|
|
−195330 |
−6496 |
−13396 |
−10092 |
−6458 |
−14959 |
−15207 |
−14692 |
−13912 |
−6176 |
|
42191 |
1403 |
2894 |
2180 |
1395 |
3231 |
3285 |
3173 |
3005 |
1334 |
Table 5.
Results for the components of when the 1st- and 2nd-order sensitivities are considered for the top 10 parameters, with uniform parameters relative standard deviations.
Table 5.
Results for the components of when the 1st- and 2nd-order sensitivities are considered for the top 10 parameters, with uniform parameters relative standard deviations.
| Ranking of parameter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Parameter |
|
|
|
|
|
|
|
|
|
|
|
−195330 |
−6496 |
−13396 |
−10092 |
−6458 |
−14959 |
−15207 |
−14692 |
−13912 |
−6176 |
|
33379 |
1110 |
2289 |
1725 |
1104 |
2556 |
2599 |
2511 |
2377 |
1055 |
Table 6.
Results for the components of when sensitivities up to 3rd-order are considered for the top 10 parameters, with uniform parameters relative standard deviations.
Table 6.
Results for the components of when sensitivities up to 3rd-order are considered for the top 10 parameters, with uniform parameters relative standard deviations.
| Ranking of parameter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Parameter |
|
|
|
|
|
|
|
|
|
|
|
−319430 |
−6519 |
−13464 |
−10136 |
−6481 |
−15039 |
−15288 |
−14767 |
−13981 |
−6199 |
|
27793 |
567 |
1171 |
882 |
564 |
1309 |
1330 |
1285 |
1216 |
539 |
Table 7.
Results for the components of when sensitivities up to 4th-order are considered for the top 10 parameters, with uniform parameters relative standard deviations.
Table 7.
Results for the components of when sensitivities up to 4th-order are considered for the top 10 parameters, with uniform parameters relative standard deviations.
| Ranking of parameter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Parameter |
|
|
|
|
|
|
|
|
|
|
|
−319430 |
−6519 |
−13464 |
−10136 |
−6481 |
−15039 |
−15288 |
−14767 |
−13981 |
−6199 |
|
21889 |
447 |
923 |
695 |
444 |
1031 |
1048 |
1012 |
958 |
425 |
Table 8.
Results for the components of when only the 1st-order sensitivities are considered for the top 10 parameters, with uniform parameters relative standard deviations .
Table 8.
Results for the components of when only the 1st-order sensitivities are considered for the top 10 parameters, with uniform parameters relative standard deviations .
| Ranking of parameter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Parameter |
|
|
|
|
|
|
|
|
|
|
|
−1220812 |
−40598 |
−83724 |
−63075 |
−40362 |
−93494 |
−95043 |
−91823 |
−86952 |
−38598 |
|
51544 |
1714 |
3535 |
2663 |
1704 |
3947 |
4013 |
3877 |
3671 |
1630 |
Table 9.
Results for the components of when the 1st- and 2nd-order sensitivities are considered for the top 10 parameters, with uniform parameters relative standard deviations .
Table 9.
Results for the components of when the 1st- and 2nd-order sensitivities are considered for the top 10 parameters, with uniform parameters relative standard deviations .
| Ranking of parameter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Parameter |
|
|
|
|
|
|
|
|
|
|
|
−1220812 |
−40598 |
−83724 |
−63075 |
−40362 |
−93494 |
−95043 |
−91823 |
−86952 |
−38598 |
|
17091 |
568 |
1172 |
883 |
565 |
1309 |
1331 |
1285 |
1217 |
540 |
Table 10.
Results for the components of when sensitivities up to 3rd-order are considered for the top 10 parameters, with uniform parameters relative standard deviations.
Table 10.
Results for the components of when sensitivities up to 3rd-order are considered for the top 10 parameters, with uniform parameters relative standard deviations.
| Ranking of parameter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Parameter |
|
|
|
|
|
|
|
|
|
|
|
−6068475 |
−41512 |
−86401 |
−64793 |
−41281 |
−96626 |
−98217 |
−94783 |
−89638 |
−39528 |
|
8771 |
60 |
125 |
94 |
60 |
140 |
142 |
137 |
130 |
57 |
Table 11.
Results for the components of when sensitivities up to 4th-order are considered for the top 10 parameters, with uniform parameters relative standard deviations.
Table 11.
Results for the components of when sensitivities up to 4th-order are considered for the top 10 parameters, with uniform parameters relative standard deviations.
| Ranking of parameter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Parameter |
|
|
|
|
|
|
|
|
|
|
|
−6068475 |
−41512 |
−86401 |
−64793 |
−41281 |
−96626 |
−98217 |
−94783 |
−89638 |
−39528 |
|
4189 |
29 |
60 |
45 |
28 |
67 |
68 |
65 |
62 |
27 |
Table 12.
Best-estimate parameter values , for the top 10 parameters, with uniform parameters relative standard deviations .
Table 12.
Best-estimate parameter values , for the top 10 parameters, with uniform parameters relative standard deviations .
| Ranking |
|
|
|
|
|
|
| 1 |
|
29.542 |
29.346 |
29.550 |
29.549 |
29.604 |
| 2 |
|
6.971 |
6.965 |
6.972 |
6.971 |
6.973 |
| 3 |
|
16.182 |
16.169 |
16.183 |
16.183 |
16.185 |
| 4 |
|
12.279 |
12.268 |
12.279 |
12.279 |
12.281 |
| 5 |
|
7.928 |
7.921 |
7.928 |
7.928 |
7.929 |
| 6 |
|
18.571 |
18.556 |
18.571 |
18.571 |
18.574 |
| 7 |
|
19.697 |
19.681 |
19.697 |
19.697 |
19.700 |
| 8 |
|
20.158 |
20.143 |
20.158 |
20.158 |
20.160 |
| 9 |
|
20.334 |
20.320 |
20.335 |
20.334 |
20.337 |
| 10 |
|
9.186 |
9.179 |
9.186 |
9.186 |
9.187 |
Table 13.
Best-estimate parameter values , for the top 10 parameters, with uniform parameters relative standard deviations .
Table 13.
Best-estimate parameter values , for the top 10 parameters, with uniform parameters relative standard deviations .
| Ranking |
|
|
|
|
|
|
| 1 |
|
29.542 |
29.302 |
29.985 |
29.770 |
30.070 |
| 2 |
|
6.971 |
6.963 |
6.986 |
6.973 |
6.975 |
| 3 |
|
16.182 |
16.166 |
16.213 |
16.186 |
16.190 |
| 4 |
|
12.279 |
12.266 |
12.301 |
12.281 |
12.284 |
| 5 |
|
7.928 |
7.920 |
7.942 |
7.929 |
7.931 |
| 6 |
|
18.571 |
18.552 |
18.604 |
18.574 |
18.579 |
| 7 |
|
19.697 |
19.678 |
19.731 |
19.700 |
19.705 |
| 8 |
|
20.158 |
20.139 |
20.191 |
20.161 |
20.166 |
| 9 |
|
20.334 |
20.317 |
20.366 |
20.338 |
20.342 |
| 10 |
|
9.186 |
9.178 |
9.199 |
9.187 |
9.189 |
Table 14.
Nominal values of the components of for the top 10 parameters, with uniform parameters relative standard deviations .
Table 14.
Nominal values of the components of for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
0.3491 |
0.000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0194 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.1047 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0603 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0251 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.1379 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.1552 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.1625 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.1654 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0337 |
Table 15.
Results for : when only the 1st-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 15.
Results for : when only the 1st-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
0.1304 |
−0.0073 |
−0.0150 |
−0.0113 |
−0.0072 |
−0.0167 |
−0.0170 |
−0.0164 |
−0.0156 |
−0.0069 |
|
−0.0073 |
0.0192 |
−0.0005 |
−0.0004 |
−0.0002 |
−0.0006 |
−0.0006 |
−0.0005 |
−0.0005 |
−0.0002 |
|
−0.0150 |
−0.0005 |
0.1037 |
−0.0008 |
−0.0005 |
−0.0011 |
−0.0012 |
−0.0011 |
−0.0011 |
−0.0005 |
|
−0.0113 |
−0.0004 |
−0.0008 |
0.0597 |
−0.0004 |
−0.0009 |
−0.0009 |
−0.0008 |
−0.0008 |
−0.0004 |
|
−0.0072 |
−0.0002 |
−0.0005 |
−0.0004 |
0.0249 |
−0.0006 |
−0.0006 |
−0.0005 |
−0.0005 |
−0.0002 |
|
−0.0167 |
−0.0006 |
−0.0011 |
−0.0009 |
−0.0006 |
0.1367 |
−0.0013 |
−0.0013 |
−0.0012 |
−0.0005 |
|
−0.0170 |
−0.0006 |
−0.0012 |
−0.0009 |
−0.0006 |
−0.0013 |
0.1539 |
−0.0013 |
−0.0012 |
−0.0005 |
|
−0.0164 |
−0.0005 |
−0.0011 |
−0.0008 |
−0.0005 |
−0.0013 |
−0.0013 |
0.1613 |
−0.0012 |
−0.0005 |
|
−0.0156 |
−0.0005 |
−0.0011 |
−0.0008 |
−0.0005 |
−0.0012 |
−0.0012 |
−0.0012 |
0.1643 |
−0.0005 |
|
−0.0069 |
−0.0002 |
−0.0005 |
−0.0004 |
−0.0002 |
−0.0005 |
−0.0005 |
−0.0005 |
−0.0005 |
0.0335 |
Table 16.
Results for : when both 1st- and 2nd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 16.
Results for : when both 1st- and 2nd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
0.1761 |
−0.0058 |
−0.0119 |
−0.0089 |
−0.0057 |
−0.0132 |
−0.0135 |
−0.0130 |
−0.0123 |
−0.0055 |
|
−0.0058 |
0.0192 |
−0.0004 |
−0.0003 |
−0.0002 |
−0.0004 |
−0.0004 |
−0.0004 |
−0.0004 |
−0.0002 |
|
−0.0119 |
−0.0004 |
0.1039 |
−0.0006 |
−0.0004 |
−0.0009 |
−0.0009 |
−0.0009 |
−0.0008 |
−0.0004 |
|
−0.0089 |
−0.0003 |
−0.0006 |
0.0598 |
−0.0003 |
−0.0007 |
−0.0007 |
−0.0007 |
−0.0006 |
−0.0003 |
|
−0.0057 |
−0.0002 |
−0.0004 |
−0.0003 |
0.0249 |
−0.0004 |
−0.0004 |
−0.0004 |
−0.0004 |
−0.0002 |
|
−0.0132 |
−0.0004 |
−0.0009 |
−0.0007 |
−0.0004 |
0.1369 |
−0.0010 |
−0.0010 |
−0.0009 |
−0.0004 |
|
−0.0135 |
−0.0004 |
−0.0009 |
−0.0007 |
−0.0004 |
−0.0010 |
0.1541 |
−0.0010 |
−0.0010 |
−0.0004 |
|
−0.0130 |
−0.0004 |
−0.0009 |
−0.0007 |
−0.0004 |
−0.0010 |
−0.0010 |
0.1616 |
−0.0009 |
−0.0004 |
|
−0.0123 |
−0.0004 |
−0.0008 |
−0.0006 |
−0.0004 |
−0.0009 |
−0.0010 |
−0.0009 |
0.1645 |
−0.0004 |
|
−0.0055 |
−0.0002 |
−0.0004 |
−0.0003 |
−0.0002 |
−0.0004 |
−0.0004 |
−0.0004 |
−0.0004 |
0.0336 |
Table 17.
Results for : when 1st-, 2nd- and 3rd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 17.
Results for : when 1st-, 2nd- and 3rd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
0.1135 |
−0.0048 |
−0.0099 |
−0.0075 |
−0.0048 |
−0.0111 |
−0.0113 |
−0.0109 |
−0.0103 |
−0.0046 |
|
−0.0048 |
0.0193 |
−0.0002 |
−0.0002 |
−0.0001 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
|
−0.0099 |
−0.0002 |
0.1043 |
−0.0003 |
−0.0002 |
−0.0005 |
−0.0005 |
−0.0005 |
−0.0004 |
−0.0002 |
|
−0.0075 |
−0.0002 |
−0.0003 |
0.0601 |
−0.0002 |
−0.0004 |
−0.0004 |
−0.0003 |
−0.0003 |
−0.0001 |
|
−0.0048 |
−0.0001 |
−0.0002 |
−0.0002 |
0.0250 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
|
−0.0111 |
−0.0002 |
−0.0005 |
−0.0004 |
−0.0002 |
0.1374 |
−0.0005 |
−0.0005 |
−0.0005 |
−0.0002 |
|
−0.0113 |
−0.0002 |
−0.0005 |
−0.0004 |
−0.0002 |
−0.0005 |
0.1546 |
−0.0005 |
−0.0005 |
−0.0002 |
|
−0.0109 |
−0.0002 |
−0.0005 |
−0.0003 |
−0.0002 |
−0.0005 |
−0.0005 |
0.1620 |
−0.0005 |
−0.0002 |
|
−0.0103 |
−0.0002 |
−0.0004 |
−0.0003 |
−0.0002 |
−0.0005 |
−0.0005 |
−0.0005 |
0.1649 |
−0.0002 |
|
−0.0046 |
−0.0001 |
−0.0002 |
−0.0001 |
−0.0001 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0002 |
0.0337 |
Table 18.
Results for : when 1st- through 4th-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 18.
Results for : when 1st- through 4th-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
0.1636 |
−0.0038 |
−0.0078 |
−0.0059 |
−0.0038 |
−0.0087 |
−0.0089 |
−0.0086 |
−0.0081 |
−0.0036 |
|
−0.0038 |
0.0194 |
−0.0002 |
−0.0001 |
−0.0001 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
|
−0.0078 |
−0.0002 |
0.1044 |
−0.0002 |
−0.0002 |
−0.0004 |
−0.0004 |
−0.0004 |
−0.0003 |
−0.0002 |
|
−0.0059 |
−0.0001 |
−0.0002 |
0.0601 |
−0.0001 |
−0.0003 |
−0.0003 |
−0.0003 |
−0.0003 |
−0.0001 |
|
−0.0038 |
−0.0001 |
−0.0002 |
−0.0001 |
0.0251 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
|
−0.0087 |
−0.0002 |
−0.0004 |
−0.0003 |
−0.0002 |
0.1375 |
−0.0004 |
−0.0004 |
−0.0004 |
−0.0002 |
|
−0.0089 |
−0.0002 |
−0.0004 |
−0.0003 |
−0.0002 |
−0.0004 |
0.1548 |
−0.0004 |
−0.0004 |
−0.0002 |
|
−0.0086 |
−0.0002 |
−0.0004 |
−0.0003 |
−0.0002 |
−0.0004 |
−0.0004 |
0.1621 |
−0.0004 |
−0.0002 |
|
−0.0081 |
−0.0002 |
−0.0003 |
−0.0003 |
−0.0002 |
−0.0004 |
−0.0004 |
−0.0004 |
0.1650 |
−0.0002 |
|
−0.0036 |
−0.0001 |
−0.0002 |
−0.0001 |
−0.0001 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0002 |
0.0337 |
Table 19.
Nominal values of the components of for the top 10 parameters with 5% parameter relative standard deviations.
Table 19.
Nominal values of the components of for the top 10 parameters with 5% parameter relative standard deviations.
| |
|
|
|
|
|
|
|
|
|
|
|
2.1820 |
0.000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.1215 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.6547 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.3769 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.1571 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.8622 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.9699 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
1.0158 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
1.0337 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.2109 |
Table 20.
Results for : when only the 1st-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 20.
Results for : when only the 1st-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
0.5123 |
−0.0555 |
−0.1145 |
−0.0863 |
−0.0552 |
−0.1279 |
−0.1300 |
−0.1256 |
−0.1189 |
−0.0528 |
|
−0.0555 |
0.1197 |
−0.0038 |
−0.0029 |
−0.0018 |
−0.0043 |
−0.0043 |
−0.0042 |
−0.0040 |
−0.0018 |
|
−0.1145 |
−0.0038 |
0.6468 |
−0.0059 |
−0.0038 |
−0.0088 |
−0.0089 |
−0.0086 |
−0.0082 |
−0.0036 |
|
−0.0863 |
−0.0029 |
−0.0059 |
0.3725 |
−0.0029 |
−0.0066 |
−0.0067 |
−0.0065 |
−0.0061 |
−0.0027 |
|
−0.0552 |
−0.0018 |
−0.0038 |
−0.0029 |
0.1553 |
−0.0042 |
−0.0043 |
−0.0042 |
−0.0039 |
−0.0017 |
|
−0.1279 |
−0.0043 |
−0.0088 |
−0.0066 |
−0.0042 |
0.8524 |
−0.0100 |
−0.0096 |
−0.0091 |
−0.0040 |
|
−0.1300 |
−0.0043 |
−0.0089 |
−0.0067 |
−0.0043 |
−0.0100 |
0.9598 |
−0.0098 |
−0.0093 |
−0.0041 |
|
−0.1256 |
−0.0042 |
−0.0086 |
−0.0065 |
−0.0042 |
−0.0096 |
−0.0098 |
1.0064 |
−0.0089 |
−0.0040 |
|
−0.1189 |
−0.0040 |
−0.0082 |
−0.0061 |
−0.0039 |
−0.0091 |
−0.0093 |
−0.0089 |
1.0252 |
−0.0038 |
|
−0.0528 |
−0.0018 |
−0.0036 |
−0.0027 |
−0.0017 |
−0.0040 |
−0.0041 |
−0.0040 |
−0.0038 |
0.2093 |
Table 21.
Results for : when both 1st- and 2nd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 21.
Results for : when both 1st- and 2nd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
1.6284 |
−0.0184 |
−0.0380 |
−0.0286 |
−0.0183 |
−0.0424 |
−0.0431 |
−0.0416 |
−0.0394 |
−0.0175 |
|
−0.0184 |
0.1209 |
−0.0013 |
−0.0010 |
−0.0006 |
−0.0014 |
−0.0014 |
−0.0014 |
−0.0013 |
−0.0006 |
|
−0.0380 |
−0.0013 |
0.6521 |
−0.0020 |
−0.0013 |
−0.0029 |
−0.0030 |
−0.0029 |
−0.0027 |
−0.0012 |
|
−0.0286 |
−0.0010 |
−0.0020 |
0.3754 |
−0.0009 |
−0.0022 |
−0.0022 |
−0.0022 |
−0.0020 |
−0.0009 |
|
−0.0183 |
−0.0006 |
−0.0013 |
−0.0009 |
0.1565 |
−0.0014 |
−0.0014 |
−0.0014 |
−0.0013 |
−0.0006 |
|
−0.0424 |
−0.0014 |
−0.0029 |
−0.0022 |
−0.0014 |
0.8589 |
−0.0033 |
−0.0032 |
−0.0030 |
−0.0013 |
|
−0.0431 |
−0.0014 |
−0.0030 |
−0.0022 |
−0.0014 |
−0.0033 |
0.9665 |
−0.0032 |
−0.0031 |
−0.0014 |
|
−0.0416 |
−0.0014 |
−0.0029 |
−0.0022 |
−0.0014 |
−0.0032 |
−0.0032 |
1.0127 |
−0.0030 |
−0.0013 |
|
−0.0394 |
−0.0013 |
−0.0027 |
−0.0020 |
−0.0013 |
−0.0030 |
−0.0031 |
−0.0030 |
1.0309 |
−0.0012 |
|
−0.0175 |
−0.0006 |
−0.0012 |
−0.0009 |
−0.0006 |
−0.0013 |
−0.0014 |
−0.0013 |
−0.0012 |
0.2104 |
Table 22.
Results for : when 1st-, 2nd- and 3rd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 22.
Results for : when 1st-, 2nd- and 3rd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
0.7697 |
−0.0097 |
−0.0201 |
−0.0151 |
−0.0096 |
−0.0225 |
−0.0229 |
−0.0221 |
−0.0209 |
−0.0092 |
|
−0.0097 |
0.1214 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
−0.0001 |
|
−0.0201 |
−0.0001 |
0.6544 |
−0.0002 |
−0.0001 |
−0.0003 |
−0.0003 |
−0.0003 |
−0.0003 |
−0.0001 |
|
−0.0151 |
−0.0001 |
−0.0002 |
0.3768 |
−0.0001 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
|
−0.0096 |
−0.0001 |
−0.0001 |
−0.0001 |
0.1570 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
−0.0001 |
|
−0.0225 |
−0.0002 |
−0.0003 |
−0.0002 |
−0.0002 |
0.8618 |
−0.0004 |
−0.0004 |
−0.0003 |
−0.0001 |
|
−0.0229 |
−0.0002 |
−0.0003 |
−0.0002 |
−0.0002 |
−0.0004 |
0.9695 |
−0.0004 |
−0.0003 |
−0.0001 |
|
−0.0221 |
−0.0002 |
−0.0003 |
−0.0002 |
−0.0002 |
−0.0004 |
−0.0004 |
1.0155 |
−0.0003 |
−0.0001 |
|
−0.0209 |
−0.0001 |
−0.0003 |
−0.0002 |
−0.0001 |
−0.0003 |
−0.0003 |
−0.0003 |
1.0334 |
−0.0001 |
|
−0.0092 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
0.2109 |
Table 23.
Results for : when 1st- through 4th-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 23.
Results for : when 1st- through 4th-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
1.5075 |
−0.0046 |
−0.0096 |
−0.0072 |
−0.0046 |
−0.0107 |
−0.0109 |
−0.0105 |
−0.0100 |
−0.0044 |
|
−0.0046 |
0.1215 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
|
−0.0096 |
−0.0001 |
0.6545 |
−0.0001 |
−0.0001 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
−0.0001 |
|
−0.0072 |
−0.0001 |
−0.0001 |
0.3768 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
|
−0.0046 |
−0.0001 |
−0.0001 |
−0.0001 |
0.1571 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
|
−0.0107 |
−0.0001 |
−0.0002 |
−0.0001 |
−0.0001 |
0.8620 |
−0.0002 |
−0.0002 |
−0.0002 |
−0.0001 |
|
−0.0109 |
−0.0001 |
−0.0002 |
−0.0001 |
−0.0001 |
−0.0002 |
0.9697 |
−0.0002 |
−0.0002 |
−0.0001 |
|
−0.0105 |
−0.0001 |
−0.0002 |
−0.0001 |
−0.0001 |
−0.0002 |
−0.0002 |
1.0156 |
−0.0002 |
−0.0001 |
|
−0.0100 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0002 |
−0.0002 |
−0.0002 |
1.0336 |
−0.0001 |
|
−0.0044 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
−0.0001 |
0.2109 |
Table 24.
Nominal values of the components of for the top 10 parameters, for 10% relative standard deviations.
Table 24.
Nominal values of the components of for the top 10 parameters, for 10% relative standard deviations.
| |
|
|
|
|
|
|
|
|
|
|
|
8.7280 |
0.000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.4860 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
2.6187 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
1.5076 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.6285 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
3.4487 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
3.8796 |
0.0000 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
4.0633 |
0.0000 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
4.1348 |
0.0000 |
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.8437 |
Table 25.
Results for : when only the 1st-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 25.
Results for : when only the 1st-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
1.8307 |
−0.2294 |
−0.4730 |
−0.3564 |
−0.2280 |
−0.5282 |
−0.5370 |
−0.5188 |
−0.4913 |
−0.2181 |
|
−0.2294 |
0.4784 |
−0.0157 |
−0.0119 |
−0.0076 |
−0.0176 |
−0.0179 |
−0.0173 |
−0.0163 |
−0.0073 |
|
−0.4730 |
−0.0157 |
2.5862 |
−0.0244 |
−0.0156 |
−0.0362 |
−0.0368 |
−0.0356 |
−0.0337 |
−0.0150 |
|
−0.3564 |
−0.0119 |
−0.0244 |
1.4892 |
−0.0118 |
−0.0273 |
−0.0277 |
−0.0268 |
−0.0254 |
−0.0113 |
|
−0.2280 |
−0.0076 |
−0.0156 |
−0.0118 |
0.6209 |
−0.0175 |
−0.0178 |
−0.0172 |
−0.0162 |
−0.0072 |
|
−0.5282 |
−0.0176 |
−0.0362 |
−0.0273 |
−0.0175 |
3.4083 |
−0.0411 |
−0.0397 |
−0.0376 |
−0.0167 |
|
−0.5370 |
−0.0179 |
−0.0368 |
−0.0277 |
−0.0178 |
−0.0411 |
3.8378 |
−0.0404 |
−0.0382 |
−0.0170 |
|
−0.5188 |
−0.0173 |
−0.0356 |
−0.0268 |
−0.0172 |
−0.0397 |
−0.0404 |
4.0242 |
−0.0369 |
−0.0164 |
|
−0.4913 |
−0.0163 |
−0.0337 |
−0.0254 |
−0.0162 |
−0.0376 |
−0.0382 |
−0.0369 |
4.0998 |
−0.0155 |
|
−0.2181 |
−0.0073 |
−0.0150 |
−0.0113 |
−0.0072 |
−0.0167 |
−0.0170 |
−0.0164 |
−0.0155 |
0.8368 |
Table 26.
Results for : when both 1st- and 2nd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
Table 26.
Results for : when both 1st- and 2nd-order sensitivities are considered; for the top 10 parameters, with uniform parameters relative standard deviations .
| |
|
|
|
|
|
|
|
|
|
|
|
7.9885 |
−0.0246 |
−0.0507 |
−0.0382 |
−0.0244 |
−0.0566 |
−0.0576 |
−0.0556 |
−0.0527 |
−0.0234 |
|
−0.0246 |
0.4852 |
−0.0017 |
−0.0013 |
−0.0008 |
−0.0019 |
−0.0019 |
−0.0018 |
−0.0018 |
−0.0008 |
|
−0.0507 |
−0.0017 |
2.6152 |
−0.0026 |
−0.0017 |
−0.0039 |
−0.0039 |
−0.0038 |
−0.0036 |
−0.0016 |
|
−0.0382 |
−0.0013 |
−0.0026 |
1.5057 |
−0.0013 |
−0.0029 |
−0.0030 |
−0.0029 |
−0.0027 |
−0.0012 |
|
−0.0244 |
−0.0008 |
−0.0017 |
−0.0013 |
0.6277 |
−0.0019 |
−0.0019 |
−0.0018 |
−0.0017 |
−0.0008 |
|
−0.0566 |
−0.0019 |
−0.0039 |
−0.0029 |
−0.0019 |
3.4444 |
−0.0044 |
−0.0043 |
−0.0040 |
−0.0018 |
|
−0.0576 |
−0.0019 |
−0.0039 |
−0.0030 |
−0.0019 |
−0.0044 |
3.8751 |
−0.0043 |
−0.0041 |
−0.0018 |
|
−0.0556 |
−0.0018 |
−0.0038 |
−0.0029 |
−0.0018 |
−0.0043 |
−0.0043 |
4.0591 |
−0.0040 |
−0.0018 |
|
−0.0527 |
−0.0018 |
−0.0036 |
−0.0027 |
−0.0017 |
−0.0040 |
−0.0041 |
−0.0040 |
4.1311 |
−0.0017 |
|
−0.0234 |
−0.0008 |
−0.0016 |
−0.0012 |
−0.0008 |
−0.0018 |
−0.0018 |
−0.0018 |
−0.0017 |
0.8430 |
Table 27.
Best-estimate values for , ; parameters relative standard deviations .
Table 27.
Best-estimate values for , ; parameters relative standard deviations .
| Skewness |
|
|
|
|
|
8.595 × 10−1 |
−2.604 × 10−2 |
−1.147 × 10−2 |
−1.224 × 10−1 |
|
1.805 × 100 |
−4.713 × 10−2 |
−4.888 × 10−2 |
−4.508 × 10−1 |
|
1.424 × 10−1 |
−4.741 × 10−3 |
−2.417 × 10−3 |
−2.654 × 10−2 |
|
1.263 × 10−1 |
−4.207 × 10−3 |
−2.149 × 10−3 |
−2.361 × 10−2 |
Table 28.
Best-estimate values for , ; parameters relative standard deviations .
Table 28.
Best-estimate values for , ; parameters relative standard deviations .
| Skewness |
|
|
|
|
|
1.229 × 10−1 |
−2.154 × 10−1 |
−2.178 × 10−2 |
−5.061 × 10−2 |
|
1.050 × 100 |
−1.079 × 100 |
−7.916 × 10−1 |
−1.366 × 100 |
|
6.963 × 10−2 |
−1.267 × 10−1 |
−1.334 × 10−2 |
−3.102 × 10−2 |
|
6.176 × 10−2 |
−1.125 × 10−1 |
−1.196 × 10−2 |
−2.781 × 10−2 |
Table 29.
Best-estimate values for , ; parameters relative standard deviations .
Table 29.
Best-estimate values for , ; parameters relative standard deviations .
| Kurtosis |
|
|
|
|
|
5.260 |
4.364 |
3.599 |
3.548 |
|
4.885 |
3.001 |
3.002 |
3.134 |
|
3.013 |
3.000 |
3.000 |
3.000 |
|
3.011 |
3.000 |
3.000 |
3.000 |
Table 30.
Best-estimate values for , ; parameters relative standard deviations .
Table 30.
Best-estimate values for , ; parameters relative standard deviations .
| Kurtosis |
|
|
|
|
|
3.280 |
3.116 |
3.009 |
3.004 |
|
3.695 |
3.732 |
3.404 |
4.138 |
|
3.003 |
3.011 |
3.000 |
3.001 |
|
3.003 |
3.008 |
3.000 |
3.001 |