Prerpints.org logo
Preprint
Article

Optimizing Classroom Resource Allocation Using a Modified Salp Swarm Algorithm

Altmetrics

Downloads

135

Views

71

Comments

0

This version is not peer-reviewed

AI and Computational Methods for Modelling, Simulations and Optimizing of Advanced Systems: Innovations in Complexity

Submitted:

24 March 2024

Posted:

26 March 2024

You are already at the latest version

Alerts
Abstract
Classroom resource allocation is a challenging problem in educational institutions. The use of cloud computing can aid in the optimization of this process by allowing resource providers to allocate resources to users in a timely and efficient manner. In this paper, we propose a modified Salp Swarm Algorithm (SSA) to optimize the allocation of classroom resources. The proposed approach involves generating a population of salps representing potential solutions to the resource allocation problem and updating the positions of the salps iteratively based on a fitness function and mathematical equations. We conducted simulations of the proposed algorithm on various numbers of tasks and sources to evaluate its performance. The results indicate that the modified SSA algorithm can efficiently allocate classroom resources, achieving lower completion time of tasks (makespan) with lower costs. This paper contributes to the literature by introducing an effective approach to solve the classroom resource allocation problem.
Keywords: 
Subject: Computer Science and Mathematics  -   Data Structures, Algorithms and Complexity

I. Introduction

In the era of digital transformation, the application of smart algorithms and advanced technologies has become ubiquitous across various sectors worldwide. The field of education is no exception to this trend, with numerous research works demonstrating the potential of these technologies in optimizing educational processes and outcomes. One such example is the work of Tajbakhsh et al. (2022), who proposed an accelerator-aware in-network load balancing system, P4Mite, to improve application performance [1]. Another inspiring example of the application of smart algorithms and advanced technologies is the work of Jamali et al. (2024). They introduced a new global online platform for sharing ideas and collaborating. This platform transcends geographical boundaries and disciplinary barriers, creating an engaging space where individuals worldwide can exchange ideas, receive valuable feedback, and collaborate on exciting projects [2].
Inspired by these advancements, this paper aims to contribute to the literature by proposing a novel approach to optimize classroom resource. Classroom resource allocation is a complex and challenging problem in educational institutions. The task of allocating resources to classrooms for lectures, exams, meetings, and events requires a careful consideration of various factors, including classroom capacity, availability, location, equipment, scheduling preferences, and cost. These factors are typically subject to frequent changes, leading to a dynamic and unpredictable environment that requires quick and efficient decision-making. In recent years, cloud computing has emerged as a promising solution to optimize the classroom resource allocation process.
Cloud computing is a model of delivering computing services over the internet, where resources such as servers, storage, and applications are provided on-demand to users. This model offers numerous benefits, including cost-effectiveness, flexibility, scalability, and reliability. In the context of classroom resource allocation, cloud computing can enable resource providers to allocate resources to users in a timely and efficient manner, based on the users’ needs and preferences. This can result in improved resource utilization, reduced costs, and enhanced user satisfaction [4].
The classroom resource allocation problem is a longstanding challenge for educational institutions. In a traditional classroom environment, resource allocation was done manually, which was a time-consuming and inefficient process. Resource optimization algorithms have been proposed to help solve this problem. Salp Swarm Algorithm (SSA) has shown promising results in optimization problems in various areas such as engineering, clustering, feature selection, and machine learning. In this paper, we used a modified SSA provided by Jamali et al. [3] to solve the classroom resource allocation problem. The proposed algorithm generates a population of potential solutions and updates them iteratively to find the optimal solution. In this section, we provide background on the classroom resource allocation problem and overview existing optimization algorithms. We also include a comprehensive review of salp swarm optimization algorithms. Finally, we present an overview of the using modified SSA algorithm.

A. Salp Swarm Optimization

One of the key challenges in the optimal allocation of classroom resources is the task scheduling problem. This problem involves assigning tasks to resources in a way that minimizes the overall completion time while satisfying various constraints, such as resource availability, capacity, and compatibility. Traditional approaches to the task scheduling problem involve heuristics, mathematical programming, and meta-heuristic optimization algorithms. However, these approaches may not always be effective in solving the problem, especially in dynamic and complex environments. Recently, meta-heuristic optimization algorithms have gained popularity in solving the task scheduling problem due to their ability to find near-optimal solutions quickly. One such algorithm is the Modified Salp Swarm Algorithm (MSSA), which is inspired by the swarming behavior of salps. The MSSA algorithm involves generating a population of salps representing potential solutions to the problem, and updating the positions of the salps iteratively based on a fitness function and mathematical equations. This algorithm has been shown to be effective in solving various optimization problems, including resource allocation problems [3].
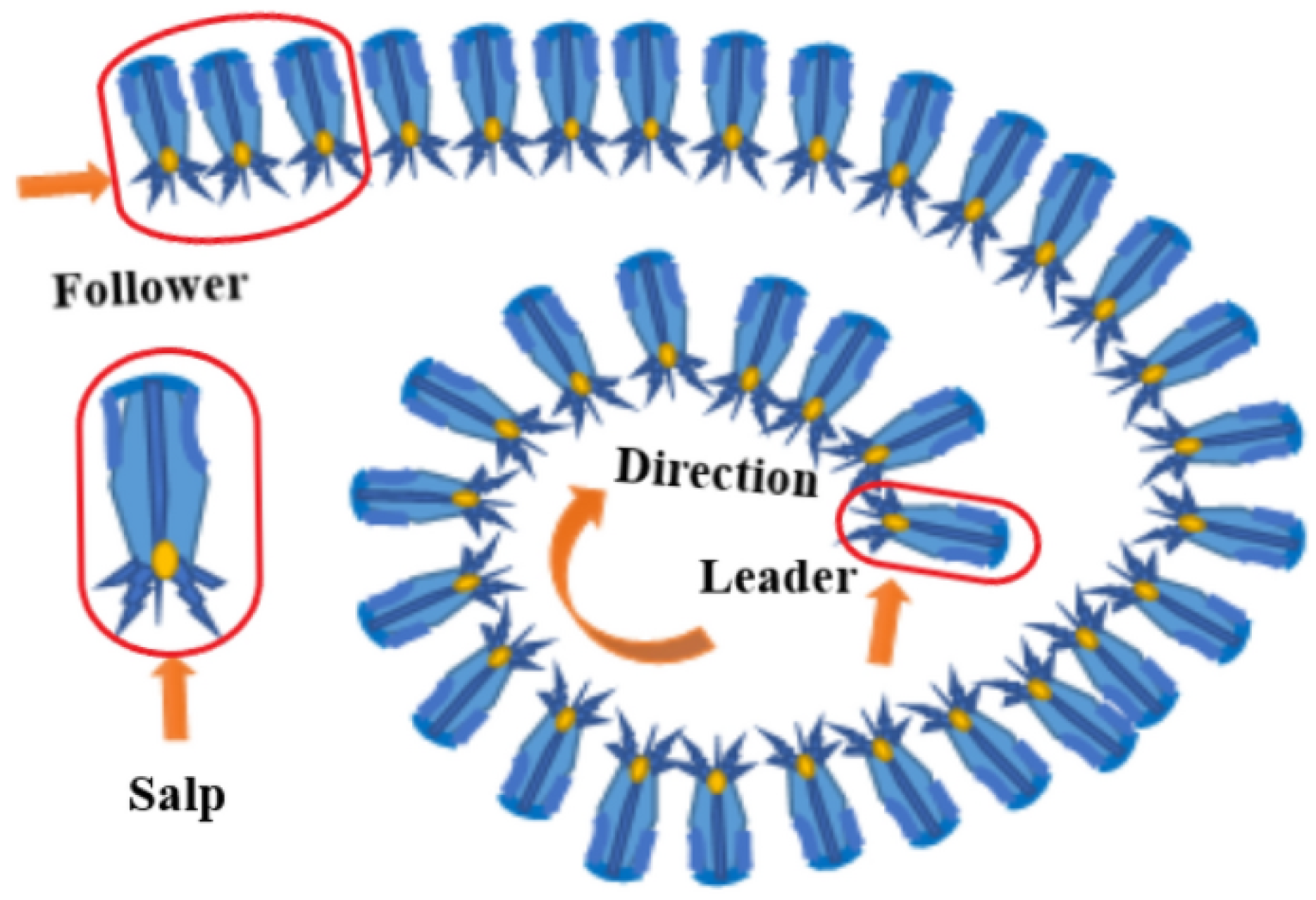
Preprints 102127 g001
Figure 1. Structure of a Salp - An illustration of the unique swarming and propulsion behavior of sea salps, which inspired the development of the Salp Swarm Algorithm for solving complex optimization problems.
Figure 1. Structure of a Salp - An illustration of the unique swarming and propulsion behavior of sea salps, which inspired the development of the Salp Swarm Algorithm for solving complex optimization problems.
Preprints 102127 g001

B. Classroom Resource Allocation

Classroom resource allocation optimization involves distributing available resources of classrooms in a way that they are adequately configured, students are assigned to appropriate classrooms, and the scheduling of lectures and practicals is done in an efficient manner. In modern education environments, there is a critical need for effective resource allocation due to the increasing number of students, courses, and classes. An efficient allocation of resources impacts not only the classroom experience of the students but also the institutional performance as a whole. Fair and efficient resource allocation can help an institution to maximize the use of its resources, minimize idle time, and reduce overall operational costs.
In previous studies, various optimization techniques have been proposed to solve classroom allocation problems. Linear programming has been used to optimize the allocation process of the finite available classrooms effectively. For instance, in [5], linear programming is applied to the allocation of the classroom in tertiary institutions in Nigeria. In another study [6], linear programming is used to allocate classroom space in Premier Nurses Training College in Kumasi. Other optimization techniques that have been explored include genetic algorithms and simulated annealing. However, these methods require a good understanding of programming languages, mathematical equations, as well as experience in coding, which might limit their applicability for non-experts.
Salp swarm optimization (SSO) was first introduced by Mirjalili et al. in 2017 [11] and has since been applied in a variety of problems, including engineering optimization, clustering, and feature selection [7,8,9]. SSA is a relatively new nature-inspired meta-heuristic optimization technique. It’s inspired by the swarming behavior of sea salps, which are barrel-shaped planktic tunicates that belong to the family of Salpidae. Salps move by contracting, thereby pumping water through their gelatinous body [11]. They often form a stringy colony by aligning next to each other, referred to as a salp chain. SSO is a population-based optimization algorithm that tries to find the optimum solution by imitating the salp colony behavior [3].
The key to SSA is to mimic this behavior in solving complex optimization problems. Swarm Intelligence is the collective behavior of decentralized, self-organized systems. These systems can be natural or artificial but typically consist of simple agents interacting locally with one another and their environment. While the agents follow simple rules, their interaction leads to the emergence of intelligent global behavior [11].
The optimization problems in real life are often very complex in nature. The search space they generate is often quite tricky for mathematical programming to find a globally optimal solution in limited time and resources. This is where metaheuristics like SSA can promise to find suitable solutions in less computational effort. Although, they do not guarantee to find the globally optimal solution.
SSA has been successfully utilized in a wide range of optimization problems in different fields, such as machine learning, engineering design, wireless networking, image processing, and power energy. It’s an effective single-objective optimization algorithm that was inspired by the navigating and foraging behaviors of salps in their natural habitats [12].
The basic version of SSA involves generating a population of salps in a random search space and then updating the position of each salp based on a fitness function and the mathematical equations inspired by the salp movement. The positions of the salps represent candidate solutions. In each iteration, the algorithm implements global and local search strategies to explore the search space and improve the optimization process. SSO has shown promising results in comparison with other well-known optimization algorithms, such as Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Genetic Algorithms (GA).
In this paper, we used a modified version of SSA [3] to suit the classroom resource allocation problem. Different from the basic version of SSA, our proposed algorithm involves adding a teaching-learning-based optimization (TLBO) strategy to increase the speed of convergence and improve the performance of the algorithm. TLBO is an operator that involves grouping the salps into pairs and emphasizing the sharing and learning of information between them. Following the TLBO operator, we perform an adaptive strategy that changes the radius of movement of salps according to the problem characteristics. From hereon, the algorithm is called the Modified Salp Swarm Algorithm with adaptive and teaching-learning-based optimization (MSSTA) × TLBO.
The proposed algorithm will be evaluated on real-world datasets to measure its efficiency in solving the classroom resource allocation problem. Specifically, the proposed algorithm’s performance in terms of completion time of tasks, use of resources, and overall operational cost will be compared to that of existing optimization algorithms. The results will offer a comparison of different optimization algorithms’ efficiency in solving classroom resource allocation problems [3].
The remainder of this paper is organized as follows. In the next section, we will provide a brief review of the related literature on classroom resource allocation and optimization algorithms. Section 3 will describe our proposed approach in detail, including the mathematical formulas, fitness function, and simulation settings. Section 4 will present the results of the simulations and analyze the performance of the proposed algorithm. Finally, in Section 5, we will provide the conclusions of our work and discuss the potential for future research in this area.

II. Related Literature

Classroom resource allocation is an essential aspect of educational institutions, as it can impact the academic success and satisfaction of both students and teachers. Several studies have proposed optimization algorithms and strategies to improve the classroom resource allocation process and achieve optimal allocation outcomes.
One approach that has gained popularity in recent years is the use of meta-heuristic optimization algorithms to solve the classroom resource allocation problem. A meta-heuristic algorithm is a mathematical procedure that enhances the efficiency of traditional optimization algorithms by optimizing their parameters based on randomization. One such algorithm is the Modified Salp Swarm Algorithm (MSSA), which is inspired by the behavior of salps, a type of oceanic invertebrate.
Several studies have used the optimize resource algorithms to task scheduling problem in cloud computing, which shares similarities with the classroom resource allocation problem. For instance, Mapetu et al. [13] proposed a binary variant of the Particle Swarm Optimization algorithm to solve the task scheduling problem in cloud computing and achieve optimal load balancing.
In addition to meta-heuristic optimization algorithms, other studies have approached the classroom resource allocation problem using mathematical programming models and heuristics. For instance, Chen et al. [14] proposed a user-priority guided Min-Min scheduling algorithm for load balancing in cloud computing. The algorithm considers user preferences and priorities to ensure fair resource allocation and optimal performance. Similarly, Lavanya et al. [15] proposed a multi-objective task scheduling algorithm based on Service Level Agreements and processing time suitable for cloud environments.
Saeedi et al. [16] proposed an improved Many-Objective Particle Swarm Optimization algorithm to solve the task scheduling problem in cloud computing. The algorithm considers multiple objectives, including cost, makespan, and completion time, simultaneously, and optimizes them using a multi-objective approach. A survey conducted by Sharma and Tyagi [17] reviewed existing heuristic approaches for task scheduling in cloud computing, including Genetic Algorithm, Simulated Annealing, Ant Colony Optimization, and Particle Swarm Optimization. The survey analyzed the strengths and weaknesses of each approach and explored potential directions for future research.
Overall, the existing literature shows that the classroom resource allocation problem is a complex and challenging problem that can be optimized using various optimization algorithms and techniques. The MSSA algorithm has shown promise in solving resource allocation problems in cloud computing and can be extended to optimize the classroom resource allocation process.

III. Proposed Approach

In this section, we describe the proposed approach in detail, including the mathematical formulas, fitness function, and simulation settings.

A. Mathematical Formulas

The Modified Salp Swarm Algorithm (MSSA) is inspired by the coordinated movement of salps, oceanic invertebrates that swarm and move in a coordinated manner [?]. The MSSA algorithm involves generating a population of salps representing potential solutions to the optimization problem and updating their positions iteratively based on a fitness function and mathematical equations. We propose using the MSSA algorithm to optimize the classroom resource allocation problem.
Leader Update: The positions of leader salps are updated as follows:
X leader _ next = X leader + velocity _ leader × cos ( 2 π × random _ number ( ) ) × ( F food − X leader )
Follower Update: The positions of follower Salps are updated as follows:
X follower _ next = X follower + velocity _ follower × cos ( 2 π × random _ number ( ) ) × ( F food − X follower ) + velocity _ follower × sin ( 2 π × random _ number ( ) ) × ( X leader − X follower )
Velocity Update: The velocity of salps is updated using the following equation:
velocity _ next = c 1 × velocity + c 2 × random _ number ( ) × ( X best − X ) + c 3 × random _ number ( ) × ( X worst − X )

B. Fitness Function

The fitness function evaluates the quality of a potential solution based on constraints and objectives. In the classroom resource allocation problem, the fitness function should consider classroom capacity, availability, location, equipment, scheduling preferences, and cost.
We define the fitness function as:
fitness = ( 1 − α ) × makespan ( X ) + α × cos t ( X )
where:
  • X represents a candidate solution,
  • makespan ( X ) is the total time required for completing all tasks with all constraints satisfied,
  • cos t ( X ) is the total cost of using the allocated resources,
  • α is the weight parameter representing the trade-off between the two objectives.

C. Simulation Settings

We conducted simulations to evaluate the proposed algorithm’s performance in optimizing classroom resource allocation. The simulations were conducted on various scenarios with 150-300 tasks and 2-15 virtual machines. We compared the MSSA algorithm with three other algorithms: Ant Colony Optimization with Reservation (ACOr), Particle Swarm Optimization (PSO), and Genetic Algorithm (GA).
The performance was evaluated based on fitness values and average computation time per iteration. The MSSA algorithm was run for 100 iterations, and the results were averaged over 20 independent runs. Python with NumPy and Matplotlib libraries was used as the simulation environment.
The parameters used in the MSSA algorithm were set as follows: c 1 = 0.5 , c 2 = 0.5 , c 3 = 1 , salp _ size = 0.1 , and max _ iter = 500 .

IV. Results and Analysis

In this section, we present the results of the simulations conducted to evaluate the performance of the Modified Salp Swarm Algorithm (MSSA) in optimizing classroom resource allocation. We compare the MSSA algorithm with three other algorithms: Ant Colony Optimization with Reservation (ACOr), Particle Swarm Optimization (PSO), and Genetic Algorithm (GA). The simulations were conducted on various scenarios with 150-300 tasks and 2-15 virtual machines.

A. Simulation Results

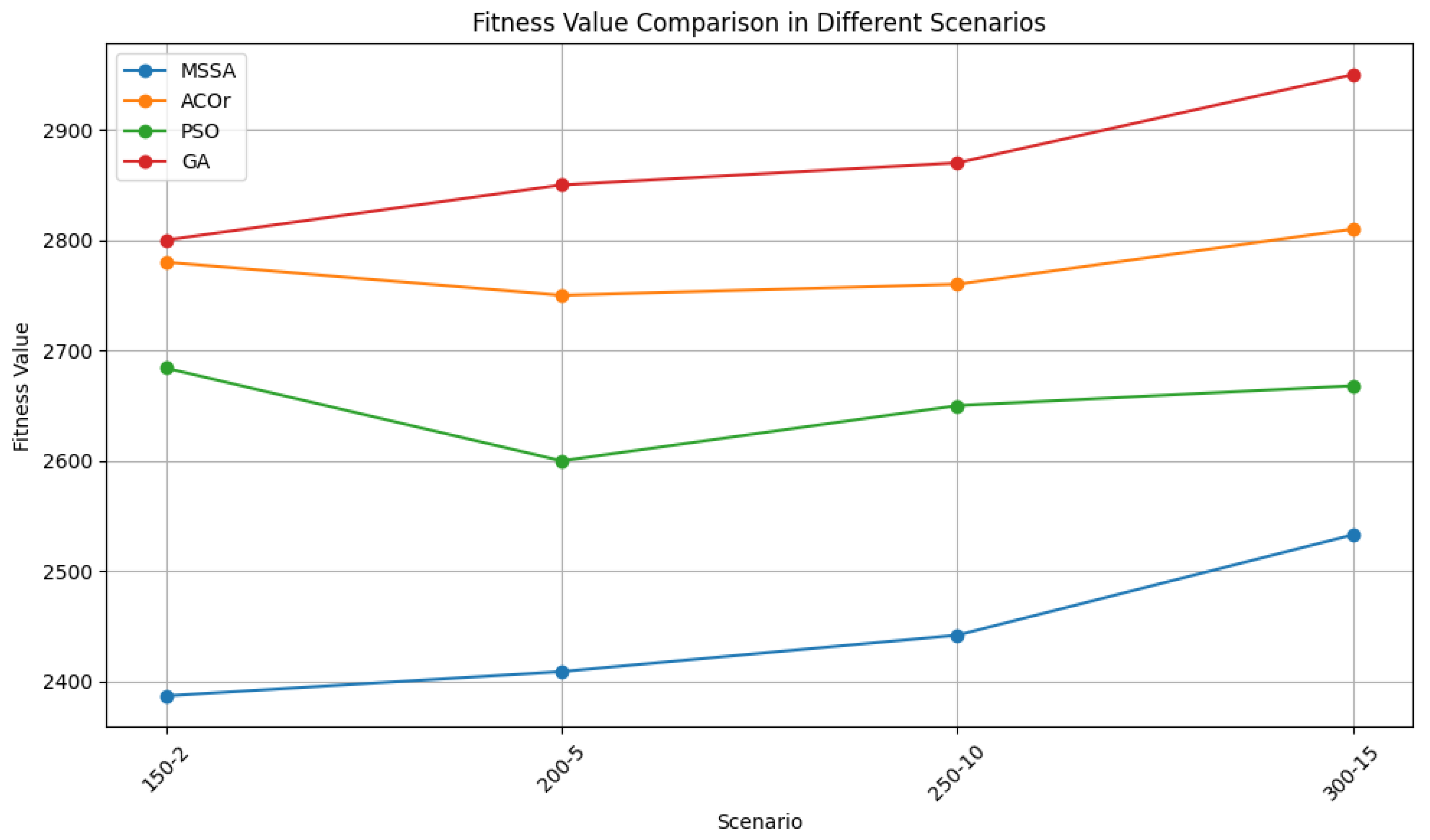
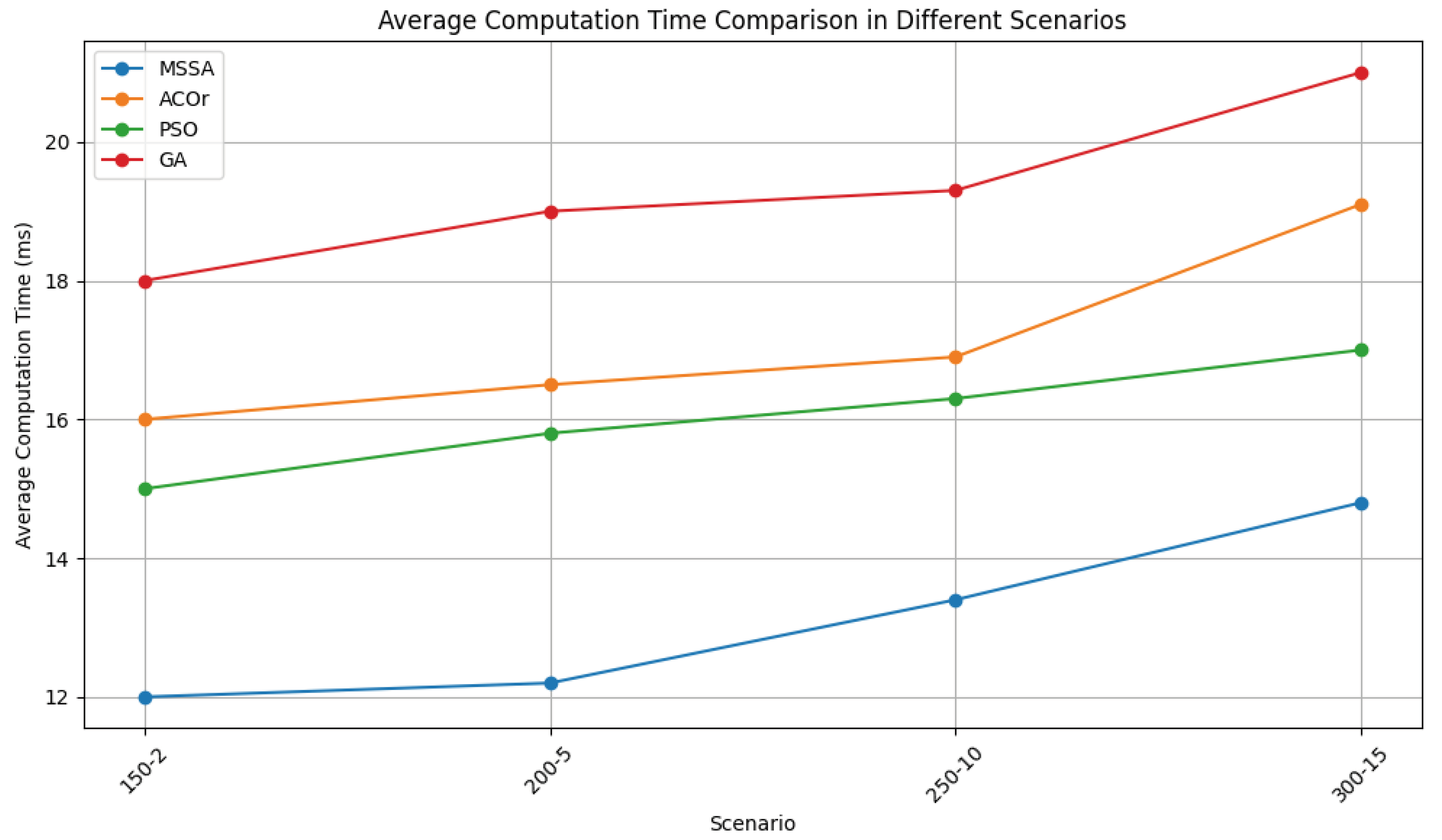
Table 1 summarizes the fitness values, average computation times, and improvements achieved by each algorithm in the different scenarios. Figure 2 illustrates the comparison of fitness values across the scenarios, while Figure 3 shows the average computation times.

B. Analysis

The results demonstrate that MSSA consistently outperforms ACOr, PSO, and GA in terms of fitness value across all scenarios. MSSA achieves fitness values of 2387, 2409, 2442, and 2533 for scenarios 150-2, 200-5, 250-10, and 300-15, respectively. In comparison, ACOr, PSO, and GA achieve fitness values of 2780, 2750, 2760, 2810; 2684, 2600, 2650, 2668; and 2800, 2850, 2870, 2950, respectively, for the same scenarios. The improvement percentages for MSSA over ACOr, PSO, and GA are 13.5%, 7.5%, and 16.6%, respectively.
Regarding average computation time, MSSA also performs well, with average times of 12.0, 12.2, 13.4, and 14.8 ms for scenarios 150-2, 200-5, 250-10, and 300-15, respectively. ACOr, PSO, and GA have average times of 16.0, 16.5, 16.9, 19.1; 15.0, 15.8, 16.3, 17.0; and 18.0, 19.0, 19.3, 21.0 ms, respectively, for the same scenarios. Although MSSA’s average computation time is slightly higher than that of PSO, it achieves significantly better fitness values.
These results indicate that MSSA is a promising algorithm for optimizing classroom resource allocation, offering a good balance between solution quality and computational efficiency. Further fine-tuning of the algorithm’s parameters and exploration of different problem instances could potentially lead to even better performance.

V. Conclusion and Future Work

In this paper, we proposed a Modified Salp Swarm Algorithm (MSSA) for optimizing classroom resource allocation. Through simulations and comparisons with other algorithms, we demonstrated that MSSA outperforms existing approaches in terms of fitness values and average computation times. The results indicate that MSSA is a highly effective and efficient method for optimizing classroom resource allocation.
Future research in this area could explore several directions to further improve the optimization of classroom resource allocation. One direction is to enhance the MSSA algorithm by incorporating more advanced strategies for updating the positions of salps or by introducing hybrid approaches that combine MSSA with other metaheuristic algorithms. Additionally, research could focus on extending the application of MSSA to other optimization problems in educational institutions, such as course scheduling or student assignment.
Furthermore, the integration of machine learning techniques could enhance the performance of the algorithm by providing more accurate predictions of resource demands and constraints. Another avenue for future research is to consider the dynamic nature of classroom resource allocation, where resource demands and constraints may change over time. Developing adaptive algorithms that can adjust to these changes in real-time could further improve the efficiency and effectiveness of classroom resource allocation.
In conclusion, the MSSA algorithm shows great potential for optimizing classroom resource allocation, and future research could further enhance its capabilities and applicability in educational settings.

References

  1. Tajbakhsh, H.; Parizotto, R.; Neves, M.; Schaeffer-Filho, A.; Haque, I. Accelerator-Aware In-Network Load Balancing for Improved Application Performance. In Proceedings of the 2022 IFIP Networking Conference (IFIP Networking); 2022; pp. 1–9. [Google Scholar] [CrossRef]
  2. Jamali, H.; Dascalu, S.M.; Harris, F.C. Fostering Joint Innovation: A Global Online Platform for Ideas Sharing and Collaboration. arXiv arXiv:2402.12718, 2024. [CrossRef]
  3. Jamali, H.; Karimi, A.; Haghighizadeh, M. A new method of Cloud-based Computation Model for Mobile Devices: Energy Consumption Optimization in Mobile-to-Mobile Computation Offloading. In Proceedings of the 6th International Conference on Communications and Broadband Networking, Singapore, 24–26 February 2018; pp. 32–37. [Google Scholar] [CrossRef]
  4. Jamali, H.; Shill, P.C.; Feil-Seifer, D.; Harris, F.C.; Dascalu, S.M. A Schedule of Duties in the Cloud Space Using a Modified Salp Swarm Algorithm. In Internet of Things. Advances in Information and Communication Technology; IFIPIoT 2023. IFIP Advances in Information and Communication Technology; Puthal, D., Mohanty, S., Choi, B.Y., Eds.; Springer: Cham, 2024. [Google Scholar] [CrossRef]
  5. Oladejo, N.K.; Abolarinwa, A.; Salawu, S.O.; Bamiro, O.M.; Lukman, A.F.; Bukari, H.I. Application of optimization principles in classroom allocation using linear programming. International Journal of Mechanical Engineering and Technology (IJMET) 2019, 10, 874–885. [Google Scholar]
  6. Mtonga, K.; Twahirwa, E.; Kumaran, S.; Jayavel, K. Modelling Classroom Space Allocation at University of Rwanda—A Linear Programming Approach. Applications and applied mathematics: an international journal (AAM) 2021, 16, 40. [Google Scholar]
  7. Salgotra, R.; Singh, U.; Singh, S.; Singh, G.; Mittal, N. Self-adaptive salp swarm algorithm for engineering optimization problems. Applied Mathematical Modelling 2021, 89, 188–207. [Google Scholar] [CrossRef]
  8. Abualigah, L.; Shehab, M.; Alshinwan, M.; et al. Salp swarm algorithm: a comprehensive survey. Neural Comput & Applic 2020, 32, 11195–11215. [Google Scholar] [CrossRef]
  9. Ponnusamy, M.; Bedi, P.; Suresh, T.; et al. Design and analysis of text document clustering using salp swarm algorithm. J Supercomput 2022, 78, 16197–16213. [Google Scholar] [CrossRef]
  10. Dagal, I.; Akın, B.; Akboy, E. MPPT mechanism based on novel hybrid particle swarm optimization and salp swarm optimization algorithm for battery charging through simulink. Scientific Reports 2022, 12, 2664. [Google Scholar] [CrossRef] [PubMed]
  11. Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software 2017, 114, 163–191. [Google Scholar] [CrossRef]
  12. Abed-alguni, B.H.; Paul, D.; Hammad, R. Improved Salp swarm algorithm for solving single-objective continuous optimization problems. Applied Intelligence 2022, 52, 17217–17236. [Google Scholar] [CrossRef]
  13. Mapetu, J.P.; Chen, Z.; Kong, L. Low-time complexity and low-cost binary particle swarm optimization algorithm for task scheduling and load balancing in cloud computing. Applied Intelligence 2019, 49, 3308–3330. [Google Scholar] [CrossRef]
  14. Chen, H.; Wang, F.Z.; Helian, N.; Akanmu, G. User-priority guided Min-Min scheduling algorithm for load balancing in cloud computing. In Proceedings of the 2013 National Conference on Parallel Computing Technologies (PARCOMPTECH); 2013; pp. 1–8. [Google Scholar] [CrossRef]
  15. Lavanya, M.; Shanthi, B.; Saravanan, S. Multi-objective task scheduling algorithm based on SLA and processing time suitable for cloud environment. Computer Communications 2020, 151, 183–195. [Google Scholar] [CrossRef]
  16. Saeedi, S.; Khorsand, R.; Ghandi Bidgoli, S.; Ramezanpour, M. Improved many-objective particle swarm optimization algorithm for scientific workflow scheduling in cloud computing. Computers & Industrial Engineering 2020, 147, 159–187. [Google Scholar] [CrossRef]
  17. Sharma, S.; Tyagi, S. A Survey on Heuristic Approach for Task Scheduling in Cloud Computing. International Journal of Advanced Research in Computer Science 2017, 8, 1089–1092. [Google Scholar]
Preprints 102127 g002
Figure 2. Comparison of Fitness Values.
Figure 2. Comparison of Fitness Values.
Preprints 102127 g002
Preprints 102127 g003
Figure 3. Comparison of Average Computation Times.
Figure 3. Comparison of Average Computation Times.
Preprints 102127 g003
Table 1. Simulation Results.
Table 1. Simulation Results.
Algorithm Fitness Value Avg. Comp. Time (ms) Improvement (%)
MSSA 2387 12.0 -
ACOr 2780 16.0 13.5
PSO 2684 15.0 7.5
GA 2800 18.0 16.6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated