A New Look at Physico-Chemical Causes of Changing Climate: Is Strong Acid Production Lowering the Surface pH Value a Continuing Cause of Increasing pCO2 in the Earth’s Atmosphere?

A testable hypothesis with quantitative predictions is put forward, proposing that strong acids produced on land at a rate correlated with global population are an increas-ing cause of increasing atmospheric CO2 pressure (pCO2). This hypothesis widens the imbalance assumed between the global uptake of CO2 by photosynthesis and emissions of CO2 from all sources, including the combustion of fossil fuels, causing greater atmos-pheric pCO2. Our modelling tests for reactions of dissolved inorganic carbon show that increasing atmospheric CO2 is caused thermodynamically by falling land surface pH values, but only with bicarbonate present. Strong acids generated by oxygen from re-duced inorganic compounds of nitrogen and sulphur emit CO2 almost stoichiometrically from dissolved bicarbonate in the pH range of most global soils, between 6 to above 8. We show that each decrease of aqueous pH value of 0.01 units from acidification of sur-face water near pH 8 potentially increases the pCO2 in the atmosphere by about 7 ppmv. The surface pH value of the ocean near 8.10 in 2000 has been shown to decrease at this rate, a result of equilibrating with the rising atmospheric pCO2. Therefore, our qualita-tive estimates of increasing atmospheric CO2 driven by irreversible acidification on land are critical and need broad scale validation. Unfortunately, these acidifying processes on land from excessive nitrogen fertiliser, export of alkaline produce from farmlands and other processes were not considered by previous biogeochemical reviews. However, several very recent research studies showing CO2 emissions from soil during nitrifica-tion are consistent with our hypothesis. Despite counter measures to curb excessive CO2 emissions, including carbon capture and geological storage, the increasing Keeling curve for pCO2 may continue to rise because zero carbon policies do not address these causes. We recommend that this hypothesis be further tested by in situ experiments in neutral soils and water, designed to compare CO2 emissions under the acidifying conditions de-scribed in this article. Corrective counter measures can then be designed and applied.

Keywords:

Subject: Environmental and Earth Sciences - Environmental Science

1. Introduction

The environmental chemistry of carbon cycling is well understood to be regulated by global thermodynamic factors, such as temperature and the pH value in water affecting chemical equilibrium, although rarely achieved. Our recent article [1] tested the physico-chemical hypothesis that seasonal variation in seawater temperature was a probable cause of changing atmospheric pCO₂. The Thermal model linked seasonal variations in the temperature of the ocean’s surface layer as causing differences between the relative thermodynamic fugacity of CO₂ in surface seawater [1] and in air, also affecting the solubility of calcite. Particularly in the northern hemisphere oceans, calcite precipitation in warming surface water in summer must lower pH, increasing seawater CO₂ fugacity (fCO2) as atmospheric pCO₂ becomes lowest, promoting CO₂ transfer to air as winter progresses, a process reversing [1] as about 1-2 mg per litre (10-20 μM) of surface calcite redissolves in cooling seawater, raising pH values and causing higher CO₂ in the atmosphere until early spring. Non-equilibrium transport processes at the interface between air and the surface of the ocean explain [1] most of the seasonal oscillation in pCO₂ (Figure 1), even up to the 15 ppmv variation observed by Keeling [2] at Point Barrow in the Arctic. Therefore, the pCO₂ oscillation is not exclusively a result of regional seasonal imbalances in photosynthesis and respiration. Van’t Hoff analyses of the variation of equilibrium constants with temperature showed [1] that the enthalpy of formation of bicarbonate and carbonate is endothermic, favored by summer warming consistent with Le Chatelier’s principle. This seasonal oscillation in pCO₂ on Mauna Loa is shown in the subset of Figure 1. We estimated [1] that about 15 Gtonnes of CO₂ is now exchanged annually between the sea mixing layer and the atmosphere, particularly in the northern hemisphere, on a seasonal basis. The CO₂ transfer is similar in magnitude to the total annual emission of fossil fuels, some 5% of the total CO₂ emissions from all sources For each square metre of the Earth’s surface [3], almost 50 moles of carbon per square metre are emitted and reabsorbed photosynthetically on land and 23 over the ocean, an average globally of 30 moles per square metre [3].

Against this background research that established a firm role for temperature in regulating seasonal flows of CO₂ between the ocean and the atmosphere we felt justified in investigating the role of another control of the dissolved inorganic carbon (DIC) system easily observed in the laboratory, the pH value. To what extent did the pH value of the land surface influence or control the flows of CO₂ at the boundary layer? The high sensitivity of equilibrium pCO₂ to changes in pH value in seawater suggested that similar controls might occur with land waters and with moist soil. In this article, we intend to show that pH changes from acidification because of human activities can also be a significant control factor for atmospheric CO₂. In the 20th century, such acidifying processes were studied intensively, for remediation of soil and the environment at large [4]. Where soils are poorly buffered against pH change or anthropogenic activities expose soils to oxygen producing sulphuric and nitric acids from reduced forms of these compounds, serious impacts on environmental ecology are apparent [4]. Past research on acidification has focused on loss of nutrients of effects of toxicity from aluminium and manganese ions at more acid pH.

In this article, we will examine less challenging effects of acidification in soils well buffered with dissolved inorganic carbon (DIC) like bicarbonate (HCO₃^-); an unexpected result may be strong emissions of CO₂. Understanding the causes and magnitude of this source of CO₂ emissions is important in mitigating any effect on global warming or climate change and for the strategy of using the soil system as a means of diminishing atmospheric pCO₂, recognising the important role of surface soils in the carbon cycle.

1.1. Background Inorganic Chemistry and Responses to Changing Water pH Values

This article tests a second physico-chemical hypothesis regarding the Keeling curve, proposing that decreasing land surface pH values cause a long-term planetary trend for increasing atmospheric pCO₂. Our article will first investigate whether there are likely anthropogenic reasons for such a trend, the environmental production of strong acid (H⁺) causing the following Reactions (1) and (2). The equilibrium constants are shown inversely to those for reversed reactions of those given in our previous article [1].

H⁺ + HCO₃^- ⇄ H₂O + CO₂ (1/K₁)

(1)

H⁺ + CO₃^2- ⇄ HCO₃^- (1/K₂)

(2)

Reaction (3) forming bicarbonate directly is normally very slow, except at very high pH values where the concentration of hydroxyl ions [OH^-] from the dissociation of water is high.

CO₂ + OH^- ⇄ HCO₃^- (K_a)

(3)

This reaction is possible on land, but only with highly alkaline materials such as in sodic soils with pH greater than 10. Such soil conditions do occur, but rarely.

The equilibrium constant K_a is given in Equation (4).

K_a=[HCO₃^-]/{[CO₂][OH^-]}

(4)

Reaction (2) does not generate CO₂ reflecting the greater alkalinity or charge of the carbonate ion (CO₃^2-). The probability that acid as hydrated hydrogen ions (H⁺)_aq will react with bicarbonate (Equation 1) or carbonate (Equation (2)) is statistical, depending on the ratio of their concentrations in water. Only at pH values (-log₁₀[H⁺]) greater than 9 does carbonate exceed bicarbonate. At pH 8, bicarbonate is expected to be in strong excess. For most of the world’s soils and even in seawater, the pH value is probably near 8 or less. Thus, the addition of an equivalent of strong acid to water buffered with DIC will emit CO₂ almost stoichiometrically, as shown in Equation (1).

The Henry coefficient (K₀) indicates the equilibrium for the distribution between the concentration of dissolved CO₂ in water [CO₂] and the equilibrium pressure of carbon dioxide [pCO₂ ]_atm, as atmospheric CO₂.

[CO₂]_aq/[pCO₂ ]_atm = K₀

(5)

The Henry coefficient has mixed physical units, by convention for oceanographers of mM [CO₂] and pCO₂ as atmospheres, currently about 0.00042. At 278.15, 288.15 and 298.15 K in seawater we showed [1] that K₀ has values of 0.05213, 0.03746 and 0.02839 respectively, this large decrease in relative solubility of CO₂ with temperature change being mainly governed by the ideal gas law. By contrast, the partition constant for distribution of CO₂ concentration ([CO₂]) between seawater and air is close to unity.

We can also express the equilibrium constant for Equation (1) as a composite of K_a and K_w, where the latter is equal to the product of water dissociation [H⁺][OH^-].

K₁ = KaKw) = [HCO₃-][H⁺]/[CO₂]

(6)

The different forms in DIC, carbonate (CO₃^2-), bicarbonate (HCO₃^-) and carbon dioxide (CO₂), are constituents of an important pH buffering systems in sea water and in water on land in soil, streams and rivers and lakes, as well as in biological systems.

In this article we will first establish the credibility of our hypothesis that the land surface pH controls the pCO₂ in air, caused anthropogenically in a similar way to acid precipitation [3,4] known as acid rain. All forms of fossil fuels contain a few percent of sulphur and nitrogen, to varying extents [3,4]. Coal is formed by geological compression on land of plant material containing sulphur as well as nutrient ions such as calcium, magnesium, and potassium, with organic molecules as negative counterions balancing their positive charge. Oils are usually of marine origin produced for flotation of photosynthesizing calcite cells, deposited in limestone sediments but also containing other nutrient cations as well as charge balancing organic anions [3]. Natural gas as methane (CH₄) formed in highly anaerobic environments sometimes contains hydrogen sulphide gas (H₂S), dependent on anaerobic microbial activity reducing the main oxidant in anoxic water, sulphate. On combustion with oxygen, sulphur generates gaseous sulphur dioxide that can be oxidised to sulphurous and sulphuric acid and in very hot furnaces, organic nitrogen can be converted to gaseous oxides of nitrogen, precursors for nitrous and nitric acid [4].

1.2. Lifetime of Fossil Fuel Emissions in the Atmosphere

Despite a thermodynamic seasonal variation of atmospheric pCO2 that can reach 15 ppmv at Point Barrow [1,2] numerous claims have been made that excess CO₂ emissions can persist for many centuries, even millennia. Answering this question is highly important for deciding the significance of such emissions and how they can be managed. Processes that can diminish the rate of increase of atmospheric pCO₂ include reaction with the surface layer of the Earth, on land or sea, rates of photosynthesis or longer-term processes like dissolution of limestone (CaCO₃) itself taking thousands of years. Archer et al. [5] claim that the longevity of the increased CO₂ correlated with anthropogenic global warming has been underestimated. From their modelling they claim that 20-35% of the fossil emissions remain in the atmosphere after equilibration with the ocean for 200 to 2,000 years. In their model, neutralization by reaction with CaCO₃ can draw the airborne fraction down further but only on timescales of 3 to 7 Kyr.

However, the rapid decline of radioactive atmospheric ¹⁴CO₂ from nuclear testing is not consistent with this conclusion, given ¹⁴Cs much longer half-life. Lags in Δ¹⁴C of heterotrophic respiration fell behind that of the atmosphere because of finite residence time in biota. It is well known that radioactive carbon mimics ¹²C very well so the rapid equilibrations observed from the bomb test data do not support the idea that fossil emissions of ¹²CO₂ will persist in the atmosphere. Post-bomb Δ¹⁴C Juniper tree data obtained by Ely et al. for river sediments in western USA showed a half-life decay from a peak in 1963 to half this value in 1973, ten years later, showing how rapidly ¹⁴CO₂ was declining [6]. Southern hemisphere troposphere ¹⁴CO₂ concentrations only lagged northern hemisphere values for several years in the later 1960s [7]. Very rapid oscillations in radioactive carbon soon after the test ban treaty were largely caused by stratosphere-troposphere mixing, bomb ¹⁴C being injected into the troposphere in winter and spring. Later, major exchanges of radioactivity between the ocean biota and air were measured at many sites, with results also affected by local generation of fossil CO₂ devoid of radioactivity, almost absent in the tropics. Such a rapid decline has even enabled estimates of varying turnover times of carbon in molecules in different tissues [8]. These data are consistent with the 145 moles of CO₂ above each square metre of the Earth’s surface being highly active, with some 35 moles per square metre being recycled biologically on land and sea annually. Given that fossil fuel emissions are only 1.6 moles of CO₂ per square metre annually, some 816x10¹² moles globally, about 1% of that in each column, it seems possible that the system might be flexible enough to absorb such a small increment.

We conclude that long residence times for increasing atmospheric pCO₂ are highly speculative. Alkaline runoff such as riverine sodium bicarbonate can raise ocean seawater pH values, increasing carbonate and the propensity to absorb CO₂; this is necessarily a slow process, a function of the rate of erosion of alkaline rocks on land [4] so absorption in the ocean is slow. Our earlier research [1] showed that variation in temperature can affect the seasonal distribution of CO₂ between the ocean and the atmosphere but this cannot be responsible for the increasing trend of pCO₂ in air. We claim that another important short term thermodynamic control factor may have been overlooked. This control is the variable acidity of the surface of the Earth, that has been declining in pH value at an increasing rate with human population since the beginning of the industrial age [4].

This is advanced as another testable physicochemical hypothesis, needing both data on hand and results from future experimentation.

2. Experimental Methods

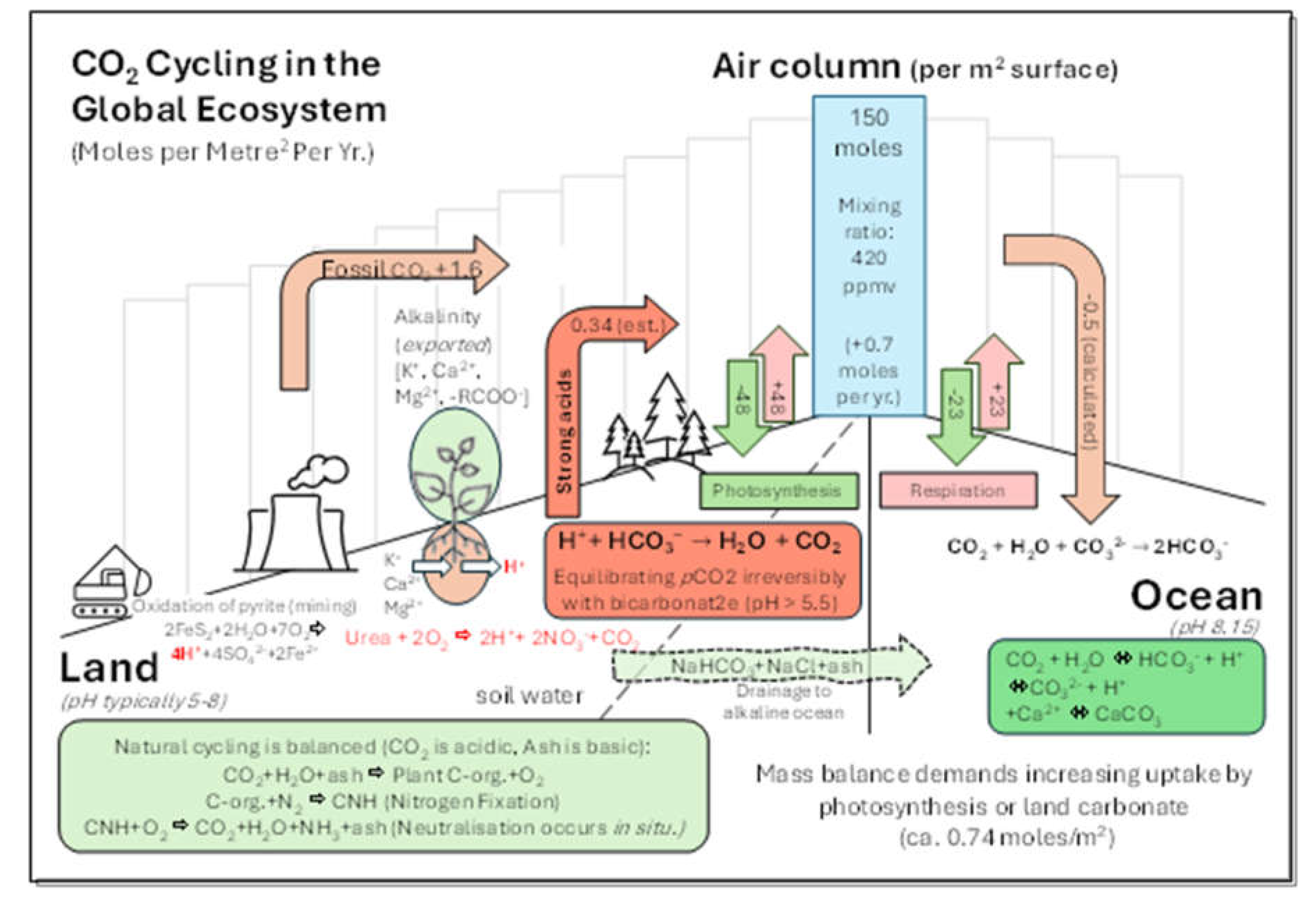
2.1. Modelling a Terrestrial Acidification Hypothesis

The ocean surface is considered as having an active mixing zone varying from about 25 metres depth near the equator to 100 metres or more at high latitudes, with little or no penetration deeper except on much longer time scales [3]. This assumption of a separate well mixed compartment from the bulk of the deeper ocean was very useful for short term modelling of the increasing level of pCO₂ in the atmosphere [1]. At least in the short term of 12 months, composition globally is approximately homogeneous, so that we were able to model the influence of seasonal variation in temperature on the pCO₂ in the atmosphere [1].

On land, no such general assumption can be made regarding DIC species, given the high local variability of pH in soil and associated water. A soil scientist might object that the soil-water dynamic is much more complex, depending not only on chemical characteristics but also by physical factors in different soil layers affecting water movement, as remarked on by a reviewer of this article. Only heterogeneous equilibria are possible between the DIC species shown in Figure 2 and the CO₂ in the atmosphere. Nevertheless, as long as the pH value falls from between 6.5 and 9.0 bicarbonate (HCO₃^-) will be the predominant species and irresistible thermodynamic action as a function of temperature and pH value will ensure that a tendency to equilibrium will exist, despite this being less easily achieved in the ocean. In all such cases, the generation of strong acid species will result in CO₂ evolution and below pH 8, this will be almost equal to the equivalents of acid generated. A quantitative relationship between soil acidifying processes such as nitrification and decreases in soil pH has been well established [4] but experimental tests in laboratory and field are still needed to test the main hypothesis advanced in this article. Rather than attempt to model such a heterogeneous system which would be possible, we preferred to use conditions in seawater to establish relationships between additions of strong acid and weak acid like carbonic. While salt concentration will affect the activity of species such as carbonate and calcium ions, we are able to calculate such effects approximately using available algorithms described in this section.

Our hypothesis regarding the influence of falling surface pH on the increasing trend of atmospheric pCO₂ will be tested with our model Titrate (Figure 2), similar in programming structure to the Thermal model [1]. School laboratory chemistry usually includes dropwise titrations from burettes of one chemical solution with another; an indicator shows colour changes of pH value when the solution is near neutrality in hydrogen ion concentration. Equations (1) and (2) are possible for absorption of strong acid, with only (1) directly yielding emission of CO₂. The relative concentration of carbonate and bicarbonate determines the statistical stoichiometry for the reaction. At pH 8.2 in sea water, this ratio is about 1 in 8 and the destruction of alkalinity at each pH by each equivalent of hydrogen ions will be partitioned in this ratio, considering the double alkalinity of carbonate. To a small extent given its concentration of only 0.5 mM, borate in sea water will also absorb acidity without CO₂ emission, having most effect at its pK value of 8.7, but less in seawater near 8.2.

By comparison with water on land, seawater is relatively strongly buffered in pH value with more than 2 mM bicarbonate as DIC. As a result, freshwater pH values can change more rapidly with processes like photosynthesis. Below pH 7.5 in seawater and even at the lower acidity of pH 8.0 in freshwater as shown later, nearly all destruction of alkalinity involves stoichiometric conversion of bicarbonate to an equivalent of weakly acid CO₂. To the extent that the concentration and fugacity of CO₂ generated exceeds that allowed by the Henry coefficient at the water temperature, CO₂ will be transferred to the atmosphere at a rate dictated by the ratio of fugacities in water and air, a function of temperature as explained earlier [1]. It is likely that heterogeneous equilibria on land will be achieved on an annual timescale, not requiring longer times to establish clear trends between acidification and atmospheric pCO₂, certainly not many years. We will examine how this thermodynamic principle affects the fate of emissions of CO₂ from fossil fuels in this article.

For seasonal temperature variations the DIC equilibria in Figure 2 displace towards carbonate (CO₃^2-) and calcite (CaCO₃) formation in summer while acidifying seawater, raising the fugacity of CO₂ [1], with this calcification process assisted by biota. Similar seasonal effects of temperature will occur in land and soil water, leading to precipitation of calcium carbonate. In winter, these processes will reverse, dissolving any calcite present, raising soil water of CO₂ [CO₂]. Any addition of strong acid to this soil system will displace the equilibrium towards CO₂ formation, releasing it to the atmosphere to an extent indicated by the Henry coefficient. Thermodynamic interaction of atmospheric CO₂ will occur with the highly heterogenous land surface to an extent governed by the variable hydration of soil as well as by reaction with DIC in lakes and river systems. Some absorption of CO₂ in highly alkaline waters will also occur erratically though continuously. For a hypothesis to be credible as shown in Figure 2, the possible rates of strong acid production must have a rational quantitative relationship with the observed increases of CO₂ in the atmosphere. In a closed system, each aliquot of acid will eventually generate an exact pCO₂ depending on concentrations of DIC and temperature. In an open system like the global environment, this is true within the constraints of variable conditions of temperature in water and air and other factors, with the actual pCO₂ in air usually in disequilibrium with that in water, but with transfer rates between the liquid and gaseous phases dependent on the extent of this disequilibrium condition. We will make estimates of the scale of this acidifying condition and predict time constants for these processes in Section 4.1 this article.

Our modelling strategy includes demonstrating the capability of the Titrate model to estimate equilibrium values, considering alkalinity (A), total dissolved inorganic carbon species (C), and pH values in surface waters and pCO₂ values in air at equilibrium. As in all environmental systems, equilibrium is rarely achieved, subject to macroscopic variations in conditions such as temperature, density or pressure and process rates of chemical reaction. On different time scales systems will evolve showing a natural tendency to increase their action and entropy in their approach to equilibrium [6], including for gases in the troposphere. Using the Titrate model, rates of acidification in seawater, soil water or in lakes and rivers on land can be examined, to gauge the possible effects of adding strong acids on the pCO₂ (ppmv) in air. Finally, these possibilities will be tested for their global significance, using available data to predict risk and the validity of the IPCC models for control of global pCO₂. Readers are advised to consult the previous article [1] for a more comprehensive account of the background inorganic chemistry and thermodynamics regarding CO₂. Most of the chemical processes of inorganic nitrogen and sulphur were considered in the earlier treatise entitled Acid Soil and Acid Rain [4], although the magnitude of CO₂ emissions was not then of interest with focus at the time on aluminium ion toxicity, released below pH 5.

For modelling processes, robust algorithms [1] previously established by oceanographic authorities performing research on seawater were employed (Figure 3). These include those described by Dickson and Millero [9] in documents of the United States Department of Energy [10,11,12,13]. We employed the algorithms used to calculate fluctuations in key equilibrium constants with temperature or salt concentration given by Emerson and Hedges [13] shown in Supplementary Materials. There are at least 10 computing packages available for calculating key inorganic properties of DIC in seawater [14] based on the principle of setting input pairs of variables to values and then calculating all other values of interest. These models all give similar results with minor exceptions, as modifications of the methods recommended by Dickson and Millero [9], employed mainly for accuracy in data collection and recording.

A more flexible approach for inputs and outputs was adopted here in the various programs called collectively Titrate (Figure 3). When executed this program first estimates as functions of temperature and salt concentration all key constants (Henry coefficient K_o, the equilibrium of bicarbonate with dissolved CO₂, K₁; the equilibrium of carbonate with bicarbonate, K₂; the solubility product for calcite, K_sp occurring in key reactions. Then levels are estimated (μmoles per kg of water) of inorganic intermediates ([CO₂]=a; [HCO₃^-] = b; [CO₃^2-]=c) under the prevailing conditions of temperature and pH value as controlled by alkalinity (A) or atmospheric pCO₂. Where reiterations for inputs of acid and CO₂ are included in programs, a unique quadratic solution is used to obtain new values of bicarbonate using simultaneous equations. This solution was given in more detail in our earlier study [1] on the seasonal oscillations in atmospheric pCO₂ caused by variations in seawater temperature.

Reiterative processes with time for injections of acids (or bases), both strong and weak were established, to yield effects from variations of pH, pCO₂ (atm), residual alkalinity and for inorganic carbon (A_c). A uniform mixing zone in seawater of 65 m depth was assumed for calculations, although this depth is known to vary with latitude and is generally deeper in the southern hemisphere [1,3]. This may mean that CO₂ equilibration is faster in southern waters, from a stronger gradient. For soil systems to 1 metre depth and surface waters on land, representative values for temperature, salt concentration and pH are assumed.

A key difference between seawater and water on land or in soils is its pH value, generally held near 8.1-8.2 in the ocean surface, but far more variable in soil, often below pH 7 and as low as pH 4, depending on histories of soil development and methods of cultivation [4]. A second difference is the salt (NaCl) concentration, generally ca. 3.5% (S=35‰) in seawater except where diluted by rivers but highly variable in water on land, usually with much less salt.

Millero [12,15] has cautioned that algorithmic methods for estimating constants with seawater become less accurate with saline content less than 0.5%, so we do not expect similar accuracy for freshwater in this article, while continuing to use the same computer code as for seawater. However, refinement would only make marginal differences in the values, not important enough for the purpose of this article. Specific details of the programs used to obtain numerical results are given in Supplementary Materials. including all computer coding.

Soil acidification has been a major area of research in agricultural science for hundreds of years [4]. This problem is typical of poorly buffered soils, with pH values less than 5. Methods to investigate rates of acidification from farming have employed measurements of inputs and outputs [16] or by measures of rates of acidifying processes such as nitrification [4]. This enables any requirements for liming of soil [16] to prevent acidification to be estimated. However, in this article the effects of acidification are not related to toxic acid soils but to neutral soils containing significant DIC as bicarbonate and carbonate. Only these well buffered soils can emit CO₂. This subtle difference in location of acidification is a key feature of the hypothesis.

However, more realistic environmental distributions for DIC in sea and land are investigated in Results and Discussion. Initially, an analysis of possible rates of acidification from fossil fuel emissions will be made. Then, modelling effects of strong acidification on the fugacity of CO₂ in the mixing zone of seawater will be executed. Finally, acidification processes on land will be examined before weighing the overall evidence for a significant role of surface pH in regulating atmospheric pCO₂.

3. Results

The increase in global atmospheric pCO₂ shown in Figure 1 is regarded as commencing when the industrial age began. In 1750 each square metre of the Earth’s surface contained a total of 95.6 moles of CO₂ in the column of air to the top of the atmosphere. This corresponded to 280 ppmv or 0.00028 atm, a ratio of concentration maintained to the top of the atmosphere. In 2020, this has risen to 420 ppmv [17] or 150 moles above each square metre (Table 1). At present, each global emission of 1 mole per m² corresponds to 3 ppmv, about 30% more than the current annual addition to the atmosphere [1].

3.1. The Possible Acidic Effect of Anthropogenic Combustion of Fossil Fuels since 1750

The total production of CO₂ from fossil fuels since the industrial age began around 1750 with the invention of the steam engine is estimated by numerous sources to be about 2.5 trillion tonnes from combusting about 680 billion tonnes of organic carbon (Table 2). Assuming a sulphur content of 5%, this is equivalent to some 2.1 moles of SO₂ for each square metre of the Earth’s surface since 1750. In 1750, each square metre had about 96 moles of CO₂ suspended in the atmosphere above it, diluted with altitude by the interaction between gravity and the gas law [4] from 280 ppmv. By 2020, at a surface concentration near 420 ppmv, this has risen to the current 150 moles of gravitationally suspended CO₂. We suggest that expression of CO₂ as ppmv can give the misleading impression that the amount of CO₂ in the atmospheric column of air is small: the magnitude of the amount of CO₂ present is much more apparent when expressed on a molar basis for the total air column above each square metre of the earth’s surface.

Dependent on surface pH value, with bicarbonate present in water between pH 8 and 5, each mole of sulphuric acid has the potential as shown in Table 2 to evolve 4.2 moles of CO₂ from bicarbonate by Equation (1), given sulphuric acid is divalent in acidic strength. This would be equivalent to an increase of 12.6 ppmv, calculated for the average atmospheric pCO₂ value of 350 ppmv between 1750 and 2020. In our previous paper [1] we showed that a variation in seawater pH in the mixing layer of 0.01 units corresponds to a pCO₂ change of 5-10 ppmv, so we would expect a decrease in seawater pH of 0.02 units from this sulphuric acid, assuming there was no mixing with deeper water. The current trend of declining pH at the ALOHA Station between 1990 and 2002 of about 0.005 units per year [19] is consistent with this rate of decline, considering the current consumption of fossil fuels is now about four times the average annual consumption in the past 270 years. In 2020, 3.68x10¹⁰ tonnes of CO₂ were emitted by combustion [17], containing sulphur sufficient to produce 0.061 moles of CO₂ above each square metre of the Earth’s surface, or 4% of the actual total CO₂ emissions.

Since 2000, many of the Earth’s power stations are required by law to use limestone in smokestacks to trap SO₂ emitted from coal, forming gypsum (CaSO₄), as shown in Equation (7). This would reduce the emissions of CO₂ from this source to half, the strong acid reacting with carbonate rather than bicarbonate.

CaCO₃ + H₂SO₄ → CaSO₄ + CO₂ + H₂O

(7)

Given that the increase of CO₂ in the atmosphere in 2020 was 2.5 ppmv or 4.421x10¹⁴ moles of CO_2, 52.9% of estimated fossil emissions, the proportion from sulphuric acid production should be increased to 9.0% of the net emissions to the atmosphere. The comparison here is for CO₂ emissions controlled by system surface pH buffering value with gross emission of CO₂ by combustion. We rule out any conclusion that sulphur in coal was solely responsible for the increase in pCO₂. Nonetheless, our monograph [4] established that the regional damage caused by acid rain in the industrial era was severe, because of its property of releasing toxic aluminium ions from soil below pH 5 and from leaching of nutrients from vegetation and soils. Remarkably, the lakes of Norway lost all their stocks of fish early in the 20th century, requiring remediation with powdered limestone [4].

Several assumptions are involved in these estimates. The evolution of CO₂ from bicarbonate is stoichiometric, although this depends on the ratio of bicarbonate to carbonate in water. In fresh water at pH 8 this ratio is greater than 10. Even in seawater, the ratio is large as shown later in Section 3.2. Another assumption is that the rate of deposition in sulphuric acid in precipitation matches the rate of CO₂ evolution. However, oxides of nitrogen in combustion products also contribute to nitric acid production in the atmosphere [4]. The percentage of nitrogen in coal is about 2.5%, also variable. As a worst case, this could double the production of strong acid if combustion occurs at high temperature. For reactions with bicarbonate, nitric acid has half the emitting power of sulphuric acid per mole being monovalent (HNO₃ versus H₂SO₄). Together, these combustions could mean that up to 20% of the increase in atmospheric pCO₂ before stricter emission controls were legislated by 2000 was from combustion of fossil fuels containing sulphur, reducing CO₂ emissions to half.

We consider the estimates for CO₂ emission in Table 2 establish a prima-facie case for our hypothesis that atmospheric pCO₂ could be in part controlled thermodynamically. Assuming the validity of our acidifying hypothesis as causing CO₂, emissions, what other sources might contribute to strong acids globally? We will explore this question in more detail, in considering both agricultural and environmental acid production.

3.2. Modelling Acidification of Sea or Land Water

Although increasing CO₂ consumes natural alkalinity as hydroxyl ions (OH^-) without change in charge by forming bicarbonate (HCO₃^-), its effect from inputs over many years (Table 2) would differ from the effect of strong acids such as nitric acid and sulphuric acids, both consuming alkalinity stoichiometrically. Fully dissociated strong nitric and sulphuric acids have the same effect on CO₂ emission, with sulphuric twice as potent, reducing alkalinity and pH values of surface waters in proportion to the equivalents of acidity added shown in Table 2. It is important to realise that most of the time courses for acidification given in this article are only predictions of the maximum extent of acidification, occurring in the absence of feedback responses. Natural processes can be expected to lessen any predicted impacts, such as by mixing with more alkaline deeper seawater or by slower dissolution of limestone. Initially, we model and analyse whether rates of acidification of seawater could explain increases in atmospheric pCO₂ during the past century. aiming to predict the scale of possible emissions of CO₂ from seawater and of absorption, because of processes regulating pH values. First, we ask the question whether seawater is a potential long-term source for emission of CO₂ to the atmosphere.

3.3. Titration of Seawater Alkalinity by Strong Acids and Atmospheric CO₂

Modelling of acidification of seawater is of interest to determine the quantities of strong acids needed to have significant effects of pCO₂ and pH values, the main topic of this section. The model Titrate makes several assumptions that differ for titration either by increasing pCO₂ or by possible ingress of strong acids such as nitric or sulphuric acid; CO₂ can be considered as reacting with hydroxyl ions to form bicarbonate according to Equation (3) This reaction will be slower as hydroxyl activity and pH fall, but it may be catalysed biologically by carbonic anhydrase in the surface water [1].

Reaction (1) can also be written as the dissociation of carbonic acid yielding bicarbonate and a hydrogen ion. But the thermodynamic state and chemical potentials of reactants are independent of the path used to generate them. Only about 0.1% of CO₂ interacting within seawater is in the form of carbonic acid (H₂CO₃). However, provided the equilibrium constant for the dissociation of water (K_w) is included as shown for K₁= K_aK_w above, the same result is obtained thermodynamically.

Deposition of strong acids such as nitric acid onto the sea surface will reduce the carbon-based alkalinity as follows in Equations (8) and (9), with relative magnitude a function of pH value determining the ratio of [HCO₃^-] to [CO₃^2-].

2HNO₃ + CO₃^2- ⇄ CO₂ + H₂O + 2NO₃^-

(8)

HNO₃ + HCO₃^- ⇄ CO₂ + H₂O + NO₃^-

(9)

The anionic alkalinity (A_c) of DIC is replaced by that of nitrate (NO₃^-). Deciding how the equivalents of strong acids deposited will be distributed to different buffering systems including borate and DIC may seem daunting. However, reflection seems to provide a solution in that, to an approximation as indicated in Equation (8), every two equivalents of strong acid will evolve one molecule of CO₂, whereas only one equivalent is required for evolution from bicarbonate. But at pH 8, reaction with bicarbonate is some 7-10 times more likely than reaction with carbonate, based on number density, lower in seawater than fresh water. The obligatory evolution of CO₂ follows from the decreased DIC alkalinity caused by acidification and the decrease in inorganic carbon (C) inferred in an open system. The equivalents of alkalinity from inorganic carbon sources (A_c) are given by Equation (9).

A_c = [HCO₃^-] + 2[CO₃^2-]

(10)

Then absorption of CO₂ converting carbonate (CO₃^2-) to two molecules of bicarbonate (HCO₃^-) shown in Equation (11) will preserve alkalinity in Equation (2), effectively including Equation (4), carbonate extracting hydroxyl ions from water by its hydrolysis. However, the likelihood that carbonic alkalinity will persist as exactly constant is small, given the complexity of oceanic processes.

CO_{2 +} H₂O + CO₃^2- ⇄ 2HCO₃^-

(11)

Each micro-equivalent of strong acid will reduce the alkalinity (A_c) in proportion, reducing the carbonate and increasing the concentration of bicarbonate by the same amount, but only if CO₂ cannot escape. In an open system where CO₂ exchange is possible, the following Equation (12) must be adjusted indicating the total CO_2-yielding DIC constituents (C) in seawater.

C = [CO₂] + [HCO₃^-] + [CO₃^2-]

(12)

Any change in the concentration or number density of bicarbonate will disturb the equilibria between carbonate and CO₂, if reducing the pH value, increasing [CO₂] causes venting to the atmosphere in seeking equilibrium according to the Henry coefficient (K₀). In a closed system where the CO₂ fugacity is regarded as held constant, all the effect of adding acid can be accommodated in a new distribution of carbonate and bicarbonate. But in a real open system such as in seawater, CO₂ must be evolved, migrating into the air and into the atmospheric column. Indeed, the Titrate model automatically vents CO₂ at a rate only slightly less than equality with strong acid added. The exact stoichiometry is set by the ratio of bicarbonate to carbonate (b/c) and the pH value.

It is obvious that the relationship between the pCO₂ in air and the pH of seawater must be strong. The observation since 2000 of the decreasing seawater pH shown in the ALOHA dataset [1,19] suggests that this exchange of CO₂ between air and seawater is both rapid and near equilibrium, at least in the mixing zone.

In Table 3 are shown values for DIC estimated for different salt concentrations equivalent to seawater and freshwater on land giving the distribution between CO₂, bicarbonate and carbonate in equilibrium with 420 ppmv atmospheric pCO₂ in the pH range 8.2 to 5.2 covering most land surfaces. By Reactions (7) and (8), these will be affected by addition of strong acid, venting CO₂ to the atmosphere in almost equivalent amounts. In freshwater at pH 8.2, the ratio of bicarbonate to carbonate is 25.7, about three times greater than in sea water. It is predicted that the likelihood of reaction with bicarbonate or carbonate is statistical, based on concentration and at pH 7.2 and below, very little carbonate remains. Therefore, it is reasonable to claim that this evolution of CO₂ is close to stoichiometric with any strong acid production.

Below neutrality at pH 7, carbonate is absent. Only above pH 8.7 does the double alkalinity of carbonate play a major role in resisting pH change by acidifying reactions. The irrelevance of a Bjerrum plot of molar ratios for DIC, or a constant value for total DIC (C) in a closed system containing CO₂, is obvious from the data given in Table 4. While the different compartments containing inorganic carbon are never completely in equilibrium and each compartment will have a different turnover rate depending on its size there can be no doubt that the atmospheric pCO₂ value also tends to equilibrate rapidly with exposed waters on land. The time scale for such exchange is likely to be no more than weeks or months for surface waters.

Figure 4 is a replot of data in Table 4 emphasising the variation with pH in the concentrations of DIC for water as salty and seawater and for freshwater in equilibrium with a pCO₂ of 420 ppmv in the atmosphere. Equilibrium constants for reactions of DIC are calculated at 288 K, assumed not to affected by changes in pH value. The pH range between pH 5.2 and 8.2 is regarded as typical of most of the world’s productive soils, showing how rapidly DIC falls in concentration with fall in pH or increased acidity. The Bjerrum diagram for response to pH by DIC often referred to for a constant value of 2 mM DIC is highly misleading for water on land, referring to the fugacity (fCO₂) for CO₂ with no gas space. In fact, if the Earth’s atmosphere was in equilibrium with 2 mM DIC at pH 5.2 it would predict a pressure near 42,000 ppmv, 100 times greater than at present.

3.3. Titrate Modelled Stoichiometry of CO₂ Formation from Addition of Strong Acid

The trials shown in Table 3 and in Supplementary Materials reveal that the direct release of CO₂ to the atmosphere from addition of strong acids to seawater are pH dependent. Although the weak acid CO₂ in water will react with carbonate ions according to Equation (10) forming bicarbonate, thus increasing the inorganic carbon content (C), strong acids added at pH values less than 8 can produce CO₂ emissions almost equivalent to the micro-equivalents of acid added, resulting in an ongoing depletion in inorganic carbon in solution and a stoichiometric decrease in inorganic carbon alkalinity (A_c). This direct evolution of CO₂ is not prevented by the alkalinity unless pH exceeds 8.5 but depends on the carbonate/bicarbonate ratio as a function of pH.

A more advanced version of the Titrate model used for Figure 5 estimated increases in pCO₂ caused in the long term by increases in pCO₂ (ppmv) from fossil fuels. Additions of stronger acids depleting the DIC (C) by strong acid was programmed to directly generate stoichiometric increases in pCO₂, not used for the trials depicted in Table 3 and Figure 5. In any case, an assumption is needed regarding the maximum size of the mixed layer depleted [1], taken as 65,000 kg of seawater per m². Model data generated indicate that about 5 μmoles of CO₂ was emitted per kg of mixed zone seawater annually, but more is likely nearer the surface, with replenishment of inorganic carbon mixed from below. To estimate the pCO₂ increase in atmospheres the mass of seawater must be multiplied by a factor indicating the mmoles of extra CO₂ needed to raise its air content by 1 ppmv or 10^-6 atm. A water column 65 m deep producing 325 mmoles of gas in total per m² would raise the pCO₂ in air by 1 ppmv or 0.000001 atm.

In seawater, boric acid is of most significance with its more easily dissociated proton (pK_b = 8.7) being available for buffering by its concentration about 25% of DIC of bicarbonate plus carbonate.

B(OH)₃ + H₂O ⇄ B(OH)₄^- + H⁺

(13)

This very reaction with a purple Tashiro’s indicator turning clear green is well-known to those with experience of titrating ammonia from Kjeldahl distillations, often ¹⁵N-labelled; boric acid solution is used to trap distilled ammonia and then back-titrated for quantitation. In seawater, the following temperature sensitive equilibrium constants are involved (reactions 14-16) all included in the program Titrate.

K_B = [B(OH)₄^-][H⁺]/[B(OH)₃] = [H+][p/q]

(14)

K₁ = [HCO₃^-][H⁺]/[CO₂] = [H⁺][b/a]

(15)

K₂ = [CO₃^2-][H⁺]/[HCO₃^-] = [H+][c/b]

(16)

We can equate [H⁺] = K_bq/p = K₁a/b = K₂b/c and so pH = pK_b − log(p/q) = pK₁ − log(a/b) = pK₂ − log(b/c), enabling the respective ratios to be calculated for any pH value. The total inorganic borate buffer system B equals [p + q], is less than 20% of the total buffering capacity in seawater, estimated as proportional to sodium chloride concentration expressed from 0 to 35‰ or 35 parts per thousand. The salt (NaCl) strongly affects the activity of other chemical species and K values, by increasing the entropy of water, dissociating its clusters. Other minor pH buffering systems like inorganic phosphate also contribute, depending on local conditions [4], but are usually minor and can be ignored. The buffering capacity is pH dependent and as a result near pH 8.1-8-2, less than 10% extra acid is required to convert B(OH)₄ to B(OH)₃ as pH fell, during all the titrations given here.

A titration with strong acid must be modelled with its acid equivalents distributed continuously between all three reactions (14-16). At higher pH values near 10 or above that can occur temporarily during photosynthetic algal growth in lake water, another dissociation reaction of boric acid must be considered, but this is not important in seawater. The resultant change in pH will depend on the combined effect of all systems, corresponding to their current buffering capacity (BC). More acid can be absorbed near the pK value for the dissociation where the buffering capacity is greatest. Then the greater the BC at a stated pH for a system, the greater the proportion of additional acid or base that will be consumed by that system. Note that the different (pK − pH) values equate to the log(x/y) so that the nearer the ratio is to 1.0 or its log to zero, the greater the buffer capacity. So, the decrease in alkalinity as acid is added can be assigned to each system in proportion to this ratio.

Figure 5 models the effect with time on p-CO₂ from annual additions of strong acid (micromoles per kg) or liming (left-hand side) or of strong acid with increasing emissions of CO₂. Because atmospheric CO₂ reacts with carbonate in seawater, these additions are not additive with respect to increasing p-CO₂. The buffering capacity (BC) in any system is measured [4] by the rate of adding acid or base compared to the rate of change in pH value (BC= dA/dpH). The Titrate model output (Figure 5 and Figure 6 and Table 3) also shows that adding CO₂ locally to air by combustion will temporarily affect the carbon equilibria in land and seawater. However, the rate of decrease of pH and [CO₂] activity will be about half that for each milliequivalent of strong acid. In the latter case there are two effects involved; one lowers pH while destroying alkalinity and the other is a thermodynamic response to the higher atmospheric pCO₂. These curves are all “worst case” predictions and would be expected to encounter negative feedback opposing them such as slow mixing with more alkaline water from deeper in the ocean, or by dissolution of calcite shown as liming (L) in Figure 5 and Figure 6.

The purpose of these trials in the Titrate model was to show evolution of CO₂ from sea water by titration with strong acids, the opposite of the absorption of CO₂ now occurring. Figure 6 shows decreasing pH values at different rates of addition of strong acid. A fall of about 0.25 pH units corresponds to an increase in pCO₂ of 175 ppmv, about 7 ppmv per 0.01 units. A similar rate of pH change is shown with pCO₂ when increased rates of addition to the atmosphere were modelled. As a reversible system, significant evolution of CO₂ by acidification will also cause the pH value of sea water to fall, as discussed in detail earlier [1].

While the rates of pCO₂ addition and strong acid production both significantly decreased pH values in the surface seawater, increasing alkalinity even at the strongest addition of strong acid ameliorated the pH fall strongly. Without information on rates of acid inflows or dissolution of CaCO₃ it is not possible to be definite about probable rates of pH falls. The results given in this section are valid for rates of increase in pCO₂ but there is no evidence for such high rates of acidification in sea water.

3.4. Global Significance Possible for Rates of Acidification in Seawater

Exact modelling for acidification of seawater is not claimed here, given that confounding factors like rates of precipitation and dissolution of calcite or aragonite are unclear. Nonetheless, Figure 6 shows that strong acid absorption on a scale of 50 μequiv per kg of surface seawater could cause the emission of CO₂ to current pCO₂ pressure, like the annual rates of 1-2 ppmv over more than a century in the more recent industrial age. However, this would require 1.17x10¹⁵ gram-equivalents of strong nitric or sulphuric acid reacting with seawater to a depth of 65 m for an oceanic area of 3.61x10¹⁴ m². Total CO₂ emissions from fossil fuels in 2020 post Covid 19 were 34 Gt [17], 7.727x10¹⁴ moles of carbon. If we assume that about 1% of this amount is emitted as sulphuric or nitric acid from coal or oil, despite more recent legal restrictions imposed on acid emissions in most countries since 2000, some 10¹³ equivalents of atmospheric acid rain in the 20th century seems feasible. Overall, some 2.5 trillion tonnes or 5.7x10¹⁶ moles of CO₂ are said to have been emitted industrially since 1750 at the beginning of the steam age (Table 2).

Offsetting this strong acid production would be gradual mixing of surface layers with seawater at greater depth, or dissolution of CaCO₃ suspended in seawater as calcite and aragonite. It is true that increased pCO₂ in air from combustion will cause a decrease in seawater pH as shown in Figure 6, almost as great as from strong acid. However, whatever the cause of increasing CO₂ in the atmosphere to its current quantity of ca. 150 moles above every square metre of the Earth’s surface, a decrease in seawater surface pH of 0.15 pH units would sustain a pCO₂ about 150 ppmv greater than in 1750 when Thomas Newcomen and James Watt were inventing thermodynamics. However, the higher ¹³C-content of carbon in surface seawater suggests that the major source of CO₂ emissions to the atmosphere could be terrestrial where much of the acid deposition from combustion of fossil fuels occurs.

3.5. Modelling Acid Titrations in Fresh Water on Land Resulting from Farming

Depending on the mode of nitrogen nutrition in plants, typically there is an excess of cations taken up from the soil environment [4]. This requires that hydrogen ions or protons be excreted to the soil solution as shown in Figure 7. If the soil is neutral or alkaline in pH value, this will result in evolution of CO₂ from reaction with bicarbonate. Where soils are acid and treated with limestone (CaCO₃) to prevent soil becoming too acid for plant growth, CO₂ will still be evolved. The strong acid excreted because of photosynthesis is replaced by the weak carbonic acid, vented to the atmosphere. If plants are decomposed locally in pasture or forest soils, the negatively charged carboxylate compounds are oxidised to CO₂ and water, consuming a proton from the soil solution thus rendering the soil neutral. However, if produce in exported from rural areas to urban areas, or overseas, the alkalinity of the negatively charged compounds like organic acids and pectates is also exported, leaving the soil acidified to the same extent.

Because there is usually an excess of cation uptake by plants over anions, charge balance requires the biosynthesis of negatively charged counterions, such as citrate, malate and fumarate. In breakdown of plant vegetative material, these weak carbon acids are oxidised as respiratory substrates shown in Equation (17) for acetate, considered as balanced with K⁺ maintaining osmolarity and plant turgor.

CH₃COO^- + H⁺ + 2O₂ => 2CO₂ + 2H₂O

(17)

Four carbon compounds like malate will yield twice as much CO₂, consuming two hydrogen ions and three molecules of oxygen, thus slightly rasing the pH value of the soil solution. The content of such acid-consuming compounds in agricultural produce can be estimated quantitatively as ash alkalinity, a term first described by Justus von Liebig, the German agricultural chemist of the 19th century [4]. This will be discussed in more detail in Section 4.2, where we estimate a mean value for alkalinity equivalent to 25 kg CaCO₃ per tonne of agricultural produce, depending on the content of cationic nutrients such as K⁺ and Ca²⁺. Eight billion humans together with needs of an equivalent population of livestock could consume 2x10¹⁰ tonnes of exported produce annually. This is equivalent to 0.020 moles of CO₂ emission for each square metre of the Earth’s surface. Even livestock production in feed lots will contribute to such export of alkalinity, if all alkalinity excreted is not returned to land but instead to land fill or marine locations.

In an earlier treatise [4] the potential for acidification resulting from various scenarios for different inputs for agricultural production were considered in N-flux diagrams (Figure 8). Processes considered included biological nitrogen fixation, fertilisation with nitrogen compounds, denitrification, leaching, bicarbonate formation and so on. The most acidifying ecosystem examined (Case B in Figure 8) was dairy cattle on grass with ammonium sulphate fertilization, producing 33.4 kilo-equivalents of acid requiring 1670 kg of limestone as CaCO₃ per ha to maintain a constant pH value in soil. Using a clover-grass ley pasture for dairy cattle producing milk reduced this acidification to 12 keq of acid requiring 600 kg of limestone annually. By comparison, a mature natural forest suffering minor acid rain produced 4.4 keq acid and needed 220 kg of limestone annually to maintain soil pH if fully effective.

Many regional pasture and cropping soils have been allowed to acidify without effective rectification by liming, with pH falling several units over a century while soil organic carbon is reduced to less than half [20] in pasture-crop rotations involving N₂-fixing clovers fertilized with superphosphate. Such soils lose cation nutrients such as K⁺, Ca²⁺ and Mg²⁺ with anions such as nitrate and sulphate by leaching, being replaced by hydrogen ions (H⁺); eventually aluminium ions (Al³⁺) at pH less than 5. They may become too acid to grow cereal crops because of aluminium ion toxicity at pH values near 4. The decline in organic carbon requires protons from acidification that are replaced on negatively charged clay particles by aluminium ions. Many million ha of soils globally have suffered this fate, with substantial emissions of CO₂ to the atmosphere, even without the practice of liming to prevent lowered pH values. The true nature of the degradation of such soils as being a result of Al³⁺ toxicity [4] is often not recognised.

3.6. The Scale of Acidic Depositions on the Terrestrial Surface

Acidification of soil and runoff water is an ancient problem except in subsistence agriculture agriculture where all produce is consumed and recycled to soil locally. Where produce is exported this is no longer the case and acidification are more likely. In countries with poorly buffered granitic soils the introduction of nutrients like nitrogen and phosphorus can lead to strong acidification, particularly if nitrate is leached from soil to ground and river water [19]. Millions of hectares of such soils have been lost to cropping of cereals as a result [4]. Not only are cationic nutrients such as K⁺, Ca²⁺ and Mg²⁺ replaced with H⁺ but toxic aluminium and manganese ions are released, toxic to energy metabolism in plants. Weakly acidic carbonic acid cannot diminish the alkalinity of bicarbonate-carbonate (A_c). However, significant quantities of strong acids of nitrogen and sulphur are released into the global environment [4], both to soil systems on land and sea. The values estimated for the global population in 2021 in Table 4 compare the approximate magnitude of these, showing they are a significant fraction of the total CO₂ emissions. Once in the atmosphere, it is impossible to distinguish the reactivities of CO₂ from different sources, although with lower mass and higher chemical potential, fossil fuel emissions should be slightly more reactive. Whatever the case, these strong acids must diminish alkalinity somewhere, only evolving CO₂ from the global surface reservoir of bicarbonate and carbonate. The estimates given in Table 4 need confirmation regionally, though these are based on IPCC reports [21,22] or United Nations agencies including FAO.

Table 4. Calculated global values for potential annual generation of environmental acids in 2021.

Acid	Source	Estimated total moles H⁺ and CO₂	Annual acid meq/m² globally
Hydrogen ions (H⁺) [4,16]	Croplands, 15x10¹² m² sown alkalinity export	10.0x10¹²	19.6
“	Forestry, 50x10¹² m² harvested alkalinity export	5.0x10¹²	9.8
“	Rangelands, 100x10¹² m² alkalinity export	5.0x10¹²	9.8
Nitric, HNO₃ [4,19]	Nitrification 1.5x10⁸ t NH₃ plus leached legume-N	20x10¹²	39.2
	Agriculture total	37.5 x10¹²	78.4
Sulphuric, H₂SO₄ [4]	Coal, oil, gas, wood combustion	16x10¹²	64.0
Sulphuric, H₂SO₄ or sulphurous [3,4]	Anaerobic sulphate respiration [4] from ca. 10¹³ moles C annually in sewage, discharged mainly to the ocean ; UV oxidation H₂S and DMS [4]; oxidation of sulphides in aerated acid sulphate soils by drainage in urban habitation Stone & Ahern [23]	25x10¹²	98.0
Carbonic acid H₂CO₃	Global respiration = assumed photosynthesis [3]	15,300x10¹²	30,000.0
Carbonic acid “[	Coal, oil and gas fossil emissions [17]	816x10¹²	1,599.7
Carbonic acid “	Increasing wildfires with population	100x10¹²	392.1
Nitric, sulphuric, acids	From increasing combustion in wildfires, ash countering acidification in forests	16x10¹²	64.0
Carbonic acid H₂CO₃ [3]	Cement, construction [3, Schulz]		104.6
Total emissions	Approximate estimate only ±10%		32,316.2
Weak acid	H₂CO₃	pK 6.5, 8.9	31,991.8
Total strong acids (H⁺)	C-fuels, agriculture, fire, smelting ores with sulphides (20 mequiv/m²)	pK ca. 0-1	324.4
	Wildfires 1.76 billion tonnes
Greening scenario [27]	1% greater photosynthesis annually	+150x10¹²	300.0
Photosynthesis	All sources + CO₂ fertilisation	15,600x10¹²	-34,650.1
Net CO₂	Weak acid—photosynthesis	150x10¹²	-1297.1
CO₂ to atmosphere	Current increase per annum 2.0 ppmv		664.0

Total weak and strong acid production is estimated annually of as CO₂ per square metre. Each square metre now has ca. 150 moles CO₂ in the air column to space at 420 ppmv over a total area of 5.101x10¹⁴ m². From FAO data, ca. 40% of 6x10¹³ m² total of land is devoted to agriculture and ca. 2x10¹³ m² to crops, say half exported away from soil; potential dimethylsulfide (DMS) or related reduced sulphur emissions, oxidised rapidly in air, absorbed by seawater; a change of 1 ppmv of CO₂ in air is equivalent to 2.13 Gt C globally.

Strong acidification anywhere displaces the equilibrium towards bicarbonate and aqueous CO₂, lessening the quantity of carbonate because the lenses of calcite in soil are dissolved. The pool of CO₂ in the atmosphere moving over the Earth’s surface can act as a conduit for environmental impacts from strong acids, attributing declining seawater pH values to the farmer’s use of powdered limestone (AgLime) on land that evolves equivalent CO₂ to rectify acidity from exporting produce to distant markets (Table 4). Limestone suspended in water gives an equilibrium pH value near 8 [4] so soil solutions below pH 5 to which limestone is normally applied to counter aluminium ion toxicity will not prevent CO₂ emission in the way that soluble carbonate at pH 9 will. A conclusion that there may be reduced CO₂ emission from applying limestone on soils in the United States [24] may be mistaken. The release at acid pH should be stoichiometric, given that AgLime is only applied to soil values at pH values well below 6 when very little bicarbonate is available, except that generated by dissolving limestone. Limestone particles are slow to dissolve and can persist in soil but once dissolved in acid soil water must eventually give CO₂ stoichiometrically.

4. Discussion

4.1. Confirming Our Prima-Facie Case for Ongoing CO₂ Emission from Acidification of Soil Inorganic Carbon

The Results section makes a logical case for significant CO₂ evolution caused by acidification of bicarbonate, as strong acids are formed in the soil solution. In Table 4 these were calculated for agricultural, pastoral and forestry ecosystems and exposure of surface materials to air in mining or for for human habitation. As chemical processes, these emissions can be pH buffered near neutrality, not affecting plant production or attracting attention as acidification in poorly buffered systems. Yet they are the same anthropogenic processes, irrespective of system pH. Any for any hypothesis, however well based, there is a need to conduct tests to confirm their quantitative significance.

By coincidence, other research laboratories in soil and environmental chemistry have conducted such tests while this article was being prepared. Zamanian et al. [25] made a global assessment of the effect of nitrogen fertilisation and nitrification on CO₂ efflux from inorganic carbon, promoted by ammonia reduced by methane in the Haber process [4]. In some areas, liquid ammonia is piped to farms and injected into soil in corn fields for growing stock feed and processed foods for humans. Otherwise, powdered urea is the major fertiliser applied for cereal crops at sowing or later as required. Both forms of reduced nitrogen require microbial oxidation to nitrate for plant growth, the nutrient favoured for ccreal plants

Soil organic carbon (SOC) is a major component on land, said to contain several times the 150 moles of CO₂ per m² of the atmosphere. Hopes are often expressed that by raising SOC content, the CO₂ in the atmosphere can be sequestered, perhaps reducing global warming. Far less focus has been placed on the soil inorganic carbon in soil as shown in a comprehensive review [26]. While the relationship of these two means of carbon storage is close, given they are interconvertible biologically, there is no direct equilibrium between the two. Paradoxically, soil organic carbon can increase by incorporation of photosynthate from increased growth of crops while pH is falling, possibly with DIC declining from CO₂ emission, as shown in a recent study for mid-latitudes in China [27].

Excessive nitrogen fertiliser leading to nitrification and partial leaching of nitrate is well known to cause acidification [4], also confirmed in field experiments [28] leading to loss of soil carbon in Californian soil. Raza et al. [29] explain how inorganic carbon losses by soil acidification jeopardise global efforts on carbon sequestration, with 273x10¹² g of carbon in limestone each year neutralizing acidity. This could emit a maximum of 0.036 moles CO₂ per square metre averaged over the Earth’s surface emitted from highly acidic soils. As late as 2024, Huang et al. [30] discuss the vulnerability of global soil carbon, associated with nitrogen additions to soil systems. Tao et al. [31] study nitrification-induced acidity and CO₂ emissions from soil carbonates in experiments. A recent study on tundra has shown that rates of respiration are increasing with increasing global temperature [32]. Could this too, also be associated with acidification caused by increasing temperature?

However, none of these studies suggest that small declines in pH of neutral soils might be a major influence on the atmospheric pCO₂ value. Our modelling in Results showed that, whatever the cause, there is a thermodynamic relationship between increasing CO₂ in the atmosphere with the corresponding decrease in the pH of water of about 7 ppmv for each decrease of 0.01 pH units. Such processes are reversible and a similar highly sensitive reverse relationship between soil and water pH values on land must therefore be possible. These recent studies on nitrification [23,24,25,26,27,28,29,30,31] as just one cause of acidification that we have identified validate our hypothesis, though its scale in the overall increase in the Keeling curve in Figure 1 still needs better quantification. Unless this acidification on land is corrected or prevented, any artificial or geological process of CO₂ sequestration from the atmosphere will fail given that neutral soils will emit CO₂ from DIC as bicarbonate and carbonate controlled by the pH value.

A comprehensive field study conducted Scanes et al. [33] showed widespread acidification of Australian river systems and estuaries in the recent warming period. This 12-year study in the Australian coastline involved 6200 observations for 166 estuaries on more than 1100 kn, all rivers acidifying to variable extents, reflecting the regional geochemical environment. Bicarbonate can be the major anion in such waters when draining from basic or volcanic landscapes, but greater falls in the pH value of water will occur in unbuffered water. The changes observed were considered [33] an order of magnitude faster than global ocean and atmospheric models, not relevant locally. However, the trend of increasing acidity obviously results from regional activities, such as agriculture and forestry and urban. Even though acidifying processes outlined in Table 4 occur in the local ecosystem, their effects on the pH of water flowing to the ocean may be felt off-site as shown in these quality-assured measurements [33].

4.2. Intergovernmental Panel for Climate Change Reports

According to the IPCC report of 2001 [21], CO₂ from fossil fuel burning was virtually certain to be the dominant factor determining CO₂ concentrations during the 21st century. This report on the global carbon cycle emphasises modelling and projections, pointing out that the ocean has a declining capacity to absorb anthropogenic emissions as carbonate is converted to bicarbonate as ocean surface pH falls, perhaps about 0.15 units since 1900. Changes in management practices such as deforestation and land clearing for agriculture are very likely to have significant effects on the terrestrial carbon cycle. Low tillage agriculture may reduce the soil carbon lost when land is cleared. There was no agreement on how to model reactive nitrogen deposition and increased vegetation productivity.

No mention is made in recent IPCC reports [21,22] of any thermodynamic relationship between atmospheric pCO₂ and surface pH values, except for unknown effects of “soil acidification due to deposition of NO₃^- and SO₄^2-“. This conclusion shows a lack of understanding by the report authors in that these anions eventually may have an alkaline effect in ecosystems in anaerobic nitrate and sulphate respiration [4] but it is their deposition as strong nitric and sulphuric acids as in acid rain that is detrimental. However, as late as 2013, the Ciais et al. IPCC Report [21] began to show more appreciation that the ocean surface water was being acidified, shown by a fall in pH value of 0.10 units attributed solely to the reaction of increasing pCO₂ with carbonate ions in the surface layer, increasing the bicarbonate concentration but with no change in the DIC alkalinity. This was regarded as mainly a result of absorption of anthropogenic CO₂ emissions from industry, with negligible pH declines attributed to strong acids such as acid rain [4]. Obviously, this conclusion implies a significant tendency towards equilibrium of CO₂ in the atmosphere with that in the ocean, as indicated by the Henry coefficient. We can assert that this tendency to equilibrium must also apply on the land surface.

The main purpose of this article is to challenge the assumption that the increasing atmospheric pCO₂ is predominantly from fossil fuels and to show other significant sources of anthropogenic CO₂ summarised in Table 4 have been overlooked in the IPCC reports. If so, IPCC conclusions should include CO₂ produced by acidification in the land surface, proposed here to have a continuing role in the increase in the Keeling curve in Figure 1.

4.3. Integrating Rates of Acidifying Processes

The operation of the model Titrate provides an elementary Equation for the rate of increase of atmospheric pCO₂ as a function of the rates of the underlying processes. Although the tendency to equilibrium plays a part in determining the rates of these processes, the increase (or decrease) is a matter of kinetics. The sensitivity of lakes to acidification is usually given as a function of their alkalinity, expressed as constituent soluble ions or a balance of charge as in Equation (18), where A^- here represents organic anions [4], not alkalinity.

Alkalinity = 2Ca²⁺ + 2Mg²⁺ + Na⁺ + K⁺ +NH₄⁺ − 2SO₄^2- − Cl^- − NO₃^- − A^-

(18)

An equivalent approximate expression for seawater is given in Equation (18), neglecting the major salts.

Alkalinity = HCO₃^- + 2CO₃^2- + OH^- + B(OH)₄^- + A^- − H⁺

(19)

An equivalent approximate expression for seawater is given in Equation (18), neglecting the major salts.

To the extent that the scale of the processes producing equivalents of acidity shown in Table 4 can be verified, the net rate of production of CO₂ from strong acid indicated in Equation (20) could theoretically be most of the decline of alkalinity, varying depending on local surface pH on land and the current alkalinity. Estimates of total photosynthesis and respiration are fraught with difficulty [3] and the only meaningful measurement may be the current stocks of fixed carbon and their rates of increase or decline. Obviously these two processes occur simultaneously, dominated by season in higher latitudes. Claims of up to 100 Pmoles of CO₂ fixed occur in the literature. However, this implies a turnover time for CO₂ in the atmosphere of less than a year whereas about four years is implied by the assumptions in Table 5. The evidence discussed earlier regarding decay of long-lived ¹⁴CO₂ increased in the atmosphere by nuclear testing allow estimation of the half turnover time of ten years [6].

d[H⁺]/dt = -dAlk/dt = d[CO₂]/dt ≡ d(pCO₂)/dt

(20)

Given an annual 0.5% increase in pCO₂ in 2021, assimilation by RuBisco could be increased almost proportionately. Taken with a 1% increased need for food production, matching the increase in global human population, even a 1% annual increase in assimilation by photosynthesis is possible, though optimistic. At 0.5% increased photosynthesis (see Table 4) overall greening can be justified. Such a greening effect would operate on all sources of CO₂ emission.

In contrast to the main hypothesis of this article, a review by Doney et al. [34] concluded that strong acidity generated anthropogenically was essentially irrelevant in affecting the pH of global seawater. Their estimate for contributions to global acidity from ammonia deposition and nitrification was 4.11 Tequiv per year that they compared to 138 Tequiv from partial absorption of CO₂ from industry, apparently allowing the scale of ammonia’s effect to be dismissed if absorbed by seawater. However, most of the effects of ammonia such as nitrification are exerted specifically on the land surface and we estimate up to 10 Tequiv of impacts from ammonia alone, given 150 million tonnes of Haber process ammonia synthesised annually. Their order of magnitude calculation depicts all fossil emissions of CO₂ as interacting first with the ocean rather than partially mixing with the current 7.14x10¹⁶ moles of CO₂ in the atmosphere, a maximum possible dilution factor of about 114-fold that should not be dealt with separately from the tendency towards pH equilibrium. Furthermore, extra emissions of CO₂ to the atmosphere can react strongly with much rarer soils above pH 8.5-9 by formation of bicarbonate from carbonate in proportion to the relative surface areas.

Doney et al. [34] failed to consider all the other possible sources of acidity listed in Table 4. They assumed that anthropogenic CO₂ emissions or production of strong acids operate in separate compartments, whereas they are eventually well mixed with the background atmospheric CO₂. Only then can the effect of additional CO₂ can be estimated − not by attributing all its effect on seawater pH with its buffering acting in a separate parcel. The fossil fuel parcel can be substantially diminished by interaction with the total biosphere on land and not only seawater. For example, a study of the contribution of Baltic shipping to acidification [35] also concluded that the problem could readily be managed − partly by exports of acid to the North Sea.

Table 5 summarises the possible annual contribution of CO₂ to the atmosphere by global acidification. This estimates global CO₂ emissions from surface waters as shown, though the data can only be taken with moderate confidence. More accurate data will not rule out acidification as a highly significant cause of CO₂ increase. Much of the data in Table 5 is based on known magnitudes of agricultural produce and fertiliser applications, as well as processes involving sulphur [4].

The CO₂ estimated as emitted from agriculture and forestry calculated in Table 4 as 73.6 meq per square metre shown above can be compared with the current world market for agricultural limestone in 2024 of about one billion tonnes. As moles of CaCO₃ this can neutralise 40 meq per square metre. Only part of the world’s soils receive limestone annually, but as orders of magnitude, these are very similar estimates justifying the statistical confidence shown of moderate. Soils well buffered with DIC near pH 7 releasing CO₂ from bicarbonate in the soil solution will not need treatment with limestone.

Further to Table 4, there may be other sources of strong acids not listed, or negative effects on acidification by alkaline effects of sodic soils, for example. More research and better use of existing process data sets is needed. Despite these uncertainties, the fact that the acidic effects are of similar order to the observed increases of CO₂ in the atmosphere suggests it is even possible that CO₂ emissions from fossil fuels per se may be having no effect on the ever-increasing Keeling curve, since additional photosynthesis and absorption of CO₂ in the ocean as discussed earlier may remove all these emissions, replaced by new emissions from acidifying soil. A valid question that can be posed is whether the current atmospheric pCO₂ is partly controlled by overall surface pH values, with total photosynthetic productivity a compromise between this and availability of plant nutrients and water. If so, the current economic policies and practical methods to achieve carbon neutrality may prove ineffective, as long as processes of strong acidification continue unabated.

It is important to emphasise that CO₂ production from strong acids reacting with bicarbonate is stoichiometric and irreversible. By contrast, fossil fuel emissions of CO₂ may be reversibly assimilated by photo-assimilation as well as by chemosynthetic organisms [4] and by soils and water at pH values greater than 8, including sea water. Assuming that the missing fossil emissions in the atmosphere is solely a result of absorption in the ocean may be highly misleading.

4.4. Export of Produce as a Major Acidification Factor in CO₂ Emission from Bicarbonate by Soils

Any effect on climate of increasing pCO₂ in the atmosphere must be attributed to all its sources on the Earth’s surface or interior, including farming and aerobic and anaerobic sewage disposal. From this sum any increased assimilation of CO₂ such as by greening fertilisation [33] of photosynthesis or absorption in strongly alkaline soils, which are widespread, must be subtracted. Strong acids emitted and generated more strongly by industry near coastlines but deposited globally also make their contribution to the effect on seawater. As modelled earlier in Section 3.5, farming acidifies all soils to the extent that alkalinity in produce is exported (Figure 8), between 5 to 30 kilo-equivalents per hectare annually [4]. Below pH 8 to pH 5, there is almost a stochiometric release of CO₂ per equivalent of acid excreted or deposited on the soil by reaction with bicarbonate in neutral soils or with limestone slowly dissolving in acid soils below pH 5. Extractive forestry and pasturelands also contribute strong acids, because plants acquire their cationic nutrients by energetic expulsion of protons from their roots, balancing charge. Obviously, the scale of these processes is closely correlated with increasing world population. Even when farmers rectify acidification with powdered limestone or more rarely by liming with calcium hydroxide, carbon dioxide is released, as soil alkalinity is increased. These farmer practices are based on experience thousands of years old.

Some estimates [4,36] of rates of alkali depletion for export of different products are given in Table 6, showing the expected formation of strong acid formed in soil for each crop harvested. This is a function of the nutrient cations exported in each product and the amount of highly alkaline oxides such as CaO, K₂O, and MgO that will be formed if the product is ashed by ignition at high temperatures; this must be sufficient to decompose carbonates. It is of interest that the German agricultural chemistry Justus von Liebig initiated such analyses in the 19th century [4], to establish nutrient requirements proving that plants needed more than water and CO₂ for growth. A mean value for produce alkalinity of 25 kg CaCO₃ for each tonne of produce exported was assumed for the calculation performed in Table 4. However, farmers will not need to apply CaCO₃ as limestone if the soil is formed from basic volcanic or sedimentary rocks with ample bicarbonate and carbonate buffering pH changes, as modelled in Figure 4, Figure 5 and Figure 6 in Section 3.

The total strong acidification in Table 4 from export of produce and nitric acid formation in agriculture is estimated as ca. 37.5x10¹² equivalents, capable of generating the same number of moles of CO₂ from bicarbonate in soil water, or 0.45x10¹⁵ g of carbon.(0.45 Pg) from Agriculture, compared to fossil fuel emissions of 9.792x10¹² g (9.8 Pg) annually, as shown in Table 4

There is uncertainty in the scale of total carbon cycling in global ecosystems Chen et al. [37] showed in a global carbon disequilibrium flux inversion model using ¹³CO₂ measurements at 73 stations for 39 land regions and 11 ocean regions that direct CO₂ measurement overestimated the total land carbon sink by some 0.9 Pg C per year whereas for the ocean it increased the ocean carbon sink by the same amount. This infers additional low ¹³CO₂ emissions from land of the same magnitude as that proposed in Table 4. Given that the reverse was found in the Amazon indicating its carbon capture was underestimated, other sources of strong acid deposition must be proposed. More research on this issue is justified, as the claims that fossil fuel emissions are uniquely depleted in the heavy carbon isotope have been questioned [1].

The significance of the bicarbonate-carbonate system in providing pH buffering capacity in neutral to alkaline soils has been illustrated for a 3600 km transect in northern China [38]. Highly sodic soils with pH values above 9 can absorb CO₂ by reaction with carbonate forming bicarbonate. Such strongly alkaline soils are common in northern India and Pakistan and the rate and scale of such CO₂ absorption needs consideration as a land factor. Whenever the pH value of such soils is altered, CO₂ is either absorbed or emitted to join the global atmospheric sink. It is unclear to what extent the acidifying effect of CO₂ from fossil fuels shown in Table 4 should be discounted but this ranges from zero in case of no other sources of assimilation to 1.0 if the Earth’s biosphere either biologically or chemically capably assimilates all the extra CO₂ and the increasing level in the atmosphere is all generated by strong acids. However, such high efficiency would require adequate nutrients for plant growth.

The alkalinity of the ocean and of the land surface involves a variable state of quasi-equilibrium for CO₂, between bicarbonate and carbonate in solution and CO₂ in the atmosphere. Clearly, thermodynamics must influence the atmospheric concentration (Figure 6), but the current extent of disequilibrium is uncertain. Processes to sequester CO₂ such as agroforestry or other more expensive forms of CO₂ capture can act to reduce the CO₂ in the ocean, even raising the pH value of seawater. This may protect coral reefs from erosion but questions the effectiveness of direct removal of CO₂ from the atmosphere, given the ability of the huge store of DIC in the ocean that will respond to disturbance of this equilibrium. Sequestration by any means would also involve interaction with the pH state of surface materials on land or in the ocean.

4.5. Nitrification of Ammonia and Oxidation of Sulphur to Sulphuric Acid

Globally, approaching 150 million tonnes of ammonia (NH₃) is manufactured annually in the Haber process using hydrogen gas generated from natural gas (CH₄) and steam and atmospheric dinitrogen (N₂). This is the world’s major global chemical industry, used to prepare fertilisers such as urea and explosives. Ultimately, as a worst-case scenario, all this reduced inorganic-N in contact with the atmosphere can be oxidised to nitric acid in processes like nitrification or oxidation in the atmosphere, evolving CO₂ if bicarbonate and carbonate are available in systems above pH 6 [4]. Püspök et al. [28] had found in 2022 that experimental addition of ammonium fertilizers to soils led to emission of CO₂ from soil rather than an increase in soil organic carbon, as predicted by the main hypothesis of this article from nitrification. The overall process for nitrification of urea by microbial reactions with oxygen [4] is summarised in Reaction (21).

H₂N-CO-NH₂ + 2O₂ => CO₂ + 2H⁺ + 2NO₃^-

(21)

The source of urea is reaction of ammonia with CO₂ so this major product of the chemical industry does not generate its net emission. However, by Reaction (1) with bicarbonate and the protons generated by oxygen, strong emissions must occur.

Intensive crop and pasture legumes can also add an uncertain amount of excess reduced nitrogen to soils as leachate, capable of nitrification by soil microbes exposed to oxygen. Although soybeans can fix nitrogen if effectively nodulated with Bradyrhizobium japonicum they are often also fertilised with anhydrous ammonia sometimes delivered by pipeline or injected into soil to maximise yields. The expansion of the soybean industry into Latin America means global production is approaching 500 million tonnes annually, some 2 x 10¹¹ moles of acid production in soils given ash alkalinity of 400 moles per tonne (see Table 6) possibly yielding a similar amount of CO₂ emissions and 3 x 10¹² moles of nitrogen released as ammonia that may be nitrified to twice that amount of acid if excreted from livestock and leached to the ocean as nitrate. The annual algal blooming seen from satellites in the Gulf of Mexico is testament to this process. Unless a substantial part of the nitrate generated in nitrification is denitrified under anaerobic conditions to molecular nitrogen (N₂) there is no mechanism for nitrogen storage except in biota.

Sulphuric acid is partly a product of the burning of fossil fuels, depending on their sulphur content, often greater than 3%. Sulphate respiration [4] by strict anaerobic microbes (e.g., Desulfomonas) at low very O₂ tension involves the reduction of sulphate to hydrogen sulphide (H₂S), a process typical of stagnant waterlogged soils when all traces of O₂, or nitrate being denitrified to N₂O, have been consumed [4]. Fermentation yielding methane requires even more strictly anaerobic conditions. Global sewage nearly all reaching the ocean includes about 2.5x10¹⁴ g of reduced carbon compounds annually, augmented by food waste in wealthy countries. This is equivalent to about 2x10¹³ moles of carbon compounds capable of reducing sulphate to hydrogen sulphide as shown with glucose in Equation (22). Released to the atmosphere, H₂S is rapidly oxidised to sulphur dioxide (SO₂) by ultraviolet radiation, producing a similar number of moles of sulphurous and sulphuric acid [4].

C₆H₁₂O₆ + 6H⁺ + 3SO₄^2- 3H₂S (g) + 6CO₂ (g) + 6H₂O

(22)

Another possibly major source of deposition of oxides of sulphur or sulphuric acid into the ocean surface layer but difficult to quantify because of local cycling is sulphate respiration from sewerage or detritus of marine algae or phytoplankton below the oxygenated zone [4,39,40], producing volatile dimethylsulfide (DMS) or similar reduced sulphur compounds as a continuous source of sulphurous and sulphuric acids. This process is probably also catalysed by disposal of sewage into the ocean and ultraviolet radiation. The rates given in Table 4 depends on the rate of disposal of reduced carbon in sewage to O₂-limited lakes, rivers or deeper in the ocean. However, sulphate can be a major oxidant in the ocean at depth if oxygen does not penetrate to water at depth. Like borate, sulphate is distributed through the water column. While sulphate respiration will increase alkalinity where it occurs in an anoxic zone at depth, its volatile products following oxidation in the atmosphere can have an acidic effect in the oxic surface layer. Conversely, acid sulphate soils if exposed to air such as by urban drainage of the sulphide containing soils common in rice paddies can then be a potent source of sulphuric acid [40]. A recent trend to more aerobic growth of rice may be increasing acidification. Furthermore, sulphide oxidising bacteria can grow at very low environmental pH values even below 2, given the very large thermodynamic potential [4]. All these soil and atmospheric processes in the sulphur cycle are difficult to quantify so the rate of acidification in Table 4 is speculative, but it could be an underestimate. Quantification is clearly warranted.

An average increase in pCO₂ of about 2 ppmv per year in air is equivalent to adding some 4.26 Gt of carbon to the atmosphere from 0.696 equivalents of acid to every square metre of the Earth’s surface, obviously greater than is occurring. However, a productive farming system producing milk by dairy farming, using urea as nitrogen fertiliser to make casein, can produce about 33 kiloequiv. of strong acid in soil per ha (3.3 equiv./m²) annually, requiring 1.67 tonnes of limestone to neutralise the acidity and restore nutrient calcium exported [4]. This acid production is reduced to one-third if the nitrogen source is N₂-fixing clovers or medics. It is obvious that such strong acid production is directly related to the increasing human population or intensive animal production. To the extent that increasing acidification and lowered surface pH value is a function of sources other than fossil fuels, substituting other sources of renewable energy can have no influence on the rate of increase of pCO₂ in the atmosphere.

4.6. Photosynthesis Reaction Kinetics and Increasing Temperature Affecting Greening

Given that the K_m value of ribulose bisphosphate carboxylase (RuBisco) in C₃-plants [4] is around 20 μM, the enzyme fixing CO₂ in photosynthesis, is less than the current pCO₂ it is expected that this process should increase annually as the pCO₂ level rises on the Michaelis-Menten curve towards saturation at 1000-1300 ppm. Harvey [3] estimated a 25% increase in photosynthesis from the increase in atmospheric CO₂ from 280 up to 380 ppmv by 2000. Such a percentage increase amounts to less than the increase in emissions, but the assimilation of CO₂ by enhanced photosynthesis at least partly keeps these processes in balance.

It can be noted that a pCO₂ fertilising effect on carbon assimilation has not been shown to be strong for marine organisms. Their access to CO₂ may be by dissociation of bicarbonate (Figure 2), releasing alkalinity as hydroxyl ions, but as the models in this paper amply demonstrate, the concentration of bicarbonate is not highly sensitive to variation in pCO₂.

Furthermore, the assimilation of CO₂ by the biosphere on land may have been underestimated because of adaptive responses [42,43]; these studies have shown that water use efficiency increases significantly as C₃ plants on land have less need to keep open stomates to obtain adequate CO₂. It is not clear what proportion of the emissions may be assimilated biologically on land and sea, but increasing water use efficiency is being observed, leading to the arid zone greening observed from space [44]. If significant, the value in acid equivalents of acidity per annum from fossil fuels noted in Table 4 for CO₂ should be reduced for its effect on surface seawater, perhaps to a small fraction of the value shown.

The thesis that the seasonal oscillations most noticeable in the northern hemisphere are caused by imbalance between photosynthesis and respiration depended on a significant uncoupling of these two processes, to the extent of 10¹⁵ moles, 1 Pmole or 12 Gt of carbon absorbed globally in mid-summer. Claims have been made that increasing temperature will favour more respiration, depleting the global stock of biologically fixed carbon. However, it should be appreciated that these processes consuming and emitting CO₂ are not independent processes globally. The reactions of photosynthesis are highly improbable processes, without any biological means of activation of CO₂ and water. The catalysis by RuBisco, the most prolific protein on Earth, is essential for photosynthesis, together with specific quanta from the Sun. Synthesis of glucose can be represented in the reversible Equation (23).

6CO₂ + 6H₂O ⇄ C₆H₁₂O₆ +6O₂

(23)

Under mean surface conditions the products of this reaction are in a highly improbable or unstable state compared to the reactants. The resultant pressure of 21% oxygen in the atmosphere causes all forms of reduced carbon, nitrogen and sulphur to be vulnerable to oxidation. It seems improbable that unlimited sources of rapidly growing microorganisms capable of degrading reduced carbon compounds such as sugars will delay their activity to the next winter, except to some extent for durable polymers like cellulose and lignin.From the thermodynamic theory of action [4], the rate (k_f) of an uncatalysed reaction is given by Equation (24), where -ΔG* is the decrease in molar chemical potential for vibration of bonds in reactant molecules in a standard state (1 molal), reaching their activated transition states, leading to formation of products,

k_f = kT/h.e^-ΔG*of/RT

(24)

(kT/h is a harmonised vibration frequency; e^-ΔG*of/RT= N*/N_o) and that of the reverse direction is given by Equation (25).

k_r = kT/h.e^-ΔG*or

(25)

Thus, k_f/k_r = K_eq = e ^-ΔGo/RT

For a reaction far from equilibrium with non-standard, there are still two effects of temperature on reaction rate shown in Equations (17) and (18). For a change of 1 ^oC in mean temperature, a change in reaction rate of about 10-20% is expected, a result also obtained even when catalysed by RuBisco when the ratio k_f/k_r remains the same but both k_f and k_r are amplified.

To the extent that increased photosynthesis occurs as pCO₂ rises [41,42,43], including the kinetic contribution from increased temperature (Equations (24) and (25)), the relative significance of possible strong acid sources to increasing pCO₂ becomes greater. However, there is great uncertainty regarding such estimates of deposition [3]. As the degree of penetration of acids into seawater is uncertain it is important to estimate the likely rate and profile of absorption from estimates of chemical potential and fugacity. Such methods are available [45] for intermedia transport of chemicals, including diffusive processes based on differences in fugacity between phases such as would occur when fossil CO₂ is added to the atmosphere. Our own research on the variation in surface temperature in the ocean can catalyse seasonal transfers between sea water and air sufficient to explain the seasonal variation in the Keeling curve [1].

In considering exchange of CO₂ with the ocean and its capacity to absorb this product of fossil fuel combustion [4], no mention was made of the effect of pH value of seawater on this process. Focus has mainly been given to the extent of the net flux of CO₂ into the ocean [2]. However, by 2005 a Royal Society report was commissioned to assess the likely effect of CO₂ on the pH of the ocean using the data provided by Station ALOHA as proof of declining pH values in surface waters [19]. Between 1989 and 2010, a pH change of 0.002 units per year was observed in this region. This would correspond to an annual increase in atmospheric pCO₂ 1.4 ppmv or 7 ppmv per 0.01 units, as shown by our modelling of titration with increasing pCO₂ in Figure 5 and Figure 6.

Indeed, these flows in both cases may best be considered as governed by effects on pH of the mixing zone.

4.7. Unbalanced Acidification in Ecosystems

The specific societal focus on CO₂ and so-called carbon credits and carbon pricing is perhaps unfortunate, given that the task of managing pCO₂ in Earth’s atmosphere is much broader and will require more than a focus on energy generation. The major issue identified here is the local separation of alkalinity and acidity by processes such as sale of produce and disposal of waste elsewhere. The property that should be discouraged to reduce its impact is acidity or less frequently, excessive alkalinity. As a plant product formed by geological compression on land, coal has strong alkalinity based mainly on its metallic calcium, magnesium and potassium content, as oxides. These were charge balanced predominantly by organic anions such as pectins in plant cell walls, citrate and malate. On high temperature combustion as in a furnace, these evolve CO₂ forming fly ash including CaO, MgO and K₂O, with strong alkaline reactions.

Figure 9 illustrates land and ocean cycling of CO₂ in 2021, including effects of strong acidification shown in Table 4. Other increasing sources of emissions such as changes in land use or deforestation are not included. For the latter part of the 20th century, fossil fuel emissions were equivalent to an annual increase about 2 ppmv. Currently, an annual increase in pCO₂ about 0.7 moles per m² or 2 ppmv with 1.6 moles of fossil emissions of which about one third is modelled (Figure 6) as absorbed by the ocean, forming bicarbonate from carbonate (Equation 11). About 0.4 moles per m² annually is suggested to be derived from acidification (see Table 5). Fossil emissions with acid emissions are about five percent of the CO₂ emitted in global respiration. Figure 9 shows that a mean of about 30 moles of the 150 moles in each air column is recycled annually corrected for relative area of land and sea, consistent with the short turnover time of several years, discussed in Section 1.2. On land, 48 moles per square metre of CO₂ absorbed by plants annually [3] corresponds to about 3 tonnes of dry matter per ha annually. A stand of plants well supplied with water and nutrients can accumulate 10 tonnes of dry matter per ha, as suggested for lucerne in Table 6. As was pointed out three decades ago [4], the lack of local recycling results in separation of acidity and alkalinity. Where organic sewage is discharged into land water without aeration and into the deep ocean, gaseous reduced sulphur and nitrogen compounds such as H₂S or oxides of nitrogen including N₂O may be voided into the atmosphere where reactive oxygen may generate strong sulphuric and nitric acids, ultimately deposited on the surfaces of land and ocean.

Combustion of natural gas such as methane and petroleum oils yield no such alkalinity, these hydrocarbons being formed as biological products usually associated with deposition of CaCO₃ in limestone or MgCO₃ in dolomitic materials. Anthropogenically, two major processes proportional to population increase occur should be observed in Figure 9. These are export of alkalinity in produce and overfertilization with reduced nitrogen chemical fertilisers like ammonia and urea. Formation of nitrogen fertilisers on the current scale now approaching 200 million tonnes of nitrogen annually is unprecedented on Earth, all subject to the risk of formation of nitric acid given the high content of oxygen in the Earth’s atmosphere. Our estimate is that up to half of the reduced nitrogen in fertilisers is converted to nitric acid in runoff or groundwater, eventually contributing one mole of CO₂ from NH₃ and two from NH₄⁺ to the atmosphere. Nitrogen use efficiency is a key goal in agriculture, but difficult to achieve as shown by the annual blooms of algae in the Gulf of Mexico from runoff visible from space.

The atmospheric column in Figure 9 shows the scale of CO₂ emissions and reabsorption in these global processes, using one square metre on the surface as the area involved. For the calculated mean value of 0.34 moles per square metre of strong acid globally, the diagram suggests an increasing excess of 0.3 moles of photosynthesis, corresponding to a 1% increase in CO₂ assimilation for modelling purposes.

As recommended previously, recycling of waste products to their source allows alkalinity and acidity to compensate each other. Plant products, particularly dicotyledonous crops acidify soil by excreting positively charged hydrogen ions in exchange for nutrient cations. This is traditionally neutralised by treatment with powdered limestone, but that generates equivalent CO₂. Plants synthesise organic acids by oxidising sugar to replenish cytoplasmic hydrogen ions, thus balancing internal change with carboxylate anions. When combusted, organic anions consume hydrogen ions evolving CO₂ and water, leaving metallic oxides as the ash alkalinity content. Ash alkalinity can be quantitatively established by back titration with sodium hydroxide solution, after treatment with acid [4]. This ash alkalinity is analogous to the alkalinity of fly ash from burning coal often wasted in land fill instead of being usefully returned to the active biosphere that could be employed [46,47,48,49]. Natural sources of sodium carbonate such as the mineral trona used in glass manufacture are also a possible means of restoring alkalinity in soil or water with less CO₂ formation given the greater alkalinity of soluble carbonate. The Solvay process for manufacture of sodium carbonate from CO₂ by adjusting the reaction pH with ammonia is also a way of recovering alkalinity, converting half of the CO₂ fixed into the more durable alkaline form.

The process of biological nitrogen fixation for agriculture and forestry including agroforestry [50,51] could have a major role in limiting the production of acids formed from industrially fixed nitrogen and in new forest growth not limited by nitrogen. The fertilisation effect of higher pCO₂ may be limited by insufficient nutrients, particularly nitrogen and phosphorus [52] but nitrogen-fixing species have a competitive advantage, also minimising nitrogen runoff. Active programs of greening to restore cleared forests has been conducted in China and elsewhere and the encouragement of agroforestry for durable products as global precipitation increases in a warming Earth should be encouraged; rock phosphate for fertiliser manufacture is plentiful, though more expensive to manufacture; high quality organic sources from bird droppings called guano are largely exhausted as a source of phosphorus.

Excess N-fertiliser application and poor nutrient use efficiency is an acknowledged source of environmental pollution and eventually, all the industrially fixed ammonia is likely to form nitric acid in global precipitation. This alone could have contributed to 10-20% of the emissions of CO₂ in the 20th century. The application of plant-growth promoting organisms [53,54] to cereal crops also contributes to better nitrogen-use efficiency by plants and less nitric acid production from leaching and runoff.

Soil pH is a heterogeneous property with great local variance. Figure 10 indicates in the top panel that strongly acid soils below pH 5 are less frequent. Farming practice does acidify soil and application of powdered limestone, or calcium hydroxide less frequently, is widespread to improve productivity [16]. Clearly, soils of pH 6.4 or greater are more frequent, to the extent that they contain bicarbonate, able to emit CO₂ when acidified. Soils already less than pH 5.5 are effectively devoid of bicarbonate unless limestone is added. Highly productive areas harvested areas are generally well watered and around pH 6-7. It can be concluded that soils emitting CO₂ from bicarbonate are almost universal wherever harvesting crops is possible. Where soils or waters are above pH 9, absorption of CO₂ becomes possible.

5. Conclusions

Understanding the causes of CO₂ emissions because of acidification is essential in mitigating effects on global warming or climate change and for the strategy of using the soil system as a means of diminishing atmospheric pCO₂. This recognises the important role of surface soils in the carbon cycle. Where soils are poorly buffered against falling pH values to becoming toxic from aluminium and manganese, modern farming has always sought the cheapest solution, raising pH with powdered limestone. As shown in Reaction (7), the slowly soluble CaCO₃ has the advantage of being divalent, able to consume two equivalents of acidity for each mole of limestone as discussed for Table 6 regarding ash alkalinity of produce. Where bicarbonate is a major agent near pH 7, the release of CO₂ per equivalent of acid is twice as great. Qualitatively, all the causes of acidification given in Table 4 must operate to some extent. Quantitative research using existing data and new experiments is required for certainty and to design corrective measures. A new industry has arisen in world agriculture, farmers gaining carbon credits by practices that raise soil carbon, already storing many times the carbon in the atmosphere [24], in the tillage surface alone. Although pH values for moist soil and water on land vary widely, equilibration of DIC by Henry’s coefficient, independent of pH as a function of temperature with the pCO₂ in the atmosphere must also occur, following the relationships shown in Equation (5), Table 4 and Figure 2 and Figure 4.

Soils below pH 5.5 contain very little bicarbonate in solution, but addition of limestone by farmers [16] to maintain Ca fertility and raise soil pH, overcoming the insidious aluminium toxicity, also increases CO₂ emissions, requiring accurate quantification. Given that the ongoing loss of nutrients and alkalinity from soils mined by export of agricultural produce involves disposal to landfill or to marine ecosystems in sewage with little recycling, our crude estimate (Table 5) of the scale of strong acid release of CO₂ could be a substantial part of the atmospheric increase. Effects on soil pH are irreversible in the short term and could eventually lead to global depletion of soil carbonates. Most of these acidifying processes were identified in the monograph Acid Soil and Acid Rain [4] but it is possible that other oxidative sources of acidity need to be considered. In contrast, biological processes conducted anaerobically in soils and water have an alkaline effect, reducing anions such as nitrate or sulphate tending to balance the global biosystem, suggested in Figure 9. Understanding the kinetic rates of such processes whether biotic or abiotic will be important for future solutions limiting unwanted CO₂ emissions.

We suggest that the opinion that the global ecosystem is unable to cope with moderate rates of fossil fuel emissions may have been based on a false assumption underestimating rates of increased photosynthesis. A proposal that harvesting one quarter annually from 10 million hectares of fast growing woody N₂-fixing casuarinas in profitable agroforestry would fix sufficient CO₂ to match Australia’s emissions from burning coal illustrates the scope of photosynthetic CO₂ sequestration to be accelerated [56]. By comparison, Australia harvests 25 million ha of annual crops. This paper’s main thesis infers that the increasing pCO₂ in air is an inevitable thermodynamic result of decreasing global land surface pH values, largely independent of the general capacity for accumulation of biomass. Recent research showing the greening of dry areas on land [27] and even more recently of greening of the subtropical and tropical ocean by Cael et al. [57] inferring increasing chlorophyll in phytoplankton in the last 20 years, could be demonstrating this response of increasing productivity, also reviewed by Canadell et al. [58]. If so, as this paper shows in theory, CO₂ is thermodynamically bound to distribute between the air and Earth’s ocean and land surfaces.

In our earlier study [1] it was demonstrated for the northern Pacific gyre near the ALOHA station that thermal calcification with falling pH is important in raising the fugacity of CO₂ in surface seawater in summer to the point it exceeds that above the surface in air, as shown expertly by Chen et al. [59]; this increasing fugacity in spring and summer promotes photosynthesis but also the transfer of CO₂ from seawater to the atmosphere during autumn and winter, the net atmospheric pCO₂ reaching a maximum in May. This area showed an increased chlorophyll signal observed from the MODIS satellite near 500 nm [1]. Conversely, if the pH of the land surface and ocean could rise sufficiently to absorb CO₂ on a net basis, CO₂ could decline in the ocean surface and in the atmosphere. We have suggested this may even have been a factor in decreasing CO₂ in ice cores in the recent millennial ice ages [60]. Even if fossil fuel emissions of CO₂ are partly the cause of falling pH values in seawater, we claim that the quasi-equilibrium with the pH value of the Earth’s surface materials must be the logical focus for efforts at mitigation.

If this hypothesis regarding minor change in pH on land withstands analysis, not considering such a cross-disciplinary process until recently is a significant omission. Perhaps it proves the criticism by John Maddox, former chief editor of Nature in 1998 [61], that an assumption that fossil fuel emissions were solely to blame for the shape of the Keeling curve shown in Figure 1 was too simplistic. To quote Maddox, “The IPCC’s scientific assessments would be more persuasive if they were plainly the products of an independent organization”, rather than an intergovernmental panel also likely to guide research funding. Properly funded but independent scientific institutes would be better equipped to establish causation before commissioning reports on methods to mitigate climate change. We have attempted to do this in our recent article on tropospheric thermodynamics [62]. The only consensus really required is on how to manage effects of warming and climate change, but only when a high probability of the effectiveness of such measures can be shown. If the hypothesis advanced here on significant acidification is verified, attempting to use zero carbon policies regarding fossil fuels could be a futile waste of resources in halting the increasing Keeling curve.

All the acidifying processes listed in Table 5 provide a guide for future research. Particularly for sulphur, the global production of sulphuric acid in oxygenic soils or because of venting of hydrogen sulphide, allowing ultraviolet oxidation to acid in the atmosphere needs quantification [4]. For soil systems, research is needed to establish what proportion of reduced nitrogen fertiliser is eventually converted to nitric acid by nitrification in the global ecosystem. Nitrate can be denitrified to nitrous oxide, itself a potent greenhouse gas [63], but Escherichia coli and other microbes reform ammonia as a product of using nitrate as an anerobic electron acceptor. Ideally, the reduced nitrogen content in fertilisers would be best evolved as atmospheric N₂, but the extent to which this occurs is unknown. The extent to which the alkalinity in exported produce is returned to crop producing soils is another issue, given that most of this benefit may be lost to the ocean in sewage, in part countering ocean acidification.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Table S1, CO2TIT1/Cal program data for titration of seawater with strong acid and CO₂ at 278.15, 288.15 and 298.15 K; Table S2, CO2TIT3/Cal program Titrate data, I iterations, U -meq acid, A=alkalinity, T=meq alkalinity, P=pH value, K=temperature Kelvin, S=35 ‰; Table S3, Program Code for CO2TIT1/Cal; Table S4, Program Code for CO2TIT3; Table S5, Program Code for CO2TIT4; Table S6, Emerson (2012) Inorganic Carbon Chemistry.

Author Contributions

Conceptualization, I.K.; J.R.; R.R.; methodology, I.K.; R.R.; software, I.K.; validation, A.N.C.; data curation, I.K.; writing—original draft preparation, I.K.; review and editing, R.R.; A.N.C.; J.R.; I.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no research funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data is given in the article or in Supplementary Materials.

Acknowledgments

We dedicate this article to the late James Raven FRS of the University of Dundee, Scotland, for his long guidance in matters related to charge balancing and effects of pH values. Our thanks for help in preparing this manuscript also go to colleagues Edward Cocking, FRS Philip Kuchel, Rafe Champion, Nikolas Crossan and Peter Smith (abstract). We also acknowledge ongoing infrastructure support from the University of Sydney and the Prince Songkla University of Phuket, Thailand.

Conflicts of Interest

The authors declare no conflict of interest.

References

Kennedy, I.R.; Runcie, J.W.; Zhang, S.; Ritchie, R.J. A New Look at physico-chemical causes of changing climate: Is the seasonal variation in seawater temperature a significant factor in establishing the partial pressure of carbon dioxide in the Earth’s atmosphere? Thermo 2022, 2, 401–434. [Google Scholar] [CrossRef]
Keeling, C.D. ; TP, Wahlen M. ; van der Plicht, J. Interannual extremes in the rate of rise of atmospheric carbon dioxide since 1980. Nature 1995, 375, 666–670. [Google Scholar]
Harvey, L.D. Global Warming 2000, The Hard Science. Prentice Hall, Harlow UK.
Kennedy, I.R. Acid Soil and Acid Rain. 1992, Wiley, United Kingdom.
Archer, D.; Eby, M.; Brovkin, V.; Ridgwell, A.; Cao, L.; Mikolajewicz, U.; Caldeira, K.; Matsumoto, K.; Munhoven, G.; Montenegro, A.; Tokos, K. Atmospheric lifetime of fossil fuel carbon dioxide. Annu. Rev. Earth Planet. Sci. 2009, 37, 117–134. [Google Scholar] [CrossRef]
Ely, L.L.; Webb, R.H.; Enzel, R.H. Accuracy of post-bomb ¹³⁷Cs and ¹⁴C in dating fluvial deposits. Quatern. Res. 1992, 38, 38,196–204. [Google Scholar] [CrossRef]
Randerson, J.T.; Enting, I.G.; Schuur, A.G.; Calderia, K.; Fung, I.Y. Seasonal and latitudinal variability of troposphere Δ¹⁴CO₂: Post bomb contributions from fossil fuels, oceans, the stratosphere, and the terrestrial biosphere. Glob. Biogeochem. Cyc. 2002, 16, 1112. [Google Scholar] [CrossRef]
Bernard, S.; Frisén, J.; Spalding, K.L. A mathematical model for the interpretation of nuclear bomb test derived ¹⁴C incorporation in biological systems. Nucl. Instrum. Methods Phys. Res. Sect. B: Beam Interact. Mater. At. 2010, 268, 1295– 1298.
Dickson, A.G.; Millero, F.J. x A comparison of the equilibrium constants for dissociation of carbonic acid in seawater media. Deep Sea Res. Contrib. 2019, 34, 1733–1743. [Google Scholar] [CrossRef]
Millero, F.J.; Graham, T.B.; Huang, F.; Bustos-Serrano, H.; Pierrot, D. Dissociation constants of carbonic acid in seawater as a function of salinity and temperature. Mar. Chem. 2006, 100, 80–94. [Google Scholar] [CrossRef]
Millero, F.; Huang, F.; Graham, T.; Pierrot, D. The dissociation of carbonic acid in NaCl solutions as a function of concentration and temperature. Geochim. 2007, 71, 46–55. [Google Scholar] [CrossRef]
Millero, F.J. ; Thermodynamics of the carbon dioxide system in the oceans. Geochim. Cosmochim. Acta 1995, 59, 661–677. [Google Scholar] [CrossRef]
Emerson, S.; Hedges, J. Carbonate Chemistry. In Chemical Oceanography and Marine Carbon Cycle, 2008, pp. 101–133, Cambridge University Press.
Orr, J.C.; Epitalon, J.M.; Gattuso, J.P. Comparison of the packages that compute ocean carbonate chemistry. Biogeosci. 2007, 12, 1483–1510. [Google Scholar] [CrossRef]
Millero, F.J. Carbonate constants for estuarine waters. Mar. Freshwater Res. 2010, 61, 139–142. [Google Scholar] [CrossRef]
Goulding, K.W.T. Soil acidification and the importance of liming agricultural soils with particular reference to the United Kingdom. Soil Use Man. 2016, 32, 390–399. [Google Scholar] [CrossRef] [PubMed]
Le Quéré, C.; Peters, G.P.; Jones, M.W. Fossil CO₂ emissions in the post-COVID-19 era. Nature Clim. Change 2020, 11, 197–199. [Google Scholar] [CrossRef]
Trenberth, K.E.; Smith, L. The mass of the atmosphere. J. Clim. 2005, 18, 864–875. [Google Scholar] [CrossRef]
Dore, J.E.; Sadler, D.W.; Church, M.J.; Karl, D.M. ; Physical and biogeochemical modulation of ocean acidification in the central North Pacific. PNAS USA 2009, 106, 12235–12240. [Google Scholar] [CrossRef]
Bromfield, S.M.; Cumming, R.W.; David, D.J.; Williams, C.H. Changes in soil pH, manganese and aluminium under subterranean pasture. Aust. J. Exp. Agric. Anim. Husb. 1988, 23, 181–191. [Google Scholar] [CrossRef]
Prentice, I.C.; Farquhar, M.J.R.; Fasham, M.L.; Goulden, M.L.; Heimann, M.; Jarmilla, V.J.; Kheshgi, H.S.; Le Quere, C.; Scholes, R.J.; Wallace, D.W.R. The carbon cycle and atmospheric carbon dioxide. In Climate Change 2001, Chapter 3 The Scientific Basis, Contribution to the Third Assessment Report of the IPCC.
Ciais, P.; Sabine, C.; Balu, G.; Bopp, L.; Brovkin, V.; Canadell, J.; Chabra, A. ; Defries. R.; Galloway J.; Heimann, M.; Jones, C.; Le Quere C.; Myneni, R.B.; Piao, S.; Thornton, P. Carbon and other biogeochemical cycles. 2013, In: Climate Change 2013: The Physical Basis Contribution of Working Group 1 to Fifth Assessment Report of the IPCC, Cambridge Press UK, USA.
Stone, Y.; Ahern, C.R.; Blunden, B. Acid Sulfate Soil Manual. 1998, NSW Agriculture, Wollongbar, NSW 2477, Australia.https://www.epa.nsw.gov.au/~/media/EPA/Corporate%20Site/resources/epa/Acid-sulfate-Manual-1998.ashx.
West, T.O.; McBride, A.C. The contribution of agricultural lime to carbon dioxide emissions in the United States: dissolution, transport and net emissions. Agric. Ecosys. Environ. 2005, 108, 145–154. [Google Scholar] [CrossRef]
Zamanian, K.; Zarebanaadkouki, M.; Kuzyakov, Y. Nitrogen fertilization raises CO₂ efflux from inorganic carbon: A global assessment. Glob. Change Biol. 2018, 24, 2810–2817. [Google Scholar] [CrossRef]
Sharififar, A.; Minasny, B.; Arruays, D.; et al. Soil inorganic carbon, the other and equally important soil carbon pool: Distribution, controlling factors and the impact of climate change. Adv. Agron. 2023, 178, 165–231. [Google Scholar] [CrossRef]
Sun, X.l.; Minasny, B.; Wu, Y.J.; Wang, H.L.; Fan, X.H.; Zhang, G.L. Soil organic carbon content increase in the east and south of China is accompanied by soil acidification. Sci. Total Env. 2022, 8587, 159253. [Google Scholar] [CrossRef]
Püspök, J.F.; Zhao, S.; Calma, A.D.; Vourlitis, G.L.; Allison, S.D.; Aronson, E.L.; Schimel, J.P.; Hamam, E.J.; Homyak, P.M. Effects of experimental nitrogen deposition on soil organic carbon storage in Southern California drylands. Glob. Change Biol. 2022. [CrossRef] [PubMed]
Raza, S.; Zamanian, K.; Ullah, S.; Kuzyakov, Y.; Virto, I.; Zhou, J. Inorganic carbon losses by soil acidification jeopardize global efforts on carbon sequestration and climate change mitigation. J. Clean. Prod. 2024, 315, 128036. [Google Scholar] [CrossRef]
Huang, Y.; Song, X.; Wang, Y.P. : Canadell, J.G.; Luo, Y.; Ciais, P.: et al., Size, distribution, and vulnerability of the global soil inorganic carbon. Science 2024, 384, 233–239. [Google Scholar] [CrossRef] [PubMed]
Tao, J.; Fan, L.; Zhou, J.; Banfield, C.C.; Kuzyakov, Y.; Zamanian, K. Nitrification-induced acidity controls CO₂ emission from soil carbonates. Soil Biol. Biochem. 2024, 192, 10939. [Google Scholar] [CrossRef]
Maes, S.L.; Dietrich, J.; Midolo, G.; Schwieger, S.; Kummu, M.; et al. Environmental drivers of increased ecosystem respiration in a warming tundra. Nature 2024, 629, 105–113. [Google Scholar] [CrossRef] [PubMed]
Scanes, E.; Scanes, P.R.; Ross, P.M. Climate change rapidly warms and acidifies Australian estuaries. Nature Commun. 2020, 11, 1803–1814. [Google Scholar] [CrossRef] [PubMed]
Doney, S.C.; Mahowald, N.; Lima, I.; Feely, R.A.; Mackenzie, F.T.; Lamarque, J.F.; Rasch, P.J. Impact of anthropogenic atmospheric nitrogen and sulphur deposition on ocean acidification and the inorganic carbon system. PNAS 2007, 104, 14580–14585. [Google Scholar] [CrossRef] [PubMed]
Turner, D.R.; Edman, M.; Gallego-Urrea, J.A.; Claremor, B.; Hasselöv, I.M.; Omstedt, A.; Rutgersson, A. The potential future contribution of shipping to acidification of the Baltic Sea. Ambio 2018, 47, 368–378. [Google Scholar] [CrossRef] [PubMed]
Slattery, W.J.; Ridley, A.M.; Windsor, S.M. Ash alkalinity of animal and plant products. 1991, Austral. J. Exp. Agric. 31, No. 3.
Chen, J.M.; Mo, G.; Deng, F. A joint global carbon inversion system using both CO₂and ¹³CO₂ atmospheric concentration data. Geosci. Model Develop. 2017, 10, 1131–1156. [Google Scholar] [CrossRef]
Luoi, W.T.; Nelson, P.N.; Li, M.H.; Cai, J.P.; Zhang, Y.Y.; Zhang, Y.G.; Yang, S.; Wang, R.Z.; Wang, Z.W.; Wu, Y.N.; Han, X.G.; Jiang, Y. Contrasting pH buffering patterns in neutral-alkaline soils along a 3600 km transect in northern China. Biogeosci 2015, 12, 7047–7056. [Google Scholar] [CrossRef]
Yoch, D. Dimethylsulfoniopropionate: Its sources, role in the marine food web, and biological degradation to dimethylsulfide. Appl. Environ. Micro. 2002, 68, 5804–5815. [Google Scholar] [CrossRef] [PubMed]
Keller, M.D. Dimethyl sulfide production and marine phytoplankton: The importance of species composition and cell size. Biol. Ocean. 1989, 6, 375–382. [Google Scholar]
Farquhar, G.D.; Ehleringer, J.R.; Hubick, K.T. Carbon isotope discrimination and photosynthesis. Ann. Rev. Plant Biol. 1994, 40, 503–537. [Google Scholar] [CrossRef]
Wright, G.C.; Rao, R.C.N.; Farquhar, G.D. Water-use efficiency and carbon isotope discrimination in peanut under water deficit conditions. Crop Sci. 1994, 34, 92–97. [Google Scholar] [CrossRef]
Barbour, M.M.; Farquhar, G.D. (2001) Relative humidity-and ABA-induced variation in carbon and oxygen isotope ratios of cotton leaves. Plant Cell Environ. 2001, 23, 473–485. [Google Scholar] [CrossRef]
Piao, S.; Wang, X.; Park, T.; Chen, C.; Lian, X.; He, Y.; Bjerke, J.W.; Chen, A.; Ciais, P.; Tømmervik, H.; Nemani, R.R.; Myneni, R.B. Characteristics, drivers and feedbacks of global greening. Nature Rev. 2020, 1, 14–27. [Google Scholar] [CrossRef]
Mackay, D. Multimedia Environmental Models; The Fugacity Approach. 2001, 2nd Edition Lewis Publishers, Boca Raton.
Im-Erb, R.; Bamroongrugsa, N.; Kawashima, K.; Amano, T.; Kato, S. Utilisation of coal ash to improve acid soil. J. Sci. Technol. 2004, 26, 697–708. [Google Scholar]
Ukwattage, N.L.; Ranjith, P.G. Accelerated carbonation of coal combustion fly ash for atmospheric carbon dioxide sequestration and soil amendment. J. Poll. Effec. Contain. 2018, 6, 210–217. [Google Scholar]
Back, S.K.; Mojannal, A.H.M.; Jo, H.H.; Kim, J.H.; Jeong, M.J.; Seo, Y.C.; Joung, H.T.; Kim, S.H. Increasing seawater alkalinity using fly ash to restore the pH and the effect of temperature on seawater flue gas desulphurization. J. Mater. Cyc. Waste Manag. 2019, 21, 962–973. [Google Scholar]
Kim, A.G. (1999) The reaction of acid mine drainage with fly ash from coal combustion. 1999, Proc. Amer. Soc. Mining data Reclamation pp. 111–117.
Ganguli, N.; Kennedy, I.R. (2013) Indigenous actinorhizal plants of Australia. J. Biosci. 2013, 38, 749–759. [Google Scholar] [CrossRef]
Haruthaithanasan, M.; Pinyopusarerk, K.; Nicodemus, A.; Bush, D.; Thomson, L. Casuarinas for green economy and environmental sustainability. 2020, Proc.Sixth Inter. Casuarina Workshop, Krabi Thailand. Kasetsart Agricultural and Agro-Industrial Product Improvement Institute, Kasetsart University: Bangkok. 306 pp. ISBN 978-616-278-583-2.
Bashan, Y.; Holguin, G.; de-Bashan, LE. Azospirillum-plant relationships: physiological, molecular, agricultural, and environmental advances (1997-2003) Can. J. Microbiol. 2004, 50, 521–577. [Google Scholar] [CrossRef] [PubMed]
Kennedy, I.R.; Choudhury, A.; Kecskés, M.L. Non-symbiotic bacterial diazotrophs in crop-farming systems: can their potential for plant growth promotion be better exploited? Soil Biol. Biochem. 2004, 36, 1229–1244. [Google Scholar] [CrossRef]
Seneviratne, G.; Zavahir, J.S.; Bandara, W.R.S.M.; Weerasekara, M. Fungal-bacterial biofilms: their development for novel biotechnological applications. World J. Microbiol. Biotech. 2007, 24, 739–743. [Google Scholar] [CrossRef]
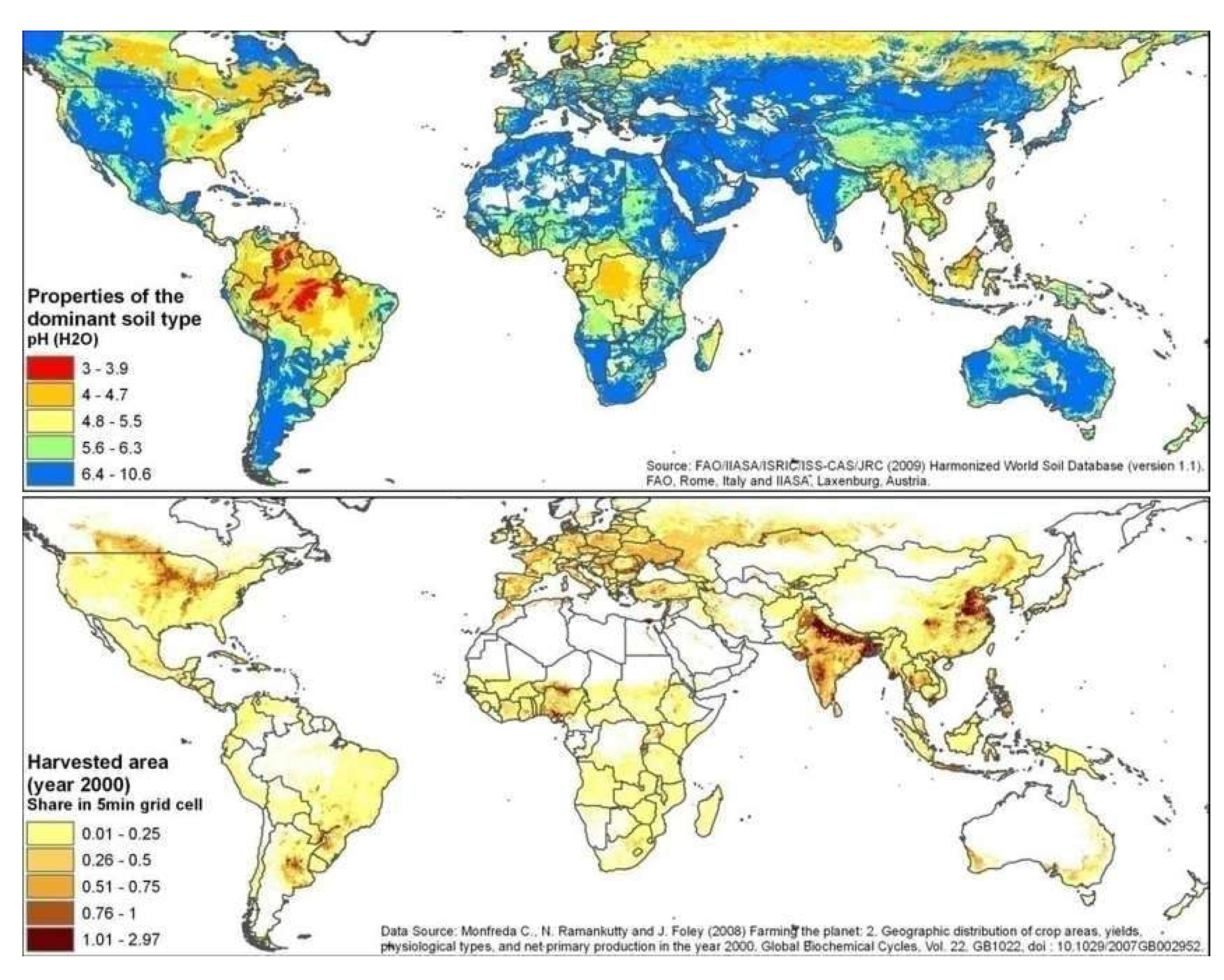
Monfreda, C.; Ramankutty, N.; Foley, J. Farming the planet: 2. Geographic distribution of crop areas, yields, physiological types and net primary production in the year. Glob. Biochem. Cycl, 1022. [Google Scholar] [CrossRef]
Kennedy, I.R.; Ganguli, N. N₂-fixing trees for profitable farm-forestry. Agric. For. 2016, 62, 29–36. [Google Scholar] [CrossRef]
Cael, B.B.; Bisson, K.; Boss, E.; Dutkiewicz, S.; Henson, S. Global climate-change trends detected in indicators of ocean ecology. 2023. [CrossRef]
Canadell, J.G.; et al. , Contributions to accelerating atmospheric CO₂ growth from economic activity, carbon intensity and efficiency of natural sinks. Proc. Natl. Acad. Sci. USA 2007, 104, 18–866. [Google Scholar] [CrossRef] [PubMed]
Chen, S.; Sutton, A.J.; Hu, C. Quantifying the atmospheric CO₂ forcing effect on surface ocean pCO₂ in the North Pacific subtropical gyre in the past two decades. Front. Mar. Sci. 2021, 8, 636861. [Google Scholar] [CrossRef]
Hodzic, M.; Kennedy, I. R Kalman filter harmonic bank for Vostok ice core data analysis and climate predictions. 2021, Glaciers and the Polar Environment, Kanao, M., Godone, D., Dematteis, N. /: htpps. [CrossRef]
Maddox, J. What remains to be discovered. p. 340, Macmillan 1998, London United Kingdom.
Kennedy, I.R.; Hodzic, M. Applying the action principle of classical mechanics to the thermodynamics of the troposphere. Appl. Mech. 2023, 4, 729–775. [Google Scholar] [CrossRef]
Mothapo, N.; Chen, H.; Cubeta, M.A.; Grossman, J.M.; Fuller, F.; Shi, W. Phylogenetic, taxonomic and functional diversity of fungal denitrifiers and associated N₂O production efficacy. Soil Biol. Biochem. 2015, 83, 160–175. [Google Scholar] [CrossRef]

Figure 1. The Keeling curve for molar fraction of atmospheric CO₂ at 3200 m on Mauna Loa, Hawaii. Data from Dr. Pieter Tans, NOAA/ESRL and Dr. Ralph Keeling, Scripps Institution of Oceanography. CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=40636957. Note the surge in pCO₂ around 1990 and its increasing rate since.

Figure 2. Terrestrial titration hypothesis from strong acid causing increasing _pCO_2. in air. As pH decreases from strong acid production by oxidation of reduced sulphur and nitrogen, the DIC equilibria move towards CO₂ formation, though pH changes more slowly if nearer pK values. As we have shown [1], as T varies, K_SP, K₁, K_2, K_o, K_SP vary, towards carbonate (c) and solid CaCO₃ if warmer and towards bicarbonate and dissolved CO₂ (a) if colder.

Figure 3. Flow sheet for the CO₂ Titrate program. The model allocates acidity to titrating alkalinity of carbonate and bicarbonate according to their relative concentrations at the current pH value. The Program includes a novel quadratic equation to solve for bicarbonate (b) concentration responding to inputs of other forms of DIC. Program details are given in Supplementary Materials.

Figure 4. Effect of water pH value on bicarbonate and carbonate concentration in seawater and freshwater, equilibrated with the current atmospheric pCO₂ of 420 ppmv estimated with the Titrate model (Supplementary Materials, CO2MOD4, Table S5).

Figure 5. Time courses (X-axis, years) for p-CO₂ (C), strong acid (A) or calcite (L) titrations (μequiv/kg), generating increased pCO₂ values (Y-axis ppmv). Primary data including a, b, c, C, A_c, A_b, Ω is included in Supplementary Materials Table S3.

Figure 6. Effect on pH of (i) strong acid on solubility of calcite (33.3 acid plus 10 ppmv, 33.3 or 66.6 acid μequiv/kg per 10 years (plots on left); (ii) increased mixing ratio of atmospheric pCO₂ per decade (plots on right).

Figure 7. Strong acidification of soil from balancing charge in plant growth. Protons (H⁺) are excreted in proportion to the extent that nutrient cations exceed anions taken up by plants. If plant or animal produce is then exported, soils in the rural environment will be acidified in proportion. Applying powdered limestone on farms releases CO₂ to air.

Figure 8. Acidification from nitrogen cycling and export of produce in dairy farming with nitrogen supplied as ammonium sulphate [4]. Different annual keq per ha rates (A, B, C) of nitrification (18, 25.2, 25.2), denitrification (5, 5, 12.2), nitrogen fixation (0.8), and ammonification (8.8, 16, 16) are shown, with nitrate leaching (2.2, 9.4, 2.2) producing the same ammonia vaporization (6) and milk production (5.2). Net acid production.

Figure 9. Rates per square metre in global carbon cycling between land water, the atmosphere and the ocean, illustrating the pH-acidification hypothesis. Quantities shown are moles per square metre of the Earth, for a mixing ratio of 420 ppmv in 2021 shown in the central column bridging land and ocean. The values are derived from the data given in Figure 6 and Table 4 and 5 and [3], assuming photosynthesis is equal to respiration. Soils below pH 5 also contribute CO₂ from the land surface if they are treated with limestone to raise pH values discussed in 3.4 to prevent aluminium toxicity [4]. The land area of Earth is 1.48x10¹⁴ m², the oceans is 3.62x10¹⁴ m², 5.10 x10¹⁴ m² in total., represented as a mean value in the central air column.

Figure 10. FAO world map of surface soil pH and crop harvesting [55] showing a preponderance of soils with significant concentration of bicarbonate, able to evolve CO₂ from strong acid production; pH from FAO Harmonized world soil database (2009).

Table 1. Increasing anthropogenic atmospheric CO₂ content.

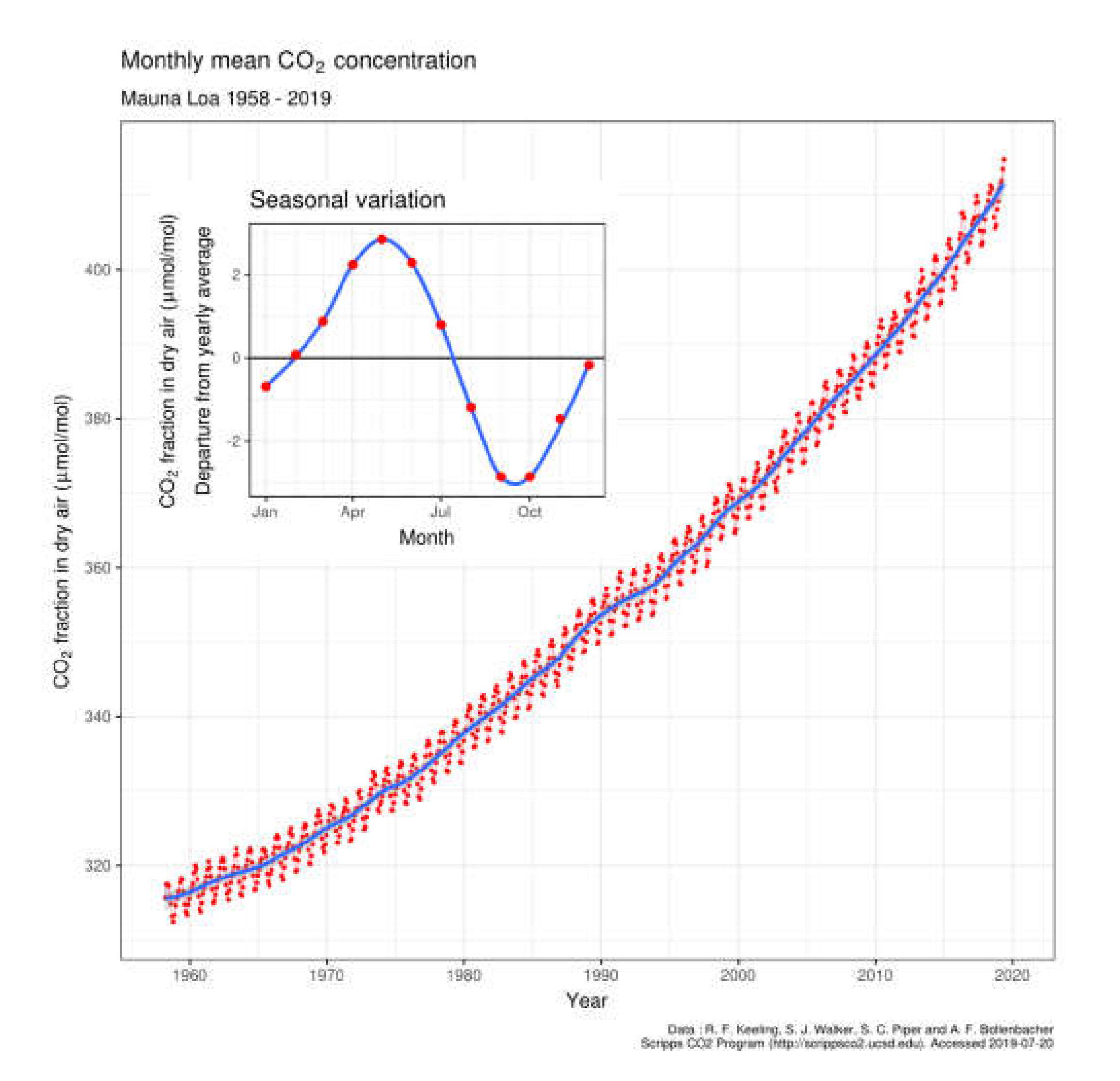
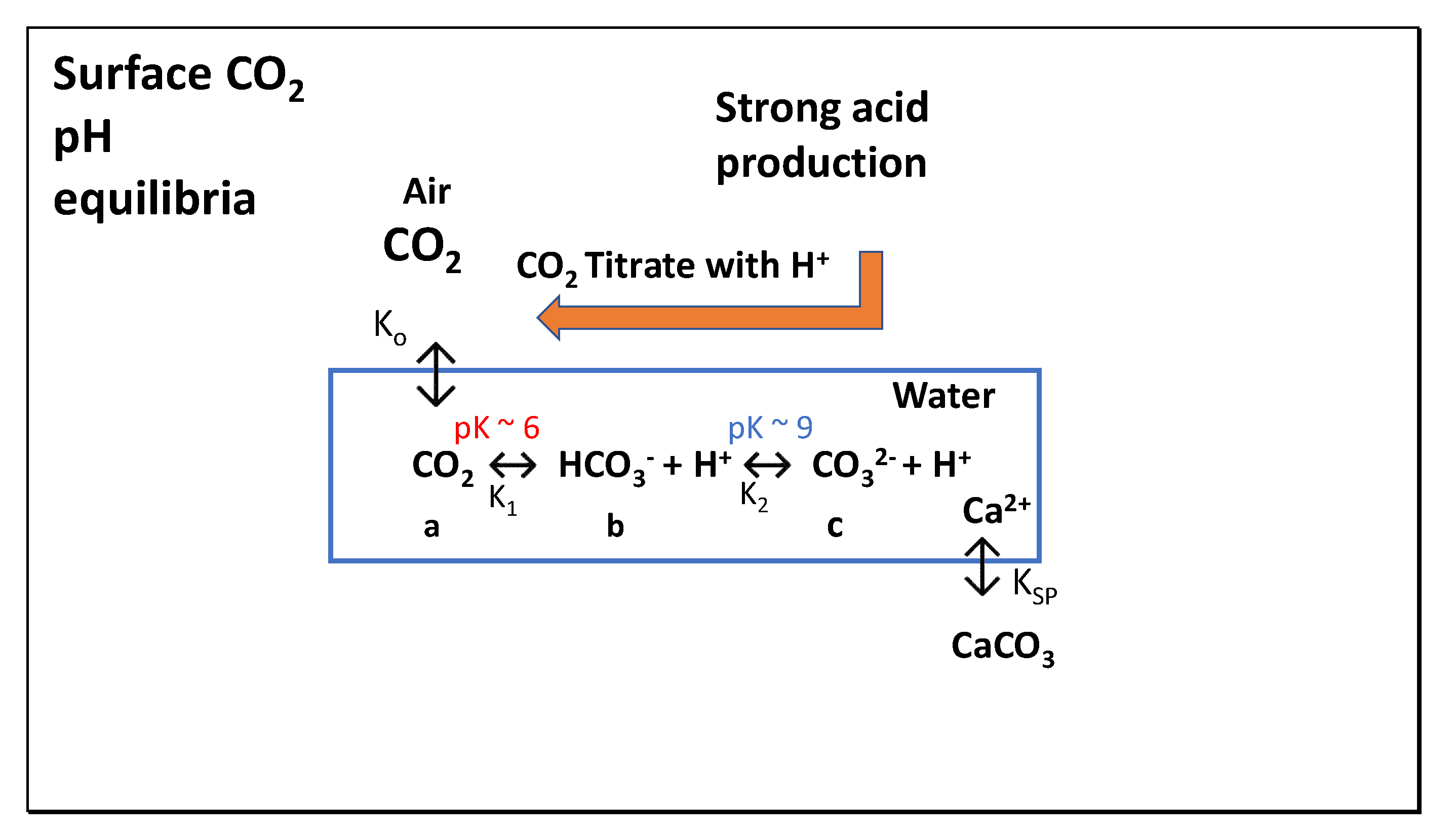
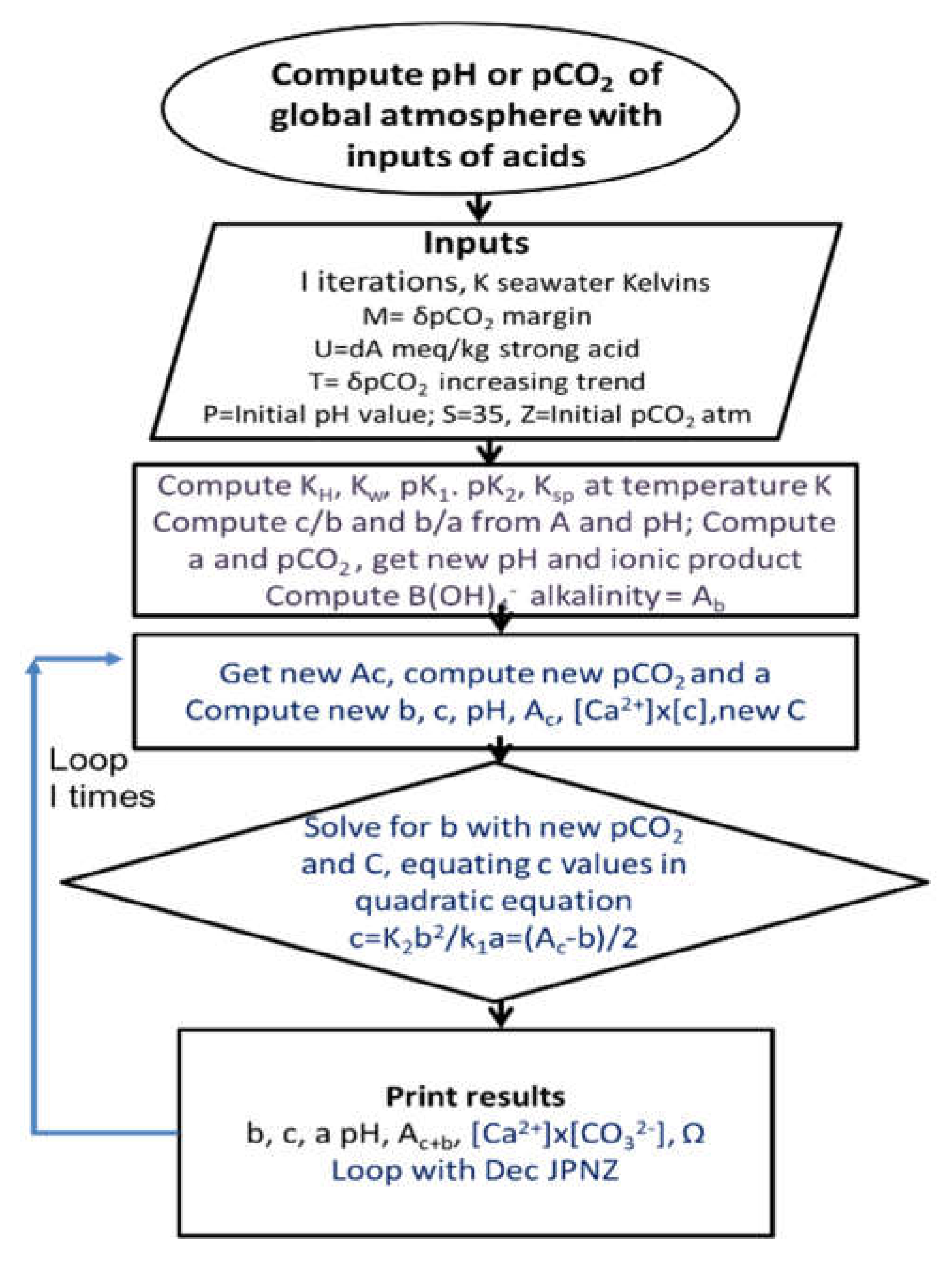
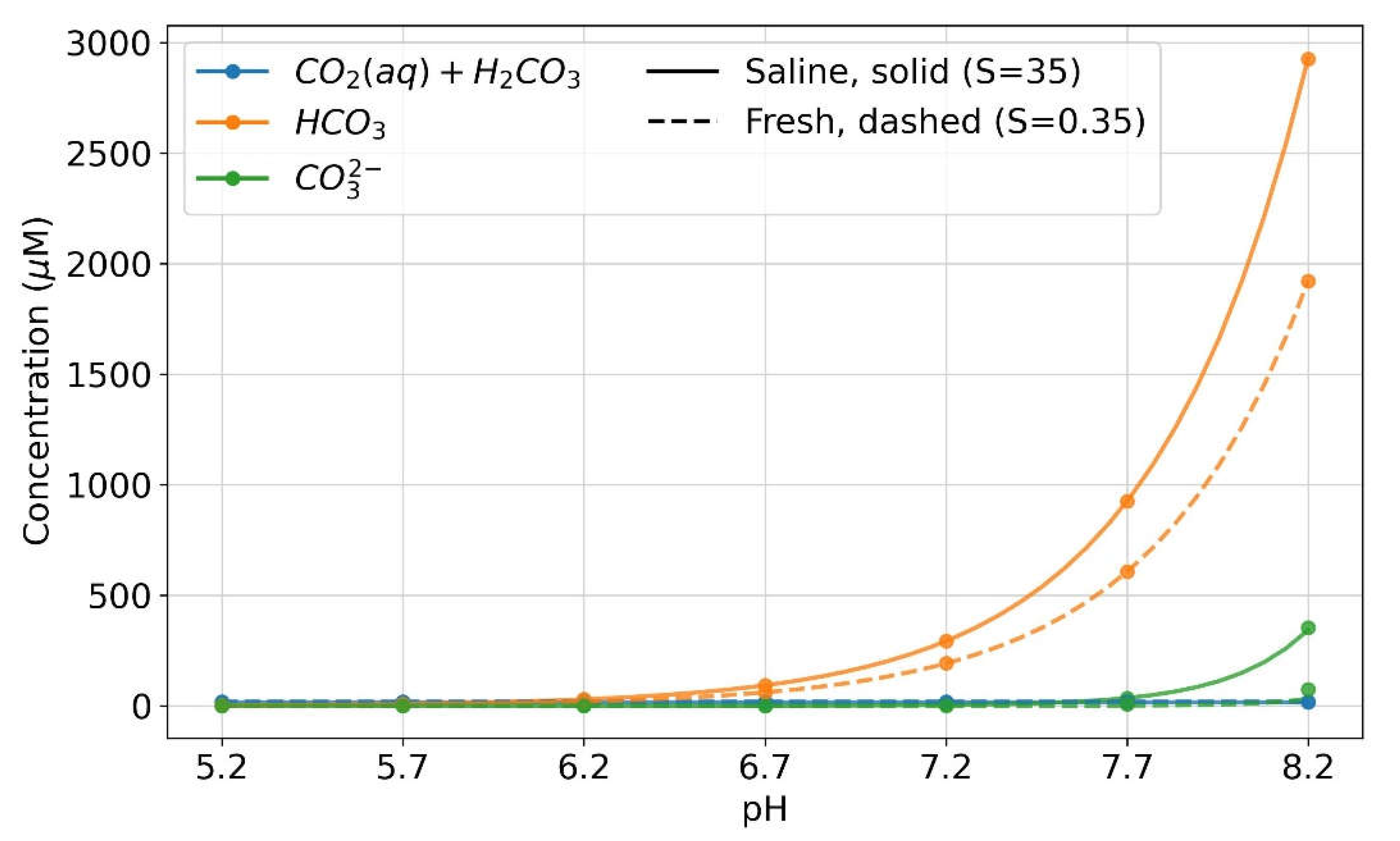
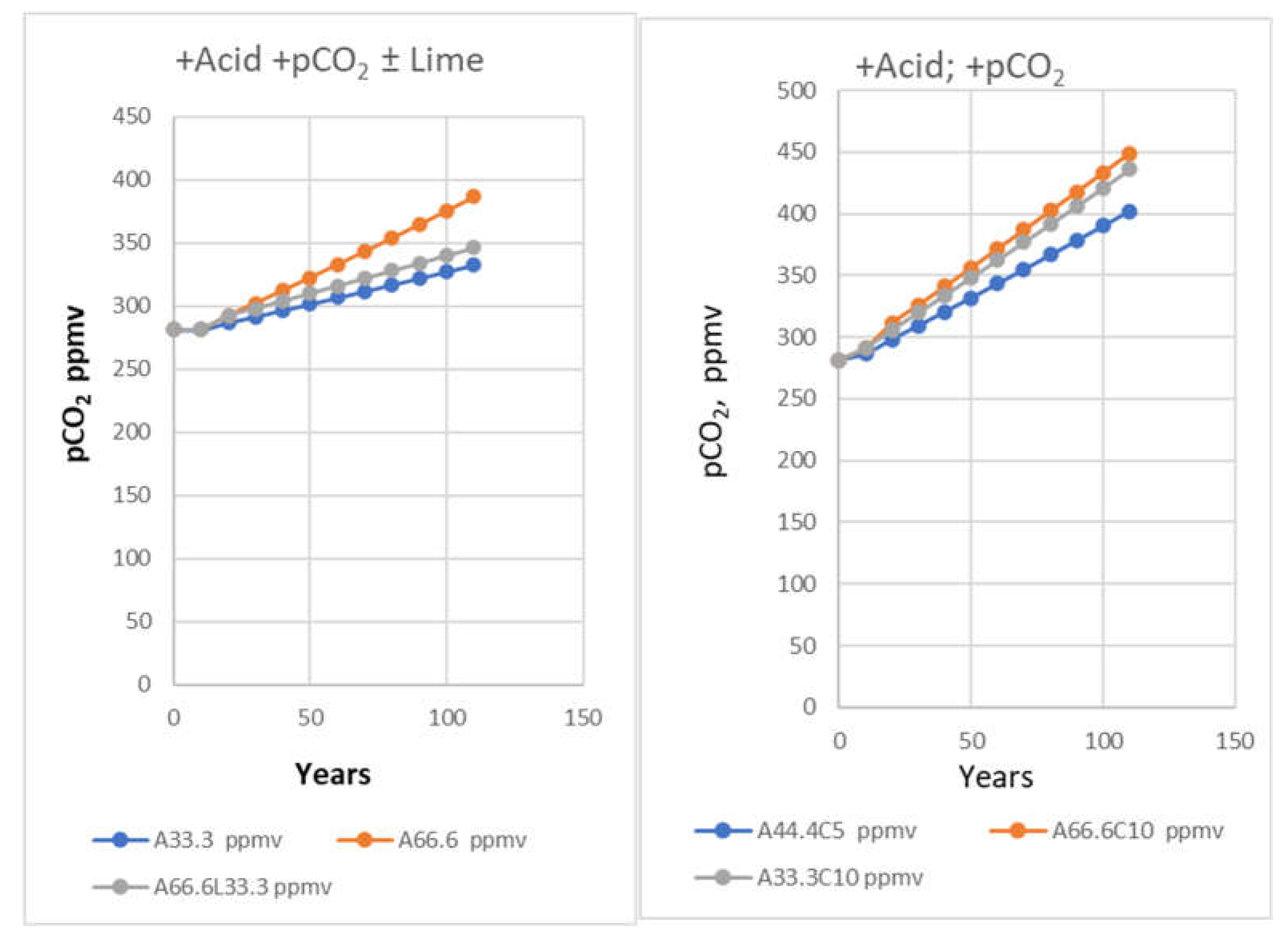
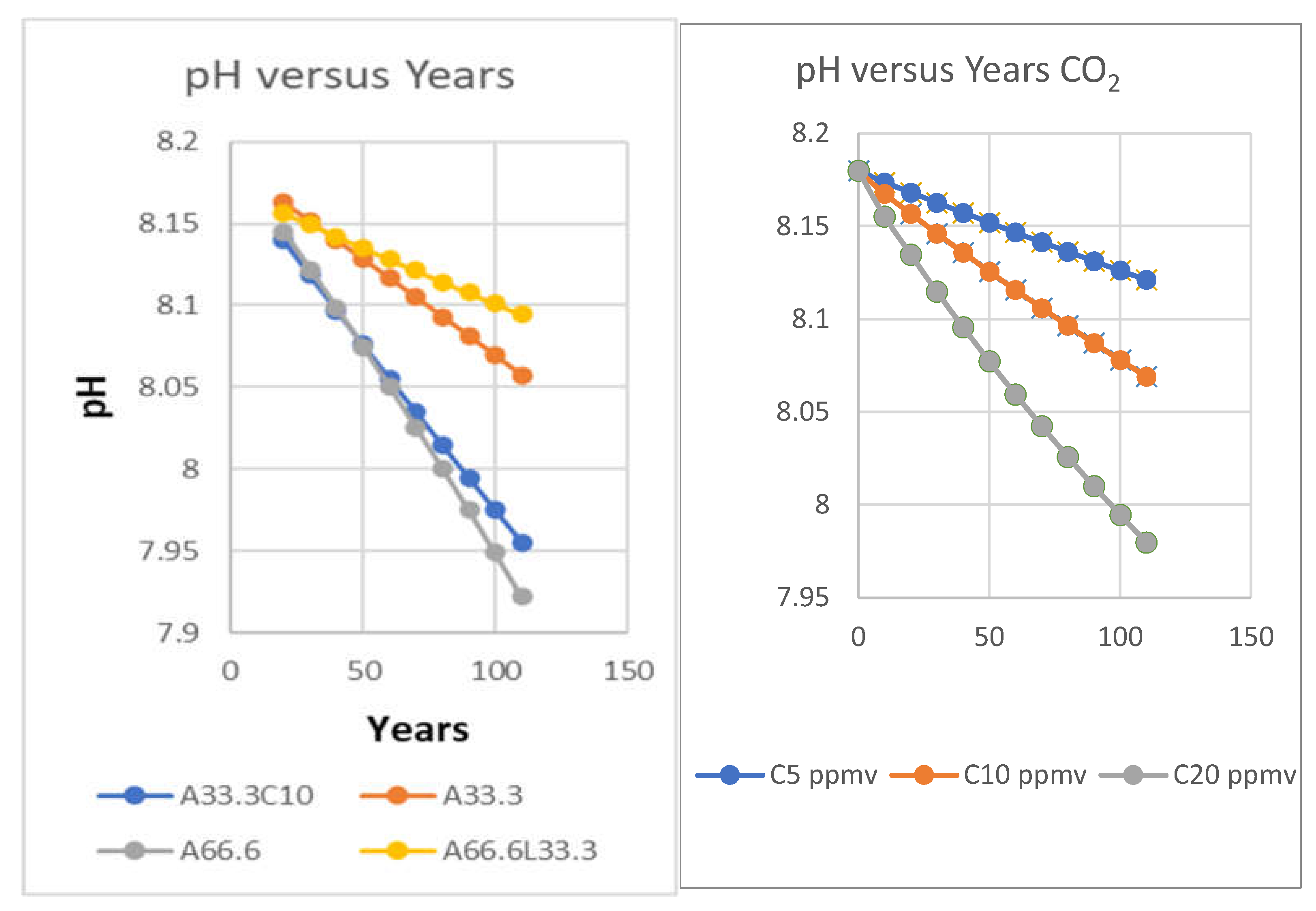
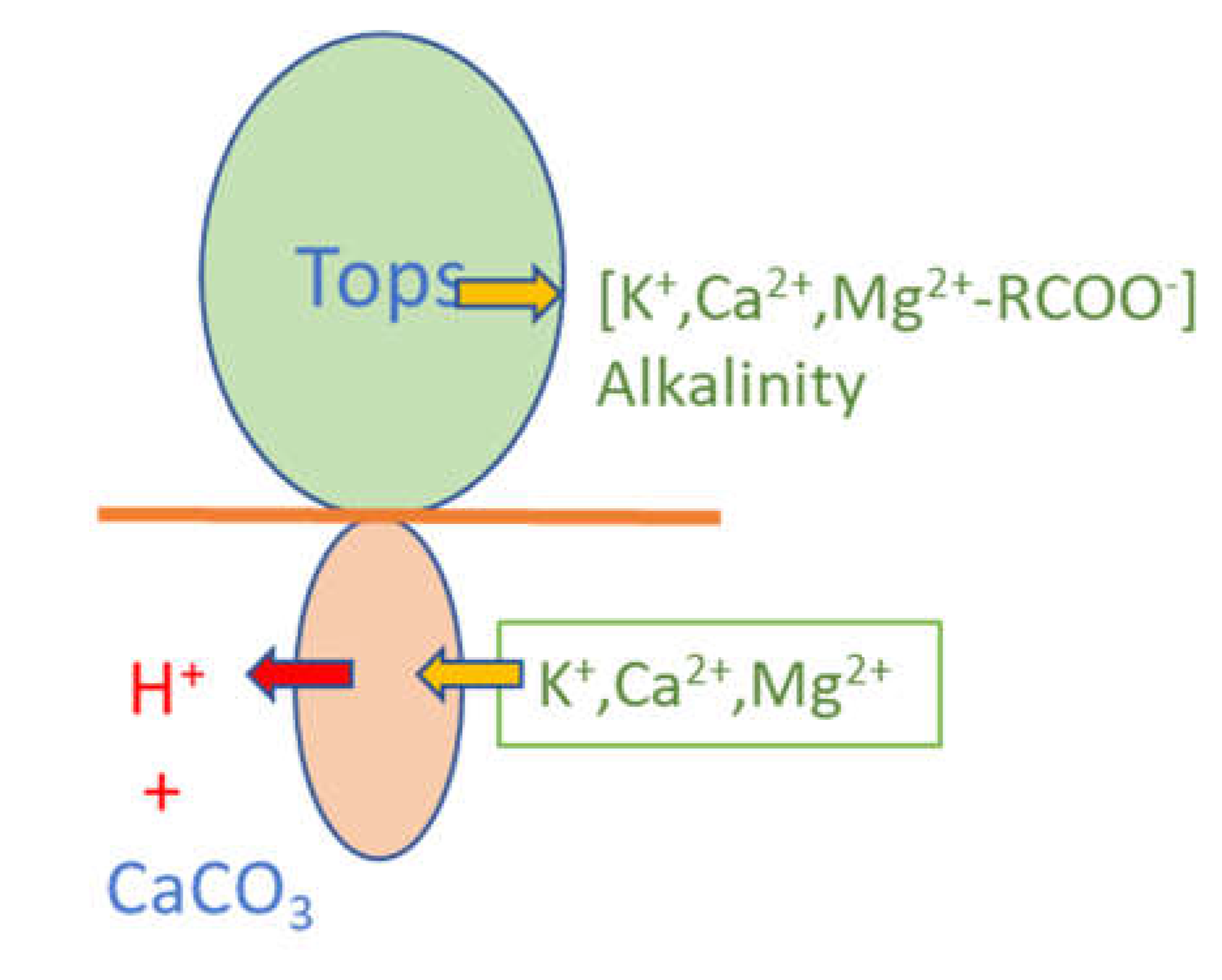
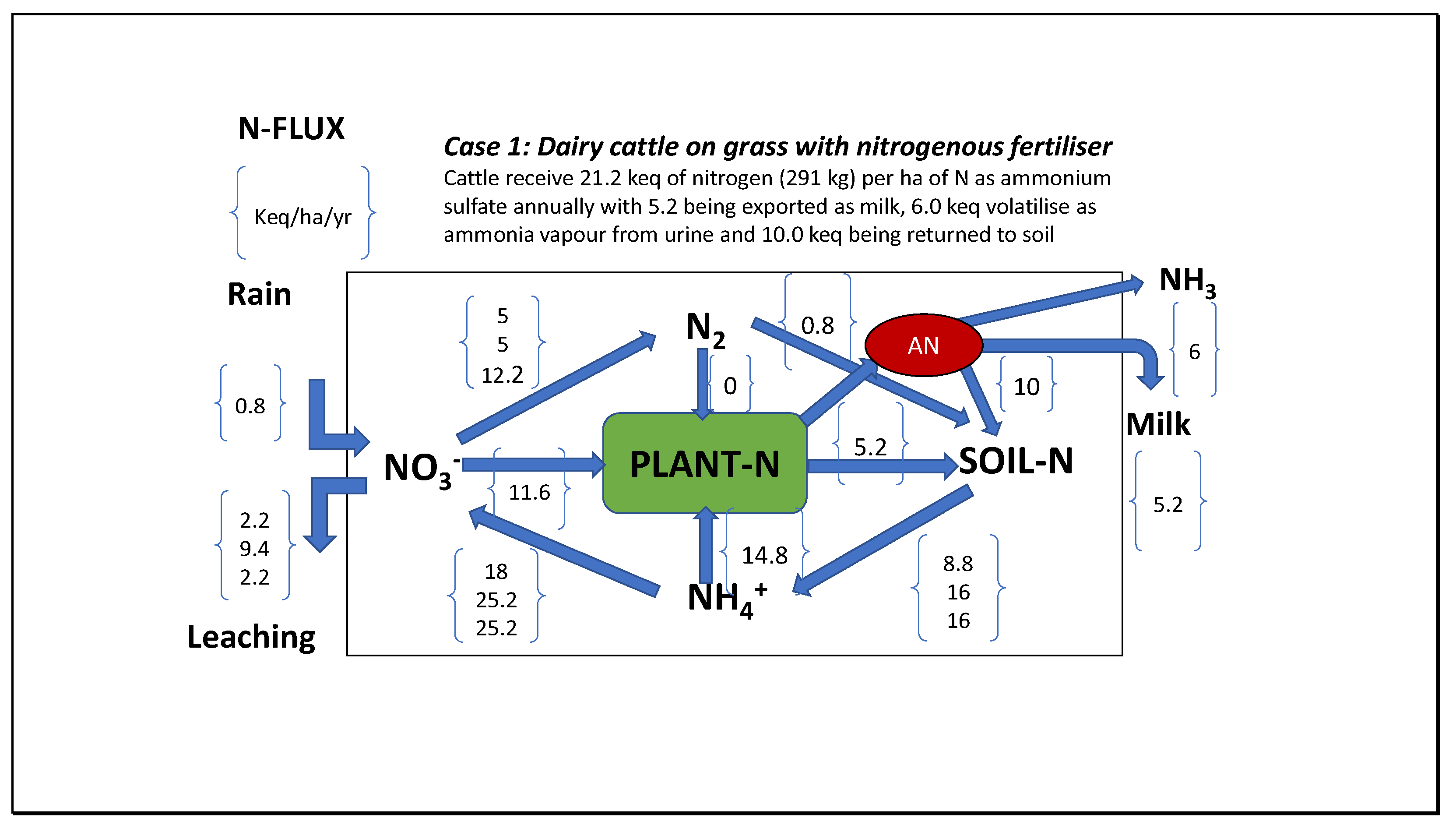
Year	ppmv.	Moles atmospheric CO₂/m²	Increase moles/m²	Total global atmospheric CO₂ Teratonnes (10¹²)
1750	280	95.61	0	2.1459
2015	400	140.00	44.390	3.1422

510.1 million km² global surface area; 148.326 million km² land area. The Earth’s atmosphere weighs about 5x10²¹ g or 1.7x10²⁰ moles of gas averaging 29 Daltons per molecule, with CO₂ shown as 400 ppmv by molecular proportion, not by weight, a factor 0.659 less, Trenberth and Smith [18].

Table 2. Anthropogenic CO₂ emissions from acidification of bicarbonate by oxidised sulphur in fossil fuels.

Fuel	Tonnes	Gram CO₂	Moles C	Moles S (5%)	Moles SO₂/m²	Total acidic moles CO₂/m²
Total global CO₂ emissions since 1750	2.5x10¹²	2.5x10¹⁸	5.682x10¹⁶	1.065x10¹⁵	2.130	4.26
Annual CO₂ emissions Statistica^TM 2020	3.7x10¹⁰	3.68x10¹⁶	8.364x10¹⁴	1.55x10¹³	0.032*	0.06

https://www.statista.com/statistics/264699/worldwide-co2-emissions/. Earth is 510.1 million km² global area; *in 2021 for 150 moles/m² as 420 ppmv, multiply moles SO₂ increase by 6.0 to estimate increased ppmv; 5.101x10¹⁴ m² global land area.

Table 3. Equilibrium concentrations of DIC modelled in seawater (S=35) and in fresh land water (S=0.35) at given pH values and salt concentrations (temperature 288 K, pCO2=420 ppmv).

Salt (NaCl ‰)	35	35	35	35	0.35	0.35	0.35	0.35
pH	8.2	7.2	6.2	5.2	8.2	7.2	6.2	5.2
[CO₂] μM = a	15.8	15.8	15.8	15.8	19.2	19.2	19.2	19.2
[HCO₃^-] μM = b	2930.2	293.0	29.3	0.93	1924.7	192.5	19.2	1.92
[CO₃^2-] μM = c	352.1	0.35	0.0004	0.000	74.3	0.07	0.001	0.000
[HCO₃^-]/[CO₃^2-]	8.27	82.7	827.4	8274.4	25.7	257.5	2574.9	25749.1
C=a+b+c μM	3298.1	312.3	45.1	16.7	2018.2	217.4	38.4	21.12

Computed using the CO2TIT4 program given in Table S5 in Supplementary Materials.

Table 5. Summary of sources of global annual atmospheric CO₂ emissions.

Acidifying process	Moles of global strong acid production	Moles of CO₂ increase (meq/m²)	Statistical confidence
Increase in atmospheric CO₂ (2021)		664.0	Strong
Sources of strong acid production	Sulphuric, nitric	, protons
Fossil fuels (2% fossil CO₂ moles untrapped SO₂)	32.8x10¹²	64.0±10	Moderate
Acidification from agriculture and forestry	37.5x10¹²	78.4±10	Moderate
Increasing wildfire acidification S and N	44x10¹²	64.0±20	Low
Anaerobic sulphate respiration, H₂S, DMS	25x10¹²	98.0±20	Low
Mining exposure, refining metal, sulfides, pyrites	10x10¹²	20.0±50	Low
Total decrease in alkalinity from strong acids	197x10¹²	324.4±110	Approximate

Table 6. Ash alkalinity of farm produce exported and resultant acidification.

Product exported	Ash alkalinity mmoles H⁺/kg	CaCO₃ equivalent kg/tonne	Estimated limestone kg/ha	H⁺ per m² per crop
Lamb	340	17	1700 (1 t/ha)	0.34
Milk	80	4	400 (1 t/ha	0.08
Clover	822	41	41,100 (5t/ha)
Lucerne	1203	60	60.000 (10t/ha)	6.00
Wheat	184	9	9,000 (5t/ha)	0.90
Lupin	404	20	20,000 (5 t/ha)	2.0

Data recalculated from Slattery et al. [36].

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer