Prerpints.org logo
Preprint
Article

Modelling of Real Gas Compression Using the Finite Volume Thermofluid Network Methodology and Mean-Line Approach for Centrifugal Compressors

Altmetrics

Downloads

141

Views

59

Comments

0

This version is not peer-reviewed

Enhanced Heat Transfer and Advanced Energy Conversion Technology

Submitted:

25 March 2024

Posted:

27 March 2024

You are already at the latest version

Alerts
Abstract
A novel compressible real gas 1D finite volume thermofluid network modelling methodology is proposed that can be applied in the analysis of supercritical CO2 (sCO2) power cycles. It is applied to simulate centrifugal compressor performance via a mean line approach that directly solves the mass, energy, and momentum balance equations for the discretized flow channels within the machine along with the associated loss models, component characteristics, and applicable compressible real gas equation of state. This can be integrated seamlessly with the rest of the power cycle components like pipes, valves, heat exchangers, etc., thereby eliminating the need for static performance maps and the associated difficulties to ensure similarity over the whole range of operation. This direct simulation of the internal flows also makes it possible to do integrated cycle design optimization that includes the geometry of the compressors, and to simulate fast transients for dynamic analysis. The methodology was applied to simulate well-documented air and sCO2 centrifugal compressors and compared the generated results with that of conventional thermofluid network incompressible and compressible ideal gas approaches. The results indicate that the proposed compressible real gas approach can capture the stagnation pressure changes and isentropic efficiencies with good accuracy for both cases over the whole range of mass flow rates and shaft rotational speeds. In contrast, the conventional thermofluid network incompressible and compressible ideal gas approaches are only applicable in selected regions of the fluid property regime and suffer from discretization errors and inappropriate treatment of the relationship between stagnation and static pressures. Furthermore, comparative analyses between the newly proposed approach and the traditional mechanical energy balance method are performed, showing that the latter approach needs to be discretized more finely through the compression process to correctly capture the polytropic compression path shape, whereas the former more accurately captures the stagnation pressure changes through the analyzed compressors with only a single increment per compressor component.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Simulation plays an important role in the design, analysis, and control of complex thermofluid systems such as aircraft gas turbines and power plants. Many thermofluid systems, specifically power generation plants, consist of numerous interconnected devices such as compressors, pipes, valves, and heat exchangers [1] all significantly varying in characteristics and size. To perform time-dependent or multiple successive steady-state three dimensional (3D) simulations of such complex interconnected energy systems using computational fluid dynamics (CFD) requires prohibitive computational resources [2]. A well-established approach to efficiently simulate these large energy systems is using the thermofluid network methodology. This methodology is based on the finite volume procedure of solving the discretized mass, energy, and momentum balance equations on a network structure consisting of nodes and one dimensional (1D) flow elements (branches), as opposed to cell volumes and faces traditionally used in CFD. Due to the usefulness of the thermofluid network approach a series of commercial and research codes have been released in recent years such as Flownex SE [3], GFSSP (Generalized Fluid System Simulation Program by NASA) [2], AxSTREAM System [4] and APROS [5]. The extensive utilization of the thermofluid network modelling approach can be observed in the development of next generation energy technologies such as pebble-bed nuclear reactor cycles [6,7] and supercritical carbon-dioxide (sCO2) Brayton power cycles [8,9].
When integrated thermofluid network simulations of sCO2 cycles are performed, static maps are typically used for the turbomachinery as a simplified simulation method, since the fluid inertia of the machines is significantly faster than that of the heat exchangers [10]. The utilization of static maps does not provide a direct simulation of the internal flows and dynamic behavior through the machines. Therefore, the approach using static maps cannot be applied when performing integrated cycle design optimization [11,12,13] which includes machine dimensions such as impeller diameters and vane angles as independent design parameters, or when the fast transient response [14] of the turbomachinery systems is to be investigated. Furthermore, the conventional scaling rules based on corrected mass flow and corrected speed on which static maps are based do not necessarily ensure similarity in the case of sCO2 [15]. To mitigate this, one can directly solve the mass, energy, and momentum balance equations [16] for the discretized flow channels within a turbomachine along with the associated loss models [17], component characteristics (velocity triangles), and applicable equation of state (ideal gas or real gas). Such turbomachine models could be integrated seamlessly with the rest of the cycle components like pipes, valves, heat exchangers, etc., thereby eliminating the need for static performance maps.
When applying the thermofluid network method to solve the balance equations, it is convenient to directly solve for the stagnation conditions at the nodes using the network implicit pressure correction method (IPCM) [7,18]. This enables the use of zero-dimensional (0D) nodes to represent flow junctions and splits, which eliminates the need for two-dimensional (2D) flow elements [19] to describe these bifurcations in the flow network. The energy balance equations at the nodes are therefore written in terms of stagnation enthalpy rather than static enthalpy, and the momentum balance equations are written in terms of stagnation pressure rather than static pressure. Suitable formulations must be provided to derive the values of stagnation enthalpy from the static enthalpy and stagnation pressure from the static pressure, and vice versa, since other fluid properties are dependent on the static enthalpy and static pressure. These formulations describe the fictitious isentropic process taking place between the stagnation and static conditions at the network nodes and are not the same for compressible ideal gases and compressible real gases. The derivation of the momentum balance equation is also not independent of the choice of equation of state. The final form of the equations that must be solved therefore depends on whether the fluid is assumed to be incompressible liquid, compressible ideal gas, or a two-phase flow mixture. Therefore, the formulation of the balance equations for the real gas thermofluid network approach to model turbomachinery, requires careful consideration.
A challenge encountered in the analysis of sCO2 power cycles is that the real gas effects should be correctly accounted for in process-level (1D) mean line simulations [20], especially when operating close to the critical point where the deviation from ideal gas theory is significant. The conventional approach found in the literature [9,21,22,15] to calculate the stagnation pressure rise in a real gas (sCO2) centrifugal compressor is to calculate the exit stagnation enthalpy as the difference between the inlet stagnation enthalpy, the shaft work and lost work, at constant entropy. This relation can also be thought of as the mechanical energy balance across the entire turbomachine [23] where the reversible work is equated to the difference between the shaft work and lost work. To find the compressor exit stagnation pressure, the mechanical energy, mass, and the thermodynamic energy balance equations are implicitly solved along with the required thermodynamic property relations and component characteristics. Although this approach of performing a mechanical energy balance for the entire compression process yields reasonable accuracy at low pressure ratios and rotational speeds, it does not account for the polytropic compression path shape and fails to consider the effect of diverging pressure iso-lines of the T-s and Mollier diagrams. Moreover, it only uses the inlet thermodynamic conditions of the compressor along with the shaft and lost work to find the pressure rise [24]. Therefore, the mechanical energy balance method does not correctly consider the effect of increasing entropy and temperature on the compression process. This leads to an overprediction of pressure rise and machine efficiencies in centrifugal real gas compressors at high pressure ratios. To address this error, Aungier [25] proposed a correction factor that should be applied to the sum of the machine enthalpy losses (lost work) for ideal gas centrifugal compressors operating at high pressure ratios. Alternatively, for real gas machines, the compression process path should be discretized into sequential small-step compression processes, and the mechanical energy balance equations solved for these incremental steps [24] to ensure that the correct stagnation pressure and machine efficiency is found. With regards to the 1D finite volume thermofluid network approach, partial workarounds to model real gas compression exist in industry, but to the best of the authors’ knowledge a suitable formulation of the momentum balance equation for the IPCM network method using real gas properties has not been proposed in literature. It should be noted, one can conduct computational fluid dynamics (CFD) simulations of the compressors, which accurately consider the interactions among fluid flow, energy transfer, and lost work, as demonstrated in the research by Toni et al. [26] and Hosangadi et al. [27]. However, the drawback of CFD lies in the high computational costs associated with iterative calculations common in turbomachinery design. This is where accurate process-level mean line analysis tools which accounts for real gas effects are typically useful and commonly employed.
In the present work, a 1D finite volume thermofluid network modelling approach using the IPCM will be presented that can solve various types of fluid flow scenarios including incompressible, compressible ideal gas, and compressible real gas, including operation close to the critical point. The methodology will be demonstrated and validated by applying it to the well-documented Eckardt air centrifugal compressor [28], as well as the Sandia National Laboratories (SNL) [29] sCO2 centrifugal compressor experimental datasets at different shaft speeds. For these two case study compressors, the results of the newly proposed real gas thermofluid network method will be compared to those obtained using traditional incompressible and compressible ideal gas thermofluid network formulations, to highlight the generalizability of the newly proposed method. Additionally, the results obtained from the newly proposed method will also be compared to the conventional single-step mechanical energy method, commonly used in literature for sCO2 compressors, to highlight the importance of accounting for the polytropic compression path shape at high rotational speeds and compression ratios. The simulations performed in the current work were developed using the Python 3.9.12 programming language along with the opensource NumPy, SciPy, Pandas and CoolProp packages.

2. Materials and Methods

2.1. Finite Volume Thermofluid Network Methodology Balance Equations

The thermofluid network methodology entails the simultaneous solution of the 1D forms of the mass, energy, and momentum balance equations. The closure equations for the balance equations include models for the component specific characteristics such as the rate of heat transfer, power, frictional pressure drop, or pressure rise due to work input. The network method discretizes a flow system into nodes and elements. The elements are control volumes representing components such as pipes, heat exchangers, or compressors in the fluid system. Each element has only one inlet and one outlet and fluid properties in the element are assumed to be taken as some weighted average between the inlet and outlet values. The nodes in the network represent connection points between elements and have multiple inlets and outlets with the fluid properties assumed to be uniform within the node. The mass and energy balance equations are solved for each node in the network, whereas the momentum balance equation is solved for each element in the network.
The differential form of the 1D steady-state mass, energy and momentum balance equations are given by
∂ ( ρ u ) ∂ x = 0
∂ ( ρ u ( h + 1 2 u 2 + g z ) ) ∂ x = q ‴ − w ‴
∂ ( ρ u u ) ∂ x = − ∂ p ∂ x − ρ g ∂ z ∂ x + ∂ p 0 , W ∂ x − ∂ p 0 , L ∂ x
In Equations (1)–(3), ρ is the fluid density, u is the fluid velocity, x is the 1D spatial dimension, h is the static fluid enthalpy, g is the gravitational acceleration constant, z is the elevation, q ‴ is the volumetric heat transfer rate to the fluid control volume from its surroundings, w ‴ is the volumetric work exertion by the fluid on its surroundings, p is the fluid static pressure, p 0 , W is the total pressure rise due to work done on the fluid, and p 0 , L is the total pressure loss. Using the chain rule together with the differential form of the mass balance equation, and neglecting the elevation term, Equation (4) can be written as
ρ u ∂ u ∂ x = − ∂ p ∂ x + ∂ p 0 , W ∂ x − ∂ p 0 , L ∂ x
The spatially integrated mass and energy balances that are solved for each node in the network are given by Equations (5) and (6), while ignoring the potential energy term.
∑ m ˙ e − ∑ m ˙ i = 0
∑ m ˙ e h 0 , e − ∑ m ˙ i h 0 , i = Q ˙ − W ˙
In the above equations, m ˙ is the mass flow rate and the subscripts e and i indicate the flows into and out of the node respectively. For the energy balance equation, Q ˙ is the heat transfer rate into the fluid elements flowing into the node, h 0 is the stagnation enthalpy and W ˙ is the power (work rate) exerted by the fluid elements flowing into node on its surroundings. For a compressor element W ˙ < 0 , while for a turbine element W ˙ > 0 .
In Equation (7), the fundamental definition of stagnation enthalpy is used, namely
h 0 = h + 1 2 u 2
which is valid for incompressible fluids, compressible ideal gases, and compressible real gases.
As mentioned previously, the network IPCM method solves the stagnation pressures, and Equation (4) should be cast accordingly. We therefore need to find the appropriate formulation for stagnation pressure as a function of static pressure for compressible real gas applications, which will be different from those for ideal gases or incompressible fluids. Knowing that T d s = d h − ( 1 / ρ ) d p for all fluids, we may characterize any isentropic process by d p = ρ d h . Therefore, we integrate between the static and stagnation states as follows:
∫ p p 0 d p = ∫ h h 0 ρ ( p , h ) d h
In the case of compressible real gases, the density will not remain constant between the stagnation and static states, and since we cannot apply the ideal gas assumption, the density cannot be expressed in simple form to enable direct integration. We circumvent this difficulty by adopting a constant value for the density while ensuring that we assign the appropriate mean value between the stagnation and static states. We therefore define the mean stagnation density ρ s as shown in the equation below, where the subscript s implies an isentropic process.
ρ s = [ p 0 − p h 0 − h ] s
Given this, the real gas stagnation pressure can be expressed in terms of static pressure as follows:
p 0 = p + ρ s ( h 0 − h ) = p + 1 2 ρ s u 2
In the application of the network methodology the value of the mean stagnation density in each node can be obtained with the sequence provided in Equation (11) as follows: (i) determine the entropy at the stagnation conditions using the known values of stagnation enthalpy and stagnation pressure with the aid of a suitable real gas fluid property library (such as CoolProp); (ii) determine the static enthalpy from the stagnation enthalpy and the velocity; (iii) obtain the static pressure using the known values of static enthalpy and entropy (which is the same value as at the stagnation conditions) with the aid of a suitable real gas fluid property library; (iv) determine the value of the mean stagnation density from Equation (11).
s = f ( h 0 , p 0 ) →   h = h 0 − 1 2 u 2 →   p = f ( s , h ) →   ρ s = p 0 − p h 0 − h
The formulation of the momentum balance Equation (4) may now be manipulated for compressible real gases as follows:
∂ p ∂ x + ρ u ∂ u ∂ x = ∂ p 0 , W ∂ x − ∂ p 0 , L ∂ x ∂ p ∂ x + 1 2 ρ ∂ u 2 ∂ x + 1 2 ∂ ( ρ s u 2 ) d x − 1 2 ∂ ( ρ s u 2 ) d x = ∂ p 0 , W ∂ x − ∂ p 0 , L ∂ x ∂ ( p + 1 2 ρ s u 2 ) ∂ x + 1 2 ρ ∂ u 2 ∂ x − 1 2 ∂ ( ρ s u 2 ) d x = ∂ p 0 , W ∂ x − ∂ p 0 , L ∂ x
and then expressed in terms of stagnation pressure as
∂ p 0 ∂ x + 1 2 ρ ∂ u 2 ∂ x − 1 2 ∂ ( ρ s u 2 ) ∂ x = ∂ p 0 , W ∂ x − ∂ p 0 , L ∂ x
For a one-dimensional fluid control volume with a well-defined single inlet (i) and single outlet (e) Equation (13) can be integrated to get
p 0 , e − p 0 , i + 1 2 ρ a v g ( u e 2 − u i 2 ) − 1 2 ( ρ s , e u e 2 − ρ s , i u i 2 ) = Δ p 0 , W − Δ p 0 , L
where ρ a v g is the average density inside the fluid element, Δ p 0 , W is the total pressure rise due to the work input, and Δ p 0 , L is the total pressure drop due to lost work, i.e., irreversibilities. Note that for a compressor Δ p 0 , W > 0 and for a turbine Δ p 0 , W < 0 , while we always have Δ p 0 , L > 0 .
The simultaneous solution of (5) and (6) for each node and (14) for each element in the network, together with appropriate boundary conditions will yield the nodal stagnation pressures and enthalpies as well as the elemental mass flow rates. Following this the static properties can be obtained from equation (11), which can then be used to determine all the other fluid properties with the aid of a suitable real gas fluid property library. Once all the fluid property values are known for the nodes, the appropriate mean values can also be determined for the elements, which in turn can be used in the calculation of the component characteristics ( Δ p 0 , W , Δ p 0 , L , Q ˙ and W ˙ ), which are required as inputs to the solution of the energy balance and momentum balance equations. For the current work this compressible real gas approach will be designated as M1.
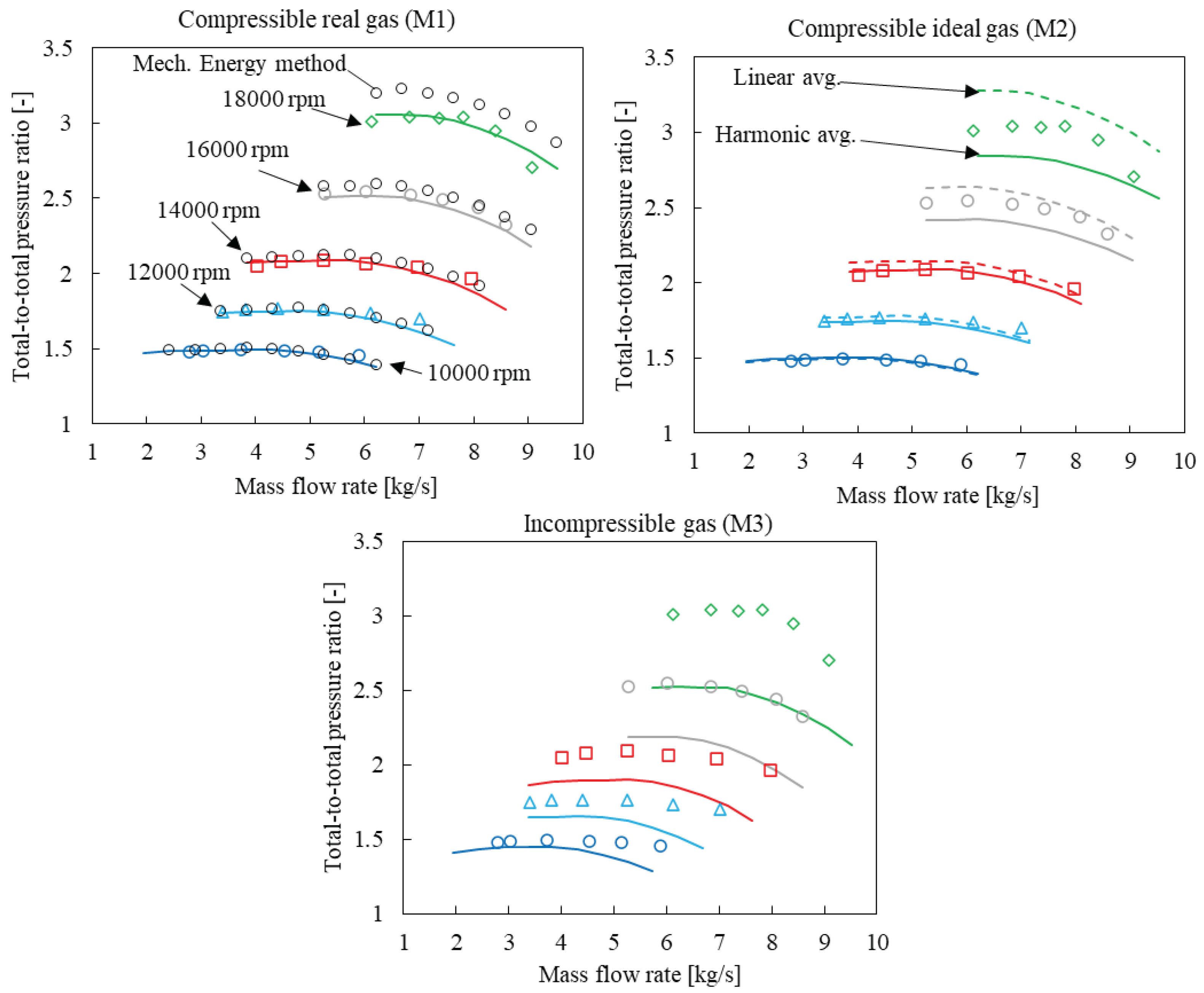
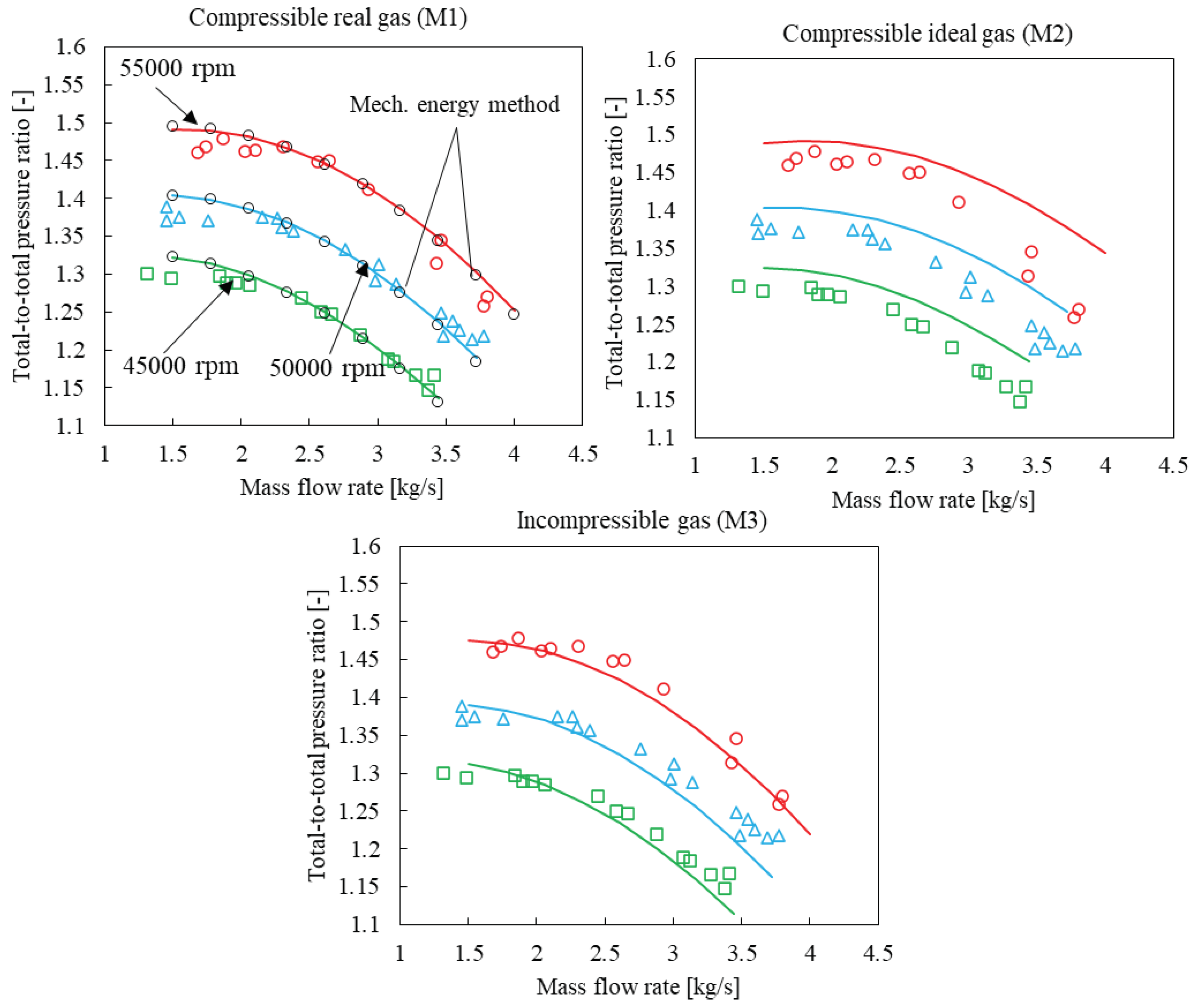
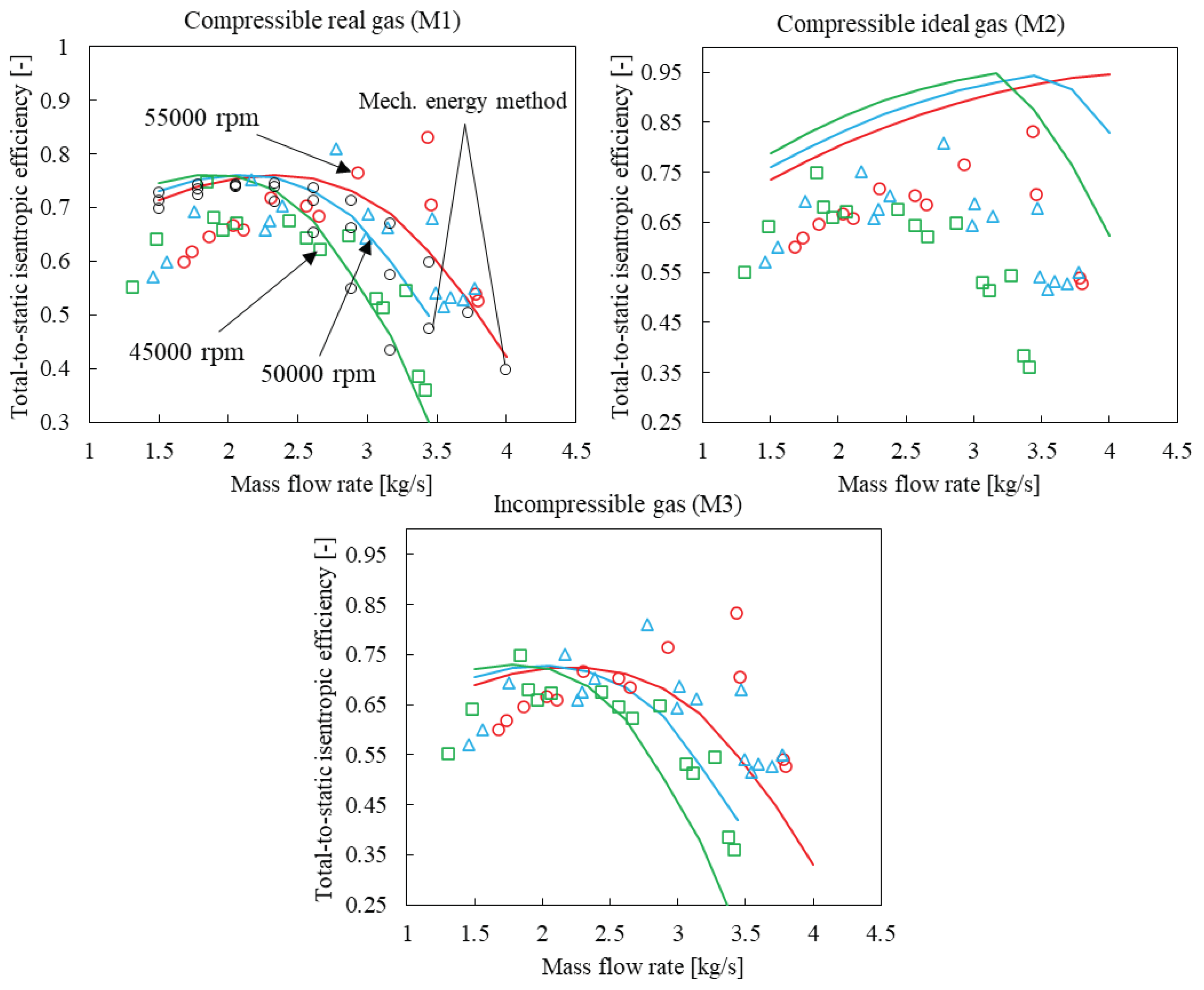
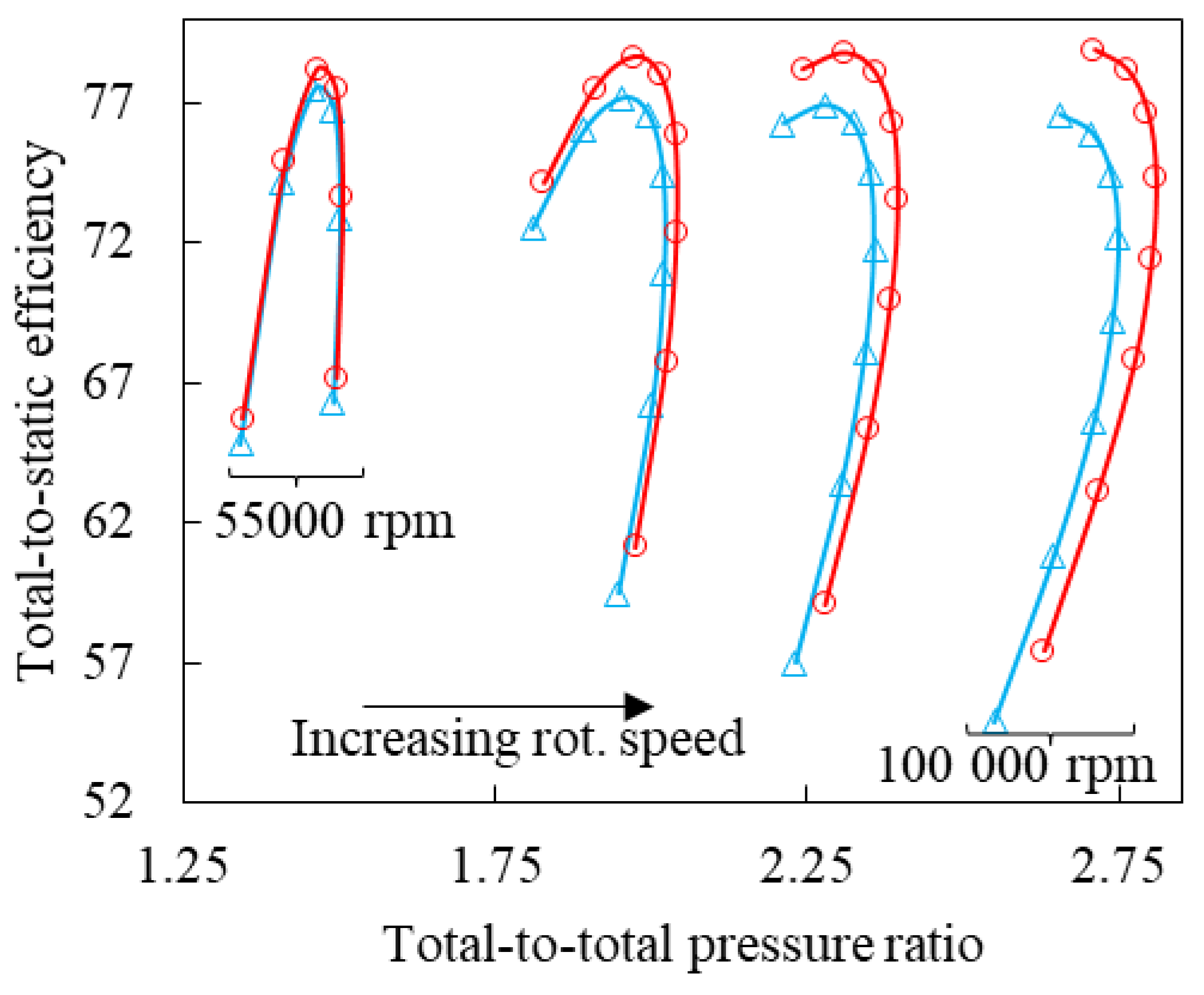
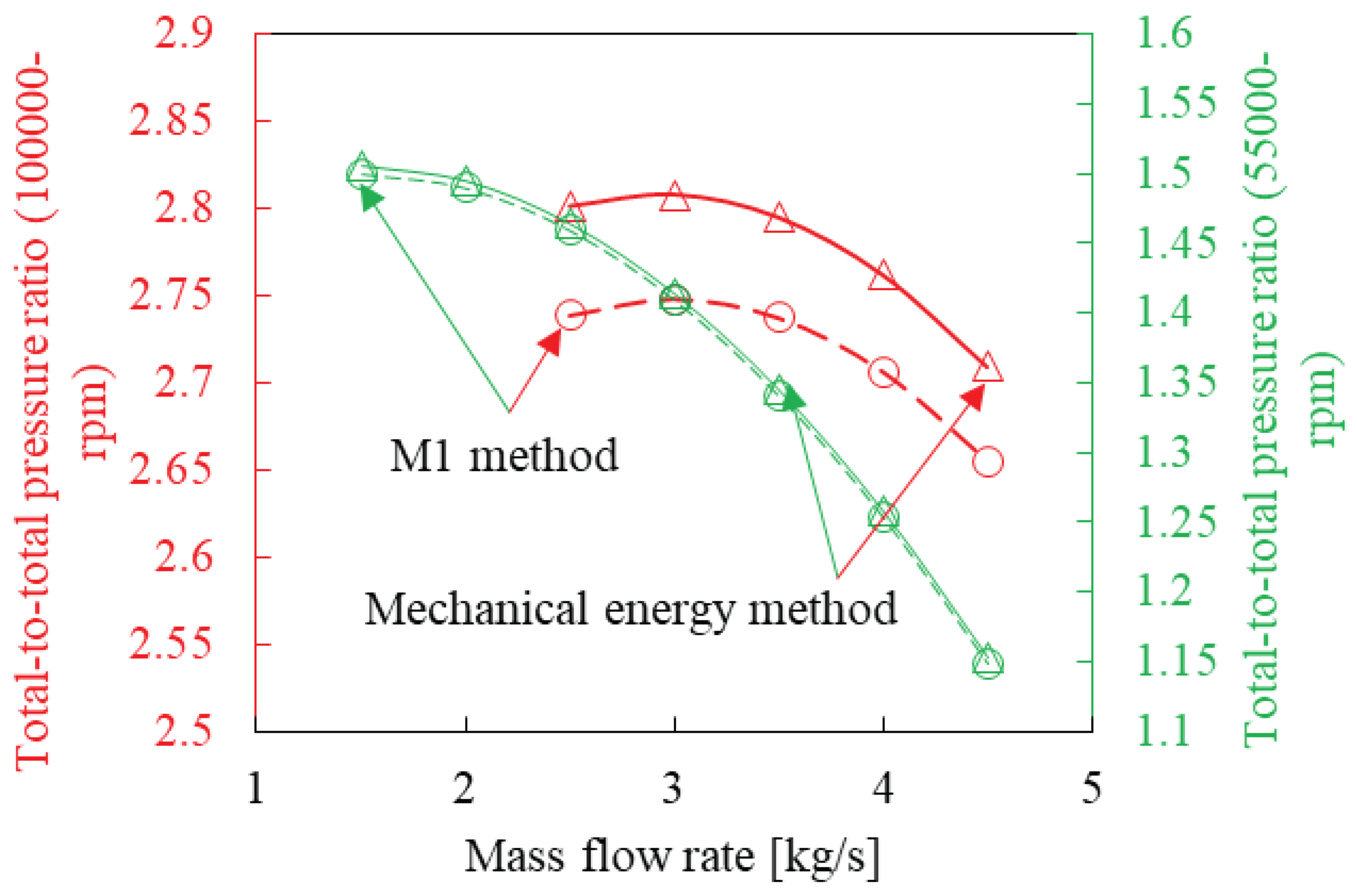
To showcase the accuracy and benefits of this approach, the results for the SNL and Eckardt compressors will not only be compared to experimental data but also to results generated with the conventional incompressible and compressible ideal gas thermofluid network IPCM approaches.
The compressible ideal gas approach is designated M2. It is based on the same mass and energy balance equations used in M1. The discretized integral momentum balance equation for M2 is given by [30]
p a v g p 0 , a v g ( p 0 , e − p 0 , i ) + 1 2 ρ a v g u a v g 2 1 T 0 , a v g ( T 0 , e − T 0 , i ) = Δ p 0 , W − Δ p 0 , L
In the above equation, T 0 is the stagnation temperature of the fluid and is evaluated using the stagnation pressure, stagnation enthalpy and the fluid property database. To find the static pressure using the stagnation pressure the conventional isentropic perfect gas relation between static and stagnation pressure and temperature, covered in many textbooks, can be used. Close to the critical point of a fluid, as is the case for the SNL sCO2 compressor, the variation in fluid properties is highly non-linear with pressure and enthalpy and the behavior of the fluid is non-ideal. Therefore, applying the ideal gas law to calculate the nodal densities will result in values far below the actual values. For example, the actual SNL compressor inlet density is approximately ∼ 590   k g m 3 , whereas the density calculated using the ideal gas law and corresponding inlet temperature and pressure is approximately ∼ 100   k g m 3 . These underpredictions of density have a detrimental effect on the model to calculate the correct fluid velocities and other fluid properties. Therefore, to generate reasonable results using the SNL compressor M2 model, the CoolProp fluid property database is used to calculate the required fluid properties such as ρ , T , T 0 and γ using the predicted velocities and stagnation conditions. To estimate the static pressure from the stagnation pressure the well isentropic ideal gas relation will be used, p 0 / p = ( T 0 / T ) γ / γ − 1 .
The conventional incompressible IPCM approach is designated M3. The fluid is assumed to be weakly compressible, therefore, density is only a function of the local thermodynamic conditions. M3 also employes Equations (5) and (6) for the mass and energy balances respectively. The discretized integral momentum balance equation for M3 is given by [3]:
p 0 , e − p 0 , i = Δ p 0 , W − Δ p 0 , L
For the incompressible approach, the relationship between stagnation pressure and static pressure is governed by p 0 = p + 1 2 ρ u 2 .
In Equations (14) and (15) various mean values of fluid properties are required such as p 0 , a v g , T 0 , a v g and ρ a v g . Since the velocity and property distributions through a centrifugal compressor are not linear, the harmonic mean values are utilized. For example, the mean density is calculated as follows:
ρ a v g = [ 1 2 ( 1 ρ i + 1 ρ e ) ] − 1
By solving the mass(5), energy (6) and momentum balance equations [(14) or (15) or (16)] for the compressor impeller and downstream components such as the vaneless space, the mass flow rates, stagnation enthalpy changes and stagnation pressure changes through the system can be calculated.

2.2. Mechanical Energy Equation Approach to Estimate Compressor Stagnation Pressure Rise

The reversible work produced by a working fluid undergoing a thermodynamic process can be written in the mechanical energy form as Δ w r e v = Δ w + ∑ Δ h L [23], where Δ w r e v is the reversible work produced by the fluid, Δ w is the actual work produced by the working fluid, which in the case of a compressor is the Euler work, and ∑ Δ h L is the lost work due to aerodynamic losses such frictional pressure drop. The mechanical energy equation can be used to estimate the stagnation pressure at the outlet of the compressor by replacing the reversible work term with the change in isentropic stagnation enthalpy as shown in equation (18). In the below equation, h 0 s , e ( s , p 0 ) is the element exit isentropic stagnation enthalpy based on the inlet entropy, s i , and outlet stagnation pressure, p 0 , e .
h 0 s , e ( s i , p 0 , e ) = h 0 , i ( s i , p 0 , i ) − Δ w − ∑ Δ h L
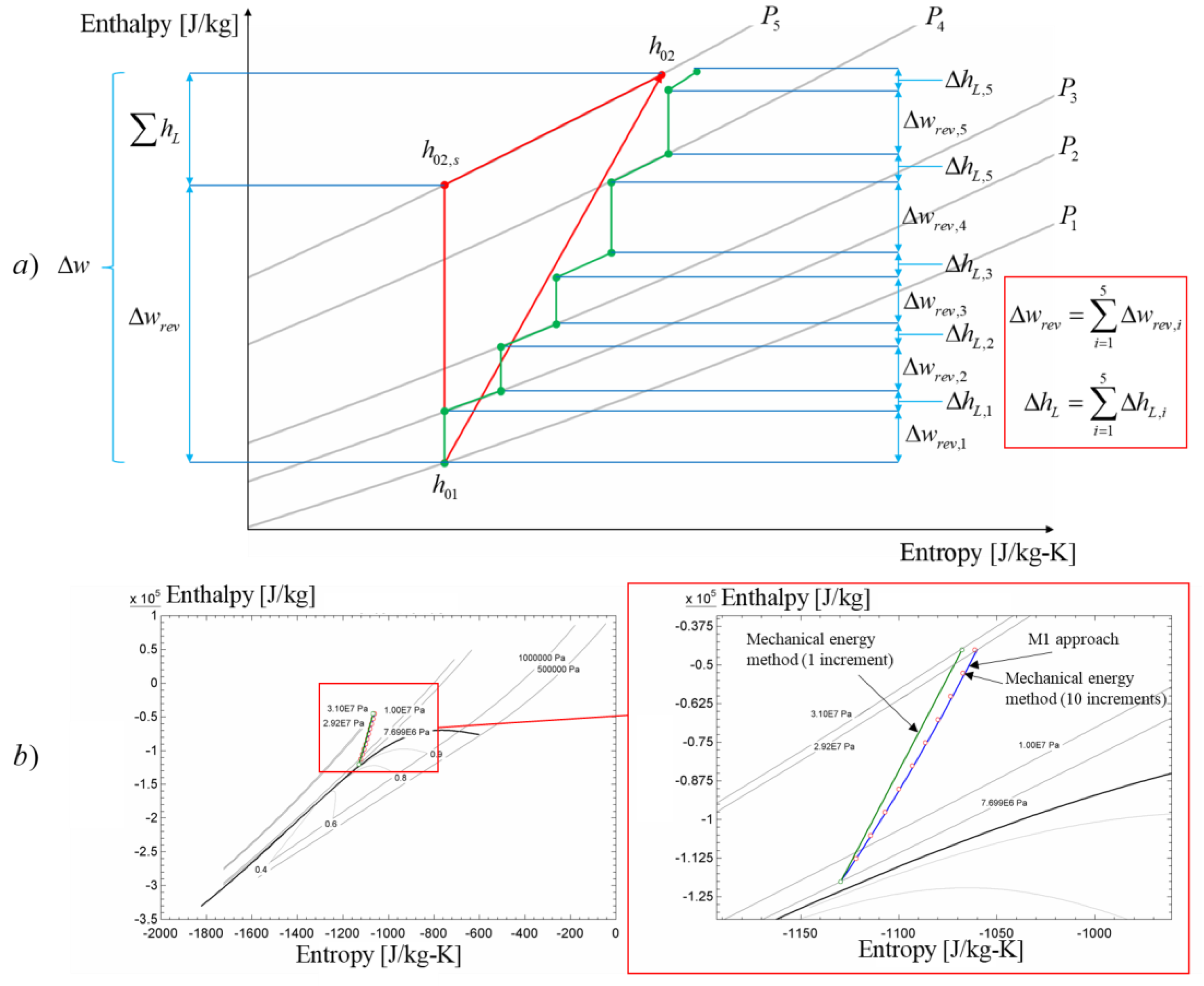
The application of Equation (18) to estimate compressor outlet pressure, for high pressure ratios, using only the inlet thermodynamic conditions of the compressor would lead to significant overprediction, due to the fact that the polytropic compression path shape was not taken into consideration. The shape of the polytropic path on the T-s diagram which illustrates the temperature and entropy increase during compression, can significantly influence the amount of pressure rise for specified amounts of actual work, Δ w , and lost work, ∑ Δ h L . This occurs because as the fluid undergoes compression, the temperature increases due the dissipation of lost work, which in turn increases the compression work requirements. Consequently, the pressure gain diminishes for a given amount of reversible work. This phenomenon can also be observed in the divergence of pressure iso-lines on T-s and Mollier diagrams as entropy increases. Hence, if Equation (18) is applied to a real gas compressor operating at high pressure ratios, it only accounts for the inlet thermodynamic conditions ( s i , p 0 , i ) when calculating the exit stagnation pressure, neglecting the effects of entropy and temperature increase along the polytropic path. To circumvent this shortcoming of the mechanical energy method, the compression process can be discretised into multiple small-step compression processes and Equation (18) applied to each step, thereby accounting for the effect of temperature and entropy increases along the compression path. This is illustrated in the sketch shown in Figure 1a, where the compression process using both single-step and multi-step mechanical energy methods is depicted on the Mollier diagram. As shown in Figure 1a, the total amount of lost work and reversible work remains constant between the single- and multi-step variations. However, due to the diverging pressure iso-lines, a lower final pressure is achieved at an increased entropy value. Aungier [25] mentioned that not accounting for the entropy increase would result in significant overprediction of pressure ratios and therefore under designing of the compressor. To correct this Aungier proposed the use of an ideal gas pressure rise correction factor which works well up to pressure ratios of 3.5.
To demonstrate the effect of not capturing the correct polytropic path shape using the single-step mechanical energy method and only the compressor inlet conditions, as applied by many researchers in the literature, a numerical experiment simulating a toy compression process is conducted. For this numerical experiment, the results generated using the single step mechanical energy method, the M1 approach and the multi-step mechanical energy method are compared. The experiment consists of a single small conduit supplied by CO2 at inlet conditions of 35 ⁰C and 7.687 MPa. Constant specific work of 75 kJ/kg is supplied to the fluid while the lost work is set to a constant value of 25 kJ/kg. Figure 1b shows the results for this toy problem on the CO2 Mollier diagram. The results show that the exit stagnation pressure predicted by the single step mechanical energy method (1 increment) is 31 MPa, whereas the M1 approach and the multi-step mechanical energy method (10 increments) predicts exit stagnation pressures of 29.26 MPa and 29.38 MPa respectively. The relative percentage difference between the results of the M1 approach and the single-step and multi-step mechanical energy methods are 6% and 0.4% respectively. As the number of increments for the multi-step approach is increased to 50, the relative percentage difference between the multi-step mechanical energy method and the M1 approach reduces to 0.1%, indicating that the multi-step method converges to the results of the M1 approach. It should be noted that the M1 approach only utilizes a single increment to model the compression process, therefore, it can be concluded that it is a numerically more robust approach compared to the mechanical energy balance method. One potential reason for the ability of the M1 approach to predict the exit stagnation pressure close to that of a multi-step mechanical energy method, with only a single step, could be that the pressure rise and drop due to actual work input and lost work respectively are included in the momentum equation, which then directly solves for the stagnation pressure change across the component.
For the remainder of the work, only the single-step mechanical energy method will be utilized for comparison with the M1 approach results. The motivation behind this decision is that a significant number of researchers are employing this approach to model sCO2 centrifugal compressors.

2.3. Component Characteristic Models

In the current work we will assume that all processes through the compressor are adiabatic, i.e., Q ˙ = 0 . However, a crucial part of the analysis is to determine the appropriate relationship between the rate of work input to the fluid and the total pressure rise due to this work, i.e., Δ p 0 W = f ( W ˙ ) , and between the rate of lost work and the total pressure drop due to the lost work, i.e., Δ p 0 L = f ( W ˙ L ) . We start by writing the energy balance equation for steady flow through a control volume in difference form as follows:
d h + 1 2 d u 2 + g d z = δ q − δ w
Where in the above equation δ q [kJ/kg] is the incremental specific heat transfer to the fluid from its surroundings with q = Q ˙ m ˙ , and δ w [kJ/kg] is the incremental specific work done by the fluid on its surroundings with w = W ˙ m ˙ . Similarly, we write the entropy balance for steady flow through a control volume in difference form as T d s = δ q + δ w L where δ w L [kJ/kg] is the incremental specific lost work with w L = W ˙ L m ˙ , which is always positive. Inserting T d s = d h − 1 ρ d p into this entropy balance equation and then subtracting it from Equation (19) we get
1 2 ρ d u 2 + ρ g d z + d p = − ρ ( δ w + δ w L )
We now manipulate Equation (20) as follows:
1 2 ρ d u 2 + ρ g d z + d p + 1 2 d ( ρ s u 2 ) − 1 2 d ( ρ s u 2 ) = − ρ ( δ w + δ w L )
Then, inserting the definition of stagnation pressure for compressible real gases we get
d p 0 + 1 2 ρ d u 2 − 1 2 d ( ρ s u 2 ) + ρ g d z = − ρ ( δ w + δ w L )
Integrating Equation (22) over a one-dimensional fluid element between the inlet and outlet while neglecting the elevation term leads to
p 0 , e − p 0 , i + 1 2 ρ a v g ( u e 2 − u i 2 ) − 1 2 ( ρ s , e u e 2 − ρ s , i u i 2 ) = − ρ a v g m ˙ ( W ˙ + W ˙ L )
By comparing Equation (23) with the momentum balance Equation (14) we see that Δ p 0 W = − ( ρ a v g / m ˙ ) W ˙ = − ρ a v g w and Δ p 0 L = ( ρ a v g / m ˙ ) W ˙ L = ρ a v g w L . In the present work, both the Eckardt and SNL centrifugal compressor models consist of an impeller and vaneless space. Additionally, the SNL compressor has a vaned diffuser located downstream of the vaneless diffuser. For each of these sections the applicable source terms are defined below.
The net change in specific angular momentum over the impeller fluid control volume can be determined using the well-known Euler turbomachinery Equation (24), where X is the specific angular momentum, r is the radius with the subscripts 1 and 2 indicating the impeller inlet and outlet tip stations (nodes) respectively, and u θ is the absolute tangential velocity component of the fluid flow.
X = r 2 u θ , 2 − r 1 u θ , 1
A positive value of X implies a driving torque on the fluid as in a compressor, while a negative value implies a braking torque on the fluid as in a turbine. The various impeller inlet and outlet velocity components are calculated using the respective velocity triangles and the mean line method approach discussed in [31]. The Wiesner slip factor model [32] is implemented in the current work.
To calculate the required specific work input into the impeller control volume, which we will refer to as the Euler specific work, the following is applied w E u = − ω X , with ω = 2 π N 60 where N is the rotational speed of the impeller. To convert the Euler specific work to the total pressure rise the previous relation is used, Δ p 0 , W , 1 = − ρ a v g w E u where the subscript 1 refers to the impeller element.
The total internal pressure loss experienced by the fluid within the impeller element due to irreversibilities is calculated using Equation (25).
Δ p 0 , L , 1 = Δ p 0 , i n c + Δ p 0 , d i f f + Δ p 0 , b l d + Δ p 0 , s f + Δ p 0 , c l r + Δ p 0 , c h o k e + Δ p 0 , m i x
Many of the loss models found in literature express the internal impeller losses as enthalpy losses ( Δ h L ) rather than pressure losses. These enthalpy losses are transformed to pressure losses using Δ p 0 , L , i = ρ a v g Δ h L , i where the subscript i indicates the specific loss contribution, for example the incidence loss for the impeller element is Δ p 0 , i n c , 1 = ρ a v g Δ h i n c . The various empirical internal impeller loss models used for the case study compressors are shown in Table 1.
Besides the losses experienced by the fluid within the impeller element there are also parasitic losses in the flow around the impeller that require additional power input to the impeller element. The total required power input to the impeller is given by
W ˙ = m ˙ ( w E u − Δ w L , 1 )
In Equation (26), Δ w L , 1 is the combined specific work loss due to parasitic losses which consists of the disk friction, recirculation, and leakage losses for the impeller element designated with subscript 1. The values of individual specific work losses are obtained from empirical correlations. The three main sources of parasitic work considered in the current work are disk friction loss, recirculation loss and leakage loss [33]. In the present work the disk friction, recirculation and leakage losses are calculated using the approach proposed by Daily and Nece [40], Coppage et al. [36] and Aungier [34] respectively. The combined parasitic loss is expressed as Δ w L , 1 = Δ w d f + Δ w r e + Δ w l k .
For the case study compressors, the impeller is followed by a vaneless diffuser element. The vaneless diffuser inlet velocity vector and fluid properties are simply taken as the absolute velocity and properties at the outlet of the impeller element. To calculate the vaneless diffuser outlet velocity vector the conservation of angular momentum is applied [41]. The only pressure drop considered for the vaneless diffuser element is the skin friction loss, which is calculated using the hydraulic diameter and average velocity for the vaneless space [34]. The typical mean line method approach is utilized to calculate the outlet velocity vector for the vaned diffuser element given the vaned diffuser blade angles α b , 3 and α b , 4 . To estimate the stagnation pressure drop experienced by the flow through the vaned diffuser, the incidence and skin friction losses were accounted for, since these are assumed to be the dominant pressure drop mechanisms [15].

2.4. Solution Strategy

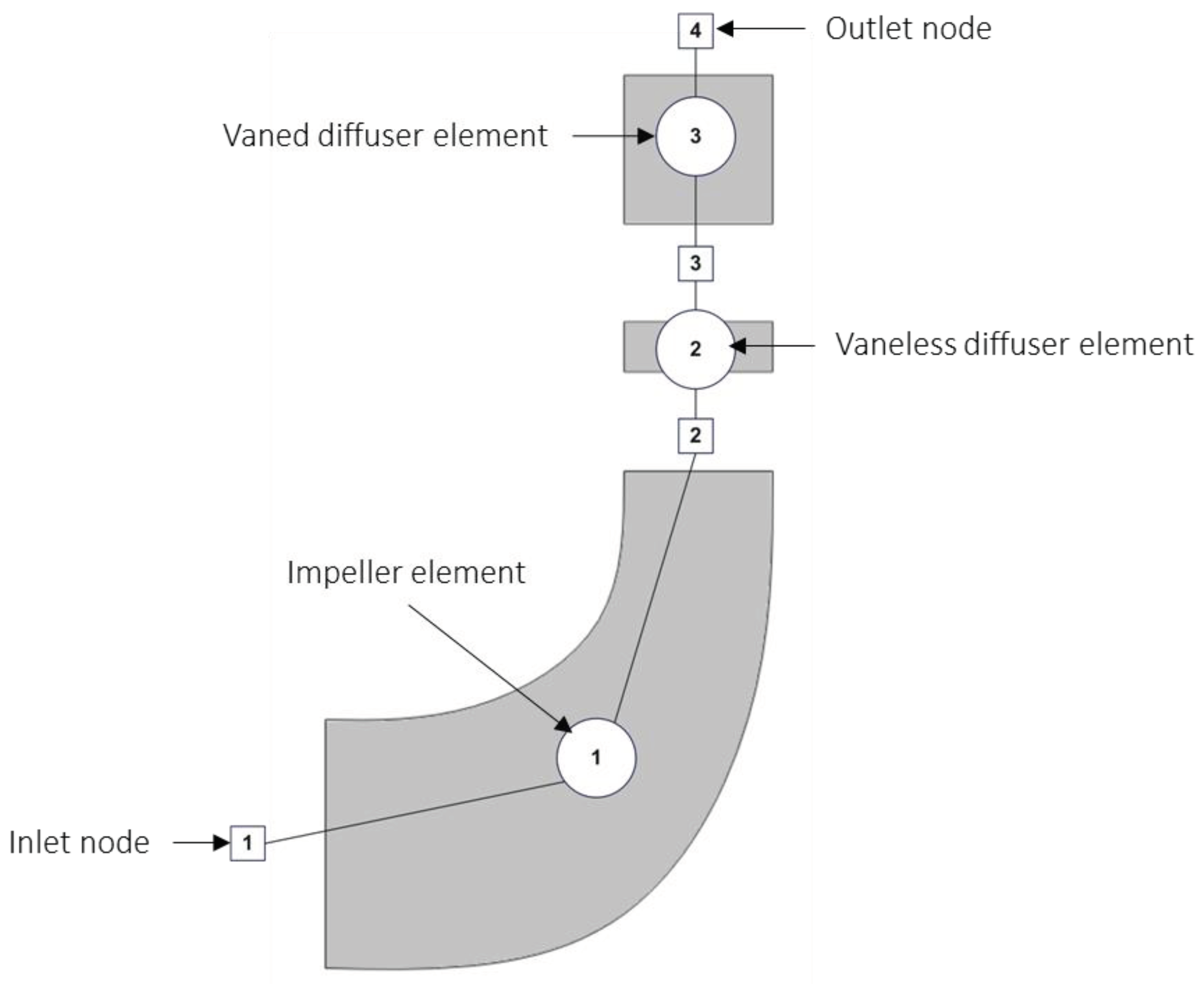
The two case study compressors both consist of three flow elements and four nodes. The three flow elements are the impeller, vaneless diffuser space and the vaned diffuser, designated elements 1, 2 and 3 respectively. The discretized thermofluid network model of the compressors is shown in Figure 2. For the Eckardt compressor the vaned diffuser element is simply a dummy component where no pressure drop or fluid direction change is induced. For each flow element the 1D momentum balance equation is solved based on the selected model namely M1, M2 or M3. The mass and energy balance equations are solved for each node along with the fluid property relations. The solver routine uses a combination of the Newton-Raphson and successive substitution numerical schemes to solve the steady-state discretized equations [2].
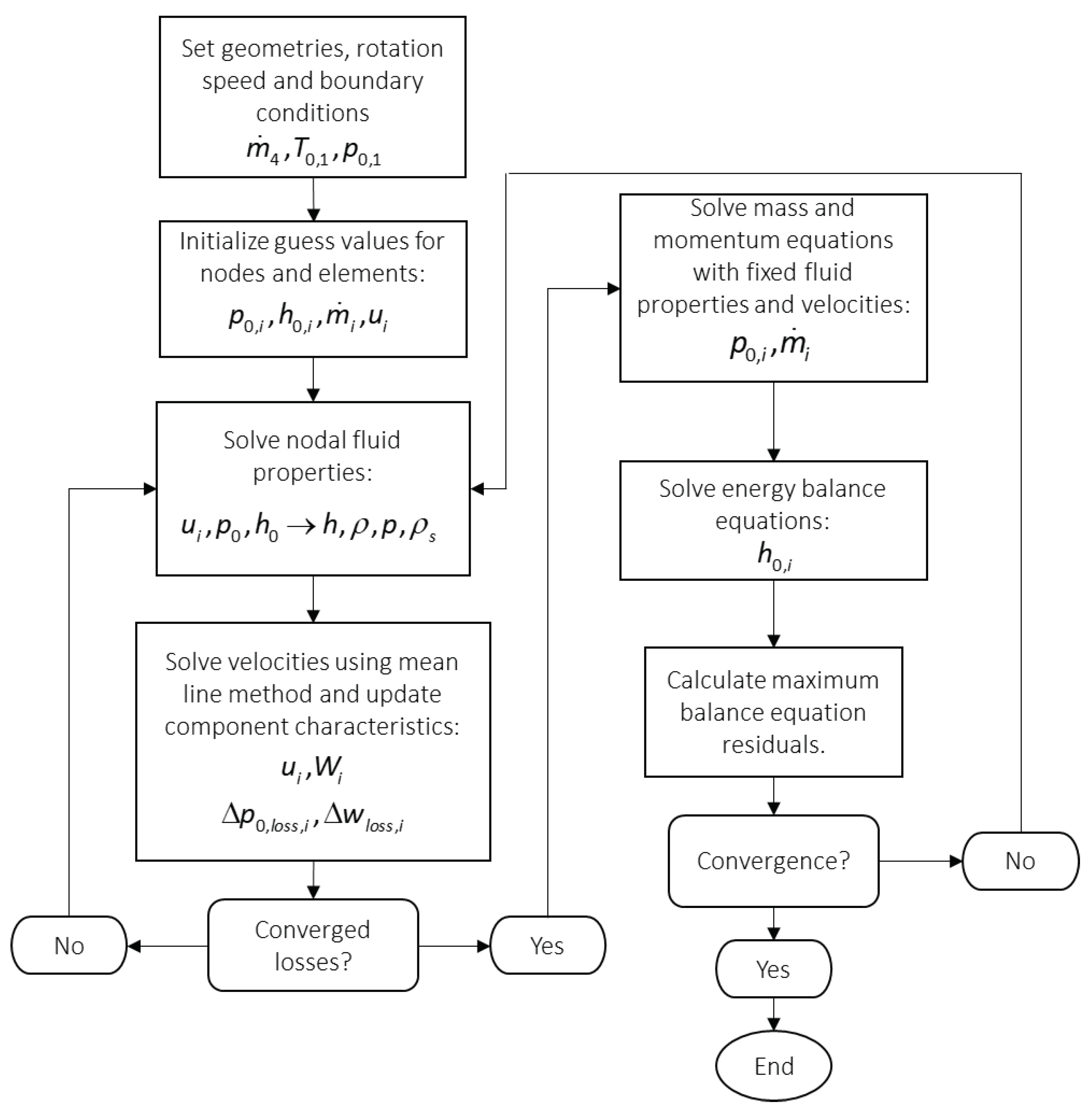
The algorithm initiates with user-specified geometric features, boundary conditions, and rotational speed for compressor components. Inlet stagnation temperature, pressure, and outflow node conditions are defined. Flow element mass flow rates are set to unity, and nodal properties are initialized based on inlet conditions. Fluid properties are iteratively solved using guessed values, employing fluid property relations. The mean line method calculates velocity vector values for each flow element. Component characteristic source terms are estimated, and the process repeats until energy and momentum balance equations converge. Converged fluid properties and characteristics are used to simultaneously solve mass and momentum balance equations with a Newton Raphson solver. Energy balance equations are solved via successive substitution once the mass and momentum equations are solved for a given iteration. Residuals are checked for convergence, using a user-specified criterion (1e-3). The solver loop iterates through fluid property and source term updates until overall convergence is achieved for stagnation pressure, stagnation enthalpy, and mass flow rates.
A flow diagram of the solver process is shown in Figure 3, where the subscripts indicate the nodal and elemental indices.
Table 2 below contains the discretized network balance equations solved for the M1 model approach. Similar sets of equations can be derived for approaches M2 and M3 using Equations (15) and (16) respectively. As previously indicated, the mass and energy balance equations remain unchanged for the three approaches studied in the current work.
designates the boundary condition.

2.5. Case Studies

The Eckart compressor experimental setup consisted of an unshrouded impeller plus casing and a vaneless diffuser space for which the compressor maps were generated. The second compressor selected for the current study is the sCO2 compressor built and tested by Sandia National Laboratories [42]. This compressor consists of a centrifugal impeller, vaneless diffuser, and vaned diffuser. Experimental total-to-total pressure ratio and isentropic efficiency of the Eckardt compressor at 14000 rpm and three mass flow rates (4.53, 5.31, and 6.09 kg/s) will be compared with predictions from models M1, M2, and M3. Furthermore, model-predicted total-to-total pressure ratios will be compared to measurements at five speeds and various mass flow rates.
The experimental values of total-to-total pressure ratio and isentropic efficiency for the Eckardt compressor will be compared with the predicted results from the three developed models (M1, M2, and M3). This comparison will be conducted at the design speed of 14000 rpm and three different mass flow rates: 4.53 kg/s, 5.31 kg/s, and 6.09 kg/s. Additionally, the predicted total-to-total pressure ratio values from the models will be compared to measurements collected at five different speeds and a range of mass flow rates.
The experimental values of total-to-total pressure ratio and total-to-static isentropic efficiency for the SNL compressor will be compared with the predicted values from the three developed models. This comparison will be conducted using data collected at three different rotational speeds and mass flow rates ranging from 1 to 4 kg/s. The geometric dimensions and thermodynamic boundary conditions for both compressors can be found in Table 3.

3. Results and Discussions

3.1. Eckardt Air Compressor

Table 4 and Table 5 show the predicted results for total-to-total stagnation pressure ratio and total-to-total isentropic efficiency predicted by models M1, M2 and M3 together with the measurement data. The total-to-total stagnation pressure ratio is simply calculated as P R t t = p 0 , 3 / p 0 , 1 where p 0 , 3
is the pressure at the outlet of the vaneless diffuser and p 0 , 1 is the inlet stagnation pressure. The isentropic efficiency values are calculated using Equation (22), where h 0 , 3 s ( s 1 , p 0 , 3 ) is the isentropic outlet stagnation enthalpy calculated using the predicted outlet stagnation pressure and inlet entropy.
η t t = h 0 , 3 s ( s 1 , p 0 , 3 ) − h 0 , 1 h 0 , 3 − h 0 , 1
The results in Table 4 and Table 5 show that the M1 approach can predict the experimental values with an average absolute error percentage of 0.2% on pressure ratio and 0.3% on efficiency. The M2 approach performs slightly worse with average differences of 2% and 2.5% on pressure ratio and efficiency respectively. This shows that both the compressible real gas approach and the compressible ideal gas approach are suitable for use with air in the region where the ideal gas assumption is valid. The M3 approach performs significantly worse compared to the other approaches with percentage differences of 9.7% and 14.5% on pressure ratio and efficiency respectively.
Figure 4 below shows the pressure ratio maps generated with the three approaches along with the experimental data taken from [43]. To further highlight the applicability of the proposed IPCM approach, the calculated pressure ratio and isentropic efficiency results using the M1 approach are compared to a model which uses the conventional mechanical energy equation to calculate the stagnation pressure changes across the compressor.
The presented M1 method is based on the fundamental balance equations and does not have a pressure ratio limitation as the correction factor proposed by Aungier. The results of the mechanical energy method are also shown in Figure 4 and are indicated as grey markers. It is seen that the results generated using the M1 approach can accurately capture the experimental trends for the different rotational speeds and mass flow rates. The average percentage difference between the model predictions and the experimental data considering all the speed lines is 1.2% with the largest average difference of 1.32% observed for the 18000 rpm data. For the M1 approach, changing the averaging of the density term from harmonic to linear has less than a 0.3% effect on the results for the 18000 rpm speed line. Comparing the results for the design speed data (14000 rpm) between the M1 approach and the mechanical energy approach (black circle markers), the average percentage difference is 2% for the pressure ratios.
For the 18000 rpm case, it is seen that average pressure ratio differences between M1, and the mechanical energy method increases to 5.9% and it is clearly seen that the mechanical energy method overpredicts the measured pressure ratios. This could be attributed to the fact that the implemented conventional method does not correctly account for the increase in entropy and associated temperatures occurring at higher pressure ratios as mentioned by Aungier [24] and Taher and Evans [24], whereas the M1 method, as shown through the derivations and above examples, implicitly accounts for this effect more accurately.
For the compressible ideal gas (M2) approach the average percentage differences between the model predictions and experimental datapoints considering the data for all the speed lines is 3.1% with the maximum average difference of 6.1% observed for the 18000 rpm data. As the rotational speed increases the results deviate more from the experimental trends. A possible cause for this observation is discretization error, whereby the harmonic averaged quantities used, such as p 0 , a v g , p a v g , T 0 , a v g , T a v g , u a v g and ρ a v g , in Equation (15) do not accurately capture the true mean inside the impeller at high rotational speeds, therefore, necessitating the need for more fluid elements in the passage. It should be noted that all fluid properties are calculated and stored at nodes and averaged quantities per element are calculated using fluid properties at the adjacent nodes. To demonstrate the sensitivity of the M2 results on the averaged element quantities, the simulated cases were recalculated but using the linear averaging approach. These results are shown in Figure 4 as dashed lines. Where the harmonic mean values previously underestimated the pressure ratio values at high rotational speeds, the linear averaged approach overpredicts the pressure ratio values. This emphasizes how the accuracy of the M2 model is influenced by the chosen method of averaging and the degree of discretization. For the M1 model, by changing the averaging of the density term from harmonic to linear no significant change in the results were observed (less than 0.5%). From this it can be concluded that the M1 approach is more robust when compared to the current IPCM compressible ideal gas approach (M2), since it is capable of capturing the observed trends with only a single element, due to the fact that the only average quantity used in the momentum Equation (15) is ρ a v g . It should be stated that the M2 modelling error, is not due to the ideal gas assumption but rather the formulation of the compressible ideal gas momentum equation shown Equation (15). As expected, the M3 results shown in Figure 4, indicate that the incompressible momentum equation formulation is unable to capture the rise in stagnation pressure through the impeller.

3.2. SNL sCO2 Compressor Results

Figure 5 below shows the experimental and predicted pressure ratio values for the sCO2 compressor at rotational speeds of 45000, 50000 and 55000 rpm. The experimental data was taken from the work of Jeong et al. [13]. From the results it is seen that models M1, M2 and M3 can all, with relative accuracy, capture the experimental trends. The average percentage difference between the predictions and experimental data considering all the measurements are 1.07%, 3.2% and 1.5% for models M1, M2 and M3 respectively. The reason why the predicted pressure ratio values for the three models closely align with each other is attributed to the low absolute velocities within the compressor. This results in the flow being categorized as weakly compressible, with a Mach number below 0.3. For example, the absolute inlet and outlet Mach numbers for the sCO2 compressor impeller at 55000 rpm and 3.53 kg/s are 0.12 and 0.26 respectively.
The weak compressibility of the flow will result in terms 2 and 3 on the left-hand side (LHS) of Equation (14) being relatively small compared to the change in stagnation pressure, thereby simplifying to equation (16). Similarly, for M2 approach, p / p 0 ≈ 1  and p 0 , e − p 0 , i > > 1 2 ρ a v g u a v g 2 1 T 0 , a v g ( T 0 , e − T 0 , i ) , thus Equation (15) also simplifies to the momentum equation used for the M3 approach. Conversely, for the Eckardt impeller the inlet and outlet Mach numbers for the design mass flow rate (5.31 kg/s) and rotational speed (14000 rpm) are 0.24 and 0.77 respectively. The high outlet Mach number underpins the need to consider compressibility effects thereby nullifying the previously mentioned simplification observed for the SNL compressor. Nonetheless, it is observed that the M2 model results slightly over predict the measurements. The M2 approach utilized the harmonic averaging of fluid properties for the SNL compressor case. Due to the low-pressure ratios for the SNL compressor, there was little variation in M2 results between harmonic and linear averaging cases, similar to the low rotational speed cases of the air compressor.
Figure 6 below shows the measured and predicted total-to-static isentropic efficiencies for the SNL sCO2 compressor. The total-to-static isentropic efficiency is calculated using Equation (28) and the corresponding computer model outputs.
η t s = h 4 s ( s 1 , p 4 ) − h 0 , 1 h 0 , 4 − h 0 , 1
The results from Figure 6 indicate that the M1 and M3 approaches can capture the general trends observed for the measured data. The average percentage difference between the M1 model results and the experimental data is 15% whereas the M3 results produce an average percentage difference of 15.9%. Due to the incompressible flow assumption being valid for the SNL compressor, the calculation of h 4 s ( s 1 , p 4 )  using the definition of incompressible stagnation pressure p 4 = p 0 , 4 − 1 2 ρ 4 u 4   2  as implemented in the M3 approach produce correct results.
Although these mentioned percentage difference values are relatively high, it should be noted that a significant amount of scatter is observed in the measurements. The random uncertainty of the experimental data was estimated using the 95% confidence band and quadratic trend and it was found that the M1 and M3 results fall well within this band. The M2 results in Figure 6 show that the model is unable to accurately recover the measured values. While the M2 approach accurately captures the change in stagnation pressures through the compressor, there is an error in the conversion from stagnation pressure to static pressure when estimating the total-to-static isentropic efficiencies. This error arises from the use of the ideal gas definition of stagnation pressure in Equation (15) which does not accurately capture the fluid property changes near the critical point. The average percentage error between the M2 approach efficiency results and the measured values is 29%. For the SNL compressor it is seen that the mechanical energy method results closely matches with the M1 results due to the relatively low machine pressure ratios, which aligns with the observations in the air compressor for low rotational speeds. Similar to the air compressor analysis, the results of the M1 approach for the 55000 rpm case are compared to the pressure ratio and efficiency values calculated using the steady-state mechanical energy method shown in Equation (18). The average percentage difference between the M1 approach and the mechanical energy method for the pressure ratio and isentropic efficiency values are 0.2% and 2.5% respectively. For the 45000 rpm case, the average percentage difference between the M1 and mechanical energy method are 0.3% and 9% respectively for the pressure ratio and efficiency values.
To demonstrate the differences between the M1 approach and the mechanical energy method results at higher pressure ratios, the SNL compressor is simulated at rotational speeds exceeding the experimental values. Figure 7 illustrates the total-to-total pressure ratio and total-to-static isentropic efficiency results for rotational speeds ranging from 55000 rpm to 100000 rpm and mass flow rates of 1 kg/s to 4.5 kg/s for both modeling approaches. The findings indicate that at 55000 rpm (as depicted in Figure 4 and Figure 5), the M1 and mechanical energy approaches yield comparable results.
However, as rotational speed—and subsequently pressure ratios—increase, larger disparities between the modeling approaches become apparent. The average percentage difference in isentropic efficiency between the two approaches increases from 0.8% at 55000 rpm to 2.3% at 100000 rpm.
Figure 8 illustrates the impact of rotational speed on predicted pressure ratios as a function of mass flow rate through the compressor. The results show the peak percentage difference between the mechanical energy and M1 methods increases from 0.4% to 3.5% as the rotational speed is increased from 55000 rpm to 100000 rpm.

4. Conclusions

A new unified compressible real gas implicit pressure correction methodology for thermofluid network modelling is proposed that can be applied in the analysis of sCO2 power cycles. In the present work the accuracy of the method was demonstrated for both an air and sCO2 compressor. The proposed method enables the mean-line simulation of real gas compressors operating at low- and high-pressure ratios. The results presented in this work indicate that, for relatively low-pressure ratios, the conventional mechanical energy method and compressible real gas thermofluid network approach yield similar results for both air and sCO2 compressors. However, at high pressure ratios and rotational speeds, the mechanical energy method tends to overpredict the resultant pressure rise, and relevant isentropic efficiencies compared to the newly defined thermofluid network approach and experimental data (for air only). This discrepancy arises from the inability of the latter method to compensate for entropy increase effects on pressure rise.

References

  1. Alobaid, F.; Mertens, N.; Starkloff, R.; Lanz, T.; Heinze, C.; Epple, B. Progress in dynamic simulation of thermal power plants. Progress in Energy and Combustion Science 2017, 59, 79–162. [Google Scholar] [CrossRef]
  2. Majumdar, A. A Finite Volume Procedure for Thermofluid System Analysis in a Flow Network. In 50 Years of CFD in Engineering Sciences, 2020, pp. 231—265. [CrossRef]
  3. 3. Flownex Genral User Manual.
  4. Inc., S. Inc., S. Streamline System Performance - AxSTREAM System Simulation Overview. Availabe online: https://www.softinway.com/software-applications/streamline-system-performance-with-axstreamsystem-simulation/.
  5. Silvennoinen, E.; Juslin, K.; Hanninen, M.; Tiihonen, O.; Kurki, J.; Porkholm, K. The APROS software for process simulation and model development Laboratory of Electrical and Automation Engineering. 1989.
  6. Rousseau, P.G.; Du Toit, C.G.; Jun, J.S.; Noh, J.M. Code-to-code comparison for analysing the steady-state heat transfer and natural circulation in an air-cooled RCCS using GAMMA+ and Flownex. Nuclear Engineering and Design 2015, 291, 71–89. [Google Scholar] [CrossRef]
  7. Greyvenstein, G.P. The application of system CFD to the design and optimization of high-temperature gas-cooled nuclear power plants. J Eng Gas Turbine Power 2008, 130. [Google Scholar] [CrossRef]
  8. Herrera, M.; Heim, D. Dynamic Modeling for the 10 MWe sCO2 Test Facility Program. In Proceedings of The 7th International Supercritical CO2 Power Cycles Symposium.
  9. Persico, G.; Giostri, A.; Gaetani, P.; Romei, A. The Role of Turbomachinery Performance in the Optimization of Supercritical Carbon Dioxide Power Systems. Journal of Turbomachinery 2020, 142. [Google Scholar] [CrossRef]
  10. Wei, D.; Lu, X.; Lu, Z.; Gu, J. Dynamic modeling and simulation of an Organic Rankine Cycle (ORC) system for waste heat recovery. Appl Therm Eng 2008, 28, 1216–1224. [Google Scholar] [CrossRef]
  11. Juangphanich, P.; De Maesschalck, C.; Paniagua, G. Turbine passage design methodology to minimize entropy production-A two-step optimization strategy. Entropy 2019, 21. [Google Scholar] [CrossRef]
  12. Ntonas, K., et al., 1D multi-point marine turbocharger design, for optimal performance recovery. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2022.
  13. Chen, J.; Liu, C. Efficient one-dimensional turbomachinery design method based on transfer learning and Bayesian optimization. SN Appl Sci 2022, 4. [Google Scholar] [CrossRef]
  14. Botros, K.K.; Campbell, P.J.; Mah, D.B. Dynamic Simulation of Compressor Station Operation Including Centrifugal Compressor and Gas Turbine. J Eng Gas Turbine Power 1991, 113, 300–311. [Google Scholar] [CrossRef]
  15. Jeong, Y.; Son, S.; Cho, S.K.; Baik, S.; Lee, J.I. Evaluation of supercritical CO2 compressor off-design performance prediction methods. Energy 2020, 213. [Google Scholar] [CrossRef]
  16. Gonzalez Gonzalez, J. Modelling Axial Turbomachinery for Compressed Air Energy Storage. University of Waterloo, 2018.
  17. Zhang, C.; et al. A method to select loss correlations for centrifugal compressor performance prediction. Aerosp Sci Technol 2019, 93. [Google Scholar] [CrossRef]
  18. Greyvenstein, G.P. An implicit method for the analysis of transient flows in pipe networks. Int J Numer Methods Eng 2002, 53, 1127–1143. [Google Scholar] [CrossRef]
  19. Li, Q.; Liang, Q.; Xia, X. A novel 1D-2D coupled model for hydrodynamic simulation of flows in drainage networks. Adv Water Resour 2020, 137. [Google Scholar] [CrossRef]
  20. Wang, X.; et al. Dynamic simulation study of the start-up and shutdown processes for a recompression CO2 Brayton cycle. Energy 2022, 259. [Google Scholar] [CrossRef]
  21. Xia, W.; Zhang, Y.; Yu, H.; Han, Z.; Dai, Y. Aerodynamic design and multi-dimensional performance optimization of supercritical CO2 centrifugal compressor. Energy Conversion and Management 2021, 248. [Google Scholar] [CrossRef]
  22. Ren, H.; Schuster, S.; Hacks, A.; Brillert, D. Mean-line analysis for supercritical CO2 centrifugal compressors by using enthalpy loss coefficients. In Proceedings of The 4th European sCO2 Conference for Energy Systems Online Conference.
  23. Marco Gambini, M.V. Turbomachinery: Fundamentals, Selection and Preliminary Design, 1 ed. 2: SPringer, 2020. [Google Scholar] [CrossRef]
  24. Taher, M.; Evans, F. Centrifugal Compressor Polytropic Performance—Improved Rapid Calculation Results—Cubic Polynomial Methods. International Journal of Turbomachinery, Propulsion and Power 2021, 6, 15. [Google Scholar] [CrossRef]
  25. Aungier, R.H. Mean Streamline Aerodynamic Performance Analysis of Centrifugal Compressors. Journal of Turbomachinery 1995, 117, 360–366. [Google Scholar] [CrossRef]
  26. Toni, L.; Bellobuono, E.F.; Valente, R.; Romei, A.; Gaetani, P.; Persico, G. Computational and Experimental Assessment of a MW-Scale Supercritical CO2 Compressor Operating in Multiple Near-Critical Conditions. Journal of Engineering for Gas Turbines and Power 2022, 144. [Google Scholar] [CrossRef]
  27. Hosangadi, A.; Weathers, T.; Liu, J.; Pelton, R.; Wygant, K.; Wilkes, J. Numerical Predictions of Mean Performance and Dynamic Behavior of a 10 MWe SCO2 Compressor With Test Data Validation. Journal of Engineering for Gas Turbines and Power 2022, 144. [Google Scholar] [CrossRef]
  28. Eckardt, D. Detailed Flow Investigations Within a High-Speed Centrifugal Compressor Impeller. J Fluids Eng 1976, 98, 390–399. [Google Scholar] [CrossRef]
  29. Wright, S.A.; Radel, R.F.; Vernon, M.E.; Rochau, G.E.; Pickard, P.S. SANDIA REPORT Operation and Analysis of a Supercritical CO 2 Brayton Cycle; 2020.
  30. Rousseau, P.G.; Du Toit, C.G.; Landman, W.A. Validation of a transient thermal-fluid systems CFD model for a packed bed high temperature gas-cooled nuclear reactor. Nuclear Engineering and Design, 1016. [Google Scholar] [CrossRef]
  31. Japikse, D.; Baines, N. Introduction to Turbomachinery; Concepts ETI Inc: 1997.
  32. Wiesner, F.J. A Review of Slip Factors for Centrifugal Impellers. Journal of Engineering for Power 1967, 89, 558–566. [Google Scholar] [CrossRef]
  33. Conrad, O.; Raif, K.; Wessels, M. The calculation of performance maps for centrifugal compressors with vane-island diffusers. In Proceedings of Proceedings of the Twenty-fifth Annual International Gas Turbine Conference and Exhibit and Twenty-second Annual Fluids Engineering Conference, New Orleans.
  34. Aungier, R.H. Centrifugal Compressors: A Strategy for Aerodynamic Design and Analysis; ASME Press: 2000; 10.1115/1.800938.
  35. Jansen, W. A method for calculating the flow in a centrifugal impeller when entropy gradients are present. In Proceedings of Royal Society Conference on Internal Aerodynamics (Turbomachinery).
  36. Coppage, J.; Dallenbach, F.; Eichenberger, H.; Hlavaka, G.; Knoernschild, E.; Van Lee, N. Study of supersonic radial compressors for refrigeration and pressurization systems; Wright Air Development Center: 1956.
  37. Krylov, E.; Spunde, Y. About the Influence of the Clearance between the Working Blades and Housing of a Radial Turbine on Its Exponent. 1967.
  38. Rodgers, C. A cycle analysis technique for small gas turbines. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy.
  39. Johnston, J.P.; Dean, R.C. Losses in Vaneless Diffusers of Centrifugal Compressors and Pumps: Analysis, Experiment, and Design. Journal of Engineering for Power 1966, 88, 49–60. [Google Scholar] [CrossRef]
  40. Daily, J.W.; Nece, R.E. Chamber Dimension Effects on Induced Flow and Frictional Resistance of Enclosed Rotating Disks. Journal of Basic Engineering 1960, 82, 217–230. [Google Scholar] [CrossRef]
  41. De Bellis, F.; Grimaldi, A.; Rubino, D.T.; Amirante, R.; Distaso, E. Accurate Radial Vaneless Diffuser One-Dimensional Model. J Eng Gas Turbine Power 2015, 137. [Google Scholar] [CrossRef]
  42. Wright, S.A.; Radel, R.F.; Vernon, M.E.; Rochau, G.E.; Pickard, P.S. Operation and Analysis of a Supercritical CO 2 Brayton Cycle; 2018.
  43. Lee, J.; Lee, J.I.; Yoon, H.J.; Cha, J.E. Supercritical Carbon Dioxide turbomachinery design for water-cooled Small Modular Reactor application. Nuclear Engineering and Design 2014, 270, 76–89. [Google Scholar] [CrossRef]
Preprints 102211 g001
Figure 1. a) Single-step and multi-step polytropic compression processes; b) results for toy compression problem.
Figure 1. a) Single-step and multi-step polytropic compression processes; b) results for toy compression problem.
Preprints 102211 g001
Preprints 102211 g002
Figure 2. Discretized thermofluid network model compressors.
Figure 2. Discretized thermofluid network model compressors.
Preprints 102211 g002
Preprints 102211 g003
Figure 3. Model solver loop.
Figure 3. Model solver loop.
Preprints 102211 g003
Preprints 102211 g004
Figure 4. Eckardt compressor map data and predicted results (markers – exp. data, solid lines – predicted results, black markers – mechanical energy method results).
Figure 4. Eckardt compressor map data and predicted results (markers – exp. data, solid lines – predicted results, black markers – mechanical energy method results).
Preprints 102211 g004
Preprints 102211 g005
Figure 5. sCO2 SNL compressor map data and predicted results (markers – exp. data, solid lines – predicted results, black markers – mechanical energy method results).
Figure 5. sCO2 SNL compressor map data and predicted results (markers – exp. data, solid lines – predicted results, black markers – mechanical energy method results).
Preprints 102211 g005
Preprints 102211 g006
Figure 6. sCO2 SNL total-to-static isentropic efficiency map data and predicted results (markers - exp. data, solid lines - predicted results, black markers – mechanical energy method results).
Figure 6. sCO2 SNL total-to-static isentropic efficiency map data and predicted results (markers - exp. data, solid lines - predicted results, black markers – mechanical energy method results).
Preprints 102211 g006
Preprints 102211 g007
Figure 7. Pressure-ratio and efficiency results for SNL compressor at higher rotational speeds (red – mechanical energy method, blue – M1 method).
Figure 7. Pressure-ratio and efficiency results for SNL compressor at higher rotational speeds (red – mechanical energy method, blue – M1 method).
Preprints 102211 g007
Preprints 102211 g008
Figure 8. Pressure-ratios as a function of mass flow rates for SNL compressor at 55000 rpm and 100000 rpm (triangles – mechanical energy method, circles – M1 method).
Figure 8. Pressure-ratios as a function of mass flow rates for SNL compressor at 55000 rpm and 100000 rpm (triangles – mechanical energy method, circles – M1 method).
Preprints 102211 g008
Table 1. Applied aerodynamic loss models.
Table 1. Applied aerodynamic loss models.
Internal losses sCO2 (SNL) Air (Eckart)
Incidence loss, Δ h i n c Conrad et al. [33] Aungier [34]
Inlet diffusion loss, Δ h d i f f Aungier [34]
Skin friction loss, Δ h s f Jansen [35]
Blade loading loss, Δ h b l d Aungier [34] Coppage et al. [36]
Tip clearance loss, Δ h c l r Krylov and Spunde [37] Rodgers [38]
Choke loss, Δ h c h o k e Aungier [34]
Wake mixing loss, Δ h m i x Dean [39] Aungier [34]
Table 2. Compressor model equations using compressible real gas formulation (M1). In the table subscript b c
Table 2. Compressor model equations using compressible real gas formulation (M1). In the table subscript b c
Node/element Discretized equations
Nodal mass balance equations: m ˙ 2 − m ˙ 1 = 0 , m ˙ 3 − m ˙ 2 = 0 , m ˙ 4 − m ˙ 3 = 0 m ˙ b c − m ˙ 4 = 0
Element momentum balance equations: p 0 , 1 − p 0 , b c = 0 p 0 , 2 − p 0 , 1 + 1 2 ρ a v g , 1 ( u 2 2 − u 1 2 ) − 1 2 ( ρ s , 2 u 2 2 − ρ s , 1 u 1 2 ) − Δ p 0 , W , 1 + Δ p 0 , L , 1 = 0 p 0 , 3 − p 0 , 2 + 1 2 ρ a v g , 2 ( u 3 2 − u 2 2 ) − 1 2 ( ρ s , 3 u 3 2 − ρ s , 2 u 2 2 ) + Δ p 0 , L , 2 = 0 p 0 , 4 − p 0 , 3 + 1 2 ρ a v g , 3 ( u 4 2 − u 3 2 ) − 1 2 ( ρ s , 4 u 4 2 − ρ s , 3 u 3 2 ) + Δ p 0 , L , 3 = 0 where Δ p 0 , L , i is the combined internal losses for element i .
Nodal energy balance equations: h 0 , 1 = h 0 , b c h 0 , 2 = ( 1 2 [ m ˙ 1 + m ˙ 2 ] ⋅ [ − w E u + Δ w L , 1 ] + m ˙ 1 h 0 , 1 ) / m ˙ 2 h 0 , 3 = ( 1 2 [ m ˙ 2 + m ˙ 3 ] ⋅ [ Δ w L , 2 ] + m ˙ 2 h 0 , 2 ) / m ˙ 3 h 0 , 4 = ( 1 2 [ m ˙ 3 + m ˙ 4 ] ⋅ [ Δ w L , 3 ] + m ˙ 3 h 0 , 3 ) / m ˙ 4 where Δ w L , i is the combined parasitic (external) losses for element i .
Table 3. Eckart and SNL compressor thermodynamic and machine dimensions.
Table 3. Eckart and SNL compressor thermodynamic and machine dimensions.
Parameter Eckardt SNL
Boundary conditions
Fluid Air sCO2
Inlet stagnation temperature, T 0 , b c 288.1 [K] 305.3 [K]
Inlet stagnation pressure, p 0 , b c 101300 [Pa] 7687000 [Pa]
Design mass flow rate, m ˙ b c 4.53 [kg/s] 3.53 [kg/s]
Rotational speeds, N 10000-18000 [rpm] 45000-55000 [rpm]
Geometric conditions
Blade inlet angle at tip, β b , t , 1 -63 [deg] -50 [deg]
Blade inlet angle at hub, β b , h , 1 -32 [deg] -50 [deg]
Blade outlet angle, β b , 2 0 [deg] -50 [deg]
Number of full-length impeller blades, Z r 20 [-] 6 (6 splitters) [-]
Radius at inlet hub, r h , 1 0.045 [m] 0.002537 [m]
Radius at inlet tip, r t , 1 0.14 [m] 0.009372 [m]
Radius at outlet, r 2 0.2 [m] 0.01868 [m]
Inlet passage height, b 1 0.095 [m] 0.006835 [m]
Outlet passage depth, b 2 0.026 [m] 0.001712 [m]
Clearance, c 0.0005 [m] 0.000254 [m]
Throat area, A t h 0.0320801 [m2] 0.0002557* [m2]
Vaneless diffuser outlet radius, r 3 0.21 [m] 0.02 [m]
Vaneless diffuser outlet passage height, b 3 0.026 [m] 0.001712 [m]
Vaned diffuser outlet radius, r 4 - 0.03 [m]
Vaned diffuser outlet passage height, b 4 - 0.001712 [m]
Vaned diffuser blade angle, β b , 34 - 71.5 [deg]
Table 4. Eckardt compressor design speed data comparison to computer model predicted values for pressure ratios.
Table 4. Eckardt compressor design speed data comparison to computer model predicted values for pressure ratios.
Mass flow rate [kg/s] Exp. M1 M2 M3
4.53 2.086 2.08 2.049 1.9
5.31 2.094 2.09 2.053 1.9
6.09 2.086 2.081 2.04 1.86
Table 5. Eckardt compressor design speed data comparison to computer model predicted values for efficiencies.
Table 5. Eckardt compressor design speed data comparison to computer model predicted values for efficiencies.
Mass flow rate [kg/s] Exp. [%] M1 [%] M2 [%] M3 [%]
4.53 86.5 86.7 84.8 75.03
5.31 88 87.5 85.4 75.4
6.09 87 86.9 84.7 73.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated