Prerpints.org logo
Preprint
Article

Predictive Modeling of Postpartum Haemorrhage Using Early Risk Factors: A Comparative Analysis of Statistical and Machine Learning Models

Altmetrics

Downloads

99

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 March 2024

Posted:

28 March 2024

You are already at the latest version

Alerts
Abstract
Postpartum haemorrhage (PPH) is a significant cause of maternal morbidity and mortality worldwide, particularly in low-resource settings. This study aimed to develop a predictive model for PPH using early risk factors and rank their importance in terms of predictive ability. The dataset was obtained from an observational case-control study in Northern Rwanda. Various statistical models and machine learning techniques were evaluated, including logistic regression, logistic re-gression with elastic-net regularisation, Random Forest, Extremely Randomized Trees, and gradient boosted trees with XGBoost. Random Forest emerged as the best predictive model for PPH across three different train-test data partitions. The important predictors identified in the study were haemoglobin level during labour and maternal age. However, there were differences in PPH risk factor importance in different data partitions, highlighting the need for further investigation. These findings contribute to understanding PPH risk factors, highlight the importance of considering different data partitions and implementing cross-validation in predictive modelling, and emphasise the value of identifying the appropriate prediction model for the application. Effective PPH pre-diction models are essential for improving maternal health outcomes on a global scale. This study provides valuable insights for healthcare providers to develop predictive models for PPH to identify high-risk women and implement targeted interventions
Keywords: 
Subject: Public Health and Healthcare  -   Public Health and Health Services

1. Introduction

The historical definition of postpartum haemorrhage (PPH) was based on specific blood loss thresholds after vaginal or caesarean delivery. For vaginal delivery, it was defined as blood loss of 500mL or more, while for caesarean section, it was defined as blood loss of over 1000mL [1]. However, in 2017, the American College of Obstetrics and Gynaecology revised this definition. The new definition includes any blood loss exceeding 1000mL accompanied by hypovolemia symptoms within 24 hours post-delivery, regardless of the delivery method. This revision was prompted by the routine underestimation of blood loss during delivery [2].
PPH primarily occurs within the first 24 hours after delivery but can also manifest up to 12 weeks post-delivery [3]. Bleeding within the initial 24 hours is referred to as primary PPH while bleeding occurring between 24 hours and 12 weeks post-delivery is termed secondary PPH [3].
Globally, pregnancy-related fatalities pose a significant concern and lead to the premature loss of around 500,000 women each year [4]. Among these fatalities, approximately one-fourth are linked to PPH [5]. Despite an overall reduction in maternal mortality rates [6], PPH remains a significant threat, affecting 1-5% of deliveries worldwide and standing as the leading cause of maternal morbidity and mortality [2]. Additionally, for every PPH-related death, there are at least 10 cases of "maternal near misses," which encompass severe complications such as multiorgan dysfunction, multiple blood transfusions, or peripartum hysterectomy [7]. Therefore, accurate identification of women at higher risk of PPH is crucial for improving intervention strategies and reducing maternal deaths and adverse outcomes.
The present research builds upon a previous study conducted in 2021 that utilised the same dataset from Rwanda [8]. The primary objective of the earlier investigation was to identify risk factors for PPH and determine its prevalence, which was found to be 25.5%. This prevalence exceeds the global estimated prevalence of 1-5% of deliveries [2]. The 2021 study employed descriptive statistics to assess the overall prevalence of PPH and utilised inferential statistics, specifically a modified Poisson regression model with robust error variance, to identify risk factors for PPH.
The study considered various risk factors related to social and demographic aspects, pregnancy, obstetrics, and factors during and immediately after childbirth. Significant early risk factors were identified, including having no medical insurance, multiple foetuses, pre-labour bleeding, intrauterine foetal death, and haemoglobin level at labour, all at a 5% significance level. Maternal age, Body Mass Index (BMI), multiparity, and a history of PPH were also found to be statistically significant.
While many of these factors are well-known contributors to PPH, Bazirete et al. [8] emphasised the significance of pre-labour haemorrhage and intrauterine foetal death. They recommended further examination of these factors in subsequent predictive models for PPH.
Findings from research conducted in various Eastern African countries both support and challenge the conclusions of Bazirete et al. [8]. A cross-sectional study conducted at a university hospital in Eastern Ethiopia confirmed the significant roles of maternal age, multiparity, and a history of PPH as risk factors for PPH, utilising logistic regression in their analysis [9]. In contrast, a prospective cohort study from Uganda did not establish a significant association between the risk of PPH and factors such as anaemia during pregnancy, a history of PPH, or multiparity based on their logistic regression analysis [10]. However, it was found that multiple pregnancy constituted a significant risk factor for PPH in the case of vaginal delivery, although this was not a consistent risk factor across all delivery methods.
The variations in findings regarding risk factors underscore the need for further exploration of these divergent outcomes. The discrepancies observed may be attributed to the use of different research methodologies and statistical models, highlighting the importance of considering these factors when interpreting the results.
This study aims to develop an optimal predictive model for PPH using early risk factors. It employs both statistical and machine learning models, each with unique advantages [11]. According to these authors, statistical models assume data is generated by a known stochastic model, allowing for direct modelling. Machine learning (ML) approaches consider the data generation process as largely unknown. Statistical models predetermine features and their interactions, while ML models offer adaptability and flexibility, allowing for feature selection and minimizing their impact. ML models often outperform statistical models in predictive performance but can be less interpretable.
A review by Christodoulou et al. [12] examined 71 studies and concluded that ML techniques did not significantly improve predictive performance compared to logistic regression in clinical prediction modelling with binary outcomes. However, ML models outperformed logistic regression in high-bias situations. Venkatesh et al. [13] emphasised the transparency of statistical models, making them more suitable for clinical practice, while hybrid techniques combining statistical modelling and ML methods provide interpretable alternatives.
Venkatesh et al. [13] conducted a study using data from the United States Consortium for Safe Labor Study to develop predictive models for postpartum haemorrhage (PPH). ML techniques, specifically Random Forest and gradient boosted trees with XGBoost, exhibited superior discriminative power in predicting PPH compared to statistical models such as logistic regression with/without LASSO regularisation. The study validated the models using phased and multi-site data, further reinforcing their findings.

2. Materials and Methods

2.1. Dataset

This project utilises a dataset from a study carried out by Bazirete et al. [8] in Rwanda, aimed at identifying risk factors for postpartum haemorrhage (PPH) and determining its prevalence, established at 25.5%. The study incorporated a population of 5,362 women admitted to five healthcare facilities in Rwanda's Northern Province, who gave birth from January to June 2020. A random sample of 430 women, aged 18 or older and at least 32 weeks pregnant, was chosen from this population, encompassing 108 primary PPH cases and 322 controls without primary PPH.
As the goal of this study was to construct the most effective predictive model for early PPH detection, risk factors known upon labour admission or during labour were considered as the primary variables of interest for predicting PPH. These variables were selected based on the findings of Bazirete et al. [8], Mesfin et al. [9], and Ononge et al. [10].
However, some pre-labour risk factors were extremely rare within the study population, with an incidence of less than 1.5%. As the classification performance depends on having features that clearly differentiate between the majority and minority classes, it is crucial to evaluate whether a variable of interest contains enough information to achieve this separation [14].
As a result, certain variables like uterine anomaly, uterine surgery, gestational diabetes mellitus, polyhydramnios, anticoagulant medication, and severe preeclampsia were not considered for this study due to their low prevalence in the dataset. Their limited presence inhibits the clear separation between cases of PPH and the control group based on these variables.
The risk factors of postpartum haemorrhage (PH) retained for analysis included maternal age, haemoglobin level during labour (Haem), body mass index (BMI), multiparity (MP), multiple pregnancy (MU), medical insurance (IN), previous PPH (Pre), pre-labour haemorrhage (AH), and intrauterine foetal death (IFD).

2.2. Statistical Analysis

In this study, we utilised two statistical models: logistic regression and penalised logistic regression with elastic-net regularisation. Penalised regression applies a penalty to variables with high variance, resulting in a reduction of the number of variables in the model and an improvement in prediction quality. Elastic net regularisation is a combination of L1 and L2 penalty terms weighted by a mixing parameter [15].
In addition, this study used three distinct tree-based ensemble learning techniques to construct predictive models for postpartum haemorrhage (PPH): Random Forest, Extremely Randomised Trees, and gradient boosted trees utilising the XGBoost library. Tree-based ensembles work by creating a collection of decision trees and then consolidating their predictions [16].
At their core, decision trees are simple models that anticipate outcomes from data observations through recursive binary splits on features within the dataset. The binary splits are determined based on optimising a certain splitting criterion. This process effectively partitions the feature space into unique, non-overlapping predictive sub-regions as per a branching set of decision rules [17]. Each partition results in a node in the decision tree, grouping observations deemed similar as per the decision rule.
Final predictions are made at terminal nodes when the space can no longer be partitioned further, or when a particular stopping condition is met. For regression trees, these predictions are continuous in nature and reflect the mean of the target response for the observations partitioned within the terminal node [16]. Conversely, classification trees predict class probabilities and class labels. Hence, the prediction of PPH cases and their probabilities using tree-based methods would be viewed as a classification problem. Here, all observations within a terminal node are classified according to the majority class of the observations partitioned within that node.
Random Forest and Extremely Randomised Trees (ERT) both train trees on random subsets of features rather than the full feature sets. However, while Random Forest identifies split points based on a prespecified splitting condition, ERT selects split point at random. Due to the randomization of the splits, ERT is often observed to perform better than Random Forest in classification problems with noisy data [18]. ERT's sampling approach differs from Random Forest’s bootstrap resampling as trees are trained on random samples drawn without replacement from the full set of training observations [18]. On the other hand, gradient boosted trees use a stochastic gradient boosting algorithm to train a tree-based ensemble model by optimising an objective function [19].
This study employed a 40-60 data separation, with 60% of the data used for training and the remaining 40% for validation (30%) and testing (10%). All candidate models were trained, tested, and validated on the same data separation. As recommended by Mehrnoush et al. [20], while various separations and approaches for train and test data can be utilised, it is crucial to maintain consistent separation across all algorithms for meaningful comparisons.
Hyperparameter tuning was performed via grid search. Four hyperparameters were considered for Random Forest and ERT: the number of random features considered at each split, the number of trees in the ensemble, the minimum size of terminal nodes and the maximum depth of each tree in the ensemble. The following seven hyperparameters were considered for gradient boosted trees with XGBoost: the learning rate, the minimum loss reduction, the number of boosting iterations, minimum child weight, maximum tree depth, proportion of features sub-sampled per tree, and the proportion of training observations sub-sampled per tree.
All candidate models were trained to maximise the area under the ROC curve and were evaluated using sensitivity to PPH cases and specificity to controls as comparative measures. The misclassification rate was also reported for the final model.
The area under the Receiver Operating Characteristic (ROC) curve is a widely recognised metric in machine learning [21]. The ROC curve plots the true positive rate (TPR) against the false positive rate (FPR) at different probability thresholds. In this application, the ROC curve plots the proportion of correctly predicted PPH cases against the proportion of incorrectly predicted PPH cases. The area under this ROC curve is then used to assess the performance of a classification model at different probability thresholds.
Sensitivity refers to the proportion of true PPH cases accurately predicted by a given model, while specificity denotes the proportion of true PPH controls accurately predicted. On the other hand, the misclassification rate (MR) describes the proportion of all predictions that were incorrectly classified.
Data analysis was performed using RStudio [22]. As classification performance often varies with different training sets, this study identifies the model with the best classification performance across three different data partitions over 5-fold cross-validation. These data partitions were created using the tidymodels package [23]. To encourage balanced training sets with respect to the target variable (PPH), training set partitioning was stratified by the target variable. Each training set consisted of 24.9% PPH cases, but the proportions of PPH cases differed in validation and test sets. Candidate models were trained with 5-fold cross-validation using the caret package [24] and probabilities of PPH were predicted. For each candidate model and each data partition, the classification probability threshold providing the optimal trade-off between sensitivity and specificity was identified graphically.

3. Results

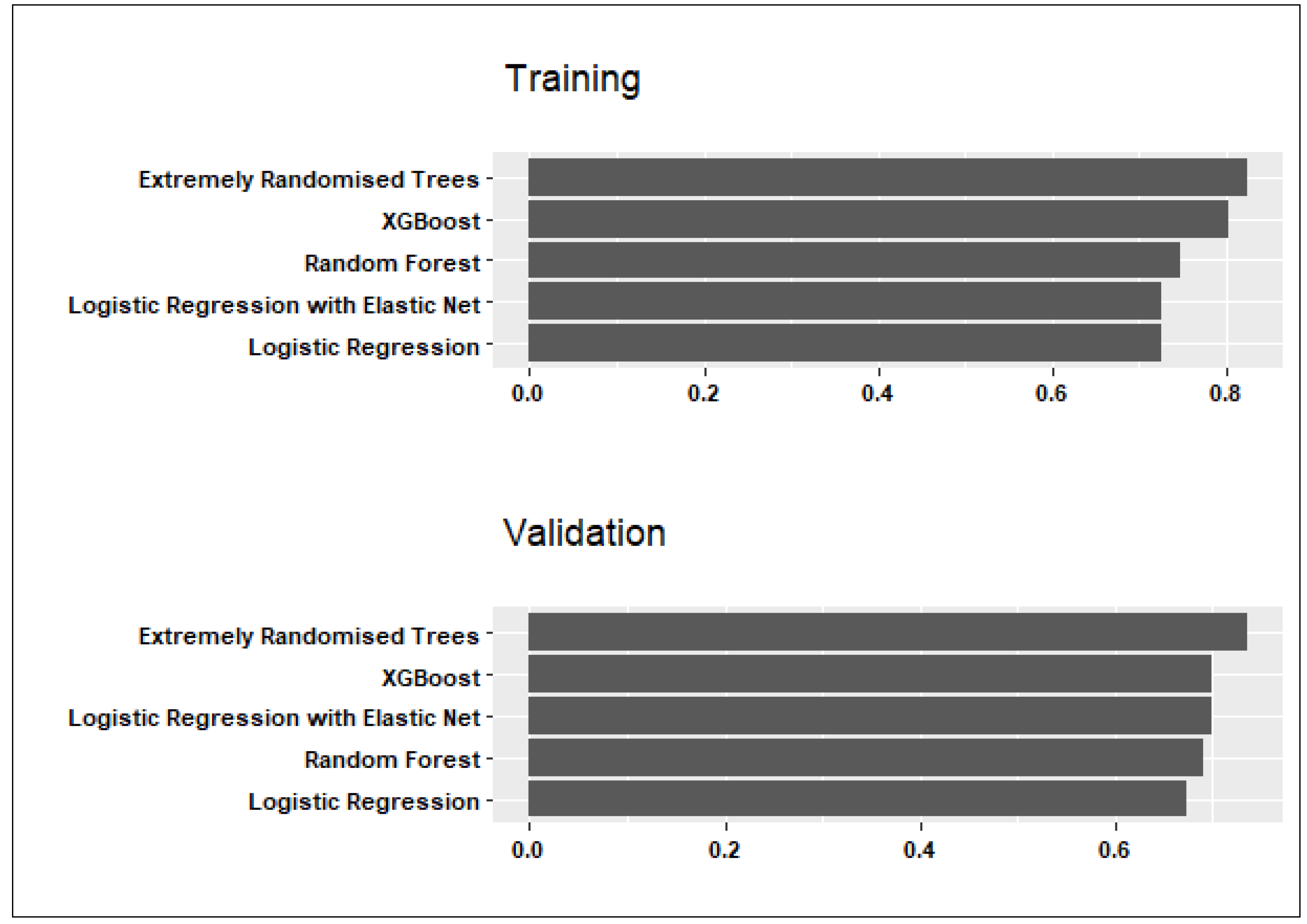
The performance of candidate models was compared in both the training and validation sets. Figure 1 and Figure 2 show candidate models’ performance averaged across the three data partitions, considering sensitivity and specificity. Below is a summary of the findings and conclusions:
Considering both training and validation sets in Figure 1, the Random Forest model exhibited the highest sensitivity to PPH cases with average values of 0.79 in training and 0.71 in validation. The average specificity to controls was similar (0.76 in training; 0.70 in validation).
Although the Extremely Randomised Trees model had the highest specificity values of 0.81 in training and 0.74 in validation (see Figure 2), the average sensitivity to predicting PPH cases was somewhat lower than in the Random Forest model (0.74 in training and 0.70 in validation).
Considering these results, the Random Forest model was selected as the final predictive model for PPH due to good average sensitivity to PPH cases and comparable specificity to controls in training and validation. The Random Forest hyperparameters that maximised ROC for each data partition are summarised in Table 1.
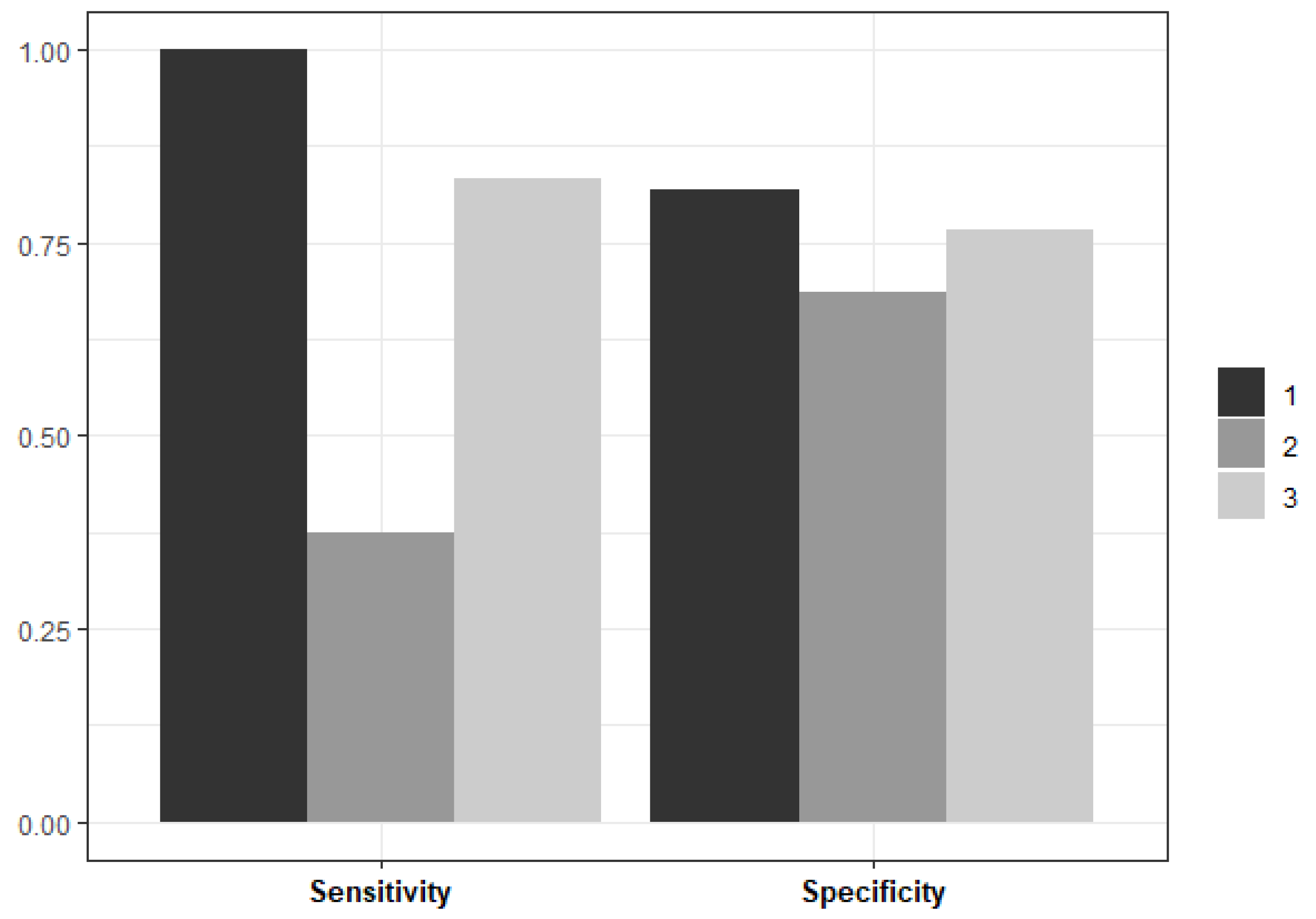
The number of random features considered at each split was consistent across data partitions (n = 2). However, there were some differences in the minimum size of terminal nodes with a minimum size of 20 in two data partitions and a minimum size of 25 in the remaining partition. The Random Forest model performance metrics on unseen test data, averaged across three data partitions, are plotted in Figure 3.
In two out of the three data partitions, the Random Forest model performed well on unseen data – both in terms of its sensitivity to PPH cases and its specificity to controls. The average sensitivity across all partitions is 0.81 and the average specificity is 0.71. The average misclassification rate is 12.19%, and most misclassifications correspond to controls misclassified as PPH cases.
After identifying the best predictive model for PPH, the next objective was to rank the importance of features in predicting PPH. Relative feature importance was estimated using the caret package by applying the final models to the test data for each data partition [24]. For Random Forest models, feature importance was determined using Gini impurity. This metric considers how many times a feature is used to create a partition (weighted by the number of bootstrap samples including that partition), then averages the decreases in Gini impurity resulting from splitting on that feature over all trees in the ensemble [25]. Estimates are scaled between 0 and 100 within each partition for comparison.
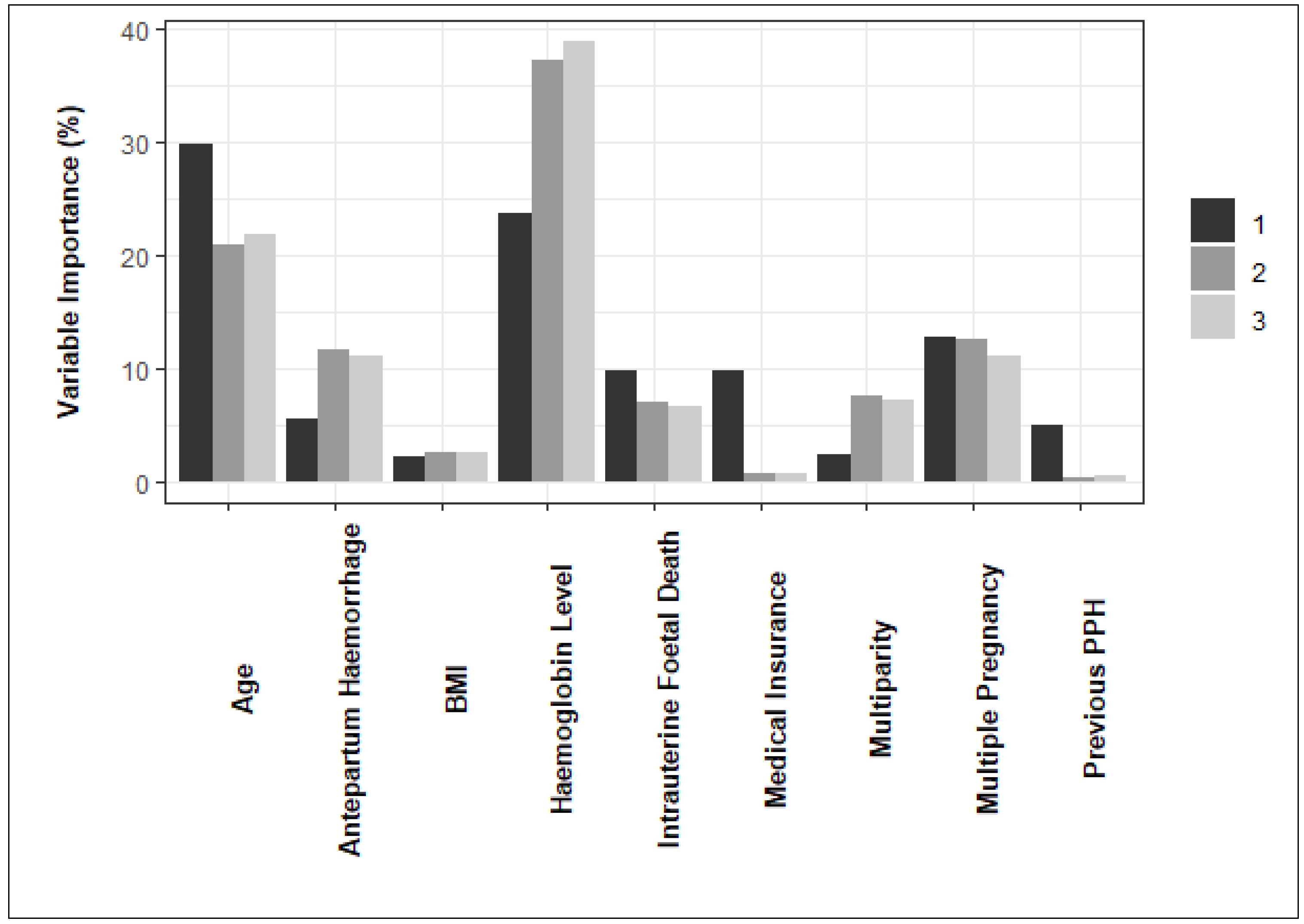
The variable importance estimates obtained from the final model for each data partition are summarized in Figure 4. According to the figure, haemoglobin level and maternal age are influential features in predicting PPH across all partitions.
Maternal age has a higher relative importance in the first data partition than the second and third partitions. On the other hand, haemoglobin level during labour had a lower relative importance in the first data partition than in the second and third partitions. The importance of maternal BMI, intrauterine foetal death and multiple pregnancy is lower but more consistent across data partitions.

4. Discussion

The research evaluated various predictive models - logistic regression, logistic regression using elastic net, Random Forest, Extremely Randomised Trees, and XGBoost's gradient boosted trees - for predicting Postpartum Haemorrhage (PPH). The Random Forest model emerged as the most effective classifier for PPH. Upon assessment with unseen test data, this model demonstrated impressive performance across three data partitions. It achieved an average sensitivity of 80.7% in identifying PPH cases, a specificity of 71.3% in recognising controls, and maintained an average misclassification rate of 12.19%.
Previous comparative studies by Venkatesh et al. [13] demonstrated that tree-based ensemble techniques, such as gradient boosted trees with XGBoost and Random Forest, outperformed statistical models like logistic regression and lasso regression in predicting PPH. Similar findings were observed in other studies comparing various machine learning techniques in clinical predictive modelling for diseases, where tree-based ensemble techniques showed excellent predictive performance compared to neural networks, Support Vector Machines, and Bayesian approaches [26,27].
Machine learning techniques offer greater flexibility which appears necessary in this application to achieve the required separability between PPH cases and controls for good predictive performance.
The variable importance of the final model did not completely align with the expectations based on the original study by Bazirete et al. [8] and other literature reviewed at the beginning of this study. Bazirete et al. [8] found pre-labour haemorrhage and having no medical insurance to be significantly associated with PPH based on the p-values (p < 0.05) associated with the estimated risk ratios. Maternal age, haemoglobin level during labour, BMI, and multiparity were also found to be statistically significant in the original study. Mesfin et al. [9] identified a maternal age of 35 years and older as a significant risk factor of PPH when considering specific maternal age categories. However, features such as intrauterine foetal death and multiple pregnancy, which were highly significant in Bazirete et al. [8], had lower relative importance in the final model. The previous history of PPH, although identified as a significant risk factor for PPH by Bazirete et al. [8], was not considered an important predictor in the final model.

5. Conclusions

The objective of this project was to develop an accurate predictive model for postpartum haemorrhage (PPH) using early risk factors and rank the most significant predictors. The dataset consisted of 430 observations from a previous study in Rwanda. Models, including logistic regression, elastic-net-regularized logistic regression, Random Forest, Extremely Randomized Trees, Extreme Gradient Boosting, were trained and evaluated using cross-validation in three different train-test data partitions. The Random Forest model performed the best, demonstrating good sensitivity, specificity, and misclassification rate.
The most important predictors of PPH identified by the model were maternal age and haemoglobin level during labour. This was observed across all data partitions, despite a higher relative importance for maternal age and a lower relative importance for haemoglobin level in the first partition. The importance of maternal BMI, intrauterine foetal death and multiple pregnancy is lower but more consistent across data partitions. The variations in findings regarding risk factors underline the need for further exploration of these divergent outcomes. The discrepancies observed may be attributed to the use of different research methodologies and statistical models, highlighting the importance of considering these factors when interpreting the results.
The analysis has limitations, including a narrow focus on variables before and at labour admission as well as a small dataset, limiting generalisability. Given the small dataset, certain variables with low prevalences could not be considered, including uterine anomaly, uterine surgery, gestational diabetes mellitus, polyhydramnios, anticoagulant medication, and severe preeclampsia.
To address these limitations, it is recommended to validate the findings with larger datasets and diverse populations. Validation using data from different time periods and conducting a cross-sectional study using medical records would enhance reliability. Furthermore, incorporating more intrapartum and immediate postpartum features should be considered for improved predictive performance, requiring further analysis and comparison of modelling techniques. Validating the findings in different settings and populations, including additional features, would strengthen the reliability and applicability of the developed predictive model for PPH.

Author Contributions

Conceptualization, Innocent Karangwa and Francesca Little; data curation, Oliva Bazirete, formal analysis, Shannon Holcroft and Joelle Behoor; investigation, Shannon Holcroft and Joelle Behoor; methodology, Shannon Holcroft, Joelle Behoor, Innocent Karangwa and Francesca Little; supervision, Innocent Karangwa and Francesca Little; writing – original draft, Shannon Holcroft; writing – review and editing, Shannon Holcroft, Innocent Karangwa and Francesca Little.

Funding

Please add: This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We extend our thanks to the University of Rwanda for providing the dataset used in this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hamm, R.F.; Wang, E.; Romanos, A.; O'Rourke, K.; Srinivas, S.K. Implementation of Quantification of Blood Loss Does Not Improve Prediction of Hemoglobin Drop in Deliveries with Average Blood Loss. Am. J. Perinatol. 2018, 35, 134–139. [Google Scholar] [CrossRef] [PubMed]
  2. Committee on Practice Bulletins-Obstetrics. Practice bulletin no. 183: Postpartum haemorrhage. Obstet. Gynecol. 2017, 130, e168–e186. [CrossRef]
  3. Knight, M.; Callaghan, W.M.; Berg, C.; et al. Trends in postpartum haemorrhage in high resource countries: A review and recommendations from the International postpartum haemorrhage Collaborative group. BMC Pregnancy Childbirth 2009, 9, 55. [Google Scholar] [CrossRef] [PubMed]
  4. Say, L.; Chou, D.; Gemmill, A.; et al. Global causes of maternal death: A WHO systematic analysis. Lancet Glob. Health 2014, 2, e323–e333. [Google Scholar] [CrossRef] [PubMed]
  5. Boujarzadeh, B.; Ranjbar, A.; Banihashemi, F.; Mehrnoush, V.; Darsareh, F.; Saffari, M. Machine learning approach to predict postpartum haemorrhage: A systematic review protocol. BMJ Open 2023, 13, e067661. [Google Scholar] [CrossRef]
  6. Creanga, A.A.; Berg, C.J.; Ko, J.Y.; et al. Maternal mortality and morbidity in the United States: Where are we now? J. Women's Health 2014, 23, 3–9. [Google Scholar] [CrossRef] [PubMed]
  7. Chandraharan, E.; Krishna, A. Diagnosis and management of postpartum haemorrhage. BMJ 2017, 358, j3875. [Google Scholar] [CrossRef]
  8. Bazirete, O.; Nzayirambaho, M.; Umubyeyi, A.; Karangwa, I.; Evans, M. Risk factors for postpartum haemorrhage in the Northern Province of Rwanda: A case control study. PLoS ONE 2022, 17, e0263731. [Google Scholar] [CrossRef]
  9. Mesfin, S.; Dheresa, M.; Fage, S.G.; Tura, A.K. Assessment of postpartum hemorrhage in a university hospital in Eastern Ethiopia: A cross-sectional study. Int. J. Women's Health 2021, 663–669. [Google Scholar] [CrossRef]
  10. Ononge, S.; et al. Incidence and risk factors for postpartum hemorrhage in Uganda. Reprod. Health 2016, 13, 1. [Google Scholar] [CrossRef]
  11. Boulesteix, A.L.; Schmid, M. Machine learning versus statistical modeling. Biometrical J. 2014, 56, 588–593. [Google Scholar] [CrossRef] [PubMed]
  12. Christodoulou, E.; Ma, J.; Collins, G.S.; Steyerberg, E.W.; Verbakel, J.Y.; Van Calster, B. A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models. J. Clin. Epidemiol. 2019, 110, 12–22. [Google Scholar] [CrossRef] [PubMed]
  13. Venkatesh, K.K.; Strauss, R.A.; Grotegut, C.; et al. Machine learning and statistical models to predict postpartum hemorrhage. Obstet. Gynecol. 2020, 135, 935. [Google Scholar] [CrossRef]
  14. Zhou, P.; Hu, X.; Li, P.; Wu, X. Online feature selection for high-dimensional class-imbalanced data. Knowl.-Based Syst. 2017, 136, 187–199. [Google Scholar] [CrossRef]
  15. Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
  16. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  17. Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
  18. Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
  19. Chen, T.; He, T.; Benesty, M.; et al. Xgboost: Extreme gradient boosting. R package version 2015, 0.4-2, 1–4. [CrossRef]
  20. Mehrnoush, V.; Ranjbar, A.; Farashah, M.V.; Darsareh, F.; Shekari, M.; Jahromi, M.S. Prediction of postpartum hemorrhage using traditional statistical analysis and a machine learning approach. AJOG Glob. Rep. 2023, 3, 100185. [Google Scholar] [CrossRef]
  21. Søreide, K. Receiver-operating characteristic curve analysis in diagnostic, prognostic and predictive biomarker research. J. Clin. Pathol. 2009, 62, 1–5. [Google Scholar] [CrossRef] [PubMed]
  22. RStudio Team. RStudio: Integrated Development for R. RStudio, PBC. 2021. Available online: https://www.rstudio.com/.
  23. Kuhn, M.; Wickham, H. Tidymodels: A collection of packages for modeling and machine learning using tidyverse principles. 2020. Available online: https://www.tidymodels.org.
  24. Kuhn, M. caret: Classification and Regression Training. R package version 6.0-88. 2022. Available online: https://CRAN.R-project.org/package=caret.
  25. Wright, M.N.; Wager, S.; Probst, P.; Wright, M.M.N. Package ‘ranger’. Version 0.11.2. 2019. Available online: https://CRAN.R-project.org/package=ranger.
  26. Khalilia, M.; Chakraborty, S.; Popescu, M. Predicting disease risks from highly imbalanced data using random forest. BMC Med. Inform. Decis. Mak. 2011, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
  27. Ghiasi, M.M.; Zendehboudi, S. Application of decision tree-based ensemble learning in the classification of breast cancer. Comput. Biol. Med. 2021, 128, 104089. [Google Scholar] [CrossRef] [PubMed]
Preprints 102458 g001
Figure 1. Comparison of candidate model sensitivity averaged across the training sets produced by three different data partitions.
Figure 1. Comparison of candidate model sensitivity averaged across the training sets produced by three different data partitions.
Preprints 102458 g001
Preprints 102458 g002
Figure 2. Comparison of candidate model specificity averaged across the training sets produced by three different data partitions.
Figure 2. Comparison of candidate model specificity averaged across the training sets produced by three different data partitions.
Preprints 102458 g002
Preprints 102458 g003
Figure 3. Summary of the final model’s performance on unseen data, averaged across the three data partitions.
Figure 3. Summary of the final model’s performance on unseen data, averaged across the three data partitions.
Preprints 102458 g003
Preprints 102458 g004
Figure 4. Ranking the importance of features in predicting PPH.
Figure 4. Ranking the importance of features in predicting PPH.
Preprints 102458 g004
Table 1. Random Forest hyperparameters that maximised ROC for each data partition.
Table 1. Random Forest hyperparameters that maximised ROC for each data partition.
Data Partition Number of random features Minimum terminal node size
1 2 20
2 2 25
3 2 20
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated