Design of Mixed-Mode Analog PID Controller with CFOAs

The design of a mixed-mode proportional-integral-derivative (PID) controller circuit using current-feedback operational amplifiers (CFOAs) as active components is proposed. With the same circuit topology, the proposed configuration of three CFOAs, four resistors, and two capacitors is capable of performing the PID controller in all four operation modes: namely voltage mode, trans-admittance mode, current mode, and trans-impedance mode. Numerous mathematical analyses are conducted to determine the controller performance under ideal and non-ideal conditions. Additionally, the mixed-mode second-order lowpass filter is suggested, and also used to examine the workability of the proposed mixed-mode PID controller in a feedback control structure. The proposed PID controller is implemented with the commercially available IC-type CFOA AD844, and the simulation results are presented to illustrate the functionality of the controller and its closed-loop control system.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The proportional-integral-derivative (PID) controllers are the most significant control components used in numerous industrial processes [1]. It is estimated that PID controllers are utilized in over 90% of all dynamical control systems [2]. With its three-term functionality involving proportional, integral, and derivative actions, the PID controller handles the treatment of transient and steady-state responses and adjusts the level of system stability, which are effective solutions for a wide range of real-world control problems [3]. It also offers simplicity, robustness, wide applicability, and simple parameter tuning. Consequently, the prevalence of PID control has increased considerably.

Literature review reveals that the PID controller implementation includes a wide variety of designs based on the use of different active elements [4,5,6,7,8,9,10,11,12,13,14,15,16,17]. In [4], voltage-feedback operational amplifiers (OAs) are extensively used to implement conventional voltage-mode (VM) PID controllers. The realized controller, however, requires a significant number of active and passive components. Its response time is also limited by the constant gain bandwidth product and low slew rate of the OA. To overcome these limitations, some current-mode (CM) active components, such as operational transconductance amplifier (OTA), current differencing buffered amplifier (CDBA), operational transresistance amplifier (OTRA), second-generation current conveyor (CCII), voltage differencing current conveyor (VDCC), and current-feedback operational amplifier (CFOA), are suggested for PID controller implementations. The OTA-based PID controller in [5] uses two grounded capacitors and eight OTAs. It supplies the output voltage signal at the high-impedance terminal, which is incompatible with cascading in VM. The PID controller designed with CDBAs requires four active and ten passive components, and lacks high input impedance [6]. In [7], the VM PID controller circuit is constructed with two OTRAs, four floating resistors, and three floating capacitors, but it does not have both high input and low output impedances. Based on CCIIs, the PID controller circuits are proposed in [8,9,10]. The works of [8,9] present two distinct configurations for VM and CM operations, while [10] only discusses CM operation. However, none of the CCII-based VM PID designs have low output impedance, and neither of the CM PID designs have low input impedance. As described in [11], a single VDCC-based VM PID controller circuit with a single input and two output terminals is realized with four resistors and two capacitors. It can simultaneously implement non-inverting and inverting control signals. However, the configuration does not fully utilize the differential input property of the VDCC because one of the differential inputs is not employed. This could be the result of input noise injection. Also, a recent VM PID controller using a single active component was reported in [12], but its limitations are the same to those in [11]. Three DDCCs and five passive elements are used in the construction of VM PID controllers [13]. At the inputs of all DDCCs, the high input impedance and capability of arithmetic operations are not fully utilized. Some earlier works do not exhibit high-input and low-output impedances for VM [14,15], or low-input and high-output impedances for CM [16]. In addition, all of the proposed PID controllers in [4,5,6,7,8,9,10,11,12,13,14,15,16] are capable of operating in either VM or CM. In real-world process control applications, mixed-signal processing PID controllers are required to interact between CM and VM circuits. To satisfy this requirement, the trans-admittance-mode (TAM) and trans-impedance-mode (TIM) PID controller circuits are also used to interface between CM and VM units without any distortion. Only one of those controllers suggests a transconductor-capacitor-based mixed-mode PID design [17]. The active blocks used in the design are not commercially available. Note that implementing the controller with commercially available elements is advantageous from both a practical and a simplicity aspect.

This work describes a mixed-mode PID controller circuit that utilizes three CFOAs as active components in addition to four resistors and two capacitors as passive components. In a single topology, the proposed controller can implement mixed-mode PID control responses, i.e., VM, CM, TAM, and TIM. Table 1 provides a detailed comparison between the proposed circuit and earlier PID controllers [4,5,6,7,8,9,10,11,12,13,14,15,16,17].

2. Proposed Mixed-Mode PID Controller Configuration

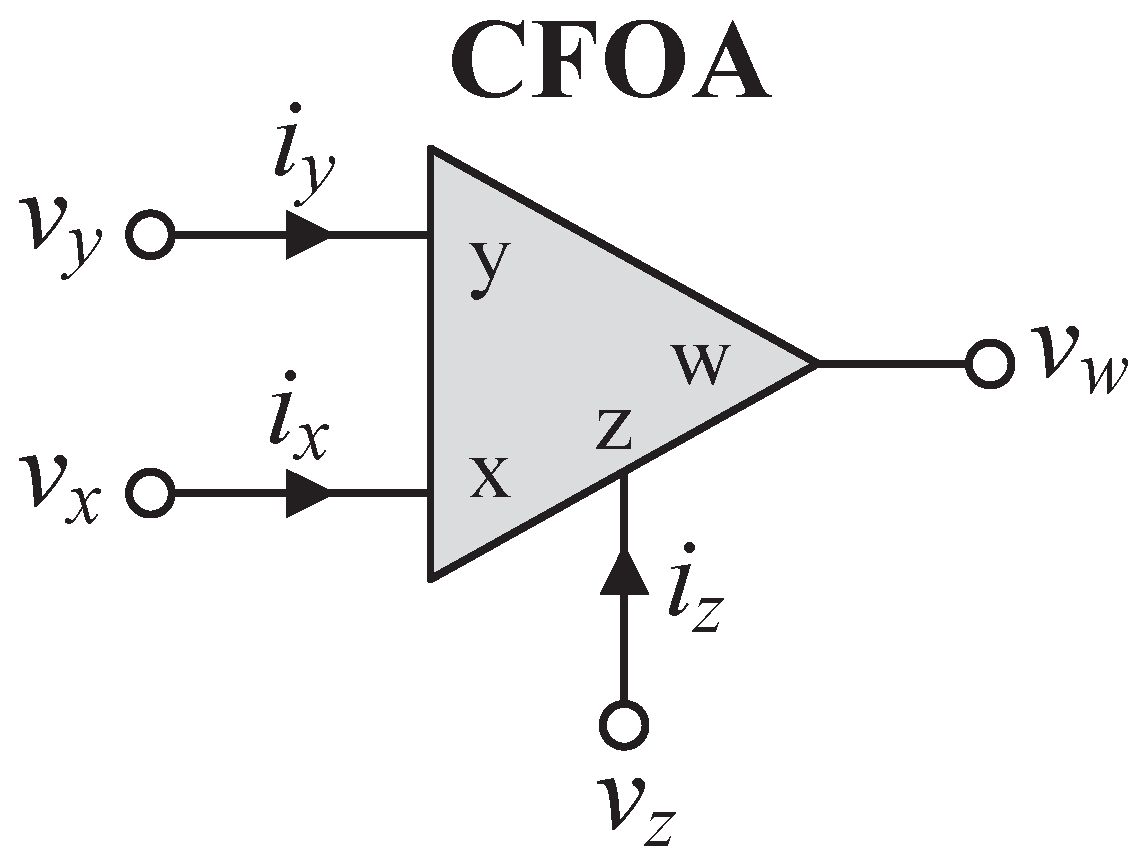
The CFOA is a four-terminal active device represented symbolically in Figure 1. Its ideal characteristic is defined by i_y = 0, v_x = v_y, i_z = i_x, and v_w = v_z. In addition, the characteristics of the CFOA with non-ideal transfer gains can be defined by the following terminal relations:

i_y = 0, v_x = βv_y, i_z = αi_x, and v_w = γv_z,

(1)

where β = (1 - ε_β), α = (1 - ε_α), and γ = (1 - ε_γ). Further, ε_β (|ε_β| << 1) is the input-voltage tracking error, ε_α (|ε_α| << 1) is the input-current tracking error, and ε_γ (|ε_γ| << 1) is the output-voltage tracking error. All of the parameters β, α, and γ should ideally equal one.

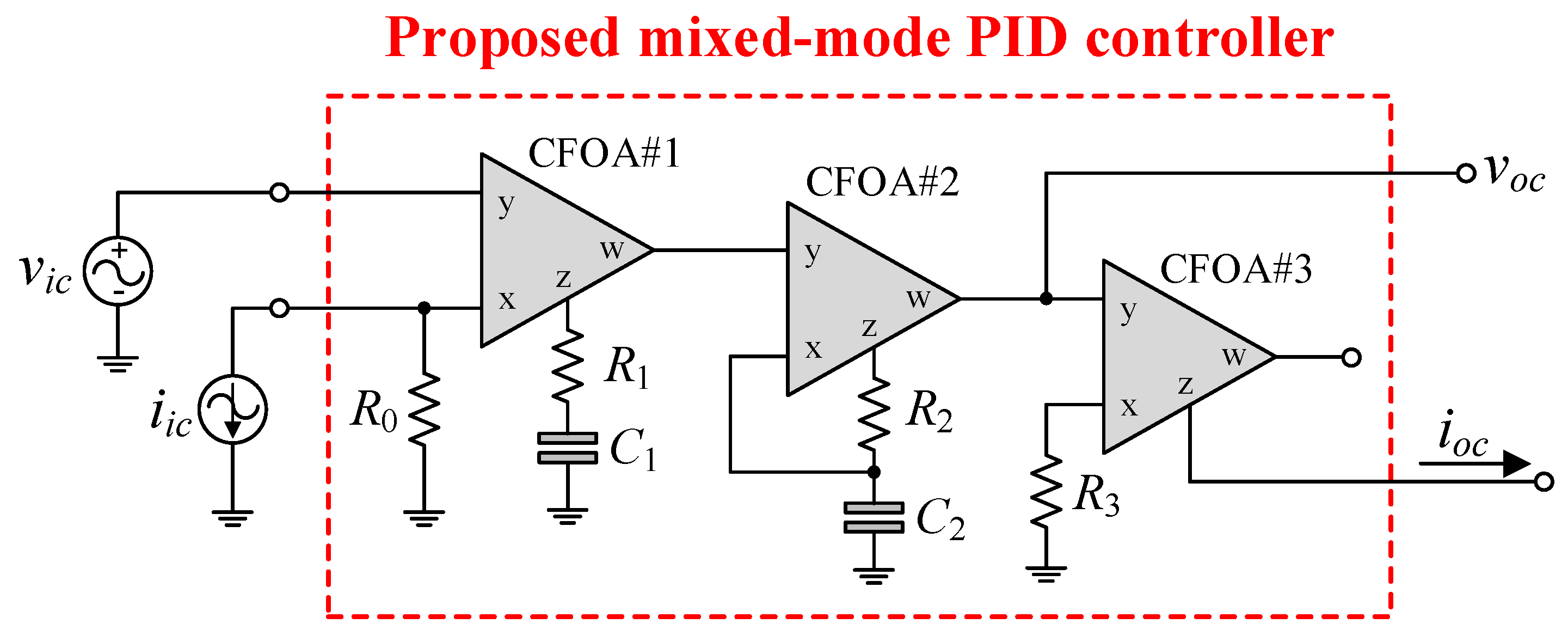
Figure 2 depicts the configuration of the proposed mixed-mode PID controller, which consists of two input terminals (v_ic and i_ic), and two output terminals (v_oc and i_oc). For the VM signal, the circuit provides high input and low output impedance, while for the CM signal, it provides low input and high output impedance. By appropriately employing the relevant input signals via v_ic and i_ic, the proposed PID controller can realize all four possible modes of operation, VM, TIM, CM, and TAM, in a single topology. Consequently, it is a mixed-mode PID controller.

The general transfer function of the PID controller can be expressed as:

\begin{matrix}  \end{matrix} G_{V} (s) = K_{P} + \frac{K_{I}}{s} + s K_{D} \begin{matrix}  \end{matrix}

(2)

where the parameters K_P, K_I and K_D are the proportional gain, integral gain, and derivative gain of the controller, respectively.

2.1. VM and TAM Operations

From Figure 2, if i_ic = 0, one can derive the following generalized transfer function for VM:

\begin{matrix}  \end{matrix} G_{V} (s) = \frac{v_{o c}}{v_{i c}} = \frac{R_{1}}{R_{0}} (1 + \frac{R_{2} C_{2}}{2 R_{1} C_{1}}) + (\frac{1}{s R_{0} C_{1}}) + (\frac{s R_{1} R_{2} C_{2}}{2 R_{0}}) \begin{matrix}  \end{matrix} .

(3)

Comparing Equation (3) to Equation (2), the important gain coefficients of the proposed VM PID controller are obtained as follows:

\begin{matrix}  \end{matrix} K_{P V} = \frac{R_{1}}{R_{0}} (1 + \frac{R_{2} C_{2}}{2 R_{1} C_{1}}) \begin{matrix}  \end{matrix},

(4a)

\begin{matrix}  \end{matrix} K_{I V} = \frac{1}{R_{0} C_{1}} \begin{matrix}  \end{matrix},

(4b)

and

\begin{matrix}  \end{matrix} K_{D V} = \frac{R_{1} R_{2} C_{2}}{2 R_{0}} \begin{matrix}  \end{matrix} .

(4c)

In Equation (4), the parameters K_PV, K_IV and K_DV are the gains K_P, K_I, and K_D for VM, respectively.

Similarly, the transfer function of the proposed TAM PID controller is also obtained as:

\begin{matrix}  \end{matrix} G_{Y} (s) = \frac{i_{o c}}{v_{i c}} = \frac{R_{1}}{R_{0} R_{3}} (1 + \frac{R_{2} C_{2}}{2 R_{1} C_{1}}) + (\frac{1}{s R_{0} R_{3} C_{1}}) + (\frac{s R_{1} R_{2} C_{2}}{2 R_{0} R_{3}}) \begin{matrix}  \end{matrix},

(5)

where

\begin{matrix}  \end{matrix} K_{P Y} = \frac{R_{1}}{R_{0} R_{3}} (1 + \frac{R_{2} C_{2}}{2 R_{1} C_{1}}) \begin{matrix}  \end{matrix},

(6a)

\begin{matrix}  \end{matrix} K_{I Y} = \frac{1}{R_{0} R_{3} C_{1}} \begin{matrix}  \end{matrix},

(6b)

and

\begin{matrix}  \end{matrix} K_{D Y} = \frac{R_{1} R_{2} C_{2}}{2 R_{0} R_{3}} \begin{matrix}  \end{matrix} .

(6c)

Since the primary objective of this communication is to design an analog PID controller with all four modes of operation in a single configuration, orthogonal adjustment of the control gain parameters K_PV(Y), K_IV(Y), and K_DV(Y) derived from Equations (4) and (6) is not anticipated. However, independent tuning of K_IV(Y) and K_DV(Y) is possible via R₀ and C₂, respectively, by adjusting R₀, R₁, C₁, and C₂ simultaneously in order that R₁/R₀ and C₂/C₁ remain constant.

2.2. CM and TIM Operations

Furthermore, by applying i_in while connecting v_ic to ground (v_ic = 0), the proposed circuit in Figure 2 can be used for CM PID control. As a consequence, the realized transfer function of the CM PID controller is

\begin{matrix}  \end{matrix} G_{I} (s) = \frac{i_{o c}}{i_{i c}} = \frac{R_{1}}{R_{3}} (1 + \frac{R_{2} C_{2}}{2 R_{1} C_{1}}) + (\frac{1}{s R_{3} C_{1}}) + (\frac{s R_{1} R_{2} C_{2}}{2 R_{3}}) \begin{matrix}  \end{matrix} .

(7)

For R₀ = R₃, the gain parameters K_PI, K_II, and K_DI of the CM PID controller in Equation (7) are the exact same as K_PV, K_IV, and K_DV in Equation (4).

It is also observed that the transfer function of the proposed TIM PID controller is found as:

\begin{matrix}  \end{matrix} G_{Z} (s) = \frac{v_{o c}}{i_{i c}} = (R_{1} + \frac{R_{2} C_{2}}{2 C_{1}}) + (\frac{1}{s C_{1}}) + (\frac{s R_{1} R_{2} C_{2}}{2}) \begin{matrix}  \end{matrix},

(8)

where

\begin{matrix}  \end{matrix} K_{P Z} = R_{1} + \frac{R_{2} C_{2}}{2 C_{1}} \begin{matrix}  \end{matrix},

(9a)

\begin{matrix}  \end{matrix} K_{I Z} = \frac{1}{C_{1}} \begin{matrix}  \end{matrix},

(9b)

and

\begin{matrix}  \end{matrix} K_{D Z} = \frac{R_{1} R_{2} C_{2}}{2} \begin{matrix}  \end{matrix} .

(9c)

According to Equations (4), (6), and (9), it can be observed that the relative element sensitivities of the control coefficients are low, in that their values are all less than unity, as given below:

\begin{matrix}  \end{matrix} S_{R_{0}}^{K_{P V}} = S_{R_{0}, R_{3}}^{K_{P Y}} = S_{R_{3}}^{K_{P I}} = - 1 \begin{matrix}  \end{matrix},

(10)

\begin{matrix}  \end{matrix} S_{R_{1}}^{K_{P V}, K_{P Y}, K_{P I}, K_{P Z}} = \frac{1}{(1 + \frac{R_{2} C_{2}}{2 R_{1} C_{1}})} < 1 \begin{matrix}  \end{matrix},

(11)

\begin{matrix}  \end{matrix} S_{R_{2}, C_{2}}^{K_{P V}, K_{P Y}, K_{P I}, K_{P Z}} = - S_{C_{1}}^{K_{P V}, K_{P Y}, K_{P I}, K_{P Z}} = \frac{1}{(1 + \frac{2 R_{1} C_{1}}{R_{2} C_{2}})} < 1 \begin{matrix}  \end{matrix},

(12)

\begin{matrix}  \end{matrix} S_{R_{0}, C_{1}}^{K_{I V}} = S_{R_{0}, R_{3}, C_{1}}^{K_{I Y}} = S_{R_{3}, C_{1}}^{K_{I I}} = S_{C_{1}}^{K_{I Z}} = - 1 \begin{matrix}  \end{matrix},

(13)

and

\begin{matrix}  \end{matrix} S_{R_{0}}^{K_{D V}} = S_{R_{0}, R_{3}}^{K_{D Y}} = S_{R_{3}}^{K_{D I}} = - S_{R_{1}, R_{2}, C_{2}}^{K_{D V}, K_{D Y}, K_{D I}, K_{D Z}} = - 1 \begin{matrix}  \end{matrix} .

(14)

3. Non-Ideality Effects of CFOA Parasitic Gains

In practice, the CFOA may take into account the non-ideal transfer gains β, α, and γ. According to Equation (1), when β ≠ α ≠ γ ≠ 1, the following are the practical gain parameters of the proposed PID controller in Figure 2.

For VM operation, the control parameters K_PV, K_IV, and K_DV are nonideally obtained as:

\begin{matrix}  \end{matrix} K_{P V} = \frac{β_{1} β_{2} α_{1} γ_{1} γ_{2} R_{1}}{R_{0}} [1 + \frac{α_{2} R_{2} C_{2}}{(1 + α_{2}) R_{1} C_{1}}] \begin{matrix}  \end{matrix},

(15a)

\begin{matrix}  \end{matrix} K_{I V} = \frac{β_{1} β_{2} α_{1} γ_{1} γ_{2}}{R_{0} C_{1}} \begin{matrix}  \end{matrix},

(15b)

and

\begin{matrix}  \end{matrix} K_{D V} = \frac{β_{1} β_{2} α_{1} α_{2} γ_{1} γ_{2} R_{1} R_{2} C_{2}}{(1 + α_{2}) R_{0}} \begin{matrix}  \end{matrix},

(15c)

where the multiplication coefficients β_i, α_i, and γ_i (i = 1, 2, 3) denote the non-ideal gains β, α, and γ of the i-th CFOA, respectively.

For TAM operation, the non-ideal control parameters K_PY, K_IY, and K_DY can be expressed as:

\begin{matrix}  \end{matrix} K_{P Y} = \frac{β_{1} β_{2} β_{3} α_{1} α_{3} γ_{1} γ_{2} R_{1}}{R_{0} R_{3}} [1 + \frac{α_{2} R_{2} C_{2}}{(1 + α_{2}) R_{1} C_{1}}] \begin{matrix}  \end{matrix},

(16a)

\begin{matrix}  \end{matrix} K_{I Y} = \frac{β_{1} β_{2} β_{3} α_{1} α_{3} γ_{1} γ_{2}}{R_{0} R_{3} C_{1}} \begin{matrix}  \end{matrix},

(16b)

and

\begin{matrix}  \end{matrix} K_{D Y} = \frac{β_{1} β_{2} β_{3} α_{1} α_{2} α_{3} γ_{1} γ_{2} R_{1} R_{2} C_{2}}{(1 + α_{2}) R_{0} R_{3}} \begin{matrix}  \end{matrix} .

(16c)

For CM and TIM operations, the non-ideal control parameters can be determined, respectively, as follows:

\begin{matrix}  \end{matrix} K_{P I} = \frac{β_{2} β_{3} α_{1} α_{3} γ_{1} γ_{2} R_{1}}{R_{3}} [1 + \frac{α_{2} R_{2} C_{2}}{(1 + α_{2}) R_{1} C_{1}}] \begin{matrix}  \end{matrix},

(17a)

\begin{matrix}  \end{matrix} K_{I I} = \frac{β_{2} β_{3} α_{1} α_{3} γ_{1} γ_{2}}{R_{3} C_{1}} \begin{matrix}  \end{matrix},

(17b)

\begin{matrix}  \end{matrix} K_{D I} = \frac{β_{2} β_{3} α_{1} α_{2} α_{3} γ_{1} γ_{2} R_{1} R_{2} C_{2}}{(1 + α_{2}) R_{3}} \begin{matrix}  \end{matrix},

(17c)

and

\begin{matrix}  \end{matrix} K_{P Z} = β_{2} α_{1} γ_{1} γ_{2} [R_{1} + \frac{α_{2} R_{2} C_{2}}{(1 + α_{2}) C_{1}}] \begin{matrix}  \end{matrix},

(18a)

\begin{matrix}  \end{matrix} K_{I Z} = \frac{β_{2} α_{1} γ_{1} γ_{2}}{C_{1}} \begin{matrix}  \end{matrix},

(18b)

\begin{matrix}  \end{matrix} K_{D Z} = \frac{β_{2} α_{1} α_{2} γ_{1} γ_{2} R_{1} R_{2} C_{2}}{(1 + α_{2})} \begin{matrix}  \end{matrix} .

(18c)

According to Equations (15)-(18), the gain parameters of the proposed PID controller differ slightly owing to the non-ideal transfer gains β_i, α_i, and γ_i. Inspecting these equations implies that all sensitivities of the PID control coefficients with respect to non-ideal transfer gains of the CFOA are not greater than unity in absolute value.

4. Non-Ideality Effects of CFOA Parasitic Impedances

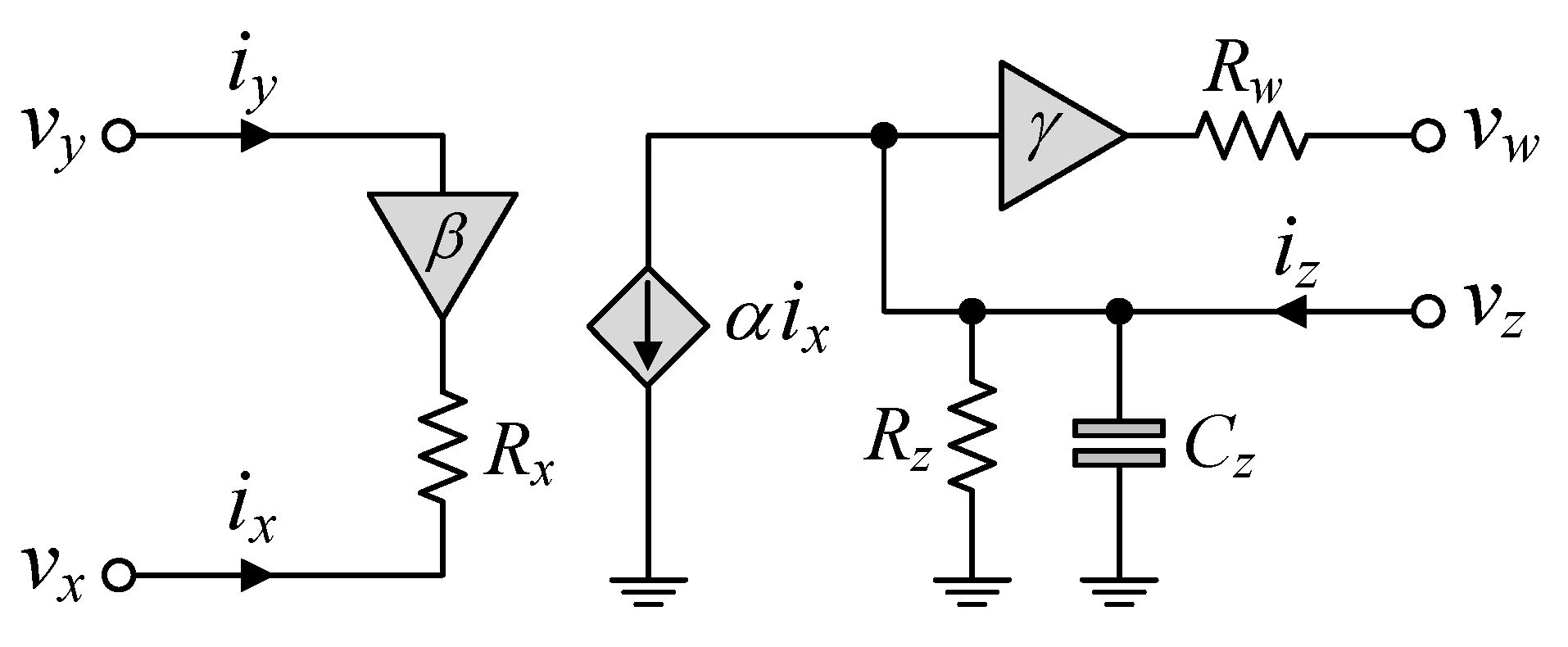
Figure 3 shows the non-ideal behavior model of the practical CFOA, including the typical parasitic impedances. In accordance with this model, R_x and R_w are the low-level parasitic resistances, R_z is the high-level parasitic resistance, and C_z is the parasitic capacitance, associated with the corresponding terminals. For example, the parasitic element values for the commercially available integrated circuit (IC) AD844 CFOA are as follows: R_x = 50 Ω, R_w = 15 Ω, R_z = 3 MΩ, and C_z = 4.5 pF [18].

Considering the dominant parasitic effects of the CFOA on the performance of the proposed mixed-mode PID controller in Figure 2, the following additional assumptions can be defined under the conditions that β ≅ α ≅ γ ≅ 1:

\begin{matrix}  \end{matrix} |R_{1} + \frac{1}{j ω C_{1}}| < < |R_{z 1} / / \frac{1}{j ω C_{z 1}}| \begin{matrix}  \end{matrix},

(19)

and

\begin{matrix}  \end{matrix} |R_{2} + (R_{x 2} / / \frac{1}{j ω C_{2}})| < < |R_{z 2} / / \frac{1}{j ω C_{z 2}}| \begin{matrix}  \end{matrix} .

(20)

It is important to note that, in practice, the impact of the parasitic resistances R_x₁ and R_x₃ is negligible due to the fact that R₀ >> R_x₁ and R₃ >> R_x₃. The expression in Equation (19) can be rewritten as:

\begin{matrix}  \end{matrix} \sqrt{1 + {(ω R_{1} C_{1})}^{2}} < < \frac{ω R_{z 1} C_{1}}{\sqrt{1 + {(ω R_{z 1} C_{z 1})}^{2}}} \begin{matrix}  \end{matrix} .

(21)

When the parasitic capacitance C_z₁ is minimal, the operating frequency is limited to the following range:

\begin{matrix}  \end{matrix} f > > \frac{1}{2 π (\sqrt{R_{z 1}^{2} - R_{1}^{2}}) C_{1}} \Rightarrow f_{1} \begin{matrix}  \end{matrix} .

(22)

Additionally, from Equation (21), if R_z₁ is negligible, the range of applicable frequency is as follows:

\begin{matrix}  \end{matrix} f < < \frac{\sqrt{{(\frac{C_{1}}{C_{z 1}})}^{2} - 1}}{2 π R_{1} C_{1}} \Rightarrow f_{2} \begin{matrix}  \end{matrix} .

(23)

For instance, if the commercially available IC AD844 CFOA is employed with R₁ = 5 kΩ, and C₁ = 1 nF, the useful operating frequencies found from Equations (22) and (23) are around f₁ ≅ 53 Hz, and f₂ ≅ 7.07 MHz.

Assuming that R₂ >> R_x₂, Equation (20) can be rearranged as:

\begin{matrix}  \end{matrix} \sqrt{1 + {(ω R_{z 2} C_{z 2})}^{2}} < < \frac{R_{z 2}}{R_{2}} \begin{matrix}  \end{matrix} .

(24)

In the same manner, the practical frequency range in this case is limited to

\begin{matrix}  \end{matrix} f < < \frac{\sqrt{{(\frac{R_{z 2}}{R_{2}})}^{2} - 1}}{2 π R_{z 2} C_{z 2}} \Rightarrow f_{3} \begin{matrix}  \end{matrix} .

(25)

By utilizing R₂ = 5 kΩ, R_z₂ = 3 MΩ, and C_z₂ = 4.5 pF, it is possible to determine the frequency location of f₃ ≅ 7.07 MHz.

By combining Equations (22), (23), and (25), the proposed mixed-mode PID controller shown in Figure 2 can be effectively utilized over the following frequency range:

\begin{matrix}  \end{matrix} m a x \{f_{1}\} < < f < < m i n \{f_{2}, f_{3}\} \begin{matrix}  \end{matrix} .

(26)

5. Functional Simulation and Discussion

In order to validate the theoretical analysis presented in the previous section, the proposed mixed-mode PID controller circuit depicted Figure 2 was investigated using PSPICE program with model parameters of the commercial CFOA IC-type AD844 available from Analog Devices company [18]. All the AD844 ICs were biased with symmetrical power supplies of ±9 V. The passive components for the controller were set as: R₀ = 1 kΩ, R₁ = R₂ = R₃ = 5 kΩ, and C₁ = C₂ = 1 nF. For the specified component values, the controller parameters were calculated as follows:

K_PV = 7.5, K_IV = 1 Ms^-1, and K_DV = 12.5 μs for VM;
K_PY = 1.5 m, K_IY = 200 s^-1, and K_DY = 2.5 ns for TAM;
K_PI = 1.5, K_II = 0.2 Ms^-1, and K_DI = 2.5 μs for CM;
K_PZ = 7.5 k, K_IZ = 1 Gs^-1, and K_DZ = 12.5 ms for TIM.

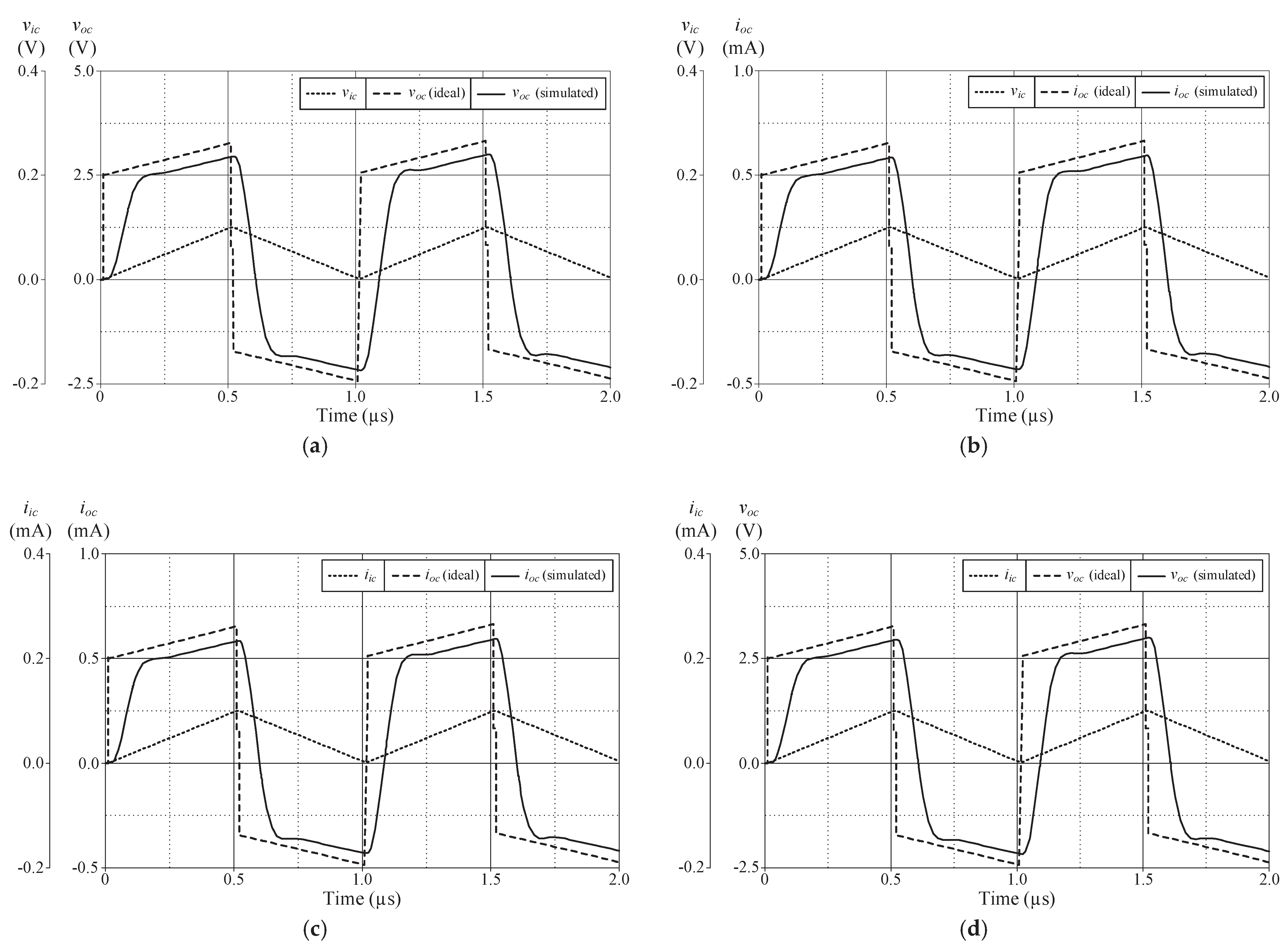
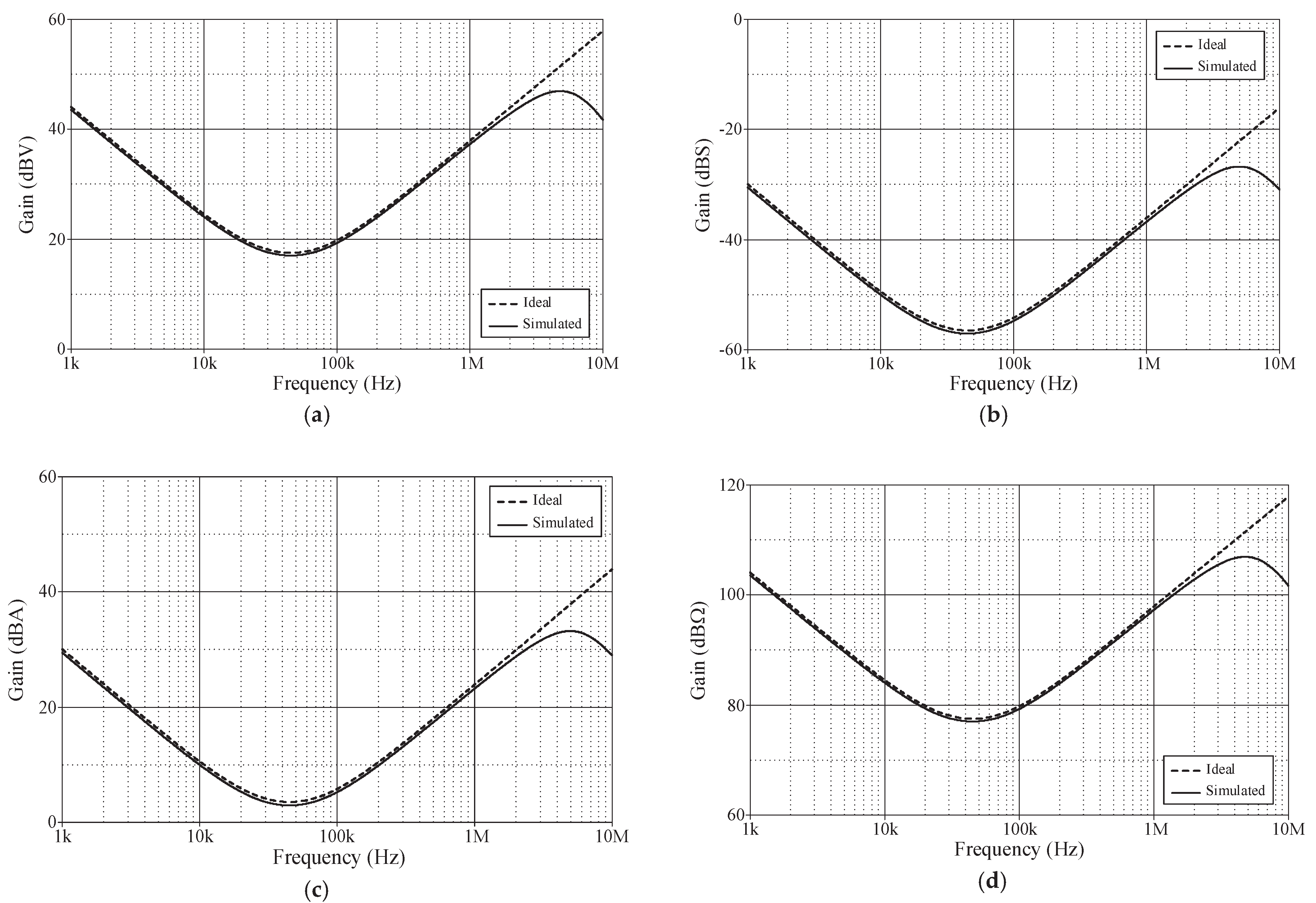
Figure 4 illustrates the time-domain simulation responses of the VM, TAM, CM and TIM PID controllers in comparison to the ideal responses. As shown in Figure 4, the controller was applied with a 100-mV triangular input signal with a frequency of 1 MHz. Figure 5 additionally illustrates the ideal and simulated frequency-domain characteristics of the proposed mixed-mode PID controller with the exact same components. It is evident from these responses that the gain-frequency limitation of the controller occurs predominantly at more than 5 MHz. This phenomenon can be attributed to the dominant pole frequencies of parasitic impedances, as expected in the previous section. The total power consumption of the controller is approximately 0.348 W.

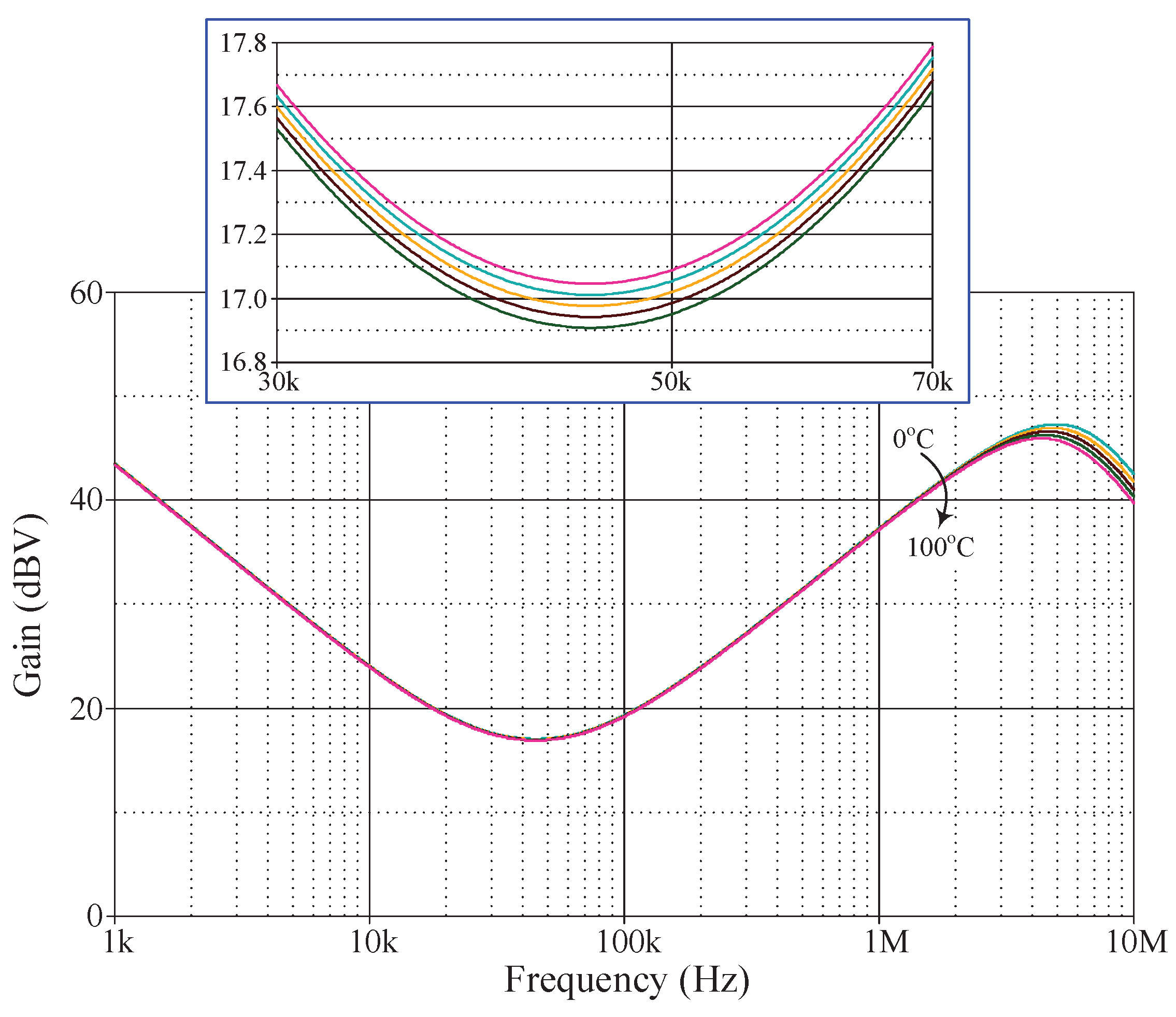
A further analysis was conducted on the gain response variation in the proposed VM PID controller with respect to ambient temperature. The temperature analysis was performed at the following temperatures: T = 0°C, 25°C, 50°C, 75°C, and 100°C. The simulation results of the analysis of ambient temperature are illustrated in Figure 6, while Table 2 provides the controller gain values for various temperatures. Based on the data given in Table 2, the controller gain change with respect to temperature variation (ΔdBV/ΔT) is determined to be 0.137%, 0.138%, and 0.179% at f = 10 kHz, 100 kHz, and 1 MHz, respectively.

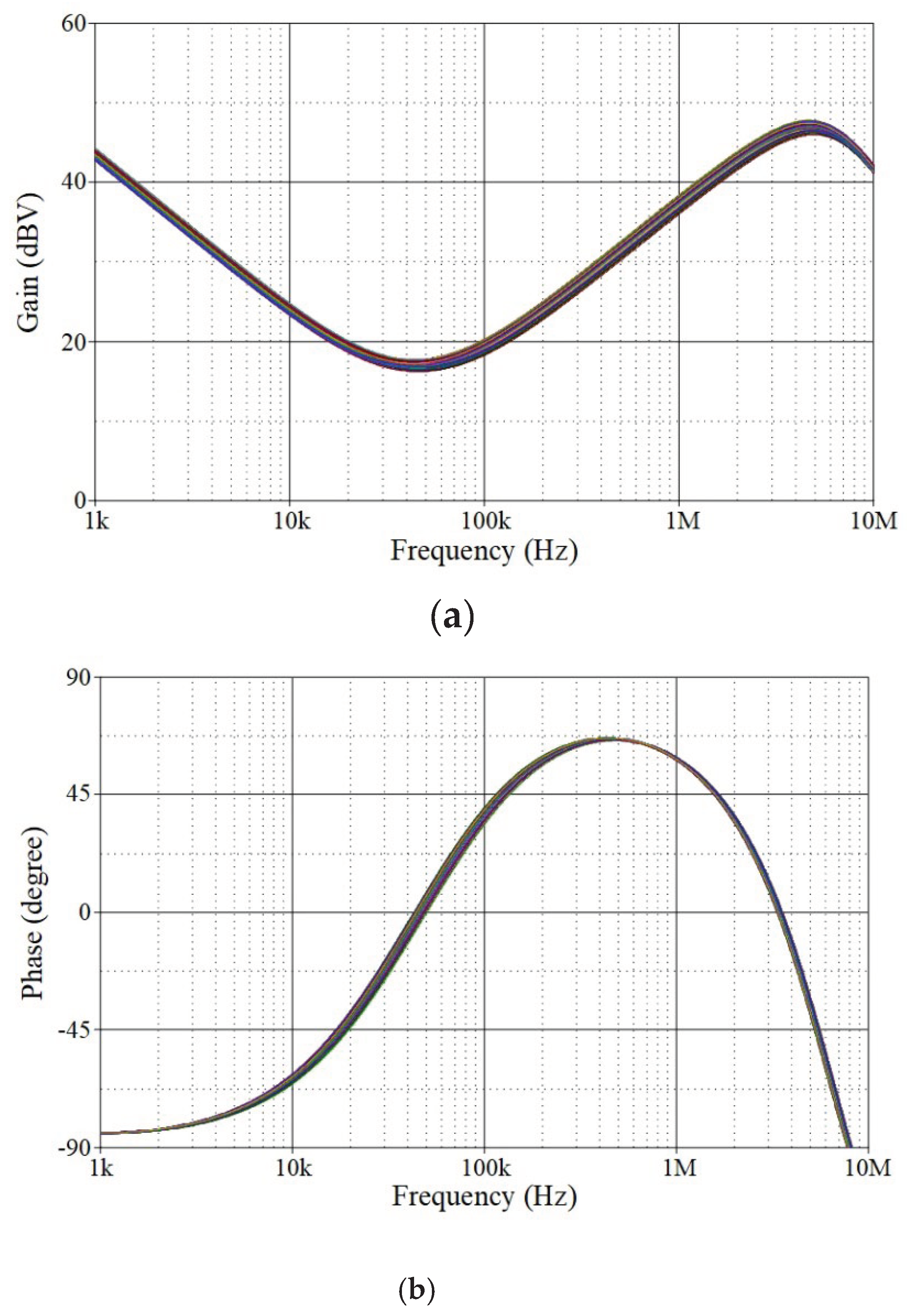
Additionally, Monte Carlo statistical analysis has been performed to demonstrate the robustness of the proposed controller. The analysis was conducted using 200 simulation runs in which the resistor and capacitor values were subject to a 5% Gaussian deviation. The Monte Carlo analysis results are shown in Figure 7. The results indicate that a change in the passive component has no significant effect on the phase or gain responses of the controller.

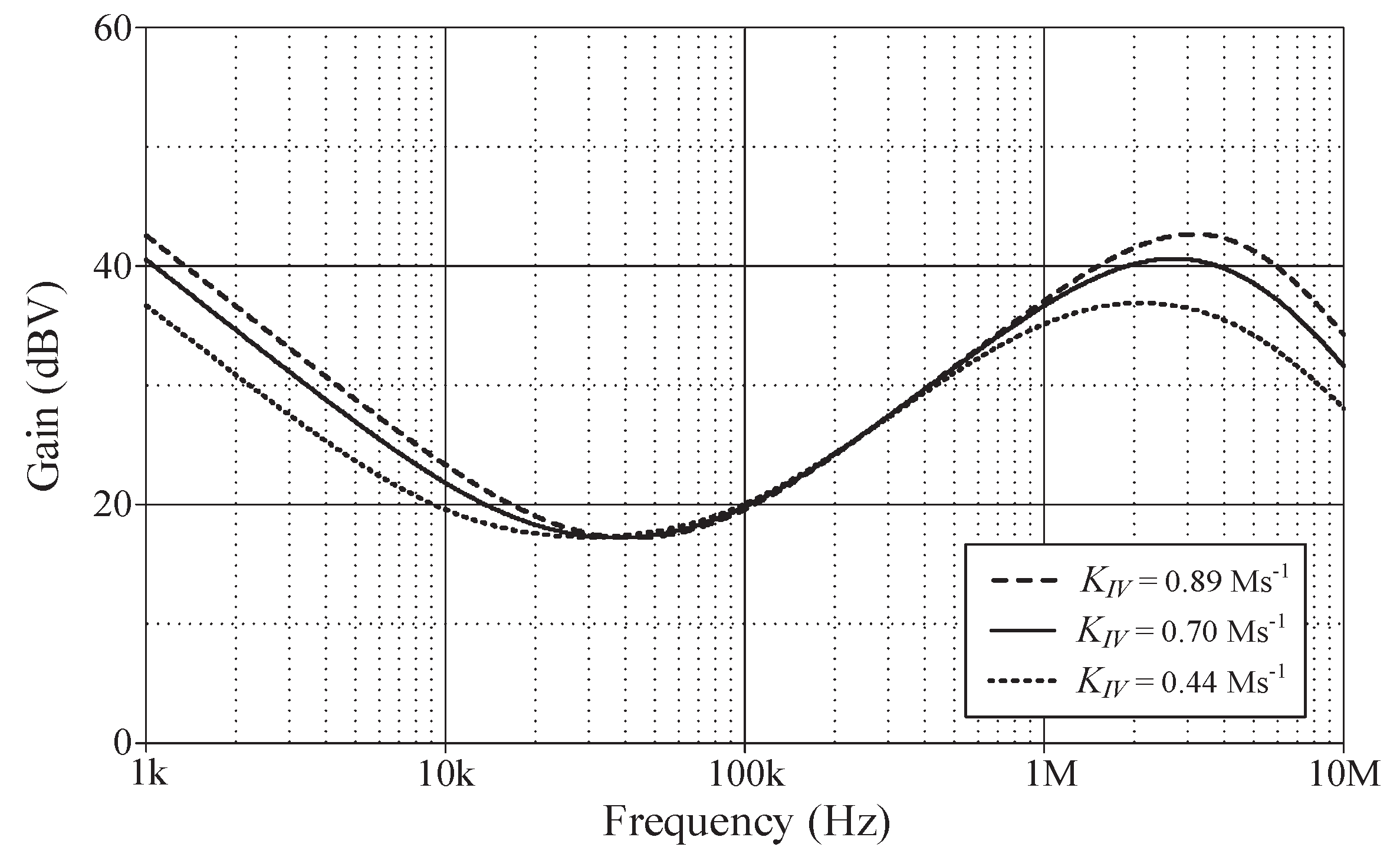
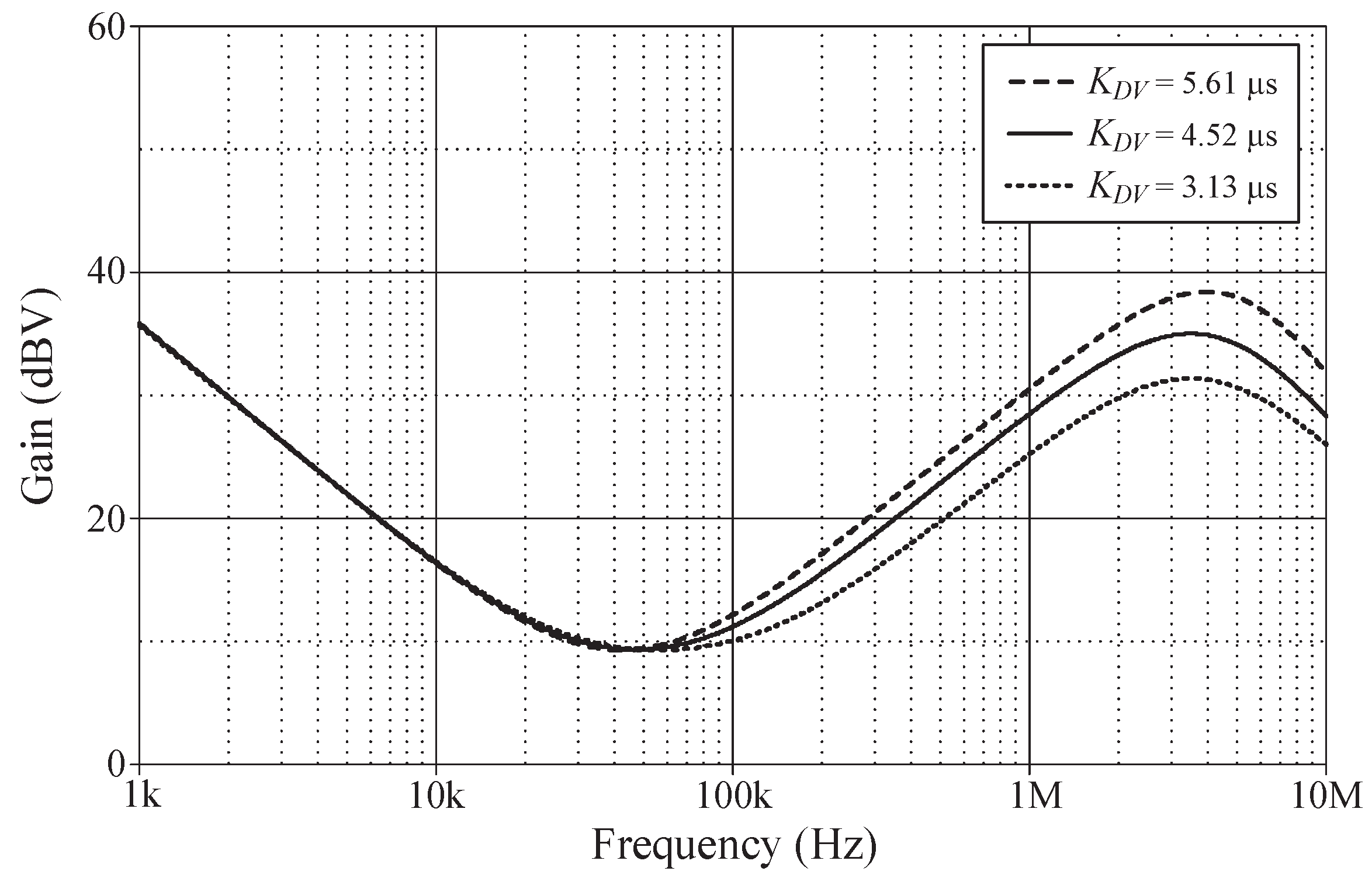
In order to evaluate of the tuning performance, the simulations have been carried out by varying the coefficients K_PV, K_IV and K_DV of the VM controller. For our first tuning example, the values of various controller components for the variation in controller coefficient K_PV, while holding K_IV and K_DV constant, are given in Table 3. As evident in Figure 8, the parameter K_PV influences the entire operational range as it appears from the gain response of the controller. The variations in the K_IV and K_DV values resulting from the use of different component values are also provided in Table 4 and Table 5. For the specified set parameters, the gain responses of the VM PID controller with tuning K_IV and K_DV are illustrated in Figure 9 and Figure 10, respectively.

6. Performance Verification with Closed-Loop Control Implementation

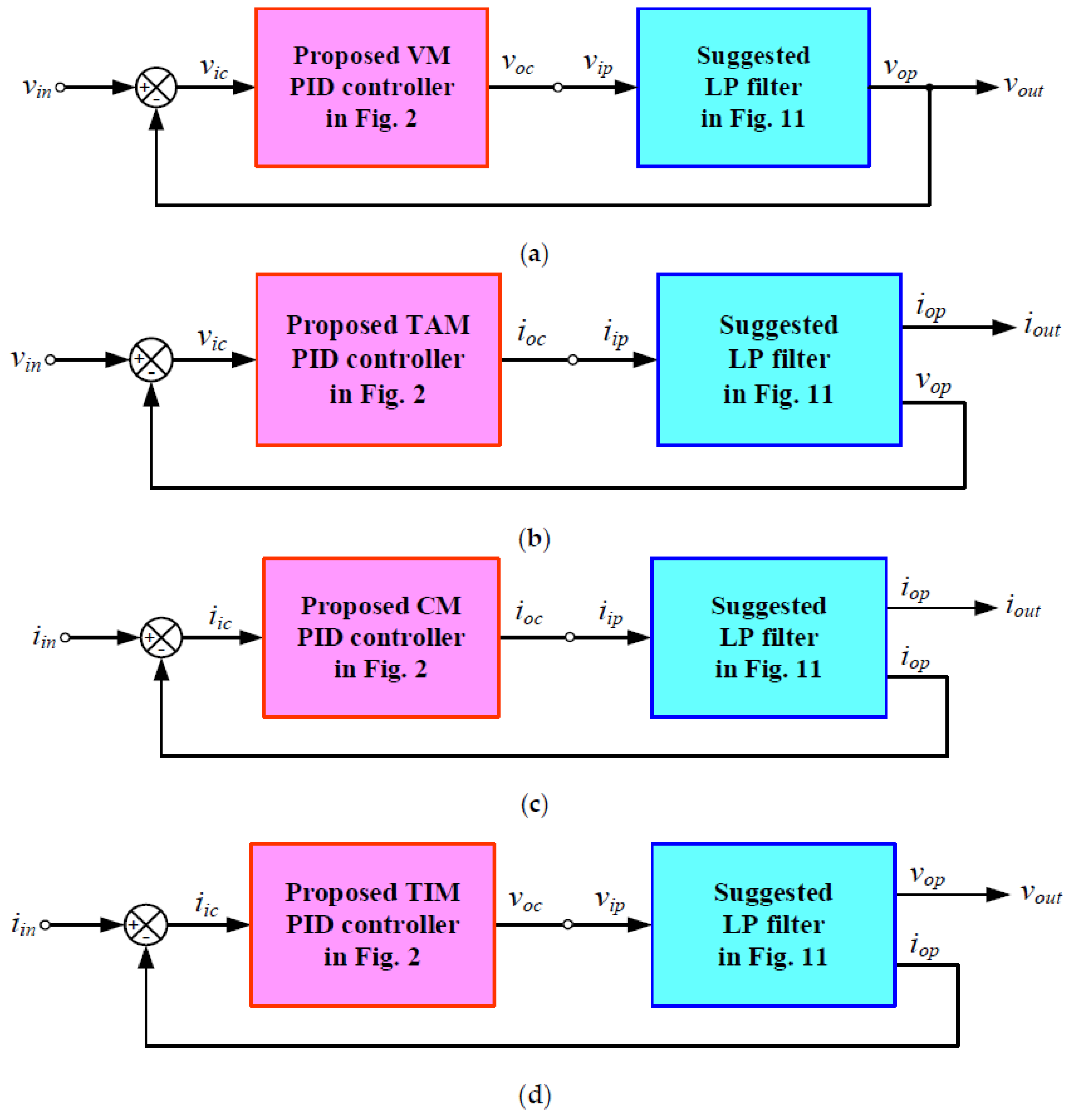
In order to assess the effectiveness of the proposed mixed-mode PID controller in Figure 2, the mixed-mode second-order lowpass (LP) filter depicted in Figure 11 is suggested as a plant for implementing a closed-loop control system. The suggested LP filter can be realized for all four-mode LP filters with the following transfer functions:

\begin{matrix} VM : \end{matrix} T_{V} (s) = \frac{v_{o p}}{v_{i p}} = \frac{(\frac{1}{R_{p 0} R_{p 2} C_{p 1} C_{p 2}})}{D (s)},

(27)

\begin{matrix} TAM : \end{matrix} T_{Y} (s) = \frac{i_{o p}}{v_{i p}} = \frac{(\frac{1}{R_{p 0} R_{p 2} R_{p 3} C_{p 1} C_{p 2}})}{D (s)},

(28)

\begin{matrix} CM : \end{matrix} T_{I} (s) = \frac{i_{o p}}{i_{i p}} = \frac{(\frac{1}{R_{p 2} R_{p 3} C_{p 1} C_{p 2}})}{D (s)},

(29)

\begin{matrix} TIM : \end{matrix} T_{Z} (s) = \frac{v_{o p}}{i_{i p}} = \frac{(\frac{1}{R_{p 2} C_{p 1} C_{p 2}})}{D (s)},

(30)

where

\begin{matrix}  \end{matrix} D (s) = s^{2} + s (\frac{1}{R_{p 1} C_{p 1}} + \frac{1}{R_{p 2} C_{p 2}}) + (\frac{1}{R_{p 1} R_{p 2} C_{p 1} C_{p 2}}) \begin{matrix}  \end{matrix} .

(31)

From Equations (27)-(31), the natural angular frequency (ω_n) and the quality factor (Q) for the filter are respectively obtained as:

\begin{matrix}  \end{matrix} ω_{n} = 2 π f_{n} = \frac{1}{\sqrt{R_{p 1} R_{p 2} C_{p 1} C_{p 2}}} \begin{matrix}  \end{matrix},

(32)

and

\begin{matrix}  \end{matrix} Q = \frac{\sqrt{R_{p 1} R_{p 2} C_{p 1} C_{p 2}}}{R_{p 1} C_{p 1} + R_{p 2} C_{p 2}} \begin{matrix}  \end{matrix} .

(33)

The implemented closed-loop systems, as depicted in Figure 12, utilize the mixed-mode PID controller proposed in Figure 2 and the filter plant suggested in Figure 11. The configurations depicted in Figure 12a–d were constructed for the performance assessment of VM, TAM, CM, and TIM controllers, correspondingly. The component values for the filters are as follows: R_p₀ = R_p₁ = R_p₂ = R_p₃ = 1 kΩ and C_p₁ = C_p₂ = 1 nF; thus, f_n = 159 kHz and Q = 0.5 are obtained. All implemented controllers utilized R₁ = R₃ = 5 kΩ and C₁ = C₂ = 200 pF.

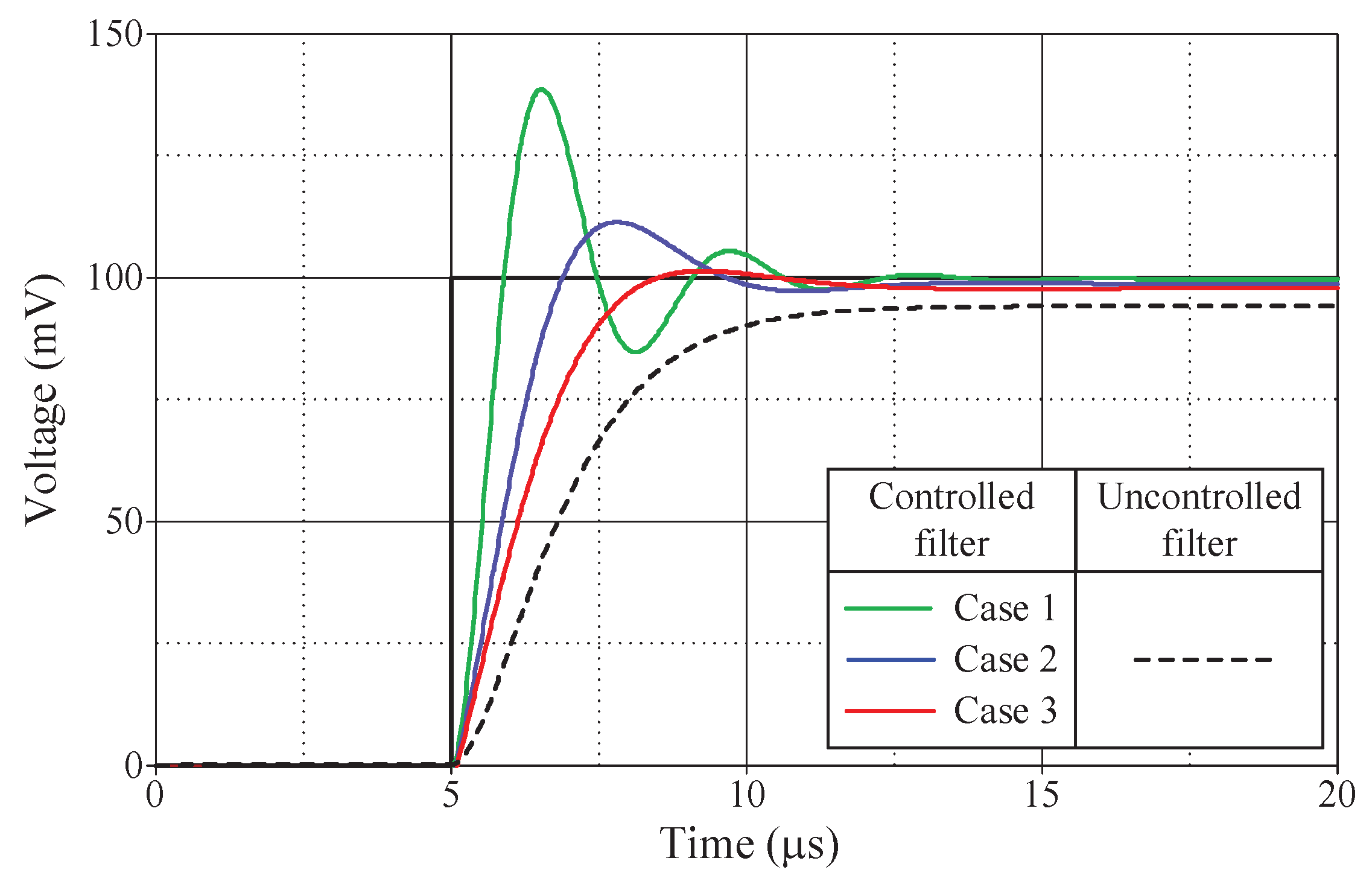
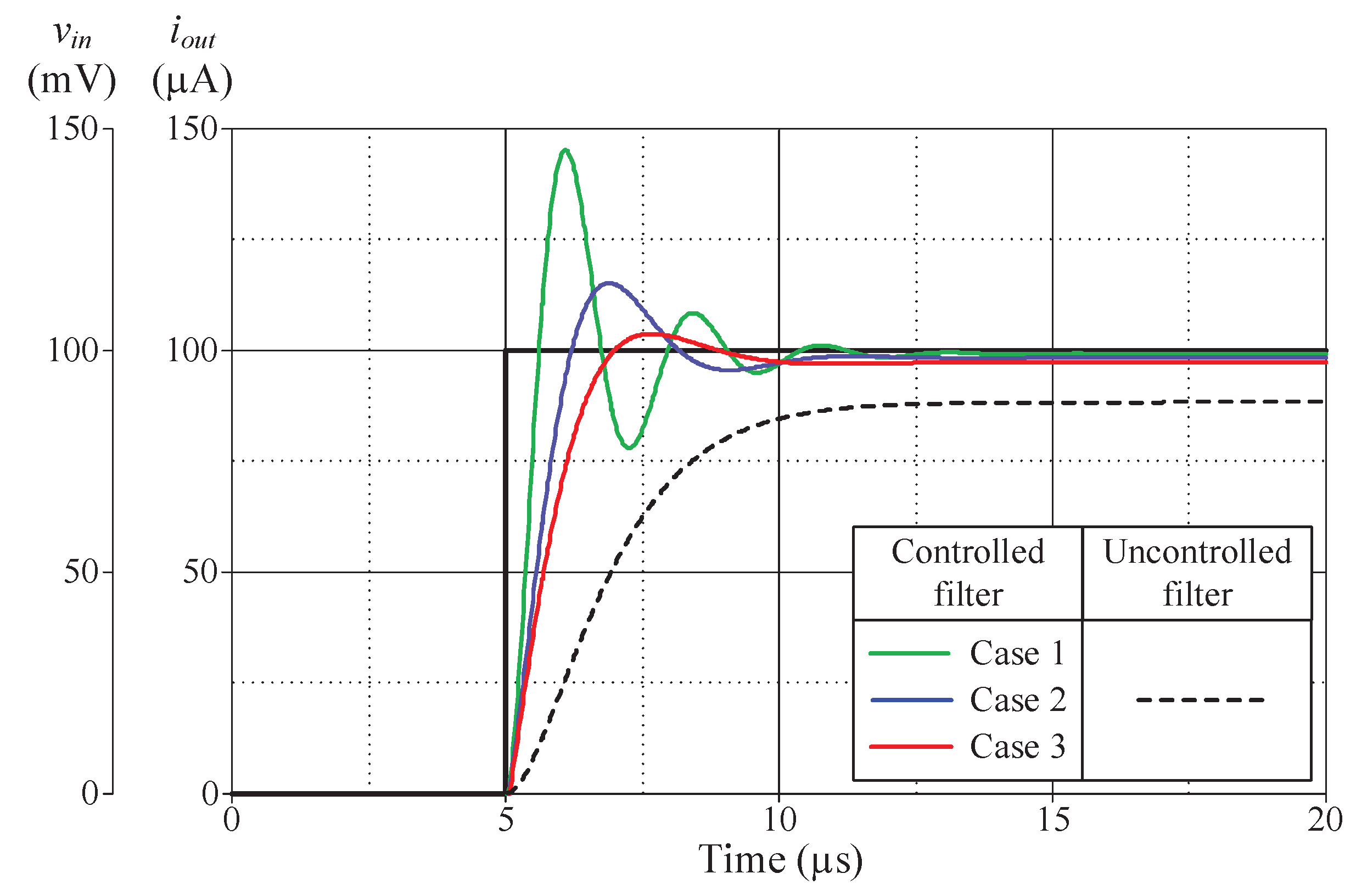
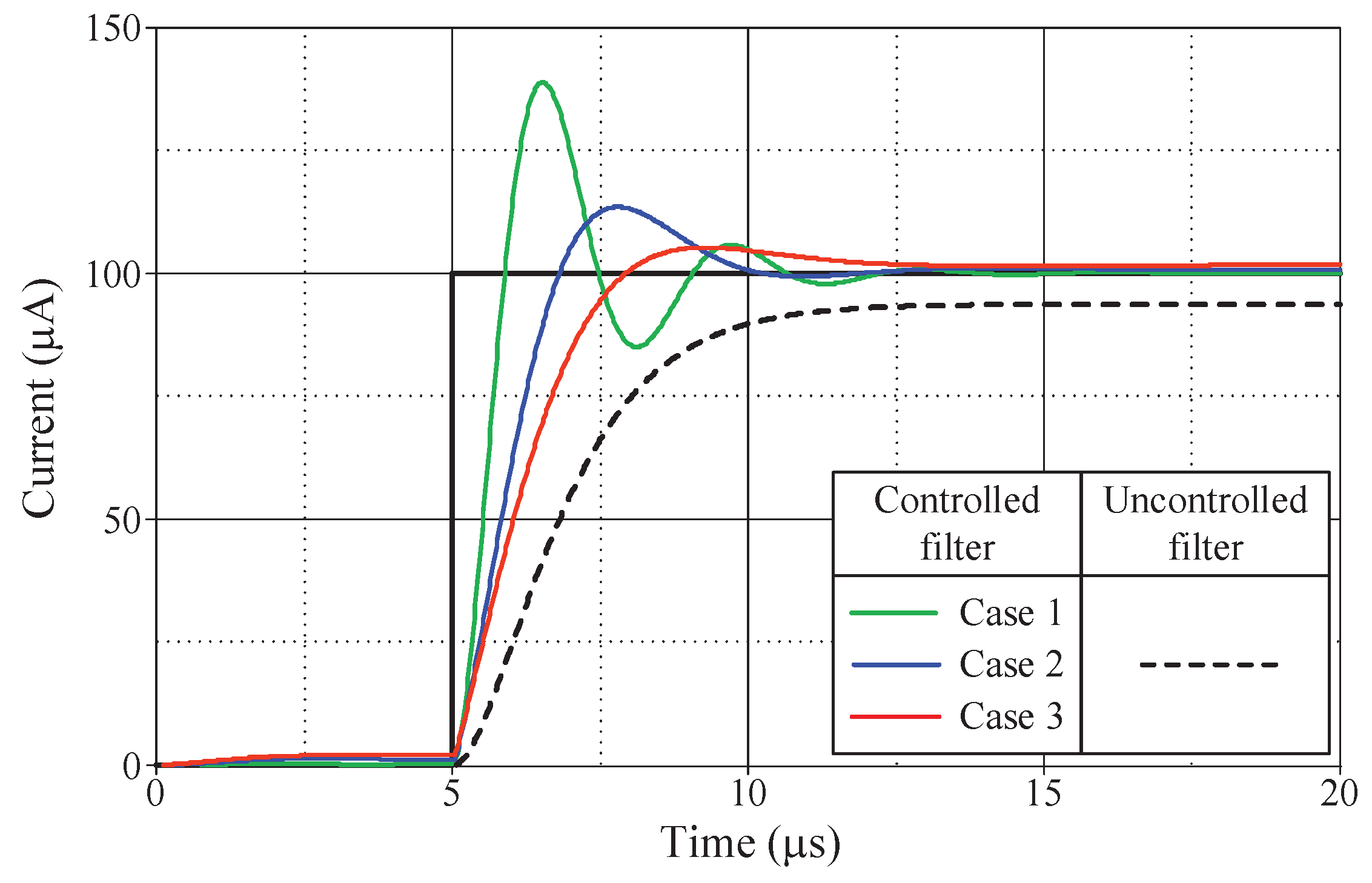
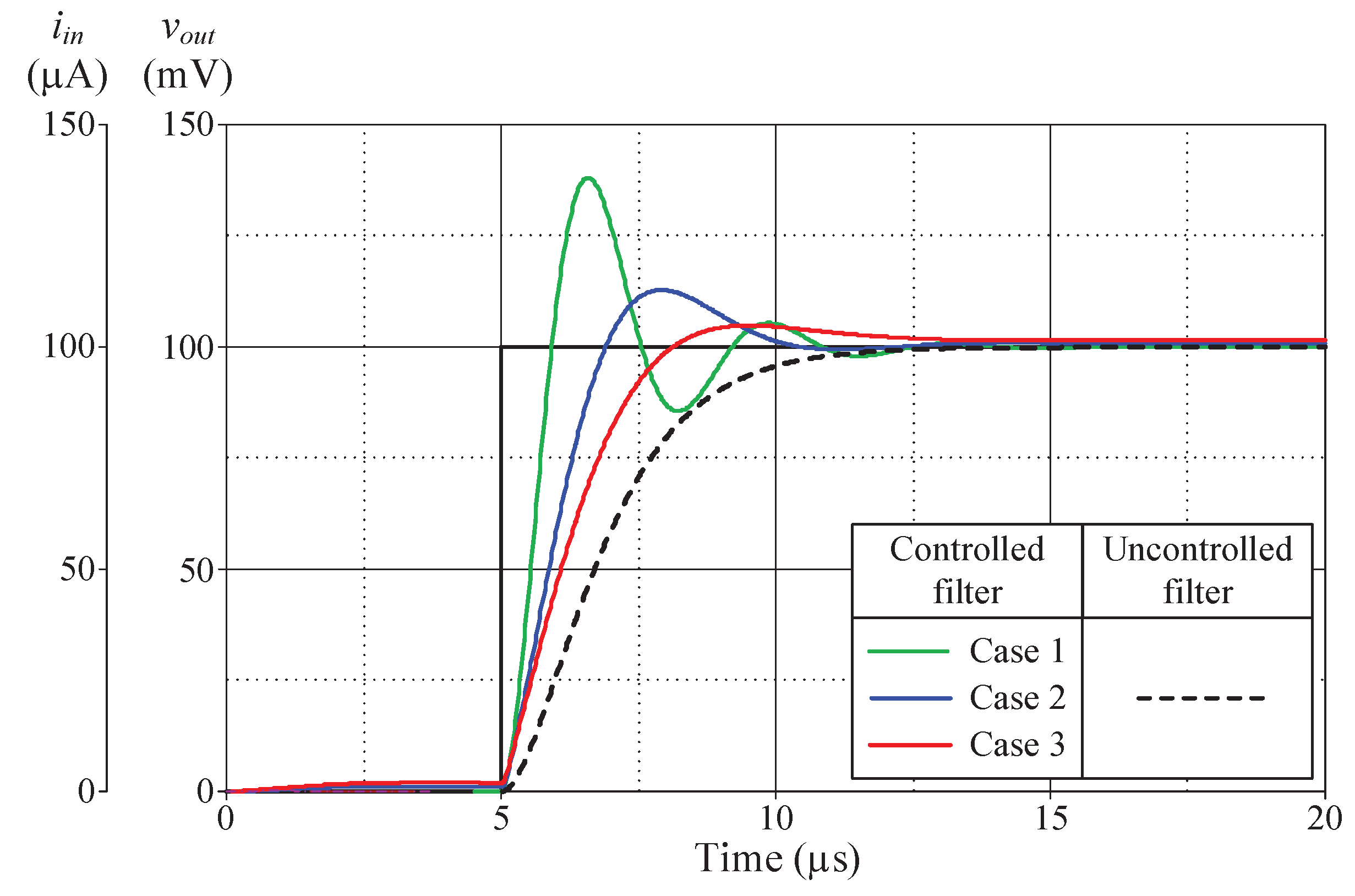
Figure 13, Figure 14, Figure 15 and Figure 16 illustrate the step responses of the uncontrolled filter and PID-controlled filter systems for Figure 12a–d, respectively. The controller parameters employed to evaluate the step response, along with the characteristics derived from the responses for each of the four modes, are also documented in Table 6, Table 7, Table 8 and Table 9. It is evident from the tables that the proposed PID controllers improve the time response of the closed-loop control filter systems, particular for t_d, t_r, t_p, and t_s. Additionally, the controlled filters enter the steady-state faster than the uncontrolled filters, and track the step-input with a reduced stead-state error.

7. Conclusions

This work presents the tunable mixed-mode PID controller implemented with commercially available integrated circuits (ICs), the current-feedback operational amplifiers (CFOAs). The presented PID controller circuit employs three CFOAs, four resistors, and two capacitors. All four operational mode PID controllers, namely VM, TAM, CM, and TIM, can be performed with a single proposed circuit topology. The important parameters of the proposed PID controllers, namely, K_P, K_I, and K_D, are modifiable as desired. Since the proposed controller is designed using only off-the-shelf ICs together with some passive components, it has advantages in terms of practicality and simplicity. Analyses of non-ideal transfer gain and parasitic effects on the controller performance have also been examined in detail. In addition, to evaluate the practical applicability of the proposed mixed-mode PID controller, the mixed-mode second-order lowpass filter is designed to be a testing plant for a mixed-mode closed-loop control system. A simulation study demonstrates the performance of the circuits.

Author Contributions

Conceptualization, N.R., J.S., and W.T.; methodology, N.R., J.S., T.P., and W.T.; software, N.R. and J.S.; validation, N.R., J.S., T.P., and W.T.; formal analysis, N.R., J.S. and W.T.; investigation, N.R., J.S., T.P., and W.T.; resources, N.R., J.S., T.P., and W.T.; data curation, N.R., J.S., and W.T.; writing—original draft preparation, N.R., J.S., and W.T.; writing—review and editing, T.P. and W.T.; visualization, N.R., J.S., and W.T.; supervision, T.P. and W.T.; project administration, T.P. and W.T. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by King Mongkut’s Institute of Technology Ladkrabang [2567-02-01-067].

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data supporting the results presented in this work are available on request from the authors.

Conflicts of Interest

The authors declare no conflict of interest.

References

Michael, A. J.; Mohammad, H. M. PID Control New Identification and Design Methods, Springer, Berlin, 2005.
Astrom, K. J.; Hagglund, T. The future of PID control. Control Eng. Practice. 2001, 9, 1163–1175. [Google Scholar] [CrossRef]
Astrom, K. J.; Hagglund, T. PID Controllers: Theory, Design and Tuning, 2nd ed.; Instrument Society of America: Research Triangle Park, USA, 1995. [Google Scholar]
Franco, S. Design with operational amplifiers and analog integrated circuits, 3rd ed.; McGraw-Hill: Boston, 2002. [Google Scholar]
Erdal, C.; Toker, A.; Acar, C. OTA-based proportional-integral-derivative (PID) controller and calculating optimum parameter tolerances. Turk. J. Elec. Engin. 2001, 9, 189–198. [Google Scholar]
Keskin, A. U. Design of PID controller circuit employing CDBAs. Int. J. Electr. Eng. Educ. 2006, 43, 48–56. [Google Scholar] [CrossRef]
Pandey, R.; Pandey, N.; Chitranshi, S.; Paul, S. K. Operational transresistance amplifier based PID controller. Adv. Electr. Electron. Eng. 2015, 13, 171–181. [Google Scholar] [CrossRef]
Yuce, E.; Tokat, S.; Minaei, S.; Cicekoglu, O. Low-component-count insensitive current-mode and voltage-mode PID, PI and PD controllers. Frequenz 2006, 60, 65–69. [Google Scholar] [CrossRef]
Yuce, E.; Tokat, S.; Kizilkaya, A.; Cicekoglu, O. CCII-based PID controllers employing grounded passive components. AEU - Int. J. Electron. Commun. 2006, 60, 399–403. [Google Scholar] [CrossRef]
Yuce, E.; Minaei, S. New CCII-based versatile structure for realizing PID controllers and instrumentation amplifier. Microelectron. J. 2010, 41, 311–316. [Google Scholar] [CrossRef]
Ozer, E.; Kacar, F. Design of voltage-mode PID controller using a single voltage differencing current conveyor (VDCC). Analog Integr. Circuits Signal Process. 2021, 109, 11–27. [Google Scholar] [CrossRef]
Shrivastava, P.; Surendra, S.; Ranjan, R. K.; Shrivastav, A.; Priyadarshini, B. PI, PD and PID controllers using single DVCCTA. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 673–685. [Google Scholar] [CrossRef]
Yuce, E.; Alpaslan, H. DDCC+ based voltage-mode PID controller employing only grounded passive components. Indian J. Eng. Mater. Sci. 2016, 23, 120–128. [Google Scholar]
Tangsrirat, W. Voltage-mode analog PID controller using a single z-copy current follower transconductance amplifier (ZC-CFTA). Informacije MIDEM 2015, 45, 175–179. [Google Scholar]
Mongkolwai, P.; Tangsrirat, W.; Suesut, T. Novel voltage-Mode PID controller using a single CCTA and all grounded passive components. Informacije MIDEM 2022, 52, 169–179. [Google Scholar] [CrossRef]
Taskıran, Z. G. Ç.; Sedef, H.; Anday, F. A new PID controller circuit design using CFOAs. Circuits, Syst. Signal Process. 2021, 40, 1166–1182. [Google Scholar] [CrossRef]
Silaruam, V.; Lorsawatsiri, A.; Wongtaychatham, C. Novel resistorless mixed-mode PID controller with improved low-frequency performance. Radioengineering 2013, 22, 932–940. [Google Scholar]
Analog Devices, AD844: 60 MHz, 2000 V/μs, Monolithic op amp with Quad Low Noise. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD844.pdf (accessed on 29 June 2022).

Figure 1. CFOA circuit representation.

Figure 2. Proposed mixed-mode PID controller configuration using CFOAs.

Figure 3. Non-ideal behavior model of the CFOA.

Figure 4. Ideal and simulated time-domain responses of the proposed controller in Figure 2: (a) VM; (b) TAM; (c) CM; (d) TIM.

Figure 5. Ideal and simulated frequency-domain responses of the proposed controller in Figure 2: (a) VM; (b) TAM; (c) CM; (d) TIM.

Figure 6. Simulated frequency responses of the proposed VM PID controller with ambient temperature variation.

Figure 7. Monte Carlo statistical analysis results of the proposed VM PID controller: (a) gain response; (b) phase response.

Figure 8. Gain-frequency responses of the proposed VM PID controller when adjusting K_PV while keeping K_IV and K_DV constant.

Figure 9. Gain-frequency responses of the proposed VM PID controller when adjusting K_IV while keeping K_PV and K_DV constant.

Figure 10. Gain-frequency responses of the proposed VM PID controller when adjusting K_DV while keeping K_PV and K_IV constant.

Figure 11. Suggested mixed-mode lowpass filter.

Figure 12. Closed-loop control system implementation: (a) VM; (b) TAM; (c) CM; (d) TIM.

Figure 13. Step-responses of the uncontrolled and controlled filters in Figure 12(a).

Figure 14. Step-responses of the uncontrolled and controlled filters in Figure 12(b).

Figure 15. Step-responses of the uncontrolled and controlled filters in Figure 12(c).

Figure 16. Step-responses of the uncontrolled and controlled filters in Figure 12(d).

Table 1. Comparison features of the proposed controller circuit with the earlier PID controllers [4,5,6,7,8,9,10,11,12,13,14,15,16,17].

Ref.	Active component	Passive component	Mixed-mode operation	Operating modes				Technology	Supply voltage (V)
Ref.	Active component	Passive component	Mixed-mode operation	VM	CM	TAM	TIM	Technology	Supply voltage (V)
[4]	OA = 4	R = 8, C = 2	no	yes	no	no	no	NA	NA
[5]	OTA = 8	C = 2	no	yes	no	no	no	0.8-μm CMOS	±5, (-2 ~ 4)
[6]	CDBA = 4	R = 8, C = 2	no	yes	no	no	no	0.8-μm CMOS	±2.5, ±1
[7]	OTRA = 2	R = 4, C = 3	no	yes	no	no	no	0.18-μm CMOS	±1.5
[8]	CCII = 2	R = 4, C = 2	no	yes	yes	no	no	AD844	NA
[9]	CCII = 1, DO-CCII = 1	R = 3, C = 2	no	yes	yes	no	no	0.35-μm CMOS	±1.5, +0.5
[10]	DO-CCII = 1	R = 2, C = 2	no	no	yes	no	no	0.13-μm CMOS	±1, +0.4
[11]	VDCC = 1	R = 4, C = 2	no	yes	no	no	no	0.18-μm CMOS	±0.9
[12]	DVCCTA = 1	R = 3, C = 2	no	yes	no	no	no	0.25-μm CMOS	±1.5, -1
[13]	DCCC = 3	R = 3, C = 2	no	yes	no	no	no	0.13-μm CMOS	±0.75, +0.37
[14]	ZC-CFTA = 1	R = 2, C = 2	no	yes	no	no	no	0.35-μm CMOS	±1
[15]	CCTA = 1	R = 2, C = 2	no	yes	no	no	no	0.35-μm CMOS	±1.5
[16]	CFOA = 2	R = 3, C = 2 for VM, R = 5, C = 2 for CM	no	yes	yes	no	no	AD844	±12
[17]	Transconductor = 6	C = 2	yes	yes	yes	yes	yes	0.18-μm CMOS	±0.9
Proposed controller	CFOA = 2	R = 4, C = 2	yes	yes	yes	yes	yes	AD844	±9

Abbreviations: R = Resistor, C = Capacitor, NA = Not Available, OA = operational amplifier, OTA = operational transconductance amplifier, CDBA = current differencing buffered amplifier, OTRA = operational transresistance amplifier, CCII = second-generation current conveyor, DO-CCII = dual-output CCII, VDCC = voltage differencing current conveyor, CCTA = current conveyor transconductance amplifier, DVCCTA = differential voltage CCTA, DDCC = differential difference current conveyor, ZC-CFTA = z-copy current follower transconductance amplifier, CFOA = current feedback operational amplifier

Table 2. Temperature dependence of the gain value for the proposed VM PID controller.

Temperature (°C)	Controller VM gain (dBV)
Temperature (°C)	f = 10 kHz	f = 100 kHz	f = 1 MHz
0	24.090	19.350	37.336
25	24.056	19.315	37.293
50	24.021	19.281	37.249
75	23.987	19.246	37.204
100	23.953	19.212	37.157

Table 3. Different component values for the variation in controller coefficient K_PV.

K_PV	K_IV (Ms^-1)	K_DV (μs)	R₀ (kΩ)	R₁ = R₂ = R₃ (kΩ)	C₁ (nF)	C₂ (nF)
8.25	1	12.5	2.5	5	0.40	2.5
10.05			3.5	5	0.29	3.5
15.54			6.0	5	0.17	6.0

Table 4. Different component values for the variation in controller coefficient K_IV.

K_PV	K_IV (Ms^-1)	K_DV (μs)	R₀ (kΩ)	R₁ = R₂ = R₃ (kΩ)	C₁ (nF)	C₂ (nF)
7.5	0.89	12.5	2.5	5	0.45	2.5
	0.70		3.5	5	0.41	3.5
	0.44		6.0	5	0.38	6.0

Table 5. Different component values for the variation in controller coefficient K_DV.

K_PV	K_IV (Ms^-1)	K_DV (μs)	R₀ (kΩ)	R₁ = R₂ = R₃ (kΩ)	C₁ (nF)	C₂ (nF)
3	0.4	5.61	3.5	5	0.72	1.57
		4.52	6	5	0.42	2.17
		3.13	10	5	0.25	2.50

Table 6. Controller parameters and the resulting characteristics of the uncontrolled filter and controlled filter systems shown in Figure 12(a).

		R₀ = R₂ (kΩ)	K_PV	K_IV (Ms^-1)	K_DV (μs)	Delay time, t_d (μs)	Rise time, t_r (μs)	Peak time, t_p (μs)	Settling time, t_s (μs)		Maximum overshoot, M_p (mV)	Steady- state error (mV)
		R₀ = R₂ (kΩ)	K_PV	K_IV (Ms^-1)	K_DV (μs)	Delay time, t_d (μs)	Rise time, t_r (μs)	Peak time, t_p (μs)	5%	2%	Maximum overshoot, M_p (mV)	Steady- state error (mV)
PID- controlled filter	Case 1	1	5.50	5.00	0.5	5.52	5.89	6.53	9.97	11.52	138.63	0.20
	Case 2	3	2.17	1.67	0.5	5.86	6.88	7.81	9.06	9.52	111.43	1.19
	Case 3	5	1.50	1.00	0.5	6.12	8.50	9.28	7.66	10.66	101.40	2.19
Uncontrolled filter						6.79	11.69	11.69	9.72	10.83	94.19	5.81

Table 7. Controller parameters and the resulting characteristics of the uncontrolled filter and controlled filter systems shown in Figure 12(b).

		R₀ = R₂ (kΩ)	K_PY	K_IY (Ms^-1)	K_DY (μs)	Delay time, t_d (μs)	Rise time, t_r (μs)	Peak time, t_p (μs)	Settling time, t_s (μs)		Maximum overshoot, M_p (μA)	Steady- state error (μA)
		R₀ = R₂ (kΩ)	K_PY	K_IY (Ms^-1)	K_DY (μs)	Delay time, t_d (μs)	Rise time, t_r (μs)	Peak time, t_p (μs)	5%	2%	Maximum overshoot, M_p (μA)	Steady- state error (μA)
PID- controlled filter	Case 1	1	11	10	1	5.36	5.61	6.09	8.83	10.04	145.23	0.72
	Case 2	3	4.33	3.33	1	5.56	6.21	6.89	7.92	9.64	115.20	1.68
	Case 3	5	3	2	1	5.69	6.98	7.68	8.28	9.09	103.76	2.63
Uncontrolled filter						6.92	14.30	14.30	9.64	10.76	88.36	11.64

Table 8. Controller parameters and the resulting characteristics of the uncontrolled filter and controlled filter systems shown in Figure 12(c).

		R₀ = R₂ (kΩ)	K_PI	K_II (Ms^-1)	K_DI (μs)	Delay time, t_d (μs)	Rise time, t_r (μs)	Peak time, t_p (μs)	Settling time, t_s (μs)		Maximum overshoot, M_p (μA)	Steady- state error (μA)
		R₀ = R₂ (kΩ)	K_PI	K_II (Ms^-1)	K_DI (μs)	Delay time, t_d (μs)	Rise time, t_r (μs)	Peak time, t_p (μs)	5%	2%	Maximum overshoot, M_p (μA)	Steady- state error (μA)
PID- controlled filter	Case 1	1	1.1	1	0.1	5.52	5.89	6.53	9.99	11.45	138.92	0.10
	Case 2	3	1.3	1	0.3	5.83	6.81	7.80	9.06	9.51	113.53	0.90
	Case 3	5	1.5	1	0.5	6.03	7.98	9.26	7.66	10.66	105.29	1.71
Uncontrolled filter						6.81	11.63	11.63	9.72	10.83	93.74	6.26

Table 9. Controller parameters and the resulting characteristics of the uncontrolled filter and controlled filter systems shown in Figure 12(d).

		R₀ = R₂ (kΩ)	K_PZ	K_IZ (Ms^-1)	K_DZ (μs)	Delay time, t_d (μs)	Rise time, t_r (μs)	Peak time, t_p (μs)	Settling time, t_s (μs)		Maximum overshoot, M_p (mV)	Steady- state error (mV)
		R₀ = R₂ (kΩ)	K_PZ	K_IZ (Ms^-1)	K_DZ (μs)	Delay time, t_d (μs)	Rise time, t_r (μs)	Peak time, t_p (μs)	5%	2%	Maximum overshoot, M_p (mV)	Steady- state error (mV)
PID- controlled filter	Case 1	1	5.50	5	0.5	5.54	5.92	6.59	10.06	11.62	138.03	0.001
	Case 2	3	6.5	5	1.5	5.87	6.91	7.91	9.19	9.67	112.82	0.782
	Case 3	5	7.5	5	2.5	6.09	8.13	9.51	7.81	10.79	104.79	1.579
Uncontrolled filter						6.70	11.81	11.81	9.79	10.91	99.92	0.085

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Design of Mixed-Mode Analog PID Controller with CFOAs

Abstract

1. Introduction

2. Proposed Mixed-Mode PID Controller Configuration

2.1. VM and TAM Operations

2.2. CM and TIM Operations

3. Non-Ideality Effects of CFOA Parasitic Gains

4. Non-Ideality Effects of CFOA Parasitic Impedances

5. Functional Simulation and Discussion

6. Performance Verification with Closed-Loop Control Implementation

7. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe