Information in the Three Dimensions of Time

Preprint

Article

Information in the Three Dimensions of Time

Altmetrics

Downloads

132

Views

Comments

seyed kazem mousavi^*,

Jerzy Zbigniew Achimowicz

seyed kazem mousavi^*,

Jerzy Zbigniew Achimowicz

This version is not peer-reviewed

This preprints belongs to the Topic

Quantum Information and Quantum Computing, 2nd Volume

Submitted:

31 March 2024

Posted:

02 April 2024

You are already at the latest version

Alerts

Abstract

The relationship between physics and information processing is a topic of great significance in the realm of science and technology. The laws of physics, which govern the behavior of matter and energy, also have a profound influence on the way information is processed and utilized. While the mathematics governing information processing has not extensively utilized the laws of physics, it is evident that there is potential for these laws to play a more significant role, particularly in the context of quantum systems. based on the equivalence between information and energy, we can explore how other laws of physics can effectively contribute to more efficient and advanced information processing techniques. This research sheds light on the interconnectedness of physics and information processing, and its findings have the potential to significantly enhance our ability to process information, particularly in cutting-edge quantum systems. By recognizing and leveraging the influence of physics, we can pave the way for further advancements in information processing technologies.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

In the realm of information theory, it is imperative to recognize that all the laws of physics apply [1,2]. Information, in its various forms, is subject to the fundamental principles that govern the physical world [3,4]. From the conservation of energy to the second law of thermodynamics, the entire framework of physics is intertwined with the transmission, storage, and processing of information [5,6]. At its core, the laws of physics are a collection of information over time. The acquisition of information is a process that unfolds gradually over time. It is not an instantaneous event, but rather a function of the passage of time. As time progresses, new data is gathered, analyzed, and synthesized, leading to the formation of knowledge and understanding. This gradual accumulation of information allows for a more comprehensive and nuanced perspective on a given subject [7,8]. The behavior of particles, the propagation of waves, and the dynamics of systems all contribute to a vast reservoir of knowledge about the physical world. This knowledge is encoded in the form of laws and principles that describe the behavior of matter and energy. In turn, these laws provide the foundation for understanding and manipulating information in a wide range of contexts.[8] One of the most fundamental principles that underpins the relationship between physics and information is the concept of entropy. In thermodynamics, entropy is a measure of the disorder or randomness in a system [8]. It is also intimately linked to the amount of information that is required to fully describe the state of a system. As systems evolve over time, their entropy tends to increase, leading to a corresponding increase in the amount of information needed to characterize their state. This connection between entropy and information has profound implications for fields as diverse as communication theory, cryptography, and computational complexity [9,10,11]. Furthermore, the laws of physics also dictate the fundamental limits on the transmission and processing of information. For example, the speed of light imposes a fundamental limit on the rate at which information can be transmitted across space. Similarly, quantum mechanics places constraints on the accuracy with which certain types of information can be measured and processed. These limitations, rooted in the laws of physics, have significant implications for the design and operation of communication systems, computing devices, and information processing algorithms [12]. In addition to these fundamental constraints, the laws of physics also offer opportunities for leveraging physical phenomena to store and process information in novel ways [13,14]. For instance, emerging technologies such as quantum computing and spintronics exploit the unique properties of quantum mechanics and spin dynamics to perform computations and store data in fundamentally different ways than traditional electronic devices [15,16,17]. These developments not only push the boundaries of what is possible in terms of information processing, but also deepen our understanding of the underlying physical principles that govern these processes. In conclusion, the laws of physics are indeed a collection of information over time, and this insight has profound implications for our understanding and manipulation of information in all its forms. By recognizing the deep connections between physical principles and information theory, we can continue to push the boundaries of what is possible in fields as diverse as communication, computation, and data storage [18]. As we continue to explore and exploit these connections, we are likely to uncover new opportunities for innovation and discovery at the intersection of physics and information theory. The concept of six-dimensional space-time allows for the examination of the equivalence between distance in space and time with density, leading to a new perspective on information [19,20]. This viewpoint suggests that information can be considered equivalent to inertial mass, as is the case with the equivalence between inertial mass and gravitational mass. As a result, the limitations that govern physical laws may diminish over time. This understanding opens up new possibilities for how we perceive and interact with the world around us, and may have implications for the future development of technology and scientific exploration.

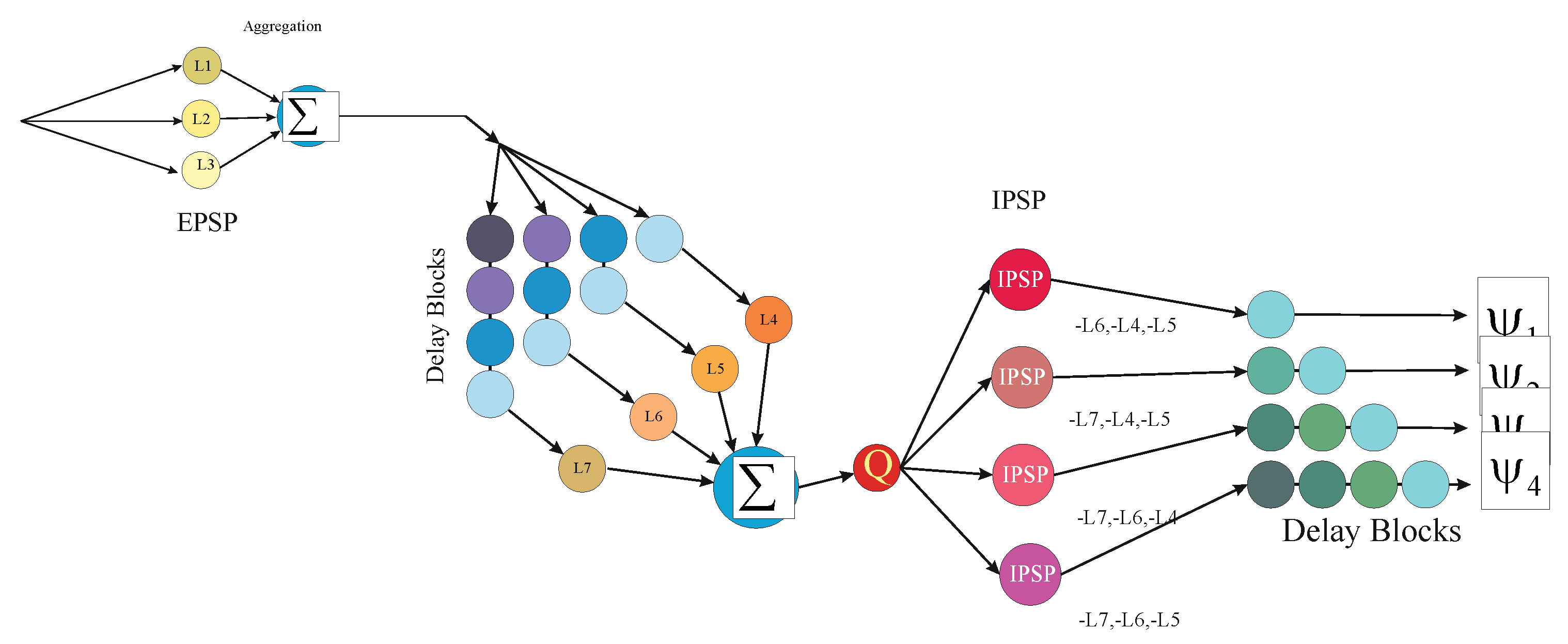
2. Method

The movement of all objects is inherently linked to the dimension of time. It is observed that the speed of an object's movement in the time dimension is directly influenced by its density. When an object moves through space, it experiences a decrease in its movement in the dimension of time, accompanied by an increase in its mass. This phenomenon is commonly known as time dilation in the context of special relativity. Conversely, an increase in mass and density leads to a decrease in the object's speed in the time dimension. It is important to note that there exists a direct correlation between gravitational mass and the passage of time. Without the passage of time, gravitational mass ceases to exist, and consequently, objects do not experience a gravitational pull. This intricate relationship between movement, density, and time underscores the fundamental principles governing the behavior of objects within the fabric of spacetime (2.1).

\sin 0 = 0 \Rightarrow x, t \neq c ξ = s i n (\cos^{- 1} (\frac{∆ x}{c})) + s i n (\cos^{- 1} (\frac{∆ y}{c})) + s i n (\cos^{- 1} (\frac{∆ z}{c})) t = \frac{t_{0}}{ξ} \equiv t = t_{0} \sqrt{1 - \frac{2 G M}{r c^{2}}} \Rightarrow c ({η^{2}}_{1} + {η^{2}}_{2} + {η^{2}}_{3}) = r_{x, ρ} c \Rightarrow s i n (\cos^{- 1} (\frac{\sqrt{2 G M}}{c \sqrt{r}})) \equiv s i n ϕ t = \frac{t_{0}}{η}, l = \frac{l_{0}}{η}, m = \frac{m_{0}}{η} m^{t} = \frac{h ν}{c^{2}}, {(ρ c)}^{\frac{1}{2}} = ∆ \overset{´}{x}, r_{x, ρ} = ∆ x + ∆ \overset{´}{x}, (m^{t} + m_{x}) = \frac{m^{t}}{η} \to s i n θ = s i n (\cos^{- 1} (\frac{Δ x}{c})) = η = \frac{m^{t}}{m^{t} + m_{x}}

(2.1)

(ρ c) = {∆ \overset{´}{x}}^{2}, (\frac{c}{ρ}) = {∆ \overset{´}{t}}^{2}

ρ = (\frac{m^{t}}{2 π^{2} r^{3}}), m / ρ = \frac{2 π^{2} r^{3}}{η}, \frac{h ν}{c^{2}} = m^{t}, \frac{F}{a} = m_{x}

The concept of information is intricately linked to the passage of time, as it requires energy for its production. This association between information and energy suggests a weak equivalence between the two. In a similar vein, the well-established equivalence between mass and energy posits that they can be interconverted. However, it is important to note that information, unlike mass and energy, is contingent upon the passage of time and is equivalent to inertial mass (2.2).

P^{2} = {m_{x}}^{2} v^{2} \equiv I^{2} \frac{ρ c}{Δ t^{2}} \Rightarrow Δ t^{2} = \frac{1}{ρ c} \Rightarrow I^{2} {(ρ c)}^{2} \Rightarrow E_{k} = m_{x} c^{2} (\frac{1}{s i n θ} - 1) E = m_{x} c^{2} \Rightarrow E = \frac{P^{2}}{2 m_{x}} = n h ν = \frac{I^{2} {(ρ c)}^{2}}{2 m_{x}} \Rightarrow I^{2} {(ρ c)}^{2} = n h ν 2 m_{x}

(2.2)

The concept of density can be likened to a spatial and temporal length that revolves around the density field. Figure 1. The length of the density is equal to the radius of the field. The existence of density causes heterogeneity in the structure of space-time. Accordingly, when the speed of the object increases, the density and the radius of the object's density field change.

The basis of information is based on zero and one. Analog information is also based on signal strength and weakness. The equivalence between mass and energy is violated over time. Consequently, the definition of negative density becomes imperative to counterbalance the absence of matter in both the future and the past (2.3).

T_{μ ν} = [\begin{matrix} - ρ & 0 & 0 & 0 & 0 & 0 \\ 0 & - ρ & 0 & 0 & 0 & 0 \\ 0 & 0 & ρ & 0 & 0 & 0 \\ 0 & 0 & 0 & P & 0 & 0 \\ 0 & 0 & 0 & 0 & P & 0 \\ 0 & 0 & 0 & 0 & 0 & P \end{matrix}]

(2.3)

The tensor described in equation (2.3) depicts the representation of three spatial dimensions and three temporal dimensions. This concept allows for a comprehensive understanding of the interplay between space and time within the framework of physics. Furthermore, by introducing a six-dimensional momentum and energy tensor, a new definition of information can be established (2.4).

I^{2} {(ρ c)}^{2} = n h ν 2 m_{x}, \frac{m}{ρ} = \frac{2 π^{2} r^{3}}{η} \Rightarrow I^{2} = \frac{n h ν 4 π^{2} r^{3}}{Δ {\overset{´}{x}}^{2} c (\sin ({c o s}^{- 1} \frac{Δ x}{c}))}

(2.4)

c (\sin ({c o s}^{- 1} \frac{Δ x}{c})) = Δ t, c (\cos ({c o s}^{- 1} \frac{Δ x}{c})) = Δ x \int_{- ρ}^{+ ρ} \int_{- t}^{+ t} \int_{- \infty}^{+ \infty} {|ψ (ρ, t, x)|}^{2} d ρ d t d x = 1

Each information unit has a wave function. Figure 2. The wave function consists of smaller packets that exist over time. These packets are a complete period of rotation of the density around the mass field (2.5)

|Ψ⟩ = b_{1} |{\tilde{ψ}}_{1}⟩ + b_{2} |{\tilde{ψ}}_{2}⟩ + \dots + b_{n} |{\tilde{ψ}}_{n}⟩ |\tilde{ψ}⟩ = α_{1} |A_{1}⟩ + α_{2} |A_{2}⟩ + α_{3} |A_{3}⟩ + α_{4} |A_{4}⟩ + α_{5} |A_{5}⟩ + α_{6} |A_{6}⟩ b_{μ} = x_{μ} + t i, X_{μ} = (x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}) \Rightarrow b_{μ} {b_{μ}}^{*} = (\frac{1}{3})

(2.5)

\int_{0}^{2 π} {|ψ (x, t))|}^{2} d x = 1 \to \frac{2 π}{6} ⟹ \{(\frac{π}{3}) + i (\frac{2 π}{3})\}, \{(\frac{2 π}{3}) + i (\frac{4 π}{3})\}, \{(π) + (i)\}, {(\frac{4 π}{3}) + i (\frac{5 π}{3}), \{(\frac{5 π}{3}) + i (1)\}, \{(2 π) + i (2 π)\}

Based on this, we can introduce the wave function tensor that can affect the wave function (2.6). however, defining a tensor, we can account for the multidimensional nature of the wave function and its interactions. The wave function tensor provides a powerful tool for describing quantum mechanical systems and can offer valuable insights into the behavior of particles and waves in various physical scenarios.

Ψ_{μ ν} = [\begin{matrix} {c o s}^{2} θ {c o s}^{2} ϕ & A_{ι} & A_{ι} & A_{ι} & A_{ι} & A_{ι} \\ A_{ι} & {c o s}^{2} ϕ & A_{ι} & A_{ι} & A_{ι} & A_{ι} \\ A_{ι} & A_{ι} & e^{- i π φ} & A_{ι} & A_{ι} & A_{ι} \\ A_{ι} & A_{ι} & A_{ι} & e^{i π φ} & A_{ι} & A_{ι} \\ A_{ι} & A_{ι} & A_{ι} & A_{ι} & {s i n}^{2} θ & A_{ι} \\ A_{ι} & A_{ι} & A_{ι} & A_{ι} & A_{ι} & {s i n}^{2} θ {s i n}^{2} ϕ \end{matrix}]

(2.6)

A_{σ} = \pm (\frac{π}{3}) + i z, A_{2} = \pm (\frac{2 π}{3}) + i z, A_{3} = \pm (π) + i z, A_{4} = \pm (\frac{4 π}{3}) + i z, A_{5} = \pm (\frac{5 π}{3}) + i z, A_{6} = \pm (2 π) + i z

The speed of phase change of the wave function is indeed influenced by the density, as indicated in Figure 2. An increase in information will result in a larger area for the circle, consequently leading to a longer phase change. This relationship highlights the significance of density in determining the speed of phase change within the wave function.

Furthermore, it is essential to recognize that the space metric varies for each moving observer (2.7). This variation emphasizes the dynamic nature of space and its interaction with moving observers, further underscoring the complexity of wave function behaviour. In conclusion, the interplay between density and phase change, as well as the variability of space metrics for moving observers, underscores the intricate nature of wave function dynamics. These considerations are crucial for a comprehensive understanding of wave function behaviour and its implications in various contexts.

g_{μ ν} = [\begin{matrix} r a^{2} {c o s}^{2} θ {c o s}^{2} ϕ & 0 & 0 & 0 & 0 & 0 \\ 0 & r^{2} a^{2} {c o s}^{2} θ & 0 & 0 & 0 & 0 \\ 0 & 0 & r^{2} a^{2} & 0 & 0 & 0 \\ 0 & 0 & 0 & {a^{2} r}^{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & a^{2} r^{2} {s i n}^{2} θ & 0 \\ 0 & 0 & 0 & 0 & 0 & {a r}^{2} {s i n}^{2} θ {s i n}^{2} ϕ \end{matrix}]

(2.7)

The field is the approach of the states of the wave function to each other. Figure 3. Density creates a field over time in six-dimensional space-time. Information also has a field and shows the general equation of this field. The K tensor represents the spin electromagnetics for the field. (2.8)

m = \frac{2 G M}{c^{2}} \frac{h e^{φ^{2}} G e^{π^{3}} r}{∆ {\overset{´}{x}}^{2}} = \frac{{2 h}^{2} G^{2} e^{{(φ)}^{2} π^{3}} ν}{c^{4} ∆ {\overset{´}{x}}^{2}} = \frac{2 Λ c}{c^{4} λ ∆ {\overset{´}{x}}^{2}} \Rightarrow \frac{Λ}{{∆ {\overset{´}{x}}^{3} c}^{3} π} K_{μ ν} = [\begin{matrix} \frac{r_{t}}{π c} & A_{ι} & A_{ι} & A_{ι} & A_{ι} & A_{ι} \\ A_{ι} & \frac{{r_{t} h e}^{π^{3}}}{c} & A_{ι} & A_{ι} & A_{ι} & A_{ι} \\ A_{ι} & A_{ι} & \frac{r_{t} \sqrt{G} h e^{φ^{2}}}{c} & A_{ι} & A_{ι} & A_{ι} \\ A_{ι} & A_{ι} & A_{ι} & \frac{\sqrt{G}}{r_{x}} & A_{ι} & A_{ι} \\ A_{ι} & A_{ι} & A_{ι} & A_{ι} & \frac{\sqrt{G}}{r_{x}} & A_{ι} \\ A_{ι} & A_{ι} & A_{ι} & A_{ι} & A_{ι} & \frac{\sqrt{G}}{r_{x}} \end{matrix}] R = \frac{15}{a^{2} r^{3} ({{c o s}^{2} θ c o s}^{2} ϕ)} \Rightarrow (\frac{5}{r^{2}}) (\frac{3}{{r a}^{2} ({{c o s}^{2} θ c o s}^{2} ϕ)})

(2.8)

G_{μ ν} = [\begin{matrix} \frac{10}{r^{2}} & 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{4}{{r c o s}^{2} ϕ} & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{4}{r {{c o s}^{2} θ c o s}^{2} ϕ} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{4}{r {{c o s}^{2} θ c o s}^{2} ϕ} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{4 \sin^{2} θ}{{{r c o s}^{2} θ c o s}^{2} ϕ} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{4 \sin^{2} θ \sin^{2} ϕ}{{{r a c o s}^{2} θ c o s}^{2} ϕ} \end{matrix}]

Achimowicz-Mousavi equation proposes that information fields exhibit a geometric structure across spacetime, suggesting a fundamental connection between information and the fabric of the universe (2.9). This equation challenges conventional notions of causality by suggesting that information can have an impact on events in both the past and the future, implying a non-linear relationship between cause and effect in the fields of information. Within the framework of Achimowicz-Mousavi equation, determinism plays a central role in shaping the arrow of time and the concept of entropy, offering a new perspective on the fundamental principles governing the evolution of physical systems.

G_{μ ν} = R_{μ ν} - \frac{1}{2} R g_{μ ν} = I_{μ ν} Ψ_{μ ν} + I_{μ ν} + Λ g_{μ ν} = {(\frac{π - 2}{2})}^{6} (\frac{h e}{c}) T_{μ ν} + K_{μ ν}

(2.9)

3. Result

Based on this research, it is evident that all physical attributes such as speed, momentum, thrust, force, and acceleration can be viewed as pairs. Furthermore, each of these attributes can be paired with a corresponding aspect in the dimension of time. Consequently, the accumulation of information over time can potentially form the basis for a novel approach to the field of physics. This insight opens up new possibilities for understanding the fundamental principles governing the physical world.

Each unit of information has an associated wave function, which is expanded over time. As a result, information can be stored in a compressed form over time in a pulse and every spike represents the collapse of a wave function. Figure 4. Due to the presence of related fields in the wave function, information is compressed and decoded based on the structure of these fields. Based on this, the relationship between inductance, resistance and intensity of electric current depending on the electric field in data compression and decoding has been investigated [14]. And the proposed plan can be examined in the case of quantum computer qubits.

There is evidence for the existence of this method in nature, and experiments have been conducted based on the transmission of compressed information by the brain [21]. Based on this, information can be transmitted faster than the speed of light in the present, past or future. There is a violation of causality about information, and evidence has been observed in clinical trials and sleep REM.

Compression and decoding of information in compressed pulses requires following equation (2.9). Using inhibitory neurons as negative density in momentum and energy tensor can be effective in decoding information. The general block diagram of information compression and decoding shows the presence of multidimensional and same-phase factors in information decoding Figure 5 and Figure 6.

The wave function has two directions. Information can be compressed from the past to the future or from the future to the past in the wave function. As a result, the information stored in the memory is stored in reverse. And with each memory recall, these inverted compressed pulses are compared with new and similar information. The difference between these two pulses calls up a new pulse from the memory, which can represent an event in the past or the future. This information processing is the stage of dreaming in sleep. that is an allegory of the future or the past. In essence, the wave function's capacity to encode and manipulate information embodies a profound duality that transcends traditional notions of temporal linearity. This phenomenon underscores the intricate interplay between memory, perception, and the conceptualization of time within the framework of quantum mechanics. This research can open a big window in the field of physics and quantum information for researchers. Based on this, it is suggested to test the transmission and decoding of information based on photons by adding the entanglement phenomenon to the blog diagram in Figure 5. This addition will allow for a more comprehensive examination of the capabilities and implications of utilizing photon-based systems for communication and data processing. Furthermore, incorporating entanglement into the diagram will provide a visual representation of how this phenomenon can be harnessed to advance the field of quantum communication.

Acknowledgments

The authors appreciate the guidance and support of all those who contributed to this research.

References

Gershenfeld, N. (2000). The physics of information technology. Cambridge University Press.
Paredes, O. , Farfán-Ugalde, E., Gómez-Márquez, C., Borrayo, E., Mendizabal, A. P., & Morales, J. A. (2024). The calculus of codes-From entropy, complexity, and information to life. Biosystems, 236, 105099. [CrossRef]
Bouwmeester, D. , & Zeilinger, A. (2000). The physics of quantum information: basic concepts. In The physics of quantum information: quantum cryptography, quantum teleportation, quantum computation (pp. 1-14). Berlin, Heidelberg: Springer Berlin Heidelberg. [CrossRef]
Naruse, M., Tate, N., Aono, M., & Ohtsu, M. (2013). Information physics fundamentals of nanophotonics. Reports on Progress in Physics, 76(5), 056401. [CrossRef]
Landauer, R. (1996). The physical nature of information. Physics letters A, 217(4-5), 188-193. [CrossRef]
Landauer, R. (1991). Information is physical. Physics Today, 44(5), 23-29. [CrossRef]
Borgmann, A. (1999). Holding on to Reality: The Nature of Information at the Turn of the Millennium. University of Chicago press.
Parrondo, J. M., Horowitz, J. M., & Sagawa, T. (2015). Thermodynamics of information. Nature physics, 11(2), 131-139. [CrossRef]
Rényi, A. (1961, January). In On measures of entropy and information. In Proceedings of the fourth Berkeley symposium on mathematical statistics and probability, volume 1: contributions to the theory of statistics (Vol. 4; pp. 547–562.
Edrisi, A. , Patwa, H., & Morales Escalante, J. A. (2024). A Numerical Study of Quantum Entropy and Information in the Wigner–Fokker–Planck Equation for Open Quantum Systems. Entropy, 26(3), 263. [CrossRef]
Pires, C. , Vannitsem, S., & Docquier, D. (2024). Evaluation of Shannon Entropy-based Information transfer in nonlinear systems (No. EGU24-4315). Copernicus Meetings. [CrossRef]
Mastriani, M. Relativistic entanglement and the Theory of Dilated Locality.
Sengupta, N. , & Kasabov, N. (2017). Spike-time encoding as a data compression technique for pattern recognition of temporal data. Information Sciences, 406, 133-145.
Mousavi, S. K. Compression And Decoding Of Data In The Spike Current. Researchgate 2023, 9. [Google Scholar] [CrossRef]
Awschalom, D. , & Loss, D. (2002). Semiconductor spintronics and quantum computation. Springer Science & Business Media.
Qin, J., Sun, B., Zhou, G., Guo, T., Chen, Y., Ke, C., ... & Zhao, Y. (2023). From Spintronic Memristors to Quantum Computing. ACS Materials Letters, 5(8), 2197-2215.
Monakhov, K. Y. (2024). Oxovanadium electronics for in-memory, neuromorphic, and quantum computing applications. Materials Horizons.
Tao, P. , Hao, X., Cheng, J., & Chen, L. (2023). Predicting time series by data-driven spatiotemporal information transformation. Information Sciences, 622, 859-872.
Seyed Kazem Mousavi. (2024). General Balance in the Six-Dimensions of Space-Time. Qeios. [CrossRef]
Mousavi, S. K. (2023). The balance In the six dimensions of space-time description of quantum mechanics phenomena and nature of time. journal physics theories and applications, 7(1), 95-114. [CrossRef]
Seyed Kazem Mousavi. (2024). Information Transfer based on Brains Entanglement. Qeios. [CrossRef]

Figure 1. Density or velocity can cause heterogeneity in the space-time structure. Density is a length over time. This length is rotating around the field. The field of Möbius space transfers the properties of lower dimensions to higher dimensions. This heterogeneity in higher dimensions follows the laws of homogeneity and isotropy.

Figure 2. The wave function in the time dimension is the sum of the small packets that make up the mass field.

Figure 3. The relationship between the electric field and the magnetic field with the gravitational field is when the states of the wave function approach each other. Accordingly, there are three fields of information. which can be introduced in an information unit.

Figure 4. Each pulse contains compressed information.

Figure 5. Different pulses are stored in memory after integration, aggregation and compression of information. Each spike current represents a unique wave function containing distinct pieces of information.

Figure 6. Each compressed pulse can be decomposed into constituent units.

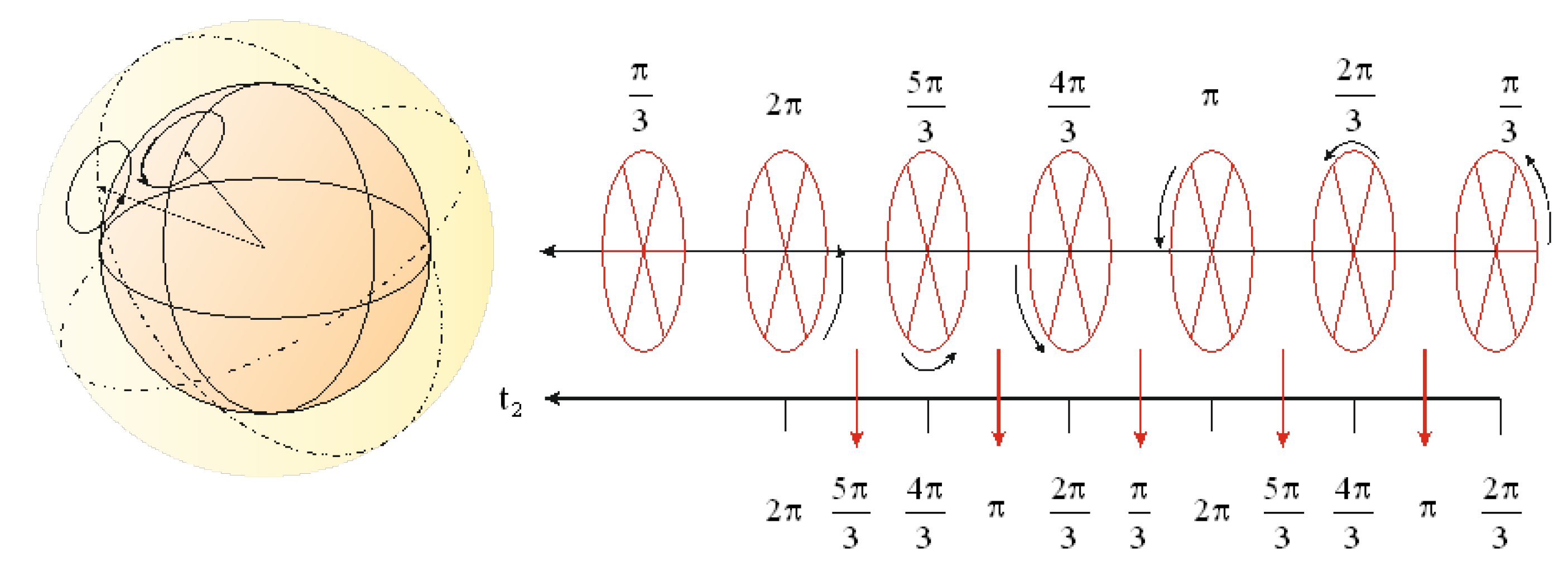
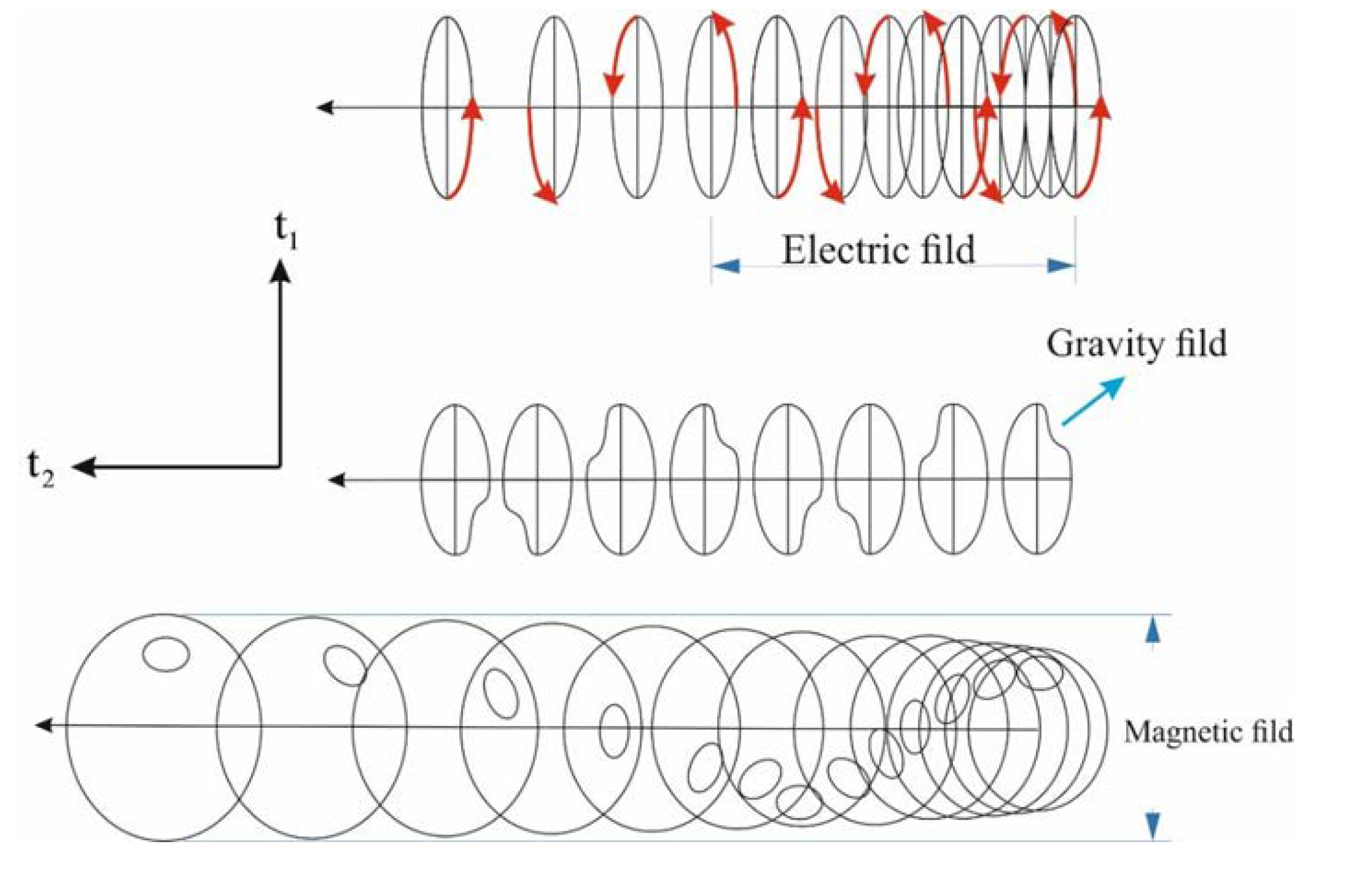
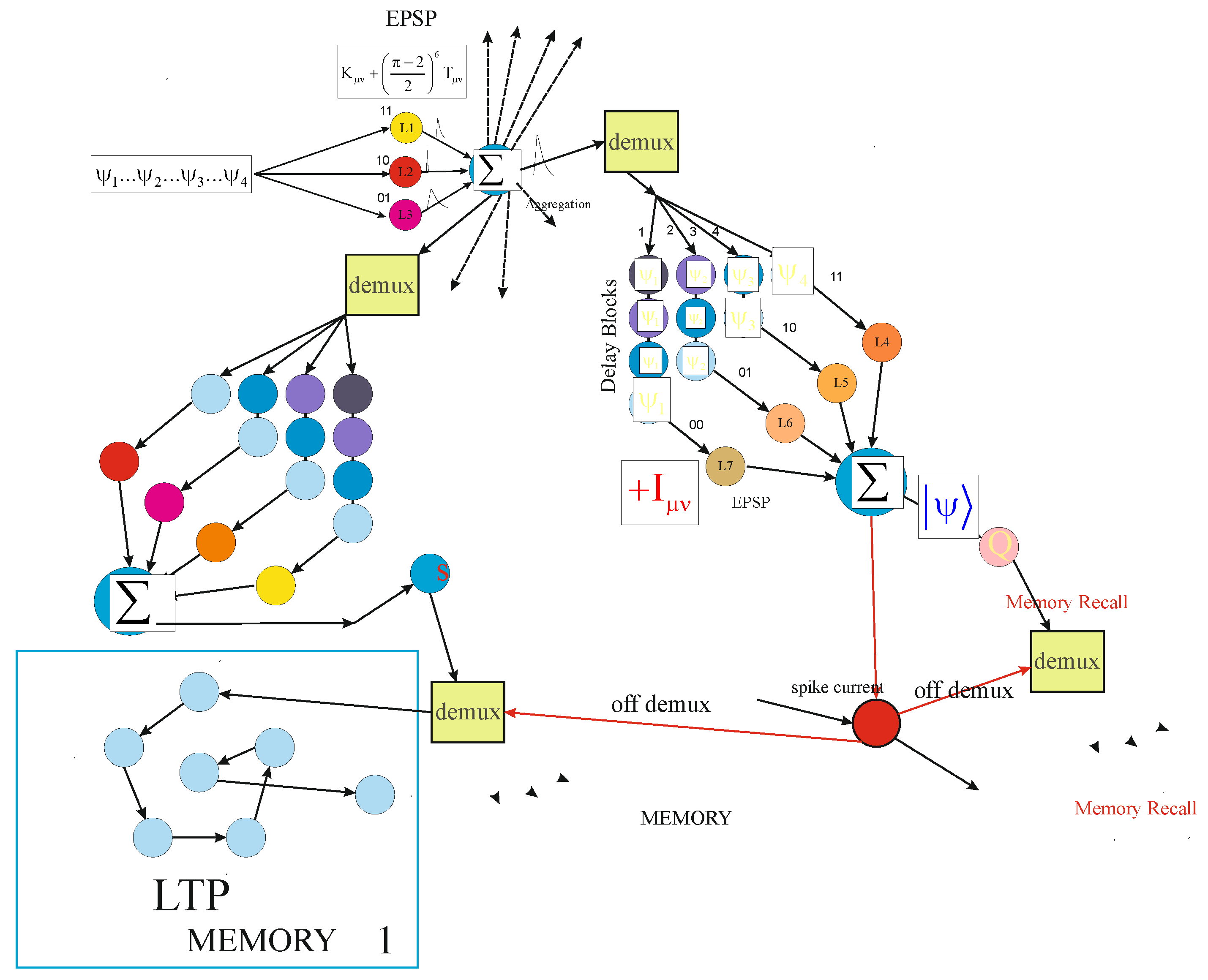
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Information in the Three Dimensions of Time

Abstract

1. Introduction

2. Method

3. Result

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe