Prerpints.org logo
Preprint
Article

Phase transition thermodynamics of 1,3,5-tris-(α-naphthyl)benzene: theory and experiment

Altmetrics

Downloads

82

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (180.79KB )

Submitted:

02 April 2024

Posted:

03 April 2024

You are already at the latest version

Alerts
Abstract
1,3,5-Tris-(α-naphthyl)benzene is an organic non-electrolyte with notable stability of an amorphous phase. Its glassy and supercooled liquid states were previously studied by spectroscopic and calorimetric methods. However, the thermodynamic parameters of phase transitions available from the literature are inconsistent. In this work, the heat capacities of crystalline and liquid phases, the temperature dependence of the saturated vapor pressures, fusion and vaporization enthalpies were determined using differential and fast scanning calorimetry and verified using the estimates based on solution calorimetry. The structural features of 1,3,5-tris-(α-naphthyl)benzene are discussed based on the computations performed and the data on the molecular refractivity. The consistency between the values obtained by independent techniques was demonstrated. The deviations in the previously published data were attributed to possible polymorphism.
Keywords: 
Subject: Chemistry and Materials Science  -   Physical Chemistry

1. Introduction

Over the last 60 years, 1,3,5-tris-(α-naphthyl)benzene (C36H24, TNB) and its isomers proved to be important model objects in the studies of the glass transition phenomenon and crystallization [1,2,3,4,5,6,7,8,9]. TNB has a notably stable amorphous phase, so its glassy and supercooled liquid states can be investigated by a variety of spectroscopic and calorimetric methods. More recently, it was shown to form ultrastable glass upon physical vapor deposition onto a cold substrate [10,11,12,13]. Although precise data on the thermodynamic parameters of fusion below the melting point (Tm) is needed when describing the glass and supercooled liquid properties using modern approaches [14], there are significant deviations between the literature values of the fusion enthalpies at Tm [1,4,9]. The cause of this inconsistency is not yet understood. Also, the difference between the heat capacities of condensed phases determined in Refs. [2,4] is ca. 5 %. Re-evaluation of these data is needed to obtain reliable estimates of the temperature dependences of the fusion enthalpy and entropy. On the other hand, the thermodynamic parameters of vaporization, whose knowledge is useful for planning the vapor deposition process [15,16], have been measured in the region of thermal instability only [17]. The extremely low volatility of TNB impedes studying crystal-vapor and liquid-vapor equilibria by most conventional techniques.
The goal of the present work is to provide a consistent set of thermodynamic parameters of phase transitions of TNB. Its fusion enthalpy and the heat capacities of crystal and liquid states were measured by differential scanning calorimetry (DSC), while the temperature dependence of the saturated vapor pressure, and the vaporization enthalpy were determined by fast scanning calorimetry (FSC). The solution enthalpy in benzene was determined and its agreement with the fusion enthalpy at 298.15 K calculated using Kirchhoff’s law of Thermochemistry was demonstrated. The optimized geometry of the TNB molecule in the gaseous state, fundamental vibrational frequencies, and potential energy surface for the intramolecular rotations were computed and the ideal gas phase heat capacities as a function of temperature were calculated, which, together with the measured liquid state heat capacity, enabled to establish the vaporization enthalpy at 298.15 K. On the other hand, the molecular refractivity of TNB was derived using refractometry and densitometry. This parameter was used to provide an alternative estimate of the vaporization enthalpy at 298.15 K, and it was found to agree with the experimental results.
The cause of the large discrepancy between the literature values of Tm and fusion enthalpies of crystalline TNB is discussed.

2. Results

Below, the results of the experimental measurements of the fusion and vaporization enthalpies, vapor pressures, and heat capacities are provided together with the literature data. Before the measurement, TNB was purified by fractional sublimation under reduced pressure of 10-3 Torr onto a substrate at T = 283 K. The vapor-deposited compound was mechanically removed from a sublimation apparatus, placed into a glass beaker, and annealed at 443 K for 24 h in vacuo to ensure complete crystallization. Powder X-ray diffraction (PXRD) was employed to characterize the crystal structure (Figure S1). The patterns were the same for the commercial and purified samples. The purity (mole fraction >0.997) was determined using high-performance liquid chromatography. The information on the sample characterization is provided in Section 4.1 and Table S1.

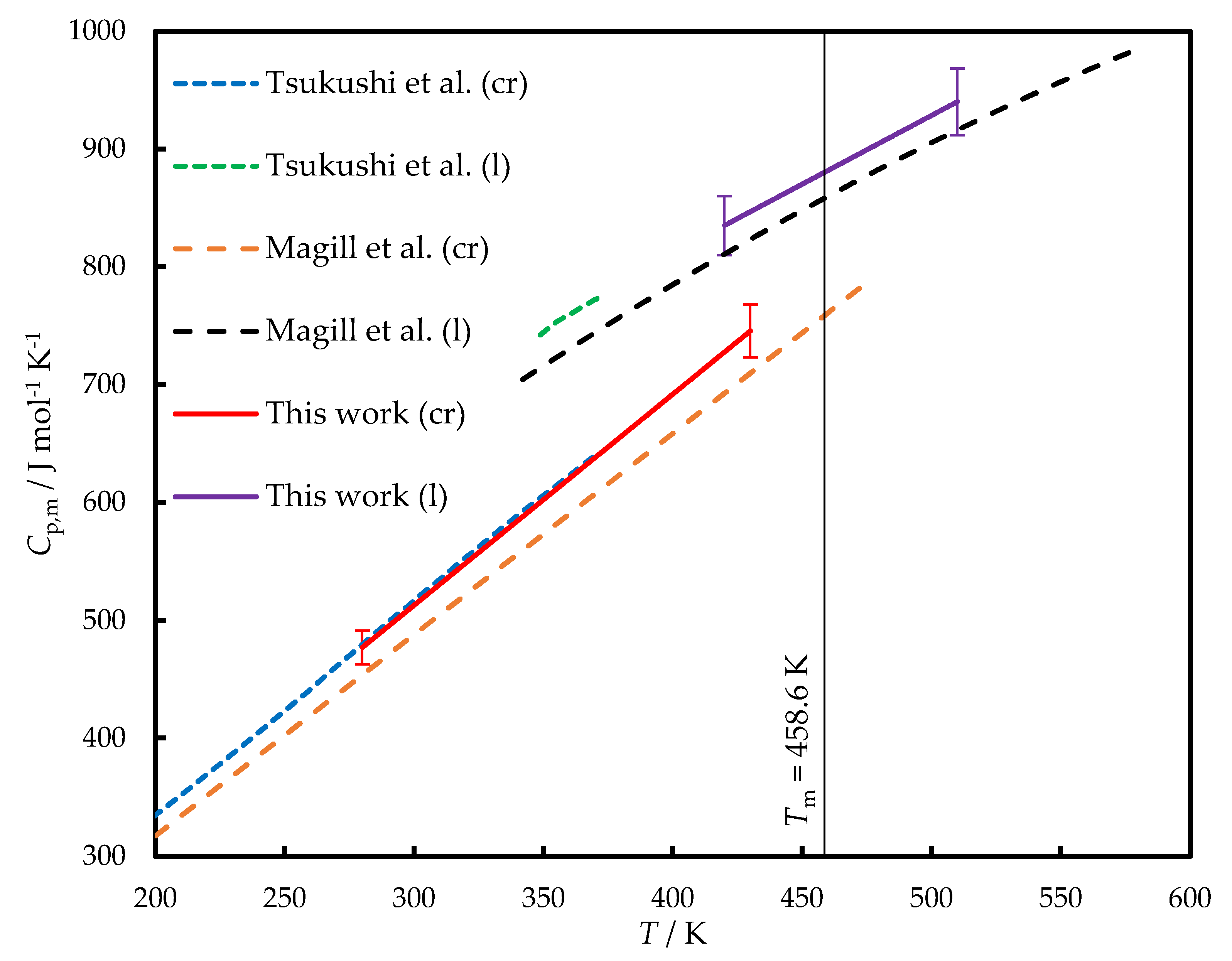
2.1. Thermodynamics of Fusion

The fusion enthalpy at Tm ( Δ cr l H ( T m ) ) determined in this work is shown in Table 1. The value corresponds to the average of the first heating scans to 493 K at 10 K·min-1 of the samples purified by vacuum sublimation and annealed at 443 K as described above. Variation of the heating rate during the first scan did not change Δ cr l H or Tm. The completely molten samples did not crystallize during further thermal cycling in DSC pans at (323-493) K at 10 K·min-1 and exhibited the glass transition at 353.0±0.5 K (half-step glass transition temperature on heating). The commercial samples initially melted with slightly lower enthalpy (28-31 kJ·mol-1) but after isothermal annealing at 443 K the effect raised to ~33 kJ·mol-1.
The values determined in Refs. [4,9] substantially exceed the results of this work and Ref. [1]. The possible reasons are discussed in Section 3.1.

2.2. Condensed phase heat capacities

The low crystallization tendency of TNB enables the determination of its heat capacity (Cp,m) in the liquid state below Tm using conventional methods. The heat capacities of liquid (l) and crystalline (cr) TNB measured in this work and available from the literature [2,4] are provided in Figure 1.
In Ref. [2] Tsukushi et al. applied adiabatic calorimetry to measure the heat capacities of crystalline and glassy TNB; the latter measurements also included a narrow range of supercooled liquid phase. For both crystal and liquid (in the case of linear extrapolation) phases, the agreement is within ±1 %.
Magill et al. [4] measured the heat capacities of crystalline and liquid TNB using DSC. The latter data were provided in graphical form and extracted from the printed figure for the sake of comparison; we estimate that the error of the procedure does not exceed 10 J mol-1 K-1. Both Cp,m of crystal and liquid determined in Ref. [4] were lower by 5 % than in this work and in Ref. [2]. Importantly, the difference of the same magnitude is also exhibited in the liquid state, so it cannot be explained solely by the possibly different polymorphic state of crystal.
During the further calculation of the temperature dependences of the phase transition enthalpies, we used Cp,m of crystal and liquid obtained in this work and fitted by a linear function of temperature:
Cp,m(cr)/ J mol-1 K-1 = 1.791 · (T/K) – 24.3, (280 < T/K < 430), Ur,tot < 0.03
Cp,m(l)/ J mol-1 K-1 = 1.166 · (T/K) + 345.3, (420 < T/K < 510), Ur,tot < 0.03
Ur,tot is expanded uncertainty (0.95 level of confidence), including reproducibility of the measurement and calibration uncertainty.

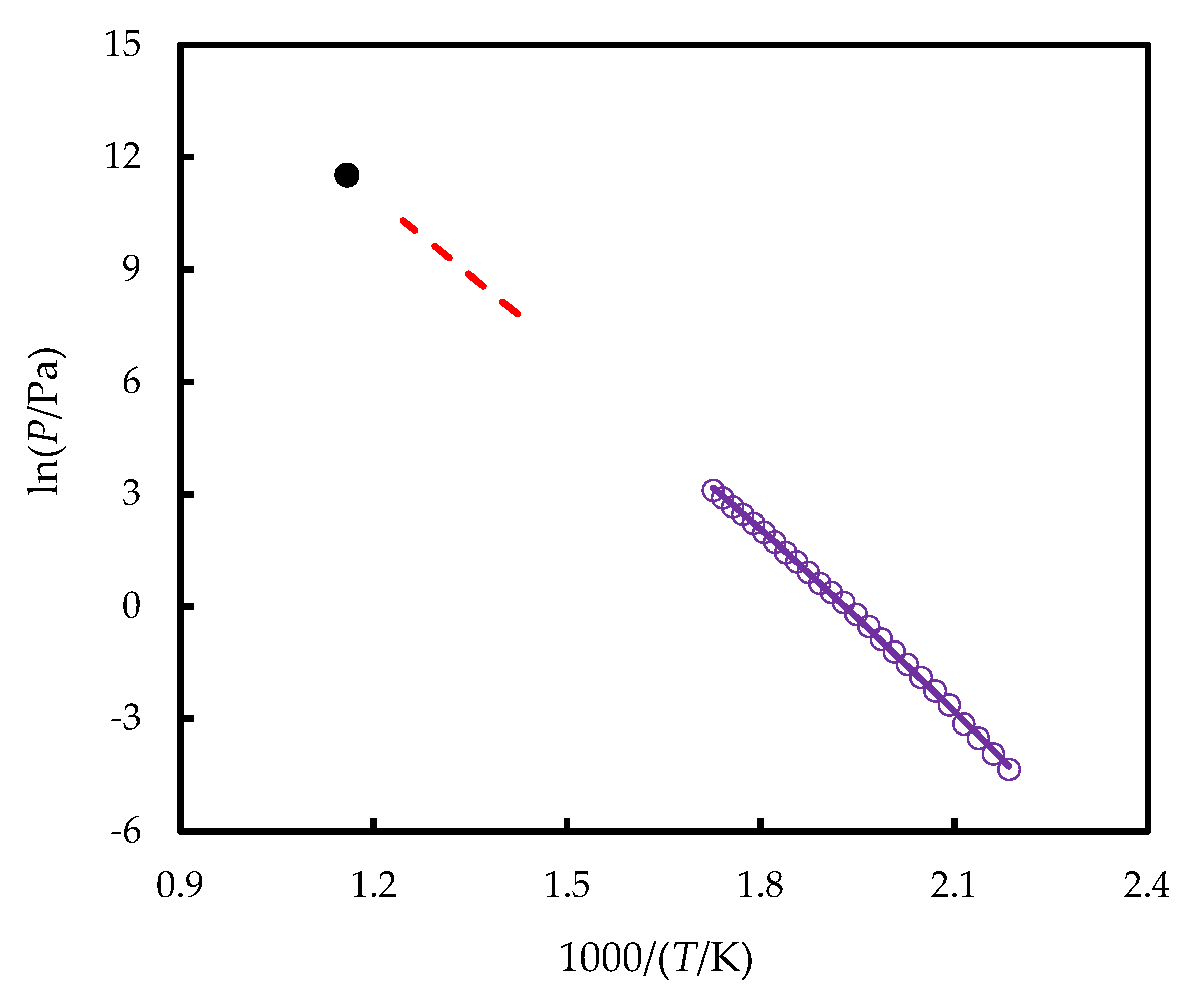
2.3. Vapor Pressures and Vaporization Enthalpies

The vapor pressures (p) of TNB measured in this work are provided in Figure 2. Magill and Ubbelohde [17] studied vaporization of TNB between 703 and 803 K using ebuliometry; however, the authors stated that the compound tended to decompose above 723 K. They did not report numerical values of vapor pressures and provided only the vaporization enthalpy Δ l g H = 116.7 kJ mol-1 at the mean experimental temperature of 753 K. Later, these authors reported an estimate of the normal boiling point of TNB equal to 863 K [9]; the latter was found by extrapolation of p-T data from Ref. [17]. Combining these data, one can estimate that p(l) measured in Ref. [17] varied between 2·103 and 3·104 Pa. These values are provided in graphical form in Figure 2 for the sake of comparison.

3. Discussion

In this section, the temperature dependences of the fusion and vaporization enthalpies are analyzed and the consistency of the values at 298.15 K with the estimates from solution enthalpy in benzene and molecular refractivity is checked. The cause of the deviations in the literature data on the fusion of TNB is discussed.

3.1. Discrepancy of the Fusion Data

The temperature and enthalpy values determined in this work agree with those reported by Tsukushi et al. [1]. The authors [1] also performed a PXRD measurement of the crystal, which matches the pattern obtained in this work.
At the same time, Magill et al. [4,9] reported the greater Δ cr l H and Tm values. The authors [9] mentioned X-ray analysis of the sample, which implies that TNB is not prone to polymorphism; however, no XRD pattern or atomic coordinates were provided in this work. Dawson et al. [10] also measured Δ cr l H of TNB but did not publish the results explicitly. Authors [10] state that the measured values are within 5 % of Δ cr l H reported in [1] and [4], although the latter differ by 27 %.
The melting points of TNB, available from the Reaxys database, vary between 428 and 476 K [18]. Although no XRD measurements could be found in the literature, except [1], it is reasonable to assume that the scatter of available Tm and Δ cr l H is associated with polymorphism of TNB. The reason for the formation of different polymorphs in the above studies and the present work is likely different crystal preparation methods. Tsukushi et al. did not report the crystallization conditions in Ref. [1] but pointed out that crystallization from chloroform-hexane mixture was performed in the later calorimetric study [2]. Magill et al. used benzene as a solvent for recrystallization [9].
The difference between the heat capacities determined by Tsukushi and in this work, and the data from Magill, is observed in both crystal and liquid states as TNB. If the discrepancy had been caused by the systematic error of the heat flow, it would further increase the difference in the fusion enthalpy values.
It is interesting to note that the fusion entropy values at T m, which can be calculated based on the data in Table 1, are also significantly different: 72 J mol-1 K-1 (this work and Ref. [1], 89 J mol-1 K-1 (Refs. [4,9]). Given that the liquid state is the same, the difference corresponds to different entropies of the crystal states, with the one studied by Magill having the lower entropy.

3.1. Fusion and Solution Thermochemistry at 298.15 K

In a series of our previous works [19,20,21], we showed that solution calorimetry enables the independent estimation of the fusion enthalpy at 298.15 K of organic non-electrolytes. In order to do this, Hess’s law is applied to the solution process:
Δ cr l H A ( 298.15   K ) = Δ soln H A / S ( c r ,   298.15   K ) − Δ soln H A / S ( l ,   298.15   K )  
where Δ soln H A / S ( c r ,   298.15   K ) is the solution enthalpy of a crystal compound A in a solvent S at 298.15 K, and Δ soln H A / S ( l ,   298.15   K ) corresponds to the dissolution of a hypothetical quasi-equilibrium liquid A at 298.15 K, i.e. supercooled liquid obtained under equilibrium conditions. Δ soln H A / S ( c r ,   298.15   K ) is measured experimentally, while Δ soln H A / S ( l ,   298.15   K ) can be often estimated. It is usually close to 0 when A and S are structurally similar compounds (“like dissolves like”). Particularly, Δ soln H A / S ( l ,   298.15   K ) equals 1±1 kJ·mol-1 when non-hydrogen-bonded aromatic compounds are dissolved in benzene [22]. In this work Δ soln H TNB / C 6 H 6 ( cr ,   298 . 15   K ) = 15.1±0.4 kJ·mol-1 was determined (for details see Section 4.2 and Table S5). From Eq. (3), one can find Δ cr l H ( 298.15   K ) = 14.1±1.1 kJ·mol-1. Determination of the solution enthalpy of amorphous TNB would be also of interest; monitoring of its enthalpy relaxation throughout experiment is necessary.
On the other hand, one can calculate the temperature dependence of the fusion enthalpy according to Kirchhoff’s law of Thermochemistry. In the absence of phase transitions between 298.15 K and Tm, Eq. (4) is valid:
Δ cr l H A ( 298.15   K ) = Δ cr l H A ( T m ) + ∫ T m 298.15 [ C p , m A ( l ) − C p , m A ( cr )   ] d T
Linear temperature dependence of Cp,m(l) between 298.15 K and Tm was assumed when calculating the ∫ T m 298.15 [ C p , m A ( l ) − C p , m A ( cr )   ] d T value. The validity of such an approximation was previously demonstrated for more than 50 compounds [23]. Using Δ cr l H ( T m ) = 32.9±0.5 kJ·mol-1 determined in this work and the heat capacities given by Eqs. (1-2), one arrives at Δ cr l H ( 298.15   K ) = (32.9±0.5) – (21.4±4.4) kJ·mol-1 = 11.5±4.4 kJ·mol-1.
The Δ cr l H ( 298.15   K ) values found according to Eqs. (3) and (4) agree within the limits of the propagated uncertainty, confirming the reliability of each experimental magnitude in the combined Hess’s and Kirchhoff’s law:
Δ cr l H A ( 298.15   K ) = Δ cr l H A ( T m ) + ∫ T m 298.15   K [ C p , m A ( l ) − C p , m A ( cr )   ] d T = Δ soln H A / S ( c r ,   298.15   K ) − Δ soln H A / S ( l ,   298.15   K )  
The measured Δ cr l H ( T m ) value and heat capacity temperature dependences given by Eqs. (1, 2) can be implemented for estimating the thermodynamic stability of the supercooled liquid, as well as various glassy phases of TNB, which can be obtained by melt quenching, crystal milling, or vapor deposition, and parametrization of the kinetic parameters of crystallization/nucleation [14].
Earlier the solution enthalpy of TNB (a form with Tm = 472 K) in benzene was evaluated from the temperature dependence of the solubility between 433 and 465 K [9]. From these measurements, Δ soln H A / S ( c r ,   449   K ) = 38.1 kJ·mol-1. This value should be nearly equal to the fusion enthalpy under the same conditions, considering that the solution enthalpy of hypothetical liquid TNB in benzene should be close to 0 at elevated temperatures as well. The heat capacity integral ∫ 449   K 472   K [ C p , m A ( l ) − C p , m A ( cr )   ] d T evaluated using Eqs. (1, 2) equals 1.9 kJ·mol-1, so using the data by Magill et al.  Δ cr l H ( 449   K ) is expected to be 39.9 kJ·mol-1, closely agreeing with the solution enthalpy under the same conditions.
The crystal parameters obtained in this work correspond to the form with Tm = 458.6 K. The measured Δ cr l H ( T m ) value and heat capacity temperature dependences given by Eqs. (1, 2) can be implemented for estimating the thermodynamic stability of the supercooled liquid, as well as various glassy phases of TNB, which can be obtained by melt quenching, crystal milling, or vapor deposition, with respect to this crystal form, and parametrization of the kinetic parameters of crystallization/nucleation [14].

3.2. Vaporization and Sublimation Thermochemistry

The temperature dependence of the vapor pressure of TNB determined in this work was fitted by Clarke-Glew equation:
ln ( p / Pa ) = ln ( p ( T ref ) / Pa ) − Δ l g H ( T ref ) R ( 1 T − 1 T ref ) + Δ l g C p , m R ( T ref T − 1 + ln ( T T ref ) )
where the difference between the heat capacities of the ideal gas and liquid ( Δ l g C p , m ) was calculated based on the experimental (Secs. 2.2, 4.3) Cp,m(l) and computed (4.5) Cp,m(g) values. In the temperature range of vapor pressure measurement, – Δ l g C p , m varied between 154 and 164 J·K-1·mol-1, being 158 J·K-1·mol-1 on average. The middle of the measurement range was chosen as the reference temperature Tref = 518 K. From the fitting, Δ l g H ( 518   K ) = 134.1±3.2 kJ·mol-1 was derived (the standard uncertainty of the vaporization enthalpy, which includes the standard uncertainties of the vapor pressures and measurement temperatures, was evaluated as previously [24,25]).
Extrapolation of the vapor pressure temperature dependence to 703-803 K, where Magill and Ubbelohde [17] performed ebuliometric measurements, results in p values agreeing with Ref. [17] within ±50 %. Such agreement may be considered satisfactory, given the total uncertainty of the method. However, Δ l g H ( 753   K ) = 116.7 kJ mol-1 reported in Ref. [17] appears to be overestimated, compared with Δ l g H ( 518   K ) = 134.1±3.2 kJ·mol-1 obtained above. Adjusting of the previous value to 518 K according to Kirchhoff’s law (Eq. 7) using – Δ l g C p , m of 158 J·K-1·mol-1 leads to Δ l g H ( 518   K ) = 154 kJ·mol-1:
Δ cr l H ( T 2 ) = Δ cr l H ( T 1 ) + ∫ T 1 T 2 Δ l g C p , m d T
Δ l g C p , m depends on temperature, but that of TNB increases above 500 K, so the consideration of Δ l g C p , m temperature dependence would likely increase the heat capacity integral, causing a greater disagreement between the present work and measurements in Ref. [17]. It is reasonable to assume that the thermal decomposition above 700 K reported by Magill and Ubbelohde leads to an overestimation of ln p vs. 1/T dependence slope.
We also applied Eq. (7) to the calculation of Δ l g H ( 298 . 15   K ) . Cp,m(l) at T = (298.15 – 518.00) K was described by Eq. (2) and Cp,m(g) from Table S9 was fitted to a quadratic polynomial. The resulting Δ l g H ( 298 . 15   K ) value equaled (134.1±3.2) + (38.5±5.6) = 172.6±6.4 kJ·mol-1. One can compare the latter with the estimates based on “molecular addivity” [26] and the correlation between the solvation enthalpy (enthalpy of transition from from the ideal gas to an infinitely diluted solution, Δ solv H ) and the molecular refraction (MR) [27].
First, it is fruitful to compare the vaporization enthalpies of 1-phenylnaphthalene and TNB. Previously, the average literature Δ l g H ( 298 . 15   K ) = 81.9±1.0 kJ·mol-1 was derived for 1-phenylnaphthalene [27]. Then Δ l g H ( 298 . 15   K ) of TNB can be evaluated as (81.9 – 34.8) · 3 + 34.8 kJ·mol-1 = 176.1 kJ·mol-1. It agrees with the experimental value within the measurement uncertainty. Such an estimate implies that phenyl and naphthalene rings exhibit the same conjugation between isolated aromatic fragments in 1-phenylnaphthalene and TNB. Our computations show that phenyl-naphthyl dihedral angle in the optimized molecular structure of TNB equals (60.2±0.2)°. In 1-phenylnaphthalene, the same angle equals (58±4)° [28]. The potential energy surfaces also qualitatively agree (see Figure S2 for potential surface computed for TNB), suggesting a similar level of conjugation in these molecules.
Molecular refractivity is a measure of molecule polarizability. Previously, it was shown that Δ solv H ( 298 . 15   K ) of organic non-electrolytes in various organic solvents linearly correlate with MR. Particularly, for aromatic hydrocarbons dissolved in benzene Eq. (8) is valid (root-mean-square deviation 0.8 kJ·mol-1 [27]):
− Δ solv H A / C 6 H 6 ( 298 . 15   K ) / ( kJ · mol - 1 ) = 1.088 ⋅ M R / ( cm 3 · mol - 1 ) + 6.86
In its turn, the sublimation and vaporization enthalpies at 298.15 K can be found as the difference between the solution and solvation enthalpies:
Δ cr / l g H A ( 298.15   K ) = Δ soln H A / C 6 H 6 ( cr / l ,   298.15   K ) − Δ solv H A / C 6 H 6 ( 298.15   K )  
In this work, MR = 154.5±3.2 cm3·mol-1 was calculated from the densities (d) and refractive indices (n) of TNB solutions in benzene. MR of a pure compound can be found according to Eq. (10) (M is a molecular weight):
M R = M d ( n 2 − 1 n 2 + 2 )
MR of a solute is found according to Eq. (11), considering that the molecular refractivities of solution components are additive:
M R = 1 x [ M ⋅ x + M C 6 H 6 ⋅ ( 1 − x ) d ( n 2 − 1 n 2 + 2 ) − M R C 6 H 6 ⋅ ( 1 − x ) ]
where x and M correspond to the molar fraction and molecular weight of a solute.
From the literature, MR of 160.0 cm3·mol-1 is available [29]. However, both the refractometer and densimeter used in Ref. [29] had an accuracy lower by an order of magnitude, compared to the present work. Therefore, MR = 154.5±3.2 cm3·mol-1 was used in the further calculations. From Eq. (8), one can find Δ solv H A / C 6 H 6 ( 298 . 15   K ) = –175.0±3.6 kJ·mol-1. From this value, Δ cr g H ( 298 . 15   K ) = 190.1±3.6 kJ·mol-1 can be found using the experimental Δ soln H A / C 6 H 6 ( cr ,   298.15   K ) = 15.1±0.4 kJ·mol-1. On the other hand, using an average estimate of Δ soln H A / C 6 H 6 ( l ,   298.15   K ) = 1±1 kJ·mol-1 for non-hydrogen-bonded aromatic compounds, one can calculate Δ l g H ( 298 . 15   K ) = 176.0±3.7 kJ·mol-1. The latter value agrees with the experimental data and the estimate based on the “molecular additivity” approach.
A comparison of MR of 1-phenylnaphthalene (69.1±1.0 cm3·mol-1 [27]) and TNB (154.5±3.2 cm3·mol-1) with group-contribution-derived values is also be useful. From MR of benzene (26.18 cm3·mol-1), naphthalene (44.37 cm3·mol-1) and bond-refraction data (C-C, C-H) [29], MR(calc) of 1-phenylnaphthalene equals 68.5 cm3·mol-1, indicating weak conjugation between phenyl and naphthyl rings in this molecule. On the other hand, MR(calc) of TNB would be 153.1 cm3·mol-1. It also agrees with the experimental MR obtained in this work. Thus, it is likely that both TNB and 1-phenylnaphthalene exhibit weak conjugation between naphthyl and phenyl fragments. It is consistent with the observed vaporization enthalpies, which also reflect the polarizability of a molecule.

4. Materials and Methods

4.1. Materials

TNB (1,3,5-tri(1-naphthyl)benzene, C36H24, CAS № 7059-70-3, Hotspot Biotechnology, China) was purchased and purified by sublimation under reduced pressure. The final purity of 0.997 (mole fraction) was determined by HPLC using Dionex Ultimate 3000 chromatograph (Thermo Fisher Scientific, USA) equipped with a UV detector (254 nm), Dionex Acclaim 120 chromatographic column (C18-bonded silica, 5 μm, 120 Å, 4.6 × 250 mm) and 100% acetonitrile was used as an eluent. Benzene used for solution calorimetry (C6H6, CAS № 71-43-2) was purified according to [30]. Its final purity determined by gas chromatography (Agilent 7890 B, USA) exceeded 0.999 (mass fraction). The characterization of the samples and auxiliary compounds used for calibration of the instruments is provided in Table S1.

4.2. Solution calorimetry

The solution enthalpy of TNB in benzene was measured using an isothermal precision dissolution calorimeter TAM III (TA Instruments, USA). The measuring procedure was as follows: the crystalline samples with masses of ca. 40 mg were placed in glass ampoules. Subsequently, the ampoules were immersed in a calorimetric cell filled with 100 mL of benzene. Thereafter, the solution enthalpy was determined after the ampoule was broken in the pre-thermostated cells. Before and after the breaking of the ampoule, electrical calibrations were performed. Infinite dilution conditions were confirmed by monitoring the concentration dependence of the solution enthalpy (molality ranged from 1 to 6.5 mmol·kg-1). The accuracy of the technique was verified by the measurement of the solution enthalpy of 1-propanol in bidistilled water [31]. The obtained values of the solution enthalpies are provided in Table S4 of the Supplementary Materials.

4.3. Differential scanning calorimetry

The heat capacities, fusion enthalpy, and melting temperature of TNB were measured using a DSC 8500 calorimeter (Perkin Elmer, USA) at 10 K min-1. The heat capacities were measured using a three-step method, with measurements taken for empty crucibles, sapphire, and the sample. The temperature program involves two isothermal segments of 3 min at Tmin and Tmax, and one dynamic segment. For the crystalline phase, the measurements were performed between Tmin = 280 and Tmax = 430 K, while for the liquid phase, the range was 420 to 510 K. The fusion enthalpy was determined during the first heating scan between (Tm – 20 K) and (Tm + 20 K). The heat capacities of the liquid determined below Tm correspond to the supercooled phase obtained by cooling the melt at a rate of 40 K/min. No crystallization or other effects were observed on the cooling heat flow curves.
The DSC was calibrated according to the manufacturer's recommendations using zinc and indium samples. Verification of the quality of the DSC used in the heat capacity measurements with standard samples was performed previously [2]. All experiments were performed in 40 ml aluminum crucibles in a dynamic nitrogen atmosphere (Nurgas, Russia; volume fraction of nitrogen > 0.99999) with a gas flow rate of 30 mL min-1.
Measurements of the heat capacity and fusion enthalpy were repeated for 3 samples. The experimental values are provided in Table S2 and Table S3 of the Supplementary Materials.

4.4. Fast Scanning Calorimetry

The vapor pressures of TNB were measured using thermogravimetry – fast scanning calorimetry method based on the relationship between evaporation rate and vapor pressure [32] as previously described [33] using Mettler Toledo Flash DSC1 (Switzerland). UFS1 chip sensor was calibrated using anthracene, benzoic acid and biphenyl as temperature standards [34]. Measurement was performed between 455 K and 580 K under a nitrogen atmosphere (Nurgas, Russia; volume fraction of nitrogen >0.99999) using samples with a typical mass of 50 ng in liquid and supercooled liquid states. No tendency to crystallize was observed during the measurements. The mass change during isothermal steps was calculated using Cp,m(liq) measured in this work by DSC. Sample geometry (height and radius of the droplet) was determined using an optical microscope BX3M (Olympus, Japan). The diffusion volume of TNB needed to estimate its diffusion coefficient according to procedure [35] was calculated additively [36] and found to be 536.4 cm3 mol-1.
Measurements at each temperature were reproduced 10 times. Experimental values of the measured vapor pressures are provided in Table 2.

4.5. Computations

The heat capacities of TNB in the ideal gas phase between 200 and 800 K were calculated using methods of quantum chemistry and statistical thermodynamics.
First, the torsion angles between the benzene ring and naphthyl substituents were determined during a combined low-level/high-level conformational search algorithm implemented in the TorsiFlex software package [38]. A low-level search was conducted at the HF/3-21G theory level with the use of preconditioned and stochastic strategies. The preconditioned structures were made by a 30-degree rotation of the naphthyl substituents. Then, the high-level search was performed at the B3LYP/6-31+G(d,p) theory level, which is also used for all the subsequent computations in this work. The optimized geometry of TNB is shown in Figure 3, its cartesian coordinates are provided in Table S5. The correspondence of this structure to the global minimum was subsequently confirmed by the absence of negative vibrational frequencies and lower energy structures formed by internal rotation.
After that, a set of fundamental vibrational frequencies of TNB was obtained. The frequencies corresponding to internal rotation were identified with a method proposed by Ayala [39] and excluded from further calculations. All the other frequencies were scaled by a factor of 0.9795 below 2000 cm-1 and 0.9566 above 2000 cm-1 following the recommendations from Ref. [40]. The resulting set of frequencies was used for the calculation of the vibrational contribution to the ideal gas heat capacity with Eq. (S1).
The one-dimensional (1-D) hindered rotor model was utilized for the treatment of the internal rotation motion to the heat capacities of the ideal gas phase. The algorithm described in Ref. [41] was used for this purpose, with the reduced moment of inertia of the naphthyl rotating top, Ir = 431.56 ± 0.14 amu Å2, calculated according to Kilpatrick and Pitzer [42]. For the determination of the potential energy surface (PES), a 360-degree optimized scan was performed with a step size of 10°. The obtained PES was used for the calculation of the energy levels of internal rotation with the Fourier grid Hamiltonian (FGH) method [43,44,45]. The contribution of hindered rotation to the ideal gas heat capacity of TNB is calculated from these energy levels with Eq. (S2) [41].
The implementation of the 1-DHR approach for the internal rotor treatment in combination with two scaling factors for vibrational frequencies allows for the determination of the ideal gas heat capacity with an average absolute percentage deviation σr of 1.5 % at 300 K and 1 % at 800 K [46].
All the data used for the determination of the ideal gas heat capacities of TNB and the calculated values of Cp,m(g) between 200 and 800 K are presented in Tables S5-S9 and Eqs. (S1-S3) of the Supplementary Materials.

4.6. Molecular Refractivity

For the determination of the molar refractivity value of TNB, the densities and refractive indices of its solutions in benzene were measured at 298.15 K.
An automatic digital refractometer RX-9000 alpha (Atago Co., Ltd.) calibrated with de-ionized water was used for the determination of refractive indices of the TNB solutions in benzene at 298.15 K with an accuracy of 0.00010 in the range of measurements.
The densities of benzene solutions of TNB at 298.15 K were measured using a vibrat-ing-tube densimeter Anton Paar DSA 5000 M with an accuracy of 0.000007 g∙cm-3. Prior to the experiments, it was calibrated with air and deionized water.
Obtained refractive indices and densities of benzene solutions of TNB, as well as calculated values of molar refractivity, are presented in Table S9 of Supplementary Materials.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: PXRD pattern of TNB sample studied in this work; Figure S2: Potential energy surface for internal rotation of naphthyl substituents in TNB; Table S1: Provenance and purity of the materials; Table S2: Enthalpies and temperatures of fusion of TNB measured in this work at 105 Pa; Table S3: Isobaric heat capacities of crystalline and liquid TNB measured in this work using DSC at the pressure of 0.1 MPa; Table S4: Experimental enthalpies of solution of TNB in benzene measured in this work at 298.15 K and 0.1 MPa; Table S5: Cartesian coordinates for TNB optimized with B3LYP/6-31+G(d,p); Table S6: Computed fundamental vibrational wavenumbers of TNB used in the calculation of the ideal-gas heat capacities; Table S7: Energy levels of hindered rotation of naphthyl substituents in TNB; Table S8: Contributions of vibration and internal rotation to the heat capacities of TNB, as well as isochoric and isobaric heat capacities calculated in this work; Table S9: Molar refractions of TNB derived according to Eq. (10) of the manuscript and experimentally measured densities and refractive indices of TNB solutions in benzene at 298.15 K required for its calculation.

Author Contributions

Conceptualization, M.I.Ya.; methodology, M.I.Ya. and D.N.B.; software, A.A.S.; validation, D.N.B., B.N.S.; formal analysis, A.A.N.; investigation, I.S.B., A.A.N., A.A.S..; writing—original draft preparation, M.I.Ya., D.N.B.; writing—review and editing, T.A.M., D.N.B., A.A.S., A.A.N., B.N.S.; visualization, A.A.S. and D.N.B.; supervision, B.N.S.; project administration, M.I.Ya. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Russian Science Foundation, Project No 23-73-10014.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article and supplementary material, further inquiries can be directed to the corresponding authors.

Acknowledgments

Authors help Mr. Alexander D. Kachmarzhik for the assistance in experiments on HPLC and Mrs. Liana S. Zubaidullina for the assistance in experiments on PXRD.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Tsukushi, I.; Yamamuro, O.; Matsuo, T. Solid state amorphization of organic molecular crystals using a vibrating mill. Solid State Commun. 1995, 94, 1013–1018. [Google Scholar] [CrossRef]
  2. Tsukushi, I.; Yamamuro, O.; Ohta, T.; Matsuo, T.; Nakano, H.; Shirota, Y. A calorimetric study on the configurational enthalpy and low-energy excitation of ground amorphous solid and liquid-quenched glass of 1, 3, 5-tri--naphthylbenzene. J. Phys. Cond. Matt. 1996, 8, 245. [Google Scholar] [CrossRef]
  3. Magill, J.H.; Plazek, D.J. Crystallization Kinetics of 1 : 3 :5 Tri-α-naphthyl Benzene. Nature 1966, 209, 70–71. [Google Scholar] [CrossRef]
  4. Magill, J. Physical Properties of Aromatic Hydrocarbons. III. A Test of the Adam—Gibbs Relaxation Model for Glass Formers Based on the Heat-Capacity Data of 1, 3, 5-tri-α-Naphthylbenzene. J. Chem. Phys. 1967, 47, 2802–2807. [Google Scholar] [CrossRef]
  5. Ngai, K.; Magill, J.; Plazek, D. Flow, diffusion and crystallization of supercooled liquids: Revisited. J. Chem. Phys. 2000, 112, 1887–1892. [Google Scholar] [CrossRef]
  6. Swallen, S.F.; Bonvallet, P.A.; McMahon, R.J.; Ediger, M. Self-diffusion of tris-naphthylbenzene near the glass transition temperature. Phys. Rev. Lett. 2003, 90, 015901. [Google Scholar] [CrossRef] [PubMed]
  7. Hofer, K.; Perez, J.; Johari, G.P. Detecting enthalpy ‘cross-over’ in vitrified solids by differential scanning calorimetry. Philos. Mag. Lett. 1991, 64, 37–43. [Google Scholar] [CrossRef]
  8. Whitaker, C.M.; McMahon, R.J. Synthesis and characterization of organic materials with conveniently accessible supercooled liquid and glassy phases: Isomeric 1, 3, 5-tris (naphthyl) benzenes. J. Phys. Chem. 1996, 100, 1081–1090. [Google Scholar] [CrossRef]
  9. Magill, J.; Plazek, D. Physical Properties of Aromatic Hydrocarbons. II. Solidification Behavior of 1, 3, 5-Tri-α-Naphthylbenzene. J. Chem. Phys. 1967, 46, 3757–3769. [Google Scholar] [CrossRef]
  10. Dawson, K.; Zhu, L.; Kopff, L.A.; McMahon, R.J.; Yu, L.; Ediger, M. Highly stable vapor-deposited glasses of four tris-naphthylbenzene isomers. J. Phys. Chem. Lett. 2011, 2, 2683–2687. [Google Scholar] [CrossRef]
  11. Whitaker, K.R.; Ahrenberg, M.; Schick, C.; Ediger, M. Vapor-deposited α, α, β-tris-naphthylbenzene glasses with low heat capacity and high kinetic stability. J. Chem. Phys. 2012, 137, 154502. [Google Scholar] [CrossRef]
  12. Liu, T.; Cheng, K.; Salami-Ranjbaran, E.; Gao, F.; Li, C.; Tong, X.; Lin, Y.-C.; Zhang, Y.; Zhang, W.; Klinge, L.; et al. The effect of chemical structure on the stability of physical vapor deposited glasses of 1,3,5-triarylbenzene. J. Chem. Phys. 2015, 143, 084506. [Google Scholar] [CrossRef]
  13. Ediger, M.D.; Swallen, S.; Kearns, K.; Yu, L.; Wu, T. Unusually stable glasses and methods for forming same. US Patent 2012. [Google Scholar]
  14. Gutzow, I.; Schmelzer, J. The vitreous state; Springer: 2015; 576 p.
  15. Costa, J.C.S.; Rocha, R.M.; Vaz, I.C.M.; Torres, M.C.; Mendes, A.; Santos, L.M.N.B.F. Description and Test of a New Multilayer Thin Film Vapor Deposition Apparatus for Organic Semiconductor Materials. J. Chem. Eng. Data 2015, 60, 3776–3791. [Google Scholar] [CrossRef]
  16. Lima, C.F.; Costa, J.C.; Silva, A.M.; Mendes, A.; Santos, L.M. Solid–Liquid–Gas Phase Equilibria for Small Phenylene-Thiophene Co-Oligomers. J. Chem. Eng. Data 2022, 67, 3033–3045. [Google Scholar] [CrossRef]
  17. Magill, J.; Ubbelohde, A. Interlocking of polyphenyl molecules in the pre-freezing region. Trans. Faraday Soc. 1958, 54, 1811–1821. [Google Scholar] [CrossRef]
  18. Elseiver. https://www.reaxys.com/ Reaxys. 2024.
  19. Yagofarov, M.I.; Nagrimanov, R.N.; Solomonov, B.N. New aspects in the thermochemistry of solid-liquid phase transitions of organic non-electrolytes. J. Mol. Liq. 2018, 256, 58–66. [Google Scholar] [CrossRef]
  20. Bolmatenkov, D.N.; Yagofarov, M.I.; Sokolov, A.A.; Ziganshin, M.A.; Solomonov, B.N. The heat capacities and fusion thermochemistry of sugar alcohols between 298.15 K and Tm: The study of D-sorbitol, D-mannitol and myo-inositol. J. Mol. Liq. 2021; 115545. [Google Scholar]
  21. Sokolov, A.A.; Yagofarov, M.I.; Balakhontsev, I.S.; Nizamov, I.I.; Mukhametzyanov, T.A.; Solomonov, B.N.; Yurkshtovich, Y.N.; Stepurko, E.N. Thermodynamic Properties of 3-and 4-Ethoxyacetanilides between 80 and 480 K. Molecules 2023, 28, 7027. [Google Scholar] [CrossRef]
  22. Solomonov, B.N.; Yagofarov, M.I. An approach for the calculation of vaporization enthalpies of aromatic and heteroaromatic compounds at 298.15 K applicable to supercooled liquids. J. Mol. Liq. 2020, 319, 114330. [Google Scholar] [CrossRef]
  23. Yagofarov, M.I.; Solomonov, B.N. Interpolation of the temperature dependence of the fusion enthalpy of aromatic compounds between 298.15 K and the melting temperature. Int. J. Thermophys. 2022, 43, 90. [Google Scholar] [CrossRef]
  24. Cebe, P.; Thomas, D.; Merfeld, J.; Partlow, B.P.; Kaplan, D.L.; Alamo, R.G.; Wurm, A.; Zhuravlev, E.; Schick, C. Heat of fusion of polymer crystals by fast scanning calorimetry. Polymer 2017, 126, 240–247. [Google Scholar] [CrossRef]
  25. Bolmatenkov, D.N.; Yagofarov, M.I.; Valiakhmetov, T.F.; Rodionov, N.O.; Solomonov, B.N. Vaporization enthalpies of benzanthrone, 1-nitropyrene, and 4-methoxy-1-naphthonitrile: prediction and experiment. J. Chem. Thermodyn. 2021, 168, 106744. [Google Scholar] [CrossRef]
  26. Solomonov, B.N.; Yagofarov, M.I.; Nagrimanov, R.N. Additivity of vaporization enthalpy: group and molecular contributions exemplified by alkylaromatic compounds and their derivatives. J. Mol. Liq. 2021, 342, 117472. [Google Scholar] [CrossRef]
  27. Solomonov, B.N.; Varfolomeev, M.A.; Nagrimanov, R.N.; Novikov, V.B.; Zaitsau, D.H.; Verevkin, S.P. Solution calorimetry as a complementary tool for the determination of enthalpies of vaporization and sublimation of low volatile compounds at 298.15 K. Thermochim. Acta 2014, 589, 164–173. [Google Scholar] [CrossRef]
  28. Biswas, N.; Dey, G.; Das, L.; Das, S.; Ruidas, N.; Chakraborty, A. Geometry, vibrations and torsional potential of 1-phenyl naphthalene: A combined ab-initio and experimental study. J. Mol. Struct. 2024, 1296, 136844. [Google Scholar] [CrossRef]
  29. Le Fevre, R.; Sundaram, A.; Sundaram, K. 593. Molecular polarisability. The molar Kerr constants and conformations of eight polyaryls as solutes. J. Chem. Soc. 1963, 3180–3188. [Google Scholar] [CrossRef]
  30. Armarego, W.L. Purification of laboratory chemicals; Butterworth-Heinemann: 2017.
  31. Yagofarov, M.I.; Sokolov, A.A.; Balakhontsev, I.S.; Nizamov, I.I.; Solomonov, B.N. Thermochemistry of fusion, solution and hydrogen bonding in benzamide, N-methylbenzamide, and acetanilide. Thermochim. Acta 2023, 728, 179579. [Google Scholar] [CrossRef]
  32. Buzyurov, A.V.; Nagrimanov, R.N.; Zaitsau, D.H.; Mukhametzyanov, T.A.; Abdelaziz, A.; Solomonov, B.N.; Schick, C. Application of the Flash DSC 1 and 2+ for vapor pressure determination above solids and liquids. Thermochim. Acta 2021, 706, 179067. [Google Scholar] [CrossRef]
  33. Bolmatenkov, D.N.; Yagofarov, M.I.; Valiakhmetov, T.F.; Rodionov, N.O.; Solomonov, B.N. Vaporization enthalpies of benzanthrone, 1-nitropyrene, and 4-methoxy-1-naphthonitrile: Prediction and experiment. J. Chem. Thermodyn. 2022, 168, 106744. [Google Scholar] [CrossRef]
  34. Yagofarov, M.I.; Lapuk, S.E.; Mukhametzyanov, T.A.; Ziganshin, M.A.; Schick, C.; Solomonov, B.N. Application of fast scanning calorimetry to the fusion thermochemistry of low-molecular-weight organic compounds: Fast-crystallizing m-terphenyl heat capacities in a deeply supercooled liquid state. Thermochim. Acta 2018, 668, 96–102. [Google Scholar] [CrossRef]
  35. Fuller, E.N.; Schettler, P.D.; Giddings, J.C. New Method for Prediction of Binary Gas-Phase Diffusion Coefficients. Ind. Eng. Chem. 1966, 58, 18–27. [Google Scholar] [CrossRef]
  36. Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The properties of gases and liquids; McGraw-Hill, Inc.: New York:, 1987. [Google Scholar]
  37. Buzyurov, A.V.; Nagrimanov, R.N.; Zaitsau, D.H.; Mukhametzyanov, T.A.; Solomonov, B.N.; Abdelaziz, A.; Schick, C. Application of the Flash DSC 1 and 2+ for vapor pressure determination above solids and liquids. Thermochim. Acta 2021, 706, 179067. [Google Scholar] [CrossRef]
  38. Ferro-Costas, D.; Fernández-Ramos, A. A combined systematic-stochastic algorithm for the conformational search in flexible acyclic molecules. Frontiers Chem. 2020, 8, 16. [Google Scholar] [CrossRef] [PubMed]
  39. Ayala, P.Y.; Schlegel, H.B. Identification and treatment of internal rotation in normal mode vibrational analysis. J. Chem. Phys. 1998, 108, 2314–2325. [Google Scholar] [CrossRef]
  40. Cervinka, C.; Fulem, M.; Ruzicka, K. Evaluation of accuracy of ideal-gas heat capacity and entropy calculations by density functional theory (DFT) for rigid molecules. J. Chem. Eng. Data 2012, 57, 227–232. [Google Scholar] [CrossRef]
  41. Pfaendtner, J.; Yu, X.; Broadbelt, L.J. The 1-D hindered rotor approximation. Theor. Chem. Acc. 2007, 118, 881–898. [Google Scholar] [CrossRef]
  42. Kilpatrick, J.E.; Pitzer, K.S. Energy levels and thermodynamic functions for molecules with internal rotation. III. Compound rotation. J. Chem. Phys. 1949, 17, 1064–1075. [Google Scholar] [CrossRef]
  43. Marston, C.C.; Balint-Kurti, G.G. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions. J. Chem. Phys. 1989, 91, 3571–3576. [Google Scholar] [CrossRef]
  44. Balint-Kurti, G.G.; Ward, C.L.; Marston, C.C. Two computer programs for solving the Schrödinger equation for bound-state eigenvalues and eigenfunctions using the Fourier grid Hamiltonian method. Comput. Phys. Commun. 1991, 67, 285–292. [Google Scholar] [CrossRef]
  45. Balint-Kurti, G.G.; Dixon, R.N.; Marston, C.C. Grid methods for solving the Schrödinger equation and time dependent quantum dynamics of molecular photofragmentation and reactive scattering processes. Int. Rev. Phys. Chem. 1992, 11, 317–344. [Google Scholar] [CrossRef]
  46. Cervinka, C.; Fulem, M.; Růžička, K.t. Evaluation of uncertainty of ideal-gas entropy and heat capacity calculations by density functional theory (DFT) for molecules containing symmetrical internal rotors. J. Chem. Eng. Data 2013, 58, 1382–1390. [Google Scholar] [CrossRef]
Preprints 102923 g001
Figure 1. The heat capacities of TNB. Dashed orange line – crystal, Ref. [4]; dashed blue line – crystal, Ref. [2]; solid red line – crystal, this work; dashed black line – liquid, Ref. [4]; dotted green line – liquid, Ref. [2]; solid violet line – liquid, this work.
Figure 1. The heat capacities of TNB. Dashed orange line – crystal, Ref. [4]; dashed blue line – crystal, Ref. [2]; solid red line – crystal, this work; dashed black line – liquid, Ref. [4]; dotted green line – liquid, Ref. [2]; solid violet line – liquid, this work.
Preprints 102923 g001
Preprints 102923 g002
Figure 2. The vapor pressures of TNB measured in this work (violet line – values fitted by Clarke-Glew equation, circles – experimental points) and calculated based on Refs. [9,17] (dashed red line – p at (703 – 803) K, black point – normal boiling point at 863 K).
Figure 2. The vapor pressures of TNB measured in this work (violet line – values fitted by Clarke-Glew equation, circles – experimental points) and calculated based on Refs. [9,17] (dashed red line – p at (703 – 803) K, black point – normal boiling point at 863 K).
Preprints 102923 g002
Preprints 102923 g003
Figure 3. Optimized geometry of TNB in the gas phase obtained at B3LYP/6-31+G(d,p) theory level.
Figure 3. Optimized geometry of TNB in the gas phase obtained at B3LYP/6-31+G(d,p) theory level.
Preprints 102923 g003
Table 1. The enthalpies and temperatures of fusion of TNB.
Table 1. The enthalpies and temperatures of fusion of TNB.
Tm / K ∆ c r l H (Tm)/ kJ mol-1 Ref.
458.6±0.4 a 32.9±0.5 a This work
456.3 33.3 [1]
472 42.4±0.6 [4]
472.2 41.8 [9]
a The uncertainties include the expanded uncertainty of the mean U (0.95 level of confidence, coverage factor of 2.0) and reproducibility of calibration.
Table 2. The vapor pressures above liquid TNB measured in this work.
Table 2. The vapor pressures above liquid TNB measured in this work.
T / K pa / Pa T / K pa / Pa T / K pa / Pa
457.6 1.29·10-2 503.3 4.19·10-1 548.9 5.59
462.7 1.95·10-2 508.3 5.85·10-1 554.0 7.22
467.8 2.95·10-2 513.4 8.03·10-1 559.0 9.15
472.8 4.33·10-2 518.5 1.11 564.1 11.6
477.9 7.24·10-2 523.5 1.45 569.2 14.3
483.0 1.05·10-1 528.6 1.86 574.3 18.3
488.1 1.50·10-1 533.7 2.49 579.3 22.2
493.1 2.14·10-1 538.8 3.29
498.2 2.99·10-1 543.8 4.19
a The estimated uncertainties (standard uncertainty (u) at a level of confidence of 68%) of vapor pressure reported inside Table S4 were below 20 % and included the uncertainty of sample mass determination, sample area determination, the uncertainty of diffusion coefficient and uncertainty of temperature (1 K). Analysis of the uncertainties was made as described in Ref. [37].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Phase transition thermodynamics of 1,3,5-tris-(α-naphthyl)benzene: theory and experiment

Mikhail I. Yagofarov

et al.

,

2024

The Phase Diagram of the API Benzocaine and Its Highly Persistent, Metastable Crystalline Polymorphs

Ivo B. Rietveld

et al.

,

2023

Polymorph Dependent Initial Thermal Decay Mechanism of 1,1-Diamino-2,2-Dinitroethylene (FOX-7)

Huaiyu Jiang

et al.

,

2023

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated