Chaotic Interaction between Thermodynamic Systems

Preprint

Article

Chaotic Interaction between Thermodynamic Systems

Altmetrics

Downloads

131

Views

145

Comments

EKREM AYDINER^*

This version is not peer-reviewed

Submitted:

02 April 2024

Posted:

03 April 2024

You are already at the latest version

Alerts

Abstract

In the previous work in Ref.[1], we presented a new interaction scheme that describes the interaction of thermodynamic systems. Using this interaction scheme, we showed that the interactions of dark matter and dark energy are chaotic. We also predicted that the results could be generalized to all particle and thermodynamic systems. In addition, we gave physical definitions of the concepts of chaos and self-organization. More importantly, we proposed a new law of physics based on interacting systems. In this study, we will consider two thermodynamic systems interacting under different conditions to prove the universality of the physical law we propose. We will show that these systems also have chaotic interaction dynamics.

Keywords:

Subject: Physical Sciences - Thermodynamics

1. Introduction

In the previous study [1], our main aim in the previous study was to prove that the interaction in the dark side is chaotic. In Ref. [1], we introduce a new interaction schema for dark components and we show that the interaction between dark matter and dark energy is chaotic. In Ref. [1], we consider dark matter and dark energy as a thermodynamic system and we studied the interaction two open systems under conditions

δ Q \neq 0

δ N \neq 0

and

d V = 0

. By generalized these results to the thermodynamic systems, we introduced an new physics law:

"The dynamics of all coupled interacting particle and thermodynamic systems are chaotic."

In the previous study, we studied the interaction condition

δ Q \neq 0

δ N \neq 0

and

d V = 0

for two interacting thermodynamic systems. The proposed law should be valid for all interacting thermodynamic systems. For this reason, we will consider two different situations in this study: i)

δ Q \neq 0

δ N = 0

and

d V = 0

and ii)

δ Q \neq 0

δ N \neq 0

and

d V \neq 0

. By using the same interaction schema In Ref. [1], in this study, we will consider these cases We will analyse the dynamics of this coupling system.

This work is organized as fallows: In Section II, we consider a case for

δ Q \neq 0

δ N = 0

and

d V = 0

. In Section III, we consider a case for

δ Q \neq 0

δ N \neq 0

and

d V \neq 0

. In the both sections, we introduce new interaction equations for two cases and we will analyses the phase space and chaos behaviours of the interacting systems. In Section IV, we discuss some remarkable results and finally, in the last section, conclusion are presented.

2. The Model

The energy exchange for any open thermodynamic systems is given by

\begin{matrix} d U = δ Q + \sum_{i = 1}^{N} δ W_{i} \end{matrix}

(1)

where

d U

corresponds to energy exchange in the system,

δ Q

is heat changes, and

δ W_{i}

denotes work which is done ont he system. The energy exchanges for two coupled interacting systems can be given in the form

\begin{matrix} d U_{1} (x_{2}) = δ Q_{1} (x_{1}) + δ W_{1} (x_{1}) + δ N_{1} (x_{1}) \end{matrix}

(2a)

\begin{matrix} d U_{2} (x_{1}) = δ Q_{2} (x_{2}) + δ W_{2} (x_{2}) + δ N_{2} (x_{2)} \end{matrix}

(2b)

where

d U_{1} (x_{2})

and

d U_{2} (x_{1})

denote the energy exchanges on the system 1 and 2, respectively.

Here,

x_{1}

is considered as the energy flux passing through system 1, and

x_{2}

is considered as the energy flux passing through system 2. In energy exchanges between systems, the total energy will be conserved:

\begin{matrix} \oint d U (x_{i}) = 0 \end{matrix}

(3)

where

i = 1, 2

. At the same time, total energy is conservative:

\begin{matrix} \sum_{i = 1} E_{i} = c o n s t \end{matrix}

(4)

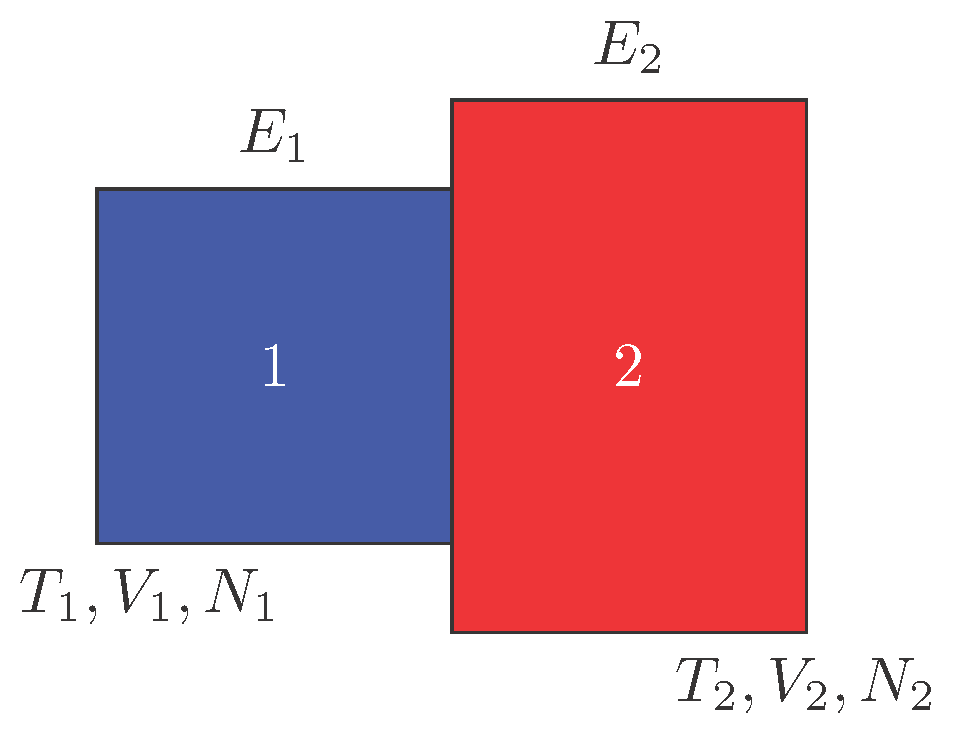
Let us imagine that two separate thermodynamic systems with different energies, temperatures, volumes, and number of particles are in contact with each other, as in Figure 1. According to the traditional thermodynamic approach, if these two systems are not in equilibrium, that is, for example,

T_{1} \neq T_{2}

p_{1} \neq p_{2}

μ_{1} \neq μ_{2}

are met, the systems are far from equilibrium and will continue to interact with each other until they reach equilibrium. Internal energy changes in both systems can be derived from Equations (2) and (3).

Figure 1. Two thermodynamic systems in contact.

E_{1, 2}

are the energies of the systems,

T_{1, 2}

denote the temperatures,

V_{1, 2}

represents the volumes, and

N_{1, 2}

are the number of particles.

Figure 1. Two thermodynamic systems in contact.

E_{1, 2}

are the energies of the systems,

T_{1, 2}

denote the temperatures,

V_{1, 2}

represents the volumes, and

N_{1, 2}

are the number of particles.

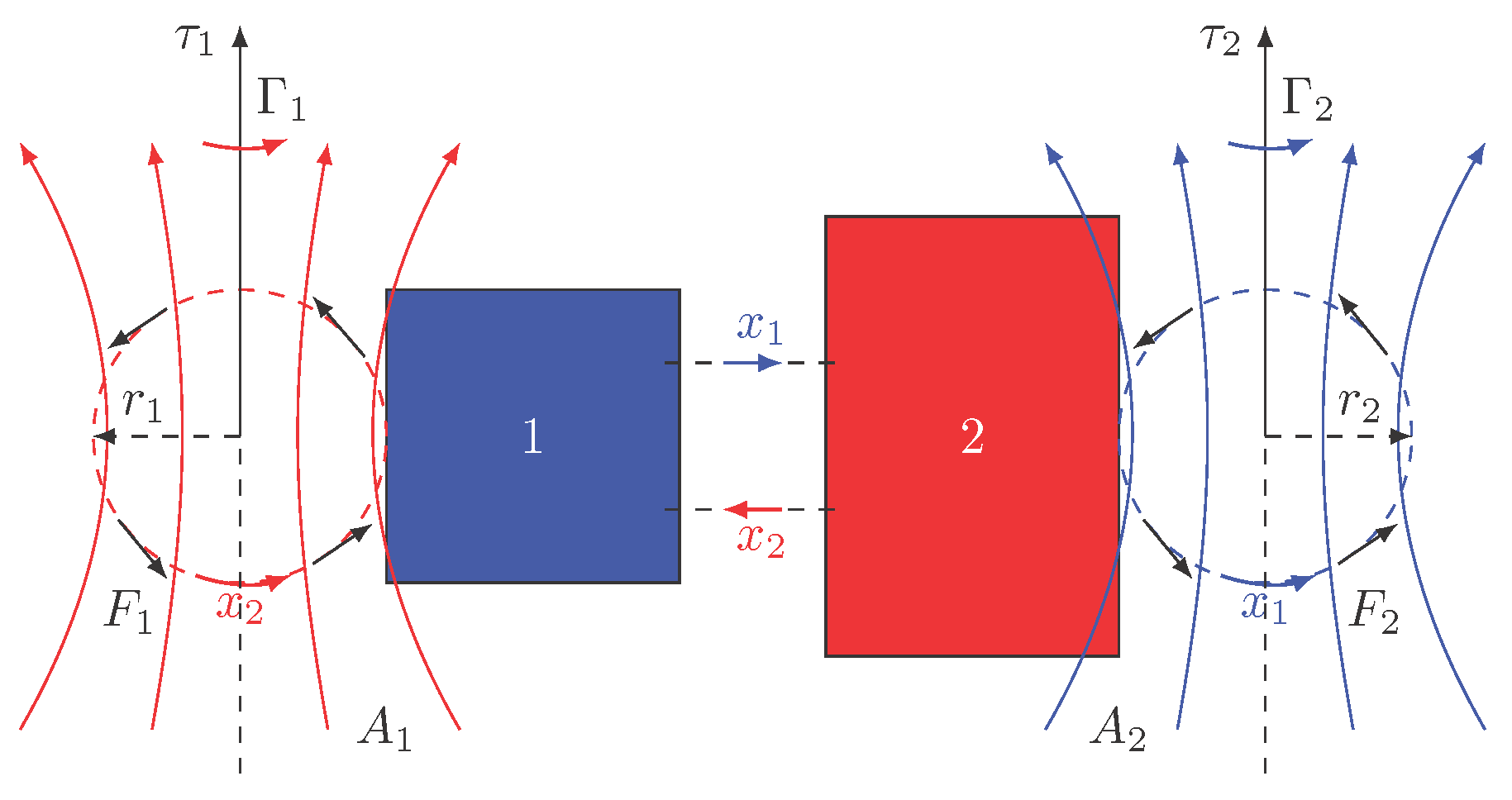
Figure 2. Schematic representation of two thermodynamic systems interacting in contact. The vectorial attractor fields and torque behavior on the self-interacting loops.

Γ_{1, 2}

denotes non-holonomic variables in Equation (5).

{\vec{A}}_{1, 2}

are the attractor vectorial fields caused by driven force

{\vec{F}}_{1, 2}

and

{\vec{τ}}_{1, 2}

correspond to torque on the loops. These variables are defined in Ref. [1].

Figure 2. Schematic representation of two thermodynamic systems interacting in contact. The vectorial attractor fields and torque behavior on the self-interacting loops.

Γ_{1, 2}

denotes non-holonomic variables in Equation (5).

{\vec{A}}_{1, 2}

are the attractor vectorial fields caused by driven force

{\vec{F}}_{1, 2}

and

{\vec{τ}}_{1, 2}

correspond to torque on the loops. These variables are defined in Ref. [1].

In this study, two models are

δ Q \neq 0

δ N = 0

d V = 0

and

δ Q \neq 0

δ N \neq 0

d V \neq 0

. We will consider different situation. Since the interactions in the self-interaction loops will remain the same for both cases, we will focus only on the mutual interaction in the next section. As it is known, the mutual and self-interaction scheme is as follows:

Self-interactions of two coupled thermodynamic system given in Ref. [1] are

\frac{d Γ_{1}}{d t} = 1 - x_{1} x_{2}, \frac{d Γ_{2}}{d t} = 1 - x_{1} x_{2}

(5)

For solid systems that are assumed not to rotate while in contact, Equation (5) can be written as

\begin{matrix} \frac{d Γ_{1}}{d t} = - x_{1} x_{2}, \frac{d Γ_{2}}{d t} = - x_{1} x_{2} . \end{matrix}

(6)

Self-interaction loops are not defined in standard statistical thermodynamics. Therefore, the interaction picture still needs to be completed. The mutual interactions do not formally connect the interacting systems. However, systems behave each other as sources. We show that in the previews study [1] that the self-interaction loops connect resources in the interaction schema. Therefore, the self-interact loops have new hidden variables and vectorial fields unlike classical interaction schema. It is clear that both the new interaction schema and new concepts strongly indicate the presence of the new thermodynamic laws.

Self-infraction loops represent the hidden attractors. When looking at the literature, it can be seen that the idea of hidden attractor is not new and appears in dynamic systems. The concept of hidden attractors was first introduced in connection with Hilbert’s 16th problem formulated in 1900 [2]. Kuznetsov et al. reported the chaotic hidden attractor in Chua’s circuit [3,4,5]. This research has since led to further efforts to locate hidden attractors in various examples [6,7,8,9,10,11].

3. Case I: $δ Q \neq 0$ , $δ N = 0$ and $dV = 0$

For the case

δ Q \neq 0

δ N = 0

and

d V = 0

the mutual interaction equation as

\frac{d x_{1}}{d t} = Γ_{1} x_{2}, \frac{d x_{2}}{d t} = Γ_{2} x_{1}

(7)

where

Γ_{1, 2}

are the non-holonomic variables which are denote energy transfer velocity.

By using Equations (5) and (7) we obtain interaction equation for the coupled and interacting two canonical ensembles i.e. thermodynamic systems as

\begin{matrix} \frac{d x_{1}}{d t} & = & x_{2} x_{3} \\ \frac{d x_{2}}{d t} & = & (x_{3} - q) x_{1} \\ \frac{d x_{3}}{d t} & = & 1 - x_{1} x_{2} \end{matrix}

(8)

where q is the control parameters

q = Γ_{1} - Γ_{2}

. Equation 8 is a non-linear and which describes the dynamics of the interacting systems via only heat transfer.

Using the Runga-Kutta method and the linearized algorithm [12], we numerically solved Equation (8) with FORTRAN 90. We obtained phase space solutions and Lyapunov exponents belonging to the coupling equations. Phase trajectories and Lyapunov exponents are given in Figure 3, Figure 4 and Figure 5 and Figure 6, respectively.

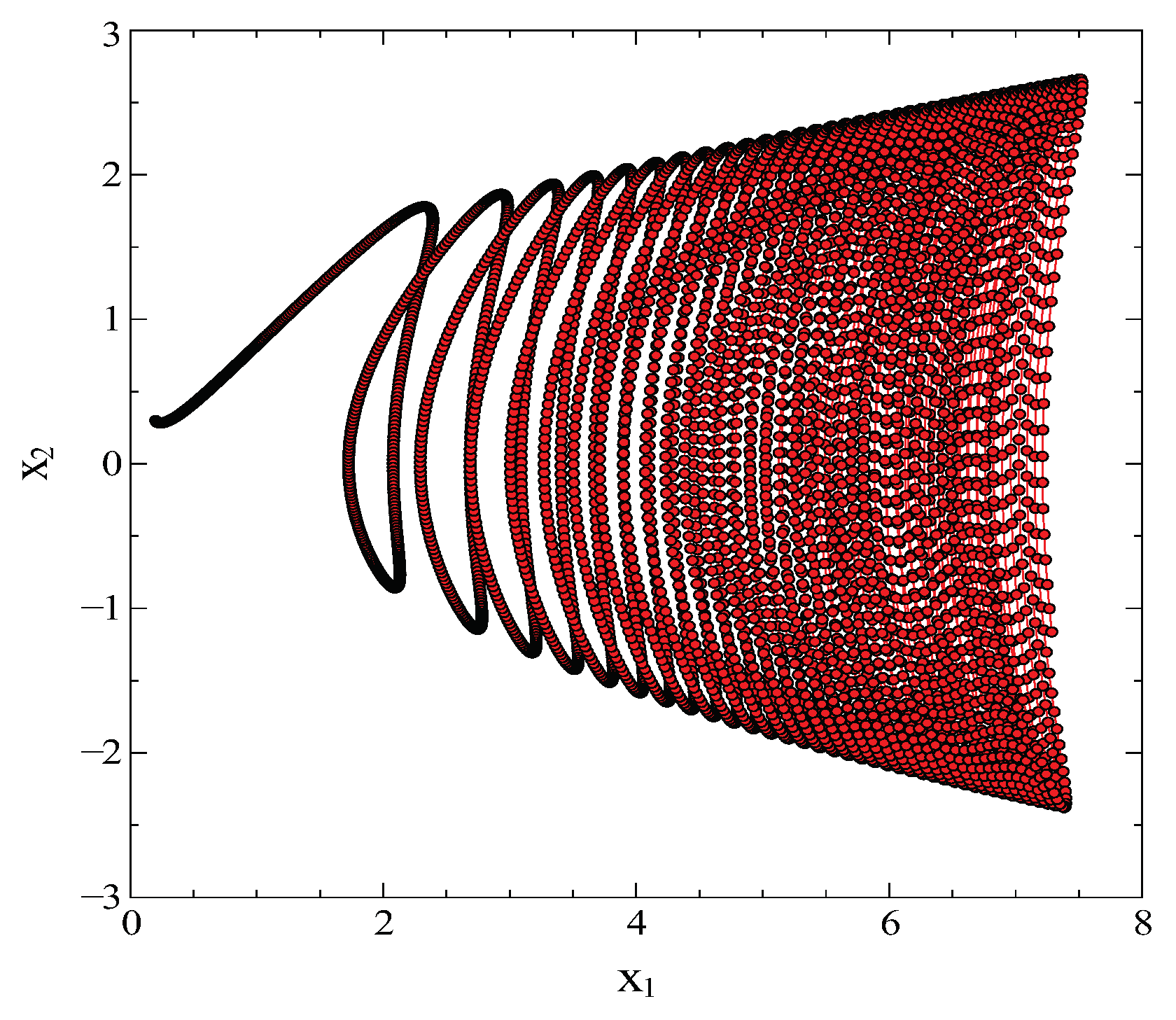
Solutions of the

x_{1}

and

x_{2}

for the control parameters

q = 3.46

are given in Figure 3. It is clearly seen that trajectory in the

x_{1} - x_{2}

plane does not intersect and repeated itself in the attractor basin. One can see that attractor appears around

x_{2} = 0

and trajectory proceeds in the

x_{1}

direction.

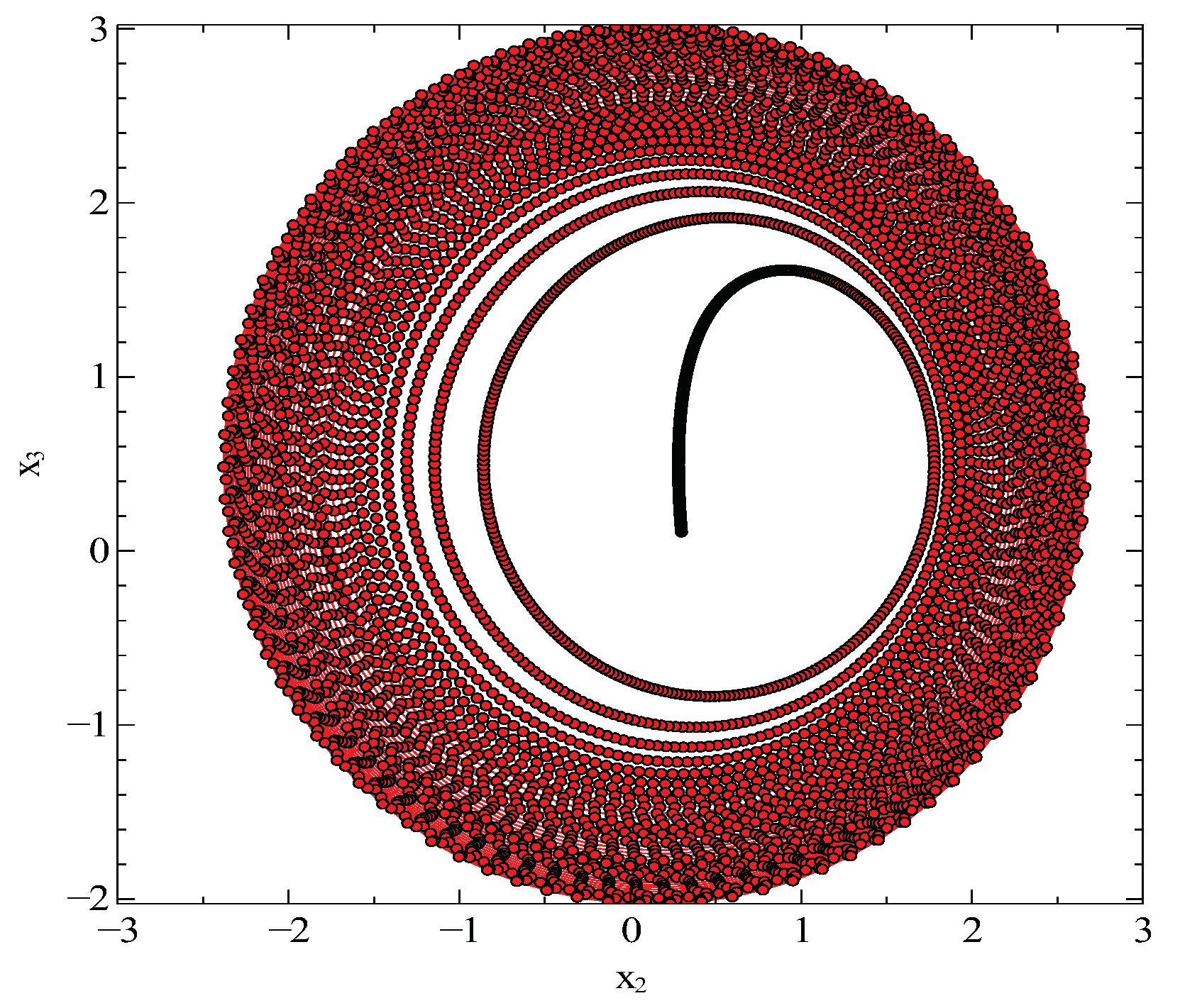
Similarly, solutions of the

x_{1}

and

x_{3}

for the control parameters

q = 3.46

are given in Figure 4, the attractor appears in

x_{1} - x_{3}

plane around

x_{3} = 0

. One can see that orbit does non periodic and moves on the

x_{1}

direction without cutting itself. Indeed, the attractor behaviors in Figure 3 and Figure 4 can be seen clearly in Figure 5. Indeed, the attractor and trajectory appear around

x_{2} = 0

and

x_{3}

on the

x_{2} - x_{3}

in Figure 5.

Additionally, we have tested that character of phase space solution do not change for the various running step time. Chaotic attractor is localized at only one fixed point.

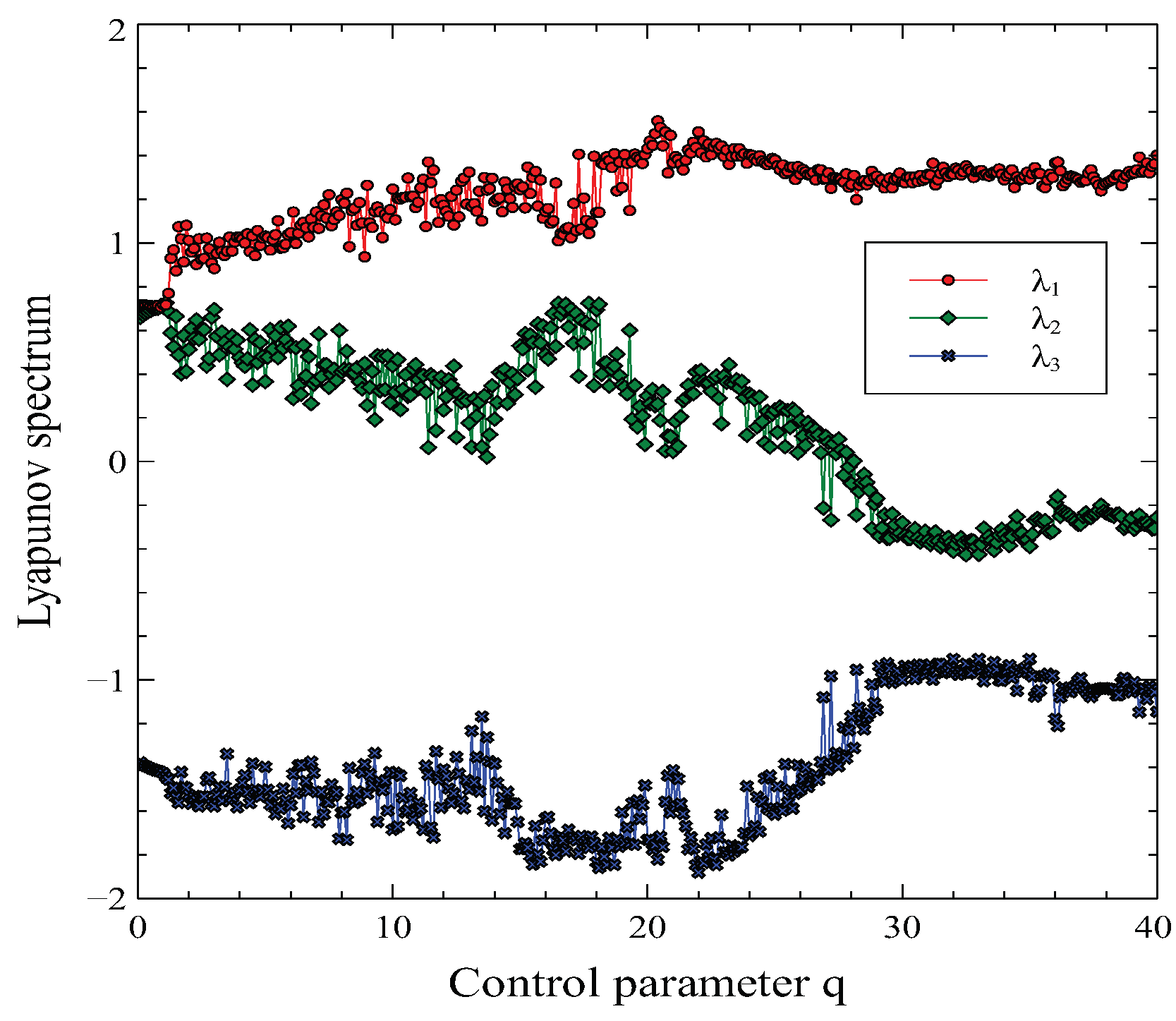
Now we discuss the Lyapunov spectrum of the system in Equation (8). It is known that positive Lyapunov exponents indicate the chaotic behavior of the system. We obtained the Lyapunov spectrum using the Wolf algorithm and plotted it in Figure 6. One can see that the system produces three positive Lyapunov exponents in this interaction schema. As seen from Figure 6, one of the exponents which are given a red curve is always positive for all q values. However, the other two Lyapunov exponents (yellow and blue curves) take negative and positive values for the different q values. It is strongly provided that the dynamics of the two coupled and interacting canonical or close thermodynamic systems are chaotic like two grand canonical systems [1].

4. Case II: $δ Q \neq 0$ , $δ N \neq 0$ and $dV \neq 0$

In this section, we will also consider volume changes. As a result of the interaction, the volume of the systems may change and this prevents work on the system. The work done on the system is defined as

δ W = - p d V

. In this case, the equations Equation (8) can be written in the following form:

\begin{matrix} \frac{d x_{1}}{d t} & = & x_{2} x_{3} - x_{1} - \int_{0}^{τ} x_{1} (t) d t \\ \frac{d x_{2}}{d t} & = & (x_{3} - q) x_{1} - x_{2} - \int_{0}^{τ} x_{2} (t) d t \\ \frac{d x_{3}}{d t} & = & 1 - x_{1} x_{2} \end{matrix}

(9)

The integral terms in the expression Equation (9) represent the energy storage capacity in systems. Integral expressions do not contain non-linear terms. Therefore, the contributions from these terms can be considered as constant contributions in the numerical solution. For simplicity, we define these integrals as

δ_{1, 2}

, where

δ_{1} = \int_{0}^{τ} x_{1} (t) d t

and

δ_{2} = \int_{0}^{τ} x_{2} (t) d t

we can simplify the solution. We can think of

δ_{1, 2}

as control parameters that measure the energy storage capacity. In this case, instead of getting lost in the details of the numerical solution, it would be appropriate to include the behavior of the system depending on the

δ_{1, 2}

parameter for a fixed q value. Because, as can be seen in Figure 6, the system behaves chaotic for all q values. However, the chaotic dynamics in the system can be controlled depending on the energy storage capacity.

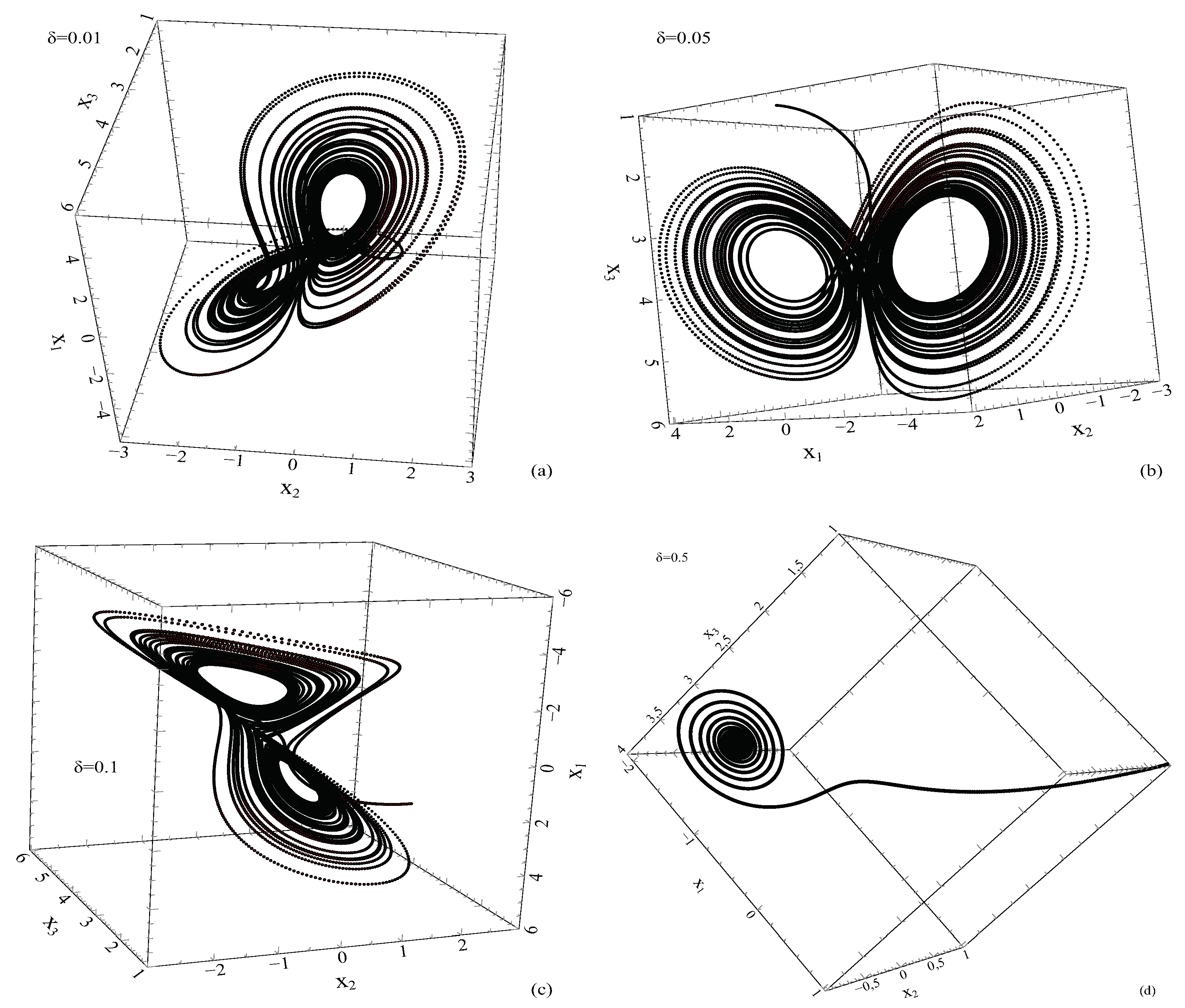
In order to maintain simplicity in the numerical solution, we will take

δ = δ_{1} = δ_{2}

and solve Equation (9) numerically for different

δ

values. Using the Runga-Kutta method and the linearised algorithm

δ

values are given in Figure 7.

Figure 7 (a)-(d) for four different delta values

δ = 0.01

δ = 0.05

δ = 0.1

and

δ = 0.5

are plotted. As can be seen in Figure 7 (a)-(c), the existence of chaotic attractors in the phase space is observed for small values of

δ

. But for

δ = 0.5

the chaotic attractors disappear. We did not look for a critical value for

δ

here. However, we only wanted to show that for large values of the

δ

parameter, chaotic dynamics will disappear and the system will go to a periodic or aperiodic solution. Here

δ

acts as a control parameter.

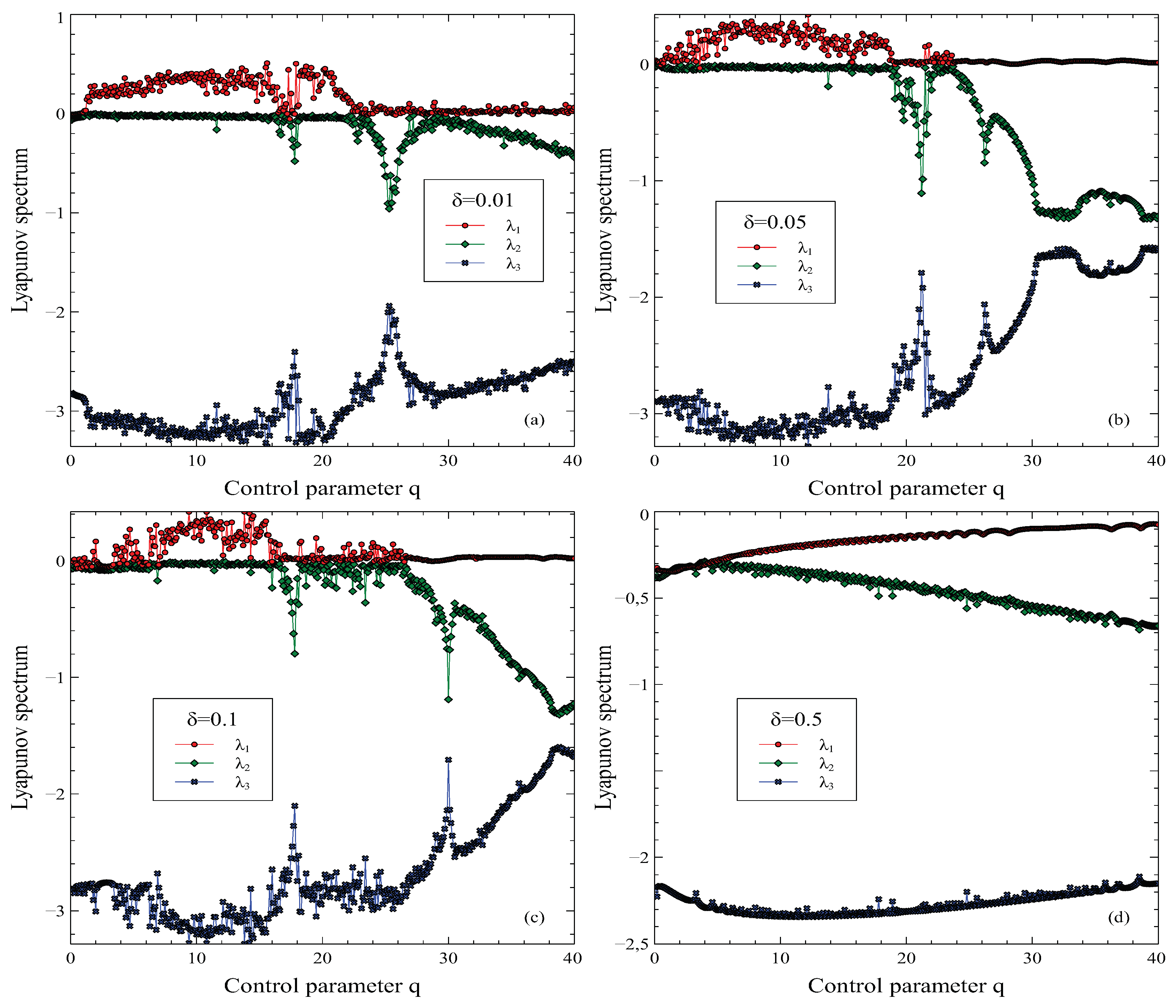
Similarly, we calculated the Lyapunov exponents for the same

δ

values and gave them in Figure 8. As can be seen in Figure 8 (a) and (c), there is at least one positive Lyapunov exponent in the spectrum for

δ = 0.01

δ = 0.05

and

δ = 0.1

For

δ = 0.5

, in Figure 8 (a), all exponents do not take negative values. As will be remembered, to say that the dynamics of the system are chaotic, there must be at least one positive exponent in the Lyapunov spectrum.

We would like to point out another important difference. For example, for the condition

δ Q \neq 0

δ N = 0

and

d V = 0

, only one chaotic attractor appears in the phase space, while for case

δ Q \neq 0

δ N \neq 0

It is seen that it is a chaotic attractor in the condition and

d V \neq 0

. The reason for this can be expressed as the system of equations given in Equation (9) has a more complex structure.

Another important point is that

δ = δ_{1} = δ_{2}

was chosen. Instead, if different values of

δ_{1}

and

δ_{2}

had been studied, two control parameters would have been included in the system. However, it is obvious that for small

δ_{1}

and

δ_{2}

values, the system given by Equation (9) will produce chaotic dynamics. Another point is that the expressions

δ_{1}

and

δ_{2}

could be written as a function of time. But it is clear that in any case, the quantitative analysis will not change.

5. Conclusion

In this study, we considered thermodynamic systems interacting with each other under conditions

δ Q \neq 0

δ N = 0

d V = 0

δ Q \neq 0

δ N \neq 0

d V \neq 0

. Using the interaction schema presented in Ref.[1], we obtained Equation (8) for

δ Q \neq 0

δ N = 0

d V = 0

and Equation (9) for

δ Q \neq 0

δ N \neq 0

d V \neq 0

. We obtained numerical solutions by solving the equations with FORTRAN 90.

Equation (8) It is understood from the Lyapunov spectrum given in Figure 6 that the interaction dynamics of two closed thermodynamic systems interacting only through heat transfer is chaotic. Similarly, by including heat exchange and work done on the system into the equation, it has been shown that the interactions of the open thermodynamic system given in Equation (8) will be chaotic. The results obtained here are in agreement with the results obtained in Ref.[1]. In other words, the results obtained confirm the universality of the new physics law we proposed.

Additionally, we should point out that case II gives slightly newer, more interesting results. However, the integral terms in the equation system Equation (9) work as control parameters and can be used to remove the dynamics of the system from chaos. This parameter will be possible to determine the chaotic threshold of the system. Large values of this parameter may suppress other interactions in the interacting system. Such interactive systems may require further investigation.

This study is complementary to the work presented in Ref.[1]. The results obtained in the previous study and in this study suggest that the dynamics of interacting thermodynamic systems will be chaotic. In other words, the results obtained support the comprehensiveness and universality of the proposed physical law. Finally, we would like to point out that, leaving the physics aside, Equations (8) and (9) are mathematically interesting in themselves. The fact that equations in this form produce chaos is a meaningful and important result in itself.

References

Aydiner, E. Chaotic interactions between dark matter and dark energy. arXiv 2023, arXiv:2304.06614. [Google Scholar]
Hilbert, D. Lecture delivered before the international congress of mathematicians at Paris in 1900. Bull. Amer. Math. Soc. 1901-1902, 8, 437–479. [Google Scholar] [CrossRef]
Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. from hidden oscillations in hilbert–kolmogorov, aizerman, and kalman problems to hidden chaotic attractor in chua circuits. International Journal of Bifurcation and Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
Leonov, G.; Kuznetsov, N.; Vagaitsev, V. Hidden attractor in smooth Chua systems. Physica D: Nonlinear Phenomena 2012, 241, 1482–1486. [Google Scholar] [CrossRef]
Leonov, G.; Kuznetsov, N.; Mokaev, T. Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion: Homoclinic orbits, and self-excited and hidden attractors. The European Physical Journal Special Topics 2015, 224, 1421–1458. [Google Scholar] [CrossRef]
Leonov, G.; Kuznetsov, N.; Vagaitsev, V. Localization of hidden Chua’s attractors. Physics Letters A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
Dudkowski, D.; Prasad, A.; Kapitaniak, T. Perpetual points and hidden attractors in dynamical systems. Physics Letters A 2015, 379, 2591–2596. [Google Scholar] [CrossRef]
Kuznetsov, N.; Leonov, G. Hidden attractors in dynamical systems: systems with no equilibria, multistability and coexisting attractors. IFAC Proceedings Volumes 2014, 47, 5445–5454. [Google Scholar] [CrossRef]
Kumarasamy, S.; Banerjee, M.; Varshney, V.; Shrimali, M.D.; Kuznetsov, N.V.; Prasad, A. Saddle-Node Bifurcation of Periodic Orbit Route to Hidden Attractors in Nonlinear Dynamical Systems. arXiv 2023, arXiv:2303.09888. [Google Scholar]
Kuznetsov, N.; Mokaev, T.; Ponomarenko, V.; Seleznev, E.; Stankevich, N.; Chua, L. Hidden attractors in Chua circuit: mathematical theory meets physical experiments. Nonlinear Dyn 2023, 111, 5859–5887. [Google Scholar] [CrossRef]
Jafari, S.; Sprott, J.; Nazarimehr, F. Recent new examples of hidden attractors. The European Physical Journal Special Topics 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D: Nonlinear Phenomena 1985, 16, 285–317. [Google Scholar] [CrossRef]

Figure 3. Non-periodic orbital in

x_{1} - x_{2}

plane for

q = 3.46

and attractor basin.

Figure 3. Non-periodic orbital in

x_{1} - x_{2}

plane for

q = 3.46

and attractor basin.

Figure 4. Chaotic attractor and trajectory in

x_{1} - x_{3}

plane for

q = 3.46

Figure 4. Chaotic attractor and trajectory in

x_{1} - x_{3}

plane for

q = 3.46

Figure 5. Chaotic attractor and trajectory in

x_{2} - x_{3}

plane for

q = 3.46

Figure 5. Chaotic attractor and trajectory in

x_{2} - x_{3}

plane for

q = 3.46

Figure 6. Three Lyapunov exponents versus control parameter q.

Figure 7. Three Lyapunov exponents which depends on q for two close interacting thermodynamic systems.

Figure 8. Three Lyapunov exponents for various

δ

parameter.

Figure 8. Three Lyapunov exponents for various

δ

parameter.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Chaotic Interaction between Thermodynamic Systems

Abstract

1. Introduction

2. The Model

3. Case I: δ Q ≠ 0 , δ N = 0 and dV = 0

4. Case II: δ Q ≠ 0 , δ N ≠ 0 and dV ≠ 0

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

3. Case I: $δ Q \neq 0$ , $δ N = 0$ and $dV = 0$

4. Case II: $δ Q \neq 0$ , $δ N \neq 0$ and $dV \neq 0$