1. Introduction
A notable feature of the current period is that the classical value of science as the pursuit of the truth, independently of other interests, is gradually being abandoned [
2]. People pride themselves on being scientists and (political) activists at the same time [
3], while calls for political actions to “save the planet”, including enhanced global governance mechanisms, are published even in scientific journals (e.g. [
4]). A relevant example is provided by the high-profile journal
Nature, which declares that it is “committed to supporting the research enterprise” [
5], but admits being involved in politics and proclaims that this is the right thing [
6,
7], even though it is recognized that this affects scientific credibility and causes loss of confidence in science [
8,
9]. It is thus natural to wonder if articles published in scientific journals promote the truth or political aims, perhaps hiding or distorting the truth, and even reversing cause and effect [
10,
11,
12,
13].
Seeking truth may have been even more difficult due to a recent development, the appearance of artificial intelligence (AI) bots, which certainly affects common opinion, as well as scientific perception and advancement. Assuming that AI bots more or less reflect the common perception in the scientific community and the general public, the Microsoft Bing’s Chat bot was asked the following question:
Which gas determines the greenhouse effect on Earth?
The bot provided the following answer (also supporting it with references [
14,
15,
16]):
The greenhouse effect is the process through which heat is trapped near Earth’s surface by substances known as ‘greenhouse gases.’ These gases consist of carbon dioxide, methane, ozone, nitrous oxide, chlorofluorocarbons, and water vapor. Water vapor, which reacts to temperature changes, is referred to as a ‘feedback’, because it amplifies the effect of forces that initially caused the warming. Scientists have determined that carbon dioxide plays a crucial role in maintaining the stability of Earth’s atmosphere. If carbon dioxide were removed, the terrestrial greenhouse effect would collapse, and Earth’s surface temperature would drop significantly, by approximately 33°C (59°F).
A literature search reveals that the AI bot essentially (and selectively) reproduces the following statements by Lacis et al. [
17]:
Noncondensing greenhouse gases, which account for 25% of the total terrestrial greenhouse effect, thus serve to provide the stable temperature structure that sustains the current levels of atmospheric water vapor and clouds via feedback processes that account for the remaining 75% of the greenhouse effect. Without the radiative forcing supplied by CO₂ and the other noncondensing greenhouse gases, the terrestrial greenhouse would collapse, plunging the global climate into an icebound Earth state. […]
If the global atmospheric temperatures were to fall to as low as TS = TE [where TE = 255 K is the global mean effective temperature] the Clausius-Clapeyron relation would imply that the sustainable amount of atmospheric water vapor would become less than 10% of the current atmospheric value.
On the other hand, Koutsoyiannis and Vournas [
18] recently examined longwave radiation observations extending over a period of 100 years and found that the observed increase of the atmospheric dioxide concentration ([CO₂]; from 300 to 420 ppm) has not altered, in a discernible manner, the greenhouse effect, which remains dominated by the quantity of water vapour in the atmosphere. Naturally, given the uproar about the enhancement of greenhouse effect due to human emissions by fossil fuel combustion, this finding appeared surprising to many. Some (including a knowledgeable reviewer of [
18]) postulated that this would be expected for the downwelling longwave (LW) radiation flux, which was the subject of Koutsoyiannis and Vournas [
18], but would not be the case for the outgoing radiation, where the effect of [CO₂] increase would be substantial. However, no long data series exist to verify such a conjecture and hence this question was not investigated in [
18], whose scope was to make inference based on data.
Hence the following research questions are raised:
We will examine these questions below, noting that the first one refers to a fictitious case (removal of atmospheric CO₂) for which no empirical data can exist. Rather, paleoclimatic studies and geological facts suggest that CO₂ existed, mostly in much higher concentrations than today, in most periods of Earth’s history, and also before oxygen appeared in the atmosphere. Also, the second question cannot be studied on an empirical basis, as no long-term data exist (systematic satellite measurements of outgoing LW flux have only been made in the 21
st century). Therefore, to study these questions we need to resort to theoretical arguments and analyses. We will do this by applying the established greenhouse theory and by enrolling standard models, without considering doubts that have been cast on the validity of the theory or alternative hypotheses (e.g. [
19,
20]).
Human CO₂ emissions are 4% of the total [
13] but there are also human H₂O emissions over the terrestrial part of Earth of a comparable percentage [
21]. Specifically, according to Koutsoyiannis [
22] the quantity of evaporation and transpiration over land is 91 400 km
3/year. According to Food and Agriculture Organization of the United Nations [
23], the human water withdrawal in 2010, including the evaporation from reservoirs, was 4.3 km
3/year, of which 69% and 19% were for agricultural and industrial use, respectively. Considering the fact that almost all of agricultural and a large part of industrial water are evaporated, as well as the increasing trend in water withdrawal, with simple calculations we may conclude that the current human addition to natural water cycle over land is about 4%. One could speculate that each of these 4% additions might influence climate to a degree comparable to that percentage, but the reasons that only the influence of CO₂ is investigated and highlighted by the scientific community, being regarded a driver of climate, despite the fact that H₂O is much stronger as a greenhouse gas, should be non-scientific.
We may note, though, that this percentage becomes lower, of the order of 1%, if we also consider the evaporation over oceans. However, it appears reasonable for this estimate of human water emissions to consider only the terrestrial part of Earth, because of the high local variability and the small residence time of atmospheric water. Indeed, the mean residence time of atmospheric water is a few days (specifically, 12 250 km
3 / (522 700 km
3/year) = 0.23 years = 6.6 d, where the total volume of liquid water in the atmosphere, 12 250 km
3, was taken as the average atmospheric water content, 24.0 kg/m
3, as estimated from the ERA5 Reanalysis over the globe for the period 1950-2023, while the atmospheric inflow volume of water, 522 700 km
3/year, was taken from [
22]). In contrast, CO₂ is well mixed as it has a much higher residence time, of a few years (specifically, 870 Gt / (226.9 Gt/year) = 3.8 years, where the total mass of atmospheric CO₂, 870 Gt was taken from the Intergovernmental Panel on Climate Change (IPCC) report [
24], namely its figure 5.12, while the atmospheric inflow mass, 226.9 Gt/year, was taken from [
13]).
The thesis expressed in this paper is that none of these anthropogenic additions to hydrological and carbon cycle drives climate. On the other hand, both H₂O and CO₂ are important elements of climate and their quantities and fluxes are determined by natural processes, with the human factor being rather negligible. Both are elixirs of life and in this respect they act complementary to each other. Thus, it may be pointless to compare them to each other. Yet this comparison is the main focus of this paper, as lately the scientific efforts to study each of them has been inversely proportional to their respective importance.
By its definition by UNESCO [
25], hydrology is the science which deals with the waters of the Earth, and its domain covers the entire history of the cycle of water on the Earth. Water is a critical element of life and of climate as well. While climate has become a hot topic and its research a top priority, it is odd that hydrology has lost importance, as evident from the abundance of papers examining climate change impacts and applying model projections for the future based on CO₂ emission scenarios. This totally misses the fact that water is the dominant element on Earth in driving climate and that the hydrological cycle is self-ruling rather than a feedback or impact of another cycle—namely the carbon cycle, which has also been downgraded to an issue governed by human carbon emissions (the 4% of the total).
By emphasizing the relative importance of water in climate, in comparison to carbon dioxide, this paper tries to show that the picture of Earth’s climatic system may have been distorted, and to give prominence to hydrology (and its branch of hydrometeorology) in climate. The paper is made as a stand-alone and therefore it includes a synopsis of the related theoretical concepts and a model (
Section 2). Its foundation is not only theoretical, but also empirical, utilizing observed data (
Section 3). By combining the model and data, it extracts simple macroscopical empirical relationships representing the greenhouse effect as accurately as the detailed model whose results are based upon (
Section 4). These relationships are tested against observational data (
Section 5) and their simple and analytical expressions, which enable extraction of partial derivatives, allow the comparison of the effect of water relative to other greenhouse gases (
Section 6). The findings are put in a more general context (
Section 7) and allow drawing relevant conclusions (
Section 8).
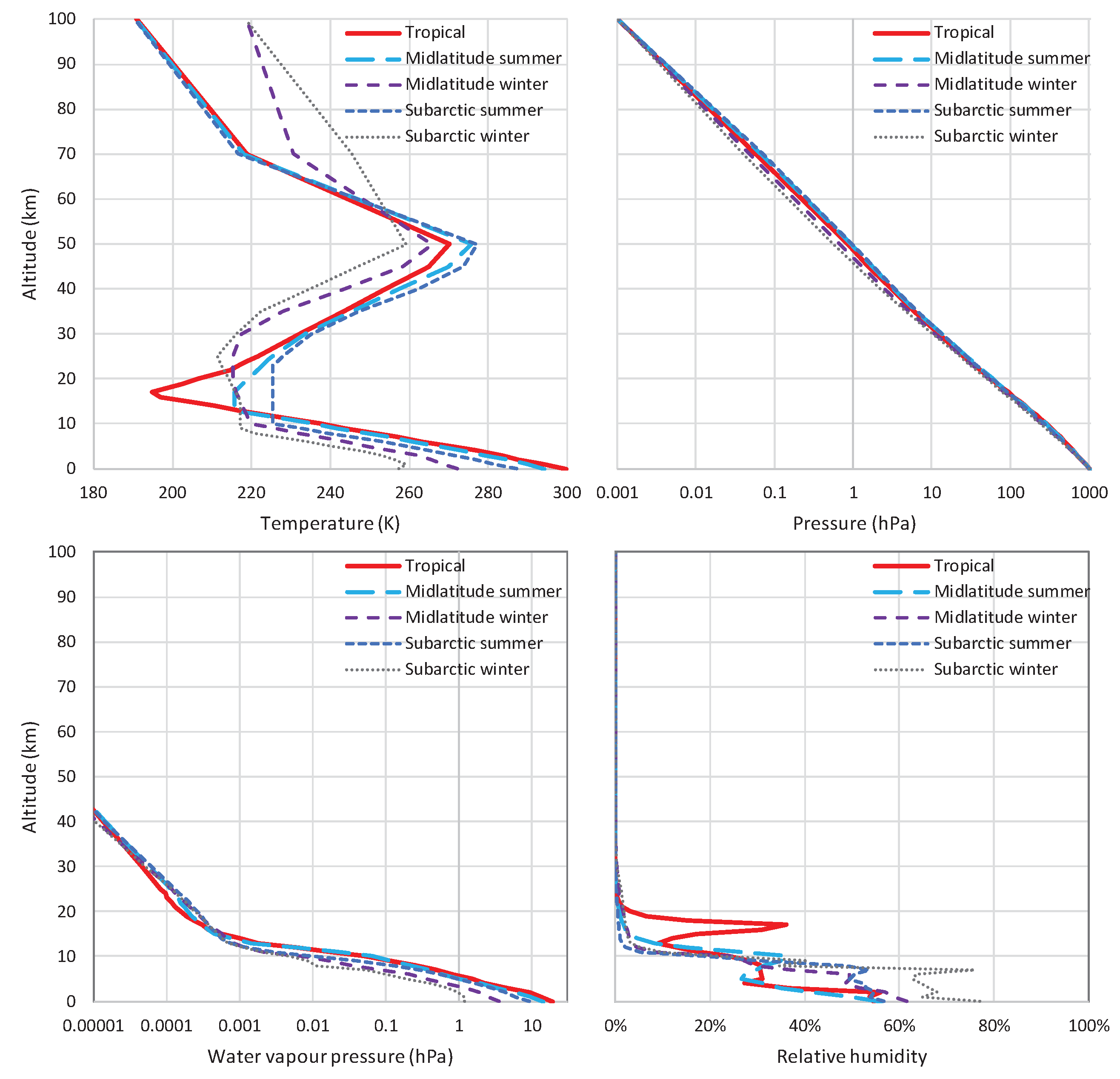
3. Data
To compare MODTRAN results to observed radiation profiles in the atmosphere, we need radiosonde data. While radiosondes are routinely made in several hundreds of sites across the world, they typically measure temperature, humidity, pressure and wind. Radiation radiosonde measurements are rare, yet it is useful to make at least a single comparison to get a general idea. Here we use a couple of radiosondes from a day and a night flight on 23 September 2011, in cloud-free conditions, at the aerological station in Payerne, Switzerland (6.9440° E, 46.8130°, +491 m a.s.l.). In these, in-situ measurements of downward and upward radiation fluxes were taken through the troposphere and into the stratosphere, exceeding 32 km of altitude. They were presented by Philipona et al. [
49] in graphical form in their
Figure 2, which was digitized here to recover the measurements.
For the downwelling LW radiation flux, there have been numerous measurements at specific sites and for a period of more than a century [
18]. These were the basis for the derivation of the empirical or semiempirical formulae for the calculation of the downwelling radiation flux, discussed in
Section 2.2. Considering that these formulae reflect the data that was based upon, here we use the formulae, instead of the data, for comparisons with MODTRAN.
Information for the radiation fluxes at the top of the atmosphere (TOA), including the LW fluxes, are provided by satellite instruments. These are available only for the 21st century from the ongoing project Clouds and the Earth’s Radiant Energy System (CERES), a part of NASA’s Earth Observing System, designed to measure both solar-reflected and Earth-emitted radiation from the TOA (in CERES defined at the altitude of 20 km) to the surface.
The specific product used here is the CERES SSF1deg monthly averaged TOA LW radiative fluxes at a 1°-regional grid, constant-meteorology-temporally-interpolated [
50,
51,
52]. The TOA fluxes are provided for clear-sky and all-sky conditions. Both these observational data are available online [
53] and were retrieved here for their entire time span of complete years, i.e., from January 2001 to December 2022 from the Terra platform. The same CERES product provides information on clouds, which was also retrieved (monthly averaged for both day and night).
In addition, the CERES project provides LW fluxes for the surface, both downwelling and upgoing, through the product CERES_EBAF_Ed4.2, where EBAF stands for “Energy Balanced and Filled” [
54,
55]. However these are computed gridded values rather than observational data. They are publicly available [
56] and were also retrieved here.
The CERES data are associated with considerable uncertainties. According to CERES [
57], the combined regional all-sky LW flux uncertainty is 2.4 W/m² and the daily regional all-sky LW diurnal uncertainty is 8 W/m². According to CERES [
58]; Table 6.1], the uncertainties in the 1°×1° regional monthly TOA fluxes are 4.6 W/m² for clear sky and 2.5 W/m² for all sky. In addition, as also noted in CERES [
58], with the most recent CERES instrument calibration improvements, there still is a net imbalance of ~4.3 W/m², much larger than the expected observed ocean heating rate which CERES assumes to be ~0.71 W/m². It is noted though that, according to the calculations by Koutsoyiannis [
22], the latter imbalance value, again inferred from ocean heating data, is even lower, 0.37 W/m². The EBAF dataset adjusts the observations to remove the above inconsistency. All this information suggests that the observational uncertainties are far too high to allow calculations of Earth’s imbalance and of temporal climatic changes, yet they are quite useful for the scope of this study.
Additional atmospheric variables used here, namely temperature and water vapour pressure, are taken from the ERA5 and NCEP/NCAR Reanalyses at monthly scale. ERA5 stands for the fifth-generation atmospheric reanalysis of the European Centre for Medium-Range Weather Forecasts (ECMWF; ECMWF ReAnalysis). Its data are publicly available for the period 1940 onwards at a spatial resolution of 0.5°. NCEP/NCAR stands for Reanalysis 1 by the National Centers for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR). Its data are publicly available from 1948 to the present at a horizontal resolution of 1.88° (∼ 210 km). Both data sets can be retrieved from the Climexp platform [
59] and from the Physical Sciences Laboratory platform of the US National Oceanic and Atmospheric Administration (NOAA) [
60]. Finally [CO₂] data were retrieved for the most well-known station, Mauna Loa, again from the Climexp platform.
The gridded CERES SSF1deg TOA LW data are presented in
Figure 2, averaged over the period of observations. The cloud information (cloud area fraction) of the same data product is shown in
Figure 3. The zonal distribution of the LW radiation data are shown in
Figure 4, along with that of temperature, and, as expected, the distributions of the two variables are similar.
Figure 5, constructed from the data of
Figure 4 shows that the torrid zone (between 23.4° S and 23.4° N) contributes 43% of Earth’s outgoing LW radiation flux, and together with the two temperate zones (between 23.4° and 66.6° S and N) radiates 94% of the total, leaving only 6% for the frigid zones (between 66.6° and 90° S and N).
Figure 6 better depicts the relationship of outgoing LW radiation flux and surface temperature, for each month of the 22 years of data availability separately, but areally averaged over geographical zones of 15° latitude. This graph allows two important observations. First, the individual monthly values align very well with the average zonal distribution. Second, at the high end of temperature variation, around 300 K, there appears a stagnancy, or even regression of radiation with respect to temperature.
7. Discussion and Further Results
In view of the above results, we may revisit Lacis et al.’s [
17] statements quoted in the Introduction, leaving aside the fact they refer to imaginary-world conditions. Specifically, even if we removed the CO₂ from the atmosphere, again there would be new emissions from volcanos and outgassing from the oceans, even if the biosphere was also removed. In the relatively recent glacial periods, covered by Vostok proxy data, the CO₂ concentration did not fall below 180 ppm. This value is perhaps the absolute low for the entire history of Earth. What would disappear from Earth in the imaginary-world case of CO₂ removal is not the greenhouse effect but life as we know it. For plants may not survive at CO₂ levels below 150 ppm [
71] while without the photosynthesis performed by plants the entire biosphere would collapse. On the opposite side, the increase in CO₂ is beneficial for plant growth. As recently reported and as a result of the recent increase, global greening is an “indisputable fact”, and even its rate has increased slightly [
72].
Furthermore, even the 10% of the current atmospheric value of water vapour for
, given in the quoted statement by Lacis et al., would produce a greenhouse effect and hence would imply the inequality
, thus leading to absurd. That greenhouse effect would not be 10% or close to it, but closer to its current magnitude. Indeed, according to Brutsaert’s equation (13), for
= 255/288 (with 288 K being the current average temperature used by Brutsaert) and vapour pressure ratio
= 0.1, the resulting emissivity ratio
would be (0.1 / (255/288))
1/7 = 0.73. An emissivity
means that we would again have the greenhouse effect produced by water vapour. (See also
Table 5 and its discussion in
Section 6.1.) And even in an “
icebound Earth state”, thermodynamics implies the presence of water vapour in the atmosphere, due to sublimation. Remarkably, though, geological evidence presented by Veizer [
73,
74,
75] suggests the presence of running water as far back as we have a record, up to 3.8 or even 4.2 billion years, despite the much smaller solar irradiance (the faint young sun puzzle). All these imply that the argument is mistaken and so is the popular result that is being widely reproduced.
The distinction between feedbacks and forcings, also appearing in the quoted statements by Lacis et al. (and the bot), is problematic. Both H₂O and CO₂ are “native” and abundant on Earth, and both are greenhouse gases, with the difference being that the former is the determinant, as already demonstrated. Calling CO₂ forcing and H₂O feedback is like claiming that the tail wags the dog.
Water has more roles in climate than examined above. The greenhouse effect slows down the rate of Earth’s cooling by LW radiation. However, Earth’s surface cooling and its reaction, i.e., atmosphere’s warming, is not only due to LW radiation. According to Trenberth et al. [
76], the contribution of the LW radiation is 396 – 333 = 63 W/m
2, a value generally consistent with the results of this paper. This low value is due to the action of greenhouse gases, and, as we have seen, it is dominated by the presence of water vapour in the atmosphere. However, the greatest contribution in Earth’s surface cooling, namely 80 W/m
2 [
10,
76], is due to the latent heat from evaporation (phase change of water from liquid to gaseous phase).
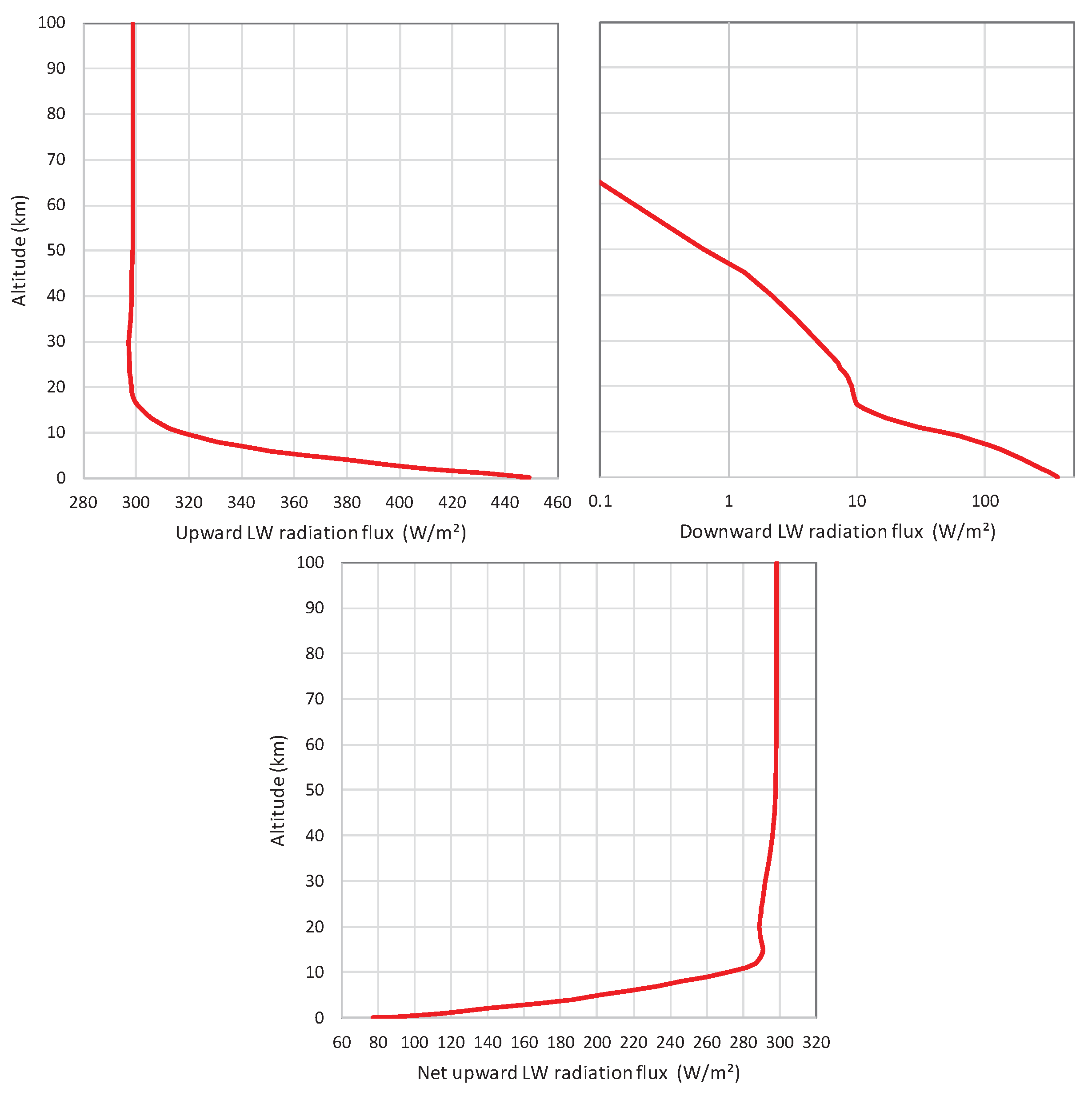
Surface cooling and atmosphere warming are reflected in the vertical profile of the net upgoing radiation flux, seen in
Figure 25. Here the SW radiation was also considered, calculated by RRTM. The net radiation minus the absorbed SW radiation in the atmosphere is increasing with altitude. As, on the long term, the energy is not stored in the atmosphere, the total heat transfer should be the same at all altitudes. The deficit of heat transfer in low altitudes is recovered by sensible and latent heat transfer, which warm the atmosphere.
Figure 26 shows diagrammatically the contribution of each of these mechanisms to Earth’s cooling and atmosphere’s warming.
Figure 25.
(
left) Vertical profile of net LW radiation flux for default conditions and standard tropical atmospheric profile (
T = 299.7 K; [CO₂] = 400 ppm;
= 369.26 W/m²;
= 298.49 W/m²), as calculated by MODTRAN, and its difference from the net SW profile, as calculated by the RRTM Earth's Energy Budget (
https://climatemodels.uchicago.edu/rrtm/). (
right) MODTRAN’s standard tropical atmospheric profile of temperature, compared with the dry adiabatic profile (with a gradient of 9.8 K/km); the arrows indicated the heating of the atmosphere due to the latent heat released by condensation of water vapour, accumulated over elevation.
Figure 25.
(
left) Vertical profile of net LW radiation flux for default conditions and standard tropical atmospheric profile (
T = 299.7 K; [CO₂] = 400 ppm;
= 369.26 W/m²;
= 298.49 W/m²), as calculated by MODTRAN, and its difference from the net SW profile, as calculated by the RRTM Earth's Energy Budget (
https://climatemodels.uchicago.edu/rrtm/). (
right) MODTRAN’s standard tropical atmospheric profile of temperature, compared with the dry adiabatic profile (with a gradient of 9.8 K/km); the arrows indicated the heating of the atmosphere due to the latent heat released by condensation of water vapour, accumulated over elevation.
Interestingly, heat exchange by evaporation (and hence the latent heat transfer from the Earth’s surface to the atmosphere) is the Earth’s natural locomotive, with the total energy involved in the hydrological cycle being 1290 ZJ/year, corresponding to an energy flux density of 80 W/m
2. Compared to human energy production, the total energy of the natural locomotive is 2100 times higher than that of the human locomotive [
10].
In addition to regulating the LW radiation flux and the latent heat flux, water vapour and clouds also regulate the SW radiation and Earth’s albedo. Other properties of water, as listed in Koutsoyiannis [
10], are also determinant for climate. First is its unique property to appear on Earth in
all three phases and in different formations, with spectacular differences among them in properties related to climate. Remarkable is its
abundance on Earth, as only the part that is in turbulent motion amounts to 1.34 × 10
9 Gt (not counting quantities that are stored in the soil, ground and glaciers), 260 times larger than the total mass of the atmosphere. The
turbulent motion of water, which is intrinsically uncertain, generates climatic phenomena at all scales, from large-scale coupled ocean–atmosphere fluctuations, such as the El Niño–Southern Oscillation (ENSO), Atlantic Multidecadal Oscillation (AMO) and Interdecadal Pacific Oscillation (IPO), to regional droughts and floods. The high specific heat (or
heat capacity) of water, particularly in its liquid phase, combined with its abundance, makes water the climatic thermostat of the Earth, i.e., the element that determines the heat storage and through it the climate of the Earth. The high
specific latent heat of vaporization (calculated from Equation (6)) combined with the water occurrence on Earth in all three phases, makes water the thermodynamic regulator of climate. Finally, the fact that water is a universal solvent makes it an
elixir of life, complementary to the CO₂ which is the other elixir of life, as through the photosynthesis it is responsible for the organic matter on which life on Earth is based.
Thus, the biosphere strongly depends on both CO₂ and H₂O. In particular, the presence of water determines the type and extent of ecosystems. In turn, the ecosystems affect climate at large through the carbon and oxygen cycles (where the vast majority of the CO₂ and O₂ emissions are products of life, through respiration and photosynthesis, respectively), and their contribution in the water cycle (transpiration) and in the energy cycle (photosynthesis). Humans, as part of the biosphere, also interact with water and climate, affecting them and being affected by them. Excluding human influences, the processes of the biosphere determine the vast majority (96%) of CO₂ emissions and partly, in the terrestrial part, the emission of H₂O by the transpiration process. And as Koutsoyiannis et al. [
12,
13] have shown, it is the relationship between temperature and biosphere that has determined the recent increase in the atmospheric [CO₂].
Considering all these facts, it is stunning that the whole “climate project”, including climate modelling, is based on hypotheses and scenarios about human CO₂ emissions.
Figure 1.
Output of the MODTRAN model for the standard tropical atmospheric profile, in comparison to the case that the standard [CO₂] of 400 ppm is replaced by that of 800 ppm. The outgoing radiation corresponds to the level of 100 km above the ground. The ground temperature is 299.7 K (26.55 °C) and the total outgoing LW flux is 298.52 W/m² for [CO₂] = 400 ppm and 295.129 W/m² for [CO₂] = 800 ppm (difference –3.36 W/m²). Graph generated from
https://climatemodels.uchicago.edu/modtran/.
Figure 1.
Output of the MODTRAN model for the standard tropical atmospheric profile, in comparison to the case that the standard [CO₂] of 400 ppm is replaced by that of 800 ppm. The outgoing radiation corresponds to the level of 100 km above the ground. The ground temperature is 299.7 K (26.55 °C) and the total outgoing LW flux is 298.52 W/m² for [CO₂] = 400 ppm and 295.129 W/m² for [CO₂] = 800 ppm (difference –3.36 W/m²). Graph generated from
https://climatemodels.uchicago.edu/modtran/.
Figure 3.
Geographical distribution of cloud area fraction averaged over the period of 2000 – 2022 as given by the CERES data. Data source and graph generation as in
Figure 2.
Figure 3.
Geographical distribution of cloud area fraction averaged over the period of 2000 – 2022 as given by the CERES data. Data source and graph generation as in
Figure 2.
Figure 5.
Graphical depictions of the relative intensity of outgoing LW radiation averaged over the period of 2000 – 2022 as given by the CERES data, as a function of the latitude; (left) ratio of intensity at latitude φ (S or N) to that at the equator; (right) cumulative flux between latitudes φ S and φ N to the total outgoing radiation.
Figure 5.
Graphical depictions of the relative intensity of outgoing LW radiation averaged over the period of 2000 – 2022 as given by the CERES data, as a function of the latitude; (left) ratio of intensity at latitude φ (S or N) to that at the equator; (right) cumulative flux between latitudes φ S and φ N to the total outgoing radiation.
Figure 6.
Depiction of monthly variability of outgoing LW radiation, as given by the CERES data; each point is the monthly value, spatially averaged over a geographical zone of 15° latitude, during the period of 2000 – 2022; the zonal distributions (temporal averages for the entire period as in
Figure 4) are also shown for each hemisphere (SH and NH).
Figure 6.
Depiction of monthly variability of outgoing LW radiation, as given by the CERES data; each point is the monthly value, spatially averaged over a geographical zone of 15° latitude, during the period of 2000 – 2022; the zonal distributions (temporal averages for the entire period as in
Figure 4) are also shown for each hemisphere (SH and NH).
Figure 7.
Changes in the downwelling LW radiation, , as calculated by MODTRAN, due to changes in temperature (converted to blackbody radiation, ), and (upper) water vapour pressure () and (lower) carbon dioxide concentration ([CO₂]). The calculations were made for the tropical profile, no clouds and default other settings. For the upper graph it was assumed [CO₂] = 400 ppm and for the lower graph = 19 hPa. Notice that the scale of the vertical axis is linear in the upper graph (with range ±10% of the central value) and logarithmic in the lower graph (with range from half to twice the central value).
Figure 7.
Changes in the downwelling LW radiation, , as calculated by MODTRAN, due to changes in temperature (converted to blackbody radiation, ), and (upper) water vapour pressure () and (lower) carbon dioxide concentration ([CO₂]). The calculations were made for the tropical profile, no clouds and default other settings. For the upper graph it was assumed [CO₂] = 400 ppm and for the lower graph = 19 hPa. Notice that the scale of the vertical axis is linear in the upper graph (with range ±10% of the central value) and logarithmic in the lower graph (with range from half to twice the central value).
Figure 8.
As in
Figure 7 but for the outgoing LW radiation,
.
Figure 8.
As in
Figure 7 but for the outgoing LW radiation,
.
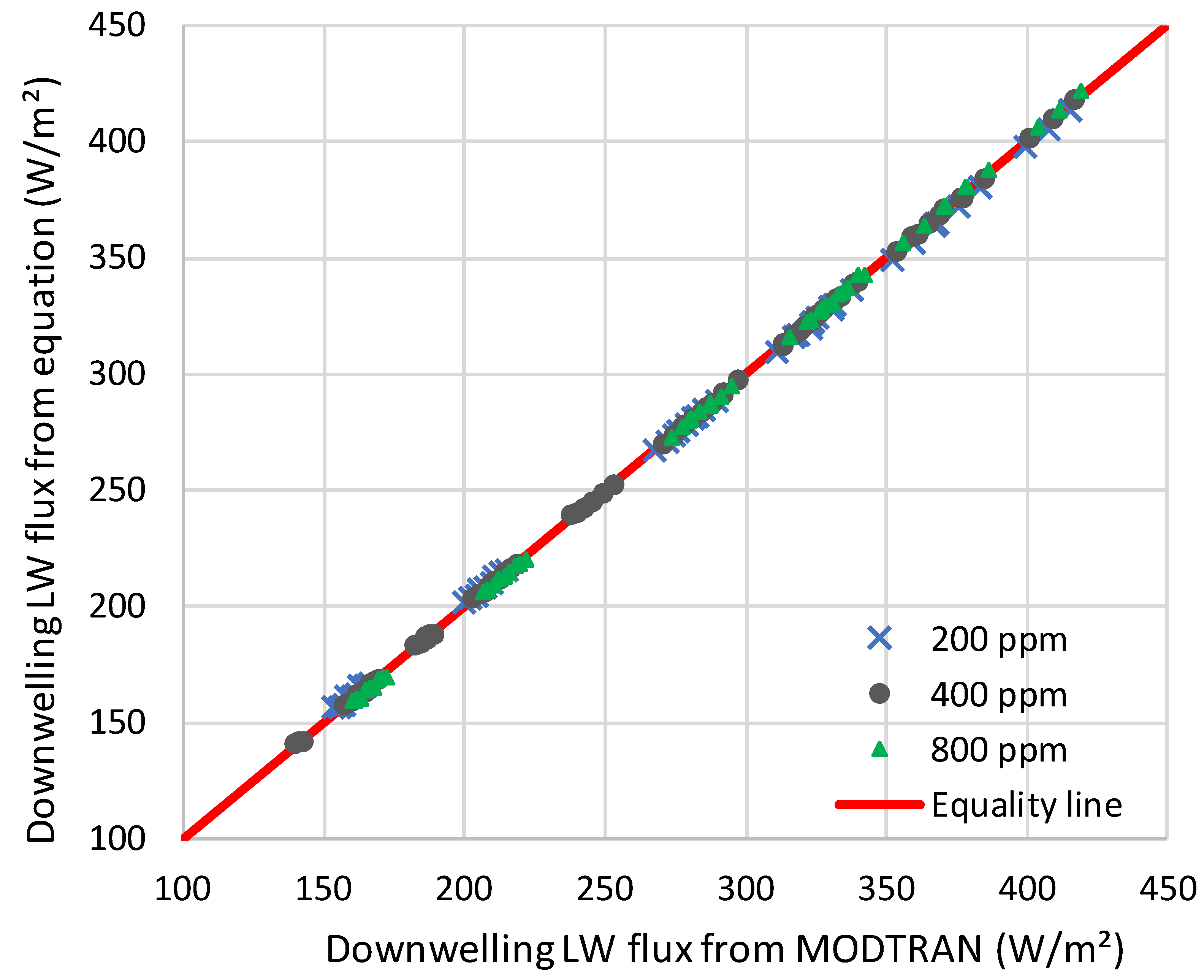
Figure 9.
Comparison of downwelling LW radiation flux, , as computed by MODTRAN and by Equation (21).
Figure 9.
Comparison of downwelling LW radiation flux, , as computed by MODTRAN and by Equation (21).
Figure 10.
Comparison of outgoing LW radiation flux, , as computed by MODTRAN and by Equation (21).
Figure 10.
Comparison of outgoing LW radiation flux, , as computed by MODTRAN and by Equation (21).
Figure 11.
Comparison of outgoing LW radiation flux, , as computed by MODTRAN and by Equation (22), based on the downwelling flux, .
Figure 11.
Comparison of outgoing LW radiation flux, , as computed by MODTRAN and by Equation (22), based on the downwelling flux, .
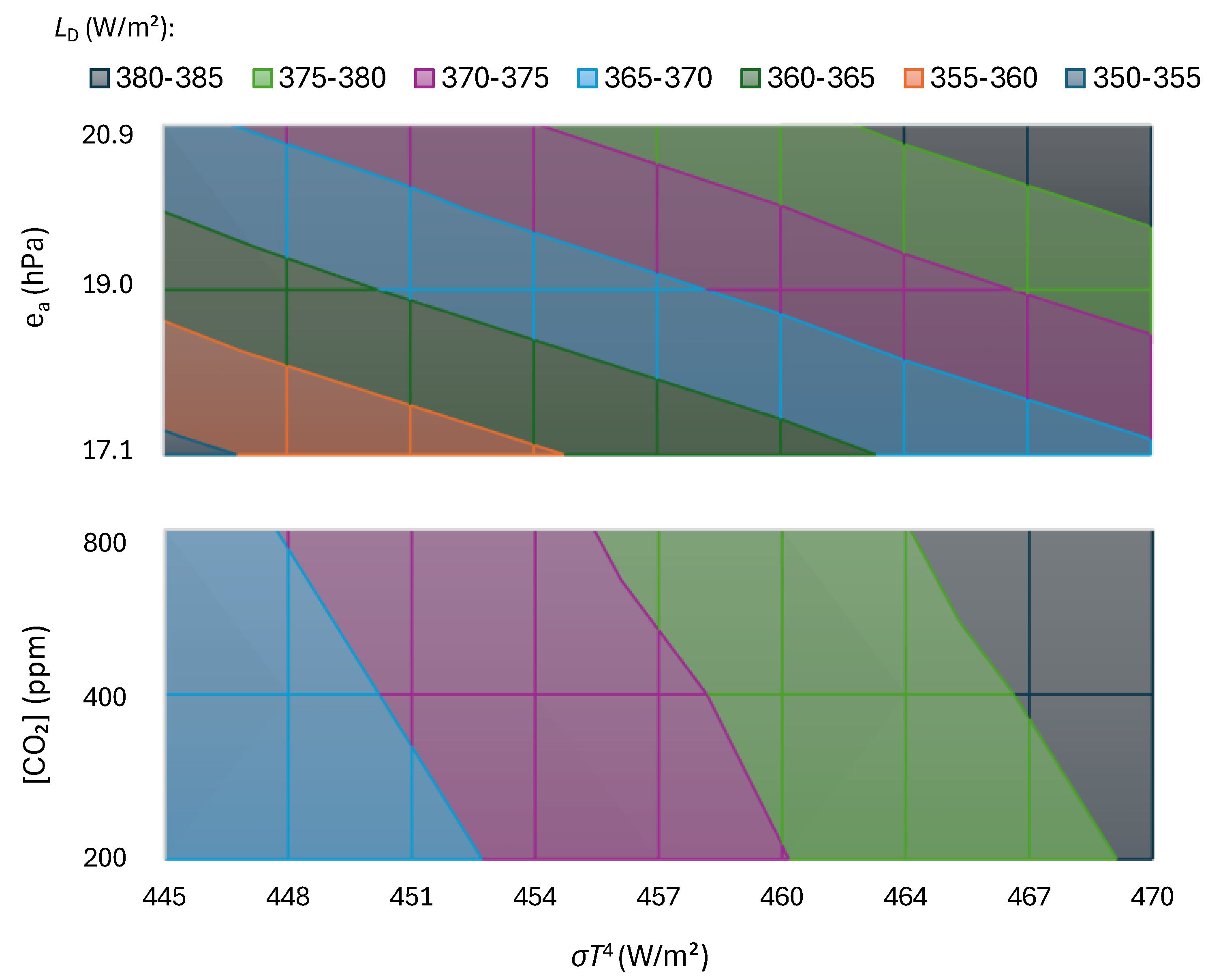
Figure 12.
Comparison of outgoing LW radiation flux,
, as computed from MODTRAN and from Equation (21), fitted only for the tropical profile and for
T = 299.7 ± 2 K,
= 19 ± 1.9 hPa, and [CO₂] range of 200 – 800 ppm. The parameters of Equation (21) were reoptimized for these ranges, and the values
= 56.2 K and
0.00683 hPa were found, while all others remained the same as in
Table 1. The case of cumulus clouds is also plotted in the graph, with abscissae as derived by MODTRAN and ordinates equal to the values of Equation (21) for clear sky multiplied by 0.904.
Figure 12.
Comparison of outgoing LW radiation flux,
, as computed from MODTRAN and from Equation (21), fitted only for the tropical profile and for
T = 299.7 ± 2 K,
= 19 ± 1.9 hPa, and [CO₂] range of 200 – 800 ppm. The parameters of Equation (21) were reoptimized for these ranges, and the values
= 56.2 K and
0.00683 hPa were found, while all others remained the same as in
Table 1. The case of cumulus clouds is also plotted in the graph, with abscissae as derived by MODTRAN and ordinates equal to the values of Equation (21) for clear sky multiplied by 0.904.
Figure 13.
Effect of clouds to outgoing radiation, expressed as
, i.e. the deviation from 1 of the ratio of longwave radiation for all sky (
) to that for clear sky (
), vs. the cloud fraction,
C. The slopes of homogenous linear regressions,
are also shown. Each plotted point corresponds to one of the 64 800 grid points of the CERES grids of clear-sky and all-sky radiation (
Figure 2), and cloud area fraction (
Figure 3), where the average over the period 2001-2022 was taken.
Figure 13.
Effect of clouds to outgoing radiation, expressed as
, i.e. the deviation from 1 of the ratio of longwave radiation for all sky (
) to that for clear sky (
), vs. the cloud fraction,
C. The slopes of homogenous linear regressions,
are also shown. Each plotted point corresponds to one of the 64 800 grid points of the CERES grids of clear-sky and all-sky radiation (
Figure 2), and cloud area fraction (
Figure 3), where the average over the period 2001-2022 was taken.
Figure 14.
Comparison of LW radiation components calculated by MODTRAN to radiosonde measurements by Philipona et al. [
49].
Figure 14.
Comparison of LW radiation components calculated by MODTRAN to radiosonde measurements by Philipona et al. [
49].
Figure 15.
Comparison of emissivity calculated by MODTRAN to that calculated by Equation (21).
Figure 15.
Comparison of emissivity calculated by MODTRAN to that calculated by Equation (21).
Figure 16.
Comparison of emissivity calculated by MODTRAN to that calculated by each of the indicated formulae; the explained variance (EV) is also shown for each case.
Figure 16.
Comparison of emissivity calculated by MODTRAN to that calculated by each of the indicated formulae; the explained variance (EV) is also shown for each case.
Figure 17.
Downwelling LW radiation flux vs. temperature, as calculated by MODTRAN for the five indicated locality profiles and default settings (points with crosses) as well as with temperature offsets from the default values of up to ±25 K (all other points), in comparison to the CERES EBAF zonal distribution shown in
Figure 4.
Figure 17.
Downwelling LW radiation flux vs. temperature, as calculated by MODTRAN for the five indicated locality profiles and default settings (points with crosses) as well as with temperature offsets from the default values of up to ±25 K (all other points), in comparison to the CERES EBAF zonal distribution shown in
Figure 4.
Figure 18.
Outgoing LW radiation flux vs. temperature, as calculated by MODTRAN for the five indicated locality profiles and default settings (points with crosses) as well as with temperature departing from the default values by up to ±25 K (all other points), in comparison to the observed zonal distribution (CERES SSF1) as shown in
Figure 4 and
Figure 6.
Figure 18.
Outgoing LW radiation flux vs. temperature, as calculated by MODTRAN for the five indicated locality profiles and default settings (points with crosses) as well as with temperature departing from the default values by up to ±25 K (all other points), in comparison to the observed zonal distribution (CERES SSF1) as shown in
Figure 4 and
Figure 6.
Figure 19.
Time series of the indicated variables, averaged over the torrid zone. The values plotted are monthly averages, while the 11-year averages are also plotted in thicker lines.
Figure 19.
Time series of the indicated variables, averaged over the torrid zone. The values plotted are monthly averages, while the 11-year averages are also plotted in thicker lines.
Figure 20.
(upper) Time series of outgoing clear-sky LW radiation flux, averaged over the torrid zone, as given by CERES data and as predicted by Equation (21) with temperature, water vapour and [CO₂] data from the ERA5 and NCEP/NCAR Reanalyses. (lower) Time series outgoing all-sky LW radiation flux, averaged over the torrid zone, as given by CERES data and as predicted by the CERES clear-sky data and Equation (21) with CERES cloud area fraction. The values plotted are monthly averages, while the 11-year averages are also plotted in thicker lines.
Figure 20.
(upper) Time series of outgoing clear-sky LW radiation flux, averaged over the torrid zone, as given by CERES data and as predicted by Equation (21) with temperature, water vapour and [CO₂] data from the ERA5 and NCEP/NCAR Reanalyses. (lower) Time series outgoing all-sky LW radiation flux, averaged over the torrid zone, as given by CERES data and as predicted by the CERES clear-sky data and Equation (21) with CERES cloud area fraction. The values plotted are monthly averages, while the 11-year averages are also plotted in thicker lines.
Figure 21.
Output of the MODTRAN model, with the red curves in both panels produced for default settings (for the standard tropical atmospheric profile; T = 299.7 K; [CO₂] = 400 ppm; = 298.49 W/m²), and the blue curves produced for zero concentrations of all greenhouse gases except water vapour, assuming constant relative humidity and conditions such as to much the total outgoing LW flux of the red curves, namely: (left) temperature lower than default by 15 K (T = 284.7 K); (right) temperature equal to the default (T = 299.7 K) but water vapour scale increased to 1.3, accompanied by cumulus clouds.
Figure 21.
Output of the MODTRAN model, with the red curves in both panels produced for default settings (for the standard tropical atmospheric profile; T = 299.7 K; [CO₂] = 400 ppm; = 298.49 W/m²), and the blue curves produced for zero concentrations of all greenhouse gases except water vapour, assuming constant relative humidity and conditions such as to much the total outgoing LW flux of the red curves, namely: (left) temperature lower than default by 15 K (T = 284.7 K); (right) temperature equal to the default (T = 299.7 K) but water vapour scale increased to 1.3, accompanied by cumulus clouds.
Figure 22.
Difference of LW radiation flux from the values at the default settings of the standard tropical atmospheric profile (T = 299.7 K; [CO₂] = 400 ppm; = 369.26 W/m²; = 298.49 W/m²), as calculated by MODTRAN for the cases of (left) zero concentrations of all greenhouse gases except water vapour, assuming constant relative humidity and (right) as left but with [CO₂] = 200 ppm.
Figure 22.
Difference of LW radiation flux from the values at the default settings of the standard tropical atmospheric profile (T = 299.7 K; [CO₂] = 400 ppm; = 369.26 W/m²; = 298.49 W/m²), as calculated by MODTRAN for the cases of (left) zero concentrations of all greenhouse gases except water vapour, assuming constant relative humidity and (right) as left but with [CO₂] = 200 ppm.
Figure 23.
Difference of LW radiation flux for the indicated conditions of [CO₂] from the respective values at the default settings of the standard tropical atmospheric profile (T = 299.7 K; [CO₂] = 400 ppm; = 369.26 W/m²; = 298.49 W/m²), as calculated by MODTRAN.
Figure 23.
Difference of LW radiation flux for the indicated conditions of [CO₂] from the respective values at the default settings of the standard tropical atmospheric profile (T = 299.7 K; [CO₂] = 400 ppm; = 369.26 W/m²; = 298.49 W/m²), as calculated by MODTRAN.
Figure 24.
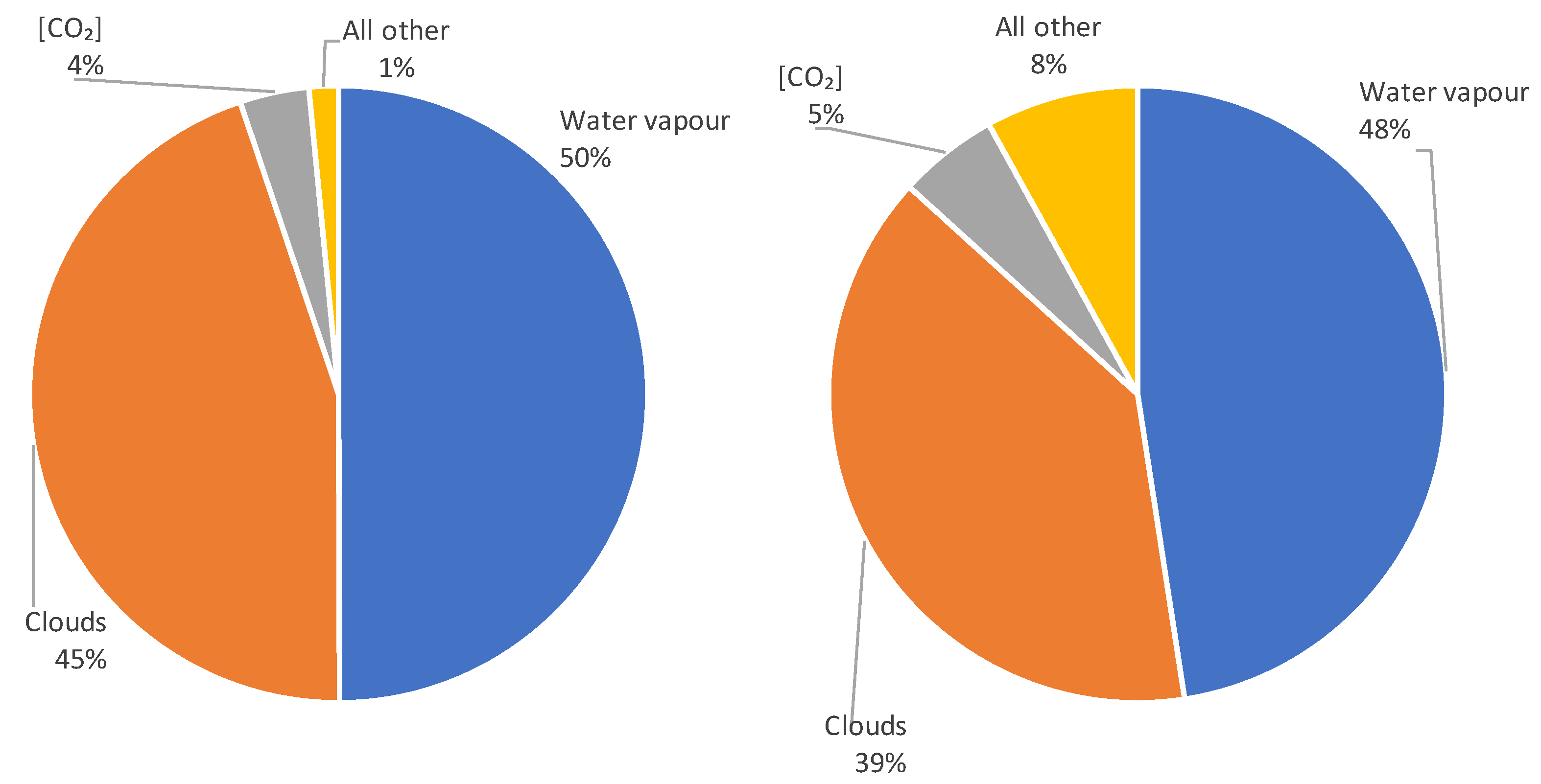
Contribution of the greenhouse drivers to the LW radiation fluxes, (left) downwelling and (right) outgoing.
Figure 24.
Contribution of the greenhouse drivers to the LW radiation fluxes, (left) downwelling and (right) outgoing.
Figure 26.
Contribution of (
left) the three mechanisms responsible for the cooling of Earth’s surface and (
right) the four mechanisms responsible for the warming of Earth’s atmosphere, based on the energy balance by Trenberth et al. [
76].
Figure 26.
Contribution of (
left) the three mechanisms responsible for the cooling of Earth’s surface and (
right) the four mechanisms responsible for the warming of Earth’s atmosphere, based on the energy balance by Trenberth et al. [
76].
Table 1.
Fitted parameters of Equation (21) for ranges of temperature 247.2 – 309.7 K (–26.0 – 36.6 °C), water vapour pressure 1.08 – 20.9 hPa and CO₂ concentration 200 – 800 ppm.
Table 1.
Fitted parameters of Equation (21) for ranges of temperature 247.2 – 309.7 K (–26.0 – 36.6 °C), water vapour pressure 1.08 – 20.9 hPa and CO₂ concentration 200 – 800 ppm.
| |
Sign†
|
(W/m²) |
(K) |
(hPa) |
(ppm)‡ |
|
|
|
§
|
|
+ |
27 |
181 |
6.36 |
400 |
4.5 |
1 |
0.015 |
0.34 |
|
– |
1 |
55 |
0.00302 |
400 |
3.5 |
0.5 |
0.015 |
0.15 |
Table 2.
Performance indices of Equations (21) (with parameters as in
Table 1) and (22), fitted for ranges of temperature 247.2 – 309.7 K (–26.0 – 36.6 °C), water vapour pressure 1.08 – 20.9 hPa and CO₂ concentration 200 – 800 ppm, and clear sky.
Table 2.
Performance indices of Equations (21) (with parameters as in
Table 1) and (22), fitted for ranges of temperature 247.2 – 309.7 K (–26.0 – 36.6 °C), water vapour pressure 1.08 – 20.9 hPa and CO₂ concentration 200 – 800 ppm, and clear sky.
| Equation, variable |
(W/m2) |
(W/m2) |
(%) |
(%) |
(%) |
|
140.0 – 419.5 |
1.3 |
99.97 |
0.5 |
1.9 |
|
170.6 – 351.1 |
1.3 |
99.79 |
0.7 |
1.9 |
| (22) |
170.6 – 351.1 |
3.6 |
99.24 |
1.5 |
4.5 |
Table 3.
Ratios of outgoing LW radiation under cloudy sky to that for clear sky, for the indicated types of clouds and locality profiles, as determined by MODTRAN for default settings (the lowest value is highlighted in bold).
Table 3.
Ratios of outgoing LW radiation under cloudy sky to that for clear sky, for the indicated types of clouds and locality profiles, as determined by MODTRAN for default settings (the lowest value is highlighted in bold).
Locality profile
→
Cloud type ↓ |
Tropical |
Midlatitude summer |
Subarctic summer |
Midlatitude winter |
Subarctic winter |
| Cumulus |
0.904 |
0.899 |
0.889 |
0.910 |
0.95 |
| Altostratus |
0.901 |
0.896 |
0.887 |
0.907 |
0.948 |
| Stratus |
0.966 |
0.973 |
0.962 |
0.973 |
1.016 |
| Stratus/Stratocumulus |
0.939 |
0.945 |
0.931 |
0.950 |
0.989 |
| Nimbostratus |
0.98 |
0.984 |
0.977 |
0.984 |
1.024 |
| Standard Cirrus |
0.93 |
0.939 |
0.957 |
0.95 |
0.974 |
| NOAA Cirrus |
0.937 |
0.945 |
0.963 |
0.956 |
0.98 |
Table 4.
Comparison of observed data and MODTRAN results for the average conditions of each of the indicated two periods. The observed data are global averages. The MODTRAN results are for the average observed temperature and [CO₂] of each period, and for the same water vapour scales in the two periods, estimated so as to (approximately) match the outgoing clear-sky LW flux of CERES for the first period, while holding fixed relative humidity for the two periods.
Table 4.
Comparison of observed data and MODTRAN results for the average conditions of each of the indicated two periods. The observed data are global averages. The MODTRAN results are for the average observed temperature and [CO₂] of each period, and for the same water vapour scales in the two periods, estimated so as to (approximately) match the outgoing clear-sky LW flux of CERES for the first period, while holding fixed relative humidity for the two periods.
| Period → |
2001-11 |
2012-22 |
Difference |
| Observations (averages over each period) |
|
|
|
| Temperature from ERA5 (K) |
287.21 |
287.49 |
+0.28 |
| [CO₂] from Mauna Loa (ppm) |
381.83 |
406.48 |
+24.65 |
| Outgoing TOA (20 km) clear-sky LW from CERES (W/m2) |
268.33 |
268.27 |
–0.08 |
|
Outgoing clear-sky LW radiation by MODTRAN at 20 km altitude (W/m2) |
|
|
| Tropical profile, water vapour scale 0.82 |
268.34 |
268.72 |
+0.38 |
| Midlatitude summer profile, water vapour scale 1.08 |
268.34 |
268.78 |
+0.44 |
| Midlatitude winter profile, water vapour scale 1.14 |
268.28 |
268.78 |
+0.50 |
| Subarctic summer profile, water vapour scale 2.56 |
268.31 |
268.91 |
+0.60 |
Table 5.
Results of MODTRAN calculations for temperature of 288 K (the value of current global temperature used by Brutsaert [
32] and tropical profile and extreme (imaginary-world) cases of greenhouse gas concentrations.
Table 5.
Results of MODTRAN calculations for temperature of 288 K (the value of current global temperature used by Brutsaert [
32] and tropical profile and extreme (imaginary-world) cases of greenhouse gas concentrations.
| [CO₂] relative to the default value of 400 ppm |
Water vapour scale relative to the default tropical profile |
Other greenhouse gases concentration relative to default |
Downward IR heat flux at surface (W/m²) |
Upward IR heat flux at surface (W/m²) |
Outgoing LW radiation flux at 100 km altitude (W/m²) |
| 1 |
1 |
1 |
325.6 |
381.5 |
249.5 |
| 1 |
1 |
0 |
324.0 |
381.5 |
256.7 |
| 0 |
0 |
0 |
1.7 |
380.3 |
379.0 |
| 1 |
0 |
0 |
68.2 |
380.3 |
340.7 |
| 2500*
|
0 |
0 |
215.7 |
381.5 |
257.1 |
| 0 |
0.0015 |
0 |
78.8 |
380.3 |
366.4 |
| 0 |
0.04 |
0 |
157.8 |
380.6 |
340.7 |
| 0 |
0.2 |
0 |
212.5 |
380.9 |
319.3 |
| 0 |
1 |
0 |
319.7 |
381.5 |
284.7 |
| 0 |
2.2 |
0 |
372.1 |
381.8 |
257.7 |
Table 6.
Relative changes of LW radiation fluxes at standard conditions, equal to the global averages, T = 288.6 K, = 15.2 hPa, = 400 ppm, C = 0.671, as calculated analytically and numerically by Equation (21).
Table 6.
Relative changes of LW radiation fluxes at standard conditions, equal to the global averages, T = 288.6 K, = 15.2 hPa, = 400 ppm, C = 0.671, as calculated analytically and numerically by Equation (21).
| Case of relative change |
Relative change expression |
Numerical value of relative change |
| Downwelling flux |
Outgoing flux |
|
|
3.18 |
4.44 |
|
|
0.207 |
–0.136 |
|
|
0.015 |
–0.015 |
|
|
0.186 |
–0.112 |
|
(see text) |
0.006 |
–0.023 |
Table 7.
Relative changes of LW radiation fluxes at standard conditions, equal to the global averages, T = 288.6 K, = 15.2 hPa, C = 0.671 (or C = 0 for clear sky), and with the indicated values of [CO₂] as calculated analytically and numerically by Equation (21). In parentheses are the values directly calculated by MODTRAN assuming midlatitude summer profile matching the above values of T and , and altostratus clouds for the cloudy case.
Table 7.
Relative changes of LW radiation fluxes at standard conditions, equal to the global averages, T = 288.6 K, = 15.2 hPa, C = 0.671 (or C = 0 for clear sky), and with the indicated values of [CO₂] as calculated analytically and numerically by Equation (21). In parentheses are the values directly calculated by MODTRAN assuming midlatitude summer profile matching the above values of T and , and altostratus clouds for the cloudy case.
| [CO₂] increase |
Sky |
|
|
|
mean* |
% change |
|
mean* |
% change |
| From 300 to 420 |
Cloudy |
1.93
(0.31) |
382.4
(374.1) |
0.5%
(0.1%) |
–1.18
(–1.00) |
235.1
(238.0) |
–0.5%
(–0.4%) |
| From 300 to 420 |
Clear |
1.57
(0.79) |
311.3
(309.6) |
0.4%
(0.3%) |
–1.32
(–1.32) |
261.5
(265.7) |
–0.5%
(–0.5%) |
| From 300 to 800 |
Cloudy |
5.63
(0.63) |
384.2
(374.3) |
1.5%
(0.2%) |
–3.45
(–2.89) |
234.0
(237.0) |
–1.5%
(–1.2%) |
| From 300 to 800 |
Clear |
4.59
(2.45) |
312.8
(310.5) |
1.2%
(0.8%) |
–3.84
(–3.89) |
260.2
(264.4) |
–1.5%
(–1.5%) |