Prerpints.org logo
Preprint
Article

Spatial Distribution Mechanism of Soil Water-Salt Coupling Effect in Arid Saline-Alkali Farmland

Altmetrics

Downloads

91

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

05 April 2024

Posted:

05 April 2024

You are already at the latest version

Alerts
Abstract
Revealing the spatial distribution mechanism of the coupling effect between soil water and salt is essential for managing saline-alkali farmland. This study utilized the multifractal method to analyze soil water and salt under varying water content levels in arid saline-alkali farmland. Soil samples were collected on the second (S1), fifth (S2), eighth (S3), eleventh (S4), and fourteenth (S5) days after a rainfall event. The findings showed that a significant decrease in soil water content, contrasting with an increase in soil salt content throughout the soil layers post-rainfall. As water content decreased, the spatial variability of soil water initially increased from S1-3 and then decreased, while the spatial variability of soil salt decreased. The spatial distribution between soil water and salt exhibited a high correlation at S3-4 (with relative water content of soil ranging from 0.52 to 0.75) due to their coupling effect. However, soil salt was unevenly leached by rainfall at high water content levels (S1-2) and precipitated at low water content levels (S5), resulting in low spatial variability correlations between soil water and salt. This study elucidated the coupling process of soil water and salt, identifying their spatiotemporal distribution mechanism in dryland agricultural areas.
Keywords: 
Subject: Environmental and Earth Sciences  -   Soil Science

1. Introduction

Soil salinization is a significant factor contributing to land desertification and degradation on a global scale [1]. This issue not only leads to the depletion of resources and substantial losses in agricultural output but also presents a threat to the biosphere and ecological systems. The impact of soil salinization extends to human survival, social stability, agricultural productivity, natural resources, and the pursuit of environmentally sustainable development [2,3,4]. The total area of saline-alkali land worldwide is approximately 9.3×108 ha, and the area of secondary soil salinization in arid and semi-arid areas is approximately 8×107 ha [5,6]. Soil salinization is caused by the movement of soil water and salt. Over time, soil water and salt show varying spatial distribution patterns [7]. Understanding the spatiotemporal distribution of soil water and salt is crucial for managing and preventing soil salinization [8].
Soil water plays a crucial role in the transport of salt, as the leaching and accumulation of soil salt depend on the presence of water [9,10]. When salt dissolves in liquid water, the relative humidity of pores decreases and the volume of pores also decreases, impacting soil water transport [11]. Walter et al. [12] showed that a close correlation is observed between soil water and salt. The soil salt distribution between top and subsoil reflected the leaching of dissolved salt by soil water and the capillary rise of dissolved soil salt by increasing evaporation. Cao et al. [13] reported that soil water and salt both revealed “island” distribution and they presented a strong or moderate spatial dependency in a semi-arid saline environment. These results indicated that spatial distributions of soil water and salt may affect by their coupling. Therefore, we assumed that the spatial variability between soil water and salt were correlative. In addition, Yuan et al. [14] and Dong et al. [15] also showed that soil salt accumulation exhibited differences in soil layer under varying irrigation amounts. Ren et al. [7]) reported that soil salt distribution was dominated by quantities, and the uniformity of field irrigation at the field scale. These results implied that spatial distribution of soil salt may be affected by different soil water content levels. Therefore, it is necessary to determine the spatial distribution of soil water and salt at different water content levels.
The spatial variability of variables has always been a primary focus for scholars, and the topic can be explained by various methods [16–18]. Teng et al. [19] and Wang et al. [20] showed that the spatial distribution characteristics of soil organic carbon were described thoroughly by the semi-variance function and Kriging method. Vidana Gamage et al. [21] also achieved useful results in their study of spatial and temporal variation of soil properties using geostatistics. These methods showed good results in spatial variability analysis. The multifractal method is a powerful method used to characterize variability across scales, and is widely used in determining spatial patterns and variability of soil properties [18,22]. Qi et al. [23] used the multifractal method to study soil particle size distribution and showed that the differences between different vegetation types were quantitatively characterized by multifractal parameters. Jing et al. [24] also used the multifractal method to multidimensionally characterize the spatial variability of soil physical properties under different treatments. Wang et al. [25] showed that multifractal parameters can quantify the spatial variability of the soil particle size distribution range, concentration degree, non-uniformity, and non-symmetry. In addition, the joint multifractal method has been applied in previous studies to explore the correlations among several paired soil properties at different scales [17]. Bertol et al. [26] reported joint multifractal analysis that showed that the relationships between soil and water losses were scale-dependent across the studied temporal domain, and that their respective scaling indices had various degrees of association under different tillage treatments. Therefore, we suggest that the multifractal and joint multifractal method characterizes the spatial variability of soil water and salt and their correlations in different soil layers.
Currently, there is a lack of research focusing on the spatial variability correlations between soil water and salt. Furthermore, the use of multifractal and joint multifractal methods in studying the spatial variability of soil water and salt is limited. Therefore, the objectives of our experiments were: 1) to analyze the spatiotemporal distributions of soil water and salt at various water content levels; 2) to assess the spatial variability correlation between soil water and salt at different water content levels.

2. Materials and Methods

2.1. Information of Study Area

The experimental site is located in the farmland in the typical loess hilly region of China (40°14′11′′N – 42°27′42′′N, 75°33′16′′E – 80°59′7′′E). The region has a semi-arid continental monsoon climate with the mean annual rainfall of 505.3 mm and the mean annual potential evaporation of 1463 mm [16,27]. The experimental plot is laid in the farmland which planted alfalfa (Medicago sativa Linn). The soil physical properties are summarized in Table 1. The soil texture was classified as loam according to the international standard for soil texture classification. The soils at the experimental site are suffering from slight salinization [27,28].

2.2. Experimental Design and Sample Collection

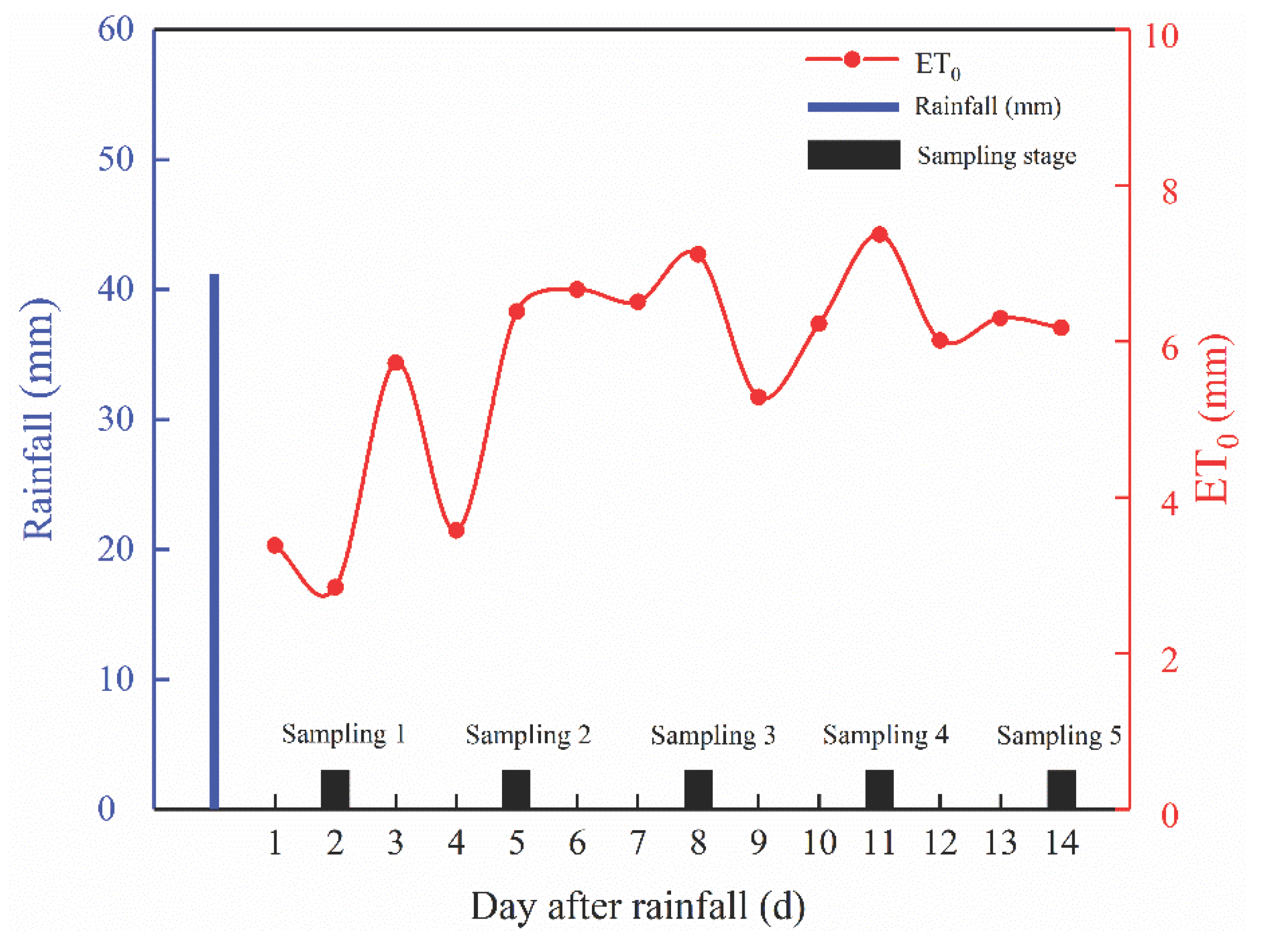
The spatial distribution of soil water and salt and their correlations were determined at different water content levels under the natural soil conditions. Range of soil water content should meet as possible from wilting coefficient to field capacity. For this purpose, we designed that soil samples collected at different stages after a heavy rainfall event. Surface soil water content could reach field capacity with > 30 mm rainfall according to Zhang et al. [29]. In addition, our experiment was conducted during high evaporation in the area for enabling soil water content to reach the withering coefficient in short monitoring periods. Therefore, a rainfall event was selected with a total precipitation of 41.2 mm on June 5, 2019 by an automatic meteorological station (FRT-X06A, Fuotong Technology [Beijing] Co. Ltd., China) installed in the experimental field site. 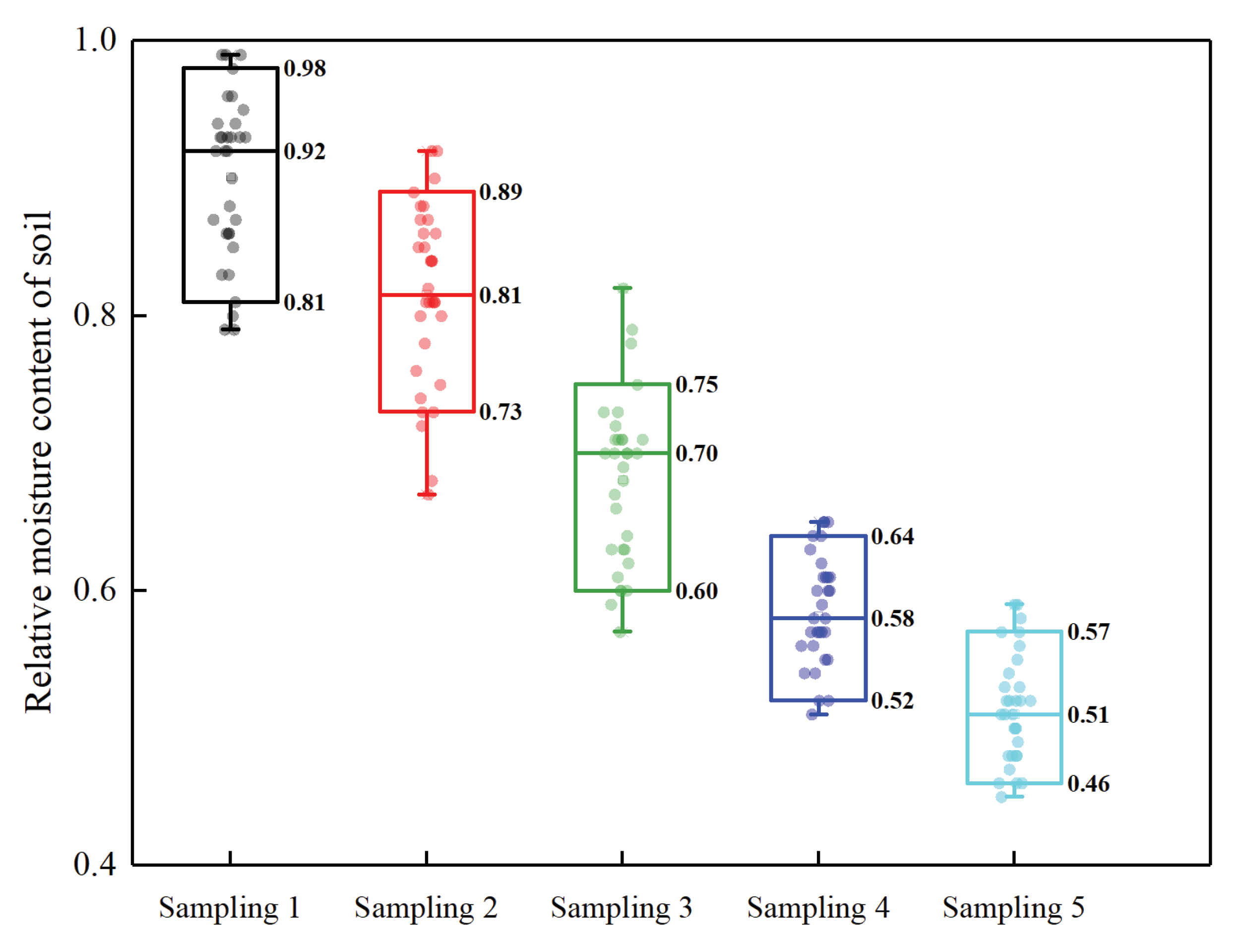Soil samples were collected on the second, fifth, eighth, eleventh and fourteenth day after the rainfall event, which were defined as the sampling 1 (S1), sampling 2 (S2), sampling 3 (S3), sampling 4 (S4), and sampling 5 (S5) stages, respectively (Figure 1). The distribution range of relative water content of soil at different sampling stages was shown in Figure 2.
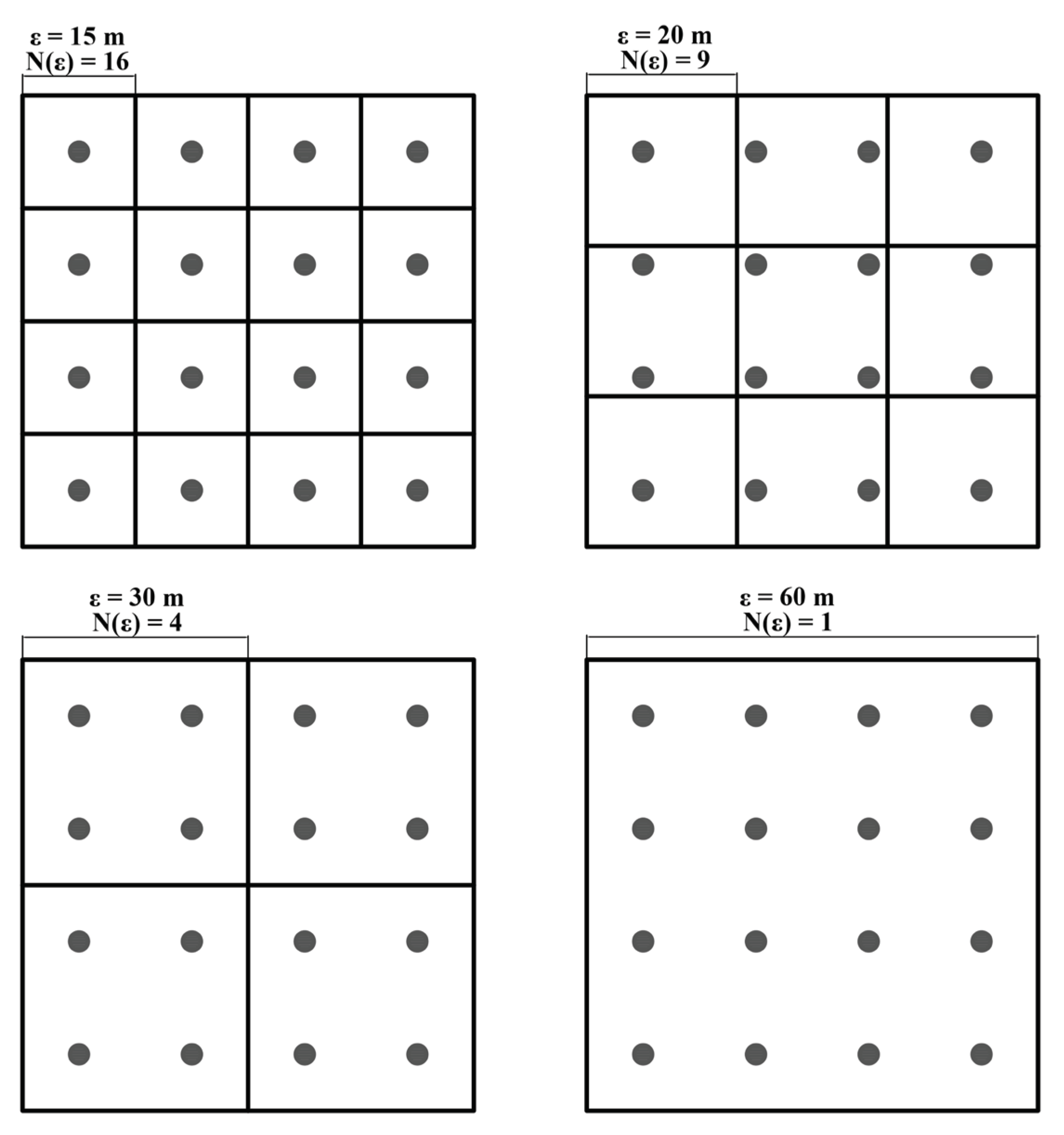
A square plot (3, 600 m2) was evenly divided into 16 grids (grid size, 15 m×15 m) (Figure 3) in this study. All grids were sampled at different stages after the rainfall event. Each sampling site was located at the center of the point in the grid. The center point was determined by tape measure and labeled with the plastic sticks. Soil samples were obtained using a soil auger (4 cm in diameter with a retractable extended drill stem) in the 0–20 and 20–40 cm layers. The holes were backfilled with soil after sampling completed.

2.3. Sample Measurement

Soil samples were filled into an aluminum box and dried at a constant temperature of 105°C until a constant weight for determining soil water content (Bao, 2005). Soil soluble salt content was determined using the weight-based method described previously [31]. The soil electric conductivity (EC) was determined using an EC meter (DDS-307A, Shanghai Yidian Scientific Instrument Co. Ltd., China). The detail was showd in Ke et al. [9] and the fitted equation between the soil soluble salt (g kg–1) and EC (μs m–1) is as follows: Soil salt content = 0.0042 EC−0.1032, n = 40, and P < 0.01. Then, EC values were converted into the soil soluble salt contents.
The soil physical properties were measured in each layer with six replications. The methods of bulk density, field capacity, and saturated hydraulic conductivity referred to Li and Shao [32]. Soil particle size was employed for laser diffraction analysis (Mastersizer 2000, Malvern Company, UK).

2.4. Reference Crop Evapotranspiration (ET0) in the Sampling Period

Reference crop evapotranspiration (ET0) was calculated using the Penma–Monteith method (FAO-56) [33]. Weather data were obtained from an automatic meteorological station (FRT-X06A, Fuotong Technology (Beijing) Co. Ltd., China) in the experimental area. The daily ET0 was shown in Figure 1. The entire sampling period had high evaporation and without precipitation.

2.5. Fractal Methods

2.5.1. Multifractal Method

The multifractal method was used to characterize the spatial variability of soil water and salt between the 0–20 and 20–40 cm layers in the plot. A square grid of size ε covered by a part of the space containing soil water and salt was used to calculate generalized dimension Dq. Because the scale of three sampled plots was 60 m×60 m and the size of each sampling point was 15 m×15 m, four grid sizes ε (i.e., 15 m, 20 m, 30 m and 60 m) were considered in the study, with the total number of grids (N (ε)) in the plot being 16, 9, 4, and 1, respectively (Figure 4) [24]. The values of soil water and salt in each grid were the mean values of all sampling points.
The following steps were defined to conduct the multifractal analysis. First, the probability mass function was calculated as follows,
p i   ε = Z i ∑ i = 1 N ( ε ) Z i ,
Where Z i is the value of a given size ε and N (ε) is the number of grids when the scale is ε .
Second, the generalized fractal dimension Dq is defined as follows,
D q = l i m ⁡ ε → 0 1 q − 1 × lg ⁡ ( ∑ i = 1 N ( ε ) p i ( ε ) q ) lg ⁡ ε   q ≠ 1 ,   a n d
D 1 = l i m ε → 0   ×   ∑ i = 1 N ( ε ) p i ε lg ⁡ p i ε lg ⁡ ε   q = 1 ,
where q represents integers in [−10, 10], i.e., the probability density weight index. D q was determined by least square method at different grid sizes. D1 is the information dimension. A high D1 value indicates that the values of the soil water and salt are distributed over a relatively small domain and exhibit relatively low spatial variability, whereas a low of D1 value indicates that the soil water and salt values are concentrated over a relatively large domain with a relatively high spatial variability [24,34]. ΔD (D−10−D10) can reflect the degree of spatial variability of the soil water and salt in a local distribution, and the lower the ΔD, the lower the variability [35].

2.5.2. Joint Multifractal Method

Spatial distribution correlations of soil water and salt were analyzed using joint multifractal method in different sampling stages. Joint multifractal method between soil water and salt in the 0–20 cm layer was an example of analysis, as follow.
First, the normalized joint partition function, μ i = (q1, q2, ε), is calculated as follows [22],
μ i = ( q 1 , q 2 , ε ) = p i 1 ( ε ) q 1 p i 2 ( ε ) q 2 ∑ i = 1 N ( ε ) p i 1 ( ε ) q 1 p i 2 ( ε ) q 2 ,
where N( ε ) is the number of grids when the scale is ε . q1 and q2 represent the moment orders of soil water and salt, respectively, and p i 1 ( ε ) and p i 2 ( ε ) represent the normalized probability mass function of soil water and salt, respectively [17].
Second, the Hólder exponents of soil water and salt are calculated as follows,
α 1 q 1 ,   q 2 = - ∑ i = 1 N ( ε ) [ μ i q 1 ,   q 2 ,   ε   lg p i 1 ( ε ) lg   N ( ε ) , a n d
α 1 q 1 ,   q 2 = - ∑ i = 1 N ( ε ) [ μ i q 1 ,   q 2 ,   ε   lg p i 1 ( ε ) lg   N ( ε ) , a n d
where α1 and α2 are the Hólder exponents of soil water and salt, respectively, and
f α 1 , α 2 = − ∑ i = 1 N ( ε ) [ μ i q 1 ,   q 2 ,   ε   lg μ i q 1 ,   q 2 ,   ε ] lg   N ( ε ) ,
where dimension f(α1, α2) represents a set in which α1 and α2 represent the mean local exponents of soil water and salt, respectively.
The image composed of α 1 q 1 ,   q 2 , α 2 q 1 ,   q 2 , and f α 1 , α 2 is the joint multifractal spectrum. The correlation between soil water and salt can be qualitatively described through the shape of the gray-scale. Increasing in the extension and concentration of a gray image along a diagonal line will result in a stronger correlation between soil water and salt in the 0–20 cm layer. Conversely, if the distribution of gray values on the image is discrete, indicating a low spatial dependency [36,37].

2.6. Statistical Analysis

The mean values and standard deviation of soil water and salt were calculated using Microsoft Excel. Analysis of variance was conducted on soil water and salt levels at different sampling stages and soil layers using least significant difference tests at P<0.05 (SPSS 23.0, Chicago, USA). Graphs were generated using Origin Pro 8.0 (Electronic Arts Inc., USA).

3. Results

3.1. Descriptive Statistics of the Soil Water and Salt

The relative water content of soil in S1, S2, S3, S4, and S5 ranged from 0.81–0.98, 0.73–0.89, 0.60–0.75, 0.52–0.64, and 0.46–0.57, respectively (Figure 2). Table 2 showed the mean values and significant differences of soil water and salt in the 0−20 cm and 20−40 cm layers in different sampling stages after rainfall. Over time, average soil water content decreased significantly due to high ET0 (Figure 1) in the following order: S1 (22.44%) > S2 (20.31%) > S3 (16.97%) > S4 (14.5%) > S5 (12.73%) in the entire layer (P<0.05). In contrast, average soil salt content increased significantly in the following order: S1 (0.71 g kg−1) < S2 (0.84 g kg−1) < S3 (0.96 g kg−1) < S4 (1.11 g kg−1) < S5 (1.18 g kg−1) in the entire layer (P<0.05). Soil water in the 0−20 cm layer showed significant differences with respect to the 20−40 cm layer (P<0.05), except for the S3. Soil salt content in the 0−20 cm layer demonstrated significant differences with respect to the 20−40 cm layer under S2−5 (P<0.05).

3.2. Spatial Variability of the Soil Water and Salt

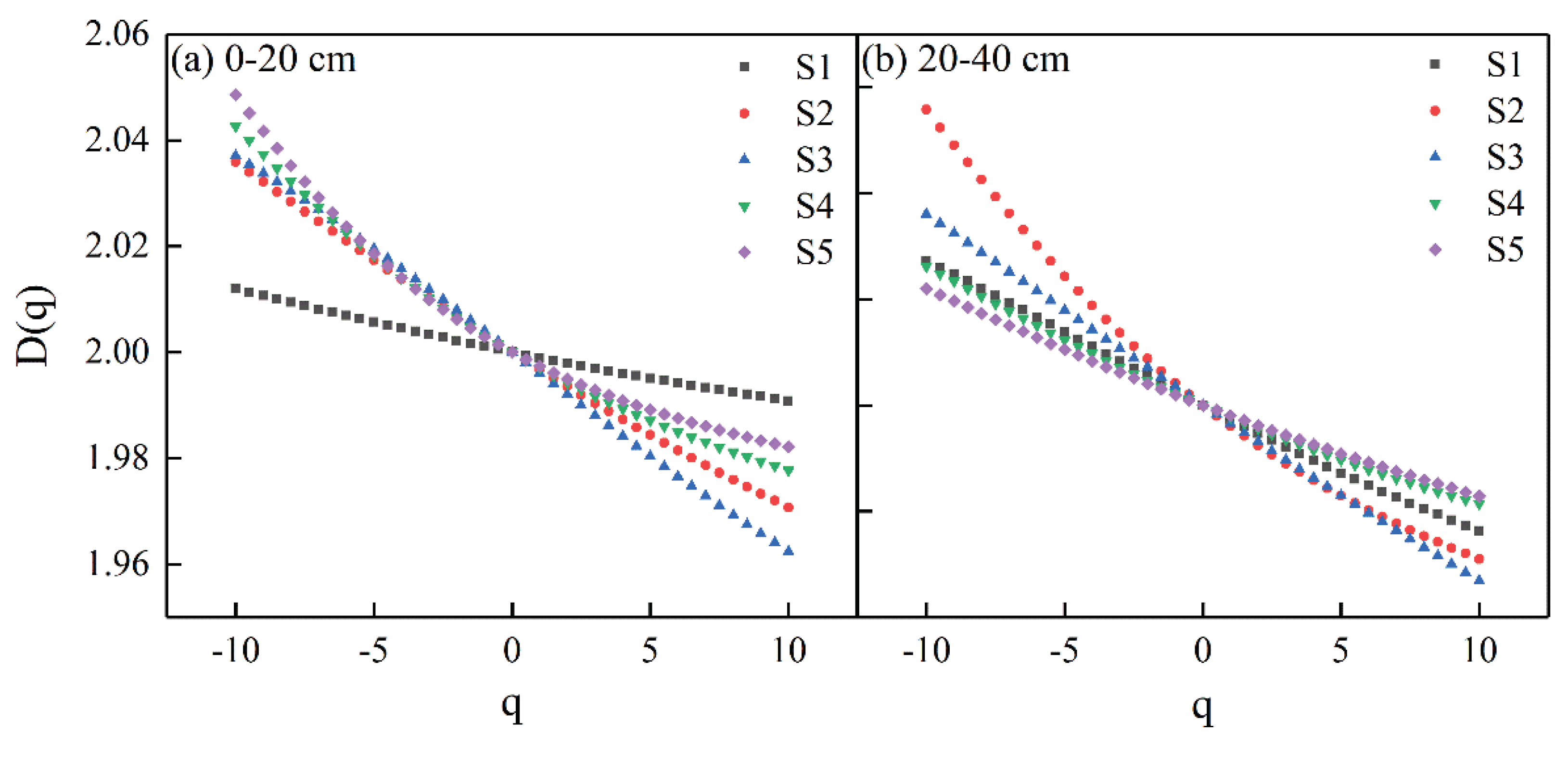
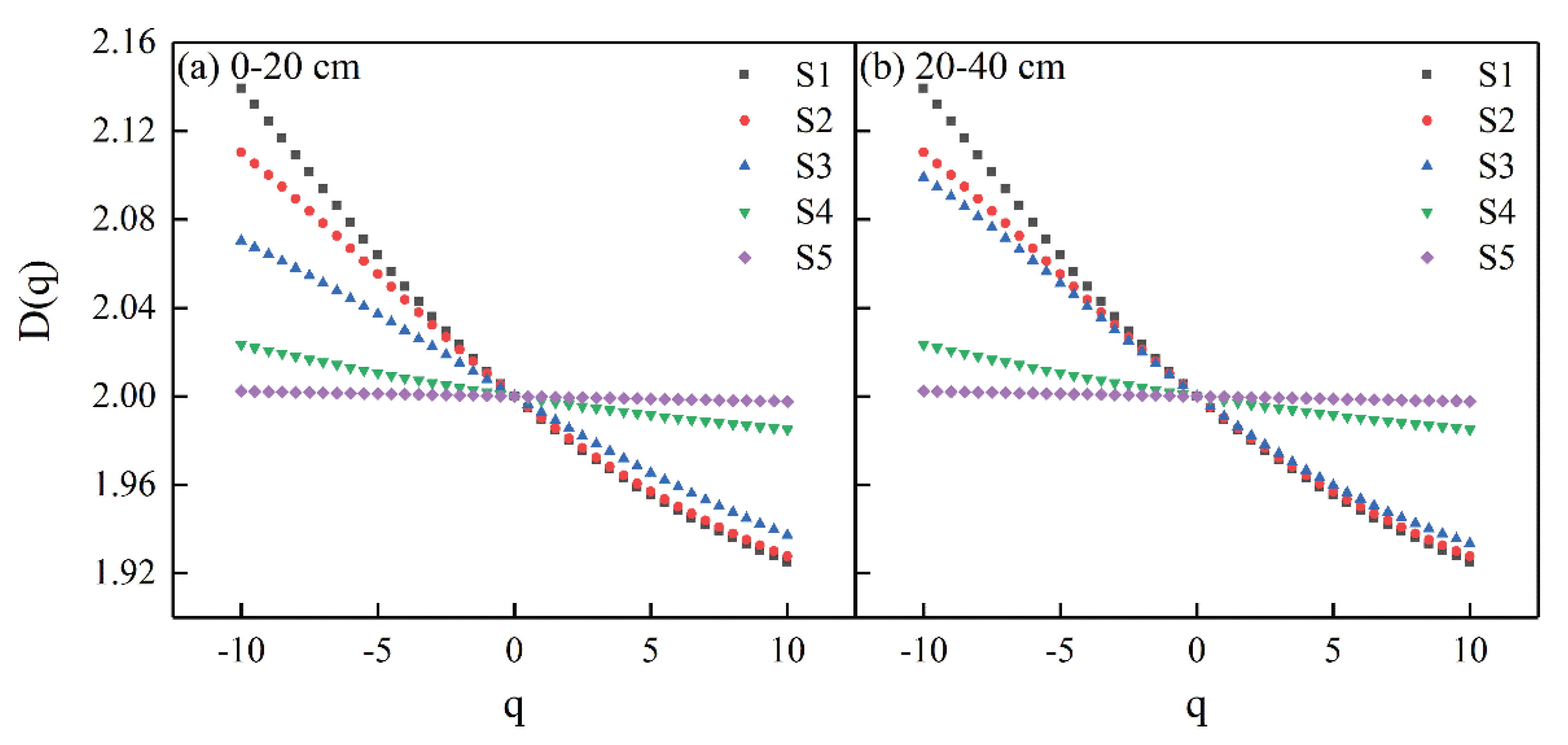
D(q) values decreased with increasing q values, which indicated the variables with multifractal characteristics [38]. Generalized dimension spectra of soil water and salt between the 0−20 cm and 20−40 cm layers at different sampling stages are shown in Figure 4 and Figure 5. We found that soil water and salt had multifractal characteristics at different sampling stages in the entire layer.
Table 3 shows the multifractal parameters of soil water and salt. The mean D1 values of soil water in the entire layer were S1 (1.9982), S2 (1.9964), S3 (1.9963), S4 (1.9975) and S5 (1.9978), respectively, which indicated that spatial variability of soil water over a relatively large domain showed an increasing trend under S1−3 and then a decreasing trend under S3−5 with water content declines. The mean ΔD values of soil water in the entire layer were S1 (0.0360), S2 (0.0750), S3 (0.0720), S4 (0.0549) and S5 (0.0528), respectively, which indicated that spatial variability of soil water in a local distribution showed an increasing trend under S1−2 and then a decreasing trend under S2−5 with water content declines. Spatial variability of soil water over a relatively large domain and in a local distribution was lower in 0−20 cm than the 20−40 cm layer under S1−2 and high under S3−5.
The mean D1 values of soil salt showed S1 (1.9885), S2 (1.9897), S3 (1.9918), S4 (1.9964) and S5 (1.9997), and mean ΔD values showed S1 (0.2202), S2 (0.1825), S3 (0.1493), S4 (0.0691) and S5 (0.0066) in the entire layer, which indicated that spatial variability of soil salt over a relatively large domain and in a local distribution showed a decreasing trend with water content declines. Spatial variability of soil salt over a relatively large domain and in a local distribution was lower in 0−20 cm than 20−40 cm layer in all sampling stages.

3.3. Spatial Distribution Correlations between Soil Water and Salt

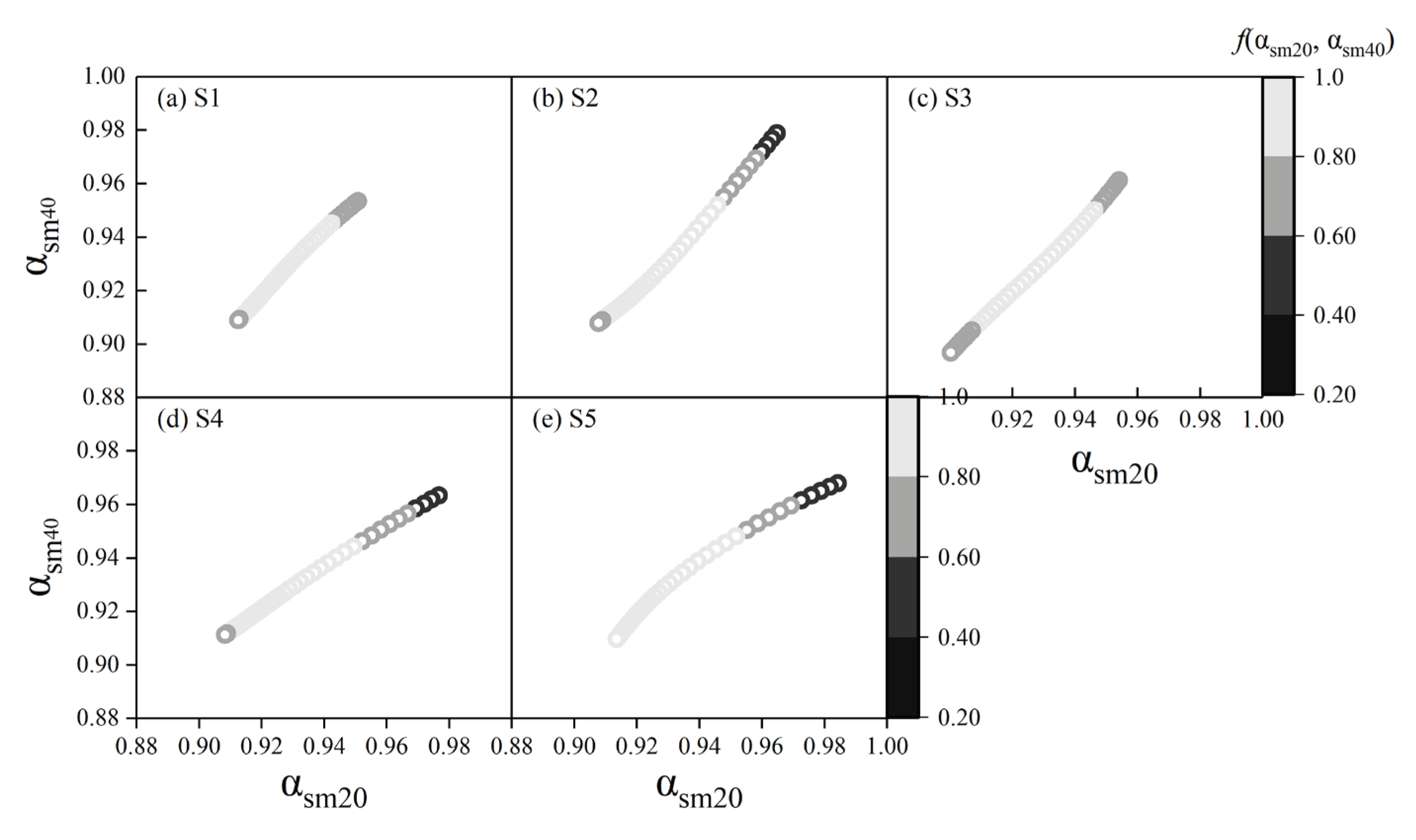
Gray-scale images of the joint multifractal spectrum of soil water and salt in the 0−20 cm layer are shown in Figure 6a–e. The αsm20 and αss20 values represent the singularity index of soil water and salt in the 0−20 cm layer, respectively. The f(αsm20, αss20) values represent a joint dimension distribution function of soil water and salt in the 0−20 cm layer. The gray-scale image was diagonal and concentrated in Figure 6c,d, which indicated that the spatial distribution of soil water and salt in the 0−20 cm layer had a relatively high correlation under S3−4. However, the gray-scale image outlines in Figure 6a,b,e were not diagonal and tended to be scattered, which indicated that the spatial distribution correlation of soil water and salt in the 0−20 cm layer was low under S1−2 and S5.
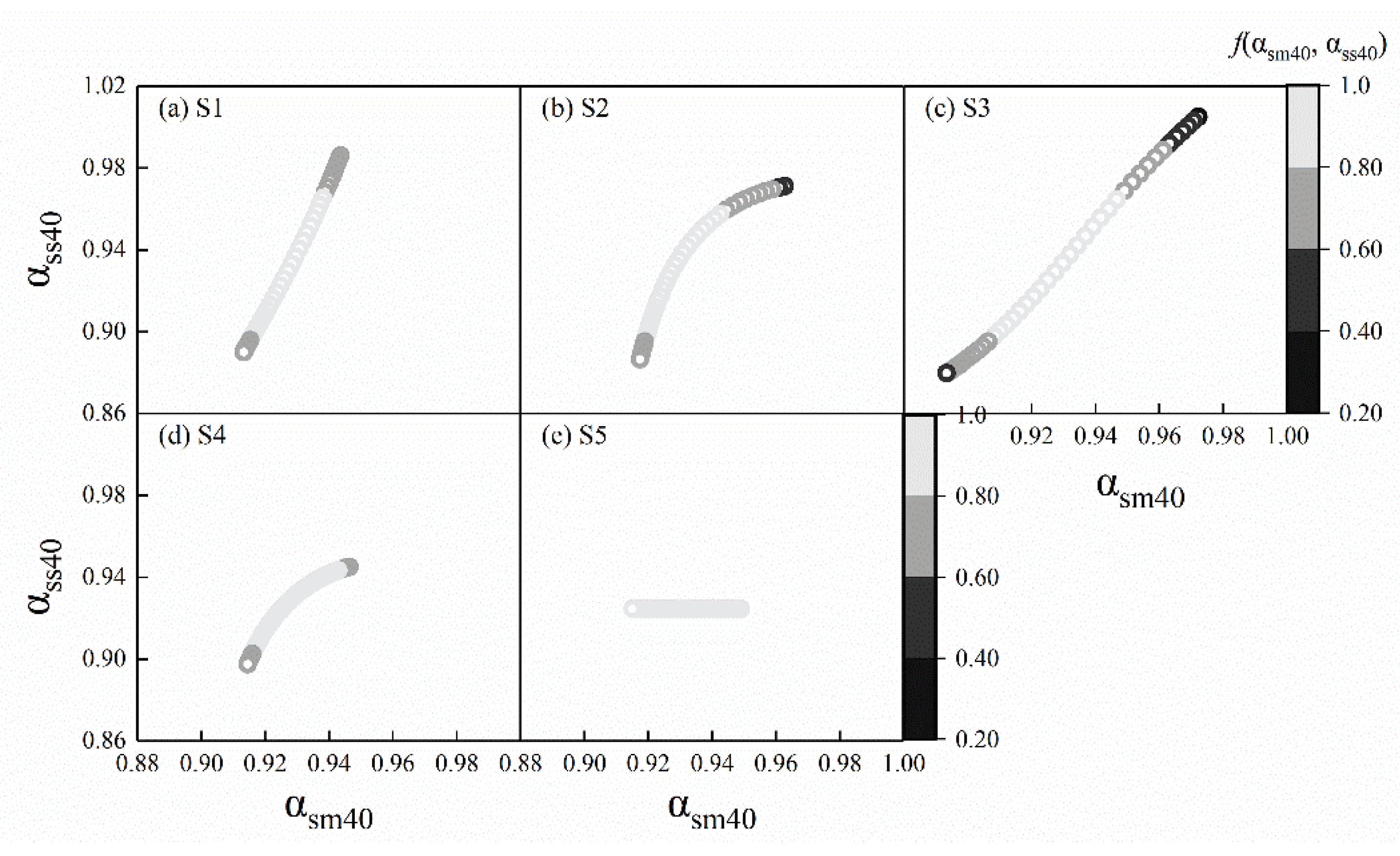
Gray-scale images of the joint multifractal spectrum of soil water and salt in the 20−40 cm layer are shown in Figure 7a–e. The αsm40 and αss40 values represent the singularity index of soil water and salt in the 20−40 cm layer, respectively. The f(αsm40, αss40) values represent a joint dimension distribution function of soil water and salt in the 20−40 cm layer. The gray-scale images were diagonal and concentrated in Figure 7a–d, which indicated that the spatial distribution of soil water and salt in the 20−40 cm layer had a relatively high correlation under the S1−4. However, the gray-scale image outlines in Figure 7e was not diagonal and tended to be scattered, which indicated that the spatial distribution correlation of soil water and salt in the 20−40 cm layer was low under S5.

4. Discussion

The soil water and salt contents fluctuate over time [39]. In this experiment, following a rainfall event, the average soil water content exhibited a significant decreasing trend over time (Table 2). Initially, the water content was highest at S1, as this soil layer received a substantial amount of rainfall, but subsequently decreased due to high ET0 levels (Figure 1). Furthermore, the average soil salt content showed a significant increasing trend over time following the rainfall event (Table 2). Ke et al. [9] noted that soil salt is initially leached after rainfall, then accumulates with continuous evapotranspiration. In our study, soil salt accumulated consistently from S1 to S5 throughout the entire layer, indicating a leaching process before S1 and an accumulation process after S1 (Table 2).
The spatial distribution of soil water and salt also varies with time [40,41]. Our findings indicate that as water content decreases, the variability of soil water distribution initially increases under S1−3 and then decreases under S3−5 throughout the layer (Table 3 and Figure 4). Following rainfall, capillary pores were saturated with water, resulting in high water content throughout the layer and low spatial variability under S1. Zhu and Lin [42] also showed that high soil water content resulted in low spatial variability. Soil water was consumed in large quantities during the strong evapotranspiration, and soil water demonstrated high spatial variability under S3 because of the variable water-holding capacity at different points. Along with further evapotranspiration, soil water remained at a low level, soil water conservation at different points decreased gradually, and thus low spatial variability was shown under S5. Previous studies correlate with our results, whereby soil texture, capillary pores, organic matter and aggregates affected soil water content and distribution, and their effects will be relatively decreased as soil water was at a low level [43−45]. Thus, the low water content level also led to its low spatial variability. In addition, with water content declines, spatial variability of soil salt showed a decreasing trend in the entire layer (Table 3 and Figure 5). The spatial variability of salt was high under S1 due to uneven leaching caused by rainfall. Zhang et al. [46] demonstrated that differences in soil wetting front under irrigation conditions supported this finding. Salt in soil continuously migrated to the surface through capillary pores under S1−5 (Table 2), leading to uneven accumulation of salt at the surface. As water content decreased throughout the layer, the spatial variability of soil salt gradually decreased.
Spatial distribution of soil water and salt in the entire layer only showed a high correlation under S3−4 (Figure 6 and Figure 7). This can be attributed to the coupling effect between soil water and salt. Wen et al. [11] reported that soil water is a carrier of soil salt transport, whereas the precipitated and dissolved salt had a certain impact on the water migration, for example, the pores relative humidity decreases as salt dissolve in liquid water and the pores volume reduces as salt precipitate from liquid water and then lead to change of physical and mechanical properties of soil. Therefore, the spatial distribution between soil water and salt were correlative. In addition, the water content level in soil was the main reason affecting the spatial distribution correlation of soil water and salt. At S1−2, range of relative water content of soil was 0.73−0.98 (Figure 2), and soil soluble salt could be fully dissolved by water. Spatial distribution of soil water and salt were low and high, respectively, due to the uneven leaching of salt by rainfall (Table 3, Figure 4 and Figure 5). Thus, a low correlation in spatial distribution of soil water and salt occurred in the stage. As the water content decreased further (S3−4), soil water migration mainly occurred in the capillary pores, thereby determining the dynamic distribution of salt [7,39]. Spatial variability of soil water and salt decreased gradually, leading to a high correlation during this stage (Figure 6 and Figure 7). At S5, the average relative water content of the soil was 0.51% (Figure 2). The precipitation of soil salt may occur due to low soil water content, leading to solid crystallization that blocks capillary pores in soil. This phenomenon suggests a low correlation in the spatial distribution of soil water and salt throughout the entire layer during this stage (Figure 6 and Figure 7). Our findings provide valuable insights into the spatiotemporal distribution characteristics of soil water and salt, as well as their correlations.

5. Conclusions

This study analyzed the spatiotemporal distribution of soil water and salt, as well as their correlations, using multifractal and joint multifractal methods across different soil layers and water content levels. The findings revealed that as water content decreased, spatial variability of soil water increased in layers S1−3 and then decreased in the entire layer under S3−5, while spatial variability of soil salt decreased. The main factor influencing the spatial distribution correlation of soil water and salt was the water content level in soil. The correlation between soil water and salt was high with a relative water content range of 0.52−0.75 (S3−4) in the entire layer due to their coupling effect. Spatial distribution between soil water and salt in the 0−40 cm layer could be reflected by the 0−20 cm layer when the range of relative water content of soil was 0.52−0.89. These results contribute to a better understanding of the spatial coupling effect of soil water and salt.

Author Contributions

Zengming Ke: Writing−original draft. Lihui Ma: Investigation. Nan Shen: Conceptualization.

Funding

Financial support for this research was provided by the China Postdoctoral Science Foundation (2021M702681), the Natural Science Basic Research Program of Shaanxi (2024JC-YBQN-0588), and the National Key Research and Development Program of China (2017YFD0800502).

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wang, Q.; Jin, H.; Yuan, Z.; Yang, C. Synergetic variations of active layer soil water and salt in a permafrost-affected meadow in the headwater area of the Yellow River, northeastern Qinghai–Tibet plateau. Int. Soil Water Conse. 2021, 10(2), 284-292. [CrossRef]
  2. Qiu, Y.; Wang, Y.; Fan, Y.; Hao, X.; Li, S.; Kang, S. Root, Yield, and Quality of Alfalfa Affected by Soil salt in Northwest China. Agriculture. 2023, 13, 750. [CrossRef]
  3. Heng, T.; Ma, Y.; Ai, P.; Liu, Z.; Wu, M.; Liu, C. The Effects of Soil Salt Stress on the Nitrogen Uptake, Yield Response and Nitrogen Use Efficiency of Cotton in Arid Areas. Agronomy. 2024, 14, 229. [CrossRef]
  4. Yu, C.; Shi, H.; Miao, Q.; Gonçalves, J.M.; Yan, Y.; Hu, Z.; Hou, C.; Zhao, Y. Water–Salt Migration Patterns among Cropland–Wasteland–Fishponds in the River-Loop Irrigation Area. Agronomy. 2024, 14, 107. [CrossRef]
  5. Ghassemi, F.; Close, A.; Kellett, J.R. Numerical models for the management of land and water resources salinisation. Math. Comput. Simulat. 1997, 43, 323-329. [CrossRef]
  6. Rengasamy, P. World salinization with emphasis on Australia. J. Exp. Bot. 2006, 57, 1017-1023. [CrossRef]
  7. Ren, D.; Wei, B.; Xu, X.; Engel, B.; Li, G.; Huang, Q.; Xiong, Y.; Huang, G. Analyzing spatiotemporal characteristics of soil salt in arid irrigated agro-ecosystems using integrated approaches. Geoderma. 2019, 356, 113935. [CrossRef]
  8. Gorji, T.; Yildirim, A.; Hamzehpour, N.; Tanik, A.; Sertel, E. Soil salt analysis of Urmia Lake Basin using Landsat-8 OLI and Sentinel-2A based spectral indices and electrical conductivity measurements. Ecol. Indic. 2020, 112, 106173. [CrossRef]
  9. Ke, Z.; Liu, X.; Ma, L.; Feng, Z.; Tu, W.; Dong, Q.g.; Jiao, F.; Wang, Z. Rainstorm events increase risk of soil salinization in a loess hilly region of China. Agric. Water Manag. 2021, 256, 107081. [CrossRef]
  10. Mastrocicco, M.; Colombani, N.; Soana, E.; Vincenzi, F.; Castaldelli, G. Intense rainfalls trigger nitrite leaching in agricultural soils depleted in organic matter. Sci. Total Environ. 2019, 665, 80-90. [CrossRef]
  11. Wen, W.; Lai, Y.; You, Z. Numerical modeling of water–heat–vapor–salt transport in unsaturated soil under evaporation. Int. J. Heat. Mass Tran. 2020, 159, 120114. [CrossRef]
  12. Walter, J.; Lück, E.; Bauriegel, A.; Facklam, M.; Zeitz, J. Seasonal dynamics of soil salt in peatlands: A geophysical approach. Geoderma. 2018, 310, 1-11.
  13. Cao, Q.; Yang, B.; Li, J.; Wang, R.; Liu, T.; Xiao, H. Characteristics of soil water and salt associated with Tamarix ramosissima communities during normal and dry periods in a semi-arid saline environment. CATENA. 2020,193, 104661. [CrossRef]
  14. Yuan, C.; Feng, S.; Huo, Z.; Ji, Q. Effects of deficit irrigation with saline water on soil water-salt distribution and water use efficiency of maize for seed production in arid Northwest China. Agric. Water Manag. 2019, 212, 424-432. [CrossRef]
  15. Dong, Q.; Yang, Y.; Zhang, T.; Zhou, L.; He, J.; Chau, H.W.; Zou, Y.; Feng, H. Impacts of ridge with plastic mulch-furrow irrigation on soil salt, spring maize yield and water use efficiency in an arid saline area. Agric. Water Manag. 2018, 201, 268-277. [CrossRef]
  16. Ke, Z.; Ma, L.; Jiao, F.; Liu, X.; Liu, Z.; Wang, Z. Multifractal parameters of soil particle size as key indicators of the soil water distribution. J. Hydrol. 2021, 595, 125988. [CrossRef]
  17. Wang, F.; Wang, J.; Wang, Y. Using multi-fractal and joint multi-fractal methods to characterize spatial variability of reconstructed soil properties in an opencast coal-mine dump in the Loess area of China. CATENA. 2019, 182, 104111. [CrossRef]
  18. Wang, J.; Zhang, C.; Wu, Z.; Wharton, J.; Ren, L. Numerical study on reduction of aerodynamic noise around an airfoil with biomimetic structures. J. Sound. Vib. 2017, 394, 46-58. [CrossRef]
  19. Teng, M.; Zeng, L.; Xiao, W.; Huang, Z.; Zhou, Z.; Yan, Z.; Wang, P. Spatial variability of soil organic carbon in Three Gorges Reservoir area, China. Sci. Total Environ. 2017, 599-600, 1308-1316. [CrossRef]
  20. Wang, T.; Kang, F.; Cheng, X.; Han, H.; Bai, Y.; Ma, J. Spatial variability of organic carbon and total nitrogen in the soils of a subalpine forested catchment at Mt. Taiyue, China. CATENA. 2017, 155, 41-52. [CrossRef]
  21. Vidana Gamage, D.N.; Biswas, A.; Strachan, I.B. Spatial variability of soil thermal properties and their relationships with physical properties at field scale. Soil. Till. Res. 2019, 193, 50-58. [CrossRef]
  22. Zeleke, T.B.; Si, B.C. Characterizing scale-dependent spatial relationships between soil properties using multifractal techniques. Geoderma. 2006, 134, 440-452. [CrossRef]
  23. Qi, F.; Zhang, R.; Liu, X.; Niu, Y.; Zhang, H.; Li, H.; Li, J.; Wang, B.; Zhang, G. Soil particle size distribution characteristics of different land-use types in the Funiu mountainous region. Soil and Tillage Research 184, 45-51.Jing, Z.; Wang, J.; Wang, R.; Wang, P.; 2019. Using multi-fractal analysis to characterize the variability of soil physical properties in subsided land in coal-mined area. Geoderma. 2018, 114054.
  24. Wang, F.; Wang, J.; Wang, Y. Using multi-fractal and joint multi-fractal methods to characterize spatial variability of reconstructed soil properties in an opencast coal-mine dump in the Loess area of China. CATENA. 2019, 182, 104111. [CrossRef]
  25. Bertol, I.; Schick, J.; Bandeira, D.H.; Paz-Ferreiro, J.; Vázquez, E.V. Multifractal and joint multifractal analysis of water and soil losses from erosion plots: A case study under subtropical conditions in Santa Catarina highlands, Brazil. Geoderma. 2017, 287, 116-125. [CrossRef]
  26. Jin, Z.; Guo, L.; Wang, Y.; Yu, Y.; Lin, H.; Chen, Y.; Chu, G.; Zhang, J.; Zhang, N. Valley reshaping and damming induce water table rise and soil salinization on the Chinese Loess Plateau. Geoderma. 2019, 339, 115-125. [CrossRef]
  27. Yu, Y.; Lin, H.; zhao, J.; Guangchen, C.; Jin, Z. Ammonia dynamics in reservoirs in response to rainfall events in a gully-filled loess catchment in Yan’an City, Shaanxi Province. Quatern. Sci. 2017, 37 (6), 1204–1218. [CrossRef]
  28. Zhang, J.; Wang, X.; Wang, Y.; Jin, S.; Dong, J.; Wang, Z. Regularities of Rainfall Infiltration and Water Migration in Woodland Drying Soil in the Loess Hilly Region. J. Soil Water Conse. 2017, 31, 231-238. [CrossRef]
  29. Zhang, J.; Wang, X.; Wang, Y.; Jin, S.; Dong, J.; Wang, Z. Regularities of Rainfall Infiltration and Water Migration in Woodland Drying Soil in the Loess Hilly Region. J. Soil Water Conse. 2017, 31, 231-238. [CrossRef]
  30. Bao, S.D. Soil Analysis in Agricultural Chemistry (in chinese). China Agricultural Press, Beijing. 2005.
  31. Li, Y.Y.; Shao, M.A. Change of soil physical properties under long-term natural vegetation restoration in the Loess Plateau of China. J. Arid Environ. 2006, 64, 77-96. [CrossRef]
  32. Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration - Guidelines for computing crop water requirements - FAO Irrigation and drainage paper 56. FAO, Rome. 1998, 300 (9), D05109.
  33. Evertsz, C.J.G.; Mandelbrot, B.B. Multifractal measures. Chaos & Fractals New Frontiers of Science, Springer-Verlag. 1992, 984.
  34. Zhou, H.; Li, B.; Lv, Y.; Liu, W. Multifractal characteristics of soil porestructure under different tillage systems. Acta Pedologica Sinica. 2010, 47, 1094–1100. [CrossRef]
  35. Jiménez-Hornero, F.J.; Gutiérrez de Ravé, E.; Ariza-Villarverde, A.B.; Giráldez, J.V. Description of the seasonal pattern in ozone concentration time series by using the strange attractor multifractal formalism. Environ. Monit. Assess. 2010, 160, 229-236. [CrossRef]
  36. Si, B.C.; Kachanoski, R.G. Estimating Soil Hydraulic Properties During Constant Flux Infiltration: Inverse Procedures. Soil Sci. Soc. Am. J. 2000, 64, 439-449. [CrossRef]
  37. Vázquez, E.V.; Miranda, J.G.V.; Paz-Ferreiro, J. A multifractal approach to characterize cumulative rainfall and tillage effects on soil surface micro-topography and to predict depression storage. Biogeosciences. 2010, 7, 2989–3004. [CrossRef]
  38. Akça, E.; Aydin, M.; Kapur, S.; Kume, T.; Nagano, T.; Watanabe, T.; Çilek, A.; Zorlu, K. Long-term monitoring of soil salt in a semi-arid environment of Turkey. CATENA. 2020, 193, 104614. [CrossRef]
  39. Benslama, A.; Khanchoul, K.; Benbrahim, F.; Boubehziz, S.; Chikhi, F.; Navarro-Pedreno, J. Monitoring the Variations of Soil salt in a Palm Grove in Southern Algeria. Sustainability. 2020, 12, 19.
  40. Han, J.; Mammadov, Z.; Kim, M.; Mammadov, E.; Lee, S.; Park, J.; Mammadov, G.; Elovsat, G.; Ro, H.M. Spatial distribution of salt and heavy metals in surface soils on the Mugan Plain, the Republic of Azerbaijan. Environ. Monit. Assess. 2021, 193, 20.
  41. Zhu, Q.; Lin, H. Influences of soil, terrain, and crop growth on soil water variation from transect to farm scales. Geoderma. 2011, 163, 45-54. [CrossRef]
  42. Pollacco, J.A.P.; Fernández-Gálvez, J.; Carrick, S. Improved prediction of water retention curves for fine texture soils using an intergranular mixing particle size distribution model. J. Hydrol. 2020, 584, 124597. [CrossRef]
  43. Suh, H.S.; Kang, D.H.; Jang, J.; Kim, K.Y.; Yun, T.S. Capillary pressure at irregularly shaped pore throats: Implications for water retention characteristics. Adv. Water Resour. 2017, 110, 51-58. [CrossRef]
  44. Zhang, C.; Wang, H. A brief review of advances in soil water research. Agricul. Res. Arid Area. 2003, (08), 13-18.
  45. Zhang, T.; Dong, Q.g.; Zhan, X.; He, J.; Feng, H. Moving salts in an impermeable saline-sodic soil with drip irrigation to permit wolfberry production. Agric. Water Manag. 2019, 213, 636-645. [CrossRef]
Preprints 103181 g001
Figure 1. Rainfall, sampling stages, and reference crop evapotranspiration (ET0) after the rainfall event.
Figure 1. Rainfall, sampling stages, and reference crop evapotranspiration (ET0) after the rainfall event.
Preprints 103181 g001
Preprints 103181 g002
Figure 2. Distribution range of relative water content of soil at different sampling stages after the rainfall.
Figure 2. Distribution range of relative water content of soil at different sampling stages after the rainfall.
Preprints 103181 g002
Preprints 103181 g003
Figure 3. Experimental plot and squared gird layout used to conduct multifractal analysis at different size ε (i.e., 15 m, 20 m, 30 m, and 60 m).
Figure 3. Experimental plot and squared gird layout used to conduct multifractal analysis at different size ε (i.e., 15 m, 20 m, 30 m, and 60 m).
Preprints 103181 g003
Preprints 103181 g004
Figure 4. Spectra of generalized dimensions for the q moment range [−10, 10] of soil water in the 0–20 cm and 20–40 cm layers at different stage after the rainfall event. S1, S2, S3, S4, and S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively.
Figure 4. Spectra of generalized dimensions for the q moment range [−10, 10] of soil water in the 0–20 cm and 20–40 cm layers at different stage after the rainfall event. S1, S2, S3, S4, and S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively.
Preprints 103181 g004
Preprints 103181 g005
Figure 5. Spectra of generalized dimensions for the q moment range [−10, 10] of soil salt in the 0–20 cm and 20–40 cm layers at different stage after the rainfall event. S1, S2, S3, S4, and S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively.
Figure 5. Spectra of generalized dimensions for the q moment range [−10, 10] of soil salt in the 0–20 cm and 20–40 cm layers at different stage after the rainfall event. S1, S2, S3, S4, and S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively.
Preprints 103181 g005
Preprints 103181 g006
Figure 6. Joint multi-fractal spectra gray scale images of the 0−20 cm soil layer between soil water and salt at different stage after the rainfall event. (a) S1, (b) S2, (c) S3, (d) S4, and (e) S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively. αsm20, soil water at the layer of 0−20 cm; αss20, soil salt at the layer of 0−20 cm; f(αsm20, αss20), the values of joint dimension distribution function of the soil water and salt at the layer of 0−20 cm.
Figure 6. Joint multi-fractal spectra gray scale images of the 0−20 cm soil layer between soil water and salt at different stage after the rainfall event. (a) S1, (b) S2, (c) S3, (d) S4, and (e) S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively. αsm20, soil water at the layer of 0−20 cm; αss20, soil salt at the layer of 0−20 cm; f(αsm20, αss20), the values of joint dimension distribution function of the soil water and salt at the layer of 0−20 cm.
Preprints 103181 g006
Preprints 103181 g007
Figure 7. Joint multi-fractal spectra gray scale images of the 20−40 cm soil layer between soil water and salt at different stage after the rainfall event. (a) S1, (b) S2, (c) S3, (d) S4, and (e) S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively. αsm40, soil water at the layer 20−40 cm;αss40, soil salt at the layer 20−40 cm; f(αsm40, αss40), the values of joint dimension distribution function of the soil water and salt at layer of 20−40 cm.
Figure 7. Joint multi-fractal spectra gray scale images of the 20−40 cm soil layer between soil water and salt at different stage after the rainfall event. (a) S1, (b) S2, (c) S3, (d) S4, and (e) S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively. αsm40, soil water at the layer 20−40 cm;αss40, soil salt at the layer 20−40 cm; f(αsm40, αss40), the values of joint dimension distribution function of the soil water and salt at layer of 20−40 cm.
Preprints 103181 g007
Table 1. Soil basic properties in the experimental plot.
Table 1. Soil basic properties in the experimental plot.
Soil layers
(cm)		 Bulk density
(g cm-3)		 Field capacity
(%)		 Saturated hydraulic
Conductivity (cm min-1)		 Soil texture
classification
0–20 1.17 24.80 0.57 Loam
20–40 1.26 25.00 0.36 Loam
Table 2. Descriptive statistics for soil water and salt in the 0–20 cm and 20–40 cm layers at different stage after the rainfall event.
Table 2. Descriptive statistics for soil water and salt in the 0–20 cm and 20–40 cm layers at different stage after the rainfall event.
Soil properties Soil layer
(cm)		 S1 (Mean±SD) S2
(Mean±SD)		 S3
(Mean±SD)		 S4
(Mean±SD)		 S5
(Mean±SD)
Soil water
content (%)		 0−20 22.56 ± 1.37Aa 19.57 ± 1.36Bb 16.23 ± 1.26Bc 13.92 ± 1.07Bd 12.02 ± 0.85Be
20−40 22.31 ± 1.64Aa 21.05 ± 1.66Ab 17.70 ± 1.49Ac 15.08 ± 1.01Ad 13.43 ± 1.03Ae
Mean 22.44 ± 1.49 20.31 ± 1.67 16.97 ± 1.55 14.50 ± 1.18 12.73 ± 1.17
Soil salt
content (g kg-1)		 0−20 0.64 ± 0.09Be 0.79 ± 0.10Bd 0.98 ± 0.10Ac 1.25 ± 0.08Ab 1.38 ± 0.03Aa
20−40 0.79 ± 0.11Ac 0.89 ± 0.12Ab 0.94 ± 0.13Aab 0.97 ± 0.09Ba 0.97 ± 0.03Ba
Mean 0.71 ± 0.12 0.84 ± 0.12 0.96 ± 0.12 1.11 ± 0.16 1.18 ± 0.21
Notes: S1, S2, S3, S4, and S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively. SD indicates standard deviation. Different capital letters indicate significant differences between 0−20 and 20−40cm layers in the same stage (P<0.05). Different lower-case letters indicate significant differences between sampling stages in the same soil layer (P<0.05).
Table 3. Multifractal parameters for soil water and salt in the 0–20 cm and 20–40 cm layers at different stage after the rainfall event.
Table 3. Multifractal parameters for soil water and salt in the 0–20 cm and 20–40 cm layers at different stage after the rainfall event.
Soil properties Soil layers (cm) S1 S2 S3 S4 S5 　
D1 ∆D D1 ∆D D1 ∆D D1 ∆D D1 ∆D
Soil water 0−20 1.9990 0.0211 1.9967 0.0651 1.9960 0.0748 1.9971 0.0649 1.9974 0.0665
20−40 1.9973 0.0509 1.9961 0.0848 1.9965 0.0692 1.9978 0.0448 1.9981 0.0391
Mean 1.9982 0.0360 1.9964 0.0750 1.9963 0.0720 1.9975 0.0549 1.9978 0.0528
Soil salt 0−20 1.9896 0.2139 1.9902 0.1826 1.9927 0.1331 1.9976 0.0482 1.9998 0.0046
20−40 1.9874 0.2264 1.9892 0.1824 1.9908 0.1654 1.9951 0.0900 1.9996 0.0085
Mean 1.9885 0.2202 1.9897 0.1825 1.9918 0.1493 1.9964 0.0691 1.9997 0.0066
Notes: S1, S2, S3, S4, and S5 indicate sampling 1, sampling 2, sampling 3, sampling 4, and sampling 5 stages, respectively.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated